Antinormality and m-isometry of shift on weighted trees

Abstract

The shift operator and its various generalizations are amongst the most widely studied operators on a Hilbert space. In this paper, we characterize antinormal and m-isometric shift operator S on the Hilbert space $L^2({\mathcal {T}},\lambda )$ associated with a locally finite directed weighted tree ${\mathcal {T}}$. We also discuss interesting connections between antinormality and m-isometry of S.

1 Introduction

Throughout this paper, we denote the set of all natural numbers, the set of all integers, the set of all real numbers and the set of all complex numbers by ${\mathbb {N}}, \ {\mathbb {Z}}, \ {\mathbb {R}}$ and ${\mathbb {C}}$ respectively. We denote the set of all non-negative integers and set of all non-positive integers by $\mathbb {Z^+}$ and $\mathbb {Z^-}$, respectively. For a given set A, ${\text {card}}(A)$ denotes the cardinality of A. Let H denote a separable complex Hilbert space and, ${\mathcal {B}}(H)$ and ${\mathcal {N}}$, respectively, be the set of all linear bounded operators on H and the set of all normal operators on H. For a $T\in {\mathcal {B}}(H)$, $T^*$ denotes Hilbert adjoint of T.

A fascinating problem in the Hilbert space operator theory is to determine the distance between a particular operator and a collection of operators. Important examples of such collections are the set of all unitary operators, the set of all self adjoint operators, the set of all normal operators and the set of all compact operators. In this setting, a deep and interesting case is whether there exists a best approximation. Holmes [8] studied best normal approximation and introduced the notion of “antinormal operator”. A particularly simple but interesting example of an antinormal operator is the classical right shift operator of multiplicity one on the Hilbert space $l^2({\mathbb {N}})$. Antinormal operators have been extensively studied by several authors. For the historical details, we refer to [9, 11,12,13, 15, 16].

Jabłoński et al. [10] introduced weighted shifts on directed trees. Martńez-Avendaño [14] analyzed the dynamical property of shift operator on weighted directed trees. In this paper, we completely characterize the antinormality of shift operator on weighted directed trees.

The natural generalization of an isometric operator is the m-isometric operator on Hilbert space. The notion of m-isometric operator was introduced by Agler [5]. As stated by Agler and Stankus [3, 4, 6] the concept of m-isometries in case when $m>1$ is interesting and deep as its requires ideas from many areas of mathematics such as distribution theory and function theory. Abdullah and Le [1] gave a result on m-isometry of unilateral weighted shift. We extend their result on the shift on a weighted directed tree. We also relate antinormality and m-isometry of the shift on a weighted directed tree. We now state various definitions and results relevant to our study.

Definition 1.1

[8] An operator $T\in {\mathcal {B}}(H)$ is said to be antinormal if $d(T,{\mathcal {N}}) = \inf \nolimits _{ N\in {\mathcal {N}}} \Vert T-N\Vert = \Vert T\Vert$.

Observe that an operator $T\in {\mathcal {B}}(H)$ is antinormal if and only if $0\in {\mathcal {B}}(H)$ is the best normal approximation. We note that antinormality of an operator $T\in {\mathcal {B}}(H)$ is necessary as well as sufficient for antinormality of $T^*$.

Definition 1.2

[7] An operator $T\in {\mathcal {B}}(H)$ is said to be Fredholm operator if ${\text {range}}(T)$ is closed and dimension of both $\mathrm{ker}(T)$ and $\mathrm{ker}(T^*)$ are finite.

Definition 1.3

[2] The essential spectrum of an operator $T\in {\mathcal {B}}(H)$ is defined as $\sigma _e(T) = \{\alpha \in {\mathbb {C}} : T-\alpha I \ is \ not \ Fredholm\}$.

Definition 1.4

The essential minimum modulus of an operator $T\in {\mathcal {B}}(H)$ is defined as $m_e(T)=\inf \{\alpha \ge 0:\alpha \in \sigma _e(|T|)\}$, where $|T|=(T^*T)^{1/2}$.

Definition 1.5

For an operator $T\in {\mathcal {B}}(H)$, index of T is defined as

$$\begin{aligned} i(T) = {\left\{ \begin{array}{ll} \dim (\mathrm{ker}(T))-\dim (\mathrm{ker}(T^*)), &{} \hbox {if} \dim (\mathrm{ker}(T))<\infty \hbox {or} \dim (\mathrm{ker}(T^*)) <\infty \\ 0, &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

Remark 1.6

[9] If $i(T)=0$ then T is not antinormal.

Theorem 1.7

[9] Let $T\in {\mathcal {B}}(H)$ with $i(T)<0$. Then the following conditions are equivalent:

• (1) T is antinormal.

• (2) $m_e(T)=\Vert T\Vert$.

• (3) $d(T,{\mathcal {U}})=1+\Vert T\Vert$, where ${\mathcal {U}}$ is the class of all unitary operators in ${\mathcal {B}}(H)$.

Definition 1.8

[5] Let m be a natural number and $T\in {\mathcal {B}}(H)$. Then T is said to be an m-isometry if T satisfies the following equation:

$$\begin{aligned} \sum \limits _{k=0}^m(-1)^k\left( {\begin{array}{c}m\\ k\end{array}}\right) {T^*}^kT^k=0. \end{aligned}$$

(1.1)

Moreover, T is said to be strictly m-isometry if m is the smallest natural number for which Eq. (1.1) holds.

Definition 1.9

Let V be a non-empty set and E be a subset of $V\times V$. Then (V, E) is known as directed graph. An element of V is called a vertex and an element of E is called an edge.

In this paper we restrict to the case when V is a countable set. In a directed graph (V, E), ${\text {card}}(\{u\in V : (u,v) \in E\})$ and ${\text {card}}(\{u\in V : (v,u) \in E\})$ are respectively called indegree of v and outdegree of v. A directed graph (V, E) is said to be locally finite if for every vertex in V both the indegree and the outdegree are finite. A directed graph (V, E) is said to be connected if its underlying graph is connected [17]. A finite sequence $\{u_1 ,u_2 , \ldots ,u_k\}$ for some $k\ge 2$, of distinct vertices in V is called a directed circuit of (V, E) if $(u_i ,u_{i+1} )\in E$ for each $i=1,2, \ldots ,k-1$ and $(u_k ,u_1 )\in E$.

Definition 1.10

A directed graph ${\mathcal {T}}:=(V,E)$ is called a directed tree if ${\mathcal {T}}$ does not have any directed circuits, ${\mathcal {T}}$ is connected and the indegree of every vertex in ${\mathcal {T}}$ is at most one.

Definition 1.11

In a directed tree ${\mathcal {T}}$ a vertex is called a root if its indegree is zero. If the outdegree of a vertex is zero then it is called a leaf.

We have adopted various notations introduced in [14]. Let ${\mathcal {T}}$ be a directed tree. For an edge $(u,v) \in E$, we define $u = {\text {par}}(v)$ and call v as a child of u. For a vertex $v\in V$, ${\text {par}}^2(v)$ denotes ${\text {par}}({\text {par}}(v))$ and for $n\ge 3$ ${\text {par}}^n (v) = {\text {par}}({\text {par}}^{n-1}(v))$ whenever ${\text {par}}^{n-1} (v)$ is not a root. For $u\in V$ define ${\text {chi}}(u)=\{v\in V \ : \ u = {\text {par}}(v)\}$ and for $n\ge 2$, ${\text {chi}}^n (u) = \{u\in V : {\text {par}}^n (v) = u\}$. Also, for $u\in V$, $\gamma (u)$ denotes the cardinality of ${\text {chi}}(u)$.

Remark 1.12

Let $u,v,w\in V$. If ${\text {chi}}(u)=\{v\}$, then v is also denoted by ${\text {chi}}(u)$. Similarly, if ${\text {chi}}^n(u)=\{w\}$ for some $n\ge 2$, then w is also denoted by ${\text {chi}}^n(u)$.

Definition 1.13

Two directed trees ${\mathcal {T}}=(V,E)$ and $\tilde{{\mathcal {T}}}=({\tilde{V}},{\tilde{E}})$ are said to be isomorphic if there exists a one-to-one correspondence $\psi$ from V onto ${\tilde{V}}$ such that $(u,v)\in E$ if and only if $(\psi (u),\psi (v))\in {\tilde{E}}$.

Definition 1.14

Let $G=(V,E)$ be a directed graph and $W\subseteq V$. Then, $G\setminus W$ denotes the directed graph by removing all vertices of W from G and all edges whose at least one end vertex is in W.

Definition 1.15

Let ${\mathcal {T}}$ be a directed tree and $\lambda = \{\lambda _v \in {\mathbb {R}} : \ \lambda _v>0, \ v \in V \}$ be a set. We call $\lambda$ weight on the vertex set V. We denote by $L^2({\mathcal {T}},\lambda )$ the space of complex valued functions $f:V\rightarrow {\mathbb {C}}$ such that

$$\begin{aligned} \sum \limits _{v\in V}|f(v)|^2\lambda _v<\infty . \end{aligned}$$

This is a Hilbert space endow with the inner product

$$\begin{aligned} \langle f,g\rangle =\sum \limits _{v\in V}f(v)\overline{g(v)}\lambda _v, \ \ f,g\in L^2({\mathcal {T}},\lambda ). \end{aligned}$$

Throughout this paper by “tree", we mean a locally finite directed tree. Also $\mathbb {Z_{{\mathcal {T}}}^+}$ and $\mathbb {Z_{{\mathcal {T}}}^-}$, respectively, denote the trees $(\mathbb {Z^+},\{(i,i+1):i\in \mathbb {Z^+} \})$ and $(\mathbb {Z^-},\{(i,i-1):i\in \mathbb {Z^-} \})$. For a tree ${\mathcal {T}}=(V,E)$ we define $V_{{\text {leaves}}}$ as the set of all leaves, $V_{\ge 2}$ as the set $\{u\in V : \ \gamma (u)\ge 2 \}$ and ${\text {chi}}(V_{\ge 2})$ as the set $\bigcup \nolimits _{v\in V_{\ge 2}}{\text {chi}}(v)$. Also, we assign a integer value $\delta _{\mathcal {T}}$ to the tree ${\mathcal {T}}$ as follows:

$$\begin{aligned} \delta _{\mathcal {T}} = \left\{ \begin{array}{@{}l@{ }l} 1, &{} \text{ if } \text{ tree } \text{ has } \text{ a } \text{ root } \\ 0, &{} \text{ otherwise. }\\ \end{array} \right. \end{aligned}$$

Let $\Delta : V\rightarrow (0,\infty )$ be such that $\Delta (u)=\bigg (\frac{1}{\lambda _u}\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v\bigg )^{\frac{1}{2}},$ for every $u\in V$. And a sequence in $\Delta$ is a sequence of the form $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ , where $\mu :{\mathbb {N}}\rightarrow V$ is an injective function.

Definition 1.16

Let ${\mathcal {T}}$ be a tree and $\lambda$ be weight on V. Then the shift $S : L^2({\mathcal {T}},\lambda )\rightarrow L^2({\mathcal {T}},\lambda )$ is the operator defined as

$$\begin{aligned} (Sf)(u) = {\left\{ \begin{array}{ll} f({\text {par}}(u)), &{} u \text{ is } \text{ not } \text{ a } \text{ root } \\ 0, &{} \text{ otherwise, } \end{array}\right. } \end{aligned}$$

where $f \in L^2({\mathcal {T}},\lambda )$.

Theorem 1.17

[14] Let ${\mathcal {T}}$ be a tree and $\lambda$ be weight on V. The shift $S:L^2({\mathcal {T}},\lambda )\rightarrow L^2({\mathcal {T}},\lambda )$ is bounded if and only if

$$\begin{aligned} \sup \limits _{u\in V}\bigg (\frac{1}{\lambda _u}\sum \limits _{v\in {\text {chi}}(u)}\lambda _{v}\bigg )<\infty . \end{aligned}$$

In either case,

$$\begin{aligned} \Vert S\Vert =\sup \limits _{u\in V}\bigg (\frac{1}{\lambda _u}\sum \limits _{v\in {\text {chi}}(u)}\lambda _{v}\bigg )^{1/2}. \end{aligned}$$

Hilbert adjoint of S [14]: The Hilbert adjoint $S^*$ of the shift operator S on $L^2({\mathcal {T}},\lambda )$ is given by

$$\begin{aligned} (S^*g)(u)=\frac{1}{\lambda _u}\sum \limits _{v\in {\text {chi}}(u)}g(v)\lambda _v, \end{aligned}$$

for each $g\in L^2({\mathcal {T}},\lambda )$ and $u\in V$.

2 Antinormality of the shift operator

Prior to our investigations on antinormality of S, we state some results. From the definition of S and $S^*$, we have $\mathrm{ker}(S)=\{f\in L^2({\mathcal {T}},\lambda ) : \ f(u)=0, \ for \ each \ u \in V{\setminus } V_{{\text {leaves}}}\}$ and $\mathrm{ker}(S^*)=\big \{f\in L^2({\mathcal {T}},\lambda ) : \ \sum \nolimits _{v\in {\text {chi}}(u)}f(v)\lambda _v=0, \ for \ each \ u \in V\big \}$. Thus, $\mathrm{ker}(S)$ is collection of all $f\in L^2({\mathcal {T}},\lambda )$ such that . Hence, $\dim (\mathrm{ker}(S))$ is finite if and only if ${\text {card}}(V_{{\text {leaves}}})$ is finite. Further, if ${\text {card}}(V_{{\text {leaves}}})$ is finite then $\dim (\mathrm{ker}(S))={\text {card}}(V_{{\text {leaves}}})$.

Lemma 2.1

Dimension of $\mathrm{ker}(S^*)$ is finite if and only if ${\text {card}}(V_{\ge 2})$ is finite. Moreover, if ${\text {card}}(V_{\ge 2})$ is finite, then $\dim (\mathrm{ker}(S^*))={\text {card}}({\text {chi}}(V_{\ge 2}))-{\text {card}}(V_{\ge 2})+\delta _{\mathcal {T}}$.

Proof

Let . Then,

(2.1)

If $v\in V_{\ge 2}$, then $\gamma (v)\ge 2$. Let ${\text {chi}}(v)=\{w_1,w_2, \ldots ,w_l\}$ and satisfying $\sum \nolimits _{i=1}^{l}f(w_i)\lambda _{w_i} =0$ then from Eq. (2.1) $f\in \mathrm{ker}(S^*)$. Clearly, the collection of all such f forms a subspace of dimension $\gamma (v)-1\ge 1$, which is contained in $\mathrm{ker}(S^*)$. Also, for $u_1\not =u_2$, ${\text {chi}}(u_1)$ and ${\text {chi}}(u_2)$ are disjoint sets. Therefore, $\dim (\mathrm{ker}(S^*))\ge {\text {card}}(V_{\ge 2})$. Hence, if ${\text {card}}(V_{\ge 2})$ is not finite, then $\dim (\mathrm{ker}(S^*))$ is also not finite.

Now assume that ${\text {card}}(V_{\ge 2})$ is finite. If $V_{\ge 2}$ is empty, then the result obviously holds. Let $V_{\ge 2}=\{v_1,v_2, \ldots ,v_k\}$ and for each $v_j\in V_{\ge 2}, \ {\text {chi}}(v_j)=\{w_1^j,w_2^j, \ldots ,w_{m_j}^j\}$. We now consider the case when the tree has a root. Let . Then, from Eq. (2.1), $f(w)=0$ whenever ${\text {par}}(w)$ has unique child viz. w. Thus, $f(w)=0$, whenever $w\in V{\setminus }({\text {chi}}(V_{\ge 2})\cup \{{\text {root}}\}$. Hence

Therefore, f is linear combination of with $k (={\text {card}}(V_{\ge 2}))$ extra conditions

$$\begin{aligned} \sum \limits _{i=1}^{m_j}f(w_{i}^{j})\lambda _{w_{i}^{j}} =0, \ 1\le j \le k. \end{aligned}$$

This implies that , where $V_{\ge 2}=\{v_1,v_2, \ldots ,v_k\}$ and for each $v_j\in V_{\ge 2}, \ {\text {chi}}(v_j)=\{w_1^j,w_2^j, \ldots ,w_{m_j}^j\}$. Consequently,

$$\begin{aligned} \dim (\mathrm{ker}(S^*))=1+{\text {card}}({\text {chi}}(V_{\ge 2}))-{\text {card}}(V_{\ge 2}). \end{aligned}$$

(2.2)

Preceding arguments also implies that if ${\text {card}}(V_{\ge 2})$ is finite and the tree has no root then , where $V_{\ge 2}=\{v_1,v_2, \ldots ,v_k\}$ and for each $v_j\in V_{\ge 2}, \ {\text {chi}}(v_j)=\{w_1^j,w_2^j, \ldots ,w_{m_j}^j\}$. Therefore,

$$\begin{aligned} \dim (\mathrm{ker}(S^*))={\text {card}}({\text {chi}}(V_{\ge 2}))-{\text {card}}(V_{\ge 2}). \end{aligned}$$

(2.3)

Hence from Eqs. (2.2) and (2.3), we get

$$\begin{aligned} \dim (\mathrm{ker}(S^*))={\text {card}}({\text {chi}}(V_{\ge 2}))-{\text {card}}(V_{\ge 2})+\delta _{\mathcal {T}}. \end{aligned}$$

$\square$

Remark 2.2

• (1) It is worth noting that, if tree is not locally finite, then

  $$\begin{aligned} \dim (\mathrm{ker}(S^*))=\sum \limits _{u\in {\text {chi}}(V_{\ge 2})}[{\text {card}}({\text {chi}}(V_{\ge 2}))-1]+\delta _{\mathcal {T}}. \end{aligned}$$

• (2) In view of preceding definitions and the above lemma, the following statements follow easily.

  • (i) If ${\text {card}}(V_{\ge 2})$ is finite then ${\text {card}}(V_{{\text {leaves}}})$ is also finite.

  • (ii) The ${\text {card}}(V_{\ge 2})$ is finite if and only if ${\text {card}}({\text {chi}}(V_{\ge 2}))$ is finite.

  • (iii) $2\cdot {\text {card}}(V_{\ge 2})\le {\text {card}}({\text {chi}}(V_{\ge 2}))$.

We now give a relation between ${\text {card}}(V_{\ge 2})$, ${\text {card}}({\text {chi}}(V_{\ge 2}))$ and ${\text {card}}(V_{{\text {leaves}}})$.

Proposition 2.3

In a tree ${\mathcal {T}}$, ${\text {card}}(V_{{\text {leaves}}})+{\text {card}}(V_{\ge 2})\le {\text {card}}({\text {chi}}(V_{\ge 2}))+1$.

Proof

First consider the case when the tree ${\mathcal {T}}$ is finite. In this case, using induction on number of vertices we prove that the above inequality is an equality. Clearly equality holds for the tree with 1 and 2 vertices. Let the assertion be true for the tree with $k(\ge 2)$ vertices. Now, consider a tree ${\mathcal {T}}$ with $k+1$ vertices. Then ${\mathcal {T}}$ has a leaf $v^*$. Consequently, the tree $\tilde{{\mathcal {T}}}=({\tilde{V}},{\tilde{E}})={\mathcal {T}}{\setminus }\{v^*\}$ has k vertices with two possibilities:

• (1) If $v^*\in {\text {chi}}(V_{\ge 2})$, then ${\text {card}}({{\tilde{V}}_{{\text {leaves}}}})={\text {card}}(V_{{\text {leaves}}})-1$. Further, in this case, we have following two possibilities:

  • (a) If $\gamma ({\text {par}}(v^*))=2$ then ${\text {card}}(\tilde{V_{\ge 2}})={\text {card}}(V_{\ge 2})-1$ and ${\text {card}}({\text {chi}}(\tilde{V_{\ge 2}}))={\text {card}}({\text {chi}}(V_{\ge 2}))-2$. Since equality holds for a tree with k vertices, therefore

    $$\begin{aligned} {\text {card}}({\tilde{V}}_{{\text {leaves}}})+{\text {card}}({\tilde{V}}_{\ge 2})= {\text {card}}({\text {chi}}({\tilde{V}}_{\ge 2}))+1. \end{aligned}$$

    This implies

    $$\begin{aligned} {\text {card}}({V}_{{\text {leaves}}})-1+{\text {card}}({V}_{\ge 2})-1= {\text {card}}({\text {chi}}({V}_{\ge 2}))-2+1. \end{aligned}$$

    Thus,

    $$\begin{aligned} {\text {card}}({V}_{{\text {leaves}}})+{\text {card}}({V}_{\ge 2})= {\text {card}}({\text {chi}}({V}_{\ge 2}))+1. \end{aligned}$$

  • (b) If $\gamma ({\text {par}}(v^*))\ge 3$ then ${\text {card}}(\tilde{V_{\ge 2}})={\text {card}}(V_{\ge 2})$ and ${\text {card}}({\text {chi}}(\tilde{V_{\ge 2}}))={\text {card}}({\text {chi}}(V_{\ge 2}))-1$. Therefore,

    $$\begin{aligned} {\text {card}}({\tilde{V}}_{{\text {leaves}}})+{\text {card}}({\tilde{V}}_{\ge 2})= {\text {card}}({\text {chi}}({\tilde{V}}_{\ge 2}))+1. \end{aligned}$$

    Which gives

    $$\begin{aligned} {\text {card}}({V}_{{\text {leaves}}})+{\text {card}}({V}_{\ge 2})= {\text {card}}({\text {chi}}({V}_{\ge 2}))+1. \end{aligned}$$

• (2) If $v^*\notin {\text {chi}}(V_{\ge 2})$ then ${\text {card}}({{\tilde{V}}_{{\text {leaves}}}})={\text {card}}(V_{{\text {leaves}}})$, ${\text {card}}(\tilde{V_{\ge 2}})={\text {card}}(V_{\ge 2})$ and ${\text {card}}({\text {chi}}(\tilde{V_{\ge 2}}))={\text {card}}({\text {chi}}(V_{\ge 2}))$. Therefore ${\text {card}}({V}_{{\text {leaves}}})+{\text {card}}({V}_{\ge 2})={\text {card}}({\text {chi}}({V}_{\ge 2}))+1$.

Thus, equality also holds for a tree with $k+1$ vertices. Hence, it holds for any finite tree.

Now consider the case when the tree ${\mathcal {T}}$ is not finite. Let us split this case into two parts as follows:

• (1) If ${\text {card}}(V_{\ge 2})$ is not finite then ${\text {card}}({\text {chi}}(V_{\ge 2}))$ is also not finite. Thus in this case the result holds.

• (2) If ${\text {card}}(V_{\ge 2})$ is finite (which implies ${\text {card}}(V_{{\text {leaves}}})$ is also finite) then we can choose a finite subset $W\subseteq V$ such that $\tilde{{\mathcal {T}}}=\big (W,E\cap (W\times W)\big )$ is a tree with the properties that $V_{\ge 2}, {\text {chi}}(V_{\ge 2})$ and $V_{{\text {leaves}}}$ are all contained in W and the directed graph ${\mathcal {T}}{\setminus } W$ is collection of finite number of linear trees each of which is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ or $\mathbb {Z_{{\mathcal {T}}}^-}$. Further, let $W_{\ge 2}=\{w\in W :\gamma (w)>1\}$ and $W_{{\text {leaves}}}=\{w\in W :w \ is \ leaf \ of \ \tilde{{\mathcal {T}}}\}$. Then $W_{\ge 2}=V_{\ge 2}$, ${\text {chi}}(W_{\ge 2})={\text {chi}}(V_{\ge 2})$ and we have exactly two scenarios:

  • (a) ${\mathcal {T}}{\setminus } W$ contains a linear tree which is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ and ${\text {card}}(W_{{\text {leaves}}})>{\text {card}}(V_{{\text {leaves}}})$.

  • (b) ${\mathcal {T}}{\setminus } W$ does not contain any linear tree which is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ (in this case ${\mathcal {T}}{\setminus } W$ is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^-}$)and ${\text {card}}(W_{{\text {leaves}}})={\text {card}}(V_{{\text {leaves}}})$.

  Thus, we have ${\text {card}}(V_{{\text {leaves}}})\le {\text {card}}(W_{{\text {leaves}}})$. Therefore,

  $$\begin{aligned} {\text {card}}({V}_{{\text {leaves}}})+{\text {card}}({V}_{\ge 2})\le & {} {\text {card}}({W}_{{\text {leaves}}})+{\text {card}}({W}_{\ge 2})\\= & {} {\text {card}}({\text {chi}}({W}_{\ge 2}))+1\\= & {} {\text {card}}({\text {chi}}({V}_{\ge 2}))+1. \end{aligned}$$

Hence, the result holds for every tree ${\mathcal {T}}$. $\square$

Remark 2.4

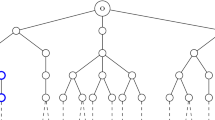
Above proposition can be visualized in the following trees. Figure 1 is a finite tree for which the inequality of Proposition 2.3 becomes an equality. In Figure 2 tree ${\mathcal {T}}$ is not finite but ${\text {card}}(V_{\ge 2})$ is finite. In this tree, if we take W as collection of all the vertices such that $V_{\ge 2}, {\text {chi}}(V_{\ge 2})$ and $V_{{\text {leaves}}}$ are all contained in W, then ${\mathcal {T}}{\setminus } W$ is collection of finite number of linear trees each of which is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ or $\mathbb {Z_{{\mathcal {T}}}^-}$.

Fig. 1

A Finite tree

Fig. 2

Infinite tree in which card ($V\ge 2$) is finite

Corollary 2.5

For the $S:L^2({\mathcal {T}},\lambda )\rightarrow L^2({\mathcal {T}},\lambda )$, $i(S)\le 1$.

Proof

Consider the case when $\dim (\mathrm{ker}(S))$ and $\dim (\mathrm{ker}(S^*))$ are both infinite then by definition, $i(S)=0$. The Remark 2.2 precludes the possibility that $\dim (\mathrm{ker}(S))$ is infinite and $\dim (\mathrm{ker}(S^*))$ is finite. If $\dim (\mathrm{ker}(S))$ is finite but $\dim (\mathrm{ker}(S^*))$ is infinite then $i(S)=-\infty$. Now if $\dim (\mathrm{ker}(S))$ and $\dim (\mathrm{ker}(S^*))$ both are finite, then

$$\begin{aligned} i(S)= & {} \dim (\mathrm{ker}(S))-\dim (\mathrm{ker}(S^*))\\= & {} {\text {card}}({V}_{{\text {leaves}}})-[{\text {card}}({\text {chi}}({V}_{\ge 2}))-{\text {card}}({V}_{\ge 2})+\delta _{\mathcal {T}}]\\\le & {} 1-\delta _{\mathcal {T}}\\= & {} \left\{ \begin{array}{@{}l@{ }l} 1, &{} \text{ if } \text{ the } \text{ tree } \text{ is } \text{ without } \text{ a } \text{ root } \\ 0, &{} \text{ otherwise. }\\ \end{array} \right. \end{aligned}$$

Thus, $i(S)\le 1$. $\square$

Remark 2.6

If $i(S)=1$, then tree is not finite and by Corollary 2.5$\delta _{\mathcal {T}}=0$. This implies that tree has no root. Again by Corollary 2.5${\text {card}}(V_{\ge 2})$ is finite and ${\text {card}}(V_{{\text {leaves}}})={\text {card}}({\text {chi}}(V_{\ge 2}))-{\text {card}}(V_{\ge 2})+1$. Now repeating the arguments of Proposition 2.3 above, it follows that there exists $W\subseteq V$ such that ${\mathcal {T}}{\setminus } W$ is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^-}$. In all other cases, the $i(S)\le 0$.

We now have the following propositions.

Proposition 2.7

If $i(S)<0$ then S is antinormal if and only if for every $\epsilon >0$, there exists a finite subset $U\subset V$ such that $\big |\Delta (v)-\Vert S\Vert \big |<\epsilon$ for each $v\in V{\setminus } U$.

Proof

Let $i(S)<0$. Then, $V_{{\text {leaves}}}$ must be finite. For if, $V_{{\text {leaves}}}$ is an infinite set then $V_{\ge 2}$ is also an infinite set. Hence both the $\dim (\mathrm{ker}(S))$ and $\dim (\mathrm{ker}(S^*))$ are infinite. Consequently $i(S)=0$, which is a contradiction.

Now consider $T=(S^*S)^{\frac{1}{2}}$. Since

therefore,

Thus, T is a diagonal operator. Hence, essential minimum modulus of S is

$$\begin{aligned} m_e(S)= & {} \inf \{\alpha \ge 0 \ : \alpha \in \sigma _e(T) \}\\= & {} \inf \{\alpha \ge 0 \ : \ T-\alpha I \ \text{ is } \text{ not } \text{ Fredholm }\}\\= & {} \inf \{\alpha \ge 0 : \text{ either } \dim (\mathrm{ker}(T-\alpha I)) \text{ is } \text{ not } \text{ finite } \text{ or } {\text {range}}(T-\alpha I) \text{ is } \text{ not } \text{ closed }\}\\= & {} \inf \{\alpha \ge 0 \ : \alpha \text{ is } \text{ a } \text{ limit } \text{ of } \text{ some } \text{ convergent } \text{ sequence } \text{ in } \Delta \}, \end{aligned}$$

Now $\Vert S\Vert =\sup \limits _{u\in V}\big (\frac{1}{\lambda _u}\sum \limits _{v\in {\text {chi}}(u)}\lambda _{v}\big )^{\frac{1}{2}}$ and $i(S)<0$. Hence S is antinormal if and only if $m_e(S)=\Vert S\Vert$. This is equivalent to $\Delta$ has a convergent sequence and every convergent sequence in $\Delta$ converge to $\Vert S\Vert$. As $\sup \nolimits _{v\in V}\Delta (v)=\Vert S\Vert$, therefore S is antinormal if and only if for every $\epsilon >0$, there exists a finite subset $U\subset V$ such that $\big |\Delta (v)-\Vert S\Vert \big |<\epsilon$ for each $v\in V{\setminus } U$. $\square$

Proposition 2.8

If $i(S)=1$ then S is antinormal if and only for every $\epsilon >0$, there exists a finite subset $U\subset V$ such that $\big |\Delta (v)-\Vert S\Vert \big |<\epsilon$ for each $v\in V{\setminus } U$.

Proof

Let $i(S)=1$. Then by Remark 2.6, the tree ${\mathcal {T}}$ has no root and there exists a set of finite vertices $W=\{w_1,w_2, \ldots ,w_l\}$ such that the tree ${\mathcal {T}}{\setminus } W$ is isomorphic to the $\mathbb {Z_{{\mathcal {T}}}^-}$. Hence any sequence in $\big \{\big (\frac{1}{\lambda _u}\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v\big )^{1/2} :u\in V\big \}$ will lie eventually in $\big \{\big (\frac{1}{\lambda _u}\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v\big )^{\frac{1}{2}}: u\in V{\setminus } W \big \}$. Also $i(S^*)=-i(S)=-1<0$. Consider $T=(SS^*)^{\frac{1}{2}}$. A simple computation shows that

Therefore,

The above equation can also be expressed as

Using the fact that W is finite set and T is diagonal operator on $V{\setminus } W$, we get

$$\begin{aligned} m_e(S^*)= & {} \inf \{\alpha \ge 0 \ : \alpha \in \sigma _e(T) \}\\= & {} \inf \{\alpha \ge 0 \ : T-\alpha I \text{ is } \text{ not } \text{ Fredholm }\}\\= & {} \inf \{\alpha \ge 0 : \text{ either } \dim (\mathrm{ker}(T-\alpha I)) \text{ is } \text{ not } \text{ finite } \text{ or } {\text {range}}(T-\alpha I) \text{ is } \text{ not } \text{ closed }\}\\= & {} \inf \big \{\alpha \ge 0 \ : \hbox {} \alpha \hbox {is a limit of some convergent sequence in} \bigg \{\bigg (\frac{1}{\lambda _u}\sum \limits _{v\in {\text {chi}}(u)}\lambda _v \bigg )^{\frac{1}{2}}: u\in V{\setminus } W\big \} \bigg \},\\= & {} \inf \{\alpha \ge 0 \ : \alpha \text{ is } \text{ a } \text{ limit } \text{ of } \text{ some } \text{ convergent } \text{ sequence } \text{ in } \Delta \}, \end{aligned}$$

Since $i(S^*)<0$, therefore $S^*$ is antinormal if and only if $m_e(S^*)=\Vert S^*\Vert$. Also S is antinormal if and only if $S^*$ is antinormal. Hence, S is antinormal if and only if $m_e(S^*)=\Vert S\Vert$. Consequently S is antinormal if and only for every $\epsilon >0$, there exists a finite subset $U\subset V$ such that $\big |\Delta (v)-\Vert S\Vert \big |<\epsilon$ for each $v\in V{\setminus } U$. $\square$

Combining above two propositions and Remark 1.6 we obtain the following result.

Theorem 2.9

S is antinormal if and only if $i(S)\not =0$, for every $\epsilon >0$, there exists a finite subset $U\subset V$ such that $\big |\Delta (v)-\Vert S\Vert \big |<\epsilon$ for each $v\in V{\setminus } U$.

3 m-isometry of the shift operator

In this section, we investigate the m-isometry of the shift operator and relate it to its antinormality. From the definition of m-isometry we have the following result.

Proposition 3.1

S is an m-isometry if and only if for every $u\in V$ the following holds:

$$\begin{aligned} \lambda _u-\left( {\begin{array}{c}m\\ 1\end{array}}\right) \sum \limits _{v\in {\text {chi}}(u)}\lambda _v+\left( {\begin{array}{c}m\\ 2\end{array}}\right) \sum \limits _{v\in {\text {chi}}^2(u)}\lambda _v-\cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) \sum \limits _{v\in {\text {chi}}^m(u)}\lambda _v=0. \end{aligned}$$

(3.1)

Remark 3.2

If S is an m-isometry for any $m\ge 1$, then the tree is without leaves.

Proposition 3.3

S is an m-isometry if and only if for every $u \in V$, there exists a polynomial $P_u$ of degree at most $m-1$ such that $\sum \nolimits _{v\in {\text {chi}}^n(u)}\lambda _v=P_u(n)$, for every $n\in {\mathbb {N}}\cup \{0\}$.

Proof

Assume that S is an m-isometry. Let $u \in V$, define, $b_{n}^{u}= \sum \nolimits _{v\in {\text {chi}}^n(u)}\lambda _v$, $n\ge 1$ and $b_{0}^{u}=\lambda _u$. Then, Eq. (3.1) becomes

$$\begin{aligned} b_{0}^{u}-\left( {\begin{array}{c}m\\ 1\end{array}}\right) b_{1}^{u}+\left( {\begin{array}{c}m\\ 2\end{array}}\right) b_{2}^{u}- \cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) b_{m}^{u}=0. \end{aligned}$$

More generally for every $n\ge 0$, we have

$$\begin{aligned} b_{n}^{u}-\left( {\begin{array}{c}m\\ 1\end{array}}\right) b_{n+1}^{u}+\left( {\begin{array}{c}m\\ 2\end{array}}\right) b_{n+2}^{u}- \cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) b_{n+m}^{u}=0. \end{aligned}$$

(3.2)

Now using theory of difference equations, the auxiliary equation of the recursive Eq. (3.2) is

$$\begin{aligned} 1-\left( {\begin{array}{c}m\\ 1\end{array}}\right) r+\left( {\begin{array}{c}m\\ 2\end{array}}\right) r^{2}- \cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) r^{m}=0. \end{aligned}$$

Above equation has 1 as the only zero with multiplicity m. Therefore, the general solution of Eq. (3.2) is

$$\begin{aligned} b_{n}^{u}=A_0(1)^n+A_1n(1)^n+A_2n^2(1)^n+ \cdots +A_{m-1}n^{m-1}(1)^n. \end{aligned}$$

Thus,

$$\begin{aligned} b_{n}^{u}=\sum \limits _{v\in {\text {chi}}^n(u)}\lambda _v=A_0+A_1n+A_2n^2+ \cdots +A_{m-1}n^{m-1}, \ for \ each \ n\ge 0, \end{aligned}$$

(3.3)

where $A_0,A_1, \ldots ,A_{m-1}$ are real constants which can be determined by m initial conditions

$$\begin{aligned} b_{i}^{u}=\sum \limits _{v\in {\text {chi}}^i(u)}\lambda _v, \ 0\le i\le m-1. \end{aligned}$$

Conversely, let $u\in V$. Then, there exists a polynomial $P_u$ of degree at most $m-1$ such that $b_n^u=\sum \nolimits _{v\in {\text {chi}}^n(u)}\lambda _v=P_u(n)$ for every $n\in {\mathbb {N}}\cup \{0\}$.Let

$$\begin{aligned} P_u(n)=C_0+C_1n+C_2n^2+\cdots +C_kn^{k}, C_k\not =0 \ and \ 0\le k\le m-1. \end{aligned}$$

This implies

$$\begin{aligned} b_n^u=C_0+C_1n+C_2n^2+ \cdots +C_kn^{k}, C_k\not =0 \ and \ 0\le k\le m-1. \end{aligned}$$

Then, the sequence $\{b_n^u\}_{n=0}^{\infty }$ can be recursively obtained by

$$\begin{aligned} b_{n}^{u}-\left( {\begin{array}{c}k+1\\ 1\end{array}}\right) b_{n+1}^{u}+\left( {\begin{array}{c}k+1\\ 2\end{array}}\right) b_{n+2}^{u}- \cdots +(-1)^{k+1}\left( {\begin{array}{c}k+1\\ k+1\end{array}}\right) b_{n+k+1}^{u}=0. \end{aligned}$$

Since $k+1\le m$, therefore for every $n\ge 0$

$$\begin{aligned} b_{n}^{u}-\left( {\begin{array}{c}m\\ 1\end{array}}\right) b_{n+1}^{u}+\left( {\begin{array}{c}m\\ 2\end{array}}\right) b_{n+2}^{u}- \cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) b_{n+m}^{u}=0. \end{aligned}$$

In particular,

$$\begin{aligned} b_{0}^{u}-\left( {\begin{array}{c}m\\ 1\end{array}}\right) b_{1}^{u}+\left( {\begin{array}{c}m\\ 2\end{array}}\right) b_{2}^{u}- \cdots +(-1)^m\left( {\begin{array}{c}m\\ m\end{array}}\right) b_{m}^{u}=0. \end{aligned}$$

Thus, S is an m-isometry. $\square$

Corollary 3.4

Suppose S is an m-isometry. Then, S is strictly m-isometry if and only if $\max \{\mathrm{{deg}}(P_u):u\in V\}=m-1$.

Now onwards, whenever we talk about a polynomial $P_u$ of a vertex u then it is presumed that S is an m-isometry for some $m\ge 1$.

Remark 3.5

If $u \in V$ and $v_1,v_2, \ldots ,v_l \in {\text {chi}}(u)$, then $P_u(1)=\sum \nolimits _{i=1}^{l}\lambda _{v_i}==\sum \nolimits _{i=1}^{l}P_{v_i}(0)$. Similarly, $P_u(n+1)=\sum \nolimits _{i=1}^{l}P_{v_i}(n)$.

In [10, Proposition 8.1.6] Zenon Jan Jabłoński et al. characterized the normality of weighted shift operator on trees. We state an equivalent form of this result as Proposition 3.6.

Proposition 3.6

S is normal if and only if the following conditions are satisfied.

• (1) Tree is rootless and has no leaves,

• (2) for every $u \in V, \ \gamma (u)=1$ and

• (3) for every $u \in V,\frac{\lambda _u}{\lambda _{{\text {par}}(u)}}=\beta$ for some positive real number $\beta$.

Remark 3.7

Suppose S is an m-isometry and for a vertex u, $\mathrm{{deg}}(P_u)=k$. Then, the following statements hold.

• (1) For every $n\in {\mathbb {N}}$ and for every $v\in {\text {chi}}^n(u)$, $\mathrm{{deg}}(P_v)\le k$.

• (2) For every $n\in {\mathbb {N}}$ there exists a $v\in {\text {chi}}^n(u)$, $\mathrm{{deg}}(P_v)=k$.

Using the above remarks, we have the following result.

Proposition 3.8

If S is an m-isometry and there exists $u_0\in V$ such that $P_{u_0}$ is constant polynomial, then there are infinitely many u in V such that $P_u$ is constant polynomial (in other words we have a sequence $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ in $\Delta$ with $\Delta (\mu (n))=1$ for each $n\ge 1)$.

We now investigate a connection between antinormality and m-isometry of S. Recall that, if S is antinormal then $i(S)\not =0$. Hence, either $i(S)=1$ or $i(S)<0$. If $i(S)=1$, then the tree must have a leaf. Consequently S can not be m-isometry for any $m\ge 1$.

Theorem 3.9

If S is antinormal and $i(S)=-k$ for some $k\in {\mathbb {N}}$ then S is an m-isometry for some $m\ge 2$ if and only if it is an isometry.

Proof

One way the implication is trivial. On the other hand, suppose that S is antinormal and an m-isometry for some $m\ge 2$. As S is antinormal, there is a sequence $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ in $\Delta$ which converges to $\Vert S\Vert$. Also, since $i(S)=-k$, therefore ${\text {card}}(V_{\ge 2})$ is finite, and the tree has no leaves. This implies that we can choose a finite set $W\subseteq V$ such that ${\mathcal {T}}{\setminus } W$ is finite collection of trees each of which is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ or $\mathbb {Z_{{\mathcal {T}}}^-}$. Therefore there exists a tree $\tilde{{\mathcal {T}}}=({\tilde{V}},{\tilde{E}})$ in ${\mathcal {T}}{\setminus } W$ such that a subsequence of $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ which lies in $\big \{\big (\frac{1}{\lambda _u}\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v\big )^{\frac{1}{2}} : u\in {\tilde{V}}\big \}$. Without loss of generality, let us assume that $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ lie in $\big \{\big (\frac{1}{\lambda _u}\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v\big )^{\frac{1}{2}} : u\in {\tilde{V}}\big \}$. Now assume that $\tilde{{\mathcal {T}}}$ be isomorphic to $\mathbb {Z_{{\mathcal {T}}}^+}$ with root $u_0$. Since for every $m\in {\mathbb {N}}$, $\frac{P_{u_0}(m+1)}{P_{u_0}(m)}=\frac{\lambda _{{\text {chi}}^{(m+1)}{u_0}}}{\lambda _{{\text {chi}}^{m}{u_0}}}$, therefore for each $n\in {\mathbb {N}}$ there exists a $m_n\in {\mathbb {N}}$ such that $\frac{P_{u_0}(m_n +1)}{P_{u_0}(m_n)}=\Delta (\mu (n))^2$. Further, choose a sequence $(n_l)_{l=1}^{\infty }$ in ${\mathbb {N}}$ such that $(m_{n_l})_{l=1}^{\infty }$ is an increasing sequence in ${\mathbb {N}}$. Since $\Delta (\mu (n))(n_l)^2$ converges to $\Vert S\Vert ^2$, so $\frac{P_{u_0}(m_{n_l}+1)}{P_{u_0}(m_{n_l})}$ converge to $\Vert S\Vert ^2$. But $P_{u_0}$ is a non-zero polynomial, hence $\frac{P_{u_0}(m_{n_l}+1)}{P_{u_0}(m_{n_l})}$ converges to 1. Therefore, $\Vert S\Vert =1$. Now consider the case that $\tilde{{\mathcal {T}}}$ is isomorphic to $\mathbb {Z_{{\mathcal {T}}}^-}$ with leaf $w_0$. Since for each vertex w in $\tilde{{\mathcal {T}}}$, $P_w(n)>0$ therefore using Remark 3.5 we get $P_{{\text {par}}(w)}(n)=P_w(n-1)$. Consequently $P_{w_0}(-n)=\lambda _{{\text {par}}^n(w_0)}$ for every $n\in {\mathbb {N}}$. Hence, $\Vert S\Vert =1$. Thus S is an isometry. $\square$

Remark 3.10

It is worth noting that, if $i(S)=-k$, then tree must be locally finite. Therefore in the above theorem, we can relax the condition that tree is locally finite.

Finally, we give some examples and counterexamples. In the following Figs. 3, 4, 5 and 6, a “$\bullet$" represents a vertex labeled by their corresponding weights and a line joining two vertices represent an edge with an arrow pointing from vertex ${\text {par}}(u)$ to vertex u.

Example 3.11

The shift operator on the following weighted tree is strictly 2-isometry but is not antinormal. This follows from Corollary 3.4 and Theorem 2.9.

Fig. 3

Tree on which shift operator is strictly 2-isometry but not antinormal

Example 3.12

Consider the shift operator S on the following weighted tree. It can be readily seen from Theorem 2.9 that S is antinormal. However, since weights of vertices grow exponentially, so S is not an m-isometry for any $m\in {\mathbb {N}}$.

Fig. 4

Tree on which shift operator is antinormal but not m-isometry ($\forall m \ge 1)$

Example 3.13

The shift operator on the following weighted tree is antinormal as well as an isometry. This is because $\sum \nolimits _{v\in {\text {chi}}(u)}\lambda _v=\lambda _u$, for every vertex u in the following weighted tree.

Fig. 5

Tree on which shift operator is antinormal as well as an isometry

Fig. 6

Tree on which shift operator is antinormal as well as strictly 3-isometry

The following example shows that when $i(S)=-\infty$ and S is antinormal as well as an m-isometry then it need not be an isometry.

Example 3.14

In the following figure a vertex $u\in V$ is labeled by $P_u(n)$, where $P_u$ is the polynomial corresponding to u and $q_j$ denotes the jth prime number.

Since the above tree has no leaves, therefore $\dim (\mathrm{ker}(S))=0$. Also ${\text {card}}(V_{\ge 2})=\infty \$. Hence $i(S)=-\infty$. For a vertex $w\in V$ such that ${\text {card}}({\text {chi}}({\text {par}}(w)))=1$, its corresponding polynomial $P_w$ is determined by Remark 3.5. For example $P_{w_1}(n)=(n+1)+3-\frac{1}{7}=n+4-\frac{1}{7}$. Since $\max \nolimits _{u\in V}\mathrm{{deg}}(P_u)=2$, therefore S is strictly 3-isometry. We also note that $P_u(0)$ is the weight of the vertex u. Further, from Theorem 2.9 it follows that the shift operator S on the above tree is antinormal.

Finally, we obtain the following proposition followed by its corollary.

Proposition 3.15

If S is antinormal and strictly m-isometry for $m\ge 2$ then for every $u\in V$ $\mathrm{{deg}}(P_u)\ge 1$.

Proof

On the contrary, suppose there exists a $u_0$ in V such that $\mathrm{{deg}}(P_{u_0})=0$. Since S is strictly m-isometry for $m\ge 2$. Therefore $\Vert S\Vert >1$. As $\mathrm{{deg}}(P_{u_0})=0$, by Proposition 3.8 there exists a sequence $\{\Delta (\mu (n))\}_{n=1}^{\infty }$ in $\Delta$ with $\Delta (\mu (n))=1$ for each $n\ge 1$. Consequently, from Theorem 2.9$\Vert S\Vert =1$. This is a contradiction. $\square$

Corollary 3.16

If S is an antinormal m-isometry for some $m\ge 2$ and $i(S)=-\infty$ then S is an isometry if and only if there exists a vertex $u_0$ in V such that $\lambda _{u_0}=\sum \nolimits _{v\in {\text {chi}}^n(u_0)}\lambda _v$ for every $n\in {\mathbb {N}}$.