1 Introduction

Collapse is one of the fascinating effects in physics, that can be observed in astrophysics, nonlinear optics, quantum physics, etc. The collapse of the Bose–Einstein condensates (BEC) can be investigated both theoretically [1, 13, 14] and experimentally [5]. The collapse of the BEC can be obtained due to the attraction of particles with negative scattering length \(a_{s}\) flipped from the positive by Feshbach resonance [4]. The collapse process strongly depends on the interatomic interaction, since, observation for one-dimensional space is impossible with cubic nonlinearity and with quintic nonlinearity is still can occur [2]. The collapse of the condensate with cubic nonlinearity for two-dimensional space occurs above a critical number of particles, while for three-dimensional case, it always occurs at sufficiently long time.

Synthetic spin–orbit coupling (SOC) and optically produced pseudospin-1/2 [10] is one of the most interesting phenomena of the BEC physics with intriguing effects based on “anomalous” spin-dependent velocity. Effect of this “anomalous” velocity in the collapse of BEC was considered in various SOC and interatomic interaction regimes [9, 11].

Here, we study the collapse of a quasi-two-dimensional spin-orbit coupled BEC with the cubic nonlinearity. We concentrate only in symmetrized Dresselhaus [7, 8] SOC with pseudospin-1/2. We demonstrate dynamical properties of the collapse of spin–orbit coupled condensate, where, as a result, for sufficiently strong anomalous spin-dependent velocity the collapse process is modified. All demonstrated results will be obtained from the direct numerical solution of the Gross–Pitaevskii equation.

2 Model and main parameters of collapse

We assume at zero temperature an initial state of the condensate is prepared in a ground state form of the quantum harmonic potential:

$$\begin{aligned} {\varvec{\psi } }(\mathbf{r},t=0) \equiv \frac{\sqrt{N/\pi }}{a(0)} \exp \left[ -\frac{r^{2}}{2a^{2}(0)}\right] \left[ \begin{array}{c} 1 \\ 0 \end{array}\right] , \end{aligned}$$
(2.1)

where a(0) is the initial width of the condensate and an initial spin state is along z axis. At \(t>0\), the confining potential is switched off [6] and the SOC and the attraction between the atoms are switched on. The subsequent dynamics of the spin–orbit coupled condensate with pseudospin-1/2 is described by a wave function \(\varvec{\psi }=\left[ \varvec{\psi }_{1}({\mathbf {r}},t),\varvec{\psi }_{2}({\mathbf {r}},t)\right] ^\mathrm{T}\), where \(\mathbf{r} \equiv (x,y)\), normalized to the total number of particles N. The evolution of the wavefunction is described by Gross–Pitaevskii equation

$$\begin{aligned} i\hbar \frac{\partial {\varvec{\psi } }}{\partial t}=\left[ -\frac{\hbar ^{2}}{2M}\Delta +H_{\mathrm {so}} -g\left| \varvec{\psi } \right| ^{2}\right] {\varvec{\psi } }, \end{aligned}$$
(2.2)

where M is the particle mass, \(H_{\mathrm {so}}\) is the SOC Hamiltonian. In Eq. (2.2), the interaction constant is given by \(g=-4\pi \hbar ^{2}a_{s}/Ma_{z}\), where \(a_{z}\) is the condensate size along the \(z-\) axis, and \(a_{s}\) is negative [1, 12, 14].

Below, we use the units \(\hbar \equiv M\equiv 1\) and the dimensionless interaction \({\widetilde{g}}\equiv -4\pi {a_{s}}/a_{z}\). The unit of length a(0) is chosen arbitrarily, and the corresponding unit of time is \(a^{2}(0)\).

For the spin-independent collapse of the condensate the total energy is defined by

$$\begin{aligned} \displaystyle E= -\frac{1}{2} \int \left[ \varvec{\psi }^{\dagger }\Delta \varvec{\psi }+ {\widetilde{g}}\left| \varvec{\psi }\right| ^{4}\right] \mathrm{d}x\mathrm{d}y. \end{aligned}$$
(2.3)

To demonstrate the evolution of the collapse, we use variational approach based on Gaussian ansatz [1]

$$\begin{aligned} {\varvec{\psi } }(\mathbf{r},t) = \frac{\sqrt{N/\pi }}{{\widetilde{a}}}\exp \left[ -\frac{r^{2}}{2{\widetilde{a}}^{2}}\left( 1+i{\widetilde{b}}\right) \right] \left[ \begin{array}{c} 1 \\ 0 \end{array}\right] , \end{aligned}$$
(2.4)

where the \({\widetilde{b}}\equiv {\widetilde{b}}(t)\) and \({\widetilde{a}}\equiv {\widetilde{a}}(t)\) are the chirp and characteristic width of the packet, respectively. By using ansatz function (2.4) in Eq. (2.3), we find the total energy

$$\begin{aligned} \displaystyle E= \frac{N}{2{\widetilde{a}}^2} \left( 1-\frac{{\widetilde{g}}N}{2\pi }\right) . \end{aligned}$$
(2.5)
Fig. 1
figure 1

Plot of the total energy vs inverse width of the condensate defined by Eq. (2.5). One can see that, if the attraction between particles is sufficiently strong, the width of the condensate tends to zero, the total energy tends to minus infinity and the condensate collapses. Otherwise, the condensate is stable

Full size image

The Eq. (2.5) and the Fig. 1 clearly show that the condensate can collapse if \({\widetilde{g}}N\) parameter exceeds the threshold value \(\lambda =2\pi \). The equation of motion for \({\widetilde{a}}\) becomes \(\overset{..}{{\widetilde{a}}}=-{\Lambda }/{{\widetilde{a}}^{3}}\), where \(\Lambda =\left( {\widetilde{g}}N-\lambda \right) /2\). The solution of this equation is

$$\begin{aligned} {\widetilde{a}}(t)=a(0)\sqrt{1-\frac{\Lambda t^{2}}{a^{4}(0)}}. \end{aligned}$$
(2.6)

From the Eq. (2.6), the collapse time \(T_{c}\equiv a^{2}(0)/\sqrt{\Lambda }\), and the characteristic collapse velocity is \(v_{c}\equiv a(0)/T_{c}=\sqrt{\Lambda }/a(0)\).

Now, we consider effect of spin–orbit coupling in the collapse process by writing the modified velocity including the anomalous spin-dependent term [3]

$$\begin{aligned} {{\mathbf {v}}}={{\mathbf {k}}}+\frac{\partial }{\partial \mathbf{k}}H_{\mathrm{so}}, \end{aligned}$$
(2.7)

where \({{\mathbf {k}}}\equiv \left( k_{x},k_{y}\right) \) and \({{\mathbf {k}}}= -i\partial /\partial {{\mathbf {r}}}\). In Eq. (2.7), the last term is directly related to the particle spin. The resulting evolution of the probability density \(\rho ={\varvec{\psi } }^{\dagger }{\varvec{\psi } }\) and components of the flux density

$$\begin{aligned} {\mathbf {J}}({\mathbf {r}},t)=\frac{i}{2}\left[ {\varvec{\psi } }{\varvec{\nabla }}{\varvec{\psi } }^{\dagger }-{\varvec{\psi } }^{\dagger }{\varvec{\nabla }}{\varvec{\psi }}\right] +{\varvec{\psi } }^{\dagger }\left[ \frac{\partial }{\partial \mathbf{k}}H_{\mathrm{so}}\right] {\varvec{\psi }}, \end{aligned}$$
(2.8)

are related by the continuity equation

$$\begin{aligned} \frac{\partial \rho }{\partial t}+{\varvec{\nabla }}\cdot {\mathbf {J}}({\mathbf {r}},t)=0. \end{aligned}$$
(2.9)

To characterize collapse of the condensate we use the width defined by

$$\begin{aligned} a(t) = \frac{N}{\sqrt{2\pi }} \left[ \int \left| \varvec{\psi } \right| ^{4}\mathrm{d}x\mathrm{d}y \right] ^{-1/2}. \end{aligned}$$
(2.10)
Fig. 2
figure 2

Dynamics of width of the condensate defined by Eq. (2.10) and direct numerical solution of Eq. (2.2). The curves correspond to marked values of coupling constant \(\alpha \) and interaction parameter is \({\widetilde{g}}N=8\pi \)

Full size image

3 The symmetrized Dresselhaus spin–orbit coupling and collapse

The symmetrized Dresselhaus coupling Hamiltonian, we choose in the form

$$\begin{aligned} H_{\mathrm {so}} = \alpha \left( k_{x}\sigma _{x}+k_{y}\sigma _{y}\right) , \end{aligned}$$
(3.1)

where \(\alpha \) is coupling constant, and \(\sigma _{x}, \sigma _{y}\) are the Pauli matrices. From Eq. (2.7), the corresponding spatial components of the velocity become

$$\begin{aligned} v_{x}=k_{x}+{\alpha }\sigma _{x} ,\quad v_{y}=k_{y}+{\alpha }\sigma _{y}. \end{aligned}$$
(3.2)

and the characteristic distance to flip the spin is defined by \(L_{\mathrm {so}}=1/\alpha \).

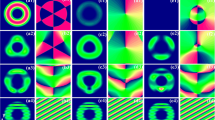
Since the initial spin is perpendicular to the SOC field, the spin precession angle is of the order of \(a(0)/L_{\mathrm{so}}\) and spin-dependent anomalous velocity is \(\propto \alpha ^2 a(0)\) for weak SOC. From Eq. (2.6) follows that at short time \(t \ll T_c\) attraction velocity \(v_c \sim t\) while anomalous spin-dependent velocity is \(\alpha \sim t^2\). As a results, the width a(t) of the condensate does not depend on the spin. Figure 2 clearly shows at short time constant width for all values of \(\alpha \) and following interplay between attraction and anomalous velocities. One can see, after critical value of SOC \(\alpha _c \approx 0.75 v_{c}\) collapse of the condensate is prevented.

Fig. 3
figure 3

Plots of the density flux defined by Eq. (2.8) for \(\alpha =v_{c}\), \({\widetilde{g}}N=8\pi \) and different values of time

Full size image
Fig. 4
figure 4

Cross-section density profiles of the condensate for value of coupling constant \(\alpha =v_{c}\) and \({\widetilde{g}}N=8\pi \)

Full size image

To prevent the collapse of BEC, it is sufficient to take \(\alpha =v_{c}\). The symmetrized Dresselhaus SOC with present initial spin state causes a density flux leaving the center of the BEC is presented in the Fig. 3. Hence, the density profile of the condensate becomes ring-shaped with \(a(t)\sim \sqrt{R(t)w(t)}\), where R(t) is radius and w(t) is width of the ring that after finite time clearly presented in Fig. 4 by a cross-section of density profiles along the y and x axes.

4 Conclusions

We have demonstrated in the presence of symmetrized Dresselhaus SOC the spin-dependent “anomalous” velocity works against squeezing of the collapsing condensate. For a weak SOC, the condensate can collapse at long time, while a sufficiently strong SOC leads to flux leaving the center of the BEC and density of the condensate becomes in ring-shaped. As a result, condensate cannot squeeze and attraction of particles decreases in the ring-shaped condensate. These results demonstrate the SOC can stop the collapse of the BEC leading to the stable condensates.