Abstract
Black holes represent outstanding astrophysical laboratories to test the strong gravity regime, since alternative theories of gravity may predict black hole solutions whose properties may differ distinctly from those of general relativity. When higher curvature terms are included in the gravitational action as, for instance, in the form of the Gauss–Bonnet term coupled to a scalar field, scalarized black holes result. Here we discuss several types of scalarized black holes and some of their properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The existence of black holes in the Universe, following gravitational collapse, is a genuine prediction of general relativity (GR) [61]. However, in GR their properties are highly constrained, when one assumes the standard model of particle physics for the allowed matter fields and considers astrophysically relevant black holes. The expectation of astrophysical black holes being (basically) uncharged, then leads to the conclusion that they are (in good approximation) all described by the Kerr family of rotating black holes, i.e., asymptotically flat black hole solutions of the vacuum Einstein equations.
Kerr black holes are uniquely characterized by their mass and their angular momentum (see, e.g. [21]) and thus they carry no hair. All their multipole moments are given in terms of these two quantities. Also, Kerr black holes are subject to a bound on their angular momentum, which is reached in the extremal limit. Beyond this bound only naked singularities reside. The no-hair hypothesis that astrophysical black holes are indeed described by the family of Kerr black holes is tested in current and future observations [19].
So far all observations are in agreement with the Kerr hypothesis, be it the motion of stars around the supermassive black hole at the center of the Milky Way (2020 Nobel Prize), the observation of gravitational waves from black hole mergers (2017 Nobel Prize) or the observation of the shadow of the supermassive black hole at the center of M87 (EHT collaboration). However, it is expected that GR will be superseded by a new gravitational theory, that will include quantum mechanics, and that might as well explain (part of) the cosmological dark components, dark matter and dark energy. Overviews of alternative theories of gravity are found, for instance, in [11, 34, 64, 73].
A particularly attractive type of alternative theories of gravity are theories that contain higher curvature terms in the form of the Gauss–Bonnet invariant, as they arise, for instance, in string theories [36, 54, 79]. Since in four dimensions the Gauss–Bonnet term corresponds to a topological term, that does not contribute to the field equations, this term has to be coupled to another field in order to make its presence count. In string theory this field is a scalar field, a so-called dilaton, that arises with a specific exponential coupling function to the Gauss–Bonnet term in the low energy limit of string theory. We will refer to these theoretically well motivated theories in the following as Einstein–dilaton–Gauss–Bonnet (EdGB) theories. EdGB theories do not allow for GR black hole solutions. Instead all EdGB black hole solutions carry dilatonic hair [4, 5, 14, 15, 23, 37, 43,44,45,46, 50, 53, 59, 60, 71, 76, 78].
In recent years, other interesting coupling functions for the scalar field have been suggested [1, 2, 27, 66, 68, 69]. In the following we will call such theories simply Einstein–scalar–Gauss–Bonnet (EsGB) theories. Like the EdGB theories, the EsGB theories possess the attractive features that they give rise to second order equations of motion, and do not possess Ostrogradsky instabilities and ghosts [20, 42, 47].
By allowing for more general coupling functions of the scalar field a new interesting phenomenon was observed: curvature induced spontaneous scalarization of black holes [1,2,3, 6,7,8, 13, 16,17,18, 22, 24, 27, 29, 30, 40, 52, 55,56,57, 66, 67]. In that case an appropriate choice of coupling function allows the GR black holes to remain solutions of the EsGB equations, while, at critical values of the coupling, GR black holes develop a tachyonic instability where new branches of spontaneously scalarized black holes arise. Moreover, in the case of rotation, there can exist two types of spontaneously scalarized black holes. Those, that arise simply from the static black holes in the limit of slow rotation, and those that arise only for fast rotation and are termed spin induced spontaneously scalarized black holes [12, 26, 31, 32, 39, 41, 77].
This paper is organized as follows: In Sect. 2 we briefly recall some properties of black holes in GR. We discuss black holes in EdGB theories in Sect. 3 and black holes in EsGB theories in Sect. 4. In both cases we will address first the static and then the rotating black holes, where in the EsGB case we then differentiate between those, that emerge continuously from the static limit, and the spin induced ones. We end in Sect. 5 with our conclusions.
2 Black holes in general relativity
Since our aim is to address deviations of the properties of black holes in certain alternative theories of gravity from the properties of black holes in GR, we will start with a brief recap of some basic properties of black holes that arise as solutions of the Einstein field equations in vacuum
with Einstein tensor \(G_{\mu \nu }\), Ricci tensor \(R_{\mu \nu }\), curvature scalar R and metric tensor \(g_{\mu \nu }\).
The asymptotically flat, static, spherically symmetric black hole solutions of these vacuum field equations are the Schwarzschild black holes. The corresponding set of rotating black holes is the family of Kerr black holes. For these vacuum black holes there is the well-known no-hair theorem [21], stating that a Kerr black hole is uniquely characterized in terms of only two global parameters: the mass M and the angular momentum J. For the static Schwarzschild black hole the angular momentum vanishes, so the mass is the only parameter.
Moreover, all the multipole moments of Kerr black holes are given in terms of these two quantities, the mass M and the angular momentum J [35, 38, 70]
with mass \(M_0=M\), and angular momentum \(S_1=J\), and multipole number l. The quadrupole moment Q is then given by \(M_2 = Q = - \frac{J^2}{M} \).
Kerr black holes are subject to a bound on their angular momentum,
the so-called Kerr bound, reached in the extremal limit, when the two horizons of the Kerr black holes coincide. Solutions beyond the Kerr bound represent naked singularities. The Kerr black holes have been analyzed in many further respects. Their shadow, for instance, was obtained first by Bardeen [9] and recently revisited numerous times, because of its significance for the EHT observations.
3 Black holes in Einstein–dilaton–Gauss–Bonnet theories
We now turn to black holes in EdGB theories, providing first the theoretical settings, and presenting then the static and rotating solutions and some of their properties.
3.1 Theoretical settings
The effective action for EdGB and EsGB theories reads
where R is the curvature scalar, \(\phi \) is the scalar field, \(F(\phi )\) is the coupling function, and \(U(\phi )\) is the potential, and
is the Gauss–Bonnet term.
Variation of the action with respect to the metric and the scalar field leads to the Einstein equations and to the scalar field equation, respectively,
where the dot denotes the derivative with respect to the scalar field \(\phi \). The stress–energy tensor in the gravitational field equation is an effective one, since it contains not only the usual contributions from the scalar field, but also contributions from the Gauss–Bonnet term. It is given by the expression
where \(\tilde{R}^{\rho \gamma }_{\alpha \beta }=\eta ^{\rho \gamma \sigma \tau } R_{\sigma \tau \alpha \beta }\) and \(\eta ^{\rho \gamma \sigma \tau }= \epsilon ^{\rho \gamma \sigma \tau }/\sqrt{-g}\). As mentioned above, this resulting set of coupled field equations is of second order. Also note, that in four spacetime dimensions the coupling of the Gauss–Bonnet term to another field is really needed in order to allow for solutions that differ from those of GR.
Since in this section we will discuss dilatonic black holes, we now specify the coupling function to the dilatonic coupling function
where \(\alpha \) is the Gauss–Bonnet coupling constant, and \(\gamma \) is the dilaton coupling constant with string theory value \(\gamma =1\). For this coupling function \(\dot{F}(\phi ) \ne 0\) unless \(\phi \rightarrow \infty \). Therefore the dilaton field equation (7) does not allow a constant value of \(\phi \) as a solution, if the Gauss–Bonnet term is non-vanishing, as it would be the case for a Schwarzschild black hole. Consequently, the Schwarzschild black hole cannot be a solution of EdGB theory, and neither can the Kerr black hole: all EdGB black hole solutions necessarily carry dilaton hair.
3.2 Dilatonic black holes
Static, spherically symmetric black hole solutions of EdGB theory were first obtained by Kanti et al. [43]. Because of symmetry one can choose the ansatz
for the metric, with two metric functions \(\Phi (r)\) and \(\Lambda (r)\), that depend only on the radial coordinate, like the dilaton function \(\phi (r)\). While the EdGB black hole solutions have not been found in closed form, numerical integration has yielded their domain of existence and their properties [43].
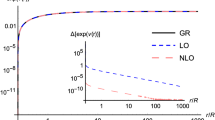
We show in Fig. 1 the scaled horizon radius versus the scaled mass and compare with the Schwarzschild black hole.
Clearly, for large masses, the EdGB black holes approach the Schwarzschild black holes, whereas for small masses the deviation from the Schwarzschild black holes becomes large. Surprisingly, one finds a minimal value of the mass for these EdGB black holes. The reason can be found in the expansion of the functions at the horizon. Here a square root appears
whose radicand vanishes at the minimal value of the mass. We will refer to such solutions as critical solutions. Depending on the value of the dilaton coupling constant \(\gamma \), a tiny second branch may exist, where the mass increases again slightly until the horizon becomes singular [37, 71].
The static EdGB black holes can be generalized to include rotation, either perturbatively or by non-perturbative numerical calculations [4, 5, 44,45,46, 53, 59, 60]. The non-perturbative solutions can for instance be obtained with the stationary axially symmetric line element [44,45,46]
with quasi-isotropic radial coordinate r. The metric functions f, m, l and \(\omega \) depend on r and \(\theta \) only, and the scalar field is also a function of r and \(\theta \) only, \(\phi =\phi (r,\theta )\).
We present the domain of existence of these rotating EdGB black holes in Fig. 2. In Fig. 2a the scaled horizon area \(A_H/16 \pi r_H^2\) is shown versus the scaled angular momentum \(J/M^2\). For a fixed value of the coupling constant, black holes exist in the shaded region. The boundary of this region consists of the static black holes (left vertical boundary), the Kerr black holes (mostly upper boundary) and the critical black holes (mostly lower boundary). Very close to the Kerr bound \(J/M^2=1\) these two boundaries cross and interchange. The last boundary is only seen in the inset in the figure, and shows the extremal black holes, which are not regular, however, in the EdGB case. Clearly, in a small part of the domain of existence the Kerr bound is slightly exceeded by almost extremal EdGB black holes. The curves inside the plot represent curves of constant horizon angular velocity.
Figure 2b shows the entropy of these black holes. In GR black holes possess an entropy that is simply a quarter of the event horizon area. However, in the presence of a Gauss–Bonnet term, coupled to a scalar field, the entropy of the EdGB black holes acquires an extra contribution [72]. Then the total entropy can be written in Wald’s form as an integral over the event horizon
where h is the determinant of the induced metric on a spatial cross section of the horizon and \({\tilde{R}}\) is the event horizon curvature. The figure shows, that the dilatonic black holes have larger entropy than the Kerr black holes, while they have smaller horizon area.
Considering further properties of the rotating EdGB black holes we note, that they can possess much larger quadrupole moments than Kerr black holes, and their ISCOs and orbital frequencies can deviate appreciably from the respective Kerr values, as well. Since their horizon area is smaller than for Kerr black holes, one might also expect considerable deviations for their shadow as compared to the Kerr black hole shadow. However, these deviations turn out to be rather small [23]. Also the X-ray reflection spectrum of accreting EdGB black holes shows only small deviations from the Kerr case [76].
3.3 Linear mode analysis: quasi-normal modes
To investigate stability of black holes under small perturbations, a linear mode analysis can be performed. Here we will directly address the formalism for quasi-normal modes. Since in gravity small perturbations will typically lead to the emission of gravitational waves the frequencies that are found in perturbation theory also contain an imaginary part, which explains the terminology. From an observational point of view, such quasi-normal modes will appear in the ringdown spectra of black holes after merger. This makes their study most relevant in connection with current and future gravitational wave observations.
While we refrain from a full derivation of these quasi-normal modes and refer to the literature [10, 48, 49, 58, 62], we briefly recall some of the relevant aspects. To this end we consider lowest order perturbation theory in the metric
and in the scalar field
where \(g_{\mu \nu }^{(0)}\) and \(\phi _0\) are the metric and the scalar field of the background black hole, respectively, and \(h_{\mu \nu }\) and \(\delta \phi \) are the perturbations. \(\epsilon \) is the small perturbation parameter.
Symmetry allows for a decomposition of the perturbations into even-parity and odd-parity perturbations. The scalar field has even parity, therefore it decouples in the case of odd-parity perturbations, which are therefore pure spacetime modes. The even-parity modes are also called polar modes, while the odd-parity modes are also termed axial modes. Besides the decomposition with respect to parity, we can also make a multipolar decomposition of the modes, characterized by the angular parameter l.
There are quasi-normal modes for all values of the angular parameter l. Because of the scalar field also modes with angular parameter \(l=0\) and \(l=1\) arise, corresponding to radial modes (monopole modes) and dipole modes. For \(l=2\) quadrupole modes arise, which are also present in GR. But because of the scalar field, there will now be two types of such modes: \(l=2\) modes dominated by the scalar field, which in the limit of vanishing Gauss–Bonnet coupling would correspond to modes of the scalar field in the background of a Schwarzschild black hole, and \(l=2\) modes dominated by the gravitational field, which would correspond to the lowest Schwarzschild quadrupolar modes. We will refer to the first set of modes as scalar-led modes, and to the second set as grav-led modes in the following.
The time dependence of the modes is factored out by an exponential
which shows that the real part \(\omega _R\) is the frequency and the imaginary part \(\omega _I\) is the inverse damping time if \(\omega _I>0\), otherwise, for \(\omega _I<0\), it signals an instability. (Note, that the overall sign choice in the exponent is only convention.) For a given parity and angular parameter l the complex frequency \(\omega \) is obtained by solving the respective resulting system of coupled differential equations, subject to proper boundary conditions. At the black hole horizon the wave must be purely ingoing, and at infinity purely outgoing.
As an interesting example we show in Fig. 3 the quasi-normal polar \(l=2\) modes for the static EdGB black holes, normalized to the respective Schwarzschild values for vanishing coupling constant. Figure 3a shows the real part of \(\omega \), and Fig. 3b the imaginary part versus the scaled Gauss–Bonnet coupling constant \(\zeta =\alpha /M^2\). We note a distinctly different behavior for the grav-led and the scalar-led modes. We also note, that the presence of the scalar field in the polar modes breaks isospectrality of the modes, i.e., the degeneracy of the axial and polar \(l=2\) gravitational modes in the Schwarzschild case.
Quasi-normal polar \(l=2\) modes of static EdGB black holes \((\gamma =1)\): a scaled frequency \(\omega _R/\omega _R^S\) vs scaled Gauss–Bonnet coupling constant \(\zeta =\alpha /M^2\); b scaled inverse damping time \(\omega _I/\omega _I^S\) vs scaled Gauss–Bonnet coupling constant \(\zeta =\alpha /M^2\)
4 Black holes in Einstein–scalar–Gauss–Bonnet theories
Whereas EdGB theories are already considerably constrained from observations, this is much less the case for EsGB theories with more general coupling functions. We now turn to the black holes in these theories and focus on coupling functions which allow for spontaneous scalarization.
4.1 Curvature induced spontaneous scalarization
The phenomenon of spontaneous scalarization was discovered for neutron stars in scalar-tensor theories [25], where GR neutron stars can develop a scalar field when the solutions become sufficiently compact. Here the trigger for the scalarization is the highly compact matter. Therefore the spontaneous scalarization is referred to as matter induced spontaneous scalarization. The absence of matter for Schwarzschild and Kerr black holes therefore precludes this phenomenon for these black holes.
Only a few years ago it was realized that spontaneous scalarization can also be curvature induced and therefore arise for black holes in EsGB theories [1, 2, 27, 66]. In order to allow for such spontaneous scalarization the coupling function should possess certain properties. First of all, the GR black hole solutions should remain solutions of the theory. This is of course the case, when the Gauss–Bonnet term does not contribute in the field equations. So if we choose a coupling function \(F(\phi )\) such that
then the source term in the scalar field equation
vanishes for \(\phi =0\), and \(\phi =0\) is a solution. Note, that we have assumed a vanishing scalar field potential \(U(\phi )\) at the moment. The Einstein equations then also receive no contribution from the Gauss–Bonnet term, and therefore the GR solutions remain solutions of such EsGB theories. However, the GR solutions are not the only black hole solutions in certain parameter ranges, that depend on the coupling function. Here black holes with scalar hair arise, and this hair is curvature induced.
To understand this mechanism, we consider the Gauss–Bonnet term for the metric of a Schwarzschild black hole
which is solely coming from the Kretschmann scalar. Clearly, this curvature term can become rather big. We now choose the simple coupling function
When we insert this into the scalar field equation, we see, that we can identify an effective mass squared \(m^2_\mathrm{eff}\) in this equation
and this effective mass squared is negative, i.e., tachyonic, for positive coupling constant \(\eta \). Therefore the Gauss–Bonnet curvature term triggers a tachyonic instability of the Schwarzschild solution, when its contribution is strong enough, and a branch of scalarized black holes bifurcates from the Schwarzschild solution.
4.2 Static black holes
We now consider the coupling function [27]
which for small \(\phi \) becomes simply a quadratic coupling, \(F(\phi )= (\lambda ^2/8) \phi ^2\). The tachyonic instability then arises at \(M/\lambda =0.587\), where a branch of scalarized black holes emerges. Since this is the first bifurcation, we refer to this branch as the fundamental or \(n=0\) branch. But this branch is not the only one, and at smaller values of \(M/\lambda \) further branches arise. These are radially excited branches, where the scalar field function possesses n nodes. Thus on the first excited branch (\(n=1\)), which arises at \(M/\lambda =0.226\), the scalar field has one node, on the second excited branch (\(n=2\): \(M/\lambda =0.140\)) it has two nodes, etc. When one follows these scalarized branches, as shown in Fig. 4a, one notes, that only the fundamental branch extends from the bifurcation all the way to vanishing mass (\(M=0\)). The excited branches all have finite extent, and they are the shorter the higher n. Note, that in the figure the scaled scalar charge \(D/\lambda \), which is read off from the asymptotic behavior of the scalar field (\(\phi \sim D/r\)) is shown versus the scaled mass \(M/\lambda \). To highlight the bifurcations, also the Schwarzschild black hole is shown, which of course carries no scalar charge.
Static EsGB black holes: a scaled scalar charge \(D/\lambda \) vs scaled mass \(M/\lambda \) for the fundamental (\(n=0\)) and radially excited (\(n>0\)) solutions; b scaled imaginary frequency \(\omega _I M^2/\lambda \) of the unstable radial modes vs scaled mass \(M/\lambda \) for the fundamental (\(n=0\)) and radially excited (\(n>0\)) solutions. The Schwarzschild solution and its unstable modes are also shown for comparison
Let us now consider the stability of these solutions, in particular, we would like to know, whether the fundamental scalarized solution is stable, when it emerges from the Schwarzschild solution, since the Schwarzschild solution has to become unstable to develop scalar hair (tachyonic instability). A first indication of stability is easily obtained by evaluating the entropy of the fundamental scalarized solution and comparing it to the entropy of the Schwarzschild solution [27]. This shows, that the \(n=0\) solution has higher entropy, and should therefore be (thermodynamically) preferred.
The next step is to consider radial (\(l=0\)) perturbations [16], which are polar perturbations involving the scalar field. When the Schrödinger-like master equation for the eigenvalue \(\omega \) is solved for the Schwarzschild background, a zero mode is found precisely at the first bifurcation point. As \(M/\lambda \) is further decreased, this zero modes turns into a negative mode, as seen in Fig. 4b. In fact, at each bifurcation, where a new branch of radially excited scalarized black holes arises, another zero mode of the Schwarzschild solution appears, that turns into another unstable mode for smaller values of \(M/\lambda \).
When we solve the Schrödinger-like master equation for the radial perturbations in the background of the fundamental scalarized black hole solutions, however, no radially unstable modes are found in the region from the bifurcation up to a critical value of \(M/\lambda \), that is marked by the vertical dashed line in Fig. 4b. Here the perturbation equation loses hyperbolicity and the employed formalism breaks down. Let us denote this point by S1 for later reference and turn to the radially excited branches.
Figure 4b also shows the radially unstable modes for the excited branches. Since these branches emerge from the Schwarzschild black hole at their respective bifurcation point, continuity at this bifurcation point demands, that the unstable modes of the radially excited black holes also bifurcate there from the Schwarzschild zero and unstable mode(s). So for the \(n=1\) solution we observe two unstable modes, one starting at the bifurcation point at the zero mode and one starting at the first unstable Schwarzschild mode. For the \(n=2\) solution we then have three unstable modes, etc.
While it is expected that radially excited solution are unstable, it would be nice, if the fundamental branch really were stable. So far we have only considered the \(l=0\) modes. Therefore we now turn to modes with higher l. These were analyzed in [13, 17]. Since axial modes do not involve perturbations of the scalar field, they start with the quadrupolar case \(l=2\). The analysis shows, that no further instability arises here, however, hyperbolicity of the equations is lost slightly earlier than in the radial case. Denoting this second point of loss of hyperbolicity by S2, we note, that there is no axial mode instability between the bifurcation point and S2 for the fundamental branch. Similarly, when the polar modes with \(l=1\) (dipole) and \(l=2\) quadrupole are considered, no further instability is encountered. Thus we conclude, that the fundamental branch is mode stable in the region between its bifurcation point and the point S2.
While there are no new unstable modes, there are of course numerous stable modes, where the imaginary part of the eigenvalue is positive and corresponds to an inverse damping time. As an example we exhibit the lowest such axial and polar grav-led \(l=2\) (quadrupole) modes in Fig. 5. The figure nicely shows the degeneracy of these modes for the Schwarzschild case, i.e., the isospectrality of the Schwarzschild modes. In contrast, for the fundamental scalarized black holes isospectrality is broken and the axial and polar modes generically differ.
Polar and axial \(l=2\) grav-led modes of static EsGB and Schwarzschild black holes: a scaled real part \(\omega _R/\lambda \) vs scaled mass \(M/\lambda \) for the fundamental (\(n=0\)) solution; b scaled imaginary part \(\omega _I/\lambda \) vs scaled mass \(M/\lambda \) for the fundamental (\(n=0\)). Note the isospectrality of the Schwarzschild modes
A similar analysis can, in principle, also be performed for other coupling functions. The simplest coupling function is of course the quadratic one, Eq. (20). Here already the entropy indicates instability of the fundamental branch of scalarized black holes, and a radial mode analysis shows, that the scalarized static spherically symmetric black holes are indeed all unstable including the fundamental branch [16]. Moreover, this branch is rather short, and oriented toward larger values of \(M/\lambda \) unlike the fundamental branch for the exponential coupling function, Eq. (22). Obviously, stability and length depend significantly on the coupling function. Including higher order terms in the coupling function with an appropriate sign can stabilize the solutions, as demonstrated in [67]. Another way to stabilize the solutions is to allow for an appropriate self-interaction potential \(U(\phi )\) of the scalar field, as shown in [52] for a quartic self-interaction.
4.3 Rotating black holes
With applications to astrophysics in mind, one has to include rotation of the black holes, and thus consider the phenomenon of curvature induced scalarization in the presence of rotation. Here the GR solution is of course the Kerr black hole. Therefore we have to inspect the source term in the scalar field equation, Eq. (18), i.e., the Gauss–Bonnet term for a Kerr black hole
where a is the usual Kerr specific angular momentum. Recalling Eq. (21) for the effective mass (with positive coupling constant \(\eta \)) and inserting the above expression for the Gauss–Bonnet term, we conjecture that the presence of the new terms that depend on the angular momentum suppresses the scalarization for large rotation, since the source term becomes weaker in (part of) the region with large curvature.
We begin the discussion of the rotating black hole solutions and their properties by considering the quadratic coupling function, Eq. (20), constructed in [22]. We exhibit the domain of existence of the fundamental scalarized branch in Fig. 6a, where the scaled angular momentum \(J/\lambda ^2\) is shown versus the scaled mass \(M/\lambda \), and we have introduced the coupling constant \(\eta =\lambda ^2/8\), while keeping a vanishing self-interaction potential \(U(\phi )=0\). The figure contains three curves showing the extremal Kerr solutions, the existence line for the scalarized black holes and the critical line for the scalarized black holes (from left to right). The existence line marks the onset of spontaneous scalarization, while the critical line shows where the scalarized black holes cease to exist. Whereas the domain of Kerr black holes is the whole area below the extremal curve, the domain of scalarized black holes is only the small band between the existence line and the critical line. As conjectured, the band becomes thinner when the angular momentum is increased, i.e., angular momentum indeed suppresses the scalarization.
In Fig. 6b we show the scaled area \(a_H=A_H/16 \pi r_H^2\) versus the scaled angular momentum \(j=J/M^2\) for the fundamental solution and for the \(n=1\) radial excitation. The scaled entropy \(s=S/4\pi M^2\) is also shown. In this representation the Kerr black holes form the upper limiting curve, for which area and entropy agree. As in the static case with quadratic coupling the entropy of the rotating fundamental black holes is smaller than the entropy of the Kerr black holes. Thus the instability persists for the fundamental scalarized black holes with a quadratic coupling function and no self-interaction when rotation is included.
Rotating EsGB black holes \((\eta >0)\): a scaled angular momentum \(J/\lambda ^2\) vs scaled mass \(M/\lambda \) for the existence line and the critical line, and also for the extremal Kerr black holes, b scaled area \(a_H=A_H/16 \pi r_H^2\) and scaled entropy \(s=S/4\pi M^2\) vs scaled angular momentum \(j=J/M^2\) for the fundamental and first radially excited black holes
In [24] the rotating fundamental scalarized black holes were obtained for the exponential coupling function, Eq. (22). Here the static fundamental branch is much larger and (at least to a large extent) also stable. Starting from this large interval of static solutions, the domain of existence is therefore much larger for the rotating solutions for this coupling function. However, for fast rotation, the domain narrows again strongly, leaving only a small band of rapidly rotating scalarized black holes. We note, that an interesting consequence of the broad range of slowly rotating black holes is the possibility to obtain a limit on the Gauss–Bonnet coupling constant, by comparing the EsGB black hole shadow with observations [24].
Let us now consider a final twist concerning curvature induced rotating scalarized black holes. To that end we return to the Gauss–Bonnet term evaluated for a Kerr black hole, Eq. (23). Above we have noticed the strong suppressive effect of fast rotation for spontaneous scalarization. Now we would like to make use of this effect in a new constructive way. As noticed in [26] and further elaborated on in [31, 32, 41, 77], a new way of inducing the tachyonic instability in the scalar field equation is obtained for sufficiently fast rotation, when a negative coupling constant \(\eta <0\) is chosen in the coupling function \(F(\phi )\). Therefore this type of spontaneous scalarization is termed spin induced spontaneous scalarization. Its onset happens at a Kerr rotation parameter of \(j=0.5\).
Following this interesting observation the associated rotating scalarized black holes were constructed in [39] for the exponential coupling function and in [12] for the quadratic one. Whereas the exponential coupling function did not yield any surprises, the quadratic one did. Namely for the spin induced rotating scalarized black holes the entropy is larger than the Kerr entropy also for the simple quadratic coupling. Therefore these solutions could be stable, as well. We illustrate the domain of existence of the spin induced rotating scalarized black holes with quadratic coupling in Fig. 7.
Already for the onset of the scalarization several different modes were studied [26], where besides even parity modes also odd parity modes were included (which do not exist in the spherically symmetric case, of course). In the two parity sectors the scalar field transforms as \(\varphi (\pi -\theta ) = + \varphi (\theta )\) and \(\varphi (\pi -\theta ) = - \varphi (\theta )\), respectively. The fundamental rotating scalarized black holes have even parity and a monopolar scalar field at infinity, whereas the odd parity black holes represent excited solutions whose lowest term at infinity is a dipole term. Therefore one can associate a monopole or scalar charge D to the even parity solutions, and a dipole charge P to the odd parity solutions.
In Fig. 7a we show the scaled scalar charge D/M and the scaled dipole charge P/M versus the scaled coupling constant \(-\eta /4M^2\) for the quadratic coupling function and no self-interaction [12]. Both types of solutions represent the lowest solutions in their respective parity sector. At vanishing scalar and dipole charge, the bifurcation from the Kerr solutions takes place. The critical line then marks the upper boundary of the domain of existence of even (D/M) and odd (P/M) rotating scalarized black holes. The various curves threading the domain of existence correspond to fixed values of the horizon angular velocity of the black holes.
Figure 7b demonstrates that the parity is indeed larger for these rotating scalarized black holes than for the Kerr black holes. Here the scaled entropy \(S/2\pi M^2\) is shown versus the scaled angular momentum j, again for the lowest solutions in both parity sectors. Clearly, the Kerr bound \(j \le 1\) can be violated for such rapidly rotating scalarized black holes. The inset of the figure shows the scaled horizon area \(A_H/16 \pi r_H^2\), for comparison, for both parity sectors.
5 Conclusions
Among the numerous alternative theories of gravity EdGB and EsGB theories are theoretically very attractive, since they are motivated from quantum gravity theories, possess second order field equations, and avoid Ostrogradsky instabilities and ghosts. Here a dilaton or a general scalar field is coupled to the Gauss–Bonnet term, which is quadratic in curvature. While there are already significant constraints on EdGB theories, EsGB theories are much less constrained.
Black holes in EdGB theories have been studied since the nineties, first the static black holes and later the rotating black holes. Because of the specific dilatonic coupling of the scalar field to the Gauss–Bonnet term, all black hole solutions in EdGB theories carry dilatonic hair, while the GR black holes do not solve the set of EdGB field equations.
This is different for EsGB theories, when the coupling function satisfies appropriate conditions. Then the GR black holes remain solutions of the EsGB field equations. However, they undergo tachyonic instabilities, where branches of curvature induced scalarized black holes arise. In the rotating case even two types of scalarized black holes are present, those with a static limit, and those, that exist only for rapid rotation, which are called spin induced EsGB black holes.
Since these EsGB theories have so far survived the constraints that have emerged in the GW emission during binary mergers, when the scalar coupling function allows for a vanishing scalar field in the cosmological context, and thus leads to the same cosmological solutions as the standard cosmological \(\Lambda \)CDM model [63], this makes them attractive also for dynamical numerical relativity studies. Recently several groups have already done work in this direction, studying, e.g., dynamical scalarization and descalarization in binary BH mergers, dynamics of rotating BH scalarization, or dynamical formation of scalarized BHs through stellar core collapse [28, 33, 51, 65, 74, 75].
References
Antoniou, G.; Bakopoulos, A.; Kanti, P.: Evasion of no-hair theorems and novel black-hole solutions in Gauss–Bonnet theories. Phys. Rev. Lett. 120(13), 131102 (2018)
Antoniou, G.; Bakopoulos, A.; Kanti, P.: Evasion of no-hair theorems and novel black-hole solutions in Gauss–Bonnet theories. Phys. Rev. D 97(8), 084037 (2018)
Antoniou, G.; Bakopoulos, A.; Kanti, P.: Black-hole solutions with scalar hair in Einstein–Scalar–Gauss–Bonnet theories. Phys. Rev. D 97(8), 084037 (2018)
Ayzenberg, D.; Yunes, N.: Slowly-rotating black holes in Einstein–Dilaton–Gauss–Bonnet gravity: quadratic order in spin solutions. Phys. Rev. D 90, 044066 (2014)
Ayzenberg, D.; Yagi, K.; Yunes, N.: Linear stability analysis of dynamical quadratic gravity. Phys. Rev. D 89(4), 044023 (2014)
Bakopoulos, A.; Antoniou, G.; Kanti, P.: Novel black-hole solutions in Einstein–scalar–Gauss–Bonnet theories with a cosmological constant. Phys. Rev. D 99(6), 064003 (2019)
Bakopoulos, A.; Kanti, P.; Pappas, N.: Existence of solutions with a horizon in pure scalar–Gauss–Bonnet theories. Phys. Rev. D 101(4), 044026 (2020)
Bakopoulos, A.; Kanti, P.; Pappas, N.: Large and ultra-compact Gauss–Bonnet black holes with a self-interacting scalar field. Phys. Rev. D 101(8), 084059 (2020)
Bardeen, J.M.: Timelike and null geodesics in the Kerr metric. In: DeWitt, C., DeWitt, B.S. (eds.) Black Holes (Les Astres Occlus), p. 215. Gordon and Breach, New York (1973)
Berti, E.; Cardoso, V.; Starinets, A.O.: Quasinormal modes of black holes and black branes. Class. Quantum Gravity 26, 163001 (2009)
Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al.: Testing general relativity with present and future astrophysical observations. Class. Quantum Gravity 32, 243001 (2015)
Berti, E.; Collodel, L.G.; Kleihaus, B.; Kunz, J.: Spin-induced black-hole scalarization in Einstein–scalar–Gauss–Bonnet theory. Phys. Rev. Lett. 126(1), 011104 (2021)
Blàzquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S.: Polar quasinormal modes of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 102 (10), 024086 (2020)
Blázquez-Salcedo, J.L.; Macedo, C.F.B.; Cardoso, V.; Ferrari, V.; Gualtieri, L.; Khoo, F.S.; Kunz, J.; Pani, P.: Perturbed black holes in Einstein–dilaton–Gauss–Bonnet gravity: stability, ringdown, and gravitational-wave emission. Phys. Rev. D 94(10), 104024 (2016)
Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J.: Quasinormal modes of Einstein–Gauss–Bonnet–dilaton black holes. Phys. Rev. D 96(6), 064008 (2017)
Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S.: Radial perturbations of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 98(8), 084011 (2018)
Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S.: Axial perturbations of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 101(10), 104006 (2020)
Brihaye, Y.; Ducobu, L.: Hairy black holes, boson stars and non-minimal coupling to curvature invariants. Phys. Lett. B 795, 135 (2019)
Cardoso, V.; Gualtieri, L.: Testing the black hole ‘no-hair’ hypothesis. Class. Quantum Gravity 33(17), 174001 (2016)
Charmousis, C.; Copeland, E.J.; Padilla, A.; Saffin, P.M.: General second order scalar–tensor theory, self tuning, and the Fab Four. Phys. Rev. Lett. 108, 051101 (2012)
Chrusciel, P.T.; Lopes Costa, J.; Heusler, M.: Stationary black holes: uniqueness and beyond. Living Rev. Relativ. 15, 7 (2012)
Collodel, L.G.; Kleihaus, B.; Kunz, J.; Berti, E.: Spinning and excited black holes in Einstein–scalar–Gauss–Bonnet theory. Class. Quantum Gravity 37(7), 075018 (2020)
Cunha, P.V.P.; Herdeiro, C.A.R.; Kleihaus, B.; Kunz, J.; Radu, E.: Shadows of Einstein–dilaton–Gauss–Bonnet black holes. Phys. Lett. B 768, 373 (2017)
Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E.: Spontaneously scalarized Kerr black holes in extended scalar–tensor–Gauss–Bonnet gravity. Phys. Rev. Lett. 123(1), 011101 (2019)
Damour, T.; Esposito-Farese, G.: Nonperturbative strong field effects in tensor–scalar theories of gravitation. Phys. Rev. Lett. 70, 2220–2223 (1993)
Dima, A.; Barausse, E.; Franchini, N.; Sotiriou, T.P.: Spin-induced black hole spontaneous scalarization. Phys. Rev. Lett. 125(23), 231101 (2020)
Doneva, D.D.; Yazadjiev, S.S.: New Gauss–Bonnet black holes with curvature induced scalarization in the extended scalar–tensor theories. Phys. Rev. Lett. 120(13), 131103 (2018)
Doneva, D.D.; Yazadjiev, S.S.: Dynamics of the nonrotating and rotating black hole scalarization. Phys. Rev. D 103(6), 064024 (2021)
Doneva, D.D.; Kiorpelidi, S.; Nedkova, P.G.; Papantonopoulos, E.; Yazadjiev, S.S.: Charged Gauss–Bonnet black holes with curvature induced scalarization in the extended scalar–tensor theories. Phys. Rev. D 98(10), 104056 (2018)
Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S.: Gauss–Bonnet black holes with a massive scalar field. Phys. Rev. D 99(10), 104045 (2019)
Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S.: Black hole scalarization induced by the spin: 2 + 1 time evolution. Phys. Rev. D 102(10), 104027 (2020)
Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S.: Spin-induced scalarization of Kerr black holes with a massive scalar field. Eur. Phys. J. C 80(12), 1205 (2020)
East, W.E.; Ripley, J.L.: Dynamics of spontaneous black hole scalarization and mergers inEinstein–scalar–Gauss–Bonnet gravity. Phys. Rev. Lett. (10), 127 101102 (2021)
Faraoni, V.; Capozziello, S.: Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics. Springer, Dordrecht (2011)
Geroch, R.P.: Multipole moments. II. Curved space. J. Math. Phys. 11, 2580–2588 (1970)
Gross, D.J.; Sloan, J.H.: The quartic effective action for the heterotic string. Nucl. Phys. B 291, 41 (1987)
Guo, Z.K.; Ohta, N.; Torii, T.: Black holes in the dilatonic Einstein–Gauss–Bonnet theory in various dimensions. I. Asymptotically flat black holes. Prog. Theor. Phys. 120, 581 (2008)
Hansen, R.O.: Multipole moments of stationary space-times. J. Math. Phys. 15, 46–52 (1974)
Herdeiro, C.A.R.; Radu, E.; Silva, H.O.; Sotiriou, T.P.; Yunes, N.: Spin-induced scalarized black holes. Phys. Rev. Lett. 126(1), 011103 (2021)
Hod, S.: Spontaneous scalarization of Gauss–Bonnet black holes: analytic treatment in the linearized regime. Phys. Rev. D 100(6), 064039 (2019)
Hod, S.: Onset of spontaneous scalarization in spinning Gauss–Bonnet black holes. Phys. Rev. D 102(8), 084060 (2020)
Horndeski, G.W.: Second-order scalar–tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 10, 363 (1974)
Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E.: Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 54, 5049 (1996)
Kleihaus, B.; Kunz, J.; Radu, E.: Rotating black holes in dilatonic Einstein–Gauss–Bonnet theory. Phys. Rev. Lett. 106, 151104 (2011)
Kleihaus, B.; Kunz, J.; Mojica, S.: Quadrupole moments of rapidly rotating compact objects in dilatonic Einstein–Gauss–Bonnet theory. Phys. Rev. D 90(6), 061501 (2014)
Kleihaus, B.; Kunz, J.; Mojica, S.; Radu, E.: Spinning black holes in Einstein–Gauss–Bonnet–dilaton theory: nonperturbative solutions. Phys. Rev. D 93(4), 044047 (2016)
Kobayashi, T.; Yamaguchi, M.; Yokoyama, J.: Generalized G-inflation: inflation with the most general second-order field equations. Prog. Theor. Phys. 126, 511 (2011)
Kokkotas, K.D.; Schmidt, B.G.: Quasinormal modes of stars and black holes. Living Rev. Rel. 2, 2 (1999)
Konoplya, R.A.; Zhidenko, A.: Quasinormal modes of black holes: from astrophysics to string theory. Rev. Mod. Phys. 83, 793–836 (2011)
Konoplya, R.; Zinhailo, A.; Stuchlík, Z.: Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein–dilaton–Gauss–Bonnet black hole. Phys. Rev. D 99(12), 124042 (2019)
Kuan, H.J.; Doneva, D.D.; Yazadjiev, S.S.: Dynamical formation of scalarized black holes and neutron stars through stellar core collapse. Phys. Rev. Lett. (16), 127 161103 (2012)
Macedo, C.F.B.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P.: Self-interactions and spontaneous black hole scalarization. Phys. Rev. D 99(10), 104041 (2019)
Maselli, A.; Pani, P.; Gualtieri, L.; Ferrari, V.: Rotating black holes in Einstein–Dilaton–Gauss–Bonnet gravity with finite coupling. Phys. Rev. D 92(8), 083014 (2015)
Metsaev, R.R.; Tseytlin, A.A.: Order alpha-prime (two loop) equivalence of the string equations of motion and the sigma model Weyl invariance conditions: dependence on the dilaton and the antisymmetric tensor. Nucl. Phys. B 293, 385 (1987)
Minamitsuji, M.; Ikeda, T.: Scalarized black holes in the presence of the coupling to Gauss–Bonnet gravity. Phys. Rev. D 99(4), 044017 (2019)
Myung, Y.S.; Zou, D.: Quasinormal modes of scalarized black holes in the Einstein–Maxwell–Scalar theory. Phys. Lett. B 790, 400–407 (2019)
Myung, Y.S.; Zou, D.C.: Black holes in Gauss–Bonnet and Chern–Simons–scalar theory. Int. J. Mod. Phys. D 28(09), 1950114 (2019)
Nollert, H.P.: Topical review: quasinormal modes: the characteristic ‘sound’ of black holes and neutron stars. Class. Quantum Gravity 16, R159–R216 (1999)
Pani, P.; Cardoso, V.: Are black holes in alternative theories serious astrophysical candidates? The case for Einstein–Dilaton–Gauss–Bonnet black holes. Phys. Rev. D 79, 084031 (2009)
Pani, P.; Macedo, C.F.B.; Crispino, L.C.B.; Cardoso, V.: Slowly rotating black holes in alternative theories of gravity. Phys. Rev. D 84, 087501 (2011)
Penrose, R.: Gravitational collapse and space-time singularities. Phys. Rev. Lett. 14, 57–59 (1965)
Rezzolla, L.: Gravitational waves from perturbed black holes and relativistic stars. ICTP Lect. Notes Ser. 14, 255–316 (2003)
Sakstein, J.; Jain, B.: Implications of the neutron star merger GW170817 for cosmological scalar–tensor theories. Phys. Rev. Lett. 119(25), 251303 (2017)
Saridakis, E.N.; et al.: Modified gravity and cosmology: an update by the CANTATA network. CANTATA. arXiv:2105.12582 [gr-qc]
Silva, H.O.; Witek, H.; Elley, M.; Yunes, N.: Dynamical scalarization and descalarization in binary black hole mergers. Phys. Rev. Lett. (3), 127 031101 (2021)
Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E.: Spontaneous scalarization of black holes and compact stars from a Gauss–Bonnet coupling. Phys. Rev. Lett. 120(13), 131104 (2018)
Silva, H.O.; Macedo, C.F.B.; Sotiriou, T.P.; Gualtieri, L.; Sakstein, J.; Berti, E.: Stability of scalarized black hole solutions in scalar–Gauss–Bonnet gravity. Phys. Rev. D 99(6), 064011 (2019)
Sotiriou, T.P.; Zhou, S.Y.: Black hole hair in generalized scalar–tensor gravity. Phys. Rev. Lett. 112, 251102 (2014)
Sotiriou, T.P.; Zhou, S.Y.: Black hole hair in generalized scalar–tensor gravity: an explicit example. Phys. Rev. D 90, 124063 (2014)
Thorne, K.S.: Multipole expansions of gravitational radiation. Rev. Mod. Phys. 52, 299–339 (1980)
Torii, T.; Yajima, H.; Maeda, K.I.: Dilatonic black holes with Gauss-Bonnet term. Phys. Rev. D 55, 739 (1997)
Wald, R.M.: Black hole entropy is the Noether charge. Phys. Rev. D 48(8), R3427–R3431 (1993)
Will, C.M.: The Confrontation between general relativity and experiment. Living Rev. Relativ. 9, 3 (2006)
Witek, H.; Gualtieri, L.; Pani, P.; Sotiriou, T.P.: Black holes and binary mergers in scalar Gauss–Bonnet gravity: scalar field dynamics. Phys. Rev. D 99(6), 064035 (2019)
Witek, H.; Gualtieri, L.; Pani, P.: Towards numerical relativity in scalar Gauss–Bonnet gravity: \(3+1\) decomposition beyond the small-coupling limit. Phys. Rev. D 101(12), 124055 (2020)
Zhang, H.; Zhou, M.; Bambi, C.; Kleihaus, B.; Kunz, J.; Radu, E.: Testing Einstein–dilaton–Gauss–Bonnet gravity with the reflection spectrum of accreting black holes. Phys. Rev. D 95(10), 104043 (2017)
Zhang, S.J.; Wang, B.; Wang, A.; Saavedra, J.F.: Object picture of scalar field perturbation on Kerr black hole in scalar–Einstein–Gauss–Bonnet theory. Phys. Rev. D 102(12), 124056 (2020)
Zinhailo, A.: Quasinormal modes of Dirac field in the Einstein–Dilaton–Gauss–Bonnet and Einstein–Weyl gravities. Eur. Phys. J. C 79(11), 912 (2019)
Zwiebach, B.: Curvature squared terms and string theories. Phys. Lett. 156B, 315 (1985)
Acknowledgements
We would like to thank our collaborators: Emanuele Berti, Vitor Cardoso, Lucas G. Collodel, Daniela D. Doneva, Valeria Ferrari, Leonardo Gualtieri, Sarah Kahlen, Panagiota Kanti, Fech Scen Khoo, Caio F. B. Macedo, Sindy Mojica, Petya Nedkova, Paolo Pani, Eugen Radu, Kalin V. Staykov, Stoytcho S. Yazadjiev. We gratefully acknowledge support by the DFG Research Training Group 1620 Models of Gravity and the COST Actions CA15117 and CA16104. JLBS would like to acknowledge support from FCT project PTDC/FIS-AST/3041/2020.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blázquez-Salcedo, J.L., Kleihaus, B. & Kunz, J. Scalarized black holes. Arab. J. Math. 11, 17–30 (2022). https://doi.org/10.1007/s40065-021-00349-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-021-00349-7