1 Introduction

The main goal of this work is to give, in the framework of the \(H^{0}\)-convergence notion (the generalization of the H-convergence to perforated domains), a general homogenization result of a type of quasilinear equations with a mixed Neumann-Dirichlet boundary conditions, beyond the periodic setting. More precisely, we study the asymptotic behaviour of the solution of the following problem:

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{\varepsilon }(\cdot ,u^{\varepsilon }) \nabla u^{\varepsilon } )=f\;\; \text{ in } \Omega {\setminus } T_{\varepsilon }, \\ A^{\varepsilon }(\cdot ,u^{\varepsilon }) \nabla u^{\varepsilon }\cdot \nu =0\;\; \text{ on } \partial T_{\varepsilon } , \\ u^{{\varepsilon } }=0\;\; \text{ on } \partial \Omega , \end{array} \right. \end{aligned}$$

where \(\Omega \) is a bounded open subset of \(\mathbb {R}^{n}\), \(\{T_{\varepsilon }\}\) is sequence of compact subsets of \(\Omega \), not necessarily periodically distributed, and where \(f\in L^{2}(\Omega )\), \(A^{\varepsilon }:(x,d)\in (\Omega ,\mathbb {R})\longmapsto A^{\varepsilon }(x, t)\in \mathbb {R}^{n\times n}\) is a sequence of Caratheodory functions uniformly coercive, uniformly bounded and uniformly equicontinuous matrix fields in the variable d. We show that, under a suitable conditions on the equicontinuity modulus and \(L^{p}\)-estimate assumption, there exists a subsequence of \({\varepsilon }\) (still denoted by \({\varepsilon }\)), a positive function \(\chi ^{0}\in L^{\infty }(\Omega )\) and a matrix field \(A^{0}(\cdot ,\cdot )\) which satisfies the same properties as \(A^{\epsilon }(\cdot ,\cdot )\) such that \(\chi ^{\varepsilon }\;\rightharpoonup \;\chi ^{0}\) weakly \(^\star \) in \(L^{\infty }(\Omega )\),

$$(A^{\varepsilon }(\cdot ,d),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(\cdot ,d)\;\;\;{\text {in}}\;\Omega ,\; \forall d\in \mathbb {R}^{n},$$

and, if we denote by \(\;\widetilde{\cdot }\;\) the extension by 0 from \(\Omega _{\varepsilon }\) to \(\Omega \), we have

$$\begin{aligned} \left\{ \begin{array}{l} \widetilde{u^{\varepsilon }}\; \rightharpoonup \;\chi ^{0} u^{0}\; {\text{ weakly }} \;{\text{ in }} \;L^{2}(\Omega ), \\ \widetilde{A^{\varepsilon }( u^{\varepsilon })\nabla u^{\varepsilon }}\;\rightharpoonup \;A^{0}(u^{0})\nabla u^{0}\; {\text{ weakly }} \;{\text{ in }} \;L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$

where \(u^{0}\) is the solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{0}(\cdot ,u^{0})\nabla u^{0} )=\chi ^{0}f\;\; \text{ in } \Omega , \\ u^{0}=0\;\; \text{ on } \partial \Omega . \end{array} \right. \end{aligned}$$

We complete our study by giving two applications of the established compactness results. The first application is for the classical periodic case, where the obtained result coincides (in our framework) with a result given in [7]. While, the second one which concerns a non-periodic case introduced in [5] is an original result.

Our work generalizes that of Murat–Bocardo given in [4] which treated in the general framework of H-convergence the same type of quasilinear equations in fixed domains without holes. The periodic case with Lipschitz continuous coefficients was subsequently processed by Artola–Duvaut in [1]. On the other hand, for periodically perforated domains, the same type of quasilinear equations was firstly studied in Bendib [2] and Bendib–Tcheugoué Teboué [3], with Lipschitz continuous coefficients and linear Robin conditions. After this Cabarrubias–Donato have studied in [7] this equation with a nonlinear Robin condition boundary of the holes and the module of equicontinuity satisfies a suitable assumption introduced by Chipot in [9], but not assumed to be Lipschitz continuous. For the homogenization of other type of Neumann quasilinear equations in perforated domains with data satisfying a general assumptions of abstract homogenization, see for example [8, 13] among others.

This article is organized as follows: Sect. 2 is devoted to some preliminary results on the \(H^{0}\)-convergence as introduced by [5]. This notion generalizes that of H-convergence in fixed domains due to Murat–Tartar (see [12, 14]). We give at the end of this section, a new result about a pointwise estimate of the dierence of two \(H^{0}\)-limits. In Sect. 3, we present our main compactness results for a class of quasilinear equations in perforated domains in the general framework of \(H^{0}\)-convergence. Section 4 is devoted to the proofs of our results. Finally, in Sect. 5, we give two applications of the obtained compactness results, namely the classical periodic case and a certain non-periodic case.

2 Notations and preliminary results

2.1 Notations

  • \(\left\{ {\varepsilon } \right\} \) denotes a strictly decreasing sequence converging to zero,

  • if \(\zeta =\left( \zeta _{i}\right) _{1\le i\le n}\) and \(\xi =\left( \xi _{i}\right) _{1\le i\le n}\) are two vectors, we set

    $$\begin{aligned} \zeta \cdot \xi =\overset{n}{\sum _{i=1}}\zeta _{i}\xi _{i}\;\; \text{ and } \;\left| \xi \right| =\left( \overset{n}{\sum _{i=1}}\xi _{i}^{2}\right) ^{ \frac{1}{2}},\end{aligned}$$

  • for matrix A in \(R^{n\times n}\), we set

    $$\begin{aligned} |A|={\text {sup}}\{ | A\xi |\; \;{\text {s.t.}}\;\;|\xi |=1\;\;{\text {and}}\;\;\xi \in \mathbb {R}^{n}\}, \end{aligned}$$

  • \(\chi _{\mathcal {O}} \) denotes the characteristic function of a subset \(\mathcal {O}\) of \(\mathbb {R}^{n}\),

  • for two real numbers \(\alpha \) and \(\beta \) such that \(0<\alpha <\beta \), \(M\left( \alpha , \beta ; \Omega \right) \) is the set of the matrix fields \(A=\left( A_{ij}\right) _{1\le i, j\le n}\) defined on \(\Omega \) such that almost everywhere in \(\Omega \), we have

    $$\begin{aligned} \left\{ \begin{array}{l} {\text {(i)}} \;A_{ij}\in L^{\infty }\left( \Omega \right) ,\; {\text {for}} \;i, j=1,\ldots , n, \\ {\text {(ii)}} \;\alpha \left| \xi \right| ^{2}\le A \xi \cdot \xi ,\; {\text {for}}\;\xi \in \mathbb {R}^{n}, \\ {\text {(iii)}}\; A^{-1}\xi \cdot \xi \ge \beta ^{-1} | \xi |^{2},\; {\text {for}}\;\xi \in \mathbb {R}^{n}. \end{array} \right. \end{aligned}$$

2.2 Preliminary results on the H-convergence for perforated domains

Since we work in the framework of the \(H^{0}\)-convergence, we recall in this subsection some preliminary results about this notion and we give at the end a useful new result on the pointwise estimate of the dierence of two \(H^{0}\)-limits.

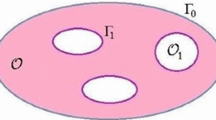
We introduce the perforated domain by

$$\begin{aligned} \Omega _{\varepsilon }=\Omega \text { }\backslash \text { }T_{\varepsilon }, \end{aligned}$$

where \(\{T_{\varepsilon }\}\) is a sequence of compact subsets of \(\Omega \) and set

$$\begin{aligned} V_{\varepsilon }=\left\{ v \in H^{1}( \Omega _{\varepsilon }) \; s.t. \;v=0\;\;on\;\partial \Omega \right\} . \end{aligned}$$

We denote by \(\widetilde{\;\cdot \;}\) the extension by 0 from \(\Omega _{\varepsilon }\) to \(\Omega \) and set \(\chi ^{\varepsilon }=\chi _{_{\Omega _{\varepsilon }}}\). In the following \(\nu \) denotes the outward normal unit vector to the boundary of \(\Omega _{\varepsilon }\).

Definition 2.1

([5]) The sequence \(\{T_{\varepsilon }\}\) is said to be admissible (in \(\Omega \)) if i) every \(L^{\infty }\) weak \(^\star \) limit point of \(\{\chi ^{\varepsilon }\}\) is positive almost everywhere in \(\Omega \), ii) there exists a positive real C, independent of \({\varepsilon } \), and a sequence \(\left\{ P_{\varepsilon }\right\} \) of linear extension operators such that for each \({\varepsilon } \)

$$\begin{aligned} \left\{ \begin{array}{l} P_{\varepsilon }\in \mathcal {L}(V_{\varepsilon }, H_{0}^{1}(\Omega )), \\ \left( P_{\varepsilon }v \right) _{\left| _{\Omega _{\varepsilon }}\right. }={v} , \;\; \forall {v} \in V_{\varepsilon }, \\ \left\| \nabla P_{\varepsilon }v \right\| _{L^{2}(\Omega )^{n}}\le C\left\| \nabla {v} \right\| _{L^{2}(\Omega _{\varepsilon })^{n}}, \;\; \forall {v} \in V_{\varepsilon }. \end{array} \right. \end{aligned}$$

We denote by \(P_{\varepsilon }^{\star }\) the adjoint operator of \(P_{\varepsilon }\), which is defined from \(H^{-1}(\Omega )\) to \(V'_{\varepsilon }\) (dual of \(V_{\varepsilon }\)) with \(P_{\varepsilon }^{\star }\) given for every \(g\in H^{-1}(\Omega ) \) by

$$\begin{aligned} \forall v\in V_{\varepsilon },\;\langle P_{\varepsilon }^{\star }g,v\rangle _{V'_{\varepsilon },V_{\varepsilon }}= \langle g,P_{\varepsilon }v\rangle _{H^{-1}(\Omega ),H_{0}^{1}(\Omega )}. \end{aligned}$$

Definition 2.2

([5]) Let \( A^{\varepsilon }\in M\left( \alpha , \beta ; {\Omega }\right) \) and \(T_{\varepsilon }\) be admissible in \(\Omega \). We say that the pair \((A^{{\varepsilon } }, T_{\varepsilon })\) \(H^{0}\)-converges to the matrix \(A^{0}\in M\left( \alpha ^{\prime }, \beta ^{\prime }; \Omega \right) \) and we write \(\left( A^{{\varepsilon } }, T_{\varepsilon }\right) \; \overset{H^{0}}{ \rightharpoonup }\;A^{0}\) in \(\Omega \) if and only if for every function g of \(L^{2}(\Omega )\), and every subsequence of \(\varepsilon \) (still denoted by \(\varepsilon \)) such that \(\chi ^{\varepsilon }\;\rightharpoonup \;\chi ^{0}\) weakly \(^\star \) in \(L^{\infty }(\Omega )\) (\(\chi ^{0}\)depending upon the subsequence), the solution \(v^{\varepsilon }\) of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{{\varepsilon } }\nabla v^{{\varepsilon } } )=g \;\; \text{ in } \Omega _{\varepsilon }, \\ (A^{{\varepsilon } }\nabla v^{{\varepsilon } } )\cdot \nu =0\;\; \text{ on } \partial T_{\varepsilon }, \\ v^{{\varepsilon } }=0\;\; \text{ on } \partial \Omega , \end{array} \right. \end{aligned}$$
(2.1)

satisfies the weak convergence

$$\begin{aligned} \left\{ \begin{array}{l} i) \;P_{\varepsilon }(v^{{\varepsilon } })\; \rightharpoonup \;v^{0}\; {\text {weakly}} \;{\text {in}} \;H_{0}^{1}(\Omega ), \\ ii) \;A^{{\varepsilon } }\widetilde{\nabla v^{{\varepsilon } } } \;\rightharpoonup \;A^{0}\nabla v^{0}\; {\text {weakly}} \;{\text {in}} \;L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$
(2.2)

where \(v^{0}\) is the unique solution of the problem

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{0}\nabla v^{0} )=\chi ^{0}g\;\; \text{ in } \Omega , \\ v^{0}=0\;\; \text{ on } \partial \Omega . \end{array} \right. \end{aligned}$$
(2.3)

Remark 2.3

  1. (1)

    In [5] the definition of \(H^{0}\)-convergence is given for \(f\in H^{-1}(\Omega ) \). This latter and Definition 2.2 are equivalent in view of [5, Theorem 1.5].

  2. (2)

    In the case of \(T_{\varepsilon }=\emptyset \), this definition reduces to the definition of H-convergence.

The main properties of the \(H^{0}\)-convergence are given by the results below.

Theorem 2.4

(Compactness [5]) Let \(A^{{\varepsilon } }\in M\left( \alpha , \beta ; \Omega \right) \) and \(T_{\varepsilon }\) be admissible in \(\Omega \). Then, there exists a subsequence of \(\left\{ {\varepsilon } \right\} \) (still denoted by \(\lbrace \varepsilon \rbrace )\) and a matrix \(A^{0}\in M\left( \frac{\alpha }{C^{2}},\beta ; {\Omega }\right) \) such that \(\left\{ (A^{{\varepsilon } }, T_{\varepsilon })\right\} \) \(H^{0}\)-converges to \(A^{0}\).

Proposition 2.5

[5] The pair \( (A^{{\varepsilon } }, T_{\varepsilon })\) \(H^{0}\)-converges to \(A^{0}\) if and only if \((^{t}A^{{\varepsilon } }, T_{\varepsilon })\) \(H^{0}\)-converges to \(^{t}A^{0}\).

Finally, we complete the preliminary results by giving a pointwise estimate of the dierence of two \(H^{0}\)-limits. This result needs the following lemma (which is a directly consequence of [5, Proposition 1.14]):

Lemma 2.6

Assume that \((A^{\varepsilon },T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}\) in \(\Omega \) and suppose that for every \(\lambda \in \mathbb {R}^{n\times n}\), there exists a sequence \(\{ v_{\lambda }^{{\varepsilon } }\}\) bounded in \(H^{1} (\Omega )\) such that

$$\begin{aligned} \left\{ \begin{array}{l} {\text {(i)}}\;\left\{ \begin{array}{l} -\mathrm{{div}}\;(\chi ^{\varepsilon }A^{{\varepsilon } }\nabla \left( v_{\lambda }^{{\varepsilon } }\right) )=P_{\varepsilon }^{\star }g_{\Lambda }^{{\varepsilon } }\text { in }\Omega _{\varepsilon },\\ {\text {with}} \;g_{\lambda }^{\varepsilon }\;{\text {is}}\;{\text {in}}\;{\text {a}}\;{\text {compact}}\;subset\;{\text {of}}\;H^{-1}(\Omega ), \end{array} \right. \\ {\text {(ii)}}\;v_{\lambda }^{{\varepsilon } }\;\rightharpoonup \; \lambda x\; {\text {weakly}} \;{\text {in}} \;H^{1}\left( \Omega \right) . \end{array} \right. \end{aligned}$$
(2.4)

Then, if we set

$$\begin{aligned} N^{\varepsilon }\lambda =\nabla v_{\lambda }^{\varepsilon },\;\forall \lambda \in \mathbb {R}^{n}, \end{aligned}$$
(2.5)

we will have \(\chi ^{\varepsilon }A^{\varepsilon }N^{\varepsilon }\;\rightharpoonup \; A^{0}\lambda \) weakly in \( L^{2}(\Omega )^{n}\) and \( N^{\varepsilon }\) is a corrector for the pair \((A^{\varepsilon },T_{\varepsilon })\) in the sense that

$$\begin{aligned} \underset{\varepsilon \rightarrow 0}{\lim }\Vert \nabla v^{\varepsilon }- N^{\varepsilon } v^{0}\Vert _{L^{1}(\Omega _{\varepsilon })^{n}}=0, \end{aligned}$$

where \(v^{\varepsilon }\) and \(v^{0}\) are solutions of (2.1) and (2.3) respectively.

We are now able to give a pointwise estimate of the dierence of two \(H^{0}\)-limits.

Theorem 2.7

Let \(T_{\varepsilon }^{1}\) and \(T_{\varepsilon }^{2}\) be admissible in \(\Omega \), \(A_{1}^{\varepsilon }\in \mathcal {M}( \alpha , \beta ;\Omega )\) and \(A_{2}^{\varepsilon }\in \mathcal {M}( \alpha ' , \beta ';\Omega )\) such that

$$\begin{aligned} \left\{ \begin{array}{l} (A_{1}^{\varepsilon },T_{\varepsilon }^{1})\;\overset{H^{0}}{\rightharpoonup }\;A_{1}^{0}\;\;\;\text { in } \Omega ,\\ (A_{2}^{\varepsilon },T_{\varepsilon }^{2})\;\overset{H^{0}}{\rightharpoonup }\;A_{2}^{0}\;\;\;\text { in } \Omega ,\\ \chi ^{\varepsilon }_{2}|A_{1}^{\varepsilon }(x)-A_{2}^{\varepsilon }(x)|\le h^{\varepsilon }(x) \;\;{\text {a.e.}}\;{\text {in}}\; \Omega ,\\ {\text {with}} \;h^{\varepsilon }\;\longrightarrow \;h^{0}\;\;\; {\text {strongly}} \;{\text {in}}\;L^{1}(\Omega ). \end{array} \right. \end{aligned}$$

Assume that

  1. (i)

    \(\chi ^{\varepsilon }_{1}- \chi ^{\varepsilon }_{2}\;\rightarrow \;0\;\;\; strongly \;in\;L^{1}(\Omega ) \),

  2. (ii)

    \( \left( A_{1}^{{\varepsilon } }, T_{\varepsilon }^{1}\right) \) admits a corrector satisfying (2.4)–(2.5),

  3. (iii)

    \( \left( A_{2}^{{\varepsilon } }, T_{\varepsilon }^{2}\right) \) admits a corrector \(N^{\varepsilon } \) satisfying (2.4)–(2.5) and

    $$\begin{aligned} \left\{ \begin{array}{l} \exists p>2,\text { such that } \Vert N^{\varepsilon }\Vert _{L^{p}(\Omega )^{n\times n}}\le \rho ,\\ \text { with } \rho >0 \text { is independent of }\varepsilon . \end{array} \right. \end{aligned}$$

Then,

$$\begin{aligned} |A_{1}^{0}-A_{2}^{0}|\le \sqrt{\frac{\beta \beta '}{\alpha \alpha '}}\;h^{0}\;\;\;\;a.\;e.\;{\text {in}}\;\Omega . \end{aligned}$$
(2.6)

Proof

The proof is obtained by using Lemma 2.6 and Proposition 2.5, and by following the same techniques used to prove a similar result given for the elasticity case in [11, Theorem 28]. \(\square \)

Remark 2.8

Assumptions

  • (i)–(iii) of Theorem 2.7 are reasonable. Indeed,

  • -(i) is obviously satisfied when \(T_{\varepsilon }^{1}=T_{\varepsilon }^{2}\) for every \(\varepsilon \),

  • -(ii) is satisfied when there exists a bounded domain O in \(\mathbb {R}^{n}\) in which \(\Omega \) is relatively compact and for which \(T_{\varepsilon }\) is admissible (see the proof of [5, Proposition 1.15]),

  • -(iii) is satisfied for the classical periodic case and also for the non-periodic case considered in [5].

3 Statement of compactness results

In this section, we give our compactness results for the \(H^{0}\)-convergence of a class of elliptic and uniformly equicontinuous operators in perforated domains. Firstly, we introduce the set \(\mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;\Omega )\) in the following definition :

Definition 3.1

For two real numbers \(\alpha ,\;\beta \) such that \(0<\alpha <\beta \) and \(\omega \) a function defined from \(\mathbb {R}^{+}\) to \(\mathbb {R}^{+}\) nondecreasing and continuous at 0, \(\mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;\Omega )\) denotes the set of all Caratheodory functions

$$A:(x,d)\in (\Omega ,\mathbb {R})\longmapsto A(x, d)\in \mathbb {R}^{n\times n}$$

satisfying the following assumptions:

  1. (i)

    for every \(d\in \mathbb {R},\;\;\;A(d)\doteq A(\cdot ,d)\in \mathcal {M}(\alpha ,\beta ;\Omega )\),

  2. (ii)

    for almost every x in \(\Omega \) and for every \(d,d'\in \mathbb {R}\), one has

    $$\begin{aligned}|A(x,d)-A(x,d')|\le \omega (|d-d'|). \end{aligned}$$

Our first main result is the following:

Theorem 3.2

Let \(\{T_{\varepsilon }\}\) be a sequence admissible in \(\Omega \) and \(\{A^{\varepsilon }\}\) be a sequence of elements of \(\mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;\Omega )\). Assume that \(\omega (0)=0\) and

$$\begin{aligned} \left\{ \begin{array}{l} \forall d\in \mathbb {R}, \;\exists p>2 \text { s.t. } \left( A^{\varepsilon }(d), T_{\varepsilon }\right) \text { admits a corrector which}\\ \text {satisfies (2.4)-(2.5) and is bounded in }L^{p}(\Omega ) \text { independently of }\varepsilon . \end{array} \right. \end{aligned}$$
(3.1)

Then, there exists a subsequence of \(\{ {\varepsilon }\} \) (still denoted by \(\lbrace \varepsilon \rbrace \)), and an element \(A^{0}\in \mathcal {M}_{Equi}(\frac{\alpha }{C^{2}},\beta ,\frac{\beta }{\alpha }\omega ;\Omega )\) such that

$$\begin{aligned} (A^{\varepsilon }(d),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(d)\;\;\;in\;\Omega ,\;\;\forall d\in \mathbb {R}. \end{aligned}$$
(3.2)

Moreover, if we suppose that there exists a bounded domain O in \(\mathbb {R}^{n}\) in which \(\Omega \) is relatively compact and for which \(T_{\varepsilon }\) is also admissible, we have

$$\begin{aligned} \;(A^{\varepsilon }(v),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(v)\;\;\;in\;\Omega ,\; \forall v\in L^{1}(\Omega ). \end{aligned}$$
(3.3)

Remark 3.3

  1. (i)

    A similar property to (3.2) is given in [14] in the case of fixed domain when the mapping \(d\rightarrow A^{\varepsilon }(\cdot , d)\) is of class \(C^{k}\) (or real analytic) from an open set D of \(\mathbb {R}^{p}\) into \( L^{\infty }\left( \Omega ;L(\mathbb {R}^{n};\mathbb {R}^{n})\right) \) for every \(p\in \mathbb {N}^{*}\).

  2. (ii)

    Theorem 3.2 still holds if \(d\in \mathbb {R}^{p}\) and \(v\in L^{1}(\Omega )^{p}\) for every \(p\in \mathbb {N}^{*}\).

As a consequence of Theorem 3.2, we obtained a general homogenization result for some quasilinear equations in perforated domain beyond periodic setting.

Theorem 3.4

Let \(\{T_{\varepsilon }\}\) be a sequence admissible in \(\Omega \) and suppose that there exists a bounded domain O in \(\mathbb {R}^{n}\) in which \(\Omega \) is relatively compact and for which \(T_{\varepsilon }\) is also admissible. Let \(\{A^{\varepsilon }\}\) be a sequence in \(\mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;\Omega )\) which satisfies (3.1). Assume that \(\omega \) is continuous with \(\omega (d)>0\;\forall d>0\) and

$$\begin{aligned} \text {for any }r>0,\;\;\,\underset{s\rightarrow 0}{\lim }\int _{s}^{r}\dfrac{\mathrm{{d}}t}{\omega (t)}=+\infty . \end{aligned}$$
(3.4)

Then, there exists subsequence of \(\{\varepsilon \}\) (still denoted by \(\{\varepsilon \})\) with \(\chi ^{\varepsilon }\) converges to a some \( \chi ^{0}\) weakly \(^\star \) in \(L^{\infty }(\Omega )\), such that for every function f of \(L^{2}(\Omega )\), the (unique) solution \(u^{{\varepsilon } }\) of the problem:

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{\varepsilon }(u^{\varepsilon }) \nabla u^{\varepsilon } )=f\;\; \text{ in } \Omega _{\varepsilon }, \\ A^{\varepsilon }(u^{\varepsilon }) \nabla u^{\varepsilon }\cdot \nu =0\;\; \text{ on } \partial T_{\varepsilon } , \\ u^{{\varepsilon } }=0\;\; \text{ on } \partial \Omega , \end{array} \right. \end{aligned}$$
(3.5)

satisfies

$$\begin{aligned} \left\{ \begin{array}{l} {\text{(i) }} \; P_{\varepsilon }(u^{{\varepsilon } })\; \rightharpoonup \;u^{0}\; {\text{ weakly }} \;{\text{ in }} \;H_{0}^{1}(\Omega ), \\ {\text{(ii) }}\; \widetilde{u^{\varepsilon }}\; \rightharpoonup \;\chi ^{0} u^{0}\; {\text{ weakly }} \;{\text{ in }} \;L^{2}(\Omega ), \\ {\text{(iii) }} \; \widetilde{A^{\varepsilon }( u^{\varepsilon })\nabla u^{\varepsilon }}\;\rightharpoonup \;A^{0}(u^{0})\nabla u^{0}\; {\text{ weakly }} \;{\text{ in }} \;L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$
(3.6)

where \(u^{0}\) is the (unique) solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{0}(u^{0})\nabla u^{0} )=\chi ^{0}f\;\; \text{ in } \Omega , \\ u^{0}=0\;\; \text{ on } \partial \Omega . \end{array} \right. \end{aligned}$$
(3.7)

with \(A^{0}\) the family of matrices given by Theorem 3.2.

Remark 3.5

Assumption (3.4) introduced initially in [9] implies that \(\underset{d\rightarrow 0}{\lim }\;\omega (d)=0\). If this assumption is replaced by just the fact that \(\underset{d\rightarrow 0}{\lim }\;\omega (d)=0\), the uniqueness will no longer be guaranteed for the solutions of (3.5) and (3.7).

4 Proofs of compactness results

We give in this section the proofs of our main results. The proofs are an adaptation of the similar ones given in [4] for fixed domains.

Proof of Theorem 3.2

We give the proof in two steps.

Step 1. Let us prove that there exists \(A^{0}\in \mathcal {M}_{Equi}(\frac{\alpha }{C^{2}},\beta ,\frac{\beta }{\alpha }\omega ;\Omega )\) which satisfies convergence (3.2) up to subsequence. Using Theorem 2.4 and the diagonal subsequence procedure, we extract a subsequence of \(\{\varepsilon \}\) (still denoted by \(\{\varepsilon \}\)) such that, for every \(d\in \mathbb {Q}\), we will have

$$\begin{aligned} (A^{\varepsilon }(d),T_{\varepsilon })\;H^{0} \text {-converges to a limit}\;A^{0}(d)\in \mathcal {M}\left( \frac{\alpha }{C^{2}},\beta ;\Omega \right) . \end{aligned}$$
(4.1)

Hence, by the fact that \(A^{\varepsilon }\in \mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;\Omega )\), Assumption (3.1) and Theorem 2.7, we obtain

$$\begin{aligned} |A^{0}(x,d)-A^{0}(x,d')|\le \frac{\beta }{\alpha }\;\omega (|d-d'|)\;\;\;{\text {a.e.}}\; x\in \Omega ,\;\forall d,\;d'\in \mathbb {Q}. \end{aligned}$$

Thus, the mapping

$$\begin{aligned} A^{0}:\;&\mathbb {Q}&\longrightarrow \mathbb {L}^{\infty }(\Omega )^{n\times n},\\&d&\longmapsto A^{0}(d) \end{aligned}$$

is uniformly continuous. Hence, it is extensible to a mapping (denoted again by \(A^{0}\)) defined and uniformly continuous on all \(\mathbb {R}\) (since \(\mathbb {Q}\) is dense in \(\mathbb {R}\)), namely

$$\begin{aligned} |A^{0}(x,d)-A^{0}(x,d')|\le \frac{\beta }{\alpha }\;\omega (|d-d'|),\;\;\;{\text {a.e.}}\; x\in \Omega ,\;\forall d,\;d'\in \mathbb {R}. \end{aligned}$$
(4.2)

On the other hand, let \(d\in \mathbb {R}\) and \(\{d_{m}\}\) be a sequence in \(\mathbb {Q}\) which converges to d as \(m\;\rightarrow \;\infty \). Thanks to Theorem 2.4, there exists a subsequence of \(\{\varepsilon \}\) (still denoted by \(\{\varepsilon \}\)) such that

$$\begin{aligned} (A^{\varepsilon }(d),T_{\varepsilon })\;H^{0}\text {-converges to some }A\in \mathcal {M}\left( \frac{\alpha }{C^{2}},\beta ;\Omega \right) . \end{aligned}$$
(4.3)

Since, for every \(\varepsilon >0\), we have

$$\begin{aligned} |A^{\varepsilon }(x,d)-A^{\varepsilon }(x,d_{m})|\le \;\omega (|d-d_{m}|),\;\;\;\;{\text {a.e.}}\; x\in \Omega , \end{aligned}$$

then from this, (4.1), (4.3), Assumption (3.1) and Theorem 2.7, it comes

$$\begin{aligned} |A(x)-A^{0}(x,d_{m})|\le \frac{\beta }{\alpha }\omega (|d-d_{m}|),\;\;\;{\text {a.e.}}\; x\in \Omega . \end{aligned}$$

This, with (4.2) and by the triangle inequality, we deduce that for almost every x in \(\Omega \)

$$\begin{aligned} |A(x)-A^{0}(x,d)|\le & {} |A(x)-A^{0}(x,d_{m})|+|A^{0}(x,d)-A^{0}(x,d_{m})|\\\le & {} 2 \frac{\beta }{\alpha }\;\omega (|d-d_{m}|). \end{aligned}$$

Using the continuity of \(\omega \) at 0, passing to the limit in this inequality as \(m\;\rightarrow \;\infty \), we find

$$\begin{aligned} A(x)=A^{0}(x,d),\;\;\;{\text {a.e.}}\; x\in \Omega . \end{aligned}$$

Step 2. We now show property (3.3). Let \(v\in L^{1}(\Omega )\). Then, \(A^{\varepsilon }(v(\cdot ))\doteq A^{\varepsilon }(\cdot ,v(\cdot ))\) belongs to \(\mathcal {M}(\alpha ,\beta ;\Omega )\). Hence, taking into account Theorem 2.4, there exists \(B^{0}\in \mathcal {M}(\frac{\alpha }{C^{2}},\beta ;\Omega )\) such that to up a subsequence, we have

$$\begin{aligned} (A^{\varepsilon }(v),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;B^{0}. \end{aligned}$$
(4.4)

On the other hand, since \(v\in L^{1}(\Omega )\), there exists a sequence of step functions \(\{ v^{m}\}\) such that \(v^{m}\;\rightarrow \; v\) strongly in \(L^{1}(\Omega )\), and \(v^{m}\) is of the form

$$\begin{aligned} v^{m}=\underset{i=1}{\overset{i=k}{\sum }}\, l^{m}_{i}\chi _{_{Y_{i}}},\;\;\;{\text {a.e.}}\;{\text {in}}\;\Omega , \end{aligned}$$
(4.5)

where \(\{Y_{i}\}_{1 \le i\le k}\) is a family of disjoint rectangles of \(\mathbb {R}^{n}\) included in \(\Omega \) and \(l^{m}_{i}\) real constants. Set

$$\begin{aligned} \left\{ \begin{array}{l} Y_{0}=\Omega {\setminus } \underset{1 \le i\le k}{\cup }\overline{Y_{i}},\\ \chi _{_{i}}=\chi _{_{Y_{i}}}\\ \chi _{_{0}}=\chi _{_{Y_{0}}}. \end{array} \right. \end{aligned}$$

We have

$$\begin{aligned} \left\{ \begin{array}{l} \forall i\in \{1,...,k\},\;|A^{\varepsilon }(x,v(x))-A^{\varepsilon }(x,l^{m}_{i})|\le \omega (|v(x)-l^{m}_{i}|)\;\;\;{\text {a.e.}}\,{\text {in}}\,\Omega ,\\ |A^{\varepsilon }(x,v(x))-A^{\varepsilon }(x,0)|\le \omega (|v(x)-0|)\;\;\;{\text {a.e.}}\,{\text {in}}\,\Omega , \end{array} \right. \end{aligned}$$
(4.6)

and (3.2) gives

$$\begin{aligned} \left\{ \begin{array}{l} A^{\varepsilon }(l^{m}_{i},T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(l^{m}_{i}), \\ A^{\varepsilon }((0),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(0). \end{array} \right. \end{aligned}$$
(4.7)

Hence, using (4.4), (4.6), (4.7), Assumption (3.1), point (ii) of Remark 2.8 and by Theorem 2.7, we obtain

$$\begin{aligned} \left\{ \begin{array}{l} \forall i\in \{1,...,k\},\;|B^{0}(x)-A^{0}(x,l^{m}_{i})|\le \frac{\beta }{\alpha }\; \omega (|v(x)-l^{m}_{i}|)\;\;\;{\text {a.e.}}\,{\text {in}}\,\Omega ,\\ |B^{0}(x)-A^{0}(x,0)|\le \frac{\beta }{\alpha }\;\omega (|v(x)-0|)\;\;\;{\text {a.e.}}\,in\,\Omega , \end{array} \right. \end{aligned}$$

which implies that for almost every x in \( \Omega \)

$$\begin{aligned} |B^{0}(x)-A^{0}(x,v^{m})|= & {} |B^{0}(x)- \underset{i=1}{\overset{i=k}{\sum }}{} \mathbf{A}^{0}(x,l^{m}_{i})\chi _{i}(x)+ A^{0}(x,0)\chi _{_{0}}(x) | \\\le & {} \underset{i=1}{\overset{i=k}{\sum }}{} \mathbf \chi _{i}(x) \frac{\beta }{\alpha }\;\omega (|v(x)-l^{m}_{i}|)+ \chi _{_{0}}(x)\frac{\beta }{\alpha }\;\omega (|v(x)-0|) \\= & {} \frac{\beta }{\alpha }\;\omega (|v(x)-v^{m}(x)|). \end{aligned}$$

Moreover, thanks to (4.2), we have

$$\begin{aligned} |A^{0}(x,v(x))-A^{0}(x,v^{m}(x))|\le \frac{\beta }{\alpha }\;\omega (|v(x)-v^{m}(x)|)\;\;\;{\text {a.e.}}\,{\text {in}}\;\Omega . \end{aligned}$$

Hence, from this two latter inequalities, it follows from triangle inequality that

$$\begin{aligned} |B^{0}(x)-A^{0}(x,v(x))|\le & {} |B^{0}(x)-A^{0}(x,v^{m}(x))|+|A^{0}(x,v^{m}(x))-A^{0}(x,v(x))| \\\le & {} 2\frac{\beta }{\alpha }\;\omega (|v(x)-v^{m}(x)|)\;\;\;{\text {a.e.}}\,{\text {in}}\;\Omega . \end{aligned}$$

Since \(\omega \) is continuous at 0, passing to the limit in this inequality when \(m\;\rightarrow \;\infty \), one obtains

$$B^{0}(x)=A^{0}(x,v(x))\;\;{\text {a.e.}}\;{\text {in}}\;\Omega ,$$

which, with (4.4), gives ( 3.3). \(\square \)

Proof of Theorem 3.4

First, note that problem (3.5) (respect. (3.7) has a unique solution in \(H_{0}^{1}(\Omega _{\varepsilon } )\) (respect. \(H_{0}^{1}(\Omega )\)) thanks to [6].

Second, taking \(u^{\varepsilon }\) as a test function in the variational formulation of (3.5), we obtain

$$\Vert P_{\varepsilon }u^{\varepsilon }\Vert _{H^{1}_{0}(\Omega )}\le C\Vert u^{\varepsilon }\Vert _{H^{1}_{0}(\Omega _{\varepsilon })}\le \frac{C}{\alpha }\Vert f\Vert _{L^{2}(\Omega _{}\varepsilon )}.$$

Hence, we can extract a subsequence of \(\{\varepsilon \}\) (still denoted by \(\{\varepsilon \}\)), such that

$$\begin{aligned} P_{\varepsilon }u^{\varepsilon }\;\rightharpoonup \; u^{0}\;\;\;{\text {weakly}}\;{\text {in}}\;H^{1}_{0}(\Omega ), \end{aligned}$$

hence

$$\begin{aligned} P_{\varepsilon }u^{\varepsilon }\;\rightarrow \;u^{0}\;\;\;{\text{ strongly }}\;{\text{ in }}\;L^{2}(\Omega ). \end{aligned}$$

This implies, for every m, that

$$\begin{aligned} P_{\varepsilon }u^{\varepsilon }-v^{m}\;\rightarrow \; u^{0}-v^{m}\;\;\;{\text {strongly}}\;{\text {in}}\;L^{2}(\Omega ), \end{aligned}$$

where \(\{v^{m}\}\) is a sequence of functions introduced in (4.5) such that \( v^{m}\;\rightarrow \; u^{0}\) strongly in \(L^{1}(\mathbb {R})\). So, thanks to continuity of \(\omega \), we get

$$\begin{aligned} \omega (|P_{\varepsilon }u^{\varepsilon }-v^{m}|)\;\rightarrow \;\omega (|u^{0}-v^{m}|)\;\;\;\;{\text {strongly}}\;{\text {in}}\;L^{1}(\Omega ). \end{aligned}$$
(4.8)

On the other hand, since \(A^{\varepsilon }(P_{\varepsilon }u^{\varepsilon })\doteq A^{\varepsilon }(\cdot ,P_{\varepsilon }u^{\varepsilon }(\cdot ))\in \mathcal {M}(\alpha ,\beta ;\Omega )\), there exists a subsequence of \(\{\varepsilon \}\) (still denoted by \(\{\varepsilon \}\)) and \(C^{0}\in \mathcal {M}(\frac{\alpha }{C^{2}},\beta ;\Omega )\), such that

$$\begin{aligned} (A^{\varepsilon }(P_{\varepsilon }u^{\varepsilon }),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;C^{0}, \end{aligned}$$
(4.9)

but

$$\begin{aligned} \forall \varepsilon >0,\;|A^{\varepsilon }(x,P_{\varepsilon }u^{\varepsilon }(x))-A^{\varepsilon }(x,v^{m}(x))|\le \omega (|P_{\varepsilon }u^{\varepsilon }(x)-v^{m}(x)|),\;{\text {a.e.}}\;{\text {in}}\;\Omega , \end{aligned}$$

hence by this last inequality, (4.8), (4.9), Theorem 3.2, Assumption (3.1), point (ii) of Remark 2.8 and Theorem 2.7, it comes

$$\begin{aligned} |C^{0}(x)-A^{0}(x,v^{m}(x))|\le \frac{\beta }{\alpha }\;\omega (|u^{0}(x)-v^{m}(x)|),\;{\text {a.e.}}\;{\text {in}}\;\Omega . \end{aligned}$$

This gives

$$\begin{aligned} |C^{0}(x)-A^{0}(x,u^{0}(x))|\le & {} |C^{0}(x)-A^{0}(x,v^{m}(x))|+|A^{0}(x,v^{m}(x))-A^{0}(x,u^{0}(x))|\\\le & {} 2\frac{\beta }{\alpha }\;\omega (|u^{0}(x)-v^{m}(x)|)\;\;\;{\text {a.e.}}\,{\text {in}}\;\Omega . \end{aligned}$$

Since \(\lim \limits _{d\rightarrow 0} \;\omega (d)=0\), passing to the limit in this inequality when \(m\;\rightarrow \;\infty \), we obtain

$$\begin{aligned} C^{0}(x)=A^{0}(x,u^{0}(x))\;\;\;{\text {a.e.}}\;{\text {in}}\;\Omega . \end{aligned}$$

Then, from this and (4.9), we find

$$\begin{aligned} (A^{\varepsilon }(P_{\varepsilon }u^{\varepsilon }),T_{\varepsilon }) \;\overset{H^{0}}{\rightharpoonup }\;A^{0}(\cdot ,u^{0}(\cdot )), \end{aligned}$$

which implies by the definition of the \(H^{0}\)-convergence and the uniqueness of the solutions of (3.5) and (3.7) that

$$\begin{aligned} \left\{ \begin{array}{l} P_{\varepsilon }u^{\varepsilon }\; \rightharpoonup \; u^{0}\; {\text{ weakly }} \;{\text{ in }} \;H_{0}^{1}(\Omega ), \\ \widetilde{A^{\varepsilon }( u^{\varepsilon })\nabla u^{\varepsilon }}\;\rightharpoonup \;A^{0}(u^{0})\nabla u^{0}\; {\text{ weakly }} \;{\text{ in }} \;L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$

where \(u^{0}\) is the solution of (3.7), which completes proof of (i) and (iii) of (3.6).

Finally, we deduce (3.6)ii) from the fact that

$$\begin{aligned} \chi ^{\varepsilon }\;\rightharpoonup \;\chi ^{0}\;\;\; {\text {weakly}} \; ^{\star }\;\; {\text {in}} \;\; L^{\infty }(\Omega ) \end{aligned}$$

and

$$\begin{aligned} P_{\varepsilon }u^{\varepsilon } \;\rightarrow \; u^{0}\;\;{\text {strongly}} \;{\text {in}} \;L^{2}(\Omega ). \end{aligned}$$

\(\square \)

5 Applications

As an application of our results, we consider the classical periodic case and a non-periodic case.

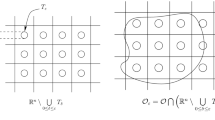
Let \(\theta \) a diffeomorphism of class \(C^{2}\) from \(\mathbb {R}^{n}\) onto \(\mathbb {R}^{n}\) and introduce the holes \(T_{\varepsilon }\) defined by

$$\begin{aligned} \left\{ \begin{array}{l} T_{\varepsilon }=\underset{k\in \mathbb {Z}^{n}}{\cup }\left\{ S_{\varepsilon }^{k}\;\;s.t.\;\;S_{\varepsilon }^{k}\subset \Omega , \;{\text {dist}}(\theta (k\varepsilon ),\partial \Omega )>2\varepsilon \right\} ,\\ \text {with }S_{\varepsilon }^{k}=\left\{ x\in \mathbb {R}^{n}\;\;s.t. \;\;|x-\theta (k\varepsilon )|\le \delta \varepsilon \right\} ,\; k\in \mathbb {Z}^{n}, \end{array} \right. \end{aligned}$$

where \(\delta \in ]0,1]\). Let \(Y=[-\frac{1}{2},\frac{1}{2}]^{n}\) and set

$$\begin{aligned} A^{\varepsilon }(x,d))=A\left( \frac{\theta ^{-1}(x)}{\varepsilon }\right) , \end{aligned}$$

with \(A\in \mathcal {M}_{Equi}(\alpha ,\beta ,\omega ;Y)\). Assume that \(\omega \) is continous with \(\omega (d)>0\;\forall d>0\) and

$$\begin{aligned} \text {for any }r>0,\;\;\,\underset{s\rightarrow 0}{\lim }\int _{s}^{r}\dfrac{\mathrm{{d}}t}{\omega (t)}=+\infty . \end{aligned}$$

In what follows, the spherical geometry of the holes can be generalized to the case where a regular boundary hole with a finite number of connected components replace a ball.

5.1 Classical periodic case

Take here \(\theta =Id_{\mathbb {R}^{n}}\) and \( \delta =\frac{1}{3}\). Then, the pair \((A^{\varepsilon }(\cdot ,\cdot ),T_{\varepsilon })\) satisfies all assumptions of Theorem 3.4 and it is well-known that in this case (see [10])

$$\begin{aligned} \left\{ \begin{array}{l} \forall d\in \mathbb {R},\; (A^{\varepsilon }(\cdot ,d),T_{\varepsilon })\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(d),\\ \chi ^{\varepsilon } \;\rightharpoonup \; \frac{|Y^{*}|}{|Y|}\; {\text {weakly}} \;^\star \; {\text {in}}\; L^{\infty }(\Omega ), \end{array} \right. \end{aligned}$$

with \(A^{0}(d)\) is independent of x and given by

$$\begin{aligned} \forall \lambda \in \mathbb {R}^{n},\;\;A^{0}(d)\lambda = \frac{1}{|Y|}\underset{Y^{\star }}{\int }A(y,d)\nabla _{y}v_{\lambda }(y,d)\mathrm{{d}}y, \end{aligned}$$
(5.1)

where

$$\begin{aligned} Y^{*}=Y{\setminus } T,\;\;\;T= \left\{ x\in \mathbb {R}^{n}\;\;s.t.\;\;|x|\le \frac{1}{3} \right\} ,\;\;\; \end{aligned}$$

and for all \( \lambda \in \mathbb {R}^{n}\), \(y\longmapsto v_{\lambda }(y,d)\) be the solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;\left( A(y,d) \nabla v_{\lambda }(y,d)\right) )=0\;\; \text{ in } Y^{\star }, \\ (A(y,d) \nabla v_{\lambda }(y,d) \nabla u^{\varepsilon }\cdot \nu =0\;\; \text{ on } \partial T, \\ v_{\lambda }(y,d)-\lambda \cdot y \;\;is\;Y-\text{ periodic } \text{ with } \text{ mean } \text{ value } 0.\end{array} \right. \end{aligned}$$

In this framework, we have the following result about the convergence of problem (3.5):

Proposition 5.1

For every \(f\in L^{2}(\Omega )\), the solution \(u^{\varepsilon } \) of problem (3.5) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} {\text{(i) }}\; P_{\varepsilon }(u^{{\varepsilon } })\; \rightharpoonup \;u^{0}\;\; \text{ weakly } \text{ in } H_{0}^{1}(\Omega ), \\ {\text{(ii) }} \;\widetilde{u^{\varepsilon }}\; \rightharpoonup \;\chi ^{0} u^{0}\;\; \text{ weakly } \text{ in } L^{2}(\Omega ), \\ {\text{(iii) }} \; \widetilde{A^{\varepsilon }( u^{\varepsilon })\nabla u^{\varepsilon }}\;\rightharpoonup \;A^{0}(u^{0})\nabla u^{0}\;\; \text{ weakly } \text{ in } L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$

where \(u^{0}\) is the solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(A^{0}(u^{0})\nabla u^{0} )=\chi ^{0}f\;\; \text{ in } \Omega , \\ u^{0}=0\;\; \text{ on } \partial \Omega . \end{array} \right. \end{aligned}$$

and where \(A^{0}\) defined by (5.1) belongs to \(\mathcal {M}_{Equi}(\frac{\alpha }{C^{2}},\beta ,\frac{\beta }{\alpha }\omega ;\Omega )\).

Remark 5.2

In the geometric framework of this example, Proposition 5.1 coincides with a result given in [7] by using the periodic unfolding, when the nonlinear Robin boundary condition on the holes reduces to the homogeneous Neumann condition.

5.2 Non-periodic case

Consider here the non-periodic perforated domain introduced in [5, Section 3] when studying the corresponding linear case. We suppose that \(\theta ^{-1}\) has a Lipschitz constant \(\kappa ^{-1}\) with \(\kappa >2\) and take \( \delta =1\). In this case, from [5, Sections 3-4], we deduce easily that for every \(d\in \mathbb {R}\), the pair \((A^{\varepsilon },T_{\varepsilon })\) satisfies all assumptions of Theorem 3.4 and

$$\begin{aligned} \left\{ \begin{array}{l} \forall d\in \mathbb {R},\;(A^{\varepsilon }(\cdot ,d),T_{\varepsilon }))\;\overset{H^{0}}{\rightharpoonup }\;A^{0}(\cdot ,d)\;in\;\Omega ,\\ \chi ^{\varepsilon }(\cdot ) \;\rightharpoonup \;\frac{|Y^{*}(\cdot )|}{|Y(\cdot )|} \;{\text {weakly}}\; ^\star \; {\text {in}} \; L^{\infty }(\Omega ), \end{array} \right. \end{aligned}$$

with

$$A^{0}(x,d)=B^{0}_{x}(d),$$

where \(B^{0}_{x}(d)\) is defined by

$$\begin{aligned} \forall \lambda \in \mathbb {R}^{n},\;\;B^{0}_{x}(d)\lambda = \frac{1}{|Y(x)|}\underset{Y(x)^{\star }}{\int }B(x,y,d)\nabla _{y}v_{\lambda }(x,y,d)\mathrm{{d}}y, \end{aligned}$$
(5.2)

and where we have

$$\begin{aligned} \left\{ \begin{array}{l} B(x,y,d)=A\left( \left[ \nabla \theta (\theta ^{-1}(x))\right] ^{-1}y,d\right) ,\\ Y(x)=\{\nabla \theta (\theta ^{-1}(x))z\;\;s.t.\;\;z\in Y\},\\ T_{1}=\left\{ z\in \mathbb {R}^{n}\;\;s.t.\;\;|z|\le 1 \right\} ,\\ Y(x)^{\star }=Y(x){\setminus } T_{1}\end{array} \right. \end{aligned}$$

and for all \( \lambda \in \mathbb {R}^{n}\), \(y\longmapsto v_{\lambda }(x,y,d)\) be the solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;\left( B(x,y,d) \nabla v_{\lambda }(x,y,d)\right) )=0\;\; \text{ in } Y(x)^{\star }, \\ (B(x,y,d) \nabla v_{\lambda }(x,y,d)\cdot \nu =0\;\; \text{ on } \partial T_{1}, \\ v_{\lambda }(x,y,d)-\lambda \cdot y \;\;is\;Y(x)-\text{ periodic } \text{ with } \text{ mean } \text{ value } 0. \end{array} \right. \end{aligned}$$

In this framework, we have the following result about the convergence of problem (3.5):

Proposition 5.3

For every \(f\in L^{2}(\Omega )\), the solution \(u^{\varepsilon } \) of problem (3.5) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} {\text{(i) }}\; P_{\varepsilon }(u^{{\varepsilon } })\; \rightharpoonup \;u^{0}\;\; \text{ weakly } \text{ in } H_{0}^{1}(\Omega ), \\ {\text{(ii) }} \;\widetilde{u^{\varepsilon }}\; \rightharpoonup \;\chi ^{0} u^{0}\;\; \text{ weakly } \text{ in } L^{2}(\Omega ), \\ {\text{(iii) }} \; \widetilde{A^{\varepsilon }( u^{\varepsilon })\nabla u^{\varepsilon }}\;\rightharpoonup \;B^{0}_x(u^{0})\nabla u^{0}\;\; \text{ weakly } \text{ in } L^{2}(\Omega )^{n}, \end{array} \right. \end{aligned}$$

where \(u^{0}\) is the solution of

$$\begin{aligned} \left\{ \begin{array}{l} -\mathrm {{div}}\;(B^{0}_{x}(u^{0}(x))\nabla u^{0}(x) )= \frac{|Y^{*}(x)|}{|Y(x)|}f(x)\;\; \text{ in } \Omega , \\ u^{0}(x)=0\;\; \text{ on } \partial \Omega \end{array} \right. \end{aligned}$$

and where \((x,d)\mapsto B^{0}_{x}(d)\) defined by (5.2) belongs to \(\mathcal {M}_{Equi}(\frac{\alpha }{C^{2}},\beta ,\frac{\beta }{\alpha }\omega ;\Omega )\).