1 Introduction

During the past few decades, wavelets have found their ways in the fields of signal processing, time-frequency analysis, image processing, quantum mechanics, and data compression. Wavelets have been also used as basis functions to estimate the solutions of integral and differential equations.

The approximation of a function belonging to some class by wavelet method has been discussed by many researchers like Devore [7], Morlet [11, 12], Meyer [10] and Debnath [6], etc. Sripathy et al. [14] discussed the Chebyshev wavelet based approximation for solving linear and non-linear differential equation. Adibi et al. [1] works on the numerical solution of Fredholm integral equation by first kind Chebyshev wavelet. As per our knowledge, no work seems for the approximation of the function belonging to generalized Hölder’s class by first and second kind Chebyshev wavelet method. In this paper, first and second kind Chebyshev wavelet approximation of function f belonging to generalized Hölder’s classes \(H^{(\chi )}_{\alpha } [0, 1)\) and \(H^{(w)}[0, 1)\) have been determined. Abel’s integral equations are solved by first and second kind Chebyshev wavelet method. Several methods are known for approximating the solution of the integral equations and differential equations. Capobianco [4] discussed the method for solving first kind integral equation. Yousefi [16] presented the numerical solution of Abel integral equation by Legendre wavelet method. Chebyshev wavelets method for solving system of Volterra integral equations has been discussed by Iqbal et al. [8]. Abel integral equation has been studied by many researcher and some numerical methods were developed. In this paper, another wavelet, Chebyshev wavelet of first and second kind are applied for the solution of Abel’s integral equation. The solutions obtained by first and second kind Chebyshev wavelet method are compared with their exact solutions and the known Legendre wavelet method. It is observed that second kind Chebyshev wavelet method gives more accurate solutions of the integral equations in comparison to first kind Chebyshev wavelet method and the Legendre wavelet method. First and second kind Chebyshev wavelet approximations established in this paper are new, sharper and best possible in wavelet analysis.

2 Definitions and preliminaries

2.1 First kind Chebyshev wavelet

Chebyshev wavelet of first kind, denoted by \(T_{n,m}\), is defined over the interval [0, 1) as

$$\begin{aligned} T_{n,m}(x)= & {} \left\{ \begin{array}{ll@{}l@{}r} 2^\frac{k}{2}{\tilde{T}} _{m}(2^kx-2n+1),\ \ \ \dfrac{n-1}{2^{k-1}}\le x <\dfrac{n}{2^{k-1}}; \\ 0 ,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \qquad \text {otherwise}, \end{array} \right. \\ \\ \text {where} \ \ {\tilde{T}}_{m}(x)= & {} \left\{ \begin{array}{lc@{}c@{}r} \frac{1}{\sqrt{\pi }},\ \ \ \ \ \ \ \ \ \ \ \qquad m=0; \\ \sqrt{\frac{2}{\pi }} T_{m}(x), \ \ \ \quad m \ne 0 , \end{array} \right. \ \ \ \ \ \ \ \ \ \ \end{aligned}$$

\(n=1,\ 2,\ \dotsc ,\ 2^{k-1},\ m=0,\ 1,\ 2,\ 3,\ \dotsc , \ M\) and k is the positive integer. Here \(T_{m}(x)\) are Chebyshev polynomials of the first kind of degree m which are orthogonal with respect to the weight function \( w(x)=\frac{1}{\sqrt{1- x^2}}\) on \([-1, 1]\), and satisfy the following recursive formula\(:\) \(T_{0}(x)=1, \ T_{1}(x)=x,\ \text {and} \ T_{m+1}(x)=2xT_{m}(x)-T_{m-1}(x),\ m=1,\ 2,\ 3, \dotsc \) [3].

2.2 Second kind Chebyshev wavelet

Chebyshev wavelet of second kind, denoted by \(U_{n,m}\), is defined over the interval [0, 1) as

$$\begin{aligned} U_{n,m}(x)= & {} \left\{ \begin{array}{lc@{}c@{}r} 2^\frac{k+3}{2}{U} _{m}\left( 2^{k+1}x-2n-1 \right) ,\ \ \ \dfrac{n}{2^{k}}\le x <\dfrac{n+1}{2^{k}}; \\ 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \quad \qquad \text {otherwise}, \end{array} \right. \end{aligned}$$

where \(n=0,\ 1,\ 2,\ \dotsc ,\ 2^{k}-1,\ m=0,\ 1,\ 2,\ \dotsc ,\ M\) and x is the normalized time. The polynomials \(U_{m}(x)\) are second kind Chebyshev polynomials of degree m orthogonal with respect to the weight function \(s(x)=\sqrt{1-x^2}\) on the interval \([-1,1]\), and satisfy the following recursive formula\(:\) \(U_{0}(x)=1,\ U_1(x)=2x,\ U_{m+1}(x)=2xU_m(x)-U_{m-1}(x),\ m=1,\ 2,\ 3,\ \dotsc \) [13].

2.3 Function of \(H_{\alpha }[0, 1)\)lass

A continuous function f \(\in \) \(H_{\alpha }[0, 1)\) if f satisfies the inequality \(|f(x+t)-f(x)|=O(|t|^\alpha ),\ \text {for} \ 0 <\alpha \le 1\) and \(\forall \ x,\ t,\ x+t \in [0, 1)\) [5].

2.4 Generalized Hölder’s class

2.4.1 \(H^{(\chi )}_{\alpha } [0, 1)\) class

Let \(\chi \) be a positive, monotonic increasing function of t such that \(\frac{|t|^{\alpha }}{\chi (\frac{1}{|t|})}\rightarrow 0 \) as \(t\rightarrow 0\). A continuous function f \(\in \) \(H^{(\chi )}_{\alpha } [0, 1)\) if f satisfies the inequality

$$\begin{aligned} |f(x+t)-f(x)|=O\left( \frac{|t|^{\alpha }}{\chi \big (\frac{1}{|t|}\big )}\right) , \ \text {for} \ 0 <\alpha \le 1 \ \text {and} \ \forall \ x, \ t, \ x+t \in [0, 1). \end{aligned}$$

Remark

It is important to note that if \(\chi (t)=1\), then class \(H^{(\chi )}_{\alpha }[0, 1)\) class coincides with the known Hölder’s class \(H_{\alpha }[0, 1)\) [5].

2.4.2 \(H^{(\phi )}[0, 1)\) class

Let \(\phi \) be a positive, monotonic increasing function defined on [0, 1) such that \(\phi (|t|) \rightarrow 0\) as \(t \rightarrow 0\). A continuous function f \(\in \) \(H^{(\phi )}[0, 1)\) if f satisfies the inequality \( |f(x+t)-f(x)|= O \big (\phi (|t|)\big ),\ \text {for} \ 0 <\alpha \le 1 \ \text {and} \ \forall \ x, \ t, \ x+t \in [0, 1)\) [15].

Remark

It is important to note that if \(\phi (|t|)=|t|^{\alpha }, \ 0< \alpha \le 1\), then \(H^{(\phi )}[0, 1)\) class reduces to known Hölder’s class \(H_{\alpha }[0, 1)\) [5].

Remark

If \(\phi (|t|)=\frac{|t|^{\alpha }}{\chi (\frac{1}{|t|})}\) then \(H^{(\phi )}[0,1)\) class reduces to \(H^{(\chi )}_{\alpha }[0, 1)\) class.

2.5 Chebyshev wavelet function approximation

The function \(f\in L^2[0, 1)\) is expressed in the form of Chebyshev wavelet series as

$$\begin{aligned} f(x)= \sum _{n=0}^{\infty } \sum _{m=0}^{\infty }c_{n,m}\psi _{n,m}(x), \end{aligned}$$
(2.1)

where \(c_{n,m}= \langle f(x),\psi _{n,m}(x)\rangle \), in which \(\langle .,.\rangle \) denotes the \(L^{2}\) inner product.

If infinite series in (2.1) is truncated then it is written as

$$\begin{aligned} S_{2^{k-1},M}f(x)= \sum _{n=0}^{2^{k-1}} \sum _{m=0}^{M} c_{n,m} \psi _{n,m}(x) = C^{ \top }\psi (x), \end{aligned}$$
(2.2)

where C and \(\psi (x)\) are \(2^{k-1}(M+1)\) column vectors of the form

$$\begin{aligned} C=[c_{0,0},c_{0,1}, \dotsc , c_{0,M}, c_{1,0},c_{1,1}, \dotsc , c_{1,M}, \dotsc , c_{2^{k-1},0}, \dotsc , c_{2^{k-1},M}]^{\top }, \end{aligned}$$

and

$$\begin{aligned} \psi (x)=[\psi _{0,0},\psi _{0,1}, \dotsc , \psi _{0,M},\psi _{1,0},\psi _{1,1}, \dotsc ,\psi _{1,M}, \dotsc ,\psi _{2^{k-1},0}, \dotsc , \psi _{2^{k-1},M}]^{\top }. \end{aligned}$$

The Chebyshev wavelet approximation \(E_{2^{k-1},M}(f)\) of a function f by \((2^{k-1},\ M+1)^{th} \) partial sums \(S_{2^{k-1},M}(f)\) of its Chebyshev wavelet series is given by

$$\begin{aligned} E_{2^{k-1},M}(f) = {\min _{{S_{2^{k-1},M}(f)}}}\Vert f-S_{2^{k-1},M}(f)\Vert _2. \end{aligned}$$

If \( E_{2^{k-1},M}(f)\rightarrow 0 \) as \( k \rightarrow \infty ,\ M \rightarrow {\infty }\), then \(E_{2^{k},M}(f)\) is called the best approximation of f of order \( (2^{k},\ M+1) \)([17], pp.115).

3 Theorem

In this paper, we prove the following Theorems:

Theorem 3.1

Let f \(\in \) \(H^{(\chi )}_{\alpha }[0, 1)\) class such that \(\frac{|t|^{\alpha }}{\chi (\frac{1}{|t|})} \rightarrow 0\) as \(t \rightarrow 0 \) and its general first kind Chebyshev wavelet expansion be \(f(x)=\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }c_{n,m}T_{n,m}(x),\) having \(\left( 2^{k-1},\ M+1 \right) th\) partial sums \((S_{2^{k-1},M}f)(x)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M}c_{n,m}T_{n,m}(x).\) Then the first kind Chebyshev wavelet approximation of f is given by:

  1. 1.

    \(E^{(1)}_{2^{k-1},0}(f)=min||f-\sum _{n=1}^{2^{k-1}}c_{n,0}T_{n,0}(x)||_{2}=O\left( \frac{1}{2^{(k-1) \alpha } \chi (2^{k-1})} \right) ,\ k \ge 1\).

  2. 2.

    \(E^{(2)}_{2^{k-1},M}(f)=min||f-\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M}c_{n,m}T_{n,m}(x)||_{2}=O\left( \frac{1}{ 2^{k\alpha } \chi (2^{k}) \sqrt{M+1} } \right) , \ M \ge 1 \).

Theorem 3.2

Let f \(\in \) \(H^{(\phi )}[0, 1)\) class such that \(\phi (|t|) \rightarrow 0\) as \(t \rightarrow 0\) and its general first kind Chebyshev wavelet expansion be \(f(x)=\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }c^{'}_{n,m}T_{n,m}(x)\) having \((2^{k-1},\ M+1)th\) partial sums \((S_{2^{k-1},M}f)(x)=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M}c^{'}_{n,m}T_{n,m}(x).\) Then the first kind Chebyshev wavelet approximation of f is given by:

  1. 1.

    \(E^{(3)}_{2^{k-1},0}(f)=min||f-\sum _{n=1}^{2^{k-1}}c^{'}_{n,0}T_{n,0}(x)||_{2}=O \left( \phi \left( \frac{1}{2^{k-1} } \right) \right) ,\ k \ge 1\).

  2. 2.

    \(E^{(4)}_{2^{k-1},M}(f)=min||f-\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M}c^{'}_{n,m}T_{n,m}(x)||_{2}=O\left( \frac{\phi \left( \frac{1}{2^{k}}\right) }{\sqrt{M+1}} \right) ,\ M \ge 1\).

Theorem 3.3

Let f \(\in \) \(H^{(\chi )}_{\alpha }[0, 1)\) class such that \(\frac{|t|^{\alpha }}{\chi (\frac{1}{|t|})} \rightarrow 0\) as \(t \rightarrow 0 \) and its general second kind Chebyshev wavelet expansion be \(f(x)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }c^{*}_{n,m}U_{n,m}(x)\) having \((2^k,\ M+1)th\) partial sums \((S_{2^k,M}f)(x)=\sum _{n=0}^{2^k-1}\sum _{m=0}^{M}c^{*}_{n,m}U_{n,m}(x)\). Then the second kind Chebyshev wavelet approximation of f is given by:

  1. 1.

    \(E^{(5)}_{2^k,0}(f)=min||f-\sum _{n=0}^{2^k-1}c^{*}_{n,0}U_{n,0}(x)||_{2}=O\left( \frac{1}{2^{k \alpha } \chi (2^{k})}\right) \).

  2. 2.

    \(E^{(6)}_{2^k,M}(f)=min||f-\sum _{n=0}^{2^k-1}\sum _{m=0}^{M}c^{*}_{n,m}U_{n,m}(x)||_{2}=O\left( \frac{1}{2^{(k+1)\alpha } \chi (2^{k+1}) \sqrt{M+1} } \right) ,\ M \ge 1 \).

Theorem 3.4

Let f \(\in \) \(H^{(\phi )}[0, 1)\) class such that \(\phi (|t|) \rightarrow 0\) as \(t \rightarrow 0\) and its general second kind Chebyshev wavelet expansion be \(f(x)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }c^{''}_{n,m}U_{n,m}(x)\) having \((2^{k},\ M+1)th\) partial sums \((S_{2^{k},M}f)(x)=\sum _{n=0}^{2^{k}-1}\sum _{m=0}^{M}c^{''}_{n,m}U_{n,m}(x).\) Then the first kind Chebyshev wavelet approximation of f is given by:

  1. 1.

    \(E^{(7)}_{2^{k},0}(f)=min||f-\sum _{n=0}^{2^{k}-1}c^{''}_{n,0}U_{n,0}(x)||_{2}=O \left( \phi \left( \frac{1}{2^{k} } \right) \right) \).

  2. 2.

    \(E^{(8)}_{2^{k},M}(f)=min||f-\sum _{n=0}^{2^{k}-1}\sum _{m=0}^{M}c^{''}_{n,m}U_{n,m}(x)||_{2}=O\left( \frac{\phi \left( \frac{1}{2^{k+1}}\right) }{ \sqrt{M+1} } \right) ,\ M \ge 1 \).

4 Proof of the theorems

4.1 Proof of Theorem 3.1

(i) Error between f(x) and its first kind Chebyshev wavelet expansion in \(\left[ \frac{n-1}{2^{k-1}}, \frac{n}{2^{k-1}}\right) \) is given by:

$$\begin{aligned} e_{n}^{'}(x)= & {} c_{n,0}T_{n,0}(x) -f(x), \ \forall x \in \left[ \frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\right) . \\ ||e_{n}^{'}||^2_{2}= & {} \int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} |e_{n}^{'}(x)|^{2}|w_{n}(x)|\mathrm{d}x =\int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}|c_{n,0}T_{n,0}(x) -f(x)|^2 |w_{n}(x)|\mathrm{d}x \\= & {} \left( \frac{2^{\frac{k}{2}}}{\sqrt{\pi }}c_{n,0}-f(\zeta _{n})\right) ^2 \int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} |w_{n}(x)|\mathrm{d}x , \ \zeta _{n} \in \left[ \frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\right) ,\ \text {by weighted mean value theorem}. \end{aligned}$$
$$\begin{aligned} \int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} |w_{n}(x)|dx= & {} \int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} w(2^kx-2n+1)\mathrm{d}x = \int _{-1}^{1} |w(t)|\frac{\mathrm{d}t}{2^k}=\int _{-1}^{1}\frac{1}{\sqrt{1-t^2}}\frac{\mathrm{d}t}{2^k} \nonumber \\= & {} 2\int _{0}^{1}\frac{1}{\sqrt{1-t^2}}\frac{\mathrm{d}t}{2^k}=\frac{\pi }{2^k}. \nonumber \\ \text {Then}, \ ||e_{n}^{'}||^2_{2}= & {} \left( \frac{2^{\frac{k}{2}}}{\sqrt{\pi }}c_{n,0}-f(\zeta _{n})\right) ^2\frac{\pi }{2^{k}}. \end{aligned}$$
(4.1)
$$\begin{aligned} \text {Now}, \ c_{n,0}= & {} \int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}f(x)T_{n,0}(x) w_{n}(x)\mathrm{d}x= \frac{2^{\frac{k}{2}}}{\sqrt{\pi }}\int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}f(x) w_{n}(x)dx \nonumber \\= & {} \frac{2^{\frac{k}{2}}}{\sqrt{\pi }}f(\eta _{n})\int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} w_{n}(x) \mathrm{d}x = {\frac{\sqrt{\pi }}{2^{\frac{k}{2}}}}f(\eta _{n}),\ \eta _{n}\in \left[ \frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\right) . \end{aligned}$$
(4.2)

By Eqs. (4.1) and (4.2), we have for \( f \in H^{(\chi )}_{\alpha }[0, 1)\)

$$\begin{aligned} ||e_n^{'}||_{2}^2= & {} (f(\eta _n)-f(\zeta _{n})^2 {\frac{\pi }{2^{k}}} =\frac{M_{1}^{2}|\zeta _n -\eta _{n}|^{2\alpha }}{\chi ^{2}\left( |\frac{1}{\zeta _n -\eta _{n}}|\right) }{\frac{\pi }{2^{k}}} \nonumber \\\le & {} \left( \frac{M_{1}^{2} \pi }{2^{k}2^{2(k-1) \alpha }\chi ^{2}(2^{k-1})}\right) = \frac{M_{1}^{2} \pi }{2^{k} 2^{2(k-1) \alpha } \chi ^{2}(2^{k-1})}. \end{aligned}$$
(4.3)

Lastly, by Eq. (4.3),

$$\begin{aligned} (E^{(1)}_{2^{k-1},0} (f))^2= & {} \int \limits _{0}^{1}\left( \sum \limits _{n=1}^{2^{k-1}}e_n^{'}(x) \right) ^2w_{n}(x) \mathrm{d}x \\= & {} \int \limits _{0}^{1}\sum \limits _{n=1}^{2^{k-1}}(e_n^{'}(x))^2w_{n}(x) dx+2\sum \limits _{1\le n}^{}\sum \limits _{\ne n'\le 2^{k-1} }^{}\int \limits _{0}^{1}e_n^{'}(x)e_{n^{'}}^{'}(x)w_{n}(x)\mathrm{d}x \\= & {} \sum \limits _{n=1}^{2^{k-1}}\int \limits _{0}^{1}(e_n^{'}(x))^2w_{n}(x) \mathrm{d}x, \text { due to disjointness of support of }\ e_n^{'} \ \text {and} \ e_{n^{'}}^{'} \\= & {} \sum \limits _{n=1}^{2^{k-1}}||e_n^{'}||_2 ^2 \le \sum \limits _{n=1}^{2^{k-1}} \left( \frac{M_{1}^{2} \pi }{2^{k} 2^{2(k-1) \alpha }\chi ^{2}(2^{k-1})}\right) = \frac{M_{1}^{2} \pi \times 2^{k-1}}{2^{k} 2^{2(k-1) \alpha \chi ^{2}(2^{k-1})}} \le \frac{2M_{1}^{2} \pi }{ 2^{2(k-1) \alpha \chi ^{2}(2^{k-1})}}. \\ \text {Therefore}, \ E^{(1)}_{2^{k-1},0} (f)\le & {} \frac{\sqrt{2}M_{1} \sqrt{\pi }}{2^{(k-1)\alpha } \chi (2^{k-1})} = O\left( \frac{1}{2^{(k-1)\alpha } \chi (2^{k-1})} \right) , \ k \ge 1. \end{aligned}$$

(ii) Consider

$$\begin{aligned} f(x)= & {} \sum \limits _{n=1}^{\infty }\sum \limits _{m=0}^{\infty }c_{n,m}T_{n,m}(x) \\ c_{n,m}= & {} \left\langle f,T_{n,m}\right\rangle _{w_{n}(x)}=\int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}f(x)T _{n,m}(x)w_{n}(x)\mathrm{d}x \\= & {} \frac{2^{\frac{k+1}{2}}}{\sqrt{\pi }}\int \limits _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}} f(x)T_m(2^{k} x-2n+1) w(2^{k} x-2n+1)\mathrm{d}x \\= & {} \frac{2^{\frac{k+1}{2}}}{\sqrt{\pi }}\int \limits _{0}^{\pi }f\left( \frac{\mathrm{cos}\theta +2n-1}{2^{k}}\right) T_m(\mathrm{cos}\theta ) w(\mathrm{cos}\theta ) \frac{\mathrm{sin}\theta }{2^{k}} \mathrm{d}\theta ,\ 2^{k} x-2n+1=cos\theta \\= & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{0}^{ \pi }\left( f\left( \frac{\mathrm{cos}\theta +2n-1}{2^{k}}\right) -f \left( {\frac{2n-1}{2^{k}}}\right) \right) \mathrm{cos}(m\theta ) \mathrm{d}\theta ,\ w(\mathrm{cos}\theta )=\frac{1}{sin\theta }. \end{aligned}$$

Hence, for \(f \in H^{(\chi )}_{\alpha }[0, 1)\),

$$\begin{aligned} |c_{n,m}|\le & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{0}^{ \pi }\left| f\left( \frac{\mathrm{cos}\theta +2n-1}{2^{k}}\right) -f \left( {\frac{2n-1}{2^{k}}}\right) \right| \left| \mathrm{cos}(m\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{2}}{\sqrt{\pi }2^{\frac{k-1}{2}}} \int \limits _{0}^{ \pi } \left| \frac{\mathrm{cos} \theta }{2^{k}} \right| ^{\alpha } \frac{1}{ \chi |\frac{2^{k}}{\mathrm{cos} \theta }|} \left| cos(m\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha }} \int \limits _{0}^{ \pi } \frac{|\mathrm{cos} \theta |^{\alpha }}{\chi |\frac{2^{k}}{\mathrm{cos} \theta }|} |\mathrm{cos}( m \theta )| \mathrm{d} \theta \le \frac{M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi } 2^{k \alpha }} \int \limits _{-\frac{ \pi }{2}}^{ \frac{\pi }{2}} \frac{|\mathrm{sin}t |^{\alpha }}{\chi |\frac{2^{k}}{\mathrm{sin} t}|} (|\mathrm{cos} (mt)| \nonumber \\&+|\mathrm{sin} (mt)|) \mathrm{d}t,\ \theta =\frac{\pi }{2}-t \nonumber \\= & {} \frac{2M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha }} \int \limits _{0}^{ \frac{\pi }{2}} \frac{(\mathrm{sin}t )^{\alpha }}{\chi |\frac{2^{k}}{sin t}|} (|\mathrm{cos} (mt)|+|\mathrm{sin} (mt)|) \mathrm{d}t \nonumber \\\le & {} \frac{2M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi } 2^{k \alpha } \chi (2^{k})} \int \limits _{0}^{ \frac{\pi }{2}} (\mathrm{sin}t) ^{\alpha }(|\mathrm{cos} (mt)| +|\mathrm{sin} (mt)|) \mathrm{d}t \nonumber \\\le & {} \frac{2M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha } \chi (2^{k})} \left[ \left\{ (sint)^{\alpha } \left( \left| \frac{\mathrm{sin}(mt)}{m} \right| +\left| \frac{\mathrm{cos}(mt)}{m} \right| \right) \right\} _{0}^{\frac{\pi }{2}} \right. \nonumber \\&\left. +\int \limits _{0}^{ \frac{\pi }{2}} \alpha (sint)^{\alpha -1} \mathrm{cos}t \left( \left| \frac{\mathrm{sin}(mt)}{m} \right| + \left| \frac{\mathrm{cos}(mt)}{m} \right| \right) \mathrm{d}t \right] \hbox { integrating by parts} \nonumber \\\le & {} \frac{2M_{2}}{2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha } \chi (2^{k})} \left[ \frac{1}{m}+\frac{2}{m}\int \limits _{0}^{ \frac{\pi }{2}} \alpha (\mathrm{sin}t)^{\alpha -1} \mathrm{cos}t \mathrm{d}t \right] \le \frac{6M_{2}}{m2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha } \chi (2^{k})}. \end{aligned}$$
(4.4)

Now

$$\begin{aligned} f(x)-S_{2^{k-1},M}(f)= & {} \sum \limits _{n=1}^{\infty }\sum \limits _{m=0}^{\infty }c_{n,m}T_{n,m}(x) -\sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=0}^{M}c_{n,m}T_{n,m}(x) \\= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }c_{n,m}T_{n,m}(x),\ \text {by definition of}\ T_{n,m}. \\ \left( f(x)-(S_{2^{k-1},M}f)(x)\right) ^{2}= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }c^{2}_{n,m}\left( T_{n,m}(x)\right) ^{2}+\sum \limits _{n=1}^{2^{k-1} }\sum \limits _{M+1\le m\ne }^{}\sum \limits _{m'\le \infty }^{}c_{n,m}c_{n,m'}T_{n,m}(x)T_{n,m'}(x) \\&+\sum \limits _{1\le n\ne }^{}\sum \limits _{n'\le 2^{k-1}}^{}\sum \limits _{m=M+1}^{\infty }c_{n,m}c_{n',m}T_{n,m}(x)T_{n',m}(x) \\&+\sum \limits _{1\le n\ne }^{}\sum \limits _{n'\le 2^{k-1}}^{}\sum \limits _{M+1\le m}^{}\sum \limits _{\ne m'\le \infty }^{}c_{n,m}c_{n',m'}T_{n,m}(x)T_{n',m'}(x). \\ \text {Then} \ \ \ \ \ (E^{(2)}_{2^{k-1},M}(f))^2= & {} ||f- S_{2^{k-1},M}(f)||_{2}^2 \\= & {} \int \limits _{0}^{1}\left( f(x)-(S_{2^{k-1},M}f)(x)\right) ^{2}w_{n}(x)\mathrm{d}x \\= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }|c_{n,m}|^2,\ \text {by orthonormality property of} \ T_{n,m}(x) \\\le & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }\left[ \frac{6M_{2}}{m2^{\frac{k-1}{2}}\sqrt{\pi }\ 2^{k \alpha } \chi (2^{k})} \right] ^2,\ \hbox { by Eq.}\ (4.4) \\= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty } \frac{36M_{2}^{2}}{m^{2}2^{k-1}\pi 2^{2k \alpha } \chi ^{2}(2^{k})} = \sum \limits _{m=M+1}^{\infty } \frac{36M_{2}^{2}}{m^{2}\pi 2^{2k \alpha } \chi ^{2}(2^{k})} \\= & {} \frac{36M_{2}^{2}}{\pi 2^{2k \alpha } \chi ^{2}(2^{k})} \sum \limits _{m=M+1}^{\infty } \frac{1}{m^{2}} \le \frac{36M_{2}^{2}}{\pi 2^{2k \alpha } (M+1) \chi ^{2}(2^{k})}. \\ \text {Therefore},\ E^{(2)}_{2^{k-1},M}(f)\le & {} \frac{6M_{2}}{ \sqrt{\pi }\ 2^{k \alpha } \sqrt{M+1} \chi (2^{k})} = O \left( {\frac{1}{2^{k\alpha } \chi (2^{k})\sqrt{M+1} }}\right) ,\ M \ge 1. \end{aligned}$$

4.2 Proof of Theorem 3.2

(i) Following the proof of the Theorem 3.1(i) and for \(f \in H^{(\phi )}[0, 1)\), we have

$$\begin{aligned} ||e_n^{'}||_{2}^2= & {} (f(\eta _n)-f(\zeta _{n}))^2 {\frac{\pi }{2^{k}}} \le \left[ M_{5} \phi (|\eta _n-\zeta _{n}|)\right] ^{2}{\frac{\pi }{2^{k}}} \le \frac{M_{5}^{2} \pi \phi ^{2}(|\eta _n-\zeta _{n}|)}{2^{k} } \nonumber \\\le & {} \frac{M_{5}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k-1}}\right) }{2^{k}}. \end{aligned}$$
(4.5)

Lastly, by Eq. (4.5)

$$\begin{aligned} (E^{(3)}_{2^{k-1},0} (f))^2= & {} \sum \limits _{n=1}^{2^{k-1}}||e_n^{'}||_2 ^2 \le \sum \limits _{n=1}^{2^{k-1}} \frac{M_{5}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k-1}}\right) }{2^{k} } = \frac{M_{5}^{2} \phi ^{2} \left( \frac{1}{2^{k-1}}\right) \pi \times 2^{k-1}}{2^{k}} = \frac{M_{5}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k-1}}\right) }{2}. \\ \text {Therefore}, \ \ E^{(3)}_{2^{k-1},0} (f)\le & {} \frac{M_{5} \phi \left( \frac{1}{2^{k-1}}\right) \sqrt{\pi } }{\sqrt{2} }= O\left( \phi \left( \frac{1}{2^{k-1}}\right) \right) ,\ k \ge 1. \end{aligned}$$

(ii) Following the proof of the Theorem 3.1(ii),

$$\begin{aligned} |c^{'}_{n,m}|\le & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{0}^{ \pi }\left| f\left( \frac{\mathrm{cos}\theta +2n-1}{2^{k}}\right) -f \left( {\frac{2n-1}{2^{k}}}\right) \right| \left| \mathrm{cos}(m\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{6}}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{0}^{ \pi } \phi \left( \left| \frac{\mathrm{cos} \theta }{2^{k}} \right| \right) \left| \mathrm{cos}(m\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{6}}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{\frac{- \pi }{2}}^{ \frac{\pi }{2}} \phi \left( \left| \frac{\mathrm{sin} t}{2^{k}} \right| \right) \left( \left| \mathrm{cos}(mt) \right| + \left| \mathrm{sin}(mt) \right| \right) \mathrm{d}t, \ \theta =\frac{\pi }{2}-t \nonumber \\= & {} \frac{2M_{6}}{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \int \limits _{0}^{ \frac{\pi }{2}} \phi \left( \left| \frac{sin t}{2^{k}} \right| \right) \left( \left| \mathrm{cos}(mt) \right| + \left| \mathrm{sin}(mt) \right| \right) \mathrm{d}t \nonumber \\\le & {} \frac{2M_{6} \phi \left( \frac{1}{2^{k}} \right) }{\sqrt{\pi }\ 2^{\frac{k-1}{2}}} \left[ \left| \frac{\mathrm{sin}(mt)}{m} \right| + \left| \frac{\mathrm{cos}(mt)}{m} \right| \right] _{0}^{\frac{\pi }{2}} \le \frac{4M_{6} \phi \left( \frac{1}{2^{k}} \right) }{m \sqrt{\pi }\ 2^{\frac{k-1}{2}}}.\\ (E^{(4)}_{2^{k-1},M}(f))^2= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }|c^{'}_{n,m}|^2,\ \text {by orthonormality property of} \ T_{nm}(x) \nonumber \\\le & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty }\left[ \frac{4M_{6} \phi \left( \frac{1}{2^{k}} \right) }{m \sqrt{\pi }.2^{\frac{k-1}{2}}} \right] ^2,\ \text {by Eq. }(4.6) \nonumber \\= & {} \sum \limits _{n=1}^{2^{k-1}}\sum \limits _{m=M+1}^{\infty } \frac{16M_{2}^{2} \phi ^{2} \left( \frac{1}{2^{k}} \right) }{m^{2} \pi 2^{k-1} } = \sum \limits _{m=M+1}^{\infty } \frac{16M_{2}^{2} \phi ^{2} \left( \frac{1}{2^{k}} \right) }{m^{2} \pi } = \frac{16M_{6}^{2} \phi ^{2} \left( \frac{1}{2^{k}} \right) }{ \pi } \sum \limits _{m=M+1}^{\infty } \frac{1}{m^{2}}\nonumber \\\le & {} \frac{16M_{6}^{2} \phi ^{2} \left( \frac{1}{2^{k}} \right) }{ \pi (M+1) }. \nonumber \\ \text {Therefore}, \ E^{(4)}_{2^{k-1},M}(f)\le & {} \frac{4M_{6} \phi \left( \frac{1}{2^{k}} \right) }{ \sqrt{\pi } \sqrt{M+1} } = O \left( {\frac{ \phi \left( \frac{1}{2^{k}} \right) }{\sqrt{M+1} }}\right) ,\ M \ge 1.\nonumber \end{aligned}$$
(4.6)

4.3 Proof of Theorem 3.3

(i) Error between f(x) and its second kind Chebyshev wavelet expansion in interval \(\left[ \frac{n}{2^{k}}, \frac{n+1}{2^{k}}\right) \) is given by:

$$\begin{aligned} e_{n}^{''}(x)= & {} c^{*}_{n,0}U_{n,0}(x) -f(x), \ \forall x \in \left[ \frac{n}{2^{k}},\frac{n+1}{2^{k}}\right) . \\ ||e_{n}^{''}||^2_{2}= & {} \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} |e_{n}^{''}(x)|^{2}|s_{n}(x)|\mathrm{d}x=\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}|c^{*}_{n,0}U_{n,0}(x) -f(x)|^2 |s_{n}(x)|\mathrm{d}x \\= & {} \left( \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}c^{*}_{n,0}-f(\zeta _{n}^{'})\right) ^2 \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} |s_{n}(x)|\mathrm{d}x , \ \zeta _{n}^{'} \in \left[ \frac{n}{2^{k}},\frac{n+1}{2^{k}}\right) , \text { by weighted mean value theorem}. \end{aligned}$$
$$\begin{aligned} \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} |s_{n}(x)|\mathrm{d}x= & {} \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}\sqrt{-2^{2k}x^2+2^k(1+2n)x-(n+n^2)} \mathrm{d}x \nonumber \\= & {} \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} \sqrt{(2^{k}x-n)-(2^{k}x-n)^{2}} dx,\ 2^{k}x-n=t \nonumber \\= & {} \frac{1}{2^{k}} \int _{0}^{1} \sqrt{t-t^{2}}=\frac{1}{2^{k}} \int _{0}^{1}\sqrt{\left( \frac{1}{2}\right) ^{2}-\left( t-\frac{1}{2}\right) ^{2}} \mathrm{d}t \nonumber \\= & {} \frac{1}{2^{k}} \left[ \frac{\left( t-\frac{1}{2}\right) }{2}\sqrt{\left( \frac{1}{2}\right) ^{2}-\left( t-\frac{1}{2}\right) ^{2}} +\frac{1}{8} sin^{-1} \left( \frac{\left( t-\frac{1}{2}\right) }{\frac{1}{2}} \right) \right] _{0}^{1}\nonumber \\= & {} \frac{1}{2^{k+3}} \left[ sin^{-1}(1)-sin^{-1}(-1)\right] =\frac{\pi }{2^{k+3}}.\nonumber \\ \text {Then}, \ \ ||e_{n}^{''}||^2_{2}= & {} \left( \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}c^{*}_{n,0}-f(\zeta _{n}^{'})\right) ^2\frac{\pi }{2^{k+3}}. \end{aligned}$$
(4.7)
$$\begin{aligned} \text {Now},\ c^{*}_{n,0}= & {} \int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}f(x)U_{n,0}(x) s_{n}(x)\mathrm{d}x = \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}f(x) s_{n}(x)\mathrm{d}x \nonumber \\= & {} \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}f(\eta _{n}^{'})\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} s_{n}(x) \mathrm{d}x,\ \eta _{n}^{'}\in \left[ \frac{n}{2^{k}},\frac{n+1}{2^{k}}\right) \nonumber \\= & {} \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}f(\eta _{n}^{'})\left( \frac{\pi }{2^{k+3}}\right) ={\frac{\sqrt{\pi }}{2^{\frac{k+3}{2}}}}f(\eta _{n}^{'}). \end{aligned}$$
(4.8)

By Eqs. (4.7) and (4.8) and for \( f \in H^{(\chi )}_{\alpha }[0, 1)\), we have

$$\begin{aligned} ||e_n^{''}||_{2}^2 = (f(\eta _n^{'})-f(\zeta _{n}^{'}))^2 {\frac{\pi }{2^{k+3}}} \le \left[ \frac{M_{3}|\zeta _n^{'} -\eta _{n}^{'}|^{\alpha }}{ \chi \left( \frac{1}{|\zeta _n^{'} -\eta _{n}^{'}|}\right) }\right] ^{2}{\frac{\pi }{2^{k+3}}} \le \frac{M_{3}^{2} \pi }{2^{k} 2^{2k \alpha }\chi ^{2}(2^{k})}. \end{aligned}$$
(4.9)

Following the proof of Theorem 3.1(i)

$$\begin{aligned} (E^{(5)}_{2^{k},0} (f))^2= & {} \sum \limits _{n=1}^{2^{k}-1}||e_n^{''}||_2 ^2 \le \sum \limits _{n=1}^{2^{k}-1} \frac{M_{3}^{2} \pi }{2^{k} 2^{2k \alpha }\chi ^{2}(2^{k})},\ \hbox { by Eq.}\ (4.9) \\= & {} \frac{M_{3}^{2} \pi }{2^{2 \alpha k }\chi ^{2}(2^{k})}. \\ \text {Therefore},\ \ E^{(5)}_{2^{k},0} (f)\le & {} \frac{M_{3} \sqrt{\pi }}{2^{\alpha k}\chi (2^{k}) }=O\left( \frac{1}{2^{k \alpha } \chi (2^{k})}\right) ,\ k \ge 1. \end{aligned}$$

(ii) Consider

$$\begin{aligned} f(x)= & {} \sum \limits _{n=0}^{\infty }\sum \limits _{m=0}^{\infty }c^{*}_{n,m}U_{n,m}(x) \\ \text {and} \ s_{n}(x)= & {} \sqrt{-2^{2k}x^2+2^k(1+2n)x-(n+n^2)} \\ c^{*}_{n,m}= & {} \left\langle f,U_{n,m}\right\rangle _{s_{n}(x)}=\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}f(x)U _{n,m}(x)s_{n}(x)\mathrm{d}x = \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}f(x)U_m(2^{k+1} x-2n-1) s_{n}(x)\mathrm{d}x \\= & {} \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}\int \limits _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}}f(x)U_m(2^{k+1} x-2n-1) \sqrt{-2^{2k}x^2+2^k(1+2n)x-(n+n^2)}\mathrm{d}x \\= & {} \frac{2^{\frac{k+3}{2}}}{\sqrt{\pi }}\int \limits _{0}^{\pi }f\left( \frac{\mathrm{cos}\theta +2n+1}{2^{k+1}}\right) U_m(\mathrm{cos}\theta ) \left( \frac{\mathrm{sin}\theta }{2} \right) \left( \frac{sin\theta }{2^{k+1}} \right) \mathrm{d}\theta ,\ 2^{k+1} x-2n-1=\mathrm{cos}\theta \\= & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k+1}{2}}}\int \limits _{0}^{\pi }f\left( \frac{\mathrm{cos}\theta +2n+1}{2^{k+1}}\right) \mathrm{sin}\theta \mathrm{sin}((m+1)\theta ) \mathrm{d}\theta \\= & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k+1}{2}}}\int \limits _{0}^{\pi }f\left( \frac{\mathrm{cos}\theta +2n+1}{2^{k+1}}\right) \left( \frac{\mathrm{cos}(m\theta ) -\mathrm{cos}((m+2) \theta )}{2} \right) \mathrm{d}\theta \\= & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k+1}{2}}} \int \limits _{0}^{ \pi }\left( f\left( \frac{\mathrm{cos}\theta +2n+1}{2^{k+1}}\right) -f \left( {\frac{2n+1}{2^{k+1}}}\right) \right) \left( \frac{\mathrm{cos}(m\theta ) -\mathrm{cos}((m+2) \theta )}{2} \right) \mathrm{d}\theta ,\ m \ge 1. \end{aligned}$$

Then, for \(f \in H^{(\chi )}_{\alpha }[0, 1) \),

$$\begin{aligned} |c^{*}_{n,m}|\le & {} \frac{1}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{0}^{ \pi }\left| f\left( \frac{\mathrm{cos}\theta +2n+1}{2^{k+1}}\right) -f \left( {\frac{2n+1}{2^{k+1}}}\right) \right| \left| \mathrm{cos}(m\theta ) -\mathrm{cos}((m+2) \theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{4}}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{0}^{ \pi } \left| \frac{\mathrm{cos} \theta }{2^{k+1}} \right| ^{\alpha } \frac{1}{ \chi |\frac{2^{k+1}}{\mathrm{cos} \theta }|} \left| \mathrm{cos}(m\theta )-\mathrm{cos}((m+2) \theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{4}}{2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha }} \int \limits _{0}^{ \pi } \frac{|\mathrm{cos} \theta |^{\alpha }}{\chi |\frac{2^{k+1}}{\mathrm{cos} \theta }|} (|\mathrm{cos}( m \theta )|+|\mathrm{cos} ((m+2) \theta )|) \mathrm{d}\theta \nonumber \\= & {} \frac{M_{4}}{2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha }} \int \limits _{-\frac{ \pi }{2}}^{ \frac{\pi }{2}} \frac{|sint |^{\alpha }}{\chi |\frac{2^{k+1}}{sin t}|} (|\mathrm{cos} (mt)|+|\mathrm{cos} ((m+2)t)| \nonumber \\&+|\mathrm{sin}( mt)|+|\mathrm{sin} ((m+2)t)|) \mathrm{d}t,\ \theta =\frac{\pi }{2}-t \nonumber \\= & {} \frac{2M_{4}}{2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha } \chi (2^{k+1})} \int \limits _{0}^{ \frac{\pi }{2}} (\mathrm{sin}t )^{\alpha } (|\mathrm{cos}(mt)| +|\mathrm{cos} ((m+2)t)| \nonumber \\&+|\mathrm{sin} (mt)|+|\mathrm{sin} ((m+2)t)|) \mathrm{d}t \nonumber \\\le & {} \frac{2M_{4}}{2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha } \chi (2^{k+1})} \left[ \left\{ (\mathrm{sin}t)^{\alpha } \left( \left| \frac{\mathrm{sin}(mt)}{m} \right| \right. \right. \right. \nonumber \\&\left. \left. \left. +\left| \frac{\mathrm{sin}((m+2)t)}{m+2} \right| +\left| \frac{\mathrm{cos}(mt)}{m} \right| +\left| \frac{\mathrm{sin}((m+2)t)}{m+2} \right| \right) \right\} _{0}^{\frac{\pi }{2}} \right. \nonumber \\+ & {} \left. \!\!\int \limits _{0}^{ \frac{\pi }{2}} \!\alpha (\mathrm{sin}t)^{\alpha -1} \mathrm{cos}t \left( \left| \frac{\mathrm{sin}(mt)}{m} \right| \!+\!\left| \frac{sin((m+2)t)}{m+2} \right| \!+\!\left| \frac{\mathrm{cos}(mt)}{m} \right| \!+\!\left| \frac{\mathrm{sin}((m+2)t)}{m+2} \right| \right) \mathrm{d}t\!\! \right] ,\ \text {integrating by parts} \nonumber \\\le & {} \frac{2M_{4}}{2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha } \chi (2^{k+1})} \left[ \frac{2}{m}+\frac{4}{m}\int \limits _{0}^{ \frac{\pi }{2}} \alpha (\mathrm{sin}t)^{\alpha -1} \mathrm{cos}t \mathrm{d}t \right] \nonumber \\\le & {} \frac{12M_{4}}{m2^{\frac{k+3}{2}}\sqrt{\pi }\ 2^{(k+1) \alpha } \chi (2^{k+1})}. \end{aligned}$$
(4.10)

Following the procedure of the Theorem 3.1(ii),

$$\begin{aligned} (E^{(6)}_{2^{k},M}(f))^2= & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty }|c^{*}_{n,m}|^2,\ \text {by orthonormality property of}\ U_{n,m}(x) \\\le & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty }\left[ \frac{12M_{4}}{m2^{\frac{k+3}{2}}\sqrt{\pi } 2^{(k+1) \alpha } \chi (2^{k+1})} \right] ^2,\ \text {by Eq. (4.10)} \\= & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty } \frac{144 M_{4}^{2}}{m^{2}\pi 2^{2(k+1)\alpha } 2^{(k+3)} \chi ^{2}(2^{k+1})} \\= & {} \frac{18 M_{4}^{2}}{m^{2}\pi 2^{2(k+1)\alpha } \chi ^{2}(2^{k+1})} \sum \limits _{m=M+1}^{\infty } \frac{1}{m^{2}} \le \frac{18 M_{4}^{2}}{(M+1)\pi 2^{2(k+1)\alpha } \chi ^{2}(2^{k+1})}. \\ \text {Therefore},\ E^{(6)}_{2^{k},M}(f)\le & {} \frac{\sqrt{18} M_{4}}{\sqrt{M+1}\sqrt{\pi } 2^{(k+1)\alpha } \chi (2^{k+1})} =O \left( {\frac{1}{2^{(k+1)\alpha } \chi (2^{k+1})\sqrt{M+1} }}\right) , \ \ M \ge 1. \end{aligned}$$

4.4 Proof of Theorem 3.4

(i) Following the proof of the Theorem 3.3(i) and for \(f \in H^{(\phi )}[0, 1)\), we have

$$\begin{aligned} ||e_n^{''}||_{2}^2= & {} (f(\eta _n^{'})-f(\zeta _{n}^{'}))^2 {\frac{\pi }{2^{k+3}}} \le \left[ M_{7} \phi (|\eta _n^{'}-\zeta _{n}^{'}|)\right] ^{2}{\frac{\pi }{2^{k+3}}} \nonumber \\\le & {} \frac{M_{7}^{2} \pi \phi ^{2}(|\eta _n^{'}-\zeta _{n}^{'}|)}{2^{k+3} } \le \frac{M_{7}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k}} \right) }{2^{k+3} }. \end{aligned}$$
(4.11)

Lastly, by Eq. (4.11),

$$\begin{aligned} (E^{(7)}_{2^{k},0} (f))^2= & {} \sum \limits _{n=0}^{2^{k}-1}||e_n^{''}||_2 ^2 \le \sum \limits _{n=0}^{2^{k}-1} \frac{M_{7}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k}}\right) }{2^{k+3} } \\= & {} \frac{M_{7}^{2} \phi ^{2} \left( \frac{1}{2^{k}}\right) \pi \times 2^{k}}{2^{k+3}} \le \frac{M_{7}^{2} \pi \phi ^{2} \left( \frac{1}{2^{k}}\right) }{8} .\\ \text {Therefore} \ \ E^{(7)}_{2^{k},0} (f)\le & {} \frac{M_{7} \phi \left( \frac{1}{2^{k}}\right) \sqrt{\pi } }{\sqrt{8} } =O\left( \phi \left( \frac{1}{2^{k}}\right) \right) . \end{aligned}$$

(ii) Following the proof of the Theorem 3.3(ii),

$$\begin{aligned} |c^{''}_{n, m}|\le & {} \frac{1}{\sqrt{\pi }2^{\frac{k+3}{2}}} \int \limits _{0}^{ \pi }\left| f\left( \frac{\mathrm{cos}\theta +2n-1}{2^{k}}\right) -f \left( {\frac{2n-1}{2^{k}}}\right) \right| \left| \mathrm{cos}(m\theta ) -\mathrm{cos}((m+2)\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{8}}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{0}^{ \pi } \phi \left( \left| \frac{\mathrm{cos} \theta }{2^{k+1}} \right| \right) \left| \mathrm{cos}(m\theta ) -\mathrm{cos}((m+2)\theta ) \right| \mathrm{d}\theta \nonumber \\\le & {} \frac{M_{8}}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{0}^{ \pi } \phi \left( \left| \frac{\mathrm{cos} \theta }{2^{k+1}} \right| \right) \left( \left| \mathrm{cos}(m\theta ) \right| + \left| \mathrm{cos}((m+2)\theta ) \right| \right) d\theta \nonumber \\= & {} \frac{M_{8}}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{\frac{- \pi }{2}}^{ \frac{\pi }{2}} \phi \left( \left| \frac{\mathrm{sin} t}{2^{k+1}} \right| \right) \left( \left| \mathrm{cos}(mt) \right| + \left| \mathrm{sin}(mt) \right| +\left| \mathrm{cos}((m+2)t) \right| \right. \nonumber \\&\left. + \left| \mathrm{sin}((m+2)t) \right| \right) \mathrm{d}t,\ \theta =\frac{\pi }{2}-t \nonumber \\= & {} \frac{2M_{8}}{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \int \limits _{0}^{ \frac{\pi }{2}} \phi \left( \left| \frac{sin t}{2^{k+1}} \right| \right) \left( \left| \mathrm{cos}(mt) \right| + \left| \mathrm{sin}(mt) \right| + \left| \mathrm{cos}((m+2)t) \right| + \left| \mathrm{sin}((m+2)t) \right| \right) \mathrm{d}t \nonumber \\\le & {} \frac{2M_{8} \phi \left( \frac{1}{2^{k+1}} \right) }{\sqrt{\pi }\ 2^{\frac{k+3}{2}}} \left[ \left| \frac{\mathrm{sin}(mt)}{m} \right| + \left| \frac{\mathrm{cos}(mt)}{m} \right| +\left| \frac{\mathrm{sin}((m+2)t)}{m+2} \right| + \left| \frac{\mathrm{cos}((m+2)t)}{m+2} \right| \right] _{0}^{\frac{\pi }{2}} \nonumber \\\le & {} \frac{8M_{8} \phi \left( \frac{1}{2^{k+1}} \right) }{m \sqrt{\pi }\ 2^{\frac{k+3}{2}}}. \end{aligned}$$
(4.12)
$$\begin{aligned} (E^{(8)}_{2^{k-1},M}(f))^2= & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty }|c^{''}_{n,m}|^2,\ \text {by orthonormality property of} \ T_{n,m}(x) \\\le & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty }\left[ \frac{8M_{8} \phi \left( \frac{1}{2^{k+1}} \right) }{m \sqrt{\pi }.2^{\frac{k+3}{2}}} \right] ^2,\ \text {by Eq. }~(4.12) \\= & {} \sum \limits _{n=0}^{2^{k}-1}\sum \limits _{m=M+1}^{\infty } \frac{64M_{8}^{2} \phi ^{2} \left( \frac{1}{2^{k+1}} \right) }{m^{2} \pi 2^{k+3} } = \sum \limits _{m=M+1}^{\infty } \frac{64M_{8}^{2} \phi ^{2} \left( \frac{1}{2^{k+1}} \right) }{8m^{2} \pi } \\= & {} \frac{8M_{8}^{2} \phi ^{2} \left( \frac{1}{2^{k+1}} \right) }{ \pi } \sum \limits _{m=M+1}^{\infty } \frac{1}{m^{2}} \le \frac{8M_{8}^{2} \phi ^{2} \left( \frac{1}{2^{k}} \right) }{ \pi (M+1) }. \\ \text {Therefore},\ E^{(8)}_{2^{k},M}(f)\le & {} \frac{\sqrt{8}M_{8} \phi \left( \frac{1}{2^{k+1}} \right) }{ \sqrt{\pi } \sqrt{M+1} } =O \left( {\frac{ \phi \left( \frac{1}{2^{k+1}} \right) }{\sqrt{M+1} }}\right) ,\ M \ge 1. \end{aligned}$$

5 Corollary

Following Corollaries can be deduced from Theorems 3.1 to 3.4:

Corollary 5.1

If f \(\in \) \(H_{\alpha }[0, 1)\), then \(E^{(1)}_{2^{k-1},0}(f) = O\left( \frac{1}{2^{(k-1) \alpha } } \right) ,\ k \ge 1\) and \(E^{(2)}_{2^{k-1},M}(f) = O\left( \frac{1}{ 2^{k\alpha } \sqrt{M+1} } \right) , M \ge 1 \).

Proof of the Corollary 5.1

can be developed parallel to the proof of Theorem 3.1 by taking \(\chi (t)=1\), \(\forall \) t \(\in \) [0, 1) . \(\square \)

Corollary 5.2

If f \(\in \) \(H_{\alpha }[0, 1)\), then \(E^{(3)}_{2^{k-1},0}(f) = O\left( \frac{1}{2^{(k-1) \alpha } } \right) ,\ k \ge 1\) and \(E^{(4)}_{2^{k-1},M}(f) = O\left( \frac{1}{ 2^{k\alpha } \sqrt{M+1} } \right) , M \ge 1 \).

Proof of the Corollary 5.2

can be developed parallel to the proof of Theorem 3.2 by taking \(\phi (t)=c|t|^\alpha \), \( c>0\), \(\forall \) t \(\in \) [0, 1) . \(\square \)

Corollary 5.3

If f \(\in \) \(H_{\alpha }[0, 1)\), then \(E^{(5)}_{2^{k},0}(f) = O\left( \frac{1}{2^{k\alpha } } \right) ,\ k \ge 1\) and \(E^{(6)}_{2^{k},M}(f) = O\left( \frac{1}{ 2^{(k+1)\alpha } \sqrt{M+1} } \right) ,\ M \ge 1 \).

Proof of the Corollary 5.3

can be developed parallel to the proof of Theorem 3.3 by taking \(\chi (t)=1\), \(\forall \) t \(\in \) [0, 1) . \(\square \)

Corollary 5.4

If f \(\in \) \(H_{\alpha }[0, 1)\), then \(E^{(7)}_{2^{k},0}(f) = O\left( \frac{1}{2^{k\alpha } } \right) ,\ k \ge 1\) and \(E^{(8)}_{2^{k},M}(f) = O\left( \frac{1}{ 2^{(k+1)\alpha } \sqrt{M+1} } \right) ,\ M \ge 1 \).

Proof of the Corollary 5.4

can be developed parallel to the proof of Theorem 3.4 by taking \(\phi (t)=c|t|^\alpha \), \( c>0\), \(\forall \) t \(\in \) [0, 1) . \(\square \)

6 Method for solving Abel’s integral equations by first and second kind Chebyshev wavelet

In this section, first and second kind Chebyshev wavelets method for solving Abel integral equations are demonstrated. Abel’s integral equation [2] has two forms:

First Kind:

$$\begin{aligned} \int _{0}^{x} \frac{y(t)}{\sqrt{x-t}}\mathrm{d}t=f(x). \end{aligned}$$
(6.1)

Second Kind:

$$\begin{aligned} y(x)=\int _{0}^{x} \frac{y(t)}{\sqrt{x-t}}\mathrm{d}t+f(x), \end{aligned}$$
(6.2)

where f(x) is a given function and y(t) is an unknown function.

At first, the functions f(x) and y(x) are approximated with Chebyshev wavelets as:

$$\begin{aligned} y(x)= Y^{\top }\Psi (x) \ \text {and} \ f(x)= F^{\top }\Psi (x), \end{aligned}$$
(6.3)

where \(\Psi (x)\) is T(x) or U(x), Y is \(2^{k-1}(M+1)\) or \(2^{k}(M+1) \) unknown column vector defined similarly to C in (2.2) and (2.4) and coefficients of F is known.

Substituting equation (6.3) in equations (6.1) and (6.2), the integral equations are transformed as:

First Kind:

$$\begin{aligned} \int _{0}^{x} \frac{Y^{\top }\Psi (t)}{\sqrt{x-t}}\mathrm{d}t=F^{\top }\Psi (x). \end{aligned}$$
(6.4)

Second Kind:

$$\begin{aligned} Y^{\top }\Psi (x)=\int _{0}^{x} \frac{Y^{\top }\Psi (x)}{\sqrt{x-t}}\mathrm{d}t+F^{\top }\Psi (x), \end{aligned}$$
(6.5)

Now we need to calculate the integral \(\int _{0}^{x} \frac{Y^{\top }\Psi (t)}{\sqrt{x-t}}\mathrm{d}t\).

Since the basis of Chebyshev wavelets is polynomials, it is sufficient to calculate the integral:

$$\begin{aligned} \int _{0}^{x} \frac{t^{n}}{\sqrt{x-t}}\mathrm{d}t. \end{aligned}$$

. This basis integral is solved as:

$$\begin{aligned} \int _{0}^{x} \frac{t^{n}}{\sqrt{x-t}}\mathrm{d}t=\frac{\sqrt{\pi }x^{(\frac{1}{2}+n) }\Gamma (n+1)}{\Gamma (n+\frac{3}{2})},\ \text {where} \ \Gamma (n)=(n-1)! \ \text {for positive integer}~n. \end{aligned}$$

Based on the above equation, the integral \(\int _{0}^{x} \frac{Y^{\top }\Psi (t)}{\sqrt{x-t}}\mathrm{d}t\) can be obtained as:

$$\begin{aligned} \int _{0}^{x} \frac{\Psi (t)}{\sqrt{x-t}}\mathrm{d}t=L \Psi (x), \end{aligned}$$

where L is the operational matrix obtained from first or second kind Chebyshev wavelets. With the calculated L, the unknown coefficient vector \(Y^{\top }\) can be calculated from using equation (6.4), (6.5) and the above equation:

First Kind:

$$\begin{aligned} Y^{\top }=F^{\top }L^{-1}. \end{aligned}$$

Second Kind:

$$\begin{aligned} Y^{\top }=F^{\top }(I-L)^{-1}. \end{aligned}$$

The unknown function \(y(x)=Y^{\top }\Psi (x)\), where \(\Psi (x)\) is T(x) or U(x), is the required approximate solution.

Fig. 1
figure 1

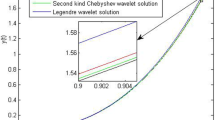
Comparison of Legendre wavelet and Chebyshev wavelet solutions of example 7.1

Full size image

7 Illustrative examples

In this section, we applied Chebyshev wavelet method described in previous Section for solving integral equations and solve some examples.

Example 7.1

Consider the following Abel’s integral equation of the first kind:

$$\begin{aligned} \int _{0}^{x} \frac{y(t)}{\sqrt{x-t}}\mathrm{d}t=\frac{2\sqrt{x}(15+10x+8x^{2})}{15} \end{aligned}$$
(7.1)

having the exact solution \( y(x)= x^{2}+x+1 \).

Consider the approximate solution as \(y(x)= \sum _{m=0}^{9}c_{0,m}\Psi _{0,m}(x) \).

The integral equation has been solved by applying the procedure described in Sect. 6 by first and second kind Chebyshev wavelets by taking \( M=9 \ and \ k=0. \)

Table 1 Comparisons between the exact solution and estimated numerical solutions for various values of x
Full size table

The graphs of the obtained numerical solution through wavelet methods and the exact solution of example 7.1 are shown in the Fig. 1:

It is observed from the table and figure that the numerical solution obtained by the second kind Chebyshev wavelet is approximately same as the exact solution.

Example 7.2

Consider the following Abel’s integral equation of the second kind:

$$\begin{aligned} y(x)=4x^{\frac{3}{2}}-\int _{0}^{x} \frac{y(t)}{\sqrt{x-t}}\mathrm{d}t \end{aligned}$$
(7.2)

having the exact solution \( y(x)= \frac{-6\sqrt{x}}{\pi }+3x+\frac{3(1-erfc(\sqrt{\pi x}))}{\pi }\).

Fig. 2
figure 2

Comparison of Legendre wavelet and Chebyshev wavelet solutions of example 7.1

Full size image

Consider the approximate solution as \(y(x)= \sum _{m=0}^{9}c_{0,m}U_{0,m}(x) \). The integral equation has been solved by applying the procedure described in Sect. 6 for second kind Abel’s integral equation by taking \( M=9 \ and \ k=0. \)

Table 2 Comparisons between the exact solution and numerical solutions for various values of x
Full size table

The graphs of the estimated numerical solution through wavelet methods and the exact solution of example 7.2 are shown in the Fig. 2:

It is observed from the table and figure that the numerical solution obtained by the second kind Chebyshev wavelet is sufficiently close to the exact solution.

8 Comparison of results of Chebyshev wavelet of first kind and second kind with Legendre wavelet

8.1 Legendre wavelet

Legendre wavelet over the interval [0,1) is defined as

$$\begin{aligned} \psi _{n,m}(x)=\left\{ \begin{array}{lc@{}c@{}r} \sqrt{m+\frac{1}{2}} \ \ 2^\frac{k}{2}P_m(2^kx-{\hat{n}}),\ \ \ \dfrac{{\hat{n}}-1}{2^k}\le x <\dfrac{{\hat{n}}+1}{2^k}; \\ 0 , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {otherwise}, \end{array} \right. \end{aligned}$$

where \(n=1,2,\ldots , 2^{k-1}\), \(m=0,1,2,\ldots , M-1\) and \({\hat{n}}=2n-1\) [9].

Comparisons are shown in Figs. 1 and 2. By the figures, it is observed that the numerical results obtained by the Chebyshev wavelet of second kind are quite close to the exact solution. Due to the weight functions \(w(x)=\frac{1}{\sqrt{1- x^2}}\) and \(s(x)=\sqrt{1- x^2}\) of Chebyshev polynomial of first kind and second kind respectively, the absolute errors at end points in case of Chebyshev wavelet of first kind and second kind is less than those of Legendre wavelet. Therefore, Chebyshev wavelet of second kind gives better result as compared to the Legendre wavelet and Chebyshev wavelet of first kind.

9 Superiority of Chebyshev wavelet of second kind to first kind

In Chebyshev wavelet of first kind, the weight function is \( w(x)=\frac{1}{\sqrt{1- x^2}}\) and the weight function in the Chebyshev wavelet of second kind is \( s(x)=\sqrt{1- x^2}\). Weight function of Chebyshev wavelet of second kind is more convenient and applicable than the weight function of Chebyshev wavelet of first kind. Furthermore, Chebyshev polynomial of second kind in the definition of second kind Chebyshev wavelet is more effective and significant in mathematical premises than the Chebyshev polynomial of first kind in the definition of first kind Chebyshev wavelet. In view of the above mentioned observation, Chebyshev wavelet of second kind is better than the Chebyshev wavelet of first kind.

10 Conclusions

10.1 The approximation obtained in the Theorems 3.1, 3.2, 3.3 and 3.4 are given below:

$$\begin{aligned} E^{(1)}_{2^{k-1},0}(f)= & {} O\left( \frac{1}{2^{(k-1) \alpha } \chi (2^{k-1})} \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \\ E^{(2)}_{2^{k-1},M}(f)= & {} O\left( \frac{1}{ 2^{k\alpha } \chi (2^{k}) \sqrt{M+1} } \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \ M \rightarrow \infty , \\ E^{(3)}_{2^{k-1},0}(f)= & {} O \left( \phi \left( \frac{1}{2^{k-1} } \right) \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \\ E^{(4)}_{2^{k-1},M}(f)= & {} O\left( \frac{\phi \left( \frac{1}{2^{k}}\right) }{ \sqrt{M+1} } \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \ M \rightarrow \infty , \\ E^{(5)}_{2^k,0}(f)= & {} O\left( \frac{1}{2^{k \alpha } \chi (2^{k})} \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \\ E^{(6)}_{2^k,M}(f)= & {} O\left( \frac{1}{ 2^{(k+1)\alpha } \chi (2^{k+1}) \sqrt{M+1} } \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \ M \rightarrow \infty , \\ E^{(7)}_{2^{k},0}(f)= & {} O \left( \phi \left( \frac{1}{2^{k} } \right) \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \\ E^{(8)}_{2^{k},M}(f)= & {} O\left( \frac{\phi \left( \frac{1}{2^{k+1}}\right) }{ \sqrt{M+1} } \right) \rightarrow 0 \ \text {as} \ k \rightarrow \infty , \ M \rightarrow \infty . \end{aligned}$$

These estimators are best possible in wavelet analysis.

10.2 \(E^{(2)}_{2^{k-1},M}(f) \le E^{(1)}_{2^{k-1},0}(f)\) and \(E^{(6)}_{2^k,M}(f) \le E^{(5)}_{2^k,0}(f)\).

Thus, Chebyshev wavelet estimator is better and sharper if a large number of terms of the expansion of the function is considered.

10.3 Abel’s integral equations are solved by first and second kind Chebyshev wavelets method and it is seen that second kind Chebyshev wavelet method gives better solution as compared to first kind Chebyshev wavelet method.

10.4 \(\chi (2^{k+1}) 2^{(k+1)\alpha } \sqrt{M+1} \ge \chi (2^{k}) 2^{k\alpha } \sqrt{M+1}\), \(\frac{1}{\chi (2^{k+1}) 2^{(k+1)\alpha } \sqrt{M+1} } \le \frac{1}{ \chi (2^{k}) 2^{k\alpha } \sqrt{M+1}} \Rightarrow E^{(6)}_{2^{k},M}(f) \le E^{(2)}_{2^{k-1},M}(f)\).

Therefore, second kind Chebyshev wavelet approximation is better and sharper as compared to first kind Chebyshev wavelet approximation.

10.5 The second kind Chebyshev wavelet method is superior to Legendre wavelet [16] and other wavelet method. It is verified by the numerical examples and their graphs in this research paper.

10.6 The results of this paper are significant achievements in wavelet analysis and its applications.