Strong consistency of local linear estimation of a conditional density function under random censorship

Abstract

In this paper, we study nonparametric local linear estimation of the conditional density of a randomly censored scalar response variable given a functional random covariate. We establish under general conditions the pointwise almost sure convergence with rates of this estimator under $\alpha$-mixing dependence. Finally, to show interests of our results, on the practical point of view, we have conducted a computational study, first on a simulated data and, then on some real data concerning Kidney transplant data.

1 Introduction

Conditional density plays an important role; not only in exploring relationships between responses and covariates, but also in financial econometrics (see Ait-Sahalia [1]). A vast variety of papers use the estimators of conditional densities as building blocks. These papers include those of Robinson [20], Tjøstheim [23], among others. However, in all of these papers, the conditional density function is indirectly estimated. Hyndman et al. [13] have studied the kernel estimator of conditional density estimator and its bias corrected version. There are many advantages of using local linear regression, such as the lack of boundary modifications, high minimax efficiency, and ease of implementation. Then, Bashtannyk and Hyndman [3] have suggested several simple and useful rules for selecting bandwidths for conditional density estimation. Hall et al. [11] applied the cross-validation technique to estimate the conditional density. Fan and Yim [9] proposed a consistent data-driven bandwidth selection procedure for estimating the conditional density functions.

In the last decade, the kernel method has been largely used for nonparametric functional data study; in this context, we refer to the monograph of Ferraty and Vieu [10]. Since then, many interesting publications have appeared. According to the literature, results on the local linear modeling in the functional data setting are limited. Baillo and Grané [4] proposed a local linear estimator (LLE) of the regression operator when the explanatory variable takes values in a Hilbert space, and then when the explanatory variable takes values in a semi-metric space. Demongeot et al. [7] presented local linear estimation of the conditional density when the data are functional. Furthermore, Messaci et al. [19] used the same approach to estimate the conditional quantile of a scalar response given a functional explanatory variable in the i.i.d. case. In these papers, it is assumed that the observations are complete.

Censored data analysis is a major issue in survival studies. Censored data, truncated data, missing data, and current status data are among the complex data structures in which only partial information on the variable of interest is available (see Kaplan and Meier [14]). In real data applications, censoring is a condition in which the value of a measurement or observation is only partially known. For this, we observe the censored lifetime $(C_i)$ for $i=1,\ldots , n$ of the variable under study instead of the real lifetime $(Y_i)$ for $i=1,\ldots , n$ (which has a continuous cumulative function (cdf) F(.)). We assume that $\{Y_i, i\ge 1\}$ is a stationary sequence of lifetimes and $\{C_i, i\ge 1\}$ is a sequence of i.i.d censoring random variable with common unknown continuous (cdf) G(.), and we observe only the n pairs $\{(T_i, \, \delta _i), \, i=1,\ldots , n\}$, where $T_i=Y_i\wedge C_i$ and (with $\wedge$ denoting minimum and denoting the indicator function on a set A).

The distinguishing characteristic of censoring has attracted the attention of many researchers. Beran [5] introduced a nonparametric estimate of the conditional survival function and showed some consistency results. Many other properties of the conditional distribution have been broadly studied in the literature (see Stute [22]). Furthermore, in the same context, many results on conditional quantile and conditional mode have been given (see Horrigue and Ould Saïd [12], Khardani and Thiam [15]).

The present study extends the result of Demongeot et al. [7] to censored data under general conditions. We establish the almost sure consistencies with convergence rates of the conditional density estimator when the explanatory variable is of functional type.

The paper is organized as follows. Section 2 is devoted to the presentation of our estimator. In Sect. 3, we introduce notations and assumptions, and state the main results. In Sect. 4, we conduct a simulation study that shows the performance of the considered estimator. Finally, proofs of our results are gathered in Sect. 5.

2 Construction of the conditional density estimator

Consider n pairs of random variables $(X_i, Y_i)$ for $i=1,\ldots , n$ drawn from the pair (X, Y) with values in $\mathcal {F}\times R$, where $\mathcal {F}$ is a semi-metric space equipped with a semi-metric d. In this paper, we consider the problem of nonparametric estimation of the conditional Y given $X=x$ when the responses variable $(Y_i)$ for $i=1,\ldots , n$ are right censored and when the observations $(X_i, Y_i)$ for $i=1,\ldots , n$ are strongly mixing. Furthermore, we denote by $(C_i)$ for $i=1,\ldots , n$ the censoring random variables which are independent and identically distributed with a common unknown continuous distribution function G. Thus, we observe the triplets $(X_i, T_i, \delta _i)$ for $i=1,\ldots , n$, where $T_i=Y_i\wedge C_i$ and $\delta _i={1}_{{\{Y_i\le C_i\}}}$ (with $\wedge$ denoting minimum and ${1}_A$ denoting the indicator function on a set A). We suppose that $(Y_i)$ for $i=1,\ldots , n$ and $(C_i)$ for $i=1,\ldots , n$ are independent which ensures the identifiability of the model. In the case of complete data, we adopt the fast functional locally modeling, introduced by Barrientos-Marin et al. [2] for regression analysis, that is, we estimate the conditional density $\zeta (.|x)$ by $\widehat{a}$ which is obtained by minimizing the following quantity:

$$\begin{aligned} \min _{(a,b)\in R^{2}}\sum _{i=1}^n \left( h_H^{-1} H(h_H^{-1}(y-T_i))-a-b\beta (X_i,x)\right) ^2K(h_K^{-1}\delta (x,X_i)), \end{aligned}$$

where $\beta (.,.)$ is a known function from $\mathcal {F}^2$ into R,  such that $\forall \xi \in \mathcal {F}$, $\beta (\xi , \xi )=0$, where K and H are kernels, $h_K=h_{K,n}$ (resp. $h_H=h_{H,n}$) is a sequence of positive real numbers, and $\delta (.,.)$ is chosen as a function of $\mathcal {F}\times \mathcal {F},$ such that $d(.,.)=|\delta (.,.)|$. Here, we denote $\widehat{a}$ by $\zeta _{n}(.|x).$ Then, the expression of $\zeta _{n}(.|x)$ is given as:

$$\begin{aligned} \zeta _{n}(y|x)=\frac{\sum _{{i,j=1}}^n W_{ij}(x) H(h_H^{-1}(y-T_i))}{h_H\sum _{{i,j=1}}^n W_{ij}(x)}, \end{aligned}$$

where

$$\begin{aligned} W_{ij}(x)=\beta (X_i,x)\left[ \beta (X_i,x)-\beta (X_j,x)\right] K(h_K^{-1}\delta (x,X_i))K(h_K^{-1}\delta (x,X_j)), \end{aligned}$$

with the convention ${0}/{0}=0$.

We assume that there exists a certain compact set , such that $\zeta (y|x)$ has an unique mode $\theta (x)$ on $\Omega$, where:

$$\begin{aligned} \theta (x)=\arg \sup _{y\in \Omega }\zeta (y|x). \end{aligned}$$

In the censored case, we adapt the idea of Carbonez et al. (1995), Kohler et al. (2002), and Khardani et al. (2010) to the infinite dimension case using a smooth distribution function H(.) instead of a step function. Then, we get the "pseudo"-estimator of $\zeta (.|x)$:

$$\begin{aligned} {\tilde{\zeta }}_{n}(y|x)=\frac{\sum _{{i,j=1}}^n \delta _i \overline{G}^{-1} (T_i) W_{ij}(x) H(h_H^{-1}(y-T_i))}{h_H\sum _{{i,j=1}}^n W_{ij}(x)}\doteqdot \dfrac{{\tilde{f}}^{x}_{n}(y)}{\gamma _{n}(x)}, \end{aligned}$$

where

and

The cumulative distribution function G, of the censoring random variables, is estimated by the Kaplan–Meier (1958) estimator defined as:

where $T_{(1)}< T_{(2)}< \cdots < T_{(n)}$ are the order statistics of $T_i$ and $\delta _{(i)}$ is the concomitant of $T_{(i)}$, which is known to be uniformly convergent to $\bar{G}$.

Therefore, a feasible estimator of $\zeta (.|x)$ is given by:

$$\begin{aligned} \widehat{\zeta }_{n}(y|x)=\dfrac{\widehat{f}^{x}_{n}(y)}{\gamma _{n}(x)}, \end{aligned}$$

where

Then, a natural estimator of $\theta (x)$ is defined by:

$$\begin{aligned} \widehat{\theta }_{n}(x)=\arg \sup _{y\in \Omega }\widehat{\zeta }_{n}(y|x). \end{aligned}$$

3 Assumptions and main results

Let $\mathcal {F}_{i}^{k}(Z)$ denote the $\sigma -$ algebra generated by $\left\{ Z_{j},i\le j\le k\right\}$.

Definition 3.1

Let $\left\{ Z_{i},i=1,2,\ldots \right\}$ be a strictly stationary sequence of random variables. Given a positive integer n, set:

The sequence is said to be $\alpha$-mixing (strong mixing) if the mixing coefficient $\alpha (n)\rightarrow 0$ as $n\rightarrow \infty .$

This condition was introduced in 1956 by Rosenblatt. The strong-mixing condition is reasonably weak and has many practical applications (see Doukhan [8], for more details).

3.1 Almost sure consistency of the conditional density estimator

Our first result concerns the almost sure convergence of the LLE of the conditional density. We introduce some conditions that are required to state our asymptotic result. Throughout the paper, x denotes a fixed point in $\mathcal{{F}}$; $N_x$ denotes a fixed neighborhood of x. For any df L, let $\tau _{L}:={\text {sup}} \lbrace y:L(y)<1\rbrace$ be its support’s right endpoint and assume that $\theta (x) \in \Omega \subset (-\infty ,\tau ],$ where $\tau < \tau _{G} \wedge \tau _{F}$, $B(x,r)=\left\{ x'\in \mathcal {F}/|\delta (x',x)|\le r\right\}$ and .

Note that our nonparametric model is quite general in the sense that we just need the following assumptions:

• (H1) For any $r>0$, $\phi _x(r):=\phi _x(-r,r)>0$ 

• (H2)

  • (i) The conditional density $\zeta ^{x}$ is such that: there exist $b_1>0,\, b_2>0$, $\forall (y_1,y_2) \in \Omega ^2$, and $\forall (x_1,x_2)\in N_x\times N_x$:

    $$\begin{aligned} |\zeta (y_{1}|x_{1})-\zeta (y_{2}|x_{2})|\le C_x\left( |\delta ^{b_1}(x_1,x_2)|+|y_1-y_2|^{b_2}\right) , \end{aligned}$$

    where $C_x$ is a positive constant depending on x.

  • (ii) $\zeta (.|x)$ is twice differentiable, its second derivative $\zeta ^{(2)}(.|x)$ is continuous on a neighborhood of $\theta (x)$ and $\zeta ^{(2)}(\theta (x)|x)<0$.

• (H3) The function $\beta (.,.)$ is such that:

  $$\begin{aligned} \forall x^{\prime } \in \ \mathcal {F},\; C_1\, |\delta (x,x^{\prime } )|\le |\beta (x,x^{\prime } )|\le C_2\, |\delta (x,x^{\prime } )|,\hbox { where } C_1>0,\, C_2>0. \end{aligned}$$

• (H4) The sequence $(X_i, Y_i)_{i\in \mathbb {N}}$ satisfies: $\exists a>0, \exists c>,0 \ \forall n\in \mathbb {N} \ \alpha (n)\le cn^{-a}$ and:

  

• (H5) The conditional density of $(Y_i,Y_j)$ given $(X_i,X_j)$ exists and is bounded.

• (H6) K is a positive, differentiable function with support $[-1,1]$.

• (H7) H is a positive, bounded, Lipschitzian continuous function, such that:

  $$\begin{aligned} \int |t|^{b_2}H(t){\text {d}}t< \infty \hbox { and } \int H^2(t){\text {d}}t<\infty . \end{aligned}$$

• (H8) The bandwidth $h_K$ satisfies: there exists an integer $n_0$, such that:

  $$\begin{aligned} \forall n>n_0, \; -\frac{1}{\phi _x(h_K)}\int _{-1}^1\phi _x(zh_K,h_K)\frac{{\text {d}}}{{\text {d}}z}\left( z^2K(z)\right) {\text {d}}z>C_3>0, \end{aligned}$$

  and

  $$\begin{aligned} h_K\int _{B(x,h_K)}\beta (u,x){\text {d}}P(u)=o\left( \int _{B(x,h_K)}\beta ^2(u,x)\, {\text {d}}P(u)\right) , \end{aligned}$$

  where ${\text {d}}P(x)$ is the cumulative distribution.

• (H9) $\displaystyle \lim _{n\rightarrow \infty }h_H = 0 \text{ and } \exists \beta _1>0, \text{ such } \text{ that } \lim _{n\rightarrow \infty } n^{\beta _1}\, h_H=\infty$.

• (H10)

  • (i) $\displaystyle \lim _{n\rightarrow \infty } h_K = 0,$ $\displaystyle \lim _{n\rightarrow \infty }\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\ \phi _x^2(h_K)}=0.$

  • (ii) $C n^{\frac{(3-a)}{(a+1)}+\frac{3\beta _1+1}{a+1}}\log n[\log _{2} n]^{6/(a+1)}\le h_H\chi _x^{1/2}(h_K),$ where $\chi _x(h)=\max (\phi _x^2(h),\varphi _x(h)).$

Remarks on the assumptions Most of the assumptions are common in nonparametric functional data analysis (NFDA) context. More precisely, assumption (H1) is usually used in NFDA and it is linked with the topological structure of the functional space, $\mathcal F$, of the explanatory variable X (see Ferraty and Vieu [10] for more discussions). Furthermore, assumptions (H2) and (H3) are mild regularity assumptions on the conditional density function. Finally, conditions (H4), (H5), and (H10) are technical assumptions (see Ferraty and Vieu [10] for the constant local method case).

Theorem 3.2

Under assumptions (H1)–(H10), we have:

$$\begin{aligned} \sup _{y\in \Omega }|\widehat{\zeta }_{n}(y|x)-\zeta (y|x)| = O\left( h_K^{b_1}+h_H^{b_2}\right) +O\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\ \phi _x^2(h_K)}}\right) , \; a.s. \end{aligned}$$

Proof of Theorem 3.2

The proof is a direct consequence of the following decomposition $\forall y\in \Omega :$

(1)

where

and

and the following Lemmas 3.3–3.6. $\square$

Lemma 3.3

(cf. [7])

Under assumptions (H1), (H3), (H4),(H6), (H8), and (H10), we have¹

$$\begin{aligned} 1-\gamma _{n}(x)=O\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\, \phi _x^2(h_K)}}\right) ,\; a.co., \end{aligned}$$

and

Lemma 3.4

Under assumptions (H1), (H2), and (H7), we obtain:

$$\begin{aligned} \sup _{y\in \Omega }\left| E[{\tilde{f}}^{x}_{n}(y)]-\zeta (y|x) \right| =O\left( h_K^{b_1}+h_H^{b_2}\right) , \; a.s. \end{aligned}$$

Lemma 3.5

Under assumptions of Theorem 3.2, we get:

Lemma 3.6

Under assumptions (H1), (H6), (H8),(H9), and (H10), we have:

$$\begin{aligned} \sup _{y\in \Omega }\left| \widehat{f}^{x}_{n}(y)-{\tilde{f}}^{x}_{n}(y) \right| =O\left( \sqrt{\frac{\log (\log n)}{n}}\right) ,\; a.s. \end{aligned}$$

3.2 Almost sure consistency of the conditional mode estimator

The convergence rate of the LLE of the conditional mode is a direct consequence of the previous result. Thus, in addition to the previous conditions, we assume that:

• (H11) There exists $\theta (x) \subset \Omega$, such that $\zeta (y|x)<\zeta (\theta (x)|x),$ for all $y\ne \theta (x), y\in \Omega$.

Then, the asymptotic behaviour of $\widehat{\theta }(x)$ is given in the following Theorem.

Theorem 3.7

Assume that (H1)–(H11) hold. We have:

$$\begin{aligned} |\widehat{\theta }_{n}(x)-\theta (x)| = O\left( h_K^{b_1/2}+h_H^{b_2/2}\right) +O\left( \left( \frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\ \phi _x^2(h_K)}\right) ^{\dfrac{1}{4}}\right) , \; a.s. \end{aligned}$$

Proof of Theorem 3.7

We easily can show that:

$$\begin{aligned} \vert \zeta (\widehat{\theta }_{n}(x)|x)-\zeta (\theta (x)|x)\vert \le 2 \sup _{y\in \Omega } \vert \widehat{\zeta }_{n}(y|x)-\zeta (y|x)\vert . \end{aligned}$$

(2)

Making use of a Taylor expansion of the function $\zeta (.|x),$ we get:

$$\begin{aligned} \zeta (\widehat{\theta }_{n}(x)|x)-\zeta (\theta (x)|x)= \dfrac{1}{2}(\widehat{\theta }_{n}(x)-\theta (x))^{2}\zeta ^{(2)}(\theta ^{*}(x)|x), \end{aligned}$$

(3)

where $\theta ^{*}(x)$ is between $\theta (x)$ and $\widehat{\theta }_{n}(x)$

Combining Eqs. (22) and (23), we find:

$$\begin{aligned} \vert \widehat{\theta }_{n}(x)-\theta (x) \vert \le 2 \sqrt{\dfrac{\sup _{y\in \Omega } \vert \widehat{\zeta }_{n}(y|x)-\zeta (y|x)\vert }{\zeta ^{(2)}(\theta ^{*}(x)|x)}}. \end{aligned}$$

The almost sure consistency of $\widehat{\theta }_{n}(x)$ is an immediate consequence of Theorem 3.2. $\square$

4 Computational studies

4.1 On simulated data

In this subsection, a simulation study is carried out to investigate the finite sample performance of the local linear estimator $f_{LL}(y|x)$ of the conditional density function under right-censored and functional-dependent data. As common to all, the applicability of asymptotic normality result requires a practical estimation of the asymptotic bias and variance. For this, we neglect the bias term and we use a plug-in approach to construct an estimator of the asymptotic variance of the conditional density function given by:

$$\begin{aligned} \overline{G}^{-1}(y)\dfrac{f^{x}(y)}{h_{H}} \frac{{\varvec{{M}}}_{2}}{{\varvec{{M}}}^{2}_{1}n\phi _{x}(h_{K})}\int H^{2}(t){\text {d}}t. \end{aligned}$$

(4)

To test the effectiveness of the asymptotic normality result and to attain this purpose, let us consider the following regression model where the response is a scalar: $Y_i= r(X_i) + \epsilon _i$, $i=1, \dots , n,$, where $\epsilon _i$ is the error generated by an autoregressive model defined by:

$$\begin{aligned} \epsilon _i = \frac{1}{\sqrt{2}}\left( \epsilon _{i-1} + \eta _i \right) , \quad i=1, \dots , n, \end{aligned}$$

with $\{\eta _i\}_i$ is a sequence of i.i.d. random variables normally distributed with a variance equal to 0.1. The explanatory variables are constructed by:

$$\begin{aligned} X(t) = A(2-\cos (\pi t W)) + (1-A) \cos (\pi t W), \quad t\in [0,1], \end{aligned}$$

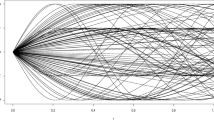
where W is generated from a Gaussian distribution $\mathcal {N}(0,1)$ and A is a random variable Bernoulli distributed with parameter $p=0.5$. $X_i's$ are generated from 300 curves and are plotted in Fig. 1.

Fig. 1

A set of 300 simulated curves

On the other hand, n i.i.d. random variables $(C_i)_i$ are simulated through the exponential distribution $\mathcal {E}(\lambda )$ and for $i=1, \dots , n=300,$, the scalar response $Y_i$ is computed by considering the following operator:

$$\begin{aligned} r(X) = 4\exp \left\{ \frac{1}{2+\int _{0}^{\pi /2}|X_i(t)|^2}\right\} . \end{aligned}$$

Given $X=x$, we can easily see that Y is as a gaussian distribution $\mathcal {N}\left( r(x), 0.2\right)$. Then, we can get the corresponding conditional density, which is explicitly defined by

$$\begin{aligned} f^{Y|X} (y|x)= \frac{1}{\sqrt{2\pi \times 0.3}} \exp \left\{ -\frac{1}{2\times 0.3}(y-r(x)^2\right\} \end{aligned}$$

Fig. 2

Distribution of the MSE obtained for different CR for $n=300$

Therefore, the conditional mode, the conditional mean r(x),  and the conditional median functions will coincide and will be equal to r(x), for any fixed x. Our purpose, now, consists in evaluating the accuracy of the conditional mode function estimator based on randomly censored data. The computation of this estimator is based on the observed data $\left( X_i, T_i, \delta _i \right) _{i=1, \dots , n},$ where $T_i = {\min }(Y_i, C_i)$ and .

In this simulation study, we present only results of the case where $i = 2$ and $q = 1$. For this, we take and . Elsewhere, as it is well known in FDA, the choice of the metric and the smoothing parameters have crucial roles in the computational issues. To optimize these choices on this illustration, we use the local cross-validation procedure method in the aim of choosing smoothing parameters $h_K$ and $h_H$ (see Laksaci et al. [17]).

Another important point for insuring good behavior of the considered methods is to use locating functions $\delta$ and/or $\beta$ that are well adapted to the kind of data that we have to deal with. Here, it is clear that the shape of the curves (cf. Fig. 1) allows us to use the locating functions $\sigma$ and $\beta$ defined by the derivatives of the curves. More precisely, we take:

$$\begin{aligned} \delta (x,x') =\left( \int _0^1 (x^{(i)}(t)-x'^{(i)}(t))^2 {\text {d}}t\right) ^{1/2}\,\ \hbox {and} \,\ \beta (x,x') =\int _0^1 \alpha (t)(x_i(t)-x'_i(t))^2 {\text {d}}t, \end{aligned}$$

where $x^{(i)}$ denotes the ith derivative of the curve x and $\alpha$ is the eigenfunction of the empirical covariance operator $\frac{1}{n}\sum _{i=1}^n (X_j^{(i)} -\bar{X^{(i)}}) (X_j^{(i)} -\bar{X^{(i)}})$ associated with the q-greatest eigenvalues. The performance of the conditional mode estimator $\widehat{\theta }_{n}(x)$ is evaluated on $N=400$ replications using different sample sizes $n=50,100, 200,$ and 300. The mean square error (MSE) is considered here, such that, for a fixed x,  ${\text {MSE}} = \frac{1}{400}\sum _{m=1}^{400} \left( \widehat{\theta }_{n,m}(x) - r(x)\right) ^2$. Figure 2 displays the distribution of the obtained MSE given by the N replications. It can be observed that the proposed estimator performs well, especially when the sample size increases. This conclusion is confirmed by Table 1 which provides a numerical summary of the distribution of the MSE, with different censored rates (CR).

In the second part of the simulation studies, we are interested in the evaluation of the prediction accuracy of the conditional median with different censored rates (CR). A sample $(X_i, Y_i)_{i=1, \dots , 550}$ of size $n=550$ generated from the model described above, is considered for this purpose. We split this sample into two parts: a learning subsample $\{(X_i, Y_i); i=1, \dots , 500 \}$ which is used to calculate the predictor (the conditional mode in this case) and a testing subsample $\{(X_i, Y_i); i=501, \dots , 550\}$ used to evaluate the performance of the predictor. The prediction accuracy is measured, for different values of CR, using the Mean Absolute Error (MAE), defined as ${\text {MAE}} = \frac{1}{50}\sum _{i=501}^{550} |Y_i - \widehat{\theta }_{n}(X_i)|$, as well as the Mean Square Error (MSE), such that ${\text {MSE}} = \frac{1}{50}\sum _{i=501}^{550} \left( Y_i - \widehat{\theta }_{n}(X_i)\right) ^2$. We can see that the prediction accuracy of the conditional mode decreases as the censored rate increases. For censoring distributions $\mathcal {E}(2)-1, (CR=7\%, {\text {MAE}}=0.204, {\text {MSE}}=0.483)$, $\mathcal {E}(2), (CR=16\%, {\text {MAE}}=0.363, {\text {MSE}}=0.62),$ and $\mathcal {E}(2)+5, (CR=49\%, {\text {MAE}}=1.052, {\text {MSE}}=2.291)$.

Table 1 Numerical summary of the distribution of the MSE, for ${N}=400$, obtained for $n=50, 100,200$ and 300

4.2 Real data application

A useful tool in survival analysis is the hazard rate, which reflects the instantaneous probability that a duration will end within the next time instant. Among the most used examples in survival analysis: survival times of patients, Stanford Heart Transplant, durations between subsequent transactions in a financial security,$\ldots$. For application on real data, we apply the local linear method via the Kidney transplant data (see Klein and Moeschberger [16] and https://www.agence-biomedecine.fr). The bandwidth selection is given by plug-in rules and more advanced selection methods like cross-validation are likely to further improve the performance of the local linear hazard rate estimator. To use the Kidney transplant data, we need to describe three fundamental parameters that are (1) the survival times in days of patients following kidney transplant as the response, (2) race (black/white), and (3) age in years for each patient as the covariate. We propose a new method based on the functional local linear approach. More precisely, we use the conditional hazard rate. The methodology of this study is given by the following description: in the first, we consider the subsamples of white males and white females. At the second step, we take 432 patients as the first group and have a censoring rate of $83\%$. The second group involves 280 patients with a $86\%$ censoring rate. The survival times of white patients vary between 1 day and 9.4 years. The average age of the male patients is slightly less than 44 years, whereas the female patients are almost 41 years old on average. We find only small differences between the various plug-in bandwidths for the conditional hazard rate, where we have taken age as the conditioning variable.

Fig. 3

Estimates of the conditional hazard rate after the transplantation

In conclusion, we find only small differences between the various plug-in bandwidths for the conditional hazard rate, where we have taken age as the conditioning variable (see Fig. 3). Figure (A) and Figure (D), based on the normal reference rule, depict the conditional hazard rate as a function of time and consider several values of age. Figure (A) and Figure (B) zoom in on the period shortly after the transplantation, whereas Figure (C) and Figure (D) display the hazard rate over a longer time. We see that the hazard rate is strongly no monotonic for both male and female patients. As expected, the hazard rate is higher for older patients. Interestingly, the differences in the hazard rates of younger and older women diminish after about 150 days. For men, the differences between the various age groups persist longer. Also, the risk of dying shortly after the transplantation is higher for men than for women. On the other hand, for female patients, the risk of dying in a later stage is lower than for males.

5 Proofs

In what follows, when no confusion is possible, we will denote by C and $C'$ some strictly positive generic constants. Moreover, we put, for any $x\in \mathcal {F}$, and for all $i=1,\ldots ,n:$

$$\begin{aligned} K_i(x)=K(h^{-1}\delta (x,X_i)), \; \beta _i(x)=\beta (X_i,x) \hbox { and } H_i(y)=H(h_{H}^{-1}(y-Y_{i})). \end{aligned}$$

Proposition 5.1

(Ferraty and Vieu [10], page 237)

Assume that $\left\{ U_{i}, i\ge 1\right\}$ are identically distributed, with strong mixing coefficient $\alpha (n)=O(n^{-a}), a>1$, such that $|U_{1}|$ is bounded. Then, for each $r>1$ and $\varepsilon >0$:

$$\begin{aligned} P\left\{ \left| \sum ^{n}_{i=1}U_{i}\right| >\varepsilon \right\} \le C \left( 1+\dfrac{\varepsilon ^{2}}{rS^{2}_{n}}\right) ^{-r/2} + Cnr^{-1}\left( \dfrac{2r}{\varepsilon }\right) ^{a+1}, \end{aligned}$$

where

$$\begin{aligned} S_{n}^{2}=\sum _{1 \le i,j \le n}|cov(U_{i}, U_{j})|. \end{aligned}$$

Proof of Lemma 3.4

The bias term is not affected by the dependence condition of $(X_i,Y_i)$. Therefore, by the equiprobability of the couples $(X_i,Y_i),$ we have:

$$\begin{aligned} E[{\tilde{f}}^{x}_{n}(y)]-\zeta (y|x)= & {} \frac{1}{h_H E[W_{12}(x)]}E\left[ \delta _1 \overline{G}^{-1} (T_1)W_{12}(x)H_{i}(y)\right] -\zeta (y|x). \end{aligned}$$

Using conditional expectation properties and the fact that:

(5)

for any measurable function $\varphi$, we have:

Since

and

$$\begin{aligned} E[H_{i}(y)|X_1]=\int _{{\mathbb {R}}}H\left( \frac{y-z}{h_H}\right) \zeta (z|X){\text {d}}z=h_H \int _{{\mathbb {R}}}H(t)\zeta (y-h_Ht|X){\text {d}}t, \end{aligned}$$

then by assumptions (H2) and (H7), we get:

$$\begin{aligned} \vert E[{\tilde{f}}^{x}_{n}(y)]-\zeta (y|x)\vert= & {} \left| \frac{1}{h_HE[W_{12}(x)]}E\left[ W_{12}(x)h_H \int _{{\mathbb {R}}}H(t)\zeta (y-h_Ht|X){\text {d}}t \right] -\zeta (y|x) \right| \\= & {} \left| \int _{{\mathbb {R}}}H(t)(\zeta (y-h_Ht|X)-\zeta (y|x)){\text {d}}t \right| \\\le & {} \int _{{\mathbb {R}}}H(t)\vert \zeta (y-h_Ht|X)-\zeta (y|x)\vert {\text {d}}t \\\le & {} C \int _{{\mathbb {R}}}H(t)(h_{K}^{{b_{1}}}+\vert t\vert ^{{b_{2}}} h_{H}^{{b_{2}}}){\text {d}}t\\= & {} O\left( h_K^{b_1}\right) +O\left( h_H^{b_2}\right) ,\\ \end{aligned}$$

which proves Lemma 3.4. $\square$

Proof of Lemma 3.5

Let $\Omega$ be a compact set. It can be covered by a finite number $s_n$ of intervals of length $l_n$ at some points $(z_k)_{k=1, \ldots , s_n}$, that is:

$$\begin{aligned} \Omega \subset \bigcup _{k=1}^{s_n}(z_k-l_n,~z_k+l_n), \end{aligned}$$

with $l_n=n^{-\frac{3\gamma }{2}-\frac{1}{2}}$ and $s_n=O(l_n^{-1})$. Let

$$\begin{aligned} \displaystyle z_y=\arg \min _{z\in \{z_1,\ldots ,z_{s_n}\}}|y-z|, \end{aligned}$$

(6)

and consider the following decomposition:

From (6) we have $|y-z_y|\le l_n,$ then under (H9) and Lemma 3.4, we get:

$$\begin{aligned} \mathfrak {I}_{1,n}=o_{a.co.}\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\, \phi _x^2(h_K)}}\right) . \end{aligned}$$

(7)

In the same way, we find:

$$\begin{aligned} \mathfrak {I}_{3,n}=o_{a.co.}\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\, \phi _x^2(h_K)}}\right) . \end{aligned}$$

(8)

Next, let us prove that:

$$\begin{aligned} \mathfrak {I}_{2,n}=o_{a.co.}\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\, \phi _x^2(h_K)}}\right) . \end{aligned}$$

For all $\eta >0,$ we have:

Then, we have to show that:

For this, we consider the following decomposition:

which implies that:

where

and

Therefore, our claimed result is direct consequences of the following assertions:

(9)

(10)

(11)

and

$$\begin{aligned} Cov(T_4,T_5)=o_{a.co.}\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\, \phi _x^2(h_K)}}\right) . \end{aligned}$$

(12)

Concerning (9): Observe that for $i=3, 5$ has been already obtained in Lemma 3.3. Thus, we focus only on the case where $i=2, 4$. For this, we use proposition 5.1.

For $1\le i\le n$ and $k=0,1,$ let:

(13)

Then, it can be seen that:

Under assumptions (H1), (H3), (H5), and (H7), we have:

(14)

Next, let us calculate:

$$\begin{aligned} S_{n}^{2}=\displaystyle \sum _{i=1}^{n}\displaystyle \sum _{j=1}^n {\text {Cov}}(\nabla _{i}^k,\nabla _{j}^k)=S_{n}^{2*}+n {\text {Var}}[\nabla _{1}^k], \end{aligned}$$

where

$$\begin{aligned} S_{n}^{2*}=\displaystyle \sum _{i=1}^{n}\displaystyle \sum _{i\ne j} {\text {Cov}}(\nabla _{i}^k,\nabla _{j}^k). \end{aligned}$$

Using Eqs. (5) and (14), and the conditional expectation properties, we have:

Finally, using the fact that:

we get:

$$\begin{aligned} n{\text {Var}}[\nabla _{1}^k]=O(nh_H\chi _x^{(1/2)}(h_K)). \end{aligned}$$

Then, from Eq. (13), using again the conditional expectation, and from the fact that:

we get under (H4) and (H5), for $i \ne j$:

(15)

Now, following Masry [18], we define:

$$\begin{aligned} S_1=\{ (i,j)\;\ \text{ such } \text{ that }\; \ 1\le i-j\le m_n\}, \end{aligned}$$

and

$$\begin{aligned} S_2=\{ (i,j)\; \ \text{ such } \text{ that }\;\ m_n+1\le i-j\le n-1\}, \end{aligned}$$

where $m_n\rightarrow \infty , \text{ as } n\rightarrow \infty .$

Thus:

$$\begin{aligned} s_n^{2*}\le \sum _{S_1}{\text {Cov}}(\nabla _{i}^k,\nabla _{j}^k)+\sum _{S_2} {\text {Cov}}(\nabla _{i}^k,\nabla _{j}^k):= \curlyvee _{1,n} + \curlyvee _{2,n}. \end{aligned}$$

We then get from Eq. (15):

$$\begin{aligned} \curlyvee _{1,n} \le C nm_n h_H^2\chi _x(h_K). \end{aligned}$$

For $\curlyvee _{2,n},$ we use the Davydov–Rio’s inequality for bounded mixing processes:

$$\begin{aligned} \forall i\not =j \ \ \vert {\text {Cov}}(\nabla _{i}^k,\nabla _{j}^k)\vert \le C\alpha (|i-j|). \end{aligned}$$

Therefore, using $\sum _{j\ge x+1}j^{-a}\le \int _{u\ge x}u^{-a}=\left[ (a-1)x^{a-1}\right] ^{-1},$ and the first part of (H4), we get:

$$\begin{aligned} \curlyvee _{2,n} \le Cnm_n^{-a+1}. \end{aligned}$$

Thus:

$$\begin{aligned} s_n^{2*}\le C( nm_n h_H^2\chi _x(h_K)+ nm_n^{1-a}). \end{aligned}$$

By choosing $m_n=\left( h_H^2\chi _x(h_K)\right) ^{-1/a},$ we obtain:

$$\begin{aligned} s_n^{2*}=O(nh_H^2\chi _x(h_K))^{(a-1)/a}). \end{aligned}$$

Finally, as $a>2,$ then:

$$\begin{aligned} S_{n}^{2}=O(nh_H\chi _x^{1/2}(h_K)). \end{aligned}$$

(16)

Taking $\varepsilon =\eta \frac{ \sqrt{S_{n}^{2} \log n }}{nh_{H}\phi _x(h_K)},$ making use of Proposition 5.1 and Eq. (16), we get:

(17)

Next, using Eq. (17) with $r=C\log n(\log _{2} n)^{\frac{1}{a}}$ and Taylor series expansion of $\log (1+x),$ we obtain:

$$\begin{aligned} \wp _1\le C\exp \left( -C\eta ^2\log n\right) =Cn^{-C\eta ^2}, \end{aligned}$$

(18)

and

$$\begin{aligned} \wp _2\le C n^{(1-a)/2}\eta ^{-(a+1)}(h_{H}\chi ^{1/2}_x(h_K))^{-(a+1)/2}(\log n)^{(a-1)/2}\log _{2}n. \end{aligned}$$

(19)

Now, from Eqs. (18) and (19), using assumption (H10)(ii), we have $s_{n} \wp _2=O(n^{-1}\log ^{-1}n \log _{2}^{-2}n)$ which is the general term of a convergent Bertrand series.

In the same way, we can choose $\eta$, such that $s_{n} \wp _1$ is the general term of a convergent series.

Finally, we find:

Concerning (10): from Demongeot et al. [7], we have:

Now, we have to study the case where $i=2, 4.$

Since the pairs $(X_{i},Y_{i}), i = 1,...,n$ are identically distributed, we obtain:

and

We have to evaluate:

Using the conditional expectation properties and Eq. (5), we have for all $l=0,1:$

Using Lemma 3 given in Barrientos-Marin et al. [2], we obtain

(20)

From Eq. (20), we find:

Concerning (11) and (12): following similar steps as in the proof of (16), we get:

$$\begin{aligned}&{\text {Cov}}(T_2,T_3)=O\left( \frac{\chi _x^{(1/2)}(h_K)}{n\,\phi _x^2(h_K)}\right) =o\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\phi _x^2(h_K)}}\right) \\&\quad \text{ and } {\text {Cov}}(T_4,T_5)=O\left( \frac{\chi _x^{(1/2)}(h_K)}{n\,\phi _x^2(h_K)}\right) =o\left( \sqrt{\frac{\chi _x^{(1/2)}(h_K)\log n}{n\,h_H\phi _x^2(h_K)}}\right) . \end{aligned}$$

Hence:

(21)

Finally, proof of Lemma 3.5 can be achieved by considering Eqs. (7), (8), and (21). $\square$

Proof of Lemma 3.6

Observe that:

$$\begin{aligned} \left| \widehat{f}^{x}_{n}(y)-{\tilde{f}}^{x}_{n}(y)\right|\le & {} \frac{1}{n(n-1)h_H E\left[ W_{12}(x)\right] }\sum _{i\not =j} \left| \delta _i W_{ij}(x)H_{i}(y)\left( \frac{1}{\overline{G}_n(T_i)}-\frac{1}{\overline{G}(T_i)}\right) \right| \\\le & {} \frac{\sup _{y\in \Omega }|\overline{G}_n(t)-\overline{G}(t)|}{\overline{G}_n(\tau )}\frac{1}{n(n-1)h_H E\left[ W_{12}(x)\right] }\sum _{i\not =j} \delta _i \overline{G}^{-1}(T_i) W_{ij}(x)H_{i}(y)\\= & {} \frac{\sup _{y\in \Omega }|\overline{G}_n(t)-\overline{G}(t)|}{\overline{G}_n(\tau )} {\tilde{f}}^{x}_{n}(y). \end{aligned}$$

Since $\overline{G}(\tau ) > 0$ in conjunction with the strong law of large numbers and the law of the iterated logarithm on the censoring law (see formula (4.28) in Deheuvels and Einmahl [6]), the result is an immediate consequence of Lemmas 3.4 and 3.5$\square$

Proof of Theorem 3.7

One can easily show that:

$$\begin{aligned} \vert \zeta (\widehat{\theta }_{n}(x)|x)-\zeta (\theta (x)|x)\vert \le 2 \sup _{y\in \Omega } \vert \widehat{\zeta }_{n}(y|x)-\zeta (y|x)\vert . \end{aligned}$$

(22)

Using Taylor’s expansion $\zeta (.|x),$ we get:

$$\begin{aligned} \zeta (\widehat{\theta }_{n}(x)|x)-\zeta (\theta (x)|x)=\dfrac{1}{2}(\widehat{\theta }_{n}(x) -\theta (x))^{2}\zeta ^{(2)}(\theta ^{*}(x)|x), \end{aligned}$$

(23)

where $\theta ^{*}(x)$ is between $\theta (x)$ and $\widehat{\theta }_{n}(x).$

Combining Eqs. (22) and (23), we obtain:

$$\begin{aligned} \vert \widehat{\theta }_{n}(x)-\theta (x) \vert \le 2 \sqrt{\dfrac{\sup _{y\in \Omega } \vert \widehat{\zeta }_{n}(y|x)-\zeta (y|x)\vert }{\zeta ^{(2)}(\theta ^{*}(x)|x)}}. \end{aligned}$$

The almost sure consistency of $\widehat{\theta }_{n}(x)$ follows, then, immediately from Theorem 3.2. $\square$