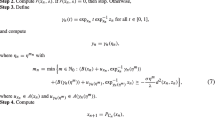Solving Yosida inclusion problem in Hadamard manifold

Abstract

We consider a Yosida inclusion problem in the setting of Hadamard manifolds. We study Korpelevich-type algorithm for computing the approximate solution of Yosida inclusion problem. The resolvent and Yosida approximation operator of a monotone vector field and their properties are used to prove that the sequence generated by the proposed algorithm converges to the solution of Yosida inclusion problem. An application to our problem and algorithm is presented to solve variational inequalities in Hadamard manifolds.

1 Introduction

Variational inequalities introduced by Hartman and Stampacchia have been studied in different spaces, namely Hilbert spaces, Banach spaces, see for example [2, 6, 7, 15, 23]. There are various problems in applied sciences which can be formulated as variational inequalities or boundary value problems on manifolds. Therefore, the extensions of the concepts and techniques of the theory of variational inequalities and related topics from Euclidean spaces to Riemannian or Hadamard manifolds are natural and interesting but not easy.

Németh introduced the concept of variational inequalities on Hadamard manifold: Find $x\in K$ such that

$$\begin{aligned} \langle F(x), {\exp }_x^{-1} y\rangle \ge 0, \quad \forall ~y\in K, \end{aligned}$$

where K is nonempty closed, convex subset of Hadamard manifold ${\mathbb {M}}$. $F:K \rightarrow T{\mathbb {M}}$ is a vector field, that is $F(x)\in T_x{\mathbb {M}}$ for each $x\in K$ and $\mathrm{exp}^{-1}$ is the inverse of exponential mapping. Németh generalized some basic existence and uniqueness results of the classical theory of variational inequality from Euclidean space to Hadamard manifold which is simply connected complete Riemannian manifold with nonpositive sectional curvature. Li et al. [12] studied the variational inequality problem on Riemannian manifolds. Fang and Chen [8] proved the convergence of projection algorithm to estimate the solution of set-valued variational inequalities on Hadamard manifolds. Noor et al. [17] studied Two-steps methods to solve variational inequalities in Hadamard manifolds.

An important generalization of variational inequalities is variational inclusion. The inclusion problem $0\in B(x)$ for set-valued monotone operator B on Hilbert space ${\mathbb {H}}$ is formulated as mathematical model of many problems arising in operation research, economics, physics, etc. It is well known that set-valued monotone operator can be regularized into a single-valued monotone operator by the process known as the Yosida approximation. Yosida approximation is a tool to solve a variational inclusion problem using non-expansive resolvent operator. Due to the fact that the zeros of maximal monotone operator are the fixed point sets of resolvent operator, the resolvent associated with a set-valued maximal monotone operator plays an important role to find the zeros of monotone operators. Many authors have discussed how to find the zeros of monotone operators, see for example [4, 5, 9, 11, 18,19,20].

Recently, many authors have extended the results related to the zeros of monotone operators from linear spaces to Riemannian manifolds. Li et al. [13] proved the convergence of proximal point algorithm on Hadamard manifolds using the fact that the zeros of maximal monotone operator are fixed point of associated resolvent. The idea of firmly nonexpansive mapping, resolvent of a set-valued monotone vector field and Yosida approximation operator was introduced in [14]. Furthermore, Tang and Huang [24] studied a variant of Korpelevich’s method for pseudomonotone variational inequalities. Recently, Ansari et al. [3] introduced Korpelevich’s method for variational inclusion problems on Hadamard manifolds.

Motivated by the work of Tang and Huang, Ansari et al. and ongoing research in this direction, our motive in this paper is to study the following Yosida inclusion problem in Hadamard manifolds: Find $x\in K$ such that

$$\begin{aligned} 0\in J^{B}_{\lambda }(x) + B(x), \end{aligned}$$

(1)

where K is a nonempty closed and convex subset of Hadamard manifold $\mathbb {M}$; $B: \mathbb {M}\rightrightarrows \mathbb {M}$ is a set-valued monotone vector field and $J^{B}_{\lambda }$ be the Yosida approximation operator of B. Ahmad et al. [1] have investigated the solution of similar Yosida inclusion problem in Banach spaces.

2 Preliminaries

Let $\mathbb {M}$ be a finite dimensional differentiable manifold. For a given $x\in \mathbb {M}$, the tangent space of $\mathbb {M}$ at x is denoted by $T_x\mathbb {M}$ and the tangent bundle is denoted by $T\mathbb {M}=\cup _{x\in \mathbb {M}}T_x\mathbb {M}$, which is naturally a manifold. An inner product $\mathfrak {R}_x(.,.)$ on $T_x\mathbb {M}$ is called the Riemannian metric on $T_x\mathbb {M}$. A tensor field $\mathfrak {R}(.,.)$ is said to be Riemannian metric on $\mathbb {M}$ if for every $x\in \mathbb {M}$, the tensor $\mathfrak {R}_x(.,.)$ is a Riemannian metric on $T_x \mathbb {M}$. The norm corresponding to the inner product on $T_x \mathbb {M}$ is denoted by $\Vert .\Vert _x$. A differentiable manifold $\mathbb {M}$ endowed with the Riemannian metric $\mathfrak {R}(.,.)$ is called a Riemannian manifold. Given a piecewise smooth curve $\gamma :[a, b]\rightarrow \mathbb {M}$ joining x to y$(i.e., \gamma (a)=x {~\mathrm and~} \gamma (b)=y)$, we can define the length of $\gamma$ by $L(\gamma )=\int _{a}^{b}\Vert \gamma ^{'}(t)\Vert \mathrm{d}t$. The Riemannian distance d(x, y), which included the original topology on $\mathbb {M}$, is the minimal length over the set of all such curves joining x to y.

Let $\varDelta$ be the Levi–Civita connection associated with Riemannian manifold $\mathbb {M}$. Let $\gamma$ be a smooth curve on $\mathbb {M}$. A vector field X is said to be parallel along $\gamma$ if $\varDelta _{\gamma ^{'}}X=0$. If $\gamma ^{'}$ is parallel along $\gamma$, i.e., $\varDelta _{\gamma ^{'}}\gamma ^{'}=0$, then $\gamma ^{'}$ is said to be geodesic and in this case $\Vert \gamma ^{'}\Vert$ is a constant. When $\Vert \gamma ^{'}\Vert =1$, $\gamma$ is said to be normalized. A geodesic joining x and y in $\mathbb {M}$ is said to be minimal geodesic if its length is equal to d(x, y).

A Riemannian manifold is complete if for any $x\in \mathbb {M}$, all geodesic emanating from x are defined for all $t\in (-\infty , \infty )$. We know by Hopf–Rinow Theorem [22] that if $\mathbb {M}$ is complete, then any pair of point in $\mathbb {M}$ can be joined by a minimal geodesic. Furthermore, $(\mathbb {M}, d)$ is a complete metric space and hence, all bounded closed subsets are compact.

Assuming $\mathbb {M}$ is complete, the exponential mapping $\mathrm{exp}_x:T_x\mathbb {M}\rightarrow \mathbb {M}$ at x is defined by $\mathrm{exp}_x(v)=\gamma _v(1, x)$ for each $v\in T_x\mathbb {M}$, where $\gamma (.)= \gamma _v(., x)$ is the geodesic starting at x with velocity v$(i.e. \gamma (0)=0~\mathrm{and} ~\gamma ^{'}(0)=v).$ It is known that $\mathrm{exp}_x(tv)=\gamma _v(t, x)$ for each real number t.

The parallel transport on the tangent bundle $T\mathbb {M}$ along with $\gamma$ with respect to $\varDelta$ is denoted by $\mathcal {P}_{\gamma ,.,.}$ and is defined as

$$\begin{aligned} \mathcal {P}_{\gamma ,\gamma (a),\gamma (b)}(v)=V(\gamma (b)),~~\forall ~a,b\in \mathbb {R}~\mathrm{and}~v\in T_{\gamma (a)}\mathbb {M}, \end{aligned}$$

where V is the unique vector field satisfying $\varDelta _{\gamma ^{'}(t)}V=0$ for all t and $V(\gamma (a))=v$. Then for any $a, b\in \mathbb {R}, \mathcal {P}_{\gamma ,\gamma (a),\gamma (b)}$ is an isometry from $T_{\gamma (a)}\mathbb {M}$ to $T_{\gamma (b)}\mathbb {M}$. When $\gamma$ is a minimal geodesic joining x to y, we write $\mathcal {P}_{y, x}$ instead of $\mathcal {P}_{\gamma , y, x}$.

A complete, simply connected Riemannian manifold of non-positive sectional curvature is called a Hadamard manifold. Throughout the remainder of the paper, we will assume that $\mathbb {M}$ is a finite-dimensional Hadamard manifold with constant curvature.

Proposition 2.1

[22] Let $\mathbb {M}$ be a Hadamard manifold and $x\in \mathbb {M}$. Then ${\exp }_x:T_x\mathbb {M}\rightarrow \mathbb {M}$ is a diffeomorphism and for any two points x and $y\in \mathbb {M}$, there exists a unique normalized geodesic joining x to y, which is in fact a minimal geodesic.

If $\mathbb {M}$ is a finite-dimensional manifold with dimension n, the above proposition shows that $\mathbb {M}$ is diffeomorphism to the Euclidean space $\mathbb {R}^n$. Thus, we see that $\mathbb {M}$ has the same topology and differential structure as $\mathbb {R}^n$. Moreover, Hadamard manifolds and Euclidean spaces have some similar geometrical properties. We describe some of them in the following results.

Recall that a geodesic triangle $\varDelta (x_1, x_2, x_3)$ of Riemannian manifold is a set consisting of three points $x_1, x_2$ and $x_3$ and the three minimal geodesic $\gamma _i$ joining $x_i$ to $x_{i+1}$, where $\mathrm{i=1,2,3~ mod~(3)}.$

Proposition 2.2

(Comparison Theorem for Triangle) [22] Let $\varDelta (x_1, x_2, x_3)$ be a geodesic triangle. Denote, for each $\mathrm{i=1,2,3~ mod~(3)}$, by ${\gamma }_i:[0, l_i]\rightarrow \mathbb {M}$ geodesic joining $x_i$ to $x_{i+1}$ and set $l_i=L(\gamma _i), \alpha _1=\angle (\gamma _i^{'}(0), -\gamma _{i-1}^{'}(l_{i-1}))$. Then

$$\begin{aligned} \alpha _1+\alpha _2+\alpha _3\le & {} \pi , \end{aligned}$$

(2)

$$\begin{aligned} l_{i}^{2}+l_{i+1}^{2}-2 l_{i}l_{i+1} \cos {\alpha }_{i+1}\le & {} l_{i-1}^{2}. \end{aligned}$$

(3)

In terms of distance and exponential mapping, Inequality (3) can be rewritten as

$$\begin{aligned} d^2(x_i, x_{i+1})+d^2(x_{i+1}, x_{i+2})-2\langle \mathrm{\exp }_{x_{i+1}}^{-1} x_i, \mathrm{\exp }_{x_{i+1}}^{-1} x_{i+2}\rangle \le d^2(x_{i-1}, x_i), \end{aligned}$$

(4)

since

$$\begin{aligned} \langle \mathrm{\exp }_{x_{i+1}}^{-1} x_i, \mathrm{\exp }_{x_{i+1}}^{-1} x_{i+2}\rangle =d(x_i, x_{i+1})d(x_{i+1}, x_{i+2})\cos {\alpha _{i+1}}. \end{aligned}$$

(5)

A subset $K\subset \mathbb {M}$ is said to be convex if for any two points $x, y\in K$, the geodesic joining x and y is contained in K, that is, if $\gamma :[a, b]\rightarrow \mathbb {M}$ is a geodesic such that $x=\gamma (a)$ and $y=\gamma (b)$, then $\gamma (1-t)a+tb\in K$ for all $t\in [0, 1]$. From now on, $K\subset \mathbb {M}$ will denote a nonempty, closed and convex subset of a manifold $\mathbb {M}$. The projection of v onto K is defined by

$$\begin{aligned} P_{K}(v)=\{ u\in K: d(v, u)\le d(v, w),~\forall ~w\in K\},~\forall ~v\in \mathbb {M}. \end{aligned}$$

(6)

Lemma 2.3

[13] Let $x_0\in \mathbb {M}$ and $\{x_n\}\subset \mathbb {M}$ with $x_n\rightarrow x_0$. Then, the following assertions hold:

• (i) For any $y\in \mathbb {M}$, we have

  $$\begin{aligned} \mathrm{exp}_{x_n}^{-1} y\rightarrow \mathrm{exp}_{x_0}^{-1} y ~\mathrm{and~} \mathrm{exp}_y^{-1} {x_n}\rightarrow \mathrm{exp}_y^{-1} {x_0}. \end{aligned}$$

• (ii) If $v_n\in T_{x_n}\mathbb {M}$ and $v_n\rightarrow v_0$, then $v_0\in T_{x_0}\mathbb {M}$.

• (iii) Given $u_n, v_n\in T_{x_n}\mathbb {M}$ and $u_0, v_0\in T_{x_0}\mathbb {M}$, if $u_n\rightarrow u_0$ and $v_n\rightarrow v_0$, then $\mathfrak {R}( u_n, v_n) \rightarrow \mathfrak {R}( u_0, v_0)$.

• (iv) For any $u\in T_{x_0}\mathbb {M}$, the function $F: \mathbb {M}\rightarrow T\mathbb {M}$ defined by $F(x)=\mathcal {P}_{x, x_0}u$ for each $x\in \mathbb {M}$ is continuous on $\mathbb {M}$.

Lemma 2.4

[24] Let K be a nonempty closed convex subset of $\mathbb {M}$. Then,

$$\begin{aligned} d^2(P_{K}(x), x^*)\le d^2(x, x^*)-d^2(x, P_{K}(x)),~~\forall ~x\in \mathbb {M}, x^*\in K. \end{aligned}$$

Proposition 2.5

[25] If $x\in \mathbb {M}$ and $P_{K}$ is singleton, then

$$\begin{aligned} \mathfrak {R}( \mathrm{exp}_{{P_K}(x)}^{-1}x, \mathrm{exp}_{{P_K}(x)}^{-1}y )\le 0, \quad \forall ~y\in \mathbb {M}. \end{aligned}$$

Lemma 2.6

[9] Let $\mathbb {M}$ be a Riemannian manifold with constant curvature. For given $x\in \mathbb {M}$ and $u\in T_x\mathbb {M}$, the set

$$\begin{aligned} L_{x, u}=\{y\in \mathbb {M}:\mathfrak {R}(\mathrm{exp}_{x}^{-1}y, u )\le 0\}, \end{aligned}$$

is convex.

The set of all single-valued vector fields on $\mathbb {M}$ is denoted by $\varOmega (\mathbb {M})$. We denote the set of all set-valued vector fields on $\mathbb {M}$ by $\chi (\mathbb {M})$. Let $B\in \mathbb {M}$. Then $B\rightrightarrows T\mathbb {M}$ such that $B(x)\subseteq T_x(\mathbb {M})$ for all $x\in D(B)$, where D(B) is the domain of B defined as $D(B)=\{x\in \mathbb {M}:B(x)\ne \phi \}.$

Definition 2.7

A vector field $F\in \varOmega (\mathbb {M})$ is said to be

• (i) monotone if for all $x, y\in \mathbb {M}$,

  $$\begin{aligned} \mathfrak {R}\big (F(x), \mathrm{exp}_{x}^{-1}y \big )\le \mathfrak {R}\big (F(y), -\mathrm{exp}_{y}^{-1}x \big ); \end{aligned}$$

• (ii) pseudomonotone if for all $x, y\in \mathbb {M}$,

  $$\begin{aligned} \mathfrak {R}\big (F(x), \mathrm{exp}_{x}^{-1}y \big ) \ge 0 \Rightarrow \mathfrak {R}\big (F(y), \mathrm{exp}_{y}^{-1}x\big )\le 0; \end{aligned}$$

• (iii) Firmly nonexpansive if for all $x, y\in K \subseteq \mathbb {M}$, the mapping $\varphi :[0,1]\rightarrow [0, \infty ]$ defined by

  $$\begin{aligned} \varphi (t)=d(\mathrm{exp}_{x}~t~ \mathrm{exp}_{x}^{-1} F(x), \mathrm{exp}_{y}~t~\mathrm{exp}_{y}^{-1} F(y)),~\forall ~t\in [0,1], \end{aligned}$$

  is nonincreasing.

Definition 2.8

A vector field $B\in \chi (\mathbb {M})$ is said to be

• (i) monotone if for all $x, y\in D(\mathbb {M})$,

  $$\begin{aligned} \mathfrak {R}\big (u, \mathrm{exp}_{x}^{-1}y \big )\le \mathfrak {R}\big (v, -\mathrm{exp}_{y}^{-1}x \big ),~\forall ~u\in B(x), v\in B(y); \end{aligned}$$

• (ii) pseudomonotone if for all $x, y\in D(\mathbb {M})$ and $\forall ~u\in B(x)$ and $\forall ~v\in B(y)$

  $$\begin{aligned} \mathfrak {R}\big (u, \mathrm{exp}_{x}^{-1}y \big ) \ge 0 \Rightarrow \mathfrak {R}\big (v, \mathrm{exp}_{y}^{-1}x\big )\le 0; \end{aligned}$$

• (iii) maximal monotone if it is a monotone and for all $x\in \mathbb {M}$ and all $u\in T_x\mathbb {M}$, the condition

  $$\begin{aligned} \mathfrak {R}\big (u, \mathrm{exp}_{x}^{-1}y \big )\le \mathfrak {R}\big (v, -\mathrm{exp}_{y}^{-1}x \big ),~\forall ~y\in D(B), v\in B(y), \end{aligned}$$

  implies that $u\in B(x)$.

Definition 2.9

[14] Given $\lambda >0$ and $B\in \chi (\mathbb {M})$, the resolvent and the Yosida approximation of B of order $\lambda$ are set-valued mappings $R_{\lambda }^{B}:\mathbb {M}\rightarrow 2^\mathbb {M}$ and $J_{\lambda }^{B}:\mathbb {M}\rightarrow 2^\mathbb {M}$ defined respectively by

$$\begin{aligned} R_{\lambda }^{B}(x)=\{ z\in \mathbb {M}:x\in \mathrm{exp}_{z}\lambda B(z) \}, \quad \forall ~x\in \mathbb {M}, \end{aligned}$$

and

$$\begin{aligned} J_{\lambda }^{B}(x)=-\frac{1}{\lambda } \mathrm{exp}_x^{-1}R_{\lambda }^{B}(x), ~~\forall ~x\in \mathbb {M}. \end{aligned}$$

We can see that the Yosida approximation of B is the complementary vector field of the corresponding resolvent multiplied by the constant $\frac{1}{\lambda }$.

Theorem 2.10

[14] Let $\lambda >0$ and $B\in \chi (\mathbb {M})$. Then the following assertions hold:

• (i) The vector field B is monotone if and only if $R_{\lambda }^{B}$ is single valued and firmly nonexpansive.

• (ii) If $D(B)=\mathbb {M}$, the vector field B is maximal monotone if and only if $R_{\lambda }^{B}$ is single valued, firmly nonexpansive and domain $D(R_{\lambda }^{B})=\mathbb {M}$.

• (iii) If B is monotone, then so is the Yosida approximation $J_{\lambda }^{B}$. Moreover, if B is maximal monotone with $D(B)=\mathbb {M}$, then so is $J_{\lambda }^{B}$.

Németh give the following version of Brouwer’s fixed point theorem in the setting of Hadamard manifolds.

Lemma 2.11

[16] If K is a compact subset of $\mathbb {M}$, then every continuous function $f:K \rightarrow K$ has a fixed point.

Definition 2.12

[10] Let X be a complete metric space and $E\subset X$ be a nonempty set. A sequence $\{x_n\}\subset X$ is called Fej$\acute{e}$r convergent to E if for all $y\in E$

$$\begin{aligned} d(x_{n+1}, y)\le d(x_n, y),~~\forall ~n\in \mathbb {N}. \end{aligned}$$

Lemma 2.13

[10] Let X be a complete metric space. If $\{x_n\}\subset X$ is a Fejér convergent to a nonempty set $E\subset X$, then $\{x_n\}$ is bounded. Moreover, if a cluster point x of $\{x_n\}$ belongs to E, then $\{x_n\}$ converges to x.

3 Main results

Let $B \in \chi (\mathbb {M})$ such that B is monotone then by Theorem 1(i), resolvent and hence Yosida approximation $J_{\lambda }^{B}$ of B is single valued, that it $J_{\lambda }^{B}\in \varOmega (\mathbb {M})$. The set of singularities of $J_{\lambda }^{B}+B$ is denoted by $S=\{x\in \mathbb {M}:0\in J_{\lambda }^{B}(x)+B(x)\}$.

First, we handle the following results which are used in the main theorem.

Lemma 3.1

If $B \in \chi (\mathbb {M})$ is a monotone vector field on K, then for any $x\in K$

$$\begin{aligned}&d^2\big (x, R^B_{\lambda }(\mathrm{exp}_{x}(-\lambda J^B_{\lambda }(x)))\big )\nonumber \\&\quad \le -\lambda \mathfrak {R}\big (J^B_{\lambda }(x)+v_x, \mathrm{exp}^{-1}_x\big [R^B_{\lambda }(\mathrm{exp}_x(-\lambda J^B_{\lambda }(x)))\big ]\big ), \end{aligned}$$

(7)

where $v_x\in B(x)$, $R_{\lambda }^{B}$ and $J_{\lambda }^{B}$ are resolvent and Yosida approximation of B, respectively.

Proof

Let $x\in {{\mathbb {M}}}$. Consider the geodesic triangle $\triangle (x,y,z)$, where

$$\begin{aligned} z=\mathrm{exp}_x(-\lambda J^B_{\lambda }(x))~~ \mathrm{and}~~y=R_{\lambda }^{B}(z). \end{aligned}$$

From Inequality (3), we have

$$\begin{aligned} d^2(x, y)+d^2(z,y) -2 \mathfrak {R}\big (\mathrm{exp}^{-1}_{y} x, \mathrm{exp}^{-1}_{y} z \big )\le d^2(x, z), \end{aligned}$$

(8)

and

$$\begin{aligned} d^2(x, y)+d^2(x,z) -2\mathfrak {R}\big (\mathrm{exp}^{-1}_{x} z, \mathrm{exp}^{-1}_{x} y\big )\le d^2(z, y). \end{aligned}$$

(9)

Since $y=R^{B}_{\lambda }(z)$, this implies that $\frac{1}{\lambda }\mathrm{exp}_{y}^{-1}z\in B(y).$ By monotonicity of B, we have for all $v_x\in B(x)$

$$\begin{aligned} \mathfrak {R}\bigg (\frac{1}{\lambda }\mathrm{exp}_{y}^{-1}z, \mathrm{exp}^{-1}_{y} x\bigg )\le \mathfrak {R}(v_x, -\mathrm{exp}^{-1}_{x} y). \end{aligned}$$

(10)

Combining (8) and (9), we have

$$\begin{aligned} d^2(x, y)\le -\lambda \mathfrak {R}(J^B_{\lambda }(x), \mathrm{exp}^{-1}_{x} y)+ \mathfrak {R}(\mathrm{exp}^{-1}_{y} z, \mathrm{exp}^{-1}_{y} x). \end{aligned}$$

(11)

From (10) to (11), we have

$$\begin{aligned} d^2(x, y)\le -\lambda \mathfrak {R}(J^B_{\lambda }(x), \mathrm{exp}^{-1}_{x} y)+ \lambda \mathfrak {R}(v_x, -\mathrm{exp}^{-1}_{x} y), \end{aligned}$$

that is

$$\begin{aligned} d^2 (x, R^{B}_{\lambda }(\mathrm{exp}_x(-\lambda J^B_{\lambda }(x))))\le -\lambda \mathfrak {R}(J^B_{\lambda }(x)+v_x, \mathrm{exp}^{-1}_{x} y). \end{aligned}$$

This completes the proof. $\square$

Proposition 3.2

Let $B \in \chi (\mathbb {M})$ be a monotone vector field and $x\in K$. The following statements are equivalent:

• (i) x is a solution of Problem (1).

• (ii) $x=R^{B}_{\lambda }(\mathrm{exp}_x(-\lambda J^B_{\lambda }(x)))$, for all $\lambda >0$.

• (iii) $r_\lambda (x)=0$, where $r_\lambda (x_k)$ is defined by

  $$\begin{aligned} r_\lambda (x)= \mathrm{exp}_x^{-1}\big [ R^{B}_{\lambda } (\mathrm{exp}_x(-\lambda J^B_{\lambda }(x)))\big ]. \end{aligned}$$

Proof

$(i)\Leftrightarrow (ii)$

$$\begin{aligned} x&= R^{B}_{\lambda }(\mathrm{exp}_x(-\lambda J^B_{\lambda }(x)))\\&\Leftrightarrow \mathrm{exp}_x(-\lambda J^B_{\lambda }(x))\in \mathrm{exp} _x(\lambda B(x)) \\&\Leftrightarrow -\lambda J^B_{\lambda }(x)\in \lambda B(x)\\&\Leftrightarrow 0\in J^B_{\lambda }(x)+B(x) \\&\Leftrightarrow x \mathrm{is \, a \, solution \, of \, problem} (1) \end{aligned}$$

$(ii) \Leftrightarrow (iii)$ It follows directly by the definition of exponential mapping. $\square$

Proposition 3.3

Let K be a nonempty bounded closed and convex subset of Hadamard manifold $\mathbb {M}$ with constant curvature. If $B\in \chi (\mathbb {M})$ is a maximal monotone vector field on K, then Problem (1) has a solution.

Proof

K is compact convex subset of Hadamard manifold by Hopf–Rinow Theorem. Since B is maximal monotone, hence by Theorem 2.10, $R^{B}_{\lambda }$ and $J^B_{\lambda }$ is single valued and also continuous with compact domain. Therefore, by Lemma 2.11, $R^{B}_{\lambda }(\mathrm{exp}_x(-\lambda J^B_{\lambda }(\cdot )))$ has a fixed point. In view of Proposition 3.2, the proof is complete. $\square$

Now, we describe the algorithm to compute the approximate solution of Yosida inclusion problem (1).

Algorithm 3.4

Let K be a nonempty bounded, closed and convex subset of Hadamard manifold ${\mathbb {M}}$ and $B\in \chi ({{\mathbb {M}}})$ be a maximal monotone vector field on K.

$\mathbf{Step 0.}$ Choose any $\lambda>0, \zeta >1$, $s\in (0, 1)$ and initial point $x_0\in K$

Set k=0, where $k\in \mathbb {N}\cup \{0\}$,

$\mathbf{Step 1.}$ Compute $r_\lambda (x_k)$. If $r_\lambda (x_k)=0$ for some $x_k\in {{\mathbb {M}}}$ then stop.

Otherwise, compute

$$\begin{aligned} \gamma _k(s)=\mathrm{exp}_{x_k} s~\mathrm{exp}_{x_k}^{-1} [ R^{B}_{\lambda } (\mathrm{exp}(-\lambda J^{B}_{\lambda }(x_k)))] \end{aligned}$$

(12)

and

$$\begin{aligned} y_k=\gamma _k(\psi _k), \end{aligned}$$

where

$$\begin{aligned} \psi _k= \zeta ^{-j(k)} \end{aligned}$$

with

$$\begin{aligned} j(k)= & {} \min \bigg \{ j\in {{\mathbb {N}}}_{+} : \mathfrak {R}( J^{B}_{\lambda }({\gamma _k (\zeta ^{-j})})+v_{\gamma _k (\zeta ^{-j})},~~ \gamma ^{'}_{k}(\zeta ^{-j})) \nonumber \\\le & {} -\frac{1}{\lambda } d^2 (x_k,~~ R^{B}_{\lambda } (\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k))))\bigg \}, \end{aligned}$$

(13)

where $v_{\gamma _k (\zeta ^{-j})}\in B({\gamma _k (\zeta ^{-j})})$. For $v_{y_k}\in B(y_k)$, Compute

$$\begin{aligned} \mathrm {Q_k}= \{ x\in {{\mathbb {M}}} :\mathfrak {R}\big ( J^{B}_{\lambda }({y_k})+v_{y_k},~\mathrm{exp} _{y_k}^{-1} x \big )\le 0 \}, \end{aligned}$$

(14)

define

$$\begin{aligned} x_{k+1}=\mathbf {P}_{\mathrm {Q_k}}(x_k). \end{aligned}$$

(15)

Update k=k+1 and return to Step 1.

In the following proposition, we show that Algorithm 3.4 is well defined.

Proposition 3.5

Let $\{x_k\}$ and $\{y_k\}$ be the sequences defined in Algorithm 3.4. Then the following assertions hold:

• (i) If $r_\lambda (x_k)=0$, then current term $x_k$ is a solution of Problem (1).

• (ii) If $r_\lambda (x_k)\ne 0$ then j(k) is well defined and $y_k\in K$.

• (iii) ${\mathrm {Q_k}}$ is nonempty, closed and convex and $x_{k+1}$ is well defined.

Proof

(i):

This proof is obvious and follows directly by Proposition 3.2.

(ii):

Since $R^B_{\lambda }$ and $J^B_{\lambda }$ are continuous, and

$$\begin{aligned} \gamma _k^{'}(s)= & {} \mathcal {P}_{\gamma _k (s), x_k }\mathrm{exp}^{-1}_{x_k} [ R^B_{\lambda } \mathrm{exp}_{x_k}(-\lambda J^B_{\lambda }(x_k))]. \end{aligned}$$

Since the parallel transport is an isometry and using Lemma 2.3 (iv) and Lemma 3.1, we have

$$\begin{aligned}&\lim \limits _{j\rightarrow \infty }\mathfrak {R}\big ( J^{B}_{\lambda }({\gamma _k (\zeta ^{-j})})+v_{\gamma _k(\zeta ^{-j})}, \gamma _{k}^{\prime }(\zeta ^{-j}) \big )\nonumber \\&\quad =\mathfrak {R}\big ( J^{B}_{\lambda }(x_k)+v_{x_k}, \mathrm{exp}_{x_k}^{-1}\big [ R^{B}_{\lambda } \mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k))) \big ] \big ) \nonumber \\&\quad \le -\frac{1}{\lambda } d^2 \big (x_k, R^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k))) \big ). \end{aligned}$$

(16)

If $r(x_k)\ne 0,$ then $d \big (x_k, R^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k)))\big )>0$. It follows from the inequality that whatever we choose large j, the inequality (15) holds good. Thus, j(k) is well defined. Moreover, $y_k=\gamma _k(\mu _k)$ is geodesic joining $x_k$ and $R^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k))$ and $x_k\in K$. It follows from the convexity of K and the definition of $y_k$ that $y_k\in K$.

(iii) To prove that $x_{k+1}$ is well defined, it is enough to show that ${\mathrm {Q_k}}$ is nonempty, closed and convex subset of Hadamard manifold. ${\mathrm {Q_k}}$ is closed by Lemma 2.3 (i) and $J^{B}_{\lambda }(y_k)+v_{y_k}\in T_{y_k}\mathbb {M}$. In view of Lemma 2.6, we conclude that ${\mathrm {Q_k}}$ is convex and $y_k\in {\mathrm {Q_k}}.$ This completes the proof. $\square$

Theorem 3.6

Let K be a nonempty bounded, closed and convex subset of Hadamard Manifold $\mathbb {M}$ with constant curvature and $B\in \chi (\mathbb {M})$ be a maximal monotone vector field on K. Then, the sequence $\{x_k\}$ generated by Algorithm 3.4 converges to a solution of Problem (1).

Proof

Let $x^*$ be a solution of Problem (1) such that $0\in J^{B}_{\lambda }(x^*)+B(x^*)$, that is $-J^{B}_{\lambda }(x^*)\in B(x^*)$. Using monotonicity of B, for any $x\in \mathbb {M}$ and any $v_x\in B(x)$, we have

$$\begin{aligned} \mathfrak {R}(v_x, \mathrm{exp}^{-1}_x x^*)\le \mathfrak {R}(J^{B}_{\lambda }(x^*), \mathrm{exp}^{-1}_{x^*} x). \end{aligned}$$

(17)

Also, since $J^{B}_{\lambda }$ is monotone, then

$$\begin{aligned} \mathfrak {R}(J^{B}_{\lambda }(x^*), \mathrm{exp}^{-1}_{x^*} x)\le \mathfrak {R}(J^{B}_{\lambda }(x), -\mathrm{exp}^{-1}_x{x^*}). \end{aligned}$$

(18)

Adding (17) and (18), we have

$$\begin{aligned} \mathfrak {R}(J^{B}_{\lambda }(x)+v_x, \mathrm{exp}^{-1}_x{x^*})\le 0. \end{aligned}$$

(19)

In particular, $v_{y_k}\in B(y_k)$, we have

$$\begin{aligned} \mathfrak {R}(J^{B}_{\lambda }({y_k})+v_{y_k}, \mathrm{exp}^{-1}_{y_k}{x^*})\le 0. \end{aligned}$$

(20)

Keeping in mind (14), we conclude that $x^*\in \mathrm {Q}_{k}$ and $x_{k+1}=\mathbf {P}_{\mathrm {Q_k}}(x_k)$. By Lemma 2.4, we have

$$\begin{aligned} d^2(x_{k+1}, x^*)+ d^2(x_k, x_{k+1})\le d^2(x_k, x^*). \end{aligned}$$

(21)

This implies that

$$\begin{aligned} d^2(x_{k+1}, x^*)\le d^2(x_k, x^*). \end{aligned}$$

(22)

Thus, the sequence generated by Algorithm 3.4 is Fe$\acute{j}$er’s convergent with respect to S. This implies that $\{x_k\}$ is bounded. Also from (21), we have

$$\begin{aligned} d^2(x_{k}, x_{k+1})\le d^2(x_k, x^*)- d^2( x_{k+1}, x^*), \end{aligned}$$

(23)

Since $\{x_k\}$ is bounded, it implies that $\{ d(x_k, x^*)\}$ is nonincreasing and bounded and hence convergent. Therefore, by (23), we have

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } d(x_{k+1}, x_k) =0. \end{aligned}$$

(24)

Boundedness of $\{x_k\}$ implies that there exists a subsequence $\{x_{k_j}\}$ converging to $\bar{x}.$ Furthermore, since $R_{\lambda }^{B}$ is nonexpansive, we have $\{ R^B_{\lambda }( \mathrm{exp}(-\lambda J^B_{\lambda }(x_k)))\}$ is also bounded and so $\{y_k\}$ and $J_{\lambda }^{B}(y_k)$ are bounded.

To complete the proof, it is sufficient to show that any cluster point $\bar{x}$ of $\{x_k\}$ belongs to S. We have $\lim _{j\rightarrow \infty } x_{k_j} =\bar{x}.$ By (24), we can also have $\lim _{j\rightarrow \infty } x_{{k_j}+1} =\bar{x}.$

Since $\{\mathfrak {R}(J^{B}_{\lambda }{y_k}+v_{y_k}, \mathrm{exp}^{-1}_{y_k} x_k \}$ is bounded, we can easily obtain that $\lim _{j\rightarrow \infty }\mathfrak {R}(J^{B}_{\lambda }({y_{k_j}})+v_{y_{k_j}}, \mathrm{exp}^{-1}_{y_{k_j}} x_{k_j})$ exists. From (13), we have

$$\begin{aligned} \mathfrak {R}(J^{B}_{\lambda }({y_k})+v_{y_k}, \gamma _{k}^{'}(\psi _{k}))\le & {} -\frac{1}{\lambda }d^2\big (x_k, R^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k)))\big )\nonumber \\ \mathfrak {R}(J^{B}_{\lambda }({y_k})+v_{y_k}, -\psi _k \gamma _{k}^{'}(\psi _{k}))\ge & {} \frac{\psi _k}{\lambda }d^2\big (x_k, J^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k)))\big ). \end{aligned}$$

(25)

Define $\varphi _{k}(t)= \gamma _k(1-t)\psi _{k},~\forall ~t\in [0,1].$ Then, $\varphi _{k}(t)$ is a geodesic joining $y_k$ and $x_k$ and

$$\begin{aligned} \varphi _{k}^{'}(t)=-\psi _k \gamma _k^{'}(\psi _k), \end{aligned}$$

(26)

and $\varphi _{k}(t)=\mathrm{exp}_{y_k} t {~\mathrm exp}_{y_k}^{-1} x_k,~~\forall ~t\in [0,1]$ is also a geodesic joining $y_k$ to $x_k$ and

$$\begin{aligned} \varphi _{k}^{'}(0)=-\mathrm{exp}_{y_k}^{-1}x_k. \end{aligned}$$

(27)

From (25), (26) and (27), we have

$$\begin{aligned} \mathfrak {R}(J^{B}_{\lambda }({y_k})+v_{y_k}, \mathrm{exp}_{y_k}^{-1}x_k) \ge \frac{\psi _k}{\lambda }d^2\big (x_k, J^{B}_{\lambda }(\mathrm{exp}_{x_k}(-\lambda J^{B}_{\lambda }(x_k)))\big ). \end{aligned}$$

(28)

From (13) and (14), we have that

$$\begin{aligned} x_{k_{j+1}}\in \mathrm {Q}_{k_j}= \{ x\in {{\mathbb {M}}} :\mathfrak {R}\big ( J^{B}_{\lambda }({y_{k_j}})+v_{y_{k_j}},~\mathrm{exp} _{y_{k_j}}^{-1} x \big )\le 0 \}, \end{aligned}$$

(29)

we have $\lim _{j\rightarrow \infty }x_{k_j}=x_{k_{j+1}}=\bar{x}.$ From (29) and Lemma 2.3 (i), we have

$$\begin{aligned} \lim \limits _{j\rightarrow \infty }\mathfrak {R}\big ( J^{B}_{\lambda }({y_{k_j}})+v_{y_{k_j}},~\mathrm{exp} _{y_{k_j}}^{-1} x \big )\le & {} \lim \limits _{j\rightarrow \infty }\mathfrak {R}\big ( J^{B}_{\lambda }({y_{k_j}})+v_{y_{k_j}},~\mathrm{exp} _{y_{k_j}}^{-1} x_{k_j+1} \big )\nonumber \\\le & {} 0 \end{aligned}$$

(30)

From (28) and (30), we obtained

$$\begin{aligned} \lim \limits _{j\rightarrow \infty }\psi _{k_j} d(x_{k_j}, R_{\lambda }^{B}(\mathrm{exp}_{x_{k_j}}(-\lambda J^{B}_{\lambda }(x_{k_j})))=0. \end{aligned}$$

(31)

Now, we have two possible cases.

Suppose first that $\psi _{k_j}\nrightarrow 0$. Then there exists $\psi >0$ such that $\psi _{k_j}>\psi$ for all j. Thus following (31), we have

$$\begin{aligned} \lim \limits _{j\rightarrow \infty } d(x_{k_j}, R_{\lambda }^{B}(\mathrm{exp}_{x_{k_j}}(-\lambda J^{B}_{\lambda }(x_{k_j}))=0, \end{aligned}$$

(32)

and so

$$\begin{aligned} d(\bar{x}, R_{\lambda }^{B}(\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x})))=0, \end{aligned}$$

(33)

that is $\bar{x}\in S$.

Suppose now that $\lim _{j\rightarrow \infty } d(x_{k_j}, J_{\lambda }^{B}(\mathrm {exp}_{x_{k_j}}(-\lambda J_{\lambda }^{B}(x_{k_j})))\ne 0$. Then $\lim _{j\rightarrow \infty }\psi _{k_j}= 0.$ From the definition of j(k), we have

$$\begin{aligned} \mathfrak {R}\big (J^{B}_{\lambda }(\gamma _k (\psi _{k_j})+v_{\gamma _{k_j}(\psi _{k_j})}, \gamma _{k_j}^{'}(\psi _{k_j})\big )> -\frac{1}{\lambda } d^2 ( x_{k_j}, R_{\lambda }^{B}(\mathrm{exp}_{x_{k_j}}(-\lambda J_{\lambda }^{B}(x_{k_j})))). \end{aligned}$$

(34)

Taking into account that

$$\begin{aligned} \gamma _{k_j}^{'}(s)= \mathcal {P}_{\gamma _{k_j}(s)x_{k_j}} \{ \mathrm{exp}^{-1}_{x_{k_j}}\big [ R^B_{\lambda } \mathrm{exp}_{x_{k_j}}(-\lambda J_{\lambda }^{B}(x_{k_j}))\big ]\}, \end{aligned}$$

(35)

we have

$$\begin{aligned}&\mathfrak {R}\big ( J^{B}_{\lambda }({\gamma _k (\psi _{k_j})})+v_{\gamma _{k_j}{(\psi _{k_j})}}, \mathcal {P}_{\gamma _{k_j}(\psi _{k_j})x_{k_j}} \big \{ \mathrm{exp}^{-1}_{x_{k_j}}\big [ R^B_{\lambda } \mathrm{exp}_{x_{k_j}}(-\lambda J_{\lambda }^{B}(x_{k_j}))\big ]\big \}\big ) \nonumber \\&\quad >-\frac{1}{\lambda } d^2 ( x_{k_j}, R^{B}_{\lambda } (\mathrm{exp}_{k_j}(-\lambda J_{\lambda }^{B}(x_{k_j}))). \end{aligned}$$

(36)

Since the parallel transport is an isometry, letting $\lim _{j\rightarrow \infty }$ in (36), we have

$$\begin{aligned}&-\lambda \mathfrak {R}(\bar{x}+v_{\bar{x}},\mathrm{exp}^{-1}_{\bar{x}}\big [ R^{B}_{\lambda }(\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x}))\big ])\nonumber \\&\quad < d^2 (\bar{x}, R^{B}_{\lambda }[\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x}))]). \end{aligned}$$

(37)

Taking together (37) and (7), we have

$$\begin{aligned} d^2(\bar{x}, \big [ R^{B}_{\lambda }(\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x}))\big ])\le & {} -\lambda \mathfrak {R}({\bar{x}}+v_{\bar{x}}, \mathrm{exp}^{-1}_{\bar{x}}\big [ R^{B}_{\lambda }(\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x}))\big ])\\< & {} d^2 (\bar{x}, R^{B}_{\lambda }[\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda } (\bar{x}))] ), \end{aligned}$$

which is a contradiction to our assumption. Hence

$$\begin{aligned} d (\bar{x}, R^{B}_{\lambda }[\mathrm{exp}_{\bar{x}}(-\lambda J^{B}_{\lambda }(\bar{x}))])=0. \end{aligned}$$

Thus $\bar{x}\in S$. This completes the proof. $\square$

Remark 3.7

If $\mathbb {M}=X$, a Banach space, C is a nonempty, closed and convex subset of X, and set $J^{\partial I_K}_{\lambda }=A$, an accretive operator and B be monotone operator. Then, Problem (1) is equivalent to the variational inclusion problem:

$$\begin{aligned} \mathrm{Find} ~z\in C ~ \mathrm{such~ that}~ 0\in Az+Bz, \end{aligned}$$

which was studied by Sahu et al. [21]. They use the prox-Tikhonov-like forward–backward method to estimate the above variational inclusion problem.

4 Application

Let K be a nonempty, closed and convex subset of Hadamard manifold $\mathbb {M}$ and $F:\mathbb {M}\rightarrow T\mathbb {M}$ be a single-valued vector field. Then, the variational inequality problem VI(F, K) is to find $x\in K$ such that

$$\begin{aligned} \langle F(x), \mathrm{exp}_x^{-1}y \rangle \ge 0, \forall ~y\in K. \end{aligned}$$

(38)

It can be easily seen that $x\in K$ is a solution of VI(F, K) if and only if x satisfies (see [13])

$$\begin{aligned} 0\in F(x)+N_{K}(x), \end{aligned}$$

(39)

where $N_{K}(x)$ denotes the normal cone to K at $x\in K$, defined as

$$\begin{aligned} N_{K}(x)=\{u\in T_x\mathbb {M}:\mathfrak {R}(u, \mathrm{exp}_x^{-1}y)\le 0,~\forall ~y\in K\}. \end{aligned}$$

Let $I_{K}$ be the indicator function of K, i.e.,

$$\begin{aligned} I_{K}(x)={\left\{ \begin{array}{ll} ~0, ~~~~~~if x \in K, \\ +\infty , ~if x \notin K. \end{array}\right. } \end{aligned}$$

Since $I_{K}x$ is proper, lower semicontinuous, the differential $\partial I_{K}(x)$ of $I_{K}$ is maximal monotone, defined by

$$\begin{aligned} \partial I_{K}(x)= \{v\in T_x\mathbb {M}: \mathfrak {R}(v, \mathrm{exp}_x^{-1}y)\le I_{K}(y)-I_{K}(x)\}. \end{aligned}$$

(40)

Since $I_{K}(x)=I_{K}(y)=0,~\forall ~x,y\in K$. From (40), we have

$$\begin{aligned} \partial I_{K}(x)= & {} \{v\in T_x\mathbb {M}: \mathfrak {R}(v, \mathrm{exp}_x^{-1}y)\le 0\}.\nonumber \\= & {} N_{K}(x). \end{aligned}$$

(41)

Let $R^{\partial I_K}_{\lambda }$ be the resolvent of $\partial I_{K}$, defined as

$$\begin{aligned} R^{\partial I_K}_{\lambda }(x)=\{w\in \mathbb {M}:x\in \mathrm{exp}_w\lambda \partial I_{K}(w) \}=P_{K}(x),~\forall x\in \mathbb {M}, \lambda >0, \end{aligned}$$

and thus the complimentary vector field, i.e., the Yosida approximation of $\partial I_{K}$, is defined by

$$\begin{aligned} J^{\partial I_K}_{\lambda }(x)= & {} -\frac{1}{\lambda } \mathrm{exp}_x^{-1} R^{\partial I_K}_{\lambda }(x),~\forall x\in \mathbb {M},\nonumber \\= & {} -\frac{1}{\lambda } \mathrm{exp}_x^{-1}P_{K}(x). \end{aligned}$$

(42)

since ${\partial I_K}$ is monotone, $J^{\partial I_K}_{\lambda }$ is single-valued and monotone. For more details, see [3, 13, 14]. Following (38),(39), (41) and (42), we conclude that by replacing and relaxing Yosida approximation operator $J^{\partial I_K}_{\lambda }$ by a pseudomonotone vector field F, B by $\partial I_K$ and resolvent $R^{\partial I_K}_{\lambda }$ by projection operator $P_K$ in Algorithm 3.4, we get Algorithm 4.1, studied by Tang and Huang [24] for the convergence of Korpelevich’s method for variational inequality problem VI(F, K).

5 Conclusion

This paper is devoted to the study of Yosida inclusion problem in Hadamard manifolds. We prove the convergence of Korpelevich-type algorithm to solve a Yosida inclusion problem using Yosida approximation and the resolvent of a set-valued monotone vector field B. Our problem is a new one and more general than a variational inequality problem VI(K, F) in Hadamard manifolds [24], and extends Yosida inclusion problem [2] and zeros of sum of accretive and monotone operators from Banach spaces to Hadamard manifolds [21] .