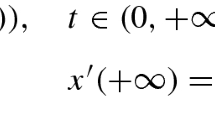Abstract
In this paper, we establish existence of solutions for the following boundary value problem on the half-line: \((q(t)u''(t))' = g(t, u(t), u'(t), u''(t)),\;\;\; t \in (0, \infty )\) subject to the boundary conditions \( u'(0) = \sum ^{m}_{i=1}\alpha _i\int ^{\xi _i}_0 u(t)\mathrm{d}t, u(0) = 0,\; \lim _{t\rightarrow \infty }q(t)u''(t)=0.\) We establish sufficient conditions for the existence of at least one solution using coincidence degree arguments. An example is provided to validate our result.

Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Agarwal, R.P.; O’Regan, D.: Infinite Interval Problems for Differential, Difference and Integral Equations. Kluwer, Dordrecht (2001)
Agarwal, R.P.; Cetin, E.: Unbounded solutions of third order three-point boundary value problems on a half-line. Adv. Nonlinear Anal. 5(2), 105–119 (2016)
Frioui, A.; Guezane-Lakud, A.; Khaldi, R.: Higher order boundary value problems at resonance on an unbounded interval. Electron. J. Differ. Equ. 2016(29), 110 (2016). http://ejde.math.txstate.edu
Kosmatov, N.: Multipoint boundary value problems on an unbounded domain at resonance. Nonlinear Anal. 65, 2158–2171 (2008)
Lian, H.R.; Ge, W.G.: Solvability for second order three-point boundary value problems at resonance on a half-line. J. Math. Anal. Appl. 337, 1171–1181 (2007)
Liu, Y.; Li, D.; Fang, M.: Solvability for second order m-point boundary value problems at resonance on the half-line. Electron. J. Differ. Equ. 2009(13), 1–11 (2009). http://ejde.math.txstate.edu
Liu, B.M.; Liu, L.S.; Wu, Y.H.: Unbounded solutions for three point boundary value problems with non-linear boundary conditions on \([0, \infty )\). Nonlinear Anal. 23, 2923–2932 (2010)
Mawhin, J.: Topological Degree Methods in Nonlinear Boundary Value Problems, NSF-CBMS Regional Conference Series in Mathematics. American Mathematical Society, Providence (1979).
O’Regan, D.; Yan, B.; Agarwal, R.P.: Solutions in weighted spaces of singular boundary value problems on the half-line. J. Comput. Appl. Math. 205, 751–763 (2007)
Shi, H.; Pei, M.: Solvability of a third-order three-point boundary value problem on half-line. Bull. Malays. Math. Sci. Soc. 38, 909–926 (2015)
Yan, B.Q.; Liu, Y.S.: Unbounded solutions of singular boundary value problems for second order differential equations on the half-line. Appl. Math. Comput. 147, 629–644 (2004)
Zima, M.: On positive solutions of boundary value-problems on the half-line. J. Math. Anal. Appl. 259, 127–136 (2001)
Acknowledgements
The author wishes to express his gratitude to the anonymous referees for their useful suggestions and corrections.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Iyase, S.A. On a third-order boundary value problem at resonance on the half-line. Arab. J. Math. 8, 43–53 (2019). https://doi.org/10.1007/s40065-018-0209-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-018-0209-5