Abstract
Given a marked \(\infty \)-category \(\mathcal {D}^{\dagger }\) (i.e. an \(\infty \)-category equipped with a specified collection of morphisms) and a functor \(F: \mathcal {D}\rightarrow {\mathbb {B}}\) with values in an \(\infty \)-bicategory, we define  , the marked colimit of F. We provide a definition of weighted colimits in \(\infty \)-bicategories when the indexing diagram is an \(\infty \)-category and show that they can be computed in terms of marked colimits. In the maximally marked case \(\mathcal {D}^{\sharp }\), our construction retrieves the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\). In the specific case when
, the marked colimit of F. We provide a definition of weighted colimits in \(\infty \)-bicategories when the indexing diagram is an \(\infty \)-category and show that they can be computed in terms of marked colimits. In the maximally marked case \(\mathcal {D}^{\sharp }\), our construction retrieves the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\). In the specific case when  , the \(\infty \)-bicategory of \(\infty \)-categories and \(\mathcal {D}^{\flat }\) is minimally marked, we recover the definition of lax colimit of Gepner–Haugseng–Nikolaus. We show that a suitable \(\infty \)-localization of the associated coCartesian fibration \({\text {Un}}_{\mathcal {D}}(F)\) computes
, the \(\infty \)-bicategory of \(\infty \)-categories and \(\mathcal {D}^{\flat }\) is minimally marked, we recover the definition of lax colimit of Gepner–Haugseng–Nikolaus. We show that a suitable \(\infty \)-localization of the associated coCartesian fibration \({\text {Un}}_{\mathcal {D}}(F)\) computes  . Our main theorem is a characterization of those functors of marked \(\infty \)-categories \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) which are marked cofinal. More precisely, we provide sufficient and necessary criteria for the restriction of diagrams along f to preserve marked colimits
. Our main theorem is a characterization of those functors of marked \(\infty \)-categories \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) which are marked cofinal. More precisely, we provide sufficient and necessary criteria for the restriction of diagrams along f to preserve marked colimits
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of \(\infty \)-categories is, by now, well-established as an excellent way to treat coherence and higher homotopical data. However, the mere presence of this higher data means that many properties which can be explored most easily by explicit computation in the ordinary categorical setting are best accessed by universal properties in the \(\infty \)-categorical setting. Consequently, general constructions exhibiting universal properties take on an even greater importance in the study of higher category theory. Among such constructions, the theories of limits and colimits form an essential core around which many of the results in higher category theory are built. In the developing theory of \(\infty \)-bicategories, as in its strict 1-categorical analogue, these theories must be extended to allow for laxness—loosely, allowing cones over a functor to commute up to non-invertible 2-morphism.
This paper is a new entry in this story, dealing with lax colimits which depend on a collection of marked morphisms in the source. These morphisms can be viewed as “controlling the laxness” of the colimit in question. Such collections of marked morphisms arise throughout the study of higher categories—in localizations, cartesian fibrations, etc. The theory of marked colimits and marked cofinality developed in this paper represents a new technology for treating such objects. Along the way to \(\infty \)-cofinality, we will also see that the theory of weighted colimits expounded in [6] can be viewed as one instance of the general theory of marked colimits, and will note a fundamental relation to the Grothendieck construction, generalizing extant results for lax colimits and usual \(\infty \)-colimits.
A comment from the author (22/06/20): After completion of this work, a prepint [4] appeared proving Theorem 3 below. This result was achieved independently by both authors using completely different methods of proof. In this work, the definition of marked colimit provided is characterized by a 2-dimensional universal property. By the time the paper [4] was uploaded I was working in the proof of Proposition 2 in order to show that the definition of weighted colimits appearing in [6] satisfies this 2-dimensional universal property. The reader not willing to take Proposition 2 on faith can adapt the proof to the definition of lax colimit provided in the aforementioned papers.
Update (28/09/20): The proof of Proposition 2 can be now found in [2].
Marked colimits in 2-categories. Let \({F: {\mathbb {C}} \rightarrow {\mathbb {B}}}\) be a 2-functor. A lax cone for F with vertex point \(b \in {\mathbb {B}}\) is given by the following data
-
For every object \(c \in C\) a morphism \({\alpha _c:F(c) \rightarrow b}\).
-
For every morphism \({u:c \rightarrow c'}\) in C a 2-morphism \({\theta _u: \alpha _c \Rightarrow \alpha _{c'} \circ F(u)}\) depicted by a 2-commutative diagram

These data must satisfy the following set of axioms
(I) Unitality: \(\theta _{{\text {id}}_c}={\text {id}}_{\alpha _c}\) for every \(c \in {\mathbb {C}}\). (II) Composability: Given \({u: c \rightarrow c'}\) and \({v: c' \rightarrow c'' }\) the following equation holds

(III) Compatibility with 2-morphisms: For every 2-morphism \({\eta :u \Rightarrow u'}\) in \({\mathbb {C}}\) the following equation holds

A morphism of lax cones  with vertex point b is given by a family of 2-morphisms
with vertex point b is given by a family of 2-morphisms  such that for every \({f: c \rightarrow c'}\) the following equation holds
such that for every \({f: c \rightarrow c'}\) the following equation holds

One can then show that this defines a category of lax cones for F with vertex b. Furthermore, we can arrange the previous definitions into a 2-functor with values in the 2-category of categories

The laxcolimit of F is then defined as an object  correpresenting the functor above (see [7] for a classical reference on lax limits). In practice it is common to work with a category C (resp. 2-category \({\mathbb {C}}\)) equipped with a collection of chosen morphisms containing the identities (marked categories, resp. marked 2-categories) that one wants to formally invert. It is thus desirable to have a theory of colimits adapted to accomodate the extra information present in marked (2)-categories.
correpresenting the functor above (see [7] for a classical reference on lax limits). In practice it is common to work with a category C (resp. 2-category \({\mathbb {C}}\)) equipped with a collection of chosen morphisms containing the identities (marked categories, resp. marked 2-categories) that one wants to formally invert. It is thus desirable to have a theory of colimits adapted to accomodate the extra information present in marked (2)-categories.
Let \({\mathbb {C}}^{\dagger }\) be a marked 2-category. We define a marked cone for F to be a lax cone such that the 2-morphisms \(\theta _f\) are invertible whenever f is a marked morphism in \({\mathbb {C}}^{\dagger }\). Paralleling the construction above, we obtain the notion of the marked colimit of F. This definition was already present in the literature under the name of \(\sigma \)-colimits [5], where it was succesfully applied to define a 2-dimensional theory of flat pseudofunctors. Although similar in spirit, our definition of marked colimits presented in Sect. 3 will depart from that of Descotte et al. The main cause of this difference is our use of weighted colimits as the jumping-off point of our theory, rather than using different levels of laxness (see Definition 2.4.3 in [5]) in the natural transformation defining a marked cone. We have opted for this approach since to our eyes is the one that is better suited for developing the cofinality theory that we will now introduce.
Marked colimits in \(\infty \)-bicategories. Let  denote the \(\infty \)-bicategory of \(\infty \)-categories. Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and
denote the \(\infty \)-bicategory of \(\infty \)-categories. Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and  be functors where \(\mathcal {C}\) is an \(\infty \)-category and \({\mathbb {B}}\) is an \(\infty \)-bicategory. In Sect. 3 we define \(W \otimes F\), the colimit of F weighted by W. Once this basic theory is established we embark upon the main construction of this work, the definition of marked colimits, appearing in Sect. 4. Given a marked \(\infty \)-category \(\mathcal {C}^{\dagger }\) we define a functor
be functors where \(\mathcal {C}\) is an \(\infty \)-category and \({\mathbb {B}}\) is an \(\infty \)-bicategory. In Sect. 3 we define \(W \otimes F\), the colimit of F weighted by W. Once this basic theory is established we embark upon the main construction of this work, the definition of marked colimits, appearing in Sect. 4. Given a marked \(\infty \)-category \(\mathcal {C}^{\dagger }\) we define a functor

where \({\text {L}}_{W}\left( \mathcal {C}^{\dagger }_{c/}\right) \) stands for the \(\infty \)-localization of the slice category \(\mathcal {C}_{c/}\) with respect to the marking induced by \(\mathcal {C}^{\dagger }\). This allows us to define the marked colimit of a functor \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) as \({\mathfrak {C}}^{\dagger }_{\mathcal {C}/} \otimes F\). The definition presented naturally extends the notion of \(\infty \)-colimits appearing in [3, 10], as demonstrated by the following result.
Theorem 1
Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and suppose that  exists. Then the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\) exists and there is an equivalence
exists. Then the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\) exists and there is an equivalence

In particular, both universal properties coincide if \({\mathbb {B}}=\mathcal {B}\).
The rest of Sect. 4 is devoted to computational results. First, we show that weighted colimits indexed by an \(\infty \)-category \(\mathcal {C}\) can be computed in terms of marked colimits. Let  be a weight functor. Let us observe that its associated Cartesian fibration \({\mathcal {W}}\) comes equipped with a canonical marking given by the Cartesian edges. We denote this marked category by \({\mathcal {W}}^{\natural }\). With the aid of this observation, we can then prove:
be a weight functor. Let us observe that its associated Cartesian fibration \({\mathcal {W}}\) comes equipped with a canonical marking given by the Cartesian edges. We denote this marked category by \({\mathcal {W}}^{\natural }\). With the aid of this observation, we can then prove:
Theorem 2
Let \({F:\mathcal {C}\rightarrow {\mathbb {B}}}\) and  . Let \({p:\mathcal {W} \rightarrow \mathcal {C}}\) denote the Cartesian fibration classifying W. Suppose that \(W \otimes F\) exists. Then
. Let \({p:\mathcal {W} \rightarrow \mathcal {C}}\) denote the Cartesian fibration classifying W. Suppose that \(W \otimes F\) exists. Then  exists and there is an equivalence in \({\mathbb {B}}\)
exists and there is an equivalence in \({\mathbb {B}}\)

We conclude Sect. 4 by providing a thorough analysis of marked colimits in  . To achieve this goal, we will employ the Grothendieck construction in its \(\infty \)-categorical incarnation as the unstraightening functor (see chapter 3 in [10]), as the “universal recipe” to compute colimits of diagrams in \(\infty \)-categories. This is witnessed by two results already known in the literature: in [6] the authors define lax colimits in \(\infty \)-categories and show in Theorem 7.4 that given a functor F with values in \(\infty \)-categories its associated coCartesian fibration computes the lax colimit. Let us remark that our definition in the minimally marked case \(\mathcal {C}^{\flat }\) particularizes to that of Gepner et al. If we focus our attention on the maximally marked case \(\mathcal {C}^{\sharp }\), we note that Corollary 3.3.4 in [10] shows that the colimit of a functor F with values in \(\infty \)-categories can be computed as the \(\infty \)-localization of its associated coCartesian fibration at the collection of coCartesian edges.
. To achieve this goal, we will employ the Grothendieck construction in its \(\infty \)-categorical incarnation as the unstraightening functor (see chapter 3 in [10]), as the “universal recipe” to compute colimits of diagrams in \(\infty \)-categories. This is witnessed by two results already known in the literature: in [6] the authors define lax colimits in \(\infty \)-categories and show in Theorem 7.4 that given a functor F with values in \(\infty \)-categories its associated coCartesian fibration computes the lax colimit. Let us remark that our definition in the minimally marked case \(\mathcal {C}^{\flat }\) particularizes to that of Gepner et al. If we focus our attention on the maximally marked case \(\mathcal {C}^{\sharp }\), we note that Corollary 3.3.4 in [10] shows that the colimit of a functor F with values in \(\infty \)-categories can be computed as the \(\infty \)-localization of its associated coCartesian fibration at the collection of coCartesian edges.
Therefore, we observe that the two extremal cases \(\mathcal {C}^{\flat }\) resp. \(\mathcal {C}^{\sharp }\), are already well understood. It is then natural to ask ourselves if there is a generalization of both results which can be seen through the lens of marked colimits. We provide an affirmative answer to this question in the following result which can be found as Theorem 8 in the main body of this article.
Theorem 3
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category. Given  there is a equivalence of \(\infty \)-categories
there is a equivalence of \(\infty \)-categories

where \( {\text {L}}_W \left( {\text {Un}}^{{\text {co}}}_{\mathcal {C}}(F)^{\natural (\dagger )}\right) \) denotes the \(\infty \)-localization at the collection of coCartesian edges lying over marked edges of \(\mathcal {C}^{\dagger }\).
A cofinality criterion: Theorem A\(^{\dagger }\). Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marking-preserving functor. We call f a marked cofinal functor if for every diagram \({F:\mathcal {D}\rightarrow {\mathbb {B}}}\) the canonical comparison mapFootnote 1

is an equivalence in \({\mathbb {B}}\). The main result of this work is a characterization of this higher notion of cofinality.
Theorem 4
Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marking-preserving functor of \(\infty \)-categories. Then f is marked cofinal if and only if for every \(d \in \mathcal {D}\) the canonical map \({\mathcal {C}_{d/}^{\dagger } \rightarrow \mathcal {D}^{\dagger }_{d/}}\) induces an equivalence on localized \(\infty \)-categories,
As a corollary we obtain a generalization of Theorem A in [12] to marked \(\infty \)-categories.
Corollary 1
(Theorem A\(^{\dagger }\)) Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marking-preserving functor of \(\infty \)-categories. If the canonical map \({{\text {L}}_W\left( \mathcal {C}_{d/}^{\dagger }\right) \xrightarrow {\simeq } {\text {L}}_W\left( \mathcal {D}_{d/}^{\dagger }\right) }\) is an equivalence of \(\infty \)-categories for every \(d \in \mathcal {D}\), then the induced functor on \(\infty \)-localizations
is an equivalence of \(\infty \)-categories.
In previous work, (see [1] for general background and notation) we generalized Quillen’s Theorem A to (strict) marked 2-categories.
Theorem 5
Let \({F:{\mathbb {C}}^\dagger \rightarrow {\mathbb {D}}^\dagger }\) be a functor of marked 2-categories. Suppose that,
- 1.:
-
For every object \(d\in {\mathbb {D}}\), there exists a morphism \({g_d: d\rightarrow F(c)}\) which is initial in both
 and
and  .
. - 2.:
-
Every marked morphism
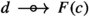 is initial in
is initial in  .
. - 3.:
-
For any marked morphism
 in \({\mathbb {D}}\), the induced functors
in \({\mathbb {D}}\), the induced functors  preserve initial objects.
preserve initial objects.
Then the induced functor \({F_{W}: {\text {L}}_{W}({\text {N}}_2({\mathbb {C}}^\dagger ))\rightarrow {\text {L}}_{W}({\text {N}}_2({\mathbb {D}}^\dagger ))}\) is an equivalence of \(\infty \)-categories.
We also claimed that the conditions of the previous theorem should control the notion of higher cofinality for \(\infty \)-bicategories. This work can be understood as a partial result towards proving the cofinality conjecture as stated in [1]. This will be justified in Theorem 9 where we show that the hypotheses of Theorem 4 are equivalent to the analogous conditions of Theorem 5 for \(\infty \)-categories.
The importance of Theorem 4 becomes apparent when combined with Theorem 2. The use of weighted colimits permeates throughout category theory. Many essential constructions, for example, Kan extensions, are best formulated in terms of weighted (co)limits. However, to the author’s knowledge the general theory was lacking tools that allow us to simplify the computations of weighted colimits. Marked colimits are devised as an equivalent language to that of their weighted counterparts that allows for transparent cofinality statements. Let us consider for example a functor \(f: \mathcal {C}\rightarrow \mathcal {D}\) between \(\infty \)-categories. A common situation that we might encounter ourselves in is to try to determine whether the restriction functor
is fully faithful. An elegant sufficient criterion to check is to show that for every \(d \in \mathcal {D}\) the induced morphism is \(\mathcal {C}_{d/} \rightarrow \mathcal {D}_{d/}\) is cofinal in the usual sense. Once our cofinality theory is developed to its full 2-category potential such statements will be available to the public allowing a better access to complicated constructions such as functor \(\infty \)-bicategories.
2 Preliminaries
In this section, we collect notation, definitions and background necessary for our constructions and proofs. We assume basic familiarity with the theory of \(\infty \)-categories as in [3, 10]. We will use scaled simplicial sets as a model for \(\infty \)-bicategories following [9]. We refer the reader to [8] for the basics of enriched category theory including weighted (co)limits.
Notation 1
We will denote ordinary strict 1-categories by capital letters (A, B, C) and \(\infty \)-categories by caligraphic letters \((\mathcal {A},\mathcal {B},\mathcal {C})\). We will generally (see Remark 1 below for an exception) denote \(\infty \)-bicategories by boldface letters \(({\mathbb {A}},{\mathbb {B}},{\mathbb {C}})\).
Remark 1
Following the previous convention we will denote by \({\text {Cat}}_{\infty }\) the full subcategory of the 1-category of simplicial sets consisting of \(\infty \)-categories. We will use the notation \(\mathcal {C}\!{\text {at}}_{\infty }\) to denote the \(\infty \)-category of \(\infty \)-categories. We will denote the \(\infty \)-bicategory of \(\infty \)-categories by  .
.
Notation 2
We will extensively use marked simplicial sets as a model for \(\infty \)-categories. Given a simplicial set X we denote by \(X^{\flat } \in {{\text {Set}}_{\Delta }^+}\) the marked simplicial set with only degenerate edges marked and by \(X^{\sharp }\) the marked simplicial set with all edges marked.
Notation 3
Given a simplicial set X we denote by \(X_{\flat } \in {\text {Set}}_{\Delta }^{{\text {sc}}}\) the scaled simplicial set with only degenerate 2-simplices being thin and by \(X_{\sharp }\) the scaled simplicial set with all 2-simplices being thin. We will identify \(\infty \)-categories with maximally scaled simplicial sets that are fibrant in the bicategorical model structure.
Notation 4
Given an \(\infty \)-bicategory \({\mathbb {B}}\) and objects \(x,y \in {\mathbb {B}}\), we denote by  the mapping category. For every \(y \in {\mathbb {B}}\) we denote by \({\mathbb {B}}(\mathord {-},y)\) the functor
the mapping category. For every \(y \in {\mathbb {B}}\) we denote by \({\mathbb {B}}(\mathord {-},y)\) the functor

Notation 5
Given \(\infty \)-bicategories \({\mathbb {B}},{\mathbb {C}}\) and functors \({F,G: {\mathbb {C}} \rightarrow {\mathbb {B}}}\) we denote by \({\text {Nat}}_{{\mathbb {B}}}(F,G)\) the mapping category of \({\text {Fun}}\left( {\mathbb {C}},{\mathbb {B}}\right) \). We denote by \({\text {Nat}}_{{\mathbb {B}}}^{\simeq }(F,G)\) the underlying Kan complex.
Notation 6
Given an \(\infty \)-bicategory \({\mathbb {B}}\) we denote by \({\mathcal {Y}}_{{\mathbb {B}}}\) the \(\infty \)-bicategorical Yoneda embedding

Notation 7
Given a functor \({F:\mathcal {C}\rightarrow \mathcal {C}\!{\text {at}}_{\infty }}\) we will denote by \({\text {Un}}^{{\text {co}}}_\mathcal {C}(F)\) the value of the (coCartesian) unstraightening functor as defined (with the adequate dualization) in 3.2.1 [10]. Since \({\text {Un}}^{{\text {co}}}_\mathcal {C}\) induces an equivalence of \(\infty \)-categories between \({\text {Fun}}(\mathcal {C},\mathcal {C}\!{\text {at}}_{\infty })\) and the \(\infty \)-category of coCartesian fibrations over \(\mathcal {C}\) we will often call \({\text {Un}}^{{\text {co}}}_\mathcal {C}(F)\) the “coCartersian fibration associated to F”.
2.1 Marked \(\infty \)-categories and localizations
Definition 1
Let \({U:{{\text {Set}}_{\Delta }^+}\rightarrow {\text {Set}}_{\Delta }}\) be the forgetful functor. We define \({\text {Cat}}_{\infty }^{\dagger }\) (see Remark 1) as the full subcategory of \({{\text {Set}}_{\Delta }^+}\) on those objects \(X^{\dagger } \in {{\text {Set}}_{\Delta }^+}\) such that \(U(X^{\dagger })\) is an \(\infty \)-category. We call the objects of \({\text {Cat}}_{\infty }^{\dagger }\) marked \(\infty \)-categories and its morphisms marked functors.
Definition 2
Let \({f: \mathcal {C}^{\dagger }\rightarrow \mathcal {D}^{\dagger }}\) be a marked functor. Given \(d \in \mathcal {D}\) we define a marking on \(\mathcal {C}_{d/}\) by declaring an edge \({\sigma : \Delta ^1 \rightarrow \mathcal {C}_{d/}}\) to be marked if an only if its image under the canonical map is marked in \(\mathcal {C}^{\dagger }\). We denote this marked simplicial set by \(\mathcal {C}^{\dagger }_{d/} \in {{\text {Set}}_{\Delta }^+}\).
Notation 8
Given a marked \(\infty \)-category \(\mathcal {C}^{\dagger }\) we denote its \(\infty \)-categorical localization with respect to its marked edges by \({\text {L}}_{W}(\mathcal {C}^{\dagger })\). Given \(\mathcal {X}\in \mathcal {C}\!{\text {at}}_{\infty }\) we define \({\text {Fun}}^{\dagger }(\mathcal {C}, \mathcal {X})\) to be the full subcategory of \({\text {Fun}}(\mathcal {C},\mathcal {X})\) on those functors mapping marked edges of \(\mathcal {C}\) to equivalences in \(\mathcal {X}\).
Remark 2
Note that the universal property of localizations implies that we have an equivalence of \(\infty \)-categories \({\text {Fun}}^{\dagger }(\mathcal {C}, \mathcal {X})\simeq {\text {Fun}}\left( {\text {L}}_W (\mathcal {C}^{\dagger }), \mathcal {X}\right) \). We remind the reader that a model for the localization of \(\mathcal {C}^{\dagger }\) is given by its fibrant replacement in the model structure on marked simplicial sets.
2.2 Free fibrations
In this section, we review the main results of [6] regarding free Cartesian fibrations and their relation to marked \(\infty \)-categories.
Definition 3
Given \(\mathcal {C}\in \mathcal {C}\!{\text {at}}_{\infty }\) let \(\mathcal {C}\!{\text {at}}_{\infty / \mathcal {C}}^{{\text {cart}}}\) be the subcategory of the undercategory \(\mathcal {C}\!{\text {at}}_{\infty / \mathcal {C}}\), whose objects are Cartesian fibrations, and whose morphisms are functors which preserve Cartesian morphisms.
Remark 3
There is an obvious forgetful functor \({{\mathfrak {U}}: \mathcal {C}\!{\text {at}}_{\infty / \mathcal {C}}^{{\text {cart}}} \rightarrow \mathcal {C}\!{\text {at}}_{\infty / \mathcal {C}} }\).
Notation 9
Given an \(\infty \)-category \(\mathcal {C}\) and two Cartesian fibrations
we denote by \({\text {Fun}}^{{\text {cart}}}_{\mathcal {C}}(\mathcal {X},\mathcal {Y})\) the full subcategory of functors over \(\mathcal {C}\) that preserve Cartesian morphisms.
Definition 4
Let \(\mathcal {C}\) be an \(\infty \)-category. For \({p: \mathcal {E} \rightarrow \mathcal {C}}\) any functor of \(\infty \)-categories, let \({{\mathfrak {F}}(p): {\mathfrak {F}}(\mathcal {E}) \rightarrow \mathcal {C}}\) denote the map \({\mathcal {E}\times _{\mathcal {C}} \mathcal {C}^{\Delta ^{1}} \rightarrow \mathcal {C}}\), where the pullback is along the target fibration \({\mathcal {C}^{\Delta ^{1}} \rightarrow \mathcal {C}}\) given by evaluation at \(1 \in \Delta ^1\), and the projection \({\mathfrak {F}}(p)\) is induced by evaluation at 0. We call the projection map \({\mathcal {E}\times _{\mathcal {C}} \mathcal {C}^{\Delta ^{1}} \rightarrow \mathcal {C}}\) the free Cartesian fibration on p. The Cartesian edges of \({\mathfrak {F}}(p)\) are precisely those which are mapped to equivalences under the projection to \(\mathcal {E}\). Then \({\mathfrak {F}}\) defines a functor
Remark 4
Let \({p:\mathcal {E} \rightarrow \mathcal {C}}\). Then the objects of \({\mathfrak {F}}(\mathcal {E})\) are given by edges of \(\mathcal {C}\) of the form \(c \rightarrow p(e)\) where \(e \in \mathcal {E}\). A morphism is given by a commutative diagram in \(\mathcal {C}\)

where f is an morphism in \(\mathcal {E}\).
Remark 5
Composition with the degeneracy map \({s_0: \Delta ^1 \rightarrow \Delta ^0}\) induces a functor \({\mathcal {C}\rightarrow \mathcal {C}^{\Delta ^1}}\) which is a section to both of the evaluation maps. Given a functor \({\mathcal {E}\rightarrow \mathcal {C}}\), this section gives a natural map
over \(\mathcal {C}\), inducing a unit natural transformation \({\eta :{\text {id}} \Rightarrow {\mathfrak {U}} \circ {\mathfrak {F}}}\).
Proposition 1
Given a map of \(\infty \)-categories \({\mathcal {E}\rightarrow \mathcal {C}}\) then the unit natural transformation \({\mathcal {E}\rightarrow {\mathfrak {F}}(\mathcal {E})}\) induces an equivalence of \(\infty \)-categories
Proof
This is Proposition 4.11 in [6]. \(\square \)
Definition 5
Let \({p:\mathcal {E}\rightarrow \mathcal {C}}\) be a functor of \(\infty \)-categories. Suppose that \(\mathcal {E}\) is a marked \(\infty \)-category and denote it by \(\mathcal {E}^{\dagger }\). We declare an edge of \(\mathcal {E}\times _{\mathcal {C}} \mathcal {C}^{\Delta ^1}\) to be marked if and only if its projection to \(\mathcal {E}\) is marked. We denote this marked \(\infty \)-category over \(\mathcal {C}\) by \({\mathfrak {F}}(\mathcal {E})^{\dagger }\).
Remark 6
Observe that in the previous definition, we can identify the fibers  with the marked slice \(\mathcal {E}_{c/}^{\dagger }\) where we declare an edge marked if and only if it is marked in \(\mathcal {E}^{\dagger }\).
with the marked slice \(\mathcal {E}_{c/}^{\dagger }\) where we declare an edge marked if and only if it is marked in \(\mathcal {E}^{\dagger }\).
Definition 6
Let \({p: \mathcal {E}\rightarrow \mathcal {C}}\) be a functor of \(\infty \)-categories and assume further that \(\mathcal {E}\) is a marked \(\infty \)-category. Given a Cartesian fibration \({\mathcal {X}\rightarrow \mathcal {C}}\) we define \({\text {Fun}}^{\dagger }_{\mathcal {C}}(\mathcal {E},\mathcal {X})\) to be the full subcategory on those functors mapping marked edges in \(\mathcal {E}^{\dagger }\) to Cartesian morphisms in \(\mathcal {X}\). If p is a Cartesian fibration we define \({\text {Fun}}^{{\text {cart}},\dagger }_{\mathcal {C}}(\mathcal {E},\mathcal {X})\) to be the full subcategory of \({\text {Fun}}^{\dagger }_{\mathcal {C}}(\mathcal {E},\mathcal {X})\) on those functors which also preserve the Cartesian edges of \(\mathcal {E}\).
Lemma 1
Let \(\mathcal {E}^{\dagger }\) be a marked \(\infty \)-category together with a functor \({p:\mathcal {E}\rightarrow \mathcal {C}}\). Consider \({\mathfrak {F}}(\mathcal {E})^{\dagger }\) as in Definition 5. Then the unit map \(\eta \) induces a commutative diagram in \(\mathcal {C}\!{\text {at}}_{\infty }\)

where the vertical maps are fully faithful and the horizontal maps are equivalences of \(\infty \)-categories.
Proof
The vertical maps are fully faithful by definition. Since the bottom horizontal map is an equivalence by Proposition 1 it will suffice to compute its essential image when restricted to \({\text {Fun}}^{{\text {cart}},\dagger }_{\mathcal {C}}({\mathfrak {F}}(\mathcal {E}),\mathcal {X})\). It is clear that the image of this restricted map lands in \({\text {Fun}}^{\dagger }_{\mathcal {C}}(\mathcal {E},{\mathfrak {U}}(\mathcal {X}))\). Now suppose that we are given a functor of Cartesian fibrations \({L:{\mathfrak {F}}(\mathcal {E}) \rightarrow \mathcal {X}}\) such that its image under the unit map lands in \({\text {Fun}}^{\dagger }_{\mathcal {C}}(\mathcal {E},{\mathfrak {U}}(\mathcal {X}))\). Consider a marked edge in \({\sigma : \Delta ^1 \rightarrow {\mathfrak {F}}(\mathcal {E})}\) represented by a commutative diagram

where \({\alpha : \Delta ^1 \rightarrow \mathcal {E}}\) is a marked morphism. We claim that \(L(\sigma )\) is a Cartesian edge of \(\mathcal {X}\). First we observe that we have an inner horn \({\theta :\Lambda ^2_1 \rightarrow \mathcal {X}}\) given by

Using Proposition 2.4.1.7 in [10] we see that since both edges of the horn are Cartesian in \(\mathcal {X}\) it follows that any composite of those two edges must be Cartesian in \(\mathcal {X}\). We consider another horn \({\Xi : \Lambda ^2_1 \rightarrow \mathcal {X}}\)

First we observe that the restriction \({\Delta ^{\{1,2 \}} \rightarrow \Lambda ^1_2 \rightarrow [\Xi ] \mathcal {X}}\) is a Cartesian edge and that the restriction of \(\Xi \) to \(\Delta ^{\{0,1 \}}\) is \(L(\sigma )\). Finally one notes that any composite of the morphisms in \(\theta \) must be homotopic to any composite of the morphisms in \(\Xi \). Again by Proposition 2.4.1.7 in [10] this implies that \(L(\sigma )\) is Cartesian in \(\mathcal {X}\). \(\square \)
Definition 7
Let \({\pi :\mathcal {X}\rightarrow \mathcal {C}}\) be a Cartesian fibration and assume that \(\mathcal {X}^{\dagger }\) is a marked \(\infty \)-category. A fiberwise localization of \(\pi \) at the collection of marked edges of \(\mathcal {X}\) is a Cartesian fibration \({{\text {L}}_W^{\mathcal {C}}(\pi ^{\dagger }) \rightarrow \mathcal {C}}\) together with a map of Cartesian fibrations \({\iota :\mathcal {X}\rightarrow {\text {L}}_W^{\mathcal {C}}(\pi ^{\dagger })}\) such that
-
The map \(\iota \) sends marked edges in \(\mathcal {X}\) to Cartesian edges in \({\text {L}}_W^{\mathcal {C}}(\pi ^{\dagger })\).
-
For any Cartesian fibration \({\mathcal {Y} \rightarrow \mathcal {C}}\) the induced functor \({{\text {Fun}}^{{\text {cart}}}_{\mathcal {C}}({\text {L}}_W^{\mathcal {C}}(\pi ^{\dagger }),\mathcal {Y}) \rightarrow {\text {Fun}}^{{\text {cart}},\dagger }_{\mathcal {C}}(\mathcal {X},\mathcal {Y})}\) is an equivalence of \(\infty \)-categories.
Remark 7
Given \({\pi :\mathcal {X}\rightarrow \mathcal {C}}\) as above let \(\mathcal {X}^{\diamond }\) denote the marked simplicial set over \(\mathcal {C}\) where an edge is marked if it is Cartesian or if it is marked in \(\mathcal {X}^\dagger \). Then a fibrant replacement in the model structure for Cartesian fibrations over \(\mathcal {C}\) gives a model for \({\text {L}}_W^{\mathcal {C}}(\pi ^{\dagger })\).
Lemma 2
Let \(\mathcal {E}^{\dagger }\) be a marked \(\infty \)-category together with a functor \({p:\mathcal {E}\rightarrow \mathcal {C}}\). Consider \({{\mathfrak {F}}(p)^{\dagger }:{\mathfrak {F}}(\mathcal {E})^{\dagger } \rightarrow \mathcal {C}}\) as in Definition 5. Then for every vertex \(c \in \mathcal {C}\) there is an equivalence of \(\infty \)-categories

Proof
Let \({\mathfrak {E}}_{\mathcal {C}/}\) denote the functor classifying \({\mathfrak {F}}(\mathcal {E})\). It is not hard to verify that this functor maps each \(c\in \mathcal {C}\) to the \(\infty \)-category \(\mathcal {E}_{c/}\) and that its action on morphisms is induced by precomposition in \(\mathcal {C}\). Therefore we define \(\widetilde{{\mathfrak {E}}}_{\mathcal {C}/}^{\dagger }\) to be the functor sending each c to \(\mathcal {E}^{\dagger }_{c/}\). It is clear that we have an equivalence of Cartesian fibrations
In addition, we observe that the right-hand side can be modeled by a fibrant replacement of \(\widetilde{{\mathfrak {E}}}_{\mathcal {C}/}^{\dagger }\) in the projective model structure of \({{\text {Set}}_{\Delta }^+}\)-valued functors. This finally implies

\(\square \)
3 Weighted colimits in \(\infty \)-bicategories
Definition 8
Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and  . We define a functor as the composite
. We define a functor as the composite

Definition 9
Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and  . We say that an object \(b \in {\mathbb {B}}\) is the colimit of F weighted by W if there exists an equivalence of functors
. We say that an object \(b \in {\mathbb {B}}\) is the colimit of F weighted by W if there exists an equivalence of functors

Remark 8
Since weighted colimits are unique up to equivalence we will often speak of “the weighted colimit” and denote it by \(W \otimes F\).
Definition 10
Let \(\mathcal {C}\) be an \(\infty \)-category. The twisted arrow \(\infty \)-category \({\text {Tw}}(\mathcal {C})\) of \(\mathcal {C}\) is the simplicial set given by \({\text {Hom}}_{{\text {Set}}_{\Delta }}(\Delta ^n,{\text {Tw}}(\mathcal {C}))\simeq {\text {Hom}}_{{\text {Set}}_{\Delta }}(\Delta ^n \star (\Delta ^n)^{{{\text {op}}}},\mathcal {C})\). Note that \({\text {Tw}}(\mathcal {C})\) comes equipped with a projection functor \({{\text {Tw}}(\mathcal {C}) \rightarrow \mathcal {C}\times \mathcal {C}^{{{\text {op}}}}}\) which is a right fibration by Proposition 5.2.1.3 in [11], so that \({\text {Tw}}(\mathcal {C})\) is an \(\infty \)-category.
We present now two of the main results obtained in [2] that will allow us to understand weighted colimits in  . The proofs can be found in the aforementioned document as Theorem 4.3 and*** Theorem 4.28.
. The proofs can be found in the aforementioned document as Theorem 4.3 and*** Theorem 4.28.
Proposition 2
Let \(\mathcal {C}\) be a \(\infty \)-category and \({\mathbb {D}}\) an \(\infty \)-bicategory. Then for every pair of functors \({F,G: \mathcal {C}\rightarrow {\mathbb {D}}}\) there exists a equivalence of \(\infty \)-categories
which is natural in each variable.
Corollary 2
Let  and
and  . Then there is an equivalence of \(\infty \)-categories
. Then there is an equivalence of \(\infty \)-categories

We finish the section by relating conical weighted colimits, i.e. those with weight constant on the terminal category, with ordinary colimits.
Proposition 3
Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and let  denote the constant functor with value the terminal \(\infty \)-category. Suppose that \(\underline{*}\otimes F\) exists. Then
denote the constant functor with value the terminal \(\infty \)-category. Suppose that \(\underline{*}\otimes F\) exists. Then  exists and there is an equivalence in \(\mathcal {B}\)
exists and there is an equivalence in \(\mathcal {B}\)

where the right-hand side is given by the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\).
Proof
Let \({\Xi : {\mathbb {B}}(\underline{*}\otimes F,\mathord {-}) \xrightarrow {\simeq } {\text {Nat}}_{\mathcal {C}^{{{\text {op}}}}}(\underline{*},{\mathbb {B}}(F(\mathord {-}),\mathord {-}))}\) be the natural equivalence exhibiting \(\underline{*}\otimes F\) as the weighted colimit of F and let \(\iota ^{*}\Xi \) denote its restriction to \(\mathcal {B}\). Observe that \(\iota ^{*}\Xi \) factors through \(\mathcal {C}\!{\text {at}}_{\infty }\). We will abuse notation by viewing \(\iota ^{*}\Xi \) as a functor with target \(\mathcal {C}\!{\text {at}}_{\infty }\). Now we consider the following composite
where k denotes the underlying Kan complex functor. It is clear that we have produced a natural equivalence \({\mathcal {B}(\underline{*}\otimes F,\mathord {-})\xrightarrow {\simeq } {\text {Nat}}_{\mathcal {C}^{{{\text {op}}}}}(\underline{*},\mathcal {B}(F(\mathord {-}),\mathord {-}))}\). Observe that due to Proposition 2 we have the following natural equivalence of spaces for every \(b \in \mathcal {B}\)
where \(\underline{b}\) denotes the constant functor with value \(b \in \mathcal {B}\). We have thus produced equivalences of functors
We note that \(\mathcal {B}_{/\underline{*}\otimes F}\) is the left fibration classifying the functor \(\mathcal {B}(\underline{*}\otimes F,\mathord {-})\) and that it has an initial object. Therefore the left fibration classifying \({\text {Nat}}_{\mathcal {C}}\left( F,\underline{(\mathord {-})}\right) \) has an initial object. This exhibits \(\underline{*}\otimes F\) as the colimit of \({F: \mathcal {C}\rightarrow \mathcal {B}}\). \(\square \)
4 Marked colimits
4.1 Definitions and general properties
Definition 11
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category and consider \({{\mathfrak {F}}({\text {id}}_{\mathcal {C}}):{\mathfrak {F}}(\mathcal {C})^{\dagger } \rightarrow \mathcal {C}}\) as in Definition 5. Given the Cartesian fibration \({\text {L}}^{\mathcal {C}}_{W}\left( {\mathfrak {F}}({\text {id}}_\mathcal {C})^{\dagger }\right) \) discussed in Definition 7 we let

be its associated functor. As we noted in Lemma 2, the functor \({\mathfrak {C}}^{\dagger }_{\mathcal {C}/}\) sends each \(c \in \mathcal {C}\) to the localized comma category \({\text {L}}_W\left( \mathcal {C}^{\dagger }_{c/}\right) \)
Definition 12
Given a marked \(\infty \)-category \(\mathcal {C}^{\dagger }\) and a diagram \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) we define

and call it the marked colimit of F.
Remark 9
Using Corollary 2 we see that if  and the marking of \(\mathcal {C}\) consists only of equivalences our definition coincides with the definition of lax colimit given in [6].
and the marking of \(\mathcal {C}\) consists only of equivalences our definition coincides with the definition of lax colimit given in [6].
Theorem 6
Let \({F: \mathcal {C}\rightarrow {\mathbb {B}}}\) and suppose that  exists. Then the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\) exists and there is an equivalence
exists. Then the \(\infty \)-categorical colimit of F in the underlying \(\infty \)-category \(\mathcal {B}\subseteq {\mathbb {B}}\) exists and there is an equivalence

Proof
Let \({t: {\mathfrak {C}}_{\mathcal {C}/}^{\sharp } \Rightarrow \underline{*}}\) denote the unique map to the terminal functor. By Proposition 3 it will suffice to show that t is a levelwise equivalence. This follows immediately from Lemma 2 and the fact that slice categories \(\mathcal {C}_{c/}\) are all contractible. \(\square \)
Remark 10
It is natural to ask ourselves, whether Theorem 6 admits a converse. The answer to this question is no and it is already well documented (see for example 3.54 in [8]). For the sake of completeness we will include an example here. Let \({\mathbb {B}}\) be the following 2-category

Then it is clear that c is the coproduct of a and b in the underlying 1-category \(\mathcal {B}\). However c fails to satisfy the 2-dimensional universal property because the identity morphism on c has no non-trivial 2-morphisms.
Corollary 3
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category and consider a functor \({F: \mathcal {C}^{\dagger } \rightarrow \mathcal {B}}\) with \(\mathcal {B}\) an \(\infty \)-category. Then  exists if and only if the colimit of F exists and there is an equivalence in \(\mathcal {B}\)
exists if and only if the colimit of F exists and there is an equivalence in \(\mathcal {B}\)

Proof
It follows from Theorem 6 after noting that since the mapping categories in \(\mathcal {B}\) are Kan complexes then any natural transformation \({{\mathfrak {C}}^{\dagger }_{\mathcal {C}/} \Rightarrow \mathcal {B}(F(\mathord {-}),b)}\) must factor through \({\mathfrak {C}}^{\sharp }_{\mathcal {C}/}\). Thus concluding that both universal properties are the same. \(\square \)
Proposition 4
Let \({\pi :\mathcal {X}\rightarrow \mathcal {C}}\) be a Cartesian fibration where we view \(\mathcal {X}\) as a marked category (denoted by \(\mathcal {X}^{\natural }\)) by marking the Cartesian edges. Consider the base change adjunction
Then for every Cartesian fibration \({\mathcal {Y}\rightarrow \mathcal {C}}\) there is an equivalence of \(\infty \)-categories
natural in \(\mathcal {Y}\). In particular, there is an equivalence of Cartesian fibrations \(\pi _! {\text {L}}_W^{\mathcal {X}}\)\(\left( {\mathfrak {F}}({\text {id}}_\mathcal {X})^{\natural }\right) \simeq \mathcal {X}\).
Proof
We can produce the following natural equivalences
where the third equivalence is given by the non-Cartesian base change adjunction. The result follows. \(\square \)
Theorem 7
Let \({F:\mathcal {C}\rightarrow {\mathbb {B}}}\) and  . Let \({p:\mathcal {W} \rightarrow \mathcal {C}}\) denote the Cartesian fibration classifying W. Suppose that \(W \otimes F\) exists. Then
. Let \({p:\mathcal {W} \rightarrow \mathcal {C}}\) denote the Cartesian fibration classifying W. Suppose that \(W \otimes F\) exists. Then  exists and there is an equivalence in \({\mathbb {B}}\)
exists and there is an equivalence in \({\mathbb {B}}\)

Proof
Let \({\mathfrak {W}}_{\mathcal {W}/}^{\natural }\) denote the weight functor in the definition of the colimit of \(F \circ p\). By Proposition 4 we know that \(p_!{\mathfrak {W}}_{\mathcal {W}/}^{\natural } \simeq W \). This shows that there is a map
which is levelwise an equivalence on the underlying Kan complexes. Combining Proposition 2 and Proposition 6.9 in [6] we obtain for every \(b \in {\mathbb {B}}\) the following commutative diagram

where \(\mathcal {Y}\) is the Cartesian fibration classifying \({\mathbb {B}}(F(\mathord {-}),b)\). Since the bottom horizontal map is an equivalence due to Proposition 4 we conclude by 2-out-of-3. \(\square \)
4.2 Marked colimits in the \(\infty \)-bicategory of \(\infty \)-categories.
In this section we show how to compute marked colimits of functors with values in \(\infty \)-categories. Our strategy will be a direct generalization of the arguments presented in [6] where the authors show that the unstraightening functor (see Notation 7) computes the lax colimit of a functor.
Definition 13
Let \({F: \mathcal {C}\rightarrow \mathcal {C}\!{\text {at}}_{\infty }}\) be a functor and denote by \({\mathcal {F} \rightarrow \mathcal {C}}\) its associated coCartesian fibration. Given \(\mathcal {X}\in \mathcal {C}\!{\text {at}}_{\infty }\) we define a simplicial set \(\Phi ^{\mathcal {F}}_{\mathcal {X}}\) over \(\mathcal {C}\) via the universal property \({\text {Hom}}_{\mathcal {C}}(K, \Phi ^{\mathcal {F}}_{\mathcal {X}})\simeq {\text {Hom}}(K \times _{\mathcal {C}}\mathcal {F},\mathcal {X})\).
Remark 11
As a special case of (the dual of) Corollary 3.2.2.12 in [10] we see that \({\Phi ^{\mathcal {F}}_{\mathcal {X}} \rightarrow \mathcal {C}}\) is a Cartesian fibration. An edge \({\Delta ^1 \rightarrow \Phi ^{\mathcal {F}}_{\mathcal {X}}}\) is Cartesian if and only if the associated functor \({\Delta ^1 \times _{\mathcal {C}} \mathcal {F}\rightarrow \mathcal {X}}\) maps coCartesian edges in \(\Delta ^1 \times _{\mathcal {C}} \mathcal {F}\) to equivalences in \(\mathcal {X}\).
Proposition 5
The Cartesian fibration \({\Phi ^{\mathcal {F}}_{\mathcal {X}} \rightarrow \mathcal {C}}\) classifies the functor
Proof
This is Proposition 7.3 of [6]. \(\square \)
Definition 14
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category and consider a Cartesian (resp. coCartesian) fibration \({\mathcal {X}\rightarrow \mathcal {C}}\). We equip \(\mathcal {X}\) with a marking by declaring an edge marked if and only if it is Cartesian (resp. coCartesian) and its image in \(\mathcal {C}\) is marked. We will denote this marked \(\infty \)-category over \(\mathcal {C}\) by \(\mathcal {X}^{\natural (\dagger )}\).
Remark 12
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category and consider a functor \({F: \mathcal {C}\rightarrow \mathcal {C}\!{\text {at}}_{\infty }}\). Denote its associated coCartesian fibration by \(\mathcal {F}\). Then given \(\mathcal {X}\in \mathcal {C}\!{\text {at}}_{\infty }\) we have a natural equivalence of \(\infty \)-categories
where the first equivalence is the universal property of the localization (see Notation 8) and the second is given by the universal property of \(\Phi ^{\mathcal {F}}_{\mathcal {X}}\).
Proposition 6
Let \(\mathcal {C}\) be an \(\infty \)-category. Given \({F,G: \mathcal {C}^{{{\text {op}}}} \rightarrow {\text {Cat}}_{\infty }}\) classified by the Cartesian fibrations \(\mathcal {F}\) and \(\mathcal {G}\) respectively, there is a natural equivalence of \(\infty \)-categories
Proof
See Proposition 6.9 in [6]. \(\square \)
Theorem 8
Let \(\mathcal {C}^{\dagger }\) be a marked \(\infty \)-category. Given  there is a equivalence of \(\infty \)-categories
there is a equivalence of \(\infty \)-categories

Proof
We fix the notation \({\text {Un}}^{{\text {co}}}_{\mathcal {C}}(F)^{\natural (\dagger )}=\mathcal {F}^{\natural (\dagger )}\). We have a natural equivalence of \(\infty \)-categories provided by Lemmas 1 and 12
Propositions 5 and 6 in turn imply
Combining these two natural equivalences, the result follows from the Yoneda lemma and Corollary 2. \(\square \)
Corollary 4
Let \(\mathcal {C}\) be an \(\infty \)-category. Given  there is an equivalence of \(\infty \)-categories
there is an equivalence of \(\infty \)-categories

Proof
This follows by observing that a coCartesian edge lying over a degenerate edge must be an equivalence. \(\square \)
As a consequence of Theorem 8, we obtain an alternative proof of Corollary 3.3.4.3 in [10].
Corollary 5
Let \({F: \mathcal {C}\rightarrow \mathcal {C}\!{\text {at}}_{\infty }}\) then there is an equivalence of \(\infty \)-categories
Proof
Combine Theorem 8 with \(\mathcal {C}^{\sharp }\) and Proposition 3. \(\square \)
5 A cofinality criterion
The goal of this section is to extend the preexisting theory of cofinality to the setting of marked colimits. Our main result, Theorem 9, is a generalization of the characterization of cofinal functors appearing in Theorem 4.1.3.1 in [10]. As an immediate corollary we obtain a generalization of Quillen’s theorem A for marked \(\infty \)-categories.
Definition 15
Let \({f: \mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marked functor and consider \({{\mathfrak {F}}(f): {\mathfrak {F}}(\mathcal {C})^{\dagger } \rightarrow \mathcal {D}}\) as in Definition 5. We denote by

the functor classifying the Cartesian fibration \({\text {L}}^{\mathcal {D}}_W\left( {\mathfrak {F}}(f)^{\dagger }\right) \).
Remark 13
Observe that we have a natural transformation \({{\mathcal {A}}_{f}:{\mathfrak {C}}^{\dagger }_{\mathcal {D}/} \Rightarrow {\mathfrak {D}}^{\dagger }_{\mathcal {D}/}}\). We will abuse notation by also denoting by \({\mathcal {A}}_f\) the associated map of Cartesian fibrations.
Proposition 7
Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marked functor and let \(f_{!}\dashv f^{*}\) denote the base change adjunction
Then there is a natural equivalence of \(\infty \)-categories
In particular, we have \({f_{!}{\text {L}}_W^{\mathcal {C}}\left( {\mathfrak {F}}({\text {id}}_{\mathcal {C}})^{\dagger }\right) \xrightarrow {\simeq } {\text {L}}^{\mathcal {D}}_W\left( {\mathfrak {F}}(f)^{\dagger }\right) }\).
Proof
Let \({\mathcal {X}\rightarrow \mathcal {D}}\) be a Cartesian fibration. We observe that we have natural equivalences
where the second equivalence is given by the non-Cartesian base change adjunction \(f_* \dashv f^{*}\). It is clear that the right-hand side is equivalent to \({\text {Fun}}_{\mathcal {D}}^{{\text {cart}}}\left( {\text {L}}^{\mathcal {D}}_W\left( {\mathfrak {F}}(f)^{\dagger }\right) , \mathcal {X}\right) \) and the result follows. \(\square \)
Given a marked functor \({f: \mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) it follows that for every functor  we can produce the following natural transformations
we can produce the following natural transformations

where the last map is a natural equivalence by virtue of Proposition 7. It follows that when \(G={\mathbb {B}}(F(\mathord {-}),b)\) for some diagram \(F:{\mathcal {D}\rightarrow {\mathbb {B}}}\), we obtain a map

which we will call the canonical comparison map whenever both are defined.
Definition 16
A functor \({f: \mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) of marked \(\infty \)-categories is said to be marked cofinal if for every functor \({F:\mathcal {D}\rightarrow {\mathbb {B}}}\), the following conditions hold:
-
The marked colimit F exists if and only the marked colimit of \((F \circ f)\) exists.
-
The canonical comparison map
 is an equivalence in \({\mathbb {B}}\).
is an equivalence in \({\mathbb {B}}\).
Proposition 8
Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marked functor. For every diagram  we have a commutative diagram in \(\mathcal {C}\!{\text {at}}_{\infty }\) given by
we have a commutative diagram in \(\mathcal {C}\!{\text {at}}_{\infty }\) given by

where the leftmost vertical map is induced by pullback along f.
Proof
This follows as a corollary of Theorem 8. \(\square \)
Proposition 9
A functor \({f: \mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) of marked \(\infty \)-categories is marked cofinal if and only if the natural transformation
is a levelwise equivalence.
Proof
Suppose f is marked cofinal. Given an object \(d \in \mathcal {D}\) we define the composite
where first functor is given by \({\text {Map}}_{\mathcal {D}}(d,\mathord {-})\) and the second functor is the inclusion of the full subcategory of spaces. Then using Corollary 8 we obtain an equivalence of \(\infty \)-categories

Using Lemma 2 we identify this map with the fiber of the map \({\mathcal {A}}_f\) over d. Since equivalences of Cartesian fibrations can be detected fiberwise it follows that \({\mathcal {A}}_f\) is an equivalence. The converse follows immediately. \(\square \)
Remark 14
Suppose \({f:\mathcal {C}^{\sharp } \rightarrow \mathcal {D}^{\sharp }}\) is cofinal for the maximal marking. Since f is cofinal we obtain an equivalence after \(\infty \)-groupoid completion
Then it follows that f satisfies the hypothesis of Theorem 4.1.3.1 in [10] and so pullback along f preserves all \(\infty \)-limits.
Corollary 6
(Theorem \(\text {A}^{\dagger }\)) Let \({f:\mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a marked cofinal functor. Then there exists an equivalence of \(\infty \)-categories
Proof
By Theorem 8 we can identify \({\text {L}}_{W}\left( \mathcal {D}^{\dagger }\right) \) with the marked colimit of the constant point valued functor. The result then follows from Corollary 8. \(\square \)
Remark 15
For the rest of this section, we will abuse notation by denoting the Cartesian fibration \({\text {L}}_{W}^{\mathcal {D}}\left( {\mathfrak {F}}(f)^{\dagger }\right) \) by \({\mathfrak {C}}^{\dagger }_{\mathcal {D}/}\) and similarly for the other fiberwise localizations of free fibrations already mentioned.
Lemma 3
Let \(\mathcal {D}^{\dagger }\) be a marked \(\infty \)-category and consider the Cartesian fibration \({{\mathfrak {D}}^{\dagger }_{\mathcal {D}/} \rightarrow \mathcal {D}}\). Then the following hold
-
For every \(d \in \mathcal {D}\) there exists an initial object in
 .
. -
Every object in
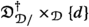 represented by a marked morphism is initial.
represented by a marked morphism is initial.
Proof
The proof is analogous to the proof of Lemma 4.0.3 in [1]. \(\square \)
Proposition 10
Let \({\pi :\mathcal {X}\rightarrow \mathcal {D}}\) be a Cartesian fibration of simplicial sets. Assume that for each vertex \(c\in \mathcal {C}\), the \(\infty \)-category \(\mathcal {X}_d\) has an initial object. Denote by \(\mathcal {X}^\prime \subset \mathcal {X}\) the full simplicial subset of \(\mathcal {X}\) spanned by those x which are initial objects in \(\mathcal {X}_{\pi (x)}\). Then
is a trivial Kan fibration of simplicial sets. Moreover, a section s of \(\pi :\mathcal {X}\rightarrow \mathcal {C}\) is initial in the \(\infty \)-category \({\text {Fun}}_{\mathcal {C}}(\mathcal {C},\mathcal {X})\) if and only if s factors through \(\mathcal {X}^\prime \).
Proof
See Proposition 2.4.4.9 in [10]. \(\square \)
Theorem 9
Let \({f: \mathcal {C}^{\dagger } \rightarrow \mathcal {D}^{\dagger }}\) be a functor of marked \(\infty \)-categories. Then f is marked cofinal if and only the following conditions hold
-
1.
For every \(d \in \mathcal {D}\) there is a morphism \({g_d:d \rightarrow f(c)}\) which is initial in \({\text {L}}_W\left( \mathcal {C}_{d/}^{\dagger }\right) \) and in \({\text {L}}_W\left( \mathcal {D}_{d/}^{\dagger }\right) \).
-
2.
Every object in \({\text {L}}_W\left( \mathcal {C}_{d/}^{\dagger }\right) \) represented by a marked morphism in \(\mathcal {D}^{\dagger }\) is initial.
-
3.
There exists a Cartesian morphism providing a solution to the lifting problem

if the image of \(\sigma \) consists in two initial objects in their respective fibers.
Proof
By Proposition 9 it will suffice to show that \({\mathcal {A}}_f\) is an equivalence of Cartesian fibrations precisely when the conditions above are satisfied.
Suppose that \({\mathcal {A}}_f\) is an equivalence and pick an inverse \({\Xi :{\mathfrak {D}}^{\dagger }_{\mathcal {D}/} \rightarrow {\mathfrak {C}}^{\dagger }_{\mathcal {D}/} }\) over \(\mathcal {D}\). First we see that the first 2 conditions can be checked by noting that \({\mathcal {A}}_f\) induces an equivalence of \(\infty \)-categories upong passage to fibers. The existence of \(\Xi \) implies the existence of a section \({s_{f}:\mathcal {D}\rightarrow {\mathfrak {C}}^{\dagger }_{\mathcal {D}/}}\) mapping each object of \(\mathcal {D}\) to an initial object in the fiber and mapping marked edges to Cartesian edges. To finish the proof of this implication we will show that condition (3) holds. We start by picking a Cartesian lift of u denoted by \({\hat{u}}\) such that \({\hat{u}}(1)=\sigma (1)\). Then since \(\sigma (0)\) is initial we obtain a morphism from \(\sigma (0) \rightarrow {\hat{u}}(0)\). Note that if we show that \({\hat{u}}(0)\) is initial its corresponding fibre then we can finish our argument by picking an adequate composite \(\sigma (0) \rightarrow {\hat{u}}(0) \rightarrow {\hat{u}}(1)=\sigma (1)\). Since \({\mathcal {A}}_f\) is an equivalence it will suffice that \({\mathcal {A}}_f({\hat{u}}(0))=y\) is initial. We note that y is equivalent to the morphism u viewed as an object of \({\mathfrak {D}}^{\dagger }_{\mathcal {D}/}\), therefore the conclusion follows from Lemma 3.
To show the converse we first observe that condition (1) together with Proposition 10 imply the existence of a section \({s_{f}:\mathcal {D}\rightarrow {\mathfrak {C}}^{\dagger }_{\mathcal {D}/}}\) such that for every \(d \in \mathcal {D}\) both \(s_{f}(d)\) and \({\mathcal {A}}_f(s_{f}(d))\) are initial in their respective fibers. We claim that \(s_{f}\) maps marked edges to Cartesian edges in \({\mathfrak {C}}^{\dagger }_{\mathcal {D}/}\). To see this given \({\alpha :(\Delta ^1)^{\sharp } \rightarrow \mathcal {D}^{\dagger }}\) we denote by \({\widetilde{\alpha }}\) the Cartesian lift provided by condition (3). One immediately checks that there exists an equivalence in \({\Delta ^1 \xrightarrow {u} {\mathfrak {C}}^{\dagger }_{\mathcal {D}/}}\) such that \(s_f(\alpha )\sim u \circ {\widetilde{\alpha }} \) and thus \(s_f(\alpha )\) is Cartesian. In particular we obtain a map of Cartesian fibrations
We fix the notation
and observe that both the identity functor on \( {\mathfrak {D}}^{\dagger }_{\mathcal {D}/ }\) and \({\mathcal {A}}_f \circ \Xi \) get mapped under \(\Gamma _{\mathcal {D}}\) to sections landing in initial objects in the fibers. It follows from Proposition 10 that \({\mathcal {A}}_f \circ \Xi \sim id\).
Similarly we consider
and observe that \(\Gamma _{\mathcal {C}}(\Xi \circ {\mathcal {A}}_f)(c)=s_f(f(c))\) which is initial in the fiber by construction. Similarly the image of the identity functor under \(\Gamma _{\mathcal {C}}\) sends \(c \in \mathcal {C}\) to an object represented by a marked morphism. Condition (2) implies that this object is initial. Since both maps can factored through the pullback

we can apply Proposition 10 to their factorizations. This shows that \(\Xi \circ {\mathcal {A}}_f \sim {\text {id}}\) and thus finishes the proof. \(\square \)
Remark 16
Let \({{\mathfrak {C}}_{\mathcal {D}/}^{\dagger }: \mathcal {D}^{{{\text {op}}}} \rightarrow \mathcal {C}\!{\text {at}}_{\infty }}\). Note that condition (3) in Theorem 9 holds if and only if for every marked edge  in \(\mathcal {D}\) the functor \({\mathfrak {C}}_{\mathcal {D}/}^{\dagger }(u)\) preserves initial objects.
in \(\mathcal {D}\) the functor \({\mathfrak {C}}_{\mathcal {D}/}^{\dagger }(u)\) preserves initial objects.
Availability of data and material
Not applicable.
Notes
See Sect.5 for a precise definition of the comparison map.
References
Abellán, G.F., Stern, W.: Theorem A for marked 2-categories. 2020 arXiv: 2002.12817
Abellán, G.F., Stern, W.: Enhanced twisted arrow categories. arXiv:2009.11969 (2020)
Cisinski, D.: Higher Categories and Homotopical Algebra. Cambridge University Press, Cambridge (2019)
Berman, J.: On lax colimits in \(\infty \)-categories. arXiv: 2006.10851 (2020)
Descotte, M.E., Dubuc, E.J., Szyld, M.: Sigma limits in 2-categories and flat pseudofunctors. Adv. Math. 718, 266–313 (2018). https://doi.org/10.1016/j.aim.2018.05.021
Gepner, D., Haugseng, R., Nikolaus, T.: Lax colimits and free fibrations in \(\infty \)-categories. Doc. Math. 22, 1225–1266 (2015)
Gray, J.: The existence and construction of Lax limits. Cahiers Topol. Géométr. Différ. Catégoriques Tome 21(3), 277–304 (1980)
Kelly, G.M.: Basic concepts of enriched category theory. Reprints Theory Appl. Categ. 10, 20 (2005)
Lurie, J.: \((\infty , 2)\)-categories and the Goodwillie Calculus. 2009. arXiv: 0905.0462
Lurie, J.: Higher Topos Theory. Princeton University Press, Princeton (2009)
Lurie, J.: Higher Algebra. http://people.math.harvard.edu/~lurie/papers/HA.pdf (2017) The author’s webpage
Quillen, D.: Higher Algebraic K-Theory I Higher K-Theories Lecture Notes in Mathematics, vol. 341. Springer, Berlin (1973). https://doi.org/10.1007/BFb0067053
Acknowledgements
I would like to thank Tobias Dyckerhoff for the guidance and support offered throughout this process. It is also a pleasure to thank Walker Stern for all the careful revisions of the draft and the many improvements suggested. I am grateful to an anonymous referee for the very careful reading which helped improve the article. The author acknowledges the support of the VolkswagenStiftung through the Lichtenberg Professorship Programme.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL. The author acknowledges the support of the VolkswagenStiftung through the Lichtenberg Professorship Programme.
Author information
Authors and Affiliations
Contributions
Not applicable
Corresponding author
Ethics declarations
Conflicts of interest
Not applicable.
Code availability
Not applicable.
Additional information
Communicated by Emily Riehl.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abellán García, F. Marked colimits and higher cofinality. J. Homotopy Relat. Struct. 17, 1–22 (2022). https://doi.org/10.1007/s40062-021-00296-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-021-00296-2



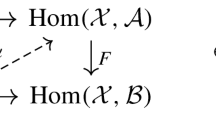

 and
and  .
.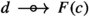 is initial in
is initial in  .
. in
in  preserve initial objects.
preserve initial objects. is an equivalence in
is an equivalence in  .
.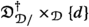 represented by a marked morphism is initial.
represented by a marked morphism is initial.