Abstract
We exploit the equivalence between t-structures and normal torsion theories on a stable \(\infty \)-category to show how a few classical topics in the theory of triangulated categories, i.e., the characterization of bounded t-structures in terms of their hearts, their associated cohomology functors, semiorthogonal decompositions, and the theory of tiltings, as well as the more recent notion of Bridgeland’s slicings, are all particular instances of a single construction, namely, the tower of a morphism associated with a J-slicing of a stable \(\infty \)-category  , where J is a totally ordered set equipped with a monotone \(\mathbb {Z}\)-action.
, where J is a totally ordered set equipped with a monotone \(\mathbb {Z}\)-action.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
If you’re going to read this, don’t bother.
C. Palahniuk
An elementary and yet fundamental theorem in algebraic topology asserts that every sufficiently nice connected topological space X fits into a “tower”
where each \(X_n\) is n-connected and each map \(X_n\longrightarrow X_{n-1}\) is a fibration that induces isomorphisms in \(\pi _{>n}\), and has an Eilenberg–MacLane space \(K(\pi _{n}(X),n-1)\) as its fiber. This result admits an immediate generalization to an arbitrary ambient category which is “good enough” for homotopy theory. It is indeed a statement about the decomposition of an initial morphism \(* \longrightarrow X\) into a tower of fibrations whose fibers have homotopy concentrated in a single degree. It is nevertheless only in the setting of \((\infty ,1)\)-category theory that this result can be given its cleanest conceptualization: the tower of a pointed object X is the result of the factorization of \(* \longrightarrow X\) with respect to the collection of factorization systems \((n\textsc {-conn}, n\textsc {-trunc})\) whose right classes are given by n-truncated morphisms [17, 5.2.8.16].
Of course, a similar construction can be exported to stable homotopy theory, where the analogue of the factorization system \((n\textsc {-conn}, n\textsc {-trunc})\) is given by the canonicalt-structure \(\mathfrak {t}\) on the category of spectra, determined by the objects whose homotopy groups vanish in negative an non-negative degree, respectively,
together with all its shifts\(\mathfrak {t}_n=\mathfrak {t}[n]\).Footnote 1 In this context, it becomes natural to consider the whole \(\{\mathfrak {t}_n\mid n\in {\mathbb {Z}}\}\) as a single object, namely the orbit of \(\mathfrak {t}\) under the canonical action of the group of integers on the class \(\text {ts}(\mathcal {S}\text {p})\) of t-structures on the category of spectra. A closer look at this example makes it evident that this action is also monotone with respect to the natural structure of partially ordered class of \(\text {ts}(\mathcal {S}\text {p})\), and the natural total order of \({\mathbb {Z}}\): more formally, the group homomorphism \({\mathbb {Z}}\longrightarrow \text {Aut}(\text {ts}(\mathcal {S}\text {p}))\) defining the action is also a monotone mapping.
The aim of this paper is to investigate the consequences of taking this point of view further on the classical theory of t-structures. In particular, we describe all the terminology we need about partially ordered groups and their actions in Sect. 2, and then we specialize the discussion to \(\mathbb {Z}\)-actions on partially ordered sets. This is motivated by the fact that the class of t-structures on a given stable \(\infty \)-category carries a natural choice of such an action.
Even if we employ a rather systematic approach, we do not aim at reaching a complete generality, but instead at gathering a number of useful results and nomenclature we can refer to along the present article. Among various possible choices, we mention specialized references as [2, 8, 10] for an extended discussion of the theory of actions on ordered groups.
We introduce the definition of a slicing of a poset J (Definition 3.1) and of a J-slicing of a stable \(\infty \)-category  (Definition 3.11) in Sect. 3: of course these are not original definitions, as the notion is classical in order theory under different names; our only purpose here is to collect the minimal amount of theory for the sake of clarity. Namely, in the same spirit of Dedekind’s construction of real numbers, we consider decompositions of a poset J (more often than not, a totally ordered one) into an upper and lower set, and associate with each such a decomposition a t-structure on an ambient \((\infty ,1)\)-category
(Definition 3.11) in Sect. 3: of course these are not original definitions, as the notion is classical in order theory under different names; our only purpose here is to collect the minimal amount of theory for the sake of clarity. Namely, in the same spirit of Dedekind’s construction of real numbers, we consider decompositions of a poset J (more often than not, a totally ordered one) into an upper and lower set, and associate with each such a decomposition a t-structure on an ambient \((\infty ,1)\)-category  . The totally ordered set J will be assumed to be equipped with a monotone action of \(\mathbb {Z}\) and the correspondence
. The totally ordered set J will be assumed to be equipped with a monotone action of \(\mathbb {Z}\) and the correspondence

will be monotone and \({\mathbb {Z}}\)-equivariant.
Now, following [1], (bounded) t-structures on a triangulated category can be seen as the datum of a set of (co)homological functors indexed by integers; thus a J-slicings can be seen as a generalization to “fractal” or “ non-integer” cohomological dimensions now indexed by J and not by \(\mathbb {Z}\). Namely, each J-slicing induces local cohomology objects depending on an interval, as discussed in Sect. 4.
In this framework many homological features appear as a shadow of clear constructions with totally ordered sets with \(\mathbb {Z}\)-actions. For instance, when the totally ordered set J has a heart \(J^\heartsuit \), i.e., when there’s a \(\mathbb {Z}\)-equivariant monotone morphism \(J \longrightarrow {\mathbb {Z}}\), a J-slicing on a stable \(\infty \)-category  is precisely the datum of a t-structure on
is precisely the datum of a t-structure on  together with a collection of torsion theories parametrized by \(J^\heartsuit \) on the heart of
together with a collection of torsion theories parametrized by \(J^\heartsuit \) on the heart of  , which turns out to be an abelian \(\infty \)-category. This is shown Sects. 5 and 7.
, which turns out to be an abelian \(\infty \)-category. This is shown Sects. 5 and 7.
In Sect. 6, we recover the theory of classical semi-orthogonal decompositions by considering the case when \({\mathbb {Z}}\) acts trivially on J. Semi-orthogonal decompositions and J-slicing with hearts are essentially the only two interesting classes, as shown by the structure theorem we prove in section Sect. 8: under suitable finiteness assumptions, the datum of a J-slicing on a stable \(\infty \)-category  is equivalent to the datum of a finite type semi-orthogonal decomposition of
is equivalent to the datum of a finite type semi-orthogonal decomposition of  , together with bounded t-structures on the slices and collections of torsion theories on the hearts of these t-structures (Theorem 8.2). It is worth mentioning that, under the finiteness conditions of Theorem 8.2, when \(J={\mathbb {R}}\) the notion of J-slicing as discussed in the present paper actually becomes a reinterpretation of Bridgeland’s definition of slicing of a triangulated category [5]. This can be better appreciated by switching to the general approach to ‘stability data’ introduced by [9].
, together with bounded t-structures on the slices and collections of torsion theories on the hearts of these t-structures (Theorem 8.2). It is worth mentioning that, under the finiteness conditions of Theorem 8.2, when \(J={\mathbb {R}}\) the notion of J-slicing as discussed in the present paper actually becomes a reinterpretation of Bridgeland’s definition of slicing of a triangulated category [5]. This can be better appreciated by switching to the general approach to ‘stability data’ introduced by [9].
Finally, in Sect. 7 we show how the functoriality of the association \(J\mapsto \{\text {J-slicings}\}\) gives rise to an elegant and synthetic reformulation of classical tilting theory [12].
1.1 Notation and conventions
We will work within the framework of stable \(\infty \)-categories in the sense of [18]. The reader who prefers to work in the more traditional framework of triangulated categories will find no difficulty in pretending that all higher categories are instead categories and that all fiber sequences are distinguished triangles; indeed, many of our statements and constructions are actually adjustments of classical arguments valid in triangulated categories. However a few proofs become more natural when stated in the language of stable \(\infty \)-categories (for example, theorems whose proof involves a certain universal property unavailable in the triangulated world).
To make the article more self-contained and enjoyable to a reader with no previous exposure to stable \(\infty \)-categories, we recall here the minimal amount of \(\infty \)-categorical notions we will make use of. As in [17], we will call ‘\(\infty \)-category’ an \((\infty ,1)\)-category, i.e. an higher category whose k-morphisms are invertible (up to homotopy) for any \(k>1\). In colloquial terms, this means that an \(\infty \)-category has objects, morphisms, homotopies between morphisms, homotopies between homotopies, etc., and such homotopies are all invertible. As shown in [13, 17], the entire theory of categories transports to \(\infty \)-categories. In particular, an \(\infty \)-category  can have finite co/limits.
can have finite co/limits.
Definition
(Stable\(\infty \)-category) An \(\infty \)-category  is said to be stable if it has all finite limits and all finite colimits, and if in addition it satisfies the so-called pullout axiom: a diagram
is said to be stable if it has all finite limits and all finite colimits, and if in addition it satisfies the so-called pullout axiom: a diagram

in  (or, more formally, an object of the functor category
(or, more formally, an object of the functor category  ) is a pushout if and only if it is a pullback.
) is a pushout if and only if it is a pullback.
We will henceforth call these diagrams pullout diagrams or simply pullouts. The pullout axiom is inherently \(\infty \)-categorical: the only ordinary category with finite limits and colimits satisfying it is the trivial category (i.e. the terminal additive category with a single zero object \(\mathbf{0}\)). It is also extremely powerful: if  is a stable \(\infty \)-category, then its homotopy category
is a stable \(\infty \)-category, then its homotopy category  is triangulated. In other words, this single and extremely simple axiom subsumes all of the axiomatic of triangulated categories (the notorious octahedral axiom included).
is triangulated. In other words, this single and extremely simple axiom subsumes all of the axiomatic of triangulated categories (the notorious octahedral axiom included).
Unfortunately not every triangulated category can be realized as the homotopy category of a stable \(\infty \)-category, see [20]; stable \(\infty \)-categories therefore only give rise to ‘well-behaved’ triangulated categories. It should however be remarked that ill-behaved ones are often artificial: the reader can then safely assume that essentially every ‘reasonable’ triangulated category is the homotopy category  of some stable \(\infty \)-category
of some stable \(\infty \)-category  .
.
As already said, a particularly pleasant consequence of this good behaviour is the fact that in a stable \(\infty \)-category the notions of t-structure [1] and of normal factorization system (or normal torsion theory) [6] are naturally equivalent; this remains true in a triangulated category, although the equivalence is much less transparent (see [19], where this issue is framed in a fairly more general environment). This equivalence will be used several times along the discussion, as well as the following result from [7]:
Lemma
(Sator lemma) If \((\mathcal {E},\mathcal {M})\) is a factorization system on a stable \(\infty \)-category  , with the property that both \(\mathcal {E}\) and \(\mathcal {M}\) saisfy the ‘two out of three’ property, then for every object
, with the property that both \(\mathcal {E}\) and \(\mathcal {M}\) saisfy the ‘two out of three’ property, then for every object  an initial arrow \(0\longrightarrow A\) lies in \(\mathcal {E}\) (resp. in \(\mathcal {M}\)) if and only if the terminal arrow \(A\longrightarrow 0\) of the same object lies in \(\mathcal {E}\) (resp. in \(\mathcal {M}\)).
an initial arrow \(0\longrightarrow A\) lies in \(\mathcal {E}\) (resp. in \(\mathcal {M}\)) if and only if the terminal arrow \(A\longrightarrow 0\) of the same object lies in \(\mathcal {E}\) (resp. in \(\mathcal {M}\)).
A final line to conclude this introductory subsection: not to spoil the reader’s fun, while avoiding to to hide them their meaning, translations of the quotes opening each section are provided immediately before the bibliography.
2 Posets with \(\mathbb {Z}\)-actions

This section introduces the terminology about partially ordered groups and their actions, and then specializes the discussion to \(\mathbb {Z}\)-actions. We do not aim at a complete generality, but instead at gathering a number of useful results and nomenclature which is useful to have at hand. Among various possible choices, we mention specialized references as [2, 8, 10] for an extended discussion of the theory of actions on ordered groups.
We begin by recalling the well known fact that the category  of partially ordered sets and monotone maps is cartesian closed. Namely, the product order on the cartesian product \(P\times Q\) of two posets \((P,\le )\) and \((Q,\le )\), given by \((x,y)\le (x',y')\) if and only if \(x\le x'\) and \(y\le y'\) makes \((P\times Q,\le )\) together with the projections on the factors satisfy the universal property of the product in the category of posets. Moreover, the set
of partially ordered sets and monotone maps is cartesian closed. Namely, the product order on the cartesian product \(P\times Q\) of two posets \((P,\le )\) and \((Q,\le )\), given by \((x,y)\le (x',y')\) if and only if \(x\le x'\) and \(y\le y'\) makes \((P\times Q,\le )\) together with the projections on the factors satisfy the universal property of the product in the category of posets. Moreover, the set  of monotone maps from \((P,\le )\) to \((Q,\le )\) has a natural order on it given by \(f\le g\) if and only if \(f(x)\le g(x)\) for every x in P. With this order one has an adjunction
of monotone maps from \((P,\le )\) to \((Q,\le )\) has a natural order on it given by \(f\le g\) if and only if \(f(x)\le g(x)\) for every x in P. With this order one has an adjunction

Remark 2.1
The product order is not the only standard order one puts on the product \(P\times Q\) of two posets P and Q. Another commonly used one is the lexicographic order defined by \((x,y)\le _{{\text {lex}}} (x',y')\) if and only if \(x< x'\) or \(x=x'\) and \(y\le y'\). The lexicographic order does not make \(P\times Q\) be the product of P and Q in the category of posets, but it still has a few peculiar properties that, as we are going to see, are relevant to the theory of slicings.
Remark 2.2
Let \((P,\le )\) be a poset, and let \(\sim \) be an equivalence relation on the set P. One says that \(\sim \) is compatible with the order relation if \(x\le y\), \(x\sim x'\) and \(y\sim y'\) imply \(x'\le y'\) or \(x'\sim y'\). When this happens the quotient set \(P/_{\!\sim }\) inherits a order relation from P by \([x]\le [y]\) if and only if \(x\le y\) or \(x\sim y\). Moreover the projection to the quotient \(P\longrightarrow P/_{\!\sim }\) is a morphism of posets.
Definition 2.3
A partially ordered group (“po-group” for short) is a pair \((G, \le )\) consisting of a group G and of a partial order relation \(\le \) on G such that the group multiplication \(\cdot :G\times G\longrightarrow G\) is a map of posets, where \(G\times G\) is endowed with the product order: for any two pairs (g, h) and \((g',h')\) with \(g\le g'\) and \(h\le h'\) we have \(gg' \le hh'\).
Remark 2.4
In the literature on the subject it is customary draw a distinction between a left po-group and a right po-group. We choose to ignore this subtlety, since all the po-groups we will be dealing with will be ordered by two-sided congruences.
Remark 2.5
If \((G,\le )\) is a po-group, the inversion  is an antitone antiautomorphism of groups, i.e. we have that \(g\le h\) if and only if \(h^{-1}\le g^{-1}\). Moreover the set \(G^+\) of positive elements, i.e. the set \(\{g\in G\mid 1\le g\}\) is closed under conjugation.
is an antitone antiautomorphism of groups, i.e. we have that \(g\le h\) if and only if \(h^{-1}\le g^{-1}\). Moreover the set \(G^+\) of positive elements, i.e. the set \(\{g\in G\mid 1\le g\}\) is closed under conjugation.
Example 2.6
Let \((P,\le )\) be a poset, and let  be the automorphism group of P as a poset, i.e., the set of monotone bijections of p into itself. Then
be the automorphism group of P as a poset, i.e., the set of monotone bijections of p into itself. Then  inherits an order relation by its inclusion in the poset
inherits an order relation by its inclusion in the poset  , and this makes
, and this makes  a partially ordered group. This is the standard po-group structure on
a partially ordered group. This is the standard po-group structure on  .
.
Remark 2.7
Any group G can be seen as a po-group with the trivial order relation \(g\le h\) if and only if \(g=h\). It is worth noticing that on finite groups the trivial order is the only possible po-group structure. Namely, assume \(g\le h\) and let \(k=g^{-1}h\). Then we have \(1\le k\le k^2\le k^2\le \cdots \le k^{\text {ord}(k)}=1\) and so \(k=1\), i.e., \(g=h\).
Definition 2.8
A homomorphism of po-groups consists of a group morphism \(f:G\longrightarrow H\) which is also a monotone mapping. This defines a category \(\mathcal {PoGrp}\) of partially ordered groups and their homomorphisms.
Definition 2.9
Let \((G,\le )\) be a po-group. A G-poset is a partially ordered set \((P, \le )\) endowed with a po-group homomorphism  to the group of order isomorphisms of P with its standard po-group structure.
to the group of order isomorphisms of P with its standard po-group structure.
Remark 2.10
Equivalently, a G-poset is a partially ordered set P together with a group action \(G\times P\longrightarrow P\) which is a morphism of posets, where on \(G\times P\) one has the product order.
Example 2.11
Every po-group G is a G-poset with the multiplication action of G on itself.
Remark 2.12
An equivalence relation \(\sim \) on a G-poset P is said to be compatible with the G-action if \(x\sim y\) implies \(g\cdot x\sim g\cdot y\) for any g in G. If \(\sim \) is compatible both with the order and with the G-action then the quotient set \(P/_{\!\sim }\) is naturally a G-poset with the G-action \(g\cdot [x]=[g\cdot x]\). Moreover the projection to the quotient is a morphism of G-posets.
We now specialize our discussion to the case \(G=\mathbb {Z}\)
Definition 2.13
A \(\mathbb {Z}\)-poset is a partially ordered set \((P,\le )\) together with a group action
which is a morphism of partially ordered sets, when \(\mathbb {Z}\) is regarded with its usual total order.
Remark 2.14
It is immediate to see that a \(\mathbb {Z}\)-poset is equivalently the datum of a poset \((P,\le )\) together with a monotone bijection \(\rho :P\longrightarrow P\) such that \(x\le \rho (x)\) for any x in P. The function \(\rho \) and the action are related by the identity \(\rho (x)=x+_P1\).
Notation 2.15
To avoid a cumbersome accumulation of indices, the action \(+_P\) will be often denoted as a simple “\(+\)”. This is meant to evoke in the reader the most natural example of a \(\mathbb {Z}\)-poset, given by \({\mathbb {Z}}\) itself, and to simplify our notation for the axioms of an action:
We will also write \(x-n\) for \(x+_P(-n)\).
Example 2.16
The poset \((\mathbb {Z},\le )\) of integers with their usual order is a \(\mathbb {Z}\)-poset with the action given by the usual sum of integers. The poset \((\mathbb {R},\le )\) of real numbers with their usual order is a \(\mathbb {Z}\)-poset for the action given by the sum of real numbers with integers (seen as a subring of real numbers).
Example 2.17
Given any poset \((P,\le )\), the poset \(\mathbb {Z}\times _{\text {lex}}P\) carries a natural \({\mathbb {Z}}\)-action given by \((n,x)+1=(n+1,x)\), i.e., by the standard \(\mathbb {Z}\)-action on the first factor and by the trivial \(\mathbb {Z}\)-action on the second factor.
Remark 2.18
If \((P,\le )\) is a finite poset, then the only \(\mathbb {Z}\)-action it carries is the trivial one. Indeed, if \(\rho :P\longrightarrow P\) is the monotone bijection associated with the \(\mathbb {Z}\)-action, one sees that \(\rho \) is a finite order element in  , by the finiteness of P. Therefore there exists an \(n\ge 1\) such that \(\rho ^n=\text {id}_P\). It follows that, for any x in P,
, by the finiteness of P. Therefore there exists an \(n\ge 1\) such that \(\rho ^n=\text {id}_P\). It follows that, for any x in P,
and so \(x=x+1\).
Remark 2.19
An obvious terminology: a G-fixed point for a G-poset P is an element \(p\in P\) kept fixed by all the elements of G under the G-action. Clearly, an element x of a \(\mathbb {Z}\)-poset P is a \(\mathbb {Z}\)-fixed point if and only if \(x+ 1 = x\), or equivalently \(x-1=x\). From this it immediately follows that if \(x\in P\) is a \(\le \)-maximal or \(\le \)-minimal element in the \(\mathbb {Z}\)-poset P, then it is a \(\mathbb {Z}\)-fixed point.
Remark 2.20
Given a poset P we can always define a partial order on the set \(P_{\! \mathchoice{\lhd \rhd }{\lhd \rhd }{\lhd \rhd }{\lhd \rhd } } = P\cup \{-\,\infty ,+\,\infty \}\) which extends the partial order on P by the rule \(-\infty \le x\le +\infty \) for any \(x\in P\).
Lemma 2.21
If \((P,\le )\) is a \(\mathbb {Z}\)-poset, then \((P_{\! \mathchoice{\lhd \rhd }{\lhd \rhd }{\lhd \rhd }{\lhd \rhd } },\le )\) carries a natural \(\mathbb {Z}\)-action extending the \(\mathbb {Z}\)-action on P, by declaring both \(-\infty \) and \(+\infty \) to be \(\mathbb {Z}\)-fixed points.
Proof
Adding a fixed point always gives an extension of an action, so we only need to check that the extended action is compatible with the partial order. This is equivalent to checking that also on \(P_{\! \mathchoice{\lhd \rhd }{\lhd \rhd }{\lhd \rhd }{\lhd \rhd } }\) the map \(x\mapsto x+1\) is a monotone bijection such that \(x\le x+1\), which is immediate. \(\square \)
Posets with \(\mathbb {Z}\)-actions naturally form a category  , whose morphisms are \(\mathbb {Z}\)-equivariant morphisms of posets. More explicitly, if P and Q are \(\mathbb {Z}\)-posets with actions \(+_P\) and \(+_Q\), then a morphism of \(\mathbb {Z}\)-posets between them is a morphism of posets \(\varphi :P\longrightarrow Q\) such that
, whose morphisms are \(\mathbb {Z}\)-equivariant morphisms of posets. More explicitly, if P and Q are \(\mathbb {Z}\)-posets with actions \(+_P\) and \(+_Q\), then a morphism of \(\mathbb {Z}\)-posets between them is a morphism of posets \(\varphi :P\longrightarrow Q\) such that
for any \(x\in P\) and any \(n\in \mathbb {Z}\).
Remark 2.22
If P and Q are \(\mathbb {Z}\)-posets, then the hom-set  is naturally a \(\mathbb {Z}\)-poset. Namely, as we have already remarked,
is naturally a \(\mathbb {Z}\)-poset. Namely, as we have already remarked,  is naturally a poset, and so
is naturally a poset, and so  inherits the poset structure as a subset. The \(\mathbb {Z}\)-action is given by \((\varphi +n)(x)=\varphi (x) +_Q n\). This makes
inherits the poset structure as a subset. The \(\mathbb {Z}\)-action is given by \((\varphi +n)(x)=\varphi (x) +_Q n\). This makes  a closed category.
a closed category.
Remark 2.23
Every poset can be seen as a \(\mathbb {Z}\)-poset with the trivial \(\mathbb {Z}\)-action. Since every monotone mapping is \(\mathbb {Z}\)-equivariant with respect to the trivial \(\mathbb {Z}\)-action, this gives a fully faithful embedding  .
.
Lemma 2.24
The choice of an element x in a \(\mathbb {Z}\)-poset P is equivalent to the datum of a \(\mathbb {Z}\)-equivariant morphism \(\varphi :(\mathbb {Z},\le )\longrightarrow (P,\le )\). Moreover x is a \(\mathbb {Z}\)-fixed point if and only if the corresponding morphism \(\varphi \) factors \(\mathbb {Z}\)-equivariantly through \((*,\le )\), where \(*\) denotes the terminal object of  .
.
Proof
To the element x one associates the \(\mathbb {Z}\)-equivariant morphism \(\varphi _x\) defined by \(\varphi _x(n)=x+n\). To the \(\mathbb {Z}\)-equivariant morphism \(\varphi \) one associates the element \(x_\varphi =\varphi (0)\). It is immediate to check that the two constructions are mutually inverse. The proof of the second part of the statement is straightforward. \(\square \)
Lemma 2.25
Let \(\varphi :(\mathbb {Z},\le )\longrightarrow (P,\le )\) be a \(\mathbb {Z}\)-equivariant morphism of \(\mathbb {Z}\)-posets. Then \(\varphi \) is either injective or constant.
Proof
Assume \(\varphi \) is not injective. then there exist two integers n and m with \(n>m\) such that \(\varphi (n)=\varphi (m)\). By \(\mathbb {Z}\)-equivariancy we therefore have
with \(n-m\ge 1\) and \(x_\varphi =\varphi (0)\). The conclusion then follows by the same argument used in Remark 2.18. \(\square \)
Lemma 2.26
Let \(\varphi :(P,\le )\longrightarrow (Q,\le )\) be a morphism of \(\mathbb {Z}\)-posets. Assume Q has a minimum and a maximum. Then \(\varphi \) extends to a morphism of \(\mathbb {Z}\)-posets \((P_{\! \mathchoice{\lhd \rhd }{\lhd \rhd }{\lhd \rhd }{\lhd \rhd } },\le )\longrightarrow (Q,\le )\) by setting \(\varphi (-\,\infty )=\min (Q)\) and \(\varphi (+\,\infty )=\max (Q)\).
Proof
Since \(\min (Q)\) and \(\max (Q)\) are \(\mathbb {Z}\)-fixed points by Remark 2.19, the extended \(\varphi \) is a morphism of \(\mathbb {Z}\)-posets. Moreover, since \(\min (Q)\) and \(\max (Q)\) are the minimum and the maximum of Q, respectively, the extended \(\varphi \) is indeed a morphism of posets, and so it is a morphism of \(\mathbb {Z}\)-posets. \(\square \)
All of the above applies in particular to totally ordered sets. We will denote by  the full subcategory of totally ordered sets, and by
the full subcategory of totally ordered sets, and by  the full subcategory of \(\mathbb {Z}\)-actions on totally ordered sets.
the full subcategory of \(\mathbb {Z}\)-actions on totally ordered sets.
Lemma 2.27
Let \((P, \le )\) be a totally ordered \({\mathbb {Z}}\)-poset. The relation \(x\sim y\) if and only if there are integers \(a,b \in {\mathbb {Z}}\) such that \(x + a \le y \le x + b \) is an equivalence relation on P compatible with both the order and the \({\mathbb {Z}}\)-action. It therefore induces a morphism of \({\mathbb {Z}}\)-posets \(P\longrightarrow P/_{\!\sim }\) given by the projection to the quotient. Moreover, \(P/_{\!\sim }\) is totally ordered and the \({\mathbb {Z}}\)-action on the quotient is trivial.
Proof
Checking that \(\sim \) is an equivalence relation is immediate: reflexivity is manifest; symmetry reduces to noticing that \(x + a \le y \le x + b \) is equivalent to \(y-b\le x\le y-a\); transitivity follows by the fact that \(x + a \le y \le x + b \) and \(y + c \le z \le y + d\) together imply \(x+ (a+ c) \le z \le x+(b + d)\). To see that \(\sim \) is compatible with the order relation, let \(x\le y\) and let \(x\sim x'\) and \(y\sim y'\). Then there exist a, b, c and d in \({\mathbb {Z}}\) such that \(x + a \le x' \le x + b \) and \(y + c \le y' \le y + d\). Since P is totally ordered, either \(x'\le y'\) or \(y'\le x'\). In the second case we have \(y'\le x' \le x + b\le y+b \le y'+b-c\), and so \(x'\sim y'\) by definition of the relation \(\sim \). The compatibility of \(\sim \) with the \({\mathbb {Z}}\)-action is straightforward. Therefore by Remarks 2.2 and 2.12 we see that the projection to the quotient \(P\longrightarrow P/_{\!\sim }\) is a morphism of \({\mathbb {Z}}\)-posets. Since the order on P is total, so is also the order induced by \(\sim \) on the quotient set. Finally, to see that the \({\mathbb {Z}}\) action on \(P/_{\!\sim }\) is trivial, just notice that for any x in P, we have \(x\le x+1\le x+1\) and so \([x]+1=[x]\). \(\square \)
Remark 2.28
If the \({\mathbb {Z}}\)-action on the totally ordered set P is trivial, then the equivalence relation from Lemma 2.27 is trivial as well: \(x\sim y\) if and only if \(x=y\).
Lemma 2.29
Let \((P, \le )\) be a totally ordered \({\mathbb {Z}}\)-poset, and let \(\sim \) be the equivalence relation from Lemma 2.27. Then either \([x]=\{x\}\) or \([x]={\mathbb {Z}}\times _{\text {lex}}[x,x+1)\), where \([x,x+1)=\{y\in P\mid x\le y<x+1\}\)
Proof
Let \(x\in P\); then either \(x=x+1\) or \(x<x+1\). In the first case x is a fixed point for the \(\mathbb {Z}\)-action on P and so the equivalence relation \(\sim \) is the trivial one: \(y\sim x\) if and only if \(y=x\). If \(x<x+1\) then the interval \([x,x+1)\) is nonempty, as \(x\in [x,x+1)\).
Let \(\varphi :{\mathbb {Z}}\times _{\text {lex}}[x,x+1)\longrightarrow P\) the map defined by \((n,y)\mapsto y+n\). The map \(\varphi \) is a morphism of \(\mathbb {Z}\)-posets.
Indeed, if \((n,y)\le _{\text {lex}} (n',y')\) either \(n<n'\) or \(n=n'\) and \(y\le y'\). In the first case we have \(n+1\le n'\) and so \(y+n< x+1+n\le x+n'\le y'+n'\), whereas in the second case we have \(y+n\le y'+n=y'+n'\). The map \(\varphi \) is also injective.
To conclude we only need to show that \(\varphi :{\mathbb {Z}}\times _{\text {lex}}[x,x+1)\longrightarrow [x]\) is surjective. Let \(z\in [x]\). By definition of the equivalence relation there exist a, b in \({\mathbb {Z}}\) such that \(x+a\le z\le x+b\). Since x is not a \(\mathbb {Z}\)-fixed point, we have \(a\le b\) and \(z\in [x+a,x+b+1)\). Writing
we see that there exists \(n\in \mathbb {Z}\) such that \(z\in [x,x+1)+n\), i.e., \(z=\varphi (n,y)\) for some y in \([x,x+1)\). \(\square \)
Proposition 2.30
The fully faithful embedding  given by trivial \(\mathbb {Z}\)-actions on totally ordered sets has a left adjoint.
given by trivial \(\mathbb {Z}\)-actions on totally ordered sets has a left adjoint.
Proof
For any totally ordered \(\mathbb {Z}\)-poset P, let \(\iota (P)\) be the \({\mathbb {Z}}\)-poset \(P/_{\!\sim }\), where \(\sim \) is the equivalence relation from Lemma 2.27. Then  is a functor, since if \(f:P\longrightarrow Q\) is a morphism of \({\mathbb {Z}}\)-posets then \(x+a\le y\le x+b\) implies
is a functor, since if \(f:P\longrightarrow Q\) is a morphism of \({\mathbb {Z}}\)-posets then \(x+a\le y\le x+b\) implies
and so f induces a well defined morphism of sets \({\tilde{f}}:\iota (P)\longrightarrow \iota (Q)\). It is immediate to see that \({\tilde{f}}\) is actually a morphism of \(\mathbb {Z}\)-posets and that \(f\rightsquigarrow {\tilde{f}}\) preserves identities and compositions of morphisms. Finally, to see that I is a right adjoint to the trivial action embedding  , let P be a a totally ordered \({\mathbb {Z}}\)-poset and Q be a totally ordered set. Since I is a functor, a morphism of \({\mathbb {Z}}\)-posets \(f:P\longrightarrow Q^\flat \) induces a morphism of posets \({\tilde{f}}:\iota (P)\longrightarrow \iota (Q^\flat )\). Moreover, since the \({\mathbb {Z}}\)-action on \(Q^\flat \) is trivial, we have \(\iota (Q^\flat )\cong Q\), see Remark 2.28. Therefore, \(f\mapsto {\tilde{f}}\) defines a map
, let P be a a totally ordered \({\mathbb {Z}}\)-poset and Q be a totally ordered set. Since I is a functor, a morphism of \({\mathbb {Z}}\)-posets \(f:P\longrightarrow Q^\flat \) induces a morphism of posets \({\tilde{f}}:\iota (P)\longrightarrow \iota (Q^\flat )\). Moreover, since the \({\mathbb {Z}}\)-action on \(Q^\flat \) is trivial, we have \(\iota (Q^\flat )\cong Q\), see Remark 2.28. Therefore, \(f\mapsto {\tilde{f}}\) defines a map

which we want to show is a bijection. Assume \({\tilde{f}}_1={\tilde{f}}_2\). Then, for any x in P we have \(f_1(x)\sim f_2(x)\) in \(Q^\flat \). Since the equivalence relation on \(Q^\flat \) is trivial, this means \(f_1=f_2\), so \(f\rightsquigarrow {\tilde{f}}\) is injective. Let now \(\varphi \) be a morphism of posets, \(\varphi :\iota (P)\longrightarrow Q\), and let \(f=\varphi \circ \pi \) where \(\pi :P\longrightarrow \iota (P)\) is the projection to the quotient. We have \({\tilde{f}}([x])=[f(x)]=f(x)=\varphi (\pi (x))=\varphi ([x])\), and so \(\varphi ={\tilde{f}}\), i.e., \(f\rightsquigarrow {\tilde{f}}\) is surjective. \(\square \)
3 Histoire d’\(\mathcal {O}(J)\)
Sa liberté était pire que n’importe quelle chaîne
D. Aury
Recall that a lower set in a poset J is a subset \(L\subseteq J\) such that if \(x\in L\) and \(y\le x\) then \(y\in L\); the set of lower sets of J is denoted \({\downharpoonleft } J\) and it naturally a partially ordered set. Dually, one defines upper sets and the set \({\upharpoonleft }J\) of upper sets with its natural partial order.
Definition 3.1
Let J be a poset. A slicing of J is a pair (L, U), where L is a lower set in J, U is an upper set, \(L\cap U=\emptyset \) and \(L\cup U=J\). The collection of all slicings of J will be denoted by \(\mathcal {O}(J)\).
Remark 3.2
Since the complement of an upper set is a lower set and vice versa, the projection on the second factor is a bijection
This induces a natural partial order on \(\mathcal {O}(J)\): we set \((L_1,U_1)\le (L_2,U_2)\) if and only if \(U_2\subseteq U_1\). Notice that \(\mathcal {O}(J)\) has a minimum given by the slicing \((\emptyset ,J)\) and a maximum given by the slicing \((J,\emptyset )\).
Remark 3.3
If J is totally ordered, then so is \(\mathcal {O}(J)\). Namely, let \(U_1\) and \(U_2\) two upper sets in J and assume that \(U_1\) is not a subset of \(U_2\). Then there exists an element x in \(U_1\) which is not in \(U_2\). If \(y\in U_2\) then either \(y\le x\) or \(y\ge x\) since J is totally ordered. But since \(U_2\) is an upper set \(y\le x\) would imply \(x\in U_2\) against our assumption. This means that \(y\ge x\) and, since \(U_1\) is an upper set, this implies \(y\in U_1\). Therefore if \(U_1\) is not a subset of \(U_2\) we have that \(U_2\subseteq U_1\).
Remark 3.4
If J is a \({\mathbb {Z}}\)-poset, then so is \(\mathcal {O}(J)\). The natural \({\mathbb {Z}}\)-action on \(\mathcal {O}(J)\) is given by
where \(L+n=\{x+n\,|\, x\in L\}\) and \(U+n=\{x+n\,|\, x\in U\}\).
Remark 3.5
Every element x in J determines two slicings of J: \(((-\infty ,x),[x,+\infty ))\) and \(((-\infty ,x],(x,+\infty ))\). Here \((-\infty ,x)\) is the lower set \(\{y\in J\,|\, y<x\}\), and similarly for \((-\infty ,x]\), \((x,+\infty )\) and \([x,+\infty )\). This gives two natural morphisms of posets \(J\longrightarrow \mathcal {O}(J)\). If J is a \({\mathbb {Z}}\)-poset, then these morphisms are \({\mathbb {Z}}\)-equivariant.
The construction of \(\mathcal {O}(J)\) is actually functorial in J so that we have the following
Lemma 3.6
The map \(J\rightsquigarrow \mathcal {O}(J)\) defines a functor

where  denotes the category of \(\mathbb {Z}\)-posets with minimum and maximum and with \(\mathbb {Z}\)-morphism of posets preserving them (these maps are called \(\{0,1\}\)-homomorphisms in lattice theory, see [11]).
denotes the category of \(\mathbb {Z}\)-posets with minimum and maximum and with \(\mathbb {Z}\)-morphism of posets preserving them (these maps are called \(\{0,1\}\)-homomorphisms in lattice theory, see [11]).
Proof
By the above remarks the only thing we have to prove is functoriality. For any morphism of \(\mathbb {Z}\)-posets \(f:J_1\longrightarrow J_2\), we set \(\mathcal {O}(f):U\longrightarrow f^{-1}(U)\). It is immediate to see that \(f^{-1}(U)\) is an upper set in \(J_2\) for any upper set U in \(J_1\) an that \(f^{-1}(U+1)=f^{-1}(U)+1\), so that \(\mathcal {O}(f)\) is indeed a morphism of \(\mathbb {Z}\)-posets from \(\mathcal {O}(J_2)\) to \(\mathcal {O}(J_1)\). Moreover we have \(\mathcal {O}(\text {id}_J)=\text {id}_{\mathcal {O}(J)}\) and \(\mathcal {O}(fg)=\mathcal {O}(g)\mathcal {O}(f)\), and \(\mathcal {O}(f)(\emptyset )=\emptyset \) and \(\mathcal {O}(f)(J_2)=J_1\). \(\square \)
Remark 3.7
Since the minimum and the maximum of a \(\mathbb {Z}\)-poset, when they exist, are necessarily fixed points of the \(\mathbb {Z}\)-action, we see that the inclusion  induces a \(\mathbb {Z}\)-poset structure on
induces a \(\mathbb {Z}\)-poset structure on  making this inclusion a morphism of \(\mathbb {Z}\)-posets.
making this inclusion a morphism of \(\mathbb {Z}\)-posets.
Example 3.8
The morphism \(n\mapsto [n,+\infty )\) induces an isomorphism of \({\mathbb {Z}}\)-posets \({\mathbb {Z}}_{ \mathchoice{\lhd \rhd }{\lhd \rhd }{\lhd \rhd }{\lhd \rhd } }\xrightarrow {\sim } \mathcal {O}({\mathbb {Z}})\). The morphisms \(x\mapsto (x,+\infty )\) and \(x\mapsto [x,+\infty )\) together induce an isomorphism of posets \({\mathbb {Z}}\)-posets
where \([\mathbf 1 ]\) is the totally ordered set \(\{0 < 1\}\).
Definition 3.9
Before introducing the main definition of this section, let us recall that a t-structure on a stable \(\infty \)-category  consists of a pair
consists of a pair  of full sub-\(\infty \)-categories satisfying the following properties:
of full sub-\(\infty \)-categories satisfying the following properties:
-
(i)
orthogonality:
 is contractible for each
is contractible for each  ,
,  ;
; -
ii)
one has
 and
and  ;
; -
(iii)
Any object
 fits into a (homotopy) fiber sequence
fits into a (homotopy) fiber sequence  , with
, with  in
in  and
and  in
in  .
.
We introduce further terminology as a separate remark:
Remark 3.10
The categories  and
and  are called the lower sub-\(\infty \)-category and the upper sub-\(\infty \)-category of the t-structure \(\mathfrak {t}\), respectively.
are called the lower sub-\(\infty \)-category and the upper sub-\(\infty \)-category of the t-structure \(\mathfrak {t}\), respectively.
The collection  of all t-structures on a stable \(\infty \)-category
of all t-structures on a stable \(\infty \)-category  is a poset with respect to following order relation: given two t-structures
is a poset with respect to following order relation: given two t-structures  and
and  , one has \(\mathfrak {t}_1 \le \mathfrak {t}_2\) if and only if
, one has \(\mathfrak {t}_1 \le \mathfrak {t}_2\) if and only if  .
.
The ordered group \(\mathbb {Z}\) acts on  in a way that is fixed by the action of the generator \(+1\); this maps a t-structure
in a way that is fixed by the action of the generator \(+1\); this maps a t-structure  to the shiftedt-structure
to the shiftedt-structure  . Since \(\mathfrak {t}\le \mathfrak {t}[1]\) one sees that
. Since \(\mathfrak {t}\le \mathfrak {t}[1]\) one sees that  is naturally a \(\mathbb {Z}\)-poset. Finally, the poset
is naturally a \(\mathbb {Z}\)-poset. Finally, the poset  has a minimum and a maximum given by
has a minimum and a maximum given by  and
and  , respectively. These are called the trivialt-structures.
, respectively. These are called the trivialt-structures.
Definition 3.11
Let \((J,\le )\) be a \(\mathbb {Z}\)-poset. A J-slicing of a stable \(\infty \)-category  is a \(\mathbb {Z}\)-equivariant morphism of posets
is a \(\mathbb {Z}\)-equivariant morphism of posets  respecting minima and maxima on both sides. We denote as
respecting minima and maxima on both sides. We denote as  the class of all J-slicings of the category
the class of all J-slicings of the category  ;Footnote 2
;Footnote 2
More explicitly, a J-slicing is a family \(\{\mathfrak {t}_{(L,U)}\}_{(L,U)\in \mathcal {O}(J)}\) of t-structures on  such that
such that
-
(i)
\(\mathfrak {t}_{(L_1,U_1)}\le \mathfrak {t}_{(L_2,U_2)}\) if \((L_1,U_1)\le (L_2,U_2)\) in \(\mathcal {O}(J)\);
-
(ii)
\(\mathfrak {t}_{(L,U)+1}=\mathfrak {t}_{(L,U)}[1]\) for any \((L,U)\in \mathcal {O}(J)\).
-
(iii)
 and
and  .
.
Remark 3.12
Of course,  : this, together with 3.6 and 3.7, gives that
: this, together with 3.6 and 3.7, gives that  is a functor.
is a functor.
Notation 3.13
We will denote the lower and the upper sub-\(\infty \)-categories of the t-structure \(\mathfrak {t}_{(L,U)}\) by  and
and  , respectively, i.e., we write
, respectively, i.e., we write  . For \(i\in J\), we will write
. For \(i\in J\), we will write  ,
,  ,
,  and
and  for
for  and
and  , respectively. Note that, by \(\mathbb {Z}\)-equivariancy, we have
, respectively. Note that, by \(\mathbb {Z}\)-equivariancy, we have  , and similarly for the other cases.
, and similarly for the other cases.
Example 3.14
By Lemma 2.24 and Example 3.8, a \(\mathbb {Z}\)-slicing on  is equivalent to the datum of a t-structure
is equivalent to the datum of a t-structure  . One has
. One has  for any \(n\in {\mathbb {Z}}\), consistently with the Notation 3.13,
for any \(n\in {\mathbb {Z}}\), consistently with the Notation 3.13,  and
and  . Notice that by our Remark 2.18, as soon as
. Notice that by our Remark 2.18, as soon as  is a proper subcategory of
is a proper subcategory of  , then the inclusion
, then the inclusion  is proper for all \(n\in \mathbb {Z}\), i.e. the orbit \(\mathfrak {t}+ \mathbb {Z}\) is an infinite set. The equivalence between t-structures and \(\mathbb {Z}\)-slicings can also be seen in the light of Remark 3.12: for every \(\mathbb {Z}\)-poset P with minimum and maximum one has a distinguished isomorphism
is proper for all \(n\in \mathbb {Z}\), i.e. the orbit \(\mathfrak {t}+ \mathbb {Z}\) is an infinite set. The equivalence between t-structures and \(\mathbb {Z}\)-slicings can also be seen in the light of Remark 3.12: for every \(\mathbb {Z}\)-poset P with minimum and maximum one has a distinguished isomorphism  given by \(\varphi \mapsto \varphi ([0,+\infty ))\)
given by \(\varphi \mapsto \varphi ([0,+\infty ))\)
Example 3.15
By Example 3.8, an \(\mathbb {R}\)-slicing on  is the datum of two t-structures
is the datum of two t-structures  and
and  on
on  for any \(\lambda \in \mathbb {R}\) in such a way that
for any \(\lambda \in \mathbb {R}\) in such a way that  , etc., and with the inclusions
, etc., and with the inclusions  for any \(\lambda \in {\mathbb {R}}\) and
for any \(\lambda \in {\mathbb {R}}\) and

for any \(\lambda _1<\lambda _2\) in \({\mathbb {R}}\). \({\mathbb {R}}\)-slicings have been introduced in [5], where they are called simply “slicings”. Actually [5] imposes more restrictive conditions to ensure “compactness” of the factorization, we will come back to this later. Compare also [9].
Remark 3.16
Since the subcategories  and
and  are the lower and the upper subcategories of a t-structure \(\mathfrak {t}_{(L,U)}\) they are reflexive and coreflective, respectively. In particular we have reflection and coreflection functors
are the lower and the upper subcategories of a t-structure \(\mathfrak {t}_{(L,U)}\) they are reflexive and coreflective, respectively. In particular we have reflection and coreflection functors

For X an object in  we will occasionally write \(X_L\) for \(R_LX\) and \(X_U\) for \(S_UX\), and similarly for morphisms. Finally, by composing \(R_L\)and \(S_U\) with the inclusions of
we will occasionally write \(X_L\) for \(R_LX\) and \(X_U\) for \(S_UX\), and similarly for morphisms. Finally, by composing \(R_L\)and \(S_U\) with the inclusions of  and
and  in
in  , we can look at \(R_L\) and \(S_U\) as endofunctors of
, we can look at \(R_L\) and \(S_U\) as endofunctors of  .
.
In order to investigate properties of the (co-)reflections S and R, we recall the main result from [7]: there is an equivalence between t-structures on  and normal factorization systems on
and normal factorization systems on  , so that \(\mathfrak {t}\) can equivalently be seen as a \(\mathbb {Z}\)-equivariant morphism
, so that \(\mathfrak {t}\) can equivalently be seen as a \(\mathbb {Z}\)-equivariant morphism  , where
, where  denotes the \({\mathbb {Z}}\)-poset of normal factorization systems of
denotes the \({\mathbb {Z}}\)-poset of normal factorization systems of  . Explicitly, this equivalence is given as follows: given a t-structure
. Explicitly, this equivalence is given as follows: given a t-structure  on
on  , the corresponding factorization system \((\mathcal {E},\mathcal {M})\) is characterized by
, the corresponding factorization system \((\mathcal {E},\mathcal {M})\) is characterized by

Since we are going to use this fact several times, we recall that both the class \(\mathcal {E}\) and the class \(\mathcal {M}\) have the 3-for-2 property. In particular this implies the Sator lemma:
For further information on normal factorization systems in stable \(\infty \)-categories we address the reader to [7, 16].
Remark 3.17
Notice that the left class \(\mathcal {E}\) of the normal factorization system \((\mathcal {E},\mathcal {M})\) corresponds to the right class  of the corresponding t-structure
of the corresponding t-structure  . One could avoid this position switch by writing the pair of classes in a t-structure as
. One could avoid this position switch by writing the pair of classes in a t-structure as  , however we preferred to keep the upper class on the right to agree with the standard orientation on the line of real numbers.
, however we preferred to keep the upper class on the right to agree with the standard orientation on the line of real numbers.
Remark 3.18
Since \((\mathcal {E},\mathcal {M})\) are a factorization system, the class \(\mathcal {M}\) is closed under pullbacks and the class \(\mathcal {E}\) is closed under pushouts. Together with the Sator lemma this implies that  and
and  are extension closed.
are extension closed.
Lemma 3.19
Let \(\mathfrak {t}\) be a J-slicing of  and let \((L_0,U_0)\) and \((L_1,U_1)\) two slicings of J with \((L_0,U_0)\le (L_1,U_1)\). Then we have the natural isomorphisms
and let \((L_0,U_0)\) and \((L_1,U_1)\) two slicings of J with \((L_0,U_0)\le (L_1,U_1)\). Then we have the natural isomorphisms
-
(i)
\(R_{L_0}R_{L_1}\cong R_{L_1}R_{L_0}\cong R_{L_0}\);
-
(ii)
\( S_{U_0}S_{U_1}\cong S_{U_1}S_{U_0}\cong S_{U_1}\);
-
(iii)
\(R_{L_0}S_{U_1}\cong S_{U_1}R_{L_0}\cong 0\).
Proof
It is enough to prove (i) and (iii), as the proof of (ii) is dual to (i).
We denote \(\mathfrak {t}_0\) and \(\mathfrak {t}_1\) the t-structures corresponding to \((L_0,U_0)\) and \((L_1,U_1)\), respectively, and by \((\mathcal {E}_0,\mathcal {M}_0)\) and \((\mathcal {E}_1,\mathcal {M}_1)\) the corresponding normal torsion theories. Since \((L_0,U_0)\le (L_1,U_1)\) we have \(\mathcal {M}_{0} \subseteq \mathcal {M}_{1}\) and \(\mathcal {E}_1\subseteq \mathcal {E}_0\).
The object \(S_1X\) is obtained by \((\mathcal {E}_1, \mathcal {M}_1)\)-factoring the arrow \(0\longrightarrow X\) as \(0\xrightarrow {\mathcal {E}_1}S_1X\xrightarrow {\mathcal {M}_1}X\). Since \(\mathcal {E}_1\subseteq \mathcal {E}_0\), this shows that \(0\longrightarrow S_1X\) is in \(\mathcal {E}_0\) and so, by the Sator lemma, also \(S_1X\longrightarrow 0\) is in \(\mathcal {E}_0\). Now the object \(R_0S_1X\) is obtained by the \((\mathcal {E}_0, \mathcal {M}_0)\)-factorization of the terminal morphism \(S_1X\longrightarrow 0\) as \(S_1X\xrightarrow {\mathcal {E}_0}R_0S_1X\xrightarrow {\mathcal {M}_0}0\).
By the 3-for-2 property for \(\mathcal {E}_0\) we see that \(R_0S_1X \longrightarrow 0\) lies in \(\mathcal {E}_{0}\cap \mathcal {M}_{0}\), hence it an isomorphism, so that \(R_0S_1 X\cong 0\). The proof that \(S_1R_0X\cong X\) is perfectly dual. This proves (iii).
The proof of (i) goes as follows. The reflection \(R_0R_1 X\) is defined by the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization \(R_1X\xrightarrow {\mathcal {E}_0}R_0R_1X\xrightarrow {\mathcal {M}_0}0\). Since \(\mathcal {E}_1\subseteq \mathcal {E}_0\) and \(X\longrightarrow R_1X\) is in \(\mathcal {E}_1\) we see that \(X\longrightarrow R_0R_1X\longrightarrow 0\) is already the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of \(X\longrightarrow 0\) and so by uniqueness of the factorization we have \(R_0R_1X\cong R_0X\). Finally, the reflection \(R_1R_0 X\) is defined by the \((\mathcal {E}_1,\mathcal {M}_1)\)-factorization \(R_0X\xrightarrow {\mathcal {E}_1}R_1R_0X\xrightarrow {\mathcal {M}_1}0\). Since \(R_0X\longrightarrow 0\) is in \(\mathcal {M}_0\subseteq \mathcal {M}_1\), by the 3-for-2 property we have that \(R_0X\longrightarrow R_1R_0X\) is in \(\mathcal {E}_1\cap \mathcal {M}_1\) and so it is an isomorphism. \(\square \)
Remark 3.20
Notice how, in the proof of the above lemma, one sees that applying \(R_{L_0}\) to the natural morphism \(R_{L_1}X\longrightarrow 0\) we get a natural morphism \(R_{L_1}X\longrightarrow R_{L_0} X\), an so one has a natural transformation \(R_{L_1}\longrightarrow R_{L_0}\). Dually, we have a natural transformation \(S_{U_1}\longrightarrow S_{U_0}\).
Lemma 3.21
Let \(\mathfrak {t}\) be a J-slicing of  and let \((L_0,U_0)\) and \((L_1,U_1)\) two slicings of J with \((L_0,U_0)\le (L_1,U_1)\). Then we have natural isomorphisms
and let \((L_0,U_0)\) and \((L_1,U_1)\) two slicings of J with \((L_0,U_0)\le (L_1,U_1)\). Then we have natural isomorphisms
Moreover \(S_{U_0}R_{L_1}\) is the fiber of the natural transformation \(R_{L_1}\longrightarrow R_{L_0}\) and \(R_{L_1}S_{U_0}\) is the cofiber of the natural transformation \(S_{U_1}\longrightarrow S_{U_0}\)
Proof
In the same notation as in the proof of Lemma 3.19 we have that \(\mathcal {E}_1\subseteq \mathcal {E}_0\) and \(\mathcal {M}_0\subseteq \mathcal {M}_1\). Since both \((\mathcal {E}_0,\mathcal {M}_0)\) and \((\mathcal {E}_1,\mathcal {M}_1)\) are normal factorization systems, the isomorphisms of Lemma 3.19 give the diagram

where every square is a pullout. The fact that each class \(\mathcal {E}_i\) is closed under pushout and each \(\mathcal {M}_i\) is closed under pullback now gives that the arrows \(S_0X \longrightarrow F \longrightarrow 0\) and \(0\longrightarrow F \longrightarrow R_1X\) are respectively the \((\mathcal {E}_1, \mathcal {M}_1)\)-factorization of \(S_0X\longrightarrow 0\) and the \((\mathcal {E}_0, \mathcal {M}_0)\)-factorization of \(0\longrightarrow R_1X\), so that \(R_1 S_0 X \cong F \cong S_0 R_1 X\).
To prove the second part of the statement, notice that by definition of normal factorization system associated to the slicing \((L_0,U_0)\) we have a fiber sequence

and the conclusion follows from the natural isomorphism \(R_0R_1X\cong R_0X\). Dually one proves the statement on the cofiber of \(S_{U_0}\longrightarrow S_{U_1}\). \(\square \)
3.1 A tale of intervals
Although a few of the statements we are going to prove hold more generally for arbitrary \({\mathbb {Z}}\)-posets, for the remainder of this section we will restrict our attention to \({\mathbb {Z}}\)-posets which are totally ordered sets.
Definition 3.22
Let J be a poset. An interval in J is a subset \(I\subseteq J\) such that if \(x,y\in I\) and \(x\le z\le y\) in J, then \(z\in I\).
Example 3.23
Let J be a totally ordered \({\mathbb {Z}}\)-poset, and let \(\sim \) be the equivalence relation from Lemma 2.27. For \(i\in J\), let \(I_i\) be the equivalence class of i. Then \(I_i\) is an interval. Namely, id \(x,y\in I_i\) then there exist integers a, b with \(i+a\le x\) and \(y\le i+b\) so if \(x\le z\le y\) then \(i+a\le z\le i_b\) and so \(z\sim i\).
Clearly, the intersection of a lower set and an upper set is an interval. Remarkably, in totally ordered sets also the converse is true. Although this is a classical (and easy) result, we recall its proof for completeness.
Lemma 3.24
Let J be a totally ordered set. Then a subset \(I\subseteq J\) is an interval if and only if I can be written as the intersection of an upper set and a lower set.
Proof
Let
Then clearly \(L_I\) is a lower set, \(U_I\) is an upper set and we have \(I\subseteq L_I\cap U_I\). Moreover, if \(y\in L_I\cap U_I\) then there exist \(x_0,x_1\) in I such that \(y\in (-\infty ,x_1]\cap [x_0,+\infty )=[x_0,x_1]\). Since \(x_0\le y\le x_1\) and I is an interval, we have \(y\in I\), and so \(L_I\cap U_I\subseteq I\). \(\square \)
Lemma 3.25
In a totally ordered set, the upper set and the lower set intersecting in a nonempty interval I are uniquely determined by I.
Proof
Let \(I\subseteq J\) be a interval and let
with U and L ranging over the upper sets and the lower sets in J containing I, respectively. Then it is clear that \(I\subseteq U_I\cap L_I\) and we want to show that actually \(I=U_I\cap L_I\) and that if \(I={\tilde{U}}\cap {\tilde{L}}\) then \({\tilde{U}}=U_I\) and \({\tilde{L}}=L_I\). By Lemma 3.24 there exist an upper set \({\tilde{U}}\) and a lower set \({\tilde{L}}\) such that \(I={\tilde{U}}\cap {\tilde{L}}\). By definition of \(U_I\) and \(L_I\) we have \(U_I\subseteq {\tilde{U}}\) and \(L_I\subseteq {\tilde{L}}\). Therefore \(I\subseteq L_I\cap U_I\subseteq {\tilde{L}}\cap {\tilde{U}}=I\) and so \(I=U_I\cap L_I\). Now we want to show that \(U_I={\tilde{U}}\). Since \(U_I\subseteq U_0\) we only need to show that \({\tilde{U}}\subseteq U_I\). Let \(x\in {\tilde{U}}\) and let \(y\in I\). Since J is totally ordered, either \(x\le y\) or \(x\ge y\). In the first case, since \(L_0\) is a lower set, we have \(x\in {\tilde{L}}\) and so \(x\in {\tilde{L}}\cup {\tilde{U}}=I\subseteq U_I\). In the second case, since \(U_I\) is an upper set, we have directly \(x\in U_I\). \(\square \)
By the above lemma, the following definition is well-posed.
Definition 3.26
Let J be a totally ordered \({\mathbb {Z}}\)-poset and let  be a J-slicing on a stable \(\infty \)-category
be a J-slicing on a stable \(\infty \)-category  . For every nonempty interval \(I=L_I\cap U_I\) in J we set
. For every nonempty interval \(I=L_I\cap U_I\) in J we set

We also set  .
.
Remark 3.27
The whole of J is an interval, with \(L_J=U_J=J\). From Definition 3.26 we obtain  , as expected. Also, every upper set U is an interval, with \(U_U=U\) and \(L_U=J\). So from Definition 3.26 we find that the subcategory of
, as expected. Also, every upper set U is an interval, with \(U_U=U\) and \(L_U=J\). So from Definition 3.26 we find that the subcategory of  associated to U as an interval is precisely the subcategory
associated to U as an interval is precisely the subcategory  associated to U as an upper set. The same happens for lower sets. This shows that the notation introduced in Definition 3.26 is consistent with the notation for J-slicings.
associated to U as an upper set. The same happens for lower sets. This shows that the notation introduced in Definition 3.26 is consistent with the notation for J-slicings.
Example 3.28
For every i, j in J with \(i\le j\) one has the four intervals (i, j), (i, j], [i, j), [i, j] and consequently the four subcategories  and
and  of
of  . In particular for every \(i\in J\) we have the interval [i, i] consisting of the single element i. To avoid cumbersome notation, we will always write
. In particular for every \(i\in J\) we have the interval [i, i] consisting of the single element i. To avoid cumbersome notation, we will always write  for
for  . The subcategories
. The subcategories  with i ranging in J are called the slices of the J-slicing \(\mathfrak {t}\).
with i ranging in J are called the slices of the J-slicing \(\mathfrak {t}\).
Definition 3.29
Let \(\mathfrak {t}\) be a J-slicing on  . We say that
. We say that  is J-bounded if
is J-bounded if

Similarly, we say that  is J-left-bounded if
is J-left-bounded if  and J-right-bounded if
and J-right-bounded if  .
.
Remark 3.30
This notion is well known in the classical as well as in the quasicategorical setting: see [1, 18]. In particular, when \(\mathfrak {t}\) is a \(\mathbb {Z}\)-family of t-structures on  , then
, then  is \(\mathbb {Z}\)-bounded (resp., \(\mathbb {Z}\)-left-bounded, \(\mathbb {Z}\)-right-bounded) if and only if
is \(\mathbb {Z}\)-bounded (resp., \(\mathbb {Z}\)-left-bounded, \(\mathbb {Z}\)-right-bounded) if and only if  is bounded (resp., left-bounded, right-bounded) with respect to the t-structure \(\mathfrak {t}_0\), agreeing with the classical definition of boundedness as given, e.g., in [1].
is bounded (resp., left-bounded, right-bounded) with respect to the t-structure \(\mathfrak {t}_0\), agreeing with the classical definition of boundedness as given, e.g., in [1].
Remark 3.31
Since  one immediately sees that
one immediately sees that  is J-bounded if and only if
is J-bounded if and only if  is both J-left- and J-right-bounded.
is both J-left- and J-right-bounded.
The following remark is the first step towards the definition of factorization of morphisms associated with interval decompositions of J.
Remark 3.32
A nonempty interval in a totally ordered set J is equivalent to the datum of a pair of upper sets \(U_0\) and \(U_1\) with \(U_1\subseteq U_0\), i.e., to the datum of a strictly monotone morphism of posets \([\mathbf 1 ]\longrightarrow \mathcal {O}(J)\). Namely, we have seen that I is equivalent to the datum of an upper set \(U_I\) and a lower set \(L_I\), which are uniquely determined by I. Let us set \(U_0=U_I\) and \(U_1=J\setminus L_I\). Then, since \(\mathcal {O}(J)\) is totally ordered by Remark 3.3, we have either \(U_0\subseteq U_1\) or \(U_1\subseteq U_0\). If \(U_0\subseteq U_1\) then we have \(I=U_0\cap L_I\subseteq U_I\cap L_I=\emptyset \) against the assumption on I. So \(U_1\subseteq U_0\) and \(i\mapsto U_i\) for \(i=0,1\) defines a monotone map from \([\mathbf 1 ]\) to \(\mathcal {O}(J)\). Moreover this map is strictly monotone since we have excluded the possibility \(U_0\subseteq U_1\) and so we can’t have \(U_0=U_1\). By removing the assumption that I is nonempty, we can say that an interval in J is given by a (non necessarily strictly monotone) morphism of posets \([\mathbf 1 ]\longrightarrow \mathcal {O}(J)\). Actually this is not completely accurate, since all constant maps from \([\mathbf 1 ]\) to \(\mathcal {O}(J)\) will correspond to the empty interval. Yet it will be extremely convenient to always think of intervals as monotone maps to \(\mathcal {O}(J)\), so we will systematically adopt this point of view in what follows. In other words we will identify a monotone map \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) with the interval \(I=U_0\cap L_1\), where \(I(0)=(L_0,U_0)\) and \(I(1)=(L_1,U_1)\).
Remark 3.33
If \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) is an interval in a totally ordered set J, then \([U_0,U_1]\) is an interval in the totally ordered set \({\mathcal {O}}(J)\). It is easy to see that intersecting with I defines a bijection of totally ordered sets
Lemma 3.34
Let \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) be an interval in J, and let  be the corresponding subcategory of
be the corresponding subcategory of  , for a given J-slicing. Then the restriction of \(S_{U_0}\) to
, for a given J-slicing. Then the restriction of \(S_{U_0}\) to  and the restriction of \(R_{L_1}\) to
and the restriction of \(R_{L_1}\) to  both take values in
both take values in  .
.
Proof
We split the proof in two cases. If \(I=\emptyset \) then \(U_0=U_1\) and so for any X in  we have \(S_0X\cong S_1X=\mathbf{0 }\). So
we have \(S_0X\cong S_1X=\mathbf{0 }\). So  does take its values in
does take its values in  in this case. If \(I\ne \emptyset \), then \(U_1\subseteq U_0\). Since \(S_{0}\) takes values in
in this case. If \(I\ne \emptyset \), then \(U_1\subseteq U_0\). Since \(S_{0}\) takes values in  , we only need to show that it maps
, we only need to show that it maps  into itself. In other words we want to show that if
into itself. In other words we want to show that if  then \(S_0X\xrightarrow {\sim } R_1S_0X\). From the fiber sequence
then \(S_0X\xrightarrow {\sim } R_1S_0X\). From the fiber sequence

we see we are reduced to showing that \(S_1S_0X\cong \mathbf{0 }\). Since \(U_1\subseteq U_0\), we have \(S_1S_0X\cong S_1X\). But, since  we have \(S_1X\cong \mathbf{0 }\). This concludes the proof in the case \(I\ne \emptyset \). The proof for \(R_{L_1}\) is completely analogous. \(\square \)
we have \(S_1X\cong \mathbf{0 }\). This concludes the proof in the case \(I\ne \emptyset \). The proof for \(R_{L_1}\) is completely analogous. \(\square \)
By the above lemma and by Lemma 3.21 we can give the following
Definition 3.35
Let \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) be an interval in J, and let  be a J-slicing on a stable \(\infty \)-category
be a J-slicing on a stable \(\infty \)-category  . The functor
. The functor

is defined as the composition \({\mathcal {H}}^I=R_{L_1}S_{U_0}=S_{U_0}R_{L_1}\).
As for the functors \(R_L\) and \(S_U\) we will often implicitly compose \({\mathcal {H}}^I\) with the inclusion  and look at it as an endofunctor of
and look at it as an endofunctor of  . Notice that if I is the empty interval then \({\mathcal {H}}^I\) is the zero functor.
. Notice that if I is the empty interval then \({\mathcal {H}}^I\) is the zero functor.
Remark 3.36
By looking at a lower set L and to an upper set U as intervals, the above definition gives \({\mathcal {H}}^L=R_L\) and \({\mathcal {H}}^U=S_U\). In particular we find
and, by Lemma 3.21, \({\mathcal {H}}^I\) is the cofiber of the natural transformation \({\mathcal {H}}^{U_1}\longrightarrow {\mathcal {H}}^{U_0}\).
Remark 3.37
Let \(I,{\tilde{I}}\subseteq J\) two intervals, with \(I\subseteq {\tilde{I}}\). Then
Namely, if I is empty, then there is nothing to prove. If I is nonempty, as I is a sub-interval of \({\tilde{I}}\) we have \(U_0\subseteq {\tilde{U}}_0\) and \(L_1\subseteq {\tilde{L}}_1\). Therefore \(({\tilde{L}}_0,{\tilde{U}}_0)\le (L_0,U_0)\le (L_1,U_1)\le ({\tilde{L}}_1,{\tilde{U}}_1)\), and so \(S_{U_0}R_{{\tilde{L}}_1}=R_{{\tilde{L}}_1}S_{U_0}\) by Lemma 3.21 as well as \(R_{L_1}R_{{\tilde{L}}_1}=R_{L_1}\) and \(S_{U_0}S_{{\tilde{U}}_0}=S_{U_0}\) by Lemma 3.19. Therefore,
The proof that \({\mathcal {H}}^{{\tilde{I}}}{\mathcal {H}}^I={\mathcal {H}}^I\) is similar.
Remark 3.38
If I and \({\tilde{I}}\) are two disjoint intervals in the totally ordered set J then either every element of I is strictly smaller than every element of \({\tilde{I}}\) or vice versa. If we are in the first case, then  is right-orthogonal to
is right-orthogonal to  , i.e.,
, i.e.,  is contractible whenever
is contractible whenever  and
and  . Namely, by the assumption on I and \({\tilde{I}}\) we have \({\tilde{U}}_0\subseteq U_1\) and so
. Namely, by the assumption on I and \({\tilde{I}}\) we have \({\tilde{U}}_0\subseteq U_1\) and so  . On the other hand,
. On the other hand,  and
and  is right-orthogonal to
is right-orthogonal to  by definition of t-structure.
by definition of t-structure.
Remark 3.39
If I and \({\tilde{I}}\) are two disjoint intervals in the totally ordered set J , then
Indeed, the statement is trivial if either I or \({\tilde{I}}\) are empty. When they are nonempty, up to exchanging the role of I and \({\tilde{I}}\) we may assume that every element of I is strictly smaller than every element of \({\tilde{I}}\) . Then we have \((L_0,U_0)\le (L_1,U_1)\le ({\tilde{L}}_0,{\tilde{U}}_0)\le ({\tilde{L}}_1,{\tilde{U}}_1)\) and so
by lemma 3.19. Similarly one shows that \({\mathcal {H}}^{{\tilde{I}}}{\mathcal {H}}^I=0\).
The above Remarks 3.36 and 3.39 are actually two particular instances of the following general result. The proof is completely analogous to those in the remarks above, and so it is omitted.
Proposition 3.40
Let I and \({\tilde{I}}\) be two intervals in a \({\mathbb {Z}}\)-toset, and let  be a J-slicing on a stable \(\infty \)-category
be a J-slicing on a stable \(\infty \)-category  . Then
. Then
We conclude this section with a notational convention, which will be useful later.
Notation 3.41
Consistently with the notation from Example 3.28, for every i in J we write \({\mathcal {H}}^i\) for \({\mathcal {H}}^{[i,i]}\).
4 Interval decompositions and towers

Remark 4.1
For the whole section \((J,\le )\) will be a fixed totally ordered \(\mathbb {Z}\)-poset and  will be a J-slicing.
will be a J-slicing.
Definition 4.2
A \((k+2)\)-fold interval decomposition of J is a morphism of posets \(I_{[\mathbf k ]}:[\mathbf k ]\longrightarrow \mathcal {O}(J)\).
Notation 4.3
When no ambiguity is possible, the image of \(j\in \{0,1,\ldots ,k\}\) via \(I_{[\mathbf k ]}\) will be denoted simply by \((L_j,U_j)\). For every \(j=0,\ldots ,k+1\) the interval \(I_j=U_{j-1}\cap L_j\) is called the j-th interval in the decomposition, with the convention that \(U_{-1}=J=L_{k+1}\).
The factorization system associated with \((L_j,U_j)\) will be denoted by \((\mathcal {E}_j,\mathcal {M}_j)\). Notice that, since \(I_{[\mathbf k ]}\) is a morphism of posets we have \(\mathcal {E}_{j+1}\subseteq \mathcal {E}_j\) and \(\mathcal {M}_{j+1}\supseteq \mathcal {M}_j\).
This implies that the composition  is a k-fold factorization system; in other words
is a k-fold factorization system; in other words
Lemma 4.4
Let \((\mathcal {E}_j, \mathcal {M}_j)\) as above. Then every arrow \(f:X\longrightarrow Y\) in  can be uniquely factored into a composition
can be uniquely factored into a composition
Proof
Since \((\mathcal {E}_k,\mathcal {M}_k)\) is a factorization system, we have a (unique) factorization \(X \xrightarrow {\mathcal {E}_{k}} Z_{k} \xrightarrow {\mathcal {M}_{k}} Y\). Since \((\mathcal {E}_{k-1},\mathcal {M}_{k-1})\) is a factorization system, we can (uniquely) factor \(Z_k\longrightarrow Y\) as \(Z_k \xrightarrow {\mathcal {E}_{k-1}} Z_{k-1} \xrightarrow {\mathcal {M}_{k-1}} Y\). Since \(\mathcal {M}_{k-1}\subseteq \mathcal {M}_k\), the morphism \(Z_{k-1} \longrightarrow Y\) is also in \(\mathcal {M}_k\) and so, by the 3-for-2 property, also \(Z_k \longrightarrow Z_{k-1}\) is in \(\mathcal {M}_k\). Therefore \(Z_k \xrightarrow {\mathcal {E}_{k-1}} Z_{k-1}\) is in \(\mathcal {E}_{k-1}\cap \mathcal {M}_k\). then one concludes iterating this argument. \(\square \)
Definition 4.5
The sequence of morphism in the factorization of \(f:X\longrightarrow Y\) in Lemma 4.4 is called the \(I_{[\mathbf k ]}\)-tower of f, and it is denoted  , or simply by
, or simply by  when the interval decomposition \(I_{[\mathbf k ]}\) is clear from the context.
when the interval decomposition \(I_{[\mathbf k ]}\) is clear from the context.
Remark 4.6
When  is the stable \(\infty \)-category of spectra and \(X\longrightarrow 0\) and \(0\longrightarrow X\) are the terminal and the initial morphism of X, respectively, the above notation and construction is in line with the classical Postnikov and Whitehead towers of X, i.e., with the sequences
is the stable \(\infty \)-category of spectra and \(X\longrightarrow 0\) and \(0\longrightarrow X\) are the terminal and the initial morphism of X, respectively, the above notation and construction is in line with the classical Postnikov and Whitehead towers of X, i.e., with the sequences
of factorizations obtained from the (stable image of) the n-connected factorization system of [14].
Remark 4.7
If both X and Y are in  , then the morphism \(X\longrightarrow Z_{k}\) in
, then the morphism \(X\longrightarrow Z_{k}\) in  is an isomorphism. Indeed, by construction the morphism \(Z_{k}\longrightarrow Y\) is in \(\mathcal {M}_{k}\). Since both \(X\longrightarrow 0\) and \(Y\longrightarrow 0\) are in \(\mathcal {M}_{k}\) then also \(X\longrightarrow Y\) is in \(\mathcal {M}_{k}\) by 3-for-2, and so also \(X\longrightarrow Z_{k}\) in in \(\mathcal {M}_{k}\) again by 3-for-2. But by construction \(X\longrightarrow Z_{k}\) is in \(\mathcal {E}_{k}\), so it is an isomorphism. By the same argument one sees that if both X and Y are in
is an isomorphism. Indeed, by construction the morphism \(Z_{k}\longrightarrow Y\) is in \(\mathcal {M}_{k}\). Since both \(X\longrightarrow 0\) and \(Y\longrightarrow 0\) are in \(\mathcal {M}_{k}\) then also \(X\longrightarrow Y\) is in \(\mathcal {M}_{k}\) by 3-for-2, and so also \(X\longrightarrow Z_{k}\) in in \(\mathcal {M}_{k}\) again by 3-for-2. But by construction \(X\longrightarrow Z_{k}\) is in \(\mathcal {E}_{k}\), so it is an isomorphism. By the same argument one sees that if both X and Y are in  , then the morphism \(Z_{0}\longrightarrow Y\) is an isomorphism.
, then the morphism \(Z_{0}\longrightarrow Y\) is an isomorphism.
Corollary 4.8
Let \(I_{[\mathbf k ]}\) be a \((k+2)\)-fold interval decomposition of J. Then for any object Y in  , the tower
, the tower  is
is
Moreover, the arrows \(f_j:{\mathcal {H}}^{U_j}Y\longrightarrow {\mathcal {H}}^{U_{j-1}}Y\) in  are such that
are such that  , for \(j=0,\ldots ,k+1\).
, for \(j=0,\ldots ,k+1\).
Proof
From the \((k+2)\)-fold factorization
and from the fact that \(\mathcal {E}_{0}\supseteq \mathcal {E}_{1} \supseteq \dots \supseteq \mathcal {E}_{k}\) and each class \(\mathcal {E}_{j}\) is closed for composition, we see that \(0\longrightarrow Y_{j}\longrightarrow Y\) is the \((\mathcal {E}_j,\mathcal {M}_j)\)-factorization of \(0\longrightarrow Y\) and so \(Y_{j}=S_{U_j}Y={\mathcal {H}}^{U_j}Y\). One concludes by Lemma 3.21. \(\square \)
The above corollary motivates the following
Definition 4.9
Let \(f:X\longrightarrow Y\) be a morphism in  . A \(I_{[\mathbf k ]}\)-weaved factorization for f is a factorization of f of the form
. A \(I_{[\mathbf k ]}\)-weaved factorization for f is a factorization of f of the form
with  , for \(j=0,\ldots ,k+1\).
, for \(j=0,\ldots ,k+1\).
Remark 4.10
If we call  the class of \(I_{[\mathbf k ]}\)-weaved factorizations for a morphism \(f :X\longrightarrow Y\), it is immediate to see that we have a canonical identification
the class of \(I_{[\mathbf k ]}\)-weaved factorizations for a morphism \(f :X\longrightarrow Y\), it is immediate to see that we have a canonical identification

Moreover Corollary 4.8 precisely states that  is an \(I_{[\mathbf k ]}\)-weaved factorization, and so we have the existence of \(I_{[\mathbf k ]}\)-weaved factorizations for arbitrary morphisms. The remainder of this section is devoted to proving the uniqueness of \(I_{[\mathbf k ]}\)-weaved factorizations. This reduces to proving the uniqueness of \(I_{[\mathbf k ]}\)-weaved factorizations for initial morphism, i.e., to showing that the only possible \(I_{[\mathbf k ]}\)-weaved factorization of \(0\longrightarrow Y\) is its tower.
is an \(I_{[\mathbf k ]}\)-weaved factorization, and so we have the existence of \(I_{[\mathbf k ]}\)-weaved factorizations for arbitrary morphisms. The remainder of this section is devoted to proving the uniqueness of \(I_{[\mathbf k ]}\)-weaved factorizations. This reduces to proving the uniqueness of \(I_{[\mathbf k ]}\)-weaved factorizations for initial morphism, i.e., to showing that the only possible \(I_{[\mathbf k ]}\)-weaved factorization of \(0\longrightarrow Y\) is its tower.
Lemma 4.11
In the above notation, let \(f:X\longrightarrow Y\) be a morphism in  . If X is in
. If X is in  and \({{\,\mathrm{cofib}\,}}(f)\) is in
and \({{\,\mathrm{cofib}\,}}(f)\) is in  then \(0\longrightarrow X\xrightarrow {f}Y\) is the \((\mathcal {E}_j,\mathcal {M}_j)\)-factorization of the initial morphism \(0\longrightarrow Y\) and Y is in
then \(0\longrightarrow X\xrightarrow {f}Y\) is the \((\mathcal {E}_j,\mathcal {M}_j)\)-factorization of the initial morphism \(0\longrightarrow Y\) and Y is in  . In particular f is in \(\mathcal {E}_{j-1}\cap \mathcal {M}_j\).
. In particular f is in \(\mathcal {E}_{j-1}\cap \mathcal {M}_j\).
Proof
Since X is in  , the morphism \(0\longrightarrow X\) is in \(\mathcal {E}_j\), and so to show that \(0\longrightarrow X\xrightarrow {f} Y\) is the \((\mathcal {E}_j,\mathcal {M}_j)\)-factorization of \(0\longrightarrow Y\) we are reduced to showing that \(f:X\longrightarrow Y\) is in \(\mathcal {M}_j\). Since \({{\,\mathrm{cofib}\,}}(f)\) is in
, the morphism \(0\longrightarrow X\) is in \(\mathcal {E}_j\), and so to show that \(0\longrightarrow X\xrightarrow {f} Y\) is the \((\mathcal {E}_j,\mathcal {M}_j)\)-factorization of \(0\longrightarrow Y\) we are reduced to showing that \(f:X\longrightarrow Y\) is in \(\mathcal {M}_j\). Since \({{\,\mathrm{cofib}\,}}(f)\) is in  , we have in particular that \({{\,\mathrm{cofib}\,}}(f)\longrightarrow 0\) is in \(\mathcal {M}_j\) and so \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) is in \(\mathcal {M}_j\) by the Sator lemma. Then we have a homotopy pullback diagram
, we have in particular that \({{\,\mathrm{cofib}\,}}(f)\longrightarrow 0\) is in \(\mathcal {M}_j\) and so \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) is in \(\mathcal {M}_j\) by the Sator lemma. Then we have a homotopy pullback diagram

and so f is in \(\mathcal {M}_j\) by the fact that \(\mathcal {M}_j\) is closed under pullbacks. To show also that \(f\in \mathcal {E}_{j-1}\) let \(X\longrightarrow T\longrightarrow Y\) be the \((\mathcal {E}_{j-1},\mathcal {M}_{j-1})\)-factorization of f. Then, since \(\mathcal {E}_j\subseteq \mathcal {E}_{j-1}\), \(0\longrightarrow T\longrightarrow Y\) is the \((\mathcal {E}_{j-1},\mathcal {M}_{j-1})\)-factorization of \(0\longrightarrow Y\). So, by the normality of \((\mathcal {E}_{j-1},\mathcal {M}_{j-1})\) we get the diagram

where all the squares are pullouts, and where we have used the Sator lemma, the fact that \({{\,\mathrm{cofib}\,}}(f)\longrightarrow 0\) is in \(\mathcal {M}_j\), that the classes \(\mathcal {E}\) are closed for pushouts while the classes \(\mathcal {M}\) are closed for pullbacks, and the 3-for-2 property for both classes. Since by hypothesis \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) is in \(\mathcal {E}_{j-1}\), we see that \(V=0\) and so \(T=Y\). Therefore,  and \(f\in \mathcal {E}_{j-1}\cap \mathcal {M}_j\). \(\square \)
and \(f\in \mathcal {E}_{j-1}\cap \mathcal {M}_j\). \(\square \)
Corollary 4.12
Let Y an object in  and let
and let
be an \(I_{[\mathbf k ]}\)-weaved factorization for \(0\longrightarrow Y\). Then 
Proof
By uniqueness of the k-fold factorization we only need to prove that \(f_j\in \mathcal {E}_{i_{k-1}}\cap \mathcal {M}_{i_k}\), which is immediate by repeated application of Lemma 4.11. \(\square \)
Remark 4.13
It’s an unavoidable temptation to think of the \(I_{[\mathbf k ]}\)-weaved factorization of a morphism f as of its tower  . As the following counterexample shows, when f is not an initial morphism this is in general not true. Let \(J=\mathbb {Z}\), let \(k=0\) and let \(I_{[\mathbf 0 ]}:[\mathbf 0 ]\longrightarrow \mathcal {O}(\mathbb {Z})\) be the slicing \(U_0=[0,+\infty )\). Now take a morphism \(f:X\longrightarrow Y\) between two elements in
. As the following counterexample shows, when f is not an initial morphism this is in general not true. Let \(J=\mathbb {Z}\), let \(k=0\) and let \(I_{[\mathbf 0 ]}:[\mathbf 0 ]\longrightarrow \mathcal {O}(\mathbb {Z})\) be the slicing \(U_0=[0,+\infty )\). Now take a morphism \(f:X\longrightarrow Y\) between two elements in  . The object \({{\,\mathrm{cofib}\,}}(f)\) will lie in
. The object \({{\,\mathrm{cofib}\,}}(f)\) will lie in  , since \(\mathcal {E}_0[-1]\) is closed for pushouts, but in general it will not be an element in
, since \(\mathcal {E}_0[-1]\) is closed for pushouts, but in general it will not be an element in  . In other words, we will have, in general, a nontrivial \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of the initial morphism \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\), i.e., a nontrivial tower
. In other words, we will have, in general, a nontrivial \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of the initial morphism \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\), i.e., a nontrivial tower  . Pulling this back along \(Y\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) we obtain the \(I_{[\mathbf 0 ]}\)-weaved factorization \(X\xrightarrow {f_2} Z\xrightarrow {f_1} Y\) of f, and this factorization will be nontrivial since its pushout is nontrivial. It follows that \((f_2,f_1)\), cannot be
. Pulling this back along \(Y\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) we obtain the \(I_{[\mathbf 0 ]}\)-weaved factorization \(X\xrightarrow {f_2} Z\xrightarrow {f_1} Y\) of f, and this factorization will be nontrivial since its pushout is nontrivial. It follows that \((f_2,f_1)\), cannot be  , which is the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of f. Indeed, by the 3-for-2 property of \(\mathcal {M}_0\), the morphism f is in \(\mathcal {M}_0\), so its \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization is trivial.
, which is the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of f. Indeed, by the 3-for-2 property of \(\mathcal {M}_0\), the morphism f is in \(\mathcal {M}_0\), so its \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization is trivial.
Remark 4.14
Let \(I_{[\mathbf k' ]}:[\mathbf k' ]\longrightarrow {\mathcal {O}}(J)\) be a refinement of an interval decomposition \(I_{[\mathbf k ]}:[\mathbf k ]\longrightarrow {\mathcal {O}}(J)\). This means that for every \(i=0,\ldots ,k+1\) we have an interval decomposition \(I_{[\mathbf{k }_i]}:[\mathbf{k }_i]\longrightarrow {\mathcal {O}}(I_{[\mathbf k ];i})\), where \(I_{[\mathbf k ];i}\) denotes the i-th interval in the subdivision \(I_{[\mathbf k ]}\). By the pasting law for pullouts it is immediate to see that for any morphism \(f:X \longrightarrow Y\) we have a canonical identification

4.1 Bridgeland slicings
Definition 4.15
A J-slicing  of a stable \(\infty \)-category
of a stable \(\infty \)-category  is called discrete if for any object X in
is called discrete if for any object X in  one has \({\mathcal {H}}^i(X)=\mathbf{0 }\) for every i in J if and only if \(X=\mathbf{0 }\). A discrete J-slicing is said to be of finite type if for any object X one has \({\mathcal {H}}^i(X)\ne \mathbf{0 }\) only for finitely many elements \(i\in J\).
one has \({\mathcal {H}}^i(X)=\mathbf{0 }\) for every i in J if and only if \(X=\mathbf{0 }\). A discrete J-slicing is said to be of finite type if for any object X one has \({\mathcal {H}}^i(X)\ne \mathbf{0 }\) only for finitely many elements \(i\in J\).
Example 4.16
A finite type discrete \({\mathbb {Z}}\)-slicing on  is precisely the datum of a bounded t-structure on
is precisely the datum of a bounded t-structure on  .
.
Suppose now that \(\mathfrak {t}\) is of finite type, so that for each  one has \({\mathcal {H}}^i(X)=\mathbf{0 }\) but for a finite set \(\{ i_1^X< \cdots < i_{k_X}^X \} \subseteq J\) of indices i, depending on X. We can then build up a \((k+2)\)-fold interval decomposition \(I_{[ \mathbf{k }_X ]}^X\), depending on the object X, by setting \(U_j^X=(i_j, +\infty )\). As we are assuming J to be totally ordered, we have \(L_j^X=(-\infty , i_j]\). The next proposition shows that the tower of the initial morphism \(\mathbf{0 } \longrightarrow X\) associated to this interval decomposition is indeed the “finest one”.
one has \({\mathcal {H}}^i(X)=\mathbf{0 }\) but for a finite set \(\{ i_1^X< \cdots < i_{k_X}^X \} \subseteq J\) of indices i, depending on X. We can then build up a \((k+2)\)-fold interval decomposition \(I_{[ \mathbf{k }_X ]}^X\), depending on the object X, by setting \(U_j^X=(i_j, +\infty )\). As we are assuming J to be totally ordered, we have \(L_j^X=(-\infty , i_j]\). The next proposition shows that the tower of the initial morphism \(\mathbf{0 } \longrightarrow X\) associated to this interval decomposition is indeed the “finest one”.
Proposition 4.17
Let  be a J-slicing of finite type and let X an object of
be a J-slicing of finite type and let X an object of  . Then for all j we have
. Then for all j we have
Proof
Let us write \(i_j\), \(I_j\) and \(S_j\) for \(i_j^X\), \(I_j^X\) and \(S_{U_j}^X\), respectively. Now, for each \(\varphi \in J\), using By, Proposition 3.40 we have
But \({\mathcal {H}}^iX=\mathbf{0 }\) for \(i \not = i_1 , \ldots , i_{k_X}\), and so \({\mathcal {H}}^{i}({\mathcal {H}}^{(i_{j-1}, i_{j})}X)=\mathbf{0 }\) for all \(i \in J\). Since \(\mathfrak {t}\) is discrete, this gives \({\mathcal {H}}^{(i_{j-1}, i_{j})}X= \mathbf{0 }\), proving the second part of the statement. To prove the first part, recall that by Lemma 3.21, \({\mathcal {H}}^{I_j}(X)\) is the cofiber of \(S_{j}X\longrightarrow S_{j-1}X\), while \({\mathcal {H}}^{i_j}(X)\) is the cofiber of \(S_jX\longrightarrow S_{[i_j,+\infty )}X\). So we are reduced to show that \(S_{j-1}X=S_{[i_j,+\infty )}X\). Since \(i_{j} > i_{j-1}\) we have \([i_{j},+\infty )\subseteq (i_{j-1},+\infty )=U_{j-1}^X\) and so, by Lemma 3.19, \(S_{[i_j,+\infty )}X=S_{[i_j,+\infty )}S_{j-1}X\). Thus, we are reduced to show that \(S_{j-1}X=S_{[i_j,+\infty )}S_{j-1}X\), i.e., equivalently, that \(R_{(-\infty ,i_j)}S_{j-1}X=\mathbf{0 }\). This is immediate as \( R_{(-\infty ,i_j)}S_{j-1}X={\mathcal {H}}^{(i_{j-1}, i_j)}X\). \(\square \)
In particular the above tells us that, writing \(\varphi _j\) for \(i_{k_X-j}\), the cofiber of the j-th morphism of  is
is  . In other words, these towers are weaved factorizations with cofibers in the subcategories
. In other words, these towers are weaved factorizations with cofibers in the subcategories  and so they correspond to the Harder-Narasimhan filtrations from [5]. That is, Bridgeland’s slicings (in their generalized version from [9]) are precisely the slicings of finite type in our sense. We show this in detail below.
and so they correspond to the Harder-Narasimhan filtrations from [5]. That is, Bridgeland’s slicings (in their generalized version from [9]) are precisely the slicings of finite type in our sense. We show this in detail below.
Definition 4.18
A BridgelandJ-slicing on  is a collection
is a collection  of full extension closed sub-\(\infty \)-subcategories satisfying:
of full extension closed sub-\(\infty \)-subcategories satisfying:
-
(i)
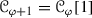 for each \(\varphi \in J\);
for each \(\varphi \in J\); -
(ii)
orthogonality:
 is contractible for each
is contractible for each  ,
,  for \(\varphi > \psi \) in J;
for \(\varphi > \psi \) in J; -
(iii)
for each object
 there is a finite set \(\{ \varphi _1> \cdots > \varphi _n \}\) and a factorization of the initial morphism \(\mathbf{0 } \longrightarrow X\)$$\begin{aligned} \mathbf{0 }=X_0 \xrightarrow {\alpha _1} \cdots \xrightarrow {\alpha _n} X_n=X \end{aligned}$$
there is a finite set \(\{ \varphi _1> \cdots > \varphi _n \}\) and a factorization of the initial morphism \(\mathbf{0 } \longrightarrow X\)$$\begin{aligned} \mathbf{0 }=X_0 \xrightarrow {\alpha _1} \cdots \xrightarrow {\alpha _n} X_n=X \end{aligned}$$with
 for all \(i = 1, \ldots , n\).
for all \(i = 1, \ldots , n\).
Notation 4.19
For \(\mathcal {S}\) a subcategory of  , we write \(\langle \mathcal {S}\rangle \) for the smallest extension closed full subcategory of
, we write \(\langle \mathcal {S}\rangle \) for the smallest extension closed full subcategory of  containing \(\mathcal {S}\). If \(M \subseteq J\) is a subset and
containing \(\mathcal {S}\). If \(M \subseteq J\) is a subset and  is a Bridgeland J-slicing on
is a Bridgeland J-slicing on  , we denote
, we denote  the extension-closed subcategory generated by
the extension-closed subcategory generated by  with \(\varphi \in M\), i.e., we set
with \(\varphi \in M\), i.e., we set

Remark 4.20
Set \(\langle \mathcal {S}\rangle _0=\mathbf{0 }\), define \(\langle \mathcal {S}\rangle _1\) as the full subcategory of  generated by \(\mathcal {S}\) and \(\mathbf{0 }\), and define inductively \(\langle \mathcal {S}\rangle _n\) as the full subcategory of
generated by \(\mathcal {S}\) and \(\mathbf{0 }\), and define inductively \(\langle \mathcal {S}\rangle _n\) as the full subcategory of  on those objects X which fall into a homotopy fiber sequence
on those objects X which fall into a homotopy fiber sequence

with \(h,k\ge 1\), \(X_h\) in \(\langle \mathcal {S}\rangle _h\), \(X_k\) in \(\langle \mathcal {S}\rangle _k\) and \(h+k=n\). One clearly has
Moreover \(\bigcup _n \langle \mathcal {S}\rangle _n\) is clearly extension closed, so that
Lemma 4.21
Let \(\mathcal {S}_1,\mathcal {S}_2\) be two subcategories of  with
with  , i.e., such that
, i.e., such that  is contractible for any \(X\in \mathcal {S}_1\) and any \(Y\in \mathcal {S}_2\). Then
is contractible for any \(X\in \mathcal {S}_1\) and any \(Y\in \mathcal {S}_2\). Then  and
and  , and so
, and so 
Proof
By Remark 4.20, to prove the first statement we are reduced to show that, if \(X\in \mathcal {S}_1\) and \(Y\in \langle \mathcal {S}_2\rangle _n\) then  is contractible. We prove this by induction on n. For \(n=0,1\) there is nothing to prove by the assumption
is contractible. We prove this by induction on n. For \(n=0,1\) there is nothing to prove by the assumption  . For \(n\ge 2\), consider a fiber sequence \(Y_h\longrightarrow Y\longrightarrow Y_k\) with \(1\le h,k\) and \(h+k=n\) as in Remark 4.20. Since
. For \(n\ge 2\), consider a fiber sequence \(Y_h\longrightarrow Y\longrightarrow Y_k\) with \(1\le h,k\) and \(h+k=n\) as in Remark 4.20. Since  preserves homotopy fiber sequences, we get a homotopy fiber sequence of \(\infty \)-groupoids
preserves homotopy fiber sequences, we get a homotopy fiber sequence of \(\infty \)-groupoids

By the inductive hypothesis both  and
and  are contractible, so
are contractible, so  also is. The proof of the second statement is perfectly dual, due to the fact that in
also is. The proof of the second statement is perfectly dual, due to the fact that in  every fiber sequence is also a cofiber sequence, and
every fiber sequence is also a cofiber sequence, and  transforms a cofiber sequence into a fiber sequence. \(\square \)
transforms a cofiber sequence into a fiber sequence. \(\square \)
Lemma 4.22
Let (L, U) be a slicing of J, and let  and
and  be defined according to Notation 4.19. Then
be defined according to Notation 4.19. Then  .
.
Proof
Since by definition  for \(\varphi >\psi \), the statement immediately follows from Lemma 4.21. \(\square \)
for \(\varphi >\psi \), the statement immediately follows from Lemma 4.21. \(\square \)
Lemma 4.23
In the above hypothesis and notation, every object Y of  sits into a homotopy fiber sequence \(Y_{U}\longrightarrow Y\longrightarrow Y_{L}\) with
sits into a homotopy fiber sequence \(Y_{U}\longrightarrow Y\longrightarrow Y_{L}\) with  and
and  .
.
Proof
Let
a factorization of the initial morphism \(\mathbf{0 } \longrightarrow X\) with  for all \(i = 1, \cdots , n\), with \(\varphi _i>\varphi _{i+1}\) and with \(\varphi _{{\bar{\imath }}}\in U\) and \(\varphi _{{\bar{\imath }}+1}\in L\) (with \({\bar{\imath }}=-1\) or n when all of the \(\varphi _i\) are in L or in U, respectively). Consider the pullout diagram
for all \(i = 1, \cdots , n\), with \(\varphi _i>\varphi _{i+1}\) and with \(\varphi _{{\bar{\imath }}}\in U\) and \(\varphi _{{\bar{\imath }}+1}\in L\) (with \({\bar{\imath }}=-1\) or n when all of the \(\varphi _i\) are in L or in U, respectively). Consider the pullout diagram

together with the
and
The first factorization shows that  while the second factorization shows that
while the second factorization shows that  . \(\square \)
. \(\square \)
Lemma 4.24
In the above hypothesis and notation, one has  and
and  .
.
Proof
Since the shift functor commutes with pushouts, if an object X is obtained by iterated extensions by objects in  with \(\varphi \in U\), then X[1] is obtained by iterated extensions by objects in
with \(\varphi \in U\), then X[1] is obtained by iterated extensions by objects in  with \(\varphi \in U\). In other words, X[1] is an object in
with \(\varphi \in U\). In other words, X[1] is an object in  . Since U is an upper set, \(U+1\subseteq U\) and so
. Since U is an upper set, \(U+1\subseteq U\) and so  . This proves that
. This proves that  . The proof for
. The proof for  is perfectly analogous. \(\square \)
is perfectly analogous. \(\square \)
The above Lemmas together give the following
Proposition 4.25
In the above hypothesis and notation, the map  defines a J-slicing of
defines a J-slicing of  , i.e., \(\mathfrak {t}\) is a \({\mathbb {Z}}\)-equivariant map of posets
, i.e., \(\mathfrak {t}\) is a \({\mathbb {Z}}\)-equivariant map of posets  .
.
Proof
Lemmas 4.22–4.24 together precisely say that  is a t-structure on
is a t-structure on  . Equivariancy of the map is the fact that, as remarked in the proof of Lemma 4.24, one has
. Equivariancy of the map is the fact that, as remarked in the proof of Lemma 4.24, one has  . Finally, if \((L_0,U_0)\le (L_1,U_1)\) then we have \(U_1\subseteq U_0\) and so
. Finally, if \((L_0,U_0)\le (L_1,U_1)\) then we have \(U_1\subseteq U_0\) and so  , which shows that the map \(\mathfrak {t}\) is a morphism of posets. \(\square \)
, which shows that the map \(\mathfrak {t}\) is a morphism of posets. \(\square \)
Proposition 4.26
Let J be a totally ordered \({\mathbb {Z}}\)-poset and let  be a stable \(\infty \)-category. Then we have a bijection
be a stable \(\infty \)-category. Then we have a bijection

Proof
The only thing left to be proven is that the above construction actually produces a discrete slicing of finite type. This is actually immediate once one realizes that the factorization \(\mathbf{0 }=X_0 \xrightarrow {\alpha _1} \cdots \xrightarrow {\alpha _n} X_n=X\) of the initial morphism \(0\longrightarrow X\) provided by the definition of Bridgeland slicing is actually the weaved factorization corresponding to the interval decomposition of J associated with the decreasing sequence \(\varphi _1> \cdots > \varphi _n\). One then directly sees that the two constructions indicated in the statement of the proposition are inverse each other. \(\square \)
Remark 4.27
Using the orthogonality condition  for \(\varphi >\psi \), is not hard to prove by induction on the length of the factorizations that Definition 4.18 actually implies uniqueness of Bridgeland factorizations
for \(\varphi >\psi \), is not hard to prove by induction on the length of the factorizations that Definition 4.18 actually implies uniqueness of Bridgeland factorizations
of initial morphisms \(0\longrightarrow X\). As a consequence one has well defined functors

given by
As it is natural to expect, in the correspondence given by Proposition 4.26 the functor \({\mathcal {H}}^\varphi _B\) is identified with the functor \({\mathcal {H}}^\varphi \) associated with the discrete J-slicing. Moreover, one easily sees that

so that the correspondence of Proposition 4.26 can be defined sending the pair  into
into  , with inverse
, with inverse

5 Hearts of J-slicings
I watched a snail crawl along the edge of a straight razor. That’s my dream. That’s my nightmare. Crawling, slithering, along the edge of a straight razor...and surviving.
Col. W. E. Kurtz
Recall the equivalence relation \(x\sim y\) if and only if there are integers \(a,b \in \mathbb {Z}\) with \(a\le b\) such that \(x + a \le y \le x + b\) on a \(\mathbb {Z}\)-toset J from Lemma 2.27.
Lemma 5.1
The following are equivalent:
-
(i)
the \(\mathbb {Z}\)-toset J consists of a single equivalence class with respect to the equivalence relation \(\sim \);
-
(ii)
there exists an interval I in J such that the map \(\varphi :(n,x)\mapsto x+n\) is an isomorphism of \(\mathbb {Z}\)-tosets \(\mathbb {Z}\times _{\text {lex}}I\xrightarrow {\sim } J\) (where the \(\mathbb {Z}\)-action on I is the trivial one and the \(\mathbb {Z}\)-action on \(\mathbb {Z}\) is the translation).
Proof
That (i) implies (ii) is an immediate consequence of 2.29. To prove the converse implication notice that since \(\varphi \) is surjective every element in J is equivalent to an element in I. So we are reduced to show that all elements in I are equivalent each other. Let \(x,y\in I\). We can assume \(x\le y\). Since J is totally ordered we have either \(y\le x+1\) or \(x+1\le y\). In the latter case we have \(x\le x+1\le y\) and so \(x+1\in I\), since I is an interval. But then \(\varphi (1,x)=\varphi (0,x+1)\) against the hypothesis on \(\varphi \). So we are left with \(x\le y\le x+1\) which implies \(x\sim y\). \(\square \)
Definition 5.2
Let J be a \(\mathbb {Z}\)-toset. A heart for J is an interval \(J^\heartsuit \subseteq J\) such that \(\varphi :(n,x)\mapsto x+n\) is an isomorphism of \(\mathbb {Z}\)-tosets \(\mathbb {Z}\times _{\text {lex}}J^\heartsuit \xrightarrow {\sim } J\).
Remark 5.3
Of course, not every \(\mathbb {Z}\)-toset has a heart. It is easy to see that J has an heart if and only if there is a morphism of \(\mathbb {Z}\)-tosets \(\pi _\heartsuit :J \longrightarrow \mathbb {Z}\). An heart of J is given by \(\pi _\heartsuit ^{-1}(0)\) in this case.
Remark 5.4
It is immediate from the definition that \(J^\heartsuit \) is a heart of J if and only if \(J^\heartsuit +n\) is a heart of J, for every \(n\in \mathbb {Z}\).
Example 5.5
If \(J=\mathbb {Z}\), with the standard \(\mathbb {Z}\)-toset structure, the hearts of J are the singletons \(\{n\}\) with \(n\in \mathbb {Z}\). In particular \(\{0\}\) is the standard heart of \(\mathbb {Z}\), and all the other hearts are shifts of this. If \(J={\mathbb {R}}\), with the standard \(\mathbb {Z}\)-toset structure, then the hearts of J are the intervals of the form \([x,x+1)\) and those of the form \((x,x+1]\), with \(x\in {\mathbb {R}}\).
Example 5.6
Let \((J, \le )\) be a totally ordered \({\mathbb {Z}}\)-poset, and let \(\sim \) be the equivalence relation from Lemma 2.27. For every \(i\in J\) let \(I_i\) be the equivalence class of i. This is an interval in J, see Example 3.23. Moreover, by Lemma 2.29, \(I_i\) has a heart precisely when i is not a fixed point of the \(\mathbb {Z}\)-action.
Lemma 5.7
Let \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) be a heart of J. Then \(I(1)=I(0)+1\), i.e., \(U_1=U_0+1\) (equivalently, \(L_1=L_0+1\)).
Proof
Assume \(U_1\nsubseteq U_0+1\). Then there exists an element x in \(U_1\cap (L_0+1)\). Since I is a heart, there exists an element y in I and an integer n such that \(x=y+n\). If \(n\ge 1\) we have \(y+n\in U_0+n\subseteq U_0+1\) and so \(x\in (U_0+1)\cap (L_0+1)\), which is impossible. If \(n\le 0\) we have \(y+n\in L_1+n\subseteq L_1\) and so \(x\in L_1\cap U_1\) which again is impossible. Therefore \(U_1\subseteq U_0+1\). Now assume \(U_0+1\nsubseteq U_1\). Then there exists an element \(x\in (U_0+1)\cap L_1\). Let \(y=x-1\). Then \(y\in U_0\cap (L_1-1)\subseteq U_0\cap L_1=I\). Since \(U_0+1\subseteq U_0\) we also have \(x\in I\), and so \(\varphi (-1,x)=\varphi (0,y)\), which is impossible. Therefore \(U_1= U_0+1\). \(\square \)
Definition 5.8
Let \(J^\heartsuit \subseteq J\) be a heart of J and let  be a J-slicing on a stable \(\infty \)-category
be a J-slicing on a stable \(\infty \)-category  . The subcategory
. The subcategory  of
of  will be called a heart of the J-slicing \(\mathfrak {t}\) and will be denoted
will be called a heart of the J-slicing \(\mathfrak {t}\) and will be denoted  .
.
Notation 5.9
We denote the canonical projection to the heart as  ; see Definition 3.35.
; see Definition 3.35.
Example 5.10
We have seen in Example3.14 that a a \(\mathbb {Z}\)-slicing on a stable \(\infty \)-category  is the same thing as the datum of a t-structure
is the same thing as the datum of a t-structure  on
on  . The standard heart
. The standard heart  is called the heart of the t-structure \(\mathfrak {t}\). The projection to the heart is the functor \({\mathcal {H}}^0\); see Notation 3.41.
is called the heart of the t-structure \(\mathfrak {t}\). The projection to the heart is the functor \({\mathcal {H}}^0\); see Notation 3.41.
From 4.8 we immediately get the following
Proposition 5.11
Let  be a bounded t-structure on a stable \(\infty \)-category
be a bounded t-structure on a stable \(\infty \)-category  , and let
, and let  be its standard heart. Then \(\mathfrak {t}\) is completely determined by the functors
be its standard heart. Then \(\mathfrak {t}\) is completely determined by the functors  (and so by the functor \({\mathcal {H}}^0\) alone). More precisely,
(and so by the functor \({\mathcal {H}}^0\) alone). More precisely,  is the full subcategory of
is the full subcategory of  on the objects Y such that \({\mathcal {H}}^jY=0\) for any \(j< 0\), while
on the objects Y such that \({\mathcal {H}}^jY=0\) for any \(j< 0\), while  is the full subcategory of
is the full subcategory of  on those objects Y for which \({\mathcal {H}}^jY=0\) for any \(j\ge 0\).
on those objects Y for which \({\mathcal {H}}^jY=0\) for any \(j\ge 0\).
Remark 5.12
There is a rather evocative pictorial representation of the heart  of an \({\mathbb {R}}\)-slicing, manifestly inspired by [5]: if we depict
of an \({\mathbb {R}}\)-slicing, manifestly inspired by [5]: if we depict  and
and  as contiguous half-planes (refer to Fig. 1) then the action of the shift functor can be represented as an horizontal shift, and the closure properties of the two classes
as contiguous half-planes (refer to Fig. 1) then the action of the shift functor can be represented as an horizontal shift, and the closure properties of the two classes  under positive and negative shifts are a direct consequence of the shape of these areas. With these notations, an object Z is in the heart
under positive and negative shifts are a direct consequence of the shape of these areas. With these notations, an object Z is in the heart  if it lies in a “boundary region”, i.e. if it lies in
if it lies in a “boundary region”, i.e. if it lies in  , but \(Z[-1]\) lies in
, but \(Z[-1]\) lies in  .
.
Let now \(J^\heartsuit \subseteq J\) be a heart, and let  be the corresponding subcategory of C, relative to a given J-slicing \(\mathfrak {t}\). Writing I as \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\), for any \(n\in \mathbb {Z}\) and any \(k\ge 0\) we can consider the interval decomposition \(I_{[\mathbf k ]}:[\mathbf k ]\longrightarrow \mathcal {O}(J)\) defined by setting \(I_{[\mathbf k ]}(j)=I(0)+j+n\) for \(0\le j\le k\). By Lemma 5.7, this corresponds to the collection of n contiguous intervals \(I+n,I+n+1,\ldots ,I+n+k-1\subseteq J\). The corresponding subcategories of
be the corresponding subcategory of C, relative to a given J-slicing \(\mathfrak {t}\). Writing I as \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\), for any \(n\in \mathbb {Z}\) and any \(k\ge 0\) we can consider the interval decomposition \(I_{[\mathbf k ]}:[\mathbf k ]\longrightarrow \mathcal {O}(J)\) defined by setting \(I_{[\mathbf k ]}(j)=I(0)+j+n\) for \(0\le j\le k\). By Lemma 5.7, this corresponds to the collection of n contiguous intervals \(I+n,I+n+1,\ldots ,I+n+k-1\subseteq J\). The corresponding subcategories of  will be
will be  ,
,  ,...,
,..., .
.
The existence and uniqueness of \(I_{[\mathbf k ]}\)-weaved factorizations then specializes to the following statement
Proposition 5.13
Let \(f:X\longrightarrow Y\) be a morphism in  . Then for any integer n and any positive integer k there exists a unique factorization
. Then for any integer n and any positive integer k there exists a unique factorization
of f such that \({{\,\mathrm{cofib}\,}}(f_j)\in \mathcal {C}^\heartsuit [j]\) for any \(j=n,\ldots ,n+k-1\),  and
and  .
.
The content of Proposition 5.13 becomes more interesting when  is bounded with respect to the J-slicing \(\mathfrak {t}\) (see Definition 3.29), as in this case \({{\,\mathrm{cofib}\,}}(f)\) lies in
is bounded with respect to the J-slicing \(\mathfrak {t}\) (see Definition 3.29), as in this case \({{\,\mathrm{cofib}\,}}(f)\) lies in  for \(n\ll 0\) and in
for \(n\ll 0\) and in  for \(n\gg 0\) . Namely, if
for \(n\gg 0\) . Namely, if  is J-bounded, then \({{\,\mathrm{cofib}\,}}(f)\) lies in
is J-bounded, then \({{\,\mathrm{cofib}\,}}(f)\) lies in  for some \(i\in J\). Since \(J^\heartsuit \) is a heart, there exists an element \(x\in I\) and an integer \(n_0\) such that \(i=x+n_0\), so that
for some \(i\in J\). Since \(J^\heartsuit \) is a heart, there exists an element \(x\in I\) and an integer \(n_0\) such that \(i=x+n_0\), so that  . As \(x\in I\) we have \(x\in U_0\) and so \([x,+\infty )\subseteq U_0\) therefore
. As \(x\in I\) we have \(x\in U_0\) and so \([x,+\infty )\subseteq U_0\) therefore  and so
and so  for any \(n\le n_0\). Dually one proves the statement for \(n\gg 0\). As an immediate consequence, by Remark 4.7 we see that in the J-bounded case if \(f:X\longrightarrow Y\) is any morphism in
for any \(n\le n_0\). Dually one proves the statement for \(n\gg 0\). As an immediate consequence, by Remark 4.7 we see that in the J-bounded case if \(f:X\longrightarrow Y\) is any morphism in  , then the morphisms \(0 \longrightarrow {{\,\mathrm{cofib}\,}}(f)_{n+k-1}\) and \({{\,\mathrm{cofib}\,}}(f)_{n} \longrightarrow {{\,\mathrm{cofib}\,}}(f)\) in
, then the morphisms \(0 \longrightarrow {{\,\mathrm{cofib}\,}}(f)_{n+k-1}\) and \({{\,\mathrm{cofib}\,}}(f)_{n} \longrightarrow {{\,\mathrm{cofib}\,}}(f)\) in  are isomorphisms for \(n\ll 0\) and \(k \gg 0\). Since
are isomorphisms for \(n\ll 0\) and \(k \gg 0\). Since  is the \(I_{[\mathbf k ]}\)-weaved factorization of \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) by Corollary 4.8, and since isomorphisms are preserved by pullouts we see that both \(X \xrightarrow {f_{n+k}} Z_{n+k-1} \) and \(Z_{n} \xrightarrow {f_{n-1}} Y\) are isomorphisms.
is the \(I_{[\mathbf k ]}\)-weaved factorization of \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) by Corollary 4.8, and since isomorphisms are preserved by pullouts we see that both \(X \xrightarrow {f_{n+k}} Z_{n+k-1} \) and \(Z_{n} \xrightarrow {f_{n-1}} Y\) are isomorphisms.
This leads to the following
Proposition 5.14
Let  be a stable \(\infty \)-category which is bounded with respect to a given J-slicing \(\mathfrak {t}\). Let \(J^\heartsuit \subseteq J\) be a heart for J and let
be a stable \(\infty \)-category which is bounded with respect to a given J-slicing \(\mathfrak {t}\). Let \(J^\heartsuit \subseteq J\) be a heart for J and let  be the corresponding heart in
be the corresponding heart in  . Then for any morphism \(f:X\longrightarrow Y\) in
. Then for any morphism \(f:X\longrightarrow Y\) in  there exists an integer \(n_0\) and a positive integer \(k_0\) such that for any integer \(n\le n_0\) and any positive integer k with \(k\ge n_0-n+k_0\) there exists a unique factorization of f
there exists an integer \(n_0\) and a positive integer \(k_0\) such that for any integer \(n\le n_0\) and any positive integer k with \(k\ge n_0-n+k_0\) there exists a unique factorization of f
such that  for any \(j=n,\ldots ,n+k-1\).
for any \(j=n,\ldots ,n+k-1\).
Remark 5.15
By uniqueness in Proposition 5.14, one has a well defined \(\mathbb {Z}\)-factorization
with j ranging over the integers,  for any \(j\in \mathbb {Z}\) and with \(f_m\) being an isomorphism for \(|j|\gg 0\). We will refer to this factorization as the
for any \(j\in \mathbb {Z}\) and with \(f_m\) being an isomorphism for \(|j|\gg 0\). We will refer to this factorization as the  -weaved factorization of f. Notice how the boundedness of
-weaved factorization of f. Notice how the boundedness of  has played an essential role: when
has played an essential role: when  is not bounded, one still has towers for interval decomposition \(I_{[\mathbf k ]}:j\mapsto I(0)+j+n\) for arbitrary k and n, but in general they do not stabilize.
is not bounded, one still has towers for interval decomposition \(I_{[\mathbf k ]}:j\mapsto I(0)+j+n\) for arbitrary k and n, but in general they do not stabilize.
Remark 5.16
Let \(J^\heartsuit \subseteq J\) be a heart, and let (L, U) be the slicing \(J^\heartsuit (0)\) of J and  be the corresponding t-structure on
be the corresponding t-structure on  . By Lemma 5.7 the standard heart of \(\mathfrak {t}\) is precisely
. By Lemma 5.7 the standard heart of \(\mathfrak {t}\) is precisely  . Moreover, by Corollaries 4.8 and 4.12, the
. Moreover, by Corollaries 4.8 and 4.12, the  -weaved factorization
-weaved factorization
of an initial morphism \(0\longrightarrow Y\) is such that \({{\,\mathrm{cofib}\,}}(f_j)={\mathcal {H}}^jY\) for any \(j\in \mathbb {Z}\). Therefore we see that the t-structure  can be completely read from
can be completely read from  -weaved factorizations: an object Y is in
-weaved factorizations: an object Y is in  if and only if the
if and only if the  -weaved factorization of \(0\longrightarrow Y\) satisfies \({{\,\mathrm{cofib}\,}}(f_j)=0\) for any \(j< 0\), while Y is in
-weaved factorization of \(0\longrightarrow Y\) satisfies \({{\,\mathrm{cofib}\,}}(f_j)=0\) for any \(j< 0\), while Y is in  if and only if \({{\,\mathrm{cofib}\,}}(f_j)=0\) for any \(j\ge 0\). We are going to use this fact later to characterize hearts of t-structures among full subcategories of
if and only if \({{\,\mathrm{cofib}\,}}(f_j)=0\) for any \(j\ge 0\). We are going to use this fact later to characterize hearts of t-structures among full subcategories of  .
.
Remark 5.17
The content of Remark 5.16 can be elegantly expressed in terms of the functoriality of slicings (Remark 3.12). Namely, by Remark 5.3, to give a heart \(J^\heartsuit \) of J is equivalent to giving a \(\mathbb {Z}\)-equivariant morphism of \(\pi _\heartsuit :\mathbb {Z}\)-tosets \(J\longrightarrow \mathbb {Z}\), and by functoriality this induces a map

The heart  of a J-slicing \(\mathfrak {t}\) on
of a J-slicing \(\mathfrak {t}\) on  is then the standard heart of the corresponding t-structure \(\pi _\heartsuit (\mathfrak {t})\). Moreover, one easily sees that \(\mathfrak {t}\) is a bounded J-slicing if and only if \(\pi _\heartsuit (\mathfrak {t})\) is a bounded t-structure. Indeed, since \(\pi _\heartsuit \) is a morphism of tosets, for any \(i_1\le i_2\) in J we have \([i_1,i_2]\subseteq \pi _\heartsuit ^{-1}[\pi _\heartsuit (i_1),\pi _\heartsuit (i_2)]\). Vice versa, since \(\pi _\heartsuit \) is \(\mathbb {Z}\)-equivariant, for every \(j\in J\) we have \(\pi _\heartsuit (j+n)=\pi _\heartsuit (j)+n\) and so for every \(n_1\le n_2\) in \(\mathbb {Z}\) there exist \(j_1\le j_2\) in J such that \(\pi _\heartsuit (j_1)< n_1\) and \(\pi _\heartsuit (j_2)> n_2\). Let \(j\in J\) be such \(n_1\le \pi _\heartsuit (j)\le n_2\). If \(j>j_2\) then we would have \(\pi _\heartsuit (j)\ge \pi _\heartsuit (j_2)>n_2\), and so \(j\le j_2\). Similarly \(j\ge j_1\) and so \(\pi _{\heartsuit }^{-1} [n_1,n_2]\subseteq [j_1,j_2]\).
is then the standard heart of the corresponding t-structure \(\pi _\heartsuit (\mathfrak {t})\). Moreover, one easily sees that \(\mathfrak {t}\) is a bounded J-slicing if and only if \(\pi _\heartsuit (\mathfrak {t})\) is a bounded t-structure. Indeed, since \(\pi _\heartsuit \) is a morphism of tosets, for any \(i_1\le i_2\) in J we have \([i_1,i_2]\subseteq \pi _\heartsuit ^{-1}[\pi _\heartsuit (i_1),\pi _\heartsuit (i_2)]\). Vice versa, since \(\pi _\heartsuit \) is \(\mathbb {Z}\)-equivariant, for every \(j\in J\) we have \(\pi _\heartsuit (j+n)=\pi _\heartsuit (j)+n\) and so for every \(n_1\le n_2\) in \(\mathbb {Z}\) there exist \(j_1\le j_2\) in J such that \(\pi _\heartsuit (j_1)< n_1\) and \(\pi _\heartsuit (j_2)> n_2\). Let \(j\in J\) be such \(n_1\le \pi _\heartsuit (j)\le n_2\). If \(j>j_2\) then we would have \(\pi _\heartsuit (j)\ge \pi _\heartsuit (j_2)>n_2\), and so \(j\le j_2\). Similarly \(j\ge j_1\) and so \(\pi _{\heartsuit }^{-1} [n_1,n_2]\subseteq [j_1,j_2]\).
5.1 Abelianity of the heart
In the following section we present a proof of the fact that a heart  of a J-slicing on a stable \(\infty \)-category
of a J-slicing on a stable \(\infty \)-category  is an abelian \(\infty \)-category.
is an abelian \(\infty \)-category.
In other words,  is homotopy equivalent to its homotopy category
is homotopy equivalent to its homotopy category  , which is an abelian category; this is the higher-categorical counterpart of a classical result, first proved in [1, Thm. 1.3.6], which only relies on properties stated in terms of normal torsion theories in a stable \(\infty \)-category.
, which is an abelian category; this is the higher-categorical counterpart of a classical result, first proved in [1, Thm. 1.3.6], which only relies on properties stated in terms of normal torsion theories in a stable \(\infty \)-category.
We begin with the following
Definition 5.18
(Additive \(\infty \)-category) An additive\(\infty \)-category is an additive category regarded as an \(\infty \)-category.
Remark 5.19
Equivalently, an additive \(\infty \)-category is a quasicategory \(\mathcal {A}\) such that
-
(i)
the hom space \(\mathcal {A}(X,Y)\) is a homotopically discrete infinite loop space for any X, Y, i.e., there exists an infinite sequence of \(\infty \)-groupoids \(\Xi _0, \Xi _1,\Xi _2,\ldots \), with
 and homotopy equivalences \(\Xi _i\cong \Omega \Xi _{i+1}\) for any \(i\ge 0\), such that \(\pi _n \Xi _0=0\) for any \(n\ge 1\);
and homotopy equivalences \(\Xi _i\cong \Omega \Xi _{i+1}\) for any \(i\ge 0\), such that \(\pi _n \Xi _0=0\) for any \(n\ge 1\); -
(ii)
\(\mathcal {A}\) has a zero object, and (homotopy) biproducts.
Remark 5.20
If  is a full additive \(\infty \)-subcategory of a stable \(\infty \)-category
is a full additive \(\infty \)-subcategory of a stable \(\infty \)-category  , then
, then  for any \(n_1>n_2\). Namely, for an additive
for any \(n_1>n_2\). Namely, for an additive  , let
, let  and
and  . Then \(X=Z_1[n_1]\) and \(Y=Z_2[n_2]\) for suitable
. Then \(X=Z_1[n_1]\) and \(Y=Z_2[n_2]\) for suitable  and so
and so

where in the last equality we used the fact that  is full. Since \(n_1-n_2>0\), the space
is full. Since \(n_1-n_2>0\), the space  is contractible by definition of additive \(\infty \)-category.
is contractible by definition of additive \(\infty \)-category.
Remark 5.21
In the triangulated setting one does not have the compatibility between the looping operation on objects and on spaces of morphisms  and so the othogonality condition
and so the othogonality condition  for \(n_1>n_2\), when needed, has to be imposed by hands. This is nothing but the usual vanishing of negative Ext’s one frequently meets as a property of ‘good’ additive subcategories of a triangulated category.
for \(n_1>n_2\), when needed, has to be imposed by hands. This is nothing but the usual vanishing of negative Ext’s one frequently meets as a property of ‘good’ additive subcategories of a triangulated category.
Definition 5.22
(Abelian\(\infty \)-category) An abelian\(\infty \)-category is an abelian category regarded as an \(\infty \)-category.
Remark 5.23
Equivalently, an abelian \(\infty \)-category is an additive \(\infty \)-category \(\mathcal {A}\) such that
-
(i)
\(\mathcal {A}\) has (homotopy) kernels and cokernels;
-
(ii)
for any morphism f in \(\mathcal {A}\), the natural morphism from the coimage of f to the image (see Definition 5.31) of f is an equivalence.
The rest of the section is devoted to the proof of the following result:
Theorem 5.24
Let  be a heart of a J-slicing \(\mathfrak {t}\) on a stable \(\infty \)-category
be a heart of a J-slicing \(\mathfrak {t}\) on a stable \(\infty \)-category  . Then
. Then  is an abelian \(\infty \)-category.
is an abelian \(\infty \)-category.
Remark 5.25
If \(J=\mathbb {Z}\), so that \(\mathfrak {t}\) is the datum of a t-structure on  , and
, and  is the standard heart of
is the standard heart of  , the the homotopy category
, the the homotopy category  is the abelian category arising as the standard heart of the t-structure \(h(\mathfrak {t})\) on the triangulated category
is the abelian category arising as the standard heart of the t-structure \(h(\mathfrak {t})\) on the triangulated category  .
.
In what follows, let \(I:[\mathbf 1 ]\longrightarrow \mathcal {O}(J)\) be an interval such that  . The two factorization systems associated with I will be denoted by \((\mathcal {E}_0,\mathcal {M}_0)\) and \((\mathcal {E}_1,\mathcal {M}_1)\), respectively. By Lemma 5.7 we have \(\mathcal {M}_1=\mathcal {M}_0[1]\) and \(\mathcal {E}_1=\mathcal {E}_0[1]\).
. The two factorization systems associated with I will be denoted by \((\mathcal {E}_0,\mathcal {M}_0)\) and \((\mathcal {E}_1,\mathcal {M}_1)\), respectively. By Lemma 5.7 we have \(\mathcal {M}_1=\mathcal {M}_0[1]\) and \(\mathcal {E}_1=\mathcal {E}_0[1]\).
Lemma 5.26
For any X and Y in  , the hom space
, the hom space  is a homotopically discrete infinite loop space.
is a homotopically discrete infinite loop space.
Proof
Since  is a full subcategory of
is a full subcategory of  , we have
, we have  , which is an infinite loop space since
, which is an infinite loop space since  is a stable \(\infty \)-category.
is a stable \(\infty \)-category.
So we are left to prove that  for \(n\ge 1\). Since
for \(n\ge 1\). Since  , this is equivalent to showing that
, this is equivalent to showing that  is contractible. Since X and Y are objects in
is contractible. Since X and Y are objects in  , we have
, we have  and
and  . But
. But  is right object-orthogonal to
is right object-orthogonal to  , therefore
, therefore  is contractible. \(\square \)
is contractible. \(\square \)
The subcategory  inherits the 0 object and biproducts (in fact, all finite limits) from
inherits the 0 object and biproducts (in fact, all finite limits) from  , so in order to prove it is is abelian we are left to prove that it has kernels and cokernels, and that the canonical morphism from the coimage to the image is an equivalence.
, so in order to prove it is is abelian we are left to prove that it has kernels and cokernels, and that the canonical morphism from the coimage to the image is an equivalence.
Lemma 5.27
Let \(f:X\longrightarrow Y\) be a morphism in  . Then \(\text {fib}(f)\) is in
. Then \(\text {fib}(f)\) is in  and \({{\,\mathrm{cofib}\,}}(f)\) is in
and \({{\,\mathrm{cofib}\,}}(f)\) is in  .
.
Proof
Since both \(X\longrightarrow 0\) and \(Y\longrightarrow 0\) are in \(\mathcal {M}_1\), by the 3-for-2 property also f is in \(\mathcal {M}_1\). Since \(\mathcal {M}_1\) is closed for pullbacks, \(\text {fib}(f)\longrightarrow 0\) is in \(\mathcal {M}_1\) and so \(\text {fib}(f)\) is in  . The proof for \({{\,\mathrm{cofib}\,}}(f)\) is completely dual. \(\square \)
. The proof for \({{\,\mathrm{cofib}\,}}(f)\) is completely dual. \(\square \)
Definition 5.28
Denote by

the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of the morphism \(0\longrightarrow {{\,\mathrm{fib}\,}}(f)\) and by

the \((\mathcal {E}_1,\mathcal {M}_1)\)-factorization of the morphism \({{\,\mathrm{cofib}\,}}(f)\longrightarrow 0\). We call \(\ker (f)\) and \({{\,\mathrm{coker}\,}}(f)\) respectively the kernel and the cokernel of f in  .
.
Remark 5.29
Since \({{\,\mathrm{cofib}\,}}(f)[-1]\cong {{\,\mathrm{fib}\,}}{f}\) and \((\mathcal {M}_1,\mathcal {E}_1)[-1]=(\mathcal {M}_0,\mathcal {E}_0)\), one can equivalently define \({{\,\mathrm{coker}\,}}(f)\) by declaring the \((\mathcal {E}_0,\mathcal {M}_0)\)-factorization of \({{\,\mathrm{fib}\,}}(f)\longrightarrow 0\) to be \({{\,\mathrm{fib}\,}}(f)\xrightarrow {\mathcal {E}_0}{{\,\mathrm{coker}\,}}(f)[-1]\xrightarrow {\mathcal {M}_0} 0\). Similarly, one can define \(\ker (f)\) by declaring the \((\mathcal {E}_1,\mathcal {M}_1)\)-factorization of \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) to be \(0\xrightarrow {\mathcal {E}_1}\ker (f)[1]\xrightarrow {\mathcal {M}_1} {{\,\mathrm{cofib}\,}}(f)\). By normality of the factorization system we therefore have the homotopy commutative diagram

whose square sub-diagram is a homotopy pullout.
Lemma 5.30
Both \(\ker (f)\) and \({{\,\mathrm{coker}\,}}(f)\) are in  .
.
Proof
By construction \(\ker (f)\) is in  , so we only need to show that \(\ker (f)\) is in
, so we only need to show that \(\ker (f)\) is in  . By definition of \(\ker (f)\), we have that \(\ker (f)\longrightarrow {{\,\mathrm{fib}\,}}(f)\) is in \(\mathcal {M}_0\). Since \(\mathcal {M}_0[-1]\subseteq \mathcal {M}_0\), we have that also \(\ker (f)[-1]\longrightarrow {{\,\mathrm{fib}\,}}(f)[-1]\) is in \(\mathcal {M}_0\). By Lemma 5.27, \({{\,\mathrm{fib}\,}}(f)[-1]\longrightarrow 0\) is in \(\mathcal {M}_1[-1]=\mathcal {M}_0\) and so we find that also \(\ker (f)[-1]\longrightarrow 0\) is in \(\mathcal {M}_0\). The proof for \({{\,\mathrm{coker}\,}}(f)\) is perfectly dual. \(\square \)
. By definition of \(\ker (f)\), we have that \(\ker (f)\longrightarrow {{\,\mathrm{fib}\,}}(f)\) is in \(\mathcal {M}_0\). Since \(\mathcal {M}_0[-1]\subseteq \mathcal {M}_0\), we have that also \(\ker (f)[-1]\longrightarrow {{\,\mathrm{fib}\,}}(f)[-1]\) is in \(\mathcal {M}_0\). By Lemma 5.27, \({{\,\mathrm{fib}\,}}(f)[-1]\longrightarrow 0\) is in \(\mathcal {M}_1[-1]=\mathcal {M}_0\) and so we find that also \(\ker (f)[-1]\longrightarrow 0\) is in \(\mathcal {M}_0\). The proof for \({{\,\mathrm{coker}\,}}(f)\) is perfectly dual. \(\square \)
By definition of \(\ker (f)\) and \({{\,\mathrm{coker}\,}}(f)\), the defining diagram of \({{\,\mathrm{fib}\,}}(f)\) and \({{\,\mathrm{cofib}\,}}(f)\) can be enlarged as

where \(k_f\) and \(c_f\) are morphisms in  .
.
Definition 5.31
Let \(f:X\longrightarrow Y\) be a morphism in  . The image\({{\,\mathrm{\textsf {im}}\,}}(f)\) and the coimage\({{\,\mathrm{\textsf {coim}}\,}}(f)\) of f are defined as \({{\,\mathrm{\textsf {im}}\,}}(f)=\ker (c_f)\) and \({{\,\mathrm{\textsf {coim}}\,}}(f)={{\,\mathrm{coker}\,}}(k_f)\).
. The image\({{\,\mathrm{\textsf {im}}\,}}(f)\) and the coimage\({{\,\mathrm{\textsf {coim}}\,}}(f)\) of f are defined as \({{\,\mathrm{\textsf {im}}\,}}(f)=\ker (c_f)\) and \({{\,\mathrm{\textsf {coim}}\,}}(f)={{\,\mathrm{coker}\,}}(k_f)\).
The following lemma shows that \(\ker (f)\) does indeed have the defining property of a kernel:
Lemma 5.32
The homotopy commutative diagram

is a pullback diagram in  .
.
Proof
A homotopy commutative diagram

between objects in the heart is in particular a homotopy commutative diagram in  so it is equivalent to the datum of a morphism \(k':K\longrightarrow {{\,\mathrm{fib}\,}}(f)\) in
so it is equivalent to the datum of a morphism \(k':K\longrightarrow {{\,\mathrm{fib}\,}}(f)\) in  , with K an object in
, with K an object in  . By the orthogonality of \((\mathcal {E}_0,\mathcal {M}_0)\), this is equivalent to a morphism \({\tilde{k}}:K\longrightarrow \ker (f)\):
. By the orthogonality of \((\mathcal {E}_0,\mathcal {M}_0)\), this is equivalent to a morphism \({\tilde{k}}:K\longrightarrow \ker (f)\):

\(\square \)
There is, obviously, a dual result showing that \({{\,\mathrm{coker}\,}}(f)\) is indeed a cokernel.
Lemma 5.33
The homotopy commutative diagram

is a pushout diagram in  .
.
Proposition 5.34
A homotopy commutative diagram

with vertices in  is a pullout diagram in
is a pullout diagram in  if and only if it is a pullout diagram in
if and only if it is a pullout diagram in  .
.
Proof
Since  is a full subcategory of
is a full subcategory of  it is clear that if the given diagram is a pullout in
it is clear that if the given diagram is a pullout in  then it is automatically also a pullout in
then it is automatically also a pullout in  . Conversely, assume the given diagram is a pullout in
. Conversely, assume the given diagram is a pullout in  . This means that \(X=\ker (g)\) and \(Z={{\,\mathrm{coker}\,}}(f)\). By definition of \(\ker \) and \({{\,\mathrm{coker}\,}}\) this implies that we have the following homotopy commutative diagram in
. This means that \(X=\ker (g)\) and \(Z={{\,\mathrm{coker}\,}}(f)\). By definition of \(\ker \) and \({{\,\mathrm{coker}\,}}\) this implies that we have the following homotopy commutative diagram in  where each square is a pullout (in
where each square is a pullout (in  ):
):

Here \(X\longrightarrow \mathbf 0 \) is in \(\mathcal {E}_0\) by definition of \(\ker (g)\) and by the Sator lemma, and so also \({{\,\mathrm{fib}\,}}(g)\longrightarrow W\) is in \(\mathcal {E}_0\) since \(\mathcal {E}_0\) is closed under pushouts. The morphism \({{\,\mathrm{cofib}\,}}(f)\longrightarrow Z\) is in \(\mathcal {E}_1\) by definition of \({{\,\mathrm{coker}\,}}(f)\). From the pullout diagram in 

and the fact \(\mathcal {E}_1\) is closed under pushouts that follows that \(\mathbf 0 \longrightarrow W[1]\) is in \(\mathcal {E}_1\). Therefore \(\mathbf 0 \longrightarrow W\) is in \(\mathcal {E}_1[-1]=\mathcal {E}_0\) and so \(W\longrightarrow \mathbf 0 \) is in \(\mathcal {E}_0\). This shows that \({{\,\mathrm{fib}\,}}(g)\longrightarrow \mathbf 0 \) is in \(\mathcal {E}_0\) and so \(X\longrightarrow {{\,\mathrm{fib}\,}}(g)\) is an isomorphism. Therefore the given diagram is a pullback in  and so a pullout in
and so a pullout in  . \(\square \)
. \(\square \)
Lemma 5.35
For \(f:X\longrightarrow Y\) a morphism in  , there is a homotopy commutative diagram where all squares are homotopy pullouts:
, there is a homotopy commutative diagram where all squares are homotopy pullouts:

uniquely determining an object  .
.
Proof
Define \(Z_f\) as the homotopy pullout

Here the vertical arrow on the right is in \(\mathcal {E}_0\) since the vertical arrow on the left is in \(\mathcal {E}_0\) by definition of \({{\,\mathrm{coker}\,}}(f)\) (see Remark 5.29) and \(\mathcal {E}_0\) is preserved by pushouts. Next, paste on the left of this diagram the pullout given by Remark 5.29 and build the rest of the diagram by taking pullbacks or pushouts, recalling that \((\mathcal {E}_0,\mathcal {M}_0)[1]=(\mathcal {E}_1,\mathcal {M}_1)\). Use again Remark 5.29 and the fact that \(\mathcal {M}_1\) is closed under pullbacks to see that \(Z_f\longrightarrow Y\) is in \(\mathcal {M}_1\). Finally, we have
and so \(Z_f\) is in  . \(\square \)
. \(\square \)
Proposition 5.36
There is an isomorphism \({{\,\mathrm{\textsf {im}}\,}}(f)\cong {{\,\mathrm{\textsf {coim}}\,}}(f)\).
Proof
By definition, \({{\,\mathrm{\textsf {im}}\,}}(f)\) and \({{\,\mathrm{\textsf {coim}}\,}}(f)\) are defined by the factorizations

and

The diagram in Lemma 5.35 shows that we have \({{\,\mathrm{fib}\,}}(c_f)=Z_f={{\,\mathrm{cofib}\,}}(k_f)\). Therefore, what we need to exhibit are the \((\mathcal {E}_0,\mathcal {M}_0)\) factorizations of \(0\longrightarrow Z_f\) and the \((\mathcal {E}_1,\mathcal {M}_1)\) factorization of \(Z_f\longrightarrow 0\). Since \(Z_f\) is an object in  , these are
, these are
and
respectively, thus giving \({{\,\mathrm{\textsf {im}}\,}}(f)\cong Z_f\cong {{\,\mathrm{\textsf {coim}}\,}}(f)\). \(\square \)
5.2 Abelian subcategories as hearts.
By the results in the previous section and by Corollary 5.11 we see that hearts of bounded t-structures are very peculiar subcategories of a stable \(\infty \)-category  : they are abelian and every morphism in
: they are abelian and every morphism in  admits a unique
admits a unique  -weaved factorization. As we are going to show, these two properties precisely characterize hearts among full subcategories of
-weaved factorization. As we are going to show, these two properties precisely characterize hearts among full subcategories of  .
.
Definition 5.37
Let \(f:X\longrightarrow Y\) be a morphism in  , and let
, and let  be an additive \(\infty \)-subcategory of
be an additive \(\infty \)-subcategory of  . An
. An  -weaved factorization of f is a factorization
-weaved factorization of f is a factorization
with j ranging over the integers,  for any \(j\in \mathbb {Z}\) and with \(f_m\) being an isomorphism for \(|j|\gg 0\).
for any \(j\in \mathbb {Z}\) and with \(f_m\) being an isomorphism for \(|j|\gg 0\).
Proposition 5.38
Let  be an additive full \(\infty \)-subcategory of a stable \(\infty \)-category
be an additive full \(\infty \)-subcategory of a stable \(\infty \)-category  such that any morphism \(f:X\longrightarrow Y\) in
such that any morphism \(f:X\longrightarrow Y\) in  has an
has an  -weaved factorization. Then the collection of subcategories
-weaved factorization. Then the collection of subcategories  is a Bridgeland \(\mathbb {Z}\)-slicing of
is a Bridgeland \(\mathbb {Z}\)-slicing of  .
.
Proof
Looking at Definition 4.18, the only thing we need to prove is that  for \(n_1>n_2\). This is Remark 5.20. \(\square \)
for \(n_1>n_2\). This is Remark 5.20. \(\square \)
From Proposition 4.26 and Remark 4.27 we then immediately have the following converse of Corollary 5.11, corresponding to [5, Lemma 3.2].
Proposition 5.39
Let  be a full additive \(\infty \)-subcategory of a stable \(\infty \)-category
be a full additive \(\infty \)-subcategory of a stable \(\infty \)-category  , such that any morphism in
, such that any morphism in  has a
has a  -weaved factorization, and let
-weaved factorization, and let  be the functors given by taking the cofibers of the n-th morphism in the
be the functors given by taking the cofibers of the n-th morphism in the  -weaved factorization of the initial morphisms. Let
-weaved factorization of the initial morphisms. Let  be the full subcategory of
be the full subcategory of  on those objects X such that \({\mathcal {H}}^j_B(X)=0\) for any \(j< 0\), and let
on those objects X such that \({\mathcal {H}}^j_B(X)=0\) for any \(j< 0\), and let  be the full subcategory of
be the full subcategory of  on those objects X such that \({\mathcal {H}}^j_B(X)=0\) for any \(j\ge 0\). Then
on those objects X such that \({\mathcal {H}}^j_B(X)=0\) for any \(j\ge 0\). Then  is a t-structure on
is a t-structure on  , the stable \(\infty \)-category
, the stable \(\infty \)-category  is bounded with respect to
is bounded with respect to  , and the standard heart of
, and the standard heart of  is (equivalent to)
is (equivalent to)  . In particular
. In particular  is abelian.
is abelian.
Proof
The only thing left to prove is that the standard heart of  is
is  . To see this notice that an object Y lies in
. To see this notice that an object Y lies in  if and only if the
if and only if the  -weaved factorization
-weaved factorization
of its initial morphism has \(\text {cofib}(f_j)=0\) for every \(j\ne 0\), and so it is of the form
with  . \(\square \)
. \(\square \)
6 Semi-orthogonal decompositions
La vie c’est ce qui se décompose à tout moment; c’est une perte monotone de lumière, une dissolution insipide dans la nuit, sans sceptres, sans auréoles, sans nimbes.
E. Cioran
In the previous section we have investigated the case when the equivalence relation \(\sim \) from Lemma 2.27 had a single equivalence class. At the opposite end is the case when each equivalence class consists of a single element. As \(x\sim x+1\) for any \(x\in J\), this is equivalent to requiring that the \(\mathbb {Z}\)-action is trivial. As noticed in Remark 2.18 this in particular happens when J is a finite finite totally ordered set. As we are going to show, this is another well investigated case in the literature: J-families of t-structures with a finite J capture the notion of semi-orthogonal decompositions for the stable \(\infty \)-category  (see [3, 15] for the notion of semi-orthogonal decomposition in the classical triangulated context).
(see [3, 15] for the notion of semi-orthogonal decomposition in the classical triangulated context).
To fix notations for this section, let \(J=[\mathbf k ]\) be the totally ordered set on \((k+1)\) elements, i.e., \(J=\{0,1,\ldots ,k\}\), and let  be a \([\mathbf k ]\)-slicing on
be a \([\mathbf k ]\)-slicing on  . We have the maximal interval decomposition on \([\mathbf k ]\) given by intervals \(I_i=\{i\}\) for \(i=0,\ldots ,k\). This corresponds to the morphism of posets \([\mathbf k-1 ]\longrightarrow {\mathcal {O}}([\mathbf k ])\) given by \(i\mapsto \{x\ge i+1\}\). Using this decomposition we have that any morphism \(f:X\longrightarrow Y\) in
. We have the maximal interval decomposition on \([\mathbf k ]\) given by intervals \(I_i=\{i\}\) for \(i=0,\ldots ,k\). This corresponds to the morphism of posets \([\mathbf k-1 ]\longrightarrow {\mathcal {O}}([\mathbf k ])\) given by \(i\mapsto \{x\ge i+1\}\). Using this decomposition we have that any morphism \(f:X\longrightarrow Y\) in  has a unique factorization
has a unique factorization
with  , and
, and  , for any \(0\le h <i\le k\).
, for any \(0\le h <i\le k\).
What we are left to investigate are therefore the special features of the t-structures  coming from the triviality of the \(\mathbb {Z}\)-action on \([\mathbf k ]\), and so on \({\mathcal {O}}([\mathbf k ])\). By \(\mathbb {Z}\)-equivariancy of the map
coming from the triviality of the \(\mathbb {Z}\)-action on \([\mathbf k ]\), and so on \({\mathcal {O}}([\mathbf k ])\). By \(\mathbb {Z}\)-equivariancy of the map  , this implies that all the t-structures \(\mathfrak {t}_{i}\) are \(\mathbb {Z}\)-fixed points for the natural \(\mathbb {Z}\)-action on
, this implies that all the t-structures \(\mathfrak {t}_{i}\) are \(\mathbb {Z}\)-fixed points for the natural \(\mathbb {Z}\)-action on  . Now, a rather pleasant fact is that fixed points of the \(\mathbb {Z}\)-action on
. Now, a rather pleasant fact is that fixed points of the \(\mathbb {Z}\)-action on  are precisely those t-structures
are precisely those t-structures  for which
for which  is a stable sub-\(\infty \)-category of
is a stable sub-\(\infty \)-category of  . We will make use of the following
. We will make use of the following
Lemma 6.1
Let \(\mathcal {B}\) be a full sub-\(\infty \)-category of the stable \(\infty \)-category  ; then, \(\mathcal {B}\) is a stable sub-\(\infty \)-category of
; then, \(\mathcal {B}\) is a stable sub-\(\infty \)-category of  if and only if \(\mathcal {B}\) is closed under shifts in both directions and under pushouts in
if and only if \(\mathcal {B}\) is closed under shifts in both directions and under pushouts in  .
.
Proof
The “only if” part is trivial, so let us prove the “if” part. First of all let us see that under these assumptions \(\mathcal {B}\) is closed under taking fibers of morphisms. This is immediate: if \(f:X\longrightarrow Y\) is an arrow in \(\mathcal {B}\) (i.e. an arrow of  between objects of \(\mathcal {B}\), by fullness), then \(f[-1]\) is again in \(\mathcal {B}\) since \(\mathcal {B}\) is closed with respect to the left shift. Since \(\mathcal {B}\) is closed under pushouts in
between objects of \(\mathcal {B}\), by fullness), then \(f[-1]\) is again in \(\mathcal {B}\) since \(\mathcal {B}\) is closed with respect to the left shift. Since \(\mathcal {B}\) is closed under pushouts in  , also \({{\,\mathrm{fib}\,}}(f)={{\,\mathrm{cofib}\,}}(f[-1])\) is in \(\mathcal {B}\). It remains to show how this implies that \(\mathcal {B}\) is actually stable, i.e. it is closed under all finite limits and satisfies the pullout axiom. Unwinding the assumptions on \(\mathcal {B}\), this boils down to showing that in the square
, also \({{\,\mathrm{fib}\,}}(f)={{\,\mathrm{cofib}\,}}(f[-1])\) is in \(\mathcal {B}\). It remains to show how this implies that \(\mathcal {B}\) is actually stable, i.e. it is closed under all finite limits and satisfies the pullout axiom. Unwinding the assumptions on \(\mathcal {B}\), this boils down to showing that in the square

the pullback B of \(f,g \in \hom (\mathcal {B})\) done in  is actually an object of \(\mathcal {B}\); indeed, once this is shown, the square above will satisfy the pullout axiom in
is actually an object of \(\mathcal {B}\); indeed, once this is shown, the square above will satisfy the pullout axiom in  , so a fortiori it will have the universal property of a pushout in \(\mathcal {B}\). To this aim, let us consider the enlarged diagram of pullout squares in
, so a fortiori it will have the universal property of a pushout in \(\mathcal {B}\). To this aim, let us consider the enlarged diagram of pullout squares in 

The objects \(Z[-1], {{\,\mathrm{fib}\,}}(f)\) and \({{\,\mathrm{fib}\,}}(g)\) lie in \(\mathcal {B}\) by the first part of the proof, so the square \((\star )\) is in particular a pushout of morphism in \(\mathcal {B}\); by assumption, this entails that \(B\in \mathcal {B}\). \(\square \)
Remark 6.2
Obviously, a completely dual statement can be proved in a completely dual fashion: a full sub-\(\infty \)-category \(\mathcal {B}\) of a stable \(\infty \)-category  is a stable sub-\(\infty \)-category if and only if it is closed under shifts in both directions and under pullbacks in
is a stable sub-\(\infty \)-category if and only if it is closed under shifts in both directions and under pullbacks in  .
.
Proposition 6.3
Let  be a t-structure on a stable \(\infty \)-category
be a t-structure on a stable \(\infty \)-category  , and let \((\mathcal {E},\mathcal {M})\) be the normal torsion theory associated to \(\mathfrak {t}\); then the following conditions are equivalent:
, and let \((\mathcal {E},\mathcal {M})\) be the normal torsion theory associated to \(\mathfrak {t}\); then the following conditions are equivalent:
-
(1)
\(\mathfrak {t}\) is a fixed point for the \(\mathbb {Z}\)-action on \(\text {ts}(\mathcal {C})\), i.e., \(\mathfrak {t}[1]=\mathfrak {t}\) (or equivalently,
 , or equivalently
, or equivalently  );
); -
(2)
 is a stable sub-\(\infty \)-category of
is a stable sub-\(\infty \)-category of  .
. -
(3)
 is a stable sub-\(\infty \)-category of
is a stable sub-\(\infty \)-category of  .
. -
(4)
\(\mathcal {E}\) is closed under pullback;
-
(5)
\(\mathcal {M}\) is closed under pushout.
Proof
‘(2) implies (1)’ is obvious. Namely, if  is a stable sub-\(\infty \)-category of
is a stable sub-\(\infty \)-category of  , then it is closed under shifts in both directions. Therefore
, then it is closed under shifts in both directions. Therefore  , and so
, and so  . Since, by definition of t-structure,
. Since, by definition of t-structure,  , we have
, we have  . To prove that ‘(1) implies (2)’, assume
. To prove that ‘(1) implies (2)’, assume  . This implies
. This implies  , so
, so  is closed under shifts in both directions. By Lemma 6.1, we then have only to show that
is closed under shifts in both directions. By Lemma 6.1, we then have only to show that  is closed under pushouts in
is closed under pushouts in  to conclude that
to conclude that  is a stable \(\infty \)-subcategory of
is a stable \(\infty \)-subcategory of  . Consider a pushout diagram
. Consider a pushout diagram

in  with A, B and C in
with A, B and C in  . Since A and C are in
. Since A and C are in  we have that both \(0\longrightarrow A\) and \(0\longrightarrow C\) are in \(\mathcal {E}\). But \(\mathcal {E}\) has the 3-for-2 property, so also \(A\longrightarrow C\) is \(\mathcal {E}\). Since \(\mathcal {E}\) is closed for pushouts, this implies that also \(B\longrightarrow P\) is in \(\mathcal {E}\). But \(0\longrightarrow B\) in in \(\mathcal {E}\) since B is in
we have that both \(0\longrightarrow A\) and \(0\longrightarrow C\) are in \(\mathcal {E}\). But \(\mathcal {E}\) has the 3-for-2 property, so also \(A\longrightarrow C\) is \(\mathcal {E}\). Since \(\mathcal {E}\) is closed for pushouts, this implies that also \(B\longrightarrow P\) is in \(\mathcal {E}\). But \(0\longrightarrow B\) in in \(\mathcal {E}\) since B is in  , and therefore also \(0\longrightarrow P\) is in \(\mathcal {E}\), i.e., P is in
, and therefore also \(0\longrightarrow P\) is in \(\mathcal {E}\), i.e., P is in  .
.
We now prove that ‘(1) is equivalent to (4)’. Assume \(\mathcal {E}\) is closed under pullbacks. Then for any X in  we have that \(0\longrightarrow X\) is in \(\mathcal {E}\), and so \(X[-1]\longrightarrow 0\) is in \(\mathcal {E}\). By the Sator lemma this implies that \(0\longrightarrow X[-1]\) is in \(\mathcal {E}\), i.e., that \(X[-1]\) is in
we have that \(0\longrightarrow X\) is in \(\mathcal {E}\), and so \(X[-1]\longrightarrow 0\) is in \(\mathcal {E}\). By the Sator lemma this implies that \(0\longrightarrow X[-1]\) is in \(\mathcal {E}\), i.e., that \(X[-1]\) is in  . This shows that
. This shows that  and therefore that \(\mathfrak {t}[1]= \mathfrak {t}\). Conversely, assume \(\mathfrak {t}[1]=\mathfrak {t}\), and consider a morphism \(f:X\longrightarrow Y\) in \(\mathcal {E}\). For any morphism \(B\longrightarrow Y\) in
and therefore that \(\mathfrak {t}[1]= \mathfrak {t}\). Conversely, assume \(\mathfrak {t}[1]=\mathfrak {t}\), and consider a morphism \(f:X\longrightarrow Y\) in \(\mathcal {E}\). For any morphism \(B\longrightarrow Y\) in  consider the diagram
consider the diagram

where all the squares are pullouts in  . Since f is in \(\mathcal {E}\) and \(\mathcal {E}\) is closed for pushouts, also \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) is in \(\mathcal {E}\). This means that \({{\,\mathrm{cofib}\,}}(f)\) is in
. Since f is in \(\mathcal {E}\) and \(\mathcal {E}\) is closed for pushouts, also \(0\longrightarrow {{\,\mathrm{cofib}\,}}(f)\) is in \(\mathcal {E}\). This means that \({{\,\mathrm{cofib}\,}}(f)\) is in  and so, since we are assuming that
and so, since we are assuming that  , also \(\text {fib}(f)={{\,\mathrm{cofib}\,}}(f)[-1]\) is in
, also \(\text {fib}(f)={{\,\mathrm{cofib}\,}}(f)[-1]\) is in  , i.e., \(0\longrightarrow \text {fib}(f)\) is in \(\mathcal {E}\). By the Sator lemma, \(\text {fib}(f)\longrightarrow 0\) is in \(\mathcal {E}\), which is closed for pushouts, and so \(A\longrightarrow B\) is in \(\mathcal {E}\). The proofs that ‘(1) if and only if (3)’ and ‘(1) if and only if (5)’ are perfectly dual. \(\square \)
, i.e., \(0\longrightarrow \text {fib}(f)\) is in \(\mathcal {E}\). By the Sator lemma, \(\text {fib}(f)\longrightarrow 0\) is in \(\mathcal {E}\), which is closed for pushouts, and so \(A\longrightarrow B\) is in \(\mathcal {E}\). The proofs that ‘(1) if and only if (3)’ and ‘(1) if and only if (5)’ are perfectly dual. \(\square \)
Remark 6.4
A factorization system \((\mathcal {E},\mathcal {M})\) for which the class \(\mathcal {E}\) is closed for pullbacks is sometimes called an exact reflective factorization, see, e.g., [6]. This is equivalent to saying that the associated reflection functor is left exact (this is called a localization in the jargon of [6]). Dually, one characterizes co-localizations of a category  with an initial object as co-exact coreflective factorizations where the right class \(\mathcal {M}\) is closed under pushouts. Therefore, in the stable \(\infty \)-case, we see that a \(\mathbb {Z}\)-fixed point in
with an initial object as co-exact coreflective factorizations where the right class \(\mathcal {M}\) is closed under pushouts. Therefore, in the stable \(\infty \)-case, we see that a \(\mathbb {Z}\)-fixed point in  is a t-structure
is a t-structure  such that the truncation functors
such that the truncation functors  and
and  respectively form a co-localizations and a localization of
respectively form a co-localizations and a localization of  . In the terminology of [4] we therefore find that in the stable \(\infty \)-case \(\mathbb {Z}\)-fixed point in
. In the terminology of [4] we therefore find that in the stable \(\infty \)-case \(\mathbb {Z}\)-fixed point in  correspond to hereditary torsion pairs on
correspond to hereditary torsion pairs on  . Since we have seen that for a \(\mathbb {Z}\)-fixed point in
. Since we have seen that for a \(\mathbb {Z}\)-fixed point in  both
both  and
and  are stable \(\infty \)-categories, this result could be deduced also from [18, Prop. 1.1.4.1]: a left (resp., right) exact functor between stable \(\infty \)-categories is also right (resp., left) exact.
are stable \(\infty \)-categories, this result could be deduced also from [18, Prop. 1.1.4.1]: a left (resp., right) exact functor between stable \(\infty \)-categories is also right (resp., left) exact.
We can now precisely relate semi-orthogonal decompositions in a stable \(\infty \)-category  to \([\mathbf k ]\)-slicings of
to \([\mathbf k ]\)-slicings of  . The only thing we still need is the following definition, which is an immediate adaptation to the stable setting of the classical definition given for triangulated categories (see, e.g., [3, 15]).
. The only thing we still need is the following definition, which is an immediate adaptation to the stable setting of the classical definition given for triangulated categories (see, e.g., [3, 15]).
Definition 6.5
Let  be a stable \(\infty \)-category. A semi-orthogonal decomposition with \(k+1\) classes on
be a stable \(\infty \)-category. A semi-orthogonal decomposition with \(k+1\) classes on  is the datum of \(k+1\) stable \(\infty \)-subcategories
is the datum of \(k+1\) stable \(\infty \)-subcategories  ,...,
,...,  of
of  such that
such that
-
(1)
one has
 for \(h<i\) (semi-orthogonality);
for \(h<i\) (semi-orthogonality); -
(2)
for any object Y in
 there exists a unique
there exists a unique 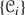 -weaved tower, i.e., a factorization of the initial morphism \(0\longrightarrow Y\) as $$\begin{aligned} 0 \xrightarrow {f_{k}} Y_{k-1} \xrightarrow {f_{k-1}}Y_{{k-2}}\longrightarrow \cdots \longrightarrow Z_{{1}} \xrightarrow {f_1} Y_{0} \xrightarrow {f_0} Y, \end{aligned}$$
-weaved tower, i.e., a factorization of the initial morphism \(0\longrightarrow Y\) as $$\begin{aligned} 0 \xrightarrow {f_{k}} Y_{k-1} \xrightarrow {f_{k-1}}Y_{{k-2}}\longrightarrow \cdots \longrightarrow Z_{{1}} \xrightarrow {f_1} Y_{0} \xrightarrow {f_0} Y, \end{aligned}$$with
 for any \(i=0,\ldots , k\).
for any \(i=0,\ldots , k\).
Since  -weaved towers are preserved by pullouts, one can equivalently require that any morphism \(f:X\longrightarrow Y\) in
-weaved towers are preserved by pullouts, one can equivalently require that any morphism \(f:X\longrightarrow Y\) in  has a unique factorization of has a unique factorization
has a unique factorization of has a unique factorization
with  , and this immediately leads to the following
, and this immediately leads to the following
Proposition 6.6
Let  be a stable \(\infty \)-category. Then the datum of a semi-orthogonal decompositions with \(k+1\) classes on
be a stable \(\infty \)-category. Then the datum of a semi-orthogonal decompositions with \(k+1\) classes on  is equivalent to the datum of a \([\mathbf k ]\)-slicing on
is equivalent to the datum of a \([\mathbf k ]\)-slicing on  .
.
Proof
The only missing piece of information to show that a \([\mathbf k ]\)-slicing is a semi-orthogonal decompositions is the fact that the sub-\(\infty \)-categories  are stable. But
are stable. But  and both
and both  and
and  are stable by Proposition 6.3. Therefore, also
are stable by Proposition 6.3. Therefore, also  is stable (see [18]). Conversely, given a semi-orthogonal decomposition this defines a \([\mathbf k ]\)-slicing by means of the cofiber functors
is stable (see [18]). Conversely, given a semi-orthogonal decomposition this defines a \([\mathbf k ]\)-slicing by means of the cofiber functors  , by the same argument in the proof of Proposition 5.39. \(\square \)
, by the same argument in the proof of Proposition 5.39. \(\square \)
Remark 6.7
By Remark 6.4, we recover in the stable \(\infty \)-setting the well known fact (see [4, IV.4]) that semi-orthogonal decompositions with a single class correspond to hereditary torsion pairs on the category.
Proposition 6.6 immediately suggests to generalize the definition of semi-orthogonal decomposition to the case of an arbitrary toset of indices, not necessarily finite.
Definition 6.8
Let I be a toset, and let \(I^\flat \) be the \(\mathbb {Z}\)-toset given by I endowed with the trivial \(\mathbb {Z}\)-action (see 2.30). An \(I^\flat \)-slicing of a stable \(\infty \)-category  is called a I-semi-orthogonal decomposition of
is called a I-semi-orthogonal decomposition of  . The class of all I-semi-orthogonal decompositions of
. The class of all I-semi-orthogonal decompositions of  will be denoted by
will be denoted by  , i.e.
, i.e.  .
.
Remark 6.9
If an I-semi-orthogonal decomposition of  is given, then all the subcategories
is given, then all the subcategories  are stable, for any i in I.
are stable, for any i in I.
Remark 6.10
Let J be a \({\mathbb {Z}}\)-toset, and let \(\iota (J)\) be the toset of equivalence classes of J, for the equivalence relation \(\sim \) of Lemma 2.27. Then every J-slicing of a stable \(\infty \)-category  induces an \(\iota (J)\)-semi-orthogonal decomposition of
induces an \(\iota (J)\)-semi-orthogonal decomposition of  . Namely, by Proposition 2.30, \(J\rightsquigarrow \iota (J)\) is the left adjoint of the fully faithful embedding
. Namely, by Proposition 2.30, \(J\rightsquigarrow \iota (J)\) is the left adjoint of the fully faithful embedding  , and the the projection to the quotient is a \(\mathbb {Z}\)-equivariant morphism
, and the the projection to the quotient is a \(\mathbb {Z}\)-equivariant morphism
which is the unit of this adjunction. By functoriality of the slicings (Remark 3.12) we therefore have a natural map

7 Abelian slicings and tiltings
Quando si vuole uccidere un uomo bisogna colpirlo al cuore, e un Winchester è l’arma più adatta.
R. Rojo
We now review the abelian counterpart of the notion of J-slicing and relate slicings on hearts of a stable \(\infty \)-category  with slicings of
with slicings of  . First of all recall the notion of torsion pair on an abelian \(\infty \)-category, which is the abelian counterpart of the notion of t-structure on a stable \(\infty \)-category.
. First of all recall the notion of torsion pair on an abelian \(\infty \)-category, which is the abelian counterpart of the notion of t-structure on a stable \(\infty \)-category.
Definition 7.1
(torsion theory on an abelian\(\infty \)-category) Let  be an abelian \(\infty \)-category. A torsion pair on an abelian \(\infty \)-category
be an abelian \(\infty \)-category. A torsion pair on an abelian \(\infty \)-category  is a pair
is a pair  of full sub-\(\infty \)-subcategories of
of full sub-\(\infty \)-subcategories of  satisfying:
satisfying:
-
(i)
orthogonality:
 is contractible for each
is contractible for each  ,
,  ;
; -
(ii)
any object
 fits into a pullout diagram
fits into a pullout diagram 
with
 and
and  .
.
The subcategories  and
and  are called the torsion class and the torsion free class, respectively.
are called the torsion class and the torsion free class, respectively.
Notation 7.2
We denote by  the set of torsion theories on
the set of torsion theories on  ; this set has a natural choice for a partial order:
; this set has a natural choice for a partial order:  if and only if
if and only if  , or equivalently
, or equivalently  .
.
The poset  has a top and a bottom element, given by
has a top and a bottom element, given by  and
and  , respectively. The following definition is directly inspired by [21].
, respectively. The following definition is directly inspired by [21].
Definition 7.3
(Abelian slicing) Let \((I, \le )\) be a poset. An abelianI-slicing on  is a morphism of posets
is a morphism of posets  that preserve the top and bottom element. The image of \((\Lambda ,\Upsilon )\in {\mathcal {O}}(I)\) by \(\mathcal {T}\) will be denoted
that preserve the top and bottom element. The image of \((\Lambda ,\Upsilon )\in {\mathcal {O}}(I)\) by \(\mathcal {T}\) will be denoted 
Remark 7.4
Notice that, since there is no choice of a shift functor in an abelian \(\infty \)-category, there is no \(\mathbb {Z}\)-action on I or \(\mathbb {Z}\)-equivariancy condition involved in the above definition.
Remark 7.5
(The abelian slicings functor) By analogy with Remark 3.12, for any \(\infty \)-category \(\mathcal {A}\) we have a functor  mapping a poset I to the poset of abelian I-slicings of
mapping a poset I to the poset of abelian I-slicings of  .
.
Lemma 7.6
Let  be a t-structure on
be a t-structure on  with heart
with heart  , and let \(\mathfrak {t}_1=\mathfrak {t}_0[1]\). Also let
, and let \(\mathfrak {t}_1=\mathfrak {t}_0[1]\). Also let  be another t-structure with \(\mathfrak {t}_0 \le \mathfrak {t}\le \mathfrak {t}_1\). Then
be another t-structure with \(\mathfrak {t}_0 \le \mathfrak {t}\le \mathfrak {t}_1\). Then

is a torsion theory on  .
.
Proof
Clearly,  and
and  . Moreover,
. Moreover,  and
and  , and so
, and so  . Now, pick
. Now, pick  and consider the fiber sequence
and consider the fiber sequence

induced by the t-structure \(\mathfrak {t}\). From it we get the fiber sequence

We have  and
and  . Since \(\mathcal {L}_1\) is closed by extensions (see Remark 3.18), this implies that
. Since \(\mathcal {L}_1\) is closed by extensions (see Remark 3.18), this implies that  . Therefore
. Therefore  . An analogous argument shows that
. An analogous argument shows that  . \(\square \)
. \(\square \)
Proposition 7.7
Let \((J,\le )\) be a \({\mathbb {Z}}\)-toset, and let \(J^\heartsuit \) a heart of J. Then a J-slicing on  induces a t-structure on
induces a t-structure on  together with an abelian \(J^\heartsuit \)-slicing on
together with an abelian \(J^\heartsuit \)-slicing on  .
.
Proof
Let  be a fixed J-slicing on
be a fixed J-slicing on  , and let \(J^\heartsuit =U_0\cap L_1\) for some (unique) upper set \(U_0\) and lower set \(L_1\) in J. Finally, let \(\mathfrak {t}_0\) be the t-structure on
, and let \(J^\heartsuit =U_0\cap L_1\) for some (unique) upper set \(U_0\) and lower set \(L_1\) in J. Finally, let \(\mathfrak {t}_0\) be the t-structure on  corresponding to the slicing \((L_0,U_0)\) of J. Then we know from Remark 5.15 that
corresponding to the slicing \((L_0,U_0)\) of J. Then we know from Remark 5.15 that  is the standard heart of \(\mathfrak {t}_0\). Let \(\mathfrak {t}_1\) be the t-structure on
is the standard heart of \(\mathfrak {t}_0\). Let \(\mathfrak {t}_1\) be the t-structure on  corresponding to the slicing \((L_1,U_1)\) of J. By Lemma 5.7 we know that \(\mathfrak {t}_1=\mathfrak {t}_0[1]\). Moreover we know from Remark 3.33 that every upper set \(\Upsilon \) of \(J^\heartsuit \) is of the form \(\Upsilon =U\cap J^\heartsuit \) for a unique upper set U in J with \(U_0\le U\le U_1\). Let (L, U) be the slicing of J determined by U. By Lemma 7.6,
corresponding to the slicing \((L_1,U_1)\) of J. By Lemma 5.7 we know that \(\mathfrak {t}_1=\mathfrak {t}_0[1]\). Moreover we know from Remark 3.33 that every upper set \(\Upsilon \) of \(J^\heartsuit \) is of the form \(\Upsilon =U\cap J^\heartsuit \) for a unique upper set U in J with \(U_0\le U\le U_1\). Let (L, U) be the slicing of J determined by U. By Lemma 7.6,

defines an abelian \(J^\heartsuit \)-slicing on  . \(\square \)
. \(\square \)
As we are going to show, in the bounded case we also have the converse of the above proposition.
Lemma 7.8
Suppose that \(\mathfrak {t}\) is a bounded t-structure on  with heart
with heart  . Then a torsion theory
. Then a torsion theory  on
on  induces a bounded \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\)-slicing on
induces a bounded \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\)-slicing on  .
.
Proof
Since every interval of the form \([n_0,n_1]\) in \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\) is finite, a bounded \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\)-slicing is discrete of finite type. Therefore, by Proposition 4.26 we are reduced to showing that a torsion theory \(\mathcal {T}\) on  induces a Bridgeland \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\)-slicing on
induces a Bridgeland \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\)-slicing on  . Since
. Since  is a torsion theory of
is a torsion theory of  , we have that
, we have that  is a torsion theory of
is a torsion theory of  for any \(n\in {\mathbb {Z}}\). Consider the full subcategories
for any \(n\in {\mathbb {Z}}\). Consider the full subcategories

Since the \(\mathbb {Z}\)-action on \(\mathbb {Z}\times _{\text {lex}}[\mathbf 1 ]\) is \((n,i)+1=(n+1,i)\), it is immediate to see that  for every (n, i) in \(\mathbb {Z}\times _{\text {lex}}[\mathbf 1 ]\). Let now
for every (n, i) in \(\mathbb {Z}\times _{\text {lex}}[\mathbf 1 ]\). Let now  and
and  with \((n_1,i_1)>(n_2,i_2)\). Since the order is the lexicographic one, we either have \(n_1>n_2\) or \(n_1=n_2\) and \(i_1=1\) and \(i_2=0\). In the first case
with \((n_1,i_1)>(n_2,i_2)\). Since the order is the lexicographic one, we either have \(n_1>n_2\) or \(n_1=n_2\) and \(i_1=1\) and \(i_2=0\). In the first case  and
and  with \(n_1>n_2\) and so
with \(n_1>n_2\) and so  ; in the second case
; in the second case  and
and  and so again
and so again  . Finally, we have to show that for every object X of
. Finally, we have to show that for every object X of  we have a factorization of the initial morphism \(0\longrightarrow X\) into morphisms whose cofibers are in
we have a factorization of the initial morphism \(0\longrightarrow X\) into morphisms whose cofibers are in  for a decreasing sequence of indices (n, i)’s in the lexicographic order on \({\mathbb {Z}} \times [\mathbf 1 ]\). To see this, let X be an object in
for a decreasing sequence of indices (n, i)’s in the lexicographic order on \({\mathbb {Z}} \times [\mathbf 1 ]\). To see this, let X be an object in  and consider the
and consider the  -weaved tower of its initial morphism. Keeping only the nontrivial morphisms in this tower we are reduced to a finite factorization of the form
-weaved tower of its initial morphism. Keeping only the nontrivial morphisms in this tower we are reduced to a finite factorization of the form
with  for a suitable sequence of decreasing integers \(n_0>n_1>\cdots > n_k\). Since
for a suitable sequence of decreasing integers \(n_0>n_1>\cdots > n_k\). Since  is a torsion theory on
is a torsion theory on  , for each l we have a pullout diagram
, for each l we have a pullout diagram

in  . By Proposition 5.34, this is a pullout diagram in
. By Proposition 5.34, this is a pullout diagram in  and so we can consider the commutative diagram
and so we can consider the commutative diagram

where each square is a pullout in  . As l ranges from 0 to k the sequence
. As l ranges from 0 to k the sequence
gives a factorization of \(0\longrightarrow X\) into morphisms whose cofibers are in  for a decreasing sequence of indices (n, i)’s. \(\square \)
for a decreasing sequence of indices (n, i)’s. \(\square \)
Remark 7.9
The nontrivial upper sets in \(\mathbb {Z}\times _{\text {lex}} [\mathbf 1 ]\) are easily described: they are all of the form \([(n,i),+\infty )\) for some \(n\in \mathbb {Z}\) and \(i\in [\mathbf 1 ]\). In the notation of Lemma 7.8, the t-structures on  corresponding to these upper sets are easily described by means of Remark 4.27. We have
corresponding to these upper sets are easily described by means of Remark 4.27. We have

Equivalently,

Definition 7.10
Let  be a bounded t-structure on
be a bounded t-structure on  and let
and let  be its standard heart. For every torsion theory \(\mathcal {T}\) on
be its standard heart. For every torsion theory \(\mathcal {T}\) on  , the t-structure
, the t-structure  is said to be obtained tilting (it’s a verb)
is said to be obtained tilting (it’s a verb)  with \(\mathcal {T}\) (see [4]).
with \(\mathcal {T}\) (see [4]).
Remark 7.11
One immediately sees that the tilting of a t-structure  by the bottom torsion theory
by the bottom torsion theory  is the trivial tilting, while tilting by the the top torsion theory
is the trivial tilting, while tilting by the the top torsion theory  correspond to shifting by 1:
correspond to shifting by 1:
-
 ,
, -
 .
.
Remark 7.12
The construction of Lemma 7.8 gives a map

and the explicit description in Remark 7.9 show that this is a morphism of posets. Namely, if \(\mathcal {T}_1\le \mathcal {T}_2\) then  and so
and so  for every (n, i). In particular, tilting defines a morphism of posets
for every (n, i). In particular, tilting defines a morphism of posets

This construction can be seen as a byproduct of the functoriality of slicings as follows. The \({\mathbb {Z}}\)-toset \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\) has an obvious \({\mathbb {Z}}\)-equivariant morphism of posets to \({\mathbb {Z}}\) given by the projection \(\pi \) on the first factor. However, and remarkably, there is also another less trivial \({\mathbb {Z}}\)-equivariant morphism
given by the composition of the projection \(\pi \) with the \({\mathbb {Z}}\)-equivariant automorphism of the poset \({\mathbb {Z}} \times _{\text {lex}} [\mathbf 1 ]\) defined by
Since taking slicings of a fixed stable \(\infty \)-category with respect to a \(\mathbb {Z}\)-toset J is functorial in J (Remark 3.12), we have a morphism of \(\mathbb {Z}\)-tosets

Composing this with the morphism of posets  gives the tilting map.
gives the tilting map.
The proposition below can be found in [4] for \(J={\mathbb {Z}} \times _{\text {{lex}}} [\mathbf 1 ]\) and in [5] for \(J={\mathbb {R}}\).
Proposition 7.13
Let J be a \({\mathbb {Z}}\)-toset, and let \(J^\heartsuit \) be a heart of J. Then giving a bounded J-slicing on  is equivalent to giving a bounded t-structure
is equivalent to giving a bounded t-structure  on
on  together with an abelian \(J^\heartsuit \)-slicing on the standard heart
together with an abelian \(J^\heartsuit \)-slicing on the standard heart  of
of  . Moreover the bounded J-slicing on
. Moreover the bounded J-slicing on  is discrete if and only if the abelian \(J^\heartsuit \)-slicing of
is discrete if and only if the abelian \(J^\heartsuit \)-slicing of  is discrete.
is discrete.
Proof
In one direction this is the content of Proposition 7.7. Vice versa, assume we have a bounded t-structure  on
on  and an abelian \(J^\heartsuit \)-slicing \(\mathcal {T}\) on its standard heart
and an abelian \(J^\heartsuit \)-slicing \(\mathcal {T}\) on its standard heart  . By definition this is a morphism of posets
. By definition this is a morphism of posets  . By Remark 7.12, tilting a fixed t-structure gives a morphism of posets
. By Remark 7.12, tilting a fixed t-structure gives a morphism of posets  , and so by composition we get a morphism of posets
, and so by composition we get a morphism of posets

Recalling the identification of \({\mathcal {O}}(J^\heartsuit )\) with the interval \([U_0,U_1]\) of \({\mathcal {O}}(J)\) from Remark 3.33, and that \(U_1=U_0+1\) from Lemma 5.7, this is a morphism of posets  and so it induces a uniquely determined \(\mathbb {Z}\)-equivariant morphism of \(\mathbb {Z}\)-tosets
and so it induces a uniquely determined \(\mathbb {Z}\)-equivariant morphism of \(\mathbb {Z}\)-tosets

By Remark 7.11, \(\mathfrak {t}_{(1,U_0)}=\mathfrak {t}_{(0,U_0)}[1]=\mathfrak {t}_{(0,U_0+1)}\) and so \(\mathfrak {t}\) factors through the natural morphism of \(\mathbb {Z}\)-tosets
given by \((n,U)\mapsto U+n\). In other words, \(\mathfrak {t}\) uniquely defines a J-slicing on  , which is bounded since the t-structure
, which is bounded since the t-structure  is, by Remark 5.17. Finally, the construction manifestly preserves finite types. \(\square \)
is, by Remark 5.17. Finally, the construction manifestly preserves finite types. \(\square \)
8 Concluding remarks
That’s all, folks!
Bosko
We have explored two classes of J-slicings so far: those for which J has a heart, and those for which \({\mathbb {Z}}\) acts trivially on J. In this section, we show how these two cases are fundamental building blocks for all other J-slicings.
Lemma 8.1
Let \(\mathfrak {t}\) be a J-slicing on a stable \(\infty \)-category  , and let \(I_i\subseteq J\) be the equivalence class of \(i\in J\) with respect to the equivalence relation \(\sim \) of Lemma 2.27. For every \((\Lambda ,\Upsilon )=(L\cap I_{i},U\cap I_{i})\) in \({\mathcal {O}}(I_i)\), let
, and let \(I_i\subseteq J\) be the equivalence class of \(i\in J\) with respect to the equivalence relation \(\sim \) of Lemma 2.27. For every \((\Lambda ,\Upsilon )=(L\cap I_{i},U\cap I_{i})\) in \({\mathcal {O}}(I_i)\), let  . Then \(\mathfrak {t}_i:(\Lambda ,\Upsilon )\longrightarrow \mathfrak {t}_{i;\Lambda ,\Upsilon }\) is a \(I_i\)-slicing of
. Then \(\mathfrak {t}_i:(\Lambda ,\Upsilon )\longrightarrow \mathfrak {t}_{i;\Lambda ,\Upsilon }\) is a \(I_i\)-slicing of  .
.
Proof
By Remark 6.10, the J-slicing \(\mathfrak {t}\) induces an \(\iota (J)\)-semi-orthogonal decomposition of  : for every equivalence class [i] in \(\iota (J)\) the corresponding slice in this semi-orthogonal decomposition is the subcategory
: for every equivalence class [i] in \(\iota (J)\) the corresponding slice in this semi-orthogonal decomposition is the subcategory  of
of  determined by the J-slicing \(\mathfrak {t}\), where \(I_i\subseteq J\) is the equivalence class of i with respect to the equivalence reltion \(\sim \), as a subset of J. As they are the slices of a semi-orthogonal decomposition, the subcategories
determined by the J-slicing \(\mathfrak {t}\), where \(I_i\subseteq J\) is the equivalence class of i with respect to the equivalence reltion \(\sim \), as a subset of J. As they are the slices of a semi-orthogonal decomposition, the subcategories  are stable (this can also be seen directly from the definition of the \(\mathcal {C}_{I_i}\)’s). As shown in Example 3.23, \(I_i\) is an interval of J and a sub-\(\mathbb {Z}\)-toset of J, simply by definition of the equivalence relation. For every i, we can therefore write \(I_i=U_{i;0}\cap L_{i;1}\). By Remark 3.33 every slicing \((\Lambda ,\Upsilon )\) of \(I_i\) is of the form \(\Lambda =L\cap I_{i}\) and \(\Upsilon =U\cap I_{i}\) for a unique slicing (L, U) of J with \(U_{i;0}\le U\le U_{i;1}\). This gives an isomorphism of tosets between \({\mathcal {O}}(I_i)\) and the interval \([U_{i;0},U_{i;1}]\) in \({\mathcal {O}}(J)\). Now, to show that \(\mathfrak {t}_{i;\Lambda ,\Upsilon }\) is a t-structure on
are stable (this can also be seen directly from the definition of the \(\mathcal {C}_{I_i}\)’s). As shown in Example 3.23, \(I_i\) is an interval of J and a sub-\(\mathbb {Z}\)-toset of J, simply by definition of the equivalence relation. For every i, we can therefore write \(I_i=U_{i;0}\cap L_{i;1}\). By Remark 3.33 every slicing \((\Lambda ,\Upsilon )\) of \(I_i\) is of the form \(\Lambda =L\cap I_{i}\) and \(\Upsilon =U\cap I_{i}\) for a unique slicing (L, U) of J with \(U_{i;0}\le U\le U_{i;1}\). This gives an isomorphism of tosets between \({\mathcal {O}}(I_i)\) and the interval \([U_{i;0},U_{i;1}]\) in \({\mathcal {O}}(J)\). Now, to show that \(\mathfrak {t}_{i;\Lambda ,\Upsilon }\) is a t-structure on  one verbatim repeats the proof of Lemma 7.6 to get orthogonality of the classes and the existence of the relevant fiber sequences. Next, to show that
one verbatim repeats the proof of Lemma 7.6 to get orthogonality of the classes and the existence of the relevant fiber sequences. Next, to show that  notice that, since \(I_i\) is an equivalence class, we have \(I_i+1=I_i\) and so
notice that, since \(I_i\) is an equivalence class, we have \(I_i+1=I_i\) and so
This shows that \(\mathfrak {t}_i\) is a morphism of sets  and it is immediate to see that this is actually a morphism of tosets. Finally, \(\mathbb {Z}\) equivariance is obtained by noticing that \(\Upsilon +1=(U\cap I_i)+1=(U+1)\cap I_i\) and \(\Lambda +1=(L+1)\cap I_i\), so that
and it is immediate to see that this is actually a morphism of tosets. Finally, \(\mathbb {Z}\) equivariance is obtained by noticing that \(\Upsilon +1=(U\cap I_i)+1=(U+1)\cap I_i\) and \(\Lambda +1=(L+1)\cap I_i\), so that

where we used that  is a stable subcategory of
is a stable subcategory of  and so
and so  . \(\square \)
. \(\square \)
We can now state and prove our main result, summarising and putting together the various pieces constructed so far. To make a self-standing statement, we explicitly recall the definition of the equivalence relation \(\sim \) from Lemma 2.27 in the statement of the theorem below.
Theorem 8.2
Let \((J,\le )\) a \(\mathbb {Z}\)-toset. A finite type J-slicing on a stable \(\infty \)-category  is equivalent to the following data:
is equivalent to the following data:
-
(i)
a finite type semi-orthogonal decomposition of
 whose slices
whose slices  are stable \(\infty \)-subcategories of
are stable \(\infty \)-subcategories of  indexed by equivalence classes in J with respect to the equivalence relation \(x\sim y\) if and only if there exist integers \(n_1\) and \(n_2\) with \(x+n_1\le y\le x+n_2\);
indexed by equivalence classes in J with respect to the equivalence relation \(x\sim y\) if and only if there exist integers \(n_1\) and \(n_2\) with \(x+n_1\le y\le x+n_2\); -
(ii)
a bounded t-structure \(\mathfrak {t}_{[x]}\) on
 for each [x] in \(J/_{\!\sim }\);
for each [x] in \(J/_{\!\sim }\); -
(iii)
a finite type abelian \([x,x+1)\)-slicing on
 for every [x] in \(J/_{\!\sim }\) such that x is not a fixed point of the \(\mathbb {Z}\)-action on J.
for every [x] in \(J/_{\!\sim }\) such that x is not a fixed point of the \(\mathbb {Z}\)-action on J.
Proof
By Lemma 8.1, a J-slicing on a stable \(\infty \)-category induces semi-orthogonal decomposition of  whose slices
whose slices  are stable \(\infty \)-subcategories of
are stable \(\infty \)-subcategories of  indexed by equivalence classes \(I_i\) in J with respect to the equivalence relation \(\sim \), together with \(I_i\)-slicings of these subcategories. If i is a fixed point for the \(\mathbb {Z}\)-action on J, then \(I_i=\{i\}\) and \({\mathcal {O}}(I_i)=[\mathbf 1 ]\) so that a \(I_j\)-slicing is trivial. On the other hand, by Example 5.6, precisely when i is not a fixed point of the \(\mathbb {Z}\)-action the interval \(I_i\) has a heart \(I_i^\heartsuit \) which can be identified with the interval \([i,i+1)\) of J. Therefore, by Proposition 7.7 an \(I_i\)-slicing on
indexed by equivalence classes \(I_i\) in J with respect to the equivalence relation \(\sim \), together with \(I_i\)-slicings of these subcategories. If i is a fixed point for the \(\mathbb {Z}\)-action on J, then \(I_i=\{i\}\) and \({\mathcal {O}}(I_i)=[\mathbf 1 ]\) so that a \(I_j\)-slicing is trivial. On the other hand, by Example 5.6, precisely when i is not a fixed point of the \(\mathbb {Z}\)-action the interval \(I_i\) has a heart \(I_i^\heartsuit \) which can be identified with the interval \([i,i+1)\) of J. Therefore, by Proposition 7.7 an \(I_i\)-slicing on  induces a t-structure on
induces a t-structure on  together with an abelian \([i,i+1)\)-slicing on the standard heart
together with an abelian \([i,i+1)\)-slicing on the standard heart  . Moreover, by Proposition 7.13, in the finite type case an \(I_i\)-slicing on
. Moreover, by Proposition 7.13, in the finite type case an \(I_i\)-slicing on  is precisely equivalent to this datum of a bounded t-structure on
is precisely equivalent to this datum of a bounded t-structure on  with an abelian \(I_i^\heartsuit \)-slicing on
with an abelian \(I_i^\heartsuit \)-slicing on  .
.
Vice versa, given the data (i)-(iii), we want to define a J-slicing of  . For every upper set U of J, we can write
. For every upper set U of J, we can write
and, by Proposition 7.13 again, the data (i)-(iii) define \(\infty \)-subcategories  of
of  . Defining
. Defining  as the extension closed \(\infty \)-subcategory of
as the extension closed \(\infty \)-subcategory of  generated by the
generated by the  ’s provides a map
’s provides a map  which is immediate to see it is montone and \({\mathbb {Z}}\)-equivariant and so is a J-slicing of
which is immediate to see it is montone and \({\mathbb {Z}}\)-equivariant and so is a J-slicing of  . Moreover, this J-slicing is of finite type as all the slicings provided by the data are of finite type, and manifestly this way of constructing finite type J-slicings out of data (i)-(iii) provides an inverse to the construction described in the first part of the proof. \(\square \)
. Moreover, this J-slicing is of finite type as all the slicings provided by the data are of finite type, and manifestly this way of constructing finite type J-slicings out of data (i)-(iii) provides an inverse to the construction described in the first part of the proof. \(\square \)
8.1 Translations of the opening quotes.
-
§2.)
These are the first three verses of Tao te Ching’s chapter 63: “Act without action / work without work / taste without taste.”
-
§3.)
This is a quote from Histoire d’O: “her freedom was worse than any chain.”
-
§4.)
This is Genesis 11:7: “let us go down, and there confound their language, that they may not understand one another’s speech.”
-
§6.)
This is a quote from E. Cioran’s Brief history of decay: “Life is what decomposes at every moment; it is a monotonous loss of light, an insipid dissolution in the darkness, without scepters, without halos.”
-
§7.)
This is a famous line Ramon Rojo says in S. Leone’s movie A fistful of dollars: “When you want to kill a man you must shoot for his heart and a Winchester is the best weapon.”
Notes
Here and in the rest of the paper we are implicitly using the equivalence between t-structures and normal torsion theories: if
 is a stable \(\infty \)-category with a terminal object, there exists an antitone Galois connection between the poset
is a stable \(\infty \)-category with a terminal object, there exists an antitone Galois connection between the poset  of reflective subcategories of
of reflective subcategories of  and the poset \(\text {pf}(\mathcal {C})\) of prefactorization systems on
and the poset \(\text {pf}(\mathcal {C})\) of prefactorization systems on  such that \(r(\mathbb {F})\) is a 3-for-2 class. This adjunction induces a bijective correspondence between the class of certain reflective and coreflective factorization systems called normal torsion theories and the class of t-structures on (the homotopy category of)
such that \(r(\mathbb {F})\) is a 3-for-2 class. This adjunction induces a bijective correspondence between the class of certain reflective and coreflective factorization systems called normal torsion theories and the class of t-structures on (the homotopy category of)  : this statement is the central result of [7] where it is called the Rosetta stone theorem, and motivates our choice to state our main results in the setting of stable \((\infty ,1)\)-categories.
: this statement is the central result of [7] where it is called the Rosetta stone theorem, and motivates our choice to state our main results in the setting of stable \((\infty ,1)\)-categories.The Japanese verb
 (“kiru”, to cut) contains the radical
(“kiru”, to cut) contains the radical 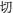 , the same of katana.
, the same of katana.
References
Beilinson, A.A., Bernstein, J., Deligne, P.: Faisceaux Pervers, Analysis and Topology on Singular Spaces, I (Luminy, 1981), Astéérisque, vol. 100, Soc. Math. France, Paris, pp. 5–171 (1982)
Blyth, T.S.: Lattices and Ordered Algebraic Structures. Universitext. Springer, London (2005)
Bondal, A., Orlov, D.: Semiorthogonal decomposition for algebraic varieties. arXiv preprint arXiv:alg-geom/9506012 (1995)
Beligiannis, A., Reiten, I.: Homological and homotopical aspects of torsion theories. Mem. Am. Math. Soc. 188(883), viii+207 (2007)
Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. (2) 166(2), 317–345 (2007)
Cassidy, C., Hébert, M., Kelly, G.M.: Reflective subcategories, localizations and factorization systems. J. Austral. Math. Soc. Ser. A 38(3), 287–329 (1985)
Fiorenza, D., Loregiàn, F.: t-structures are normal torsion theories. Appl. Categ. Struct. 24(2), 181–208 (2016)
Fuchs, L.: Partially Ordered Algebraic Systems. Pergamon Press, Oxford (1963)
Gorodentsev, A.L., Kuleshov, S.A., Rudakov, A.N.: \(t\)-stabilities and \(t\)-structures on triangulated categories. Izv. R. Akad. Nauk Ser. Mat. 68, 117–150 (2004)
Glass, A.M.W.: Partially Ordered Groups, Series in Algebra, vol. 7. World Scientific Publishing Co. Inc, River Edge (1999)
Grätzer, G.: Lattice Theory: Foundation. Springer Science & Business Media, Berlin (2011)
Happel, D., Reiten, I., Smalø, S.O.: Tilting in abelian categories and quasitilted algebras, vol. 575. American Mathematical Society, Providence (1996)
Joyal, A.: The Theory of Quasi-categories and its Applications. Lectures at the CRM (Barcelona) (2008). http://mat.uab.cat/~kock/crm/hocat/advanced-course/Quadern45-2.pdf
Joyal, A.: The Theory of Quasi-Categories and its Applications. Citeseer, Princeton (2008)
Kuznetsov, A.: Base change for semiorthogonal decompositions. Compos. Math. 147(3), 852–876 (2011)
Loregian, F.: \(t\)-structures in stable \((\infty ,1)\)-categories, Ph.D. thesis, sissa, 2016. http://urania.sissa.it/xmlui/handle/1963/35202
Lurie, J.: Higher Topos Theory, Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton (2009)
Lurie, J.: Higher algebra, online version September 18 (2017)
Loregian, F., Virili, S.: Factorization systems on (stable) derivators (2017). arXiv:1705.08565
Muro, Fernando, Schwede, Stefan, Strickland, Neil: Triangulated categories without models. Invent. Math. 170(2), 231–241 (2007)
Rudakov, A.: Stability for an abelian category. J. Algebra 197(1), 231–245 (1997)
Acknowledgements
Open access funding provided by Max Planck Society. We thank the anonymous referee for useful comments that helped us to improve the overall exposition.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Walter Tholen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fiorenza, D., Loregian, F. & Marchetti, G.L. Hearts and towers in stable \(\infty \)-categories. J. Homotopy Relat. Struct. 14, 993–1042 (2019). https://doi.org/10.1007/s40062-019-00237-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-019-00237-0




 is contractible for each
is contractible for each  ,
,  ;
; and
and  ;
; fits into a (homotopy) fiber sequence
fits into a (homotopy) fiber sequence  , with
, with  in
in  and
and  in
in  .
. and
and  .
.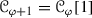 for each
for each  is contractible for each
is contractible for each  ,
,  for
for  there is a finite set
there is a finite set  for all
for all 
 and homotopy equivalences
and homotopy equivalences  , or equivalently
, or equivalently  );
); is a stable sub-
is a stable sub- .
. is a stable sub-
is a stable sub- .
. for
for  there exists a unique
there exists a unique 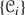 -weaved tower, i.e., a factorization of the initial morphism
-weaved tower, i.e., a factorization of the initial morphism  for any
for any  is contractible for each
is contractible for each  ,
,  ;
; fits into a pullout diagram
fits into a pullout diagram 
 and
and  .
. ,
, .
. whose slices
whose slices  are stable
are stable  indexed by equivalence classes in J with respect to the equivalence relation
indexed by equivalence classes in J with respect to the equivalence relation 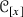 for each [x] in
for each [x] in  for every [x] in
for every [x] in  is a stable
is a stable  of reflective subcategories of
of reflective subcategories of  and the poset
and the poset  such that
such that  : this statement is the central result of [
: this statement is the central result of [ (“kiru”, to cut) contains the radical
(“kiru”, to cut) contains the radical  , the same of katana.
, the same of katana.