Abstract
This paper is the first in a series in which we offer a new framework for hermitian \({\text {K}}\)-theory in the realm of stable \(\infty \)-categories. Our perspective yields solutions to a variety of classical problems involving Grothendieck-Witt groups of rings and clarifies the behaviour of these invariants when 2 is not invertible. In the present article we lay the foundations of our approach by considering Lurie’s notion of a Poincaré \(\infty \)-category, which permits an abstract counterpart of unimodular forms called Poincaré objects. We analyse the special cases of hyperbolic and metabolic Poincaré objects, and establish a version of Ranicki’s algebraic Thom construction. For derived \(\infty \)-categories of rings, we classify all Poincaré structures and study in detail the process of deriving them from classical input, thereby locating the usual setting of forms over rings within our framework. We also develop the example of visible Poincaré structures on \(\infty \)-categories of parametrised spectra, recovering the visible signature of a Poincaré duality space. We conduct a thorough investigation of the global structural properties of Poincaré \(\infty \)-categories, showing in particular that they form a bicomplete, closed symmetric monoidal \(\infty \)-category. We also study the process of tensoring and cotensoring a Poincaré \(\infty \)-category over a finite simplicial complex, a construction featuring prominently in the definition of the \({\text {L}}\)- and Grothendieck-Witt spectra that we consider in the next instalment. Finally, we define already here the 0th Grothendieck-Witt group of a Poincaré \(\infty \)-category using generators and relations. We extract its basic properties, relating it in particular to the 0th \({\text {L}}\)- and algebraic \({\text {K}}\)-groups, a relation upgraded in the second instalment to a fibre sequence of spectra which plays a key role in our applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quadratic forms are among the most ubiquitous notions in mathematics. In a pioneering paper [75], Witt suggested a way to understand quadratic forms over a field k in terms of an abelian group \({\text {W}}^{\text {q} }(k)\), now known as the Witt group of quadratic forms. By definition, the Witt group is generated by isomorphism classes [V, q] of finite dimensional k-vector spaces equipped with a unimodular quadratic form q, where we impose the relations \([V \oplus V',q \perp q'] = [V,q]+[V',q']\) and declare as trivial the classes of hyperbolic forms \([V \oplus V^*,h]\) given by the canonical pairing between V and its dual \(V^*\). In arithmetic geometry the Witt group became an important invariant of fields, related to their Milnor \({\text {K}}\)-theory and Galois cohomology via the famous Milnor conjecture. The definition of the Witt group naturally extends from fields to commutative rings R, where one replaces vector spaces by finitely generated projective R-modules. More generally, instead of starting with a commutative ring R and taking R-valued forms, one can study unimodular hermitian forms valued in an invertible \((R \otimes R)\)-module M equipped with an involution, a notion which makes sense also for non-commutative R. This includes for example the case of a ring R with anti-involution by considering \(M=R\), and also allows to consider skew-quadratic forms by changing the involution on M by a sign. Quadratic forms at this level of generality also show up naturally in the purely geometric context of surgery theory through the quadratic \({\text {L}}\)-groups of the group ring \({\mathbb {Z}}[\pi _1(X)]\) for a topological space X. The latter groups, whose name, coined by Wall, suggests their relation with algebraic \({\text {K}}\)-theory, are a sequence of groups \({\text {L}}^\text {q} _i\) associated to a ring with anti-involution R, or more generally, a ring equipped with an invertible \((R \otimes R)\)-module with involution M as above, with \({\text {L}}^{\text {q} }_0(R,M)\) being the Witt group of M-valued quadratic forms over R. They are 4-periodic, or more precisely, satisfy the skew-periodic relation \({\text {L}}^{\text {q} }_{n+2}(R,M) \cong {\text {L}}^{\text {q} }_{n}(R,-M)\), where \(-M\) is obtained from M by twisting the involution by a sign. In particular, for a ring with anti-involution R the even quadratic \({\text {L}}\)-groups consist of the Witt groups of quadratic and skew-quadratic forms.
To obtain richer information about quadratic forms over a given R, the Witt group \({\text {W}}^{\text {q} }(R,M)\) was often compared to the larger group generated by the isomorphism classes of unimodular quadratic M-valued forms [P, q] over R under the relation \([P \oplus P',q \perp q'] = [P,q]+[P',q']\), but without taking the quotient by hyperbolic forms. The latter construction leads to the notion of the Grothendieck-Witt group \({\text {GW}}^{\text {q} }_0(R,M)\) of quadratic forms. The Witt and Grothendieck-Witt groups are then related by an exact sequence
where the first term denotes the orbits for the \({{\text {C} }_{\textrm{2}}}\)-action on the \({\text {K}}\)-theory group \({\text {K}}_0(R)\) which sends the class of a finitely generated projective R-module P to the class of its M-dual \({\text {Hom}}_R(P,M)\). The left hand map then sends [P] to the class of the associated hyperbolic form on \(P \oplus {\text {Hom}}_{R}(P,M)\), and is invariant under this \({{\text {C} }_{\textrm{2}}}\)-action. The sequence (1) can often be used to compute \({\text {GW}}^{\text {q} }_0(R,M)\) from the two outer groups, and consequently obtain more complete information about quadratic forms. For example, in the case of the integers this sequence is split short exact and we have an isomorphism \({\text {W}}^{\text {q} }({\mathbb {Z}}) \cong {\mathbb {Z}}\) given by taking the signature divided by 8 and an isomorphism \({\text {K}}_0({\mathbb {Z}})_{{{\text {C} }_{\textrm{2}}}} \cong {\mathbb {Z}}\) given by the dimension.
In this paper we begin a four-part investigation revisiting classical questions about Witt, Grothendieck-Witt, and \({\text {L}}\)-groups of rings from a new perspective. One of our main motivating applications is to extend the short exact sequence (1) to a long exact sequence involving Quillen’s higher \({\text {K}}\)-theory and the higher Grothendieck-Witt groups \({\text {GW}}^\text {q} _i(R,M)\) introduced by Karoubi and Villamayor [39], see below for more details. In this paper we, among many other things, define abelian groups \({\text {L}}_i^{\text {gq} }(R,M)\), called genuine quadratic \({\text {L}}\)-groups, which are the correct higher Witt groups from this point of view: We show in Paper [3] that we have \({\text {L}}_0^{\text {gq} }(R,M) = {\text {W}}^{\text {q} }(R,M)\) and that the sequence (1) can be extended to a long exact sequence involving the groups \({\text {L}}_i^{\text {gq} }(R,M)\) which starts off as
The groups \({\text {L}}_i^{\text {gq} }(R,M)\) are generally different from Wall’s quadratic \({\text {L}}\)-groups, and in particular are usually not 4-periodic. They are, however, relatively accessible for study by means of algebraic surgery. Combining this with the above long exact sequence allows us to obtain many new results about the Grothendieck-Witt groups \({\text {GW}}^\text {q} _i(R)\) of rings in Paper [3]. For example, we obtain an essentially complete calculation of these groups in the case of the integers \(R = {\mathbb {Z}}\). In what follows we give more background, outline our approach and its main applications, and elaborate more on the content of the present paper.
1.1 Background
The higher Grothendieck-Witt groups \({\text {GW}}^\text {q} _i(R,M)\) mentioned above were first defined by Karoubi and Villamayor [39] by applying Quillen’s foundational techniques from algebraic \({\text {K}}\)-theory. This is done by producing a homotopy-theoretical refinement of the 0th Grothendieck-Witt group into a Grothendieck-Witt space and then defining \({\text {GW}}_i(R,M)\) as the ith homotopy group of this space. Given R and M as above, one organises the collection of unimodular quadratic M-valued forms (P, q) into a groupoid \(\text {Unimod} ^{\text {q} }(R,M)\), which is viewed as an \({\text {E} _\infty }\)-space using the symmetric monoidal structure on \(\text {Unimod} ^{\text {q} }(R)\) arising from the orthogonal sum. One can then take its group completion to obtain an \({\text {E} _\infty }\)-group

whose group of components is the Grothendieck-Witt group described above. Here the subscript \(\text {cl} \) stands for classical, and is meant to avoid confusion with the constructions of the present paper series. This construction can equally well be applied for other interesting types of forms, such as symmetric bilinear, or symmetric bilinear forms which admit a quadratic refinement, also known as even forms, and these can be taken with values in an arbitrary invertible module with involution M as above. Taking the polarisation of a quadratic form determines maps

which are equivalences if 2 is a unit in R. In this latter case Grothendieck-Witt groups are generally much more accessible. For example, if 2 is invertible in R, Schlichting [59] has produced a (generally non-connective) delooping of the Grothendieck-Witt space to a Grothendieck-Witt spectrum \({\text {GW}}_{\text {cl} }(R,M)\), in which case the forgetful and hyperbolic maps can be refined to spectrum level \({{\text {C} }_{\textrm{2}}}\)-equivariant maps
He then showed in loc. cit. that the cofibre of the induced map
has 4-periodic homotopy groups, whose even values are given by the Witt groups \({\text {W}}(R,M)\) and \({\text {W}}(R,-M)\). More precisely, Schlichting’s identification of these homotopy groups matches the \({\text {L}}\)-groups of Ranicki–Wall, which has lead to the folk theorem that, if 2 is a unit in R, then the cofibre of (2) is naturally equivalent to Ranicki’s \({\text {L}}\)-spectum \({\text {L}}^q(R,M)\) from [58]. This allows one to produce an extension of (1) to a long exact sequence, whenever 2 is invertible, and obtain information about higher Grothendieck-Witt groups from information about higher \({\text {K}}\)- and \({\text {L}}\)-groups. A closely related connection between Grothendieck-Witt spaces with coefficients in \(\pm M\) when 2 is invertible was established by Karoubi in his influential paper [37], where he proved what is now known as Karoubi’s fundamental theorem, forming one of the conceptual pillars of hermitian \({\text {K}}\)-theory, as well as part of its standard tool kit. It permits, for example, to inductively deduce results on higher Grothendieck-Witt groups from information about algebraic \({\text {K}}\)-theory and about the low order Grothendieck-Witt groups \({\text {GW}}_{0}(R,\pm M)\) and \({\text {GW}}_1(R,\pm M)\).
By contrast, when 2 is not invertible none of these assertions hold as stated. In particular, the relation between Grothendieck-Witt theory and \({\text {L}}\)-theory remained, in this generality, completely mysterious. Karoubi, in turn, conjectured in [38] that his fundamental theorem should have an extension to general rings, relating Grothendieck-Witt spaces for two different form parameters, as was also suggested earlier by Giffen [74]. In the context of motivic homotopy theory, crucial properties such as dévissage and \({{\textbf {A}}}^1\)-invariance of Grothendieck-Witt theory were only known to hold when 2 is invertible by the work of Schlichting and Hornbostel [34, 36]. Consequently, hermitian \({\text {K}}\)-theory was available to study as a motivic spectrum exclusively over \({\mathbb {Z}}[\tfrac{1}{2}]\), see [35]. Finally, while all the above tools could be used to calculate Grothendieck-Witt groups of rings in which 2 is invertible, such as the ring \({\mathbb {Z}}[\tfrac{1}{2}]\) whose Grothendieck-Witt groups were calculated by Berrick and Karoubi in [13], higher Grothendieck-Witt groups of general rings remain largely unknown.
1.2 Hermitian \({\text {K}}\)-theory of Poincaré \(\infty \)-categories
The goal of the present paper series is to offer new foundations for hermitian \({\text {K}}\)-theory in a framework that unites its algebraic and surgery theoretic incarnations and that is robustly adapted to handle the subtleties involved when 2 is not invertible. We begin by situating hermitian \({\text {K}}\)-theory in the general framework of Poincaré \(\infty \)-categories, a notion suggested by Lurie in his treatise of \({\text {L}}\)-theory [45]. A Poincaré \(\infty \)-category consists of a stable \(\infty \)-category \({\mathcal {C}}\) together with a functor  which is quadratic in the sense of Goodwillie calculus and satisfies a suitable unimodularity condition, the latter determining in particular a duality
which is quadratic in the sense of Goodwillie calculus and satisfies a suitable unimodularity condition, the latter determining in particular a duality  on \({\mathcal {C}}\). We refer to such a
on \({\mathcal {C}}\). We refer to such a  as a Poincaré structure on \({\mathcal {C}}\). Roughly speaking, the role of the Poincaré structure
as a Poincaré structure on \({\mathcal {C}}\). Roughly speaking, the role of the Poincaré structure  is to encode the flavour of forms that we want to consider. For example, for a commutative ring R one may take \({\mathcal {C}}={{\mathcal {D}}}^\text {p} (R)\) to be the perfect derived category of R. One should then think of the mapping spectrum \({\text {hom}}_{{{\mathcal {D}}}^\text {p} (R)}(X \otimes _R X, R)\) as the spectrum of bilinear forms on the chain complex X, which acquires a natural \({{\text {C} }_{\textrm{2}}}\)-action by flipping the components in the domain term. In this case the Poincaré structure
is to encode the flavour of forms that we want to consider. For example, for a commutative ring R one may take \({\mathcal {C}}={{\mathcal {D}}}^\text {p} (R)\) to be the perfect derived category of R. One should then think of the mapping spectrum \({\text {hom}}_{{{\mathcal {D}}}^\text {p} (R)}(X \otimes _R X, R)\) as the spectrum of bilinear forms on the chain complex X, which acquires a natural \({{\text {C} }_{\textrm{2}}}\)-action by flipping the components in the domain term. In this case the Poincaré structure

encodes a homotopy coherent version of the notion of symmetric bilinear forms, while

encodes a homotopy coherent version of quadratic forms. Both these Poincaré structures have the same underlying duality, given by \(X \mapsto {\text {Hom}}^{\textrm{cx}}_R(X,R)\).
Alternatively, as we develop in the present paper, one may also obtain Poincaré structures on \({{\mathcal {D}}}^\text {p} (R)\) by taking a non-abelian derived functor associated to a quadratic functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\) from finitely generated projective modules to abelian groups. For example, taking the functors which associate to a projective module P the abelian groups of quadratic, even and symmetric forms on P one obtains Poincaré structures  and
and  on \({{\mathcal {D}}}^\text {p} (R)\), respectively. We call these the genuine quadratic, even and symmetric functors, and consider them as encoding the classical, rigid notions of hermitian forms in the present setting, whereas
on \({{\mathcal {D}}}^\text {p} (R)\), respectively. We call these the genuine quadratic, even and symmetric functors, and consider them as encoding the classical, rigid notions of hermitian forms in the present setting, whereas  and
and  encode their homotopy coherent counterparts. More generally, one can apply this construction to any associative ring R equipped with an invertible \((R \otimes R)\)-module with involution M as above. The resulting Poincaré structures are then all related by a sequence of natural transformations
encode their homotopy coherent counterparts. More generally, one can apply this construction to any associative ring R equipped with an invertible \((R \otimes R)\)-module with involution M as above. The resulting Poincaré structures are then all related by a sequence of natural transformations

which encode the polarisation map between the quadratic, even and symmetric flavours of hermitian forms and at the same time the comparison between homotopy coherent and rigid variants of such forms. The fact that these two types of distinctions are not entirely unrelated leads to some of the more surprising applications of our approach. When 2 is invertible in R, all these maps are equivalences.
The fundamental invariant of a Poincaré \(\infty \)-category is its space  of Poincaré objects, which are pairs \((x,q)\) consisting of an object \(x\in {\mathcal {C}}\) and a point
of Poincaré objects, which are pairs \((x,q)\) consisting of an object \(x\in {\mathcal {C}}\) and a point  whose associated map
whose associated map  is an equivalence. These are the avatars in the present context of the notion of a unimodular hermitian form. From this raw invariant one may produce two principal spectrum valued invariants—the Grothendieck-Witt spectrum
is an equivalence. These are the avatars in the present context of the notion of a unimodular hermitian form. From this raw invariant one may produce two principal spectrum valued invariants—the Grothendieck-Witt spectrum  and \({\text {L}}\)-theory spectrum
and \({\text {L}}\)-theory spectrum  . The \({\text {L}}\)-theory spectrum was transported by Lurie from the classical work of Wall–Ranicki to the context of Poincaré \(\infty \)-categories in [45]. In particular, the \({\text {L}}\)-theory spectrum
. The \({\text {L}}\)-theory spectrum was transported by Lurie from the classical work of Wall–Ranicki to the context of Poincaré \(\infty \)-categories in [45]. In particular, the \({\text {L}}\)-theory spectrum  and
and  coincide with Ranicki’s 4-periodic quadratic and symmetric \({\text {L}}\)-theory spectra, respectively. When applied to the genuine Poincaré structures this yields new types of \({\text {L}}\)-theory spectra \({\text {L}}^{\text {gq} }(R,M), {\text {L}}^{\text {ge} }(R,M)\) and \({\text {L}}^{\text {gs} }(R,M)\). It turns out that these are in fact not entirely new: We show in Paper [3] that for the genuine symmetric structure the homotopy groups of \({\text {L}}^{\text {gs} }(R,M)\) coincide with Ranicki’s original non-periodic variant of symmetric \({\text {L}}\)-groups, as defined in [57]. Somewhat surprisingly, the genuine quadratic \({\text {L}}\)-theory spectrum \({\text {L}}^{\text {gq} }(R,M)\) is a 4-fold shift of \({\text {L}}^{\text {gs} }(R,M)\).
coincide with Ranicki’s 4-periodic quadratic and symmetric \({\text {L}}\)-theory spectra, respectively. When applied to the genuine Poincaré structures this yields new types of \({\text {L}}\)-theory spectra \({\text {L}}^{\text {gq} }(R,M), {\text {L}}^{\text {ge} }(R,M)\) and \({\text {L}}^{\text {gs} }(R,M)\). It turns out that these are in fact not entirely new: We show in Paper [3] that for the genuine symmetric structure the homotopy groups of \({\text {L}}^{\text {gs} }(R,M)\) coincide with Ranicki’s original non-periodic variant of symmetric \({\text {L}}\)-groups, as defined in [57]. Somewhat surprisingly, the genuine quadratic \({\text {L}}\)-theory spectrum \({\text {L}}^{\text {gq} }(R,M)\) is a 4-fold shift of \({\text {L}}^{\text {gs} }(R,M)\).
The Grothendieck-Witt spectrum  of a Poincaré \(\infty \)-category is defined in Paper [2], though in the present paper we already introduce its zeroth homotopy group
of a Poincaré \(\infty \)-category is defined in Paper [2], though in the present paper we already introduce its zeroth homotopy group  , namely, the Grothendieck-Witt group. The underlying infinite loop space
, namely, the Grothendieck-Witt group. The underlying infinite loop space

is then called the Grothendieck-Witt space of  . If 2 is invertible in R, we show in Paper [2] that
. If 2 is invertible in R, we show in Paper [2] that  is equivalent to the Grothendieck-Witt spectrum defined by Schlichting in [59] (where
is equivalent to the Grothendieck-Witt spectrum defined by Schlichting in [59] (where  is any of the Poincaré structures considered above, which coincide due to the invertibility condition on 2). When 2 is not invertible, the fourth and ninth author show in the companion paper [28] that the Grothendieck-Witt spaces of \({{\mathcal {D}}}^\text {p} (R)\) with respect to the genuine Poincaré structures
is any of the Poincaré structures considered above, which coincide due to the invertibility condition on 2). When 2 is not invertible, the fourth and ninth author show in the companion paper [28] that the Grothendieck-Witt spaces of \({{\mathcal {D}}}^\text {p} (R)\) with respect to the genuine Poincaré structures  and
and  coincide with the classical Grothendieck-Witt spaces of quadratic, even and symmetric M-valued forms, respectively. On the other hand, the Grothendieck-Witt spectra of
coincide with the classical Grothendieck-Witt spaces of quadratic, even and symmetric M-valued forms, respectively. On the other hand, the Grothendieck-Witt spectra of  and
and  are actually new invariants of rings, which are based on the homotopy coherent avatars of quadratic and symmetric forms. These sometimes have better formal properties. For example, in the upcoming work [16], the first, third and seventh authors show that the \({\text {GW}}\)- and \({\text {L}}\)-theory spectra associated to the symmetric Poincaré structures
are actually new invariants of rings, which are based on the homotopy coherent avatars of quadratic and symmetric forms. These sometimes have better formal properties. For example, in the upcoming work [16], the first, third and seventh authors show that the \({\text {GW}}\)- and \({\text {L}}\)-theory spectra associated to the symmetric Poincaré structures  satisfy \({{\textbf {A}}}^{1}\)-invariance, and can further be encoded via motivic spectra over the integers. This statement does not hold for any of the other Poincaré structures above, including the genuine symmetric one.
satisfy \({{\textbf {A}}}^{1}\)-invariance, and can further be encoded via motivic spectra over the integers. This statement does not hold for any of the other Poincaré structures above, including the genuine symmetric one.
One of the principal results we prove in Paper [2] is that the relation between Grothendieck-Witt-, \({\text {L}}\)- and algebraic \({\text {K}}\)-theory is governed by the fundamental fibre sequence

where the first term is the homotopy orbits of the algebraic \({\text {K}}\)-theory spectra of \({\mathcal {C}}\) with respect to the \({{\text {C} }_{\textrm{2}}}\)-action induced by the duality of  . In the case of the genuine symmetric Poincaré structure
. In the case of the genuine symmetric Poincaré structure  , this gives a relation between classical symmetric Grothendieck-Witt groups and Ranicki’s non-periodic symmetric \({\text {L}}\)-groups, which to our knowledge is completely new. In the case of the genuine quadratic structure the consequence is even more surprising: The resulting long exact sequence in homotopy groups extends the classical exact sequence (1) to a long exact sequence involving a shifted copy of Ranicki’s non-periodic \({\text {L}}\)-groups.
, this gives a relation between classical symmetric Grothendieck-Witt groups and Ranicki’s non-periodic symmetric \({\text {L}}\)-groups, which to our knowledge is completely new. In the case of the genuine quadratic structure the consequence is even more surprising: The resulting long exact sequence in homotopy groups extends the classical exact sequence (1) to a long exact sequence involving a shifted copy of Ranicki’s non-periodic \({\text {L}}\)-groups.
The main role of the present instalment is to lay down the mathematical foundations that enable the arguments of the next three papers, and eventually their fruits, to take place. In particular, we carefully develop the main concepts of Poincaré \(\infty \)-categories and Poincaré objects, discuss hyperbolic objects and Lagrangians, and prove a version of Ranicki’s algebraic Thom construction in the present setting. We also define the \({\text {L}}\)-groups and zeroth Grothendieck-Witt group of a Poincaré \(\infty \)-category, and conduct a thorough investigation of the global structural properties enjoyed by the \(\infty \)-category of Poincaré \(\infty \)-categories. In addition to the general framework, we also introduce and study important constructions of Poincaré \(\infty \)-categories, which give rise to our motivating examples of interest. In particular:
-
i)
We classify all Poincaré structures in the case where \({\mathcal {C}}\) is the \(\infty \)-category of perfect modules over a ring spectrum, and show that they can be efficiently encoded by the notion of a module with genuine involution.
-
ii)
When \({\mathcal {C}}\) is the perfect derived category of a discrete ring, we develop the procedure of deriving Poincaré structures used to produce the genuine Poincaré structures above. Here, we pick up on some recent ideas of Brantner, Glasman and Illusie, and show that Poincaré structures on \({\mathcal {C}}\) are in fact uniquely determined by their values on projective modules. This allows for the connection between the present set-up and Grothendieck-Witt theory of rings in [28], through which the applications of Paper [2] and Paper [3] to classical problems can be carried out.
-
iii)
We develop in some detail the example of visible Poincaré structures on \(\infty \)-categories of parametrised spectra, which allows us to reproduce visible \({\text {L}}\)-theory as well as \(\text {LA} \)-theory of Weiss–Williams in the present setting. This leads to applications in surgery theory, which we will pursue in future work.
-
iv)
Following Lurie’s treatment of \({\text {L}}\)-theory we study the process of tensoring and cotensoring a Poincaré \(\infty \)-category over a finite simplicial complex. This construction is later exploited in Paper [2] to define and study the Grothendieck-Witt spectrum.
-
v)
We show that the \(\infty \)-category of Poincaré \(\infty \)-categories has all limits and colimits. This enables one, for example, to produce new Poincaré \(\infty \)-categories by taking fibres and cofibres of Poincaré functors, and enables the notion of additivity, which lies at the heart of Grothendieck-Witt theory, to be properly set-up in Paper [2].
-
vi)
We show that Poincaré \(\infty \)-categories can be tensored with each other. This can be used to produce new Poincaré \(\infty \)-categories from old, but also to identify additional important structures, such as a Poincaré symmetric monoidal structure, which arises in many examples of interest and entails the refinement of their Grothendieck-Witt and \({\text {L}}\)-theory spectra to \({\text {E} _\infty }\)-rings. This last claim is proven in Paper [4], though we construct the consequent multiplicative structure on the Grothendieck-Witt and \({\text {L}}\)-groups already in the present paper.
1.3 Applications
Our framework of Poincaré \(\infty \)-categories is motivated by a series of applications which we extract in the following instalments, many of which pertain to classical questions in hermitian \({\text {K}}\)-theory. To give a brief overview of what’s ahead, we first mention that a key feature of the Grothendieck-Witt spectrum we construct in Paper [2] is its additivity. In the setting of Poincaré \(\infty \)-categories, this can be neatly phrased by saying that the functor  sends split bifibre sequences
sends split bifibre sequences

of Poincaré \(\infty \)-categories to bifibre sequences of spectra, where a split bifibre sequence is one in which \({{{\mathcal {C}}}'}\rightarrow {{{\mathcal {C}}}''}\) admits both a left and a right adjoint. One of the main results of Paper [2] is that \({\text {GW}}\) is additive, and is, furthermore, universally characterised by this property as initial among additive functors from Poincaré \(\infty \)-categories to spectra equipped with a natural transformation from \(\Sigma ^{\infty }\text {Pn} \). This is analogous to the universal property characterising algebraic \({\text {K}}\)-theory of stable \(\infty \)-categories established in [14]. In fact, we show in Paper [2] that \({\text {GW}}\) is not only additive but also Verdier localising, a property formulated as above but with the splitness condition removed. This will be used in [16] by the first, third and seventh author in order to show that the \({\text {GW}}\)-spectrum satisfies Nisnevich descent over smooth schemes. It also plays a key role in the study of Grothendieck-Witt theory of Dedekind rings in Paper [3].
One major consequence of additivity is that the hyperbolic and forgetful maps fit to form the Bott–Genauer sequence

where  is the shifting operation on Poincaré functors. Such a sequence was established in the setting of rings in which 2 is invertible by Schlichting [59], who used it to produce another proof of Karoubi’s fundamental theorem. The same argument then yields a version of Karoubi’s fundamental theorem in the setting of Poincaré \(\infty \)-categories. When applied to the genuine Poincaré structures we construct in the present paper, this yields an extension of Karoubi’s fundamental theorem to rings in which 2 is not assumed invertible, establishing, in particular, a conjecture of Karoubi and Giffen.
is the shifting operation on Poincaré functors. Such a sequence was established in the setting of rings in which 2 is invertible by Schlichting [59], who used it to produce another proof of Karoubi’s fundamental theorem. The same argument then yields a version of Karoubi’s fundamental theorem in the setting of Poincaré \(\infty \)-categories. When applied to the genuine Poincaré structures we construct in the present paper, this yields an extension of Karoubi’s fundamental theorem to rings in which 2 is not assumed invertible, establishing, in particular, a conjecture of Karoubi and Giffen.
The fundamental fibre sequence (3) is heavily exploited in Paper [3] to obtain applications for classical Grothendieck-Witt groups of rings. In particular, improving a comparison bound of Ranicki we show in Paper [3] that, if R is Noetherian of global dimension d, the maps
are equivalences in degrees past \(d+2,d\) and \(d-2\), respectively. Thus, even though the genuine \({\text {L}}\)-theory spectra are not 4-periodic, they become so in degrees sufficiently large compared to the global dimension. In addition, when combined with the fundamental fibre sequence (3) this implies that the maps of classical Grothendieck-Witt spaces

are isomorphisms on homotopy groups in sufficiently high degrees. This is a new and quite unexpected result about classical Grothendieck-Witt groups and, to the best of our knowledge, it is the first time that the global dimension of a ring has been related in any way to the gap between its quadratic and symmetric \({\text {GW}}\)-groups. Combined with our extension of Karoubi’s fundamental theorem this implies that in the case of finite global dimension Karoubi’s fundamental theorem holds in its classical form in sufficiently high degrees, allowing for many of the associated arguments to be picked up in this context. In a different direction, for such rings one can eventually deduce results about classical symmetric \({\text {GW}}\)-groups from results on the corresponding homotopy coherent symmetric \({\text {GW}}\)-groups, allowing one to exploit some of the useful properties of the latter, such as a dévissage property we prove in Paper [3] and the \({{\textbf {A}}}^1\)-invariance, which will be established in [16], for the benefit of the former. We exploit these ideas in Paper [3] to solve the homotopy limit problem for number rings, show that their Grothendieck-Witt groups are finitely generated, and produce an essentially complete calculation of the quadratic and symmetric Grothendieck-Witt groups (and their skew variants) of the integers, affirming, in particular, a conjecture of Berrick and Karoubi from [13].
1.4 Organisation of the paper
Let us now describe the structure and the content of the present paper in more detail. In Sect. 1 we define Poincaré \(\infty \)-categories. As indicated before, a Poincaré \(\infty \)-category is a stable \(\infty \)-category \({\mathcal {C}}\) equipped with a quadratic functor  which is perfect in a suitable sense. We give the precise definition in Sect. 1.2, after a discussion of quadratic functors in Sect. 1.1. We also consider the weaker notion of a hermitian \(\infty \)-category, obtained by removing the perfectness condition on
which is perfect in a suitable sense. We give the precise definition in Sect. 1.2, after a discussion of quadratic functors in Sect. 1.1. We also consider the weaker notion of a hermitian \(\infty \)-category, obtained by removing the perfectness condition on  , and explain how to extract from a Poincaré structure
, and explain how to extract from a Poincaré structure  a duality
a duality  . In Sect. 1.3 we describe how one can classify hermitian and Poincaré structures on a given stable \(\infty \)-category in terms of their linear and bilinear parts. Finally, in Sect. 1.4 we discuss the functorial dependence of hermitian structures on the underlying stable \(\infty \)-category, and relate it to the classification discussed in Sect. 1.3.
. In Sect. 1.3 we describe how one can classify hermitian and Poincaré structures on a given stable \(\infty \)-category in terms of their linear and bilinear parts. Finally, in Sect. 1.4 we discuss the functorial dependence of hermitian structures on the underlying stable \(\infty \)-category, and relate it to the classification discussed in Sect. 1.3.
In Sect. 2 we define the notion of a Poincaré object in a given Poincaré \(\infty \)-category  . Such a Poincaré object consists of an object \(x\in {\mathcal {C}}\) together with a map
. Such a Poincaré object consists of an object \(x\in {\mathcal {C}}\) together with a map  , to be thought of as a form in X, such that a certain induced map
, to be thought of as a form in X, such that a certain induced map  is an equivalence. The precise definition is given in Sect. 2.1. We then proceed to discuss hyperbolic Poincaré objects in Sect. 2.2, and in Sect. 2.3 the slightly more general notion of metabolic Poincaré objects, that is, Poincaré objects that admit a Lagrangian. We show how one can understand metabolic Poincaré objects via Poincaré objects in a certain Poincaré \(\infty \)-category
is an equivalence. The precise definition is given in Sect. 2.1. We then proceed to discuss hyperbolic Poincaré objects in Sect. 2.2, and in Sect. 2.3 the slightly more general notion of metabolic Poincaré objects, that is, Poincaré objects that admit a Lagrangian. We show how one can understand metabolic Poincaré objects via Poincaré objects in a certain Poincaré \(\infty \)-category  constructed from
constructed from  . The notion of metabolic Poincaré objects is the main input in the definition of the \({\text {L}}\)-groups of a given Poincaré \(\infty \)-category, which we also give in this section. Finally, in Sect. 2.5 we define the Grothendieck-Witt group
. The notion of metabolic Poincaré objects is the main input in the definition of the \({\text {L}}\)-groups of a given Poincaré \(\infty \)-category, which we also give in this section. Finally, in Sect. 2.5 we define the Grothendieck-Witt group  of a given Poincaré \(\infty \)-category and develop its basic properties.
of a given Poincaré \(\infty \)-category and develop its basic properties.
In Sect. 3 we study Poincaré structures on the \(\infty \)-category \({\text {Mod}}^{\omega }_{A}\) of perfect modules over a ring spectrum A. To this end, we introduce the notion of a module with involution in Sect. 3.1 and show how it can be used to model bilinear functors on module \(\infty \)-categories. We then refine this notion in Sect. 3.2 to a module with genuine involution, that allows us to encode not only bilinear functors but also hermitian and Poincaré structures. Then, in Sect. 3.4 we discuss the basic operations of restriction and induction of modules with genuine involution along maps of ring spectra.
In Sect. 4 we discuss several examples of interest of Poincaré \(\infty \)-categories in further detail. We begin in Sect. 4.1 with the important example of the universal Poincaré \(\infty \)-category  , which is characterised by the property that Poincaré functors out of it pick out Poincaré objects in the codomain. In Sect. 4.2 we consider perfect derived \(\infty \)-categories of ordinary rings and show how to translate the classical language of forms on projective modules into that of the present paper via the process of deriving quadratic functors. In Sects. 4.3 and 4.4 we explain how to construct Poincaré structures producing visible \({\text {L}}\)-theory as studied by Weiss [70], Ranicki [58], and more recently Weiss–Williams [73].
, which is characterised by the property that Poincaré functors out of it pick out Poincaré objects in the codomain. In Sect. 4.2 we consider perfect derived \(\infty \)-categories of ordinary rings and show how to translate the classical language of forms on projective modules into that of the present paper via the process of deriving quadratic functors. In Sects. 4.3 and 4.4 we explain how to construct Poincaré structures producing visible \({\text {L}}\)-theory as studied by Weiss [70], Ranicki [58], and more recently Weiss–Williams [73].
In Sect. 5 we show that the tensor product of stable \(\infty \)-categories refines to give a symmetric monoidal structure on the \(\infty \)-category \(\text {Cat} ^{\textrm{p}}_\infty \) of Poincaré \(\infty \)-categories. The precise definition and main properties of this monoidal product are spelt out in Sects. 5.1 and 5.2. In Sect. 5.3 we analyse what it means for a Poincaré \(\infty \)-category to be an algebra with respect to this structure, and use this analysis in Sect. 5.4 in order to identify various examples of interest of symmetric monoidal Poincaré \(\infty \)-categories.
In Sect. 6 we study the global structural properties of the \(\infty \)-categories \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) of Poincaré and hermitian \(\infty \)-categories, respectively. We begin in Sect. 6.1 by showing that these two \(\infty \)-categories have all small limits and colimits, and describe how these can be computed. In Sect. 6.2 we prove that the symmetric monoidal structures on \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) constructed in Sect. 5.2 are closed, that is, admit internal mapping objects. We then show in Sects. 6.3 and 6.4 that \(\text {Cat} ^{\textrm{h}}_\infty \) is tensored and cotensored over \(\text {Cat} _\infty \). A special role is played by indexing diagrams coming from the poset of faces of a finite simplicial complex, which we study in Sect. 6.5 and 6.6, showing in particular that in this case this procedure preserves Poincaré \(\infty \)-categories. The cotensor construction is used in Paper [2] to define the hermitian \({\text {Q}}\)-construction and eventually Grothendieck-Witt theory, while the tensor construction plays a role in proving the universal property of Grothendieck-Witt theory.
In Sect. 7 we consider the relationship between \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \), and between both of them and various coarser variants, such as bilinear and symmetric bilinear \(\infty \)-categories. By categorifying the relationship between Poincaré forms, hermitian forms and bilinear forms we construct in Sect. 7.2 and 7.3 left and right adjoints to all relevant forgetful functors. In Sect. 7.3 we also prove a generalised version of the algebraic Thom construction, which is used in Paper [2] for the formation of algebraic surgery. In Sect. 7.4 we use this to study \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) from the perspective of \({{\text {C} }_{\textrm{2}}}\)-category theory as developed by Barwick and collaborators, and set-up some of the foundations leading to the genuine \({{\text {C} }_{\textrm{2}}}\)-refinement of the Grothendieck-Witt spectrum we construct in Paper [2]. Finally, in Sect. 7.5 we show that the Grothendieck-Witt group and the \({\text {L}}\)-groups are lax symmetric monoidal functors with respect to the tensor product of Poincaré \(\infty \)-categories.
2 Poincaré categories
In this section we introduce the principal notion of this paper, namely that of Poincaré \(\infty \)-categories. These were first defined by Lurie in [45], though no name was chosen there. Succinctly stated, Poincaré \(\infty \)-categories are stable \(\infty \)-categories \({\mathcal {C}}\) equipped with a quadratic functor  to spectra, which is perfect in a sense we explain below. We then refer to
to spectra, which is perfect in a sense we explain below. We then refer to  as a Poincaré structure on \({\mathcal {C}}\). It is also convenient to consider the more general setting where
as a Poincaré structure on \({\mathcal {C}}\). It is also convenient to consider the more general setting where  is not necessarily perfect, leading to a notion that we call a hermitian \(\infty \)-category. We present both of these in Sect. 1.2, after devoting Sect. 1.1 to surveying quadratic functors and their basic properties. In Sect. 1.3 we describe how one can classify hermitian and Poincaré structures on a given stable \(\infty \)-category in terms of their linear and bilinear parts. This is a particular case of the general structure theory of Goodwillie calculus, but we elaborate the details relevant to the case at hand, as we rely on this classification very frequently, both in explicit constructions of examples and in general arguments. Finally, in Sect. 1.4 we discuss the functorial dependence of hermitian structures on the underlying stable \(\infty \)-category, and relate it to the classification discussed in Sect. 1.3.
is not necessarily perfect, leading to a notion that we call a hermitian \(\infty \)-category. We present both of these in Sect. 1.2, after devoting Sect. 1.1 to surveying quadratic functors and their basic properties. In Sect. 1.3 we describe how one can classify hermitian and Poincaré structures on a given stable \(\infty \)-category in terms of their linear and bilinear parts. This is a particular case of the general structure theory of Goodwillie calculus, but we elaborate the details relevant to the case at hand, as we rely on this classification very frequently, both in explicit constructions of examples and in general arguments. Finally, in Sect. 1.4 we discuss the functorial dependence of hermitian structures on the underlying stable \(\infty \)-category, and relate it to the classification discussed in Sect. 1.3.
2.1 Quadratic and bilinear functors
In this subsection we will recall the notions of quadratic and bilinear functors, and survey their basic properties. These notions fit most naturally in the context of Goodwillie calculus, as adapted to the \(\infty \)-categorical setting in [47, §6]. Our scope of interest here specializes that of loc. cit. in two ways: first, we will only consider the Goodwillie calculus up to degree 2, and second, we will focus our attention on functors from a stable \(\infty \)-category \({\mathcal {C}}\) to the stable \(\infty \)-category \({{\mathcal {S}}{p}}\) of spectra. This highly simplifies the general theory, and will allow us to give direct arguments for most claims, instead of quoting [47, §6]. The reader should however keep in mind that the discussion below is simply a particular case of Goodwillie calculus, to which we make no claim of originality.
Recall that an \(\infty \)-category \({\mathcal {C}}\) is said to be pointed if it admits an object which is both initial and terminal. Such objects are then called zero objects. A functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) between two pointed \(\infty \)-categories is called reduced if it preserves zero objects. Given two pointed \(\infty \)-categories \({\mathcal {C}},{\mathcal {D}}\) we will denote by \({\text {Fun}}_{*}({\mathcal {C}},{\mathcal {D}}) \subseteq {\text {Fun}}({\mathcal {C}},{\mathcal {D}})\) the full subcategory spanned by the reduced functors. A stable \(\infty \)-category is by definition a pointed \(\infty \)-category which admits pushouts and pullbacks and in which a square is a pushout square if and only if it is a pullback square. To avoid breaking the symmetry one then refers to such squares as exact. Any stable \(\infty \)-category is canonically enriched in spectra, and we will denote by \({\text {hom}}_{{\mathcal {C}}}(x,y)\) the mapping spectrum from x to y. It is related to the corresponding mapping space in \({\mathcal {C}}\) by the formula \({\text {Map}}_{{\mathcal {C}}}(x,y) = \Omega ^{\infty }{\text {hom}}_{\mathcal {C}}(x,y)\).
A functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) between two stable \(\infty \)-categories is called exact if it preserves zero objects and exact squares. We note that stable \(\infty \)-categories automatically admit all finite limits and colimits, and that a functor between stable \(\infty \)-categories is exact if and only if it preserves finite colimits, and if and only if it preserves finite limits. If \({\mathcal {D}}\) is a stable \(\infty \)-category and \({\mathcal {C}}\subseteq {\mathcal {D}}\) is a full subcategory which is closed under finite limits and finite colimits then \({\mathcal {C}}\) is also stable and the inclusion \({\mathcal {C}}\subseteq {\mathcal {D}}\) is an exact functor. In this case we will say that \({\mathcal {C}}\) is a stable subcategory of \({\mathcal {D}}\). Given two stable \(\infty \)-categories \({\mathcal {C}},{\mathcal {D}}\) with \({\mathcal {C}}\) small we will denote by \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {D}}) \subseteq {\text {Fun}}({\mathcal {C}},{\mathcal {D}})\) the full subcategory spanned by the exact functors. We note that when \({\mathcal {C}}\) and \({\mathcal {D}}\) are stable one has that \({\text {Fun}}({\mathcal {C}},{\mathcal {D}})\) is also stable and \({\text {Fun}}_*({\mathcal {C}},{\mathcal {D}})\) and \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {D}})\) are stable subcategories. We will denote by \(\text {Cat} _\infty ^\text {ex} \) the (non-full) subcategory of \(\text {Cat} _\infty \) spanned by the stable \(\infty \)-categories and exact functors between them.
If one considers stable \(\infty \)-categories as a categorified version of a vector space, then reduced functors correspond to zero-preserving maps, while exact functors correspond to linear maps. If a functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) is only required to preserves exact squares, but is not necessarily reduced, then one says that f is 1-excisive. More generally, if \({\mathcal {C}}\) is an \(\infty \)-category with finite colimits and \({\mathcal {D}}\) an \(\infty \)-category with finite limits, then \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) is said to be 1-excisive if it sends pushout squares to pullback squares. In the above analogy with linear algebra, these correspond to affine maps, that is, maps which contain a linear part and a constant term, or said differently: polynomial maps of degree 1. In the theory of Goodwillie calculus this point of view is generalized to higher degrees as follows:
Definition 1.1.1
A 3-cube \(\rho :(\Delta ^1)^3 \rightarrow {\mathcal {C}}\) is said to be cartesian if it exhibits \(\rho (0,0,0)\) as the limit of the restriction of \(\rho \) to the subsimplicial set of \((\Delta ^1)^3\) spanned by the complement of (0, 0, 0). Such a 3-cube \(\rho \) is called strongly cartesian if its restriction to each 2-dimensional face of \((\Delta ^1)^3\) is a cartesian square. In particular, strongly cartesian 3-cubes are cartesian. Dually, \(\rho \) is said to be (strongly) cocartesian if \(\rho ^{\text {op} }\) is a (strongly) cartesian cube in \({\mathcal {C}}^{\text {op} }\). A functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) whose domain admits finite colimits and whose target admits finite limits is called 2-excisive if it sends strongly cocartesian 3-cubes to cartesian 3-cubes.
If \({\mathcal {C}}\) is stable then a 3-cube is (strongly) cartesian if and only if it is (strongly) cocartesian, in which case we simply say that \(\rho \) is (strongly) exact. A functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) between stable \(\infty \)-categories is then 2-excisive if it sends strongly exact 3-cubes to exact 3-cubes.
Remark 1.1.2
Though in the present paper we will focus almost entirely on the case of stable \(\infty \)-categories, we chose to formulate the above definition in the slightly more general setting where \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) is a functor from an \(\infty \)-category with finite colimits to an \(\infty \)-category with finite limits. This level of generality, in which most of Goodwillie calculus can be carried out, will be used in Sect. 4.2, but will otherwise not be needed in the present paper.
We note that every 1-excisive functor is in particular 2-excisive. If the former are analogous to affine maps between vector spaces, the latter are then analogous to maps between vector spaces which are polynomial of degree 2, that is, contain a homogeneous quadratic part, a linear part, and a constant term. If we restrict attention to 2-excisive functors which are reduced, then we get the analogue of maps with terms in degrees 1 and 2, but no constant term. These are going to be the functors we consider in this paper.
In the present work it will be convenient to take a slightly different route to the definition of reduced 2-excisive functors, which proceeds as follows. Given a small stable \(\infty \)-category \({\mathcal {C}}\), let us denote by \({\text {BiFun}}({\mathcal {C}}) \subseteq {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) the full subcategory spanned by those reduced functors \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) such that \(\text {B} (x,y) \simeq 0\) if either \(x\) or \(y\) is a zero object. Such functors may be referred to as bi-reduced. Then \({\text {BiFun}}({\mathcal {C}})\) is closed under all limits and colimits in \({\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), and hence the inclusion of the former in the latter admits both a left and a right adjoint. These left and right adjoints are in fact canonically equivalent, and can be described by the following explicit formula: given a reduced functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) we have a canonically associated retract diagram
where \(0 \in {\mathcal {C}}\) is a chosen zero object, and all the maps are induced by the essentially unique maps \(0 \rightarrow x\rightarrow 0\) and \(0 \rightarrow y\rightarrow 0\). The composition of these two maps is the identity thanks to the assumption that \(\text {B} \) is reduced, that is, \(\text {B} (0,0) \simeq 0\). The above retract diagram then induces a canonical splitting
where \(\text {B} ^{\text {red} }(x,y)\) can be identified with both the cofibre of the left map in (4) and the fibre of the right map in (4). We note that by construction the resulting functor
is bi-reduced. The following lemma records the fact that the association \(\text {B} \mapsto \text {B} ^{\text {red} }\) yields both a left and a right adjoint to the inclusion \({\text {BiFun}}({\mathcal {C}}) \subseteq {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
Lemma 1.1.3
The split inclusion \(\text {B} ^{\text {red} }(-,-) \Rightarrow \text {B} (-,-)\) is universal among natural transformations to \(\text {B} \) from a bi-reduced functor, while the projection \(\text {B} (-,-) \Rightarrow \text {B} ^{\text {red} }(-,-)\) is universal among natural transformations from \(\text {B} \) to a bi-reduced functor. In particular, the association \(\text {B} \mapsto \text {B} ^{\text {red} }\) is both left and right adjoint to the full inclusion \({\text {BiFun}}({\mathcal {C}}) \subseteq {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
Proof
Given that \({\text {Fun}}_*({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) is stable and \({\text {BiFun}}({\mathcal {C}})\) is a stable full subcategory, to prove both claims it suffices to show that for \(\text {B} \in {\text {Fun}}_*({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), the associated functors
considered as functors in \({\text {Fun}}_*({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) have a trivial mapping spectrum to any and from any bi-reduced functor. Indeed, since \(0 \in {\mathcal {C}}^{\text {op} }\) is both final and initial it follows that the inclusion \({\mathcal {C}}^{\text {op} }\times \{0\} \subseteq {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) is both left and right adjoint to the projection \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times \{0\}\), and hence restricting along this inclusion is both left and right adjoint to restricting along this projection. The same statement holds for the inclusion \(\{0\} \times {\mathcal {C}}^{\text {op} }\subseteq {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) of the second factor. The mapping spectrum between any bi-reduced functor and a functor restricted along either projection is consequently trivial. \(\square \)
Definition 1.1.4
Let \({\mathcal {C}}\) be a stable \(\infty \)-category and  a reduced functor. We will denote by
a reduced functor. We will denote by  the bi-reduced functor
the bi-reduced functor

obtained by taking the universal bi-reduced replacement described above of the reduced 2-variable functor  . Following the terminology of Goodwillie calculus we will refer to
. Following the terminology of Goodwillie calculus we will refer to  as the cross effect of
as the cross effect of  . The formation of cross effects then yields a functor
. The formation of cross effects then yields a functor
sending  to
to  .
.
Remark 1.1.5
In [45] the term polarization is used for what we called above cross effect, though in [47, §6] the term cross effect is employed.
Remark 1.1.6
If \(f,g:{\mathcal {C}}\rightarrow {\mathcal {D}}\) are reduced functors then the associated restriction functor
along \((f \times g)^{\text {op} }:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {D}}^{\text {op} }\times {\mathcal {D}}^{\text {op} }\) sends the retract diagram
to the retract diagram
where we have used the symbols \(x\) and \(y\) to distinguish the two entries. It then follows that the universal bi-reduction procedure described above commutes with restriction (along pairs of reduced functors). Similarly, if \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) furthermore preserves direct sums, then the formation of cross effects is compatible with restriction along f, that is, the square

naturally commutes.
Given a stable \(\infty \)-category \({\mathcal {C}}\), the diagonal functor \(\Delta :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) induces a pullback functor
In what follows, for any \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), we will denote by \(\text {B} ^{\Delta } := \Delta ^*\text {B} \) the restriction of \(\text {B} \) along the diagonal. Now the maps  and
and  induced by the diagonal \(\Delta _{x}:x\rightarrow x\oplus x\) and collapse map \(\nabla _{x}:x\oplus x\rightarrow x\) induce natural maps
induced by the diagonal \(\Delta _{x}:x\rightarrow x\oplus x\) and collapse map \(\nabla _{x}:x\oplus x\rightarrow x\) induce natural maps

which can be considered as natural transformations

The formation of cross effects then enjoys the following universal property:
Lemma 1.1.7
The two natural transformations in (7) act as a unit and counit exhibiting the cross effect functor (5) as left and right adjoint respectively to the restriction functor \(\Delta ^* :{\text {BiFun}}({\mathcal {C}}) \rightarrow {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
Proof
The direct sum functor \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\) realizes both the product and coproduct (since \({\mathcal {C}}^{\text {op} }\) is stable) and is hence both left and right adjoint to \(\Delta :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\), with units and counits given by the diagonal and collapse maps of the objects in \({\mathcal {C}}\). It then follows that restriction along the direct sum functor is both right and left adjoint to restriction along \(\Delta \), with unit and counit induced by the diagonal and collapse maps. The desired result now follows from Lemma 1.1.3. \(\square \)
Remark 1.1.8
The two sided adjunction of Lemma 1.1.7 is obtained by composing a pair of two-sided adjunctions
where the one on the left is induced by the two sided adjunction  witnessing the existence of biproducts in \({\mathcal {C}}^{\text {op} }\), and the one of the right exhibits the full subcategory \({\text {BiFun}}({\mathcal {C}})\subseteq {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) as reflective and coreflective (Lemma 1.1.3). In particular, we may express the unit and counit of the two sided adjunction \({\text {Fun}}_{*}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \leftrightarrows {\text {BiFun}}({\mathcal {C}})\) which are not specified in Lemma 1.1.7 via the unit \((x,y) \rightarrow (x\oplus y,x\oplus y)\) of the adjunction
witnessing the existence of biproducts in \({\mathcal {C}}^{\text {op} }\), and the one of the right exhibits the full subcategory \({\text {BiFun}}({\mathcal {C}})\subseteq {\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) as reflective and coreflective (Lemma 1.1.3). In particular, we may express the unit and counit of the two sided adjunction \({\text {Fun}}_{*}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \leftrightarrows {\text {BiFun}}({\mathcal {C}})\) which are not specified in Lemma 1.1.7 via the unit \((x,y) \rightarrow (x\oplus y,x\oplus y)\) of the adjunction  and counit \((x\oplus y,x\oplus y) \rightarrow (x,y)\) of the adjunction
and counit \((x\oplus y,x\oplus y) \rightarrow (x,y)\) of the adjunction  , which are all given by the corresponding component inclusions and projections. Unwinding the definitions, we get that the unit of the adjunction
, which are all given by the corresponding component inclusions and projections. Unwinding the definitions, we get that the unit of the adjunction  is given by the induced map
is given by the induced map
and the counit of the adjunction  is given by the induced map
is given by the induced map
Lemma 1.1.9
Let  be a reduced functor. Then the cross effect
be a reduced functor. Then the cross effect  is symmetric, i.e. it canonically refines to an element of \({\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{{\text {hC} }_{\textrm{2}}}\), where the cyclic group with two elements \({{\text {C} }_{\textrm{2}}}\) acts by flipping the two input variables.
is symmetric, i.e. it canonically refines to an element of \({\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{{\text {hC} }_{\textrm{2}}}\), where the cyclic group with two elements \({{\text {C} }_{\textrm{2}}}\) acts by flipping the two input variables.
Proof
By [47, Proposition 6.1.4.3, Remark 6.1.4.4] the bi-reduction functor
discussed above refines to a compatible functor
on \({{\text {C} }_{\textrm{2}}}\)-equivariant objects. It will hence suffice to show that the functor  naturally refines to a \({{\text {C} }_{\textrm{2}}}\)-equivariant object. For this, it suffices to note that the direct sum functor \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\) is equipped with a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure with respect to the flip action on \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) and the trivial action on \({\mathcal {C}}^{\text {op} }\). Indeed, this is part of the symmetric monoidal structure afforded to the direct sum, canonically determined by its universal description as the coproduct in \({\mathcal {C}}^{\text {op} }\). \(\square \)
naturally refines to a \({{\text {C} }_{\textrm{2}}}\)-equivariant object. For this, it suffices to note that the direct sum functor \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\) is equipped with a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure with respect to the flip action on \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) and the trivial action on \({\mathcal {C}}^{\text {op} }\). Indeed, this is part of the symmetric monoidal structure afforded to the direct sum, canonically determined by its universal description as the coproduct in \({\mathcal {C}}^{\text {op} }\). \(\square \)
Keeping in mind the proofs of Lemmas 1.1.7 and 1.1.9, we now note that the diagonal functor \(\Delta :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\), which is both left and right adjoint to the \({{\text {C} }_{\textrm{2}}}\)-equivariant direct sum functor, is also canonically invariant under the \({{\text {C} }_{\textrm{2}}}\)-action on the right hand side switching the two components. This means that the associated restriction functor
is equivariant for the trivial \({{\text {C} }_{\textrm{2}}}\)-action on the target, and so the restricted functor  becomes a \({{\text {C} }_{\textrm{2}}}\)-object of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). In particular,
becomes a \({{\text {C} }_{\textrm{2}}}\)-object of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). In particular,  is naturally a spectrum with a \({{\text {C} }_{\textrm{2}}}\)-action for every \(x\in {\mathcal {C}}\). Explicitly, this action is induced by the canonical action of \({{\text {C} }_{\textrm{2}}}\) on \(x\oplus x\) by swapping the components.
is naturally a spectrum with a \({{\text {C} }_{\textrm{2}}}\)-action for every \(x\in {\mathcal {C}}\). Explicitly, this action is induced by the canonical action of \({{\text {C} }_{\textrm{2}}}\) on \(x\oplus x\) by swapping the components.
Lemma 1.1.10
The natural transformations in (7) both naturally refine to \({{\text {C} }_{\textrm{2}}}\)-equivariant maps with respect to the above \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {B} ^{\Delta }\). In particular, the maps (7) induces natural transformations

Proof
Inspecting the construction of the natural transformations in (7) we see that it will suffice to put a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the diagonal and collapse natural transformations
of functors \({\mathcal {C}}\rightarrow {\mathcal {C}}\). This in turn follows from the fact that the direct sum monoidal structure is both cartesian and cocartesian and every object is canonically a commutative algebra object with respect to coproducts ([47, Proposition 2.4.3.8]). \(\square \)
Definition 1.1.11
For \({\mathcal {C}},{\mathcal {D}}\) and \({\mathcal {E}}\) stable \(\infty \)-categories, we will say that a functor \(b:{\mathcal {C}}\times {\mathcal {D}}\rightarrow {\mathcal {E}}\) is bilinear if it is exact in each variable separately. For a stable \(\infty \)-category \({\mathcal {C}}\) we will denote by \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) the full subcategory spanned by the bilinear functors. We note that this full subcategory is closed under, and hence inherits, the flip action of \({{\text {C} }_{\textrm{2}}}\). We will then denote by \({\text {Fun}}^{\textrm{s}}({\mathcal {C}}) := [{\text {Fun}}^{\textrm{b}}({\mathcal {C}})]^{{{\text {hC} }_{\textrm{2}}}}\) the \(\infty \)-category of \({{\text {C} }_{\textrm{2}}}\)-equivariant objects in \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) with respect to the flip action in the entries, and refer to them as symmetric bilinear functors on \({\mathcal {C}}\).
Example 1.1.12
Suppose that \({\mathcal {C}}\) is a stable \(\infty \)-category equipped with a monoidal structure which is exact in each variable separately. Then for every object \(a \in {\mathcal {C}}\) we have an associated bilinear functor \(\text {B} _a:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) defined by
where \({\text {hom}}_{{\mathcal {C}}}(-,-)\) refers to the canonical enrichment of \({\mathcal {C}}\) in spectra. If the monoidal structure refines to a symmetric one then \(\text {B} _a\) refines to a symmetric bilinear functor. Natural examples of interest to keep in mind are when \({\mathcal {C}}\) is the perfect derived category of a commutative ring (or, more generally, an \({\text {E} _\infty }\)-ring spectrum), or the \(\infty \)-category of perfect quasi-coherent sheaves on a scheme.
Proposition 1.1.13
Let  be a reduced functor. Then the following are equivalent:
be a reduced functor. Then the following are equivalent:
-
i)
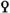 is 2-excisive;
is 2-excisive; -
ii)
the cross effect
 is bilinear and the fibre of the natural transformation
is bilinear and the fibre of the natural transformation  from (8) is an exact functor in \(x\);
from (8) is an exact functor in \(x\); -
iii)
the cross effect
 is bilinear and the cofibre of the natural transformation
is bilinear and the cofibre of the natural transformation  from (8) is an exact functor in \(x\).
from (8) is an exact functor in \(x\).
Proof
Since \({{\mathcal {S}}{p}}\) is stable the property of being reduced and 2-excisive is preserved under limits and colimits of functors \({\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\). It then follows that both ii) and iii) imply i), since exact functors and diagonal restrictions of bilinear functors are in particular reduced and 2-excisive (see [47, Cor. 6.1.3.5]).
In the other direction, if  is 2-excisive then its cross effect is bilinear by [47, Pr. 6.1.3.22]. Moreover, since taking the cross effect commutes with fibres and cofibres, the functors in the statement of ii) and iii) have trivial cross effect. But they are also reduced and 2-excisive by the first part of the argument, and are hence exact by [47, Pr. 6.1.4.10]. \(\square \)
is 2-excisive then its cross effect is bilinear by [47, Pr. 6.1.3.22]. Moreover, since taking the cross effect commutes with fibres and cofibres, the functors in the statement of ii) and iii) have trivial cross effect. But they are also reduced and 2-excisive by the first part of the argument, and are hence exact by [47, Pr. 6.1.4.10]. \(\square \)
Definition 1.1.14
We will say that  is quadratic if it satisfies the equivalent conditions of Proposition 1.1.13. For a small stable \(\infty \)-category \({\mathcal {C}}\) we will then denote by \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) the full subcategory spanned by the quadratic functors.
is quadratic if it satisfies the equivalent conditions of Proposition 1.1.13. For a small stable \(\infty \)-category \({\mathcal {C}}\) we will then denote by \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) the full subcategory spanned by the quadratic functors.
Remark 1.1.15
It follows from the first criterion in Proposition 1.1.13 that \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is closed under limits and colimits in \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). Since the latter is stable it follows that \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is stable as well.
In light of Lemma 1.1.9 and Proposition 1.1.13, the cross effect functor refines to a functor
We will then refer to  as the symmetric bilinear part of
as the symmetric bilinear part of  , and refer to the underlying bilinear functor of
, and refer to the underlying bilinear functor of  as the bilinear part of
as the bilinear part of  .
.
Examples 1.1.16
-
i)
Any exact functor \({\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is quadratic. These are exactly the quadratic functors whose bilinear part vanishes. In particular, we have an exact full inclusion of stable \(\infty \)-categories \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\).
-
ii)
If \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is a bilinear functor then the functor \(\text {B} ^{\Delta }(x) = \text {B} (x,x)\) is a quadratic functor ([47, Cor. 6.1.3.5]). Its symmetric bilinear part is given by the symmetrization \((x,y) \mapsto \text {B} (x,y) \oplus \text {B} (y,x)\) of \(\text {B} \), equipped with its canonical symmetric structure.
Example 1.1.17
If \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) is a symmetric bilinear functor then the functors

and

are both quadratic functors. Indeed, this follows from the previous example by noting that the symmetry induces a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {B} ^{\Delta }\) and invoking Remark 1.1.15. Since taking cross-effects commutes with all limits and colimits the symmetric bilinear parts of these functors are given respectively by
which are both canonically equivalent to \(\text {B} \) itself: indeed, when \(\text {B} \) is symmetric its symmetrization canonically identifies with \(\text {B} [{{\text {C} }_{\textrm{2}}}] = \text {B} \oplus \text {B} \) as a \({{\text {C} }_{\textrm{2}}}\)-object in \({\text {Fun}}^{\textrm{s}}({\mathcal {C}})\), which, since the latter is stable, is the \({{\text {C} }_{\textrm{2}}}\)-object both induced and coinduced from \(\text {B} \).
The superscript \((-)^{\text {q} }\) and \((-)^{\text {s} }\) above refer to the relation between these constructions and the notions of quadratic and symmetric forms in algebra. To see this, consider the case where \({\mathcal {C}}:= {{\mathcal {D}}}^\text {p} (R)\) is the perfect derived \(\infty \)-category of a commutative ring R, that is, the \(\infty \)-categorical localisation of the category of bounded complexes of finitely generated projective R-modules by quasi-isomorphisms. We then have a natural choice of a bilinear functor \(\text {B} _R:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) given by
where \(\otimes _R\) denotes the (derived) tensor product over R. A point \(\beta \in \Omega ^{\infty }\text {B} _{R}(X,Y)\) then corresponds to a map \(X \otimes _R Y \rightarrow R\), which we can consider as a bilinear form on the pair (X, Y). If X, Y are ordinary projective modules then \(\pi _0\text {B} _R(X,Y)\) is simply the abelian group of bilinear forms on (X, Y) in the ordinary sense. For a projective R-module X we may then identify the \({{\text {C} }_{\textrm{2}}}\)-fixed subgroup \(\pi _0\text {B} _R(X,X)^{{{\text {C} }_{\textrm{2}}}}\) with the group of symmetric bilinear forms on X, while the \({{\text {C} }_{\textrm{2}}}\)-quotient group \(\pi _0\text {B} _R(X,X)_{{{\text {C} }_{\textrm{2}}}}\) can be identified with the group of quadratic forms on X via the map sending the orbit of bilinear form \(b:X \otimes _R X \rightarrow R\) to the quadratic form \(q_b(x) = b(x,x)\). In this case the quadratic functors  and
and  defined as above can be considered as associating to a perfect R-complex X a suitable spectrum of quadratic and symmetric forms on X, respectively.
defined as above can be considered as associating to a perfect R-complex X a suitable spectrum of quadratic and symmetric forms on X, respectively.
Remark 1.1.18
By definition the cross effect of a quadratic functor is bilinear, and on the other hand by Example 1.1.16ii) the diagonal restriction of any bilinear functor is quadratic. It then follows from Lemma 1.1.7 that diagonal restriction \(\Delta ^*:{\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) determines a two-sided adjoint to the bilinear part functor \(\text {B} _{(-)}:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\), with unit and counit given by the natural maps

By Remark 1.1.8 the other unit and counit are given by the component inclusion and projections
As quadratic functors are only 2-excisive, but not 1-excisive, they generally don’t preserve exact squares. Their failure to preserve exact squares is however completely controlled by the associated symmetric bilinear parts. More precisely, we have the following:
Lemma 1.1.19
Let  be a quadratic functor with bilinear part
be a quadratic functor with bilinear part  and let
and let

be an exact square in \({\mathcal {C}}\). Then in the diagram

both squares are exact. In particular, there is a natural equivalence

Proof
Consider the following pair of maps between commutative squares

where the left one is induced by the strongly cocartesian cube

Here, the map \(x\oplus x\rightarrow x\) is the collapse map, the map \(z\oplus y \rightarrow w\) is the one whose components are \(\alpha \) and \(\beta \), and the maps \(x\oplus y\rightarrow y\) and \(x\oplus z\rightarrow z\) have one component the identity and one component \(\alpha '\) or \(\beta '\), respectively. Since  is quadratic it is in particular 2-excisive by the first characterization in Proposition 1.1.13, and so
is quadratic it is in particular 2-excisive by the first characterization in Proposition 1.1.13, and so  maps (12) to a cartesian cube of spectra. This means that the first map in (11) induces an equivalence on total fibres. On the other hand, the second map in (11) also induces an equivalence on total fibres since its cofibre is the square
maps (12) to a cartesian cube of spectra. This means that the first map in (11) induces an equivalence on total fibres. On the other hand, the second map in (11) also induces an equivalence on total fibres since its cofibre is the square

whose total fibre is trivial. We then deduce that the composite of the two maps in (11) induces an equivalence on total fibres, and hence the left square in (10) is exact. Finally, the right square in (10) is exact because \(\text {B} (-,-)\) is exact in each variable separately and hence the total fibre of the right most square in (11) identifies with \(\text {B} ({\text {cof}}(\beta '),{\text {cof}}(\alpha '))\) via the natural map \(\text {B} ({\text {cof}}(\beta '),{\text {cof}}(\alpha ')) \rightarrow \text {B} (z,y)\). \(\square \)
Remark 1.1.20
Lemma 1.1.19 admits a natural dual variant. Given a quadratic functor  with bilinear part
with bilinear part  and an exact square as in (9), one may form instead the diagram
and an exact square as in (9), one may form instead the diagram

obtained using the maps on the left hand side of (6) instead of the right. The dual of the argument in the proof of Lemma 1.1.19 then shows that (13) consists of two exact squares, yielding a natural equivalence

Applying Lemma 1.1.19 in the case where \(z=0\) we obtain:
Corollary 1.1.21
(cf. [45, Lecture 9, Theorem 5]) For an exact sequence \(x\rightarrow y\rightarrow w\) in \({\mathcal {C}}\), the natural map

from  to the total fibre of the square on the right, is an equivalence.
to the total fibre of the square on the right, is an equivalence.
Definition 1.1.22
For a quadratic functor  we will denote by
we will denote by  the cofibre of the natural transformation
the cofibre of the natural transformation  , which is exact by Proposition 1.1.13, and refer to it as the linear part of
, which is exact by Proposition 1.1.13, and refer to it as the linear part of  . By construction, the linear part
. By construction, the linear part  sits in an exact sequence
sits in an exact sequence

The formation of linear parts can be organized into a functor
whose post-composition with the inclusion \({\text {Fun}}^{\text {ex} }({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) carries a natural transformation from the identity  , corresponding to the second arrow in (14).
, corresponding to the second arrow in (14).
Remark 1.1.23
It follows from Remark 1.1.6 that the formation of linear parts naturally commutes with restriction along an exact functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\).
Lemma 1.1.24
The natural map  is a unit exhibiting \(\Lambda _{(-)}\) as left adjoint to the inclusion
is a unit exhibiting \(\Lambda _{(-)}\) as left adjoint to the inclusion
Proof
Since \({\text {Fun}}^{\text {ex} }({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is a full inclusion it will suffice to show that  induces an equivalence on mapping spectra to every exact functor. Since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is stable this is the same as saying that the fibre of
induces an equivalence on mapping spectra to every exact functor. Since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is stable this is the same as saying that the fibre of  maps trivially to any exact functor. This fibre is
maps trivially to any exact functor. This fibre is  by construction, and so it will hence suffice to show that
by construction, and so it will hence suffice to show that  maps trivially to any exact functor. Indeed, this follows from the adjunction of Remark 1.1.18 since the bilinear part of every linear functor vanishes. \(\square \)
maps trivially to any exact functor. Indeed, this follows from the adjunction of Remark 1.1.18 since the bilinear part of every linear functor vanishes. \(\square \)
Let us also remark that equivalences of quadratic functors can be detected on their connective covers.
Lemma 1.1.25
Let \({\mathcal {C}}\) be a stable \(\infty \)-category and  be a quadratic functor. Suppose that for every \(x\in {\mathcal {C}}\) the spectrum
be a quadratic functor. Suppose that for every \(x\in {\mathcal {C}}\) the spectrum  is coconnective. Then
is coconnective. Then  is the zero functor. In particular, if a natural transformation of quadratic functors
is the zero functor. In particular, if a natural transformation of quadratic functors  is an equivalence after applying \(\Omega ^\infty \), then it is itself an equivalence.
is an equivalence after applying \(\Omega ^\infty \), then it is itself an equivalence.
Proof
First suppose that  is exact. Then, for every \(x\in {\mathcal {C}}\) and \(n\in {\mathbb {Z}}\),
is exact. Then, for every \(x\in {\mathcal {C}}\) and \(n\in {\mathbb {Z}}\),  , and so
, and so  .
.
Let us now prove the general case. For every \(x,y\in {\mathcal {C}}\), the spectrum  is a direct summand of
is a direct summand of  . In particular it is also coconnective. Hence, if we fix an \(x\in {\mathcal {C}}\), then
. In particular it is also coconnective. Hence, if we fix an \(x\in {\mathcal {C}}\), then  is an exact functor taking values in coconnective spectra, and therefore the zero functor by the previous argument. The cross-effect
is an exact functor taking values in coconnective spectra, and therefore the zero functor by the previous argument. The cross-effect  is therefore the zero functor. In particular,
is therefore the zero functor. In particular,  is exact, and is hence the zero functor by the same argument.
is exact, and is hence the zero functor by the same argument.
The final statement follows by applying the previous argument to the fibre of f. \(\square \)
We finish this subsection with a discussion of the left and right adjoints to the inclusion of quadratic functors inside reduced functors.
Construction 1.1.26
Let \({\mathcal {E}}\) be a stable \(\infty \)-category. Given a quadratic functor  , Lemma 1.1.19 applied in the case where both z and y are zero objects implies that the sequence
, Lemma 1.1.19 applied in the case where both z and y are zero objects implies that the sequence

is exact, and hence that the natural map

is an equivalence. This map itself is however defined for any reduced  , and is natural in
, and is natural in  . In particular, given a stable \(\infty \)-category we may define a functor
. In particular, given a stable \(\infty \)-category we may define a functor
which sends a reduced functor \({\mathcal {R}}:{\mathcal {E}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) to the reduced functor
The operation \(\text {T} ^{{\mathcal {E}}}_2\) is equipped with a natural map
which is an equivalence when \({\mathcal {R}}\) is quadratic by Lemma 1.1.19. Unwinding the definitions, we see that the association \({\mathcal {R}}\mapsto \text {T} ^{{\mathcal {E}}}_2({\mathcal {R}})\) identifies with the one defined in [47, Construction 6.1.1.22] for \({\mathcal {C}}= {\mathcal {E}}^{\text {op} }\) and \({\mathcal {D}}= {{\mathcal {S}}{p}}\). Since \({{\mathcal {S}}{p}}\) is stable and admits small colimits it is in particular differentiable in the sense of [47, Definition 6.1.1.6]. By [47, Theorem 6.1.1.10] we may then conclude that the association
gives a left adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {E}}) \subseteq \textrm{Fun}_*({\mathcal {E}}^{op},Sp)\). This procedure is often referred to as 2-excisive approximation.
In a dual manner, if we use Remark 1.1.20 instead of Lemma 1.1.19 then we get that for a quadratic functor  the sequence
the sequence

is exact, and so the natural map

is an equivalence. As above, for a general reduced functor \({\mathcal {R}}\) we can define the functor
equipped with a natural map
which is an equivalence when \({\mathcal {R}}\) is quadratic. We may also identify \(\text {T} ^2_{{\mathcal {E}}}\) with the result of [47, Construction 6.1.1.22] applied to \({\mathcal {C}}= {\mathcal {E}}\) and \({\mathcal {D}}={{\mathcal {S}}{p}}^{\text {op} }\). Since \({{\mathcal {S}}{p}}^{\text {op} }\) is also differentiable by the same argument it follows from [47, Theorem 6.1.1.10] that the association
provides a right adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {E}}) \subseteq \textrm{Fun}_*({\mathcal {E}}^{op},Sp)\).
2.2 Hermitian and Poincaré \(\infty \)-categories
In this subsection we introduce the key player in this paper—the notion of a Poincaré \(\infty \)-category. For this, it will be convenient to pass first through the following weaker notion:
Definition 1.2.1
A hermitian \(\infty \)-category is a pair  where \({\mathcal {C}}\) is a small stable \(\infty \)-category and
where \({\mathcal {C}}\) is a small stable \(\infty \)-category and  is a quadratic functor in the sense of Definition 1.1.14. We will then also refer to
is a quadratic functor in the sense of Definition 1.1.14. We will then also refer to  as a hermitian structure on \({\mathcal {C}}\). The collection of hermitian \(\infty \)-categories can be organized into a (large) \(\infty \)-category \(\text {Cat} ^{\textrm{h}}_\infty \), obtained as the cartesian Grothendieck construction of the functor
as a hermitian structure on \({\mathcal {C}}\). The collection of hermitian \(\infty \)-categories can be organized into a (large) \(\infty \)-category \(\text {Cat} ^{\textrm{h}}_\infty \), obtained as the cartesian Grothendieck construction of the functor
(here \(\text {CAT} _\infty \) stands for the \(\infty \)-category of possibly large \(\infty \)-categories). We shall also refer to its morphisms as hermitian functors.
Unpacking this definition, we find that a hermitian functor from  to
to  consists of an exact functor \(f :{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) and a natural transformation
consists of an exact functor \(f :{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) and a natural transformation  . We will thus generally denote hermitian functors as pairs \((f,\eta )\) of this form. If
. We will thus generally denote hermitian functors as pairs \((f,\eta )\) of this form. If  is a hermitian functor then by Remark 1.1.6 we have a natural equivalence
is a hermitian functor then by Remark 1.1.6 we have a natural equivalence  , and consequently the natural transformation \(\eta \) determines a natural transformation
, and consequently the natural transformation \(\eta \) determines a natural transformation

which we then denote by \(\beta _{\eta }\).
The notion of Poincaré \(\infty \)-category is obtained from that of a hermitian \(\infty \)-category  by requiring
by requiring  to satisfy two non-degeneracy conditions. Both of these conditions depend only on the underlying symmetric bilinear part
to satisfy two non-degeneracy conditions. Both of these conditions depend only on the underlying symmetric bilinear part  . To formulate the first one we first note that the exponential equivalence
. To formulate the first one we first note that the exponential equivalence
restricts to an equivalence
We then consider the following condition:
Definition 1.2.2
We will say that a bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is right non-degenerate if the associated exact functor
takes values in the essential image of the stable Yoneda embedding
where \({\text {Fun}}^{\text {lex} }\) denotes left exact (that is, finite limit preserving) functors, and the equivalence to the last term is by [47, Corollary 1.4.2.23]. In other words, if for each \(y\in {\mathcal {C}}\) the presheaf of spectra \(\text {B} (-,y)\) is representable by an object in \({\mathcal {C}}\). In this case we can factor (22) essentially uniquely as a functor
followed by \({\mathcal {C}}\hookrightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), so that we obtain an equivalence
Similarly, \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is called left non-degenerate if the associated exact functor \(x\mapsto \text {B} (x,-)\) takes values in the essential image of the stable Yoneda embedding. If \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is left and right non-degenerate, then it is called non-degenerate. In this case the two resulting dualities are, essentially by definition, adjoint to each other.
We will say that a symmetric bilinear functor is non-degenerate if the underlying bilinear functor is. In this case it of course suffices to check that it is right non-degenerate. The two dualities are in this case equivalent and we will refer to the representing functor \(\text {D} _{\text {B} }\) as the duality associated to the non-degenerate symmetric bilinear functor \(\text {B} \) (though we point out that \(\text {D} _{\text {B} }\) is not in general an equivalence). Given a hermitian structure  on a stable \(\infty \)-category \({\mathcal {C}}\), we will say that
on a stable \(\infty \)-category \({\mathcal {C}}\), we will say that  is non-degenerate if its underlying bilinear part is. In this case we will also say that
is non-degenerate if its underlying bilinear part is. In this case we will also say that  is a non-degenerate hermitian \(\infty \)-category and will denote the associated duality by
is a non-degenerate hermitian \(\infty \)-category and will denote the associated duality by  .
.
The full subcategories of \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}),{\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) and \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) spanned by the non-degenerate functors will be denoted \({\text {Fun}}^{\textrm{nb}}({\mathcal {C}}),{\text {Fun}}^{\textrm{ns}}({\mathcal {C}})\) and \({\text {Fun}}^{\textrm{nq}}({\mathcal {C}})\), respectively. The bilinear exponential equivalence (21) then restricts to an equivalence
where \({\text {Fun}}^{\textrm{R}}\) denotes the right adjoint functors. To see this it suffices to observe that \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is non-degenerate precisely if it is right non-degenerate and the resulting duality admits a left adjoint. Under this equivalence the \({{\text {C} }_{\textrm{2}}}\)-action on the left corresponds to the \({{\text {C} }_{\textrm{2}}}\)-action on the right given by passing to adjoints and taking opposites, so that we get an equivalence
Both of these equivalences will be denoted by \(\text {B} \mapsto \text {D} _{\text {B} }\). Similarly, we will also denote the composition
by  .
.
Let us make these adjointability statements explicit: if \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) is a non-degenerate symmetric bilinear functor with associated duality \(\text {D} = \text {D} _{\text {B} }:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) then the symmetric structure of \(\text {B} \) determines a natural equivalence
where \(\text {D} ^{\text {op} }:{\mathcal {C}}\rightarrow {\mathcal {C}}^{\text {op} }\) is the functor induced by \(\text {D} \) upon taking opposites. Such a natural equivalence exhibits in particular \(\text {D} ^{\text {op} }\) as left adjoint to \(\text {D} \). We will denote by
the unit of this adjunction, and refer it as the evaluation map of \(\text {D} \). Its individual components
are then the maps corresponding to identity \(\text {D} ^{\text {op} }(x) \rightarrow \text {D} ^{\text {op} }(x)\) under the equivalence (23). The counit of this adjunction is given again by natural transformation (24), but interpreted as an arrow from \(\text {D} ^{\text {op} }\text {D} \) to the identity in the \(\infty \)-category \({\text {Fun}}({\mathcal {C}}^{\text {op} },{\mathcal {C}}^{\text {op} }) \simeq {\text {Fun}}({\mathcal {C}},{\mathcal {C}})^{\text {op} }\).
Remark 1.2.3
The process of viewing the equivalence (23) as an adjunction between \(\text {D} \) and \(\text {D} ^{\text {op} }\) and extracting its unit as above can be reversed: knowing that \(\text {ev} \) is a unit of an adjunction we can reproduce the equivalence \({\text {hom}}_{{\mathcal {C}}}(y,\text {D} (x)) \simeq {\text {hom}}_{{\mathcal {C}}}(x,\text {D} (y))\) as the composite
where the last map is induced by pre-composition with the evaluation map.
Lemma 1.2.4
Let  be two non-degenerate hermitian \(\infty \)-categories with associated dualities
be two non-degenerate hermitian \(\infty \)-categories with associated dualities  and
and  , and let \(f,g :{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) be two exact functors. Then there is a natural equivalence
, and let \(f,g :{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) be two exact functors. Then there is a natural equivalence

where \({\text {nat}}\) stands for the spectrum of (non-symmetric) natural transformations, on the left between two spectrum valued functors on \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\), and on the right between two functors \({\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}'\).
Proof
Consider the left Kan extension functor
which is left adjoint to the corresponding restriction functor. Natural transformations

then correspond under this adjunction to natural transformations

Now for \(y\in {\mathcal {C}}\) we have

as can be seen by the pointwise formula for left Kan extension. Since  is represented by
is represented by  and left Kan extension preserves representable functors it then follows that
and left Kan extension preserves representable functors it then follows that

for \((x',y) \in {{{\mathcal {C}}}'}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\). On the other hand, we have  , and so by the fully-faithfulness of the Yoneda embedding we thus obtain
, and so by the fully-faithfulness of the Yoneda embedding we thus obtain

as desired. \(\square \)
Definition 1.2.5
Given a hermitian functor  , we will denote by
, we will denote by

the natural transformation corresponding to the natural transformation  of (20), via Lemma 1.2.4.
of (20), via Lemma 1.2.4.
Remark 1.2.6
In the situation of Definition 1.2.5, it follows from the triangle identities of the adjunction \((f \times \text {id} )_! \dashv (f \times \text {id} )^*\) that the natural transformation  can be recovered from
can be recovered from  as the composite
as the composite

where the two middle maps are induced by the action of f on mapping spectra and post-composition with \(\tau _{\eta }\), respectively.
Definition 1.2.7
A hermitian functor  between non-degenerate hermitian \(\infty \)-categories is called duality preserving if the transformation
between non-degenerate hermitian \(\infty \)-categories is called duality preserving if the transformation  constructed above is an equivalence.
constructed above is an equivalence.
Definition 1.2.8
A symmetric bilinear functor \(\text {B} \) is called perfect if the evaluation map \(\text {id} _{\mathcal {C}}\Rightarrow \text {D} _{\text {B} }\text {D} _{\text {B} }^{\text {op} }\) of (24) is an equivalence. An hermitian structure  is called Poincaré if the underlying bilinear functor of
is called Poincaré if the underlying bilinear functor of  is perfect. In this case we will say that
is perfect. In this case we will say that  is a Poincaré \(\infty \)-category. We will denote by
is a Poincaré \(\infty \)-category. We will denote by
the (non-full) subcategory spanned by the Poincaré \(\infty \)-categories and duality preserving functors, and will generally refer to duality-preserving hermitian functors between Poincaré \(\infty \)-categories as Poincaré functors. For a stable \(\infty \)-category \({\mathcal {C}}\), we will denote by
the subcategory spanned by those hermitian structures which are Poincaré, and those natural transformations  which are duality preserving, that is, for which the associated hermitian functor
which are duality preserving, that is, for which the associated hermitian functor  is Poincaré.
is Poincaré.
Remark 1.2.9
A symmetric bilinear functor \(\text {B} \) is perfect if and only if it is non-degenerate and \(\text {D} _{\text {B} } :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) is an equivalence of categories. Indeed, an adjunction consists of a pair of inverse equivalences if and only if its unit and counit are equivalences.
If \(\text {B} \) is a perfect bilinear functor on \({\mathcal {C}}\) then the duality \(\text {D} _{\text {B} }:{\mathcal {C}}^{\text {op} }\xrightarrow {\simeq }{\mathcal {C}}\) is not just an equivalence of \(\infty \)-categories, but carries a significant amount of extra structure. To make this precise note that there is a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Cat} _\infty ^\text {ex} \) given by sending \({\mathcal {C}}\mapsto {\mathcal {C}}^{\text {op} }\). This can be seen by using simplicial sets as a model where taking the opposite gives an action on the nose. Alternatively one can also use that the space of autoequivalences of \(\text {Cat} _\infty ^\text {ex} \) is equivalent to the discrete group \({{\text {C} }_{\textrm{2}}}\) as shown in [67], see also [44, Theorem 4.4.1].
Definition 1.2.10
A stable \(\infty \)-category with perfect duality is a homotopy fixed point of \(\text {Cat} _\infty ^\text {ex} \) with respect to the \({{\text {C} }_{\textrm{2}}}\)-action given by taking the opposite \(\infty \)-category. Equivalently, it is, a section \(\text {B} {{\text {C} }_{\textrm{2}}}\rightarrow \widetilde{\text {Cat} _\infty ^\text {ex} }\) of the fibration \(\widetilde{\text {Cat} _\infty ^\text {ex} } \rightarrow \text {B} {{\text {C} }_{\textrm{2}}}\) encoding the \({{\text {C} }_{\textrm{2}}}\)-action on the \(\infty \)-category \(\text {Cat} _\infty ^\text {ex} \) given by taking opposites.
We note that a stable \(\infty \)-category with perfect duality consists in particular of a stable \(\infty \)-category \({\mathcal {C}}\) and an equivalence \(\text {D} :{\mathcal {C}}\rightarrow {\mathcal {C}}^{\text {op} }\), equipped with additional coherence structure of being a homotopy \({{\text {C} }_{\textrm{2}}}\)-fixed point. For example, the composition \(\text {D} \text {D} ^{\text {op} }\) is equipped with a natural equivalence \(\text {ev} :\text {id} \simeq \text {D} \text {D} ^{\text {op} }\), which itself carries higher coherence homotopies relating it with its opposite, and so forth. By a perfect duality on a given stable \(\infty \)-category \({\mathcal {C}}\) we will mean a refinement of \({\mathcal {C}}\) to a homotopy \({{\text {C} }_{\textrm{2}}}\)-fixed point of \(\text {Cat} _\infty ^\text {ex} \). We may also identify the notion of a perfect duality with that of a \({{\text {C} }_{\textrm{2}}}\)-fixed equivalence \({\mathcal {C}}^{\text {op} }\xrightarrow {\simeq } {\mathcal {C}}\), where the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Fun}}^{\textrm{R}}({\mathcal {C}}^{\text {op} },{\mathcal {C}})\) is obtained via its identification with the \(\infty \)-category \({\text {Fun}}^{\textrm{nb}}({\mathcal {C}})\) of non-degenerate bilinear functors. We will often abuse notation and denote a perfect duality simply by its underlying equivalence \(\text {D} :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\).
In their work on \(\infty \)-categories with duality, Heine–Lopez–Avila–Spitzweck prove that the duality functor \(\text {D} _{\text {B} }\) associated to a perfect bilinear functor \(\text {B} \) on a stable \(\infty \)-category \({\mathcal {C}}\), naturally refines to a perfect duality on \({\mathcal {C}}\) in the above sense. Furthermore, the association \(\text {B} \mapsto \text {D} _{\text {B} }\) determines an equivalence between perfect bilinear functors on \({\mathcal {C}}\) and perfect dualities on \({\mathcal {C}}\) see [29, Corollary 7.3], and [63, Proposition 2.1] for the stable variant. Together with Lemma 1.2.4, this association determines a forgetful functor

from Poincaré \(\infty \)-categories to stable \(\infty \)-categories with perfect duality. This provides a key link between the present setup and the existing literature on stable \(\infty \)-categories with duality.
Definition 1.2.11
Given a stable \(\infty \)-category and a symmetric bilinear functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) we will refer to the hermitian structures  of Example 1.1.17 as the symmetric and quadratic hermitian structures associated to \(\text {B} \), respectively. As the symmetric bilinear parts of both
of Example 1.1.17 as the symmetric and quadratic hermitian structures associated to \(\text {B} \), respectively. As the symmetric bilinear parts of both  and
and  are canonically equivalent to \(\text {B} \), these hermitian structures are Poincaré if and only if \(\text {B} \) is perfect.
are canonically equivalent to \(\text {B} \), these hermitian structures are Poincaré if and only if \(\text {B} \) is perfect.
Example 1.2.12
Let R be an ordinary commutative ring and let \({\mathcal {C}}= {{\mathcal {D}}}^\text {p} (R)\) be the perfect derived \(\infty \)-category of R. Similar as in Example 1.1.17 we may then consider the symmetric bilinear functor \(\text {B} _R \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) given by
with symmetric structure induced by the symmetric structure of the tensor product \(\otimes \). This bilinear functor is perfect with duality given by
where the right hand side stands for the internal mapping complex. An element \(\beta \in \Omega ^{\infty }\text {B} _{R}(X,Y)\) then corresponds to a map \(X \otimes _R Y \rightarrow R\), which we can consider as a bilinear form on the pair (X, Y). To this perfect bilinear functor we can associate the corresponding symmetric and quadratic Poincaré structures

as in Definition 1.2.11. The space  is then the space of (homotopy) \({{\text {C} }_{\textrm{2}}}\)-fixed points of \(\Omega ^{\infty }\text {B} _{R}(X,X)\), which should be viewed as the homotopical counterpart of the notion of a symmetric form on X. The space
is then the space of (homotopy) \({{\text {C} }_{\textrm{2}}}\)-fixed points of \(\Omega ^{\infty }\text {B} _{R}(X,X)\), which should be viewed as the homotopical counterpart of the notion of a symmetric form on X. The space  , on the other hand, is the space of (homotopy) \({{\text {C} }_{\textrm{2}}}\)-orbits of \(\Omega ^{\infty }\text {B} _{R}(X,X)\), which we can consider as a homotopical analogue of that a quadratic form on X, see Example 1.1.17.
, on the other hand, is the space of (homotopy) \({{\text {C} }_{\textrm{2}}}\)-orbits of \(\Omega ^{\infty }\text {B} _{R}(X,X)\), which we can consider as a homotopical analogue of that a quadratic form on X, see Example 1.1.17.
Example 1.2.13
In the situation of Example 1.2.12 we could also consider the symmetric bilinear functor \(\text {B} _{-R}\) whose underlying bilinear functor is \(\text {B} _{R}\) but whose symmetric structure is twisted by the sign action of \({{\text {C} }_{\textrm{2}}}\). In other words, the symmetry equivalence \(\text {B} _{-R}(X \otimes _R Y,R) \xrightarrow {\simeq } \text {B} _{-R}(Y \otimes _R X,R)\) of \(\text {B} _{-R}\) is minus the one of \(\text {B} _R\). This bilinear functor is again perfect with duality which coincides with \(\text {D} _R\) on the level of the underlying equivalence \({{\mathcal {D}}}^\text {p} (R)^{\text {op} }\rightarrow {{\mathcal {D}}}^\text {p} (R)\), but which has a different double dual identification. We may then consider the corresponding symmetric and quadratic Poincaré structures

as in Definition 1.2.11. The space  is then a homotopical counterpart of the notion of an anti-symmetric form on X, while
is then a homotopical counterpart of the notion of an anti-symmetric form on X, while  is its quadratic counterpart.
is its quadratic counterpart.
Example 1.2.14
In the spirit of Example 1.2.12, one may also fix a scheme X and consider the stable \(\infty \)-category \({{\mathcal {D}}}^\text {p} (X)\) of perfect complexes of quasi-coherent sheaves on X. Given a line bundle L on X we have an associated bilinear form \(\text {B} _L\) on \({{\mathcal {D}}}^\text {p} (X)\) given by
which is perfect with duality
To this perfect duality we can then associate the corresponding symmetric and quadratic Poincaré structures

Example 1.2.15
Let \({{\mathcal {S}}{p}}^{\text {f} }\) be the \(\infty \)-category of finite spectra. We define a hermitian structure on \({{\mathcal {S}}{p}}^{\text {f} }\) via the pullback square

where \(\text {D} (X)={\text {hom}}(X,{\mathbb {S}})\) denotes the Spanier–Whitehead dual and the right vertical map is the Tate diagonal \(\text {D} X\rightarrow (\text {D} X\otimes \text {D} X)^{{{\text {tC} }_{\textrm{2}}}}\) of \(\text {D} X\). This hermitian structure is then Poincaré with duality given by Spanier–Whitehead duality. We note that this Poincaré structure is neither quadratic nor symmetric (Definition 1.2.11). The superscript \(\text {u} \) is suggestive for universal, see Sect. 4.1. The Poincaré \(\infty \)-category also functions as the unit of the symmetric monoidal structure on Poincaré \(\infty \)-categories that we will construct in Sect. 5.
Defining hermitian structures as spectrum valued functors allows us to easily implement various useful manipulations. One of them, which plays a recurring role in this paper, is the procedure of shifting hermitian structures:
Definition 1.2.16
Let \({\mathcal {C}}\) be a stable \(\infty \)-category and  a quadratic functor. For \(n \in {\mathbb {Z}}\) we will denote by
a quadratic functor. For \(n \in {\mathbb {Z}}\) we will denote by  the n-fold suspension of
the n-fold suspension of  , given by
, given by

We note that  is again a quadratic functor with bilinear part
is again a quadratic functor with bilinear part  and linear part
and linear part  ; indeed, \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is a stable subcategory of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) and \(\text {B} _{(-)}\) and \(\Lambda _{(-)}\) are both exact functors. In particular, if
; indeed, \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is a stable subcategory of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) and \(\text {B} _{(-)}\) and \(\Lambda _{(-)}\) are both exact functors. In particular, if  non-degenerate or perfect then so is
non-degenerate or perfect then so is  with duality
with duality  . We refer to
. We refer to  as the n-fold shift of
as the n-fold shift of  , and to the hermitian \(\infty \)-category
, and to the hermitian \(\infty \)-category  as the n-fold shift of
as the n-fold shift of  .
.
Remark 1.2.17
The hermitian \(\infty \)-category  is Poincaré if and only if
is Poincaré if and only if  is.
is.
Example 1.2.18
In the situation of Example 1.2.12, if we shift the Poincaré structures  and
and  on \({{\mathcal {D}}}^\text {p} (R)\) by \(n \in {\mathbb {Z}}\) then we get Poincaré structures
on \({{\mathcal {D}}}^\text {p} (R)\) by \(n \in {\mathbb {Z}}\) then we get Poincaré structures

and

respectively, which we consider as encoding n-shifted symmetric and quadratic forms. Here, R[n] denotes the R-complex which is R in degree n and zero everywhere else.
We note that the full subcategories of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) spanned by non-degenerate and perfect functors respectively are not preserved under pullback along exact functors \(f:{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\). For example, the hermitian structure  on \({{\mathcal {D}}}^\text {p} ({\mathbb {Q}})\) is perfect (see Example 1.2.12), but its pullback to \({{\mathcal {D}}}^\text {p} ({\mathbb {Z}})\) is not even non-degenerate. A notable exception to this is however the following:
on \({{\mathcal {D}}}^\text {p} ({\mathbb {Q}})\) is perfect (see Example 1.2.12), but its pullback to \({{\mathcal {D}}}^\text {p} ({\mathbb {Z}})\) is not even non-degenerate. A notable exception to this is however the following:
Observation 1.2.19
If  is a non-degenerate hermitian or Poincaré \(\infty \)-category and \({\mathcal {D}}\subseteq {\mathcal {C}}\) is a full stable subcategory such that the duality
is a non-degenerate hermitian or Poincaré \(\infty \)-category and \({\mathcal {D}}\subseteq {\mathcal {C}}\) is a full stable subcategory such that the duality  maps \({\mathcal {D}}\) to itself then
maps \({\mathcal {D}}\) to itself then  is again non-degenerate with
is again non-degenerate with  . In particular, if
. In particular, if  is Poincaré then
is Poincaré then  is again Poincaré.
is again Poincaré.
Example 1.2.20
If  is a non-degenerate hermitian \(\infty \)-category then the full subcategory \({\mathcal {C}}^{\text {refl} } \subseteq {\mathcal {C}}\) spanned by those objects \(x\in {\mathcal {C}}\) for which the evaluation map \(\text {ev} _{x}:x\rightarrow \text {D} ^{\text {op} }\text {D} (x)\) is an equivalence is preserved under the duality by the triangle identities, and hence the hermitian \(\infty \)-category
is a non-degenerate hermitian \(\infty \)-category then the full subcategory \({\mathcal {C}}^{\text {refl} } \subseteq {\mathcal {C}}\) spanned by those objects \(x\in {\mathcal {C}}\) for which the evaluation map \(\text {ev} _{x}:x\rightarrow \text {D} ^{\text {op} }\text {D} (x)\) is an equivalence is preserved under the duality by the triangle identities, and hence the hermitian \(\infty \)-category  is again non-degenerate, and even Poincaré, since the evaluation map is now an equivalence by construction.
is again non-degenerate, and even Poincaré, since the evaluation map is now an equivalence by construction.
2.3 Classification of hermitian structures
In this section we discuss the classification of hermitian and Poincaré structures on a fixed stable \(\infty \)-category \({\mathcal {C}}\), in terms of their linear and bilinear parts. For the hermitian part, this is essentially the \(n=2\) case classification of n-excisive functors in Goodwillie calculus, and is also a particular instance of the structure theory of stable recollements (see [47, §A.8], [12, 55]). For the purpose of self containment we however provide full proofs of the statements that we need in the present setting. In order to formulate these statements we first need to better understand the role played by the quadratic and symmetric hermitian structures  associated to a given symmetric bilinear form \(\text {B} \).
associated to a given symmetric bilinear form \(\text {B} \).
Lemma 1.3.1
Let  be a quadratic functor on a small stable \(\infty \)-category \({\mathcal {C}}\). Then the following are equivalent:
be a quadratic functor on a small stable \(\infty \)-category \({\mathcal {C}}\). Then the following are equivalent:
-
i)
The map
 of (8) is an equivalence for every \(x\in {\mathcal {C}}\).
of (8) is an equivalence for every \(x\in {\mathcal {C}}\). -
ii)
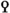 is equivalent to a quadratic functor of the form
is equivalent to a quadratic functor of the form  for some symmetric bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) (see Example 1.1.17).
for some symmetric bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) (see Example 1.1.17). -
iii)
The spectrum of natural transformations
 is trivial for any exact functor \({\text {L}}\in {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\).
is trivial for any exact functor \({\text {L}}\in {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\).
Definition 1.3.2
Following the conventions of Goodwillie calculus, we will refer to quadratic functors  which satisfy the equivalent conditions of Lemma 1.3.1 as homogeneous. We will denote by \({\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) the full subcategory spanned by the homogeneous functors.
which satisfy the equivalent conditions of Lemma 1.3.1 as homogeneous. We will denote by \({\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) the full subcategory spanned by the homogeneous functors.
Proof
(Proof of Lemma 1.3.1) Clearly i) \(\Rightarrow \) ii). If we assume ii) then iii) follows from Lemma 1.1.24 since the linear part of  vanishes by definition. Similarly if we assume iii) then i) follows by Lemma 1.1.24 since the linear part vanishes. \(\square \)
vanishes by definition. Similarly if we assume iii) then i) follows by Lemma 1.1.24 since the linear part vanishes. \(\square \)
Corollary 1.3.3
(cf. [47, Proposition 6.1.4.14]) The functor

is fully-faithful and its essential image is spanned by those quadratic functors which are homogeneous in the above sense.
Proof
By Lemma 1.3.1 the functor (28) takes values in homogeneous functors, and hence determines a functor \(\varphi :{\text {Fun}}^{\textrm{s}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\), where the latter denotes the full subcategory spanned by homogeneous quadratic functors. On the other hand, the formation of cross effects determines a functor in the other direction \(\psi :{\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\). By Lemma 1.3.1 the composed functor \(\varphi \circ \psi :{\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{hom}}({\mathcal {C}})\) is naturally equivalent to the identity, and by Examples 1.1.17 the composite \(\psi \circ \varphi \) is naturally equivalent to the identity \({\text {Fun}}^{\textrm{s}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) as well. It then follows that \(\varphi \) is an equivalence from \({\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) to \({\text {Fun}}^{\textrm{hom}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\), as desired. \(\square \)
The notion of a homogeneous quadratic functor has a dual counterpart, which consists of the quadratic functors which have a trivial mapping spectrum from any exact functor. The argument of Lemma 1.3.1 then runs in a completely dual manner to show that this property is equivalent to the canonical map  being an equivalence and is satisfied by quadratic functors of the form
being an equivalence and is satisfied by quadratic functors of the form  for any \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\). We will refer to such functors as cohomogeneous, and denote by \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) the full subcategory spanned by the cohomogeneous functors. The argument of Corollary 1.3.3 then runs in a completely dual manner to show that the functor
for any \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\). We will refer to such functors as cohomogeneous, and denote by \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) the full subcategory spanned by the cohomogeneous functors. The argument of Corollary 1.3.3 then runs in a completely dual manner to show that the functor

is fully-faithful and its essential image is spanned by the cohomogeneous quadratic functors.
Remark 1.3.4
Given a bilinear functor \(\text {B} \), the quadratic functor \(x\mapsto \text {B} (x,x)\) is both homogeneous and cohomogeneous.
Proposition 1.3.5
The natural transformation  exhibits
exhibits  as final among homogeneous functors equipped with a map to
as final among homogeneous functors equipped with a map to  . Dually, the natural transformation
. Dually, the natural transformation  exhibits
exhibits  as initial among cohomogeneous functors equipped with a map from
as initial among cohomogeneous functors equipped with a map from  .
.
Proof
This first statement is equivalent to Lemma 1.1.24 and the second is dual. \(\square \)
Corollary 1.3.6
For a small stable \(\infty \)-category \({\mathcal {C}}\) the functor
admits left and right adjoints, both of which are fully faithful, given by sending \(\text {B} \) to  and
and  respectively.
respectively.
Remark 1.3.7
By Corollary 1.3.6 with Lemma 1.1.24 the pair of fully-faithful inclusions

form a recollement in the sense of [47, Definition A.8.1], and more precisely a stable recollement in the sense of [12] and [55] since all \(\infty \)-categories involved are stable and all functors involved are exact.
Given a symmetric bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\), Lemma 1.3.1 implies that the linear part of the quadratic functor  is trivial. This however need not be the case for the quadratic functor
is trivial. This however need not be the case for the quadratic functor  . To identify the linear part of the latter, recall that the symmetric bilinear part of
. To identify the linear part of the latter, recall that the symmetric bilinear part of  is canonically identified with \(\text {B} \) itself (see Example 1.1.17), and so by Corollary 1.3.6 natural transformations
is canonically identified with \(\text {B} \) itself (see Example 1.1.17), and so by Corollary 1.3.6 natural transformations  correspond to natural transformations \(\text {B} \Rightarrow \text {B} \). In particular, there is a distinguished transformation
correspond to natural transformations \(\text {B} \Rightarrow \text {B} \). In particular, there is a distinguished transformation

which corresponds to the identity \(\text {B} \Rightarrow \text {B} \). In terms of the adjunctions of Corollary 1.3.6, this map can also be identified with the counit of the adjunction \((-)^{\Delta }_{{{\text {hC} }_{\textrm{2}}}} \dashv \text {B} _{(-)}\) evaluated at  , or the unit of \(\text {B} _{(-)} \dashv ((-)^{\Delta })^{{{\text {hC} }_{\textrm{2}}}}\) evaluated at
, or the unit of \(\text {B} _{(-)} \dashv ((-)^{\Delta })^{{{\text {hC} }_{\textrm{2}}}}\) evaluated at  .
.
Lemma 1.3.8
For \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) the map (30) is canonically equivalent to the trace map associated to the \({{\text {C} }_{\textrm{2}}}\)-action on the object \(\text {B} ^{\Delta } \in {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\).
Proof
Given the bijective correspondence between natural transformations  and natural transformations \(\text {B} \Rightarrow \text {B} \) it will suffice to construct an identification between the map \(\text {B} \Rightarrow \text {B} \) induced by the trace map of \(\text {B} ^{\Delta }\) and the identity on \(\text {B} \). For this, note that since the functor \(\text {B} _{(-)}:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) preserves all limits and colimits it also sends trace maps to trace maps. In particular, the map \(\text {B} \Rightarrow \text {B} \) induced on bilinear parts by the trace map
and natural transformations \(\text {B} \Rightarrow \text {B} \) it will suffice to construct an identification between the map \(\text {B} \Rightarrow \text {B} \) induced by the trace map of \(\text {B} ^{\Delta }\) and the identity on \(\text {B} \). For this, note that since the functor \(\text {B} _{(-)}:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) preserves all limits and colimits it also sends trace maps to trace maps. In particular, the map \(\text {B} \Rightarrow \text {B} \) induced on bilinear parts by the trace map  is itself the trace map
is itself the trace map
associated to the \({{\text {C} }_{\textrm{2}}}\)-action on the symmetric bilinear part of \(\text {B} ^{\Delta }\), which we identify with the induced/coinduced \({{\text {C} }_{\textrm{2}}}\)-object \(\text {B} \oplus \text {B} \) as in Example 1.1.17. The desired result now follows from the following completely general property of trace maps: given a semi-additive \(\infty \)-category \({\mathcal {D}}\) and an object \(x\in {\mathcal {D}}\), the trace map of the induced/coinduced \({{\text {C} }_{\textrm{2}}}\)-object \(x\oplus x\) identifies with the identity \(\text {id} :x\rightarrow x\) under the canonical identifications \((x\oplus x)_{{{\text {hC} }_{\textrm{2}}}} \simeq x\simeq (x\oplus x)^{{{\text {hC} }_{\textrm{2}}}}\). \(\square \)
Remark 1.3.9
Lemma 1.3.8 implies that  naturally lifts to a functor with values in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. We will discuss this issue in greater detail and precision in Sect. 7.4.
naturally lifts to a functor with values in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. We will discuss this issue in greater detail and precision in Sect. 7.4.
Corollary 1.3.10
For a symmetric bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) the linear part of  is naturally equivalent to the Tate construction \((\text {B} ^{\Delta })^{{{\text {tC} }_{\textrm{2}}}}(x) = \text {B} (x,x)^{{{\text {tC} }_{\textrm{2}}}}\). In particular, the latter is always an exact functor.
is naturally equivalent to the Tate construction \((\text {B} ^{\Delta })^{{{\text {tC} }_{\textrm{2}}}}(x) = \text {B} (x,x)^{{{\text {tC} }_{\textrm{2}}}}\). In particular, the latter is always an exact functor.
By virtue of Lemma 1.3.8 and Corollary 1.3.10, any quadratic functor  on \({\mathcal {C}}\) determines a diagram of quadratic functors
on \({\mathcal {C}}\) determines a diagram of quadratic functors

in which the right square is exact and the right most vertical map is obtained from the middle vertical map by taking linear parts. Conversely, by Proposition 1.1.13 a symmetric bilinear functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), an exact functor \(\Lambda :{\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) and a natural transformation \(\tau :\Lambda \Longrightarrow (\text {B} ^{\Delta })^{{\text {tC} }_{\textrm{2}}}\) together determine a quadratic functor  by declaring the square
by declaring the square

cartesian. This observation leads to a well-known classification of quadratic functors, which we now explain. To formulate it, let us first note that for a quadratic functor  , Lemma 1.1.24 tells us that the natural transformation
, Lemma 1.1.24 tells us that the natural transformation  is universally characterized by the property that it induces an equivalence on mapping spectra to every exact functor. In particular, if
is universally characterized by the property that it induces an equivalence on mapping spectra to every exact functor. In particular, if  is any map from
is any map from  to an exact functor \(\Lambda \) which induces an equivalence on mapping spectra to any exact functor, then \(\varphi \) factors through an equivalence
to an exact functor \(\Lambda \) which induces an equivalence on mapping spectra to any exact functor, then \(\varphi \) factors through an equivalence  in an essentially unique manner. In this case, we will also say that \(\varphi \) exhibits \(\Lambda \) as the linear part of
in an essentially unique manner. In this case, we will also say that \(\varphi \) exhibits \(\Lambda \) as the linear part of  . Similarly, we will say that a map
. Similarly, we will say that a map  exhibits
exhibits  as the cohomogeneous part of
as the cohomogeneous part of  if
if  is cohomogeneous and \(\psi \) induces an equivalence on mapping spectra to any cohomogeneous functor. In this case, Corollary 1.3.6 tells us that \(\psi \) factors through an essentially unique equivalence
is cohomogeneous and \(\psi \) induces an equivalence on mapping spectra to any cohomogeneous functor. In this case, Corollary 1.3.6 tells us that \(\psi \) factors through an essentially unique equivalence  . Let us now denote by \({\mathcal {E}}\subseteq {\text {Fun}}(\Delta ^1 \times \Delta ^1,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) the full subcategory spanned by those squares of quadratic functors
. Let us now denote by \({\mathcal {E}}\subseteq {\text {Fun}}(\Delta ^1 \times \Delta ^1,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) the full subcategory spanned by those squares of quadratic functors

which are exact and for which the top horizontal map exhibits \(\Lambda \) as the linear part of  and the left vertical map exhibits
and the left vertical map exhibits  as the cohomogeneous part of
as the cohomogeneous part of  . In particular, any square in \({\mathcal {E}}\) is equivalent to a square as of the form appearing on the right side of (31) in an essentially unique way. We may consider \({\mathcal {E}}\) as the \(\infty \)-category of quadratic functors equipped with a “cohomogeneous-linear decomposition”.
. In particular, any square in \({\mathcal {E}}\) is equivalent to a square as of the form appearing on the right side of (31) in an essentially unique way. We may consider \({\mathcal {E}}\) as the \(\infty \)-category of quadratic functors equipped with a “cohomogeneous-linear decomposition”.
Proposition 1.3.11
The evaluation at \((0,0) \in \Delta ^1 \times \Delta ^1\) map \({\mathcal {E}}\rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sending a square as in (32) to  is an equivalence of \(\infty \)-categories. In particular, every quadratic functor can be written as a pullback of cohomogeneous and exact functors.
is an equivalence of \(\infty \)-categories. In particular, every quadratic functor can be written as a pullback of cohomogeneous and exact functors.
Proof
Given Remark 1.3.7 this can be deduced from [12, Lemma 9]. We however spell out the details for completeness. Let \({\mathcal {E}}\ulcorner \subseteq {\text {Fun}}(\Lambda ^2_0,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) be the full subcategory spanned by those \(\Lambda ^2_0\)-diagrams

for which the top horizontal map exhibits \(\Lambda \) as the linear part of  and the left vertical map exhibits
and the left vertical map exhibits  the cohomogeneous part of
the cohomogeneous part of  . Then the restriction of any square in \({\mathcal {E}}\) to \(\Lambda ^2_0 \subseteq \Delta ^1 \times \Delta ^1\) lies in \({\mathcal {E}}\ulcorner \) and the resulting projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\ulcorner \) is a trivial Kan fibration since every square in \({\mathcal {E}}\) is exact and hence a left Kan extension of its restriction to \(\Lambda ^2_0\). It will hence suffice to show that the projection \({\mathcal {E}}\ulcorner \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sending a diagram as in (33) to
. Then the restriction of any square in \({\mathcal {E}}\) to \(\Lambda ^2_0 \subseteq \Delta ^1 \times \Delta ^1\) lies in \({\mathcal {E}}\ulcorner \) and the resulting projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\ulcorner \) is a trivial Kan fibration since every square in \({\mathcal {E}}\) is exact and hence a left Kan extension of its restriction to \(\Lambda ^2_0\). It will hence suffice to show that the projection \({\mathcal {E}}\ulcorner \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sending a diagram as in (33) to  is an equivalence. Now the \(\infty \)-category \({\mathcal {E}}\ulcorner \) can be embedded in the larger \(\infty \)-category \({\mathcal {E}}' \subseteq {\text {Fun}}(\Lambda ^2_0,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) consisting of those diagrams as in (33) for which \(\Lambda \) is exact and
is an equivalence. Now the \(\infty \)-category \({\mathcal {E}}\ulcorner \) can be embedded in the larger \(\infty \)-category \({\mathcal {E}}' \subseteq {\text {Fun}}(\Lambda ^2_0,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) consisting of those diagrams as in (33) for which \(\Lambda \) is exact and  is cohomogeneous. Then the projection \({\mathcal {E}}' \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sending (33) to
is cohomogeneous. Then the projection \({\mathcal {E}}' \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sending (33) to  is a cartesian fibration classified by the functor sending
is a cartesian fibration classified by the functor sending  to the product of the comma category of exact functors under
to the product of the comma category of exact functors under  and the comma category of cohomogeneous functors under
and the comma category of cohomogeneous functors under  . We may then identify \({\mathcal {E}}\ulcorner \) with the full subcategory of \({\mathcal {E}}'\) spanned by those objects which are initial in their fibres. It then follows that the projection \({\mathcal {E}}\ulcorner \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is a trivial Kan fibration, and so the proof is complete. \(\square \)
. We may then identify \({\mathcal {E}}\ulcorner \) with the full subcategory of \({\mathcal {E}}'\) spanned by those objects which are initial in their fibres. It then follows that the projection \({\mathcal {E}}\ulcorner \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is a trivial Kan fibration, and so the proof is complete. \(\square \)
We may now deduce the classification theorem for hermitian structures (cf. the general classification of recollements [47, Proposition A.8.11]):
Corollary 1.3.12
(Classification of hermitian structures) The square

is cartesian. Here the lower horizontal functor sends \(\text {B} \) to \((\text {B} ^{\Delta })^{{\text {tC} }_{\textrm{2}}}\) and the right vertical functor sends an arrow to its target.
Proof
Let \({\mathcal {E}}\lrcorner \subseteq {\text {Fun}}(\Lambda ^2_2,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) be the full subcategory spanned by those \(\Lambda ^2_2\)-diagrams

for which  is cohomogeneous, \(\Lambda \) is exact and the bottom horizontal map exhibits \(\Lambda '\) as the linear part of
is cohomogeneous, \(\Lambda \) is exact and the bottom horizontal map exhibits \(\Lambda '\) as the linear part of  . Then restriction along \(\Lambda ^2_2 \subseteq \Delta ^1 \times \Delta ^1\) sends every square in \({\mathcal {E}}\) to a square in \({\mathcal {E}}\lrcorner \). On the other hand, if we complete a diagram of the form (35) which belongs to \({\mathcal {E}}\lrcorner \) to a cartesian square, then this square will belong to \({\mathcal {E}}\): indeed, this follows from the fact that a map
. Then restriction along \(\Lambda ^2_2 \subseteq \Delta ^1 \times \Delta ^1\) sends every square in \({\mathcal {E}}\) to a square in \({\mathcal {E}}\lrcorner \). On the other hand, if we complete a diagram of the form (35) which belongs to \({\mathcal {E}}\lrcorner \) to a cartesian square, then this square will belong to \({\mathcal {E}}\): indeed, this follows from the fact that a map  from a quadratic to an exact functor exhibits the latter as the linear part of the former if and only if its fibre maps trivially to any exact functor, that is, if its fibre is homogeneous. We then conclude that the projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\lrcorner \) induced by restriction along \(\Lambda ^2_2\) is a trivial Kan fibration. On the other hand, the \(\infty \)-category \({\mathcal {E}}\lrcorner \) is by construction a fibre product \({\text {Ar}}({\text {Fun}}^{\textrm{ex}}({\mathcal {C}})) \times _{{\text {Fun}}^{\textrm{ex}}({\mathcal {C}})} {\mathcal {E}}''\) where \({\mathcal {E}}''\) is the full subcategory of \({\text {Fun}}(\Delta ^1,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) spanned by those arrows
from a quadratic to an exact functor exhibits the latter as the linear part of the former if and only if its fibre maps trivially to any exact functor, that is, if its fibre is homogeneous. We then conclude that the projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\lrcorner \) induced by restriction along \(\Lambda ^2_2\) is a trivial Kan fibration. On the other hand, the \(\infty \)-category \({\mathcal {E}}\lrcorner \) is by construction a fibre product \({\text {Ar}}({\text {Fun}}^{\textrm{ex}}({\mathcal {C}})) \times _{{\text {Fun}}^{\textrm{ex}}({\mathcal {C}})} {\mathcal {E}}''\) where \({\mathcal {E}}''\) is the full subcategory of \({\text {Fun}}(\Delta ^1,{\text {Fun}}^{\textrm{q}}({\mathcal {C}}))\) spanned by those arrows  such that
such that  is cohomogeneous and \(\psi \) exhibits \(\Lambda '\) as the linear part of
is cohomogeneous and \(\psi \) exhibits \(\Lambda '\) as the linear part of  . As in the proof of Proposition 1.3.11 the projection \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{coh}}({\mathcal {C}})\) sending
. As in the proof of Proposition 1.3.11 the projection \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{coh}}({\mathcal {C}})\) sending  to
to  is a trivial Kan fibration onto the full subcategory \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) spanned by the cohomogeneous functors, and the section is given by sending a cohomogeneous functor
is a trivial Kan fibration onto the full subcategory \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) spanned by the cohomogeneous functors, and the section is given by sending a cohomogeneous functor  to the arrow
to the arrow  . We hence see that the projection \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) is equivalent as an arrow to the functor \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) taking linear parts. Finally, by Corollary 1.3.6 and Corollary 1.3.10 the latter arrow is also equivalent to the arrow \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) sending \(\text {B} \) to \((\text {B} ^{\Delta })^{{{\text {tC} }_{\textrm{2}}}}\). Since \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) is a categorical fibration the fibre product \({\mathcal {E}}\lrcorner \) is a model for the homotopy fibre product in the square (34). The desired result now follows from Proposition 1.3.11 and the fact that the projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\lrcorner \) is an equivalence. \(\square \)
. We hence see that the projection \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) is equivalent as an arrow to the functor \({\text {Fun}}^{\textrm{coh}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) taking linear parts. Finally, by Corollary 1.3.6 and Corollary 1.3.10 the latter arrow is also equivalent to the arrow \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) sending \(\text {B} \) to \((\text {B} ^{\Delta })^{{{\text {tC} }_{\textrm{2}}}}\). Since \({\mathcal {E}}'' \rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}})\) is a categorical fibration the fibre product \({\mathcal {E}}\lrcorner \) is a model for the homotopy fibre product in the square (34). The desired result now follows from Proposition 1.3.11 and the fact that the projection \({\mathcal {E}}\rightarrow {\mathcal {E}}\lrcorner \) is an equivalence. \(\square \)
Finally, let us also deduce an analogous classification for Poincaré structures. For this, let us denote by \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) the non-full subcategory spanned by the perfect bilinear functors and duality preserving natural transformations, that is, the natural transformations \(\beta :\text {B} \Rightarrow \text {B} '\) for which the associated transformation \(\tau _{\beta }:\text {D} _{\text {B} } \Rightarrow \text {D} _{\text {B} '}\) is an equivalence. We then define \({\text {Fun}}^{\textrm{ps}}({\mathcal {C}})\) to be the \(\infty \)-category sitting in the pullback square

It then follows directly from the definitions that the subcategory inclusion \({\text {Fun}}^{\textrm{p}}({\mathcal {C}})\subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) (see Definition 1.2.8) features in a commutative diagram

in which both squares are pullback squares. The following is now a direct consequence of Corollary 1.3.12:
Corollary 1.3.13
(Classification of Poincaré structures) The square

is cartesian.
2.4 Functoriality of hermitian structures
In this subsection, we discuss the functorial dependence of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) on \({\mathcal {C}}\) from the perspective of the classification described in Sect. 1.3, not only contravariantly via restriction along exact functors, but also covariantly via left Kan extensions. Recall that in Sect. 1.2 we defined \(\text {Cat} ^{\textrm{h}}_\infty \) as the total \(\infty \)-category of the cartesian fibration
which classifies the functor \({\mathcal {C}}\mapsto {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\). In particular, being a cartesian fibration, the projection (37) encodes the contravariant dependence of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) in \({\mathcal {C}}\). We will now show that \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) also depends covariantly in \({\mathcal {C}}\) via the formations of left Kan extensions. In particular, it will follow that the projection (37) is also a cocartesian fibration. Since we constantly work with contravariant functors to spectra let us employ the following notation: given a functor \(g:{\mathcal {D}}\rightarrow {\mathcal {E}}\) between \(\infty \)-categories we denote by \(g_!:{\text {Fun}}({\mathcal {D}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {E}}^{\text {op} },{{\mathcal {S}}{p}})\) the operation of left Kan extension along \(g^{\text {op} }:{\mathcal {D}}^{\text {op} }\rightarrow {\mathcal {E}}^{\text {op} }\).
Lemma 1.4.1
-
i)
If \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) is an exact functor between stable \(\infty \)-categories then the associated left Kan extension functor
$$\begin{aligned} f_!:{\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {D}}^{\text {op} },{{\mathcal {S}}{p}}) \end{aligned}$$sends exact functors to exact functors.
-
ii)
If \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) and \(g:{\mathcal {A}}\rightarrow {\mathcal {B}}\) are exact functors between stable \(\infty \)-categories then the associated left Kan extension functor
$$\begin{aligned} (f \times g)_!:{\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {A}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {D}}^{\text {op} }\times {\mathcal {B}}^{\text {op} },{{\mathcal {S}}{p}}) \end{aligned}$$sends bilinear functors to bilinear functors.
-
iii)
If \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) is an exact functor between stable \(\infty \)-categories then the associated left Kan extension functor
$$\begin{aligned} f_!:{\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {D}}^{\text {op} },{{\mathcal {S}}{p}}) \end{aligned}$$sends quadratic functors to quadratic functors.
Proof
We first note that left Kan extension along any functor between pointed \(\infty \)-categories preserve reduced functors by the pointwise formula for left Kan extension. Let now \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) be an exact functor and \({\mathcal {R}}:{\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) a reduced functor. Consider the following commutative diagram of stable \(\infty \)-categories

Then the bottom arrow admits a left adjoint \(g :{\text {Pro}}({\mathcal {D}}) \longrightarrow {\text {Pro}}({\mathcal {C}})\), which corresponds to restriction along \({\mathcal {C}}\rightarrow {\mathcal {D}}\) under the identification of \({\text {Pro}}(-) \simeq {\text {Ind}}((-)^{\text {op} })^{\text {op} }\) with (the opposite category of) right exact functors to spaces. Now since the Yoneda embedding \(j:{\mathcal {D}}\rightarrow {\text {Pro}}({\mathcal {D}})\) is fully faithful we have that \(j^*j_!:{\text {Fun}}({\mathcal {D}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {D}}^{\text {op} },{{\mathcal {S}}{p}})\) is equivalent to the identity, and so
Moreover, since g is left adjoint to \(\widetilde{f}\) we have that the left Kan extension functor \(\widetilde{f}_!:{\text {Fun}}^{\textrm{ex}}({\text {Pro}}({\mathcal {C}})^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}^{\textrm{ex}}({\text {Pro}}({\mathcal {D}})^{\text {op} },{{\mathcal {S}}{p}})\) is equivalent to restriction along \(g^{\text {op} }:{\text {Pro}}({\mathcal {D}})^{\text {op} }\rightarrow {\text {Pro}}({\mathcal {C}})^{\text {op} }\), and so
Applying [47, Proposition 6.1.5.4] we now get that \(i_!{\mathcal {R}}\) is exact (resp. quadratic) if \({\mathcal {R}}\) is exact (resp. quadratic). Precomposition with the exact functor gj then preserve the properties of being exact or quadratic, and so \(f_!{\mathcal {R}}\) is exact (resp. quadratic) if \({\mathcal {R}}\) is exact (resp. quadratic). This proves i) and iii). To prove ii), we now argue as follows. By the compatibility of left Kan extensions with composition of functors we may reduce to the case where either f or g are the identity functor. By symmetry it will suffice to assume that it is f which is the identity \({\mathcal {C}}\rightarrow {\mathcal {C}}\). For any functor \({\mathcal {R}}:{\mathcal {C}}^{\text {op} }\times {\mathcal {A}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) and every \(x\in {\mathcal {C}}\) we then have
as can be seen by the pointwise formula for left Kan extension. We may then conclude that under the exponential equivalences
the left Kan extension functor \((\text {id} \times g)_!\) corresponds to post-composing with the left Kan extension functor \(g_!:{\text {Fun}}({\mathcal {A}}^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}({\mathcal {B}}^{\text {op} },{{\mathcal {S}}{p}})\). Under the same equivalence the bilinear functors correspond to those functor \({\mathcal {C}}^{\text {op} }\rightarrow {\text {Fun}}({\mathcal {A}}^{\text {op} },{{\mathcal {S}}{p}})\) which are exact and which take values in \({\text {Fun}}^{\textrm{ex}}({\mathcal {A}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}({\mathcal {A}}^{\text {op} },{{\mathcal {S}}{p}})\). Since \(g_!\) preserve exact functors by the first part of the lemma and post-composition with \(g_!\) preserves exact functors since \(g_!\) is colimit preserving (being a left adjoint), it now follows that \((\text {id} \times g)_!\) preserves bilinear functors, as desired. \(\square \)
Corollary 1.4.2
The projection
is also a cocartesian fibration, with pushforward along \(f :{\mathcal {C}}\longrightarrow {\mathcal {D}}\) given by  .
.
Let us now discuss the compatibility of restriction and left Kan extensions with the decomposition of the \(\infty \)-category of quadratic functors given by Corollary 1.3.12. We first observe that, given an exact functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\), the associated restriction functor \(f^*:{\text {Fun}}^{\textrm{q}}({\mathcal {D}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) respects the square (34) in its entirety: indeed, taking linear and bilinear parts is compatible with restriction by Remarks 1.1.6 and 1.1.23, and the bottom functor in (34) is also visibly compatible with restriction. We then get that if  is a quadratic functor on \({\mathcal {D}}\) with bilinear part \(\text {B} \), linear part \(\Lambda \) and structure map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\), then
is a quadratic functor on \({\mathcal {D}}\) with bilinear part \(\text {B} \), linear part \(\Lambda \) and structure map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\), then  is the quadratic functor with bilinear part \((f \times f)^*\text {B} \), linear part \(f^*\Lambda \) and structure map
is the quadratic functor with bilinear part \((f \times f)^*\text {B} \), linear part \(f^*\Lambda \) and structure map
We now give a similar statement for left Kan extensions:
Proposition 1.4.3
Let \(f:{\mathcal {C}}\longrightarrow {\mathcal {D}}\) be an exact functor between stable \(\infty \)-categories and let  be a quadratic functor on \({\mathcal {C}}\). Then the natural transformations
be a quadratic functor on \({\mathcal {C}}\). Then the natural transformations

and

are equivalences.
Proof
Let \(i:{\mathcal {C}}\rightarrow {\text {Pro}}({\mathcal {C}})\) and \(j:{\mathcal {D}}\rightarrow {\text {Pro}}({\mathcal {D}})\) be the respective Yoneda embeddings. Arguing as in the proof of Lemma 1.4.1 using that \((j \times j)^*(j \times j)_!\) is equivalent to the identity and that restriction commutes with taking bilinear parts (Remark 1.1.6) we may identify the first map in (38) with the restriction along \(gj \times gj:{\mathcal {D}}\times {\mathcal {D}}\rightarrow {\text {Pro}}({\mathcal {C}}) \times {\text {Pro}}({\mathcal {C}})\) of

We may hence assume without loss of generality that \({\mathcal {D}}={\text {Pro}}({\mathcal {C}})\) and \(f = i\). To prove the latter special case, we see that the component of the transformation (39) at a pair of pro-objects \(\{x_{\alpha }\}_{\alpha \in {\mathcal {I}}},\{y_\beta \}_{\beta \in {\mathcal {J}}}\) in \({\mathcal {C}}\) identifies with the natural map

Now since \({\mathcal {I}}\) and \({\mathcal {J}}\) are cofiltered the projections \({\mathcal {I}}^{\text {op} }\times {\mathcal {J}}^{\text {op} }\rightarrow {\mathcal {I}}^{\text {op} }\) and \({\mathcal {I}}^{\text {op} }\times {\mathcal {J}}^{\text {op} }\rightarrow {\mathcal {J}}^{\text {op} }\) are cofinal and hence we can also rewrite the above map as

and so the desired result follows from the commutation of finite limits and filtered colimits in \({{\mathcal {S}}{p}}\). This also implies that the second map in (38) is an equivalence since the formation of linear parts is obtained by  and left Kan extension commutes with colimits. Finally, the proof that the map
and left Kan extension commutes with colimits. Finally, the proof that the map

is an equivalence is obtained via the same argument by reducing to the case of \({\mathcal {D}}={\text {Pro}}({\mathcal {C}})\) and using that the formation of infinite loop spaces commutes with filtered colimits. \(\square \)
Proposition 1.4.3 tells us that the formation of linear and bilinear parts is compatible with left Kan extensions. The situation is however slightly less simple then with restriction, since the bottom arrow in (34) does not commute with left Kan extensions. This is essentially due to the fact that the formation of symmetric hermitian structures  does not commute with left Kan extension. Instead, given \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) we have a natural map
does not commute with left Kan extension. Instead, given \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) we have a natural map

which is generally not an equivalence. This leads to the following description of the behavior of structure maps under left Kan extensions:
Corollary 1.4.4
Let \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) be an exact functor. If  is a quadratics functor on \({\mathcal {C}}\) with bilinear part \(\text {B} \), linear part \(\Lambda \) and structure map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\) then
is a quadratics functor on \({\mathcal {C}}\) with bilinear part \(\text {B} \), linear part \(\Lambda \) and structure map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\) then  is the quadratic functor on \({\mathcal {D}}\) with bilinear part \(f_!\text {B} \), linear part \(f_!\Lambda \), and structure map the composite
is the quadratic functor on \({\mathcal {D}}\) with bilinear part \(f_!\text {B} \), linear part \(f_!\Lambda \), and structure map the composite
which is the map induced on linear parts by the composite

Remark 1.4.5
In the situation of Corollary 1.4.4 we can also identify the second map in (40) with the Beck–Chevalley transformation on the lax commuting square on the right

which is obtained from the commuting square on the left by replacing the vertical restriction functors \((f \times f)^*\) and \(f^*\) by their left adjoints \((f \times f)_!\) and \(f_!\), respectively.
3 Poincaré objects
In this section we introduce and study another key element of the present paper, the notion of a Poincaré object in a given Poincaré \(\infty \)-category  . As reflected by Examples 1.2.12 and 1.2.13, we think of a Poincaré structure on a given stable \(\infty \)-category \({\mathcal {C}}\) as a way of encoding a particular notion of hermitian form, e.g., quadratic, symmetric, or anti-symmetric forms on modules over rings. In the context of a general Poincaré \(\infty \)-category
. As reflected by Examples 1.2.12 and 1.2.13, we think of a Poincaré structure on a given stable \(\infty \)-category \({\mathcal {C}}\) as a way of encoding a particular notion of hermitian form, e.g., quadratic, symmetric, or anti-symmetric forms on modules over rings. In the context of a general Poincaré \(\infty \)-category  and an object \(x\in {\mathcal {C}}\), we will consequently call points in the underlying infinite loop space
and an object \(x\in {\mathcal {C}}\), we will consequently call points in the underlying infinite loop space  hermitian forms on \(x\). Such a form determines in particular a map \(x\rightarrow \text {D} x\) from \(x\) to its dual, and we say that a form is Poincaré if this map is an equivalence. A Poincaré object is then the abstract analogue of a module equipped with (some flavour of) a hermitian form which is unimodular.
hermitian forms on \(x\). Such a form determines in particular a map \(x\rightarrow \text {D} x\) from \(x\) to its dual, and we say that a form is Poincaré if this map is an equivalence. A Poincaré object is then the abstract analogue of a module equipped with (some flavour of) a hermitian form which is unimodular.
We begin in Sect. 2.1 by introducing the main definitions and establishing a few basic consequences. One of the simplest forms of Poincaré objects are the hyperbolic ones, which are the abstract analogue of the notion of hyperbolic quadratic forms. We discuss these types of Poincaré objects in Sect. 2.2 and see how their formation can be encoded as the action of a suitable Poincaré functor \({\text {Hyp}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\) from a certain Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\) constructed from \({\mathcal {C}}\). The Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\) displays the interesting property that its Poincaré objects correspond to just objects in \({\mathcal {C}}\), and we study it in further depth in Sect. 7. We also exploit this construction in order to prove that Poincaré objects with respect to symmetric Poincaré structures (Definition 1.2.11) correspond to \({{\text {C} }_{\textrm{2}}}\)-fixed objects in \({\mathcal {C}}\) (see Proposition 2.2.11 below). In Sect. 2.3 we study another important kind of Poincaré objects-the metabolic Poincaré objects. These correspond to metabolic forms in the classical sense, that is, forms which admit a Lagrangian. Similarly to the hyperbolic case we show how one can understand metabolic Poincaré objects via Poincaré objects in a certain Poincaré \(\infty \)-category  constructed from
constructed from  . The notion of metabolic Poincaré objects is the main input in the definition of the \({\text {L}}\)-groups of a given Poincaré \(\infty \)-category (see Definition 2.3.11 below). These are in fact the homotopy groups of the \({\text {L}}\)-theory spectrum which was classically defined and studied in the seminal work of Ranicki [58], and transported to the context of Poincaré \(\infty \)-categories by Lurie [45]. A key technique in studying \({\text {L}}\)-groups is Ranicki’s algebraic Thom construction, which we present in Sect. 2.4 in the setting of Poincaré \(\infty \)-categories, and revisit in greater depth in Sect. 7.3.
. The notion of metabolic Poincaré objects is the main input in the definition of the \({\text {L}}\)-groups of a given Poincaré \(\infty \)-category (see Definition 2.3.11 below). These are in fact the homotopy groups of the \({\text {L}}\)-theory spectrum which was classically defined and studied in the seminal work of Ranicki [58], and transported to the context of Poincaré \(\infty \)-categories by Lurie [45]. A key technique in studying \({\text {L}}\)-groups is Ranicki’s algebraic Thom construction, which we present in Sect. 2.4 in the setting of Poincaré \(\infty \)-categories, and revisit in greater depth in Sect. 7.3.
A key role in the present series of papers is played by the Grothendieck-Witt spectrum of a Poincaré \(\infty \)-category, an invariant we will construct using the framework of cobordism categories in Paper [2]. The zero’th homotopy group of the Grothendieck-Witt spectrum, also known as the Grothendieck-Witt group, was classically defined in the context of rings as the group completion of the groupoid of unimodular forms (with respect to orthogonal sum). We will see how to define the Grothendieck-Witt group in the abstract setting of Poincaré \(\infty \)-categories in Sect. 2.5, and extract some of its basic properties. In particular, the Grothendieck-Witt group  of a Poincaré \(\infty \)-category
of a Poincaré \(\infty \)-category  sits in an exact sequence
sits in an exact sequence

between the zero’th \({\text {L}}\)-group of  and the \({{\text {C} }_{\textrm{2}}}\)-orbits of the algebraic \({\text {K}}\)-theory of \({\mathcal {C}}\). This exact sequence is in fact the tail of a long exact sequence issued from a fibre sequence of spectra
and the \({{\text {C} }_{\textrm{2}}}\)-orbits of the algebraic \({\text {K}}\)-theory of \({\mathcal {C}}\). This exact sequence is in fact the tail of a long exact sequence issued from a fibre sequence of spectra

that we will construct in Paper [2]. The existence of the above fibre sequence in this generality is a principal novelty of our approach to hermitian \({\text {K}}\)-theory, and yields a variety of consequences we will exploit in Paper [2], Paper [3] and Paper [4].
3.1 Hermitian and Poincaré objects
In this section we will present the notions of hermitian and Poincaré objects and extract some of their basic properties.
Definition 2.1.1
Let  be a hermitian \(\infty \)-category and \(x\in {\mathcal {C}}\) an object. By a hermitian form on \(x\) we will mean a point q in the space
be a hermitian \(\infty \)-category and \(x\in {\mathcal {C}}\) an object. By a hermitian form on \(x\) we will mean a point q in the space  . We will then refer to the pair \((x,q)\) as a hermitian object in
. We will then refer to the pair \((x,q)\) as a hermitian object in  . Hermitian objects can be organized into an \(\infty \)-category given by the total \(\infty \)-category of the right fibration
. Hermitian objects can be organized into an \(\infty \)-category given by the total \(\infty \)-category of the right fibration

classified by the functor  . We will refer to
. We will refer to  as the \(\infty \)-category of hermitian objects in
as the \(\infty \)-category of hermitian objects in  . We will denote by
. We will denote by  the maximal subgroupoid of
the maximal subgroupoid of  , and refer to it as the space of hermitian objects.
, and refer to it as the space of hermitian objects.
Lemma 2.1.2
The assignment  canonically extends to a functor \(\text {He} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty \), together with a natural transformation to the forgetful functor
canonically extends to a functor \(\text {He} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty \), together with a natural transformation to the forgetful functor  , whose component for a given
, whose component for a given  is the defining right fibration
is the defining right fibration  .
.
Proof
The functor \(\text {Cat} _\infty ^\text {ex} \hookrightarrow \text {Cat} _\infty \), together with the composed natural transformation

where \(\Omega ^{\infty }_*\) denotes post-composition with the infinite loop space functor \(\Omega ^{\infty }:{{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\), together induces under unstraightening a functor
Invoking (the dual of) [23, Corollary A.31], we may identify the Grothendieck construction on the right as
where \({\text {RFib}}({\mathcal {C}})\) denotes the \(\infty \)-category of right fibrations over \({\mathcal {C}}\) and \({\text {RFib}}\subseteq {\text {Ar}}(\text {Cat} _\infty )\) is the full subcategory of the arrow category of \(\text {Cat} _\infty \) consisting of right fibrations. The resulting functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\text {RFib}}\rightarrow {\text {Ar}}(\text {Cat} _\infty )\) then associates to a hermitian \(\infty \)-category  the right fibration
the right fibration  , yielding the desired functoriality. \(\square \)
, yielding the desired functoriality. \(\square \)
We will mostly be interested in hermitian forms which satisfy a unimodularity condition. To formulate it, we need to assume that  is non-degenerate. In that case any hermitian object \((x,q)\) determines a map
is non-degenerate. In that case any hermitian object \((x,q)\) determines a map  as the image of q under
as the image of q under

Definition 2.1.3
We will say that a hermitian form q on \(x\in {\mathcal {C}}\) is Poincaré if the associated map  is an equivalence. In this case we will also say that \((x,q)\) is a Poincaré object. We will denote by
is an equivalence. In this case we will also say that \((x,q)\) is a Poincaré object. We will denote by  the full subgroupoid of
the full subgroupoid of  spanned by the Poincaré objects. We will refer to
spanned by the Poincaré objects. We will refer to  as the space of Poincaré objects in
as the space of Poincaré objects in  .
.
Remark 2.1.4
Similarly to the \(\infty \)-category  one could also form an \(\infty \)-category of Poincaré objects as a full subcategory of
one could also form an \(\infty \)-category of Poincaré objects as a full subcategory of  . This construction is rather poorly behaved formally and will not play any role in this paper. Therefore we will only consider the space
. This construction is rather poorly behaved formally and will not play any role in this paper. Therefore we will only consider the space  of Poincaré objects here.
of Poincaré objects here.
Lemma 2.1.5
If  is a duality preserving hermitian functor between non-degenerate hermitian \(\infty \)-categories then the induced functor
is a duality preserving hermitian functor between non-degenerate hermitian \(\infty \)-categories then the induced functor

preserves Poincaré objects, that is, it maps the full subgroupoid  to the full subgroupoid
to the full subgroupoid  . In particular, the association
. In particular, the association  thus extends to a functor
thus extends to a functor
It is this functor \(\text {Pn} \) that plays a pivotal role in the rest of the paper.
Proof of Lemma 2.1.5
By Remark 1.2.6 the natural transformation  determines a commutative diagram
determines a commutative diagram

In particular, if \((f,\eta )\) is duality preserving then \(\tau _{\eta }\) is an equivalence and hence the top horizontal arrow sends Poincaré forms on \(x\) to Poincaré forms on \(f(x)\). \(\square \)
Remark 2.1.6
The map  factors as
factors as  , see (8). It then follows that for any hermitian form q on \(x\) the corresponding map
, see (8). It then follows that for any hermitian form q on \(x\) the corresponding map  is self-dual, that is, it is invariant under the \({{\text {C} }_{\textrm{2}}}\)-action on
is self-dual, that is, it is invariant under the \({{\text {C} }_{\textrm{2}}}\)-action on  . In particular, by Remark 1.2.3 there is a canonical homotopy rendering the diagram
. In particular, by Remark 1.2.3 there is a canonical homotopy rendering the diagram

commutative.
Remark 2.1.7
Every Poincaré form q on \(x\) gives rise to a form \({\hat{q}}\) on  via the inverse of the induced map
via the inverse of the induced map  . By construction
. By construction  is an equivalence in
is an equivalence in  and from Remark 2.1.6 we find
and from Remark 2.1.6 we find  . In particular, \(q_\sharp ^{-1} \simeq \text {ev} _{x}^{-1} \circ {\hat{q}}_{\sharp }\).
. In particular, \(q_\sharp ^{-1} \simeq \text {ev} _{x}^{-1} \circ {\hat{q}}_{\sharp }\).
Example 2.1.8
Let M be a compact oriented topological n-manifold with boundary \(\partial M \subseteq M\) and fundamental class \([M]\in H_n(M,\partial M)\). Then the fundamental class together with the cup-product induces a \((-n)\)-shifted hermitian form

sending \((\varphi ,\psi )\) to \((\varphi \cup \psi )([M])\). We note that we are working with homological grading conventions, so that, for example, the complex \(C^*(M,\partial M)\) is concentrated in non-positive degrees with trivial homology outside the range \([-n,0]\). The associated map \(q^{[M]}_{\sharp }\) from \(C^*(M,\partial M)\) to its dual can then be identified with the canonical map
which is an equivalence if and only if \(C^*(\partial M) \simeq 0\), i.e., if and only if \(\partial M\) is empty. In particular, the hermitian form \(q^{[M]}\) is Poincaré if and only if M is closed.
3.2 Hyperbolic and symmetric Poincaré objects
Given a Poincaré \(\infty \)-category  , the space of Poincaré objects
, the space of Poincaré objects  is related to the underlying space of objects \(\iota {\mathcal {C}}\) in two different ways. First, one can of course take a Poincaré object and forget its Poincaré form, yielding a forgetful map
is related to the underlying space of objects \(\iota {\mathcal {C}}\) in two different ways. First, one can of course take a Poincaré object and forget its Poincaré form, yielding a forgetful map  . There is however also an interesting construction in the other direction, which takes an object \(x\in {\mathcal {C}}\) and associates to it the object \(x\oplus \text {D} x\) endowed with its hyperbolic Poincaré form, leading to a map
. There is however also an interesting construction in the other direction, which takes an object \(x\in {\mathcal {C}}\) and associates to it the object \(x\oplus \text {D} x\) endowed with its hyperbolic Poincaré form, leading to a map  . Though these constructions seem different in nature, they are in fact closely related, and will both occupy our attention in this present section. A common feature they both share is equivariance with respect to the \({{\text {C} }_{\textrm{2}}}\)-action on \(\iota {\mathcal {C}}\) induced by the duality. In the final part of this section we will show that when the Poincaré structure is symmetric the resulting map
. Though these constructions seem different in nature, they are in fact closely related, and will both occupy our attention in this present section. A common feature they both share is equivariance with respect to the \({{\text {C} }_{\textrm{2}}}\)-action on \(\iota {\mathcal {C}}\) induced by the duality. In the final part of this section we will show that when the Poincaré structure is symmetric the resulting map  is an equivalence. We will further study the relationship between the hyperbolic and forgetful functors in Sect. 7.4 in the setting of \({{\text {C} }_{\textrm{2}}}\)-categories.
is an equivalence. We will further study the relationship between the hyperbolic and forgetful functors in Sect. 7.4 in the setting of \({{\text {C} }_{\textrm{2}}}\)-categories.
Definition 2.2.1
Let  be a Poincaré \(\infty \)-category with duality \(\text {D} \). Given an object \(x\in {\mathcal {C}}\) we will denote by
be a Poincaré \(\infty \)-category with duality \(\text {D} \). Given an object \(x\in {\mathcal {C}}\) we will denote by  the Poincaré object whose underlying object is \(x\oplus \text {D} x\) and whose Poincaré form is given by the image of the identity under
the Poincaré object whose underlying object is \(x\oplus \text {D} x\) and whose Poincaré form is given by the image of the identity under

Unwinding the definitions one easily checks that this indeed defines a Poincaré object. We will refer to \(\text {hyp} (x)\) as the hyperbolic Poincaré object on \(x\).
To understand systematically the role played by hyperbolic Poincaré objects in \({\mathcal {C}}\) it is most useful to describe them as Poincaré objects in another Poincaré \(\infty \)-category built from \({\mathcal {C}}\).
Definition 2.2.2
Let \({\mathcal {C}}\) be a stable \(\infty \)-category. We define its hyperbolic category \({\text {Hyp}}({\mathcal {C}})\) to be the hermitian \(\infty \)-category whose underlying stable \(\infty \)-category is \({\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\), equipped with the hermitian structure  .
.
Unwinding the definitions, we see that the symmetric bilinear functor associated to the hyperbolic hermitian structure is given by
and its linear approximation is trivial. In particular, the bilinear functor \(\text {B} _{\text {hyp} }\) is perfect with associated duality \( \text {D} _{\text {hyp} }(x,y) = (y,x) \) and consequently \({\text {Hyp}}({\mathcal {C}})\) is always a Poincaré \(\infty \)-category.
Remark 2.2.3
By construction, the quadratic functor  is obtained by diagonally restricting the bilinear functor \(((x,y),(x',y')) \mapsto {\text {hom}}_{{\mathcal {C}}}(x,y')\). It then follows that the canonical maps
is obtained by diagonally restricting the bilinear functor \(((x,y),(x',y')) \mapsto {\text {hom}}_{{\mathcal {C}}}(x,y')\). It then follows that the canonical maps

are given by the collapse and diagonal maps
and  coincides with both the quadratic and symmetric Poincaré structure associated to the symmetric bilinear functor \(\text {B} _{\text {hyp} }\).
coincides with both the quadratic and symmetric Poincaré structure associated to the symmetric bilinear functor \(\text {B} _{\text {hyp} }\).
Remark 2.2.4
The Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\) is shift-invariant: for every \(n \in {\mathbb {Z}}\) the functor \(\Sigma ^n\times \text {id} :{\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) refines to an equivalence  , see Definition 1.2.16.
, see Definition 1.2.16.
For  a Poincaré \(\infty \)-category with duality \(\text {D} \), the associated hyperbolic category \({\text {Hyp}}({\mathcal {C}})\) relates to \({\mathcal {C}}\) via Poincaré functors
a Poincaré \(\infty \)-category with duality \(\text {D} \), the associated hyperbolic category \({\text {Hyp}}({\mathcal {C}})\) relates to \({\mathcal {C}}\) via Poincaré functors

in both directions. Here the functor on the left in (42) is given by the exact functor \((x,y) \mapsto x\oplus \text {D} y\), promoted to a hermitian functor via the natural transformation

while the second functor is given by the exact functor \(x\mapsto (x,\text {D} x)\), promoted to a hermitian functor via the natural transformation

By definition, the \(\infty \)-category \(\text {He} ({\text {Hyp}}({\mathcal {C}}))\) sits in a right fibration
classified by the functor \({\mathcal {C}}^{\text {op} }\oplus {\mathcal {C}}\rightarrow {\mathcal {S}}\) sending \((x,y)\) to the mapping space \({\text {Map}}_{{\mathcal {C}}}(x,y)\). But this functor is already known to classify the right fibration
where \({\text {TwAr}}({\mathcal {C}})\) is the twisted arrow category of \({\mathcal {C}}\) (see, e.g., [47, §5.2.1]), and we consequently obtain an equivalence
over \({\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\). In particular, hermitian objects in \({\text {Hyp}}({\mathcal {C}})\) are simply given by arrows \(\alpha :x\rightarrow y\) in \({\mathcal {C}}\), while morphisms between hermitian objects correspond to diagrams in \({\mathcal {C}}\) of the form

Proposition 2.2.5
For a stable \(\infty \)-category \({\mathcal {C}}\), the composite
is an equivalence of spaces. Here the first map is induced by the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) and the second is given by the projection onto the first factor. Under this equivalence, the natural map \(\text {Pn} ({\text {Hyp}}({\mathcal {C}})) \rightarrow \text {He} ({\text {Hyp}}({\mathcal {C}}))\) corresponds to the map
Proof
An object \([\alpha :x\rightarrow y] \in {\text {TwAr}}({\mathcal {C}})\) viewed as hermitian object \((x,y,\alpha )\) in \({\text {Hyp}}({\mathcal {C}})\), has as associated self dual map \((x,y) \rightarrow \text {D} (x,y) = (y,x)\) the map \(\alpha \) on both factors (viewed as either a map \(x\rightarrow y\) in \({\mathcal {C}}\) or a map \(y\rightarrow x\) in \({\mathcal {C}}^{\text {op} }\)). Consequently, the hermitian form \((x,y,\alpha )\) is Poincaré if and only if \(\alpha \) is an equivalence. Together with the fact that right fibrations detect equivalences we obtain that
We finish the proof by observing that the projection \({\text {TwAr}}(\iota {\mathcal {C}}) \rightarrow \iota {\mathcal {C}}\) is an equivalence since \(\iota {\mathcal {C}}\) is an \(\infty \)-groupoid. \(\square \)
Remark 2.2.6
We will show in Sect. 7.4 that the association \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) organizes into a functor \(\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) which is both left and right adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \), with unit and counit given by (42), see Corollary 7.2.21. Together with the corepresentability of \(\text {Pn} \) (Proposition 4.1.3) this will give another proof of Proposition 2.2.5.
In light of Proposition 2.2.5 the Poincaré functors (42) now induce a pair of maps

Unwinding the definitions we see that the functor on the left sends an object \(x\) to the associated hyperbolic Poincaré object \(\text {hyp} (x)\), while, the functor on the right sends a Poincaré object \((x,q)\) to the underlying object \(x\). A key feature of both these maps is that they are \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the \({{\text {C} }_{\textrm{2}}}\)-action on \(\iota {\mathcal {C}}\) induced by the duality of  and the trivial action on
and the trivial action on  . To make this idea precise we will first construct this action on the level of the Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\).
. To make this idea precise we will first construct this action on the level of the Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\).
Construction 2.2.7
Let  be a Poincaré \(\infty \)-category with associated duality
be a Poincaré \(\infty \)-category with associated duality  . We construct a \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}}) \in \text {Cat} ^{\textrm{p}}_\infty \) as follows. To begin, consider the equivalence of stable \(\infty \)-categories
. We construct a \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}}) \in \text {Cat} ^{\textrm{p}}_\infty \) as follows. To begin, consider the equivalence of stable \(\infty \)-categories
Transporting the flip \({{\text {C} }_{\textrm{2}}}\)-action on \({\mathcal {C}}\times {\mathcal {C}}\) to \({\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) we thus obtain a \({{\text {C} }_{\textrm{2}}}\)-action on \({\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\), given informally by the formula \((x,y) \mapsto (\text {D} y,\text {D} ^{\text {op} }x)\). We wish to promote this action to a \({{\text {C} }_{\textrm{2}}}\)-action on the Poincaré \(\infty \)-category \({\text {Hyp}}({\mathcal {C}})\). Since every equivalence in \(\text {Cat} ^{\textrm{h}}_\infty \) is a Poincaré functor we may equivalently construct a \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}})\) as a hermitian \(\infty \)-category. By the construction of \(\text {Cat} ^{\textrm{h}}_\infty \) as the unstraightening of the functor \({\mathcal {C}}\mapsto {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\), lifting the above \({{\text {C} }_{\textrm{2}}}\)-action on \({\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) to \({\text {Hyp}}({\mathcal {C}})\) is equivalent to giving a \({{\text {C} }_{\textrm{2}}}\)-fixed point structure on  with respect to the induced \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}}^{\text {op} })\). Since the relevant \({{\text {C} }_{\textrm{2}}}\)-action was transported from the flip action on \({\mathcal {C}}\times {\mathcal {C}}\) via the equivalence \((\text {id} ,\text {D} ^{\text {op} })\) we may equivalently construct a \({{\text {C} }_{\textrm{2}}}\)-fixed point structure on the quadratic functor
with respect to the induced \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}}^{\text {op} })\). Since the relevant \({{\text {C} }_{\textrm{2}}}\)-action was transported from the flip action on \({\mathcal {C}}\times {\mathcal {C}}\) via the equivalence \((\text {id} ,\text {D} ^{\text {op} })\) we may equivalently construct a \({{\text {C} }_{\textrm{2}}}\)-fixed point structure on the quadratic functor  . The latter is readily discovered to be
. The latter is readily discovered to be

and so we need to construct a \({{\text {C} }_{\textrm{2}}}\)-fixed point structure on  , considered as an object of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}})\). But
, considered as an object of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}})\). But  lies in the full subcategory \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}})\), where it is equipped with a \({{\text {C} }_{\textrm{2}}}\)-fixed structure by virtue of Lemma 1.1.9.
lies in the full subcategory \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \subseteq {\text {Fun}}^{\textrm{q}}({\mathcal {C}}\times {\mathcal {C}})\), where it is equipped with a \({{\text {C} }_{\textrm{2}}}\)-fixed structure by virtue of Lemma 1.1.9.
Remark 2.2.8
The \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}})\) constructed in 2.2.7 induces a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {He} ({\text {Hyp}}({\mathcal {C}})) \simeq {\text {TwAr}}({\mathcal {C}})\). Unwinding the definitions, this action sends an arrow \([x\rightarrow y] \in {\text {TwAr}}({\mathcal {C}})\) to the dual arrow  . Similarly, this \({{\text {C} }_{\textrm{2}}}\)-action determines an action on \(\text {Pn} ({\text {Hyp}}({\mathcal {C}}))\). Under the identification \({\text {Pn}}({\text {Hyp}}({\mathcal {C}})) \simeq \iota {\mathcal {C}}\) of Proposition 2.2.5 this action can be written simply by
. Similarly, this \({{\text {C} }_{\textrm{2}}}\)-action determines an action on \(\text {Pn} ({\text {Hyp}}({\mathcal {C}}))\). Under the identification \({\text {Pn}}({\text {Hyp}}({\mathcal {C}})) \simeq \iota {\mathcal {C}}\) of Proposition 2.2.5 this action can be written simply by  . Here we point out that since \(\iota {\mathcal {C}}\) is an \(\infty \)-groupoid it is canonically equivalent to its opposite via an equivalence which sends every arrow to its inverse. Hence the contravariant equivalence \(\text {D} \) becomes a self-equivalence on the level of \(\iota {\mathcal {C}}\). We may also state this as follows: the \({{\text {C} }_{\textrm{2}}}\)-action \((-)^{\text {op} }:\text {Cat} _\infty \rightarrow \text {Cat} _\infty \) admits a canonical trivialization along the full subcategory \({\mathcal {S}}\subseteq \text {Cat} _\infty \) (in fact, the space of self-equivalences of \({\mathcal {S}}\) is contractible by its universal property [43, Theorem 5.1.5.6]), yielding an identification \({\mathcal {S}}^{{{\text {hC} }_{\textrm{2}}}} \simeq {\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},{\mathcal {S}})\). The duality
. Here we point out that since \(\iota {\mathcal {C}}\) is an \(\infty \)-groupoid it is canonically equivalent to its opposite via an equivalence which sends every arrow to its inverse. Hence the contravariant equivalence \(\text {D} \) becomes a self-equivalence on the level of \(\iota {\mathcal {C}}\). We may also state this as follows: the \({{\text {C} }_{\textrm{2}}}\)-action \((-)^{\text {op} }:\text {Cat} _\infty \rightarrow \text {Cat} _\infty \) admits a canonical trivialization along the full subcategory \({\mathcal {S}}\subseteq \text {Cat} _\infty \) (in fact, the space of self-equivalences of \({\mathcal {S}}\) is contractible by its universal property [43, Theorem 5.1.5.6]), yielding an identification \({\mathcal {S}}^{{{\text {hC} }_{\textrm{2}}}} \simeq {\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},{\mathcal {S}})\). The duality  then induces a duality on \(\iota {\mathcal {C}}\) and hence a \({{\text {C} }_{\textrm{2}}}\)-action.
then induces a duality on \(\iota {\mathcal {C}}\) and hence a \({{\text {C} }_{\textrm{2}}}\)-action.
Lemma 2.2.9
Let  be a Poincaré \(\infty \)-category with duality
be a Poincaré \(\infty \)-category with duality  . Then the functors
. Then the functors

both admit a distinguished refinement to \({{\text {C} }_{\textrm{2}}}\)-equivariant maps with respect to the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}})\) constructed in 2.2.7 and the trivial action on  .
.
Corollary 2.2.10
The induced maps on Poincaré objects (which we denote by the same name)

are \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the duality induced action on \(\iota {\mathcal {C}}\) and the trivial action on  .
.
Proof of Lemma 2.2.9
We first construct the \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the underlying exact functors. For this, note that since the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}{(\mathcal {C})}\) was constructed by transporting the flip action along the equivalence \(\text {id} \times \text {D} ^{\text {op} }:{\mathcal {C}}\times {\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) and \(\text {D} ^{\text {op} }\text {D} \simeq \text {id} \) it will suffice to to promote the resulting exact functors
to \({{\text {C} }_{\textrm{2}}}\)-equivariant exact functors. Indeed, these are just the diagonal and fold map of \({\mathcal {C}}\) as an object in the semi-additive \(\infty \)-category \(\text {Cat} _\infty ^\text {ex} \), which are both canonically \({{\text {C} }_{\textrm{2}}}\)-equivariant. To lift the resulting \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on \((\text {id} ,\text {D} ^{\text {op} }):{\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) to a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the Poincaré functor \(\text {fgt} \) we need to promote the associated natural transformation

to a \({{\text {C} }_{\textrm{2}}}\)-equivariant map in \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\). Transporting the problem again along the equivalence \(\text {id} \times \text {D} ^{\text {op} }\) we need to put a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the natural transformation

where \(\Delta :{\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}\) is the diagonal. Indeed, this is established in Lemma 1.1.10. By the same argument we see that in order to obtain the desired \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on \(\text {hyp} \) it will suffice to put a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the natural transformation

where \(\nabla :{\mathcal {C}}\oplus {\mathcal {C}}\rightarrow {\mathcal {C}}\) is the collapse functor \((x,y) \mapsto x\oplus y\). Using the adjunction between restriction and left Kan extension we may instead put a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on the adjoint transformation

where we used that left Kan extension along \(\nabla ^{\text {op} }\) is obtained by restriction along its right adjoint \(\Delta ^{\text {op} }:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\). The desired \({{\text {C} }_{\textrm{2}}}\)-equivariant structure was again established in Lemma 1.1.10. \(\square \)
Let us now focus on the Poincaré functor  . Upon taking hermitian and Poincaré objects (and using Proposition 2.2.5) this Poincaré functor induces a commutative diagram
. Upon taking hermitian and Poincaré objects (and using Proposition 2.2.5) this Poincaré functor induces a commutative diagram

in which the vertical maps inherit from \(\text {fgt} \) a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure with respect to the trivial action on their domains and the \({{\text {C} }_{\textrm{2}}}\)-action induced by the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Hyp}}({\mathcal {C}})\) on the target. Here the left square consists only of spaces and the horizontal maps are (up to equivalence) inclusions of components: for the upper left map these are the components of  consisting of Poincaré objects and for the lower left map these are the components of \(\iota {\text {TwAr}}({\mathcal {C}})\) consisting of those arrows \([x\rightarrow y]\) which are equivalences. Since by definition a hermitian object \((x,q)\) is Poincaré if and only if \(q_{\sharp }\) is an equivalence we see in particular that the left square is cartesian. Now by the \({{\text {C} }_{\textrm{2}}}\)-equivariance above the external rectangle in (44) induces a commutative square
consisting of Poincaré objects and for the lower left map these are the components of \(\iota {\text {TwAr}}({\mathcal {C}})\) consisting of those arrows \([x\rightarrow y]\) which are equivalences. Since by definition a hermitian object \((x,q)\) is Poincaré if and only if \(q_{\sharp }\) is an equivalence we see in particular that the left square is cartesian. Now by the \({{\text {C} }_{\textrm{2}}}\)-equivariance above the external rectangle in (44) induces a commutative square

Proposition 2.2.11
If  is a symmetric Poincaré structure of some symmetric bilinear form \(\text {B} \) then the vertical maps in (45) are equivalences.
is a symmetric Poincaré structure of some symmetric bilinear form \(\text {B} \) then the vertical maps in (45) are equivalences.
Proof
Consider the extended diagram

in which the external rectangle of the left column is cartesian as observed above. In addition, since the fibres of the map \({\text {TwAr}}(\iota {\mathcal {C}}) \rightarrow \iota {\text {TwAr}}({\mathcal {C}})\) are \((-1)\)-truncated the bottom left square is cartesian as well, and hence the top left square is cartesian. Similarly, since the map from the homotopy fixed point is conservative, the bottom central square and therefore the top central square, are cartesian.
Now the map \({\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) is equivalent as a \({{\text {C} }_{\textrm{2}}}\)-equivariant arrow to the diagonal inclusion \({\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}\), which exhibits the \({{\text {C} }_{\textrm{2}}}\)-object \({\mathcal {C}}\times {\mathcal {C}}\) as coinduced from \({\mathcal {C}}\). This implies in particular that the top right vertical map in (46) is an equivalence. Thus to conclude it suffices to show that the top right square is cartesian.
Now consider the right most column in (46). Since homotopy fixed points commute with fibre products the fibres of the middle horizontal map over a fixed object in \({\mathcal {C}}\) is the homotopy fixed points of the corresponding fibre of the bottom horizontal map in the same column. We hence obtain that the map on horizontal fibre in the top right square can be identified with the induced map

which is an equivalence by the assumption that  for some \(\text {B} \). It then follows that the second and third vertical arrows in the top of (46) are equivalences. The left most vertical map in that row is consequently an equivalence as well since the top left square is cartesian. \(\square \)
for some \(\text {B} \). It then follows that the second and third vertical arrows in the top of (46) are equivalences. The left most vertical map in that row is consequently an equivalence as well since the top left square is cartesian. \(\square \)
3.3 Metabolic objects and \({\text {L}}\)-groups
In this section we will introduce the notion of a metabolic Poincaré object and use it to define the \({\text {L}}\)-groups of a Poincaré \(\infty \)-category. In the context of modules over rings these were first defined by Wall and Ranicki in their seminal work on surgery theory [69], and were transported to the setting of Poincaré \(\infty \)-categories in [45]. We will then develop an analogue of Ranicki’s algebraic Thom construction [57, Proposition 3.4] in this context. This construction will play an important role in the framework of algebraic surgery which we will set up in Paper [2].
Definition 2.3.1
Let  be a Poincaré \(\infty \)-category and \((x,q)\) a Poincaré object. By an isotropic object over \(x\) we will mean a pair \((f:w\rightarrow x,\eta )\) where \(f:w\rightarrow x\) is a map in \({\mathcal {C}}\) and
be a Poincaré \(\infty \)-category and \((x,q)\) a Poincaré object. By an isotropic object over \(x\) we will mean a pair \((f:w\rightarrow x,\eta )\) where \(f:w\rightarrow x\) is a map in \({\mathcal {C}}\) and  is a null-homotopy of the restriction of q to \(w\). We will say that an isotropic object \((w\rightarrow x,\eta )\) is a Lagrangian if the null-homotopy of \(w\rightarrow x\simeq \text {D} x\rightarrow \text {D} w\) given by the image of \(\eta \) in
is a null-homotopy of the restriction of q to \(w\). We will say that an isotropic object \((w\rightarrow x,\eta )\) is a Lagrangian if the null-homotopy of \(w\rightarrow x\simeq \text {D} x\rightarrow \text {D} w\) given by the image of \(\eta \) in  exhibits the sequence
exhibits the sequence
as exact. We will say that \((x,q)\) is metabolic if it admits a Lagrangian.
Example 2.3.2
If  is a Poincaré \(\infty \)-category and \(x\in {\mathcal {C}}\) an object then the associated hyperbolic Poincaré object \(\text {hyp} (x)\) is metabolic with Lagrangian given by the component inclusion \(x\rightarrow x\oplus \text {D} x\).
is a Poincaré \(\infty \)-category and \(x\in {\mathcal {C}}\) an object then the associated hyperbolic Poincaré object \(\text {hyp} (x)\) is metabolic with Lagrangian given by the component inclusion \(x\rightarrow x\oplus \text {D} x\).
Example 2.3.3
In \({{\mathcal {D}}}^\text {p} ({\mathbb {F}}_2)\), let V be a 2-dimensional \({\mathbb {F}}_2\)-vector space with basis v, u equipped with the symmetric bilinear form \(b:V \otimes _{{\mathbb {F}}_2} V \rightarrow {\mathbb {F}}_2\) given by \(b(v,v)=0\) and \(b(v,u)=b(u,v)=b(u,u)=1\). Then the Poincaré object  is metabolic with Lagrangian \(L = \left<v\right> \hookrightarrow V\) but (V, b) is not isomorphic to \(\text {hyp} (U)\) for any \(U \in {{\mathcal {D}}}^\text {p} ({\mathbb {F}}_2)\). Indeed, since any object in \({{\mathcal {D}}}^\text {p} ({\mathbb {F}}_2)\) breaks as a direct sum of shifts of \({\mathbb {F}}_2\) the only possible candidate is \(U = {\mathbb {F}}_2\), but (V, b) is not isomorphic to \(\text {hyp} ({\mathbb {F}}_2)\). In particular, not every metabolic object is hyperbolic.
is metabolic with Lagrangian \(L = \left<v\right> \hookrightarrow V\) but (V, b) is not isomorphic to \(\text {hyp} (U)\) for any \(U \in {{\mathcal {D}}}^\text {p} ({\mathbb {F}}_2)\). Indeed, since any object in \({{\mathcal {D}}}^\text {p} ({\mathbb {F}}_2)\) breaks as a direct sum of shifts of \({\mathbb {F}}_2\) the only possible candidate is \(U = {\mathbb {F}}_2\), but (V, b) is not isomorphic to \(\text {hyp} ({\mathbb {F}}_2)\). In particular, not every metabolic object is hyperbolic.
Example 2.3.4
Let M be a closed oriented n-manifold with fundamental class \([M] \in H_n(M;{\mathbb {Z}})\), so that we have a symmetric Poincaré form  as in Example 2.1.8. If W is now an oriented \((n+1)\)-manifold with boundary M then the relative fundamental class \([W] \in H_{n+1}(W,M)\) can be used to promote the map
as in Example 2.1.8. If W is now an oriented \((n+1)\)-manifold with boundary M then the relative fundamental class \([W] \in H_{n+1}(W,M)\) can be used to promote the map
to a Lagrangian of \((C^*(M),q^{[M]})\). This can be considered as an algebraic reflection of the fact that W exhibits M as a boundary. In particular, if \((C^*(M),q^{[M]})\) is not metabolic then M is not the boundary of any oriented \((n+1)\)-manifold, that is, M is not (oriented-ly) null-cobordant.
As in the case of hyperbolic Poincaré objects, it would be desirable to have a description of metabolic Poincaré objects in terms of Poincaré objects in another Poincaré \(\infty \)-category constructed from  .
.
Definition 2.3.5
For a Poincaré \(\infty \)-category  , we define the associated metabolic category
, we define the associated metabolic category  to be the hermitian \(\infty \)-category with underlying \(\infty \)-category \({\text {Ar}}({\mathcal {C}}) = {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) and hermitian structure
to be the hermitian \(\infty \)-category with underlying \(\infty \)-category \({\text {Ar}}({\mathcal {C}}) = {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) and hermitian structure

whose value on arrows is  .
.
Unwinding the definitions we see that the underlying symmetric bilinear functor of  is
is

From this formula we see that if  is perfect with duality \(\text {D} \) then \(\text {B} _{\text {met} }\) is perfect with duality
is perfect with duality \(\text {D} \) then \(\text {B} _{\text {met} }\) is perfect with duality
so that  is Poincaré whenever
is Poincaré whenever  is so. We note that by definition a hermitian form on \([f:w\rightarrow x]\) with respect to
is so. We note that by definition a hermitian form on \([f:w\rightarrow x]\) with respect to  consists of a form
consists of a form  together with a null-homotopy \(\eta \) of
together with a null-homotopy \(\eta \) of  . Such a
. Such a  -form \((q,\eta )\) is Poincaré if and only if the associated self dual map encoded by the horizontal maps of the square
-form \((q,\eta )\) is Poincaré if and only if the associated self dual map encoded by the horizontal maps of the square

is an equivalence. Here \(q_{\sharp }\) is the self dual map determined by q and we denoted by \(\eta _{\sharp }\) the map corresponding to the null-homotopy of the composed map \(w\rightarrow x\rightarrow \text {D} x\rightarrow \text {D} w\) determined by the image of \(\eta \) in  . We then see that (47) constitutes an equivalence between the vertical arrows if and only if \(q_{\sharp }:x\rightarrow \text {D} x\) is an equivalence and the resulting sequence \(w\rightarrow x\simeq \text {D} x\rightarrow \text {D} w\) is exact, that is, if \((f:w\rightarrow x,\eta )\) is a Lagrangian. We may thus conclude that Poincaré objects in
. We then see that (47) constitutes an equivalence between the vertical arrows if and only if \(q_{\sharp }:x\rightarrow \text {D} x\) is an equivalence and the resulting sequence \(w\rightarrow x\simeq \text {D} x\rightarrow \text {D} w\) is exact, that is, if \((f:w\rightarrow x,\eta )\) is a Lagrangian. We may thus conclude that Poincaré objects in  correspond to metabolic objects in
correspond to metabolic objects in  , or, more precisely, to Poincaré objects in \({\mathcal {C}}\) equipped with a specified Lagrangian.
, or, more precisely, to Poincaré objects in \({\mathcal {C}}\) equipped with a specified Lagrangian.
Definition 2.3.6
For a Poincaré \(\infty \)-category  we will denote by
we will denote by

the space of Poincaré objects in  , which we consider as above as the space of Poincaré objects equipped with a specified Lagrangian.
, which we consider as above as the space of Poincaré objects equipped with a specified Lagrangian.
Lemma 2.3.7
The maps

given respectively by \(i(x)=[x\rightarrow 0]\) and \(\text {met} ([w\rightarrow x])=x\) extend to morphisms in \(\text {Cat} ^{\textrm{p}}_\infty \).
Proof
For the first we observe that the map i is fully faithful, that  and that the image of i is closed under the duality in
and that the image of i is closed under the duality in  , so the result follows from Observation 1.2.19. For the second map we take the hermitian structure associated to the canonical map
, so the result follows from Observation 1.2.19. For the second map we take the hermitian structure associated to the canonical map

By the explicit description of the duality above we see that the resulting hermitian functor is Poincaré. \(\square \)
Unwinding the definitions we see that the map

induced by the right hand Poincaré functor in (48) corresponds to the forgetful map which takes a Poincaré object equipped with a Lagrangian and forgets the Lagrangian. In particular, a Poincaré object in  is metabolic if and only if it is in the image of (49)
is metabolic if and only if it is in the image of (49)
As observed earlier, every hyperbolic form is metabolic, but not every metabolic object is equivalent to the associated hyperbolic form on its Lagrangian. This relation between metabolic and hyperbolic objects is best expressed by relating the Poincaré \(\infty \)-categories  and \({\text {Hyp}}({\mathcal {C}})\) via suitable Poincaré functors.
and \({\text {Hyp}}({\mathcal {C}})\) via suitable Poincaré functors.
Construction 2.3.8
Let  be a Poincaré \(\infty \)-category. We define Poincaré functors
be a Poincaré \(\infty \)-category. We define Poincaré functors

and

via the indicated formulas on the level of the underlying exact functors, and with hermitian structures as follows. For the two functors on the left hand side the hermitian structure is obtained via the identification

whose target visibly projects to both  and
and  . For the functors on the right hand side the hermitian structure is given by the natural transformation
. For the functors on the right hand side the hermitian structure is given by the natural transformation

where we recognize the target as naturally equivalent to both \({\text {lag}}^*\text {B} _{\text {hyp} }\) and \(\text {dlag} ^*\text {B} _{\text {hyp} }\). The preservation of the duality by these hermitian functors is visible by the explicit descriptions of \(\text {D} _{\text {met} }\) and \(\text {D} _{\text {hyp} }\) above. We also note that the composites

and

are naturally equivalent to the identity, and so exhibit \({\text {Hyp}}({\mathcal {C}})\) as a retract of  in \(\text {Cat} ^{\textrm{p}}_\infty \).
in \(\text {Cat} ^{\textrm{p}}_\infty \).
Remark 2.3.9
The Poincaré functors \({\text {lag}},\text {dlag} :{\text {Met}}({\mathcal {C}}) \rightarrow {\text {Hyp}}({\mathcal {C}})\) are closely related: they differ by post-composition with the Poincaré involution \({\text {Hyp}}({\mathcal {C}}) \xrightarrow {\simeq } {\text {Hyp}}({\mathcal {C}})\) of Construction 2.2.7. Similarly, the Poincaré functors \(\text {can} ,\text {dcan} :{\text {Hyp}}({\mathcal {C}}) \rightarrow {\text {Met}}({\mathcal {C}})\) differ by pre-composition with this involution. It then follows from Lemma 2.2.9 that the composite

is independent of whether the first functor is \({\text {lag}}\) or \(\text {dlag} \). The action of this composed functor on \(\text {Pn} (-)\) sends a Poincaré object \((x,q)\) equipped with a Lagrangian \(w\rightarrow x\) to the associated hyperbolic object \(\text {hyp} (w) \simeq \text {hyp} (\text {D} w)\). The difference between a metabolic Poincaré object and its hyperbolic counterpart plays a key role in the definition of the Grothendieck-Witt group, see Sect. 2.5 below. On the other hand, we also observe that the composite Poincaré functor

coincides with the functor \(\text {hyp} \) of (42), independently of whether the first functor is \(\text {can} \) or \(\text {dcan} \). On the level of Poincaré objects we may interpret this as the observation that a hyperbolic Poincaré object \(\text {hyp} (w)\) can be considered as a metabolic object in two canonical ways: one via the Lagrangian \(w\rightarrow w\oplus \text {D} w\) and one via the Lagrangian \(\text {D} w\rightarrow w\oplus \text {D} w\).
A fundamental invariant of Poincaré \(\infty \)-categories is their \({\text {L}}\)-groups. To define them, we first observe that the set  of equivalence classes of Poincaré objects carries a natural commutative monoid structure, with sum given by
of equivalence classes of Poincaré objects carries a natural commutative monoid structure, with sum given by

for  , where
, where

corresponds to the tuple \((q,q',0)\). Though this commutative monoid is generally not a group, every element is invertible up to the class of a metabolic object. More precisely, we have the following:
Lemma 2.3.10
Let  be a Poincaré \(\infty \)-category. Then the cokernel of the map
be a Poincaré \(\infty \)-category. Then the cokernel of the map  in the category of commutative monoids is a group. Explicitly, the inverse to \([x,q]\) is given by \([x,-q]\).
in the category of commutative monoids is a group. Explicitly, the inverse to \([x,q]\) is given by \([x,-q]\).
Proof
This follows from the fact that  is metabolic with Lagrangian given by the diagonal inclusion \(x \rightarrow x \oplus x\) with the canonical null-homotopy \(q+ (-q) \sim 0\). \(\square \)
is metabolic with Lagrangian given by the diagonal inclusion \(x \rightarrow x \oplus x\) with the canonical null-homotopy \(q+ (-q) \sim 0\). \(\square \)
Definition 2.3.11
Let  be a Poincaré \(\infty \)-category. For \(n \in {\mathbb {Z}}\) we define the n’th \({\text {L}}\)-group of
be a Poincaré \(\infty \)-category. For \(n \in {\mathbb {Z}}\) we define the n’th \({\text {L}}\)-group of  by
by

which is an abelian group by Lemma 2.3.10.
Remark 2.3.12
A standard description of cokernels in commutative monoids gives that  map to the same class in
map to the same class in  if and only if there exists metabolic Poincaré objects \([y,p],[y',p']\) such that \([x,q] + [y,p] = [x',q'] + [y',p']\) in
if and only if there exists metabolic Poincaré objects \([y,p],[y',p']\) such that \([x,q] + [y,p] = [x',q'] + [y',p']\) in  . In particular, \([x,q]\) maps to zero in
. In particular, \([x,q]\) maps to zero in  if and only if it is stably metabolic, that is \([x,q] + [y,p]\) is metabolic for some metabolic Poincaré object \([y,p]\). In the setting of Poincaré \(\infty \)-categories this property is actually equivalent to \([x,q]\) itself being metabolic. Indeed, suppose that \(z\rightarrow y\) is a Lagrangian for \(p\) and \(z'\rightarrow x\oplus y\) is a Lagrangian for
if and only if it is stably metabolic, that is \([x,q] + [y,p]\) is metabolic for some metabolic Poincaré object \([y,p]\). In the setting of Poincaré \(\infty \)-categories this property is actually equivalent to \([x,q]\) itself being metabolic. Indeed, suppose that \(z\rightarrow y\) is a Lagrangian for \(p\) and \(z'\rightarrow x\oplus y\) is a Lagrangian for  . Setting \(w= [x\oplus z] \times _{x\oplus y} z'\) and using the null-homotopies of \(p|_{z}\) and
. Setting \(w= [x\oplus z] \times _{x\oplus y} z'\) and using the null-homotopies of \(p|_{z}\) and  we then obtain
we then obtain

and one can verify that this null-homotopy exhibits \(w\) as a Lagrangian for \(q\), so that \([x,q]\) is metabolic. It then follows from Lemma 2.3.10 that  map to the same class in
map to the same class in  if and only if the Poincaré object
if and only if the Poincaré object  is metabolic.
is metabolic.
Remark 2.3.13
It follows from Lemma 2.3.10 that if  is a Poincaré functor then the two induced abelian group homomorphisms
is a Poincaré functor then the two induced abelian group homomorphisms

differ by a sign, where \(-\eta \) is an additive inverse to \(\eta \) in the \({\text {E} _\infty }\)-group of natural transformations  (well-defined up to homotopy).
(well-defined up to homotopy).
Remark 2.3.14
We note that the Poincaré functor

constructed in Lemma 2.3.7 is fully-faithful and the natural transformation  is an equivalence. It then follows that the induced map
is an equivalence. It then follows that the induced map  is injective. Since the essential image of i coincides with the full subcategory spanned by those objects whose image under
is injective. Since the essential image of i coincides with the full subcategory spanned by those objects whose image under  is zero it follows that the sequence of monoids
is zero it follows that the sequence of monoids

is exact. We may consequently identify  with the “middle homology” of the sequence of monoids
with the “middle homology” of the sequence of monoids

The terminology of \({\text {L}}\)-groups goes back to Wall [69], who defined the quadratic \({\text {L}}\)-groups of a (not necessarily commutative) ring with anti-involution. These play a key role in the surgery theoretic classification of higher dimensional manifolds. In the case of fields the zero’th quadratic \({\text {L}}\)-group was first studied by Witt [75], and later became known in this context as the Witt group. The zero’th \({\text {L}}\)/Witt group of fields plays an important role in arithmetic geometry through its relation to Milnor’s K-theory and Galois cohomology, as formulated in Milnor’s conjecture and eventually proven by Voevodsky. For more on the relation between classical \({\text {L}}\)-groups of rings and the ones defined above, see Example 2.3.17 and Remark 4.2.25.
The notion of \({\text {L}}\)-groups was subsequently generalized from rings to categories by various authors: by Ranicki [58] for categories of bounded complexes over an additive category equipped with a chain duality, and later by Weiss and Williams [72] for Waldhausen categories equipped with a Spanier–Whitehead product. Higher \({\text {L}}\)-groups were also studied by Balmer [9] under the name higher Witt groups in the context of triangulated categories. When applied to the triangulated bounded derived categories of \({\mathbb {Z}}[\tfrac{1}{2}]\)-linear categories with chain duality these agree with Ranicki’s \({\text {L}}\)-groups, and the latter are a particular case of the construction in [72] (see Example 1.A.1 of loc. cit.). Let us hence briefly explain how to compare the definition of \({\text {L}}\)-groups given in [72] with the one considered here.
Recall that in [72] Weiss and Williams consider a Waldhausen category \({\mathcal {E}}\) satisfying certain additional axioms. In particular, \({\mathcal {E}}\) is equipped with an initial object \(\emptyset \in {\mathcal {E}}\) and two distinguished classes of morphisms, called cofibrations and weak equivalences, and the additional axioms ensure that this structure exhibits \({\mathcal {E}}\) as a category of cofibrant objects in the sense of [17]. One may then view \({\mathcal {E}}\) as a model for the \(\infty \)-category \({\mathcal {E}}_{\infty } = {\mathcal {E}}[W^{-1}]\) obtained by localising at the weak equivalences, and the auxiliary structure given by the cofibrations allows one to access certain aspects of \({\mathcal {E}}_{\infty }\) while working entirely within \({\mathcal {E}}\). For example, the initial object of \({\mathcal {E}}\) is also initial in \({\mathcal {E}}_{\infty }\) (this is true in any localisation) and one can compute pushouts in \({\mathcal {E}}_{\infty }\) by forming in \({\mathcal {E}}\) pushouts with one leg cofibration. In fact, the axioms of a category with cofibrant objects ensure that any map in \({\mathcal {E}}_{\infty }\) can be represented by a cofibration in \({\mathcal {E}}\) (and this is true even if we fix the domain), and so all homotopy pushouts in \({\mathcal {E}}_{\infty }\) can be computed in this way.
In the case considered in [72] the \(\infty \)-category \({\mathcal {E}}_{\infty }\) obtained by localised \({\mathcal {E}}\) at the weak equivalences is assumed to be stable, so that one can contemplate the constructions of the present paper for \({\mathcal {E}}_{\infty }\). We then point out a second difference with [72]: while here we consider forms on objects \(x\in {\mathcal {E}}_{\infty }\), which can then be restricted along maps, in [72] one works with the dual notion of co-forms on a given object, which roughly correspond to forms on the dual object. In particular, the rule which associates to any object its space (or spectrum) of co-forms is encoded by a covariant, rather than a contravariant functor on the underlying category. In addition, if one is working with the 1-categorical model \({\mathcal {E}}\) for the stable \(\infty \)-category \({\mathcal {E}}_{\infty }\) then it is natural to also work with a 1-categorical model for spaces or spectra, which in [72] is done by using the category \(\text {Top} \) of compactly generated Hausdorff spaces and the category \({{\mathcal {S}}{p}}^{\Omega }\) of sequential \(\Omega \)-spectra in such. When localised at the class of weak homotopy equivalences these yield the \(\infty \)-categories of spaces and spectra, respectively, and we will treat the former as models for the latter. By a stable Spanier–Whitehead (SW) product the authors of [72] then mean a symmetric functor
which is invariant under weak equivalences and exact in each variable, that is, for each \(x\in {\mathcal {E}}\) the functor \(\text {B} (x,-)\) sends initial objects to zero \(\Omega \)-spectra and pushout squares with one leg cofibration to homotopy pullback squares of \(\Omega \)-spectra. In particular, by the above discussion we see that a stable SW-product always descends to symmetric bilinear functor
in the sense of Sect. 1.1. Weiss and Williams then require that the resulting functor
is represented in \({\text {Ho}}({\mathcal {E}})\) by an equivalence \(\text {D} :{\text {Ho}}({\mathcal {E}}) \rightarrow {\text {Ho}}({\mathcal {E}})^{\text {op} }\). This condition is implied by the condition that \(\text {B} _{\infty }\) is perfect in the sense of Definition 1.2.8, and so to compare [72] with the present setting we simply assume that \(\text {B} _{\infty }\) is perfect. One may then speak of symmetric Poincaré objects in \({\mathcal {E}}\), which are objects \(x\in {\mathcal {E}}\) equipped with a point \(q\in \Omega ^{\infty }\text {B} (x,x)^{{{\text {hC} }_{\textrm{2}}}}\) whose corresponding map \(\text {D} x\rightarrow x\) in \({\text {Ho}}({\mathcal {E}})\) is an isomorphism. In [72] these are simply considered as a set \(\text {sp} _0({\mathcal {E}})\), which one can endow with a commutative monoid structure via orthogonal sums.
The notion of a metabolic Poincaré object can naturally be set in the context of [72] by associating to the Waldhausen category \({\mathcal {E}}\) the Waldhausen category \({\text {Met}}({\mathcal {E}})\) whose objects are cofibrations \(x\rightarrow w\), the weak equivalences are defined levelwise, and the cofibrations are the Reedy cofibrations. One may then put a stable SW-product on \({\text {Met}}({\mathcal {E}})\) by setting \(\text {B} ([x\rightarrow w,x'\rightarrow w']) = {\text {hofib}}[\text {B} (x,x') \rightarrow \text {B} (w,w')]\), so that one has a functor of Waldhausen categories with stable SW-products
A Poincaré object \((x,q)\) in the context of Weiss–Williams is then identified as metabolic if it is the image of a Poincaré object in \({\text {Met}}({\mathcal {E}})\). Though not explicitly defined in this manner, the zero’th \({\text {L}}\)-group of [72] can be identified with the quotient of \(\text {sp} _0({\mathcal {E}})\) by the sub-monoid of metabolic objects. These constructions naturally compare with those of the present paper, and one obtains a commutative diagram of commutative monoids

where  is the symmetric Poincaré structure associated to the bilinear functor \(\text {B} _\infty \). Here, the composite of the two maps in every row is zero, and the bottom row is exact by Remark 2.3.12. We then have the following comparison statement:
is the symmetric Poincaré structure associated to the bilinear functor \(\text {B} _\infty \). Here, the composite of the two maps in every row is zero, and the bottom row is exact by Remark 2.3.12. We then have the following comparison statement:
Proposition 2.3.15
The right most vertical map  is an isomorphism.
is an isomorphism.
Proof
To begin, note that \({\mathcal {E}}\rightarrow {\mathcal {E}}_{\infty }\) is essentially surjective by virtue of being a localisation. In addition, for every \(x\in {\mathcal {E}}\) with image \(\overline{x} \in {\mathcal {E}}_{\infty }\) one has \(\text {B} (x,x)^{{{\text {hC} }_{\textrm{2}}}} \simeq \text {B} _{\infty }(\overline{x},\overline{x})^{{{\text {hC} }_{\textrm{2}}}}\) essentially by definition, and since the functor \({\mathcal {E}}\rightarrow {\text {Ho}}({\mathcal {E}})\) is conservative we have that a given co-form on \(x\) is Poincaré in \({\mathcal {E}}\) if and only if the corresponding form on \(\text {D} \overline{x}\) is Poincaré in \({\mathcal {E}}_\infty ^{\text {op} }\). Combining all this yields that the map of monoids  is surjective, and so the map
is surjective, and so the map  is surjective. To show that the last map is also injective it will now suffice to show that for every \((x,q) \in \text {sp} _0({\mathcal {E}})\), the map
is surjective. To show that the last map is also injective it will now suffice to show that for every \((x,q) \in \text {sp} _0({\mathcal {E}})\), the map

is surjective. Arguing as for the surjectivity on Poincaré objects, it will suffice to show that the induced functor
is essentially surjective, which amounts in this case to showing that every map \(\overline{x} \rightarrow y\) out of \(\overline{x}\) in \({\mathcal {E}}_\infty \) can be represented by a cofibration \(x\rightarrow y\) out of \(x\) in \({\mathcal {E}}\). This is a general property of categories of cofibrant objects: indeed, since these admit a left calculus of fractions [17, §7.2] one may represent \(\overline{x} \rightarrow y\) by some map \(x\rightarrow y\) in \({\mathcal {E}}\), which can then be replaced by a cofibration by using the factorization axiom for such categories (which assures that every map can be written as a composite of a cofibration followed by a weak equivalence). \(\square \)
Remark 2.3.16
In [72] Weiss and Williams also define quadratic \({\text {L}}\)-groups associated to a Waldhausen category with a Spanier–Whitehead product, by replacing homotopy fixed points by homotopy orbits in the definition of co-forms. The proof of Proposition 2.3.15 then adapts verbatim to show that the quadratic \({\text {L}}\)-groups of [72] identify with the \({\text {L}}\)-groups of the Poincaré structure  .
.
Example 2.3.17
Let R be a commutative ring and \({\text {Ch}}^{\textrm{b}}(R)\) the category of bounded complexes of finitely generated projective R-modules. Then \({\text {Ch}}^{\textrm{b}}(R)\) has the structure of a Waldhausen category with cofibrations being the maps which are levelwise injective with projective cokernel, and weak equivalences the collection \(\text {qIso} \) of quasi-isomorphisms. We may endow this Waldhausen category with a Spanier–Whitehead product \(\text {B} ^{\otimes }(X,Y) := \text {H} (X \otimes _R Y)\) which sends X, Y to the Eilenberg–Maclane spectrum of \(X \otimes _R Y\). The symmetric and quadratic \({\text {L}}\)-groups associated to this Spanier–Whitehead product by [72] then coincide with Ranicki’s (4-periodic) symmetric and quadratic \({\text {L}}\)-groups, respectively, see [72, Example 1.A.1]. Let \({{\mathcal {D}}}^\text {p} (R) = {\text {Ch}}^{\textrm{b}}(R)[\text {qIso} ^{-1}]\) be the perfect derived \(\infty \)-category of R obtained by taking the \(\infty \)-categorical localisation of \({\text {Ch}}^{\textrm{b}}(R)\) by the quasi-isomorphisms. Then under the equivalence \(\text {D} _R:{{\mathcal {D}}}^\text {p} (R)^{\text {op} }\simeq {{\mathcal {D}}}^\text {p} (R)\) the descended bilinear functor \(\text {B} ^{\otimes }_{\infty }\) identifies with the bilinear functor \(\text {B} _R\) of Example 1.2.12. By Proposition 2.3.15 and Remark 2.3.16 we may then identify Ranicki’s symmetric and quadratic \({\text {L}}\)-groups with the \({\text {L}}\)-groups of the Poincaré structures  and
and  described in that example. More generally, the same holds (for the same reason) over a not-necessarily-commutative ring R with respect to a fixed invertible module with involution M, see Sect. 4.2.
described in that example. More generally, the same holds (for the same reason) over a not-necessarily-commutative ring R with respect to a fixed invertible module with involution M, see Sect. 4.2.
Remark 2.3.18
The collection of \({\text {L}}\)-groups are in fact the homotopy groups of a spectrum valued invariant  , known as the \({\text {L}}\)-theory spectrum. A definition in the setting of Poincaré \(\infty \)-categories was given in [45], but was defined much earlier in the setting of rings with anti-involution by Ranicki [58], and plays a key role in surgery theory. We will recall the definition of this invariant in Paper [2], prove its main properties and characterize it by a universal property. The interaction between the \({\text {L}}\)-spectrum and the closely related Grothendieck-Witt spectrum is one of the principal themes of the present series of papers.
, known as the \({\text {L}}\)-theory spectrum. A definition in the setting of Poincaré \(\infty \)-categories was given in [45], but was defined much earlier in the setting of rings with anti-involution by Ranicki [58], and plays a key role in surgery theory. We will recall the definition of this invariant in Paper [2], prove its main properties and characterize it by a universal property. The interaction between the \({\text {L}}\)-spectrum and the closely related Grothendieck-Witt spectrum is one of the principal themes of the present series of papers.
3.4 The algebraic Thom construction
Given a Poincaré \(\infty \)-category  , the map
, the map

induced by the Poincaré functor of Lemma 2.3.7 sends a \((-1)\)-shifted Poincaré object \((x,q)\) to the metabolic Poincaré object 0 equipped with \(x\) as its Lagrangian. In particular, the data of a Lagrangian of 0 is equivalent to that of a Poincaré object with respect to the shifted Poincaré structure  . This idea fits in the more general paradigm of the algebraic Thom isomorphism developed by Ranicki [57, Proposition 3.4], under which Poincaré objects in
. This idea fits in the more general paradigm of the algebraic Thom isomorphism developed by Ranicki [57, Proposition 3.4], under which Poincaré objects in  equipped with a Lagrangian can equivalently be encoded via a hermitian object with respect to
equipped with a Lagrangian can equivalently be encoded via a hermitian object with respect to  . To discuss this equivalence, it will be useful to introduce the following construction:
. To discuss this equivalence, it will be useful to introduce the following construction:
Definition 2.4.1
Let  be a Poincaré \(\infty \)-category. We will denote by
be a Poincaré \(\infty \)-category. We will denote by  the hermitian \(\infty \)-category whose underlying stable \(\infty \)-category is the arrow category \({\text {Ar}}({\mathcal {C}})\) and whose quadratic functor
the hermitian \(\infty \)-category whose underlying stable \(\infty \)-category is the arrow category \({\text {Ar}}({\mathcal {C}})\) and whose quadratic functor  sits in a pullback diagram
sits in a pullback diagram

where the vertical map is the canonical one from a quadratic functor to its diagonally restricted bilinear part while the bottom horizontal map is the natural transformation whose component at f is given by restriction along f.
Remark 2.4.2
For \([z\rightarrow w] \in {\text {Ar}}({\mathcal {C}})\), the commutative square

determines a natural map  . From Corollary 1.1.21 we then get that for an exact sequence \(z\rightarrow w\rightarrow x\) the associated sequence
. From Corollary 1.1.21 we then get that for an exact sequence \(z\rightarrow w\rightarrow x\) the associated sequence

is exact.
Unwinding the definitions we see that the underlying symmetric bilinear functor of  sits in a fibre square
sits in a fibre square

from which we see that when  is perfect with duality \(\text {D} \) then \(\text {B} _{\text {ar} }\) is perfect with duality
is perfect with duality \(\text {D} \) then \(\text {B} _{\text {ar} }\) is perfect with duality
In this case, identifying  , we see that a hermitian form on an arrow \([f:z\rightarrow w] \in {\text {Ar}}({\mathcal {C}})\) consists of a triple \((q,g,\eta )\) where q is a hermitian form on \(z\) with respect to
, we see that a hermitian form on an arrow \([f:z\rightarrow w] \in {\text {Ar}}({\mathcal {C}})\) consists of a triple \((q,g,\eta )\) where q is a hermitian form on \(z\) with respect to  , \(g:w\rightarrow \text {D} z\) is a map in \({\mathcal {C}}\), and \(\eta \) is a homotopy \(q_{\sharp } \sim g\circ f\) between the resulting two maps from \(z\) to \(\text {D} z\). The self-dual map \([z\rightarrow w] \rightarrow [\text {D} w\rightarrow \text {D} z]\) associated to such a triple can then be expressed as the map between the two vertical arrows in the square
, \(g:w\rightarrow \text {D} z\) is a map in \({\mathcal {C}}\), and \(\eta \) is a homotopy \(q_{\sharp } \sim g\circ f\) between the resulting two maps from \(z\) to \(\text {D} z\). The self-dual map \([z\rightarrow w] \rightarrow [\text {D} w\rightarrow \text {D} z]\) associated to such a triple can then be expressed as the map between the two vertical arrows in the square

In particular, a triple \((q,g,\eta )\) constitutes a Poincaré form if and only if g is an equivalence. We now note that the map  appearing in the defining square (50) promotes the domain projection
appearing in the defining square (50) promotes the domain projection
to a hermitian functor and hence determines a map

given on the level of tuples as above by \((z\rightarrow w,q,g,\eta ) \mapsto (z,q)\). We then have the following:
Proposition 2.4.3
The map (51) restricts to an equivalence

An explicit inverse is given by the association \((z,q) \mapsto (q_{\sharp }:z\rightarrow \text {D} z,q,\text {id} ,\text {id} )\).
Concisely stated, Proposition 2.4.3 says that for a Poincaré \(\infty \)-category  , hermitian objects in \({\mathcal {C}}\) can be described via Poincaré objects in its arrow category. Though a direct proof is perfectly possible at the moment, we will postpone it to Sect. 7.3, where we will prove this statement in a more general context in Proposition 7.3.5. Meanwhile, let us connect the present conclusions to the above discussion of metabolic objects.
, hermitian objects in \({\mathcal {C}}\) can be described via Poincaré objects in its arrow category. Though a direct proof is perfectly possible at the moment, we will postpone it to Sect. 7.3, where we will prove this statement in a more general context in Proposition 7.3.5. Meanwhile, let us connect the present conclusions to the above discussion of metabolic objects.
Notation 2.4.4
For a stable \(\infty \)-category \({\mathcal {C}}\) we will denote by \({\text {Seq}}({\mathcal {C}}) \subseteq {\text {Fun}}(\Delta ^1 \times \Delta ^1,{\mathcal {C}})\) the full subcategory spanned by the exact squares of the form

In other words, \({\text {Seq}}({\mathcal {C}})\) is the \(\infty \)-category of exact sequences \([z\rightarrow w\rightarrow x]\) in \({\mathcal {C}}\), where we will often omit the null-homotopy encoded by the commutative square (52) to simplify notation.
We have two projections

Lemma 2.4.5
The projections (53) are both equivalences. In addition, the restrictions of  and
and  to \({\text {Seq}}({\mathcal {C}})\) via the left and right projection respectively, are naturally equivalent.
to \({\text {Seq}}({\mathcal {C}})\) via the left and right projection respectively, are naturally equivalent.
Proof
The first claim follows from the fact that exact squares as in (52) are both left Kan extended from their restriction to \(\Lambda ^2_0 \subseteq \Delta ^1\times \Delta ^1\) and right Kan extended from their restriction to \(\Lambda ^2_2 \subseteq \Delta ^1 \times \Delta ^1\). The natural homotopy between  and
and  is then encoded by the 4-fold exact sequence of quadratic functors on \({\text {Seq}}({\mathcal {C}})\) given by
is then encoded by the 4-fold exact sequence of quadratic functors on \({\text {Seq}}({\mathcal {C}})\) given by

where the last exact sequence is by Remark 2.4.2. \(\square \)
Lemma 2.4.5 identifies the Poincaré \(\infty \)-category  with the Poincaré \(\infty \)-category
with the Poincaré \(\infty \)-category  up to a shift of the Poincaré structure. We note however that
up to a shift of the Poincaré structure. We note however that  , that is, the formation of arrow Poincaré \(\infty \)-categories commutes with shifting the Poincaré structure. Using Lemma 2.4.5 and Proposition 2.4.3 we then obtain a sequence of equivalences
, that is, the formation of arrow Poincaré \(\infty \)-categories commutes with shifting the Poincaré structure. Using Lemma 2.4.5 and Proposition 2.4.3 we then obtain a sequence of equivalences

Unwinding the definitions, this composed map sends a tuple \((w\rightarrow x,q,\eta )\), consisting of a Poincaré object \((x,q)\) equipped with a Lagrangian \((w\rightarrow x,\eta )\), to the object \(z:= {\text {fib}}(w\rightarrow x)\), equipped with the shifted hermitian structure encoded by the pair of null-homotopies of \(q|_{z}\) (one restricted from \(\eta \) and one induced by the null-homotopy of the composed map \(z\rightarrow w\rightarrow x\)).
Corollary 2.4.6
(The algebraic Thom isomorphism) The association \([w\rightarrow x] \mapsto {\text {fib}}(w\rightarrow x)\) underlines a natural equivalence of spaces

between Poincaré objects in \({\mathcal {C}}\) equipped with a Lagrangian and \((-1)\)-shifted hermitian objects in \({\mathcal {C}}\).
Remark 2.4.7
Combining Remark 2.3.14 with the algebraic Thom isomorphism of Corollary 2.4.6 we may identify the \({\text {L}}\)-groups of  with the homology monoids of the chain complex of monoids of the form
with the homology monoids of the chain complex of monoids of the form

where the map  sends an \((-i)\)-fold hermitian object \((x,q)\) to its Ranicki boundary
sends an \((-i)\)-fold hermitian object \((x,q)\) to its Ranicki boundary  , endowed with its associated \((-i+1)\)-fold Poincaré form.
, endowed with its associated \((-i+1)\)-fold Poincaré form.
We finish this section by framing the observation that the hyperbolic and arrow constructions naturally commute with each other
Lemma 2.4.8
For a stable \(\infty \)-category \({\mathcal {C}}\), the natural equivalence
in which the second equivalence sends \((f:z\rightarrow w,f':z'\rightarrow w')\) to  , extends to an equivalence of Poincaré \(\infty \)-categories
, extends to an equivalence of Poincaré \(\infty \)-categories
Proof
Transporting the Poincaré structure of \({\text {Ar}}({\text {Hyp}}({\mathcal {C}}))\) along the equivalence (54) yields the quadratic functor

We thus finish the proof by recognizing the last term as the quadratic functor of \({\text {Hyp}}({\text {Ar}}({\mathcal {C}}))\). \(\square \)
Combining Lemma 2.4.8 with Lemma 2.4.5 and Remark 2.2.4 we immediately conclude
Corollary 2.4.9
For a stable \(\infty \)-category \({\mathcal {C}}\) there is a natural equivalence of Poincaré \(\infty \)-categories
which, on the underlying stable \(\infty \)-categories, is given by the equivalence
where the second equivalence is the product of the identity of \({\text {Ar}}({\mathcal {C}})\) and the equivalence \({\text {Ar}}({\mathcal {C}}^{\text {op} })\simeq {\text {Ar}}({\mathcal {C}})^{\text {op} }\) which sends an arrow \(x\leftarrow w:g\) in \({\mathcal {C}}^{\text {op} }\) to the canonical arrow \({\text {fib}}(g)\rightarrow w\). In particular, the Poincaré functor \(\text {met} :{\text {Met}}{\text {Hyp}}({\mathcal {C}})\rightarrow {\text {Hyp}}({\mathcal {C}})\) from Lemma 2.3.7 (applied to \({\text {Hyp}}({\mathcal {C}})\)) admits a section in \(\text {Cat} ^{\textrm{p}}_\infty \).
3.5 The Grothendieck-Witt group
In this section we define the Grothendieck-Witt group of a Poincaré \(\infty \)-category. In the setting of ordinary rings, the Grothendieck-Witt group was classically defined as the group completion of the monoid of isomorphism classes of pairs (P, q) where P is a finite dimensional projective module and q is a non-degenerate hermitian form of some flavour (symmetric, quadratic, anti-symmetric, etc.). It was later extended to more general contexts such as vectors bundles over algebraic varieties [41] and forms in abstract additive categories with duality [54]. In doing so it was realized that the simple definition via group completion needs to be slightly modified to take into account information coming from non-split short exact sequences. In particular, one had to quotient out the group completion by the relation \([x,q] \sim [\text {hyp} (w)]\) identifying the class of a metabolic object with Lagrangian \(w\) with that of the associated hyperbolic object. In fact, the latter relation already implies the group property for the resulting quotient (as we will see below in our context), and hence can be done on the level of monoids without explicitly group completing. On the other hand, in the case of modules over rings (or, more generally, in contexts in which all short exact sequences split) the relation \([x,q] \sim [\text {hyp} (w)]\) automatically holds in the group completion since every metabolic object is stably hyperbolic.
In the present section we will give a definition of the Grothendieck-Witt group in the context of Poincaré \(\infty \)-categories, and extract some of its basic properties. Using the work of the fourth and ninth authors [28], this definition can be compared with the classical one in the case of modules over rings using suitable Poincaré structures on \({{\mathcal {D}}}^\text {p} (R)\), see Remark 4.2.28 below for the precise statement.
For the following definition, recall the map  induced on Poincaré objects by the Poincaré functor
induced on Poincaré objects by the Poincaré functor  under the equivalence \(\text {Pn} ({\text {Hyp}}({\mathcal {C}})) \simeq \iota {\mathcal {C}}\) of Proposition 2.2.5. Explicitly, this map sends an object \(x\in {\mathcal {C}}\) to the Poincaré object \(\text {hyp} (x) = x\oplus \text {D} x\) equipped with its canonical Poincaré form, see Sect. 2.2.
under the equivalence \(\text {Pn} ({\text {Hyp}}({\mathcal {C}})) \simeq \iota {\mathcal {C}}\) of Proposition 2.2.5. Explicitly, this map sends an object \(x\in {\mathcal {C}}\) to the Poincaré object \(\text {hyp} (x) = x\oplus \text {D} x\) equipped with its canonical Poincaré form, see Sect. 2.2.
Definition 2.5.1
Let  be a Poincaré \(\infty \)-category. We define
be a Poincaré \(\infty \)-category. We define  to be the quotient in the category of commutative monoids of
to be the quotient in the category of commutative monoids of  (with its commutative monoid structure given by direct sums) by the relations
(with its commutative monoid structure given by direct sums) by the relations
for every Poincaré object \((x,q)\) with Lagrangian \(w\rightarrow x\).
Remark 2.5.2
By definition we may identify  with the coequalizer of the pair of maps
with the coequalizer of the pair of maps

where the first map is induced by the Poincaré functor  and the second is induced by the composed Poincaré functor
and the second is induced by the composed Poincaré functor  discussed in Remark 2.3.9.
discussed in Remark 2.3.9.
We quickly summarize a few properties which follow directly from the definition of \({\text {GW}}_0\).
Lemma 2.5.3
-
i)
For every exact sequence \(z'\rightarrow z\rightarrow z''\) in \({\mathcal {C}}\) the relation
$$\begin{aligned}{}[\text {hyp} (z)] \sim [\text {hyp} (z')] + [\text {hyp} (z'')] \end{aligned}$$holds in
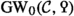 .
. -
ii)
For every Poincaré object
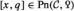 the relation $$\begin{aligned}{}[x,q] + [x,-q] + [\text {hyp} (\Omega x)] \sim [\text {hyp} (x)] + [\text {hyp} (\Omega x)] \sim 0 \end{aligned}$$
the relation $$\begin{aligned}{}[x,q] + [x,-q] + [\text {hyp} (\Omega x)] \sim [\text {hyp} (x)] + [\text {hyp} (\Omega x)] \sim 0 \end{aligned}$$holds in
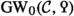 .
.
Proof
For i) note that if \(z'\rightarrow z\rightarrow z''\) is an exact sequence in \({\mathcal {C}}\) then  is naturally a Lagrangian in \(\text {hyp} (z)\), and \(\text {hyp} (w) \simeq \text {hyp} (z') \oplus \text {hyp} (z'')\).
is naturally a Lagrangian in \(\text {hyp} (z)\), and \(\text {hyp} (w) \simeq \text {hyp} (z') \oplus \text {hyp} (z'')\).
To prove ii), the first identification is given by (55) applied to the metabolic object \((x\xrightarrow {\Delta } x\oplus x, q \oplus -q)\) and the second relation is given by i) applied to the exact sequence \(\Omega x\rightarrow 0 \rightarrow x\). \(\square \)
Corollary 2.5.4
The commutative monoid  is always a group. We refer to it as the Grothendieck-Witt group of
is always a group. We refer to it as the Grothendieck-Witt group of  .
.
Example 2.5.5
For a stable \(\infty \)-category \({\mathcal {C}}\), the isomorphism
induced on components of the equivalence of Proposition 2.2.5, descends to a group isomorphism
Indeed, the isomorphism (56) relates the class of \(z\in {\mathcal {C}}\) to the Poincaré class of \((z,z) \in {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) equipped with its canonical Poincaré form  . An isotropic object in \(((z,z),\text {id} _{z})\) is then given by a pair of maps \(z'\rightarrow z,z\rightarrow z''\) in \({\mathcal {C}}\), such that the composite \(z'\rightarrow z\rightarrow z''\), which corresponds to the pullback of the Poincaré form \(\text {id} _{z}\) to
. An isotropic object in \(((z,z),\text {id} _{z})\) is then given by a pair of maps \(z'\rightarrow z,z\rightarrow z''\) in \({\mathcal {C}}\), such that the composite \(z'\rightarrow z\rightarrow z''\), which corresponds to the pullback of the Poincaré form \(\text {id} _{z}\) to  , vanishes. Such an isotropic object is a Lagrangian precisely when the resulting sequence \(z'\rightarrow z\rightarrow z''\) is exact. Moreover the hyperbolic object on \((z',z'')\) is given by the object \((z'\oplus z'', z'\oplus z'') \in {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\). It then follows that under the isomorphism (56), the defining relations of the Grothendieck-Witt group can be written as \([z] = [z'] + [z'']\) for every exact sequence \(z'\rightarrow z\rightarrow z''\), which are exactly the relations defining the quotient \(\pi _0\iota ({\mathcal {C}}) \twoheadrightarrow {\text {K}}_0({\mathcal {C}})\).
, vanishes. Such an isotropic object is a Lagrangian precisely when the resulting sequence \(z'\rightarrow z\rightarrow z''\) is exact. Moreover the hyperbolic object on \((z',z'')\) is given by the object \((z'\oplus z'', z'\oplus z'') \in {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\). It then follows that under the isomorphism (56), the defining relations of the Grothendieck-Witt group can be written as \([z] = [z'] + [z'']\) for every exact sequence \(z'\rightarrow z\rightarrow z''\), which are exactly the relations defining the quotient \(\pi _0\iota ({\mathcal {C}}) \twoheadrightarrow {\text {K}}_0({\mathcal {C}})\).
Recall from Definition 2.3.11 that the zero’th \({\text {L}}\)-group  is defined as the cokernel of the monoid homomorphism
is defined as the cokernel of the monoid homomorphism  . In particular, the quotient map
. In particular, the quotient map  sends the class of any metabolic object (and in particular any hyperbolic object) to zero, and hence factors through a group homomorphism
sends the class of any metabolic object (and in particular any hyperbolic object) to zero, and hence factors through a group homomorphism

which is necessarily surjective, as we can identify  with the quotient group of
with the quotient group of  by the subgroup spanned by the classes of metabolic objects. To obtain more information about this kernel, we note that the map
by the subgroup spanned by the classes of metabolic objects. To obtain more information about this kernel, we note that the map

induced by the Poincaré functor  of Construction 2.3.8, is surjective: any object \(z\in {\mathcal {C}}\) is a Lagrangian in the Poincaré object \(\text {hyp} (z)\). In addition, the canonical map
of Construction 2.3.8, is surjective: any object \(z\in {\mathcal {C}}\) is a Lagrangian in the Poincaré object \(\text {hyp} (z)\). In addition, the canonical map
to the zero’th algebraic \({\text {K}}\)-theory group of \({\mathcal {C}}\) is surjective as well: we may identify \({\text {K}}_0({\mathcal {C}})\) with the quotient of \(\pi _0(\iota {\mathcal {C}})\) in the category of commutative monoids by the relations \([z] \sim [z'] + [z'']\) for every exact sequence \(z'\rightarrow z\rightarrow z''\). By Lemma 2.5.3i) the homomorphism  then descends to a homomorphism of abelian groups
then descends to a homomorphism of abelian groups

which by Example 2.5.5 we may also identify with the map induced on \({\text {GW}}_0\) by the Poincaré functor \(\text {hyp} :{\text {Hyp}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\). Comparing the relevant universal properties we then see that  sits in a pushout square of commutative monoids of the form
sits in a pushout square of commutative monoids of the form

where \([{\text {lag}}]\) denotes the composed map  . It then follows that
. It then follows that  can equivalently be obtained as the cokernel of the map of abelian groups
can equivalently be obtained as the cokernel of the map of abelian groups  . On the other hand, by Corollary 2.2.10 the map \([\text {hyp} ]\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the induced \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {K}}_0\) and the trivial \({{\text {C} }_{\textrm{2}}}\)-action on
. On the other hand, by Corollary 2.2.10 the map \([\text {hyp} ]\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the induced \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {K}}_0\) and the trivial \({{\text {C} }_{\textrm{2}}}\)-action on  . We then obtain an induced exact sequence of abelian groups
. We then obtain an induced exact sequence of abelian groups

In Paper [2] we will show that this sequence comes from an exact sequence of spectra

the Tate exact sequence, encoding the fundamental relationship between these three invariants. In particular, this allows one to extend (59) to a long exact sequence involving the higher \({\text {L}}\)-groups and higher Grothendieck-Witt groups, yielding a powerful tool for computing the latter. In Paper [3] we will exploit these ideas for computing the higher Grothendieck-Witt groups of the integers.
4 Poincaré structures on module categories
In this section we discuss hermitian and Poincaré structures on \(\infty \)-categories of modules over ring spectra. In particular, we fix a base \({\text {E} _\infty }\)-ring spectrum k and consider an \({\text {E} _1}\)-algebra A in the symmetric monoidal \(\infty \)-category \({\text {Mod}}_k\) of k-module spectra. We denote by \(\text {Alg} _{{\text {E} _1}} := \text {Alg} _{{\text {E} _1}}({\text {Mod}}_k)\) the \(\infty \)-category of \({\text {E} _1}\)-algebra objects in \({\text {Mod}}_k\), which we simply refer to as \({\text {E} _1}\)-algebras. Given an \({\text {E} _1}\)-algebra \(A \in \text {Alg} _{{\text {E} _1}}\), we denote by \({\text {Mod}}_A\) the \(\infty \)-category of left A-module objects in \({\text {Mod}}_k\), which we refer to as A-modules. Our goal is to describe and study hermitian and Poincaré structures on the full subcategory \({\text {Mod}}^{\omega }_{A} \subseteq {\text {Mod}}_A\) of compact A-modules in \({\text {Mod}}_k\), as these account for many examples of interest motivating the present work (see also Sect. 4 for some more specific examples). More generally, one often wishes to consider a dense stable subcategory of \({\text {Mod}}^{\omega }_{A}\), that is, a stable (and in particular full) subcategory which generates all of \({\text {Mod}}^{\omega }_{A}\) under retracts. For example, one may consider the stable subcategory \(\text {Mod} ^{\text {f} }_{A} \subseteq {\text {Mod}}^{\omega }_{A}\) of finitely presented A-module spectra, which is the smallest stable subcategory containing the A-module A. By the work of Thomason [65], the dense stable subcategories of \({\text {Mod}}^{\omega }_{A}\) are classified by subgroups \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\), where to such a c corresponds the dense subcategory \({\text {Mod}}^c_A \subseteq {\text {Mod}}^{\omega }_{A}\) consisting of those compact A-modules M whose class \([M] \in {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) lies in c. In this context, let us point out that studying hermitian and Poincaré structures on \({\text {Mod}}^c_A\) for a general \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) is not really more complicated then studying hermitian and Poincaré structures in the maximal case of \({\text {Mod}}^{\omega }_{A}\). Indeed, by Lemma 1.4.1 left Kan extension and restriction form an adjunction

and \({\text {Mod}}^c_A \subseteq {\text {Mod}}^{\omega }_{A}\) being a dense full subcategory implies that this adjunction is an equivalence (cf. [2], Remark 1.3.4). As will follow from our more detailed analysis below, this equivalence identifies the \(\infty \)-category \({\text {Fun}}^{\textrm{p}}({\text {Mod}}^c_A)\) of Poincaré structures on \({\text {Mod}}^c_A\) with the full subcategory of \({\text {Fun}}^{\textrm{p}}({\text {Mod}}^{\omega }_{A})\) spanned by those Poincaré structures whose associated duality preserves \({\text {Mod}}^c_A\), or, equivalently, preserves the subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) (see Remark 3.3.4).
The present section is organised as follows. We begin in Sect. 3.1 by introducing the notion of a k-module with involution, and show how it can be used to construct bilinear functors on module \(\infty \)-categories. We then extend this notion in Sect. 3.2 to a k-module with genuine involution, which allows us to refine the associated bilinear functor to a hermitian or Poincaré structure. The basic operations of restriction and induction of modules with genuine involution along maps of ring spectra are discussed in Sect. 3.4.
We point out that the \(\infty \)-categories \({\text {Mod}}^c_A\) we will consider do not depend on k, that is, they only depend on the underlying \({\text {E} _1}\)-ring spectrum of A. However, the notion of a k-module with (genuine) involution does depend on k, and affects the type of hermitian structures on \({\text {Mod}}^c_A\) one can obtain in this way. More precisely, we will see in Sect. 3.3 that when \(k={\mathbb {S}}\), modules with genuine involution precisely correspond to hermitian structure on \({\text {Mod}}^{\omega }_{A}\), while for a general k one recovers hermitian structures equipped with a certain additional k-linear structure, the precise meaning of which is described in Remark 3.3.2 and Example 5.4.13. The reader who wishes to avoid this additional layer of structure is invited to assume \(k={\mathbb {S}}\) throughout. On the other hand, the reader who prefers to reason in terms of chain-complexes instead of spectra is invited to consider \(k={\mathbb {Z}}\). The latter case (and more generally, that of a complex-oriented k) also leads to better periodicity properties, as we discuss Sect. 3.5.
4.1 Ring spectra and involutions
In this section we will define the notion of a k-module with involution over an \({\text {E} _1}\)-algebra A and show how it can be used to construct bilinear functors on \({\text {Mod}}^{\omega }_{A}\). We will identify the k-modules with involution which lead to perfect bilinear functors as those which are invertible in a suitable sense. An important class of invertible k-modules with involution arise from \({\text {E} _1}\)-algebras with anti-involutions, a case for which we will present a convenient recognition criterion, see Proposition 3.1.14.
To begin, we note that since \(\otimes _k\) is a symmetric monoidal structure on \({\text {Mod}}_k\) the monoidal product
itself refines to a monoidal functor, which then sends the algebra object (A, A) in \({\text {Mod}}_k \times {\text {Mod}}_k\) to the algebra object \(A \otimes _k A\) in \({\text {Mod}}_k\), and thus refines to a functor
In addition, since \(\otimes _k\) is a symmetric monoidal structure the functor \(\otimes _k:{\text {Mod}}_k \times {\text {Mod}}_k \rightarrow {\text {Mod}}_k\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect the flip action on the domain and trivial action on the target, and consequently (60) inherits a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure with respect to the flip action on the domain and the \({{\text {C} }_{\textrm{2}}}\)-action on the target induced by the flip action on \(A \otimes _k A\). Given an \((A \otimes _k A)\)-module M, let us denote by
the resulting bilinear form. The association \(M \mapsto \text {B} _M\) then assembles to form a functor
which by the above inherits a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure with respect to the flip-induced \({{\text {C} }_{\textrm{2}}}\)-actions on both sides.
Definition 3.1.1
Let A be an \({\text {E} _1}\)-algebra over k. By a k-module with involution over A we will mean an object M of the \(\infty \)-category \(({\text {Mod}}_{A\otimes _k A})^{{{\text {hC} }_{\textrm{2}}}}\), where as above \({{\text {C} }_{\textrm{2}}}\) acts on \({\text {Mod}}_{A \otimes _k A}\) via its flip action on \(A \otimes _k A\). When \(k={\mathbb {S}}\) we will often omit k and simply write module with involution.
Concretely, a k-module with involution over A consists of a spectrum M with a \({{\text {C} }_{\textrm{2}}}\)-action and an \((A\otimes _k A)\)-module structure, such that the involution is linear over the ring map \(A\otimes _k A \rightarrow A\otimes _k A\) which switches the two factors. Since (61) is \({{\text {C} }_{\textrm{2}}}\)-equivariant the bilinear functor
on \({\text {Mod}}^{\omega }_{A}\) associated to M consequently inherits the structure of a symmetric bilinear functor.
Definition 3.1.2
Let M be a k-module with involution over an \({\text {E} _1}\)-algebra A. We denote by

the quadratic and symmetric hermitian structures associated to the symmetric bilinear functor \(\text {B} _{M} \in {\text {Fun}}^{\textrm{s}}({\text {Mod}}^{\omega }_{A})\) as in Example 1.1.17 and Definition 1.2.11.
If M is a k-module with involution over A, these are given explicitly by the formulas

Remark 3.1.3
Given a subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) we may restrict \(\text {B} _M\) to obtain a symmetric bilinear functor on \({\text {Mod}}^c_A\), and similarly for the associated hermitian structures  and
and  . For simplicity we will generally not distinguish in notation between these functors and their respective restrictions to \({\text {Mod}}^c_A\) for a given c.
. For simplicity we will generally not distinguish in notation between these functors and their respective restrictions to \({\text {Mod}}^c_A\) for a given c.
We may consider an \((A \otimes _k A)\)-module M as a k-module spectrum equipped with two commuting actions of A. The first A-action then promotes M to an object of \({\text {Mod}}_A\), while the second action refines to an action of A on M via A-module maps. In particular, the second A-action can be encoded via a map
If M is a k-module with involution over A then the involution determines an equivalence between the two different A-module structures. In particular, in this case it does not matter which action is considered first and which is considered second.
Definition 3.1.4
We will say that a k-module with involution M over A is invertible if it is compact as an A-module (with respect to either the first or the second A-action) and the map (62) is an equivalence.
Notation 3.1.5
If M is a k-module with involution over A then for every A-module X we may form the mapping spectrum \({\text {hom}}_A(X,M)\), where we consider M as an A-module via its first A-action. This spectrum then carries an A-action via the residual second A-action on M, and so we may view \({\text {hom}}_A(X,M)\) as an A-module. In what follows we will always consider \({\text {hom}}_A(X,M)\) as an A-module in this manner, without indicating it explicitly in the notation.
Proposition 3.1.6
Let A be an \({\text {E} _1}\)-algebra and M a k-module with involution over A. Then for a subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) the following statements hold:
-
i)
The restriction of \(\text {B} _M\) to \({\text {Mod}}^c_A\) is non-degenerate if and only if the A-module \({\text {hom}}_A(X,M)\) (see Notation 3.1.5) belongs to \({\text {Mod}}^c_A\) for every \(X \in {\text {Mod}}^c_A\).
-
ii)
When the equivalent conditions of i) hold the associated duality on \({\text {Mod}}^c_A\) is given by
$$\begin{aligned} \text {D} _M(X) := {\text {hom}}_A(X,M). \end{aligned}$$This duality is furthermore an equivalence if and only if M is in addition invertible.
Remark 3.1.7
In the situation of Proposition 3.1.6, if \({\text {Mod}}^c_A\) contains A then the condition in i) necessitates in particular that M belongs to \({\text {Mod}}^c_A\) (take \(X=A\)). If \({\text {Mod}}^c_A\) is either \({\text {Mod}}^{\omega }_{A}\) or \(\text {Mod} ^{\text {f} }_{A}\) then M belonging to \({\text {Mod}}^c_A\) is also sufficient: for \(\text {Mod} ^{\text {f} }_{A}\) this is because A generates \(\text {Mod} ^{\text {f} }_{A}\) under finite colimits and desuspensions and for \({\text {Mod}}^{\omega }_{A}\) it is because A generates \({\text {Mod}}^{\omega }_{A}\) under finite colimits, desuspensions and retracts, and \({\text {Mod}}^{\omega }_{A}\) is furthermore idempotent complete.
Remark 3.1.8
It follows from Proposition 3.1.6 and Remark 3.1.7 that M is invertible if and only if it is compact as an A-module and the contravariant functor \(X \mapsto {\text {hom}}_A(X,M)\) from \({\text {Mod}}^{\omega }_{A}\) to itself is an equivalence. Now for any \({\text {E} _1}\)-algebra A the functor \(X \mapsto {\text {hom}}_A(X,A)\) determines an equivalence
In addition, for M compact the natural map \({\text {hom}}_A(X,A) \otimes _A M \rightarrow {\text {hom}}_A(X,M)\) is an equivalence. It then follows that for a k-module with involution M which is compact as an A-module the condition of being invertible is equivalent to the condition that
is an equivalence of \(\infty \)-categories.
Proof of Proposition 3.1.6
We begin with the first claim. For a fixed compact A-module Y, the functor \(X \mapsto {\text {hom}}_{A \otimes _k A}(X \otimes _k Y,M)\) from \({\text {Mod}}_A^{\text {op} }\) to \({{\mathcal {S}}{p}}\) is represented by the A-module \({\text {hom}}_A(Y,M)\), where the latter is considered as an A-module via its second A-action. Since the functor \({\text {Mod}}_A \rightarrow {\text {Ind}}({\text {Mod}}^c_A) = {\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^c_A)^{\text {op} },{{\mathcal {S}}{p}})\) sending a module to the presheaf it represents on \({\text {Mod}}^c_A\) is fully-faithful (in fact, it is an equivalence) it follows that \(\text {B} _M(-,Y)\) is representable in \({\text {Mod}}^c_A\) if and only if \({\text {hom}}_A(Y,M)\) lies in \({\text {Mod}}^c_A\), in which case \({\text {hom}}_A(Y,M)\) serves as a representing object already in \({\text {Mod}}^c_A\). This proves i) and the first part of ii).
To prove the second part of ii) let now suppose that the condition in i) holds, that is, \({\text {hom}}_A(X,M)\) belongs to \({\text {Mod}}^c_A\) for every \(X \in {\text {Mod}}^c_A\). This means in particular that \({\text {hom}}_A(X,M)\) is compact for every \(X \in {\text {Mod}}^c_A\). Since \({\text {Mod}}^c_A\) is dense in \({\text {Mod}}^{\omega }_{A}\) it follows that A is a retract of an object in \({\text {Mod}}^c_A\), and hence \(M = {\text {hom}}_A(A,M)\) is compact as well. We now wish to show that the evaluation map
is an equivalence for every \(X \in {\text {Mod}}^c_A\) if and only if M is furthermore invertible. Using again that \({\text {Mod}}^c_A\) generates \({\text {Mod}}^{\omega }_{A}\) under retracts the above evaluation map is an equivalence on \({\text {Mod}}^c_A\) if and only if it is an equivalence on all of \({\text {Mod}}^{\omega }_{A}\). On the other hand, since \({\text {Mod}}^{\omega }_{A}\) is generated under finite colimits and retracts by A it will suffice to check the component of the evaluation map at \(X=A\), in which case it becomes the map
which by definition is an equivalence if and only if M is invertible. \(\square \)
We now consider some examples. An \({\text {E} _1}\)-algebra with anti-involution (over k) is an object of \(\text {Alg} _{{\text {E} _1}}^{{{\text {hC} }_{\textrm{2}}}} = \text {Alg} _{{\text {E} _1}}({\text {Mod}}_k)^{{{\text {hC} }_{\textrm{2}}}}\), where the action of \({{\text {C} }_{\textrm{2}}}\) on the \(\infty \)-category of \({\text {E} _1}\)-algebras is given by sending an algebra A to its opposite \(A^{\text {op} }\).
Example 3.1.9
Let A be an \({\text {E} _1}\)-algebra with anti-involution \(\tau :A^{\text {op} }\rightarrow A\). Then A can be naturally considered as an invertible k-module with involution over itself. Indeed, by using that the forgetful functor \(\text {Alg} _{{\text {E} _1}} \rightarrow {{\mathcal {S}}{p}}\) is equivariant with respect to the trivial action on the target, we obtain a functor \(\text {Alg} _{{\text {E} _1}}^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},{{\mathcal {S}}{p}})\), which allows us to view A as a spectrum with \({{\text {C} }_{\textrm{2}}}\)-action. In addition, by construction this action switches between the canonical left and right actions of A on itself. More precisely, viewing A as an \((A \otimes _k A^{\text {op} })\)-module, this \({{\text {C} }_{\textrm{2}}}\)-action is linear over the \({{\text {C} }_{\textrm{2}}}\)-action on \(A \otimes _k A^{\text {op} }\) which flips the two components and applies the anti-involution \(\tau \). Equivalently, the anti-involution determines an equivalence of \({\text {E} _1}\)-algebras \(A \otimes _k A^{\text {op} }\simeq A \otimes _k A\) intertwining the above \({{\text {C} }_{\textrm{2}}}\)-action with the flip action on \(A \otimes _k A\), and we may hence view A as an object of \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\). Informally, the \(A \otimes _k A\)-action on A is given by \((a\otimes b)\cdot x = a\cdot x \cdot \tau (b)\). We may then recover the anti-involution \(\tau \) as the induced map of \({\text {E} _1}\)-algebras \(A \rightarrow {\text {hom}}_A(A,A)=A^{\text {op} }\). The latter is therefore an equivalence, and so A is invertible.
Example 3.1.10
The restriction of the \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Alg} _{{\text {E} _1}}\) to \({\text {E} _\infty }\)-algebras is canonically trivialised, so that we obtain a functor
In particular, \({\text {E} _\infty }\)-algebras with \({{\text {C} }_{\textrm{2}}}\)-actions give rise to an \({\text {E} _1}\)-algebra with involution. For example, any \({\text {E} _\infty }\)-algebra equipped with the trivial \({{\text {C} }_{\textrm{2}}}\)-action, determines an \({\text {E} _1}\)-algebra with involution.
More generally, when A is an \({\text {E} _\infty }\)-algebra, any A-module M with \({{\text {C} }_{\textrm{2}}}\)-action canonically defines a k-module with involution over A, with \(A \otimes _k A\) acting via the multiplication map \(A \otimes _k A \rightarrow A\). By Remark 3.1.8, the invertibility condition from 3.1.4 is in this case equivalent to the \(\otimes _A\)-invertibility of M, or in other words to \(M \in {\text {Pic}}(A)\) upon disregarding \({{\text {C} }_{\textrm{2}}}\)-actions.
Example 3.1.11
An important source of \({\text {E} _1}\)-algebras with anti-involution arises from the group algebra construction. We will study this example and its relation to visible \({\text {L}}\)-theory in further detail in Sect. 4.3.
Examples 3.1.12
Let R be an ordinary associative ring. Using the Eilenberg–Mac Lane embedding \(\text {H} :{\mathcal {A}}b\hookrightarrow {{\mathcal {S}}{p}}\) we may associate to R an \({\text {E} _1}\)-ring spectrum \(\text {H} R\), and by [47, Theorem 7.1.2.1] we have a natural equivalence
between the \(\infty \)-category of compact \(\text {H} R\)-module spectra and the perfect derived \(\infty \)-category of R, defined as in Example 1.2.12. An anti-involution on \(\text {H} R\) is then the same as an anti-involution on R, that is, an isomorphism \(\tau :R \rightarrow R^{\text {op} }\) such that \(\tau ^2 = \text {id} \). We will study this case in further detail in Sect. 4.2. Ordinary rings which carry anti-involutions are then fairly common, see Examples 4.2.7.
Example 3.1.13
As in Example 3.1.12, suppose that R is an ordinary associative ring. Recall that a Wall anti-structure [68] on R consists of an anti-automorphism \(\tau :R \rightarrow R^{\text {op} }\) and a unit \(\epsilon \in R^*\) such that \(\tau (r) = \epsilon ^{-1} r\epsilon \) and \(\tau (\epsilon )=\epsilon ^{-1}\). The most common type of these are the central Wall anti-structures, namely, those in which \(\epsilon \) is in the center and \(\tau \) is an anti-involution. Given a Wall anti-structure we can consider R as an \((R \otimes _{{\mathbb {Z}}} R)\)-module via the action \((a \otimes b)(c) = ab\tau (c)\), and endow it with an involution given by \(x \mapsto \epsilon \tau (x)\). Applying the Eilenberg–Mac Lane functor this results in an invertible k-module with involution over the \({\text {E} _1}\)-ring spectrum \(\text {H} R\), whose underlying \(\text {H} R\)-module is \(\text {H} R\), but which is generally not the one associated to any anti-involution on \(\text {H} R\).
The following lemma gives a recognition criterion for k-modules with involution over A which come from anti-involutions of A. Essentially, it reflects the idea that the datum of an anti-involution on A is equivalent to that of a perfect duality \(\text {D} :{\text {Mod}}^{\omega }_{A} \rightarrow ({\text {Mod}}^{\omega }_{A})^{\text {op} }\) together with a symmetric Poincaré form \(u \in {\text {hom}}_A(A,\text {D} (A))^{{{\text {hC} }_{\textrm{2}}}}\) on the A-module A:
Proposition 3.1.14
Let A be an \({\text {E} _1}\)-algebra and M a k-module with involution over A. Then M comes from an anti-involution on A as in Example 3.1.9 if and only if there exists a \({{\text {C} }_{\textrm{2}}}\)-equivariant map of spectra \(u:{\mathbb {S}}\rightarrow M\) (where \({{\text {C} }_{\textrm{2}}}\)-acts trivially on \({\mathbb {S}}\)) such that the induced A-module map \(A \rightarrow M\) (using, say the first A-action on M), is an equivalence. In this case, the anti-involution on A can be recovered via the map \(A \rightarrow {\text {hom}}_A(M,M) \simeq {\text {hom}}_A(A,A) = A^{\text {op} }\) associated to the second A-action on M.
The proof of Proposition 3.1.14 will require some preparation. Given a stable \(\infty \)-category \({\mathcal {C}}\), the formation of mapping spectra allows one to consider \({\mathcal {C}}\) as an \(\infty \)-category enriched in spectra, see [22, Example 7.4.14]. This enrichment is functorial in \({\mathcal {C}}\), that is, it can be organised into a functor
where the latter is the \(\infty \)-category of \({{\mathcal {S}}{p}}\)-enriched \(\infty \)-categories, see [14, Proposition 4.10] (and [26, Theorem 1.1] for the comparison of the model categorical and \(\infty \)-categorical approaches to spectrally enriched categories). The functor (63) is in fact fully-faithful and exhibits \(\text {Cat} _\infty ^\text {ex} \) as an accessible localisation of \(\text {Cat} _{{{\mathcal {S}}{p}}}\) by the collection of triangulated equivalences, see [14, Theorem 4.22].
Remark 3.1.15
Every spectrally enriched \(\infty \)-category has an “underlying \(\infty \)-category” obtained by applying the functor \(\Omega ^{\infty } = {\text {Map}}({\mathbb {S}},-):{{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\) to all mapping spectra. In particular, the underlying \(\infty \)-category of the spectrally enriched category \({\mathcal {C}}_{{{\mathcal {S}}{p}}}\) is just \({\mathcal {C}}\) itself (or rather, its image in \(\text {Cat} _\infty \)). More formally, the functor (63) constitutes a lift of the inclusion \(\text {Cat} _\infty ^\text {ex} \hookrightarrow \text {Cat} _\infty \) along the underlying \(\infty \)-category functor \(\text {Cat} _{{{\mathcal {S}}{p}}}\rightarrow \text {Cat} _\infty \).
Let \(\text {Cat} ^\text {ex} _{\infty ,*}:= \text {Cat} _\infty ^\text {ex} \times _{\text {Cat} _\infty } (\text {Cat} _\infty )_{\Delta ^0/}\) denote the \(\infty \)-category of stable \(\infty \)-categories \({\mathcal {C}}\) equipped with a distinguished object \(x\in {\mathcal {C}}\), and similarly, let \(\text {Cat} _{{{\mathcal {S}}{p}},*}= \text {Cat} _{{{\mathcal {S}}{p}}}\times _{\text {Cat} _\infty } (\text {Cat} _\infty )_{\Delta ^0/}\) denote the \(\infty \)-category of spectrally enriched categories equipped with a distinguished object. Then we may consider the composite
where the first functor is induced from (63) and the second is the functor of [22, Theorem 6.3.2(iii)], which can be described on objects as sending a pointed spectrally enriched category \(({\mathcal {D}},x)\) to the endomorphism spectrum \({\text {Map}}_{{\mathcal {D}}}(x,x)\). As shown in loc. cit. this functor has a fully-faithful left adjoint \(\text {B} :\text {Alg} _{{\text {E} _1}} \rightarrow \text {Cat} _{{{\mathcal {S}}{p}},*}\) which sends a ring spectrum A to the pointed spectrally enriched category \((\text {B} A,x)\) containing a single object \(x\) whose endomorphism ring is A. The essential image of \(\text {B} \) is then given by those pointed spectrally enriched categories \(({\mathcal {D}},x)\) for which \(x\) is the only object up to equivalence.
Proposition 3.1.16
Let  be a Poincaré \(\infty \)-category and \((x,q)\) a Poincaré object in \({\mathcal {C}}\). Then the image \({\text {hom}}_{{\mathcal {C}}}(x,x) \in \text {Alg} _{{\text {E} _1}}\) of \(({\mathcal {C}},x)\) under (64) inherits a canonical anti-involution, that it, it lifts to an object of \(\text {Alg} _{{\text {E} _1}}^{h{{\text {C} }_{\textrm{2}}}}\).
be a Poincaré \(\infty \)-category and \((x,q)\) a Poincaré object in \({\mathcal {C}}\). Then the image \({\text {hom}}_{{\mathcal {C}}}(x,x) \in \text {Alg} _{{\text {E} _1}}\) of \(({\mathcal {C}},x)\) under (64) inherits a canonical anti-involution, that it, it lifts to an object of \(\text {Alg} _{{\text {E} _1}}^{h{{\text {C} }_{\textrm{2}}}}\).
Proof
We first note that the spectral enrichment functor (63) commutes with taking opposites. Indeed, since (63) is fully-faithful and its essential image, spanned by the pre-triangulated spectrally enriched categories, is closed under opposites, the \(\text {op} \) action on \(\text {Cat} _{{{\mathcal {S}}{p}}}\) induces a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Cat} _\infty ^\text {ex} \). This action then coincides with the action induced by the inclusion of \(\text {Cat} _\infty ^\text {ex} \) in \(\text {Cat} _\infty \) by Remark 3.1.15 and the fact that the underlying \(\infty \)-category functor \(\text {Cat} _{{{\mathcal {S}}{p}}}\rightarrow \text {Cat} _\infty \) visibly commutes with opposites since it is induced by a functor \({{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\) on the level of enriching \(\infty \)-categories.
Now since \(\Delta ^0 \simeq (\Delta ^0)^{\text {op} }\) via an essentially unique isomorphism the \(\text {op} \) action on \(\text {Cat} _\infty ^\text {ex} \) induces a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Cat} ^\text {ex} _{\infty ,*}\), which can be described on objects by the formula \(({\mathcal {C}},x)\mapsto ({\mathcal {C}}^{\text {op} },x)\). Similarly, the \(\text {op} \) action on \(\text {Cat} _{{{\mathcal {S}}{p}}}\) induces a \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Cat} _{{{\mathcal {S}}{p}},*}\). In addition, the endomorphism functor \(\text {Cat} _{{{\mathcal {S}}{p}},*}\rightarrow \text {Alg} _{{\text {E} _1}}\) in (64) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the \(\text {op} \) actions on both sides, as can be seen by the fact that it admits a fully-faithful right adjoint \(\text {B} :\text {Alg} _{{\text {E} _1}} \rightarrow \text {Cat} _{{{\mathcal {S}}{p}},*}\) which is itself compatible with taking opposites essentially by construction. Now consider the diagram

in which both arrows are \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the \(\text {op} \) action. The perfect duality  promotes \({\mathcal {C}}\) to a \({{\text {C} }_{\textrm{2}}}\)-fixed object of \(\text {Cat} _\infty ^\text {ex} \) (see (27)). The fibre of \(\text {Cat} ^\text {ex} _{\infty ,*}\rightarrow \text {Cat} _\infty ^\text {ex} \) over \({\mathcal {C}}\) can be identified with \(\iota {\mathcal {C}}\), with its \({{\text {C} }_{\textrm{2}}}\)-action induced by
promotes \({\mathcal {C}}\) to a \({{\text {C} }_{\textrm{2}}}\)-fixed object of \(\text {Cat} _\infty ^\text {ex} \) (see (27)). The fibre of \(\text {Cat} ^\text {ex} _{\infty ,*}\rightarrow \text {Cat} _\infty ^\text {ex} \) over \({\mathcal {C}}\) can be identified with \(\iota {\mathcal {C}}\), with its \({{\text {C} }_{\textrm{2}}}\)-action induced by  . To finish the proof it will suffice to show that \(x\in \iota {\mathcal {C}}\) refines to a \({{\text {C} }_{\textrm{2}}}\)-fixed point. Indeed, this now follows from Corollary 2.2.10. \(\square \)
. To finish the proof it will suffice to show that \(x\in \iota {\mathcal {C}}\) refines to a \({{\text {C} }_{\textrm{2}}}\)-fixed point. Indeed, this now follows from Corollary 2.2.10. \(\square \)
Proof of Proposition 3.1.14
The only if direction is clear, since any anti-involution on A preserves the unit map \(u :{\mathbb {S}}\rightarrow A\). To prove the other direction, suppose that M is a k-module with involution over A and we are given a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \(u:{\mathbb {S}}\rightarrow M\) with respect to the trivial \({{\text {C} }_{\textrm{2}}}\)-action on \({\mathbb {S}}\), such that the induced A-module map \(A \rightarrow M\) is an equivalence. Since u is \({{\text {C} }_{\textrm{2}}}\)-invariant it follows that this condition holds for both the first and second A-actions. On the other hand, it also holds for the \(A^{\text {op} }\)-action on A that the analogously defined map is an equivalence. The corresponding statement also holds for the \({\text {hom}}_A(M,M)\)-action on M. We hence obtain a commutative diagram

in which both vertical maps (induced by the base point \(u:{\mathbb {S}}\rightarrow M\)) are equivalences, and the bottom horizontal map is the involution on M. It then follows that the top horizontal map \(A \rightarrow {\text {hom}}_A(M,M)\) is an equivalence as well. In particular, M is invertible and hence the induced bilinear functor on \({\text {Mod}}^{\omega }_{A}\) is perfect by Lemma 3.1.6, with associated duality \(X \mapsto {\text {hom}}_A(X,M)\) on \({\text {Mod}}^{\omega }_{A}\). The \({{\text {C} }_{\textrm{2}}}\)-equivariant map \(u:{\mathbb {S}}\rightarrow M\) then determines a form

which is Poincaré by the condition that the induced map \(A \rightarrow M = \text {D} (A)\) is an equivalence. We may then identify the top horizontal equivalence in (65) as the underlying equivalence of the anti-involution on \({\text {hom}}_A(A,A) = {\text {hom}}_A(\text {D} (A),\text {D} (A))^{\text {op} }\) induced by the Poincaré form \(q_u\) by Proposition 3.1.16. \(\square \)
4.2 Modules with genuine involution
Our goal in this section is to refine the definition of a k-module with involution studied in Sect. 3.1 above in order to obtain a notion capable of encoding not just bilinear but also quadratic functors on \({\text {Mod}}^{\omega }_{A}\), and similarly on \({\text {Mod}}^c_A\) for a given subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\). To begin, recall that for a spectrum X there is a canonical map \(X \rightarrow (X \otimes _{{\mathbb {S}}} X)^{{{\text {tC} }_{\textrm{2}}}}\), known as the Tate diagonal, which enjoys a variety of favourable formal properties, see [53]. If X is now a k-module then we can consider the composite map
where the second map is induced by the lax monoidal structure of the forgetful functor \({\text {Mod}}_k \rightarrow {{\mathcal {S}}{p}}\). For \(X=k\) the map (66) gives the composite map
which is known as the Tate Frobenius map. For a k-module spectrum X we may then consider the spectrum \((X \otimes _k X)^{{{\text {tC} }_{\textrm{2}}}}\), which is naturally a \(k^{{{\text {tC} }_{\textrm{2}}}}\)-module, as a k-module spectrum, by restricting structure along the Tate Frobenius. With this k-module structure the map (66) becomes k-linear, and we will henceforth refer to it as the k-linear Tate diagonal.
Remark 3.2.1
The functor \(\text {id} :{{\mathcal {S}}{p}}\rightarrow {{\mathcal {S}}{p}}\) is stably corepresented by \({\mathbb {S}}\), and so for any exact functor \(F:{{\mathcal {S}}{p}}\rightarrow {{\mathcal {S}}{p}}\), the space of natural transformations \(\text {id} \Rightarrow F\) identifies, via evaluation at \({\mathbb {S}}\), with the space \(\Omega ^{\infty } F({\mathbb {S}})\) of maps \({\mathbb {S}}\rightarrow F({\mathbb {S}})\). Under this identification, the Tate diagonal \(\text {id} \Rightarrow ((-) \otimes (-))^{{{\text {tC} }_{\textrm{2}}}}\) corresponds to the image in \(\Omega ^{\infty }[{\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}]\) of the unit \(e \in [\Omega ^{\infty }{\mathbb {S}}]^{{{\text {hC} }_{\textrm{2}}}} = \Omega ^{\infty }[{\mathbb {S}}^{{{\text {hC} }_{\textrm{2}}}}]\) (where we consider \(\Omega ^{\infty }{\mathbb {S}}= {\text {Map}}({\mathbb {S}},{\mathbb {S}})\) as a monoid with respect to composition, and the \({{\text {C} }_{\textrm{2}}}\)-equivariant structure, as the \({{\text {C} }_{\textrm{2}}}\)-action on \({\mathbb {S}}\), is constant). On the other hand, the functor \(\Omega ^{\infty }:{{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\) is the space valued functor corepresented by \({\mathbb {S}}\), and hence natural transformations \(\Omega ^{\infty } \Rightarrow G\) identify with maps \(*\rightarrow G({\mathbb {S}})\) for any functor \(G :{{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\). The point \(e \in [\Omega ^{\infty }{\mathbb {S}}]^{{{\text {hC} }_{\textrm{2}}}}\) then determines a factorization of \(\Omega ^{\infty }\Delta :\Omega ^{\infty }(-) \Rightarrow \Omega ^{\infty }[((-) \otimes (-))^{{{\text {tC} }_{\textrm{2}}}}]\) as
Furthermore, since e is a monoid unit it lifts along \(\Omega ^{\infty }{\mathbb {S}}\times \Omega ^{\infty }{\mathbb {S}}\rightarrow \Omega ^{\infty }{\mathbb {S}}\) to the point (e, e), and this can be done also on the level of \({{\text {C} }_{\textrm{2}}}\)-homotopy fixed points where \({{\text {C} }_{\textrm{2}}}\) acts on the domain by flipping the components. We conclude that the above factorization of \(\Omega ^{\infty }\Delta :\Omega ^{\infty }(-) \Rightarrow \Omega ^{\infty }[((-) \otimes (-))^{{{\text {tC} }_{\textrm{2}}}}]\) refines to a factorization
where the first map is simply the \({{\text {C} }_{\textrm{2}}}\)-equivariant diagonal. We will use this observation in the proof of Lemma 67 below.
Warning 3.2.2
Since k is the unit of \({\text {Mod}}_k\) the flip \({{\text {C} }_{\textrm{2}}}\)-action on \(k \otimes _k k \simeq k\) is trivial. However, the Tate Frobenius \(k \rightarrow k^{{{\text {tC} }_{\textrm{2}}}}\) is generally not equivalent to the composite \(k \rightarrow k^{{{\text {hC} }_{\textrm{2}}}} \rightarrow k^{{{\text {tC} }_{\textrm{2}}}}\). In particular, if we were to endow \((X \otimes _k X)^{{{\text {tC} }_{\textrm{2}}}}\) with the k-module structure restricted from its \(k^{{{\text {tC} }_{\textrm{2}}}}\)-module structure along \(k \rightarrow k^{{{\text {hC} }_{\textrm{2}}}} \rightarrow k^{{{\text {tC} }_{\textrm{2}}}}\) (which would be the k-module structure we would obtain by applying to \(X \otimes _k X\) the Tate construction internally in \({\text {Mod}}_k\)) then (66) would generally not be k-linear.
Definition 3.2.3
Let A be a \({\text {E} _1}\)-algebra. A module with genuine involution over A is a triple \((M,N,\alpha )\) which consists of
-
a k-module with involution M over A in the sense of Definition 3.1.1,
-
an A-module N, and
-
an A-linear map \(f:N \rightarrow M^{{{\text {tC} }_{\textrm{2}}}}\)
Here we view \(M^{{{\text {tC} }_{\textrm{2}}}}\), which is canonically an \((A\otimes _k A)^{{{\text {tC} }_{\textrm{2}}}}\)-module, as an A-module through the k-linear Tate diagonal \(A \rightarrow (A\otimes _k A)^{{{\text {tC} }_{\textrm{2}}}}\).
Remark 3.2.4
When \(k={\mathbb {S}}\) the data of a module with genuine involution over A can equivalently be described as a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum equipped with an action of the Hill–Hopkins–Ravenel norm \(\text {N} A\) of A, first introduced in [31] and later reinterpreted from the \(\infty \)-categorical perspective in [11]. The genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum \(\text {N} A\) has as underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum \(A\otimes _{{\mathbb {S}}} A\) with the flip \({{\text {C} }_{\textrm{2}}}\)-action, geometric fixed points A, and reference map \(A \rightarrow (A\otimes _{{\mathbb {S}}} A)^{{{\text {tC} }_{\textrm{2}}}}\) the Tate-diagonal considered in [53]. It is an algebra object with respect to the symmetric monoidal structure on genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, and the data of a module over this algebra object consists exactly of an \((A\otimes _{{\mathbb {S}}} A)\)-module with \({{\text {C} }_{\textrm{2}}}\)-action (which is M in our case), a module over the geometric fixed points A (which is N in our case), and a reference map \(\alpha :N \rightarrow M^{{{\text {tC} }_{\textrm{2}}}}\) refining M to a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum with geometric fixed points N.
More generally, for an arbitrary base \({\text {E} _\infty }\)-ring spectrum k and \({\text {E} _1}\)-algebra A over k, the notion of a k-module with genuine involution over A is equivalent to that of a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum equipped with an action of the k-linear norm \(\text {N} _k A\) of A: this is the genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum whose underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum is \(A\otimes _k A\) with the flip \({{\text {C} }_{\textrm{2}}}\)-action, whose geometric fixed point spectrum is A, and whose reference map \(A \rightarrow (A\otimes _k A)^{{{\text {tC} }_{\textrm{2}}}}\) is the k-linear Tate-diagonal mentioned above.
Lemma 3.2.5
For \(M \in {\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) and \(X \in {\text {Mod}}^{\omega }_{A}\) there is an equivalence
natural in M and X.
Proof
Consider the functor \(F:({\text {Mod}}^{\omega }_{A})^{^{\text {op} }} \rightarrow {{\mathcal {S}}{p}}\) given by \(X \mapsto {\text {hom}}_{A \otimes _k A}(X \otimes _k X,M)^{{{\text {tC} }_{\textrm{2}}}}\). This functor is exact, thus by Morita theory it is of the form \({\text {hom}}_A(X, N)\) for some A-module N. Setting \(X = A\) we find that \(N = M^{{{\text {tC} }_{\textrm{2}}}}\) as a spectrum. Furthermore, the right action of \(\Omega ^\infty A\) on A translates under the functor F to the diagonal action of \(\Omega ^\infty A\) on \(M^{{{\text {tC} }_{\textrm{2}}}}\), i.e., the action through the composite
which at the same time also underlines the k-linear Tate diagonal by Remark 3.2.1. Applying the same observation to shifts of A and using exactness then fully identifies the A-module structure on \(M^{{{\text {tC} }_{\textrm{2}}}}\), showing the claim. \(\square \)
Construction 3.2.6
Let \((M,N,\alpha )\) be a k-module with genuine involution over A. We define a quadratic functor  on perfect A-modules by the pullback
on perfect A-modules by the pullback

where the lower horizontal map is given by the composite

where the last equivalence is via Lemma 3.2.5.
By construction the underlying bilinear part of  is \(\text {B} _M\), and hence the condition that
is \(\text {B} _M\), and hence the condition that  is Poincaré depends only on M, via the criterion of Proposition 3.1.6. In addition, by Lemma 1.1.10 the trace map
is Poincaré depends only on M, via the criterion of Proposition 3.1.6. In addition, by Lemma 1.1.10 the trace map  factors canonically as
factors canonically as

If \(M^{{{\text {tC} }_{\textrm{2}}}}=0\), for example if A is an \({\mathbb {S}}[\tfrac{1}{2}]\)-algebra, then  .
.
Example 3.2.7
Let M be a k-module with involution over an \({\text {E} _1}\)-algebra A. The k-modules with genuine involution \((M,0,0\rightarrow M^{{{\text {tC} }_{\textrm{2}}}})\) and \((M,M^{{{\text {tC} }_{\textrm{2}}}}, M^{{{\text {tC} }_{\textrm{2}}}}=M^{{{\text {tC} }_{\textrm{2}}}})\) give rise respectively to the quadratic and symmetric functors  and
and  of Definition 3.1.2.
of Definition 3.1.2.
Example 3.2.8
Let M be a k-module with involution over an \({\text {E} _1}\)-algebra A and assume that A is connective (so that the truncation of an A-module admits a canonical A-module structure). Then there is for every \(m \in {\mathbb {Z}}\) a k-module with genuine involution given by
with the reference map being the m-connective cover. Applying Construction 3.2.6 these give rise to quadratic functors  that sit between the quadratic and the symmetric one, i.e., there are maps
that sit between the quadratic and the symmetric one, i.e., there are maps

If \(M^{{{\text {tC} }_{\textrm{2}}}}\) vanishes, e.g. if 2 is invertible in A, then all of these maps are equivalences. The limit and colimit of these diagrams of Poincaré structures are given by

and

Indeed, inspecting the defining pullback squares (68) for  and using that pullbacks and mapping spectra out of compact A-modules respect both limits and colimits this follows from the fact that \(\lim \tau _{\ge m} M^{{{\text {tC} }_{\textrm{2}}}} = 0\) while the induced map \(\mathop {{\text {colim} }}\tau _{\ge m} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M^{{{\text {tC} }_{\textrm{2}}}}\) is an equivalence. We may hence consider the tower (69) as interpolating between the quadratic and symmetric Poincaré structures on \({\text {Mod}}^{\omega }_{A}\). We will study this construction in further detail in Sect. 4.2 in the case where A is (the Eilenberg–Mac Lane spectrum of) an ordinary ring.
and using that pullbacks and mapping spectra out of compact A-modules respect both limits and colimits this follows from the fact that \(\lim \tau _{\ge m} M^{{{\text {tC} }_{\textrm{2}}}} = 0\) while the induced map \(\mathop {{\text {colim} }}\tau _{\ge m} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M^{{{\text {tC} }_{\textrm{2}}}}\) is an equivalence. We may hence consider the tower (69) as interpolating between the quadratic and symmetric Poincaré structures on \({\text {Mod}}^{\omega }_{A}\). We will study this construction in further detail in Sect. 4.2 in the case where A is (the Eilenberg–Mac Lane spectrum of) an ordinary ring.
Example 3.2.9
Let A be a \({\text {E} _1}\)-algebra with anti-involution. In Example 3.1.9 we have seen that A can be considered as an invertible k-module with involution over itself. In order to promote A to a k-module with genuine involution we need an A-module N and a map \(N \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) of A-modules. Such a triple \((A,N,\alpha )\) is called an \({\text {E} _1}\)-algebra with genuine anti-involution. Any such \({\text {E} _1}\)-algebra with genuine anti-involution has an underlying genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum, the module N taking the role of the geometric fixed points. Since A is invertible as a k-module with involution by Proposition 3.1.6 and Remark 3.1.7 imply that the associated hermitian structure  on \({\text {Mod}}^{\omega }_{A}\) and on \(\text {Mod} ^{\text {f} }_{A}\) are both Poincaré.
on \({\text {Mod}}^{\omega }_{A}\) and on \(\text {Mod} ^{\text {f} }_{A}\) are both Poincaré.
Example 3.2.10
Let A be an orthogonal ring spectrum with anti-involution in the sense of [20]. This gives rise to a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum whose underlying spectrum with \({{\text {C} }_{\textrm{2}}}\)-action is the underlying spectrum of A, whose geometric fixed points \(A^{{\varphi {{\text {C} }_{\textrm{2}}}}}\) is canonically an A-module, and where the map \(\alpha :A^{{\varphi {{\text {C} }_{\textrm{2}}}}} \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) is A-linear. We therefore obtain a ring spectrum with genuine anti-involution \((A,A^{{\varphi {{\text {C} }_{\textrm{2}}}}},\alpha )\).
Example 3.2.11
Consider the sphere spectrum \({\mathbb {S}}\) with the trivial \({{\text {C} }_{\textrm{2}}}\)-action. We may then view \({\mathbb {S}}\) as an associative ring spectrum with anti-involution, and refine it to a ring spectrum with genuine anti-involution using as reference map the composite \({\mathbb {S}}\rightarrow {\mathbb {S}}^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}\), which also agrees in this case with the Tate diagonal. The Poincaré structure associated to this genuine anti-involution on \({\mathbb {S}}\) is the universal Poincaré structure  of Example 1.2.15.
of Example 1.2.15.
Example 3.2.12
Let A be an \({\text {E} _\infty }\)-k-algebra equipped with a \({{\text {C} }_{\textrm{2}}}\)-action. We may then view A as an associative k-algebra with anti-involution, and refine it to a k-algebra with genuine anti-involution using as reference map the composite
where the first map is the k-linear Tate diagonal and the second map is induced by the \({{\text {C} }_{\textrm{2}}}\)-equivariant commutative k-algebra map \(A \otimes _k A \rightarrow A\) whose restriction to the first component is the identity \(A \rightarrow A\) and restriction to the second component is given by the generator of the \({{\text {C} }_{\textrm{2}}}\)-action. This yields a Poincaré structure on \({\text {Mod}}^{\omega }_{A}\), which we denote by  , and refer to as the Tate Poincaré structure associated to the given \({{\text {C} }_{\textrm{2}}}\)-action. The universal Poincaré structure
, and refer to as the Tate Poincaré structure associated to the given \({{\text {C} }_{\textrm{2}}}\)-action. The universal Poincaré structure  on \({{\mathcal {S}}{p}}^{\text {f} }\) then corresponds to the case where \(A=k={\mathbb {S}}\) and the \({{\text {C} }_{\textrm{2}}}\)-action is trivial.
on \({{\mathcal {S}}{p}}^{\text {f} }\) then corresponds to the case where \(A=k={\mathbb {S}}\) and the \({{\text {C} }_{\textrm{2}}}\)-action is trivial.
Example 3.2.13
Given an \({\text {E} _1}\)-algebra A we may form the \({\text {E} _1}\)-algebra with anti-involution \(A \oplus A^{\text {op} }\) where the involution flips the two factors. We may then refine this involution to a genuine one by taking the zero map \(0 \rightarrow (A \oplus A^{\text {op} })^{{{\text {tC} }_{\textrm{2}}}} = 0\), which at the same time is also an equivalence. The resulting Poincaré structure  on \({\text {Mod}}^{\omega }_{A \oplus A^{\text {op} }}\) is then both quadratic and symmetric (see Example 3.2.7). We now note that the projections \(A \oplus A^{\text {op} }\rightarrow A\) and \(A \oplus A^{\text {op} }\rightarrow A^{\text {op} }\) induce an equivalence
on \({\text {Mod}}^{\omega }_{A \oplus A^{\text {op} }}\) is then both quadratic and symmetric (see Example 3.2.7). We now note that the projections \(A \oplus A^{\text {op} }\rightarrow A\) and \(A \oplus A^{\text {op} }\rightarrow A^{\text {op} }\) induce an equivalence
under which the Poincaré structure in question corresponds to the hyperbolic structure of Definition 2.2.2, and so

4.3 Classification of hermitian structures
We shall henceforth focus on the case where \(k={\mathbb {S}}\) is the sphere spectrum. We will show that in this case, modules with genuine involution do not only provide a convenient way of producing hermitian structures on \({\text {Mod}}_{A}^\omega \) but that these two notions become in fact equivalent. To formulate this more precisely, we proceed to organise modules with genuine involution over A into an \(\infty \)-category \({\text {Mod}}_{\text {N} A}\), defined as the pullback

of the arrow category \({\text {Ar}}({\text {Mod}}_A)\) and the \(\infty \)-category \(({\text {Mod}}_{A\otimes _{{\mathbb {S}}} A})^{{{\text {hC} }_{\textrm{2}}}}\) of modules with involution. The right vertical map is the projection onto the target, and the bottom horizontal map sends a module with involution M to the Tate construction \(M^{{{\text {tC} }_{\textrm{2}}}}\), considered as an A-module via the Tate diagonal map \(A\rightarrow (A\otimes _{{\mathbb {S}}} A)^{{{\text {tC} }_{\textrm{2}}}}\).
We would like to relate \({\text {Mod}}_{\text {N} A}\) and \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) by constructing a commutative diagram

where the front square is the pullback square of Corollary 1.3.12 which exhibits the analogous decomposition of the \(\infty \)-category of quadratic functors \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) into linear and bilinear parts. We then define the right face of (71) to be the square induced by the Yoneda map
and the bottom arrow in the left face is the functor
introduced above. The commuting homotopy in the bottom square of (71) is then provided by Lemma 3.2.5. The cube is then uniquely determined by the fact that its front face is a cartesian square.
Theorem 3.3.1
The cube (71), considered as a natural transformation from its back face to its front face, is an equivalence. In particular, the resulting arrow
is an equivalence of \(\infty \)-categories, whose action on objects is given by  .
.
Remark 3.3.2
For a general k one can still define the pullback of \(\infty \)-categories
and construct a functor
which in general will not be an equivalence. Here we use the notation \({\text {Mod}}_{\text {N} _k A}\) to indicate that we may think of this as the \(\infty \)-category of modules in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra over the k-linear norm \(\text {N} _k A\) of A, see Remark 3.2.4. Alternatively, we may also identify \({\text {Mod}}_{\text {N} _k A}\) with the \(\infty \)-category of hermitian structures on \({\text {Mod}}^{\omega }_{A}\) equipped with an action of the Tate hermitian structure  of Example 3.2.12. Here we have that \({\text {Mod}}^{\omega }_{k}\) acts on \({\text {Mod}}^{\omega }_{A}\) by the fact that A is a k-algebra, and this induces an action of \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{k})\) on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) by means of Day convolution, see Sect. 5.3 and Example 5.4.13. The functor (72) then corresponds to forgetting the
of Example 3.2.12. Here we have that \({\text {Mod}}^{\omega }_{k}\) acts on \({\text {Mod}}^{\omega }_{A}\) by the fact that A is a k-algebra, and this induces an action of \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{k})\) on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) by means of Day convolution, see Sect. 5.3 and Example 5.4.13. The functor (72) then corresponds to forgetting the  -module structure.
-module structure.
Proof of Theorem 3.3.1
Since the back and front faces are both cartesian squares it will suffice to show that its right and back faces determine equivalences from their back edge to their front edge. For this, it will suffice to show that the functors
are equivalences. For the former, we note that since \({{\mathcal {S}}{p}}\) is stable we have that post-composition with \(\Omega ^{\infty }:{{\mathcal {S}}{p}}\rightarrow {\mathcal {S}}\) induces an equivalence
and consequently the claim follows from the fact that \({\text {Mod}}_A\) is generated by \({\text {Mod}}^{\omega }_{A}\) under colimits. For the second map, by its construction it will suffice to show that the functor
is an equivalence of \(\infty \)-categories. For this, recall that by [47, Theorem 4.8.5.16] and [47, Remark 4.8.5.19] the association \(A \mapsto {\text {Mod}}_A\) refines to a symmetric monoidal functor
from \({\text {E} _1}\)-ring spectra to the \(\infty \)-category of \({{\mathcal {S}}{p}}\)-modules in presentable \(\infty \)-categories, and the latter can be identified with the full subcategory of \(\text {Pr} ^{\text {L} }\) spanned by the stable presentable \(\infty \)-categories. In particular, the bilinear functor
induces an equivalence
where \(\otimes _{{{\mathcal {S}}{p}}}\) denotes the tensor product of stable presentable \(\infty \)-categories (which can also be viewed as \({{\mathcal {S}}{p}}\)-modules in presentable \(\infty \)-categories). Since \({\text {Mod}}_A\) and \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}\) are compactly generated by \({\text {Mod}}^{\omega }_{A}\) and \({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} A}\) respectively and the bilinear functor \((X,Y) \mapsto X \otimes _{{\mathbb {S}}} Y\) maps a pair of compact A-modules to a compact \((A \otimes _{{\mathbb {S}}} A)\)-module we see that the equivalence (74) is induced on Ind-categories by the functor
induced by the same bilinear functor \((X,Y) \mapsto X \otimes _{{\mathbb {S}}} Y\), where \(\otimes \) is the tensor product of stable \(\infty \)-categories, and we use the fact that \({\text {Ind}}(-)\) is symmetric monoidal. It then follows that restriction along (75) induces an equivalence
Since the Yoneda map \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A} \rightarrow {\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} A})^{\text {op} },{{\mathcal {S}}{p}})\) is an equivalence by the argument above we may now conclude that (73) is an equivalence, and so the proof is complete. \(\square \)
Remark 3.3.3
As explained in the introduction of the present section, left Kan extension and restriction determine inverse equivalences between \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^c_A)\) and \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) for every subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\). Theorem 3.3.1 then implies that the association  also determines an equivalence \({\text {Mod}}_{\text {N} A} \simeq {\text {Fun}}^{\textrm{q}}({\text {Mod}}^c_A)\) for every \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\).
also determines an equivalence \({\text {Mod}}_{\text {N} A} \simeq {\text {Fun}}^{\textrm{q}}({\text {Mod}}^c_A)\) for every \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\).
Remark 3.3.4
It follows from Theorem 3.3.1 and Proposition 3.1.6 that the association  determines a bijective correspondence between equivalence classes of invertible modules with genuine involution \((M,N,\alpha ) \in {\text {Mod}}_{\text {N} A}\) and equivalence classes of Poincaré structures on \({\text {Mod}}^{\omega }_{A}\). More generally, for a given subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) we obtain a classification of Poincaré structures on \({\text {Mod}}^c_A\) via invertible modules with genuine involution \((M,N,\alpha )\) such that the associated duality \(\text {D} _M = {\text {hom}}_A(-,M)\) on \({\text {Mod}}^{\omega }_{A}\) preserves \({\text {Mod}}^c_A\) (or, equivalently, preserves \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\)). In the case of \(\text {Mod} ^{\text {f} }_{A}\) the last condition amounts to M itself being in \(\text {Mod} ^{\text {f} }_{A}\), see Remark 3.1.7. We note that under these correspondences maps of Poincaré structures (see Definition 1.2.8) correspond to those maps \((M,N,\alpha ) \rightarrow (M',N',\alpha ')\) in \({\text {Mod}}_{\text {N} A}\) for which the map \(M \rightarrow M'\) is an equivalence.
determines a bijective correspondence between equivalence classes of invertible modules with genuine involution \((M,N,\alpha ) \in {\text {Mod}}_{\text {N} A}\) and equivalence classes of Poincaré structures on \({\text {Mod}}^{\omega }_{A}\). More generally, for a given subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) we obtain a classification of Poincaré structures on \({\text {Mod}}^c_A\) via invertible modules with genuine involution \((M,N,\alpha )\) such that the associated duality \(\text {D} _M = {\text {hom}}_A(-,M)\) on \({\text {Mod}}^{\omega }_{A}\) preserves \({\text {Mod}}^c_A\) (or, equivalently, preserves \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\)). In the case of \(\text {Mod} ^{\text {f} }_{A}\) the last condition amounts to M itself being in \(\text {Mod} ^{\text {f} }_{A}\), see Remark 3.1.7. We note that under these correspondences maps of Poincaré structures (see Definition 1.2.8) correspond to those maps \((M,N,\alpha ) \rightarrow (M',N',\alpha ')\) in \({\text {Mod}}_{\text {N} A}\) for which the map \(M \rightarrow M'\) is an equivalence.
4.4 Restriction and induction
In the present subsection we keep the assumption that \(k = {\mathbb {S}}\) and consider the functorial dependence of \({\text {Mod}}_{\text {N} A}\) in A, and the compatibility of this functoriality with the one for hermitian structures along the equivalence of Theorem 3.3.1. Let \(\phi :A \rightarrow B\) be a map of \({\text {E} _1}\)-algebras and let
be the induction functor sending X to \(B \otimes _A X\). Then the restriction functor
corresponds, under the equivalence of Theorem 3.3.1, to a functor
which we consider as the restriction of structure operation for modules with genuine involution. As explained in Sect. 1.3, restriction of quadratic functors commutes with taking linear and bilinear parts and with the formation of symmetric Poincaré structures, that is, it acts compatibly on the entire pullback square

Under the equivalence of Theorem 3.3.1 we obtain the same for the restriction functor (77), that is, it extends to the entire defining squares (70) for A and B. On the other hand, the Yoneda equivalences \({\text {Mod}}_A \simeq {\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^{\omega }_{A})^{\text {op} },{{\mathcal {S}}{p}})\) and \({\text {Mod}}_{B} \simeq {\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^{\omega }_{B})^{\text {op} },{{\mathcal {S}}{p}})\) fit into a commutative square

in which the top horizontal arrow is the forgetful functor from B-modules to A-modules and the bottom horizontal functor is restriction along \(p_{\phi }\). Indeed, the commutativity is given by the adjunction equivalence \({\text {hom}}_B(p_{\phi }X,M) \simeq {\text {hom}}_A(X,\phi ^*M)\). Similarly, the equivalences \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A} \simeq {\text {Fun}}^{\textrm{b}}({\text {Mod}}^{\omega }_{A})\) and \({\text {Mod}}_{B \otimes _{{\mathbb {S}}} B} \simeq {\text {Fun}}^{\textrm{b}}({\text {Mod}}^{\omega }_{B})\) fit into a commutative square

We may thus conclude that for \((M,N,\alpha ) \in {\text {Mod}}_{\text {N} B}\) the restriction functor (77) is obtained by simply restricting the \((B \otimes _{{\mathbb {S}}} B)\)-module structure on M to \(A \otimes _{{\mathbb {S}}} A\), the B-module structure on N to A, and viewing \(\alpha \) as a map of A-modules by forgetting its compatibility with the B-module structures on its domain and codomain.
We now proceed to discuss how the operation of left Kan extension is mirrored along the equivalence of Theorem 3.3.1. Recall that by Lemma 1.4.1 the operation of left Kan extensions \({\text {Fun}}(({\text {Mod}}^{\omega }_{A})^{\text {op} },{{\mathcal {S}}{p}}) \rightarrow {\text {Fun}}(({\text {Mod}}^{\omega }_{B})^{\text {op} },{{\mathcal {S}}{p}})\) preserves quadratic functors, and the resulting functor
is compatible with taking linear and bilinear parts, that is

By Lemma 1.4.1 and Corollary 1.4.4 we may then conclude the following:
Corollary 3.4.1
Under the equivalence of Theorem 3.3.1, the left Kan extension functor (81) corresponds to the functor
sending a module with genuine involution \((M,N,\alpha ) \in {\text {Mod}}_{\text {N} A}\) to the module with genuine involution
where \(\phi _!\alpha \) is given by the composite
of \(B \otimes _A \alpha \) and the Beck–Chevalley transformation on the lax commuting square on the right

which is obtained from the commuting square on the left after replacing the vertical forgetful functors by their left adjoints \(B \otimes _A (-)\) and \((B \otimes _{{\mathbb {S}}} B) \otimes _{A \otimes _{{\mathbb {S}}} A} (-)\), respectively.
We now wish to apply the above discussion in order to obtain explicit data which permits us to refine \(p_{\phi }:{\text {Mod}}^{\omega }_{A} \rightarrow {\text {Mod}}^{\omega }_{B}\) to a hermitian functor with respect to a pair of hermitian structures coming from modules with genuine involution \((M_A,N_A,\alpha ) \in {\text {Mod}}_{\text {N} A}\) and \((M_B,N_B,\beta ) \in {\text {Mod}}_{\text {N} B}\). In terms of quadratic functors, this data is a natural transformation

Under the above equivalences, the transformation \(\eta \) corresponds to a map \((M_A,N_A,\alpha ) \rightarrow \phi ^*(M_B,N_B,\beta )\) in \({\text {Mod}}_{\text {N} A}\), or equivalently by adjunction, to a map \(\phi _!(M_A,N_A,\alpha ) \rightarrow (M_B,N_B,\beta )\). Let us summarise the situation in explicit terms as follows:
Corollary 3.4.2
Keeping the notation above, the data of a hermitian functor  covering the induction functor \(p_{\phi }\) can be encoded by a triple \((\delta ,\gamma ,\sigma )\) where \(\delta :M_A \rightarrow M_B\) and \(\gamma :N_A \rightarrow N_B\) in \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}^{{{\text {hC} }_{\textrm{2}}}}\) and \({\text {Mod}}_A\) respectively, and \(\sigma \) is a commutation homotopy in the square
covering the induction functor \(p_{\phi }\) can be encoded by a triple \((\delta ,\gamma ,\sigma )\) where \(\delta :M_A \rightarrow M_B\) and \(\gamma :N_A \rightarrow N_B\) in \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}^{{{\text {hC} }_{\textrm{2}}}}\) and \({\text {Mod}}_A\) respectively, and \(\sigma \) is a commutation homotopy in the square

Equivalently, we may provide the adjoints \(\overline{\delta }:(B \otimes _{{\mathbb {S}}} B) \otimes _{A \otimes _{{\mathbb {S}}} A}M_A \rightarrow M_B\) and \(\overline{\gamma }:B \otimes _A N_A \rightarrow N_B\) in \({\text {Mod}}_{B \otimes _{{\mathbb {S}}} B}^{{{\text {hC} }_{\textrm{2}}}}\) and \({\text {Mod}}_B\) respectively, together with a commutative square of the form

where the left lower horizontal map is the Beck–Chevalley map (82). It can also be identified with the composition of the Tate diagonal and the lax monoidal structure of \((-)^{{{\text {tC} }_{\textrm{2}}}}\).
Lemma 3.4.3
In the situation of Corollary 3.4.2, the hermitian functor

associated to a map \((\delta ,\gamma ,\sigma ):(M_A,N_A,\alpha ) \rightarrow \phi ^*(M_B,N_B,\beta )\) is Poincaré if and only if the composite
is an equivalence, where the first map is induced by the left unit \(B \rightarrow B \otimes _{{\mathbb {S}}} B\).
Proof
By definition, the hermitian functor \((p_{\varphi },\eta )\) is Poincaré if and only if the induced map
is an equivalence of B-modules for every perfect A-module X. Since \({\text {Mod}}^{\omega }_{A}\) is generated under finite colimits and retracts by A this map is an equivalence for every \(X \in {\text {Mod}}^{\omega }_{A}\) if and only if it is an equivalence for \(X = A\). But this is exactly the statement that the induced map
is an equivalence, as desired. \(\square \)
Definition 3.4.4
In the situation of Lemma 3.4.3, when the condition that the induced map \(B \otimes _A M_A \rightarrow M_B\) is an equivalence holds, we say that the morphism \((\delta ,\gamma ,\sigma )\) is \(\phi \)-invertible. In particular, Lemma 3.4.3 says that the hermitian functor induced by \((\delta ,\gamma ,\sigma )\) is Poincaré if and only if \((\delta ,\gamma ,\sigma )\) is \(\phi \)-invertible.
Example 3.4.5
Suppose that \((\phi ,\tau ):(A,N_A,\alpha ) \rightarrow (B,N_B,\beta )\) is a map of \({\text {E} _1}\)-algebras with genuine anti-involution (Example 3.2.9), so that \(\phi :A \rightarrow B\) is a map of rings with anti-involution and \(\tau :N_A\rightarrow \phi ^*N_B\) is a map of A-modules. Then both \((A,N_A,\alpha )\) and \((B,N_B,\beta )\) are invertible as modules with genuine involution over A and B respectively and \(\tau \) is \(\phi \)-invertible. In particular, in this situation we always obtain an induced Poincaré functor  .
.
Example 3.4.6
Suppose that \(\phi :A \rightarrow B\) is a map of \({\text {E} _1}\)-algebras. A module with involution \(M_A \in ({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A})^{{{\text {hC} }_{\textrm{2}}}}\) then determines a symmetric bilinear functor with associated quadratic hermitian structure  on A encoded by the module with genuine involution \((M_A,0,0\rightarrow M_A^{{{\text {tC} }_{\textrm{2}}}})\). The left Kan extension of
on A encoded by the module with genuine involution \((M_A,0,0\rightarrow M_A^{{{\text {tC} }_{\textrm{2}}}})\). The left Kan extension of  to \({\text {Mod}}^{\omega }_{B}\) is then encoded by the module with genuine involution \((M_B, 0,0 \rightarrow M_B^{{{\text {tC} }_{\textrm{2}}}})\) for \(M_B := M_A\otimes _{A\otimes _{{\mathbb {S}}} A}(B\otimes _{{\mathbb {S}}} B)\), and so
to \({\text {Mod}}^{\omega }_{B}\) is then encoded by the module with genuine involution \((M_B, 0,0 \rightarrow M_B^{{{\text {tC} }_{\textrm{2}}}})\) for \(M_B := M_A\otimes _{A\otimes _{{\mathbb {S}}} A}(B\otimes _{{\mathbb {S}}} B)\), and so

On the other hand, the associated symmetric hermitian structure  is encoded by the module with genuine involution \((M_A,M_A^{{{\text {tC} }_{\textrm{2}}}},\text {id} :M_A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M_A^{{{\text {tC} }_{\textrm{2}}}})\), and hence its left Kan extension to \({\text {Mod}}^{\omega }_{B}\) is encoded by the module with genuine involution \((M_B, B \otimes _A M_A^{{{\text {tC} }_{\textrm{2}}}}, B \otimes _A M_A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M_B^{{{\text {tC} }_{\textrm{2}}}})\), which is generally not the symmetric hermitian structure
is encoded by the module with genuine involution \((M_A,M_A^{{{\text {tC} }_{\textrm{2}}}},\text {id} :M_A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M_A^{{{\text {tC} }_{\textrm{2}}}})\), and hence its left Kan extension to \({\text {Mod}}^{\omega }_{B}\) is encoded by the module with genuine involution \((M_B, B \otimes _A M_A^{{{\text {tC} }_{\textrm{2}}}}, B \otimes _A M_A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M_B^{{{\text {tC} }_{\textrm{2}}}})\), which is generally not the symmetric hermitian structure  , unless B is perfect as an \(A^{\text {op} }\)-module (indeed, for a fixed M the underlying map of spectra \(B \otimes _A M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow (B\otimes _A M)^{{{\text {tC} }_{\textrm{2}}}}\) can be considered as a natural transformation between two exact functors in the argument \(B \in {\text {Mod}}^{\omega }_{A^{\text {op} }}\) which is an equivalence on \(B=A^{\text {op} }\) and hence on any perfect B). As a counter-example consider \({\mathbb {S}}\rightarrow {\mathbb {S}}[\frac{1}{2}]\): by Lin’s theorem [42] one has that \({\mathbb {S}}^{{\text {tC} }_{\textrm{2}}}\simeq {\mathbb {S}}^\wedge _2\) so \({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}^{{\text {tC} }_{\textrm{2}}}\simeq \text {H} {\mathbb {Q}}_2\) whereas \(({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}[\frac{1}{2}])^{{\text {tC} }_{\textrm{2}}}\simeq 0\) since 2 is invertible on \({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}[\frac{1}{2}] \simeq {\mathbb {S}}[\frac{1}{2}]\).
, unless B is perfect as an \(A^{\text {op} }\)-module (indeed, for a fixed M the underlying map of spectra \(B \otimes _A M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow (B\otimes _A M)^{{{\text {tC} }_{\textrm{2}}}}\) can be considered as a natural transformation between two exact functors in the argument \(B \in {\text {Mod}}^{\omega }_{A^{\text {op} }}\) which is an equivalence on \(B=A^{\text {op} }\) and hence on any perfect B). As a counter-example consider \({\mathbb {S}}\rightarrow {\mathbb {S}}[\frac{1}{2}]\): by Lin’s theorem [42] one has that \({\mathbb {S}}^{{\text {tC} }_{\textrm{2}}}\simeq {\mathbb {S}}^\wedge _2\) so \({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}^{{\text {tC} }_{\textrm{2}}}\simeq \text {H} {\mathbb {Q}}_2\) whereas \(({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}[\frac{1}{2}])^{{\text {tC} }_{\textrm{2}}}\simeq 0\) since 2 is invertible on \({\mathbb {S}}[\frac{1}{2}] \otimes _{\mathbb {S}}{\mathbb {S}}[\frac{1}{2}] \simeq {\mathbb {S}}[\frac{1}{2}]\).
4.5 Ranicki periodicity
In this final section we will discuss the effect of shifting Poincaré structures on module \(\infty \)-categories. In the case of ordinary rings, this is the basis for the classical 4-fold periodicity in \({\text {L}}\)-theory. To unravel the essence of this phenomenon, we introduce the notion of an \(n\sigma \)-orientation on modules with involution, and explain how it combines with shifting to yield a 2n-fold periodicity effect on the level of \({\text {L}}\)-groups. In Paper [2] we will extend these results to the level of both \({\text {L}}\)-spectra and Grothendieck-Witt spectra, yielding in particular a generalisation of Karoubi’s fundamental theorem. For the remainder of this subsection we fix an arbitrary base \({\text {E} _\infty }\)-ring k.
Recall that for a quadratic functor  on a stable \(\infty \)-category \({\mathcal {C}}\), and an integer \(n \in {\mathbb {Z}}\), we denoted by
on a stable \(\infty \)-category \({\mathcal {C}}\), and an integer \(n \in {\mathbb {Z}}\), we denoted by  the quadratic functor on \({\mathcal {C}}\) given by
the quadratic functor on \({\mathcal {C}}\) given by  (see Definition 1.2.16). Since the formation of linear and bilinear parts is exact the shifted quadratic functor
(see Definition 1.2.16). Since the formation of linear and bilinear parts is exact the shifted quadratic functor  has bilinear part
has bilinear part  , linear part
, linear part  , and structure map
, and structure map  induced by the structure map of
induced by the structure map of  on n-fold suspensions. If \({\mathcal {C}}\) is now of the form \({\text {Mod}}^{\omega }_{A}\) for some \({\text {E} _1}\)-algebra A over k and
on n-fold suspensions. If \({\mathcal {C}}\) is now of the form \({\text {Mod}}^{\omega }_{A}\) for some \({\text {E} _1}\)-algebra A over k and  for some k-module with genuine involution \((M,N,\alpha )\) over A, then
for some k-module with genuine involution \((M,N,\alpha )\) over A, then  is the quadratic functor associated to the k-module with genuine involution \((\Sigma ^n M,\Sigma ^n N,\Sigma ^n\alpha )\), and we write
is the quadratic functor associated to the k-module with genuine involution \((\Sigma ^n M,\Sigma ^n N,\Sigma ^n\alpha )\), and we write

A second natural operation we can perform on the quadratic functor  is to pre-compose it with \(\Sigma ^n\). In this case the hermitian \(\infty \)-category
is to pre-compose it with \(\Sigma ^n\). In this case the hermitian \(\infty \)-category  is canonically equivalent to
is canonically equivalent to  via the functor \(\Sigma ^n:{\text {Mod}}^{\omega }_{A} \rightarrow {\text {Mod}}^{\omega }_{A}\). However, the reparametrised quadratic functor
via the functor \(\Sigma ^n:{\text {Mod}}^{\omega }_{A} \rightarrow {\text {Mod}}^{\omega }_{A}\). However, the reparametrised quadratic functor  is also directly identified with the quadratic functor associated to another k-module with genuine involution. To determine it, let us introduce some notation. Given a finite dimensional real representation V for the group \({{\text {C} }_{\textrm{2}}}\), let us denote by \(S^V\) the associated one-point compactification of V, which is a sphere of dimension \(\dim (V)\) equipped with a based \({{\text {C} }_{\textrm{2}}}\)-action. Similarly, we will denote by \({\mathbb {S}}^{V} = \Sigma ^{\infty }(S^V)\) the associated suspension spectrum with \({{\text {C} }_{\textrm{2}}}\)-action. Given a spectrum X with a \({{\text {C} }_{\textrm{2}}}\)-action, we will denote by \(\Sigma ^V X := {\mathbb {S}}^V \otimes _{{\mathbb {S}}} X\) the smash product of \({\mathbb {S}}^{V}\) and X equipped with its diagonal \({{\text {C} }_{\textrm{2}}}\)-action. Similarly, the \(\infty \)-category \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) of k-modules with involution over A is naturally tensored over spectra with \({{\text {C} }_{\textrm{2}}}\)-action, and given a k-module with involution M over A we will denote by \(\Sigma ^VM = {\mathbb {S}}^V \otimes _{{\mathbb {S}}} M\) the associated tensor of M by \({\mathbb {S}}^V\). We will denote by \(\sigma \) the 1-dimensional sign representation of \({{\text {C} }_{\textrm{2}}}\) and \(\rho \) the 2-dimensional regular representation of \({{\text {C} }_{\textrm{2}}}\). In particular, \(\rho \) decomposes of the direct sum of a trivial representation and a sign representation, which we write as \(\rho = 1+\sigma \). More generally, we will denote by \(a + b\rho + c\sigma \) the direct sum of a copies of the 1-dimensional trivial representation, b copies of \(\rho \), and c copies of \(\sigma \).
is also directly identified with the quadratic functor associated to another k-module with genuine involution. To determine it, let us introduce some notation. Given a finite dimensional real representation V for the group \({{\text {C} }_{\textrm{2}}}\), let us denote by \(S^V\) the associated one-point compactification of V, which is a sphere of dimension \(\dim (V)\) equipped with a based \({{\text {C} }_{\textrm{2}}}\)-action. Similarly, we will denote by \({\mathbb {S}}^{V} = \Sigma ^{\infty }(S^V)\) the associated suspension spectrum with \({{\text {C} }_{\textrm{2}}}\)-action. Given a spectrum X with a \({{\text {C} }_{\textrm{2}}}\)-action, we will denote by \(\Sigma ^V X := {\mathbb {S}}^V \otimes _{{\mathbb {S}}} X\) the smash product of \({\mathbb {S}}^{V}\) and X equipped with its diagonal \({{\text {C} }_{\textrm{2}}}\)-action. Similarly, the \(\infty \)-category \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) of k-modules with involution over A is naturally tensored over spectra with \({{\text {C} }_{\textrm{2}}}\)-action, and given a k-module with involution M over A we will denote by \(\Sigma ^VM = {\mathbb {S}}^V \otimes _{{\mathbb {S}}} M\) the associated tensor of M by \({\mathbb {S}}^V\). We will denote by \(\sigma \) the 1-dimensional sign representation of \({{\text {C} }_{\textrm{2}}}\) and \(\rho \) the 2-dimensional regular representation of \({{\text {C} }_{\textrm{2}}}\). In particular, \(\rho \) decomposes of the direct sum of a trivial representation and a sign representation, which we write as \(\rho = 1+\sigma \). More generally, we will denote by \(a + b\rho + c\sigma \) the direct sum of a copies of the 1-dimensional trivial representation, b copies of \(\rho \), and c copies of \(\sigma \).
We will require the following lemma:
Lemma 3.5.1
Let X be a spectrum with a \({{\text {C} }_{\textrm{2}}}\)-action. Then the map
induced by the \({{\text {C} }_{\textrm{2}}}\)-equivariant map \(S^0 \rightarrow S^{\sigma }\), is an equivalence. In particular, the Tate construction is invariant under tensoring with the sign representation sphere spectrum \({\mathbb {S}}^{\sigma }\).
Proof
The cofibre of the map \(S^0 \rightarrow S^{\sigma }\) is given by the pointed \(C_2\)-space \(\Sigma (C_2)_+\) and so the cofibre of \(X \rightarrow \Sigma ^{\sigma } X\) is given by \(\Sigma ^{\infty +1}_+(C_2) \otimes _{{\mathbb {S}}} X\). The claim now follows since the latter is an induced \(C_2\)-spectrum and thus its Tate construction vanishes. \(\square \)
Remark 3.5.2
Instead of tensoring with the map \(S^0 \rightarrow S^{\sigma }\) we may also cotensor with it, yielding a map \(\Omega ^{\sigma }X \rightarrow X\), which induces an equivalence on Tate constructions since its fibre is an induced \(C_2\)-spectrum by the same argument as in the proof of Lemma 3.5.1. Iterating these constructions we then obtain for every non-negative n equivalences of the form \(X^{{{\text {tC} }_{\textrm{2}}}} \xrightarrow {\simeq } (\Sigma ^{n\sigma }X)^{{{\text {tC} }_{\textrm{2}}}}\) and \((\Omega ^{n\sigma }X)^{{{\text {tC} }_{\textrm{2}}}} \xrightarrow {\simeq } X^{{{\text {tC} }_{\textrm{2}}}}\).
Proposition 3.5.3
Let \((M,N,\alpha )\) be a k-module with genuine involution over an \({\text {E} _1}\)-algebra A. Then for \(n \in {\mathbb {Z}}\) there are equivalences of quadratic functors

where the right hand side is the quadratic functor associated to the k-module with genuine involution
defined using the identification \((\Sigma ^{m-n\sigma }M)^{{{\text {tC} }_{\textrm{2}}}} \simeq \Sigma ^{m} M^{{{\text {tC} }_{\textrm{2}}}}\) issued from Lemma 3.5.1 and Remark 3.5.2. In particular, the functor \(\Omega ^{n}:{\text {Mod}}^{\omega }_{A} \rightarrow {\text {Mod}}^{\omega }_{A}\) refines to an equivalence

of hermitian \(\infty \)-categories (or Poincaré when M is invertible). The same statement holds if we replace \({\text {Mod}}^{\omega }_{A}\) by \({\text {Mod}}^c_A\) for some subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\).
Proof
In light of (83) it will suffice to prove the case \(m=-n\). In this case we need to show that  . Replacing \((M,N,\alpha )\) by \((\Sigma ^{n\rho }M,\Sigma ^nN,\Sigma ^n\alpha )\) we observe that the claim for n implies the same for \(-n\), and so we may assume that n is positive. Arguing by induction, it is then enough to prove the case \(n=1=-m\). Inspecting the explicit formula for the linear and bilinear parts one directly sees that they commute with pre-composing with \(\Sigma ^{\text {op} }\), that is, for a quadratic functor
. Replacing \((M,N,\alpha )\) by \((\Sigma ^{n\rho }M,\Sigma ^nN,\Sigma ^n\alpha )\) we observe that the claim for n implies the same for \(-n\), and so we may assume that n is positive. Arguing by induction, it is then enough to prove the case \(n=1=-m\). Inspecting the explicit formula for the linear and bilinear parts one directly sees that they commute with pre-composing with \(\Sigma ^{\text {op} }\), that is, for a quadratic functor  we have natural equivalences
we have natural equivalences

It then follows that the canonical interchange map  induces an equivalences on linear parts, and on bilinear parts gives the corresponding interchange map
induces an equivalences on linear parts, and on bilinear parts gives the corresponding interchange map

associated to  , where here we view
, where here we view  as a functor in a single input, the tuple (X, Y). If we however break this input into two separate variables and take into account the symmetric structure of \(\text {B} \), then the above interchange map factors as a composite
as a functor in a single input, the tuple (X, Y). If we however break this input into two separate variables and take into account the symmetric structure of \(\text {B} \), then the above interchange map factors as a composite

where the second map is induced by cotensoring along the “smash diagonal” \(S^1 \rightarrow S^{\rho }\), and the first arises from the interchange map of each variable separately, which is an equivalence since  is bilinear. If we now evaluate at \(Y=X\) then we obtain a composite of \({{\text {C} }_{\textrm{2}}}\)-equivariant maps
is bilinear. If we now evaluate at \(Y=X\) then we obtain a composite of \({{\text {C} }_{\textrm{2}}}\)-equivariant maps

which induces an equivalence on Tate constructions by Lemma 3.5.1 and Remark 3.5.2 (indeed, under the representation sphere isomorphism \(S^{\rho } \cong S^{1+\sigma }\), the smash diagonal identifies with the suspension of the map \(S^0 \rightarrow S^{\sigma }\)). We therefore conclude that the interchange map  identifies the reference map
identifies the reference map  of
of  with the desuspension of the reference map
with the desuspension of the reference map  of
of  . We summarize the above arguments in the following commutative diagram
. We summarize the above arguments in the following commutative diagram

which may be viewed as an equivalence between the top left square and the external rectangle. As such, it identifies the classifying square of  with one having bilinear term
with one having bilinear term  , linear term
, linear term  , and reference map \(\Omega \alpha \). Applying this in the case of
, and reference map \(\Omega \alpha \). Applying this in the case of  we now conclude that
we now conclude that  is represented by the module with genuine involution \((\Omega ^{\rho }M,\Omega N,\Omega \alpha )\) defined using the identification \((\Omega ^{\rho }M)^{{{\text {tC} }_{\textrm{2}}}} \simeq \Omega M^{{{\text {tC} }_{\textrm{2}}}}\), as desired. \(\square \)
is represented by the module with genuine involution \((\Omega ^{\rho }M,\Omega N,\Omega \alpha )\) defined using the identification \((\Omega ^{\rho }M)^{{{\text {tC} }_{\textrm{2}}}} \simeq \Omega M^{{{\text {tC} }_{\textrm{2}}}}\), as desired. \(\square \)
Remark 3.5.4
We will show in Sect. 7.4 (see Corollary 7.4.17) that any quadratic functor  canonically refines to the genuine fixed points of a functor
canonically refines to the genuine fixed points of a functor  to genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. Thus one can make sense of tensoring any quadratic functor with \({\mathbb {S}}^{n-m\sigma }\), equipped with its genuine \({{\text {C} }_{\textrm{2}}}\)-structure in which the geometric fixed points are \({\mathbb {S}}^n\). A version of the above calculations also holds in this generality, see Proposition 7.4.19. For example, one finds that twisting a quadratic functor by \({\mathbb {S}}^{1-\sigma }\) corresponds to the operation
to genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. Thus one can make sense of tensoring any quadratic functor with \({\mathbb {S}}^{n-m\sigma }\), equipped with its genuine \({{\text {C} }_{\textrm{2}}}\)-structure in which the geometric fixed points are \({\mathbb {S}}^n\). A version of the above calculations also holds in this generality, see Proposition 7.4.19. For example, one finds that twisting a quadratic functor by \({\mathbb {S}}^{1-\sigma }\) corresponds to the operation  , while twisting by \({\mathbb {S}}^{\sigma -1}\) corresponds to the operation
, while twisting by \({\mathbb {S}}^{\sigma -1}\) corresponds to the operation  . We shall see in the examples below that these really are two inequivalent operations.
. We shall see in the examples below that these really are two inequivalent operations.
Our next goal is to use the above calculations to deduce periodicity properties for the \({\text {L}}\)-groups of certain rings. For this, we will use the notion of orientation, suitably adapted to the present setting.
Construction 3.5.5
Suppose given an \({\text {E} _1}\)-group G and a spherical character of G, that is, a map of \({\text {E} _1}\)-groups \(\chi :G \rightarrow \text {gl} _1({\mathbb {S}}) = {\text {Aut}}_{{{\mathcal {S}}{p}}}({\mathbb {S}})\). We may consequently view G as acting on the sphere spectrum \({\mathbb {S}}\), and will write \({\mathbb {S}}^{\chi }\) for the associated G-spectrum. Moreover, since every stable \(\infty \)-category \({\mathcal {C}}\) is canonically tensored over \({{\mathcal {S}}{p}}^{\text {f} }\), the character \(\chi \) determines an action of G on any object \(X \in {\mathcal {C}}\), by identifying X with the underlying object of \(X^{\chi } := {\mathbb {S}}^{\chi } \otimes X\). More generally, if X is already equipped with a G-action, then we may tensor X with \({\mathbb {S}}^{\chi }\) to obtain a new G-object \(X^{\chi } = {\mathbb {S}}^{\chi } \otimes X\) with the same underlying object X, that which can be called twisting X by \(\chi \). Even more generally, if \({\mathcal {C}}\) itself admits a G-action, then we can similarly twist a G-fixed object \(X \in {\mathcal {C}}^{\text {h} G}\) by \(\chi \) to obtain a new G-fixed object \(X^{\chi } \in {\mathcal {C}}^{\text {h} G}\). By a \(\chi \)-orientation on such a G-fixed object X we will then mean an equivalence
of G-fixed objects, refining the identity \(X=X\) in \({\mathcal {C}}\). When the G-action on both \({\mathcal {C}}\) and X is trivial and \({\mathcal {C}}\) admits quotients for G-objects, the data of a \(\chi \)-orientation can equivalently by encoded via a factorisation
of the identity \(X = X\), where the first map is the canonical map from the underlying object to the quotient.
Given an \({\text {E} _1}\)-group G and a spherical character \(\chi :G \rightarrow \text {gl} _1({\mathbb {S}})\), we will refer to the homotopy quotient \({\mathbb {S}}^{\chi }_{\text {h} G}\) as the Thom spectrum of \(\chi \), and will denote it also by \(\text {Th} (\chi )\). Recall that \(\text {B} \text {gl} _1({\mathbb {S}})\) identifies with the classifying space for stable spherical fibrations. In particular, it carries the universal stable spherical fibration \(\gamma \) and the definition above coincides with the usual Thom spectrum for \((\text {B} \chi )^*(\gamma )\). In particular, when \(\chi \) factors over the J-homomorphism
the spectrum \(\text {Th} (\chi )\) is indeed the Thom spectrum of the associated stable vector bundle. If \({\mathcal {C}}\) is now a cocomplete, stable \(\infty \)-category, so that the action of \({{\mathcal {S}}{p}}^{\text {f} }\) extends to all of \({{\mathcal {S}}{p}}\) in a colimit preserving manner, then we may use the Thom spectrum to describe orientations, at least for objects with trivial G-action. In particular, a \(\chi \)-orientation on such an \(X \in {\mathcal {C}}\) is equivalent to the data of a factorisation of the identity map \(X=X\) as
where the first map is the tensor with X of the map to the quotient \({\mathbb {S}}\rightarrow {\mathbb {S}}^{\chi }_{\text {h} G} = \text {Th} (\chi )\) induced by the initial \({\text {E} _1}\)-group map \(*\rightarrow G\). In that case, an orientation also determines an equivalence \(X^{\chi }_{\text {h} G} = \text {Th} (\chi ) \otimes X \simeq \text {B} G \otimes X = X_{\text {h} G}\), a generalisation of the classical Thom isomorphism, where the last term refers to the homotopy quotient of X by the trivial G-action.
Notation 3.5.6
Let G be an \({\text {E} _1}\)-group equipped with a spherical character \(\chi \). By a \(\chi \)-oriented \({\text {E} _\infty }\)-ring spectrum we will mean an \({\text {E} _\infty }\)-ring spectrum E, which, when considered as a module over itself acted trivially upon by G, is equipped with a \(\chi \)-orientation. In particular, identifying \({\text {hom}}_E(E,E) = {\text {hom}}_{{{\mathcal {S}}{p}}}({\mathbb {S}},E)\) such a \(\chi \)-orientation is equivalent to a refinement of the unit map \({\mathbb {S}}\rightarrow E\) to a G-equivariant map \({\mathbb {S}}\rightarrow E^{\chi }\), where \({\mathbb {S}}\) is considered as having trivial G-action. As above, may also encode this data as a factorisation of the unit map as a composite \({\mathbb {S}}\rightarrow \text {Th} (\chi ) \rightarrow E\).
Remark 3.5.7
Let G be an \({\text {E} _1}\)-group equipped with a spherical character \(\chi \) and \({\mathcal {C}}\) a stable presentable \(\infty \)-category (so that \({{\mathcal {S}}{p}}\) acts on \({\mathcal {C}}\)). If E is a \(\chi \)-oriented \({\text {E} _\infty }\)-ring spectrum (in the sense of Notation 3.5.6) then any E-module object in \({\mathcal {C}}^{\text {h} G}\) is automatically \(\chi \)-oriented. Indeed, for such an X the \(\chi \)-orientation of E induces a \(\chi \)-orientation \( X^{\chi } = {\mathbb {S}}^{\chi } \otimes X = ({\mathbb {S}}^{\chi } \otimes _{{\mathbb {S}}} E) \otimes _E X \xrightarrow {\simeq } E \otimes _E X = X \).
Example 3.5.8
Consider the \({\text {E} _1}\)-group \(\text {U} (1)\) together with its standard spherical character \(\chi :\text {U} (1) \rightarrow \text {gl} _1({\mathbb {S}})\) coming from the tautological complex representation of \(\text {U} (1)\). As the Thom space of the associated line bundle on \(\text {B} \text {U} (1) = {\mathbb {C}}P^{\infty }\) is equivalent via the zero section to \({\mathbb {C}}P^{\infty }\) one has
For an \({\text {E} _\infty }\)-ring spectrum E, the data of a \(\chi \)-orientation on E (as an E-module with constant action, see Notation 3.5.6) is given by a factorisation in the \(\infty \)-category of spectra
of the 2-fold suspended unit \({\mathbb {S}}\rightarrow E\), a structure otherwise known as a complex orientation on E.
Remark 3.5.9
Suppose that G is not just an \({\text {E} _1}\)-group but an \({\text {E} _\infty }\)-group, and that \(\chi :G \rightarrow \text {gl} _1({\mathbb {S}})\) is an \({\text {E} _\infty }\)-map. Then the corresponding Thom spectrum \( \text {Th} (\chi ) = {\mathbb {S}}^{\chi }_{\text {h} G} \) inherits the structure of an \({\text {E} _\infty }\)-ring with unit the canonical map \({\mathbb {S}}\rightarrow {\mathbb {S}}^{\chi }_{\text {h} G} = \text {Th} (\chi )\) to the quotient. This unit then tautologically factors through \(\text {Th} (\chi )\), and hence \(\text {Th} (\chi )\) is canonically \(\chi \)-oriented. This means, in particular, that any \({\text {E} _\infty }\)-algebra over \(\text {Th} (\chi )\) is canonically \(\chi \)-oriented. We note however that the structure of a \(\text {Th} (\chi )\)-algebra (that is, the structure of an \({\text {E} _\infty }\)-map \(\text {Th} (\chi ) \rightarrow E\)) is generally finer then that of a \(\chi \)-orientation, which in turn corresponds to a map \(\text {Th} (\chi ) \rightarrow E\) merely on the level of plain spectrum under \({\mathbb {S}}\). This is a reflection of the fact that G has a much richer structure than just an \({\text {E} _1}\)-group, namely, an \({\text {E} _\infty }\)-group structure. One may take this additional structure into account by defining a suitable notion of an \({\text {E} _\infty }\)-\(\chi \)-orientation on an \({\text {E} _\infty }\)-ring spectra E, in which case one would obtain a notion equivalent to that of an \({\text {E} _\infty }\)-algebra over \(\text {Th} (\chi )\).
Example 3.5.10
For concrete examples of the previous remark, consider the diagram of \({\text {E} _\infty }\)-groups

yielding by restriction spherical characters on all the appearing \({\text {E} _\infty }\)-groups. We then have that the corresponding Thom spectra \(\text {MSp} ,\text {MU} ,\text {MString} ,\text {MSpin} ,\text {MSpin} ^{\text {c}},\text {MSO} \) and \(\text {MO} \) are each oriented with respect to its respective spherical character. Similarly, any \({\text {E} _\infty }\)-algebra over any of these Thom spectra will inherit the corresponding orientation.
Remark 3.5.11
The notions of a complex (or \({\text {U}}(1)\)-) orientation appearing in Example 3.5.8 and the notion of a \({\text {U}}\)-orientation appearing in Example 3.5.10 are closely related. On the one hand, the \({\text {E} _1}\)-group map \({\text {U}}(1) \rightarrow {\text {U}}\) allows one to restrict any \({\text {U}}\)-orientation to a \({\text {U}}(1)\)-orientation. In concrete terms, this means that any map \(\text {MU} \rightarrow E\) on the level of plain spectra under \({\mathbb {S}}\) restricts to a map \(\text {MU} (1) = \Sigma ^{\infty -2}{\mathbb {C}}P^{\infty } \rightarrow E\) of the same nature. On the other hand, it is a well-known consequence of the splitting principle that any complex orientation \(\text {MU} (1) \rightarrow E\) extends to a map \(\text {MU} \rightarrow E\), which is furthermore compatible with the ring spectrum structure on both sides up to (non-coherent) homotopy, see [5, Part II], or [48, Lecture 6]. In particular, the map from the space of \({\text {U}}\)-orientations on E to the space of complex orientations on E is surjective on components, though is generally not an equivalence. Both these structures are weaker than that of being an \({\text {E} _\infty }\)-algebra over \(\text {MU} \), which would correspond, as in Remark 3.5.9, to a suitable \({\text {E} _\infty }\)-enhancement of the notion of a \({\text {U}}\)-orientation, see [32].
We now return to our context of modules with involutions and hermitian structures.
Definition 3.5.12
For \(n \ge 0\) we will use the term \(n\sigma \)-orientation to refer to an orientation with respect to the spherical character \(\chi _{n\sigma }:{{\text {C} }_{\textrm{2}}}\rightarrow \text {gl} _1({\mathbb {S}})\) determined by \({\mathbb {S}}^{n\sigma -n}\).
Fixing an \({\text {E} _1}\)-algebra over k, we will be interested in the notion of \(n\sigma \)-orientation for k-modules with involution M over an \({\text {E} _1}\)-algebra A over k, viewed as \({{\text {C} }_{\textrm{2}}}\)-fixed objects with respect to the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Mod}}_{A \otimes _k A}\). We note that for \(A=k\), the notion of an \(n\sigma \)-orientation on \(M=k\) with trivial \({{\text {C} }_{\textrm{2}}}\)-action reduces to that of an \(n\sigma \)-orientation on the \({\text {E} _\infty }\)-ring k in the sense of Notation 3.5.6.
Remarks 3.5.13
-
i)
Every object in \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) is canonically a k-module object, and so by Remark 3.5.7 we have that an \(n\sigma \)-orientation on k itself determines such an orientation on any k-module with involution over any \({\text {E} _1}\)-algebra A over k.
-
ii)
An \(n\sigma \)-orientation determines an \(N\sigma \)-orientation for any multiple N of n.
-
iii)
By Lemma 3.5.1 the Tate construction swallows sign suspensions, and so if M is \({n}\sigma \)-oriented then \(M^{{{\text {tC} }_{\textrm{2}}}}\) is n-periodic, that is \(\Sigma ^n M^{{{\text {tC} }_{\textrm{2}}}} \simeq M^{{{\text {tC} }_{\textrm{2}}}}\).
Of particular importance are the cases \(n=1,2\). In particular, a \(2\sigma \)-orientation determines a refinement of the identity map \(M = M\) to a \({{\text {C} }_{\textrm{2}}}\)-equivariant map
and we shall denote this common value by \(-M\). If the \(2\sigma \)-orientation comes from a \(\sigma \)-orientation, then \(-M \simeq M\).
Examples 3.5.14
-
i)
If k is an \({\text {E} _\infty }\)-algebra over \(\text {H} {\mathbb {Z}}\) (e.g., \(k=\text {H} R\) for some discrete ring R) then k admits a \(2\sigma \)-orientation. Indeed, it suffices to check this for \(k=\text {H} {\mathbb {Z}}\). Since \({\text {Map}}_{\text {H} {\mathbb {Z}}}(\text {H} {\mathbb {Z}},\text {H} {\mathbb {Z}}) = {\mathbb {Z}}\) is discrete and the action of the generator of \({{\text {C} }_{\textrm{2}}}\) on \({\mathbb {S}}^{2\sigma -2}\) is homotopic to the identity, it follows that the induced action on \({\mathbb {S}}^{2-2\sigma } \otimes _{{\mathbb {S}}} \text {H} {\mathbb {Z}}\) is trivial, and consequently \(1 \in {\mathbb {Z}}\) admits a unique lift to a fixed point. For such a k we then have by Remark 3.5.7 that any k-module with involution M over any k-\({\text {E} _1}\)-algebra A is \({2}\sigma \)-oriented. More generally, even if k itself is not an \({\text {E} _\infty }\)-algebra over \(\text {H} {\mathbb {Z}}\), it is still true that any \(\text {H} {\mathbb {Z}}\)-module object in \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) is canonically \(2\sigma \)-oriented, see Remark 3.5.7. When M is furthermore discrete (that is, in the image of the Eilenberg–Mac Lane functor) the meaning of \(-M\) reduces to the naive one, that simply inserts a sign into the involution.
-
ii)
If k is an \({\text {E} _\infty }\)-algebra over \(\text {H} {\mathbb {F}}_2\) then the same argument applied to \({\mathbb {S}}^{\sigma }\) provides a \(\sigma \)-orientation, since the action of the generator of \({{\text {C} }_{\textrm{2}}}\) on \({\mathbb {S}}^\sigma \) is the negative of the identity. Any k-module with involution over any k-\({\text {E} _1}\)-algebra A is then \(\sigma \)-oriented. More generally, even if k itself is not an \({\text {E} _\infty }\)-algebra over \(\text {H} {\mathbb {F}}_2\), it still true that any \(\text {H} {\mathbb {F}}_2\)-module object in \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\) is canonically \(\sigma \)-oriented, see Remark 3.5.7.
-
iii)
As a partial converse to the above we note that if the \({\text {E} _\infty }\)-ring k is \(\sigma \)-oriented then at least the underlying \(\text {E}_2\)-algebra of k refines to a \(\text {E}_2\)-\(\text {H} {\mathbb {F}}_2\)-algebra, and hence any module with involution over any \({\text {E} _1}\)-k-algebra A is canonically an \(\text {H} {\mathbb {F}}_2\)-module object in \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\). This is because any \(\sigma \)-orientation on k determines a homotopy \(2 \sim 0\) on it, and by Mahowald’s theorem \(\text {H} {\mathbb {F}}_2\) is the initial \(\text {E}_2\)-ring spectrum with a homotopy \(2 \sim 0\) (see [6, Theorem 5.1] for a recent treatment, where we recall that for \(p=2\) no completion is necessary).
-
iv)
The module with involution \(\text {H} {\mathbb {F}}_2 \otimes _{{\mathbb {S}}} \text {H} {\mathbb {F}}_2\) over \(\text {H} {\mathbb {F}}_2\) (equipped with the flip action) does not admit an \(n\sigma \)-orientation for any n, even though the underlying spectrum of M is an \(\text {H} {\mathbb {F}}_2\)-module. Indeed, by Lin’s theorem [42] (see [53, Theorem III.1.7] for a treatment in the present language), the Tate diagonal provides an equivalence
$$\begin{aligned} \text {H} {\mathbb {F}}_2 \longrightarrow (\text {H} {\mathbb {F}}_2 \otimes _{{\mathbb {S}}} \text {H} {\mathbb {F}}_2)^{{\text {tC} }_{\textrm{2}}}. \end{aligned}$$In particular, the latter spectrum is not periodic, and so \(\text {H} {\mathbb {F}}_2 \otimes _{{\mathbb {S}}} \text {H} {\mathbb {F}}_2\) cannot be \({n}\sigma \)-oriented, see Remark 3.5.13iii). We note that this does not contradict Remark 3.5.7, since the \(\text {H} {\mathbb {F}}_2\)-action on the underlying spectrum of M is not compatible with its \({{\text {C} }_{\textrm{2}}}\)-action.
-
v)
In a similar vein, the sphere does not admit an \(n\sigma \)-orientation for any n, since we would obtain an equivalence
$$\begin{aligned} {\mathbb {S}}^n \otimes _{{\mathbb {S}}} ({\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}) \simeq ({\mathbb {S}}^n)^{{{\text {tC} }_{\textrm{2}}}} \simeq ({\mathbb {S}}^{n\sigma })^{{\text {tC} }_{\textrm{2}}}\simeq {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}, \end{aligned}$$but from Segal’s conjecture (a consequence of Lin’s theorem) \({\mathbb {S}}^{{\text {tC} }_{\textrm{2}}}\) is the 2-completion of \({\mathbb {S}}\), which is not periodic.
-
vi)
The \({\text {E} _\infty }\)-ring \({\mathbb {S}}[1/2]\) admits a unique \(2\sigma \)-orientation. To see this, one can compute \(\pi _*({\mathbb {S}}^{n\sigma -n}[1/2])^{{\text {hC} }_{\textrm{2}}}\) using the (collapsing) homotopy fixed point spectral sequence, to see
$$\begin{aligned} \pi _*({\mathbb {S}}^{n\sigma -n}[1/2])^{{\text {hC} }_{\textrm{2}}}= \pi _*({\mathbb {S}}[1/2])^{{\text {C} }_{\textrm{2}}}. \end{aligned}$$But if n is even, the induced \({{\text {C} }_{\textrm{2}}}\)-action on \(\pi _*({\mathbb {S}}[1/2])\) is trivial, so we in particular get that the forgetful map
$$\begin{aligned} ({\mathbb {S}}^{2\sigma -2}[1/2])^{{\text {hC} }_{\textrm{2}}}\longrightarrow {\mathbb {S}}[1/2] \end{aligned}$$is an equivalence, so \({\mathbb {S}}[1/2]\) admits a unique \(2\sigma \)-orientation. It follows that if k is an \({\mathbb {S}}[1/2]\)-algebra (that is, 2 acts invertibly on k) then any k-module with involution over any k-\({\text {E} _1}\)-algebra A is \({2}\sigma \)-oriented. More generally, it is enough to assume that 2 acts invertibly on M itself, rather than on k. Indeed, in this case M refines to an \({\mathbb {S}}[1/2]\)-module object in \({\text {Mod}}_{A \otimes _k A}^{{{\text {hC} }_{\textrm{2}}}}\), and is hence \({2}\sigma \)-oriented by Remark 3.5.7.
-
vii)
The representation \(\sigma \) being real we find that the spherical character \(\chi _{\sigma }\) factors through the \({\text {E} _\infty }\)-group map \(\chi _{\text {O} }:\text {O} \rightarrow \text {gl} _1({\mathbb {S}})\), and so any \(\chi _{\text {O} }\)-orientation determines a \(\sigma \)-orientation. By Example 3.5.10 we consequently deduce that \(\text {MO} \), as well as any \({\text {E} _\infty }\)-algebra over \(\text {MO} \), is \(\sigma \)-oriented.
-
viii)
Similarly, the representation \(2\sigma \) refines to a complex representation and the spherical character \(\chi _{2\sigma }\) factors through \({\text {U}}\). By Example 3.5.10 we consequently deduce that \(\text {MU} \), as well as any \({\text {E} _\infty }\)-algebra over \(\text {MU} \), is \(2\sigma \)-oriented. Since the map \(\text {U} \rightarrow \text {O} \) factors through \(\text {Spin} ^{\text {c}}\), this applies in particular to any \({\text {E} _\infty }\)-algebra over \(\text {MSpin} ^{\text {c}}\), such as \(\text {ku} \) or \(\text {KU} \). More generally, since \(\chi _{\sigma }\) actually factors through \({\text {U}}(1)\), any complex orientation on k determines a \(2\sigma \)-orientation on it, see Example 3.5.8 and Remark 3.5.11. In particular, if k is a complex oriented \({\text {E} _\infty }\)-ring spectrum (e.g., \(k=\text {MU} , \text {ku} ,\text {KU} \) or any of the Lubin–Tate spectra) then any k-module with involution M over any k-\({\text {E} _1}\)-algebra A is \({2}\sigma \)-oriented.
-
ix)
Further up, the representation \(4\sigma \) is quaternion and the spherical character \(\chi _{4\sigma }\) factors through \(\text {Sp} \), and so any \({\text {E} _\infty }\)-algebra over \(\text {MSp} \), is \(4\sigma \)-oriented. Since the map \(\text {Sp} \rightarrow \text {O} \) factors through \(\text {Spin} \), this applies in particular to any \({\text {E} _\infty }\)-algebra over \(\text {MSpin} \), such as \(\text {ko} \) or \(\text {KO} \). Finally, the representation \(8\sigma \) refines to a string representation since its Steifel–Whitney classes vanish in degrees \(< 8\) and \(H^4({{\text {C} }_{\textrm{2}}},{\mathbb {Z}}) = H^4({{\text {C} }_{\textrm{2}}},{\mathbb {Z}}/2)\), and so any \({\text {E} _\infty }\)-algebra over \(\text {MString} \) (such as \(\text {tmf}\)) is \(8\sigma \)-oriented.
We can now specialise Proposition 3.5.3 to the case of oriented modules with involutions.
Corollary 3.5.15
Let A be an \({\text {E} _1}\)-algebra and let \((M,N,\alpha :N \rightarrow M^{{{\text {tC} }_{\textrm{2}}}})\) be an invertible k-module with genuine involution over A, such that M is \({n}\sigma \)-oriented, and \(c \subseteq K_0(A)\) a subgroup closed under the induced involution. Then the n-fold loop functor \(\Omega ^n\) refines to an equivalence of Poincaré \(\infty \)-categories

If \(n=2\), e.g., if k is discrete or complex oriented, or if 2 acts invertibly on M, then the loop functor \(\Omega \) furthermore refines to an equivalence

Proof
Apply Proposition 3.5.3 with \(m=n\) and use that \(\Sigma ^{n\sigma -n}M \simeq M\) when M is \({n}\sigma \)-oriented. The second claim is essentially by definition (but is useful to note nonetheless, since \(-M := \Sigma ^{\sigma -1}M\) is explicitly given by a sign twist when M is discrete). \(\square \)
Corollary 3.5.16
Let A be an \({\text {E} _1}\)-algebra over k and let M be an invertible k-module with involution over A, such that M is \({n}\sigma \)-oriented, and \(c \subseteq K_0(A)\) a subgroup closed under the induced involution. Then the n-fold loop functor \(\Omega ^n\) refines to give equivalences of Poincaré \(\infty \)-categories

For \(n=2\), e.g., if k is discrete or complex oriented, or if 2 acts invertibly on M, then the loop functor \(\Omega \) refines to give equivalences of Poincaré \(\infty \)-categories

Corollary 3.5.17
Let A be an \({\text {E} _1}\)-algebra over k and let M be an invertible k-module with involution over A, such that M is \({n}\sigma \)-oriented and \(c \subseteq K_0(A)\) a subgroup closed under the induced involution. Then the n-fold loop functor \(\Omega ^n\) refines to give equivalences of Poincaré \(\infty \)-categories

For \(n=2\), e.g., if k is discrete or complex oriented, or if 2 acts invertibly on M, then the loop functor \(\Omega \) refines to give equivalences of Poincaré \(\infty \)-categories

Proof
This is a particular case of Corollary 3.5.15 since the operation \(\alpha \mapsto \Sigma ^n\alpha \) sends the m-connective cover map \(\tau _{\ge m}M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow M^{{{\text {tC} }_{\textrm{2}}}}\) to the \((m+n)\)-connective cover map \(\tau _{\ge m+n}(\Sigma ^nM^{{{\text {tC} }_{\textrm{2}}}}) \rightarrow \Sigma ^nM^{{{\text {tC} }_{\textrm{2}}}}\). \(\square \)
The following periodicity result for \({\text {L}}\)-groups immediately follows (see also Remark 4.2.25 for the relation with classical \({\text {L}}\)-group periodicity):
Corollary 3.5.18
(Ranicki periodicity) Let A be an \({\text {E} _1}\)-algebra over k and let M be a \({n}\sigma \)-oriented invertible k-module with involution over A, and \(c \subseteq K_0(A)\) a subgroup closed under the induced involution. Then for \(d \in {\mathbb {Z}}\) we have canonical isomorphisms

and when A is connective, for \(d,m \in {\mathbb {Z}}\) we have canonical isomorphisms

If \(n=2\) (e.g, k is discrete or complex oriented, or if 2 acts invertibly on M) then we also have canonical isomorphisms

and when A is connective, for \(d,m \in {\mathbb {Z}}\) we have canonical isomorphisms

In summary, the quadratic and symmetric \({\text {L}}\)-groups of discrete (or complex oriented) rings are 4-periodic, and those of \(\text {H} {\mathbb {F}}_2\)-algebras are 2-periodic. In other cases, such as \(\text {MSp} \)- or \(\text {MSpin} \)-algebras, one has 8-periodic \({\text {L}}\)-groups, while \(\text {MString} \)-algebras have 16-periodic \({\text {L}}\)-groups. For example, \({\text {L}}_{*}^\text {s} (\text {ku} ), {\text {L}}_{*}^\text {s} (\text {ko} )\) and \({\text {L}}_{*}^\text {s} (\text {tmf})\) are 4, 8 and 16 periodic, respectively, and similarly for the non-connective variants. We will upgrade these periodicity results to the spectrum level in the second instalment, and show that it neatly combines with a spectrum-level Karoubi periodicity yielding what we call Karoubi–Ranicki periodicity, see [2], §4.5.
Regarding the quadratic \({\text {L}}\)-groups let us also mention that for a connective ring spectrum R, the algebraic \(\pi \)-\(\pi \)-theorem of Weiss and Williams from [71] implies that generally \({\text {L}}_*^\text {q} (R) \cong {\text {L}}_*^\text {q} (\pi _0(R))\), so that the quadratic \({\text {L}}\)-groups in fact end up 4-periodic; we give an account of this result in [3], Corollary 1.2.33.
5 Examples
In this section we discuss several examples of interest of Poincaré \(\infty \)-categories in further detail. We begin in Sect. 4.1 with the important example of the universal Poincaré \(\infty \)-category  , which is characterized by the property that Poincaré functors out of it pick out Poincaré objects in the codomain. In Sect. 4.2 we consider perfect derived \(\infty \)-categories of ordinary rings and show how to translate the classical language of forms on projective modules into that of the present paper via the process of deriving quadratic functors. These examples form the main link between the present work and classical hermitian \({\text {K}}\)-theory, and will be the main focus of applications in Paper [3]. In Sect. 4.3 we turn to a specific family of ring spectra with anti-involution, the group ring spectra, which carries a special interest due to its relation with surgery theory. In particular, we explain how to construct modules with genuine involution over such ring spectra whose associated \({\text {L}}\)-groups capture various flavours of visible \({\text {L}}\)-groups, for example, the visible symmetric \({\text {L}}\)-groups defined by [70] (see Example 4.3.6). Finally, in Sect. 4.4 we discuss the closely related case of parametrised spectra, which serves as a base-point-free version of group rings, and show how to construct Poincaré structures producing the parametrised spectra variant of visible \({\text {L}}\)-theory as studied in [73] (see Corollary 4.4.14).
, which is characterized by the property that Poincaré functors out of it pick out Poincaré objects in the codomain. In Sect. 4.2 we consider perfect derived \(\infty \)-categories of ordinary rings and show how to translate the classical language of forms on projective modules into that of the present paper via the process of deriving quadratic functors. These examples form the main link between the present work and classical hermitian \({\text {K}}\)-theory, and will be the main focus of applications in Paper [3]. In Sect. 4.3 we turn to a specific family of ring spectra with anti-involution, the group ring spectra, which carries a special interest due to its relation with surgery theory. In particular, we explain how to construct modules with genuine involution over such ring spectra whose associated \({\text {L}}\)-groups capture various flavours of visible \({\text {L}}\)-groups, for example, the visible symmetric \({\text {L}}\)-groups defined by [70] (see Example 4.3.6). Finally, in Sect. 4.4 we discuss the closely related case of parametrised spectra, which serves as a base-point-free version of group rings, and show how to construct Poincaré structures producing the parametrised spectra variant of visible \({\text {L}}\)-theory as studied in [73] (see Corollary 4.4.14).
5.1 The universal Poincaré category
In this section we discuss the Poincaré \(\infty \)-category  of Example 1.2.15, which we call the universal Poincaré \(\infty \)-category. This term is motivated by the following mapping property which we will prove below: the Poincaré \(\infty \)-category
of Example 1.2.15, which we call the universal Poincaré \(\infty \)-category. This term is motivated by the following mapping property which we will prove below: the Poincaré \(\infty \)-category  corepresents the functor \(\text {Pn} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\mathcal {S}}\) which assigns to a Poincaré \(\infty \)-category its space of Poincaré forms. To exhibit this, consider the map
corepresents the functor \(\text {Pn} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\mathcal {S}}\) which assigns to a Poincaré \(\infty \)-category its space of Poincaré forms. To exhibit this, consider the map

given by the identity \({\mathbb {S}}\rightarrow \text {D} {\mathbb {S}}= {\mathbb {S}}\) on the linear part and by the unit map \({\mathbb {S}}\rightarrow (\text {D} {\mathbb {S}}\otimes \text {D} {\mathbb {S}})^{{{\text {hC} }_{\textrm{2}}}} = {\mathbb {S}}^{{{\text {hC} }_{\textrm{2}}}}\) on the bilinear part. These two maps canonically lead to the ‘same’ map to \((\text {D} {\mathbb {S}}\otimes \text {D} {\mathbb {S}})^{{{\text {tC} }_{\textrm{2}}}} = {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}\) since the Tate diagonal of \({\mathbb {S}}\) agrees with the composite \({\mathbb {S}}\rightarrow {\mathbb {S}}^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}}\) by construction. In particular, the composite  is the identity. We then note that the map (84) corresponds to a hermitian form
is the identity. We then note that the map (84) corresponds to a hermitian form  such that \(q^{\text {u} }_{\sharp }:{\mathbb {S}}\rightarrow \text {D} {\mathbb {S}}={\mathbb {S}}\) is the identity, and in particular \(q^{\text {u} }\) is Poincaré. We will refer to it as the universal Poincaré form.
such that \(q^{\text {u} }_{\sharp }:{\mathbb {S}}\rightarrow \text {D} {\mathbb {S}}={\mathbb {S}}\) is the identity, and in particular \(q^{\text {u} }\) is Poincaré. We will refer to it as the universal Poincaré form.
Lemma 4.1.1
For every quadratic functor  , the map
, the map

induced by the universal form (84), is an equivalence of spectra.
Proof
Since the collection of  for which (85) is an equivalence is closed under limits it will suffice by Proposition 1.3.11 to prove the claim whenever
for which (85) is an equivalence is closed under limits it will suffice by Proposition 1.3.11 to prove the claim whenever  is either exact or of the form
is either exact or of the form  for some symmetric bilinear functor \(\text {B} \). In the former case, the claim follows since the linear part of
for some symmetric bilinear functor \(\text {B} \). In the former case, the claim follows since the linear part of  is \(\text {D} \) by construction and the composite
is \(\text {D} \) by construction and the composite  exhibits \(\text {D} \) as (stably) represented by \({\mathbb {S}}\). On the other hand, if
exhibits \(\text {D} \) as (stably) represented by \({\mathbb {S}}\). On the other hand, if  is of the form \(\text {B} (x,x)\) for some symmetric bilinear functor \(\text {B} \) then the result follows from Lemma 1.1.7 since the image of the universal form (84) in
is of the form \(\text {B} (x,x)\) for some symmetric bilinear functor \(\text {B} \) then the result follows from Lemma 1.1.7 since the image of the universal form (84) in

corresponds to the identity \({\mathbb {S}}\rightarrow {\mathbb {S}}\) by construction, and thus exhibits the underlying bilinear part

as stably represented by \({\mathbb {S}}\) as well. \(\square \)
Lemma 4.1.2
The sphere spectrum \({\mathbb {S}}\in {{\mathcal {S}}{p}}^{\text {f} }\) exhibits \({{\mathcal {S}}{p}}^{\text {f} }\) as corepresenting the core groupoid functor
Proof
Let \({{\mathcal {S}}^{\textrm{fin}}_{*}}\) be the \(\infty \)-category of finite pointed spaces. Then the inclusion \({{\mathcal {S}}^{\textrm{fin}}_{*}}\rightarrow {{\mathcal {S}}{p}}^{\text {f} }\) exhibits \({{\mathcal {S}}{p}}^{\text {f} }\) as the Spanier–Whitehead stabilisation of \({{\mathcal {S}}^{\textrm{fin}}_{*}}\), and in particular, for every stable \(\infty \)-category \({\mathcal {D}}\) the restriction functor
is an equivalence, where \({\text {Fun}}^{\text {rex} }(-,-) \subseteq {\text {Fun}}(-,-)\) denotes the full subcategory spanned by the right exact (i.e., finite colimits preserving) functors, see, e.g., [46, Proposition C.1.1.7]. On the other hand, for \({\mathcal {D}}\) stable we may identify right exact functors \({{\mathcal {S}}^{\textrm{fin}}_{*}}\rightarrow {\mathcal {D}}\) with those which are reduced and excisive, and hence with spectrum objects in \({\mathcal {D}}\). We thus obtain that for \({\mathcal {D}}\) stable the evaluation functor
is an equivalence, and hence induces an equivalence
on the level of core groupoids. \(\square \)
We now come to the main result of this section:
Proposition 4.1.3
(Universality of the universal Poincaré \(\infty \)-category) The universal Poincaré object \(({\mathbb {S}},q^{\text {u} })\) exhibits  as corepresenting the functor \(\text {Pn} \). Similarly, when considered as a hermitian \(\infty \)-category, the underlying universal hermitian object exhibits
as corepresenting the functor \(\text {Pn} \). Similarly, when considered as a hermitian \(\infty \)-category, the underlying universal hermitian object exhibits  as corepresenting the functor \(\text {Fm} \).
as corepresenting the functor \(\text {Fm} \).
Proof
We begin with the second claim. We need to show that for every  the map
the map

sending  to \((f({\mathbb {S}}),\eta _{{\mathbb {S}}}(q^{\text {u} }))\) is an equivalence. Consider the commutative square
to \((f({\mathbb {S}}),\eta _{{\mathbb {S}}}(q^{\text {u} }))\) is an equivalence. Consider the commutative square

furnished by Lemma 2.1.2, where the bottom horizontal map is the one induced by the object \({\mathbb {S}}\in \iota {{\mathcal {S}}{p}}^{\text {f} }\), which is an equivalence by Lemma 4.1.2. It will hence suffice to show that for every exact functor \(f:{{\mathcal {S}}{p}}^{\text {f} }\rightarrow {\mathcal {C}}\) the top horizontal map in (86) induces an equivalence on vertical fibres. Now by the construction of \(\text {Cat} ^{\textrm{h}}_\infty \) as a cartesian fibration we have that the fibre of the left vertical map over \(f:{{\mathcal {S}}{p}}^{\text {f} }\rightarrow {\mathcal {C}}\) is given by the space of natural transformations  . On the other hand, the fibres of the right vertical map over \(f({\mathbb {S}})\) is the space
. On the other hand, the fibres of the right vertical map over \(f({\mathbb {S}})\) is the space  of hermitian forms on \(f({\mathbb {S}}) \in {\mathcal {C}}\) by construction. Lemma 4.1.1 then implies that the induced map
of hermitian forms on \(f({\mathbb {S}}) \in {\mathcal {C}}\) by construction. Lemma 4.1.1 then implies that the induced map

on vertical fibres is an equivalence. This shows that \(({\mathbb {S}},q^{\text {u} })\) exhibits  as corepresenting the functor \(\text {Fm} \) in \(\text {Cat} ^{\textrm{h}}_\infty \). To obtain the analogous claim for Poincaré forms we observe that the corresponding map
as corepresenting the functor \(\text {Fm} \) in \(\text {Cat} ^{\textrm{h}}_\infty \). To obtain the analogous claim for Poincaré forms we observe that the corresponding map

induced by the image of the universal Poincaré form in  , identifies under Lemma 1.2.4 with the map
, identifies under Lemma 1.2.4 with the map

which sends a natural transformation  to the composite
to the composite

Since \(q^{\text {u} }_{\sharp }\) is an equivalence this map sends natural equivalences  to equivalences
to equivalences  . To finish the proof it will hence suffice to show that (87) also detects equivalences. Indeed, since \(q^{\text {u} }_{\sharp }\) is an equivalence, this follows from the fact that \({\mathbb {S}}\) generates \({{\mathcal {S}}{p}}^{\text {f} }\) under finite colimits and so a natural transformation between two exact functors on \({{\mathcal {S}}{p}}^{\text {f} }\) is an equivalence if and only if it evaluates to an equivalence on \({\mathbb {S}}\). \(\square \)
. To finish the proof it will hence suffice to show that (87) also detects equivalences. Indeed, since \(q^{\text {u} }_{\sharp }\) is an equivalence, this follows from the fact that \({\mathbb {S}}\) generates \({{\mathcal {S}}{p}}^{\text {f} }\) under finite colimits and so a natural transformation between two exact functors on \({{\mathcal {S}}{p}}^{\text {f} }\) is an equivalence if and only if it evaluates to an equivalence on \({\mathbb {S}}\). \(\square \)
5.2 Ordinary rings and derived structures
In this section we consider the case of ordinary rings and explain how classical inputs for Grothendieck-Witt- and \({\text {L}}\)-theory can be encoded as Poincaré structures on the \(\infty \)-category of perfect chain complexes. Our main result (see Proposition 4.2.18 below) is that such Poincaré structures are essentially uniquely determined by their values on projective modules. This leads to the formation of derived versions of classical notions of hermitian forms, constituting the main link through which the point of view taken in this paper series interacts with its classical counterpart.
Let R be an ordinary associative ring. Recall the Eilenberg–MacLane inclusion
of abelian groups as the heart of the canonical t-structure on spectra. Since this t-structure is compatible with tensor products the functor \(\text {H} \) is naturally lax symmetric monoidal, and consequently \(\text {H} R\) is naturally an \({\text {E} _1}\)-ring spectrum, or more precisely, an \({\text {E} _1}\)-algebra over the \({\text {E} _\infty }\)-ring spectrum \(\text {H} {\mathbb {Z}}\). We then have natural equivalences [47, Theorem 7.1.2.1]
between the \(\infty \)-categories of \(\text {H} {\mathbb {Z}}\)-module spectra and compact \(\text {H} R\)-modules in \(\text {H} {\mathbb {Z}}\)-module spectra, as considered in Sect. 3, and the derived and perfect derived \(\infty \)-categories of \({\mathbb {Z}}\) and R, respectively, see Example 1.2.12 and Example 3.1.12. Similarly, we have an equivalence \(\text {Mod} ^{\text {f} }_{\text {H} R} \simeq {{\mathcal {D}}}^{\text {f} }(R)\) between the \(\infty \)-category of finitely presented R-modules in \({\text {Mod}}_{\text {H} {\mathbb {Z}}}\) and the finitely presented derived category \({{\mathcal {D}}}^{\text {f} }(R)\), obtained from the category of bounded complexes of finitely generated free R-modules by inverting quasi-isomorphisms.
Notation 4.2.1
In what follows we will need to consider both the ordinary tensor product over \({\mathbb {Z}}\) and the tensor product of \(\text {H} {\mathbb {Z}}\)-module spectra over \(\text {H} {\mathbb {Z}}\), which corresponds, under the equivalence (88), to the derived tensor product \(\otimes ^{{\text {L}}}_{\mathbb {Z}}\) of complexes over \({\mathbb {Z}}\). We will consequently write \(\otimes _{{\mathbb {Z}}}\) for the former and \(\otimes _{\text {H} {\mathbb {Z}}}\) for the latter. In particular, for two ordinary R-modules M and N one has a canonical map
which is generally not an isomorphism, though it does exhibit its target as the 0th truncation of its domain, and in particular determines an isomorphism
As described in Sect. 3, we may construct bilinear functors on \({\text {Mod}}^{\omega }_{\text {H} R}\) from \(\text {H} {\mathbb {Z}}\)-modules with involution over \(\text {H} R\) (Definition 3.1.1), and hermitian structures on \({\text {Mod}}^{\omega }_{\text {H} R}\) from \(\text {H} {\mathbb {Z}}\)-modules with genuine involution over \(\text {H} R\) (Definition 3.2.3). In this context, it is natural to focus attention on \(\text {H} {\mathbb {Z}}\)-modules with involution which arise by taking Eilenberg–MacLane spectra of ordinary \({\mathbb {Z}}\)-modules with involutions, by which we mean:
Definition 4.2.2
By a \({\mathbb {Z}}\)-module with involution over R we will mean an \((R \otimes _{\mathbb {Z}}R)\)-module M in the ordinary sense together with an involution of abelian groups \(\sigma :M \xrightarrow {\simeq } M\) which is linear over the flip isomorphism \(R \otimes _{\mathbb {Z}}R \xrightarrow {\simeq } R \otimes _{\mathbb {Z}}R\), that is, which satisfies \(\sigma ((a \otimes b)x) = (b \otimes a)\sigma (x)\).
We will generally write such \({\mathbb {Z}}\)-modules with involution as pairs \((M,\sigma )\). We will then denote by \(\text {B} _M\) the bilinear functor on \({{\mathcal {D}}}^\text {p} (R)\) corresponding to the bilinear functor \(\text {B} _{\text {H} M}\) on \({\text {Mod}}_{\text {H} R}\) via the equivalence (88). The following lemma ensures that the value of this bilinear form on projective modules is of a classical nature:
Lemma 4.2.3
For \(P,Q \in \text {Proj} (R)\) the canonical map
is an equivalence. In particular, \(\text {B} _M\) sends pairs of projective modules to (Eilenberg–MacLane spectra of) abelian groups.
Proof
For \(P \in \text {Proj} (R)\) the condition that (89) is an equivalence is closed under direct sums and retracts, and so it suffices to check it for \(R=P\), where it can be identified with the identity map
\(\square \)
The bilinear functor \(\text {B} _M\) is perfect if and only if \(\text {H} M\) is invertible, that is, \(\text {H} M\) is perfect as an \(\text {H} R\)-module and the map \(\text {H} R \rightarrow {\text {End}}_{\text {H} R}(\text {H} M)\) is an equivalence (see Definition 3.1.4).
Definition 4.2.4
We will say that a \({\mathbb {Z}}\)-module with involution M over R (in the sense of Definition 4.2.2) is invertible if \(\text {H} M\) is invertible as an H\(\mathbb {Z}\)-module with involution over \(\text {H} R\) and in addition M is projective as an R-module.
Remark 4.2.5
For a \({\mathbb {Z}}\)-module with involution M over R which is projective as an R-module we have \({\text {hom}}_{\text {H} R}(\text {H} M,\text {H} M) = \text {H} {\text {Hom}}_R(M,M)\), and so for such modules invertibility is equivalent to the map \(R \rightarrow {\text {Hom}}_R(M,M)\) being an isomorphism.
The projectivity assumption in Definition 4.2.2 is meant to insure that the duality \(\text {D} _M:{{\mathcal {D}}}^\text {p} (R)^{\text {op} }\xrightarrow {\simeq } {{\mathcal {D}}}^\text {p} (R)\) associated to the perfect bilinear functor \(\text {B} _M\) preserves the (ordinary) full subcategory \(\text {Proj} (R) \subseteq {{\mathcal {D}}}^\text {p} (R)\) of finitely generated projective R-modules, and determines in particular a duality of ordinary categories
where \({\text {Hom}}_R(X,M)\) is given an R-module structure using the second R-action. This is also consistent with the classical terminology concerning invertible modules, see, e.g., Example 4.2.6 just below.
Example 4.2.6
If R is commutative then any R-module M can be considered as an \((R \otimes _{\mathbb {Z}}R)\)-module via the multiplication homomorphism \(R \otimes _{\mathbb {Z}}R \rightarrow R\). In particular, the two R-actions coincide, and we may endow M with the trivial involution. For a projective M this results in an invertible \({\mathbb {Z}}\)-module with involution if and only if M is invertible as an object in the symmetric monoidal category \(\text {Proj} (R)\). From the perspective of algebraic geometry, such modules correspond to line bundles over \(\text {spec} (R)\).
Examples 4.2.7
Suppose that R is equipped with an anti-involution, that is, an abelian group involution \(\overline{\bullet }:R \xrightarrow {\simeq } R\) which satisfies \(\overline{ab} = \overline{b}\overline{a}\). In this case R can be considered as a \({\mathbb {Z}}\)-module with involution over itself via the \((R \otimes _{\mathbb {Z}}R)\)-action \((a \otimes b)x = ax\overline{b}\) and the involution \(\sigma = \overline{\bullet }\). Some examples of interest of such rings include:
-
i)
Any commutative ring with an automorphism of order 2 gives rise to a ring with anti-involution. For example, the field \({\mathbb {C}}\) of complex numbers can be considered as a ring with anti-involution via complex conjugation.
-
ii)
The group ring \({\mathbb {Z}}[G]\) associated to a discrete group G carries a natural anti-involution given on additive generators by \(g \mapsto g^{-1}\). This example is a recurring one in geometric applications of \({\text {L}}\)-theory (see also Sect. 4.3). More generally one can consider an orientation character \(\chi :G \rightarrow C_2 = \{\pm 1\}\) and define the \(\chi \)-twisted anti-involution by setting \(g \mapsto \chi (g) g^{-1}\).
-
iii)
For a commutative ring k the k-algebra of \(n \times n\)-matrices \(\text {Mat} _n(k)\) admits an anti-involution \(A \mapsto A^{t}\) given by sending a matrix to its transpose. This more generally works for k a ring with anti-involution.
-
iv)
For a commutative ring k and \(a,b \in k\), the quaternion k-algebra \({\text {Q}}_k(a,b)\) is the algebra generated over k by elements i, j under the relation \(i^2=a,j^2=b,ij=-ji\). It admits an anti-involution sending i to \(-i\) and j to \(-j\).
Another common source of invertible \({\mathbb {Z}}\)-modules with involution is the following. Recall that an anti-structure in the sense of Wall [68] on a ring R consists of a ring isomorphism
together with a unit \(\epsilon \in R^*\), such that \(\overline{\epsilon }=\epsilon ^{-1}\) and  . In particular, if \(\epsilon \) belongs to the center of R then \(\overline{\bullet }\) is an anti-involution, and this is arguably the most common case studied in the literature. Specifically, one often considers the case where \(\epsilon =\pm 1\), which, for example, in the case of the integers \({\mathbb {Z}}\), are also the only .
. In particular, if \(\epsilon \) belongs to the center of R then \(\overline{\bullet }\) is an anti-involution, and this is arguably the most common case studied in the literature. Specifically, one often considers the case where \(\epsilon =\pm 1\), which, for example, in the case of the integers \({\mathbb {Z}}\), are also the only .
Given a Wall anti-structure \((\overline{\bullet },\epsilon )\), we may consider R as an \((R \otimes _{\mathbb {Z}}R)\)-module with action given by \((a\otimes b) \cdot r=ar\overline{b}\). The map \(a \mapsto \epsilon \overline{a}\) is then an involution on R which is linear over the flip action on \(R \otimes _{\mathbb {Z}}R\), and so we obtain the structure of a \({\mathbb {Z}}\)-module with involution. This \({\mathbb {Z}}\)-module with involution is always invertible: the induced map \(R \rightarrow {\text {Hom}}_R(R,R)\cong R^{\text {op} }\) identifies with \(r \mapsto \overline{r}\) (see Remark 4.2.5).
Remark 4.2.8
A Wall anti-structure captures the most general form of an invertible \({\mathbb {Z}}\)-module with involution over R whose underlying R-module is R. Indeed, giving the R-module R a second commuting R-action is equivalent to providing a ring homomorphism \(\overline{\bullet }:R \rightarrow {\text {Hom}}_R(R,R) = R^{\text {op} }\), which is furthermore an isomorphism if the desired \((R \otimes _{\mathbb {Z}}R)\)-module is to be invertible (see Remark 4.2.5). The \((R \otimes _{\mathbb {Z}}R)\)-action can then be written in terms of \(\overline{\bullet }\) by \((a \otimes b)(c) = ac\overline{b}\). If \(\sigma :R \rightarrow R\) is now an abelian group isomorphism which switches the two R-actions then \(\sigma \) is completely determined by the value \(\epsilon := \sigma (1) \in R\), in terms of which \(\sigma \) can be written as
Since \(\sigma \) and \(\overline{\bullet }\) are both isomorphisms of abelian groups so is the map \(r \mapsto \epsilon \cdot r\), and hence \(\epsilon \) must be a unit. In addition, since \(\sigma \) switches the two R-actions we also have

and hence  . Finally, the condition that \(\sigma \) is an involution implies that
. Finally, the condition that \(\sigma \) is an involution implies that
and hence \(\overline{\epsilon } = \epsilon ^{-1}\). In particular, the pair \((\overline{\bullet },\epsilon )\) is a Wall anti-structure on R and the \({\mathbb {Z}}\)-module with involution we obtain is the one associated to that structure.
Remark 4.2.9
If \((\overline{\bullet },\epsilon )\) is a Wall anti-structure on a ring R and \(u \in R^*\) is a unit then we can obtain a new Wall anti-structure by replacing \(\overline{\bullet }\) with \(u^{-1}\overline{\bullet }u\) and \(\epsilon \) with \(\epsilon \big (\overline{u}\big )^{-1}u\). One then says that the two Wall anti-structures \((\overline{\bullet },\epsilon )\) and \((u^{-1}\overline{\bullet }u,\epsilon \big (\overline{u}\big )^{-1}u)\) are conjugated. In this case the associated \({\mathbb {Z}}\)-modules with involution over R are isomorphic via the map \(R \rightarrow R\) sending x to xu. In fact, any isomorphism between the \({\mathbb {Z}}\)-modules with involution associated to two Wall anti-structures is of this form, and so two Wall anti-structures are conjugated if and only if their associated \({\mathbb {Z}}\)-modules with involution are isomorphic as such.
The construction below, which was shared with the authors by Uriya First, gives an example of a Wall anti-structure which is not conjugated to any central Wall anti-structure:
Example 4.2.10
Let K be a field which admits an automorphism \(\sigma :K \rightarrow K \) of order 4. Define \(R = K[x,x^{-1};\sigma ^2]\) to be the twisted Laurent polynomial ring generated over K by an invertible generator x which satisfies the relation \(x^{-1}\alpha x = \sigma ^2(\alpha )\) for \(\alpha \in K\). We may then extend \(\sigma \) to an anti-automorphism on R defined on monomials by
Then  and \(x\overline{x} = 1\), so that we obtain a Wall anti-structure \((\overline{\bullet },\epsilon )\) with \(\epsilon = x\). This Wall anti-structure is not conjugated to any central Wall anti-structure: indeed, the units of R are exactly the monomials \(\alpha x^i\), and if we conjugate the above Wall anti-structure by \(\alpha x^i\) then the new \(\epsilon \) will be of the form \(\beta x^{2i+1}\) for a suitable \(\beta \in K\), and as such cannot be in the center, since it does not commute with \(K \subseteq R\).
and \(x\overline{x} = 1\), so that we obtain a Wall anti-structure \((\overline{\bullet },\epsilon )\) with \(\epsilon = x\). This Wall anti-structure is not conjugated to any central Wall anti-structure: indeed, the units of R are exactly the monomials \(\alpha x^i\), and if we conjugate the above Wall anti-structure by \(\alpha x^i\) then the new \(\epsilon \) will be of the form \(\beta x^{2i+1}\) for a suitable \(\beta \in K\), and as such cannot be in the center, since it does not commute with \(K \subseteq R\).
Let us now also give a non-commutative example of an invertible \({\mathbb {Z}}\)-module with involution whose underlying module is not the ring itself:
Example 4.2.11
Let \(B={\text {Q}}_{{\mathbb {Q}}}(-5,-13)\) be the quaternion algebra over \({\mathbb {Q}}\) and let \(A \subseteq B\) be the subring generated over \({\mathbb {Z}}\) by 1, i, j and \(\beta = \frac{1+i+j+ij}{2}\). Then A is a maximal order in the quaternion algebra B, that is, it is finitely generated as a \({\mathbb {Z}}\)-module and is not contained in any other subring with this property. Invertible bimodules over maximal orders are relatively well understood, and can all be realized as invertible two-sided ideals in A. In particular, the two-sided ideal \(I \subseteq A\) which is generated by \(2,i-1,j-1\) is an invertible ideal of index 4 in A (the quotient \(A/I\cong {\mathbb {F}}_2[\beta ]/(\beta ^2-\beta +1)\) is a finite field of order 4). One can then verify that this ideal is not principal by checking that A contains no elements of norm 2, and so this A-bimodule is not isomorphic to A as a left A-module. At the same time, the involution on B sending i to \(-i\) and j to \(-j\) restricts to an involution on A, through which we can consider I as an \(A \otimes A\)-module, and since this involution preserves I it endows it with the structure of an involution which is linear over the flip map \(A \otimes A \rightarrow A \otimes A\). Then I gives an invertible \({\mathbb {Z}}\)-module with involution over A which is not isomorphic to A as a left A-module.
We now fix a ring R and an invertible \({\mathbb {Z}}\)-module with involution M over R. Let us say that a Poincaré structure  on \({{\mathcal {D}}}^\text {p} (R)\) is compatible with M if its associated duality is given by \(\text {D} _M\) (equivalently, if its symmetric bilinear part is \(\text {B} _M\)).
on \({{\mathcal {D}}}^\text {p} (R)\) is compatible with M if its associated duality is given by \(\text {D} _M\) (equivalently, if its symmetric bilinear part is \(\text {B} _M\)).
Example 4.2.12
As in Definition 3.1.2 we have the quadratic and symmetric Poincaré structures  and
and  associated to the bilinear functor \(\text {B} _M\), which are compatible with M by construction.
associated to the bilinear functor \(\text {B} _M\), which are compatible with M by construction.
Example 4.2.13
As in Example 3.2.8, for an integer \(m\in {\mathbb {Z}}\) one can consider the associated \(\text {H} {\mathbb {Z}}\)-module with genuine involution
over \(\text {H} R\), where \(t_m:\tau _{\ge m}\text {H} M^{{{\text {tC} }_{\textrm{2}}}}\rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}}\) is the m-connective cover of \(\text {H} M^{{{\text {tC} }_{\textrm{2}}}}\). The associated Poincaré structure

defined as in Construction 3.2.6, is then compatible with M.
Remark 4.2.14
By Theorem 3.3.1 the data of a Poincaré structure on \({{\mathcal {D}}}^\text {p} (R)\) compatible with M is equivalent to that of an \(\text {H} R\)-module spectrum N equipped with a map of \(\text {H} R\)-module spectra \(N \rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}}\). The above examples then correspond to the case where this map is the identity (the symmetric structure), the map from the zero module (the quadratic structure), or the various connective covers.
Warning 4.2.15
In the construction above, the \(\text {H} R\)-module \(\text {H} M^{{{\text {tC} }_{\textrm{2}}}}\) is such that the induced R-module structure on \(\pi _0(\text {H} M)^{{{\text {tC} }_{\textrm{2}}}} = \hat{\text {H}}_0({{\text {C} }_{\textrm{2}}},M) = \text {coker} [\text {T} _{{{\text {C} }_{\textrm{2}}}}:M_{{{\text {C} }_{\textrm{2}}}} \rightarrow M^{{{\text {C} }_{\textrm{2}}}}]\) is given by
where [m] is the class mod norms of a \({{\text {C} }_{\textrm{2}}}\)-fixed element \(m \in M\). This can lead to some confusion when R is commutative and the involution on M is R-linear. In this case, another natural action of R on M is available by realizing the Tate construction in \(\text {H} R\)-modules. The associated action on homotopy groups is then given by \(r[m] = [rm]\), which is generally different from the action above (see also Warning 3.2.2).
Remark 4.2.16
By construction the linear part of the Poincaré structure  is given by the formula \(X \mapsto {\text {hom}}_{\text {H} R}(X,\tau _{\ge m}\text {H} M^{{{\text {tC} }_{\textrm{2}}}})\), where in the last term we have identified X with the corresponding \(\text {H} R\)-module spectrum via the equivalence (88). In particular,
is given by the formula \(X \mapsto {\text {hom}}_{\text {H} R}(X,\tau _{\ge m}\text {H} M^{{{\text {tC} }_{\textrm{2}}}})\), where in the last term we have identified X with the corresponding \(\text {H} R\)-module spectrum via the equivalence (88). In particular,  sits in an exact sequence of spectra
sits in an exact sequence of spectra

which can be used to obtained connectivity estimates on the gap between  and
and  . On the other hand, from the fibre sequence \(\tau _{\ge m}\text {H} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow \tau _{\le m-1}\text {H} M^{{{\text {tC} }_{\textrm{2}}}}\) we see that
. On the other hand, from the fibre sequence \(\tau _{\ge m}\text {H} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}} \rightarrow \tau _{\le m-1}\text {H} M^{{{\text {tC} }_{\textrm{2}}}}\) we see that  also sits in an exact sequence of spectra
also sits in an exact sequence of spectra

and this can be used to obtain coconnectivity estimates on the gap between  and
and  .
.
Our principal goal in this section to construct a link between Poincaré structures on \({{\mathcal {D}}}^\text {p} (R)\) compatible with a given M and the classical framework of M-valued forms on projective R-modules. For this, let \({\text {Ch}}^{\textrm{b}}(\text {Proj} (R))\) be the category of bounded chain complexes of finitely generated projective R-modules, so that the \(\infty \)-category \({{\mathcal {D}}}^\text {p} (R)\) can be identified with the \(\infty \)-categorical localisation of \({\text {Ch}}^{\textrm{b}}(\text {Proj} (R))\) by the collection of quasi-isomorphisms. The inclusion \(\text {Proj} (R) \subseteq {\text {Ch}}^{\textrm{b}}(\text {Proj} (R))\) as chain-complexes concentrated in degree 0 determines a fully-faithful functor
We also point out that the category \(\text {Proj} (R)\) is additive, and the inclusion (90) is additive in the sense that it preserves direct sums. One can then show that (90) exhibits \({{\mathcal {D}}}^\text {p} (R)\) as the initial stable \(\infty \)-category equipped with additive functor from \(\text {Proj} (R)\). It is also sometimes called the stable envelope of \(\text {Proj} (R)\).
The following definition is originally due to Eilenberg and MacLane [21, Theorem 9.11].
Definition 4.2.17
Let \({\mathcal {C}},{\mathcal {D}}\) be additive \(\infty \)-categories. We will say that a reduced (that is, zero object preserving) functor  is polynomial of degree 2 if its cross-effects
is polynomial of degree 2 if its cross-effects  (defined as in Definition 1.1.4 as the kernel of the split surjection
(defined as in Definition 1.1.4 as the kernel of the split surjection  ) preserves direct sums in each variable separately. We will denote by
) preserves direct sums in each variable separately. We will denote by
the full subcategory spanned by reduced functors which are polynomial of degree 2.
We now arrive to the main result of this section:
Proposition 4.2.18
Let R be an associative ring. Then restriction along the inclusion \(\text {Proj} (R) \subseteq {{\mathcal {D}}}^\text {p} (R)\) yields an equivalence of \(\infty \)-categories
Since the Eilenberg–MacLane embedding \(\text {H} :{\mathcal {A}}b\hookrightarrow {{\mathcal {S}}{p}}\) is fully-faithful and additive, Proposition 4.2.18 implies in particular that if  is a reduced polynomial functor of degree 2 then the composed functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\rightarrow {{\mathcal {S}}{p}}\) extends to a quadratic functor
is a reduced polynomial functor of degree 2 then the composed functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\rightarrow {{\mathcal {S}}{p}}\) extends to a quadratic functor  in an essentially unique manner. We will refer to such an extension
in an essentially unique manner. We will refer to such an extension

as the derived quadratic functor of  .
.
Remark 4.2.19
For perfect complexes \(X \in {{\mathcal {D}}}^\text {p} (R)\) concentrated in non-negative degrees one can express the value of the derived functor  as follows. One first translates X to a simplicial R-module using the Dold–Kan correspondence. Applying the functor
as follows. One first translates X to a simplicial R-module using the Dold–Kan correspondence. Applying the functor  levelwise yields a cosimplicial abelian group which one can then re-translate into a non-positively graded chain complex over \({\mathbb {Z}}\), and consequently into a spectrum. This is the classical description of non-abelian derived functors on non-negatively graded complexes due to Dold and Puppe [19].
levelwise yields a cosimplicial abelian group which one can then re-translate into a non-positively graded chain complex over \({\mathbb {Z}}\), and consequently into a spectrum. This is the classical description of non-abelian derived functors on non-negatively graded complexes due to Dold and Puppe [19].
The proof of Proposition 4.2.18 will be given below. Before, let us explore some of its consequences. As their higher categorical counterparts, reduced degree 2 polynomial functors \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\) can be used to encode various types of hermitian forms. To make this more explicit, consider for a projective module \(P \in \text {Proj} (R)\) the abelian group \({\text {Hom}}_{R\otimes R}(P\otimes _{{\mathbb {Z}}} P,M)\) of M-valued R-bilinear forms \(\beta :P \otimes _{\mathbb {Z}}P\rightarrow M\). This abelian group carries an involution which sends a form \(\beta \) to the form
where \(\sigma :M \rightarrow M\) is the involution of M. The \({{\text {C} }_{\textrm{2}}}\)-orbits and \({{\text {C} }_{\textrm{2}}}\)-fixed points of \(\sigma \) are then related via the trace map
which sends an orbit to the sum of its representatives.
Definition 4.2.20
Let R be a ring and \((M,\sigma )\) an invertible \({\mathbb {Z}}\)-module with involution over R. We define functors \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\) by the formulas

and

For \(P \in \text {Proj} (R)\) we will refer to these as the abelian groups of \(\sigma \)-quadratic, \(\sigma \)-symmetric, and \(\sigma \)-even forms on P, respectively. These functors are visibly reduced and the cross-effect of each of them is \((P,Q) \mapsto {\text {Hom}}_{R \otimes _{\mathbb {Z}}R}(P \otimes _{\mathbb {Z}}Q,M)\), which is additive in each variable separately. In particular, they are polynomial of degree 2.
Remark 4.2.21
It follows from Lemma 4.2.3 that

and similarly

By definition, a \(\sigma \)-symmetric form is an R-bilinear form \(\phi :P \otimes _{\mathbb {Z}}P \rightarrow M\) such that \(\phi (b,a) = \sigma (\phi (a,b))\). On the other hand, the data of a \(\sigma \)-quadratic form, or a \({{\text {C} }_{\textrm{2}}}\)-orbit \([\beta ] \in {\text {Hom}}_{R\otimes R}(P\otimes _{{\mathbb {Z}}} P,M)_{{\text {C} }_{\textrm{2}}}\), is equivalent to that of a pair \((\phi ,q)\), where \(\phi \in {\text {Hom}}_{R\otimes R}(P\otimes _{{\mathbb {Z}}} P,M)^{{{\text {C} }_{\textrm{2}}}}\) is a \(\sigma \)-symmetric form and \(q:P \rightarrow M_{{{\text {C} }_{\textrm{2}}}}\) is a set-theoretic function which satisfies
-
i)
\(q(v+u)-q(v)-q(u) = [\phi (v,u)] \in M_{{{\text {C} }_{\textrm{2}}}}\) for \(v,u \in P\);
-
ii)
\(q(r v) = (r \otimes r)q(v)\) for \(v \in P\) and \(r \in R\);
-
iii)
the image of q(v) under the trace map \(M_{{{\text {C} }_{\textrm{2}}}} \rightarrow M^{{{\text {C} }_{\textrm{2}}}}\) is the \({{\text {C} }_{\textrm{2}}}\)-fixed element \(\phi (v,v)\) for \(v \in P\).
To obtain this description, note that the abelian group of such pairs \((\phi ,q)\) forms a reduced degree 2 polynomial functor  , which receives a natural transformation
, which receives a natural transformation  sending
sending  to the pair \((\phi ,q)\), where \(\phi = \text {T} _{{{\text {C} }_{\textrm{2}}}}[\beta ]\) is the trace of \(\beta \) and \(q(x) = [\beta (x,x)] \in M_{{{\text {C} }_{\textrm{2}}}}\). One can then verify in a straightforward manner that this natural transformation induces an isomorphism on cross-effects and an isomorphism on the value on \(P=R\), and is hence an isomorphism on every \(P \in \text {Proj} (R)\) (see also [68, Theorem 1], where this argument is elaborated in the case where M comes from a Wall anti-structure).
to the pair \((\phi ,q)\), where \(\phi = \text {T} _{{{\text {C} }_{\textrm{2}}}}[\beta ]\) is the trace of \(\beta \) and \(q(x) = [\beta (x,x)] \in M_{{{\text {C} }_{\textrm{2}}}}\). One can then verify in a straightforward manner that this natural transformation induces an isomorphism on cross-effects and an isomorphism on the value on \(P=R\), and is hence an isomorphism on every \(P \in \text {Proj} (R)\) (see also [68, Theorem 1], where this argument is elaborated in the case where M comes from a Wall anti-structure).
When R is commutative and \(M=R\) with trivial involution the above notion of a quadratic form identifies with the usual one. In this case even forms are symmetric forms which admit a quadratic refinement in the classical sense (which is not kept as part of the structure). For example, when \(M=R={\mathbb {Z}}\) with trivial involution then a symmetric bilinear form b on P admits a quadratic refinement if and only if \(b(x,x) \in 2{\mathbb {Z}}\) for all \(x\in P\), hence the terminology “even forms”. In this case the quadratic refinement is even unique, though this is by no means the case in general. If R is commutative and \(M=R\) with involution \(\sigma (x)=-x\) then \(\sigma \)-symmetric forms are skew-symmetric forms, while the \(\sigma \)-even forms are the alternating ones. For non-commutative R this way of viewing quadratic forms was first devised by Tits [66] for central simple algebras, and later generalized by Wall [68] to arbitrary rings with anti-structure as above.
By Proposition 4.2.18 each of the functors  and
and  extends in an essentially unique manner to its corresponding derived quadratic functor \({{\mathcal {D}}}^\text {p} \rightarrow {{\mathcal {S}}{p}}\). The following proposition identifies these in terms of Poincaré structures we have already encountered:
extends in an essentially unique manner to its corresponding derived quadratic functor \({{\mathcal {D}}}^\text {p} \rightarrow {{\mathcal {S}}{p}}\). The following proposition identifies these in terms of Poincaré structures we have already encountered:
Proposition 4.2.22
The derived quadratic functors of  and
and  are canonically equivalent to the Poincaré structures
are canonically equivalent to the Poincaré structures  and
and  , respectively.
, respectively.
Proof
By Lemma 4.2.3 we have that for \(P \in \text {Proj} (P)\) the spectrum \(\text {B} _M(P[0],P[0])\) belongs to \({{\mathcal {S}}{p}}^{\heartsuit }\) and so  is connective and
is connective and  is coconnective. By Remark 4.2.16 we then get that for \(m=0,1,2\) the spectrum
is coconnective. By Remark 4.2.16 we then get that for \(m=0,1,2\) the spectrum  is both connective and coconnective, and hence lies in the heart as well. Now consider the pair of maps
is both connective and coconnective, and hence lies in the heart as well. Now consider the pair of maps

By Remark 4.2.16 the first map above is an isomorphism when \(m=2\) and the second map is an isomorphism when \(m=0\). Finally, when \(m=1\) the same remark gives that the first map is surjective and the second is injective. In light of Remark 4.2.21 we now get an identification of  for \(m=0,1,2\) with
for \(m=0,1,2\) with  and
and  respectively. By the uniqueness of Proposition 4.2.18 we may identify
respectively. By the uniqueness of Proposition 4.2.18 we may identify  for \(m=0,1,2\) with the desired derived quadratic functors. \(\square \)
for \(m=0,1,2\) with the desired derived quadratic functors. \(\square \)
Notation 4.2.23
In light of Proposition 4.2.22 we will denote the Poincaré structures  ,
,  and
and  also by
also by  ,
,  and
and  , and refer to them as the genuine quadratic, genuine even and genuine symmetric Poincaré structures on R associated to M.
, and refer to them as the genuine quadratic, genuine even and genuine symmetric Poincaré structures on R associated to M.
Combining Proposition 4.2.22 with Corollary 3.5.17 we conclude:
Corollary 4.2.24
The loop functor \(\Omega :{{\mathcal {D}}}^\text {p} (R) \rightarrow {{\mathcal {D}}}^\text {p} (R)\) refines to equivalences of Poincaré \(\infty \)-categories

and

Remark 4.2.25
The \({\text {L}}\)-groups of \({{\mathcal {D}}}^\text {p} (R)\) with respect to the Poincaré structures  and
and  identify with Ranicki’s 4-periodic quadratic and symmetric \({\text {L}}\)-groups, see Example 2.3.17. The \({\text {L}}\)-groups of the genuine Poincaré structures
identify with Ranicki’s 4-periodic quadratic and symmetric \({\text {L}}\)-groups, see Example 2.3.17. The \({\text {L}}\)-groups of the genuine Poincaré structures  are generally not 4-periodic, though one has the relation
are generally not 4-periodic, though one has the relation

by Corollary 4.2.24. We will show in Paper [3] that the \({\text {L}}\)-groups of the genuine symmetric Poincaré structure actually rediscover an older non-periodic variant of the symmetric \({\text {L}}\)-groups, originally introduced by Ranicki [57] using n-dimensional Poincaré complexes to define the n’th \({\text {L}}\)-group.
The notions of \(\sigma \)-symmetric, \(\sigma \)-even and \(\sigma \)-quadratic M-valued forms were generalized by Bak [8] to the setting where one is given, in addition to M, a subgroup \(Q\subseteq M^{{{\text {C} }_{\textrm{2}}}}\) containing the image of the trace map \(M_{{{\text {C} }_{\textrm{2}}}} \rightarrow M^{{{\text {C} }_{\textrm{2}}}}\), and closed under the quadratic action of R on \(M^{{{\text {C} }_{\textrm{2}}}}\) given by \((a,m) \mapsto (a \otimes a)m\). Here we use the term quadratic action to designate the fact that it is encoded by a quadratic monoid map \((R,\cdot ,1,0) \mapsto {\text {End}}_{{\mathbb {Z}}}(M^{{{\text {C} }_{\textrm{2}}}})\), rather than a ring homomorphism. In particular, the cross effect
of this action is not trivial, but instead given by a bilinear map \(R \otimes R \rightarrow {\text {End}}_{{\mathbb {Z}}}(M^{{{\text {C} }_{\textrm{2}}}})\), which in this case is induced by the symmetrization of the \((R \otimes R)\)-action on M. We will refer to abelian groups equipped with this kind of action as quadratic modules. This notion was subsequently generalized by Schlichting [60] by removing the condition that \(Q\) injects in M:
Definition 4.2.26
(Schlichting) Let R be a ring equipped with an invertible \({\mathbb {Z}}\)-module with involution M. A form parameter \(\lambda \) on (R, M) is a quadratic R-module \(Q\) lying in a sequence of quadratic modules
whose composition is the trace map, and such that the cross-effect of the R-action on \(Q\) satisfies \((a\perp b)x = \tau ((a\otimes b)\rho (x))\).
We note that any reduced degree 2 polynomial functor  with cross-effect
with cross-effect  determines a form parameter on
determines a form parameter on  by taking
by taking  , with the maps
, with the maps

induced by the \({{\text {C} }_{\textrm{2}}}\)-equivariant diagonal and collapse maps relating R and \(R \oplus R\). Schlichting then proves (see [60, Lemma A.16]) that the association  determines an equivalence between the category \({\text {Fun}}^{2-\text {poly} }_*(\text {Proj} (R)^{\text {op} },{\mathcal {A}}b)\) and the category of form parameters as above (more precisely, Schlichting proves this for \(\text {Proj} (R)\) replaced with the category of finitely generated free R-modules, but \({\text {Fun}}^{2-\text {poly} }_*(-,{\mathcal {A}}b)\) is invariant under idempotent completion). Explicitly, an inverse to this map is given by sending a form parameter \(\lambda = [M_{{{\text {C} }_{\textrm{2}}}} \xrightarrow {\tau } Q\xrightarrow {\rho } M^{{{\text {C} }_{\textrm{2}}}}]\) to the functor
determines an equivalence between the category \({\text {Fun}}^{2-\text {poly} }_*(\text {Proj} (R)^{\text {op} },{\mathcal {A}}b)\) and the category of form parameters as above (more precisely, Schlichting proves this for \(\text {Proj} (R)\) replaced with the category of finitely generated free R-modules, but \({\text {Fun}}^{2-\text {poly} }_*(-,{\mathcal {A}}b)\) is invariant under idempotent completion). Explicitly, an inverse to this map is given by sending a form parameter \(\lambda = [M_{{{\text {C} }_{\textrm{2}}}} \xrightarrow {\tau } Q\xrightarrow {\rho } M^{{{\text {C} }_{\textrm{2}}}}]\) to the functor

which associates to a projective R-module P its group of \(\lambda \)-hermitian forms, which by definition consists of pairs \((\phi ,q)\) where \(\phi :P \otimes _{{\mathbb {Z}}} P \rightarrow M\) is a \(\sigma \)-symmetric M-valued form and \(q:P \rightarrow Q\) is a map of sets such that
-
i)
\(q(r v) = rq(v)\) for \(v \in P\) and \(r \in R\), where rq(v) stands for the (quadratic) action of r on \(q(v) \in Q\).
-
ii)
\(q(v+u)-q(v)-q(u) = \tau (\phi (v,u)) \in Q\) for \(v,u \in P\);
-
iii)
\(\rho q(v) = \phi (v,v)\).
The cross effect of  is then given by \((P,P') \mapsto {\text {Hom}}_R(P \otimes _{{\mathbb {Z}}} P',M)\). In particular, for \(Q=M^{{{\text {C} }_{\textrm{2}}}}\) we get the notion of a \(\sigma \)-symmetric M-valued form, for \(Q=M_{{{\text {C} }_{\textrm{2}}}}\) we get the notion of a \(\sigma \)-quadratic M-valued form, and for \(Q=\text {im} [M_{{{\text {C} }_{\textrm{2}}}} \rightarrow M^{{{\text {C} }_{\textrm{2}}}}]\) we get the notion of a \(\sigma \)-even M-valued form. Using Proposition 4.2.18 we may extend the composite functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\hookrightarrow {{\mathcal {S}}{p}}\) to a quadratic functor
is then given by \((P,P') \mapsto {\text {Hom}}_R(P \otimes _{{\mathbb {Z}}} P',M)\). In particular, for \(Q=M^{{{\text {C} }_{\textrm{2}}}}\) we get the notion of a \(\sigma \)-symmetric M-valued form, for \(Q=M_{{{\text {C} }_{\textrm{2}}}}\) we get the notion of a \(\sigma \)-quadratic M-valued form, and for \(Q=\text {im} [M_{{{\text {C} }_{\textrm{2}}}} \rightarrow M^{{{\text {C} }_{\textrm{2}}}}]\) we get the notion of a \(\sigma \)-even M-valued form. Using Proposition 4.2.18 we may extend the composite functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\hookrightarrow {{\mathcal {S}}{p}}\) to a quadratic functor

in an essentially unique manner. By Lemma 4.2.3 the bilinear part of  is \(\text {B} _M\) and it is hence Poincaré and compatible with M. Writing
is \(\text {B} _M\) and it is hence Poincaré and compatible with M. Writing  for the linear part of
for the linear part of  and evaluating at \(R \in {{\mathcal {D}}}^\text {p} (R)\) we obtain a fibre sequence
and evaluating at \(R \in {{\mathcal {D}}}^\text {p} (R)\) we obtain a fibre sequence

which we may rewrite as
This determines the linear part of  to be \(\Lambda ^{{\text {g} \lambda }}_{M} \simeq {\text {hom}}_R(-,N)\), where the underlying spectrum of N is given by the cofibre of the composed map \(M_{{{\text {hC} }_{\textrm{2}}}} \rightarrow M_{{{\text {C} }_{\textrm{2}}}} \rightarrow Q\). In particular, in the classification of Theorem 3.3.1 the Poincaré structure
to be \(\Lambda ^{{\text {g} \lambda }}_{M} \simeq {\text {hom}}_R(-,N)\), where the underlying spectrum of N is given by the cofibre of the composed map \(M_{{{\text {hC} }_{\textrm{2}}}} \rightarrow M_{{{\text {C} }_{\textrm{2}}}} \rightarrow Q\). In particular, in the classification of Theorem 3.3.1 the Poincaré structure  corresponds to the module with genuine involution
corresponds to the module with genuine involution
Remark 4.2.27
To clarify the relation between form parameters and modules with genuine involution one may use the framework of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. Recall from Remark 3.2.4 that modules with genuine involution over the \({\text {E} _1}\)-ring spectrum \(\text {H} R\) can be identified with module objects in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra over the Hill–Hopkins–Ravenel norm \(\text {N} \text {H} R\), the latter being the genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum whose underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum is \(\text {H} R\otimes _{{\mathbb {S}}} \text {H} R\) with the flip \({{\text {C} }_{\textrm{2}}}\)-action, whose geometric fixed point spectrum is \(\text {H} R\), and whose reference map \(\text {H} R \rightarrow (\text {H} R\otimes _{{\mathbb {S}}} \text {H} R)^{{{\text {tC} }_{\textrm{2}}}}\) is the Tate-diagonal. We then note that the stable \(\infty \)-category of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra admits a t-structure whose connective objects are those whose underlying spectrum and geometric fixed points are both connective. In particular, \(\text {N} \text {H} R\) is a connective algebra object in \({{\text {C} }_{\textrm{2}}}\)-spectra, and so its \(\infty \)-category of modules inherits a t-structure created by the forget-the-action functor. Let us now switch to viewing genuine \({{\text {C} }_{\textrm{2}}}\)-spectra as \({{\mathcal {S}}{p}}\)-valued Mackey functors, that is, product preserving functors from the span \(\infty \)-category of finite \({{\text {C} }_{\textrm{2}}}\)-sets to \({{\mathcal {S}}{p}}\), see [10] and [11]. In this framework the above t-structure is the objectwise one: indeed, the condition that the underlying spectrum and the geometric fixed points spectrum are both connective is equivalent to the condition that the underlying spectrum and genuine fixed points being both connective. As a result, the heart of this t-structure can be identified with the category of \({\mathcal {A}}b\)-valued Mackey functors, and similarly the heart of the induced t-structure on \(\text {N} \text {H} R\)-modules can be identified with \({\mathcal {A}}b\)-valued Mackey functors which are modules over \(\pi _0\text {N} \text {H} R\). The latter can be computed by translating \(\text {N} \text {H} R\) into an \({{\mathcal {S}}{p}}\)-valued Mackey functor and then taking \(\pi _0\) objectwise. This computation was carried out in [20, Proposition 5.5] yielding the \({\mathcal {A}}b\)-valued Mackey functor encoded by the arrows
where W is the abelian group whose underlying set of elements is \(R \times (R \otimes _{{\mathbb {Z}}} R)_{{{\text {C} }_{\textrm{2}}}}\), and whose addition law is given by
Here, the map \(\tau \) is the inclusion \(v \mapsto (0,v)\) and the map \(\rho \) sends (a, v) to \((a \otimes a) + \text {T} _{{{\text {C} }_{\textrm{2}}}}(v)\), where \(\text {T} _{{{\text {C} }_{\textrm{2}}}}\) is the trace map from \((R \otimes _{{\mathbb {Z}}} R)_{{{\text {C} }_{\textrm{2}}}}\) to \((R \otimes _{{\mathbb {Z}}} R)^{{{\text {C} }_{\textrm{2}}}}\). Now on the level of spectral Mackey functors the tensor product of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra is determined by Day convolution along the symmetric monoidal structure induced on the level of spans by the cartesian product of finite \({{\text {C} }_{\textrm{2}}}\)-sets. The Mackey object (91) inherits from \(\text {N} \text {H} R\) an associative algebra structure with respect to this monoidal structure, and this means in particular that \(W \rightarrow (R \otimes _{{\mathbb {Z}}} R)^{{{\text {C} }_{\textrm{2}}}}\) is a map of associative algebras and that \((R \otimes _{{\mathbb {Z}}} R)_{{{\text {C} }_{\textrm{2}}}} \rightarrow W\) is a map of W-bimodules (where W acts on \((R \otimes _{{\mathbb {Z}}} R)_{{{\text {C} }_{\textrm{2}}}}\) via the action of \((R \otimes _{{\mathbb {Z}}} R)^{{{\text {C} }_{\textrm{2}}}}\) on the latter inherited from its equivariant action on \(R \otimes _{{\mathbb {Z}}} R\)). The ring structure on W was also calculated in [20, Proposition 5.5] and is given by
Unwinding the definitions, we then see that the notion of a module over W corresponds exactly to that of an abelian group equipped with a quadratic R-action, and that the data of a module over (91) in \({\mathcal {A}}b\)-valued Mackey functors corresponds exactly to the notion of a form parameter as in Definition 4.2.26. In summary, we may reproduce the category of form parameters as the heart under the above t-structure of the \(\infty \)-category \({\text {Mod}}_{\text {N} \text {H} R}\) of \(\text {N} \text {H} R\)-modules in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, or, equivalently, of modules with genuine involution over \(\text {H} R\). The latter identifies with \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{\text {H} R})\) under the equivalence of Theorem 3.3.1, and in that setting we may identify the heart with the full subcategory spanned by the derived quadratic functors, that is, those quadratic functors \({\text {Mod}}^{\omega }_{\text {H} R} \rightarrow {{\mathcal {S}}{p}}\) which send \(\text {Proj} (R)\) to \({\mathcal {A}}b= {{\mathcal {S}}{p}}^{\heartsuit }\) (and to which Proposition 4.2.18 pertains). In particular, the derived quadratic functor corresponding to a given form parameter \(\lambda = [M_{{{\text {C} }_{\textrm{2}}}} \rightarrow Q \rightarrow M^{{{\text {C} }_{\textrm{2}}}}]\) is exactly  , and the corresponding \(\text {H} {\mathbb {Z}}\)-module with genuine involution \((\text {H} M,{\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q], {\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q] \rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}})\) is then obtained by extracting the underlying spectrum and geometric fixed points of the Mackey functor \(\text {H} \lambda \) associated to \(\lambda \), where the \(\text {H} R\)-action on the geometric fixed points \({\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q]\) is induced by the action of \(\text {N} \text {H} R\) (whose geometric fixed points is \(\text {H} R\)) on \(\text {H} \lambda \).
, and the corresponding \(\text {H} {\mathbb {Z}}\)-module with genuine involution \((\text {H} M,{\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q], {\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q] \rightarrow \text {H} M^{{{\text {tC} }_{\textrm{2}}}})\) is then obtained by extracting the underlying spectrum and geometric fixed points of the Mackey functor \(\text {H} \lambda \) associated to \(\lambda \), where the \(\text {H} R\)-action on the geometric fixed points \({\text {cof}}[\text {H} M_{{\text {hC} }_{\textrm{2}}}\rightarrow \text {H} Q]\) is induced by the action of \(\text {N} \text {H} R\) (whose geometric fixed points is \(\text {H} R\)) on \(\text {H} \lambda \).
Remark 4.2.28
In [28] the fourth and ninth authors show that the Grothendieck-Witt groups (the one defined in Sect. 2.5 as well as the higher ones we will define in Paper [2]) of derived Poincaré structures as above can be described in terms of the group completion of the corresponding monoid of Poincaré forms on projective modules. It then follows that for an invertible \({\mathbb {Z}}\)-module with involution \((M,\sigma )\) over R the Grothendieck-Witt groups of  coincide with the Grothendieck-Witt groups of \(\lambda \)-hermitian forms as defined and studied by Bak [8], see also [38] and [60]. In particular, the Grothendieck-Witt groups of \({{\mathcal {D}}}^\text {p} (R)\) with respect to the genuine quadratic, genuine even and genuine symmetric Poincaré structures are the classical \(\sigma \)-quadratic, \(\sigma \)-even and \(\sigma \)-symmetric Grothendieck-Witt groups of R with coefficients in M.
coincide with the Grothendieck-Witt groups of \(\lambda \)-hermitian forms as defined and studied by Bak [8], see also [38] and [60]. In particular, the Grothendieck-Witt groups of \({{\mathcal {D}}}^\text {p} (R)\) with respect to the genuine quadratic, genuine even and genuine symmetric Poincaré structures are the classical \(\sigma \)-quadratic, \(\sigma \)-even and \(\sigma \)-symmetric Grothendieck-Witt groups of R with coefficients in M.
We now show how to extend the equivalences of Corollary 4.2.24 to more general form parameters. For this, as explained in [60], note that to a form parameter \(M_{{{\text {C} }_{\textrm{2}}}} \rightarrow Q\rightarrow M^{{{\text {C} }_{\textrm{2}}}}\) may associate another form parameter
Indeed, this construction is well-defined since \(\text {im} (\rho )\) is contained in the kernel of the map \(1-\sigma :M \rightarrow M\) and contains the image of the map \(1+\sigma :M \rightarrow M\). Hermitian forms with respect to the form parameter \({\check{\lambda }}\) on \(-M\) then correspond to what Bak [8] called \(\lambda \)-quadratic forms.
Proposition 4.2.29
Let \((Q,\rho ,\tau )\) be a form parameter on M in which \(\rho :Q\rightarrow M^{{{\text {C} }_{\textrm{2}}}}\) is injective. Then the loop functor \(\Omega :{{\mathcal {D}}}^\text {p} (R) \rightarrow {{\mathcal {D}}}^\text {p} (R)\) refines to an equivalence of Poincaré \(\infty \)-categories

Proof
Applying Corollary 1.1.21 in the case where \(y=0\) we get for \(P \in \text {Proj} (R)\) an equivalence

Now since \(\rho :Q\rightarrow M^{{{\text {C} }_{\textrm{2}}}}\) is injective the notion of a \(\lambda \)-hermitian form \((\phi ,q)\) on P simply reduces to a symmetric M-valued form \(\phi \) such that \(\phi (v,v) \in Q\) for \(v \in P\) (from which the data of q is uniquely determined). It then follows that the map  is injective, and so its cofiber in \({{\mathcal {S}}{p}}\) is just the Eilenberg–MacLane spectrum of its cokernel in \({\mathcal {A}}b\). By the equivalence of Proposition 4.2.18 we now conclude that the Poincaré structure
is injective, and so its cofiber in \({{\mathcal {S}}{p}}\) is just the Eilenberg–MacLane spectrum of its cokernel in \({\mathcal {A}}b\). By the equivalence of Proposition 4.2.18 we now conclude that the Poincaré structure  is the derived Poincaré structure of the degree 2 polynomial functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\) given by
is the derived Poincaré structure of the degree 2 polynomial functor \(\text {Proj} (R)^{\text {op} }\rightarrow {\mathcal {A}}b\) given by

We now claim that  is naturally equivalent to
is naturally equivalent to  . Indeed, unwinding the definitions we see that the transfer map
. Indeed, unwinding the definitions we see that the transfer map

vanishes on  and hence determines a natural transformation
and hence determines a natural transformation

One then readily verifies that this natural transformation is an equivalence on cross effects (which on both sides identify with bilinear forms to \(-M\)). It will hence suffice to check that this natural transformation evaluates to an isomorphism on the projective R-module R. Indeed, its component at R is the tautological identification

\(\square \)
Remark 4.2.30
In Paper [2] we prove a version of Karoubi’s fundamental theorem in the setting of Poincaré \(\infty \)-categories. When applied to the various derived Poincaré structures on \({{\mathcal {D}}}^\text {p} (R)\) mentioned above (and using the comparison statement of Remark 4.2.28), this yields a complete solution to both conjectures made by Karoubi in [38] concerning potential generalizations of his fundamental theorem to the case where 2 is not assumed invertible. More precisely, when combined with Corollary 4.2.24 one obtains the statement of [38, Conjecture 1], and when combined with Proposition 4.2.29 the statement of [38, Conjecture 2]. We point out that while these conjectures pertain to the classical theory of forms as encoded by the various polynomial functors above, the equivalences of Poincaré \(\infty \)-categories appearing in Corollary 4.2.24 and Proposition 4.2.29 are only visible after deriving these into Poincaré structures on \({{\mathcal {D}}}^\text {p} (R)\).
We now turn to the proof of Proposition 4.2.18. Let \(\Delta _{\le n} \subseteq \Delta \) be the full subcategory spanned by those totally ordered sets with at most \(n+1\) elements.
Definition 4.2.31
Let \({\mathcal {C}}\) and \({\mathcal {D}}\) be small \(\infty \)-categories.
-
i)
A diagram \(p:\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) is called finite if it is left Kan extended from its restriction to \(\Delta ^{\text {op} }_{\le n}\) for some n. A colimit over such a diagram is called a finite geometric realisation. Dually, a diagram \(\Delta \rightarrow {\mathcal {C}}\) is called finite if it is right Kan extended from its restriction to \(\Delta _{\le n}\) for some n. A limit over such a diagram is called a finite totalization.
-
ii)
An \(\infty \)-category \({\mathcal {C}}\) is said to admit finite geometric realizations if every finite diagram \(\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) in \({\mathcal {C}}\) admits a colimit. Dually, \({\mathcal {C}}\) is said to admit finite totalizations if every finite diagram \(\Delta \rightarrow {\mathcal {C}}\) admits a limit.
-
iii)
A functor \(f :{\mathcal {C}}\rightarrow {\mathcal {D}}\) is said to preserve finite geometric realizations if its sends colimit cones \(\overline{p}:(\Delta ^{\text {op} })^{\triangleright } \rightarrow {\mathcal {C}}\) over finite diagrams \(p:\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) to colimit cones in \({\mathcal {D}}\). Here, it is not required that \(f \circ p:\Delta ^{\text {op} }\rightarrow {\mathcal {D}}\) remains finite in the above sense. Dually, a functor f is said to preserve finite totalizations if its sends limit cones \(\overline{p}:(\Delta ^{\text {op} })^{\triangleleft } \rightarrow {\mathcal {C}}\) over finite diagrams \(p:\Delta \rightarrow {\mathcal {C}}\) to limit cones in \({\mathcal {D}}\). Again, it is not required that \(f \circ p:\Delta ^{\text {op} }\rightarrow {\mathcal {D}}\) remains finite.
We will denote by \({\text {Fun}}^{\Delta ^{\text {op} }_\text {fin} }({\mathcal {C}},{\mathcal {D}}) \subseteq {\text {Fun}}({\mathcal {C}},{\mathcal {D}})\) the full subcategory spanned by the functors which preserve finite geometric realizations.
Remark 4.2.32
If an \(\infty \)-category \({\mathcal {C}}\) admits finite colimits then it admits finite geometric realizations, since the \(\infty \)-category \(\Delta _{\le n}^{\text {op} }\) is finite (see e.g. Example 6.5.3 below) and colimits of left Kan extended diagrams \(X :\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) can be calculated on their restriction to \(\Delta _{\le n}^{\text {op} }\). In addition, if \({\mathcal {C}}\) and \({\mathcal {D}}\) are \(\infty \)-categories with finite colimits and \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) preserves finite colimits then f sends finite diagrams \(X:\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) to finite diagrams; indeed, this follows from the pointwise formula for left Kan extensions since for each \([m] \in \Delta ^{\text {op} }\) the comma category \((\Delta ^{\text {op} }_{\le n})_{/_{[m]}}\) is finite. It then follows that such an f also preserves finite geometric realizations. A similar statement holds for finite totalizations under the analogous assumptions concerning finite limits.
Lemma 4.2.33
Let \({\mathcal {C}}\) be an \(\infty \)-category which admits finite colimits and \({\mathcal {D}}\) an \(\infty \)-category which admits sifted colimits. Then restriction along the Yoneda embedding \({\mathcal {C}}\rightarrow {\text {Ind}}({\mathcal {C}})\) induces an equivalence
between the full subcategory of functors \({\text {Ind}}({\mathcal {C}}) \rightarrow {\mathcal {D}}\) which preserve sifted colimits on the left hand side and functors \({\mathcal {C}}\rightarrow {\mathcal {D}}\) which preserve finite geometric realizations on the right.
Proof
We first note that by the universal property of ind-categories [43, Proposition 5.3.5.10] we have that \({\text {Ind}}({\mathcal {C}})\) admits filtered colimits and restriction along \(\iota :{\mathcal {C}}\hookrightarrow {\text {Ind}}({\mathcal {C}})\) determines an equivalence
where the left hand side stands for the full subcategory of \({\text {Fun}}({\text {Ind}}({\mathcal {C}}),{\mathcal {D}})\) spanned by the functors which preserves filtered colimits. It will hence suffice to show that if \(f:{\text {Ind}}({\mathcal {C}}) \rightarrow {\mathcal {D}}\) is a functor which preserves filtered colimits then f preserves sifted colimits if and only if \(f \circ \iota \) preserves finite geometric realizations. To begin, note that if \(f:{\text {Ind}}({\mathcal {C}}) \rightarrow {\mathcal {D}}\) preserves sifted colimits then it preserves in particular finite geometric realizations. Since the inclusion \(\iota :{\mathcal {C}}\rightarrow {\text {Ind}}({\mathcal {C}})\) preserves finite colimits it preserves finite diagrams and finite geometric realizations by Remark 4.2.32. It then follows that in this case \(f \circ \iota \) preserves finite geometric realizations. To prove the other direction, let us now suppose that \(f:{\text {Ind}}({\mathcal {C}}) \rightarrow {\mathcal {D}}\) is a functor which preserves filtered colimits such that \(f\circ \iota \) preserves finite geometric realizations. We wish to show that f preserves all sifted colimits. By [43, Corollary 5.5.8.17] it will suffice to show that f preserves geometric realizations. Let \(t_n:\Delta ^{\text {op} }_{\le n} \rightarrow \Delta ^{\text {op} }\) be the inclusion. Then every \(\Delta ^{\text {op} }\)-diagram \(\rho :\Delta ^{\text {op} }\rightarrow {\text {Ind}}({\mathcal {C}})\) can be written as a sequential (and in particular filtered) colimit of finite diagrams of the form
Since f preserves filtered colimits it will suffice to prove that f preserves finite geometric realizations. Now let \(\rho _n:\Delta ^{\text {op} }_{\le n} \rightarrow {\text {Ind}}({\mathcal {C}})\) be a diagram indexed on \(\Delta ^{\text {op} }_{\le n}\). We claim that \(\rho _n\) can be written as a filtered colimit of \(\Delta ^{\text {op} }_{\le n}\)-diagrams taking values in \({\mathcal {C}}\). To see this, consider the smallest full subcategory \({\mathcal {E}}\subseteq {\text {Fun}}(\Delta ^{\text {op} }_{\le n},{\text {Ind}}({\mathcal {C}}))\) which contains the left Kan extended functors \((i_k)_!\iota (x)\), where \(x\in {\mathcal {C}}\) is an object and \(i_k:\{[k]\} \hookrightarrow \Delta ^{\text {op} }_{\le n}\) is the inclusion of the object [k], and closed under finite colimits. Then \({\mathcal {E}}\) forms a collection of compact generators for \({\text {Fun}}(\Delta ^{\text {op} }_{\le n},{\text {Ind}}({\mathcal {C}}))\) and hence every diagram \(\rho _n:\Delta ^{\text {op} }_{\le n} \rightarrow {\text {Ind}}({\mathcal {C}})\) is a filtered colimit of diagrams in \({\mathcal {E}}\). Since the mapping sets in \(\Delta ^{\text {op} }_{\le n}\) are finite the functors \((i_k)_!\iota (x)\) takes values in the image of \({\mathcal {C}}\), and hence factor through \(\Delta ^{\text {op} }_{\le n}\)-diagrams in \({\mathcal {C}}\). It will hence suffice to show that f preserves finite geometric realizations of simplicial diagrams which factor through \(\iota :{\mathcal {C}}\hookrightarrow {\text {Ind}}({\mathcal {C}})\). Indeed, since \({\mathcal {C}}\) admits finite geometric realizations which are preserved by \(\iota \) this follows from the assumption that \(f \circ \iota \) preserves finite geometric realizations. \(\square \)
Lemma 4.2.34
Any quadratic functor  preserves finite geometric realizations and finite totalizations.
preserves finite geometric realizations and finite totalizations.
Proof
It suffices to show the claim for the special cases where  is either exact or of the form \(x\mapsto \text {B} (x,x)\) for a bilinear functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), since these generate all quadratic functors under both limits and colimits: indeed, a general quadratic functor
is either exact or of the form \(x\mapsto \text {B} (x,x)\) for a bilinear functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), since these generate all quadratic functors under both limits and colimits: indeed, a general quadratic functor  is both the fibre of a map from
is both the fibre of a map from  to an exact functor and the cofibre of a map from an exact functor to
to an exact functor and the cofibre of a map from an exact functor to  . The case where
. The case where  is exact follows from Remark 4.2.32. We hence suppose that
is exact follows from Remark 4.2.32. We hence suppose that  for some bilinear \(\text {B} \), and let \(X:\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) be a finite diagram. Since \(\Delta \) is sifted we then have
for some bilinear \(\text {B} \), and let \(X:\Delta ^{\text {op} }\rightarrow {\mathcal {C}}\) be a finite diagram. Since \(\Delta \) is sifted we then have

Now for each fixed \(x \in {\mathcal {C}}\) the functor \(\text {B} (x,-)\) is exact and hence preserves finite geometric realizations by Remark 4.2.32. Similarly, for each fixed \(y\in {\mathcal {C}}\) the functor \(\text {B} (-,y)\) preserves finite geometric realizations. We hence get that
Using again that \(\Delta \) is sifted we consequently get  , as desired. \(\square \)
, as desired. \(\square \)
Our strategy for the proof of Proposition 4.2.18 is to break the inclusion \(\text {Proj} (R) \hookrightarrow {{\mathcal {D}}}^\text {p} (R)\) into the composite of two inclusions
where \({{\mathcal {D}}}^\text {p} (R)_{\ge 0} \subseteq {{\mathcal {D}}}^\text {p} (R)\) is the image under the localisation functor \({\text {Ch}}^{\textrm{b}}(\text {Proj} (R)) \rightarrow {{\mathcal {D}}}^\text {p} (R)\) of the full subcategory \({\text {Ch}}^{\textrm{b}}_{\ge 0}(\text {Proj} (R)) \subseteq {\text {Ch}}^{\textrm{b}}(\text {Proj} (R))\) spanned by the complexes concentrated in non-negative degrees. To make this strategy work we would like to have a notion of a (contravariant) quadratic functor from \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) to spectra.
Recall from Definition 1.1.1 that a functor  is said to be 2-excisive if it sends strongly cocartesian cubes in \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) to exact cubes in \({{\mathcal {S}}{p}}^{\text {op} }\). We will denote by
is said to be 2-excisive if it sends strongly cocartesian cubes in \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) to exact cubes in \({{\mathcal {S}}{p}}^{\text {op} }\). We will denote by
the full subcategory spanned by the reduced 2-excisive functors \({{\mathcal {D}}}^\text {p} (R)_{\ge 0} \rightarrow {{\mathcal {S}}{p}}^{\text {op} }\).
Remark 4.2.35
It follows from [47, Proposition 6.1.3.22] that the cross effect of any reduced 2-excisive functor  is reduced and 1-excisive in each variable separately.
is reduced and 1-excisive in each variable separately.
Lemma 4.2.36
Restriction along the inclusion \({{\mathcal {D}}}^\text {p} (R)_{\ge 0} \subseteq {{\mathcal {D}}}^\text {p} (R)\) yields an equivalence
Proof
Consider the composite
where the first functor is given by right Kan extension along the inclusion \(\iota :{{\mathcal {D}}}^\text {p} (R)_{\ge 0}^{\text {op} }\hookrightarrow {{\mathcal {D}}}^\text {p} (R)^{\text {op} }\) (a procedure which preserves reduced functors by the pointwise formula for Kan extensions) and the second by the right adjoint \(\text {P} ^2\) to the inclusion \({\text {Fun}}^{\textrm{q}}({{\mathcal {D}}}^\text {p} (R)) \subseteq {\text {Fun}}_*({{\mathcal {D}}}^\text {p} (R)^{\text {op} },{{\mathcal {S}}{p}})\) described in Construction (1.1.26). Since (93) is a composite of right adjoints it is itself right adjoint to the composite
Since (94) factors through the full subcategory of quadratic functors the unit and counit of the adjunction between (93) and (94) also yield an adjunction

where the right adjoint is obtained by restricting the domain of (93) and the left adjoint is the restriction functor (92) under consideration. We claim that the adjunction (95) is an equivalence. To begin, we first show that for  the counit
the counit  is an equivalence. We note that this counit is given itself by a composite
is an equivalence. We note that this counit is given itself by a composite

where the second map is the counit of \(\iota ^* \dashv \iota _*\), which is an equivalence since \(\iota \) is fully-faithful. The first map in turn is the one obtained by applying \(\iota ^*\) to the counit  . We hence need to show that the component
. We hence need to show that the component

is an equivalence for X in the image of the inclusion \({{\mathcal {D}}}^\text {p} (R)_{\ge 0} \subseteq {{\mathcal {D}}}^\text {p} (R)\). For this we recall that \(\text {P} ^2\) is defined via a sequential limit
where \({\mathcal {T}}^2({\mathcal {R}})(X) = \Sigma {\text {cof}}[\text {B} _{{\mathcal {R}}}(\Sigma X,\Sigma X) \rightarrow {\mathcal {R}}(\Sigma X)]\), see Construction 1.1.26. It will then suffice to show that for \(X \in {{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) the sequence

is exact. Indeed, this follows by the exact same argument as the dual version of Lemma 1.1.19 (see Remark 1.1.20) in the case where z and w are zero objects, using that  is assumed to be reduced and 2-excisive on \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\).
is assumed to be reduced and 2-excisive on \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\).
As the counit is an equivalence, to finish the proof it will suffice to show that \(\iota ^*\) is conservative, or equivalently (since its domain is stable), detects zero objects. In particular, we need to show that if  is a quadratic functor which vanishes on \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) then
is a quadratic functor which vanishes on \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) then  is the zero functor. Indeed, for such a
is the zero functor. Indeed, for such a  we will have that
we will have that  vanishes on \(({{\mathcal {D}}}^\text {p} (R))_{\ge -n} := \Sigma ^{-n}{{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) and hence that
vanishes on \(({{\mathcal {D}}}^\text {p} (R))_{\ge -n} := \Sigma ^{-n}{{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) and hence that

since any \(X \in {{\mathcal {D}}}^\text {p} (R)\) lies in \({{\mathcal {D}}}^\text {p} (R)_{\ge -n}\) for some n. \(\square \)
Lemma 4.2.37
Restriction along the inclusion \(\text {Proj} (R) \subseteq {{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) yields an equivalence
Proof
Let \({\mathcal {D}}(R)_{\ge 0} \subseteq {\mathcal {D}}(R)\) denote the full subcategory spanned by the objects represented by non-negatively graded complexes. By [47, Proposition 1.3.3.14] restriction along the inclusion \(\text {Proj} (R) \rightarrow {\mathcal {D}}(R)_{\ge 0}\) yields an equivalence
where the left hand side denotes the full subcategory of \({\text {Fun}}({\mathcal {D}}(R)_{\ge 0}^{\text {op} },{{\mathcal {S}}{p}})\) spanned by the functors which preserve sifted limits. It then follows from Lemma 4.2.33 that restriction along the inclusion \(\text {Proj} (R) \rightarrow {{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) induces an equivalence
where on the left hand side we have the \(\infty \)-category of functors \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) which preserve finite geometric realizations. By Lemma 4.2.34 the latter contains \({\text {Fun}}^{2-\text {exc} }_*({{\mathcal {D}}}^\text {p} (R)_{\ge 0})\) as a full subcategory. We now claim that under the equivalence (98) the reduced 2-excisive functors on the left hand side correspond to the functors that are reduced and polynomial of degree 2 on the right hand side. First, since the inclusion \(\text {Proj} (R) \rightarrow {{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) is additive and reduced 2-excisive functors have cross effects which are reduced and 1-excisive in each variable separately (see [47, Proposition 6.1.3.22]) it follows that reduced 2-excisive functors restrict to reduced functors which are polynomial of degree 2. Conversely, suppose that \({\mathcal {R}}:{{\mathcal {D}}}^\text {p} (R)_{\ge 0}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is a functor which preserves finite geometric realizations whose restriction to \(\text {Proj} (R)^{\text {op} }\) is reduced and polynomial of degree 2. Since \(\text {Proj} (R)\) contains the zero object of \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) we have that \({\mathcal {R}}\) is reduced. To show that \({\mathcal {R}}\) is 2-excisive we need to show that it sends strongly cocartesian cubes in \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) to exact cubes of spectra. For this, let \(\rho :(\Delta ^1)^3 \rightarrow {{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) be a strongly cocartesian cube. We want to reduce to the case where \(\rho \) takes values in the subcategory of finite projective modules and injections. Let us identify \((\Delta ^1)^3\) with the nerve of the poset \({\mathcal {P}}([2])\) of subsets of \([2] = \{0,1,2\}\). Let \({\mathcal {P}}_{\le 1}([2]) \subseteq {\mathcal {P}}([2])\) be the full subposet spanned by \(\{\},\{0\},\{1\},\{2\}\). Since \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) is the localisation of the cofibration category \({\text {Ch}}^{\textrm{b}}_{\ge 0}(\text {Proj} (R))\) it follows from [17, Theorem 7.6.17] that we can represent \(\rho |_{{\mathcal {P}}_{\le 1}([2])}\) by a diagram \(\tau :{\mathcal {P}}_{\le 1}([2]) \rightarrow {\text {Ch}}^{\textrm{b}}_{\ge 0}(\text {Proj} (R))\) in which each map \(c_i:\tau (\{\}) \rightarrow \tau (\{i\})\) is levelwise injective with projective kernel. The Dold–Kan correspondence then associates to \(\tau \) a diagram \(\tau ':{\mathcal {P}}_{\le 1}([2]) \rightarrow \text {Proj} (R)^{\Delta ^{\text {op} }}\) of simplicial R-modules such that each of the maps \(c_i:\tau (\{\}) \rightarrow \tau (\{i\})\) is levelwise injective with projective cokernel (see [56, §II.4.12]). In addition, since \(\tau \) takes values in bounded complexes we can find an \(n \ge 0\) such that it takes values in complexes concentrated in degrees 0 to n. Under the Dold–Kan correspondence such complexes map to simplicial R-modules which are left Kan extended from their restriction to \(\Delta _{\le n}^{\text {op} }\). Switching the simplicial dimension with the \({\mathcal {P}}_{\le 1}([2])\)-dimension we may conclude that \(\tau |_{{\mathcal {P}}_{\le 1}([2])}\) can be written as a finite geometric realisation of a simplicial family of diagrams \(\tau '_{n}:{\mathcal {P}}_{\le 1}([2]) \rightarrow \text {Proj} (R)\) such that each \(\tau '_n\) has the property that \(\tau '_n(\{\}) \rightarrow \tau '_n(\{i\})\) is a split injective map of projective modules. Left Kan extending from \({\mathcal {P}}_{\le 1}([2])\) we obtain a representation of \(\rho \) as a finite geometric realisation of a simplicial family of strongly cocartesian cubes \(\rho _n:{\mathcal {P}}([2]) \rightarrow \text {Proj} (R)\) such that each \(\rho _n(\{\}) \rightarrow \rho _n(\{i\})\) is a split injective map of projective modules. Since \({\mathcal {R}}\) preserves finite geometric realizations it will suffice to show that \({\mathcal {R}}\) sends each \(\rho _n\) to an exact cube of spectra. Now since \(\text {Proj} (R)\) is closed in \({{\mathcal {D}}}^\text {p} (R)_{\ge 0}\) under pushouts with one leg split injective it follows that each \(\rho _n\) is a strongly cocartesian cube in \(\text {Proj} (R)\). More explicitly, we may pick projective modules \(X_n,Y_n^0,Y_n^1,Y_n^2\) such that \(\tau '_n(\{\}) = X^n\) and \(\tau '_n(\{i\}) = X_n \oplus Y_n^i\) for \(i=0,1,2\), in which case \(\rho _n:{\mathcal {P}}([2]) \rightarrow {{\mathcal {D}}}^\text {p} (R)\) is given by
To finish the proof we need to show that the resulting cube of spectra
is exact. Let \(\text {B} (-,-)\) be the cross-effect of \({\mathcal {R}}\). The assumption that \({\mathcal {R}}|_{\text {Proj} (R)}\) is polynomial of degree 2 means that the restriction of \(\text {B} \) to \(\text {Proj} (R) \times \text {Proj} (R)\) preserve direct sums in each variable separately. The cube of spectra \({\mathcal {R}}\circ \rho _n\) thus decomposes as a direct sum of four components
The first component is constant and is hence an exact cube, and the second and third components are visibly exact. Finally, the fourth component \(S \mapsto \oplus _{i < j \in S} \text {B} (Y_n^i,Y_n^j)\) is also an exact cube since it vanishes on S of size smaller than 2 and exhibits its value at \(S=\{0,1,2\}\) as the product of its values on \(\{0,1\},\{1,2\}\) and \(\{0,2\}\). We have thus showed that the cube of spectra (99) is exact, and so the proof is complete. \(\square \)
Proof of Proposition 4.2.18
Combine Lemma 4.2.36 and Lemma 4.2.37. \(\square \)
5.3 Group-rings and visible structures
In this section we will consider group rings, and more generally, group ring spectra, which provide important examples of rings with anti-involutions, and whose various types of \({\text {L}}\)-groups play a role in surgery theory and manifold classification, see Example 4.3.6. As in the work of Weiss–Williams [73], these geometric applications are sometimes better serviced by replacing modules over group rings by parametrised spectra, a point of view we will take up in Sect. 4.4.
Recall that for an ordinary group G equipped with a homomorphism \(\chi :G \rightarrow \{-1,1\}\), one may endow the group ring \({\mathbb {Z}}G\) with the associated \(\chi \)-twisted involution \(\tau _{\chi }:{\mathbb {Z}}G \xrightarrow {\cong } ({\mathbb {Z}}G)^{\text {op} }\), defined by sending \(g \in {\mathbb {Z}}G\) to \(\chi (g)g^{-1}\). In what follows we will consider a generalization of this setup where G is replaced by an \({\text {E} _1}\)-group, that is, a group-like \({\text {E} _1}\)-monoid in spaces, and instead of \({\mathbb {Z}}\) the coefficients are taken in the sphere spectrum. More precisely, for such a G the suspension spectrum \({\mathbb {S}}[G] := \Sigma ^{\infty }_+G\) inherits the structure of an \({\text {E} _1}\)-ring spectrum, which is called the group ring spectrum of G. This \({\text {E} _1}\)-ring spectrum is characterized by the fact that its module spectra correspond to spectra with a G-action, a notion which we will call here (naive) G-spectra, and consequently also use the notations \({\text {Mod}}_G := {\text {Mod}}_{{\mathbb {S}}[G]}\) and \({\text {Mod}}^{\omega }_{G} := {\text {Mod}}^{\omega }_{{\mathbb {S}}[G]}\), as well as the shorthand \(\otimes _G\) for \(\otimes _{{\mathbb {S}}[G]}\). In this section we consider data giving rise to Poincaré structures on \({\text {Mod}}^{\omega }_{{\mathbb {S}}[G]}\). We also consider variants for the group algebras \(A[G] := A \otimes _{{\mathbb {S}}} {\mathbb {S}}[G]\) with coefficients in some \({\text {E} _1}\)-ring spectrum A. A closely related construction involving parametrised spectra over a space will be explored in Sect. 4.4.
Recall that a spectrum \(E \in {{\mathcal {S}}{p}}\) is called invertible if there exists a spectrum \(E'\) such that \(E \otimes _{{\mathbb {S}}} E' \simeq {\mathbb {S}}\). In this case E is necessarily of the form \(\Sigma ^n{\mathbb {S}}\) for a unique \(n \in {\mathbb {Z}}\), to which we refer as the rank of E. By a character of an \({\text {E} _1}\)-group G we will mean a pair \((E,\chi )\) where E is an invertible spectrum and \(\chi :G \rightarrow {\text {Aut}}(E) \simeq \text {gl} _1({\mathbb {S}})\) is a homomorphism of \({\text {E} _1}\)-groups, encoding an action of G on E.
Construction 4.3.1
Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\). We define a module with genuine involution on the group ring \({\mathbb {S}}[G]\) as follows. First, since the diagonal map \(G \rightarrow G \times G\) is naturally equivariant with respect to the flip \({{\text {C} }_{\textrm{2}}}\)-action on \(G \times G\) and the trivial action on G, it follows that the induction functor
refines to a functor
where \({{\text {C} }_{\textrm{2}}}\) acts on \({\text {Mod}}_{G \times G}\) via its flip action on \(G \times G\). In particular, the \(G \times G\)-spectrum
induced from the G-spectrum E is naturally a \({{\text {C} }_{\textrm{2}}}\)-equivariant object of \({\text {Mod}}_{G \times G}\). Identifying \({\mathbb {S}}[G] \otimes _{{\mathbb {S}}} {\mathbb {S}}[G]\) with \({\mathbb {S}}[G \times G]\) we then see that the Tate diagonal
is given by the composite \({\mathbb {S}}[G] \rightarrow {\mathbb {S}}[G \times G]^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\mathbb {S}}[G \times G]^{{{\text {tC} }_{\textrm{2}}}}\) in which the first map is induced by the \({{\text {C} }_{\textrm{2}}}\)-equivariant diagonal \(G \rightarrow G \times G\). In particular, the G-action on \(E[G^{-}]^{{{\text {tC} }_{\textrm{2}}}}\) is induced by the G-action on \(E[G^{-}]\) restricted from \(G \times G\) along the diagonal, and we may then consider the composite map of G-spectra
and we call the resulting module with genuine involution \((E[G^{-}],E,\eta )\) the \(\chi \)-twisted visible module. We will denote the corresponding hermitian structure on \({\text {Mod}}^{\omega }_{G}\) by  and refer to it as the \(\chi \)-twisted visible structure on \({\text {Mod}}^{\omega }_{G}\). Similarly, for a given subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{G})\) we may restrict
and refer to it as the \(\chi \)-twisted visible structure on \({\text {Mod}}^{\omega }_{G}\). Similarly, for a given subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{G})\) we may restrict  to obtain the corresponding visible hermitian structure on \({\text {Mod}}^c_G\).
to obtain the corresponding visible hermitian structure on \({\text {Mod}}^c_G\).
Lemma 4.3.2
Let n be such that \(E \simeq \Sigma ^n{\mathbb {S}}\) as spectra. Then the \(({\mathbb {S}}[G] \otimes _{{\mathbb {S}}} {\mathbb {S}}[G])\)-module \(E[G^{-}]\) is invertible and equivalent to \(\Sigma ^n{\mathbb {S}}[G]\) as an \({\mathbb {S}}[G]\)-module. Furthermore, under this equivalence the involution on \(E[G^{-}]\) corresponds to the n-fold suspension of a ring spectrum anti-involution
so that \((\Sigma ^{-n}E[G^{-}],\Sigma ^{-n}E,\Sigma ^{-n}\eta )\) promotes \({\mathbb {S}}[G]\) to a genuine ring with involution. In particular, the visible structure  on both \({\text {Mod}}^{\omega }_{G}\) and \(\text {Mod} ^{\text {f} }_{G}\) is Poincaré (see Example 3.2.9).
on both \({\text {Mod}}^{\omega }_{G}\) and \(\text {Mod} ^{\text {f} }_{G}\) is Poincaré (see Example 3.2.9).
We will use the notation \({\mathbb {S}}_{\chi }[G]\) to denote the group ring of G considered with the anti-involution \(\tau _{\chi }:{\mathbb {S}}[G] \rightarrow {\mathbb {S}}[G]^{\text {op} }\) of Lemma 4.3.2. Explicitly, \(\tau _{\chi }\) is the ring map induced by the composed map
in which the first map is given by \(g \mapsto (\chi (g),g^{-1})\). In particular, on \(\pi _0{\mathbb {S}}[G] \cong {\mathbb {Z}}[\pi _0 G]\) this involution can be written as \(\sum _i a_i g_i \mapsto \sum _i a_i\chi _0(g_i)g_i^{-1}\), where
is the induced homomorphism on \(\pi _0\).
Proof of Lemma 4.3.2
By Proposition 3.1.14 it will suffice to exhibit a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \(u:{\mathbb {S}}\rightarrow \Sigma ^{-n}E[G^{-}]\) which freely generates \(\Sigma ^{-n}E[G^{-}]\) as an \({\mathbb {S}}[G]\)-module. Indeed, this is given by the \({{\text {C} }_{\textrm{2}}}\)-equivariant map
induced by the diagonal map \(G \rightarrow G \times G\). This map exhibits \(\Sigma ^{-n}E[G^{-}]\) as a free \({\mathbb {S}}[G]\)-module on a single generator since the shear map \(G \times G \rightarrow G \times G\) (given informally by \((g,h) \mapsto (g,gh)\)) is an equivalence by the group-like property. \(\square \)
The following variant is also of interest:
Variant 4.3.3
(Visible structures with coefficients) Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\) and let \((A,N,\alpha )\) be an \({\text {E} _1}\)-ring spectrum with genuine involution. The \({\text {E} _1}\)-ring
can be endowed with a module with genuine involution by tensoring the visible module \((E[G^{-}], E,\eta )\) of Construction 4.3.1 with \((A,N,\alpha )\), using the monoidal structure on genuine \({{\text {C} }_{\textrm{2}}}\)-spectra (see Remark 3.2.4). Explicitly, this yields the module with genuine involution
where
is obtained via the lax monoidal structure map of the Tate construction. We will denote the corresponding hermitian structure on \({\text {Mod}}^{\omega }_{A[G]}\) by  , and refer to it as the \(\chi \)-twisted visible structure on \({\text {Mod}}^{\omega }_{A[G]}\). It then follows from Lemma 4.3.2 that this hermitian structure is Poincaré and identifies up to a shift with the Poincaré structure associated to a genuine refinement of the anti-involution \(\tau _{A,\chi }:A[G] \xrightarrow {\simeq } (A[G]){^{\text {op} }}\) induced by the anti-involution of A and \(\chi \)-twisted anti-involution of \({\mathbb {S}}[G]\). We will refer to \(\tau _{A,\chi }\) as the \(\chi \)-twisted anti-involution on A[G].
, and refer to it as the \(\chi \)-twisted visible structure on \({\text {Mod}}^{\omega }_{A[G]}\). It then follows from Lemma 4.3.2 that this hermitian structure is Poincaré and identifies up to a shift with the Poincaré structure associated to a genuine refinement of the anti-involution \(\tau _{A,\chi }:A[G] \xrightarrow {\simeq } (A[G]){^{\text {op} }}\) induced by the anti-involution of A and \(\chi \)-twisted anti-involution of \({\mathbb {S}}[G]\). We will refer to \(\tau _{A,\chi }\) as the \(\chi \)-twisted anti-involution on A[G].
Example 4.3.4
When G is discrete a common choice of a twisting is via a sign homomorphism \(\chi :G \rightarrow \{-1,1\}\). This can be made into a G-character \((E,\chi )\) once we fix what is meant by the sign action on \({\mathbb {S}}\). Here (at least) two equally natural options are possible: one can either take \(E = {\mathbb {S}}^{\sigma -1}\) to be the desuspension of the sign representation sphere, or take \(E = {\mathbb {S}}^{1-\sigma }\) to be its inverse. These are generally not equivalent as spectra with \({{\text {C} }_{\textrm{2}}}\)-action, see Example 3.5.14 iii).
Example 4.3.5
Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\). If \((A,0,0 \rightarrow A^{{{\text {tC} }_{\textrm{2}}}})\) is an \({\text {E} _1}\)-ring spectrum with genuine involution associated to the quadratic genuine refinement of an anti-involution on A, then the associated \(\chi \)-twisted visible Poincaré structure on \({\text {Mod}}^{\omega }_{A}\) coincides with the quadratic Poincaré structure associated to the \(\chi \)-twisted duality on \({\text {Mod}}^{\omega }_{A[G]}\).
Example 4.3.6
(The visible symmetric structure) Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\) and let A be an \({\text {E} _1}\)-ring spectrum with anti-involution. We refer to the \(\chi \)-twisted Poincaré structure on \({\text {Mod}}^{\omega }_{A[G]}\) associated to the \({\text {E} _1}\)-ring spectrum with genuine involution \((A,A^{{{\text {tC} }_{\textrm{2}}}},\text {id} :A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow A^{{{\text {tC} }_{\textrm{2}}}})\) as the visible symmetric Poincaré structure, and denote it by  . Its reference map \(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \rightarrow A_{\chi }[G^-]^{{{\text {tC} }_{\textrm{2}}}}\) can then be factored as a composite
. Its reference map \(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \rightarrow A_{\chi }[G^-]^{{{\text {tC} }_{\textrm{2}}}}\) can then be factored as a composite
where \(\alpha \) is induced by the Tate diagonal of \({\mathbb {S}}[G]\) and the lax symmetric monoidal structure of \((-)^{{{\text {tC} }_{\textrm{2}}}}\), and \(\beta \) is the canonical interchange map between \((-) \otimes _G E\) and \((-)^{{{\text {tC} }_{\textrm{2}}}}\). When G and A are discrete the \({\text {L}}\)-groups of this Poincaré structure recover the visible symmetric \({\text {L}}\)-groups A[G], first defined by Weiss [70]. Indeed, translating the definition of [70] to the present setting gives a Poincaré structure with linear part classified by the A[G]-module \(A[G \times G]^{{{\text {tC} }_{\textrm{2}}}} \otimes _G E\) with reference map \(\beta \) as above. To compare the two it will hence suffice to show that \(\alpha \) is an equivalence when G and A are discrete. Indeed, we can factor \(\alpha \) as a composite
where the first map is an equivalence in this case since the Tate construction preserves filtered colimits of discrete spectra and the second map is an equivalence since the cofibre of the map \({\mathbb {S}}[G] \rightarrow {\mathbb {S}}[G \times G]\) is an induced \({{\text {C} }_{\textrm{2}}}\)-module when G is discrete.
Example 4.3.7
(The visible genuine structure) Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\) and let A be a connective \({\text {E} _1}\)-ring spectrum with anti-involution. We will refer to the \(\chi \)-twisted Poincaré structure on \({\text {Mod}}^{\omega }_{A[G]}\) associated to the \({\text {E} _1}\)-ring spectrum with genuine involution \((A,\tau _{\ge m}A^{{{\text {tC} }_{\textrm{2}}}},t_m)\) as the visible genuine Poincaré structure, and denote it by  . Its linear part is then classified by the A[G]-module \(\tau _{\ge m}A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \simeq \tau _{\ge n+m}(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E)\), where n is the rank of E.
. Its linear part is then classified by the A[G]-module \(\tau _{\ge m}A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \simeq \tau _{\ge n+m}(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E)\), where n is the rank of E.
In some circumstances, the visible symmetric Poincaré structure on A[G] identifies with the symmetric one:
Lemma 4.3.8
Let A be an \({\text {E} _1}\)-ring spectrum with anti-involution, G an \({\text {E} _1}\)-group and \((E,\chi )\) a G-character of rank n. If either \(\text {B} G\) is a finitely dominated space or G is a discrete group with no non-trivial 2-torsion then the comparison map  is an equivalence.
is an equivalence.
Remarks 4.3.9
-
i)
The two different conditions considered in Lemma 4.3.8 are not completely unrelated: if G is a discrete group then the condition that \(\text {B} G\) is finitely dominated implies that G has no non-trivial torsion (indeed, for such a G the constant module \({\mathbb {Z}}\) admits a finite projective resolution, and so all subgroups of G have finite cohomological dimension, see, e.g., [15, Corollary VIII.2.5]).
-
ii)
The proof of Lemma 4.3.8 in the case of G discrete with no non-trivial 2-torsion extends to more general groups: the same argument works for example for Lie groups with no non-trivial 2-torsion which are sufficiently nice in the sense G is a finite dimensional \({{\text {C} }_{\textrm{2}}}\)-CW-complex considered with respect to the \({{\text {C} }_{\textrm{2}}}\)-action \(g \mapsto g^{-1}\).
In the circumstances of Lemma 4.3.2, the visible genuine Poincaré structure on A[G] also identifies with the truncated structure of Example 3.2.8, up to a shift in the truncation point by the rank of E:
Corollary 4.3.10
Let A be a connective \({\text {E} _1}\)-ring spectrum with anti-involution, G an \({\text {E} _1}\)-group and \((E,\chi )\) a G-character of rank n. If either \(\text {B} G\) is a finitely dominated space or G is a discrete group with no 2-torsion then

Proof of Lemma 4.3.8
The comparison claim is equivalent to the statement that under the given assumptions the reference map \(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \rightarrow A_{\chi }[G^{-}]^{{{\text {tC} }_{\textrm{2}}}}\) of the visible symmetric structure is an equivalence.
Assume first that G is a discrete group with no 2-torsion. Then we may identify \(A_{\chi }[G^{-}] \simeq \oplus _{g \in G} [A \otimes _{{\mathbb {S}}} E]\) with the involution acting by applying the involution of A on each factor and then switching the component associated to \(g \in G\) with the component associated to \(g^{-1}\). Under the identification \(A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} E \simeq (A \otimes _{{\mathbb {S}}} E)^{{{\text {tC} }_{\textrm{2}}}}\) the reference map is then induced on Tate objects by the inclusion of the component of \(1 \in G\). When G has no 2-torsion the cofibre of this inclusion is an induced \({{\text {C} }_{\textrm{2}}}\)-module, and so the induced map on Tate objects is an equivalence.
Now assume that \(\text {B} G\) is a compact space. We then factor the reference map of the visible symmetric structure as in (100). Since \(\text {B} G\) is compact it follows that E, which can be written as a \(\text {B} G\)-indexed colimit of free \({\mathbb {S}}[G]\)-modules, is itself a compact \({\mathbb {S}}[G]\)-module, and so the arrow \(\beta \) in (100) is an equivalence. Now consider the exact functor \(T:{\text {Mod}}_A \rightarrow {{\mathcal {S}}{p}}\) given by \(T(X) \mapsto (\overline{X} \otimes _A X)^{{{\text {tC} }_{\textrm{2}}}}\), where \(\overline{X}\) denotes X, but considered as a right A-module via the involution on A. In particular, we have a canonical equivalence \(T(A) \simeq A^{{{\text {tC} }_{\textrm{2}}}}\). Then the interchange map \(T(A) \otimes _{{\mathbb {S}}} E \rightarrow T(A \otimes _{{\mathbb {S}}} E)\) is an equivalence since E is finite as a spectrum, but can also be factored as a composite of interchange maps
in which the second interchange map is an equivalence since E is perfect as an \({\mathbb {S}}[G]\)-module. It then follows that the first interchange map
is an equivalence as well. Unwinding the definitions, this map can be identified with \(\alpha \), and so the desired result is obtained. \(\square \)
Remark 4.3.11
Let G be an \({\text {E} _1}\)-group equipped with a character \((E,\chi )\). Consider the universal Poincaré structure  on \({{\mathcal {S}}{p}}^{\text {f} }\) associated to the module with genuine involution \(({\mathbb {S}},{\mathbb {S}},{\mathbb {S}}\rightarrow {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}})\). Since any stable \(\infty \)-category is tensored over \({{\mathcal {S}}{p}}\) the character \(\chi \) induces an action of G on
on \({{\mathcal {S}}{p}}^{\text {f} }\) associated to the module with genuine involution \(({\mathbb {S}},{\mathbb {S}},{\mathbb {S}}\rightarrow {\mathbb {S}}^{{{\text {tC} }_{\textrm{2}}}})\). Since any stable \(\infty \)-category is tensored over \({{\mathcal {S}}{p}}\) the character \(\chi \) induces an action of G on  , and hence on
, and hence on  . Using the point of view of parametrised spectra, we will show in Sect. 6.1 that the visible Poincaré structure
. Using the point of view of parametrised spectra, we will show in Sect. 6.1 that the visible Poincaré structure  on finitely presented \({\mathbb {S}}[G]\)-modules can be universally characterized as the quotient of
on finitely presented \({\mathbb {S}}[G]\)-modules can be universally characterized as the quotient of  by G in \(\text {Cat} ^{\textrm{p}}_\infty \) (see Proposition 6.1.9 and Example 4.4.5). The Poincaré \(\infty \)-category
by G in \(\text {Cat} ^{\textrm{p}}_\infty \) (see Proposition 6.1.9 and Example 4.4.5). The Poincaré \(\infty \)-category  can then be identified with the corresponding quotient only computed in idempotent complete Poincaré \(\infty \)-categories.
can then be identified with the corresponding quotient only computed in idempotent complete Poincaré \(\infty \)-categories.
More generally, if \((A,N,\alpha )\) is an \({\text {E} _1}\)-ring spectrum with genuine anti-involution then  represents the quotient of the associated G-action on
represents the quotient of the associated G-action on  ; this can be deduced from the above claim by identifying
; this can be deduced from the above claim by identifying  with a suitable tensor product of
with a suitable tensor product of  and
and  , see Sect. 5.2 and Example 5.1.6.
, see Sect. 5.2 and Example 5.1.6.
Variant 4.3.12
Construction 4.3.1 can be generalized by introducing the following additional pieces of data: a \({{\text {C} }_{\textrm{2}}}\)-action \(\tau :{{\text {C} }_{\textrm{2}}}\rightarrow {\text {Aut}}(G)\) on G, an additional \({\text {E} _1}\)-group H, and a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \(H \rightarrow G\), where \({{\text {C} }_{\textrm{2}}}\) acts trivially on H. We may consider such a structure as a genuine \({{\text {C} }_{\textrm{2}}}\)-action on G. The data of a character \((E,\chi )\) for G then needs to be promoted to that of \({{\text {C} }_{\textrm{2}}}\)-equivariant character \(\chi :G \rightarrow {\text {Aut}}(E)\) (where \({{\text {C} }_{\textrm{2}}}\)-acts trivially on the target), and the induced \({{\text {C} }_{\textrm{2}}}\)-action on the restricted character \(\chi |_{H}\) should be equipped with a trivialization. To all this data one can associate a module with genuine involution \((E[G^{-\tau }],E[G/H],\eta )\) where \(E[G^{-\tau }] := E[G\times G]\otimes _G E\) is the \((G \times G)\)-spectrum induced from E, this time along the \(\tau \)-diagonal \((\tau ,\text {id} ):G \rightarrow G \times G\), and E[G/H] is the G-module induced from the H-character \((E,\chi |_{H})\) along the map \(H \rightarrow G\). Since the map \((\tau ,\text {id} )\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to flip action on \(G \times G\), and \(\chi \) is \({{\text {C} }_{\textrm{2}}}\)-equivariant, the \((G \times G)\)-module \(E[G^{-\tau }]\) inherits an involution compatible with the flip involution of \(G \times G\), and hence the structure of a module with involution over \({\mathbb {S}}[G]\). At the same time, since the usual diagonal \(G \rightarrow G \times G\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the trivial action on the domain, and coincides with the \(\tau \)-diagonal when restricted to H, it induces a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \({\mathbb {S}}[G] \otimes _H E \rightarrow {\mathbb {S}}[G \times G]\otimes _{G} E\) with respect to the trivial action on the domain. The composed map
then constitutes a structure map exhibiting \((E[G^{\tau }],E[G/H],\eta )\) as a module with genuine involution over \({\mathbb {S}}[G]\), yielding a hermitian structure  on \({\text {Mod}}^{\omega }_{G}\), or on \({\text {Mod}}^c_G\) for some subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{G})\). The case of Construction 4.3.1 can be recovered as corresponding to the trivial involution on G with \(H=G\) and \(H \rightarrow G\) the identity map. Arguing as in the proof of Lemma 4.3.2 we can check that this module with genuine involution is invertible and corresponds, up to a shift, to a genuine refinement of a suitable anti-involution on \({\mathbb {S}}[G]\), whose underlying equivalence \({\mathbb {S}}[G] \rightarrow {\mathbb {S}}[G]^{\text {op} }\) is induced by the map \(G \rightarrow \text {gl} _1({\mathbb {S}})\times G\) given by \(g \mapsto (\chi (g),\tau (g)^{-1})\). As in Remark 4.3.11 the Poincaré \(\infty \)-category
on \({\text {Mod}}^{\omega }_{G}\), or on \({\text {Mod}}^c_G\) for some subgroup \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{G})\). The case of Construction 4.3.1 can be recovered as corresponding to the trivial involution on G with \(H=G\) and \(H \rightarrow G\) the identity map. Arguing as in the proof of Lemma 4.3.2 we can check that this module with genuine involution is invertible and corresponds, up to a shift, to a genuine refinement of a suitable anti-involution on \({\mathbb {S}}[G]\), whose underlying equivalence \({\mathbb {S}}[G] \rightarrow {\mathbb {S}}[G]^{\text {op} }\) is induced by the map \(G \rightarrow \text {gl} _1({\mathbb {S}})\times G\) given by \(g \mapsto (\chi (g),\tau (g)^{-1})\). As in Remark 4.3.11 the Poincaré \(\infty \)-category  can be characterized as a certain colimit in \(\text {Cat} ^{\textrm{p}}_\infty \). This can be interpreted as reflecting the structure of \(\text {Cat} ^{\textrm{p}}_\infty \) as a \({{\text {C} }_{\textrm{2}}}\)-category, see Sect. 7.4, which admits quotients by actions of genuine \({{\text {C} }_{\textrm{2}}}\)-groups.
can be characterized as a certain colimit in \(\text {Cat} ^{\textrm{p}}_\infty \). This can be interpreted as reflecting the structure of \(\text {Cat} ^{\textrm{p}}_\infty \) as a \({{\text {C} }_{\textrm{2}}}\)-category, see Sect. 7.4, which admits quotients by actions of genuine \({{\text {C} }_{\textrm{2}}}\)-groups.
5.4 Parametrised spectra
In this section we will discuss Poincaré structures on the \(\infty \)-category of compact parametrised spectra over a space X, whose \({\text {L}}\)-groups reproduces the visible \({\text {L}}\)-groups of [73] (see Corollary 4.4.14 below). We will then show how to construct visible signatures for Poincaré duality spaces in this setting.
Let us begin by establishing some terminology. We write \({{\mathcal {S}}{p}}_X := {\text {Fun}}(X,{{\mathcal {S}}{p}})\) for the \(\infty \)-category of functors \(X \rightarrow {{\mathcal {S}}{p}}\), to which we will refer to as local systems of spectra, or as parametrised spectra over X. We then denote by \({{\mathcal {S}}{p}}_X^{\omega } \subseteq {{\mathcal {S}}{p}}_X\) the full subcategory spanned by the compact objects, and by \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}_X^{\omega }\) the smallest full stable subcategory containing the local systems \(x_!E\) left Kan extended from finite spectra \(E \in {{\mathcal {S}}{p}}^{\text {f} }\) along point inclusions \(\{x\} \subseteq X\). We then note that \({{\mathcal {S}}{p}}_X^{\omega }\) is idempotent complete and the inclusion \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}_X^{\omega }\) is dense, and so exhibits \({{\mathcal {S}}{p}}_X^{\omega }\) is the idempotent completion of \({{\mathcal {S}}{p}}^{\text {f} }_X\). When X is connected and pointed we may identify these subcategories with those of compact and finitely presented \({\mathbb {S}}[\Omega X]\)-modules, respectively. The situation then renders in the context of Sect. 4.3, and we may consider the visible Poincaré structures associated to various \(\Omega X\)-characters. The point of view of parametrised spectra has however the advantage of working without a preferred base point, and not being restricted to connected spaces. The unpointed setting is more natural, for example, when the input is a Poincaré duality space, as arising in the surgery classification of manifolds. The unpointed analogue of a \(\Omega X\)-character is then given by a spherical fibration, that is, a local system \(\xi :X \rightarrow {{\mathcal {S}}{p}}\) which takes values in the full subgroupoid \({\text {Pic}}({\mathbb {S}}) \subseteq \iota {{\mathcal {S}}{p}}\) spanned by the invertible spectra.
Construction 4.4.1
Let X be a space and \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\) a spherical fibration on X. We associate to \(\xi \) a symmetric bilinear functor on \({{\mathcal {S}}{p}}_X^{\omega } = {\text {Fun}}(X,{{\mathcal {S}}{p}})^\omega \) by setting
where the mapping spectra takes place in the \(\infty \)-category \({\text {Fun}}(X \times X,{{\mathcal {S}}{p}})\), \(\boxtimes \) is the exterior tensor product, and \(\Delta _!\) is left Kan extension along the diagonal \(\Delta :X \rightarrow X\times X\). The associated symmetric and quadratic hermitian structure on \( {{\mathcal {S}}{p}}_X^{\omega }\) are then given by

and

respectively. By abuse of notation, we will also denote by  and
and  the respective restrictions of these functors to the dense subcategory \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}^{\omega }_X\).
the respective restrictions of these functors to the dense subcategory \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}^{\omega }_X\).
The above construction is functorial in X in the following sense. Let us call a map of spaces with spherical fibrations a pair \((f,\tau )\) where \(f:X \rightarrow Y\) is a map between spaces equipped with spherical fibrations \(\xi _X\) and \(\xi _Y\) respectively, and \(\tau :\xi _X \rightarrow f^*\xi _Y\) is a natural transformation. We may then associate to f the corresponding left Kan extension functors
The natural transformation \(\tau \) then induces a map
which is natural in L and \(L'\), so that we obtained an induced symmetric functor
covering the left Kan extension functor \(f_!\).
Our first goal is to show that the above construction gives a perfect bilinear functor and identify the associated duality. For this, note that for a fixed local system \(L \in {{\mathcal {S}}{p}}_X\) the association \(L'\mapsto L \boxtimes L' \in {{\mathcal {S}}{p}}_{X \times X}\) is colimit preserving and hence admits a right adjoint
which we can compute explicitly to be
where \(x:*\rightarrow X\) is the insertion of the point x and \(j_x:X \times \{x\} \rightarrow X \times X\) is the corresponding insertion of the horizontal slice at height x.
Lemma 4.4.2
For a spherical fibration \(\xi \), the bilinear functor (101) is non-degenerate with duality
Furthermore, if \((f,\tau ):(X,\xi _X) \rightarrow (Y,\xi _Y)\) is a map of spaces with spherical fibrations such that \(\tau :\xi _X \rightarrow f^*\xi _Y\) is an equivalence then the induced symmetric functor (102) is duality preserving.
Proof
Indeed, by adjunction we have
and so \(\text {B} _{\xi _X}\) is non-degenerate. To see the second claim, fix a map \(f:X \rightarrow Y\) and an equivalence \(\tau :\xi _X \rightarrow \xi _Y\). Since \({{\mathcal {S}}{p}}^{\omega }_X\) is compactly generated by the collection of objects \(x_!{\mathbb {S}}\), for \(x:*\rightarrow X\) a point, it suffices to check that the induced map \(f_!\text {D} L \rightarrow \text {D} f_!L\) is an equivalence for \(L=x_!{\mathbb {S}}\). For this, it will suffice to prove the claim for the maps \(x:*\rightarrow X\) and \(f(x):*\rightarrow Y\). In other words, we may as well assume that \(X=*\) and f is the inclusion of a point \(y \in Y\). Let \(\xi _y \in {{\mathcal {S}}{p}}\) be the value of \(\xi _Y\) at y, so that the goal becomes showing that the canonical symmetric functor
is duality preserving. We now observe that if \(E \in {{\mathcal {S}}{p}}^{\omega }\) is a compact spectrum then we can factor the map \(y_!\text {D} _{\xi _y}(E) \rightarrow \text {D} _{\xi _Y}(y_!E)\) as the composite
where the fourth equivalence is by the formula in (103) and the third arrow is the Beck–Chevalley transformation for the square

where the top horizontal map picks the point \((y,y) \in \{y\} \times Y\). This transformation is an equivalence since the square is cartesian. \(\square \)
Corollary 4.4.3
For a spherical fibration \(\xi \), the \(\xi \)-twisted duality
is perfect. In particular, the associated symmetric and quadratic hermitian structures  and
and  are Poincaré, and their restrictions to \({{\mathcal {S}}{p}}^{\text {f} }_X\) are Poincaré as well.
are Poincaré, and their restrictions to \({{\mathcal {S}}{p}}^{\text {f} }_X\) are Poincaré as well.
Proof
We need to show that the evaluation map \(L \rightarrow \text {D} ^{\text {op} }\text {D} L\) is an equivalence for any \(L \in {{\mathcal {S}}{p}}_X^{\omega }\). Since \({{\mathcal {S}}{p}}^{\omega }_X\) is compactly generated by the collection of objects \(x_!{\mathbb {S}}\), for \(x:*\rightarrow X\) a point, it suffices to check this for \(L=x_!{\mathbb {S}}\). Invoking Lemma 4.4.2 it will suffice to show that the duality \(\text {D} _{\xi _x}\) on \({{\mathcal {S}}{p}}^{\omega }_{\{x\}} = {{\mathcal {S}}{p}}^{\omega }\) is non-degenerate, that is, we may assume that X is a point. But then for any invertible spectrum \(E \in {\text {Pic}}({\mathbb {S}})\) we have that \(\text {D} _E(-) \simeq E \otimes _{{\mathbb {S}}} \text {D} _{{\mathbb {S}}}\) and is hence a perfect duality, the case of \(\text {D} _{{\mathbb {S}}}\) being the usual Spanier–Whitehead duality. Finally,  and
and  also restrict to Poincaré structures on \({{\mathcal {S}}{p}}^{\text {f} }_X\) by Observation 1.2.19; indeed, the equivalence \(\text {D} _{\xi }x_!E \simeq x_!\text {D} _{\xi _x}E\), implies that \({{\mathcal {S}}{p}}^{\text {f} }_X\) is closed under the duality in \({{\mathcal {S}}{p}}^{\omega }_X\). \(\square \)
also restrict to Poincaré structures on \({{\mathcal {S}}{p}}^{\text {f} }_X\) by Observation 1.2.19; indeed, the equivalence \(\text {D} _{\xi }x_!E \simeq x_!\text {D} _{\xi _x}E\), implies that \({{\mathcal {S}}{p}}^{\text {f} }_X\) is closed under the duality in \({{\mathcal {S}}{p}}^{\omega }_X\). \(\square \)
Out next goal is to construct a Poincaré structure on \({{\mathcal {S}}{p}}^{\omega }_{X}\), which in some sense interpolates between the quadratic and symmetric structures. This structure is called the visible Poincaré structure. To construct it, we first need to identify the linear part of the symmetric Poincaré structure  . By definition, it is given by the formula
. By definition, it is given by the formula
which consequently constitutes an exact (contravariant) functor on \({{\mathcal {S}}{p}}^{\omega }_X\). Such functors are always represented by an object in \({\text {Ind}}({{\mathcal {S}}{p}}^{\omega }_X) \simeq {{\mathcal {S}}{p}}_X\), and so there exists a (possibly non-compact) parametrised spectrum \(N:X \rightarrow {{\mathcal {S}}{p}}\) such that
for \(L \in {{\mathcal {S}}{p}}^{\omega }_X\). To identify it, it suffices to check the values of (104) at the generators \(x_!{\mathbb {S}}\) of \({{\mathcal {S}}{p}}^{\omega }_X\). In particular, N is canonically identified with the parametrised spectrum
or simply, \(N = (\Delta ^*\Delta _!\xi )^{{{\text {tC} }_{\textrm{2}}}}\). We thus obtain a natural transformation
which is an equivalence for \(L \in {{\mathcal {S}}{p}}^{\omega }_X\).
Definition 4.4.4
Let X be space and \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\) a spherical fibration on X. We define the \(\xi \)-twisted visible Poincaré structure  by the top pullback square
by the top pullback square

where the right vertical map is induced by the canonical map \(\xi \rightarrow (\Delta ^*\Delta _!\xi )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow (\Delta ^*\Delta _!(\xi ))^{{{\text {tC} }_{\textrm{2}}}}\), which we can also identify with the composite \(\xi \rightarrow \xi ^{{{\text {tC} }_{\textrm{2}}}} \rightarrow (\Delta ^*\Delta _!(\xi ))^{{{\text {tC} }_{\textrm{2}}}}\) (the first Tate construction being taken with respect to the trivial action). By abuse of notation, we will also denote by  its restriction to the duality invariant dense subcategory \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}^{\omega }_X\). By construction, the linear part of
its restriction to the duality invariant dense subcategory \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}^{\omega }_X\). By construction, the linear part of  is given by
is given by
Example 4.4.5
If X is connected with base point \(x \in X\) then \({{\mathcal {S}}{p}}^{\text {f} }_X\) and \({{\mathcal {S}}{p}}_X^{\omega }\) are naturally equivalent to \(\text {Mod} ^{\text {f} }_{\Omega _xX}\) and \({\text {Mod}}^{\omega }_{\Omega _xX}\), respectively, and \(\xi \) can be encoded via a suitable \(\Omega _xX\)-character \(\chi \). Under this equivalence, the visible Poincaré structure  corresponds to the visible Poincaré structure
corresponds to the visible Poincaré structure  of Construction 4.3.1.
of Construction 4.3.1.
Remark 4.4.6
Given a map \((f,\tau ):(X,\xi _X) \rightarrow (Y,\xi _Y)\) of spaces with spherical fibrations, the functoriality of Construction 4.4.1 together with the naturality of the maps \(\xi \rightarrow (\Delta ^*\Delta _!\xi )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow (\Delta ^*\Delta _!(\xi ))^{{{\text {tC} }_{\textrm{2}}}}\) in \(\xi \) combine to yield induced hermitian functors

These are furthermore Poincaré when \(\tau :\xi _X \rightarrow f^*\xi _Y\) is an equivalence by Lemma 4.4.2.
Proposition 4.4.7
Let X be a space equipped with a spherical fibration \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\), and for \(x \in X\) consider the associated maps \((x,\text {id} ):(\{x\},\xi _x) \rightarrow (X,\xi )\) of spaces with spherical fibrations obtained by embedding the various x inside X. Then the natural transformation

induced by the associated Poincaré functors  of Remark 4.4.6, is an equivalence of quadratic functors on \({{\mathcal {S}}{p}}^{\omega }_X\).
of Remark 4.4.6, is an equivalence of quadratic functors on \({{\mathcal {S}}{p}}^{\omega }_X\).
Remark 4.4.8
Since \({{\mathcal {S}}{p}}^{\text {f} }_X \subseteq {{\mathcal {S}}{p}}^{\omega }_X\) is a full inclusion through which all the exact functors \(\lambda _x:{{\mathcal {S}}{p}}^{\text {f} }\rightarrow {{\mathcal {S}}{p}}^{\omega }_X\) factor, the pointwise formula for left Kan extensions shows that the statement made in Proposition 4.4.7 about the Poincaré structure  on \({{\mathcal {S}}{p}}^{\omega }_X\) is also inherited by its restriction to \({{\mathcal {S}}{p}}^{\text {f} }_X\). In other words, that restriction is in turn given by the corresponding colimit of left Kan extensions of
on \({{\mathcal {S}}{p}}^{\omega }_X\) is also inherited by its restriction to \({{\mathcal {S}}{p}}^{\text {f} }_X\). In other words, that restriction is in turn given by the corresponding colimit of left Kan extensions of  along the various \(\lambda _x:{{\mathcal {S}}{p}}^{\text {f} }_{\{x\}} \rightarrow {{\mathcal {S}}{p}}^{\text {f} }_X\).
along the various \(\lambda _x:{{\mathcal {S}}{p}}^{\text {f} }_{\{x\}} \rightarrow {{\mathcal {S}}{p}}^{\text {f} }_X\).
Remark 4.4.9
The universal property of the visible Poincaré structure  described in Proposition 4.4.7 also determines universal properties of a similar nature for
described in Proposition 4.4.7 also determines universal properties of a similar nature for  and
and  as Poincaré \(\infty \)-categories. More precisely, we will prove in Sect. 6.1 that the collection of Poincaré functors
as Poincaré \(\infty \)-categories. More precisely, we will prove in Sect. 6.1 that the collection of Poincaré functors  exhibits
exhibits  as the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram
as the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram  , see Proposition 6.1.9. Similarly,
, see Proposition 6.1.9. Similarly,  is the colimit of the same diagram, but calculated inside idempotent complete Poincaré \(\infty \)-categories. We will discuss idempotent completion of Poincaré \(\infty \)-categories in further details in Paper [2].
is the colimit of the same diagram, but calculated inside idempotent complete Poincaré \(\infty \)-categories. We will discuss idempotent completion of Poincaré \(\infty \)-categories in further details in Paper [2].
Remark 4.4.10
Denoting by \({\mathbb {S}}_X\) the constant spherical fibration on X with value \({\mathbb {S}}\), the proof of Proposition 4.4.7 given below also establishes an identification
as symmetric bilinear functors \({{\mathcal {S}}{p}}^{\omega }_X \times {{\mathcal {S}}{p}}^{\omega }_X \rightarrow {{\mathcal {S}}{p}}\) (in \(L,L'\)), and an equivalence
as functors \({{\mathcal {S}}{p}}^{\omega }_X \rightarrow {{\mathcal {S}}{p}}\). Under these equivalences the defining pullback square of  becomes
becomes

where the right vertical map is given by the composite
using the Tate diagonal of \(L_x\).
Proof of Proposition 4.4.7
Being a map of quadratic functors, it suffices by Corollary 1.3.12 to show that (106) induces an equivalence on bilinear and linear parts. Since taking linear and bilinear parts commutes with colimits, and by Proposition 1.4.3 also with left Kan extensions, the two maps that we need to consider are
Let \(\widetilde{\text {B} }_{\xi _x}\) and \(\widetilde{\Lambda }^{\text {v} }_{\xi _x}\) be the left Kan extensions of \(\text {B} _{\xi _x}\) and \(\Lambda ^{\text {v} }_{\xi _x}\) to \({\text {Pro}}({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\times {\text {Pro}}({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\) and \({\text {Pro}}({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\), respectively. As in the proof of Lemma 1.4.1, we may compute the left Kan extensions of \(\text {B} _{\xi _x}\) and \(\Lambda ^{\text {v} }_{\xi _x}\) along \(\lambda _x \times \lambda _x\) and \(\lambda _x\) respectively by restricting \(\widetilde{\text {B} }_{\xi _x}\) and \(\widetilde{\Lambda }^{\text {v} }_{\xi _x}\) along a given pro-left adjoint
that is, a restriction to \({{\mathcal {S}}{p}}^{\omega }_X\) of a left adjoint to the induced functor \({\text {Pro}}(\lambda _x):{\text {Pro}}({{\mathcal {S}}{p}}^{\text {f} }) \rightarrow {\text {Pro}}({{\mathcal {S}}{p}}^{\omega }_X)\). To produce such a pro-left adjoint, we note that for every \(x \in X\), the duality \(\text {D} _{\xi _x}:({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\xrightarrow {\simeq } {{\mathcal {S}}{p}}^{\text {f} }\) induces an equivalence
Now since evaluation at x is right adjoint to left Kan extension \({{\mathcal {S}}{p}}\rightarrow {{\mathcal {S}}{p}}_X\) along \(\{x\} \subseteq X\) it now follows that a pro-left adjoint for \(\lambda _x\) is given by the composite
Using this pro-left adjoint to express the left Kan extension of \(\text {B} _{\xi _x}\) along \((\lambda _x \times \lambda _x)\) we now obtain
and
To compute these terms further, let us first unwind the pre-compositions of \(\text {B} _{\xi _x}\) and \(\Lambda ^{\text {v} }_{\xi _x}\) with the duality \(\text {D} _{\xi _x}\). For finite spectra \(E,E',E''\) we have
and
Now the two expressions on the right hand sides are well-defined for \(E,E',E''\) which are not necessarily finite, and are colimit preserving in each of these inputs separately. These formulas hence also describe the left Kan extensions of \(\text {B} _{\xi _x}(\text {D} _{\xi _x}(-),\text {D} _{\xi _x}(-))\) and \(\Lambda ^{\text {v} }_{\xi _x}(\text {D} _{\xi _x}(-))\) to \({{\mathcal {S}}{p}}\times {{\mathcal {S}}{p}}\) and \({{\mathcal {S}}{p}}\), respectively. We may consequently conclude that
and
Combining all the above with the equivalences
supplied by (103) and the Beck–Chevalley property, we now conclude that for local systems \(L,L'\in {{\mathcal {S}}{p}}^{\omega }_X\) we have
and
We may now finally identify the maps (107) in explicit terms as follows. The first map in (107) identifies with the composite
where \(\alpha _{L,L'}\) is induced on colimits by the functoriality of \(\boxtimes \) and the identification \(x_!{\mathbb {S}}\boxtimes x_!{\mathbb {S}}\simeq (x,x)_!{\mathbb {S}}\), and \(\beta _{L,L'}\) is given by post-composition with the map \([(x,x)_!{\mathbb {S}}] \otimes \xi _x \simeq (x,x)_!\xi _x \simeq \Delta _!(x_!\xi _x) \rightarrow \Delta _!\xi \) induced by the counit maps \(x_!\xi _x \rightarrow \xi \). In a similar manner, the second map in (107) now becomes the map
induced by the counit maps \(x_!\xi _x \rightarrow \xi \). We now note that the collection of counit maps \(x_!\xi _x \rightarrow \xi \) exhibit \(\xi \) as the colimit in \({{\mathcal {S}}{p}}^{\omega }_X\) of the diagram \(x \mapsto x_!\xi _x\). Indeed, identifying \(x_!\xi _x\) back with \(\Delta _!\xi |_{X \times \{x\}}\), this is just the statement that the map \(\Delta _!\xi \rightarrow \pi _1^*\xi \) exhibits \(\xi \) as the left Kan extension of \(\Delta _!\xi \) along the projection \(\pi _1:X \times X \rightarrow X\) on the first argument, which is clear since \(\pi _1\Delta \simeq \text {id} \). We then conclude that \(\beta _{L,L'}\) and \(\gamma _{L''}\) are equivalences when \(L,L',L''\) are perfect since in this case the functors \({\text {hom}}_{X \times X}(L \boxtimes L',-)\) and \({\text {hom}}_X(L'',-)\) are colimit preserving. To see that \(\alpha _{L,L'}\) is an equivalence, we note that since it is a natural transformation of bilinear functors in \(L,L'\), to check that it is an equivalence on perfect \(L,L'\) it suffices to verify the case where \(L=y_!E\) and \(L'=y'_!E'\) for points \(y,y' \in X\), since local systems of this form generate all perfect local systems under finite colimits and retracts. Then \(\alpha _{y_!E,y'_!E'}\) can be identified with the map
which is an equivalence since the maps
are equivalences for every \(x \in X\). \(\square \)
Let us now pause to explain the relation between the Poincaré \(\infty \)-category  with the construction used in Weiss–Williams [73] to define visible \({\text {L}}\)-theory. To simplify the discussion, let us consider the case where \(\xi ={\mathbb {S}}_X\), though the argument in the general case proceeds in a similar manner. To begin, recall first that the straightening-unstraightening equivalence \({\text {Fun}}(X,{\mathcal {S}}) \simeq {\mathcal {S}}_{/X}\) induces an equivalence
with the construction used in Weiss–Williams [73] to define visible \({\text {L}}\)-theory. To simplify the discussion, let us consider the case where \(\xi ={\mathbb {S}}_X\), though the argument in the general case proceeds in a similar manner. To begin, recall first that the straightening-unstraightening equivalence \({\text {Fun}}(X,{\mathcal {S}}) \simeq {\mathcal {S}}_{/X}\) induces an equivalence
where \({\mathcal {S}}_{X//X} := ({\mathcal {S}}_{/X})_{\text {id} _X/}\) is the \(\infty \)-category of retractive spaces over X. This restricts to an equivalence between the full subcategory \({{\mathcal {S}}{p}}^{\omega }_X \subseteq {{\mathcal {S}}{p}}_X\) of perfect parametrised spectra and the full subcategory of \({{\mathcal {S}}{p}}({\mathcal {S}}_{X//X})\) spanned by the suspension spectra of finitely dominated retractive spaces \([X \rightarrow Y \rightarrow X] \in {\mathcal {S}}^{\text {fd} }_{X//X}\). Here the full subcategory \({\mathcal {S}}^{\text {fd} }_{X//X} \subseteq {\mathcal {S}}_{X//X}\) of finitely dominated retractive spaces is the closure under retracts of the full subcategory of \({{\mathcal {S}}{p}}_{X//X}\) spanned by the retractive spaces \(X \rightarrow Y \rightarrow X\) such that \(X \rightarrow Y\) can be represented by an inclusion of simplicial sets with Y having only finitely many non-degenerated simplices not in X. In particular, we may identify \({{\mathcal {S}}{p}}_X^{\omega }\) with the Spanier–Whitehead stabilisation of \({\mathcal {S}}^{\text {fd} }_{X//X}\).
If we now represent X by a CW-complex then the \(\infty \)-category \({\mathcal {S}}^{\text {fd} }_{X//X}\) can be modelled by the Waldhausen category \({\mathcal {R}}(X)\) of finitely dominated retractive topological spaces \(X \rightarrow Y \rightarrow X\) such that \(X \rightarrow Y\) is a Serre cofibration, with weak equivalences W the weak homotopy equivalences, that is, \({\mathcal {S}}^{\text {fd} }_{X//X} \simeq {\mathcal {R}}(X)[W^{-1}]\). Indeed, this is a standard consequence of the fact that \({\mathcal {S}}_{X//X}\) is presented by the Serre model structure on \(\text {Top} _{X//X}\), and \({\mathcal {R}}(X) \subseteq \text {Top} _{X//X}\) is a full subcategory consisting of cofibrant objects and closed under weak equivalences between cofibrant objects. From this one may obtain a Waldhausen model \(\text {s} {\mathcal {R}}(X)\) for the Spanier–Whitehead stabilisation by considering the category whose objects are pairs (Y, k) where \(X \rightarrow Y \rightarrow X\) is a finitely dominated retractive topological space over X and \(k\in {\mathbb {Z}}\) is an integer, with the set of maps from (Y, k) to \((Y',k')\) being
The object (Y, k) should be considered as the formal k’th desuspension of \(X \xrightarrow {i} Y \xrightarrow {f} X\). Endowing \(\text {s} {\mathcal {R}}(X)\) with the collection sW of stable weak homotopy equivalences, that is, the maps \((Y,k) \rightarrow (Y',k')\) which can be represented by a weak homotopy equivalence \(\Sigma ^{n-k}Y \rightarrow \Sigma ^{n-k'}Y'\) for some n, one obtains a model for perfect parametrised spectra, in the sense that \(\text {s} {\mathcal {R}}(X)[sW^{-1}] \simeq {{\mathcal {S}}{p}}^{\omega }_X\). Indeed, this is a formal consequence of the above and the commutation of localisation with colimits:
where we note that the sequential colimit on the left hand side (before localisation) is given by \(\text {s} {\mathcal {R}}(X)\) both as ordinary categories and as \(\infty \)-categories. In this presentation, the object (Y, k) corresponds to the local system \(x \mapsto \Sigma ^{\infty -k}Y_x\), where \(Y_x\) denotes the homotopy fibre of \(f:Y \rightarrow X\) over x, considered as a pointed space using the map \(X \rightarrow Y\). The Waldhausen category \(\text {s} {\mathcal {R}}(X)\) is equipped with a stable Spanier–Whitehead product (see discussion at the end of Sect. 2.3):
given by
that is, by (the implicit \(\Omega \)-spectrum replacement of) the shifted suspension spectrum of the pointed space
the symbol \(/\) standing for collapsing a subspace to a point. Here \(X^I\) is the space of paths in X, used here to form an explicit functorial model for the homotopy fibre product. This Spanier–Whitehead product preserves weak equivalences in each entry and thus descends to a bilinear functor
which we can now compare with the bilinear functor on parametrised spectra considered here:
Lemma 4.4.11
The bilinear functor \(\text {B} ^{\text {WW} }_{\text {v} }\) is naturally equivalent to the bilinear functor
Proof
Since \(\Sigma ^\infty \) is colimit preserving and symmetric monoidal for \(\wedge \) we have
where the last equivalence is by Remark 4.4.10. Since \(\text {s} {\mathcal {R}}(X) \rightarrow {{\mathcal {S}}{p}}^{\omega }_X\) is a localisation functor this natural equivalence descends to a natural equivalence \(\text {B} ^{\text {WW} }_{\text {v} }(L,L') \simeq \text {B} _{{\mathbb {S}}_X}(\text {D} _{{\mathbb {S}}_X}L,\text {D} _{{\mathbb {S}}_X}L')\), as desired. \(\square \)
Combining Lemma 4.4.11 with Proposition 2.3.15 and Remark 2.3.16 we now deduce
Corollary 4.4.12
The symmetric and quadratic \({\text {L}}\)-groups associated to the Spanier–Whitehead product \(\odot _\bullet \) are naturally equivalent to the \({\text {L}}\)-groups of the Poincaré structures  and
and  of Construction 4.4.1.
of Construction 4.4.1.
We would like to extend this comparison to visible \({\text {L}}\)-groups. These are defined in [73] by replacing the notion of symmetric co-forms on (Y, k), given by the homotopy fixed points spectrum \(((Y,k) \odot _\bullet (Y,k))^{{{\text {hC} }_{\textrm{2}}}}\), with the corresponding genuine fixed points \(((Y,k) \odot _\bullet (Y,k))^{{{\text {C} }_{\textrm{2}}}}\), where \((Y,k) \odot _\bullet (Y,k)\) is considered as a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum by identifying it with the shifted suspension \({{\text {C} }_{\textrm{2}}}\)-spectrum \(\Sigma ^{\infty -k\rho }(Y \wedge ^h_X Y)\). Here \(\rho \) is the regular \({{\text {C} }_{\textrm{2}}}\)-representation and \(Y \wedge ^h_X Y\) is considered as a genuine \({{\text {C} }_{\textrm{2}}}\)-space whose \({{\text {C} }_{\textrm{2}}}\)-fixed points are its point-set level fixed points
The natural map \(((Y,k) \odot _\bullet (Y,k))^{{{\text {C} }_{\textrm{2}}}} \rightarrow ((Y,k) \odot _\bullet (Y,k))^{{{\text {hC} }_{\textrm{2}}}}\) then enables one to define unimodular visible co-forms and hence visible \({\text {L}}\)-groups by applying the machinery of [72]. We note that the functor \((Y,k) \mapsto ((Y,k) \odot _\bullet (Y,k))^{{{\text {C} }_{\textrm{2}}}}\) preserves weak equivalences and hence descends to a functor

which we would like to compare with the visible Poincaré structure on parametrised spectra considered here:
Proposition 4.4.13
The functor  is naturally equivalent to the quadratic functor
is naturally equivalent to the quadratic functor  .
.
Before we come to the proof of Proposition 4.4.13, let first recall that the notion of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra admits a variety of point-set models, among which are orthogonal \({{\text {C} }_{\textrm{2}}}\)-spectra [50, 61], symmetric \({{\text {C} }_{\textrm{2}}}\)-spectra [49], prespectra indexed over the poset of finite dimensional sub-representations of a complete \({{\text {C} }_{\textrm{2}}}\)-universe [50], or alternatively over a submonoid of the representation ring of \({{\text {C} }_{\textrm{2}}}\) [49], this last model being the one employed in [71] using the submonoid spanned by the regular representation. All these models are known to be Quillen equivalent to each other, see [50, Theorem 4.16], [49, Theorem 6.2] and [49, Theorem 10.2]. On the other, the notion of \({{\text {C} }_{\textrm{2}}}\)-spectra can also be defined \(\infty \)-categorically using either Mackey functors or the stabilisation of \({{\text {C} }_{\textrm{2}}}\)-spaces along the regular representation sphere [10, 11, 51, 62], and this approach is equivalent to the model categorical one by [51, Theorem A.4]. The last equivalence between the \(\infty \)-categorical and model categorical approaches is furthermore compatible with the formation of genuine fixed points on the one hand, and the formation of suspension \({{\text {C} }_{\textrm{2}}}\)-spectra on the other. In particular, the construction of Weiss and Williams can be performed using any of these models by simply implementing the formation of genuine fixed points and suspension \({{\text {C} }_{\textrm{2}}}\)-spectra in the relevant context. We consequently may and will freely apply ideas and results from the theory of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra in the setting of [73].
Proof of Proposition 4.4.13
Since \(\text {s} {\mathcal {R}}(X)[sW^{-1}] \rightarrow {{\mathcal {S}}{p}}^{\omega }_X\) is a localisation functor it will suffice to construct, naturally in a given retractive space \(X \xrightarrow {i} Y \xrightarrow {f} X \in \text {s} {\mathcal {R}}(X)\), an equivalence

Now since \((Y,k) \odot _{\bullet } (Y,k)\) is a shifted suspension \({{\text {C} }_{\textrm{2}}}\)-spectrum its geometric fixed points are given by
and its isotropy separation square is

where the right vertical map is the k-fold desuspension of the composite
induced by the \({{\text {C} }_{\textrm{2}}}\)-equivariant diagonal \(Y/X \rightarrow Y \wedge ^h_X Y= [Y \times ^h_X Y]/[Y \coprod _X Y]\). To construct the desired equivalence we would like to compare this isotropy separation square with the square

produced by Remark 4.4.10. Indeed, since in the \(\infty \)-category of pointed spaces we have \(\mathop {{\text {colim} }}_x Y_x \simeq Y/X\) and \(\mathop {{\text {colim} }}_x Y_x \wedge Y_x \simeq Y \wedge ^h_X Y\), and since \(\Sigma ^\infty \) is colimit preserving and symmetric monoidal for \(\wedge \), we may proceed as in the proof of Lemma 4.4.11 to identify the three bottom right corners in the two squares, as well as the map from the homotopy fixed points to the corresponding Tate object, which in both cases is the component of the natural transformation \((-)^{{{\text {hC} }_{\textrm{2}}}} \Rightarrow (-)^{{{\text {tC} }_{\textrm{2}}}}\). To obtain an induced equivalence on the top left corner it is will now suffice to identify the right vertical map in the two squares. Peeling away the k-fold desuspension and using the fact that the Tate diagonal of \(\Sigma ^{\infty }Y_x\) is induced by the diagonal \(Y_x \rightarrow Y_x \wedge Y_x\) on the level of pointed spaces, the desired identification is now encoded by the following canonical commutative diagram

\(\square \)
Corollary 4.4.14
The visible \({\text {L}}\)-groups of [73] are naturally equivalent to the \({\text {L}}\)-groups of the visible Poincaré structure  .
.
Proof
The visible \({\text {L}}\)-groups are (litterally) defined in [73] by invoking the construction of [73] and replacing everywhere symmetric Poincaré objects by visible ones. The proof of the present corollary is then identical to that of Proposition 2.3.15, replacing everywhere symmetric Poincaré objects by visible ones, using Proposition 4.4.13. \(\square \)
Variant 4.4.15
Let X be a space with a spherical fibration \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\) and let \((A,N,\alpha )\) be a ring spectrum with genuine involution. We may then form a Poincaré structure  on the \(\infty \)-category \({\text {Fun}}(X,{\text {Mod}}_A)^{\omega }\) of compact local systems of A-modules by the top pullback square
on the \(\infty \)-category \({\text {Fun}}(X,{\text {Mod}}_A)^{\omega }\) of compact local systems of A-modules by the top pullback square

Here we note that the \({{\text {C} }_{\textrm{2}}}\)-equivariant structure of \(\Delta _!\xi \otimes _{{\mathbb {S}}} A\) with respect to the flip action on \(X \times X\) is induced by the equivariant structure of \(\Delta _!\xi \) and the involution on A. Arguing as in Lemma 4.4.2 and Corollary 4.4.3 one sees again that the hermitian \(\infty \)-category  is functorial in maps \((f,\tau ) :(X,\xi _X) \rightarrow (Y,\xi _Y)\) of spaces with spherical fibrations and that
is functorial in maps \((f,\tau ) :(X,\xi _X) \rightarrow (Y,\xi _Y)\) of spaces with spherical fibrations and that  is again Poincaré with underlying perfect duality \(L \mapsto {\text {hom}}^{\boxtimes }_A(L,\Delta _!(\xi )\otimes _{{\mathbb {S}}} A)\), where \({\text {hom}}^{\boxtimes }_A(L,-)\) denotes the right adjoint of the functor
is again Poincaré with underlying perfect duality \(L \mapsto {\text {hom}}^{\boxtimes }_A(L,\Delta _!(\xi )\otimes _{{\mathbb {S}}} A)\), where \({\text {hom}}^{\boxtimes }_A(L,-)\) denotes the right adjoint of the functor
Remark 4.4.16
In addition to its functoriality in maps of spaces with spherical fibrations, the construction of Variant 4.4.15 is also functorial in maps in \((A,N,\alpha ) \rightarrow (B,K,\beta )\) of rings with genuine involution. In fact, the Poincaré \(\infty \)-category  depends functorially on the pair of Poincaré \(\infty \)-categories
depends functorially on the pair of Poincaré \(\infty \)-categories  : we may identify it with their tensor product
: we may identify it with their tensor product  , a construction we will study in Sect. 5. As in Remark 4.4.9, one can then identify
, a construction we will study in Sect. 5. As in Remark 4.4.9, one can then identify  with the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram
with the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram  . The Poincaré structures
. The Poincaré structures  are then the ones associated to the module with genuine involution \((A,N,\alpha )\otimes _{{\mathbb {S}}} \xi _x = (A \otimes _{{\mathbb {S}}} \xi _x, N \otimes _{{\mathbb {S}}} \xi _x,\alpha _x)\), where \(\alpha _x\) is the composed map \(N \otimes _{{\mathbb {S}}} \xi _x \rightarrow A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} \xi _x^{{{\text {tC} }_{\textrm{2}}}} \rightarrow (A \otimes _{{\mathbb {S}}} \xi _x)^{{{\text {tC} }_{\textrm{2}}}}\).
are then the ones associated to the module with genuine involution \((A,N,\alpha )\otimes _{{\mathbb {S}}} \xi _x = (A \otimes _{{\mathbb {S}}} \xi _x, N \otimes _{{\mathbb {S}}} \xi _x,\alpha _x)\), where \(\alpha _x\) is the composed map \(N \otimes _{{\mathbb {S}}} \xi _x \rightarrow A^{{{\text {tC} }_{\textrm{2}}}} \otimes _{{\mathbb {S}}} \xi _x^{{{\text {tC} }_{\textrm{2}}}} \rightarrow (A \otimes _{{\mathbb {S}}} \xi _x)^{{{\text {tC} }_{\textrm{2}}}}\).
For the remainder of this section we will show how to construct visible signatures for Poincaré duality spaces in the present context. We take a purely homotopy theoretical approach to Poincaré duality spaces and their Spivak normal fibration following [40]. Let X be a finite space (that is, a space which can be realized by a simplicial set with only finitely many non-degenerate simplices). The right Kan extension functor \(r_*:{{\mathcal {S}}{p}}_X \rightarrow {{\mathcal {S}}{p}}\) along \(r:X \rightarrow *\) is given by taking the limit along X, which is in particular a finite limit and hence preserves colimits by the stability of \({{\mathcal {S}}{p}}_X\). It is thus equivalent to a functor of the form \(r_!({\mathcal {F}}_X \otimes (-))\) for an essentially unique \({\mathcal {F}}_X\), which is then called the dualizing complex of X. Here \(\otimes \) stands for the pointwise tensor product of X-parametrised spectra. We say that X is a Poincaré duality space if the parametrised spectrum \({\mathcal {F}}_X:X\rightarrow {{\mathcal {S}}{p}}\) factors through the full subgroupoid \({\text {Pic}}({\mathbb {S}}) \subseteq \iota {{\mathcal {S}}{p}}\) of invertible objects. In this case we denote the resulting spherical fibration by \(\nu := {\mathcal {F}}_X\), and call it the Spivak normal fibration of X. We note that the identification of \(r_!(\nu \otimes (-))\) with \(r_*\) can equivalently be encoded via a unit map
exhibiting \(r_!(\nu \otimes (-))\) as right adjoint to \(r^*\). Since \({\text {Fun}}^{\textrm{ex}}({{\mathcal {S}}{p}}^{\text {f} },{{\mathcal {S}}{p}}^{\text {f} }) \simeq {{\mathcal {S}}{p}}^{\text {f} }\) via evaluation at \({\mathbb {S}}\) the natural transformation \(c_{(-)}\) is canonically of the form \(c \otimes _{{\mathbb {S}}} (-)\), where
is its component at \({\mathbb {S}}\). One may then say that a map \(c :{\mathbb {S}}\rightarrow r_!(\nu )\) exhibits \(\nu \) as the Spivak normal fibration of X if the associated natural transformation
exhibits \(r_!(\nu \otimes (-))\) as right adjoint to \(r^*\). The map c is then called the Thom–Pontryagin map of \(\nu \).
Example 4.4.17
If M is a closed smooth manifold then the underlying space of M is a Poincaré duality space. Furthermore, if \(\iota :M \hookrightarrow {\mathbb {R}}^{N}\) is a smooth embedding with normal bundle \(E = TM^{\perp } \subseteq \iota ^*T{\mathbb {R}}^N\) and associated spherical fibration \(\xi _E\), and \(M \subseteq U \subseteq {\mathbb {R}}^N\) is a chosen tubular neighborhood, then the Thom–Pontryagin collapse map
induces a map of spectra
that exhibits \(\Sigma ^{-N}\xi _E\) as the Spivak normal fibration of M. Since \(E \oplus TM =\iota ^*T{\mathbb {R}}^N\) is a trivial N-dimensional vector bundle we can identify \(\Sigma ^{-N}\xi _E \simeq \xi _{TM}^{-1}\), where \(\xi _{TM}\) is the spherical fibration underlying the tangent bundle.
Remark 4.4.18
Let X be a finite space with Spivak normal fibration \(\nu \) and Thom–Pontryagin map c. Suppose that \({\mathcal {E}}\) is a stable \(\infty \)-category, so that \({\mathcal {E}}\) is canonically tensored over \({{\mathcal {S}}{p}}^{\text {f} }\). We may then consider the restriction functor \(r^*:{\mathcal {E}}\rightarrow {\text {Fun}}(X,{\mathcal {E}})\), together with the associated left and right Kan extensions \(r_!,r_*:{\text {Fun}}(X,{\mathcal {E}}) \rightarrow {\mathcal {E}}\) (which exist because X is finite and every stable \(\infty \)-category admits finite limits and colimits). The Thom–Pontryagin map then determines a natural transformation of functors from \({\mathcal {E}}\) to itself whose component at \(A \in {\mathcal {E}}\) is
This natural transformation then exhibits \(r_!(\nu \otimes (-))\) as right adjoint to \(r^*\). Indeed, for \(A \in {\mathcal {E}}\) and \(B:X \rightarrow {\mathcal {E}}\) the composed map
is an equivalence, as can be seen by comparing it with the composed map
where \(B^A\) is the local system \(x \mapsto {\text {hom}}_{{\mathcal {E}}}(A,B_x)\), and we are using that
since X is finite and each \(\nu _x\) is a finite spectrum.
We now proceed to construct the visible signature of a Poincaré duality spaces X. Let \(p_1,p_2:X \times X \rightarrow X\) denote the two projections. Applying Remark 4.4.18 to \({\mathcal {E}}= {{\mathcal {S}}{p}}_X\) we obtain that the natural map
for \(L \in {{\mathcal {S}}{p}}_X\) acts as a unit exhibiting \((p_2)_!((p_1)^*\nu \otimes (-))\) as right adjoint to \((p_2)^*\). Since \((p_1)^*\nu \) is invertible tensoring with it is left and right inverse to tensoring with \((p_1)^*\nu ^{-1}\), and hence the above map also acts as a unit exhibiting \((p_2)_!:{{\mathcal {S}}{p}}_{X \times X} \rightarrow {{\mathcal {S}}{p}}_X\) as right adjoint to \((p_1)^*\nu \otimes (p_2)^*(-) = \nu \boxtimes (-)\). We consequently obtain a canonical equivalence
of functors \({{\mathcal {S}}{p}}_{X \times X} \rightarrow {{\mathcal {S}}{p}}_X\). Evaluating at \(\Delta _!\xi \) for some spherical fibration \(\xi \) we obtain a canonical equivalence
In other words, for every spherical fibration \(\xi \) on X, the \(\xi \)-twisted duality switches between \(\xi \) and \(\nu \). Taking \(\xi = \nu \) we then get
that is, \(\nu \) is equivalent to its own \(\nu \)-twisted dual. We now claim that this equivalence is induced by a canonical Poincaré form  . To see this, note that by Remark 4.4.10 and the equivalence (110) we have a \({{\text {C} }_{\textrm{2}}}\)-equivariant equivalence
. To see this, note that by Remark 4.4.10 and the equivalence (110) we have a \({{\text {C} }_{\textrm{2}}}\)-equivariant equivalence
where the \({{\text {C} }_{\textrm{2}}}\)-action on the third term is by switching the two \({\mathbb {S}}\) factors, and the \({{\text {C} }_{\textrm{2}}}\)-action on the last two terms is trivial. In particular, the \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {B} _{\xi }(\nu ,\nu )\) is equivalent to a constant action. Taking \(\xi = \nu \) we then obtain:
Corollary 4.4.19
The equivalence \(\nu \rightarrow \text {D} _{\nu }\nu \) constructed above canonically refines to a self-dual equivalence, yielding in particular a symmetric Poincaré form  .
.
We would like to lift the symmetric form \(q_{\text {s} }\) from  to a visible form
to a visible form  . For this, we note that by using the second formula in Remark 4.4.10 we obtain an equivalence
. For this, we note that by using the second formula in Remark 4.4.10 we obtain an equivalence
and so we can write the pullback square defining the visible Poincaré structure evaluated at \(\nu \) as

where the \({{\text {C} }_{\textrm{2}}}\)-fixed points and Tate construction are performed with respect to the trivial action on \(r_!\xi \), and the right vertical map is given by the composite \(r_!\xi \rightarrow (r_!\xi )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow (r_!\xi )^{{{\text {tC} }_{\textrm{2}}}}\). Taking again \(\xi = \nu \) we then obtain:
Corollary 4.4.20
Then the symmetric Poincaré form of Corollary 4.4.19 canonically lifts to a visible Poincaré form  .
.
The Poincaré object  is called the visible signature of the Poincaré duality space X.
is called the visible signature of the Poincaré duality space X.
Remark 4.4.21
Since X is finite any spherical fibration \(\xi \) is a finite colimit \(\xi \simeq \mathop {{\text {colim} }}_{x \in X}x_!\xi _x\), and hence belongs to \({{\mathcal {S}}{p}}^{\text {f} }_X\). It then follows that the visible signature \((\nu ,q_{\text {v} })\) is naturally a Poincaré object in  .
.
6 Monoidal structures and multiplicativity
In this section we will show that the tensor product of stable \(\infty \)-categories refines to give symmetric monoidal structures on the \(\infty \)-categories \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \). We give a careful analysis of algebra objects in \(\text {Cat} ^{\textrm{p}}_\infty \), and use it to show that many examples of interest, such as the symmetric and genuine symmetric Poincaré structures on perfect derived categories of commutative rings, admit such an algebra structure. The significance of this fact is that for an algebra object in \(\text {Cat} ^{\textrm{p}}_\infty \), the \({\text {L}}\)-groups and the Grothendieck-Witt group inherit the structure of rings. We will show in Paper [4] that this phenomenon extends to an \({\text {E} _\infty }\)-structure on the level of Grothendieck-Witt- and \({\text {L}}\)-theory spectra, a structure which plays a key role in the study of these invariants in the commutative setting.
This section is organized as follows. In Sect. 5.1 we define the tensor product of hermitian and Poincaré \(\infty \)-categories and give a formula for the linear and bilinear parts of the hermitian structure on the tensor product in term of the linear and bilinear parts of the individual terms. In Sect. 5.2 we show that this operation organizes into a symmetric monoidal structure on the \(\infty \)-categories \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \), such that the forgetful functors \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) are symmetric monoidal. In Sect. 5.3 we analyse what it means for a hermitian or Poincaré \(\infty \)-category to be an algebra with respect to this structure, and use this analysis in Sect. 5.4 in order to identify various examples of interest of symmetric monoidal Poincaré \(\infty \)-categories. Finally, in Sect. 7.5 we show that the Grothendieck-Witt group and zero’th \({\text {L}}\)-group are symmetric monoidal functors on \(\text {Cat} ^{\textrm{p}}_\infty \), and hence their values on a given symmetric monoidal Poincaré \(\infty \)-category are rings. Similarly, we show that in this case the collection of all \({\text {L}}\)-groups acquires the structure of a graded-commutative ring.
6.1 Tensor products of hermitian \(\infty \)-categories
In this first part we define the tensor product of hermitian \(\infty \)-categories on the level of objects and show that the tensor product of Poincaré \(\infty \)-categories is again Poincaré.
We begin by recalling the tensor product of stable \(\infty \)-categories due to Lurie.
Construction 5.1.1
Applying the construction of [47, §4.8.1] with respect to the collection \({\mathcal {K}}\) of finite simplicial sets yields a symmetric monoidal structure on the \(\infty \)-category \(\text {Cat} _\infty ^\text {rex} \), whose objects are small \(\infty \)-categories with finite colimits and whose morphisms are functors which preserve finite colimits. For a pair of \(\infty \)-categories with finite colimits \({\mathcal {C}}\) and \({{{\mathcal {C}}}'}\), their tensor product \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\in \text {Cat} _\infty ^\text {rex} \) is equipped with a functor \({\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) which preserves finite colimits in each variable, and is initial with this property. Now the \(\infty \)-category \(\text {Cat} _\infty ^\text {ex} \) embeds fully-faithful in \(\text {Cat} _\infty ^\text {rex} \), and is furthermore a reflective subcategory: a left adjoint to the inclusion \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty ^\text {rex} \) is given by tensoring with \({{\mathcal {S}}{p}}^{\text {f} }\). To see this, observe that for an \(\infty \)-category \({\mathcal {C}}\) with finite colimits, the tensor product of \({\mathcal {C}}\) and \({{\mathcal {S}}{p}}^{\text {f} }\) yields an \(\infty \)-category with finite colimits \({\mathcal {C}}\otimes {{\mathcal {S}}{p}}^{\text {f} }\in \text {Cat} _\infty ^\text {rex} \) which is a module over \({{\mathcal {S}}{p}}^{\text {f} }\). Since \(0 \in {{\mathcal {S}}{p}}^{\text {f} }\) is a self-dual object it acts via a self-adjoint functor and hence \({\mathcal {C}}\otimes {{\mathcal {S}}{p}}^{\text {f} }\) is pointed. In addition, since the object \(\Sigma {\mathbb {S}}\in {{\mathcal {S}}{p}}^{\text {f} }\) is invertible we get that suspension is invertible on \({\mathcal {C}}\otimes {{\mathcal {S}}{p}}^{\text {f} }\) and so the latter is furthermore stable. To see that this operation gives a left adjoint to the inclusion \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty ^\text {rex} \) we note that for every stable \(\infty \)-category \({\mathcal {D}}\) the restriction functor
is an equivalence by Lemma 4.1.2. It then follows from [47, Proposition 4.1.7.4] that the symmetric monoidal structure \(\otimes \) descends to \(\text {Cat} _\infty ^\text {ex} \). In particular, the unit of \(\text {Cat} _\infty ^\text {ex} \) is given by \({{\mathcal {S}}{p}}^{\text {f} }\), and if \({\mathcal {C}},{{{\mathcal {C}}}'}\) are stable then \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) is universal among stable \(\infty \)-categories receiving a bilinear functor \(\beta :{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\): given a stable \(\infty \)-category \({\mathcal {D}}\), restriction along \(\beta \) induces an equivalence between the \(\infty \)-category of exact functors from \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\rightarrow {\mathcal {D}}\) and the \(\infty \)-category of bilinear functors \({\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {D}}\). We will refer to \({\text {E} _\infty }\)-algebra objects in \((\text {Cat} _\infty ^\text {ex} )^{\otimes }\) as stably symmetric monoidal \(\infty \)-categories. Concretely, this means a symmetric monoidal \(\infty \)-category whose underlying \(\infty \)-category is stable and the tensor product is exact in each variable.
We now refine this construction to the level of hermitian \(\infty \)-categories.
Construction 5.1.2
For a pair of hermitian \(\infty \)-categories  and
and  , we define their tensor product
, we define their tensor product

to be the hermitian \(\infty \)-category whose underlying stable \(\infty \)-category is the tensor product of the underlying stable \(\infty \)-categories, and whose hermitian structure

is obtained by applying the 2-excisive approximation functor of Construction 1.1.26 to the left Kan extension along \(\beta :{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) of the ‘external’ tensor product

Here we note that  is already reduced since
is already reduced since  is reduced and \(\beta \) preserve zero objects, and so Construction 1.1.26 is applicable to it.
is reduced and \(\beta \) preserve zero objects, and so Construction 1.1.26 is applicable to it.
Note that the tensor product  carries by design a similar universal property to the tensor product \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) of stable \(\infty \)-categories: for any hermitian \(\infty \)-category
carries by design a similar universal property to the tensor product \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) of stable \(\infty \)-categories: for any hermitian \(\infty \)-category  , maps from the tensor product
, maps from the tensor product  to
to  correspond to bilinear maps \(b:{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {{{\mathcal {C}}}''}\) together with a natural transformation
correspond to bilinear maps \(b:{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {{{\mathcal {C}}}''}\) together with a natural transformation  , i.e. a natural transformation in the square
, i.e. a natural transformation in the square

Our next goal is to identify the linear and bilinear parts of the hermitian structure on  in more explicit terms. To this end, let
in more explicit terms. To this end, let  denote the linear parts and
denote the linear parts and  the bilinear parts of the hermitian structures
the bilinear parts of the hermitian structures  and
and  , respectively. The functor
, respectively. The functor

is then bilinear, and therefore extends along \(\beta \) to a linear functor  in an essentially unique manner. Similarly, the multilinear functor
in an essentially unique manner. Similarly, the multilinear functor

extends to a bilinear functor

The symmetric structures of  and
and  then determine a \({{\text {C} }_{\textrm{2}}}\)-fixed structure on
then determine a \({{\text {C} }_{\textrm{2}}}\)-fixed structure on  with respect to the \({{\text {C} }_{\textrm{2}}}\)-action which permutes the two \({\mathcal {C}}^{\text {op} }\)-coordinates and the two \({{{\mathcal {C}}}'}{^{\text {op} }}\)-coordinates. This structure then descends to a symmetric structure on
with respect to the \({{\text {C} }_{\textrm{2}}}\)-action which permutes the two \({\mathcal {C}}^{\text {op} }\)-coordinates and the two \({{{\mathcal {C}}}'}{^{\text {op} }}\)-coordinates. This structure then descends to a symmetric structure on  by its universal characterization.
by its universal characterization.
Proposition 5.1.3
For hermitian \(\infty \)-categories  there is a canonical pullback square
there is a canonical pullback square

of functors \({\mathcal {C}}{^{\text {op} }}\otimes {{{\mathcal {C}}}'}{^{\text {op} }}\rightarrow {{\mathcal {S}}{p}}\). In particular the linear part of  is given by
is given by  and its symmetric bilinear part by
and its symmetric bilinear part by  .
.
Proof
By definition the functor  is characterized by the fact that for every quadratic functor
is characterized by the fact that for every quadratic functor  the natural map
the natural map

is an equivalence. Using this universal mapping property the commutative square (111) is then obtained from the external square in the diagram

where the top square is obtained by taking the external product of the classifying squares of  and
and  , and the bottom square witnesses the lax symmetric monoidal structure of the homotopy fixed points functor and the projection to the Tate construction. To show that the resulting square (111) is a pullback square we need to show that the induced map
, and the bottom square witnesses the lax symmetric monoidal structure of the homotopy fixed points functor and the projection to the Tate construction. To show that the resulting square (111) is a pullback square we need to show that the induced map

is an equivalence for any quadratic functor  . Let us analyse both sides of the map (112). We start with the following claim (see Sect. 1.3 for the terminology of homogeneous and cohomogeneous and their basic properties):
. Let us analyse both sides of the map (112). We start with the following claim (see Sect. 1.3 for the terminology of homogeneous and cohomogeneous and their basic properties):
Claim 1:
if either
is exact and
is cohomogeneous or
is homogeneous and
is exact.
To see this claim we note that for a fixed object \(c' \in {{{\mathcal {C}}}'}\) we have that the space of natural transformations

(natural in \((-)\)) vanishes under these assumptions since the left hand functor is exact (resp. homogeneous) and the right hand functor is cohomogeneous (resp. exact). But the space  can be written as a limit of these spaces over the twisted arrow category of \({{{\mathcal {C}}}'}\) so that the claim follows. We also have the following claim
can be written as a limit of these spaces over the twisted arrow category of \({{{\mathcal {C}}}'}\) so that the claim follows. We also have the following claim
Claim 2:
if either
is exact and
is cohomogeneous or
is homogeneous and
is exact.
which follows by the same argument as above since under the assumptions the pullback is either  or
or  .
.
Together the last two claims show that the map (111) is an equivalence under the assumption that either  is exact and
is exact and  is cohomogeneous or
is cohomogeneous or  is homogeneous and
is homogeneous and  is exact. Now
is exact. Now  can be fit in an exact sequence between a homogeneous functor and an exact functor, and
can be fit in an exact sequence between a homogeneous functor and an exact functor, and  can be fit in an exact sequence between an exact and a cohomogeneous functors. Since both sides of (111) are natural and exact in
can be fit in an exact sequence between an exact and a cohomogeneous functors. Since both sides of (111) are natural and exact in  and
and  we can thus assume without loss of generality that
we can thus assume without loss of generality that  and
and  are both exact or
are both exact or  is homogeneous and
is homogeneous and  is cohomogeneous. Since everything is symmetric in
is cohomogeneous. Since everything is symmetric in  and
and  we can also make the same reduction in this variable so that we only need to show the fact that (111) is a pullback under the following assumptions:
we can also make the same reduction in this variable so that we only need to show the fact that (111) is a pullback under the following assumptions:
Claim 3: Either all three functors
are exact or
and
are homogeneous and
is cohomogeneous.
In the first case the statement unwinds to the universal property of \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) and in the second case it unwinds (also using the universal property) to the statement that maps from a homogeneous functor to a cohomogeneous functor are equivalent to maps between the associated symmetric bilinear functors. \(\square \)
Corollary 5.1.4
If  and
and  are Poincaré with duality functors
are Poincaré with duality functors  then
then  is Poincaré with duality functor
is Poincaré with duality functor  .
.
Proof
We get from Proposition 5.1.3 that the cross effect of the quadratic functor on \({\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) is given by  , which coincides with the left Kan extension of
, which coincides with the left Kan extension of  along the map
along the map
where

We want to show that this is represented by the functor  . Now the left Kan extension along \(\beta \times \beta \) can be computed by composing left Kan extensions along \(\beta \times \text {id} \) and \(\text {id} \times \beta \). Then for \(y\in {\mathcal {C}},y'\in {{{\mathcal {C}}}'}\) we then have
. Now the left Kan extension along \(\beta \times \beta \) can be computed by composing left Kan extensions along \(\beta \times \text {id} \) and \(\text {id} \times \beta \). Then for \(y\in {\mathcal {C}},y'\in {{{\mathcal {C}}}'}\) we then have

and the left Kan extension along \(\beta \) of the functor  is
is  . \(\square \)
. \(\square \)
Proposition 5.1.5
Recall the universal Poincaré \(\infty \)-category  of Sect. 4.1. Then we have a natural equivalence
of Sect. 4.1. Then we have a natural equivalence

for  .
.
Proof
We first note that \({{\mathcal {S}}{p}}^{\text {f} }\) is the unit with respect to the tensor product of stable \(\infty \)-categories (see Construction 5.1.1), and that \(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\simeq {{\mathcal {S}}{p}}^{\text {f} }\) through Spanier–Whitehead duality. By definition, the linear part of  is Spanier–Whitehead duality \(\text {D} \) and the bilinear part is the composite
is Spanier–Whitehead duality \(\text {D} \) and the bilinear part is the composite
which also corresponds to Spanier Whitehead duality \(({{\mathcal {S}}{p}}^{\text {f} }){^{\text {op} }} \rightarrow {{\mathcal {S}}{p}}^{\text {f} }\) under the equivalence \(({{\mathcal {S}}{p}}^{\text {f} }){^{\text {op} }} \otimes ({{\mathcal {S}}{p}}^{\text {f} }){^{\text {op} }} \simeq ({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\). Now using Proposition 5.1.3 the claim is reduced to the statement that for any exact functor \(\Lambda :{\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) the functor
is equivalent to \(\Lambda \). Indeed, the composite \({\mathcal {C}}^{\text {op} }= ({\mathcal {C}}\otimes {{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\otimes ({{\mathcal {S}}{p}}^{\text {f} }){^{\text {op} }}\) sends \(c \in {\mathcal {C}}^{\text {op} }\) to \(c \otimes {\mathbb {S}}\). \(\square \)
Example 5.1.6
Let A, B be \({\text {E} _1}\)-ring spectra equipped with modules with genuine involutions \((M_A,N_A,\alpha )\) and \((M_B,N_B,\beta )\) respectively (see Sect. 3.2). As discussed in the proof of Theorem 3.3.1, it follows from [47, Theorem 4.8.5.16 and Remark 4.8.5.19] that the exact functor
induced by the bilinear functor \((X,Y) \mapsto X \otimes Y\), yields an equivalence  upon passing to Ind-categories, where \(\otimes _{{{\mathcal {S}}{p}}}\) denotes the tensor product of stable presentable \(\infty \)-categories. In particular, the functor (113) is necessarily a dense full inclusion, which is therefore an equivalence since its image contains \(A \otimes B\) and its target contains no proper stable subcategories with that property. More generally, given subgroups \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) and \(d \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{B})\) we obtain an equivalence
upon passing to Ind-categories, where \(\otimes _{{{\mathcal {S}}{p}}}\) denotes the tensor product of stable presentable \(\infty \)-categories. In particular, the functor (113) is necessarily a dense full inclusion, which is therefore an equivalence since its image contains \(A \otimes B\) and its target contains no proper stable subcategories with that property. More generally, given subgroups \(c \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A})\) and \(d \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{B})\) we obtain an equivalence
where \(e \subseteq {\text {K}}_0({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} B})\) is the image of \(c \otimes d\) under the induced map \({\text {K}}_0({\text {Mod}}^{\omega }_{A}) \otimes {\text {K}}_0({\text {Mod}}^{\omega }_{B}) \rightarrow {\text {K}}_0({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} B})\). We note that in general e might fail to be all of \({\text {K}}_0({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} B})\), even if c and d are all of \({\text {K}}_0({\text {Mod}}^{\omega }_{A})\) and \({\text {K}}_0({\text {Mod}}^{\omega }_{B})\), respectively. It then follows from Proposition 5.1.3 that

where the reference map on the right hand side is the composite
obtained using the lax monoidal structure of the Tate construction.
6.2 Construction of the symmetric monoidal structure
In this section we will show that the notion of tensor product constructed in Sect. 5.1 above can be enhanced to symmetric monoidal structures on \(\text {Cat} ^{\textrm{h}}_\infty \) and on \(\text {Cat} ^{\textrm{p}}_\infty \). The construction is somewhat technical and can be skipped on a first read.
Construction 5.2.1
For an \(\infty \)-category \({\mathcal {D}}\) we will denote by
the cartesian fibration classified by the functor
We will refer to \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) as the lax slice over \({\mathcal {D}}\). The objects of \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) are given by functors \({\mathcal {C}}\rightarrow {\mathcal {D}}\) and the morphisms by diagrams

filled by a non-invertible 2-cell \(p \Rightarrow qf\). The actual slice \((\text {Cat} _\infty )_{/{\mathcal {D}}}\) is a non-full subcategory of \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) which contains all objects but only those 1-morphisms for which the natural transformation \(p \Rightarrow qf\) is an equivalence.
Remark 5.2.2
The \(\infty \)-category \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) can be characterized by the following universal mapping property: the data of a functor from \({\mathcal {E}}\) to \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) is equivalent to the data of a diagram in \(\text {Cat} _\infty \) of the form

with p a cocartesian fibration. In this description functors from \({\mathcal {E}}\) to the actual slice \((\text {Cat} _\infty )_{/{\mathcal {D}}}\) correspond to diagrams as above where the functor \({\mathcal {C}}\rightarrow {\mathcal {D}}\) send p-cocartesian lifts to equivalences in \({\mathcal {D}}\). This description also uniquely determines \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) since it describes the represented functor \({\text {Ho}}(\text {Cat} _\infty )^{\text {op} }\rightarrow \text {Set} \).
Lemma 5.2.3
Let \({\mathcal {D}}\) be a symmetric monoidal \(\infty \)-category. Then \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) admits a symmetric monoidal refinement \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) with the following properties:
-
i)
The tensor product of \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) and \(g:{\mathcal {C}}' \rightarrow {\mathcal {D}}\) in \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) is given by the composite
$$\begin{aligned} {\mathcal {C}}\times {\mathcal {C}}' \xrightarrow {f \times g} {\mathcal {D}}\times {\mathcal {D}}\xrightarrow {\otimes } {\mathcal {D}}, \end{aligned}$$and the tensor unit by the functor \(\text {pt} \rightarrow {\mathcal {D}}\) corresponding to the tensor unit of \({\mathcal {D}}\).
-
ii)
The forgetful functor \((\text {Cat} _\infty )_{//{\mathcal {D}}} \rightarrow \text {Cat} _\infty \) admits a symmetric monoidal refinement \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \rightarrow \text {Cat} _\infty ^\times \) with respect to the cartesian symmetric monoidal structure on \(\text {Cat} _\infty \).
-
iii)
For any \(\infty \)-operad \({\mathcal {O}}^\otimes \), the space of \({\mathcal {O}}\)-algebras in \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) is naturally equivalent to the space of diagrams of \(\infty \)-operads
where p is a cocartesian fibration of \(\infty \)-operads (see [47, Definition 2.1.2.13]). In other words, a pair consisting of an \({\mathcal {O}}\)-monoidal \(\infty \)-category \({\mathcal {C}}\) together with a lax \({\mathcal {O}}\)-monoidal functor from \({\mathcal {C}}\) to \({\mathcal {D}}\), where the latter is consider as an \({\mathcal {O}}\)-monoidal \(\infty \)-category by pullback along the terminal map of \(\infty \)-operads \({\mathcal {O}}\rightarrow {\text {E} _\infty }\).
Remark 5.2.4
Property iii) of Lemma 5.2.3 determines the symmetric monoidal \(\infty \)-category \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) uniquely. Indeed, a symmetric monoidal \(\infty \)-category is uniquely determined by its underlying \(\infty \)-operad, and Property iii) determines the functor
represented by the underlying \(\infty \)-operad \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \). One can in fact show that the first two properties of the lemma are direct consequences of the third (see the arguments in the proof of Lemma 5.2.3 below).
Proof of Lemma 5.2.3
For a fixed symmetric monoidal \(\infty \)-category \({\mathcal {D}}\) with underlying \(\infty \)-operad \({\mathcal {D}}^\otimes \), we consider the \(\infty \)-category \({\mathcal {X}}\) whose objects are given by diagrams of \(\infty \)-operads of the form

where p is a cocartesian fibration of \(\infty \)-operads. The morphisms in \({\mathcal {X}}\) are those maps of such diagrams which are the identity on \({\mathcal {D}}^\otimes \) and preserve p-cocartesian arrows in the \({\mathcal {C}}^\otimes \) component. Projecting to the \({\mathcal {O}}^\otimes \)-component defines a functor \({\mathcal {X}} \rightarrow \text {Op} _\infty \) which is a cartesian fibration classified by some functor \(\text {Op} _\infty ^{\text {op} }\rightarrow \text {Cat} _\infty \). Postcomposing the latter with the groupoid core functor we obtain a functor
sending an \(\infty \)-operad \({\mathcal {O}}\) to the space consisting of pairs of a cocartesian fibration \(p:{\mathcal {C}}^\otimes \rightarrow {\mathcal {O}}^\otimes \) of \(\infty \)-operads together with a map \({\mathcal {C}}^\otimes \rightarrow {\mathcal {D}}^\otimes \) of \(\infty \)-operads. We now claim that the functor q is representable by an \(\infty \)-operad. To see this we use that \(\text {Op} _\infty \) is a presentable \(\infty \)-category by [47, Section 2.1.4] so that we have to check that the functor q preserves limits by [43, Proposition 5.5.2.2]. This can be seen as follows: a cocartesian fibration \({\mathcal {C}}^\otimes \rightarrow {\mathcal {O}}^\otimes = \mathop {{\text {colim} }}_i {\mathcal {O}}_i^\otimes \) over a colimit of \(\infty \)-operads is classified by a map of \(\infty \)-operads \(\chi :\mathop {{\text {colim} }}_i {\mathcal {O}}_i^\otimes \rightarrow \text {Cat} _\infty ^\times \) where \(\text {Cat} _\infty ^\times \) is equipped with the structure of an \(\infty \)-operad induced by the cartesian symmetric monoidal structure on \(\text {Cat} _\infty \) (see [47, Remark 2.4.2.6]). The space of such functors is thus a limit of the spaces of maps of \(\infty \)-operads \(\chi _i:{\mathcal {O}}_i^\otimes \rightarrow \text {Cat} _\infty ^\times \). In particular the space of cocartesian fibrations over \(\mathop {{\text {colim} }}_i {\mathcal {O}}_i^\otimes \) is the limit of the spaces of cocartesian fibrations over \({\mathcal {O}}_i^\otimes \). In addition, for every cocartesian fibration \({\mathcal {C}}^{\otimes } \rightarrow {\mathcal {O}}^{\otimes }\) of \(\infty \)-operads the natural map
is an equivalence of \(\infty \)-operads, where \({\mathcal {C}}_i^\otimes := {\mathcal {C}}^\otimes \times _{{\mathcal {O}}^\otimes } {{\mathcal {O}}_i^\otimes }\) is the corresponding fibre product (computed in \(\text {Op} _\infty \)). This follows from the fact that the functor
commutes with colimits of \(\infty \)-operads since it has a right adjoint given by the relative Day convolution \({\text {Fun}}^{{\mathcal {O}}}({\mathcal {C}}, -)^\otimes \), see [47, Construction 2.2.6.7 and Remark 2.2.6.8]. The colimit description of (116) then implies that the space of maps \({\mathcal {C}}^\otimes \rightarrow {\mathcal {D}}^\otimes \) of \(\infty \)-operads is given by the limit of the space of maps \({\mathcal {C}}_i^\otimes \rightarrow {\mathcal {D}}^\otimes \). Together this shows that the functor q preserves limits and is thus representable. We denote the representing object by \((\text {Cat} _\infty ^\otimes )_{//{\mathcal {D}}}\). We note that by Remark 5.2.2 the underlying \(\infty \)-category \(\big ((\text {Cat} _\infty ^{\otimes })_{//{\mathcal {D}}}\big )_{\left<1\right>}\) identifies with \((\text {Cat} _\infty )_{//{\mathcal {D}}}\); indeed, when \({\mathcal {O}}^{\otimes }\) is the image of an \(\infty \)-category \({\mathcal {E}}\) under the full inclusion \(\text {Cat} _\infty \subseteq \text {Op} _\infty \), the data of a diagram as in (115) with p a cocartesian fibration of \(\infty \)-operads reduces to that of a diagram of the form (114), with p a cocartesian fibration of \(\infty \)-categories. To show \((\text {Cat} _\infty ^{\otimes })_{//{\mathcal {D}}}\) is a symmetric monoidal structure on \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) we will need a more explicit description of the multi-mapping spaces in \((\text {Cat} _\infty ^\otimes )_{//{\mathcal {D}}}\).
Let \(C_n\) (sometimes called the n-corolla) be the \(\infty \)-operad freely generated by a single n-ary operation \(x_1,\ldots , x_n \rightarrow x\) with colours \(x_1,\ldots ,x_n\) and x.Footnote 1 The space of maps \(C_n^\otimes \rightarrow (\text {Cat} _\infty ^\otimes )_{//{\mathcal {D}}}\) is then by the defining property of \((\text {Cat} _\infty ^\otimes )_{//{\mathcal {D}}}\) the classifying space of pairs of a \(C_n\)-monoidal \(\infty \)-category \({\mathcal {C}}\) and a lax \(C_n\)-monoidal functor \({\mathcal {C}}\rightarrow {\mathcal {D}}\). As the \(\infty \)-operad \(C_n\) is free a \(C_n\)-monoidal \(\infty \)-category is simply given by a sequence \(\{{\mathcal {C}}_1,\ldots ,{\mathcal {C}}_n;{\mathcal {C}}\}\) of \(\infty \)-categories together with a functor \(\alpha :{\mathcal {C}}_1 \times \ldots \times {\mathcal {C}}_n \rightarrow {\mathcal {C}}\), and a lax \(C_n\)-monoidal functor from this to \({\mathcal {D}}\) corresponds to a collection of functors \(\{f_1:{\mathcal {C}}_1 \rightarrow {\mathcal {D}}, \ldots , f_n:{\mathcal {C}}_n \rightarrow {\mathcal {D}}; f:{\mathcal {C}}\rightarrow {\mathcal {D}}\}\) together with a transformation in the square

As a result we find that the corresponding multi-mapping space, which can be identified with the pullback

is given by the spaces of maps in \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) from the object
to the object \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\). In particular, this multi-mapping space is corepresented by the object (117) and so the \(\infty \)-operad \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) is corepresentable in the sense of [47, Definition 6.2.4.3], that is, the functor \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \rightarrow \text {Fin}_*\) is a locally cocartesian fibration. To see that it is actually cocartesian, i.e. \((\text {Cat} _\infty )_{//D}^\otimes \) is symmetric monoidal, we have to additionally verify that the induced maps from [47, Example 6.2.4.9] are equivalences. This is however clear in the case at hand.
Finally, let us verify that \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) satisfies the required Properties i)-iii). Indeed, Property iii) is satisfied by construction and Property i) follows from the explicit description of multi-mapping spaces above. To prove Property ii) we note that the \(\infty \)-operad \(\text {Cat} _\infty ^\times \) represents the functor \(\text {Op} _\infty ^{\text {op} }\rightarrow {\mathcal {S}}\) which sends an \(\infty \)-operad \({\mathcal {O}}^{\otimes }\) to the space of cocartesian fibrations \({\mathcal {E}}^{\otimes } \rightarrow {\mathcal {O}}^{\otimes }\) (this follows from [47, Remark 2.4.2.6]). The functor \((\text {Cat} _\infty )_{//D} \rightarrow \text {Cat} _\infty \) which forgets the map refines to a transformation of represented functors \(\text {Op} _\infty ^{\text {op} }\rightarrow {\mathcal {S}}\) (again given by forgetting the map to \({\mathcal {D}}^\otimes \)). Thus we get a lax symmetric monoidal structure on the functor \((\text {Cat} _\infty )_{//{\mathcal {D}}} \rightarrow \text {Cat} _\infty \) and by the description of the tensor product given above it follows that this functor is actually symmetric monoidal as opposed to merely lax symmetric monoidal. \(\square \)
Remark 5.2.5
It is also possible to give a direct construction of the symmetric monoidal \(\infty \)-category \((\text {Cat} _\infty )_{//{\mathcal {D}}}^\otimes \) as follows. Let \(\text {LaxAr} \subseteq (\text {Cat} _\infty )_{/\Delta ^1}\) be the full subcategory spanned by the cartesian fibrations \({\mathcal {M}}\rightarrow \Delta ^1\). We note that such a cartesian fibration encodes the data of an functor \((\Delta ^1)^{\text {op} }\rightarrow \text {Cat} _\infty \), corresponding to an arrow \({\mathcal {M}}_1 \rightarrow {\mathcal {M}}_0\) in \(\text {Cat} _\infty \), where \({\mathcal {M}}_i := {\mathcal {M}}\times _{\Delta ^1} \Delta ^{\{i\}}\) is the fibre of \({\mathcal {M}}\) over \(i \in \{0,1\}\). By definition the morphisms in \(\text {LaxAr} (\text {Cat} _\infty )\) simply correspond to functors \({\mathcal {M}}\rightarrow {\mathcal {M}}'\) over \(\Delta ^1\), and these are not required to preserve cartesian edges. As a result, morphisms in \(\text {LaxAr} \) correspond to lax natural transformations of arrows, that is, to squares which commute up to a specified transformation. We then endow \(\text {LaxAr} \) with the cartesian monoidal structure \(\text {LaxAr} ^{\times }\), which is simply given by fibre product over \(\Delta ^1\) (since cartesian fibrations are closed under fibre products) and we define \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) to be the fibre of the functor
over \({\mathcal {D}}\). Since \(f_0\) is product preserving and \({\mathcal {D}}\) is an \({\text {E} _\infty }\)-monoid object in \(\text {Cat} _\infty \) the fibre \((\text {Cat} _\infty )_{//{\mathcal {D}}}\) inherits a symmetric monoidal structure, which we denote by \((\text {Cat} _\infty )_{//{\mathcal {D}}}^{\otimes }\). We now claim that the underlying \(\infty \)-operad of \((\text {Cat} _\infty )_{//{\mathcal {D}}}^{\otimes }\) represents the same functor described in Property iii), and hence identifies with the construction given above. To see this, let us first identify the functor represented by \(\text {LaxAr} ^{\times }\). For \({\mathcal {O}}\) an \(\infty \)-operad, \({\mathcal {O}}\)-algebra objects in \(\text {LaxAr} ^{\times }\) correspond to \({\mathcal {O}}\)-monoids, which are simply functors \({\mathcal {O}}^{\otimes } \rightarrow \text {LaxAr} \) in which certain diagrams are cartesian. But the \(\infty \)-category of functors \({\mathcal {O}}^{\otimes } \rightarrow \text {LaxAr} \) embeds in the \(\infty \)-category of functors \({\mathcal {O}}^{\otimes } \rightarrow (\text {Cat} _\infty )_{/\Delta ^1}\), and the latter correspond via unstraightening to cocartesian fibrations \(p:{\mathcal {E}}\rightarrow {\mathcal {O}}^{\otimes }\) equipped with a map \({\mathcal {E}}\rightarrow \Delta ^1\) which sends p-cocartesian edges to equivalences. The condition that the associated functor \({\mathcal {O}}^{\otimes } \rightarrow (\text {Cat} _\infty )_{/\Delta ^1}\) lands in \(\text {LaxAr} \) corresponds in these terms to the condition that for every x in \({\mathcal {O}}^{\otimes }\) the restricted map \({\mathcal {E}}_x \rightarrow \Delta ^1\) is a cartesian fibration. By the dual of [43, Corollary 4.3.1.15], this is equivalent to saying that \({\mathcal {E}}\rightarrow \Delta ^1\) is a cartesian fibration whose cartesian edges all map to equivalences in \({\mathcal {O}}^{\otimes }\). Straightening over \(\Delta ^1\), this data is equivalent to that of a map \({\mathcal {E}}_1 \rightarrow {\mathcal {E}}_0\) of \(\infty \)-categories over \({\mathcal {O}}^{\otimes }\) such that the maps \({\mathcal {E}}_0 \rightarrow {\mathcal {O}}^{\otimes }\) and \({\mathcal {E}}_1 \rightarrow {\mathcal {O}}^{\otimes }\) are cocartesian fibrations. The monoid condition is then equivalent to the condition that for \(i=0,1\) the cocartesian fibration \({\mathcal {E}}_i \rightarrow {\mathcal {O}}^{\otimes }\) exhibits \({\mathcal {E}}_i\) as an \({\mathcal {O}}\)-monoidal \(\infty \)-category and that the functor \({\mathcal {E}}_1 \rightarrow {\mathcal {E}}_0\) preserves inert maps. We hence get that the data of an \({\mathcal {O}}\)-algebra object in \(\text {LaxAr} ^{\times }\) is equivalent to that of a pair of \({\mathcal {O}}\)-monoidal \(\infty \)-categories \({\mathcal {E}}_0,{\mathcal {E}}_1\) equipped with a lax \({\mathcal {O}}\)-monoidal functor \({\mathcal {E}}_1 \rightarrow {\mathcal {E}}_0\). We may then conclude that the data of an \({\mathcal {O}}\)-algebra object in \((\text {Cat} _\infty )_{//D}\) is equivalent to that of an \({\mathcal {O}}\)-monoidal \(\infty \)-category \({\mathcal {E}}_1\) equipped with a lax \({\mathcal {O}}\)-monoidal functor \({\mathcal {E}}_1 \rightarrow {\mathcal {D}}\).
We will now apply the construction of Lemma 5.2.3 to the category \({\mathcal {D}}= {{\mathcal {S}}{p}}\) of spectra, equipped with its symmetric monoidal structure given by the tensor product of spectra, and form the pullback along the autoequivalence \((-)^{\text {op} }:\text {Cat} _\infty \rightarrow \text {Cat} _\infty \). More precisely we define a symmetric monoidal \(\infty \)-category \(\left( (\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}}\right) ^\otimes \) as the pullback

Objects of this symmetric monoidal \(\infty \)-category are given by pairs  consisting of an \(\infty \)-category \({\mathcal {C}}\) and a functor
consisting of an \(\infty \)-category \({\mathcal {C}}\) and a functor  . Morphisms
. Morphisms

in \(\left( (\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}}\right) ^\otimes \) are given by pairs \((f,\eta )\) of a functor \(f:{\mathcal {C}}_1 \times \ldots \times {\mathcal {C}}_n \rightarrow {\mathcal {C}}'\) and a natural transformation  . This description also holds for \(n = 0\).
. This description also holds for \(n = 0\).
Construction 5.2.6
We define the \(\infty \)-operad \((\text {Cat} ^{\textrm{h}}_\infty )^\otimes \) as the suboperad of
\(\left( (\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}}\right) ^\otimes \) spanned by those objects  such that each \({\mathcal {C}}_i\) is stable and each
such that each \({\mathcal {C}}_i\) is stable and each  is quadratic, and those maps \((f,\eta )\) as above such that \(f:{\mathcal {C}}_1 \times \ldots \times {\mathcal {C}}_n \rightarrow {{{\mathcal {C}}}'}\) is exact in each variable.
is quadratic, and those maps \((f,\eta )\) as above such that \(f:{\mathcal {C}}_1 \times \ldots \times {\mathcal {C}}_n \rightarrow {{{\mathcal {C}}}'}\) is exact in each variable.
We note that the underlying \(\infty \)-category of \((\text {Cat} ^{\textrm{h}}_\infty )^\otimes \) is indeed given by \(\text {Cat} ^{\textrm{h}}_\infty \) since it is, essentially by definition, the Grothendieck construction of the functor \({\mathcal {C}}\mapsto {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) which is a subcategory of the lax slice \((\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}}\).
By definition we have that the composed lax symmetric monoidal functor
factors through the suboperad
spanned by the tuples of stable \(\infty \)-categories and tuples of functors which are exact in each variable.
Theorem 5.2.7
-
i)
The \(\infty \)-operad \((\text {Cat} ^{\textrm{h}}_\infty )^\otimes \) is symmetric monoidal with tensor product given by the tensor product of Construction 5.1.2 and tensor unit given by
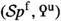 .
. -
ii)
The resulting map \(p^{\otimes }:(\text {Cat} ^{\textrm{h}}_\infty )^\otimes \rightarrow (\text {Cat} _\infty ^\text {ex} )^\otimes \) is a cocartesian fibration of \(\infty \)-operads and in particular a symmetric monoidal functor.
-
iii)
This symmetric monoidal structure on \(\text {Cat} ^{\textrm{h}}_\infty \) restricts to a symmetric monoidal structure on the subcategory \(\text {Cat} ^{\textrm{p}}_\infty \).
Proof
By design, the hermitian \(\infty \)-category  of Construction 5.1.2 corepresents the binary multi-mapping space functor
of Construction 5.1.2 corepresents the binary multi-mapping space functor

Similarly, the object  corepresents the nullary operations
corepresents the nullary operations
since the morphisms  exhibits the target as the initial hermitian \(\infty \)-category under \((\text {pt} , {\mathbb {S}})\) by Proposition 4.1.3. These constructions thus produce locally cocartesian lifts for the active arrows \(\langle 0 \rangle \rightarrow \langle 1 \rangle \) and \(\langle 2 \rangle \rightarrow \langle 1 \rangle \), and more generally for every active arrow \(\alpha :\langle n\rangle \rightarrow \langle m\rangle \) whose fibres are of size \(\le 2\). Since the latter generate all maps in \(\text {Com} \), to prove i) it will now suffice to show that these locally cocartesian lifts are cocartesian. Taking into account the decomposition of mapping spaces in \(\infty \)-operads it will be enough to verify that the induced maps
exhibits the target as the initial hermitian \(\infty \)-category under \((\text {pt} , {\mathbb {S}})\) by Proposition 4.1.3. These constructions thus produce locally cocartesian lifts for the active arrows \(\langle 0 \rangle \rightarrow \langle 1 \rangle \) and \(\langle 2 \rangle \rightarrow \langle 1 \rangle \), and more generally for every active arrow \(\alpha :\langle n\rangle \rightarrow \langle m\rangle \) whose fibres are of size \(\le 2\). Since the latter generate all maps in \(\text {Com} \), to prove i) it will now suffice to show that these locally cocartesian lifts are cocartesian. Taking into account the decomposition of mapping spaces in \(\infty \)-operads it will be enough to verify that the induced maps

and

are equivalences of functors \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\mathcal {S}}\). We will give the argument for the first assertion, the second works similar. The first assertion unwinds to the statement that natural transformations from the functor

to any functor \( ({\mathcal {C}}_1 \otimes {\mathcal {C}}_2) \times {\mathcal {C}}_3 \times \ldots \times {\mathcal {C}}_n \rightarrow {{\mathcal {S}}{p}}\) pulled back from a quadratic functor \({\mathcal {C}}_1 \otimes \ldots \otimes {\mathcal {C}}_n \rightarrow {{\mathcal {S}}{p}}\) are equivalent to natural transformations from

to the restriction of the same functor. After fixing objects \(x_3 \in {\mathcal {C}}_3, x_4 \in {\mathcal {C}}_4,\ldots \) it is certainly true that the space of natural transformations between the restricted functors along
agree by the universal properties of left Kan extension \(\beta _!\) and 2-excisive approximation \(\text {P} _2\). The claim then follows since the space of transformations is a limit over these restricted spaces.
To see ii) first observe that the operad map \(p^{\otimes }:(\text {Cat} ^{\textrm{h}}_\infty )^\otimes \rightarrow (\text {Cat} _\infty ^\text {ex} )^\otimes \) preserves cocartesian edges, as is visible by the explicit formula for the tensor product above. In particular, it is a symmetric monoidal functor. Since the functor on underlying \(\infty \)-categories \(p:\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is a cocartesian fibration by Corollary 1.4.2 it now follows from [43, Proposition 2.4.2.11] that \(p^{\otimes }\) is a locally cocartesian fibration. To show that \(p^{\otimes }\) is a cocartesian fibration one needs to additionally verify that for every arrow in \(\alpha :\langle n \rangle \rightarrow \langle m \rangle \) in \(\text {Com} ^{\otimes }\), the associated transition functor \(\alpha _!:(\text {Cat} ^{\textrm{h}}_\infty )^{\otimes }_{\langle n \rangle } \rightarrow (\text {Cat} ^{\textrm{h}}_\infty )^{\otimes }_{\langle m \rangle }\) sends locally \(p^{\otimes }_{\langle n \rangle }\)-cocartesian edges to locally \(p^{\otimes }_{\langle m \rangle }\)-cocartesian edges (indeed, by the explicit description of locally \(p^{\otimes }\)-cocartesian edges provided in [43, Proposition 2.4.2.11], this would imply that these are closed under composition, and are hence all \(p^{\otimes }\)-cocartesian by [43, Proposition 2.4.2.8]). Unwinding the definitions and using Corollary 1.4.2 we observe that this statement is straightforward when \(\alpha \) is inert, and for \(\alpha \) active amounts to verifying that for every commutative square of the form

and every collection of quadratic functors  , the natural map
, the natural map

is an equivalence. Since \(f_1 \otimes \cdots \otimes f_n\) is exact, restriction along it preserves quadratic functors and hence left Kan extension along it commutes with \(\text {P} _2\). We may consequently identify the above map with the image under \(\text {P} _2\beta _!\) of the map

The latter is then easily seen to be an equivalence by the pointwise formula for left Kan extension and the fact that tensor products of spectra commute with colimits in each variable.
For Assertion iii) about \(\text {Cat} ^{\textrm{p}}_\infty \), since every equivalence between Poincaré \(\infty \)-categories belongs to \(\text {Cat} ^{\textrm{p}}_\infty \) it suffice to check that the tensor product of \((\text {Cat} ^{\textrm{h}}_\infty )^{\otimes }\) preserves Poincaré \(\infty \)-categories, which is Corollary 5.1.4, and that the tensor unit  is Poincaré, which was already observed in Example 1.2.15. \(\square \)
is Poincaré, which was already observed in Example 1.2.15. \(\square \)
Corollary 5.2.8
The functors \(\text {Pn} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\mathcal {S}}\) and \(\text {He} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\mathcal {S}}\) admit canonical lax symmetric monoidal structures.
Proof
By Theorem 5.2.7 and Proposition 4.1.3 both of these functors are corepresented by the respective tensor units, so that the result immediately follows from [52, Corollary 3.10]. \(\square \)
We now point out that both
are subcategory inclusions, and hence induce subcategory inclusions
on the level of algebras for every \(\infty \)-operad \({\mathcal {O}}\). By Lemma 5.2.3 an \({\mathcal {O}}\)-algebra in \(\left( (\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}}\right) ^\otimes \) consists of an \({\mathcal {O}}\)-monoidal \(\infty \)-category \({\mathcal {C}}\) equipped with a lax \({\mathcal {O}}\)-monoidal functor  . By construction, such an \({\mathcal {O}}\)-algebra belongs to the essential image of \(\text {Alg} _{{\mathcal {O}}}(\text {Cat} ^{\textrm{h}}_\infty )\) if and only if the following conditions hold:
. By construction, such an \({\mathcal {O}}\)-algebra belongs to the essential image of \(\text {Alg} _{{\mathcal {O}}}(\text {Cat} ^{\textrm{h}}_\infty )\) if and only if the following conditions hold:
-
i)
for every colour \(t \in {\mathcal {O}}\) the corresponding \(\infty \)-category \({\mathcal {C}}_{t}\) is stable and the functor
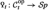 is quadratic;
is quadratic; -
ii)
for every multi-map \(\alpha :\{t_1,\dots , t_n\} \rightarrow t'\) in \({\mathcal {O}}\) the induced functor
$$\begin{aligned} \alpha _*:{\mathcal {C}}_{t_1} \times \ldots \times {\mathcal {C}}_{t_n} \rightarrow {\mathcal {C}}_{t'} \end{aligned}$$is exact in each variable.
In addition, such an \({\mathcal {O}}\)-algebra is further in the essential image of \(\text {Alg} _{{\mathcal {O}}}(\text {Cat} ^{\textrm{p}}_\infty )\) if and only if for every colour \(t \in {\mathcal {O}}\), the corresponding hermitian \(\infty \)-category  is Poincaré, and for every multi-map \(\alpha :\{t_1,\dots , t_n\} \rightarrow t'\) in \({\mathcal {O}}\) and each tuple \(x_1 \in {\mathcal {C}}_{t_1}, \ldots , x_n \in {\mathcal {C}}_{t_n}\) of objects the corresponding hermitian functor
is Poincaré, and for every multi-map \(\alpha :\{t_1,\dots , t_n\} \rightarrow t'\) in \({\mathcal {O}}\) and each tuple \(x_1 \in {\mathcal {C}}_{t_1}, \ldots , x_n \in {\mathcal {C}}_{t_n}\) of objects the corresponding hermitian functor

is Poincaré.
Notation 5.2.9
For an \(\infty \)-operad \({\mathcal {O}}\), we will refer to \({\mathcal {O}}\)-algebra objects  in \(\text {Cat} ^{\textrm{h}}_\infty \) with respect to the symmetric monoidal structure of Theorem 5.2.7 as \({\mathcal {O}}\)-monoidal hermitian \(\infty \)-categories, and similarly to \({\mathcal {O}}\)-algebra objects in \(\text {Cat} ^{\textrm{p}}_\infty \) as \({\mathcal {O}}\)- monoidal Poincaré \(\infty \)-categories. We will then refer to the hermitian (resp. Poincaré) structure
in \(\text {Cat} ^{\textrm{h}}_\infty \) with respect to the symmetric monoidal structure of Theorem 5.2.7 as \({\mathcal {O}}\)-monoidal hermitian \(\infty \)-categories, and similarly to \({\mathcal {O}}\)-algebra objects in \(\text {Cat} ^{\textrm{p}}_\infty \) as \({\mathcal {O}}\)- monoidal Poincaré \(\infty \)-categories. We will then refer to the hermitian (resp. Poincaré) structure  as an \({\mathcal {O}}\)-monoidal hermitian (resp. Poincaré) structure. When \({\mathcal {O}}=\text {Com} \) we will replace as customary the term \({\mathcal {O}}\)-monoidal by symmetric monoidal.
as an \({\mathcal {O}}\)-monoidal hermitian (resp. Poincaré) structure. When \({\mathcal {O}}=\text {Com} \) we will replace as customary the term \({\mathcal {O}}\)-monoidal by symmetric monoidal.
6.3 Day convolution of hermitian structures
In this section we will analyse in more explicit terms symmetric monoidal hermitian and Poincaré structures over a fixed stably symmetric monoidal \(\infty \)-category \({\mathcal {C}}\), and show that they can be encoded in terms of their linear and bilinear parts. To this end, recall that for two symmetric monoidal \(\infty \)-categories \({\mathcal {E}},{\mathcal {D}}\), there is an associated \(\infty \)-operad \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) with underlying \(\infty \)-category \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\), called the Day convolution \(\infty \)-operad, see [24, 47, §2.2.6], and [18] for the classical counterpart. It is characterized by the following universal property: there is an evaluation map of \(\infty \)-operads
refining the usual evaluation map, such that for every \(\infty \)-operad \({\mathcal {O}}^{\otimes }\), the composed map
is an equivalence of \(\infty \)-categories. Here, we may identify \(\text {Alg} _{{\mathcal {E}}\times _{\text {Com} } {\mathcal {O}}}({\mathcal {D}}) \simeq \text {Alg} _{{\mathcal {E}}\times _{\text {Com} } {\mathcal {O}}/{\mathcal {O}}}({\mathcal {D}}\times _{\text {Com} }{\mathcal {O}})\) with the \(\infty \)-category of lax \({\mathcal {O}}\)-monoidal functors from \({\mathcal {E}}\) to \({\mathcal {D}}\), both considered as \({\mathcal {O}}\)-monoidal \(\infty \)-categories by pulling back along \({\mathcal {O}}\rightarrow \text {Com} \). In particular, for \({\mathcal {O}}^{\otimes }=\text {Com} ^{\otimes }\) we get an equivalence between commutative algebra objects in \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) and lax symmetric monoidal functors \({\mathcal {E}}\rightarrow {\mathcal {D}}\). On the other hand, taking \({\mathcal {O}}^{\otimes }\) to be the underlying \(\infty \)-operad of a symmetric monoidal \(\infty \)-category \({\mathcal {C}}\), we get that lax symmetric monoidal functors \({\mathcal {C}}\rightarrow {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) correspond to lax symmetric monoidal functors \({\mathcal {C}}\times {\mathcal {E}}\rightarrow {\mathcal {D}}\).
By [47, Corollary 2.2.6.12] the multi-mapping space in \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) from a collection \(\{\varphi _i:{\mathcal {E}}\rightarrow {\mathcal {D}}\}_{i=1,\ldots ,n}\) to \(\psi :{\mathcal {E}}\rightarrow {\mathcal {D}}\) is given by the space of natural transformations in the square

If \({\mathcal {E}}\) is small, \({\mathcal {D}}\) admits small colimits, and the tensor product in \({\mathcal {D}}\) preserves small colimits in each variable, then \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) is a symmetric monoidal \(\infty \)-category, with tensor product \(\varphi _1 \otimes \varphi _2:{\mathcal {E}}\rightarrow {\mathcal {D}}\) given by the left Kan extension of \(\varphi _1 \boxtimes \varphi _2:{\mathcal {E}}\times {\mathcal {E}}\rightarrow {\mathcal {D}}\times {\mathcal {D}}\rightarrow {\mathcal {D}}\) along \({\mathcal {E}}\times {\mathcal {E}}\rightarrow {\mathcal {E}}\) (see [47, Proposition 2.2.6.16]). Furthermore, in this case \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) admits small colimits and the Day convolution product preserves small colimits in each variable [24, Lemma 2.13].
Remark 5.3.1
Comparing universal properties we see that if \({\mathcal {C}},{\mathcal {E}}\) are small symmetric monoidal \(\infty \)-categories and \({\mathcal {D}}\) is an \(\infty \)-category with small colimits which is endowed with a symmetric monoidal structure which preserves colimits in each variable, then there is a natural equivalence of symmetric monoidal \(\infty \)-categories
where the left hand side is equipped with the Day convolution structure, and the right hand side with the twice nested Day convolution structure.
We now relate this concept to the constructions we made in the previous sections. Given a small symmetric monoidal \(\infty \)-category \({\mathcal {C}}\), consider the pullback square of \(\infty \)-operads

refining the pullback square of \(\infty \)-categories which identifies \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) as the fibre of the cartesian fibration \((\text {Cat} _\infty )_{\text {op} //{{\mathcal {S}}{p}}} \rightarrow \text {Cat} _\infty \) over \({\mathcal {C}}\in \text {Cat} _\infty \). We then have the following:
Lemma 5.3.2
Let \({\mathcal {C}}\) be a small stably symmetric monoidal \(\infty \)-category. Then the \(\infty \)-operad \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) is a symmetric monoidal \(\infty \)-category. Furthermore, we may identify the symmetric monoidal structure on \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) with Day convolution. In particular, for an \(\infty \)-operad \({\mathcal {O}}\), the data of an \({\mathcal {O}}\)-algebra structure on  corresponds, naturally in \({\mathcal {O}}\), to that of a lax \({\mathcal {O}}\)-monoidal refinement of
corresponds, naturally in \({\mathcal {O}}\), to that of a lax \({\mathcal {O}}\)-monoidal refinement of  , where \({\mathcal {C}}\) and \({{\mathcal {S}}{p}}\) are considered as \({\mathcal {O}}\)-monoidal \(\infty \)-categories by pulling back along \({\mathcal {O}}\rightarrow \text {Com} \).
, where \({\mathcal {C}}\) and \({{\mathcal {S}}{p}}\) are considered as \({\mathcal {O}}\)-monoidal \(\infty \)-categories by pulling back along \({\mathcal {O}}\rightarrow \text {Com} \).
Remark 5.3.3
It follows from Lemma 5.3.2 that the tensor product of  is given by the left Kan extension of the functor
is given by the left Kan extension of the functor  along \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\).
along \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\).
Proof
Since \(\left( (\text {Cat} _\infty )_{\text {op} //{\mathcal {D}}}\right) ^{\otimes } \rightarrow \text {Cat} _\infty ^\times \) is a cocartesian fibration it follows that \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^\otimes \rightarrow {\text {E} _\infty }\) is also a cocartesian fibration, so that \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^\otimes \) is a symmetric monoidal \(\infty \)-category. By the description of algebra objects in \(\left( (\text {Cat} _\infty )_{\text {op} //{\mathcal {D}}}\right) ^{\otimes }\) given in Lemma 5.2.3iii) and the fact that taking algebra objects is compatible with limits of \(\infty \)-operads we get that \({\mathcal {O}}\)-algebras in \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes }\) are given by lax \({\mathcal {O}}\)-monoidal functors \({\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), and this description is natural in \({\mathcal {O}}\), which allows us to identify the monoidal structure on \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) with Day convolution. \(\square \)
We now wish to understand in similar terms the hermitian context, in which one considers quadratic functors \({\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\). For this, let us consider the setting of Day convolution when the target \({\mathcal {D}}\) is a presentably symmetric monoidal \(\infty \)-category, that is, it is presentable and the tensor product preserves small colimits in each variable. In this case, for a small \(\infty \)-category \({\mathcal {E}}\), the functor category \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) is again presentably symmetric monoidal with respect to Day convolution. Suppose now that \({\mathcal {I}}= \{\overline{p}_{\alpha }:K_{\alpha }^{\triangleright } \rightarrow {\mathcal {E}}\}\) is a small collection of diagrams in \({\mathcal {E}}\). Let \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}}) \subseteq {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) be the full subcategory spanned by those functors \({\mathcal {E}}\rightarrow {\mathcal {D}}\) which send every diagram in \({\mathcal {I}}\) to a limit diagram. We claim that \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\) is an accessible localisation of \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\). Indeed, choose a small set of generators T for \({\mathcal {D}}\), and for \(\alpha \in {\mathcal {I}}\) let us denote by \(p_{\alpha } := (\overline{p}_{\alpha })|_{K_{\alpha }}\) the corresponding restriction. Then for every \(a \in T\) and \(\alpha \in {\mathcal {I}}\) the diagram \(\overline{p}_{\alpha }\) induces a map
where \(j:{\mathcal {E}}^{\text {op} }\rightarrow {\text {Fun}}({\mathcal {E}},{\mathcal {S}})\) is the Yoneda embedding and \(\otimes \) denotes the canonical bifunctor \({\text {Fun}}({\mathcal {E}},{\mathcal {S}}) \times {\mathcal {D}}\rightarrow {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) induced levelwise by the tensoring of the presentable \(\infty \)-category \({\mathcal {D}}\) over spaces. Let \(S = \{s_{\alpha ,a}\}_{\alpha \in {\mathcal {I}}, a \in T}\). We may then identify \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}}) \subseteq {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) with the full subcategory spanned by the S-local objects. Since S is a set it follows from [43, Proposition 5.5.4.15] that \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\) is also presentable and its inclusion admits a left adjoint
We then have that L exhibits \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\) as the localisation of \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) by the set of maps S. Since L is a left adjoint functor we also refer to it as a left Bousfield localisation.
We now consider the above setup in the context of Day convolution. Recall that in general, a left Bousfield localisation functor \(L:{\mathcal {A}}\rightarrow {\mathcal {B}}\), with fully-faithful right adjoint \(R:{\mathcal {B}}\hookrightarrow {\mathcal {A}}\), is said to be compatible with respect to a given symmetric monoidal structure \({\mathcal {A}}^{\otimes }\) on \({\mathcal {A}}\), if for every \(f:x\rightarrow y\) in \({\mathcal {A}}\) such that L(f) is an equivalence, and every \(z\in {\mathcal {A}}\), the map \(L(z\otimes f)\) is again an equivalence. By [47, Proposition 2.2.1.9] the \(\infty \)-category \({\mathcal {B}}\) then inherits a symmetric monoidal structure \({\mathcal {B}}^{\otimes }\) such that L refines to a symmetric monoidal functor \(L^{\otimes }:{\mathcal {A}}^{\otimes } \rightarrow {\mathcal {B}}^{\otimes }\) and R refines to a fully-faithful inclusion of \(\infty \)-operads \(R^{\otimes }:{\mathcal {B}}^{\otimes } \rightarrow {\mathcal {A}}^{\otimes }\). In addition, the symmetric monoidal functor \(L^{\otimes }\) exhibits \({\mathcal {B}}^{\otimes }\) as universal among symmetric monoidal \(\infty \)-categories receiving a symmetric monoidal functor from \({\mathcal {A}}\) which inverts the maps inverted by L. Indeed, the symmetric monoidal functor \(L^{\otimes }\) must factor through such a symmetric monoidal localisation by [47, Proposition 4.1.7.4], and the resulting comparison between the two symmetric monoidal \(\infty \)-categories under \({\mathcal {A}}^{\otimes }\) is an equivalence since it is an equivalence on the level of underlying \(\infty \)-categories. We will consequently refer to \(L^{\otimes }\) as a symmetric monoidal Bousfield localisation.
Lemma 5.3.4
Given \({\mathcal {E}},{\mathcal {D}}\) and \({\mathcal {I}}\) be as above, let us denote by \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})^{\otimes } \subseteq {\text {Fun}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) the full suboperad spanned by \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\). Suppose that \({\mathcal {I}}\) is closed under post-composition with \(x\otimes (-):{\mathcal {E}}\rightarrow {\mathcal {E}}\) for every \(x\in {\mathcal {E}}\), that is, if \(p_\alpha \in {\mathcal {I}}\) then \((x\otimes (-)) \circ p_\alpha \) is also in \({\mathcal {I}}\). Then the left Bousfield localisation functor L is compatible with Day convolution, and hence extends to a symmetric monoidal localisation Bousfield localisation functor
In particular, \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) inherits a symmetric monoidal \(\infty \)-category, universally obtained from \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) by inverting the set of maps S.
Remark 5.3.5
In the situation of Lemma 5.3.4, the tensor product \(\otimes _{{\mathcal {I}}}\) in \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) can be expressed in terms of the tensor product \(\otimes _{\text {Day} }\) in \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})^{\otimes }\) and the localisation functor. Explicitly, the tensor product of \(\varphi ,\psi \in {\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\) is given by \(L(\varphi \otimes _{\text {Day} } \psi )\).
Remark 5.3.6
In the situation of Lemma 5.3.4, since Day convolution preserves small colimits in each variable and L preserves colimits it follows from Remark 5.3.5 that the localised tensor product on \({\text {Fun}}_{{\mathcal {I}}}({\mathcal {E}},{\mathcal {D}})\) also preserves small colimits in each variable.
Proof of Lemma 5.3.4
Let W be the collection of all maps in \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\) whose image under L is an equivalence. We need to show that W is closed under Day convolution against objects, that is, to show that for \(\tau \in W\) and \(\varphi \in {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\), we have that \(\tau \otimes _{\text {Day} } \varphi \) is again in W. By [43, Proposition 5.5.4.15] we have that W is generated as a strongly saturated class by the set \(S = \{s_{\alpha ,a}\}\) above, and so it will suffice to show that S is closed under Day convolution against \(\varphi \in {\text {Fun}}({\mathcal {E}},{\mathcal {D}})\). Since Day convolution preserves colimits in each variable we may as well check this for a generating set of \({\text {Fun}}({\mathcal {E}},{\mathcal {D}})\). Such a generating set is given, for example, by the functors of the form \(j(x) \otimes a\), for \(x\in {\mathcal {E}}\) and \(a \in T\), where j is the Yoneda embedding as above. Since j is symmetric monoidal ([24, §3] or [47, Corollary 4.8.1.12 and Remark 4.8.1.13]) and using again that Day convolution preserves colimits in each variable, the closure of S under Day convolution with these generators now follows from our condition that \({\mathcal {I}}\) is closed under post-composition with \(x\otimes (-)\) for every \(x\in {\mathcal {E}}\). \(\square \)
We now apply the above ideas in the context of quadratic functors. For a given stable \(\infty \)-category \({\mathcal {C}}\), the \(\infty \)-category \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) sits in a diagram

in which all squares are pullbacks. We then refine this diagram to a diagram of \(\infty \)-operads

by extending the lower and right part and defining the \(\infty \)-operads \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes }\), \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^{\otimes }\) as the respective pullbacks. Since taking algebra objects is compatible with limits in the target it follows that for an \(\infty \)-operad \({\mathcal {O}}\) we have a pullback square

and so \({\mathcal {O}}\)-algebras in \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) correspond to \({\mathcal {O}}\)-monoidal hermitian \(\infty \)-categories refining the underlying \({\mathcal {O}}\)-monoidal \(\infty \)-category of \({\mathcal {C}}\). On the other hand, since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) is a full inclusion and the monoidal structure on the latter identifies with Day convolution by Lemma 5.3.2, we may identify the data of an \({\mathcal {O}}\)-algebra structure on a given quadratic functor  with that of a lax \({\mathcal {O}}\)-monoidal structure. We will refer to such
with that of a lax \({\mathcal {O}}\)-monoidal structure. We will refer to such  as \({\mathcal {O}}\)-monoidal hermitian refinements of \({\mathcal {C}}\).
as \({\mathcal {O}}\)-monoidal hermitian refinements of \({\mathcal {C}}\).
Corollary 5.3.7
Let \({\mathcal {C}}\) be a small stably symmetric monoidal \(\infty \)-category. Then the full inclusion of \(\infty \)-operads
admits a symmetric monoidal left adjoint exhibiting \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^\otimes \) as a symmetric monoidal localisation of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes }\). In particular, the \(\infty \)-operad \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^\otimes \) is a symmetric monoidal \(\infty \)-category.
Remark 5.3.8
It follows from Corollary 5.3.7 that the tensor product of  is given by their Day convolution followed by an application of the left adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). Since
is given by their Day convolution followed by an application of the left adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). Since  are in particular reduced the result of this left Kan extension is reduced and hence the left adjoint in question can be implemented via the 2-excisive approximation of Construction 1.1.26. Comparing this description with Construction 5.1.2 we may equivalently describe the tensor product of
are in particular reduced the result of this left Kan extension is reduced and hence the left adjoint in question can be implemented via the 2-excisive approximation of Construction 1.1.26. Comparing this description with Construction 5.1.2 we may equivalently describe the tensor product of  as the left Kan extension of the quadratic functor
as the left Kan extension of the quadratic functor  along \({\mathcal {C}}^{\text {op} }\otimes {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\).
along \({\mathcal {C}}^{\text {op} }\otimes {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\).
Proof of Corollary 5.3.7
This is a particular case of Lemma 5.3.4 since the condition of being a quadratic functor is equivalent to that of being reduced and 2-excisive (Proposition 1.1.13) which in turn can be formulated as sending a suitable set of diagrams in \({\mathcal {C}}^{\text {op} }\) (consisting of the constant diagram on 0 and all strongly exact 3-cubes) to limit diagrams. \(\square \)
Our next goal is to understand the monoidal structure on \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^{\otimes }\) in terms of decomposition into linear and bilinear components, as described in Corollary 5.3.14 below. Towards this end, we begin with the following direct application of Lemma 5.3.4:
Corollary 5.3.9
Let \({\mathcal {C}}\) be a small stably symmetric monoidal \(\infty \)-category \({\mathcal {C}}\). Then the following holds:
-
i)
The full suboperad \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes } \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes }\) is a symmetric monoidal localisation of the Day convolution product on \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
-
ii)
The full suboperad \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes } \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})^{\otimes }\) is a symmetric monoidal localisation of the Day convolution product on \({\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
Proof
In case i) we apply Lemma 5.3.4 with respect to the collection of diagrams in \({\mathcal {C}}^{\text {op} }\) consisting of the constant diagram on 0 and all exact squares. For ii) we apply Lemma 5.3.4 with respect to the collection of diagrams in \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\) consisting of the constant diagrams on \((x,0)\) and \((0,x)\) for all \(x\in {\mathcal {C}}^{\text {op} }\) and all squares of the form \(\{x\} \times \sigma \) and \(\sigma \times \{x\}\) where \(\sigma :\Delta ^1 \times \Delta ^1 \rightarrow {\mathcal {C}}^{\text {op} }\) is an exact square. \(\square \)
Remark 5.3.10
As in Remark 5.3.5, the tensor product of \(\Lambda ,\Lambda '\in {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) is obtained by taking their Day convolution \(\Lambda \otimes _{\text {Day} } \Lambda '\) and applying to it the left adjoint to the inclusion \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). Similarly, in ii) the tensor product of \(\text {B} ,\text {B} '\in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is obtained by taking their Day convolution \(\text {B} \otimes _{\text {Day} } \text {B} '\) as functors \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), and then applying to it the left adjoint to the inclusion \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\).
Remark 5.3.11
It follows from Remark 5.3.6 that the tensor products on  ,
,  and \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) of Corollaries 5.3.7 and 5.3.9 all preserve small colimits in each variable.
and \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) of Corollaries 5.3.7 and 5.3.9 all preserve small colimits in each variable.
Combining Corollaries 5.3.7 and 5.3.9 we obtain
Corollary 5.3.12
The linear part functor \(\Lambda _{(-)}\) refines to a symmetric monoidal localisation functor
We would like to establish a similar property for the bilinear part functor. To this end, consider the commutative diagram

in which the horizontal arrows are the relevant inclusions and the vertical arrows are all induced by restriction along the diagonal \({\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\). An application of Lemma 5.3.4 shows that all \(\infty \)-categories in this diagram inherit symmetric monoidal structures from the Day convolution product on the functor \(\infty \)-categories in the right most column, and such that all horizontal inclusions admit symmetric monoidal left adjoints, which are also localisation functors. In addition, the right most vertical functor, given by restriction along the diagonal \({\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\), admits a left adjoint via the corresponding left Kan extension. Since the diagonal is symmetric monoidal, so is the corresponding left Kan extension. In addition, since the diagonal admits itself a two sided adjoint via the direct sum functor \(\oplus :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\) this left Kan extension is just given by restriction along \(\oplus \). By the universal property of all the appearing localisations it then follows that the vertical arrows in (121) admit symmetric monoidal left adjoints and we consequently obtain a diagram of symmetric monoidal \(\infty \)-categories and symmetric monoidal functors

in which all horizontal functors are symmetric monoidal localisations and all vertical functors are given by restriction along \(\oplus :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}^{\text {op} }\) followed by the projection to the relevant full subcategory of \({\text {Fun}}_{*}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\). In particular, the top middle horizontal arrow in (122) is the bi-reduction functor of Lemma 1.1.3 and the second from the left vertical functor in (122) is the cross-effect functor of Definition 1.1.4. Since the cross-effect of any quadratic functor is bilinear this formula also holds for the left most vertical arrow, that is, we may identify it with the bilinear part functor \(\text {B} _{(-)}\). Arguing as in the proof of Lemma 1.1.9 we see that this symmetric monoidal refinement of \(\text {B} _{(-)}\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the flip action on \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }\) and the trivial action on \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^{\otimes }\), and consequently refines to a symmetric monoidal functor
where the target is endowed with the symmetric monoidal structure obtained by taking the \({{\text {C} }_{\textrm{2}}}\)-fixed points of \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }\) in the \(\infty \)-category of symmetric monoidal \(\infty \)-categories.
Now recall that the symmetric bilinear part functor
is also a left Bousfield localisation functor, since it admits a fully-faithful right adjoint (in fact, it admits fully-faithful adjoints from both sides). We now verify that the same holds for its symmetric monoidal refinement just constructed:
Lemma 5.3.13
The symmetric monoidal functor (123) is a symmetric monoidal localisation functor.
Proof
It will suffice to show that the localisation functor \(\text {B} _{(-)}\) is compatible with the symmetric monoidal structure (the resulting comparison between the corresponding localisation and \(\text {B} _{(-)}^{\otimes }\) is then necessarily an equivalence since it is an equivalence on the level of underlying \(\infty \)-categories). Now the maps that are sent to equivalences by \(\text {B} _{(-)}\) are exactly the maps whose cofibre is exact. Since left Kan extensions along exact functors preserve exact functors (Lemma 1.4.1) it will suffice to show that if  are such that
are such that  is exact then
is exact then  (defined as in Construction 5.1.2) is exact. Indeed, its bilinear part is
(defined as in Construction 5.1.2) is exact. Indeed, its bilinear part is  by Proposition 5.1.3. \(\square \)
by Proposition 5.1.3. \(\square \)
We now combine the symmetric monoidal structures of Corollaries 5.3.7 and 5.3.9 to enhance the classification of hermitian structures of Corollary 1.3.12 to a symmetric monoidal one:
Corollary 5.3.14
(Monoidal classification of hermitian structures) The pullback square of Corollary 1.3.12 refines to a pullback square in \(\text {Op} _\infty \)

in which all corners are symmetric monoidal \(\infty \)-categories and the vertical functors are symmetric monoidal. Here the left vertical arrow is (123), the bottom right corner is endowed with the symmetric monoidal structure of Corollary 5.3.9, and the arrow category carries the corresponding pointwise symmetric monoidal structure.
Concretely, this means that for a given \(\infty \)-operad \({\mathcal {O}}\), the data of an \({\mathcal {O}}\)-monoidal hermitian refinement of a stably symmetric monoidal \({\mathcal {C}}\) can be identified with that of a triple \((\text {B} ,\Lambda ,\alpha :\Lambda \Rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}})\) where \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is a lax \({\mathcal {O}}\)-monoidal symmetric bilinear functor, \(\Lambda :{\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is a lax \({\mathcal {O}}\)-monoidal exact functor, and \(\Lambda \Rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\) is a lax \({\mathcal {O}}\)-monoidal transformation.
Proof of Corollary 5.3.14
Recall from Remark 1.3.7 that the pair of fully-faithful exact functors

form a stable recollement. We may then invoke the theory of monoidal recollements as developed in [55] to promote our classification of hermitian structures to a monoidal one. More precisely, combining Corollary 5.3.12 and Lemma 5.3.13 it follows that the above stable recollement is symmetric monoidal in the sense of [55, Definition 1.19]. The symmetric monoidal refinement of the classification square is then a consequence of [55, Proposition 1.26]. \(\square \)
Recall from Definition 1.2.8 that for a given stable \(\infty \)-category \({\mathcal {C}}\), the \(\infty \)-category \({\text {Fun}}^{\textrm{p}}({\mathcal {C}})\) is the non-full subcategory of \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) consisting of the Poincaré structures on \({\mathcal {C}}\) and the duality preserving natural transformations between them. We can refine this inclusion to a (non-full) inclusion of \(\infty \)-operads by extending (120) to a commutative diagram of \(\infty \)-operads

in which all squares are pullbacks. For an \(\infty \)-operad \({\mathcal {O}}\), the data of an \({\mathcal {O}}\)-algebra structure on a given Poincaré structure  then corresponds to that of an \({\mathcal {O}}\)-monoidal structure on
then corresponds to that of an \({\mathcal {O}}\)-monoidal structure on  which refines the underlying \({\mathcal {O}}\)-monoidal structure of \({\mathcal {C}}\).
which refines the underlying \({\mathcal {O}}\)-monoidal structure of \({\mathcal {C}}\).
Construction 5.3.15
Applying Remark 5.3.1 and the uniqueness of localised symmetric monoidal structures we deduce that the equivalence
refines to a symmetric monoidal equivalence
where the domain is endowed with the localised Day convolution product and the target with the corresponding nested localised Day convolution. Passing to non-degenerate bilinear functors we obtain an equivalence
between the full suboperad of \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }\) spanned by the non-degenerate bilinear functors and the full suboperad of the Day convolution \(\infty \)-operad \(\textrm{Fun}(\mathcal {C}^\textrm{op},\mathcal {C})^\otimes \) spanned by the exact functors. We note that the latter may fail to be a symmetric monoidal \(\infty \)-category since \({\mathcal {C}}\) generally does not admit small colimits. To avoid confusion, let us try to make the equivalence (126) more explicit. Given non-degenerate bilinear functors \(\text {B} _1,\ldots ,\text {B} _n\) and \(\text {B} '\), a multi-map \(\{\text {B} _1,\ldots ,\text {B} _n\} \rightarrow \text {B} '\) in \({\text {Fun}}^{\textrm{nb}}({\mathcal {C}})^{\otimes }\) is given by a natural transformation
where \(m:{\mathcal {C}}\times \ldots \times {\mathcal {C}}\rightarrow {\mathcal {C}}\) is the symmetric monoidal product of \({\mathcal {C}}\), and \(\widetilde{m}:{\mathcal {C}}\otimes \ldots \otimes {\mathcal {C}}\rightarrow {\mathcal {C}}\) is the exact functor induced by it. Here we point out that the domain in (127) is generally not non-degenerate, which is why \({\text {Fun}}^{\textrm{nb}}({\mathcal {C}})^{\otimes }\) is usually not a symmetric monoidal \(\infty \)-category. By adjunction we may equivalently describe the data of (127) via a natural transformation in the square

By Corollary 5.1.4 (and its proof), the bilinear functor \(\text {B} _1 \otimes \ldots \otimes \text {B} _n\) is non-degenerate and represented by \(\text {D} _{\text {B} _1} \otimes \ldots \text {D} _{\text {B} _n}:{\mathcal {C}}^{\text {op} }\otimes \ldots \otimes {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\otimes \ldots \otimes {\mathcal {C}}\), where \(\text {D} _{\text {B} _i}:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) is the exact functor representing the non-degenerate bilinear functor \(\text {B} _i\). The corresponding multi-map on the right hand side of (126) is then given by the map
induced by the natural transformation in the square

associated to (128) by Lemma (1.2.4).
We now define \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})^{\otimes } \hookrightarrow {\text {Fun}}^{\textrm{nb}}({\mathcal {C}})^{\otimes }\) to be the non-full suboperad spanned by the perfect bilinear functors and those multi-maps whose corresponding natural transformation (129) is an equivalence. Similarly, we define \({\text {Fun}}^{\textrm{ps}}({\mathcal {C}})^{\otimes }\) to be the suboperad of the symmetric monoidal \(\infty \)-category \({\text {Fun}}^{\textrm{s}}({\mathcal {C}})^{\otimes } = [{\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }]^{{{\text {hC} }_{\textrm{2}}}}\) sitting in the pullback square

We note that by construction, the underlying \(\infty \)-categories of \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})^{\otimes }\) and \({\text {Fun}}^{\textrm{ps}}({\mathcal {C}})^{\otimes }\) are the subcategories \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})\) and \({\text {Fun}}^{\textrm{ps}}({\mathcal {C}})\) of \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) and \({\text {Fun}}^{\textrm{s}}({\mathcal {C}})\) respectively, spanned by the perfect (symmetric) bilinear functors respectively and duality preserving (symmetric) transformations between them.
Lemma 5.3.16
The pullback square

refines to a pullback square of \(\infty \)-operads

Proof
Since \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})^{\otimes } \hookrightarrow {\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }\) is a suboperad this follows from the fact that a hermitian functor

lying over the monoidal product \(\widetilde{m}:{\mathcal {C}}\otimes \ldots \otimes {\mathcal {C}}\rightarrow {\mathcal {C}}\) of \({\mathcal {C}}\) is Poincaré exactly when the corresponding natural transformation

is an equivalence, where we have used the identification of the duality on a Poincaré tensor product of Corollary 5.1.4. \(\square \)
Corollary 5.3.17
(Monoidal classification of Poincaré structures) The pullback square of Corollary 1.3.13 refines to a pullback square in \(\text {Op} _\infty \)

in which all corners are symmetric monoidal \(\infty \)-categories and the vertical functors are symmetric monoidal.
Corollary 5.3.18
Let \({\mathcal {C}}\) be a stably symmetric monoidal \(\infty \)-category, \({\mathcal {O}}\) an \(\infty \)-operad and  a lax \({\mathcal {O}}\)-monoidal quadratic functor, so that
a lax \({\mathcal {O}}\)-monoidal quadratic functor, so that  and
and  inherit lax \({\mathcal {O}}\)-monoidal structures by Corollary 5.3.14. Then the corresponding \({\mathcal {O}}\)-monoidal hermitian \(\infty \)-category
inherit lax \({\mathcal {O}}\)-monoidal structures by Corollary 5.3.14. Then the corresponding \({\mathcal {O}}\)-monoidal hermitian \(\infty \)-category  is \({\mathcal {O}}\)-monoidal Poincaré if and only if the following holds:
is \({\mathcal {O}}\)-monoidal Poincaré if and only if the following holds:
-
i)
The underlying hermitian \(\infty \)-category
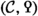 is Poincaré.
is Poincaré. -
ii)
The lax \({\mathcal {O}}\)-monoidal structure on
 induced from that of
induced from that of 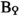 via Construction 5.3.15 is (strongly) \({\mathcal {O}}\)-monoidal. In particular,
via Construction 5.3.15 is (strongly) \({\mathcal {O}}\)-monoidal. In particular, 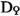 is an equivalence of \({\mathcal {O}}\)-monoidal \(\infty \)-categories.
is an equivalence of \({\mathcal {O}}\)-monoidal \(\infty \)-categories.
Concretely, Corollary 5.3.18 implies that for a stably symmetric monoidal \(\infty \)-category \({\mathcal {C}}\), providing a compatible \({\mathcal {O}}\)-monoidal Poincaré structure on \({\mathcal {C}}\) is equivalent to providing a self-dual equivalence of \({\mathcal {O}}\)-monoidal \(\infty \)-categories \(\text {D} :{\mathcal {C}}^{\text {op} }\xrightarrow {\simeq }{\mathcal {C}}\), a lax \({\mathcal {O}}\)-monoidal exact functor \(\Lambda :{\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\), and a lax \({\mathcal {O}}\)-monoidal transformation \(\Lambda (-) \Rightarrow [{\text {hom}}(-,\text {D} (-))]^{{{\text {tC} }_{\textrm{2}}}}\).
Proof of Corollary 5.3.18
In light of Corollary 5.3.17 it will suffice to show that for a lax \({\mathcal {O}}\)-monoidal bilinear functor \(\text {B} \), the corresponding \({\mathcal {O}}\)-algebra object in \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{\otimes }\) lies in the non-full subcategory \(\text {Alg} _{{\mathcal {O}}}({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})) \subseteq \text {Alg} _{{\mathcal {O}}}({\text {Fun}}^{\textrm{b}}({\mathcal {C}}))\) if and only if \(\text {B} \) is perfect and the associated lax \({\mathcal {O}}\)-monoidal structure on \(\text {D} _{\text {B} }\) is strongly \({\mathcal {O}}\)-monoidal. To see this, note that under the equivalence (126) of Construction 5.3.15, the suboperad \({\text {Fun}}^{\textrm{pb}}({\mathcal {C}})^{\otimes }\) corresponds to the suboperad \({\text {Fun}}^{\circ }({\mathcal {C}}^{\text {op} },{\mathcal {C}})^{\otimes } \subseteq {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{\mathcal {C}})^{\otimes }\) spanned by the colours corresponding to equivalences \(\text {D} :{\mathcal {C}}^{\text {op} }\xrightarrow {\simeq }{\mathcal {C}}\) and the multi-maps \(\{\text {D} _1,\ldots \text {D} _n\} \rightarrow \text {D} '\) corresponding to natural transformations
which are equivalences. We now observe that by the universal property of the tensor product of stable \(\infty \)-categories, such a natural transformation of exact functors is an equivalence if and only if it is sent to an equivalence of multi-linear maps after pre-composing both sides with the functor
We may hence equivalently define this suboperad of \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{\mathcal {C}})^{\otimes }\) to be spanned by the colours corresponding to equivalences and the multi-maps \(\{\text {D} _1,\ldots \text {D} _n\} \rightarrow \text {D} '\) corresponding to natural equivalences
where m is the composite \({\mathcal {C}}\times \ldots \times {\mathcal {C}}\rightarrow {\mathcal {C}}\otimes \ldots \otimes {\mathcal {C}}\xrightarrow {\simeq } {\mathcal {C}}\). It then follows directly from the definitions that \({\mathcal {O}}\)-algebra objects in this suboperad correspond to equivalences \(\text {D} :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) equipped with strong \({\mathcal {O}}\)-monoidal structures, as desired. \(\square \)
6.4 Examples
In this section we want to give some examples of algebras and modules in \(\text {Cat} ^{\textrm{p}}_\infty \).
Example 5.4.1
Consider the Poincaré \(\infty \)-category  . It is the tensor unit of \(\text {Cat} ^{\textrm{p}}_\infty \) and thus admits a structure of commutative algebra. This algebra structure is given by the usual smash product on \({{\mathcal {S}}{p}}^{\text {f} }\) and the canonical commutative algebra structure on the universal quadratic functor
. It is the tensor unit of \(\text {Cat} ^{\textrm{p}}_\infty \) and thus admits a structure of commutative algebra. This algebra structure is given by the usual smash product on \({{\mathcal {S}}{p}}^{\text {f} }\) and the canonical commutative algebra structure on the universal quadratic functor  induced by it being the image under the symmetric monoidal left adjoint \({\text {Fun}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} },{\mathcal {S}}) \rightarrow {\text {Fun}}^{\textrm{q}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} },{\mathcal {S}})\) of the Yoneda image of \({\mathbb {S}}\in {{\mathcal {S}}{p}}^{\text {f} }\).
induced by it being the image under the symmetric monoidal left adjoint \({\text {Fun}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} },{\mathcal {S}}) \rightarrow {\text {Fun}}^{\textrm{q}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} },{\mathcal {S}})\) of the Yoneda image of \({\mathbb {S}}\in {{\mathcal {S}}{p}}^{\text {f} }\).
Example 5.4.2
Since the forgetful functor \(U:\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is symmetric monoidal by Theorem 5.2.7 every symmetric monoidal Poincaré \(\infty \)-category  yields a stably symmetric monoidal \(\infty \)-category \({\mathcal {C}}\) upon forgetting
yields a stably symmetric monoidal \(\infty \)-category \({\mathcal {C}}\) upon forgetting  . In the other direction, we will show in Sect. 7.2 that the formation of hyperbolic categories \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) (see Sect. 2.2) gives both a left and a right adjoint to U, and hence \({\text {Hyp}}\) is both lax and oplax monoidal, see Remark 7.2.23 below. It then follows in particular that if \({\mathcal {C}}\) is a stably symmetric monoidal \(\infty \)-category then \({\text {Hyp}}({\mathcal {C}})\) inherits a symmetric monoidal structure. Unwinding the definitions, this structure is given explicitly by the operation \((x,y) \otimes (x',y') = (x\otimes x',y\otimes y')\) with the canonical lax monoidal structure on
. In the other direction, we will show in Sect. 7.2 that the formation of hyperbolic categories \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) (see Sect. 2.2) gives both a left and a right adjoint to U, and hence \({\text {Hyp}}\) is both lax and oplax monoidal, see Remark 7.2.23 below. It then follows in particular that if \({\mathcal {C}}\) is a stably symmetric monoidal \(\infty \)-category then \({\text {Hyp}}({\mathcal {C}})\) inherits a symmetric monoidal structure. Unwinding the definitions, this structure is given explicitly by the operation \((x,y) \otimes (x',y') = (x\otimes x',y\otimes y')\) with the canonical lax monoidal structure on  . Similarly, if
. Similarly, if  is a symmetric monoidal Poincaré \(\infty \)-category then the Poincaré functor
is a symmetric monoidal Poincaré \(\infty \)-category then the Poincaré functor

sending \(x\) to \((x,\text {D} x)\) (see Sect. 2.2) is canonically a symmetric monoidal Poincaré functor, since \(\text {fgt} \) acts as the unit of the symmetric monoidal adjunction \(U \dashv {\text {Hyp}}\), see Remark 7.2.22. On the other hand, the Poincaré functor  sending \((x,y)\) to \(x\oplus \text {D} y\) (see Sect. 2.2) is not symmetric monoidal in general, though we will show below that it is a morphism of
sending \((x,y)\) to \(x\oplus \text {D} y\) (see Sect. 2.2) is not symmetric monoidal in general, though we will show below that it is a morphism of  -module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
-module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
Example 5.4.3
We will show below (see Remark 7.3.18) that the association  from \(\text {Cat} ^{\textrm{p}}_\infty \) to \(\text {Cat} ^{\textrm{p}}_\infty \) (see Definition 2.4.1) refines to a lax symmetric monoidal functor. It then follows that if
from \(\text {Cat} ^{\textrm{p}}_\infty \) to \(\text {Cat} ^{\textrm{p}}_\infty \) (see Definition 2.4.1) refines to a lax symmetric monoidal functor. It then follows that if  is a Poincaré \(\infty \)-category then
is a Poincaré \(\infty \)-category then  inherits a symmetric monoidal structure. On the level of underlying objects this is given simply by the levelwise product of arrows: \([x\rightarrow y] \otimes [x' \rightarrow y'] = [x\otimes x' \rightarrow y\otimes y']\). The Poincaré functor
inherits a symmetric monoidal structure. On the level of underlying objects this is given simply by the levelwise product of arrows: \([x\rightarrow y] \otimes [x' \rightarrow y'] = [x\otimes x' \rightarrow y\otimes y']\). The Poincaré functor

then inherits the structure of a symmetric monoidal Poincaré functor by its role as a unit of a symmetric monoidal adjunction, see Remark 7.3.17.
We now consider the case of modules over ring spectra studied in Sect. 3. We will specialize to the case where A is an \({\text {E} _\infty }\)-ring spectrum, that is, an algebra object in \({{\mathcal {S}}{p}}\) over the commutative \(\infty \)-operad, and the base \({\text {E} _\infty }\)-ring k is just the sphere spectrum (though see Example 5.4.13 for a perspective incorporating a general k). The \(\infty \)-category \({\text {Mod}}^{\omega }_{A}\) then carries a symmetric monoidal structure given by tensoring over A. We then consider the data needed in order to promote \(({\text {Mod}}^{\omega }_{A})^{\otimes }\) to a symmetric monoidal hermitian or Poincaré \(\infty \)-category.
To begin, by Corollary 5.3.7 and Remark 5.3.8, the \(\infty \)-category \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) inherits a symmetric monoidal structure, given by Day convolution followed by 2-excisive approximation, such that symmetric monoidal hermitian refinements of \({\text {Mod}}^{\omega }_{A}\) correspond to algebra objects  . By Theorem 3.3.1 we have a natural equivalence \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A}) \simeq {\text {Mod}}_{\text {N} A}\) between the \(\infty \)-category of hermitian structures on \({\text {Mod}}^{\omega }_{A}\) and that of modules with genuine involution over A, and so by transport of structure the symmetric monoidal structure on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) induces one on \({\text {Mod}}_{\text {N} A}\).
. By Theorem 3.3.1 we have a natural equivalence \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A}) \simeq {\text {Mod}}_{\text {N} A}\) between the \(\infty \)-category of hermitian structures on \({\text {Mod}}^{\omega }_{A}\) and that of modules with genuine involution over A, and so by transport of structure the symmetric monoidal structure on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) induces one on \({\text {Mod}}_{\text {N} A}\).
Definition 5.4.4
For an \({\text {E} _\infty }\)-ring spectrum A and an \(\infty \)-operad \({\mathcal {O}}\), we refer to an \({\mathcal {O}}\)-algebra object in \({\text {Mod}}_{\text {N} A}\) with respect to the above symmetric monoidal structure as an \({\mathcal {O}}\)-algebra with genuine involution over A.
Warning 5.4.5
Notation 5.4.4 for \({\mathcal {O}}= {\text {E} _1}\) should not be confused with that of an \({\text {E} _1}\)-algebra with genuine anti-involution as in Example 3.2.9.
As described in the proof of Corollary 5.3.14, the recollement \(\left( {\text {Fun}}^{\textrm{s}}({\text {Mod}}^{\omega }_{A}),{\text {Fun}}^{\textrm{ex}} (({\text {Mod}}^{\omega }_{A})^{\text {op} },{{\mathcal {S}}{p}})\right) \) on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\) is compatible with the symmetric monoidal structure and hence the same holds for the recollement \(({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}^{{{\text {hC} }_{\textrm{2}}}},{\text {Mod}}_A)\) on \({\text {Mod}}_{\text {N} A}\). It then follows that the square

refines to a square of symmetric monoidal \(\infty \)-categories and lax symmetric monoidal functors, such that the equivalence (71) becomes a symmetric monoidal one. To identify the resulting symmetric monoidal structure on the individual components \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}^{{{\text {hC} }_{\textrm{2}}}},{\text {Mod}}_A\) we have the following:
Lemma 5.4.6
Let A be an \({\text {E} _\infty }\)-ring spectrum.
-
i)
Under the equivalence \({\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^{\omega }_{A})^{\text {op} },{{\mathcal {S}}{p}}) \simeq {\text {Mod}}_{A}\) the symmetric monoidal structure on the left hand side induced by Day convolution corresponds to the symmetric monoidal structure \(\otimes _A\) on \({\text {Mod}}_{A}\).
-
ii)
Under the equivalence \({\text {Fun}}^{\textrm{b}}({\text {Mod}}^{\omega }_{A}) \simeq {\text {Fun}}^{\textrm{ex}}(({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} A})^{\text {op} },{{\mathcal {S}}{p}}) \simeq {\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}\) the symmetric monoidal structure on the left hand side induced by Day convolution corresponds to the symmetric monoidal structure \(\otimes _{A \otimes _{{\mathbb {S}}} A}\) on \({\text {Mod}}_{A \otimes _{{\mathbb {S}}} A}\).
Proof
We begin with i). By Corollary [47, Corollary 4.8.1.14] there is a unique symmetric monoidal structure on \({\text {Ind}}({\text {Mod}}^{\omega }_{A})\) which preserves filtered colimits in each variable and such that the inclusion \({\text {Mod}}^{\omega }_{A} \hookrightarrow {\text {Ind}}({\text {Mod}}^{\omega }_{A})\) is symmetric monoidal. These two properties are satisfied by the tensor product on \({\text {Mod}}_{A}\), and by Remark 5.3.11 the first property holds for the localised Day convolution product. To finish the proof it is hence left to verify that for a stable \(\infty \)-category \({\mathcal {E}}\) the stable Yoneda embedding \({\mathcal {E}}\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {E}}^{\text {op} },{{\mathcal {S}}{p}})\) admits a symmetric monoidal structure. Indeed, it follows from [52, Proposition 6.3] that the stable Yoneda embedding coincides with the composite
where the first arrow is the ordinary Yoneda embedding, which is naturally symmetric monoidal [24, §3], the second is post-composition with the symmetric monoidal suspension infinity functor \(\Sigma ^{\infty }_+\), and the last one is the left adjoint of the inclusion \({\text {Fun}}^{\textrm{ex}}({\mathcal {E}}^{\text {op} },{{\mathcal {S}}{p}}) \subseteq {\text {Fun}}({\mathcal {E}}^{\text {op} },{\mathcal {S}})\), which is symmetric monoidal by Corollary 5.3.9.
We now prove ii). In light of i), it will suffice to show the localised Day convolution structures on \({\text {Fun}}^{\textrm{b}}({\text {Mod}}^{\omega }_{A})\) and \({\text {Fun}}^{\textrm{ex}}({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} A})\) coincide. For this we consider the commutative square

where the horizontal maps are induced by restriction along the bifunctor \((X,Y) \mapsto X \otimes _{{\mathbb {S}}} Y\) from \({\text {Mod}}^{\omega }_{A} \times {\text {Mod}}^{\omega }_{A}\) to \({\text {Mod}}^{\omega }_{A}\), and the vertical maps are the relevant full inclusions. Passing to left adjoints and using the universal property of localisation we obtain a commutative square

in which the horizontal maps are induced by left Kan extension along \((X,Y) \mapsto X \otimes _{{\mathbb {S}}} Y\), followed by projection to \({\text {Fun}}^{\textrm{ex}}({\text {Mod}}^{\omega }_{A \otimes _{{\mathbb {S}}} A})\) in case of the top arrow. In particular, all arrows carry a natural symmetric monoidal structure, and so the top horizontal equivalence identifies the localised Day convolution structures on both sides. \(\square \)
Corollary 5.4.7
Let A be an \({\text {E} _\infty }\)-ring spectrum and \({\mathcal {O}}\) an \(\infty \)-operad. Then the data of an \({\mathcal {O}}\)-monoidal hermitian refinement of \(({\text {Mod}}^{\omega }_{A})^{\otimes }\) corresponds to a triple \((B,C,\alpha :C \rightarrow B^{{{\text {tC} }_{\textrm{2}}}})\) where \(B \in \text {Alg} _{A \otimes _{{\mathbb {S}}} A}^{{{\text {hC} }_{\textrm{2}}}}\) is an \({\mathcal {O}}\)-\((A \otimes _{{\mathbb {S}}} A)\)-algebra equipped with a symmetry with respect to the flip action on \(A \otimes _{{\mathbb {S}}} A\), C is an \({\mathcal {O}}\)-A-algebra, and \(\alpha \) is a map of \({\mathcal {O}}\)-A-algebras.
Corollary 5.4.8
Let A be an \({\text {E} _\infty }\)-ring spectrum and \({\mathcal {O}}\) an \(\infty \)-operad. Suppose that \({\mathcal {O}}\) is unital. Then B, an \({\mathcal {O}}\)-algebra with genuine involution over A, determines an \({\mathcal {O}}\)-monoidal Poincaré structure on \(({\text {Mod}}^{\omega }_{A})^{\otimes }\) if and only if the underlying \({\mathcal {O}}\)-A-algebra of B (with respect to either of the two component inclusions \(A \rightarrow A \otimes _{{\mathbb {S}}} A\), this makes no difference due to the symmetry of B) is initial.
Remark 5.4.9
In the situation of Corollary 5.4.8, the initiality condition on B can be more explicitly formulated by saying that for every colour \(t \in {\mathcal {O}}\) the composed map \(A \rightarrow A \otimes _{{\mathbb {S}}} A \rightarrow B_t\) associated to the essentially unique null-operation \(\{\} \rightarrow t\) and either of the two component inclusions \(A \rightarrow A \otimes _{{\mathbb {S}}} A\), is an equivalence.
Proof of Corollary 5.4.8
Let  be the \({\mathcal {O}}\)-monoidal hermitian structure on \({\text {Mod}}^{\omega }_{A}\) associated to the \({\mathcal {O}}\)-algebra with genuine involution \((B,C,\alpha :C \rightarrow B^{{{\text {tC} }_{\textrm{2}}}})\). By Corollary 5.3.18 this hermitian structure is \({\mathcal {O}}\)-monoidal Poincaré if and only if
be the \({\mathcal {O}}\)-monoidal hermitian structure on \({\text {Mod}}^{\omega }_{A}\) associated to the \({\mathcal {O}}\)-algebra with genuine involution \((B,C,\alpha :C \rightarrow B^{{{\text {tC} }_{\textrm{2}}}})\). By Corollary 5.3.18 this hermitian structure is \({\mathcal {O}}\)-monoidal Poincaré if and only if  is Poincaré and the associated lax \({\mathcal {O}}\)-monoidal functor \(\text {D} _{B} = {\text {hom}}_A(-,B)\) is \({\mathcal {O}}\)-monoidal. This condition requires in particular that the map
is Poincaré and the associated lax \({\mathcal {O}}\)-monoidal functor \(\text {D} _{B} = {\text {hom}}_A(-,B)\) is \({\mathcal {O}}\)-monoidal. This condition requires in particular that the map
in question is an equivalence. On the other hand, when this condition holds we get from Proposition 3.1.14 that \((B,C,\alpha )\) is induced by an anti-involution on A, and hence in particular  is Poincaré by Example 3.1.9. In addition, in this case we may write the duality as a composition of the standard duality \(\text {D} _A\) and the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Mod}}^{\omega }_{A}\) induced by the involution on \(B=A\), both of which are \({\mathcal {O}}\)-monoidal. \(\square \)
is Poincaré by Example 3.1.9. In addition, in this case we may write the duality as a composition of the standard duality \(\text {D} _A\) and the \({{\text {C} }_{\textrm{2}}}\)-action on \({\text {Mod}}^{\omega }_{A}\) induced by the involution on \(B=A\), both of which are \({\mathcal {O}}\)-monoidal. \(\square \)
Taking \({\mathcal {O}}={\text {E} _\infty }\) in Corollary 5.4.8, we note that the data of a symmetric \({\text {E} _\infty }\)-\((A \otimes _{{\mathbb {S}}} A)\)-algebra whose underlying A-algebra is initial is the same as the data of a \({{\text {C} }_{\textrm{2}}}\)-action on A as an \({\text {E} _\infty }\)-ring spectrum. We hence get that symmetric monoidal Poincaré refinements of \(({\text {Mod}}^{\omega }_{A})^{\otimes }\) correspond to the data of a \({{\text {C} }_{\textrm{2}}}\)-action on A as an \({\text {E} _\infty }\)-ring spectrum, together with a map of \({\text {E} _\infty }\)-A-algebras \(C \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\). Here \(A^{{{\text {tC} }_{\textrm{2}}}}\) is considered as a \({\text {E} _\infty }\)-A-ring spectrum via the Tate Frobenius \(A \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\). We will refer to such a triple \((A,C,C \rightarrow A^{{{\text {tC} }_{\textrm{2}}}})\) as an \({\text {E} _\infty }\)-ring spectrum with genuine involution.
Examples 5.4.10
Let \(A \in \text {Alg} _{{\text {E} _\infty }}^{{{\text {hC} }_{\textrm{2}}}}\) be an \({\text {E} _\infty }\)-ring spectrum equipped with an involution. We then have the following examples of genuine refinements of interest:
-
i)
The map \(\text {id} :A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) determines an \({\text {E} _\infty }\)-ring spectrum with genuine involution \((A,A^{{{\text {tC} }_{\textrm{2}}}},\text {id} )\), and hence a symmetric monoidal refinement of the associated symmetric Poincaré structure
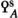 on \({\text {Mod}}^{\omega }_{A}\).
on \({\text {Mod}}^{\omega }_{A}\). -
ii)
If A is connective then the commutative A-algebra map \(t_0 :\tau _{\ge 0}A^{{{\text {tC} }_{\textrm{2}}}} \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) determines an \({\text {E} _\infty }\)-ring spectrum with genuine involution \((A,\tau _{\ge 0}A^{{\text {tC} }_{\textrm{2}}}, t_0)\), and hence a symmetric monoidal refinement of the Poincaré \(\infty \)-category
 of Example 3.2.8. When A is discrete, this is the genuine symmetric Poincaré structure, see 4.2.
of Example 3.2.8. When A is discrete, this is the genuine symmetric Poincaré structure, see 4.2. -
iii)
The twisted Tate Frobenius map \(\text {t} :A \rightarrow (A \otimes _{{\mathbb {S}}} A)^{{{\text {tC} }_{\textrm{2}}}} \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\), which in this context is also the unit map of the \({\text {E} _\infty }\)-A-algebra \(A^{{{\text {tC} }_{\textrm{2}}}}\), determines an \({\text {E} _\infty }\)-ring spectrum with genuine involution \((A,A,\text {t} )\), and hence a symmetric monoidal refinement of the Poincaré structure
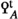 of Example 3.2.12.
of Example 3.2.12.
We now consider some examples where \({\mathcal {O}}\) is not the commutative \(\infty \)-operad, but instead the operad \(\text {MCom} \) whose algebras are pairs (A, M) of a commutative algebra and a module over it [47, Definition 3.3.3.8]. In particular, the data of an \({\mathcal {O}}\)-monoidal hermitian (resp. Poincaré) \(\infty \)-category consists of a pair  where
where  is a symmetric monoidal hermitian (resp. Poincaré) \(\infty \)-category and
is a symmetric monoidal hermitian (resp. Poincaré) \(\infty \)-category and  is a module over
is a module over  in \(\text {Cat} ^{\textrm{h}}_\infty \) (resp. \(\text {Cat} ^{\textrm{p}}_\infty \)). Consider the case where \({\mathcal {E}}\) is \({\mathcal {C}}\) considered as a module over itself, so that
in \(\text {Cat} ^{\textrm{h}}_\infty \) (resp. \(\text {Cat} ^{\textrm{p}}_\infty \)). Consider the case where \({\mathcal {E}}\) is \({\mathcal {C}}\) considered as a module over itself, so that  is a module over
is a module over  in \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^{\otimes }\). By Corollary 5.3.14 the data of such a
in \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})^{\otimes }\). By Corollary 5.3.14 the data of such a  -module corresponds to a choice of
-module corresponds to a choice of  -module \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\), a
-module \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\), a  -module \(\Lambda \in {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), and a
-module \(\Lambda \in {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), and a  -module map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\). For example, we may always take
-module map \(\alpha :\Lambda \rightarrow [\text {B} ^{\Delta }]^{{{\text {tC} }_{\textrm{2}}}}\). For example, we may always take  considered as a module over itself. In this case, if
considered as a module over itself. In this case, if  is a symmetric monoidal Poincaré \(\infty \)-category then all the structure maps in the \(\text {MCom} \)-algebra structure on
is a symmetric monoidal Poincaré \(\infty \)-category then all the structure maps in the \(\text {MCom} \)-algebra structure on  are Poincaré, since on the level of the underlying bilinear forms these maps come from the structure of
are Poincaré, since on the level of the underlying bilinear forms these maps come from the structure of  as a module over itself. Similarly, any commutative triangle
as a module over itself. Similarly, any commutative triangle

of  -modules in \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) induces a morphism
-modules in \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) induces a morphism  of
of  -module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
-module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
Example 5.4.11
Let  be a symmetric monoidal hermitian \(\infty \)-category with underlying bilinear part
be a symmetric monoidal hermitian \(\infty \)-category with underlying bilinear part  . Then the associated quadratic hermitian \(\infty \)-category
. Then the associated quadratic hermitian \(\infty \)-category  is canonically a module over
is canonically a module over  , and the natural hermitian functor
, and the natural hermitian functor

is a map of  -module objects in \(\text {Cat} ^{\textrm{h}}_\infty \). In addition, if
-module objects in \(\text {Cat} ^{\textrm{h}}_\infty \). In addition, if  is Poincaré then
is Poincaré then  is a module over
is a module over  in \(\text {Cat} ^{\textrm{p}}_\infty \) and the corresponding Poincaré functor (131) is a morphism of
in \(\text {Cat} ^{\textrm{p}}_\infty \) and the corresponding Poincaré functor (131) is a morphism of  -module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
-module objects in \(\text {Cat} ^{\textrm{p}}_\infty \).
When \({\mathcal {C}}= {\text {Mod}}^{\omega }_{A}\) for some \({\text {E} _\infty }\)-algebra A and  for some \({{\text {C} }_{\textrm{2}}}\)-action on A and some map of \({\text {E} _\infty }\)-A-algebras \(\alpha :C \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) then Corollary 5.4.8 tells us that the notion of a
for some \({{\text {C} }_{\textrm{2}}}\)-action on A and some map of \({\text {E} _\infty }\)-A-algebras \(\alpha :C \rightarrow A^{{{\text {tC} }_{\textrm{2}}}}\) then Corollary 5.4.8 tells us that the notion of a  -module in \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^\mathrm{{op}},{{\mathcal {S}}{p}})\) is equivalent to that of a C-module D equipped with a C-module map to \(A^{{{\text {tC} }_{\textrm{2}}}}\).
-module in \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^\mathrm{{op}},{{\mathcal {S}}{p}})\) is equivalent to that of a C-module D equipped with a C-module map to \(A^{{{\text {tC} }_{\textrm{2}}}}\).
Example 5.4.12
Let A be a connective \({\text {E} _\infty }\)-ring spectrum equipped with an involution. Then for every \(m \in {\mathbb {Z}}\) the truncated Poincaré structure  of Example 3.2.8 is canonically a module over the symmetric monoidal Poincaré \(\infty \)-category
of Example 3.2.8 is canonically a module over the symmetric monoidal Poincaré \(\infty \)-category  of Example 5.4.10ii). Indeed, this follows from the above since \(\tau _{\ge m}A^{{{\text {tC} }_{\textrm{2}}}}\) is canonically a module over the algebra \(\tau _{\ge 0}A^{{{\text {tC} }_{\textrm{2}}}}\) for every m. Similarly, the canonical Poincaré functor
of Example 5.4.10ii). Indeed, this follows from the above since \(\tau _{\ge m}A^{{{\text {tC} }_{\textrm{2}}}}\) is canonically a module over the algebra \(\tau _{\ge 0}A^{{{\text {tC} }_{\textrm{2}}}}\) for every m. Similarly, the canonical Poincaré functor

refines to a map of  -modules.
-modules.
Example 5.4.13
Let k be an \({\text {E} _\infty }\)-ring spectrum and A an \({\text {E} _1}\)-algebra over k. Then \({\text {Mod}}^{\omega }_{k}\) is a symmetric monoidal \(\infty \)-category which acts on \({\text {Mod}}^{\omega }_{A}\), giving an \(\text {MCom} ^{\otimes }\)-algebra object in \(\text {Cat} _\infty ^\text {ex} \). The fibre product \((\text {Cat} ^{\textrm{h}}_\infty )^{\otimes } \times _{(\text {Cat} _\infty ^\text {ex} )^{\otimes }} \text {MCom} ^{\otimes }\) then encodes the Day convolution symmetric monoidal structure on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{k})\) and an action of this structure on \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\). On the level of modules with genuine involution this is an action of \({\text {Mod}}_{\text {N} k}\) on \({\text {Mod}}_{\text {N} A}\), which can also be encoded via the action of \(\text {N} k\) on \(\text {N} A\) in \({{\text {C} }_{\textrm{2}}}\)-spectra. By Example 5.4.10iii) the Tate Poincaré structure  is a commutative algebra object in \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{k}) \simeq {\text {Mod}}_{\text {N} k}\) corresponding to the Tate Frobenius triple \(k^{\text {Fr} } := (k,k,k \rightarrow k^{{{\text {tC} }_{\textrm{2}}}})\) encoding a commutative algebra object in modules with genuine involution over k, or, equivalently, a commutative \(\text {N} k\)-algebra object in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. We may then identify the k-linear norm \(\text {N} _k A\) of A (see Remark 3.2.4 and Remark 3.3.2) with the tensor product \(\text {N} A \otimes _{\text {N} k} k^{\text {Fr} }\), and deduce that \(\text {N} _k A\)-modules in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra correspond to \(k^{\text {Fr} }\)-modules in \(\text {N} A\)-modules, and hence to
is a commutative algebra object in \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{k}) \simeq {\text {Mod}}_{\text {N} k}\) corresponding to the Tate Frobenius triple \(k^{\text {Fr} } := (k,k,k \rightarrow k^{{{\text {tC} }_{\textrm{2}}}})\) encoding a commutative algebra object in modules with genuine involution over k, or, equivalently, a commutative \(\text {N} k\)-algebra object in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. We may then identify the k-linear norm \(\text {N} _k A\) of A (see Remark 3.2.4 and Remark 3.3.2) with the tensor product \(\text {N} A \otimes _{\text {N} k} k^{\text {Fr} }\), and deduce that \(\text {N} _k A\)-modules in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra correspond to \(k^{\text {Fr} }\)-modules in \(\text {N} A\)-modules, and hence to  -module objects in \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\). In summary, the hermitian structures on \({\text {Mod}}^{\omega }_{A}\) associated to k-modules with genuine involution as in Sect. 3.2 (with base \({\text {E} _\infty }\)-ring k) are exactly hermitian structures on \({\text {Mod}}^{\omega }_{A}\) which are
-module objects in \({\text {Fun}}^{\textrm{q}}({\text {Mod}}^{\omega }_{A})\). In summary, the hermitian structures on \({\text {Mod}}^{\omega }_{A}\) associated to k-modules with genuine involution as in Sect. 3.2 (with base \({\text {E} _\infty }\)-ring k) are exactly hermitian structures on \({\text {Mod}}^{\omega }_{A}\) which are  -modules, and so such k-modules with genuine involution classify refinements of \({\text {Mod}}^{\omega }_{A}\) to
-modules, and so such k-modules with genuine involution classify refinements of \({\text {Mod}}^{\omega }_{A}\) to  -module objects in \(\text {Cat} ^{\textrm{h}}_\infty \).
-module objects in \(\text {Cat} ^{\textrm{h}}_\infty \).
7 The category of Poincaré categories
In the present section we study the global structural properties of the \(\infty \)-categories \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \). We begin in Sect. 6.1 by showing that \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) have all limits and colimits, and that those are preserved by the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \hookrightarrow \text {Cat} ^{\textrm{h}}_\infty \) and by the forgetful functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \). In Sect. 6.2 we prove that the symmetric monoidal structures on \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) constructed in Sect. 5.2 are closed, that is, they are equipped with a compatible notion of internal mapping objects, which we refer to as internal functor categories. This implies, in particular, that these monoidal structures preserve colimits in each variable separately. We then show in Sects. 6.3 and 6.4 that \(\text {Cat} ^{\textrm{h}}_\infty \) is tensored and cotensored over \(\text {Cat} _\infty \) in a manner compatible with its closed symmetric monoidal structure. Taken together, these properties imply that \(\text {Cat} ^{\textrm{h}}_\infty \) (just like \(\text {Cat} _\infty \)) can be viewed as an \((\infty ,2)\)-category, that is furthermore enriched over itself. Though this point of view does not directly extend to \(\text {Cat} ^{\textrm{p}}_\infty \), in some special cases, such as poset of faces of finite simplicial complexes, the tensor and cotensor constructions do preserve Poincaré \(\infty \)-categories. We prove this in the final Sect. 6.6, after dedicating Sect. 6.5 to the role played by imposing certain finiteness conditions on the (co)tensoring \(\infty \)-category.
In addition to its conceptual aspect, we will also make concrete use of the material of this section in a variety of contexts, including Sect. 7.3 in the present paper, and later in Paper [2], notably via the \({\text {Q}}\)-construction which is used in the definition of the Grothendieck-Witt spectrum, and the dual \({\text {Q}}\)-construction which is used in establishing its universal property.
7.1 Limits and colimits
In this section we prove that \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \) have all small limits and colimits and that the functors \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) preserve these limits and colimits. Since the former is conservative it follows automatically that it also detects limits and colimits. We then verify a few (co)limit-related results which will be useful later on, including the semi-additivity of \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \), and the fact that the functors \(\text {Pn} \) and \(\text {Fm} \) preserve filtered colimits.
We begin by recording the following statement, to which we could not find a reference in this form:
Proposition 6.1.1
The \(\infty \)-category \(\text {Cat} _\infty ^\text {ex} \) admits all small limits and colimits. Limits and filtered colimits are preserved by the inclusion \(\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} _\infty \).
Proof
The statement for limits is [47, Theorem 1.1.4.4] and for filtered colimits is given by [47, Proposition 1.1.4.6]. For general colimits we consider the fully-faithful embedding of \(\text {Cat} _\infty ^\text {ex} \) inside the \(\infty \)-category \(\text {Cat} _\infty ^\text {rex} \) of \(\infty \)-categories with finite colimits and right exact functors between them. The latter admits small colimits by [43, Lemma 6.3.4.4]. On the other hand, the embedding \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty ^\text {rex} \) admits a left adjoint given by tensoring with \({{\mathcal {S}}{p}}^{\text {f} }\), see Construction 5.1.1. It then follows that \(\text {Cat} _\infty ^\text {ex} \) has small colimits obtained by forming colimits in \(\text {Cat} _\infty ^\text {rex} \) and then tensoring with \({{\mathcal {S}}{p}}^{\text {f} }\). \(\square \)
Proposition 6.1.2
The \(\infty \)-category \(\text {Cat} ^{\textrm{h}}_\infty \) admits all small limits and colimits, and these are preserved by the forgetful functor \(\pi :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \).
Proof
By construction the forgetful functor \(\pi :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is a cartesian fibration classified by the functor \({\mathcal {C}}\mapsto {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\). By Corollary 1.4.2 we have that \(\pi \) is also a cocartesian fibration and by Remark 1.1.15 the fibres \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) of \(\pi \) admits small limits and colimits. Given an exact functor \(f:{\mathcal {C}}\rightarrow {\mathcal {D}}\) the associated cartesian transition functor \(f^*:{\text {Fun}}^{\textrm{q}}({\mathcal {D}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) preserves limits and the cocartesian transition functor \(f_!:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {D}})\) preserves colimits (indeed \(f_!\) is left adjoint to \(f^*\)). Now the base \(\text {Cat} _\infty ^\text {ex} \) of this bicartesian fibration admits small limits and colimits by Proposition 6.1.1. It then follows from [43, 4.3.1.11] and [43, 4.3.1.5.(2)] that \(\text {Cat} ^{\textrm{h}}_\infty \) admits all small limits and colimits and that these are preserved by \(\pi \). \(\square \)
Remark 6.1.3
To make the content (and proof) of Proposition 6.1.2 more explicit, let K be a simplicial set and \(p:K \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) a diagram. Then the limit of p is computed as follows: one first extends the diagram \(q := \pi p:K \rightarrow \text {Cat} _\infty ^\text {ex} \) of stable \(\infty \)-categories to a limit diagram \(\overline{q}:K^{\triangleleft } \rightarrow \text {Cat} _\infty ^\text {ex} \). Let \({\mathcal {C}}_{\infty } = \overline{q}(\infty )\) be the image of the cone point (which we denote by the symbol \(\infty \)), so that \(\overline{q}\) exhibits \({\mathcal {C}}_{\infty }\) as the limit of q in \(\text {Cat} _\infty ^\text {ex} \). Interpreting \(\overline{q}\) as a natural transformation with target \(q:K \rightarrow \text {Cat} _\infty ^\text {ex} \) and domain the constant diagram \(K \rightarrow \text {Cat} _\infty ^\text {ex} \) with value \({\mathcal {C}}_{\infty }\), we may lift it to a pointwise \(\pi \)-cartesian natural transformation with target p and domain some diagram \(p_{\infty }:K \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) which is concentrated in the fibre of \({\mathcal {C}}_{\infty }\). In other words, \(p_{\infty }\) encodes a diagram \(p_{\infty }:K \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\). The hermitian \(\infty \)-category \(({\mathcal {C}}_{\infty },\lim _{K} p_{\infty })\) is then the limit of the original diagram p. Somewhat informally, though more explicitly, we may describe the diagram \(p_{\infty }\) via the formula  , where
, where  is the hermitian \(\infty \)-category associated to k by the diagram p and \(r_k:{\mathcal {C}}_{\infty } \rightarrow {\mathcal {C}}_k\) is the exact functor associated to the map \(\infty \rightarrow k\) in \(K^{\triangleleft }\) by the limit diagram \(\overline{p}\). Since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\) is closed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\) under limits the limit of \(p_{\infty }\) can also be computed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\), that is, object-wise. Similarly, in order to compute the colimit of p we first extend \(q=\pi p\) to a colimit diagram \(\overline{q}:K^{\triangleright } \rightarrow \text {Cat} _\infty ^\text {ex} \). Let \({\mathcal {C}}_{\infty } = \overline{q}(\infty )\) be the image of the cone point, and \(i_k:{\mathcal {C}}_k \rightarrow {\mathcal {C}}_{\infty }\) the exact functor associated to the arrow \(k \rightarrow \infty \) in \(K^{\triangleright }\). Then as above we can “push” the diagram p to the fibre over \({\mathcal {C}}_{\infty }\), yielding a diagram \(p_{\infty }:K \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\) given by the formula
is the hermitian \(\infty \)-category associated to k by the diagram p and \(r_k:{\mathcal {C}}_{\infty } \rightarrow {\mathcal {C}}_k\) is the exact functor associated to the map \(\infty \rightarrow k\) in \(K^{\triangleleft }\) by the limit diagram \(\overline{p}\). Since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\) is closed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\) under limits the limit of \(p_{\infty }\) can also be computed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\), that is, object-wise. Similarly, in order to compute the colimit of p we first extend \(q=\pi p\) to a colimit diagram \(\overline{q}:K^{\triangleright } \rightarrow \text {Cat} _\infty ^\text {ex} \). Let \({\mathcal {C}}_{\infty } = \overline{q}(\infty )\) be the image of the cone point, and \(i_k:{\mathcal {C}}_k \rightarrow {\mathcal {C}}_{\infty }\) the exact functor associated to the arrow \(k \rightarrow \infty \) in \(K^{\triangleright }\). Then as above we can “push” the diagram p to the fibre over \({\mathcal {C}}_{\infty }\), yielding a diagram \(p_{\infty }:K \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\) given by the formula  . The colimit of p in \(\text {Cat} ^{\textrm{h}}_\infty \) is then given by
. The colimit of p in \(\text {Cat} ^{\textrm{h}}_\infty \) is then given by

where the colimit of \(p_{\infty }\) is computed in \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\). This last colimit can also be computed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\) since \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{\infty })\) is closed in \({\text {Fun}}({\mathcal {C}}_{\infty }^{\text {op} },{{\mathcal {S}}{p}})\) under colimits (see Remark 1.1.15).
Proposition 6.1.4
The \(\infty \)-category \(\text {Cat} ^{\textrm{p}}_\infty \) has small limits and colimits and the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) preserves small limits and colimits.
The proof of Proposition 6.1.4 will require the following lemma.
Lemma 6.1.5
Let \(\overline{p}:K^\triangleright \rightarrow \text {Cat} _\infty ^\text {ex} \) be a colimit diagram of stable \(\infty \)-categories and let \(f:{\mathcal {C}}_\infty := \overline{p}(\infty )\rightarrow {\mathcal {D}}\) be an exact functor to a cocomplete stable \(\infty \)-category. Then the canonical map
is an equivalence, where \(i_k:{\mathcal {C}}_k := \overline{p}(k)\rightarrow {\mathcal {C}}_\infty \) is the map associated to \(k \rightarrow \infty \) by \(\overline{p}\).
Proof
For any diagram \(\overline{p}:K^\triangleright \rightarrow \text {Cat} _\infty ^\text {ex} \), the functor
sending f to \(\{f\circ i_k\}_{k\in K}\) has a left adjoint given by
Indeed, this follows for example by the general formula of [33, Theorem B]. Our claim is then equivalent to the statement that the counit
is an equivalence if \(\overline{p}\) is a colimit diagram. But \({\text {Fun}}^{\textrm{ex}}(-,{\mathcal {D}}):(\text {Cat} _\infty ^\text {ex} )^{\text {op} }\rightarrow \text {Cat} _\infty ^\text {ex} \) is a right adjoint (in fact, its own right adjoint) and so it preserves all limits. Hence \(i^*\) is an equivalence of \(\infty \)-categories and in particular the counit is an equivalence of exact functors. \(\square \)
Proof of 6.1.4
We begin with the case of colimits. Let \(p: K \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) be a diagram. By Proposition 6.1.2 we may find a colimit diagram \(\overline{p}:K^\triangleright \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) in \(\text {Cat} ^{\textrm{h}}_\infty \) extending (the image of) p. We will show that the image of \(\overline{p}\) is contained in \(\text {Cat} ^{\textrm{p}}_\infty \) and forms a colimit diagram there. Let  be the image of the cone point and for \(k \in K\) let
be the image of the cone point and for \(k \in K\) let  be the hermitian functor associated to the map \(k \rightarrow \infty \) in \(K^{\triangleright }\) by \(\overline{p}\). In particular, the collection of natural transformations
be the hermitian functor associated to the map \(k \rightarrow \infty \) in \(K^{\triangleright }\) by \(\overline{p}\). In particular, the collection of natural transformations  exhibits
exhibits  as the colimit of the diagram
as the colimit of the diagram  . Our argument proceeds in two steps:
. Our argument proceeds in two steps:
Step 1. The hermitian \(\infty \)-category  is Poincaré, and all the hermitian functors
is Poincaré, and all the hermitian functors  are Poincaré.
are Poincaré.
Let \(\text {D} _k:{\mathcal {C}}_k^{\text {op} }\rightarrow {\mathcal {C}}_k\) be the duality associated to  . Let \(q := \pi p:K \rightarrow \text {Cat} _\infty ^\text {ex} \) be the underlying diagram of stable \(\infty \)-categories and let us denote by \(q_{\text {op}}:K \rightarrow \text {Cat} _\infty ^\text {ex} \) the composite of q and the equivalence \((-)^{\text {op} }:\text {Cat} _\infty ^\text {ex} \xrightarrow {\simeq } \text {Cat} _\infty ^\text {ex} \). Since the diagram p takes values in Poincaré \(\infty \)-categories and duality preserving functors the functors \(\text {D} _k\) form the components of a natural transformation \(q_{\text {op}} \Rightarrow q\), which consequently induce a functor
. Let \(q := \pi p:K \rightarrow \text {Cat} _\infty ^\text {ex} \) be the underlying diagram of stable \(\infty \)-categories and let us denote by \(q_{\text {op}}:K \rightarrow \text {Cat} _\infty ^\text {ex} \) the composite of q and the equivalence \((-)^{\text {op} }:\text {Cat} _\infty ^\text {ex} \xrightarrow {\simeq } \text {Cat} _\infty ^\text {ex} \). Since the diagram p takes values in Poincaré \(\infty \)-categories and duality preserving functors the functors \(\text {D} _k\) form the components of a natural transformation \(q_{\text {op}} \Rightarrow q\), which consequently induce a functor
where we note that \((-)^{\text {op} }:\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} _\infty ^\text {ex} \) preserves colimits since it is an equivalence. We claim that \(\text {D} _{\infty }\) represents the bilinear part of  . Indeed, since bilinear parts commute with left Kan extensions (Lemma 1.4.3) and colimits (by Lemma 1.1.7) the bilinear part of
. Indeed, since bilinear parts commute with left Kan extensions (Lemma 1.4.3) and colimits (by Lemma 1.1.7) the bilinear part of  is given by
is given by

where the last equivalence is by Lemma 6.1.5. We have thus established that the hermitian \(\infty \)-category  is non-degenerate and all the hermitian functors
is non-degenerate and all the hermitian functors  are duality preserving. To finish the proof it will hence suffice to show that
are duality preserving. To finish the proof it will hence suffice to show that  is perfect. But this follows from Remark 1.2.9 since \(\text {D} _{\infty }\) is an equivalence, being the functor induced on limits by a natural equivalence of diagrams \(q_{\text {op}} \Rightarrow q\).
is perfect. But this follows from Remark 1.2.9 since \(\text {D} _{\infty }\) is an equivalence, being the functor induced on limits by a natural equivalence of diagrams \(q_{\text {op}} \Rightarrow q\).
Step 2. If \(({\mathcal {D}},\Phi )\) is a Poincaré \(\infty \)-category then a hermitian functor  is Poincaré if and only if \((f\circ i_k,i_k^*\eta )\) is Poincaré for every \(k\in K\).
is Poincaré if and only if \((f\circ i_k,i_k^*\eta )\) is Poincaré for every \(k\in K\).
The hermitian functor \((f,\eta )\) is a Poincaré functor if and only if the associated natural transformation
is an equivalence. Since \({\mathcal {C}}_{\infty }\) is the colimit of p in \(\text {Cat} _\infty ^\text {ex} \) the natural transformation (132) is an equivalence if and only if the natural transformation
is an equivalence for all \(k\in K\). But, since the \(i_k\) are all Poincaré functors, there is a commutative diagram

Thus, (132) is an equivalence if and only if \((f\circ i_k,i_k^*\eta )\) is a Poincaré functor for all \(k\in K\).
The case of limits is similar and slightly easier. Indeed, as above, the natural equivalence of diagrams \(q_{\text {op}} \Rightarrow q\) induced by the collection of dualities \(\text {D} _k\) induces an equivalence
This time, showing that \(\text {D} _\infty \) represents the bilinear form of  (where \(r_k:{\mathcal {C}}_{\infty } \rightarrow {\mathcal {C}}_k\) are the canonical maps) is even simpler. Indeed, since taking bilinear forms commutes with restriction (Remark 1.1.6), and limits (by Lemma 1.1.7), the bilinear part of
(where \(r_k:{\mathcal {C}}_{\infty } \rightarrow {\mathcal {C}}_k\) are the canonical maps) is even simpler. Indeed, since taking bilinear forms commutes with restriction (Remark 1.1.6), and limits (by Lemma 1.1.7), the bilinear part of  is given by
is given by

and this concludes the proof of Step 1 in the case of limits. The proof of Step 2 is completely dual to that of colimits. \(\square \)
Remark 6.1.6
By Proposition 6.1.4 the \(\infty \)-category \(\text {Cat} ^{\textrm{p}}_\infty \) has small limits and colimits, and those are preserved by the inclusion in \(\text {Cat} ^{\textrm{h}}_\infty \), which itself also has small limits and colimits. Since the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) is conservative, it also detects limits and colimits. One then says that limits and colimits in \(\text {Cat} ^{\textrm{p}}_\infty \) are computed in \(\text {Cat} ^{\textrm{h}}_\infty \).
Proposition 6.1.7
The \(\infty \)-categories \(\text {Cat} _\infty ^\text {ex} \), \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \) are all semi-additive, i.e. finite products and coproducts agree.
Proof
For \(\text {Cat} _\infty ^\text {ex} \), as in the proof of Proposition 6.1.1 we can embed \(\text {Cat} _\infty ^\text {ex} \) as a reflective full subcategory of \(\text {Cat} _\infty ^\text {rex} \). It will then suffice to verify that \(\text {Cat} _\infty ^\text {rex} \) is semi-additive, which in turn follows from [43, Lemma 7.3.3.4]. In particular, the coproduct of \({\mathcal {C}}\) and \({{{\mathcal {C}}}'}\) in \(\text {Cat} _\infty ^\text {ex} \) is given by the product \({\mathcal {C}}\times {{{\mathcal {C}}}'}\), and exhibited by the two inclusions

Turning to the other two cases, we first observe that since limits and colimits in \(\text {Cat} ^{\textrm{p}}_\infty \) are computed in \(\text {Cat} ^{\textrm{h}}_\infty \) (Remark 6.1.6) it is in fact sufficient to show that \(\text {Cat} ^{\textrm{h}}_\infty \) is semi-additive. We first observe that \(\text {Cat} ^{\textrm{h}}_\infty \) is pointed. Indeed, the hermitian \(\infty \)-category \((\{0\},0)\), whose underlying stable \(\infty \)-category consists of a single object 0, equipped with the hermitian structure which sends 0 to the zero spectrum, is both initial and final in \(\text {Cat} ^{\textrm{h}}_\infty \).
Now let  and
and  be two hermitian \(\infty \)-categories. By the explicit description of Remark 6.1.3 we have that the coproduct of
be two hermitian \(\infty \)-categories. By the explicit description of Remark 6.1.3 we have that the coproduct of  and
and  in \(\text {Cat} ^{\textrm{h}}_\infty \) is given by
in \(\text {Cat} ^{\textrm{h}}_\infty \) is given by  , while the product is given by
, while the product is given by  , where \(p,p'\) are the projections on \({\mathcal {C}}\) and \({{{\mathcal {C}}}'}\), respectively. It will hence suffice to show that the canonical natural transformation
, where \(p,p'\) are the projections on \({\mathcal {C}}\) and \({{{\mathcal {C}}}'}\), respectively. It will hence suffice to show that the canonical natural transformation

is an equivalence. But, since i is also right adjoint to p and \(i'\) is right adjoint to \(p'\) we have natural equivalences

under which the canonical map (133) becomes the identity, since \(p \circ i\) and \(p' \circ i'\) are the respective identities while \(p \circ i'\) and \(p' \circ i\) are the zero functors. \(\square \)
The following result will be useful for us in Paper [4] for proving that \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) are compactly generated presentable \(\infty \)-categories:
Proposition 6.1.8
The functors \(\text {Fm} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\mathcal {S}}\) and \(\text {Pn} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\mathcal {S}}\) commute with filtered colimits. In particular, the object  which corepresents these functors (Proposition 4.1.3) is compact in both \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \).
which corepresents these functors (Proposition 4.1.3) is compact in both \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \).
Proof
Let us first prove the statement for \(\text {Fm} \). Let \({\mathcal {E}}\rightarrow \text {Cat} _\infty \) be the presentable fibration classified by the functor \(\text {Cat} _\infty \rightarrow \text {CAT} _\infty \) sending \({\mathcal {C}}\) to \({\text {Psh}}({\mathcal {C}})\), so the objects of \({\mathcal {E}}\) are given by a pair \(({\mathcal {C}},S)\) where \(S:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {S}}\) is a presheaf, and morphisms are pairs \((f,\eta )\) where \(f:{\mathcal {C}}\rightarrow {\mathcal {C}}'\) is a functor and \(\eta :S\rightarrow f^*S'\) is a natural transformation. There is a functor \(\Phi :\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\mathcal {E}}\) lying above the inclusion \(\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} _\infty \) sending  to
to  . Then we can factor \(\text {Fm} (-)\) as
. Then we can factor \(\text {Fm} (-)\) as
where the second functor is the functor corepresented by the final object \(*:=(\Delta ^0,*:\Delta ^0\rightarrow {\mathcal {S}})\) in \({\mathcal {E}}\). Note that \(\Phi \) is a morphism of cocartesian fibrations by Proposition 1.4.3 and that it preserves filtered colimits fibrewise. Moreover it lies above the inclusion \(\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} _\infty \), which preserves filtered colimits by [47, Proposition 1.1.4.6]. Hence the functor \(\Phi \) preserves filtered colimits. It will hence suffice to show that \(*\) is compact in \({\mathcal {E}}\). Now by the naturality of the straightening-unstraightening equivalence as recorded in [23, Corollary A.31], the unstraightening procedure determines an equivalence \({\mathcal {E}}\simeq {\text {RFib}}\), where \({\text {RFib}}\subseteq {\text {Ar}}(\text {Cat} _\infty )\) is the full subcategory spanned by the right fibrations. It will hence suffice to show that the final object in \({\text {RFib}}\) is compact. This object corresponds to the identity right fibration \(\Delta ^0 \rightarrow \Delta ^0\), which is compact when considered as an object of \({\text {Ar}}(\text {Cat} _\infty )\) since \(\Delta ^0\) is compact in \(\text {Cat} _\infty \). It will hence suffice to show that the inclusion \({\text {RFib}}\subseteq {\text {Ar}}(\text {Cat} _\infty )\) is closed under filtered colimits. Indeed, the condition of being a right fibration can be phrased as being local with respect to the maps in \({\text {Ar}}(\text {Cat} _\infty )\) encoded by the squares of the form

with \(0 < i \le n\). This is an arrow between two compact objects of \({\text {Ar}}(\text {Cat} _\infty )\) and hence the locality condition it defines is closed under filtered colimits.
Now we want to prove the statement for \(\text {Pn} \). We know that the functors \(\text {Cat} _\infty ^\text {ex} \rightarrow {\mathcal {S}}\) sending \({\mathcal {C}}\) to \(\iota {\mathcal {C}}\) and \({\mathcal {C}}\mapsto \iota {\text {TwAr}}({\mathcal {C}}) \simeq \iota {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) commute with filtered colimits since \(\Delta ^0\) and \(\Delta ^1\) are compact in \(\text {Cat} _\infty \) and the inclusion \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty \) preserves filtered colimits by [47, Proposition 1.1.4.6]. We then consider the cartesian square (see (44))

where we identify \({\text {TwAr}}(\iota {\mathcal {C}})\) with the subspace of \(\iota {\text {TwAr}}({\mathcal {C}})\) spanned by those arrows that are equivalences in \({\mathcal {C}}\). Since all the corners of the square except \(\text {Pn} \) preserve filtered colimits in \(\text {Cat} ^{\textrm{h}}_\infty \) (and so in \(\text {Cat} ^{\textrm{p}}_\infty \)), so does \(\text {Pn} \). \(\square \)
We finish this subsection by describing an example of a colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) arising from visible Poincaré structures on parametrised spectra. Recall from Sect. 4.4 that given a space X and a spherical fibration \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\), one may endow the \(\infty \)-category \({{\mathcal {S}}{p}}^{\text {f} }_X\) of finitely presented parametrised spectra over X with the \(\xi \)-twisted visible Poincaré structure  , whose \({\text {L}}\)-groups are the associated visible \({\text {L}}\)-groups studied in [73] (see Corollary 4.4.14). We now show that this construction actually produces the colimit of a suitable diagram of Poincaré \(\infty \)-categories. Note first that, as inspecting the definitions reveals, for every \(x \in X\) the Poincaré structure
, whose \({\text {L}}\)-groups are the associated visible \({\text {L}}\)-groups studied in [73] (see Corollary 4.4.14). We now show that this construction actually produces the colimit of a suitable diagram of Poincaré \(\infty \)-categories. Note first that, as inspecting the definitions reveals, for every \(x \in X\) the Poincaré structure  on \({{\mathcal {S}}{p}}^{\text {f} }_{\{x\}} = {{\mathcal {S}}{p}}^{\text {f} }\) identifies with the tensor
on \({{\mathcal {S}}{p}}^{\text {f} }_{\{x\}} = {{\mathcal {S}}{p}}^{\text {f} }\) identifies with the tensor  , defined using the action of \({{\mathcal {S}}{p}}^{\text {f} }\) on \({\text {Fun}}^{\textrm{q}}({{\mathcal {S}}{p}}^{\text {f} })\) canonically determined by the stability of the latter. We may then consider the composite diagram
, defined using the action of \({{\mathcal {S}}{p}}^{\text {f} }\) on \({\text {Fun}}^{\textrm{q}}({{\mathcal {S}}{p}}^{\text {f} })\) canonically determined by the stability of the latter. We may then consider the composite diagram

where the last arrow places the fibre of the cartesian fibration \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) over \({{\mathcal {S}}{p}}^{\text {f} }\in \text {Cat} _\infty ^\text {ex} \). This diagram can then be viewed as a diagram in \(\text {Cat} ^{\textrm{p}}_\infty \): indeed, each  is Poincaré by Corollary 4.4.3 and all the hermitian functors involved are equivalences in \(\text {Cat} ^{\textrm{h}}_\infty \) and hence in particular duality preserving.
is Poincaré by Corollary 4.4.3 and all the hermitian functors involved are equivalences in \(\text {Cat} ^{\textrm{h}}_\infty \) and hence in particular duality preserving.
Proposition 6.1.9
Let X be a space equipped with a spherical fibration \(\xi :X \rightarrow {\text {Pic}}({\mathbb {S}})\). Then the collection of Poincaré functors

associated by Remark 4.4.6 to the various point inclusions \(\{x\} \hookrightarrow X\), exhibits  as the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram
as the colimit in \(\text {Cat} ^{\textrm{p}}_\infty \) of the diagram

constructed in (134).
Remark 6.1.10
In the situation of Proposition 6.1.9, if \(\xi = {\mathbb {S}}_X\) is the constant spherical fibration with value \({\mathbb {S}}\) then the composed diagram (134) is constant with value  , and we may view the statement of the proposition as identifying
, and we may view the statement of the proposition as identifying  with the tensor of the Poincaré \(\infty \)-category
with the tensor of the Poincaré \(\infty \)-category  and the space X. We will discuss such tensors from a more general perspective in Sect. 6.4 below.
and the space X. We will discuss such tensors from a more general perspective in Sect. 6.4 below.
Proof of Proposition 6.1.9
By Proposition 6.1.4 it will suffice to check that the underlying hermitian functors exhibit  as the colimit in \(\text {Cat} ^{\textrm{h}}_\infty \) of the diagram in question. By the explicit description of colimits in \(\text {Cat} ^{\textrm{h}}_\infty \) given in Remark 6.1.3 and the fact that we have already established this colimit property on the level of quadratic functors in Proposition 4.4.7 (see Remark 4.4.8), all that is left is to check that the collection of exact functors \(\lambda _x:{{\mathcal {S}}{p}}^{\text {f} }\rightarrow {{\mathcal {S}}{p}}^{\text {f} }_X\) exhibit \({{\mathcal {S}}{p}}^{\text {f} }_X\) as the colimit in \(\text {Cat} _\infty ^\text {ex} \) of the constant X-indexed diagram with value \({{\mathcal {S}}{p}}^{\text {f} }\). We now note that the equivalence \((-)^{\text {op} }:\text {Cat} _\infty \xrightarrow {\simeq } \text {Cat} _\infty \) preserves stable \(\infty \)-categories and exact functors, and hence restricts to an equivalence \((-)^{\text {op} }:\text {Cat} _\infty ^\text {ex} \xrightarrow {\simeq } \text {Cat} _\infty ^\text {ex} \). We may hence show instead that the diagram in question becomes a colimit diagram after applying \((-)^{\text {op} }\). We now observe that
as the colimit in \(\text {Cat} ^{\textrm{h}}_\infty \) of the diagram in question. By the explicit description of colimits in \(\text {Cat} ^{\textrm{h}}_\infty \) given in Remark 6.1.3 and the fact that we have already established this colimit property on the level of quadratic functors in Proposition 4.4.7 (see Remark 4.4.8), all that is left is to check that the collection of exact functors \(\lambda _x:{{\mathcal {S}}{p}}^{\text {f} }\rightarrow {{\mathcal {S}}{p}}^{\text {f} }_X\) exhibit \({{\mathcal {S}}{p}}^{\text {f} }_X\) as the colimit in \(\text {Cat} _\infty ^\text {ex} \) of the constant X-indexed diagram with value \({{\mathcal {S}}{p}}^{\text {f} }\). We now note that the equivalence \((-)^{\text {op} }:\text {Cat} _\infty \xrightarrow {\simeq } \text {Cat} _\infty \) preserves stable \(\infty \)-categories and exact functors, and hence restricts to an equivalence \((-)^{\text {op} }:\text {Cat} _\infty ^\text {ex} \xrightarrow {\simeq } \text {Cat} _\infty ^\text {ex} \). We may hence show instead that the diagram in question becomes a colimit diagram after applying \((-)^{\text {op} }\). We now observe that
and consequently
Under the last equivalence, the full subcategory \(({{\mathcal {S}}{p}}^{\text {f} }_X)^{\text {op} }\) of finitely presented parametrised spectra corresponds to the full subcategory \((({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} })_X \subseteq {\text {Fun}}(X^{\text {op} }, {\text {Pro}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }))\) generated under finite limits by the functors \(X^{\text {op} }\rightarrow {\text {Pro}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} })\) right Kan extended along point inclusions \(\{x\} \subseteq X^{\text {op} }\) from functors \(\{x\} \rightarrow {\text {Pro}}(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} })\) with value in \(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\). The desired result now follows from the fact that the functor
exhibits \((({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} })_X\) as the tensor of \(({{\mathcal {S}}{p}}^{\text {f} })^{\text {op} }\) over X in \(\text {Cat} _\infty ^\text {ex} \), see Remark 6.4.2 below. \(\square \)
7.2 Internal functor categories
In the present section we will show that the symmetric monoidal structures on \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \) constructed in Sect. 5.2 are closed. In particular, for two hermitian \(\infty \)-categories  and
and  , we will promote the stable \(\infty \)-category \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\) of exact functors from \({\mathcal {C}}\) to \({{{\mathcal {C}}}'}\) to a hermitian \(\infty \)-category
, we will promote the stable \(\infty \)-category \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\) of exact functors from \({\mathcal {C}}\) to \({{{\mathcal {C}}}'}\) to a hermitian \(\infty \)-category  , characterized by a natural equivalence
, characterized by a natural equivalence

for  . Furthermore, if
. Furthermore, if  and
and  are Poincaré \(\infty \)-categories, then the hermitian \(\infty \)-category
are Poincaré \(\infty \)-categories, then the hermitian \(\infty \)-category  is Poincaré as well and satisfies
is Poincaré as well and satisfies

The internal functor category  enjoys the following useful property: its hermitian objects correspond exactly to the hermitian functors
enjoys the following useful property: its hermitian objects correspond exactly to the hermitian functors  , and when
, and when  and
and  are Poincaré the Poincaré objects in
are Poincaré the Poincaré objects in  correspond to Poincaré functors
correspond to Poincaré functors  . In particular, this allows one to view the notions of hermitian functors and hermitian objects in a unified setting, and describe the relation between hermitian and Poincaré functors in terms of that which holds between hermitian and Poincaré objects.
. In particular, this allows one to view the notions of hermitian functors and hermitian objects in a unified setting, and describe the relation between hermitian and Poincaré functors in terms of that which holds between hermitian and Poincaré objects.
Definition 6.2.1
Let  and
and  be two hermitian \(\infty \)-categories. We set
be two hermitian \(\infty \)-categories. We set

where \({\text {nat}}\) denotes the spectrum of natural transformations between two spectrum valued functors.
Proposition 6.2.2
The functor  is quadratic. Its bilinear part is given by
is quadratic. Its bilinear part is given by

and its linear part makes the diagram

cartesian, where the left bottom equivalence is by the adjunction of Lemma 1.1.7. Here, as in Sect. 1.1, for a bilinear form \(\text {B} \) we denote by \(\text {B} ^{\Delta } = \Delta ^*\text {B} \) its pre-composition with the diagonal. If both  and
and  are non-degenerate, so is
are non-degenerate, so is  with duality given by
with duality given by

Finally, if both  and
and  are perfect, then so is
are perfect, then so is  .
.
Proof
We begin by computing the cross effect of  . It is given by
. It is given by

where the last equivalence is by the adjunction of Lemma 1.1.7. In particular, the cross effect of  is bilinear. Taking \(f=g\) we similarly get that
is bilinear. Taking \(f=g\) we similarly get that

and hence

Since  is exact by Proposition 1.1.13 it then follows that (136) is exact in f, and hence by the same proposition we have that
is exact by Proposition 1.1.13 it then follows that (136) is exact in f, and hence by the same proposition we have that  is quadratic.
is quadratic.
We now compute the linear part of  . Applying
. Applying  to the classifying square of
to the classifying square of  and using the equivalence (135) and the equivalence
and using the equivalence (135) and the equivalence  given by Lemma 1.1.24 we obtain an exact square
given by Lemma 1.1.24 we obtain an exact square

in which the terms on the left hand side are quadratic in f and the terms on the right hand side are exact in f. The desired formula for  is now obtained by taking linear parts.
is now obtained by taking linear parts.
Now suppose that  and
and  are non-degenerate. Applying Lemma 1.2.4 and the adjunction between
are non-degenerate. Applying Lemma 1.2.4 and the adjunction between  and
and  we obtain natural equivalences
we obtain natural equivalences

which shows that  is non-degenerate with duality
is non-degenerate with duality  . If
. If  and
and  are in addition perfect then the dualities
are in addition perfect then the dualities  and
and  are equivalences and hence so is
are equivalences and hence so is  by the above formula. The hermitian structure
by the above formula. The hermitian structure  is then also perfect, as desired. \(\square \)
is then also perfect, as desired. \(\square \)
Definition 6.2.3
For hermitian \(\infty \)-categories  we will denote by
we will denote by

the hermitian \(\infty \)-category given by Proposition 6.2.2. We will refer to  as the internal functor category from
as the internal functor category from  to
to  .
.
Remark 6.2.4
If  and
and  are Poincaré then
are Poincaré then  is Poincaré. This follows from the last part of Proposition 6.2.2.
is Poincaré. This follows from the last part of Proposition 6.2.2.
Example 6.2.5
Let  be a hermitian \(\infty \)-category. Then under the natural equivalence \({\text {Fun}}^{\textrm{ex}}({{\mathcal {S}}{p}}^{\text {f} },{\mathcal {C}})\simeq {\mathcal {C}}\) given by evaluation at the sphere spectrum, the functor
be a hermitian \(\infty \)-category. Then under the natural equivalence \({\text {Fun}}^{\textrm{ex}}({{\mathcal {S}}{p}}^{\text {f} },{\mathcal {C}})\simeq {\mathcal {C}}\) given by evaluation at the sphere spectrum, the functor  corresponds to
corresponds to  by virtue of Lemma 4.1.1. We consequently obtain a natural equivalence
by virtue of Lemma 4.1.1. We consequently obtain a natural equivalence

of hermitian \(\infty \)-categories.
Construction 6.2.6
For two hermitian \(\infty \)-categories  we construct a hermitian functor
we construct a hermitian functor

as follows. We first observe that by definition of the monoidal structure on \(\text {Cat} ^{\textrm{h}}_\infty \), specifying such a hermitian functor is equivalent to specifying a functor \(f:{\mathcal {C}}\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'}) \rightarrow {{{\mathcal {C}}}'}\) which is exact in each variable separately, together with a natural transformation

of functors \({\mathcal {C}}^{\text {op} }\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\). In the case at hand we then take as f the usual evaluation functor \(\text {ev} :{\mathcal {C}}\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'}) \rightarrow {{{\mathcal {C}}}'}\). To construct \(\eta \) we use the curry-equivalence
and pull the evaluation transformation

back along the postcomposition functor

which is the curry of  .
.
Proposition 6.2.7
Let  and
and  be two hermitian \(\infty \)-categories. Then the evaluation functor \((\text {ev} ,\eta )\) of Construction 6.2.6 exhibits
be two hermitian \(\infty \)-categories. Then the evaluation functor \((\text {ev} ,\eta )\) of Construction 6.2.6 exhibits  as the internal mapping object in the symmetric monoidal \(\infty \)-category \(\text {Cat} ^{\textrm{h}}_\infty \). That is, for any
as the internal mapping object in the symmetric monoidal \(\infty \)-category \(\text {Cat} ^{\textrm{h}}_\infty \). That is, for any  hermitian \(\infty \)-category the composite
hermitian \(\infty \)-category the composite

is an equivalence of spaces.
By the Yoneda lemma we immediately find:
Corollary 6.2.8
The association  canonically extends to a functor \((\text {Cat} ^{\textrm{h}}_\infty )^{\text {op} }\times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) in a way that renders the evaluation map of Construction 6.2.6 a natural transformation.
canonically extends to a functor \((\text {Cat} ^{\textrm{h}}_\infty )^{\text {op} }\times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) in a way that renders the evaluation map of Construction 6.2.6 a natural transformation.
Corollary 6.2.9
The symmetric monoidal structures on \(\text {Cat} ^{\textrm{h}}_\infty \) constructed in Sect. 5.2 is closed.
Corollary 6.2.10
The symmetric monoidal product on \(\text {Cat} ^{\textrm{h}}_\infty \) preserves small colimits in each variable.
Remark 6.2.11
Since the hermitian evaluation functor of Construction 6.2.6 refines by definition the usual evaluation functor of \(\text {Cat} _\infty ^\text {ex} \), it follows that the forgetful functor \(\text {U} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is not only symmetric monoidal (Theorem 5.2.7ii), but also closed symmetric monoidal, that is, for  the composed map
the composed map

exhibits  as the internal mapping object in \(\text {Cat} _\infty ^\text {ex} \) from
as the internal mapping object in \(\text {Cat} _\infty ^\text {ex} \) from  to
to  . In other words, the transposed map
. In other words, the transposed map

is an equivalence.
Proof of Proposition 6.2.7
The forgetful functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) induces a commutative diagram

in which the bottom horizontal arrow is an equivalence since on the level of stable \(\infty \)-categories, the bilinear functor \(\text {ev} :{\mathcal {C}}\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'}) \rightarrow {{{\mathcal {C}}}'}\) already exhibits \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'}) \in \text {Cat} _\infty ^\text {ex} \) as the internal mapping object from \({\mathcal {C}}\) to \({{{\mathcal {C}}}'}\) in \(\text {Cat} _\infty ^\text {ex} \). It will hence suffice to show that the map induced by (137) on vertical homotopy fibres is an equivalence. Let us thus fix a linear functor \(g:{{{\mathcal {C}}}''}\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\), and write \(\overline{g}:{\mathcal {C}}\otimes {{{\mathcal {C}}}''}\rightarrow {{{\mathcal {C}}}'}\) for its image in the bottom right corner of (137). Since \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is a cartesian fibration the induced map on vertical fibres in (137) can be identified with the composed map of spaces of natural transformations

where the second map is induced by the natural transformation  of Construction 6.2.6, restricted along \((\text {id} ,g):{\mathcal {C}}\times {{{\mathcal {C}}}''}\rightarrow {\mathcal {C}}\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\). Let us now identify functors \(({\mathcal {C}}\times {{{\mathcal {C}}}''})^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) with functors \({{{\mathcal {C}}}''}^{\text {op} }\rightarrow {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), and write
of Construction 6.2.6, restricted along \((\text {id} ,g):{\mathcal {C}}\times {{{\mathcal {C}}}''}\rightarrow {\mathcal {C}}\times {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\). Let us now identify functors \(({\mathcal {C}}\times {{{\mathcal {C}}}''})^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) with functors \({{{\mathcal {C}}}''}^{\text {op} }\rightarrow {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\), and write  for the curried functor determined by
for the curried functor determined by  . Unwinding the definitions we may rewrite (138) as
. Unwinding the definitions we may rewrite (138) as

where we understand  as the functor obtained by applying
as the functor obtained by applying  levelwise. To finish the proof it will hence suffice to show that the evaluation natural transformation
levelwise. To finish the proof it will hence suffice to show that the evaluation natural transformation

exhibits

as left adjoint to

Indeed, this is simply the adjunction induced by the canonical adjunction

encoding the structure of \({\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) as tensored over \({{\mathcal {S}}{p}}\). \(\square \)
Specializing Proposition 6.2.7 to the unit Poincaré \(\infty \)-category  and using Proposition 4.1.3 we recover a natural equivalence
and using Proposition 4.1.3 we recover a natural equivalence

which by comparing with the analogous claim for \(\text {Cat} _\infty ^\text {ex} \) we can place in a commutative square

In particular, the equivalence (139) is of a somewhat tautological nature: a hermitian object in  consists of a pair \((f,\eta )\), where \(f:{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) is an exact functor and
consists of a pair \((f,\eta )\), where \(f:{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) is an exact functor and  is a form for
is a form for  , that which by definition means a natural transformation
, that which by definition means a natural transformation  . The equivalence (139) then associates to this hermitian object the same pair \((f,\eta )\), now considered as a hermitian functor from
. The equivalence (139) then associates to this hermitian object the same pair \((f,\eta )\), now considered as a hermitian functor from  to
to  . Consulting the proof of Proposition 6.2.2 we observe that when
. Consulting the proof of Proposition 6.2.2 we observe that when  and
and  are non-degenerate the map
are non-degenerate the map

associated to a hermitian object \((f,\eta )\), corresponds to the map

(see Definition 1.2.5) via the adjunction between pre-composition with  and pre-composition with
and pre-composition with  . When
. When  is an equivalence we thus have that \(\eta _{\sharp }\) is an equivalence if and only if \(\tau _{\eta }\) is an equivalence. In particular, for Poincaré \(\infty \)-categories
is an equivalence we thus have that \(\eta _{\sharp }\) is an equivalence if and only if \(\tau _{\eta }\) is an equivalence. In particular, for Poincaré \(\infty \)-categories  we have that a hermitian object \((f,\eta )\) in
we have that a hermitian object \((f,\eta )\) in  is Poincaré if and only if the corresponding hermitian functor
is Poincaré if and only if the corresponding hermitian functor  is Poincaré. In particular, in this case the equivalence (139) restricts to an equivalence
is Poincaré. In particular, in this case the equivalence (139) restricts to an equivalence

We may summarize the situation as follows:
Corollary 6.2.12
For a hermitian \(\infty \)-category  , the hermitian object
, the hermitian object  in
in  corresponding to the identity under the equivalence (139), exhibits
corresponding to the identity under the equivalence (139), exhibits  as corepresenting the functor
as corepresenting the functor

in \(\text {Cat} ^{\textrm{h}}_\infty \). In addition, if  is Poincaré then
is Poincaré then  is Poincaré and exhibits
is Poincaré and exhibits  as corepresenting the functor
as corepresenting the functor

in \(\text {Cat} ^{\textrm{p}}_\infty \).
Corollary 6.2.13
Let  and
and  be hermitian \(\infty \)-categories. Then there is an equivalence of hermitian \(\infty \)-categories
be hermitian \(\infty \)-categories. Then there is an equivalence of hermitian \(\infty \)-categories

which is natural in  . In addition, for
. In addition, for  this equivalence sends the hermitian object on the left hand side corresponding to the identity to the hermitian object on the right side corresponding to the evaluation functor of Construction 6.2.6.
this equivalence sends the hermitian object on the left hand side corresponding to the identity to the hermitian object on the right side corresponding to the evaluation functor of Construction 6.2.6.
Proof
This is a formal consequence of the Yoneda lemma that holds true in any closed symmetric monoidal \(\infty \)-category. Indeed, embedding both sides in presheaves to spaces we may use Proposition 6.2.7 and Corollary 6.2.8 to construct natural equivalences between the resulting presheaves

The additional claim in the case  can be obtained by taking
can be obtained by taking  and tracing through the equivalences on both sides. \(\square \)
and tracing through the equivalences on both sides. \(\square \)
Taking Poincaré objects in (141) and using the equivalence (140) we thus conclude:
Corollary 6.2.14
Let  and
and  be two Poincaré \(\infty \)-categories. Then the evaluation functor \((\text {ev} ,\eta )\) of Construction 6.2.6 is Poincaré and exhibits
be two Poincaré \(\infty \)-categories. Then the evaluation functor \((\text {ev} ,\eta )\) of Construction 6.2.6 is Poincaré and exhibits  as the internal mapping objects in the symmetric monoidal category \(\text {Cat} ^{\textrm{p}}_\infty \). In particular, it determines an equivalence of spaces
as the internal mapping objects in the symmetric monoidal category \(\text {Cat} ^{\textrm{p}}_\infty \). In particular, it determines an equivalence of spaces

for  .
.
Corollary 6.2.15
The symmetric monoidal structure on \(\text {Cat} ^{\textrm{p}}_\infty \) constructed in Sect. 5.2 is closed.
Corollary 6.2.16
The association  canonically extends to a functor \((\text {Cat} ^{\textrm{p}}_\infty )^{\text {op} }\times \text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) in a way that renders the evaluation map of Construction 6.2.6 a natural transformation.
canonically extends to a functor \((\text {Cat} ^{\textrm{p}}_\infty )^{\text {op} }\times \text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) in a way that renders the evaluation map of Construction 6.2.6 a natural transformation.
Corollary 6.2.17
The symmetric monoidal product on \(\text {Cat} ^{\textrm{p}}_\infty \) preserves small colimits in each variable.
Remark 6.2.18
Since the evaluation functor used in Corollary 6.2.14 to exhibit internal functor categories in \(\text {Cat} ^{\textrm{p}}_\infty \) is the same as the one that was used to exhibit internal functor categories in \(\text {Cat} ^{\textrm{h}}_\infty \) it follows formally that the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \hookrightarrow \text {Cat} ^{\textrm{h}}_\infty \) is not only symmetric monoidal (Theorem 5.2.7iii)), but also closed symmetric monoidal, that is, preserves internal functor categories. It then follows from Remark 6.2.11 that the composed functor
is closed symmetric monoidal as well.
Definition 6.2.19
For hermitian \(\infty \)-categories  and
and  we define the category of hermitian functors from
we define the category of hermitian functors from  to
to  to be
to be

Remark 6.2.20
Combining Corollary 6.2.13 and Corollary 6.2.12 we deduce that for hermitian \(\infty \)-categories  and
and  , the evaluation functor of Construction 6.2.6 determines a natural equivalence
, the evaluation functor of Construction 6.2.6 determines a natural equivalence

Remark 6.2.21
Proposition 6.2.7 tells us that \(\text {Cat} ^{\textrm{h}}_\infty \) is a closed monoidal category, so we can turn it into an \(\infty \)-category enriched over itself via [22, Cor. 7.4.10]. In particular, for three hermitian \(\infty \)-categories  and
and  we have natural composition hermitian functors
we have natural composition hermitian functors

which one can of course also easily write down without using enriched technology. Applying [22, Cor. 5.7.6] to the lax monoidal functor \(\text {He} :\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty \) we see that \(\text {Cat} ^{\textrm{h}}_\infty \) is canonically endowed with an enrichment over \(\text {Cat} _\infty \), with composition functors

and identities given by the tautological hermitian objects  of Corollary 6.2.12. In particular, one should consider \(\text {Cat} ^{\textrm{h}}_\infty \) as an \((\infty ,2)\)-category, with mapping categories given by \({\text {Fun}}^{\textrm{h}}(-,-)\). Though we will not make explicit use of this point of view, these hermitian functor categories will play a role in Sects. 6.3–6.4 when we study the tensor-cotensor constructions, a structure most naturally viewed with the \((\infty ,2)\)-categorical perspective in mind.
of Corollary 6.2.12. In particular, one should consider \(\text {Cat} ^{\textrm{h}}_\infty \) as an \((\infty ,2)\)-category, with mapping categories given by \({\text {Fun}}^{\textrm{h}}(-,-)\). Though we will not make explicit use of this point of view, these hermitian functor categories will play a role in Sects. 6.3–6.4 when we study the tensor-cotensor constructions, a structure most naturally viewed with the \((\infty ,2)\)-categorical perspective in mind.
7.3 Cotensoring of hermitian categories
Given a hermitian \(\infty \)-category  and an \(\infty \)-category \({\mathcal {I}}\), our goal in this section is to promote the diagram category \({\mathcal {C}}^{{\mathcal {I}}} := {\text {Fun}}({\mathcal {I}},{\mathcal {C}})\) to a hermitian \(\infty \)-category
and an \(\infty \)-category \({\mathcal {I}}\), our goal in this section is to promote the diagram category \({\mathcal {C}}^{{\mathcal {I}}} := {\text {Fun}}({\mathcal {I}},{\mathcal {C}})\) to a hermitian \(\infty \)-category  , which we call the cotensor of
, which we call the cotensor of  by \({\mathcal {I}}\). We will characterize the resulting hermitian \(\infty \)-category by a universal property, see Proposition 6.3.10 below, which can be considered as witnessing it being the cotensor structure of \(\text {Cat} ^{\textrm{h}}_\infty \) over \(\text {Cat} _\infty \) with respect to the enrichment of the former in the latter described in Sect. 6.2. This construction will feature prominently in Paper [2] via the hermitian \({\text {Q}}\)-construction.
by \({\mathcal {I}}\). We will characterize the resulting hermitian \(\infty \)-category by a universal property, see Proposition 6.3.10 below, which can be considered as witnessing it being the cotensor structure of \(\text {Cat} ^{\textrm{h}}_\infty \) over \(\text {Cat} _\infty \) with respect to the enrichment of the former in the latter described in Sect. 6.2. This construction will feature prominently in Paper [2] via the hermitian \({\text {Q}}\)-construction.
Construction 6.3.1
Let \({\mathcal {I}}\) be a small \(\infty \)-category and  a hermitian \(\infty \)-category. We will denote by \({\mathcal {C}}^{{\mathcal {I}}} := {\text {Fun}}({\mathcal {I}},{\mathcal {C}})\) the stable \(\infty \)-category of functors \({\mathcal {I}}\rightarrow {\mathcal {C}}\). Let \(\text {ev} :{\mathcal {I}}\times {\mathcal {C}}^{{\mathcal {I}}} \rightarrow {\mathcal {C}}\) be the evaluation functor, which, under the exponential equivalence
a hermitian \(\infty \)-category. We will denote by \({\mathcal {C}}^{{\mathcal {I}}} := {\text {Fun}}({\mathcal {I}},{\mathcal {C}})\) the stable \(\infty \)-category of functors \({\mathcal {I}}\rightarrow {\mathcal {C}}\). Let \(\text {ev} :{\mathcal {I}}\times {\mathcal {C}}^{{\mathcal {I}}} \rightarrow {\mathcal {C}}\) be the evaluation functor, which, under the exponential equivalence
corresponds to the functor which associates to \(i \in {\mathcal {I}}\) the evaluation-at-i functor \(\text {ev} _i:{\mathcal {C}}^{{\mathcal {I}}} \rightarrow {\mathcal {C}}\). Define a functor  by
by

On a given diagram \(\varphi \in {\mathcal {C}}^{{\mathcal {I}}}\) the functor  is given by the formula
is given by the formula

Proposition 6.3.2
The functor  is quadratic. Its bilinear part is given by
is quadratic. Its bilinear part is given by

and the linear part \(\Lambda ^{{\mathcal {I}}}\) makes the square

cartesian. If  is non-degenerate and \({\mathcal {C}}\) admits \(({\mathcal {I}}_{i/})^{\text {op} }\)-shaped limits for all \(i \in {\mathcal {I}}\), then
is non-degenerate and \({\mathcal {C}}\) admits \(({\mathcal {I}}_{i/})^{\text {op} }\)-shaped limits for all \(i \in {\mathcal {I}}\), then  is also non-degenerate with duality given by
is also non-degenerate with duality given by

Remark 6.3.3
If \({\mathcal {I}}\) is a finite \(\infty \)-category then  , since the bottom horizontal map in (142) is then an equivalence.
, since the bottom horizontal map in (142) is then an equivalence.
Proof of Proposition 6.3.2
The functor  is defined as a limit of the functors
is defined as a limit of the functors  , each of which is quadratic since
, each of which is quadratic since  itself is quadratic and each \(\text {ev} _i\) is exact. Since the collection of quadratic functors is closed under limits (Remark 1.1.15) it follows that
itself is quadratic and each \(\text {ev} _i\) is exact. Since the collection of quadratic functors is closed under limits (Remark 1.1.15) it follows that  is quadratic. Since the formation of bilinear parts is compatible with restriction (Remark 1.1.6) and commutes with limits (e.g, by Lemma 1.1.7), it follows that
is quadratic. Since the formation of bilinear parts is compatible with restriction (Remark 1.1.6) and commutes with limits (e.g, by Lemma 1.1.7), it follows that

and in particular

The formation of linear parts however does not commute with limits. To compute it, we apply \(\lim _{{\mathcal {I}}^{\text {op} }}\) to the square classifying  via Corollary 1.3.12, yielding the square
via Corollary 1.3.12, yielding the square

of quadratic functors in \(\varphi \) whose left hand side consists of exact functors. Taking linear parts we then get the desired description of \(\Lambda ^{{\mathcal {I}}}\).
We now prove the desired formula for the duality. For this, we henceforth assume that  is non-degenerate and that \({\mathcal {C}}\) admits \(({\mathcal {I}}_{/i})^{\text {op} }\)-indexed limits for every \(i \in {\mathcal {I}}\). Let \(s:{\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}\) and \(t:{\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}^{\text {op} }\) be the source and target functors, respectively. Define \(\text {D} ^{{\mathcal {I}}}:({\mathcal {C}}^{{\mathcal {I}}})^{\text {op} }\rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) by the composite formula
is non-degenerate and that \({\mathcal {C}}\) admits \(({\mathcal {I}}_{/i})^{\text {op} }\)-indexed limits for every \(i \in {\mathcal {I}}\). Let \(s:{\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}\) and \(t:{\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}^{\text {op} }\) be the source and target functors, respectively. Define \(\text {D} ^{{\mathcal {I}}}:({\mathcal {C}}^{{\mathcal {I}}})^{\text {op} }\rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) by the composite formula

where \(s_*\) stands for right Kan extension. This right Kan extension indeed exists: since \(s:{\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}\) is a cartesian fibration classified by the functor \(i \mapsto ({\mathcal {I}}_{i/})^{\text {op} }\) this right Kan extension is given by the explicit formula

where the required limits exist in \({\mathcal {C}}\) by assumption. We now claim that \(\text {D} ^{{\mathcal {I}}}\) represents the bilinear functor \(\text {B} ^{{\mathcal {I}}}\). To prove this, note first that since the right Kan extension functor \(s_*\) is right adjoint to the corresponding restriction functor \(s^*\) we get that

where we have used the standard formula for the spectrum of natural transformations as a limit over the twisted arrow category. We wish to show that the last limit above is equivalent to  . For this we will make use of several cofinality arguments. To facilitate readability in what follows, we invite the reader to visualize an object \([\sigma :\alpha \Rightarrow \beta ] \in {\text {TwAr}}({\text {TwAr}}({\mathcal {I}}))^{\text {op} }\) as a diagram of the form
. For this we will make use of several cofinality arguments. To facilitate readability in what follows, we invite the reader to visualize an object \([\sigma :\alpha \Rightarrow \beta ] \in {\text {TwAr}}({\text {TwAr}}({\mathcal {I}}))^{\text {op} }\) as a diagram of the form

To begin, consider the commutative diagram

Since \((s \times t):{\text {TwAr}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) is a right fibration it induces an equivalence on over categories. It then follows that the commutative square on the left is cartesian, and hence the induced map
is an equivalence. In particular, the projection
is a cartesian fibration whose fibres have terminal objects, being pulled back from the (target) cartesian fibration \({\text {TwAr}}({\mathcal {I}}^{\text {op} }) \rightarrow {\mathcal {I}}\) given by \([l \leftarrow k] \mapsto k\) which has this property. By [43, Lemma 4.1.3.2] it then follows that the functor (143) is cofinal. To avoid confusion, we note that in the fibre product in (143), the map \({\text {TwAr}}({\mathcal {I}}) \rightarrow {\mathcal {I}}^{\text {op} }\) is the target projection \([i \rightarrow j] \mapsto j\) and the map \({\text {TwAr}}({\mathcal {I}})^{\text {op} }\rightarrow {\mathcal {I}}^{\text {op} }\) is the opposite of the source projection \([j \rightarrow k] \mapsto j\). Now the composed functor
is cocartesian fibration, being a composition of a left fibration and a constant cocartesian fibration. By compatibility with base change we see that this cocartesian fibration is classified by the functor \(k \mapsto {\text {TwAr}}({\mathcal {I}}) \times _{{\mathcal {I}}^{\text {op} }} ({\mathcal {I}}_{/k})^{\text {op} }\). Since the projection \({\mathcal {I}}_{/k} \rightarrow {\mathcal {I}}\) is a right fibration it follows by the same argument as above that the map \({\text {TwAr}}({\mathcal {I}}_{/k}) \rightarrow {\text {TwAr}}({\mathcal {I}}) \times _{{\mathcal {I}}^{\text {op} }} ({\mathcal {I}}_{/k})^{\text {op} }\) (induced by the target projection) is an equivalence. The cocartesian (144) is hence also classified by the equivalent functor \(k \mapsto {\text {TwAr}}({\mathcal {I}}_{/k})\). Now consider the map of cocartesian fibrations (over \({\mathcal {I}}\))
induced by the source projections \({\text {TwAr}}({\mathcal {I}}_{/k}) \rightarrow {\mathcal {I}}_{/k}\). Then (145) is a map of cocartesian fibrations which is fibrewise cofinal by Lemma [43, Lemma 4.1.3.2] and is hence itself cofinal. Since cofinal maps are closed under composition we may now conclude that the composed projection
is cofinal. On the other hand the canonical inclusion \({\mathcal {I}}\rightarrow {\text {Ar}}({\mathcal {I}})\) sending \(x\) to \(\text {id} _x\) is also cofinal since it has a left adjoint (the target functor). We may therefore conclude that

and so \(\text {D} _{{\mathcal {I}}}\) represents  , as desired. \(\square \)
, as desired. \(\square \)
Definition 6.3.4
For a hermitian \(\infty \)-category  and an \(\infty \)-category \({\mathcal {I}}\) we will denote by
and an \(\infty \)-category \({\mathcal {I}}\) we will denote by  the \(\infty \)-category given by Proposition 6.3.2. We will refer to it as the cotensor of
the \(\infty \)-category given by Proposition 6.3.2. We will refer to it as the cotensor of  by \({\mathcal {I}}\).
by \({\mathcal {I}}\).
Remark 6.3.5
If \({\mathcal {I}}\) is a finite poset then the comma \(\infty \)-categories \({\mathcal {I}}_{/i}\) are finite for every \(i \in {\mathcal {I}}\), and hence every stable \(\infty \)-category admits \(({\mathcal {I}}_{/i})^{\text {op} }\) indexed limits. In particular, in this case  is non-degenerate as soon as
is non-degenerate as soon as  is non-degenerate.
is non-degenerate.
Example 6.3.6
For \({\mathcal {I}}= {\text {TwAr}}(\Delta ^1)\) we may identify \({\mathcal {C}}^{{\mathcal {I}}}\) with the \(\infty \)-category of spans \(x\leftarrow w\rightarrow y\) in \({\mathcal {C}}\), with  given by
given by

and the duality (when  is non-degenerate) given by
is non-degenerate) given by

It is then straightforward to verify that this duality is perfect whenever  is perfect, in which case
is perfect, in which case  is Poincaré. This example will feature prominently in subsequent parts of the present paper in the context of the cobordism category of a Poincaré \(\infty \)-category, where we will view the above duality as an algebraic incarnation of Lefschetz duality for manifolds.
is Poincaré. This example will feature prominently in subsequent parts of the present paper in the context of the cobordism category of a Poincaré \(\infty \)-category, where we will view the above duality as an algebraic incarnation of Lefschetz duality for manifolds.
Warning 6.3.7
For a Poincaré  and \({\mathcal {I}}\) arbitrary, the hermitian \(\infty \)-category
and \({\mathcal {I}}\) arbitrary, the hermitian \(\infty \)-category  might fail to be Poincaré, even if \({\mathcal {I}}\) is a finite poset. This happens for example if \({\mathcal {I}}\) has a final object but is not itself equivalent to a point; indeed, in this case the image of \(\text {D} ^{{\mathcal {I}}}\) is the full subcategory of \({\mathcal {C}}^{\mathcal {I}}\) spanned by the constant diagrams. On the other hand, we will see in Sect. 6.4 that cotensor by \({\mathcal {I}}\) does preserve Poincaré \(\infty \)-categories when \({\mathcal {I}}\) is the poset of faces of a finite simplicial complex.
might fail to be Poincaré, even if \({\mathcal {I}}\) is a finite poset. This happens for example if \({\mathcal {I}}\) has a final object but is not itself equivalent to a point; indeed, in this case the image of \(\text {D} ^{{\mathcal {I}}}\) is the full subcategory of \({\mathcal {C}}^{\mathcal {I}}\) spanned by the constant diagrams. On the other hand, we will see in Sect. 6.4 that cotensor by \({\mathcal {I}}\) does preserve Poincaré \(\infty \)-categories when \({\mathcal {I}}\) is the poset of faces of a finite simplicial complex.
We go on to establish the universal property of these hermitian diagram categories, from which we will also deduce their functoriality. We will require the following lemma:
Lemma 6.3.8
Let \({\mathcal {I}}\) be a small \(\infty \)-category and \({\mathcal {C}},{{{\mathcal {C}}}'}\) be two hermitian \(\infty \)-categories. Then the fibre of the map

over a functor \(f:{\mathcal {I}}\times {\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) is naturally equivalent to the space  of natural transformations
of natural transformations  , where \(p_{{\mathcal {C}}}:{\mathcal {I}}\times {\mathcal {C}}\rightarrow {\mathcal {C}}\) denotes the projection to \({\mathcal {C}}\).
, where \(p_{{\mathcal {C}}}:{\mathcal {I}}\times {\mathcal {C}}\rightarrow {\mathcal {C}}\) denotes the projection to \({\mathcal {C}}\).
Proof
We want to describe the space of dotted lifts

Recall that the vertical map above is the right fibration classified by functor  , and so by [43, Corollary 3.3.3.2], the space of sections of this right fibration coincides with the limit
, and so by [43, Corollary 3.3.3.2], the space of sections of this right fibration coincides with the limit

On the other hand, we have

since right Kan extensions along \(p_{{\mathcal {C}}}\) are computed by taking the limit fibrewise, as can be seen from the pointwise formula for right Kan extensions. Hence the two constructions are naturally equivalent. \(\square \)
Construction 6.3.9
For a hermitian \(\infty \)-category  and an \(\infty \)-category \({\mathcal {I}}\) we define a functor
and an \(\infty \)-category \({\mathcal {I}}\) we define a functor

as follows. Let \(p :{\mathcal {I}}^{\text {op} }\times ({\mathcal {C}}^{{\mathcal {I}}})^{\text {op} }\rightarrow ({\mathcal {C}}^{{\mathcal {I}}})^{\text {op} }\) be the projection on the second factor and
the evaluation. By Lemma 6.3.8 the additional data needed in order to define \(\overline{\text {ev} }\) is a natural transformation

We then define \(\tau \) by taking the counit transformation
currying it into morphism in \({\text {Fun}}({\mathcal {I}}^{\text {op} }\times {\text {Fun}}({\mathcal {I}}^{\text {op} },{{\mathcal {S}}{p}}),{{\mathcal {S}}{p}})\) and finally pre-composing with the functor
induced by  .
.
Proposition 6.3.10
Let  and
and  be two hermitian \(\infty \)-categories and \({\mathcal {I}}\) a small \(\infty \)-category. Then the composite map
be two hermitian \(\infty \)-categories and \({\mathcal {I}}\) a small \(\infty \)-category. Then the composite map

defined using the functor \(\overline{\text {ev} }\) of Construction 6.3.9 and the composition functor of Remark 6.2.21, determines an equivalence of \(\infty \)-categories

and in particular an equivalence

We will give the proof of Proposition 6.3.10 at the end of this subsection. Before let us explore some of its consequences. First, as in the case of internal functor categories, the Yoneda lemma immediately implies:
Corollary 6.3.11
The association  extends canonically to a functor \(\text {Cat} _\infty ^{\text {op} }\times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) that renders the equivalence from Proposition 6.3.10 natural.
extends canonically to a functor \(\text {Cat} _\infty ^{\text {op} }\times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) that renders the equivalence from Proposition 6.3.10 natural.
Remark 6.3.12
Unwinding the definitions, if \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) is a functor of small \(\infty \)-categories and  is a hermitian \(\infty \)-category then the hermitian functor
is a hermitian \(\infty \)-category then the hermitian functor

issued via the functoriality of Corollary 6.3.11 is given by the usual restriction functor \(\alpha ^*:{\mathcal {C}}^{{\mathcal {J}}} \rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) on the underlying stable \(\infty \)-categories accompanied by the usual restriction-induced map

on limits.
Remark 6.3.13
As pointed out in Warning 6.3.7, the cotensor construction does not restrict to a functor \(\text {Cat} _\infty ^{\text {op} }\times \text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \). In particular, while this construction is best understood by considering \(\text {Cat} ^{\textrm{h}}_\infty \) as an \((\infty ,2)\)-category, the \((\infty ,2)\)-categorical perspective does not seem to extend to \(\text {Cat} ^{\textrm{p}}_\infty \) in a meaningful manner.
Remark 6.3.14
It follows from Proposition 6.3.10 that when \({\mathcal {I}}\) is an \(\infty \)-groupoid the cotensor  coincides with the limit in \(\text {Cat} ^{\textrm{h}}_\infty \) of the constant \({\mathcal {I}}\)-diagram with value
coincides with the limit in \(\text {Cat} ^{\textrm{h}}_\infty \) of the constant \({\mathcal {I}}\)-diagram with value  . In particular, it follows form Proposition 6.1.4 that for such an \({\mathcal {I}}\) the functor
. In particular, it follows form Proposition 6.1.4 that for such an \({\mathcal {I}}\) the functor  does preserve Poincaré \(\infty \)-categories.
does preserve Poincaré \(\infty \)-categories.
Taking  in Proposition 6.3.10 yields:
in Proposition 6.3.10 yields:
Corollary 6.3.15
There is a natural equivalence  .
.
Remark 6.3.16
We know of no analogous formula for the Poincaré objects of  when the latter happens to be Poincaré. It is certainly not true, for example, that the individual objects of a Poincaré diagram are Poincaré objects themselves, as demonstrated by the case \({\mathcal {I}}= {\text {TwAr}}(\Delta ^1)\), see Example 6.3.6.
when the latter happens to be Poincaré. It is certainly not true, for example, that the individual objects of a Poincaré diagram are Poincaré objects themselves, as demonstrated by the case \({\mathcal {I}}= {\text {TwAr}}(\Delta ^1)\), see Example 6.3.6.
The following is again a formal consequence:
Corollary 6.3.17
For any hermitian \(\infty \)-categories  and any \(\infty \)-category \({\mathcal {I}}\) there is a canonical equivalence
and any \(\infty \)-category \({\mathcal {I}}\) there is a canonical equivalence

of hermitian \(\infty \)-categories.
Proposition 6.3.18
Let  be non-degenerate and \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) a functor between small categories, such that
be non-degenerate and \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) a functor between small categories, such that  admits both \(({\mathcal {I}}_{i/})^{\text {op} }\)- and \(({\mathcal {J}}_{j/})^{\text {op} }\)-shaped limits for all \(i\in {\mathcal {I}}\) and \(j \in {\mathcal {J}}\). If the induced maps \({\mathcal {I}}_{i/} \rightarrow {\mathcal {J}}_{\alpha (i)/}\) are cofinal for every \(i \in {\mathcal {I}}\) then the hermitian functor
admits both \(({\mathcal {I}}_{i/})^{\text {op} }\)- and \(({\mathcal {J}}_{j/})^{\text {op} }\)-shaped limits for all \(i\in {\mathcal {I}}\) and \(j \in {\mathcal {J}}\). If the induced maps \({\mathcal {I}}_{i/} \rightarrow {\mathcal {J}}_{\alpha (i)/}\) are cofinal for every \(i \in {\mathcal {I}}\) then the hermitian functor

is duality preserving. In particular, if  and
and  are Poincaré then \((\alpha ^*,\eta ^{\alpha })\) is a Poincaré functor.
are Poincaré then \((\alpha ^*,\eta ^{\alpha })\) is a Poincaré functor.
Proof
This follows directly from the explicit description of the duality in Proposition 6.3.2. \(\square \)
Remark 6.3.19
In the situation of Proposition 6.3.18, if \(\alpha \) is a map of posets, then the given criterion for preservation of duality can be rephrased more explicitly by saying that for every \(i \in {\mathcal {I}}\) and \(j \in {\mathcal {J}}\) with \(j \ge \alpha (i)\), the realisation of the poset \(\{k \in {\mathcal {I}}\mid i \le k, j \le \alpha (k)\}\) is contractible.
Proof of Proposition 6.3.10
We argue similarly to the proof of Proposition 6.2.7. The forgetful functor determines a commutative diagram of \(\infty \)-categories

in which the vertical maps are right fibrations and where the bottom arrow is an equivalence since the functor \(\text {ev} ':{\mathcal {I}}\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\mathcal {I}},{{{\mathcal {C}}}'})\) underlying \(\overline{\text {ev} }\) already exhibits \({\mathcal {C}}^{\mathcal {I}}\) as the cotensor of \({\mathcal {C}}\) over \({\mathcal {I}}\) in \(\text {Cat} _\infty ^\text {ex} \). It will hence suffice to show the map induced by (149) on vertical fibres is an equivalence. Let us hence fix an exact functor \(g:{{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}^{\mathcal {I}}\) and let \(g_{\mathcal {I}}:= \{g_i\}: {\mathcal {I}}\rightarrow {\text {Fun}}^{\textrm{ex}}({{{\mathcal {C}}}'},{\mathcal {C}})\) be its image in the bottom right corner of (149). Now the fibre of the right vertical map in (149) over \(g_{\mathcal {I}}\) is the space of sections of the base change

where the fibre product is taken with respect to the map \(g_{\mathcal {I}}\). By the compatibility of base change and straightening we see that (150) is the right fibration classified by the functor  . By [43, Corollary 3.3.3.2] evaluation at the various \(i \in {\mathcal {I}}\) exhibits the space of sections of (150) as the limit
. By [43, Corollary 3.3.3.2] evaluation at the various \(i \in {\mathcal {I}}\) exhibits the space of sections of (150) as the limit  . We may then identify the map induced by (149) from the fibre over g to the fibre of \(g_{\mathcal {I}}\) with the map
. We may then identify the map induced by (149) from the fibre over g to the fibre of \(g_{\mathcal {I}}\) with the map

whose components  are induced by the components
are induced by the components  of (146). Since pulling back functors preserves limits the desired result now follows from the fact that the collection of maps
of (146). Since pulling back functors preserves limits the desired result now follows from the fact that the collection of maps  exhibit
exhibit  as the limit of the diagram
as the limit of the diagram  , by definition. \(\square \)
, by definition. \(\square \)
7.4 Tensoring of hermitian categories
In this section we will consider the dual of the cotensor construction studied in Sect. 6.3, which we will refer to as tensoring a Poincaré \(\infty \)-category  by an \(\infty \)-category \({\mathcal {I}}\). In general this construction is somewhat less accessible then the cotensor construction, but we will be able to say more about it when \({\mathcal {I}}\) satisfies certain finiteness conditions, see Sect. 6.5 below. We will exploit the tensor construction in Paper [2] in order to form the dual \({\text {Q}}\)-construction, which is needed in the proof of the universal property of the Grothendieck-Witt spectrum.
by an \(\infty \)-category \({\mathcal {I}}\). In general this construction is somewhat less accessible then the cotensor construction, but we will be able to say more about it when \({\mathcal {I}}\) satisfies certain finiteness conditions, see Sect. 6.5 below. We will exploit the tensor construction in Paper [2] in order to form the dual \({\text {Q}}\)-construction, which is needed in the proof of the universal property of the Grothendieck-Witt spectrum.
Construction 6.4.1
Let  be a hermitian \(\infty \)-category and \({\mathcal {I}}\) a small \(\infty \)-category. For \(i \in {\mathcal {I}}\) and \(x\in {\mathcal {C}}\), let us denote by \(R_{i,x} :{\mathcal {I}}^{\text {op} }\rightarrow {\text {Pro}}({\mathcal {C}})\) the functor \(R_{i,x} = (\iota _i)_*(x)\) right Kan extended along the inclusion \(\iota _i:\{i\} \hookrightarrow {\mathcal {I}}^{\text {op} }\) of i from the functor \(\{i\} \rightarrow {\text {Pro}}({\mathcal {C}})\) with value \(x\in {\mathcal {C}}\subseteq {\text {Pro}}({\mathcal {C}})\). We then let \({\mathcal {C}}_{\mathcal {I}}\subseteq {\text {Pro}}({\mathcal {C}})^{{\mathcal {I}}^{\text {op} }}\) be the smallest full subcategory containing \(R_{i,x}\) for \(i \in {\mathcal {I}}\) and \(x\in {\mathcal {C}}\) and closed under finite limits. Then \({\mathcal {C}}_{\mathcal {I}}\) is also closed under suspensions (since the collection \(R_{i,x}\) is, as suspension in \({\mathcal {C}}\) commutes with finite limits) and is hence stable. It is also equipped by construction with a functor
be a hermitian \(\infty \)-category and \({\mathcal {I}}\) a small \(\infty \)-category. For \(i \in {\mathcal {I}}\) and \(x\in {\mathcal {C}}\), let us denote by \(R_{i,x} :{\mathcal {I}}^{\text {op} }\rightarrow {\text {Pro}}({\mathcal {C}})\) the functor \(R_{i,x} = (\iota _i)_*(x)\) right Kan extended along the inclusion \(\iota _i:\{i\} \hookrightarrow {\mathcal {I}}^{\text {op} }\) of i from the functor \(\{i\} \rightarrow {\text {Pro}}({\mathcal {C}})\) with value \(x\in {\mathcal {C}}\subseteq {\text {Pro}}({\mathcal {C}})\). We then let \({\mathcal {C}}_{\mathcal {I}}\subseteq {\text {Pro}}({\mathcal {C}})^{{\mathcal {I}}^{\text {op} }}\) be the smallest full subcategory containing \(R_{i,x}\) for \(i \in {\mathcal {I}}\) and \(x\in {\mathcal {C}}\) and closed under finite limits. Then \({\mathcal {C}}_{\mathcal {I}}\) is also closed under suspensions (since the collection \(R_{i,x}\) is, as suspension in \({\mathcal {C}}\) commutes with finite limits) and is hence stable. It is also equipped by construction with a functor
We then promote \({\mathcal {C}}_{\mathcal {I}}\) to a hermitian \(\infty \)-category by endowing it with the quadratic functor

obtained by taking the left Kan extension of  along \(\iota ^{\text {op} }:{\mathcal {C}}^{\text {op} }\times {\mathcal {I}}^{\text {op} }\rightarrow {\mathcal {C}}_{{\mathcal {I}}}^{\text {op} }\), which results in a reduced functor, and then applying to it the 2-excisive approximation of Construction 1.1.26, left adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{{\mathcal {I}}}) \subseteq {\text {Fun}}_{*}({\mathcal {C}}_{{\mathcal {I}}}^{\text {op} },{{\mathcal {S}}{p}})\) (in fact, we will see in the proof of Proposition 6.4.3 that this 2-excisive approximation is not needed, that is, the result of the left Kan extension is already 2-excisive). Here we denote by \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) projection to \({\mathcal {C}}\). We then set
along \(\iota ^{\text {op} }:{\mathcal {C}}^{\text {op} }\times {\mathcal {I}}^{\text {op} }\rightarrow {\mathcal {C}}_{{\mathcal {I}}}^{\text {op} }\), which results in a reduced functor, and then applying to it the 2-excisive approximation of Construction 1.1.26, left adjoint to the inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}_{{\mathcal {I}}}) \subseteq {\text {Fun}}_{*}({\mathcal {C}}_{{\mathcal {I}}}^{\text {op} },{{\mathcal {S}}{p}})\) (in fact, we will see in the proof of Proposition 6.4.3 that this 2-excisive approximation is not needed, that is, the result of the left Kan extension is already 2-excisive). Here we denote by \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) projection to \({\mathcal {C}}\). We then set

and refer to it as the tensor of  by \({\mathcal {I}}\). By construction the functor
by \({\mathcal {I}}\). By construction the functor  supports a natural transformation
supports a natural transformation

where \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) is the projection to \({\mathcal {C}}\), and by Lemma 6.3.8 this transformation determines a functor

which to \(i \in {\mathcal {I}}\) associates the exact functor \(x\mapsto R_{i,x},\) equipped with the natural transformation  given by the construction of
given by the construction of  .
.
Remark 6.4.2
The functor \(\text {coev} :{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}_{{\mathcal {I}}}\) exhibits \({\mathcal {C}}_{{\mathcal {I}}}\) as universal among stable \(\infty \)-categories equipped with a functor from \({\mathcal {C}}\times {\mathcal {I}}\) which is exact in the first entry. To see this, we may replace the term “exact” by “finite limit preserving”. In other words, it will suffice to show that (151) is universal among maps from \({\mathcal {C}}\times {\mathcal {I}}\) to a finitely complete \(\infty \)-category which preserve finite limits in the first variable. Such universal constructions are explicitly described in [43, §5.3.6]. In particular, it will suffice to show that \({\mathcal {C}}_{\mathcal {I}}\) coincides with the construction appearing in the proof of [43, Proposition 5.3.6.2]. To see this, note that \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) identifies with the full subcategory of \({\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})^{\text {op} }\) spanned by those functors which preserve finite limits in the \({\mathcal {C}}\)-variable. This full inclusion then admits a right adjoint
and what we need to check is that \({\mathcal {C}}_{\mathcal {I}}\subseteq {\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) identifies with the full subcategory generated under finite limits by the images under R of the corepresentable functors \({\text {Map}}_{{\mathcal {C}}\times {\mathcal {I}}}((x,i),-):{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {S}}\). In light of the definition of \({\mathcal {C}}_{\mathcal {I}}\) this amounts to showing that \(R_{i,x} \simeq R({\text {Map}}_{{\mathcal {C}}\times {\mathcal {I}}}((x,i),-))\). Indeed, both these objects represent the functor
To describe  more explicitly, let
more explicitly, let  be the left Kan extension of
be the left Kan extension of  along the Yoneda embedding \({\mathcal {C}}^{\text {op} }\hookrightarrow {\text {Pro}}({\mathcal {C}})^{\text {op} }\). Then
along the Yoneda embedding \({\mathcal {C}}^{\text {op} }\hookrightarrow {\text {Pro}}({\mathcal {C}})^{\text {op} }\). Then  is quadratic by [47, Proposition 6.1.5.4]. Its bilinear part then coincides with the essentially unique bilinear functor
is quadratic by [47, Proposition 6.1.5.4]. Its bilinear part then coincides with the essentially unique bilinear functor  which extends \(\text {B} \) and preserve colimits in each variable separately, and its linear part is the essentially unique colimit preserving functor
which extends \(\text {B} \) and preserve colimits in each variable separately, and its linear part is the essentially unique colimit preserving functor  extending
extending  .
.
Proposition 6.4.3
Let  be a hermitian \(\infty \)-category and \({\mathcal {I}}\) a small \(\infty \)-category. Then the quadratic functor
be a hermitian \(\infty \)-category and \({\mathcal {I}}\) a small \(\infty \)-category. Then the quadratic functor  of Construction 6.4.1 is given explicitly by the formula
of Construction 6.4.1 is given explicitly by the formula

Its bilinear and linear parts are given by

respectively.
Proof
To establish the formula for  we first note that
we first note that  is quadratic, being a colimit of the quadratic functors
is quadratic, being a colimit of the quadratic functors  for \(i \in {\mathcal {I}}^{\text {op} }\), see Remark 1.1.15. Its linear and bilinear parts are then given by the indicated formulas since taking linear and bilinear parts commutes with colimits. It will hence suffice to identify
for \(i \in {\mathcal {I}}^{\text {op} }\), see Remark 1.1.15. Its linear and bilinear parts are then given by the indicated formulas since taking linear and bilinear parts commutes with colimits. It will hence suffice to identify  with the left Kan extension of
with the left Kan extension of  along \(\iota ^{\text {op} }\). For this, consider the commutative square
along \(\iota ^{\text {op} }\). For this, consider the commutative square

where the left vertical map j is the Yoneda embedding and the bottom horizontal map is the left adjoint to the inclusion \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\hookrightarrow {\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})\) induced by the inclusion \({\text {Pro}}({\mathcal {C}}) \hookrightarrow {\text {Fun}}({\mathcal {C}},{\mathcal {S}})^{\text {op} }\) as the full subcategory spanned by left exact functors. Since the right vertical map is fully-faithful we may compute  by further Kan extending to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\) and then restricting back to \({\mathcal {C}}_{{\mathcal {I}}}^{\text {op} }\). By the commutativity of the above square the left Kan extension to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\) can be performed by first left Kan extending to \({\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})\) and then left Kan extending to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\), the latter given by restriction along the right adjoint \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\hookrightarrow {\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})\). Now the left Kan extension of
by further Kan extending to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\) and then restricting back to \({\mathcal {C}}_{{\mathcal {I}}}^{\text {op} }\). By the commutativity of the above square the left Kan extension to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\) can be performed by first left Kan extending to \({\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})\) and then left Kan extending to \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\), the latter given by restriction along the right adjoint \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))^{\text {op} }\hookrightarrow {\text {Fun}}({\mathcal {C}}\times {\mathcal {I}},{\mathcal {S}})\). Now the left Kan extension of  along the Yoneda embedding results in the coend construction
along the Yoneda embedding results in the coend construction

where \(\otimes \) denotes the tensor of spectra over spaces. Now, in the case where our functor \({\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {S}}\) is of the form \(\rho _{\varphi }(x,i) = {\text {Map}}_{{\mathcal {C}}}(\varphi (i),x)\) for some \({\text {Pro}}({\mathcal {C}})\)-valued presheaf \(\varphi :{\mathcal {I}}^{\text {op} }\rightarrow {\text {Pro}}({\mathcal {C}})\), then its left Kan extension along \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) is given by
We may then conclude that

As this expression is already 2-excisive in \(\varphi \) we deduce that

as desired. \(\square \)
We shall now address the universal property of the tensor construction.
Proposition 6.4.4
Let  and
and  be hermitian \(\infty \)-categories and \({\mathcal {I}}\) a small \(\infty \)-category. Then the composed map
be hermitian \(\infty \)-categories and \({\mathcal {I}}\) a small \(\infty \)-category. Then the composed map

induces an equivalence

and in particular an equivalence

As in the case of the cotensor construction the universal characterization implies functoriality:
Corollary 6.4.5
The association  extends canonically to a functor \(\text {Cat} _\infty \times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) that renders the equivalence from Proposition 6.4.4 natural.
extends canonically to a functor \(\text {Cat} _\infty \times \text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) that renders the equivalence from Proposition 6.4.4 natural.
Remark 6.4.6
Comparing universal properties, we see that there are canonical equivalences of hermitian \(\infty \)-categories

Remark 6.4.7
Comparing universal properties we see that there are canonical equivalences of hermitian \(\infty \)-categories

Remark 6.4.8
It follows from Remarks 6.4.6, 6.4.7 and 6.2.4 that for a given small \(\infty \)-category \({\mathcal {I}}\) the conditions
-
i)
the functor
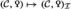 preserves Poincaré \(\infty \)-categories;
preserves Poincaré \(\infty \)-categories; -
ii)
the hermitian \(\infty \)-category
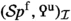 is Poincaré;
is Poincaré;
are equivalent, and that when these equivalent conditions hold the functor  preserves Poincaré \(\infty \)-categories as well.
preserves Poincaré \(\infty \)-categories as well.
Remark 6.4.9
If \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) is a map between small \(\infty \)-categories then the hermitian functor
resulting from the functoriality of Corollary 6.4.5 must induce the associated restriction functor

under the equivalence of Proposition 6.4.4, upon mapping into any  . The underlying exact functor is consequently the essentially unique one (see Remark 6.4.2) making the diagram
. The underlying exact functor is consequently the essentially unique one (see Remark 6.4.2) making the diagram

commute, and must therefore coincide with the restriction to \({\mathcal {C}}_{\mathcal {I}}\) of the right Kan extension functor
By a slight abuse of notation we will denote this restriction by \(\alpha _*:{\mathcal {C}}_{{\mathcal {I}}} \rightarrow {\mathcal {C}}_{{\mathcal {J}}}\) as well. Using the formula of Proposition 6.4.3 the hermitian structure on \(\alpha _*\) is then given by the natural map

for \(\varphi \in {\mathcal {C}}_{{\mathcal {I}}}\).
Remark 6.4.10
The natural equivalences (148) and (154) exhibit \((-)_{\mathcal {I}}\) as left adjoint to \((-)^{\mathcal {I}}\). Furthermore, if \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) is a map of finite posets then this adjunction intertwines the restriction functor  with the (restricted) right Kan extension functor
with the (restricted) right Kan extension functor  .
.
Proof of Proposition 6.4.4
The forgetful functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) determines a commutative square of \(\infty \)-categories

in which the vertical maps are right fibrations. By Remark 6.4.2 the bottom horizontal map is an equivalence. It will hence suffice to show that (155) induces an equivalence on vertical fibres. Let \(g:{\mathcal {C}}_{\mathcal {I}}\rightarrow {{{\mathcal {C}}}'}\) be an exact functor and let \(g_{\mathcal {I}}= \{g_i\}:{\mathcal {I}}\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\) be its image in the bottom right corner of (155). To identify the fibre on the left side, let  be the composed functor, so that \(g_0\) corresponds to \(g_{\mathcal {I}}\) under the identification of functors \({\mathcal {I}}\rightarrow {\text {Fun}}({\mathcal {C}},{{{\mathcal {C}}}'})\) and functors \({\mathcal {C}}\times {\mathcal {I}}\rightarrow {{{\mathcal {C}}}'}\). In light of the definition of
be the composed functor, so that \(g_0\) corresponds to \(g_{\mathcal {I}}\) under the identification of functors \({\mathcal {I}}\rightarrow {\text {Fun}}({\mathcal {C}},{{{\mathcal {C}}}'})\) and functors \({\mathcal {C}}\times {\mathcal {I}}\rightarrow {{{\mathcal {C}}}'}\). In light of the definition of  via left Kan extensions and 2-excisive approximations we may identify the fibre of the left vertical arrow in (155) over g with
via left Kan extensions and 2-excisive approximations we may identify the fibre of the left vertical arrow in (155) over g with  , where \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) is the projection. The map between the vertical fibres in (155) can then be identified with the map of spaces
, where \(p_{{\mathcal {C}}}:{\mathcal {C}}\times {\mathcal {I}}\rightarrow {\mathcal {C}}\) is the projection. The map between the vertical fibres in (155) can then be identified with the map of spaces

whose i’th component  is given by restricting to \({\mathcal {C}}\times \{i\}\subseteq {\mathcal {C}}\times {\mathcal {I}}\). This map is an equivalence by Lemma 6.3.8, and so the proof is complete. \(\square \)
is given by restricting to \({\mathcal {C}}\times \{i\}\subseteq {\mathcal {C}}\times {\mathcal {I}}\). This map is an equivalence by Lemma 6.3.8, and so the proof is complete. \(\square \)
7.5 Finite tensors and cotensors
In this section we will consider the tensor and cotensor constructions in the case where the \(\infty \)-category \({\mathcal {I}}\) satisfies strong finiteness conditions, e.g., when \({\mathcal {I}}\) is a finite poset. In this case the tensor construction admits a more accessible description, and sends non-degenerate Poincaré \(\infty \)-categories to non-degenerate ones, with explicit induced duality, see Proposition 6.5.8. In addition, we will show that under these conditions the functor  is not only right adjoint to
is not only right adjoint to  , but also left adjoint to it, and extract some useful consequences. Finally, in this case both the tensor and cotensor constructions are functorial not only in maps \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\), but also in cofinal maps \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) going in the other direction, a phenomenon we refer to as exceptional functoriality, see Construction 6.5.14.
, but also left adjoint to it, and extract some useful consequences. Finally, in this case both the tensor and cotensor constructions are functorial not only in maps \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\), but also in cofinal maps \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) going in the other direction, a phenomenon we refer to as exceptional functoriality, see Construction 6.5.14.
To begin, recall that an \(\infty \)-category \({\mathcal {I}}\) is said to be finite if it is categorically equivalent to a simplicial set with only finitely many non-degenerate simplices. If \({\mathcal {I}}\) is a space then the condition that \({\mathcal {I}}\) is finite as an \(\infty \)-category is equivalent to the condition that \({\mathcal {I}}\) is finite as a space, that is, that it is weakly equivalent to a simplicial set with finitely many non-degenerate simplices. We will use the term finite (co)limits to refer to (co)limits indexed by finite \(\infty \)-categories. We recall that any stable \(\infty \)-category admits finite limits and colimits, and that these are preserved by any exact functor. In particular, in any stable \(\infty \)-category which admits small (co)limits, the latter automatically commute with finite (co)limits.
Definition 6.5.1
We will say that an \(\infty \)-category \({\mathcal {I}}\) is strongly finite if it is finite, and in addition for every \(i,j \in {\mathcal {I}}\) the mapping space \({\text {Map}}_{{\mathcal {I}}}(i,j)\) is finite.
Example 6.5.2
Any finite poset is strongly finite.
Example 6.5.3
Any Reedy category with finitely many objects and finitely many morphisms is strongly finite. This follows by induction from [43, Proposition A.2.9.14]. For example, the full subcategory \(\Delta _{\le n} \subseteq \Delta \) spanned by the ordinals [k] for \(k \le n\) is strongly finite.
Remark 6.5.4
If \({\mathcal {I}}\rightarrow {\mathcal {J}}\) is a cartesian or cocartesian fibration such that \({\mathcal {J}}\) is finite and the fibres \({\mathcal {I}}_j\) are finite for every \(j \in {\mathcal {J}}\) then \({\mathcal {I}}\) is finite. This follows from the explicit description of cartesian fibrations over the n-simplex via generalized mapping cones, see [43, §3.2.3]. It then follows that for a strongly finite \(\infty \)-category \({\mathcal {I}}\) the twisted arrow category \({\text {TwAr}}({\mathcal {I}})\) is finite. Similarly, if \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) is a functor between strongly finite \(\infty \)-categories then all the comma \(\infty \)-categories of \(\alpha \) are finite.
Remark 6.5.5
Any localisation of a finite \(\infty \)-category by a finite set of arrows is finite, since it can be written as a pushout of finite \(\infty \)-categories. In particular, if \({\mathcal {I}}\) is an \(\infty \)-category such that \({\text {TwAr}}({\mathcal {I}})\) is finite then \({\mathcal {I}}\) is finite, since \({\mathcal {I}}\) can be written as a localisation of \({\text {TwAr}}({\mathcal {I}})\) by a collection of arrows of the form \([f:x\rightarrow y] \rightarrow [\text {id} :x\rightarrow x]\) where f runs over a set of representatives of equivalence types in \({\text {TwAr}}({\mathcal {I}})\). Combining this with Remark 6.5.4 it follows that the condition that \({\mathcal {I}}\) is strongly finite is equivalent to the condition that \({\text {TwAr}}({\mathcal {I}})\) is finite and all mapping space in \({\mathcal {I}}\) are finite.
Lemma 6.5.6
Let \({\mathcal {I}}\) be a small \(\infty \)-category and \({\mathcal {C}}\) a stable \(\infty \)-category. Then the following holds:
-
i)
If the mapping spaces of \({\mathcal {I}}\) are finite then \({\mathcal {C}}_{\mathcal {I}}\) is contained in \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\).
-
ii)
If the twisted arrow category \({\text {TwAr}}({\mathcal {I}}^{\text {op} })\) is finite then \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\mathcal {C}})\) is contained in \({\mathcal {C}}_{\mathcal {I}}\).
In particular, if \({\mathcal {I}}\) is a strongly finite \(\infty \)-category then \({\mathcal {C}}_{{\mathcal {I}}} = {\text {Fun}}({\mathcal {I}}^{\text {op} },{\mathcal {C}})\) as full subcategories of \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\).
Remark 6.5.7
The objects \(R_{x,i}\) are cocompact in \({\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) and generate it under limits. Since \({\mathcal {C}}_{{\mathcal {I}}}\) is by definition the closure of \(R_{x,i}\) under finite limits it follows that the inclusion \({\mathcal {C}}_{{\mathcal {I}}} \subseteq {\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) induces an equivalence \({\text {Pro}}({\mathcal {C}}_{{\mathcal {I}}}) \simeq {\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\). When \({\mathcal {I}}\) is strongly finite Lemma 6.5.6 then gives an equivalence
This generalizes [43, Proposition 5.3.5.15] (in the case of \(\kappa =\omega \)) from finite posets to all strongly finite \(\infty \)-categories.
Proof of Lemma 6.5.6
To prove i) it will suffice to show that \({\mathcal {C}}^{{\mathcal {I}}^{\text {op} }}\), which is closed under finite limits in \({\text {Pro}}({\mathcal {C}})^{{\mathcal {I}}^{\text {op} }}\), contains the objects \(R_{i,x}\) for every \((i,x) \in {\mathcal {I}}\times {\mathcal {C}}\). Indeed \(R_{i,x}(j) = x^{{\text {Map}}_{\mathcal {I}}(i,j)}\) is contained in \({\mathcal {C}}\subseteq {\text {Pro}}({\mathcal {C}})\) since \(x\) is in \({\mathcal {C}}\), \({\text {Map}}_{\mathcal {I}}(i,j)\) is a finite space, and \({\mathcal {C}}\) is closed inside \({\text {Pro}}({\mathcal {C}})\) under finite limits.
Let us now prove ii). We need to show that if \({\text {TwAr}}({\mathcal {I}})^{\text {op} }\) is finite then any \({\mathcal {C}}\)-valued presheaf \(\varphi :{\mathcal {I}}^{\text {op} }\rightarrow {\mathcal {C}}\) is a finite limit of cofree presheaves of the form \(R_{i,x}\). But it is a standard fact that any presheaf \(\varphi \) is canonically the limit of the composed \({\text {TwAr}}({\mathcal {I}})^{\text {op} }\)-indexed diagram

which takes values in cofree presheaves. To see this note that the \({\text {TwAr}}({\mathcal {I}})^{\text {op} }\)-indexed family of maps \(c_{[i \rightarrow j]}:\varphi (j)\rightarrow \varphi (i)\) determines a \({\text {TwAr}}({\mathcal {I}})^{\text {op} }\)-indexed family of maps \(\varphi \Rightarrow R_{j,\varphi (i)}\), and hence a map
Evaluating at \(k \in {\mathcal {I}}^{\text {op} }\), the resulting map
is then seen to be an equivalence by the cofinality of the functors \({\text {TwAr}}({\mathcal {I}}_{/k})\xrightarrow {\text {dom} } {\mathcal {I}}_{/k} \leftarrow \{\text {id} _k\}\). \(\square \)
Proposition 6.5.8
Let \({\mathcal {I}}\) be a strongly finite \(\infty \)-category (e.g., any finite poset). Then under the identification
of Lemma 6.5.6, the quadratic functor  corresponds to the functor
corresponds to the functor

Its bilinear and linear parts are then given by

respectively. In addition, if  is non-degenerate then
is non-degenerate then  is non-degenerate with duality
is non-degenerate with duality

Proof of Proposition 6.5.8
The identification of  together with its linear and bilinear parts follows directly from Proposition 6.4.3 and Lemma 6.5.6. Now assume that
together with its linear and bilinear parts follows directly from Proposition 6.4.3 and Lemma 6.5.6. Now assume that  is non-degenerate. To prove the formula for the duality, we need to show that for diagrams \(\varphi ,\psi :{\mathcal {I}}^{\text {op} }\rightarrow {\mathcal {C}}\) there is an equivalence
is non-degenerate. To prove the formula for the duality, we need to show that for diagrams \(\varphi ,\psi :{\mathcal {I}}^{\text {op} }\rightarrow {\mathcal {C}}\) there is an equivalence
natural in \(\varphi ,\psi \), where \(\text {D} _{{\mathcal {I}}}\) is given by (157). Expanding the right hand side and using the standard formula for natural transformations we obtain

where we have used the finiteness of \({\text {TwAr}}({\mathcal {I}})\) and \({\text {Map}}_{\mathcal {I}}(-,-)\) to commute limits and colimits and the cofinality of the maps \({\text {TwAr}}({\mathcal {I}}_{k/}) \xrightarrow {\text {cod} } {\mathcal {I}}_{k/}^{\text {op} }\leftarrow \{\text {id} _k\}\). \(\square \)
We now turn our attention to some structural properties of the tensor and cotensor constructions which are special to the strongly finite case. Recall from Remark 6.4.10 that for a fixed \(\infty \)-category \({\mathcal {I}}\), the functor \((\) is right adjoint to the functor  . Our next goal is to show that when \({\mathcal {I}}\) is strongly finite the functor
. Our next goal is to show that when \({\mathcal {I}}\) is strongly finite the functor  is also left adjoint to the functor
is also left adjoint to the functor  . To exhibit this, consider for hermitian \(\infty \)-categories
. To exhibit this, consider for hermitian \(\infty \)-categories  the evaluation hermitian functor
the evaluation hermitian functor

from Construction 6.2.6. By the universal property of internal functor categories this transposes to a hermitian functor

and consequently induces for \({\mathcal {I}}\in \text {Cat} _\infty \) a hermitian functor

where we have used the equivalence of Remark 6.4.6. The resulting functor then transposes twice to give a hermitian functor

On the other hand, using the equivalence of Remark 6.4.7 the evaluation functor (158) induces a hermitian functor

which transposes to give a hermitian functor

Combining the above constructions we hence obtain a pair of hermitian functors

natural in  and \({\mathcal {I}}\) (indeed, all the operations used above have already been proven natural in Sects. 6.2, 6.3 and 6.4 through the various universal properties they encode).
and \({\mathcal {I}}\) (indeed, all the operations used above have already been proven natural in Sects. 6.2, 6.3 and 6.4 through the various universal properties they encode).
Proposition 6.5.9
If \({\mathcal {I}}\) is strongly finite then the hermitian functors in (159) are equivalences of hermitian \(\infty \)-categories. Passing to hermitian objects (see (139)) they then determine a natural equivalence

exhibiting \((-)^{{\mathcal {I}}}\) as left adjoint to \((-)_{{\mathcal {I}}}\).
Proof
To begin, we note that on the level of underlying stable \(\infty \)-categories both functors in (159) are equivalences by Lemma 6.5.6. Indeed, replacing \({\mathcal {I}}\) with \({\mathcal {I}}^{\text {op} }\) these identify with the equivalences of stable \(\infty \)-categories
underlying those of Remark 6.4.6. Explicitly, the equivalence on the left hand side of (160) associates to a diagram \(\varphi :{\mathcal {I}}^{\text {op} }\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\) the exact functor \(g_{\varphi }:{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}^{{\mathcal {I}}^{\text {op} }} = {{{\mathcal {C}}}'}_{{\mathcal {I}}}\) given by \([g_{\varphi }(x)](i) = \varphi _i(x)\). Unwinding the definitions, the hermitian structure of the left hand side functor in (159) is given by the map

which is indeed an equivalence since \({\mathcal {I}}\) is finite and  is an exact functor.
is an exact functor.
Similarly, the equivalence on the right hand side of (160) associates to a diagram \(\varphi :{\mathcal {I}}^{\text {op} }\rightarrow {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{{{\mathcal {C}}}'})\) an exact functor \(h_{\varphi }:{\mathcal {C}}_{{\mathcal {I}}^{\text {op} }}={\mathcal {C}}^{{\mathcal {I}}} \rightarrow {{{\mathcal {C}}}'}\) such that \(\varphi \) can be recovered from \(h_{\varphi }\) as \(\varphi _i(x) = h_{\varphi }(R_{i,x})\). Let us denote by \(\text {ev} _i:{\mathcal {C}}^{{\mathcal {I}}} \rightarrow {\mathcal {C}}\) the evaluation at \(i \in {\mathcal {I}}\) functor and by \(\text {ran} _i:{\mathcal {C}}\rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) its right adjoint, given by right Kan extension. In particular, we have \(\text {ran} _i(x) = R_{i,x}\) by definition. Unwinding the definitions, the hermitian structure of the right hand side functor in (159) is then given by the map

which is indeed an equivalence since \({\mathcal {I}}\) is finite and  is an exact functor.
is an exact functor.
\(\square \)
Corollary 6.5.10
Let \({\mathcal {I}}\) be a strongly finite \(\infty \)-category. Then the functor  from \(\text {Cat} ^{\textrm{h}}_\infty \) to itself preserves all limits and the functor
from \(\text {Cat} ^{\textrm{h}}_\infty \) to itself preserves all limits and the functor  preserves all colimits.
preserves all colimits.
Corollary 6.5.11
For a fixed strongly finite \(\infty \)-category \({\mathcal {I}}\), the functor  is internally corepresented by
is internally corepresented by  . More precisely, there is an equivalence of hermitian \(\infty \)-categories
. More precisely, there is an equivalence of hermitian \(\infty \)-categories

natural in  and \({\mathcal {I}}\).
and \({\mathcal {I}}\).
Corollary 6.5.12
For a strongly finite \(\infty \)-category \({\mathcal {I}}\) the following conditions are equivalent:
-
i)
the operation
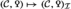 preserves Poincaré \(\infty \)-categories and Poincaré functors.
preserves Poincaré \(\infty \)-categories and Poincaré functors. -
ii)
the hermitian \(\infty \)-category
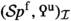 is Poincaré;
is Poincaré; -
iii)
the operation
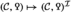 preserves Poincaré \(\infty \)-categories and Poincaré functors.
preserves Poincaré \(\infty \)-categories and Poincaré functors. -
iv)
the hermitian \(\infty \)-category
 is Poincaré;
is Poincaré;
In a similar spirit, we may deduce that the criterion for duality preservation of Proposition 6.3.18 holds for tensors as well in the strongly finite case:
Corollary 6.5.13
Let \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\) be a map of strongly finite \(\infty \)-categories and  a non-degenerate hermitian \(\infty \)-category. If the induced map \({\mathcal {I}}_{i/} \rightarrow {\mathcal {J}}_{\alpha (i)/}\) is cofinal for every \(i \in {\mathcal {I}}\) then the induced hermitian functor
a non-degenerate hermitian \(\infty \)-category. If the induced map \({\mathcal {I}}_{i/} \rightarrow {\mathcal {J}}_{\alpha (i)/}\) is cofinal for every \(i \in {\mathcal {I}}\) then the induced hermitian functor  is duality preserving. In particular, if
is duality preserving. In particular, if  and
and  are Poincaré then \((\alpha _*,\eta _{\alpha })\) is a Poincaré functor.
are Poincaré then \((\alpha _*,\eta _{\alpha })\) is a Poincaré functor.
Proof
Identify  with
with  as a functor of \({\mathcal {I}}\) using Corollary 6.5.11 and apply Proposition 6.3.18. \(\square \)
as a functor of \({\mathcal {I}}\) using Corollary 6.5.11 and apply Proposition 6.3.18. \(\square \)
We now describe some additional functoriality exhibited by the tensor and cotensor constructions in the strongly finite case.
Construction 6.5.14
(Exceptional functoriality) Let \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) be a functor between strongly finite \(\infty \)-categories. Then by Lemma 6.5.6 the full subcategory \({\mathcal {C}}_{{\mathcal {I}}} \subseteq {\text {Fun}}({\mathcal {I}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) is sent into \({\mathcal {C}}_{{\mathcal {J}}} \subseteq {\text {Fun}}({\mathcal {J}}^{\text {op} },{\text {Pro}}({\mathcal {C}}))\) by restriction along any functor \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\). On the cotensor side, the comma categories of \(\beta \) are all finite by Remark 6.5.4 and hence the operation of right Kan extension \(\beta _*:{\mathcal {C}}^{{\mathcal {J}}} \rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) exists for any stable \({\mathcal {C}}\). Now suppose that \(\beta \) is cofinal. Then we can refine \(\beta ^*:{\mathcal {C}}_{{\mathcal {I}}} \rightarrow {\mathcal {C}}_{{\mathcal {J}}}\) and \(\beta _*:{\mathcal {C}}^{{\mathcal {J}}} \rightarrow {\mathcal {C}}^{{\mathcal {I}}}\) to hermitian functors as follows. In the tensor case we simply note that the cofinality of \(\beta \) yields a natural equivalence

and so we obtain a hermitian functor  in which
in which  is an equivalence. For cotensors we consider the counit \(\beta ^*\beta _*\psi \Rightarrow \psi \) and use the coinitiality of \(\beta ^{\text {op} }\) to obtain a map
is an equivalence. For cotensors we consider the counit \(\beta ^*\beta _*\psi \Rightarrow \psi \) and use the coinitiality of \(\beta ^{\text {op} }\) to obtain a map

giving a hermitian refinement  .
.
Example 6.5.15
A common source of cofinal maps are maps \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) which admit a left adjoint \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\). Unwinding the definitions and using Remarks 6.3.12 and 6.4.9, we see that in this case the exceptional hermitian functors \((\beta ^*,\vartheta ^{\beta })\) and \((\beta _*,\vartheta _{\beta })\) of Construction 6.5.14 coincide with the direct hermitian functors \((\alpha _*,\eta _{\alpha })\) and \((\alpha ^*,\eta ^{\alpha })\), respectively.
Remark 6.5.16
Let \({\mathcal {I}},{\mathcal {J}}\) be two strongly finite \(\infty \)-categories and  a Poincaré \(\infty \)-category. The identification
a Poincaré \(\infty \)-category. The identification

of Remark 6.4.6, being natural in \({\mathcal {I}}\), identifies, for every map \(\alpha :{\mathcal {I}}\rightarrow {\mathcal {J}}\), the associated hermitian functor  with the one induced from
with the one induced from  upon taking internal functor categories to
upon taking internal functor categories to  . Similarly, the identification
. Similarly, the identification

of Corollary 6.5.11 identifies the hermitian functor  with the one induced from
with the one induced from  . Unravelling all definitions, and observing the similarity between the formulas for the direct and exceptional functorialities, we see that the equivalence (161) also identifies for every \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) the exceptional hermitian functor
. Unravelling all definitions, and observing the similarity between the formulas for the direct and exceptional functorialities, we see that the equivalence (161) also identifies for every \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) the exceptional hermitian functor  with the one induced from the exceptional functor
with the one induced from the exceptional functor  upon taking internal functor categories to
upon taking internal functor categories to  , and similarly the equivalence (162) also identifies the exceptional hermitian functor
, and similarly the equivalence (162) also identifies the exceptional hermitian functor  with the one induced from
with the one induced from  .
.
Remark 6.5.17
Like the ordinary functoriality of the tensor and cotensor constructions, the exceptional functorialities are compatible with composition. More precisely, if \({\mathcal {K}}\xrightarrow {\beta '} {\mathcal {J}}\xrightarrow {\beta } {\mathcal {I}}\) are a pair of composable cofinal maps then the hermitian functor  is naturally equivalent to the composite of \((\beta ^*,\vartheta ^{\beta })\) and \(((\beta ')^*,\vartheta ^{\beta '})\) and the hermitian functor
is naturally equivalent to the composite of \((\beta ^*,\vartheta ^{\beta })\) and \(((\beta ')^*,\vartheta ^{\beta '})\) and the hermitian functor  is naturally equivalent to the composite of \((\beta _*,\vartheta _{\beta })\) and \((\beta '_*,\vartheta _{\beta '})\). Indeed, by Remark 6.5.16 it will suffice to check this for the tensor construction, where it amounts to the fact the Beck–Chevalley transformation relating restriction and colimits is compatible with composition of restriction maps.
is naturally equivalent to the composite of \((\beta _*,\vartheta _{\beta })\) and \((\beta '_*,\vartheta _{\beta '})\). Indeed, by Remark 6.5.16 it will suffice to check this for the tensor construction, where it amounts to the fact the Beck–Chevalley transformation relating restriction and colimits is compatible with composition of restriction maps.
Remark 6.5.18
Comparing the explicit formulas of the direct and exceptional functorialities we see that if \(\beta :{\mathcal {J}}\rightarrow {\mathcal {I}}\) is a cofinal map then the resulting hermitian structure on the exceptional-direct composite  is given by the map
is given by the map

induced by the counit \(\beta ^*\beta _*\psi \Rightarrow \psi \). Similarly, the resulting hermitian structure on the direct-exceptional composite  is induced by the counit of
is induced by the counit of  in a similar manner. In particular, if \(\beta \) is fully-faithful then these counits are equivalences, in which case we get that the exceptional functoriality of \(\beta \) gives a one sided inverse to its direct functoriality. More generally, it can be checked that for any cofinal \(\beta \) the exceptional functoriality \((\beta _*,\vartheta _{\beta })\) is right adjoint to the direct functoriality \((\beta ^*,\eta ^{\beta })\), and the exceptional functoriality \((\beta ^*,\vartheta ^{\beta })\) is left adjoint to the direct functoriality \((\beta _*,\eta _{\beta })\), when these terms are understood with respect to the \((\infty ,2)\)-categorical structure of \(\text {Cat} ^{\textrm{h}}_\infty \) determined by the internal functor categories of Sect. 6.2.
in a similar manner. In particular, if \(\beta \) is fully-faithful then these counits are equivalences, in which case we get that the exceptional functoriality of \(\beta \) gives a one sided inverse to its direct functoriality. More generally, it can be checked that for any cofinal \(\beta \) the exceptional functoriality \((\beta _*,\vartheta _{\beta })\) is right adjoint to the direct functoriality \((\beta ^*,\eta ^{\beta })\), and the exceptional functoriality \((\beta ^*,\vartheta ^{\beta })\) is left adjoint to the direct functoriality \((\beta _*,\eta _{\beta })\), when these terms are understood with respect to the \((\infty ,2)\)-categorical structure of \(\text {Cat} ^{\textrm{h}}_\infty \) determined by the internal functor categories of Sect. 6.2.
7.6 Finite complexes and Verdier duality
In this final section we explore the particular case when \({\mathcal {I}}\) is the poset of simplices of a finite simplicial complex. In this context the tensor construction plays a central role in [45], where its duality functor is identified as a form of Verdier duality. Filling in the details in some of the arguments of loc. cit., we will show that tensoring and cotensoring by the poset of faces of a finite simplicial complex preserves Poincaré \(\infty \)-categories, and that the hermitian functors associated to maps of simplicial complexes (direct functoriality) and refinements of triangulations (exceptional functoriality) are Poincaré.
Recall that a finite simplicial complex K consists of a finite set of vertices \(K_0\) and a collection \({\mathcal {I}}_{K}\) of non-empty subsets \(S \subseteq K_0\), called faces, which contain all singletons and are downwards closed in the sense that if S is a face of K and \(S'\subseteq S\) then \(S'\) is a face of K as well. The dimension of a face S is by definition \(\dim (S) := |S|-1\). We may realise a simplicial complex K geometrically as the subspace |K| of the full simplex on \(K_0\) obtained as the union of the given faces. For a finite simplicial complex K we will consider \({\mathcal {I}}_K\) as a poset, and consequently a category, by inverse inclusion, that is, there is a unique morphism \(S \rightarrow S'\) if \(S'\subseteq S\). A map of simplicial complexes \(K \rightarrow L\) is by definition a map of sets \(K_0 \rightarrow L_0\) which sends every face of K to a face of L. In particular, such a map determines a map of posets \(\alpha :{\mathcal {I}}_{K} \rightarrow {\mathcal {I}}_{L}\). If K is a simplicial complex then a refinement of K consists of a simplicial complex L together with a homeomorphism \(|L| \xrightarrow {\cong } |K|\) which carries the realisation of every face of L into the realisation of a face of K, and such that the realisation of every face of K in |K| is a union of faces of L. We note that such a homeomorphism determines in particular a map of posets \(\beta :{\mathcal {I}}_L \rightarrow {\mathcal {I}}_K\) which sends every face of L to the face of K containing it under the homeomorphism \(|L| \cong |K|\).
Proposition 6.6.1
([45, Lecture 19, Proposition 3]) Let  be a Poincaré \(\infty \)-category and K a finite simplicial complex with poset of faces \({\mathcal {I}}_K\). Then the hermitian \(\infty \)-categories
be a Poincaré \(\infty \)-category and K a finite simplicial complex with poset of faces \({\mathcal {I}}_K\). Then the hermitian \(\infty \)-categories  and
and  are Poincaré.
are Poincaré.
Proof
By Corollary 6.5.12 it will suffice to prove the claim for  . We need to show that for every \(\varphi \in {\mathcal {C}}_{{\mathcal {I}}_K}\) the map
. We need to show that for every \(\varphi \in {\mathcal {C}}_{{\mathcal {I}}_K}\) the map
is an equivalence. To do so it suffices to show it for a system of objects that generate under colimits. We choose the set \(\varphi =R_{x,S}\) for \(S\in {\mathcal {I}}_K\) and \(x\in {\mathcal {C}}\). Now the face S corresponds to an injective map of simplicial complexes \(\Delta ^n \rightarrow K\) which in turn determines an inclusion of posets \(\alpha :{\mathcal {I}}_{\Delta ^n} \subseteq {\mathcal {I}}_K\) such that \(\alpha ([n]) =S\) and \(R_{x,S}\) is the right Kan extension along \(\alpha ^{\text {op} }\) of the constant diagram \(\varphi _{x}:{\mathcal {I}}_{\Delta ^n}^{\text {op} }\rightarrow {\mathcal {C}}\) with value \(x\). Now the map \(\alpha \) satisfies the hypothesis of Corollary 6.5.13 (in fact, the map that needs to be cofinal is an isomorphism of posets, see also Proposition 6.6.2 below), and so the hermitian functor \((\alpha _*,\eta _{\alpha }):{\mathcal {C}}_{{\mathcal {I}}_{\Delta ^n}} \rightarrow {\mathcal {C}}_{{\mathcal {I}}_K}\) is duality preserving. We can hence reduce to the case of \(K=\Delta ^n\) and \(\varphi =\varphi _x\). Using Proposition 6.5.8 we now have

To calculate this colimit let us denote by \(\iota :{\mathcal {I}}^S_{\Delta ^n} \subseteq {\mathcal {I}}_{\Delta ^n}\) the subposet spanned by those \(T \subseteq [n]\) such that  . Then the functor whose colimit is calculated in (164) can be identified with the cofibre of the map \(\iota ^*\iota _!\varphi _x \rightarrow \varphi _x\), and so we get that
. Then the functor whose colimit is calculated in (164) can be identified with the cofibre of the map \(\iota ^*\iota _!\varphi _x \rightarrow \varphi _x\), and so we get that
Now since \({\mathcal {I}}^S_{\Delta ^n}\) is closed under subfaces in \({\mathcal {I}}_{\Delta ^n}\) it corresponds to some subcomplex \(\Delta ^n\), which we readily identify as the join \(\partial \Delta ^S *\Delta ^{S'}\), where \(S'= [n]- S\) is the complement of S, and we have used the notation \(\Delta ^S\) and \(\Delta ^{S'}\) to denote the corresponding faces, considered as subcomplexes. The poset \({\mathcal {I}}^S_{\Delta ^n}\) is hence weakly contractible if \(S' \ne \emptyset \), that is, if \(S \ne [n]\), and is weakly equivalent to \(\partial \Delta ^n\) if \(S=[n]\). We thus conclude that
By the same argument we then have

so that \(\text {D} _{{\mathcal {I}}_{\Delta ^n}}\text {D} _{{\mathcal {I}}_{\Delta ^n}}\varphi _{x}\) is constant with value \(\Sigma ^n\text {D} \Sigma ^n\text {D} x\simeq x\), and is in particular equivalent to \(\varphi _{x}\). We need however to make sure that specifically the evaluation map is an equivalence. Since both \(\text {D} _{{\mathcal {I}}_{\Delta ^n}}\text {D} _{{\mathcal {I}}_{\Delta ^n}}\varphi _{x}\) and \(\varphi _{x}\) are constant it will suffice to show that the component of the evaluation map at \(S=[n]\) is an equivalence. Unwinding the definitions, this is the composed map
whose component at level \(T'\) is 0 for \(T'\ne [n]\) and is the inclusion of the \(T=[n]\) component in the colimit otherwise. The invertibility of this map then reduces to the fact that in a stable \(\infty \)-category an n-cube is cartesian if and only if it is cocartesian. \(\square \)
The perfectness of hermitian structures asserted in Proposition 6.6.1 is accompanied by the following duality preservation statement:
Proposition 6.6.2
[45, Lecture 19] Let  be a Poincaré \(\infty \)-category.
be a Poincaré \(\infty \)-category.
-
i)
If \(K \rightarrow L\) is a map of finite simplicial complexes with \(\alpha :{\mathcal {I}}_K \rightarrow {\mathcal {I}}_L\) the induced map of posets of faces then the induced hermitian functors
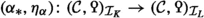 and
and 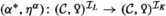 are Poincaré.
are Poincaré. -
ii)
If L is a refinement of a simplicial complex K and \(\beta :{\mathcal {I}}_{L} \rightarrow {\mathcal {I}}_{K}\) is the associated map of posets of faces then \(\beta \) is cofinal and the exceptional hermitian functors
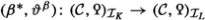 and
and 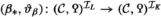 are Poincaré.
are Poincaré.
Proof
By Remark 6.5.16 it will suffice to prove the tensor case. For the first statement we observe that the functor \(\alpha :{\mathcal {I}}_{K} \rightarrow {\mathcal {I}}_{L}\) satisfies the criterion of Corollary 6.5.13, since for every face \(S \in {\mathcal {I}}_{K}\) the functor \(({\mathcal {I}}_{K})_{S/} \rightarrow ({\mathcal {I}}_{L})_{\alpha (S)/}\) admits a left adjoint sending \(T \subseteq \alpha (S)\) to its inverse image in S.
To prove the second statement, we begin by showing that \(\beta \) is cofinal. Indeed for any simplex \(S\in {{\mathcal {I}}_K}\) the poset \({{\mathcal {I}}_L}\times _{{\mathcal {I}}_K} ({\mathcal {I}}_K)_{S/}\) has geometric realisation homeomorphic to a simplex and so it is weakly contractible. To prove that \((\beta ^*,\vartheta ^{\beta })\) is Poincaré, it will suffice to show that for every generator \(R_{x,S} \in {\mathcal {C}}_{{\mathcal {I}}_K}\) the associated map
is an equivalence. Now the face S corresponds to an injective map of simplicial complexes \(\Delta ^S \rightarrow K\) (where \(\Delta ^S\) denotes the full simplex with vertex set S), which in turn determines an inclusion of posets \(\alpha :{\mathcal {I}}_{\Delta ^S} \subseteq {\mathcal {I}}_K\) such that \(R_{x,S}\) is the right Kan extension along \(\alpha \) of the constant diagram \(\varphi _{x}:{\mathcal {I}}_{\Delta ^S} \rightarrow {\mathcal {C}}\) with value \(x\). The inverse image of \({\mathcal {I}}_{\Delta ^S}\) in \({\mathcal {I}}_L\) then determines a subcomplex \(L_S \subseteq L\) which is a refinement of \(\Delta ^S\).
Let us denote by \(\beta _S:{\mathcal {I}}_{L_S} \rightarrow {\mathcal {I}}_{\Delta ^S}\) the induced refinement map and by \(\widetilde{\alpha }:{\mathcal {I}}_{L_S} \hookrightarrow {\mathcal {I}}_L\) the inclusion. Since \({\mathcal {I}}_{\Delta ^S}\) and \({\mathcal {I}}_{L_S}\) are downward closed the pointwise formula for right Kan extensions implies that the square

commutes. Since the vertical hermitian functors are Poincaré by the first part we may reduce to the case where K is the n-simplex \(\Delta ^n\), L is some refinement of \(\Delta ^n\), and \(\varphi = \varphi _{x}\). Now for \(T \in {\mathcal {I}}_L\) let us denote by \({\mathcal {I}}^T_L \subseteq {\mathcal {I}}_L\) the subposet spanned by those faces which do not contain T, and by \({\mathcal {J}}^T_L \subseteq {\mathcal {I}}^T_L\) the subposet spanned by those faces whose image in \({\mathcal {I}}_K\) does not contain \(\beta (T)\). We note that both of these subposets are downward closed and correspond to subcomplexes of L. In particular, \({\mathcal {I}}^T_L\) corresponds to the subcomplex \(L^T \subseteq L\) obtained by removing all faces which contain T, and \({\mathcal {J}}^T_L\) corresponds to the subcomplex \(L^T_0 \subseteq L^T\) obtained by removing all faces whose image in K contains T. We also note that \(L^T_0\) is a refinement of the subcomplex \(\partial \Delta ^{\beta (T)} *\Delta ^{[n]-\beta (T)} \subseteq \Delta ^n\) obtained from \(\Delta ^n\) by removing all the faces which contain \(\beta (T)\). Calculating as in the proof of Proposition 6.6.1 and using that refinement maps are cofinal as established above we may identify the cofibre of the map
for \(T \in {\mathcal {I}}_L\) with the total cofibre of the square

To finish the proof it will hence suffice to show that \(|L^0_T| \rightarrow |L_T|\) is a weak homotopy equivalence. Let \(p \in |\Delta ^n|\) be a point in the interior of the face T (and hence also in the interior of the face \(\beta (T)\)). Then we have a sequence of inclusions \( |L^0_T| \subseteq |L_T| \subseteq U \) where \(U \subseteq |\Delta ^n|\) is the complement of p. The desired result now follows from the fact that both \(|L^0_T| \subseteq U\) and \(|L_T| \subseteq U\) are deformation retracts; this is a general property of simplicial complexes: if one removes a point from the realisation of a simplicial complex then the result deformation retracts to the subcomplex spanned by all the simplices which do not contain that point. \(\square \)
8 Hyperbolic and metabolic Poincaré categories
From a conceptual view point, it is arguably tempting to regard hermitian structures on stable \(\infty \)-categories as categorified versions of hermitian forms on modules. Similarly, Poincaré \(\infty \)-categories correspond to modules equipped with a unimodular hermitian form. Inspired by this informal perspective, in this section we identify a surprisingly comprehensive variety of such categorified counterparts, including the categorified analogues of bilinear forms, perfect bilinear forms, hyperbolic objects, metabolic objects and the algebraic Thom construction. Beyond its conceptually pleasing effect, it turns out that many of the constructions encountered via this perspective give explicit left and right adjoints to various natural functors, a feature which we will repeatedly exploit in subsequent instalments of this project. In particular, the main practical outcomes of our categorified stroll will include the following:
-
i)
After exploring the categorified counterparts of bilinear forms in Sect. 7.2, we deduce that the association \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) described in Sect. 2.2 is both left and right adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \), with unit and counit given on the side of \(\text {Cat} ^{\textrm{p}}_\infty \) by the Poincaré functors
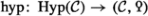 and
and 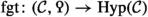 described in Sect. 2.2. In addition, we show that \({\text {Hyp}}\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the \(\text {op} \) action on \(\text {Cat} _\infty ^\text {ex} \) and the trivial action on \(\text {Cat} ^{\textrm{p}}_\infty \), and that \(\text {hyp} \) and \(\text {fgt} \) are equivariant natural transformations. All this information is best organised in the setting of \({{\text {C} }_{\textrm{2}}}\)-categories and Mackey functors, which we explore in Sect. 7.4. This will also be the basis for our organization in Paper [2] of algebraic \({\text {K}}\)-theory, Grothendieck-Witt theory and \({\text {L}}\)-theory into a single functor taking values in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, which we call the real \({\text {K}}\)-theory spectrum.
described in Sect. 2.2. In addition, we show that \({\text {Hyp}}\) is \({{\text {C} }_{\textrm{2}}}\)-equivariant with respect to the \(\text {op} \) action on \(\text {Cat} _\infty ^\text {ex} \) and the trivial action on \(\text {Cat} ^{\textrm{p}}_\infty \), and that \(\text {hyp} \) and \(\text {fgt} \) are equivariant natural transformations. All this information is best organised in the setting of \({{\text {C} }_{\textrm{2}}}\)-categories and Mackey functors, which we explore in Sect. 7.4. This will also be the basis for our organization in Paper [2] of algebraic \({\text {K}}\)-theory, Grothendieck-Witt theory and \({\text {L}}\)-theory into a single functor taking values in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, which we call the real \({\text {K}}\)-theory spectrum. -
ii)
While forming the categorified analogue of metabolic objects, Lagrangians, and the algebraic Thom construction in Sect. 7.3, we deduce an explicit formula for the left and right adjoints to the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \). This will be exploited in Paper [2] when setting up the framework of algebraic surgery in the context of Poincaré \(\infty \)-categories, and in analysing the effect of additive and bordism invariant functors applied to the \({\text {Q}}\)-construction. We will also use it in Paper [4] for constructing the localised analogue of the Grothendieck-Witt spectrum and for proving that \(\text {Cat} ^{\textrm{p}}_\infty \) is compactly generated.
The present section is organised as follows. We begin in Sect. 7.1 with some preliminary material on bifibrations, a notion used for encoding space valued bifunctors which are covariant in one entry and contravariant in the other. By translating results from [47, §5.2.1] to the context of bifibrations we deduce in particular that the \(\infty \)-category of perfect symmetric bifibrations is equivalent to \(\text {Cat} _\infty ^{{{\text {hC} }_{\textrm{2}}}}\). In Sect. 7.2 we specialise to the setting of stable \(\infty \)-categories and replace space valued bifunctors by spectrum valued ones. This leads to the notion of bilinear \(\infty \)-categories as analogous of pairs of modules equipped with a bilinear form. We also consider the variants of requiring the form to be perfect and/or symmetric, and identify, using Sect. 7.1, the notion of a perfect symmetric \(\infty \)-category with that of a stable \(\infty \)-category equipped with a perfect duality. All these notions accept natural forgetful functors from either \(\text {Cat} ^{\textrm{p}}_\infty \) (in the perfect case) or \(\text {Cat} ^{\textrm{h}}_\infty \). Studying all of them on equal footing allows one to efficiently identify left and right adjoints to these forgetful functors, which constitutes the main content of Sect. 7.2. In particular, we will see that the association \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) described in Sect. 2.2 gives a two-sided adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \). In Sect. 7.3 we discuss the categorified analogous of metabolic objects and Lagrangians, and show that the categorified analogue of the Thom construction enables one to produce both a left and a right adjoint to the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \). We also prove a generalization of the non-categorified Thom construction, thus providing in particular a proof for Proposition 2.4.3 which was stated in Sect. 2.4. Finally, in Sect. 7.4 we discuss \({{\text {C} }_{\textrm{2}}}\)-categories and Mackey functors, and show how to view various players in the present paper in that context. In particular, we show that the relations between quadratic and bilinear functors, between hermitian and bilinear \(\infty \)-categories, and between Poincaré and stable \(\infty \)-categories, can all be understood on the same footing, giving another take on the categorified perspective. The results of Sect. 7.4 will be primarily used in Paper [2] in order to define the real \({\text {K}}\)-theory spectrum, but the \({{\text {C} }_{\textrm{2}}}\)-equivariant properties of the hyperbolic construction resulting from it are useful for a variety of other purposes as well.
8.1 Preliminaries: pairings and bifibrations
Let \({\mathcal {A}},{\mathcal {B}}\) be two \(\infty \)-categories. By a correspondence on the pair \(({\mathcal {A}},{\mathcal {B}})\) we will simply mean a functor \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\). In particular, we think of a correspondence as a space valued functor on pairs \((x,y)\) with \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\), which is contravariant in \(x\) and covariant in y. The prototypical example to have in mind is taking \({\mathcal {A}}= {\mathcal {B}}= {\mathcal {C}}\) for some \(\infty \)-category \({\mathcal {C}}\), with \(b(x,y) = {\text {Map}}_{{\mathcal {C}}}(x,y)\). Given a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) and \(y\in {\mathcal {B}}\), evaluation at \(y\) yields a presheaf of spaces \(b(-,y)\) on \({\mathcal {A}}\), which we can unstraighten to obtain a right fibration
Since the presheaf \(b(-,y) \in {\text {Fun}}({\mathcal {A}}^{\text {op} },{\mathcal {S}})\) depends functorially on \(y\), so does the domain of (165). In fact, we can identify the arrow (165) with the map \(\int ^{x\in {\mathcal {A}}} b(x,y) \rightarrow \int ^{x\in {\mathcal {A}}}*\) associated to the terminal map of correspondences \(b \rightarrow *\), and so the entire arrow (165) depends functorially on \(y\). Equivalently, we may view it as a natural transformation between two \(\text {Cat} _\infty \)-valued functors on \({\mathcal {B}}\), the second of which is constant with value \({\mathcal {A}}\). We then define
to be the \(\infty \)-category over \({\mathcal {A}}\times {\mathcal {B}}\) obtained by unstraightening (165) over \({\mathcal {B}}\). The \(\infty \)-category \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) can informally be described as having objects triples \((x,y,\beta )\) where \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) are objects and \(\beta \in b(x,y)\) is a b-valued pairing on \(x\) and \(y\). A map from \((x,y,\beta )\) to \((x',y',\beta ')\) is then given by maps \(f:x\rightarrow x',g:y\rightarrow y'\) and a homotopy \(\eta :g_*\beta \sim f^*\beta ' \in b(x,y')\), where \(f^*\) and \(g_*\) encode the contravariant and covariant dependence of b on \(x\) and \(y\), respectively.
We point out that since the above construction involves both the cartesian unstraightening \(\int ^{x\in {\mathcal {A}}}\) and the cocartesian straightening \(\int _{y\in {\mathcal {B}}}\), the resulting arrow in (166) is neither a cartesian nor a cocartesian fibration. We can nonetheless describe it as follows: recall that a bifibration (see [43, Definition 2.4.7.2]) is a pair of maps
consisting of a cartesian fibration \(q:{\mathcal {X}}\rightarrow {\mathcal {A}}\) and a cocartesian fibration \(p:{\mathcal {X}}\rightarrow {\mathcal {B}}\), such that the q-cartesian edges are exactly those projecting to equivalences in \({\mathcal {B}}\) and the p-cocartesian edges are exactly those projecting to equivalences in \({\mathcal {A}}\). Equivalently, the pair of maps p, q forms a bifibration if and only if \((q,p):{\mathcal {X}}\rightarrow {\mathcal {A}}\times {\mathcal {B}}\) is a map of cocartesian fibrations over \({\mathcal {B}}\) whose fibres are right fibrations, and if and only if \((q,p):{\mathcal {X}}\rightarrow {\mathcal {A}}\times {\mathcal {B}}\) is map of cartesian fibrations over \({\mathcal {A}}\) whose fibres are left fibrations. In particular, one readily verifies that for a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\), the pair of projections
constitutes a bifibration. In fact, this association determines an equivalence between correspondences \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) and bifibrations \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) (see [64] and [7, §4]), and can be considered as a bivariant form of the space-valued straightening-unstraightening equivalence. In particular, using the coherent compatibility of the straightening-unstraightening equivalence with base change as established in [23, Corollary A.31], this equivalence integrates to an equivalence
where \(\text {BiFib} \subseteq {\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\) is the full subcategory spanned by the bifibrations.
Example 7.1.1
In the case of \({\mathcal {B}}={\mathcal {A}}={\mathcal {C}}\) and the canonical correspondence \(m_{{\mathcal {C}}} := {\text {Map}}_{{\mathcal {C}}}(-,-):{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}\rightarrow {\mathcal {S}}\), the \(\infty \)-category \({\text {Pair}}({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\) canonically identifies with the arrow category \({\text {Ar}}({\mathcal {C}}) := {\text {Fun}}(\Delta ^1,{\mathcal {C}})\).
Remark 7.1.2
The notion of a correspondence \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) can equivalently be encoded by a right fibration \({\mathcal {M}}\rightarrow {\mathcal {A}}\times {\mathcal {B}}^{\text {op} }\). Right fibrations of this form were studied in [47, §5.2.1] under the name pairings. In particular, the \(\infty \)-category \(\text {CPair}\) of [47, Construction 5.2.1.14] of pairings is naturally equivalent to \(\text {BiFib} \), since both are equivalent to \(\int ^{{\mathcal {A}},{\mathcal {B}}\in \text {Cat} _\infty }{\text {Fun}}({\mathcal {A}}^{\text {op} }\times {\mathcal {B}},{\mathcal {S}})\). Under this equivalence, the canonical bifibration \({\mathcal {C}}\leftarrow {\text {Ar}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\) of Example 7.1.1 encoding the mapping space correspondence corresponds to the right fibration \({\text {TwAr}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\).
Remark 7.1.3
The notion of a bifibration was generalised in [26, 27] to that of an orthofibration, which the authors show encodes the data of a functor \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow \text {Cat} _\infty \). In particular, an explicit dualisation procedure transforming an orthofibration over \({\mathcal {A}},{\mathcal {B}}\) to that of a cartesian fibration over \({\mathcal {A}}\times {\mathcal {B}}^{\text {op} }\) is constructed in loc. cit.; when applied in the case of bifibrations, this enables one to identify them directly with pairings as in Remark 7.1.2 without passing through straightening and unstraightening. For example, this dualisation procedure shows directly that the bifibration \({\mathcal {C}}\leftarrow {\text {Ar}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\) corresponds to the right fibration \({\text {TwAr}}({\mathcal {C}}) \rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\). The machinery of [27] also shows that the identification of functors \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow \text {Cat} _\infty \) with orthofibrations (and hence of functors \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) with bifibrations), is independent of whether we first unstraighten the contravariant part, and then covariant one (as we did above), or the other way around.
Definition 7.1.4
We say that a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is right-representable if the associated map \({\mathcal {B}}\rightarrow {\text {Psh}}({\mathcal {A}})\) factors through the image of the Yoneda embedding \(\iota :{\mathcal {A}}\hookrightarrow {\text {Psh}}({\mathcal {A}})\). In this case the resulting functor \(d:{\mathcal {B}}\rightarrow {\mathcal {A}}\) is characterised by a natural equivalence \({\text {Map}}_{{\mathcal {A}}}(x,d(y)) \simeq b(x,y)\).
Remark 7.1.5
If a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is right-representable then \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) naturally identifies with the fibre product \({\text {Ar}}({\mathcal {A}}) \times _{{\mathcal {A}}} {\mathcal {B}}\) along the target projection \({\text {Ar}}({\mathcal {A}}) \rightarrow {\mathcal {A}}\) and \(d:{\mathcal {B}}\rightarrow {\mathcal {A}}\). More generally, if we Yoneda embed \({\mathcal {A}}\) in \({\text {Psh}}({\mathcal {A}}) = {\text {Fun}}({\mathcal {A}}^{\text {op} },{\mathcal {S}})\), then b becomes tautologically right representable by the functor \(\widetilde{d}:{\mathcal {B}}\rightarrow {\text {Psh}}({\mathcal {A}})\) sending \(y\in {\mathcal {B}}\) to \(b(-,y) \in {\text {Psh}}({\mathcal {A}})\). We may then write
where the fibre product is taken along the Yoneda embedding \({\mathcal {A}}\rightarrow {\text {Psh}}({\mathcal {A}})\) and \(\widetilde{d}:{\mathcal {B}}\rightarrow {\text {Psh}}({\mathcal {B}})\), and \({\text {Ar}}({\text {Psh}}({\mathcal {A}}))\) projects to the domain on the left hand side and to the target on the right hand side.
Definition 7.1.6
We say that a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is perfect if b is right-representable and the associated representing functor \(d:{\mathcal {B}}\rightarrow {\mathcal {A}}\) is an equivalence. In this case, we say that a pairing \((x,y,\beta ) \in {\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) is perfect if the map \(x\rightarrow d(y)\) determined by \(\beta \) is an equivalence. Similarly, we say that a bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) is perfect if its classifying correspondence \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is. In this case we say that an object in \({\mathcal {X}}\) is perfect if it corresponds to a perfect pairing under the identification of \({\mathcal {X}}\) with \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\). We then say that a map of bifibration
is perfect if it sends perfect objects of \({\mathcal {X}}\) to perfect objects of \({\mathcal {X}}'\). We denote by \({\hbox {BiFib}^{\textrm{p}}}\subseteq \text {BiFib} \) the (non-full) subcategory spanned by the perfect bifibrations and the perfect maps between them.
While \({\hbox {BiFib}^{\textrm{p}}}\subseteq \text {BiFib} \) is not a full subcategory, it does satisfy the following weaker property [46, Definition 20.1.1.2]:
Definition 7.1.7
Let \({\mathcal {C}}\) be an \(\infty \)-category and \({\mathcal {C}}' \subseteq {\mathcal {C}}\) a subcategory. We say that \({\mathcal {C}}'\) is replete if for every \(x\in {\mathcal {C}}'\) and \(y\in {\mathcal {C}}\) such that there is an equivalence \(\alpha :x\xrightarrow {\simeq }y\) in \({\mathcal {C}}\), then \(y\in {\mathcal {C}}'\) and there exists an equivalence \(\beta :x\xrightarrow {\simeq } y\) in \({\mathcal {C}}'\) whose image in \({\mathcal {C}}\) is homotopic to \(\alpha \).
Remark 7.1.8
The condition of being a replete subcategory \({\mathcal {C}}'\subseteq {\mathcal {C}}\) is detected on the level of the homotopy categories: it is equivalent to saying that \({\text {Ho}}{\mathcal {C}}'\) is closed under isomorphisms and for every \(x,y\in {\mathcal {C}}'\) the subset \({\text {Hom}}_{{\text {Ho}}{\mathcal {C}}'}(x,y) \subseteq {\text {Hom}}_{{\text {Ho}}{\mathcal {C}}}(x,y)\) contains all isomorphisms from \(x\) to \(y\) in \({\mathcal {C}}\).
Example 7.1.9
The subcategory \({\hbox {BiFib}^{\textrm{p}}}\subseteq \text {BiFib} \) is replete. This follows from the observation that any equivalence between perfect bifibrations is necessarily a perfect map.
Example 7.1.10
The subcategory \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty \) is replete.
Remark 7.1.11
For any subcategory \({\mathcal {C}}'\subseteq {\mathcal {C}}\) the induced map \({\text {Map}}_{{\mathcal {C}}'}(x,y) \rightarrow {\text {Map}}_{{\mathcal {C}}}(x,y)\) is a \((-1)\)-truncated map of spaces for every \(x,y\in {\mathcal {C}}'\), that is, its fibres are either empty or contractible. If the subcategory \({\mathcal {C}}'\) is replete then the induced map \(\iota {\mathcal {C}}'\rightarrow \iota {\mathcal {C}}\) on core groupoids is also \((-1)\)-truncated. This implies that every replete subcategory inclusion \({\mathcal {C}}' \hookrightarrow {\mathcal {C}}\) is \((-1)\)-truncated as a map in \(\text {Cat} _\infty \), that is, for every test \(\infty \)-category \({\mathcal {D}}\) the induced map
is \((-1)\)-truncated. In many contexts, this property is what makes replete subcategories behave more like “subobjects” than general subcategories.
The following proposition records the content of [47, Remark 5.2.1.20] in the context of bifibrations:
Proposition 7.1.12
The composite

is an equivalence of \(\infty \)-categories. An inverse is given by \({\mathcal {C}}\mapsto [{\mathcal {C}}\leftarrow {\text {Ar}}({\mathcal {C}}) \rightarrow {\mathcal {C}}]\).
Proof
Since the association \({\mathcal {C}}\mapsto [{\mathcal {C}}\leftarrow {\text {Ar}}({\mathcal {C}}) \rightarrow {\mathcal {C}}]\) is visibly a one-sided inverse to (168) we see that the latter is in particular essentially surjective, and it will hence suffice to show that it is also fully-faithful, On the other hand, if \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) is a perfect bifibration then it is equivalent in \(\text {BiFib} \) to \({\mathcal {A}}\leftarrow {\text {Ar}}{\mathcal {A}}\rightarrow {\mathcal {A}}\) via the associated functor \(d:{\mathcal {B}}\rightarrow {\mathcal {A}}\) and the natural equivalence \(b(x,y) \simeq {\text {hom}}_{{\mathcal {A}}}(x,d(y))\). It will hence suffice to show that for every \({\mathcal {C}}\in \text {Cat} _\infty \) and every perfect bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) the induced map
is an equivalence. But this now follows from [47, Proposition 5.2.1.18] under the equivalence between bifibrations as above and pairings in the sense of [47, Definition 5.2.1.5], see Remark 7.1.2. \(\square \)
The \(\infty \)-category \(\text {BiFib} \subseteq {\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\) of bifibrations carries a natural action of \({{\text {C} }_{\textrm{2}}}\) induced by the action of \({{\text {C} }_{\textrm{2}}}\) on \(\Lambda ^2_0\) switching the vertices \(\Delta ^{\{1\}}\) and \(\Delta ^{\{2\}}\) and post-composing with the \(\text {op} \) action on \(\text {Cat} _\infty \). Explicitly, this action sends a bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) to the bifibration \({\mathcal {B}}^{\text {op} }\leftarrow {\mathcal {X}}^{\text {op} }\rightarrow {\mathcal {A}}^{\text {op} }\) (indeed, the latter is again a bifibration since taking opposites switches cartesian and cocartesian fibrations). A \({{\text {C} }_{\textrm{2}}}\)-fixed structure on a given bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) can then be described as a duality \(\text {D} :{\mathcal {X}}\xrightarrow {\simeq } {\mathcal {X}}^{\text {op} }\) on \({\mathcal {X}}\), an equivalence \({\mathcal {A}}\simeq {\mathcal {B}}^{\text {op} }\), and a duality-preserving refinement of \({\mathcal {X}}\rightarrow {\mathcal {A}}\times {\mathcal {B}}\simeq {\mathcal {A}}\times {\mathcal {A}}^{\text {op} }\). We refer to such a structure as a \(\Lambda ^2_0\)-duality on \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\), and call a bifibration equipped with a \(\Lambda ^2_0\)-duality a symmetric bifibration.
Proposition 7.1.13
The \({{\text {C} }_{\textrm{2}}}\)-fixed \(\infty \)-category \(\text {BiFib} ^{{{\text {hC} }_{\textrm{2}}}}\) participates in a cartesian fibration
classified by the functor \({\mathcal {C}}\mapsto {\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{\mathcal {S}})^{{{\text {hC} }_{\textrm{2}}}}\).
Proof
Equipping \(\Delta ^{\{1\}} \coprod \Delta ^{\{2\}}\) with the swap action and restricting along the \({{\text {C} }_{\textrm{2}}}\)-equivariant inclusion \(\Delta ^{\{1\}} \coprod \Delta ^{\{2\}} \subseteq \Lambda ^2_0\) we get that the cocartesian fibration
naturally refines to a \({{\text {C} }_{\textrm{2}}}\)-equivariant functor, where \({{\text {C} }_{\textrm{2}}}\) acts on the target by flipping the factors and taking opposites. Since cartesian fibration are preserved under limits, taking \({{\text {C} }_{\textrm{2}}}\)-fixed points results in a cartesian fibration
We now observe that the equivalence
intertwines the flip-op action on the left hand side with the flip action on the right hand side, and so the target of (169) is a coinduced \({{\text {C} }_{\textrm{2}}}\)-object. We may consequently identify the target of (170) with \(\text {Cat} _\infty \) and write it as a cocartesian fibration
Since taking fibres commutes with fixed points we may identify the fibres of (171) with the \({{\text {C} }_{\textrm{2}}}\)-fixed points of the corresponding fibres of (169). Now \({\mathcal {C}}\in \text {Cat} _\infty \) corresponds to the fixed object \(({\mathcal {C}},{\mathcal {C}}^{\text {op} }) \in \text {Cat} _\infty \times \text {Cat} _\infty \), and so the fibre of (171) over \({\mathcal {C}}\) is the \({{\text {C} }_{\textrm{2}}}\)-fixed points of \({\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{\mathcal {S}})\), as claimed. \(\square \)
Construction 7.1.14
By Proposition 7.1.13 we may identify the notion of a symmetric bifibration with that of a pair \(({\mathcal {C}},b)\) where \({\mathcal {C}}\) is an \(\infty \)-category and \(b\in {\text {Fun}}({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} },{\mathcal {S}})^{{\text {hC} }_{\textrm{2}}}\) is a symmetric functor. Given \(({\mathcal {C}},b)\), the associated symmetric bifibration is
equipped with its \(\Lambda ^2_0\)-duality which we denote by \(\text {D} _{\text {pair} }\). It is given explicitly by the duality
on \({\text {Pair}}({\mathcal {C}},{\mathcal {C}}^{\text {op} },b)\), where \(\sigma _{x,y}:b(x,y) \xrightarrow {\simeq } b(y,x)\) is given by the symmetric structure of b, equipped with the tautological duality-preserving structure of the projection \({\text {Pair}}({\mathcal {C}},{\mathcal {C}}^{\text {op} },b) \rightarrow {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\).
Proposition 7.1.15
The \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {BiFib} \) restricts to a \({{\text {C} }_{\textrm{2}}}\)-action on \({\hbox {BiFib}^{\textrm{p}}}\). Under the equivalence \({\hbox {BiFib}^{\textrm{p}}}\simeq \text {Cat} _\infty \) of Proposition 7.1.12, this action corresponds to the \(\text {op} \)-action on \(\text {Cat} _\infty \). In particular, we may identify the notion of a perfect symmetric bifibration with that of an \(\infty \)-category equipped with a perfect duality.
Proof
We claim that the functor
admits a natural \({{\text {C} }_{\textrm{2}}}\)-equivariant structure, where \({{\text {C} }_{\textrm{2}}}\) acts on \(\text {Cat} _\infty \) via the \(\text {op} \)-action. To see this, it will suffice to construct a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure for the composite map \(\text {Cat} _\infty \rightarrow \text {BiFib} \hookrightarrow {\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\). This composite is by definition given by mapping out of the diagram \(e := [\Delta ^{\{0\}} \rightarrow \Delta ^1 \leftarrow \Delta ^{\{1\}}]\), and so it will suffice to put a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on \(e:(\Lambda ^2_0)^{\text {op} }\rightarrow \text {Cat} _\infty \). Such an equivariant structure is then given by the canonical duality on \(\text {D} _{\Delta ^1}:\Delta ^1 \rightarrow (\Delta ^1)^{\text {op} }\) which switches \(\{0\}\) and \(\{1\}\) (since \(\Delta ^1\) is the nerve of an ordinary category not much coherence is needed in order to verify this fact).
By Proposition 7.1.12 it now follows in particular that the \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {BiFib} \) preserves the subcategory \({\hbox {BiFib}^{\textrm{p}}}\). This subcategory is replete by Example 7.1.9, and so by Remark 7.1.11 the \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {BiFib} \) restricts to an essentially unique \({{\text {C} }_{\textrm{2}}}\)-action on \({\hbox {BiFib}^{\textrm{p}}}\) making the inclusion \({\hbox {BiFib}^{\textrm{p}}}\hookrightarrow \text {BiFib} \) equivariant. By the above this action must then coincide with the \(\text {op} \)-action via the equivalence \({\hbox {BiFib}^{\textrm{p}}}\simeq \text {Cat} _\infty \), as desired. \(\square \)
Example 7.1.16
In the situation of Construction 7.1.14, if the symmetric correspondence \(b:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {S}}\) is perfect with duality \(\text {D} :{\mathcal {C}}^{\text {op} }\xrightarrow {\simeq } {\mathcal {C}}\) then the associated symmetric bifibration identifies by Proposition 7.1.12 with
and by Proposition 7.1.15 (and its proof) the associated \(\Lambda ^2_0\)-duality \(\text {D} _{\text {pair} }\) corresponds to the arrow duality \([x\rightarrow y] \mapsto [\text {D} y\rightarrow \text {D} x]\) induced on the functor category \({\text {Ar}}({\mathcal {C}}) = {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) from the dualities of \(\Delta ^1\) and \({\mathcal {C}}\).
The remainder of this section is devoted to producing an explicit formula expressing the mapping spaces in \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) in terms of b and the mapping spaces in \({\mathcal {A}}\times {\mathcal {B}}\). This will be useful for us in Sect. 7.3 when we will need to upgrade the pairings construction to the hermitian setting. To begin, consider the following diagram in \({\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\):

Here, left going internal arrows are all given on vertices by \([0 \mapsto 0],[1 \mapsto 1],[2 \mapsto 1]\) and all the right going internal arrows are given by \([0 \mapsto 1],[1 \mapsto 1], [2\mapsto 2]\), while the external arrows always preserve the vertex labels. The upper square is cocartesian, as can be tested levelwise using the standard categorical equivalence \(\Delta ^{\{0,1\}} \coprod _{\Delta ^{\{1\}}} \Delta ^{\{1,2\}} \xrightarrow {\simeq } \Delta ^2\). In addition, all entries in this square carry compatible \(\Lambda ^2_0\)-dualities, induced by the canonical duality \(\Delta ^2 \xrightarrow {\simeq } (\Delta ^2)^{\text {op} }\) which switches between 0 and 2 and between \(\Delta ^{\{0,1\}}\) and \((\Delta ^{\{1,2\}})^{\text {op} }\). Mapping out of the above diagram now yields a \({{\text {C} }_{\textrm{2}}}\)-equivariant functor \({\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty ) \rightarrow {\text {Fun}}(\Lambda ^2_0 \times \Delta ^1,\text {Cat} _\infty )\) sending \([{\mathcal {A}}\xleftarrow {q} {\mathcal {X}}\xrightarrow {p} {\mathcal {B}}]\) to the diagram

in which the top square is cartesian. In addition, using that all entries in this diagram compatibly project to \({\mathcal {X}}^{\Delta ^{\{0\}}}\) and \({\mathcal {X}}^{\Delta ^{\{2\}}}\) we will view this as a diagram in \((\text {Cat} _\infty )_{/{\mathcal {X}}\times {\mathcal {X}}}\).
Proposition 7.1.17
When \([{\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}]\) is a bifibration the bottom vertical arrows in (172) are equivalences. In particular, inverting these and taking the external rectangle yields a \({{\text {C} }_{\textrm{2}}}\)-equivariant functor \(\text {BiFib} \rightarrow {\text {Fun}}(\Delta ^1 \times \Delta ^1,{\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty ))\) which sends \([{\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}]\) to a cartesian square (173) of the form

in \((\text {Cat} _\infty )_{/{\mathcal {X}}\times {\mathcal {X}}}\). Here, the two projections to \({\mathcal {X}}\) are given by the domain and codomain projections in the case of \({\text {Ar}}({\mathcal {X}})\) and by the projection to the two extremal factors in the three other cases. In addition, this functor takes values in \({\text {Fun}}(\Delta ^1 \times \Delta ^1,\text {BiFib} )\) after post-composing with the inclusion \((\text {Cat} _\infty )_{/{\mathcal {X}}\times {\mathcal {X}}} \rightarrow {\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\).
Writing \({\mathcal {X}}= {\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) for some correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) the square of bifibrations (173) corresponds to a cartesian square of correspondences \({\mathcal {X}}^{\text {op} }\times {\mathcal {X}}\rightarrow {\mathcal {S}}\) of the form

giving, in particular, an explicit pullback formula for the mapping spaces in \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\).
Remark 7.1.18
In the situation of Proposition 7.1.17, the \({{\text {C} }_{\textrm{2}}}\)-equivariance of the functor in question means in particular that if a bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) carries a \(\Lambda ^2_0\)-duality then all the entries in the square (173) inherit such a duality and all arrows in the square are duality preserving.
Proof of Proposition 7.1.17
By definition the arrows in \({\mathcal {X}}\) which map to equivalences in \({\mathcal {A}}\) are exactly the p-cocartesian arrows, and the arrows which map to equivalences in \({\mathcal {B}}\) are exactly the q-cartesian arrows. It then follows that the projections
and
are equivalences, and so the right bottom vertical arrow in (172) (which is the fibre product of these two maps over the identity on \({\mathcal {A}}\times {\mathcal {B}}\)) is an equivalence. Similarly, the projections
are both equivalences, from which it follows that the left bottom vertical arrow in (172), which is a base change of the above composite, is an equivalence. \(\square \)
8.2 Bilinear and symmetric \(\infty \)-categories
In the present section we define and study the notion of bilinear and perfect bilinear \(\infty \)-categories. We then show that the notion of an \(\infty \)-category equipped with a symmetric bilinear form, which we call a symmetric \(\infty \)-category, can be identified with a \({{\text {C} }_{\textrm{2}}}\)-fixed bilinear \(\infty \)-category, and similarly in the perfect case. Using the results of Sect. 7.1 we then identify the \(\infty \)-category of perfect bilinear \(\infty \)-categories with \(\text {Cat} _\infty ^\text {ex} \) itself, through which we also deduce an equivalence between \(\infty \)-categories with perfect dualities and \({{\text {C} }_{\textrm{2}}}\)-fixed objects of \(\text {Cat} _\infty ^\text {ex} \) with respect to the \(\text {op} \)-action. We then construct left and right adjoints to the forgetful functors from hermitian to symmetric to bilinear \(\infty \)-categories, and similarly in the Poincaré/perfect case, where we finally recover the hyperbolic construction \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) acting as both left and right adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \).
Let \({\mathcal {A}},{\mathcal {B}}\) be stable \(\infty \)-categories. We say that a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is left biexact if it preserves finite limits in each variable separately. Such a correspondence lifts in an essentially unique manner to a bilinear functor \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {{\mathcal {S}}{p}}\). More precisely, post-composition with the infinite loop space functor induces an equivalence between bilinear functors \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {{\mathcal {S}}{p}}\) and left biexact correspondences \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\).
Definition 7.2.1
We denote by \({\text {Fun}}^{\textrm{b}}({\mathcal {A}},{\mathcal {B}}) \subseteq {\text {Fun}}({\mathcal {A}}^{\text {op} }\times {\mathcal {B}},{{\mathcal {S}}{p}})\) the full subcategory spanned by the bilinear functors and write
for the \(\infty \)-category of triples \(({\mathcal {A}},{\mathcal {B}},\text {B} )\) where \({\mathcal {A}},{\mathcal {B}}\) are stable \(\infty \)-categories and \(\text {B} :{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {{\mathcal {S}}{p}}\) is a bilinear functor. We will refer to the object \(({\mathcal {A}},{\mathcal {B}},\text {B} )\) of \({\textrm{Cat}^\textrm{b}_\infty }\) as bilinear categories.
Example 7.2.2
For a stable \(\infty \)-category \({\mathcal {C}}\) the mapping correspondence \(m_{{\mathcal {C}}}:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}\rightarrow {\mathcal {S}}\) of Example 7.1.1 is left biexact. We may hence consider the triple \(({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\) as a bilinear \(\infty \)-category.
Example 7.2.3
Let \({\mathcal {A}},{\mathcal {B}}\) be stable \(\infty \)-categories. If a correspondence \(b:{\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\rightarrow {\mathcal {S}}\) is right representable by an exact functor \(d:{\mathcal {A}}\rightarrow {\mathcal {B}}\) then b is left biexact.
Example 7.2.4
Let \({\mathcal {C}}\) be a stable \(\infty \)-category. Consider the \(\infty \)-category \({\text {Seq}}({\mathcal {C}})\) of exact sequences in \({\mathcal {C}}\) (see Notation 2.4.4). The pair of projections

then constitute a bifibration. Indeed, a map of exact sequences

is a cocartesian lift of \(y\rightarrow y'\) if and only if the left square is exact, or, equivalently, if the map \(x\rightarrow x'\) is an equivalence, and similarly forms a cartesian lift of \(x\rightarrow x'\) if and only if its component \(y\rightarrow y'\) is an equivalence. To identify the correspondence \(\text {seq} _{{\mathcal {C}}}:{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}\rightarrow {\mathcal {S}}\) associated to this bifibration we use the fact that every exact square as in (52) extends in an essentially unique manner to a diagram

in which all squares except the top right one are exact. We note that such a diagram determines in particular equivalences \(x' \simeq \Omega x\) and \(y' \simeq \Sigma y\). At the same time, the forgetful functor sending a diagram as a above to its external square

is an equivalence as well. In particular, if we denote by \({\text {Ar}}^{\Omega }({\mathcal {C}}) \subseteq {\text {Fun}}(\Delta ^1 \times \Delta ^1,{\mathcal {C}})\) the full subcategory spanned by the squares of the form (175) then we obtain an equivalence of bifibrations

The correspondence associated to \({\text {Ar}}^{\Omega }({\mathcal {C}})\) can then be identified with \((x',y') \mapsto \Omega {\text {Map}}_{{\mathcal {C}}}(x',y')\), and so the correspondence associated to \({\text {Seq}}\) can be written as \(\text {seq} _{{\mathcal {C}}}(x,y) = \Omega {\text {Map}}(\Omega x,\Sigma y)\). In particular, it is left biexact.
Remark 7.2.5
It follows from Lemma 1.4.1 that the defining cartesian fibration \({\textrm{Cat}^\textrm{b}_\infty }\rightarrow \text {Cat} _\infty ^\text {ex} \times \text {Cat} _\infty ^\text {ex} \) is also a cocartesian fibration. Applying the precise same argument as in the proof of Proposition 6.1.2 we may consequently conclude that \({\textrm{Cat}^\textrm{b}_\infty }\) has all small limits and colimits, and that those are preserved by the projection to \(\text {Cat} _\infty ^\text {ex} \times \text {Cat} _\infty ^\text {ex} \).
Given a bilinear category \(({\mathcal {A}},{\mathcal {B}},\text {B} )\) we may consider the pairings \(\infty \)-category associated to the underlying left biexact correspondence \(\Omega ^{\infty }\text {B} \). To simplify notation we set
We note that since \(\Omega ^{\infty }\text {B} \) is left biexact the functor \(y\mapsto \widetilde{d}(y) = \Omega ^{\infty }\text {B} (-,y)\) from \({\mathcal {B}}\) to \({\text {Psh}}({\mathcal {A}})\) takes values in the full subcategory \({\text {Ind}}({\mathcal {A}}) \subseteq {\text {Psh}}({\mathcal {A}})\) spanned by the left exact presheaves. In addition, in this case \({\text {Ind}}({\mathcal {A}})\) is also stable, the Yoneda embedding \({\mathcal {A}}\rightarrow {\text {Ind}}({\mathcal {A}})\) is exact, and the functor \(\widetilde{d}:{\mathcal {B}}\rightarrow {\text {Ind}}({\mathcal {A}})\) given by \(\Omega ^{\infty }\text {B} \) is exact as well. As in Remark 7.1.5 we may then identify
a description from which we see that \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},\text {B} )\) is stable and that exact squares in \({\text {Pair}}({\mathcal {A}},{\mathcal {B}},\text {B} )\) are detected in \({\mathcal {A}}\times {\mathcal {B}}\). This means in particular that any map of bifibrations
whose component \({\mathcal {A}}\rightarrow {\mathcal {A}}',{\mathcal {B}}\rightarrow {\mathcal {B}}'\) are exact, is also exact on \({\text {Pair}}(-,-,-)\). Invoking again the coherent compatibility of the straightening-unstraightening equivalence with base change as established in [23, Corollary A.31], we may consequently assemble the association \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto {\text {Pair}}({\mathcal {A}},{\mathcal {B}},\text {B} )\) to a functor
taking values in stable \(\infty \)-categories and exact functors between them. It then follows that the bivariant straightening equivalence (167) restricts to a (non-full) subcategory inclusion
whose image is spanned by those bifibrations \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) for which \({\mathcal {A}},{\mathcal {B}}\) are stable and the associated correspondence is left biexact and by those maps of bifibrations whose components are exact functors.
Remark 7.2.6
The subcategory inclusion (177) is replete (see Definition 7.1.7).
Remark 7.2.7
The association in (177) can also be viewed as a functor from \({\textrm{Cat}^\textrm{b}_\infty }\) to \({\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty ^\text {ex} )\). As such, it is fully-faithful and its image is spanned by those diagrams \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) in \(\text {Cat} _\infty ^\text {ex} \) which are bifibrations with associated correspondence left biexact. From this description we see that \({\textrm{Cat}^\textrm{b}_\infty }\) is closed under finite products in \({\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty ^\text {ex} )\), and hence inherits from its the property of being semiadditive, see Proposition 6.1.7.
Definition 7.2.8
We say that a bilinear category \(({\mathcal {A}},{\mathcal {B}},\text {B} )\) is perfect if its corresponding bifibration is perfect in the sense of Definition 7.1.6, and say that a map of perfect bilinear categories is perfect if the corresponding map of bifibrations is so. We denote by \({\textrm{Cat}^\textrm{pb}_\infty }\subseteq {\textrm{Cat}^\textrm{b}_\infty }\) the (non-full) subcategory spanned by the perfect bilinear categories and perfect maps between them.
Remark 7.2.9
As in Example 7.1.9, the subcategory inclusion \({\textrm{Cat}^\textrm{pb}_\infty }\subseteq {\textrm{Cat}^\textrm{b}_\infty }\) is replete.
By construction we have a commutative diagram

in which both squares are cartesian (the right one because (bi)exact functors to spectra are determined by their underlying space-valued functors) and all vertical arrows, as well as the horizontal arrows in the left square, are replete subcategory inclusions.
Proposition 7.2.10
The composite functor

is an equivalence of \(\infty \)-categories. An inverse is given by \({\mathcal {A}}\mapsto ({\mathcal {A}},{\mathcal {A}},m_{{\mathcal {A}}})\).
Proof
This follows directly from Proposition 7.1.12 since a perfect bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) belongs to the image of \({\textrm{Cat}^\textrm{pb}_\infty }\) if and only if \({\mathcal {A}}\simeq {\mathcal {B}}\) is stable (in which case the associated correspondence is automatically left biexact by Example 7.2.3). \(\square \)
Recall from Sect. 7.1 that the \(\infty \)-category \(\text {BiFib} \subseteq {\text {Fun}}(\Lambda ^2_0,\text {Cat} _\infty )\) of bifibrations carries a natural action of \({{\text {C} }_{\textrm{2}}}\) induced by the action of \({{\text {C} }_{\textrm{2}}}\) on \(\Lambda ^2_0\) switching the vertices \(\Delta ^{\{1\}}\) and \(\Delta ^{\{2\}}\) and post-composing with the \(\text {op} \) action on \(\text {Cat} _\infty \). Explicitly, this action sends a bifibration \({\mathcal {A}}\leftarrow {\mathcal {X}}\rightarrow {\mathcal {B}}\) to the bifibration \({\mathcal {B}}^{\text {op} }\leftarrow {\mathcal {X}}^{\text {op} }\rightarrow {\mathcal {A}}^{\text {op} }\). Since taking opposites also preserves stable \(\infty \)-categories and exact functors, the above action induces a \({{\text {C} }_{\textrm{2}}}\)-action on the replete subcategory \({\textrm{Cat}^\textrm{b}_\infty }\hookrightarrow \text {BiFib} \). Explicitly, the resulting \({{\text {C} }_{\textrm{2}}}\)-action sends a triple \(({\mathcal {A}},{\mathcal {B}},\text {B} )\) to the triple \(({\mathcal {B}}^{\text {op} },{\mathcal {A}},\text {B} _{\text {swap} })\), where \(\text {B} _{\text {swap} }:{\mathcal {B}}\times {\mathcal {A}}^{\text {op} }\rightarrow {\mathcal {S}}\) is \(\text {B} \) pre-composed with the swap equivalence \({\mathcal {B}}\times {\mathcal {A}}^{\text {op} }\simeq {\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\).
Definition 7.2.11
We denote by \(\text {Cat} ^{\textrm{sb}}_\infty := ({\textrm{Cat}^\textrm{b}_\infty })^{{{\text {hC} }_{\textrm{2}}}}\) the \(\infty \)-category of homotopy fixed points in \({\textrm{Cat}^\textrm{b}_\infty }\) with respect to the above \({{\text {C} }_{\textrm{2}}}\)-action.
Proposition 7.2.12
The \(\infty \)-category \(\text {Cat} ^{\textrm{sb}}_\infty \) participates in a cartesian fibration
classified by the functor \({\mathcal {C}}\mapsto {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\).
Proof
The claim follows from its unstable counterpart Proposition 7.1.13 since the restriction along exact functors preserves left biexact correspondences. \(\square \)
By Proposition 7.2.12 we may identify the objects of \(\text {Cat} ^{\textrm{sb}}_\infty \) with pairs \(({\mathcal {C}},\text {B} )\) where \({\mathcal {C}}\) is a small stable \(\infty \)-category and \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) is a symmetric bilinear functor, that is an object of the \(\infty \)-category \({\text {Fun}}^{\textrm{s}}({\mathcal {C}}) = {\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{{{\text {hC} }_{\textrm{2}}}}\). We refer to such a pair as a symmetric \(\infty \)-category. We refer to morphisms \(({\mathcal {C}},\text {B} ) \rightarrow ({{{\mathcal {C}}}'},\text {B} ')\) in \(\text {Cat} ^{\textrm{sb}}_\infty \) as symmetric functors. Using again Proposition 7.2.12 we may identify these with pairs \((f,\beta )\) where \(f:{\mathcal {C}}\rightarrow {{{\mathcal {C}}}'}\) is an exact functor and \(\beta :\text {B} \rightarrow (f \times f)^*\text {B} '\) is a natural transformation.
Definition 7.2.13
We say that a symmetric bilinear \(\infty \)-category \(({\mathcal {C}},\text {B} )\) is non-degenerate if \(\text {B} \) is non-degenerate in the sense of Definition 1.2.2. In this case \(\text {B} \) is induced by a (possibly imperfect) duality \(\text {D} _{\text {B} }:{\mathcal {C}}\rightarrow {\mathcal {C}}^{\text {op} }\), and every symmetric functor \((f,\beta ):({\mathcal {C}},\text {B} ) \rightarrow ({{{\mathcal {C}}}'},\text {B} ')\) induces a natural transformation \(\tau _{\beta }:f\text {D} _{\text {B} } \Rightarrow \text {D} _{\text {B} '}f^{\text {op} }\) via Lemma 1.2.4. We say that such a symmetric functor \((f,\beta )\) is duality preserving if \(\tau _{\beta }\) is an equivalence. We say that \(({\mathcal {C}},\text {B} )\) is perfect if \(\text {D} \) is an equivalence. We then denote by \(\text {Cat} ^{\textrm{ps}}_\infty \subseteq \text {Cat} ^{\textrm{sb}}_\infty \) the (non-full) subcategory spanned by the perfect symmetric \(\infty \)-categories and duality preserving functors between them.
Lemma 7.2.14
The \({{\text {C} }_{\textrm{2}}}\)-action on \({\textrm{Cat}^\textrm{b}_\infty }\) preserves the replete subcategory \({\textrm{Cat}^\textrm{pb}_\infty }\) of perfect bilinear \(\infty \)-categories. In addition, on the level of homotopy fixed points the resulting replete subcategory
coincides with the replete subcategory \(\text {Cat} ^{\textrm{ps}}_\infty \) of perfect symmetric bilinear \(\infty \)-categories.
Proof
We need to verify two things:
-
i)
If \(({\mathcal {C}},\text {B} )\) is a symmetric \(\infty \)-category then \(\text {B} \) is perfect in the sense of Definition 7.2.13 if and only if the left biexact correspondence \(\Omega ^{\infty }\text {B} \) is perfect in the sense of Definition 7.1.6.
-
ii)
A symmetric functor \((f,\beta ):({\mathcal {C}},\text {B} ) \rightarrow ({{{\mathcal {C}}}'},\text {B} ')\) between perfect symmetric \(\infty \)-categories is duality preserving if and only if the induced functor \({\text {Pair}}({\mathcal {C}},{\mathcal {C}}^{\text {op} },\text {B} ) \rightarrow {\text {Pair}}({{{\mathcal {C}}}'},{{{\mathcal {C}}}'}^{\text {op} },\text {B} ')\) preserves perfect pairings.
To prove i) we need to show that \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) can be written as \(\text {B} (x,y) \simeq {\text {hom}}_{{\mathcal {C}}}(x,\text {D} y)\) for some equivalence \(\text {D} :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) if and only if \(\Omega ^{\infty }\text {B} \) can be written as \({\text {Map}}_{{\mathcal {C}}}(x,\text {D} y)\) for some equivalence \(\text {D} :{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\). Clearly the former implies the latter, but the latter also implies the former since post-composition with \(\Omega ^{\infty }\) induces an equivalence between bilinear functors \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) and left biexact correspondences \({\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {S}}\). To verify ii), consider the commutative diagram

furnished by Remark 1.2.6. We then see that the map \(f\text {D} _{\text {B} }(y) \rightarrow \text {D} _{\text {B} '}f(y)\) is an equivalence if and only if f sends the tautological perfect pairing \((\text {D} _{\text {B} }(y),y,\iota ) \in {\text {Pair}}({\mathcal {C}},{\mathcal {C}}^{\text {op} },\text {B} )\) to a perfect pairing in \({{{\mathcal {C}}}'}\). Since every perfect pairing is equivalent to a tautological perfect pairing \((\text {D} _{\text {B} }(y),y,\iota )\) for some y we may thus conclude that \(\tau _{\beta }:f\text {D} _{\text {B} } \Rightarrow \text {D} _{\text {B} '}f^{\text {op} }\) is an equivalence if and only if the induced functor \({\text {Pair}}({\mathcal {C}},{\mathcal {C}}^{\text {op} },\text {B} ) \rightarrow {\text {Pair}}({{{\mathcal {C}}}'},{{{\mathcal {C}}}'}^{\text {op} },\text {B} ')\) preserves perfect pairings, as desired. \(\square \)
Remark 7.2.15
Under the equivalence \({\textrm{Cat}^\textrm{pb}_\infty }\simeq \text {Cat} _\infty ^\text {ex} \) of Proposition 7.2.10, the restricted \({{\text {C} }_{\textrm{2}}}\)-action on \({\textrm{Cat}^\textrm{pb}_\infty }\) recovers the \(\text {op} \)-action on \(\text {Cat} _\infty ^\text {ex} \). Indeed, this follows from the corresponding unstable statement on the level of \({\hbox {BiFib}^{\textrm{p}}}\) and \(\text {Cat} _\infty \) (see Proposition 7.1.15) since in both cases the \({{\text {C} }_{\textrm{2}}}\)-action is the restricted one (uniquely determined since the inclusions \({\textrm{Cat}^\textrm{pb}_\infty }\subseteq {\hbox {BiFib}^{\textrm{p}}}\) and \(\text {Cat} _\infty ^\text {ex} \subseteq \text {Cat} _\infty \) are both replete).
Combining Proposition 7.2.10, Lemma 7.2.14 and Remark 7.2.15 and we now obtain the following statement, versions of which were previously established in [29] and [30]:
Corollary 7.2.16
The forgetful functor \(\text {Cat} ^{\textrm{ps}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) lifts to an equivalence
where \({{\text {C} }_{\textrm{2}}}\) acts on \(\text {Cat} _\infty ^\text {ex} \) by the \(\text {op} \)-action.
The constructions we have made so far can now be summarised by the following commutative diagram

in which the vertical arrows in the top row are replete subcategory inclusions, the top squares are cartesian, the vertical arrows in the bottom row are cartesian fibrations, and the horizontal arrows in the middle row preserve cartesian edges. In fact, all the vertical maps in the bottom row are also cocartesian fibrations and the horizontal arrows in the middle row also preserve cocartesian edges, see Corollary 1.4.2 and Proposition 1.4.3. We also recall that the \({{\text {C} }_{\textrm{2}}}\)-action on \(\text {Cat} _\infty ^\text {ex} \times \text {Cat} _\infty ^\text {ex} \) is given by \(({\mathcal {A}},{\mathcal {B}}) \mapsto ({\mathcal {B}}^{\text {op} },{\mathcal {A}}^{\text {op} })\) and the composite \(\text {Cat} _\infty ^\text {ex} \rightarrow \text {Cat} _\infty ^\text {ex} \times \text {Cat} _\infty ^\text {ex} \) along the bottom and right sides both equivalent to the diagonal map.
A useful feature of the diagram (179) is that all arrows in it admit both left and right adjoints, and in particular all arrows preserve all limits and colimits. For the vertical functors on the bottom row, these are all cartesian and cocartesian fibrations and their fibres admit zero objects, thus the zero section gives a two sided adjoint in all three cases. The left and right adjoints of the horizontal functors in (179) will be studied in this section, with special interest given to the resulting adjoints of the composite arrow \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) on the top row, which are both given by the construction \({\mathcal {C}}\mapsto {\text {Hyp}}({\mathcal {C}})\) of Sect. 2.2. The left and right adjoint to the top left vertical inclusion \(\text {Cat} ^{\textrm{p}}_\infty \hookrightarrow \text {Cat} ^{\textrm{h}}_\infty \) will be produced in Sect. 7.3 below using the pairings construction. Left and right adjoints to the top middle vertical inclusion then follow by formal considerations, while left and right adjoints to the top right inclusion can be constructed in a similar manner, see Remarks 7.3.19 and 7.3.24.
The remainder of this section is dedicated to the construction of left and right adjoints to the horizontal functors in (179). We begin with the top left square:
Proposition 7.2.17
The functor
admits fully-faithful left and right adjoints, given by sending  and
and  , respectively. Furthermore, the units and counits of these adjunctions project to equivalences in \(\text {Cat} _\infty ^\text {ex} \).
, respectively. Furthermore, the units and counits of these adjunctions project to equivalences in \(\text {Cat} _\infty ^\text {ex} \).
Proof
We have a diagram

where p and q are cartesian fibrations and the forgetful functor f preserves cartesian edges. The functor f has fibrewise left and right adjoints by Corollary 1.3.6, and so by [47, Proposition 7.3.2.6] f admits a left adjoint whose unit transformation is sent to an equivalence in \(\text {Cat} _\infty ^\text {ex} \). The counit of the adjunction is given by the fibrewise counit and thus is an equivalence by Corollary 1.3.6, according to which the fibrewise left adjoint is fully faithful. On the other hand, by Corollary 1.4.2 and Remark 7.2.5 the maps p, q are also cocartesian fibrations, and by Proposition 1.4.3 the map f preserves cocartesian edges. Applying the dual of [47, Proposition 7.3.2.6] we now conclude that f admits a right adjoint whose associated unit is mapped to an equivalence in \(\text {Cat} _\infty ^\text {ex} \) and whose counit is an equivalence in \(\text {Cat} ^{\textrm{sb}}_\infty \). \(\square \)
Proposition 7.2.18
The fully-faithful adjoints of Proposition 7.2.17 map \(\text {Cat} ^{\textrm{ps}}_\infty \) to \(\text {Cat} ^{\textrm{p}}_\infty \), and yield fully-faithful left and right adjoints to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{ps}}_\infty \).
Proof
Since the left and right adjoints constructed in Proposition 7.2.17 are fully-faithful and since the condition for a hermitian \(\infty \)-category of being non-degenerate is defined via the non-degeneracy of the underlying symmetric bilinear form we see that these adjoints send non-degenerate symmetric \(\infty \)-categories to non-degenerate hermitian \(\infty \)-categories and similarly perfect symmetric \(\infty \)-categories to Poincaré \(\infty \)-categories. For the same reason these adjoints also send duality-preserving symmetric functors to duality preserving functors. To see that these now yield left and right adjoints to \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{ps}}_\infty \) it is enough to check that all the units and counits are contained in the respective subcategories. Now on the side of \(\text {Cat} ^{\textrm{ps}}_\infty \) these units and counits are equivalences, and so by triangle identities these units and counits in \(\text {Cat} ^{\textrm{p}}_\infty \) map to equivalences in \(\text {Cat} ^{\textrm{ps}}_\infty \). This implies that they are duality preserving, as desired. \(\square \)
Definition 7.2.19
Given a perfect bilinear functor \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {C}})\), the images of \(({\mathcal {C}},\text {B} )\) under the fully-faithful left adjoint and right adjoint of Proposition 7.2.18 are, as in the case of Proposition 7.2.17, given by  and
and  , respectively. We refer to Poincaré \(\infty \)-categories of this form as quadratic and symmetric Poincaré \(\infty \)-categories, respectively.
, respectively. We refer to Poincaré \(\infty \)-categories of this form as quadratic and symmetric Poincaré \(\infty \)-categories, respectively.
Taking now the top external rectangle in (179) we obtain a square

in which the right vertical arrow is given by

Proposition 7.2.20
In the square (180) both horizontal arrows admit left and right adjoints, both compatible with the vertical subcategory inclusions. In addition, both adjoints of the bottom horizontal arrow are equivalent and given by the formula \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto ({\mathcal {A}}\times {\mathcal {B}}^{\text {op} },\text {B} )\).
Pre-composing the formula of Proposition 7.2.20 with the functor (181) we conclude
Corollary 7.2.21
The forgetful functor \(\text {U} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) admits both a left and a right adjoint. The two are equivalent and given by the association \({\mathcal {A}}\mapsto ({\mathcal {A}}\times {\mathcal {A}}^{\text {op} },m_{{\mathcal {A}}}) = {\text {Hyp}}({\mathcal {A}})\).
Remark 7.2.22
The unit exhibiting \({\text {Hyp}}\) as right adjoint to \(\text {U} \) and the counit exhibiting \({\text {Hyp}}\) as left adjoint to \(\text {U} \) are given respectively by the Poincaré functors

of (42). The counit \(\text {U} {\text {Hyp}}({\mathcal {C}}) = {\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\) exhibiting \({\text {Hyp}}\) as right adjoint to \(\text {U} \) is then given by the projection on the first fact and the unit \({\mathcal {C}}\rightarrow \text {U} {\text {Hyp}}({\mathcal {C}}) = {\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\) exhibiting \({\text {Hyp}}\) as left adjoint to \(\text {U} \) is given by the inclusion into the first summand. Here we are using the direct sum notation keeping in mind that \(\text {Cat} _\infty ^\text {ex} \) is semi-additive, see Proposition 6.1.7.
Remark 7.2.23
By [47, Corollary 7.3.2.7] the functor \({\text {Hyp}}\) inherits a lax symmetric monoidal structure by virtue of being right adjoint to the symmetric monoidal functor \(\text {U} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) (see Theorem 5.2.7). In particular, \(\text {U} \dashv {\text {Hyp}}\) is a symmetric monoidal adjunction. Applying the same argument to the symmetric monoidal functor \(\text {U} ^{\text {op} }:(\text {Cat} ^{\textrm{p}}_\infty )^{\text {op} }\rightarrow (\text {Cat} _\infty ^\text {ex} )^{\text {op} }\) we get that the adjunction \(\text {U} ^{\text {op} }\dashv {\text {Hyp}}^{\text {op} }\) (opposite to \({\text {Hyp}}\dashv \text {U} \)) is symmetric monoidal and \({\text {Hyp}}\) also carries an oplax symmetric monoidal structure.
Remark 7.2.24
The symmetric monoidal structure on the forgetful functor \(\text {U} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) yields for every  a commutative square
a commutative square

Passing to right adjoints using Corollaries 7.2.21 and 6.2.15 we obtain a commutative square

In particular, we have a natural equivalence of Poincaré \(\infty \)-categories

Proof of Proposition 7.2.20
We first observe that the square (180) is also the external top rectangle in (179). Propositions 7.2.17 and 7.2.18 provide left and right adjoints to the horizontal arrows in the top left square of (179), which are furthermore compatible with the vertical subcategory inclusions. In the same diagram, the horizontal arrows in the top middle square are equivalences, and the horizontal arrows in the top right square have left and right adjoints as well. Indeed, in both cases these are the natural maps from \({{\text {C} }_{\textrm{2}}}\)-fixed points to underlying objects, which admit left and right adjoints since \(\text {Cat} _\infty ^\text {ex} \) and \({\textrm{Cat}^\textrm{b}_\infty }\) admits products and coproducts (see Proposition 6.1.1 and Remark 7.2.5). In addition, since \(\text {Cat} _\infty ^\text {ex} \) is semiadditive (Proposition 6.1.7) these products and coproducts coincide, and we get that the left and right adjoints of \((\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow \text {Cat} _\infty ^\text {ex} \) are both give by the formula \({\mathcal {C}}\mapsto {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\). This implies that the left and right adjoints for the horizontal maps in the top right square in (179) are compatible with the vertical replete subcategory inclusions, and hence we may conclude that the horizontal arrows in (180) admit left and right adjoints, both compatible with the vertical subcategory inclusions.
It is left to obtain the desired explicit formula. First by semi-additivity, the left and right adjoints of \(\text {Cat} ^{\textrm{sb}}_\infty \rightarrow {\textrm{Cat}^\textrm{b}_\infty }\) are both given by the formula
where \(\text {B} _{\text {sym}}\in {\text {Fun}}^{\textrm{s}}({\mathcal {A}}\times {\mathcal {B}}^{\text {op} })\) is the symmetrisation of \(\text {B} \), given by
We note that this symmetric bilinear form is both induced and coinduced from \(\text {B} \). In particular,  and
and  both canonically identify with \(\text {B} \) itself, when the latter is viewed as a single entry functor on \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\). By Propositions 7.2.17 the left and right adjoints of the bottom horizontal map in (180) are consequently both given by the formula \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto ({\mathcal {A}}\times {\mathcal {B}}^{\text {op} },\text {B} )\). \(\square \)
both canonically identify with \(\text {B} \) itself, when the latter is viewed as a single entry functor on \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\). By Propositions 7.2.17 the left and right adjoints of the bottom horizontal map in (180) are consequently both given by the formula \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto ({\mathcal {A}}\times {\mathcal {B}}^{\text {op} },\text {B} )\). \(\square \)
8.3 The categorical Thom isomorphism
In Sect. 2.4 we described the algebraic Thom construction, an operation introduced by Ranicki which allows one to identify the notion of a metabolic Poincaré object  equipped with a prescribed Lagrangian \((w\rightarrow x,\eta )\), with the data of a hermitian object \((z,r)\) in \({\mathcal {C}}\) with respect to the shifted Poincaré structure
equipped with a prescribed Lagrangian \((w\rightarrow x,\eta )\), with the data of a hermitian object \((z,r)\) in \({\mathcal {C}}\) with respect to the shifted Poincaré structure  . In this section we will see that this procedure naturally fits in a more general perspective. We begin by refining the construction of pairing \(\infty \)-categories described in Sect. 7.2 above to the context of hermitian \(\infty \)-categories. This results in a construction which takes a hermitian \(\infty \)-category
. In this section we will see that this procedure naturally fits in a more general perspective. We begin by refining the construction of pairing \(\infty \)-categories described in Sect. 7.2 above to the context of hermitian \(\infty \)-categories. This results in a construction which takes a hermitian \(\infty \)-category  and produces a Poincaré \(\infty \)-category
and produces a Poincaré \(\infty \)-category  . When
. When  is Poincaré this construction reproduces that of the arrow category
is Poincaré this construction reproduces that of the arrow category  described in Sect. 2.4. We then prove that Poincaré objects in
described in Sect. 2.4. We then prove that Poincaré objects in  correspond to hermitian objects in
correspond to hermitian objects in  , yielding in particular a proof of Proposition 2.4.3 upon taking
, yielding in particular a proof of Proposition 2.4.3 upon taking  to be Poincaré.
to be Poincaré.
The Poincaré \(\infty \)-categories of the form  can be considered as a categorified form of the notion of a metabolic Poincaré object: they contain a stable full subcategory on which the Poincaré structure vanishes and which is equivalent to its own orthogonal complement, a property which can be considered as a categorical analogue of the notion of a Lagrangian. From this point of view, we may consider the association
can be considered as a categorified form of the notion of a metabolic Poincaré object: they contain a stable full subcategory on which the Poincaré structure vanishes and which is equivalent to its own orthogonal complement, a property which can be considered as a categorical analogue of the notion of a Lagrangian. From this point of view, we may consider the association  as a categorified form of the Thom construction, taking a hermitian \(\infty \)-category and producing a Poincaré \(\infty \)-category with a canonical choice of Lagrangian. We show that this process is reversible: given a Poincaré \(\infty \)-category
as a categorified form of the Thom construction, taking a hermitian \(\infty \)-category and producing a Poincaré \(\infty \)-category with a canonical choice of Lagrangian. We show that this process is reversible: given a Poincaré \(\infty \)-category  with a Lagrangian, one can reconstruct a hermitian \(\infty \)-category
with a Lagrangian, one can reconstruct a hermitian \(\infty \)-category  such that
such that  . We consider this as a categorical form of the Thom isomorphism. Relying on these results we then use the pairing construction in order to produce both a left and a right adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \). This adjunction ties together all the above results in a conceptual manner, and at the same time is quite useful in practice. In particular, the results of this section will be used in subsequent instalments of this project, for example in setting up the theory of algebraic surgery in Paper [2], and in proving that \(\text {Cat} ^{\textrm{p}}_\infty \) is compactly generated in Paper [4].
. We consider this as a categorical form of the Thom isomorphism. Relying on these results we then use the pairing construction in order to produce both a left and a right adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \). This adjunction ties together all the above results in a conceptual manner, and at the same time is quite useful in practice. In particular, the results of this section will be used in subsequent instalments of this project, for example in setting up the theory of algebraic surgery in Paper [2], and in proving that \(\text {Cat} ^{\textrm{p}}_\infty \) is compactly generated in Paper [4].
We now proceed to introduce the main construction of the current section:
Construction 7.3.1
Given a stable \(\infty \)-category \({\mathcal {C}}\), any bilinear functor \(\text {B} :{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}\) determines a left biexact correspondence on the pair \(({\mathcal {C}},{\mathcal {C}}^{\text {op} })\), given by \((x,y) \mapsto \Omega ^{\infty }\text {B} (x,y)\). We then denote by
the associated \(\infty \)-category of pairings. Given a hermitian structure  on \({\mathcal {C}}\), we define an associated hermitian structure
on \({\mathcal {C}}\), we define an associated hermitian structure  on
on  via the pullback square
via the pullback square

where the bottom horizontal map is given by the association \([f:x\rightarrow y] \mapsto f^*\beta \in \text {B} (x,x)\), canonically extended from mapping spaces to mapping spectra. We denote the resulting hermitian \(\infty \)-category by  .
.
Lemma 7.3.2
The hermitian structure  is Poincaré. Its bilinear part sits in the pullback square of symmetric bilinear forms
is Poincaré. Its bilinear part sits in the pullback square of symmetric bilinear forms

and its associated duality coincides with the duality
of Construction 7.1.14, which encodes the symmetric structure of \(\text {B} \).
Proof
Substituting in (182) the direct sum of  we obtain the square
we obtain the square

which yields the square (183) upon passing to bireduced replacements. On the other hand, working backwards from the required duality, we note that \(\text {D} _{\text {pair} }\) is part of a \(\Lambda ^2_0\)-duality of the associated bifibration

Applying Proposition 7.1.17 and Remark 7.1.18 to this bifibration we obtain a cartesian square of symmetric bilinear forms

where we are again silently identifying exact functors valued in spectra with left exact functors valued in spaces. Comparing this square with (183) we thus get that \(\text {B} _{\text {pair} }\) is perfect with duality \(\text {D} _{\text {pair} }\). \(\square \)
Examples 7.3.3
-
i)
For a stable \(\infty \)-category \({\mathcal {C}}\) equipped with the zero hermitian structure, the Poincaré \(\infty \)-category \({\text {Pair}}({\mathcal {C}},0)\) is naturally equivalent to \({\text {Hyp}}({\mathcal {C}})\).
-
ii)
If the hermitian \(\infty \)-category
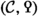 is Poincaré with associated duality \(\text {D} \), then the correspondence
is Poincaré with associated duality \(\text {D} \), then the correspondence 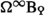 on the pair \(({\mathcal {C}},{\mathcal {C}}^{\text {op} })\) is equivalent to the correspondence \({\text {Map}}_{{\mathcal {C}}}(-,-)\) on the pair \(({\mathcal {C}},{\mathcal {C}})\) via $$\begin{aligned} (\text {id} ,\text {D} ):{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\xrightarrow {\simeq } {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}, \end{aligned}$$
on the pair \(({\mathcal {C}},{\mathcal {C}}^{\text {op} })\) is equivalent to the correspondence \({\text {Map}}_{{\mathcal {C}}}(-,-)\) on the pair \(({\mathcal {C}},{\mathcal {C}})\) via $$\begin{aligned} (\text {id} ,\text {D} ):{\mathcal {C}}^{\text {op} }\times {\mathcal {C}}^{\text {op} }\xrightarrow {\simeq } {\mathcal {C}}^{\text {op} }\times {\mathcal {C}}, \end{aligned}$$and so
 is naturally equivalent to the arrow category \({\text {Ar}}({\mathcal {C}})\) of Definition 2.4.1. Under this equivalence, the Poincaré structure
is naturally equivalent to the arrow category \({\text {Ar}}({\mathcal {C}})\) of Definition 2.4.1. Under this equivalence, the Poincaré structure 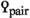 directly translates to the Poincaré structure
directly translates to the Poincaré structure 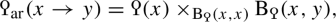
and so we obtain a natural equivalence
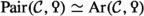 .
. -
iii)
Combining the previous example with Lemma 2.4.5 we obtain a natural identification of Poincaré \(\infty \)-categories
 whenever
whenever 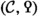 is Poincaré.
is Poincaré.
Remark 7.3.4
Combining Example 7.3.3(ii), Example 7.1.16 and Lemma 7.3.2, we obtain that for  Poincaré, the underlying duality \(\text {D} _{\text {ar} }\) of
Poincaré, the underlying duality \(\text {D} _{\text {ar} }\) of  is equivalent to the one induced on \({\text {Ar}}({\mathcal {C}}) \simeq {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) by the duality
is equivalent to the one induced on \({\text {Ar}}({\mathcal {C}}) \simeq {\text {Fun}}(\Delta ^1,{\mathcal {C}})\) by the duality  on \({\mathcal {C}}\) and the canonical duality of \(\Delta ^1\).
on \({\mathcal {C}}\) and the canonical duality of \(\Delta ^1\).
By construction, the underlying stable \(\infty \)-category of  sits in a bifibration
sits in a bifibration

so that q is a cartesian fibration and p is a cocartesian fibration. The fact that \({\mathcal {C}}\) is pointed and  is bireduced implies that these fibrations have fully-faithful adjoints
is bireduced implies that these fibrations have fully-faithful adjoints

More precisely, q has a fully-faithful right adjoint  sending \(x\) to \((x,0,0)\). Indeed, the canonical arrows \((x,y,\beta ) \rightarrow (x,0,0)\) in
sending \(x\) to \((x,0,0)\). Indeed, the canonical arrows \((x,y,\beta ) \rightarrow (x,0,0)\) in  induce an equivalence on mapping spaces into any triple of the form \((x',0,0)\), and thus assemble to form a unit exhibiting j as right adjoint to q. Similarly, the collection of arrows \((0,y,0) \rightarrow (x,y,\beta )\) assemble to form a counit exhibiting the functor
induce an equivalence on mapping spaces into any triple of the form \((x',0,0)\), and thus assemble to form a unit exhibiting j as right adjoint to q. Similarly, the collection of arrows \((0,y,0) \rightarrow (x,y,\beta )\) assemble to form a counit exhibiting the functor  sending \(y\) to \((0,y,0)\) as left adjoint to p, and we observe that the image of i coincides with the kernel of q and the image of j with the kernel of p.
sending \(y\) to \((0,y,0)\) as left adjoint to p, and we observe that the image of i coincides with the kernel of q and the image of j with the kernel of p.
We now observe that  naturally extends to a hermitian functor
naturally extends to a hermitian functor

with  given by the natural projection furnished directly from the definition of
given by the natural projection furnished directly from the definition of  . In generalisation of the algebraic Thom isomorphism we then have:
. In generalisation of the algebraic Thom isomorphism we then have:
Proposition 7.3.5
For every hermitian \(\infty \)-category  the composite map
the composite map

is an equivalence. In particular, Poincaré objects in  classify hermitian objects in
classify hermitian objects in  .
.
Remark 7.3.6
Applied in the case where  is Poincaré, Proposition 7.3.5 reduces to the statement of Proposition 2.4.3 via the identification
is Poincaré, Proposition 7.3.5 reduces to the statement of Proposition 2.4.3 via the identification  of Examples 7.3.3.
of Examples 7.3.3.
Proposition 7.3.5 is a direct consequence of the following lemma:
Lemma 7.3.7
Let  be a hermitian \(\infty \)-category. Then the functor
be a hermitian \(\infty \)-category. Then the functor

induced by (185) is a cartesian fibration whose fibres admit final objects. In addition, a hermitian object \(((x,y,\beta ),q)\) in  is final in its fibre over
is final in its fibre over  if and only if it is Poincaré.
if and only if it is Poincaré.
Given Lemma 7.3.7, the proof of Proposition 7.3.5 is immediate:
Proof of Proposition 7.3.5
By Lemma 7.3.7 the homotopy fibres of

are contractible, and so the desired result follows. \(\square \)
Proof of Lemma 7.3.7
Consider the commutative square

where the vertical arrows are the defining right fibrations of \(\text {He} (-)\). Since the bottom horizontal map is a cartesian fibration (by the construction of  as a bifibration) we obtain that the composite dotted map is a cartesian fibration, and hence we can view the top horizontal map is a map of cartesian fibrations over \({\mathcal {C}}\) whose target is a right fibration. Such a map is automatically a cartesian fibration (up to equivalence), which gives us the first claim of the lemma. We now verify that its fibres contain final objects. Let
as a bifibration) we obtain that the composite dotted map is a cartesian fibration, and hence we can view the top horizontal map is a map of cartesian fibrations over \({\mathcal {C}}\) whose target is a right fibration. Such a map is automatically a cartesian fibration (up to equivalence), which gives us the first claim of the lemma. We now verify that its fibres contain final objects. Let

be the right fibration classifying the contravariant functor \((x,y,\alpha ) \mapsto {\text {Map}}_{{\mathcal {C}}}(x,y)\). The defining fibre square (182) then determines a commutative square

of \(\infty \)-categories in which (using the same argument as above) the vertical maps are right fibrations and the horizontal maps are cartesian fibrations. In addition, the top square in (186) is cartesian; indeed, base changing the right fibrations on the right from \({\mathcal {C}}\) to  yields a fibre square of right fibrations which is the straightening of the defining square (182) (after taking \(\Omega ^{\infty }\)). It will hence suffice to show that the fibres of the middle horizontal cartesian fibration have final objects. Fix an object
yields a fibre square of right fibrations which is the straightening of the defining square (182) (after taking \(\Omega ^{\infty }\)). It will hence suffice to show that the fibres of the middle horizontal cartesian fibration have final objects. Fix an object  . Then the fibre \({\mathcal {X}}_{(x,\beta )}\) of the middle horizontal map sits in a right fibration
. Then the fibre \({\mathcal {X}}_{(x,\beta )}\) of the middle horizontal map sits in a right fibration

where the middle term stands for the fibre of the bottom horizontal map over \(x\in {\mathcal {C}}\). Using the pullback formula (174) for the mapping spaces in  we now calculate
we now calculate

from which we see that the right fibration (187) is visibly represented by \((x,x,\beta )\), so that \({\mathcal {X}}_{(x,\beta )}\) has a final object.
To finish the proof we now need to verify that a hermitian object \(((x,y,\beta ),q)\) in  is Poincaré if and only if it is final in the fibre. The top square in (186) being cartesian it will suffice to show that \(((x,y,\beta ),q)\) is Poincaré if and only if its image in \({\mathcal {X}}\) is final in its fibre over
is Poincaré if and only if it is final in the fibre. The top square in (186) being cartesian it will suffice to show that \(((x,y,\beta ),q)\) is Poincaré if and only if its image in \({\mathcal {X}}\) is final in its fibre over  . Indeed, a hermitian form q on \((x,y,\beta )\) determines a self dual map \(q_{\sharp }:(x,y,\beta ) \rightarrow \text {D} _{\text {pair} }(x,y,\beta ) = (y,x,\beta )\) with components \(f:x\rightarrow y\) and \(y\leftarrow x:g\) (the latter considered as a map from \(y\) to \(x\) in \({\mathcal {C}}^{\text {op} }\)). The form q is then Poincaré if and only if f and g are equivalences. But since \(q_{\sharp }\) is self-dual the components f and g are homotopic to each other. We then get that q is Poincaré if and only if the map g is an equivalence. But g (or f) is exactly the image of q in \({\text {Map}}_{{\mathcal {C}}}(x,y)\) via the vertical map in the defining square (182), and so the image of \(((x,y,\beta ),q)\) in \({\mathcal {X}}\) is \(((x,y,\beta ),g)\). The latter object lies over
. Indeed, a hermitian form q on \((x,y,\beta )\) determines a self dual map \(q_{\sharp }:(x,y,\beta ) \rightarrow \text {D} _{\text {pair} }(x,y,\beta ) = (y,x,\beta )\) with components \(f:x\rightarrow y\) and \(y\leftarrow x:g\) (the latter considered as a map from \(y\) to \(x\) in \({\mathcal {C}}^{\text {op} }\)). The form q is then Poincaré if and only if f and g are equivalences. But since \(q_{\sharp }\) is self-dual the components f and g are homotopic to each other. We then get that q is Poincaré if and only if the map g is an equivalence. But g (or f) is exactly the image of q in \({\text {Map}}_{{\mathcal {C}}}(x,y)\) via the vertical map in the defining square (182), and so the image of \(((x,y,\beta ),q)\) in \({\mathcal {X}}\) is \(((x,y,\beta ),g)\). The latter object lies over  and corresponds to the object
and corresponds to the object

We may then conclude that \(((x,y,\beta ),q)\) is Poincaré if and only if g is an equivalence, and so if and only if (188) is final, as desired. \(\square \)
The following almost immediate corollary of Lemma 7.3.7 will also be useful for us later:
Corollary 7.3.8
The natural transformation

exhibits  as the left Kan extension of
as the left Kan extension of  along
along  .
.
Proof
By Proposition 1.4.3 and Lemma 1.1.25 it will suffice to show that \(\Omega ^{\infty }\eta \) exhibits  as the left Kan extension of
as the left Kan extension of  . Since \(q^{\text {op} }\) is a cocartesian fibration left Kan extensions along \(q^{\text {op} }\) are calculated by colimits along the fibres. In particular, we need to show that for every \(x\in {\mathcal {C}}\) the map
. Since \(q^{\text {op} }\) is a cocartesian fibration left Kan extensions along \(q^{\text {op} }\) are calculated by colimits along the fibres. In particular, we need to show that for every \(x\in {\mathcal {C}}\) the map

induced by \(\eta \), is an equivalence of spaces. Since colimits in spaces are universal it will suffice to show that for every point  the space
the space

is contractible. Indeed, this space can in turn be identified with the geometric realisation of the fibre of  over \((x,\beta )\), and the latter has an initial object by Lemma 7.3.7, so its realisation is contractible. \(\square \)
over \((x,\beta )\), and the latter has an initial object by Lemma 7.3.7, so its realisation is contractible. \(\square \)
We now take a closer look at the Poincaré \(\infty \)-categories of the form  . We wish to make the argument that they constitute a categorical analogue of the notion of a metabolic Poincaré object, making the passage from
. We wish to make the argument that they constitute a categorical analogue of the notion of a metabolic Poincaré object, making the passage from  to
to  an analogue of the algebraic Thom construction. To identify further key properties we introduce the following piece of notation:
an analogue of the algebraic Thom construction. To identify further key properties we introduce the following piece of notation:
Definition 7.3.9
Let  be a Poincaré \(\infty \)-category and \({\mathcal {L}}\subseteq {\mathcal {D}}\) a full subcategory. We will denote by \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) the full subcategory spanned by the objects \(y\in {\mathcal {D}}\) such that
be a Poincaré \(\infty \)-category and \({\mathcal {L}}\subseteq {\mathcal {D}}\) a full subcategory. We will denote by \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) the full subcategory spanned by the objects \(y\in {\mathcal {D}}\) such that  for every \(x\in {\mathcal {L}}\). We will refer to \({\mathcal {L}}^{\perp }\) as the orthogonal complement of \({\mathcal {L}}\).
for every \(x\in {\mathcal {L}}\). We will refer to \({\mathcal {L}}^{\perp }\) as the orthogonal complement of \({\mathcal {L}}\).
Using the notion of orthogonal complements, we may identify the following additional properties held by the full subcategory inclusion  :
:
-
i)
The restriction of the quadratic functor
 to \({\mathcal {C}}^{\text {op} }\) vanishes.
to \({\mathcal {C}}^{\text {op} }\) vanishes. -
ii)
The inclusion \(i{\mathcal {C}}^{\text {op} }\subseteq (i{\mathcal {C}}^{\text {op} })^{\perp }\), furnished by i) above, is an equivalence.
-
iii)
i admits a right adjoint
 given by \((x,y,\beta ) \mapsto y\) (see (184) and the discussion below it).
given by \((x,y,\beta ) \mapsto y\) (see (184) and the discussion below it).
The validity of i) above is evident from the fibre square (182) defining  . To see that ii) holds, note that
. To see that ii) holds, note that
and hence \((x,y,\beta ) \in (i{\mathcal {C}}^{\text {op} })^{\perp }\) if and only if \(x=0\), i.e., if and only if \((x,y,\beta ) \in i{\mathcal {C}}^{\text {op} }\). This motivates the following definition:
Definition 7.3.10
Let  be a Poincaré \(\infty \)-category and \({\mathcal {L}}\subseteq {\mathcal {D}}\) a full subcategory. We will say that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\) if it satisfies Properties i), ii) and iii) above. In other words, if
be a Poincaré \(\infty \)-category and \({\mathcal {L}}\subseteq {\mathcal {D}}\) a full subcategory. We will say that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\) if it satisfies Properties i), ii) and iii) above. In other words, if  vanishes when restricted to \({\mathcal {L}}\), the orthogonal complement \({\mathcal {L}}^{\perp }\subseteq {\mathcal {D}}\) coincides with \({\mathcal {L}}\) itself and the inclusion \({\mathcal {L}}\subseteq {\mathcal {D}}\) admits a right adjoint. We will say that a Poincaré \(\infty \)-category is metabolic if it admits a Lagrangian.
vanishes when restricted to \({\mathcal {L}}\), the orthogonal complement \({\mathcal {L}}^{\perp }\subseteq {\mathcal {D}}\) coincides with \({\mathcal {L}}\) itself and the inclusion \({\mathcal {L}}\subseteq {\mathcal {D}}\) admits a right adjoint. We will say that a Poincaré \(\infty \)-category is metabolic if it admits a Lagrangian.
In particular, the Poincaré \(\infty \)-category  contains \({\mathcal {C}}^{\text {op} }\) as a Lagrangian. We now claim that this property completely characterises Poincaré \(\infty \)-categories of the form
contains \({\mathcal {C}}^{\text {op} }\) as a Lagrangian. We now claim that this property completely characterises Poincaré \(\infty \)-categories of the form  . To see this, let
. To see this, let  be a Poincaré \(\infty \)-category with underlying duality \(\text {D} \), and let \(i:{\mathcal {L}}\hookrightarrow {\mathcal {D}}\) be a Lagrangian with right adjoint \(p:{\mathcal {D}}\rightarrow {\mathcal {L}}\). Let \(j:{\mathcal {L}}^{^{\text {op} }} \subseteq {\mathcal {D}}\) be the inclusion sending \(z\) to \(\text {D} (i(z))\). Then
be a Poincaré \(\infty \)-category with underlying duality \(\text {D} \), and let \(i:{\mathcal {L}}\hookrightarrow {\mathcal {D}}\) be a Lagrangian with right adjoint \(p:{\mathcal {D}}\rightarrow {\mathcal {L}}\). Let \(j:{\mathcal {L}}^{^{\text {op} }} \subseteq {\mathcal {D}}\) be the inclusion sending \(z\) to \(\text {D} (i(z))\). Then
and j admits a left adjoint \(q:{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\) given by the formula \(q(x) = p(\text {D} x)\).
We then have the following:
Proposition 7.3.11
(Recognition principle for pairing Poincaré categories) Let  be a Poincaré \(\infty \)-category admitting a Lagrangian \(i :{\mathcal {L}}\hookrightarrow {\mathcal {D}}\) with right adjoint \(p:{\mathcal {D}}\rightarrow {\mathcal {L}}\), and let the adjunction
be a Poincaré \(\infty \)-category admitting a Lagrangian \(i :{\mathcal {L}}\hookrightarrow {\mathcal {D}}\) with right adjoint \(p:{\mathcal {D}}\rightarrow {\mathcal {L}}\), and let the adjunction  be as above. Let
be as above. Let  be the left Kan extension of
be the left Kan extension of  along \(q^{\text {op} }:{\mathcal {D}}^{\text {op} }\rightarrow {\mathcal {L}}\) and
along \(q^{\text {op} }:{\mathcal {D}}^{\text {op} }\rightarrow {\mathcal {L}}\) and  the unit natural transformation. Then there exists a canonical diagram of hermitian \(\infty \)-categories
the unit natural transformation. Then there exists a canonical diagram of hermitian \(\infty \)-categories

in which the middle vertical arrow is an equivalence of Poincaré \(\infty \)-categories. Here the top row consists of the underlying bifibration (184) of \({\text {Pair}}({\mathcal {L}}^{\text {op} },\text {B} _{\Pi })\) promoted to the level of hermitian \(\infty \)-categories trivially on the right and as in (185) on the left.
Remark 7.3.12
The recognition principle of Proposition 7.3.11 could also be formulated in the bilinear setting of Sect. 7.2. In particular, given a stable \(\infty \)-category \({\mathcal {D}}\), equivalences of the form \({\mathcal {D}}\simeq {\text {Pair}}({\mathcal {A}},{\mathcal {B}},b)\) for \(({\mathcal {A}},{\mathcal {B}},b) \in {\textrm{Cat}^\textrm{b}_\infty }\) correspond to fully-faithful embeddings \(i:{\mathcal {B}}\hookrightarrow {\mathcal {D}}\) which admit a right adjoint \(p:{\mathcal {D}}\rightarrow {\mathcal {B}}\), in which case \({\mathcal {A}}\) is recovered as the kernel of p, and b is recovered as the restriction of the correspondence \(\text {seq} _{{\mathcal {D}}}:{\mathcal {D}}^{\text {op} }\times {\mathcal {D}}\rightarrow {\mathcal {S}}\) of Example 7.2.4 to \({\mathcal {A}}^{\text {op} }\times {\mathcal {B}}\). The proof of this claim essentially amounts to the first half of the proof of Proposition 7.3.11 below.
Proof of Proposition 7.3.11
Let \({\text {Seq}}({\mathcal {D}},{\mathcal {L}}) \subseteq {\text {Seq}}({\mathcal {D}})\) denote the full subcategory spanned by those exact sequences \([y\rightarrow z\rightarrow x]\) such that \(y\in i({\mathcal {L}})\) and \(x\in j({\mathcal {L}}^{\text {op} })\). We claim that the projection
is an equivalence. To see this, consider first the map \({\text {Seq}}({\mathcal {D}},{\mathcal {L}}) \rightarrow {\text {Ar}}({\mathcal {D}}) \times _{{\mathcal {D}}} j({\mathcal {L}}^{\text {op} })\) sending \([y\rightarrow z\rightarrow x]\) to \([z\rightarrow x]\). By [43, Proposition 4.3.2.15] this map is fully-faithful, with essential image the full subcategory of \({\text {Ar}}({\mathcal {D}}) \times _{{\mathcal {D}}} j({\mathcal {L}}^{\text {op} })\) spanned by those arrows \(z\rightarrow x\) with \(x\in j({\mathcal {L}}^{\text {op} })\) whose fibre lies in \(i({\mathcal {L}})\). Now since \(i({\mathcal {L}}) = \ker (q)\) the condition that the fibre of \(z\rightarrow x\) lies in \(i({\mathcal {L}})\) is equivalent to the condition that \(q(z) \rightarrow q(x) \simeq x\) is an equivalence. Now the projection \({\text {Ar}}({\mathcal {D}}) \times _{{\mathcal {D}}} j({\mathcal {L}}^{\text {op} }) \rightarrow {\mathcal {D}}\) sending \(z\rightarrow x\) to z is a cartesian fibration whose fibre over \(z\in {\mathcal {D}}\) is equivalent to the comma category \({\mathcal {D}}_{z/} \times _{{\mathcal {D}}} j({\mathcal {L}}^{\text {op} })\). This comma category is equivalent by adjunction to \({\mathcal {L}}^{\text {op} }_{q(z)/}\), and the above condition shows that under this equivalence the full subcategory \({\text {Seq}}({\mathcal {D}},{\mathcal {L}}) \subseteq {\text {Ar}}({\mathcal {D}}) \times _{{\mathcal {D}}} j({\mathcal {L}}^{\text {op} })\) consists of exactly those objects which are initial in their fibres. The projection \({\text {Seq}}({\mathcal {D}},{\mathcal {L}}) \rightarrow {\mathcal {D}}\) is consequently an equivalence.
We note that under the equivalence between bifibrations and correspondences, base changes on the cartesian side correspond the restriction along the first entry, while base changes on the cocartesian side correspond to restriction in the second entry. In particular, we may identify \({\text {Seq}}({\mathcal {D}},{\mathcal {L}})\) with \({\text {Pair}}({\mathcal {L}}^{\text {op} },{\mathcal {L}},(\text {seq} _{{\mathcal {D}}})|_{{\mathcal {L}}\times {\mathcal {L}}})\) as full subcategories of \({\text {Pair}}({\mathcal {D}},{\mathcal {D}},\text {seq} _{{\mathcal {D}}})\), and so the projections

form a bifibration classified by the restricted correspondence \((\text {seq} _{{\mathcal {D}}})|_{{\mathcal {L}}\times {\mathcal {L}}}:{\mathcal {L}}\times {\mathcal {L}}\rightarrow {\mathcal {S}}\). Under this equivalence \({\text {Seq}}({\mathcal {D}},{\mathcal {L}}) \simeq {\mathcal {D}}\) these projections correspond to adjoints \(p:{\mathcal {D}}\rightarrow {\mathcal {L}}\) and \(q :{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\) to the inclusions \(i:{\mathcal {L}}\hookrightarrow {\mathcal {D}}\) and \(j:{\mathcal {L}}^{\text {op} }\hookrightarrow {\mathcal {D}}\). We now observe that for \(x\in {\mathcal {L}}^{\text {op} }\) and \(y\in {\mathcal {L}}\) we have

and so if we let \(\Pi :{\mathcal {L}}\rightarrow {{\mathcal {S}}{p}}\) be the quadratic functor given by the formula  then we obtain an equivalence
then we obtain an equivalence
on the level of stable \(\infty \)-categories, which is compatible with the inclusions from and projections to \({\mathcal {L}}\) and \({\mathcal {L}}^{\text {op} }\) on both sides.
We now address the comparison of Poincaré structures. For every \(x\in {\mathcal {D}}\) the counit of \(i \dashv p\) and unit of \(q \dashv j\) yield a sequence
whose composite admits an essentially unique null-homotopy, since \(jq(x) \in \ker (p)\) and hence \({\text {hom}}_{{\mathcal {C}}}(ip(x),jq(x))= {\text {hom}}_{{\mathcal {L}}}(p(x),pjq(x))= 0\). This null-homotopy exhibits (189) as exact. Indeed, this sequence maps to an exact sequence by both p and q and these two functors are jointly conservative since \(\ker (p) \cap \ker (q) \simeq \text {im} (j) \cap \ker (q) =0\). Since  the shifted exact sequence \(\Omega jq(x) \rightarrow ip(x) \rightarrow x\) determines an exact square
the shifted exact sequence \(\Omega jq(x) \rightarrow ip(x) \rightarrow x\) determines an exact square

which, having set  , we can write as
, we can write as

Comparing the exact square (190) with the exact square (182) we then conclude that the equivalence \({\mathcal {D}}\simeq {\text {Pair}}({\mathcal {L}}^{\text {op} },\text {B} _{\Pi })\) refines to an equivalence of Poincaré \(\infty \)-categories  . By Corollary 7.3.8 we then get that the natural transformation
. By Corollary 7.3.8 we then get that the natural transformation  furnished by the top row of the square (190) exhibits \(\Pi \) as the left Kan extension of
furnished by the top row of the square (190) exhibits \(\Pi \) as the left Kan extension of  along \(q^{\text {op} }:{\mathcal {D}}^{\text {op} }\rightarrow {\mathcal {L}}\). We hence an equivalence
along \(q^{\text {op} }:{\mathcal {D}}^{\text {op} }\rightarrow {\mathcal {L}}\). We hence an equivalence

compatible with the projections to (and hence also the embedding of) the \(\infty \)-categories \({\mathcal {L}}\) and \({\mathcal {L}}^{\text {op} }\) on both sides. \(\square \)
Given a Poincaré \(\infty \)-category  admitting a Lagrangian
admitting a Lagrangian

with associated projection \(q= p\text {D} :{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\), Proposition 7.3.11 yields an equivalence of Poincaré \(\infty \)-categories

In particular, the association  takes values in metabolic Poincaré \(\infty \)-categories, and every metabolic Poincaré \(\infty \)-category is obtained in this manner.
takes values in metabolic Poincaré \(\infty \)-categories, and every metabolic Poincaré \(\infty \)-category is obtained in this manner.
In what follows, it will be useful to observe that the hermitian structure  on \({\mathcal {L}}^{\text {op} }\) can also be recovered using the inclusion \(j:{\mathcal {L}}^{\text {op} }\rightarrow {\mathcal {D}}\) right adjoint to q. To avoid a potential confusion we emphasise that \(\Pi \) does not coincide with the restriction of
on \({\mathcal {L}}^{\text {op} }\) can also be recovered using the inclusion \(j:{\mathcal {L}}^{\text {op} }\rightarrow {\mathcal {D}}\) right adjoint to q. To avoid a potential confusion we emphasise that \(\Pi \) does not coincide with the restriction of  along j. Instead, let \(\Pi _{\text {pair} }(x,y,\beta ) = \Pi (x) \times _{\text {B} (x,x)}{\text {hom}}(x,y)\) be the quadratic functor on \({\text {Pair}}({\mathcal {L}}^{\text {op} },\Pi )\) as in Construction 7.3.1. Under the equivalence (191) the functor \(j:{\mathcal {L}}^{\text {op} }\hookrightarrow {\mathcal {D}}\) sends \(x\) to \((x,0,0) \in {\text {Pair}}({\mathcal {L}}^{\text {op} },\text {B} _{\Pi })\) and we have
along j. Instead, let \(\Pi _{\text {pair} }(x,y,\beta ) = \Pi (x) \times _{\text {B} (x,x)}{\text {hom}}(x,y)\) be the quadratic functor on \({\text {Pair}}({\mathcal {L}}^{\text {op} },\Pi )\) as in Construction 7.3.1. Under the equivalence (191) the functor \(j:{\mathcal {L}}^{\text {op} }\hookrightarrow {\mathcal {D}}\) sends \(x\) to \((x,0,0) \in {\text {Pair}}({\mathcal {L}}^{\text {op} },\text {B} _{\Pi })\) and we have

where the last equivalence is issued from Lemma 1.1.19 and Example 1.1.21. It will consequently be convenient to introduce the following terminology:
Definition 7.3.13
Let \({\mathcal {C}}\) be a stable \(\infty \)-category and  a quadratic functor on \({\mathcal {C}}\). We denote by
a quadratic functor on \({\mathcal {C}}\). We denote by  and
and  the quadratic functors obtained by pre- and post-composing with \(\Omega \) and \(\Sigma \), respectively. We note that the operations
the quadratic functors obtained by pre- and post-composing with \(\Omega \) and \(\Sigma \), respectively. We note that the operations  and
and  are inverse to each other, and in particular adjoint (in both directions). By Lemma 1.1.19 we have natural equivalences
are inverse to each other, and in particular adjoint (in both directions). By Lemma 1.1.19 we have natural equivalences

yielding in particular a natural transformation  and an adjoint transformation
and an adjoint transformation  .
.
Remark 7.3.14
For a hermitian \(\infty \)-category  , the underlying symmetric bilinear form of
, the underlying symmetric bilinear form of  is given by \((x,y) \mapsto \Omega \text {B} (\Omega x,\Omega y) \simeq \Sigma ^{\sigma }\text {B} (x,y)\), where \(\Sigma ^{\sigma }\) is the operation of tensoring by the sign representation sphere, see discussion in Sect. 3.5. In other words,
is given by \((x,y) \mapsto \Omega \text {B} (\Omega x,\Omega y) \simeq \Sigma ^{\sigma }\text {B} (x,y)\), where \(\Sigma ^{\sigma }\) is the operation of tensoring by the sign representation sphere, see discussion in Sect. 3.5. In other words,  has as underlying bilinear form
has as underlying bilinear form  , but the symmetric structure is twisted by a sign, see Remark 3.5.4. Similarly,
, but the symmetric structure is twisted by a sign, see Remark 3.5.4. Similarly,  has underlying bilinear form \(\Omega \text {B} \), but the symmetric structure is twisted by a sign.
has underlying bilinear form \(\Omega \text {B} \), but the symmetric structure is twisted by a sign.
The identification (192) can be succinctly stated as  , or equivalently,
, or equivalently,  . We may summarise this discussion by extending (191) to
. We may summarise this discussion by extending (191) to

We now use the pairing construction in order to form left and right adjoints to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \).
Proposition 7.3.15
For every hermitian \(\infty \)-category  and Poincaré \(\infty \)-category
and Poincaré \(\infty \)-category  , the map
, the map

induced by post-composition with the hermitian functor  of (185), is an equivalence of spaces. In particular, the association
of (185), is an equivalence of spaces. In particular, the association  assembles to form a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) which is right adjoint to \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \).
assembles to form a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) which is right adjoint to \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \).
Remark 7.3.16
Though one can show directly that the association  organises into a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \), Proposition 7.3.15 is formulated in a way that does not require knowing this in advance, and on the other hand implies this functoriality via general principles of adjunctions; indeed, knowing that the comma category
organises into a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \), Proposition 7.3.15 is formulated in a way that does not require knowing this in advance, and on the other hand implies this functoriality via general principles of adjunctions; indeed, knowing that the comma category  has a final object is enough to imply the existence of the desired adjoints, which then must coincide with the given formula on objects.
has a final object is enough to imply the existence of the desired adjoints, which then must coincide with the given formula on objects.
Remark 7.3.17
In the situation of Proposition 7.3.15, if  is also Poincaré then we have a natural equivalence
is also Poincaré then we have a natural equivalence  (see Example 7.3.3 iii)) under which the hermitian functor of (185) becomes the domain projection
(see Example 7.3.3 iii)) under which the hermitian functor of (185) becomes the domain projection  . The unit of the adjunction furnished by Proposition 7.3.15 then corresponds to the essentially unique Poincaré functor
. The unit of the adjunction furnished by Proposition 7.3.15 then corresponds to the essentially unique Poincaré functor  for which the composite with the domain projection is the identity on
for which the composite with the domain projection is the identity on  . In particular, the unit must coincide with the fully-faithful inclusion
. In particular, the unit must coincide with the fully-faithful inclusion

endowed with the natural equivalence  .
.
Remark 7.3.18
By [47, Corollary 7.3.2.7] the functor \({\text {Pair}}(-)\) inherits a lax symmetric monoidal structure by virtue of being right adjoint to the symmetric monoidal functor \(\iota :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) (see Theorem 5.2.7). In particular, the adjunction \(\iota \dashv {\text {Pair}}(-)\) of Proposition 7.3.15 is a symmetric monoidal adjunction. It then follows from the equivalence of Example 7.3.3(ii) that the functor \({\text {Ar}}(-):\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) is lax symmetric monoidal as well.
Remark 7.3.19
In the situation of Proposition 7.3.15, if  is the quadratic Poincaré \(\infty \)-category associated to a symmetric bilinear form \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {E}})\), then by Propositions 7.2.17 and 7.2.18 the arrow (194) identifies with the arrow
is the quadratic Poincaré \(\infty \)-category associated to a symmetric bilinear form \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {E}})\), then by Propositions 7.2.17 and 7.2.18 the arrow (194) identifies with the arrow

and so we may conclude that the association \(({\mathcal {C}},\text {B} ) \mapsto ({\text {Pair}}({\mathcal {C}},\text {B} ),\text {B} _{\text {pair} })\) assembles to form a right adjoint to the inclusion \(\text {Cat} ^{\textrm{ps}}_\infty \rightarrow \text {Cat} ^{\textrm{sb}}_\infty \). Identifying \(\text {Cat} ^{\textrm{ps}}_\infty \) with \((\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}}\) via Corollary 7.2.16 and using Lemma 7.3.2 we may also reformulate this as saying that the association \(({\mathcal {C}},\text {B} ) \mapsto ({\text {Pair}}({\mathcal {C}},\text {B} ),\text {D} _{\text {pair} })\) gives a right adjoint to the functor \((\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow \text {Cat} ^{\textrm{sb}}_\infty \) sending \(({\mathcal {C}},\text {D} )\) to \(({\mathcal {C}},\text {B} _{\text {D} })\). This last conclusion could also be obtained from the opposite direction by showing that the association \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto {\text {Pair}}({\mathcal {A}},{\mathcal {B}},\text {B} )\) gives a \({{\text {C} }_{\textrm{2}}}\)-equivariant right adjoint to the functor \(\text {Cat} _\infty ^\text {ex} \rightarrow {\textrm{Cat}^\textrm{b}_\infty }\) sending \({\mathcal {C}}\) to \(({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\), and hence induces a right adjoint on the level of \({{\text {C} }_{\textrm{2}}}\)-fixed objects on both sides. In fact, \({\text {Pair}}(-,-,-)\) being right adjoint to \({\mathcal {C}}\mapsto ({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\) is a statement that holds also in the non-stable setting and can be proven using the setting of bifibrations as described in Sect. 7.1. Alternatively, an argument in the stable setting can be mounted along the lines of the proof of Proposition 7.3.15 below, using Remark 7.3.12 in place of Proposition 7.3.11.
Proof of Proposition 7.3.15
Fix a hermitian \(\infty \)-category  and a Poincaré \(\infty \)-category \(({\mathcal {E}},\Psi )\), and let
and a Poincaré \(\infty \)-category \(({\mathcal {E}},\Psi )\), and let

be the corresponding internal hom Poincaré \(\infty \)-category constructed in Sect. 6.2. We will use Proposition 7.3.11 in order to identify \(({\mathcal {D}},\Phi )\) with the pairing Poincaré \(\infty \)-category associated to the internal hom hermitian \(\infty \)-category  , thus reducing Proposition 7.3.15 to the algebraic Thom isomorphism of Proposition 7.3.5. Indeed, define
, thus reducing Proposition 7.3.15 to the algebraic Thom isomorphism of Proposition 7.3.5. Indeed, define
and let \(i_*:{\mathcal {L}}\rightarrow {\mathcal {D}}\) stand for post-composition with  . Since i is fully-faithful and admits a right adjoint
. Since i is fully-faithful and admits a right adjoint  we have that \(i_*\) is fully-faithful and admits a right adjoint \(p_*:{\mathcal {D}}\rightarrow {\mathcal {L}}\) obtained by post-composing with p. In addition, the restriction of
we have that \(i_*\) is fully-faithful and admits a right adjoint \(p_*:{\mathcal {D}}\rightarrow {\mathcal {L}}\) obtained by post-composing with p. In addition, the restriction of  to \({\mathcal {L}}\) vanishes because if
to \({\mathcal {L}}\) vanishes because if  is an exact functor which factors through \({\mathcal {C}}^{\text {op} }\) then
is an exact functor which factors through \({\mathcal {C}}^{\text {op} }\) then  (since
(since  vanishes on \({\mathcal {C}}^{\text {op} }\)) and so
vanishes on \({\mathcal {C}}^{\text {op} }\)) and so  . Finally, the orthogonal complement \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) consists of those exact functors
. Finally, the orthogonal complement \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) consists of those exact functors  such that \(p_*\text {D} _{{\mathcal {D}}}(f) = 0\), that is, such that \(p\text {D} _{\text {pair} }f\text {D} _{{\mathcal {E}}}(x) = 0\) for every \(x\in {\mathcal {E}}\). This is just equivalent to saying that f takes values in the orthogonal complement \((i{\mathcal {C}}^{\text {op} })^{\perp }\), which coincides with \(i{\mathcal {C}}^{\text {op} }\) itself since \(i{\mathcal {C}}^{\text {op} }\) is a Lagrangian. We may then conclude that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\).
such that \(p_*\text {D} _{{\mathcal {D}}}(f) = 0\), that is, such that \(p\text {D} _{\text {pair} }f\text {D} _{{\mathcal {E}}}(x) = 0\) for every \(x\in {\mathcal {E}}\). This is just equivalent to saying that f takes values in the orthogonal complement \((i{\mathcal {C}}^{\text {op} })^{\perp }\), which coincides with \(i{\mathcal {C}}^{\text {op} }\) itself since \(i{\mathcal {C}}^{\text {op} }\) is a Lagrangian. We may then conclude that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\).
Now, if we identify \({\mathcal {L}}^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {E}},{\mathcal {C}}^{\text {op} })^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {E}}^{\text {op} },{\mathcal {C}})\) with \({\text {Fun}}^{\textrm{ex}}({\mathcal {E}},{\mathcal {C}})\) via pre-composition with the duality of \({\mathcal {E}}\), then the inclusion \({\mathcal {L}}^{\text {op} }\rightarrow {\mathcal {D}}\) sending f to \(\text {D} _{{\mathcal {D}}}(i_*f)\) identifies with \(f \mapsto j_*f\), where \(j_*\) denotes post-composition with  . The left adjoint of \(j_*\) is then given by post-composition with
. The left adjoint of \(j_*\) is then given by post-composition with  , which we denote by \(q_*\). Let
, which we denote by \(q_*\). Let  be the quadratic functor obtained by left Kan extending
be the quadratic functor obtained by left Kan extending  along \(q_*:{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\). As in (193) we may also identify \(\Pi \) with the quadratic functor
along \(q_*:{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\). As in (193) we may also identify \(\Pi \) with the quadratic functor  . We may then compute
. We may then compute

and identify the natural map

for \(f \in {\mathcal {D}}\) with the map

obtained post-composition with  . Invoking Proposition 7.3.11 we now get an identification
. Invoking Proposition 7.3.11 we now get an identification

of  as the pairings Poincaré category of the hermitian \(\infty \)-category
as the pairings Poincaré category of the hermitian \(\infty \)-category  , under which the associated cartesian fibration
, under which the associated cartesian fibration

identifies with post-composition with  . Proposition 7.3.20 consequently follows from Proposition 7.3.5. \(\square \)
. Proposition 7.3.20 consequently follows from Proposition 7.3.5. \(\square \)
To obtain a left adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) we first promote j to a hermitian functor

using the equivalence \(\vartheta \) appearing in Definition 7.3.13.
Proposition 7.3.20
For every Poincaré \(\infty \)-category  , the map
, the map

induced by pre-composition with (195), is an equivalence of spaces. In particular, substituting  instead of
instead of  we deduce that the association
we deduce that the association  assembles to form a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) which is left adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \).
assembles to form a functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{p}}_\infty \) which is left adjoint to the forgetful functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \).
Remark 7.3.21
In the situation of Proposition 7.3.20, if  is also Poincaré then by Example 7.3.3 iii) we have a natural equivalence
is also Poincaré then by Example 7.3.3 iii) we have a natural equivalence

where the last equivalence covers the exact functor \([w\rightarrow x] \mapsto [\Omega w\rightarrow \Omega x]\). Under this equivalence the hermitian functor (195) becomes the inclusion

The counit of the adjunction furnished by Proposition 7.3.20 then corresponds to the essentially unique Poincaré functor  for which the pre-composing with this unit gives the identity on
for which the pre-composing with this unit gives the identity on  . In particular, the counit must coincide with the projection
. In particular, the counit must coincide with the projection

of Lemma 2.3.7.
Remark 7.3.22
For a Poincaré \(\infty \)-category  , applying the functor \({\text {Pair}}(-,(-)^{[\sigma ]})\) to the canonical hermitian functors
, applying the functor \({\text {Pair}}(-,(-)^{[\sigma ]})\) to the canonical hermitian functors  and
and  yields, using Remark 7.3.21, the Poincaré functors
yields, using Remark 7.3.21, the Poincaré functors

and

of Construction 2.3.8, respectively. This gives, in particular, a certain abstract justification for the appearance of these Poincaré functors.
Remark 7.3.23
It follows from Proposition 7.3.20 and Remark 7.3.21 that the association  carries the structure of a comonad on \(\text {Cat} ^{\textrm{p}}_\infty \), with the Poincaré functors
carries the structure of a comonad on \(\text {Cat} ^{\textrm{p}}_\infty \), with the Poincaré functors  assembling to form the counit of this monad. A formal consequence of this which we record here for later use is that the resulting comultiplication Poincaré functor
assembling to form the counit of this monad. A formal consequence of this which we record here for later use is that the resulting comultiplication Poincaré functor  gives a section for either of the two projections
gives a section for either of the two projections

the first being the counit evaluated at  and the second obtained by applying \({\text {Met}}\) to the counit evaluated at
and the second obtained by applying \({\text {Met}}\) to the counit evaluated at  .
.
Remark 7.3.24
In the situation of Proposition 7.3.20, if  is the symmetric Poincaré \(\infty \)-category associated to a symmetric bilinear form \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {E}})\), then by Propositions 7.2.17 and 7.2.18 and Remark 7.3.14, the arrow (196) identifies with the arrow
is the symmetric Poincaré \(\infty \)-category associated to a symmetric bilinear form \(\text {B} \in {\text {Fun}}^{\textrm{s}}({\mathcal {E}})\), then by Propositions 7.2.17 and 7.2.18 and Remark 7.3.14, the arrow (196) identifies with the arrow

As in Remark 7.3.19 we may then conclude that the association \(({\mathcal {C}},\text {B} ) \mapsto ({\text {Pair}}({\mathcal {C}},\Sigma ^{\sigma }\text {B} ),\text {D} _{\text {pair} })\) assembles to form a left adjoint to the functor \((\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow \text {Cat} ^{\textrm{sb}}_\infty \) sending \(({\mathcal {C}},\text {D} )\) to \(({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\). This conclusion could also be obtained differently by showing first that the association \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto {\text {Pair}}({\mathcal {A}},{\mathcal {B}},\Sigma \text {B} )\) gives \({{\text {C} }_{\textrm{2}}}\)-equivariant left adjoint to the functor \(\text {Cat} _\infty ^\text {ex} \rightarrow {\textrm{Cat}^\textrm{b}_\infty }\) sending \({\mathcal {C}}\) to \(({\mathcal {C}},{\mathcal {C}},m_{{\mathcal {C}}})\) (though the \({{\text {C} }_{\textrm{2}}}\)-equivariant structure here involves a somewhat subtle sign). The last claim can be proven using an argument similar to that of the proof of Proposition 7.3.20 below, by replacing the recognition principle of Proposition 7.3.11 by its bilinear version (see Remark 7.3.12). We leave the details to the motivated reader.
Proof of Proposition 7.3.20
Fix a hermitian \(\infty \)-category  and a Poincaré \(\infty \)-category
and a Poincaré \(\infty \)-category  , and let
, and let

be the corresponding internal hom Poincaré \(\infty \)-category. As in the proof of Proposition 7.3.15 we will use Proposition 7.3.11 in order to identify \({\mathcal {D}}\) with a pairing Poincaré \(\infty \)-category associated to the internal hom hermitian \(\infty \)-category  , thus reducing Proposition 7.3.20 to the algebraic Thom isomorphism of Proposition 7.3.5. For this, define
, thus reducing Proposition 7.3.20 to the algebraic Thom isomorphism of Proposition 7.3.5. For this, define
and let \(p^*:{\mathcal {L}}\rightarrow {\mathcal {D}}\) stand for pre-composition with  . Since p has a fully-faithful left adjoint
. Since p has a fully-faithful left adjoint  we get that \(p^*\) is fully-faithful and admits a right adjoint \(i^*:{\mathcal {D}}\rightarrow {\mathcal {L}}\) given by pre-composition with i. In addition, the restriction of
we get that \(p^*\) is fully-faithful and admits a right adjoint \(i^*:{\mathcal {D}}\rightarrow {\mathcal {L}}\) given by pre-composition with i. In addition, the restriction of  to \({\mathcal {L}}\) vanishes because if
to \({\mathcal {L}}\) vanishes because if  for some \(g:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {E}}\) then
for some \(g:{\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {E}}\) then

where the identification  is since \(i^{\text {op} }\) is right adjoint to \(p^{\text {op} }\). Finally, the orthogonal complement \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) consists of those exact functors
is since \(i^{\text {op} }\) is right adjoint to \(p^{\text {op} }\). Finally, the orthogonal complement \({\mathcal {L}}^{\perp } \subseteq {\mathcal {D}}\) consists of those exact functors  such that \(i^*\text {D} _{{\mathcal {D}}}(f) = 0\), that is, such that \(\text {D} _{{\mathcal {E}}}f\text {D} _{\text {pair} }(i(x)) = 0\) for every \(x\in {\mathcal {C}}^{\text {op} }\). This is just equivalent to saying that f vanishes on \(\text {im} (j)=\ker (p)\), which is equivalent to saying that f factors through p. We may then conclude that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\).
such that \(i^*\text {D} _{{\mathcal {D}}}(f) = 0\), that is, such that \(\text {D} _{{\mathcal {E}}}f\text {D} _{\text {pair} }(i(x)) = 0\) for every \(x\in {\mathcal {C}}^{\text {op} }\). This is just equivalent to saying that f vanishes on \(\text {im} (j)=\ker (p)\), which is equivalent to saying that f factors through p. We may then conclude that \({\mathcal {L}}\) is a Lagrangian in \({\mathcal {D}}\).
Let us now identify \({\mathcal {L}}^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {C}}^{\text {op} },{\mathcal {E}})^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {E}}^{\text {op} })\) with \({\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {E}})\) via post-composition with the duality of \({\mathcal {E}}\). Then the inclusion \({\mathcal {L}}^{\text {op} }\rightarrow {\mathcal {D}}\) sending f to \(\text {D} _{{\mathcal {D}}}(p^*f)\) identifies with \(f \mapsto q^*f\), where \(q^*\) denotes pre-composition with the cartesian projection  , and the left adjoint of \(q^*\) is given by pre-composition with
, and the left adjoint of \(q^*\) is given by pre-composition with  . Let \(\Pi := (j^*)_!\Psi \in {\text {Fun}}^{\textrm{q}}({\mathcal {L}}^{\text {op} })\) be the quadratic functor obtained by left Kan extension \(\Psi \) along \(j^*:{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\), so that by (193) we can also write as
. Let \(\Pi := (j^*)_!\Psi \in {\text {Fun}}^{\textrm{q}}({\mathcal {L}}^{\text {op} })\) be the quadratic functor obtained by left Kan extension \(\Psi \) along \(j^*:{\mathcal {D}}\rightarrow {\mathcal {L}}^{\text {op} }\), so that by (193) we can also write as  for \(g \in {\mathcal {L}}^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {E}})\). Using Corollary 7.3.8 we then compute
for \(g \in {\mathcal {L}}^{\text {op} }= {\text {Fun}}^{\textrm{ex}}({\mathcal {C}},{\mathcal {E}})\). Using Corollary 7.3.8 we then compute

The canonical map

for \(f \in {\mathcal {D}}\) then identifies with the map

obtained by restricting along j using the equivalence  . Invoking Proposition 7.3.11 we now get an identification
. Invoking Proposition 7.3.11 we now get an identification

of  as the pairings Poincaré category of the hermitian \(\infty \)-category
as the pairings Poincaré category of the hermitian \(\infty \)-category  , under which the associated cartesian fibration
, under which the associated cartesian fibration

identifies with pre-composition with  . Proposition 7.3.15 consequently follows from Proposition 7.3.5. \(\square \)
. Proposition 7.3.15 consequently follows from Proposition 7.3.5. \(\square \)
We take the point of view that the functor  is a categorical analogue of the algebraic Thom construction studied in Sect. 2.4. Recall that the latter takes a hermitian object and returns a metabolic Poincaré object with respect to a shifted Poincaré structure. In the algebraic setting we saw that this association determines an equivalence
is a categorical analogue of the algebraic Thom construction studied in Sect. 2.4. Recall that the latter takes a hermitian object and returns a metabolic Poincaré object with respect to a shifted Poincaré structure. In the algebraic setting we saw that this association determines an equivalence

between hermitian object in  and Poincaré objects in
and Poincaré objects in  equipped with a prescribed Lagrangian. To make the categorical analogue complete we would like to argue that \({\text {Pair}}(-)\) determines an equivalence between \(\text {Cat} ^{\textrm{h}}_\infty \) and a suitable \(\infty \)-category whose objects are Poincaré \(\infty \)-categories
equipped with a prescribed Lagrangian. To make the categorical analogue complete we would like to argue that \({\text {Pair}}(-)\) determines an equivalence between \(\text {Cat} ^{\textrm{h}}_\infty \) and a suitable \(\infty \)-category whose objects are Poincaré \(\infty \)-categories  equipped with a Lagrangian \({\mathcal {L}}\subseteq {\mathcal {D}}\), and whose maps are Poincaré functors which preserve the given Lagrangians. While we will not make this completely precise, the gist of this claim amounts to the following two facts:
equipped with a Lagrangian \({\mathcal {L}}\subseteq {\mathcal {D}}\), and whose maps are Poincaré functors which preserve the given Lagrangians. While we will not make this completely precise, the gist of this claim amounts to the following two facts:
-
i)
The essential image of the functor
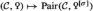 consists of the metabolic Poincaré \(\infty \)-categories. This follows from Proposition 7.3.11.
consists of the metabolic Poincaré \(\infty \)-categories. This follows from Proposition 7.3.11. -
ii)
Given two hermitian \(\infty \)-categories
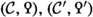 , Poincaré functors
, Poincaré functors 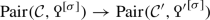
sending the Lagrangian
 to the Lagrangian
to the Lagrangian 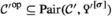 are in bijection with hermitian functors
are in bijection with hermitian functors  . Indeed, by Proposition 7.3.20 Poincaré functors
. Indeed, by Proposition 7.3.20 Poincaré functors  correspond to hermitian functors
correspond to hermitian functors  , and such a hermitian functor takes values in the full subcategory
, and such a hermitian functor takes values in the full subcategory  if and only if the corresponding Poincaré functor
if and only if the corresponding Poincaré functor  sends \({\mathcal {C}}\) to \({{{\mathcal {C}}}'}\), which is equivalent to sending the Lagrangian
sends \({\mathcal {C}}\) to \({{{\mathcal {C}}}'}\), which is equivalent to sending the Lagrangian 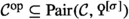 to the Lagrangian
to the Lagrangian  since \({\mathcal {C}}\) and \({\mathcal {C}}^{\text {op} }\) are two full subcategories of
since \({\mathcal {C}}\) and \({\mathcal {C}}^{\text {op} }\) are two full subcategories of  which are switched by the duality, and the same holds for \({{{\mathcal {C}}}'}\) and \({{{\mathcal {C}}}'}^{\text {op} }\).
which are switched by the duality, and the same holds for \({{{\mathcal {C}}}'}\) and \({{{\mathcal {C}}}'}^{\text {op} }\).
8.4 Genuine semi-additivity and spectral Mackey functors
In this section we explain how various categorical structures appearing in the theory of Poincaré \(\infty \)-categories can neatly be encoded in the framework of \({{\text {C} }_{\textrm{2}}}\)-categories and Mackey functors, as developed by Barwick and collaborators in the setting of parametrised higher category theory, see [10, 11, 51, 62]. The material of this section, and in particular the hyperbolic Mackey functor constructed in Corollary 7.4.18 below, will form the basis to the formation of the real \({\text {K}}\)-theory spectrum in Paper [2].
To begin, let \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) be the orbit category of \({{\text {C} }_{\textrm{2}}}\), that is, the category of transitive \({{\text {C} }_{\textrm{2}}}\)-sets and \({{\text {C} }_{\textrm{2}}}\)-equivariant maps. We note that \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) has two objects, \({{\text {C} }_{\textrm{2}}}/{{\text {C} }_{\textrm{2}}}= *\) and \({{\text {C} }_{\textrm{2}}}/e = {{\text {C} }_{\textrm{2}}}\), such that \(*\) is terminal, \({\text {Hom}}_{{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}}({{\text {C} }_{\textrm{2}}},{{\text {C} }_{\textrm{2}}}) = {{\text {C} }_{\textrm{2}}}\) and there are no maps from \(*\) to \({{\text {C} }_{\textrm{2}}}\). A \({{\text {C} }_{\textrm{2}}}\)-category is by definition a cocartesian fibration
which by the straightening-unstraightening equivalence is the same data as a functor \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow \text {Cat} _\infty \). A \({{\text {C} }_{\textrm{2}}}\)-functor between \({{\text {C} }_{\textrm{2}}}\)-categories is then a functor over \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) which preserves cocartesian edges. We note that by the above explicit description of \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) we see that it is isomorphic to the categorical cone on the category \(\text {B} {{\text {C} }_{\textrm{2}}}\). As a result, the data of a functor \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {{\text {C} }_{\textrm{2}}}\) is equivalent to that of an \(\infty \)-category \({\mathcal {E}}_{*}\) (the image of the “cone point” \(*\)), an \(\infty \)-category \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) with \({{\text {C} }_{\textrm{2}}}\)-action (the image of \({{\text {C} }_{\textrm{2}}}\) with the \({{\text {C} }_{\textrm{2}}}\)-action induced by its automorphisms) and a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) where the domain is considered with the trivial \({{\text {C} }_{\textrm{2}}}\)-action. Since \(\text {Cat} _\infty \) admits limits the data of a \({{\text {C} }_{\textrm{2}}}\)-equivariant map \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) can equivalently be encoded via a map \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}^{{{\text {hC} }_{\textrm{2}}}}\).
Example 7.4.1
If \({\mathcal {C}}\) is an \(\infty \)-category with a \({{\text {C} }_{\textrm{2}}}\)-action then we can right Kan extend the functor \(\text {B} {{\text {C} }_{\textrm{2}}}\rightarrow \text {Cat} _\infty \) encoding this action to a functor \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow \text {Cat} _\infty \), which we can then straighten to obtain a \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) with fibres \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \simeq {\mathcal {C}}\) and \({\mathcal {E}}_{*} \simeq {\mathcal {C}}^{{{\text {hC} }_{\textrm{2}}}}\), and structure map \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}^{{{\text {hC} }_{\textrm{2}}}}\) the identity. This construction embeds \({\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},\text {Cat} _\infty )\) as a full subcategory of \({{\text {C} }_{\textrm{2}}}\)-categories.
Example 7.4.2
In the situation of Example 7.4.1, if \({\mathcal {C}}\) is of the form \({\mathcal {D}}\times {\mathcal {D}}\) with the flip action then \({\mathcal {C}}^{{{\text {hC} }_{\textrm{2}}}} \simeq {\mathcal {D}}\) and the \({{\text {C} }_{\textrm{2}}}\)-equivariant functor \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) is the diagonal \({\mathcal {D}}\rightarrow {\mathcal {D}}\times {\mathcal {D}}\).
The examples we are interested in are the following:
Examples 7.4.3
-
i)
For a stable \(\infty \)-category \({\mathcal {C}}\) the functor of taking symmetric bilinear parts \(\text {B} _{(-)}:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{s}}({\mathcal {C}}) = {\text {Fun}}^{\textrm{b}}({\mathcal {C}})^{{{\text {hC} }_{\textrm{2}}}}\) determines a \({{\text {C} }_{\textrm{2}}}\)-category
$$\begin{aligned} \underline{\hbox {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\end{aligned}$$whose fibre over \(*\) is \({\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) and whose fibre over \({{\text {C} }_{\textrm{2}}}\) is \({\text {Fun}}^{\textrm{b}}({\mathcal {C}})\).
-
ii)
The functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} ^{\textrm{sb}}_\infty = ({\textrm{Cat}^\textrm{b}_\infty })^{{{\text {hC} }_{\textrm{2}}}}\) sending a hermitian \(\infty \)-category
 to its underlying symmetric category \(({\mathcal {C}},\text {B} )\) determines a \({{\text {C} }_{\textrm{2}}}\)-category $$\begin{aligned} \underline{\textrm{Cat}}^\textrm{h}_\infty \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\end{aligned}$$
to its underlying symmetric category \(({\mathcal {C}},\text {B} )\) determines a \({{\text {C} }_{\textrm{2}}}\)-category $$\begin{aligned} \underline{\textrm{Cat}}^\textrm{h}_\infty \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\end{aligned}$$whose fibre over \(*\) is \(\text {Cat} ^{\textrm{h}}_\infty \) and whose fibre over \({{\text {C} }_{\textrm{2}}}\) is \({\textrm{Cat}^\textrm{b}_\infty }\).
-
iii)
The functor \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{ps}}_\infty = (\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}}\) sending a Poincaré \(\infty \)-category
 to its underlying \(\infty \)-category with perfect duality determines a \({{\text {C} }_{\textrm{2}}}\)-category $$\begin{aligned} \underline{\textrm{Cat}}^\textrm{p}_\infty \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\end{aligned}$$
to its underlying \(\infty \)-category with perfect duality determines a \({{\text {C} }_{\textrm{2}}}\)-category $$\begin{aligned} \underline{\textrm{Cat}}^\textrm{p}_\infty \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\end{aligned}$$whose fibre over \(*\) is \(\text {Cat} ^{\textrm{p}}_\infty \) and whose fibre over \({{\text {C} }_{\textrm{2}}}\) is \(\text {Cat} _\infty ^\text {ex} \).
For a \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) one may consider the \({{\text {C} }_{\textrm{2}}}\)-variants of the usual notions of limits and colimits, defined for a given \({{\text {C} }_{\textrm{2}}}\)-functor \(p:{\mathcal {I}}\rightarrow {\mathcal {E}}\). If \({\mathcal {I}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is equivalent to a projection \(K \times {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) for some K then a \({{\text {C} }_{\textrm{2}}}\)-colimit of \(p:{\mathcal {I}}\rightarrow {\mathcal {E}}\) is given by a cocartesian section \(s:{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {\mathcal {E}}\) together with a natural transformation \(\eta :p \Rightarrow s|_{K}\) which exhibits s as a colimit fibrewise, and dually for limits. For example, a \({{\text {C} }_{\textrm{2}}}\)-initial object is given by a section \(s:{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {\mathcal {C}}\) which is fibrewise initial. We shall refer to these as fibrewise \({{\text {C} }_{\textrm{2}}}\)-colimits. By [51, Proposition 2.11] a \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {E}}\) has all fibrewise \({{\text {C} }_{\textrm{2}}}\)-colimits indexed by \(K \times {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) if and only if the fibres \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) and \({\mathcal {E}}_{*}\) both have K-indexed colimits and the functor \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) preserves K-indexed colimits. In particular, all the examples in 7.4.3 have all fibrewise \({{\text {C} }_{\textrm{2}}}\)-limits and \({{\text {C} }_{\textrm{2}}}\)-colimits, since in all three cases the individual fibres have all limits and colimits and the cocartesian transition functor preserves all limits and colimits.
For an indexing \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {I}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) which is not of the form \(K \times {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) the notion of a \({{\text {C} }_{\textrm{2}}}\)-colimit is a bit more involved. The underlying data is still given by that of s and \(\eta \), but the condition these are required to satisfy is more complicated, and is neither weaker nor stronger than being a fibrewise colimit. To avoid a technical digression let us avoid giving the general definition, referring the reader to [62, Definition 5.2]. The simplest type of non-fibrewise \({{\text {C} }_{\textrm{2}}}\)-(co)limits are finite \({{\text {C} }_{\textrm{2}}}\)-(co)products, and these will be the only type of non-fibrewise \({{\text {C} }_{\textrm{2}}}\)-(co)limits that we will consider here. These are \({{\text {C} }_{\textrm{2}}}\)-(co)limits indexed by finite \({{\text {C} }_{\textrm{2}}}\)-sets, that is, \({{\text {C} }_{\textrm{2}}}\)-categories \({\mathcal {I}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) which are finite direct sums of corepresentable left fibrations. We may decompose them as a disjoint union of the finite \({{\text {C} }_{\textrm{2}}}\)-set \([*\rightarrow *]\) (standing for the left fibration over \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) corepresented by \(*\)) and the finite \({{\text {C} }_{\textrm{2}}}\)-set \([\emptyset \rightarrow {{\text {C} }_{\textrm{2}}}]\) (standing for the left fibration corepresented by \({{\text {C} }_{\textrm{2}}}\)).
We wish to verify that our examples of interest 7.4.3 all have finite \({{\text {C} }_{\textrm{2}}}\)-products and coproducts. For this we will use a convenient criterion from [51]. Before we can state it, we point out the following observation: if \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is a \({{\text {C} }_{\textrm{2}}}\)-category with associated \({{\text {C} }_{\textrm{2}}}\)-equivariant functor \(f:{\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\), and \(g:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\) is a left or right adjoint to f, then g inherits a canonical \({{\text {C} }_{\textrm{2}}}\)-equivariant structure. In fact, the entire adjunction carries a \({{\text {C} }_{\textrm{2}}}\)-action, so that the unit and counit are \({{\text {C} }_{\textrm{2}}}\)-equivariant natural transformations. This essentially follows from the uniqueness of adjoints given their existence. Otherwise put, the functor that forgets an adjunction to its left adjoint is fully-faithful and hence any \({{\text {C} }_{\textrm{2}}}\)-action can be lifted along it. One can also see this as follows. If f admits a right adjoint then the cocartesian fibration \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is also locally cartesian (since \({{\text {C} }_{\textrm{2}}}\rightarrow *\) is the only arrow that is not an isomorphism in \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\)), and hence a cartesian fibration. This cartesian fibration then encodes the data of a \({{\text {C} }_{\textrm{2}}}\)-equivariant functor \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\), which is right adjoint to f. If a left adjoint to f is considered then the same argument can be made using the dual cartesian fibration \({\hat{{\mathcal {E}}}} \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\), that is, the cartesian fibration classified by the same functor as \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\).
The following lemma is just an adaptation of [51, Proposition 2.11] to the case at hand:
Lemma 7.4.4
Let \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{^{\text {op} }}\) be a \({{\text {C} }_{\textrm{2}}}\)-category such that the fibres \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}},{\mathcal {E}}_{*}\) admit finite coproducts and the functor \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) preserves finite coproducts. Write \(\sigma :{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) for the action of the generator of \({{\text {C} }_{\textrm{2}}}\). Then the following are equivalent:
-
i)
\({\mathcal {E}}\) admits all finite \({{\text {C} }_{\textrm{2}}}\)-coproducts.
-
ii)
\({\mathcal {E}}\) admits \({{\text {C} }_{\textrm{2}}}\)-colimits for \({{\text {C} }_{\textrm{2}}}\)-diagrams indexed by the corepresentable \({{\text {C} }_{\textrm{2}}}\)-set \([\emptyset \rightarrow {{\text {C} }_{\textrm{2}}}]\).
-
iii)
The functor \(f:{\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) admits a left adjoint \(g:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\) such that for \(x\in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) the map
$$\begin{aligned} x\coprod \sigma (x) \rightarrow fg(x) \end{aligned}$$adjoint to the fold map \(g(x\coprod \sigma (x)) \simeq g(x) \coprod g(\sigma (x)) \simeq g(x) \coprod g(x) \rightarrow g(x)\) is an equivalence.
Proof
The equivalence of i) and ii) follows from the fact that under the assumptions of the lemma \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) has fibrewise coproducts (that is, coproducts for diagrams indexed by finite direct sums of \([*\rightarrow *]\)) by [51, Proposition 2.11] and so the existence of all \({{\text {C} }_{\textrm{2}}}\)-coproducts reduces to the case of the corepresentable ones, of which \([*\rightarrow *]\) is trivial. The equivalence of i) and iii) follows from [51, Proposition 2.11] since iii) is simply a reformulation of the Beck–Chevalley criterion given there in the case of the unique non-invertible edge \({{\text {C} }_{\textrm{2}}}\rightarrow *\) of \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\). \(\square \)
Remark 7.4.5
Lemma 7.4.4 has a dual version which is proven exactly the same way. It says that \({\mathcal {E}}\) has a all finite \({{\text {C} }_{\textrm{2}}}\)-products if and only if it has \({{\text {C} }_{\textrm{2}}}\)-limits for diagrams indexed by \([\emptyset \rightarrow {{\text {C} }_{\textrm{2}}}]\), and that the latter is equivalent to f having a right adjoint \(g:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\) such that for \(x\in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) the map
adjoint to the diagonal \(g(x) \rightarrow \text {g} (x) \times g(x) \simeq g(x) \times g(\sigma (x)) \simeq g(x\times \sigma (x))\) is an equivalence.
Remark 7.4.6
Diagrams in \({\mathcal {E}}\) indexed by \([\emptyset \rightarrow {{\text {C} }_{\textrm{2}}}]\) are determined by the data of an object \(x\in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\). When the equivalent conditions of Lemma 7.4.4 hold then the \({{\text {C} }_{\textrm{2}}}\)-coproduct of such a diagram is given by the cocartesian section \(s:{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {\mathcal {E}}\) whose value at \(*\) is g(x) and whose value at \({{\text {C} }_{\textrm{2}}}\) is \(x \coprod \sigma (x)\). The existence of such a cocartesian section is insured by iii) above. Similarly, the \({{\text {C} }_{\textrm{2}}}\)-product of such a diagram, when exists, is given by a cocartesian section \(s:{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {\mathcal {E}}\) whose value at \(*\) is g(x) and whose value at \({{\text {C} }_{\textrm{2}}}\) is \(x \times \sigma (x)\).
Example 7.4.7
In the situation of Example 7.4.2, the resulting \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) has finite \({{\text {C} }_{\textrm{2}}}\)-products (resp. \({{\text {C} }_{\textrm{2}}}\)-coproducts) if and only if \({\mathcal {D}}\) has finite products (resp. coproducts).
Proposition 7.4.8
The \({{\text {C} }_{\textrm{2}}}\)-categories of Examples 7.4.3 all have finite \({{\text {C} }_{\textrm{2}}}\)-products and coproducts.
Proof
We will use the criterion of Lemma 7.4.4. For this we first verify that the fibres over \({{\text {C} }_{\textrm{2}}}\) and \(*\) have finite (co)products and that the transition functors preserve finite (co)products. In Example i) the fibres are stable and the transition functors are exact. For Example ii) the existence of limits and colimits is established in Proposition 6.1.2 and Remark 7.2.5, and the preservation of limits and colimits by the transition functors is a consequence of Proposition 7.2.20. For Example iii) the same is established in Proposition 6.1.1, Proposition 6.1.4 and Corollary 7.2.21. We now verify that all three examples satisfy Criterion iii) of Lemma 7.4.4. In the case of Example i) it follows from Lemma 1.1.7 and Remark 1.1.18 that the functor \(\text {B} \mapsto \text {B} ^{\Delta }\) gives both a left and a right adjoint to the bilinear part functor  . We now need to verify that for \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) the maps
. We now need to verify that for \(\text {B} \in {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) the maps
and
are equivalences. Indeed, this follows directly from the bilinearity of \(\text {B} \). For Example ii) we have by Proposition 7.2.20 that the association \(({\mathcal {A}},{\mathcal {B}},\text {B} ) \mapsto ({\mathcal {A}}\times {\mathcal {B}}^{\text {op} },\text {B} )\) gives both a left and a right adjoint to the functor \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\textrm{Cat}^\textrm{b}_\infty }\). Criterion iii) can then be deduced from its validity for Example i) and for Example 7.4.7 with \({\mathcal {D}}= \text {Cat} _\infty ^\text {ex} \). Finally, the case of Example iii) follows from that of ii) since the former maps to the latter via a \({{\text {C} }_{\textrm{2}}}\)-functor which is a fibrewise replete subcategory inclusion, so the two-sided adjoint of \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\textrm{Cat}^\textrm{b}_\infty }\) restricts to give two sided adjoints for \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) by Proposition 7.2.20. \(\square \)
It will be important for us in subsequent instalments of this project to know that the \({{\text {C} }_{\textrm{2}}}\)-categories of Examples 7.4.3 don’t just admit finite \({{\text {C} }_{\textrm{2}}}\)-products and coproducts but that they are furthermore \({{\text {C} }_{\textrm{2}}}\)-semiadditive, see [51, Definition 5.3]. To explain what this means let \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) be a \({{\text {C} }_{\textrm{2}}}\)-category which admits finite \({{\text {C} }_{\textrm{2}}}\)-products and coproducts, so that by Lemma 7.4.4f admits both a left adjoint \(g:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\) and a right adjoint \(h:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\), and these satisfy \(fg(x) \simeq x\coprod \sigma (x)\) and \(fh(x) \simeq x\times \sigma (x)\). Suppose that the fibres \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) and \({\mathcal {E}}_{*}\) are both semiadditive, so that we may identify products and coproducts and write them as direct sums
Then we have natural candidate for a comparison map
which is adjoint to the map
corresponding to the inclusion of the component \(x\).
The following definition is an adaptation of [51, Definition 5.3] to the particular case where the base is \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\), making use of the fact that \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) has a unique non-invertible arrow, given by \({{\text {C} }_{\textrm{2}}}\rightarrow *\).
Definition 7.4.9
Let \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) be a \({{\text {C} }_{\textrm{2}}}\)-category which admits finite \({{\text {C} }_{\textrm{2}}}\)-products and finite \({{\text {C} }_{\textrm{2}}}\)-coproducts. Then \({\mathcal {E}}\) is called \({{\text {C} }_{\textrm{2}}}\)-semiadditive if the following holds:
-
i)
The fibres \({\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) and \({\mathcal {E}}_{*}\) are semiadditive.
-
ii)
The comparison map (197) between the left and right adjoints of f is an equivalence.
Example 7.4.10
In the situation of Example 7.4.2, the resulting \({{\text {C} }_{\textrm{2}}}\)-category \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is semiadditive if and only if \({\mathcal {D}}\) is semiadditive.
Proposition 7.4.11
The \({{\text {C} }_{\textrm{2}}}\)-categories of Example 7.4.3 are all \({{\text {C} }_{\textrm{2}}}\)-semiadditive.
Proof
We first verify that in all the examples in 7.4.3 the fibres are semi-additive. For Example i) the fibres are stable and in particular semiadditive. For Examples ii) and iii) this was established in Proposition 6.1.7 and Remark 7.2.7.
We now establish the second condition of Definition 7.4.9. Arguing as in the proof of Proposition 7.4.8 using Example 7.4.10 in place of Example 7.4.7 we see that it will suffice to establish the second condition for Example i). Now by Remark 1.1.18 the diagonal restriction functor \(\Delta ^*:{\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}})\) is both left and right adjoint to the cross effect functor \(\text {B} _{(-)}:{\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) and we already saw in the proof of Proposition 7.4.8 that the composite \({\text {Fun}}^{\textrm{b}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {\text {Fun}}^{\textrm{b}}({\mathcal {C}})\) is naturally equivalent to the functor \(\text {B} \mapsto \text {B} \oplus \text {B} _{\text {swap} }\). Unwinding the definitions, to establish the second condition it will suffice to show that unit of the adjunction \(\Delta ^* \dashv \text {B} _{(-)}\) is given by the component inclusion
and the counit of the adjunction \(\text {B} _{(-)} \dashv \Delta ^*\) is given by the component projection
Indeed, this is established in Remark 1.1.18. \(\square \)
Remark 7.4.12
If \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is a \({{\text {C} }_{\textrm{2}}}\)-semiadditive \({{\text {C} }_{\textrm{2}}}\)-category then the \({{\text {C} }_{\textrm{2}}}\)-product and \({{\text {C} }_{\textrm{2}}}\)-coproduct of a \([\emptyset \rightarrow {{\text {C} }_{\textrm{2}}}]\)-indexed \({{\text {C} }_{\textrm{2}}}\)-diagram in \({\mathcal {E}}\) corresponding to an object \(x\in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) are both given by the cocartesian section \(s:{{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\rightarrow {\mathcal {E}}\) whose value at \(*\) is g(x) and whose value at \({{\text {C} }_{\textrm{2}}}\) is \(x \oplus \sigma (x)\), cf. Remark 7.4.6.
Remark 7.4.13
If \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) is a \({{\text {C} }_{\textrm{2}}}\)-semiadditive \({{\text {C} }_{\textrm{2}}}\)-category then the functor \(f:{\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) admits a two sided adjoint g. The \({{\text {C} }_{\textrm{2}}}\)-equivariant structure induces a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure on g in a priori two different ways: one by the uniqueness of g as a left adjoint of f and once by its uniqueness as a right adjoint. The comparison map (197) is however a natural transformation of \({{\text {C} }_{\textrm{2}}}\)-equivariant functors (since the component inclusion \(x\rightarrow x\oplus \sigma (x)\) is such), and so it identifies the left and right adjoints of f also as \({{\text {C} }_{\textrm{2}}}\)-equivariant functors. Similarly, the induced functor \(\overline{g}:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},{\mathcal {E}}_{*})\) is a two sided adjoint to the induced functor \(\overline{f}:{\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},{\mathcal {E}}_{*}) \rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}^{{{\text {hC} }_{\textrm{2}}}}\).
Remark 7.4.14
Specializing to the case of the \({{\text {C} }_{\textrm{2}}}\)-category \(\underline{\textrm{Cat}}^\textrm{p}_\infty \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) we now get that the functor \({\text {Hyp}}\) inherits a \({{\text {C} }_{\textrm{2}}}\)-equivariant structure making it a two-sided \({{\text {C} }_{\textrm{2}}}\)-equivariant adjoint to \(\text {U} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \), and similarly the induced functor \({\text {Hyp}}^{{{\text {hC} }_{\textrm{2}}}}:(\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}} \rightarrow {\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}},\text {Cat} ^{\textrm{p}}_\infty )\) is a two-sided adjoint to \(\text {U} ^{{{\text {hC} }_{\textrm{2}}}}:{\text {Fun}}(\text {B} {{\text {C} }_{\textrm{2}}}, \text {Cat} ^{\textrm{p}}_\infty ) \rightarrow (\text {Cat} _\infty ^\text {ex} )^{{{\text {hC} }_{\textrm{2}}}}\). The composite
then determines a \({{\text {C} }_{\textrm{2}}}\)-action on  for a Poincaré \(\infty \)-category. For a fixed
for a Poincaré \(\infty \)-category. For a fixed  , this is the \({{\text {C} }_{\textrm{2}}}\)-action of Construction 2.2.7, but now promoted to be natural in \({\mathcal {C}}\). Similarly, the \({{\text {C} }_{\textrm{2}}}\)-equivariance of the maps
, this is the \({{\text {C} }_{\textrm{2}}}\)-action of Construction 2.2.7, but now promoted to be natural in \({\mathcal {C}}\). Similarly, the \({{\text {C} }_{\textrm{2}}}\)-equivariance of the maps

constructed in Lemma 2.2.9 is now exhibited as the components of two natural transformations of \({{\text {C} }_{\textrm{2}}}\)-equivariant functors in  .
.
Remark 7.4.15
In the situation of Remark 7.4.14, the functors \(\text {U} \) and \(\text {U} ^{{{\text {hC} }_{\textrm{2}}}}\) participate in a commutative square of forgetful functors

Passing to left adjoints, we obtain a commutative square

At the same time, since \(\text {Cat} _\infty ^\text {ex} \) is semi-additive the top horizontal functor in (198) is given by the symmetrisation \({\mathcal {C}}\mapsto {\mathcal {C}}\times {\mathcal {C}}^{\text {op} }\) associated to the \(\text {op} \)-action on \(\text {Cat} _\infty ^\text {ex} \). But \(\underline{\textrm{Cat}}^\textrm{p}_\infty \) having finite \({{\text {C} }_{\textrm{2}}}\)-coproducts (Proposition 7.4.8) means that this symmetrisation is identified with \(\text {U} \circ {\text {Hyp}}\) as a functor \(\text {Cat} _\infty ^\text {ex} \rightarrow (\text {Cat} _\infty ^\text {ex} )^{{{\text {C} }_{\textrm{2}}}}\). Since \(\text {Cat} ^{\textrm{p}}_\infty \) is also semi-additive (Proposition 6.1.7) it then follows from the commutativity of the above square that the functor

is naturally equivalent to the functor sending  to \({\text {Hyp}}({\mathcal {C}}) \times {\text {Hyp}}({\mathcal {C}})\), equipped with the flip \({{\text {C} }_{\textrm{2}}}\)-action.
to \({\text {Hyp}}({\mathcal {C}}) \times {\text {Hyp}}({\mathcal {C}})\), equipped with the flip \({{\text {C} }_{\textrm{2}}}\)-action.
We now wish to use the \({{\text {C} }_{\textrm{2}}}\)-semiadditivity of the examples in 7.4.3 in order to extract extra structures in terms of Mackey functors. For this, let \({\text {Span}}({{\text {C} }_{\textrm{2}}})\) be the span \(\infty \)-category of finite \({{\text {C} }_{\textrm{2}}}\)-sets, as defined in [10, Df. 3.6]. A Mackey object in an additive \(\infty \)-category \({\mathcal {A}}\) is by definition a product preserving functor from \({\text {Span}}({{\text {C} }_{\textrm{2}}}) \rightarrow {\mathcal {A}}\). If \({\mathcal {A}}\) is taken to be \({{\mathcal {S}}{p}}\), then [51, Theorem A.4] shows that the arising \(\infty \)-category underlines the various (Quillen equivalent) model categories classically used for the definition of genuine \({{\text {C} }_{\textrm{2}}}\)-spectra. Taking spectral Mackey functors as the definition of the latter we set
Evaluation at the finite \({{\text {C} }_{\textrm{2}}}\)-sets \({{\text {C} }_{\textrm{2}}}\) then defines the functor \(u :{{\mathcal {S}}{p}}^{\text {g} {{\text {C} }_{\textrm{2}}}}\rightarrow {{\mathcal {S}}{p}}^{{{\text {hC} }_{\textrm{2}}}}\), by retaining the action of the span \({{\text {C} }_{\textrm{2}}}\xleftarrow {\text {id} } {{\text {C} }_{\textrm{2}}}\xrightarrow {+1} {{\text {C} }_{\textrm{2}}}\). Evaluation at the one-point \({{\text {C} }_{\textrm{2}}}\)-set defines the genuine fixed points \((-)^{gC_2} :{{\mathcal {S}}{p}}^{\text {g} {{\text {C} }_{\textrm{2}}}}\rightarrow {{\mathcal {S}}{p}}\). The datum of a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum thus is equivalent to the datum of the pair of spectra \((E^{g{{\text {C} }_{\textrm{2}}}},E)\), together with a \({{\text {C} }_{\textrm{2}}}\)-action on E and restriction and transfer maps
coming from the spans
with a host of compatibility data, and similarly for other target categories.
Proposition 7.4.16
Let \({\mathcal {E}}\rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) be a \({{\text {C} }_{\textrm{2}}}\)-semiadditive \(\infty \)-category with transition functor \(f:{\mathcal {E}}_*\rightarrow {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}}\) and two-sided adjoint \(g:{\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \rightarrow {\mathcal {E}}_{*}\). Then the identity functor \({\mathcal {E}}_{*} \rightarrow {\mathcal {E}}_{*}\) canonically lifts to a functor

where the vertical arrow is given by evaluation at \(*\). In addition the composite
where \(\text {ev} _{{{\text {C} }_{\textrm{2}}}}\) denotes evaluation at \({{\text {C} }_{\textrm{2}}}\in {\text {Span}}({{\text {C} }_{\textrm{2}}})\), is naturally equivalent to the functor \(x\mapsto gf(x)\).
Proof
Let  be the \({{\text {C} }_{\textrm{2}}}\)-Burnside \(\infty \)-category of [51, Df. 4.12]. The objects of
be the \({{\text {C} }_{\textrm{2}}}\)-Burnside \(\infty \)-category of [51, Df. 4.12]. The objects of  are given by arrows \(U \rightarrow V\) where U is a finite \({{\text {C} }_{\textrm{2}}}\)-set and \(V \in {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) is a \({{\text {C} }_{\textrm{2}}}\)-orbit, and morphisms in
are given by arrows \(U \rightarrow V\) where U is a finite \({{\text {C} }_{\textrm{2}}}\)-set and \(V \in {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) is a \({{\text {C} }_{\textrm{2}}}\)-orbit, and morphisms in  from \([U \rightarrow V]\) to \([U' \rightarrow V']\) are given by diagrams of the form
from \([U \rightarrow V]\) to \([U' \rightarrow V']\) are given by diagrams of the form

The functor  is then given by \([U \rightarrow V] \mapsto V\), and is a cocartesian fibration whose fibre over \(V \in {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) is the span \(\infty \)-category of finite \({{\text {C} }_{\textrm{2}}}\)-sets over V. Combining [51, Pr. 5.11] and [51, Th. 6.5] we have that the evaluation at the object
is then given by \([U \rightarrow V] \mapsto V\), and is a cocartesian fibration whose fibre over \(V \in {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) is the span \(\infty \)-category of finite \({{\text {C} }_{\textrm{2}}}\)-sets over V. Combining [51, Pr. 5.11] and [51, Th. 6.5] we have that the evaluation at the object  yields an equivalence
yields an equivalence

Now the action of every \({{\text {C} }_{\textrm{2}}}\)-product preserving \({{\text {C} }_{\textrm{2}}}\)-functor  on fibres over \(*\) is again a product-preserving functor from \({\text {Span}}({{\text {C} }_{\textrm{2}}})\) to \({\mathcal {E}}_{*}\). Base change along \(\{*\} \subseteq {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) then determines a functor
on fibres over \(*\) is again a product-preserving functor from \({\text {Span}}({{\text {C} }_{\textrm{2}}})\) to \({\mathcal {E}}_{*}\). Base change along \(\{*\} \subseteq {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) then determines a functor

equipped with a natural equivalence
by construction. Furthermore, for \(x\in {\mathcal {E}}_{*}\) the Mackey functor \({\mathcal {R}}(x):{\text {Span}}({{\text {C} }_{\textrm{2}}}) \rightarrow {\mathcal {E}}_{*}\) is obtained in particular by restricting a \({{\text {C} }_{\textrm{2}}}\)-functor  , i.e., a functor over \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) which preserves cocartesian edges. Since
, i.e., a functor over \({{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}^{\text {op} }\) which preserves cocartesian edges. Since  sends \([*\rightarrow *]\) to \(x \in {\mathcal {E}}_*\subseteq {\mathcal {E}}\) by construction it must send the object
sends \([*\rightarrow *]\) to \(x \in {\mathcal {E}}_*\subseteq {\mathcal {E}}\) by construction it must send the object  to \(f(x) \in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \subseteq {\mathcal {E}}\). Since
to \(f(x) \in {\mathcal {E}}_{{{\text {C} }_{\textrm{2}}}} \subseteq {\mathcal {E}}\). Since  furthermore preserves \({{\text {C} }_{\textrm{2}}}\)-biproducts it must therefore send
furthermore preserves \({{\text {C} }_{\textrm{2}}}\)-biproducts it must therefore send  to \(gf(x)\), see Remark 7.4.12. \(\square \)
to \(gf(x)\), see Remark 7.4.12. \(\square \)
Applying Proposition 7.4.16 in the case of the \({{\text {C} }_{\textrm{2}}}\)-category \(\underline{\hbox {Fun}}^{\textrm{q}}({\mathcal {C}}) \rightarrow {{\textbf {O}}}_{{{\text {C} }_{\textrm{2}}}}\) of Example 7.4.3 i) we obtain:
Corollary 7.4.17
The inclusion \({\text {Fun}}^{\textrm{q}}({\mathcal {C}}) \subseteq {\text {Fun}}({\mathcal {C}}^{\text {op} },{{\mathcal {S}}{p}})\) admits a canonical lift to a functor
In particular, every quadratic functor  lifts canonically to a functor
lifts canonically to a functor  valued in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, such that
valued in genuine \({{\text {C} }_{\textrm{2}}}\)-spectra, such that  has underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum
has underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum  , geometric fixed points
, geometric fixed points  and genuine fixed points
and genuine fixed points  .
.
Proof
Only the claim about the geometric fixed point is not immediate from the application of Proposition 7.4.16 to Example 7.4.3 i), but it follows from the defining cofibre sequence

which by construction matches the cofibre sequence

\(\square \)
Corollary 7.4.18
(The hyperbolic Mackey functor) The construction of hyperbolic categories canonically refines to a functor
together with natural equivalences of Poincaré \(\infty \)-categories

and a natural \({{\text {C} }_{\textrm{2}}}\)-equivariant equivalence of Poincaré \(\infty \)-categories

In addition, the resulting \({{\text {C} }_{\textrm{2}}}\)-equivariant functors

associated to the spans of (199) are given by the functors \(\text {hyp} \) and \(\text {fgt} \) of (42) which are the unit and counit of the two-sided adjunctions between \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} _\infty ^\text {ex} \) of Corollary 7.2.21.
Using 7.4.17 we can now also extend the periodicity considerations for Poincaré structures on module categories of Sect. 3.5 to the general case. Specifically, we have:
Proposition 7.4.19
For a hermitian structure  on a stable category \({\mathcal {C}}\), there is a natural equivalence
on a stable category \({\mathcal {C}}\), there is a natural equivalence

of functors \({\mathcal {C}}^{\text {op} }\rightarrow {{\mathcal {S}}{p}}^{\text {g} {{\text {C} }_{\textrm{2}}}}\), and so in particular \(\Omega ^n :{\mathcal {C}}\rightarrow {\mathcal {C}}\) refines to an equivalence

Proof
The proof is essentially identical to that of 3.5.3. It clearly suffices to treat the case \(m=-n\), as both sides display the same behaviour under shifting, and since pre-composition with \(\Sigma \) can be inverted and iterated, one may reduce to proving the case \(n=1=-m\). Let  be the reference map of
be the reference map of  . Arguing as in the proof of Proposition 3.5.3 one obtains a natural commutative diagram
. Arguing as in the proof of Proposition 3.5.3 one obtains a natural commutative diagram

which may be viewed as an equivalence between the top left square and the external rectangle. As such, it identifies the classifying square of  with one having bilinear term
with one having bilinear term  , linear term
, linear term  , and reference map \(\Omega \alpha \). But these are precisely the underlying spectrum, geometric fixed point, and glueing map of
, and reference map \(\Omega \alpha \). But these are precisely the underlying spectrum, geometric fixed point, and glueing map of  . We immediately obtain that
. We immediately obtain that  agrees with the genuine fixed points of
agrees with the genuine fixed points of  , and thus the second part (which suffices for all our applications) follows. But it is a folklore result that a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum is in fact naturally determined by the data we have computed above, namely, the diagram
, and thus the second part (which suffices for all our applications) follows. But it is a folklore result that a genuine \({{\text {C} }_{\textrm{2}}}\)-spectrum is in fact naturally determined by the data we have computed above, namely, the diagram

where u takes the underlying \({{\text {C} }_{\textrm{2}}}\)-spectrum and t extracts the target of an arrow is cartesian; a proof of this fact can also be found in [2], Remark 3.7.5. This implies the full statement of the proposition. \(\square \)
8.5 Multiplicativity of Grothendieck-Witt and \({\text {L}}\)-groups
In this section we prove that the invariants \({\text {L}}_0(-)\) and \({\text {GW}}_0(-)\) defined in Sect. 2.3 and 2.5 are lax symmetric monoidal functors. In addition, the higher \({\text {L}}\)-groups organise into a symmetric monoidal functor to the category of graded abelian groups (with its Koszul symmetric monoidal structure). As a result, they carry a graded-commutative algebra structure when applied to symmetric monoidal Poincaré \(\infty \)-categories, such as those described in Sect. 5.4.
To begin, we first note that by Corollary 5.2.8 the functor \(\pi _0\text {Pn} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Set} \) admits a canonical lax symmetric monoidal structure. This lax symmetric monoidal structure can be made quite explicit. Indeed, consider the assignment

For a pair of Poincaré objects (x, q) and \((x',q')\) we get the Poincaré object \((x \otimes x', q \otimes q')\) in  , where \(x \otimes x' \in {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) is the image of \((x,x') \in {\mathcal {C}}\times {{{\mathcal {C}}}'}\) under the universal bilinear functor \(\beta :{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\), and \(q \otimes q'\) denotes the map
, where \(x \otimes x' \in {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\) is the image of \((x,x') \in {\mathcal {C}}\times {{{\mathcal {C}}}'}\) under the universal bilinear functor \(\beta :{\mathcal {C}}\times {{{\mathcal {C}}}'}\rightarrow {\mathcal {C}}\otimes {{{\mathcal {C}}}'}\), and \(q \otimes q'\) denotes the map  obtained as the composite
obtained as the composite

This object is Poincaré because its underlying bilinear form is given in light of Proposition 5.1.3 by the combination of the underlying bilinear forms of q and \(q'\).
We now wish to upgrade the above lax symmetric monoidal structure to the level of \({\text {E} _\infty }\)-spaces. For this, first note that since \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) are semi-additive (Proposition 6.1.7) the corepresentable functors \(\text {Pn} \) and \(\text {Fm} \) canonically refine to functors with values in \({\text {E} _\infty }\)-spaces. Recall (see, e.g., [52, Proposition 5.6]) that the \(\infty \)-category \({\text {Mon}}_{{\text {E} _\infty }}\) of \({\text {E} _\infty }\)-monoids carries a canonical symmetric monoidal structure such that the free-forgetful adjunction

becomes symmetric monoidal (that is, its left adjoint is symmetric monoidal from which the right adjoint inherits a lax symmetric monoidal structure). We now claim that the \({\text {E} _\infty }\)-refinement \(\widetilde{\text {Pn} }:\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\text {Mon}}_{{\text {E} _\infty }}\) and \(\widetilde{\text {Fm} }:\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\text {Mon}}_{{\text {E} _\infty }}\) also carry lax symmetric monoidal structures. This is in fact a completely formal consequence of the fact that the monoidal structure on \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) preserves direct sums:
Lemma 7.5.1
Let \({\mathcal {E}}\) be a small semi-additive \(\infty \)-category equipped with a symmetric monoidal structure \(\otimes \) which preserves direct sums in each variable. Then the lax symmetric monoidal structure of \({\text {Map}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-)\) canonically lifts to its \({\text {E} _\infty }\)-refinement \(\widetilde{{\text {Map}}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-):{\mathcal {E}}\rightarrow {\text {Mon}}_{{\text {E} _\infty }}\).
Corollary 7.5.2
The lax symmetric monoidal structure of \(\text {Pn} \) and \(\text {Fm} \) canonically lifts to their \({\text {E} _\infty }\)-refinements \(\widetilde{\text {Pn} }:\text {Cat} ^{\textrm{p}}_\infty \rightarrow {\text {Mon}}_{{\text {E} _\infty }}\) and \(\widetilde{\text {Fm} }:\text {Cat} ^{\textrm{h}}_\infty \rightarrow {\text {Mon}}_{{\text {E} _\infty }}\).
Proof
By possibly enlarging the universe we may assume that \(\text {Cat} ^{\textrm{p}}_\infty \) and \(\text {Cat} ^{\textrm{h}}_\infty \) are small. The claim then follows from Lemma 7.5.1. \(\square \)
Proof of Lemma 7.5.1
The full subcategory \({\text {Fun}}^{\times }({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }}) \subseteq {\text {Fun}}({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }})\) spanned by the product-preserving functors is an accessible localisation of \({\text {Fun}}({\mathcal {E}}, {\text {Mon}}_{{\text {E} _\infty }})\) with a left adjoint which we denote by \(L:{\text {Fun}}({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }}) \rightarrow {\text {Fun}}^{\times }({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }})\). By Lemma 5.3.4 this localisation is compatible with Day convolution and extends to a symmetric monoidal localisation
where the codomain is endowed with the structure inherited from being a full suboperad of \({\text {Fun}}({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }})^{\otimes }\). Now the identification \({\text {Map}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-) \simeq \text {U} \widetilde{{\text {Map}}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-)\) transposes to give a natural transformation of the form \(\text {F} \circ {\text {Map}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-)\Rightarrow \widetilde{{\text {Map}}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-)\). Since \(\widetilde{{\text {Map}}}_{{\mathcal {E}}}(1_{{\mathcal {E}}},-)\) is product preserving this natural transformation induces a natural transformation
We claim that this last transformation is an equivalence. Note that this implies the desired claim via the symmetric monoidal structures of L and \(\text {F} \). Now, to prove the claim, it will suffice to show that for every product-preserving functor \({\mathcal {G}}:{\mathcal {E}}\rightarrow {\text {Mon}}_{{\text {E} _\infty }}\) the induced map
is an equivalence of spaces. Indeed, by adjunction we may also identify this map with the map
induced by \(\text {U} \circ (-)\). This last map is an equivalence since the forgetful functor \(\text {U} \circ (-):{\text {Fun}}^{\times }({\mathcal {E}},{\text {Mon}}_{{\text {E} _\infty }}) \rightarrow {\text {Fun}}^{\times }({\mathcal {E}},{\mathcal {S}})\) is an equivalence on product-preserving functors. \(\square \)
We now come to the main result of this subsection:
Proposition 7.5.3
The functors \({\text {L}}_0, {\text {GW}}_0:\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {CMon} \) admit unique lax symmetric monoidal structures such that the transformations
are symmetric monoidal, where \(\text {CMon} \) stands for the (ordinary) symmetric monoidal category of commutative monoids.
Remark 7.5.4
The full subcategory \({\mathcal {A}}b\subseteq \text {CMon} \) spanned by abelian groups is a full suboperad and a symmetric monoidal localisation of \(\text {CMon} \). Since \({\text {GW}}_0\) and \({\text {L}}_0\) take values in \({\mathcal {A}}b\) the lax monoidal structures on \({\text {GW}}_0,{\text {L}}_0\) and the map \({\text {GW}}_0 \Rightarrow {\text {L}}_0\) equally applies if we consider \({\text {GW}}_0\) and \({\text {L}}_0\) as functors to \({\mathcal {A}}b\). The reason for working with the larger category of commutative monoids is to be able to make arguments pertaining to the natural transformation from \(\pi _0\text {Pn} \).
The proof of Proposition 7.5.3 will require knowing certain multiplicative properties of the adjunctions  and
and  , which we now verify.
, which we now verify.
Lemma 7.5.5
The adjunction  of Proposition 7.3.20, in which the right adjoint \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) is symmetric monoidal, satisfies the projection formula: for
of Proposition 7.3.20, in which the right adjoint \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) is symmetric monoidal, satisfies the projection formula: for  and
and  the Poincaré functor
the Poincaré functor

associated under this adjunction to the hermitian functor

induced by the unit hermitian functor  , is an equivalence of Poincaré \(\infty \)-categories.
, is an equivalence of Poincaré \(\infty \)-categories.
Proof
This is a formal consequence of (and actually equivalent to) the fact that the right adjoint \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) is closed symmetric monoidal, that is, preserves internal mapping objects, see Remark 6.2.18. Explicitly, it will suffice to show that for every Poincaré \(\infty \)-category  the restriction map
the restriction map

is an equivalence of spaces. Indeed, since the Poincaré \(\infty \)-category  serves as an internal mapping object in both \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \) we may identify this map with the map
serves as an internal mapping object in both \(\text {Cat} ^{\textrm{h}}_\infty \) and \(\text {Cat} ^{\textrm{p}}_\infty \) we may identify this map with the map

which is an equivalence by adjunction. \(\square \)
Taking  in Lemma 7.5.5 and using Remark 7.2.22 we immediately find:
in Lemma 7.5.5 and using Remark 7.2.22 we immediately find:
Corollary 7.5.6
The adjunction \({\text {Hyp}}\dashv \text {U} \) satisfies the projection formula: for  and \({{{\mathcal {C}}}'}\in \text {Cat} ^{\textrm{h}}_\infty \) the Poincaré functor
and \({{{\mathcal {C}}}'}\in \text {Cat} ^{\textrm{h}}_\infty \) the Poincaré functor

induced by the component inclusion
is an equivalence of Poincaré \(\infty \)-categories.
Remark 7.5.7
One can also deduce Corollary 7.5.6 from the fact that the forgetful functor \(\text {U} :\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \) is closed symmetric monoidal, being the composition of the inclusion \(\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {Cat} ^{\textrm{h}}_\infty \) and the closed symmetric monoidal projection \(\text {Cat} ^{\textrm{h}}_\infty \rightarrow \text {Cat} _\infty ^\text {ex} \), see Remark 6.2.11 and the final part of Remark 6.2.18. In particular, the adjunction  also satisfies the projection formula, as is visible from the equivalence
also satisfies the projection formula, as is visible from the equivalence  .
.
Remark 7.5.8
In the situation of Lemma 7.5.5, when  is also Poincaré then by the triangle identities the projection formula equivalence (200) fits into a commutative triangle
is also Poincaré then by the triangle identities the projection formula equivalence (200) fits into a commutative triangle

where the diagonal arrows are obtained from the counit of the adjunction  at
at  and
and  , respectively. Using Example 7.3.3 iii) and Remark 7.3.21 we may also write this commutative triangle as
, respectively. Using Example 7.3.3 iii) and Remark 7.3.21 we may also write this commutative triangle as

Applying the same argument for the projection formula of Corollary 7.5.6 we similarly have the commutative triangle

Remark 7.5.9
The commutative triangle (201) taken with  yields an equivalence
yields an equivalence  of Poincaré \(\infty \)-categories over
of Poincaré \(\infty \)-categories over  . It then follows that when
. It then follows that when  is a symmetric monoidal Poincaré \(\infty \)-category the Poincaré \(\infty \)-category
is a symmetric monoidal Poincaré \(\infty \)-category the Poincaré \(\infty \)-category  acquires the structure of a module object over
acquires the structure of a module object over  (specifically, the free
(specifically, the free  -module generated from
-module generated from  ) such that the functor
) such that the functor

is a map of (free)  -modules. Similarly, the commutative triangle (202) taken with
-modules. Similarly, the commutative triangle (202) taken with  yields an equivalence
yields an equivalence  over
over  , and so when
, and so when  is symmetric monoidal Poincaré we get that
is symmetric monoidal Poincaré we get that  acquires the structure of a module object over
acquires the structure of a module object over  (freely generated by \({\text {Hyp}}({{\mathcal {S}}{p}}^{\text {f} })\)) and
(freely generated by \({\text {Hyp}}({{\mathcal {S}}{p}}^{\text {f} })\)) and

is a map of free  -modules.
-modules.
Proof of Proposition 7.5.3
The uniqueness is clear since the maps  are surjective (and surjectivity is stable under tensor products in \(\text {CMon} \)). It will hence suffice to show that for every pair of Poincaré \(\infty \)-categories
are surjective (and surjectivity is stable under tensor products in \(\text {CMon} \)). It will hence suffice to show that for every pair of Poincaré \(\infty \)-categories  the dotted arrows
the dotted arrows

exists to make the diagram commute, where the tensor products in the top row is that of commutative monoids.
Let us first treat the case of the functor \({\text {L}}_0\). For this it will suffice to show that for a pair of Poincaré objects \((x, q)\) and \((x',q')\) such that \((x',q')\) is metabolic the associated Poincaré object \((x,q) \otimes (x',q')\) is metabolic in  (the rest follows by symmetry). But this follows directly from the commutativity of the diagram
(the rest follows by symmetry). But this follows directly from the commutativity of the diagram

given by the commutative triangle (201).
We now turn to \({\text {GW}}_0\). For the well-definedness of the middle dotted arrow in (203) we have to show that the relation \([\text {hyp} (w)] \sim [x,q]\) for a Lagrangian \(w \rightarrow x\) is preserved under tensoring with some Poincaré object \((x',q')\). Given the commutativity of the diagram (204) above, it will suffice to show that the diagram

is commutative as well, where the vertical arrows in the top rows are induced by the Poincaré functor \(\text {dlag} :{\text {Met}}(-)\rightarrow {\text {Hyp}}(-)\) of Construction 2.3.8. Here, the squares on the right hand side are commutative as they are given by the lax monoidal structure on \(\pi _0 \text {Pn} \), and the bottom left triangle is induced by the commutative triangle (202). It will suffice to show that the top left square commutes. Indeed, this square is obtained by applying \(\pi _0\text {Pn} \) to the square of Poincaré \(\infty \)-categories

which commutes since it is obtained by evaluating the natural transformation (200) of the projection formula at the arrow  in \(\text {Cat} ^{\textrm{h}}_\infty \), see Remark 7.3.22. \(\square \)
in \(\text {Cat} ^{\textrm{h}}_\infty \), see Remark 7.3.22. \(\square \)
Corollary 7.5.10
The functor \({\text {L}}_{\bullet }:\text {Cat} ^{\textrm{p}}_\infty \rightarrow \text {gr}{\mathcal {A}}b\) admits a lax symmetric monoidal structure, where \(\text {gr}{\mathcal {A}}b\) denotes the category of \({\mathbb {Z}}\)-graded abelian groups with the symmetric monoidal structure using the Koszul sign rules.
Proof
By definition we have that  . Thus the claim follows by combining Proposition 7.5.3, Remark 2.3.13, and the fact that \({\mathbb {S}}^{-{\tiny \bullet }}\) is a graded commutative algebra in the homotopy category of spectra. Concretely, the structure maps are simply given by
. Thus the claim follows by combining Proposition 7.5.3, Remark 2.3.13, and the fact that \({\mathbb {S}}^{-{\tiny \bullet }}\) is a graded commutative algebra in the homotopy category of spectra. Concretely, the structure maps are simply given by

and the fact that it is symmetric follows as explained above. \(\square \)
Corollary 7.5.11
If  is a monoidal \(\infty \)-category then
is a monoidal \(\infty \)-category then  acquires a ring structure and
acquires a ring structure and  a graded ring structure such that the natural map
a graded ring structure such that the natural map

is a ring homomorphism. If the monoidal structure is symmetric then  is commutative and
is commutative and  is graded commutative.
is graded commutative.
Example 7.5.12
Let \(A \in \text {Alg} _{{\text {E} _\infty }}^{{{\text {hC} }_{\textrm{2}}}}\) be a commutative ring spectrum equipped with a \({{\text {C} }_{\textrm{2}}}\)-action. Then the Grothendieck-Witt groups  ,
,  and
and  of the symmetric monoidal Poincaré \(\infty \)-categories of Examples 5.4.10 carry natural commutative ring structures, and similarly the corresponding graded \({\text {L}}\)-groups
of the symmetric monoidal Poincaré \(\infty \)-categories of Examples 5.4.10 carry natural commutative ring structures, and similarly the corresponding graded \({\text {L}}\)-groups  ,
,  and
and  carry canonical graded-commutative ring structures.
carry canonical graded-commutative ring structures.
Combining Proposition 7.5.3 with Example 2.5.5, Example 5.4.2 and Remark 7.5.9 we also get:
Corollary 7.5.13
If  is a symmetric monoidal \(\infty \)-category then
is a symmetric monoidal \(\infty \)-category then

is a map of rings and

is a map of \({\text {GW}}_0({\mathcal {C}})\)-modules.
Remark 7.5.14
In the situation of Corollary 7.5.13, the  -module structure on \({\text {K}}_0({\mathcal {C}})\) could be considered ambiguous: on the one hand we have the module structure determined by the ring structure of \({\text {K}}_0({\mathcal {C}})\) via the ring map
-module structure on \({\text {K}}_0({\mathcal {C}})\) could be considered ambiguous: on the one hand we have the module structure determined by the ring structure of \({\text {K}}_0({\mathcal {C}})\) via the ring map  , and on the other we have the module structure induced by the
, and on the other we have the module structure induced by the  -module structure on \({\text {Hyp}}({\mathcal {C}})\) of Remark 7.5.9 via the identification \({\text {K}}_0({\mathcal {C}}) \cong {\text {GW}}_0({\text {Hyp}}({\mathcal {C}}))\). These two modules structures however coincide. Indeed, unwinding the definitions we see that the former structure is induced via the lax monoidal structure of \({\text {GW}}_0\) and the symmetric monoidal structure of
-module structure on \({\text {Hyp}}({\mathcal {C}})\) of Remark 7.5.9 via the identification \({\text {K}}_0({\mathcal {C}}) \cong {\text {GW}}_0({\text {Hyp}}({\mathcal {C}}))\). These two modules structures however coincide. Indeed, unwinding the definitions we see that the former structure is induced via the lax monoidal structure of \({\text {GW}}_0\) and the symmetric monoidal structure of  by the Poincaré functor
by the Poincaré functor

corresponding via the adjunction \(\text {U} \dashv {\text {Hyp}}\) to the exact functor \({\mathcal {C}}\otimes [{\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }] \rightarrow {\mathcal {C}}\otimes {\mathcal {C}}\) induced by the projection \({\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\rightarrow {\mathcal {C}}\), while the latter module structure is induced in the same manner by the inverse of the Poincaré equivalence

of Corollary 7.5.6, corresponding via the adjunction \({\text {Hyp}}\dashv \text {U} \) to the exact functor \({\mathcal {C}}\otimes {\mathcal {C}}\rightarrow {\mathcal {C}}\otimes [{\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }]\) induced by the inclusion \({\mathcal {C}}\rightarrow {\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }\). It will hence suffice to verify that these Poincaré functors determine inverse equivalences between \({\text {Hyp}}({\mathcal {C}}\otimes {\mathcal {C}})\) and  . However, since Poincaré functors from (or to) \({\text {Hyp}}\) are determined by their underlying exact functors, it suffices to check that these underlying exact functors determine inverse equivalences between \({\mathcal {C}}\otimes [{\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }]\) and \([{\mathcal {C}}\otimes {\mathcal {C}}] \oplus [{\mathcal {C}}^{\text {op} }\otimes {\mathcal {C}}^{\text {op} }]\). The latter is however a formal consequence of the fact that the monoidal structure on \(\text {Cat} _\infty ^\text {ex} \) preserves direct sums in each variable.
. However, since Poincaré functors from (or to) \({\text {Hyp}}\) are determined by their underlying exact functors, it suffices to check that these underlying exact functors determine inverse equivalences between \({\mathcal {C}}\otimes [{\mathcal {C}}\oplus {\mathcal {C}}^{\text {op} }]\) and \([{\mathcal {C}}\otimes {\mathcal {C}}] \oplus [{\mathcal {C}}^{\text {op} }\otimes {\mathcal {C}}^{\text {op} }]\). The latter is however a formal consequence of the fact that the monoidal structure on \(\text {Cat} _\infty ^\text {ex} \) preserves direct sums in each variable.
Invoking Examples 5.4.11 and Example 5.4.12 we also have the following two corollaries:
Corollary 7.5.15
Let  be a symmetric monoidal hermitian \(\infty \)-category with underlying bilinear part
be a symmetric monoidal hermitian \(\infty \)-category with underlying bilinear part  . Then the quadratic Grothendieck-Witt group
. Then the quadratic Grothendieck-Witt group  is canonically a module over the ring
is canonically a module over the ring  and the map
and the map

is a map of  -modules. Similarly, the quadratic \({\text {L}}\)-groups
-modules. Similarly, the quadratic \({\text {L}}\)-groups  form a graded module over the graded ring
form a graded module over the graded ring  and the map
and the map

is a map of graded  -modules.
-modules.
Corollary 7.5.16
Let A be a connective commutative ring spectrum equipped with an involution. Then for every \(m \in {\mathbb {Z}}\) the Grothendieck-Witt group  of the truncated Poincaré structure of Example 3.2.8 is canonically a module over the \({\text {GW}}_0\)-ring
of the truncated Poincaré structure of Example 3.2.8 is canonically a module over the \({\text {GW}}_0\)-ring  of the Poincaré structure of Example 5.4.10 ii).
of the Poincaré structure of Example 5.4.10 ii).
Notes
This is in fact the nerve of an ordinary operad which can for example be seen using the theory of dendroidal sets, but we shall not need this fact here.
References
This paper series
Calmes, B., Dotto, E., Harpaz, Y., Hebestreit, F., Land, M., Nardin, D., Moi, K., Nikolaus, T., Steimle, W.: Hermitian K-theory for stable \(\infty \)-categories, part I: Foundations. arXiv:2009.07223 (2020)
Calmes, B., Dotto, E., Harpaz, Y., Hebestreit, F., Land, M., Nardin, D., Moi, K., Nikolaus, T., Steimle, W.: Hermitian K-theory for stable \(\infty \)-categories, part II: Cobordism categories and additivity. arXiv:2009.07224 (2020)
Calmes, B., Dotto, E., Harpaz, Y., Hebestreit, F., Land, M., Nardin, D., Moi, K., Nikolaus, T., Steimle, W.: Hermitian K-theory for stable \(\infty \)-categories, part III: Grothendieck-Witt groups of rings. arXiv:2009.07225 (2020)
Calmes, B., Dotto, E., Harpaz, Y., Hebestreit, F., Land, M., Nardin, D., Moi, K., Nikolaus, T., Steimle, W.: Hermitian K-theory for stable \(\infty \)-categories, part IV: Poincare motives and Karoubi–Grothendieck–Witt groups (in preparation)
Other references
Adams, J.F.: Stable Homotopy and Generalised Homology. University of Chicago Press, Chicago (1974)
Antolín-Camarena, O., Barthel, T.: A simple universal property of Thom ring spectra. J. Topol. 12(1), 56–78 (2019)
Ayala, D., Francis, J.: Fibrations of \(\infty \)-categories. High. Struct. 4(1), 168–265 (2020)
Bak, A.: K-Theory of Forms, vol. 98. Princeton University Press, Princeton (1981)
Balmer, P.: Witt groups. Handbook of K-Theory, pp. 539–576. Springer, Berlin (2005)
Barwick, C.: Spectral Mackey functors and equivariant algebraic K-theory (I). Adv. Math. 304, 646–727 (2017)
Barwick, C., Dotto, E., Glasman, S., Nardin, D., Shah, J.: Parametrized higher category theory and higher algebra: a general introduction (2016). arXiv:1608.03654
Barwick, C., Glasman, S.: A note on stable recollements (2016). arXiv:1607.02064
Berrick, A.J., Karoubi, M.: Hermitian K-theory of the integers. Amer. J. Math. 127(4), 785–823 (2005)
Blumberg, A.J., Gepner, D., Tabuada, G.: A universal characterization of higher algebraic K-theory. Geom. Topol. 17(2), 733–838 (2013)
Brown, K.S.: Cohomology of groups, Graduate Texts in Mathematics, vol. 87. Springer, New York (1994) (Corrected reprint of the 1982 original)
Calmès, B., Harpaz, Y., Nardin, D.: A motivic spectrum representing Hermitian K-theory (in preparation)
Cisinski, D.-C.: Higher Categories and Homotopical Algebra, vol. 180. Cambridge University Press, Cambridge (2019)
Day, B. J.: Construction of biclosed categories. Ph.D. Thesis (1970)
Dold, A., Puppe, D.: Non-additive functors, their derived functors, and the suspension homomorphism. Proc. Natl. Acad. Sci. U.S.A. 44, 1065–1068 (1958). https://doi.org/10.1073/pnas.44.10.1065
Dotto, E., Moi, K., Patchkoria, I., Reeh, S.P.: Real topological Hochschild homology. J. Eur. Math. Soc. 23(1), 63–152 (2021). https://doi.org/10.4171/jems/1007
Eilenberg, S., Mac Lane, S.: On the groups H(\(\Pi \), n), II: methods of computation. Ann. Math. 60, 49–139 (1954)
Gepner, D., Haugseng, R.: Enriched \(\infty \)-categories via non-symmetric \(\infty \)-operads. Adv. Math. 279, 575716 (2015)
Gepner, D., Haugseng, R., Nikolaus, T.: Lax colimits and free fibrations in \(\infty \)-categories. Doc. Math. 22, 1225–1266 (2017)
Glasman, S.: Day convolution for \(\infty \)-categories. Math. Res. Lett. 23(5), 1369–1385 (2016)
Haugseng, R.: Rectification of enriched\(\infty \)-categories. Algebr. Geom. Topol. 15(4), 1931–1982 (2015)
R. Haugseng, F. Hebestreit, S. Linskens, J. Nuiten.: Lax monoidal adjunctions, two-variable fibrations and the calculus of mates (2021). arXiv:2011.08808v2
R. Haugseng, F.Hebestreit, S. Linskens, J. Nuiten.: Two-variable fibrations, factorisation systems and \(\infty \)-categories of spans (2022). arXiv:2011.11042v2
Hebestreit, F., Steimle, W.: Stable moduli spaces of Hermitian forms (2021). arXiv:2103.13911v1
Heine, H., Lopez-Avila, A., Spitzweck, M.: Infinity categories with duality and hermitian multiplicative infinite loop space machines (2016). arXiv:1610.10043
Heine, H., Spitzweck, M., Verdugo, P.: Real K-theory for Waldhausen infinity categories with genuine duality (2019). arXiv: 1911.11682
Hill, M.A., Hopkins, M.J., Ravenel, D.C.: On the nonexistence of elements of Kervaire invariant one. Ann. Math. 184, 1–262 (2016)
Hopkins, M., Lawson, T.: Strictly commutative complex orientation theory. Math. Z. 290(1), 83101 (2018)
Horev, A., Yanovski, L.: On conjugates and adjoint descent. Topol. Appl. 232, 140–154 (2017)
Hornbostel, J.: Constructions and devissage in hermitian K-theory. K-Theory 26(2), 139–170 (2002)
Hornbostel, J.: \({\mathbb{A}}^{{1}}\) -Representability of Hermitian K-theory and Witt groups. Topology 44(3), 661–687 (2005)
Hornbostel, J., Schlichting, M.: Localization in Hermitian K-theory of rings. J. Lond. Math. Soc. 70(1), 77–124 (2004)
Karoubi, M.: Le théorème fondamental de la K-théorie hermitienne. Ann. Math. (2) 112(2), 259–282 (1980)
Karoubi, M.: Periodicity theorems and conjectures in Hermitian K-theory [appendix to MR2538715]. J. K-Theory 4(1), 67–75 (2009)
Karoubi, M., Villamayor, O.: K-théorie hermitienne. Comptes Rendus de l’Académie des Sciences, Paris, Sér. A-B 272, A1237–A1240 (1971)
Klein, J.R.: The dualizing spectrum of a topological group. Math. Ann. 319(3), 421–456 (2001). https://doi.org/10.1007/PL00004441
Knebusch, M.: Symmetric bilinear forms over algebraic varieties. Publ. Math. Debr. 46, 103–283 (1977)
Lin, W.-H.: On conjectures of Mahowald, Segal and Sullivan. Math. Proc. Cambr. Philos. Soc. 87, 449–458 (1980)
Lurie, J.: Higher Topos Theory, Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton, NJ (2009)
Lurie, J.: (\(\infty \), 2)-categories and the Goodwillie calculus I (2009). Available from https://www.math.ias.edu/~lurie/papers/GoodwillieI.pdf
Lurie, J.: Lecture notes on algebraic L-theory and surgery (2011). Available from https://people.math.harvard.edu/~lurie/287x.html
Lurie, J.: Spectral algebraic geometry (2016). Available from https://www.math.ias.edu/~lurie/papers/SAG-rootfile.pdf
Lurie, J.: Higher algebra (2017). Available from https://people.math.harvard.edu/~lurie/papers/HA.pdf
Lurie, J.: Lecture notes on chromatic homotopy theory (2010). Available from https://www.math.ias.edu/~lurie/252x.html
Mandell, M.A.: Equivariant symmetric spectra. Contemp. Math. 346, 399–452 (2004)
Mandell, M.A., May, J.P.: Equivariant orthogonal spectra and S-modules. American Mathematical Society, Providence (2002)
Nardin, D.: Parametrized higher category theory and higher algebra: expose IV—stability with respect to an orbital \(\infty \)-category (2016). arXiv:1608.07704
Nikolaus, T.: Stable \(\infty \)-operads and the multiplicative Yoneda lemma (2016). arXiv:1608.02901
Nikolaus, T., Scholze, P.: On topological cyclic homology. Acta Math. 221(2), 203–409 (2018)
Quebbemann, H.-G., Scharlau, W., Schulte, M.: Quadratic and Hermitian forms in additive and Abelian categories. J. Algebra 59(2), 264–289 (1979)
Quigley, J.D., Shah, J.: On the parametrized Tate construction and two theories of real p-cyclotomic spectra (2019). arXiv:1909.03920
Quillen, D.: Homotopical Algebra, vol. 43. Springer, Berlin (2006)
Ranicki, A.: The algebraic theory of surgery. I. Foundations. Proc. Lond. Math. Soc. (3) 40(1), 87–192 (1980)
Ranicki, A.: Algebraic L-Theory and Topological Manifolds, Cambridge Tracts in Mathematics, vol. 102. Cambridge University Press, Cambridge (1992)
Schlichting, M.: Hermitian K-theory, derived equivalences and Karoubi’s fundamental theorem. J. Pure Appl. Algebra 221(7), 1729–1844 (2017)
Schlichting, M.: Higher K-theory of forms I. From rings to exact categories. J. Inst. Math. Jussieu 20, 1–69 (2019)
Schwede, S.: Global Homotopy Theory, vol. 34. Cambridge University Press, Cambridge (2018)
Shah, J.: Parametrized higher category theory and higher algebra: Exposé II—indexed homotopy limits and colimits (2018). arXiv:1809.05892
Spitzweck, M.: A Grothendieck–Witt space for stable infinity categories with duality (2016). arXiv:1610.10044
Stevenson, D.: Model structures for correspondences and bifibrations (2018). arXiv:1807.08226
Thomason, R.W.: The classification of triangulated subcategories. Compos. Math. 105(1), 1–27 (1997)
Tits, J.: Formes quadratiques, groupes orthogonaux et algebres de Clifford. Invent. Math. 5(1), 19–41 (1968)
Toën, B.: Towards an axiomatization of the theory of higher categories (2004). arXiv:math/0409598
Wall, C.T.C.: On the axiomatic foundations of the theory of Hermitian forms. Math. Proc. Cambr. Philos. Soc. 67, 243–250 (1970)
Wall, C.T.C.: Surgery on Compact Manifolds. American Mathematical Society, Providence (1999)
Weiss, M.: Visible L-theory. Forum Math. 4(5), 465–498 (1992)
Weiss, M., Williams, B.: Automorphisms of manifolds and algebraic K-theory. II. J. Pure Appl. Algebra 62(1), 47–107 (1989)
Weiss, M., Williams, B.: Duality in Waldhausen categories. Forum Math. 10(5), 533–603 (1998)
Weiss, M., Williams, B.: Automorphisms of manifolds and algebraic K-theory: part III. Mem. Am. Math. Soc. 231(1084), vi+110 (2014)
Williams, B.: Quadratic K-theory and geometric topology. Handb. K-theory 1(2), 611–651 (2005)
Witt, E.: Theorie der quadratischen Formen in beliebigen Körpern. J. Reine Angew. Math. 176, 31–44 (1937)
Acknowledgements
For useful discussions about our project, we heartily thank Tobias Barthel, Clark Barwick, Lukas Brantner, Mauricio Bustamante, Denis-Charles Cisinski, Dustin Clausen, Uriya First, Rune Haugseng, André Henriques, Lars Hesselholt, Gijs Heuts, Geoffroy Horel, Marc Hoyois, Max Karoubi, Daniel Kasprowski, Ben Knudsen, Manuel Krannich, Achim Krause, Henning Krause, Sander Kupers, Wolfgang Lück, Ib Madsen, Cary Malkiewich, Mike Mandell, Akhil Mathew, Lennart Meier, Irakli Patchkoria, Nathan Perlmutter, Andrew Ranicki, Oscar Randal-Williams, George Raptis, Marco Schlichting, Peter Scholze, Stefan Schwede, Graeme Segal, Markus Spitzweck, Jan Steinebrunner, Georg Tamme, Ulrike Tillmann, Michael Weiss, Christoph Winges and Maria Yakerson. Furthermore, we owe a tremendous intellectual debt to Jacob Lurie for creating the framework we exploit here, and to Søren Galatius for originally spotting the overlap between various separate projects of ours; his insight ultimately led to the present collaboration.
The authors would also like to thank the Hausdorff Center for Mathematics at the University of Bonn, the Newton Institute at the University of Cambridge, the University of Copenhagen and the Mathematical Research Institute Oberwolfach for hospitality and support while parts of this project were undertaken.
Funding
Open Access funding enabled and organised by Projekt DEAL. BC was supported by the French National Centre for Scientific Research (CNRS) through a “délégation” at LAGA, University Paris 13. ED was supported by the German Research Foundation (DFG) through the priority program “Homotopy theory and Algebraic Geometry” (DFG grant no. SPP 1786) at the University of Bonn and WS by the priority program “Geometry at Infinity” (DFG grant no. SPP 2026) at the University of Augsburg. YH and DN were supported by the French National Research Agency (ANR) through the grant “Chromatic Homotopy and K-theory” (ANR grant no. 16-CE40-0003) at LAGA, University of Paris 13. FH is a member of the Hausdorff Center for Mathematics at the University of Bonn (DFG grant no. EXC 2047 390685813) and TN of the cluster “Mathematics Münster: Dynamics-Geometry-Structure” at the University of Münster (DFG grant no. EXC 2044 390685587). FH, TN and WS were further supported by the Engineering and Physical Sciences Research Council (EPSRC) through the program “Homotopy harnessing higher structures” at the Isaac Newton Institute for Mathematical Sciences (EPSRC grants no. EP/K032208/1 and EP/R014604/1). FH was also supported by the European Research Council (ERC) through the grant “Moduli spaces, Manifolds and Arithmetic” (ERC grant no. 682922) and KM by the grant “\({\text {K}}\)-theory, \({\text {L}}^2\)-invariants, manifolds, groups and their interactions” (ERC grant no. 662400). ML and DN were supported by the collaborative research centre “Higher Invariants” (DFG grant no. SFB 1085) at the University of Regensburg. ML was further supported by the research fellowship “New methods in algebraic K-theory” (DFG grant no. 424239956) and by the Danish National Research Foundation (DNRF) through the Center for Symmetry and Deformation (DNRF grant no. 92) and the Copenhagen Centre for Geometry and Topology (DNRF grant no. 151) at the University of Copenhagen. KM was also supported by the K &A Wallenberg Foundation.
Author information
Authors and Affiliations
Corresponding author
Additional information
To Andrew Ranicki.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Calmès, B., Dotto, E., Harpaz, Y. et al. Hermitian K-theory for stable \(\infty \)-categories I: Foundations. Sel. Math. New Ser. 29, 10 (2023). https://doi.org/10.1007/s00029-022-00758-2
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-022-00758-2




 is 2-excisive;
is 2-excisive;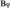 is bilinear and the fibre of the natural transformation
is bilinear and the fibre of the natural transformation  from (
from ( is bilinear and the cofibre of the natural transformation
is bilinear and the cofibre of the natural transformation  from (
from ( of (
of ( is equivalent to a quadratic functor of the form
is equivalent to a quadratic functor of the form 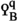 for some symmetric bilinear functor
for some symmetric bilinear functor  is trivial for any exact functor
is trivial for any exact functor 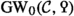 .
.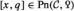 the relation
the relation 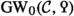 .
. if either
if either  is exact and
is exact and  is cohomogeneous or
is cohomogeneous or  is homogeneous and
is homogeneous and  is exact.
is exact. if either
if either  is exact and
is exact and  is cohomogeneous or
is cohomogeneous or  is homogeneous and
is homogeneous and  is exact.
is exact. are exact or
are exact or  and
and  are homogeneous and
are homogeneous and  is cohomogeneous.
is cohomogeneous.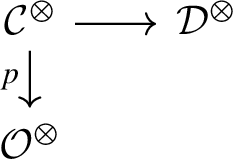
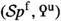 .
.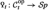 is quadratic;
is quadratic;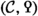 is Poincaré.
is Poincaré. induced from that of
induced from that of 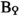 via Construction
via Construction 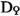 is an equivalence of
is an equivalence of 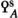 on
on  of Example
of Example 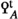 of Example
of Example 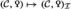 preserves Poincaré
preserves Poincaré 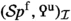 is Poincaré;
is Poincaré;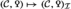 preserves Poincaré
preserves Poincaré 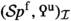 is Poincaré;
is Poincaré;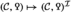 preserves Poincaré
preserves Poincaré  is Poincaré;
is Poincaré;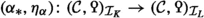 and
and 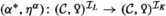 are Poincaré.
are Poincaré.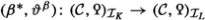 and
and 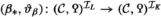 are Poincaré.
are Poincaré.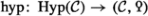 and
and 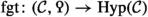 described in Sect.
described in Sect. 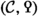 is Poincaré with associated duality
is Poincaré with associated duality 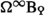 on the pair
on the pair  is naturally equivalent to the arrow category
is naturally equivalent to the arrow category 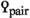 directly translates to the Poincaré structure
directly translates to the Poincaré structure 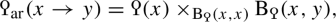
 .
. whenever
whenever  is Poincaré.
is Poincaré. to
to  given by
given by  consists of the metabolic Poincaré
consists of the metabolic Poincaré 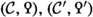 , Poincaré functors
, Poincaré functors 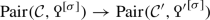
 to the Lagrangian
to the Lagrangian 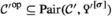 are in bijection with hermitian functors
are in bijection with hermitian functors 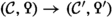 . Indeed, by Proposition
. Indeed, by Proposition 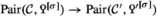 correspond to hermitian functors
correspond to hermitian functors  , and such a hermitian functor takes values in the full subcategory
, and such a hermitian functor takes values in the full subcategory 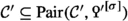 if and only if the corresponding Poincaré functor
if and only if the corresponding Poincaré functor 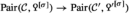 sends
sends 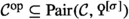 to the Lagrangian
to the Lagrangian  since
since  which are switched by the duality, and the same holds for
which are switched by the duality, and the same holds for  to its underlying symmetric category
to its underlying symmetric category  to its underlying
to its underlying