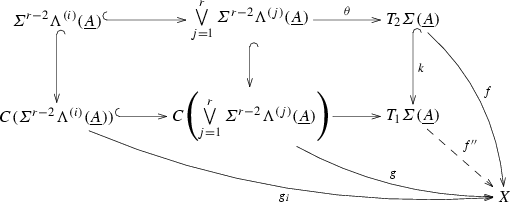On the higher Whitehead product

Abstract

Porter’s approach is used to derive some properties of higher order Whitehead products, similar to those ones for triple products obtained by Hardie. Computations concerning the higher order Whitehead product for spheres and projective spaces are presented as well.

1 Introduction

Whitehead products play an important role in algebraic topology and its applications. The classical Whitehead product [f, g] of (homotopy classes of) maps $f:\mathbb {S}^m\rightarrow X$ and $g:\mathbb {S}^n\rightarrow X$ is (the homotopy class) represented by a map $h:\mathbb {S}^{m+n-1}\rightarrow X$ and defined by means of the so called Whitehead map $\omega :\mathbb {S}^{m+n-1}\rightarrow \mathbb {S}^m\vee \mathbb {S}^n$, the attaching map for the $(m+n)$-cell of $\mathbb {S}^m\times \mathbb {S}^n$.

Arkowitz [2] constructed a generalization $\omega :\varSigma (A\wedge B)\rightarrow \varSigma A\vee \varSigma B$ of the Whitehead map to define the generalized Whitehead product [f, g] of maps $f :\varSigma A\rightarrow X$ and $g :\varSigma B\rightarrow X$. Then Zeeman [13] and Hardie [8] generalized the Whitehead product in a different context, that is, they defined a triple spherical Whitehead product $[f_1,f_2,f_3]$ of maps $f_i:\mathbb {S}^{m_i}\rightarrow X$ for $i=1,2,3$. The main result from [8] deals with the rth order spherical Whitehead product $[f_1,\ldots ,f_r]$ for maps $f_i : \mathbb {S}^{m_i}\rightarrow X$ with $r\ge 3$ defined in [9], and in particular, it states that the triple product $[f_1,f_2,f_3]$ is a coset of a subgroup of $\pi _{m-1}(X)$, where $m=m_1+m_2+m_3$. Many properties which hold for the classical Whitehead product still hold for the triple one as well.

Porter’s approach [15] was to construct the Whitehead map $\omega _r$ for more than two spaces (see Eq. (5)). Hardie’s construction from [9] was generalized in [15], where the rth order generalized Whitehead product of maps $f_i:\varSigma A_i\rightarrow X$ for $i=1,\ldots ,r$, with $r\ge 2$ was introduced. Then the 2nd order Whitehead product coincides with the generalized Whitehead product studied by Arkowitz [2].

Higher order Whitehead products are secondary, tertiary, etc. analogues of ordinary Whitehead products. They first appeared in the late 1960’s as a part of a research theme studying higher products, or simply higher structures, in homotopy theory. They are vital for understanding the homotopy theory of certain basic objects, such as an iterated product of spaces, and their maps into other spaces. Recently, higher Whitehead products have re-emerged as key players in the homotopy theory of polyhedral products. These are important objects in toric topology and are being increasingly used in geometric group theory and graph theory. Porter’s construction is very useful in many mathematical constructions. For example, given a simplicial complex K on n vertices, Davis and Januszkiewicz [6] associated two fundamental objects of toric topology: the moment–angle complex $\mathcal {Z}_K$ and the Davis–Januszkiewicz space $DJ_K$. The homotopy fibration sequence

$$\begin{aligned} \mathcal {Z}_K\xrightarrow {\tilde{\omega }}DJ_K\rightarrow \textstyle \prod \limits ^n_{i=1}\mathbb {C}P^\infty \end{aligned}$$

and its generalization have been studied in [7, 11], respectively to show that $\tilde{\omega } : \mathcal {Z}_K\rightarrow DJ_K$ is a sum of higher and iterated Whitehead products for appropriate complexes K.

Next, let $\mathcal {F}(\mathbb {R}^{n+1},m)$ be the Euclidean ordered configuration space. By Salvatore [17, Theorem 7], the homotopy type of $\mathcal {F}(\mathbb {R}^{n+1},m)$ for $n \ge 2$ admits a minimal cellular model

$$\begin{aligned} *=X_0\subseteq X_n\subseteq X_{2n}\subseteq {\cdots }\subseteq X_{mn} \end{aligned}$$

whose cells are attached via higher order Whitehead products.

In this paper, we work with triple and rth order Whitehead products. The aim of Sect. 1 is to fix some notations, recall definitions and necessary results from [1, 2] and present properties on separation elements, and the relative generalized Whitehead product as well. Section 2 expounds the main facts from [15] on rth Whitehead products which are used to discuss the main result from [8]. In Sect. 3, based on some relations from [20], (5.5), (5.8) and Proposition 5.11], we prove Proposition 4, the main result of that section, which deals with the non-triviality problem of the triple product $[\eta _4,\eta _4^2,2\iota _4]\subseteq \pi _{14}(\mathbb {S}^4)$, stated by Hardie [8, Section 5]. The main result of Sect. 4 is Theorem 4 which extends the result [8, Theorem 4.3] to higher order Whitehead products. Finally, Sect. 5 is devoted to some computations concerning the rth order Whitehead product for spheres and projective spaces. In particular, Proposition 5 shows that there are spaces X such that the rth order generalized Whitehead product $[0_1,\ldots ,0_r]$ contains a non-trivial element provided $0_i : \mathbb {S}^{m_i}\rightarrow X$ are trivial for $i=1,\ldots ,r$ with $r\ge 4$.

2 Preliminaries

Denote by $\pi (X,Y)$ the set of (based) homotopy classes of (based) maps $X\rightarrow Y$. In the sequel we do not distinguish between a map and its homotopy class. Write $C(-)$ and $\varSigma (-)$ for the reduced cone and the reduced suspension functors, respectively. As in Toda [20], p. 16], $\iota _n:\mathbb {S}^n\rightarrow \mathbb {S}^n$ denotes the identity map of the n-sphere $\mathbb {S}^n$, and $\eta _n=\varSigma ^{n-2}\eta _2:\mathbb {S}^{n+1}\rightarrow \mathbb {S}^n$ for $n\ge 2$, is the iterated suspension of the Hopf map $\eta _2:\mathbb {S}^3\rightarrow \mathbb {S}^2$. We also use freely other symbols from [20], pp. 39–50 and pp. 172–185] and write $\iota _X$ for the identity map on a space X.

2.1 Relative generalized Whitehead product

Let A and B be spaces. Given maps $f:\varSigma A\rightarrow X$ and $g: \varSigma B \rightarrow X$, Arkowitz constructed in [2] the Whitehead map

$$\begin{aligned} \omega :\varSigma (A\wedge B) \rightarrow \varSigma A\vee \varSigma B \end{aligned}$$

(1)

to define the generalized Whitehead product [f, g] as the map $\nabla (f\vee g) \omega :\varSigma (A\wedge B)\rightarrow X$, where $\nabla : X\vee X \rightarrow X$ is the folding map and $A\wedge B$ is the smash product. Also, from [2, Proposition 3.3], the product is anti-commutative, that is, $[g,f]=-(\varSigma \sigma )^*[f,g]$, where $\sigma : B\wedge A\rightarrow A\wedge B$ is the homeomorphism determined by the map $B\times A\rightarrow A\times B$.

In [1], Ando defined the relative generalized Whitehead product, briefly described as follows. Let $i_Z:Z\hookrightarrow CZ$ be the inclusion map. Given $k:X\rightarrow Y$, we say that $(h_1,h_2):i_Z\rightarrow k$ is a pair-map provided the diagram

is commutative. Write $\pi _1(Z,k)$ for the set of homotopy classes of pair-maps $(h_1,h_2):i_Z\rightarrow k$.

Note that if $Z=\varSigma Z'$ then the standard co-H-structure $\nu : \varSigma Z'\rightarrow \varSigma Z'\vee \varSigma Z'$ leads to a pair-map

which determines a group structure on $\pi _1(Z,k)$. Moreover, this group is abelian provided $Z'=\varSigma Z''$. In particular, if $k:X_0\hookrightarrow X$ is an inclusion map and $Z=\mathbb {S}^n$, we obtain the ordinary relative homotopy groups $\pi _1(\mathbb {S}^n,k)=\pi _{n+1}(X,X_0)=[(\mathbb {D}^{n+1},\mathbb {S}^n),(X,X_0)]$, where $\mathbb {D}^{n+1}=C\mathbb {S}^n$ is the $(n+1)$-disc.

Further, the map $k:X\rightarrow Y$ implies the dual Puppe long exact sequence

$$\begin{aligned} \dots \rightarrow \pi (\varSigma ^2Z,X) \xrightarrow {k_*} \pi (\varSigma ^2Z,Y) \xrightarrow {j_*} \pi _1(\varSigma Z,k) \xrightarrow {\delta _*} \pi (\varSigma Z,X) \xrightarrow {k_*} \cdots . \end{aligned}$$

(2)

For $k=i_{\varSigma A}\vee \iota _{\varSigma B}$, according to [1, Section 2(b)], there is a commutative diagram

where the vertical maps $\kappa _i$ for $i=1,2$ are induced by the inclusions of the wedge into the product, and the top row is exact.

By [15, Theorem (2.3)], $(i_{\varSigma A}\times \iota _{\varSigma B})_*\kappa _1(\omega )=0$ and by the commutativity of the diagram above, and the fact that $\kappa _2$ is isomorphism, $(i_{\varSigma A}\vee \iota _{\varSigma B})_*(\omega )=0$. Note that $(i_{\varSigma A}\vee \iota _{\varSigma B})_*: \pi (\varSigma Z,\varSigma A\vee \varSigma B)\rightarrow \pi (\varSigma Z,C(\varSigma A) \vee \varSigma B)$ is an epimorphism, and so $\delta _*$ is a monomorphism. Thus, by the exactness of the top row, there is a unique element $\overline{\omega }\in \pi _1(\varSigma Z,i_{\varSigma A}\vee \iota _{\varSigma B})$ such that $\delta _*(\overline{\omega })=\omega$.

Let $k:X\rightarrow Y$ and $Z=A\wedge B$ in the above. Then, given $f=(f_1,f_2)\in \pi _1(\varSigma A,k)$ and $g\in \pi (\varSigma B,X)$, the element $\overline{\omega }$ determines a pair-map $(\omega ',\omega )$ commuting the diagram

As in [1], the relative generalized Whitehead product $[f,g]_R\in \pi _1(\varSigma (A\wedge B),k)$ is defined by the pair-map

$$\begin{aligned} \bigl (\nabla (f_1\vee kg),\nabla (f_2\vee g)\bigr )_*(\overline{\omega })=\bigl (\nabla (f_1\vee kg)\omega ',\nabla (f_2\vee g)\omega \bigr ). \end{aligned}$$

Also therein, Ando compares his construction to the one introduced by Hardie in [8]. We describe that here to obtain Proposition 2.

First, since the generalized Whitehead product [0, g] is trivial and the product $\varSigma A\times \varSigma B$ is a push-out, we obtain a map $\lambda _A(g):C\varSigma (A\wedge B)\rightarrow X$ commuting the diagram

where $p_B:\varSigma A\times \varSigma B\rightarrow \varSigma B$ is the projection map.

Let $[f_1,kg]':C\varSigma (A\wedge B)\rightarrow Y$ be given by

$$\begin{aligned} \, [f_1,kg]' [y,t]={\left\{ \begin{array}{ll} \lambda _A(kg)[y,2t], &{} 0\le t\le \frac{1}{2}, \\ \, [f_1\sigma '_{2t-1},kg](y), &{} \frac{1}{2} \le t \le 1, \end{array}\right. } \end{aligned}$$

where $y\in \varSigma (A\wedge B)$, and $\sigma '_{2t-1}:\varSigma A\rightarrow C\varSigma A$ is given by $\sigma '_{2t-1}(x)=[x,2t-1]$ for $x\in \varSigma A$. Thus, by [1, Theorem (4.6)] we obtain

$$\begin{aligned} \, [f,g]_R = \bigl ( [f_1,kg]', [f_2,g] \bigr ). \end{aligned}$$

(3)

Further,

$$\begin{aligned} \varphi [f_1,kg]'=[\varphi f_1,\varphi kg]' \end{aligned}$$

(4)

for $\varphi : Y\rightarrow Z$ and

$$\begin{aligned} \, [(C\varSigma \alpha )^*f_1,(\varSigma \beta )^*kg]' = (C\varSigma (\alpha \wedge \beta ))^*[f_1,kg]' \end{aligned}$$

for $\alpha : A'\rightarrow A$ and $\beta : B'\rightarrow B$.

Next, suppose that $A=\varSigma A'$ and consider $[f_2,g]'':\varSigma (A\wedge B)\rightarrow X$ given by

$$\begin{aligned} \, [f_2,g]'' [y,t]={\left\{ \begin{array}{ll} \lambda _A(g)[y,4t], &{} 0\le t\le \frac{1}{4}, \\ \, [f_2\sigma _{\frac{1}{2}(4t-1)},g](y), &{} \frac{1}{4} \le t \le \frac{3}{4}, \\ \lambda _A(g)[y,4-4t], &{} \frac{3}{4}\le t\le 1, \end{array}\right. } \end{aligned}$$

where $y\in \varSigma (A\wedge B)$, and $\sigma _{\frac{1}{2}(4t-1)}:A\rightarrow \varSigma A$ is given by $\sigma _{\frac{1}{2}(4t-1)}(a)=[a,\frac{1}{2}(4t-1)]$ for $a\in A$. Note that for $t=\frac{1}{4}$, $f_2\sigma _0=0$ and $\lambda _A(g)[y,1]=[0,g](y)$, and the same for $t=\frac{3}{4}$. So, the map $[f_2,g]''$ is well defined and $[f_2,g]''= [f_2,g]$ (cf. [8, Theorem (2.4)]).

Remark 1

We work with relative Whitehead products for an inclusion map $k:X_0\hookrightarrow X$. It means that (homotopy classes of) maps $f: (C\varSigma A,\varSigma A)\rightarrow (X,X_0)$ and $g: \varSigma B \rightarrow X_0$ determine the map of pairs

$$\begin{aligned} \, [f,g]_R: (C\varSigma (A\wedge B),\varSigma (A\wedge B)) \rightarrow (X,X_0). \end{aligned}$$

We finish this section with some properties of the relative product $[-{,}-]_R$.

Let $f,f_i\in \pi _1(\varSigma A,k)$ and $g,g_i\in \pi (\varSigma B,X)$ for $i=1,2$. According to [1, Proposition (4.5)], if A and B are suspensions then $[f,g_1+g_2]_R=[f,g_1]_R+[f,g_2]_R$ and $[f_1+f_2,g]_R=[f_1,g]_R+[f_2,g]_R$. Also, [1, Theorem (4.8)] states that $[g,f]_R=-(C\varSigma \sigma ,\varSigma \sigma )^*[f,g]_R$, where $\sigma :B\wedge A\rightarrow A\wedge B$ is the canonical homeomorphism.

2.2 Generalized separation element

Given maps $f,g: CA \rightarrow X$ such that $f_{\vert A}=g_{\vert A}$, following James [12, Section 10] and Tsuchida [21, Section 3], we define the generalized separation element as (the homotopy class of) the map $d(f,g):\varSigma A \rightarrow X$ given by:

$$\begin{aligned} d(f,g)[a,t]={\left\{ \begin{array}{ll} f[a,2t], &{} 0\le t\le \frac{1}{2}, \\ g[a,2-2t], &{} \frac{1}{2}\le t\le 1. \end{array}\right. } \end{aligned}$$

Further, if $A=\varSigma A'$ then we consider

$$\begin{aligned} f+g :C\varSigma A'\xrightarrow {C\nu } C(\varSigma A')\vee C(\varSigma A')\xrightarrow {\nabla (f\vee g)} X. \end{aligned}$$

Then, following (mutatis mutandis) Hardie [8, Section 1] and James [12, Section 10], we may state:

Proposition 1

Let $f,g,h:CA\rightarrow X$ be maps such that $f_{\vert A}=g_{\vert A}=h_{\vert A}$, and let $k:X\rightarrow Y$ be any map. Then:

• (i) triviality: $d(f,f)=0$;

• (ii) triangularity: $d(f,g)+d(g,h)=d(f,h)$;

• (iii) antisymmetry: $d(g,f)=-d(f,g)$;

• (iv) naturality: $d(k f,k g)=k d(f,g)$;

• (v) co-naturality: $d((C\alpha )^*f,(C\alpha )^*g)=(\varSigma \alpha )^*d(f,g)$ for $\alpha :A'\rightarrow A$.

Moreover, let $f_i,g_i:C\varSigma A\rightarrow X$ be maps for $i=1,2$ such that $f_{1\vert \varSigma A}=f_{2\vert \varSigma A}$ and $g_{1\vert \varSigma A}=g_{2\vert \varSigma A}$. Then:

• (vi) $d(f_1+g_1,f_2+g_2)=d(f_1,f_2)+d(g_1,g_2)$;

• (vii) if $\varphi : \varSigma A \rightarrow X$ then there exists $f':CA\rightarrow X$ such that $f'_{\vert A}=f_{\vert A}$ and $-\varphi =d(f,f')$;

Let $j_*$ and $\delta _*$ be the maps as in the exact sequence (2). Then:

• (viii) if $\delta _*(f',f'')=0$ for some $(f',f'')\in \pi _1(\varSigma A,k)$ and $g\in \pi (C\varSigma A,X)$ such that $g_{\vert \varSigma A}=f'_{\vert \varSigma A}$ then $j_*d(f',kg)=(f',f'')$. In addition for any $h\in j_*^{-1}(f',f'')$ there exists $g'\in \pi (C\varSigma A,X)$ with $g'_{\vert \varSigma A}=f'_{\vert \varSigma A}$ such that $h=d(f',kg')$.

Proof

Since the items (i)–(vi) follow directly from the definition of d, we just prove (vii) and sketch a proof of (viii).

For (vii), let $q:A\times I \rightarrow CA$ be the quotient map such that the inclusion $A\hookrightarrow CA$ is given by $a\mapsto q(a,1)=[a,1]$ for $a\in A$. Define $f':CA\rightarrow X$ by

$$\begin{aligned} f'[a,t]={\left\{ \begin{array}{ll} \varphi [a,2t], &{} 0\le t \le \frac{1}{2},\\ f q (a,2t-1), &{} \frac{1}{2}\le t \le 1, \end{array}\right. } \end{aligned}$$

and note that for $t=\frac{1}{2}$, $\varphi [a,1]=*=f q(a,0)$, and for $t=1$, $f'[a,1]=f q(a,1)=f[a,1]$, that is, $f_{\vert A}=f'_{\vert A}$. After some computations and changes of parameters we can show that:

$$\begin{aligned} d(f,f')[a,t]={\left\{ \begin{array}{ll} f[a,\frac{8}{3}t], &{} 0\le t \le \frac{3}{8}, \\ f[a,2-\frac{8}{3}t], &{} \frac{3}{8}\le t \le \frac{3}{4}, \\ \varphi [a,4(1-t)], &{} \frac{3}{4}\le t \le 1. \end{array}\right. } \end{aligned}$$

Since the first two parts provide a map homotopic to $d(f,f)=0$ and the third part is homotopic to $-\varphi$, we obtain $-\varphi = d(f,f')$.

For (viii), we note that the map $j_*:\pi (\varSigma ^2A,Y)\rightarrow \pi _1(\varSigma A,k)$ is determined by the map $(C\varSigma A,\varSigma A)\rightarrow (\varSigma ^2A,*)$. Then, we simply mimic the proof of [8, Theorem 1.9]. $\square$

We finish this section by stating a relation between the separation element and the products defined in Sect. 1.1 (cf. [8, (2.7)]).

Proposition 2

Let $f=(f_1,f_2)$, $f'=(f_1',f_2')\in \pi _1(\varSigma A,k)$ and $g\in \pi (\varSigma B,X)$, where $k:X\rightarrow Y$. Suppose that $f_2=f_2':\varSigma A\rightarrow X$. Then

$$\begin{aligned} d\bigl ( [f_1,kg]', [f_1',kg]' \bigr )= [ d(f_1,f_1') ,kg ]:\varSigma ^ 2(A\wedge B)\rightarrow Y. \end{aligned}$$

Proof

Just observe that the restrictions of $[f_1,kg]'$ and $[f_1',kg]'$ to $\varSigma (A\wedge B)$ are equal to $k_*[f_2,g]$ and $k_*[f_2',g]$, respectively. Since $f_2=f_2'$, we get $k_*[f_2,g]=k_*[f_2',g]$ and $d\bigl ( [f_1,kg]', [f_1',kg]' \bigr )$ is defined. Then by the definition of the generalized separation element and the discussion above

$$\begin{aligned} d\bigl ( [f_1,kg]', [f_1',kg]' \bigr )=[ d(f_1,f_1') ,kg ]''=[ d(f_1,f_1') ,kg ], \end{aligned}$$

and the proof follows. $\square$

3 Higher order generalized Whitehead product

Let $r\ge 2$ be an integer and denote by $\underline{A}=(A_1,\ldots ,A_r)$ an r-tuple of topological spaces with base points $*$. The fat wedge of $\underline{A}$ is the space

$$\begin{aligned} FW(\underline{A})=\bigl \{(a_1,\ldots ,a_r)\in A_1\times \cdots \times A_r \mid \text {at least one }a_i=*\bigr \}. \end{aligned}$$

If $r=2$, then $FW(\underline{A})=A_1\vee A_2$ is the wedge sum.

Following Porter’s notation [15], let $T_0(\underline{A})= A_1\times \cdots \times A_r$ and $T_s(\underline{A}) \subseteq T_0(\underline{A})$ be the subset of points $(a_1,\ldots ,a_r)$ with at least s coordinates $a_i=*$ for $s=1,\ldots ,r$. Thus, $T_{r-1}(\underline{A})= A_1\vee \cdots \vee A_r$ is the wedge sum and $T_1(\underline{A})=FW(\underline{A})$ is the fat wedge. Also, we write $\Lambda (\underline{A})=A_1\wedge \cdots \wedge A_r$ and $\varSigma (\underline{A})=(\varSigma A_1,\ldots ,\varSigma A_r)$.

Remark 2

In the sequel, we need to take some coordinate $a_{i_0}=*$. To do this, we define

$$\begin{aligned} T_0^{(i)}(\underline{A}) = \textstyle \prod \limits _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{r} A_j, \quad \Lambda ^{(i)}(\underline{A})=\textstyle \bigwedge \limits _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{r} A_j \end{aligned}$$

for $i=1,\ldots ,r$. In this way, the subset $T_s^{(i)}(\underline{A}) \subseteq T_0^{(i)}(\underline{A})$ is defined for $s=1,\ldots ,r-1$ and has a self-explanatory notation. Also, there are canonical embeddings $\Psi _s^{(i)}:T_s^{(i)}(\underline{A}) \hookrightarrow T_{s+1}(\underline{A})$ for any $s=0,\ldots ,r-1$.

In [15], Porter constructed the generalized Whitehead map (cf. (1))

$$\begin{aligned} \omega _r : \varSigma ^{r-1}\Lambda (\underline{A})\rightarrow T_1\varSigma (\underline{A}) \end{aligned}$$

(5)

to define the rth order generalized Whitehead product $\omega _r(f)\in \pi (\varSigma ^{r-1}\Lambda (\underline{A}),X)$ of a map $f:T_1\varSigma (\underline{A}) \rightarrow X$ as the composite

$$\begin{aligned} \omega _r(f): \varSigma ^{r-1}\Lambda (\underline{A}) \xrightarrow {\omega _r} T_1\varSigma (\underline{A}) \mathop {\longrightarrow }\limits ^{f} X. \end{aligned}$$

Given $f_i:\varSigma A_i \rightarrow X$ for $i=1,\ldots ,r$, let $f_1\vee \cdots \vee f_r:T_{r-1}\varSigma (\underline{A}) \rightarrow X$ be the wedge sum map. The (possibly empty) set

$$\begin{aligned} \, [f_1,\ldots ,f_r]=\bigl \{\omega _r(f)\in \pi (\varSigma ^{r-1}\Lambda (\underline{A}),X) \bigr \}, \end{aligned}$$

for all $f:T_1\varSigma (\underline{A}) \rightarrow X$ extending $f_1\vee \cdots \vee f_r$, is called the rth order generalized Whitehead product of $f_1,\ldots ,f_r$. Hardie [9] gave the definition of $[f_1,\ldots ,f_r]$ when all the $A_i$’s are spheres (called the rth order spherical Whitehead product).

In virtue of [15, Theorem (2.7)], it is non-empty if and only if all the lower products $[f_{m_1},\ldots ,f_{m_k}]$ for $1\le m_1\le \cdots \le m_k\le r$ with $k=2,\ldots , r-1$ contain the zero element 0. We note that the set $[f_1,\ldots ,f_r]$ can be empty even if $f_i=0$ for some i. This is the case for $[0,\iota _2,\iota _2]$, since the classical Whitehead product $[\iota _2,\iota _2]=2\eta _2\ne 0$, by [20, p. 39].

Remark 3

In the sequel we will use the same notation $\sigma$ for a permutation of the set $\{1,\ldots ,r\}$ and for its induced homeomorphism $A_1\wedge \cdots \wedge A_r\rightarrow A_{\sigma (1)}\wedge \cdots \wedge A_{\sigma (r)}$.

Proposition 3

Let $f_i:\varSigma A_i \rightarrow X$ for $i=1,\ldots ,r$ and $\sigma \in S_r$ be a permutation of the set $\{1,\ldots ,r\}$. Then

$$\begin{aligned} \, [f_{\sigma (1)},\ldots ,f_{\sigma (r)}]=\mathrm{sgn}(\sigma )(\varSigma ^{r-1}\sigma )^*[f_1,\ldots ,f_r]. \end{aligned}$$

Proof

Denote by $\sigma \underline{A}=(A_{\sigma (1)},\ldots ,A_{\sigma (r)})$ the image of $\underline{A}$ under the permutation $\sigma \in S_r$. It is clear that there is a commutative diagram

Let $f_{\sigma (1)}\vee \cdots \vee f_{\sigma (r)}=(T_{r-1}\varSigma \sigma )^*(f_1\vee \cdots \vee f_r): T_{r-1}\varSigma (\sigma \underline{A})\rightarrow X$. So, if $f:T_1\varSigma (\underline{A})\rightarrow X$ is an extension of $f_{1}\vee \cdots \vee f_{r}$ then $\sigma f=(T_1\varSigma \sigma )^*(f):T_1\varSigma (\sigma \underline{A})\rightarrow X$ is an extension of $f_{\sigma (1)}\vee \cdots \vee f_{\sigma (r)}$. Finally, note that $\sigma \omega _r(\sigma f)=\mathrm{sgn}(\sigma )(\varSigma ^{r-1}\sigma )^*(\omega _r(f))$ and the proof follows. $\square$

According to [15, Theorem (2.3)] there is a homotopy equivalence

$$\begin{aligned} T_1\varSigma (\underline{A})\cup _{\omega _r} C(\varSigma ^{r-1}\Lambda (\underline{A}))\xrightarrow {\simeq } T_0\varSigma (\underline{A}). \end{aligned}$$

(6)

So, we have a pair-map $(\Omega _r,\omega _r)$ commuting the diagram

Considering the spaces and inclusions as in Remark 2, let

$$\begin{aligned} \theta : \textstyle \bigvee \limits _{i=1}^r \varSigma ^{r-2}\Lambda ^{(i)} (\underline{A}) \rightarrow T_2\varSigma (\underline{A}) \end{aligned}$$

be given by $\theta _{\vert \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})}=\Psi _1^{(i)} \omega _r^{(i)}$, where $\omega _r^{(i)}:\varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})\rightarrow T_1^{(i)}\varSigma (\underline{A})$ is the generalized Whitehead map. Then, as a particular case of [15, Theorem (2.6)], we have:

Theorem 1

The following spaces are homotopy equivalent:

• (i) $T_1\varSigma (\underline{A})$;

• (ii) $T_2\varSigma (\underline{A})\cup _\theta C\left( \textstyle \bigvee \limits _{i=1}^r \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})\right)$;

• (iii) $T_2\varSigma (\underline{A})\cup _\theta \textstyle \bigvee \limits _{i=1}^r C( \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A}))$.

Now, we discuss some results on the rth order generalized Whitehead product $[f_1,\ldots ,f_r]$ of maps $f_i:\varSigma A_i\rightarrow X$ for $i=1,\ldots ,r$. First, we recall [15, Theorems (2.1)(d), (2.4), (2.5) and Remark (4)] and present a corollary of [15, Theorem (2.3)].

Theorem 2

• (i) (Naturality) Let $f_i:\varSigma A_i\rightarrow \varSigma B_i$, $g_i:\varSigma B_i\rightarrow X$ and $k:X\rightarrow Y$ be maps for $i=1,\ldots , r$. Then, $k_*[g_1,\ldots ,g_r]\subseteq [k g_1,\ldots ,k g_r]$.

• (ii) If X is an H-space then $\omega _r(f)=0$.

• (iii) Let $f_i:\varSigma A_i\rightarrow X$ be maps for $i=1,\ldots ,r$. Then $0\in [f_1,\ldots ,f_r]$ if and only if $f_1\vee \cdots \vee f_r:T_{r-1}\varSigma (\underline{A})\rightarrow X$ has an extension to $T_0\varSigma (\underline{A})$. Further, $\varSigma \omega _r(f)=0$ for $f:T_1\varSigma (\underline{A}) \rightarrow X$ extending $f_1\vee \cdots \vee f_r$.

Corollary 1

If $[f_1,\ldots ,f_r]\ne \emptyset$ and $f_{i_0}=0_{i_0}$ for some $1\le i_0\le r$ then $0\in [f_1,\ldots ,f_r]$.

Proof

In virtue of Proposition 3, we can suppose that $i_0=1$. By hypothesis the map $0\vee f_2\vee \cdots \vee f_r: T_{r-1}\varSigma (\underline{A}) \rightarrow X$ has an extension $F_1:T_1\varSigma (\underline{A})\rightarrow X$. Define $F: T_0\varSigma (\underline{A}) \rightarrow X$ by $F(x_1,\ldots ,x_r)= F_1(*,x_2,\ldots ,x_r)$ for $(x_1,\ldots ,x_r)\in T_0\varSigma (\underline{A})$. Then, F is an extension of $0_1\vee f_2\vee \cdots \vee f_r$, and the result follows by Theorem 2(iii). $\square$

Recall from [19] that a space X is called a G -space if for any map $f : \mathbb {S}^n\rightarrow X$ and $n\ge 1$ the map $\nabla (\iota _X \vee f): X\vee \mathbb {S}^n \rightarrow X$ extends to $F: X \times \mathbb {S}^n \rightarrow X$. According to [19, Theorem 3.2], any rth order spherical Whitehead product of a G-space contains zero.

Now, let $\mathcal {G}(A, X)\subseteq \pi (A,X)$ be the set of (homotopy classes of) maps $f:A \rightarrow X$ such that the maps $\nabla (\iota _X \vee f): X\vee A \rightarrow X$ extend to $F: X \times A \rightarrow X$. A space X is called a G -space with respect to the space A if $\mathcal {G}(A, X)=\pi (A,X)$.

Lemma 1

If X is a G-space with respect to the spaces $A_1,\ldots , A_r$ then any map $\iota _X\vee f_1\vee \cdots \vee f_r : X\vee A_1\vee \cdots \vee A_r\rightarrow X$ extends to $F: X\times A_1\times \cdots \times A_r\rightarrow X$.

Proof

The proof is by induction on r. Let $r=2$ and $F_i:X\times A_i\rightarrow X$ extending $\iota _X\vee f_i:X\vee A_i\rightarrow X$ for $i=1,2$. Then $F_2(F_1\times \iota _{ A_2}):X\times A_1\times A_2\rightarrow X$ extends $\iota _X\vee f_1\vee f_2: X\vee A_1\vee A_2 \rightarrow X$.

Suppose that the statement is true for ${r-1}$, that is, there exists $F:X\times A_1\times \cdots \times A_{r-1}\rightarrow X$ extending $\iota _X\vee f_1\vee \cdots \vee f_{r-1}$.

Finally, let $F_r:X\times A_r\rightarrow X$ extending $\iota _X\vee f_r:X\vee A_r\rightarrow X$ and then the composite $F_r (F\times \iota _{ A_r}): X\times T_0(\underline{A})\rightarrow X$ extends $\iota _X\vee f_1\vee \cdots \vee f_r$, which completes the proof. $\square$

Referring to Williams [22], we say that a space X has property $P_r$ if for every $f_i : \varSigma A_i\rightarrow X$ with $i=1,\ldots ,r$, we have $0\in [f_1,\ldots ,f_r]$. Certainly, in view of Theorem 2(ii), any H-space has not only property $P_r$ for all $r\ge 2$ but 0 is the only element of $[f_1,\dots ,f_r]$. (Williams [22]: We note at this point that it is unresolved conjecture as to whether X has property $P_r$ implies that 0 is the only element of $[f_1,\ldots ,f_r]$.)

Directly from Theorem 2(iii) and Lemma 1 it follows:

Corollary 2

Every G-space X with respect to any $\varSigma A_1,\ldots ,\varSigma A_r$ has property $P_r$. In particular, if $f : \varSigma A\rightarrow X$ and X is a G-space with respect to any $\varSigma A$ then $0\in [f,\overset{\times r}{\cdots {}},f]$ for any $r\ge 2$.

In general, the generalized Whitehead product is not additive. But, in the sequel, we need an addition operation defined in [15] for some particular functions. We say that maps $f,g:T_1\varSigma (\underline{A})\rightarrow X$ are compatible off the ith coordinate if $f\Psi _0^{(i)}= g\Psi _0^{(i)}:T_0^{(i)}\varSigma (\underline{A})\rightarrow X$. If $A_i=\varSigma A_i'$ is a suspension one defines an addition $+^{(i)}$ by

$$\begin{aligned}&(f+^{(i)}g)(x_1,\ldots ,[t_i,[u,a_i']],\ldots ,x_r)\\&\quad ={\left\{ \begin{array}{ll} f(x_1,\ldots ,[t_i,[2u,a_i']],\ldots ,x_r), &{} 0\le u \le \frac{1}{2}, \\ g(x_1,\ldots ,[t_i,[2u-1,a_i']],\ldots ,x_r), &{} \frac{1}{2}\le u \le 1. \end{array}\right. } \end{aligned}$$

Also, one defines ${-^{(i)}}f$ by

$$\begin{aligned} (-^{(i)}f)(x_1,\ldots ,[t_i,[u,a_i']],\ldots ,x_r)=f(x_1,\ldots ,[t_i,[1-u,a_i']],\ldots ,x_r). \end{aligned}$$

Then, in view of [15, Theorem (2.13)], we can state:

Theorem 3

• (i) $\omega _r(f+^{(i)}g)=\omega _r(f)+\omega _r(g)$;

• (ii) $\omega _r({-^{(i)}}f)=-\omega _r(f)$.

From this, it follows:

Corollary 3

If $f_i : \varSigma A_i\rightarrow X$ for $i=1,\ldots ,r$ then

$$\begin{aligned} \, [f_1,\ldots ,nf_i,\ldots ,f_r]\subseteq n[f_1,\ldots ,f_i,\ldots ,f_r] \end{aligned}$$

for any integer n and $i=1,\ldots ,r$.

4 Triple spherical Whitehead products

Zeeman [13, Section 3.3] associated with a triple of elements $f\in \pi _p(X)$, $g\in \pi _q(X)$ and $h\in \pi _r(X)$ ($p,q,r\ge 2$), whose Whitehead products taken in pairs all vanish, a certain subset $[f,g,h]'$ of $\pi _{p+q+r-1}(X)$. Hardie [8] sharpened this construction defining the triple spherical Whitehead product $[f,g,h]\subseteq [f,g,h]'$ and proving in [8, Theorem 0.1] that [f, g, h] is a coset of the subgroup

$$\begin{aligned} J(f,g,h)=[\pi _{q+r}(X),f]+ [\pi _{p+r}(X),g]+[\pi _{p+q}(X),h] \end{aligned}$$

of $\pi _{p+q+r-1}(X)$. Thus, a trivial triple spherical Whitehead product means $[f,g,h]=J(f,g,h)$ or equivalently, $0\in [f,g,h]$. Hardie stated in [8, Section 5]: We do not know of a case when the triple (spherical) product [f, g, h] is non-trivial for a sphere, and for $X=\mathbb {S}^4$, the triple product $[\eta _4,\eta _4^2,2\iota _4]\subseteq \pi _{14}(\mathbb {S}^4)$ is possibly non-trivial. Proposition 4 below shows that it is non-empty and has order fifteen. In order to prove this, we need to check first that all lower products vanish. We keep below the standard notations from Toda’s book [20, pp. 39–50 and pp. 172–185].

Lemma 2

Given $\eta _4\in \pi _5(\mathbb {S}^4)$, $\eta _4^2\in \pi _6(\mathbb {S}^4)$, and $\iota _4\in \pi _4(\mathbb {S}^4)$, the following classical Whitehead products vanish:

$$\begin{aligned} \, [\eta _4,2\iota _4]&=0, \quad&[\eta _4^2,2\iota _4]&=0, \quad&[\eta _4,\eta _4^2]&=0. \end{aligned}$$

Proof

Certainly, $[\eta _4,2\iota _4]=[2\eta _4,\iota _4]=0$ and $[\eta _4^2,2\iota _4]=[2\eta _4^2,\iota _4]=0$. Further, by [20, (5.9), p. 44], $\eta _3\circ \nu _4=\nu '\circ \eta _6$, by [20, (5.5), p. 42], $4\nu _n=\eta _n^3$ for $n\ge 5$, and by [20, Proposition 5.6, p. 42], $\varSigma \nu '$ has order four.

But $[\eta _4,\eta _4^2] = \eta _4 \circ [\iota _5,\eta _5] = \eta _4 \circ [\iota _5,\iota _5] \circ \eta _9$ and $[\iota _5,\iota _5]=\nu _5\circ \eta _8$, by [20, (5.10), p. 44]. Thus $[\eta _4,\eta _4^2]= (\eta _4\circ \nu _5) \circ \eta _8 \circ \eta _9 = \varSigma \nu ' \circ \eta _7 \circ \eta _8 \circ \eta _9 = \varSigma \nu ' \circ 4 \nu _7 = 4\varSigma \nu '\circ \eta _7=0$. $\square$

To prove the next proposition, we recall from [20, (13.1), p. 172 and Proposition 13.6, p. 179] that

$$\begin{aligned} \pi _{11}(\mathbb {S}^4)=\mathbb {Z}_3\{\alpha _2(4)\}\oplus \mathbb {Z}_5\{\alpha _1(4)\} \end{aligned}$$

and for the 2-primary components, in view of [20, Propositions 5.9, p. 44 and 5.11, p. 46], we have:

$$\begin{aligned} \pi _{9}^4&=\mathbb {Z}_2\{\nu _4\circ \eta _7^2\}\oplus \mathbb {Z}_2\{\varSigma \nu '\circ \eta _7^2\},&\pi _{10}^4&=\mathbb {Z}_8\{\nu _4^2\}. \end{aligned}$$

Moreover, from [18, Proposition IV.5], Serre’s isomorphism for any odd p-primary components

$$\begin{aligned} \pi _{i-1}(\mathbb {S}^{2m-1};p)\oplus \pi _i(\mathbb {S}^{4m-1};p)\simeq \pi _i(\mathbb {S}^{2m};p) \end{aligned}$$

is given by $(f,g)\mapsto \varSigma f+[\iota _{2m},\iota _{2m}]\circ g$.

Proposition 4

The groups $[\pi _{9}(\mathbb {S}^4),\eta _4^2]$ and $[\pi _{10}(\mathbb {S}^4),\eta _4]$ are trivial. In particular, $J(\eta _4,\eta _4^2,2\iota _4)=[\pi _{11}(\mathbb {S}^4),2\iota _4]$ and it is a subgroup of $\pi _{14}(\mathbb {S}^4)$ with order fifteen. In addition, the triple spherical Whitehead product

$$\begin{aligned} \, [\eta _4,\eta _4^2,2\iota _4]=(4x(\nu _4\circ \sigma ')+2y(\varSigma \varepsilon '))+J(\eta _4,\eta _4^2,2\iota _4) \end{aligned}$$

for some $x,y\in \{0,1\}$.

Proof

First, recall that for $f\in \pi _k(\mathbb {S}^m)$ and $g\in \pi _l(\mathbb {S}^m)$ with relatively prime orders, the Whitehead product $[f,g]=0$. Hence, because the orders of $\eta _4$ and $\eta _4^2$ are two, we can restrict to $\pi _{9}^4$ and $\pi _{10}^4$ only.

For the first statement notice that

$$\begin{aligned} \, [\nu _4^2,\eta _4]=[\nu _4,\iota _4]\circ \varSigma (\nu _6\wedge \eta _3) \end{aligned}$$

and

$$\begin{aligned} \, [\nu _4\circ \eta _7^2,\eta _4^2]=[\nu _4,\iota _4]\circ \varSigma (\eta _6^2\wedge \eta _3^2). \end{aligned}$$

Because $[\nu _4,\iota _4]=\pm 2\nu _4^2$ ([3, Corollary (7.4)]), we derive that $[\nu _4^2,\eta _4]=0$ and $[\nu _4\circ \eta _7^2,\eta _4^2]=0$.

Next, $[\varSigma \nu ',\iota _4]=[\iota _4,\iota _4]\circ \varSigma \nu '$ and [20, (5.5), p. 42 and Proposition 5.11, p. 46] implies $[\varSigma \nu ',\iota _4]=\pm 4\nu _2^2$. Consequently,

$$\begin{aligned}{}[\varSigma \nu '\circ \eta _7^2,\iota _4\circ \eta _4^2]=[\varSigma \nu ',\iota _4]\circ \varSigma (\eta _6^2\wedge \eta _3^2)=0. \end{aligned}$$

This proves that $J(\eta _4,\eta _4^2,2\iota _4)=[\pi _{11}(\mathbb {S}^4),2\iota _4]$.

To determine its order, notice that by means of Serre’s isomorphisms

$$\begin{aligned} \pi _{13}(\mathbb {S}^3;p)\oplus \pi _{14}(\mathbb {S}^7;p)\simeq \pi _{14} (\mathbb {S}^4;p) \end{aligned}$$

for $p=3,5$, the orders of $[\alpha _2(4),\iota _4]=[\iota _4,\iota _4]\circ \alpha _2(7)$ and $[\alpha _1(4),\iota _4]= [\iota _4,\iota _4]\circ \alpha _1(7)$ are three and five, respectively. This implies that the order of $J(\eta _4,\eta _4^2,2\iota _4)$ is fifteen.

Finally, let $\alpha \in \pi _{14}(\mathbb {S}^4)$ be such that $[\eta _4,\eta _4^2,2\iota _4]=\alpha +J(\eta _4,\eta _4^2,2\iota _4)$. Since $2\eta _4=0$, in view of Corollaries 1 and 3, we deduce that

$$\begin{aligned} 0\in [2\eta _4,\eta _4^2,2\iota _4]\subseteq 2[\eta _4,\eta _4^2,2\iota _4]= 2\alpha +J(\eta _4, \eta _4^2,2\iota _4). \end{aligned}$$

Consequently, $2\alpha \in J(\eta _4,\eta _4^2,2\iota _4)$ and so $30\alpha =0$. Hence, $\alpha =a\alpha '+b\beta$ for $\alpha '\in \pi _{14}^4$ with order two and $\beta \in J(\eta _4,\eta _4^2,2\iota _4)$ for some $a\in \{0,1\}$ and $b\in \{0,\ldots ,14\}$. This implies that $[\eta _4,\eta _4^2,2\iota _4]=\alpha +J(\eta _4,\eta _4^2,2\iota _4)=a\alpha '+J(\eta _4,\eta _4^2,2\iota _4)$ and $a\alpha '\in [\eta _4,\eta _4^2,2\iota _4]$.

In view of [20, Theorem 7.3, p. 66], it holds $\pi _{14}^4=\mathbb {Z}_8\{\nu _4\circ \sigma '\}\oplus \mathbb {Z}_4\{\varSigma \varepsilon '\}\oplus \mathbb {Z}_2\{\eta _4\circ \mu _5\}$. Then, we derive that $\alpha '=4x'(\nu _4\circ \sigma ')+2y'(\varSigma \varepsilon ')+z'(\eta _4\circ \mu _5)$ for some $x',y',z'\in \{0,1\}$. Because $\alpha '\in [\eta _4,\eta _4^2,2\iota _4]$, we get from Theorem 2(iii) that $0=\varSigma \alpha '=4x'(\nu _5\circ \varSigma \sigma ')+2y'(\varSigma ^2\varepsilon ')+z'(\eta _5\circ \mu _6)$. But, by [20, (7.10), p. 67 and (7.16), p. 69], it holds $2(\nu _5\circ \sigma _8)=\pm \varSigma ^2\varepsilon '$ and $2(\nu _5\circ \sigma _8)=\nu _5\circ \varSigma \sigma '$. Thus, $z'(\eta _5\circ \mu _6)=0$, so $z'=0$ and $\alpha '=4x'(\nu _4\circ \sigma ')+2y'(\varSigma \varepsilon ')$ for some $x',y'\in \{0,1\}$ which completes the proof. $\square$

5 Main result

Theorem 1 provides the following commutative diagram

which lead to pair-maps

$$\begin{aligned} (h_i',h_i''): \bigl (C(\varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})), \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A}) \bigr ) \rightarrow (T_1\varSigma (\underline{A}), T_2\varSigma (\underline{A}) ), \end{aligned}$$

(7)

for $i=1,\ldots ,r$.

Let $\Theta _i=(h_i',h_i'')\in \pi _1(\varSigma ^{r-2}\Lambda ^{(i)}(\underline{A}),k)$ and $\jmath _i:\varSigma A_i \hookrightarrow T_2\varSigma (\underline{A})$ be the canonical inclusion map for $i=1,\ldots ,r$, where $k:T_2\varSigma (\underline{A})\hookrightarrow T_1\varSigma (\underline{A})$ is the inclusion map. Then each relative generalized Whitehead product

$$\begin{aligned}&\, [\Theta _i,\jmath _i]_R : \bigl ( C(\varSigma (\varSigma ^{r-3}\Lambda ^{(i)}(\underline{A})\wedge A_i)), \varSigma (\varSigma ^{r-3}\Lambda ^{(i)}(\underline{A}) \wedge A_i) \bigr )\\&\qquad \qquad \qquad \rightarrow (T_1\varSigma (\underline{A}),T_2\varSigma (\underline{A})) \end{aligned}$$

simplifies to

$$\begin{aligned} \tau _i^*[\Theta _i,\jmath _i]_R : \bigl (C(\varSigma ^{r-2}\Lambda (\underline{A}) ) , \varSigma ^{r-2}\Lambda (\underline{A})\bigr ) \rightarrow (T_1\varSigma (\underline{A}), T_2\varSigma (\underline{A}) ), \end{aligned}$$

where $\tau _i=(C\varSigma ^{r-2}\sigma _i,\varSigma ^{r-2}\sigma _i)$ for $i=1,\ldots ,r$, and $\sigma _i\in S_r$ is the permutation inducing the homeomorphism $\sigma _i: \Lambda (\underline{A})\rightarrow \Lambda ^{(i)}(\underline{A})\wedge A_i$.

Hence, we got the relative generalized Whitehead products $\tau _i^*[\Theta _i,\jmath _i]_R\in \pi _1(\varSigma ^{r-2}\Lambda (\underline{A}), k)$ for $i=1,\ldots ,r$.

Next, consider the commutative diagram

where $k:T_2\varSigma (\underline{A})\hookrightarrow T_1\varSigma (\underline{A})$ and $k':T_1\varSigma (\underline{A})\hookrightarrow T_0\varSigma (\underline{A})$ are inclusion maps, $\delta _{*1},\delta _{*2}$ are boundaries and $j_*$ is the obvious map.

Since the bottom row is exact and $\delta _{*1}(\Omega _r,\omega _r)=\omega _r$, we obtain $\partial (\Omega _r,\omega _r)=j_*(\omega _r)$ and so $\delta _{*2}\partial (\Omega _r,\omega _r)=\delta _{*2} j_*(\omega _r)=0$.

Following mutatis mutandis the result due to Nakaoka–Toda [14, Lemma (1.2)] for spheres and a proof of its generalization [10, Formula (0.1)], we may state for suspensions:

Lemma 3

If $h=\sum \nolimits _{i=1}^{r} \tau _i^* [\Theta _i,\jmath _i]_R \in \pi _1(\varSigma ^{r-2}\Lambda (\underline{A}),k)$ then $h=\partial (\Omega _r,\omega _r)$.

Notice that in view of the formula (3), we have

$$\begin{aligned} \, [\Theta _i,\jmath _i]_R=\bigl ([h'_i,k\jmath _i]',[h''_i,\jmath _i]\bigr ) \end{aligned}$$

for $i=1,\ldots ,r$. Consequently,

$$\begin{aligned} \textstyle h= (h',h'') =\left( \sum \limits _{i=1}^{r}(C\varSigma ^{r-2}\sigma _i)^*[h'_i,k\jmath _i]',\sum \limits _{i=1}^{r}(\varSigma ^{r-2}\sigma _i)^*[h''_i,\jmath _i] \right) . \end{aligned}$$

Now, we are in a position to generalize the main result of [8, Theorem 4.3].

Theorem 4

Let $f:T_2\varSigma (\underline{A})\rightarrow X$ be any map, $\jmath _i:\varSigma A_i \hookrightarrow T_2\varSigma (\underline{A})$ be the canonical inclusion maps, and $f_i=f \jmath _i:\varSigma A_i\rightarrow X$ for $i=1,\ldots ,r$.

• (i) If $f',f'':T_1\varSigma (\underline{A}) \rightarrow X$ are extensions of f then

  $$\begin{aligned} \omega _r({f'})-\omega _r({f''}) \in \textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ], \end{aligned}$$

  where $\sigma _i\in S_r$ is the permutation inducing the homeomorphism $\sigma _i: \Lambda (\underline{A}) \rightarrow \Lambda ^{(i)}(\underline{A})\wedge A_i$ for $i=1,\ldots ,r$.

• (ii) If $f': T_1\varSigma (\underline{A})\rightarrow X$ is an extension of f then for any

  $$\begin{aligned} \gamma \in \textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ], \end{aligned}$$

  there exists $f'': T_1\varSigma (\underline{A})\rightarrow X$ an extension of f such that $\gamma =\omega _r({f'})-\omega _r({f''})$.

Proof

• (i) By Lemma 3 and commutativity of the diagram above, $h=\partial (\Omega _r,\omega _r)=j_*(\omega _r)$ so that $\omega _r\in j_*^{-1}(h)$. In view of Proposition 1(viii), there exists $g':C\varSigma ^{r-2}\Lambda (\underline{A})\rightarrow T_2\varSigma (\underline{A})$ with $g'_{\vert \varSigma ^{r-2}\Lambda (\underline{A})}=h'_{\vert \varSigma ^{r-2}\Lambda (\underline{A})}=h''$ such that $\omega _r=d(h',kg')\in \pi (\varSigma ^{r-1}\Lambda (\underline{A}),T_1\varSigma (\underline{A}))$. Since $f'k=f''k=f$, by (4) and Propositions 1–2, we get

  $$\begin{aligned}&\omega _r(f')-\omega _r(f'') = d(f' h',f' k g')- d(f'' h',f'' k g') \\&\quad = d(f' h',f'' h') \\&\quad = d\left( \textstyle \sum \limits _{i=1}^{r} f'\bigl ((C\varSigma ^{r-2}\sigma _i)^*[h'_i,k\jmath _i]'\bigr ), \textstyle \sum \limits _{i=1}^{r} f''\bigl ((C\varSigma ^{r-2}\sigma _i)^*[h'_i,k\jmath _i]'\bigr )\right) \\&\quad = \textstyle \sum \limits _{i=1}^{r} d\bigl ((C\varSigma ^{r-2}\sigma _i)^*[f'h'_i,f'k \jmath _i]',(C\varSigma ^{r-2}\sigma _i)^*[f''h'_i,f''k\jmath _i]'\bigr ) \\&\quad = \textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^* [d(f'h'_i,f''h'_i),f_i]\\&\quad \in \textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ]. \end{aligned}$$

• (ii) Let $\gamma =\textstyle \sum \nolimits _{i=1}^{r}(\varSigma ^{r-1}\sigma _i)^*[\gamma _i,f_i]$, with $\gamma _i: \varSigma ^{r-1}\Lambda ^{(i)}(\underline{A})\rightarrow X$. By (7), we obtain $f' h'_i:C(\varSigma ^{r-2}\Lambda ^{(i)}(\underline{A}))\rightarrow X$ and then, in view of Proposition 1(vii), there exist maps $g_i:C(\varSigma ^{r-2}\Lambda ^{(i)}(\underline{A}))\rightarrow X$ such that the restrictions ${g}_{i\vert \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})}=f h''_{i\vert \varSigma ^{r-2}\Lambda ^{(i)}(\underline{A})}$ and $d(f' h'_i,g_i)=\gamma _i$ for $i=1,\ldots ,r$.

  Note that the maps $g_i$ determine a map

  $$\begin{aligned} g=g_1\vee \cdots \vee g_r:C\left( \textstyle \bigvee \limits _{j=1}^r \varSigma ^{r-2}\Lambda ^{(j)}(\underline{A})\right) \rightarrow X. \end{aligned}$$

  Since, by Theorem 1, the space $T_1\varSigma (\underline{A})$ is a push-out, the universal property guarantees the existence of $f'':T_1\varSigma (\underline{A})\rightarrow X$ with $f''_{\vert T_2\varSigma (\underline{A})}=f'_{\vert T_2\varSigma (\underline{A})}=f$ and $f'' h'_i=g_i$.

  

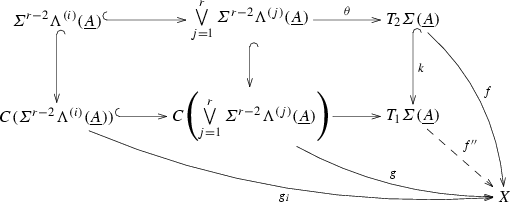
  The same computations as in (i) show that $\gamma =\omega _r(f')-\omega _r(f'')$ and the proof is complete.$\square$

Corollary 4

• (i) Let $f_i:\varSigma A_i\rightarrow X$ be any maps for $i=1,\ldots ,r$. Suppose that $[f_1,\ldots ,f_r]\ne \emptyset$. Then for any $\beta \in [f_1,\dots ,f_r]$ there is an inclusion

  $$\begin{aligned} \beta + \textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ] \subseteq [f_1,\ldots ,f_r]. \end{aligned}$$

• (ii) If $\omega _r(f)\in [f_1,\ldots ,f_r]$ for $f: T_1\varSigma (\underline{A})\rightarrow X$ then

  $$\begin{aligned}&\textstyle \sum \limits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ]=\\&\qquad \qquad \bigl \{ \omega _r(f')-\omega _r(f);\ f': T_1\varSigma (\underline{A})\rightarrow X \ \mathrm{with} \ f'_{\vert T_2\varSigma (\underline{A})}={f}_{\vert T_2\varSigma (\underline{A})} \bigr \}. \end{aligned}$$

• (iii) If $[f_1,f_2,f_3]\ne \emptyset$ then it is a coset of the subgroup

  $$\begin{aligned}&(\varSigma ^2\sigma _1)^*[\pi (\varSigma ^2\Lambda ^{(1)}(\underline{A}),X),f_1]+ (\varSigma ^2\sigma _2)^*[\pi (\varSigma ^2\Lambda ^{(2)}(\underline{A}),X),f_2]\\&\qquad \qquad +\,(\varSigma ^2\sigma _3)^*[ \pi (\varSigma ^2\Lambda ^{(3)}(\underline{A}),X ),f_3 ]\subseteq \pi (\varSigma ^2\Lambda (\underline{A}),X). \end{aligned}$$

Proof

• (i) First, for simplicity, let $\Gamma =\textstyle \sum \nolimits _{i=1}^{r} (\varSigma ^{r-1}\sigma _i)^*[ \pi (\varSigma ^{r-1}\Lambda ^{(i)}(\underline{A}),X ),f_i ]$. Next, let $f':T_1\varSigma (\underline{A})\rightarrow X$ be a map such that $\beta =\omega _r(f')$. Let $f=f'_{\vert T_2\varSigma (\underline{A})}:T_2\varSigma (\underline{A})\rightarrow X$ so that $f'$ extends f, obviously. By Theorem 4(ii), for any $\gamma \in \Gamma$ there exists $f'': T_1\varSigma (\underline{A})\rightarrow X$ an extension of f such that $\gamma =\omega _r({f'})-\omega _r({f''})$, or equivalently, $\beta +(-\gamma )=\omega _r(f'')$. Finally, since $f''$ extends the wedge sum map $f_1\vee \cdots \vee f_r$, then $\omega _r(f'')\in [f_1,\ldots ,f_r]$ and the result follows.

• (ii) This follows directly from Theorem 4.

• (iii) This is a consequence of (i) and (ii). $\square$

6 Some computations for spheres and projective spaces

Because $0\in [0_1,0_2,0_3]$, Corollary 4(iii) implies $[0_1,0_2,0_3]=0$ (modulo indeterminacy). Further, we can easily show:

Lemma 4

Let $0_i : \varSigma A_i\rightarrow X$ be trivial maps for $i=1,\ldots ,r$ with $r\ge 3$. The following are equivalent:

• (i) $[0_1,\ldots ,0_r]=0$ (modulo indeterminacy) for any space X;

• (ii) the composition

  $$\begin{aligned} \varSigma ^{r-1} \Lambda (\underline{A})\xrightarrow {\omega _r}T_1\varSigma (\underline{A})\xrightarrow {p} T_1\varSigma (\underline{A}){\mathbin {/}}T_{r-1}\varSigma (\underline{A}) \end{aligned}$$

  is trivial, where p is the quotient map;

• (iii) there is a retraction

  $$\begin{aligned} T_0\varSigma (\underline{A}){\mathbin {/}}T_{r-1}\varSigma (\underline{A}) \xrightarrow {\rho } T_1\varSigma (\underline{A}) {\mathbin {/}} T_{r-1}\varSigma (\underline{A}) \end{aligned}$$

  for the map

  $$\begin{aligned} T_1\varSigma (\underline{A}){\mathbin {/}}T_{r-1}\varSigma (\underline{A}) \xrightarrow {\bar{k}} T_0\varSigma (\underline{A}) {\mathbin {/}} T_{r-1}\varSigma (\underline{A}) \end{aligned}$$

  induced by the inclusion $k: T_1\varSigma (\underline{A}) \hookrightarrow T_0\varSigma (\underline{A})$.

Proposition 5

If $r\ge 4$ and $\underline{\mathbb {S}}=(\mathbb {S}^{m_1-1},\ldots ,\mathbb {S}^{m_r-1})$ with $m_i\ge 1$ for $i=1,\ldots ,r$ then the quotient map $T_1\varSigma (\underline{\mathbb {S}})\rightarrow T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})$ leads to a non-trivial element of the rth order generalized Whitehead product $[0_1,\ldots ,0_r]$.

Proof

¹Suppose that the quotient map $T_1\varSigma (\underline{\mathbb {S}})\rightarrow T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})$ yields a trivial element of the rth order generalized Whitehead product $[0_1,\ldots ,0_r]$ for $r\ge 4$. Then, by Lemma 4(iii), there is a retraction

$$\begin{aligned} T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}) \xrightarrow {\rho } T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}) \end{aligned}$$

for the map

$$\begin{aligned} T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}) \xrightarrow {\bar{k}} T_0\varSigma (\underline{A}){\mathbin {/}}T_{r-1}\varSigma (\underline{A}) \end{aligned}$$

induced by the inclusion $k: T_1\varSigma (\underline{\mathbb {S}}) \hookrightarrow T_0\varSigma (\underline{\mathbb {S}})$.

This leads to homomorphisms of cohomology algebras

$$\begin{aligned} \rho ^*: H^*(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\rightarrow H^*(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

and

$$\begin{aligned} \bar{k}^*: H^*(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\rightarrow H^*(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

over integers with $\bar{k}^*\rho ^*=\mathrm {id}_{H^*(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))}$. In particular, $\rho ^*$ is monomorphism. The long exact sequence for the triple $T_{r-1}\varSigma (\underline{\mathbb {S}})\subseteq T_1\varSigma (\underline{\mathbb {S}})\subseteq T_0\varSigma (\underline{\mathbb {S}})$ yields homomorphisms

$$\begin{aligned} \bar{k}^*: H^n(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\rightarrow H^n(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

(8)

which is an isomorphism for $n<m_1+\cdots +m_r-1$, and a monomorphism for $n<m_1+\cdots +m_r$.

Let now $i :T_{r-1}\varSigma (\underline{\mathbb {S}})\hookrightarrow T_0\varSigma (\underline{\mathbb {S}})$ and $q: T_0\varSigma (\underline{\mathbb {S}})\rightarrow T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})$ be the inclusion and quotient maps, respectively. Thus, the Künneth Theorem implies that the induced cohomology maps $i^*: H^n(T_0\varSigma (\underline{\mathbb {S}}))\rightarrow H^n(T_{r-1}\varSigma (\underline{\mathbb {S}}))$ are splitting epimorphisms for $n\ge 0$, and consequently

$$\begin{aligned} q^*: H^*(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\rightarrow H^*(T_0\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

is a monomorphism of cohomology algebras.

Now, consider the non-trivial elements $\alpha \in H^{m_1+m_2}(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))$ and $\beta \in H^{m_3+\cdots +m_r}(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))$ determined by cocycles associated to the cells $e^{m_1}\times e^{m_2}$ and $e^{m_3}\times \cdots \times e^{m_r}$, respectively. Then, the cup-product $\alpha \smile \beta \in H^{m_1+\cdots +m_r}(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))=0$ and consequently, $\rho ^*(\alpha \smile \beta )=\rho ^*(\alpha )\smile \rho ^*(\beta )=0$.

On the other hand, since $\rho ^*$ and $q^*$ are monomorphisms, the elements $q^*\rho ^*(\alpha )$ and $q^*\rho ^*(\beta )$ are non-trivial as well. Further, in view of (8), the map

$$\begin{aligned} \bar{k}^*: H^n(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\xrightarrow {\cong } H^n(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

is an isomorphism with the inverse

$$\begin{aligned} \rho ^*=(\bar{k}^*)^{-1} : H^n(T_1\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}}))\xrightarrow {\cong } H^n(T_0\varSigma (\underline{\mathbb {S}}){\mathbin {/}}T_{r-1}\varSigma (\underline{\mathbb {S}})) \end{aligned}$$

for $n=m_1+m_2$ and $n=m_3+\cdots +m_r$.

Then, the cohomology algebra structure

$$\begin{aligned} H^*(T_0\varSigma (\underline{\mathbb {S}}))\xrightarrow {\cong }H^*(\mathbb {S}^{m_1})\otimes \cdots \otimes H^*(\mathbb {S}^{m_r}) \end{aligned}$$

and $r\ge 4$ lead to the non-trivial cup-product

$$\begin{aligned} q^*\rho ^*(\alpha )\smile q^*\rho ^*(\beta )=q^*(\rho ^*(\alpha )\smile \rho ^*(\beta ))\in H^{m_1+\cdots +m_r}(T_0\varSigma (\underline{\mathbb {S}})). \end{aligned}$$

Consequently, $\rho ^*(\alpha )\smile \rho ^*(\beta )\in H^{m_1+\cdots +m_r}(T_0\varSigma (\underline{\mathbb {S}}) {\mathbin {/}} T_{r-1}\varSigma (\underline{\mathbb {S}}))$ is non-trivial as well. This contradiction completes the proof. $\square$

Remark 4

The generalized Whitehead map $\omega _r:\varSigma ^{r-1}\Lambda (\underline{\mathbb {S}})\rightarrow T_1\varSigma (\underline{\mathbb {S}})$ is non-trivial for any $r\ge 2$. Indeed, if $\omega _r$ is trivial then it factors through the cone $C\varSigma ^{r-1}\Lambda (\underline{\mathbb {S}})$. Hence, in view of (6), there exists a retraction $\rho : T_0\varSigma (\underline{\mathbb {S}})\rightarrow T_1\varSigma (\underline{\mathbb {S}})$ for the inclusion map $k: T_1\varSigma (\underline{\mathbb {S}}) \hookrightarrow T_0\varSigma (\underline{\mathbb {S}})$.

Let $\alpha \in H^{m_1}(T_1\varSigma (\underline{\mathbb {S}}))$ and $\beta \in H^{m_2+\cdots +m_r}(T_1\varSigma (\underline{\mathbb {S}}))$ be non-trivial elements determined by cocycles associated to the cells $e^{m_1}$ and $e^{m_2}\times \cdots \times e^{m_r}$, respectively. Thus,

$$\begin{aligned} \alpha \smile \beta \in H^{m_1+\cdots +m_r}(T_1\varSigma (\underline{\mathbb {S}}))=0. \end{aligned}$$

But, $\rho ^*(\alpha ),\rho ^*(\beta )\in H^{*}(T_0\varSigma (\underline{\mathbb {S}}))$ satisfy

$$\begin{aligned} \rho ^*(\alpha )\smile \rho ^*(\beta )=\rho ^*(\alpha \smile \beta )\ne 0 \end{aligned}$$

and since $\rho ^*$ is monomorphism, it holds $\alpha \smile \beta \ne 0$. This contradiction guarantees that $\omega _r$ is non-trivial.

Let $\mathbb {R}$ and $\mathbb {C}$ be the fields of real and complex numbers, respectively and $\mathbb {H}$ the skew $\mathbb {R}$-algebra of quaternions. Denote by $\mathbb {F}P^n$ the n-projective space over $\mathbb {F}=\mathbb {R}$, $\mathbb {C}$ or $\mathbb {H}$, put $d=\dim _\mathbb {R}\mathbb {F}$ and set $i_{n\mathbb {F}} : \mathbb {S}^d\hookrightarrow \mathbb {F}P^n$ for the inclusion map. Let $\gamma _{n\mathbb {F}}:\mathbb {S}^{(n+1)d-1}\rightarrow \mathbb {F}P^n$ be the canonical quotient map. In view of [3, Corollary (7.4)] and [4, (4.1–3)], we obtain a key formula:

Lemma 5

Let $h_0f\in \pi _k(\mathbb {S}^{2n-1})$ be the 0th Hopf–Hilton invariant for $f\in \pi _k(\mathbb {S}^n)$. Then:

$$\begin{aligned} \, [\gamma _{n\mathbb {R}} f,i_{n\mathbb {R}}] ={\left\{ \begin{array}{ll} 0, &{} \text {for odd }\,n,\\ (-1)^k\gamma _{n\mathbb {R}}(-2f+[\iota _n,\iota _n]\circ h_0f), &{} \text {for even }\,n. \end{array}\right. } \end{aligned}$$

Now, let $f: T_1\varSigma (\underline{\mathbb {S}})\rightarrow \mathbb {S}^2$ for $\underline{\mathbb {S}}=(\mathbb {S}^{m_1-1},\ldots ,\mathbb {S}^{m_r-1})$. Recall that by [5, Satz], we have $\omega _r(f)=0$ provided $m_1+\cdots +m_r\ne 4$. Further, Lemma 5 implies that $[\pi _{r-1}(\mathbb {R}P^2),i_{2\mathbb {R}}]\ne 0$ in general. This yields the following result.

Proposition 6

Let $f: T_1\varSigma (\underline{\mathbb {S}})\rightarrow \mathbb {R}P^2$ for $\underline{\mathbb {S}}=(\mathbb {S}^{m_1-1},\dots ,\mathbb {S}^{m_r-1})$.

• (i) If $m_i\ge 2$ for $i=1,\dots ,r$ with $r\ge 2$, then $\omega _r(f)=0$ provided $m_1+\cdots +m_r\ne 4$.

• (ii) $[\pi _{r-1}(\mathbb {R}P^2),i_{2\mathbb {R}}]\subseteq [f_1,\ldots ,f_r]$ for $f_i : \mathbb {S}^1\rightarrow \mathbb {R}P^2$ with $i=1,\ldots ,r$ and $f_{i_0}=i_{2\mathbb {R}}$ for at least one $1\le i_0\le r$. In particular, $2\pi _2(\mathbb {R}P^2) =[0,0,i_{2\mathbb {R}}]=[0,i_{2\mathbb {R}}, i_{2\mathbb {R}}]=[i_{2\mathbb {R}},i_{2\mathbb {R}}, i_{2\mathbb {R}}]$.

Proof

• (i) Since $m_i\ge 2$ for $i=1,\ldots ,r$, the space $T_1\varSigma (\underline{\mathbb {S}})$ is 1-connected. Hence, any map $f:T_1\varSigma (\underline{\mathbb {S}})\rightarrow \mathbb {R}P^2$ lifts to $\widetilde{f}: T_1\varSigma (\underline{\mathbb {S}})\rightarrow \mathbb {S}^2$ via the quotient map $\gamma _{2\mathbb {R}}:\mathbb {S}^{2}\rightarrow \mathbb {R}P^2$. Consequently, in view of [5, Satz], $\omega _r(f)=0$.

• (ii) Certainly, in view of Corollary 1, it holds $0\in [f_1,\dots ,f_r]$ if at least $f_{i_0}=0$ for some $1\le i_0\le r$. Further, because the circle $\mathbb {S}^1$ is a topological group, we have $[\iota _1,\overset{\times r}{\cdots {}},\iota _1]=0$. Hence, by Theorem 2(i), $0=(i_{2\mathbb {R}})_*[\iota _1,\overset{\times r}{\cdots {}},\iota _1]\in [i_{2\mathbb {R}},\overset{\times r}{\cdots {}}, i_{2\mathbb {R}}]$. Then, Corollary 4 leads to the inclusion $[\pi _{r-1}(\mathbb {R}P^2),i_{2\mathbb {R}}]\subseteq [f_1,\ldots , f_r]$ if $f_{i_0}=i_{2\mathbb {R}}$ for at least one $1\le i_0\le r$. Finally, Lemma 5 and [8, Theorem 0.1] lead to $[\pi _2(\mathbb {R}P^2),i_{2\mathbb {R}}]= 2\pi _2(\mathbb {R}P^2)= [0,0,i_{2\mathbb {R}}]=[0,i_{2\mathbb {R}},i_{2\mathbb {R}}]=[i_{2\mathbb {R}},i_{2\mathbb {R}},i_{2\mathbb {R}}]$ and the proof is complete. $\square$

Notice that we can also state:

Remark 5

• (i) $0\in [i_{n\mathbb {R}},\overset{\times r}{\cdots {}}, i_{n\mathbb {R}}]\subseteq \pi _{r-1}(\mathbb {R}P^n)$ for $r\ge 2$. In particular, $[i_{n\mathbb {R}},\overset{\times r}{\cdots {}}, i_{n\mathbb {R}}]=0$ for $r\le n$ and $2\pi _{r-1}(\mathbb {R}P^{2n})\subseteq [i_{2n\mathbb {R}},\overset{\times r}{\cdots {}}, i_{2n\mathbb {R}}]\subseteq \pi _{r-1}(\mathbb {R}P^{2n})$ for $r<4n$.

• (ii) $[i_{r\mathbb {C}},\overset{\times (r+1)}{\dots \cdots {}}, i_{r\mathbb {C}}]=(r+1)! \gamma _{r\mathbb {C}}$ for $r\ge 2$ ([16, Corollary 2]).

• (iii) It is known that $[i_{1\mathbb {H}},i_{1\mathbb {H}}]=[\iota _4,\iota _4]=\pm (2\nu _4-\varSigma \nu ')$ and $[i_{n\mathbb {H}},i_{n\mathbb {H}}]=(i_{n\mathbb {H}})_{*}[\iota _4,\iota _4]=\pm i_{n\mathbb {H}}(\varSigma \nu ')\ne 0$ for $n\ge 2$. Hence, $[i_{n\mathbb {H}},\overset{\times r}{\cdots {}},i_{n\mathbb {H}}]=\emptyset$ for $r\ge 3$ and $n\ge 1$.