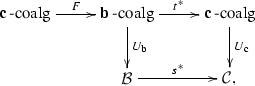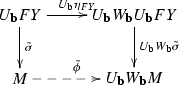A recognition principle for the existence of descent data

Abstract

Suppose $R\rightarrow S$ is a faithfully flat ring map. Given an $S$-module $N$, does there exists some $R$-module $M$ such that $S\otimes _R M\cong N$? In this paper we work out (as a special case of a more general question about extensions of comonads) a criterion for the existence of such an $R$-module $M$, under some reasonable hypotheses on the map $R\rightarrow S$.

1 Introduction

Suppose $R\rightarrow S$ is an effective descent morphism of rings, for example, a faithfully flat morphism. We will write ${{\mathrm{\mathrm{Rep}}}}(R),{{\mathrm{\mathrm{Rep}}}}(S)$ for the representation semirings of $R$ and $S$, that is, the isomorphism classes of finitely generated $R$-modules and $S$-modules, respectively. Here addition is given by direct sum and multiplication by tensor product. We have a base-change (“tensoring-up”) map

$$\begin{aligned} {{\mathrm{\mathrm{Rep}}}}(R) \mathop {\longrightarrow }\limits ^{f} {{\mathrm{\mathrm{Rep}}}}(S). \end{aligned}$$

This map may fail to be injective, but we have excellent control over its failure to be injective. If $N\in {{\mathrm{\mathrm{im\,}}}}f$, then descent theory identifies the preimage $f^{-1}(N)$ with the set of $S/R$-descent data that $N$ admits. When this set is nonempty, there are useful and classical cohomological descriptions of it. See [4] for a nice exposition of some results of this kind. A modern, very general version is in Mesablishvili’s paper [1].

If one wants to understand the map ${{\mathrm{\mathrm{Rep}}}}(R)\mathop {\longrightarrow }\limits ^{f}{{\mathrm{\mathrm{Rep}}}}(S)$, however, something is missing from this picture: one needs to get some control over the failure of $f$ to be surjective. In other words, we do not know how to recognize which elements of ${{\mathrm{\mathrm{Rep}}}}(S)$ are indeed in the image of $f$. Another way of putting it is that we want to know, given a finitely generated $S$-module $N$, whether there exists any $S/R$-descent datum on $N$ at all. Equivalently, we want to have a simple criterion for determining whether $N\cong S\otimes _R M$ for some $R$-module $M$. Such a recognition principle, along with the descent theory described above, is what one needs in order to understand the relationship between ${{\mathrm{\mathrm{Rep}}}}(R)$ and ${{\mathrm{\mathrm{Rep}}}}(S)$, or more generally, to understand how the module theory of a ring changes under faithfully flat extension of that ring.

The purpose of this note is to describe and prove such a recognition principle (Theorem 2.4). Our recognition principle is an abstract statement about extensions of comonads, and as such, it has sufficient generality to be applied to many nonclassical situations (e.g. cases in which the rings $R,S$ are not commutative, and may have gradings that we insist the modules respect; and there may perhaps be interesting applications which are not of an algebraic nature at all). A short list of the easiest cases to see that this recognition principle applies in is Theorem 3.2, with consequences listed in Corollaries 3.5 and 3.6.

The most familiar setting in which our main result applies is the case in which we have a pair of maps

$$\begin{aligned} A \rightarrow B\rightarrow k\otimes _A B \end{aligned}$$

(1.1)

of finite-dimensional commutative augmented algebras over a field $k$, such that the map $A\rightarrow B$ is a split monomorphism as a map of $A$-modules, and such that, whenever $a\in A$ is in the kernel of the augmentation map $A \rightarrow k$, then $ba\in A$ for all $b\in B$. Then our Corollary 3.5 states that a $B$-module $M$ is of the form $B\otimes _A N$ for some $A$-module $N$ if and only if $(k\otimes _A B)\otimes _B M \cong k\otimes _B M$ is a free $k\otimes _A B$-module. In other words, we have our criterion for the existence of a $B/A$-descent datum on a finitely-generated $B$-module $M$: such a descent datum exists if and only if $(k\otimes _A B)\otimes _B M$ is a free $k\otimes _A B$-module.

Consequently, if every finitely generated projective $A$-module is free and every finitely-generated projective $B$-module is free (both of which are often satisfied in cases of interest—for example, when $A,B$ are both Artin $k$-algebras, since they are then nilpotent extensions of $k$ and hence local rings), then we get an exact sequence of commutative monoids

$$\begin{aligned} {{\mathrm{\mathrm{StableRep}}}}(A) \rightarrow {{\mathrm{\mathrm{StableRep}}}}(B) \rightarrow {{\mathrm{\mathrm{StableRep}}}}(B\otimes _A k)\rightarrow 0, \end{aligned}$$

where we write ${{\mathrm{\mathrm{StableRep}}}}$ for the commutative monoid of stable equivalence classes of finitely generated modules. This is our Corollary 3.6.

We use these results in our work on stable representation theory and stable algebraic $G$-theory, [3].

We note that the initial version of this paper was entirely in terms of “extensions of abelian categories,” and an anonymous referee suggested rephrasing and generalizing the results to be in basically the level of generality of Definition 2.1. Namely: one has two comonads ${{\mathrm{\mathbf{b}}}},{{\mathrm{\mathbf{c}}}}$ on categories $\mathcal {B},\mathcal {C}$ and a commutative diagram

and given an object $X$ of $\mathcal {B}$ such that $s^*X$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra, one wants to know whether $X$ admits the structure of a ${{\mathrm{\mathbf{b}}}}$-coalgebra. Our Theorem 2.4 gives necessary and sufficient conditions for this to be so, and it in turns implies our main result with algebraic applications, Theorem 3.2. It would be interesting to know if there exist non-algebraic applications for our Theorem 2.4.

We are grateful to the anonymous referee for their apt and helpful suggestions, and also to C. Weibel for his editorial help.

2 The main definitions and the main result

Definition 2.1

Let $\mathcal {C}$ be a category, ${{\mathrm{\mathbf{c}}}}$ a comonad on $\mathcal {C}$. By a pointed extension of ${{\mathrm{\mathbf{c}}}}$ we mean the following data:

• a category $\mathcal {B}$ and a comonad ${{\mathrm{\mathbf{b}}}}$ on $\mathcal {B}$, and

• functors $F,t^*,s^*$ which admit right adjoints $G,t_*,s_*$, respectively, which fit into the following diagram and make it commute:

  

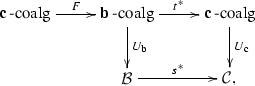
  where by ${{\mathrm{\mathbf{c}}}}{{\mathrm{\mathrm{-coalg}}}}$ and ${{\mathrm{\mathbf{b}}}}{{\mathrm{\mathrm{-coalg}}}}$ we mean the categories of ${{\mathrm{\mathbf{c}}}}$-coalgebras and ${{\mathrm{\mathbf{b}}}}$-coalgebras, respectively, and by $U_{{{\mathrm{\mathbf{c}}}}},U_{{{\mathrm{\mathbf{b}}}}}$ we mean the usual forgetful functors. (In what follows, we will write $W_{{{\mathrm{\mathbf{c}}}}}, W_{{{\mathrm{\mathbf{b}}}}}$ for the usual right adjoints to these functors.)

The above data is required to satisfy the following conditions:

• (Pointedness) $t^{*} \circ F \simeq {{\mathrm{\mathrm{id}}}}_{{{\mathrm{\mathbf{c}}}}{{\mathrm{\mathrm{-coalg}}}}}$.

• (Beck-Chevalley condition) $U_{{{\mathrm{\mathbf{b}}}}}\circ t_* = s_*\circ U_{{{\mathrm{\mathbf{c}}}}}$.

• (Affineness) The functors $G$ and $W_{{{\mathrm{\mathbf{b}}}}}$ preserve epimorphisms.

• (Semisimplicity) Every epimorphism in the category of ${{\mathrm{\mathbf{c}}}}$-coalgebras is split.

• (Nakayama axiom) The unit map $X \rightarrow s_*s^*X$ of the adjunction is an epimorphism for all objects $X$ of $\mathcal {B}$, and $s_*s^*$ has the property that if $s_*s^*f$ is an isomorphism, then $f$ is an epimorphism.

The names of the axioms which suggest a geometric origin are because these axioms are motivated by, and satisfied in, algebraic situations of geometric interest. Specifically, in the case where we have a field $k$, an augmented commutative $k$-algebra $R$, and a monomorphism of commutative $k$-algebras $R \rightarrow S$, we let $\mathcal {B}$ be the category of $S$-modules and we let $\mathcal {C}$ be the category of $k\otimes _R S$-modules, with $t^*$ the base change functor $M \mapsto (k\otimes _R S)\otimes _S M$. We let ${{\mathrm{\mathbf{b}}}}$ be the base-change comonad $M \mapsto S\otimes _R M$ on $S$-modules, and we let ${{\mathrm{\mathbf{c}}}}$ be the base-change comonad $M \mapsto (k\otimes _R S)\otimes _k M$ on $k\otimes _R S$-modules. Then the category of ${{\mathrm{\mathbf{c}}}}$-coalgebras is equivalent to the category of $k$-modules (thanks to the anonymous referee, who pointed out this useful fact!), and the category of ${{\mathrm{\mathbf{b}}}}$-coalgebras is equivalent to the category of $R$-modules if the morphism $R\rightarrow S$ is an effective descent morphism.

In that situation, the pointedness axiom in Definition 2.1 is satisfied because of $R$ being an augmented, i.e., pointed, $k$-algebra. The affineness axiom is satisfied because the scheme morphisms ${{\mathrm{\mathrm{Spec}}}}S \rightarrow {{\mathrm{\mathrm{Spec}}}}R$ and ${{\mathrm{\mathrm{Spec}}}}R \rightarrow {{\mathrm{\mathrm{Spec}}}}k$ are affine morphisms, so their induced direct image functors on the quasicoherent module categories are right exact, i.e., preserve epimorphisms. The semisimplicity axiom is satisfied because the category of $k$-vector spaces is semisimple. On restricting to the finitely-generated module categories, the Nakayama condition is satisfied when the kernel of $S\rightarrow k\otimes _R S$ is contained in the Jacobson radical of $S$, by Nakayama’s lemma.

Now we define what it means for an object to be “formally supported” by a comonad. The definition looks technical at a glance, but it has two advantages: first, the objects $X$ formally supported by a comonad ${{\mathrm{\mathbf{b}}}}$ have the property that they admit the structure of a ${{\mathrm{\mathbf{b}}}}$-coalgebra if and only if $s^*X$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra. See Theorem 2.4 for this result. Second, the condition required for an object to be formally supported by a comonad is actually concrete enough that it is checkable in situations of concrete interest, and frequently holds for all objects on which the comonad is defined. See our Theorem 3.2, where we verify that all objects are formally supported by certain base-change comonads arising in a wide class of very concrete and explicit algebraic cases of interest.

Definition 2.2

Let ${{\mathrm{\mathbf{c}}}}$ be a comonad and $({{\mathrm{\mathbf{b}}}}, F,t^*,s^*)$ a pointed extension of ${{\mathrm{\mathbf{c}}}}$. (Our notation is as in Definition 2.1.) We say that an object $M$ of $\mathcal {B}$ is formally supported by ${{\mathrm{\mathbf{b}}}},F,t^*,s^*,{{\mathrm{\mathbf{c}}}}$, or formally supported by ${{\mathrm{\mathbf{b}}}}$ for short, if the following condition is satisfied:

• (Lifting axiom) For every ${{\mathrm{\mathbf{c}}}}$-coalgebra $Y$ and every epimorphism $\tilde{\sigma }: U_{{{\mathrm{\mathbf{b}}}}} FY \rightarrow M$ such that $s^*\tilde{\sigma }$ is an isomorphism, there exists a map $\tilde{\phi }: M \rightarrow U_{{{\mathrm{\mathbf{b}}}}}W_{{{\mathrm{\mathbf{b}}}}}M$ making the diagram

  

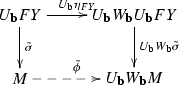
  commute.

If enough objects are formally supported by a comonad, we say that the pointed extension of comonads is short:

Definition 2.3

Let ${{\mathrm{\mathbf{c}}}}$ be a comonad and $({{\mathrm{\mathbf{b}}}}, F,t^*,s^*)$ a pointed extension of ${{\mathrm{\mathbf{c}}}}$. We say that ${{\mathrm{\mathbf{b}}}}$ is an short extension of ${{\mathrm{\mathbf{c}}}}$ if, whenever $M$ is an object of $\mathcal {B}$ such that $s^*M$ is isomorphic to $s^*U_{{{\mathrm{\mathbf{b}}}}}FY$ for some ${{\mathrm{\mathbf{c}}}}$-coalgebra $Y$, we have that $M$ is formally supported by ${{\mathrm{\mathbf{b}}}}$.

Now here is our main technical result, which implies the concrete results in the next section:

Theorem 2.4

Let ${{\mathrm{\mathbf{c}}}}$ be a comonad and $({{\mathrm{\mathbf{b}}}}, F,t^*,s^*)$ a pointed extension of ${{\mathrm{\mathbf{c}}}}$. $($Our notation is as in Definition 2.1.$)$ Suppose $M$ is an object of $\mathcal {B}$ which is formally supported by ${{\mathrm{\mathbf{b}}}}$. Then $M$ admits the structure of a ${{\mathrm{\mathbf{b}}}}$-coalgebra if and only if $s^*M$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra.

Proof

Suppose $s^*M$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra. Then we can choose a ${{\mathrm{\mathbf{c}}}}$-coalgebra $Y$ such that $U_{{{\mathrm{\mathbf{c}}}}} Y = s^*M$ in $\mathcal {C}$. Let $\sigma : U_{{{\mathrm{\mathbf{b}}}}}FY\rightarrow s_*s^*M$ be the composite

(2.1)

i.e., $s = \eta _{U_{{{\mathrm{\mathbf{b}}}}}FY}$.

We have the commutative diagram of hom-sets

(2.2)

in which the bottom horizontal map is split epic, since $M \rightarrow s_*s^*M$ is epic by the Nakayama axiom in Definition 2.1, since $G,W_{{{\mathrm{\mathbf{b}}}}}$ both preserve epimorphisms by the affineness axiom in Definition 2.1, and since every epimorphism in ${{\mathrm{\mathbf{c}}}}$-coalgebras is split by the semisimplicity axiom in Definition 2.1. So the top horizontal map in diagram (2.2) is also a split epimorphism. So the map $\sigma \in \hom _{\mathcal {B}}(U_{{{\mathrm{\mathbf{b}}}}}FY, s_*s^*M)$ lifts to a map $\tilde{\sigma }\in \hom _{\mathcal {B}}(U_{{{\mathrm{\mathbf{b}}}}}FY, M)$ which fills in the dotted arrow in diagram (2.1).

We claim that $\tilde{\sigma }$ is epic. By the commutativity of diagram (2.1), $s_*s^*\tilde{\sigma }$ makes the diagram

commute, hence $s_*s^*\tilde{\sigma }$ is an isomorphism. Now since $s_*s^*\tilde{\sigma }$ is an isomorphism, $\tilde{\sigma }$ is an epimorphism by the Nakayama axiom.

We now have the diagram in $\mathcal {B}$:

(2.3)

and the lifting axiom in Definition 2.2 now guarantees the existence of a map $\tilde{\psi }$ filling in the dotted arrow and making the diagram commute.

We claim that $\tilde{\psi }$ is in fact a ${{\mathrm{\mathbf{b}}}}$-coalgebra structure map on $M$. To prove this claim, we must check that it is counital and coassociative. But this follows automatically from $\tilde{\sigma }$ being an epimorphism, from commutativity of the diagram (2.3), and from $U_{{{\mathrm{\mathbf{b}}}}}\eta ^{{{\mathrm{\mathbf{b}}}}}_{FY}$ being a ${{\mathrm{\mathbf{b}}}}$-coalgebra structure map.

Conversely, if $M$ is a ${{\mathrm{\mathbf{b}}}}$-coalgebra, then $M$ is in the image of $U_{{{\mathrm{\mathbf{b}}}}}$. Choose $N$ in the category of ${{\mathrm{\mathbf{b}}}}$-coalgebras such that $M = U_{{{\mathrm{\mathbf{b}}}}}(N)$. Then we have

$$\begin{aligned} s^*M&= s^*U_{{{\mathrm{\mathbf{b}}}}} N \\&= U_{{{\mathrm{\mathbf{c}}}}}t^* N, \end{aligned}$$

so $s^*M$ is in the image of $U_{{{\mathrm{\mathbf{c}}}}}$. So $s^*M$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra. $\square$

Corollary 2.5

Let ${{\mathrm{\mathbf{c}}}}$ be a comonad and let ${{\mathrm{\mathbf{b}}}}$ be an short extension of ${{\mathrm{\mathbf{c}}}}$. Then an object $M$ of $\mathcal {B}$ admits the structure of a ${{\mathrm{\mathbf{b}}}}$-coalgebra if and only if $s^*M$ admits the structure of a ${{\mathrm{\mathbf{c}}}}$-coalgebra.

Corollary 2.5 makes it clear that the relationship between ${{\mathrm{\mathbf{c}}}}$-coalgebras and ${{\mathrm{\mathbf{b}}}}$-coalgebras is very simple when ${{\mathrm{\mathbf{b}}}}$ is an short extension of ${{\mathrm{\mathbf{c}}}}$. We claim that short extensions of comonads are actually not unusual, in fact occuring in practical, concrete situations. See Theorem 3.2 for a wide class of examples.

3 Special cases and applications

Now we introduce a useful definition which plays an essential role in Theorem 3.2.

Definition 3.1

Suppose $k$ is a field, and $A,B$ are $k$-algebras. Suppose $A$ is equipped with a $k$-algebra augmentation map $\epsilon : A\rightarrow k$. We say that a monomorphism $f: A\rightarrow B$ of $k$-algebras is (right) short if, for each element $b\in B$ and each element $a\in \ker \epsilon$, the element $ba\in B$ is in ${{\mathrm{\mathrm{im\,}}}}f\subseteq B$.

One can define a “left short” morphism by simply swapping right-multiplication out for left-multiplication in Definition 3.1.

Note that any short morphism $R \rightarrow S$ has the property that $S\rightarrow S\otimes _R k$ is a (right) square-zero extension of algebras, but the converse is not necessarily true: if $S\rightarrow S\otimes _R k$ is a right square-zero extension, it is not always true that $R \rightarrow S$ is a right short morphism, even when $R\rightarrow S$ is injective. For example, let $S = k[x]/x^4$ and let $R = k[y]/y^2$, and let $R\rightarrow S$ send $y$ to $x^2$. This map is not short, but $S \rightarrow S\otimes _R k$ is a square-zero extension. On the other hand, the map of $k$-algebras $k[y]/y^2 \rightarrow k[x]/x^3$ sending $y$ to $x^2$ is a good example of a short morphism.

Here are some examples of pointed extensions of comonads, to which Theorem 2.4 applies.

Theorem 3.2

Suppose $k$ is a field. Suppose $A$ is an augmented commutative algebra over $k$, and $f: A\rightarrow B$ is an effective descent morphism of commutative $k$-algebras. Suppose both $A$ and $B$ are finite-dimensional as $k$-vector spaces. Let $C$ be the algebra $B\otimes _A k$, and suppose the kernel of the ring map $B\rightarrow B\otimes _A k$ is contained in the Jacobson radical of $B$. Then the commutative diagram of categories and functors

expresses ${{\mathrm{\mathbf{b}}}}$ as a pointed extension of ${{\mathrm{\mathbf{c}}}}$, where we are writing ${{\mathrm{\mathbf{b}}}}$ for the base change comonad $M \mapsto {{\mathrm{\mathbf{b}}}}M = M\otimes _A B$ on ${{\mathrm{\mathrm{fgMod}}}}(B)$, and ${{\mathrm{\mathbf{c}}}}$ for the base-change comonad $M \mapsto {{\mathrm{\mathbf{c}}}}M = M\otimes _B C$ on ${{\mathrm{\mathrm{fgMod}}}}(C)$. Here $F,U_{{{\mathrm{\mathbf{b}}}}},U_{{{\mathrm{\mathbf{c}}}}},t^*$ are all the obvious base-change $($tensoring-up$)$ functors.

Furthermore, if $f$ is short, then ${{\mathrm{\mathbf{b}}}}$ is an short extension of ${{\mathrm{\mathbf{c}}}}$.

Proof

Suppose $A$ is an augmented commutative algebra over $k$, and $f: A\rightarrow B$ is an effective descent morphism of commutative $k$-algebras. Suppose both $A$ and $B$ are finite-dimensional as $k$-vector spaces. Let $C$ be the algebra $B\otimes _A k$. Then the category of ${{\mathrm{\mathbf{c}}}}$-coalgebras is naturally equivalent to the category of $k$-vector spaces, since the unit $k$-algebra map $k\rightarrow C$ is clearly faithfully flat, hence an effective descent morphism. Furthermore, the category of ${{\mathrm{\mathbf{b}}}}$-coalgebras is naturally equivalent to the category of $A$-modules, by the assumption that $f$ is an effective descent morphism. It is trivial that these statements remain true with the adjective “finitely generated” included throughout.

Now we check the relevant conditions, from Definition 2.1, for ${{\mathrm{\mathbf{b}}}}$ to be a pointed extension of ${{\mathrm{\mathbf{c}}}}$.

• Pointedness is immediate from the composite of the $k$-algebra maps $k \rightarrow C \rightarrow k$ being the identity on $k$.

• The Beck-Chevalley condition is a classical property of restriction and induction of scalars.

• The affineness condition is classical: the restriction of scalars functor induced by a map of rings (or $k$-algebras) is exact.

• Semisimplicity is due to $k$ being a field, hence the category of $k$-modules (or of finitely-generated $k$-modules) is semisimple.

• For the Nakayama condition: since the morphism of $k$-algebras $B \rightarrow C$ is surjective, we have that $M \cong B\otimes _B M \rightarrow C\otimes _B M \cong s_*s^*M$ is surjective for all $B$-modules $M$. So the unit map ${{\mathrm{\mathrm{id}}}}\rightarrow s_*s^*$ is always an epimorphism, satisfying the first part of the Nakayama condition. For the second part, we must use the assumption that all our modules are finitely generated. Now the functor $s_*s^*$ is the functor

  $$\begin{aligned} M\mapsto M\otimes _B (B\otimes _{A} k)\cong M\otimes _A k\cong M/M(\ker f). \end{aligned}$$

  If $M/M(\ker g)\cong 0$, then the inclusion $M(\ker g)\hookrightarrow M$ is an isomorphism. Nakayama’s Lemma now applies: since $(\ker g)$ is contained in the Jacobson radical of $B$, $(\ker g)M = M$ and $M$ finitely generated together imply that $M = 0$.

Now suppose that $f$ is short, and suppose that $M$ is a finitely-generated $B$-module equipped with an epimorphism $U_{{{\mathrm{\mathbf{b}}}}}FY = Y\otimes _k B \mathop {\longrightarrow }\limits ^{i} M$ of $B$-modules such that $s^*i = i\otimes _B C$ is an isomorphism, where $Y$ is a finitely-generated $k$-module. We will write $\epsilon : A \rightarrow k$ for the augmentation map on $A$. Then $\ker i$ consists entirely of elements of the free $B$-module $Y\otimes _k B$ which are divisible by elements in $\ker \epsilon$, that is, $\ker i$ consists entirely of elements of the form $ya$ for some $y\in Y\otimes _k B$ and some $a\in \ker \epsilon$.

Now we choose a basis $y_1,\ldots ,y_n$ for $Y$. If $ya$ is some element of $\ker i$, we write it in the form

$$\begin{aligned} ya = \left( \sum _{j=1}^n \alpha _j y_j\right) a \end{aligned}$$

and we observe that, since $f$ is short, each element $\alpha _j y_ja\in B\{ y_j\}\cong B$ is contained in ${{\mathrm{\mathrm{im\,}}}}f$. Hence $ya$ is contained in

$$\begin{aligned} Y\otimes _k {{\mathrm{\mathrm{im\,}}}}f : Y\otimes _k A\rightarrow Y\otimes _k B. \end{aligned}$$

Hence, in the commutative diagram

(3.1)

there exists a map as in the dotted arrow which makes the diagram commute. Since the row in diagram (3.1) is exact and since the middle column in diagram (3.1) is a short exact sequence, the composite map $\ker i \rightarrow M\otimes _A B$ is zero, hence there exists a map $M \rightarrow M\otimes _A B = s_*s^*M$ fitting into the bottom row of diagram (3.1) and making the diagram commute. This is precisely the lifting axiom in Definition 2.2. So if $M \otimes _B C$ is a free $B$-module, then $M$ is formally supported by ${{\mathrm{\mathbf{b}}}}$. So ${{\mathrm{\mathbf{b}}}}$ is an short extension of ${{\mathrm{\mathbf{c}}}}$. $\square$

A version of Theorem 3.2 also holds for the categories of graded modules, under the additional assumption that all algebras in question are graded, and the algebra homomorphisms preserve the gradings.

It is convenient to have a characterization of effective descent morphisms which is applicable to short $k$-algebra morphisms, so that one can use Theorem 3.2 in practical situations. One knows, from classical descent theory, that faithfully flat ring morphisms are effective descent morphisms. This is not so helpful, however, since it is very rare for a short $k$-algebra map to be flat. Instead, the more general Joyal-Tierney theorem is quite helpful for determining when a short morphism of commutative $k$-algebras is an effective descent morphism. See [2] for the following result, which Mesablishvili attributes to Joyal and Tierney, but which was apparently never written up by Joyal and Tierney themselves:

Theorem 3.3

(Joyal-Tierney) Suppose $f: R \rightarrow S$ is a homomorphism of commutative rings. Then $f$ is an effective descent morphism if and only if $f$ is a pure monomorphism.

We remind the reader that a monomorphism of $R$-modules $f: M \rightarrow N$ is said to be pure if, for every $R$-module $M_0$, the tensor product $M_0\otimes _R f: M_0 \otimes _R M\rightarrow M_0\otimes _R N$ is a monomorphism. So the condition of Theorem 3.3 is that the map $R\rightarrow S$ is a pure monomorphism, as a map of $R$-modules.

The following is a corollary of the Joyal-Tierney theorem but is also not hard to prove directly.

Corollary 3.4

Suppose $f: R\rightarrow S$ is a homomorphism of commutative rings which is a split monomorphism as a map of $R$-modules. Then $f$ is an effective descent morphism.

Proof

If $f$ is a split monomorphism as a map of $R$-modules, we can write $S$ as $R \oplus M$ for some $R$-module $M$, with the map $f$ being the inclusion of the summand $R$. Then, for any $R$-module $M_0$, the map

$$\begin{aligned} M_0 \cong M_0\otimes _R R \mathop {\longrightarrow }\limits ^{M_0\otimes _R f} M_0\otimes _R (R\oplus M)\cong M\oplus M_0\otimes _R M \end{aligned}$$

is also inclusion of a summand, hence still a monomorphism. Hence $f$ is a pure monomorphism, hence an effective descent morphism by Theorem 3.3.

Now we can list some more corollaries of Theorem 3.2.

Corollary 3.5

Suppose, for any ring $R$, we write ${{\mathrm{\mathrm{Rep}}}}(R)$ for the commutative monoid of isomorphism classes of finitely-generated right $R$-modules, with addition given by direct sum. Suppose $k$ is a field, $A$ is an augmented commutative $k$-algebra, and $B$ is a commutative $k$-algebra equipped with a short $k$-algebra monomorphism $f: A\rightarrow B$. Suppose $A,B$ are both finite-dimensional as $k$-vector spaces, and suppose that $f$, when regarded as a map of $A$-modules, is a split monomorphism. Finally, suppose the kernel of the ring map $B\rightarrow B\otimes _A k$ is contained in the Jacobson radical of $B$. Then the image of the base-change $($“tensoring up”$)$ map of monoids ${{\mathrm{\mathrm{Rep}}}}(A)\rightarrow {{\mathrm{\mathrm{Rep}}}}(B)$ consists of exactly the isomorphism classes of $B$-modules $M$ such that $M\otimes _A k$ is a free $B\otimes _A k$-module.

Corollary 3.6

Suppose $k,A,B,f$ are as in Corollary 3.5. Write ${{\mathrm{\mathrm{StableRep}}}}(A)$ (resp. ${{\mathrm{\mathrm{StableRep}}}}(B)$) for the stable representation monoid of $A$ (resp. $B$), that is, the monoid of stable equivalence classes of finitely generated $A$-modules ($resp. finitely generated$B$-modules$). Suppose every finitely generated projective $B\otimes _A k$-module is free. Then the sequence of monoid maps

$$\begin{aligned} {{\mathrm{\mathrm{StableRep}}}}(A) \rightarrow {{\mathrm{\mathrm{StableRep}}}}(B) \rightarrow {{\mathrm{\mathrm{StableRep}}}}(B\otimes _A k)\rightarrow 0 \end{aligned}$$

(3.2)

is exact.

We would be very interested in knowing whether there is any natural way to extend exact sequence (3.2) to the left. This would make Corollary 3.6 quite useful for making very concrete computations of stable representation rings of Artin algebras.

Warning 3.7

The reader should be careful to note that, while the sequence 3.2 is an exact sequence of commutative monoids—that is, the image of each map is equal to the kernel of the next—the same is not necessarily true after one takes the Grothendieck group completion of those monoids. Furthermore, exact sequences of commutative monoids really are quite different from exact sequences of abelian groups. In particular, ${{\mathrm{\mathrm{StableRep}}}}(B)$ is capable of being non-finitely-generated even when both ${{\mathrm{\mathrm{StableRep}}}}(A)$ and ${{\mathrm{\mathrm{StableRep}}}}(B\otimes _A k)$ are finitely generated. This actually occurs in the case where $A\rightarrow B$ is the short morphism $k[y]/y^2 \hookrightarrow k[x,y]/x^2,xy,y^2$.