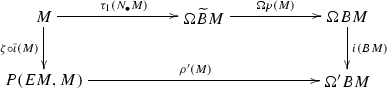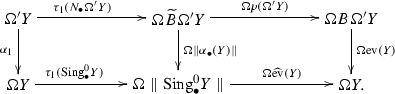Homotopy homomorphisms and the classifying space functor

Abstract

We show that the classifying space functor $B:\mathcal {M}on \rightarrow {\mathcal {T}\! op}^*$ from the category of topological monoids to the category of based spaces is left adjoint to the Moore loop space functor $\Omega ':{\mathcal {T}\! op}^*\rightarrow \mathcal {M}on$ after we have localized $\mathcal {M}on$ with respect to all homomorphisms whose underlying maps are homotopy equivalences and ${\mathcal {T}\! op}^*$ with respect to all based maps which are (not necessarily based) homotopy equivalences. It is well-known that this localization of ${\mathcal {T}\! op}^*$ exists, and we show that the localization of $\mathcal {M}on$ is the category of monoids and homotopy classes of homotopy homomorphisms. To make this statement precise we have to modify the classical definition of a homotopy homomorphism, and we discuss the necessary changes. The adjunction is induced by an adjunction up to homotopy $B:\mathcal {H}\mathcal {M}on^{w}\leftrightarrows {\mathcal {T}\! op}^w:\Omega '$ between the category of well-pointed monoids and homotopy homomorphisms and the category of well-pointed spaces. This adjunction is shown to lift to diagrams. As a consequence, the well-known derived adjunction between the homotopy colimit and the constant diagram functor can also be seen to be induced by an adjunction up to homotopy before taking homotopy classes. As applications we among other things deduce a more algebraic version of the group completion theorem and show that the classifying space functor preserves homotopy colimits up to natural homotopy equivalences.

1 Introduction

Let $\mathcal {T}\! op$ denote the category of $k$-spaces, ${\mathcal {T}\! op}^*$ the category of based $k$-spaces, and ${\mathcal {T}\! op}^w$ the category of well-pointed $k$-spaces. Recall that a space $X$ is a k-space if $A\subset X$ is closed iff $p^{-1}(A)$ is closed in $C$ for each map $p:C\rightarrow X$ where $C$ is a compact Hausdorff space, and that a space is called well-pointed if the inclusion of the base point is a closed cofibration.

Let $\mathcal {M}on$ denote the category of topological monoids and continuous homomorphisms, and $\mathcal {M}on^{w}$ and $\mathcal {C}\mathcal {M}on$ the full subcategories of well-pointed, respectively, commutative monoids. A monoid is canonically based by its unit.

We are interested in the relationship between Milgram’s classifying space functor $B: \mathcal {M}on\rightarrow {\mathcal {T}\! op}^*$ and the Moore loop space functor $\Omega ':{\mathcal {T}\! op}^*\rightarrow \mathcal {M}on$ (for explicit definitions see Sect. 4).

The related question for commutative monoids is easily answered: it is well-known that the classifying space $BM$ of a commutative monoid is a commutative monoid [16], so that we have a functor $B:\mathcal {C}\mathcal {M}on\rightarrow \mathcal {C}\mathcal {M}on$. The usual loop space functor induces a functor $\Omega : \mathcal {C}\mathcal {M}on\rightarrow \mathcal {C}\mathcal {M}on$ by defining the multiplication in $\Omega M$ by point-wise multiplication in $M$. The category $\mathcal {C}\mathcal {M}on$ is enriched over ${\mathcal {T}\! op}^*$ in an obvious way, and it is tensored and cotensored (for definitions see [6] or Sect. 3). The cotensor $M^K$ of $M\in \mathcal {C}\mathcal {M}on$ and $K\in {\mathcal {T}\! op}^*$ is the function space with point-wise multiplication. It is well-known that $B(M)\cong M\boxtimes S^1$, the tensor of $M$ and $S^1$. Since $-\boxtimes K$ is left adjoint to $(-)^K$ we obtain:

Proposition 1.1

The functors

$$\begin{aligned} B:\mathcal {C}\mathcal {M}on\rightleftarrows \mathcal {C}\mathcal {M}on:\Omega \end{aligned}$$

form a ${\mathcal {T}\! op}^*$-enriched adjoint pair.

In the non-commutative case there is no hope for a similar result. A candidate for a right adjoint of the classifying functor

$$\begin{aligned} B: \mathcal {M}on\rightarrow {\mathcal {T}\! op}^*\end{aligned}$$

is the Moore loop space functor

$$\begin{aligned} \Omega ':{\mathcal {T}\! op}^*\rightarrow \mathcal {M}on, \end{aligned}$$

but $\Omega '$ does not preserve products. In fact, there is no product preserving functor

$$\begin{aligned} F:{\mathcal {T}\! op}^*\rightarrow \mathcal {M}on\end{aligned}$$

such that $F(X)\simeq \Omega (X)$ for all $X$ [5, Prop. 6.1].

Remark 1.2

In [8] Fiedorowicz showed that the Moore loop space functor into a different target category is right adjoint to what he called the Moore suspension functor: let ${\mathcal {T}\! op}^*[\mathbb {R}_+]$ be the category whose objects are based spaces $X$ together with a continuous map $p:X\rightarrow \mathbb {R}_+$ (the non-negative real numbers) such that $p^{-1}(0)=*$ and whose morphisms are maps over $\mathbb {R}_+$. Then

$$\begin{aligned} \Omega ':{\mathcal {T}\! op}^*\rightarrow {\mathcal {T}\! op}^*[\mathbb {R}_+],\quad X\mapsto (\Omega 'X,l), \end{aligned}$$

where $l$ is the length function, has this Moore suspension functor as left adjoint.

The Moore loop space funtor $\Omega ':{\mathcal {T}\! op}^*\rightarrow \mathcal {M}on$ preserves products up to natural homotopy. So one might expect it to be a right adjoint of $B$ after formally inverting homotopy equivalences. We will prove this in this paper.

We will have to localize our categories $\mathcal {C}$, and it is a priori not clear that these localizations exist. A common procedure is to define a Quillen model structure on $\mathcal {C}$ such that the morphisms we want to invert are the weak equivalences in these structures. The localization then is the homotopy category ${\mathrm{Ho}}\mathcal {C}$ associated with this model structure.

There are two standard model structures on $\mathcal {T}\! op$: the structure due to Quillen [19] whose weak equivalences are weak homotopy equivalences and whose fibrations are Serre fibrations, and the structure due to Strøm [23] whose weak equivalences are homotopy equivalences, whose fibrations are Hurewicz fibrations, and whose cofibrations are closed cofibrations.

Although mainstream homotopy theory usually works with the Quillen model structure and the proofs of our results would be considerably shorter in this context (because we could use the rich literature, in particular, the results of Fiedorowicz [8]), we choose the Strøm setting because we share Puppe’s [18] point of view: “frequently a weak homotopy equivalence is considered as good as a genuine one, because for spaces having the homotopy type of a $CW$-complex there is no difference and most interesting spaces in algebraic topology are of that kind. I am not going to argue against this because I agree with it, but I do think that the methods by which we establish the genuine homotopy equivalences give some new insight into homotopy theory”. Moreover, there are spaces of interest which rarely have the homotopy type of a $CW$ complex such as function spaces and spaces of foliations, which account for a growing interest in results in the Strøm setting.

So we call a based map in ${\mathcal {T}\! op}^*$ a weak equivalence if it is a not necessarily based homotopy equivalence, and a homomorphism in $\mathcal {M}on$ a weak equivalence if the underlying map of spaces is a weak equivalence in ${\mathcal {T}\! op}^*$. Let ${\mathrm{Ho}}{\mathcal {T}\! op}^*$ and ${\mathrm{Ho}}\mathcal {M}on$ be the categories obtained from ${\mathcal {T}\! op}^*$ respectively $\mathcal {M}on$ by formally inverting weak equivalences.

Theorem 1.3

The categories ${\mathrm{Ho}}{\mathcal {T}\! op}^*$ and ${\mathrm{Ho}}\mathcal {M}on$ exist and the classifying space functor and the Moore loop space functor induce a derived adjoint pair

$$\begin{aligned} {\mathrm{Ho}}B:{\mathrm{Ho}}\mathcal {M}on\rightleftarrows {\mathrm{Ho}}{\mathcal {T}\! op}^*:{\mathrm{Ho}}\Omega ' \end{aligned}$$

Remark 1.4

This contrasts the situation in the simplicial category: the loop group functor $G: \mathcal {SS}ets\rightarrow \mathcal {SG}roups$ from simplicial sets to simplicial groups is left adjoint to the simplicial classifying space functor $\overline{W}: \mathcal {SG}roups \rightarrow \mathcal {SS}ets$ (e.g. see [11, Lemma V.5.3]).

With our choice of weak equivalences the Strøm model structure on $\mathcal {T}\! op$ lifts to ${\mathcal {T}\! op}^*$ so that ${\mathrm{Ho}}{\mathcal {T}\! op}^*$ exists, but in contrast to the Quillen model structure, it is not known that the Strøm model structure lifts to $\mathcal {M}on$ (there is a model structure on $\mathcal {M}on$ whose weak equivalences are homotopy equivalences in $\mathcal {M}on$ rather than homotopy equivalences of underlying spaces; this follows from work of Cole [7] and Barthel and Riel [1]).

In the construction of ${\mathrm{Ho}}\mathcal {M}on$ in the Strøm setting homotopy homomorphisms between monoids come into play: a topological monoid can be considered as an algebra over the operad $\mathcal {A}ss$ of monoid structures or as a topologically enriched category with one object. The homotopy homomorphisms of this paper are based on the enriched category aspect and describe “functors up to coherent homotopies”. They were introduced for monoids by Sugawara [24] and extensively studied by Fuchs [9]. Homotopy homomophisms of $\mathcal {A}ss$-algebras were introduced in [4], and we will indicate their relation to the ones considered in this paper in Sect. 2. An extension of our results to arbitrary category objects in $\mathcal {T}\! op$ may be of separate interest.

If we define a semigroup to be a topological space with a continuous associative multiplication, an inspection of the definition shows that a homotopy homomorphism $f:M\rightarrow N$ of monoids is nothing but a semigroup homomorphism $\overline{W}M\rightarrow N$ where $\overline{W}$ is a variant of the Boardman and Vogt [4] $W$-construction (not to be confused with the functor $\overline{W}$ of Remark 1.4). If ${\mathcal {S}\mathrm{gp}}$ denotes the category of semigroups and continuous homomorphisms then $\overline{W}:{\mathcal {S}\mathrm{gp}}\rightarrow {\mathcal {S}\mathrm{gp}}$ is a functor equipped with a natural transformation $\overline{\varepsilon }:\overline{W}\rightarrow \mathrm{Id}$. The Boardman–Vogt $W$-construction $W:\mathcal {M}on\rightarrow \mathcal {M}on$ and its associated natural transformation $\varepsilon : W\rightarrow \mathrm{Id}$ are obtained from $(\overline{W},\ \overline{\varepsilon })$ by factoring out a unit relation. In particular, for any monoid $M$ there is a natural projection $\varepsilon '(M): \overline{W}M\rightarrow WM$ of semigroups such that $\varepsilon (M)\circ \varepsilon '(M)=\overline{\varepsilon }(M)$.

The lack of conditions for the unit is an indication that Sugawara’s notion of a homotopy homomorphism is not quite the correct one. So we define unitary homotopy homomorphisms from $M$ to $N$ to be monoid homomorphisms $WM\rightarrow N$; those were studied by Brinkmeier [3].

Composition of homotopy homomorphisms and their unitary versions is only associative up to homotopy. To obtain genuine categories of monoids and (unitary) homotopy homomorphisms we modify both notions: a homotopy homomorphisms from $M$ to $N$ will be a semigroup homomorphism $\overline{W}M\rightarrow \overline{W}N$ and a unitary one a monoid homomorphism $WM\rightarrow WN$. From a homotopy theoretical point of view this modification is not significant:

Proposition 1.5

If $M, N$ are monoids and $M$ is well-pointed and $G, H$ are semigroups then the maps

$$\begin{aligned} \varepsilon (N)_*&:\mathcal {M}on(WM,WN) \rightarrow \mathcal {M}on(WM,N) \\ \overline{\varepsilon }(N)_*&:{\mathcal {S}\mathrm{gp}}(\overline{W}G,\overline{W}H) \rightarrow {\mathcal {S}\mathrm{gp}}(\overline{W}G,H) \end{aligned}$$

are homotopy equivalences.

It is well-known that $WM\rightarrow M$ has the flavor of a cofibrant replacement of $M$ as known from model category theory provided $M$ is well-pointed (e.g. see [2, 26]). So it is no surprise that the category of well-pointed monoids and homotopy classes of unitary homotopy homomorphisms is the localization of $\mathcal {M}on^{w}$ with respect to its weak equivalences. If we want to construct ${\mathrm{Ho}}\mathcal {M}on$ we have to relax unitary homotopy homomorphisms to homotopy unitary homotopy homomorphisms and the corresponding statement holds. We will study these various notions of homotopy homomorphisms in Sect. 2 in detail.

The lack of the appropriate Quillen model structure in some of our categories is made up for by their topological enrichment with nice properties. This topological enrichment allows us to prove stronger results. E.g. the restriction of Theorem 1.3 to the well-pointed case is the path-component version of the following result.

Theorem 1.6

Let $\mathcal {H}\mathcal {M}on^{w}$ be the category of well-pointed monoids and unitary homotopy homomorphisms. Then the classifying space functor and the Moore loop space functor induce an adjunction up to homotopy

$$\begin{aligned} \mathcal {H}\mathcal {M}on^{w}\leftrightarrows {\mathcal {T}\! op}^w. \end{aligned}$$

In Sect. 3 we will introduce the necessary notions to make this precise. There we will also recall basic facts from enriched category theory and show that topologically enriched categories with a class of weak equivalences which admit a cofibrant replacement functor can be localized. We believe that these results are of separate interest.

In Sect. 4 we prove Theorem 1.6 and related results and hence Theorem 1.3. In Sect. 5 we draw some immediate consequences of Theorem 1.3 and of the intermediate steps in the proof of Theorem 1.6.

E.g. we obtain yet another but considerably shorter proof of a strong version of the James construction.

Definition 1.7

A Dold space is a topological space admitting a numerable cover $\{ U_\gamma ;\ \gamma \in \Gamma \}$ such that each inclusion $U_\gamma \subset X$ is nullhomotopic.

A space of the homotopy type of a $CW$-complex is a Dold space. For more details on Dold spaces see [20].

Proposition 1.8

• 1. If $X$ is a well-pointed space and $JX$ is the based free topological monoid on $X$ (the James construction), then $BJX\simeq \Sigma X$.

• 2. If $X$ is a well-pointed path-connected Dold space, then $JX\simeq \Omega \Sigma X$.

Part (2) was first proven in [25], shorter proofs can be found in [18, 20].

We also obtain a new interpretation of the group completion theorem of a monoid without any additional assumptions on the multiplication.

Definition 1.9

A topological monoid is called grouplike if it admits a continuous homotopy inversion.

A standard example of a grouplike monoid is the Moore loop space $\Omega 'X$ of a space $X$.

Theorem 1.10

Let $M$ be a well-pointed topological monoid. Then there is a unitary homotopy homomorphism $\mu _M:M\rightarrow \Omega 'BM$, natural up to homotopy, having the following universal property: given any unitary homotopy homomorphism $f:M\rightarrow N$ into a grouplike monoid $N$ there is a unitary homotopy homomorphism $\bar{f}:\Omega 'BM\rightarrow N$, unique up to homotopy, such that $\bar{f}\circ \mu _M\simeq f$. (Here homotopy means homotopy in the category, i.e. homotopy through unitary homotopy homomorphisms.)

From the intermediate steps of the proof of Theorem 1.6 we obtain the following extension and strengthening of a theorem of Fuchs [9, Satz 7.7]

Proposition 1.11

• 1. If $M$ and $N$ are well-pointed monoids and $N$ is grouplike then

  $$\begin{aligned} B:\mathcal {M}on(WM,WN)\rightarrow {\mathcal {T}\! op}^*(BWM,BWN) \end{aligned}$$

  is a homotopy equivalence.

• 2. If $X$ is a well-pointed path-connected Dold space then $W\Omega ': {\mathcal {T}\! op}^w(X,Y)\rightarrow \mathcal {M}on^{w}(W\Omega 'X,W\Omega 'Y)$ is a homotopy equivalence.

The reader may object that Fuchs considers homotopy homomorphisms while Proposition 1.11 addresses unitary homotopy homomorphisms. Since Fuchs only considers well-pointed grouplike monoids and all his spaces are of the homotopy type of $CW$-complexes the two notions are linked by

Proposition 1.12

Let $M$ and $N$ be well-pointed monoids and $N$ be grouplike. Then

$$\begin{aligned} (\varepsilon ')^*: \mathcal {M}on(WM,N)\rightarrow {\mathcal {S}\mathrm{gp}}(\overline{W}M,N) \end{aligned}$$

is a homotopy equivalence,

Section 6 deals with diagrams in topologically enriched categories $\mathcal {M}$ with weak equivalences and a “good” cofibrant replacement functor. We first show that their localizations with respect to maps of diagrams which are objectwise weak equivalences exist. We then show that the well-known derived adjunction induced by the colimit functor and the constant diagram functor is the path-component version of an adjunction up to homotopy between the homotopy colimit functor and the constant diagram functor. We believe that this is of separate interest, too. We then show that the homotopy adjunction of Theorem 1.6 lifts to a homotopy adjunction between the corresponding categories of diagrams. In contrast to strict adjunctions this is a priori not clear, because the associated unit is natural only up to homotopy and hence does not lift to diagrams. We apply this result to prove

Theorem 1.13

The classifying space functor $B:\mathcal {M}on\rightarrow {\mathcal {T}\! op}^*$ preserves homotopy colimits up to natural homotopy equivalences.

The path-component versions of most of our main results are more or less known if we restrict to grouplike monoids. The paper extends these results to general monoids and shows that they arise from stronger statements. Moreover, we show that a topological enrichment with good properties can make up for the non-existence of Quillen model structures.

2 Homotopy homomorphisms revisited

Sugawara [24] introduced the notion of a strongly homotopy multiplicative map between monoids, which we will call a homotopy homomorphism or $h$-morphism, for short.

Definition 2.1

A homotopy homomorphism, or $h$-morphism $f:M\rightarrow N$ between two monoids is a sequence of maps

$$\begin{aligned} f_n: M^{n+1}\times I^n\longrightarrow N\quad n\in \mathbb {N} \end{aligned}$$

such that $(x_i\in M, t_j\in I)$

$$\begin{aligned}&f_n(x_0, t_1, x_1,t_2,\ldots ,t_n,x_n)\\&\quad = \left\{ \begin{array}{ll} f_{n-1}(x_0,t_1,\ldots , x_{i-1}\cdot x_i, \ldots ,t_n,x_n) &{}\quad \text {if } t_i=0\\ f_{i-1}(x_0,t_1,\ldots , x_{i-1})\cdot f_{n-i}(x_i,t_{i+1},\ldots ,x_n) &{}\quad \text {if } t_i=1. \end{array} \right. \end{aligned}$$

We call $f_0:M\rightarrow N$ the underlying map of $f$.

If in addition $f_0(e_M)=e_N$ and

$$\begin{aligned}&f_n(x_0, t_1, x_1,t_2,\ldots ,t_n,x_n)\\&\quad = \left\{ \begin{array}{ll} f_{n-1}(x_1,t_2, \ldots ,x_n) &{}\quad \text {if } x_0=e_M\\ f_{n-1}(x_0,\ldots , x_{i-1},\max (t_i, t_{i+1}),x_{i+1},\ldots , x_n)&{}\quad \text {if } x_i=e_M\\ f_{n-1}(x_0, t_1,\ldots ,x_{n-1}) &{}\quad \text {if } x_n=e_M \end{array} \right. \end{aligned}$$

where $e_M\in M$ and $e_N\in N$ are the units, we call $f$ a unitary homotopy homomorphism or $uh$-morphism, for short.

Since an $h$-morphism does not pay tribute to the unit it does not seem to be the right notion for maps between monoids. E.g. if we require $f_0$ to be a based map so that it preserves the unit we would like the path

to be the constant one, if $x_0$ or $x_1$ is the unit. Unitary $h$-morphisms have this property. Nevertheless, in the past one usually considered $h$-morphisms because the additional conditions for $uh$-morphisms make it harder to work with them.

We will later find it more convenient to work with homotopy unitary homotopy homomorphisms which preserve the unit only up to homotopy. We will introduce those at the end of this section.

The most extensive study of $h$-morphisms and their induced maps on classifying spaces was done by Fuchs [9], who constructed composites of $h$-morphisms, proved that composition is homotopy associative and stated that an $h$-morphism $f:M\rightarrow N$ whose underlying map is a homotopy equivalence has a homotopy inverse $h$-morphism $g:N\rightarrow M$. In fact, he constructed $g_0$, $g_1$ and the homotopies $g\circ f\simeq \mathrm{id}$ and $f\circ g\simeq \mathrm{id}$ in dimensions 0 and 1 in [9, p. 205–p. 208], but left the rest to the reader. He produced a complete proof in [10].

We handle these problems by interpreting homotopy homomorphisms as genuine homomorphisms of a “cofibrant” replacement of $M$.

By a semigroup we will mean a $k$-space with a continuous associative multiplication. Let ${\mathcal {S}\mathrm{gp}}$ denote the category of semigroups and continuous homomorphisms.

Constructions 2.2

We will construct continuous functors

$$\begin{aligned} \overline{W}:{\mathcal {S}\mathrm{gp}}\longrightarrow {\mathcal {S}\mathrm{gp}}\quad \text {and}\quad W:\mathcal {M}on\longrightarrow \mathcal {M}on\end{aligned}$$

and natural transformations

$$\begin{aligned} \overline{\varepsilon }: \overline{W}\longrightarrow \mathrm{Id}\quad \text {and}\quad \varepsilon :W\longrightarrow \mathrm{Id}\end{aligned}$$

as follows:

$$\begin{aligned} \overline{W}M=\left( \coprod \limits ^\infty _{n=0} M^{n+1}\times I^n\right) / \sim \end{aligned}$$

with the relation

• 1. $(x_0,t_1,x_1,t_2,\ldots ,t_n,x_n)\sim (x_0,t_1,\ldots ,x_{i-1}\cdot x_i,\ldots ,t_n,x_n)$   if $t_i=0$

• 2. and $WM$ is the quotient of $\overline{W}M$ by imposing the additional relations $(x_0, t_1, x_1,t_2,\ldots ,t_n,x_n) \sim \left\{ \begin{array}{ll} (x_1,t_2, \ldots ,x_n) &{}\quad \text {if } x_0=e\\ (x_0,\ldots , x_{i-1},\max (t_i, t_{i+1}),x_{i+1},\ldots , x_n)&{}\quad \text {if } x_i=e\\ (x_0, t_1,\ldots ,x_{n-1}) &{}\quad \text {if } x_n=e \end{array} \right.$

The multiplications of $\overline{W}M$ and $WM$ are given on representatives by

$$\begin{aligned} (x_0,t_1,\ldots ,x_k)\cdot (y_0,u_1,\ldots ,y_l)=(x_0, t_1,\ldots x_k, 1, y_0, u_1,\ldots ,y_l). \end{aligned}$$

The natural transformations $\overline{\varepsilon }$ and $\varepsilon$ are defined by

$$\begin{aligned} \overline{\varepsilon }(M),\ \varepsilon (M):(x_0,t_1,\ldots ,x_n)\longmapsto x_0\cdot x_1\cdot \ldots \cdot x_n. \end{aligned}$$

Their underlying maps have natural sections

$$\begin{aligned} \bar{\iota }(M),\ \iota (M): x \longmapsto (x) \end{aligned}$$

which are not homomorphisms, and there is a homotopy over $M$

$$\begin{aligned} h_s:(x_0,t_1,x_1,\ldots ,t_n,x_n)\longmapsto (x_0,s\cdot t_1,x_1,\ldots ,s\cdot t_n,x_n) \end{aligned}$$

from $\overline{\iota }(M)\circ \overline{\varepsilon }(M)$ respectively $\iota (M)\circ \varepsilon (M)$ to the identity. In particular, $\overline{\varepsilon }(M)$ and $\varepsilon (M)$ are shrinkable as maps.

If $M$ is a monoid the projection

$$\begin{aligned} \varepsilon '(M):\overline{W}M\rightarrow WM \end{aligned}$$

is a homomorphism of semigroups satisfying

$$\begin{aligned} \bar{\varepsilon }(M)=\varepsilon (M)\circ \varepsilon '(M)\quad \text {and}\quad \varepsilon '(M)\circ \overline{\iota }(M) = \iota (M). \end{aligned}$$

By inspection we see

Observation 2.3

• 1. $h$-morphisms $(f_n): M\rightarrow N$ correspond bijectively to homomorphisms $\bar{f}:\overline{W}M\rightarrow N$ of semigroups, and $f_0=\bar{f}\circ \overline{\iota }(M)$.

• 2. $uh$-morphisms $(f_n): M\rightarrow N$ correspond bijectively to homomorphisms $f: WM\rightarrow N$ of monoids, and $f_0=f\circ \iota (M)$.

Observation 2.4

Algebraically, $\overline{W}M$ is a free semigroup and $WM$ is a free monoid. The indecomposables are precisely those elements which have a representative $(x_0,t_1,x_1,\ldots ,x_n)$ where no $t_i$ equals $1$.

2.5. The formal relation between $\overline{\mathbf{W}}$ and $\mathbf{W}$: The forgetful functor $i:\mathcal {M}on\rightarrow {\mathcal {S}\mathrm{gp}}$ has a left adjoint

$$\begin{aligned} (-)_+:{\mathcal {S}\mathrm{gp}}\rightarrow \mathcal {M}on,\quad G\mapsto G_+, \end{aligned}$$

where $G_+=G\sqcup \{*\}$ with $*$ as unit. It follows from the definitions that the diagram

commutes up to natural isomorphisms in $\mathcal {M}on$.

Both constructions have a universal property, which is a consequence of the following result. We give ${\mathcal {T}\! op}^*(X,Y)$ and $\mathcal {T}\! op(X,Y)$ the $k$-function space topology, obtained by turning the space of all maps from $X$ to $Y$ with the compact-open topology into a $k$-space. We give $\mathcal {M}on(M,N)$ and ${\mathcal {S}\mathrm{gp}}(M,N)$ the subspace topologies of the corresponding function spaces in ${\mathcal {T}\! op}^*$ respectively $\mathcal {T}\! op$.

Definition 2.6

We call a homomorphism $f:M\rightarrow N$ in $\mathcal {M}on$ or ${\mathcal {S}\mathrm{gp}}$ a weak equivalence if its underlying map of spaces is a homotopy equivalence in $\mathcal {T}\! op$. (Recall that a weak equivalence in $\mathcal {M}on$ is a homotopy equivalence of underlying spaces in ${\mathcal {T}\! op}^*$ if $M$ and $N$ are well-pointed.)

Proposition 2.7

• 1. Let $M$ be a well-pointed monoid and $p:X\rightarrow Y$ a homomorphism of monoids. Let

  $$\begin{aligned} p_*:\mathcal {M}on(WM,X)\longrightarrow \mathcal {M}on(WM,Y) \end{aligned}$$

  be the induced map. If $p$ is a fibration of underlying spaces, so is $p_*$. If $p$ is a weak equivalence, $p_*$ is a homotopy equivalence.

• 2. The same holds for $\overline{W}$ and an arbitrary object $M$ in the category ${\mathcal {S}\mathrm{gp}}$.

Proof

Let $p:X\rightarrow Y$ be a weak equivalence. By the HELP-Lemma [27] in $\mathcal {T}\! op$ with the Strøm model structure [22] we have to show: given a diagram of spaces

(A)

which commutes up to a homotopy $\bar{h}_{A,t}:\bar{g}\circ i\simeq p_*\circ \bar{f}_A$, where $i$ is a closed cofibration, there are extensions $\bar{f}:B\rightarrow \mathcal {M}on(WM,X)$ of $\bar{f}_A$ and $\bar{h}_t:B\rightarrow \mathcal {M}on(WM,Y)$ of $\bar{h}_{A,t}$ such that $\bar{h}_t: \bar{g}\simeq p_*\circ \bar{f}$.

Passing to adjoints we obtain a diagram

commuting up to a homotopy $h_{A,t}$, such that each $f_a=f_A|WM\times \{a\}$, each $g_b=g|WM\times \{b\}$, and each $h_{a,t}=h_{A,t}|WM\times \{a\}$ is a homomorphism. We have to construct extensions $f:WM\times B\rightarrow X$ and $h_t:WM\times B\rightarrow Y$ of $f_A$ and $h_{A,t}$ such that $h_t:g\simeq p\circ f$ and each $h_{b,t}$ and $f_b, \ b\in B$ is a homomorphism.

We filter $WM\times B$ by closed subspaces $F_n\times B$, where $F_n$ is the submonoid of $WM$ generated by all elements having a representative $(x_0,t_1,\ldots ,t_k,x_k)$ with $k\le n$. We put $F_{-1}=\{e\}$. Then $f$ and $h_t$ are uniquely determined on $F_{-1}\times B$.

Suppose that $f$ and $h_t$ have been defined on $F_{n-1}\times B$. An element $(x_0,t_1,\ldots ,t_n,x_n)$ represents an element in $F_{n-1}$ iff one of the following conditions holds

• some $x_i=e$   (relation 2.2.2)

• some $t_i=0$   (relation 2.2.1)

• some $t_i=1$   (it represents a product in $F_{n-1}$).

If $DM^{n+1}\subset M^{n+1}$ denotes the subspace of points with some coordinate $e$, then $f$ and $h_t$ are already defined on $(DM^{n+1}\times I^n\cup M^{n+1}\times \partial I^n)\times B\cup M^{n+1}\times I^n\times A$. The elements in $(M^{n+1}\times I^n)\backslash (DM^{n+1}\times I^n\cup M^{n+1}\times \partial I^n)$ represent indecomposables of filtration $n$, but not of lower filtration. Consider the diagram

(B)

(in abuse of notation we use $g$ for the composite $M^{n+1}\times I^n\times B\rightarrow WM\times B\rightarrow Y$). Diagram (B) commutes up to the homotopy $h_t$ and we need an extension of $f$ and $h_t$ to $M^{n+1}\times I^n\times B$. These extensions exist by the HELP-Lemma, because our assumptions ensure that $j$ is a closed cofibration. So we have defined $f$ and $h_t$ for indecomposable generators $(x_0,t_1,\ldots ,t_n,x_n)$ of $F_n$. We extend these maps to $F_n\times B$ by the conditions that each $f_b$ and $h_{b,t},\ b\in B$ be a homomorphism using Observation 2.4.

Now suppose that $p$ is a fibration. By [22, Thm. 8] we need to consider a commutative diagram (A), where $i$ is a closed cofibration and a homotopy equivalence, and we have to find an extension $\bar{f}: B\rightarrow \mathcal {M}on(WM,X)$ of $\bar{f}_A$ such that $\bar{g}=p_*\circ \bar{f}$. We proceed as above. In the inductive step we have a commutative diagram (B). Since $i$ is a closed cofibration and a homotopy equivalence so is $j$ by the pushout-product theorem for cofibrations. Hence the required extension $f:M^{n+1}\times I^n\times B\rightarrow X$ exists by [22, Thm. 8].

Part (2) is proved in the same way starting with $F_{-1}M=\emptyset$. $\square$

As an immediate consequence we obtain the

2.8. Lifting theorem: (1) Given homomorphisms of monoids

such that $p$ is a weak equivalence and $M$ is well-pointed, then there exists a homomorphism $g:WM\rightarrow X$, unique up to homotopy in $\mathcal {M}on$ (i.e. a homotopy through homomorphisms), such that $f\simeq p\circ g$ in $\mathcal {M}on$.

If, in addition, the underlying map of $p$ is a fibration there is a homomorphism $g: WM\rightarrow X$, unique up to homotopy in $\mathcal {M}on$, such that $f=p\circ g$.

(2) For $\overline{W}$ the analogous results hold in the category ${\mathcal {S}\mathrm{gp}}$.

2.9. By Proposition 2.7 the second one of the maps

$$\begin{aligned} \varepsilon (N)_*&:\mathcal {M}on(WM,WN) \rightarrow \mathcal {M}on(WM,N) \\ \overline{\varepsilon }(N)_*&:7{\mathcal {S}\mathrm{gp}}(\overline{W}M,\overline{W}N) \rightarrow {\mathcal {S}\mathrm{gp}}(\overline{W}M,N) \end{aligned}$$

is a homotopy equivalence, and the first one is a homotopy equivalence if $M$ is well-pointed.

To guarantee the well-pointedness condition we introduce the whiskering functor.

2.10. The whiskering construction: We define a functor

$$\begin{aligned} V^t:{\mathcal {T}\! op}^*\rightarrow {\mathcal {T}\! op}^w\end{aligned}$$

by $V^t(X,x_0)=(X\sqcup I)/(x_0\sim 1)$ and choose $0\in I$ as base-point of $V^{t} X$. Then $V^{t} X$ is well-pointed, and the natural map $q(X): V^tX\rightarrow X$ mapping $I$ to $x_0$ is a homotopy equivalence. Its homotopy inverse $\bar{q}(X): X\rightarrow V^tX$ is the canonical map. If $X$ is well-pointed, $q(X)$ is a based homotopy equivalence.

This functor lifts to a functor

$$\begin{aligned} V:\mathcal {M}on\rightarrow \mathcal {M}on^{w}\end{aligned}$$

defined by $V(M)=V^t(M)$ with $x_0$ replaced by $e_M$ with the multiplication

$$\begin{aligned} x\cdot y=\left\{ \begin{array}{ll} x\cdot y\in M &{}\quad \text {if } x,y\in M\\ x &{}\quad \text {if } x\in M, \ y\in I\\ y &{}\quad \text {if } y\in M, \ x\in I\\ \text {max}(x,y)&{}\quad \text {if } x,y \in I. \end{array}\right. \end{aligned}$$

Since $0\in I$ is the unit of $VM$ the monoid $VM$ is well-pointed. The natural map $q(M): VM\rightarrow M$ is a weak equivalence in $\mathcal {M}on$, but observe that $\bar{q}(M): X\rightarrow VM$ is not a homomorphism because it does not preserve the unit.

A homomorphism $f:WVM\rightarrow N$ can be considered a homotopy unitary homotopy homomorphism. Strictly speaking, the underlying map of $f:WVM\rightarrow N$ is

$$\begin{aligned} f_0=f\circ \iota (VM)\circ \bar{q}(M):M\rightarrow VM\rightarrow WVM\rightarrow N. \end{aligned}$$

We note that $f_0$ preserves the unit $e_M$ only up to homotopy.

By 2.9 the following change of our notations of homotopy homomorphisms is insignificant from a homotopy theoretic point of view:

Definition 2.11

From now on a homotopy unitary homotopy homomorphism, $huh$-morphism for short, from $M$ to $N$ is a homomorphism $f:WVM\rightarrow WVN$. Its underlying map is $q(N)\circ \varepsilon (VN)\circ f\circ \iota (VM)\circ \bar{q}(M)$.

A unitary homotopy homomorphism, $uh$-morphism for short, from $M$ to $N$ is a homomorphism $f:WM\rightarrow WN$. Its underlying map is $\varepsilon (N)\circ f\circ \iota (M)$.

A homotopy homomorphism, $h$-morphism for short, from the semigroup $M$ to the semigroup $N$ is a homomorphism $f:\overline{W}M\rightarrow \overline{W}N$. Its underlying map is $\overline{\varepsilon }(N)\circ f\circ \overline{\iota }(M)$.

This solves the problem of composition, and from 2.7 we obtain

Proposition 2.12

If $f:WM\rightarrow WN$ is a $uh$-morphism from $M$ to $N$ whose underlying map is a homotopy equivalence, and $M$ and $N$ are well-pointed, then $f$ is a homotopy equivalence in the category $\mathcal {M}on$.

If $f:WVM\rightarrow WVN$ is a $huh$-morphism from $M$ to $N$, whose underlying map is a homotopy equivalence, then $f$ is a homotopy equivalence in the category $\mathcal {M}on$.

The analogous statement in ${\mathcal {S}\mathrm{gp}}$ holds for homomorphisms $\overline{W}M\rightarrow \overline{W}N$.

Monoids are algebras over the operad $\mathcal {A}ss$ of monoid structures, and there is the notion of an “operadic” homotopy homomorphism defined by Boardman and Vogt [4]. Klioutch [15] compared the operadic notion with the one considered in this paper and could show.

Proposition 2.13

Let $M$ and $N$ be well-pointed monoids and let H$(M,N)$ be the space of operadic homotopy homomorphisms from $M$ to $N$, then there is a natural homotopy equivalence

$$\begin{aligned} \text {H}(M,N)\simeq \mathcal {M}on(WM,N). \end{aligned}$$

3 Categorical prerequisites and localizations

The functors $WV:\mathcal {M}on\rightarrow \mathcal {M}on$ and $\overline{W}:{\mathcal {S}\mathrm{gp}}\rightarrow {\mathcal {S}\mathrm{gp}}$ resemble cofibrant replacement functors as known from Quillen model category theory. Unfortunately, there is no known model category structure on $\mathcal {M}on$ with our choice of weak equivalences. This draw-back is made up by the topological enrichment of our categories as we will see in this section.

Our categories are enriched over ${\mathcal {T}\! op}^*$ or $\mathcal {T}\! op$. So we have a natural notion of homotopy. Moreover, they are tensored and cotensored. Recall that a ${\mathcal {T}\! op}^*$-enriched category $\mathcal {M}$ is tensored and cotensored (over ${\mathcal {T}\! op}^*$) if there are functors

$$\begin{aligned} {\mathcal {T}\! op}^*\times \mathcal {M}&\rightarrow \mathcal {M}, (X,M) \mapsto X\boxtimes M\\ ({\mathcal {T}\! op}^*)^{\mathrm{op}} \times \mathcal {M}&\rightarrow \mathcal {M}, (X,M) \mapsto M^X \end{aligned}$$

and natural homeomorphisms

$$\begin{aligned} \mathcal {M}(X\boxtimes M, N)\cong {\mathcal {T}\! op}^*(X,\mathcal {M}(M,N))\cong \mathcal {M}(M,N^X). \end{aligned}$$

These properties imply that for based spaces $X$ and $Y$ and objects $M\in \mathcal {M}$ there are natural isomorphisms

$$\begin{aligned} (X\wedge Y)\boxtimes M\cong X\boxtimes (Y\boxtimes M). \end{aligned}$$

The definition in the $\mathcal {T}\! op$-enriched case is similar. To distinguish between the based and the non-based case we denote the tensor over $\mathcal {T}\! op$ by $X\otimes M$. The natural isomorphism in the non-based case reads

$$\begin{aligned} (X\times Y)\otimes M\cong X\otimes (Y\otimes M). \end{aligned}$$

Forgetting base points turns a ${\mathcal {T}\! op}^*$-enriched category $\mathcal {M}$ into a $\mathcal {T}\! op$-enriched one. If $\mathcal {M}$ is tensored over ${\mathcal {T}\! op}^*$ it is also tensored over $\mathcal {T}\! op$: we define

$$\begin{aligned} X\otimes M= X_+\boxtimes M \end{aligned}$$

where $X_+=X\sqcup \{*\}$ with the additional point as base point.

Example 3.1

$\mathcal {M}on$ is ${\mathcal {T}\! op}^*$-enriched, tensored and cotensored [17, Prop. 2.10]. The cotensor $M^X$ is the $k$-function space with pointwise multiplication, $X\boxtimes M$ is more complicated: as a set, it is a free product of copies $M$, one copy for each $x\in X$ different from the base point. By the same argument as in [17] the category ${\mathcal {S}\mathrm{gp}}$ is $\mathcal {T}\! op$-enriched and tensored and cotensored over $\mathcal {T}\! op$.

If $\otimes _{{\mathcal {S}\mathrm{gp}}}$ denotes the tensor in ${\mathcal {S}\mathrm{gp}}$ and $\otimes$ the one over $\mathcal {T}\! op$ in $\mathcal {M}on$, then the universal properties of the tensor and of the adjunction of 2.5 imply that there is a natural isomorphism

$$\begin{aligned} (K\otimes _{{\mathcal {S}\mathrm{gp}}} G)_+\cong K\otimes (G_+) \end{aligned}$$

in $\mathcal {M}on$ for semigroups $G$.

Definition 3.2

Let $\mathcal {M}$ be a $\mathcal {T}\! op$-enriched category. Two morphisms $f,g:A\rightarrow X$ are called homotopic if there is a path in $\mathcal {M}(A,X)$ joining $f$ and $g$.

Clearly, the homotopy relation is an equivalence relation preserved under composition. Passing to path components we obtain the homotopy category $\pi \mathcal {M}$.

If $\mathcal {M}$ is tensored over $\mathcal {T}\! op$ it has a canonical cylinder functor $M\mapsto I\otimes M$. The associated homotopy notion coincides with the one of Definition 3.2.

Definition 3.3

Let $\mathcal {M}$ be a category and $\fancyscript{W}$ a class of morphisms in $\mathcal {M}$, which we will call weak equivalences. The localization of $\mathcal {M}$ with respect to $\fancyscript{W}$ is a category $\mathcal {M}[\fancyscript{W}^{-1}]$ with $\mathrm{ob}\mathcal {M}[\fancyscript{W}^{-1}]=\mathrm{ob}\mathcal {M}$ and a functor $\gamma : \mathcal {M}\rightarrow \mathcal {M}[\fancyscript{W}^{-1}]$ such that

• 1. $\gamma$ is the identity on objects

• 2. $\gamma (f)$ is an isomorphism for all $f\in \fancyscript{W}$

• 3. if $F:\mathcal {M}\rightarrow \mathcal {D}$ is a functor such that $F(f)$ is an isomorphism for all $f\in \fancyscript{W}$ then there exists a unique functor $\overline{F}:\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ such that $F=\overline{F}\circ \gamma$.

Proposition 3.4

Let $\mathcal {M}$ be a $\mathcal {T}\! op$-enriched tensored category and $\fancyscript{W}$ a class of morphisms in $\mathcal {M}$ such that

• 1. $\fancyscript{W}$ contains all homotopy equivalences,

• 2. there is a functor $Q:\mathcal {M}\rightarrow \mathcal {M}$ and a natural transformation $\varepsilon :Q\rightarrow \mathrm{Id}$ or a natural transformation $\eta : \mathrm{Id}\rightarrow Q$ taking values in $\fancyscript{W}$ such that $Qf$ is a homotopy equivalence for each $f\in \fancyscript{W}$. Then $\mathcal {M}[\fancyscript{W}^{-1}]$ exists. Precisely, let $\mathcal {HM}$ be the category with $\mathrm{ob}\mathcal {HM}=\mathrm{ob}\mathcal {M}$ and $\mathcal {HM}(M_1,M_2)=\mathcal {M}(QM_1,QM_2)$. Then $\mathcal {M}[\fancyscript{W}^{-1}]= \pi \mathcal {HC}$, the quotient category obtained by passing to homotopy classes. The functor $\gamma :\mathcal {M}\rightarrow \mathcal {M}[\fancyscript{W}^{-1}]$ is the identity on objects and maps a morphism $f$ to the homotopy class of $Qf$.

Proof

The proof is essentially the same as in the case of a Quillen model category (e.g. see [12, Thm 8.3.5]). We recall the construction of the localization $\mathcal {M}[\fancyscript{W}^{-1}]$ in this case. So let $\mathcal {M}$ be a Quillen model category, let $\varepsilon : C\rightarrow \mathrm{Id}$ respectively $\eta ; \mathrm{Id}\rightarrow R$ be a cofibrant respectively fibrant replacement functor. There are cylinder objects giving rise to the left homotopy relation.

Step 1 Using the fact that $RC(X)$ is fibrant and cofibrant for each object $X$ in $\mathcal {M}$ one proves that left homotopy is an equivalence relation on $\mathcal {M}(RC(A),RC(X))$ which is preserved under composition. Let $\pi \mathcal {M}(RC(A),RC(X))$ be the set of equivalence classes. One defines

$$\begin{aligned} \mathrm{ob}\mathcal {M}[\fancyscript{W}^{-1}]= \mathrm{ob}\mathcal {M}\quad \text {and}\quad \mathcal {M}[\fancyscript{W}^{-1}](A,B)= \pi \mathcal {M}(RC(A),RC(B)), \end{aligned}$$

and it follows that $\mathcal {M}[\fancyscript{W}^{-1}]$ is a category.

Step 2 One proves that $RC(f)$ is a homotopy equivalence if $f:A\rightarrow X$ is a weak equivalence. Then one defines

$$\begin{aligned} \gamma :\mathcal {M}\rightarrow \mathcal {M}[\fancyscript{W}^{-1}] \quad f\mapsto RC(f). \end{aligned}$$

In particular, $\gamma$ maps weak equivalences to isomorphisms.

Step 3 One shows that a functor $F:\mathcal {M}\rightarrow \mathcal {N}$, which maps weak equivalences to isomorphisms, maps homotopic morphisms to the same morphism.

Step 4 Given a functor $F:\mathcal {M}\rightarrow \mathcal {N}$, which maps weak equivalences to isomorphisms, then there is a unique functor $\bar{F}: \mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {N}$ such that $F=\bar{F}\circ \gamma$, and $\bar{F}$ is defined on objects by $\bar{F} (X)=F (X)$ and on morphisms $[f]\in \mathcal {M}[\fancyscript{W}^{-1}](A,X)$ by

$$\begin{aligned} \bar{F}([f]) = F (\varepsilon (X))\circ (F (\eta (CX)))^{-1}\circ F (f)\circ F (\eta (CA))\circ (F(\varepsilon (A)))^{-1}, \end{aligned}$$

where $[f]$ is the homotopy class of $f$.

We now prove Proposition 3.4. We deal with the case where we have a natural transformation $\varepsilon :Q\rightarrow \mathrm{Id}$ taking values in $\fancyscript{W}$.

Step 1 follows from the topological enrichment

$$\begin{aligned} \mathrm{ob}\mathcal {M}[\fancyscript{W}^{-1}]= \mathrm{ob}\mathcal {M}\quad \text {and}\quad \mathcal {M}[\fancyscript{W}^{-1}](A,B)= \pi \mathcal {M}(Q(A),Q(B)) \end{aligned}$$

which is a category.

Step 2 holds by Assumption 3.4.2, and we define

$$\begin{aligned} \gamma :\mathcal {M}\rightarrow \mathcal {M}[\fancyscript{W}^{-1}]\quad f\mapsto Q(f). \end{aligned}$$

$\gamma$ maps weak equivalences to isomorphisms.

For Step 3 we need the cylinder functor: the bottom and top inclusions $i_0\otimes \mathrm{id},i_1\otimes \mathrm{id}:X\cong *\otimes X\rightarrow I\otimes X$ into the cylinder are homotopy equivalences with the common homotopy inverse $r\otimes \mathrm{id}:I\otimes X\rightarrow *\otimes X\cong X$.

Step 4: given a functor $F:\mathcal {M}\rightarrow \mathcal {N}$, which maps weak equivalences to isomorphisms, we define $\bar{F}: \mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {N}$ by

$$\begin{aligned} \bar{F} (X)=F (X)\quad \text {and}\quad \bar{F}([f]) = F (\varepsilon (X))\circ F(f)\circ (F(\varepsilon (A)))^{-1} \end{aligned}$$

for $[f]\in \mathcal {M}[\fancyscript{W}^{-1}](A,X)$. The rest follows like in [12, Thm 8.3.5]. $\square$

Remark 3.5

For Proposition 3.4 we do not need that the tensor $X\otimes M$ exists for all topological spaces: it suffices that $\mathcal {M}$ is tensored over the full subcategory of $\mathcal {T}\! op$ consisting of a point $*$ and the unit interval $I$.

Notation 3.6

Following the standard convention we denote $\mathcal {M}[\fancyscript{W}^{-1}]$ by ${\mathrm{Ho}}\mathcal {M}$ if the class $\fancyscript{W}$ has been specified.

A pair $(Q,\ {\varepsilon :Q\rightarrow \mathrm{Id}})$ respectively $(Q,\ {\eta :\mathrm{Id}\rightarrow Q})$ satisfying the requirements of 3.4 will be called a cofibrant respectively fibrant replacement functor. Each $\mathcal {T}\! op$-enriched category $\mathcal {M}$ considered in this paper will have a continuous cofibrant replacement functor, and we call the category $\mathcal {H}\mathcal {M}$ the category of Q-morphisms associated with $\mathcal {M}$.

Definition 3.7

A functor $Q:\mathcal {M}\rightarrow \mathcal {M}$ together with a natural transformation $\varepsilon : Q\rightarrow \mathrm{Id}$ is called a strong cofibrant replacement functor if each $\varepsilon (M) : Q(M)\rightarrow M$ is a weak equivalence and $p_*: \mathcal {M}(QA,B)\rightarrow \mathcal {M}(QA,C)$ is a homotopy equivalence whenever $p:B\rightarrow C$ is a weak equivalence.

Clearly, a strong cofibrant replacement functor is a cofibrant replacement functor.

3.8. Examples:

• 1. Let $\fancyscript{W}\subset \mathcal {M}on$ be the class of weak equivalences in the sense of 2.6. Then $WV:\mathcal {M}on\rightarrow \mathcal {M}on$ together with $WVM\xrightarrow {\varepsilon (VM)}VM \xrightarrow {q(M)} M$ is a strong cofibrant replacement functor, and the $Q$-morphisms are the $huh$-morphisms. This follows from informations in 2.2, 2.7, 2.10, and 2.12.

• 2. Let $\fancyscript{W}\subset \mathcal {M}on^{w}$ be again the class of weak equivalences. Then $W:\mathcal {M}on^{w}\rightarrow \mathcal {M}on^{w}$ together with $\varepsilon : W\rightarrow \mathrm{Id}$ is a strong cofibrant replacement functor, and the $Q$-morphisms are the $uh$-morphisms. The required information is obtained from 2.2, 2.7, and 2.12.

• 3. Let $\fancyscript{W}\subset {\mathcal {S}\mathrm{gp}}$ be the class of weak equivalences. Then $\overline{W}:{\mathcal {S}\mathrm{gp}}\rightarrow {\mathcal {S}\mathrm{gp}}$ together with $\overline{\varepsilon }: \overline{W}\rightarrow \mathrm{Id}$ is a strong cofibrant replacement functor, and the $Q$-morphisms are the $h$-morphisms by informations from 2.2 and 2.7.

• 4. Let $\fancyscript{W}\subset {\mathcal {T}\! op}^*$ be the class of based maps which are (not necessarily based) homotopy equivalences. Then $V^t:{\mathcal {T}\! op}^*\rightarrow {\mathcal {T}\! op}^*$ together with $q:V^t\rightarrow \mathrm{Id}$ is a strong cofibrant replacement functor by the lemma below, the proof of which we leave as an exercise.

• 5. Let $\fancyscript{W}\subset {\mathcal {T}\! op}^w$ be the class of homotopy equivalences. Then $\mathrm{Id}: {\mathcal {T}\! op}^w\rightarrow {\mathcal {T}\! op}^w$ is a strong cofibrant replacement functor and each map is a $Q$-morphism.

Lemma 3.9

Let $A$ be a well-pointed space and $p:X\rightarrow Y$ a map in ${\mathcal {T}\! op}^*$ which is a not necessarily based homotopy equivalence. Then

$$\begin{aligned} p_*: {\mathcal {T}\! op}^*(A,X)\rightarrow {\mathcal {T}\! op}^*(A,Y) \end{aligned}$$

is a homotopy equivalence in $\mathcal {T}\! op$.

Proposition 3.10

The localizations of the categories of 3.8 with respect to their weak equivalences exist.

Proof

We apply 3.4 and 3.5. We have to show that our categories are tensored over the full subcategory of $\mathcal {T}\! op$ consisting of a point $*$ and the unit interval $I$, the other assumptions of 3.4 have been verified above.

We already know that $\mathcal {M}on$ and ${\mathcal {S}\mathrm{gp}}$ are tensored over $\mathcal {T}\! op$. The category ${\mathcal {T}\! op}^*$ is tensored over itself by the smash product and hence also tensored over $\mathcal {T}\! op$. For the Examples 3.8.2 and 3.8.5 it suffices to know that for any object $M$ in the category the tensor $I\otimes M$ is well-pointed (recall $*\otimes M\cong M$). This is well known for ${\mathcal {T}\! op}^w$ and holds for $\mathcal {M}on^{w}$ by [17, Prop. 7.8]. $\square$

Definition 3.11

Let $\mathcal {M}$ be a category and $\fancyscript{W}$ a class of morphisms in $\mathcal {M}$ such that $\mathcal {M}[\fancyscript{W}^{-1}]$ exists. Let $F:\mathcal {M}\rightarrow \mathcal {D}$ be a functor. A functor $\mathbf{L}F:\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ together with a natural transformation $\tau : \mathbf{L}F\circ \gamma \rightarrow F$ is called left derived functor of $F$, if given any functor $T:\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ and natural transformation $\sigma :T\circ \gamma \rightarrow F$, there is a unique natural transformation $\rho : T\rightarrow \mathbf{L}F$ such that $\sigma =\tau \circ (\rho *\gamma )$.

Dually, a functor $\mathbf{R}F:\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ together with a natural transformation $\mu : F\rightarrow \mathbf{R}F\circ \gamma$ is called right derived functor of $F$, if given any functor $G:\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ and natural transformation $\nu :F\rightarrow G\circ \gamma$, there is a unique natural transformation $\xi : \mathbf{R}F\rightarrow G$ such that $(\xi *\gamma )\circ \mu$.

Remark 3.12

• 1. A left or right derived functor is unique up to natural isomorphism if it exists.

• 2. If $F:\mathcal {M}\rightarrow \mathcal {D}$ maps weak equivalences to isomorphisms, then the induced functor $\overline{F}: \mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {D}$ is the right and left derived functor of $F$.

Proposition 3.13

Let $\mathcal {M}$ be as in Proposition 3.4, and let $F:\mathcal {M}\rightarrow \mathcal {B}$ be a functor which maps homotopy equivalences to isomorphisms. Then $\mathbf{L}F :\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {B}$ exists if $\mathcal {M}$ has a cofibrant replacement functor, and $\mathbf{R}F :\mathcal {M}[\fancyscript{W}^{-1}]\rightarrow \mathcal {B}$ exists if $\mathcal {M}$ has a fibrant replacement functor. In both cases the derived functor is induced by $F\circ Q:\mathcal {M}\rightarrow \mathcal {B}$.

Proof

The proof is the same as in the case of a model category (e.g. see [12, 8.4.]). $\square$

Let $F:\mathcal {M}\rightarrow \mathcal {B}$ be a functor between $\mathcal {T}\! op$-enriched categories admitting cofibrant replacement functors $Q_{\mathcal {M}}:\mathcal {M}\rightarrow \mathcal {M}$ and $Q_{\mathcal {B}}:\mathcal {B}\rightarrow \mathcal {B}$. Proposition 3.13 motivates the introduction of the functor

3.14. $F^{\mathcal {H}}: \mathcal {H}\mathcal {M}\rightarrow \mathcal {H}\mathcal {B}$

defined on objects by $F^{\mathcal {H}}(X)=F(Q_{\mathcal {M}}X)$ and on morphisms by

$$\begin{aligned} F^{\mathcal {H}}: \mathcal {M}(Q_{\mathcal {M}}X,Q_{\mathcal {M}}Y)\xrightarrow {Q_{\mathcal {B}}\circ F} \mathcal {B}(Q_{\mathcal {B}}FQ_{\mathcal {M}}X,Q_{\mathcal {B}}FQ_{\mathcal {M}}Y). \end{aligned}$$

If $F$ preserves homotopy equivalences, e.g. if $F$ is continuous, and $\pi _{\mathcal {B}}:\mathcal {B}\rightarrow \pi \mathcal {B}$ is the canonical functor, then $\pi _{\mathcal {B}}\circ F^{\mathcal {H}}$ induces the left derived functor

$$\begin{aligned} {\mathrm{Ho}}F:{\mathrm{Ho}}\mathcal {M}\rightarrow {\mathrm{Ho}}\mathcal {B}\end{aligned}$$

of $\pi _{\mathcal {B}}\circ F$. Following model category terminology, we call ${\mathrm{Ho}}F$ the total left derived functor of $F$.

One of the objectives of this paper is to show that the classifying space functor and the Moore loop space functor induce an adjoint derived pair (see Theorem 4.6 below). This is the path-component version of the more general result (Theorem 4.5 below) that

are a homotopically adjoint pair. To make this last statement precise we need some preparations.

Definition 3.15

Let $\mathcal {A}$ and $\mathcal {B}$ be topologically enriched categories. A functor $F:\mathcal {A}\rightarrow \mathcal {B}$ is called continuous if

$$\begin{aligned} F:\mathcal {A}(A,B)\longrightarrow \mathcal {B}(FA,FB) \end{aligned}$$

is continuous for all $A$ and $B$ in $\mathcal {A}$.

If $F,G:\mathcal {A}\rightarrow \mathcal {B}$ are continuous functors, a collection of morphisms $\{\alpha (A): FA\rightarrow GA;\; A\in \mathrm{ob}\mathcal {A}\}$ is called a natural transformation up to homotopy if the diagram

is homotopy commutative.

A pair of continuous functors

$$\begin{aligned} F:\mathcal {A}\leftrightarrows \mathcal {B}:G \end{aligned}$$

is called a homotopy adjoint pair if there is a natural transformation up to homotopy

$$\begin{aligned} \alpha (A,X):\mathcal {B}(FA,X)\rightarrow \mathcal {A}(A,GX) \end{aligned}$$

such that each $\alpha (A,X)$ is a homotopy equivalence. The homotopy equivalences are called the homotopy adjunctions.

Just as the usual notion of adjunction is equivalently encoded by the concepts of unit and counit, Proposition 3.18 below describes how a homotopy adjunction is specified by a homotopy unit and a homotopy counit.

Observe that we have chosen a strong form of a natural transformation $\alpha : F\rightarrow G$ up to homotopy: for each morphism $f:A\rightarrow B$ in $\mathcal {A}$ we have a square

commuting up to a homotopy $H(f)$ which is continuous in $f$.

The proofs of the following two lemmas are easy exercises.

Lemma 3.16

Let $S,T,U:\mathcal {A}\rightarrow \mathcal {B}$ be continuous functors of topologically enriched categories.

• 1. Each natural transformation $\alpha :S\rightarrow T$ is a natural transformation up to homotopy.

• 2. If $\varepsilon :S\rightarrow T$ and $\eta :T\rightarrow U$ are natural transformations up to homotopy, then $\eta \circ \varepsilon :S\rightarrow U$ is one.

• 3. Let $\varepsilon :S\rightarrow T$ be a natural transformation up to homotopy such that each $\varepsilon (A)$ is a homotopy equivalence. Choose a homotopy inverse $\eta (A)$ of $\varepsilon (A)$ for each $A$ in $\mathcal {A}$. Then the $\eta (A)$ form a natural transformation $\eta :T\rightarrow S$ up to homotopy.${\square }$

Lemma 3.17

Let $S,T,U,V:\mathcal {A}\rightarrow \mathcal {B}$ be continuous functors of topologically enriched categories, and let $\varepsilon :S\rightarrow T$ and $\eta :U\rightarrow V$ be natural transformations up to homotopy.

• 1. Let $F,G:\mathcal {A}^{\mathrm{op}}\times \mathcal {A}\rightarrow \mathcal {T}\! op$ be defined by $F(A,B)=\mathcal {A}(A,B)$ and $G(A,B)=\mathcal {B}(TA,TB)$. Then

  $$\begin{aligned} \tau (A,B):\mathcal {A}(A,B)\xrightarrow {T} \mathcal {B}(TA,TB) \end{aligned}$$

  is a natural transformation from $F$ to $G$.

• 2. Let $F,G:\mathcal {A}^{\mathrm{op}}\times \mathcal {A}\rightarrow \mathcal {T}\! op$ be defined by $F(A,B)=\mathcal {B}(VA,SB)$ and $G(A,B)= \mathcal {B}(UA,TB)$. Then

  $$\begin{aligned} \alpha (A,B):\mathcal {B}(VA,SB)\xrightarrow {\varepsilon (B)_*\circ \eta (A)^*} \mathcal {B}(UA,TB) \end{aligned}$$

  is a natural transformation from $F$ to $G$ up to homotopy. ${\square }$

Proposition 3.18

Let $F:\mathcal {A}\leftrightarrows \mathcal {B}:G$ be a pair of continuous functors of topologically enriched categories. Suppose there are natural transformations up homotopy

$$\begin{aligned} \mu (A): A\rightarrow GF(A)\quad \text {and}\quad \eta (X):FG(X)\rightarrow X \end{aligned}$$

such that

$$\begin{aligned} G(\eta (X))\circ \mu (GX)\simeq \mathrm{id}_{GX}\quad \text {and}\quad \eta (FA)\circ (F(\mu (A))\simeq \mathrm{id}_{FA}. \end{aligned}$$

Then $F$ and $G$ are a homotopy adjoint pair. (We call $\mu : \mathrm{Id}\rightarrow GF$ the homotopy unit and $\eta :FG\rightarrow \mathrm{Id}$ the homotopy counit of the resulting homotopy adjunction.)

Proof

We define

$$\begin{aligned} \alpha (A,X):\mathcal {B}(FA,X)\xrightarrow {G} \mathcal {A}(GFA,GX)\xrightarrow {\mu (A)^*} \mathcal {A}(A,GX) \end{aligned}$$

and

$$\begin{aligned} \beta (A,X):\mathcal {A}(A,GX)\xrightarrow {F}\mathcal {B}(FA,FGX)\xrightarrow {\eta (X)_*}\mathcal {B}(FA,X). \end{aligned}$$

By 3.17 both are natural transformations up to homotopy. The following diagram shows that $\beta (A,X)\circ \alpha (A,X)\simeq \mathrm{id}$.

The squares II and III commute and square I commutes up to homotopy, and $(F\mu (A))^*\circ \eta (FA)^*\simeq \mathrm{id}$ by assumption.

The proof that $\alpha (A,X)\circ \beta (A,X)\simeq \mathrm{id}$ is dual. $\square$

Definition 3.19

A homotopy adjunction $F: \mathcal {A}\leftrightarrows \mathcal {B}:G$ is called natural if there is a natural homotopy equivalence

$$\begin{aligned} \beta (A,X):\mathcal {A}(A,GX)\rightarrow \mathcal {B}(FA,X) \end{aligned}$$

and conatural if there is a natural homotopy equivalence

$$\begin{aligned} \alpha (A,X):\mathcal {B}(FA,X)\rightarrow \mathcal {A}(A,GX) \end{aligned}$$

(because in this case there is a natural homotopy unit, respectively, a natural homotopy counit).

4 The classifying space and the Moore loop space functor

4.1. The 2-sided bar construction: Let $\mathcal {C}$ be a small topologically enriched category, $X$ a $\mathcal {C}^{op}$-diagram and $Y$ a $\mathcal {C}$-diagram in $\mathcal {T}\! op$. We define a simplicial space $B_\bullet (X,\mathcal {C},Y)$ by

$$\begin{aligned} B_0(X,\mathcal {C},Y)&= \coprod _{A \in \mathcal {C}}X(A)\times Y(A) \\ B_n(X,\mathcal {C},Y)&= \coprod _{A,B\in \mathcal {C}} X(B)\times \mathcal {C}_n(A,B)\times Y(A)\quad \text {for } n>0, \end{aligned}$$

where $\mathcal {C}_n(A,B)$ is the space of all composable $n$-tuples of morphisms $(f_1,\ldots ,f_n)$ such that source$(f_n)\ =\ A$ and target$(f_1)\ =\ B$, with boundary and degeneracy maps given by

$$\begin{aligned} d^i(x,f_1,\ldots ,f_n,y)&= (X(f_1)(x),f_2,\cdots ,f_n,y) \quad i=0\\ d^i(x,f_1,\ldots ,f_n,y)&= (x,f_1,\ldots ,f_i\circ f_{i+1},\ldots ,f_n,y) \quad 0<i<n\\ d^i(x,f_1,\ldots ,f_n,y)&= (x,f_1,\ldots ,f_{n-1},Y(f_n)(y))\quad i=n\\ s^i(x,f_1,\ldots ,f_n,y)&= (x,f_1,\ldots ,f_i,\mathrm{id}, f_{i+1},\ldots ,f_n,y) \quad 0\le i\le n. \end{aligned}$$

Let $B(X,\mathcal {C},Y)=|B_\bullet (X,\mathcal {C},Y)|$ be its topological realization.

We consider a topological monoid as a topologically enriched category with one object and define the classifying space functor

$$\begin{aligned} B:\mathcal {M}on\longrightarrow {\mathcal {T}\! op}^*\end{aligned}$$

by $BM=B(*,M, *)$. Since $BM$ is well-pointed if $M$ is, the classifying space functor is a functor of pairs

$$\begin{aligned} B:(\mathcal {M}on,\mathcal {M}on^{w})\rightarrow ({\mathcal {T}\! op}^*,{\mathcal {T}\! op}^w). \end{aligned}$$

4.2. We will also work with the variant

$$\begin{aligned} \widetilde{B}:\mathcal {M}on\longrightarrow {\mathcal {T}\! op}^*\end{aligned}$$

where the topological realization of $B_\bullet (*,M, *)$ is replaced by the fat realization which disregards degeneracies. Since the fat realization does not make use of identities the functor $\widetilde{B}$ extends to ${\mathcal {S}\mathrm{gp}}$; moreover, $\widetilde{B}G$ is well-pointed for any semigroup $G$ so that

$$\begin{aligned} \widetilde{B}:{\mathcal {S}\mathrm{gp}}\rightarrow {\mathcal {T}\! op}^w. \end{aligned}$$

By construction, there is a natural homeomorphism $\widetilde{B}(G)\cong B(G_+)$ for semigroups $G$, and the diagram

commutes for monoids $M$, where $\kappa : M_+\rightarrow M$ is the counit of the adjunction 2.5 and $p: \widetilde{B}\rightarrow B$ is the natural projection.

It is well-known that $p(M):\widetilde{B}(M)\rightarrow B(M)$ and hence $B(\kappa (M)):B(M_+)\rightarrow B(M)$ are homotopy equivalences if $M$ is well-pointed.

4.3. The Moore path and loop space: Let $X$ be a (not necessarily based) space. The Moore path space of $X$ is the subspace $\mathrm{Path}(X)\subset X^{\mathbb {R}_+}\times \mathbb {R}_+$ consisting of all pairs $(w,r)$ such that $w(t)=w(r)$ for all $t\ge r$. We call $r$ the length of $w$ and denote it by $r=l(w)$.

For two paths $(w_1,r_1)$ and $(w_2,r_2)$ with $(w_1)(r_1)= (w_2)(0)$ we define path addition by

$$\begin{aligned} (w_1,r_1)+(w_2,r_2)=(w, r_1+r_2) \end{aligned}$$

with

$$\begin{aligned} w(t)=\left\{ \begin{array}{ll} w_1(t), &{}\quad 0\le t\le r_1,\\ w_2(t-r_1) &{}\quad r_1 \le t. \end{array}\right. \end{aligned}$$

If $(X,*)$ is a based space, the Moore loop space $\Omega '(X)\subset \mathrm{Path}(X)$ is the subspace of all pairs $(w,r)$ with $(w)(r)=(w)(0)=*$. Path addition defines a monoid structure on $\Omega 'X$ with $(c,0)$ as unit, where $c:\mathbb {R}_+\rightarrow X$ is the constant map to $*$. The usual loop space $\Omega X$ is embedded in $\Omega '(X)$ as a deformation retract.

It follows from [25, (11.3)] that $\Omega '(X)$ is well-pointed if $X$ is. Hence $\Omega '$ defines a functor of pairs

$$\begin{aligned} \Omega ': ({\mathcal {T}\! op}^*,{\mathcal {T}\! op}^w)\rightarrow (\mathcal {M}on,\mathcal {M}on^{w}). \end{aligned}$$

Following 3.14 we have pairs of continuous functors

$$\begin{aligned} B^{\mathcal {H}}: \mathcal {H}\mathcal {M}on\leftrightarrows \mathcal {H}{\mathcal {T}\! op}^*:\Omega '^{\mathcal {H}}\end{aligned}$$

and

$$\begin{aligned} B^{w{\mathcal {H}}}:\mathcal {H}\mathcal {M}on^{w}\leftrightarrows \mathcal {H}{\mathcal {T}\! op}^w={\mathcal {T}\! op}^w:\Omega '^{w{\mathcal {H}}}. \end{aligned}$$

We shall prove

Theorem 4.4

The functors

are a conatural homotopically adjoint pair: there is a continuous natural map

$$\begin{aligned} \lambda (WM,X): \mathcal {M}on(WM, W\Omega 'X)\longrightarrow {\mathcal {T}\! op}^*(BWM,X) \end{aligned}$$

which is a homotopy equivalence.

As an immediate consequence we obtain

Theorem 4.5

The functors

are a conatural homotopically adjoint pair: there is a continuous natural map

$$\begin{aligned} \lambda (WVM,V^tX): \mathcal {M}on(WVM, WV\Omega 'V^tX)\longrightarrow {\mathcal {T}\! op}^*(V^tBWVM,V^tX) \end{aligned}$$

which is a homotopy equivalence.

Proof

Replacing $M$ by $VM$ and $X$ by $V^tX$ in Proposition 4.4 we obtain a natural homotopy equivalence

$$\begin{aligned} \mathcal {M}on(WVM,WV\Omega 'V^tX)\xrightarrow {\simeq } {\mathcal {T}\! op}^*(BWVM,V^tX). \end{aligned}$$

Since $BWVM$ is well-pointed the natural map $q(BWVM):V^tBWVM \rightarrow BWVM$ is a based homotopy equivalence inducing a natural homotopy equivalence

$$\begin{aligned} q(BWVM)^*: {\mathcal {T}\! op}^*(BWVM,V^tX) \rightarrow {\mathcal {T}\! op}^*(V^tBWVM,V^tX). \end{aligned}$$

$\square$

Passing to homotopy classes (see 3.4) we obtain

Theorem 4.6

The functors

$$\begin{aligned} {\mathrm{Ho}}B:{\mathrm{Ho}}\mathcal {M}on\leftrightarrows {\mathrm{Ho}}{\mathcal {T}\! op}^*:{\mathrm{Ho}}\Omega ' \end{aligned}$$

are an adjoint pair. Moreover, ${\mathrm{Ho}}B$ is the left derived of $\gamma _{{\mathcal {T}\! op}^*}\circ B$ and ${\mathrm{Ho}}\Omega '$ the left derived of $\gamma _{\mathcal {M}on}\circ \Omega '$.

Proof

This follows from our explicit description of the localizations and the derived functors in Sect. 3. $\square$

The rest of this section is devoted to the proof of Theorem 4.4. By 3.18 it suffices to construct a homotopy unit $\mu : \mathrm{Id}_{\mathcal {H}\mathcal {M}on^{w}}\rightarrow \Omega '^{w{\mathcal {H}}}B^{w{\mathcal {H}}}$ and a homotopy counit $\eta : B^{w{\mathcal {H}}}\Omega '^{w{\mathcal {H}}}\rightarrow \mathrm{Id}_{\mathcal {H}{\mathcal {T}\! op}^w}$. Then $\lambda (WM,X)$ is the composite

$$\begin{aligned} \mathcal {M}on(WM, W\Omega 'X)\xrightarrow {B}{\mathcal {T}\! op}^*(BWM,BW\Omega 'X)\xrightarrow {\eta (X)_*} {\mathcal {T}\! op}^*(BWM,X). \end{aligned}$$

4.7. This means, we have to construct continuous homomorphisms

$$\begin{aligned} \mu (WM):WM\longrightarrow W\Omega 'BWM \end{aligned}$$

which constitute a natural transformation up to homotopy with respect to homomorphisms $WM\rightarrow WN$, and a natural transformation

$$\begin{aligned} \eta (X): BW\Omega 'X\longrightarrow X, \end{aligned}$$

such that

• 1. $W\Omega '\eta (X)\circ \mu (W\Omega 'X)\simeq \mathrm{id}_{W\Omega 'X}$ in $\mathcal {M}on^{w}$ and

• 2. $\eta (BWM)\circ B\mu (WM)\simeq \mathrm{id}_{BWM}$ in ${\mathcal {T}\! op}^w$. (For $\lambda$ to be a natural transformation we need $\eta$ to be a natural transformation.)

4.8. The homotopy counit: Let $X$ be a based space and let

$$\begin{aligned} \Delta ^n=\{(t_0,\ldots ,t_n)\in \mathbb {R}^{n+1}; \quad \sum \limits ^n_{i=0}t_i=1, \; t_i\ge 0\quad \text {for all } i\} \end{aligned}$$

denote the standard $n$-simplex. The evaluation map

$$\begin{aligned} \mathrm{ev}(X): B\Omega ' X=\left( \coprod \limits _{n\ge 0}(\Omega 'X)^n\times \Delta ^n\right) /\sim \ \longrightarrow X \end{aligned}$$

is defined by

$$\begin{aligned} \mathrm{ev}(X)((w_1,\ldots ,w_n)(t_0,\ldots ,t_n)) =(w_1+\cdots +w_n)\left( \sum \limits ^n_{i=1}t_i\cdot \sum \limits ^i_{j=1}l(w_j)\right) \end{aligned}$$

where $l(w_j)$ is the length of $w_j$.

The homotopy counit $\eta$ is the natural map

4.9. The homotopy unit: For a monoid $M$ let $EM$ denote the 2-sided bar construction $B(M,M,*)$. Then

$$\begin{aligned} z\cdot (x_0,x_1,\ldots ,x_n)=(z\cdot x_0,x_1,\ldots ,x_n) \end{aligned}$$

defines a left $M$-action on the simplicial space $B_\bullet (M,M,*)$ and hence on $EM$.

Let $P(EM)$ denote the space of Moore paths in $EM$ starting at the base-point $(e)$ in the 0-skeleton $M$ of $EM$. The endpoint projection

$$\begin{aligned} P(EM)\longrightarrow EM \end{aligned}$$

is known to be a fibration. Moreover, it is a homotopy equivalence because $P(EM)$ and $EM$ are contractible. Let $P(EM,M)$ be the pullback

where $i$ is the inclusion of the 0-skeleton, i.e. $P(EM,M)$ is the space of Moore paths in $EM$ starting at $(e)$ and ending in $M$. Then $\pi (M)$ is a fibration and a homotopy equivalence. We define a monoid structure $\oplus$ in $P(EM,M)$ by

$$\begin{aligned} w_1\oplus w_2=w_1+x\cdot w_2 \end{aligned}$$

where $+$ is the usual path addition, $x\in M$ is the endpoint of $w_1$, and $x\cdot w_2$ is the path $t\mapsto x\cdot w_2(t)$. Then $\pi (M):P(EM,M)\rightarrow M$ is a homomorphism and hence a weak equivalence of monoids.

Factoring out the operation of $M$ on $EM$ we obtain a projection

$$\begin{aligned} EM\rightarrow BM \end{aligned}$$

inducing a homomorphism

$$\begin{aligned} \rho '(M):(P(EM,M),\oplus )\longrightarrow (\Omega 'BM,+). \end{aligned}$$

Since we do not know whether or not $(P(EM,M))$ is well-pointed we apply the whiskering process to it and obtain a homomorphism

$$\begin{aligned} \rho (M): V(P(EM,M),\oplus )\xrightarrow {q((P(EM,M))} (P(EM,M),\oplus )\xrightarrow { \rho '(M)} (\Omega 'BM,+). \end{aligned}$$

The homomorphism $\sigma (M): WV(P(EM,M)\rightarrow M$ defined by

is a weak equivalence. All these constructions are functorial in $M$ and the maps between them are natural in $M$. We apply them to $WM$ rather than to $M$; in particular $\sigma (WM)$ is a homotopy equivalence in $\mathcal {M}on^{w}$.

We choose a homotopy inverse of $\sigma (WM)$ in $\mathcal {M}on^{w}$

$$\begin{aligned} \nu (WM):WM\longrightarrow WVP(EWM,WM), \end{aligned}$$

which is a natural transformation up to homotopy with respect to homomorphisms $WM\rightarrow WN$ by Lemma 3.16.

We define our homotopy unit by

which is a natural transformation up to homotopy by Lemma 3.16.

Our verification of the conditions 4.7 depends on an explicit description of an $h$-morphism $M\rightarrow \Omega 'BM$ defined by a natural homomorphism

$$\begin{aligned} \zeta '(M) :\overline{W}(M) \longrightarrow \Omega 'BM \end{aligned}$$

and the interplay of $\overline{W}(M)$ and $WM$.

We define $\zeta '(M)$ as a composite of homomorphisms

The homomorphism $\zeta (M)$ maps the element represented by $(x_0,t_1,\ldots ,x_n)$ to the path

$$\begin{aligned} v_0+v_1+\cdots +v_n \end{aligned}$$

of length $t_1+\cdots +t_n+1$ in the simplex $(e,x_0,x_1,\ldots ,x_n)\times \Delta ^{n+1}\subset EM$, where

$$\begin{aligned} v_k(s)=(e,x_0,\ldots ,x_n)\times (u_0,\ldots ,u_{n+1})\quad \text {and}\quad l(v_k)=t_{k+1} \end{aligned}$$

with

$$\begin{aligned} u_r=\left\{ \begin{array}{ll} (1-s)\cdot t_r\cdot \prod \nolimits ^k_{j=r+1}(1-t_j) &{}\quad r\le k\\ s &{}\quad r=k+1\\ 0 &{}\quad r\ge k+2 \end{array}\right. \end{aligned}$$

and the conventions that $t_0=1$ and $t_{n+1}=1$.

Observe that $+$ is the usual path addition of Moore paths in $EM$ and not the monoid structure of $P(EM,M)$.

Example: $(x_0,t_1,x_1,t_2,x_2)$ is mapped to the path $v_0+v_1+v_2$ of length $t_1+t_2+1$ given by (Fig. 1)

Fig. 1

The path $\zeta (M)(x_{0}, t_{1}, x_{1}, t_{2}, x_{2})$

4.10. By construction, $\pi (M)\circ \zeta (M)=\overline{\varepsilon }(M)$. In particular, $\zeta (M):\overline{W}M\rightarrow P(EM,M)$ is a weak equivalence of semigroups.

Remark 4.11

We will show below that $\rho '(M):P(EM,M)\rightarrow \Omega 'BM$ is a weak equivalence if $M$ is grouplike, so that $\rho '(M)\circ \zeta (M)$ is an $h$-morphism which is a weak equivalence if $M$ is grouplike. It is well-known that such an $h$-morphism exists, but to our knowledge there is no explicit description in the literature.

4.12. Consider the following diagram

where $\sigma _1(WM)=q(P(EM,M))\circ \varepsilon (VP(EM,M))$ and $f^+:G_+\rightarrow M$ is the adjoint of the homomorphism $f:G\rightarrow M$ from a semigroup into a monoid. By definition of $\nu (WM)$ and $\sigma (WM)$ the left lower triangle commutes up to homotopy in $\mathcal {M}on^{w}$ and the right lower triangle is commutative. Since

$$\begin{aligned} \pi (WM)\circ \zeta (WM)=\overline{\varepsilon }(WM)\simeq \pi (WM)\circ \sigma _1(WM)\circ \nu (WM)\circ \overline{\varepsilon }(WM) \end{aligned}$$

Proposition 2.7 implies that

$$\begin{aligned} \sigma _1(WM)\circ \nu (WM)\circ \overline{\varepsilon }(WM)\simeq \zeta (WM) \quad \text {in } {\mathcal {S}\mathrm{gp}}\end{aligned}$$

which in turn is equivalent to the saying that square I commutes up to homotopy in $\mathcal {M}on$.

We are now in the position to prove

Proposition 4.13

$\eta (BWM)\circ B\mu (WM)\simeq \mathrm{id}_{BWM}$ in ${\mathcal {T}\! op}^w$.

This result is a fairly easy consequence of

Lemma 4.14

The diagram

commutes up to homotopy.

Proof

Let $f=\mathrm{ev}(BM)\circ p(\Omega 'BM) \circ \widetilde{B}\rho '(M)\circ \widetilde{B}\zeta$ and let $g= p(M)\circ \widetilde{B}\overline{\varepsilon }(M)$. Let $z=(z_1,\ldots ,z_n)$ be an element in $(\overline{W}M )^n$, so that $z\times \Delta ^n$ is an $n$-simplex in $\widetilde{B}\overline{W}M$. If $z_j=(x_{j0},t_{j1},\ldots , x_{jr_j})$, then $f$ maps $z\times \Delta ^n$ to the image of the path $\rho '(M)\circ \zeta (z_1)+\ldots +\rho '(M)\circ \zeta (z_n)$ which lies in the simplex

$$\begin{aligned} \sigma = \sigma (z)=(x_{10},\ldots , x_{1r_1},\ldots ,x_{n0},\ldots ,x_{nr_n})\times \Delta ^{r_1+\cdots +r_n+n} \end{aligned}$$

in $BM$, while $g$ maps $z\times \Delta ^n$ identically (modulo possible degenerations) onto the simplex

$$\begin{aligned} \tau =\tau (z)=(x_{10}\cdot \ldots \cdot x_{1r_1},\ldots , x_{n0}\cdot \ldots \cdot x_{nr_n})\times \Delta ^n \end{aligned}$$

in $BM$, which is a face of $\sigma$. So $f|z\times \Delta ^n$ is homotopic to $g|z\times \Delta ^n$ by a linear homotopy. We call a homotopy from $f$ to $g$ admissible if it maps $z\times \Delta ^n$ to $\sigma (z)$ throughout the homotopy.

We are going to construct an admissible homotopy $H: \widetilde{B}\overline{W}M \times I \rightarrow BM$ from $f$ to $g$ by induction on the canonical filtration $(\widetilde{B}\overline{W}M)^{(n)}$ of $\widetilde{B}\overline{W}M$.

$(\widetilde{B}\overline{W}M)^{(0)}$ is a point, which is mapped by $f$ and $g$ to the base-point. Now suppose that we have constructed an admissible homotopy

$$\begin{aligned} H:(\widetilde{B}\overline{W}M)^{(n-1)}\times I \rightarrow BM. \end{aligned}$$

Let $z\times \Delta ^n$ be an $n$-simplex in $\widetilde{B}\overline{W}M$ as above. We define

$$\begin{aligned} q(z)=q(z_1,\ldots ,z_n)=r_1+\cdots +r_n \in \mathbb {N} \end{aligned}$$

and we extend $H$ over $(\widetilde{B}\overline{W}M)^{(n)}\times I$ by induction on $q$.

If $q=0$, then $z=(z_1,\ldots ,z_n)$ with $z_j=(x_{j0})$ for $j=1,\ldots ,n$ and $\sigma (z)=\tau (z)=(x_{10},\ldots ,x_{n0})\times \Delta ^n$. Hence the space of all $n$-simplices $z\in (\overline{W}M)^n$ with $q(z)=0$ is $M^n$. By induction, we have to find a homotopy

$$\begin{aligned} h:M^n\times \Delta ^n\times I\rightarrow M^n\times \Delta ^n \end{aligned}$$

over $M^n$ which is already determined on $M^n\times \partial (\Delta ^n\times I)$. If $b_n$ denotes the barycenter of $\Delta ^n$ we map $((x_1,\ldots ,x_n),b_n,\frac{1}{2})$ to $((x_1,\ldots ,x_n),b_n)$ and cone off.

If $q>0$ we have $q$ coordinates $t_{jk}\in I$ in $z$. So the space of all elements $z$ with $q(z)=q$ is the union of spaces of the form $M^{n+q}\times I^q$ which may intersect on their lower faces $M^{n+q}\times LI^q$ due to the relations, where $LI^q=\{(t_1,\ldots ,t_q)\in I^q; \text { some } t_i=0\}$. So possible intersections are of lower filtration. We have to find a map

$$\begin{aligned} h:M^{n+q}\times I^q\times \Delta ^n\times I\rightarrow M^{n+q}\times \Delta ^{n+q} \end{aligned}$$

over $M^{n+q}$ which is already defined on

$$\begin{aligned} M^{n+q}\times (LI^q\times \Delta ^n\times I\cup I^q\times \partial (\Delta ^n\times I)). \end{aligned}$$

Since $LI^q$ is a strong deformation retract of $I^q$, the inclusion

$$\begin{aligned} LI^q\times \Delta ^n\times I\cup I^q\times \partial (\Delta ^n\times I)\subset I^q\times \Delta ^n\times I \end{aligned}$$

is an inclusion of a strong deformation retract. Hence $h$ exists. $\square$

Proof of Proposition 4.13

Since $M$ is well-pointed, the projection $p(M):\widetilde{B}M\rightarrow BM$ is a homotopy equivalence. If $h:X\rightarrow Y$ is a weak equivalence of semigroups, then $\widetilde{B}h:\widetilde{B}X\rightarrow \widetilde{B}Y$ is a based homotopy equivalence. Hence it suffices to show that

$$\begin{aligned} \eta (BWM)\circ B\mu (WM)\circ p(WM)\circ \widetilde{B}\overline{\varepsilon }(WM) \simeq p(WM)\circ \widetilde{B}\overline{\varepsilon }(WM). \end{aligned}$$

Now

$$\begin{aligned}&\eta (BWM) \circ B\mu (WM) \circ p(WM) \circ \widetilde{B}\bar{\epsilon }(WM)\\&\quad = \mathrm{ev}(BWM) \circ B \varepsilon (\Omega 'BWM)\circ BW \rho (WM) \circ B \nu (WM) \circ p(WM) \circ \widetilde{B}\bar{\varepsilon }(WM), \end{aligned}$$

$$\begin{aligned}&\hbox {since } \eta (BWM) = \mathrm{ev}(BWM) \circ B \varepsilon (\Omega 'BWM) \hbox { and } \mu (WM)=W \rho (WM) \circ \nu (WM) ,\\&\quad = \mathrm{ev}(BWM) \circ B \varepsilon (\Omega 'BWM) \circ BW \rho (WM)\circ p(WVP(EWM,WM)) \\&\qquad \circ \widetilde{B}\nu (WM) \circ \widetilde{B}\bar{\varepsilon }(WM),\\&\hbox {by naturality of } p,\\&\quad = \mathrm{ev}(BWM) \circ B\rho (WM)\circ p(VP(EWM,WM))\circ \widetilde{B}\varepsilon (VP(EWM,WM)) \\&\qquad \circ \widetilde{B}\nu (WM) \circ \widetilde{B}\bar{\varepsilon }(WM),\\&\hbox {by naturality of }\varepsilon ,\\&\quad = \mathrm{ev}(BWM) \circ p(\Omega 'BWM)\circ \widetilde{B}\rho (WM)\\&\qquad \circ \widetilde{B}\varepsilon (VP(EWM,WM)) \circ \widetilde{B}\nu (WM) \circ \widetilde{B}\bar{\varepsilon }(WM),\\&\hbox {by naturality of }p \hbox { again},\\&\quad = \mathrm{ev}(BWM) \circ p(\Omega 'BWM)\circ \widetilde{B}\rho '(WM)\circ \widetilde{B}q(P(EWM,WM)) \\&\qquad \circ \widetilde{B}\varepsilon (VP(EWM,WM)) \circ \widetilde{B}\nu (WM) \circ \widetilde{B}\bar{\varepsilon }(WM),\\&\hbox {by the definition of }\rho (WM),\\&\quad = \mathrm{ev}(BWM) \circ p(\Omega 'BWM)\circ \widetilde{B}\rho '(WM)\circ \widetilde{B}\sigma _1(WM) \circ \widetilde{B}\nu (WM)\\&\qquad \circ \widetilde{B}\bar{\varepsilon }(WM),\\&\hbox {by the definition of } \sigma _1(WM)\hbox { from } 4.12,\\&\quad \simeq \mathrm{ev}(BWM) \circ p(\Omega 'BWM)\circ \widetilde{B}\rho '(WM) \circ \widetilde{B}\zeta (WM),\\&\hbox {by Diagram } 4.12,\\&\quad \simeq p(WM) \circ \widetilde{B}\varepsilon (WM), \end{aligned}$$

by Lemma 4.14. ${\square }$

Remark 4.15

If we use the Quillen model structure on $\mathcal {T}\! op$ rather than the Strøm structure we can construct a homotopy unit $\mu (WM)$ and deduce Proposition 4.13 fairly easily from [8, Thm. 7.3] and its proof.

The proof of the first part of 4.7 needs some preparation. Let $\mathcal {J}$ denote the category of ordered sets $[n]=\{0<1<\dots <n\}$ and order preserving injections, and let $\mathcal {J}\mathcal {T}\! op_0$ denote the category of all diagrams

$$\begin{aligned} X_\bullet : \mathcal {J}^{\mathrm{op}}\rightarrow \mathcal {T}\! op,\quad [n]\mapsto X_n \end{aligned}$$

such that $X_0$ is a single point, i.e. an object in $\mathcal {J}\mathcal {T}\! op_0$ is a reduced simplicial space without degeneracies. Of lately, such an object is called a reduced semisimplicial space. The usual fat topological realization functor

$$\begin{aligned} \mathcal {J}\mathcal {T}\! op_0 \rightarrow {\mathcal {T}\! op}^*,\quad X_\bullet \mapsto \parallel X_\bullet \parallel \end{aligned}$$

has a right adjoint, the reduced singular functor

$$\begin{aligned} \mathrm{Sing}_\bullet ^0:{\mathcal {T}\! op}^*\rightarrow \mathcal {J}\mathcal {T}\! op_0, \quad \mathrm{Sing}_n^0(Y)=\mathcal {T}\! op((\Delta ^n,\Delta ^n_0),(Y,*)) \end{aligned}$$

where $\Delta ^n_0$ is the $0$-skeleton of $\Delta ^n$. The unit of this adjunction

$$\begin{aligned} \tau _\bullet (X_\bullet ): X_\bullet \rightarrow \mathrm{Sing}_\bullet ^0\parallel X_\bullet \parallel \end{aligned}$$

sends $x\in X_n$ to the singular simplex

$$\begin{aligned} \Delta ^n\xrightarrow {i_x}\coprod _k X_k\times \Delta ^k\rightarrow \parallel X_\bullet \parallel \end{aligned}$$

where $i_x$ is the inclusion of the simplex $\{ x\}\times \Delta ^n$. The counit

$$\begin{aligned} \widehat{\mathrm{ev}}(Y): \parallel \mathrm{Sing}_\bullet ^0(Y) \parallel \rightarrow Y \end{aligned}$$

is induced by the evaluation maps $\mathrm{Sing}_n^0(Y)\times \Delta ^n\rightarrow Y$. The formula defining our evaluation map of 4.8 defines a natural semisimplicial map

$$\begin{aligned} \alpha _\bullet (Y): N_\bullet \Omega 'Y\rightarrow \mathrm{Sing}_\bullet ^0 Y \end{aligned}$$

where $N_\bullet \Omega 'Y$ is the semisimplicial nerve of $\Omega 'Y$. Let $v_0,\ldots ,v_n$ denote the vertices of $\Delta ^n$ and let $L_n\subset \Delta ^n$ denote the union of the $1$-simplexes $[v_{i-1},v_i]$, $i=1,\ldots ,n$. Then $L_n$ is a strong deformation retract of $\Delta ^n$. The composite

$$\begin{aligned} (\Omega 'Y)^n=N_n(\Omega 'Y)\xrightarrow {\alpha _n(Y)}\mathrm{Sing}_n^0(Y)\xrightarrow {r}\mathcal {T}\! op((L_n,\Delta ^n_0),(Y,*))=(\Omega Y)^n, \end{aligned}$$

where $r$ is the restriction to $L_n$, is the map normalizing the loop lengths to $1$. In particular, $\alpha _n(Y)$ is a homotopy equivalence inducing a homotopy equivalence $\parallel \alpha _\bullet (Y)\parallel$. Moreover, the diagram

4.16.

commutes.

Proposition 4.17

• 1. If $M$ is a grouplike well-pointed monoid, then $\rho '(M):P(EM,M)\rightarrow \Omega 'BM$ and hence $\mu (WM): WM\rightarrow W\Omega 'BWM$ are weak equivalences.

• 2. If $Y$ is a well-pointed path-connected Dold space (see Definition 1.7), then $\mathrm{ev}(Y): B\Omega 'Y \rightarrow Y$ is a based homotopy equivalence, and, hence so is

  $$\begin{aligned} \eta (Y) :BW\Omega 'Y\xrightarrow {B\varepsilon (\Omega 'Y)} B\Omega 'Y\xrightarrow {\mathrm{ev}(Y)} Y. \end{aligned}$$

• 3. If $Y$ is a well-pointed space, then $\Omega '\mathrm{ev}(Y): \Omega 'B\Omega 'Y \rightarrow \Omega ' Y$ is a weak equivalence. Hence so is $\Omega '\eta (Y):\Omega 'BW\Omega 'Y\rightarrow \Omega 'Y$.

• 4. If $M$ is a well-pointed monoid, then $B\mu (WM): BWM\rightarrow BW\Omega 'BWM$ is a homotopy equivalence.

Proof

• 1. The diagram

  

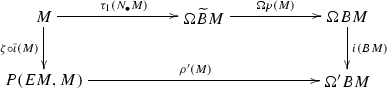
  commutes. Here $i(X):\Omega X\rightarrow \Omega 'X$ is the inclusion and $\bar{\iota } (M):M\rightarrow \overline{W}M$ the section (see 2.2). It is well known that $\tau _1(N_\bullet M)$ is a homotopy equivalence if $M$ is grouplike (e.g. see [21]). Since $p(M),\ i(BM)$, and $\zeta \circ \bar{\iota }(M)$ are homotopy equivalences in $\mathcal {T}\! op$, so is $\rho '(M)$.

• 2. In the commutative diagram 4.16 the map $p(\Omega 'Y)$ is a homotopy equivalence because $\Omega 'Y$ is well-pointed and $\widehat{\mathrm{ev}}(Y)$ is a homotopy equivalence by [20, Prop. 5.6].

• 3. Consider the following commutative diagram in $\mathcal {J}\mathcal {T}\! op_0$

  

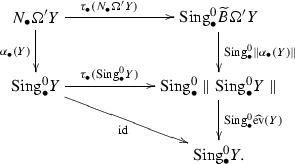
  Restricting this diagram to degree $0$ we obtain a commutative diagram of spaces

  

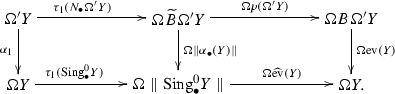
  Since $\Omega 'Y$ is grouplike, $\tau _1(N_\bullet \Omega 'Y)$ is a homotopy equivalence. Since $Y$ and hence $\Omega 'Y$ is well-pointed, $\Omega p(\Omega 'Y)$ is a homotopy equivalence. Since $\alpha _1$ and $\parallel \alpha _\bullet (Y)\parallel$ are homotopy equivalences, $\tau _1(\mathrm{Sing}_\bullet ^0Y)$ is one. Hence so is $\Omega \widehat{\mathrm{ev}}(Y)$ and hence also $\Omega \mathrm{ev}(Y)$, which implies the result.

• 4. Since $BWM$ is a well-pointed path-connected Dold space by [20, Cor. 5.2] the statement follows from Part (2) and Proposition 4.13.

$\square$

Proposition 4.18

$W\Omega '\eta (X)\circ \mu (W\Omega 'X)\simeq \mathrm{id}_{W\Omega 'X}$ in $\mathcal {M}on$.

Proof

It follows from Proposition 4.13 and the homotopy naturality of $\mu$ and $\eta$ that the following diagram commutes up to homotopy.

We obtain

$$\begin{aligned} W\Omega '\eta (X)\circ \mu (W\Omega 'X)\circ W\Omega '\eta (X) \circ \mu (W\Omega 'X)\simeq W\Omega '\eta (X)\circ \mu (W\Omega 'X). \end{aligned}$$

Since $\Omega 'X$ is grouplike $\mu (W\Omega 'X)$ and $W\Omega '\eta (X)$ are weak equivalences by Proposition 4.17. By Proposition 2.12 both homomorphisms have homotopy inverses in $\mathcal {M}on$ so that

$$\begin{aligned} W\Omega '\eta (X)\circ \mu (W\Omega 'X)\simeq \mathrm{id}_{W\Omega 'X} \end{aligned}$$

in $\mathcal {M}on$. $\square$

5 Immediate consequences

5.1 The James construction:

The underlying space functor $U:(\mathcal {M}on,\mathcal {M}on^{w})\rightarrow ({\mathcal {T}\! op}^*,{\mathcal {T}\! op}^w)$ has a left adjoint

$$\begin{aligned} J:({\mathcal {T}\! op}^*,{\mathcal {T}\! op}^w)\rightarrow (\mathcal {M}on,\mathcal {M}on^{w}) \end{aligned}$$

commonly called the James construction, which associates with each based space $X$ the free based topological monoid on $X$.

Proposition 5.1

(James [13]) For each path-connected based space there is a weak homotopy equivalence of spaces

$$\begin{aligned} JX\simeq \Omega \Sigma X. \end{aligned}$$

D. Puppe investigated the conditions which would imply for this weak homotopy equivalence to be a genuine homotopy equivalence.

Proposition 5.2

(Puppe [25]) If $X$ is a well-pointed path-connected Dold space then there is a homotopy equivalence

$$\begin{aligned} JX\simeq \Omega \Sigma X. \end{aligned}$$

Consider the diagram of functors

All functors preserve weak equivalences. Hence they induce a diagram

consisting of adjoint pairs. Since the Moore loop space functor is naturally homotopy equivalent to the usual loop space functor there is a natural transformation

$$\begin{aligned} \tau (X):U\circ \Omega '(X)\rightarrow \Omega (X) \end{aligned}$$

which is a homotopy equivalence. Hence ${\mathrm{Ho}}\Omega$ and ${\mathrm{Ho}}U\circ {\mathrm{Ho}}\Omega '$ are naturally isomorphic. Since their left adjoints are unique up to natural isomorphisms this implies that ${\mathrm{Ho}}B\circ {\mathrm{Ho}}J$ and ${\mathrm{Ho}}\Sigma$ are naturally isomorphic. We obtain

Proposition 5.3

For each $X\in {\mathcal {T}\! op}^w$ there is a homotopy equivalence

$$\begin{aligned} BJ(X)\simeq \Sigma (X) \end{aligned}$$

natural up to homotopy. $\square$

We obtain Puppe’s result by combining 5.3 with another well-known result:

Proposition 5.4

If $M$ is a well-pointed monoid whose underlying space is a Dold space and $\pi _0(M)$ is a group, then $M$ is grouplike [25, (12.7)].

Proof of 5.2

If $X$ is a path-connected Dold space, so is $JX$. Hence $JX$ is grouplike and $\mu (WJX): WJX\rightarrow W\Omega 'BWJX$ is a weak equivalence by 4.17, so that $\Omega 'B\varepsilon (JX)\circ \varepsilon (\Omega 'BJX)\circ \mu (WJX)\circ \iota (JX) :JX\rightarrow \Omega 'BJX$ is a homotopy equivalence. We have a sequence of homotopy equivalences

$$\begin{aligned} JX\simeq \Omega 'BJX\simeq \Omega BJX\simeq \Omega \Sigma X. \end{aligned}$$

Homotopical group completion:

Homotopical group completion is the replacement of a monoid by a grouplike one having a universal property. We state our result for the full subcategory ${\mathrm{Ho}}\mathcal {M}on^{w}$ of ${\mathrm{Ho}}\mathcal {M}on$ of well-pointed monoids. Since $q(M):VM\rightarrow M$ is a weak equivalence, ${\mathrm{Ho}}\mathcal {M}on^{w}$ is equivalent to ${\mathrm{Ho}}\mathcal {M}on$ so that the corresponding statement for ${\mathrm{Ho}}\mathcal {M}on$ follows.

Proposition 5.5

Let $M$ be a well-pointed monoid. The homotopy class of the homomorphism $\mu (WM):WM\rightarrow W\Omega 'BWM$, considered as a morphism in ${\mathrm{Ho}}\mathcal {M}on^{w}(M, \Omega 'BWM)$, is a group completion in the following sense: given a diagram

in ${\mathrm{Ho}}\mathcal {M}on^{w}$ with $N$ grouplike, there exists a unique morphism $[\overline{g}]:\Omega 'BWM\rightarrow N$ making the diagram commute.

Proof

Consider the homotopy commutative diagram in $\mathcal {M}on^{w}$

Since $N$ is well-pointed and grouplike $\mu (WN)$ is homotopy invertible in $\mathcal {M}on^{w}$ by 4.17. We choose a homotopy inverse $h:W\Omega 'BWN\rightarrow WN$ and define $\overline{g}=h\circ W\Omega 'Bg$. Then $\overline{g}\circ \mu (WM)\simeq g$ in $\mathcal {M}on^{w}$.

For the uniqueness of $[\overline{g}]$ suppose there is a homomorphism $g': W\Omega 'BM \longrightarrow WN$ such that $h \circ \mu (WM)\simeq g$. Put $j_1=\mu (WN)\circ g'$ and $j_2=W\Omega 'Bg$. It suffices to show that $j_1\simeq j_2$ in $\mathcal {M}on^{w}$. Since $Bj_1\circ B\mu (WM)\simeq \mu (WN)\circ Bg\simeq Bj_2\circ B\mu (WM)$ and $B\mu (WM)$ is a homotopy equivalence by 4.17, we obtain $Bj_1\simeq Bj_2$. Since $\mu (W\Omega 'BM)$ and $\mu (W\Omega 'BN)$ are homotopy equivalences in $\mathcal {M}on^{w}$ by 4.17 and $\mu$ is natural up to homotopy the following diagram is homotopy commutative and establishes the result:

$\square$

5.2 Dold spaces and grouplike monoids

For details on Dold spaces see [20]. We restrict our attention to the well-pointed case. Using the whiskering process it is easy to extend our results to the general case.

Let ${\mathcal {T}\! op}^w_{Dold}\subset {\mathcal {T}\! op}^w$ denote the full subcategory of well-pointed path-connected Dold spaces. Since $BM$ is in ${\mathcal {T}\! op}^w_{Dold}$ for any well-pointed monoid by [20, Cor. 5.2], the classifying space functor restricts to a functor

$$\begin{aligned} B:\mathcal {M}on^{w}\rightarrow {\mathcal {T}\! op}^w_{Dold}. \end{aligned}$$

Let $\mathcal {M}on^{w}_{group}\subset \mathcal {M}on^{w}$ denote the full subcategory of grouplike well-pointed monoids. Then Proposition 4.17 implies

Theorem 5.6

The functors

$$\begin{aligned} B^{w{\mathcal {H}}}:\mathcal {H}\mathcal {M}on^{w}_{group}\leftrightarrows \mathcal {H}{\mathcal {T}\! op}^w_{Dold}:\Omega '^{w{\mathcal {H}}}\end{aligned}$$

define an equivalence up to homotopy of categories, i.e. the natural transformations up to homotopy $\mu : \mathrm{Id}\rightarrow \Omega '^{w{\mathcal {H}}}\circ B^{w{\mathcal {H}}}$ and $\eta : B^{w{\mathcal {H}}}\circ \Omega '^{w{\mathcal {H}}}\rightarrow \mathrm{Id}$ take values in homotopy equivalences. In particular,

$$\begin{aligned} {\mathrm{Ho}}B:{\mathrm{Ho}}\mathcal {M}on^{w}_{group}\leftrightarrows {\mathrm{Ho}}{\mathcal {T}\! op}^w_{Dold}:{\mathrm{Ho}}\Omega ' \end{aligned}$$

define an equivalence of categories. ${\square }$

The second part is a slight extension of a well-known result (e.g. see [3, Section 4]).

The following two propositions extend and strengthen results of Fuchs [9, Satz 7.7].

The diagram

commutes up to homotopy because by 4.13,

$$\begin{aligned} (\lambda (WM,BWN)\circ \mu (WN)_*)(f)&= \eta (BWN)\circ B' \circ \mu (WN)_*)(f)\\&= \eta (BWN)\circ B\mu (WN)\circ Bf\\&\simeq Bf \;\text {continuously in } f \end{aligned}$$

with $B': \mathcal {M}on^{w}(WM,W\Omega 'BWN)\rightarrow {\mathcal {T}\! op}^w(BWM,BW\Omega 'BWN)$. If $N$ is grouplike $\mu (WN)$ is a homotopy equivalence in $\mathcal {M}on^{w}$, and we obtain

Proposition 5.7

If $N$ is a well-pointed grouplike monoid then

$$\begin{aligned} B: \mathcal {M}on^{w}(WM,WN)\rightarrow {\mathcal {T}\! op}^w(BWM,BWN) \end{aligned}$$

is a homotopy equivalence. ${\square }$

Since $\eta (X):BW\Omega 'X\rightarrow X$ is a natural transformation the following diagram commutes

Since $W\Omega 'Y$ is grouplike the map $B$ is a homotopy equivalence by 5.7. Since $\eta (Y)_*\circ B=\lambda (W\Omega 'X,Y)$ the map $\eta (Y)_*: {\mathcal {T}\! op}^w(BW\Omega 'X,BW\Omega 'Y)\rightarrow {\mathcal {T}\! op}^w(BW\Omega 'X,Y)$ is a homotopy equivalence. If $X$ is a well-pointed path-connected Dold space $\eta (X)$ is a based homotopy equivalence by 4.17. We obtain

Proposition 5.8

If $X$ is a well-pointed path-connected Dold space then $W\Omega ': {\mathcal {T}\! op}^w(X,Y)\rightarrow \mathcal {M}on^{w}(W\Omega 'X,W\Omega 'Y)$ is a homotopy equivalence. ${\square }$

5.3 Homotopy homomorphisms and unitary homotopy homomorphisms

Proposition 5.9

Let $M$ and $N$ be well-pointed monoids and $N$ be grouplike. Then $\varepsilon '(M):\overline{W}M\rightarrow WM$ induces a homotopy equivalence

$$\begin{aligned} \mathcal {M}on(WM,N)\rightarrow {\mathcal {S}\mathrm{gp}}(\overline{W}M,N). \end{aligned}$$

Proof

By 2.7 we may replace $N$ by $WN$. Since ${\mathcal {S}\mathrm{gp}}(\overline{W}M,WN)$ is naturally homeomorphic to $\mathcal {M}on(W(M_+),WN)$ by 2.5 it suffices to show that the counit $\kappa (M):M_+\rightarrow M$ induces a homotopy equivalence

$$\begin{aligned} \kappa (M)^*: \mathcal {M}on(WM,WN)\rightarrow \mathcal {M}on(W(M_+),WN) \end{aligned}$$

The diagram

commutes. By 5.7 the maps $B$ are homotopy equivalences, and by 4.2 the map $B\kappa (M)^*$ is a homotopy equivalence. Hence so is $\kappa (M)^*$. $\square$

Remark 5.10

In general we cannot expect that $\varepsilon '(M):\overline{W}M\rightarrow WM$ induces a homotopy equivalence. E.g. it can happen that a homomorphism $\overline{W}M\rightarrow N$ does not map $(e_M)$ into the path-component of $e_N$ so that there is no chance to homotop it into a homomorphism $WM\rightarrow N$.

Proposition 5.11

If $M$ is a well-pointed monoid then $Wq(M):WVM\rightarrow WM$ is a homotopy equivalence in $\mathcal {M}on^{w}$ by 2.12 inducing a homotopy equivalence

$$\begin{aligned} \mathcal {M}on(WM,N)\rightarrow \mathcal {M}on(WVM,N). \end{aligned}$$

6 Diagrams of monoids

We want to show that the homotopy adjunction of Theorem 4.5 lifts to diagram categories. This is not evident: since the unit of our homotopy adjunction is only natural up to homotopy it does not lift to diagrams.

Let $\mathcal {M}$ be a cocomplete $\mathcal {T}\! op$-enriched tensored category with a class $\fancyscript{W}$ of weak equivalences containing the homotopy equivalences. We assume that $\mathcal {M}$ has a strong cofibrant replacement functor $(Q_M,\varepsilon _M)$. We use $\otimes$ for the tensor in $\mathcal {M}$ and $Q$ for $Q_M$ as long as there is no ambiguity.

Definition 6.1

Let $\mathcal {C}$ be a small indexing category. A morphism $f:D_1\rightarrow D_2$ of $\mathcal {C}$-diagrams in $\mathcal {M}$ is called a weak equivalence if it is objectwise a weak equivalence in $\mathcal {M}$. We denote the class of weak equivalences in $\mathcal {M}^\mathcal {C}$ by $\fancyscript{W}^\mathcal {C}$.

Our first aim is to show that $\mathcal {M}^{\mathcal {C}}$ admits a strong cofibrant replacement functor in order to make additional applications of Proposition 3.4. Therefore we proceed as in 2.7 and 2.2.

We define a $\mathcal {C}\times \mathcal {C}^{\mathrm{op}}$-diagram $B(\mathcal {C},\mathcal {C},\mathcal {C})$ in $\mathcal {T}\! op$ as follows:

$$\begin{aligned} B(\mathcal {C},\mathcal {C},\mathcal {C})(b,a)=B(\mathcal {C}(-,b),\mathcal {C},\mathcal {C}(a,-)) \end{aligned}$$

where the right side is the 2-sided bar construction of 4.1.

The $\mathcal {C}\times \mathcal {C}^{\mathrm{op}}$ structure on $B_n(\mathcal {C},\mathcal {C},\mathcal {C})$ is given by

$$\begin{aligned} (g, h)\cdot (f_0,\ldots ,f_{n+1})=(g\circ f_0, f_1,\ldots , f_n, f_{n+1}\circ h) \end{aligned}$$

Analogously we define a $\mathcal {C}^{\mathrm{op}}$-diagram $B(*,\mathcal {C},\mathcal {C})$ in $\mathcal {T}\! op$, where $*$ denotes the constant $\mathcal {C}^{\mathrm{op}}$-diagram on a single point.

Lemma 6.2

Let $X$ and $Y$ be $\mathcal {C}\times \mathcal {C}^{\mathrm{op}}$-diagrams in $\mathcal {T}\! op$, let $p:X\rightarrow Y$ be a map of diagrams which is objectwise a homotopy equivalence. Then $p$ induces a homotopy equivalence

$$\begin{aligned} p_*:\mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}),X)\rightarrow \mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}),Y) \end{aligned}$$

in $\mathcal {T}\! op$.

Proof

We apply the HELP-Lemma. So given a diagram

which commutes up to a homotopy $\bar{h}_{K,t}:\bar{g}\circ i\simeq p_*\circ \bar{f}_K$, where $i$ is a closed cofibration, we have to construct extensions

$$\begin{aligned} \bar{f}: L&\rightarrow \mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}),X)\\ \bar{h}_t: L&\rightarrow \mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}),Y) \end{aligned}$$

of $\bar{f}_K$ respectively $\bar{h}_{K,t}$ such that $\bar{h}_t: \bar{g}\simeq p_*\circ \bar{f}$.

Taking adjoints the above diagram translates to the following diagram of $\mathcal {C}\times \mathcal {C}^{\mathrm{op}}$-spaces

which commutes up to a homotopy $h'_t:g\circ (i\times \mathrm{id})\simeq p\circ f'$ in $\mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}$, and it suffices to construct extensions $f: L\times B(\mathcal {C},\mathcal {C},\mathcal {C})\rightarrow X$ of $f'$ and $h_t:L\times B(\mathcal {C},\mathcal {C},\mathcal {C})\rightarrow Y$ of $h'_t$ such that $h_t: g\simeq p \circ f$ in $\mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}$.

We construct these extensions by induction on the natural filtration $F_n$ of $L\times B(\mathcal {C},\mathcal {C},\mathcal {C})$ induced by the realization of the simplicial set $B_\bullet (\mathcal {C},\mathcal {C},\mathcal {C})$. We start with $F_0=\coprod _{a,b,c} L\times \mathcal {C}(c,b)\times \mathcal {C}(a,c)$. The diagram

commutes up to a homotopy given by $h_t'$. Since $p: X(c,c)\rightarrow Y(c,c)$ is a homotopy equivalence and $K\rightarrow L$ is a closed cofibration the required extensions exist by the HELP-Lemma. We extend $f$ over all of $F_0$ by $f(l,j_0,j_1)=X(j_0,j_1)\circ f(l,\mathrm{id},\mathrm{id})$ and analogously for $h_t$.

Now suppose that $f$ and $h_t$ have been defined on $F_{n-1}$. We obtain $F_n$ from $F_{n-1}$ by attaching spaces $L\times (j_0,\ldots ,j_{n+1})\times \Delta ^n$ along $L\times (j_0,\ldots ,j_{n+1})\times \partial \Delta ^n$. Here the $j_k$ are morphisms in $\mathcal {C}$ such that the composition

$$\begin{aligned} j_0\circ \ldots j_{n+1}:a\rightarrow c_n\rightarrow \ldots \ c_0\rightarrow b \end{aligned}$$

is defined and $j_1,\ldots , j_n$ are not identities. Hence the extension $f$ and the homotopy $h_t$ are already defined on

$$\begin{aligned}&D(L\times (j_0,j_1,\ldots ,j_n,j_{n+1})\times \Delta ^n)\\&\quad = K\times (j_0,j_1,\ldots ,j_n,j_{n+1})\times \Delta ^n \cup L\times (j_0,j_1,\ldots ,j_n,j_{n+1})\times \partial \Delta ^n. \end{aligned}$$

We apply the HELP-Lemma to the homotopy commutative diagram

where $f''$ and the commuting homotopy are given by the already defined extensions. Since ${p}$ is objectwise a homotopy equivalence and the inclusion

$$\begin{aligned} D(L\times (\mathrm{id}_{c_0},j_1,\ldots ,j_n,\mathrm{id}_{c_n})\times \Delta ^n)\subset L\times (\mathrm{id}_{c_0},j_1,\ldots ,j_n,\mathrm{id}_{c_n})\times \Delta ^n \end{aligned}$$

is a closed cofibration the required extensions exist. We extend our maps to maps of diagrams as in the $F_0$-case. $\square$

Let $D$ be a $\mathcal {C}$-diagram in $\mathcal {M}$ and $X$ a $\mathcal {C}^{\mathrm{op}}$-diagram in $\mathcal {T}\! op$. We define $X\otimes _\mathcal {C} D$ to be the coequalizer in $\mathcal {M}$ of

where for $f:a\rightarrow b$ in $\mathcal {C}$ the $f$-summand $X(b)\otimes D(a)$ is mapped as follows

$$\begin{aligned} \alpha&= X(f)\otimes \mathrm{id}: X(b)\otimes D(a) \longrightarrow X(a)\otimes D(a)\\ \beta&= \mathrm{id}\otimes D(f): X(b)\otimes D(a) \longrightarrow X(b)\otimes D(b) \end{aligned}$$

We define a functor

$$\begin{aligned} R:\mathcal {M}^{\mathcal {C}}\rightarrow \mathcal {M}^{\mathcal {C}},\quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} QD \end{aligned}$$

where $B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C}D$ is the $\mathcal {C}$-diagram

$$\begin{aligned} a\mapsto B(\mathcal {C}(-,a),\mathcal {C},\mathcal {C})\otimes _\mathcal {C} D \end{aligned}$$

in $\mathcal {M}$.

Proposition 6.3

Let $D_0,\ D_1$, and $D_2$ be $\mathcal {C}$ diagrams in $\mathcal {M}$, let $p:D_1\rightarrow D_2$ be a weak equivalence in $\mathcal {M}^{\mathcal {C}}$ and $q:A_1\rightarrow A_2$ a weak equivalence in $\mathcal {M}$. Then $p$ and $q$ induce homotopy equivalences

$$\begin{aligned} p_*:\mathcal {M}^{\mathcal {C}}(R D_0,D_1)&\rightarrow \mathcal {M}^{\mathcal {C}}(R D_0,D_2)\\ q_*: \mathcal {M}(B(*,\mathcal {C},\mathcal {C})\otimes _\mathcal {C}QD_0, A_1)&\rightarrow \mathcal {M}(B(*,\mathcal {C},\mathcal {C})\otimes _\mathcal {C}QD_0, A_2) \end{aligned}$$

in $\mathcal {T}\! op$.

Proof

Since $\mathcal {M}^{\mathcal {C}}(R D_0,D_i)\cong \mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}), \mathcal {M}(QD_0,D_i))$ it follows from Lemma 6.2 with $X(b,a)=\mathcal {M}(QD_0(a),D_1(b))$ and $Y(b,a)=\mathcal {M}(QD_0(a),D_2(b))$ that $p_*$ is a homotopy equivalence.

There is a sequence of natural homeomorphisms

$$\begin{aligned} \mathcal {M}(B(*,\mathcal {C},\mathcal {C})\otimes _\mathcal {C}QD_0, A_i)&\cong \mathcal {T}\! op^{\mathcal {C}^{\mathrm{op}}}(B(*,\mathcal {C},\mathcal {C}),\mathcal {M}(QD_0,A_i)\\&\cong \mathcal {T}\! op^{\mathcal {C}^{\mathrm{op}}}(\mathrm{colim}_{\mathcal {C}} B(\mathcal {C},\mathcal {C},\mathcal {C}),\mathcal {M}(QD_0,A_i)\\&\cong \mathcal {T}\! op^{\mathcal {C}\times \mathcal {C}^{\mathrm{op}}}(B(\mathcal {C},\mathcal {C},\mathcal {C}),\mathcal {M}(QD_0,\text {const}A_i) \end{aligned}$$

where $\text {const}A_i$ are the constant $\mathcal {C}$-diagrams on $A_i$. As in the first part, it follows that $q_*$ is a homotopy equivalence. $\square$

Let $\mathcal {C}_\bullet$ denote the $\mathcal {C}\times \mathcal {C}^{\mathrm{op}}$-diagram of simplical sets sending $(b,a)$ to the constant simplicial set $\mathcal {C}(a,b)$. The maps

$$\begin{aligned} \delta _n: B_n(\mathcal {C},\mathcal {C},\mathcal {C}) (b,a)=B_n(\mathcal {C}(-,b),\mathcal {C},\mathcal {C}(a,-))&\longrightarrow \mathcal {C}(a,b)\\ (f_0,\ldots ,f_{n+1})&\longmapsto f_0\circ \ldots \circ f_{n+1} \end{aligned}$$

define a simplicial map $B_\bullet (\mathcal {C},\mathcal {C},\mathcal {C})\rightarrow \mathcal {C}_\bullet$. Let $\delta :B(\mathcal {C},\mathcal {C}, \mathcal {C})\rightarrow \mathcal {C}$ be its realization.

Proposition 6.4

$\delta (D)=\delta \otimes _\mathcal {C}\mathrm{id}_D:B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C}D\rightarrow \mathcal {C} \otimes _\mathcal {C}D\cong D$ is objectwise a homotopy equivalence in $\mathcal {M}$ and hence a weak equivalence in $\mathcal {M}^{\mathcal {C}}$.

The proposition is an immediate consequence of the following Lemma:

Lemma 6.5

For each object $b\in \mathcal {C}$ the map $\varepsilon : B(\mathcal {C},\mathcal {C},\mathcal {C})(-,b)\rightarrow \mathcal {C}(-,b)$ is a homotopy equivalence in the category $\mathcal {T}\! op^{\mathcal {C}^{\mathrm{op}}}$.

Proof

For $a\in \mathcal {C}$ let $\mathcal {X}_a$ denote the category whose objects are diagrams $a\xrightarrow {j_1} c\xrightarrow {j_0} b$ and whose morphisms from this object to $a\xrightarrow {j'_1} c'\xrightarrow {j'_0} b$ are morphisms $h:c\rightarrow c'$ in $\mathcal {C}$ making the diagram

commute. Let $\mathcal {C}(a,b)$ stand for the discrete category whose object set is $\mathcal {C}(a,b)$. Then

$$\begin{aligned} \varepsilon _a: \mathcal {X}_a\rightarrow \mathcal {C}(a,b),\quad (a\xrightarrow {j_1} c\xrightarrow {j_0} b)\mapsto (j_0\circ j_1:a\rightarrow b) \end{aligned}$$

defines a functor which has the section

$$\begin{aligned} s_a:\mathcal {C}(a,b)\rightarrow \mathcal {X}_a,\quad j\mapsto (a\xrightarrow {j} b\xrightarrow {\mathrm{id}} b). \end{aligned}$$

There is a natural transformation $\tau _a:\mathrm{Id}_{\mathcal {X}_a}\rightarrow s_a\circ \varepsilon _a$ defined by the diagram

So $\varepsilon _a$ induces a homotopy equivalence of the classifying spaces. Now $B(\mathcal {X}_a)=B(\mathcal {C},\mathcal {C},\mathcal {C}(a,b))$ and $B(\mathcal {C}(a,b))=\mathcal {C}(a,b)$. Moreover all data are natural with respect to $a\in \mathcal {C}^{\mathrm{op}}$. Hence we obtain the required result. $\square$

When we combine 6.3 and 6.4 we obtain the following corollary.

Corollary 6.6

$R:\mathcal {M}^{\mathcal {C}}\rightarrow \mathcal {M}^{\mathcal {C}}$ together with $\epsilon =\delta \otimes _{\mathcal {C}}\varepsilon _M: R\rightarrow \mathrm{Id}$ is a strong cofibrant replacement functor.

Let $\mathcal {N}$ be another cocomplete $\mathcal {T}\! op$-enriched tensored category with a class of weak equivalences containing the homotopy equivalences and a strong cofibrant replacement functor $(Q_N,\varepsilon _N)$.

Theorem 6.7

Let

$$\begin{aligned} F:\mathcal {M}\leftrightarrows \mathcal {N}:G \end{aligned}$$

be continuous functors inducing a natural homotopy equivalence

$$\begin{aligned} \lambda (Q_MA,Q_NX): \mathcal {M}(Q_MA,Q_MGQ_NX)\rightarrow \mathcal {N}(Q_NFQ_MA,Q_NX) \end{aligned}$$

so that

$$\begin{aligned} F^{\mathcal {H}}:\mathcal {H}\mathcal {M}\leftrightarrows \mathcal {H}\mathcal {N}:G^{\mathcal {H}} \end{aligned}$$

is a conatural adjunction up to homotopy. Then

$$\begin{aligned} (F^{\mathcal {C}})^{\mathcal {H}}: \mathcal {H}(\mathcal {M}^{\mathcal {C}})\leftrightarrows \mathcal {H}(\mathcal {N}^{\mathcal {C}}):(G^{\mathcal {C}})^{\mathcal {H}} \end{aligned}$$

is an adjunction up to homotopy, and hence

$$\begin{aligned} {\mathrm{Ho}}(F^{\mathcal {C}}):{\mathrm{Ho}}(\mathcal {M}^{\mathcal {C}}) \leftrightarrows {\mathrm{Ho}}(\mathcal {N}^{\mathcal {C}}):{\mathrm{Ho}}(G^{\mathcal {C}}) \end{aligned}$$

a genuine adjunction.

Proof

For diagrams $D:\mathcal {C}\rightarrow \mathcal {M}$ and $Z:\mathcal {C}\rightarrow \mathcal {N}$ we have a sequence of natural maps

By assumption $\lambda (Q_MD,Q_NZ)$ is a homotopy equivalence. Since $\delta (D)$ is objectwise a homotopy equivalence and since continuous functors preserve homotopy equivalences, $R_MG\delta (Q_NZ)$ and $R_NF\delta (Q_MD)$ are homotopy equivalences in $\mathcal {M}^{\mathcal {C}}$ by 6.3 so that $R_MG\delta (Q_NZ)_*$ and $R_NF\delta (Q_MD)^*$ are homotopy equivalences in $\mathcal {T}\! op$, and $\delta (Q_NZ)_*$ and $\delta (Q_MGQ_NZ)_*$ are homotopy equivalences in $\mathcal {T}\! op$ by 6.3. $\square$

6.8. Addendum: The last natural map in the proof of the theorem points in the wrong direction. So we cannot conclude that $(F^{\mathcal {C}})^{\mathcal {H}}$ and $(G^{\mathcal {C}})^{\mathcal {H}}$ are a conatural homotopy adjoint pair.

$$\begin{aligned} \eta (Q_NY)=\lambda (Q_MGQ_NY,Q_NY)(\mathrm{id}_{Q_MGQ_NY}):Q_NFQ_MGQ_NY\rightarrow Q_NY \end{aligned}$$

is natural with respect to morphisms $f:Q_NY_1\rightarrow Q_NY_2$ in $\mathcal {N}$. If $\eta$ extends to a natural map $\eta (Y):Q_NFQ_MGY\rightarrow Y$ for all $Y\in \mathcal {N}$ or at least for all $Y$ of the form $Y=R_NY'$ we obtain a natural map $\lambda ^{\mathcal {C}}(R_MD,R_NZ)$ defined by

which makes the diagram of the proof of the theorem commute so that $(F^{\mathcal {C}})^{\mathcal {H}}$ and $(G^{\mathcal {C}})^{\mathcal {H}}$ are a conatural homotopy adjoint pair.

For use in the next proposition we note

Lemma 6.9

Let $D: \mathcal {C}\rightarrow \mathcal {M}on^{w}$ be a diagram of well-pointed monoids. Then $B(*,\mathcal {C},\mathcal {C})\otimes _\mathcal {C} D$ is a well-pointed space, and $B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} D$ and $B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} WD$ are diagrams of well-pointed monoids.

Proof

The first part holds by [17, Prop. 7.8]. The second and third statement follow by the argument used in [17, Prop. 7.8]. $\square$

From 6.6 and 6.9 we obtain

Proposition 6.10

With the choices of weak equivalences $\fancyscript{W}$ as in 3.8 the functors

$$\begin{aligned} \begin{array}{rcll} \mathcal {M}on^{\mathcal {C}}&{} \rightarrow &{} \mathcal {M}on^{\mathcal {C}}&{}\quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} WVD\\ ( \mathcal {M}on^{w})^{\mathcal {C}}&{}\rightarrow &{}( \mathcal {M}on^{w})^{\mathcal {C}}&{} \quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} WD\\ {\mathcal {S}\mathrm{gp}}^{\mathcal {C}} &{} \rightarrow &{} {\mathcal {S}\mathrm{gp}}^{\mathcal {C}} &{}\quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})\otimes _\mathcal {C} \overline{W}D\\ ({\mathcal {T}\! op}^*)^{\mathcal {C}} &{} \rightarrow &{} ({\mathcal {T}\! op}^*)^{\mathcal {C}} &{}\quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})_+\wedge _\mathcal {C} V^tD\\ ({\mathcal {T}\! op}^w)^{\mathcal {C}} &{} \rightarrow &{} ({\mathcal {T}\! op}^w)^{\mathcal {C}} &{}\quad D\mapsto B(\mathcal {C},\mathcal {C},\mathcal {C})_+\wedge _\mathcal {C} D \end{array} \end{aligned}$$

together with the corresponding natural transformations $\epsilon$ are strong cofibrant replacement functors with respect to the weak equivalences in $\fancyscript{W}^{\mathcal {C}}$. In particular, the localizations of these categories with respect to $\fancyscript{W}^{\mathcal {C}}$ exist. (Recall that $K_+\wedge X$ is the tensor over $\mathcal {T}\! op$ in ${\mathcal {T}\! op}^*$.)

Since Addendum 6.8 applies to our situation in Sect. 4 we obtain

Theorem 6.11

The homotopy adjunctions of Theorems 4.4 and 4.5 lift to conatural homotopy adjunctions

and

There are natural adjunction homotopy equivalences

$$\begin{aligned} \lambda (RD,QZ):(\mathcal {M}on^{w})^{\mathcal {C}}(RD,R\Omega 'QZ)&\rightarrow ({\mathcal {T}\! op}^w)^{\mathcal {C}}(QBRD,QZ)\\ \lambda (RVD,QV^tZ):\mathcal {M}on^{\mathcal {C}}(RVD,RV\Omega 'QV^tZ)&\rightarrow {{\mathcal {T}\! op}^*}^{\mathcal {C}}(QV^tBRVD,QV^tZ) \end{aligned}$$

in $\mathcal {T}\! op$, where $(R,\epsilon )$ and $(Q,\epsilon ^t)$ are the cofibrant replacement functors in $(\mathcal {M}on^{w})^{\mathcal {C}}$ respectively $({\mathcal {T}\! op}^w)^{\mathcal {C}}$ of 6.10. Hence

$$\begin{aligned} {\mathrm{Ho}}B^{\mathcal {C}}: {\mathrm{Ho}}(\mathcal {M}on^{w})^{\mathcal {C}}\leftrightarrows {\mathrm{Ho}}({\mathcal {T}\! op}^w)^{\mathcal {C}}:{\mathrm{Ho}}\Omega '^{\mathcal {C}} \end{aligned}$$

and

$$\begin{aligned} {\mathrm{Ho}}B^{\mathcal {C}}: {\mathrm{Ho}}(\mathcal {M}on)^{\mathcal {C}}\leftrightarrows {\mathrm{Ho}}({\mathcal {T}\! op}^*)^{\mathcal {C}}:{\mathrm{Ho}}\Omega '^{\mathcal {C}} \end{aligned}$$

are genuine adjunctions.

Theorem 6.12

Let $\mathcal {M}$ be as above. Then the adjoint pair of functors

$$\begin{aligned} \mathrm{colim}: \mathcal {M}^{\mathcal {C}}\leftrightarrows \mathcal {M}:\text {const}\end{aligned}$$

induces a conatural adjunction up to homotopy

$$\begin{aligned} \mathrm{colim}^{\mathcal {H}}:\mathcal {H}\mathcal {M}^{\mathcal {C}}\leftrightarrows \mathcal {H}\mathcal {M}:\text {const}^{\mathcal {H}}. \end{aligned}$$

Hence we obtain a genuine adjunction

$$\begin{aligned} {\mathrm{Ho}}\mathrm{colim}: {\mathrm{Ho}}\mathcal {M}^{\mathcal {C}}\leftrightarrows {\mathrm{Ho}}\mathcal {M}:{\mathrm{Ho}}\text {const}\end{aligned}$$

Proof

We have the following sequence of natural homotopy equivalences and homeomorphisms from $\mathcal {H}\mathcal {M}^{\mathcal {C}}(D,\text {const}^{\mathcal {H}}A)=\mathcal {M}^{\mathcal {C}}(RD,R(\text {const}QA))$ to $\mathcal {H}\mathcal {M} (\mathrm{colim}^{\mathcal {H}}D,A)$ $=\mathcal {M}(Q(\mathrm{colim}RD),QA)$:

$$\begin{aligned} \begin{array}{lrcl} 1. &{} \mathcal {M}^{\mathcal {C}}(RD,R(\text {const}QA)) &{}\xrightarrow {\epsilon (\text {const}QA)_*} &{} \mathcal {M}^{\mathcal {C}}(RD, \text {const}QA)\\ 2. &{} &{}\mathop {\longrightarrow }\limits ^{\cong } &{} \mathcal {M}(\mathrm{colim}RD, QA)\\ 3. &{}&{} \xrightarrow {\varepsilon _M(\mathrm{colim}RD)^*} &{} \mathcal {M}(Q(\mathrm{colim}QD), QA). \end{array} \end{aligned}$$

The first map is a homotopy equivalence by 6.3, the second one is the adjunction homeomorphism, and the third one is a homotopy equivalence, because $\varepsilon _M(\mathrm{colim}RD): Q\mathrm{colim}RD \rightarrow \mathrm{colim}RD$ is a homotopy equivalence in $\mathcal {M}$ by 6.3. $\square$

Definition 6.13

Let $\mathcal {M}$ be a cocomplete $\mathcal {T}\! op$-enriched tensored category with a class $\fancyscript{W}$ of weak equivalences containing the homotopy equivalences and equipped with a strong cofibrant replacement functor $(Q,\varepsilon )$. Then the homotopy colimit functor $\mathrm{hocolim}: \mathcal {M}^{\mathcal {C}}\rightarrow \mathcal {M}$ is defined by

$$\begin{aligned} \mathrm{hocolim}D= \mathrm{colim}RD= B(*,\mathcal {C},\mathcal {C})\otimes _{\mathcal {C}} QD. \end{aligned}$$

Remark 6.14

In the literature one often finds the homotopy colimit defined by $\mathrm{hocolim}D =B(*,\mathcal {C},\mathcal {C})\otimes _{\mathcal {C}} D$ (e.g. see [12, 18.1.1]). This has historical reasons because homotopy colimits were first defined in categories where all object were cofibrant.

We apply these results to $\mathcal {M}on$ and prove

Theorem 6.15

The classifying space functor

$$\begin{aligned} B:(\mathcal {M}on,\mathcal {M}on^{w})\rightarrow ({\mathcal {T}\! op}^*,{\mathcal {T}\! op}^w) \end{aligned}$$

preserves homotopy colimits up to genuine homotopy equivalences. More precisely, for any diagram $D:\mathcal {C}\rightarrow \mathcal {M}on$ the natural map

$$\begin{aligned} \mathrm{hocolim}^{{\mathcal {T}\! op}^*}BD\rightarrow B(\mathrm{hocolim}^{\mathcal {M}on}D) \end{aligned}$$

is a homotopy equivalence.

Proof

By definition of the homotopy colimit functor it suffices to prove the well-pointed case.

Consider the diagram

and recall that ${\mathrm{Ho}}\mathrm{colim}$ is induced by the homotopy colimit functor. Since $B$ preserves weak equivalences in the well-pointed case, $B^{\mathcal {C}}$ induces ${\mathrm{Ho}}B^{\mathcal {C}}$ so that the left square commutes up to natural equivalence. The right square commutes up to natural equivalence, because the corresponding square of right adjoints commutes. Hence, for any diagram $D$ in $\mathcal {M}on$, the natural map

$$\begin{aligned} \mathrm{hocolim}^{{\mathcal {T}\! op}^w}BD\rightarrow B(\mathrm{hocolim}^{\mathcal {M}on^{w}}D) \end{aligned}$$

becomes an isomorphism in ${\mathrm{Ho}}{\mathcal {T}\! op}^w=\pi {\mathcal {T}\! op}^w$. $\square$