Introduction

The continued improvement of GDP performance in China has not only boosted the increase in the standard of living over the past 40 years, but also has leaded to negative effects, such as serious air pollution. The balance between economic growth and air pollution shifts as income rises. People value the quality of environment more highly, and regulatory institutions become more effective. In order to reducing air pollution, Chinese government has been implementing the strict environmental protection policies, such as the Air Pollution Prevention and Control Action Plan implemented in 2013,Footnote 1 the Environmental Protection Law of the People’s Republic of China revised in 2014,Footnote 2 and the Law of the People’s Republic of China on the Prevention and Control of Atmospheric Pollution revised in 2018.Footnote 3 China has established a network to monitor PM2.5 and industrial dust and SO2 levels nationwide. The continued improvement of air quality has demonstrated the achievements in implementing strict environmental regulation since 2012.

Several studies have shown that environmental regulation between regions influence each other and thus have strong spatial effects, which may trigger the strategic interaction between environmental regulations among different regions (Konisky 2007; Deng et al. 2012). That is to say, the air pollution status in one city can be influenced not only by local environmental regulations but also by environmental regulations in neighboring regions (Wu et al. 2020a; Chang et al. 2023). The more effective the environmental regulatory actions in one city, the more beneficial the neighboring cities. This is known as the “free-rider” behavior of neighboring cities. But keeping minds on GDP performance may impel the provincial and local officials to prefer the large-sized and high-pollution enterprises to small-and-medium-sized and low-pollution enterprises, because the large-sized and high-pollution enterprises such as the heavy and chemical industry can immediately promote the high-speed economic growth (Li and Zhou 2005; Chen et al. 2017). The pursuit of GDP performance may create a “race to the bottom”, as cities compete by lowering their environmental regulatory intensities (Chirinko and Wilson 2017).

To achieve the reduction in pollutants, Chinese government highlights the adjustment of structure in the level of macro-economy. Firstly, it includes the adjustment of industrial structure, which implies the progression from polluting industrial to clean service sector domination of the economy. The Second is the adjustment of energy structure, which emphasizes to enhance the use of gas, nuclear energy, water, wind and solar power, to reduce the dependence on coal. In terms of micro-firm level, the path to reduce pollutants includes both the energy-saving and emission-reducing. The energy-saving ways means to reduce pollution in the front-end or the process of production. The emission-reducing path usually means to add equipment to decrease pollution emission in the end-end of production.

Here, one important mediating variable is technology. The short-term effects of environmental regulation may add additional burdens to firms, however, green technological innovation through increased research expenditures can significantly reduce the firms’ cost of environmental management in the long run (Porter and van der Linde 1995). General environmental regulation have an inhibitory effect on the efficiency of technological innovation at the current period, but have a facilitating effect in the lagged period (Li et al. 2022). More targeted subsidies can also drive the innovation in higher-cost energy technologies such as solar energy (Johnstone et al. 2010). The major breakthrough of technology in wind power and solar power in China have demonstrated the achievements in subsidy in on-grid electricity price for wind power and solar power. It means that the government can guide enterprises to do more green technological innovation by imposing temporary taxes on pollution emissions or subsidizing clean technology, which will eventually lead to a decrease in pollution emissions when enterprises carry out production (Acemoglu et al. 2012). Wu et al. (2020b) find a significant U-shape relationship between environmental regulation and green total factor productivity, in which environmental decentralization plays a moderating role.

Some studies have find that environmental regulations promote the increase in environmental investment and innovation by firms in the long run, leading to an improvement in both economic and environmental performance, which in turn attracts more firms to come to this region, thus promoting industrial agglomeration (Porter and van der Linde 1995; Popp et al. 2015). There is an idea that reasonable environmental regulations can induce enterprises to conduct more R&D, which will enhance the competitiveness of enterprises, and reasonable environmental regulations are conducive to the increase in industrial agglomeration in the region (Acemoglu et al. 2012). Another idea is that strict environmental regulations can promote regional industrial development and the increase in the tertiary industry agglomeration, and the increase in clean industries brings more financing demand and promotes the synergistic development of the banking industry (Luo and Qi 2021).

Due to the high cost and uncertainty of innovation, investment, especially in highly polluting industries, tends to prefer countries and regions with more lax regulations when trade and capital can flow freely (Zeng and Zhao 2009), leading to the “pollution haven effect” (Copeland and Taylor 2004). The cost of environmental regulation is an important factor influencing firms’ decision of geographic location according to the pollution haven hypothesis (Keller and Levinson 2002; Fredriksson et al. 2003). When environmental regulation is strengthened in an area, firms will reduce the cost of pollution control by relocating. An example of this is that the strict restrictions on pollution emissions in the 11th Five-Year Plan drive enterprises to shift their production to the western Chinese regions (Wu et al. 2017). The industries with more lax environmental regulations become more competitive as a result of the U.S. Clean Air Act (Hanna 2010). Specifically, when a firm makes a decision to build a plant, it responds to changes in environmental regulations at each location, and the Pollution Haven Hypothesis becomes more pronounced especially when the stringency of environmental regulations varies from location to location (Lin and Sun 2016). For example, firms would respond to stringent environmental regulatory measures by discharging more in the downstream districts and counties of the rivers in the provinces (Cai et al. 2020).

Most of literatures examining the effects of industrial agglomeration on environmental regulation has not reached consistent conclusion. One view is that the industrial agglomeration is accompanied by the large agglomeration of industrial sectors, especially manufacturing sectors, which can lead to excessive energy use and concentrated pollution emissions, resulting in significant negative pollution externalities (Leeuw et al. 2001; Zhang and Dou 2013). Another view is that the industrial agglomeration can bring about the increasing return to scale and decreasing cost of environmental management (Copeland and Taylor 2003; Rooij and Lo 2010). The agglomeration in manufacturing enterprises can reduce input costs by sharing pollution control facilities, and the technology exchange among enterprises can promote the application of green technology, showing the “scale effect” of industrial agglomeration (Lu and Feng 2014), thus achieving the purpose of reducing pollution emissions. Some studies pay more attention on the “spatial spillover effects” of the industrial concentration, pollution dispersion and environmental ecological conditions, and find that the relationship between industrial concentration and industrial sulfur dioxide, industrial wastewater and industrial dust emissions has an inverted-U shape (Chen et al. 2020). There may be a cubic relationship between industrial SO2 and industrial smoke (dust) emission intensity and industrial agglomeration (He et al. 2014). The industrial agglomeration in local and adjacent areas can contribute to the aggravation of local haze pollution, mainly because of the high dispersion of haze pollution and the difficulties in definition of responsibility (Li et al. 2021). Air pollution firstly goes down and then goes up as local industrial agglomeration rises in the short run, but the industrial agglomeration can alleviate air pollution in city by influencing environmental regulation, technological progress and the adjustment of industry structure in the long run (Hao et al. 2022a, b). Some studies find that there are various threshold effects of industrial agglomeration on pollution emissions (Cheng et al. 2017; Zhou and Zhu 2013; Yue et al. 2015). Whether the impact of industrial agglomeration on pollution exerts a positive or negative externality is largely determined by technological progress (Yuan and Xie 2015).

The above literatures show, implicitly or explicitly, that there exists a correlation between environmental regulation and industrial agglomeration and air pollution. However, there is few studies to discuss the effects of environmental regulation and industrial agglomeration on air pollution. On the other hand, lush mountain and lucid water and clean air are as valuable as gold and silver. Chinese government has begun to shift from pursuing the single economic performance to pursuing the continued improvement in living standard and environmental quality as people’s disposable income rises. A shift in demand inspires us to investigate the theoretical mechanism both environmental regulation and industrial agglomeration affect air pollution, and the econometric evidence of effects of environmental regulation and industrial agglomeration on air pollution.

The possible contributions of this paper are threefold. Firstly, this paper collects the long panel data of 275 prefecture-level cities during 2003–2019 and believes that the results are more accurate because it has a larger sample size. Secondly, this paper combines environmental regulation with industrial agglomeration and examines transmission mechanism how environmental regulation affect industrial agglomeration, thereby affecting air pollution, and transmission mechanism how environmental regulation affect innovation, thereby affecting air pollution. Thirdly, this paper examines the effects of environmental regulation and industrial agglomeration on air pollution by using the spatial econometric model that can correctly describe the spatial spillover effects of environmental regulations and reveals successfully the effects of spatial variables on air pollution.

The remainder of this paper is organized as follows: ”Theoretical framework and hypothesis” section discusses theoretical framework and mechanism. ”Empirical model” section constructs the econometric model. ”Descriptive statistics and variable selection” section is descriptive statistics and the selection of variables. ”Results and discussion” section presents the empirical results. ”Mechanism test” section is the test on theoretical mechanism. Finally, ”Conclusion” section concludes the paper and provides corresponding policy recommendations.

Theoretical framework and hypothesis

Due to the strategic interaction of environmental regulations between regions (Deng et al. 2012), the air pollution status in one city is influenced not only by local environmental regulation measures, but also by those of neighboring regions (Wu et al. 2020a). Environmental regulations are used to achieve targets of pollution emission reduction by influencing the behavior of enterprises (Milani 2017). Based on the Porter hypothesis and the Pollution Haven hypothesis, enterprises can reduce pollution emission through the replacement of production equipment, such as substitution 1000 MW coal-fired generator for 300 MW coal-fired generator, and green technology innovation, such as substitution wind power or solar power for coal-fired power. Enterprises also can continue to produce by installing the desulfurization and denitration and dust-reducing equipment in the process of production, or by moving to an area with lax/weaker environmental regulations. Therefore, it is very important to figure out the transmission mechanism of environmental regulation and industrial agglomeration, respectively, affect air pollution, and the transmission mechanism how the stringent implementation of environmental regulations affect industrial agglomeration, thereby affecting air pollution.

Environmental regulation will change the energy-saving and emission-reducing actions of enterprises, which will further affect regional air pollution status. Firstly, based on the Porter hypothesis, strict environmental regulations will force firms to enhance economic efficiency and invest more in green technological innovation, which will further increase the concentration of clean industries in the region (Acemoglu et al. 2012; Franco and Marin 2017; Johnstone et al. 2010; Lee et al. 2011; Porter and van der Linde 1995). Specifically, as the intensity of environmental regulation increases, firms will have to increase their investment in technological research and development and take technological progress, which may improve other firms’ economic efficiency through spillover effects (Cole et al. 2006). Generally, local firms can take advantage of the economies of scale effect (Fujita and Thisse 2005) to improve economic efficiency by sharing costs of pollution control and acquiring green innovative technology from other local firms, which will attract more firms to the region and promote local industrial development. Because knowledge and innovative technology spread rapidly (Lin et al. 2017), new environmental protection technologies and green production ways are invented and developed more and more rapidly. Firms located in industrial agglomeration area are more likely to adopt the advanced environmental protection technologies (Cole et al. 2006), which will ultimately lead to the increase in agglomeration of local clean industries and the reduction in air pollution.

Secondly, the strict implementation of environmental regulations in one city may force polluting firms to move to neighboring cities with lax environmental regulation, which is known as the Pollution Haven Hypothesis (Copeland and Taylor 2004). Generally speaking, the increase in industrial agglomeration may lead to excessive energy use, and excessive pollution emission, which will aggravate air quality (Zhang and Dou 2013). Conversely, if the stringent enforcement of environmental regulations become the common activities between cities, polluting enterprises will have to choose to innovate or introduce green technology to reduce pollution emission, because they cannot avoid environmental regulations by shifting production, which will lead to synergistic growth in technology level and productivity among adjacent cities (Jin and Shen 2018).

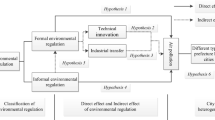
Based on the above analysis, the following hypotheses are proposed in this paper (see Fig. 1).

Fig. 1
figure 1

Theoretical framework

Full size image

Hypothesis 1

The intensity of environmental regulations (ER) in both local and neighboring cities has very different impacts on air pollution in local city.

Hypothesis 2 (Pollution Haven Hypothesis)

The strict implementation of environmental regulation in one city will lead to the relocation of polluting enterprises/industries to neighboring cities with weaker environmental regulations, which will promote a decrease in agglomeration of polluting industries and an increase in concentration of clean industries, finally improving air quality and decreasing air pollution in local city.

Hypothesis 3 (Porter Hypothesis)

When both local and neighboring cities adopt stringent environmental regulations, firms will be forced to engage in green technological innovation and achieve the reduction in pollution emission.

Material and method

Empirical model

Spatial weight matrix

The spatial weight matrix can be used to measure the spatial distance between cities, and most of studies use a 0–1 matrix (W1), i.e., if two cities are next to each other, the corresponding weight coefficient is 1; otherwise, it is 0. This paper supposes that the environmental regulation intensity (ER) is not only associated with distance between cities, but also there may be strategic ER interaction between adjacent cities. In order to reflect this spatial correlation between cities, this paper further constructs the inverted-geographic-distance weight matrix (W2) based on the 0–1 matrix (W1) and normalizes the matrix by rows.

Assuming that city i is adjacent to city j, the element \({w}_{ij}=1\) in the row i and column j in the weight matrix is defined, and if city i is not adjacent to city j or i = j, then \({w}_{ij}=0\). The constructed matrix is normalized to obtain the 0–1 matrix W1. Assuming that the spatial distance between city i and city j is \({d}_{ij}\), the element \({w}_{ij}=\{1/{d}_{ij}, i\ne j; 0, i=j\)}, and the resulting matrix is normalized by row to obtain the inverted-distance weight matrix W2. If the spatial distance between two cities is remote, the mutual spatial weights will be smaller, and therefore the mutual influence between variables in the econometric model will be smaller.

Spatial correlation test

Due to the spatial spillover effect of variables, the results may be biased. When applying the spatial econometric model, the spatial correlation of variables needs to be tested. In the model setting of this paper, air pollution emission, environmental regulation and industrial agglomeration may be spatially correlated. We use the global Moran index I to test whether there is spatial correlation among variables, and I is calculated as:

$$ {\text{Moran}}^{\prime} {\text{s}}\;I = \frac{{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} (x_{i} - \overline{x})(x_{j} - \overline{x})} } }}{{S^{2} \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }} $$
(1)

where \({S}^{2}\) is the square deviation of the sample and \({w}_{ij}\) is the element of spatial weight matrix. The Moran index I takes values (− 1, 1). Positive value (Moran’s index > 0) indicates a positive spatial correlation between variables.

Model 1: impact of ER and industrial agglomeration on air pollution

Baseline regression model

A large number of studies have shown that there is a threshold effect of environmental regulation (Li and Zou 2018; Dong and Wang 2019), so this paper adds the quadratic term of ER (ERS) to the econometric model, and the impact of ER on air pollution is tested by constructing a linear regression model without spatial effects. The model is set as follows.

$$ {\text{In}}P_{it} = \beta_{0} + \beta_{1} {\text{ER}}_{it} + \beta_{2} {\text{ERS}}_{it} + \gamma X_{it} + \delta_{t} + u_{i} + \varepsilon_{it} $$
(2)

where i denotes the city, t denotes the year, \(\mathrm{ln}{P}_{it}\) denotes the natural logarithm of the level of air pollution emission in city i in year t. \({\mathrm{ER}}_{it}\) and \({\mathrm{ERS}}_{it}\) denote the environmental regulation intensity and its quadratic term in city i in year t, respectively. The ER intensity is measured by standardizing SO2 removal rate and industrial smoke/dust removal rate and then by the weighted average method. Coefficients \({\beta }_{1}\) and \({\beta }_{2}\) measure the impact of environmental regulation on pollution emission. Xit is a series of control variables affecting pollution emission, including real per capita income, labor productivity, urbanization rate, real utilization of foreign capital, the ratio of the secondary industry value-added to GDP, population density, and green technology level, etc.\({\delta }_{t}\) denotes time fixed effects, ui denotes city fixed effects, and \({\varepsilon }_{it}\) denotes the random disturbance term.

Spatial Durbin model (SDM)

Since the key variables in this paper are significantly spatial correlated, the spatial lagged term of ER and its quadratic term are added to the baseline model, and the SDM is set as follows.

$$ \begin{aligned} {\text{In}}P_{it} = & \rho \sum\limits_{j = 1}^{n} {w_{ij} {\text{In}}P_{jt} } + \beta_{0} + \beta_{1} {\text{ER}}_{it} + \beta_{2} {\text{ERS}}_{it} \\ & \quad + \theta_{1} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ER}}_{jt} } + \theta_{2} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ERS}}_{jt} } + \gamma X_{it} + \delta_{t} + u_{i} + \varepsilon_{it} \\ \end{aligned} $$
(3)

where wij = denotes the element of spatial weight matrix, which measure the spatial proximity between different cities. \(w_{ij} {\text{In}}P_{jt}\) is the spatial lagged term of air pollution, and coefficient ρ reflects the dispersion effect of air pollution from neighboring cities to local city i. \(w_{ij} {\text{ER}}_{jt}\) and \(w_{ij} {\text{ERS}}_{jt}\) are the spatial lagged terms of ER intensity and its quadratic term. Coefficient θ1 and θ2 measure the effects of ER in neighboring cities on air pollution in local city i. The remaining control variables are consistent with those in the baseline regression model.

Model 2: mechanism analysis of environmental regulation

Effects of ER on the industrial agglomeration

Considering that environmental regulation may affect the industrial agglomeration level of local and neighboring cities through the Porter effect and Pollution Haven effect, which further affects the air pollution level in cities. The model 4 is added the spatial lagged term of ER to test the possible spatial effects. The model 4 is set as follows.

$$ \begin{aligned} {\text{Agg}}_{it} = & \beta_{0} + \beta_{1} {\text{ER}}_{it} + \beta_{2} {\text{ERS}}_{it} + \theta_{1} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ERS}}_{jt} } \\ & \quad + \theta_{2} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ERS}}_{jt} } + \gamma X_{it} + \delta_{t} + u_{i} + \varepsilon_{it} \\ \end{aligned} $$
(4)

where \({\text{Agg}}_{it}\) denotes the degree of agglomeration in manufacturing sectors or productive service sectors in city i in year t. The coefficients β1 and β2 measure the impact of ER on industrial agglomeration in local city i, and θ1 and θ2 measure the impact of ER in neighboring cities on the industrial agglomeration in local city i. \(X_{it}\) are control variables that affect industrial agglomeration, including human capital, infrastructure, market size, market potential, labor cost, etc.

Effect of ER on technological progress

In order to further test whether ER has an impact on cities’ pollution levels at the spatial level by influencing firms’ innovation decisions, this paper sets up a spatial econometric model:

$$ \begin{aligned} {\text{Patent}}_{it} = \beta_{0} + \beta_{1} {\text{ER}}_{it} + \beta_{2} {\text{ERS}}_{it} + \theta_{1} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ERS}}_{jt} } \\ & \quad + \theta_{2} \sum\limits_{j = 1}^{n} {w_{ij} {\text{ERS}}_{jt} } + \gamma X_{it} + \delta_{t} + u_{i} + \varepsilon_{it} \\ \end{aligned} $$
(5)

where \({\text{Patent}}_{it}\) is the level of innovation in city i in year t. The coefficients β1 and β2 measure the effect of ER on innovation in city i in year t. The coefficients θ1 and θ2 measure the effect of ER in neighboring cities on innovation in local city i. \(X_{it}\) are a series of control variables that affect innovation, including real GDP, human capital, labor productivity, real foreign capital use, labor force, etc.

Descriptive statistics and variable selection

Air pollution status

Figure 2 plots the average value of SO2, PM2.5, and industrial smoke (dust) in China during 2003–2019, respectively, with data from China City Statistical Yearbook. The darker the green color in Fig. 2, the severer air pollution. Figure 2 shows that air pollution between cites is significantly spatial correlated, i.e., cities with serious air pollution tend to be close to cities with serious air pollution, and vice versa, cities with low air pollution are next to cities with low air pollution. More precisely, in panel (a), cities with serious industrial SO2 emission are largely located in northern China, which indicates that urbanization in China may mainly follow the economic development pattern with excessive energy consumption and serious pollution emission. In panel (b), particulate matter in the air (PM2.5) is more serious in the northern China, especially in the Beijing-Tianjin-Hebei urban area. In panel (c), the spatial distribution of industrial smoke (dust) is almost consistent with the spatial distribution of industrial SO2 emission.

Fig. 2
figure 2

Average value of pollutant during 2003–2019: a SO2; b PM2.5; c industrial smoke (dust)

Full size image

Intensity of environmental regulation

Figure 3 plots the annual average value of industrial SO2 and industrial smoke (dust) removal rate in 2003–2019, respectively, with data from China City Statistical Yearbook, characterizing the intensity of ER in different cities. Firstly, the darker the green color, the stricter the enforcement of ER. Specifically speaking, cities located in eastern coastal and central China show the darker green color than cities located in western China, which implies that the intensity of enforcement of ER in eastern and central China is stricter than that in other less-developed cities, which are known as the second-tier and third-tier cities in China. In other words, the second-tier and third-tier cities implement lax ER for pursuing economic growth goals.

Fig. 3
figure 3

Average industrial pollutant removal rate in 2003–2019 a SO2; b industrial smoke (dust)

Full size image

Secondly, the intensity of ER enforcement shows significant spatial distribution characteristics with low-low agglomeration and high-high agglomeration. The weaker the enforcement of ER in one city, the weaker ER in neighboring cities. It can be explained by the fact that local government officials, due to priority to GDP performance, may attract the large-sized and high pollution enterprises by enforcing the weaker ER than neighboring cities (Li and Zhou 2005; Chen et al. 2017), eventually leading to a “race to the bottom” in the enforcement of ER policies (Chirinko & Wilson 2017). Conversely, the stricter the enforcement of ER in a city, the stricter the enforcement of ER in neighboring cities. Especially the economic developed cities, such as Beijing, Shanghai, Shenzhen and Guangzhou city, can improve air quality and attract the high-end and high-tech enterprises by enforcing stricter ER. As a result, it promote the mutual coordination of ER enforcement (Jin and Shen 2018).

Industrial agglomeration

This paper mainly examines the impact of industrial agglomeration on air pollution. According to the industrial division, the manufacturing sectors in the secondary industry have the most significant industrial pollutant emission. However, since the detailed data in manufacturing sectors are not reported in the China City Statistical Yearbook, this paper considers them as a whole. In the tertiary industry, considering the living service and public service industries have no significant difference in air quality due to the similarity of economic development between cities, this paper only focuses on the productive service industry, which has a significant impact on air quality. Following the study of Li and Li (2014), the productive service industry is further divided into the high-end and low-end productive service industries, and the specific division criteria are shown in Table 1.

Table 1 Industrial division
Full size table

This paper uses the “location-entropy-index” to calculate the degree of agglomeration in manufacturing and production service industries in each city, respectively, with data from China City Statistical Yearbook and draw the geographical distribution map. In Fig. 4, panels (a–d) denote the degree of agglomeration in manufacturing industry, productive service industry, the high-end and low-end productive service industries, respectively.

Fig. 4
figure 4

Distribution of industrial agglomeration degree: a manufacturing industry; b productive service industry; c high-end productive service industry; d low-end productive service industry

Full size image

As we know, the process of economic development in an area is associated with the process of industrial agglomeration. Panel (a) in Fig. 4 shows that manufacturing industries are mostly concentrated in the eastern coastal and some central cities in China, which is associated with economic development priority right in China over past four decades. More precisely, the eastern coastal areas in China and the provincial capital in every province have priority in competition of economic development among areas. Furthermore, agglomeration in manufacturing industry can not only produce a large amount of demand for production factors, including natural resources, technology and talent (human capital), but also take the scale effect.

The productive service industry spreads in different cities in China. Panel (b) shows that the agglomeration of productive service industries are largely concentrated in the provincial capital and prefecture-level city, which is largely attribute to population density and the imbalance in development between cities. At the same time, the paper finds that the productive service industry is correlated with manufacturing industry. The more developed productive service industry is usually accompanies by the more developed manufacturing industry.

This paper further decomposes the productive service industry into the high-end productive service industry and low-end productive service industry. Panel (c) shows that the high-end service industry is mostly located in economically developed areas. In contrast, the low-end productive service industry is scattered in every area, which is more relevant to people’s lives. According to Friedman’s core-periphery theory of urban agglomeration, the high-end services are concentrated in central cities, while general services are concentrated in peripheral cities. As cities develop, the demand for public resources will push up the price of production factors, such as housing rent. The high-tech industries can afford higher price because of making higher profits, while the low-end services have to move to neighboring cities as production costs rise. This results in the higher agglomeration of the high-end productive service industry than low-end productive service industry.

Selection of variables

This paper collects and uses the panel data of 275 prefecture-level cities in China in 2003–2019. The data come from the China City Statistical Yearbook, Chinese research data services platform database (CNRDS) and China Stock Market & Accounting Research Database (CSMAR). In the process of calculation, cities with mass missing data are deleted, and cities with partially missing data are treated by interpolation. Table 2 shows the descriptive statistics of key variables.

Table 2 Descriptive statistics of variables
Full size table

Dependent variable: air pollution

Due to the availability of data, industrial SO2 emission is selected as a proxy variable for air pollution, which is one of sources of air pollution and is significantly correlated with urban air pollution. The industrial smoke (dust) and PM2.5 are also selected as the proxy variable for testing robustness of the model.

Core independent variable: environmental regulation (ER)

Referring to Shen et al. (2017), a linear weighting method is used to construct the ER intensity indicator. The specific approach is as follows: first, the removal rate is calculated using the data of the emission and removal of industrial SO2 and industrial smoke (dust) from the China City Statistical Yearbook, respectively. In the process of calculation, cities with mass missing data are deleted, and cities with partially missing data are treated by interpolation, and the calculated SO2 removal rate and industrial smoke (dust) removal rate are standardized as follows.

$$ pt_{ij}^{s} = \frac{{pt_{ij} - \min (pt_{j} )}}{{\max (pt_{j} ) - \min (pt_{j} )}} $$
(6)

where \(pt_{ij}\) denotes the pollutant j removal rate in city i, \(\max (pt_{j} )\) and \(\min (pt_{j} )\) denote the maximum and minimum value of the corresponding pollutant j removal rate, respectively. \(pt_{ij}^{s}\) is the normalized value of the removal rate. The adjusted coefficient of SO2 removal rate and industrial smoke (dust) removal rate is calculated, respectively:

$$ A_{ij} = \frac{{{{P_{ij} } \mathord{\left/ {\vphantom {{P_{ij} } {\sum\limits_{i} {P_{ij} } }}} \right. \kern-0pt} {\sum\limits_{i} {P_{ij} } }}}}{{{{{\text{GDP}}_{i} } \mathord{\left/ {\vphantom {{{\text{GDP}}_{i} } {\sum\limits_{i} {{\text{GDP}}_{i} } }}} \right. \kern-0pt} {\sum\limits_{i} {{\text{GDP}}_{i} } }}}} $$
(7)

where \(A_{ij}\) is equal to that the share of pollutant j emission in city i to total emission of pollutant j in China divided by the share of city i’s GDP to Chinese total GDP. Given the same economic size, a larger value of \(A_{ij}\) indicates that the city will have more pollution emission and tend to implement the stricter environmental regulation. Finally, the ER intensity of cities is obtained by weighting the standardized value of SO2 removal rate and industrial smoke (dust) removal rate according to the adjustment factor.

$$ {\text{ER}}_{i} = \frac{{\sum\limits_{j = 1}^{2} {A_{ij} (pt_{ij}^{s} )} }}{2} $$
(8)

Core independent variable: industrial agglomeration

The measurement methods of domestic and foreign scholars on the degree of industrial agglomeration mainly include Herfindahl index, Hoover index, Gini coefficient and location quotient, etc. The most widely adopted method at present is the location entropy, mainly because it can well measure the spatial distribution of labor, capital and resource endowments while eliminating the difference in economic development between indifferent cities. The specific method of locational entropy is calculated as:

$$ {\text{Agg}}_{im} = \frac{{{{e_{im} } \mathord{\left/ {\vphantom {{e_{im} } {\sum\limits_{i} {e_{im} } }}} \right. \kern-0pt} {\sum\limits_{i} {e_{im} } }}}}{{{{\sum\limits_{m} {e_{im} } } \mathord{\left/ {\vphantom {{\sum\limits_{m} {e_{im} } } {\sum\limits_{i} {\sum\limits_{m} {e_{im} } } }}} \right. \kern-0pt} {\sum\limits_{i} {\sum\limits_{m} {e_{im} } } }}}} $$
(9)

where eim denotes the number of production factors of m industries in city i, which is generally the number of industrial workers or total value of industrial output. The numerator measures the proportion of m industries in city i, the denominator measures the proportion of all industries in city i in China, and \({\text{Agg}}_{im}\) is the agglomeration degree of m industries in city i.

In this paper, we use the number of employees from the China City Statistical Yearbook to calculate the industrial agglomeration degree, where AM represents the agglomeration degree of manufacturing industry and is calculated using the number of employee working in the manufacturing industry sectors in city. AS represents the agglomeration degree of productive service industry and is calculated using the number of employees working in the productive service industry sectors in city. To ensuring the robustness of the econometric regression result, this paper chooses the number of employee in the secondary industry to calculate the agglomeration degree of the secondary industry (AM(sec)). That is to say, we substitute AM(sec) for AM. Similarly, AS(high) and AS(low) are calculated based on the number of employee in the high-end productive service industry and the number of employees in the low-end productive service industry, respectively. That is to say, we substitute AS(high) and AS(low) for AS.

Control variables

Many papers argue that ER and industrial agglomeration may be influenced by other variables (Chen et al. 2020). Following this idea, the paper introduces control variables into the econometric model. Control variables include (shown in Panel C in Table 2):

  1. (1)

    Annual real per capita income (pgdp): measured by current annual per capita income divided by GDP index using 2003 as base year. According to the classical environmental Kuznets curve hypothesis, environmental pollution rises and then falls as per capita income rises. Therefore, this paper introduces the natural logarithm of real per capita income and its quadratic term into the regression model

  2. (2)

    Labor productivity (lp): It is measured by the natural logarithm of the ratio of non-agricultural output to the number of non-agricultural employee. The level of labor productivity affects the efficiency of energy use and actual pollution emission. In the early stage of economic development, the increase in labor productivity comes mainly from the development of the manufacturing sectors, which may be accompanied by the large amount of pollutants emission. The higher labor productivity often means the lower pollutants emission as the economy goes up to the higher level of economic development

  3. (3)

    Urbanization rate (ur): measured by the ratio of the year-end non-agricultural registered population to total population in city i in year t. The rapid acceleration of urbanization will lead to a continued increase in non-agricultural registered population and a large amount of energy consumption, which will produce more pollution emission. On the other hand, the impact of urbanization rate on air pollution depends on the pattern of economic development in city, so the impact on air pollution may be unclear

  4. (4)

    Actual utilization of foreign capital (fdi): measured by real utilization of foreign direct investment in city i in year t. Generally speaking, the inflow of FDI may bring the more advanced energy-saving and pollution-emission-reducing technologies. In order to attract the foreign direct investment, however, some cities may implement the minimum standards of environmental regulation, which may lead to the “pollution refuge effect” and exacerbate urban air pollution, so the impact of FDI on urban air pollution is uncertain

  5. (5)

    The share of the secondary industry value-added to GDP (secp): The secondary industrial sectors is the main source of pollution emission, so the higher the proportion of the secondary industry in a city, the more serious the air pollution in the city may be

  6. (6)

    Population density (pop): measured by the number of people per square kilometer. Cities with the higher population density usually means the more serious air pollution

  7. (7)

    Green technology level (green): measured by the number of green patents and green utility patents applied for by city i in year t. The more green technology used by a city, the less pollutant emission made by this city. Green technology is introduced in Model 2 and Model 3

  8. (8)

    Technology Innovation (Patent): measured by the score of the number of patents in city i. The larger the value, the stronger the innovation capability of the city, and this variable is used in the mechanism regression to measure the technological progress effect. The data comes from the Regional Innovation and Entrepreneurship Index compiled by the Enterprise Big Data Research Center of Peking University

  9. (9)

    Human capital (hr): this paper chooses the number of college students as a proxy variable of human capital, because the data is not available, such as the number of labor with higher education in prefecture-level city. The more and higher the human capital in a city, it is more beneficial to attract enterprises engaging in produce and services in this city. That is to say, the level of human capital affects the industrial agglomeration in a city. The variable of human capital is included in the mechanism regression models 4 and 5

  10. (10)

    Infrastructure (proad): measured by road area per capita. The higher the level of infrastructure in a city, the better the industrial development in the city. The variable of infrastructure is introduced into the mechanism models 4 and 5

  11. (11)

    Labor cost (salary): measured by the average salary of employees. The higher the labor cost of a city, the higher the production cost of enterprises, which in turn has an impact on the industrial development and agglomeration of the city. It is introduced into the mechanism model 4 and 5

  12. (12)

    Market potential (grate): measured by the growth rate of GDP. The market potential of a city will affect the degree of industrial agglomeration in the city, which is introduced in the mechanism regression models 4 and 5.

Results and discussion

Spatial correlation test

Table 3 shows that the Moran index I of key variables are significantly positive in all years, indicating that these variables have a strong spatial correlation. Therefore, this paper introduces the spatial lagged term into the regression model to control the possible spatial correlation.

Table 3 Global Moran index of key variables
Full size table

The impact of ER on air pollution

Table 4 reports the regression results of impact of environmental regulation (ER) on air pollution emission SO2. Columns 1 and 2 are the regression results based on the Model 2, and Columns 3 to Column 6 are the regression results based on the Model 3. To ensure the robustness of the regression results, clustering standard errors are included in the regression, and city fixed effects and time fixed effects are all controlled in regression model.

Table 4 Effects of environmental regulation (ER) on SO2
Full size table

Firstly, Table 4 shows that the coefficients of ER are significantly positive and its squared term ERS are significantly negative in all regression, which means that air pollution emission SO2 rises firstly and then falls as the ER intensity in local city i becomes stricter. That is to say, the effects of environmental regulation on air pollution are the inverted-U shape curve in terms of local city i.

Secondly, from column 3–column 6 (replacing the spatial weight matrix W1 with W2 in Columns 5 and 6), the estimated results show that the spatial lagged term of the environmental regulation (w × ER) are significantly negative and its squared term (w × ERS) are significantly positive, which means that the ER in neighboring cities j has the U-shape relationship with air pollution emission in local city i. In other words, the air pollution emission in city i may firstly fall and then rise as the ER in neighboring cities becomes more and more stringent. Therefore, the stricter enforcement of ER in neighboring cities can aggravate air pollution in local city i. One possible explanation is the “Pollution Haven effect” caused by the strategic interaction of local government environmental regulations, which will force polluting enterprises to shift from city with more stringent environmental regulations to city with less stringent environmental regulations.

Thirdly, coefficient of the spatial lagged term (ρ), and coefficient of the time–space lagged term of pollution emission (L.SO2 and L.wSO2) are both significantly positive, which implies that there exists the time lags and the spatial diffusion effect for air pollution emission. That is, if the air pollution emission is serious in the previous year, then the pollution emission in the next year maybe still serious. If air pollution in neighboring cities j are serious, the air pollution in local city i maybe also serious, which can be explained by the “air diffusion effect”.

Robustness test

This paper replaces variable SO2 with annual average value of PM2.5 and industrial dust emission, respectively, to test the robustness of the regression based on Model 2 and 3 in Table 4. Table 5 shows that the estimated coefficients of ER are still significantly positive and its squared term ERS are still significantly negative, which offers further evidence that the effects of ER on air pollution in local city are the inverted-U pattern.

Table 5 Robustness test: substitution PM2.5 and industrial dust for SO2
Full size table

Secondly, the spatial lagged term of environmental regulations (w × ER) is significantly negative and its squared term (w × ERS) is significantly positive, which provides further evidence that the effects of ER in neighboring cities j on air pollution in local city i are the U-shape curve.

Thirdly, the spatial lagged term ρ is significantly positive. All in all, the signs of coefficients of key variables in Table 5 are consistent with the signs of the estimated results in Table 4, which supports the robustness of the econometric regression results in Table 4.

Mechanism test

Effects of ER on industrial agglomeration

The regression results in Tables 4 and 5 confirm that the stricter enforcement of environmental regulations can improve air quality in local city i while worsening air quality in neighboring cities, and the interaction of environmental regulations between adjacent cities may lead to the Pollution Haven effect. This paper wants to know whether the stricter implementation of ER in neighboring city j will force polluting enterprises located in city j to engage in green innovation, or choose to move to city with less stringent ER, such as city i.

Table 6 examines the effect of ER on the agglomeration of manufacturing industry sectors (AM) based on the model 4. All estimated results show that coefficients of ER are significantly positive, coefficients of ERS are significantly negative, which implies that the effects of ER on AM is the inverted-U pattern in terms of local city i. Combined with the sign and results of ER and ERS in Tables 4 and 5, it is reasonable to infer that there exists an environmental regulations transmission mechanism. That is, in terms of local city i, the more stringent environmental regulations eventually decrease the agglomeration of manufacturing sectors (AM), which in turn reduce air pollution emission.

Table 6 Effects of ER on the agglomeration of manufacturing sectors (AM)
Full size table

Secondly, coefficients of W*ER are significantly negative and coefficients of W*ERS are significantly positive. Moreover, the signs of the estimated results remain constant when the time–space lagged term of the agglomeration of manufacturing sectors is introduced into SDM (seeing Column 4, and 7). This implies that the effects of ER in city j on AM in city i is the U-shape. More precisely, the more stringent ER in city j will lead to the first decrease and then increase (eventual increase) in agglomeration of manufacturing sectors in local city i. Combined with the sign and results of (w × ER) and (w × ERS) in Tables 4 and 5, it is reasonable to infer that there exists another environmental regulations transmission mechanism. That is, the polluting firms in city j may shift manufacturing plants to neighboring cities with less stringent ER, such as city i, thereby leading to the eventual increase in agglomeration of manufacturing sectors (AM) in city i, which in turn aggravate air pollution in city i.

Table 7 examines the effect of ER on the agglomeration of productive services industry (AS) based on Model 4. The signs of coefficients of ER, ERS, W*ER and W*ERS are exactly contrary to the signs of the estimated results in Table 6. This implies that the more stringent ER may lead to the eventual increase in agglomeration of the productive service industry in terms of local city i, which is the U-shape. The possible explanation is that the productive service industry with less pollution emission can substitute for the manufacturing industry with severe pollution, because local government officials have the strong incentive to achieve both the target of economic development, such as economic growth, employment, and accomplish the target of environmental protection, such as air pollution emission reducing.

Table 7 Impact of ER on the agglomeration of productive service sectors (AS)
Full size table

In Table 8, Columns 1–3 replace variable AM with the dependent variable AM(sec), which indicates the agglomeration of the secondary industries. Firstly, the estimated result in Column 3 shows that the more stringent ER will lead to the eventual decrease in agglomeration of the secondary industry in terms of local city i, which implies that the effects of ER on AM(sec) is the inverted-U pattern in terms of local city i. There is one more thing we have to mind, coefficients of ER are not significant in Column 1–3, and coefficient of ERS is not significant in Column 1and 2. Comparison of the regression results in Table 6 with Table 8 can verify that the effects of ER on agglomeration of manufacturing sectors (AM) will be significantly larger than that on agglomeration of the secondary industry (AM(sec)). Secondly, the more stringent ER in neighboring cities j will promote the eventual increase in agglomeration of the secondary industry in city i, which is line with the regression results in Table 6.

Table 8 Impact of ER on Agg. of the secondary industry and the high-end productive service industry
Full size table

In Table 8, Columns 4–6 replace AS with the dependent variable AS(high), which denotes the agglomeration of the high-end productive service industry. Firstly, the estimated result in Column 6 shows that the more stringent ER may promote the eventual increase in agglomeration of the high-end productive service industry in terms of local city i, which is consistent with the regression results in Table 7. Unfortunately, coefficients of the square term ERS is not significant in column 4 and 5. Secondly, the signs of the estimated coefficients of W*ER and W*ERS in column 5 and 6 in Table 8 are not consistent with the signs of the estimated value in Table 7. It implies that the effects of ER in adjacent cities j on the productive service industry or the high-end productive service industry in local city i are vague.

Effects of ER on technological progress

We assume that environmental regulations affect firms’ production and innovation behavior through the Porter hypothesis and the Pollution Haven Hypothesis. Firstly, the more stringent ER in local city i may lead to a dramatic increase in firms’ pollution control costs and investment in research and development for reducing pollution. Polluting enterprises will shift production plants to neighboring cities with weaker ER to maintain output and profits. On the other hand, the strict enforcement of environmental regulations in neighboring cities j may prevent the “pollution haven effect”. The more stringent environmental regulation in city j will force polluting enterprises to make more investment in pollution-reducing R&D, thereby making technological progress.

Table 9 examines the effect of ER on technological progress based on the Model 5. The estimated results of columns 3 and 4 show that the more stringent ER leads to the first increase and then decline in technology progress in terms of local city i. In other words, the impact of ER on technological progress is the inverted-U shape. One possible explanation is that the more stringent ER will lead to the dramatic increase in firms’ pollution-reducing costs, which have greatly exceeded the profitability of the firm. In this case, the more stringent ER will eventually inhibit green innovation.

Table 9 Effect of ER on technology progress
Full size table

Secondly, the significant positive value of (W × ERS) infer s that the more stringent ER in neighboring cities (city j) will lead to the first decrease and then increase (eventual rise) in technology progress in local city i, which supports the “pollution haven hypothesis”. That is to say, the existence of Pollution Haven effects will reduce the incentives for firms to innovate in the short run. In the long run, however, firms will eventually engage in more green innovation if polluting firms cannot relocate production plants in area with weaker ER, which means that the Pollution Haven effect does not exist.

Conclusion

Using the panel data of 275 prefecture-level cities in China in 2003–2019 and spatial econometric model, this paper examines the effects of environmental regulation (ER) and industrial agglomeration on air pollution, and explores the transmission mechanism of ER affecting agglomeration of manufacturing sectors, thereby affecting air pollution. The results are as follows.

  1. (1)

    There are differences in effects of environmental regulations on air pollution in local and neighboring city. Environmental regulation has a significant threshold effect on air pollution. On the one hand, when environmental regulations in one city are over the threshold value, which is over the turning point of the inverted-U shape curve, the more stringent environmental regulations is beneficial to the decline in air pollution in local city. On the other hand, there exists pollution transfer between cities due to difference in implementation of environmental regulations, which is known as the pollution haven effect. Specifically speaking, when the intensity of ER in local city (i) is much weaker than that in adjacent cities (j), polluting enterprises may move from neighboring cities (j) with more stringent environmental regulations to the city (i) with less stringent ER, thereby leading to the increase in air pollution in city i with lax ER

  2. (2)

    Environmental regulation affects air pollution by influencing industrial agglomeration. More precisely, in terms of local city i, the more stringent environmental regulations will eventually decrease the agglomeration of manufacturing sectors (AM), which in turn reduce air pollution emission. There also exists another environmental regulations transmission mechanism. The polluting industry in adjacent cities j may shift manufacturing plants to the local city with less stringent ER, such as city i, thereby leading to the eventual increase in agglomeration of manufacturing sectors (AM) in city i, which in turn aggravate air pollution in city i

  3. (3)

    Mechanism analysis shows that environmental regulation affects industrial agglomeration and air pollution through influencing firms’ innovation decisions. Specifically, the more stringent ER will lead to the dramatic increase in firms’ pollution-emission-reducing costs, which have exceeded the profitability of the firm. In this case, the more stringent ER may eventually inhibit green technological innovation. On the other hand, the existence of “pollution haven effects” will lead to the fall in the incentives for firms to innovate in the short run. In the long run; however, firms will eventually engage in more green innovation if polluting firms cannot relocate production plants to area with lax ER.

Our findings have two important policy implications for economic development and environmental protection. These are summarized below.

  1. (1)

    The single priority of economic performance such as real GDP should transform into the multi-dimension development goals including real GDP per capita, unemployment rate, improved air quality and pollution reduction. Because of the nature of transboundary air pollution, the more stringent implementation of environmental regulations should become a nationwide activities, such as the concentration of PM2.5 and industrial dusts at all prefecture-level cities must, respectively, reduce at least 10 percent in the 14th five-year plan period (2021–2025). The central government should strengthen coordination between cities (or administrative provinces) in air pollution control. This is essential to avoid the transfer of polluting industrial sectors (Chang et al. 2023)

  2. (2)

    Combined with local development conditions, local governments should use both stringent individual command-and-control regulation and market-based regulation, such as tradable emission, to encourage incumbent enterprises to act vigorously to heighten economic efficiency and intensify pollution emission reduction, known as the technological transformation and upgrading, which is line with the goal of high-quality development advocated by Chinese central government. On the other hand, local governments should make efforts to encourage and attract the investment in clean industries or low-pollution-emission industries such as the high-end productive service sectors if it is possible.

In terms of future works, to identify accurately the effects of environmental regulation on air pollution, more effort is devoted to collecting the data, such as daily data, monthly data and quarterly data. The annual data cannot well and truly reveal the daily and seasonal change in air pollution. The fact is that the air quality is obviously better in April–September in a year than in October–March in next year in China. The annual data on air pollution are the average value, which cannot accurately estimate the daily or seasonal change in climatic conditions including air temperature, air ventilation, wind and rain varying over day. In the future, climatic conditions will be taken into account as control variables to further investigate the influencing factors of air pollution. In addition, it is interesting to estimate the impact of specific environmental regulation on corresponding specific indicator (or composite indicator) of air pollution emission using data from micro-firm level. Frankly speaking, the reduction in air pollution comes true only until every individual emission indicator lowers the mandated minimum regulation level.