Abstract
Previous studies have examined the relationship between total e-waste generation and its determinants. However, e-waste categories have not received appropriate attention, and thus important information is missing for policymakers. This paper advances the state of knowledge by studying e-waste categories individually. Statistical data of e-waste in the EU28 + 2 countries over the period 2000–2015 is disaggregated into single categories, namely temperature exchange equipment, screens and monitors, lamps, large equipment, small equipment, and small IT and telecommunication equipment. To examine the main driving forces of e-waste in each category, the STIRPAT model (Stochastic Impacts by Regression on Population, Affluence, and Technology) and the environmental Kuznets curve (EKC) hypothesis are applied, using panel quantile regression as main method and pooled OLS to control robustness of findings. Results show that population, renewable energy consumption, trade openness, and urbanization are positively correlated with all e-waste categories. Renewable energy exploitation is a major e-waste driver of large and small equipment, screens and monitors, and small IT. Interestingly, an inverted U-shaped relationship between gross domestic product (GDP) per capita and the quantity of e-waste was found across all e-waste categories for most regressions when using the quantile regression method (28 out of 30 quantiles), and for all regressions when using the pooled OLS method. This confirms the EKC hypothesis and indicates that e-waste of all categories increases with GDP up to a certain level (turning point) but then decreases when GDP continues to grow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Technological advances have become an essential element of economic prosperity in all countries of the world (Romer 1990; Hwang and Shin 2017; Mewes and Broekel 2020; Appiah-Otoo and Song 2021). However, technological progress not only improves living standards but is also accompanied by problems such as the generation of wastes (Panambunan-Ferse and Breiter 2013; Umair et al. 2015). The last two decades have witnessed a growing interest in waste electrical and electronic equipment (WEEE), or e-waste, and the impacts of this waste stream on human health and environment have been evaluated (Chatterjee and Abraham 2017; Ahirwar and Tripathi 2021; Li and Achal 2020). Between 2014 and 2019, global e-waste generation increased from 41.8 Mt (an average of 5.8 kg per inhabitant) to 53.6 Mt (an average of 7.3 kg/inh); e-waste today represents one of the fastest-growing waste streams (Baldé et al. 2015; Forti et al. 2020; Freitas et al. 2020). Despite the dramatic rise of e-waste around the world, its main driving forces are not fully understood (Boubellouta and Kusch-Brandt 2021a).
A geographic region, where driving forces of e-waste generation can be studied in detail, is Europe. Good data availability and a relatively large number of countries characterize the region. Europe represents an economically prosperous territory with extensive technological advances, and it is one of the largest producers of e-waste in the world, both in terms of total quantity and per capita (per inhabitant) (Forti et al. 2020). European e-waste generation amounted to 15.6 kg/inh in 2014, 16.6 kg/inh in 2016, and 16.2 kg/inh in 2019 (Baldé et al. 2015, 2017; Forti et al. 2020), while the global average was less than half of this. Being a major e-waste generator, the European Union (EU) has embarked on a strategy to responsibly manage this waste stream, and through the EU WEEE Directive has set mandatory e-waste collection and recycling targets (between 50 and 85%) for the EU member states (Arduin et al. 2020; Coughlan and Fitzpatrick 2020). Identification of the main driving forces of e-waste generation could provide essential support to achieve the defined e-waste collection and valorization targets.
The most used model to study the driving forces of environmental degradation is the IPAT model, proposed by Ehrlich and Holdren (1971). The IPAT equation (Eq. 1) assumes that the socioeconomic impact on environmental degradation (I) is determined by the following three factors: population size (P); affluence (A), commonly expressed as gross domestic product (GDP) per capita; and technology (T).
This approach has been widely applied to examine the impact of population growth on the environment, and it has also been frequently exercised to analyze the main determinants of environmental pressure (Fan et al. 2006). However, the postulated proportional relationship between environmental degradation and its determinants is a key limitation of the IPAT model (Wang et al. 2017a, b). To overcome this limitation, Dietz and Rosa (1997), by reformulating IPAT, adopted the STIRPAT model (Stochastic Impacts by Regression on Population, Affluence, and Technology), which provides a quantitative framework to examine the non-proportional impact of main driving forces of environmental degradation (Wang et al. 2017a, b). It is expressed by the formula in Eq. 2, where the subscript i indicates the subject under study (observational unit) and t the time (year); I, P, A, and T are the same as in Eq. (1); a is the constant term, b, c, and d are the coefficients of P, A, and T, and e is the error term. After taking logarithms for both sides of Eq. (2), the STIRPAT form in Eq. 3 is obtained:
Over the last three decades, the STIRPAT model has been extensively employed to examine the main driving factors of pollutant emissions. According to Hashmi and Alam (2019), the SCOPUS database contains about 1300 STIRPAT-related articles, and half of these were published during the last three years. Most studies used pollutant or CO2 emissions as indicator of environmental degradation (Liu and Xiao 2018; Vélez-Henao et al. 2019), some looked at the ecological footprint (Jia et al. 2009; Wang et al. 2010; Usman and Hammar 2021), while a few researchers used solid waste (Fischer-Kowalski and Amann 2001; Arbulu et al. 2016; Cheng et al. 2020; Han et al. 2020).
For mature economies, the impact of economic growth on environmental health is more complex than simply a linear relationship. The link between economic development and environmental degradation has been analyzed under several theoretical frameworks, such as environmental Kuznets curve (EKC) hypothesis, scale hypothesis, race to the bottom hypothesis, gains from trade hypothesis, Porter hypothesis, and pollution havens hypothesis (Frankel 2009; Barnes 2019). The EKC hypothesis has evolved into one of the most applied theories. It postulates that the relationship between economic growth and environmental degradation is an inverted U-shaped curve, i.e., when economic development reaches a certain level (turning point), further economic growth will witness reduced environmental pressure put forward by Kuznets (1955), the Kuznets curve hypothesis originally referred to the relationship between income and inequality, but it has now been widely applied by researchers in many other fields, including macroeconomics, sociology, mathematics, and agriculture (Jula et al. 2015; Asumadu and Vladimir 2019). Panayotou (1993) introduced the expression “Environmental Kuznets Curve” when applying the Kuznets curve hypothesis to the environmental field, while Grossman and Krueger (1991) were the first to claim that the relationship between GDP per capita and environmental degradation is that of an inverted U-shaped curve, i.e., a Kuznets curve. Today, more than 2300 EKC studies are documented in the Web of Science database (Asumadu and Vladimir 2019).
When testing the EKC hypothesis on e-waste, the relationship between economic growth and total e-waste generation in a country was found to be that of an inverted U-curve (Boubellouta and Kusch-Brandt 2020, 2021a, b), where e-waste first increases with GDP but at high economic development stage, it starts declining. E-waste increase reflects a growing consumption of electrical and electronic equipment since all technical equipment will at some point reach its end of life (Forti et al. 2020). Such increased demand for technical equipment was reported to be caused by socioeconomic factors, in particular, economic growth and population (Kumar et al. 2017; Kusch and Hills 2017; Awasthi et al. 2018; Namlis and Komilis 2019), which is in line with the assumptions of the STIRPAT model. Other factors such as technological advances (for example through more widespread adoption of renewable energy technologies), urbanization and trade openness have received little attention. Thus, the picture regarding the main driving forces of e-waste generation is fragmented. Furthermore, previous studies have analyzed total e-waste generation only, but have not looked at different e-waste categories individually. E-waste is a material flow that contains very different types of constituents; technical devices of a variety of sizes, designs, and intended fields of applications are in use and eventually become e-waste.
In this work, e-waste generation, disaggregated into individual categories (temperature exchange equipment, screens and monitors, lamps, large equipment, small equipment, and small IT and telecommunication equipment) is conceptualized as indicator of environmental degradation. In an attempt to contribute to the existing literature, this study explores the main driving forces of the different e-waste categories and aims to close important knowledge gaps. First, this study analyzes the relationship between e-waste generation and an extended set of socioeconomic indicators, namely economic growth, population, renewable energy consumption, urbanization, and trade openness, for 30 European countries (EU28 + 2) over the period 2000–2015, at the level of e-waste categories. The individual categories are employed as dependent variables to overcome the limits of existing studies which have all used total e-waste generation. Each component is employed as an indicator of environmental degradation within the framework of the STIRPAT model. This is the first work to apply the STIRPAT model for the analysis of e-waste. Second, the EKC hypothesis for e-waste categories is examined (integrated in the STIRPAT model), while previous studies exploring the EKC hypothesis have used total e-waste only, without considering the individual categories contained in total e-waste. Knowing the nature of the relationship between economic growth and each e-waste category is useful for policymakers to design appropriate programs and measures. Third, in contrast to previous studies, this research applies a panel quantile regression model suggested by Powell (2016) to explore the main determinants of e-waste categories. The quantile regression for panel data (QRPD) method is more elaborate in terms of providing a detailed picture of determinants compared to the traditional ordinary least squares method, which estimates the average value of the sample (Wang et al. 2019); quantile regression presents the whole picture of a conditional distribution, and thus identifies the comprehensive effect of influencing factors on e-waste components across several quantiles.
The rest of this paper is organized as follows. The “Methodology” section presents the model applied and specifies the econometric estimator and data used. The “Results and discussion” section provides and discusses the results. Finally, the “Conclusion” section presents concluding remarks.
Materials and methods
Model specification
Environmental Kuznets curve hypothesis (EKC)
The EKC describes the phenomenon that during early stages of economic development environmental degradation increases with economic growth, but when GDP reaches a certain level (turning point), environmental quality improves while GDP continues to increase (Grossman and Krueger 1991; Panayotou 1993). The basic form of the EKC hypothesis is expressed by the following equation:
where I is the indicator of environmental degradation such as CO2 emissions, water pollution, or solid waste. GDP.cap is the gross domestic product per capita, X represents control variables, and ε is the error term. When the coefficient α1 is positive and the coefficient α2 is negative, and both coefficients are statistically significant, the EKC hypothesis is fulfilled, i.e., the relationship between GDP per capita and environmental degradation is an inverted U-shaped curve.
Previous studies on the EKC hypothesis have used a range of indicators of environmental degradation, such as carbon dioxide, carbon monoxide, sulfur dioxide, and greenhouse gas (Asumadu and Vladimir 2019; Shahbaz and Sinha 2019; Mehmood and Tariq 2020; Ahmad et al. 2021), but relatively few used solid waste (Waste Kuznets Curve) as an indicator. According to Boubellouta and Kusch-Brandt (2021b), there are 33 studies documented in literature, and 73% of these confirmed the WKC hypothesis. More recently, environmental abatement through recycling of solid waste was researched under the EKC hypothesis (Kasioumi and Stengos 2020). Most WKC studies used municipal solid waste as indicator, while very few looked at e-waste in the context of the EKC hypothesis. Only three studies explored e-waste under the EKC hypothesis. The work of Boubellouta and Kusch-Brandt (2020), using panel data for 28 + 2 European countries over the period 2000–2016, was the first to examine the Kuznets curve for e-waste, by applying as econometric methods generalized method of moments (GMM), two-stage least squares (2SLS), and ordinary least squares (OLS); strong evidence for the Kuznets curve hypothesis was found. Likewise, Boubellouta and Kusch-Brandt (2021a) found an inverted U-shaped relationship between GDP and e-waste generation for 174 countries for 2016. To capture the impact of economic growth on e-waste mismanagement, Boubellouta and Kusch-Brandt (2021b) used two indicators for environmental degradation, namely uncollected and non-recycled/non-reused e-waste, and looked at data from 27 European countries over the period 2008–2016, applying FMOLS and DOLS as econometric methods; the work evidenced an inverted U-shaped relationship between GDP per capita and mismanaged e-waste and thus confirmed the EKC hypothesis for mismanaged e-waste. All previous studies used total e-waste as parameter and did not consider the e-waste composition, i.e., different e-waste categories.
Expanded STIRPAT model
Since the relationship between GDP and environmental degradation can be non-linear and thus potentially comply with the pattern postulated by Kuznets (1955), the STIRPAT model has also been used to test the EKC hypothesis between GDP and CO2 emissions or other indicators of environmental degradation (Salman et al. 2019; Zhang and Zhao 2019; Cheng et al. 2020). This has not yet been trialed for solid waste. Combining EKC hypothesis and STIRPAT model could provide a powerful approach for examining the relationship between GDP and quantity of waste in each e-waste category, and for simultaneously identifying the main determinants of the e-waste category under study. A strong correlation between GDP per capita and/or population and e-waste generation is documented in literature (Kumar et al. 2017; Kusch and Hills 2017; Awasthi et al. 2018; Namlis and Komilis 2019). To minimize the omitted variable bias, in addition to population, GDP, and renewable energy consumption (representing the technology factor), this work adds further variables that could have an impact on e-waste generation. The STIRPAT model is expanded by including GDP per capita squared to account for the EKC theory and urbanization and trade openness as additional control variables. Thus, the STIRPAT model becomes as follows:
where WEEE is e-waste generation for each e-waste category, POP is the size of population, GDP.cap is the gross domestic product per capita, REC is renewable energy consumption as a proxy of technology, URB is urbanization, and OPEN is trade openness.
An energy-related parameter (energy intensity, total energy consumption, or partial energy consumption (industry, non-renewable, renewable)) is a frequent choice in the context of IPAT and STIRPAT (Ghazali and Ali 2019) to account for the technology factor. Total energy consumption is closely coupled with economic development, while the adoption of renewable energies indicates a technological innovation pathway (Ebhota and Tabakov 2021). Renewable energy was reported to be a significant determinant of both human development (Satrovic 2018) and environmental degradation (Cheng et al. 2019). In addition, renewable energy technologies are closely related to electrical and electronic equipment. Thus, renewable energy consumption is selected in this work to represent the technology factor. The model controls for urbanization to capture the effect of demographic characteristics. Urbanization has been reported to negatively impact environmental degradation when looking at CO2 emissions (Abbasi et al. 2020; Shabani et al. 2021). The impact of urbanization on e-waste has become more important because the world is more rapidly urbanizing (Lu et al. 2015; Shamim et al. 2015; Kosai et al. 2020). When rural residents move to cities, they will inevitably buy electrical and electronic devices, and the increased demand for such items leads to more e-waste. Therefore, a positive effect of urbanization on e-waste quantities is expected. The model further controls for trade openness to capture the effect of exports and imports. Satrovic et al. (2020) highlighted the need to include trade openness as control variable when exploring determinants of environmental degradation; a significant influence of this variable on CO2 emissions is documented in literature (Satrovic 2019; Mujtaba et al. 2020). According to previous studies, trade openness can affect the environment positively or negatively (Halliru et al. 2020). On the one hand, trade openness can negatively affect environmental degradation through the fact that trade liberalization enhances economic growth and such growth, in turn, helps protecting the environment as a result of increasing per capita income. On the other hand, the more elevated exports and imports resulting from higher trade openness increase the effects of emissions and waste on the environment, by rising production and consumption and by aggravating the pressure on natural resources.
Regression
Panel quantile regression model
The quantile regression approach proposed by Koenker and Bassett (1978) is employed to examine the main driving forces of e-waste. Quantile regression has been widely used in environmental economics during recent years. Compared with traditional ordinary least squares method (OLS), quantile regression has distinct advantages. First, traditional OLS focuses only on the conditional expectation (mean effect) for the whole sample, which may lead to under- or overestimating coefficients, while quantile regression focuses on the conditional quantiles and thus provides multiple regressions for the same sample (Wang et al. 2019). Second, when the data contains outliers, the quantile regression provides robust results and heavy distributions (Bera et al. 2016). Third, the traditional OLS provides inconsistent findings in the absence of normal distribution for variables of interest, while quantile regression does not require any distributional assumption (Cheng et al. 2019). A large body of studies has used panel quantile regression estimators with fixed effects (FEQR) suggested by Koenker (2004), Canay (2011), Ponomareva (2010), Rosen (2012). The fixed effect panel quantile regression estimator can be written as follows:
where y is the dependent variable, xi presents the vector of independent variables, α is the individual fixed effects, τ means the τth quantile, τ ϵ (0, 1); \(\beta_{{(\tau_{k} )}}\) is the τth quantile of coefficients to be estimated. The main advantage of additive fixed effects quantile regression is its ability to control individual effects, but it suffers from the incidental parameter problem when the time dimension of panel data is small (Baryshnikova and Pham 2019), and it is inefficient when a large number of cross-section in data is given. To address this problem, Powell (2014, 2016) proposed a quantile regression estimator for panel data (QRPD) with nonadditive fixed effects. Unlike FEQR, the QRPD approach assumes nonadditive fixed effects and the parameters to be interpreted vary based on the nonadditive disturbance term while maintaining the non-separable disturbance term, which typically corresponds with the basic quantile regression approach. In addition, the quantile regression with additive fixed effects estimates the distribution of (yit − αi)/Dit (with Dit representing the set of explanatory variables), while the panel quantile regression with nonadditive fixed effects estimates the distribution of yit/Dit, and Powell (2014, 2016) argues that the estimation method of FEQR may be inappropriate because observations registered at the highest ranks of the (yit − ai) articulation may essentially belong to the lowest levels of the yit distribution, making the outcome of the FEQR method potentially deficient in critical information. The underlying model of QRPD with nonadditive fixed effects can be written as follows:
where yit is the dependent variable, \(D_{it}^{\prime }\) is the set of independent variables, β the coefficient of variables to be estimated, and \(U_{it}^{*}\) is the error term which can be moderated by various types and manifestations of disturbances (some might be fixed, others varying in time). With the adoption of Powell’s argument, the QRPD model is linear in parameters, and \(D_{it}^{\prime } \beta_{(\tau )}\) is a strictly increasing function with respect to τ. For any individual τth quantile, the quantile regression claims the conditional restriction expressed in Eq. 8, where P, with P ϵ (0, 1), is the probability:
The conditional restriction in Eq. 8 means that the probability of the dependent variable yit is smaller or the same as the quantile function for all independent variables and equal to τ. Powell (2014, 2016) assumes that this probability varies by observed entity and even within-entity (over time) as long as such variation is orthogonal to the instruments. Accordingly, QRPD is set to depend on both a conditional and an unconditional restriction, with Di = (Di1, …, Dit) specified as follows:
Powell (2014, 2016) developed the QRPD in an instrumental variable framework, with instruments Zi = (Zi1, …, Zit), using generalized method of moments (GMM) for estimation. The sample moments are defined as follow:
where \(\overline{Z}_{i} = \frac{1}{t}\mathop \sum \limits_{i = 1}^{T} Z_{it}\).
Based on Eq. 11, the parameter set is defined as follows:
Then, the following applies:
where \(\hat{A}\) is a weighting matrix. Markov Chain Monte Carlo (MCMC) optimization method is used to implement the model.
Unit root tests
It is widely accepted that time series at macro level are non-stationary, i.e., they contain the unit root. If the time series used are nonstationary, the results could generate a spurious regression. Hence, before running the estimation procedure, it is necessary to ensure the stationarity of each variable used through the unit root test. Researchers have provided many unit root tests divided into two categories, which are common unit root tests and individual unit root tests. In this paper, the four widely used panel unit root tests are applied, regarding the common unit root the Lavin-Lin-Chu (LLC) test (Levin et al. 2002) is used, while the Im-Pesaran-Shin (IPS) (Im et al. 2003), Augmented Dicky-Fuller (ADF) (Dickey and Fuller 1979), and Philips-Perron (PP) (Phillips and Perron 1988) tests are adopted to examine the individual unit root. For all tests, the null hypothesis is that there is unit root, i.e., the variable is nonstationary, whereas the alternative hypothesis is that there is no unit root, i.e., the variable is stationary. The selection of optimum lag is based on Schwartz information criterion. In addition, it is examined whether the time series contains cross-section dependence, because in that case, the above tests become ineffective. To overcome such a situation, Pesaran (2007) proposed an alternative approach (CIPS test) which considers the cross-sectional dependencies. Applying this second-generation unit root test makes the cross-sectional independence assumption obsolete.
Panel cointegration test
Once the stationarity of the time series under study is confirmed, it is useful to determine if a long-run cointegration relationship exists among the variables of interest. In this research, three frequently used tests are applied, namely Pedroni (2004), Kao (1999), and Westerlund (2007). Pedroni (2004) suggested two categories of cointegration tests: panel tests statistics and group tests statistics. The panel tests are based on the within dimension approach which includes four statistics which are panel v-statistic, panel rho-statistic, panel PP statistic, and panel ADF-statistic. The group tests are based on the between dimension approach which includes three statistics namely group rho-statistic, group PP-statistic, and group ADF-statistic. In addition, Kao panel cointegration test follows the same estimation way compared to Pedroni test, but it includes cross-section intercepts and homogenous coefficients into the regression (Dogan and Seker 2016). Both tests assume as null hypothesis the absence of a cointegration relationship between the variables of interest versus the alternative hypothesis that there is a cointegration relationship. In addition, the co-integration test suggested by Westerlund (2007) is employed. This test is more effective compared to Padroni and Kao in the presence of cross-section dependence.
Data
For each of the six e-waste categories under study, the panel data set used in this paper consists of 480 observations, covering 30 European countries (EU28 plus Norway and Switzerland) over the period 2000–2015, i.e., 16 years. Selection of countries and study period was based on data availability. In this study, e-waste generation of each country (WEEE) is disaggregated into six distinct categories (Panels A to F), using the data provided by Huisman et al. (2017) (there based on the Global E-waste Monitor), and expressed for each year per capita (per inhabitant of the country) (WEEE.cap): temperature exchange equipment (WEEE.cap.tee, Panel A); screens and monitors (WEEE.cap.scr, Panel B); lamps and lighting equipment (WEEE.cap.lmp, Panel C), large equipment (WEEE.cap.leq, Panel D), small equipment (WEEE.cap.seq, Panel E); small IT and telecommunication equipment (WEEE.cap.sit, Panel F). A detailed description of the composition of each e-waste category is available in Huisman et al. (2017). The six e-waste categories together amount to total e-waste generation as reported in national statistics.
GDP per capita, population, renewable energy consumption, urbanization, and trade openness are from the World Development Indicators (World Bank 2020). Table 1 reports the descriptive statistics and normality tests for all variables used. GDP.cap is the gross domestic product per capita (and GDP.cap2 is the square of GDP per capita). POP is the total population in a country. URB is the urbanization measured as percentage of urban population out of the total population of a country. REC is renewable energy consumption (% of total final energy consumption). OPEN is trade openness (volume exports + imports in % of GDP).
Before implementing quantile regression, it should be ensured that the variables under study are not normally distributed. Several tests have been proposed to check the normal distribution, either through descriptive statistics or statistical tests. First, skewness is among the most used descriptive statistics of the normality test. Skewness is used to measure the symmetry of the data distribution. The data distribution follows the same as that of the normal distribution, when the third moment (skewness) is equal to 0. Results of skewness in Table 1 indicate that the coefficients of all variables of interest are significantly non-zero, this means that the variables under study are not normally distributed. Second, there are a several statistical tests to check the normality distribution. This research used two tests namely Shapiro–Wilk (Royston 1992) and Jarque–Bera's test (Jarque and Bera 1980). As shown in Table 1, the p-values for both tests are statistically significant at 1% for almost all variables, meaning that all the variables are not normally distributed. The results of these tests confirm that the quantile regression approach is a suitable and reasonable choice for examining the main determinants of e-waste categories in European countries.
Table 2 provides the correlation matrix of the data. A strong positive correlation between GDP per capita and all components of e-waste generation at 1% of significance is found, which indicates that GDP per capita has a large impact on their changes. Likewise, population and urbanization are significantly positively correlated with e-waste components at 1% of statistical significance except for lamps with population. Similar results are found between renewable energy consumption, temperature exchange equipment, screens, and lamps. The results also show a statistically non-significant correlation between trade openness and all components of e-waste.
Results and discussion
Results of unit root and cointegration tests
As described in “Unit root tests” and “Panel cointegration test” sections, the variables under study first pass through unit root tests and cointegration tests to ensure appropriateness of the regression. Before implementing panel unit tests for the variables used, it is analyzed whether a cross-sectional dependency and a slope homogeneity exist; Table 3 reports the results. Cross-sectional dependency is found for all e-waste categories (Panels A to F). In addition, the Pesaran and Yamagata (2008) slope homogeneity test suggest that slope coefficients are heterogeneous. Since heterogeneity exists across countries for the variables of interest, the panel quantile regression approach is confirmed to be a suitable method as it considers heterogeneity of the sample.
Thus, the data set represents heterogeneous panels with cross-sectional dependencies, and the Pesaran CIPS test (Pesaran 2007) is appropriate to test unit roots. The results (Table 4) show that the null hypothesis of a unit root can be rejected at the 5% and 1% statistical significance for all variables. Variables of interest were nonstationary at the level, but after taking the first difference, all variables have become stationary.
The cointegration test results of the Pedroni, Kao, and Westerlund tests can be found in Table 5. Since four out of seven statistics reject the null hypothesis of no cointegration at 1% level of statistical significance for all estimated models, the Pedroni cointegration test strongly supports existence of long-run cointegration relationships between the variables of interest for all models. Likewise, the Kao test supports existence of cointegration at 1% level of significance for e-waste components and at 5% level of significance for the WEEE.cap.sit. In addition, the Westerlund test confirms existence of long-run cointegration between the variables for all models.
Panel quantile regression results
Panel quantile regression with non-additive fixed effects (QRPD), as suggested by Powell (2016) is used in this study to investigate the main driving forces of e-waste components in European countries. The results of the quantile regression are shown in Table 6, reported for the 10th, 25th, 50th, 75th, and 90th percentiles of the conditional e-waste distribution of each e-waste category. The percentile indicates the set of data values within a specific share of the distribution of values, e.g., the 25th percentile means that 25% of data points are below this value, while the 90th percentile means that only 10% of data points are higher; therefore, low quantiles refer to countries with lower e-waste generation, while high quantiles represent countries with more elevated e-waste generation per capita. In addition to the QRPD method, for the purpose of comparison, the pooled OLS method is used for the regression, and the OLS results appear in the last column of Table 6.
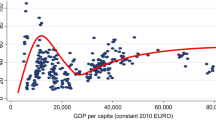
To identify whether the EKC hypothesis is fulfilled, the coefficients of GDP per capita and its square are of interest; when the first one is positive and the second is negative, and both are statistically significant, the EKC hypothesis is confirmed (see “Environmental Kuznets curve hypothesis” section), and thus an inverted U-shaped curve is found for the relationship between economic development stage (GDP per capita) and environmental degradation (quantity of WEEE of a specific category in this study). Regarding GDP per capita and its square, the results in Table 6 show that the coefficients are positive and negative, respectively, and statistically significant at 1% level across different quantiles for all e-waste categories except for two out of 30 quantiles (10th percentile for large equipment and 75th percentile for small equipment). Furthermore, pooled OLS provides similar results regarding GDP and its square compared to those obtained from quantile regression, and coefficients are statistically significant at 1% level. These results indicate existence of an inverted U-shaped relationship between GDP per capita and all e-waste categories (EKC hypothesis confirmed) for European countries at different quantiles of e-waste categories. The interpretation of this observation is as follows: when the GDP per capita exceeds a certain level (called turning point), the relationship between GDP per capita and e-waste quantity of a specific category will turn from positive to negative, and thus e-waste generation of this category will decline along further economic growth. These results are in accordance with findings of Boubellouta and Kusch-Brandt (2020), who identified an inverted U-shaped relationship between GDP per capita and total e-waste generation for European countries (using GMM estimator over the period 2000–2016), and they also agree with findings obtained by Boubellouta and Kusch-Brandt (2021a) for 39 countries of the pan-European region for the year 2016. The results are in line with the previous studies that used municipal waste as indicator of environmental degradation such as Ercolano et al. (2018) for Italy, Madden et al. (2019) for Australia, and Cheng et al. (2020) for 258 Chinese cites. The present findings expand the existing body of knowledge because none of the earlier studies attempted to disaggregate the data into individual categories of e-waste, and thus this is the first work to have examined the economic relationships of e-waste categories and to confirm the EKC hypothesis for the e-waste categories individually.
Overall, the results obtained from the panel quantile regression and the pooled OLS method are consistent across different categories of e-waste regarding the pattern of e-waste occurrence along economic development, and this consistency of results is a clear evidence for the validity of the EKC hypothesis between GDP per capita and all e-waste categories in European countries. This relationship of an inverted U-shaped curve can be clearly seen for all e-waste categories in Fig. 1.
In addition, the results show that the impact of GDP per capita square in lower quantiles (10th and 25th percentiles) is stronger than those in the upper quantiles (75th and 90th percentiles) for temperature exchange equipment, screen, large equipment, and small IT. In contrast, this impact in the middle quantiles (50th percentiles) and upper quantiles (90th percentiles) is larger than in other quantiles for lamps and small equipment.
The regression results in Table 6 enable further insights into the main determinants of each e-waste category. Earlier studies suggested that the size of population has a positive impact on e-waste generation (see “Expanded STIRPAT model” section). This assumption is supported by the majority of quantiles, and also by the pooled OLS regression. Results are statistically significant at 1% level for almost all e-waste categories. This indicates that the population number of a country is an important determinant of an increased environmental degradation through e-waste generation in European countries; similar findings have been reported by of Boubellouta and Kusch-Brandt (2020) for total e-waste generation. The results are also consistent with those of Boubellouta and Kusch-Brandt (2021b) who found a positive impact of population density on mismanaged e-waste for 27 European countries during the period 2008–2016. However, when looking in detail at the data reported in Table 6, some differences among the e-waste categories can be identified; the estimated coefficients differ across quantiles in terms of mathematical sign and magnitude. The impact of population is statistically significant and positive at lower quantiles for almost all waste categories and negative at higher quantiles for only two categories, namely temperature exchange equipment and lamps. The positive mathematical sign indicates that an increase in population is accompanied by an increased e-waste generation per capita at lower quantile levels for all e-waste categories, while the negative sign indicates that a population increase correlates with a reduced occurrence of end-of-life temperature exchange equipment and lamps at higher quantile levels. Furthermore, it is evident that the impact of population in lower quantiles (10th percentiles) is larger than in the upper quantiles (75th and 90th percentiles) for temperature exchange equipment, screen, small equipment, and small IT, while in middle (50th) and upper quantiles (90th percentiles) it is higher than in other quantiles for large equipment and lamps, respectively.
In terms of renewable energy consumption, the findings show that the estimated coefficients are mathematically positive and statistically significant at 1% level across different quantiles for almost all e-waste categories, which indicates that the expansion of renewable energy consumption increases e-waste generation in European countries. The same is found with pooled OLS. This is consistent with earlier studies, where a link between more widespread adoption of renewable energy and increased e-waste generation has been made. In the EU, end-of-life photovoltaic panels fall under e-waste legislation and represent one of the fastest-growing e-waste streams (Kusch and Alsheyab 2017). End-of-life photovoltaic panels will also increase worldwide during the coming decades, when installed panels become waste after 20 to 30 years; by 2050, annual photovoltaic panel waste could exceed 10% of total e-waste generation worldwide (IRENA 2016); however, outside the EU the quantification is not necessarily easy because photovoltaic waste in most countries worldwide does not fall under specific e-waste regulations. A report of the UK’s Department for International Development (DFID) estimated that the off-grid solar sector in 14 Sub-Saharan African countries generated about 3600 metric tons of e-waste in 2017 (Cross and Murray 2018). All form of renewable energy exploitation integrate advanced ICT schemes. In addition, the more decentralized nature of renewable energy installations will often mean the installation of technical equipment at each site, including temperature exchange equipment, engines, screens, ICT. It is therefore not surprising that renewable energy consumption is identified as a driver of e-waste generation across the different e-waste categories and most quantiles. For some categories, such as temperature exchange equipment, screens and monitors, and small IT, the effect of renewable energy consumption on e-waste generation is more pronounced in the countries with lower e-waste generation (representing the lower quantiles, such as the 10th and 25th percentiles) compared to the countries with higher e-waste generation (upper quantiles: 75th and 90th percentiles).
When looking at urbanization, the results indicate that the coefficients of urbanization are positive and statistically significant at 1% across the majority of quantiles. This means that when more people move from rural areas to urban areas, e-waste generation increases. Consumption demands of individuals during their transition to becoming city citizens, including their demand for electrical and electronic equipment, will become higher as a result of the increase in per capita income; thus, the volume of e-waste generated will eventually grow. These results are similar with those of Gui et al. (2019) and Cheng et al. (2020) for municipal solid waste in China. However, there are some differences in the impact of urbanization on e-waste categories across lower and upper quantiles (i.e., countries with lower and higher e-waste generation per capita). Specifically, at lower quantiles, such as 10th and 25th percentiles, which refer to the lower e-waste generation countries, the effect of urbanization on lamps, large equipment and small IT is larger than in higher quantiles such as 75th and 90th percentiles. On the contrary, the effect of urbanization in upper quantiles (75th and 90th percentiles) is stronger than the urbanization effect in lower quantile countries for temperature exchange equipment, small equipment, and screen.
Finally, the effect of trade openness on e-waste categories can be identified. Similar to the effect of population, the coefficients of trade openness at upper quantiles (75th and 90th percentiles) turn from positive to negative for temperature exchange equipment, while the rest of quantiles are positive and statistically significant at 1% level across the majority of quantiles for all e-waste categories. This result is in line with Hecksher–Ohlin’s trade theory, which assumes that foreign trade induces an increase in the consumption and production of goods and services, thus leading to increased environmental degradation (Sharma 2011). However, this effect differs among quantiles. When comparing the estimated coefficients of the variable OPEN (trade openness) across different quantiles, the results in Table 6 show that an increase of trade openness has a stronger effect on increasing e-waste such as temperature exchange equipment, screen, and small IT in the countries with less e-waste generation (10th percentiles) compared to the countries with higher e-waste generation. Furthermore, the effect of trade openness is a different one for lamps and large equipment; in particular, at the higher quantiles such as the 90th percentile, the coefficients of openness are larger than those in lower quantiles.
It is worth pointing out that, as documented in Table 6, the results are conclusive for both methods applied, i.e., panel quantile regression and pooled OLS, which confirms the robustness of the findings.
The observed patterns in Table 6 document correlations of variables. To better understand whether one variable is instrumental to reliably predict the change of another, the Granger causality test is applied. Results are reported in Table 7. Results show there is a bi-directional panel causality relationship between GDP per capita and its square and all e-waste categories in the European countries. The results also indicate that there is a unidirectional panel causality running from population to temperature exchange equipment and screen. A bidirectional panel causality between renewable energy consumption and screen, large equipment, small equipment, and small IT is also revealed. Bidirectional Granger causality between urbanization and large equipment is found. Regarding trade openness, the results indicate a bidirectional panel causality relationship between trade openness, temperature exchange equipment, and small equipment, while there is a unidirectional panel causality running from trade openness to screen and large equipment.
Policy implications
The results of this study provide valuable insights about the main driving forces of individual e-waste categories, which has not received much attention in previous studies, where total e-waste generation was analyzed but the different e-waste categories remained without attention. The main patterns found in this work were consistent for all e-waste categories across almost all quantiles, i.e., both for countries with low and high e-waste generation. Interestingly, a pronounced inverted U-shaped relationship between e-waste quantity and economic development stage was found for all e-waste categories, i.e., when economy reaches a certain level, it can be expected that reduced e-waste generation will be witnessed in the presence of further economic growth. While this pattern was found for total e-waste generation in earlier works (Boubellouta and Kusch-Brandt 2020, 2021a), this present study confirms that for European countries it also applies for the individual e-waste categories. However, volumes of e-waste generation are predicted to grow substantially in the future, and even after crossing the turning point where e-waste generation will no longer grow with the prosperous economy, the e-waste quantities will remain high. Therefore, e-waste management policies should take into account environmental and socio-economic aspects related to the occurring e-waste quantities. Based on the results of this study, the following suggestions are provided.
First, the robust inverted U-shaped relationship between GDP per capita and all e-waste categories is a positive finding with view to potential limits of further e-waste growth; at a lower GDP per capita e-waste generation increases, but a high income per capita can support the reduction of e-waste generation. However, focusing on increasing the GDP per capita is not enough of a strategy to solve the problems of e-waste generation and management. The role of governments is very important in setting up a framework for sound e-waste management. In this context, the individual e-waste categories merit more attention, while today it is common to look at total e-waste only. Especially with high GDP per capita, European countries should pay attention to the growth rate of e-waste for each category in order to tailor the appropriate procedures and to become aware of changing patterns of individual e-waste flows. The use of technology has become more and more integrated into all areas of our lives; thus, e-waste generation today is not only a ubiquitous phenomenon but also subject to a very high diversity among types of items and their individual characteristics, along with rapid changes. As an example, if the growth rate of some electrical and electronic devices increases due to declining prices or a shortened lifespan of devices as a result of rapid technological progress, e-waste generation may continue even though the country has reached the turning point of GDP per capita level.
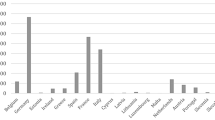
Second, the e-waste generation level of a country is not enough as an indicator to characterize a country’s challenges in establishing sound e-waste management schemes. The composition of e-waste varies among countries, and this applies both for countries with different and with similar e-waste generation levels. As an example, Norway and Luxembourg both had a very high GDP per capita in 2015 (107,235.27USD and 90,132.34USD, respectively), but the temperature exchange equipment generation was quite different, amounting to 4.82 kg/inh in Norway and 2.86 kg/inh in Luxembourg, while Slovenia with a relatively much lower GDP per capita (23,735.24USD in 2015) experienced a temperature exchange equipment generation of 3.05 kg/inh. Therefore, countries should focus on their e-waste components according to their own consumerism and consequently build an e-waste management system that fits the specifications and characteristics of the country. This further supports the earlier recommendation to focus more on the single e-waste categories and not only on total e-waste. A specific focus should be given to small e-waste; small e-waste is one of the most diverse categories (The Economist Intelligence Unit 2015), and one of the categories with the highest generation volumes (see Fig. 1), but at the same time this type of waste is characterized by the fact that major shares remain uncollected and without appropriate treatment even in countries where advanced collection schemes are in place, such as in Europe (Baldé et al. 2015).
Third, renewable energy consumption was identified to be an important driver of the generation of e-waste in categories such as IT and communication technology, and large technical equipment. The potential of renewable energy to alleviate environmental problems (greenhouse gas emission, in particular) has been highlighted in many studies (Shahnazi and Shabani 2021). Possible implications regarding e-waste generation, especially the risk of increased e-waste quantities occurring along the energy transition, have previously been mentioned (Kusch and Alsheyab 2017; Cross and Murray 2018). The results of this study provide evidence that higher renewable energy exploitation is accompanied by more e-waste across the European countries. Therefore, as technological progress will advance, environmental degradation in terms of e-waste occurrence must be expected to increase. The governments should strengthen the interlinkages between policies which focus on energy transition and policies, which focus on other areas of environmental protection. To reduce e-waste generation, energy policies must factor in their effects on waste quantity and quality.
Fourth, it should find the attention of policymakers that trade openness is positively correlated with increased e-waste generation for all e-waste categories in European countries, and it represents a main driver of most categories, including small and large technical equipment, screens and monitors, and temperature exchange equipment. More trade openness means more technical equipment that becomes waste within the country, with corresponding implications for environment, economy, and health. Increased quantities of e-waste as a result of high trade openness mean more potentially hazardous waste products to handle. Therefore, foreign trade control with a focus on reducing hazardous components contained in electrical and electronic equipment can make a viable contribution to reducing adverse environmental and health impacts of e-waste.
Conclusion
Based on panel data from 30 European countries over the period 2000–2015, this paper examined the effects of main determinants of e-waste categories, namely temperature exchange equipment, screens and monitors, lamps, large equipment, small equipment and small IT, and telecommunication equipment. The quantities of e-waste of each category served as dependent variables within the framework of the STIRPAT model and the environmental Kuznets curve (EKC) hypothesis, using panel quantile regression as main econometric method and pooled OLS to check the robustness of the results.
For both methods applied, the variables used to explore the main driving forces of e-waste categories were found to have positive and statistically significant effects for almost all e-waste types. Thus, it was confirmed that GDP per capita, population, renewable energy consumption, urbanization, and trade openness are main determinants of e-waste categories in European countries. Interestingly, GDP per capita square had a statistically significant negative effect on all e-waste categories when using pooled OLS for the regression, and in most tests (28 out of 30 quantiles) when using panel quantile regression. Therefore, the relationship between GDP per capita and the quantity of material in each e-waste category is an inverted U-shaped curve (EKC hypothesis confirmed), i.e., e-waste generation in the European countries increases for all categories with the growth of GDP per capita up to a certain level (turning point), but then e-waste generation for all categories decreases as GDP per capita continues to increase.
However, among the e-waste categories, some differences in the impact of variables used were found across quantiles. The empirical results evidenced that GDP had a greater impact on e-waste in the lower quantiles (i.e., the countries with lower e-waste generation) for temperature exchange equipment, screens and monitors, large equipment, and small IT. The impact of population in the low quantiles was greater than in the upper quantiles for temperature exchange equipment, screens and monitors, small equipment, and small IT, while an effect of population was more pronounced in the middle and upper quantiles for large equipment and lamps, respectively. Renewable energy consumption had highest impact on e-waste generation in the lower quantiles (i.e., among countries with relatively lower e-waste generation) for temperature exchange equipment, screens and monitors, and small IT. In contrast, for large and small equipment, the impact of renewable energy exploitation was stronger in the high quantiles compared to the other quantiles. The influence of trade openness in the low quantiles appeared stronger than in other quantiles for temperature exchange equipment, screens and monitors, and small IT, while for lamps and large equipment this effect was more pronounced in high quantiles than in lower quantiles.
The close relationship ascertained between renewable energy exploitation and several e-waste categories, including temperature exchange equipment, large and small equipment, and ICT, calls for more attention of policymakers on the waste-related impacts of energy transition pathways. Energy policies should be coordinated with e-waste programs. Furthermore, control of foreign trade with a focus on reducing hazardous components contained in electrical and electronic devices could make a highly relevant contribution to alleviating adverse impacts of e-waste across the European countries, since trade openness was identified as a main driver of e-waste, including small technical equipment and screens and monitors.
This research has a number of limitations. Total e-waste generation was disaggregated into six pre-defined categories due to availability of data for these categories. While the analysis of those categories provides a more detailed insight compared to total e-waste, each of the six categories still comprises a variety of technical equipment. The category “large equipment”, for example, includes technical devices from commerce but also from end-users. A link to the contents of both valuable and hazardous materials in each e-waste category was not possible based on the available data. It should also be noted that renewable energy consumption is only one possible choice to account for the technology factor in the STIRPAT model. While this was valid in the context of this work, robustness of this choice cannot necessarily be generalized. A further limitation of this work is that it considers only European countries. Whether the observed patterns also apply to other regions and can be transferred to the global level must be clarified by additional research. Especially in low-income countries, other determinants might play a vital role, which is not relevant for Europe. As an example, access to electricity is an important factor among poorer communities, while across Europe the population is largely served with electricity. Another potentially relevant control factor might be industrialization.
References
Abbasi MA, Parveen S, Khan S, Kamal MA (2020) Urbanization and energy consumption effects on carbon dioxide emissions: evidence from Asian-8 countries using panel data analysis. Environ Sci Pollut Res 27:18029–18043
Ahirwar R, Tripathi AK (2021) E-waste management: a review of recycling process, environmental and occupational health hazards, and potential solutions. Environ Nanotechnol Monit Manag 15:100409
Ahmad M, Muslija A, Satrovic E (2021) Does economic prosperity lead to environmental sustainability in developing economies? Environmental Kuznets curve theory. Environ Sci Pollut Res 28:22588–22601
Appiah-Otoo I, Song N (2021) The impact of ICT on economic growth—comparing rich and poor countries. Telecommun Policy 45:102082
Arbulu I, Lozano J, Rey-Maquieira J (2016) Waste generation flows and tourism growth: a STIRPAT model for Mallorca. J Ind Ecol 21(2):1–10
Arduin RH, Mathieux F, Huisman J, Blengini GA, Charbuillet C, Wagner M, Baldé CP, Perry N (2020) Novel indicators to better monitor the collection and recovery of (critical) raw materials in WEEE: focus on screens. Resour Conserv Recycl 157:104772
Asumadu SS, Vladimir S (2019) A review on environmental Kuznets curve hypothesis using bibliometric and meta-analysis. Sci Total Environ 649:128–145
Awasthi AK, Cucchiella F, D’Adamo I, Li J, Rosa P, Terzi S, Wei G, Zeng X (2018) Modelling the correlations of e-waste quantity with economic increase. Sci Total Environ 613–614:46–53
Baldé CP, Forti V, Gray V, Kuehr R, Stegmann P (2017) The global e-waste monitor 2017. United Nations University (UNU), International Telecommunication Union (ITU) & International Solid Waste Association (ISWA), Bonn
Baldé CP, Wang F, Kuehr R, Huisman J (2015) The global e-waste monitor 2014: quantities, flows and resources. United Nations University, IAS—SCYCLE, Bonn
Barnes S (2019) Understanding plastics pollution: the role of economic development and technological research. Environ Pollut 249:812–821
Baryshnikova NV, Pham NTA (2019) Natural disasters and mental health: a quantile approach. Econ Lett 180:62–66
Bera AK, Galvao AF, Montes-Rojas GV, Park SY (2016) Asymmetric Laplace regression: maximum likelihood, maximum entropy and quantile regression. J Econom Methods 5(1):79–101
Boubellouta B, Kusch-Brandt S (2020) Testing the environmental Kuznets curve hypothesis for e-waste in the EU28+2 countries. J Clean Prod 277:123371
Boubellouta B, Kusch-Brandt S (2021a) Cross-country evidence on environmental Kuznets curve in waste electrical and electronic equipment for 174 countries. Sustain Prod Consum 25:136–151
Boubellouta B, Kusch-Brandt S (2021b) Relationship between economic growth and mismanaged e-waste: panel data evidence from 27 EU countries analyzed under the Kuznets curve hypothesis. Waste Manag 120:85–97
Canay IA (2011) A note on quantile regression for panel data models. Economet J 14:368–386
Chatterjee A, Abraham J (2017) Efficient management of e-wastes. Int J Environ Sci Technol 14:211–222
Cheng C, Ren X, Wang Z, Yan C (2019) Heterogeneous impacts of renewable energy and environmental patents on CO2 emission—evidence from the BRIICS. Sci Total Environ 668:1328–1338
Cheng J, Shi F, Yi J, Fu H (2020) Analysis of the factors that affect the production of municipal solid waste in China. J Clean Prod 259:120808
Coughlan D, Fitzpatrick C (2020) Trialling the preparation for reuse of consumer ICT WEEE in Ireland. J Clean Prod 256:120512
Cross J, Murray D (2018) The afterlives of solar power: Waste and repair off the grid in Kenya. Energy Res Soc Sci 44:100–109
Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74(366):427–431
Dietz T, Rosa EA (1997) Effects of population and affluence on CO2 emissions. Proc Natl Acad Sci 94:175–179
Dogan E, Seker F (2016) The influence of real output, renewable and non-renewable energy, trade and financial development on carbon emissions in the top renewable energy countries. Renew Sust Energy Rev 60:1074–1085
Ebhota WS, Tabakov PY (2021) Development of domestic technology for sustainable renewable energy in a zero-carbon emission-driven economy. Int J Environ Sci Technol 18:1253–1268
Ehrlich PR, Holdren JP (1971) Impact of population growth. Science 171(80):1212–1217
Ercolano S, Gaeta G, Ghinoi S, Silvestri F (2018) Kuznets curve in municipal solid waste production: an empirical analysis based on municipal-level panel data from the Lombardy region (Italy). Ecol Indic 93:397–403
Fan Y, Liu L, Wu G, Wei Y (2006) Analyzing impact factors of CO2 emissions using the STIRPAT model. Environ Impact Assess Rev 26:377–395
Fischer-Kowalski M, Amann C (2001) Beyond IPAT and Kuznets curves: globalization as a vital factor in analysing the environmental impact of socio-economic metabolism. Popul Environ 23(1):7–47
Forti V, Baldé CP, Kuehr R, Bel G (2020) The global e-waste monitor 2020: quantities, flows and the circular economy potential. United Nations University (UNU)/United Nations Institute for Training and Research (UNITAR)—co-hosted SCYCLE Programme, International Telecommunication Union (ITU) & International Solid Waste Association (ISWA), Bonn/Geneva/Rotterdam
Frankel JA (2009) Environmental effects of international trade. HKS Faculty Research Working Paper Series RWP09-006, John F. Kennedy School of Government, Harvard University
Freitas R, Cardoso CED, Costa S, Morais T, Moleiro P, Lima AFD, Soares M, Figueiredo S, Agueda TL, Rocha P, Amador G, Soares AMVM, Pereira E (2020) New insights on the impacts of e-waste towards marine bivalves: the case of the rare earth element Dysprosium. Environ Pollut 260:113859
Ghazali A, Ali G (2019) Investigation of key contributors of CO2 emissions in extended STIRPAT model for newly industrialized countries: a dynamic common correlated estimator (DCCE) approach. Energy Rep 5:242–252
Grossman G, Krueger A (1991) Environmental impacts of a North American Free Trade Agreement. National Bureau of Economic Research, Working Paper 3194, Cambridge
Gui S, Zhao L, Zhang Z (2019) Does municipal solid waste generation in China support the Environmental Kuznets Curve? New evidence from spatial linkage analysis. Waste Manag 84:310–319
Halliru AM, Loganathan N, Hassan AAG, Mardani A, Kamyab H (2020) Re-examining the environmental Kuznets curve hypothesis in the economic community of West African States: a panel quantile regression approach. J Clean Prod 276:124247
Han X, Hu C, Lin L (2020) A study on the impact of China’s urbanization on the quantity of municipal solid waste produced. Waste Manag Res 38(2):184–192
Hashmi R, Alam K (2019) Dynamic relationship among environmental regulation, innovation, CO2 emissions, population, and economic growth in OECD countries: a panel investigation. J Clean Prod 231:1100–1109
Huisman J, Leroy P, Tertre F, Söderman ML, Chancerel P, Cassard D, Løvik AN, Wäger P, Kushnir D, Rotter VS, Mählitz P, Herreras L, Emmerich J, Hallberg A, Habib H, Wagner M, Downes S (2017) Prospecting secondary raw materials in the urban mine and mining wastes (ProSUM). Final Report, ISBN: 978-92-808-9060-0 (print), 978-92-808-9061-7, Brussels, Belgium. http://www.urbanmineplatform.eu/urbanmine/eee/weightpercapita. Accessed 15 Jan 2021
Hwang W, Shin J (2017) ICT-specific technological change and economic growth in Korea. Telecommun Policy 41(4):282–294
Im KS, Pesaran MH, Shin Y (2003) Testing for unit roots in heterogeneous panels. J Econom 115:53–74
IRENA (2016) End-of-life management—solar photovoltaic panels. International Renewable Energy Agency (IRENA) and International Energy Agency Photovoltaic Power Systems (IEA-PVPS)
Jarque CM, Bera AK (1980) Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ Lett 6(3):255–259
Jia J, Deng H, Duan J, Zhao J (2009) Analysis of the major drivers of the ecological footprint using the STIRPAT model and the PLS method—a case study in Henan Province. China Ecol Econ 68(11):2818–2824
Jula D, Dumitrescu C-I, Lie I-R, Dobrescu R-M (2015) Environmental Kuznets curve. Evidence from Romania. J Theor Appl Econom 22(1):85–96
Kao C (1999) Spurious regression and residual-based tests for cointegration in panel data. J Econ 90:1–44
Kasioumi M, Stengos T (2020) The environmental Kuznets curve with recycling: a partially linear semiparametric approach. J Risk Financ Manag 13:274
Koenker R (2004) Quantile regression for longitudinal data. J Multivar Anal 91(1):74–89
Koenker R, Bassett G (1978) Regression quantiles. Econometrica 46(1):33–50
Kosai S, Kishita Y, Yamasue E (2020) Estimation of the metal flow of WEEE in Vietnam considering lifespan transition. Resour Conserv Recy 154:104621
Kumar A, Holuszko M, Espinosa DCR (2017) E-waste: an overview on generation, collection, legislation and recycling practices. Resour Conserv Recy 122:32–42
Kusch S, Alsheyab M (2017) Waste electrical and electronic equipment (WEEE): a closer look at photovoltaic panels. In: Proceedings of the 17th international multidisciplinary scientific geoconference SGEM 2017, vol 17, no 41, pp 317–324
Kusch S, Hills CD (2017) The link between e-waste and GDP—new insights from data from the Pan-European region. Resources 6:15
Kuznets S (1955) Economic growth and income inequality. Am Econ Rev 45(1):1–28
Levin A, Lin CF, Chu CSJ (2002) Unit root tests in panel data: asymptotic and finite sample properties. J Econom 108(1):1–24
Li W, Achal V (2020) Environmental and health impacts due to e-waste disposal in China—a review. Sci Total Environ 737:139745
Liu D, Xiao B (2018) Can China achieve its carbon emission peaking? A scenario analysis based on STIRPAT and system dynamics model. Ecol Indic 93:647–657
Lu C, Zhang L, Zhong Y, Ren W, Tobias M, Mu Z, Ma Z, Geng Y, Xue B (2015) An overview of e-waste management in China. J Mater Cycles Waste Manag 17:1–12
Madden B, Florin N, Mohr S, Giurco D (2019) Using the waste Kuznet’s curve to explore regional variation in the decoupling of waste generation and socioeconomic indicators. Resour Conserv Recycl 149:674–686
Mehmood U, Tariq S (2020) Globalization and CO2 emissions nexus: evidence from the EKC hypothesis in South Asian countries. Environ Sci Pollut Res 27:37044–37056
Mewes L, Broekel T (2020) Technological complexity and economic growth of regions. Res Policy 2020:104156
Mujtaba A, Jena PK, Mukhopadhyay D (2020) Determinants of CO2 emissions in upper middle-income group countries: an empirical investigation. Environ Sci Pollut Res 27:37745–37759
Namlis K, Komilis D (2019) Influence of four socioeconomic indices and the impact of economic crisis on solid waste generation in Europe. Waste Manag 89:190–200
Panambunan-Ferse M, Breiter A (2013) Assessing the side effects of ICT development: E-waste production and management: a case study about cell phone end-of-life in Manado, Indonesia. Technol Soc 35(3):223–231
Panayotou T (1993) Empirical test and policy analysis of environmental degradation at different stages of economic development. World Employment Research Programme, Working Paper WP238, International Labour Office, Geneva
Pedroni P (2004) Panel cointegration: asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econ Theory 20(3):597–625
Pesaran MH (2007) A simple panel unit root test in the presence of cross-section dependence. J Appl Econ 22:265–312
Pesaran MH, Yamagata T (2008) Testing slope homogeneity in large panels. J Econom 142(1):50–93
Phillips PCB, Perron P (1988) Testing for a unit root in time series regression. Biometrika 75(2):335–346
Ponomareva M (2010) Quantile regression for panel data models with fixed effects and small T: Identification and estimation. Working Paper, University of Western, Ontario
Powell D (2014) Did the economic stimulus payments of 2008 reduce labor supply? Evidence from quantile panel data estimation. Working Paper WR-710-3, RAND Corporation
Powell D (2016) Quantile regression with nonadditive fixed effects. RAND Corporation
Romer P (1990) Endogenous technological change. J Political Econ 98(5):71–102
Rosen AM (2012) Set identification via quantile restrictions in short panels. J Econom 166(1):127–137
Royston P (1992) Approximating the Shapiro-Wilk W-Test for non-normality. Stat Comput 2(3):117–119
Salman M, Long X, Dauda L, Mensah CN, Muhammad S (2019) Different impacts of export and import on carbon emissions across 7 ASEAN countries: a panel quantile regression approach. Sci Total Environ 686:1019–1029
Satrovic E (2018) The human development relies on renewable energy: evidence from Turkey. In: Atmaca A (ed) 3rd International energy and engineering congress, proceedings book. Gaziantep University, Gaziantep, pp 19–27
Satrovic E (2019) Energy consumption, trade openness and growth nexus in Turkey: evidence from VECM. J Econ Adm Sci 20(1):1–12
Satrovic E, Muslija A, Abul SJ (2020) The relationship between CO2 emissions and gross capital formation in Turkey and Kuwait. South East Eur J Econ Bus 15(2):28–42
Shabani E, Hayati B, Pishbahar E, Ghorbani MA, Ghahremanzadeh M (2021) The relationship between CO2 emission, economic growth, energy consumption, and urbanization in the ECO member countries. Int J Environ Sci Technol. https://doi.org/10.1007/s13762-021-03319-w
Shahbaz M, Sinha A (2019) Environmental Kuznets curve for CO2 emission: a literature survey. J Econ Stud 46(1):106–168
Shahnazi RZ, Shabani D (2021) The effects of renewable energy, spatial spillover of CO2 emissions and economic freedom on CO2 emissions in the EU. Renew Energy 169:293–307
Shamim A, Mursheda AK, Rafiq I (2015) E-Waste trading impact on public health and ecosystem services in developing countries. Int J Waste Resour 5:188
Sharma SS (2011) Determinants of carbon dioxide emissions: empirical evidence from 69 countries. Appl Energy 88:376–382
The Economist Intelligence Unit (2015) Global e-waste systems: insights for Australia from other developed countries. The Economist Intelligence Unit, London, New York
Umair S, Björklund A, Petersen EE (2015) Social impact assessment of informal recycling of electronic ICT waste in Pakistan using UNEP SETAC guidelines. Resour Conserv Recycl 95:46–57
Usman M, Hammar N (2021) Dynamic relationship between technological innovations, financial development, renewable energy, and ecological footprint: fresh insights based on the STIRPAT model for Asia Pacific Economic Cooperation countries. Environ Sci Pollut Res 28:15519–15536
Vélez-Henao JA, Vivanco DF, Hernández-Riveros JA (2019) Technological change and the rebound effect in the STIRPAT model: a critical view. Energy Policy 129:1372–1381
Wang M, Liu J, Wang J, Zhao G (2010) Ecological footprint and major driving forces in West Jilin Province, Northeast China. Chin Geogr Sci 20:434–441
Wang C, Wang F, Zhang X, Yang Y, Su Y, Ye Y, Zhang H (2017a) Examining the driving factors of energy related carbon emissions using the extended STIRPAT model based on IPAT identity in Xinjiang. Renew Sustain Energy Rev 67:51–61
Wang Y, Zhang C, Lu A, Li L, He Y, ToJo J, Zhu X (2017b) A disaggregated analysis of the environmental Kuznets curve for industrial CO2 emissions in China. Appl Energy 190:172–180
Wang S, Zeng J, Liu X (2019) Examining the multiple impacts of technological progress on CO2 emissions in China: A panel quantile regression approach. Renew Sustain Energy Rev 103:140–150
Westerlund J (2007) Testing for error correction in panel data. Oxf Bull Econ Stat 69(6):709–748
World Bank (2020) World Bank data. https://data.worldbank.org. Retrieved 15 Nov 2020
Zhang S, Zhao T (2019) Identifying major influencing factors of CO2 emissions in China: regional disparities analysis based on STIRPAT model from 1996 to 2015. Atmos Environ 207:136–147
Funding
Open Access funding enabled and organized by Projekt DEAL. No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Editorial responsibility: Samareh Mirkia.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boubellouta, B., Kusch-Brandt, S. Determinants of e-waste composition in the EU28 + 2 countries: a panel quantile regression evidence of the STIRPAT model. Int. J. Environ. Sci. Technol. 19, 10493–10510 (2022). https://doi.org/10.1007/s13762-021-03892-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13762-021-03892-0