Abstract
Vulnerability assessment and mapping play a crucial role in disaster risk reduction and planning for adaptation to a future earthquake. Turkey is one of the most at-risk countries for earthquake disasters worldwide. Therefore, it is imperative to develop effective earthquake vulnerability assessment and mapping at practically relevant scales. In this study, a holistic earthquake vulnerability index that addresses the multidimensional nature of earthquake vulnerability was constructed. With the aim of representing the vulnerability as a continuum across space, buildings were set as the smallest unit of analysis. The study area is in İzmit City of Turkey, with the exposed human and structural elements falling inside the most hazardous zone of seismicity. The index was represented by the building vulnerability, socioeconomic vulnerability, and vulnerability of the built environment. To minimize the subjectivity and uncertainty that the vulnerability indices based on expert knowledge are suffering from, an extension of the catastrophe progression method for the objective weighing of indicators was proposed. Earthquake vulnerability index and components were mapped, a local spatial autocorrelation metric was employed where the hotspot maps demarcated the earthquake vulnerability, and the study quantitatively revealed an estimate of people at risk. With its objectivity and straightforward implementation, the method can aid decision support for disaster risk reduction and emergency management.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given the specific nature of its rapid onset, unpredictability, and destruction potential, earthquakes pose a serious threat to cities, placing their assets and inhabitants at risk. Earthquakes do not affect every country, region, city, or even part of a city equally (Wisner et al. 2004). Although developed countries are at risk for their high-valued assets, developing countries are more at-risk regarding fatalities, causalities, and short- and long-term impacts (Pelling 2003; Peduzzi et al. 2009).
Turkey is one of the developing countries highly susceptible to earthquakes. It is the most at-risk country for earthquake disasters worldwide for urban mortality and economic loss (Brecht et al. 2013). One of the most damaging earthquakes in the country, the İzmit earthquake of 1999 (Mw 7.8, also called the Marmara earthquake) caused the death of over 18,000 people and 37,000 people were injured, and about 95,000 houses were severely damaged (Bağcı et al. 2000). Even though it has not been long past 1999, an earthquake hazard is not a remote possibility for the city. A major, Mw ≤ 7.6 event is expected on the Marmara segment of the fault (west) in the next half century with a probability of approximately 50% (Şengör et al. 2005). İzmit City is expected to be affected by an earthquake in this segment.
Under the threat of a probable earthquake, the seismic risk of the city remains a critical issue to be addressed. Although the city has developed since 1999, there is still evidence of needs for improvement regarding the building stock, socioeconomic status of the inhabitants, and the built environment.
This study aimed at vulnerability assessment and mapping to demarcate vulnerable places encompassing diverse components that produce vulnerability at the part of İzmit City with very high seismicity using a data-driven approach, advancing visual communication of the results, and making a crude estimate of the inhabitants that are at the highest risk.
1.1 Disaster Risk and Vulnerability Concept
Disaster risk is a product of co-existence of hazard, exposure, and vulnerability. While hazard and exposure are components of disaster risk that are barely modifiable, vulnerability is. In this regard, there has been a shift from hazards to a vulnerability/resilience paradigm (Haque and Etkin 2006; McEntire 2012) and an increased recognition that disaster risks on human society cannot be reduced without a focus on vulnerability and its quantitative assessment.
Vulnerability is a complex and multifaceted concept (Bohle 2001), and there are many conceptualizations of the term, as gathered in the review by Diaz-Sarachaga and Jato-Espino (2019). Among many others, a widely recognized definition suggests that vulnerability reflects the susceptibility or the intrinsic predisposition to be affected or the conditions that favor or facilitate damage (Cardona 2004). These predispositions and conditions for seismic vulnerability typically exhibit physical, environmental, and socioeconomic aspects (Carreño et al. 2007; Barbat et al. 2009). We describe seismic vulnerability in this study as physical, socioeconomic, and environmental susceptibilities or conditions of limited capacity that facilitate harm in an earthquake event.
1.2 Vulnerability Assessment Method and Indices
Vulnerability assessment has become a method to communicate the disaster risk to the decision makers for risk reduction and adaptation (Birkmann 2006; Lindlay et al. 2011; Fekete 2019). A map of vulnerability supplemented with an estimate of the rate of people at risk is key to loss modeling and emergency and disaster risk management (Aubrecht et al. 2012). Vulnerability is a multidimensional construct that cannot be measured easily with a single variable (Cutter and Finch 2008). A Multi-criteria decision analysis (MCDA) with weight allocation is the most widely used technique to address urban vulnerability (Diaz-Sarachaga and Jato-Espino 2019) where a composite of multiple quantitative variables with an aggregative formula results in a single index score, called vulnerability index.
Several physical, environmental, and socioeconomic factors are considered responsible for producing the vulnerability of places (Carreño et al. 2007; Cutter and Finch 2008; Carreño et al. 2017). Although physical vulnerability that represents the fragility of the physical structures is crucial, comprehensive or holistic earthquake vulnerability covering overall predispositions is a far more encompassing concept (Barbat et al. 2009). Social vulnerability is described as socioeconomic status and characteristics that make people/societies susceptible to hazards (Cutter et al. 2003). Even though physical and social conditions may have diverse courses of change over space and time, they are considered to be inextricably linked together to produce high-risk conditions, where the former is indicative of the latter (Rashed and Weeks 2003). Socioeconomic conditions often force particular communities to live in hazard-prone areas and homes of poor structural condition (McEntire 2012) and are considered the causes of the physical vulnerability in many cases (Barbat et al. 2009). Built environment capacities, determined by the grain, density, and distribution of facilities such as parks, and so on, affects location-specific vulnerabilities (Wamsler et al. 2013). These inequalities across the space produce location-specific vulnerabilities communicated formerly as “hazard of places” (Cutter 1996).
A common interest of vulnerability assessment is representing the diversity of vulnerability across space. Congruently, mapping of earthquake vulnerability has become a trend in disaster risk reduction studies. The complex and multifaceted nature of the vulnerability concept is also reflected in a broad spectrum of spatial scales, for example, national, regional, local, and household levels (Diaz-Sarachaga and Jato-Espino 2019; Jaimes et al. 2022). Studies that assess intracity variation of vulnerabilities commonly use census units, for example, ward or neighborhood, or the census blocks, as mapping units. Studies that take smaller units as a basis, for example, buildings, are scarce and usually focus on the structural vulnerability (Zhai et al. 2019; Pavić et al. 2020), or they are based on standalone community surveys, rather than open census data (Birkmann 2006; Ebert et al. 2009). However, in urban environments of complexity, interactions across space generate spatial variations of characteristics regardless of the administrative units or census tracks that are for management purposes. Assigning an aggregate measure of characteristics of elements to units or groups, without any relation between them being demonstrated, may also lead to methodological error called “ecological fallacy” (Jones and Andrey 2007), which may cause drawing inaccurate conclusions about the vulnerability and the households/individuals that exhibit it. At the microscale, it becomes essential to represent spatial variation based on the smallest unit, that is, buildings.
In constructing a vulnerability index, the selection of indicators and the weighting are considered major challenges (Zhang et al. 2017; Ziarh et al. 2021). Although numerous studies have used equal weights (Zhang et al. 2017; Diaz-Sarachaga and Jato-Espino 2019), a common disposition is that indicators’ contribution to overall vulnerability is not equal, and weighing the indicators based on their relative importance is more likely to represent the real situation. There are broadly two approaches to weighing—the subjective and objective methods—that both have certain drawbacks. The subjective methods—the so-called knowledge-driven or expert-based methods—rely on the experts’ rankings or a consensus. The vast amount of studies that employ knowledge-driven methods such as AHP, TOPSIS, and so on, however, suffers from the subjectivity that introduces uncertainty and controversy into an index (Chen et al. 2010; Zhang et al. 2017; Rodcha et al. 2019). The objective methods—the so-called data-driven methods—attempt to overcome the subjectivity of the knowledge-based methods by determining weights based on the data. However, weights derived from data may not exactly reflect the actual weights of indicators and may deviate the results from the real situation (Zhang et al. 2021). To overcome the challenge of weighing, this study adopted the catastrophe progression (CP) method that uses relative importance of indicators, rather than direct use of hard to determine weights (Zhang et al. 2017).
Catastrophe progression, as a data-driven approach stemming from the study of dynamic systems, combines catastrophe theory with fuzzy mathematics (Cheng et al 1996) to develop a fuzzy membership function of system state (Gao et al. 2020). In CP, responses to changes in the internal values of each factor are intrinsically evaluated considering their ranking of importance that reduces subjectivity (Ahmed et al. 2015; Xue et al. 2022). Song et al. (2020) and Mostafa (2022) stated that the CP method has been demonstrated to have a unique advantage in dealing with uncertainty and is increasingly employed in holistic indices, particularly the vulnerability indices in the last decade (for example, Zhang et al. 2017; Ziarh et al. 2021; Zheng and Huang 2023). The CP method is also characterized by its perceptiveness to gradual changes in a system that may cause sudden shifts, resembling a catastrophe. Conventional data-driven methods that use calculus to reach a vulnerability index score, however, may fail to address multiple characteristics of an individual or neighborhood that interact and amplify each other to a fragile condition. We consider vulnerability as an example to this. Intrinsically, the CP method favors the relative importance of control variables where, ranking indicators regarding their importance is an issue to be addressed (Shen et al. 2020; Du et al. 2022). The CP executes hierarchical recursive calculations apt for a system tree. Therefore, rather than ranking indicators all at once, grouping indicators with shared context into categories and then ranking them is a compromise approach (Shen et al. 2020). The ranking is either knowledge-based or data-driven. By employing data-driven methods, for example, the mean square difference method (Jin and Zhang 2020), weights based on components share on total variance in principal component analysis (PCA) (Wood et al. 2010; Aksha et al. 2019), and entropy weights (Wu et al. 2022), subjectivity can be avoided. We adopted an extension of the CP method advancing entropy weights for objective ranking of the indicators.
The current study is motivated to objectively address the multidimensional nature of earthquake vulnerability. We acknowledge that earthquake vulnerability exhibits physical, socioeconomic, and environmental aspects and adopted a holistic approach that accommodates the below items as components of earthquake vulnerability index:
-
1.
Building vulnerability, as the structural fragility of the exposed residential building stock (construction system, period, plan irregularity, and so on);
-
2.
Socioeconomic vulnerability that produces susceptibilities for individuals and households (age, gender, household structure, income, and so on); and
-
3.
Vulnerability of the built environment that may reduce the coping capacity (building density, distance to assembly areas, and so on).
To conduct the analysis at a level of detail that can represent the vulnerability as a continuum across space and avoid ecological fallacy, vulnerability mapping at the microscale, taking buildings as the smallest unit of analysis, was adopted. Spatial clustering that advances communication by adding analytical abilities (Aksha et al. 2019) was employed. A classification was conducted on the vulnerability scores to reveal an estimate of the number of people that are highly vulnerable.
In the present study, indicators of earthquake vulnerability were chosen based on the relevance and availability of the data at the building and household scales. We particularly sought to employ data available or can be calculated using GIS tools at no cost.
2 Materials and Methods
A holistic earthquake vulnerability assessment and mapping at a microscale taking buildings as minimum mapping unit was proposed. The catastrophe progression (CP) method was adopted for its perceptiveness to gradual changes that may evolve into highly vulnerable conditions and merit in minimizing subjectivity. In this section, the study area and the vulnerability index components and indicators are described. The CP method and its steps are also explained.
2.1 Study Area
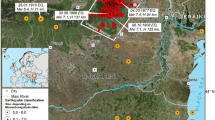
İzmit City of Kocaeli Province is located at the İzmit Bay of the Marmara Sea, in the northwest of Turkey. The city is in the hinterland of megacity Istanbul and is the industrial heart of Turkey. The city center is close to the sea level, with altitude rapidly increasing towards the north of the city where limited settlement activity has occurred, and densification has taken place in the immediate surroundings of the city center. The city is located within the North Anatolian Fault Zone (NAFZ) extending all the way in northern Turkey.
Due to the high alluvial sediment thickness (250–500 m) in the region, soil amplification is extreme (Özalaybey et al. 2008). The Vs30 velocity below 360 m/s in the study area indicates the two most hazardous soil groups, D and E, according to the NEHRP (National Earthquake Hazard Reduction Program) soil classification. The soil characteristics as sub-components of the seismic hazard suggest that a part of the city center is a 1st level seismic hazard zone (Özalaybey et al. 2008) as shown in Fig. 1b (in red). The severity significantly reduces at the surrounding parts of the zone. Therefore, the study area was restricted to the urban area intersecting with this hazard zone. As the hazard is steady across the area, all residential building stock and inhabitants within the study area are presumed to be exposed to earthquake.
The study was conducted for the residential building stock in the study area that accounts for 75% of all buildings, that is, 6540 buildings accommodating about 83 thousand people by 2021. The gross density in the study area of 6.56 km2 was 12,651 persons/km2, indicating quite a dense settlement pattern.
2.2 Earthquake Vulnerability Components and Indicators at the Microscale
Acknowledging that earthquake vulnerability exhibits physical, socioeconomic, and environmental aspects, we identified indicators for the components of earthquake vulnerability based on a literature review as follows and also in Table 1.
2.2.1 Building Vulnerability
The indicators of the building vulnerability in this study primarily stem from the building classification method of rapid visual screening (RVS). A building classification groups buildings with similar materials and seismic force-resisting systems together, facilitating the fast identification of a building’s susceptibility to an earthquake (FEMA 2015). The RVS and other more sophisticated methods use many parameters and sometimes necessitate in-situ tests, which are not practically applicable at the urban scale. Hence, quick methods of assigning vulnerability scores to buildings are often more convenient (Barbat et al. 2009; Fischer et al. 2022). Since there is no complete list of RVS indicators for the study area, available data necessary for building vulnerability assessment were used in building classifications (Silva et al. 2022; Zhang et al. 2023).
Some of the structural attributes were obtained from the local municipality, which mainly archives these for building permits and the data are stored on a building-by-building basis. “Construction system” of existing buildings readily available as FEMA building types S3, C2, C1, C3, and URM were ranked according to the basic scores of FEMA 154 (FEMA 2015) from 1 to 5 respectively, where 5 represents the highest seismic vulnerability of an existing building in the study area. Most common buildings in the study area were of C3 type (concrete frame with unreinforced masonry infill walls) with moderate to high vulnerability, and URM (unreinforced masonry bearing wall buildings) with high vulnerability. The “construction period” was available only as before and after 2007, which is a milestone of the release of the most comprehensive and legally binding regulation on seismic building codes in Turkey (DBYBHY 2007).
Other indicators are about buildings’ physical properties that may cause defects in their seismic response. They are relative position (adjacency), plan irregularity (FEMA 2015), and height/floor area ratio that makes tiny buildings highly vulnerable (Shakya et al. 2018). We calculated these indicators using metrics via GIS tools (ArcGIS 10.8) for repeatability.
“Relative position” is the type of adjacency of the building where an isolated building responds better to earthquake compared to attached buildings, and the position of a building, for example, in the middle, at the end, or at the corner of a block, matters (FEMA 2015; RYTEIE 2019). An extension of the technique “proximity” to automatically determine the relative positions of the buildings was employed. “Plan irregularity” is a geometric measure of the extent to which a building plan is regular and symmetrical to reduce torsional response (Davidson 1997). “Minimum bounding rectangle” for a convex hull of the building vertices was calculated to quantify the irregularity in plan. The “height/floor area ratio” was calculated using the building height divided by the floor area, where the higher ratio is an indication of the fragility of a building.
2.2.2 Socioeconomic Vulnerability
Most of the socioeconomic indicators in this study originate from census data at the household level of the Citizenship Affairs of the Republic of Turkey. Specific age groups or gender, namely elderly, children, and female are common groups deemed socially vulnerable in most studies (Wood et al. 2010; Armaş et al. 2017; Zhang et al. 2017; Sauti et al. 2021). Based on the census data, the occupancy rate of elderly, children, and females were calculated per building. Households with single elderly (Fischer et al. 2022), female-headed (Wood et al. 2010; McEntire 2012), and with three or more children (Armaş et al. 2017), which were considered disadvantaged, were calculated for their rate in the buildings’ total households. Rate of the disadvantaged groups ranged between 0 and 100% except for the children that may not occupy a whole building. People with low income are more susceptible to hazards (Cutter et al. 2003; Wood et al. 2010). As the income data at the household level were unavailable, two proxy indicators (Ebert et al. 2009)—the “current market value of the real estate” and “households receiving social aid”—were obtained from the municipality records.
2.2.3 Vulnerability of the Built Environment
Besides physical and socioeconomic components, the urban fabric also affects location-specific vulnerabilities (Pelling 2003). High concentration and density create susceptible conditions (Sauti et al. 2021; Jaimes et al. 2022). In this component of the human-environment interface, three density indicators—the density of buildings, the density of people, and the density of the parcel (floor/parcel ratio)—were adopted.
Greenness that was selected as an indicator is not a direct measure of vulnerability, but a proxy for the quality of the built environment and the abundance of green and tree cover that may provide services (Ebert et al. 2009). Greenness was obtained from Normalized Difference Vegetation Index (NDVI) using Landsat 8 images of July 2021. Assembly areas are of crucial importance for increasing coping capacities after an earthquake (Allan and Bryant 2011). Hence each building’s distance to assembly areas was taken as an indicator for the component. All of the indicators of the built environment component were calculated using proximity analysis. Buffers excluding the building itself (ring buffer) was produced to calculate zonal statistics for each residential building.
Earthquake vulnerability index is represented by the three components and the selected set of 18 indicators (x1, x2, ..., x18) for each case (building), as seen in Table 1. The first three physical indicators are ordinal categorical variables with rank order that are commonly used as input in CP (e.g., Jenifer and Jha 2017; Ahmed et al. 2015). The signs indicate whether the indicator is positively (+) or negatively (−) related to vulnerability.
2.3 The Catastrophe Progression Method
The CP method is based on the catastrophe theory developed by Thom (1975) and deals with discontinuous changes caused by continuous changes that typically characterize catastrophic phenomena. In the catastrophe theory, system function variables are divided into state variables (dependent), which are the internal variables of the system, and control variables (independent), which are the external influencing factors (Cheng et al. 1996). The status of the state variable is formulated regarding the relative importance of the control variables intrinsically by catastrophe models’ fuzzy membership functions (normalization) rather than user-defined weights (Ahmed et al. 2015; Zhang et al. 2017). Catastrophe progression was employed after standardization of the raw values of indicators, followed by normalization for the estimation of fuzzy membership functions for the state variable, which constitutes the core part of the CP method.
2.3.1 Standardization
For resolving incompatibility and imbalanced weighing, all indicators were standardized using the range standardization method and set to a dimensionless range between 0 and 1. As the CP method is designed for positively related control variables, all indicators positively related to vulnerability were transformed using Eq. 1, and indicators negatively related to vulnerability were transformed using Eq. 2.
where \({x}_{i}\) is the original value of the indicator \(X\), \({x}_{\text{max}}\) and \({x}_{\text{min}}\) are the maximum and minimum values of the indicator, \({x}_{i}^{\prime}\) is standard values of the indicator \(X\), and \({x}_{i}^{{\prime}}\in \left[{0,1}\right]\).
2.3.2 Normalization Using Catastrophe Models
In the CP method, the system is expressed with potential function via the state variables and the external control variables. The normalization formulas are obtained by decomposing the bifurcation set equation (Zhang et al. 2017). The descriptions and normalization formulas of the catastrophe models describe all possible discontinuities of a single state-dependent variable controlled by up to five control variables, namely fold, cusp, swallowtail, butterfly, and wigwam (Cheng et al. 1996; Wood et al. 2010) (Table 2).
As shown in Table 2, \(x\) represents response variables, and \(a\), \(b\), \(c\), \(d\), and \(e\) represent control variables. There are two principles in implementing normalized formulas: complementary and non-complementary. If there is a correlation between the control variables \((a, b, c, \dots )\), variables are assumed to fill up the deficiency of each other, and they are complementary. Therefore, their mean value can be used for the system, that is, \(x=\left({x}_{a}+{x}_{b}+{x}_{c}\right)/3\). If there is no apparent correlation between the control variables \((a, b, c, \dots )\), control variables cannot be replaced with each other, and they are non-complementary. Therefore, the smallest value of control variables is used for the system, i.e., \(x=min\left\{{x}_{a},{x}_{b},{x}_{c}\right\}\) (Jenifer and Jha 2017; Zhang et al. 2017). In catastrophe models, the system’s behavior is determined by the priority of control variables. Therefore, an essential step before normalization by catastrophe models is the sorting of control variables in priority order (Shen et al. 2020; Du et al. 2022). In an attempt to avoid the subjectivity of user-defined ranking, the entropy weights approach was adopted.
2.4 Entropy Weighted Ranking
Entropy weight employs statistical variation to determine weights of factors that control a dependent variable (Jaafari et al. 2014). The smaller the information entropy of an index, the greater the variation degree of the index value. This means that when a particular indicator has more differentiation degree, the greater its role in the holistic evaluation and hence the greater its weight (Gao et al. 2020).
The steps to calculate the entropy weight of each control variable are shown in Eqs. 3–6. The first step is the standardization of the original values. \({P}_{ij}\) is the standardized value of \({i}{\text{th}}\) index, \({j}{\text{th}}\) sample:
\({E}_{i}\) is the information entropy value of \({i}{\text{th}}\) index:
As the natural logarithm function \(\mathrm{ln}(x)\), x ∈ [R ∣ x > 0]. \(\mathrm{ln}{P}_{ij}\) is undefined where \({P}_{ij}=0\). Therefore, \(\mathrm{ln}{P}_{ij}\) is set to 0 where \({P}_{ij}=0\) for convenience (Zhu et al. 2020). \({\omega }_{i}\) is the entropy weight of the \({i}{\text{th}}\) index:
where \(n\) is the number of samples, \(m\) is the number of indicators, and \(0\le \omega j\le 1,\Sigma {\omega }_{j}=1\). Entropy weight calculation is usually followed by a final step of the comprehensive index:
However, in the present study, \({S}_{j}\) was not used, instead, weights (\({\omega }_{i}\)) were employed to rank indicators per category.
3 Results and Discussions
The system (state variable), earthquake vulnerability herein, was divided into subsystems, building vulnerability (VPhy), socioeconomic vulnerability (VSoc), and built environment vulnerability (VEnv), each comprising their own indicators. As an initial step of the catastrophe progression (CP) method, a tree-like structure of the system was established that portrays the multidimensionality and the hierarchy of the subsystems and the control variables of the earthquake vulnerability index (EVI).
3.1 Definition of the Index System
Some studies rank indicators all at once (for example, Yariyan et al. 2020). However, ranking indicators that are very different from each other, like comparing an indicator of social vulnerability with an indicator of building vulnerability, is not convenient. We followed an approach of defining an index system with categories and subcategories and ranking indicators under their parent category (Shen et al. 2020).
In the calculation of CP membership function values, the complementary and non-complementary principle applies to the correlated and uncorrelated indicators, respectively. By convention, for uncorrelated indicators, CP membership is assigned as the minimum membership value. However, the empirical results in the present study caused CP membership function values for subcategories assigned zero for many cases (buildings). This is attributed to cases with indicator values equal to zero, especially in the category of social vulnerability—for example, there may be no elderly persons in a building—and according to the non-complementary rule, zero is assigned to the upper categories in the index system, finally ending up with zero vulnerability for numerous cases. We considered this situation obscuring the real merit of the data and hence followed a course of grouping correlated indicators together that are also semantically related. We explored the correlation of the indicators besides their semantics and employed correlation information to subgroup indicators as well. Thus, we organized subgroups as child-related (x7 and x11), gender-related (x8 and x10), and elderly-related (x6 and x9) that are correlated. The other subcategory of VSoc, the income indicators, were both semantically and statistically related (x12 and x13). Some indicators under VEnv both show a semantic relationship and correlation. Hence we subgrouped those indicators as (x14, x15, and x16). On the other hand, although having correlation with other indicators, x17 and x18, were considered semantically representatives of diverse issues—for example, distance to assembly areas (x18) have no causal relationship with density indicators, such as the density of buildings or people. Hence those indicators were set independent based on semantics. Similarly, although they may correlate, indicators of VPhy represent different characteristics of buildings, making their subgrouping inapt. Therefore, all five indicators of VPhy (x1, x2, x3, x4, and x5) were set independent.
In the present study, a five-level index system was proposed; the first-level index being the target, that is EVI. Target is divided into subsystems of VPhy, VSoc, and VEnv (components), sub-categories at the 3rd and 4th levels. The indicators x1, x2, …, x18 are at the 5th and the basic level. The indicators under subcategories were ordered regarding their entropy weights (\({\omega }_{i}\)), and the subsystems as well regarding aggregate entropy weights (\(\omega\)) of their control variables. The EVI system with categories, entropy weights, and ranking of indicators is shown in Fig. 2.
3.2 The Catastrophe Progression for Earthquake Vulnerability Index, Mapping, and Evaluations
Four normalization formulas of the CP method were used in this study based on the number of control variables, named Fold catastrophe, Cusp catastrophe, Swallowtail catastrophe, and Wigwam catastrophe, respectively, as presented in Fig. 2.
Following the workflow, CP membership function values for each case (building) in the study area at multiple levels were obtained. Membership values of the buildings across the study area were mapped at selected levels of the 2nd and the 1st (the target EVI). Spatial clustering using Getis Ord Gi* on the resulting index score maps was employed to demarcate clusters of high vulnerability. Autocorrelation of each component was tested using global Moran’s I to understand the strength of the spatial context. Pearson’s correlation was employed to assess the relationship among the vulnerability components. Finally, an estimate of people at risk is provided based on the EVI classification.
3.2.1 Earthquake Vulnerability Mapping
Figures 3, 4, and 5 depict the resulting maps for each component at the 2nd level. Figure 6 depicts the comprehensive earthquake vulnerability index (EVI) maps.
The CP scores of index maps were classified to better communicate the results visually and to aid in quantifying the most vulnerable cases. However, it is difficult to determine class breaks based on synthetic CP scores as they do not refer to actual vulnerability. Studies that employ CP use various classification methods including standard deviation (Zhang et al. 2017), natural breaks (Ziarh et al. 2021; Zheng and Huang 2023), quantile (Shen et al. 2020), and bespoke classification methods (Su et al. 2011). The quantile method is adequate for evenly distributed data and natural breaks is adequate for unevenly distributed data that show clustering. The EVI scores for the study resemble a normal distribution that is attributed to several recursive normalization procedures of CP. Therefore, standard deviation classification was employed since it is best suited for data that conforms to a normal distribution (Longley et al. 2015). Standard deviation classification reveals how values are dispersed from the mean and is more reliable in terms of determining highest-vulnerability cases, whereas other methods may undesirably involve near-mean values into dispersed classes. Standard deviation classes were obtained by subtracting or adding certain standard deviation (for example, 0.5, 1, 1.5) from the mean of the dataset, which can enable results to be compared with a future situation of the same study area or with another study area given the same dataset.
Based on standard deviation classification, five categories were defined: High Vulnerability (> 1.5 Std. Dev), High-Medium Vulnerability (0.5–1.5 Std. Dev), Medium Vulnerability (− 0.5 to 0.5 Std. Dev), Medium-Low Vulnerability (− 1.5 to − 0.5 Std. Dev.), and Low Vulnerability (< − 1.5 Std. Dev). For the hotspot maps, color red represents clusters of high vulnerability, and color blue represents clusters of low vulnerability. Gray colors indicate no statistically significant clustering.
The results show that earthquake vulnerability is more concentrated in the western half of the study area in general. But the three components of vulnerability—VPhy, VSoc, and VEnv—differ in localizations for the particular vulnerabilities they present.
3.2.2 Earthquake Vulnerability Evaluations
Besides the mapping of earthquake vulnerability, spatial autocorrelation was explored for a better understanding of the extent to which the vulnerability scores correlate in relation to space, that is, expressing clustering, dispersion, or randomness. The global Moran’s I test results show that all the components have statistically significant clustering across space. Ordered from greatest to least, spatial autocorrelation degree is VEnv > VSoc > VPhy (Table 3). Built environment vulnerability (VEnv) has the greatest spatial autocorrelation, as its indicators are density-related metrics representing spatial context. The fact that VSoc's spatial autocorrelation is higher than that of VPhy is related to similar communities showing clustering, wheareas the buildings of common characteristics showing less thereof.
Pearson’s correlation of the components was also explored. The results show that building vulnerability and social vulnerability are moderately and significantly correlated (Table 3), indicating coherence between social and physical vulnerabilities. But built environment vulnerability is not correlated with the other two vulnerability dimensions (physical and social).
3.2.3 Population at Risk
Given the necessity of quantification for enhanced risk understanding, a crude estimation of the population at risk was implemented. As the vulnerability is a spatiotemporal construct due to density, human activities, and mobility (Aubrecht et al. 2012), daytime and nighttime estimates were provided (Table 4).
The number of residents in official records was used as basic data. However, people do not fully occupy their homes at all times. Nighttime occupancy is usually accepted as approximately 75% (Ara 2014; Wei et al. 2017) of total population. Daytime occupancy can be represented as “home population” that is described by people that usually stay at home, that is, elderly, children, and unemployed (Ara 2014). For this study, nighttime population was calculated as 75% of residents (official), and daytime population was calculated for each class as number of elderly (age 65+), number of children (age ≤ 5), and unemployed approximated as 13.5% of the active population (age 15–64) according to the statistical records of the city for the relevant year (TUIK 2021).
Crude estimate of people at high risk (that is, vulnerability classes high and high-medium) constitute 20% and 7.8% of the total population (82,996 people) for nighttime and daytime, respectively.
4 Conclusion
In this study, a holistic earthquake vulnerability assessment and mapping that addresses the multidimensional nature of earthquake vulnerability at the microscale was conducted. The main contributions of this study are: (1) minimizing subjectivity in the weight assignment by employing an extension of the catastrophe progression method through entropy based ranking of the indicators where the index structure was improved using correlation and semantics; (2) vulnerability mapping at the microscale taking buildings as the smallest unit that is scarce in the literature; (3) improvement of earthquake vulnerability maps using spatial clustering technique; and (4) estimation of people at risk for effective allocation of resources for emergency planning and disaster risk reduction.
Catastrophe progression method avoiding subjectivity demonstrated a unique advantage in dealing with uncertainty and provided a straightforward workflow to generate vulnerability scores. Index scores are synthetic relative representations of vulnerability calculated using the catastrophe normalization formulas. Therefore, drawing conclusions such as a building may collapse or is extremely deprived by means of the vulnerability scores on building-by-building basis is inherently flawed.
The empirical results show that the western part of the study area is highly vulnerable. Evaluating the components separately, the results show that social vulnerabilities cluster more across space compared to physical vulnerabilities of the buildings. Buildings might be renewed/reconstructed individually in time but the social context does not change as much in the study area. Physical and social vulnerabilities show bivariate correlation, which verifies coherence of physical and social vulnerabilities, formerly signified with the idea of “hazard of places.” The EVI scores classified into vulnerability classes reveal that about 20% and 7.8% of all residents are at risk at nighttime and daytime, respectively. This crude estimate of the people at risk provides a relative measure and a basis for disaster risk and emergency management initiatives.
Although the microscale analyses at the building level provide a great amount of spatial detail, the availability of data at the building and household levels is an issue. The present study needs to include some of the indicators deemed important in vulnerability assessment that were unavailable at the household level—for example, education and employment. Some of the indicators were substituted with proxies—for example, the current market value of real estate was used in the assessment instead of income that was unavailable. With all the critical indicators available, the method may more likely represent the actual situation. However, as the study intended to demarcate the localities of the vulnerability represented by the convolutions of the dimensions of vulnerability across space, the method is considered robust despite the missing data and the use of proxies.
References
AFAD (Afet ve Acil Durum Yönetimi Başkanlığı / Disaster and Emergency Management Presidency). 2023. Turkey earthquake hazard map (Türkiye Deprem Tehlike Haritası). https://tdth.afad.gov.tr/TDTH/main.xhtml. Accessed 10 Jul 2023 (in Turkish).
Ahmed, K., S. Shahid, S. Harun, T. Ismail, N. Nawaz, and S. Shamsudin. 2015. Assessment of groundwater potential zones in an arid region based on catastrophe theory. Earth Science Informatics 8(3): 539–549.
Aksha, S.K., L. Juran, L.M. Resler, and Y. Zhang. 2019. An analysis of social vulnerability to natural hazards in Nepal using a modified social vulnerability index. International Journal of Disaster Risk Science 10(1): 103–116.
Allan, P., and M. Bryant. 2011. Resilience as a framework for urbanism and recovery. Journal of Landscape Architecture 6: 34–45.
Ara, S. 2014. Impact of temporal population distribution on earthquake loss estimation: A case study on Sylhet, Bangladesh. International Journal of Disaster Risk Science 5(3): 296–312.
Armaş, I., D. Toma-Danila, R. Ionescu, and A. Gavriş. 2017. Vulnerability to earthquake hazard: Bucharest case study, Romania. International Journal of Disaster Risk Science 8(2): 182–195.
Aubrecht, C., S. Freire, C. Neuhold, A. Curtis, and K. Steinnocher. 2012. Introducing a temporal component in spatial vulnerability analysis. Disaster Advances 5(2): 48–53.
Bağcı, G., A. Yatman, S. Özdemir, and N. Altın. 2000. The earthquakes causing damage in Turkey (Türkiye’de Hasar Yapan Depremler). Earthquake Research Bulletin (Deprem Araştırma Bülteni) 69: 113–126.
Barbat, A.H., M.L. Carreño, L.G. Pujades, N. Lantada, O.D. Cardona, and M.C. Marulanda. 2009. Seismic vulnerability and risk evaluation methods for urban areas: A review with application to a pilot area. Structure and Infrastructure Engineering 6(1–2): 17–38.
Birkmann, J. 2006. Measuring vulnerability to promote disaster-resilient societies: Conceptual frameworks and definitions. In Measuring vulnerability to natural hazards: Towards disaster resilient societies, ed. J. Birkmann, 9–54. Tokyo: United Nations University Press.
Bohle, H. 2001. Vulnerability and criticality: Perspectives from social geography. IHDP Update 2(1): 3–5.
Brecht, H., U. Deichmann, and H.G. Wang. 2013. A global urban risk index. Policy research working papers 6506. Washington, DC: The World Bank.
Cardona, O.D. 2004. The need for rethinking the concepts of vulnerability and risk from a holistic perspective: A necessary review and criticism for effective risk management. In Mapping vulnerability: Disasters, development and people, ed. G. Bankoff, G. Frerks, and D. Hilhost, 37–51. London: Earthscan.
Carreño, M., O.D. Cardona, and A.H. Barbat. 2007. Urban seismic risk evaluation: A holistic approach. Natural Hazards 40(1): 137–172.
Carreño, M.L., O.D. Cardona, A.H. Barbat, D.C. Suarez, M.P. Perez, and L. Narvaez. 2017. Holistic disaster risk evaluation for the urban risk management plan of Manizales, Colombia. International Journal of Disaster Risk Science 8(2): 258–269.
Chen, Y., J. Yu, and S. Khan. 2010. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation. Environmental Modelling & Software 25(12): 1582–1591.
Cheng, C.-H., Y. Liu, and Y. Lin. 1996. Evaluating a weapon system using catastrophe series based on fuzzy scales. Proceedings of the 1996 Asian Fuzzy Systems Symposium, 11–14 December 1996, Kenting, 212–217.
Cutter, S.L. 1996. Vulnerability to environmental hazards. Progress in Human Geography 20(4): 529–539.
Cutter, S.L., and C. Finch. 2008. Temporal and spatial changes in social vulnerability to natural hazards. Proceedings of the National Academy of Sciences 105(7): 2301–2306.
Cutter, S.L., B.J. Boruff, and W.L. Shirley. 2003. Social vulnerability to environmental hazards. Social Science Quarterly 84(2): 242–261.
Davidson, R. 1997. EERI annual student paper award a multidisciplinary urban earthquake disaster risk index. Earthquake Spectra 13(2): 211–223.
DBYBHY (Deprem Bölgelerinde Yapılacak Binalar Hakkında Yönetmelik / Regulation on buildings to be constructed in earthquake zones). 2007. https://www.resmigazete.gov.tr/eskiler/2007/03/20070306-3.htm. Accessed 10 Jul 2023.
Diaz-Sarachaga, J.M., and D. Jato-Espino. 2019. Analysis of vulnerability assessment frameworks and methodologies in urban areas. Natural Hazards 100(1): 437–457.
Du, X., X. Liu, and Y. Zihang. 2022. Risk assessment of agricultural drought based on catastrophe progression method: A China case study. SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4034084.
Ebert, A., N. Kerle, and A. Stein. 2009. Urban social vulnerability assessment with physical proxies and spatial metrics derived from air and spaceborne imagery and GIS data. Natural Hazards 48(2): 275–294.
Fekete, A. 2019. Social vulnerability (re-)assessment in context to natural hazards: Review of the usefulness of the spatial indicator approach and investigations of validation demands. International Journal of Disaster Risk Science 10(2): 220–232.
FEMA (Federal Emergency Management Agency). 2015. Rapid visual screening of buildings for potential seismic hazards: A handbook, 3rd edn. https://www.fema.gov/sites/default/files/2020-07/fema_earthquakes_rapid-visual-screening-of-buildings-for-potential-seismic-hazards-a-handbook-third-edition-fema-p-154.pdf. Accessed 10 Jul 2023.
Fischer, E., A.E. Biondo, A. Greco, F. Martinico, A. Pluchino, and A. Rapisarda. 2022. Objective and perceived risk in seismic vulnerability assessment at an urban scale. Sustainability 14(15): Article 9380.
Gao, S., H. Sun, M. Ma, Y. Lu, Y. Yao, and W. Liu. 2020. Vulnerability assessment of marine economic system based on comprehensive index and catastrophe progression model. Ecosystem Health and Sustainability 6(1): Article 1834459.
Haque, C.E., and D. Etkin. 2006. People and community as constituent parts of hazards: The significance of societal dimensions in hazards analysis. Natural Hazards 41(2): 271–282.
Jaafari, A., A. Najafi, H.R. Pourghasemi, J. Rezaeian, and A. Sattarian. 2014. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran. International Journal of Environmental Science and Technology 11(4): 909–926.
Jaimes, D.L., C.R. Escudero, K.L. Flores, and A. Zamora-Camacho. 2022. Multicriteria seismic hazard and social vulnerability assessment in the Puerto Vallarta metropolitan area, Mexico: Toward a comprehensive seismic risk analysis. Natural Hazards 116(2): 2671–2692.
Jenifer, M.A., and M.K. Jha. 2017. Comparison of analytic hierarchy process, catastrophe and entropy techniques for evaluating groundwater prospect of hard-rock aquifer systems. Journal of Hydrology 548: 605–624.
Jin, X., and W. Zhang. 2020. The optimization of objective weighting method based on relative importance. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), 25–27 December 2020, Harbin, China, 1234–1237. https://doi.org/10.1109/ICMCCE51767.2020.00271.
Jones, B., and J. Andrey. 2007. Vulnerability index construction: Methodological choices and their influence on identifying vulnerable neighbourhoods. International Journal of Emergency Management 4(2): 269–295.
Lindlay, S., J. O’Neill, N. Lawson, R. Christian, and M. O’Neil. 2011. Climate change, justice and vulnerability. York: Joseph Rowntree Foundation.
Longley, P.A., M.F. Goodchild, D.J. Maguire, and D.W. Rhind. 2015. Geographic information science and systems. New York: Wiley.
McEntire, D. 2012. Understanding and reducing vulnerability: From the approach of liabilities and capabilities. Disaster Prevention and Management: An International Journal 21(2): 206–225.
Mostafa, M.M. 2022. Five decades of catastrophe theory research: Geographical atlas, knowledge structure and historical roots. Chaos, Solitons & Fractals 159: Article 112078.
Özalaybey, S., E. Zor, M.C. Tapırdamaz, A.R. Tarancıoğlu, B. Erkan, A. Karaaslan, E.M. Alpaslan, E.S. Ergintav, and E. Tan. 2008. Soil classification and seismic hazard assessment project for Kocaeli Province (Kocaeli İli için Zemin Sınıflaması ve Sismik Tehlike Değerlendirme Projesi). TÜBİTAK.
Pavić, G., M. Hadzima-Nyarko, and B. Bulajić. 2020. A contribution to a UHS-based seismic risk assessment in Croatia – A case study for the city of Osijek. Sustainability 12(5): Article 1796.
Peduzzi, P., H. Dao, C. Herold, and F. Mouton. 2009. Assessing global exposure and vulnerability towards natural hazards: The disaster risk index. Natural Hazards and Earth System Sciences 9(4): 1149–1159.
Pelling, M. 2003. The vulnerability of cities: Natural disasters and social resilience. London: Earthscan.
Rashed, T., and J. Weeks. 2003. Exploring the spatial association between measures from satellite imagery and patterns of urban vulnerability to earthquake hazards. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences XXXIV 7(W9): 144–152.
Rodcha, R., N.K. Tripathi, and R.P. Shrestha. 2019. Comparison of cash crop suitability assessment using parametric, AHP, and FAHP methods. Land 8(5): Article 79.
RYTEIE (Riskli Yapıların Tespit Edilmesine İlişkin Esaslar / Principles for identification of risky buildings). 2019. https://webdosya.csb.gov.tr/db/altyapi/icerikler/r-skl--yapilarin-tesp-t-ed-lmes-ne-il-sk-n-esaslar-20190218134628.pdf. Accessed 6 Oct 2023.
Sauti, N.S., M.E. Daud, M. Kaamin, and S. Sahat. 2021. GIS spatial modelling for seismic risk assessment based on exposure, resilience, and capacity indicators to seismic hazard: A case study of Pahang, Malaysia. Geomatics, Natural Hazards and Risk 12(1): 1948–1972.
Şengör, A.M.C., O. Tüysüz, C. İmren, M. Sakınç, H. Eyidoğan, N. Görür, X. Le Pichon, and C. Rangin. 2005. The North Anatolian Fault: A new look. Annual Reviews 33: 37–112.
Shakya, M., H. Varum, R. Vicente, and A. Costa. 2018. Seismic vulnerability assessment methodology for slender masonry structures. International Journal of Architectural Heritage 12(7–8): 1297–1326.
Shen, D., T. Qian, Y. Xia, Y. Zhang, and J. Wang. 2020. Micro-scale flood hazard assessment based on catastrophe theory and an integrated 2-D hydraulic model: A case study of Gongshuangcha detention basin in Dongting Lake area, China. ISPRS International Journal of Geo-Information 9(4): Article 206.
Silva, V., S. Brzev, C. Scawthorn, C. Yepes, J. Dabbeek, and H. Crowley. 2022. A building classification system for multi-hazard risk assessment. International Journal of Disaster Risk Science 13(2): 161–177.
Song, F., X. Yang, and F. Wu. 2020. Catastrophe progression method based on M-K test and correlation analysis for assessing water resources carrying capacity in Hubei Province. Journal of Water and Climate Change 11(2): 556–567.
Su, S., D. Li, X. Yu, Z. Zhang, Q. Zhang, R. Xiao, J. Zhi, and J. Wu. 2011. Assessing land ecological security in Shanghai (China) based on catastrophe theory. Stochastic Environmental Research and Risk Assessment 25: 737–746.
Thom, R. 1975. Structural stability and morphogenesis. Reading, MA: WA Benjamin.
TUIK (Türkiye İstatistik Kurumu / Turkish Statistical Institute). 2021. Labor force statistics, 2021. https://data.tuik.gov.tr/Bulten/Index?p=Isgucu-Istatistikleri-2021-45645. Accessed 10 Jul 2023.
Wamsler, C., E. Brink, and C. Rivera. 2013. Planning for climate change in urban areas: From theory to practice. Journal of Cleaner Production 50: 68–81.
Wei, B., G. Nie, G. Su, L. Sun, X. Bai, and W. Qi. 2017. Risk assessment of people trapped in earthquake based on km grid: A case study of the 2014 Ludian Earthquake, China. Geomatics, Natural Hazards and Risk 8(2): 1289–1305.
Wisner, B., P.M. Blaike, T. Cannon, and I. Davis. 2004. At risk: Natural hazards, people’s vulnerability and disasters. London: Routledge.
Wood, N.J., C.G. Burton, and S.L. Cutter. 2010. Community variations in social vulnerability to Cascadia-related tsunamis in the U.S. Pacific Northwest. Natural Hazards 52(2): Article 369389.
Woodcock, A. 2006. Stereographic reconstuctions of the catastrophe manifolds of the cuspoids: (4) the wigwam. In A geometrical study of the elementary catastrophes, ed. A.E.R. Woodcock, and T. Poston, 193–211. Berlin: Springer.
Wu, J., X. Chen, and J. Lu. 2022. Assessment of long and short-term flood risk using the multi-criteria analysis model with the AHP-entropy method in Poyang Lake basin. International Journal of Disaster Risk Reduction 75: Article 102968.
Xue, J., J. Yan, and C. Chen. 2022. Combining catastrophe technique and regression analysis to deduce leading landscape patterns for regional flood vulnerability: A case study of Nanjing, China. Frontiers in Ecology and Evolution 10: Article 1002231.
Yariyan, P., H. Zabihi, I.D. Wolf, M. Karami, and S. Amiriyan. 2020. Earthquake risk assessment using an integrated fuzzy analytic hierarchy process with artificial neural networks based on GIS: A case study of Sanandaj in Iran. International Journal of Disaster Risk Reduction 50: Article 101705.
Zhai, Y., S. Chen., and Q. Ouyang. 2019. GIS-based seismic hazard prediction system for urban earthquake disaster prevention planning. Sustainability 11(9): Article 2620.
Zhang, P., X. Li, and C. Liu. 2023. Impact of spatial scale and building exposure distribution on earthquake insurance rates: A case study in Tangshan, China. International Journal of Disaster Risk Science 14(1): 64–78.
Zhang, H., Y. Sun, W. Zhang, Z. Song, Z. Ding, and X. Zhang. 2021. Comprehensive evaluation of the eco-environmental vulnerability in the Yellow River Delta wetland. Ecological Indicators 125: Article 107514.
Zhang, W., X. Xu, and X. Chen. 2017. Social vulnerability assessment of earthquake disaster based on the catastrophe progression method: A Sichuan Province case study. International Journal of Disaster Risk Reduction 24: 361–372.
Zheng, J., and G. Huang. 2023. Towards flood risk reduction: Commonalities and differences between urban flood resilience and risk based on a case study in the Pearl River Delta. International Journal of Disaster Risk Reduction 86: Article 103568.
Zhu, Y., D. Tian, and F. Yan. 2020. Effectiveness of entropy weight method in decision-making. Mathematical Problems in Engineering 2020: Article 3564835.
Ziarh, G.F., M.D. Asaduzzaman, A. Dewan, M.S. Nashwan, and S. Shahid. 2021. Integration of catastrophe and entropy theories for flood risk mapping in peninsular Malaysia. Journal of Flood Risk Management 14(1): Article e12686.
Acknowledgments
This study was supported by the Disaster and Emergency Management Presidency under Project No. AFAD-UDAP-Ç-19-06.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gerçek, D., Güven, İ.T. Urban Earthquake Vulnerability Assessment and Mapping at the Microscale Based on the Catastrophe Progression Method. Int J Disaster Risk Sci 14, 768–781 (2023). https://doi.org/10.1007/s13753-023-00512-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13753-023-00512-y