1 Introduction

The most damaging natural hazard types in Indonesia are earthquakes, tsunamis, and volcanic eruptions. These events, as well as floods, landslides, and fires, have led to an estimated average annual cost of natural hazards of around 0.3% of Indonesian Gross Domestic Product (GDP) from 2005 to 2015 (GFDRR 2011). Assessing the damages caused by these events is important for numerous stakeholders—such as governments, emergency services, and aid workers—and will help them respond efficiently and maximize resource use. If local governments can model historical frequency and damages, for example, such estimates could be used to request upward adjustments in the annual fiscal transfers from the central government to the subnational governments—for example, provincial or district governments—immediately following a natural hazard, while using locally collected data right after a natural hazard and/or visually inspecting satellite images would require a considerable amount of time and is likely to be very costly.

The aim of this article is to demonstrate how one can construct local hazard damage indices for earthquakes and volcanic eruptions by using publicly available data from remotely sensed sources and physical event data. We also show that one can use nightlight intensity as a readily available proxy for local economic activity to develop more aggregated level damage indices, such as at the district level. The data used to construct the indices are free, publicly available, and published at regular intervals or—in the case of earthquakes—very shortly after an incident. This makes the proposed indices useful for governments looking for a quick and rough estimate of damages after an event. The novelty of the methods lies in their ease of implementation and in how flexible they are in terms of expanding them with additional data sets or across different spatial scales. Finally, these methods are not just useful ex post, they can also be used to assess potential damage ex ante and be useful for policymakers to simulate possible damage scenarios after an event.

Remote sensing data and techniques have already seen some use in assessing the impact of earthquakes (Fu et al. 2005; Klinger 2005; Douglas 2007; Yamazaki and Matsuoka 2007; Dong and Shan 2013; Geiß and Taubenböck 2013; Taubenböck et al. 2014; Wu et al. 2014; Wyss 2014; Geiß et al. 2015; Platt et al. 2016; Anniballe et al. 2018), and volcanic eruptions (Carn et al. 2009; Ferguson et al. 2010; Arias et al. 2019). The authors of this article have also used remote sensing techniques for both disaster types before (Skoufias et al. 2017; Tveit 2017). In this regard, the earthquake indices are more detailed and developed through on the ground validation and have seen more widespread use.

Geiß and Taubenböck (2013) provided an extensive overview of the many different approaches to using remotely sensed data both pre- and post-event for earthquakes. The primary use so far has been in risk detection pre-event and damage assessment post-event. But most studies still rely on manual damage detection, that is, someone needs to look at images to assess changes. Our article presents a potentially fully automatable procedure that can be used both pre-event to identify areas with large exposure and post-event to model areas that are likely to have experienced the most damage.

Dong and Shan (2013) delved into more detail on damage detection with remote sensing techniques, primarily focusing on the use of very high-resolution data (10 m or less) from synthetic-aperture radar (SAR), LIDAR, and satellite images. The methods described differ from our method in that the data available are usually not free, are relatively difficult to process continuously as they come from a plethora of sources, the very high resolution makes them very space and power consuming, and the focus is generally on singular events in specific areas. More recently research that incorporates machine learning algorithms to improve estimates has been published (for example, Wu et al. 2014; Cooner et al. 2016; Anniballe et al. 2018). Such methods could possibly be explored as an extension to the approach presented in this article.

Volcanic eruption damage indices are fewer and more specialized. This is partly due to the different types of damaging factors stemming from an eruption. Ideally one would want to separately model lava flows, lahars, pyroclastic flows, and ash clouds. The first two are dependent on the topography and conditions close to the volcano, whereas ash clouds and—to some extent—pyroclastic flows are more wind related and can cause damages far away from the volcano. Wilson et al. (2014) provided a detailed overview of the damages caused by volcanic eruptions to infrastructure. Remote sensing of volcanic impacts is focused mostly on ash clouds and their monitoring (Carn et al. 2009; Ferguson et al. 2010; Arias et al. 2019). The primary focus of these studies was detection and modeling of the aviation industry impact, whereas in this study we used the data as a proxy for local damages.

The construction of the two damage indices in this study followed a 4-step process: (1) finding and combining input; (2) modeling damage or intensity; (3) weighting the damage on the basis of local nightlight intensity values; and (4) aggregating the damage index to a more aggregate spatial level. The construction of the indices is currently best done with a combination of the ArcGIS/Python, Matlab, and Stata software programs, but none of these are currently freeware. However, Python without ArcGIS and R—a statistical software—is free and available packages are continuously updated, particularly with regard to spatial analysis, so that it is highly likely that the construction of the indices could be done solely using freeware in the near future.

The common data input for both the earthquake and volcano damage indices is nightlight intensity data from the Defense Meteorological Satellite Program (DMSP) satellites. The data used in this study are the stable, cloud-free series (Elvidge et al.1997). The purpose of the nightlight data is to serve as a proxy for asset exposure. Often local damage exposure data are missing, particularly in developing countries such as Indonesia. The indices constructed in this study take into account local exposure by using nightlight intensity from satellite imagery as a proxy for economic activity, as exemplified in Henderson et al. (2012), Hodler and Raschky (2014), and Michalopoulos and Papaioannou (2014).

For the earthquake index, the primary other input data consist of ShakeMaps from the United States Geological Survey (USGS), maps that provide earthquake intensities across a grid at a scale of approximately 1.5 km by 1.5 km. These maps provide physical event data and are publicly available shortly after an earthquake happens. The data come from regional seismic networks and are not remotely sensed data. We used these in conjunction with national building type distribution data and urban maps from Jaiswal and Wald (2008) and CIESIN et al. (2011), as well as fragility curves from GHI and UNCRD (2001). The ShakeMaps were used to measure earthquake intensity in a location, the nightlights were used to model the economic exposure in the affected location, and the building data and fragility curves were employed to estimate damages. Once the input data have been combined and the damage across locations has been modeled, the index can easily be aggregated up to any spatial level of choice. We conducted a small case study to compare the estimated damages with the reported damages for the 2009 West Sumatra Earthquakes. The overall fit turns out to be reasonably good for the nightlight values, whereas the impact comparison depends heavily on the size of the geographical unit, with larger units providing a better fit. If one wants to analyze specific events or small areas, local knowledge about building qualities, types of economic activity, and light use could be used to further improve the estimates.

Our volcanic eruption index is an intensity index more than a damage index and needs to be interpreted in a slightly different manner than the earthquake index. First, the index is not a direct damage index, but rather a measure of local volcanic ash intensity since we do not have equivalent fragility curves as we do for earthquakes. Second, these intensity estimates are only based on ash cloud data. As volcanoes can cause damages through other means as well, the estimates here should only be considered as capturing damages due to ash clouds and not due to lava flows or lahars, thus limiting the index’s use for damage assessment. To establish when an eruption happens, we used ash advisory data from the Volcanic Ash Advisory Centers (VAAC). These data provide the aviation industry with four levels of warnings about volcanic activity. We decided to use only the highest warning level (red) to isolate the events that are most likely to also have an effect on the ground. Once an event was deemed to be an eruption, we used satellite images containing sulfur dioxide (SO2) data from the Ozone Monitoring Instrument onboard the Aura satellite (OMI/Aura) as an input to model eruption intensity. These images have a low resolution at 13 km by 24 km. Finally, similarly to the earthquake index, one can aggregate the measurements up to administrative level.

As a case study, we constructed indices at the provincial and district levels for the case of Indonesia, a country that experiences frequent earthquakes and volcanic eruptions. Our results show that earthquakes can have a devastating effect in small areas, but that when the effects are aggregated up across larger administrative divisions, the impact is still relatively small and total damage is less than 10% of building mass. For volcanoes, we found that the 2010 Merapi eruption had by far the largest effect over our time period from 2004 to 2014. Both the earthquake and the volcanic eruption indices would benefit from local validation.

2 Earthquake and Volcano Activity in Indonesia

Indonesia experiences numerous earthquakes every year. This is primarily due to its location inside the seismically active region called the Pacific Ring of Fire. From 2001 to 2015, the Indonesian National Disaster Management Agency (BNPB) (National Disaster Management Agency 2016) registered close to 400 earthquakes. The most significant and deadliest event was the 2004 Indian Ocean Tsunami that was caused by a 9.0 Mw earthquake in the ocean close to Aceh. In addition to the over 100,000 fatalities following the tsunami, another 8,000 people were killed due to other earthquakes.

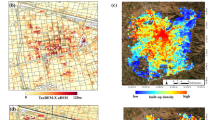
There are also close to 150 active volcanoes in Indonesia, the country with the highest number of active volcanoes in the world. Some of these volcanoes have had eruptions in recent years as well as in prior decades and centuries. There have been in excess of 60 significant volcano eruptions since 1900 and BNPB registered 92 eruptions from 2001 to 2015. The eruption on Mount Merapi in 2010 displaced over 320,000 people and killed 324. Separately from BNPB, from 2004 to 2015 the Darwin Volcanic Ash Advisory Centre (DVAAC) issued 587 red warnings. The USGS and DVAAC issue red warnings when an eruption is “imminent, underway, or suspected with hazardous activity both on the ground and in the air.”Footnote 1 A map with the volcanoes that had the largest eruptions during our 2004 to 2014 time frame is shown in Fig. 1.

Fig. 1
figure 1

Source GADM (https://gadm.org/maps/IDN.html), OMI/Aura

Map of Indonesia with provinces, major islands, and volcanoes.

Full size image

3 Nightlights

Natural hazards are inherently local phenomena in that they either affect only parts of areas and/or affect parts within areas differently, meaning that an aggregate proxy must consider different localized population and asset exposures. Preferably one would want exposures as spatially disaggregated as possible. However, for many countries—particularly in the developing world—data are often limited and at a highly spatially aggregated level.

Instead of relying on local data, one can use nightlights as a proxy for local economic activity. They have often been used—with good results—when other data or measures are lacking or missing (Henderson et al. 2012; Hodler and Raschky 2014; Michalopoulos and Papaioannou 2014). Henderson et al. (2012) used nightlights in Indonesia to show how nightlights can identify and quantify GDP changes during and after the Asian financial crisis.

Currently, there are several different data sets showing nightlights as outlined in Zhao et al. (2019). Two data sets have been used extensively: the images from the DMSP satellites and from the Visible Infrared Imaging Radiometer Suite (VIIRS) sensor on board the Suomi NPP and NOAA-20 weather satellites. The nightlight imagery used in this study comes from the DMSP because the data cover a much longer time period (since 1992) than the VIIRS data (not available until 2012). The VIIRS data are considered superior (higher-resolution images, on-board calibration, better sensors, and non-saturated measurements), and future or shorter time span research is likely to utilize the VIIRS. However, despite these advantages, Skoufias et al. (2021) found that the VIIRS data do not yield significant results either for specific hazard events or for country level regressions. This is most likely due to the inherent noise in the data and the lack of good measurements due to cloud cover in certain regions.

The DMSP data are gathered twice daily (at the same local time) from a satellite at a 101 minute near-polar, low earth orbit at an altitude of approximately 800 km. The raw data format consists of grid cells with a spatial resolution of about 1 km near the equator (30 arcseconds). Yearly values are then constructed as simple averages across daily values of the grids. These values are then normalized to a digital number from 0 to 63. We used the stable, cloud-free series (Elvidge et al. 1997), where intermittent lights such as fishing vessels and fires have been removed. The DMSP data have three corrections to exclude potential noise from observations: (1) To avoid glare and sunlight, observations are excluded based on the solar elevation angle. (2) Moonlit data are excluded based on a calculation of lunar illuminance. (3) Cloud observations are excluded based on clouds identified with the OLS thermal band data and NCEP surface temperature grids.

Despite the above corrections, some issues still persist. First, due to the normalization leading to a maximum value of 63, some cells are saturated, particularly in urban areas. This might lead to an underestimation of activity levels. Hu and Yao (2019) show how Singapore has 81.2% of cells at full saturation, and Bluhm and Krause (2020) extensively discuss the blooming effect. However, this is a problem that primarily affects wealthy countries, and in our data set only 0.2% of the observations recorded a value of 63. Second, the blooming effect can lead to an overestimation in the outer areas of urban and brightly lit areas (Shen et al. 2019). Currently, there are no easy or established fixes for this problem, and we have not tried to correct for it in this study. If one works at a smaller spatial scale than country level, it could be worthwhile to try to correct based on other local or remotely sensed data. Third, there can be cultural differences, that is, countries of similar GDP levels can differ in their light consumption. This might be an issue for Indonesia, given its size and relative heterogeneity across islands and provinces, but to our knowledge there are no ways to adjust for such differences. Finally, the images cannot distinguish what type of activity is happening on the ground, which means that one cannot identify whether the lights are due to human density or simply due to light-intensive activities such as factories. If the damage estimates are to be used with a focus on saving human lives, some local knowledge or use of secondary data sets such as population maps or satellite images such as USGS Landsat images (USGS 2019) would be necessary.

4 Constructing the Indices

The method for constructing the indices is similar for both hazard types. They primarily differ in spatial scale and how the damage is modeled. The earthquake damage index is modeled from strength of shaking in approximately 1 km2 cells, whereas ash-cloud data are used as a proxy for volcanic eruption intensity at a resolution of 13 km by 24 km. These indices are then combined with the nightlights data to obtain a proxy for economic impact. The methodology is to combine the proportional nightlight cell value—a weight—with the damage value. The weight is simply the nightlight value (0−63) over the total sum of nightlights in the administrative unit chosen, formally expressed as:

$$W_{i,p,t - 1} \equiv \frac{{L_{i,p,t - 1} }}{{\mathop \sum \nolimits_{j}^{J} L_{j,p,t - 1} }},\quad i = 1, \ldots ,I,\quad p = 1, \ldots ,P$$
(1)

which translates to the weight of the light from nightlight cell i in year t − 1 over the total amount of nightlight cell light in administrative unit p in year t − 1.

The weighted damage numbers are aggregated to find an overall economic impact in the administrative unit. The general methodology and approach are shown in Fig. 2.

Fig. 2
figure 2

General overview of the methodology for the construction of the damage indices

Full size image

5 Constructing a Damage Index for Earthquakes

Remote sensing techniques have improved the precision of event detection and intensity measurements of earthquakes. Numerous methods exist to assess earthquake damages and intensity from remotely sensed data. One strand of literature focuses on satellite images (Tralli et al. 2005; Gillespie et al. 2007; Dell’Acqua and Gamba 2012; Cooner et al. 2016; Tamkuan and Nagai 2017). Another focuses on contour maps generated by seismological ground stations (GHI and UNCRD 2001; FEMA 2006; De Groeve et al. 2008), which are not remotely sensed data per se, but can be used in combination with, for example, nightlights. Geiß and Taubenböck (2013) and Dong and Shan (2013) both provided extensive overviews of different methods and use of remotely sensed data.

In this study we chose to use contour maps from the USGS called ShakeMaps because they are freely available, have global coverage and fairly detailed spatial resolution, are easy to work with because both map files and numeric grid files are provided, and they provide any key parameter one would need to model damage. The damage index we constructed does not, however, rely on these maps, but can be used with any data source that provides spatial intensity estimates. The ShakeMaps are generated automatically after an earthquake and provide several key parameters, including peak ground velocity (PGV), peak ground acceleration (PGA), and modified Mercalli intensity (MMI). The maps themselves are constructed by using point coordinates to construct an interpolated grid. The resolution of the grids differs from earthquake to earthquake, but usually the points are 0.0167 degrees apart (roughly 1.5 km). More specifically, the ShakeMaps use data from seismic stations that are interpolated using an algorithm analogous to kriging. The algorithm is outlined in Worden et al. (2010) and combines observed ground motions and intensities with estimated peak ground motions, weighted proportionally to the inverse of their uncertainties. The intensity of each point is generated by also considering earthquake depth and ground conditions. Wald et al. (2005) noted that one should not rely only on the magnitude and epicenter location, as has often been the case historically. They expand further on this by stating that “although an earthquake has one magnitude and one epicenter, it produces a range of ground shaking levels at sites throughout the region depending on distance from the earthquake, the rock and soil conditions at sites, and variations in the propagation of seismic waves from the earthquake due to complexities in the structure of the Earth’s crust” (Wald et al. 2005, p. 13).

Intensity in a point can be estimated from different parameters such as PGA, PGV, and MMI. The former two are objective measures that quantify the maximum horizontal ground acceleration as a percentage of gravity (PGA) and the maximum horizontal ground speed in centimeters per second (PGV), while MMI is a subjective measure that is supposed to quantify the perceived intensity of the earthquake. Wald et al. (1999) estimated the conversion between the potential damage and the different parameters. Figure 3 shows the estimated damage levels, which commence at level V MMI and a PGA of 3.9% of g. These values are based on measurements found in California (Wald et al. 1999), and have been used to estimate conversion values for places both inside (Atkinson and Kaka 2006, 2007) and outside of the United States (Murphy and O’Brien 1977; Linkimer 2007). The conversion values differ from area to area, as they depend on local factors such as ground condition and building standards. The authors are not aware of any studies that have specifically measured the damage and conversion values for Indonesia. In this study, a value of 5% of g was used. This was due to two factors. First, the interest lies in detecting damage of some severity, so 3.9% of g would be too low. Second, very small damages are unlikely to be captured by nightlights. This means that any subsequent analysis with nightlight values and a very low damage threshold could lead to attenuation bias.

Fig. 3
figure 3

Source Adapted from Wald et al. 1999

ShakeMap instrumental intensity scale legend.

Full size image

Given the existence of conversion values, one can use PGA, PGV, or MMI. However, due to the objectiveness of PGA compared to the subjective measure that is MMI, the GHI and UNCRD 2001 report uses the former. The implication is that MMI is not easy to obtain reliably across the globe, nor is it a reliably consistent measure where available. Also, when the scale of the modeling is large and it is difficult to precisely model local conditions, PGA is a good proxy for earthquake intensity.

5.1 From Intensity to Damage

The construction of a damage index is based on the intensity data (PGA) described above and on building inventory data. The data set used in this study is the USGS building inventory for earthquake assessment (Jaiswal and Wald 2008), which provides country by country estimates of building type proportions (relative to total number of buildings). Overall, the data are divided into urban and rural shares and across 99 different building types. The underlying data used by the USGS to construct the building inventory differ from country to country, and in Indonesia the information regarding building type came from a survey conducted by the World Housing Encyclopedia (WHE). The survey divides the building mass into categories based on the number of people who live or work in each building type.

To define which buildings are urban and which are rural, the USGS use the urban extent map of CIESIN et al. (2011), which was constructed through a process outlined in Balk et al. (2006). The base data is a map that plots the world population on a grid based on non-spatial population estimates and administrative boundary data. From the base data, the urban extent map adds point location, collected population estimates and the approximate area and location of urban centers (places with a population above 1000), which is matched with the population estimates. The DMSP nightlight data were used to find the outline of urban areas. In cases where urban extent could not be determined, other sources were utilized. Two drawbacks of using the urban extent map are that it does not capture any temporal changes and that it is dated given the use of data from 1995. From 1995 to 2014, Indonesia’s urban population increased from 36 to 53% according to World Bank data.Footnote 2 Given how growth differs between urban and rural areas, it is difficult to correct properly for this. At the time of this study in 2016, these maps were the most recent data for Indonesia. However, if one has access to more localized or newer data, these are easy to implement with the methodology. For example, CIESIN (Center for International Earth Science Information Network) and WorldPop have released higher-resolution settlement layers for several countries across the world and these data can easily be used for the modeling.Footnote 3 Given the lack of more precise data we used the WHE survey and the CIESIN et al. (2011) map to indicate the split between urban and rural areas and the distribution of building types and mass in Indonesia. One implied assumption is that buildings are homogenously distributed within urban and rural areas.

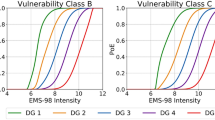
Damage curves constructed by the Global Earthquake Safety Initiative (GESI) project (GHI and UNCRD 2001) were used to derive damage by building type. These are not country-specific, but rather depend on the building data. First, the building types are divided into nine categories depending on building materials ranging from lightweight shacks to wood and steel. Next, the individual building type is given a grade depending on the quality of the design, construction, and materials. A measure of total quality is given on a scale from zero to seven, based on the total points from the three quality categories. Finally, every building is assigned one of nine damage curves depending on building type and quality classification. These nine damage curves estimate the percentage of building damage from 0 (no damage) to 1 (total destruction) over a range of 28 PGA intervals.

In the case of Indonesia, the 99 building types from the USGS building inventory were assigned to the nine building type categories of GESI. Optimally, one would want data on the building type design, construction, and material quality to allocate each building to the correct quality damage curves. Unfortunately, to the best of our knowledge, these data are not available for Indonesia. The assumption is therefore that building quality is homogenous across all building types. To account for any differences due to quality assumptions, damage curves for all eight (0 through 7) quality rating scenarios are constructed.

The damage curves for rural and urban areas in Indonesia are shown in Fig. 4. The curves show the expected damage to buildings in Indonesia—given the assumed homogenous building mass—for different assumed qualities across a range of PGA values. The assumed quality can impact the modeled damage quite extensively (Fig. 4b), in particular where a PGA of 0.75 can cause between 60% and 95% damage depending on the quality assumption.

Fig. 4
figure 4

Damage curves for rural and urban areas in Indonesia

Full size image

Damage estimation due to earthquakes in individual locations is done using data from GESI and the ShakeMaps, and by identifying each nightlight cell’s PGA by matching each earthquake point with its nearest nightlight cell. Then the nightlight cell is assigned the PGA value if the earthquake cell is closer than 1.5 km and the PGA value is in excess of 0.05g. In any other case, the nightlight cell is assigned a damage value of 0. The equation used to derive an earthquake damage index, ED, in cell i is:

$$ED_{i,q,p,t} = W_{i,p,t - 1} \cdot DR_{{i,p,k,t,pga_{k,q} }} ,\quad p = 1, \ldots ,P,\quad k = U,R,\quad q = 0, \ldots ,7$$
(2)

where DR is the damage ratio in cell i as modeled by the PGA, pga, depending on the urban (U) or rural (R) qualification, k, and the building quality q; p is the unit of analysis, typically province or district, and t is the year of the event; Wi,p,t−1 is the weights defined in Eq. 1.

Finally, we multiply the damage ratio, DR, with the weight, W, to find a proxy for the relative economic impact in the region. This means that if there is a zero nightlight value, the economic impact will be zero regardless of how strong the earthquake is. The impact value shows the damage across assets in a district or province.

The indices were created by using ArcGIS and Stata software. In both cases, underlying scripting languages (Python for ArcGIS and the in-built Stata language) were used to automate the process. Python and ArcGIS were used for the spatial mapping and combining spatial data, for example, when finding the nearest neighbors between the nightlight data and the earthquake intensity data. For the weighting and the distance calculation Stata was used, primarily because of the speed with which it can calculate distances between two points.

If one wants to use this earthquake index, it is important to remember its underlying assumptions and their implications. First, the assumption of homogenous building qualities and mass across the entire country does not take into account local differences in terms of seismic preparedness, building materials, and quality. Second, the damage function is more formally a probability function, which means that even if the underlying data and assumptions are correct, there will still be an error in the measurement. Third, by using the ShakeMap intensity data across a 1 km by 1 km grid, some local variation is lost in that each grid cell will depend only on the nearest intensity value and not on an average or a more smoothed surface. If one wants truly high-resolution damage data (resolution of 10 m and below), this methodology will not be very useful and one should probably look for a different data set, as shown in Dong and Shan (2013). Finally, the split between urban and rural cells depends on a rather old data set, and using more high-resolution land cover or population data could further refine the accuracy of the index.

5.2 Results

The results are split into a section describing the results with a focus on individual points and their estimates, a section where the results are aggregated up to provincial and district level estimates, and finally a case study of the West Sumatra Earthquake in 2009. All estimates are somewhat arbitrarily based on a building quality of 4 due to the lack of building quality information. A quality of 4 typically signifies structures that showcase some level of engineering and seismic elements in the construction and/or a certain level of quality in the material. Given the frequency of earthquakes in Indonesia, one would expect that some thought has been given to this, but lack of resources is a likely factor that will hamper the overall quality, hence an overall quality of 4 seems reasonable.

5.2.1 Point Estimates

Using estimates obtained from our method, 27 of Indonesia’s 34 provinces were damaged by earthquakes at some point in time during our 2004−2014 time period. As expected, the highest amount of damaged nightlight cells was found on Java and Sumatra (Table 1), large and densely populated islands that experience earthquakes at frequent intervals. A map showing the largest islands and all provinces is shown in Fig. 1.

Table 1 Damaged nightlight cells by province in Indonesia 2004−2014
Full size table

There were an estimated 5251 cases where an earthquake hit a lit nightlight cell, that is, hit a cell with a light value above 0. The average weight for an individual nightlight cell within a province or district is small (Table 2). However, when a cell with buildings of quality 4 is struck, the average building mass destruction is a bit more than 6%. This indicates that when earthquakes with a certain intensity strike, there is a noticeable impact. To quantify the sensitivity of the quality assumption, the same model was run with building quality assumptions of 0 and 7. Comparisons of the modeled maximum damage for a cell depending on building quality gives results that range from 84% for the worst buildings down to 33% for the best buildings, with the quality 4 buildings showing a modeled 55% maximum damage. This shows how the incorporation of good building quality information can have a large impact on the damage estimates. The impact numbers do not tell us much on their own, as the individual weights that the damage numbers have been multiplied with are very small, but they do show that no single cell has a great impact on a province. Furthermore, due to the assumptions regarding homogenous quality and mass of buildings, there is no local differentiation when it comes to damages. The damage within Indonesia will depend on whether a cell is rural or urban and the PGA in the given cell.

Table 2 Overview of weights, damage, and impact assuming building quality 4 in the earthquake damage index for Indonesia
Full size table

5.2.2 Aggregated Data

The data are aggregated directly with local nightlight values via:

$$ED_{p,q,Y} = \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{y}^{Y} ED_{i,q,p,t} ,\quad p = 1, \ldots ,P,\quad q = 0, \ldots ,7\quad y = 2004, \ldots ,2014$$
(3)

where the sum of y is the sum of all days in the year Y, i is all nightlight cells in the province or district p, and ED is the damage from Eq. 2.

A very simplistic way of looking at the aggregate value is that it shows the fall in annual nightlight value caused by earthquakes in a province or district. If one can find a way to value one unit of nightlight, one can directly compute the monetary damage. This valuation is not done in this article. However, the aggregate estimates rest on certain conditions. First, since the damage is probabilistic in nature, any potential bias or error will also be aggregated and can lead to the estimates being over- or understated. One way to correct for this would be to validate the modeled damages with good local data. Second, if there were multiple earthquake events in a year, one would be unable to model the effect of the recovery efforts that happen between different events. Given that the nightlights data are annual, it is not possible to correct or adjust for this with this methodology, and if one needs to model areas with several events annually one needs to use higher-frequency temporal data. Another potential issue with multiple events is that the range of the aggregate value is larger than 1, that is, if several very damaging events have occurred within one year one could get a damage value higher than 1. However, this is quite unlikely, because even the most damaged districts only experienced a total damage of approximately 5%. Finally, to accurately model monetary damage one needs local knowledge about value and activities to be able to connect the nightlights with monetary value. Figure 5 provides a flow chart for how the earthquake index is constructed.

Fig. 5
figure 5

Flow chart of earthquake index construction

Full size image

The weighted damage variation between provinces and across years (Table 3) shows a wide range of values as expected due to the highly random occurrence of earthquakes. For example, Yogyakarta on the island of Java was only damaged by earthquakes in 2006.Footnote 4 However, with a loss of 0.4% of the total building mass, the total monetary losses were estimated to be in excess of USD 3.1 billion. There were also an estimated 5000 fatalities, and injured and displaced people in the tens of thousands. This underlines how devastating just one large event can be for the local economy and population. The results also show that Sumatra is the most affected island, with 6 of the top 10 most damaged provinces.Footnote 5 Finally, despite the fact that several large-scale earthquakes struck Indonesia between 2004 and 2013, the maximum destruction is at approximately 1% of the building mass in a province. However, damage of that scale to building mass and infrastructure does constitute a significant portion of local budgets. For example, the West Sumatra Earthquake in September/October 2009 caused USD 2.3 billion worth of damages, with estimated repair costs and losses of USD 64 million related to government buildings (Raschky 2013).

Table 3 Aggregated earthquake impact by year and province in Indonesia
Full size table

The same analysis was conducted for districts, which—as expected—showed an increase in impact with a maximum of 5% building mass loss. Overall, we found that the methodology can identify impact from a grid cell level and up to aggregated provincial levels. However, the measurements cannot be used to directly estimate economic damage or casualties. What they do provide is an intensity estimate weighted by the assumed economic activity in an area. If one has access to validated damage data from an equivalent area, one can further refine the estimates and provide monetary damage estimates.

5.2.3 West Sumatra (Sumatera Barat) Earthquake 2009

On 30 September and 1 October 2009, West Sumatra was struck by two earthquakes of magnitudes 7.6 and 6.2. The subsequent damages were assessed and reported in a joint report by the BNPB, the National Planning Development Agency (BAPPENAS), provincial and district/city governments, and international partners (World Bank Group 2009). The report provides data on economic indicators such as Gross Regional Domestic Product (GRDP) as well as detailed damage breakdowns by district. We used these events and their reported damages to compare them to those derived from our method. Lacking the value of exposed assets, we used the percentage shares of GRDP for each district and compared them with the percentage shares of light values.Footnote 6 Columns 2−4 in Table 4 show the percentages and the correlation between GRDP and lights is strong, with some exceptions. The Kepulauan Mentawai District, for example, shows no lights. The district consists of rather small islands, and this sometimes leads to the light centroids being put in the ocean, removing them from the final grid. The over- and underestimation of Padang (the city) and Padang Pariaman is most likely related to the blooming effect of the DMSP data as well as Padang being geographically very small. For Pasaman Barat and Pesisir Selatan, the underestimation might also be related to considerable economic activity very close to the ocean and in mangrove or swamp areas that are sometimes considered water in shapefiles. To decrease this, it would be important to use up-to-date shapefiles and—if possible—a full grid and not centroids for the light values. However, when considering the aggregated numbers, the economic activity is very similar across the two data sets. The data constitute 71.6% of all lights in West Sumatra and 73.4% of the reported GRDP. The mean differs by 0.1% and the standard deviations by 0.3%.

Table 4 Comparison of the analysis data and the damage report (World Bank Group 2009) for the 2009 West Sumatra Earthquake
Full size table

Without knowing asset exposure, we cannot assign a monetary value for our estimated damages, so we defined the estimated damage as “nightlight value of district” times “earthquake impact.” For the reported damages we only included the damage values for the high impact districts. The report also lacks numbers for some sectors and some districts, which means that the totals might not be complete. Columns 5 and 6 in Table 4 show the values for estimated damage and reported damage, and the only way they can be compared is in relative terms, that is, how do the damage numbers between districts compare for the two methods. It should be noted that the reported damage numbers also include damages due to landslides that occurred following the earthquakes, and such damages are not part of our modeling approach. This is a particular problem for the district with the highest reported damages, Padang Pariaman, where landslides buried at least 3 villages. Keeping this in mind we still find a reasonable fit between our estimates and the reported damages. If one combines Padang and Padang Pariaman, 68% of the estimated total damages occurred in those two districts, while the reported damages were 65% of the total. The biggest discrepancy was found for Agam and Bukittinggi. Due to Bukittinggi’s small geographical size as a city in Agam, it is difficult to spatially disentangle the two geographical units in our analysis. Hence, if one combines the two units, one finds a much better fit. In line with prior literature, the nightlight values provide a reasonable proxy for economic activity, and the bigger the geographical units are, the better the fit seems to be.

6 Constructing a Damage Index for Volcanoes

Damage from volcanic eruptions can stem from several sources, such as lahars, lava flows, and pyroclastic flows. To properly model the movement and damage from lahars and lava flows one needs very high-resolution spatial data, making it difficult to model across large temporal and spatial areas. In general, there is not much literature that has explored large-scale modeling of all damage components following volcanic eruptions.

To model individual eruptions, at least two different software programs exist. The Volcanic Risk Information System (VORIS) (Felpeto et al. 2007) models energy cones, ash clouds, and lava flows. Due to the energy cone and lava flow modeling, VORIS needs high-resolution spatial data and is not particularly well suited for large-scale modeling across multiple events. The second software program only models air pollution dispersion and is the Hybrid Single Particle Lagrangian Integrated Trajectory Model (HYSPLIT) from Air Resources Laboratory. HYSPLIT also relies on a number of local inputs per eruption but can easily be run for multiple events if local data are available.

Apart from the dedicated software, one can rely on ash clouds as a proxy for intensity (Joyce et al. 2009). In this study, we took a two-step approach. The first step identified whether an eruption was happening or not, and the second step measured the intensity of the eruption based on ash clouds. To identify an eruption, we used ash advisory data from VAAC. This step is unnecessary if the events are already known, but in our case we wanted to identify all eruptions that occurred over a large area during a long time period. To model the intensity we used the OMI/Aura satellite images, which measure sulfur dioxide levels in the atmosphere. Carn et al. (2009) and Ferguson et al. (2010) also used the OMI/Aura data to model single event eruption intensity. The modeling only uses sulfur dioxide for intensity measures, with no estimates of lava flows or energy cones. One of the main weaknesses of relying on atmospheric data is that they might not be a good proxy for ground damage, such as damage to buildings or infrastructure. However, due to the temporal and spatial scale of the modeling and the unavailability of high-quality local data, it was not feasible to model factors that rely heavily on local factors.

An ash advisory is a warning for airplanes that details the volcano state and ash conditions in the sky through relevant data such as volcano name, position, summit height, height of clouds, and a color code that reflects the condition of the air/volcano. There are four code levels, from green, the normal state, to red, which signifies an ongoing volcanic eruption or imminent danger thereof. Ash advisories that cover Indonesia are issued by the Darwin VAAC (DVAAC). There were 12,962 warnings, over 90% code red or orange, issued by the DVAAC from 2004–2015. Eruptions of code orange or below were considered too small to be properly measured by the sulfur dioxide data. Therefore, our final data set consisted of 1785 code red events over 587 different dates.

The OMI/Aura project (Krotkov and Li 2006) provides images of sulfur dioxide measurements in the atmosphere. These have been used as a proxy for intensity and movement of ash clouds in different studies (Carn et al. 2009; Ferguson et al. 2010). The images have been collected since October 2004 and have a spatial resolution of 13 km by 24 km. The satellite orbits earth 14 or 15 times a day at an altitude of 80 km, and each orbit provides images over an area that is 2,600 km wide. The images provide SO2 vertical column densities as measured in Dobson Units (DU). Sulfur dioxide concentration at sea level is typically less than 0.02 DU in clean air. The OMI/Aura data include four column density values depending on the center of mass altitude (CMA), which is a value for the assumed altitude of the center of the distribution. The CMA values range from 0.9 to 18 km above ground.

The OMI Team (2012) recommended a CMA of 8 or 18 km for use with volcanic activity. The 8 km middle tropospheric column (TRM) is recommended for medium scale events, while the 18 km upper tropospheric and stratospheric column (STL) is used when eruptions are explosive and large. Although there are differences in these values due to the altitude assumption, one can interpolate from one to the other, essentially making them interchangeable. The main disturbance to the measurements is clouds, but both the TRM and the STL are above clouds, making them accurate to a standard deviation level of 0.1 DU over Indonesia. Due to the interchangeability and the precision of both data values, in addition to the focus on large volcanic events, this study used STL data as its intensity measure.

6.1 From Sulfur Dioxide Measures to Damage Index

To construct a damage proxy from the sulfur dioxide measures it is necessary to define limits in terms of how far away from the event damages are still likely to occur and how far away from an SO2 measure the measured value is still valid. In addition, one needs to set a lower threshold for when sulfur dioxide values are correlated with damage. Unfortunately, there are currently no articles or studies that have estimated parameter values and as far as we know there are no local damage data available, so that any limits set will be rather arbitrary.

To set a distance limit for event damage, one would preferably have information on conditions on the ground and how they relate or correlate to ash clouds. The threshold should not be based on aviation industry disturbances, as the ash cloud damage reaches very far. A good example of this is the grounding of planes over Europe during the 2010 Eyjafjallajökull eruption in Iceland, when planes more than 50 degrees of latitude or longitude away were grounded. In reality, however, the local ground effects will cover a much smaller area. We decided on a relatively flexible limit by including any point closer than 10 degrees of latitude and longitude. This is most likely too lenient, but the preference of the index is to identify all areas that are potentially impacted—it is better to misidentify a non-impacted area as being impacted than not to identify an impacted area. Figure 6 shows an example of a spreading ash cloud from the 2010 Merapi eruption and its plume seven hours after the eruption on 4 November. The map shows that the plume moved slowly (approximately 20 km/h) and that less than 300 km away from the eruption, the sulfur dioxide levels had all but dissipated at lower altitudes, indicating that the 10-degree threshold works in this instance.

Fig. 6
figure 6

Source OMI/Aura Data

Ash cloud over Java on 4 November 2010, seven hours after the Mt Merapi eruption (05.33 UTC).

Full size image

The second distance limit relates to the nightlight and sulfur dioxide data. Preferably, one would want the data to be of the same resolution and fully covering all areas. However, the OMI/Aura images are of a much lower resolution and have several missing grid cells due to cloud covers. This implies that either parts of the coverage area will have no value or—as chosen by us—one would need to interpolate the sulfur dioxide data in a way that will make all areas have a value. In our case, a value of 0 is set if a point is further away from a measure than 50 km, approximately twice the length of the longest side of an OMI cell. This is done to get a more consistent nightlight and SO2 grid. What this means is that in the cases where there is no SO2 observation over a nightlight cell due to cloud cover, we assigned the closest SO2 value to the nightlight cell if it was closer than 50 km. Our final grid had the nightlight resolution of approximately 1 km by 1 km, but the sulfur dioxide values can come from observations as far as 50 km away. This is not optimal from a modeling point of view, but we preferred to know the asset distribution over aggregating up to a lower resolution. Lastly, one needs to set a minimum SO2 value that can serve as a proxy for when damage occurs and when it does not. According to the Belgian Institute for Space Aeronomy, a typical normal SO2 level in air is 0.1 DU and a strong eruption is above 10, which is the threshold value chosen.

After defining the limits, a grid map is generated with weighted nightlight cells whose value is multiplied with the sulfur dioxide value to find a weighted intensity value. We use the equation:

$$\begin{aligned} & {\text{If}}\;{ }VSO2_{t} < 10:VD_{i,t} \equiv 0, \\ & {\text{Otherwise}}:{ }\;VD_{i,t} \equiv W_{i,p,t - 1} \cdot VSO2_{t} \\ \end{aligned}$$
(4)

which shares many similarities with Eq. 2. The date is t, i is the nightlight cell, and W is the same weight. The only new value is VSO2t, which is the sulfur dioxide value on date t.

By definition, there is no upper bound. Hence theoretically, if the index had been a direct measure of damage, one could have damage values higher than 1. However, as this is simply a measure of intensity of SO2 in the atmosphere, it is just a very rough measure of how conditions are on the ground. Ground damage is not modeled with this methodology, and the authors are not aware of any validation from SO2 intensity to damage estimates. It is also unclear whether one could properly validate damage based on the SO2 intensity alone, given that lahars and pyroclastic and lava flows are much more affected by topographic features and ground conditions than the higher up and lighter ash clouds. One would probably need to be able to distinguish what type of damage is caused by ash clouds versus flows and then use that to validate the SO2 damage. This is a distinction that would be useful, as the emergency response and aid time is likely to differ between the usually more catastrophic damages from lava and pyroclastic flows compared to the more modest damages from ash fall.

In terms of the processing of the data, the index was constructed with the use of Matlab in addition to Python/ArcGIS and Stata. Matlab was used due to the speed with which it converts raster files from the OMI/Aura to more usable csv-files. The other data processing steps were similar to what was done for the earthquake index, where Python/ArcGIS were used for spatial processing and nearest neighbor analysis, while Stata was used to weight and construct the final data set containing all the data. We believe that one could construct the index with entirely free software from packages in R and Python, but it is likely to take longer to process the images.

6.2 Results

The results are first presented through the individual point estimates and then presented by aggregating the points up to province and district level.

6.2.1 Point Estimates

With the chosen limits, there are 16 red warning days left, down from 587 dates. The biggest event during the period of analysis from 2004 to 2014, the 2010 Merapi eruption accounts for 7 of the 16. Affected nightlight cells by volcano and year are shown in Table 5,Footnote 7 and there is a strong correlation between the modeled events and the events that occurred. Apart from Merapi in 2010, the other significant volcano events were Soputan in 2004, 2005, 2007, and 2008 and Sinabung with several eruptions in 2014. Overall, Merapi is linked with more than 85% of the total affected cells, an expected result given the magnitude. The event had by far the highest number of displacements and fatalities and was one of two events with a Volcanic Explosivity Index (VEI) value of 4 during our model period. The Soputan and Sinabung events were VEI levels 2 and 3.

Table 5 Damaged nightlight cells by year and volcano in Indonesia
Full size table

The impact on provinces is shown in Table 6. Affected provinces were primarily on Sumatra and Java, with Jawa Barat and Jawa Tengah with more than 120,000 cells with a sulfur dioxide value above 10. The event responsible for the high values was the 2010 Merapi eruption while the most impacted non-Merapi related province was Sulawesi Utara, which was affected by the Soputan eruptions.

Table 6 Damaged nightlight cells by year and province in Indonesia
Full size table

The sulfur dioxide values, nightlight weights, and the weight and SO2 product are shown in Table 7. The volcanic eruptions give mean sulfur dioxide values at almost 20, close to double the eruption limit that is set at 10. The maximum value approaches 60, which is 600 times the 0.1 DU level that one normally finds, indicating that these areas are quite likely to experience an impact. Unfortunately, the interpretation of the results is not straightforward since a higher sulfur dioxide value does not necessarily relate to an equivalent increase in ground damages.

Table 7 Overview of weights, SO2 level, and Intensity
Full size table

6.2.2 Aggregated Data

The aggregation of the modeled values is done with the same equation as for earthquakes:

$$VD_{p,y} = \mathop \sum \limits_{t}^{T} \mathop \sum \limits_{i}^{I} VD_{p,i,t} ,\quad p = 1, \ldots ,P,\quad y = 2004, \ldots ,2014$$
(5)

which aggregates the nightlight values across all cells i and days t over chosen administrative level p. The different steps involved in the damage index creation are shown in Fig. 7.

Fig. 7
figure 7

Flow chart of the volcano index construction

Full size image

Table 8 lists the most impacted provinces. The 2010 Merapi eruption was responsible for the high modeled intensity in the two most affected provinces and three of the top four provinces. The top two provinces, Jawa Tengah and Yogyakarta, are just south and west and immediately next to Mount Merapi. At the same time, a province such as Jawa Timur, which is also close to Merapi, but in an eastern direction, hardly experienced any impact with our modeling.

Table 8 Provinces with the highest impact intensity from volcano eruptions in Indonesia
Full size table

The same pattern was found across districts, albeit to a larger extent. However, some of the districts closest to the Merapi volcano were not among the most impacted districts. This is most likely caused by the timing of the satellite’s orbits and potential cloud cover, leading to a lack of quality observations at critical times.

In total, the model results are satisfying in that they do show areas that are affected by the eruption. However, they also suffer from several limitations. First, we have no knowledge of intensity at the ground level or of lava and/or pyroclastic flows. This means that the actual damages can be very different from what we expect based on ash cloud data. Second, due to the spatial and temporal resolution of the SO2 data, it is unlikely to be of any use in an emergency situation when one needs to know more specific locations within short time frames. The index is more likely to be of use in a more macro-oriented perspective where one wants to get an overview of impacted areas and identify where damages due to ash fall can be expected.

7 Discussion and Conclusion

The methodologies outlined in this article are not tied to the data used. For example, DMSP global nightlights data are used for the hazards to weight the indices based on economic activity. However, for natural hazards occurring from 2012 onwards, the monthly VIIRS nightlight data can be used instead, see cases such as GDP in China (Li et al. 2013; Shi et al. 2014) and Africa (Chen and Nordhaus 2015) and for storms and floods in the United States (Cao et al. 2013; Sun et al. 2015). The VIIRS data are publicly available at a monthly rather than annual frequency and have a resolution that is roughly twice as high as the DMSP images, potentially providing better localized activity estimates. Another easily replaceable data set used in this study is the urban extent map. With the growing availability of high-resolution settlement layers across the globe, such data might provide a better source for identifying urban and rural areas and enhance the damage estimates. One is also not restricted to using our chosen software suite ArcGIS, Stata, and Matlab. It should be possible to construct both indices using only free software and packages in R or Python, though this is likely to negatively impact the ease and speed of the process. To construct the indices some programming experience and knowledge of natural hazard damage indices is recommended. The indices constructed in this study can cover any large or small area across most inhabited places on earth. The USGS ShakeMaps, for example, cover major earthquakes globally and are produced more or less instantly following an event. With the proposed index, one could have an estimate of most economically impacted areas within minutes. However, the resolution of the images at a 1 km by 1 km scale is not going to be particularly useful for identifying buildings that have collapsed or the damage difference between small city blocks. If localized data are available, one can validate the indices locally and provide more accurate damage estimates. It is also worth noting that the weights are linear, that is, each unit of nightlights has the same value irrespective of whether the value is 6 or 60—an assumption that might be overly simplistic or incorrect in some areas.

In addition to providing damage estimates and mapping, the indices can be used in research. The authors show their use in analyzing district budget redistributions ex post natural hazards in Skoufias et al. (2018) and found that the hazards caused a redistributional fiscal effect that policymakers are likely looking to avoid. The damage caused by the hazards force policymakers to move budgeted money away from the originally intended use, leading to a lack of funding in the original sector. Part of the reason for this redistribution is likely to be due to slow deployment of resources from central governments and other agencies. If policymakers can simulate and predict ex ante how much money they will need to cover hazard recovery and rebuilding, they can budget for it in advance by using indices constructed in the manner described in this article. Another area of use can be demography, where Tan et al. (2009) and Lin (2010) studied birth outcomes following earthquakes, and the indices can similarly be used in population and migration studies. Within economics access to detailed asset exposure values facilitates the conversion to monetary cost estimates that one can use for cost-benefit analysis, for example. For geographers the damage estimates can be useful for high-level analysis of surface changes. Given the flexibility of the method, the authors hope to see it used with other data and potentially to model other natural hazards such as landslides or tornadoes.