Accuracy–diversity based pruning of classifier ensembles

Abstract

Classification ensemble methods have recently drawn serious attention due to their ability to appreciably pull up prediction performance. Since smaller ensembles are preferred because of storage and efficiency reasons, ensemble pruning is an important step for construction of classifier ensembles. In this paper, we propose a heuristic method to obtain an optimal ensemble from a given pool of classifiers. The proposed accuracy–diversity based pruning algorithm takes into account the accuracy of individual classifiers as well as the pairwise diversity amongst these classifiers. The algorithm performs a systematic bottom-up search and conditionally grows sub-ensembles by adding diverse pairs of classifiers to the candidates with relatively higher accuracies. The ultimate aim is to deliver the smallest ensemble with highest achievable accuracy in the pool. The performance study on UCI datasets demonstrates that the proposed algorithm rarely misses the optimal ensemble, thus establishing confidence in the quality of heuristics employed by the algorithm.

1 Introduction

Classifier ensembles, also known as multiple classifier systems, have been recognized as better performers than their individual constituent classifiers [12, 22, 24, 27, 38, 42]. The main idea underlying classification ensembles is to combine a set of predictive models (henceforth called classifiers), each of which performs the same prediction task. The aim is to obtain a composite global model capable of more accurate and reliable decisions than the best model in the set. Dietterich has justified the superiority of ensembles over individual classifiers giving computational, statistical and representational reasons [12]. Several empirical studies have demonstrated the validity of the idea [2, 13, 14, 17, 34]. Recently, ensemble techniques have been successfully implemented for evolving/streaming datasets as well [9, 43].

An ensemble $E$ is constructed by producing a pool of classifiers from the given training set using either same or different induction algorithms, and a pre-specified generation strategy. When an unseen instance is to be predicted, each classifier in the ensemble is asked for its prediction, and finally all predictions are combined using a combiner function. Variations in the “generation methods” and “combiner functions” give rise to a variety of ensemble methods [6, 22, 27, 38].

Research in the area of ensemble methods has focused on strategies to generate pools of classifiers [2, 3, 14] and design of combiner functions [22, 27]. During the last decade, ensemble pruning has attained importance in the research related to multiple classifier systems, since smaller ensembles with comparative performance have lower overheads with respect to storage and prediction [16, 21, 29, 30, 32, 33, 35, 36, 39, 41, 44, 45].

Accuracy and size of an ensemble are two important issues in ensemble technology. Theoretically, the accuracy of an ensemble of independent classifiers asymptotically approaches 1 as its size increases [27]. Practically speaking, this notion fails when classifiers with predictions identical to previous classifier members are added to the ensemble [7, 32]. Further, Margineantu and Dietterich [30] have shown that the size of an ensemble can be substantially reduced if a slight loss of performance is acceptable. Studies have empirically verified that a systematically selected subset of classifiers in an ensemble often gives better performance than the complete set [29, 32, 33].

Ensemble pruning has also been studied as ensemble selection [3, 21, 45]/thinning [1]. The goal is to remove bulk forming classifiers, which have little or no contribution in improving the performance of the ensemble. This problem has been shown to be NP complete [39]. Several heuristic methods have been proposed to solve the problem [33, 35, 36] in addition to clustering approach [16], probabilistic approach [8], genetic programming [23, 45] and semi-definite programming [44]. Tsoumakas et al. [41] give an elaborate account of these approaches in a comprehensive survey.

Diversity amongst classifiers (both pairwise and non-pairwise) is a well-studied aspect of multiple classifier systems [5, 24, 26]. Kuncheva proved that diverse classifiers lead to uncorrelated errors, which in turn improve ensemble accuracy [25]. Bagging [2], random space method [20] and Boosting [14] induce diversity implicitly as the members of ensembles are produced. Several other algorithms explicitly use diversity to prune the ensemble [25, 30].

Though the concept of diversity in ensembles has been studied for over a decade, there is no single definition for it [26, 40]. Further, there are evidences that diversity is not necessarily strongly correlated with ensemble accuracy [23]. Accuracy–diversity trade off has been well studied [26, 40] and it is opined that accuracy need not be sacrificed for diversity in ensembles. However, recent works that study the theoretical aspects of diversity, and argue in favor of diversity for ensemble pruning have rekindled interest in diversity [11, 23, 28].

Ko et al. [23] have exploited accuracy and diversity together to prune an ensemble. They propose a compound function that takes into consideration both accuracies of individual classifiers and pairwise diversities among them. During the course of current study, we found that pairwise diversity and ensemble accuracy can be integrated in a simplistic manner to discover minimum-size, maximum-accuracy ensemble, i.e., an optimal ensemble.

In this paper, we propose a novel and conceptually simple method for ensemble pruning, which integrates the use of accuracy and diversity. The proposed accuracy–diversity pruning (ADP) algorithm takes as input a pool of classifiers ($\mathcal {E} = \lbrace h_{1}\ldots h_{T} \rbrace$) and aims to find a minimum-size, maximum-accuracy ensemble. Essentially, all the classifiers in the pool must have error rate $<$0.5 for the method to work well. ADP algorithm is independent of the method of ensemble generation, and uses majority voting with 0–1 loss function. Simplicity and effectiveness are attractive features of the algorithm. Other salient features of the proposed algorithm are:

• 1. It makes an explicit use of accuracy and diversity while growing the ensemble bottom-up. The search is purely data driven and parameterless, which is the main strength of the algorithm.

• 2. Instead of greedy hill climb, the method performs multi-pronged hill climb search while ordering the ensembles according to their accuracies, thus avoiding getting stuck in local minima (Sect. 3).

• 3. The algorithm guarantees that the resulting ensemble has accuracy greater than or equal to the best classifier in the pool (Sect. 3.2). To the best of our knowledge, this guarantee is not furnished by any existing ensemble selection method.

• 4. Unlike the published works on ensemble pruning, ADP algorithm strives to achieve optimality. Experimental evaluation in Sect. 4 demonstrates that ADP discovers optimal ensemble most of the times. Results of none of the previous algorithms have been assessed for optimality.

2 Related work

Margineantu and Dietterich [30] pointed out the drawbacks of including all the classifiers in the ensemble. There have been several research studies that aim to select classifiers from large pools to train small ensembles with high generalization accuracy [16, 21, 29, 30, 32, 33, 35, 36, 39, 41, 44, 45]. An elaborate account of various approaches for ensemble pruning is presented in [41]. We present below the works that are closely related to the two strategies employed in the proposed algorithm. Firstly, we describe works that have used Ordered aggregation approach to prune ensemble, followed by those which have demonstrated the effectiveness of incorporating diversity in ensembles.

2.1 Ordered aggregation approach for ensemble pruning

Ordered aggregation of classifiers in an ensemble has been found to be an efficient approach for ensemble pruning [33]. This method ranks the classifiers based on some performance criteria to select either a pre-specified number of classifiers [1] or select all classifiers that satisfy a pre-specified threshold [29, 32]. This strategy avoids scanning the massive search space of $\mathcal {O}(2^T)$, where $T$ is the number of classifiers under consideration. Rokach [37] proposed an ensemble pruning algorithm based on ranking method that takes into account agreement level among the members in addition to agreement level between each member’s prediction and the real label. Recently, Guo and Boukir [18] proposed ordering-based ensemble pruning method which relies on measuring the margin-based information quantity of each base classifier in the ensemble. The algorithm uses a validation set $V$ (called the pruning set in the paper) to calculate the margin of each instance in $V$. Subsequently, the margin-based criterion is computed for each classifier to order them and include the best in ensemble.

2.2 Diversity for ensemble pruning

Tang et al. [40] analyzed various diversity measures and concluded that seeking diversity in an ensemble could be viewed as an implicit way to maximize the minimum margin of the ensemble. Heuristic method based on diversity-based ensemble pruning proposed in [30] shows that 60–80 % ensemble members can be pruned out without substantial degradation in performance. Ensemble pruning methods that perform state space search using hill climbing based on diversity measures have been elaborated in [41]. Recently, diversity has been studied theoretically, and it has been shown that it is closely related to the hypothesis space complexity. It can be regarded as regularization factor on ensemble methods [28].

Ko et al. [23] examined correlation between ensemble accuracy and diversity, and established theoretically and empirically that the two are indeed correlated. They proposed compound measures based on accuracy of classifiers and different types of diversities among them, to empirically substantiate their hypothesis, which is somewhat contrary to earlier studies  [26]. This study asserts that diversity should be taken into account along with accuracy of individual classifiers for the improved performance of pruned ensemble. Experimental results demonstrate that genetic algorithm (GA)-based ensemble selection using the compound measure as objective function yields more accurate ensembles than those obtained using the diversity measures alone.

The present proposal takes cue from the conclusion of work by Ko et al. [23] and integrates accuracy and pairwise diversity for ensemble pruning. We hypothesize that classifier accuracies and pairwise diversities can be combined in more simplistic and efficient manner by embodying them in search process. This approach eliminates expensive computation of compound measures to be used as objective function during ensemble selection by GA. The proposed ADP heuristically prunes the search space while systematically including accurate and diverse classifiers in the ensemble. The search is guaranteed to yield an ensemble with accuracy not lower than the best classifier in the pool. No such guarantee is attainable for an ensemble selected using evolutionary algorithms. Thus, ADP algorithm is highly likely to discover optimal ensemble. In case the optimal is missed, the discovered sub-optimal ensemble is empirically found to be close to the optimal ensemble in terms of both accuracy and size.

3 Accu–div heuristic

As mentioned earlier, ADP algorithm strives towards an optimal ensemble by integrating accuracy and diversity while pruning a pool of classifiers. Unlike greedy hill-climbing approach, which is likely to lead to locally maximum accuracy ensemble, the proposed algorithm does a multi-pronged hill climbing and examines multiple candidate solutions (sub-ensembles) for optimality in breadth-first fashion. We are hesitant to call it beam search with variable beam width, because of its purely data-driven nature. Ensembles in the proposed approach are grown by incrementally adding a pair of high diversity classifiers. Based on the performance, at each stage it is ascertained if an ensemble is worth growing further.

3.1 Search strategy

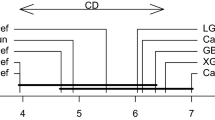
The brute force search necessitates examining $\small {\overline{2^T{-1}}}$ subsets of $\mathcal {E}$ to discover the optimal ensemble $E$. The search space can be modeled as a lattice with subset relation ($\subset$) as the ordering operator. Figure 1 shows the complete search space for a pool of five classifiers. The null ensemble is the infimum, and the complete pool is the supremum in the lattice. The optimal ensemble(s), i.e., minimum-size , maximum-accuracy ensemble, is (are) hidden in the lattice. Each node in the lattice is a potential solution (optimal ensemble) that needs to be examined. Thus in a pool of size $T$, the brute force search for optimal ensemble has computational complexity of $O(2^T)$.

Fig. 1

Complete search space for a pool of five classifiers

ADP algorithm heuristically reduces the search space by growing the ensembles incrementally and conditionally. Since the algorithm uses majority voting as combining function, ensembles are grown by adding a pair of classifiers at a time. Thus, the search is limited to examining nodes at odd-numbered levels in lattice.¹ The heuristic discipline of growing the ensemble based on accuracy and pairwise diversity, systematically discards the portions of the lattice that are not likely to contain the optimal ensemble. Though theoretical complexity of the search is still $O(2^T)$, empirical evaluation shows that the search space reduction for the experimented datasets varies from 70 to 99 %, with minor average loss of accuracy (Table 2).

Given a pool of $T$ classifiers, the algorithm performs a systematic bottom-up search starting with top 50 % accurate classifiers. Thus, the better half of the sub-ensembles of size 1 is retained and the rest are discarded. The most accurate classifier is the best accuracy sub-ensemble so far. Pairwise diversity of $T$ classifiers is computed, and top 50 % diverse pairs are retained for growing sub-ensembles. At each level of the lattice, these pairs are incrementally added to each of the retained sub-ensembles and the grown sub-ensembles are examined for improved performance. If none of the grown sub-ensembles exhibits better performance than the best accuracy sub-ensembles so far, the algorithm stops and reports the latter as the optimal ensemble. Otherwise, on an optimistic note the algorithm proceeds to the next level by retaining top 50 % sub-ensembles as potential candidates for growing.

Apparently, due to 50 % reduction at level 1, portions of lattice below these classifiers are completely missed. However, a close examination of the algorithm reveals that the discarded classifiers get a second chance to get introduced in the search space when the existing sub-ensembles are grown by addition of diverse classifier pairs. But this takes place in a purely data-driven manner.

In order to understand this aspect better, we randomly selected ten datasets from Table 1. For each of the ten datasets, we first constructed a library of 101 classifiers using bagging and J48 algorithm from Weka [19]. Then we drew random samples of sizes 11, 21 and 31, on which we executed Steps 5–8 of ADP algorithm. In a pool of size $T(=\!2k+1)$, let $C_1$ denote the top 50 % accurate classifiers, and $\overline{C_1}$ denote the remaining classifiers in the pool. We computed diversity (Q-statistic) for all $T \atopwithdelims ()2$ classifier pairs, and selected top 50 % in set DP. Next, set DP was partitioned into three mutually exclusive partitions: pairs consisting of classifiers from $C_1$(Set A), pairs consisting of classifiers from $\overline{C_1}$ (Set B) and pairs consisting of one classifier each from $C_1$ and $\overline{C_1}$ (Set $C$). Sizes of these sets are:

$$\begin{aligned} \vert A \vert =\frac{(k+1)k}{2}, \;\;\; \vert B \vert = \frac{k(k-1)}{2},\;\;\; \vert C \vert = k(k+1), \;\;\; \end{aligned}$$

(1)

In each experiment, we counted the percentage pairs in set DP belonging to sets $A, B, C$. After repeating the exercise 30 times for each dataset, we recorded the results of 900 (30 $\times$ 3 $\times$ 10) experiments. Figure 2 shows that points belonging to set $C$ constitute a compact cluster at higher percentage level. This establishes that the top 50 % diverse classifier pairs largely belong to set $C$, and the classifiers rejected in Step 5 are highly likely to be used in ensemble growing.

Table 1 UCI datasets used for experimentation

Fig. 2

Percentage composition of sets $A$, $B$ and $C$

3.2 Algorithmic details

In this subsection, we present a step by step explanation of the ADP algorithm (Algorithm 1). The algorithm takes an odd number of classifiers with their respective accuracies on validation set as input and sorts the classifiers in decreasing order of their accuracies (Step 1). In Steps 2–5, the top 50 % performing classifiers are retained in set $C_1$ and rest are discarded. They constitute the set of candidate ensembles at level 1. In addition, the highest accuracy classifier $h\_\mathrm{max}$ is noted which constitutes the highest accuracy ensemble $E$ discovered so far. In Step 6, $^{2k+1}C_{2}$ diversity pairs of $2k+1$ classifiers are generated and their diversities are calculated. In Steps 7 and 8, the classifier pairs constructed in Step 6 are sorted in decreasing order of their diversity, and top 50 % pairs are retained in set DP and rest are discarded. Steps 10–31 constitute the loop for growing the ensembles from level $\overline{2l-1}$ to level $\overline{2l+1}$ ($l\,=\,1,2, \ldots k$).

In Steps 12–20, each candidate ensemble $E_i$ from set $C_{2l-1}$ is combined with all such pairs of classifiers in set $D$, which are disjoint to $E_i$, to form candidate ensembles $X$ of size $\overline{2l+1}$ and stored in set $S$. Accuracy of each ensemble $X$ in set $S$ is also calculated. Step 21 sorts the ensembles in set $S$ in decreasing order of their accuracies. In Step 23, the accuracy of best ensemble ($e\_\mathrm{max}$) in set $S$ is compared with the maximum accuracy achieved so far $a\_\mathrm{max}$. If its accuracy is greater than the accuracy of $E$, then top 50 % performing ensembles in set $S$ are retained in set $C_{2l+1}$ for the next level, and $E$ is updated to $e\_\mathrm{max}$. Otherwise, the loop is terminated, and ensemble $E$ with accuracy $a\_\mathrm{max}$ is reported as the output.

Being a heuristic algorithm, it cannot be guaranteed that the ADP algorithm will always find the optimal ensemble. However, the algorithm guarantees that on the pessimistic side the performance of the discovered ensemble will not be lower than that of the best classifier in the pool. On the optimistic side, the discovered ensemble is same as the optimal ensemble.

Claim 1

Accuracy (on validation set) of the ensemble delivered by Algorithm 1 is not lower than the accuracy of the best classifier in the pool.

Proof

Given the pool $\mathcal E$ of $T$ classifiers, $\mathcal {E}=\{ h_1,\ldots , h_T\}$. Let $h_\mathrm{max}$ be the best performing classifier on validation set, and $E_\mathrm{adp}$ be the ensemble discovered by ADP algorithm. It is required to prove that acc$(h_\mathrm{max}) \le \mathrm{acc}(E_\mathrm{adp})$.

In Step 3 of Algorithm 1, $E_\mathrm{adp} =h_\mathrm{max}$. As the control enters the while loop, Step 23 ensures that the best accuracy ensemble at the current level is better than the previous best. Thus, acc$(h_\mathrm{max}) \le \mathrm{acc}(E_\mathrm{adp})$. $\square$

Since the classifiers are ordered on validation set accuracies, similar claim of optimality on the test set is unreasonable. Extensive experimental analysis presented in Table  3 offers evidence that ADP performs competitively on test set when compared to the optimal ensemble obtained by brute force search.

4 Experimental analysis

In this section, experimental evaluation of the proposed approach is presented. The proposed algorithm (ADP) and Brute force (BF) search were implemented using C++ and bash shell scripts, and executed on quad core machine using OpenMP shared memory model. ADP program is straight forward parallel implementation with no optimizations. Twenty-four UCI [15] datasets shown in Table 1 were used for experiments. The experimental studies were designed to answer the following research questions:

• 1. How good is the quality of heuristics employed in ADP algorithm? (Sect. 4.2)

• 2. How does ADP approach compare with other ensemble pruning methods? (Sect. 4.3)

• 3. How do mismatches and execution timings scale with increasing pool size? (Sect. 4.4)

• 4. How do the good and bad diversity components [26] vary while ADP grows the ensemble? (Sect. 4.5)

4.1 Methodology

We employed tenfold cross validation (CV) for experimental evaluation of ADP algorithm. Conforming to tenfold CV method, in each of the ten iterations, nine folds constituted the training set and the tenth fold was used as test set. To further the confidence in results, CV was carried out three times for each dataset.

In each iteration, one-third data from the training set were retained as validation set and remaining two-thirds data were used to train classifiers. Bagging was used to generate a library $L$ of 51 classifiers for each iteration. Each classifier was trained using decision tree² implementation (J48) in Weka [19], with default parameters ($C$ = 0.25, $M$ = 2).

Each experiment consisted of executing the compared pruning algorithms on the same set of classifiers. To add randomization in experimental evaluation, classifiers were picked up randomly from $L$ to construct pools of sizes 11 and 21 for pruning. Since cross-validation was carried out three times, 30 experiments were carried out for each dataset and pool size. All reported results are averaged over 30 experiments.

4.2 Evaluating quality of heuristics

To answer Q.1 above, we (i) observe how often ADP algorithm discovers the optimal ensemble (obtained by BF search), (ii) compare ADP ensemble accuracies with optimal ensemble accuracies on validation set, (iii) inspect the trend for ADP missing the optimal ensemble with increasing pool size, (iv) compare ADP ensemble accuracies with optimal ensemble accuracies on test set.

ADP algorithm and BF search were executed on pool sizes 11 and 21. Our decision to use BF search as benchmark limited the dataset size as well as pool size, because of its exponential time complexity. For each dataset and pool size, classifiers were drawn randomly from $L$. Note that during random selection, if a classifier is duplicated in a pool, its pairwise diversity with the identical classifier will be minimum and the pair will be discarded by ADP algorithm. By carrying out 30 experiments each on 24 datasets for 2 pool sizes, we performed 1,440 comparisons of ADP ensemble and optimal ensemble.

Performance comparison of ADP algorithm with BF search on validation set is presented in Table 2. Column “DS” displays the dataset, and “PS” indicates the pool size. Column “LA” reports the library accuracy. For the columns “Brute Force” and “ADP”, sub-columns “Acc” and “Size” show, respectively, the average accuracies and average sizes of discovered ensembles. It is observed from the table that average accuracy for BF ensembles is always better than the corresponding ADP ensembles, as expected. However, the sizes of ADP ensembles are generally smaller than BF ensembles hinting that loss in accuracy is often compensated by smaller-sized ensembles discovered by ADP algorithm. Further, for all datasets, average library accuracy values are much smaller than BF and ADP ensemble accuracies. This corroborates the well-accepted and understood fact that pruning leads to smaller-sized high accuracy ensembles.

Table 2 Comparison of performance of BF search and ADP algorithm on validation set

4.2.1 Cost-benefit analysis

In this subsection, we analyze the difference in quality of ADP and BF ensembles on validation set. In Table 2, column “MM” indicates the number of times ADP ensemble discovers sub-optimal ensemble, “MAL” shows the maximum loss of accuracy among the sub-optimal ADP ensembles, and “AR” shows average (%) reduction in search space while discovering an ADP ensemble. Average reduction in search space is computed as % age ensembles pruned from lattice.

Column “MM” indicates that ADP algorithm discovers optimal ensemble 1,310/1,440 (91 %) times. In the remaining cases, when it discovers sub-optimal ensembles, a close study of accuracy loss is warranted. We choose to report the “MAL” among all the sub-optimal ensembles discovered by ADP algorithm to give an idea of the upper bound on error incurred by ADP heuristic. Optimal ensemble was missed 13 times for pool size 21, for MF dataset . However, “MAL” among all the 13 sub-optimals is only 0.45 %. Close analysis of SR dataset shows maximum accuracy loss of 6.38 %, when it misses optimal only 2/30 times. Despite this heavy accuracy loss, the average performance is marginally lower than that of BF (optimal) ensembles.

It is further observed that percentage average reduction in search space varies from 70.75 to 99.87 % over all experiments. This reduction in search space translates to speedier discovery of near-optimal ensembles compared to BF search.

4.2.2 Comparison of accuracies of ADP ensembles and BF ensembles

Given a library $L$ of $T$ classifiers, let $L_{\!P}$ denote the set of $^{T\!}C_{\!P}$ pools, each pool containing $P$ classifiers. When BF search and ADP algorithm are run on all the pools in $L_{\!P}$, two distinct distributions of accuracies are obtained. Let $P^O$ denote the distribution of accuracies obtained by BF search, and $P^A$ denote the same obtained by ADP algorithm. Paired observations arise when BF search and ADP algorithm report accuracy values on the same pool. We hypothesize that the mean difference in the paired accuracy values of $P^O$ and $P^A$ is zero.

To test the hypothesis, we take a sample $S$ of size $30$ from $L_P$. Each element of $S$ is a pool of $P$ classifiers on which both algorithms are executed. Let $O=\lbrace a_1^O, \ldots a_{30}^O \rbrace$ and $A=\lbrace a_1^A, \ldots a_{30}^A \rbrace$, respectively, denote the sample accuracies of optimal ensembles and ADP ensembles. We apply paired $t$ test to show that $O$ and $A$ values do not differ significantly. The paired $t$ test investigates the differences between paired values in two samples, to determine how likely it is that the two samples belong to the same population.

For each dataset and pool size, let $\mu _D$ denote the mean of differences between the paired values, i.e., $\mu _{\!D}=\frac{1}{n} \Sigma _{i=1}^{n}(a_i^O-a_i^A)$ In consonance with our claim, the null hypothesis $H_0$: $\mu _D = 0$ is tested against the alternate hypothesis $H_1$: $\mu _D>0$. Since accuracy values reported by BF search on validation set are never less than accuracy values reported by ADP algorithm, a right-tailed paired $t$ test is carried out. MATLAB function is used to compute $p$ value for those cases which have MM $>0$.

For $28$ out of $34$ populations, the null hypothesis is accepted at $1~\%$ significance level. It can be seen from Table 2 that low $p$ values (${<} 0.01$) have been obtained for the datasets showing large number of mismatches. Thus in 28/34 cases, there was no statistical evidence for rejecting $H_0$ in favor of $H_1$.

In 6/34 experiments, the difference between the average ADP accuracies and BF accuracies is significant, and the probability of the two samples from same population showing such difference is very small. In other words, for these six datasets, ADP is not performing as well as BF, which is also evident from “MM” column in the table for these datasets.

4.2.3 Comparison of test accuracies of BF search and ADP ensembles

Performance of a classifier on the test set indicates the true capability to generalize. Accordingly, we compare the performance of BF and ADP ensembles on test set and report the results in Table 3. For 8/48 cases, all ADP ensembles exactly match the corresponding BF ensembles. Average ADP test accuracies for the remaining cases are also comparable with the corresponding average BF test accuracies.

Table 3 Comparison of test accuracies for BF search and ADP algorithm

We hypothesize that BF test accuracies are almost same as ADP test accuracies for all datasets. Since the possibility of ADP ensemble reporting higher test accuracies than BF ensemble cannot be ruled out, the null hypothesis $H_0:\mu _D=0$ is tested against the alternate hypothesis $H_1:\mu _D\ne 0$. Two-tailed paired $t$ test is applied for drawing statistical inference. The null hypothesis was tested at 1 % significance level. The last column in Table 3 shows that null hypothesis is accepted for 39/40 cases, indicating that both the approaches perform equally well. The hypothesis is rejected for one case (dataset WN pool size 11) where ADP ensembles perform much better than BF ensembles.

Thus, we conclude that generalization accuracy of ADP matches that of BF search. On the basis of this result, it is reasonable to prescribe ADP algorithm for the evaluation of any novel ensemble method with respect to optimal ensemble.

4.3 Comparison of ADP algorithm with other ensemble techniques

In this subsection, we compare the performance of ADP algorithm with complete (unpruned) ensemble (CE) and three other ensemble pruning techniques. There are two criteria on the basis of which it can be compared with other ensemble pruning methods:

• (i) Search strategy: ADP has been compared with forward selection (FS) and backward elimination (BE) methods, since these two pruning techniques search the lattice to locate the optimal ensemble, just like ADP. In FS (BE) method, a pair of classifiers is progressively added to (removed from) the ensemble and monitored for improvement in accuracy [31]. The selection (elimination) of classifiers is continued till the accuracy improves.

• (ii) Use of accuracy and diversity in heuristics: We also compare ADP algorithm with the one proposed by Ko et al. [23] which uses a compound diversity function (CDF) measure for pruning an ensemble. This measure takes into account the accuracy of each classifier member ($a_i$), as well as pairwise diversity $(d_{i\!j})$ between classifier members $\mathrm{C}_\mathrm{i}$ & $\mathrm{C}_\mathrm{j}$ in the ensemble. We use Q-statistic for diversity calculation in ADP approach and computation of CDF measure. For an ensemble of size $P$, the CDF measure is calculated as follows [23]:

  $$\begin{aligned} \mathrm{CDF}\!=\!\frac{P}{P-1}\left( \prod _{i=1}^{P}(1-a_i)\right) ^{\frac{1}{P}} \left( \prod _{i,j=1,i\ne j}^{P} d_{i\!j}\right) ^{\frac{1}{P(P-1)}}\nonumber \\ \end{aligned}$$

  (2)

  We computed CDF values for all ensembles in the search lattice, and the ensemble(s) with minimum CDF value are selected as optimal ensemble(s). This is unlike the proposal in  [23] which uses GA to select the optimal ensemble. To avoid randomization involved in GA, we carried out exhaustive search to locate the optimalensemble. The obtained optimal ensemble is then used to evaluate the test sets for the corresponding datasets.

Results of the experiments are shown in Table 4. For each dataset and pool size, the highest accuracies reported on the test set have been displayed in bold. It can be observed from the table that for 42/48 cases, pruning yields better results than the complete ensemble. Comparing the sizes of ensembles obtained by all the methods, FS reports smallest ensembles and BE the largest, although average accuracy values reported by FS ensembles are not better than ADP algorithm for majority datasets. The CDF ensembles are considerably larger than ADP ensembles with 8/48 wins.

Table 4 Comparison of ADP algorithm with other ensemble techniques on test set

To further strengthen our conclusion, we applied Friedman test for multiple comparisons. This non-parametric test is commonly used to test the null hypothesis $(\mathrm{H}_{0})$ that all classifier performances are equivalent, against the alternate $(\mathrm{H}_{1})$ that at least one classifier exhibits performance which is significantly different from others [10]. The test returns $p$ value, which is examined to draw an inference about the hypothesis. If the $p$ value is close to zero, the null hypothesis is rejected indicating that the performance of at least one classifier is significantly different from others.

Friedman test ranks the methods on the basis of ensemble accuracy for each dataset, with lower values of ranks indicating lower performance. Mean rank for a method is obtained by averaging its ranks over all datasets. It was found that mean rank for ADP algorithm was the maximum (84.11) followed by CDF (75.86) and FS (75.13). Lower ranks are reported for CE (73.47) and BE (68.93). At 95 % confidence level, very low $p$ value of $8.99886$e-19 was obtained. Consequently, the null hypothesis was not accepted, implying that sample mean accuracy of at least one method was significantly different from that of the others.

Next, Nemenyi test is employed for pairwise comparison of classifiers to detect the classifier(s) significantly different from the others. Figure 3 shows the outcome of the Nemenyi test. Mean rank of each classifier is indicated by a circle, and horizontal bars across each circle denote the intervals about these mean values. The extent of overlapping of intervals indicates the difference between two estimates being compared. It is evident from the figure that ADP algorithm is significantly different from the other methods, since it shows a smallest interval overlap with other methods. ADP scores over other algorithms because of highest mean rank (indicated by circle on ADP bar). The intervals for CDF and FS show substantial overlapping indicating similar performance, the fact is vindicated by almost equal mean ranks obtained by Friedman’s test. We attribute improved ranking of CDF to an exhaustive search for CDF ensemble (against GA-based search in [23]).

Fig. 3

Comparison of CE, CDF, ADP, FS and BE algorithms using Nemenyi test

4.4 Scalability of ADP algorithm

We also investigated if there exists a trend in execution timings and discovery of sub-optimals with increasing pool sizes. We executed BF search and ADP algorithm for pool sizes varying from 11 to 25 with increment of 2. The experiments were done for three datasets—one with heavy losses (BS), one with moderate losses (CA) and the last one with no losses (DM). For each dataset and pool size, 30 experiments were carried out (as described in Sect. 4.2).

4.4.1 Discovery of sub-optimals

We observed the number of sub-optimals discovered by ADP algorithm. The number of mismatches corresponding to each dataset and pool size is plotted in Fig. 4. Visual inspection of the graph reveals that there is no monotonic trend for losses with increasing pool size.

Fig. 4

Number of mismatches with optimal ensemble for three datasets BS, CA, DM (pool sizes 11–25)

4.4.2 Execution timings

Current ADP implementation is a straight-forward parallel implementation, with tremendous scope for optimizations. For each dataset and pool size, we recorded execution timings and plotted the graph (Fig. 5). It is clear that the execution time rises exponentially with the pool size. However, this is deceptive considering that the brute force timing could not be plotted in the same graph because of massive scale difference. For DM dataset, one ADP experiment for pool size 25 on an average took 3 s to complete, while the average time for brute force search was more than 3 min. The general improvement in timings is also indicated by column ’AR’ of Table 2, which shows massive reduction in the search space by ADP algorithm. As the pool size increases further, the difference in execution times of BF and ADP also increases exponentially.

Fig. 5

Execution times for three datasets BS, CA, DM (pool sizes 11–25)

We admit that the current implementation is suitable for medium pool sizes so much so that for pool sizes $>$21, it is slower than FS and BE.

Closer observation of execution timings reveals the two tasks that slow the algorithm. These are (i) writing of all intermediate ensembles in file and (ii) their sorting, at each level. For larger pool sizes, this problem is too acute to be tolerated. Design of smart indexing is a potential solution for the problem.

4.5 Good and bad diversity

Kuncheva and Brown established that overall diversity in majority voting ensembles can be decomposed into Good and Bad diversities  [4]. The good diversity pulls the performance of the ensemble up, while the bad diversity pulls it down. Using the notations in  [4], these two are related as follows:

$$\begin{aligned} E_{\mathrm {maj}}\!=\!\int \limits _{x} e_{\mathrm {ind}}(x) \!-\! \underbrace{\int \limits _{x+} \frac{1}{T}\sum _{t=1}^{T} \delta _t(x)}_{\mathrm {good \; diversity\;(G)}} \!+\! \underbrace{\int \limits _{x-} \frac{1}{T} \sum _{t=1}^{T} \delta _t(x)}_{\mathrm {bad \;diversity\;(B)}} \end{aligned}$$

(3)

Here, $e_{\mathrm {ind}}(x)$ is the average individual loss for classifiers in the pool. $E_{\mathrm {maj}}$ is majority voting loss, $\delta _t(x)$ is the disagreement between $t\mathrm{th}$ classifier and the ensemble, and $x-$ and $x+$ denote the data subspaces where the ensemble is correct and incorrect, respectively.

To strengthen our hypothesis of effectiveness of accuracy–diversity integration, we examined Good (G) and Bad (B) diversities at each step of growing the ensembles. In this experiment, we used pool of size 31 because ADP algorithm executed reasonably fast on this pool size. We found that the biggest ensemble of size 7 was obtained five times in BC dataset. These ensembles are denoted as $E_1, \ldots ,E_5$. We selected these ensembles for closer investigation and studied their growth at each step. For each of these five cases, the algorithm explored up to size 9 ensembles and reported size 7 ensemble as optimal. G and B were computed at each step as per Eq. 3 and plotted (Fig. 6). It can be observed that good diversity increases and bad diversity decreases till the optimal ensemble is located. Extending the ensemble beyond this point, the good diversity decreases and the bad diversity increases. Thus, the maximum value of G and minimum value of B are attained when the “optimal” ensemble is obtained.

Fig. 6

Variation in good/bad diversities for five biggest ensembles in BC dataset

4.6 Discussion

ADP algorithm is a heuristic algorithm and we do not expect it to always discover an optimal ensemble. Experimental evaluation, however, demonstrates that the quality of heuristics is reasonably good. Intuition underlying the heuristics in ADP algorithm is as follows:

• 1. Low accuracy classifiers are not likely to participate in optimal ensemble, unless paired with a high accuracy classifier. This motivates (a) rejection of 50 % low accuracy classifiers (Step 5 ), (b) rejection of 50 % low diversity classifier pairs (Step 8) and (c) extending sub-ensemble by adding relatively high diversity classifier pair (Steps 12–20).

• 2. If at the current level, the best accuracy sub-ensemble has accuracy less than or equal to that of previous level best accuracy sub-ensemble, then this cannot be the optimal ensemble. Further, it is not likely to be found at higher levels. This motivates the stopping criteria at Step 28. Close investigation reveals that this is a frequent cause of failure when a sub-optimal ensemble is discovered by ADP.

• 3. Only relatively accurate ensembles are likely to grow into an optimal ensemble. This motivates rejection of 50 % low-performing candidate sub-ensembles in the while loop (Step 26).

There are certain limitations of the experimentation, which were beyond our control and which we would like to present here.

Firstly, despite our best intention to use datasets that have been commonly used in other studies [29, 32], we had to restrict to relatively smaller datasets so that the BF search on pool size 21 and above, could be executed in reasonable time. For instance, a single experiment for pool size 31 on Magic dataset took almost 2 days to complete. With the available hardware, it was not possible to complete 30 experiments in time. Hence, the pool size was restricted.

Secondly, scalability of the algorithm is a serious issue that needs to be addressed for it to be of practical utility. The main factor that dampens the scalability is the generation of duplicate ensembles while combining candidate sub-ensembles of size $2l-1$ with disjoint classifier pairs in set DP to generate ensembles of size $2l+1$. For example, while classifier {1} can be combined with classifier pair {2, 3} to generate size 3 ensemble {1, 2, 3}. Similarly, classifiers {2} and {3} can be combined with pairs {1, 3} and {1, 2}, respectively, to generate the ensemble {1, 2, 3}. This leads to duplication of effort as an ensemble generated once need not to be generated again.

In the current implementation of ADP algorithm, duplicates are removed by sorting. This sorting is responsible for exponential rise in execution times for higher pool sizes. Therefore, there is a need to devise an efficient strategy/data structure to avoid generation of duplicates, which will lead to a substantial reduction in execution time.

5 Conclusion and future work

In this paper, we present a heuristic algorithm ADP which makes use of both accuracy and diversity for ensemble pruning. The algorithm is conceptually simple and operationally efficient in search space reduction. Using multi-pronged hill climb, ADP algorithm systematically grows ensembles by adding a pair of diverse classifiers. An ensemble is grown further if its performance has improved after addition of the pair.

Empirical evaluation of ADP algorithm shows that most of the times it discovers an optimal ensemble from the pool. In case it discovers sub-optimal ensemble, the loss of accuracy is insignificant. The growth strategy indicates that at each step, good diversity of the ensemble increases and the bad diversity decreases. Since the algorithm delivers near optimal ensembles, it can be used as a benchmark for evaluating other ensemble-pruning algorithms. However, the current implementation of the algorithm makes it unscalable. In future, we intend to overcome this limitation so that bigger pools can be pruned to obtain optimal ensembles.