Computing Euclidean Steiner trees over segments

Abstract

In the classical Euclidean Steiner minimum tree (SMT) problem, we are given a set of points in the Euclidean plane and we are supposed to find the minimum length tree that connects all these points, allowing the addition of arbitrary additional points. We investigate the variant of the problem where the input is a set of line segments. We allow these segments to have length 0, i.e., they are points and hence we generalize the classical problem. Furthermore, they are allowed to intersect such that we can model polygonal input. As in the GeoSteiner approach of Juhl et al. (Math Program Comput 10(2):487–532, 2018) for the classical case, we use a two-phase approach where we construct a superset of so-called full components of an SMT in the first phase. We prove a structural theorem for these full components, which allows us to use almost the same GeoSteiner algorithm as in the classical SMT problem. The second phase, the selection of a minimal cost subset of constructed full components, is exactly the same as in GeoSteiner approach. Finally, we report some experimental results that show that our approach is more efficient than the approximate solution that is obtained by sampling the segments.

1 Introduction

We are interested in the following problem: Given a set of segments in the Euclidean plane, connect these segments by additional segments of minimum total length, where we are allowed to use additional points, called the Steiner points. We will call this problem the Euclidean Steiner minimum tree (SMT) problem over segments and formally define it later (see Fig. 1 for an example). We allow these segments to have length 0, i.e., they are points and hence we generalize the classical problem. Furthermore, they are allowed to intersect such that we can model polygonal input. The problem at hand was motivated by the need of a geography student who wanted to connect a set of highly interconnected areas, described as polygons in a plane. The situation that parts of the network that is to be constructed is already existent can also appear in other applications, e.g., when constructing an electrical network or some pipelines.

In the classical Euclidean Steiner minimum tree problem, the input is just a set of points called the terminals. It has many applications and has been widely investigated since its introduction. The most efficient publicly available implementation is the GeoSteiner package of Juhl et al. (2018), which implements a two-phase approach first introduced by Winter (1985). In the first phase, a superset of so-called full components is generated, and in the second phase, the minimal subset of this superset is computed, leading to a Steiner tree. Algorithms for the first phase are based on an approach of Winter and Zachariasen (1997), whereas the second phase is based on an approach by Warme (1998). Alternatively, the second phase can be solved by using an algorithm for the Steiner tree problem in graphs, as shown in Polzin and Daneshmand (2003). Computational studies and several improvements are given in follow-up papers (Juhl et al. 2018; Warme et al. 1999, 2000).

Fig. 1

We are given the set of segments that are shown in bold red. The SMT consists of all shown segments, including the red ones, i.e., we define the input segments to belong to the SMT. The segments in black, blue and green were added to obtain connectivity and are called nonterminal segments, where the different colors correspond to different full components (defined in Sect. 2). The Steiner points of the SMT are the points shown in blue

The authors mentioned above considered several variants of the Euclidean Steiner tree problem, such as obstacle-avoiding Steiner trees (Zachariasen and Winter 1999), Steiner trees in other metrics like the Manhattan distance (Warme 1997) and Steiner trees that lie within polygons (Winter et al. 2002). To the best of our knowledge, the problem we are investigating has not been considered before.

Generalizing a point input to a segment input was investigated for several problems in computational geometry, like computing a segment Voronoi diagram (Karavelas 2004) or the closest-pair problem (Daescu et al. 2006).

Our algorithm is based on a structural theorem of Steiner minimum trees over segments that will allow us to use an algorithm that is very similar to the one implemented in GeoSteiner, so we can reuse their implementation of the second phase. Our approach solves the problem exactly and is more efficient than the inexact solution when we sample the given segments (see Sect. 5 for a description of the sampling approach used in the comparison).

The paper is organized as follows: In the following section, we formally define the problem and introduce necessary notations and definitions. In Sect. 3, we prove our main theorem and discuss how the algorithm for the first phase in GeoSteiner has to be modified. In Sect. 4, we show how to reduce the size of the computed superset of full components. We show some computational experiments in Sect. 5 and finally conclude in Sect. 6.

2 Basic definition and outline of the approach

We now formally define the Steiner minimum tree problem and some further basic entities. We follow the approach of Brazil and Zachariasen (2016).

A geometric network $G=(V(G), E(G))$ is a graph embedded in the plane, i.e., the vertices V(G) are points in the plane and the edges E(G) are the segments connecting two of these points.¹ The length of a geometric network is the sum of the Euclidean lengths of all segments in E(G). Notice that, in contrast to plane-embedded graphs, we do not require the edges to be nonintersecting. Although this is clearly true for the Steiner minimum tree, we do not want to argue whether this is always true when we construct geometric networks in intermediate steps.

Definition 1

Given a finite set ${\mathcal {S}}$ of segments, we define a Steiner tree T for ${\mathcal {S}}$ as a connected geometric network containing ${\mathcal {S}}$. A Steiner minimum tree (SMT) for ${\mathcal {S}}$ is a Steiner tree for ${\mathcal {S}}$ of minimal total length.

In the following, we assume that the interiors of the segments are pairwise nonintersecting, as we could otherwise split the segments at their intersections. The segments $s \in {\mathcal {S}}$ are called terminal segments, their endpoints terminal points. The open terminal segments are the terminal segments without their endpoints. A set of terminal points and terminal segments is called a connected component if it is a maximal set such that there is a connection between each pair of points within the set. Edges of a Steiner tree for ${\mathcal {S}}$ that are not in ${\mathcal {S}}$ are called nonterminal segments, and points that are not terminal points are called Steiner points. We assume that a Steiner point has degree at least three, as a Steiner point of degree 0 or 1 can be deleted (together with the incident edge for a degree one point) without increasing the length of the geometric network. If a Steiner tree contains a Steiner point p of degree 2 with neighbors q and r, we can remove p and the edges pq and pr and add an edge qr and the resulting geometric network is still a Steiner tree and its length cannot be increased. Notice that a set of segments ${\mathcal {S}}$ is a geometric network itself.

The topology of a Steiner tree is the undirected graph ${\mathcal {T}} = (V({\mathcal {T}}), E({\mathcal {T}}))$ underlying the geometric network whose vertices are labeled with the terminal points, open terminal segments and Steiner points. Hence, in a topology, the positions of the terminal points are fixed, the positions of the open terminal segments are on a segment but not on one of its endpoints and the positions of the Steiner points are free. The topology represents the nodes and edges of a graph, but without an exact statement about the length of the edges or the positions of the nodes. They only specify adjacent nodes. Notice that these definitions slightly differ from those of Brazil and Zachariasen (2016), as our problem is more general.

Notice that in this definition of a Steiner tree, the length of an SMT includes the length of the given segments. The graph underlying an SMT T for ${\mathcal {S}}$ is not necessarily a tree, as it contains cycles if and only if the given segments form them. If we contract each such cycle to a single node, it becomes a tree, denoted as $T|_{\mathcal {S}}$. The contraction of an edge (u, v) of a graph $G=(V,E)$ results in the graph $G'=(V',E')$ in which u and v are replaced by a single node [uv] and each endpoint of an edge that is either u or v is replaced by [uv]. The contraction of a cycle is the contraction of all the edges on it.

As we allow a segment to consist only of a single point, the SMT problem over segments generalizes the classical Euclidean SMT problem (over terminals) and hence the problem is NP-hard.

The following basic properties can be shown easily and are generalizations of well-known properties of SMTs over terminals.

Lemma 1

Let T be an SMT over ${\mathcal {S}}$.

• 1. Incident nonterminal segments of T form an angle of at least $2\pi /3$.

• 2. A pair of a nonterminal segment and a terminal segment meets at an angle of $\pi /2$ or greater.

• 3. Terminal points have degree at most 3 if they are not incident to a terminal segment (i.e., the corresponding terminal segment has length 0) and have at most two incident nonterminal segments otherwise.

• 4. Steiner points in T have degree 3, and each pair of incident edges meets at an angle of $2\pi /3$.

• 5. T has at most $n-2$ Steiner points and at most $2n-3$ nonterminal segments, where n is the number of connected components of the graph underlying the geometric network consisting exactly of ${\mathcal {S}}$.

Proof

(Sketch)

• 1. Assume two incident nonterminal segments pq and pr have an angle of less than $2\pi /3$. Let $q'$ be on pq and $r'$ on pr such that $|pq'|=|pr'|$. If we replace the parts $pq'$ and $pr'$ of the segments of the Steiner tree by the segments ps, $q's$ and $r's$ for s being the Fermat-Torricelli-point of the triangle $p,q',r'$, we obtain a shorter Steiner tree.

• 2. Assume a nonterminal segment pq has an angle of less than $\pi /2$ with a terminal segment pr. Choose $q'$ on pq such that the perpendicular of $q'$ to the line through p and r intersects the line on the segment pq, and let $r'$ be the intersection point. If we replace the part $pq'$ of the segment pq by $q'r'$, we obtain a shorter Steiner tree.

• 3. The next two points follow from the fact that the angles of all segments incident to a point sum up to $2\pi$. Consider a terminal point p. If all segments incident to p are nonterminal, the angles between them must be at least $2\pi /3$. Hence, there are at most 3. If there is at least one terminal segment, there cannot be three nonterminal segments, as their angle to the terminal segment is at least $\pi /2$ and the angle between them at least $2\pi /3$.

• 4. As the degree is at least 3, the angle between two segments is at least $2\pi /3$.

• 5. Consider an SMT T and contract all connected components of the graph underlying the geometric network consisting exactly of ${\mathcal {S}}$ to obtain $T'$. Clearly, $T'$ is a tree, has at most n leaves and contains all nonterminal segments. Hence, $T'$ can have at most $n-2$ Steiner points as Steiner points are not leaves and their degree is at last 3. Furthermore, the total number of edges of $T'$ is bounded by $2n-3$ as the tree has at most $n+n-2=2n-2$ nodes.

$\square$

Given a Steiner tree T for ${\mathcal {S}}$, the full topologies of T are the maximal subtrees of $T|_{\mathcal {S}}$ whose inner vertices are Steiner points. The full components of T are the geometric networks of the full topologies. Hence, the full topologies are just trees whose leaves are labeled with terminal points or open terminal segments, but do not have any geometric information. Notice that all leaves of the full components are on elements of ${\mathcal {S}}$ (see Fig. 2 for an example). Notice that there may be several full components with the same full topology. In the classical Euclidean Steiner tree problem, there is a unique minimal full component for each full topology (see, e.g., Brazil and Zachariasen 2016). Again these definitions slightly differ from those in Brazil and Zachariasen (2016), as we have a generalized problem.

Fig. 2

We show three possible full components that interconnect the four given polygons. The first two geometric networks have the same topology, whereas the topology of the third one is different, since the label of one of the vertices is different (the vertex that attaches to the segment on the top left is a terminal point in this last topology and a open terminal segment in the first two). Our structural theorem shows that we can restrict the full topologies to full topologies of at most one open terminal segment, i.e., we do not have to consider the first two, but only the third

As in the case of the classical Euclidean Steiner tree problem, we want to enumerate a superset of full components of an SMT in the first phase. In the following, we derive a property of the full components that will allow us to use almost the same algorithm for enumerating the superset of full components as in the classical SMTs.

In the second phase, we select a minimum cost subset of the enumerated full components whose union forms a Steiner tree. It works exactly as in the classical SMT. We interpret the superset of full components as weighted hyperedges in a hypergraph and compute the minimum cost spanning tree in the hypergraph. In our experiments, we used the implementation provided with Juhl et al. (2018).

As in the classical case, the number of enumerated full components cannot be bounded better than the number of possible topologies. As the minimum spanning tree in hypergraphs problem is NP-hard and we were not able to use some special structure in the instances that we construct in the analysis of the running time, we were not able to analyze the running time of the second phase better than exponential, too (the same is true for the classical case).

3 Structure of optimal Steiner trees

We now sketch (a slight modification of) the classical SMT algorithm used to enumerate a superset of full components and refer to Winter and Zachariasen (1997) for details. For two points p, q, let $e_{p,q}$ be the point obtained by rotating the point q counterclockwise around p by $\pi /3$. Hence, $e_{p,q}$ and $e_{q,p}$ are the third corners of the two equilateral triangles with corners p and q. The key insight is that for each fixed topology, there is a unique minimum cost full component with this topology which can be computed as follows.

The minimum cost full component of a topology with two terminals is just the segment connecting the two terminal points.

Any topology containing at least three terminals has two terminals u and v that have a common adjacent Steiner point s. Let t be the third point adjacent to s. It is known that s lies on the arc between u and v of the circumcircle of one of the two equilateral triangles having corners u and v and either $e_{u,v}$ or $e_{v,u}$. This arc is called the Steiner arc of the corresponding equilateral point. It is possible to compute which of the two equilateral triangles should be used, but we will not discuss this algorithm here. We simply assume that $e_{u,v}$ is the third corner of this triangle. In the algorithm, both equilateral points are enumerated.

Given a minimal full component containing u, v, s and t and its topology ${\mathcal {T}}$, if we replace the segments su, sv and st in the full component by the segment $te_{u,v}$, we get a minimal full component for ${\mathcal {T}} \setminus \{u,v,s\} \cup \{e_{u,v}\}$, i.e., where we remove the vertices u, v and s and the edges su, sv and st and add the terminal point $e_{u,v}$ and the edge $te_{u,v}$ (see Fig. 3 for illustration).

Fig. 3

We want to construct a minimal full component of the topology in which a and b are connected to a common Steiner point, called s, and c and d are both connected to $s'$. Finally, these two Steiner points are connected. To construct a minimal full component, we first construct the equilateral point $e_{c,d}$ which allows us to simplify the topology to the three terminals a, b and $e_{c,d}$. Then, we construct the equilateral point $e_{b,e_{c,d}}$ simplifying the topology to the terminals a and $e_{b,e_{c,d}}$. A minimal full component of the topology consisting only of the terminals a and $e_{b,e_{c,d}}$ is just the line between them. Then, we reverse the simplification by first replacing $e_{b,e_{c,d}}$ by the segments as, bs and $e_{c,d}s$ where s is the intersection of the segment $ae_{b,e_{c,d}}$ with the Steiner arc of $e_{b,e_{c,d}}$. Finally, we replace the segment $se_{c,d}$ by the segments $ss'$, $cs'$ and $ds'$, where $s'$ is the intersection of the segment $e_{c,d}s$ with the Steiner arc of $e_{c,d}$. The final full component is shown in black

Hence, we can iteratively construct a minimal full component for a given topology by iteratively replacing two adjacent terminals and the Steiner point by the appropriate equilateral point until only one terminal and one equilateral point are left. In this case, the minimal full component is just the line between these two points. Conversely, we can enumerate all topologies with corresponding minimal full components by iteratively constructing all equilateral points from two known ones, starting with the terminals and then connecting an equilateral point to a further terminal. Clearly, the terminals used in such a construction have to be pairwise different and hence this enumeration process is finite.

The enumeration algorithm constructs the following list of equilateral points and terminals. It starts with all terminals. For each pair p, q of points in the list, we construct the equilateral points $e_{p,q}$ and $e_{q,p}$, as long as:

• The terminals used to construct p and q are distinct.

• The potential full component cannot be excluded by pruning tests, i.e., tests showing that the potential full component cannot be part of a full component in an SMT.

Having constructed all of these equilateral points, we can construct all full components by combining one of these points p with a terminal t that is not used in the construction of p. Notice that we enumerate full components several times: We can choose an arbitrary terminal to be the one that is finally connected to an equilateral point. In Brazil and Zachariasen (2016), the algorithm is slightly different to ensure that each full component is enumerated exactly once. As we will see in the next paragraph, for our approach it is helpful that we modified the algorithm in this way.

We will show that for our problem, we can assume that each full component of an SMT of ${\mathcal {S}}$ contains at most one open terminal segment and we can use almost the same algorithm as described above. We choose the open terminal segment (if there is one) as the part of the full component that is finally connected to the equilateral point, and hence, the equilateral point is constructed only of terminal points. Hence, the construction of the list of equilateral points works exactly as for the classical SMT only starting with the terminal points instead of the terminals. Furthermore, we ensure that the terminal points used to construct an equilateral point are from different components of the geometric network consisting exactly of ${\mathcal {S}}$. For the construction of full components from an equilateral point and a terminal, we have to additionally consider the case where the terminal is an open terminal segment. In this case, we have to find the point on the open terminal segment that leads to an angle of $\pi /2$ between the open terminal segment and the constructed segment.

Lemma 2

For each set ${\mathcal {S}}$ of segments, there is a Steiner minimum tree T over ${\mathcal {S}}$ such that each full topology contains at most one vertex labeled as an open terminal segment.

Proof

Consider a Steiner minimum tree with a maximal number of full components. As long as there is at least one full component with a topology of at least two open terminal segments, we will replace such a topology and full component by a topology and full component of the same cost/length with at least one less open terminal segment.

Consider a full component F with a topology ${\mathcal {T}}$ of at least two open terminal segments, and let P be a path in ${\mathcal {T}}$ between two open terminal segments. We show that we can shift segments of the full component without changing its cost until either one (or both) endpoint(s) of P is (are) shifted into the endpoint of the segment of the open terminal segment or the full component splits into two (contradicting the fact that we consider an optimal Steiner tree with a maximal number of full components).

Let $b_0, b_1, \dots , b_n$ be the segments of P, $s_1, \dots , s_n$ the Steiner points on P, $a_1, \dots , a_n$ the third segments incident to $s_1, \dots , s_n$, and $s_0$ and $s_{n+1}$ the endpoints of P (see Fig. 4).

Assume we move the segments of the path P by moving $s_0$ on its open terminal segment (in either direction), $s_i$ along the direction of $a_i$² for $1 \le i \le n$ and finally $s_{n+1}$ on its open terminal segment such that all resulting segments are parallel to the corresponding original segments. Below, we show that the length of the full component will not change. We move until either $s_0$ or $s_{n+1}$ reaches an endpoint of the open terminal segment or until some nonterminal segment degrades to length 0. In the first case, we reduced the number of open terminal segments in the full component. The second case cannot happen, as we can see in the following. If a segment $b_i$ for $1 \le i <n$ degrades, we get a Steiner point of degree 4 without increasing the length of the full component. As we assumed that we started with a minimal full component, this full component is still minimal and hence we have a contradiction to Lemma 2 part 4. If $b_0$ or $b_n$ degrades, the angle condition on the open terminal segments (Lemma 2 part 2) is not satisfied and hence the constructed full component cannot be minimal. Finally, if a segment $a_i$ degrades, we either get an SMT with more full components (if the second endpoint of $a_i$ is a terminal), contradicting our assumption that we started with an SMT with maximal number of full components, or we get again a Steiner point of degree 4 (contradicting Lemma 2 part 4).

Fig. 4

We sketch a path $s_0, s_1, \dots , s_{n+1}$ between two open terminal segments with the segments $b_0, b_1, \dots , b_n$. If we move $s_0$ and $s_n$ along the respective open terminal segments and the Steiner points $s_i$ in direction $a_i$ for $1 \le i \le n$ such that the resulting segments of the path are parallel to the original ones, the total length of the path does not change

Hence, it remains to show that the move as defined above does not change the length of the full component. Consider a small move and construct triangles around the Steiner points $s_1, \dots , s_n$ such that for Steiner point $s_i$, the three segments of the triangle are orthogonal to $b_{i-1}$, $b_i$ and $a_i$ (see again Fig. 4). The exact sizes of these triangles do not matter, as long as the segments have nonzero length and the triangles are disjoint. Notice that these triangles are equilateral, as the angle between two of the three segments of the triangle is $2\pi /3$ each time. The total length of the parts of the full component outside the triangles does not change, as the segments of P are moved parallel and are orthogonal to the segments of the triangles. The length within the triangles does not change by Viviani’s theorem (see, e.g., Pech 2007), stating that the sum of distances of any point in an equilateral triangle to the three segments is equal to the height of the triangle, i.e., it is constant. $\square$

4 Pruning of partial topologies

Recall the algorithm to construct a superset of full components in Sect. 3. We iteratively construct all equilateral points starting from the terminal points. In this section, we show some methods to exclude many of the equilateral points from this enumeration. Each equilateral point replaces a part of a full component. We say that the topology of an equilateral point is the subtree of the topology of the full component that is replaced by the equilateral point. In the following, we consider this topology rooted at the Steiner point that lies on the Steiner arc of the equilateral point.

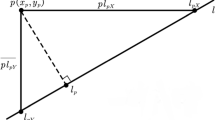
At the time of construction, we know that the Steiner point corresponding to the root of the topology of the equilateral point $e_{p,q}$ lies on the Steiner arc between p and q. For a given full topology, for a given equilateral point $e_{p,q}$ used in its enumeration, the pruning tests try to restrict the position of the Steiner point from the complete arc between p and q to some subarc between points $p'$ and $q'$ (see Fig. 5), called the feasible subarc. If a feasible subarc does not contain a point, we can prune the equilateral point, i.e., we remove it from the list of equilateral points and no equilateral point or full components can be constructed from it. If we reduce the size of a feasible subarc for one equilateral point that is used in the construction of another, it is possible that its arc can be reduced too.

Fig. 5

Assume we construct $e_{p,q}$, $p=e_{u,v}$ and the arc of $e_{u,v}$ has already been reduced to the subarc between $u'$ and $v'$. We can first restrict the arc of $e_{p,q}$ to the subarc between $p'$ and $q'$ as indicated in the picture by the necessity of the geometry. Furthermore, the subarc of $e_{u,v}$ can be reduced to the part between $p'$ and $v'$, if used within $e_{p,q}$. We try to reduce the subarcs further by additional pruning tests

When reducing the feasible subarc, we assume that the Steiner point lies on one of the two endpoints of the subarc and run some tests (see below) that can possibly exclude this position for a full component in an SMT. If this is the case, we shrink our feasible subarc by moving the endpoint we just tested toward the other until the position cannot be excluded any further.

First, we can restrict the arc due to geometry, i.e., if the Steiner point of the root lies within its feasible subarc, all other Steiner points must lie on their feasible subarcs too (see e.g., Brazil and Zachariasen 2016). Another example of a well-known pruning test is the lune property (see again Brazil and Zachariasen 2016), which works as follows. Consider an equilateral point $e_{p,q}$ and let the feasible subarc be limited by $p^{\prime }$ and $q^{\prime }$. Furthermore, let $v^{\prime }$ be the intersection of the Steiner arc of $p=e_{u,v}$ with the segment $q^{\prime }p$. If there is a terminal r not used in the construction of $e_{p,q}$ that is closer to $q^{\prime }$ and $v^{\prime }$ than the length of $q^{\prime }v^{\prime }$, then the segment $q^{\prime }v^{\prime }$ cannot be part of an SMT T and hence $q^{\prime }$ can be excluded from the feasible subarc. This is because we could remove the segment $q^{\prime }v^{\prime }$ from T and obtain two connected components with $q^{\prime }$ and $v^{\prime }$ in different components. We could then add either $q^{\prime }r$ or $v^{\prime }r$ to obtain a Steiner tree that is shorter than T. Hence, we can move $q^{\prime }$ toward p until this conflict is resolved.

Most of the pruning tests of the classical Steiner tree problem can also be used here: the bottleneck Steiner distance test, the wedge property, the projection tests and the lune property. These tests are explained in detail in Brazil and Zachariasen (2016).

There are some additional and expandable tests that use the fact that some points are already connected by the segments of the input ${\mathcal {S}}$, as explained in the following.

A first expandable test in Steiner trees over segments is the lune property. The main idea of the lune property in the classical Steiner tree problem is that given an SMT T there cannot be a terminal that is closer to both endpoints of a segment of T than the length of this segment. This can be extended as follows: If two points $p_1, p_2 \in {\mathcal {S}}$ (terminal points or points on open terminal segments) are already connected within ${\mathcal {S}}$, there can not be a segment $ab \in T$ such that a is closer to $p_1$ and b is closer to $p_2$ than the length of the segment ab. Note that the segments of ${\mathcal {S}}$ that connect $p_1$ and $p_2$ do not necessarily intersect the lune used in the classical test, as we can see in the example in Fig. 6. The correctness of the pruning test is shown in the following lemma.

Fig. 6

Assume a is one endpoint of the feasible subarc of $e_{a^{\prime },e_{u,b^{\prime }}}$. We want to remove a from the feasible subarc by considering the segment ab, which would be a segment of the full component, if a is indeed the position of the Steiner point. The point $p_1$ is closer to a than the length of the segment ab and $p_2$ is closer to b and hence, a can be removed from the feasible subarc. The input P does not intersect the lune of ab

Lemma 3

Given a finite set ${\mathcal {S}}$ of segments, consider a potential full component F. F cannot contain a nonterminal segment ab such that there are two points $p_1, p_2 \in {\mathcal {S}}$ within the same connected component of ${\mathcal {S}}$ such that $p_1$ is closer to a and $p_2$ is closer to b than the length of the segment ab.

Proof

We will prove the lemma by contradiction. Assume the nonterminal segment ab was part of the SMT and there are two points $p_1$ and $p_2$ of ${\mathcal {S}}$ part of the same connected component of ${\mathcal {S}}$ with $p_1$ closer to a than the length of ab and $p_2$ closer to b than the length of ab.

By deleting the segment ab, the SMT decomposes into two disjoint trees $t_1$ and $t_2$ with $a \in t_1$ and $b \in t_2$ by definition. Notice that $p_1$ and $p_2$ are in the same tree as they are already connected within ${\mathcal {S}}$. If $p_1 \in t_2$, we can insert the shorter edge $ap_1$ and obtain a shorter Steiner tree, a contradiction. Similarly, if $p_1 \in t_1$, we can insert the shorter edge $bp_2$. $\square$

A second test in Steiner trees over segments is based on the angle condition mentioned in Lemma 1 part 2. Each nonterminal segment incident to a terminal point p must have an angle of at least $\pi /2$ with all open terminal segments adjacent to p. This can be used to reduce the feasible subarc. In particular, if a terminal point has at least two incident open terminal segments, any equilateral point constructed from it cannot be on the side of the wedge of the two adjacent open terminal segments that has an angle of less than $\pi$. Furthermore, it cannot be that a segment of the potential full component intersects another segment of the potential full component (Lemma 1 part 3) or an open terminal segment.

5 Implementation and experimental evaluation

We implemented the algorithm to construct a superset of full components of an optimal Steiner tree in Java, using only the basic pruning tests that were known already for the classical SMT problem. For the selection of the full components of the optimal tree, we used the implementation of GeoSteiner 5.1 of Juhl et al. (2018). All experiments were done on a single core of an Intel Core i5 2430M processor with 2.40 GHz and 6 GB DDR3-SDRAM memory.

We performed three different experiments. Firstly, we solved the instance of the geographer (see Fig. 7a) and compared it against the following approach: Given a distance threshold $\epsilon$, replace each segment by a minimal number of equidistant sample points with distance at most $\epsilon$. We then solved this instance of the classical Euclidean SMT problem with GeoSteiner (see Fig. 7b). The running time of our algorithm with an input of 55 polygons took 3  s, whereas solving the sampling instance with 790 sample points with a useful $\epsilon$ took 16 s. The solution of the sampling instance has the same topology as the optimal solution when shrinking the given polygons and is only slightly larger. This is no longer true, if we decrease the sampling density. With a sampling density of a quarter of the shown instance, only the 542 endpoints of the segments of the 55 polygons remain and the running time was 12 s and the solution was not a tree when shrinking the given polygons. The main reason why the sampling approach is more expensive is that it enumerates many equilateral points that contain several terminals from the same polygon. Notice that the optimal Steiner tree of this instance is the minimum spanning tree (we will comment on this below).

Fig. 7

a We solved the instance of the geographer with our constructed Algorithm. b We used the same instance with the corresponding sampling instance and let GeoSteiner solve the problem

Secondly, we took the TSP-lib instances from Reinelt (1991) that were previously used to benchmark the GeoSteiner library for the classical SMT problem. In order to get an instance of our problem, we connected each terminal to its nearest neighbor and solved the resulting instance. We tried to solve the 46 instances with 198 up to 85900 points within 30 min. The average size of the constructed connected components was between 2.3 and 3.9 (see Fig. 8b for an example). Within 25  min, 27 instances were solved. Ten instances could be solved in less than 30 s and another 4 in less than 60 s. A total of 20 instances were solved in less than 5 min and 26 in under 11 min. The first phase of the algorithm took between 3.58 and 1318.55 s and the second phase between 0.11 and 25.79. All instances with less than 1100 points could be solved in less than 62 s. The largest solvable instance contained 3038 points, and the number of constructed equilateral points varied between 193 and 27878.

Finally, we tried to construct random instances with n polygons of at most m segments that look similar to the instance of the geographer. The construction is as follows. First, create a $k \times k$-grid of cells of size $1 \times 1$ for a given k. Then, select n of these grid cells and create a polygon within each selected grid cell as follows. Select the number $m^{\prime }$ of segments for the polygon uniformly at random from $\{3, \dots , m\}$. Fix the points $p_0=(0,0.5)$ and $p_{\lceil m^{\prime }/2 \rceil }=(1,0.5)$. Then, construct random points $p_i=(x_i,y_i)$ for $1 \le i < \lceil m^{\prime }/2 \rceil$ with $x_i$ chosen uniformly at random from the range $[(2i-1)/m^{\prime }, 2i/m^{\prime }]$ and $y_i$ in (0.5, 1]. For $\lceil m^{\prime }/2 \rceil< i < m^{\prime }$, construct random points $p_i=(x_i,y_i)$ with $x_i$ chosen uniformly at random in $[(2m^{\prime }-2i)/m^{\prime },(2m^{\prime }-2i+1)/m^{\prime }]$ and $y_i$ in [0, 0.5). The polygon $(p_0, p_1, \dots , p_{m^{\prime }-1}, p_0)$ is non-self-intersecting by construction. The value k is used to control percentage of occupied grid cells compared to the total number of grid cells, which we call the density. For example, an instance with 50 polygons and $k=10$ results in a density of 0.5 (see Fig. 8a for an example).

Fig. 8

a An instance we randomly generated. Each polygon lies within one grid cell and has a terminal point at the left and the right boundary at the half the height of the grid cell. b The instance constructed from the instance “ali535” of the TSPLIB

We were interested in measuring the running time, the number of constructed equilateral points and full components, the Steiner ratio depending on the number of polygons, the number of segments per polygon and the density in terms of the number of occupied grid cells divided by the total number of grid cells. For each of these quantities, we constructed ten random instances and took the average of the measurement.

In Fig. 9, we show the running time as a function of the number of polygons for different maximal number of segments per polygon. In this experiment, $10\%$ of the grid cells are occupied by the polygons. As we can see, for a small number of segments per polygon, we are even faster than our implementation of the algorithm for the classical case (using the instance in which we only take the first corner of each polygon as input): However, the running time increases with the number of segments in the polygons.

Fig. 9

Running time as a function of the number of polygons. The different graphs correspond to different maximal numbers of segments per polygon

This can be explained with the experiment shown in Fig. 10, where we show the number of constructed equilateral points for the same instances. For a small number of segments, this number is much smaller than in the classical Steiner tree problem, but increases with the number of segments.

Fig. 10

Number of constructed equilateral points versus the number of polygons. The different graphs correspond to different maximal number of segments per polygon. The dotted line shows the numbers of constructed equilateral points for a point input

The number of constructed full components is much smaller than the number of equilateral points and remains smaller than in the classical case, even when increasing the number of segments per polygon (see Fig. 11). The number is only slightly larger than the number of edges of a minimum spanning tree (i.e., the number of polygons minus 1).

Fig. 11

Number of constructed full components as a function of the number of polygons. The different graphs correspond to different maximal numbers of segments per polygon. The orange dotted line shows the number of constructed full components for a point input, and the gray dotted line shows the number of edges of a minimum spanning tree, i.e., the number of polygons minus 1

In Table 1, we show the Steiner ratio and the number of constructed equilateral points depending on the increasing percentage of grid cells occupied by the polygons for instances with 50 polygons of at most 10 segments. As we can see, the Steiner ratio approaches one and the number of constructed equilateral points drops below that for the classical Steiner tree problem.

We observed (see Fig. 1) that the Steiner ratio and the number of Steiner points in an optimal solution decrease with the density of the instance. In the instance of the geographer, the regions are quite large compared to their distances which explains the Steiner ratio of 1 of this instance.

Table 1 Average Steiner ratio, the average number of constructed full components, the average number of constructed equilateral points and the average number of Steiner points in the constructed optimal solution depending on the percentage of occupied grid cells. For the classical Steiner tree problem, we observed an average Steiner ration of approximately 0.9678. To compute these Steiner trees, 136.6 full components and 1376 equilateral points were constructed on average

6 Conclusion

We considered the variant of the Euclidean Steiner minimum tree problem, in which the input is a set of segments instead of a set of points. We proved a structural theorem about full components of a Steiner minimum tree that allows us to follow almost the same approach as in the classical SMT problem.

Furthermore, we implemented our algorithm and showed that it can solve moderate-sized problems in reasonable time. We give some additional pruning tests that would allow a faster implementation.

We are confident that we could extend this approach to avoid obstacles similarly to the approach in Zachariasen and Winter (1999). It would be interesting to extend the work to other metrics and to nonlinear inputs.