Introduction

Nanocrystalline (NC) materials are attractive for advanced structural applications due to their high strength resulting directly from very fine microstructure, with the grain boundaries acting as pinning points retarding dislocation mobility. Despite good strength, the small grain size implies relatively low thermal stability due to great energy stored primarily in the form of grain boundaries [1], it might be therefore expected that the grain growth will be very rapid during consolidation or service [2]. Hence, the thermal stability of NC materials is very desired to be known in order to optimize the consolidation process.

Oxide-dispersion strengthened (ODS) steels, belonging to the group of modern NC structural materials, are promising prospects for applications in field of nuclear energy, mainly due to their exceptional creep resistance at elevated temperatures [3, 4]. These alloys are predominantly fabricated via the powder metallurgy (PM) route, involving the mechanical alloying (MA) of metallic powders with the oxide of interest (Y2O3 being the most common) and subsequent compaction and sintering [5]. The incorporation of thermally stable oxides exerts a evident response on both recovery and recrystallization behavior, as the nanosized particles inhibit dislocations movement [6]. The serious amounts of excessive energy, stored in form of dislocations introduced at MA stage by plastic strain, also appreciably affect these solid-state reactions [7]. Hence, the dislocation density (\(\rho \)) along with grain size (\(D\)) are undoubtedly indispensable microstructural parameters in terms of characterizing the mechanical properties of metals and alloys.

Among several techniques used to quantify these key parameters, transmission electron microscopy (TEM) and X-ray diffraction (XRD) are the most recognized. In case of severely deformed powder materials, the choice of XRD is even more justified, as the dislocations may not be quantifiable above \(\rho \sim {10}^{15}\) m−2 threshold using TEM [8]. Although TEM provides direct view on the microstructure, it is also debatable if these measurements are representative to the whole sample studied due to very restricted area being investigated [9]. Contrary, XRD is statistically very robust, as it analyzes plenty of coherently scattering domains simultaneously. In this study, we adopted the modern whole powder pattern modeling (WPPM) approach [10] to process the diffraction line profiles, which is currently regarded as a state-of-the-art procedure for XRD microstructural analysis. Similarly to the well-known Rietveld refinement, WPPM exploits direct modeling of the entire experimental pattern by means of proper minimization algorithm [8].

It was found that proper WPPM modeling at temperatures exceeding 800 °C required the hypothesis of bimodal crystallite dispersion, which was manifested by the uncommon “super-Lorentzian” peak profiles, characterized by the narrow shape in the center accompanied with exceptionally long tails [11, 12], which is, in general, attributed to a multimodal size distribution of domains [13,14,15], or possibly monomodal with large dispersion [16]. Recently, various authors proposed the so-called “double-phase” approach to include some types of bimodal microstructure into the physical model itself. It was elaborated herein that the assumption of two twin phases of equal microstructure, but distinct sizes of crystallites can be successfully adopted to process such patterns.

This research focuses on the thermal stability of the grains with regard to the mechanically attrited ferritic ODS powder composition via XRD microstructural analysis, supported by microscopic observations and microhardness measurements. One of the biggest obstacles in powder metallurgy is transmitting the exceptional properties of nanocrystalline materials to their compacted counterparts, as the powders are exposed to more or less elevated temperatures during sintering, which tend to anneal the thoroughly malformed microstructure. For future investigations, the comprehension of annealing behavior of NC ferrous alloy would help in developing the appropriate consolidation strategy to retain as much as possible of the initial nanopowder properties. As a general rule, the thermal stability should be known in order to optimize the processing conditions, i.e. to find the compromise between minimum porosity on the one hand and grain coarsening on the other. Therefore, isothermal annealing in broad range of temperatures was applied to mechanically alloyed powder, and the microstructure features, in particular grain size and dislocation density, were investigated prior and after heat treatment (HT). Furthermore, the specific grain boundary energy along with the kinetics of the grain growth for the powder exposed to high temperatures was investigated via micromechanics approach, which considers the balance between forces acting on the grain boundary. Finally, the powders were consolidated using two dissimilar methods, i.e. classical sintering or hot isostatic pressing, in order to discuss the influence of selected consolidation process on sinter properties.

Experimental

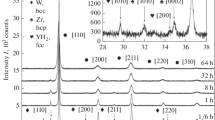
The ODS ferritic steel composition of Fe–12Cr–2W–0.3Zr–0.2Y (wt.%) consisting of commercially pure prealloyed Fe-12.5% Cr base powder (Goodfellow, England) plus elemental metallic powders of W, Zr, Y (Alfa Aesar, USA) was ground in a Fritsch Pulverisette 6 planetary ball mill, using 500 ml stainless steel bowl and 100 balls (⌀10 mm, 4.03 g each) preserving a 10:1 ball to powder mass ratio. Milling was conducted under high purity inert Ar atmosphere for 64 hours using the rotating frequency of 5 Hz. Small amounts of milled powder were sequentially collected during the process at specified time intervals. Next, they were annealed at 50–1100 °C temperature range for 1 h in tube furnace under the vacuum of 10−3 Pa to prevent excessive oxidation and finally cooled slowly within furnace. The particle size evolution during milling was controlled by laser diffraction analysis conducted in wet dispersion unit of the FRITSCH ANALYSETTE 22 MicroTec plus, which is presented in Fig. 1 in terms of volumetric distribution curves \(d{Q}_{3}(x)\) and related mean particle size \(d[\mathrm{4,3}]\) with standard deviation \({\sigma }\) in function of mechanical alloying time \(t\). According to Fig. 1, after 64 h of milling, a Gaussian-like distribution is achieved, characterized by fine mean particle size of d43 = 28.3(2) μm and narrow distribution (\({\sigma }_{p}=\) 12.5(1) μm).

Fig. 1
figure 1

Volumetric probability distribution \(d{Q}_{3}(x)\) at various stages of MA (a); (b) shows the evolution of De Brouckere mean diameter \(d[\mathrm{4,3}]\) and standard deviation \({\sigma }_{p}\) in function of MA time \(t\)

Full size image

The as-milled powder was consolidated as well using two various methods—hot isostatic pressing (HIP) and classical, pressureless sintering. Around 100 g of powder was poured into mild steel can, degassed at 650 °C, sealed, and eventually HIPed under 1150 °C and 200 MPa conditions (using Ar as the working medium). Additionally, the uniaxial pressing die (Ø 20 mm) was filled with about 10 g of powder and compacted under the pressure of 625 MPa. The powder had been additionally soft annealed at 1000 °C before it was cold pressed, since the as-milled powder exhibited very poor compressibility due to fine particle size and substantial work hardening effect. After compaction, the green compact was sintered at 1150 °C in the vacuum tube furnace for 1 h.

High-resolution X-ray powder diffractometry patterns were gathered from Bruker D8 Advance diffractometer equipped with Cu anode and operating in Bragg-Brentano focusing geometry with constant parameters of 40 kV, 25 mA, and 0.01° step size with a fixed 5 s acquisition time. The instrumental broadening of peak profiles was determined using a corundum (Al2O3) standard (NBS SRM 1976b) and processed accordingly to the Caglioti et al. formula [17], following the procedures described widely in the literature [18, 19]. Microstructural parameters were derived from XRD data using the whole pattern powder modeling (WPPM) approach implemented in PM2K crystallographic software, dedicated specifically to the line profile analysis [20]. Average contrast factor coefficients, needed to implement Wilkens’ strain anisotropy model in cubic crystals [21], were calculated considering the primary slip system 〈111〉{110} of bcc iron. Necessary single crystal \({c}_{ij}\) elastic constants of the presented alloy were evaluated by means of the Giri’s model [22], using the literature values of stiffness constants of Fe [23] and Cr [24], which yielded \({c}_{11}\) = 240, \({c}_{12}\) = 115, \({c}_{44}\) = 114 GPa, respectively.

The powder samples subjected to indentation tests were mounted to glass microscope slides using a small amount of non-viscous cyanoacrylate adhesive and left until fully cured. Then, they were gently ground using successive fine grades of abrasive papers and finally polished to a mirror finish with extra fine alumina slurry (0.05 μm). The Vickers microhardness HV of the powders was determined using a digital microhardness tester under a fixed load of 0.245 N and 15 s dwelling time. Exemplary indentation on particle surface is depicted in Fig. 2a, also including SEM morphology observations of powders (b) and energy-dispersive spectroscopy (EDS) analysis (c). Vickers hardness of sintered compacts was determined using the INNOVATEST VERZUS 750CCD device, by applying the load and dwelling time of 98.07 N and 15 s, respectively.

Fig. 2
figure 2

Vickers indentation at mounted powder sample (a), SEM photograph of powder particles after 64 h of milling (b), results of the EDS analysis of the powder (c)

Full size image

The formula relating material’s strength and dislocation density is basically known as the Bailey-Hirsch equation [25, 26]. Assuming that the hardness of material is generally 2.5 times larger than its corresponding yield strength (values ranging from 2.5 to 3 have been proposed in the literature [27]), it can be written in different forms obtained by Yin et al. [28] as follows:

$$HV=2.5{\sigma }_{0}+2.5Gb\sqrt{\rho }$$
(1)

where \({\sigma }_{0}\) is the material’s yield strength, \(G=\frac{\left({c}_{11}-{c}_{12}\right)}{2}\) shear modulus and \(b\) stands for Burgers vector (\(b={a}_{0}\sqrt{3}/2\) for bcc crystals). After grouping the constants by substituting \({HV}_{0}=2.5{\sigma }_{0}\) and \({k}_{HV}=2.5Gb\) one obtains:

$$HV={HV}_{0}+{k}_{HV}\sqrt{\rho }$$
(2)

In case of presented alloy, taking \({\sigma }_{0}\) = 0.82 GPa (estimated by the authors by means of tensile tests of a HIPed alloy), \(\alpha \) = 1, \(G\) = 62.5 GPa and \(b\) = 0.249 nm, the relation between microhardness and dislocation density is expressed as:

$$HV\left[GPa\right]=2+38.9*0.1\sqrt{\rho \left[{{10}^{16}m}^{-2}\right]}$$
(3)

Results and discussion

Mechanical alloying of the powder composition

The principal WPPM microstructural analysis results of milled powder are shown in Fig. 3. Here, the trends of the mean domain diameter \(D\) with lognormal standard deviation \(\sigma \) (Fig. 3a), dislocation density \(\rho \) (Fig. 3b), probability, and cumulative domain size distributions \(g(D)\), \(G(D)\) (Fig. 3c) were designated as a function of MA time and collated with Vickers microhardness \(HV\) plot (Fig. 3d). As can be clearly seen, MA not only causes the shift of mean diameter \(D\) to lower values, but in addition favors the distribution to narrow with milling time. Summarizing, the results presented in Fig. 3 confirm that ball milling finally led to the formation of nanocrystalline powder characterized by the narrow distribution of fine spherical domains (\(D\) = 12(3) nm) and high dislocation density reaching \(\rho =5.14(6)\times {10}^{16}\) m−2 (Fig. 3b). Severe work hardening makes the grain refinement especially effective during the initial MA stage (≤ 8 h), when the lognormal mean drops rapidly along with standard deviation, which is also accompanied with corresponding growth in the dislocation density.

Fig. 3
figure 3

Essential WPPM results of ball milled powder in function of milling time: (a) mean domain size and lognormal standard deviation; (b) dislocation density; (c) domain size distributions; (d) microhardness, compared with Bailey-Hirsch model. Error bars correspond to estimated standard deviation (ESD) of WPPM fit or standard deviation of microhardness measurement

Full size image

The work hardening of the material is witnessed by the continuous increase in microhardness with milling time, which is demonstrated in Fig. 3d. The microhardness finally increased from 2.8(1) to 10.4(7) GPa. The experimental data were compared with results obtained by Eq. 3. Model plot imitates the experimental trend quite precisely, and the theoretical values are not far from the measured ones. Also, the correlation between the defect density and microhardness is worth noting (Fig. 4). Modeling with Eq. 3 (assuming constant exponent \(n\) = 0.5) provides reasonable fit (\({R}^{2}=0.94)\) and gives set of constants \({HV}_{0}=0.92(87)\) GPa, \({k}_{HV}=45.9(5.4)\) N/m comparable to the theory. However, much better accordance (\({R}^{2} \sim 1)\) is achieved using exponential trend, i.e., in form of:

Fig. 4
figure 4

Relationship between dislocation density \(\rho \) and powder microhardness \(HV\). Dashed line presents data fitted with Bailey-Hirsch relation, while solid line represents exponential fit (Eq. 3)

Full size image
$$HV[GPa]\left(\rho [{10}^{16}{m}^{-2}]\right)=A+B{e}^{-\rho }$$
(4)

Transmission electron microscopy (TEM) can be certainly regarded as a perfect supporting tool to the present study, providing deeper insight into the actual size of the grains, thus integrating and validating results described so far. A representative overview of NC ODS alloy powder microstructure after MA can be appreciated in Fig. 5a, b. Basically, grains incline to cluster into reasonably equiaxial agglomerates with random orientation [29], which is evidenced by diffraction rings included as an inset in (b). Line scans across the gray value intensity (Fig. 5c, d, where unity corresponds to white, whereas zero is pitch black) confirm the presence of separate grains of about 12 nm in size, in good concurrence with XRD.

Fig. 5
figure 5

TEM micrographs of ball milled powder. General overview of the microstructure (a) and another with corresponding electron diffraction pattern (b); detail of the region framed by the square (c), with line scans across image intensity maxima (d). See text for further details

Full size image

Figure 6 shows the TEM size lognormal distribution obtained from circa 400 measurements, represented as equivalent-circle diameters (\({D}_{TEM}=2\sqrt{A/\pi }\), where \(A\) is the projected area [30]) and contrasted with the corresponding values obtained by WPPM (after 64h of MA, reported previously in Fig. 3c). The agreement is acceptable, particularly considering that both size results were acquired under entirely unrelated principles. Looking at the details in Fig. 6, it can be stated that major discrepancy concerns size exceeding 20 nm, since WPPM distribution is much narrower. In order to explain, distinguishing single grains from such complicated agglomerates is often problematic and somewhat subjective task. What is more, our TEM micrographs do not allow to distinct between grains and scattering domains, so the true domain size distribution is hardly obtained by TEM in an objective way.

Fig. 6
figure 6

Lognormal size distributions obtained by WPPM (\(D=12.0\left(8\right)\) nm, \(\sigma =3.1(2)\) nm) and TEM (\(D=18.1\) nm, \(\sigma =10.2\) nm)

Full size image

Annealing of the ball milled powder

Figure 7 shows the domain size and standard deviation of its distribution, respectively, of mechanically alloyed powder as a function of isochronal annealing temperature \(T\). The apparent transformation process of the (211) peak shape during annealing is illustrated in Fig. 8. However, an assumption of an unimodal model of the lognormal distribution of crystallite sizes does not provide satisfactory fit in the entire range of \(T\), as in the high-temperature region of 825-1100 °C the peaks exhibit an unusual “super-Lorentzian” profiles. Since a conventional, “single-phase” model does not particularly work in the above case, a “double-phase” model was implemented for such patterns. Moreover, the quality of refinement using the single- and double-phase models should be emphasized, respectively. As compared in Fig. 9, incorporating the second phase with distinct microstructure remarkably improves the modeling, which is indicated by reduction of statistical markers as well as features presented on residual curve (i.e., difference between the experimental pattern and model). In this study, the \({R}_{wp}\) factor (i.e., weighted profile \(R\)-factor), widely used in refinement techniques, was preferred to define the agreement between model and experimental data [31].

Fig. 7
figure 7

Mean domain size (a) and lognormal standard deviation (b) evolution in function of annealing temperature. Open dots distinguish data obtained by means of “double-phase” approach

Full size image
Fig. 8
figure 8

Shape evolution of the (211) peak after annealing in: a 500 °C; b 800 °C; c 850 °C; d 950 °C. Some data points have been skipped for better readability

Full size image
Fig. 9
figure 9

Pattern collected after annealing the powder at 850 °C and modeled by the WPPM using “single-phase” (\({R}_{wp}\) = 3.5%) and “double-phase” approach (\({R}_{wp}\) = 3,0%), respectively. Magnified insets show the two most prominent (110) and (211) peaks modeling details

Full size image

Various domain size distribution curves of the heat-treated powder are charted in Fig. 10. As suspected, the sole mean of domain size is inadequate to comprehensively describe the complex evolution of the size distribution. It can be observed that as the temperature increases, the shape changes gradually toward “long-tailed,” positively skewed dispersion (Fig. 10a), which is also reproduced by the parallel increase in the mean size and deviation. This could be an indication of growth of the new, defect-free grains, and thus, coexistence of both fine domains and coarser fraction in the material.

Fig. 10
figure 10

Probability (a) and cumulative (b, size reported in log-scale) domain diameter distributions of the annealed powder collected after: 500 °C; 900 °C; 1050 °C

Full size image

Furthermore, the occurrence of recovery should be evaluated in the heat-treated material. Figure 11a presents the dislocation density progression from heavily distorted microstructure (\(\rho\sim 6\times {10}^{16}\) m−2) up to the residual \({\sim 10}^{15}\) m−2 level, which is still in range cold-worked metals (\(\rho\,{>10}^{14}\) m−2) [32]. In more detail, the \(\rho \) is constant up to 100 °C, which can be regarded as an upper temperature stability limit of the nanostructure. Next, the slow but continuous drop of dislocation density begins, presumably as an outcome of dislocation disentanglement and annihilation processes [33], which is the clear proof of the temperature-induced recovery. Contrarily to \(\rho \), change in grain size is not apparent to the \(T \sim 800\,^\circ C\), presumably by the combined effects of strain accumulation in the grains and Zener pinning. The presence of various solutes in the grain boundary (GB) regions notably imparts drag force on the GB migration, which has been widely exemplified in various NC materials [2, 34, 35]. Consequently, the growth of grains may begin only after the certain amount of the strain has been released, which is referred to the critical density \({\rho }_{cr}\), beyond which the locking effect of dislocation is lost and grain growth becomes explicit.

Fig. 11
figure 11

Dislocation density (a) and microhardness (b) progression during annealing; relation between dislocation density and microhardness for the annealed powder (c); TEM picture of fine secondary-phase particles after annealing at 1100 °C (d).

Full size image

Thermal softening of the presented ODS steel was also verified by a change in mechanical properties. As expected, the microhardness decreases in function of annealing temperature (Fig. 11b) due to combined effects of microstructure coarsening and vanishing of defects inside the material, finally reaching 3.2(5) GPa. The recrystallization temperature \({T}_{r}\) = 780 °C was determined as the cross-point of two linear data fits (Fig. 11b), beyond which the sudden drop in \(HV\) is observed.

The heat-related \(HV\) trend was also modeled using Eq. 3, which appeared to be in rather poor agreement with the data (\({R}^{2}=0.80\), Fig. 11c), and yielded \({HV}_{0}=3.51(63)\) GPa, \({k}_{HV}=33.1(4.2)\) N/m. Again, excellent fit (\({R}^{2}=0.97\)) is obtained using Eq. 4, certainly indicating that \(HV\left(\rho \right)\) relation is exponential. Nonetheless, the strict formula relating the \(HV\) and \(\rho \) remains unknown, as it, most likely, does not only result from the \(\rho \), but is rather a complex combination of both grain size and defect content-related effects.

In the attempt to obtain a quantitative estimate of the different phenomena having impact on the grain growth during annealing, we proposed the necessary condition for the recrystallization to occur as follows:

$${\tau }_{gg}>{\tau }_{s}+{\tau }_{z}$$
(4)

when \({\tau }_{gg}\) is the thermodynamic driving force for grain growth (notice that although \({\tau }_{gg}\), \({\tau }_{s}\), \({\tau }_{z}\) are often described as driving forces, they actually have the units of pressure). Where the total amount of grain boundaries tends to be minimized, the specific energy of grain boundary \(\gamma \) with mean diameter \(D\) is given by the relationship [36]:

$${\tau }_{gg}=\frac{2\gamma }{D}$$
(5)

The resistance \({\tau }_{s}\) incorporated due to an array of dislocations can be expressed as the stress required to move against the dislocations [34, 37]:

$${\tau }_{s}=\frac{Gb\sqrt{\rho }}{8\pi \left(1-v\right)}$$
(6)

where \(v=0.26\) stands for the Poisson’s coefficient, calculated using stiffness constants (other parameters were introduced earlier in this paper). The Zener pinning stress \({\tau }_{z^\prime}\) is generally given by the equation arisen on the basis of Zener’s early (1948) calculations [38]. However, the modified mechanism proposed by Rios [39] was utilized herein, which gives a pinning force twice that of Zener’s:

$${\tau }_{z}=\frac{3\gamma f}{r}$$
(7)

where \(f\) is the volume fraction of pinning particles, and \(r\) is their mean radius. It was assumed \(f=0.01\), which was found by Oksiuta et al. for the HIP-consolidated powders of very similar chemical composition Fe–Cr–W–Ti–Y2O3 [40], while \(r=6.1\) nm, estimated using TEM (Fig. 11d).

As can be seen, \({\tau }_{gg}\) and \({\tau }_{z}\) depend on the \(\gamma \), which is unknown for the presented alloy. However, it can be easily calculated from the equilibrium of forces occurring at \({T}_{r}=780\) °C, which is expressed by:

$$\frac{2\gamma }{D}=\frac{Gb\sqrt{\rho }}{8\pi \left(1-v\right)}+\frac{3\gamma f}{r}$$
(8)

The effect of temperature on \(G\) was regarded (\(G=45.6\) GPa at 780 °C) following the dependences designated for pure iron by Adams et al. [23]. Table 1 reports the obtained components of forces favoring and retarding grain growth. The obtained \(\gamma \) value of 0.73 Jm−2 is closely related to Li et al. evaluation for pure iron (\(\gamma \) = 0.6 Jm−2) [41]. It is plausible that the domain size is mostly stabilized by the grain-boundary strain, the Zener pinning effect on the structural stability being much less relevant.

Table 1 Driving forces acting at the grain boundary at equilibrium state
Full size table

Sintering of the powder by classical sintering and hot isostatic pressing

During classical sintering, the green compact is kept at a high temperature, which initiates fusion of the particles, for a prolonged period, thereby increasing specimen’s density. Very long sintering time or the temperatures near the melting point must be applied to obtain dense material. However, the application of excessive temperature and process duration yields harsh grain growth in material, therefore losing its potentially unique properties that would be caused by nanosized structure. Contrary, during HIP, the additional utilization of high pressure induces internal stresses between the particles and their plastic deformation, which facilitates diffusion and removal of internal voids and, consequently, allows the reduction of consolidation temperature and time in comparison with pressureless sintering. Ergo, an optimal density in the sintered component, while preserving the microstructural features of milled powder, can much easier be achieved by HIP than classical sintering [42].

Samples after consolidation at 1150 ˚C had a relative density of 71% and 97% (measured by classic Archimedes principle, using digital weighting balance) in case of traditionally sintered and HIPed material, respectively.

The dependence of the consolidation method on the mean domain size is presented on Fig. 12. As can be observed, despite the high (1150 °C) temperature involved, the \(D\) size of HIPed sample is only 15.9(7) nm (Fig. 12a). For comparison, \(D\) of classically sintered sample is almost twice higher, i.e., 31.7(3.5) nm, which indicates that pressure applied during HIP might play an important role in hindering the domain growth. Nevertheless, in case of both sintering methods, a significant domain growth is avoided, which can be attributed to the pinning effects of ceramic particles [42]. However, after the heat treatment of HIPed sample, a considerable growth of domains is observed (Fig. 12).

Fig. 12
figure 12

Mean domain size and corresponding standard deviation of consolidated samples (a); probability domain diameter distributions of the sintered; HIPed and heat treated samples (b)

Full size image

The dependence of Vickers hardness and dislocation density for the sintered, as-HIPed and heat treated samples is depicted in Fig. 13. These values were also compared with the both raw and porosity-corrected Bailey-Hirsch model, the latter being obtained by an incorporation of the porosity-hardness relation found by Luo et al. [42, 43]. After considering the effect of porosity, the modified Bailey-Hirsch equation takes the following form:

$$HV_{cor} = (HV_{0} + k_{HV} \sqrt{\rho})\,\text{exp}(-5.03\,P)$$
(9)

where P is the volume fraction of porosity. The Vickers hardness of the as-HIPed material is high (6.46(8) GPa) and is also reflected in the relatively high dislocation density of \(1.51(4)\times {10}^{16}\) m−2. Previous study [44] of similar alloy reported the hardness of the as-HIPed ODS steel to be 4.17(16) GPa, which is considerably lower value. However, a few important differences should be underlined—the MA process was shorter (20 h) and conducted in reducing H2 atmosphere, which certainly resulted in lower defect and impurities content. The high hardness of the presented alloy is also attributed to the usage of prealloyed FeCr powder, which is, in general, harder than elemental due to initial solid solution strengthening [45]. After 1 h of annealing at 1150 °C, the hardness decreased to 3.89(24) GPa. Classically sintered sample is characterized by high ρ as well (ρ = 7.36(11) × 1015), although about 30% lower with regard to HIP, which is probably due to longer exposure time of the powder at elevated temperature. High porosity is obviously reflected in very poor mechanical properties—the sample has a disproportionately low hardness (1.10(12) GPa) than ρ would suggest, which can be attributed to the porosity filling phenomenon occurring beneath the loaded indenter [43, 46]. Hence, in such case the porosity-corrected Bailey-Hirsch relation must be used (Fig. 13). In fact, very little is known about the dislocation densities of the ODS steels. Renzetti et al. [47] reported the \(\rho =8\times {10}^{15}\) m−2 of the cold rolled 9% Cr ODS steel, evaluated by the modified Williamson-Hall method, a value comparable to the present study.

Fig. 13
figure 13

Dependence of Vickers hardness and dislocation density for the: classically sintered; as-HIPed and heat-treated samples

Full size image

Conclusions

The formation of nanocrystalline ODS alloy by mechanical alloying and its thermal stability and subsequent consolidation by classical sintering and HIP have been studied via the analysis of powder diffraction data by WPPM approach and supplemented by microhardness tests and microscopic observations. WPPM delivered detailed information on the evolution of crystallite size and average defect density as a function of milling time and annealing temperature. It was found that grain growth may start when lattice strain stabilizing the nanocrystalline drops below critical value, which is also manifested by the concurrent drop in microhardness. A model characterized by a bimodal distribution of crystallites, consisting of two independent crystalline phases with identical atomic structure but separate broadening patterns, was more suitable to explore the “super-Lorentzian” reflection shapes of temperature-related data. This is consistent with the typical recovery/recrystallization behavior occurring in iron alloys, where nucleation of minor grains with concurrent growth of new ones would appear, and thus, bimodal size distribution should be expected. The changes of Vickers microhardness due to severe mechanical treatment during milling and recovery/recrystallization during annealing were mirrored by the values of dislocation density obtained by WPPM. The dislocation density of the HIP-consolidated sample remained at relatively high level of \(\rho =1.5\times {10}^{16}\) m−2, comparable to the as-milled state. Finally, it is concluded that through the utilization of modern, powerful approaches as WPPM, XRD can be considered as precious complementary tool to TEM. The importance of XRD is especially pronounced in case of severely deformed (e.g., ball milled) materials, where massive quantities of defects exceeding \({10}^{15}\) m−2 can acutely limit the possibility of distinguishing the domains and dislocations, but are still perfectly quantifiable using XRD.