1 Introduction

Within the decision-making process, importance is placed on the accuracy of pertinent information, which is used as a basis for the decision. The assumption is that better data quality will lead to better decisions. However, to check this assumption the economic value of the information should be analyzed (Lawrence 1999): if the benefits obtainable from new data exceed the costs, new data should be acquired; otherwise, the decision should be made with available data. In a forestry context, the value of better quality data has been analyzed through cost-plus-loss analysis (e.g., Eid 2000; Borders et al. 2008; Mäkinen et al. 2010). The primary premise behind these analyses is that the timing of the forest operation should be optimal; thus, accrued losses are due to conducting forest management prescriptions either too early or too late. Determining the optimal timing of operations requires perfect information, which may not be possible to ascertain.

Rather than only evaluating losses from not obtaining perfect information, stochastic programming (Birge and Louveaux 2011; King and Wallace 2012) enables an analysis to evaluate the value of including uncertainty in the optimization process. Using the terms from Knight (1921) a differentiation between risk and uncertainty can be made, where risk has a known probability of occurrence and uncertainty does not. Forest management operates under uncertainty; however, through empirical testing, the probability of the uncertainty can be estimated. In a forestry context, stochastic programming has been used to schedule forest harvesting and road building decisions (Alonso-Ayuso et al. 2011; Andalaft et al. 2003), to planning the management response to forest fires (Boychuk and Martell 1996; Ntaimo et al. 2012), and to adjust to changes in timber prices (Piazza and Pagnoncelli 2014; Rios et al. 2016). For forest management planning, estimates of uncertainty can be evaluated through empirical data on inventory errors, and through time series data on growth model errors. Since inventory methods are never error free, the decision to conduct an inventory is a question of when to update the inventory to improve the quality of the data, rather than the decision to obtain perfect information. The other uncertainties (such as silvicultural and harvesting costs, timber prices or interest rate) can also be included, if estimates are available.

The appropriate level of data quality is the level where the value of the objectives of the decision maker (DM) minus the inventory cost can be maximized (e.g., Kangas 2010). To conduct mathematical optimization, the desires of the DM are formalized through the objective function. Through a stochastic programming approach, Kangas et al. (2014, 2015) examine a case where the DM can select if a particular stand needs to be measured and when the stand should be measured with an assumption that each stand can be measured separately. From those results, it is clear that the current and potential resources from the forest and the objectives of the DM affect the optimal measurement effort. For example, if the DM wishes to maximize NPV and the forest structure is heavily weighted towards very old or very young stands, the need to conduct a new inventory could be fairly low. Thus, the forest structure and preferences of the forest owner(s) impact the timing of optimal measurements.

The growth model errors also have impact on the quality of forest information. Pietilä et al. (2010) analyzed the optimal inventory interval in the presence of growth prediction errors, while Mäkinen et al. (2012) analyzed the impact of both inventory and growth prediction errors at the holding level using a cost-plus loss approach. Ståhl et al. (1994) used Bayesian theory to evaluate the optimal timing of data collection. The approaches account for the costs of the inventory of the holding and the losses due to making suboptimal decisions because of growth prediction errors. In these cases, it was assumed that the preferences of the forest owner solely depend on the NPV of the holding. The forest management preferences of the DM were not accounted for (e.g., a desire for an even flow of income, promotion of hunting opportunities), nor was the risk attitude of the DM accounted for. Thus, analysis of the optimal inventory interval for the whole holding, accounting for the preferences of the DM is still missing.

The uncertainties due to the forest inventory can be acknowledged through stochastic programming. In stochastic programming, the term “recourse” means taking intelligent actions when dealing with uncertainty. For fixed recourse, the objective function is to minimize unwanted surpluses or deficits by selecting a single set of decisions. It means we maximize the objective function while minimizing the penalized effects of exceeding thresholds of losses. For recourse, the acquisition of new information can cause the set of decisions to change, dependent on the new information. The recourse is to decide how to reduce unwanted surpluses or deficits with the new inventory information. In a forest inventory setting, if we add the possibility of additional measurements to the problem, the new measurements are a means to mitigate the risks (Kangas et al. 2014, 2015).

Solving stochastic programming problems is often done through the use of a discrete version of the stochastic problem (King and Wallace 2012). A discrete version of the stochastic problem simplifies the problem through the use of a set of scenarios, or possible futures, to represent the distribution of the estimated uncertainty. Each scenario represents one possible initial inventory state and a corresponding possibility for future growth. To represent the uncertainty of the initial inventory state, modifications can be made to the basal area and height of the stands. We use these variables as they are the input variables for the growth and yield models, and these models determine which variables are of interest (Kangas 2010). To represent growth model errors, one possible method is to match the observed empirical variation to that generated by the models (Haara and Leskinen 2009). By using both methods of representing errors, it is possible to obtain a representative set of scenarios which can be used to approximate the stochastic problem.

Risk management is an issue of individual preferences, where the DM must select how to balance the risk with their other objectives. Risk management is common in financial planning, where the balance between maximizing return while minimizing potential for losses is assessed. Risk is often interpreted as deviations away from a specific target (International Organization for Standardization, ISO Guide 73 2009); however, downside risk measures may be preferred. This is due to typical preferences of avoiding losses. The most common downside risk measures are the downside mean semideviation (Krzemienowski and Ogryczak 2005), the value at risk (VaR; Duffie and Pan 1997) and the conditional value at risk (CVaR; Rockafellar and Uryasev 2000).

This study models the forest inventory timing problem using a two-stage stochastic programming with recourse. We show how conducting the new inventory improves the quality of decisions and reduces the risks of poor incomes. We then illustrate how differences in preferences will impact the optimal timing of the next forest inventory using a small forest holding as an example.

2 Methods

2.1 Stochastic programming model

As a demonstration, we transform the deterministic even-flow harvesting problem to a stochastic framework. In a deterministic framework, the objective would be to maximize NPV with periodic constraints to ensure a nondeclining flow of resources from the forest. Transforming the problem to a stochastic framework requires additional information on how to manage the violations of these constraints. For this demonstration, we propose the use of CVaR of not achieving a specific threshold of income from harvesting operations for each period. We selected CVaR as it is a coherent risk measure (Artzner et al. 1999) and can be easily optimized (Rockafellar and Uryasev (2000). In this case, the DM desires to obtain incomes for each period, and thus, each periodic CVaR is a separate criterion for the DM. A similar problem has been formulated using a two-stage stochastic program with fixed recourse (Eyvindson and Cheng 2016); the focus here is to add an option for recourse (through updating forest information) based on the DM risk preferences. The focus of objective function is to balance between maximizing forest holding level NPV and minimizing the CVaR of not meeting the periodic flow requirement. There is an explicit trade-off between these objectives; obtaining the maximum NPV requires variable amounts harvesting actions during different periods, while obtaining a specific periodic flow implies conducting rather even amounts of harvesting during each of the periods.

Let x jkf be a decision to conduct a set of silvicultural actions for schedule k ∈ K, of stand j ∈ J, for scenario set f ∈ F. Here, sets J, K, and F are representative of the stands, schedules, and the sets of scenarios reflecting an updated forest inventory. Furthermore, let \( {\left({N}_f^t\right)}_{f\in F} \) (where F is an index set) be an exclusive partition of scenarios (represented as a set of schedules for each stand) in N for each time period (i.e.,\( {N}_{f_1}^t\cap {N}_{f_2}^t=\varnothing for\ \mathrm{all}\ {f}_1\ne {f}_2\ \mathrm{and}\ {\cup}_{f\in F}{N}_f^t=N \)). The index sets \( {N}_f^t \) mathematically models the information so that in each time period (t), there are F sets of scenarios which each represent an updated inventory. For each set (i.e., \( {N}_3^1 \), the third representation of an updated inventory at period 1), the variation represents the errors from the updated inventory. The variation between the sets at a specific time (i.e., the variation between all of the F sets in \( {N}_f^1 \)) represents the variation due to the growth model errors. The decision variable w t  ∈ {0, 1} represents the choice of an updated inventory (0 = do not measure, 1 = measure) on the holding at period t.

The objective function of the recourse problem (RP) is then

$$ \max RP=\sum_{n=1}^{\#N}\frac{{p_nNPV}_n}{\mathit{\max}\left(\mathbb{E}(NPV)\right)}-\lambda \sum_{t=1}^T\frac{CVaR_t}{\mathit{\max}(CVaR)} $$
(1)

Subject to

$$ {NPV}_n=\sum_{t=1}^T\frac{I_{nt}-{w}_th}{{\left(1+r\right)}^{\left(t\ast D-u\right)}}+\frac{PV_n}{{\left(1+r\right)}^{\left(T\ast D\right)}},for\ \mathrm{all}\ n\in N $$
(2)
$$ {L}_{nt}={\left[{I}_{nt}-{w}_th-{b}_t\right]}^{+},for\ \mathrm{all}\ n\in N,t\in T $$
(3)
$$ {CVaR}_t=\left(1-\sum_{p=1}^t{w}_p\right)\ast \left({Z}_t+\frac{1}{\left(1-\alpha \right)\#N}\sum_{n\in N}{\left[{L}_{nt}-{Z}_{ft}\right]}^{+}\right)+\left(\sum_{p=1}^t{w}_p\right)\sum_{f=1}^F\left({Z}_{ft}+\frac{1}{\left(1-\alpha \right)\#{N}_f^d}\sum_{n\in {N}_f^d}{\left[{L}_{nt}-{Z}_{ft}\right]}^{+}\right)/\#F,for\ \mathrm{all}\ t\in T $$
(4)
$$ \sum_{k=1}^{K_j}\left(\left({x}_{jkf}-{x}_{jkg}\right){s}_{jktq}\right)-\sum_{p=1}^t{w}_p\ast R\le 0,for\ \mathrm{all}\ f\in F,g\in F,j\in J,t=1,\dots, T,q\in Q,f\ne g $$
(5)
$$ \sum_{k=1}^{K_j}\left(\left({x}_{jkg}-{x}_{jkf}\right){s}_{jktq}\right)-\sum_{p=1}^t{w}_p\ast R\le 0,for\ \mathrm{all}\ f\in F,g\in F,j\in J,t=1,\dots, T,q\in Q,f\ne g $$
(6)
$$ \sum_{k=1}^{K_j}{x}_{jkf}\le 1,for\ \mathrm{all}\ j\in J,f\in F $$
(7)
$$ {I}_{nt}=\sum_{j=1}^J\sum_{k=1}^{K_j}{x}_{jkf}{c}_{jknt},for\ \mathrm{all}\ t\in T,f\in F,n\in {N}_f^d,k\in K $$
(8)
$$ {PV}_n=\sum_{j=1}^J\sum_{k=1}^{K_j}{PV}_{njkT}{x}_{jkf},for\ \mathrm{all}\ f\in F,n\in {N}_f^d,k\in K $$
(9)
$$ \sum_{t=1}^T{w}_t\le 1 $$
(10)
$$ d=\sum_{t=1}^T{w}_t\ast t $$
(11)
$$ {x}_{jkf},\in \left[0,1\right],{w}_t\in \left\{0,1\right\}\ for\ \mathrm{all}\ t\in T,f\in F,j\in J,k\in K $$
(12)

where p n is the probability of scenario n occurring, NPV n is the net present value for scenario n, λ is a risk parameter, used to balance the importance of managing the risk, CVaR t is the conditional value at risk for period t, I nt is the income associated with scenario n during period t, h is the cost associated with conducting an inventory, r is the discount rate, u is timing of the management action, D is the duration of each period; PV njkT is the productive value associated with scenario n, stand j, schedule k at the end of the planning horizon; L nt is the loss associated with scenario n at period t, b t is the income target for period t, Z t is the value at risk at period t, Z ft is the value at risk for subset f at period t, α is the confidence level for the value at risk, s jktq corresponds to the specific treatment q which was planned to be carried out in stand j for schedule k during period t, R is a very large positive number, c jknt is the income provided from stand j by conducting schedule k, and d is the period during which the next inventory is to occur.

The productive value was predicted using the models of Pukkala (2005), using a set of forest variables as explanatory variables. Depending on the interest rate, risk preferences and target for income selected, the possibility to conduct a similar amount of even-flow harvesting for periods past the planning horizon may differ significantly. If this is a key concern, an end volume constraint could be added to the model.

Equation 4 calculates the CVaR for a period t, the first portion of the constraint calculates the CVaR for those cases where new inventory has not been conducted before period t, while the second portion calculates the CVaR for the cases where the new inventory has been conducted. Constraints 5 and 6 act as a form of nonanticipavity constraints; this means that if no additional inventory is conducted prior to the conducting operations, then all of the decisions must remain the same between the subsets. Constraint 10 allows only one new inventory to be conducted during the planning horizon; this was done to ease the problem formulation. To assist in reading the model, Table 1 summarizes the variables, sets, and parameters of the models.

Table 1 A list of the notation used throughout the paper
Full size table

At the core, this model contains the key concepts and structures of the deterministic model I of Johnson and Scheurman (1977). Model I formulation requires that a set of schedules (a set of silvicultural activities) be developed for each stand, and the problem is then to select the most appropriate schedule for each stand, according to the preferences of the DM. The key difference between this model and Johnson and Scheurman’s model I is that the schedule for a particular stand can be adjusted, if a new inventory has been conducted. Additionally, in order to change the schedules of a stand, the two schedules must have the same set of silvicultural activities up to the moment the change occurs (constraints 5 and 6).

The problem developed is a two-stage stochastic programming problem formulation with recourse. The first stage allows for maximizing the NPV and minimizing the weighted CVaR to the period where a new forest inventory is to be conducted. The second stage allows for adjustments to the management plan after obtaining new information, so to best achieve the preferences of the DM. In this case, the second stage happens whenever the new inventory is conducted and the first stage can cover one or more periods. If no new inventory is conducted, the problem only considers the fixed recourse. For this case, moving to a second stage is an active decision.

The second stage problem is represented by the subset of scenarios, where each of them represents a potential updated inventory. To represent the problem, the subsets need to have a level of error which could be expected after conducting new forest inventories. For this application, when only growth model errors and inventory errors are considered, each subset must have an error relative to only inventory errors, while the entire set contains both growth model and inventory errors. To provide a comparison, the two-stage stochastic program with fixed recourse can be solved. To change the problem formulation so that all harvesting decisions must be the same for all periods (constraining the recourse problem to a fixed recourse problem), Eq. 10 is changed to

$$ \sum_{t=1}^T{w}_t=0 $$
(13)

This shift requires that no new inventory will be conducted.

2.2 Data organization

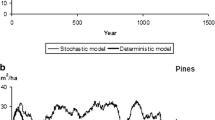
To limit the size of the scenario tree, and reduce the problem of size, the same error scenarios are used repeatedly for each time period. For a predefined number of realizations, the stand will be simulated to include both growth and inventory errors. These are then sorted into G subsets of realizations, within which the relative errors reflected the errors after conducting the new inventory. For each possible timing of the inventory, a separate sorting was carried out. Figure 1 provides an example of the results of sorting the basal area (BA).

Fig. 1
figure 1

A graphical representation of how the sorting generates subsets for the second stage. For visual clarity, only the basal area is examined and three subsets (grayscale lines) are created: a no sorting is conducted, and the planning is conducted without updating; b an inventory is conducted after period 2; c an inventory is conducted after period 4

Full size image

The aim of this algorithm is to sort the set of simulated realizations of the stand characteristics in each stand into subsets which reflect how a new inventory may resolve some of the uncertainty. As the stand grows in time, this sorting is carried out for each period where a new inventory can be carried out. However, after the inventory is carried out, the same sorting is applied to the end of the planning horizon.

  1. 1.

    For all j ∈ J, let M j be a set of all simulated instances i, i ∈ I for stand j.

  2. 2.

    Select the number of subsets that the sorting process will create (#G).

  3. 3.

    For each stand j, create empty sets \( {M}_{gt}^j \) where g ∈ G , t ∈ T;

    1. a.

      For each t, do the following steps:

      1. i.

        Calculate the average \( \frac{1}{I}{\sum}_{i=1}^{\mathrm{I}}x \)and standard deviation of the variables of interest from M j at time t.

      2. ii.

        For each g, determine a specific target average and bounds for the variables of interest. The target average should relate to the average of the set M j at time t, and the bounds should reflect the errors produced by the inventory method to be used.

      3. iii.

        For each element i in M j, evaluate if the variables of interest fall within the all targets ± the bounds set for a random g in G, if it does and \( \#{M}_{gt}^j<\frac{\#M^j}{\#G} \), add the element i into the set \( {M}_{gt}^j \), else select a new g and repeat until all potential subsets have been evaluated.

      4. iv.

        For each element i in \( {M}^j\setminus \left({\bigcup}_{g\in G}{M}_{gt}^j\right) \), evaluate if the variables of interest fall within at least one target ± the bound set for a random g in G, if it does and \( \#{M}_{gt}^j<\frac{\#M^j}{\#G} \), add the element into the set \( {M}_{gt}^j \), else select a new g and repeat until all potential subsets have been evaluated. If the element still has not been placed into a set, select a random g in G, and if \( \#{M}_{gt}^j<\frac{\#M^j}{\#G} \), add the element into the set\( {M}_{gt}^j \).

  4. 4.

    Once the stand level sorting has been completed, we can generate forest-level inventory scenarios at each period t. A forest-level inventory scenario is \( \left({N}_f^t\right) \) is a collection of stand-level sets so that \( {N}_f^t={\cup}_{j\in J}{M}_{gt}^j \), where for each j, g is a random element from the set G. The total number of forest-level scenarios can be set according to desired solution quality and computational limits.

  5. 5.

    This set of scenarios within a group g represents the situation immediately after the new inventory. If the inventory is carried out at period t, the scenario includes values for periods t + 1, …, T with increasing errors. The variation between the g groups represents the growth model error up till the new inventory.

The forest-level scenarios are created systematically; ensuring that in each set of forest-level scenarios \( \left({N}_f^t\right) \), a realization of stand from the same sorted subset is selected. In this way, we ensure that for each set of forest-level scenarios, the timing of the inventory can be evaluated.

2.3 Materials

To demonstrate the method, a small (47.3 ha, consisting of 41 stands) privately held forest holding in North Karelia, Finland, will be used. The forest holding consists primarily of Scots pine (Pinus sylvestris L.) with minority components of both Norway spruce (Picea abies (L.) Karst) and birch (Betula pendula and Betula pubescens). The age class distribution is fairly even while the diameter distribution at 1.3-m height has a large percentage of small diameter (0–5 cm) and large diameter (20–25 cm) trees. The planning horizon spans 30 years, which is broken down into six 5-year periods.

For each stand, a total of 900 instances were simulated using a Monte Carlo process using the SIMO forest simulator (Rasinmäki et al. 2009). The inventory errors were assumed to have a normal distribution, with no bias and a relative standard error of 20%. The inclusion of the growth model errors occurred as a process over time. The models simulating the growth model errors can be found in phase II of the Materials and Methods section in Pietilä et al. (2010). They separated the growth prediction error into intra-stand error (following a first-order autoregressive process—AR(1)) and inter-stand error (which was constant over the rotation period for each stand). These errors are correlated and this correlation was accounted for in the simulations. The absolute root mean square error for the BA was 1.3 and 2.2 m2 ha−1 and for height was 1.6 and 2.3 m after 5 and 10 years, respectively (Pietilä et al. 2010). Since we use the same model, the errors can be expected to be in the same range.

Using the sorting algorithm described in the “Methods” section, nine sets of 100 stand-level representations for updating the forest inventory were formulated. Stand-level inventories were sorted into nine different bins according to their mean BA and height. The targets for these two variables followed the formula

$$ \overset{-}{y}-sd,\overset{-}{y},\overset{-}{y}+sd $$
(14)

where \( \overset{-}{y} \) is the mean value and sd is the standard deviation of the set. The target value for the standard deviation was calculated in the first step of the algorithm. This process allowed for the possibility to simulate an updated inventory at each period, by ensuring that each of the nine subsets had a similar amount of variation to the initial inventory. To move from the stand level scenario to the forest holding level scenario, a random stand-level scenario is selected for all stands. This process of sorting determines the size of the second stage problem, and in this case, the total number of forest-level scenarios is fixed at 100. Based on previous research (Eyvindson and Kangas 2016), 100 scenarios were deemed to provide a sufficient solution quality for the sources of error considered in this example. The solution quality was determined through the use of the sample average approximation (Kleywegt et al. 2002), and both in-sample stability and out-of-sample stability are evaluated (Chap. 4 of King and Wallace 2012). For this case, the total number of unique second stage problems that can be created is 941 (9 bins and 41 stands) an exceptionally large number that would be time consuming to enumerate and solve with current resources. A simplification was required to ensure the tractability of the problem. The first stage problem is a collection of second stage problems, and to ensure tractability within a reasonable amount of time, we decided to use a set of 45 second stage problems.

To highlight how the preferential information influences the solution, a large number of iterations were conducted. The target for periodic (5-year period) income (b t ) was set between 60,000€ (1270€/ha) and 70,000€ (1480€/ha) with intervals of 5000€ (105€/ha), the confidence level (α) for the CVaR was set at 0.8, 0.9, and 0.95 (Fig. 2). As α increases, so does the importance of the averages of the extreme losses. For each period, a specific CVaR is evaluated, as this represents the tail risk of not achieving the required even-flow of income for that specific period. To simplify the analysis, a discount rate (r) was set at 3%; only one discount rate was used simply to ease the analysis. The risk parameter (λ) was set to indicate a nearly risk neutral DM and increased progressively to reflect a rather risk averse DM (with values close to 0 representing a risk neutral DM, and values close to 1 representing a strongly risk averse DM). Additionally, the cost to conduct a new inventory (h) was set to 500€, which corresponds to the current cost of conducting an airborne laser scanning inventory, approximately 10.5€/ha. This cost could be considered rather low if the data collection was for a single holding, but it would be rather realistic if the inventory was carried out for a larger area at the same time.

Fig. 2
figure 2

The Pareto frontier for the net present value and corresponding conditional value at risk. The λ parameter is the greatest (λ = 1) on the left of each graph and decreases towards the right of each graph (until λ = 0). To promote readability, a selection of λs were removed (specifically 0.6, 0.7, 0.8, and 0.9)

Full size image

3 Results

One of the primary results which should be highlighted is that regardless of risk preferences, the option to conduct an updated forest inventory was always used. This can be seen in Fig. 2, where the timing of the next inventory shifts from earlier to later as the importance of risk and the requirement for periodic income decreases. With a very risk averse individual with a high periodic income requirement, the timing of the next inventory should be no earlier than before the third period. With a small relaxation in either the risk or period income requirement, the next inventory should occur before the fourth period. A nearly risk neutral DM would delay the next inventory to as late as possible (in this case, before the sixth period). These results seem rather intuitive, as it highlights that risk can be reduced by conducting an inventory earlier.

Fig. 3
figure 3

The value of including the recourse option of conducting a new inventory. As risk aversion increases, the value of including the recourse option increases

Full size image

In Fig. 2, it is possible to see the absolute improvement from the two-stage programming with fixed recourse (the “+” symbols) and the two-staged programming with recourse (the solid symbols). While this net improvement seems small, the improvement can be viewed through a value of information analysis (see Chap. 4 of Birge and Louveaux 2011).

Figure 3 examines the value of shifting from a fixed recourse problem to a recourse problem. The value of formulating this as a recourse problem depends on the risk aversion of the DM. For all cases, the improvement in the solution is positive, even though the improvement is very small for the case when the DM is risk neutral (i.e., the case when the DM simply wants to maximize NPV). The improvement of the objective function (the maximum possible value for the objective value is 1) ranges from nearly 0 to 0.057, depending on the confidence level.

4 Discussion

In this paper, a two-stage stochastic program with recourse for the timing of the next forest inventory and the accompanying adjustments to the forest management plan has been developed. The first stage selected the management schedules to follow until the conduct of a new inventory, while the second stage selected management schedules for each new inventory. This analysis highlights that the timing of the new inventory is directly related to the risk preferences of the DM. If the DM is rather risk neutral (i.e., when λ = 0.05) and wants to have small periodic incomes, then the DM should conduct the next inventory before deciding which operations should occur in the 6th period. Alternatively, when the DM is rather risk averse (i.e., when λ = 1) and wants to have larger periodic incomes, then the DM should conduct a new inventory before the third or fourth period.

With a planning horizon of 30 years, there are many occasions when the timing of the inventory is at the end of the planning horizon. For some of these cases, the optimal next timing may occur at an even later period. Two options are available to the DM, either they can extend the planning horizon, or once time has passed, conduct an updated plan with the available information. Additionally, the consistency of the timing of the next inventory was checked by reducing the planning horizon. For very short planning horizons, there are cases when a new inventory is not conducted, this is because the benefits of the new inventory are less than the costs.

This analysis also compared the case when the DM could update the forest information and the case when the DM could not update the forest inventory. The comparison of these alternatives is between a two-stage stochastic program with fixed recourse and a two-stage stochastic program with recourse. Earlier studies (Eyvindson and Cheng 2016) have compared the stochastic formulation with the corresponding deterministic formulation, which highlighted the possible improvements by incorporating uncertainty. On a stand level Kangas et al. (2015) have shown the trade-off between the cost and benefits of obtaining updated data, and this depends on the quality of the new data. Adding the possibility of recourse will never be negative and the improvement depends on the risk preferences of the DM.

Modifying the problem from a stochastic problem with fixed recourse to a problem with recourse requires the construction of second stage scenario sets. The process of sorting the data is a time-consuming process, even though it was automated. Linking the sorting process with a decision support tool such as SIMO in Finland (Rasinmäki et al. 2009), or Heureka in Sweden (Wikström et al. 2011)) that utilizes basic linear programming tools can be accomplished through the addition of a module, and this can expand the functionality of these tools to include stochastic programming.

The model was structured with an aim to limit the computational processing requirements. In our model, only one update to the forest inventory can be made. To model a similar problem using multistage stochastic programming, several adjustments would need to be made, and these adjustments would substantially increase the computational processing required. Additional scenarios would need to be evaluated and increases in the amount of sorting would be required to appropriately represent the uncertainty at later stages. In our opinion, the additional computational requirements may not be justified, as the decisions proposed past the second stage would need to depend on an actual forest inventory.

The type of forest owner and the size of forest holding may impact the usefulness of this kind of information. For the forest owners’ that are risk neutral, there may not be much value in including the option for recourse. However, most forest owners have a tendency towards risk aversion and would be interested in understanding the trade-off between reducing risk and the costs of conducting a new forest inventory. For forest owners whose proportion of income is strongly linked to conducting forest operations, risk aversion may be rather strong. This can be linked to the risk aversion between small and large stakes (Rabin 2000). These kinds of forest owners could benefit by both managing and understanding the associated risks which can be provided through utilizing stochastic programming with recourse.

Additionally, the certainty of the target parameter (i.e., the desired periodic income) will have a direct impact on the value of the analysis. As the risk is linked directly to the target parameter, any uncertainty in the target parameter will impact the related risk measure. This kind of uncertainty could be included in the stochastic programming framework. For instance, Aouni et al. (2012) have focused on understanding the impact of target parameter uncertainty in stochastic goal programming.

Modifications of this model can allow for additional sources of recourse to be included in the stochastic programming problem. For instance, price uncertainty could be included through recourse. To allow for tractability this would require some simplification. For instance, price uncertainty could be included through appropriately sized bands (i.e., 5€ increments), and the management decisions could be based on how the price uncertainty is resolved. Political uncertainty could be included as a recourse option. Decisions can be set prior to the political decision, and proposed decisions can be set depending on the resolution of the political decision.

The appropriate timing of the next forest inventory depends upon the needs and desires of the DM, and this should be taken into consideration when conducting new inventories of the forest holding. In Finland, the typical interval between subsequent inventories is currently 10 years, and according to our analysis, this interval of measurements may be too frequent for most DMs. If the accuracy of the inventory increases or the cost of conducting the inventory decreases, the ideal time to update the forest inventory will change. Determining the exact optimal time for re-inventorying will remain difficult to pinpoint, as the timing will still depend upon the DM preferences, which can change through time. Even with these caveats, this research can provide a useful tool for evaluating the benefits obtained by conducting new inventories, and rather than updating the forest data as soon as the benefits exceed the costs, the inventory should be made when the benefits are optimized with consideration to the costs.