Heritabilities and genetic correlations for honey yield, gentleness, calmness and swarming behaviour in Austrian honey bees

Abstract

Heritabilities and genetic correlations were estimated for honey yield and behavioural traits in Austrian honey bees using data on nearly 15,000 colonies of the bee breeders association Biene Österreich collected between 1995 and 2014. The statistical models used distinguished between the genetic effect of workers and that of the queen of the colony. Heritability estimates for worker effect were larger than those for queen effect. Genetic correlations between both effects were negative. Heritability estimates for the sum of both effects (i.e. selection criterion) were 0.27, 0.37, 0.38 and 0.06 for honey yield, gentleness, calmness and swarming behaviour, respectively, indicating that meaningful genetic improvement is possible. Genetic correlations between these traits were generally small to medium, with large standard errors, with the exception of the high genetic correlation between gentleness and calmness. The models we present here can be used to estimate breeding values in honey bees.

1 Introduction

Genetic improvement by means of selective breeding requires knowledge of heritabilities of the relevant traits and of the genetic correlations between those traits. Estimates of heritabilities and genetic correlations indicate the prospects for genetic improvement of traits and allow the estimation of breeding values of individuals. Subsequently, estimated breeding values can be used in breeding programmes to select genetically superior individuals to become the parents of the next generation.

In honey bee breeding programmes, traits generally are observed on colony level and, therefore, the measurements are the result of a complex interplay between workers, and between queen and workers. Bienefeld and Pirchner (1990) showed that honey yield and behavioural traits, like aggressiveness and calmness, are affected by both the genotype of the workers and the genotype of the queen. Ehrhardt et al. (2010) showed the same phenomenon for two components of tolerance to varroa mites i.e. mite population growth and hygienic behaviour. Bienefeld and Pirchner (1990) analysed a small dataset. As a consequence, standard errors of the estimates of heritabilities were large. Estimates of the genetic correlations between the effects of workers and queen were strongly negative (approximately −0.9), which may have been due to the difficulty to disentangle the two effects, since both the queen and the workers are in the same colony. Separation of both effects is entirely based upon the pedigree of workers and queens. In addition to the genetic correlation between worker and queen effects, Bienefeld and Pirchner (1991) analysed the genetic correlations between honey production and other traits of economic importance. Also, here, the standard errors of the estimates were very high. It seems that the analyses of Bienefeld and Pirchner (1990, 1991) and Ehrhardt et al. (2010) are the only ones separating the effects of workers and queen, presumably because datasets are usually too small to allow such an analysis.

The approach of Bienefeld and Pirchner (1990) and also Bienefeld et al. (2007) was improved by Brascamp and Bijma (2014), while Brascamp et al. (2014) investigated the improved method for the estimation of the genetic correlation between worker and queen effects, using simulated data. The nature of the improvement is a more realistic consideration of the fact that there are full-sibs and super-sisters among the workers in a honey bee colony. Full-sibs occur because workers may descend from the same drone-producing queen, while super-sisters occur because workers may descend from the same drone. Similarly, queens and groups of drone-producing queens reared from the same colony may descend from the same drone. This phenomenon affects the genetic relationships between individuals in the population, which subsequently affects the estimation of heritabilities, genetic correlations and breeding values. The improved method has a more appropriate weighing of the information of half-sib colonies and full-sib colonies, which results in improved estimates of heritabilities and breeding values.

The purpose of this paper is to present estimates of heritabilities and genetic correlations for honey yield and behavioural traits that are based on a large amount of data and the best statistical method currently available. We used data collected in the Austrian honey bee population, a dataset that is considerably larger than those used in earlier studies, and used the method of Brascamp and Bijma (2014). We will also discuss the consequences of our findings for the estimation of breeding values.

2 Material and methods

2.1 Colonies and observations

Data on 14,948 colonies (Apis mellifera carnica) were made available by Biene Österreich, an association of bee breeders, among others responsible for a programme for testing and estimation of breeding values of honey bees in Austria. The colony records cover the period from 1995 to 2014, except the year 2002 due to organisational changes. A colony record includes the testing year, the breeder, the testing station, the queen in the colony and her mother, and also the mother of the drone-producing queens producing the drones that mated with the queen, each with identification number and year of birth. Furthermore, the records include the measurements on the traits honey yield, gentleness, calmness and swarming behaviour, measured in line with recommendations of Büchler et al. (2013). Honey yield was the weight difference of combs before and after extraction of honey. A honey yield of 0.1 kg is the lowest amount that can be entered into the recording system. Most colonies with a record of 0.1 kg actually failed to produce honey, rather than producing precisely 0.1 kg. Gentleness and calmness were measured as the average of one or more subjective scores during the season, on a scale from 1 to 4, rounded to one decimal. On this scale, higher values are desirable. Gentleness is a measure for defensive behaviour, while calmness scores the degree to which workers stay on the comb during inspection. Swarming behaviour was measured as the lowest subjective score during the season on a scale from 1 to 4. A higher value for swarming behaviour implies a lower appearance of swarming signals.

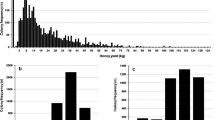
The distributions of all traits were skewed (Figure 1). The distribution of honey yield had a peak at 30 kg, a lower end of 139 colonies with 0.1 kg of honey, and a long tail to yields as high as 202 kg of honey. The higher yields were achieved by bee breeders in regions rich of flowering, who travel with their colonies. The behavioural traits generally scored 4, sometimes 3 and relatively rarely 2 or 1.

Figure 1.

Distributions of honey yield and of scores for gentleness, calmness and swarming behaviour.

For the analysis, a data file was created with an entry for each colony, containing the identification of the colony, the queen of the colony, test location and observations on the traits. From now on, we use the term “colony” to refer to the group of workers, although commonly “colony” includes workers and a queen. For the queen in the colony we use the term “dam”, as she is the mother of the workers. The group of drone-producing queens of which drones are mated with the dam is referred to as the “sire”, as they are the fathers of the workers. In that way, each worker, and also each dam and sire, has two diploid parents. This enables to build a pedigree in the usual way.

2.2 Testing procedure

Each breeder has to test yearly at least one sister group, consisting of 12 young sister queens raised from a single colony. After mating the virgin queens at a mating station, each receives a unique identification number. Of each sister group, at least six young sister queens are to be submitted to performance testing at different testing stations. The remainder is tested at the breeder’s location. For this purpose, freshly mated sister queens of each breeder are shipped within 1 week in the beginning of July to a central distribution centre and, afterwards, allocated randomly and anonymously to participating bee breeders.

2.3 Pedigree file

To allow estimation of genetic parameters from the dataset, we built a pedigree file which contained three types of individuals: colonies, dams and sires. Each entry of the pedigree file contained four elements; a unique identification number for the individual, the year of birth of the individual and the unique identification numbers of its dam and sire. For colonies and sires, additional unique identification numbers were created because these lack in the raw data, as each record contains the identification number of the dam of the colony and the dam of the sire.

The pedigree file was built stepwise, ultimately leading to dams and sires without known parents, so-called base dams and base sires. In total, there were 14,948 colonies in the pedigree file. The pedigree file contained 31,479 entries: 14,948 colonies, 15,965 dams (of which 1017 base dams), 329 sires with a colony and 237 base sires. The breeding population is fairly open and each year new dams and sires, not reared from a colony in the dataset, could be used in the breeding programme. In the last 5 years, about a quarter of the colonies had a new dam or sire.

For the statistical analysis, we calculated the genetic relationships between all members of the pedigree (see the Appendix for details).

2.4 Statistical model

Observations are affected by both the colony and the dam. To be more precise: by the worker effect of the colony and queen effect of the dam. As an example, honey yield may be affected by workers through heritable effects related to flying behaviour, while it may be affected by the dam through heritable effects related to capacity for egg laying or production of pheromones. For selection purposes, the sum of the breeding values for worker and queen effects of a colony is relevant, and called the selection criterion. Of particular interest is the selection criterion of a young queen, which equals the estimated breeding value for the selection criterion for the colony from which she is raised (Brascamp and Bijma 2014).

To estimate the worker and queen effects and their variance components, the statistical model consisted of the overall mean of a trait, the fixed effect of test location and three random effects, namely the additive genetic worker effect of the colony, the additive genetic queen effect of the dam and a residual effect. This model allowed the estimation of the variance of worker effect, the variance of queen effect, their covariance and the residual variance. From these estimates, the heritabilities for worker and queen effects and the genetic correlation between both effects were derived. Furthermore, the variance and heritability of the selection criterion were calculated. Details about the statistical model are provided in the Appendix.

2.5 Estimation of genetic parameters

To estimate genetic parameters (i.e. heritabilities and genetic correlations), we used the statistical software package ASReml (Gilmour et al. 2009), with the data file and the inverse of the matrix of pedigree relationships as input.

In a preliminary analysis using all data, we estimated genetic parameters, breeding values and the changes of average breeding values by year (so-called genetic trends). We analysed genetic trends because presence of a strong trend together with missing parents in different generations might require the use of genetic groups i.e. the grouping of base animals in groups with different genetic levels (Westell et al. 1988). Trends for worker effect, queen effect and selection criterion turned out to be low, as a result of small selection differentials. Therefore, we did not include genetic groups.

We considered 0.1 kg of honey yield for the 139 colonies not to have a genetic cause and decided to remove these records. Inspecting results of genetic trends, it appeared that for gentleness in 2006 there were 115 colonies with a common sire which had extremely high estimated breeding values. This sire also had 132 colonies with high breeding values for calmness. The sire had 159 colonies in total, and we decided to remove these records. Although the effect certainly may be genetic, we considered that these colonies were deviating so strongly from normal that including them might lead to unrealistic (over)estimates of genetic parameters. Therefore, final analyses were done with 14,650 colonies. We considered to transform the data so that distributions more resemble the normal distribution, but decided against it as the scale of the results would become more difficult to interpret.

In the final analyses, we re-estimated (co)variance components, heritabilities for worker and queen effects and their genetic correlations, and heritabilities for the selection criterion. We also estimated genetic correlations between the four traits. Estimation of genetic correlations between all traits simultaneously turned out not to be feasible (no convergence), and hence, we estimated the genetic correlations pairwise using the estimates from the single-trait models as starting values for the variances.

2.6 Validation of the model

We validated the statistical model in two ways. First, we checked whether we could adequately predict the observed phenotype of a colony when ignoring observations on that colony in the breeding value estimation. If the observation on a colony is ignored, breeding values are estimated for the colony’s worker effect and the dam’s queen effect just based on the pedigree. The sum of both estimates was taken as the prediction of the observed phenotype. The observed phenotype was defined as the difference between the observation and the estimate for the effect of test location.

The second validation method relates to planned matings. It is a desired property of the model that the estimated breeding value for the selection criterion of a planned mating (i.e. of a colony without observation) is a good prediction of the realised breeding value for the selection criterion when the colony later-on has an observation. To carry out these validations, we assigned randomly a number from 1 to 10 to each colony (creating ten groups) and performed validations by generating ten datasets, each time removing observations of one of the ten groups. We calculated the regression coefficient of the observed phenotypes and of the estimated breeding values, both on their predictions. The expectation of both regression coefficients is 1 and an outcome of 1 is considered as an indication that estimated breeding values are unbiased.

3 Results

Table I summarises the estimates for the (co)variance components and the resulting heritabilities and genetic correlations between worker and queen effects.

Table I Estimated genetic parameters. Variances (Var) of worker and queen effect, their covariance and residual and phenotypic variances. Derived from these are variance for selection criterion (σ _SC ²), estimates of heritabilities for worker effect (h _W ²), queen effect (h _Q ²), genetic correlation between worker and queen effect (r _G ) and heritabilities for selection criterion (h _SC ²). Approximate standard errors are given in brackets.

Heritabilities for worker effect were fairly high, from 0.36 for swarming behaviour to 0.70 for honey yield. Heritabilities for queen effect were moderate (0.36 and 0.25) for honey yield and swarming behaviour, and low (0.14 and 0.07) for gentleness and calmness. Considering the approximate standard errors, these latter heritabilities for the queen effect are not significantly different from zero. The estimates for the genetic correlation between queen and worker effect were negative and varied considerably, from −0.79 and −0.92 for honey yield and swarming behaviour to −0.38 and −0.36 for gentleness and calmness. The approximate standard errors for the latter estimates were high. These negative genetic correlations reduce the heritabilities for the selection criteria, which where 0.06 for swarming behaviour, 0.27 for honey yield, 0.37 for gentleness and 0.38 for calmness. The estimate for swarming behaviour is not significantly different from zero.

Table II summarises the estimated genetic correlations between the traits.

Table II Estimated genetic and residual correlations and approximate standard errors (in brackets) between honey yield, gentleness, calmness and swarming behaviour. W refers to worker effect and Q to queen effect. As an example, for the genetic correlation between honey yield and gentleness, WxQy refers to the genetic correlation between the worker effect for honey yield and the queen effect for gentleness. SC refers to the genetic correlation between the respective selection criteria.

Estimates of the genetic correlations between the respective selection criteria were low to medium, except for the combination gentleness-calmness (0.91), honey yield-swarming behaviour (−0.82) and gentleness-swarming behaviour (0.65). Approximate standard errors generally were large, however, with the exception of the combination gentleness and calmness, such that most estimates are not significantly different from zero.

Table III gives the results of the validation of the model. The results show that regression coefficients for observed phenotypes on predictions were not significantly different from 1. These results show that the model yields an unbiased prediction of future phenotypes. The accuracy of prediction of observed phenotypes (i.e. the correlation between observed phenotype and its predictor) was low, as expected since only data of other colonies was included through the pedigree. Also, the regression coefficients of the realised breeding values for selection criteria on their predictions are close to 1, which implies that the prediction of breeding values for selection criteria of planned matings is adequate.

Table III Estimates of regression coefficients of observed phenotypes and of realised breeding values (BV) for selection criteria on their predictions. Means and standard errors of regression coefficients (b) and correlation coefficients (r) are based upon the results of ten subgroups of the data.

4 Discussion

We used the method developed by Brascamp and Bijma (2014) to estimate genetic parameters in a dataset of about 15,000 colonies of Biene Österreich. Separate estimation of genetic parameters for the effects of workers and queens on honey yield, gentleness, calmness and swarming behaviour proved feasible, although by nature both effects are strongly confounded and can only be disentangled because workers and queens have a different pedigree. The estimation of genetic correlations between the traits proved feasible as well.

Just as Bienefeld and Pirchner (1990), we found negative genetic correlations between worker and queen effect, although our values are closer to zero. At first sight, this may be due to the fact that the current dataset is larger (15,000 colonies for all traits in our data vs 5300 for honey yield and 2700 for aggressiveness and calmness in Bienefeld and Pirchner (1990)). However, in a simulation study with 5000 colonies, Brascamp et al. (2014) showed that estimates of the genetic correlations were unbiased. In the German Beebreed online database (www.beebreed.eu) a far larger dataset is available (some 6000 colonies per year), but to our knowledge, no estimates of genetic parameters have been published using this dataset. Despite the negative genetic correlation between worker and queen effect, the estimates for the heritability of the selection criterion were still moderate, being 0.27 for honey yield, 0.37 for gentleness and 0.38 for calmness. These values indicate good prospects for response to selection. An even better indication of the prospects for response to selection is the additive genetic standard deviation of the selection criterion $\left(\sqrt{\sigma_{SC}^2}\right)$. In an efficient breeding programme for a single trait, a response to selection of one unit genetic standard deviation per generation is feasible. For honey yield, gentleness, calmness and swarming behaviour, these values were 11.3 kg, 0.3, 0.3 and 0.2 units, respectively.

The estimated heritability of swarming behaviour was as low as 0.06, due to the strongly negative genetic correlation between worker and queen effects (−0.92). This low value is in agreement with results of Willam and Essl (1993a), who attributed the low value to the difficulty to score the trait adequately. Our results, however, suggest that the trait can be scored adequately, because heritabilities for queen and worker effects were moderate.

Bienefeld and Pirchner (1990) published heritability estimates for worker and queen effects for honey yield, but not for the combination in the selection criterion. Their general finding was that the estimates for worker effect were larger than those for queen effect, which was confirmed by the current analysis. Despite fairly high standard errors, it appears that their estimated heritabilities for honey yield (0.26 and 0.15 for worker and queen effect, respectively) were lower than ours (0.70 and 0.36), while those for calmness (0.91 and 0.58) were higher than ours (0.43 and 0.07).

For genetic correlations between traits, a comparison of the estimates of Bienefeld and Pirchner (1991) and ours is not useful because of the large standard errors of their estimates, and often also of ours.

Data were not transformed to better resemble the normal distribution and make the variance independent of the mean. As a consequence, it might be that the more extreme estimated breeding values for the selection criterion coincide with higher estimates for the effect of test location, due to higher phenotypic variance at those locations. We investigated this issue by plotting the estimated breeding values for the selection criterion of colonies against estimates for the effect of test location. Resulting regression coefficients were close to zero, and the variation of estimated breeding values was independent from the estimated effects of test location. In other words, extreme values for the selection criterion appeared scattered across estimates for test location. Hence, we found no indication that extreme estimated breeding values are found predominantly at good test locations.

In our data, drone-producing queens have a common dam, which is quite common in situations where mating of queens is controlled. As discussed by Brascamp and Bijma (2014), the model can accommodate the situation where drone-producing queens are not sisters. It is not to be expected that estimates of heritabilities or genetic correlations will change, as these depend upon the genetic make-up of the population at hand and not upon the mating system.

The current estimation of breeding values used in Biene Österreich is based on the approach of Willam and Essl (1993b), which is a selection index method that estimates breeding values of queens by combining the trait observation on the colony of the queen (i.e. individual performance) with observations on colonies of her sister queens (i.e. family performance). The method takes into account (possible) repeated measurements and unequal family sizes. We computed the correlation between the estimates of the selection criterion for colonies from our model (i.e. single-trait animal model) and the current estimates of Biene Österreich. Specifically, we calculated the average of the correlation coefficients by year of birth, covering the whole period from 1995 to 2014. For honey yield, gentleness, calmness and swarming behaviour, these correlations were 0.70, 0.76, 0.72 and 0.47, respectively. Thus, estimates from both methods are positively correlated, but clearly different.

The single-trait animal model used here has advantages over the selection index approach of Willam and Essl (1993b). Not only the usual advantage that fixed effects (i.e. effect of test location) are better estimated but also that the model with separate worker and queen effects better reflects reality and that more family information is used. Thus, we expect that selection based on estimates from the animal model will yield greater response to selection.

Based on our results, we do not recommend to implement a multi-trait animal model, because the required genetic correlations were estimated with very high standard errors. With such inaccurate estimates of genetic correlations, the addition of observations on other traits may actually be detrimental for the estimation of breeding values (Sales and Hill 1976). On the basis of these analyses, the single-trait animal models used here are considered suitable to estimate breeding values for honey bee colonies in populations belonging to controlled breeding programmes.

Appendix

In this appendix, details are given about the statistical model, the genetic models underlying the statistical model, the matrix of additive genetic relationships among members of the pedigree (A), and the way we computed its inverse (A ⁻¹). The following summarises more extensive descriptions and derivations in Brascamp and Bijma (2014).

• 1. The statistical model

  The statistical model was

  $$ \mathbf{y}=\mathbf{X}\mathbf{b}+{\mathbf{Z}}_{\mathbf{W}}{\mathbf{a}}_{\mathbf{W}}+{\mathbf{Z}}_{\mathbf{Q}}{\mathbf{a}}_{\mathbf{Q}}+\mathbf{e} $$

  (1)

  in which y is a vector of observations, b is a vector of fixed effects (test locations), a _W the vector of breeding values for worker effect, a _Q the vector of breeding values for queen effect and e the vector of residuals. The matrices X, Z _W and Z _Q are incidence matrices connecting the observations to the vectors. Estimates for components of Eq. (1) can be found by solving the so-called Mixed Model Equations:

  $$ \left[\begin{array}{ccc}\hfill {\mathbf{X}}^{\mathbf{\prime}}\mathbf{X}\hfill & \hfill {\mathbf{X}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{W}}\hfill & \hfill {\mathbf{X}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{Q}}\hfill \\ {}\hfill {\mathbf{Z}}_{\mathbf{W}}^{\mathbf{\prime}}\mathbf{X}\hfill & \hfill {\mathbf{Z}}_{\mathbf{W}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{W}}+{\mathbf{A}}^{-\mathbf{1}}{\boldsymbol{\upalpha}}_{\mathbf{1}}\hfill & \hfill {\mathbf{Z}}_{\mathbf{W}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{Q}}+{\mathbf{A}}^{-\mathbf{1}}{\boldsymbol{\upalpha}}_{\mathbf{2}}\hfill \\ {}\hfill {\mathbf{Z}}_{\mathbf{Q}}^{\mathbf{\prime}}\mathbf{X}\hfill & \hfill {\mathbf{Z}}_{\mathbf{Q}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{W}}+{\mathbf{A}}^{-\mathbf{1}}{\boldsymbol{\upalpha}}_{\mathbf{2}}\hfill & \hfill {\mathbf{Z}}_{\mathbf{Q}}^{\mathbf{\prime}}{\mathbf{Z}}_{\mathbf{Q}}+{\mathbf{A}}^{-\mathbf{1}}{\boldsymbol{\upalpha}}_{\mathbf{3}}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{b}\hfill \\ {}\hfill {\mathbf{a}}_{\mathbf{W}}\hfill \\ {}\hfill {\mathbf{a}}_{\mathbf{Q}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathbf{X}}^{\mathbf{\prime}}\mathbf{y}\hfill \\ {}\hfill {\mathbf{Z}}_{\mathbf{W}}^{\mathbf{\prime}}\mathbf{y}\hfill \\ {}\hfill {\mathbf{Z}}_{\mathbf{Q}}^{\mathbf{\prime}}\mathbf{y}\hfill \end{array}\right] $$

  (2)

  with

  $$ \left[\begin{array}{cc}\hfill {\alpha}_1\hfill & \hfill {\alpha}_2\hfill \\ {}\hfill {\alpha}_2\hfill & \hfill {\alpha}_3\hfill \end{array}\right]={\left[\begin{array}{cc}\hfill {\sigma}_{A_W}^2\hfill & \hfill {r}_G{\sigma}_{A_W}{\sigma}_{A_Q}\hfill \\ {}\hfill {r}_G{\sigma}_{A_W}{\sigma}_{A_Q}\hfill & \hfill {\sigma}_{A_Q}^2\hfill \end{array}\right]}^{-1}{\sigma}_e^2 $$

  (3)

  where ${\sigma}_{A_W}^2$ is the variance of worker effect, ${\sigma}_{A_Q}^2$ is the variance of queen effect and r _G is the genetic correlation between worker and queen effects.

  We solved Eq. (2) using the statistical software package ASReml (Gilmour et al. 2009), which simultaneously estimates variance components ${\sigma}_{A_W}^2$, ${\sigma}_{A_Q}^2$ and σ _e ² and also r _G and gives solutions for b, a _W and a _Q .

• 2. The underlying genetic models

  Observations, in the statistical model represented by y, genetically are modelled as:

  $$ {\mathrm{P}}_{\mathrm{c}}={\overline{\mathrm{A}}}_{\mathrm{w}}^{\mathrm{W}}+{\mathrm{A}}_{\mathrm{d}}^{\mathrm{Q}}+{\mathrm{E}}_{\mathrm{c}} $$

  (4)

  The phenotype of a colony, P_c, is affected by the average breeding value for worker effect of the workers in the colony, Ā ^W_w , the breeding value for queen effect of the dam of the workers, A ^Q_d , and by environmental effects, E_c. Dropping superscripts W and Q, breeding values for colonies are modelled as

  $$ {\overline{A}}_i=\frac{1}{2}{A}_d+\frac{1}{2}{\overline{A}}_s+{\overline{\delta}}_i $$

  (5)

  where ${\overline{\delta}}_i$ is a term due to Mendelian sampling of gametes. Equation 5 illustrates that the breeding value of a colony, Ā _i , actually is the mean breeding value of many workers, and that sire’s breeding value, Ā _s , actually is the mean of the breeding value of a number of drone-producing queens. Breeding values of dams are modelled as

  $$ {A}_i=\frac{1}{2}{A}_d+\frac{1}{2}{\overline{A}}_s+{\delta}_i $$

  (6)

  while breeding values of sires are modelled as Eq. (5).

  As a result of the analysis, breeding values are estimated for all members of the pedigree. However, as explained in the body of the text, the breeding value of interest is that of a future queen raised from a colony. On average, this breeding value equals Ā _i , the mean breeding value of workers in the colony. Furthermore, the relevant selection criterion is the sum of worker and queen effects of future queens, which equals Ā ^W _i  + Ā ^Q _i .

• 3. The matrix A and its inverse

  As follows from Eq. 2, A ⁻¹ is required for the solution of the Mixed Model Equations. Usually, calculation of this inverse is included in the statistical package used, with the pedigree file as input. In honey bees, however, another route is needed because the inversion of A does not follow the usual rules for inversion of a pedigree-based relationship matrix. Thus, this inverse has to be created in advance, and provided as input to the statistical package. Summarising Brascamp and Bijma (2014), we here describe how A ⁻¹ is derived. Building upon Henderson (1976), consider the breeding value A _i of individual i, which is the sum of half the breeding value of its dam, A _d , half the breeding value of its sire, A _s , and a Mendelian-sampling term, δ _i ,

  $$ {A}_i=\frac{1}{2}{A}_d+\frac{1}{2}{A}_s+{\delta}_i $$

  (7)

  Equation 7 is a simplified version of Eqs. (5) and (6) that are actually used in the calculations but suffices to explain the principle. In matrix notation, the breeding values of all individuals in the pedigree may be represented by a vector a, such that

  $$ \mathbf{a}=\mathbf{Ma}+\mathbf{d} $$

  (8)

  In this equation, M is a matrix connecting offspring to parents, with values of ½ in the columns of both parents, and the vector d contains the Mendelian-sampling terms. Let A denote the covariance matrix of a, and D the covariance matrix of d. Then, the inverse of A can be written as

  $$ {\mathbf{A}}^{-\mathbf{1}}={\left(\mathbf{I}-\mathbf{M}\right)}^{\prime }{\mathbf{D}}^{-\mathbf{1}}\left(\mathbf{I}-\mathbf{M}\right) $$

  (9)

  In this equation I is the identity matrix. Usually D is a diagonal matrix, because the Mendelian-sampling terms for different individuals are independent. As shown by Brascamp and Bijma (2014), however, this is not the case in honey bees. In honey bees, D is a block diagonal matrix because groups of full-sibs (colonies, queens and sires with the same dam and sire) have a non-zero covariance of their Mendelian sampling terms, because members may derive from the same drone. Apart from the blocks, the matrix contains isolated diagonal terms for members of the pedigree that are not part of a full-sib group, and furthermore zeros. Numerical inversion of D is simple because the sizes of the blocks are very limited. Elements of A and D are a function of the number of drone-producing queens constituting a sire and of the number of drones mating with the queen. In the breeding programme of Biene Österreich, there are on average ten drone-producing queens at the mating stations, and we assumed that queens are mated to 12 drones on average. These 12 drones is an effective number that leads to a similar average additive genetic relationship between workers as 17 drones (Laidlaw and Page 1984) with equal expected contributions to progeny (Schlüns et al. 2005). Furthermore, the number of drones per drone-producing queen, and the number of offspring per drone, were taken to follow a Poisson distribution.

  Diagonal elements of D follow from equations 10, 18 and 21a of Brascamp and Bijma (2014). Off-diagonal elements occur only between full-sibs, and follow from equations 20 and 21a. Derivation of D needs to be preceded by derivation of A to produce inbreeding coefficients (equation 25) and additive genetic relationships between drone-producing queens (equation 24a). A requirement for the common algorithm to produce elements of A is that parents precede progeny in the pedigree file. In honey bees, we found as an additional requirement that full sisters of a queen should precede progeny of that queen.