1 Introduction

Royal jelly (RJ) production is a very particular as it requires specific conditions (Li 2000). A full-time person can hardly manage more than 40 colonies as it is a highly time-consuming work per colony, but with a short 3-month harvesting season, generally from April to June in France. In consequence, beekeepers need strains of honeybees highly improved for RJ production to reach a sufficient productivity per colony and to get a sufficient income from their activity. To our knowledge, apart from our preliminary estimates of genetic parameters for the breeding program of the French Royal Jelly Association, hereafter named GPGR (Phocas et al. 2017; Basso et al. 2022), little information is available in the technical or scientific literature on bee breeding programs for RJ production and comes mainly from China (Li 2000; Chen et al. 2002; Li and Aiping 2005) or Brazil (Ostrovski-Tomporoski et al. 2016). All these authors reported considerable improvement of RJ production through selective breeding.

To better promote the value of their product in France, five producers created the GPGR Association in the mid-90s. Since then, they have strongly selected their colonies for this production until they managed a very specific population, clearly differentiated from others breeds in France as revealed by genomic analysis (Wragg et al. 2016). The initial breeding plan was based on mass selection within beekeepers’ own seedstock. Since 2011 it has evolved through collective data recording, queen testing, and within-family selection to preserve the maternal lines’ genetic variability (Kistler et al. 2021).

For over 30 years in most farmed species, selection is no longer limited to mass selection, but integrates phenotypic information from all related animals to the selection candidates thanks to genetic and statistical models allowing the best linear unbiased prediction (BLUP) of breeding values (Henderson 1975). Due to the biological peculiarities of Apis mellifera (haplodiploidy, queen polyandry, and colony social phenotypes), the standard BLUP genetic evaluation models for livestock species could not be applied for honeybee evaluation. However, some BLUP methodologies and genetic models have been developed and used for the genetic evaluation of honeybee queens (Bienefeld et al. 2007; Brascamp and Bijma 2014, 2019a, b; Andonov et al. 2019; Guichard et al. 2020). Since 2017, RJ producers are using BLUP-estimated breeding values to rank their selection candidates considering the performance of the colony as a trait of the queen (Phocas et al. 2017), based on a so-called Queen Model in Guichard et al. (2020). Other genetic models used are either a Worker Model (Guichard et al. 2020; Du et al. 2022) or what was recently named a Colony Model (Du et al. 2022) that includes both the Queen and the Worker genetic effects in the BLUP genetic model as initially proposed by Bienefeld et al. (2007).

In order to ascertain the efficiency of the GPGR breeding program, the aims of the study were triple while accounting for the three different genetic models to describe colony performances: (i) to estimate genetic parameters of RJ production and behavioral traits; (ii) to estimate realized genetic gains; and (iii) to assess the evolution of inbreeding in the population over the last decade.

2 Material and methods

2.1 Honeybee population

Despite the fact that the GPGR data collection started in 2011, only phenotype records from queens born in years 2012 to 2021 were considered in the study (Supplementary Table S1), as consistent performance recording was only implemented since 2013. Our dataset includes information from 1420 queens of which 799 were open-mated and 621 were instrumentally inseminated.

In the GPGR breeding program, a new generation of 80 to 180 queens is produced each year from 6 to 23 1-year old breeding queens (BQs) (Supplementary Table S1). Some of them (29 to 109 virgin queens depending on the year) are instrumentally inseminated to renew the BQ pool, leading to a 1-year generation interval on the dam path. Other queens are naturally mated and part of them are used as drone-producing queens (DPQs) the year after testing. The generation interval is therefore of 2 years on the sire path. From 2020, natural mating queens are still produced but no longer phenotyped (Supplementary Table S1). Since then, the breeding program is only based on BQ phenotyping.

The same six experienced bee breeders working together since 2010 are responsible for the BQ selection nucleus and renew each year the breeding stock by exchanging genetic origins to connect their selection apiaries. In part due to this organization, only one DPQ is used by each bee breeder to inseminate the selection candidates and, when the same paternal line (i.e., same dam of the drone-producing queens) is used by different bee breeders, different DPQs are involved. On the other side, a single bee breeder produced each year all the queens which are naturally mated at the same period and place and then tested by about ten different beekeepers (8 to 18 depending on the year).

2.2 Performance testing

To ensure that all workers of each colony are daughters of the tested queens, testing starts for all surviving queens after the first winter losses (Büchler et al. 2013), whether they are potential BQs or potential DPQs. The BQs are phenotyped for all traits in their birth apiary. For DPQs, the evaluation program starts each year with production of groups of sister queens (on average 11 queens per paternal line). These groups of potential sires are sent for evaluation to 8 to 18 test apiaries each year. Queens are randomly assigned to the various beekeepers so that each paternal line is distributed across three or four apiaries and each apiary is testing three different lines with three sisters per line.

Evaluation of the queens starts in spring of the following year, using all the data records collected for BQs by bee breeders and for tested DPQs by beekeepers. As early as possible in the season, between April and May, depending on the year and the area, beekeepers start the RJ production. For this, each hive has a queen-less part in which queen cells with young larvae (stage L1) are introduced. Then, every 3 days, after removal of the queen larva, beekeepers harvest the royal jelly deposited by worker bees, using aspirators specifically designed and manufactured for GPGR beekeepers. All the queen cells from a same hive are weighed together, with 1-g precision scale, before and after royal jelly extraction, to evaluate the quantity of jelly produced by each colony. New grafted queen cells are then immediately introduced. Between 30 and 120 cell cups are introduced at the same time, depending on the colony strength and on the proportion of queen cells it accepted to rear on the previous run. If the grafting is well done with very young larvae, this 3-day-interval corresponds to the optimum between the RJ quantity not consumed by larvae (that can be harvested) and the time spent to harvest it (Chen et al. 2002).

The recorded RJ production traits consist of the first two harvests in the production season, respectively P1 and P2. P1 is the production onset. P1 is therefore not necessarily representative of the capacity of the colony to produce over the rest of the season. In contrast, it has been shown (unpublished results) that the second harvest P2 corresponds more to the cruise production rate. Limiting the phenotyping to these two first harvests enables an early selection of queens during the production season.

During the production period, gentleness (GENT) and calmness during inspection (CALM) were evaluated with a visual score ranging from 1 (worst score) to 4 (best score) according to the Beebook scoring system (Büchler et al. 2013). Due to strong differences in the number of repeated records between colonies (the median being one with one to nine records per colony), we only considered the first set of scores given in a year for all colonies of an apiary. It corresponds to scores recorded within a single week for each apiary and production period. Spring development (DEVE) was evaluated once per year, at the end of March (before the start of the production period). DEVE aims to evaluate the strength of a colony through its brood surface in comparison of the strength of all the other colonies of the same apiary. Beekeepers scored 1 the weakest colony and 4 their strongest ones.

2.3 Pedigree preparation

In the GPGR pedigree file, each record consisted of a unique identification code (ID) for the colony’s queen, the queen birth year, the queen breeder, the ID of the queen’s dam, and the testing apiary in case of a tested colony. If known, the identification of the paternal line used to mate the queen was also included in the pedigree file through the ID of the dam of the DPQ that produced the drones used to inseminate the queen.

In order to get all the information required to build the relationship matrix for BLUP evaluation (Brascamp et Bijma 2014), we considered that the number of DPQs that inseminated a queen (NS parameter) was equal to 1 for any potential breeding queen and the number of drones (ND parameter) mated to the queen was equal to 10. Unfortunately, the ID of DPQ used for insemination was not recorded, even if the DPQ was performance tested. A virtual ID of the corresponding DPQ was created through the combination of its dam ID and breeder’s name since each breeder used a different DPQ from any given dam (corresponding to a given paternal line). For any uncontrolled mated queen (i.e., a potential DPQ), the number of drone mates (ND) was set to 20 and they were supposed to come from a pool of NS = 100 DPQs assumed to come from unknown parents to mimic natural mating conditions (Tarpy and Nielsen 2002; Schlüns et al. 2005; Delaney et al. 2011; Tarpy et al. 2013).

The complete GPGR pedigree data included 4189 queens. Dam pedigree of all queens was traced back as far as possible. The founder population was composed of 22 queens born in year 2009, and there were 107 BQ with an average family size of 11 daughter queens (ranging from 1 to 37).

The pedigree file used for the BLUP genetic evaluation was created in two steps in order to run an animal model with an additional maternal genetic effect on the colony performance, i.e., to jointly evaluate the effects of the group of worker bees and of the colony’s queen as proposed by Brascamp and Bijma (2014, 2019b). Firstly, the file containing records for a unique identification number generated for the group of workers within each colony was created followed by a sire ID, dam ID (queen ID of the colony), and test year of that particular colony. Secondly, it contained raw records from the queen ID, its own sire ID, its own dam ID, and queen birth year to complete all ancestral entries. The complete BLUP pedigree file included 10,868 records.

The inverse of the pedigree relationship matrix between all entries in the pedigree was calculated using an R program (R Core team 2017) developed by Brascamp and Bijma (2019a).

2.4 Statistical analysis

Genetic parameters and genetic trends were estimated considering three different BLUP animal models to account for the genetic components playing a role on colony performance.

The model which is supposed to most accurately represent the honeybee biology is called the Colony Model (CM) in accordance with Du et al. definition (2022). This model takes into account a direct genetic effect and a maternal genetic effect.

It assumes that the phenotype Pijk of a colony composed of a worker group of bees j and a dam k is described by the following equation:

$$P_{ijk}\:=\:\mu\:+\:{\mathrm{CG}}_{i\:}+\:{\mathrm d}_j\:+\:m_k\:+\:{\mathrm e}_{ijk}\;(\mathrm{CM})$$

where μ is the general performance mean, CGi is the fixed effect of the contemporary group i (i.e., for behavioral traits, the combination of recording year × apiary effects and for the production traits the combination of recording year × apiary × harvesting period effects), dj is the direct genetic effect of the average worker bee j, mk is the maternal genetic effect of the dam k, and eijk is the CM’s residual effect.

The CM is similar to the classical model used in all livestock species as an Animal Model accounting for maternal genetic effects (Bienefeld et al. 2007).

The difference is that, in the Colony Model, the animal does not represent a single individual but the average of a group of workers.

The two other models we used are simplified models that were used because of convergence and inconsistency issues on small datasets (Guichard et al. 2020). They are used here for the very same reasons, as the restricted maximum likelihood algorithm did not converge to estimate genetic parameters under CM for behavioral traits, and CM estimates for production traits may deserve cautious attention (see Section 4). Under these models, the colony performance is only attributed to a single genetic effect, either the one of the worker group j or to the one of its queen k. This genetic effect has to be seen as a composite value that will capture genetic effects expressed by both the worker group and the queen without disentangling them (Du et al. 2022). In accordance with Guichard et al. (2020) and Du et al. (2022), we name these two models Worker Model (WM) and Queen Model (QM), respectively.

Under the Queen Model,

$$P_{ijk}\:=\:\mu\:+\:CG_i\:+\:q_k\:+\:\varepsilon_{ijk\;}(\mathrm{QM})$$

where qk is the queen effect and εijk is the residual effect in the Queen Model.

According to Du et al. (2022) formula, we can derive qk = mk + 0.5 dk.

Under the Worker Model,

$$P_{ijk}\:=\:\mu\:+\:{\mathrm{CG}}_{i\:}+\:{\mathrm w}_j\:+\:\gamma_{ijk}\;(\mathrm{WM})$$

where wj is the average genetic effect of worker group j and γijk is the WM’s residual effect.

According to Du et al. (2022) formula, we can derive

$${w_j}={d_j}+(0.5/{a_{\mathrm {ww}}})\,{m}_{j}$$

where aww corresponds to the average relationship coefficient between two workers in a colony (Brascamp and Bijma 2014, 2019a) and was estimated equal to 0.3915 in our average population and equal to 0.2775 in our base population (see Appendix A for calculation).

The phenotypic variance σ2P emerges from both the maternal genetic variance due to the single queen and the variance of the average genetic effect of the workers of the colony. Therefore, the genetic variance attributed to the worker group in the expression of σ2P is reduced by the coefficient aww compared to the variance attributed to a single worker (Brascamp and Bijma 2018, 2019a).

Therefore, in the Colony Model, the phenotypic variance is partitioned as

$$\mathrm\sigma^2\mathrm p=\mathrm\sigma^2\mathrm m+{\mathrm a}_{\mathrm{ww}}{\mathrm\sigma^2}_{\mathrm d}+{\mathrm{Cov}}_{\mathrm{dm}}+\mathrm\sigma^2\mathrm e$$

with \({\sigma^2}_{\mathrm m}\) the maternal genetic variance, \({\sigma^2}_{\mathrm d}\) the direct genetic variance, Covdm the covariance between direct and maternal genetic effects, and \({\sigma^2}_{\mathrm e}\) the CM’s residual variance.

Under CM, two heritability estimates were derived—one for the direct genetic effect of the workers (h2d = σ2d/σ2p), and another for the maternal genetic effect (h2m = σ2 m/σ2p)—while the sole heritability of the trait attributed to the queen effect (h2q) was estimated under QM, and the sole heritability of the trait attributed to the worker genetic effect (h2w) was estimated under WM.

To compare the consistency of estimates of genetic parameters between the three models, CM, WM, and QM, we recalculated the queen and worker genetic variances using CM estimates following equations detailed in Appendix B.

Bi-trait QM and WM analyses were also run to estimate genetic correlations between all traits. All analyses were performed using the AIREMLF90 program from the BLUPf90 package (Misztal et al. 2002).

3 Results

3.1 Performance testing results

The potential BQs, which are inseminated queens, show a higher RJ production on average than the potential DPQs, that are naturally mated (Table I). The average increase was +30% for P1 and even more for P2 (+36%). On the contrary, coefficients of variation of production traits were higher (~55%) for DPQs than those of BQs (~45%). The average grades on behavior traits were more similar between BQs and DPQs, but with a 20% higher variability of the scores for GENT and CALM for DPQs than for those of BQs.

Table II shows the mean and standard deviation of raw performances, as well as the phenotypic variances estimated after correction of raw performances for the fixed contemporary group effects and the phenotypic correlations between these corrected performances.

Ratios of phenotypic to raw variances indicate that the fixed effects (i.e., recording year × apiary effects) explained 50 to 53% of the variance of raw performances for all traits, except 32% for DEVE.

Table I Performance of breeding queens (BQ) and drone-producing queens (DPQ) and of full data set for all traits (P1: production at first harvest, P2: production at second harvest, GENT: gentleness, CALM: calmness during inspection, DEVE: spring development)
Full size table
Table II Variances on the diagonal and correlations above the diagonal for performances corrected for the fixed contemporary group effects estimated by ANOVA model (P1: production at first harvest, P2: production at second harvest, GENT: gentleness, CALM: calmness during inspection, DEVE: spring development)
Full size table

3.2 Estimates of genetic parameters for production traits

Table III presents the estimates of variance components for the three BLUP models CM, QM, and WM.

Regarding estimates of phenotypic variances derived as the sum of genetic and residual variances (see equations 1 to 3 in Appendix B), they varied strongly across the different genetic models (Table III) and were also markedly different from the variances derived for P1 and P2 only after correction of raw performances for the fixed contemporary group effects (Table II).

Phenotypic variances estimated between the CM and WM were very close. However, the estimates under QM were clearly lower and closer to the variances derived ignoring any genetic effects (Table II).

In addition, the phenotypic variance estimated under a WM depends on the coefficient aww. Assuming the coefficient derived for naturally mated queens (i.e., aww = 0.2775 as it happens in the base population), estimates were 155.22 and 195.79 for P1 and P2, respectively (Table III), while assuming the average aww for all the phenotyped colonies in the recorded population; the corresponding estimates were 164.06 and 209.65 (Supplementary Table S2).

Table III Estimates of variance and heritability values (h2) under respectively colony model (CM), queen model (QM), and worker model (WM) for production at first harvest (P1) and second harvest (P2) (± SE), considering only maternal half-sisters as workers in the colonies (aww = 0.2775)
Full size table

Assuming aww = 0.2775, the heritability estimates under CM were moderate for P1 (respectively 0.26 and 0.44 for the maternal genetic effects of the queen and the direct genetic effects of the workers) and high for P2 (respectively 0.53 and 0.78), but always higher for the worker effects than the queen effects. For both traits, the direct-maternal genetic correlations estimated under CM were strongly negative but with very large standard errors (Table III), rendering them neither significantly different from 0 or −1. Assuming aww = 0.3915 had little impact on heritability estimates under CM (Supplementary Table S2).

Under QM, heritability estimates were 0.19 and 0.35, respectively, for P1 and P2. Those values were lower than the heritability of maternal genetic effects under CM. Under WM, the heritability for P1 was estimated at a 5% higher value than the heritability of direct genetic effect under CM. On the contrary, the heritability for P2 under WM was estimated 20% lower than the heritability of direct genetic effects under CM.

3.3 Breeding value estimation for production traits

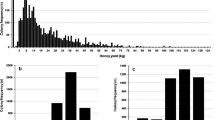
Figure 1 shows the annual trends for P2 performances as well as maternal and direct EBV standardized by genetic standard deviation for BQ and DPQ under CM.

Figure 1.
figure 1

Average phenotypic values, average direct and maternal estimated breeding values (EBV) for breeding queens (BQ) and drone-producing queens (DPQ) under the colony model for production at second harvest (P2) depending on queen birth year.

Full size image

Yearly variations in production were high, but the average performance for P2 increased respectively by 0.74 g and 1 g per year for BQ and DPQ during the observed period from year 2012 to year 2021.

Regarding EBVs based on CM, estimated direct genetic gains were two times higher for the inseminated BQ than for DPQ whose paternal path is uncontrolled (Figure 1). For BQ, direct genetic trend was estimated to 0.60 g/year, corresponding to an annual increase of ~ 7% of direct genetic standard deviation from year 2012 to year 2021. Meanwhile, no genetic trends were observed for maternal breeding values that stay stable over years for both BQ and DPQ direct breeding values (Figure 1). Note that maternal EBV reliabilities were significantly higher than direct EBV ones (Supplementary Table S3).

When considering EBVs estimated under QM and WM for P2 (Figure 2), similar differences in genetic trends were observed between DPQ and BQ as under CM with an annual increase for BQ EBVs of 8 and 9% of genetic standard deviation, respectively, under QM and WM.

Figure 2.
figure 2

Average phenotypic values and corresponding average estimated breeding values (EBV) for BQ and DPQ with queen model (QM) and worker model (WM) for production at second harvest (P2) depending on queen birth year.

Full size image

3.4 Phenotypic variance and heritability estimates for behavioral traits

Regarding estimates of phenotypic variances for behavioral traits, they show the same trend as production traits, with strong differences across the two genetic models (Table IV) and are also markedly different from the variances derived for raw performances only corrected for the fixed contemporary group effects (Table II).

Heritability estimates under QM were at moderate values for DEVE and GENT, but at a very high value of 0.76 for CALM. As for production traits, WM estimates were larger with high heritability values for the three traits. All WM estimates were reduced by 10% when considering aww = 0.3915 (Supplementary Table S4).

Table IV Estimates of variance components and heritability (h2) and associated standard errors under queen model (QM) and worker model (WM) for behavior traits (GENT: gentleness, CALM: calmness during inspection, DEVE: spring development), considering only maternal half-sisters as workers in the colonies (aww = 0.2775)
Full size table

3.5 Phenotypic and genetic correlations across all traits

The phenotypic correlation between P1 and P2 was estimated about 0.60–0.65 either on raw performances corrected for the contemporary group effects or under QM or WM BLUP genetic models (Table II; Supplementary Tables S5 and S6). Those two traits were genetically highly correlated, with estimates of correlation ranging from 0.72 under WM (Supplementary Table S6) to 0.90 under QM (Supplementary Table S5).

Phenotypic correlation between production traits and behavioral traits were close to zero regardless of the estimation method (Table II; Supplementary Tables S5 and S6). Due to large standard errors of the estimates, very few genetic correlations were significantly different from zero between behavioral traits or between these former and production traits. The only exceptions were the significant positive genetic correlations between P2 and CALM (under QM) or GENT (under QM and WM) as well as the one between CALM and GENT under QM (0.94) (Supplementary Table S5) and under WM (1.00) (Supplementary Table S6). Those two behavioral traits had very different estimates of genetic correlations with the two production traits despite the high genetic correlation estimated between P1 and P2; while positive genetic correlations were estimated with P2, negative estimates, not significantly different from 0, were derived with P1.

3.6 Estimated genetic trends for all traits and inbreeding

Regardless of the models, genetic improvement for all traits was observed (see Supplemental Figure S1), except for DEVE under WM. In the last 10 years, considering WM evaluation, P2 and CALM were improved by almost one genetic standard deviation while P1 and GENT were improved by 0.6 genetic standard deviation. Considering QM evaluation (that gave a greater weight to maternal genetic effects than to the direct genetic effects of the workers), all traits were improved in between 0.30 and 0.90 genetic standard deviation during these last 10 years.

In the same time, inbreeding increased in average by 0.8% each year from 2015 to 2021 (result not shown). As inbreeding is only derived based on the available pedigree, the inbreeding rate could not be correctly estimated for the first 4 years of the breeding program due to insufficient pedigree depth.

4 Discussion

4.1 Efficiency of the GPGR breeding program

Since 2012, we observed a clear improvement of RJ production (based on P2 records), from about 34 to 46 g for breeding queens born in 2021 (Figure 1). However, the phenotypic gain seems far much less than the one reported for the Chinese breeding program that was initiated in the 1980s to derive a high royal jelly-producing honeybee strain from Italian bees (A. mellifera ligustica). At the start of the breeding program, production of RJ was about 20 g over a 3-day period and increased to about 150 g per colony over 3 days in the early 2000s (Chen et al. 2002). In particular, a strong improvement from 30 g in 1988 to 100 g over 3 days in 1993 was observed due to an intensive selection applied over six generations at Zhejiang University to create the ‘Zhenongda No. 1’ high RJ line from a founder population of 17 lines from 1000 high-yielding colonies recorded across various high RJ-producing regions of China. We may hypothesize that the major part of this reported increase was jointly due to the extreme selection pressure to choose the 17 lines as well as a strong technical improvement in managing RJ colonies (Chen et al. 2002). In particular, French beekeepers have to respect the ISO12824:2016 standard (AFNOR 2016) for RJ production which forbid to give sugar during production. Such input can highly increase production but cause change in RJ composition (Wytrychowski et al. 2013).

As far as we know, our study is the first one trying to disentangle genetic and environmental factors that may explain the observed phenotypic increase in RJ production through the estimation of genetic trends. Despite the fact that our estimates strongly varied depending on the genetic model we considered to predict breeding values, all estimates consistently showed a strong increase in direct genetic effects of workers while no clear improvement of maternal genetic effects could be observed neither under CM (Figure 1) or comparing QM EBVs with WM EBVs (Figure 2).

Since 2017, a BLUP-QM evaluation is routinely performed to sort selection candidates of the GPGR breeding population. However, the final choice is still mainly taken through collective discussion of the bee breeders, using mainly phenotypic information for RJ production and choice within maternal families. Comparing to simulations done by Kistler et al. (2021), the operational GPGR breeding program is very close to the simulated scenario “Within family mass selection & Polyandrous mating.” In this scenario and considering a higher heritability for maternal effects than for worker direct effects, Kistler et al. (2021) predicted a higher improvement for the worker direct genetic effects than for the maternal genetic effects, which is consistent with our EBV estimates. Indeed, the variance of direct effects explaining a larger part of the phenotypic variance, selecting on phenotypes induced a stronger improvement on direct effects than on maternal ones. Kistler et al. (2021) also showed that, when a negative genetic correlation existed between direct and maternal genetic effects, the difference between the corresponding genetic gains was exacerbated.

Despite the lesser importance given to behavioral traits in the selection choices made by GPGR, they showed positive estimated genetic trends for both QM and WM EBV. Under QM, the annual direct genetic gain for CALM was estimated to 52.3% of genetic standard deviations from year 2013 to year 2021 while evolution of the maternal genetic trend was 35.5% per year. The only exception being a null trend for DEVE breeding values estimated under WM. This exception must be explained by the very negative genetic correlations estimated under WM between DEVE and P2 which is the main selection criterion (Supplementary Table S6). As the corresponding estimates were significantly closer to zero under QM, this leads us to hypothesize that the direct genetic effects for DEVE and RJ production traits are negatively correlated while probably the maternal genetic effects are not (or at least in a lesser extent).

We also gave a pedigree-based estimate of inbreeding level in the population as it is a strong concern for a small breeding population managed as an almost closed nucleus for 10 generations of selection. Using pedigree rather than genomic information, we underestimated inbreeding levels, especially the first 4 years of the breeding program as the inbreeding coefficients were directly related to the amount of pedigree information which is available. However, then we could properly estimate an annual increase of inbreeding of 0.8% from year 2015 to year 2021, which corresponded to a rate of inbreeding increase of 1.2% per generation. This estimate was close to the annual estimate (1.1%) obtained by simulation of a similar breeding program (Kistler et al. 2021). Average inbreeding coefficients for BQ born in years 2019–2021 were ranging from 7.6 to 9.5%. Recently, Druml et al. (2023) estimated inbreeding levels within the two Austrian Carnica breeding populations selected through EBVs for over the last 30 years; inbreeding of queens with full pedigree recorded over five generations was estimated about 5.5% on average in the populations of active breeding queens for the ACA (2675 BQ in 2019) and ZAC (1286 BQ in 2020) breeding programs. Both populations exhibit very moderate loss of genetic diversity in comparison to the GPGR one whose population size is very small with only 109 queens inseminated in 2020 (Supplementary Table S1).

The GPGR association should try to significantly increase the size of their breeding population to limit the risk of collapse. It is advisable to limit increasing inbreeding by 0.5 to 1% per generation in order to preserve long-term genetic gains as well as the adaptive capacities of the population in the event of a change in the environment (Felsenstein 1965). To reach the highest possible genetic gains while limiting inbreeding rate in honeybee breeding populations, further improvement of the breeding program should consider an optimum contribution selection strategy (Meuwissen 1997).

4.2 Heritability estimates according to genetic models for production traits

Regarding all models and traits studied, RJ production clearly showed moderate to high heritability, which confirms the results of Basso et al. (2022) on an earlier analysis of the GPGR breeding program. To our knowledge, there is only one other study (Faquinello et al. 2011) presenting heritability for the RJ production. This first estimate was at a very low value of 0.06 in a Brazilian small population of 174 colonies from four generations derived from 20 naturally mated Africanized queens of A. mellifera. It was based on a mixed Animal Model in which the animal was considered as the worker but the paternal pedigree was ignored. This first estimate was surprisingly low as in general production traits exhibit moderate to high heritability values whatever the farmed species considered. If we compare our estimate for RJ production to recent estimates obtained for honey production we were in the same range of the literature when considering the same genetic model (Table V).

Our negative estimate of the genetic correlation between direct and maternal genetic effects for RJ production is close to the one estimated for honey yield in a large population of Austrian Carnica bees (Brascamp et al. 2016) while, on the other hand, an almost null correlation was derived in a naturally mated Italian bee population (Andonov et al. 2019). In these two studies, higher heritability values for direct worker effects than for maternal ones were estimated for honey yield (Table V).

Table V Heritability estimates (h2 ± SE) in recent literature for honey yield, gentleness and calmness under various genetic models: queen model (QM), worker model (WM), and colony model (CM)
Full size table

Therefore, it seems that regardless of the production trait (honey or royal jelly), direct genetic effects of the workers have more impact on colony performance than the maternal genetic effects of the queen, and that both genetic effects are negatively correlated. However, those estimates of negative correlations must be taken with caution as strong biases may be induced due to uncertainties in the paternal pedigrees of the colonies (Kistler et al. 2023) and lack of data and sufficient depth of pedigree to disentangle direct and genetic effects as already reported by Andonov et al. (2019) and Guichard et al. (2020).

To assess the consistency of our results between CM and WM, we tried to rederive the genetic variances we should estimate under WM if the true direct and maternal genetic variances were the ones we estimated under CM (see Supplementary Table S7). This estimate depends on the value of the relationship coefficient aww we assume for workers in a colony. Considering aww = 0.2775, the recalculated worker genetic variance based on the CM variance estimates was close to the direct estimate under WM for P1, but it was strongly overestimated (+36%) for P2. Considering aww = 0.3915, recalculated worker genetic variances were strongly underestimated for both P1 and P2. To use relevant estimates of variance components under a WM evaluation, it is tricky to choose a proper value for aww as, in most breeding plans, both insemination and natural mating are used in varying proportions depending on year opportunities, and the numbers of DPQ and drones used to mate queens also significantly vary.

The coefficient aww is not involved in the derivation of the queen genetic variance based on the CM variance estimates. Indirect and direct estimates of the queen genetic variances were close (see Supplementary Table S7). Therefore, when data are insufficient to fit a CM, we may recommend to run a QM evaluation rather than a WM one. However, it should be noted that, doing so, bee breeders will put more emphasis on improvement on maternal genetic effects rather than on direct genetic effects on the colony performance when selecting their replacement queens on QM EBV rather than on WM EBV.

4.3 Heritability estimates for behavior traits

Our estimates of heritability for behavior traits are in the very large range of values given during the last decade in the literature for similar traits and genetic models applied to other bee populations (Table V).

As regards to GENT (also called defensive behavior), several REML estimates of heritability were given in the literature during the last decade (Table V). These previous estimates varied from very large values such as over 1 for the worker direct heritability under CM to values under QM ranging from intermediate to low values (< 0.10).

Our estimate (h2w) of heritability for CALM under WM, which are outside the range of usual values (i.e., above 1, see Table IV) is a fine illustration of the issues we have to face to present understandable estimates of genetic parameters. This value relates to the heritable variance of the effect of a colony considered as a single individual which is a measure for the scope of selection. Indeed, Bijma (2011) established that the heritable variance in traits that depend on genes from multiple individuals is not limited to phenotypic variance and can exceed the value of 1, which is a fundamental difference from classical theory. A second kind of heritability (h2 = awwh2w as reported by Brascamp et al. 2018; Guichard et al. 2020) relates to the worker effect considered as a group of bees, which reflects the part of the phenotypic variance due to the genetic effect of the worker group and has therefore 1 as theoretical upper bound.

As far as DEVE (also called spring development) is concerned, little information is available to compare our estimates with the literature. However, our heritability estimated under QM (h2q = 0.22) is close to the one derived for a Canadian honeybee population (h2q = 0.30, Maucourt et al. 2020). These moderate values estimated for the development of the colony at spring time should allow to efficiently select on this trait, which is a matter of importance to get colonies as strong as possible early in the production season since the period of honey flow tends to be reduced by climate change.

Concerning our estimates of genetic correlations, very few are significant because we only had 107 families of breeding queens with small family sizes in our study. Large sample sizes (at least several hundreds of families) are required to accurately estimate genetic correlations as shown by some empirical studies (see for instance Koots and Gibson 1996). As advised by some geneticists 30 years ago (Cheverud 1988; Roff 1995), it seems advisable to use the phenotypic correlations (presented in Table II) that are probably better estimates of the true genetic correlations, than the ones we tried to derive under the QM or WM BLUP models.

5 Conclusion

As frequently reported in the literature on genetic parameters for honeybees, we faced many doubts on the relevance of our estimates of genetic parameters because of uncertainty on paternal pedigrees and joint use of open mated and inseminated queens. When data is still insufficient to implement a BLUP-Colony Model to jointly estimate maternal and direct genetic breeding values, we recommend to run a Queen Model rather than a Worker Model to better control and understand both estimates of breeding values and genetic parameters.

Despite these challenges, our study clearly shows that selection on royal jelly production is feasible and efficient even in a very small population. Future development of the breeding scheme should try to limit the inbreeding rate through an increase in the breeding population size.