Introduction

Metals such as zinc, copper, nickel, lead, and aluminum are the main raw materials for national and international economic development and are the basis of most industries such as construction, electric, electronic, and mechanical (Zhong et al. 2019; Wang et al. 2018). In addition, with the development of technology, metals play an important role in social development (Watkins and McAleer 2004; Gargano and Timmermann 2014; Alameer et al. 2019).

The price fluctuations in supply chains that started with COVID-19 affected the metal sector as well as all other sectors. The effects of this fluctuation continue in a dramatic way. With the increase in fuel and energy prices, production costs in the mining sector have also increased. This has also triggered increases in metal prices. Metal prices are a major factor for investment decisions for such as mining, refining, and fabrication (Watkins and McAleer 2004) because metal price forecasts play a role in planning mining operations primarily and the cost–benefit balance of the manufacturing sector. Furthermore, metal prices cause variability in revenues from mining operations (Dooley and Lenihan 2005). Accurate price forecasts are necessary to determine the economic feasibility of metal exploration and mining activities (Kriechbaumer et al. 2014). As a result, there is rising demand for modeling and forecasting of metal prices, forecasting of metal prices has attracted many researchers, and these researchers have improved various approaches to forecasting. Labys (2006) used a structural time-series model to forecast monthly prices of main metals. He indicated the importance of correctly accounting for cyclicality in modeling and forecasting primary commodity prices. Kriechbaumer et al. (2014) predicted aluminum, copper, lead, and zinc prices using the mixed wavelet approach with the ARIMA method. Their study confirmed the importance of cyclicality for forecasting metal prices. Sanchez Lasheras et al. (2015) predicted copper prices by comparing the ARIMA model with the neural network approach. Their study indicated that the multilayer perceptron or Elman network produced more accurate forecasts. Drachal (2019) predicted lead, nickel, and zinc prices using Bayesian model combination schemes. He showed that model selection was more beneficial for accuracy of the forecast. Shafiee and Topal (2010) investigated the future gold price using different models. They proposed a dip diffusion model and found improved forecasting performance than the ARIMA model. He et al. (2015) studied forecasting of lead and zinc prices and they showed that the wavelet-based method delivered better forecasts than RW and ARMA. Rubaszek et al. (2020) investigated the dynamics of real prices for main non-ferrous industrial metals using four types of autoregressive model. Sohbari et al. (2021) estimated the coal prices using two-time-series combined radial basis function (RBF) neural network methods. Their suggested model has eventually approximated the coal price with acceptable precision concerning the time-series method.

In this study, aluminum, copper, lead, iron, nickel, tin, and zinc prices were analyzed by using data from 1990:1 to 2021:11. The root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) values of the models were obtained and their performances were compared to determine the appropriate model for each metal price. The main contributions of this paper are summarized as follows: a global metal price forecasting framework is proposed by using Holt, Brown, and damped exponential smoothing methods. Exponential smoothing assigns weights that decrease exponentially as the observation ages, and the prediction is very effective. Thus, the study will shed light on mining, metal sales, and other related industrial policies.

The rest of the paper is organized as follows. In the “Methodology” section, we describe the methodology. The “Data and results” section discusses the data and results. The conclusion is given in the “Conclusions” section.

Methodology

Exponential smoothing methods

A time series is statistical data about various quantitative indices of economic and social phenomena in the order of time. Time-series analysis is the analysis of dynamic series. The aim is to master the law of statistical data, based on time changes to control and predict outcomes. An important part of the forecasting method system is the time-series forecasting method. Time-series estimation methods include various estimation techniques and the most important of these techniques is the exponential smoothing estimation method. Exponential smoothing approaches are relatively simple but robust techniques that are widely used in various business applications, such as inventory control (Gardner 1985; Abderrezak et al. 2014). The accuracy and robustness of exponential smoothing estimations led to its common use in applications where multiple series are present because it requires an automated procedure (Christodoulos et al. 2011).

The formulation of exponential smoothing estimation methods emerged in the 1950s from the original work by Brown (1959, 1962) and Holt (1960) who attempted to create forecasting models for inventory control systems (Fomby 2008). The principle is to find the main improvement trend by smoothing time series to eliminate random fluctuations in historical statistical series by calculating exponential smoothing averages (Li 2013). One of the key ideas in smoothing models is to construct estimates of future values as weighted averages with more recent observations carrying more weight than observations from the more distant past in determining the predictions (Fomby 2008).

Exponential smoothing assigns weights that decrease exponentially as the observation ages. That is, recent observations are given relatively more weight in the estimation than previous observations (Christodoulos et al. 2011). Exponential smoothing models do not explicitly include model identification and parameter estimation processes, attempting to separate trends or seasonality from uneven variation (Yaffe and McGee 2000; Oni, and Akanle 2018). These methods are combination methods which assign different weights to the time series of the previous period (Sharpe et al. 2010).

In this study, Holt, Brown, and damped exponential smoothing methods are discussed.

Holt exponential smoothing

Holt exponential smoothing is a kind of linear exponential smoothing method (Li 2013). The simple exponential smoothing proposed by Holt allows for the forecasting of data with a trend (Oni and Akanle 2018). The most prominent advantage of this method is the varied trend of time series; it directly smooths the trend data and predicts the original time series without using secondary exponential smoothing. It is widely used because of a great deal of flexibility (Li 2013). Holt’s method is the most popular approach for trending series, though its linear forecast function was criticized for tending to overshoot the data beyond the short term (Christodoulos et al. 2011). It should be noted that Holt’s method performs well where only trends but no seasonality exist (Hasan and Dhali 2017). Holt is a double exponential smoothing method that has two parameters (level and trend), and, in this model, they are not constrained by each other’s values. In the weighting parameters, the new value is greater than previous observations. In addition, there is a weighted estimate of the trend of data. Generally, Holt has two smoothing constants (values between 0 and 1) (Supriatna et al. 2017). The following two coefficients (α and β) are smoothing coefficients for estimating the trend in the Holt model (Melekşen and Eyduran, 2017). The equations for Holt’s exponential smoothing are given below:

$${P}_{t}=\mathrm{\alpha }{X}_{t}+(1-\mathrm{\alpha })({P}_{t-1}+{Z}_{t-1})$$
(1)
$${Z}_{t}=\upbeta \left({P}_{t}-{P}_{t-1}\right)+(1-\upbeta ){Z}_{t-1}$$
(2)
$${F}_{t+r}={P}_{t}+r{Z}_{t}$$
(3)

where \({X}_{t}\) is the actual observed value, \({P}_{t}\) is an estimate of the level of the series at the time t, \({Z}_{t}\) is an estimate of the trend (slope) of the series at time t, \(\beta\) is also a smoothing constant between 0 and 1 and plays a role similar to that of \(\alpha\), and \({F}_{t+r}\) is the r step-ahead forecast made from forecast origin t.

Brown’s linear exponential smoothing

Another exponential smoothing method is Brown’s linear exponential smoothing method with one parameter. This method was proposed by Brown to overcome the forecasting process with data in the form of trends on a plot where the rationale of this method is similar to forecasting a linear moving average (LMA) (Muchayan 2019). The basic theory of Brown exponential smoothing is similar to the linear-quadratic mobile average method, when the trend single and double smoothing both lag behind the actual values. The difference between the values of the single and double smoothing is added to the single smoothing value, which can correct the trend (Li 2013). Estimates for this model are made using the following equations (Eqs. (4) and (5)):

$${P}_{t}^{^{\prime}}=\mathrm{\alpha }{X}_{t}+(1-\mathrm{\alpha }){P}_{t-1 }^{^{\prime}}$$
(4)
$${P}_{t}^{^{\prime\prime} }=\mathrm{\alpha }{P}_{t}^{^{\prime}}+(1-\mathrm{\alpha }){P}_{t-1 }^{^{\prime\prime} }$$
(5)

Brown’s double exponential smoothing requires the previous observations in any time period t as well as single exponential smoothing. However, Brown’s double exponential smoothing had \({P}_{t}^{^{\prime}}\) and \({P}_{t}^{^{\prime\prime} }\) where \({P}_{t}^{^{\prime}}\) is the first exponential smoothing in the period t, and \({P}_{t}^{^{\prime\prime} }\) is the second exponential smoothing in the period t based on \({P}_{t}^{^{\prime}}\). \({P}_{t-1 }^{^{\prime}}\) and \({P}_{t-1 }^{^{\prime\prime} }\) must be known to use Eqs. (4) and (5). Yet, since these values must be determined at the beginning of the period, they are not known when t = 1. To overcome this problem, it can be determined that \({P}_{t-1 }^{^{\prime}}\) and \({P}_{t-1 }^{^{\prime\prime} }\) are equal to \({X}_{1}\).

$${\mathrm{a}}_{t}=2{P}_{t}^{^{\prime}}-{P}_{t}^{^{\prime\prime} }$$
(6)
$${\mathrm{b}}_{t}=\frac{\mathrm{\alpha }}{1-\mathrm{\alpha }}({P}_{t}^{^{\prime}}-{P}_{t}^{^{\prime\prime} })$$
(7)

After \({P}_{t-1 }^{^{\prime}}\) and \({P}_{t-1 }^{^{\prime\prime} }\) are calculated, the process continues with Eqs. (6) and (7). \({b}_{t}\) is an adjustment factor to compute the slope of trend value, whereas \({a}_{t}\) is used to compute the difference between the first exponential smoothing \(2{P}_{t}^{^{\prime}}\) and the second exponential smoothing \({P}_{t}^{^{\prime\prime} }\).

$${F}_{t+m}{=a}_{t}+m{b}_{t}$$
(8)

By following Eq. (8), the forecast for the next period t is made. Here in \({F}_{t+m}\), m is the period number of the step ahead. The next forecast is the exponentially smoothed difference in the period t; \({a}_{t}\) is added to the product of the slope value \({b}_{t}\) and the period number of a step ahead m (Narotama 2022).

Holt linear exponential smoothing

Despite its popularity, empirical evidence showed that the Holt linear forecast function tends to overestimate (Gardner and McKenzie, 1985). Given this, Gardner and McKenzie (1985) described how a dampening parameter, φ, can be used within Holt’s method to provide more control over trend extrapolation (Taylor 2003). The forecasting system is based on the class of autoregressive-damping systems, also known as damped trend systems, developed by Gardner and McKenzie (1985) (Gardner 1999). In forecasting with exponential smoothing, although many attempts were made to improve this practice by selecting individual methods for each series, it is common to apply the damped trend method to every time series. They have yet to produce better forecast accuracy though method selection procedures resulting in simpler methods than the damped trend (Gardner and McKenzie 2011). In error-correction form, the damped trend is written as follows (Gardner 1999):

$${\widehat{a}}_{t}=\left(1- \alpha \right)\left({\widehat{a}}_{t-1}+\varphi {\widehat{b}}_{t-1}\right)+\alpha {d}_{t}$$
(9)
$${\widehat{b}}_{t}=\left(1- \beta \right)\varphi {\widehat{b}}_{t-1}+\beta ({\widehat{a}}_{t}-{a}_{t-1})$$
(10)
$${\widehat{d}}_{t,t+k}={\widehat{a}}_{t}+{\widehat{b}}_{t}\sum\nolimits_{i=1}^{k}{\varphi }^{i}$$
(11)

where \({a}_{t}\) is the current estimate of the level, exponentially smoothed by the constant α; φ is the damping parameter that can be interpreted as a measure of the persistence of the trend; \({d}_{t}\) is the time series being forecasted; \({b}_{t}\) is the current estimate of the trend, exponentially smoothed by the constant β; \({b}_{0}\) is the initial value of the trend, assumed to be zero, \({b}_{0}=0\); k is the number of periods ahead that the forecast is required to predict; and \({\widehat{d}}_{t,t+k}\) is the forecast, made at time t in the period t + k. The damped trend itself is defined by optimal parameters in the ranges 0 ≤ α ≤ 1, 0 < β ≤ 1, and 0 < φ < 1. When all parameters are selected from the [0, 1] interval, at least 11 different methods can be defined (Bauer 2022).

Because of the principal importance of time forecasting in many practical situations, proper care should be taken while selecting a particular model, comparing different models, and estimating forecast accuracy (Oni and Akanle 2018). In many forecasting situations, accuracy is the criterion for refusing to choose a forecasting method. In many cases, the word precision refers to the virtue of ultimately indicating how far the forecasting model can reproduce the known data (Dharmawan and Indradewi 2021).

In this study, RMSE, MAPE, and MAE criteria were used to evaluate the performance of the models.

The standard error can well reflect the precision of the measurement since the standard error is very sensitive to large or special small errors in a set of measurement data. RMSE is a measure of the deviation between the true values and the observed values. It is calculated by the following equation:

Since MAPE is widely used in cases of combining and selecting forecasts, it was selected to be the main measure in the present evaluation. Its equation is depicted below:

$$RMSE=\sqrt{\frac{\sum^{T}_{t=1}(F_t-X_t)^2}{T}}$$
(12)
$$MAPE=\frac{1}{T}\sum_{t=1}^{T}\left|\frac{\left({F}_{t}-{X}_{t}\right)}{{X}_{t}}\right|$$
(13)

where \({X}_{t}\) is the actual value at time t, T is the number of predictions, and \({F}_{t}\) is the predicted value at time t. The difference between \({X}_{t}\) and \({F}_{t}\) is divided by the actual value \({X}_{t}\) again. The absolute value of this calculation is summed for every fitted or forecast point in time and divided again by the number of fitted points.

Another popular error measure used to ensure the accuracy of results is MAE. It is calculated using the following equation (Li 2013):

$$MAE=\frac{\sum^{T}_{t=1}|F_t-X_t|}{T}$$
(14)

Data and results

This study aimed to forecast the prices of aluminum, copper, lead, iron, nickel, tin, and zinc metals with time-series analysis. The data used in the study were obtained monthly from the Federal Reserve Economic Data for the period 1990:1–2021:11 and analyses were made by taking the average price for each year (FRED 2022). Holt, Brown, and damped models, which are exponential smoothing methods within the scope of prediction methods, were applied to the data discussed in the study using the SPPS 25 program. To determine the appropriate model, the RMSE, MAE, and MAPE values of the models were obtained and their performances were compared. In total, there were 32 data for each product and the descriptive statistics of metal prices per metric ton are given in Table 1.

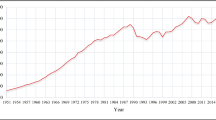
Table 1 Descriptive statistics of metal prices
Full size table

The time-series graph for each metal price used in the study was obtained and is given in Fig. 1. Moreover, the fitted values according to the methods used for each metal price and the forecast values for the period 2022–2030 are also given in Fig. 1. Figure 1 shows the time-series graph of metal prices, which is non-seasonal with observable trends. For this reason, exponential smoothing methods were applied to metal prices. To determine the appropriate exponential smoothing method, model predictions were made for each metal with Holt, Brown, and damped methods. The appropriate exponential smoothing model was determined by using the data set of each metal price and the parameters contributing to the model were selected. The exponential smoothing model parameters obtained according to the analysis results are given in Table 2.

Fig. 1
figure 1

Fit of the models and forecast graphs for metal prices

Full size image
Table 2 Exponential smoothing model parameters
Full size table

The accuracy of the models of Holt, Brown, and damped using RMSE, MAE, and MAPE refers to the magnitude of the error rate (errors) of an estimate. The smaller the value of these test statistics, the better the forecasts. The model accuracy values for the exponential smoothing methods were obtained and compared to determine the appropriate model for each metal price. The results of the evaluation of the forecasting models are shown in Table 3.

Table 3 Model accuracy statistic results for the exponential smoothing methods
Full size table

When Table 3 is examined, the smallest RMSE (328.619, 1120.858, 330.834) values for aluminum, copper, and lead metal prices, respectively, were obtained with the Holt model, while the smallest MAE (251.547, 779.263, 221.755) and MAPE (14.106, 17.759, 18.674) values, respectively, were for the damped trend model. The smallest RMSE (21.072), MAE (11.702), and MAPE (15.686) values for the iron metal price were obtained with the damped trend model. For the nickel price, the smallest RMSE (5035.768), MAE (3235.982), and MAPE (23.787) values belong to the Holt model. For the tin price, the smallest RMSE (3688.866) value belongs to the Holt model, while the smallest MAE (2385.927) and MAPE (15.902) values were from the Brown model. For the zinc price, the smallest RMSE (512.261) and MAE (304.111) values belonged to the Holt model, while the lowest MAPE (16.746) was obtained with the damped trend model. In this case, suitable forecasting model was the damped trend model for aluminum, copper, lead, and iron metal prices; the Holt model for nickel and zinc metal prices; and the Brown model for tin metal prices.

Forecasting of metal prices is the third important aspect after modeling and assessment as forecasts are useful to policymakers for contingency planning in a country. Aluminum, copper, lead, iron, nickel, tin, and zinc metal prices were forecasted by using the best-fitted models developed for this purpose. Forecasting up to 2030 was done in this study, and Table 4 and Table 5 show that forecating price for aluminum, copper, lead, iron, nickel, zinc, and tin, respectively.

Table 4 Metal price forecast results for the 2022–2030 period for aluminum, copper, lead, and iron
Full size table
Table 5 Metal price forecast results for the 2022–2030 period for nickel, zinc, and tin
Full size table

The price of aluminum rose from $1639.50 in 1990 to $2172.99 in 2010 and fell to $1704.10 in 2020. It is expected to reach $2482.02 in 2030. Similarly, the price of copper rose from $2661.34 in 1990 to $7538.36 in 2010 and declined to $6174.56 in 2020. It is expected to increase to $11,093.89 by 2030. Lead prices rose from $809.50 in 1990 to $2148.18 in 2010 and then declined to $1824.93 in 2020. It is predicted to drop to $808.56 in 2030. The price of iron rose from $14.05 in 1990 to $146.72 in 2010 and then fell to $108.07 in 2020. It is expected to reach $808.56 by 2030. Nickel prices rose from $8864.00 in 1990 to $21,810.0 in 2010 and fell to $13,790.43 in 2020. It is expected to reach $21,637.86 in 2030. The price of the zinc rose from $1517.92 in 1990 to $2160.35 in 2010 and $2266.77 in 2020. It is expected to rise to $3505.83 in 2030. The price of tin rose from $6085.38 in 1990 to $20,367.25 in 2010 and fell to $17,125.46 in 2020. It is projected to rise to $39,312.7 in 2030.

Conclusions

This study presents an analysis of the dynamics of real prices for main metals (aluminum, copper, lead, iron, nickel, tin, and zinc) by using yearly data from the period Jan 1990 to Now 2021. Holt, Brown, and damped models, which are exponential smoothing methods within the scope of prediction methods, were applied to the data. The model accuracy values (MSE, MAE, and MAPE) of the exponential smoothing methods were obtained and compared to determine the appropriate model for each metal price. In this study, in addition to exponential smoothing methods, the performances of benchmarks (Mean, Naive) and ARIMA methods were compared in order to determine the appropriate method for the data set. Mean, Naive, and ARIMA methods did not give good results. Since 7 different metal prices were examined in the study, models that did not give good results were not presented. Since presenting all applied models in the study would cause confusion, only suitable models were compared. According to the results obtained, the suitable forecasting model was the damped trend model for aluminum, copper, lead, and iron metal prices; the Holt model for nickel and zinc metal prices; and the Brown model for tin metal prices. Forecasting metal prices is useful for contingency planning by policymakers in countries. Therefore, aluminum, copper, lead, iron, nickel, tin, and zinc metal prices were forecasted up to 2030 by using the best-fitted models developed for this purpose. The prices of aluminum, copper, iron, nickel, zinc, and tin are expected to reach $2482.02, $11,093.89, $808.56, $21,637.86, $3505.83, and $39,312.7 in 2030, respectively. However, the lead price is predicted to drop to $808.56 in 2030.

Metal price movements are a key source of macroeconomic volatility in Emerging Markets and Developing Economies (Jacks et al. 2011). Metals, such as tin and copper, are critical inputs for some sectors (e.g., tin, in the electronic industry), and are important for the small number of countries that produce or export them. In addition, with the technological progress, metals are indispensable in the production cycle. Therefore, the estimation of metal prices is important for both the producing countries and the world economy. The results of the analysis in this paper provide some interesting insights for industrial advancement and will shed light on the preliminary cost analyses of some detectors. In addition, this study will encourage and stimulate further research on this vital issue, which is important for the development of countries.