Superlinear solutions of sublinear fractional differential equations and regular variation

Abstract

We consider a sublinear fractional equation of the order in the interval (1, 2). We give conditions guaranteeing that this equation possesses asymptotically superlinear solutions. We show that all of these solutions are regularly varying and establish precise asymptotic formulae for them. Further we prove non-improvability of the conditions. In addition to the asymptotically superlinear solutions we discuss also other classes of solutions, some of them having no ODE analogy. In the very special case, when the coefficient is asymptotically equivalent to a power function and the order of the equation is 2, we get known results in their full generality. We reveal substantial differences between the integer order and non-integer order case. Among other tools, we utilize the fractional Karamata integration theorem and the fractional generalized L’Hospital rule which are proved in the paper. Several examples illustrating our results but serving also in alternative proofs are given too. We provide also numerical simulations.

1 Introduction

We study asymptotic properties of solutions to the fractional differential equation of the form

$$\begin{aligned} {\mathcal {D}}^{\alpha +1}y=p(t)\varPhi _\gamma (y), \end{aligned}$$

(1.1)

$t\in [0,\infty )$, where $\varPhi _\gamma (u)=|u|^{\gamma }{\text {sgn}} u$, $\gamma \in (0,1)$ (the sublinearity condition), p is a continuous function on $[0,\infty )$, positive on $(0,\infty )$, and $\alpha \in (0,1)$. Thus the order of the equation lies in the interval (1, 2). One of our main results says that if p is regularly varying, then asymptotically superlinear solutions are regularly varying; all these concepts are recalled below in this section. For these solutions asymptotic formulae are established and some of their properties are discussed. In order to put the results into a broader context, also some other classes of solutions are treated. The conditions which are involved in the theorems are sharp and shows dependence on $\alpha$. If we formally set $\alpha = 1$, then we obtain the known results for the second order equation

$$\begin{aligned} y''=p(t)\varPhi _\gamma (y). \end{aligned}$$

(1.2)

On the other hand, in some instances we encounter new phenomena occurring only in purely fractional case. Note that for historical reasons, (1.2) is sometimes called Emden–Fowler type or Lane–Emden type or Thomas–Fermi type equation, but it appears also in another applications. Our equation (1.1) can be understood as a fractional extension of these models. Besides, equation (1.1) can be considered also in the framework of space-fractional diffusion equations, which are studied very extensively in the last years, see, e.g., [7].

By ${\mathcal {D}}^\beta$, $\beta >0$, we mean the Caputo fractional differential operator defined as ${\mathcal {D}}^\beta ={\mathcal {I}}^{\lceil \beta \rceil -\beta }{\mathcal {D}}^{\lceil \beta \rceil }$, where ${\mathcal {D}}^{n}$, $n\in \mathbb {N}$, is the classical integer order differential operator and $\lceil \cdot \rceil$ denotes the upper integer part. The symbol ${\mathcal {I}}^\beta$, $\beta >0$, denotes the Riemann–Liouville fractional integral operator and is defined by

$$\begin{aligned} {\mathcal {I}}^\beta f(t)=\frac{1}{\varGamma (\beta )}\int _0^t(t-s)^{\beta -1}f(s)\,{\textrm{d}}s, \end{aligned}$$

$t\ge 0$, where $\varGamma$ is the Gamma function. For $\beta =0$, we set ${\mathcal {I}}^0 = {\text {id}}$, the identity operator. As the main sources of basic information on fractional calculus, we use the monographs [6, 21].

By a solution y of (1.1) we mean a function $y\in C^1[0,\infty )$ such that ${\mathcal {D}}^{\alpha +1}y\in C[0,\infty )$ and y(t) satisfies (1.1) for all $t\in [0,\infty )$.

As usually, for positive f, g, the relations $f(t)\sim g(t)$ as $t\rightarrow \infty$, $f(t)\asymp g(t)$ as $t\rightarrow \infty$, $f(t)=o(g(t))$ as $t\rightarrow \infty$, and $f(t)=\mathcal {O}(g(t))$ as $t\rightarrow \infty$ mean $\lim _{t\rightarrow \infty }f(t)/g(t)=1$, $M_1 g(t)\le f(t)\le M_2 g(t)$ for large t and some $M_1>0,M_2>0$, $\lim _{t\rightarrow \infty }f(t)/g(t)=0$, and $f(t)\le M g(t)$ for large t and some $M>0$, respectively.

We are interested particularly in existence and asymptotic behavior of asymptotically superlinear solutions of (1.1), i.e., the solutions y satisfying $\lim _{t\rightarrow \infty } y'(t)=\infty$; in the ODE literature sometimes called strongly increasing solutions or fast growing solutions. The term superlinear is justified by the fact that $\lim _{t\rightarrow \infty }y(t)/t=\lim _{t\rightarrow \infty }y'(t)=\infty$. We introduce the notation for the set of asymptotically superlinear solutions by

$$\begin{aligned} \mathcal {ASL}:=\left\{ y: y \text { is a solution of (1.1), } \lim _{t\rightarrow \infty }y'(t)=\infty \right\} . \end{aligned}$$

It is easy to see that $y\in \mathcal {ASL}$ is eventually positive and eventually increasing. Sometimes we will deal with $\mathcal {ASL}$ solutions which are positive and increasing on the entire interval (and possibly start with the zero value), thus with the solutions belonging to $\mathcal {ASL}^+$, where

$$\begin{aligned} \begin{aligned} \mathcal {ASL}^+:=\big \{&y\in \mathcal {ASL}: y(t)>0 \text { on } [0,\infty ) \\ {}&\text { with } y'(0)\ge 0 \text { or } y(t)>0 \text { on } (0,\infty ) \text { with } y'(0)> 0\big \}. \end{aligned} \end{aligned}$$

Because of the sign condition on p, there are only two possible types of eventually positive increasing solutions in the ODE case, namely $\mathcal {ASL}$ solutions and asymptotically linear solutions, where the latter ones satisfy $\lim _{t\rightarrow \infty }y(t)/t=y'(t)=\textrm{const}\in (0,\infty )$; in both the cases $y'$ is eventually increasing. As a by product of our considerations, we will reveal that in the purely fractional case, there is much wider variety of the classes of eventually positive increasing solutions, see in particular Remark 2. For instance, one can have a positive increasing solution y with $\lim _{t\rightarrow \infty }y'(t)=0$ or even with $0=\liminf _{t\rightarrow \infty }y'(t)< \limsup _{t\rightarrow \infty }y'(t)=\infty$; such a behavior is excluded in the ODE case under the given setting. Note also that in contrast to the integer order case, if y is a positive solution of (1.1), then $y'$ does not need to be increasing and even under quite reasonable setting, its behavior can be complex.

It could seem that asymptotically (super)linear behavior is not peculiar to fractional order equations. But this conclusion is not true. Indeed, equation (1.1) can be written as system (4.1) where $\beta =1$, $q(t)=1$, and $\lambda =1$. In accordance with the ODE case, let us define a strongly increasing solution (x, u) of (4.1) as the solution satisfying $\lim _{t\rightarrow \infty }x(t)=\lim _{t\rightarrow \infty }u(t)=\infty$. If now $y=u$, then $y'=u'=x$, and so $\lim _{t\rightarrow \infty }y(t)=\lim _{t\rightarrow \infty }y'(t)=\infty$, thus $y\in \mathcal {ASL}$ (note that the systems where one derivative is fractional and another one is of integer order commonly appear in applications, see, e.g., [26]). In fact, such a behavior belongs among the natural ones because we consider just the Caputo operator which has the property ${\mathcal {D}}^{\alpha +1}={\mathcal {D}}^\alpha {\mathcal {D}}^1$. Anywise, this problem can be considered in a broader context of systems and derivatives in the Caputo as well as the Riemann-Liouville sense. Introducing an extension of the concept of strongly increasing solutions, we can study in parallel $\mathcal {ASL}$ solutions along with some other types of strongly increasing solutions. These ideas are described in more details at the end of the next section where we present directions for a future research.

Asymptotic analysis of the ODE of the form (1.2) has a long history. Here we mention several of the works which stay at the origin of our results. Bellman in his monograph [2] provided asymptotic formulae for solutions under the condition $p(t)=Ct^\delta$, $C\in (0,\infty )$. Kamo and Usami in [15, 16] made an analysis under the relaxed condition $p(t)\sim Ct^\delta$ as $t\rightarrow \infty$, $C\in (0,\infty )$. In [14, 24, 28], another substantial generalization was made in the sense that $p(t)\sim Ct^\delta$ as $t\rightarrow \infty$ was replaced by $p(t)=t^\delta L_p(t)$, where $L_p$ is a slowly varying function (defined below). Note that in contrast to the condition $p(t)\sim Ct^\delta$ as $t\rightarrow \infty$, the presence of a slowly varying component $L_p$ enables us to include a wider variety of qualitatively different situations. As will be shown, this concerns, among others, somehow critical (borderline) settings. In fact, we will observe that the purely fractional case even underlines the possibilities offered by the theory regular variation, and thanks to this framework new phenomena are revealed.

As for asymptotic theory of fractional differential equations, quite often the situations are studied where coefficients and/or solutions are close to power functions, in the sense of $=t^\vartheta$ or $\sim t^\vartheta$ or $o(t^\vartheta )$ or $\mathcal {O}(t^\vartheta )$ for $t\rightarrow \infty$. See [1, 8, 18, 20] for the equations of order less than one and [5, 11, 12, 17, 19, 25, 27] for the equations of order greater than one; note that the mentioned papers [17, 19] contain also a worthwhile survey of related results.

As will emerge from our observations, thanks to the concept of regular variation one can substantially generalize the power behavior setting and at the same time one can provide quite precise information about behavior of solutions. In contrast to the ODE theory (which is surveyed in the monographs [23] and [29]), regular variation seems to occur in studying the non-integer case only very rarely and more or less marginally, see [13, 22, 32, 33], although with no doubts it can serve as a powerful tool for investigation of asymptotic properties to fractional differential equations.

Our results extend in particular the ones obtained for ODEs in [16] in two ways: By fractional setting instead of integer-order one, and by regularly varying setting instead of asymptotically power one. As far as we know these type of results for nonlinear equations of order between 1 and 2 have not occurred in the literature. Moreover, we believe that the methods and observations used in our paper have a potential to be applied in a broader context and in a systematic study related to asymptotic descriptions of fractional equations of various types.

Next we recall some elements of the theory of regular variation; for more information see the monographs [3, 10, 31]. A measurable function $f:[a,\infty )\rightarrow (0,\infty )$ is called regularly varying (at infinity) of index $\vartheta$ if

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{f(\lambda t)}{f(t)}=\lambda ^\vartheta \quad \text {for every }\lambda \in (0,\infty ); \end{aligned}$$

(1.3)

we write $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$. If the limit in (1.3) is equal to 1, we speak about slowly varying functions; we write $f\in {\mathcal{S}\mathcal{V}}$, thus ${\mathcal{S}\mathcal{V}}={\mathcal{R}\mathcal{V}}(0)$. If $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$, then relation (1.3) holds uniformly on each compact $\lambda$-set in $(0,\infty )$ (this is the so-called Uniform convergence theorem, see, e.g., [3]). It is easy to see that $f \in {\mathcal{R}\mathcal{V}}(\vartheta )$ if and only if there exists a function $L \in {\mathcal{S}\mathcal{V}}$ such that $f(t) = t^{\vartheta } L(t)$ for every t. The slowly varying component of $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$ will be denoted by $L_f$, i.e.,

$$\begin{aligned} L_f(t):=\frac{f(t)}{t^{\vartheta }}, \end{aligned}$$

(1.4)

unless stated otherwise. The so-called Representation theorem (see, e.g., [3]) says the following: $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$ if and only if

$$\begin{aligned} f(t)=\varphi (t)t^\vartheta \exp \left\{ \int _a^t\frac{\psi (s)}{s}\, {\textrm{d}}s\right\} , \end{aligned}$$

(1.5)

$t\ge a$, for some $a>0$, where $\varphi , \psi$ are measurable with $\lim _{t\rightarrow \infty }\varphi (t)=C\in (0,\infty )$ and $\lim _{t\rightarrow \infty }\psi (t)=0$. Selected properties of ${\mathcal{R}\mathcal{V}}$ functions are presented in Propositions 1, 3, 4, and 5.

Among other tools which play an important role in our theory, we would like to underline the following two statements which are proved in the last section. The first one can be understood as a fractional extension of the Karamata integration theorem. Notice that in contrast to the classical Karamata theorem (see Proposition 4), the convergence of the integral is possible also in the case $\vartheta >-1$. One could establish an analogue for the Riemann–Liouville type fractional integral operator involving improper (convergent) integral $\int ^\infty$ which extends applicability of this tool, but this case is not needed in our considerations.

Proposition 1

(Fractional Karamata integration theorem) Let $\beta >0$ and $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$, where $\vartheta >-1$. Then

$$\begin{aligned} {\mathcal {I}}^\beta f(t)\sim \frac{\varGamma (\vartheta +1)}{\varGamma (\vartheta +\beta +1)} t^\beta f(t) \end{aligned}$$

as $t\rightarrow \infty$.

The case $\vartheta =-\beta$, where $0<\beta <1$ deserves a special attention. Indeed, it leads to the formula ${\mathcal {I}}^\beta f(t)\sim \varGamma (1-\beta )L_f(t)$ as $t\rightarrow \infty$, where $L_f$ is the slowly varying component of f. In the integer order case ($\beta =1$) such a formula does not hold (in contrast to the choice $\vartheta \ne -\beta$) since we find ourselves in the critical setting in the Karamata integration theorem (Proposition 4-(iii)). As we will show, this fact has interesting consequences in the framework of the analysis of equation (1.1). A variant of the fractional Karamata theorem is considered also in [32]. Note that the monograph [30] discusses asymptotic expansions of the fractional integral, but only in the case where the expansion involves the power, exponential, and logarithmic terms.

The second tool which is worthy of note is the fractional extension of the following generalized L’Hospital rule (where we assume, in particular, that $\lim _{t\rightarrow \infty }g(t)=\infty$):

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{f'(t)}{g'(t)} \le \liminf _{t\rightarrow \infty }\frac{f(t)}{g(t)} \le \limsup _{t\rightarrow \infty }\frac{f(t)}{g(t)} \le \limsup _{t\rightarrow \infty }\frac{f'(t)}{g'(t)}. \end{aligned}$$

(1.6)

Proposition 2

(Fractional L’Hospital rule) Let $0<\beta <1$, f, g be functions such that $f,g\in C[0,\infty )$, ${\mathcal {D}}^\beta f, {\mathcal {D}}^\beta g\in C(0,\infty )$, $\lim _{t\rightarrow \infty }g(t)=\infty$, and ${\mathcal {D}}^\beta g(t)$ is of one sign for large t. Then

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{{\mathcal {D}}^\beta f(t)}{{\mathcal {D}}^\beta g(t)} \le \liminf _{t\rightarrow \infty }\frac{f(t)}{g(t)} \le \limsup _{t\rightarrow \infty }\frac{f(t)}{g(t)} \le \limsup _{t\rightarrow \infty }\frac{{\mathcal {D}}^\beta f(t)}{{\mathcal {D}}^\beta g(t)}. \end{aligned}$$

It is clear from Proposition 2 that if the limit $\lim _{t\rightarrow \infty }{{\mathcal {D}}^\beta f(t)}/{{\mathcal {D}}^\beta g(t)}$ exists, then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{f(t)}{g(t)} = \lim _{t\rightarrow \infty }\frac{{\mathcal {D}}^\beta f(t)}{{\mathcal {D}}^\beta g(t)}. \end{aligned}$$

The paper is organized as follows. All the results are gathered and accompanied by comments in the next section and all the proofs are postponed into the last section. In Sect. 2 we present, in particular, the condition guaranteeing existence of $\mathcal {ASL}^+$ solution which is regularly varying. We also discuss necessity of the condition and show its optimality. Further we establish a precise asymptotic formula for regularly varying solutions in $\mathcal {ASL}^+$. By means of the so-called Asymptotic equivalence theorem we prove that all asymptotically superlinear solutions are regularly varying (and we establish their asymptotics). It is worthy of note that the method used in the proof of this result would be essentially new even in the integer order case. As already indicated, the next section contains also a series of comments where a particular emphasize is put on revealing differences between the integer order and non integer order case. The most significant differences are summarized at the end of the section where we also indicate directions for a future research. Some examples are provided too.

2 Results, comments, examples

We start with showing that under certain conditions (1.1) possesses a (positive) regularly varying asymptotically superlinear solution.

Theorem 1

Let $p\in {\mathcal{R}\mathcal{V}}(\delta )$, where $\delta \in \mathbb {R}$. Assume

$$\begin{aligned} \alpha +\gamma +\delta \ge 0 \end{aligned}$$

(2.1)

and

$$\begin{aligned} { in\; case\; of\; equality\; in\; (2.1) \;let,\; in\; addition,} \lim _{t\rightarrow \infty }L_p(t)=\infty , \end{aligned}$$

(2.2)

where $L_p$ is the slowly varying component of p. Then $\mathcal {ASL}^+\cap {\mathcal{R}\mathcal{V}}(\vartheta )\ne \emptyset$, where

$$\begin{aligned} \vartheta :=\frac{1+\alpha +\delta }{1-\gamma }. \end{aligned}$$

(2.3)

In addition, the existence of such $y\in \mathcal {ASL}^+\cap {\mathcal{R}\mathcal{V}}(\vartheta )$ is guaranteed that it satisfies any of the initial conditions $y(0)=A,y'(0)=B$, where A, B are given with $A>0,B>0$ or $A>0,B=0$ or $A=0,B>0$.

Remark 1

In [16], it is shown that under the condition $p(t)\sim t^\delta$ as $t\rightarrow \infty$ (which is a very special case of $p\in {\mathcal{R}\mathcal{V}}(\delta )$ when $L_p(t)\sim 1$ as $t\rightarrow \infty$) ODE (1.2) possesses an asymptotically superlinear solution if and only if $1+\gamma +\delta \ge 0$. Looking at Theorem 1, we see that instead of the condition $1+\gamma +\delta \ge 0$, we employ (2.1), i.e., the condition $\alpha +\gamma +\delta \ge 0$ which displays the dependence on the order $\alpha$. Because of $\alpha <1$, condition (2.1) implies $1+\gamma +\delta \ge 0$ but not vice versa. Thus the natural question is whether (2.1) can be relaxed. As we will show later, the answer is no, since (2.1) (along with the assumption on $L_p$) is not only sufficient but also necessary for the existence of asymptotically superlinear solutions in the non-integer case. It is worthy of note that the borderline case $\alpha +\gamma +\delta = 0$ is somehow delicate and solutions can exhibit very interesting behavior when allowing more general assumption $L_p\in {\mathcal{S}\mathcal{V}}$ instead of $L_p(t)\sim 1$ as $t\rightarrow \infty$. See, in particular, Remark 2.

Remark 2

As already indicated, in contrast to very special setting for p in ODE (1.2) studied in [16], we allow p to be merely regularly varying. This enables us to reach very interesting conclusions. The role of the slowly varying component $L_p$ becomes highly important especially in the critical case $\alpha +\gamma +\delta =0$. However, first let us observe that even when $L_p(t)\sim 1$ as $t\rightarrow \infty$, in the critical case we come to the discrepancy between the integer order and the non-integer case since then all positive solutions of (1.2) are asymptotically superlinear (see [16, Theorem 4.2]) while (1.1) has no $\mathcal {ASL}$ solution (see Theorem 6) and on the other hand, (1.1) possesses a solution y which is close to the asymptotically linear one, i.e., $y(t)\asymp x(t)$ as $t\rightarrow \infty$, where x is some (positive) function satisfying $\lim _{t\rightarrow \infty }x(t)/t=\lim _{t\rightarrow \infty }x'(t)=\textrm{const}\in (0,\infty )$. Indeed, we obtain such a solution practically by the same way as in the proof of Theorem 1, i.e., as a fixed point of the operator ${\mathcal {T}}u=A+{\mathcal {I}}^{\alpha +1}p\varPhi _{\gamma }(u),$ $A>0$, in the set

$$\begin{aligned} \varOmega =\left\{ u\in C[0,\infty ): K_1tL_p^{\frac{1}{1-\gamma }}(t)\le u(t)\le K_2tL_p^{\frac{1}{1-\gamma }}(t) \right\} , \end{aligned}$$

$K_1,K_2$ being as in the proof. Having a solution y in $\varOmega$, from $y'=({\mathcal {T}}y)'={\mathcal {I}}^\alpha py^\gamma$, utilizing the fractional Karamata integration theorem (Proposition 1), we obtain

$$\begin{aligned} \begin{aligned} y'(t)&=\left( {\mathcal {I}}^\alpha py^\gamma \right) (t)\asymp \left( {\mathcal {I}}^\alpha p(t)t^\gamma L_p^{\frac{\gamma }{1-\gamma }}(t)\right) (t)\\&=\left( {\mathcal {I}}^\alpha t^{-\alpha }L_p^{\frac{1}{1-\gamma }}(t)\right) (t)\sim \varGamma (1-\alpha )L_p^{\frac{1}{1-\gamma }}(t) \end{aligned} \end{aligned}$$

as $t\rightarrow \infty$. Thus $y'(t)\asymp L_p^{\frac{1}{1-\gamma }}(t)$ as $t\rightarrow \infty$. If now $L_p(t)\rightarrow 1$ (or to a positive constant) as $t\rightarrow \infty$ we come to the relation $y(t)\asymp x(t)$ as $t\rightarrow \infty$; in fact, we have $y'(t)\asymp 1$ and $y(t)\asymp t$ as $t\rightarrow \infty$.

Let us examine the role of $L_p$ in more details and in a broader context. Note that the relation $y'(t)\asymp L_p^{\frac{1}{1-\gamma }}(t)$ as $t\rightarrow \infty$ was established in the previous section under the general condition $L_p\in {\mathcal{S}\mathcal{V}}$. If now $L_p(t)\not \rightarrow \infty$ as $t\rightarrow \infty$, then $y'(t)\not \rightarrow \infty$ as $t\rightarrow \infty$, and thus y is increasing but not strongly, so it is not $\mathcal {ASL}$; note that $\lim _{t\rightarrow \infty }y(t)=\infty$ holds by Proposition 3 since $y(t)\asymp tL_p^{\frac{1}{1-\gamma }}(t)$ as $t\rightarrow \infty$ and can therefore be estimated from below by a regularly varying function of index 1. This behavior is in accordance with the necessary condition (Theorem 6). It is well known in the second order ODE case (see, e.g., [16]) that the only positive unbounded solutions of (1.2) are either asymptotically linear ($\lim _{t\rightarrow \infty }y(t)/t=\lim _{t\rightarrow \infty }y'(t)=\textrm{const}\in (0,\infty )$) or asymptotically superlinear ($\lim _{t\rightarrow \infty }y(t)/t=\lim _{t\rightarrow \infty }y'(t)=\infty$). Here we encounter a substantial difference between the integer and non-integer case. Indeed, for fractional equations, in addition to the just mentioned classes, one can have another (nonempty) classes which do not occur in the ODE case under the given general conditions (i.e., $\gamma <1$ and $p>0$). For example, if $\lim _{t\rightarrow \infty }L_p(t)=0$, then we obtain a solution y with $\lim _{t\rightarrow \infty }y(t)=\infty$ and $\lim _{t\rightarrow \infty }y'(t)=0$. Since slowly varying functions permit even the behavior like $\liminf _{t\rightarrow \infty }L_p(t)=0$, $\limsup _{t\rightarrow \infty }L_p(t)=\infty$, there exist solutions monotonically tending to infinity with the derivative behaving just in this wild way. An example of the slowly varying component causing such behavior is $L_p(t)=\exp \{(\ln t)^{1/3}\cos (\ln t)^{1/3}\}$.

Another phenomenon which occurs only in the purely fractional case is the coexistence of solutions in different asymptotic classes of increasing solutions. Let us still assume $\alpha +\delta +\gamma =0$ and take $L_p\in {\mathcal{S}\mathcal{V}}$ such that $\lim _{t\rightarrow \infty }L_p(t)=0$. In the previous paragraph we showed existence of the solution y such that $\lim _{t\rightarrow \infty }y(t)=\infty$ and $\lim _{t\rightarrow \infty }y'(t)=0$. Under the same setting consider now the operator ${\mathcal {T}}$ in the form ${\mathcal {T}}u=Bt+{\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (u)$ on the set $\varOmega =\left\{ u\in C[0,\infty ): M_1t\le u(t)\le M_2t \right\}$ where $M_1,M_2$ are certain positive constants taken similarly as in the final part of the proof of Theorem 1. Then there exists a fixed point $z\in \varOmega$, i.e. a solution of (1.1), satisfying $z(t)\rightarrow \infty$ and $z'(t)\sim B$ as $t\rightarrow \infty$ since $z'(t)= B+({\mathcal {I}}^\alpha pz^\gamma )(t)$ and

$$\begin{aligned}0<({\mathcal {I}}^\alpha pz^\gamma )(t)\le M_2^\gamma ({\mathcal {I}}^\alpha t^{\delta +\gamma }L_p)(t)\sim M_2^\gamma \varGamma (1-\alpha )L_p(t)\rightarrow 0\end{aligned}$$

as $t\rightarrow \infty$. Thus we have obtained two solutions where one is asymptotically linear while the other one is unbounded with the derivative tending to zero (the so-called intermediate solution).

The next theorem says that all regularly varying $\mathcal {ASL}$ solutions satisfy certain asymptotic formula.

Theorem 2

Let $p\in {\mathcal{R}\mathcal{V}}(\delta )$, $\delta \in \mathbb {R}$. If $y\in \mathcal {ASL}\cap {\mathcal{R}\mathcal{V}}(\varrho )$, where $\varrho \ge -(\delta +\alpha )/\gamma$, then

$$\begin{aligned} y(t)\sim {\widetilde{K}}^{\frac{1}{1-\gamma }}Q(t) \end{aligned}$$

(2.4)

as $t\rightarrow \infty$, where

$$\begin{aligned} Q(t):=t^{\frac{1+\alpha }{1-\gamma }}p^{\frac{1}{1-\gamma }}(t) \end{aligned}$$

(2.5)

and

$$\begin{aligned} \widetilde{K}:=\frac{\varGamma (\delta +\gamma \varrho +1)}{\varGamma (\delta +\gamma \varrho +\alpha +2)}. \end{aligned}$$

Moreover, $\varrho =\vartheta$,

$$\begin{aligned} {\widetilde{K}}=K:=\frac{\varGamma (\vartheta -\alpha )}{\varGamma (\vartheta +1)}, \end{aligned}$$

(2.6)

and the condition $\varrho \ge -(\delta +\alpha )/\gamma$ becomes (2.1).

Remark 3

Assume that $p(t)\sim t^\delta$ as $t\rightarrow \infty$. Supposing $1+\delta +\gamma >0$, if we formally set $\alpha = 1$, then (2.4) reduces to

$$\begin{aligned} y(t)\sim \left( \frac{t^{\delta +2}}{\vartheta (\vartheta -1)}\right) ^{\frac{1}{1-\gamma }} \end{aligned}$$

as $t\rightarrow \infty$, which is exactly the formula obtained for $\mathcal {ASL}$ solutions of ODE (1.2) in this special setting in [16]. This somehow demonstrates the sharpness of our result. Note that we have obtained this formula for (1.1) also in the borderline case $\alpha +\delta +\gamma =0$ when $p\in {\mathcal{R}\mathcal{V}}(\delta )$ with $L_p(t)\rightarrow \infty$ as $t\rightarrow \infty$ which is possible thanks to the fractional Karamata integration theorem in the critical case (see the comment after Proposition 1) and has no integer order analogy.

In the following theorem we offer an asymptotic estimate for all $\mathcal {ASL}$ solutions under relaxed conditions.

Theorem 3

Let there exist $q\in {\mathcal{R}\mathcal{V}}(\delta )$, where $\delta >-1$ satisfies $\alpha +\gamma +\delta >0$, such that $q(t)\le p(t)$ for large t.

If $y\in \mathcal {ASL}$, then

$$\begin{aligned} y(t)=\mathcal {O}\left( ({\mathcal {I}}^{\alpha +1}p)^{\frac{1}{1-\gamma }}(t)\right) \end{aligned}$$

(2.7)

as $t\rightarrow \infty$.

Specially (see the final part of the proof of Theorem 3), if $p\in {\mathcal{R}\mathcal{V}}(\delta )$ in the previous theorem, then

$$\begin{aligned} y(t)=\mathcal {O}(Q(t)) \end{aligned}$$

(2.8)

as $t\rightarrow \infty$, where Q is defined by (2.5). However, as we will see, the result in this case can be substantially improved. Indeed, thanks to the next statement (the so-called asymptotic equivalence theorem), if the coefficient p is regularly varying, then regular variation along with a precise asymptotic formula (rather than only one-sided asymptotic estimate) is guaranteed for all elements in $\mathcal {ASL}^+$. Along with (1.1) consider the equation

$$\begin{aligned} {\mathcal {D}}^{\alpha +1}x=q(t)\varPhi _\gamma (x), \end{aligned}$$

(2.9)

$t\in [0,\infty )$, where q positive and continuous on $[0,\infty )$. Let the set $\mathcal {ASL}^+_q$ for (2.9) be defined analogously as the set $\mathcal {ASL}^+=:\mathcal {ASL}^+_p$ for equation (2.9).

Theorem 4

(Asymptotic equivalence theorem) Let $x\in \mathcal {ASL}^+_q$ and $y\in \mathcal {ASL}^+_p$. Then the following hold:

• (i) If $p(t)\asymp q(t)$ as $t\rightarrow \infty$, then $y(t)\asymp x(t)$ as $t\rightarrow \infty$.

• (ii) If $p(t)\sim q(t)$ as $t\rightarrow \infty$, then $y(t)\sim x(t)$ as $t\rightarrow \infty$.

The next theorem is one of the most important conclusions of our paper.

Theorem 5

Assume that (2.1) with (2.2) hold. Let $p\in {\mathcal{R}\mathcal{V}}(\delta )$, $\delta \in \mathbb {R}$. Then $\emptyset \ne \mathcal {ASL}^+\subset {\mathcal{R}\mathcal{V}}(\vartheta )$ and each $y\in \mathcal {ASL}^+$ satisfies $y(t)\sim K^{\frac{1}{1-\gamma }}Q(t)$ as $t\rightarrow \infty$, where $\vartheta$ is defined by (2.3) and K, Q are defined in Theorem 2.

Remark 4

(i) If the assumption $p\in {\mathcal{R}\mathcal{V}}(\delta )$ in Theorem 5 is relaxed to $p(t)\asymp q(t)$ as $t\rightarrow \infty$, where q is some regularly varying function of index $\delta$, then the asymptotic formula is modified to $y(t)\asymp Q(t)$ as $t\rightarrow \infty$.

(ii) Since we work with superlinear solutions in Theorem 5, in view of Theorem 6, conditions (2.1), (2.2) are not restrictive.

The next corollary easily follows from Theorem 5 and Remark 4. An alternative way of its proof can be based on Example 1. If we set $\alpha =1$, then the corollary yields the result for ODE (1.2) in [16], see also Remark 3. However our statement is an extension of that result not only in the sense of fractional order but also in the sense of the presence of a general ${\mathcal{S}\mathcal{V}}$ component of p; for the analysis of sublinear ODEs in the framework of regular variation see also [14, 24, 28, 29].

Corollary 1

Let $\delta \in \mathbb {R}$, $\alpha +\gamma +\delta >0$, and y be a strongly increasing solution of (1.1), positive on $[0,\infty )$, with $y'(0)\ge 0$. If $p(t)\sim Ct^\delta$ $[p(t)\asymp t^\delta ]$ as $t\rightarrow \infty$, for some $C>0$, then $y(t)\sim (KC)^{\frac{1}{1-\gamma }}t^\vartheta$ $[y(t)\asymp t^\vartheta ]$ as $t\rightarrow \infty$.

Remark 5

Note that the condition $\alpha +\gamma +\delta >0$ in the previous corollary cannot be replaced by (2.1). Indeed, if we have the critical case $\alpha +\gamma +\delta =0$ and $p(t)\sim C t^\delta$ as $t\rightarrow \infty$, $C\in (0,\infty )$, then, in particular $\limsup _{t\rightarrow \infty }L_p(t)<\infty$, and thus the condition which is necessary for existence of an $\mathcal {ASL}$ solution (see Theorem 6) is not fulfilled. Here we encounter another difference between the integer order and non-integer order case. Indeed, it is known (see [16]), that if $p(t)\sim t^\delta$ as $t\rightarrow \infty$, where $1+\gamma +\delta =0$, then every positive solution y of (1.2) has the from $y(t)\sim (1-\gamma )^{1/(1-\gamma )}t(\ln t)^{1/(1-\gamma )}$ as $t\rightarrow \infty$ and, in particular is $\mathcal {ASL}$. On the other hand, from Remark 2 it follows under the critical case $\alpha +\gamma +\delta =0$, if $p(t)\asymp t^\delta$, then $y(t)\asymp t$ and $y'(t)\asymp 1$ as $t\rightarrow \infty$, thus y is not $\mathcal {ASL}$.

The next theorem provides a necessary condition for existence of $\mathcal {ASL}$ solutions. As a consequence we thus demonstrate non-improvability of the conditions posed on $\alpha +\gamma +\delta$ in the above presented results.

Theorem 6

Let $p\in {\mathcal{R}\mathcal{V}}(\delta )$, $\delta \in \mathbb {R}$. If $\mathcal {ASL}\ne \emptyset$, then $\alpha +\gamma +\delta \ge 0$ where in case of equality necessarily $\limsup _{t\rightarrow \infty }L_p(t)=\infty$.

Remark 6

A closer examination of the proof of Theorem 6 shows, that for a general p, i.e., not necessarily regularly varying, one can derive necessary condition in the integral form

$$\begin{aligned} \limsup _{t\rightarrow \infty } ({\mathcal {I}}^\alpha P_\gamma )(t)=\infty , \end{aligned}$$

where

$$\begin{aligned} P_\gamma (t):=t^\gamma p(t). \end{aligned}$$

(2.10)

Looking at Theorem 6, we see that if $p\in {\mathcal{R}\mathcal{V}}(\delta )$, then not only in the case $\alpha +\gamma +\delta >0$ but also in the critical case $\alpha +\gamma +\delta = 0$ one can have a necessary condition in the non-integral form. The latter case has no integer order analogy; the necessary condition for equation (1.2) takes the form $\int ^\infty p(t)/t\,{\textrm{d}}t=\infty$ and cannot be simplified by “removing” the integral because of the critical setting in Proposition 4.

In the following example we find an exact solution of (1.1) in a certain special case which can be used in an alternative proof of Corollary 1.

Example 1

Let $\delta$ satisfy $\alpha +\gamma +\delta >0$ and $\vartheta$ be defined by (2.3). Consider equation (2.9) where

$$\begin{aligned} q(t)=CI_t(1-\alpha ,\vartheta -1)(t+1)^\delta , \end{aligned}$$

(2.11)

$C\in (0,\infty )$, where $I_t(a,b)$ is the regularized Beta function defined by $I_t(a,b)=B(t;a,b)/B(a,b)$ with B(a, b) being the Beta function and B(t; a, b) being the incomplete Beta function; the function B(t; a, b) is considered here in the form $B(t;a,b)=\int _0^t x^{a-1}/(x+1)^{a+b}\,{\textrm{d}}x$, thus $B(\infty ;a,b)=B(a,b)$. We claim that

$$\begin{aligned} x(t)=C^{\frac{1}{1-\gamma }}K^{\frac{1}{1-\gamma }}(t+1)^\vartheta \end{aligned}$$

(2.12)

is a solution of (2.9) with the q defined by (2.11). Indeed,

$$\begin{aligned} {\mathcal {D}}^{\alpha +1}x(t)=(CK)^{\frac{1}{1-\gamma }}\frac{\vartheta (\vartheta -1)}{\varGamma (1-\alpha )} \int _0^t(t-s)^{-\alpha }(s+1)^{\vartheta -2}\,{\textrm{d}}s. \end{aligned}$$

Employing the substitution $x=(t-s)/(s+1)$ in the integral, we obtain

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^{\alpha +1}x(t)&=\frac{(CK)^{\frac{1}{1-\gamma }}\vartheta (\vartheta -1)}{\varGamma (1-\alpha )} (t+1)^{\vartheta -\alpha -1}\int _0^t\frac{x^{-\alpha }}{(x+1)^{\vartheta -\alpha }}\,{\textrm{d}}x\\&=\frac{(CK)^{\frac{1}{1-\gamma }}\vartheta (\vartheta -1)}{\varGamma (1-\alpha )} (t+1)^{\vartheta \gamma +\delta }B(t;1-\alpha ,\vartheta -1)\\&=(CK)^{\frac{\gamma }{1-\gamma }}(t+1)^{\gamma \vartheta }CK (t+1)^{\delta }\frac{\vartheta (\vartheta -1)}{\varGamma (1-\alpha )} B(t;1-\alpha ,\vartheta -1)\\&= q(t)x^\gamma (t), \end{aligned} \end{aligned}$$

where we used the identity $K\vartheta (\vartheta -1)/\varGamma (1-\alpha )=1/B(1-\alpha ,\vartheta -1)$. It is clear that $x\in \mathcal {ASL}^+_q$. Moreover, $x(t)\sim (CK)^{\frac{1}{1-\gamma }}t^\vartheta$ and $q(t)\sim C t^\delta$ as $t\rightarrow \infty$. Applying now Theorem 4 with our particular choice of q, we get the statement of Corollary 1.

The next example treats the borderline case $\alpha +\gamma +\delta =0$.

Example 2

Consider equation (2.9) where

$$\begin{aligned} q(t)= & {} C\frac{G(t)}{(t+1)^{\alpha +\gamma }\ln ^\gamma (t+1)},\nonumber \\ G(t):= & {} \int _0^t\frac{1}{\tau ^\alpha (\tau +1)^{1-\alpha }}\,{\textrm{d}}\tau ,\ C\in (0,\infty ). \end{aligned}$$

(2.13)

We claim that

$$\begin{aligned} x(t)=(C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}(t+1)\ln (t+1) \end{aligned}$$

(2.14)

is a solution of (2.9). Indeed, first note that the substitution $\tau =(t-s)/(s+1)$ in the integral yields

$$\begin{aligned} {\mathcal {I}}^{1-\alpha }\frac{1}{t+1}=\frac{1}{\varGamma (1-\alpha )}\int _0^t(t-s)^{-\alpha } (s+1)^{-1}\,{\textrm{d}}s=\frac{1}{\varGamma (1-\alpha )}(t+1)^{-\alpha }G(t). \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} ({\mathcal {D}}^{\alpha +1}x)(t)&=({\mathcal {I}}^{1-\alpha }{\mathcal {D}}^2x)(t)= (C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}({\mathcal {I}}^{1-\alpha }(t+1)^{-1})(t)\\&=q(t) (C\varGamma (1-\alpha ))^{\frac{\gamma }{1-\gamma }} (t+1)^\gamma \ln ^\gamma (t+1)=q(t)x^\gamma (t). \end{aligned} \end{aligned}$$

We have $\lim _{t\rightarrow \infty }x(t)=\infty$ and

$$\begin{aligned}\lim _{t\rightarrow \infty }x'(t)= \lim _{t\rightarrow \infty }(C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}(\ln (t+1)+1)=\infty , \end{aligned}$$

and thus x is $\mathcal {ASL}_q$ (where $\mathcal {ASL}_q$ denotes the set of asymptotically superliar solutions of (2.9)). It is easy to see that $G(t)\sim \ln t$ as $t\rightarrow \infty$. Consequently, as $t\rightarrow \infty$,

$$\begin{aligned} q(t)\sim \frac{C\ln ^{1-\gamma }t}{t^{\alpha +\gamma }}\in {\mathcal{R}\mathcal{V}}(-\alpha -\gamma ), \end{aligned}$$

and so we are indeed in the borderline case $\alpha +\gamma +\delta =0$. Since $\ln t\in {\mathcal{S}\mathcal{V}}$, we have $x\in \mathcal {ASL}_q\cap {\mathcal{R}\mathcal{V}}(1)$. According to Theorem 2 (formula (2.4)) it should hold $x(t)\sim (K t^{1+\alpha }q(t))^{\frac{1}{1-\gamma }}$ as $t\rightarrow \infty$ where $K=\varGamma (1-\alpha )/\varGamma (2)=\varGamma (1-\alpha )$, which is indeed true since

$$\begin{aligned} x(t)\sim (C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}t\ln t=\left( KCt^{1+\alpha }\frac{\ln ^{1-\gamma }t}{t^{\alpha +\gamma }}\right) ^{\frac{1}{1-\gamma }} \sim (K t^{1+\alpha }q(t))^{\frac{1}{1-\gamma }} \end{aligned}$$

as $t\rightarrow \infty$. Moreover, combining these observations with Theorem 4 (the asymptotic equivalence theorem), we obtain that if $p(t)\sim Ct^{-\alpha -\gamma }\ln ^{1-\gamma }t$ as $t\rightarrow \infty$ for some $C>0$ and $y\in \mathcal {ASL}^+$, then

$$\begin{aligned} y(t)\sim (C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}t\ln t \end{aligned}$$

(2.15)

as $t\rightarrow \infty$. Thanks to our previous results this statement can be obtained in a different manner – without knowing an exact solution of the auxiliary equation. Indeed, having $L_p(t)\sim C\ln ^{1-\gamma }t\rightarrow \infty$ as $t\rightarrow \infty$, the assumptions of Theorem 5 are fulfilled, thus it can be then utilized to guarantee that each $y\in \mathcal {ASL}^+$ satisfies $y(t)\sim K^{\frac{1}{1-\gamma }}Q(t)$ as $t\rightarrow \infty$. Since $Q(t)\sim t\ln t$ as $t\rightarrow \infty$ and $\vartheta =1$, we get (2.15).

Fig. 1

(Simulation 1, the case $\alpha +\gamma +\delta >0$) The former picture illustrates the tendency for mutual asymptotic equivalence among the exact solution x and the numerically obtained solutions y, z with different initial conditions. The latter picture illustrates the tendency for superlinearity of the solutions x, y, z

3 Numerical simulations

The simulations were performed using FDE12 Matlab code. This code was created for numerical solving fractional differential equations, for details see [9].

Simulation 1 The first simulation is pertinent to Example 1 (Fig. 1). We consider equation (2.9) with the coefficient q(t) defined by (2.11), where we take $\alpha =1/2$, $\gamma =1/5$, $\delta =1/10$, and $C=1$. Then $\alpha +\gamma +\delta >0$, thus condition (2.1) is satisfied. We consider three solutions of (2.9). The solution x is the exact solution given by (2.12). The solutions y and z are obtained numerically and their initial conditions differ from the values of x(0) and $x'(0)$. More precisely, we have $x(0)=M$ and $x'(0)=\vartheta M$, where $M:=(CK)^{\frac{1}{1-\gamma }}\approx 0.36$ and $\vartheta =2$. We set $y(0)=4M/3$, $y'(0)=\vartheta M+1/2$, $z(0)=M+1/2$, and $z'(0)=0$.

Simulation 2 This simulation is pertinent to Example 2 (Fig. 2). We consider equation (2.9) with the coefficient q(t) defined by (2.13), where we take $\alpha =4/5$, $\gamma =3/10$, and $C=1$. Since $q\in {\mathcal{R}\mathcal{V}}(-\alpha -\gamma )$, we have $\alpha +\gamma +\delta =0$, thus condition (2.1) is satisfied with the borderline value. We again consider three solutions of (2.9). The solution x is the exact solution given by (2.14). The solutions y and z are obtained numerically and their initial conditions differ from the values of x(0) and $x'(0)$. More precisely, we have $x(0)=0$ and $x'(0)=\vartheta N$, where $N:=(C\varGamma (1-\alpha ))^{\frac{1}{1-\gamma }}\approx 8.82$ and $\vartheta =2$. We set $y(0)=1$, $y'(0)=N-1/10$, $z(0)=1/5$, and $z'(0)=N+1/10$.

Fig. 2

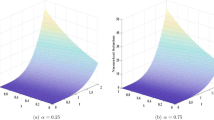
(Simulation 2, the case $\alpha +\gamma +\delta =0$) The former picture illustrates the tendency for mutual asymptotic equivalence among the exact solution x and the numerically obtained solutions y, z with different initial conditions. The latter picture illustrates the tendency for superlinearity of the solutions x, y, z

4 Conclusion

In this paper we derive, in particular, the conditions guaranteeing that the set of asymptotically superlinear solutions of (1.1) is nonempty, all its elements are regularly varying with known index, and they satisfy quite precise asymptotic formula. We also discus some other types of solutions and reveal several purely fractional phenomena; they are listed below for clarity. Moreover, we establish theoretical tools (such as the fractional Karamata integration theorem and the fractional L’Hospital rule) which are expected to find a wider use in qualitative analysis of fractional differential equations.

One of the crucial conditions in our results is the requirement on the sign of $\alpha +\gamma +\delta$; we emphasize that the expression is dependent on the order $\alpha$. Moreover, this expression becomes $1+\gamma +\delta$ when passing to $\alpha =1$, thus we obtain exactly the condition known from the ODE case. On the other hand, we have revealed several differences between the integer order and the non-integer order case. Here is the list of the most significant ones:

• In the fractional Karamata integration theorem (Proposition 1), the “critical” setting $\vartheta =-\beta$ is in fact not critical.

• If $p(t)\sim t^\delta$ as $t\rightarrow \infty$ with $\alpha +\gamma +\delta =0$, then $\mathcal {ASL}=\emptyset$ for equation (1.1) while all positive solutions of ODE (1.2) are asymptotically superlinear (see Remark 2).

• For fractional equations of the form (1.1), under the general assumptions $\gamma <1$ and $p(t)>0$, there are classes (nonempty under some settings) of solutions (like the intermediate ones) which are always empty in the corresponding integer order case $\alpha =1$. Moreover, they can coexist with some other types of classes. See Remark 2.

• Asymptotic formula (2.4) has no integer order analogy in the borderline case $1+\delta +\gamma =\alpha +\delta +\gamma =0$.

• In contrast to the ODE case, the necessary condition for the class $\mathcal {ASL}$ to be non-empty in the case $\alpha +\gamma +\delta =0$ can be written in the non-integral form, see Remark 6.

At the very end we mention some directions for a future research. We also discuss how superlinear behavior can be natural for fractional differential equations. We expect that our approach would work also when taking some generalizations of equation (1.1) such as ${\mathcal {D}}^\alpha (r(t)\varPhi _\mu (y'))=p(t)\varPhi _\gamma (y),$ where r, p are positive continuous functions and $0<\gamma <\mu$. Possibly we could replace the power nonlinearities by regularly varying nonlinearities. Moreover, instead of scalar equations we could consider a more general system such as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha x&=p(t)\varPhi _\mu (u),\\ {\mathcal {D}}^\beta u&=q(t)\varPhi _\lambda (x), \end{aligned} \end{aligned}$$

(4.1)

where $p(t)>0$, $q(t)>0$, $1<\alpha +\beta <2$, and $\mu \lambda <1$ with $\mu>0,\lambda >0$. The form of the system would enable us to examine a wider range situations concerning strongly increasing solutions which are introduced in the following extended mode. We say that (x, u) is a strongly increasing solution of (4.1) provided $\lim _{t\rightarrow \infty }x(t)=\lim _{t\rightarrow \infty }u(t)=\infty$. Such a setting then includes both type of behavior, asymptotically superlinear and also asymptotically super-$\beta$-power (i.e. “bigger than $t^\beta$”). Indeed, let us work with strongly increasing solutions of (4.1) and set $q(t)=1$ and $\lambda =1$. If $\beta =1$, then $\lim _{t\rightarrow \infty }u(t)=\infty$, $\lim _{t\rightarrow \infty }u'(t)=\lim _{t\rightarrow \infty }x(t)=\infty$, thus u is asymptotically superlinear; note that here u is automatically eventually increasing. If $\beta <1$, then $\lim _{t\rightarrow \infty }{\mathcal {D}}^\beta u(t)=\lim _{t\rightarrow \infty }x(t)=\infty$. By the fractional L’Hospital rule,

$$\begin{aligned}\lim _{t\rightarrow \infty }\frac{u(t)}{t^\beta }=\lim _{t\rightarrow \infty }\frac{{\mathcal {D}}^\beta u(t)}{\varGamma (\beta +1)}=\infty ,\end{aligned}$$

thus u is asymptotically super-$\beta$-power. Here the monotonicity of u is not guaranteed. In fact, these considerations are valid no matter what type of the fractional derivative is involved, the Caputo one or the Riemann–Liouville one. On the other hand, passing to the associated scalar equations (of the order in the interval (1, 2)) we find that while the asymptotically superlinear behavior is somehow peculiar to the Caputo derivative, the asymptotically super-$\beta$-power behavior is peculiar to the Riemann–Liouville derivative. Indeed, the equation

$$\begin{aligned}{\mathcal {D}}^{\alpha +1}u={\mathcal {D}}^\alpha {\mathcal {D}}^1 u=p(t)\varPhi _\mu (u)\end{aligned}$$

is obtained from (4.1) when $q(t)=1$, $\lambda =1$, and $\beta =1$. Taking now the Riemann–Liouville derivative (denoted by $^R{\mathcal {D}}^\beta$) instead of the Caputo one in (4.1), then the system reduces to

$$\begin{aligned}^R{\mathcal {D}}^{\beta +1}u={\mathcal {D}}^1{}^R{\mathcal {D}}^\beta u=p(t)\varPhi _\mu (u)\end{aligned}$$

provided $q(t)=1$, $\lambda =1$, and $\alpha =1$. The property of being strongly increasing means $\lim _{t\rightarrow \infty }u(t)=\lim _{t\rightarrow \infty }u'(t)=\infty$ in the former case while $\lim _{t\rightarrow \infty }u(t)=\lim _{t\rightarrow \infty }{}^R{\mathcal {D}}^\beta u(t)=\infty$ in the latter case. Moreover, u is increasing but $u'$ does not need to be monotone and may have complex behavior in the former case, while u does not need to be monotone and may have complex behavior but $^R{\mathcal {D}}^\beta u$ is increasing in the latter case.

We have dealt just with increasing type solutions (mostly the strongly ones), so this suggests to make a similar analysis for other types of solutions in the solution space. We could see that – in contrast to ODEs – even in very special cases, the solution space of fractional differential equations may show a very complicated structure. However, we expect that tools such as the Karamata theory of regular variation adapted to fractional calculus could substantially improve our knowledge of this rich structure under a fairly general setting.

It is known from the ODE theory that passing from the sublinear case $\gamma <1$ (or $\gamma <\mu$ in system (4.1)) to the superlinear one $\gamma >1$ (or $\gamma >\mu$) may substantially affect qualitative properties; the same is expected in the fractional setting. Very exceptional is then the case $\gamma =\mu$ (the so-called half-linear equations). The fact that we have successfully applied theory of regular variation makes us optimistic as for its wider use in asymptotic theory of fractional differential equations – not only in the sense of basic properties like Proposition 3 or the fractional Karamata integration theorem, but also in the sense of the tools such as Tauberian type theorems or the de Haan theory which can be understood as a refinement of the Karamata theory. The existing concept of discrete regular variation is expected to serve well in qualitative theory of fractional difference equations.

5 Proofs

We start with the auxiliary statements where selected properties of regularly varying functions are gathered.

Proposition 3

([3, 10])

• (i) If $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$, then $\ln f(t)/\ln t\rightarrow \vartheta$ as $t\rightarrow \infty$. It then clearly implies that $\lim _{t\rightarrow \infty }f(t)=0$ provided $\vartheta <0$, and $\lim _{t\rightarrow \infty }f(t)=\infty$ provided $\vartheta >0$.

• (ii) If $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$, then $f^\alpha \in {\mathcal{R}\mathcal{V}}(\alpha \vartheta )$ for every $\alpha \in \mathbb {R}$.

• (iii) If $f_i\in {\mathcal{R}\mathcal{V}}(\vartheta _i)$, $i=1,2$, $f_2(t)\rightarrow \infty$ as $t\rightarrow \infty$, then $f_1\circ f_2\in {\mathcal{R}\mathcal{V}}(\vartheta _1\vartheta _2)$.

• (iv) If $f_i\in {\mathcal{R}\mathcal{V}}(\vartheta _i)$, $i=1,2$, then $f_1+ f_2\in {\mathcal{R}\mathcal{V}}(\max \{\vartheta _1, \vartheta _2\})$.

• (v) If $f_i\in {\mathcal{R}\mathcal{V}}(\vartheta _i)$, $i=1,2$, then $f_1 f_2\in {\mathcal{R}\mathcal{V}}(\vartheta _1+\vartheta _2)$.

• (vi) If $f_1,\dots ,f_n\in {\mathcal{R}\mathcal{V}}$, $n\in \mathbb {N}$, and $R(x_1,\dots ,x_n)$ is a rational function with nonnegative coefficients, then $R(f_1,\dots ,f_n)\in {\mathcal{R}\mathcal{V}}$.

• (vii) If $L\in {\mathcal{S}\mathcal{V}}$ and $\vartheta >0$, then $t^\vartheta L(t)\rightarrow \infty ,$ $t^{-\vartheta }L(t)\rightarrow 0$ as $t\rightarrow \infty$.

• (viii) If $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$ and a measurable g is such that $g(t)\sim f(t)$ as $t\rightarrow \infty$, then $g\in {\mathcal{R}\mathcal{V}}(\vartheta )$.

The following statement (the so-called Karamata integration theorem) is of great importance in our theory. Its fractional version is presented in Proposition 1.

Proposition 4

([3, 31]) Let $L \in {\mathcal{S}\mathcal{V}}.$

• (i) If $\vartheta <-1$, then $\int _t^{\infty } s^{\vartheta }L(s)\, {\textrm{d}}s \sim t^{\vartheta + 1} L(t)/(-\vartheta - 1)$ as $t\rightarrow \infty$.

• (ii) If $\vartheta >-1$, then $\int _a^t s^{\vartheta }L(s)\,{\textrm{d}}s \sim t^{\vartheta + 1} L(t)/(\vartheta + 1)$ as $t\rightarrow \infty$.

• (iii) If $\int _a^{\infty } L(s)/s\, {\textrm{d}}s$ converges, then $\widetilde{L}(t) = \int _t^{\infty } L(s)/s\, {\textrm{d}}s$ is a ${\mathcal{S}\mathcal{V}}$ function; if $\int _a^{\infty } L(s)/s\, {\textrm{d}}s$ diverges, then ${\widetilde{L}}(t) = \int _a^t L(s)/s\, {\textrm{d}}s$ is a ${\mathcal{S}\mathcal{V}}$ function; in both cases, ${L(t)}/ {{\widetilde{L}}(t)} \rightarrow 0$ as $t\rightarrow \infty$.

Proposition 5

([31, Theorem 2.7]) Assume that $L\in {\mathcal{S}\mathcal{V}}$ is bounded on each finite subinterval of $(0,\infty )$. Let the integral $\int _0^T x^{-\eta }f(x)\,{\textrm{d}}x$ be well defined for some given function f, and given numbers $\eta> 0, T>0$. Then

$$\begin{aligned} \int _0^T f(x)L(xt)\,{\textrm{d}}x\sim L(t)\int _0^T f(x)\,{\textrm{d}}x \end{aligned}$$

as $t\rightarrow \infty$.

The previous proposition plays a role in the proof of the fractional Karamata integration theorem which is presented next.

Proof of Proposition 1

Since $f\in {\mathcal{R}\mathcal{V}}(\vartheta )$ we have $f(t)=t^\vartheta L(t)$ where $L\in {\mathcal{S}\mathcal{V}}$. The substitution $s=xt$ yields

$$\begin{aligned} \begin{aligned} {\mathcal {I}}^\beta f(t)&=\frac{1}{\varGamma (\beta )}\int _0^t (t-s)^{\beta -1}s^\vartheta L(s)\,{\textrm{d}}s\\&= \frac{1}{\varGamma (\beta )}t\int _0^1(t-xt)^{\beta -1}x^\vartheta t^\vartheta L(xt)\,{\textrm{d}}x\\&=\frac{1}{\varGamma (\beta )}t^{\beta +\vartheta }\int _0^1(1-x)^{\beta -1}x^\vartheta L(xt)\,{\textrm{d}}x\\&\sim \frac{1}{\varGamma (\beta )}t^{\beta +\vartheta }L(t)\int _0^1(1-x)^{\beta -1}x^\vartheta \,{\textrm{d}}x\\&=\frac{1}{\varGamma (\beta )} t^\beta f(t)B(\vartheta +1,\beta )\\&=\frac{\varGamma (\vartheta +1)}{\varGamma (\vartheta +\beta +1)} t^\beta f(t) \end{aligned} \end{aligned}$$

as $t\rightarrow \infty$, where the asymptotic relation in which L is put out of the integral follows from Proposition 5 (it is obvious that the desired positive $\eta$ exists); B denotes the Beta function. $\square$

Lemma 1

([21, Lemma 2.3]) Let $\beta >0$ and $\delta >0$ be such that $\beta +\delta >1$. Then ${\mathcal {I}}^\beta {\mathcal {I}}^\delta f(t)={\mathcal {I}}^{\beta +\delta }f(t)$ is satisfied at every point $t\in [0,c]$ for $f\in L^p(0,c)$, $1\le p\le \infty$.

Lemma 2

([21, Lemma 2.21]) If $\beta >0$ and $f\in C[0,c]$, then ${\mathcal {D}}^\beta {\mathcal {I}}^\beta f=f$ on [0, c].

It is worthy of note that the statement which is contained in the following lemma is an improvement of [21, Lemma 2.22] (in the sense of relaxing the smoothness assumptions, thus more useful in applications) and was established in [4, Lemma 2.6].

Lemma 3

([4, Lemma 2.6], [21, Lemma 2.22]) Let $n\in \mathbb {N}$ and $\beta \in (n-1,n]$. If $f\in C^{n-1}[0,c]$ and ${\mathcal {D}}^\beta f\in C(0,c)$, then

$$\begin{aligned}{\mathcal {I}}^\beta {\mathcal {D}}^\beta f(t)=f(t)-\sum _{k=0}^{n-1} \frac{f^{(k)}(0)}{k!}t^k\end{aligned}$$

for $t\in (0,c)$.

We can now prove the generalized fractional L’Hospital rule.

Proof of Proposition 2

First assume that $m:=\liminf _{t\rightarrow \infty }{{\mathcal {D}}^\beta f(t)}/{{\mathcal {D}}^\beta g(t)}\in \mathbb {R}$. Let $\varepsilon >0$ be arbitrary. Then ${\mathcal {D}}^\beta f(t)/{\mathcal {D}}^\beta g(t)\ge m-\varepsilon$ for large t, say $t\ge t_0$, where $t_0$ can be taken such that ${\mathcal {D}}^\beta g(t)>0$ and $g(t)>0$, $t\ge t_0$, without loss of generality. From this estimation we get ${\mathcal {D}}^\beta f(t)\ge (m-\varepsilon ){\mathcal {D}}^\beta g(t)$, $t\ge t_0$. Applying now Lemma 3, we obtain

$$\begin{aligned} f(t)-f(0)={\mathcal {I}}^\beta {\mathcal {D}}^\beta f (t)\ge (m-\varepsilon ) {\mathcal {I}}^\beta {\mathcal {D}}^\beta g (t)= (m-\varepsilon )(g(t)-g(0)), \end{aligned}$$

$t\ge t_0$. Dividing through by g(t) we have

$$\begin{aligned} \frac{f(t)}{g(t)}-\frac{f(0)}{g(t)}\ge (m-\varepsilon )\left( 1-\frac{g(0)}{g(t)} \right) , \end{aligned}$$

$t\ge t_0$. Consequently, in view of the equality $\lim _{t\rightarrow \infty }g(t)=\infty$, we get $\liminf _{t\rightarrow \infty }f(t)/g(t)\ge m-\varepsilon$. Since $\varepsilon >0$ was arbitrary, we conclude that $\liminf _{t\rightarrow \infty }f(t)/g(t)\ge m$. Similarly we obtain the inequality for $\liminf$ if we assume that $m\not \in \mathbb {R}$. The inequality

$$\begin{aligned}\limsup _{t\rightarrow \infty }\frac{f(t)}{g(t)} \le \limsup _{t\rightarrow \infty }\frac{{\mathcal {D}}^\beta f(t)}{{\mathcal {D}}^\beta g(t)}\end{aligned}$$

can be proved analogously. $\square$

Lemma 4

Let $\lambda >0$, $0<\beta <1$, and $g(t):=\lambda t$. Then $({\mathcal {D}}^\beta f\circ g)(t)=\lambda ^\beta ({\mathcal {D}}^\beta f)(\lambda t)$.

Proof

The substitution $x=\lambda s$ yields

$$\begin{aligned} \begin{aligned} ({\mathcal {I}}^\beta f\circ g )(t)&=\frac{1}{\varGamma (\beta )}\int _0^t(t-s)^{\beta -1}f(\lambda s)\,{\textrm{d}}s\\&=\frac{1}{\varGamma (\beta )\lambda ^{\beta -1}}\int _0^t(\lambda t-\lambda s)^{\beta -1}f(\lambda s)\,{\textrm{d}}s\\&=\frac{1}{\varGamma (\beta )\lambda ^{\beta }}\int _0^{\lambda t}(\lambda t-x)^{\beta -1}f(x)\,{\textrm{d}}x\\&=\frac{1}{\lambda ^\beta }({\mathcal {I}}^\beta f)(\lambda t). \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} ({\mathcal {D}}^\beta f\circ g)(t)&=({\mathcal {I}}^{1-\beta }{\mathcal {D}}f\circ g)(t)=\frac{\lambda }{\lambda ^{1-\beta }} ({\mathcal {I}}^{1-\beta }{\mathcal {D}}f)(\lambda t)=\lambda ^\beta ({\mathcal {D}}^\beta f)(\lambda t). \end{aligned} \end{aligned}$$

$\square$

Proof of Theorem 1

Let $b>0$, $A>0$ be given. Denote $\widetilde{p}(t):=\max _{s\in [0,t]}p(s)$. Since $p\in {\mathcal{R}\mathcal{V}}(\delta )$, we have $Q\in {\mathcal{R}\mathcal{V}}(\vartheta )$ by Proposition 3 where Q is defined by (2.5). Thanks to the positivity of the index $\vartheta$, there exists $N>1$ such that

$$\begin{aligned} A\le NQ(t) \end{aligned}$$

(5.1)

for $t\in [b,\infty )$. From $\gamma <1$ and $\alpha <1$ we get $(1-\alpha )\gamma <1-\alpha$, thus $\delta +\gamma \alpha +1>\delta +\gamma +\alpha \ge 0$, where the last inequality is guaranteed by (2.1). Consequently, $\delta +\gamma \alpha +1>0$ which can be shown to be equivalent to $\delta +\gamma \vartheta >-1$. From Proposition 3, we have $pQ^\gamma \in {\mathcal{R}\mathcal{V}}(\delta +\gamma \vartheta )$. Hence we may apply the fractional Karamata integration theorem (Proposition 1). Noting that $\delta +\gamma \vartheta +1=\vartheta -\alpha$, we obtain

$$\begin{aligned} ({\mathcal {I}}^{\alpha +1}pQ^\gamma )(t)\sim \frac{\varGamma (\delta +\gamma \vartheta +1)}{\varGamma (\delta +\gamma \vartheta +\alpha +2)} t^{\alpha +1+\gamma \frac{1+\alpha }{1-\gamma }}p^{1+\frac{\gamma }{1-\gamma }}(t)= KQ(t) \end{aligned}$$

(5.2)

as $t\rightarrow \infty$, where K is defined in (2.6). In view of (5.2), there exist $M_1,M_2>0$ such that

$$\begin{aligned} M_1KQ(t)\le ({\mathcal {I}}^{\alpha +1}pQ^\gamma )(t)\le M_2KQ(t) \end{aligned}$$

(5.3)

for $t\in [b,\infty )$. Set

$$\begin{aligned} \begin{aligned} K_1&= \min \left\{ \frac{A}{Q(b)}, (M_1K)^{\frac{1}{1-\gamma }} \right\} ,\\ K_2&=\max \left\{ (N+M_2K)^{\frac{1}{1-\gamma }},\left( \frac{A}{Q(b)}+\frac{b^{\alpha +1}Q^{\gamma -1}(b)\widetilde{p}(b)}{(\alpha +1)\varGamma (\alpha +1)}\right) ^{\frac{1}{1-\gamma }} \right\} . \end{aligned} \end{aligned}$$

(5.4)

Since $N>1$, we have $K_2>1$. Clearly, $K_1<K_2$. Let ${\mathcal {X}}$ be the Fréchet space of all continuous functions on $[0,\infty )$ endowed with the topology of uniform convergence on compact subintervals of $[0,\infty )$. Introduce the set

$$\begin{aligned} \varOmega =\left\{ u\in {\mathcal {X}}:u^{[1]}(t)\le u(t)\le u^{[2]}(t), t\in [0,\infty ) \right\} , \end{aligned}$$

where

$$\begin{aligned} u^{[i]}(t)= {\left\{ \begin{array}{ll} K_i Q(b) &{} \text { for }t\in [0,b),\\ K_i Q(t) &{} \text { for }t\in [b,\infty ), \end{array}\right. } \end{aligned}$$

$i=1,2$. It is not difficult to see that $\varOmega$ is a closed and convex subset of ${\mathcal {X}}$. For $u\in \varOmega$ let us define the operator ${\mathcal {T}}$ by

$$\begin{aligned} {\mathcal {T}}u=A+{\mathcal {I}}^{\alpha +1}p\varPhi _{\gamma }(u). \end{aligned}$$

Because of the form of the fractional integral it is easy to conclude that ${\mathcal {T}}$ maps $\varOmega$ into $C[0,\infty )$. Next we show that ${\mathcal {T}}\varOmega \subseteq \varOmega$. Let $u\in \varOmega$. For $t\in [0,b)$ we have $({\mathcal {T}}u)(t)\ge ({\mathcal {T}}K_1 Q(b))(t)\ge A\ge K_1 Q(b)$ by (5.4). For $t\in [b,\infty )$, using (5.3), we get

$$\begin{aligned} ({\mathcal {T}}u)(t)\ge ({\mathcal {T}}K_1 Q)(t)\ge ({\mathcal {I}}^{\alpha +1}p K_1^\gamma Q^\gamma )(t)\ge M_1 KK_1^\gamma Q(t)\ge K_1 Q(t), \end{aligned}$$

where the last inequality follows from (5.4). For $t\in [0,b)$, since $K_2>1$, we have

$$\begin{aligned} \begin{aligned} ({\mathcal {T}}u)(t)&\le ({\mathcal {T}}K_2 Q(b))(t)\le A+\frac{K_2^\gamma Q^\gamma (b)}{\varGamma (\alpha +1)}\widetilde{p}(b) \int _0^t (t-s)^\alpha {\textrm{d}}s\\&\le A+ \frac{K_2^\gamma Q^\gamma (b)\widetilde{p}(b)b^{\alpha +1}}{(\alpha +1)\varGamma (\alpha +1)}\le K_2^\gamma \left( A+ \frac{ Q^\gamma (b)\widetilde{p}(b)b^{\alpha +1}}{(\alpha +1)\varGamma (\alpha +1)}\right) \\&\le K_2^\gamma K_2^{1-\gamma }Q(b)= K_2 Q(b), \end{aligned} \end{aligned}$$

where the last inequality is guaranteed by (5.4). For $t\in [b,\infty )$, in view of (5.1), (5.3), and (5.4), we get

$$\begin{aligned} \begin{aligned} ({\mathcal {T}}u)(t)&\le {\mathcal {T}}(K_2Q)(t)\le A +M_2KK_2^\gamma Q(t)\\&\le (N_2+M_2 KK_2^\gamma )Q(t)\le (N_2+M_2 K)K_2^\gamma Q(t)\le K_2 Q(t). \end{aligned} \end{aligned}$$

Thus we have proved ${\mathcal {T}}\varOmega \subseteq \varOmega$. Next we show relative compactness of ${\mathcal {T}}\varOmega$. By Lemma 1, for $u\in \varOmega$, we have ${\mathcal {T}}u= A+{\mathcal {I}}^1{\mathcal {I}}^\alpha pu^\gamma$. Hence, $({\mathcal {T}}u)'(t)=({\mathcal {I}}^\alpha pu^\gamma )(t)$, $t\in [0,\infty )$. Since $0\le ({\mathcal {I}}^\alpha pu^\gamma )(t)\le ({\mathcal {I}}^\alpha p(u^{[2]})^\gamma )(t)$, $t\in [0,\infty )$, for every $u\in \varOmega$, we have guaranteed that the elements of ${\mathcal {T}}\varOmega$ are equicontinuous. Equiboundedness of the elements in ${\mathcal {T}}\varOmega$ easily follows from ${\mathcal {T}}\varOmega \subseteq \varOmega$. The Ascoli–Arzelà theorem now guarantees relative compactness of ${\mathcal {T}}\varOmega$. Finally we show continuity of ${\mathcal {T}}$ in $\varOmega$. To this aim it is sufficient to prove that for any sequence $u_n$ in $\varOmega$ which converges to u as $n\rightarrow \infty$ uniformly on any compact subsets [0, c] of $[0,\infty )$ it holds that ${\mathcal {T}}u_n$ tends ${\mathcal {T}}u$ as $n\rightarrow \infty$ uniformly on these subsets. Thus assume that $u_n\rightrightarrows u$ as $n\rightarrow \infty$ on [0, c], $c>0$. We have

$$\begin{aligned} |({\mathcal {T}}u_n)(t)-({\mathcal {T}}u)(t)|\le \frac{1}{\varGamma (\alpha +1)}\int _0^t(t-s)^{\alpha } p(s)|u_n^\gamma (s)-u^\gamma (s)|\,{\textrm{d}}s, \end{aligned}$$

(5.5)

$t\in [0,c]$. Clearly, there exist positive $C_1,C_2$ such that $u(t)\in [C_1,C_2]$ and $u_n(t)\in [C_1,C_2]$ for all $n\in \mathbb {N}$ and $t\in [0,c]$. From the uniform continuity of $x\mapsto x^\gamma$ on $[C_1,C_2]$ it follows that for any $\varepsilon >0$ there exists $\zeta >0$ such that if $|x_1-x_2|<\zeta$, $x_1,x_2\in [C_1,C_2]$, then

$$\begin{aligned} |x_1^\gamma -x_2^\gamma |\le \varepsilon (\alpha +1)\varGamma (\alpha +1)/(\widetilde{p}(c)c^{\alpha +1}). \end{aligned}$$

(5.6)

Since $u_n\rightrightarrows u$ on [0, c] there exists $m\in \mathbb {N}$ such that $|u_n(t)-u(t)|<\zeta$ for $t\in [0,c]$ and $n\ge m$. Hence, in view of (5.5),

$$\begin{aligned} |({\mathcal {T}}u_n)(t)-({\mathcal {T}}u)(t)|\le \frac{(\alpha +1)\varepsilon }{c^{\alpha +1}}\int _0^t(t-s)^\alpha \,{\textrm{d}}s\le \varepsilon , \end{aligned}$$

$t\in [0,c],$ for any $n\ge m$. Thus ${\mathcal {T}}u_n\rightrightarrows {\mathcal {T}}u$ on [0, c] which proves continuity of ${\mathcal {T}}$ on $\varOmega$ in the sense of the topology of the Fréchet space ${\mathcal {X}}$. Thus the Schauder–Tychonoff fixed point theorem guarantees existence of $y\in \varOmega$ such that ${\mathcal {T}}y= y$. By Lemma 2, from ${\mathcal {T}}y=y$ we get ${\mathcal {D}}^{\alpha +1}y={\mathcal {D}}^{\alpha +1}{\mathcal {T}}y=y$ and thus y satisfies (1.1) on $[0,\infty )$.

Let $\lambda >0$. Since the solution y is in $\varOmega$ and Q is regularly varying, there exist $m_1,m_2>0$ such that $m_1\le y(\lambda t)/y(t)\le m_2$ for $t\in [0,\infty )$. Therefore,

$$\begin{aligned} m_*:=\liminf _{t\rightarrow \infty }\frac{y(\lambda t)}{y(t)}\in (0,\infty )\ \ \text {and}\ \ m^*:=\limsup _{t\rightarrow \infty }\frac{y(\lambda t)}{y(t)}\in (0,\infty ). \end{aligned}$$

Since $\vartheta >0$, we have $\lim _{t\rightarrow \infty }Q(t)=\infty$ by Proposition 3, and so $\lim _{t\rightarrow \infty }y(t)=\infty$. Moreover, we have $y'={\mathcal {I}}^\alpha py^\gamma \ge {\mathcal {I}}^\alpha p(u^{[1]})^\gamma \in {\mathcal{R}\mathcal{V}}(\alpha +\delta +\gamma \vartheta )$ and

$$\begin{aligned}\left( {\mathcal {I}}^\alpha p(u^{[1]})^\gamma \right) (t)\sim C t^{\alpha +\delta +\gamma \vartheta }L_p^{\frac{1}{1-\gamma }}(t)\end{aligned}$$

as $t\rightarrow \infty$, for some $C\in (0,\infty )$, by Proposition 3 and Proposition 1, where $\alpha +\delta +\gamma \vartheta =\vartheta -1\ge 0$. Consequently, $\lim _{t\rightarrow \infty }y'(t)=\lim _{t\rightarrow \infty }({\mathcal {I}}^\alpha p(u^{[1]})^\gamma )(t)=\infty$, where in case of strict inequality in (2.1) we apply Proposition 3 while in case of equality, the infiniteness of the limit follows from the additional assumption $\lim _{t\rightarrow \infty }L_p(t)=\infty$. Proposition 2, Lemma 4, and the classical generalized L’Hospital rule (1.6) yield

$$\begin{aligned} \begin{aligned} m_*&\ge \liminf _{t\rightarrow \infty }\frac{y(\lambda t)}{y(t)}\ge \liminf _{t\rightarrow \infty }\frac{\lambda y'(\lambda t)}{y'(t)}\\&\ge \liminf _{t\rightarrow \infty }\frac{\lambda ^{1+\alpha }{\mathcal {D}}^{1+\alpha } y(\lambda t)}{{\mathcal {D}}^{1+\alpha }y(t)} =\liminf _{t\rightarrow \infty }\frac{\lambda ^{1+\alpha }p(\lambda t)y^\gamma (\lambda t)}{p(t)y^\gamma (t)} =\lambda ^{1+\alpha +\delta }m_*^\gamma , \end{aligned} \end{aligned}$$

where we used the fact that y satisfies equation (1.1) and $p\in {\mathcal{R}\mathcal{V}}(\delta )$. Hence, $m_*^{1-\gamma }\ge \lambda ^{1+\alpha +\delta }$, i.e., $m_*\ge \lambda ^\vartheta$. Similarly we obtain $m^*\le \lambda ^\vartheta$. Consequently, $\lim _{t\rightarrow \infty }y(\lambda t)/y(t)=\lambda ^\vartheta$, $\lambda \in (0,\infty )$, thus $y\in {\mathcal{R}\mathcal{V}}(\vartheta )$.

We have shown existence of $y\in \mathcal {ASL}^+\cap {\mathcal{R}\mathcal{V}}(\vartheta )$ such that $y(0)=A>0$, $y'(0)=0$. A slight modification of the operator $\mathcal {T}$ and the set $\varOmega$ would enable us to obtain an ${\mathcal{R}\mathcal{V}}$ solution with the initial conditions $y(0)=0,y'(0)=B>0$ or $y(0)=A>0,y'(0)=B>0$. We omit details. Note just that if $({\mathcal {T}}u)(t)=A+Bt+({\mathcal {I}}^{\alpha +1}p\varPhi _{\gamma }(u))(t)$, $A\ge 0$, $B\ge 0$, then $(\mathcal {T}Q)(t)=A+Bt+({\mathcal {I}}^{\alpha +1}pQ^\gamma )(t)\in {\mathcal{R}\mathcal{V}}(\max \{0,1,\vartheta \})={\mathcal{R}\mathcal{V}}(\vartheta )$ provided $\alpha +\delta +\gamma >0$. In the case $\alpha +\delta +\gamma =0$ we have to take $A>0, B=0$ – the choice which is actually covered by the first part of this proof. $\square$

Proof of Theorem 2

Let $y\in {\mathcal{R}\mathcal{V}}(\varrho )$ be a solution of (1.1). By Lemma 3 from (1.1) we get $y'(t)=B+({\mathcal {I}}^\alpha p\varPhi _\gamma (y))(t)$ and

$$\begin{aligned} \begin{aligned} y(t)&=A+Bt+({\mathcal {I}}^{\alpha +1}p\varPhi (y^\gamma ))(t)\\&= \left( \frac{A+Bt}{({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)}+1\right) ({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t) \end{aligned} \end{aligned}$$

(5.7)

with some $A,B\in \mathbb {R}$. We have $|A|\in {\mathcal{S}\mathcal{V}}$ and $|B|t\in {\mathcal{R}\mathcal{V}}(1)$. Moreover, ${\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y)\in {\mathcal{R}\mathcal{V}}(\alpha +1+\delta +\varrho \gamma )$ by Proposition 1 since $p\varPhi _{\gamma }(y)\in {\mathcal{R}\mathcal{V}}(\delta +\varrho \gamma )$ with $\delta +\varrho \gamma \ge -\alpha >-1$. If $\varrho >-(\delta +\alpha )/\gamma$, then the index satisfies $\alpha +1+\delta +\varrho \gamma > 1$, and hence $|A|+|B|t=o(({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t))$ as $t\rightarrow \infty$. If $\varrho =-(\delta +\alpha )/\gamma$, then we have again $|A|+|B|t=o(({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t))$ as $t\rightarrow \infty$ since

$$\begin{aligned} \frac{|A|+|B|t}{({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)} \sim \frac{|A|+|B|t}{\widetilde{K}tL_p(t)L_y^\gamma (t)}\sim \frac{|B|}{\widetilde{K}L_p(t)L_y^\gamma (t)} \rightarrow 0 \end{aligned}$$

as $t\rightarrow \infty$, where the last relation follows from the facts that $B+({\mathcal {I}}^\alpha p\varPhi _\gamma (y))(t)=y'(t)\rightarrow \infty$ as $t\rightarrow \infty$ and $({\mathcal {I}}^\alpha p\varPhi _\gamma (y))(t)\sim C L_p(t)L_y^\gamma (t)$ as $t\rightarrow \infty$ for some $C>0$. In view of (5.7), we have $y(t)=(1+{o}(1))({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)$ as $t\rightarrow \infty$. Proposition 1 now yields

$$\begin{aligned} y(t)\sim ({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)\sim \widetilde{K}t^{\alpha +1}p(t)y^{\gamma }(t) \end{aligned}$$

as $t\rightarrow \infty$. Thus we get, as $t\rightarrow \infty$,

$$\begin{aligned} y(t)\sim \left( \widetilde{K}t^{\alpha +1}p(t)\right) ^{\frac{1}{1-\gamma }}\in {\mathcal{R}\mathcal{V}}(\vartheta ). \end{aligned}$$

Since we assumed $y\in {\mathcal{R}\mathcal{V}}(\varrho )$, we obtain $\varrho =\vartheta$ by Proposition 3. Consequently, $\widetilde{K}=K$ and the condition $\varrho \ge -(\delta +\alpha )/\gamma$ becomes (2.1). $\square$

Proof of Theorem 3

Since $y\in \mathcal {ASL}$, there exists $t_1\ge t_0$ such that $y(t)>0$, $t\ge t_1$. From (1.1), in view of Lemma 3 and the fact that y is eventually increasing (say again for $t\ge t_1$, without loss of generality), we have

$$\begin{aligned} \begin{aligned} y(t) =&\ y(0)+y'(0)t+({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)\\ =&\ y(0)+y'(0)t+\frac{1}{\varGamma (\alpha +1)}\int _0^{t_1}(t-s)^\alpha p(s)\varPhi _\gamma (y(s))\,{\textrm{d}}s\\&+ \frac{1}{\varGamma (\alpha +1)}\int _{t_1}^t(t-s)^\alpha p(s)y^\gamma (s)\,{\textrm{d}}s\\ \le&\ |y(0)|+|y'(0)|t+\frac{\max _{s\in [0,t_1]}p(s)|y(s)|^\gamma }{\varGamma (\alpha +1)}t^\alpha \\ {}&+ \frac{y^\gamma (t)}{\varGamma (\alpha +1)}\int _{t_1}^t(t-s)^\alpha p(s)\,{\textrm{d}}s. \end{aligned} \end{aligned}$$

Since $\alpha <1$, there exists $N_1>0$ such that

$$\begin{aligned} y(t)\le N_1 t+y^{\gamma }(t)({\mathcal {I}}^{\alpha +1}p)(t), \end{aligned}$$

$t\ge t_1$. From $\lim _{t\rightarrow \infty }y'(t)=\infty$ we get existence of $M>0$ such that $y(t)\ge Mt\in {\mathcal{R}\mathcal{V}}(1)$ for large t. Therefore, in view of ${\mathcal {I}}^{\alpha +1}p\ge {\mathcal {I}}^{\alpha +1} q$, employing Proposition 1, we have that $y^\gamma {\mathcal {I}}^{\alpha +1}p$ is bigger than a regularly varying function of index $\gamma +\alpha +1+\delta$ and this index is bigger than 1. Consequently, in view of Proposition 3, there exists a positive constant $N_2$ such that

$$\begin{aligned} y(t)\le N_2y^\gamma (t)({\mathcal {I}}^{\alpha +1}p)(t), \end{aligned}$$

$t\ge t_1$. Relation (2.7) easily follows. If $p\in {\mathcal{R}\mathcal{V}}(\delta )$, then Proposition 1 guarantees existence of $N_3>0$ such that

$$\begin{aligned} y(t)\le N_2y^\gamma (t)({\mathcal {I}}^{\alpha +1}p)(t)\le N_3 y^\gamma (t)t^{\alpha +1}p(t), \end{aligned}$$

and thus we get (2.8). $\square$

To prove Theorem 4 we need the following comparison result.

Lemma 5

Let $q\le p$ on [0, c]. If y and x are positive solutions on (0, c] of equation (1.1) and (2.9), respectively, such that $x(0)\le y(0)$ and $x'(0)\le y'(0)$ where at least one of the inequalities is strict, then $x(t)<y(t)$ for $t\in (0,c]$.

Proof

Assume first $x(0)<y(0)$. Then, by the continuity, there exists $\varepsilon >0$ such that $x(t)<y(t)$ for $t\in [0,\varepsilon ]$. Assume by a contradiction that there exists $b\in (0,c]$ such that $x(t)<y(t)$ for $t\in [0,b)$ and $x(b)=y(b)$. Employing Lemma 3, from equations (1.1) and (2.9) we have

$$\begin{aligned} \begin{aligned} y(t)&= y(0)+y'(0)t+({\mathcal {I}}^{\alpha +1}py^\gamma )(t),\\ x(t)&= x(0)+x'(0)t+({\mathcal {I}}^{\alpha +1}qx^\gamma )(t), \end{aligned} \end{aligned}$$

$t\in [0,c]$. Hence,

$$\begin{aligned} \begin{aligned} 0 = y(b)-x(b) =y(0)-x(0)+y'(0)-x'(0)+[{\mathcal {I}}^{\alpha -1}(py^\gamma -qx^\gamma )](b) >0, \end{aligned} \end{aligned}$$

contradiction. If $x(0)=y(0)$ with $x'(0)<y'(0)$, then $x(t)<y(t)$, $t\in (0,\varepsilon ]$, for some $\varepsilon >0$. Similarly as before we come to contradiction when assuming that $x<y$ fails to hold on (0, c]. $\square$

Proof of Theorem 4

Take the solutions x and y of (1.1) and (2.9), respectively, satisfying the assumptions of the theorem. Then there exist $m_1>0, m_2>0$ such that

$$\begin{aligned} \begin{aligned}&m_1 x(0)\le y(0)\le m_2 x(0),\\&m_1 x'(0)\le y'(0)\le m_2 x'(0). \end{aligned} \end{aligned}$$

(i) Since $p(t)\asymp q(t)$ as $t\rightarrow \infty$, there exist $k_1>0,k_2>0$ such that $k_1^{1-\gamma }q(t)\le p(t)\le k_2^{1-\gamma } q(t)$, $t\ge 0$. Without loss of generality we can take $k_i=m_i$, $i=1,2$. The function $\widehat{x}=m_2 x$ is an $\mathcal {ASL}^+$ solution of the equation ${\mathcal {D}}^{\alpha +1}\widehat{x}= m_2^{1-\gamma }q(t)\varPhi _\gamma (\widehat{x})$. Lemma 5 yields $\widehat{x}(t)=m_2 x(t)\ge y(t)$ for $t\ge 0$. Indeed, the inequalities hold on [0, c] with $c\ge 0$ arbitrary, and thus one has validity on $[0,\infty )$. Similarly we obtain $m_1 x(t)\le y(t)$, $t\ge 0$. Hence, $x(t)\asymp y(t)$ as $t\rightarrow \infty$.

(ii) Since $p(t)\sim q(t)$ as $t\rightarrow \infty$ clearly implies $p(t)\asymp q(t)$ for $t\rightarrow \infty$, we get $x(t)\asymp y(t)$ as $t\rightarrow \infty$ as in the previous part. Consequently, $L_*:=\liminf _{t\rightarrow \infty }x(t)/y(t)\in (0,\infty )$ and $L^*:=\limsup _{t\rightarrow \infty }x(t)/y(t)\in (0,\infty )$. Applying (1.6) and Proposition 2, in view of $p(t)\sim q(t)$ as $t\rightarrow \infty$, we obtain

$$\begin{aligned} L_*\ge \liminf _{t\rightarrow \infty }\frac{x'(t)}{y'(t)}\ge \liminf _{t\rightarrow \infty }\frac{{\mathcal {D}}^{\alpha +1}x(t)}{{\mathcal {D}}^{\alpha +1}y(t)}= \liminf _{t\rightarrow \infty }\frac{q(t)x^\gamma (t)}{p(t)y^\gamma (t)}= \liminf _{t\rightarrow \infty }\frac{x^\gamma (t)}{y^\gamma (t)}= L_*^\gamma . \end{aligned}$$

Since $\gamma <1$, this implies $L_*\ge 1$. Similarly we obtain $L^*\le 1$. Hence, $\lim _{t\rightarrow \infty }x(t)/y(t)=1$, and so $x(t)\sim y(t)$ as $t\rightarrow \infty$. $\square$

Proof of Theorem 5

Let a positive continuous function q be such that $q(t)\sim p(t)$ as $t\rightarrow \infty$. Then $q\in {\mathcal{R}\mathcal{V}}(\delta )$ by Proposition 3. According to Theorem 1, applied now to equation (2.9), there exists $x\in \mathcal {ASL}_q^+$ such that $x\in {\mathcal{R}\mathcal{V}}(\vartheta )$. Theorem 2 guarantees that

$$\begin{aligned} x(t)\sim K^{\frac{1}{1-\gamma }}t^{\frac{1+\alpha }{1-\gamma }} q^{\frac{1}{1-\gamma }}(t)\sim K^{\frac{1}{1-\gamma }}t^{\frac{1+\alpha }{1-\gamma }} p^{\frac{1}{1-\gamma }}(t)= K^{\frac{1}{1-\gamma }}Q(t) \end{aligned}$$

as $t\rightarrow \infty$. From the Asymptotic equivalence theorem (Theorem 4) we get that $y(t)\sim x(t)\sim K^{\frac{1}{1-\gamma }}Q(t)$ as $t\rightarrow \infty$ for any $y\in \mathcal {ASL}^+$. Since $x\in {\mathcal{R}\mathcal{V}}(\vartheta )$, Proposition 3 guarantees that $y\in {\mathcal{R}\mathcal{V}}(\vartheta )$. $\square$

Proof of Theorem 5

Let $y\in \mathcal {ASL}$. Then $\lim _{t\rightarrow \infty }y(t)/t=\infty$. Assume by a contradiction that $\delta +\alpha +\gamma <0$ or $\delta +\alpha +\gamma =0$ with $\limsup _{t\rightarrow \infty }L_p(t)<\infty$. Thanks to Lemma 3, from equation (1.1) we have $y(t)=A+Bt+({\mathcal {I}}^{\alpha +1}p\varPhi _\gamma (y))(t)$, $t\ge 0$, for some $A,B\in \mathbb {R}$. Clearly there exists $t_0>0$ such that $y(t)>0$, $t\ge t_0$. There is $C>0$ such that for $t\ge t_0$ we have

$$\begin{aligned} \begin{aligned} y(t)\le&\ |A|+|B|t+\frac{1}{\varGamma (\alpha +1)}\int _0^{t_0}(t-s)^{\alpha }p(s)|y(s)|^\gamma \,{\textrm{d}}s\\&+\frac{1}{\varGamma (\alpha +1)}\int _{t_0}^{t}(t-s)^{\alpha }p(s)y^\gamma (s)\,{\textrm{d}}s\\ \le&\ |A|+|B|t+C{t^\alpha } +\frac{1}{\varGamma (\alpha +1)}\int _{t_0}^{t}(t-s)^{\alpha }p(s)y^\gamma (s)\,{\textrm{d}}s \end{aligned} \end{aligned}$$

Denote $z(t):=\max _{s\in [t_0,t]}y(s)/s$, $t\ge t_0$. Since $\alpha <1$, there exists $D>0$ such that for $t\ge t_0$ we have

$$\begin{aligned} \begin{aligned} \frac{y(t)}{t}&\le D+\frac{1}{t\varGamma (\alpha +1)}\int _{t_0}^t(t-s)^\alpha s^\gamma z^\gamma (s)p(s)\,{\textrm{d}}s\\&\le D +\frac{1}{t\varGamma (\alpha +1)}z^{\gamma }(t)\int _{t_0}^t(t-s)^\alpha s^\gamma p(s)\,{\textrm{d}}s. \end{aligned} \end{aligned}$$

(5.8)

Thus

$$\begin{aligned} \frac{y(t)}{t}\le D +\frac{1}{\varGamma (\alpha +1)}t^{\alpha -1}z^{\gamma }(t)\int _{t_0}^t s^\gamma p(s)\,{\textrm{d}}s. \end{aligned}$$

If either $\gamma +\delta <-1$ or $\gamma +\delta =-1$ with $\int _{t_0}^\infty s^\gamma p(s)\,{\textrm{d}}s<\infty$ holds, then clearly $t^{\alpha -1} \int _{t_0}^t s^\gamma p(s)\,{\textrm{d}}s<M$ on $[t_0,\infty )$ for some $M>0$. Hence, in view of $\lim _{t\rightarrow \infty }z(t)=\infty$, there exists $N>0$ such that

$$\begin{aligned} \frac{y(t)}{t}\le N z^\gamma (t) \end{aligned}$$

(5.9)

for $t\ge t_0$. If $\gamma +\delta = -1$ with $\int _{t_0}^\infty s^\gamma p(s)\,{\textrm{d}}s=\infty$, then Proposition 4 yields $t^{\alpha -1}\int _{t_0}^t s^\gamma p(s)\,{\textrm{d}}s\in {\mathcal{R}\mathcal{V}}(\alpha +\gamma +\delta )={\mathcal{R}\mathcal{V}}(\alpha -1)$. Because of $\alpha <1$, from Proposition 3 we have guaranteed existence of a positive constant, say again N, without loss of generality, such that (5.9) holds on $[t_0,\infty )$. It remains to consider $\gamma +\delta >-1$. From (5.8) we have

$$\begin{aligned} \frac{y(t)}{t}\le D+\frac{z^\gamma (t)}{t}({\mathcal {I}}^{\alpha +1}P_\gamma )(t), \end{aligned}$$

$t\ge t_0$, where $P_\gamma$ is defined in (2.10). Lemma 1 and the generalized L’Hospital rule (1.6) yield

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{({\mathcal {I}}^{\alpha +1}P_\gamma )(t)}{t}\le \limsup _{t\rightarrow \infty } ({\mathcal {I}}^\alpha P_\gamma )(t), \end{aligned}$$

(5.10)

where $P_\gamma$ is defined in (2.10). From Proposition 1, we get

$$\begin{aligned} ({\mathcal {I}}^\alpha P_\gamma )(t)\sim \frac{\varGamma (\gamma +\alpha +1)}{\varGamma (\gamma +\delta +\alpha +1)} t^{\gamma +\delta +\alpha }L_p(t) \end{aligned}$$

(5.11)

as $t\rightarrow \infty$. Since we assume either $\delta +\alpha +\gamma <0$ or $\delta +\alpha +\gamma =0$ with $\limsup _{t\rightarrow \infty }L_p(t)<\infty$, relations (5.10) and (5.11) guarantee existence of a positive constant D such that $({\mathcal {I}}^{\alpha +1}P_\gamma )(t)/t\ge D$ for $t\ge t_0$, and thus we again get (5.9). Thus in any case we have (5.9). Taking now maximum in (5.9) over $[t_0,t]$, noting that z is increasing, we obtain $z(t)\le N z^\gamma (t)$, i.e., $z^{1-\gamma }(t)\le N$, $t\ge t_0$. Since $\lim _{t\rightarrow \infty }z^{1-\gamma }(t)=\infty$, we come to contradiction. $\square$