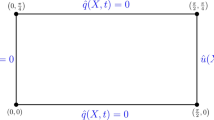General one-dimensional model of the time-fractional diffusion-wave equation in various geometries

Abstract

This paper deals with the analysis of the time-fractional diffusion-wave equation as one-dimensional problem in a large plane wall, long cylinder, and sphere. The result of the analysis is the proposal of one general mathematical model that describes various geometries and different processes. Finite difference method for solving the time-fractional diffusion-wave equation using Grünwald-Letnikov definition for homogeneous or inhomogeneous material and for homogeneous or inhomogeneous boundary conditions is described. Dirichlet, Neumann and Robin boundary conditions are considered. Implementation of numerical methods for explicit, implicit, and Crank-Nicolson scheme were realised in MATLAB. Finally, illustrative examples of simulations using the developed toolbox are presented.

1 Introduction

The fundamental phenomena, such as diffusion and wave propagation, are described by the following partial differential equations [4], i.e.

• diffusion equation:

  $$\begin{aligned} \frac{\partial u(\textbf{r},t)}{\partial t} = D \nabla ^2 u(\textbf{r},t), \end{aligned}$$

• wave equation:

  $$\begin{aligned} \frac{\partial ^2 u(\textbf{r},t)}{\partial t^2} = c^2 \nabla ^2 u(\textbf{r},t). \end{aligned}$$

Generalising the above partial differential equations by replacing the integer-order time derivatives with derivatives of fractional order $\alpha \in (0;2]$ the following time-fractional diffusion-wave equation is obtained:

$$\begin{aligned} \frac{\partial ^{\alpha } u(\textbf{r},t)}{\partial t^{\alpha }} = k^2 \nabla ^2 u(\textbf{r},t). \end{aligned}$$

The standard (integer-order) diffusion or wave equation used for the description of many materials such as visco-elastic materials, granular and porous materials, composite materials, etc., is often not sufficiently adequate. In such cases, the description requires the development of more suitable models using fractional-order derivatives [13, 22, 28, 29, 44]. The causes are mainly roughness or porosity of the material [21,22,23], fractality and chaotic behavior of systems [3, 16, 24, 42], and memory of the systems and ongoing processes [25, 26, 35, 36, 41].

The time-fractional diffusion-wave equation as an adequate model requires the creation of new methods and tools for its solution. This topic is currently relevant and many important authors have contributed to its development, such as Fourier, Abel, Leibniz, Grünwald, Letnikov, Liouville, and Riemann [18, 22, 34].

Nowadays there is a number of numerical methods for solution of time-fractional diffusion-wave equation. These methods are based on the finite difference method (FDM) [37, 39, 46], the finite element method [5, 6, 33], the random walk models [8, 14, 15], Monte Carlo simulation [7, 17, 30], the method of Adomian decomposition [10, 19], numerical quadrature [2, 12, 43], and matrix approach [9, 27,28,29]. FDM is an extended method, where explicit, implicit and Crank-Nicolson schemes are used [44]. In the case of different geometries, we know the solutions for a planar wall, a cylinder and a sphere [1, 11, 20, 31, 32, 38, 45], but for the general geometry this is not reported yet.

Therefore, the present work aims at the design, numerical solution and MATLAB implementation of the general one-dimensional model of the time-fractional diffusion-wave equation applied to the time-fractional heat conduction problem in various geometries. This is presented in Fig. , which can be considered as an outline and a graphical abstract.

Fig. 1

Graphical abstract of the present paper

2 Time-fractional heat conduction models

The one-dimensional time-fractional heat conduction model in different geometries can be expressed as follows:

• in a large plane wall

  $$\begin{aligned} \varrho c_p \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }} = \frac{\partial }{\partial r} \left( \lambda \frac{\partial T(r,t)}{\partial r} \right) , \end{aligned}$$

• in a long cylinder

  $$\begin{aligned} \varrho c_p \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }} = \frac{1}{r} \frac{\partial }{\partial r} \left( r \lambda \frac{\partial T(r,t)}{\partial r} \right) , \end{aligned}$$

• and in a sphere

  $$\begin{aligned} \varrho c_p \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }} = \frac{1}{r^2} \frac{\partial }{\partial r} \left( r^2 \lambda \frac{\partial T(r,t)}{\partial r} \right) . \end{aligned}$$

The examination of the one-dimensional time-fractional heat conduction model in large plane wall, long cylinder, and sphere reveals, that all three equations can be expressed in a compact form as a general model

$$\begin{aligned} \varrho c_p \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }} = \frac{1}{r^\gamma } \frac{\partial }{\partial r} \left( r^\gamma \lambda \frac{\partial T(r,t)}{\partial r} \right) . \end{aligned}$$

(2.1)

In the case of a constant value of the thermal conductivity $\lambda$, the general model has the form

$$\begin{aligned} \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }} = k^2 \frac{1}{r^\gamma } \frac{\partial }{\partial r} \left( r^\gamma \frac{\partial T(r,t)}{\partial r} \right) , \end{aligned}$$

(2.2)

where $\gamma$ is a geometric factor (large plane wall $\gamma =0$, long cylinder $\gamma =1$, sphere $\gamma =2$), $k^2=\lambda /(\varrho c_p)$ is the thermal diffusivity, $\varrho$ is density, and $c_p$ is specific heat capacity.

3 Initial and boundary conditions

The general time-fractional heat conduction model (2.2) requires two boundary conditions, as well as one initial condition. The initial condition specifies the temperature distribution in the material at the begin of the time, that is,

$$\begin{aligned} T(r,0) = f_0(r). \end{aligned}$$

The boundary conditions specify the temperature or the heat flux at the boundaries of the region. The following boundary conditions (Fig. ) are considered:

• 1. Dirichlet boundary conditions

  $$\begin{aligned} \left. T(r,t) \right| _{r=a} = T_{a} \quad \text{ and } \quad \left. T(r,t) \right| _{r=b} = T_{b}, \end{aligned}$$

  where $T_{a}, T_{b}$ are temperatures (K) at the boundary surface.

• 2. Neumann boundary conditions

  $$\begin{aligned} \left. - \lambda (r) \frac{\partial T(r,t)}{\partial r} \right| _{r=a} = i_{a} \quad \hbox {and} \quad \left. - \lambda (r) \frac{\partial T(r,t)}{\partial r} \right| _{r=b} = i_{b} \end{aligned}$$

  in the special case, i.e. thermal symmetry or full body (Fig. 2b)

  $$\begin{aligned} \left. \frac{\partial T(r,t)}{\partial r}\right| _{r=0} = 0, \end{aligned}$$

  where $i_{a}, i_{b}$ stand for heat flux (W$\cdot$m$^{-2}$) at the boundary surface.

• 3. Robin boundary conditions

  $$\begin{aligned} \left. - \lambda (r) \frac{\partial T(r,t)}{\partial r}\right| _{r=a}= & {} h_{a} \left( \left. T\right| _{r=a} - T_{sa}\right) \\ \textrm{and} \\ \left. - \lambda (r) \frac{\partial T(r,t)}{\partial r}\right| _{r=b}= & {} h_{b} \left( \left. T\right| _{r=b} - T_{sb}\right) , \end{aligned}$$

where $h_{a}, h_{b}$ are heat transfer coefficients (W$\cdot$m$^{-2}\cdot$K$^{-1}$); $T_{sa}, T_{sb}$ are the surrounding medium temperatures (K) at the boundary surface.

Fig. 2

Boundary conditions for (a) hollow body and (b) full symmetrical body

4 Numerical solution

The fractional derivative according to time in the general time-fractional heat conduction model (2.2) is discretised by the backward Euler method and the Grünwald-Letnikov definition

$$\begin{aligned} \left. \frac{\partial ^{\alpha } T(r,t)}{\partial t^{\alpha }}\right| _{t_p} \cong \frac{\sum _{j=0}^{N_f}c_{j}T_i^{p-j}}{\varDelta t^{\alpha }} = \frac{T_i^p + \sum _{j=1}^{N_f}c_{j}T_i^{p-j}}{\varDelta t^{\alpha }} \end{aligned}$$

by using the principle of “short memory” (Fig. ) [26], where $t_L$ is the memory length, $\varDelta t$ is the time step and the value of $N_f$ shall be determined by the following relation

$$\begin{aligned} N_f = \textrm{min} \left\{ \left[ \frac{t_0}{\varDelta t} \right] , \left[ \frac{t_L}{\varDelta t} \right] \right\} \cdot \nonumber \end{aligned}$$

For the calculation of the binomial coefficients $c_j$ the following relation can be used

$$\begin{aligned} c_0 = 1,\ c_j = \left( 1 - \frac{1+\alpha }{j} \right) c_{j-1}, \ \text {for} \ \ j\ge 1. \end{aligned}$$

Fig. 3

Time discretisation

The derivative according to the spatial coordinate (Fig. ) is discretised as follows

$$\begin{aligned}{} & {} \left. \frac{\partial T(r,t)}{\partial r}\right| _{r_{i-\frac{1}{2}}} \cong \frac{T_{i}^{p} - T_{i-1}^{p}}{\varDelta r}\\{} & {} \left. \frac{\partial T(r,t)}{\partial r}\right| _{r_{i+\frac{1}{2}}} \cong \frac{T_{i+1}^{p} - T_{i}^{p}}{\varDelta r}\\ \left. \frac{1}{r^\gamma } \frac{\partial }{\partial r} \left( r^\gamma k^2 \frac{\partial T(r,t)}{\partial r} \right) \right| _{r_i}\cong & {} \frac{1}{r_i^\gamma } \frac{ \left. r_{i+\frac{1}{2}}^\gamma k^2_i \frac{\partial T(r,t)}{\partial r}\right| _{r_{i+\frac{1}{2}}} - \left. r_{i - \frac{1}{2}}^\gamma k^2_{i-1} \frac{\partial T(r,t)}{\partial r}\right| _{r_{i-\frac{1}{2}}} }{\varDelta r} \\= & {} \frac{k^2_i \xi _i T_{i+1}^p - \left( k^2_i \xi _i + k^2_{i-1}\zeta _i \right) T_{i}^p + k^2_{i-1} \zeta _i T_{i-1}^p}{\varDelta r^2}, \end{aligned}$$

where

$$\begin{aligned} \xi _i=\left( 1+\frac{\varDelta r}{2 r_i}\right) ^{\gamma } \quad \text{ and } \quad \zeta _i = \left( 1 - \frac{\varDelta r}{2 r_i}\right) ^{\gamma }. \end{aligned}$$

The values $\xi _i$ or $\zeta _i$ represent the coefficients for calculation of the area $A_{i+\frac{1}{2}}$ or $A_{i-\frac{1}{2}}$ for the selected geometry as follows

$$\begin{aligned} A_{i+\frac{1}{2}} = A_i \xi _i \quad \text{ and } \quad A_{i-\frac{1}{2}} = A_i \zeta _i. \end{aligned}$$

Similarly, we can express the relation between area and volume as

$$\begin{aligned} V_{i+\frac{1}{2}} = A_i \frac{\varDelta r}{2} \frac{1}{\mu _i} \quad \text{ and } \quad V_{i-\frac{1}{2}} = A_i \frac{\varDelta r}{2}\frac{1}{\nu _i}, \end{aligned}$$

where

$$\begin{aligned} \mu _i = \frac{\left( \gamma +1\right) \frac{\varDelta r}{2 r_i}}{\left( 1 + \frac{\varDelta r}{2 r_i}\right) ^{\gamma +1} - 1} \quad \text{ and } \quad \nu _i = \frac{\left( \gamma +1\right) \frac{\varDelta r}{2 r_i}}{1 - \left( 1 - \frac{\varDelta r}{2 r_i}\right) ^{\gamma +1}}. \end{aligned}$$

Fig. 4

Space discretisation

4.1 Steady-state

The general time-fractional heat conduction model (2.1) for inhomogeneous material and under steady-state conditions $(\partial T/\partial t = 0)$ takes the form

$$\begin{aligned} \left. \frac{1}{r^\gamma } \frac{\partial }{\partial r} \left( r^\gamma \lambda \frac{\partial T(r,t)}{\partial r} \right) \right| _{r_i}= & {} 0,\\ \frac{1}{r_i^\gamma } \frac{ \left. r_{i+\frac{1}{2}}^\gamma \lambda _i \frac{\partial T(r,\tau )}{\partial r}\right| _{r_{i+\frac{1}{2}}} - \left. r_{i -\frac{1}{2}}^\gamma \lambda _{i-1} \frac{\partial T(r,\tau )}{\partial r}\right| _{r_{i -\frac{1}{2}}} }{\varDelta r}= & {} 0,\\ \lambda _{i-1} \zeta _i T_{i-1} - \left( \lambda _{i-1}\zeta _i + \lambda _i \xi _i \right) T_{i} + \lambda _i \xi _i T_{i+1}= & {} 0, \end{aligned}$$

and the matrix form is as follows

$$\begin{aligned} \textbf{A} \cdot \textbf{T} = \textbf{b} \end{aligned}$$

or

where the coefficients are

$$\begin{aligned} x_i= & {} \lambda _{i-1} \zeta _i, \\ y_i= & {} - \left( \lambda _{i-1} \zeta _i + \lambda _{i} \xi _i \right) , \\ z_i= & {} \lambda _{i} \xi _i, \\ w_i= & {} 0, \quad \text{ for } \quad i = 2, 3, \ldots , n-1. \end{aligned}$$

The specified temperatures of the boundary conditions are incorporated by simple assigning the given surface temperatures to the boundary nodes and therefore for the Dirichlet boundary conditions the coefficients are

$$\begin{aligned} y_1 = 1, \quad z_1 = 0, \quad w_1= & {} T_a,\\ y_n = 1, \quad x_n = 0, \quad w_n= & {} T_b. \end{aligned}$$

When other boundary conditions such as the heat flux or convection are specified at the boundary, the finite difference equation for the node at that boundary is obtained by writing an energy balance of the elementary volume at that boundary (Fig. ). The energy balance is expressed as

$$\begin{aligned} 0 = I_{1,2} + I_a \end{aligned}$$

or

$$\begin{aligned} 0 = A_{1+\frac{1}{2}} \frac{\lambda _1}{\varDelta r} \left( T_2 - T_1 \right) + A_1 i_a, \end{aligned}$$

and therefore

$$\begin{aligned} \xi _1 T_1 - \xi _1 T_2 = R_a i_a. \end{aligned}$$

For the Neumann boundary conditions the coefficients are

$$\begin{aligned} y_1 = \xi _1, \quad z_1 = - \xi _1, \quad w_1 = R_a i_a, \\ y_n = \zeta _n, \quad x_n = - \zeta _n, \quad w_n = R_b i_b, \end{aligned}$$

where $R_{a}, R_{b}$ are internal thermal resistances (m$^{2}\cdot$K$\cdot$W$^{-1}$).

In the case of Robin boundary conditions the energy balance is expressed as

$$\begin{aligned} 0 = A_{1+\frac{1}{2}} \frac{\lambda _1}{\varDelta r} \left( T_2 - T_1 \right) + A_1 h_a \left( T_{sa} - T_1 \right) \end{aligned}$$

or

$$\begin{aligned} \left( \xi _1 + \beta _a \right) T_1 - \xi _1 T_2 = \beta _a T_{sa}. \nonumber \end{aligned}$$

For the Robin boundary conditions the coefficients are

$$\begin{aligned} y_1 = \xi _1 + \beta _a, \quad z_1 = - \xi _1, \quad w_1 = \beta _a T_{sa}, \\ y_n = \zeta _n + \beta _b, \quad x_n = - \zeta _n, \quad w_n = \beta _b T_{sb}, \end{aligned}$$

where $\beta _{a}, \beta _{b}$ are Biot numbers or ratios of internal and external thermal resistances at the boundary surface.

Fig. 5

Scheme for the formulation of boundary conditions

4.2 Unsteady-state

According to the type of differential expression finite difference methods can be divided into explicit, implicit and Crank-Nicolson schemes.

4.2.1 Explicit scheme

The explicit scheme for the general time-fractional heat conduction model (2.2) has the form

$$\begin{aligned} \frac{T_i^p + \sum _{j=1}^{N_f}c_{j}T_i^{p-j}}{\varDelta t^{\alpha }} = \frac{k^2_i\xi _i T_{i+1}^{p-1}-(k^2_i\xi _i+k^2_{i-1}\zeta _i) T_i^{p-1}+k^2_{i-1}\zeta _i T_{i-1}^{p-1}}{\varDelta r^2} \end{aligned}$$

or

$$\begin{aligned} T_i^p = \tau _{i-1} \zeta _i T_{i-1}^{p-1} - \left( \tau _{i-1} \zeta _i + \tau _i \xi _i \right) T_i^{p-1} + \tau _i \xi _i T_{i+1}^{p-1} - \sum _{j=1}^{N_f} c_{j}T_i^{p-j}, \end{aligned}$$

(4.1)

where module $\tau _i$ is determined by the relation

$$\begin{aligned} \tau _i = \left( \frac{k_i}{\varDelta r}\right) ^{2} \varDelta t^\alpha , \end{aligned}$$

while the value of $\tau _i$ with respect to the stability of the solution must have values less or equal to 0.5.

The matrix form of equation (4.1) is as follows

$$\begin{aligned} \textbf{T}^p = \textbf{A} \cdot \textbf{T}^{p-1} + \textbf{b} \end{aligned}$$

or

where the coefficients are

$$\begin{aligned} x_i= & {} \tau _{i-1} \zeta _i, \\ y_i= & {} - \left( \tau _{i-1} \zeta _i + \tau _{i} \xi _i \right) , \\ z_i= & {} \tau _{i} \xi _i, \\ w_i= & {} - \sum _{j=1}^{N_f}c_{j}T_i^{p-j}, \quad \text{ for } \quad i = 2, 3, \ldots , n-1. \end{aligned}$$

For the Dirichlet boundary conditions the coefficients are

$$\begin{aligned} y_1 = 0, \quad z_1 = 0, \quad w_1 = T_a, \\ y_n = 0, \quad x_n = 0, \quad w_n = T_b. \end{aligned}$$

In the case of Neumann boundary conditions the energy balance is expressed as

$$\begin{aligned} \frac{\varDelta Q_a}{\varDelta t} = I_{1,2} + I_a \end{aligned}$$

or

$$\begin{aligned} \varrho _1 c_{p1} V_{1+\frac{1}{2}} \frac{ T_1^{p} + \sum _{j=1}^{N_f}c_{j}T_{1}^{p-j}}{\varDelta t} = A_{1+\frac{1}{2}} \frac{\lambda _1}{\varDelta r} \left( T_2^{p-1} - T_1^{p-1} \right) + A_1 i_a, \end{aligned}$$

and therefore

$$\begin{aligned} T_1^{p} = - 2 \tau _1 \mu _1 \xi _1 T_1^{p-1} + 2 \tau _1 \mu _1 \xi _1 T_2^{p-1} - \sum _{j=1}^{N_f}c_{j}T_{1}^{p-j} + 2 \tau _1 \mu _1 R_a i_a. \end{aligned}$$

For the Neumann boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} - 2\tau _1\mu _1 \xi _1, \quad z_1 = 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 R_a i_a, \\ y_n= & {} - 2\tau _{n-1}\nu _n \zeta _n, \quad x_n = 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n R_b i_b. \end{aligned}$$

In the case of Robin boundary conditions the energy balance is expressed as

$$\begin{aligned} \varrho _1 c_{p1} V_{1+\frac{1}{2}} \frac{ T_1^{p} + \sum _{j=1}^{N_f}c_{j}T_{1}^{p-j}}{\varDelta t} = A_{1+\frac{1}{2}} \frac{\lambda _1}{\varDelta r} \left( T_2^{p-1} - T_1^{p-1} \right) + A_1 h_a \left( T_{sa} - T_1^{p-1} \right) \end{aligned}$$

or

$$\begin{aligned} T_1^{p} = - 2 \tau _1 \mu _1 \left( \xi _1 + \beta _a \right) T_1^{p-1} + 2 \tau _1 \mu _1 \xi _1 T_2^{p-1} - \sum _{j=1}^{N_f}c_{j}T_{1}^{p-j} + 2 \tau _1 \mu _1 \beta _a T_{sa}. \end{aligned}$$

For the Robin boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} - 2\tau _1\mu _1 \left( \xi _1 + \beta _a \right) , \quad z_1 = 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 \beta _a T_{sa}, \\ y_n= & {} - 2\tau _{n-1}\nu _n \left( \zeta _n + \beta _b \right) , \quad x_n = 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n \beta _b T_{sb}, \end{aligned}$$

where $R_{a}, R_{b}$ are internal thermal resistances (m$^{2}\cdot$K$\cdot$W$^{-1}$); $\beta _{a}, \beta _{b}$ are Biot numbers or ratios of internal and external thermal resistances at the boundary surface.

4.2.2 Implicit scheme

The implicit scheme for the general time-fractional heat conduction model (2.2) has the form

$$\begin{aligned} \frac{T_i^p + \sum _{j=1}^{N_f}c_{j}T_i^{p-j}}{\varDelta t^{\alpha }} = \frac{k^2_i \xi _i T_{i+1}^{p} - (k^2_i \xi _i+ k^2_{i-1} \zeta _i) T_i^{p} + k^2_{i-1} \zeta _i T_{i-1}^{p}}{\varDelta r^2}, \end{aligned}$$

or

$$\begin{aligned} -\tau _{i-1}\zeta _iT_{i-1}^p+\left( 1+\tau _{i-1}\zeta _i+\tau _i\xi _i\right) T_i^p-\tau _i\xi _iT_{i+1}^p= -\sum _{j=1}^{N_f}c_{j}T_i^{p-j}. \end{aligned}$$

In matrix form this is

$$\begin{aligned} \textbf{A} \cdot \textbf{T}^p = \textbf{b} \end{aligned}$$

or

where the coefficients are

$$\begin{aligned} x_i= & {} - \tau _{i-1} \zeta _i, \\ y_i= & {} 1 +\tau _{i-1} \zeta _i + \tau _{i} \xi _i, \\ z_i= & {} - \tau _{i} \xi _i, \\ w_i= & {} - \sum _{j=1}^{N_f}c_{j}T_i^{p-j}, \quad \text{ for } \quad i = 2, 3, \ldots , n-1. \end{aligned}$$

For the Dirichlet boundary conditions the coefficients are

$$\begin{aligned} y_1 = 1, \quad z_1 = 0, \quad w_1= & {} T_a, \\ y_n = 1, \quad x_n = 0, \quad w_n= & {} T_b. \end{aligned}$$

For the Neumann boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} 1 + 2\tau _1\mu _1 \xi _1, \quad z_1 = - 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 R_a i_a, \\ y_n= & {} 1 + 2\tau _{n-1}\nu _n \zeta _n, \quad x_n = - 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n R_b i_b. \end{aligned}$$

For the Robin boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} 1 + 2\tau _1\mu _1 \left( \xi _1 + \beta _a \right) , \quad z_1 = - 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 \beta _a T_{sa}, \\ y_n= & {} 1 + 2\tau _{n-1}\nu _n \left( \zeta _n + \beta _b \right) , \quad x_n = - 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n \beta _b T_{sb}. \end{aligned}$$

4.2.3 Crank-Nicolson scheme

The Crank-Nicolson scheme for the general time-fractional heat conduction model (2.2) has the form

$$\begin{aligned} \frac{T_i^p + \sum _{j=1}^{N_f}c_{j}T_i^{p-j}}{\varDelta t^{\alpha }}= & {} \frac{1}{2} \Bigg ( \frac{k^2_i\xi _i T_{i+1}^{p-1}-(k^2_i\xi _i+k^2_{i-1}\zeta _i) T_i^{p-1}+k^2_{i-1}\zeta _i T_{i-1}^{p-1}}{\varDelta r^2} \Bigg )\\+ & {} \frac{1}{2} \Bigg ( \frac{k^2_i \xi _i T_{i+1}^{p} - (k^2_i \xi _i + k^2_{i-1} \zeta _i) T_i^{p} + k^2_{i-1} \zeta _i T_{i-1}^{p}}{\varDelta r^2} \Bigg ) \end{aligned}$$

or

$$\begin{aligned}- & {} \tau _{i-1} \zeta _i T_{i-1}^{p} + \left( 2 + \tau _{i-1} \zeta _i + \tau _i \xi _i \right) T_{i}^{p} - \tau _i \xi _i T_{i+1}^{p}\\= & {} \tau _{i-1} \zeta _i T_{i-1}^{p-1} - \left( \tau _{i-1} \zeta _i+ \tau _i \xi _i \right) T_{i}^{p-1}+ \tau _i \xi _i T_{i+1}^{p-1} - 2 \sum _{j=1}^{N_f} c_{j}T_{i}^{p-j}. \end{aligned}$$

In matrix form this is

$$\begin{aligned} \textbf{A}^p \cdot \textbf{T}^p = \textbf{A}^{p-1} \cdot \textbf{T}^{p-1} + \textbf{b} \nonumber \end{aligned}$$

or

where the coefficients are

$$\begin{aligned} x_i= & {} - \tau _{i-1} \zeta _i, \\ z_i= & {} - \tau _{i} \xi _i, \\ y_i= & {} 2 + \tau _{i-1} \zeta _i + \tau _{i} \xi _i, \\ w_i= & {} - 2 \sum _{j=1}^{N_f}c_{j}T_i^{p-j}, \quad \text{ for } \quad i = 2, 3, \ldots , n-1. \end{aligned}$$

For the Dirichlet boundary conditions the coefficients are

$$\begin{aligned} y_1 = 1, \quad z_1 = 0, \quad w_1= & {} T_a, \\ y_n = 1, \quad x_n = 0, \quad w_n= & {} T_b. \end{aligned}$$

For the Neumann boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} 1 + 2\tau _1\mu _1 \xi _1, \quad z_1 = - 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 R_a i_a, \\ y_n= & {} 1 + 2\tau _{n-1}\nu _n \zeta _n, \quad x_n = - 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n R_b i_b. \end{aligned}$$

For the Robin boundary conditions the coefficients are

$$\begin{aligned} y_1= & {} 1 + 2\tau _1\mu _1 \left( \xi _1 + \beta _a \right) , \quad z_1 = - 2\tau _1\mu _1 \xi _1, \\ w_1= & {} - \sum _{j=1}^{N_f}c_{j}T_1^{p-j} + 2\tau _1\mu _1 \beta _a T_{sa}, \\ y_n= & {} 1 + 2\tau _{n-1}\nu _n \left( \zeta _n + \beta _b \right) , \quad x_n = - 2\tau _{n-1}\nu _n \zeta _n, \\ w_n= & {} - \sum _{j=1}^{N_f}c_{j}T_n^{p-j} + 2\tau _{n-1}\nu _n \beta _b T_{sb}. \end{aligned}$$

5 Implementation

The implementation was realised in the programming environment MATLAB, in which the functions for solution of the time-fractional diffusion-wave equation in various geometries have been created. The MATLAB toolbox called Time-Fractional Diffusion-Wave Eq. in Various Geometries (TFDWEg) consists of functions for solving one-dimensional general model for various geometries with utilisation of the explicit, implicit, and Crank-Nicolson scheme, respectively. The functions implement the finite difference method for homogeneous or inhomogeneous material and for homogeneous or inhomogeneous boundary conditions. The functions headers are as follows

function [R,T,MU] = TFDWEg_exp(Uin,alpha,Nf,k,dr,a,b,dt,ts,TBC,BC,g)

function [R,T,MU] = TFDWEg_imp(Uin,alpha,Nf,k,dr,a,b,dt,ts,TBC,BC,g)

function [R,T,MU] = TFDWEg_CN (Uin,alpha,Nf,k,dr,a,b,dt,ts,TBC,BC,g)

where the function inputs are: Uin is the vector of the initial conditions, alpha is the order of the time derivative, Nf is the memory length, k is the process coefficients vector, dr is the spatial step, a and b are the left, right side coordinates of the body, respectively, dt is the time step, ts is the time of simulation, TBC is the vector of the boundary conditions type, BC are the values of the boundary condition, and g is the geometry type. The function outputs are: R is the vector of coordinates, T is the vector of time, and MU is the output values matrix. The toolbox is published at MathWorks, Inc., MATLAB Central File Exchange [40].

6 Simulations

Time-Fractional Diffusion-Wave Equation simulations in various geometries for homogeneous or inhomogeneous material and for homogeneous or inhomogeneous boundary conditions are realised using the script TFDWEg_test.m which is a part of the toolbox TFDWEg [40]. In the following examples the behaviour of temperature in space and time for various geometries is illustrated.

Let us propose an example, where the initial conditions are been defined in the form of the constant temperature ($T(r,0)=0^\circ$C) in the whole cross-section, considering copper as the material (with density $\varrho = 8900$ kg/m$^3$, thermal conductivity $\lambda = 400$ W/m/K, specific heat capacity $c_p= 380$ J/kg/K), left ($a=0.01$ m) and right ($b=0.03$ m) side coordinate. The material was divided into twenty parts in the space, with time step (0.001 s), total time simulation (2 s), and Dirichlet boundary conditions with temperatures at the edges ($T_a = 0^\circ$C and $T_b = 15^\circ$C). The simulation results using Crank-Nicolson scheme are shown in Fig. , where the left coloumn shows the behaviour of temperature in time (where the parameter is the position in space), the middle coloumn shows the behaviour of temperature in space (where the parameter is time), and the right coloumn displays 3D plots of temperatures in space and time for hollow body (Fig. 2a), i.e. large plane wall (Fig. 6a), long cylinder (Fig. 6b), and sphere (Fig. 6c). In the case of setting the left coordinate to zero ($a = 0.0$ m), it is possible to perform the same simulation but for a full symmetrical body (Fig. 2b), as shown in figure Fig. .

Fig. 6

Hollow body – (a) large plane wall, (b) long cylinder, and (c) sphere

Fig. 7

Symmetrical body – (a) large plane wall, (b) long cylinder, and (c) sphere

The graphs in Fig.  show the evolution results solving the time-fractional heat conduction using the fractional-order derivative $\alpha$ = 0.5, 1.0, and 1.5, respectively. Comparing the graphs, one can observe that the derivative of order 0.5 exhibits fast temperature rise in the beginning and slow temperature rise later. Moreover, it is evident that the temperatures propagate and diffuse with time, which means that the temperature continuously depends on the fractional derivative, therefore, when $\alpha$ = 1.5, both diffusion and wave response can be observed.

Fig. 8

Large plane wall for $\alpha$=0.5, 1.0, and 1.5

Let us use the previous settings to perform simulations demonstrating the use of different homogeneous boundary conditions for homogeneous material. The behaviour of the temperature for the Dirichlet, Neumann, and Robin boundary conditions is shown in Fig. . In the case of the Dirichlet boundary conditions, the surface temperatures are $T_a=T_b=15^\circ$C; in the case of the Neumann boundary conditions, the thermal flux and the internal thermal resistance are $i_a \cdot R_a=i_b \cdot R_b=0.75^\circ$C, and in the case of the Robin boundary conditions the surrounding media temperatures and the ratio of internal and external thermal resistances are $T_{sa}=T_{sb}=15^\circ$C, $\beta _a = \beta _b = 1$. The graphs in Fig.  show inhomogeneous boundary conditions for selected combinations, i.e. Neumann-Dirichlet, Robin-Dirichlet, and Neumann-Robin, respectively.

Fig. 9

Dirichlet, Neumann, and Robin homogeneous boundary conditions for large plane wall

Fig. 10

Neumann-Dirichlet, Robin-Dirichlet, and Neumann-Robin inhomogeneous boundary conditions

The script TFDWEg_test.m also allows to simulate homogeneous as well as inhomogeneous material. For example, in the case of thermal diffusivity for twenty layers and two materials (brass and copper) of the same thickness a twenty-component thermal diffusivity vector is needed (ten components for brass and ten components for copper). Results of the simulations are shown in Fig. a for homogeneous and in Fig. b for inhomogeneous material, where in the first half of the specimen length there is a lower temperature rise than in the other half. This is due to the fact that in the first half the material there is copper whose thermal diffusivity is about three times larger than that of brass.

Fig. 11

Large plane wall, long cylinder, and sphere for (a) homogeneous and (b) inhomogeneous material

7 Conclusion

The general one-dimensional model of the time-fractional diffusion-wave equation in various geometries is designed and described in this contribution. The numerical solution using the Grünwald-Letnikov definition of fractional derivative according to time for homogeneous and inhomogeneous boundary conditions and for homogeneous and inhomogeneous material is presented. The numerical schemes were implemented in MATLAB in the form of a library of functions. The possibilities of using this library are illustrated by examples and simulations. Additionally, besides modeling heat conduction processes, the library allows to model other processes such as diffusion, wave distribution, and so on. The library is a suitable tool for the implementation of simulations of a wide class of processes and also for the creation of complex models in the MATLAB environment. Benefits of this work are the design, numerical solution and implementation of one general mathematical model that can be used for modeling various different processes, in various geometries, materials and boundary conditions.