Abstract
We present a review on the notion of pure states and mixtures as mathematical concepts that apply for both classical and quantum physical theories, as well as for any other theory depending on statistical description. Here, states will be presented as expectation values on suitable algebras of observables, in a manner intended for the non-specialist reader; accordingly, basic literature on the subject will be provided. Examples will be exposed together with a discussion on their meanings and implications. An example will be shown where a pure quantum state converges to a classical mixture of particles as Planck’s constant tends to 0.

Similar content being viewed by others
Notes
Scalar products (or inner products) in Hilbert spaces will be always denoted here by 〈ϕ,ψ〉 rather than by 〈ϕ|ψ〉. We follow the physicists’ convention: they are antilinear in the first argument and linear in the second.
Strictly speaking one should use nets to characterise convergence in those topologies, instead of sequences. For the sake of clarity, we will use the latter. See, e.g., [17].
These rules are not supposed to hold in the case of unbounded operators acting on Hilbert spaces. See e.g. [1].
A function f ∈ C0(X) vanishes at infinite if, for any ε > 0, there is K ⊂ X compact such that |f(x)| < ε for any x ∈ X ∖ K.
Concretely, \(\tilde {\mathfrak {A}}\) is the algebra with elements \((\lambda , A) \in \mathbb {C} \times \mathfrak {A}\), involution \((\lambda , A)^{\ast } = (\overline {\lambda }, A^{\ast })\) and multiplication (λ1,A1)(λ2,A2) = (λ1λ2,λ1A2 + λ2A1 + A1A2); one easily checks that (1, 0) is an identity in \(\tilde {\mathfrak {A}}\), and the convenient way to map \(\mathfrak {A}\) into \(\tilde {\mathfrak {A}}\) is through the application A↦(0,A).
An increasing net of operators is a net such that \(A_{\nu } \geqslant A_{\mu }\) whenever \(\nu \geqslant \mu \); the operators’ order relation is defined in the following way: \(A_{\nu } \geqslant A_{\mu }\) if Aν − Aμ is a positive operator, i.e. if its spectrum is included in \(\mathbb {R}^{+}\).
The matrices
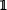 , σ1, σ2 and σ3 are a basis in the real space of the 2 × 2 self-adjoint matrices.
, σ1, σ2 and σ3 are a basis in the real space of the 2 × 2 self-adjoint matrices.With \(0 < \beta < \frac {1}{10}\), \({\varPsi }^{1}, {\varPsi }^{2} \in C_{0}^{\infty }(\mathbb {R})\), Ψ1 supported on x > 0 and suppΨ1 ∩suppΨ2 = ∅.
For any \(A,B \in \mathfrak {A}\), one has \(\omega ((AB)^{*} (AB)) \leqslant \|A\|^{2} \omega (B^{*}B)\) (see [6]), so clearly \(AB \in \mathcal {N}_{\omega }\) whenever \(B \in \mathcal {N}_{\omega }\).
If \(\mathfrak {A}\) does not have an identity, similar results can be obtained using nets converging to a unity. See e.g. [6].
When this happens, Ωω is said to be a cyclic vector.
I is the index set, the set where the indices take their values from.
References
M. Reed, B. Simon. Methods of Modern Mathematical Physics I – Functional Analysis (Academic, Cambridge, 1980)
H. Araki, Vol. 101. Mathematical theory of quantum fields, International series of monographs in Physics (Oxford University Press, London, 2009). ISBN 0 19 851773 4
R. Haag. Local Quantum Physics, 2nd edn. (Springer, Berlin, 1996). ISSN 0172-5998
C.J. Fewster, K. Rejzner, Algebraic Quantum Field Theory - an introduction. arXiv:1904.04051 [hep-th] (2019)
Gérard G. Emch. Algebraic Methods in Statistical Mechanics and Quantum Field Theory (Wiley-Interscience, New York, 1972). ISBN-13 978-0-486-47209-6
O. Bratteli, D.W. Robinson. Operator algebras and Quantum Statistical Mechanics I – C∗- and W∗-algebras, symmetry groups, decomposition of states, 2nd edn. (Springer, Berlin, 1987). ISBN 3-540-09187-4
J. Dixmier. Von Neumann algebras (North Holland, Amsterdam, 2011). ISBN-13: 978-0444557407
V. Chabu, Semiclassical analysis of the schrödinger equation with conical singularities. Asymptot. Anal. 103(4), 165–220 (2017)
V. Chabu, Semiclassical analysis of the schrödinger equation with singular potentials thèse de l’université Paris-Est (2016)
P. Gérard, P.A. Markowich, N.J. Mauser, F. Poupaud, Homogenization limits and Wigner transforms. Pure Appl. Math. 50(4), 323–379 (1997)
W. Rudin. Real And Complex Analysis. Higher Mathematics series, 3rd edn. (McCraw-Hill Education, New York, 1986). ISBN-13: 978-0070542341
P. Lions, T. Paul, Sur les mesures de Wigner. Revista Matemá,tica Iberoamericana. 9, 553–618 (1993)
M. Dimassi, S. Sjostrand, Spectral asymptotics in the semiclassical limit, London Math. Society lecture note series 268: Cambridge University Press, Cambridge (1999)
M. Zworski, Semiclassical Analysis. Graduate studies in Mathematics, Vol. 138: American Mathematical Society, Providence (2012)
G.J. Murphy. C∗-algebras and Operator Theory (Academic, Cambridge, 1990). ISBN 0-12-511360-9
J.M.G. Fell, The dual spaces of C∗-algebras. Transactions of the American Mathematical Society. https://doi.org/10.2307/1993431 (1960)
R.E. Megginson. An Introduction to Banach Space Theory (Springer, Berlin, 1998). ISBN-13: 978-1461268352
R.R. Phelps. Lectures on Choquet’s Theorem (Springer, Berlin, 2001). ISBN-13: 978-3540418344
K. Erdmann, T. Holm. Algebras and Representation Theory (Springer, Berlin, 2018). ISBN-13: 978-3319919973
K.R. Davidson. C∗-Algebras by Example. Fields Institute Monographs (American Mathematical Society, Providence, 1996). ISBN-13: 978-8185931111
W.B. Arveson. An Anvitation to C∗-Algebras (Springer, Berlin, 1998). ISBN-13: 978-1461263739
M. Kleinmann, H. Kampermann, T. Meyer, D. Bruss, Physical purification of quantum states. Phys. Rev. A. 73, 062309 (2006)
Acknowledgements
We are indebted to K.-H. Neeb for pointing us some errors in a previous version of this manuscript.
Funding
M. Brum was supported by grant 2015/02975-4, Sã o Paulo Research Foundation (FAPESP). V. Chabu was supported by grant 2017/13865-0, São Paulo Research Foundation (FAPESP).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is dedicated to the memory of Mahir S. Hussein, researcher, teacher and friend.
Appendix 1: Proof of Theorem 5
Appendix 1: Proof of Theorem 5
Here, we follow [15] closely. First, take a non-null positive linear functional \(\omega ^{\prime }\) such that, \(\forall A \in \mathfrak {A}\), \(\omega ^{\prime }(A^{*}A) \leqslant \omega (A^{*}A)\). By the Cauchy-Schwartz inequality (6),
which implies, by Riesz representation theorem (see e.g. [1]), the existence of a positive operator \(T \in {\mathcal{L}}({\mathcal{H}})\) such that \(\left \langle \pi (A){\varOmega },T\pi (B){\varOmega }\right \rangle = \omega ^{\prime }(A^{*}B)\) (remark that the sesquilinear form \((\pi (A){\varOmega },\pi (B){\varOmega }) \longmapsto \omega ^{\prime }(A^{*}B)\) may be extended to the whole \({\mathcal{H}}\), and thus the domain of T, only because Ω is cyclic). Taking \(A,B,C \in \mathfrak {A}\) arbitrary:
which implies that [T,π(B)] = 0 for any B.
As known in representation theory (as a consequence of Schur’s Lemma, see e.g. [19]), if π is an irreducible representation, any self-adjoint operator commuting with it must be a multiple of the identity and vice versa. It happens that, if  for some \(\lambda \in \mathbb {C}\), then \(\omega ^{\prime } = \lambda \omega \). Let us show an implication of this fact, that ω is a mixture if and only if π is reducible, which is enough for the theorem’s statement.
for some \(\lambda \in \mathbb {C}\), then \(\omega ^{\prime } = \lambda \omega \). Let us show an implication of this fact, that ω is a mixture if and only if π is reducible, which is enough for the theorem’s statement.
Indeed, if ω is a mixture, one may find \(\omega ^{\prime }\) such that \(\omega ^{\prime }(A^{*}A) \leqslant \omega (A^{*}A)\) which is not a multiple of ω: in this case, there is a scalar σ ∈ (0, 1) and states ω1 and ω2 (none of them multiples of ω) such that ω = σω1 + (1 − σ)ω2, so just take \(\omega ^{\prime } = \sigma \omega _{1}\). The corresponding T will not be a multiple of the identity, hence the reducibility of π.
Conversely, supposing that π is reducible, one may find a self-adjoint \(S \in \mathfrak {A}\) commuting with every π(B) and not being a multiple of  . As a consequence, any non-trivial spectral projector P of S will also commute with π, not be a multiple of the identity, and further satisfy
. As a consequence, any non-trivial spectral projector P of S will also commute with π, not be a multiple of the identity, and further satisfy  . Define the functional \(\omega ^{\prime }(A) = \left \langle {\varOmega }, P\pi (A){\varOmega }\right \rangle \) and remark that it is positive, not a multiple of ω, and that
. Define the functional \(\omega ^{\prime }(A) = \left \langle {\varOmega }, P\pi (A){\varOmega }\right \rangle \) and remark that it is positive, not a multiple of ω, and that

This implies that ω is a non-trivial mixture ω = λω1 + (1 − λ)ω2, with \(\lambda = \|\omega ^{\prime }\| \in (0, 1)\) and states \(\omega _{1} = \frac {1}{\|\omega ^{\prime }\|} \omega ^{\prime }\) and \(\omega _{2} = \frac {1}{1-\|\omega ^{\prime }\|}(\omega - \omega ^{\prime })\) (see Remark 1 for a quick justification that ∥ω2∥ = 1).
Rights and permissions
About this article
Cite this article
Barata, J.C.A., Brum, M., Chabu, V. et al. Pure and Mixed States. Braz J Phys 51, 244–262 (2021). https://doi.org/10.1007/s13538-020-00808-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13538-020-00808-0





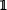 , σ1, σ2 and σ3 are a basis in the real space of the 2 × 2 self-adjoint matrices.
, σ1, σ2 and σ3 are a basis in the real space of the 2 × 2 self-adjoint matrices.