Introduction

Nowadays, considerable efforts continue to be devoted to finding ways to reduce CO2 emissions and atmospheric concentrations. Carbon sequestration, improving the efficiency of energy use, and reducing the carbon content of fuels are three major pathways that are currently being pursued to address the stabilization of greenhouse gas concentrations [1]. Carbon sequestration uses various approaches for CO2 capture, storage, and reuse [1, 2]. One such process, CO2 mineralization, uses carbonic anhydrase enzyme to convert dilute, unseparated CO2 to HCO3 and finally to everlasting calcium and magnesium carbonates. Biogenic methane is another of the carbon sequestrations; it involves geologic storage of CO2 in depleting and depleted oil and gas reservoirs, with subsequent conversion of the CO2 to CH4 via designer microbes or biomimetic systems that operate above or below ground [1]. Common among many of these concepts is the enhancement of naturally occurring biochemical and geochemical processes through the identification and replication of natural processes for the purposes of carbon sequestration.

The catalytic partial oxidation of methane into valuable products is of great scientific importance and considerable industrial, economic, and environmental interest. However, a great challenge is that in the absence of an appropriate catalyst, methane undergoes complete combustion yielding carbon dioxide and water at approximately 340 K with minimal competition with the formation of useful products that can occur at elevated temperatures. The fundamental ideas of muon-catalyzed nuclear fusion utilizing a negative muon, a deuteron, and a triton [3] are used in the proposed oxidation of CH4 to methanol for which we have selected the atomic gold anion as the catalyst. Here we propose the use of the atomic Au− ion catalyst to control the temperature of the oxidation of methane to methanol around 325 K. This has the effect of lowering the transition state (TS) by 32 % compared to the case of the absence of the catalyst for the complete oxidation of methane to methanol without carbon dioxide emission. We have employed the first principles density functional theory (DFT) and dispersion-corrected DFT calculations for the transition state on the Au− ion and analyzed the thermodynamics properties of the reactions as well.

The main motivations for the investigation are: (1) the direct synthesis of H2O2 from H2 and O2 using supported Au, Pd, and Au–Pd nanoparticle catalysts [4, 5] including the theory [6, 7] that attributed the catalytic properties of Au and Pd to the formation of negative ion resonances in low-energy electron elastic total cross sections (TCSs) for Au and Pd atoms, along with their large electron affinities (EAs); (2) the recent dispersion-corrected density functional theory transition-state calculations performed on the atomic Au− ion catalysis of water conversion to H2O2, revealing that the formation of the Au−(H2O)2 anion molecular complex in the transition state provides the fundamental mechanism for breaking up the hydrogen bonding strength in the catalysis of H2O2 using the Au− ion [8]. It is important to note that the Au− ion is employed here as a prototype for negatively charged gold clusters or surfaces. The peculiar binding energy associated with the Au− ion is of fundamental distinction as compared to that of the Au+ ion or the neutral Au atom

Contrary to bulk gold, nanogold exhibits surprisingly high activity and/or selectivity in the combustion as well as partial oxidation of various molecules and compounds [9]. Since the publication of the paper [9], there have been considerable research activities on nanogold, particularly on its catalytic properties [9–29]. The mechanisms of charge transfer [11, 12] and relativity [13] have been advanced as possible explanations for the excellent catalytic properties of gold nanoparticles. Recently, the negative ion resonances that characterize the electron elastic scattering TCSs for atomic Au have been proposed as the fundamental mechanism driving nanoscale catalysis [6, 7]. The catalytic combustion of methane, the main component of natural gas, including its conversion to useful products, has recently received extensive experimental and theoretical attention because of the potential to reduce pollutant emissions and synthesize useful chemicals [30–36] and references therein. A recent investigation demonstrated the selective conversion of a mixture of methane and oxygen to formaldehyde at temperatures below 250 K through temperature-controlled Au2+ nanocatalysis [36].

Experimentally, it has been established that the Au− anion interacts with water molecules to form the Au−(H2O)1,2 complexes, causing bond breaking and with methane to form the Au−(CH4) complex [37], thereby weakening the C–H bond. Furthermore, the strong interaction between the Au− anion and H2O is comparable to the hydrogen bonding in H2O and the Au− anion interaction with CH4 is significant as well, but the Au− ion does not interact with O2 [29]. These findings [29, 37] are vital to the fundamental understanding of nanocatalysis using Au nanoparticles. To our knowledge, our proposed approach is the first to use the Au− negative ion in the catalytic combustion of methane to useful products without the emission of CO2.

Reactions and calculation method

The complete combustion of methane leads to the formation of carbon dioxide and water:

$$ {\text{C}}{{\text{H}}_{{4}}} + {2}{{\text{O}}_{{2}}} \to {\text{C}}{{\text{O}}_{{2}}} + {2} {{\text{H}}_{{2}}}{\text{O}} $$
(1)

Possible by-products of the partial oxidation of methane are:

$$ {\text{C}}{{\text{H}}_{{4}}} + \frac{1}{2}{{\text{O}}_{{2}}} \to {\text{CO}} + {2} {{\text{H}}_{{2}}} $$
(2)
$$ {\text{C}}{{\text{H}}_{{4}}} + \frac{1}{2}{{\text{O}}_{{2}}} \to {\text{C}}{{\text{H}}_{{3}}}{\text{OH}} $$
(3)
$$ {\text{C}}{{\text{H}}_{{4}}} + {{\text{O}}_{{2}}} \to {{\text{H}}_{{2}}}{\text{CO}} + {{\text{H}}_{{2}}}{\text{O}} $$
(4)
$$ {\text{C}}{{\text{H}}_{{4}}} + {{\text{O}}_{{2}}} \to {\text{HC}}{{\text{O}}_{{2}}}{\text{H}} + {{\text{H}}_{{2}}} $$
(5)

Generally, there is little competition between the complete oxidation, reaction (1) and the selective partial oxidation (SPO), reactions (2, 3, 4, and 5), of methane. There are two reasons why the overall reaction leads to the formation of carbon dioxide and water: (1) Complete combustion of methane occurs at the lowest temperature compared to its SPO and (2) the corresponding transition state for reaction (1) is lowest compared to that of any SPO of methane to the desired products. However, the atomic Au− negative ion activates molecular oxygen in CH4 and increases the level of the SPO of methane to produce useful compounds.

Here the atomic Au− catalyst is used to control the oxidation temperature of methane around 325 K to lower the transition state by 32 % compared to the case of the absence of the catalyst for the complete oxidation of methane to methanol and further oxidize methanol to formaldehyde and formic acid without CO2 emission. We follow exactly the same procedure as in [6, 7] when applying the atomic Au− ion catalyst to each of the reactions (1, 2, 3, 4, and 5).

The proposed mechanism of catalysis using the negative Au− ion catalyst is as follows. When a slow electron collides elastically with a ground-state neutral gold atom, attachment can result, leading to the formation of a negative ion resonance due to the formation of compound atomic states. The energy position of this negative ion resonance corresponds to the stable bound state of the Au− negative ion formed during the collision as a resonance. The binding energy of the Au− ion defines the EA of atomic Au. Theoretically, it has been demonstrated that the EA of Au is right at the absolute minimum or the second R-T minimum (absolute) of the elastic TCS of Au [6, 7, 38, 39]. At this minimum and within the appropriate environment, the attachment of the Au− negative ion to the CH4 molecule results in the formation of the Au−(CH4) anionic molecular complex. This complex formation results in the disruption of the stable C–H bonds in the methane molecule. The attendant change in the Gibbs energy of the system becomes negative, thereby thermodynamically favoring the formation of methanol. The Au− ion is released after the chemical reaction. We note that the dissociative energy of the Au−(CH4) molecular complex is within the second R-T minimum of the Au elastic TCS.

We have employed the first principles calculations based on DFT and dispersion-corrected DFT approaches for the investigation. For geometry optimization of structural molecular confirmation, we utilized the gradient-corrected Perdew–Burke–Ernzerfof parameterizations [40] of the exchange correlation rectified with the dispersion corrections [41]. The double numerical plus polarization basis set was employed as implemented in the DMol3 package [42]. The dispersion correction method, coupled to suitable density functional, has been demonstrated to account for the long-range dispersion forces with remarkable accuracy. We used a tolerance of 1.0 × 10−3 eV for energy convergence. A transition-state search employing nudged elastic bands facilitates the evaluation of energy barriers [43–45]. Finally, the energy of the transition state was calculated and the thermodynamic properties of the reaction were analyzed from the DMol3 package [42]. As the calculation of the transition barrier depends crucially on the exchange correlation scheme employed, the use of reliable dispersion-corrected approach is essential. The error in extracting the transition barrier associated with the transition pathway was estimated to be less than 0.001 eV [43–45].

Results and discussion

Figures 1, 2, 3, 4, and 5 present the optimized structures of the reactants, transition states, and products of oxidation of methane leading to the formation of CO2, CO, CH3OH, H2CO, and HCO2H, respectively. The data in (a) correspond to the absence of the Au− ion catalyst while those in (b) are data when the Au− ion catalyst is present. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms. The TS and EP, both in electron volts, represent respectively the calculated transition-state energy and the energy of the products. The breaking of the stable C–H bonds in the methane molecule in the transition state resulting in the formation of methanol in the presence of O2 is attributed to the formation of the anionic Au−(CH4) complex. The role of the Au− ion is to disrupt the stable C–H bonds in the methane molecule, allowing the formation of methanol in the presence of O2. It is noted that the optimized structure corresponding to the reaction (3), namely the production of methanol, has the lowest transition-state energy (see Figs. 1b, 2b, 3b, 4b, and 5b). These results are also summarized in Table 1.

Fig. 1
figure 1

Complete oxidation of methane to carbon dioxide and water in the absence (a) and presence (b) of the Au− negative ion catalyst. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms

Full size image
Fig. 2
figure 2

Oxidation of methane to carbon monoxide and hydrogen gas in the absence (a) and presence (b) of the Au− negative ion catalyst. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms

Full size image
Fig. 3
figure 3

Oxidation of methane to methanol in the absence (a) and presence (b) of the Au− negative ion catalyst. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms

Full size image
Fig. 4
figure 4

Oxidation of methane to formaldehyde and water in the absence (a) and presence (b) of the Au− negative ion catalyst. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms

Full size image
Fig. 5
figure 5

Oxidation of methane to formic acid and hydrogen gas in the absence (a) and presence (b) of Au− negative ion catalyst. The red, white, gray, and gold spheres represent respectively oxygen, hydrogen, carbon, and gold atoms

Full size image
Table 1 TS, EP, and T represent, respectively, the calculated transition state, energy of the products and temperature of the reaction
Full size table

Understanding the results

Here we discuss the results of the complete oxidation of CH4, reaction (1), and of the SPO of CH4, reaction (3) as illustrations; the latter analysis also applies to the remaining reactions. In [6, 7] we explained the catalytic production of H2O2 from H2O, using the atomic Au− ion catalyst, in the presence of O2. Similarly, here we first apply the atomic Au− ion catalyst to the complete oxidation of CH4, reaction (1), and obtain:

$$ {\text{A}}{{\text{u}}^{ - }}\left( {{\text{C}}{{\text{H}}_{{4}}}} \right) + {2}{{\text{O}}_{{2}}} \to {\text{A}}{{\text{u}}^{ - }} + {2}{{\text{H}}_{{2}}}{{\text{O}}_{{2}}} + {\text{C}}{{\text{O}}_{{2}}} $$
(6)
$$ {\text{A}}{{\text{u}}^{ - }} + {\text{2C}}{{\text{H}}_{{4}}} + {2}{{\text{O}}_{{2}}} \to {\text{A}}{{\text{u}}^{ - }}\left( {{\text{C}}{{\text{H}}_{{4}}}} \right) + {2}{{\text{H}}_{{2}}}{{\text{O}}_{{2}}} { +}{\text{C}}{{\text{O}}_{{2}}} $$
(7)

Adding the reactions (8) and (9), we get:

$$ {\text{C}}{{\text{H}}_{{4}}} + {2}{{\text{O}}_{{2}}} \to {2}{{\text{H}}_{{2}}}{\text{O}} + {\text{C}}{{\text{O}}_{{2}}} $$
(8)

The Au− ion catalyst has changed nothing in the reaction, demonstrating complete combustion. The results of Table 1 (same TS values for the absence and presence of the catalyst) and Figs. 1 and 7 are illustrations of the complete combustion process. We note that the purpose of a catalyst is to decrease the reaction temperature to ambient temperature [46]. So, the Au− catalyst cannot be effective since the 340 K temperature (Table 1) is the ambient temperature for CO2 production.

Next we apply the Au− ion catalyst to the reaction (3) and obtain:

$$ {\text{A}}{{\text{u}}^{ - }}\left( {{\text{C}}{{\text{H}}_{{4}}}} \right) + {{{1}} \left/ {{{2}{{\text{O}}_{{2}}}}} \right.} \to {\text{A}}{{\text{u}}^{ - }} + {\text{C}}{{\text{H}}_{{3}}}{\text{OH}} $$
(9)
$$ {\text{A}}{{\text{u}}^{ - }} + {\text{2C}}{{\text{H}}_{{4}}} + {{1} \left/ {{{2}{{\text{O}}_{{2}}}}} \right.} \to {\text{A}}{{\text{u}}^{ - }}\left( {{\text{C}}{{\text{H}}_{{4}}}} \right) + {\text{C}}{{\text{H}}_{{3}}}{\text{OH}} $$
(10)

Adding the reactions (9) and (10), we have:

$$ {\text{C}}{{\text{H}}_{{4}}} + {{1} \left/ {{{2}{{\text{O}}_{{2}}}}} \right.} \to {\text{C}}{{\text{H}}_{{3}}}{\text{OH}} $$
(11)

Contrary to the complete oxidation of methane, reaction (1), the Au− ion catalyzes the SPO of CH4 to a new product, namely CH3OH without CO2 emission, reaction (11). As seen from comparing the TSs in column 2 and column 5 of Table 1, the complete oxidation leaves the TS virtually unchanged when the Au− ion catalyst is introduced. However, for the case of the SPO of CH4, reaction (3), the TSs are 4.41 and 3.01 eV in the absence and presence of the Au− ion catalyst, respectively. So, no barrier reduction is a manifestation of the complete oxidation of CH4. For this case the catalyst has no effect on reaction (1). The obtained results in Table 1 and Figs. 1, 2, 3, 4, 5, 6, and 7 can be understood from three perspectives: resonance scattering theory, thermodynamics consideration, and transition-state calculations.

Fig. 6
figure 6

a Change in the Gibbs free energy (in electron volts) versus temperature, T (in Kelvin), in the presence of the Au− ion catalyst. The first (purple squares), second (blue circles), third (red circles), fourth (green triangles), and fifth (black squares) curves correspond respectively to the reactions leading to the production of CH3OH, CO2, H2CO, CO, and HCO2H beyond the optimum temperatures. b Change in the Gibbs free energy (in electron volts) versus temperature, T (in Kelvin), in the absence of the Au− ion catalyst. The first (blue circles), second (black squares), third (red circles), fourth (purple squares), and fifth (green triangles) curves correspond respectively to the reactions leading to the production of CO2, HCO2H, H2CO, CH3OH, and CO beyond the optimum temperatures

Full size image
Fig. 7
figure 7

a Same as Fig. 6a, except that here we show the expanded region −0.50 eV ≤ ΔG ≤ 0.50 eV. b Same as Fig. 6b, except that here we show the expanded region −0.50 eV ≤ ΔG ≤ 0.50 eV. The same color scheme used for both Figures 6 and 7

Full size image

Resonance scattering approach

Most importantly, when a slow electron collides elastically with atomic Au, a stable negative Au− ion is formed almost exactly at the second deep R-T minimum of the electron elastic scattering TCS of atomic Au [38, 39]. The binding energy of this atomic Au− ion has been determined experimentally to be 2.309 eV [37, 47, 48]. This value also corresponds to the EA of atomic Au. If CH4 is introduced at the second R-T minimum of the electron elastic TCS of atomic Au, it attaches to the Au− ion forming the anionic Au−(CH4) molecular complex [29, 37], with the vertical detachment energy (VDE) of 2.34 eV [29] (incidentally, the R-T minimum is used in the creation of exotic molecules such as RbCs [49, 50]). Here we observe the remarkable characteristic of atomic Au with respect to CH4, namely the EA of Au and the VDE of Au−(CH4) are in the second R-T minimum of the Au elastic TCS. The interaction between the Au− ion and CH4 is comparable to the C–H bond strength in CH4 [29]. Thus the Au− ion weakens or disrupts the C–H bond in CH4 permitting the formation of CH3OH in the presence of O2. We note that the interaction between the Au− ion and O2 is weak [29], showing the inertness of the Au− ion toward O2. After the reaction the Au− ion catalyst is free to catalyze another reaction (the process is similar to the destruction of the ozone by the Cl− ion). This was the determining factor in our selecting the Au− ion as our catalyst. In [29] it has been remarked that the binding energies of the corresponding Au neutral complexes are significantly less than those of the anion species (for example, the complex Au−(H2O) has a binding energy that is more than an order of magnitude larger compared with that of the neutral Au(H2O) complex [29]).

Thermodynamics of reactions

Low-energy chemical reaction dynamics provides the mechanism for making and breaking bonds. In the CH4 catalysis to CH3OH using the atomic Au− ion, the C–H bond breaking has been attributed to the formation of the anionic Au−(CH4) molecular complex. The C–H bonding has a direct effect on the change in the Gibbs free energy, G(∆G = ∆H − T∆S) where H, T, and S represent respectively the enthalpy, temperature, and entropy. When the atomic Au− ion is introduced into the oxidation of CH4, the breaking of the C–H bonding occurs. Therefore, the system changes from relative order to less order. Hence, the entropy of the system increases, whereas the enthalpy of the system decreases. The overall process results in the Gibbs free energy to be negative, resulting in the spontaneous formation of methanol. To gain a deeper understanding of the process of atomic Au− ion catalysis, the rate of the reaction was calculated using Arrhenius equation [51]. In Figs. 6 and 7, the ∆G versus T for all the reactions (1, 2, 3, 4, and 5) is depicted.

What is remarkable about the effect of the Au− ion catalyst on the SPO of CH4 to CH3OH and the complete oxidation of CH4 is that whereas in the absence of the Au− ion catalyst, the production of methanol is at a much higher temperature (Table 1 and Fig. 7b). However, the introduction of the Au− ion catalyst into the reaction (3) dramatically impacts the rate of the reaction, lowering the temperature at which ∆G = 0, from 475 to 325 K (Table 1); this temperature is lower than that for the emission of CO2 (340 K). Indeed the Au− catalyst is incredibly effective in catalyzing the conversion of CH4 to CH3OH without the emission of CO2.

Transition-state calculation

Figure 1a, b presents respectively in the absence and presence of the Au− catalyst the TSs and EPs for the complete oxidation of CH4 to CO2. As already indicated, it is seen from both the figures that the TSs in the absence and presence of the Au− ion catalyst are virtually the same. Also the EPs differ only slightly. These results represent the signature of the complete combustion of CH4. Henceforth, they will be used as the benchmark for assessing the SPO of the various reactions (1, 2, 3, 4, and 5).

Figure 2a, b displays the calculated TSs and EPs, in the absence and presence of the Au− ionic catalyst, respectively, for the SPO of CH4 to CO + 2H2, reaction (2). Without the Au− ionic catalyst, the TS is 4.47 eV (Fig. 2a), while when the Au− ionic catalysts is present the TS drops down to 3.51 eV (Fig. 2b). This is to be expected since the role of the catalyst is to reduce the barrier.

Figure 3a, b presents respectively the data without and with the Au− ion catalyst for the SPO of CH4 to methane, reaction (3). The introduction of the Au− ionic catalyst drops down the TS from 4.41 eV (Fig. 3a) to 3.01 eV (Fig. 3b). We note that this dramatic reduction of the TS of the reaction (3) in the presence of the Au− ion catalyst to a value below that of the complete oxidation of CH4 is the main result of this paper. It represents a significant accomplishment in the field of catalysis using the Au− ion catalyst. The EPs are the same in both Fig. 3a, b as expected.

The results for the SPO of CH4 to H2CO + H2O without and with the Au− ion catalyst are plotted, respectively in Fig. 4a, b. Just as for the reactions (2) and (3), given in Figs. 2b and 3b, the Au− ion catalyst reduces the barrier significantly. However, the TS of 3.29 eV shown in Fig. 4b is still slightly higher than that of the complete oxidation of CH4, reaction (1). Perhaps, another atomic negative ion such as Pd− or Pt− [38] added to the Au− ion catalyst could reduce further the TS of 3.29 eV to a value significantly lower than that of the complete oxidation of CH4. We believe that with a combination of the various atomic negative ion catalysts (see for example the various figures in [38]), all the reactions (2, 3, 4, and 5) could be catalyzed directly as in the case of the reaction (3) without CO2 emission. This calls for further investigations.

Figure 5a, b contrasts the results for reaction (5), in the absence and presence of the Au− ion catalyst, respectively. Interestingly, for this reaction, the Au− ion catalyst reduces the TS by a small amount, 3.98 versus 3.71 eV. As expected, the EP remains unchanged in both figures. Comparing all the results presented in Figs. 1, 2, 3, 4, and 5, it is seen that the Au− ion catalyst has a dramatic effect on reaction (3). Namely, it reduces the TS of the reaction to a value below that obtained for the complete oxidation of methane. Hence, our main focus is on reaction (3). The results of these figures are summarized in Table 1.

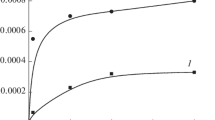
Figure 6a, b presents the results of ∆G (in electron volts) versus T (in Kelvin) for the reactions (1, 2, 3, 4, and 5). Figure 6a represents the data in the presence of the Au− ion catalyst, while Fig. 6b gives the results in the absence of the catalyst. We focus our discussion on reactions (1) and (3), namely the complete oxidation of CH4 and the production of methanol. Note the position of the curve for the complete oxidation of CH4, represented by the first curve in Fig. 6b, blue circles, and by the second curve in Fig. 6a, blue circles. In Fig. 6b, without the Au− catalyst, the production of the methanol curve occupies the position 4, purple. However, in the presence of the Au− catalyst, curve 4 jumps dramatically to position 1(Fig. 6a) ahead of the CO2 production curve; the temperature at ∆G = 0 is 325 K. This can be compared with that of the CO2 production at 340 K. Important here is that the CO2 curve does not change its position from that it occupied in Fig. 6b. This clearly demonstrates the considerable effect the catalyst has on the methanol production. Again this represents the main result of this paper.

Figure 7a, b represents respectively the magnification of the data of Fig. 6a, b in the region around ∆G = 0; the colors of the curves correspond to those of Fig. 6a, b. These data exhibit clearly the extent to which a reaction has been influenced by the presence of the Au− catalyst. By controlling the temperature around 325 K, methane can be completely oxidized to methanol, rather than to carbon dioxide (see Fig. 7a, first graph), and methanol can further oxidize to formaldehyde and formic acid.

Remarks on the results

As seen from Table 1, the thermodynamics properties agree excellently with the transition-state calculations of the complete and selective partial oxidation of methane. Combustion of methane to carbon dioxide and water in the presence and absence of the Au− ion catalyst yields almost the same transition state. However, for the selective partial oxidation of methane, there is a significant change in the transition states when we compare the results in the presence and absence of the Au− ion catalyst. The introduction of the Au− ion catalyst lowers the transition states for the formation of CO, CH3OH, H2CO, and HCO2H by 21, 32, 22, and 7 %, respectively. Also when we compare the transition states in the absence of a catalyst for the formation of carbon dioxide and methanol, we clearly see that the TS for the formation of CO2 is smaller than that for the methanol formation. This elucidates why methane undergoes complete oxidation to carbon dioxide, resulting in the increased pollutant emissions. However, if the Au− ion catalyst is used, the oxidation of methane favors the formation of methanol because its TS is lower than that of carbon dioxide. This is much like the separation of a mixture of alcohol and water through the temperature control.

In summary, this proposed catalytic process involving the use of the atomic Au− ion catalyst promises a first and a giant step toward finding and assembling nanocatalysts atom by atom for various chemical reactions, including the direct partial oxidation of methane to useful products without CO2 emission. This will certainly address the problem of greenhouse gas emissions, with considerable impact on the environment.

Discussion of results

Nanoparticles are essentially a small cluster of atoms; here we are dealing with a single atom (more specifically, its negative ion). The origin of the catalytic activity of supported gold nanoparticles is still not fully understood [52]. Turner et al. [52] investigated the catalytic behavior of very small size (approximately 1.4 nm) gold nanoparticles obtained from atomic gold clusters. They speculated that the remarkable catalytic behavior of the atomic nanoparticles was due partly to the strong electronic interaction between the gold and the titanium dioxide support. Here we use atomic gold and atomic gold anion, such as used in the experiment of Zheng et al. [37], which are obtained from laser-ablated gold foil. This completely avoids any complication associated with the support. In [6, 7] we have used a similar analysis to understand the experiments [4, 5] on the catalysis of H2O2 from H2O using Au and Pd nanoparticles.

This investigation could also help toward understanding the issue of the support since our approach uses simply atoms and atomic anions. As pointed out in [6, 7], our approach worked for the catalysis of H2O to H2O2 using the atomic Au− catalyst for the reasons: the large EA of atomic Au, the presence of the second deep R-T minimum in the electron elastic scattering TCS for atomic Au, and the existence of the VDE for the anionic Au−(H2O) complex within this R-T minimum. For CH4 catalysis the first two conditions still hold. However, the VDE (2.34 eV [37]) of the anionic Au−(CH4) complex is still within this second R-T minimum of the Au elastic TCS. To get a sense of how the proposed mechanism might be affected when small clusters are used rather than the atoms, we recently used density functional theory to investigate the structure and dynamics of small clusters of 2, 3, 4, and 5 Pt atoms [53]; the geometric optimization was achieved using the DMol package under the generalized gradient approximation with the Perdew–Wang exchange correlation functional [42].

The electron affinities for the clusters were evaluated and compared with measurement and other theoretical calculations. Our calculated EAs were found to be closer to the measurement, demonstrating the importance of careful geometric optimization of the structures. Furthermore, the EAs for the clusters did not deviate significantly from that of the atom. This implies that the proposed mechanism would still be applicable to small clusters. However, we do not know yet how far this would hold as the cluster size is increased beyond 5. Importantly, Hakkinen et al. [54] investigated the VDE for Au −7 ; they found that the calculated VDE varied between 2.75 and 3.57 eV, with their value being 3.46 eV which agrees well with the experimental value of 3.5 eV cited in [54]. Even for a cluster of this size, our analysis would work because the VDE of Au −7 is still within the effective range of the second R-T minimum of the Au elastic TCS [6, 7]. To firm this, we would need to calculate the electron elastic TCS for the Au7 cluster and identify the R-T minimum and the various resonances [38]. This will certainly be one of our future research projects.

Finally, the present paper could also lead to a better understanding of the role of the noble metal particle (Au) size and the TiO2 polymorph in the catalytic production of H2 from ethanol [55]. Notably, Au nanoparticles of size in the range 3–12 nm were found to be particularly photoreactive.

Conclusion

The atomic Au− ion catalyst is found to reduce the optimum temperature for the SPO of methane to about 325 K for CH3OH production. Consequently, in the presence of the atomic Au− ion catalyst, by controlling the temperature around 325 K, methane can be completely oxidized to methanol without the emission of the CO2, thereby broadening considerably the scope of gold’s applications. Using the Au− ion as the catalyst essentially disrupts the C–H bonding in CH4 oxidation through the ionic Au−(CH4) molecular formation, thereby eliminating the competition from the carbon dioxide formation. We conclude by recommending that the negative ions of the atoms such as those in [38] be investigated individually or in combinations for possible catalytic activities in the selective partial oxidation of methane; the Pt− negative ion will accomplish similar results as the Au− ion catalyst.