Abstract
The Paris COP21 held on December 2015 represented a step forward global GHG emission reduction: this led to intensify research efforts in renewables, including biofuels and bioliquids. However, addressing sustainable biofuels and bioliquid routes and value chains which can limit or reverse the ILUC (indirect land-use change effect) is of paramount importance. Given this background condition, the present study targets the analysis and modelling a new integrated biomass conversion pathway to produce renewable advanced fuels, enabling the issue of indirect land-use change (ILUC) of biofuels to be tackled. The bioenergy chain under investigation integrates the decentralized production of biogas through anaerobic digestion and its upgrading to biomethane, followed by a centralized conversion to liquid transport fuels, involving methane reforming into syngas, Fischer–Tropsch (FT) synthesis, and methanol synthesis. The methodology adopted in this work stem from extensive literature review of suitable bio/thermo-chemical conversion technologies and their process modelling using a commercial flow-diagram simulation software is carried out. The major significance of the study is to understand the different modelling approaches, to allow the estimation of process yields and mass/energy balances: in such a way, this work aims at providing guidance to process modellers targeting qualitative and quantitative assessments of biomass to biofuels process routes. Beyond FT products, additional process pathways have been also explored, such as MeOH synthesis from captured CO2 and direct methane to methanol synthesis (DMTM). The analysis demonstrated that it is possible to model such innovative integrated processes through the selected simulation tool. However, research is still needed as regards the DMTM process, where studies about modelling this route through the same tool have not been yet identified in the literature.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction and scope of the work
Nowadays, fossil resources still represent the main global energy source, covering about 80% of the world’s energy consumption. However, their production and use cause severe impacts on the environment, as they release carbon dioxide and other greenhouse gases (GHG), responsible for global warming and climate change: according to J. G. J. Olivier and J. A. H. W. Peters [1], fossil fuel combustion accounts for 89% of all CO2 emissions and 68% of all GHG emissions.
Climate change is today a well-recognized global concern, and the urgent need to develop and implement alternative processes for sustainable energy generation is promoting research and development worldwide.
At the international level, a major commitment to GHG emission reduction came with the adoption of the COP21 Paris Agreement in 2015, signed by 196 Parties. This binding international treaty marked the beginning of a new global effort in contrast to climate change, setting the aim of limiting global warming to well below 2 °C (possibly 1.5 °C) compared to pre-industrial levels (intended as 1850–1900) [2]. In this context, an unprecedented boost to market deployment of renewable energies is an unavoidable component of a wider climate change fighting strategy.
Along with wind and solar energy, another key solution is the use of biomass to produce transportation fuels (biofuels) replacing conventional fossil fuels, as they provide a renewable carbon-based source, being CO2 utilized by crops and forests during the natural photosynthesis process [3]. However, biofuel production itself could induce other land-related emissions, either directly and/or indirectly [4]. In fact, when biofuels are produced on existing agricultural land and conventional agronomic practices, the demand for food and feed crops might lead to the extension of agricultural land into areas with high-carbon stock such as forests, wetlands, and peatlands, to provide the same amount of feed/food replaced by biofuel production. If and when this happens, it may originate greenhouse gas emissions that will negatively impact on biofuels’ GHG balance [5] [6], and thus on climate. This effect is known as indirect land-use change (ILUC). ILUC is a very complex phenomenon, which accounting requires the understanding of a large number of different factors. It can be anyway contrasted by adopting sustainable agricultural rotations, photosynthetic intensification in agriculture, soil carbon accumulation, improved nitrogen and carbon use efficiency, etc.
The objective of this study is to investigate a novel biomass-to-liquid fuel value chain that has the potential to address the ILUC impact of biofuels. To this aim, the upstream part of the biofuels production chain under consideration refers to the Biogas Done Right (BDR) sustainable model developed by Consorzio Italiano Biogas (CIB), being this a set of agronomic practices that links anaerobic digestion to sustainable farming [7] to produce biogas. The scheme, among other elements, involves double cropping, with a primary crop for food or feed and a secondary one through crop rotation for energy production. The model is based on cover cropping, and contributes to improve the soil quality, as it is covered during the entire year, and reduces the use of fossil fertilizers, supporting in that way also the production of the main crop. In fact, BDR contrasts soil erosion and reduces nitrogen emissions, and increases the availability and use of organic fertilizers. By doing so, the BDR model ensures sustainable production of biogas, representing thus a valuable solution to the ILUC issue. Among the many possible applications, the biomethane produced through the BDR model could represent a suitable raw material for the production of sustainable biofuels, making it a good potential substitute to natural gas in several refinery processes and exploiting the natural gas pipeline infrastructure. For this reason, the value chain investigated in this paper employs biomethane as a basis to produce chemical products like Fischer–Tropsch (FT) liquids and methanol (MeOH), which, in this way, turn out to be low-ILUC-risk biofuels. Hence, the identified pathway includes the biogas production and upgrade to biomethane in decentralized farms, and integrated with a centralized biomethane-to-liquid conversion plants as FT-liquid fuels and MeOH. As said, this is approach is possible thanks to the availability of a natural gas infrastructure, where the biomethane produced through a decentralized distributed approach is injected, and the equivalent amount is collected at a centralized biorefinery site where the gas is processed into a liquid.
The natural gas network would thus be used the same way electricity from photovoltaics uses the grid. This represents a very innovative use of renewables in the current context, valorizing the use of existing infrastructures.
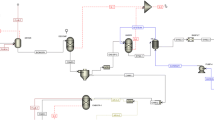
In brief, the key process steps of the selected value chain would be as follows: (i) decentralized biomethane production, based on sustainable models as the Biogas Done Right, (ii) injection of biomethane into the natural gas grid, (iii) extraction from the same volume of natural gas form the gas grid, and processing in centralized biomethane-to-liquid conversion plants, through FT synthesis and MeOH synthesis. The conceptual scheme of the whole process steps is shown in Fig. 1.
An extensive review of the conversion technologies that could be adopted in the biogas to Fischer–Tropsch fuels and MeOH production chains has been performed in this work, combined with a critical and extensive literature review on modelling the various steps identified for the selected conversion processes. The modelling approaches (assumptions, schematization, process conditions, etc.) adopted in the various papers reviewed are extensively analysed and commented. The final goal is to provide a complete set of information to study, through modelling, the efficiency, and the techno-economic feasibility of these integrated bio/thermo-chemical processes, allowing to optimize operational conditions, determine limitations, and design the distributed + centralized scheme here proposed. The current work focuses on process modelling, while the techno-economic, potential, and regulatory modelling of distributed biomethane production and centralized conversion to advanced fuels will be the subject of a subsequent research paper.
To our knowledge, no systematic review of studies encompassing all the steps of the selected value chain and their modelling has yet been published. Besides, the elements of this paper comprehensively cover an insightful analysis of a broad spectrum of industrial and novel biogas-to-liquid conversion technologies, co-product valorization, and modelling through a commercially available simulation software.
2 Materials and methods
As previously discussed, the present work investigates the state-of-the-art technology of biogas-to-liquid pathways and reviews studies modelling those technologies using a commercial simulation software by discussing essential modelling steps.
A systematic literature review of peer-reviewed journal articles and book chapters has been carried out, exploring databases such as Springer (International Journal of Energy and Environmental Engineering (IJEEE), Clean Technologies, and Environmental Policy) and Elsevier (Energy, Applied Energy, Environmental Chemical Engineering, Bioresource Technology, Energy Conversion and Management, Fuel, Chemical Engineering Research and Design, International Journal of Hydrogen Energy, Chemical Engineering & Technology, Sustainable Energy Technologies and Assessments, Fuel Processing Technology, Journal of Cleaner Production), and journals such as Energies, Chemical Engineering Transactions (CET), Energy Fuels, Fuel, Molecular Catalysis, Biomass Conversion and Biorefinery, Chemie Ingenieur Technik, Gas Processing Journal, International Journal of Chemical Reactor Engineering, Journal of Advanced Research in Biofuel and Bioenergy, and Journal of the Japan Institute of Energy. Conference papers have been also included in the research, for instance Energy Procedia, IOP Conference Series: Materials Science and Engineering, and papers of the 23rd European Biomass Conference and Exhibition. Thesis works developed within several universities have been also considered, such as Politecnico di Torino, University of Southern Denmark, University of Padua, Chalmers University of Technology, Norwegian University of Science and Technology.
Searches were limited to articles published in the last two decades, written in English, Italian, and German.
As regards the modelling papers, the first step was to choose a simulation software able to simulate all the technologies included in the identified value chain. Currently, there are lots of process modelling software packages available and used in papers in the literature, such as DWSIM, Engineering Equation Solver, COCO Simulator, Engineering Base by AUCOTEC, Aspen Plus, Aspen HYSYS, and GateCycle Software. The software chosen for this analysis is Aspen Plus, being it one of the most used process simulation tools for both industrial and research applications. The search for modelling studies has therefore been restricted to those using the selected commercial software.
After examining the titles, abstracts, and reference lists for related studies, a further screening has been also carried out, using the following inclusion criteria: (i) the application of the technologies in the papers must be similar to those of our study, (ii) clarity in modelling description and details, and (iii) in articles where the overall process is wide and complex, it must be possible to extrapolate the single technology of interest for the present study. Papers including model validation with experimental data were preferred.
The modelling studies collected have been then deeply analysed, focusing on information such as process configuration, modelling assumptions, process yield, and energy consumption of the system. Information was harmonized, i.e. data were converted to common units, to allow for effective comparisons.
3 Results
Based on the methodology described in the previous section, a comprehensive review of the conversion technologies to be applied for biogas to liquid pathways has been carried out, and 57 studies (out of 94 collected) using Aspen Plus to model them have been selected and analysed.
In this section, the findings of the present review are presented. Specifically, the paragraph is split into two main parts: in the first one, the identified biogas-to-liquid technical solutions are outlined, providing an overview of the key process parameters, whereas in the second one, the selected 57 modelling studies are described in detail, evaluating key modelling components. Challenges in process sustainability and advances are also covered.
3.1 Biogas-to-liquid pathways
3.1.1 Anaerobic digestion
Biogas is produced by the anaerobic digestion (AD) biological process. This complex microbiological path is based on the work of several groups of bacteria and archaea, working in synergy to decompose organic matter into a mixture of CH4 (53–70% vol), CO2 (30–50% vol), N2 (2–6% vol), O2 (0–5% vol), and lower fractions of H2, H2S, and NH3 [8], depending on the type of biomass digested and the process conditions. Substrates could be dedicated crops, agricultural residues, food and household wastes, animal manure, industrial wastes, etc.
The AD process consists in four crucial phases, i.e. hydrolysis, acidogenesis, acetogenesis, and methanogenesis. During the hydrolysis step, the complex substrates mainly composed by carbohydrates, fats, and proteins are hydrolyzed into their respective monomers, i.e. glucose, fatty acids, and amino acids. These monomers are then turned into volatile fatty acids (VFA), i.e. valeric, butyric, caproic, iso-valeric, iso-butyric, propionic, and acetic during the acidogenesis, and subsequently converted into acetic acid, hydrogen, and carbon dioxide (acetogenesis). Finally, methanogenesis holds the conversion of these products into methane and carbon dioxide [10]. The end-products of AD also include a slurry or solid fraction consisting of what is left of the treated substrate, referred to as digestate, rich in organic carbon and nutrients [11].
The trophic chain depends on several operational factors, such as temperature, redox potential, pH, feeding procedure, mixing, retention time, type of substrates, reactor configuration, organic loading rate, and inhibitors [12].
3.1.2 Biogas cleaning and upgrading
Biogas is by far constituted by CH4, vapour, and CO2, with other contaminants such as H2S, NH3, N2, and siloxanes, whose concentration largely depends upon the composition of the substrate digested [23]. These impurities need to be reduced, as they can cause corrosion, are toxic, can cause catalyst deactivation, and reduce gas heating value, but also to meet gas specifications and standards. Additional to the direct use in an engine for power production, in fact, biomethane can be injected into the natural gas grids. Therefore, many countries formulated standards to ensure gas quality before the injection of biomethane into the natural gas grid [24]. In Italy, the biomethane quality for injection is regulated by the Decree of the Ministry for Economic Development of 19th of February 2007, the M/475 Mandate to CEN for standards for biomethane for use in transport and injection in natural gas pipelines, and the technical report UNI/TR 11,537:2019 (updated version of UNI/TR 11,537:2016).
Typically, the purification from contaminants is referred to as “biogas cleaning”, while the CO2 and steam removal process is called “upgrading” [25]. Although some upgrading technologies separate both impurities and CO2, it can be advantageous to clean the gas before upgrading; details about biogas cleaning can be found in [11].
Currently, there are several technologies for biogas upgrading, which are continually improved, while new techniques are under development [26]. The most widespread and consolidated technologies for biogas upgrading are (i) physical absorption, using water or organic solvents, (ii) chemical absorption, using amine or saline solutions, (iii) pressure swing adsorption (PSA), (iv) membrane separation (MB), or (v) cryogenic upgrading [27].
Physical absorption techniques (i) exploit the different solubility of CH4 and CO2 (and possibly other trace compounds) in the absorbent liquid: raw biogas meets a counter flow of liquid in an absorption column, thus the leaving liquid will contain CO2 while the remaining gas stream will have an increased concentration of methane. The absorbent medium can be water, i.e. pressurized water scrubbing (PWS) technology [28], or organic, in organic solvents such as polyethylene glycol, in which CO2 is more solvent than in water. This technique is able to clean impurities such as H2S, NH3, siloxanes, and halogenated components as well [20].
In chemical absorption technologies (ii), CO2 is not only absorbed in the liquid, but also reacts chemically with the employed solutions, which can be amine, such as MEA (monoethanolamine), MDEA (methyldiethanolamine) or DEA (diethanolamine), or saline (e.g. K2CO3 solutions).
In the PSA process (iii), specific porous materials (usually activated carbon or zeolites) and high pressures are employed to adsorb CO2, but also O2, N2, and other biogas trace components, which are then released at lower pressure. When using this technique, the removal of H2S and H2O in the raw gas is essential, as they can damage the adsorbing material.
Membrane separation (iv) consists in using slight layers of materials that are permeable to CO2, H2O, and NH3, but not to CH4, which thus gets separated from the other impurities.
Cryogenic upgrading (v) is based upon the principle that, at a fixed pressure, different gases liquefy at different temperatures. This technology has seen strong interest and development in recent years.
In Europe, 35.5% of the plants employ PWS, while the 20% MEA, the 20% MB, the 17% PSA, and the remaining 8% adopt emerging technologies [24].
After cleaning and upgrading, the gas stream is called biomethane, which is a renewable source of methane (CH4 > 95%, CO2 from 1 to 5%), and can be directly used as automotive fuel or injected into the natural gas grid. [29]
3.1.3 Biomethane reforming to syngas
Both the production routes here considered to generate Fischer–Tropsch fuels and methanol are fed with syngas: therefore, in our scheme reforming of biomethane to syngas is necessary, representing a critical step of the process(Fig. 2).
Synthetic gas, or syngas, is a gaseous mixture of H2 and CO, at different ratios, that can be used as a chemical building block for the synthesis of a variety of chemical products and carbon-based fuels. The selectivity of the final products depends upon the H2/CO ratio [9]. Both Fischer–Tropsch and methanol synthesis requires H2/CO ratio equal to 2 [10] [11]. Syngas is traditionally obtained from coal, natural gas, residual oils, and petroleum, but it is possible to generate syngas also from biomass, a sustainable and renewable substitute to fossil-based syngas [12].
In this work, the syngas is obtained from biomethane, the upgraded product of anaerobic digestion of organic materials [13]. Also, it can be generated from methane extracted from the gas grid, if an equivalent amount of biomethane is injected into the gas pipeline elsewhere from the AD-biomethane production site (in a certified accounting mode, ensuring renewable carbon is not double counted through the use of guarantees of origin).
The main processes used to convert methane to syngas can be summarized as follows: (i) steam methane reforming (SMR), (ii) partial oxidation (POX), (iii) autothermal reforming (ATR), and (iv) dry methane reforming (DMR) ([10, 14, 15]).
SMR (i) is a well-established and large-scale technology, mostly used for hydrogen production from methane. In this route, CH4 and steam react in a reformer over a nickel-alumina catalyst [16], at a temperature of 1073.15 to 1173.15 K and a pressure of 15 to 30 bar. The primary reaction is:
The process is strongly endothermic [17], and the resulting H2/CO ratio is ~ 3, well above FT-synthesis requirements.
In typical industrial applications targeting H2 generation via this pathway, a second reaction also occurs, producing additional hydrogen through the water gas shift (WGS) reactor. In this case, CO and water react, producing hydrogen and carbon dioxide, as in reaction (2):
POX (ii) instead uses oxygen to convert methane. The methane partial oxidation reaction is the following:
The process is exothermic and generates H2-lean syngas (H2/CO = 1 to 1.6) and the reaction occurs at a high temperature (> 1473 K) if no catalyst is used [10]. The employment of a catalyst can lower the reaction temperature to ~ 1000 K. The catalysts employed could be divided into three groups: Ni, Co, and Fe, noble metal, and early transition metal carbide[18].
POX can be well combined with SMR reforming to achieve a H2/CO ratio in the range of 1.6 to 2.6 [10]. This process is called autothermal reforming (iii). In ATR, the heat produced by the POX is used to provide the endothermic heat of the SMR reaction.
In DMR (iv), CO2 is used as an oxidant to convert CH4 to syngas. The technology is thus very attractive from a sustainability perspective, as it uses two types of greenhouse gases, i.e. CO2 and CH4, to form a valuable product. The process is described by Eq. (3).
The syngas produced is normally characterized by a H2/CO ratio close to 1 [10]. This could also be further adjusted for methanol and Fischer–Tropsch synthesis by reacting CO with H2O to produce CO2 and H2 in water gas shift (WGS) and partial oxidation reactions [8, 14].
Catalysts for DMR can be noble metal-based (Rh, Ru), which have good activity and stability but high cost, or Ni-based ones (Ni/Al2O3), commonly used for their low cost, high H2 yield, and fast turnover rates.
This approach is particularly interesting as it can tolerate the varying concentration of CO2 associated with biomethane. Nevertheless, the commercialization of this technology is still in its preliminary stage [16, 19]. However, there are some drawbacks linked to these reforming routes, such as catalyst deactivation (mainly due to carbon deposition), and high energy demand, as the reforming reaction is endothermic and requires to be operated at high temperatures (1123.15 to 1273.15 K) to obtain higher conversion rates and minimize carbon deposition.
3.1.4 Fischer–Tropsch synthesis
Once syngas has been produced and purified, it can be used in the Fischer–Tropsch process to produce a mixture of hydrocarbons at different chain lengths, used as synthetic fuels (Fig. 3). These products may be used directly in a gas turbine or distilled into kerosene (C-10 to C-16), diesel- (C-14 to C-20), light naphtha (C-5 to C-6), heavy naphtha (C-6 to C-12) and waxes (C-20 +).
The Fischer–Tropsch synthesis is a polymerization reaction, in which CO is hydrogenated with H2 to the C-1 intermediate, which then grows to form different hydrocarbon chains of variable lengths. Syngas is thus converted into a variety of products, such as alcohols, aldehydes, olefins, paraffins, and especially liquid transportation fuels [20]. After the FT synthesis, the last stage is upgrading and separation of the FT syncrude in order to obtain high-quality products.
Fischer–Tropsch synthesis was developed in the early twentieth century by Franz Fischer and Hans Tropsch at the Kaiser Wilhelm Institute, with the aim of producing synthetic fuels from coal reserves in Germany during World War II. The process found only limited commercial application. This relatively well-known technology has recently drawn renewed interest for its application to cellulosic biomass and agricultural waste, to convert them to linear- and branched-chain synthetic hydrocarbon, representing thus a very promising and sustainable solution for the production of clean fuels at competitive costs ([21,22,23,24,25,26,27,28,29]).
The polymerization reaction requires syngas at a H2/CO ratio of 2–2.2 [30], which is processed over a metal catalyst (Fe or Co), at apressure range of 20 to 60 bar. Temperatures can be in the range of 473.15 to 523.15 K (low-temperature FT synthesis or LTFT), or 573.15 to 623.15 K (high-temperature FT synthesis or HTFT). In both cases, the process is highly exothermic, and therefore, a heat exchange system is necessary to cool the reactor and maintain control of the process temperature: it is also an energy-recovery opportunity for waste heat [31].
At first, reagents, hydrogen and carbon monoxide, form monomer units, which are then polymerized to yield a wide spectrum of products (mainly paraffin), ranging from C-1 to C-40 hydrocarbons.
The FT synthesis consists in four main reactions, shown in Eqs. (5) to (8), i.e.
-
Paraffin formation:
$$nCO+\left(2n+1\right){H}_{2}\to {C}_{n}{H}_{2n+2}+n{H}_{2}O$$(5) -
Olefin formation:
$$nCO+2n{H}_{2}\to {C}_{n}{H}_{2n}+n{H}_{2}O$$(6) -
Alcohol formation:
$$nCO+2n{H}_{2}\to {C}_{n}{H}_{2n+1}OH+(n-1){H}_{2}O$$(7) -
Carbonyl formation:
$$nCO+(2n-1){H}_{2}\to {(C{H}_{2})}_{n}O+(n-1){H}_{2}O$$(8)
Catalysts play a crucial role in FT synthesis, as they must guarantee a good conversion yield of reactants, as well as selectivity towards products. Catalysts in FT are often supported on metal oxides, typically alumina or silica [22]. Suitable catalysts for FT synthesis are group VIII elements, in particular cobalt (Co), iron (Fe), nickel (Ni), and RUTHENIUM (Ru), able to chemisorb CO dissociatively (into C and O) and H2, and have a noticeable activity. However, other elements, such as rhodium (Rh), iridium (Ir), palladium (Pd), and platinum (Pt), are also used in FT synthesis. Though the selectivity of these elements is even higher compared to Ru, Ni, Co, and Fe, they are not considered in industrial applications because of their costs [21], and only Co and Fe are used in commercial processes. Co-based catalysts are mainly used in LTFT: these are characterized by high activity, significant stability, and a tendency to produce relatively higher molar-weight hydrocarbons. On the other hand, iron-based catalysts are cheaper than Co-based ones, can be used in both HTFT and LTFT configurations, and promote a relatively higher fraction of olefins. Additionally, iron catalysts also promote the WGS secondary reaction.
There are four main different types of Fischer–Tropsch reactors: (a) fixed-bed multi-tubular reactor, (b) fluidized-bed reactor, (c) slurry-bed reactor, and (d) microchannel reactor (Fig. 4). The type of reactor influences the operational parameters of the synthesis process, the product selectivity, the product distribution with chain growth probability, the catalyst activity, and the conversion of carbon monoxide [22]. Details about the FT reactor design can be found in [32].
3.1.5 Methanol synthesis
Methanol (CH3OH) is a valuable chemical product with a variety of uses, either as a clean fuel, mixed with other conventional fuels, or as a bulk chemical building block for the synthesis of other chemicals such as acetic acid, formaldehyde, methyl methacrylate and methyl tertiary-butyl ether (MTBE), and many others [33]. CH3OH is extremely stable and liquid at room temperature, and this minimizes problems with storage and transportation, even if accidental release in soil and dwells can be a serious health risk ([34,35,36,37]).
Currently, the most used industrial route for methanol production is based on using syngas produced via reforming of natural gas, even if also biomethane can obviously be used. Nevertheless, there are also attractive routes that involve a single step, such as oxidative coupling of methane, e.g. methane partial oxidation to methanol (i.e. DMTM) [38], which will be discussed in a separate section of this work.
Methanol is obtained through the hydrogenation of carbon oxides over a suitable (copper oxide, zinc oxide, or chromium oxide-based) catalyst [39][39]. The conversion is exothermic and very selective, and the synthesis is followed by a distillation column to separate methanol from water, which is the by-product of the conversion [41].
The main reactions of methanol synthesis are [42]:
Equation (9) represents the CO hydrogenation, (10) the CO2 hydrogenation, and (11) the reverse water gas shift (RWGS) reaction. It is noted that the required H2/CO ratio of the syngas at the inlet is equal to 2.
The typical operating conditions are in the ranges of 50 to 100 bar and 493.15 to 553.15 K, depending on the catalyst supplier.
There are several commercial types of methanol synthesis reactors, i.e. quench reactor, adiabatic rectors in series, or boiling water reactors (BWR) [43]. A detailed description of reactor types is available in [44].
3.1.6 DMTM route
As an alternative to methanol synthesis from syngas, the straight conversion of methane into methanol is also a possible and interesting route. This method allows to by-pass the very energy-intensive step required to reform CH4 into CO and H2, and thus represents an economical-advantageous and environment-friendly option [45].
The technologies for the direct conversion of methane to methanol might be catalytic oxidation processes, photo-catalysis technologies, plasma technologies, supercritical water oxidation technologies, membrane technologies and other methods.
Da Silva et al. [38] and Zakaria et al. [46] performed a review of the different DMTM routes.
However, to date, this method is not yet applied at full industrial and commercial scale. The process is particularly difficult, since the target product CH3OH is more prone to oxidation than CH4, and thus, the process needs to activate the C–H bonds on one hand, and avoid over-oxidation of CH3OH on the other [47]. Moreover, the current technologies do not provide a relevant methanol yield [48].
4 Modelling biogas-to-liquid fuels
This review analyses and discusses the various plant configurations of the different studies, reporting, wherever possible, the yields and the consumptions of such steps that are used in the proposed pathway. Modelling approaches (assumptions, schematization, process conditions, etc.) are analysed and commented below.
4.1 Modelling anaerobic digestion
The AD process is an extremely complex process, involving numerous intermediate reaction mechanisms, such as bacterial metabolic reactions, parameters, inhibitors interactions, etc.
In the literature, several models have been proposed to describe anaerobic digestion [49]. These models can be single-step models [50], involving a single bacterial population with a limited description of inhibition effects, or models of intermediate complexity [51], considering a higher number of strains of bacteria with a more accurate description of inhibition factors, or, finally, complex models [52] [53] [54] [55], entailing a high number of processes, inhibition effects, and specific bacterial populations.
Among the complex AD models, Anaerobic Digestion Model No. 1 (ADM1) [52] is considered the most comprehensive one and is widely applied for AD description [56]. ADM1, developed by the International Water Association (IWA) task group, assumes that the reaction system consists of biochemical reactions (involving enzymes) and physico-chemical reactions (involving acid–base reactions and the gas–liquid transfer). The substrate fed to the digestor is assumed to be composed of carbohydrates, proteins, and fats [57]. Another important and complete complex model is the one developed by Angelidaki et al. [55], in which the substrate is assumed to be composed of basic organic components (i.e. carbohydrates, lipids, and proteins), intermediates (i.e. volatile fatty acids and long-chain fatty acids), and inorganic components (i.e. ammonia, phosphate, cations, and anions). The model includes 2 enzymatic hydrolytic steps and 8 bacterial steps and involves 19 chemical compounds [55].
Implementing modelling schemes of AD in Aspen Plus is quite challenging, as it involves microorganisms, whose microbial activity is difficult to describe in software language. In literature, several studies simulating the anaerobic digestion in Aspen Plus have however been found and are analysed below.
Al-Rubaye et al. [56] developed a two-stage simulation model: one first step for the hydrolysis phase, and a second one for the other three phases, i.e. acidogenesis, acetogenesis, and methanogenesis. The Property Method (a collection of methods and models that the software uses to compute thermodynamic and transport properties [58]) chosen for the simulation is the non-random two-liquid (NRTL). In line with ADM1, the substrate feed rate is assumed to be made of carbohydrates, proteins, and fats, and therefore the introduction of material components is treated accordingly. The feed stream is mixed with H2 and H2O through a mixer and a heat exchanger is employed to model heating of this stream, necessary to maintain the required temperature in the ranges favourable for AD. The hydrolysis step is simulated using a stoichiometric reactor (RSTOIC), in which the reaction kinetics are not considered, but stoichiometry and conversion of a reactant must be specified. Thirteen chemical reactions are considered for this step, and the reaction rates have been calculated by Aspen Plus calculator blocks, using a FORTRAN code. The subsequent AD steps have been simulated in a continuous stirred tank reactor (RCSTR), which requires the reaction kinetics to be known; thus, specifications from ADM1 and comprehensive models have been used, involving more than 33 kinetic reactions. The reaction rates have been calculated through calculator blocks, using a FORTRAN code. The RCSTR reactor releases two streams at outlet: one is the gas stream, which is the biogas and small traces of other gases, and the liquid stream. The gas stream goes through a splitter and then a flash separator, which separates the water from the biogas. Subsequently, the biogas stream passes through a gas filter, which separates the hydrogen component from the produced biogas. On the other hand, the liquid stream goes through a splitter to separate a part of it as recycle and is connected to the feed stream. The model was validated against experimental data in terms of % CH4 in the produced biogas. Three different feed cases have been tested, i.e. (i) cattle manure, (ii) cow manure, and (iii) wastewater generated from industrial and agricultural activities. Results match the literature data; in detail, the deviation from simulation results and experimental data are 5.4% for the case of cattle manure, 8.54% for the case of cow manure, and 15.83% for the case of wastewater generated from industrial and agricultural activities. In the paper, a sensitivity analysis has also been carried out to study the effect on CH4 yield in case of introduction of hydrogen in the process. The investigation revealed that, for H2 feeding rates below a maximum value, there is an increase in methane gas composition in the produced biogas.
The model developed by Rajendran et al. [59] shows similarities with Al-Rubaye’s one. Also, here, hydrolysis is separated from the other AD phases and has a separate reaction set (made of 13 reactions) including carbohydrates, proteins, and fats. Carbohydrates were modelled as cellulose, starch, and hemicelluloses, proteins as soluble proteins and insoluble proteins, while fats as tripalmate, triolein, palmito-olein, and palmitolinolein. Acidogenesis, acetogenesis, and methanogenesis are modelled using a different reaction set (made of 33 reactions) to calculate the kinetics of the reactions, whose constants were obtained following models such as ADM1 and comprehensive models. A FORTRAN code has been used to compute the reaction rates. Also, in this case, the simulation model uses NRTL as Property Method, and the reactors chosen for the hydrolysis and the other three phases are respectively a stoichiometric reactor (RSTOIC), with specified reaction extents, and a continuously stirred tank reactor (RCSTR), with specified kinetic constants. The model was validated against experimental and industrial data, using the biogas production rate as a validation parameter, for different substrates at different process conditions (7 case studies). The deviations from simulation results and experimental data span from 0.3 to 12.4% (absolute values).
Nguyen et al. [60] developed a simple one-step AD model to estimate the energy potential from the anaerobic digestion of food waste in the municipal solid waste stream of urban areas in Vietnam. A stoichiometric reactor (RSTOIC) has been chosen to simulate the digester, in which the calculations are based on the Buswell equation, describing the overall process of anaerobic degradation. The global Property Method selected for the simulation is NRTL. The resulting biogas stream is separated in a flash separator, which separates the gas components and the digestate. The gaseous phase (raw biogas) is then treated to reduce the presence of H2S and then introduced into a CHP unit, or into a boiler unit, or into an upgrading unit for biofuel production, depending on the model scenario chosen.
Scamardella et al. [61] simulated a pressurized anaerobic digestion process (PAD) using a RCSTR reactor operating at a pressure range of 1.5 to 5 bar. Reaction kinetics were taken from the ADM1 and comprehensive models. ELECNRTL (electrolyte non-random two liquid) Property Method is chosen here, as it allows to simulate dissociation equilibria that affect the CO2 solubility in the liquid phase.
Peris Serrano [57] implemented the Angelidaki and the ADM1 models. The hydrolytic step is not taken into account in this simulation, and thus, only three phases are modelled. The process consists of two stages, i.e. two digesters, in which all the AD reactions occur. The reactor type selected is the RCSTR, for which total mixed flow and constant volumes are assumed, with residence time chosen as a user-defined parameter. The kinetic reactions in the model follow the power law and kinetic constants are computed in calculation blocks written in FORTRAN. The Property Method chosen for the simulation is NRTL.
Llanes et al. [62] developed an Aspen Plus model for the AD of vinasses, which integrates ADM1, flow pattern, and biofilm characteristics with the inclusion of sulphate reduction reactions. Vinasse is usually treated in UASB (upflow anaerobic sludge blanket) reactor types instead of completely mixed flow pattern reactors, so the authors employed two stoichiometric reactors (one for the hydrolysis stage and one for the methanogenic step) and two RCSTR reactors for the other phases. Kinetics are calculated in FORTRAN programmed blocks. Here as well, cellulose, hemicellulose, and dextrose were added as carbohydrates, proteins as soluble and insoluble, while lipids comprised of tripalmate, triolein, and palmito-olein. The Property Method adopted is the NRTL. The model has been validated against experimental data for three different case studies. A mean relative error lower than ± 15% has been observed, with no significant differences between simulation results and experimental data in terms of biogas composition and methane yield.
Table 1 summarizes the main Aspen Plus models for AD reviewed in this work. The analysis has shown that the AD, though very complex to be fully described, can be simulated in Aspen Plus. Overall, the number of studies addressing AD modelling is not very large: only six Aspen Plus simulation models have been found.
4.2 Modelling biogas upgrading
Several studies simulating biogas upgrading in Aspen Plus have been retrieved in the literature.
Ashraf et al. [8] developed a model for the PWS process: absorption and stripping columns are modelled as two RADFRAC distillation blocks, which is a column type designed for general vapour-liquid multistage separation. The thermodynamic method used is electrolyte non-random two-liquid (ELECNRTL): absorption of biogas components in water is accounted for by Henry coefficients, while the dissolution of H2S and based on a first stage in which biogas is compressed to 12 bar, cooled to 313.15 K and then sent at the bottom of the absorption column, which is also fed from the top with water. The column is operated at 12 bar. Upgraded biogas leaves the column from the top of the column, and impurity-rich sour water leaves from the column bottom. Sour water is then sent to a flash separator (operated at 3 bar) to remove residual CH4,and then fed to the stripping column for regeneration at 1 bar, which uses air as a stripping medium. In the reported case study, biogas is fed at 2000 ppm of H2S. For better removal of H2S, activated carbon impregnated with ZnO is considered, and the resulting cleaned biogas has a composition characterized by less than 10 ppb of H2S and NH3, 99%, and 79% recovery of CH4 and CO2.
Cozma et al. used an Aspen Plus model to simulate a high-pressure water scrubbing (HPWS) system applied to biogas upgrading in [63] and [64] studies. The simulation model is characterized by operational conditions based on data taken from the literature (in particular, the work by Götz et al. [65]). The model is equilibrium-stage, and the thermodynamic method chosen for the analysis is a non-random two-liquid model with ideal gas and Henry’s law (NRTL); the method has been chosen based on a preliminary study in which the authors compared the performance of different thermodynamic models available in the software to calculate the solubility of the main biogas components (CO2, CH4, H2S, N2, and O2) in pure water. The simulation model assumes pressurization at 10 bar and cooling to 293.15 K of the biogas stream (60% vol CH4, 38.9% vol CO2, 300 ppm vol H2S, 0.5% vol N2, and 0.5% vol O2), which is then sent to the bottom of the absorber, which is also fed with water from the top. The scrubber is a RADFRAC column, working at T = 293.15 K, p = 10 bar. The number of stages and the absorbent flow rate required to achieve equilibrium have been determined through a preliminary study. The bottom stream (CO2-enriched water) is transferred to a flash column, where the pressure is reduced from 10 to 3 bar to minimize methane loss. The gas containing CO2, CH4, H2S, N2, O2, and water, released from the flash column is mixed with the raw biogas and re-circulated to the inlet of the compressor. After leaving the flash column, the rich solution is sent to the stripper, also modelled as a RADFRAC column, where it meets a counter flow of air. Here, CO2 and H2S are released from the water at atmospheric pressure and at a temperature of 293.15 K. Subsequently, the water is recirculated back to the top of the scrubber. Based on these conditions, it was calculated that the gas leaving the absorber contains 96.72% vol CH4, 0.937% vol CO2, 0.006 ppm vol H2S, 1.1% vol N2, and 0.976% vol O2. The calculated energy demand for producing 309.36 Nm3/h of upgraded biogas is 171.5 kWh.
The work done by Götz et al. [65], which also described and modelled in Aspen Plus the HPWS technology for biogas upgrading, represented a reference also for the studies by Cozma et al. [63] [64]. Thus, the process conditions and scheme are nearly the same for both simulation models. The model is based on equilibrium and uses ELECNRTL thermodynamic model. The calculations take into account the gas quality requirements for biogas injection according to German law. Biogas feed has a composition of 53.7% vol CH4, 45.2% vol CO2, 101.8 ppmv H2S, 0.93% vol N2, 0.19% vol O2, and 1.67% vol H2O. The gas exiting the simulated process is composed by 96.8% vol CH4, 0.47% vol CO2, < < 1 ppm vol H2S, 2.1% vol N2, 0.56% vol O2, and 0.32% vol H2O.
The PWS technology to convert biogas into biomethane has also been modelled in the thesis work by Menegon [66]. Similarly to Cozma et al. [63], the author carried out a preliminary study to select the most suitable Property Method, finally choosing the NRTL-RK model. The process conditions and scheme are very similar to those used by Cozma et al. [63]: biogas (45% vol CO2, 55% vol CH4) is compressed and cooled to 10 bar and 293.15 K and fed to an absorption column. The bottom stream is sent to a flash separator operating at 3 bar, from which gas is recirculated to the second compression stage, while liquid is sent to a stripper using air as a stripping medium. Regenerated water is sent back to the absorber. The simulation is rate-based, and the absorption and the stripping column reach a CH4 purity of 98.7% vol. The CH4 recovery is 99.08%.
The biogas water scrubbing technology has been also simulated in Aspen Plus by Bortoluzzi et al. [67]. The simulation scheme is similar to those cited above. The Property Method chosen is the Predictive Soave–Redlich–Kwong equation of state (SRK). In the simulated process, biogas is compressed to the absorption pressure of 10 bar through a two-stage intercooled compression, and water is removed via condensation. Then, biogas enters a packed column, which also receives a stream of liquid water; here, biogas upgrading occurs, thus a stream containing biomethane and a stream containing water, CO2, H2S, and small amounts of CH4. This latter stream is flashed to 3 bar to recover methane; two streams exit the flash: one, containing vapour CO2 and CH4, is recycled to the second compression stage, while the second one, liquid, is sent to a stripper. An air stream entering the stripper desorbs CO2 (and H2S) from the feed, and the solvent is then re-generated and recirculated to the absorber. The biomethane stream produced in the absorber is then dried: the CH4 recovery of the process is 99.6%. For the base case, the molar percentage of CH4 in the product stream is 98.7% mol.
The same modelling approach has been adopted also by Seman et al. [68]. Authors used the NRTL Property Method, adopting the same process conditions used in the study by Cozma et al. [64], as well as the simulation flowsheet. The specifications related to the absorption column are slightly different between the two studies, as the number of stages and the pressure is slightly higher in the work of Seman et al. [68]. This leads to a percentage of CO2 removal and biomethane purity a little higher (97.6% mol CH4 in the absorber product gas stream) in this latter case.
Ashraf et al. [8] also simulated the chemical absorption with MEA as absorption solvent for syngas upgrading (CO2 removal after desulphurization). The processing scheme is similar to water scrubbing, i.e. an absorption and a stripping column, to remove CO2 and to regenerate the solvent respectively, modelled as RADFRAC distillation columns.
Chemical absorption for biogas upgrading was simulated also by Lingelem [69], who used AMP solvent (2-amino-2-methyl-1-propanol), more specifically 30% wt AMP in aqueous solution. For the base case process, the author used the ELECNRTL thermodynamic model and RADFRAC columns (rate-based absorption, equilibrium-based desorption). The purified biogas stream is characterized by a CH4 molar concentration of 97% mol. Six modifications of the base case have been also simulated.
Gamba et al. [70] simulated both water scrubbing and chemical absorption processes for biogas upgrading by means of a rate-based approach, according to modelling details from the by Pellegrini et al. [71]. The thermodynamic model used is electrolyte-NRTL. In the PWS simulation, biogas is treated in a one packed column at 20 bar with pure water at 298.15 K. There is no water regeneration step in the process. The inlet gas composition is 60% vol CH4 and 40% vol CO2. Other components have been neglected. Concerning the chemical absorption simulation, a 30% vol and 15% vol MEA aqueous solutions have been considered. The distillation column has the same characteristics as in the case of PWS, with the only differences in the packing material (metal instead of plastic) and the absorption pressure (atmospheric pressure). Both PWS and chemical absorption have been simulated find the absorbent flowrate needed for obtaining a 98% vol biomethane concentration on a dry basis.
Gamba et al. [72] simulated water scrubbing, MEA (monoethanolamine) scrubbing, and MDEA scrubbing when applied to obtain biomethane from municipal sewage sludge AD. Also in this case, the modelling approach is rate-based, and biogas components considered are only CH4, CO2, and water. For what concerns PWS, there is no water regeneration step, and the biogas is first sent to a three-stage intercooled compression, then to the absorption column. Regarding the MEA chemical scrubbing, the model accounts for an absorption and a regeneration step in backed columns, operating at atmospheric pressure with a solution composed of 15% wt MEA. The MDEA chemical scrubbing case has the same process scheme of the MEA case. Here, absorption is carried out at 2.7 bar, using a 50% wt MDEA solution in water, and the regeneration at atmospheric pressure. All three simulated upgrading processes reach a biomethane purity higher than is 98% vol on a dry basis. For what matters in the PWS case, the upgraded biogas has a molar percentage of CH4 of 98.86% mol on a dry basis, with a methane recovery to fed biogas of 95.8%. Regarding the MEA case, the upgraded biogas has a molar percentage of CH4 of 98.71% mol on a dry basis, with a methane recovery to biogas of 99.9%. About the MDEA case, the upgraded biogas has a molar percentage of CH4 of 98.73% mol on a dry basis, with a methane recovery to fed biogas of 99.98%.
The biogas upgrading technologies of PWS and chemical absorption with alkanolamine solutions have also been simulated in Aspen Plus by Pellegrini et al. [73]. In this study, three different biogas compositions have been tested, representing landfill gas, biogas from wastewater treatments, and gas from co-fermentation. The gases considered in these feed streams are CH4, CO2, N2, and O2. The layout of the water scrubbing process takes as a reference the one developed by Bortoluzzi et al. [67]. The biogas inlet stream is first compressed to 8 bar and cooled, then purified in a packed absorption column also fed with water. The bottom stream is then sent to a flash chamber and afterwards to a stripping column using air. Compression is here carried out in more steps. In each step separation of water from methane takes place too, using flash separators. The chemical scrubbing has been simulated referring to the process scheme of the study carried out by Gamba et al. [72]. The raw biogas is fed to the absorption column (2.7 bar), after being subjected to a single-stage compression and cooling down to 308.15 K. Both the absorption and stripping columns are packed columns (packing: metal Pall rings). The column specifications have been adjusted from the ones used in a previous work [70]. In all the case studies, the total flow rate of feed biogas is such that the volumetric flow rate of biomethane leaving the plant is 500 Sm3/h, to have a common basis for an economic feasibility comparison.
Similarly, Worawimut et al. [74] used Aspen Plus to simulate and compare the processes of water scrubbing and chemical scrubbing with diethanolamine (DEA) solution with regeneration and recirculation. The studies by Cozma et al. [64] (PWS) and Niu et al. [75] (chemical absorption) have been taken as references to set process conditions and for results validation. The NRTL property method has been selected and RADFRAC distillation columns without condenser and reboiler have been used to model the absorber and the desorber, both set as equilibrium based. Biogas from swine farm wastes was used in this work, with a composition of 68% vol CH4, 24% vol CO2, 3000 ppm vol H2S, 2% vol N2, 0.1% vol O2 and 5.6% H2O. The biogas flow rate of the plant is 1000 kmol/h. Both water scrubbing and chemical scrubbing were simulated to find the absorbent flow rate needed to obtain at least 96% v/v biomethane purity. Total water flow rate of the plant is 16,000 kmol/h, which is the same amount of the total DEA solution flow rate of the plant. The product gas of the PWS process is characterized by a composition of 96.005% vol CH4, 0.32% vol CO2, < < 0.001% vol H2S, 3.098% vol N2, 0.154% vol O2, 0.424% vol H2O. The methane recovery is 89.96%, while the energy consumption of the process is 11309 kW. The product stream of the chemical absorption with DEA has a composition of: 96.026% vol CH4, 0.310% vol CO2, < < 0.001% vol H2S, 3.114% vol N2, 0.155% vol O2, 0.395% vol H2O. The process has a methane recovery equal to 89.47%, with an energy consumption of 11,331 kW.
Gangadharan et al. [16] also simulated the technology of chemical scrubbing with DEA in Aspen Plus for acid gas removal from natural gas. The simulation is rate-based, the thermodynamic property method is ELECNTRL, and also here the main blocks of the flowsheet are the absorber and stripper (RADFRAC distillation columns), but no solvent recirculation is included. The cleaned gas then enters 20-stages distillation column, operating at 44.6 bar, where methane gets separated from C-2 to C-3 components. A 99.5% mole recovery of methane is obtained from the process.
Membrane separation technique has been simulated by Scamardella et al. [61]. The authors adopted a user-defined model (user 2 block), interfacing the block with an Excel file. The Property Method selected is ELECNRTL. The model refers to Fick’s law with diffusive model assumptions. In the model, the output of the membrane are two streams, i.e. a CH4-rich gaseous stream, a CO2-rich gaseous stream, and the off-gas of the process. The resulting biomethane can reach high purity percentages (> 95% vol) for operating pressures higher than 3 bar.
As Aspen Plus is a steady state calculator, no dynamic options are available in the software. Therefore, since PSA is a dynamic process, examples of PSA process simulations have been found mainly on Aspen Adsorption, e.g. Menegon et al. [66], Abdeljaoued et al. [76]. Anyway, some studies simulating the PSA process in Aspen Plus have been found and are reported below.
Gamero et al. [34] simulated the PSA process to clean the outlet gas of gasification to obtain high quality syngas and simultaneously capture the greenhouse gases. The system consists of four units, composed by ideal column separators operating at pressure and temperature conditions (30.6 bar and 308.15 K), to separate H2 (first PSA unit), CO (second PSA unit), CO2 (third PSA unit), and CH4 (fourth PSA unit). The components obtained are then mixed, to obtain the H2/CO ratio required for the downstream utilization. Multistage compressors and valves are also used in the process. The Peng-Robinson with Boston Mathias function method was selected for the simulation. As a result, about 80% of the CO2 and 95% of CH4 fed in the PSA system were sequestrated.
Similarly, Ortiz et al. [77] simulated the PSA process to clean syngas obtained by supercritical water reforming of glycerol. The PSA system is composed by three units: in the first unit, highly pure H2 is separated as a non-adsorbed stream; in the second one, CO is separated as the adsorbed component; in the third one, separation of CO2 and CH4 occurs. The obtained gas streams are then mixed to obtain the H2/CO ratio required for downstream utilization. Distillation columns for purification and valves for depressurization are involved in the process. NRTL property method has been selected. The system reaches 95% H2 recovery, 98% CO recovery, and 90% CO2 as well as CH4 recovery.
Table 2 summarizes the Aspen Plus simulation models reviewed in this work for biogas upgrading. The analysis revealed that upgrading processes have been largely simulated in literature: more than 15 studies have been found, most of which addressing the processes of physical and chemical absorption.
4.3 Modelling methane reforming
Gangadharan et al. [16] simulated dry reforming and steam reforming for syngas production from natural gas. The simulation scheme consists of a first step dedicated to acid gas removal (H2S and CO2) from natural gas through chemical absorption with DEA, followed by methane separation from higher hydrocarbons in a distillation column, steam production in heat exchanger and finally SMR. Methane exiting the acid gas removal step is mixed with steam in a mixer, which uses heat from the SMR reactor output stream. The mixture is then sent to another heater and then to the plug flow reactor (RPLUG), where the SMR and WGS reactions take place over a Ni/Al2O3 catalyst at a constant temperature of 890 K. The output stream is then sent to a heat exchanger, used to generate steam, and then to a flash separator, where syngas and water are obtained. The thermodynamic property method selected is Peng-Robinson, and the convergence criteria have been relaxed due to issues in the PFR convergence with the default criteria. The rate expression for the catalytic reactions occurring in the PFR reactor have been modelled using the Langmuir–Hinshelwood-Hougen-Watson kinetics formulation (LHHW), obtained from the work of Xu and Froment [78]. The produced syngas is characterized by a composition of 72.22% mol H2, 21.71% mol CO, 3.56% mol H2O, 1.77% mol CO2, 0.48% mol CH4, and 0.26% mol N2. The authors also simulated a combination of SMR and DMR. In this process, the syngas generated by SMR is sent to a heat exchanger. Here, the syngas is cooled and passed through a CO2 membrane separator, separating CO2 from the syngas mixture, which contains CO, H2, CO2, H2O, and unreacted CH4. Then, the stream is sent to a flash separator, where the separation of syngas and water takes place. The CO2 separated by membrane filtering is sent to the dry reformer, where the methane reacts with CO2 for increased production of syngas. As for the SMR process, LHHW kinetic expressions are used to determine the rate of reaction of the DMR process. The resulting syngas has a composition of 73.61% mol H2, 23.85% mol CO, 1.20% mol H2O, 0.51% mol CO2, 0.55% mol CH4, and 0.27% mol N2.
Giwa et al. [79] simulated the SMR for hydrogen production. The authors modelled two different versions of the process, i.e. with and without feed (CH4 and H2O) mixer. For reforming, an equilibrium reactor was chosen, in which the stoichiometry of the reaction was specified, i.e. the reforming reaction (1) and the water–gas-shift reaction (2). Several case studies have been simulated. In the case of the reactor operating at 1173.15 K temperature and 1 bar pressure, the syngas compositions obtained in both versions of the model were characterized by the same molar composition, i.e. 62.56% mol H2, 16.06% mol CO, 17.77% mol H2O, 3.59% mol CO2, and 0.02% mol CH4.
The SMR process of natural gas has been also modelled by Amran et al. [80], using a kinetic-based approach with the Redlich-Kwong-Soave equation of state with modified Huron-Vidal mixing rules (RKSMHV2) thermodynamic model. Natural gas and steam are first mixed, fed to a heat exchanger and then to a RPLUG reactor to model the methane reforming reaction, and finally to another RPLUG reactor for WGS reaction. Both reactors follow a rearranged LHHW kinetic model. It is assumed that natural gas does not contain H2S and CO2. The modelling approach was validated against data from other published studies, showing a good agreement with the literature. A sensitivity analysis of the reaction performance has also been performed.
Gopaul et al. [81] simulated the syngas production from biogas through dry reforming. In particular, three different cases have been simulated, i.e. (i) DMR alone, (ii) DMR and POX, (iii) DMR and hydrogen oxidation (HOX). The target H2/CO ratio is 1.6–1.7, for downstream Fischer–Tropsch synthesis. The study also compares different types of biogas in terms of H2 and CO yield: landfill, corn cob, whole stillage, and combined cob and stillage. The compositions of the analysed biogas types do not include H2S or NH3. Biogas is not upgraded to biomethane prior to reforming, thus the reforming reactor is directly fed by the biogas stream. About the thermodynamic model, the Property Method chosen here is IDEAL, which uses both Raoult’s law and Henry’s law. The DMR alone case was simulated using a RGIBBS reactor, i.e. an equilibrium reactor whose output is computed following the method of Gibbs free energy minimization at specified operating conditions (pressure, temperature, flowrates). Biogas is fed into the reforming reactor at 1123.15 K and 1.01325 bar. The reactor operates at 1223.15 K and 1.01325 bar. The DMR + POX case is similar to the previous one in terms of reactor configuration and operating conditions. However, in this case, a second feed stream containing oxygen at 1.01325 bar and 473.15 K is used, and therefore the exothermic partial oxidation reaction satisfies the energy demand of the endothermic DMR process. The amount of oxygen required was determined using the Design Specification function available in Aspen Plus, taking also into account the desired syngas H2/CO ratio of 1.6–1.7. The case of DMR + HOX modelling comprises two RGIBBS reactors, one for DMR and one for H2 combustion to provide energy to the DMR process. Biogas feed and DMR reactor have the same conditions of the other two cases. The HOX reactor is fed under stoichiometric excess conditions of O2 at 473.15 K and 1.01325 bar, H2 at 1123.15 K and 1.01325 bar, and combustion occurs at 1273.15 K and 1.01325 bar. Also in this case, the required H2 and O2 feed rates were determined through the Design Specification function in Aspen Plus. The optimal process conditions to maximize syngas yield and quality were determined through a sensitivity analysis on the DMR case with landfill biogas type, which turned out to be similar also for the other biogas types. The analysis showed that, however, the desired 1.6–1.7 H2/CO ratio is found at temperatures and pressure ranges for which syngas quality is low. Therefore, other values of H2/CO ratio, slightly outside the desired range have been accepted in favour of a better CH4 conversion (from 96 to 100%) and syngas quality (meaning, for high-quality syngas, a syngas composed mainly of H2 and CO, with a minimal amount of by-products). Authors also performed an energy analysis of the processes, which are both exothermic and endothermic. DMR reactor heat duty ranges from + 14.88 to + 28.74 kWth/kmol, while the DRM + HOX process values of − 23.93 and − 4.58 kWth/kmol depending on biogas type (resulting in exothermicity); the combined DMR + POX process was able to counterbalance the high energy demand of DMR, achieving thermal-energy neutrality.
The DRM process has been modelled in Aspen Plus also by Ashraf et al. [8]. In this case, the RGIBBS reactor block was used, fed by cleaned biogas, steam, and air (to lower coke formation and external energy demand). A sensitivity study to find the optimum process conditions has also been carried out. As a result, a syngas stream characterized by a H2/CO ratio of about 1.58 was obtained, with a methane conversion of about 99%.
Er-rbib et al. [82] simulated a combination of DMR and SMR processes to produce syngas from natural gas. The reforming unit is composed by two parts: a pre-reformer and a reformer. In the pre-reformer, a complete conversion of the higher hydrocarbons of natural gas into methane occurs over a nickel catalyst at 823 K and 5 bar. Then, in the reformer, the primary SMR reaction (1), the primary DMR reaction (4), and the RWGS reaction (11) take place. The chosen reactors are equilibrium reactors, and thus no kinetic models are considered, whereas the thermodynamic model used is the Peng Robinson with Boston-Mathias alpha function (PR-BM).
Table 3 summarizes the main Aspen Plus models on upgrading processes reviewed in this work. A large number of studies were identified, most of them dealing with SMR. The analysis however revealed that there is also a good number of papers addressing the DMR, also in combination with SMR, as well as POX, while a smaller number of articles addressing ATR was found.
4.4 Modelling Fischer–Tropsch synthesis
Modelling the Fischer–Tropsch process is particularly challenging due to the high number of species existing in equilibrium, the variety of reaction products, the complexity of the CO catalyst chemistry, and the large number of process parameters relevant to the process [12]. Indeed, the identification of a plausible mechanism, as well as the formulation of a representative expression addressing the consumption rate of the primary component CO and an accurate description of the product distribution are crucial and complicated steps in modelling the Fischer–Tropsch synthesis [84] [85]. A comprehensive review of the FT kinetics has been carried out by Van Der Laan and Beenackers [86]. The Anderson-Schulz-Flory (ASF) model is normally used to represent the FT product distribution, based on one parameter, namely the chain probability factor α, which describes the addition of carbon atoms into the molecule chain [87]. However, in most cases, the real Fischer–Tropsch product selectivity does not obey the ideal ASF distribution [88], and deviations (essentially higher selectivity to CH4, and lower to C2H4 than expected in the model) are well documented in the literature [84]. Dependence of the chain probability factor α on process conditions (pressure, temperature, composition, catalyst type, etc.) has been largely studied and correlations have been formulated, e.g. [89,90,91].
In this section, different models found in literature simulating the Fischer–Tropsch synthesis in Aspen Plus are analysed.
Ashraf et al. [8] simulated the FT synthesis in a slurry reactor from bio-syngas. A RYIELD reactor block with CO conversion of 80% has been selected. This block does not require exact information about the stoichiometry or kinetics, but models a reactor by specifying the reaction yields of each component [58]. The product distribution follows the ASF distribution, with α values computed according to Kruit et al. [91] parameters. After the synthesis, the FT syncrude is then sent to a distillation column (RADFRAC) to separate products according to the following classification: C-1 to C-4 lights, C-5 to C-9 naphtha, C-10 to C-16 kerosene, C-17 to C-22 diesel, and C-22 + waxes. As the selectivity of FT-crude products depends on the reaction temperature and feed syngas (H2/CO ratio), a sensitivity study has been carried out, and these parameters optimized to maximize kerosene and diesel fraction using the solver function in MS Excel. In order to achieve 80% CO conversion and maximize kerosene and diesel yield fractions, the optimal values have been estimated between 1.6 and 2 for the H2/CO ratio, and between 473.15 and 573.15 K as regards the reaction temperature. Considering the whole process (biogas to liquid fuel conversion process using pressurized water scrubbing, dry methane reforming, and FT-synthesis), the overall carbon conversion efficiency reaches 45%, while the energy efficiency is 30%.
Adelung et al. [30] simulated the production of synthetic hydrocarbons (in particular kerosene and diesel) from syngas derived from captured CO2 and H2 obtained through water electrolysis. In the proposed approach, syngas is generated through a reverse water–gas-shift (RWGS) reaction and then converted through the FT reaction into a broad range of hydrocarbons. Product separation is performed downstream hydrocarbon production: long-chain hydrocarbons are sent to a hydrocracker to increase the yield at the desired chain length for transport fuel production (< C-22). Gas products and unreacted species are recycled to increase the carbon efficiency of the process. Operational parameters are optimized to maximize energy efficiency. In Aspen Plus, the thermodynamic method here selected is the Peng-Robinson with Boston-Mathias modifications (PR-BM), H2, CO, CO2, H2O, N2, O2 and alkanes are the chemical species considered in this model. It is assumed that carbon is not a possible product. The FT reactor is a tubular fixed bed: it has been simulated as a stoichiometric reactor (RSTOIC) with Co catalyst, without considering reaction kinetics. The reactor operates at 493.15 K and 25 bar, while the H2/CO ratio is set at 2. CO conversion is assumed equal to 40%, and inert gas share is fixed at 50%. Under these conditions, the chain growth probability factor α is equal to 0.839, calculated using the expression proposed by Vervloet et al. [90]. The stream from the reactor is first sent to a flash separator, where heavy hydrocarbons are separated, and then to a hydrocracker. The product from the hydrocracker is then subject to further separation through 8 different flashes into hydrocarbons, water, and recycling gases. The carbon efficiency of the overall process is 88%, thanks to the recycles, while the power-to-liquid efficiency for the base case is 38.7%.
Campanario et al. [77] simulated the production of low-temperature Fischer–Tropsch products from syngas obtained by supercritical water reforming of the bio-oil aqueous phase. The overall process is composed of four different sections, i.e. (i) supercritical water reforming (SCWR) of the bio-oil aqueous fraction, (ii) upgrading of the syngas to increase H2 and CO molar flow rate and to achieve the desired H2/CO ratio through water–gas-shift and dry reforming reactors and PSA systems, (iii) Fischer–Tropsch synthesis loop, and (iv) refining and upgrading of FT products by means of distillation columns and hydrocracking. Focusing on the FT synthesis section, the selected reactor is a stoichiometric one (RSTOIC) operating in a temperature range of 493.15 to 513.15 K and 20 to 40 bar, fed by syngas at 2 H2/CO ratio. FT products were assumed to be composed only of olefins and paraffins, and the probability parameter of chain growth propagation, α, has been computed using the expression obtained by Song et al. [89]. The stream leaving the FT reactor is then cooled to condense heavier hydrocarbons and separate them from the gas. The gas stream is recycled back to the FT reactor to maximize the overall CO conversion and to increase the production of liquid fuel, while the liquid phase is sent to a decanter for separating H2O from heavier hydrocarbons, which are first expanded through a valve and finally sent to the distillation section. The thermodynamic methods used are UNIQUAC for the distillation train and Peng-Robinson EOS for the FT section. The effect of the main operating parameters on the process performance, such as feed composition and operating conditions of the Fischer–Tropsch reactor, was studied by a sensitivity analysis. Optimal conditions were identified; thus, for a mass flow of aqueous phase of 60 t/h with a total organic concentration of 35% wt, biofuel production was estimated equal to 4596 kg/h (2804 kg/h FT-diesel, 1491 kg/h FT-jet fuel, and 301 kg/h FT-gasoline), the carbon efficiency with refining to 38.53% (without refining, it was estimated at 43.50%), while net electrical power was 5297 kWe.
Niassar et al. [92] simulated the FT synthesis in the context of development and optimization of an Integrated Process Configuration for IGCC Power Generation Technology, with Fischer–Tropsch fuels from coal and biomass. Basically, the process consists in a first part related to syngas generation from gasification, which is then split and sent into the FT unit, where it is converted to fuel, and the combined power cycle generates electricity and power. Focusing on the Aspen Plus model section related to the Fischer–Tropsch unit, the reactor chosen by the authors is a stoichiometric reactor (RSTOIC) in which 31 reactions have been considered. The property method selected is Peng-Robinson. The feed syngas is characterized by H2/CO ratio of about 2, and the process is carried out at about 513.15 K and 20 bar. The syngas is thus mainly converted to C-1 to C-30 hydrocarbons and water. Chemical reactions have been defined up to C-30 as the database of software does not contain hydrocarbons that are heavier than the C-30. The products of the Fischer–Tropsch reactor undergo downstream separation under gradual cooling in the three separators. Lightweight and heavyweight hydrocarbon liquids are the main products of the process, while gases are sent to the power plant for power generation. A sensitivity analysis has been carried out, and the simulation results compared with an experimental work [93, 94], indicating that the difference in results is about 4%.
In the context of assessing biogas-to-liquid processes for bagasse utilization, Michailos et al. [95] developed an Aspen Plus model to simulate the Fischer–Tropsch synthesis of bio-syngas. The studied production route included a gasifier unit, syngas quenching and cleaning, a FT synthesis reactor, product recovery and separation, and finally a heat and power generation system. The biomass, i.e. sugar cane bagasse, undergoes a pre-treatment constituted by bagasse crushing to small particles and drying before entering the system. With regards to Fischer–Tropsch modelling, authors used a product distribution reactor (RYIELD), following the Anderson-Schultz-Flory distribution model (α = 0.9), through which the mass yield of the products of the synthesis were determined. The reactor module interfaces with an Excel Spreadsheet where these calculations are carried out. The feed syngas is characterized by a H2/CO ratio of 2.05. The product stream exiting the FT unit is then sent to a flash to separate the hydrocarbons from the unconverted syngas, which is recycled back. The hydrocarbon stream is then sent to a purification zone, consisting of four distillation columns and a hydrocracking unit for waxes, with a conversion efficiency of 88%. The Property Method chosen for conventional components is the Redlich-Kwong-Soave cubic equation of state with Boston-Mathias alpha function (RKS-BM). For a feed consisting of 100 t/h of sugar cane bagasse (before being subjected to the pre-treatment process), the product flow rates of the system is 9100 kg/h diesel, 6050 kg/h gasoline, and 1175 kg/h LPG. The energy efficiency of the process is about 68%.
Hao et al. [83] used Aspen Plus to simulate a gas-to-liquid (GTL) process involving syngas generation through ATR and Fischer-Tropsh synthesis. The FTS has been simulated based on detailed kinetic models considering two kinds of industrial catalysts, i.e. iron and cobalt. The authors tested two different Aspen Plus reactor blocks, i.e. PRF (plug flow reactor) and CSTR (continuous stirred tank reactor). The detailed kinetic models for the two different catalyst types have been programmed in FORTRAN and compiled as user-defined functions for the simulation software. The authors performed a sensitivity analysis for both the catalysts to understand the performances of the two models (PFR and CSTR), by varying operating conditions and H2/CO ratio of the syngas. Different recycling options for the FT tail to the ATR have been simulated to find the optimal flowsheet structure, which was selected according to the overall thermal efficiency to crude products, the overall carbon efficiency to crude products, and the energy value of the purge gas. The study concluded that the thermal efficiency to crude products for the cobalt-based catalyst is about 60%, while for the iron-based catalyst, it is in the range of 49–55%. Additionally, FT synthesis with Fe-based catalyst generates CO2; its carbon efficiency (61–68%) turns out to be lower with regards to the cobalt-based catalyst (73–75%).
Er-rbib et al. [82] developed an Aspen Plus model to describe the production of synthetic gasoline and diesel fuels. The process consists of four different stages: (i) production of syngas from the combination of dry reforming and steam reforming of natural gas, (ii) Fischer–Tropsch synthesis to produce long chains of hydrocarbons, (iii) separation of fuel and wax hydrocracking, and (iv) recovery of hydrogen. The FT synthesis was modelled using a stoichiometric reactor (RSTOIC), specifying 42 reactions for which information about selectivity and efficiency has been found in the literature. The operating conditions are 513 K and 20 bar. In these conditions, the conversion of synthesis gas was estimated at 87%. The reactor products are cooled and separated from water and oxygen compounds, and then sent to a distillation column for the separation of heavy and light components. Waxes are finally converted into high-quality diesel through a hydrocracking unit, which has been simulated as a RYIELD reactor. The Property Method used for the reactors and the distillation columns is Peng Robinson with Boston-Mathias alpha function (PR-BM). The results show that the overall process can produce synthetic fuels composed by 72% of diesel, 26% of gasoline, and 2% of LPG.
Sudiro et al. [96] used Aspen Plus to simulate synthetic fuel production through LTFT synthesis of syngas obtained from coal and natural gas. Three processes have been simulated, i.e. (i) gas to liquid (GTL), (ii) coal to liquid (CTL), and (iii) a hybrid process coupling features of both CTL and GTL. Focusing on the Fischer–Tropsch section of the model, a RYIELD reactor block has been chosen, with syngas conversion assumed equal to 87% at 513.15 K and 15 bar operating conditions. Selectivity values (ratio between moles produced and moles of syngas converted) have been specified, taking data from the literature. Forty-four reactions of type (6) and (7), respectively olefin formation and alcohol formation, have been used for all components from CH4 to C60H122 and ethanol. Product distribution on a weight basis is gasoline (C-5 to C-11) 25.6%; diesel (C-12 to C-18) 40.3%; waxes (C-19 to C-60) 31.6%; light gases 1.6%; and oxygenated compounds 1%. The products are then subject to hydrocracking, separation, water treatment, and recycling. The Property Method used for the process parts involving reactors, distillation columns, and two-phase separators is the Peng-Robinson equation of state with Boston-Mathias alpha function, while for separations involving three phases the NRTL equation was applied. Simulated product yields for three cases are 66.7% for GTL, 32.5% for CTL, and 44.4% for the hybrid process., on a weight basis. The estimated thermal efficiency, i.e. ratio between the energy contents in the products and in the feedstock, is 54.2%.
Bao et al. [97] simulated the FT synthesis in the context of process design optimization of a GTL plant. In the study, the authors assumed a feed H2/CO ratio of ~ 2 and that the process follows the ASF product distribution, with a fixed chain growth probability factor α equal to 0.95. The syncrude is fed into a distillation column to separate LPG, naphta, and wax. NRTL-RK is the property method used, while the reactor configuration is not specified. The simulated plant converts 900,000 kg/h of natural gas into 118,000 BDP of products.
Cinti et al. [98] used Aspen Plus to model the FT synthesis as a part of a study addressing the production of synthetic green fuels through a system integrating a solid oxide electrolyzer and the Fischer–Tropsch process. The plant is divided into two main sections, i.e. (i) the electrolyzer unit and (ii) the liquid fuel synthesis unit. In (i), H2O and CO2 are converted into H2 and CO (syngas) via co-electrolysis, whereas in (ii), syngas conversion into hydrocarbons occurs. In the process modelled, the FT synthesis occurs at 20 bar and 503.15 K, and only a first FT crude separation is considered, which divides purge water from hydrocarbons and light refinery gases. The main Aspen Plus simulation blocks considered for the FT modelling part are a splitter, a stoichiometric reactor, a mixer, and a flash separator. The splitter divides the feed syngas (H2/CO = 2.1) into two streams: one enters the RSTOIC block, while the other bypasses the reactor and is mixed with the FT products. The FT reactor (Co-based) accomplishes several reactors, and the product distribution is assumed to follow the ASF products distribution model with a chain growth probability factor α equal to 0.94. The synthesis of alcohols, aromatics, and other oxygenated compounds is neglected; only alkanes and alkenes are considered products. The syncrude is then sent to a flash separator performing the separation of light gases, liquid phase, and water. For a given syngas feed characterized by a molar composition equal to 51.2% mol H2, 24.4% mol CO, 24.3% mol CO2, and 0.1% mol CH4, the products at FT reactor outlet (without any separation) is composed by 8.16% mol H2, 40.78% mol H2O, 3.58% mol CO, 43.94% mol CO2, 0.4% mol CH4, 0.24 mol C3H6, 0.38% mol C3H8, 0.06% mol C6H12, 0.32% mol C6H14, 0.06% mol C8H16, 0.57% mol C8H18, 0.01% mol C16H32, 0.94% mol C16H34, and 0.53% mol C30+. The total energy efficiency of the FT system is 52.57%; while considering the FT products deprived of light gases as a valuable product, the energy efficiency is 40.95%.
Also Pondini et al. [99] developed an Aspen Plus model considering low-temperature Fischer–Tropsch to simulate synthetic fuels production from biomass-derived syngas. The FT reactor (Co-based catalyst) has been modelled using a RSTOIC reactor, for which the fractional conversion of each reaction is imposed as calculated in an integrated Excel file according to an estimated chain-length distribution. Hydrocarbons (olefins and paraffins) with carbon numbers up to 30 are considered, and the Song et al. [89] correlation for the chain growth probability factor α is considered. The mole fraction calculations for products with carbon numbers C-1 to C-4 have been adjusted to take into account the ASF deviation (i.e. higher methane selectivity) with reference to Rane et al. [100]. Different operating conditions (H2/CO ratio, reactor pressure, temperature, CO conversion) have been tested.
Marchese et al. [101] modelled the Fischer–Tropsch synthesis in the context of analysing different power-to-liquid options, in which the FT section is integrated into a complete carbon capture and utilization from a biogas upgrading unit producing about 1 ton/h of CO2. The recovered CO2 is turned into syngas through either a reverse water gas shift reactor or to a solid oxide electrolysis unit operating in co-electrolysis mode; the produced syngas is fed to a Fischer–Tropsch reactor operating at 25 bar and 501 K, whose products are then separated into light gas, naphtha, middle distillates, light waxes, and heavy waxes. The process model implements a detailed kinetic model developed in the author’s previous study [102] based on real experimental data, which accounts for deviations from the Anderson-Schulz-Flory (ASF) distribution (i.e. higher methane and lower ethylene formation). For the implementation in Aspen Plus, a plug flow reactor (RPLUG) was selected, integrated with an external kinetic subroutine for rates definition up to C-80 for paraffins and C-40 for olefins. The Property Method chosen for the FT unit was the RKS-BM. The simulation results show that, for the case of the solid oxide electrolyzer to produce syngas, the best model configurations can reach a plant efficiency of 81.1%, while for the reverse water gas shift option, the plant efficiency reaches 71.8%.
The same modelling approach was used also in another study [103] addressing the energy and economic analysis of plant configuration integrating the direct air capture technology for CO2 recovery and the Fischer–Tropsch synthesis. In this case, the carbon number of alkanes and alkenes considered spans from C-1 to C-70.
In another study [104], aimed at analysing the techno-economic feasibility of a biomass-to-X plant, Marchese et al. modelled the FT synthesis using a different approach. The synthesis of paraffin was described up to C-40 and for olefins up to C-19, using the ASF distribution with α dependent over the temperature and syngas composition according to Song et al.’s [89] correlation. CH4 yield was assumed equal to 20%mol, in order to account for the ASF deviation for this compound. Moreover, a 90% internal recirculation for unconverted syngas was considered. The reactor configuration in Aspen Plus is not specified in the paper, while the thermodynamic method used for the FT section of the overall process is Redlich-Kwong-Soave with Boston-Mathias modification (RKS-BM) EoS.
Gabriel et al. [105] modelled the FT synthesis in the context of a GTL process composed of three sections, i.e. synthesis gas production from natural gas and conditioning, FT reaction, and FT product upgrading and separation. Different plant configurations have been evaluated; changes are limited to the syngas production technologies and conditioning sections. Focusing on the part of the process model in Aspen Plus assessing the Fischer–Tropsch synthesis, the authors used a RSTOIC reactor with a per pass conversion of 70%. The products follow the ASF distribution, with a constant α = 0.92, used along to reverse calculate the stoichiometric coefficients of the produced hydrocarbons from C-1 to C-100. Only paraffins are considered, and the stoichiometric coefficients are adjusted for the C-30 + lumping assumption. The syncrude is then sent to a refining section.
Hamad [106] developed an Aspen Plus model for the FT synthesis as part of an analysis of the solvent selection for supercritical Fischer–Tropsch synthesis reactors, in order to provide a basis for future supercritical phase simulations. The method used for this research is derived from the ASF distribution and the calculations of the stoichiometric coefficients are done in an Excel spreadsheet. For the calculation of α as temperature-dependent, the Levenberg–Marquardt algorithm was used. Products are assumed to be composed only by paraffins. The Aspen Plus reactor type chosen is not specified, as well as the Property Method used.
Dahl [107] modelled the FT process in the framework of a study evaluating a power and biomass to liquid (PBtL) process concept, which consists of biomass gasification to produce syngas, hydrogen addition to the syngas to increase its H2/CO ratio, and FT synthesis to produce hydrocarbons, which are then separated and the longer hydrocarbons cracked. The author developed two Aspen Plus models for the Fischer–Tropsch reactor: a conversion-based model, whose operating conditions were varied, and a kinetic-based model, using a plug-flow reactor (RPLUG) in which the conversion of CO is studied. The Property Method used is Peng Robinson-Boston Mathias (PR-BM). The conversion-based involves two stoichiometric reactors (RSTOIC). In the first reactor, the three main FT reactions occur (paraffin, olefin, and alcohol formation), modelled according to the ASF distribution with a method of lumping high-weight hydrocarbons described in Hillestad et al. [108]. The products are assumed to be composed by paraffins (up to C-20 with a C-21 + lump), olefins (up to C-10 with a C-11 + lump), and alcohols (up to C-5 with a C-6 + lump). Each FT product is characterized by its specific probability function α: in the case of paraffins and olefins, α is assumed to be temperature- and pressure-dependent and formulated through Todic et al.’s correlation [109], while for the oxygenates, α is assumed to be constant (i.e. equal to 0.5). To figure out the ASF underestimation of methane in the products, a stand-alone reaction describing the CH4 formation from CO and H2 is added into the reactor, as well as an additional reaction for CH4 among the olefins formation. A total CO fractional conversion has been set to 60%, which is split between the four reactions involved in the first RSTOIC reactor; its values were adjusted for each reaction in order to yield approximately the same carbon selectivities found in the experimental study carried out by Shafer et al. [110]. The second RSTOIC reactor considers the ethylene deviation, referring to Pandey et al. [84]. Computations have been performed in Aspen Plus calculation blocks. The kinetic-based model uses Langmuir–Hinshelwood (LHHW) adsorption kinetics and the consorted vinylene mechanism, a modified ASF distribution model. The model considers also ASF deviation and the effect of water over the reaction rate. The oxygenates are not included in this model. The product separation flowsheet is the same for both reactor configurations. After the Fischer–Tropsch synthesis, the liquid and gaseous FT products are separated in a FLASH at the temperature of the FT reactor outlet; in fact, at this temperature (more than 450 K), the hydrocarbons of 17 carbons or higher are liquid and unreacted syngas and hydrocarbon of 16 or lower are gaseous. The gaseous stream is then cooled in a countercurrent heat exchanger, which recovers the heat to warm the syngas feed, and then further cooled to 283.15 K. The cooled gaseous stream enters a three-outlet FLASH separator, which gives (i) a C1-C5 hydrocarbons gaseous stream, (ii) a C6-C16 hydrocarbons stream, and (iii) a water stream. The C6–C16 hydrocarbons stream undergoes further separation, involving a pressure decrease to 5 bar through a VALVE, a temperature increase to 483.15 K, in order to evaporate the C6-C7 hydrocarbons, and then a separation of the C6–C7 hydrocarbons from C8–C16 hydrocarbons in a second FLASH. Different operating conditions have been tested (i.e. 493.15 K, 27.6 bar, H2/CO = 2; 483.15 K, 25 bar, H2/CO = 1.95; 483.15 K, 25 bar, H2/CO = 1.60; 483.15 K, 20 bar, H2/CO = 1.95; 493.15 K, 25 bar, H2/CO = 1.95) for both reactor configurations, and the simulations results showed that, at the same operating conditions, the conversion-based reactor results in higher selectivity towards lower-weight hydrocarbons. For both models, carbon selectivity increases with carbon number and has a peak around C-13.
Table 4 summarizes the selected research works modelling Fischer–Tropsch synthesis in Aspen Plus. Seventeen different studies have been identified.
4.5 Methanol production from syngas modelling
In the literature, several studies for simulating methanol production in Aspen Plus can be found; these describe the conversion of syngas and CO2, to commercial-grade methanol.
4.5.1 Modelling MeOH production from syngas
Trop et al. [111] studied methanol production from a mixture of torrefied biomass and coal. In the process, gasification of biomass and coal, synthesis gas purification, and methanol synthesis from syngas have been simulated.
Authors modelled methanol synthesis as a series of plug-flow reactions occurring in a stoichiometric reactor. Products are then cooled to 303.15 K and the condensed crude methanol is sent to a flash separator and a purification system, consisting of four distillation columns, where methanol is separated from water, small amounts of ethanol, and dissolved reactants. The composition (mass fractions) of the final products is made of 0.9998 methanol, 0.0001 ethanol, and traces of H2O and CO2. For the methanol production section of the process, the Peng-Robinson thermodynamic method was chosen.
Gamero et al. [34] developed an Aspen Plus model for methanol synthesis from syngas obtained through gasified biomass and then gas cleaning through PSA. In the model, the cleaned syngas stream is compressed and heated up to the operating pressure and temperature. Then, the stream is introduced into the methanol synthesis reactor, which has been simulated as an equilibrium reactor (REQUIL). This kind of reactor requires the stoichiometry to be specified. The equations involved in the synthesis are (9) and (11), with a conversion of 36% for CO and 17% for CO2. The selected catalyst is Cu/ZnO. The reaction product is then depressurized and cooled down, and then sent to a column separator, in order to condense and separate methanol from the gas phase, getting at the bottom pure methanol as the final product. The H2/CO in the feed stream is about 2.4–2.5. As regards the thermodynamic method, the Peng-Robinson with Boston Mathias function was selected as appropriate for the process application, in particular for high-temperature gasification. Operating conditions have been varied, evaluated, and optimized through a sensitivity study. The optimal conditions were fixed at 493.15 K and 55.7 bar, yielding 32 kg/h methanol produced from a biomass feed rate of 100 kg/h.
Chein et al. [112] modelled methanol synthesis in Aspen Plus from syngas produced from biogas. After being compressed and cooled to the operating conditions for methanol synthesis (5 MPa and 523.15 K), the syngas enters the methanol reactor, modelled as an equilibrium reactor. This kind of reactor can simulate thermodynamic equilibrium reactions with good accuracy. Products (methanol and water) are expanded and then separated in a flash unit. Recycling unreacted syngas to improve the methanol yield is also performed by using a splitter with a recycle ratio. In addition, this study also estimated the performance of a green process for methanol synthesis using captured CO2 as a feedstock. Optimized conditions for obtaining 25.48% methanol yield have been found.
Ortiz et al. [39] developed an Aspen Plus simulation model for methanol synthesis from syngas obtained by supercritical water reforming of glycerol. In the model, the syngas is compressed and heated to the MeOH synthesis operating conditions (86.13 bar and 523.15 K). Then, the stream is sent to the methanol reactor, modelled as a stoichiometric (RSTOIC) gas-phase reactor, with specified CO conversion of 20% and CO2 conversion of 3%. According to the authors, this kind of reactor can better represent an industrial reactor, as an equilibrium reactor (REQUIL) would lead to a CO conversion and CO2 conversion of about 76.8% and 9.6% respectively (thermodynamic limits). In the study, it is assumed that no by-product formation occurs. The reactor effluent is then cooled down to condensate the crude methanol, and thus separated from the gas phase, which is then recompressed and recycled to increase the overall CO conversion to methanol. A fraction of the recycled gas is purged to prevent the accumulation of inert gases and sent to the furnace to support energy self-sufficiency of the process. Finally, crude methanol is sent to a distillation column, in which H2O is separated from CH3OH, with a recovery of 99%.
De María et al. [113] simulated methanol production from syngas in Aspen Plus to investigate a kinetic model developed by the authors. For this matter, an external model of the reactor was integrated into the simulation flowsheet instead of using a reactor block already available in Aspen. The reactor model was developed in Matlab and integrated into the Aspen Plus flowsheet using CAPE OPEN standard. The simulated process is constituted by a first part dedicated to syngas compression from 1 to 110 bar in a two-stage intercooled (311.15 K) compression train. Then, syngas is mixed with recycled streams, preheated in a feed-effluent heat exchanger, and then sent to a distillation column for raw methanol separation. The property method chosen for the whole process is the RK-Aspen (Redlich-Kwong), with the only exception of the distillation column, for which the NRTL-RK was set. The composition of the feed syngas is equal to 6.9% mol CO2, 23% mol CO, 0.2% mol H2O, 67.5% mol H2, 0.3% mol N2, and 2.2% mol CH4. The product stream is characterized by 98.1% mol CH3OH, 0.2% mol CO2, and 1.6% mol H2O.
4.5.2 Modelling MeOH production from CO2
Suhada et al. [114] developed an Aspen Plus simulation model to convert the CO2 separated from biogas to methanol. The methanol reactor, which is also fed by a stream of H2 obtained from an electrolysis unit, has been modelled as an equilibrium reactor type (REQUIL).
Another simulation approach for modelling methanol synthesis from captured CO2 has been developed by Atsonios et al. [115]. Two different reactor types have been investigated: a tubular catalytic reactor and a zeolite membrane reactor. The tubular catalytic reactor is composed by three main units, i.e. methanol synthesis, gas separation, and product purification. The inlet gas is constituted by H2 and CO2, with a H2/CO2 ratio of 3.0, heated to 423.15 K, and then sent to the methanol reactor. The authors do not specify which Aspen Plus reactor block has been chosen for the simulation. However, the process stoichiometry and kinetics is considered. In particular, the reactions involved are (9), (10), and (11), and the process kinetics follows the study of Graaf et al. [116], developed for a commercial Cu/Zn/Al catalyst. The composition of the stream exiting the reactor is equal to 14.5% mol CO2, 63.3% mol H2, 6.9% mol H2O, 1.8% mol CO, and 7.5% mol CH3OH. The crude methanol is then subject to a refining step, made of two flash separators and a distillation column, leading to a final product composition of 99.3% mol CH3OH, 0.1% mol H2O, and 0.6% mol CO2.
About the membrane reactor, it has been modelled as a series of equilibrium reactors with the intermediate interpolation of split separators. The split fraction of the vapours (only water and methanol) that are assumed to permeate the membrane is specified by a determined separation factor. The methanol purity of the product exiting the process is about 99.4%.
Van-Dal et al. [117] also simulated in Aspen Plus the methanol synthesis from captured CO2 via hydrogenation. In the simulation model, CO2 (1 bar, 298.15 K) is compressed to 78 bar in a series of intercooled compressors, while H2 (30 bar, 298.15 K) is compressed to 78 bar in a single stage. The two gases are mixed and then re-mixed with the recycle stream, heated to 483.15 K, and finally injected into the RPLUG reactor for methanol synthesis, which is a fixed bed adiabatic reactor. The stream leaving the reactor is then split into two streams, one used to heat the fresh feed and the other in the reboiler and to heat the feed of the distillation column. These streams are then re-mixed, cooled to 308.15 K by water, and then sent to a knock-out drum, where condensed water and methanol get separated from the non-reacted gases, which are partially purged to minimize the accumulation of inerts and by-products in the reaction loop. The crude methanol obtained (composed of CH3OH, H2O, and residual dissolved gases) is expanded to 1.2 bar through two expansion valves, fed into a flash separator where residual gases are almost completely removed, heated to 353.15 K, and finally sent to a distillation column (RADFRAC). Here, water and methanol are separated, and the resulting CH3OH stream, in gaseous form, contains 69 ppm wt. of H2O and some unreacted gases. The RPLUG reactor is packed with a fixed bed of Cu/ZnO/Al2O3 catalyst. The model of Bussche and Froment [118] describing the reactions of methanol production and the RWGS reaction with this catalyst has been chosen, with readjusted parameters of Mignard and Pritchard [119]. The kinetic constants follow the Arrhenius law, while the equilibrium constants are provided by the study of Graaf et al. [116]. In Aspen Plus, the LHHW (Langmuir–Hinshelwood-Hougen-Watson) kinetics has been selected. Achieved CO2 conversion was 33%. About the used thermodynamic method, the Redlich-Kwong-Soave equation of state with modified Huron-Vidal mixing rules (RKSMHV2) was used for streams at high pressure (> 10 bar), while for low pressure streams the NRTL-RK model was employed.
In the thesis work developed by Mantoan [120], MeOH production from CO2 hydrogenation was simulated following the model developed by Fortes et al. [121], and adopts the similar approach seen in Van-Dal et al. [117]. Also, in this case, the methanol synthesis process involves a first step, in which the feed gases are compressed up to reactor feed pressure through different intercooled compression stages; a second process step, in which the pressurized feed stream gets is heated up and sent to the reactor; and a third process step, in which MeOH is finally separated from H2O in a distillation column. As in the study of Van-Dal et al. [117], the kinetic model used is that of Bussche and Froment [118] with readjusted parameters of Mignard and Pritchard [119], the kinetic constants follow the Arrhenius law, and the equilibrium constants are given by Graaf et al. [116]. The thermodynamic models used are the RKSMHV2 for high-pressure streams (> 10 bar) and NRTL-RK for low pressure. The reactor type selected is an adiabatic ideal plug flow reactor (PFR), following Eqs. (10) and (11) and reaction rates implemented in CHEMCAD®. The CO2 conversion into CH3OH in the reactor is ~ 21%. The distillation column has been designed to yield a high MeOH purity (> 99.9% wt). The stream fed into the reactor has a composition of 13% wt H2, 75% wt CO2 and 12% wt CO. The product stream exiting the MeOH reactor has a composition of 12% wt CH3OH, 7% wt H2O, 11% wt H2, 58% wt CO2 and 12% wt CO. The product methanol stream leaving the system has a composition of: 99.96% wt CH3OH, 0.01% wt H2O and 0.03% wt CO2.
Calogero et al. [122] also simulated methanol synthesis through CO2 hydrogenation, referring to the models developed by Atsonios et al. [115] and Van-Dal et al. [117]. The process consists of two main parts, i.e. a preparation section, in which the reactants are brought to the process conditions, and a processing section, in which the synthesis reaction takes place and the separation of products and recirculation occurs. The process conditions and scheme follow those of the study developed by Atsonios et al. [115], with the aim to obtain a product methanol purity equal to 99.9% mol.
Kiss et al. [123] used Aspen Plus to simulate a process for methanol synthesis from CO2 and wet hydrogen by-product from chlor-alkali production. In the simulated process, reactants are first brought to the required temperature and pressure, mixed, and then fed to the reactor, with is simulated by a plug flow reactor (PFR) using the LHHW kinetics. The reactor outlet contains products (CH3OH and H2O) as well as unconverted reactants (COx and H2), and then this gaseous mixture is cooled and flashed to separate the condensable products from the non-condensable reactants, which are recycled. The condensed components are then separated in a distillation column, to get into lights (dissolved COx and minor light impurities), MeOH and water. The authors included a stripping unit in the process, in which wet hydrogen flows in counter-current mode with the condensed water mixture from the high-pressure low-temperature separator after the reaction. In this way, there is a complete recycle of CO2 as CO/CO2 is removed from the methanol–water mixture, and at the same time, by removing water from the wet hydrogen, there are no negative impacts on the reaction equilibrium conversion. The chosen Property Methods are the Soave–Redlich–Kwong EOS and NRTL with Henry components. The feed stream entering the PRF reactor is composed of 2.96% mol CO, 25.14% mol CO2, 71.39% mol H2, and 0.51% mol CH3OH. The product stream exiting the PRF reactor has a composition of 3.24% mol CO, 22.78% mol CO2, 63.95% mol H2, 4.74% mol H2O, and 5.29% mol CH3OH. The methanol stream exiting the system is characterized by a molar concentration of 0.01% mol H2, 0.02% mol H2O, and 99.98% mol CH3OH. The H2 conversion is 18.17%, while the CO2 conversion is 17.20% and the MeOH yield of the overall process is 99.83%. In this process, all the carbon from the CO2 feed is converted into MeOH product, whereas only two-thirds of H2 are converted into MeOH product, while the rest is converted to the water by-product.
Table 5 summarizes the reviewed studies on modelling methanol synthesis. The analysis revealed that the process (either from syngas or CO2 as main feedstock) has been largely simulated in Aspen Plus. On the other hand, no studies simulating the process of direct methane to methanol (DMTM) conversion in Aspen Plus have been found in literature, probably because the technology is still in the developing phase.
5 Preliminary quantitative assessment
In most of the reviewed modelling studies, the technologies suitable for the value chain that we investigate in the current paper were not simulated as stand-alone units, but they are embedded in wider contexts. Therefore, it was often difficult to extrapolate, whether reported, quantitative information about each specific technology Moreover, it must be underlined that each work is characterized by its own process conditions, stream compositions, plant configurations (e.g. products separation equipment, recycling streams, etc.) which can be hardly used to perform an accurate comparison among technologies. However, a preliminary quantitative assessment and use of mass balances, and thus process yields, of the models found in the literature is definitely needed to complete the overview of such conversion pathways. Therefore, considering the aforementioned limitations, and focusing on the modelling studies whose application is closer to the sustainable value chain here proposed, Table 6 has been drafted to report information regarding the mass balances of conversion technologies in the reviewed modelling studies. The table also provides extracts of mass balances related to full value chains.
The study developed by Ashraf et al. [8] is of particular interest, as the pathway encompassed is extremely coherent to that proposed in the present article. In this research, authors considered a relatively small-scale biogas to FT liquid conversion route, including biogas upgrading through PWS, biomethane reforming through DMR, syngas cleaning through chemical absorption with MEA, FT synthesis, and product upgrading in distillation columns. The study showed that, for 10,000 Nm3/h of dry biogas, the process requires 7.08 MW of power in addition to 35 of heating and 185 GJ/h for cooling, and from 4000 kg/h of methane in the biogas feed, 1602 kg/h of FT products could be produced. The process investigated is thus characterized by a carbon conversion efficiency of 45% and energy efficiency of 30%.
Another article that could be taken as a reference to study the sustainable biofuel production chain proposed is that of Bao et al. [97], even though the feedstock considered in the process is natural gas. The simulated plant converts 900,000 kg/h of natural gas to 118,000 bpd of products, through a conversion route involving reforming, FT reaction, and product upgrading.
6 Discussion
The aim of the research was to analyse a sustainable value chain, producing low-ILUC-risk biofuels (FT liquids and MeOH) and investigate the possibility to model it with a commercial software. The low-ILUC nature of the value chain is ensured by the implementation of the Biogas Done Right (BDR) model for the production of biomethane in a farm-scale decentralized configuration; the biomethane produced through this sustainable pathway serves as a basis for the production of synthetic fuels and chemicals in centralized refineries, making use of the natural gas grid to connect the two environments (farm and refinery). Existing and under-development technologies for the conversion of biomass-to-liquid fuels have been reviewed, and their modelling in the various studies available in the literature analysed, focusing on model assumptions, process conditions, applications, yields, and consumptions.
After a quality-based initial screening, a total of about 57 reviewed modelling papers were selected among the available literature; these included anaerobic digestion, biogas cleaning and upgrading to biomethane, methane reforming to syngas, syngas conversion to hydrocarbons through Fischer–Tropsch synthesis and MeOH synthesis from syngas and CO2 hydrogenation.
In the reviewed papers, many of the technologies of interest to this paper have not been modelled as stand-alone cases, but are embedded in broader contexts, with more complex flowsheets. For this reason, it was often difficult to extrapolate detailed information on yields and consumptions of the individual processes from their original framework. For example, in the study of Cinti et al. [98], aimed at simulating the production of synthetic green fuels through a system integrating solid oxide electrolyzer and FT synthesis, our analysis did not cover the electrolyzer unit, but was focused only on modelling the Fischer–Tropsch synthesis.
As discussed, the first step of the value chain under investigation foresees the anaerobic digestion process following the BDR model to produce biogas in a sustainable manner. In the literature, no studies that specifically apply this model in Aspen Plus simulation environment have been found (Fig. 5). Therefore, we searched for generalized anaerobic digestion models, which turned out to be not so numerous (i.e. 6); this could be due to the high complexity of the process, which turns out to be particularly difficult to model, especially as regards the biological activity of microorganisms. Nguyen et al. [60] and Scamardella et al. [61] opted for a one-stage model in a single reactor, in which the whole AD phases occurs. In the RSTOIC reactor (used in Nguyen et al. [60]), the reaction kinetics is not considered, whereas in the RCSTR (used in Scamardella et al. [61]) detailed information on the reactions and their kinetics must be input; this means that the first represents a more simplistic modelling approach. However, the two studies ([60] [61]) refer to different AD models (i.e. Buswell equation, ADM1, and comprehensive models), and the papers do not provide information showing a comparison with experimental data. Al-Rubaye et al. [56] and Rajendran et al. [59] adopted a very similar approach, i.e. a two-step model using a RSTOIC reactor for the hydrolytic phase and a RCSTR reactor for the other AD phases, in reference to the ADM1 and comprehensive models. The two studies have been validated against experimental data, resulting in both cases in good agreement. The AD model developed by Serrano Peris [57], which involves two RSTOIC reactors in series, does not take into account the hydrolytic step, and its application is thus limited to post-hydrolyzed wastes. Besides, a higher modelling complexity is given in that of Llanes et al. [62], which integrates ADM1, flow pattern and biofilm characteristics implemented through FORTRAN subroutines; this model is thus not limited to completely mixed flow pattern (as in the case of RCSTR reactors), and results are in agreement with experimental data.
Biogas upgrading to biomethane is a fundamental step in the proposed sustainable value chain, as biomethane must comply with strict Country-specific technical standards in order to be injected into the natural gas grid. Therefore, accurately modelling this step is crucial. In the literature, there is a relevant number of papers (i.e. 16) simulating upgrading processes; these are in large part set in the context of gas sweetening, but nevertheless, in some studies ([8, 34, 39]), the upgrading technologies are employed for syngas upgrading (i.e. CO2 removal). Many of the upgrading processes modelled in Aspen Plus turned out to be physical absorption (i.e. PWS) and chemical absorption using amine solutions (i.e. MEA, DEA, MDEA). The modelling approach of these technologies is almost the same in every paper: a distillation column for both absorption and stripping processes. The Aspen Plus distillation unit operation chosen in most of the reviewed simulations was the RADFRAC column, which is the most generic column block type. Some models have opted for an equilibrium-stage approach for both absorption and stripping column, which assumes that each plate of the column is a theoretical plate (equilibrium plate), and thus, the vapour and the liquid leave any plate at thermodynamic equilibrium [125]. In other simulations, instead, the distillation columns are rate-based, which means that the mass and energy transfer across the interface are taken into account using rate equation and mass transfer coefficients; therefore, this approach provides a more rigorous modelling of the columns. At the same time, there are studies ([66, 69]) that opted for a combined equilibrium-based and rate-based approach.
Not many models simulating the pressure swing adsorption process in Aspen Plus were found in the literature. As a matter of facts, the PSA process is a dynamic process, and as Aspen Plus is a steady state calculator, no dynamic options are available in the software. For this reason, many authors preferred to model the process in Aspen Adsorption, this being a comprehensive flowsheet simulator more specific for adsorption processes. Finally, only one study (i.e. [61]) modelling the biogas upgrading through membrane separation has been found, consisting in a user-defined model developed in Excel referring to Fick’s law with diffusive model assumptions.
About the modellization of the reforming technologies, a discrete number of studies have been found (i.e. 7), most of them assessing the SMR process, which is the most consolidated one in this matter. A good number of papers addressed the process of dry reforming, which is an emerging technology whose reaction kinetics has not been fully described yet. Anyway, there are many studies in which DMR is combined with SMR, as well as POX, while a smaller number of articles assessing the ATR process was found. Most of the reviewed models are aimed at simulating processes for hydrogen production in spite of syngas production, and consequently, in many studies, SMR is combined with WGS. The modelling approaches of the analysed studies are various: the Aspen Plus reactor blocks employed in the simulations are RGIBBS ([8, 81, 83]), REQUIL ([79, 82]), and RPLUG with Langmuir–Hinshelwood-Hougen-Watson (LHHW) kinetics ([16, 80]). The RPLUG reactor type that unlike the RGIBBS and the REQUIL, encompasses the process reaction kinetics and allows for a complete description of the process under variable conditions and proper reactor sizing; however, a suitable reaction set and the relative kinetic model and thermodynamic data must be provided [126].
A large number of studies (i.e. 17) modelling the Fischer–Tropsch process in Aspen Plus have been found in the literature. As mentioned, the FT process is particularly complex and the full understanding of all mechanisms involved has not yet been reached, though it is not a novel technology. The reference model for most of the reviewed articles is the Anderson-Schulz-Flory (ASF) distribution, a fairly simple model which gives a reasonable description of FT products by representing the synthesis as an addition polymerization reaction with chain growth probability α [127] [91]. Nevertheless, despite the mathematical simplicity of the ASF model, studies have shown that there are deviations of the FT product composition from the ideal distribution (i.e. higher methane selectivity, lower ethylene selectivity, increasing chain growth probability, and lower olefin-to-paraffin ratio with increasing carbon number) [101, 105, 107, 128]; therefore, correlations accounting for the ASF distribution deviations and dependence of α on process conditions have been developed and are well documented in the literature [89]–[84, 91, 100, 108,109,110]. In many modelling studies reviewed, the produced hydrocarbons have been assumed to be composed only by paraffins; this assumption is acceptable, as the alkanes are the main product of the FT synthesis. However, there is also a large number of studies considering olefins in the products, while only one model (i.e. Dahl [107]) among those found includes also alcohols. Moreover, it was noticed that in many studies ([95, 97, 98, 105]) the chain growth probability α has a constant value, while others use correlations to relate its values to the process conditions; the most used expression in the reviewed papers is the one derived by Song et al. [89]. Another significant parameter for determining the accuracy of a FT model is the carbon number (n) for the product chain termination; in the modelling studies reviewed, this number was found to be always higher than 20 for the main products (i.e. paraffins). Setting a high n for the hydrocarbon chain termination definitively represents a higher accuracy in describing the Fischer–Tropsch synthesis; in fact, the product slate synthesized ranges from methane up to C-120 + [88]. However, as the product selectivity significantly decreases after peaking at around C-7 to C-13 (depending on the process conditions and the catalyst), cutting the chain from n = 20 could be considered satisfactory.
Most of the reviewed Aspen Plus models employ reactor types such as RSTOIC and RYIED, in which the reaction kinetics is not explicitly considered, and the product distribution is imposed. Nevertheless, a small number of modelling studies assessing the FT synthesis reaction kinetics (through external subroutine) were also found (i.e. [83, 101, 103, 107]); these models provide higher flexibility when changing the process conditions.
As concerns the MeOH synthesis from syngas, 5 studies have been found, whose modelling procedures are diverse. Some authors did not consider the reaction kinetics, opting for a RSTOIC reactor ([39]) or for a REQUIL reactor ([34, 112]), which performs chemical and phase equilibrium reactions. At the same time, De Maria et al. [113] and Trop et al. [111] described the reaction kinetics of the catalytic reaction, using, in the former case, a user-defined reactor type developed in Matlab, and a RPLUG reactor in the latter case.
Additionally, opportunities for further pathways have been investigated, including methanol synthesis from captured CO2, which represents an excellent opportunity from an environmental sustainability point of view. Indeed, CCS and CCU technologies, if associated with bioenergy, can make the production chain considered not only carbon neutral but also carbon negative. In this perspective, in the proposed bioliquid production chain, the CO2 separated from biogas through upgrading processes represents again a further feedstock for the MeOH production, and in this way would not be dispersed in the atmosphere. Lots of studies simulating this in Aspen Plus have been found (i.e. 7), meaning that this topic is of great interest to the scientific community. The modelling approaches of the MeOH synthesis from CO2 adopted in the reviewed papers are very similar to those of in the case of syngas as a feedstock: REQUIL reactor ([112, 114]) and RPLUG reactor with LHHW kinetics ([115, 117, 120, 122, 123]).
As an alternative to MeOH synthesis from syngas, the straight conversion of methane into methanol (DMTM) could be an interesting route, as it gives the possibility to by-pass the very energy-intensive step of methane reforming, representing an economical-advantage and environment-friendly option. However, as mentioned, this method still needs to be improved to be suitable for industrial applications. As a matter of fact, no Aspen Plus models simulating this process have been found in the literature.
In view of these considerations, it can be concluded that the simulation system provides all the necessary tools to model the entire sustainable biofuel production chain selected for this work. Moreover, through browsing the suitable technologies (either consolidated or under development) that could be employed, and by analysing and commenting on the diverse options identified in literature, this study could serve as a guideline to assess the feasibility of bio-thermochemical conversion pathways.
The references collected in the literature could be used for further studies aimed at qualitatively and quantitatively assessing multiple aspects related to biofuels production, and besides the possibility to build an overall Aspen Plus simulation model of the proposed sustainable biogas-to-liquid production chain would be an interesting object for future works.
7 Conclusions
Biomass-to-fuel pathways are of interest for many sectors, in particular those relying on liquid fuels also during the short-medium term ecological transition, such as maritime and aviation. The present survey reviewed biogas-biomethane conversion pathways to Fischer–Tropsch liquids and methanol, as an alternative to fossil-based fuels. More specifically, a sustainable biofuel production chain, producing low-ILUC-risk biofuels, has been analysed, and the possibility to model it through a commercial simulation software has been explored. The low-ILUC-risk nature of the value chain is guaranteed by the implementation of the Biogas Done Right (BDR) model for the production of biomethane in decentralized farms through anaerobic digestion. The produced biomethane constitutes the base to synthesize bio-liquids and bio-chemicals in centralized conversion plants, making use of the natural gas grid to connect the farm and the refinery environments. The value chain includes thus biogas cleaning and upgrading to biomethane, injection of biomethane into the natural gas grid resulting in downstream extraction, methane reforming to syngas, and syngas conversion to hydrocarbons through Fischer–Tropsch synthesis and to methanol through MeOH synthesis. Several suitable technologies and process solutions have been reviewed and, in addition, opportunities for further pathways to be included have been investigated, in order to integrate the proposed biofuel production chain even more into a perspective of sustainability; these are methanol production from captured CO2 and direct methane to methanol (DMTM) conversion.
Moreover, a comprehensive literature review of studies modelling the identified conversion pathways using Aspen Plus process simulation software has been carried out, in order to evaluate the maturity of available simulation models. To this aim, 57 publications were selected, which have been deeply analysed from the point of view of plant configuration, modelling approach, and process yield, focusing on understanding the diverse schematizations and assumptions, as well as mass/energy balances. It has been observed that many of the technologies of interest to this article were not modelled as stand-alone studies, but were embedded in broader contexts; thus, it was often difficult to extrapolate detailed information on related yields and consumptions. Anyway, the survey showed that comprehensive and sufficiently complete kinetic data to model well-established technologies (i.e. SMR and MeOH synthesis) are available in the literature, and thus a considerable number of Aspen Plus simulation models addressing them exhaustively was found. Likewise, a large experience in modelling upgrading technologies, such as physical and chemical absorption, has been observed, as well as a remarkable coherence in the modelling approaches. At the same time, the mechanisms involved in the high-complexity processes embedded in the proposed value chain (i.e. AD and FT) still need to be fully understood, but yet studies simulating them satisfactorily and with a good match with experimental data have been found. However, the only technology for which no modelling studies were identified is DMTM, being this process still under investigation.
By investigating a broad spectrum of suitable biomass-to-liquid conversion pathways, either consolidated or under development, and by analysing and commenting on the diverse options retrieved in literature studies, this work could represent a guideline for further studies aimed to analyse qualitatively and quantitatively multiple aspects related to biofuels production.
Moreover, the review revealed that the commercial software chosen for the analysis provides the necessary tools to model the multiple technological solutions that could be employed in the identified sustainable biofuel production chain. Besides, this study contains enough references to build an overall biomass-to-liquid value chain simulation model, making it a solid basis for future works, such as optimizing operational conditions, determining limitations due to process configurations, and possibly exploiting the high potential of process waste streams to further support the sustainability of bioliquids production.
Abbreviations
- AD :
-
Anaerobic digestion
- MDEA :
-
Methyldiethanolamine
- ADM1 :
-
Anaerobic Digestion Model No.1
- MEA :
-
Monoethanolamine
- AMP :
-
Amino-methyl-propanol
- MeOH :
-
Methanol
- ASF :
-
Anderson-Schulz-Flory
- MTBE :
-
Methyl tertiary-butyl ether
- ATR :
-
Autothermal reforming
- NRTL :
-
Non-random two liquid
- BRD :
-
Biogas done right
- NRTL-RK :
-
Non-random two-liquid Redlich-Kwong
- BWR :
-
Boiling water reactor
- PAD :
-
Pressurized anaerobic digestion
- CHP :
-
Cogeneration or combined heat and power
- POX :
-
Partial oxidation
- CIB :
-
Consorzio Italiano Biogas
- PR-BM :
-
Peng Robinson with Boston-Mathias alpha function
- COP21 :
-
2015 UN Climate Change Conference
- PRF :
-
Plug flow reactor
- CSTR :
-
Continuous stirred tank reactor
- PSA :
-
Pressure swing adsorption
- CTL :
-
Coal to liquid
- PWS :
-
Pressurized water scrubbing
- DEA :
-
Diethanolamine
- RCSTR :
-
Rigorous continuous stirred tank reactor
- DME :
-
Dimethyl ether
- REQUIL :
-
Rigorous equilibrium reactor based on stoichiometric approach
- DMR :
-
Dry methane reforming
- RGIBBS :
-
Rigorous equilibrium reactor based on Gibbs free energy minimization
- DMTM :
-
Direct methane to methanol
- RK :
-
Redlich-Kwong
- ELECNRTL :
-
Electrolyte non-random two liquid
- RKSMHV2 :
-
Redlich-Kwong-Soave equation of state with modified Huron-Vidal mixing rule
- EOS :
-
Equation of state
- RPLUG :
-
Rigorous plug flow reactor with rate-controlled reactions based on known kinetics
- FT :
-
Fischer-Tropsch
- RSTOIC :
-
Stoichiometric reactor based on known fractional conversions or extents of reaction
- GHG :
-
Greenhouse gases
- RWGS :
-
Reverse water–gas shift
- GTL :
-
Gas to liquid
- RYIELD :
-
Nonstoichiometric reactor based on known yield distribution
- HPWS :
-
High-pressure water scrubbing
- SAF :
-
Sustainable aviation fuels
- HTFT :
-
High-temperature Fischer–Tropsch
- SCWR :
-
Supercritical water reforming
- IGCC :
-
Integrated gasification combined cycle
- SMR :
-
Steam methane reforming
- ILUC :
-
Indirect land-use change
- SRK-ML :
-
Soave-Redlich-Kwong equation of state with T dependent
- LHHW :
-
Langmuir-Hinshelwood-Hougen-Watson
- UASB :
-
Upflow anaerobic sludge blanked
- LPG :
-
Liquefied petroleum gas
- VFA :
-
Volatile fatty acids
- LTFT :
-
Low-temperature Fischer–Tropsch
- WGS :
-
Water-gas shift
- MB :
-
Membrane separation
References
Olivier JGJ and JAHW P (2020) “Trends in global CO2 And total greenhouse gas 2019 report”. Available: https://www.pbl.nl/sites/default/files/downloads/pbl-2020-trends-in-global-co2-and-total-greenhouse-gas-emissions-2019-report_4068.pdf
Nations U (2015) Paris Agreement. 8
Lynd LR et al (n.d.) “The role of biomass in America’s energy future: framing the analysis”. Biofuels Bioprod Biorefining 3:2. https://doi.org/10.1002/bbb.134
Overmars KP, Stehfest E, Ros JPM, Prins AG (2011) Indirect land use change emissions related to EU biofuel consumption: an analysis based on historical data. Environ Sci Policy 14(3):248–257. https://doi.org/10.1016/j.envsci.2010.12.012
Indirect Land Use Change (ILUC) (n.d.) European Commission. https://ec.europa.eu/commission/presscorner/detail/en/MEMO_12_787. Accessed 2 Feb 2022
Sustainability criteria for biofuels specified (n.d.) European Commission. https://ec.europa.eu/commission/presscorner/detail/en/MEMO_19_1656. Accessed 2 Feb 2022
Dale BE et al (2020) “The potential for expanding sustainable biogas production and some possible impacts in specific countries”. Biofuels Bioprod Biorefining 14(6):1335–1347. https://doi.org/10.1002/bbb.2134
Ashraf MT, Schmidt JE, and Oyanedel JRB (2015) “Conversion efficiency of biogas to liquids fuels through Fischer-Tropsch process”.https://doi.org/10.5071/23RDEUBCE2015-3CO.15.5
Jung S, Lee J, Moon DH, Kim KH, Kwon EE (2021) Upgrading biogas into syngas through dry reforming. Renew Sustain Energy Rev 143:110949. https://doi.org/10.1016/j.rser.2021.110949
Baltrusaitis J, Luyben WL (2015) Methane conversion to syngas for gas-to-liquids (GTL): is sustainable CO2 reuse via dry methane reforming (DMR) cost competitive with SMR and ATR processes? ACS Sustain Chem Eng 3(9):2100–2111. https://doi.org/10.1021/acssuschemeng.5b00368
10.3. SYNGAS CONVERSION TO METHANOL (n.d.) National Energy Technology Laboratory (NETL). https://netl.doe.gov/research/coal/energy-systems/gasification/gasifipedia/methanol. Accessed 2 Feb 2022
dos Santos RG, Alencar AC (2020) Biomass-derived syngas production via gasification process and its catalytic conversion into fuels by Fischer Tropsch synthesis: a review. Int J Hydrogen Energy 45(36):18114–18132. https://doi.org/10.1016/j.ijhydene.2019.07.133
GSE (n.d.) Biometano. https://www.gse.it/servizi-per-te_site/rinnovabili-per-i-trasporti_site/biometano_site/Pagine/Biometano.aspx. Accessed 2 Feb 2022
Ranjekar Y (2021) Dry reforming of methane for syngas production: a review and assessment of catalyst development and efficacy. J Indian Chem Soc 98(1):100002. https://doi.org/10.1016/j.jics.2021.100002
Yang L, and Ge X (2016) Advances in bioenergy, chapter three - biogas and syngas upgrading
Gangadharan P, Kanchi KC, Lou HH (2012) Evaluation of the economic and environmental impact of combining dry reforming with steam reforming of methane. Chem Eng Res Des 90(11):1956–1968. https://doi.org/10.1016/j.cherd.2012.04.008
Carapellucci R, Giordano L (2020) Steam, dry and autothermal methane reforming for hydrogen production: a thermodynamic equilibrium analysis. J. Power Sources 469(2019):228391. https://doi.org/10.1016/j.jpowsour.2020.228391
Zhu Q, Zhao X, Deng Y (2004) Advances in the partial oxidation of methane to synthesis gas. J Nat Gas Chem 13(4):191–203. https://doi.org/10.1016/S1003-9953-2004-13-4-191-203
Er-rbib H, Bouallou V, and Werkoff F (2012) Dry reforming of methane - review of feasibility studies. Chem Eng Trans29:163–168. April 2016. https://doi.org/10.3303/CET1229028
Ershov MA, Potanin DA, Tarazanov SV, Abdellatief TMM, Kapustin VM (2020) Blending characteristics of isooctene, MTBE, and TAME as gasoline components. Energy Fuels 34(3):2816–2823. https://doi.org/10.1021/acs.energyfuels.9b03914
Musmarra D, Mehariya S (2020) Chapter 7 - Fischer–Tropsch synthesis of syngas to liquid hydrocarbons. https://doi.org/10.1016/B978-0-12-815936-1.00007-1
Rauch R, Kiennemann A, Sauciuc A (2013) Chapter 12 - Fischer-Tropsch Synthesis to Biofuels (BtL Process). In: Triantafyllidis KS, Lappas AA, Stöcker M (eds) The role of catalysis for the sustainable production of Bio-fuels and Bio-chemicals, Elsevier, pp 397–443. https://doi.org/10.1016/B978-0-444-56330-9.00012-7
Mahmoudi H et al (2018) A review of Fischer Tropsch synthesis process, mechanism, surface chemistry and catalyst formulation. Biofuels Eng 2(1):11–31. https://doi.org/10.1515/bfuel-2017-0002
Gruber H et al (2019) Fischer-Tropsch products from biomass-derived syngas and renewable hydrogen. Biomass Convers Biorefinery 1–12. https://doi.org/10.1007/s13399-019-00459-5
Perego C, Bortolo R, Zennaro R (2009) Gas to liquids technologies for natural gas reserves valorization: the Eni experience. Catal Today 142(1–2):9–16. https://doi.org/10.1016/j.cattod.2009.01.006
Ershov MA et al (2022) An evolving research agenda of merit function calculations for new gasoline compositions. Fuel 322:124209. https://doi.org/10.1016/j.fuel.2022.124209
Ershov MA et al (2022) Perspective towards a gasoline-property-first approach exhibiting octane hyperboosting based on isoolefinic hydrocarbons. Fuel 321:124016. https://doi.org/10.1016/j.fuel.2022.124016
Abdellatief TMM, Ershov MA, Kapustin VM (2020) New recipes for producing a high-octane gasoline based on naphtha from natural gas condensate. Fuel 276:118075. https://doi.org/10.1016/j.fuel.2020.118075
Ershov MA, Abdellatief TMM, Potanin DA, Klimov NA, Chernysheva EA, Kapustin VM (2020) Characteristics of isohexene as a novel promising high-octane gasoline booster. Energy Fuels 34(7):8139–8149. https://doi.org/10.1021/acs.energyfuels.0c00945
Adelung S, Maier S, Dietrich RU (2021) Impact of the reverse water-gas shift operating conditions on the power-to-liquid process efficiency. Sustain. Energy Technol. Assessments 43:100897. https://doi.org/10.1016/j.seta.2020.100897
Méndez CI, Ancheyta J (2020) Kinetic models for Fischer-Tropsch synthesis for the production of clean fuels. Catal. Today 353:3–16. https://doi.org/10.1016/j.cattod.2020.02.012
Nassr LAIB (2013) “Simulation of Fischer-Tropsch fixed-bed reactor in different reaction media,” Texas A&M University
Yanti FM et al (2020) Methanol production from biomass syngas using Cu / ZnO / Al 2 O 3 catalyst methanol production from biomass syngas using Cu / ZnO / Al2O3 catalyst. 020006
Puig-Gamero M, Argudo-Santamaria J, Valverde JL, Sánchez P, Sanchez-Silva L (2018) Three integrated process simulation using aspen plus®: pine gasification, syngas cleaning and methanol synthesis. Energy Convers Manag 177(9):416–427. https://doi.org/10.1016/j.enconman.2018.09.088
Chein R, Chen W, Ong HC, Show PL, and Singh Y (2021) Analysis of methanol synthesis using CO2 hydrogenation and syngas produced from biogas-based reforming processes. Chem Eng J 130835. https://doi.org/10.1016/j.cej.2021.130835
Abdelaziz OY, Gadalla MA and Ashour FH (n.d.) Simulation of biomethanol production from green syngas through sustainable process design.https://doi.org/10.5220/0005002906770684
Akça A (2021) Conversion of methane to methanol on C-doped boron nitride: A DFT study. Comput. Theor. Chem. 1202:113291. https://doi.org/10.1016/j.comptc.2021.113291s
Da Silva MJ (2016) Synthesis of methanol from methane: challenges and advances on the multi-step (syngas) and one-step routes (DMTM). Fuel Process Technol 145:42–61. https://doi.org/10.1016/j.fuproc.2016.01.023
Gutiérrez Ortiz FJ, Serrera A, Galera S and Ollero P (2013) Methanol synthesis from syngas obtained by supercritical water reforming of glycerol. Fuel 105:739–751. https://doi.org/10.1016/j.fuel.2012.09.073
Kiyokawa T, Ikenaga N (2021) Oxidative dehydrogenation of n-butene to buta-1,3-diene with novel iron oxide-based catalyst: effect of iron oxide crystalline structure. Mol Catal 507:111560. https://doi.org/10.1016/j.mcat.2021.111560
Landälv I, Waldheim L, Maniatis K (2018) Continuing the work of the sub group on advanced biofuels for the RED II market deployment for Advanced Biofuels -Technology status and reliability of the value chains: 2018 Update. Available at: http://artfuelsforum.wpengine.com/wp-content/uploads/2019/04/ART-Fuels-Forum-SGAB-Biofuels-Technology-report-2018-update.pdf. Accessed 26 July 2022
Bell DA, Towler BF and Fan M (2011) Chapter 12 - Methanol and derivatives in Coal Gasification and Its Applications. 353–371
Al-Sobhi SA, Elkamel A, Erenay FS, Shaik MA (2018) Simulation-optimization framework for synthesis and design of natural gas downstream utilization networks. Energies 11(2):1–19. https://doi.org/10.3390/en11020362
Leonie L (2017) Methanol production from syngas: process modelling and design utilising biomass gasification and integrating hydrogen supply, Thesis, Delft University of Technology. Availble at: http://resolver.tudelft.nl/uuid:c0c5ebd2-c336-4f2d-85d1-014dae9fdf24. Accessed 26 July 2022
Majhi S, Pant KK (2014) Direct conversion of methane with methanol toward higher hydrocarbon over Ga modified Mo/H-ZSM-5 catalyst. J Ind Eng Chem 20(4):2364–2369. https://doi.org/10.1016/j.jiec.2013.10.014
Zakaria Z, Kamarudin SK (2016) Direct conversion technologies of methane to methanol: an overview. Renew Sustain Energy Rev 65:250–261. https://doi.org/10.1016/j.rser.2016.05.082
Ma C, Tan X, Zhang H, Shen Q, Sun N, Wei W (2020) Direct conversion of methane to methanol over Cu exchanged mordenite: effect of counter ions. Chinese Chem Lett 31(1):235–238. https://doi.org/10.1016/j.cclet.2019.03.039
Khirsariya P, Mewada RK (2013) Single step oxidation of methane to methanol - towards better understanding. Procedia Eng 51:409–415. https://doi.org/10.1016/j.proeng.2013.01.057
Ficara E, Hassam A, Allegrini A, Leva A, Malpei F, Ferretti G (2012) Anaerobic digestion models: a comparative study. IFAC Proceedings Volumes 45(2):1052–1057. https://doi.org/10.3182/20120215-3-AT-3016.00186
Graef SP, Andrews JF (1974) Stability and control of anaerobic digestion. J Water Pollut Control Fed JSTOR46. Available: http://www.jstor.org/stable/25038181. Accessed 3 Feb 2022
Bernard O et al (2001)Dynamical model development and parameter identification for an anaerobic wastewater treatment process. Biotechnol Bioeng 75(4):424–438
Batstone DJ, Keller J, Angelidaki I, Kalyuzhnyi SV, Pavlostathis SG, Rozzi A (n.d.) The IWA Anaerobic Digestion Model No 1 (ADM1). Enzyme Chem Msu Ru 1(1):65–74. Available: http://www.enzyme.chem.msu.ru/ekbio/article/ADM1-WST.pdf. Accessed 3 Feb 2022
Sötemann SW, Ristow N, Wentzel MC, Ekama G (2006) A steady state model for anaerobic digestion of sewage sludge. https://doi.org/10.4314/wsa.v31i4.5143; Available on website http://www.wrc.org.za. Accessed 26 Jul 2022
Vavilin VA., Vasiliev VB, Ponomarev AV, Rytow SV (n.d.) Simulation model ‘methane’ as a tool for effective biogas production during anaerobic conversion of complex organic matter. Bioresour Technol 48(1):1–8. https://doi.org/10.1016/0960-8524(94)90126-0
Angelidaki I, Ellegaard L, Ahring BK (1999) A comprehensive model of anaerobic bioconversion of complex substrates to biogas. Biotechnol Bioeng 63(3):363–372. https://doi.org/10.1002/(SICI)1097-0290(19990505)63:3%3c363::AID-BIT13%3e3.0.CO;2-Z
Al-Rubaye H, Karambelkar S, Shivashankaraiah MM, Smith JD (2019) Process simulation of two-stage anaerobic digestion for methane production. Biofuels 10(2):181–191. https://doi.org/10.1080/17597269.2017.1309854
Peris RS (2011) Biogas process simulation using Aspen Plus. Dep Chem Eng Biotechnol Environ Technol Syddansk Univ 1–88
Aspen Plus User Guide, Version 10.2 (2000) Aspen Technology, Inc. Available: http://www.aspentech.com. Accessed 26 Jul 2022
Rajendran K, Kankanala HR, Lundin M, Taherzadeh MJ (2014) A novel process simulation model (PSM) for anaerobic digestion using Aspen Plus. Bioresour Technol 168:7–13. https://doi.org/10.1016/j.biortech.2014.01.051
Nguyen HH, Heaven S, Banks C (2014) Energy potential from the anaerobic digestion of food waste in municipal solid waste stream of urban areas in Vietnam. Int J Energy Environ Eng 5(4):365–374. https://doi.org/10.1007/s40095-014-0133-1
Scamardella D et al (2019) Simulation and optimization of pressurized anaerobic digestion and biogas upgrading using aspen plus. Chem. Eng. Trans. 74:55–60
Lorenzo-Llanes J, Pagés-Díaz J, Kalogirou E, Contino F (2020) Development and application in Aspen plus of a process simulation model for the anaerobic digestion of vinasses in UASB reactors: hydrodynamics and biochemical reactions. J Environ Chem Eng 8(2):103540. https://doi.org/10.1016/j.jece.2019.103540
Cozma P, Ghinea C, Mǎmǎligǎ I, Wukovits W, Friedl A, Gavrilescu M (2013) Environmental impact assessment of high pressure water scrubbing biogas upgrading technology. Clean - Soil, Air, Water 41(9):917–927. https://doi.org/10.1002/clen.201200303
Cozma P, Wukovits W, Mǎmǎligǎ I, Friedl A and Gavrilescu M (2014) Modeling and simulation of high pressure water scrubbing technology applied for biogas upgrading. Clean Technol Environ Policy 17:2. https://doi.org/10.1007/s10098-014-0787-7
Götz M, Köppel W, Reimert R, Graf F (2011) Optimierungspotenzial von Wäschen zur Biogasaufbereitung: Teil 1 - Physikalische Wäschen. Chem-Ing-Tech 83(6):858–866. https://doi.org/10.1002/cite.201000211
Menegon S (2017) Tesi di Laurea Magistrale in DAL BIOGAS AL BIOMETANO: SIMULAZIONE DI PROCESSO ED ANALISI TECNO-ECONOMICA DELLE PRINCIPALI. 148
Bortoluzzi G, Gatti M, Sogni A, Consonni S (2014) Biomethane production from agricultural resources in the Italian scenario: techno-economic analysis of water wash. Chem Eng Trans 37:259–264. https://doi.org/10.3303/CET1437044
Abu Seman N and Harun N (2019) Simulation of pressurized water scrubbing process for biogas purification using Aspen Plus. IOP Conf Ser Mater Sci Eng 702:1. https://doi.org/10.1088/1757-899X/702/1/012040
Lingelem H-U (2016) Process optimization of biogas upgrading with AMP using pilot plant data and simulations with Aspen Plus, Master Thesis, NTNU (Norwegian University of Science and Technology), available at: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2411549. Accessed 26 Jul 2022
Gamba S and Pellegrini LA (2013) Biogas upgrading : analysis and comparison between water and chemical scrubbings. Chem Eng Trans32. https://doi.org/10.3303/CET1332213
Pellegrini LA, Moioli S, Gamba S (2011) Energy saving in a CO2 capture plant by MEA scrubbing. Chem Eng Res Des 89(9):1676–1683. https://doi.org/10.1016/j.cherd.2010.09.024
Gamba S, Pellegrini LA, and Langè S (2014) Energy analysis of different municipal sewage sludge-derived biogas upgrading techniques. Chem Eng Trans37. https://doi.org/10.3303/CET1437139
Pellegrini LA, De Guido G, Consonni S, Bortoluzzib G, Gatti M (2015) From biogas to biomethane: how the biogas source influences the purification costs. Chem Eng Trans 43:409–414. https://doi.org/10.3303/CET1543069
Worawimut C, Vivanpatarakij S, Watanapa A, Wiyaratn W, Assabumrungrat S (2018) Purification and upgrading from biogas to biomethane. J Japan Inst Energy 97(7):176–179. https://doi.org/10.3775/jie.97.176
Niu MW, Rangaiah GP (2014) Retrofitting amine absorption process for natural gas sweetening via hybridization with membrane separation. Int J Greenh Gas Control 29:221–230. https://doi.org/10.1016/j.ijggc.2014.08.019
Abdeljaoued A, Relvas F, Mendes A, Chahbani MH (2018) Simulation and experimental results of a PSA process for production of hydrogen used in fuel cells. J Environ Chem Eng 6(1):338–355. https://doi.org/10.1016/j.jece.2017.12.010
Campanario FJ and Gutiérrez Ortiz FJ (2017) Fischer-Tropsch biofuels production from syngas obtained by supercritical water reforming of the bio-oil aqueous phase. Energy Convers Manag150(6):599–613. https://doi.org/10.1016/j.enconman.2017.08.053
Jianguo Xu GFF (1989) Methane steam reforming, methanation and water-gas shift: I. Intrinsic kinetics. AIChE J. https://doi.org/10.1002/aic.690350109.
Giwa A, Giwa SO (2013) Simulation, sensitivity analysis and optimization of hydrogen production by steam reforming of methane using Aspen Plus. Int J Eng Res Technol 2(7):1719–1729
Amran UI, Ahmad A, Othman MR (2017) Kinetic based simulation of methane steam reforming and water gas shift for hydrogen production using aspen plus. Chem Eng Trans 56:1681–1686. https://doi.org/10.3303/CET1756281
Gopaul SG, Dutta A (2015) Dry reforming of multiple biogas types for syngas production simulated using Aspen Plus: the use of partial oxidation and hydrogen combustion to achieve thermo-neutrality. Int J Hydrogen Energy 40(19):6307–6318. https://doi.org/10.1016/j.ijhydene.2015.03.079
Er-Rbib H, Bouallou C, Werkoff F (2012) Production of synthetic gasoline and diesel fuel from dry reforming of methane. Energy Procedia 29:156–165. https://doi.org/10.1016/j.egypro.2012.09.020
Hao X, Djatmiko ME, Xu Y, Wang Y, Chang J, Li Y (2008) Simulation analysis of a gas-to-liquid process using aspen plus. Chem Eng Technol 31(2):188–196. https://doi.org/10.1002/ceat.200700336
Pandey U (2020) “Modelling Fischer-Tropsch kinetics and product distribution over a cobalt catalyst”, Nor Univ. Sci Technol
Patzlaff J, Liu Y, Graffmann C, Gaube J (2002) Interpretation and kinetic modeling of product distributions of cobalt catalyzed Fischer-Tropsch synthesis. Catal Today 71(3–4):381–394. https://doi.org/10.1016/S0920-5861(01)00465-5
Van Der Laan GP, Beenackers ACM (1999) Kinetics and selectivity of the Fischer-Tropsch synthesis: a literature review. Catal Rev Eng 41(3–4):64. https://doi.org/10.1081/CR-100101170
Damartzis T and Zabaniotou A (2011) Thermochemical conversion of biomass to second generation biofuels through integrated process design — a review. 5:366–378. https://doi.org/10.1016/j.rser.2010.08.003
Zhou L, Gao J, Hao X, Yang Y, Li Y (2021) Chain propagation mechanism of Fischer-Tropsch synthesis: experimental evidence by aldehyde, alcohol and alkene addition. Reactions 2(2):161–174. https://doi.org/10.3390/reactions2020012
Song HS, Ramkrishn D, Trinh S, Wright H (2004) Operating strategies for Fischer-Tropsch reactors: a model-directed study. Korean J Chem Eng 21(2):308–317. https://doi.org/10.1007/BF02705414
Vervloet D, Kapteijn F, Nijenhuis J, Van Ommen J (2012) Fischer-Tropsch reaction-diffusion in a cobalt catalyst particle: aspects of activity and selectivity for a variable chain growth probability. Catal Sci Technol. https://doi.org/10.1039/C2CY20060K
Kruit KD, Vervloet D, Kapteijn F, Van Ommen JR (2013) Selectivity of the Fischer-Tropsch process: deviations from single alpha product distribution explained by gradients in process conditions. Catal Sci Technol 3(9):2210–2213. https://doi.org/10.1039/c3cy00080j
Niasar MS (2019) “Development and optimization of an integrated process configuration for IGCC power generation technology with a Fischer-Tropsch fuels from coal and biomass,” January 2018. https://doi.org/10.22108/gpj.2018.112760.1038
Zheng L, Furimsky E (2003) ASPEN simulation of cogeneration plants. Energy Convers Manag 44(11):1845–1851. https://doi.org/10.1016/S0196-8904(02)00190-5
Dlugosel’skii V, Belyaev V, Mishustin N and Rybakov V (2007) Gas-turbine units for cogeneration. Therm Eng54(12):1000–1003
Michailos S, Parker D, Webb C (2017) A techno-economic comparison of Fischer-Tropsch and fast pyrolysis as ways of utilizing sugar cane bagasse in transportation fuels production. Chem Eng Res Des 118:206–214. https://doi.org/10.1016/j.cherd.2017.01.001
Sudiro M, Bertucco A (2009) Production of synthetic gasoline and diesel fuel by alternative processes using natural gas and coal: Process simulation and optimization. Energy 34(12):2206–2214. https://doi.org/10.1016/j.energy.2008.12.009
Bao B, El-Halwagi MM, Elbashir NO (2010) Simulation, integration, and economic analysis of gas-to-liquid processes. Fuel Process Technol 91(7):703–713. https://doi.org/10.1016/j.fuproc.2010.02.001
Cinti G, Baldinelli A, Di Michele A, Desideri U (2016) Integration of Solid Oxide Electrolyzer and Fischer-Tropsch: a sustainable pathway for synthetic fuel. Appl Energy 162:308–320. https://doi.org/10.1016/j.apenergy.2015.10.053
Pondini M and Ebert M (2013) “Process synthesis and design of low temperature Fischer-Tropsch crude production from biomass derived syngas,” Chalmers University of Technology
Rane S, Borg O, Rytter E, Holmen A (2012) Relation between hydrocarbon selectivity and cobalt particle size for alumina supported cobalt Fischer-Tropsch catalysts. Appl Catal A Gen 437–438:10–17. https://doi.org/10.1016/j.apcata.2012.06.005
Marchese M, Giglio E, Santarelli M and Lanzini A (2020) Energy performance of power-to-liquid applications integrating biogas upgrading, reverse water gas shift, solid oxide electrolysis and Fischer-Tropsch technologies. Energy Convers Manag X 6(1):100041. https://doi.org/10.1016/j.ecmx.2020.100041
Marchese M, Heikkinen N,.Giglio E, Lanzini A, Lehtonen J and Reinikainen M (2019) “Kinetic study based on the carbide mechanism of a Co-Pt/γ-Al2 O3 Fischer–Tropsch catalyst tested in a laboratory-scale tubular reactor,” Catalysts, vol. 9, no. 9, https://doi.org/10.3390/catal9090717.
Marchese M, Buffo G, Santarelli M and Lanzini A (2021) CO2from direct air capture as carbon feedstock for Fischer-Tropsch chemicals and fuels: energy and economic analysis. J CO2 Util46. https://doi.org/10.1016/j.jcou.2021.101487
Marchese M, Chesta S, Santarelli M, Lanzini A (2021) Techno-economic feasibility of a biomass-to-X plant: Fischer-Tropsch wax synthesis from digestate gasification. Energy 228:120581. https://doi.org/10.1016/j.energy.2021.120581
Gabriel KJ, Linke P, Jiménez-Gutiérrez A, Martínez DY, Noureldin M, El-Halwagi MM (2014) Targeting of the water-energy nexus in gas-to-liquid processes: a comparison of syngas technologies. Ind Eng Chem Res 53(17):7087–7102. https://doi.org/10.1021/ie4042998
Hamad N (2011) Safety and techno-economic analysis of solvent selection for supercritical fischer-tropsch synthesis reactors. Master’s thesis, Texas A&M University. Available electronically from https://hdl.handle.net/1969.1/ETD-TAMU-2011-12-10370. Accessed 26 Jul 2022
Dahl R (2021) Evaluation of the new Power & Biomass to Liquid (PBtL) concept for production of biofuels from woody biomass (Dissertation). Retrieved from http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-289860. Accessed 26 Jul 2022
Hillestad M (2015) Modeling the Fischer-Tropsch product distribution and model implementatioN. Chem Prod Process Model 10(3):147–159. https://doi.org/10.1515/cppm-2014-0031
Todic B, Ma W, Jacobs G, Davis BH, Bukur DB (2014) CO-insertion mechanism based kinetic model of the Fischer-Tropsch synthesis reaction over re-promoted Co catalyst. Catal Today 228:32–39. https://doi.org/10.1016/j.cattod.2013.08.008
Shafer WD et al (2019) Fischer-tropsch: Product selectivity-the fingerprint of synthetic fuels. Catalysts 9:3. https://doi.org/10.3390/catal9030259
Trop P, Anicic B, Goricanec D (2014) Production of methanol from a mixture of torrefied biomass and coal. Energy 77:125–132. https://doi.org/10.1016/j.energy.2014.05.045
Chein RY, Chen W.H, Chyuan Ong H, Loke Show P and Singh Y (2021) Analysis of methanol synthesis using CO2 hydrogenation and syngas produced from biogas-based reforming processes. Chem Eng J426(6):130835. https://doi.org/10.1016/j.cej.2021.130835
De María R, Díaz I, Rodríguez M, Sáiz A (2013) Industrial methanol from syngas: kinetic study and process simulation. Int J Chem React Eng 11(1):469–477. https://doi.org/10.1515/ijcre-2013-0061
Suhada N, Azma N, Mel M and Sulaiman S (2020) Optimization of methanol production using Aspen Plus. 1(1):1–10
Atsonios K, Panopoulos KD, Kakaras E (2016) Thermocatalytic CO2 hydrogenation for methanol and ethanol production: process improvements. Int J Hydrogen Energy 41(2):792–806. https://doi.org/10.1016/j.ijhydene.2015.12.001
Graaf GH, Stamhuis EJ, Beenackers AACM (1988) Kinetics of low-pressure methanol synthesis. Chem Eng Sci 43(12):3185–3195. https://doi.org/10.1016/0009-2509(88)85127-3
Van-Dal ÉS, Bouallou C (2013) Design and simulation of a methanol production plant from CO2 hydrogenation. J Clean Prod 57:38–45. https://doi.org/10.1016/j.jclepro.2013.06.008
VandenBussche KM, Froment GF (1996) A steady-state kinetic model for methanol synthesis and the water gas shift reaction on a commercial Cu/ZnO/Al2O3 catalyst. J Catal 161(1):1–10. https://doi.org/10.1006/jcat.1996.0156
Mignard D, Pritchard C (2008) On the use of electrolytic hydrogen from variable renewable energies for the enhanced conversion of biomass to fuels. Chem Eng Res Des 86(5):473–487. https://doi.org/10.1016/j.cherd.2007.12.008
Mantoan F, Bezzo F and Barbera E (2019) “Design and simulation of hydrogenation processes for Co 2 conversion to C-1 chemicals,” UNIVERSITÀ DEGLI STUDI DI PADOVA
Mar Pérez-Fortes JC (2016) Schöneberger, Aikaterini Boulamanti, Evangelos Tzimas, Methanol synthesis using captured CO2 as raw material: Techno-economic and environmental assessment. Appl Energy 161:718-732. https://doi.org/10.1016/j.apenergy.2015.07.067
Francesco C (2018) Methanol synthesis through CO2 hydrogenation: reactor and process modeling. Master Thesis, Politecnico di Torino. Available at: https://webthesis.biblio.polito.it/9229/. Accessed 26 Jul 2022
Kiss AA, Pragt JJ, Vos HJ, Bargeman G, de Groot MT (2016) Novel efficient process for methanol synthesis by CO2 hydrogenation. Chem Eng J 284:260–269. https://doi.org/10.1016/j.cej.2015.08.101
Cozma P, Wukovits W, Mǎmǎligǎ I, Friedl A, Gavrilescu M (2014) Modeling and simulation of high pressure water scrubbing technology applied for biogas upgrading. Clean Technol Environ Policy 17(2):373–391. https://doi.org/10.1007/s10098-014-0787-7
Almoslh A, Alobaid F, Heinze C, Epple B (2020) Comparison of equilibrium-stage and rate-based models of a packed column for tar absorption using vegetable oil. Appl Sci 10(7):8–10. https://doi.org/10.3390/app10072362
Tripodi A, Compagnoni M, Martinazzo R, Ramis G and Rossetti I (2017) Process simulation for the design and scale up of heterogeneous catalytic process: kinetic modelling issues. Catalysts 7:5. https://doi.org/10.3390/catal7050159
James OO, Chowdhury B, Mesubi MA, Maity S (2012) Reflections on the chemistry of the Fischer-Tropsch synthesis. RSC Adv 2(19):7347–7366. https://doi.org/10.1039/c2ra20519j
Prins MJ, Ptasinski KJ, Janssen FJJG (2005) Exergetic optimisation of a production process of Fischer-Tropsch fuels from biomass. Fuel Process Technol 86(4):375–389. https://doi.org/10.1016/j.fuproc.2004.05.008
Funding
Open access funding provided by Politecnico di Torino within the CRUI-CARE Agreement. This work has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No. 952872.
Author information
Authors and Affiliations
Contributions
Lorenzo Testa (lorenzo.testa@polito.it): data curation, formal analysis, investigation, methodology, visualization, writing — original draft; David Chiaramonti (david.chiaramonti@polito.it): conceptualization, writing and review — review and editing, supervision, methodology; Matteo Prussi (matteo.prussi@polito.it): writing — review and editing, conceptualization, visualization; Samir Bensaid (samir.bensaid@polito.it): writing — review and editing, visualization.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Testa, L., Chiaramonti, D., Prussi, M. et al. Challenges and opportunities of process modelling renewable advanced fuels. Biomass Conv. Bioref. 14, 8153–8188 (2024). https://doi.org/10.1007/s13399-022-03057-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13399-022-03057-0