The impact of gasification temperature on the process characteristics of sorption enhanced reforming of biomass

Abstract

Especially carbon-intensive industries are interested in a decarbonization of their processes. A technology, which can contribute to a significant reduction of the carbon footprint, is the so-called sorption enhanced reforming process. The sorption enhanced reforming process uses a dual fluidized bed reactor system with limestone as a bed material for the thermochemical conversion of biomass into a valuable nitrogen-free product gas. This product gas can be used for further synthesis processes like methanation. The dependency of the product gas composition on the gasification temperature is already a well-known fact. Nevertheless, detailed investigations and models of the effect on elemental balances (especially carbon) of the process are missing in the literature and are presented in this work. Therefore, previously published data from different pilot plants is summarized and is discussed on a mass balance. Based on this information, investigations on the product gas equilibrium composition are presented and conclusions are drawn: it can be shown that the sorption enhanced reforming process can be divided into two sub-processes, namely “carbonation dominated sorption enhanced reforming” and “water-gas shift dominated sorption enhanced reforming.” The sub-process carbonation dominated SER is characterized by a high deviation from the water-gas shift equilibrium and a nearly constant CO content in the product gas over gasification temperature (< 700 °C). The sub-process water-gas shift dominated SER can be identified by a steep increase of the CO content in the product gas over temperature and nearly equilibrium state of the water-gas shift reaction (700–760 °C).

1 Introduction

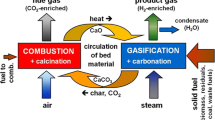
Energy security, air pollution, and climate change—these challenges raise the question of a widely available and storable, environmentally friendly, and carbon-free energy carrier. Especially, carbon-intensive industries like steel industry are interested in a decarbonization of their processes. A technology, which could contribute to a significant reduction of the carbon footprint of a steel mill could be the so-called sorption enhanced reforming (SER) process, is a variation of the dual fluidized bed (DFB) steam gasification of biomass [1]. The product of the DFB steam gasification is a nearly nitrogen-free product gas, mainly consisting of hydrogen (H₂), carbon monoxide (CO), carbon dioxide (CO₂), and methane (CH₄). Compared to the conventional DFB steam gasification process with gasification temperatures around 800–850 °C [2, 3], the SER process combines the advantages of both conventional biomass gasification and H₂ production [4,5,6]. Typically, the conventional DFB steam gasification process reaches H₂ contents in the product gas up to 45 vol.-%_db, whereas with the SER process, a H₂ content between 70 and 75 vol.-%_db can be gained. A steam-blown gasification reactor and an air-blown combustion reactor are the main parts for the process. The combustion reactor provides the necessary heat for the overall endothermic steam gasification via combustion of residual char from gasification. Due to the use of limestone as bed material and suitable temperature levels in both reactors, a decarbonization of the product gas and therefore the generation of a product gas with high H₂ contents are possible (Fig. 1). The product gas could be used as a supporting reduction agent in a blast furnace to reduce the fossil carbon share on the one hand [7]. On the other hand, it can be used for the synthesis processes like methanation [8].

Fig. 1

Principle of gasification with CO₂ capture (SER)

It has already been shown that the SER process leads to a product gas with increased reduction potential [9, 10], and further investigations were recommended to provide customized operation conditions of the process [9]. Theoretical thermodynamic investigations regarding the bed material renewable rate and bed material cycle rate have been presented in [11], and experimental considerations regarding the impact of bed material cycle rate and its influence on carbon balance have been published in [12]. Also, the description of the product gas composition in dependence of gasification temperature is well known [13]. However, a detailed characterization of the SER process over a vast temperature range is missing in the literature. Especially, the carbon balance over temperature is of great relevance for further use of the product gas.

2 Materials and methods

2.1 Sorption enhanced reforming

The main function of the bed material, which circulates between the two reactors, is the heat transport from the combustion reactor to the gasification reactor. Additionally, it acts as a transport medium of the residual char from the gasification reactor to the combustion reactor. Further, a suitable bed material is able to capture gaseous components from the product gas: in the SER process, limestone (mainly CaCO₃) is used as a bed material. In situ CO₂ capture in the gasification reactor according to Eq. (1), and its release in the combustion reactor is possible (Eq. (2)) by operating both reactors in a suitable temperature range. This allows the CO₂ capture in the gasification reactor and its release in the combustion reactor. The temperature ranges for gasification and combustion reactor during SER depend on the equilibrium partial pressure of CO₂ in Eq. (1). Typical temperatures in the gasification reactor are between 600 and 700 °C, whereas in the combustion reactor, the bed material is heated up above 830 °C. Stimulation of the water-gas shift reaction is obtained by the decreased CO₂ content in the product gas (Eq. (3)). Therefore, a product gas composition with a H₂ content up to 75 vol.-%_db and CO₂ contents of 5 vol.-%_db can be reached.

$$ CaO+C{O}_2\to CaC{O}_3\kern1.75em \Delta {H}_R^{650}=-170\ \mathrm{kJ}/\mathrm{mol} $$

(1)

$$ CaC{O}_3\to CaO+C{O}_2\kern1.5em \Delta {H}_R^{850}=167\ \mathrm{kJ}/\mathrm{mol} $$

(2)

$$ CO+{H}_2O\leftrightarrow C{O}_2+{H}_2\kern0.75em \Delta {H}_R^{650}=-36\ \mathrm{kJ}/\mathrm{mol} $$

(3)

For many synthesis processes like methanation, a certain H₂ to CO ratio is necessary. Typically, the product gas composition of the SER process is highly dependent on gasification temperature and bed material cycle rate [12, 13]. Via SER, an in situ adjustment of the H₂ to CO ratio between 2 and 9 is possible, which is clearly superior over the conventional gasification with olivine as the bed material, where only a H₂ to CO ratio up to 2 can be adjusted. Figure 2 shows the main product gas components and the H₂ to CO ratio of SER (limestone) and the conventional gasification with olivine as the bed material over temperature.

Fig. 2

Main product gas components (left) and H₂ to CO ratio of the SER process (right) over temperature (N₂-free basis and extended with internal data from the advanced 100 kW_th test plant at TU Wien from [4, 13])

2.2 Assumptions for modeling

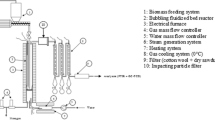
The experimental results of different pilot plants are used as the basis for the modeling approach presented in this paper [14,15,16,17]. The results include experiments with pilot plants of significant plant sizes up to 200 kW_th. Therefore, the presented values are highly representative and could also be used as a basis for scale-up to plant sizes in MW-scale. Two selected plant designs are presented in Fig. 3: TU Wien has designed an advanced dual fluidized bed test plant for the gasification of various fuels. A sketch of the plant is shown in Fig. 3 (left).

Fig. 3

Advanced 100 kWth test plant at TU Wien (left) and 200 kWth test plant at IFK Stuttgart (right)

The reactors of the 100 kW_th test plant are about 5 m high. The advanced reactor design enhances the gas-solid contact by a column with turbulent fluidized zones (upper gasification reactor), which is placed subsequent to the lower bubbling bed of the gasification reactor. The geometrical modifications in this upper part lead to an improved bed material holdup [18] and enlarge the range of applicable fuels because of higher tar and char conversion rates compared to other DFB systems. Further, gravity separators with gentle separation characteristics instead of cyclones support the use of soft bed materials such as limestone. The separation system prohibits high velocities of gas and particles and minimizes attrition effects. Additionally, a bed material cooling in the upper loop seal enables the defined setting of temperature differences between the gasification and combustion reactor for SER. A staged air input into the combustion reactor allows the effective control of the bed material cycle rate. Additional information can also be found in [12, 13, 19, 20].

A sketch of the 200 kW_th test plant at IFK Stuttgart is shown in Fig. 3 (right). According to [21, 22], the plant consists of a 6 m high gasification reactor and a 10 m high combustion reactor. The control of the bed material cycle rate is done via an L-valve, which allows the recirculation of entrained bed material from the combustion reactor directly to the combustion reactor again. Further information and details about the experimental campaigns can be found in [14, 17].

The main product gas composition in dependence of temperature from different sources [14,15,16,17] is summarized in Fig. 4. It can be seen that the results are in a narrow range. This is remarkable, since the experiments were conducted with different plants and at different universities (TU Wien, University Stuttgart) with different process conditions (biomass fuel type, steam to carbon ratio, etc.). Typically, a H₂ content about 70 vol.-%_db can be reached in the temperature range between 600 and 700 °C, whereas the lowest CO and CO₂ contents can be reached in this temperature range as well. With regard to the CH₄ content in the product gas, a nearly linear decrease of the content in the dry product gas can be observed with increasing gasification temperature. The trend for higher hydrocarbons C_xH_y including ethene, ethane, and propane is similar, but not that clear. All authors found a nearly linear increase of the product gas yield with increasing temperature. The data summarized from different sources is used as a basis for the development of a mass balance based model of the gasification reactor. The overall objective of the model is to establish a detailed description of the carbon balance of the system and, secondly, to provide investigations and a description of the process regarding chemical equilibria to further increase the understanding of the SER process. The data used for modeling is plotted in black dotted lines in Fig. 4. A significant deviation from the measured data can be observed for the assumptions of C_xH_y. No higher hydrocarbons than C₂H₄ are considered in the model. Therefore, in the model, C₂H₄ is used as a component, which compensates for all higher hydrocarbons and also tar. Thus, a significantly higher amount of C₂H₄ is used to take all the residual carbon containing components into account.

Fig. 4

Main product gas composition from different sources [14,15,16,17] and assumptions used for modeling

To calculate a full quantitative balance of the components carbon (C), hydrogen (H), and oxygen (O), information about the introduced fuel is necessary. Table 1 shows the fuel composition of different types of fuel and therefore shows that biogenic fuels (especially lignocellulosic fuels) usually have a similar fuel composition regarding the C, H, and O content. In addition, the amount of volatiles is in a narrow range for biogenic fuels (volatiles typically indicate if the amount of residual char from gasification is similar). Therefore, it can be assumed that the applied model is valid for a broad range of biogenic fuels and not only for softwood. Table 1 also shows that the results must not be used for other fuel types like lignite or plastics: the ratio between the elements C, H, and O and the volatiles are too different. C₁H_1.5O_0.7 was used as a general simple formula representing biomass for modeling of the process. This is based on the formulas published in [23], where a molar H to C ratio from 1.35 to 1.5 and a molar O to C ratio from 0.62 to 0.7 for wood are stated. Last but not least, the amount of introduced steam must be known. For all calculations, a steam to fuel ratio based on dry biomass of 0.8 kg_steam/kg_biomass is used. This is a typical value used in the SER experiments of the 100 kW_th test plant at TU Wien [13].

Table 1 Typical fuel compositions of different fuel types and composition used for modeling

2.3 Modeling

Based on the assumptions presented in Fig. 4 and Table 1, a model was invented to calculate the full quantitative balance of the main components C, H, and O for the gasification reactor over a temperature range from 600 to 850 °C (including char and CO₂ bound in CaCO₃, which leaves the gasification reactor). The model is based on the assumption that all the components introduced into the gasification reactor (fuel ${{\overset{\cdot }{N}}_i}_{,\mathrm{fuel},\mathrm{in}}$and steam ${{\overset{\cdot }{N}}_i}_{,\mathrm{H}2\mathrm{O},\mathrm{in}}$) must either leave the reactor as (i) product gas ${{\overset{\cdot }{N}}_i}_{,\mathrm{PG},\mathrm{out}}$ and (ii) steam ${{\overset{\cdot }{N}}_i}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}$ or remain as solid residuals and are subsequently transported to the combustion reactor (Eq. 4). The two possible solid types are (iii) char ${{\overset{\cdot }{N}}_i}_{,\operatorname{char},\mathrm{out}}$ and (iv) CO₂ in the bed material (as CaCO₃) ${{\overset{\cdot }{N}}_i}_{,{CO}_2\ \mathrm{in}\ {\mathrm{CaCO}}_3,\mathrm{out}}$. A simplified scheme can be found in Fig. 5. Further, pictures of bed material samples taken from the lower loop seal (after gasification reactor) and the upper loop seal (after combustion reactor) during a test run with the advanced 100 kW_th test plant at TU Wien are displayed in Fig. 5. It is obvious that for the applied conditions, approximately the whole char is burned in the combustion reactor: nearly no more black char particles are visible on the upper loop seal sample (bed material cycle rate of 7.7 h⁻¹, GR temperature of 650 °C, and maximum CR temperature of 880 °C).

Fig. 5

Simplified scheme of the flows of the quantitative balance within the gasification reactor

Fig. 6

Molar C, H, and O content in biomass char in dependence of temperature based on [24]

$$ {{\overset{\cdot }{N}}_i}_{,\mathrm{fuel},\mathrm{in}}+{{\overset{\cdot }{N}}_i}_{,\mathrm{H}2\mathrm{O},\mathrm{in}}={{\overset{\cdot }{N}}_i}_{,\mathrm{PG},\mathrm{out}}+{{\overset{\cdot }{N}}_i}_{,{\mathrm{H}}_2\mathrm{O},\mathrm{out}}+{{\overset{\cdot }{N}}_i}_{,\operatorname{char},\mathrm{out}}+{{\overset{\cdot }{N}}_i}_{,\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}}\kern1.75em i=\mathrm{C},\mathrm{H},\mathrm{O} $$

(4)

$$ {{\overset{\cdot }{N}}_C}_{,\mathrm{PG},\mathrm{out}}={Y}_{\mathrm{PG}}\times {\overset{\cdot }{m}}_{\mathrm{fuel}}/{V}_m\times \left({y}_{\mathrm{C}\mathrm{O},\mathrm{PG}}+{y}_{\mathrm{C}\mathrm{O}2,\mathrm{PG}}+{y}_{\mathrm{C}\mathrm{H}4,\mathrm{PG}}+2\times {y}_{\mathrm{C}2\mathrm{H}4,\mathrm{PG}}\right) $$

(5)

$$ {{\overset{\cdot }{N}}_H}_{,\mathrm{PG},\mathrm{out}}={Y}_{\mathrm{PG}}\times {\overset{\cdot }{m}}_{\mathrm{fuel}}/{V}_m\times \left(2\times {y}_{\mathrm{H}2,\mathrm{PG}}+4\times {y}_{\mathrm{C}\mathrm{H}4,\mathrm{PG}}+4\times {\mathrm{y}}_{\mathrm{C}2\mathrm{H}4,\mathrm{PG}}\right) $$

(6)

$$ {{\overset{\cdot }{N}}_O}_{,\mathrm{PG},\mathrm{out}}={Y}_{\mathrm{PG}}\times {\overset{\cdot }{m}}_{\mathrm{fuel}}/{V}_m\times \left({y}_{\mathrm{CO},\mathrm{PG}}+2\times {y}_{\mathrm{CO}2,\mathrm{PG}}\right) $$

(7)

$$ {{\overset{\cdot }{N}}_H}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}={{\overset{\cdot }{N}}_H}_{,\mathrm{fuel},\mathrm{in}}+{{\overset{\cdot }{N}}_H}_{,\mathrm{H}2\mathrm{O},\mathrm{in}}-{{\overset{\cdot }{N}}_H}_{,\mathrm{PG},\mathrm{out}};{{\overset{\cdot }{N}}_O}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}={{\overset{\cdot }{N}}_H}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}/2 $$

(8)

$$ {\displaystyle \begin{array}{c}{N}_{\mathrm{O},\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}}={N}_{\mathrm{O},\mathrm{fuel},\mathrm{in}}+{N}_{\mathrm{O},\mathrm{H}2\mathrm{O},\mathrm{in}}-{N}_{\mathrm{O},\mathrm{PG},\mathrm{out}}-{N}_{\mathrm{O},\mathrm{H}2\mathrm{O},\mathrm{out}};\\ {}{N}_{\mathrm{C},\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}}={N}_{\mathrm{O},\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}}/2\end{array}} $$

(9)

$$ {{\overset{\cdot }{N}}_C}_{,\operatorname{char},\mathrm{out}}={{\overset{\cdot }{N}}_C}_{,\mathrm{fuel},\mathrm{in}}-{{\overset{\cdot }{N}}_C}_{,\mathrm{PG},\mathrm{out}}-{{\overset{\cdot }{N}}_C}_{,\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}} $$

(10)

Equations 5, 6, and 7 show the equations for each component (C, H, O) in the product gas according to stoichiometric considerations. The molar flow of H and O in the gaseous water from gasification (${{\overset{\cdot }{N}}_i}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}$) can be calculated by the assumption that all the H, which is not in the dry product gas must be in the gaseous steam (Eq. 8). This is only valid if the char is modeled as pure C and therefore does not contain any H or O. Further, Eq. 9 demonstrates the calculation of the molar flow of O via bed material (CO₂ transport in CaCO₃): all the remaining O, which is not leaving the system via the product gas or the gaseous water, contributes to the molar flow of O in the bed material. Finally, the molar flow of C in the char can be calculated by subtracting the C flow in the product gas and the C flow in the bed material (Eq. 9). As already mentioned in Eqs. 8, 9, and 10, the char composition is modeled as pure C. In fact, char also contains H and O. A model for pyrolysis of biomass and the composition of the remaining char over temperature has been proposed by Neves et al. [24]. For this work, it is assumed that the model for pyrolysis is approximately valid for biomass steam gasification as well. This fact has already been verified in a previous work [25], and the used equations are presented in Eqs. 11, 12, 13, and 14. The results for Eqs. 12 to 14 are displayed in Fig. 6: the carbon content in the char typically rises with temperature:

$$ {y}_{\mathrm{total},\operatorname{char}}=\frac{0.93-0.92\times \exp \left(-0.42\times {10}^{-2}\times T\right)}{12}+\frac{0.07-0.85\times \exp \left(-0.48\times {10}^{-2}\ast T\right)}{16}+\frac{-0.41\times {10}^{-2}+0.10\times \exp \left(-0.24\times {10}^{-2}\times T\right)}{1} $$

(11)

$$ {y}_{\mathrm{C},\operatorname{char}}=\left(0.93-0.92\times \exp \left(-0.42\times {10}^{-2}\times T\right)\right)/12/{y}_{\mathrm{total},\operatorname{char}} $$

(12)

$$ {y}_{\mathrm{O},\operatorname{char}}=\left(0.07-0.85\times \exp \left(-0.48\times {10}^{-2}\times T\right)\right)/16/{y}_{\mathrm{total},\operatorname{char}} $$

(13)

$$ {y}_{\mathrm{H},\operatorname{char}}=\left(-0.41\times {10}^{-2}+0.10\times \exp \left(-0.24\times {10}^{-2}\times T\right)\right)/1/{y}_{\mathrm{total},\operatorname{char}} $$

(14)

The integration of Eqs. 11, 12, 13, and 14 into the model (Eqs. 4, 5, 6, 7, 8, 9, and 10) leads to the modification of Eqs. 8, 9, and 10 to Eqs. 15, 16, and 17. The set of equations is now nonlinear and is solved by iteration.

$$ {{\overset{\cdot }{N}}_H}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}={{\overset{\cdot }{N}}_H}_{,\mathrm{fuel},\mathrm{in}}+{{\overset{\cdot }{N}}_H}_{,\mathrm{H}2\mathrm{O},\mathrm{in}}-{{\overset{\cdot }{N}}_H}_{,\mathrm{PG},\mathrm{out}}-{{\overset{\cdot }{N}}_C}_{,\operatorname{char},\mathrm{out}}/{y}_{C,\operatorname{char}}\times {y}_{H,\operatorname{char}} $$

(15)

$$ {{\overset{\cdot }{N}}_O}_{,\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}}={{\overset{\cdot }{N}}_O}_{,\mathrm{fuel},\mathrm{in}}+{{\overset{\cdot }{N}}_O}_{,\mathrm{H}2\mathrm{O},\mathrm{in}}-{{\overset{\cdot }{N}}_O}_{,\mathrm{PG},\mathrm{out}}-{{\overset{\cdot }{N}}_O}_{,\mathrm{H}2\mathrm{O},\mathrm{out}}-{{\overset{\cdot }{N}}_C}_{,\operatorname{char},\mathrm{out}}/{y}_{C,\operatorname{char}}\times {y}_{O,\operatorname{char}} $$

(16)

$$ {{\overset{\cdot }{N}}_C}_{,\operatorname{char},\mathrm{out}}={{\overset{\cdot }{N}}_C}_{,\mathrm{fuel},\mathrm{in}}-{{\overset{\cdot }{N}}_C}_{,\mathrm{PG},\mathrm{out}}-{{\overset{\cdot }{N}}_C}_{,\mathrm{CO}2\mathrm{inCaCO}3,\mathrm{out}} $$

(17)

Further investigations focus on the calculation of chemical equilibria as well as their deviation from equilibrium state [26]. The general formula for calculation of the deviation from equilibrium pδ_eq is given in Eq. 18. One can derive from Eq. 18 that a value of zero for pδ_eq means that the equilibrium state is reached, whereas a deviation from zero indicates a deviation from the equilibrium state. A change of the algebraic sign shows a change in the reaction direction.

$$ p{\delta}_{\mathrm{eq}}\left({p}_i,T\right)={\log}_{10}\left[\frac{\prod \limits_i{p}_i^{\nu_i}}{K_P(T)}\right] $$

(18)

3 Results and discussion

3.1 Solid carbon balance

The solution of the set of equations Equations 4–10 and Equations 15–17 regarding to the carbon transport to the combustion reactor is shown in Fig. 7: at 600 °C, nearly 50% of the C in the fuel is transported to the combustion reactor via char. Further, about 30% are sorbed by the bed material as CO₂ and therefore are also transported to the combustion reactor. At 800 °C, only 30% of the C remains in the char, and practically no C is removed via the bed material as CaCO₃. This makes sense, since from a thermodynamic point of view, the SER process can take place up to 760 °C [13]. The model applied in this work shows CO₂ transport via bed material also for higher temperatures than 760 °C. This is dedicated to the fact, that the temperature distribution in the gasification reactor is not uniform in most cases. It is most likely that for an indicated gasification temperature of, e.g., 800 °C, colder spots exist, where CO₂ sorption may be possible. Last but not least, it can be seen that between 60 and 80% of the total C from the fuel can be transported to the combustion reactor at temperatures between 700 and 600 °C. It should be noticed that the char transport to the combustion reactor influences the energy balance of the total system. Therefore, an adaptation of the bed material cycle rate and/or cooling in the upper loop seal is necessary to maintain the correct temperature levels of the reactors.

Figure 7 also shows the difference between the calculation of char as pure C and as a mixture of C, H, and O according to Neves et al. [24]: the total amount of carbon, which leaves the gasification reactor, is not changed. This can be explained by the fact that all carbon which does not leave the gasification reactor in a gaseous form must leave the gasification reactor as solid to the combustion reactor. Since the change of the char composition does not change any set parameters of the product gas composition in Fig. 4, the total carbon to the combustion reactor must remain the same. However, the distribution of the carbon between char and CO₂ in CaCO₃ is changed slightly. Less char is formed, but more CO₂ is absorbed by considering C, H, and O in the char. All further calculations in this work were done with the char composition proposed by Neves et al. [24].

Fig. 7

Carbon transport to the combustion reactor

3.2 Product gas equilibrium calculation

Based on the findings of the quantitative balance the amount of elements leaving the gasification reactor as a solid (via char and as CO₂ in CaCO₃) and vice versa the amount of elements, which are present as a gas, are known now. The Gibbs free energy minimization method is applied to the remaining gaseous components in the gasification reactor to find the theoretical equilibrium composition of the product gas. The equilibrium calculation was conducted with the software HSC [27].

By considering the formation of H₂, CO, CO₂, CH₄, and H₂O as possible components for equilibrium calculation, the equilibrium results displayed in Fig. 8 are gained. Additionally, Fig. 8 contains the range of the product gas components from the experimental results of the pilot plants. One can see that especially the trends for the H₂ content and the CO content in the product gas are similar: the H₂ content decreases with increasing temperature, whereas the CO content is increasing with temperature. However, a strong deviation of the theoretical equilibrium composition and the experimentally collected data can be found for the other components. Especially, the water content and the CH₄ content in the product gas differ highly. The CH₄ content in the product gas should obviously be on a very low level according to thermodynamic equilibrium calculations. This fact has already been found by other authors and is well known [28, 29]. Schuster et al. [29] states that the devolatilization of biomass produces a high amount of CH₄ and higher hydrocarbons. These components typically do not react to the equilibrium concentrations of CO, CO₂, and H₂ under the conditions in the SER process.

Fig. 8

Equilibrium product gas composition over temperature, basis for calculations (framed): C, H, and O from (I) char and (II) in CaCO₃ transported CO₂ are eliminated for gas-gas equilibrium calculation

Therefore, as a second approach, the amount of C and H from CH₄ and C_xH_y, which is produced during the first devolatilization phase of fresh biomass particles, is eliminated for the homogeneous gas-gas equilibrium calculations. It turns out that an average of 10% of the carbon in the fuel is bound as gaseous CH₄ (Fig. 9). This value remains nearly constant over the whole temperature range. However, this is an additional proof for the theory that a constant amount of nearly inert CH₄ is released during devolatilization. Consequently, the components, which remain for the equilibrium calculation, are H₂, H₂O, CO, and CO₂. These components are all part of the water-gas shift reaction (Eq. 3), which can now be identified as governing gas-gas equilibrium reaction. Again, in Fig. 9, the results of the equilibrium calculations are displayed and are compared to the range of experimental results. Now, a very good agreement can be observed, especially for temperatures above 700 °C. For temperatures below 700 °C, a slightly higher CO₂ content and a slightly lower CO content are predicted by the equilibrium model compared to the experimental results. Nevertheless, the trend for all components is predicted correctly now by the equilibrium model.

Fig. 9

Equilibrium product gas composition over temperature, basis for calculations (framed): C, H, and O from (I) char, (II) in CaCO₃ transported CO₂, and (III) CH₄+C_xH_y are eliminated for gas-gas equilibrium calculation

To investigate the SER process in more detail based on the previous findings, the logarithmic equilibrium deviation pδ_{eq, WGS} for the water-gas shift reaction (Eq. 3) and the logarithmic equilibrium deviation pδ_{eq, Ca} for the system CaCO₃/CaO/CO₂ (Eq. 1 and 2 of the experimentally determined product gas composition (Fig. 4) is calculated and shown in Fig. 10.

Fig. 10

Characterization of sorption enhanced reforming reforming by equilibrium deviation and product gas composition

Regarding pδ_{eq, WGS} for the water-gas shift reaction, it can be seen in Fig. 10 that the experimental results are far away from the equilibrium composition at 600 °C. However, there is a steep incline until 700 °C approximately, where pδ_{eq, WGS} is already close to zero (Fig. 10, black dot number I). From there on, the incline of pδ_{eq, WGS} is small and remains close to zero. pδ_{eq, Ca} declines constantly and reaches zero at about 760 °C (Fig. 10, black dot number II). From this point on, thermodynamically, no more CO₂ sorption of the bed material is possible. These characteristic temperatures can also be found in the product gas composition. Therefore, Fig. 10 shows the experimental data for CO and CO₂ from the 100 kW_th test plant at TU Wien [7, 16] as well. From 600 to 700 °C, a more or less constant content of CO can be observed, but from 700 °C on (Fig. 10, black dot number 1), a steep increase of the CO content is visible. Considering the CO₂ content in the product gas shows that the CO₂ content is mainly increasing from 600 °C on until 760 °C is reached (Fig. 10, black dot number 2). Close to this point, where the CO₂ sorption via the bed material stops, the highest CO₂ content in the product gas can be observed.

Concluding the findings of Fig. 10 shows that the SER process can be divided into two sub-processes. The first one between 600 and 700 °C is named “carbonation dominated SER” in Fig. 10. It is mainly characterized by a high equilibrium deviation of the water-gas shift reaction pδ_{eq, WGS} and a constantly low CO content in the product gas. Further, the carbonation dominated SER process shows the highest transport rates of CO₂ via bed material (see also Fig. 7). Thus, the product gas composition is influenced significantly by the water-gas shift reaction, because removal of CO₂ from the product gas leads to enhanced consumption of CO and H₂O for the production of high H₂ contents. However, due to the dominating influence of the CO₂ removal (carbonation) of the bed material, the water-gas shift reaction does not reach an equilibrium state.

The second sub-process is called “water-gas shift dominated SER,” which points out that between 700 and 760 °C, the water-gas shift equilibrium of the product gas is almost reached. This can be traced back to the enhanced gas-gas kinetics because of higher temperatures on the one hand and the decreasing influence of the carbonation reaction on the other hand. Thus, from 700 °C on, also the CO content starts rising.

At about 760 °C, the CO₂ sorption of the bed material stops due to the thermodynamics of the system CaCO₃/CaO/CO₂. From this point on, the process is conventional, which means gasification without CO₂ transport.

4 Conclusion

Simple mathematical modeling combined with (product gas) equilibrium calculations provides a deep insight into the SER process. For the temperature range 600 to 800 °C, it has been found that between 50 and 30% of the C contained in the fuel is transported from the gasification reactor to the combustion reactor as char. In total (including C in char and in bed material), about 80% of the C in the fuel can be removed from the gasification reactor at low temperatures (~ 600 °C). By combining these findings with homogeneous gas-gas equilibrium calculations based on the general formula C₁H_1.5O_0.7 representing biomass, it turns out that CH₄ should be on a very low basis. However, due to the slow kinetics of the CH₄ reforming, a significantly higher amount of CH₄ can be found in the product gas. Therefore, by considering CH₄ as a constant component in the product gas and using the remaining main components H₂, CO, CO₂, and H₂O as reactants for gas-gas equilibrium calculations, a satisfactory agreement with experimental results can be found. A detailed analysis of the equilibrium deviation of the water-gas shift reaction and the calcination reaction of CaCO₃ shows that the SER process can be divided into the two sub-processes: (i) carbonation dominated SER and (ii) water-gas shift dominated SER. The sub-process carbonation dominated SER is characterized by a high deviation from the water-gas shift equilibrium and a constantly low CO content in the product gas over gasification temperature (< 700 °C). The sub-process water-gas shift dominated SER can be identified by a steep increase of the CO content in the product gas over temperature and nearly equilibrium state of the water-gas shift reaction (700–760 °C). Above 760 °C, conventional gasification without CO₂ transport can be found.