An empirically validated rational number sense framework

Abstract

A theoretical model describing Grade 7 students’ rational number sense was formulated and validated empirically (n = 360), hypothesizing that rational number sense is a general construct consisting of three factors: basic rational number sense, arithmetic sense, and flexibility with rational numbers. Data analysis suggested that rational-number tasks can be categorized based on the validated model. The flexibility component reflects thinking about rational numbers in terms of noticing, using, and expressing relations and properties of numbers in patterns, functions, covariation, and complicated computational tasks. It includes utilizing number structure and relational understanding of operations and numbers. Analysis identified three categories of students that represent different rational-number sense profiles. Category 1 students exhibited a limited basic profile that solved mainly traditional school-based tasks. Category 2 students reflected the basic emergent arithmetic sense profile that responded adequately in operation tasks. Category 3 students represented the flexible emergent profile, as they manipulated underlying structures in a variety of situations, indicating an emergent fundamental shift from an arithmetic to an algebraic focus. A discriminant analysis showed that basic and flexible factors could discriminate students best between the three identified profiles of rational number sense.

Introduction

Researchers and reports on mathematics education emphasize the importance of number sense (Australian Educational Council, 1991; National Council for Teachers of Mathematics, 2000; National Mathematics Advisory Panel, 2008; National Research Council, 2009; Tucker & Johnson, 2022; Yang & Sianturi, 2021; Yang et al., 2009). Student’s development of number sense is considered an important outcome and key ingredient of school curricula worldwide (Whitacre et al., 2020; Yang & Li, 2008). Research findings provided strong support to the assumption that number sense is a powerful predictor of mathematics outcomes (Hassinger-Das et al., 2014; Jordan et al., 2007). We focus on mature number sense (Whitacre et al., 2020) that refers to the flexibility with rational numbers and models the components of number sense in studies that involved primarily middle grade students (upper elementary and middle school). In contrast to early number sense that reflects skills that students typically learn in preschool and primary grades, mature number sense represents habits of mind, and ways of behaving that are considered desirable to move beyond standard algorithms. In this study, we use the term rational-number sense to make mature number sense more explicit.

The importance of rational-number sense is underlined by the fact that reasoning with fractions and decimals is important in everyday life (Jordan et al., 2013). Research findings suggest that rational numbers are among the most important and difficult topics in early mathematics education (Braithwaite et al., 2022). International assessments, such as TIMSS 2019, showed that students even in Grade 8 struggle with rational concepts (Mullis et al., 2020). Further, research findings provided evidence that understanding rational numbers, especially fractions, holds the key to future success in algebra (DeWolf et al., 2015; Siegler & Lortie-Forgues, 2014). In most countries, it is expected that students are acquainted with number concepts, operations, and problem solving that facilitate rational number sense in grades 6 and 7. Therefore, in this study, we investigate 7th grade students’ rational number sense (thirteen-year-olds) to capture the whole spectrum of the examined construct.

Most of the existing rational-number sense frameworks refer to a person’s general understanding of numbers and operations and underlie the aspect of readiness to use this understanding in flexible ways (McIntosh et al., 1992; Yang & Lin, 2015; Yang et al., 2008). The purpose of this study is to extend existing frameworks by emphasizing on the aspect of flexibility. We suggest that flexibility includes relating rational numbers by conceptualizing their structure. By the term structure sense for rational numbers, we refer to identifying properties, order structure, and additive and multiplicative relations (Freudenthal 1991). We enrich in this way the traditional descriptions of rational number sense with the flexibility component. It refers to students’ ability to notice, use, and express relations and properties of numbers and utilize number structure and relational understanding of operations and numbers (Author et al., Date; Molina & Mason, 2009).

Theoretical framework

The theoretical framework brings together notions from research in mathematics education regarding number sense in general, rational number sense, rational number knowledge, and arithmetic.

Components of number sense

Number sense consists of different and interrelated components that change with age and experience (Malofeeva et al., 2004). Whitacre et al. (2020) distinguished the construct of rational number sense from approximate number sense and early number sense. Approximate number sense includes inborn neurological abilities that concern perception and discriminations of magnitudes (Dehaene, 2001). Early number sense encompasses fundamental skills such as explicit number knowledge, number comparison, and counting (Jordan et al., 2006), while rational number sense pertains to the awareness of rational numbers in middle school and upper primary school students. It encompasses understanding the concepts, representations, computations, and applications of rational numbers (Whitacre et al., 2020).

Researchers from the mathematics cognition domain, such as Berch (2005), Case and Soweder (1990) and Jordan et al. (2006), described the nature of early number sense in terms of interrelated components. Jordan et al. (2022) showed that early number sense is a three-dimensional construct. The first dimension of this model relates to basic number skills (counting, number recognition and knowledge, number patterns, and nonverbal calculation), while the second refers to conventional arithmetic (story problems and number combinations). The third factor, number relations, entails knowledge of the relations between and among whole numbers. This model, which was empirically validated in multiple occasions (Jordan et al., 2006, 2007, 2022), could be utilized as the outset to formulate a framework describing rational-number sense because it includes the two core aspects of number knowledge and number operations and brings to the fore the perspective of number relations. However, this model should be extended to include aspects of number sense that are critical for rational numbers (Siegler & Lortie-Forgues, 2014). In the second part of the theoretical framework, we present research findings that could be utilized in the formulation of a rational number sense framework.

Rational number sense

The theoretical frameworks proposed by McIntosh et al. (1992), Markovits and Sowder (1994), and Yang et al. (2004) described rational number sense components that are commonly cited by other researchers in mathematics education. These frameworks list the following as the most important elements for rational-number sense: knowledge and flexibility with numbers and operations and applying knowledge of numbers and operations to computational settings.

Rational number knowledge

Recognizing and linking the multiple forms and interpretations of rational numbers, translating among the different notations and a quantitative understanding of rational numbers in terms of magnitude, comparison, and density are considered crucial for rational number understanding (Charalambous & Pitta-Pantazi, 2007; Van Hoof et al., 2018). In this sense, rational number knowledge includes (a) understanding of number meanings and use of multiple representations of numbers and operations and (b) recognition of relative number size, absolute magnitude of numbers, and the sense of orderliness of numbers (Markovits & Sowder, 1994; McIntosh et al., 1992).

Number meanings and representations refer to conceptualizing multiple different notations (e.g., fraction, decimal, and percentage) and multiple representations (symbolic, iconic, verbal, area models, and number line) that facilitate students’ rational number understanding. Students should go beyond recognizing the surface feature and attend to the quantitative information of rational number notation. They should understand that there is an infinite number of symbolic representations for each magnitude on the number line, and between any two magnitudes, there is an infinite number of magnitudes (Schneider & Siegler, 2010). For the case of fractions, student must coordinate two numbers working together (numerator and denominator) to yield a single magnitude, highlighting the role of multiplicative reasoning to conceptualize equivalent forms of fractions and compare fraction magnitudes (DeWolf et al., 2015; Dyson et al., 2020; Vamvakoussi, 2015). Further, the notation of fractions and decimals is visually different (fractions have a bipartite structure while decimals have a unidimensional structure) that makes organization of rational numbers more complicated as they can be grouped either by quantity or by notation (Park, 2021).

Moving across different types of rational number representations is essential to recognize that each type of representation presents a different perspective (Post et al., 1993). For instance, number lines facilitate understanding rational numbers as measures, while area models emphasize part-whole meanings and their multiplicative structure. Representations also provide equivalent numerical forms that are based on composing and decomposing rational numbers based on their structure. It is important for students to utilize an efficient representation based on the context, to manipulate different notations of rational numbers by converting a fraction to a decimal and vice versa and to apply procedures such as finding equivalent fractions (Siegler et al., 2011).

Rational numbers, irrespectively of their form, have magnitudes or numerical values so they can be ordered on the number line (Siegler et al., 2011). Understanding number magnitude for rational numbers means comparing and ordering numbers, finding which of two numbers is closer to a third one and finding numbers between two given numbers (Markovits & Sowder, 1994). Finding numbers between two given numbers is related to the notion of density (Vamvakoussi & Vosniadou, 2010). A lack of understanding of the dense structure of rational numbers leads to mistakes, such as thinking that there are no numbers between fractions with same denominators and successive nominators (e.g., 3/5 and 4/5) or decimals with successive numbers in the same decimal place (e.g., 2,5 and 2,6), due to the natural number bias (Vamvakoussi et al., 2013). Natural number bias is also accounted for common mistakes in comparing decimal numbers based on the number of decimal points and not on the value place (Van Hoof et al., 2018). Comparing and ordering rational numbers entail also appropriate use of benchmarks (Bütüner, 2018).

Rational number sense operations and applications to computational settings

Knowledge of operations entails understanding the effect of operations and mathematical properties and understanding the relationship between operations (Yang et al., 2004). Applying knowledge of numbers and operations includes a variety of abilities, such as understanding the relationship between problem context and the necessary computation; flexible estimation, mental computation, and judgment of the reasonableness of estimates of computed results (i.e., implying the use of estimation strategies without written calculations, decomposing and recomposing numbers to simplify calculations) (McIntosh et al., 1992; NCTM, 2000; Yang & Li, 2008; Yang & Siantouri, 2021); and appropriate use of benchmarks in computations (Reys et al., 1999). This aspect of number sense, referred to as applied number sense, has also been incorporated into more recent number sense frameworks (see Andrews & Sayers, 2015; Pittalis et al., 2018; Yang & Sianturi, 2021).

Students’ difficulties with rational number operations may be related to the extensive experience they encountered with natural numbers (McMullen et al., 2015). Thus, the challenge for students is to apply understandings of whole number operations to fractions and decimals, by eliminating natural number bias, and use procedures in a conceptual way. That is students apply procedures by understanding their logic and utilizing properties of operations (Fischbein et al., 1985; Greer, 1992). Understanding the relative effect of operations on numbers requires recognizing how the four basic operations affect the results and applying the properties of operations (Bütüner, 2018; González-Forte et al., 2022; Yang et al., 2008). For instance, this will facilitate understanding that the product of 49 by 0.9 is smaller than 49, because $49\times 0.9$ is equal to $0.9\times 49$ that can be interpreted as shrinking 49, since 0.9 is smaller than 1.

Research findings showed the importance of reaching absolute or approximate estimations, by using mental calculations and estimations skills and making judgements about the reasonableness of a result (Sowder, 1992). That implies that students make mental calculations without using written computation. In addition, judging the reasonableness of the result is a critical self-regulated mechanism to avoid calculation errors (Yang & Sianturi, 2019). For example, students check the correctness of a written calculation, by using estimation strategies. Research showed that applying written strategies is not sufficient for rational number calculations, but students should develop meaningful understanding and integration of written and mental estimation and calculation strategies (Yang et al., 2008; Lin et al., 2016). Further, understanding the relationship between operations is a useful tool to simplify calculations.

Applying knowledge of and facility with numbers and operations to computational settings includes also understanding the relationship between problem context and the necessary computation (McIntosh et al., 1992). This was also supported by Jordan et al. (2006) and Pittalis et al. (2018) that showed empirically that solving story problems fits in the arithmetic dimension of students’ early number sense.

The Present Study

Purpose of the study and the proposed model

Most of the studies described above provided theoretical frameworks for rational number sense and investigated aspects of rational number sense or focused on specific areas of rational number knowledge in a qualitative way. There is a need to extend previous studies by proposing and empirically validating a comprehensive framework for rational-number sense. To do so, we synthesize existing conceptions of rational-number sense (see Jordan et al., 2022; Markovits & Sowder, 1994; McIntosh et al., 1992; Yang et al, 2004) and build on researchers who have called about a relational perspective for number sense (McMullen et al., 2020; Rezat, 2019).

We assert that rational number sense for seventh graders refers to a student’s general understanding of rational numbers and relevant operations. It reflects an inclination to manipulate rational numbers and interpret and process quantitative information in a variety of situations flexibly by noticing and reflecting on underlying relations between and among rational numbers. This conception for rational-number sense is aligned with rational number concepts, processes, algorithms, and problem-solving situations that students are typically engaged in primary and middle grades (thirteen-year-old students). Further, it includes a disposition to (a) simplify or avoid complicated calculations, standard procedures, or procedural interpretations by utilizing relations in quantitative situations and (b) overcome challenges of novel and nontypical arithmetic situations. This conceptualization enriches the definition of rational number sense with a dynamic and powerful perspective that may contribute to further developing students’ arithmetic-algebraic structure sense (Pittalis, 2023; Hitt et al., 2017).

We use the three factors of Jordan et al.’s (2022) number sense model to formulate the proposed rational number sense framework. The components of rational number knowledge and arithmetic are established on the frameworks described above, by giving justice to key concepts of rational numbers, operations, and problem solving with rational numbers. The third component of number relations reflects a student’s flexibility to grasp in a variety of numerical situations the relations between and among rational numbers.

Based on this conceptualization, we suggested (see Fig. 1) that rational number sense is a general construct that consists of three distinct, but interrelated and complementary factors. We hypothesized that rational-number sense is a second-order theoretical construct made up of three first-order latent factors, namely, (a) basic rational number sense, (b) rational number arithmetic, and (c) flexibility with rational-numbers. In other words, we hypothesized that these three factors can be made accountable by a higher-level factor, which stands for rational number sense.

Fig. 1

The proposed model

The first factor, basic rational number sense, includes key elements for a typical grade 7 student and represents students’ conceptualization of rational number in respect to recognizing its symbolic form, different representations, and magnitude (Markovits & Sowder, 1994; McIntosh et al., 1992; Yang et al. (2004). In particular, basic rational number sense, consists of identifying rational numbers, conceptualizing rational number magnitude (Van Hoof et al., 2018), comparing and ordering (Siegler et al., 2011), estimating numbers in number-line, understanding rational number density, manipulating rational number representations (Schneider & Siegler, 2010), counting on and down based on rational number place value (Pittalis et al., 2018) and converting fractions to decimals and vice versa and finding equivalent fractions (DeWolf et al., 2015).

The second factor, rational number arithmetic, combines knowledge of operations and applying knowledge with numbers and operations to computational settings (Mcintosh et al., 1992). It includes calculating number combinations, understanding the effect of operations on numbers and the relationship between operations (Yang et al., 2008), using mental calculations and estimations skills (Elias et al., 2020), judge the reasonableness of computational results (Yang & Sianturi, 2019) and solving word problems (Jordan et al., 2007). Number combinations relate to students’ ability to carry out calculations with no object referents. In the present study, solving problems with rational numbers refers to conceptualizing, judging, and interpreting the meaning of operations in situational settings, without being confused by natural numbers bias (Vamvakoussi, 2015; Yang et al., 2008), especially in multiplicative situations.

The third factor, flexibility with rational numbers, manifests a student’s ability to recognize relevant arithmetic and numerical relations between a given set of numbers and integrate conceptual and procedural knowledge of numerical characteristics and relations into solutions for novel tasks. It is in line with rational number adaptive expertise. That is applying flexibly rational-number knowledge in novel contexts, as defined by McMullen et al. (2020). Further, in line with Strother (2011) and McMullen et al. (2017), flexibility reflects a structural and algebraic understanding of numbers. It opens the door for a functional approach in a variety of nontypical quantitative situations. That is extending, completing, generalizing, and building patterns (Jordan et al., 2022), exploring the functional relation between quantities (Pittalis, 2023), interpreting the growth rate of a variable/quantity, and making predictions in a variety of numerical settings, such as graphs and tables (Thompson & Carlson, 2017), and manipulating complex computational situations (McMullen et al., 2022). Exploring and generalizing the functional relation between quantities that involve rational numbers reflects a student’s self-awareness of the identified relations. Identifying patterns and expressing rational number relations in symbols are considered the two most influential factors that strengthen the relationship between number sense and algebraic thinking (Piriya et al., 2019).

Research aims

The aims of the study were to (a) examine the structure of 7th grade students’ rational-number sense through empirically validating an a priori theoretical model, (b) to identify classes of students that reflect different rational number sense profiles, and (c) to examine which of the proposed rational number sense factors discriminate students to the number sense profiles.

Participants

Three hundred sixty 7th grade students (188 girls and 172 boys) from two urban and one rural secondary school in Cyprus (N = 184) and three urban secondary schools in Greece (N = 176) participated in the study. The demographics of the school population in both countries were representative in terms of percentage of students with immigrant heritage and percentage of students with low socioeconomic status. The schools and the teachers involved participated voluntarily; thus, our sample was a sample of convenience. All participants had parental permission to participate and gave their own assent. None of them were identified by their schools as having learning disabilities or other cognitive or sensor incapacities and none of them were excluded.

The Cyprus and Greek mathematics curriculum for Grades 6–7 contain attainment targets that emphasize solving word problems with rational numbers and percentages, using mental strategies to make calculations with natural numbers, fractions, decimals, and percentages, using standard algorithms in calculations with natural numbers, fractions, and decimals, simplify fractions, find equivalent forms of rational numbers, identifying, ordering and comparing rational numbers, converting fractions to decimals and percentages and vice-versa, and interpreting fraction as part-whole, quotient, ratio and measure.

Measures

Test items were adopted or developed on the basis of previous research studies and multiple tasks were used for each presumed construct of the framework (see Markovits & Sowder, 1994; Vamvakoussi & Vosniadou, 2010). Several test items were based on those used in previous qualitative studies, teaching experiments, and intervention studies; thus, we made modifications in the format and wording of the items to meet the needs of a written test, such as transforming the task to a multiple-choice format, or reformulating the task to include a variety of rational number forms. For example, Markovits and Sowder (1994) presented two fractions and asked students to determine which one is closer to 0.5. We adapted this task into a multiple-choice format, including possible answers in both decimal and fractional forms. Appendix A presents the type of tasks used to measure each sub-component of the factors and appropriate examples.

The construct validity of the test was trialed before the main study based on the results of a pilot study (N = 45). The test was administered to two Grade 7 classes in Cyprus. The results of the pilot provided evidence regarding the appropriateness of the used items and the test, in terms of clarity, difficulty level, and time needed. Six items were removed so the test could be completed in the available time. To do so, we kept a maximum of three items for each type of task. Further, feedback was provided to make additional language and formatting corrections to other ones. Then, to strengthen the validity of our relational-structural measures, we computed the content validity index of the individual items (Taherdoost, 2016). To do so, four experts in mathematics education examined the content validity of the test items and evaluated the extent to which the proposed measures aligned with the proposed component based on a 4-point ordinal scale (Lynn, 1986). We kept only items with content validity index at least 0.75.

Basic rational number sense measures

Basic rational number sense factor was measured by six types of tasks that captured in a comprehensive way the basic aspects of rational number sense: rational number magnitude, rational number density, and rational number knowledge, counting based on place value and equivalence (McIntosh et al., 1992; Van Hoof et al., 2018). Reliability for all the items used to measure basic-rational number factor was good (Cronbach’s α = 0.87).

Rational number magnitude was measured by ordering and comparing tasks and number line estimations ones. The ordering tasks included two items ordering fractions and decimals (e.g. “Put the numbers in order from smallest to largest”: ¼, 0.5, 9/10, 0.398, and 0.8). This item was an adaptation of the task used by Stafylidou and Vosniadou (2004), as we included fractions and decimals in the same task. In each task, a fully correct answer was graded with one point and 0.2 was deduced for each mistake (reverse order of two numbers). The first comparing task asked students to compare two decimals, two fractions or a fraction and a decimal (as used by González-Forte et al., 2020). The 9 pairs of numbers were chosen based on common students’ errors and misconceptions (e.g., 5.4 vs. 5.400, 2.3 vs. 2.03, and 1/40 vs. 0.40). In the second comparing task (see Appendix A), students were asked to identify which of five numbers was closer to a given one (as proposed by Markovits & Sowder, 1994). The two items involved decimals and fractions and required multiple comparisons and conceptual understanding of the fraction relations (Dyson et al., 2020). Responses were scored as correct/incorrect for each comparison.

Number line estimation was assessed by two types of tasks. The first task was in a multiple-choice format and asked students to identify which number was marked in a number-line. In the second number-line task, students had to estimate the location of 6 rational numbers on a line marked with numbers 0 and 1 (as used by Siegler et al., 2011). Responses were scored as correct/incorrect for each task.

Rational number density was assessed using short-answer and a table-filling task (as used by Vamvakoussi & Vosniadou, 2010). The short-answer asked students to give two numbers between 2.3 and 2.4 and two numbers between ½ and 1/3. Every correct number was awarded with 0.5 point. The second task asked students to complete a table by providing a number that lies between two given ones and provide an explanation if they thought that there was not a number between them (e.g., 4.69 and 4.70 and ¼ and 1/5). Responses were scored as correct/incorrect for each sub-task.

Rational number knowledge included identifying numbers and manipulating different representations. In particular, the first type of task provided rational numbers in symbolic or verbal form and asked students to provide the other form. For example, it was asked to provide the verbal form of 0.15 and the symbolic form of “two and 7 tenths.” This task is a modified version of measures that are typically used for early number sense. In this task, each response was scored as correct/incorrect. The second task (see Apendix A) was based on the picture part of the Rankings Proportion Test and asked students to correspond 6 fractions to pictures representing fractions $\le 1$ (in circle model). A fully correct answer was graded with one point, and 1/3 of a point was deducted for each mistake, as a mistake resulted in an incorrect correspondence of two fractions. The third task emphasized in conceptualizing the meaning of numbers and their structure and reflects researchers views about conceptualizing the structure of a number in multiple ways (Hoch & Dreyfus, 2005; Zazkis & Mamolo, 2016). Students had to provide verbal statements, number sentences, or representations that correspond to a fraction and a decimal (4/5 and 1.25). Each correct response was awarded with one point.

Counting based on place value and fraction-unit was assessed with three items that asked students to count on or down from a given starting point till a target number using a specific pattern. This task is a modified version of counting measures used for early number sense. For instance, the first item asked to count on from 6.5 to 7.5 in one tenth increments. In each task, a fully correct answer was graded with one point. Deductions were made based on the number of mistakes. For instance, a deduction of 0.25 points was applied for every two mistakes.

Equivalence of fractions and fraction-decimal conversion was assessed by two tasks (as used by Dyson et al., 2020). The first one required filling an empty box (numerator or denominator) to create equivalent fractions (see Appendix A). The second one required transforming a fraction/mixed number to a decimal and vice versa (e.g., $1\frac{2}{100}$ to decimal and 3.25 to mixed number). In this task each correct response was awarded one point. A total score for each task was calculated.

Rational number arithmetic sense measures

The second factor was measured with four types of tasks that reflected students’ arithmetic sense in calculations and estimations, understanding the effect of operations on numbers, and solving word problems. Reliability for arithmetic-sense measures was good (Cronbach’s α = 0.85).

Participants were asked to solve 16 arithmetic calculations that included adding and subtracting fractions with like and unlike denominators, multiplying and dividing fractions, adding and subtracting decimals with different number of decimal points, and multiplying and dividing decimals that required mainly conceptual understanding. Each calculation was scored as correct/incorrect.

Mental calculations and estimation were measured by two types of tasks. The first one was a modified version of the tasks suggested by Van Hoof et al. (2018) and McMullen et al. (2022) and asked students to explain whether (a) dividing 51 by 0.95 gives a quotient bigger, smaller or equal to 51 and (b) multiplying 0.99 by 1001 gives a product bigger, smaller or equal to 1001. A fully correct answer that included an explanation was graded with one point, a correct answer based on calculation was graded with 0.75 points and a correct answer without explanation was graded with 0.5 points. The second type was three multi-choice questions that required judging the reasonableness of estimates, without making any calculations, as suggested by Yang et al. (2008). Each correct response was awarded one point and the total score of the task was calculated.

Understanding the effect of operations was measured by open number sentences that presented equations, equalities, and inequalities. The tasks were in a multiple-choice format and requested selecting the appropriate number so the equality or inequality holds. Students could find the answer by applying trial and error strategies or utilize the inverse relations between operations. To do so, students had to recognize how the four basic operations affect the computational results, as suggested by McIntosh et al. (1992) and Yang et al. (2008). For instance, students had to find the missing number in the open number sentence 4/8 × _ = 3/4 by conceiving that the missing number can be calculated by dividing ¾ by 4/8. In addition, students had to find the missing number in equalities, such as $\frac{3}{4}-\frac{1}{3}=1-\frac{1}{3}- \_\_$, by applying an opposite strategy, and complete missing numbers in inequalities. Each correct response was awarded one point.

Finally, problem solving was measured by two types of tasks. The first one presented three one-step (e.g., Helen has 3 kg of flour. She wants to prepare biscuits. She needs 0.15 kg of flour for each biscuit. How many biscuits can she prepare?) and one two-step (e.g., George had 4/5 L of milk. He drank 1/8 of this quantity. How much milk is left?) word problems in multiple-choice format and students had to select the number sentence that matched the problem (Pittalis et al., 2018). Each correct answer was awarded one point. The second type of tasks was story problems that involved fractions and decimals (Jordan et al., 2007). The first one required adding unlike fractions and then making a subtraction and the second one converting a decimal to a fraction, then multiplying fractions and then a subtraction (see Appendix A). A fully correct answer was awarded one point, while response in which only the first step of the problem was correct was awarded with 0.5 points.

Flexibility measures

The third factor was measured by four types of tasks that captured students’ rational-number sense in patterning situations, function machines, complex computational tasks and covariation interpreting situations based on the adopted theoretical considerations. Reliability for flexibility measures was adequate (Cronbach’s α = 0.74).

Two types of tasks were used to capture flexibility in patterning situations, that required conceiving the relations among a set of rational numbers. The first type was a traditional growing pattern that required understanding the underlying rule of the given terms to extend the pattern (Wijns et al., 2021). We used four patterns; two with an additive rule (add 0.5 and subtract 4/9), one with a multiplicate rule (multiply by 2/3), and one with a linear one (divide by two and then subtract one). In each pattern, students had to complete four terms, so each correct term was awarded with 0.25 points. The second task was developed for this study and targeted noticing the relation between a group of numbers in a novel situation, so that students could pose their own patterns by selecting numbers from the given set and describe their rule. In particular, we provided 22 rational numbers (whole numbers, fractions, and decimals). Subsets of the given numbers followed an additive (e.g., 3, 3.5, 4, $4\frac{1}{2}, ...)$ or multiplicative relation (e.g., 40, 4, 0.4, 0.04, … and$\frac{2}{3}$,$\frac{4}{9}$,$\frac{8}{27}, ...$). Students were asked to pose at least three extending pattern tasks and explain the rule of each one. Each correct pattern that included proper explanation was awarded with one point, while 0.5 points was given for a pattern without explanation.

We used three function machines to capture students’ flexibility in functional situations (Ng, 2018). For each function machine, we provided a table with input and output values so students could figure out the rule underpinning the particular set of inputs and outputs and asked them to find the output value of the function machine for two input values, and the input value for a given output value. These questions were defined as function-particular tasks (Pittalis et al., 2020). A score of 0.25 points was assigned for each correct output value, while an additional 0.5 points were granted for a correct input value, allowing for a maximum total score of one point. Further, it was asked to provide the output value when the variable x is entered in the machine. This last task (see Table 1) required expressing the generality by seeing the generality through the particular (Mason, 1996) and was defined as function-general task (Pittalis et al., 2020). A correct answer in this task was awarded one point.

Table 1 Flexibility measures

Two types of tasks were used to measure flexibility in computational settings. Both tasks required besides making calculations to consider the relations between the involved numbers and their structure in terms of place value and identify additive and multiplicative relations (Mason et al., 2009). The first one, arithmetic sentence production, was adopted by McMullen et al. (2020) and required to generate and write down as many mathematically correct arithmetic sentences as possible by using subsets of five numbers and the four operations to produce a target number (e.g., 3/2, ¾, 1.50, 0.75, and 2 to give the target number 3). Each correct arithmetic sentence was awarded with one point. The second one, developed for this study, required to group 8 given numbers into four sets, so that the sum of the numbers in each set does not exceed one (see Table 1). Each correct set was awarded with 0.25 points as a fully correct answer included four sets.

Two tasks were developed to measure flexibility in covariation interpreting situations, based on the ideas of Thomson and Carlson (2017). The first one (see Table 1) provided a linear graph that presented the cost value of a product in respect to time-years. Students had to coordinate the growth rate of the cost value in respect to time-change to make predictions regarding the cost of the product, find the cost of the product at specific time-points and find when the cost of the product will exceed a certain value. The item included in total four questions and each one was graded with 0.25 points. The second task (see Table 1) presented in a table the quantity of milk in bottle that was leaking in respect to time. Students had to coordinate the two quantities to pose questions that corresponded to given answers. Again, the item included four questions and each one was graded with 0.25 points.

Procedure and analysis

The tasks of the study were split into two parts because of the large number of items. Both parts included items from the three factors and the different sub-components, the same difficulty, and time demand. Each part was administered in the form of a written test during a 40-min school period. The two parts were administered in one-week period. Participants were not allowed to use a calculator. For each type of tasks, we calculated the mean value of the items used and then the mean value of each sub-component that was used as the observed variable measure.

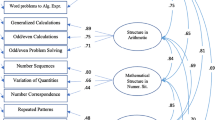
The use of confirmatory factor analysis (CFA) made sense for examining the validity of the hypothesized model, since the proposed factors of the set of variables used were based on previous research findings and theory (Brown, 2015). Our purpose was to investigate whether the established model of the three factors fits our data. CFA models are displayed by path diagrams in which rectangles represent observed variables and ovals represent the latent variables (see Fig. 2). The latent variables are manifested by the observed variables on rectangles or by lower-order latent variables. Single-headed arrows are used to imply a direction of assumed influence, and double-headed arrows represent covariance between two latent variables.

Fig. 2

Structure and standardized solution of the verified model

CFA was conducted by using MPLUS 8.0 (Muthén & Muthén, 2017). To evaluate model fit, three widely accepted fit indices were computed: x²/df should be < 2; the Comparative Fit Index should be > 0.9; and the root mean-square error of approximation (RMSEA) should be < 0.08.

We used latent profile analysis to trace categories of students reflecting different characteristics; this is a statistical method for finding sub-types of related cases (latent cases) from multivariate data. The best fitting model was chosen based on a combination of statistical indicators and substantive theory to determine the most suitable number of latent classes (Nylund et al., 2007). First, entropy values that approach 1 signify more certainty in the resulting classification and significant result of the parametric bootstrapped likelihood ratio test (BLRT) and Lo-Mendell-Rubin (LMR) test suggests support for the k-class solution in comparison with the k − 1 class solution.

After establishing categories of students, we conducted discriminant analysis to figure out on which factors of the model are the categories most different (Brown & Wicker, 2000). Discriminant analysis is a data reduction technique for analyzing data when the criterion or dependent variable is categorical and the predictor or independent variables are interval in nature. To do so, the assigned category provided by the latent profile analysis was treated as the dependent variable and the three factors of the proposed model served as predictors.

Results

The results of the study are presented in relation to its aims. Appendix B presents the covariance matrix of the sixteen manifest variables.

Grade 7 students’ rational number sense model

Confirmatory factor analysis (CFA) was used to evaluate the construct validity of the model, by validating that the a priori model matched the dataset of the present study. The descriptive-fit measures indicated support for the hypothesized model (CFI = 0.96, χ² = 198, df = 93, χ²/df = 2.13, and RMSEA = 0.05). An alternative model, hypothesizing that the three first-order factors, basic, arithmetic and flexibility do not compose a single second-order factor, resulted in a worse fitting model than the hypothesized one (Δχ²/Δdf > 2, p < 0.05). CFA showed that different rational number tasks could be categorized on the basis of the hypothesized model.

Figure 2 illustrates the way in which the various components relate to each other and presents the factors of rational number sense and their indicators. CFA showed that the factor loading of the tasks employed in the present study were statistically significant and most of them were rather large (see Fig. 2). The factor loadings ranged from 0.43 to 0.81, giving support to the assumption that all latent factors have been adequately measured by the observed variables. Thus, in accordance with our theoretical assumption, all rational number measures are clustered into three first-order factors in the expected factor loading pattern. These factors serve as the latent structure of the rational number sense model. The latent construct ‘basic rational number sense’ could accurately model students’ variances in comparison situations (including ordering and comparing tasks), understanding rational number magnitude, rational number density apprehension, knowledge of rational numbers in terms of identification and manipulating different representations, counting, and converting fractions to decimals and vice versa. In addition, the construct ‘rational number arithmetic’ could accurately explain students’ variances in number combinations, mental calculations and estimation skills, short word-problems, story problems, and conceiving the effect of operations on numbers. Finally, the theoretical construct ‘flexibility with rational numbers’ could adequately model students’ variances in patterns, covariation tasks, functional situations (particular and general tasks), and complex computational tasks.

The factor loadings of the three first-order factors that corresponded to basic, arithmetic and flexibility to the second-order factor were extremely high (ranging from 0.90 to 0.92), indicating that a higher-order general ability that refers to students’ rational number sense could explain very accurately students’ variances in these three types of situations (basic, arithmetic, and flexibility). The three first-order factors had almost the same prediction validity on the higher order factor rational number sense, indicating that the three factors are equally important. In particular, the r² of basic rational-number sense was 0.84, the r² of rational number arithmetic was 0.85 and finally the r² of flexibility was 0.81.

Profiles of rational number sense students

Latent profile analysis was used to identify categories of students based on responses to a series of continuous variables, by applying a stepwise method. To do so, we used the 16 observed variables of our model as indicators. BLRT and VLMR tests showed that the three-class model was most appropriate, as a four-class model was not better than the three-class model. A three-class model means that there are three distinct groups of students within the total sample of the study that share similar response patterns on the observed variables. Entropy for this model was 0.93, and the posterior probabilities for the classes showed that the model had high agreement with regard to placing most individuals clearly into a particular class (all latent class probabilities > 0.97).

Table 2 presents the means and standard deviations of the three classes of students in the three rational number sense factors and the observed indicators. Class 1 (n = 124) students exhibited a limited basic rational number sense (M = 0.28, SD = 0.11) and poor arithmetic (M = 0.17, SD = 0.09) and flexibility (M = 0.07, SD = 0.06). Class 2 (n = 177) students had a quite satisfactory performance in basic rational number sense (M = 0.62, SD = 0.11), limited arithmetic sense (M = 0.36, SD = 0.14), and poor flexibility (M = 0.17, SD = 0.10). Class 3 (n = 59) students were strong in basic rational number sense (M = 0.82, SD = 0.09), quite satisfactory in arithmetic (M = 0.64, SD = 0.16), and limited to moderate in flexibility (M = 0.46, SD = 0.16). Labels were assigned to the latent classes based on an interpretation of the quantitative results.

Table 2 Mean values of the three profiles in the factors and the indicator variables

Class 1 students could respond to a limited extent to basic tasks and represented the Limited Basic Sense profile. Class 2 students had above average performance in basic sense and a limited arithmetic sense; therefore, they represent the Basic Emergent Arithmetic Sense profile. Finally, Class 3 was the only group of students that exceeded the average performance in basic and arithmetic sense and approached 50% in the flexibility factor, indicating a Flexible Emergent Rational-Number Sense profile. There appeared to be a hierarchy in the three profiles suggesting that: basic sense can exist without the other two types, but the reverse does not occur, and basic and arithmetic are necessary, but not sufficient for flexible-emergent sense. In the same way, basic is necessary, but not sufficient for arithmetic. To explore the features of students’ responses that might provide an insight into the characteristics of each latent profile, Table 2 presents the mean value of each profile of students in the observed indicators. In the following section, we describe extensively the characteristics of each latent profile.

Limited basic rational number sense profile

Students that fit is this profile had in overall limited basic rational-number sense. In particular, they had a limited performance in comparison, knowledge, counting and converting tasks (0.25 < x̅ < 0.50). Their highest score was in tasks that required converting decimal numbers to fractions and vice versa. They exceeded 50% only in the task that required converting a fraction to a decimal with a ‘10’ as denominator and performed better in converting decimals to fractions than fractions to decimals. In the comparison tasks, they exceeded 50% only in the tasks that requested comparing two numbers and had an extremely poor performance in the task that requested to find the closest number to a given one from a set of numbers. In the knowledge tasks, students had a satisfactory performance only in the task that required recognizing a visual representation of a fraction. In the counting tasks, students had a satisfactory performance only in the task that involved counting-on following a decimal pattern. Students’ performance in the density and magnitude tasks was extremely poor (x̅ < 0.25). For instance, only 9% and 5% of this group provided a number between 1/8 and 2/8 and ¼ and 1/5, respectively. In the case of decimals, only 15% of this group provided a number between 4.69 and 4.7, indicating that they had difficulties understanding the density of rational numbers, independently of a number’s format. In respect to arithmetic sense, students of this class exhibited a limited performance only in operations. In particular their mean performance in additive operations was 0.40, while in the multiplicative tasks was 0.29. For instance, 74% could subtract fractions with the same denominator, 38% with the different denominator, and only 24% could subtract a fraction from an integer. In the case of decimals, 47% subtracted decimals numbers with the same number of decimal points, and only 34% subtracted a number with two decimal points from a number with one decimal point. In the multiplicative tasks, 17% responded to the multiplication $0.5x3.8$ and 19% to the division $2.5\div 0.25$ that required conceptual understanding or identifying the structure and the relations between the involved numbers. In the flexibility factor, students’ performance was poor in all types of tasks.

Basic emergent arithmetic sense profile

Students of this profile exhibited an overall satisfactory basic rational number sense, a limited arithmetic sense and poor flexibility sense. In particular, they over exceeded 50% in all types of basic tasks. Their highest score was in the converting tasks (M = 0.88) and performed quite good in the comparison tasks (M = 0.71). Their mean performance in the ordering tasks and the simple comparison tasks was over 0.85, but their mean value in the tasks that the comparison included multiple numbers was only 0.30. In respect to counting, they counted on or down successfully in the tasks that involved decimals and made mistakes in the tasks that included mixed numbers. In the knowledge tasks, students easily identified visual representations of fractions (M = 0.92), transformed symbolic to verbal and vice versa forms of rational numbers (M = 0.64), but failed to provide different representations of numbers (M = 0.26). Students performance in the density and magnitude tasks was just 0.50. In particular, they exceeded 50% in the tasks that required placing numbers on a number line (M = 0.65), but did not respond adequately in the tasks that required identifying numbers on a number line. In the density tasks, their mean score was over 50% in the tasks that included decimals and lower than 50% in the fraction ones.

In respect to the arithmetic factor, students’ overall performance was below 50%. However, students of this profile exceeded 50% in operations (M_Additive = 0.71 and M_{Multiplicative} = 0.52). Their mean score in the short problems was 0.35, because they failed in the multiplicative structure problems. In addition, their score in the mental calculation/estimation tasks was 0.36 because their performance in the division tasks was extremely low. That was also valid for the story problems and the tasks that required conceptualizing the effect of operations on numbers. Overall, students’ arithmetic profile could manage operations with rational numbers and short problems with arithmetic structure. That is the reason we considered that this group of students exhibited an emergent arithmetic sense. In respect to the flexibility tasks, their overall performance was extremely weak. Besides patterns and complicated calculations tasks that their mean score was 0.32 and 0.25, respectively, their performance was around 10%. It is worth mentioning that in the task that required posing a pattern by selecting numbers from a given set, some students of this group provided patterns with underlying structure based on either additive or multiplicative rule using whole numbers (e.g., add 1 or multiply by 2), or an additive rule using decimals/fractions (e.g., add 0.5).

Flexible emergent rational number sense profile

Students of this profile had a strong basic rational number sense, quite strong arithmetic sense, and almost sufficient flexibility sense. In particular, students of this profile had strong or moderate performance in all types of basic tasks. A distinctive characteristic compared to the other profiles is the fact that they succeeded in the comparing task that involved finding the closest number to a given one among a group of numbers (M = 0.65), in the number line identification task (M = 0.73), in the fraction-density task (M = 0.72), and in multiple representations and interpretations of rational numbers, by providing in an average 2.7 representations/interpretations for each rational number.

Students’ arithmetic sense was quite strong and especially in operations (M_Additive = 0.89 and M_{Multiplicative} = 0.70). In addition, compared to the students of the two other profiles, they responded adequately to short problems (M = 0.57) and the story ones (M = 0.61). They had a quite satisfactory performance also in mental calculation/estimation tasks. For instance, in the two tasks that asked whether a multiplication/division provides a result greater/smaller or equal to one of the terms of the calculation, not only they answered correctly but half of them provided a conceptual explanation. For instance, they explained that $51\div 1$ equals 51, so $51\div 0.95$ gives a quotient bigger than 51 as a number smaller than 1 is more than 51 times smaller than 51. That was also valid in the completing equations, equalities and inequalities tasks (M = 0.63). Thus, students’ arithmetic profile was comprehensive and multi-dimensional as students succeeded not only in simple operations or short problems (compared to students of the other profiles), but also in tasks that require conceptual understanding of arithmetic, such as estimation, reasoning on calculations and understanding the effect of the operations on numbers.

Students’ flexibility sense was moderate as their mean performance approached 50% (M = 0.46). As Fig. 3 suggests, students of this group exhibited a different profile compared to the other groups in respect to all flexibility tasks. For instance, in the patterns and the complicated calculations tasks their performance exceeded 50%. Sixty-three percent of the students of this group provided at least two pattern extension tasks and the associated rule, and 46% of them provided three patterns. Students’ performance just over exceeded 50% in the complex computational tasks. In the number sentence production task, 51% of the students produced at least three correct number sentences, while in the second computational task, 70% of the students managed to create 3 or 4 groups with sum less than one. Students’ mean performance in the two types of functional tasks was 0.42 and 0.40, but they approached 70% in the task with an additive functional rule and 20% in the task with a multiplicative rule. Finally, in the covariation tasks, about 35% of the students posed at least three appropriate questions in the table-covariation tasks, and 32% responded successfully to covariation questions based on interpreting a graph. Thus, students exhibited a flexible emergent rational number sense profile as they responded adequately to a variety of tasks. Their main obstacles were traced in manipulating multiplicative relations, either in identifying pattern rules or functional relations. For example, in identifying the rule “multiply by $\frac{3}{2}$”, in the pattern $\frac{1}{4}$, $\frac{1}{6}$, $\frac{1}{9}$, $\frac{2}{27}$ and so on.

Fig. 3

Mean performance of the three profiles in the flexibility tasks

Rational number sense factors discriminating among students based on their rational number sense profile

To address the third research aim, after classifying students into three rational -number sense profiles, a discriminant function (DF) analysis was conducted which produced two discrimination functions. The first function (DF1) distinguished the limited-basic profile from the other two profiles, while the second function (DF2) distinguished between basic-emergent arithmetic and flexible-emergent profiles. The significance of Wilks’ lambda indicated that both functions were statistically significant (p < 0.001).

The eigenvalue that emerged indicated that the first function accounted for 94% of the variance, and the second discriminant function explained the rest of variance (6%). Canonical correlations were 0.92 and 0.50 for the two discriminant factors, indicating that 85% and 25% of variances were explained by the relationship between predictors and group membership by DF1 and DF2, respectively. Because the variance explained by DF2 was smaller than 50%, only the factors that distinguished among the limited basic profile from the other two profiles were investigated. In addition, as can be inferred from Table 3, the percentage of students who were correctly classified was 88.6% (students on the diagonal). Forty-one students were misclassified: off-diagonal students (number of students that were not correctly classified based on the predictive model). As Table 4 suggests, DF 1 had the largest relationship with basic rational-number sense, followed by flexibility and arithmetic. Based on the canonical DF coefficients, the following DF (equation) was extracted:

Table 3 Classification results of rational number sense profiles

Table 4 Structure matrix based on analysis of rational number sense profile

$$D=(6.70\times \mathrm{Basic\;NS})+(1.98\times {\text{Arithmet}}.\mathrm{\;NS})+(5.95\times {\text{Flex}}.\;{\text{NS}} )-5.72$$

Discussion

The results of the study advance rational number sense literature by validating that rational number sense is a general construct that can be described as a synthesis of three distinct but interrelated components, namely, (a) basic rational-number sense, (b) rational number arithmetic, and (c) flexibility with rational numbers. The analysis showed that the three components had equal predictive validity on the general construct of number sense. Although the three components within the framework represent relatively separate dimensions, we argue that basic rational number sense, rational number arithmetic, and flexibility must be woven together since analysis showed that a model assuming the existence of a higher-order factor had a better fit than a model without a second-order factor. The innovative aspect of the proposed model is the fact that, besides the well-described components of rational-number knowledge and arithmetic, it includes the flexibility component that models students’ variances in rational number situations with patterns, functions, covariation, and complicated computational tasks. This dynamic framework highlights a student’s awareness in terms of relating numbers and recognizing and manipulating additive and multiplicative structures and avoiding unnecessary computational procedures in steps (Jacobs et al., 2007; Mason, 2021).

The proposed model provides a comprehensive description of rational-number components. First, ‘basic rational-number sense’ enriched foundational components of number sense identified by existing frameworks (see Jordan et al., 2007; Mcintosh et al., 1992) with important aspects of rational-number knowledge, such as density structure and number-line ordering and estimation. The model provides an explicit basic number sense conceptualization that reflects accurately 7th grade students’ capacity to handle a variety of number tasks that are usually used in upper primary and secondary school activities. Second, ‘rational-number arithmetic’ describes the arithmetic dimension of number sense under a new theoretical lens as we extended Jordan et al.’s conception of the arithmetic factor (2022) and incorporated students’ capacity to understand the relative effect of operations on numbers and make estimations flexibly (Bütüner, 2018; González-Forte et al., 2022; Yang et al., 2008). The flexibility factor reflects a well-connected system of numerical characteristics and arithmetic relations among rational numbers and is in line with the epistemological nature of rational numbers (Elias et al., 2020). Further, the validated structure of rational-number sense provides strong support to Mason’s (2018) assertion that to gain facility with numbers, is to think algebraically, even if not explicitly, since flexibility reflects the algebraic nature of number sense. Further, it responds to previous studies claiming that number sense and algebraic thinking work hand in hand as foundation for algebra courses (Piriya et al., 2019). This is a critical stepstone for 7th grade students’ smooth transition to algebra.

The second aim of the study was to identify categories of students with different rational number sense profiles. Analysis showed the existence of three profiles of students that describes different ways of rational number sense and clarifies distinctions between students with different profiles. The three profiles of students are hierachical in terms of students’ performance in the various components of number sense and they also represent qualitive characteristics. Particularly, students in the first profile exbibit limited basic rational number sense. They manage only procedural and traditional school-based tasks. This profile of students is in line with a vast number of research studies (Siegler & Lortie-Forgues, 2017; McIntosh et al., 1992; Van Hoof et al., 2018; Yang et al., 2004) and NAEP (National Assessment of Educational Progress) findings suggesting that fractions and decimal numbers pose large difficulties for many students, even for eight graders. Further, it corresponds to Van Hoof et al.’s (2018) initial natural number-based concept of a rational number for upper elementary school learners that includes mainly a good understanding of decimal numbers. Students of the second profile exhibit a satisfactory basic-rational number and limited arithmetic sense. They represent an arithmetic-emergent sense profile, as students’ satisfactory density, magnitude, and comparison sense (compared to the students of the first profile) seems to facilitate flexibility in operations (additive and multiplicative). This profile reflects ‘emerging operations’ state and is line with the research claim that once learners have a good understanding of the size of rational numbers, they can also develop a good understanding of operations with rational numbers (Van Hoof et al., 2018).

Finally, students of the third profile had strong basic and quite strong arithmetic rational number sense and marginally sufficient flexibility sense. Students of this profile could respond partially to tasks that required noticing and manipulating additive and multiplicative structures. This profile could be considered more advanced compared to the ‘emerging operations’ state, identified by Van Hoof et al. (2018). That is because, besides strong dense structure and arithmetic understanding, it entails flexibility with underlying structures and computational efficacy. Rational-number sense of this profile could be characterized as strong, effective, relational, and adaptive, as it responds effectively to a broad range of typical and nontypical situations (Bütüner, 2018; McMullen et al., 2020). Again, students of this profile manipulate more effectively functional relations or patterns with additive than multiplicative structure, as suggested by Siegler and Lortie-Forgues (2017). In conclusion, this profile of students represents an emergent fundamental shift from an arithmetic focus to an algebraic focus (Jacobs et al., 2007).

The importance of the proposed construct ‘flexibility’ was corroborated by the results of a discriminant analysis that identified influential factors that discriminate students best between the three identified profiles of rational number sense. Particularly, analysis showed that students’ performance in the three components of the proposed model could predict distinguishing them based on the rational-number sense profile. Further, basic and flexibility factors could better discriminate among limited basic and the other two profiles of students. Having in mind the arithmetic-emergent and the strong-arithmetic nature of the two profiles, we could argue that the level of students’ basic and flexibility sense contributes to further developing arithmetic skills. Thus, besides basic number sense, the development of the core ingredients of the flexibility factor might become the catalyst for the further development of number sense in general. This finding advances the argument that good understanding of the size of rational numbers leverages developing a good understanding of operations with rational numbers and arithmetical operations contain an algebraic dimension (Mason, 2018; Van Hoof, 2018).

Undoubtedly, the above research findings should be interpreted in the light of four study limitations. First, the proposed model is highly dependent on the adopted theoretical models regarding the definitions and conceptualizations of number sense and rational number knowledge and the tasks used. Second, the validity of the model was examined in the context of two countries with similar educational background. Third, an important limitation of the study is the exclusive use of quantitative research techniques. The use of qualitative data may have offered further insight into the identified rational number sense profiles of students by analyzing students’ processes and reasoning. A future longitudinal study could explore the invariance of the model over time, in different populations or more elaborated models that control the effect of cognitive factors. Further, a qualitative study or a mixed-design study might shed light to students’ number sense thinking processes, strategies, conceptual and procedural knowledge, cognitive or other obstacles in developing flexible rational-number sense. Finally, it would be important to investigate the teaching parameters involved in the further development of number-sense, and the description of a research-based teaching trajectory in terms of the three components, based on well-established epistemological and methodological criteria.

Conclusion

Despite the fore-mentioned limitations, the study findings have theoretical and practical implications. At a theoretical level, the study findings can be used to reconceptualize the construct of number sense for the case of rational numbers, by describing its components in an explicit way. The refined rational number sense framework is a unifying construct between numbers, arithmetic, and algebra. At a practical level, the proposed model offers educators a means to examine the complexity and multi-dimensionality of number sense. It exemplifies the importance of developing students’ rational number sense through teaching activities that involve a large variety of number sense situations. There is a need of activities that explore relations between and among numbers and prioritize key aspects of basic number sense for rational numbers, such as magnitude and dense structure. Given that rational numbers are an extensive topic, a structural-oriented teaching would provide students the opportunity to revisit time and time again many of the same rational number understandings in previous years. That is to focus on the structure of numbers by investigating key aspects such as properties of numbers, composing and decomposing, number patterns, and developing a habit of mind to see and search for structure even in simple calculations. For instance, $0.8\div 0.02$ can be interpreted as how many times bigger is 8 tenths than 2 hundredths, or as how many times bigger is 8 than 2 tenths or 80 than 2, making explicit in this way the multiplicative relation between the two given numbers and different meanings of division.

Appendices

Appendix A

	Factor	Sub-component	Type of tasks—example
1	Basic Rational-Number Sense	Rational number magnitude	Ordering Put the numbers in order from smallest to largest”: ¼; 0.5; 9/10; 0.398; 0.8 Comparing 1 Complete using the symbols >, <, or =  5.4_ 5.400; 2.3 _ 2.03; 1/40 _ 0.40 Comparing 2 Which number is the closest to 0.5? 0.6; 45/100; 0.51; 501/1000; 0.490 Number line estimation 1 Which number is marked on the number line? Number line estimation 2 Place the numbers on the number line
		Rational number density	Provide two numbers between two given ones Write two numbers that lie between 2.3 and 2.4. Explain if you think that there is no number between them Provide one number between two given ones Complete the table providing a number that lies between the two given ones. If there is not such a number, write ‘there is not’
		Rational number knowledge	Identify number Complete the symbolic or verbal form of the number Correspond fraction to picture Rankings Proportion Test Meaning of numbers Write statements, number sentences or draw pictures that represent 1.25
		Counting based on place value and fraction unit	Count on or count down Count on from 6.5 to 7.5 in one tenth increments
		Equivalence of fractions and fraction-decimal conversion	Find equivalent fractions Fill in the empty box Convert fraction to decimal and vice-versa Complete the table
2	Rational number arithmetic	Calculations	Calculations with fractions and decimals (16 tasks) Calculate 2/3 − 1/3; 4/7 − 1/2; 8 − 3/8; 1/5 + 2/3 10 0÷ 1/2; 3/8 × 1/2; 2/5 × 20; 1/2 ÷ 1/8 0.71− 0.4; 0.84 − 0.4; 3.4 + 1.02 0.2 × 3; 0.5 × 3.8; 0.3 × 0.4; 2.5 ÷ 0.25; 2 ÷ 0.5
		Mental calculations and estimation	Explain conceptually the result of a calculation (2 tasks) Explain whether dividing 51 by 0.95 gives a quotient bigger, smaller or equal to 51 Judging the reasonableness of estimates (3 tasks) Which of the following is the answer to 3.17 × 5.87? 183.226, 1832.26, 1.83226, or 18.3226
		Understanding the effect of operations	Complete open number sentences (3 tasks) Find the missing number Complete missing number in inequalities (3 tasks) Find the number that fits in the inequality
		Problem solving	Onestep and two-step word problems (4 tasks) Find the number sentence that matches each problem Helen has 3 kg of flour. She wants to prepare biscuits. She needs 0.15 kg flour for each biscuit. How many biscuits can she prepare?” (0.15 ÷ 3, 3 ÷ 0.15, 0.15 × 3, 3 ÷ 15) Story problems Solve the problem (2 tasks) A new park is being built in the town. The football playground will cover the$\frac{3}{8}$of the park and the basketball playground the$\frac{1}{3}$of the park. What part of the park will be left for other activities?
3	Flexibility*	Patterning	Complete the patterns (4 tasks) Pattern posing (1 task)
		Computation	Produce a target number (2 tasks) Creating groups (1 task)
		Function machines	Find the output value (6 tasks) Find the input value (3 tasks) Express the output value using symbols (3 tasks)
		Interpreting covariational settings	Interpreting graph with rational numbers (1 task–4 questions) Interpreting a Table (1 task–4 questions)

1. *Examples for factor 3 are provided in Table 1

Appendix B: Covariance matrix for the manifest variables

	Dens	Magn	Comp	Knowl	Count	Conv	Oper	Sh.Pr	St.Pr	Estim	Eff.Op	Patt	Cov	Fun.P	Fun.G	Comp
Dens	0.097
Magn	0.062	0.104
Comp	0.062	0.058	0.084
Knowl	0.026	0.026	0.027	0.034
Count	0.045	0.051	0.044	0.021	0.077
Conv	.044	.041	.048	.029	.043	.112
Oper	0.045	0.038	0.044	0.022	0.030	0.047	0.089
Sh.Pr	0.032	0.038	0.028	0.015	0.022	0.024	0.031	0.096
St.Pr	0.042	0.049	0.039	0.018	0.037	0.037	0.030	0.026	0.088
Estim	0.047	0.042	0.042	0.020	0.029	0.035	0.042	0.031	0.033	0.098
Eff.Op	0.034	0.038	0.029	0.014	0.027	0.024	0.025	0.017	0.033	0.028	0.093
Patt	0.036	0.045	0.032	0.021	0.040	0.036	0.030	0.022	0.041	0.028	0.031	0.077
Cov	.017	.018	.016	.015	.021	.020	.018	.011	0.021	0.018	0.017	0.022	0.046
Fun.P	0.018	0.024	0.014	0.011	0.022	0.019	0.016	0.012	0.026	0.020	0.014	0.024	0.018	0.049
Fun.G	0.019	0.022	0.013	0.011	0.023	0.020	0.018	0.010	0.023	0.020	0.015	0.022	0.021	0.044	0.058
Comp	0.023	0.030	0.023	0.014	0.025	0.022	0.019	0.016	0.027	.026	.027	.032	.011	0.021	0.021	0.051