Faster multiplication over ${\mathbb {F}}_2[X]$ using AVX512 instruction set and VPCLMULQDQ instruction

Abstract

Code-based cryptography is one of the main propositions for the post-quantum cryptographic context, and several protocols of this kind have been submitted on the NIST platform. Among them, BIKE and HQC are part of the five alternate candidates selected in the third round of the NIST standardization process in the KEM category. These two schemes make use of multiplication of large polynomials over binary rings, and due to the polynomial size (from 10,000 to 60,000 bits), this operation is one of the costliest during key generation, encapsulation, or decapsulation mechanisms. In BIKE-2, there is also a polynomial inversion which is time-consuming and this problem has been addressed in Drucker (Fast polynomial inversion for post quantum QC-MDPC cryptography, 2020). In this work, we revisit the different existing constant-time algorithms for arbitrary polynomial multiplication. We explore the different Karatsuba and Toom–Cook constructions in order to determine the best combinations for each polynomial degree range, in the context of AVX2 and AVX512 instruction sets. This leads to different kernels and constructions in each case. In particular, in the context of AVX512, we use the VPCLMULQDQ instruction, which is a vectorized binary polynomial multiplication instruction. This instruction deals with up to four polynomial (of degree up to 63) multiplications, that is four operand pairs of 64-bit words with 128-bit word storing each result, the four results being stored in one single 512-bit word. This allows to divide by roughly 3 the retired instruction number of the operation in comparison with the AVX2 instruction set implementations, while the speedup is up to 39% in terms of processor clock cycles. These results are different than the ones estimated in Drucker (Fast multiplication of binary polynomials with the forthcoming vectorized vpclmulqdq instruction, 2018). To illustrate the benefit of the new VPCLMULQDQ instruction, we used the HQC code to evaluate our approaches. When implemented in the HQC protocol, for the security levels 128, 192, and 256, our approaches provide up to 12% speedup, for key pair generation.

Appendices

Appendix A: Karatsuba algorithms

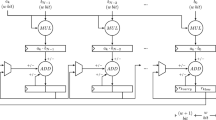
We reproduce here the Karatsuba algorithms:

• Algorithm 1 reproduces the recursive multiplication with a two halves split, from [23];

• Algorithm 2 shows the three parts split corresponding approach;

• Algorithm 3 shows the five parts split corresponding approach;

Appendix B Source code for 256-bit operand size multiplication

1.1 B.1 Source code for the $4\times 4$ 256 bit multiplication of this work based on the schoolbook approach

We present here our schoolbook AVX512 implementation of the 256 bit operand size multiplication, with comments and explanations.

These lines define the constant indexes for the _mm512_permutexvar_epi64 and _mm512_permutex2var_epi64 instructions. These instructions are explained on the fly.

The _mm512_broadcast_i64x4(*A256) instruction duplicates the 256 bits of *A256  in the A512  register, the same for the *B256.

The _mm512_permutexvar_epi64 (idx_b, tmp) spreads the 64 bit words following the index idx_b. This allows to shuffle the 64 bit words of *B256  in the B512  register, in order to prepare the elementary multiplications.

We thus have:

A512  $\leftarrow \{a_3,a_2,a_1,a_0,a_3,a_2,a_1,a_0\}$

tmp   $\leftarrow \{b_3,b_2,b_1,b_0,b_3,b_2,b_1,b_0\}$

B512  $\leftarrow \{b_1,b_0,b_3,b_2,b_3,b_2,b_1,b_0\}$

We now compute all the elementary 64 bit multiplications, providing all the 128 bit results as follows:

R0  $\leftarrow \{a_{2}\times b_{0},a_{0}\times b_{2},a_{2}\times b_{2},a_{0}\times b_{0}\}$

R1  $\leftarrow \{a_{2}\times b_{1},a_{0}\times b_{3},a_{2}\times b_{3},a_{0}\times b_{1}\}$

R2  $\leftarrow \{a_{3}\times b_{0},a_{1}\times b_{2},a_{3}\times b_{2},a_{1}\times b_{0}\}$

R3  $\leftarrow \{\underbrace{a_{3}\times b_{1}}_{128 bits},\underbrace{a_{1}\times b_{3}}_{128 bits},\underbrace{a_{3}\times b_{3}}_{128 bits},\underbrace{a_{1}\times b_{1}}_{128 bits}\}$

The tmp  register now contains all the $a_i\times b_i$ elementary products coming form the R0_512 and R3_512 registers:

tmp  $\leftarrow \{a_{3}\times b_{3},a_{2}\times b_{2},a_{1}\times b_{1},a_{0}\times b_{0}\}$

It remains now to compute the middle part of the result to be added to tmp, in order to get the final result.

The middle  register now contains the addition (XOR) between R1_512 and R2_512, reordered with the _mm512_permutexvar_epi64:

middle  $\leftarrow \{a_{0} b_{3}\oplus a_{3} b_{0},a_{2} b_{3}\oplus a_{3} b_{2},$

$~~~~~a_{1} b_{2}\oplus a_{2} b_{1},a_{1} b_{0}\oplus a_{0} b_{1}\}$

The tmp  register is added (XOR) with the elementary products of the middle  register, and nearly contains the result, except some of the products of the middle part:

The remaining products of the middle part to be added with tmp are put in place in the middle  register:

middle  $\leftarrow \{\underbrace{0x0UL}_{128 bits},a_{1} b_{3}\oplus a_{3} b_{1},a_{0} b_{2}\oplus a_{2} b_{0},\underbrace{0x0UL}_{128 bits}\}$

Out gets the final reconstruction :

Appendix C Source code for 512-bit operand size multiplications

We detail now the source code of the karat_mult_1_512_SB procedure.

First, the preamble declares the constant indexes for the _mm512_permutex2var_epi64 and _mm512_permutexvar_epi64 instructions.

Next, we compute the registers al, ah, bl, bh, sa and sb so that they contain the split parts for the 256 bit operands, and the corresponding sums for the Karatsuba 256 bit middle multiplication.

We compute now the three 256 bit multiplications in order to prepare the 512 bit registers cl, ch and cm containing their results.

These lines computes four 128 bit operand size multiplications in parallel, using a schoolbook approach. This procedure acts like the mul128x4 procedure of Drucker et al. [1], which is based on the Karatsuba algorithm².

The 512 bit registers l and h now contains the four elementary 256 bit results.

This is the schoolbook reconstruction for the first 256 bit multiplication. The register cl now contains the 512 bit result of al$\times$bl.

We now compute the same the two remaining 256 bit operand size multiplications:

The register ch now contains the 512 bit result of ah$\times$bh.

The result cm is directly added (XOR) to the other results cl and ch in order to prepare the final Karatsuba reconstruction, and cm now contains the 512 bit result of (sa$\times$sa)$\oplus$cl$\oplus$ch:

This ends the computation, the final lines stores the result: the 512 least significant bits in the memory place C[0], and the most significant bits in C[1].

Appendix D: Toom–Cook multiplication general algorithm

Several approaches to multiply two arbitrary polynomials over ${\mathbb {F}}_2[X]$ of degree at most $N-1$, using the Toom–Cook algorithm, have been presented by Bodrato in [15], Brent et al. in [28], and software implementations have been provided by Quercia and Zimmermann, in the context of the ntl and the gf2x library, see [26] and [27]. Let A and B be two binary polynomials of degree at most $N-1$. These polynomials are packed into an array of 64-bit words, whose size is $\lceil N/64\rceil$. Let $t = 3n$ with n a value ensuring $t \geqslant \lceil N/64\rceil$. Now, A and B are considered as polynomials of degree at most $64\cdot t-1$. We discuss the value of n in Sect. 3.2.

A and B are split in three parts. One wants now to evaluate the result $C = A\cdot B$ with

$$\begin{aligned} A = a_0 + a_1\cdot X^{64n} + a_2\cdot X^{2\cdot 64n} \in {\mathbb {F}}_2[X], \\ B = b_0 + b_1\cdot X^{64n} + b_2\cdot X^{2\cdot 64n} \in {\mathbb {F}}_2[X], \end{aligned}$$

(of maximum degree $64t-1$, and $a_i, b_i$ of maximum degree $64n-1$) and,

$$\begin{aligned} C = c_0 + c_1\cdot X^{64n} + c_2\cdot X^{2\cdot 64n} + c_3\cdot X^{3\cdot 64n} + c_4\cdot X^{4\cdot 64n} \end{aligned}$$

of maximum degree $6\cdot 64n-2$.

The “word-aligned” version evaluates the polynomial for the values 0, 1, $x = X^w$, $x+1 = X^w +1$, $\infty$, w being the word size, typically 64 in modern processors. Furthermore, on Intel processors, one can set $w=256$ to take advantage of the vectorized instruction set AVX-AVX2, and even $w=512$ (AVX512 extension), at the cost of a slight operand size reduction.

For the evaluation phase, one has:

$$\begin{aligned} \begin{array}{lcl} C(0) &{}=&{} a_0\cdot b_0 \\ C(1) &{}=&{} (a_0 + a_1 + a_2)\cdot (b_0 + b_1 + b_2)\\ C(x) &{}=&{} (a_0 + a_1\cdot x + a_2\cdot x^2)\cdot (b_0 + b_1\cdot x + b_2\cdot x^2) \\ C(x+1) &{}=&{} (a_0 + a_1\cdot (x + 1) + a_2\cdot (x^2 + 1))\cdot \\ &{} &{} (b_0 + b_1\cdot (x + 1)+ b_2\cdot (x^2 + 1))\\ C(\infty )&{}=&{} a_2\cdot b_2. \end{array} \end{aligned}$$

The implementation of this phase is straightforward, providing that the multiplication $a_i\cdot b_i$ is either another Toom–Cook or Karatsuba multiplication. Notice that the multiplications by x or $x^2$ are virtually free word shifts.

For the interpolation phase, one has the following equations:

$$\begin{aligned} \begin{array}{lcl} C(0) &{}=&{} c_0 \\ C(1) &{}=&{} c_0 + c_1 + c_2 + c_3 + c_4 \\ C(x) &{}=&{} c_0 + c_1\cdot x + c_2\cdot x^2 + c_3\cdot x^3 + c_4\cdot x^4 \\ C(x+1) &{}=&{} c_0 + c_1\cdot (x + 1) + c_2\cdot (x^2 + 1)\\ &{}&{} + c_3\cdot (x^3 + x^2 + x + 1) + c_4\cdot (x^4 + 1) \\ C(\infty )&{}=&{} c_4. \end{array} \end{aligned}$$

The matrix associated with this system of equations is given by:

$$\begin{aligned} M = \left( \begin{array}{ccccc} 1&{} 0&{} 0&{} 0&{} 0\\ 1&{} 1&{} 1&{} 1&{} 1\\ 1&{} x&{} x^2&{} x^3&{} x^4\\ 1&{} x + 1&{} x^2 + 1&{} x^3 + x^2 + x + 1&{} x^4 + 1\\ 0&{} 0&{} 0&{} 0&{} 1 \end{array}\right) . \end{aligned}$$

and one has:

$$\begin{aligned} M^{-1} = \left( \begin{array}{ccccc} 1&{} 0&{} 0&{} 0&{} 0\\ \frac{(x^2 + x + 1)}{(x^2 + x)}&{} 1&{} 1/x&{} \frac{1}{x + 1}&{} x^2 + x\\ 0&{} \frac{1}{x^2 + x}&{} \frac{1}{x + 1} &{} 1/x&{} x^2 + x + 1\\ \frac{1}{x^2 + x}&{} \frac{1}{x^2 + x}&{} \frac{1}{x^2 + x}&{} \frac{1}{x^2 + x} &{} 0\\ 0&{} 0&{} 0&{} 0&{} 1 \end{array}\right) . \end{aligned}$$

Finally, the interpolation phase gives :

$$\begin{aligned} \begin{array}{lcl} c_0 &{}=&{} C(0)\\ c_1 &{}=&{} (x^2 + x + 1)/(x^2 + x)\cdot C(0) + C(1) + C(x)/x \\ &{}&{} + C(x+1)/(x + 1) + (x^2 + x)\cdot C(\infty )\\ c_2 &{}=&{} C(1)/(x^2 + x) + C(x)/(x + 1) + C(x+1)/x \\ &{}&{} + (x^2 + x + 1)\cdot C(\infty )\\ c_3 &{}=&{} C(0)/(x^2 + x) + C(1)/(x^2 + x) + C(x)/(x^2 + x) \\ &{}&{} + C(x + 1)/(x^2 + x)\\ c_4 &{}=&{} C(\infty ). \end{array} \end{aligned}$$

Appendix E: experimentation procedure

Measurements were performed on a Dell Inspiron laptop with an Intel Tiger Lake processor.

The compiler is gcc version 10.2.0, the compiler options are as follows:

-O3 -g -march=tigerlake -funroll-all-loops -lm -lgf2x.

We kept the -funroll-all-loops option though it does not provide significant improvements. We follow the same kind of test procedure that the one described in [2] :

• The Turbo-Boost® is deactivated during the tests;

• 1000 runs are executed in order to “heat” the cache memory;

• One generates 50 random data sets, and for each data set the minimum of the execution clock cycle numbers over a batch of 1000 runs is recorded;

• The performance is the average of all these minimums;

• This procedure is run on console mode, to avoid system perturbations, and obtain the most accurate cycle counts.

The clock cycle counter is rdtsc and the instruction counter is rdpmc with the corresponding selection. The results for the smallest sizes (i.e., 256-bit and 512-bit operand sizes) are not very reliable since rdtsc and rdpmc are not serializing instructions (see [25]). For such sort of small functions, we wanted to avoid the insertion of a costly serializing instruction as cpuid, while the instruction count and the clock cycle number may be less than 20. We chose not to present them. The first size considered is 1024 bits, i.e., binary polynomial of degree at most 1023 operands.

Table 13 Instruction count for the 256-bit multiplication versions

Table 14 Performance comparison for Algorithm 1

Appendix F: instruction count and performances

1.1 F.1 Instruction count comparison

In Table 13, we provide the comparison between the instruction count of our schoolbook and Karatsuba versions. Moreover, we compare this two approaches with the current state-of-the-art AVX2 reference. Such an AVX2 implementation can be found in the source code of the optimized version of HQC [22]. It uses the AVX2 instruction set and the non vectorized PCLMULQDQ instruction. Finally, we also put in Table 13 the instruction number of the assembly source code for the same multiplication presented by Drucker et al. in [2]. Here are some comments on these results:

• The best version is our implementation of the schoolbook approach, dividing by more than 2 the instruction number in comparison with the state-of-the-art AVX2 implementation.

• Our Karatsuba approach presents more instructions but only 3 VPCLMULQDQ instead of 4 for the schoolbook version. Thus, the performance comparison may vary according to the latency and throughput of the instructions.

• Drucker et al.’s version has 8 VPCLMULQDQ instructions and a larger instruction number (31, instead of 19 for our implementation of the schoolbook approach). This is due to the fact that they only use 2 elementary 64-bit multiplications per VPCLMULQDQ instruction (ymmm version of the instruction), while we use 4. This also implies more XOR’s in their case.

1.2 F.2 Performances for the 256-bit level kernels

We present in Table 14 the performances of the AVX512 Karatsuba multiplications using the 256-bit kernels presented above. We also include the results of the multiplications using our 8x8 SB-512 kernel.