1 Introduction

1.1 Motivation

Cyber insurance still is a relatively new, but steadily expanding market.Footnote 1 Insurers who have recently entered the market and started to establish their cyber portfolios, exploiting the ongoing growth in demand, are becoming increasingly aware of the challenges associated with insuring cyber risk. These include the dynamically evolving threat landscape, interdependence of risks, heavy-tailed loss severities, and scarcity of reliable data to calibrate (nascent) actuarial models. Particularly the last point is repeated like a mantra; and indeed, while there are growing databases on cyber incidents and their consequences,Footnote 2 they often do not contain the information necessary for the various tasks of an actuary. In fact, the best data source which can be adjusted to contain all details to calibrate an insurer’s individual model is the insurer’s own claims-settlement department. While an increasing number of claims in cyber insurance strain insurers’ profitability margins, from the statistical point of view they should be welcomed as the detailed and reliable data whose lack is so frequently lamented. To make full use of the data collected in-house, however, the processes and systems around the underwriting of a cyber portfolio need to be aligned using a holistic approach, where risk assessment, product design, actuarial modelling, and claims settlement are treated as complementary activities interconnected by feedback loops.

In this article, we aim at illustrating the importance for insurers of using the current moment—namely when starting to underwrite cyber risk—to contemplate and establish data-collection processes in risk assessment and claims settlement which allow them to actually use the collected data to calibrate and refine their actuarial models continuously.

1.2 Literature review

In recent years, various academic papers and numerous empirical studies have been devoted to proposing stochastic models for cyber risk. Within the scope of this work, we give a concise summary of relevant research streams and refer e.g. to the excellent recent surveys [6, 14, 19] for exhaustive complementary overviews. The first models for cyber risk were mostly concerned with the behaviour of interconnected agents in simple networks, e.g. regarding equilibria of interdependent security investments with and without the existence of a cyber insurance market (e.g. [11, 43, 44]). A detailed overview of these studies is provided in [32]. Recently, more advanced models of epidemic spreading on networks have been suggested to study the development of cyber epidemics via endogenous contagion in the “global” population (e.g. [23, 48]) and via (partially) exogenous contagion in an insurance portfolio ( [28, 29]). These approaches, like models based on (marked) point processes to describe arrivals of dependent cyber losses (e.g. [9, 38, 49]) represent a useful bottom-up view, as they strive to understand and adequately formalize the underlying dynamics which originate dependence between cyber losses. On the other hand, copula approaches (e.g. [17]) have been used to analyze the scarce available empirical data, but provide no “explanation” of the underlying cause of dependencies. Finally, let us mention the steadily growing number of studies scrutinizing available empirical data (and unearthing new data sources) to derive the statistical properties of e.g. data breaches (e.g. [16, 18, 47]), general cyber incidents (e.g. [12, 20]), and with particular focus on extreme cyber losses (e.g. [13, 25]). While these studies provide valuable insights with respect to the ongoing development of actuarial models for cyber, they tend to reach diverging conclusions (e.g. on the elementary question of whether the frequency or severity of cyber losses exhibit a time trend), most likely due to the heterogeneity of the underlying data.

While numerous models of varying complexity have been suggested to capture cyber loss arrival dynamics and can yield interesting theoretical conclusions, models aimed at (actuarial) applications most often make use of Poisson processes due to their analytical tractability and well-established availability of e.g. statistical estimation techniques.Footnote 3

1.3 Contribution and structure of the paper

While this present study originated from a practical observation, it also complements the academic body of research: With very few exceptions, the existing works studying the statistical properties of cyber risk focus on the analysis of marginal distributions, i.e. the proposal of adequate frequency and severity distributions for (extreme) cyber losses and related questions (like time- or covariate-dependence of the parameters of the suggested distributions). While it is uncontested that the standard independence assumption is doubtful in the cyber context and many interesting bottom-up models including dependencies have been proposed (see above), the task of fitting these models to empirical data must usually still be postponed with a remark on the non-availability of representative data and replaced by exemplary stylized case studies. Therefore, in this work we aim to highlight the (practical and academic) necessity of data collection including dependence information in order to allow the calibration and further development of models that transcend the mere analysis of marginal distributions, the latter being already a challenging task but by no means sufficient in order to completely understand the risk from an insurance viewpoint.

The remainder of the paper is structured as follows: Sects. 2.1 and 2.2, respectively, address the cyber insurance value chain in detail to illustrate the above mentioned interconnections and to introduce one particular approach to modelling dependence in cyber, namely via common vulnerabilities.

In Sect. 3 we introduce a (purposely simplified) mathematical model capturing such a dependence structure to illustrate that straightforward, naïve data collection necessarily leads to accumulation risk being underestimated, both in the statistical and colloquial sense. We show that while this does not necessarily imply erroneous pricing of individual contracts, it may lead to a dangerous underestimation of dependence and portfolio risk. This is illustrated by comparing the common risk measures Value-at-Risk and Expected Shortfall for the total incident number in the portfolio as well as the joint loss arrival rate for any two companies in the portfolio.

Section 4 concludes and highlights the practical implications of this study for insurers.

2 Two challenges for cyber insurance

2.1 A holistic approach to cyber-insurance underwriting

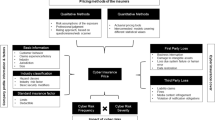
In practice, the establishment of cyber insurance as a new business line has occupied many insurers and industry subsidiaries such as brokers, see e.g. [2]. Reviews of the cyber insurance market and its development are provided e.g. in [32, 36]. Whenever a new insurance line is introduced, the central tasks for actuaries will be technical pricing of the to-be-insured risks and risk management of the resulting portfolio (or more precisely in cyber, risk management of an established portfolio, which now additionally contains risks from cyber policies). Underwriting and pricing risks can be done based on expert judgement for each risk individually or—more commonly—based on a chosen mathematical model. In other words, actuaries have to devise an answer to the question: “How (do we choose) to model cyber risk?” The extensive study of [41] provides an overview of existing cyber pricing approaches at the time, corroborating that established actuarial models for this relatively novel risk type were yet to be developed. Equally important, however, and often overlooked by academic papers, is the observation that it is not reasonable for actuaries to come up with a (no matter how accurate) answer to the above question in the isolation of an actuarial department. Instead, the chosen mathematical model needs to be simultaneously based on and itself be the basis of the business processes surrounding actuarial modelling along the entire economic insurance value chain. The development, calibration, and back-testing of an actuarial model are only sensible if they are based on information and data from risk assessment, product design, and claims settlement, as detailed below and illustrated in Fig. 1.

Fig. 1
figure 1

The diagram illustrates the interconnections between different tasks in a holistic insurance value chain. While actuaries are typically mainly involved in risk assessment and actuarial modelling, there are crucial connections to other areas which must not be overlooked. In particular, the necessity to create awareness that meaningful data, which can (and should) be tailored to the chosen actuarial model, is being collected daily in the claims-settlement department (usually by a completely disjoint group of experts, who do not have actuarial modelling aspects on their agenda of primary concerns) should be emphasized

Full size image

  • Product design: Before even starting to devise an actuarial model, a clear-cut definition and taxonomy of cyber risk(s) needs to be established in order to determine which aspects of cyber are deemed insurable (anything else should be excluded from the coverage by contract design) and which coverage components a cyber insurance policy should consist of. This product design process naturally needs to be revised regularly with the involvement of legal and market experts, as the cyber threat landscape as well as prospective clients’ coverage needs evolve dynamically.

  • Risk assessment: The risk-assessment process serves to elicit information deemed relevant to estimate a prospective policyholder’s susceptibility to cyber risk. For cyber insurance, this process should naturally include an assessment of the client’s IT infrastructure and existing cyber-security provisions. For an accurate assessment of such technical systems, cooperation with IT security experts is indispensable. However, how to adequately include extensive qualitative knowledge about an IT system’s vulnerabilities and security into a stochastic model is a complex, unresolved issue in itself. Nevertheless, the questions asked and information gathered from prospective policyholders during the risk-assessment process should depend on the actuarial model that is subsequently used for pricing of individual contracts and risk management of the cyber portfolio.

  • Actuarial modelling: The actuarial modelling step aims at developing a stochastic model which allows an estimation of the distribution of each policy’s and the overall portfolio’s loss from cyber risk. This serves as the basis for (technical) pricing and risk management. The model should be calibrated—and ideally back-tested—using adequate data (once available) and expert judgement. In summary, the choice of stochastic model depends on product design (which types of cyber losses are to be modelled) and in order to calibrate and develop it further, adequate data must be gathered through risk assessment and claims settlement.

  • Claims settlement: Claims settlement deals with incoming claims from cyber losses in existing policies. In practice, this task is often treated completely disjoint from the above-mentioned processes (except product design), and is typically conducted by legal experts whose main concern is to understand the intricacies of each individual claim well enough to judge whether and to which extent it is covered by the components of the policy. The manner of data collection and storage is mostly dictated by legal (and efficiency) concerns. For cyber it is relevant to stress that technical expertise cannot be expected in a classical claims-settlement department. However, this is a crucial shortcoming: The information that needs to be collected in order to make claims data usable for model calibration is dictated by the choice of model. Vice versa, additional information collected may uncover flaws or omissions of the actuarial model and support its continuing development. Therefore, it is important to collect historical claims information with the underlying actuarial model in mind. In cyber, it is well-established consensus that any actuarial model needs to take dependence between cyber losses into account. The exact choice of dependence model is of course an insurer’s individual decision,Footnote 4 but it is clear that if one strives to calibrate such a model based on data, the model choice needs to be reflected in the data-collection process from the insurer’s own claims experience.

Depending on the reader’s own practical experience, interconnection of the above processes and cooperation between all stakeholders may sound like a utopia or a matter of course. We agree that for established business lines, either may be the case, depending on whether systems and processes were set up and continuously monitored intentionally or rather were allowed to grow historically. It is clear that as cyber insurance is just being established, now is the moment to intentionally set up this value chain in a way that enables insurers to cope with the dynamic challenges of this new and continuously evolving risk type in the future.

2.2 Dependence in cyber via common vulnerabilities

It is uncontested that a core actuarial challenge in cyber risk is the failure of the independence assumption between claim occurrences, which underlies the diversification principle in insurance. Due to increasing interconnectivity, businesses, systems, and supply chains become ever more dependent on functional IT infrastructure and crucially, more interdependent. Therefore, including the modelling of dependence in an actuarial model for cyber risk is indispensable. The actuarial literature discusses several approaches for this, most commonly using epidemic spreading on networks / graphs (e.g. [23, 48]), based on (marked / self- or cross-exciting) point processes (e.g. [7, 38, 49]), or employing copula approaches (e.g. [27, 34, 39]).

Regardless of the concrete modelling approach, dependence between cyber losses is worrisome for insurers as it may entail accumulation risk, which can be defined e.g. as the

risk of large aggregate losses from a single event or peril due to the concentration of insured risk exposed to that single event or peril.Footnote 5

Of course, accumulation risk is not limited to cyber insurance; other lines of business typically confronted with exposure concentrated to a single event are lines subject to natural catastrophes (e.g. Hurricane Katrina has been named as the most expensive event ever to the insurance industry world-wide, see [3]) or marine insurance (see e.g. [22]). Therefore, the modelling results and their practical implications are in principle not limited to the cyber risk context, but can be useful for other lines of insurance where the assumption of independence between loss occurrences is questionable and accumulation risk due to common events causing multiple dependent incidents may be present. In our view, the particular urgency to consider this problem in the cyber context stems from the novelty of this risk type and the naturally resulting lack of experience with respect to adequate data collection and subsequent calibration of dependence models. Moreover, it seems reasonable to assume that e.g. in the context of natural catastrophes, it is generally much easier (compared to cyber) to recognize incidents as belonging to a common event.

Following the classical decomposition of risk into a combination of threat, vulnerability, and impact (see e.g. [32]), a cyber threat only manifests itself as an incident (with potential monetary impact) if there is a corresponding vulnerability in the target system. Therefore, we postulate that any cyber incident is caused by the exploitation of a vulnerability in the company’s system, where it can be distinguished between symptomatic and systemicFootnote 6 vulnerabilities (see [8, 10]), the former affecting a single company while the latter affect multiple companies simultaneously. Commonly cited examples of systemic vulnerabilities are the usage of the same operating system, cloud service provider, or payment system, affiliation with the same industry sector, or dependence on the same supplier.

Example 1

We give two recent examples of common vulnerabilities which prominently exposed many companies to a cyber threat simultaneously. The following information and more technical details on both examples can be found in the report [45]. These examples serve to illustrate that in some cases, it might be quite obvious for an insurer to determine from incoming claims data that several cyber claims are rooted in the same common vulnerability, whereas in other cases this is very difficult to detect.

  • Microsoft Exchange: In the first quarter of 2021, threat actors exploited four zero-day vulnerabilities in Microsoft Exchange Server. The attacks drew widespread media attention due to the high number of affected companies (estimates of 60.000 victims globally, see [46]) within a short time frame, enabled by the ubiquitous use and accessibility of Exchange Servers at organizations world-wide and by their ability to be chained with other vulnerabilities. Due to the massive media coverage, leading to high awareness among companies, and the relatively clear time frame (the attacks had begun in January and were rampant during the first quarter of 2021), it was relatively easy for insurers to identify whether incoming cyber claims during (or slightly after) this time frame were rooted in one of the Microsoft Exchange vulnerabilities.

  • Print Spooler / Print Nightmare: In the third quarter of 2021, several zero-day vulnerabilities were disclosed in Windows Print Spooler, another widely used service in Windows environments. As mentioned in [45], the same service was already exploited in 2010 in the so-called Stuxnet attacks. Stuxnet was a malicious worm consisting of a layered attack, where Windows systems were infected first (through zero-day vulnerabilities), but not the eventual target; i.e. the infection would have usually stayed undetected in the Windows system and seeked to propagate to certain (Siemens) PLCs (see, e.g., [24, 42]). These 2010 attacks were not immediately connected to an insurance context. However, if an analogous mechanism (e.g. through the recent Print Spooler vulnerabilities) were to cause cyber insurance claims, it would certainly be hard to attribute all claims to the same common vulnerability for two reasons: First, the eventual target system where the (economic) impact is caused differs from the system affected by the common vulnerability and second, the time frame is much less clear than in the previous example, as the delay between exploitation of the vulnerability and economic impact is somewhat arbitrary.

In any case, in order to calibrate a model that uses common vulnerabilities as the source of dependence, an insurer needs to collect at least some information about the root cause for each claim to be able to estimate the dependence structure correctly. We now give a very general overview of how information on common vulnerabilities would be reflected in the insurer’s risk modelling process, before introducing a more concrete, slightly simplified mathematical model in Sect. 3.

2.2.1 Formalization: Idiosyncratic incidents and systemic events

Assume that an insurer’s portfolio consists of \(K \in \mathbb {N}\) companies. From the viewpoint of each company, indexed \(i \in \{1,\ldots ,K\}\), cyber incidents arrive according to a simple point process with corresponding counting process \((N^{(i)}(t))_{t \ge 0} = \Big (\vert \{k \in \mathbb {N}: t^{(i)}_k \in [0,t]\} \vert \Big )_{t \ge 0}\), in the simplest case a homogeneous Poisson process with rate \(\lambda ^i > 0\). This rate may differ between companies (i.e. some are assumed to be more frequently affected than others) and the main focus of cyber risk assessment (e.g. via a questionnaire, see [26] for a blueprint, or a more extensive audit for larger risks) is to gather information about characteristics which are considered relevant to determine a prospective policyholder’s rate (classical covariates are e.g. company size, type and amount of data stored, types of business activities, see e.g. [20, 40, 41]).

As the \(\lambda ^i\) are naturally unknown, the insurer usually estimates them given past claims experience of similar policyholders (depending on the portfolio size, more or less homogeneous groups would be considered similar). The overall arrival of incoming incidents to company i is actually composed of several (assumed independent and Poisson) arrival processes (from idiosyncratic incidents and common events), i.e. the overall Poisson rate for company \(i \in \{1,\ldots ,K\}\) decomposes into

$$\begin{aligned} \lambda ^i = \lambda ^{i,\text {idio}} + \sum _{s \in S^*_i} \lambda ^{s,\text {syst}} > 0, \end{aligned}$$
(1)

where \(\lambda ^{i,\text {idio}} \ge 0\) is the rate of idiosyncratic incidents arriving to company i, possibly modelled as some function of the covariates (for example, fitting a standard GLM or GAM here would be common practice), \(S^*_i \subseteq \{1,\ldots ,S\}\) is the subset of S known systemic risk factors (any common factor through which multiple companies in the portfolio could be affected simultaneously) present at company i, and \(\lambda ^{s,\text {syst}} \ge 0\) is the overall occurrence rate of an event due to exploitation of systemic risk factor \(s \in \{1,\ldots ,S\}\). In this modelling step, several “pitfalls” could occur:

  1. (1)

    If questions about relevant covariates are omitted during risk assessment (e.g. because their influence on the frequency of cyber incidents is unknown), this may introduce a bias when estimating \(\lambda ^{i,\text {idio}}\) (in either direction, i.e. over-/underestimation depending on the covariates).

  2. (2)

    If certain systemic risk factors are unknown and therefore not inquired about during risk assessment (e.g. no question about the choice of operating system or cloud service provider) for some or all companies, an underestimation of the true rates is introduced, as the set S, resp. subsets \(S^*_i\), do not contain all possible events.

The errors (1) and (2) should be mitigated by refining risk assessment procedures continuously based on expert input and evaluation of claims data. This leads to the main point of inquiry in this article: Given (correct) assumptions about covariates and systemic risk factors, the goal is to enable the insurer to estimate the corresponding rates, both idiosyncratic and systemic, using historical claims data. As the insurer monitors incoming claims over a policy year [0, T], where typically \(T=1\), in addition to client-related data and basic claims-related data, usually a description of the incident (i.e. the order of occurrences that lead to a monetary loss) is provided by the client. This is unstructured data, and depending on the case could e.g. be given in the form of a phone conversation or e-mail report to an insurance agent or via a scanned PDF containing a report of an IT forensics expert. This information is typically reviewed by the insurance agent in order to decide whether the claim is covered, but may not or only in abbreviated form be entered into the insurer’s claims database. This means that information allowing claims to be identified as stemming from the same systemic vulnerability is often not available or (fully or partly) discarded. In the following, we illustrate the detrimental effect of this omission of information about the extent of systemic events on the estimation of dependence and portfolio risk. We again emphasize two points: When considering the underestimation of risk, one might intuitively think of incomplete information about frequency or severity of cyber incidents e.g. due to reporting bias. In this study, we aim to illustrate that even with complete and correct information on marginal frequency and severity, an underestimation of risk can be introduced by incomplete information on the dependence structure. While in a general context, such incomplete information on the underlying dependence could introduce a bias in either direction (over- or underestimation of the total risk), for the models we consider realistic in the cyber context (as formalized above and in the next section), necessarily an underestimation of portfolio risk occurs.

3 Mathematical model

To quantify the effect we have introduced and discussed on a qualitative level in Sect. 2, we now construct a simple mathematical model which captures common events (‘shocks’) and allows to analyze the effect of underestimating the extent of joint events.

3.1 An exchangeable portfolio model and the modelling of missing information

We assume that the insurer’s portfolio consists of \(K \in \mathbb {N}\) homogeneous companies and let \(\emptyset \subset I \subseteq \{1,\ldots ,K\}\) denote a non-empty subset of the portfolio affected by a common event. Assume that cyber events (to any set I) arrive according to independent, homogeneous Poisson processes.Footnote 7 In theory, each subset I could potentially have a different arrival rate of common events, leading to the prohibitive complexity of needing to estimate \(2^K-1\) rates. To avoid the curse of dimensionality, we make the following assumption.

Assumption 1

(Exchangeability: Equal rates for subsets of equal size) Assume that arrival rates only depend on the number of companies in the subset, i.e. the insurer aims at estimating a vector of K arrival rates \(\varvec{\lambda }:= (\lambda ^{|I|=1},\ldots ,\lambda ^{|I|=K})\), where \(\lambda ^{|I|=k}\) denotes the arrival rate of events affecting any subset of size \(k \in \{1,\ldots ,K\}\).

We denote as model (M) the model given these ‘true’ rates \(\varvec{\lambda }\).Footnote 8 Assumption 1 leads to homogeneous marginal arrival rates \(\lambda ^i,\; i \in \{1,\ldots ,K\}\), for each company of

$$\begin{aligned}{} & {} \lambda ^i = \sum _{k = 1}^{K} \frac{\lambda ^{|I|=k}}{\left( {\begin{array}{c}K\\ k\end{array}}\right) } \left( {\begin{array}{c}K-1\\ k-1\end{array}}\right) = \sum _{k = 1}^{K} \frac{k}{K} \lambda ^{|I|=k}\nonumber \\ {}{} & {} = \underbrace{\frac{\lambda ^{|I|=1}}{K}}_{\text {idiosyncratic incidents}} + \underbrace{\sum _{k = 2}^{K} \frac{k}{K} \lambda ^{|I|=k}.}_{\text {incidents from common events}} \end{aligned}$$
(2)

Note that (2) is a simplified formalisation of (1).

It is well-known that the maximum likelihood estimator of the rate of a homogeneous Poisson process is given by the sample mean (see e.g. [15]) over the observation period, i.e. in our case each estimator \(\hat{\lambda }^{|I|=k}\) is given by the mean total number of observed events affecting precisely k companies, i.e. for \(L > 0\) observed policy years

$$\begin{aligned} \widehat{\lambda }^{|I|=k} = \frac{1}{L} \sum _{\ell = 1}^{L} \hat{n}^{|I|=k}_\ell , \end{aligned}$$

where \(\hat{n}^{|I|=k}_\ell \) is the number of observed events to subsets of size k during policy year (or simulation run) \(\ell \in \{1,\ldots ,L\}\) and for simplicity, we have assumed policy years of length \(T=1\), during which the portfolio does not change.

Assumption 2

(Missing information on common events) Assume that, independently for each common event to a subset of any size \(|I| \ge 2\) and independently for each company in the subset, i.e. \(i \in I\), the probability that the arrival at this company is correctly identified as belonging to the common event (affecting all companies in I) is given by \(p \in [0,1]\).Footnote 9

Example 2

To illustrate Assumption 2, consider the following situation: A vulnerability in a commonly used software could be exploited, leading to hackers gaining access to confidential data which allowed them to defraud several companies throughout the policy year. After the policy year, when historical claims data is analyzed, all incidents in the database are first considered independent. Those incidents where detailed information is available, in this case that the original cause of the loss was the exploit of the common vulnerability, are then identified as belonging to a common event. If originally five companies were affected in this way, but only for three of them the required information was available, instead of (correctly) counting one observed event on a subset of five companies (contribution to the estimator \(\widehat{\lambda }^{|I|=5}\)), the insurer would (incorrectly) count one event on a subset of three companies and two independent incidents (contribution to the estimators \(\widehat{\lambda }^{|I|=3}\) and twice to \(\widehat{\lambda }^{|I|=1}\)).

Mathematically, Assumption 2 means that the Poisson arrival processes to subsets of size \(|I| = k \ge 2\) are subject to thinning (with probability \((1-p^k)\)) and superposition of \((K-k)\) other Poisson arrival processes.

Definition 1

(Model \((\widetilde{M})\) - missing information) Assumption 2 leads to a different model, denoted \((\widetilde{M})\), with Poisson arrival rates denoted \(\varvec{\widetilde{\lambda }}:= (\widetilde{\lambda }^{|I|=1},\ldots ,\widetilde{\lambda }^{|I|=K})\) given by

$$\begin{aligned} \widetilde{\lambda }^{|I|=1}&= \lambda ^{|I|=1} + \sum _{i = 2}^{K} \lambda ^{|I|=i} \Big [i \big (f_{\text {Bin}}(0;i,p) + f_{\text {Bin}}(1;i,p)\big ) \nonumber \\ {}&\quad + \sum _{j = 2}^{\max (i-1,2)} (i-j) f_{\text {Bin}}(j;i,p) \Big ], \end{aligned}$$
(3)
$$\begin{aligned} \widetilde{\lambda }^{|I|=k}&= \sum _{i = k}^{K} \lambda ^{|I|=i} f_{\text {Bin}}(k;i,p), \quad k \in \{2,\ldots ,K\}, \end{aligned}$$
(4)

where \(f_{\text {Bin}}(k;i,p) = \left( {\begin{array}{c}i\\ k\end{array}}\right) p^k (1-p)^{i-k}\) is the p.m.f. of a Binomial distribution.

Remark 1

(Interpretation of the rates \(\varvec{\widetilde{\lambda }}\)) The rates \(\varvec{\widetilde{\lambda }}\) can be interpreted as follows:

  • For \(k = K\), the rate in the model with missing information is given by

    $$\begin{aligned} \widetilde{\lambda }^{|I|=K} = \lambda ^{|I|=K} f_{\text {Bin}}(K;K,p) = \lambda ^{|I|=K} p^K, \end{aligned}$$

    i.e. the original rate thinned by the probability that all (of the K independently investigated) incidents are identified correctly. Note that for \(p \in [0,1)\), \(\widetilde{\lambda }^{|I|=K} < \lambda ^{|I|=K}\), i.e. the rate of events that jointly affect the whole portfolio is obviously lowered.

  • For \(1< k < K\), the rate in the model with missing information is given by the sum of the original rate for \(i = k\) thinned by the probability of classifying all k incidents correctly (summand for \(i = k\)) and the rates resulting from the probabilities of misclassifying events to more than k firms incorrectly such that they are counted as events to k firms (summands for \(i > k\)); compare Example 2. \(\widetilde{\lambda }^{|I|=k}\) can thus be higher or lower than \(\lambda ^{|I|=k}\), depending on \(\varvec{\lambda }\) and p. However, in general, the cumulative rate of ‘small’ events (i.e. all events up to any size k) does not decrease, i.e.

    $$\begin{aligned} \sum _{i=1}^{k} \widetilde{\lambda }^{|I|=i} \ge \sum _{i=1}^{k} \lambda ^{|I|=i}, \quad \forall k \in \{1,\ldots ,K\}. \end{aligned}$$

  • The rate for idiosyncratic incidents in model \((\widetilde{M})\) is given by the sum of the original rate (these incidents are never “misclassified”) and all the “fallout” from classifying common events incorrectly: If for an event to a subset of size i, none or only one of the firms are classified correctly, all i incidents will be counted as idiosyncratic (first part in square bracket in (3)); if \(j \ge 2\) firms are attributed correctly, the remaining \(i-j\) are classified as idiosyncratic (second part in square bracket in (3)). Therefore, for \(p \in [0,1)\), it holds \(\widetilde{\lambda }^{|I|=1} > \lambda ^{|I|=1}\), i.e. the rate of idiosyncratic incidents is increased.

Lemma 1

(Marginal rates remain unchanged) The marginal arrival rates for each company stay unchanged between model (M) and model \((\widetilde{M})\), i.e.

$$\begin{aligned} \widetilde{\lambda }^i = \lambda ^i = \sum _{k = 1}^{K} \frac{k}{K} \lambda ^{|I|=k}, \quad i \in \{1,\ldots ,K\}. \end{aligned}$$

Proof

Intuitively, the statement is clear, as an incorrect (non-)identification of common events does not lead to missing a claim, but to wrongly attributing its cause. A formal proof is given in Appendix 1. \(\square \)

The interpretation of Lemma 1 is of high practical relevance: For pricing of (cyber) insurance policies, usually only the individual loss distribution of a company is taken into account. As the marginal arrival rates stay unchanged, prices for all individual insurance contracts would stay unchanged (i.e. ‘correct’) between models (M) and \((\widetilde{M})\). This means that omitting information about common events would not lead to mispricing of individual policies. This identity of marginal rates is actually dangerous, as the crucial oversight of underestimating the extent of common events would not be evident as affecting (average) profitability, but only in a (worst-case) scenario that an unexpectedly large loss (exceeding the estimated risk measure, typically Value-at-Risk, which may be much smaller in model \((\widetilde{M})\) than the actual one in model (M), see next section) manifests.

3.2 Implications for dependence- and risk-measurement

3.2.1 Measuring portfolio risk

Despite the marginal rates staying unchanged when moving from (M) to \((\widetilde{M})\), see Lemma 1, omitting information about common events may have dangerous implications for risk management. We first illustrate how it may lead to an underestimation of portfolio risk, measured e.g. by Value-at-Risk, denoted \(\textbf{VaR}_{1-\gamma }\), of the total incident number in the portfolio in a policy year.Footnote 10\(\textbf{VaR}_{1-\gamma }\) for a r.v. X in an actuarial context (where positive values denote losses) is defined as

$$\begin{aligned} \textbf{VaR}_{1-\gamma }(X) = \inf \big \{x \in \mathbb {R}: \mathbb {P}(X \le x) \ge 1-\gamma \big \}, \quad \gamma \in (0,1). \end{aligned}$$
(5)

Note that the overall incident number in a portfolio of size K follows a compound Poisson distribution, i.e.

$$\begin{aligned}&S(T) := \sum _{i = 1}^{N(T)} Z_i,\; \quad \textit{where } N(T) \sim \text {Poi}\Big (T \sum _{k = 1}^K \lambda ^{|I|=k} \Big ),\\ {}&\{Z_i\}_{i \in \mathbb {N}}\; \textit{i.i.d. with } \mathbb {P}(Z_i = k) = \frac{\lambda ^{|I|=k}}{\sum _{k = 1}^K \lambda ^{|I|=k}},\; \forall k \in \{1,\ldots ,K\}. \end{aligned}$$

The rate \(\Big (\sum _{k = 1}^K \lambda ^{|I|=k}\Big )\) corresponds to the overall Poisson arrival rate of events (of any size), and \(\{Z_i\}_{i \in \mathbb {N}}\) correspond to the associated “jump sizes” of the total incident number, i.e. the number of companies affected in the \(i^{th}\) event. Therefore, we can use the Panjer recursion formula (based on [37], for details see Appendix 1) to compute the probability mass function (p.m.f.) and corresponding cumulative distribution function (c.d.f.) and Value-at-Risk (as in Eq. (5)) of the total incident number in a policy year under models (M) and \((\widetilde{M})\) for chosen \(\varvec{\lambda }\) and \(p \in [0,1]\). We choose an exemplary set of rates for a portfolio of size \(K=10\) as given in Table 1, where \(\varvec{\lambda }\) again denotes the rates of an original model (M) and \(\varvec{\widetilde{\lambda }}\) the rates of the corresponding model \((\widetilde{M})\) resulting from Assumption  2.

Figure 2a displays the p.m.f. under model (M) and highlights the comparison of \(\textbf{VaR}_{0.995}\) for \(p = 1\) (full information, i.e. original rates), \(p = 0.5\) (partial information about common events, compare Table 2), and \(p = 0\) (no information about common events, i.e. complete independence assumption). Figure 2b compares \(\textbf{VaR}_{1-\gamma }\) for \((1-\gamma ) \in \{0.95,0.995\}\) and \(p \in [0,1]\), based on the c.d.f. of total incident numbers under the rates \(\varvec{\lambda }\) and \(\varvec{\widetilde{\lambda }}\). This small example already highlights the importance of gathering (full!) information about the origins of cyber incidents, as otherwise the portfolio risk will be drastically underestimated.

Finally, let us mention an observation that can be made by considering the p.m.f. (and corresponding c.d.f.) for different \(p \in [0,1]\), as exemplarily depicted in Fig. 3: When moving from (M) to \((\widetilde{M})\), no events / incidents are missed completely, thus the c.d.f.s of the total incident number in the portfolio are not ordered in the sense of usual stochastic order, i.e. it does not hold that for all \(x \ge 0:\) \(F_{S_{\widetilde{M}}(T)}(x) \ge F_{S_{M}(T)}(x)\), where \(S_{M}(T)\) (resp. \(S_{\widetilde{M}}(T)\)) denotes the total incident number under model (M) (resp. \((\widetilde{M})\)).

We have observed, however, from the results illustrated in Table 2 and Fig. 2, that this ordering of c.d.f.s does hold for certain large values of x. Figure 3b shows that indeed it holds exactly for large values of x, more precisely \(x > x_0\) for some \(x_0 \ge 0\), i.e. the so-called single-crossing condition or cut-off criterion (see e.g. [35]) is fulfilled here. This is meaningful as it is a sufficient condition for another (weaker) type of stochastic order, so-called increasing convex order, which has an important connection to the class of coherent risk measures; this will be addressed more generally in a subsequent section.

Table 1 Original rates and resulting rates for \(p=0.5\) (i.e. for each event affecting a subset of at least two firms jointly, the incident at each firm is attributed correctly to this event with probability \(p=0.5\) and otherwise incorrectly seen as independent as a result of not being able to identify the common root cause) and \(p=0\). By partially omitting information about common events, the resulting idiosyncratic rates are much increased, rates of smaller common events (here up to \(|I| = 4\)) are also increased, whereas rates of larger common events (here from \(|I| = 6\) on) are lowered
Full size table
Table 2 Resulting marginal rates (homogeneous for all companies), expected total incident numbers, and risk measures \(\textbf{VaR}_{1-\gamma }(S(T))\) at three levels for \(p \in \{0,0.5,1\}\) and \(T=1\). Crucially, marginal rates and thus expected incident numbers \(\mathbb {E}[S(T)]\) do not change (by Lemma  1 and linearity), while \(\textbf{VaR}_{1-\gamma }(S(T))\) at all chosen levels is lowered when common event information is partly or fully disregarded
Full size table
Fig. 2
figure 2

Panel 2a shows the p.m.f. of the total incident number for parameters as in Table 1 and again \(T=1\). The solid vertical line depicts the corresponding \(\textbf{VaR}_{0.995}\) if full information about common events is available \((p=1)\), i.e. all incidents are classified correctly. The dashed lines depict analogously \(\textbf{VaR}_{0.995}\) for partial information (\(p=0.5\), i.e. for each event on average half of the resulting incidents are attributed correctly), and no information (\(p=0\), i.e. all incidents regarded as idiosyncratic) about common events. In both latter cases, the true risk is clearly underestimated (compare \(\textbf{VaR}_{0.995}\) for \(p=0\) with the ‘true’ underlying distribution!). Panel 2b shows \(\textbf{VaR}_{\cdot }\) for \((1-\gamma ) \in \{0.95,0.995\}\) and \(p \in [0,1]\) (in steps of \(\Delta = 0.01\)), based on underlying rates \(\varvec{\lambda }\) and \(\varvec{\widetilde{\lambda }}\). As expected, the lower the probability p of correctly identifying a common root cause, the more severe is the resulting underestimation of the risk

Full size image
Fig. 3
figure 3

Panel 3a shows the p.m.f. of the total incident number for rates \(\varvec{\lambda }\) as in Table  1, \(T=1\), and resulting rates \(\varvec{\widetilde{\lambda }}\) for \(p \in \{0,0.5\}\). Panel 3b analogously plots the c.d.f.s, illustrating that while the c.d.f.s are not ordered in the sense \(F_{S_{\widetilde{M}}(T)}(x) \ge F_{S_{M}(T)}(x),\; \forall x \ge 0\), there is a threshold value \(x_0\) s.t. this ordering holds (exactly) for large values \(x > x_0 \ge 0\), i.e. the so-called single-crossing condition is fulfilled here. In the actuarial context, one is typically interested in high quantiles of the loss distribution (\(\textbf{VaR}_{1-\gamma }\) for \((1-\gamma )\) close to 1), i.e. the region where in this case it holds for the quantile functions \(F^{\leftarrow }_{S_{\widetilde{M}}(T)}(1-\gamma ) \le F^{\leftarrow }_{S_{M}(T)}(1-\gamma )\), leading to the observations for the portfolio risk measure discussed in this section

Full size image

3.2.2 Quantifying dependence by joint loss arrival rate

From a practical viewpoint, the illustrations of the last section already emphasize the detrimental effects of missing information about common events. Theoretically, there are different quantities one might use to assess the extent of “missed / overlooked dependence” in model \((\widetilde{M})\) compared to the true model (M). From a risk management perspective, it is clear that simultaneous losses by multiple policyholders carry potentially greater risk than independent, diversifiable losses. Therefore, one might look at the instantaneous rate of two policyholders \(i,j \in \{1,\ldots ,K\},\; i \ne j\), simultaneously experiencing a cyber claim. As we are assuming an exchangeable model, one can set w.l.o.g. \(i=1,\;j=2\). As arrivals of cyber incidents to policyholder \(i \in \{1,\ldots ,K\}\) follow a Poisson process with rate \(\lambda ^i\) (see (2)), the first arrival time, denoted \(\tau _i\), follows an exponential distribution and for small \(T > 0\) it holds by a first-order Taylor expansion

$$\begin{aligned} \mathbb {P}(\tau _i \le T) = 1- e^{-\lambda ^i T} \approx 1- (1-\lambda ^i T) = \lambda ^i T \iff \frac{1}{T} \approx \frac{\lambda ^i}{\mathbb {P}(\tau _i\le T)}. \end{aligned}$$

This implies for the instantaneous joint loss arrival rate

$$\begin{aligned} \begin{aligned} \lim _{T \searrow 0} \frac{\mathbb {P}(\tau _i \le T, \tau _j \le T)}{T} \approx \lim _{T \searrow 0} \frac{\lambda ^i \mathbb {P}(\tau _i \le T, \tau _j \le T)}{\mathbb {P}(\tau _i \le T)} \\ = \lambda ^i \lim _{T \searrow 0} \mathbb {P}(\tau _j \le T \; \vert \; \tau _i \le T) = \lambda ^i \; \text {LTD}_{C}, \end{aligned} \end{aligned}$$
(6)

where \(\tau _i,\tau _j\) are the first arrival times of a cyber claim to policyholders i and j, respectively, and \(\text {LTD}_{C}\) denotes the lower tail dependence coefficient of the bivariate copula C of \((\tau _i,\tau _j)\). We know (see [31], p. 122ff) that by Assumption  1 the survival copula of the random vector of all K first claim-arrival times, \((\tau _1,\ldots ,\tau _K)\), is an exchangeable Marshall–Olkin (eMO) survival copula, and its two-margins (i.e. the survival copula of \((\tau _i,\tau _j)\)) are bivariate Cuadras–Augé copulas with parameter \(\alpha \) given by (see a previous footnote on the relation of \(\lambda ^{|I|=i}\) and \(\lambda _i\)):

$$\begin{aligned} \alpha = 1 - \frac{\sum _{i=1}^{K-1} \left( {\begin{array}{c}K-2\\ i-1\end{array}}\right) \frac{1}{\left( {\begin{array}{c}K\\ i\end{array}}\right) } \lambda ^{|I|=i}}{\sum _{i=1}^{K} \left( {\begin{array}{c}K-1\\ i-1\end{array}}\right) \frac{1}{\left( {\begin{array}{c}K\\ i\end{array}}\right) } \lambda ^{|I|=i}} = 1 - \frac{\sum _{i=1}^{K-1} \left( {\begin{array}{c}K-2\\ i-1\end{array}}\right) \lambda _i}{\sum _{i=1}^{K} \left( {\begin{array}{c}K-1\\ i-1\end{array}}\right) \lambda _i}. \end{aligned}$$
(7)

From (7), some interpretation of \(\alpha \) is immediately visible:

  • Comonotonicity occurs iff only common events to the whole portfolio occur, i.e. \(\alpha = 1 \iff \lambda _K > 0, \lambda _i = 0 \; \forall i \in \{1,\ldots ,K-1\}\);

  • Independence occurs iff only idiosyncratic incidents occur, i.e. \(\alpha = 0 \iff \lambda _1 > 0, \lambda _i = 0 \; \forall i \in \{2,\ldots ,K\}\).

Definition 2

(Bivariate Cuadras–Augé copula, [31], p. 9) For \(\alpha \in [0,1]\), let \(C_\alpha : [0,1]^2 \mapsto [0,1]\) be defined by

$$\begin{aligned} C_\alpha (u_1,u_2) := \min \{u_1,u_2\} \max \{u_1,u_2\}^{1-\alpha }, \quad u_1,u_2 \in [0,1]. \end{aligned}$$

Remark 2

[Tail dependence coefficients of Cuadras–Augé (survival) copula ( [31], p. 34f)] For a bivariate Cuadras–Augé copula \(C_\alpha \), the tail dependence coefficients are given by

$$\begin{aligned}&\text {UTD}_{C_\alpha } = \alpha , \quad \text {LTD}_{C_\alpha } = \textbf{1}_{\{\alpha =1\}}. \end{aligned}$$

Note that in general for a copula C and its survival copula \(\hat{C}\), it holds (provided existence) that \(\text {UTD}_{C} = \text {LTD}_{\hat{C}}\) and \(\text {LTD}_{C} = \text {UTD}_{\hat{C}}\), respectively.

This means for the comparison of the instantaneous joint loss arrival rate in (6), we are interested in comparing the parameter \(\alpha \) (as in (7)) for models (M) and \((\widetilde{M})\).

Remark 3

(\(LTD_{\hat{C}_\alpha }\) for constant \(\varvec{\lambda }\)) Assume \(\lambda ^{|I|=i} \equiv \bar{\lambda } > 0,\; \forall i \in \{1,\ldots ,K\}\). Then, in model (M) the lower tail dependence coefficient of the bivariate copula of \((\tau _i,\tau _j)\) is given by

$$\begin{aligned} LTD_{\hat{C}_\alpha } = \alpha = \frac{2}{3}, \end{aligned}$$

and the instantaneous joint loss arrival rate in (6) is given by

$$\begin{aligned} \lim _{T \searrow 0} \frac{\mathbb {P}(\tau _i \le T, \tau _j \le T)}{T} = \lambda ^i \alpha = \frac{\bar{\lambda } (K+1)}{2} \cdot \frac{2}{3} = \frac{\bar{\lambda } (K+1)}{3}. \end{aligned}$$

Proof

See Appendix 1. \(\square \)

Lemma 2

[Relation of \(LTD_{\hat{C}_\alpha }\) for models (M) and \((\widetilde{M})\)] Let (M) be an exchangeable model as in Assumption 1 with any vector of arrival rates \(\varvec{\lambda }\) and let \((\widetilde{M})\) be the corresponding model according to Definition 1. Let \(\alpha \) and \(\widetilde{\alpha }\) be the respective parameters of the bivariate survival copulas of (any two) first-arrival times \((\tau _i,\tau _j)\) as given in (7). Then, it holds that \(\widetilde{\alpha } \le \alpha \) and more specifically, under Assumption 2,

$$\begin{aligned} \widetilde{\alpha } = p^2 \alpha \end{aligned}$$

for any \(p \in [0,1]\).

Proof

See Appendix 1. \(\square \)

Lemma 2 implies that in model \((\widetilde{M})\), by omitting information about common events according to Assumption 2, the instantaneous joint loss arrival rate for any two companies in the portfolio is underestimated by a factor of \(p^2\), which intuitively makes sense, as this factor indicates the probability of independently not overlooking a joint event in two companies.

3.2.3 Stochastic ordering and coherent risk measures

Above, we have observed exemplarily that the portfolio risk when measured by Value-at-Risk (at ‘relevant’ levels in an actuarial context, see the remark about the single-crossing condition above and illustration in Fig. 3b) is underestimated in a model with missing information \((\widetilde{M})\) compared to an original model (M). Another important risk measure is Expected Shortfall (at level \((1-\gamma )\)), in the following denoted \(\textbf{ES}_{1-\gamma }(X)\) for a r.v. X in the actuarial context, defined as (see e.g. [1]):

$$\begin{aligned} \textbf{ES}_{1-\gamma }(X) = \frac{1}{\gamma } \int _{1-\gamma }^{1} \textbf{VaR}_z(X) \textrm{d}z, \end{aligned}$$
(8)

where \(\textbf{VaR}_z(X)\) is defined in (5). It is well-known that \(\textbf{ES}_{1-\gamma }\) possesses in a certain sense preferable analytical properties compared to \(\textbf{VaR}_{1-\gamma }\), in particular \(\textbf{ES}_{1-\gamma }\) is a coherent risk measure. We refer to the seminal work of [5] for the definition and properties of coherent risk measures and e.g. [21] for a collection of proofs of the coherence of expected shortfall.Footnote 11 The fact of \(\textbf{ES}_{1-\gamma }\) being coherent allows to draw some interesting theoretical conclusions for the present study presented below in Corollary 1. As a basis, we use the more general observation on the stochastic ordering of compound Poisson random variables summarized in the following theorem.

Theorem 1

(Increasing convex order for specific compound Poisson distributions) Let \(L > 0\) and \(\ell \in \mathbb {N}\) and consider two independent homogeneous Poisson processes with intensities \(\lambda > 0\) and \(\widetilde{\lambda }:= \ell \; \lambda > 0\), denoted \(N(t):= (N(t))_{t \ge 0}\) and \(\widetilde{N}(t)\), respectively. For any fixed \(T > 0\), let

$$\begin{aligned} S(T) := \sum _{i = 1}^{N(T)} L = L \; N(T) \quad \text {and}\quad \widetilde{S}(T) = \sum _{i = 1}^{\widetilde{N}(t)} \frac{L}{\ell } = \frac{L}{\ell } \widetilde{N}(T). \end{aligned}$$

Then, \(\mathbb {E}\big [S(T)\big ] = \mathbb {E}\big [\widetilde{S}(T)\big ]\) and

$$\begin{aligned} S(T) \ge _{icx} \widetilde{S}(T), \end{aligned}$$
(9)

where \(\ge _{icx}\) denotes ‘increasing convex order’.

Proof

See Appendix 1.Footnote 12\(\square \)

Remark 4

(Notes to Theorem 1)

  1. 1.

    Note that \(S(T) \ge _{icx} \widetilde{S}(T)\) and \(\mathbb {E}\big [S(T)\big ] = \mathbb {E}\big [\widetilde{S}(T)\big ]\) is equivalent to \(S(T) \ge _{cx} \widetilde{S}(T)\) (‘convex order’), see [35], Theorem 1.5.3.

  2. 2.

    In actuarial science, a perhaps more common, synonymous name for ‘increasing convex order’ (\(\ge _{icx}\)) is ‘stop-loss order’ (\(\ge _{sl}\)), which stems from an important characterization of \(\ge _{icx}\) by the so-called stop-loss transforms (see [35], Theorem 1.5.7):

    $$\begin{aligned} X \le _{icx} Y \iff \mathbb {E}\big [(X-t)_+\big ] \le \mathbb {E}\big [(Y-t)_+\big ] \;\; \forall t \in \mathbb {R}. \end{aligned}$$
    (10)
  3. 3.

    Note that S(T) and \(\widetilde{S}(T)\) can be interpreted as two collective risk models with equal expected total claims amount \(\mathbb {E}\big [S(T)\big ] = \mathbb {E}\big [\widetilde{S}(T)\big ]\), where

    \(\diamond \):

    S(T) is the total claims amount from a model with relatively few, large losses (of deterministic size \(L > 0\)), and

    \(\diamond \):

    \(\widetilde{S}(T)\) is the total claims amount from a model with relatively many, small losses (of deterministic size \(0< \frac{L}{\ell } < L\)).

    Thus, Theorem 1 states that the model with on average many (independent) small losses is preferable (‘less risky’) in the sense of increasing convex order compared to a model with equal expected claims amount and on average few (independent) large losses.

Corollary 1

[Expected Shortfall for models (M) and \((\widetilde{M})\)] Let \(\textbf{ES}_{1-\gamma }(\cdot )\) denote Expected Shortfall as in (8) and let \(S_M(T)\) and \(S_{\widetilde{M}}(T)\) denote the total incident number in the portfolio under models (M) and \((\widetilde{M})\), respectively, until a fixed time \(T>0\). Then, for any \(T > 0\) and any \(\gamma \in (0,1)\), it holds

$$\begin{aligned} \textbf{ES}_{1-\gamma }\big (S_M(T)\big ) \ge \textbf{ES}_{1-\gamma }\big (S_{\widetilde{M}}(T)\big ). \end{aligned}$$
(11)

Proof

See Appendix 1. \(\square \)

This implies that by omitting information about common events, the portfolio risk is necessarily underestimated when using expected shortfall (or any other coherent risk measure).

4 Conclusion

When insurers started to develop actuarial models for cyber risk, they soon emphasized that one major challenge is the lack of adequate data to calibrate and backtest their models. Many classical actuarial models are based on the assumption of independence between losses and historical data is mainly used to draw inference about individual policyholders’ loss distributions (i.e. the parameters of their loss frequency and severity distribution for a certain risk). Indeed, this is sufficient in markets where the claims are independent. Risk assessment and claims settlement therefore usually take into account this individual client-specific information. However, in the case of cyber, collecting such individual information alone is not sufficient, as not only parameters of the individual (marginal) loss distributions, but also those of an adequate model of dependence, have to be calibrated. This is only possible if information about dependence between historical claims, i.e. that losses may have stemmed from the same cause, is thoroughly collected.

This article has used a stylized mathematical model to highlight the effects on portfolio risk measurement if information on common events is fully or partly discarded. This is particularly relevant as in practice efforts are often concentrated on and limited to striving to correctly model marginal distributions. We illustrate that even with full and correct understanding of the marginal distributions, in the cyber context the portfolio risk is necessarily underestimated without a likewise full understanding of the underlying dependence structure. In practice, and we have to raise a big warning sign here, the resulting underestimation of accumulation risk would only become evident too late, namely once a (to-be-avoided) extreme portfolio loss has occurred. These results are particularly relevant in the cyber context, where the development of actuarial models and connected processes in the insurance value chain is still nascent and historical loss data is scarce, but may in principle likewise be applied to established insurance lines where accumulation risk due to common events is present.

The urgent practical implications for insurers are evident: As outlined in Sect. 2.1, actuarial modelling of cyber cannot be regarded as an isolated challenge, but as one interconnected step in the insurance value chain. Actuaries therefore must be in continuous exchange with other stakeholders, in particular legal experts (regarding insurability of cyber, product design, and requirements on the collection of claims settlement data) and information security experts. The central importance of the latter group for the actuarial modelling of cyber can hardly be overstated; their expertise is essential in tackling important challenges such as how to include an extensive qualitative assessment of a company’s IT landscape, including existing security provisions, into a stochastic actuarial model.

Only continuous interdisciplinary cooperation will allow to develop a holistic approach which allows insurers to proactively steer their cyber underwriting activities without exposing themselves to potentially starkly underestimated levels of accumulation risk.