Multivariate Lévy-type drift change detection and mortality modeling

Abstract

In this paper we give a solution to the quickest drift change detection problem for a multivariate Lévy process consisting of both continuous (Gaussian) and jump components in the Bayesian approach. We do it for a general 0-modified continuous prior distribution of the change point as well as for a random post-change drift parameter. Classically, our criterion of optimality is based on a probability of false alarm and an expected delay of the detection, which is then reformulated in terms of a posterior probability of the change point. We find a generator of the posterior probability, which in case of general prior distribution is inhomogeneous in time. The main solving technique uses the optimal stopping theory and is based on solving a certain free-boundary problem. We also construct a Generelized Shiryaev-Roberts statistic, which can be used for applications. The paper is supplemented by two examples, one of which is further used to analyze Polish life tables (after proper calibration) and detect the drift change in the correlated force of mortality of men and women jointly.

1 Introduction

The quickest detection problems (also called the disorder problems) try to answer a question: how to detect significant changes in the observed system? We assume that the system is described as a certain probabilistic model and the goal is to use appropriate statistical methods to find the change in an optimal way. First, however, it is necessary to specify what optimal means in that context. Such problems are natural in many applications, such as economics, finance or engineering. One of the classical approaches to disorder problems is based on the drift change detection and on the Bayesian approach—see Shiryaev [29, 30], where Brownian motion with linear drift is considered and the drift is changing according to an exponential distribution. The original problem was first reformulated there in terms of a free-boundary problem. Then it was solved using optimal stopping methods. All details of this analysis are also given in surveys [35, 37] (see also references therein). Apart from Baysian method, the minimax approach have also been studied in the context of detection problems. This method is based on identifying the optimal detection time based on so-called cumulative sums (CUSUM) strategy; see e.g. Page [20], Beibel [3], Shiryaev [32] or Moustakides [18] in the Wiener case, or El Karoui et al. [14] in the Poisson case. The book of Poor and Hadjiliadis [26] gathers many approaches to these quickest detection problems. In this paper we choose the first approach.

Our first main goal is to perform the analysis of the quickest drift change detection problem for multivariate processes, taking into account the dependence between components. We also allow a general 0-modified continuous prior distribution of the change point, as well as random post-change drift parameter.

Most of works on the detection problems in Bayesian setting has been devoted to the one-dimensional processes consisting of only continuous (Gaussian) part or only jumps; see e.g. Beibel [2], Shiryaev [30] or [36, Chap. 4] or Poor and Hadjiliadis [26]. Only some particular cases of jump models without diffusion component have been already analysed, e.g. by Gal’chuk and Rozovskii [11], Peskir and Shiryaev [23] or Bayraktar et al. [4] for the Poisson process, by Gapeev [12] for the compound Poisson process with the exponential jumps or by Dayanik and Sezer [7] for more general compound Poisson problem. Later, Krawiec et al. [15] allowed observed process to have, apart from diffusion ingredient, jumps as well. This is very important in many applications appearing in actuarial science, finance, etc. Lévy processes have appeared in the context of the optimal detection in other last works as well. In particular, in [5] Buonaguidi studies the disorder problem for purely jump Lévy processes with completely monotone jumps. In this case, the solution to the disorder problem for a hyperexponential process is used to approximate the one of the original problem. The efficiency of the proposed approximation scheme is investigated for some popular Lévy processes, such as the gamma, inverse Gaussian, variance-gamma and CGMY processes. Moreover, in [10] Figueroa-López and Ólafsson prove that CUSUM procedure is optimal in Lorden’s sense for change-point detection for Lévy processes. What is interesting, their approach is based on approximating the continuous-time problem by a suitable sequence of change-point problems with equispaced sampling points, and for which a CUSUM procedure is shown to be optimal. Similar ideas can be found in [6, 9, 41]. Still, all of these results concern one-dimensional case only. This paper removes this limitation.

In addition, we assume that a drift change point $\theta$ has a general 0-modified continuous prior distribution G. In most works it has been assumed that $\theta$ can have only (0-modified) exponential distribution. Such assumption makes the free-boundary problem time-homogenous due to lack of memory property, which is not true in the general case. Furthermore, similarly like in Dayanik et al. [8], we assume that the direction of disorder is a random vector $\zeta$ with known prior multivariate distribution function H(r). That is, after the change of drift, a new drift is chosen according to the law H. In the case when H is a one-point distribution we end up with the classical question where the after-change drift is fixed and different than zero. In the case when H is supported on two points in ${\mathbb R}^d$ we know that after-change drift may take one of the two possible values with known weights. Even for $d=1$ this additional feature of our model gives much more freedom and has not been analyzed in detail yet.

The methodology used in this paper is based on transferring the detection problem to a certain free-boundary problem. More formally, in this paper we consider the process $X=(X_t)_{t\ge 0}$ with

$$\begin{aligned} X_t:=\left\{ \begin{array}{ll} X^{\infty }_t, &{} t<\theta , \\ X^{\infty }_{\theta } + X^{(0,r)}_{t-\theta }, &{} t \ge \theta , \end{array} \right. \end{aligned}$$

(1)

where $X^{\infty }=(X^{\infty }_t)_{t\ge 0}$ and $X^{(0,r)}=(X^{(0,r)}_t)_{t\ge 0}$ are both independent jump-diffusion processes taking values in ${\mathbb R}^d$. We assume that $X^{\infty }$ and $X^{(0,r)}$ are related with each other via the exponential change of measure described e.g. in Palmowski and Rolski [21]. This change of measure can be seen as a form of the drift change between $X^{\infty }$ and $X^{(0,r)}$ with additional change in jump distribution. The parameter r corresponds to the rate (direction) of disorder that can be observed after time $\theta$.

Let $\theta$ has an atom at zero with mass $x>0$. We choose the classical optimality criterion based on both probability of a false alarm and a mean delay time. That is, in this paper, we are going to find an optimal detection rule $\tau ^*\in {\mathcal {T}}$ for which the following infimum is attained

$$\begin{aligned} V^*(x):=\inf _{\tau \in {\mathcal {T}}}\left\{ \overline{{\mathbb P}}^{G,H}(\tau <\theta ) + c\overline{{\mathbb E}}^{G,H}_x[(\tau -\theta )^+]\nonumber \right\} , \end{aligned}$$

where ${\mathcal {T}}$ is the family of stopping times and $c>0$ is fixed number. Measure ${\overline{{\mathbb P}}}^{G,H}$ will be formally introduced later. Firstly, we transfer above detection problem into the following optimal stopping problem

$$\begin{aligned} V^*(x)=\inf _{\tau \in {\mathcal {T}}}{\overline{{\mathbb E}}}^{G,H}_x\left[ 1-\pi _{\tau } + c\int _0^{\tau }\pi _sds\right] , \end{aligned}$$

for the a posteriori probability process $\pi =(\pi _t)_{t\ge 0}$ that also will be formally introduced later. The subscript x associated with ${\overline{{\mathbb E}}}^{G,H}$ indicates the starting position of process $\pi$ equal to x. In the next step, using the change of measure technique and stochastic calculus, we can identify the infinitesimal generator of the Markov process $\pi$. This part contains results of independent interest on properties of the posterior process $\pi$, that are related to the multidimensionality of the process X. In the classical case with exponential distribution G, $\pi$ is time-homogenous with generator ${\mathcal {A}}$. Finally, we formulate the free-boundary value problem, which in the time-homogenous case is as follows

$$\begin{aligned} \begin{aligned} {\mathcal {A}}f(x)=-cx,\quad 0\le x < A^*, \\ f(x)=1-x,\quad A^*\le x \le 1, \end{aligned} \end{aligned}$$

with the boundary conditions

$$\begin{aligned} f(A^{*-}){} & {} =1-A^* \quad \mathrm{(continuous\; fit)}, \\ f'(A^{*-}){} & {} =-1 \quad \mathrm{(smooth\; fit)}, \\ f'(0^+){} & {} =0 \quad \mathrm{(normal\; entrance)} \end{aligned}$$

for some optimal level $A^*$ which allows to identify the threshold optimal alarm rule as

$$\begin{aligned} \tau ^*=\inf \{t\ge 0:\pi _t\ge A^*\}. \end{aligned}$$

We first generalize above free-boundary problem and then solve it for two basic models: two-dimensional Brownian motion with known post-change drift and two-dimensional Brownian motion with downward exponential jumps.

Our second main goal is to apply the solution of above multivariate detection problem to the analysis of correlated change of drift in force of mortality of men and women. The life expectancies for men and women are widely recognized as dependent on each other. For example, married people live statistically longer than single ones. Since many insurance products are engineered for marriages or couples it is crucial to detect the change of mortality rate of marriages. Indeed, the observed improvements of longevity produce challenges related with the capital requirements that has to be constituted to face this long-term risk and with creating new ways to cross-hedge or to transfer part of the longevity risk to reinsurers or to financial markets. To do this we need to perform accurate longevity projections and hence to predict the change of the drift observed in prospective life tables (national or the specific ones used in insurance companies). In this paper we analyze the Polish life tables for both men and women jointly. We proceed as follows. We take logarithm of the force of mortality of men and women creating a two-dimensional process, modeled then by a jump-diffusion process. This process consists of observed two-dimensional drift that can be calibrated from the historical data and a random zero-mean Lévy-type perturbation. Based on previous theoretical work we construct a statistical and numerical procedure based on the generalized version of the Shiryaev-Roberts statistic introduced by Shiryaev [29, 30] and Roberts [27], see also Polunchenko and Tartakovsky [24], Shiryaev [33], Pollak and Tartakovsky [25] and Moustakides et al. [19]. Precisely, we start from a continuous statistic derived from the solution of the optimal detection problem in continuous time. Then we take discrete moments $0<t_1<t_2<\ldots <t_N$, construct an auxiliary statistic and raise the alarm when it exceeds certain threshold $A^*$ identified in the first part of the paper.

The set-up used in examples is, however, simplified compared to the theory presented in the previous sections. Applications focus mainly on multi-dimensionality of presented problem, to see how one can analyse mortality of men and women jointly. The distribution of change time $\theta$ is limited to classical (0-modified) exponential.

The paper is organized as follows. In Sect. 2 we describe basic setting of the problem, introduce main definitions and notation. In this section we also formulate main theoretical results of the paper. Section 3 is devoted to the construction of the Generalized Shiryaev-Roberts statistic. To apply it, we first need to find some density processes related to the processes X prior and post the drift change. This is done in Sect. 3 as well. Particular examples are analyzed in Sect. 4. Next, in Sect. 5, we give an application of the theoretical results to a real data from life tables. We finish our paper with some technical proofs given in Sect. 6.

2 Model description and main results

The main observable process is a regime-switching d-dimensional process $X=(X_t)_{t\ge 0}$. It changes its behavior at a random moment $\theta$ in the following way:

$$\begin{aligned} X_t=\left\{ \begin{array}{ll} X^{\infty }_t, &{} t<\theta , \\ X^{\infty }_{\theta } + X^{(0,r)}_{t-\theta }, &{} t \ge \theta , \end{array} \right. \end{aligned}$$

(2)

where $X^{\infty }$ and $X^{(0,r)}$ are two different independent Lévy processes related with each other via exponential change of measure specified later. The parameter r describes the drift after time $\theta$. We will also assume that in general drift r is driven by a random vector $\zeta$ with a given distribution H(r), which we formally introduce later. Moreover, this drift is chosen at time $t=0$. Further, $\theta$ is independent of the pre- and post-change random processes.

We assume the following model when the post-change drift equals r. The process that we observe after the change of drift is a d-dimensional processes $X^{(0,r)} = (X^{(0,r)}_t)_{t\ge 0} = (X^{(0,r)}_{t,1},\ldots ,X^{(0,r)}_{t,d})_{t\ge 0}$ defined as

$$\begin{aligned} X_t^{(0,r)}:=\sigma W_t^{r}+rt+\sum _{k=1}^{N_t^{(0,r)}} J_k^{(0,r)}-\mu ^r m^r t, \end{aligned}$$

(3)

where

• $W^r=(W_t^{r})_{t\ge 0}=(W_{t,1}^{r},\ldots ,W_{t,d}^{r})^T$ is a vector of standard independent Brownian motions,

• $\sigma =(\sigma _{i,j})_{i,j=1,\ldots ,d}$ is a matrix of real numbers, responsible for the correlation of the diffusion components of $X^{(0,r)}_{t,1},\ldots ,X^{(0,r)}_{t,d}$, we assume that $\sigma _{ii}>0$ for all $i=1,\ldots ,d$,

• $r=(r_1,\ldots ,r_d)^T$ is a vector of an additional drift,

• $N^{(0,r)}=(N_t^{(0,r)})_{t\ge 0}$ is a Poisson process with intensity $\mu ^r$,

• $(J_k^{(0,r)})_{k\ge 1}$ is a sequence of i.i.d. random vectors responsible for jump sizes; we denote each coordinate of $J_k^{(0,r)}$ by $J_{k,i}^{(0,r)}$ for $i=1,\ldots ,d$ and its distribution by $F^{r}_i$ with mean $m^{r}_i$; we also denote by $F^{r}$ a joint distribution of vector $J_k^{(0,r)}$ and by $m^{r}=(m^r_1,\ldots ,m^r_d)^T$ its mean.

We assume that all components of $X_t^{(0,r)}$ are stochastically independent, i.e. $W_t^{(0,r)}$, $N_t^{(0,r)}$ and the sequence $(J_k^{(0,r)})_{k=1,2,\ldots }$ are independent.

Similarly, we assume that the process that we observe prior the drift change is a d-dimensional process $X^{\infty } = (X^{\infty }_t)_{t\ge 0} = (X^{\infty }_{t,1},\ldots ,X^{\infty }_{t,d})_{t\ge 0}$ defined as

$$\begin{aligned} X_t^{\infty }:=\sigma W_t^{\infty }+\sum _{k=1}^{N_t^{\infty }} J_k^{\infty }-\mu ^{\infty } m^{\infty } t, \end{aligned}$$

(4)

where

• $W^{\infty }=(W_t^{\infty })_{t\ge 0}$ is a vector of standard independent Brownian motions,

• matrix $\sigma$ is the same as for the process $X^{(0,r)}$,

• $N^{\infty }=(N_t^{\infty })_{t\ge 0}$ is a Poisson process with intensity $\mu ^{\infty }$,

• $(J_k^{\infty })_{k\ge 1}$ is a sequence of i.i.d. random vectors, where each coordinate $J_{k,i}^{\infty }$ of $J_k^{\infty }$ has distribution $F^{\infty }_i$ with mean $m^{\infty }_i$; we also denote by $F^{\infty }$ a joint distribution of vector $J_k^{\infty }$ and by $m^{\infty }=(m^{\infty }_1,\ldots ,m^{\infty }_d)^T$ its mean.

To formally construct the model with a drift change described above, we follow the ideas of Zhitlukhin and Shiryaev [42]. Precisely, we consider a filtered measurable space $(\Omega , \mathcal {F}, \{\mathcal {F}_t\}_{t\ge 0})$ with a right-continuous filtration $\{\mathcal {F}_t\}_{t\ge 0}$, on which we define a stochastic system with disorder as follows. First, on a probability space $(\Omega , \mathcal {F}, \{\mathcal {F}_t\}_{t\ge 0})$ we introduce probability measures ${\mathbb P}^{\infty }$ and ${\mathbb P}^{(0,r)}$ for $r\in {\mathbb R}^d$ with their restrictions to ${\mathcal {F}}_t$ given by ${\mathbb P}^{\infty }_t:={\mathbb P}^{\infty }|_{\mathcal {F}_t}$ and ${\mathbb P}^{(0,r)}_t:={\mathbb P}^{(0,r)}|_{\mathcal {F}_t}$. We assume that for each $t\ge 0$ the restrictions ${\mathbb P}^{\infty }_t$ and ${\mathbb P}^{(0,r)}_t$ are equivalent. The measure ${\mathbb P}^{\infty }$ corresponds to the case when there is no drift change in the system at all and ${\mathbb P}^{(0,r)}$ describes the measure under which there is a drift r present from the beginning (i.e. from $t=0$). In the following we assume that both measures correspond to laws of the processes $X^{\infty }$ and $X^{(0,r)}$ described above, respectively. We also introduce a probability measure ${\mathbb P}$ that dominates ${\mathbb P}^{\infty }$ and ${\mathbb P}^{(0,r)}$ for each $r\in {\mathbb R}^d$ and such that the restriction ${\mathbb P}_t:={\mathbb P}|_{\mathcal {F}_t}$ is equivalent to ${\mathbb P}^{\infty }_t$ and ${\mathbb P}^{(0,r)}_t$ for each $t\ge 0$.

We define the Radon-Nikodym derivatives

$$\begin{aligned} L_t^{(0,r)}:=\frac{\textrm{d}{\mathbb P}_t^{(0,r)}}{\textrm{d}{\mathbb P}_t}, \quad L_t^{\infty }:=\frac{\textrm{d}{\mathbb P}_t^{\infty }}{\textrm{d}{\mathbb P}_t}. \end{aligned}$$

(5)

Furthermore, for $s\in (0,\infty )$ we define

$$\begin{aligned} L_t^{(s,r)}:=L_t^{\infty }I(t<s)+\frac{L_{s^-}^{\infty }}{L_{s^-}^{(0,r)}}L_t^{(0,r)}I(t\ge s). \end{aligned}$$

(6)

Finally, for any fixed $s\in (0,\infty )$ and $r\in {\mathbb R}^d$, taking a consistent family of probability measures $({\mathbb P}_t^{(s,r)})_{t\ge 0}$ defined via

$$\begin{aligned} \frac{\textrm{d}{\mathbb P}_t^{(s,r)}}{\textrm{d}{\mathbb P}_t}=L_t^{(s,r)}. \end{aligned}$$

by the Kolmogorov’s existence theorem we can define measures ${\mathbb P}^{(s,r)}$ such that ${\mathbb P}^{(s,r)}|_{\mathcal {F}_t}={\mathbb P}^{(s,r)}_t$. Note that for $t<s$ and all $r\in {\mathbb R}^d$ the following equality holds

$$\begin{aligned} {\mathbb P}_t^{\infty }={\mathbb P}_t^{(s,r)}, \end{aligned}$$

since disorder after time t does not affect the behavior of the system before time t.

We consider Bayesian framework, that is, we assume that the moment of disorder is a random variable $\theta$ with a given distribution function denoted by G(s) on $({\mathbb R}_+,\mathcal {B}({\mathbb R}_+))$. We assume that G(s) is continuous for $s>0$ with right derivative $G'(0)>0$. Similarly, we assume that the rate (direction) of disorder is a random vector $\zeta$ with multivariate distribution function H(r) on $({\mathbb R}^d,\mathcal {B}({\mathbb R}^d))$. Hence, to catch this additional randomness we have to introduce an extended filtered probability space $({\overline{\Omega }},{\overline{\mathcal {F}}},\{\overline{\mathcal {F}_t}\}_{t\ge 0},{\overline{{\mathbb P}}}^{G,H})$ such that

$$\begin{aligned}{} & {} {\overline{\Omega }}:=\Omega \times {\mathbb R}_+\times {\mathbb R}^d,\quad {\overline{\mathcal {F}}}:=\mathcal {F}\otimes \mathcal {B}({\mathbb R}_+)\otimes \mathcal {B}({\mathbb R}^d),\nonumber \\ {}{} & {} \quad {\overline{\mathcal {F}}}_t:=\mathcal {F}_t\otimes \{\emptyset ,{\mathbb R}_+\}\otimes \{\emptyset ,{\mathbb R}^d\}. \end{aligned}$$

(7)

Measure ${\overline{{\mathbb P}}}^{G,H}$ is defined for $A\in \mathcal {F}, B\in \mathcal {B}({\mathbb R}_+)$ and $C\in \mathcal {B}({\mathbb R}^d)$ as follows

$$\begin{aligned} {\overline{{\mathbb P}}}^{G,H}(A\times B\times C):=\int _C\int _B{\mathbb P}^{(s,r)}(A)\textrm{d}G(s) \textrm{d}H(r). \end{aligned}$$

On this extended space random variables $\theta$ and $\zeta$ are defined by $\theta (\omega ,s,r):=s$ and $\zeta (\omega ,s,r):=r$ with ${\overline{{\mathbb P}}}^{G,H}(\theta \le s)=G(s)$ and ${\overline{{\mathbb P}}}^{G,H}(\zeta _1\le r_1,\ldots ,\zeta _d\le r_d)=H(r)$ for $\zeta =(\zeta _1,\ldots ,\zeta _d)$ and $r=(r_1,,\ldots ,r_d)$. Observe that measure ${\overline{{\mathbb P}}}^{G,H}$ describes formally the process X defined in (2).

In the problem of the quickest detection we are looking for an optimal stopping time $\tau ^*$ that minimizes certain optimality criterion. We consider a classical criterion, which incorporates both the probability of false alarm and the mean delay time. Let $\mathcal {T}$ denote the class of all stopping times with respect to the filtration $\{\overline{\mathcal {F}_t}\}_{t\ge 0}$. Our problem can be stated as follows:

Problem 1

For a given $c>0$ calculate the optimal value function

$$\begin{aligned} V^*(x)=\inf _{\tau \in \mathcal {T}}\{\overline{{\mathbb P}}^{G,H}(\tau <\theta ) + c\overline{{\mathbb E}}^{G,H}[(\tau -\theta )^+]\} \end{aligned}$$

(8)

and find the optimal stopping time $\tau ^*$ for which above infimum is attained.

Above $\overline{{\mathbb E}}^{G,H}$ means the expectation with respect to $\overline{{\mathbb P}}^{G,H}$.

The key role in solving this problem plays a posterior probability process $\pi =(\pi _t)_{t\ge 0}$ defined as

$$\begin{aligned} \pi := \int _{{\mathbb R}^d}\pi ^r\textrm{d}H(r), \quad \textrm{where} \quad \pi ^r=(\pi _t^r)_{t\ge 0} \quad \textrm{for} \quad \pi _t^r:={\overline{{\mathbb P}}}^{G,H}(\theta \le t|{\overline{\mathcal {F}}}_t, \zeta =r).\nonumber \\ \end{aligned}$$

(9)

We denote $x:=\pi _0=G(0)$ and add a subscript x to $\overline{{\mathbb E}}^{G,H}_x$ to emphasize it. Using this posterior probability, one can reformulate criterion (8) into the following, equivalent form:

Problem 2

For a given $c>0$ find the optimal value function

$$\begin{aligned} V^*(x)=\inf _{\tau \in \mathcal {T}}\overline{{\mathbb E}}^{G,H}_x\left[ 1-\pi _{\tau }+c\int _0^{\tau }\pi _s\textrm{d}s\right] \end{aligned}$$

and the optimal stopping time $\tau ^*$ such that

$$\begin{aligned} V^*(x)=\overline{{\mathbb E}}^{G,H}_x\left[ 1-\pi _{\tau ^*}+c\int _0^{\tau ^*}\pi _s\textrm{d}s\right] . \end{aligned}$$

That is, formally, the following result holds true.

Lemma 1

The criterion given in Problem 1 is equivalent to the criterion given in Problem 2.

Although the proof follows classical arguments, we added it in Sect. 6 for completeness.

Below we formulate the main theorem that connects Problem 2 to the particular free-boundary problem. It is based on the general optimal stopping theory in the similar way as Theorem 1 in Krawiec et al. [15], which it extends. However, for the general (continuous for $s>0$ with right derivative $G'(0)>0$) distribution G(s) of the moment $\theta$, the optimal stopping problem and its solution are time-dependent. The problem reduces to time-independent case for the (0-modified) exponential distribution G. We will prove it in Sect. 6.

Theorem 1

Let $\left( \frac{\partial }{\partial t}+{\mathcal {A}}\right)$ be a Dynkin generator of the Markov process $(t,\pi _t)_{t\ge 0}$. Then the optimal value function $V^*(x)$ from the Problem 2 equals $f_0(x)$, where $f_t(x)$ solves the free-boundary problem

$$\begin{aligned} \begin{array}{cc} \left( \frac{\partial }{\partial t}+{\mathcal {A}}\right) f_t(x)=-cx,&{} 0\le x < A^*(t), \\ f_t(x)=1-x,&{} A^*(t)\le x \le 1, \end{array} \end{aligned}$$

(10)

with the boundary conditions

$$\begin{aligned} f_t(A^{*}(t)-)= & {} 1-A^*(t) \quad \mathrm{(continuous\, fit)}, \end{aligned}$$

(11)

$$\begin{aligned} f^\prime _t(A^{*}(t)-)= & {} -1 \quad \mathrm{(smooth\, fit)}. \end{aligned}$$

(12)

Furthermore, the optimal stopping time for the Problem 2 is given by

$$\begin{aligned} \tau ^*=\inf \{t\ge 0:\pi _t\ge A^*(t)\}. \end{aligned}$$

(13)

If G is the (0-modified) exponential distribution, then $V^*(x)$ solves above free-boundary problem for the unique point $A^*~\in ~(0,1]$ not depending on time with the optimal stopping time given by

$$\begin{aligned} \tau ^*=\inf \{t\ge 0:\pi _t\ge A^*\}. \end{aligned}$$

(14)

Further, in this case $f_t(x)=f_0(x)=f(x)$ and additionally the following condition holds

$$\begin{aligned} f^\prime (0+)=0 \quad \mathrm{(normal\; entrance)}. \end{aligned}$$

(15)

See also Peskir and Shiryaev [22, Chap. VI. 22], Krylov [16, p. 41], Strulovici and Szydlowski [40, Thm. 4] and [1] for details.

It is known that the Dynkin generator is an extension of an infinitesimal generator in the sense of their domains. Following [22, Chap. III] and discussion done on page 131 of [22] (see also the proof of [13, Prop. 2.6]) we can conclude that the optimal value function $V^*(t,x)$ satisfies (10) where $\left( \frac{\partial }{\partial t} + {\mathcal {A}}\right)$ is an infinitesimal generator as long as there exists unique solution of (10) lying in the domain of infinitesimal generator.

Now to formulate properly above free-boundary problem, we have to identify the infinitesimal generator $\left( \frac{\partial }{\partial t} + {\mathcal {A}}\right)$ and its domain. They are given in next theorem. We use notation $f_t(x) = f(t,x)$ for functions $f: ([0,\infty ), [0,1]) \rightarrow {\mathbb {R}}$.

Theorem 2

The infinitesimal generator of the Markov process $(t,\pi _t)_{t\ge 0}$ is given by $\frac{\partial }{\partial t}f_t(x) +{\mathcal {A}} f_t(x)$ for

$$\begin{aligned} {\mathcal {A}}f_t(x):= & {} \int _{{\mathbb R}^d}\Bigg \{f_t'(x)\bigg ( -(1-x)(\log (1-G(t)))' + x(1-x)(\mu ^{\infty }-\mu ^r) \bigg )\nonumber \\{} & {} + \frac{1}{2}f_t''(x)x^2(1-x)^2\sum _{i=1}^d\sum _{j=1}^d z_{r,i}z_{r,j}(\sigma \sigma ^T)_{ij} \nonumber \\{} & {} + \int _{{\mathbb R}^d}\left[ f_t\left( \frac{x\exp \left\{ \sum _{i=1}^dz_{r,i}u\right\} }{x\left( \exp \left\{ \sum _{i=1}^dz_{r,i}u\right\} -1\right) +1}\right) -f_t(x)\right] \nonumber \\{} & {} \cdot \left[ (1-x)\mu ^{\infty }\textrm{d}F^{\infty }(u)+x\mu ^{r}\textrm{d}F^{(0,r)}(u)\right] \Bigg \}\textrm{d}H(r) \end{aligned}$$

(16)

and for functions $f_t\in {\mathcal {C}}^2$. If G(s) is the (0-modified) exponential distribution, then $(\pi _t)_{t\ge 0}$ is a Markov process with generator ${\mathcal {A}}$ given as above with term $-(1-x)(\log (1-G(t)))'$ substituted by $G'(0)$ for functions $f_t(x)=f(x)$ not depending on $t\ge 0$.

We will prove this theorem later in Sect. 6.

Assume that we can find unique solution of (10)-(12) in the class ${\mathcal {C}}^2$ with ${\mathcal {A}}$ given in (16) then by above considerations it follows that this solution equals the value function $V^*(t,x)$. Therefore in the final step we focus on the simple time-homogeneous case of exponential time change case, then we solve uniquely (10)-(12) for some specific choice of model parameters, and finally, find the optimal threshold $A^*$ and hence the optimal alarm time. This allows us to construct a Generalized Shiryaev-Roberts statistic in this general set-up. Later we apply it to detect the changes of drift in joint (correlated) mortality of men and women based on life tables.

3 Generalized Shiryaev-Roberts statistic

Following Zhitlukhin and Shiryaev [42] and Shiryaev [31, II.7] and using the generalized Bayes theorem, the following equality for process $\pi$ defined in (9) is satisfied

$$\begin{aligned} \pi _t = \int _{{\mathbb R}^d}\frac{\int _0^tL_t^{(s,r)} \textrm{d}G(s)}{\int _0^{\infty }L_t^{(s,r)} \textrm{d}G(s)}\textrm{d}H(r). \end{aligned}$$

(17)

We will give another representation of the process $\pi$ in terms of the process $L^r=(L_t^r)_{t\ge 0}$ defined by

$$\begin{aligned} L_t^r:=\frac{L_t^{(0,r)}}{L_t^{\infty }}=\frac{\textrm{d}{\mathbb P}_t^{(0,r)}}{\textrm{d}{\mathbb P}_t^{\infty }}. \end{aligned}$$

(18)

To find above Radon-Nikodym derivative such that process X defined in (2) indeed admits representation (3) under the measure ${\mathbb P}^{(0,r)}$ and (4) under ${\mathbb P}^{\infty }$, we assume that for given $r=(r_1,\ldots ,r_d)\in {\mathbb R}^d$ the following relation holds

$$\begin{aligned} \forall _{x\in {\mathbb R}^d}\quad \mu ^r F^r(\textrm{d}y)=\frac{h_r(x+y)}{h_r(x)}\mu ^{\infty } F^{\infty }(\textrm{d}y), \end{aligned}$$

(19)

where for $x=(x_1,\ldots ,x_d)$ the function $h_r(x): {\mathbb R}^d\rightarrow {\mathbb R}$ is given by

$$\begin{aligned} h_r(x)=\exp \left\{ \sum _{j=1}^dz_{r,j}x_j\right\} . \end{aligned}$$

(20)

Above the coefficients $z_{r,1}\ldots z_{r,d}$ solve the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{lcl} r_1-\mu ^rm^{r}_1+\mu ^{\infty }m^{\infty }_1&{}=&{}\sum _{j=1}^dz_{r,j}(\sigma \sigma ^T)_{1,j}, \\ \vdots &{}\vdots &{}\vdots \\ r_d-\mu ^rm^{r}_d+\mu ^{\infty }m^{\infty }_d&{}=&{}\sum _{j=1}^dz_{r,j}(\sigma \sigma ^T)_{d,j}. \end{array}\right. \end{aligned}$$

(21)

Theorem 3

Assume that (19) holds for given $r\in {\mathbb R}^d$ and that the Radon-Nikodym derivative $L^r=(L_t^r)_{t\ge 0}$ defined in (18) is given by

$$\begin{aligned} L_t^r=\exp \left\{ \sum _{i=1}^dz_{r,i}(X_{t,i}-X_{0,i})-K_rt\right\} , \end{aligned}$$

(22)

where

$$\begin{aligned} K_r=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^dz_{r,i}z_{r,j}(\sigma \sigma ^T)_{i,j}-\sum _{i=1}^dz_{r,i}\mu ^{\infty }m^{\infty }_i+\mu ^r-\mu ^{\infty }. \end{aligned}$$

(23)

Then the process X defined in (2) admits representation (3) under the measure ${\mathbb P}^{(0,r)}$ and (4) under ${\mathbb P}^{\infty }$.

The proof will be given in Sect. 6.

Having the density process $L^r$ defined in (18) identified in above theorem, we introduce an auxiliary process

$$\begin{aligned} \psi _t^r:=\int _0^t\frac{L_t^r}{L_{s^-}^r}\textrm{d}G(s). \end{aligned}$$

(24)

Then by (6), (17) and (18) the following representation of $\pi _t$ holds true

$$\begin{aligned} \pi _t=\int _{{\mathbb R}^d}\frac{\psi _t^r}{\left[ \psi _t^r+\int _t^{\infty }\frac{L_t^{(s,r)}}{L_t^{\infty }}\textrm{d}G(s)\right] }\textrm{d}H(r)=\int _{{\mathbb R}^d}\frac{\psi _t^r}{\psi _t^r+1-G(t)}\textrm{d}H(r), \end{aligned}$$

(25)

where the last equality follows from the definition of $L_t^{(s,r)}$ in (6) for $t<s$. By the Itô’s formula applied to (24) we obtain that $\psi ^r_t$ solves the following SDE

$$\begin{aligned} \textrm{d}\psi _t^r=\textrm{d}G(t)+\frac{\psi _{t^-}^r}{L_{t}^r}\textrm{d}L_t^r. \end{aligned}$$

(26)

The construction of the classical Shiryaev-Roberts statistic (SR) is in detail described and analyzed e.g. by Shiryaev [33], Pollak and Tartakovsky [25] and Moustakides et al. [19]. In this paper we consider Generalized Shiryaev-Roberts statistic (GSR). We start the whole construction from taking the discrete-time data $X_{t_i}\in {\mathbb {R}}^d$ observed in moments $0=t_0<t_1<\ldots <t_n$, where n is a fixed integer. We assume that $t_i-t_{i-1}=1$ for $i=1,\ldots n$. Let $x_k:=X_{t_k}-X_{t_{k-1}}$ for $k=1,\ldots ,n$. Since X is a d-dimensional process, $x_k$ is a d-dimensional vector $x_k=(x_{k,1},\ldots ,x_{k,d})$.

Considering a discrete analogue of (24) we define the following statistic

$$\begin{aligned}{} & {} {\widetilde{\psi }}_n^r:= L_n^r G(0) + \sum _{j=0}^{n-1}\frac{L_n^r}{L_j^r}G'(j) = L_n^r G(0)\\ {}{} & {} + \sum _{j=0}^{n-1}\prod _{k=j+1}^n\exp \left\{ \sum _{i=1}^dz_{r,i}x_{k,i}-K_r\right\} G'(j), \end{aligned}$$

where from equation (22) we take

$$\begin{aligned} L_n^r:=\exp \left\{ \sum _{i=1}^dz_{r,i}\sum _{k=1}^nx_{k,i}-K_rn\right\} =\prod _{k=1}^n\exp \left\{ \sum _{i=1}^dz_{r,i}x_{k,i}-K_r\right\} \end{aligned}$$

for $n>0$ and $L_0^r=1$. Above $G(0)=x$ corresponds to an atom at 0.

For convenience it can be also calculated recursively as follows:

$$\begin{aligned} {\widetilde{\psi }}_{n+1}^r=({\widetilde{\psi }}_n^r+G'(n))\cdot \exp \left\{ \sum _{i=1}^dz_{r,i}x_{n+1,i}-K_r\right\} ,\quad {\widetilde{\psi }}_0^r=x. \end{aligned}$$

Recall from Theorem 1 that the optimal stopping time is given by

$$\begin{aligned} \tau ^*=\inf \{t\ge 0:\pi _t\ge A^*(t)\} \end{aligned}$$

for some optimal level $A^*$. Therefore from identity (25) we can introduce the following Generalized Shiryaev-Roberts statistic

$$\begin{aligned} {\widetilde{\pi }}_n=\int _{{\mathbb {R}}^d}\frac{{\widetilde{\psi }}_n^r}{{\widetilde{\psi }}_n^r+1-G(n)}\textrm{d}H(r) \end{aligned}$$

and raise the alarm of the drift change at the optimal time of the form

$$\begin{aligned} {\widetilde{\tau }}^*:=\inf \{n\ge 0:{\widetilde{\pi }}_n\ge A^*(n)\}. \end{aligned}$$

Note that formally, we first choose a direction of new drift r according to distribution H. Then we apply statistic ${\widetilde{\psi }}_n^r$ to identify the GSR statistic by ${\widetilde{\pi }}_n= \frac{{\widetilde{\psi }}_n^r}{{\widetilde{\psi }}_n^r+1-G(n)}$ and hence to raise the alarm at the optimal level $A^*(n)$.

We emphasize that the GSR statistic is more appropriate in longevity modeling analyzed in this article than the standard one (i.e. SR). Indeed, the classical statistic is a particular case when $\theta$ has an exponential distribution with parameter $\lambda$ tending to 0. The latter case corresponds to passing with mean value of the change point $\theta$ to $\infty$ and hence it becomes conditionally uniform, see e.g. Shiryaev [33]. Still, in longevity modeling it is more likely that life tables will need to be revised more often and therefore keeping dependence on $\lambda >0$ in our statistic seems to be much more appropriate. For the similar reasons we also prefer to fix average moment of drift change $\theta$ instead of fixing the expected moment of the revision time $\tau$.

To apply above strategy we will focus on the exponential time of drift change. In this case we have to identify the optimal alarm level $A^*$ in the first step and hence we have to solve the free-boundary value problem (10)–(12). We analyze two particular examples in the next section.

4 Examples

4.1 Two-dimensional Brownian motion

Consider the process X without jumps (i.e. with jump intensities $\mu ^{\infty }=\mu ^r=0$). In terms of processes $X^{(0,r)}$ and $X^{\infty }$ given in (3) and (4) it means that

$$\begin{aligned} X_t^{(0,r)}=\sigma W_t^r+rt \quad \text {and}\quad X_t^{\infty }=\sigma W_t^{\infty }. \end{aligned}$$

(27)

Assume that

$$\begin{aligned} \sigma =\left( \begin{array}{cc}\sigma _1 &{} 0 \\ \sigma _2\rho &{} \sigma _2\sqrt{1-\rho ^2}\end{array}\right) . \end{aligned}$$

Then the first coordinate $X^{(0,r)}_{t,1}$ is a Brownian motion with drift and with variance $\sigma ^2_1$ and the second coordinate $X^{(0,r)}_{t,2}$ is also a Brownian motion with drift and with variance $\sigma ^2_2$. The correlation of the Brownian motions on both coordinates is equal to $\rho$. Process $X^{\infty }$ has similar characteristics but without any drift.

Next, assume that, conditioned on $\theta >0$, $\theta$ is exponentially distributed with parameter $\lambda >0$, i.e.

$$\begin{aligned} {\overline{P}}^{G,H}(\theta \le t) = G(t) = x + (1-x)(1-e^{-\lambda t}), \quad t\ge 0 \end{aligned}$$

and that there is only one possible post-change drift $r_0\in {\mathbb {R}}^2$, that is

$$\begin{aligned} \textrm{d}H(r)=\delta _{r_0}(r), \end{aligned}$$

where $\delta$ means a Dirac measure. Then the generator of process $\pi$ according to (16) is equal to

$$\begin{aligned}{} & {} {\mathcal {A}}f(x)=f'(x)\lambda (1-x)+\frac{1}{2}f''(x)x^2(1-x)^2\nonumber \\ {}{} & {} \left( z_{r_{0},1}^2\sigma _1^2+z_{r_{0},2}^2\sigma _2^2+2z_{r_{0},1}z_{r_{0},2}\sigma _1\sigma _2\rho \right) , \end{aligned}$$

(28)

where $z_{r_{0},1}$ and $z_{r_{0},2}$ solve the following system

$$\begin{aligned} \left\{ \begin{array}{l} r_{0,1}=\sum _{j=1}^2z_{r_{0},j}(\sigma \sigma ^T)_{1,j}, \\ r_{0,2}=\sum _{j=1}^2z_{r_{0},j}(\sigma \sigma ^T)_{2,j}. \end{array}\right. \end{aligned}$$

Our goal is to solve the boundary value problem (10)–(12) where generator ${\mathcal {A}}$ is given by (28). Note that the system (10) takes now the following form

$$\begin{aligned} \begin{aligned} f'(x)\lambda (1-x)+\frac{1}{2}f''(x)x^2(1-x)^2\cdot B=-cx, \quad 0\le x<A^*,\\ f(x)=1-x, \quad A^*\le x \le 1, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} B:=z_{r_{0},1}^2\sigma _1^2+z_{r_{0},2}^2\sigma _2^2+2z_{r_{0},1}z_{r_{0},2}\sigma _1\sigma _2\rho . \end{aligned}$$

Observe that above equations allow us to refer to the classical Shiryaev problem, with our constant B included. Hence, from Shiryaev [29, 35] it follows that solution of above equation is given by

$$\begin{aligned} V^*(x)=\left\{ \begin{array}{ll}1-A^*-\displaystyle \int _x^{A^*}y(s)\textrm{d}s, &{} x\in [0,A^*) \\ 1-x, &{} x\in [A^*,1],\end{array}\right. \end{aligned}$$

where

$$\begin{aligned} y(s)=-\frac{2c}{B}\int _0^se^{-\frac{2\lambda }{B}[Z(s)-Z(u)]}\frac{1}{u(1-u)^2}\textrm{d}u \end{aligned}$$

for

$$\begin{aligned} Z(u)=\log \frac{u}{1-u}-\frac{1}{u}. \end{aligned}$$

The exact values of function y(x) can be found numerically, while the threshold $A^*$ can be found from the equation $y(A^*)=-1$, which is the boundary condition (12).

4.2 Two-dimensional Brownian motion with one-sided jumps

The second example concerns similar 2-dimensional Brownian motion model as in the previous example, but with additional exponential jumps. Assume that $\mu ^{\infty },\mu ^r>0$ and

$$\begin{aligned} F^{\infty }(\textrm{d}y) = \prod _{j=1}^2F_j^{\infty }(\textrm{d}y) = \prod _{j=1}^2\frac{1}{w_j}e^{-y_j/w_j}I(y_j\ge 0)\textrm{d}y. \end{aligned}$$

(29)

In other words, jump sizes on each coordinate $j\in \{1,2\}$ of process $X^{\infty }$ are independent of each other and distributed exponentially with mean $w_j>0$. Additionally, we assume as in the previous example that

$$\begin{aligned} {\overline{P}}^{G,H}(\theta \le t) = G(t) = x + (1-x)(1-e^{-\lambda t}), \quad t\ge 0 \end{aligned}$$

and that there is only one possible post-change drift $r_0\in {\mathbb {R}}^2$, that is

$$\begin{aligned} \textrm{d}H(r)=\delta _{r_0}(r). \end{aligned}$$

Jump distribution given by (29) together with Theorem 3 allows us to formulate the following lemma.

Lemma 2

Assume that jump distribution $F^{\infty }$ of the process $X^{\infty }$ is given by (29) and jump intensity is equal to $\mu ^{\infty }$. Assume also that there exists a vector $z_{r_0}=(z_{r_0,1},\ldots ,z_{r_0,d}$) satisfying the system (21) such that $(\forall _{1\le j \le 2})(|w_jz_{r_0,j}|<1)$. Then the following distribution function $F^{r_0}$ and intensity $\mu ^{r_0}$ satisfy the condition (19):

$$\begin{aligned} \begin{aligned}&F^{r_0}(\textrm{d}y) = \prod _{j=1}^2\frac{1-w_jz_{r_0,j}}{w_j}e^{-y_j/(\frac{w_j}{1-w_jz_{r_0,j}})}I(y_j\ge 0)\textrm{d}y, \\&\mu ^{r_0} = \mu ^{\infty }\prod _{j=1}^2\frac{1}{1-w_jz_{r_0,j}}. \end{aligned} \end{aligned}$$

(30)

Proof

By the combination of (19) and (20) we obtain that

$$\begin{aligned} \mu ^{r_0}F^{r_0}(\textrm{d}y) = e^{\sum _{j=1}^2z_{r_0,j}y_j}\mu ^{\infty }F^{\infty }(\textrm{d}y) = \mu ^{\infty }\prod _{j=1}^2\frac{1}{w_j}e^{-y_j/(\frac{w_j}{1-w_jz_{r_0,j}})}I(y_j\ge 0)\textrm{d}y, \end{aligned}$$

which can be rearranged to

$$\begin{aligned} \mu ^{\infty }\prod _{j=1}^2\frac{1}{1-w_jz_{r_0,j}}\cdot \prod _{j=1}^2\frac{1-w_jz_{r_0,j}}{w_j}e^{-y_j/(\frac{w_j}{1-w_jz_{r_0,j}})}I(y_j\ge 0)\textrm{d}y. \end{aligned}$$

Now it is sufficient to observe that above formula is equal to the product $\mu ^{r_0} F^{r_0}$ given by (30) and that $F^{r_0}$ is indeed a proper distribution by the assumption that $(\forall _{1\le j \le 2})$ $(|w_jz_{r,j}|<1)$. $\square$

Remark 1

Considering the jump distributions $F^{\infty }$ and $F^{r_0}$ given by (29) and (30), the system (21) consists of equations

$$\begin{aligned} r_{0,k}+\mu ^{\infty }m_k^{\infty }-\mu ^{r_0}m_k^{r_0}-\sum _{j=1}^2z_{r_0,j}(\sigma \sigma ^T)_{k,j}=0, \quad k=1,\ldots ,2, \end{aligned}$$

where

$$\begin{aligned} \mu ^{\infty }m^{\infty }_k = \mu ^{\infty }w_k \end{aligned}$$

and

$$\begin{aligned} \mu ^{r_0}m^{r_0}_k = \mu ^{\infty }\frac{w_k}{1-w_kz_{r_0,k}}\prod _{j=1}^2\frac{1}{1-w_jz_{r_0,j}}. \end{aligned}$$

Remark 2

Distribution $F^{r_0}$ given by (30) has similar characteristics to $F^{\infty }$. More precisely: jumps on both coordinates $X^{(0,r_0)}_{t,1}$ and $X^{(0,r_0)}_{t,2}$ are independent, exponentially distributed with means $\frac{w_1}{1-w_1z_{r_0,1}}$ and $\frac{w_2}{1-w_2z_{r_0,2}}$, respectively.

The generator ${\mathcal {A}}$ given by (16) for jump distributions specified above can be expressed as

$$\begin{aligned} \begin{aligned} {\mathcal {A}}f(x)&=f'(x)\left( \lambda (1-x)+x(1-x)(\mu ^{\infty }-\mu ^{r_0})\right) \\&\quad +\frac{1}{2}f''(x)x^2(1-x)^2\left[ z_{r_0,1}^2\sigma _1^2+z_{r_0,2}^2\sigma _2^2+2z_{r_0,1}z_{r_0,2}\sigma _1\sigma _2\rho \right] -f(x) \\&\quad + \int _{[0,\infty )^2} f\left( \frac{x\exp \{\sum _{i=1}^2z_{r_0,i}y_i\}}{x(\exp \{\sum _{i=1}^2z_{r_0,i}y_i\}-1)+1}\right) \\&\quad \cdot \left[ (1-x)\mu ^{\infty }\prod _{j=1}^2\frac{1}{w_j}e^{-y_j/w_j}+x\mu ^{r_0}\prod _{j=1}^2\frac{1-w_jz_{r_0,j}}{w_j}e^{-y_j/\frac{w_j}{1-w_jz_{r_0,j}}}\right] \textrm{d}y. \end{aligned} \end{aligned}$$

(31)

The integral part of ${\mathcal {A}}$ can be further simplified. For $\alpha _1,\alpha _2>0$ we define the following integrals

$$\begin{aligned} I_+^r(x):=\int _{[0,\infty )^2}f\left( \frac{x\exp \{\sum _{i=1}^2z_{r,i}y_i^r\}}{x(\exp \{\sum _{i=1}^2z_{r,i}y_i^r\}-1)+1}\right) \prod _{j=1}^2\alpha _je^{-\alpha _jy_j}\textrm{d}y \end{aligned}$$

and

$$\begin{aligned} I_-^r(x):=\int _{(-\infty ,0]^2}f\left( \frac{x\exp \{\sum _{i=1}^2z_{r,i}y_i^r\}}{x(\exp \{\sum _{i=1}^2z_{r,i}y_i^r\}-1)+1}\right) \prod _{j=1}^2\alpha _je^{\alpha _jy_j}\textrm{d}y. \end{aligned}$$

Lemma 3

Assume that $\alpha _1, \alpha _2, z_{r,1}, z_{r,2} > 0$ and $\frac{\alpha _1}{z_{r,1}}\ne \frac{\alpha _2}{z_{r,2}}$. Then for $x\in (0,1]$,

$$\begin{aligned} \begin{aligned} I_+^r(x)=f(x)&-\frac{\beta _1}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{-\beta _2}\int _x^1f'(v)\left( \frac{v}{1-v}\right) ^{-\beta _2}\textrm{d}v \\&+\frac{\beta _2}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{-\beta _1}\int _x^1f'(v)\left( \frac{v}{1-v}\right) ^{-\beta _1}\textrm{d}v \end{aligned} \end{aligned}$$

for $\beta _1=\frac{\alpha _1}{z_{r,1}}$ and $\beta _2=\frac{\alpha _2}{z_{r,2}}$ and

$$\begin{aligned} \begin{aligned} I_-^r(x)=f(x)&+\frac{\beta _1}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{\beta _2}\int _0^xf'(v)\left( \frac{v}{1-v}\right) ^{\beta _2}\textrm{d}v \\&- \frac{\beta _2}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{\beta _1}\int _0^xf'(v)\left( \frac{v}{1-v}\right) ^{\beta _1}\textrm{d}v. \end{aligned} \end{aligned}$$

Using similar arguments like in Krawiec et al. [15] that there exists unique solution of the system equations (10)-(12), hence whole estimation procedure can be applied.

Remark 3

In Lemma 3 we restrict calculations to the case $\beta _1\ne \beta _2$, but similar transformations of the integral may be made for the case $\beta _1=\beta _2$ as well. The difference will appear in the distribution of random variable $S^r$ present in the proof (see Sect. 6) being the sum of two exponential random variables.

Denote $\gamma _i:=\frac{1}{z_{r_0,i}w_i}$ for $i\in \{1,2\}$. Then from Lemma 3 the generator ${\mathcal {A}}$ given in (31) can be rewritten as follows

$$\begin{aligned} {\mathcal {A}}f(x)= & {} f(x)\left[ (1-x)\mu ^{\infty }+x\mu ^{r_0}-1\right] + f'(x)\left( \lambda (1-x)+x(1-x)(\mu ^{\infty }-\mu ^{r_0})\right) \nonumber \\{} & {} +\frac{1}{2}f''(x)x^2(1-x)^2\left[ z_{r_0,1}^2\sigma _1^2+z_{r_0,2}^2\sigma _2^2+2z_{r_0,1}z_{r_0,2}\sigma _1\sigma _2\rho \right] \nonumber \\{} & {} -(1-x)^{-\gamma _2+1}x^{\gamma _2}\int _x^1f'(v)\left[ \mu ^{\infty }\frac{\gamma _1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{-\gamma _2}+\mu ^{r_0}\frac{\gamma _1-1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{-\gamma _2+1}\right] \textrm{d}v \nonumber \\{} & {} +(1-x)^{-\gamma _1+1}x^{\gamma _1}\int _x^1f'(v)\left[ \mu ^{\infty }\frac{\gamma _2}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{-\gamma _1}+\mu ^{r_0}\frac{\gamma _2-1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{-\gamma _1+1}\right] \textrm{d}v.\nonumber \\ \end{aligned}$$

(32)

Equation ${\mathcal {A}}f(x)=-cx$ in the free-boundary value problem can be further simplified to get rid of the integrals and then solved numerically to find the threshold $A^*$. We believe that this particular case may be finally solved numerically in a similar way as in the numerical analysis described in Krawiec et al. [15], since here we obtain equation of the same order and similar characteristics. However, in this article we focus our applications on the previous example, which is used in practice in the next section.

Remark 4

The results of above example are derived under the assumption of positive exponential jumps. However, the whole analysis can be also conducted for negative exponential jumps, i.e. for the distribution

$$\begin{aligned} F^{\infty }(\textrm{d}y) = \prod _{j=1}^2\frac{1}{w_j}e^{y_j/w_j}I(y_j\le 0)\textrm{d}y. \end{aligned}$$

Then we can use part of Lemma 3 concerning $I_-^r(x)$ to derive the generator ${\mathcal {A}}$ given by

$$\begin{aligned}{} & {} {\mathcal {A}}f(x)=f(x)\left[ (1-x)\mu ^{\infty }+x\mu ^{r_0}-1\right] + f'(x)\left( \lambda (1-x)+x(1-x)(\mu ^{\infty }-\mu ^{r_0})\right) \\{} & {} \quad +\frac{1}{2}f''(x)x^2(1-x)^2\left[ z_{r_0,1}^2\sigma _1^2+z_{r_0,2}^2\sigma _2^2+2z_{r_0,1}z_{r_0,2}\sigma _1\sigma _2\rho \right] \\{} & {} \quad +(1-x)^{\gamma _2+1}x^{-\gamma _2}\int _0^xf'(v)\left[ \mu ^{\infty }\frac{\gamma _1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{\gamma _2}+\mu ^{r_0}\frac{\gamma _1+1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{\gamma _2+1}\right] \textrm{d}v \\{} & {} \quad -(1-x)^{\gamma _1+1}x^{-\gamma _1}\int _0^xf'(v)\left[ \mu ^{\infty }\frac{\gamma _2}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{\gamma _1}+\mu ^{r_0}\frac{\gamma _2+1}{\gamma _2-\gamma _1}\left( \frac{v}{1-v}\right) ^{\gamma _1+1}\right] \textrm{d}v. \end{aligned}$$

5 Application to the force of mortality

Now we are going to give an important example of applications, which concerns modeling of the force of mortality process. We will analyze the joint force of mortality for both men and women. We observe this process over the past decades and check if and when there have been significant changes of drift.

To achieve this goal, we introduce two-dimensional process of the force of mortality $\mu :=(\mu _t)_{t\ge 0}=((\mu _t^1,\mu _t^2))_{t\ge 0}$. We interpret this process as follows:

• the first coordinate $\mu _t^1$ represents force of mortality of men, while the second one $\mu _t^2$ represents force of mortality of women (of course they are correlated),

• the time t runs through consecutive years of life tables, e.g. if $t=0$ corresponds to the year 1990, then $t=10$ corresponds to the year 2000,

• the age of people is fixed for a given process $\mu$, i.e. if $\mu _0$ concerns 50-year old men and women, then $\mu _{10}$ also concerns 50-year old men and women, but in another year.

The representation of the force of mortality process is given by

$$\begin{aligned} \log \mu _t=\log {\bar{\mu }}_t+X_t, \end{aligned}$$

(33)

where $\log {\bar{\mu }}_t:=(\log \mu _t^1, \log \mu _t^2)$ is a deterministic part equal to

$$\begin{aligned} \log {\bar{\mu }}_t=a_0+a_1t. \end{aligned}$$

Above $a_0=(a_0^1, a_0^2)$ is a known initial force of mortality vector of men and women and $a_1=(a_1^1, a_1^2)$ is a vector of a historical drift per one year. It is worth to mention here that our model is similar to the Lee-Carter model (for fixed age $\omega$, cf. [17] ):

$$\begin{aligned} \log \mu _{\omega ,t}=a_{\omega }+b_{\omega }k_t+\epsilon _{\omega ,t}, \end{aligned}$$

where $a_{\omega }$ is a chosen number, $k_t$ is certain univariate time series and $\epsilon _{\omega ,t}$ is a random error. However, Lee-Carter method focuses on modeling the deterministic part of the force of mortality, while our detection procedure concerns controlling the random perturbation in time, precisely the moment when it substantially changes. This model is univariate as well in contrast to our two-dimensional mortality process.

In our numerical analysis the stochastic part $X_t$ will be modeled by the two-dimensional Brownian motion analyzed in Example 4.1. We apply this model to the life tables downloaded from the Statistics Poland website [39]. We would like to emphasize that in this article we focus our applications on multivariate modeling of both men and women jointly. For this reason we simplify other assumptions here, such as the distribution of $\theta$, random post-change drift or adding jumps into the model. However, as we have mentioned in Example 4.2, adding jumps into the model is also possible, but results in much more difficult equations to solve. To apply model from Example 4.2 one needs to solve the equation with generator given by (32). This equation has similar form to the one that was solved in Krawiec et al. [15] for the univariate case. There it has been solved numerically after the thorough analysis. Similar method should be applicable here for the model introduced in Example 4.2.

The first step concerns the model calibration. We start with some historical values of the force of mortality ${\hat{\mu }}_0,\ldots ,{\hat{\mu }}_n$, where each ${\hat{\mu }}_i=({\hat{\mu }}_{i,1},{\hat{\mu }}_{i,2})$ is a two-dimensional vector (one coordinate for women and one for men). We estimate $a_1$ as a mean value of log-increments of ${\hat{\mu }}_0,\ldots ,{\hat{\mu }}_n$. Precisely,

$$\begin{aligned} \hat{a}_1:= \frac{1}{n}\sum _{i=1}^ny_i, \end{aligned}$$

where

$$\begin{aligned} y_i:= \log {\hat{\mu }}_i - \log {\hat{\mu }}_{i-1},\quad i=1,\ldots ,n. \end{aligned}$$

A little more attention is needed to calibrate the stochastic part X, which includes correlation. Denote

$$\begin{aligned} {\hat{X}}_i = \log {\hat{\mu }}_i - a_0 - {\hat{a}}_1i, \quad i=0,\ldots ,n \end{aligned}$$

(34)

and the increments

$$\begin{aligned} x_i:= {\hat{X}}_{i+1}-{\hat{X}}_i, \quad i=1,\ldots ,n. \end{aligned}$$

(35)

We estimate $\sigma _1$ as a standard deviation of the vector $(x_{1,1},x_{2,1},\ldots ,x_{n,1})$. Similarly, $\sigma _2$ is calculated as a standard deviation of a vector $(x_{1,2},x_{2,2},\ldots ,x_{n,2})$. Finally, we calculate $\rho$ as the sample Pearson correlation coefficient of vectors $(x_{1,1},x_{2,1},\ldots ,x_{n,1})$ and $(x_{1,2},x_{2,2},\ldots ,x_{n,2})$.

There are still some model parameters that have to be chosen a priori. In particular, we have to declare the anticipated incoming drift $r_0$, the probability $x=\pi _0={\overline{{\mathbb P}}}^{G,H}(\theta =0)$ that the drift change occurs immediately, the parameter $\lambda >0$ of the exponential distribution of $\theta$ and parameter c present in criterion stated in the Problem 2.

We assume their values at the following level:

• $\lambda =0.1$. It is the reciprocal of the mean value of $\theta$ distribution conditioned to be strictly positive. Such choice reflects the expectation that the drift will change in 10 years on average.

• $x (={\overline{{\mathbb P}}}^{G,H}(\theta =0))=0.1$. This parameter should be rather small (unless we expect the change of drift very quickly).

• $c=0.1$. It is the weight of the mean delay time inside the optimality criterion stated in the Problem 1. It reflects how large delay we can accept comparing to the risk of false alarm. We have chosen rather small value and connected it to $\lambda$ by choosing $c=\lambda$.

• Drift incoming after the moment $\theta$—we have connected the anticipated value of $r_0$ to $\sigma$ by $r_0=(\sigma _1,\sigma _2)$. In practice we suggest to adjust the choice of $r_0$ to the analysis of sensitivity of e.g. price of an insurance contract.

In Table 1 we sum up all parameters that were used (both calibrated and arbitrary chosen ones) in the numerical analysis. The calibration interval was set to years 1990–2000.

Table 1 Parameters used to drift change detection

Fig. 1

Force of mortality of women aged 60 in 1990-2017

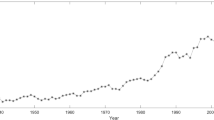
In the Fig. 1 we present exemplary plot of the force of mortality for women at age 60 through years 1990–2017. Most of the time it is decreasing, but we can observe a stabilization period around years 2002–2009. According to (33) we first take logarithm of the force of mortality, separate deterministic linear part and then model the remaining part by the process X given by (27). Figure 2 presents historical observations of this remaining part for the same data as in the Fig. 1.

Fig. 2

Historical values of X for women aged 60 in 1990-2017

Fig. 3

Drift change detection jointly for men and women aged 60 in 1990-2017

The results of the detection algorithm for the force of mortality of 60-year old men and women jointly are presented in the Fig. 3. The change of drift for given parameters was detected in year 2006 (red vertical line in the first two plots). The threshold $A^*$ for the optimal stopping time is here equal to 0.85, which is indicated by the red horizontal line in the third plot presenting values of $\pi =(\pi _t)_{t\in \{1990,\ldots ,2017\}}$.

Note that calibration of parameters (including historical drift) has been done for interval 1990–2000, when the force of mortality was mostly decreasing. After year 2002 it stayed at a stable level for several years, which was detected as a change of drift. This change of behavior is even more evident in the Fig. 2, where we can observe that process X is mostly increasing through the years 2002–2009. This example shows that our detection method does not necessarily rise the alarm after the first observed deviation, but rather after it becomes more evident, that the change of drift actually has happened. Therefore, it copes well with cases of gradually changing drift, as long as eventually observed process significantly deviates from the model.

An important note need to be given at the end. This procedure is strongly dependent on parameters chosen to the model—e.g. post-change drift vector $r_0$, which was chosen depending on $\sigma _1$ and $\sigma _2$, to give appropriate order of magnitude. Furthermore, the theoretical results contained in this article allows us to consider random drift. One good example may be a distribution of drift concentrated on several points around $\sigma _1$ and $\sigma _2$ at each coordinate. It gives much more freedom since it is not clear if the fixed magnitude of drift change equal to the historical standard deviation is enough.

Similarly, one may assume more general distribution of $\theta$ or—assuming (0-modified) exponential distribution—connect $\lambda$ to historically observed mean time between significant drift changes. Of course, it may be impossible if there were none or very few changes observed in the past. Thorough analysis of such cases is out of the scope of this article. However, as far as the applications are concerned, the goal should be to choose parameters allowing to detect drift change before it is too late. So if there is not enough historical data then one may arbitrary choose rather small mean of the prior distribution (e.g. 10 years as in our example), which should result in quicker detection. Then in the worst case scenario one will recalibrate the model too soon, obtaining similar parameters as before the recalibration.

A full analysis of the impact of individual parameters on the results should be the subject of further research, developing the applications of the detection method described in our paper.

6 Proofs

Proof of Lemma 1

Note that

$$\begin{aligned} {\overline{{\mathbb P}}}^{G,H}(\tau<\theta )= & {} {\overline{{\mathbb E}}}^{G,H}_x[{\overline{{\mathbb E}}}^{G,H}_x[I(\tau <\theta )|{\overline{\mathcal {F}}}_t]]\nonumber \\= & {} {\overline{{\mathbb E}}}^{G,H}_x[1-{\overline{{\mathbb P}}}^{G,H}(\theta \le \tau |{\overline{\mathcal {F}}}_t)]={\overline{{\mathbb E}}}^{G,H}_x[1-\pi _{\tau }]. \end{aligned}$$

(36)

Moreover, observe that by Tonelli’s theorem we have:

$$\begin{aligned} \begin{aligned} {\overline{{\mathbb E}}}^{G,H}_x[(\tau -\theta )^+]&= \int _{{\mathbb R}_+}{\overline{{\mathbb E}}}^{G,H}_x[(t-\theta )^+]{\overline{{\mathbb P}}}^{G,H}(\tau \in \textrm{d}t) \\&= \int _{{\mathbb R}_+}{\overline{{\mathbb E}}}^{G,H}_x\left[ \int _0^tI(\theta \le s)\textrm{d}s\right] {\overline{{\mathbb P}}}^{G,H}(\tau \in \textrm{d}t) \\&= \int _{{\mathbb R}_+}\int _0^t{\overline{{\mathbb E}}}^{G,H}_x\left[ {\overline{{\mathbb E}}}^{G,H}_x\left[ I(\theta \le s)|{\overline{\mathcal {F}}}_t\right] \right] \textrm{d}s{\overline{{\mathbb P}}}^{G,H}(\tau \in \textrm{d}t) \\&= \int _{{\mathbb R}_+}\int _0^t{\overline{{\mathbb E}}}^{G,H}_x[\pi _s]\textrm{d}s{\overline{{\mathbb P}}}^{G,H}(\tau \in \textrm{d}t) \\&= \int _{{\mathbb R}_+}{\overline{{\mathbb E}}}^{G,H}_x\left[ \int _0^t\pi _s\textrm{d}s\right] {\overline{{\mathbb P}}}^{G,H}(\tau \in \textrm{d}t) = {\overline{{\mathbb E}}}^{G,H}_x\left[ \int _0^{\tau }\pi _s\textrm{d}s\right] . \end{aligned} \end{aligned}$$

(37)

Putting together (36) and (37) completes the proof. $\square$

Proof of Theorem 1

We start from the observation that process $((s,\pi _s))_{s\ge 0}$ is Markov which follows from Theorem 2. Let

$$\begin{aligned} V^*(t,x):=\inf _{\tau \in \mathcal {T}, \tau \ge t}\overline{{\mathbb E}}^{G,H}\left\{ \left[ 1-\pi _{\tau }+c\int _0^{\tau }\pi _s\textrm{d}s\right] \bigg |\pi _t=x\right\} . \end{aligned}$$

Then $V^*(x)=V^*(0,x)$. Moreover, for fixed $t\ge 0$ the optimal value function $V^*(t,x)$ is concave, which follows from [15, Lem. 3] and the assumption that distribution function G(t) of $\theta$ is continuous for $t>0$. Observe that from Theorem 2 it follows that $((s,\pi _s))_{s\ge 0}$ is stochastically continuous and thus function $(t, x)\rightarrow \overline{{\mathbb E}}^{G,H}\left\{ \left[ 1-\pi _{\tau }+c\int _0^{\tau }\pi _s\textrm{d}s\right] \bigg |\pi _t=x\right\}$ is continuous for any fixed stopping time $\tau$. Thus from [22, Rem. 2.10, p. 48] we know that the value function $V^*(t,x)$ is lsc. Let

$$\begin{aligned} C=\{x: V^*(t,x)> 1-x\} \end{aligned}$$

be an open a continuation set and $D = C^c$ be a stopping set. From [22, Cor. 2.9, p. 46] we know that $C=[0,A^*(t))$ and that the stopping rule given by

$$\begin{aligned} \tau ^*=\inf \{t\ge 0:\pi _t\in D\} \end{aligned}$$

is optimal for Problem 2. Moreover, we have

$$\begin{aligned} {\mathbb P}_x(\tau ^*<\infty )=1 \end{aligned}$$

(38)

and by [22, Chap. III] the optimal value function $V^*(t,x)$ satisfies the following system

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \frac{\partial }{\partial t}+{\mathcal {A}}\right) V^*(t,x)=-cx,&{}(t,x)\in C,\\ V^*(t,x)=1-x,&{}(t,x)\in D,\end{array}\right. \end{aligned}$$

(39)

where ${\mathcal {A}}$ is a Dynkin generator. Using the same arguments like in the proofs of [15, Lem. 6 and Lem. 7] we can prove the boundary conditions $f_t(A^{*}(t)-)=1-A^*(t)$ and $f^\prime _t(A^{*}(t)-)=-1$.

Finally, if G is exponential, then $(\pi _s)_{s\ge 0}$ is Markov by Theorem 2. Now we can do the same arguments but taking simply $V^*(x)$ instead $V^*(t,x)$ above. Moreover, (15) follows from the same arguments like in the proof of [15, Lem. 6]. This completes the proof. $\square$

Proof of Theorem 2

First, we will find the SDE which is satisfied by process $\pi _t^r$. By the definition of the process X for each $i=1,\ldots ,d$, we get

$$\begin{aligned} \textrm{d}X_{t,i}= & {} \sum _{j=1}^d\sigma _{ij}\textrm{d}W_{t,j}+\Delta X_{t,i}+r_iI(t\ge \theta )\textrm{d}t\\ {}{} & {} - \left( \mu ^{\infty }m_i^{\infty }I(t<\theta )+\mu ^rm_i^rI(t\ge \theta )\right) \textrm{d}t. \end{aligned}$$

Denote the continuous part of the process by an additional upper index c. Then

$$\begin{aligned} \textrm{d}\left<X_{t,i}^{c},X_{t,k}^{c}\right> = \sum _{j=1}^d\sigma _{ij}\sigma _{kj}\textrm{d}t = (\sigma \sigma ^T)_{ik}\textrm{d}t. \end{aligned}$$

For the process $L^r$ given in (22), by the Itô’s formula we obtain

$$\begin{aligned} \begin{aligned} \textrm{d}L_t^r&= \left\{ \mu ^{\infty }-\mu ^r + \sum _{i=1}^dz_{r,i}(r_i+\mu ^{\infty }m_i^{\infty }-\mu ^rm_i^r)I(\theta \le t)\right\} L_t^r\textrm{d}t \\&\quad + \sum _{i=1}^dz_{r,i}\sum _{j=1}^d\sigma _{ij}L_t^r \textrm{d}W_{t,j} + \Delta L_t^r, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \Delta L_t^r=L_{t^-}^r\left( \frac{L_t^r}{L_{t^-}^r}-1\right) = L_{t^-}^r\left( e^{\sum _{i=1}^dz_{r,i}\Delta X_{t,i}}-1\right) . \end{aligned}$$

By (26) we conclude that

$$\begin{aligned} \begin{aligned} \textrm{d}\psi _t^r&= \textrm{d}G(t)+\left\{ \mu ^{\infty }-\mu ^r+\sum _{i=1}^dz_{r,i}(r_i+\mu ^{\infty }m_i^{\infty }-\mu ^rm_i^r)I(\theta \le t)\right\} \psi _t^r\textrm{d}t \\&\quad +\sum _{i=1}^dz_{r,i}\sum _{j=1}^d\sigma _{ij}\psi _t^r\textrm{d}W_{t,j}+\psi _{t^-}^r\left( e^{\sum _{i=1}^dz_{r,i}\Delta X_{t,i}}-1\right) . \end{aligned} \end{aligned}$$

Recall that by (25) we have

$$\begin{aligned} \pi _t^r=\frac{\psi _t^r}{\psi _t^r+1-G(t)}. \end{aligned}$$

Then, using Itô’s formula once again we obtain

$$\begin{aligned} \textrm{d}\pi _t^r = \frac{\pi _t^r(1-\pi _t^r)}{1-G(t)}\textrm{d}G(t)+\frac{(1-\pi _t^r)^2}{1-G(t)}\textrm{d}\psi _t^{r,c} - \frac{(1-\pi _t^r)^3}{(1-G(t)^2}\textrm{d}\left<\psi ^{r,c},\psi ^{r,c}\right>_t + \Delta \pi _t. \end{aligned}$$

Moreover,

$$\begin{aligned} \textrm{d}\left<\psi ^{r,c},\psi ^{r,c}\right>_t=\sum _{i=1}^d\sum _{j=1}^dz_{r,i}z_{r,j}(\sigma \sigma ^T)_{ij}(\psi _t^r)^2\textrm{d}t. \end{aligned}$$

Together with the system of equations (21) it produces

$$\begin{aligned} \begin{aligned} \textrm{d}\pi _t^r&= \frac{1-\pi _t^r}{1-G(t)}\textrm{d}G(t) + \frac{(1-\pi _t^r)^2}{1-G(t)}(\mu ^{\infty }-\mu ^r)\psi _t\textrm{d}t \\&\quad + \frac{(1-\pi _t^r)^2}{1-G(t)}\sum _{i=1}^dz_{r,i}\sum _{j=1}^d\sigma _{ij}\psi _t^r\textrm{d}W_{t,j} \\&\quad + \frac{(1-\pi _t^r)^2}{1-G(t)}\sum _{i=1}^d\sum _{j=1}^dz_{r,i}z_{r,j}(\sigma \sigma ^T)_{ij}I(\theta \le t)\psi _t^r\textrm{d}t \\&\quad - \frac{(1-\pi _t^r)^3}{(1-G(t))^2}\sum _{i=1}^d\sum _{j=1}^dz_{r,i}z_{r,j}(\sigma \sigma ^T)_{ij}(\psi _t^r)^2\textrm{d}t + \Delta \pi _t^r. \end{aligned} \end{aligned}$$

Jump part of $\pi _t$ is equal to $\int _{{\mathbb R}^d}\Delta \pi _t^r\textrm{d}H(r)$, where

$$\begin{aligned} \Delta \pi _t^r = \pi _{t^-}^r\left( \frac{\psi _t^r}{\psi _{t^-}^r}\frac{\psi _{t^-}^r+1-G(t)}{\psi _t^r+1-G(t)}-1\right) = \frac{\pi _{t^-}^r\left( \exp \{\sum _{i=1}^dz_{r,i}\Delta X_{t,i}\}-1\right) (1-G(t))}{\psi _{t^-}^r\exp \{\sum _{i=1}^dz_{r,i}\Delta X_{t,i}\}+1-G(t)}. \end{aligned}$$

Using the Itô’s formula one more time completes the proof. $\square$

Proof of Theorem 3

The proof is based on the technique of exponential change of measure described in Palmowski and Rolski [21].

Firstly, we will prove that the process $(L_t^r)_{t\ge 0}$ satisfies the following representation

$$\begin{aligned} L_t^r=\frac{h(X_t)}{h(X_0)}\exp \left( -\int _0^t\frac{({\mathcal {A}}^{\infty }h)(X_s)}{h(X_s)}\textrm{d}s\right) \end{aligned}$$

(40)

for the function $h(x):=h_r(x)$ given in (20), where ${\mathcal {A}}^{\infty }$ is an extended generator of the process X under ${\mathbb P}^{\infty }$ and h is in its domain since it is twice continuously differentiable. Then from Theorem 4.2 by Palmowski and Rolski [21] it follows that the generator of X under ${\mathbb P}^{(0,r)}$ is related with ${\mathcal {A}}^{\infty }$ by

$$\begin{aligned} {\mathcal {A}}^r f=\frac{1}{h}\left[ {\mathcal {A}}^{\infty }(fh)-f{\mathcal {A}}^{\infty }h\right] . \end{aligned}$$

(41)

On the other hand, from the definition of the infinitesimal generator or using the Theorem 31.5 in Sato [28] it follows that for twice continuously differentiable function $f(x_1,\ldots ,x_d):{\mathbb R}^d\rightarrow {\mathbb R}$ generators ${\mathcal {A}}^{\infty }$ and ${\mathcal {A}}^r$ are given by

$$\begin{aligned} \begin{aligned} {\mathcal {A}}^{\infty }f(x)&=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^d\frac{\partial ^2f}{\partial x_i\partial x_j}(x)(\sigma \sigma ^T)_{i,j}-\sum _{i=1}^d\frac{\partial f}{\partial x_i}(x)\mu ^{\infty }m^{\infty }_i \\&\quad + \int _{{\mathbb R}^d}\left( f(x+y)-f(x)\right) \mu ^{\infty } F^{\infty }(\textrm{d}y), \end{aligned} \end{aligned}$$

(42)

$$\begin{aligned} \begin{aligned} {\mathcal {A}}^{r}f(x)&=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^d\frac{\partial ^2f}{\partial x_i\partial x_j}(x)(\sigma \sigma ^T)_{i,j}-\sum _{i=1}^d\frac{\partial f}{\partial x_i}(x)\left( \mu ^rm^{r}_i-r_i\right) \\&\quad + \int _{{\mathbb R}^d}\left( f(x+y)-f(x)\right) \mu ^r F^r(\textrm{d}y). \end{aligned} \end{aligned}$$

(43)

For $h_r(x)$ given by (20) we obtain

$$\begin{aligned} \frac{h_r(X_t)}{h_r(X_0)}=\exp \left\{ \sum _{j=1}^dz_{r,j}\left( X_{t,j}-X_{0,j}\right) \right\} . \end{aligned}$$

Further, since

$$\begin{aligned} \frac{\partial h_r}{\partial x_i}=z_{r,i}h_r \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb R}^d}\frac{h(X_s+y)-h(X_s)}{h(X_s)}\mu ^{\infty }F^{\infty }(dy)=\int _{{\mathbb R}^d}\mu ^rF^r(dy)-\int _{{\mathbb R}^d}\mu ^{\infty }F^{\infty }(dy) = \mu ^r-\mu ^{\infty }, \end{aligned}$$

then

$$\begin{aligned} \frac{({\mathcal {A}}^{\infty }h_r)(X_s)}{h(X_s)}=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^d z_{r,i}z_{r,j}(\sigma \sigma ^T)_{i,j}-\sum _{i=1}^dz_{r,i}\mu ^{\infty }m^{\infty }_i + \mu ^r-\mu ^{\infty }=K_r. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \begin{aligned} L_t^r&=\exp \left\{ \sum _{j=1}^dz_{r,j}(X_{t,j}-X_{0,j})\right\} \cdot \exp \left\{ -\int _0^tK_r\textrm{d}s\right\} \\&= \exp \left\{ \sum _{j=1}^dz_{r,j}(X_{t,j}-X_{0,j})-K_rt\right\} \end{aligned} \end{aligned}$$

and thus $L_t^r$ given in (22) indeed satisfies the representation (40) for function $h_r(x)$ given by (20).

To finish the proof it is sufficient to show that the generator ${\mathcal {A}}^r$ given by (43) indeed coincides with the generator given in (41) for $h(x)=h_r(x)$. First, by (23) we get

$$\begin{aligned} \frac{1}{h}\left[ {\mathcal {A}}^{\infty }(fh)-f{\mathcal {A}}^{\infty }h\right] =\frac{{\mathcal {A}}^{\infty }(fh)}{h}-\frac{f{\mathcal {A}}^{\infty }h}{h}=\frac{{\mathcal {A}}^{\infty }(fh)}{h}-fK_r. \end{aligned}$$

Second, (42) produces

$$\begin{aligned}{} & {} \frac{{\mathcal {A}}^{\infty }(fh)}{h}=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^d\left( \frac{\partial ^2f}{\partial x_i\partial x_j}+\frac{\partial f}{\partial x_i}z_{r,j}+\frac{\partial f}{\partial x_j}z_{r,i}+fz_{r,j}z_{r,i}\right) (\sigma \sigma ^T)_{i,j} \\{} & {} \quad - \sum _{i=1}^d\left( \frac{\partial f}{\partial x_i}+fz_{r,i}\right) \mu ^{\infty }m^{\infty }_i + \int _{{\mathbb R}^d}\frac{f(x+y)h(x+y)-f(x)h(x)}{h(x)}\mu ^{\infty }F^{\infty }(dy). \end{aligned}$$

Hence

$$\begin{aligned}{} & {} \frac{{\mathcal {A}}^{\infty }(fh)}{h}-fK_r=\frac{1}{2}\sum _{i=1}^d\sum _{j=1}^d\frac{\partial ^2f}{\partial x_i\partial x_j}(\sigma \sigma ^T)_{i,j} \\{} & {} +\sum _{i=1}^d\frac{\partial f}{\partial x_i}\sum _{j=1}^d\left( z_{r,j}(\sigma \sigma ^T)_{i,j}-\mu ^{\infty }m^{\infty }_i\right) + \int _{{\mathbb R}^d}(f(x+y)-f(x))\mu ^rF^r(dy). \end{aligned}$$

Finally, using the system of equations (21) completes the proof. $\square$

Proof of Lemma 3

First observe that $I_+^r(x)$ is equal to the expectation

$$\begin{aligned} {\mathbb {E}}\left[ f\left( \frac{x\exp \{\sum _{i=1}^2z_{r,i}T_i\}}{x(\exp \{\sum _{i=1}^2z_{r,i}T_i\}-1)+1}\right) \right] , \end{aligned}$$

(44)

where $T_1$ and $T_2$ are two independent random variables with exponential distributions $\textrm{Exp}(\alpha _1)$ and $\textrm{Exp}(\alpha _2)$, respectively. Then $z_{r,1}T_1\sim \textrm{Exp}\left( \frac{\alpha _1}{z_{r,1}}\right)$, $z_{r,2}T_2\sim \textrm{Exp}\left( \frac{\alpha _2}{z_{r,2}}\right)$ and the density of $S^r:=\sum _{i=1}^2z_{r,i}T_i$ is given by

$$\begin{aligned} f_{S^r}(y)=\frac{\beta _1\beta _2}{\beta _1-\beta _2}\left( e^{-\beta _2y}-e^{-\beta _1y}\right) I(y\ge 0)\textrm{d}y. \end{aligned}$$

Hence, the expectation (44) equals

$$\begin{aligned} {\mathbb {E}}\left[ f\left( \frac{xe^{S^r}}{x(e^{S^r}-1)+1}\right) \right] = \int _0^{\infty }f\left( \frac{xe^y}{x(e^y-1)+1}\right) \frac{\beta _1\beta _2}{\beta _1-\beta _2}\left( e^{-\beta _2y}-e^{-\beta _1y}\right) \textrm{d}y. \end{aligned}$$

Next, we can integrate above integral by parts to obtain

$$\begin{aligned}{} & {} f(x)-\int _0^{\infty }f'\left( \frac{xe^y}{x(e^y-1)+1}\right) \frac{\textrm{d}}{\textrm{d}y}\left( \frac{xe^y}{x(e^y-1)+1}\right) \\ {}{} & {} \qquad \cdot \left( \frac{\beta _1}{\beta _2-\beta _1}e^{-\beta _2y}-\frac{\beta _2}{\beta _2-\beta _1}e^{-\beta _1y}\right) \textrm{d}y \end{aligned}$$

and by substitution $v:=\frac{xe^y}{x(e^y-1)+1}$ (hence $y=\ln \left( \frac{v(1-x)}{x(1-v)}\right)$) we derive

$$\begin{aligned} \begin{aligned} f(x)&-\frac{\beta _1}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{-\beta _2}\int _x^1f'(v)\left( \frac{v}{1-v}\right) ^{-\beta _2}\textrm{d}v \\&+\frac{\beta _2}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{-\beta _1}\int _x^1f'(v)\left( \frac{v}{1-v}\right) ^{-\beta _1}\textrm{d}v, \end{aligned} \end{aligned}$$

which completes the first part of the proof.

The formula for $I_-^r(x)$ can be derived by substitution $u:=-y$ to get

$$\begin{aligned} I_-^r(x)=\int _{(0,\infty )^2}f\left( \frac{x\exp \{-\sum _{i=1}^2z_{r,i}u_i^r\}}{x(\exp \{-\sum _{i=1}^2z_{r,i}u_i^r\}-1)+1}\right) \prod _{j=1}^2\alpha _je^{-\alpha _ju_i^r}\textrm{d}y, \end{aligned}$$

which, by the same arguments as for $I_+^r(x)$, is equal to

$$\begin{aligned} {\mathbb {E}}\left[ f\left( \frac{xe^{-S^r}}{x(e^{-S^r}-1)+1}\right) \right] = \int _0^{\infty }f\left( \frac{xe^{-y}}{x(e^{-y}-1)+1}\right) \frac{\beta _1\beta _2}{\beta _1-\beta _2}\left( e^{-\beta _2y}-e^{-\beta _1y}\right) \textrm{d}y. \end{aligned}$$

Integration by parts together with substitution of $v:=\frac{xe^{-y}}{x(e^{-y}-1)+1}$ $\Bigg (\text {hence}\, y=-\ln \left( \frac{v(1-x)}{x(1-v)}\right) \Bigg )$ gives

$$\begin{aligned} \begin{aligned} f(x)&+\frac{\beta _1}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{\beta _2}\int _0^xf'(v)\left( \frac{v}{1-v}\right) ^{\beta _2}\textrm{d}v \\&- \frac{\beta _2}{\beta _2-\beta _1}\left( \frac{1-x}{x}\right) ^{\beta _1}\int _0^xf'(v)\left( \frac{v}{1-v}\right) ^{\beta _1}\textrm{d}v \end{aligned} \end{aligned}$$

which completes the second part of the proof. $\square$