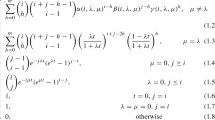A Numerical Approach for Evaluating the Time-Dependent Distribution of a Quasi Birth-Death Process

Abstract

This paper considers a continuous-time quasi birth-death (qbd) process, which informally can be seen as a birth-death process of which the parameters are modulated by an external continuous-time Markov chain. The aim is to numerically approximate the time-dependent distribution of the resulting bivariate Markov process in an accurate and efficient way. An approach based on the Erlangization principle is proposed and formally justified. Its performance is investigated and compared with two existing approaches: one based on numerical evaluation of the matrix exponential underlying the qbd process, and one based on the uniformization technique. It is shown that in many settings the approach based on Erlangization is faster than the other approaches, while still being highly accurate. In the last part of the paper, we demonstrate the use of the developed technique in the context of the evaluation of the likelihood pertaining to a time series, which can then be optimized over its parameters to obtain the maximum likelihood estimator. More specifically, through a series of examples with simulated and real-life data, we show how it can be deployed in model selection problems that involve the choice between a qbd and its non-modulated counterpart.

1 Introduction

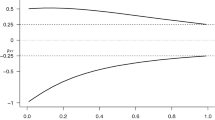
Birth-death (bd) processes are continuous-time Markov processes where transitions can only increase or decrease the state by one—usually referred to as births and deaths, respectively. These well-known processes are widely used and have applications in many areas such as biology, epidemiology and operations research. In some real life systems, however, it is likely that there is a higher variability in the birth- and/or the death rates than modelled by a conventional bd process. Observe for example the data in Fig. 1, displaying the annual counts of the female population of the whooping crane (see Stratton (2020) for the original data, and Davison et al. (2020) for the female counts). There are some fluctuations visible in the evolution of the population size, which could be indicative of a higher variability in some, or all, model parameters. One wonders whether specific generalizations of the bd process could be more suitable for this data. The major aim of this paper is to develop methodologies that can be used to rigorously compare the fit of a conventional bd process with more general alternatives.

Fig. 1

Yearly population count of female whooping cranes arriving in Texas each autumn

An example of a more general alternative to the conventional bd process is the quasi birth-death (qbd) process. The population process, called the level process, in a qbd process is given by a bd process of which the transition rates are modulated by a continuous-time Markov chain, called the phase process. This means that the transition rates of the qbd process switch between multiple distinct values at the jump times of the phase process. Together, the level and the phase process form a bivariate Markov process. In an even more general qbd process, the number of states of the phase process can depend on the current value of the level process. This leads to a so-called level-dependent qbd process, which is the process that we consider in this paper. Over the years, various properties of level-dependent qbd processes have been studied. We refer to e.g. (Bright and Taylor 1995) for calculations concerning the equilibrium distribution, Ramaswami and Taylor (1996) for the computation of certain matrices that play an important role in the qbd context, and Mandjes and Taylor (2016) for a characterization of the process’ running maximum.

In the above whooping crane example, one would like to statistically compare the scenario of the data stemming from a conventional bd process with that of the data stemming from the more general qbd process. In order to do so, a prerequisite is that we have a methodology to compute, for both models, the likelihood of our dataset. This, in turn, requires techniques for the evaluation of the time-dependent probabilities corresponding to bd and qbd processes. In this paper we investigate different approaches to compute the time-dependent probabilities of the joint Markov process of level and phase in the level-dependent qbd process. In particular, we propose, justify and test an approach based on the so-called Erlangization principle, which we compare with existing alternatives. Then we point out through a series of experiments, including the whooping crane example, how such techniques can be used in determining whether a bd process or a qbd process yields the better fit.

In order to numerically evaluate probabilities pertaining to bd and qbd processes, various methods have been developed. For all practical purposes, it is natural to let the underlying Markov chain live on a finite state space. A commonly applied approach to compute the time-dependent distribution boils down to computing the matrix exponential of the transition rate matrix, say Q, of the corresponding Markov chain (of which the states, in the qbd case, encode all level/phase combinations). More precisely, the (i, j)-th entry of e^Qt provides us with the probability of being in state j at time t given that the initial state was i, where in the qbd context, i and j correspond to specific phase/level combinations. It is known, however, that the computation of matrix exponentials may involve various numerical complications. We refer to e.g. the survey (Moler and Van Loan 2003), where about all approaches available at that time, it is stated that ‘none are completely satisfactory’. We remark that since the publication of Moler and Van Loan (2003) substantial progress has been made in order to resolve the numerical issues: various novel, more sophisticated approaches are being developed (Al-Mohy and Higham 2009). Alternatively, one could solve the linear system of differential equations resulting from the Kolmogorov equations. As argued in e.g. Reibman and Trivedi (1988), this method has various intrinsic problems as well. Most notably, if the underlying system is large, the Q matrix is ill-conditioned, or the differential equations are stiff, the evaluation can be slow and/or inaccurate.

Owing to the special structure of the transition rate matrix (i.e., the Q-matrix having non-negative off-diagonal entries, row sums equal to 0), another approach is possible. In the uniformization technique the continuous-time Markov chain is converted to a discrete-time Markov chain (say with transition matrix P) of which the jump times correspond to a Poisson process with a constant rate (say σ). Here P and σ are chosen in such a way that the newly defined process and the original continuous-time Markov chain are statistically identical, i.e. all distributional properties are equivalent. The distribution of the continuous-time Markov chain at time t can thus be obtained by weighing matrices P^k by the probabilities that the Poisson process has jumped k times in [0,t], and summing these over k (k = 0,1,…). This method performs well in many cases, but it has disadvantages as well. Evidently, in numerical computations the above summation has to be truncated at some finite threshold, where the issue is to choose this threshold high enough to make sure that the error made is negligible. In addition, to compute all k-step transition matrices P^k, the corresponding matrix multiplications need to be executed, which may make the procedure prohibitively slow. Uniformization was introduced in the 1950s in Jensen (1953); see also Grassmann (1991), Gross and Miller (1984), and Melamed and Yadin (1984) for other seminal contributions; an extensive discussion on its pros and cons can be found in van Dijk et al. (2018).

In this paper we discuss an alternative approach, based on the Erlangization principle, which has previously been explored (in other contexts) in e.g. Asmussen et al. (2002), Ramaswami et al. (2008), and Mandjes and Taylor (2016). It uses the fact that, although the computation of the distribution of the state of the Markov chain at a deterministic time is challenging, its counterpart at an exponentially distributed epoch just requires solving a system of linear equations. A second observation is that the sum of k independent exponentially distributed random variables with mean t/k—corresponding to an Erlang distribution with scale parameter k and shape parameter k/t—converges to the deterministic number t as k grows large. Combining these two properties, the idea is to evaluate the transition probabilities at an exponentially distributed epoch with parameter k/t, and to raise the resulting matrix to the power k. It is tempting to believe that our deterministic-time transition probabilities are accurately approximated by this procedure as long as k is chosen large enough. This approach has the inherent advantage that the number of matrix multiplications is limited: if k is a power of two, it suffices to square the exponential-time transition matrix $\log _{2} k$ times. Importantly, we can prove the theoretical correctness of the approach, in that we show that it becomes increasingly precise as $k\to \infty$, with an argumentation that relies on large-deviations theory. By means of a series of numerical examples, we also show that this approach is in many settings computationally faster than the approaches based on the matrix exponential and uniformization, without compromising the accuracy.

Going back to the whooping crane data from Fig. 1, an interesting question remains if a qbd process indeed provides a better fit to the data than a conventional bd process, as one might suspect from the graph. In the last section of this paper we investigate this type of model selection problems, both with simulated and real-life data. By the techniques discussed in this paper, we can compute the likelihood pertaining to a time series, thus enabling the evaluation of maximum likelihood estimates. In this respect, note that all three approaches (i.e., matrix exponential, uniformization, Erlangization) can be applied in the qbd as well as the bd setting. As the class of qbd processes contains the class of bd processes, evidently the former by definition leads to a better fit, but this comes at the price of additional parameters. To ‘fairly’ compare the two models, taking into account the corresponding numbers of parameters, we perform the model selection relying on the celebrated Akaike information criterion (aic).

The remainder of this paper is organized as follows. The level-dependent qbd process and its corresponding time-dependent distribution are defined in Section 2. Section 3 shows how the transition probabilities at an exponentially distributed epoch can be computed by solving a system of linear equations. The findings of Section 3 are then used in Section 4 to motivate the Erlangization approach; in addition the theoretical correctness of this approach is established. Section 5 experimentally investigates the performance of the three approaches discussed above. Section 6 discusses the model selection problem of choosing between bd processes and qbd processes, using examples with simulated as well as real-life data, with all likelihood computations relying on Erlangization. We conclude the paper, in Section 7, with a brief discussion.

2 Model and Preliminaries

In this section we introduce the class of qbd processes that will be considered in this paper. Next, we define the object of our study, viz. the time-dependent distribution of the corresponding bivariate Markov process, and briefly discuss established approaches to numerically evaluate it.

2.1 Model

A qbd process is a bivariate process comprising levels and phases. The level process, in the sequel denoted by $\{M_{t}\}_{t\geqslant 0}$, attains values in {0,1,…,C} for some $C\in {\mathbb N}$. The phase process is denoted by $\{X_{t}\}_{t\geqslant 0}$; when the level M_t equals m, the phase X_t attains values in {1,…,d_m}, for some $d_{m}\in {\mathbb N}$. In many applications the number of phases is uniform in the level, or, more concretely, $d_{m}=d\in {\mathbb N}$ for all m ∈{0,…,C}. The birth-death nature of the process is reflected by the fact that at any transition the level can increase or decrease by at most 1.

We provide a more precise description of the model $\{M_{t}, X_{t}\}_{t\geqslant 0}$ by formally defining the corresponding transition rates.

• In the first place, Q^(m), for m ∈{0,1,…,C}, is a transition rate matrix of dimension d_m × d_m that corresponds to a continuous-time Markov chain living on the state space {1,…,d_m}. Its elements are denoted by $q^{(m)}_{ij}$; they are non-negative for i≠j and in addition the row sums are zero. Whenever M_t = m, a jump from phase i to phase j that leaves the level unchanged occurs with rate $q^{(m)}_{ij}$, for i≠j. In addition, we define the total rate out of phase i (while the level remains at m),

  $$q^{(m)}_{i}:=-q^{(m)}_{ii}=\sum\limits_{j\not=i} q^{(m)}_{ij};$$

  here the sum on the right hand side should be understood to be over all j ∈{1,…,d_m} such that j≠i.

• In the second place, there are transitions in which the level goes up by 1, while at the same time the phase potentially changes as well. For m ∈{0,1,…,C − 1}, the matrix Λ^(m) has dimension d_m × d_m+ 1. Its (i, j)-th element contains the rate $\lambda ^{(m)}_{ij}\geqslant 0$ at which the level increases by 1 while simultaneously the phase jumps from i to j; note that i = j is allowed (under the proviso that $i\leqslant \min \limits \{d_{m},d_{m+1}\}$). Throughout this paper we write

  $$\lambda^{(m)}_{i}:=\sum\limits_{j=1}^{d_{m+1}} \lambda^{(m)}_{ij},$$

  to denote the total rate corresponding to an increase in level from phase i, with i ∈{1,…,d_m}.

• Finally, there are transitions in which the level goes down by 1, again potentially simultaneously with a phase change. The (i, j)-th element of the matrix ${\mathcal M}^{(m)}$, which has dimension d_m × d_m− 1 for m ∈{1,2,…,C}, contains the rate $\mu ^{(m)}_{ij}\geqslant 0$ at which the level decreases by 1 while the phase jumps from i to j; again, i = j is allowed (if $i\leqslant \min \limits \{d_{m-1},d_{m}\}$). We compactly write for the total rate of a decrease in level from phase i, with i ∈{1,…,d_m},

  $$\mu^{(m)}_{i}:=\sum\limits_{j=1}^{d_{m-1}} \mu^{(m)}_{ij}.$$

In this work we assume that the matrices Q^(m), Λ^(m), and ${\mathcal M}^{(m)}$ are such that the joint Markov process {M_t, X_t}_t≥ 0 is irreducible, implying that, with positive probability any level/phase pair can be reached from any other level/phase pair in any amount of time. The number of states of this process is $D:={\sum }_{m=0}^{C} d_{m}$. We let Q be the D × D transition rate matrix of {M_t, X_t}_t≥ 0, that is,

$$Q :=\left( \begin{array}{cccccc}\bar Q^{(0)}&{\Lambda}^{(0)}&0&\cdots&0&0\\ {\mathcal M}^{(1)}&\bar Q^{(1)}&{\Lambda}^{(1)}&\cdots&0&0\\ 0&{\mathcal M}^{(2)}&\bar Q^{(2)}&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&\bar Q^{(C-1)}&{\Lambda}^{(C-1)}\\ 0&0&0&\cdots&{\mathcal M}^{(C)}&\bar Q^{(C)} \end{array}\right),$$

where $\bar Q^{(m)}$ is defined as Q^(m) with the diagonal entries adapted such that the row sums of Q are zero. More precisely, the definition of $\bar Q^{(m)}$ entails that the diagonal of Q consists of entries of the form $-\sigma ^{(m)}_{i}$, where (for m ∈{0,1,…,C} and i ∈{1,…,d_m})

$$ \begin{array}{@{}rcl@{}} \sigma^{(m)}_{i}:= q^{(m)}_{i}+ \lambda^{(m)}_{i} 1_{\{m<C\}}+ \mu^{(m)}_{i} 1_{\{m>0\}} . \end{array} $$

(1)

These rates $\sigma ^{(m)}_{i}$ are to be interpreted as the ‘total flux’ when the level is m and the phase is i. For later reference we define the largest entry among these fluxes by

$$ \sigma:=\max\limits_{m\in\{0,1,\ldots,C\}} \left( \max\limits_{i\in\{1,\ldots,d_{m}\}}\sigma_{i}^{(m)}\right). $$

(2)

We finally introduce the D × D matrix P_t that describes the process’ time-dependent distribution. It contains probabilities of the type

$$ \begin{array}{@{}rcl@{}} p_{ij}(m,m^{\prime};t) := {\mathbb P}(M_{t}= m^{\prime}, X_{t} = j | M_{0} = m, X_{0} = i), \end{array} $$

(3)

with the states ordered in the same way as is done in Q. The remainder of this section is devoted to describing two often used methods to numerically evaluate P_t, with which we compare our method in Section 5.

2.2 Time-Dependent Probabilities: Matrix Exponential

It is commonly known that P_t, as given in Eq. 3, can be expressed as a matrix exponential, i.e., P_t = e^Qt. As argued extensively in (Moler and Van Loan 2003), the numerical evaluation of such matrix exponentials is a delicate issue. In numerical computing environments various types of algorithms have been implemented. Matlab’s implementation (⋅) is based on the algorithm developed in Higham (2005), and is claimed to be highly accurate; see also the further refinements in Al-Mohy and Higham (2009).

Approximation 1 (Matrix exponential)

P_t is approximated by

$$ \begin{array}{@{}rcl@{}} P_{t}^{\text{(m)}} := \mathtt{expm}(Qt), \end{array} $$

(4)

based on Matlab’s implementation (⋅).

2.3 Time-Dependent Probabilities: Uniformization

An alternative existing approach to obtain time-dependent probabilities relies on uniformization. The main idea is to convert the continuous-time Markov chain to a discrete-time Markov chain of which the jump times follow a Poisson process with a constant rate. For the qbd process we let this uniform rate be σ, as defined in Eq. 2. Define, with self-evident notation,

$$ {\mathscr P}_{(m,i),(m^{\prime},j)}:= \left\{\begin{array}{ll}\sigma^{-1} Q_{(m,i),(m^{\prime},j)} &\text{if} (m,i)\not=(m^{\prime},j),\\ 1- \sigma^{-1}{\sum}_{(m^{\prime},j)\not=(m,i)}Q_{(m,i),(m^{\prime},j)} &\text{if} (m,i)=(m^{\prime},j), \end{array}\right. $$

or, equivalently, $Q=\sigma {\mathscr P} -\sigma I$. Observe that by definition of σ all these entries are in [0,1]; in fact, ${\mathscr P}$ is a transition probability matrix of a discrete-time Markov chain. Sampling the number of jumps in (0,t] of this discrete-time Markov chain according to a Poisson distribution with parameter σt, we find that

$$ {P}_{t} = e^{Qt} = e^{(\sigma{\mathscr P}-\sigma I)t}=\sum\limits_{k=0}^{\infty} e^{-\sigma t}\frac{(\sigma t)^{k}}{k!} {\mathscr P}^{k}, $$

The following approximation is based on this representation.

Approximation 2 (Uniformization)

For a given $\ell \in {\mathbb N}$, P_t is approximated by

$$ {P}_{t}^{(\mathrm{u},\ell)} := \sum\limits_{k=0}^{\ell} e^{-\sigma t}\frac{(\sigma t)^{k}}{k!} {\mathscr P}^{k}. $$

(5)

A question is: how to select a value of ℓ to make sure that the error made is below some allowable threshold δ > 0? While in practical situations one typically relies on pragmatic criteria to determine ℓ, a formally justified, but potentially somewhat conservative, approach is the following. Realize that, trivially, as $\ell \to \infty$,

$$ 0\leqslant p_{ij}(m,m^{\prime};t)- {p}^{(\mathrm{u}, \ell)}_{ij}(m,m^{\prime};t) \leqslant {\mathbb P}(\text{Pois}(\sigma t) \geqslant \ell+1)\to 0, $$

where Pois(σt) denotes a Poisson random variable with mean σt. This bound entails that one could use for example the Chernoff bound to find the ℓ for which ${\mathbb P}(\text {Pois}(\sigma t) \geqslant \ell +1) < \delta$:

$$ \begin{array}{@{}rcl@{}}{\mathbb P}(\text{Pois}(\sigma t) \geqslant \ell+1) &\leqslant& \inf_{\theta>0} e^{-\theta (\ell+1)} {\mathbb E} e^{\theta \text{Pois}(\sigma t)}\\ &=& \inf_{\theta>0} e^{-\theta (\ell+1)} e^{\sigma t(e^{\theta}-1)} =\left( \frac{\sigma t}{\ell+1}\right)^{\ell+1} e^{\ell+1-\sigma t}; \end{array} $$

(6)

equating the right-hand side to δ yields an ℓ with the desired property.

Note that an important advantage of uniformization is its implementational simplicity: the matrix ${\mathscr P}$ is trivially computed from Q, and it is straightforward to evaluate its powers. The main disadvantage of uniformization is that many matrix multiplications are needed, as the approximation uses all matrices ${\mathscr P}^{k}$ for k = {0,1,…,ℓ}; particularly when σ is relatively large, implying that ℓ has to be chosen large as well, the procedure may become rather time consuming. To remedy this disadvantage of uniformization, we pursue an alternative approach, based on the concept of Erlangization. This approach combines two ideas: (i) if the time horizon is exponentially distributed rather than deterministic, then the corresponding transition probability follows simply by solving a linear system of equations, and (ii) one can approximate a deterministic number by a sum of a large number of independent exponentially distributed random variables with an appropriately chosen parameter. Section 3 first elaborates on property (i). Then, in Section 4, it is pointed out how, based on these two properties, P_t can be efficiently and accurately approximated. In Section 5 we numerically compare the performance of Erlangization with the matrix exponential approach (4) and uniformization (5).

3 Time-Dependent Probabilities at Exponential Epochs

The main goal of this section is to show that the evaluation of the distribution of {M_t, X_t} at an exponentially distributed epoch essentially reduces to solving a linear system of equations. Let T_η be an exponentially distributed random variable with mean η^− 1 (with η > 0), independent of $\{M_{t},X_{t}\}_{t\geqslant 0}$. We define

$$ \pi_{ij}(m,m^{\prime};\eta):= {\mathbb P}(M_{T_{\eta}}= m^{\prime}, X_{T_{\eta}} = j | M_{0} = m, X_{0} =i). $$

We now point out how to compute these probabilities $\pi _{ij}(m,m^{\prime };\eta )$, with $m,m^{\prime }\in \{0,1,\ldots ,C\}$, i ∈{1,…,d_m}, and $j\in \{1,\ldots ,d_{m^{\prime }}\}$. Recall the definition of $\sigma ^{(m)}_{i}$ in Eq. 1. The standard ‘Markovian reasoning’ yields

$$ \begin{array}{@{}rcl@{}} \pi_{ij}(m,m^{\prime};\eta)\!&=&\!\sum\limits_{i^{\prime}=1,i^{\prime}\not= i}^{d_{m}} \frac{q^{(m)}_{ii^{\prime}}}{\sigma^{(m)}_{i} + \eta} \pi_{i^{\prime}j}(m,m^{\prime};\eta) + \sum\limits_{i^{\prime}=1}^{d_{m+1}} \frac{\lambda^{(m)}_{ii^{\prime}}}{\sigma^{(m)}_{i} + \eta} \pi_{i^{\prime}j}(m + 1,m^{\prime};\eta) \!1_{\{m<C\}} \\ &&+ \sum\limits_{i^{\prime}=1}^{d_{m-1}}\frac{\mu^{(m)}_{ii^{\prime}}}{\sigma^{(m)}_{i} + \eta} \pi_{i^{\prime}j}(m-1,m^{\prime};\eta) 1_{\{m>0\}} + \frac{\eta}{\sigma^{(m)}_{i} + \eta} 1_{\{m=m^{\prime}, i=j\}}. \end{array} $$

Multiplying both sides of the equation with $\sigma ^{(m)}_{i} + \eta$ results in

$$ \begin{array}{@{}rcl@{}} (\sigma^{(m)}_{i} + \eta) \pi_{ij}(m,m^{\prime};\eta)\!&=&\!\sum\limits_{i^{\prime}=1,i^{\prime}\not= i}^{d_{m}} \!q^{(m)}_{ii^{\prime}} \pi_{i^{\prime}j}(m,m^{\prime};\eta) + \sum\limits_{i^{\prime}=1}^{d_{m+1}} \lambda^{(m)}_{ii^{\prime}} \pi_{i^{\prime}j}(m + 1,m^{\prime};\eta) \!1_{\{m<C\}} \\ &&+\sum\limits_{i^{\prime}=1}^{d_{m-1}} \mu^{(m)}_{ii^{\prime}} \pi_{i^{\prime}j}(m-1,m^{\prime};\eta) 1_{\{m>0\}} + \eta 1_{\{m=m^{\prime}, i=j\}}. \end{array} $$

(7)

The sum of the coefficients on the right equals $\sigma ^{(m)}_{i}+\eta$, making this system of linear equations strictly diagonally dominant, and therefore non-singular (Horn and Johnson 2013, Thm 6.1.10). As a consequence, the system can be numerically solved in $\pi _{ij}(m,m^{\prime };\eta )$ through various efficient evaluation techniques, such as the iterative Jacobi and Gauss-Seidel methods (Atkinson 1989, Section VIII.6).

The above linear system can be written in a compact matrix form. Define the $d_{m}\times d_{m^{\prime }}$ matrix ${\Pi }_{\eta }(m,m^{\prime })$ as the matrix whose (i, j)-th entry is $\pi _{ij}(m,m^{\prime };\eta )$. In addition, let ${\Sigma }^{(m)}:=\text {diag}\{\sigma _{1}^{(m)},\ldots ,\sigma ^{(m)}_{d_{m}}\}$ and $\check Q^{(m)}:=\text {diag}\{q_{1}^{(m)},{\ldots } q^{(m)}_{d_{m}}\}$; the matrix I^(m) is an identity matrix of dimension d_m. We thus obtain

$$ \begin{array}{@{}rcl@{}} ({\Sigma}^{(m)}+\eta I^{(m)}){\Pi}_{\eta}(m,m^{\prime}) &=& (Q^{(m)}+\check Q^{(m)}){\Pi}_{\eta}(m,m^{\prime}) + {\Lambda}^{(m)}{\Pi}_{\eta}(m+1,m^{\prime}) 1_{\{m<C\}}\\ &&+ {\mathcal M}^{(m)}{\Pi}_{\eta}(m-1,m^{\prime}) 1_{\{m>0\}} +\eta I^{(m)}1_{\{m=m^{\prime}\}}. \end{array} $$

We define π_η as a D × D matrix, which is a block matrix of which the components are the matrices ${\Pi }_{\eta }(m,m^{\prime })$:

$$ \begin{array}{@{}rcl@{}} {\Pi}_{\eta} :=\left( \begin{array}{ccccc}{\Pi}_{\eta}(0,0)&{\Pi}_{\eta}(0,1)&{\Pi}_{\eta}(0,2)&\cdots&{\Pi}_{\eta}(0,C)\\ {\Pi}_{\eta}(1,0)&{\Pi}_{\eta}(1,1)&{\Pi}_{\eta}(1,2)&\cdots&{\Pi}_{\eta}(1,C)\\ {\Pi}_{\eta}(2,0)&{\Pi}_{\eta}(2,1)&{\Pi}_{\eta}(2,2)&\cdots&{\Pi}_{\eta}(2,C)\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ {\Pi}_{\eta}(C,0)&{\Pi}_{\eta}(C,1)&{\Pi}_{\eta}(C,2)&\cdots&{\Pi}_{\eta}(C,C) \end{array}\right). \end{array} $$

(8)

Observe that in the linear equations (7) both the ‘destination level’ (namely, $m^{\prime }$) and the ‘destination phase’ are constant. This means that we can write the equations in Eq. 7 corresponding to a given phase j and level $m^{\prime }$, as a system of the form $A {\boldsymbol x}_{jm^{\prime }} = {\boldsymbol b}_{jm^{\prime }}$, where ${\boldsymbol b}_{jm^{\prime }}$ is a known vector of dimension D, ${\boldsymbol x}_{jm^{\prime }}$ is an unknown vector of dimension D, and A is known matrix of dimension D × D. Importantly, the matrix A does not depend on j and $m^{\prime }$, and can be checked to equal Q − ηI^(D). As a consequence, with ${\boldsymbol x}_{jm^{\prime }} =A^{-1} {\boldsymbol b}_{jm^{\prime }}$, we have to compute (for this specific $(j,m^{\prime })$-pair, that is) the matrix A^− 1 just once. In case the linear system is solved in the conventional way, this takes time O(D³). This means that, due to the elementary structure of ${\boldsymbol b}_{jm^{\prime }}$ (containing one entry with value − η and zeroes elsewhere), the computational effort of evaluating the full matrix π_η is O(D³).

The above reasoning can be compactly rephrased differently as follows. It is readily verified from Eq. 7 that π_η can be rewritten as − η(Q − ηI^(D))^− 1, and computing the inverse (Q − ηI^(D))^− 1 requires O(D³) time. This matrix π_η will appear in the approximation of P_t based on Erlangization, introduced in the next section.

4 Erlangization

In this section, we discuss the approach based on Erlangization to approximate P_t. We first introduce the approximation and then provide the theoretical correctness of this approach. Let S_{ℓ, t} be an Erlang-distributed random variable with rate parameter ℓ/t and shape parameter ℓ. Let $P_{t}^{(\mathrm {e},\ell )}$ be a D × D matrix with entries

$$p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) := {\mathbb{P}}(M_{S_{\ell,t}} = m^{\prime}, X_{S_{\ell,t}} = j | M_{0} = m, X_{0} = i). $$

It is clear that $P_{t}^{(\mathrm {e},\ell )} = ({\Pi }_{\ell /t})^{\ell }$, with π_η as defined in Eq. 8, owing to the fact that an Erlang random variable with rate parameter μ and shape parameter k can be written as the sum of k independent and identically distributed exponential random variables with rate μ. We propose the following approximation.

Approximation 3 (Erlangization)

For a given $\ell \in {\mathbb N}$, P_t is approximated by,

$$ P_{t}^{(\mathrm{e},\ell)} = ({\Pi}_{\ell/t})^{\ell}. $$

(9)

As we will argue below, $P_{t}^{(\mathrm {e},\ell )}$ converges to P_t as $\ell \to \infty$. The above idea is usually referred to as ‘Erlangization’: the time $t\geqslant 0$ is approximated by the Erlang time S_{ℓ, t}. This distribution has mean t and variance t²/ℓ, so that the corresponding coefficient of variation converges to 0 as $\ell \to \infty$.

Our goal is to assess how much $p_{ij}(m,m^{\prime };t)$ differs from $p^{(\mathrm {e}, \ell )}_{ij}(m,m^{\prime };t)$. The resulting bounds are then used to show that this difference vanishes as ℓ grows large. We start by establishing an upper bound. For any given δ ∈ (0,t),

$$ \begin{array}{@{}rcl@{}} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t)& =&{\mathbb{P}}(M_{S_{\ell,t}} = m^{\prime}, X_{S_{\ell,t}} = j \big| |S_{\ell,t}-t|\leqslant\delta, M_{0} = m, X_{0} =i) {\mathbb{P}}(|S_{\ell,t}-t|\leqslant\delta) \\ &&+{\mathbb{P}}(M_{S_{\ell,t}} = m^{\prime}, X_{S_{\ell,t}} = j \big| |S_{\ell,t}-t|>\delta, M_{0} = m, X_{0} =i) {\mathbb{P}}(|S_{\ell,t}-t|>\delta)\\ &\leqslant& {\mathbb{P}}(M_{S_{\ell,t}}= m^{\prime}, X_{S_{\ell,t}} = j | |S_{\ell,t} - t|\leqslant\delta, M_{0} = m, X_{0} =i)+{\mathbb{P}}(|S_{\ell,t}\!-t|\!>\!\delta). \end{array} $$

Note that ${\mathbb {P}}(M_{S_{\ell ,t}}= m^{\prime }, X_{S_{\ell ,t}} = j | |S_{\ell ,t}-t|\!\leqslant \!\delta , M_{0} = m, X_{0} = i)$ is equal to the transition probability $p_{ij}(m,m^{\prime }; S_{\ell ,t})$ additionally imposing the condition that $|S_{\ell ,t}-t|\leqslant \delta$. The difference between this probability and $p_{ij}(m,m^{\prime };t)$ can thus be at most δ times the maximum slope of $p_{ij}(m,m^{\prime };s)$ for s in [t − δ, t + δ]. Hence

$$ \begin{array}{@{}rcl@{}} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) \leqslant p_{ij}(m,m^{\prime};t) + \delta\left( \sup_{s\in[t-\delta,t+\delta]} \left|\frac{\mathrm{d}}{\mathrm{d}s} p_{ij}(m,m^{\prime}; s)\right|\right) +{\mathbb P}(|S_{\ell,t}-t|>\delta). \end{array} $$

Recall that Q is the transition rate matrix of the D-dimensional continuous-time Markov process $\{M_{t}, X_{t}\}_{t\geqslant 0}$ and $\sigma :=\max \limits _{m,i} \sigma _{i}^{(m)}$. Then, using the Kolmogorov equations in combination with the triangle inequality, uniformly in $s\geqslant 0$,

$$\left|\frac{\mathrm{d}}{\mathrm{d}s} p_{ij}(m,m^{\prime};s) \right|\leqslant\sum\limits_{m^{\prime\prime},j^{\prime}} p_{ij^{\prime}}(m,m^{\prime\prime};s) \left|Q_{(m^{\prime\prime},j^{\prime}),(m^{\prime},j)} \right| \leqslant\sum\limits_{m^{\prime\prime},j^{\prime}} p_{ij^{\prime}}(m,m^{\prime\prime};s) \sigma = \sigma .$$

We proceed by finding an upper bound on ${\mathbb P}(|S_{\ell ,t}-t|>\delta )$. Noting that S_{ℓ, t} can be written as ℓ^− 1 times an Erlang random variable $\bar S_{\ell ,t}$ with rate parameter 1/t and shape parameter ℓ,

$$ \begin{array}{@{}rcl@{}} {\mathbb{P}}(|S_{\ell,t}-t|\!>\!\delta) = {\mathbb{P}}(|\ell^{-1} \bar S_{\ell,t} - t|\!>\!\delta) = {\mathbb{P}}(\ell^{-1} \bar S_{\ell,t} - t \!<\! -\delta) + {\mathbb{P}}(\ell^{-1} \bar S_{\ell,t}-t \!>\! \delta). \end{array} $$

(10)

We can majorize both probabilities on the right-hand side by using the Chernoff bound. Starting with ${\mathbb {P}}(\ell ^{-1} \bar S_{\ell ,t}-t > \delta )$, we have

$$ {\mathbb{P}}(\ell^{-1} \bar S_{\ell,t}-t > \delta) = {\mathbb{P}}(\bar S_{\ell,t} > \ell(\delta + t) )\leqslant \inf_{\theta >0} {e^{-\theta \ell(\delta+t)}}{{\mathbb E} e^{\theta\bar S_{\ell,t}}}. $$

Using the moment generating function of the Erlang distribution, we find that

$$ {e^{-\theta \ell(\delta+t)}}{{\mathbb E} e^{\theta\bar S_{\ell,t}}}= \left( \frac{e^{-\theta(\delta+t)}}{1-t\theta} \right)^{\ell}, $$

implying that

$$ {\mathbb{P}}(\ell^{-1} \bar S_{\ell,t}-t > \delta) \leqslant \underset{\theta>0}{\inf} \left( \frac{e^{-\theta(\delta+t)}}{1-t\theta} \right)^{\ell} = \left( \underset{\theta>0}{\inf} \frac{e^{-\theta(\delta+t)}}{1-t\theta}\right)^{\ell} = e^{-\ell\delta/t} \left( 1+\frac\delta{t}\right)^{\ell}. $$

In a similar way we can majorize ${\mathbb {P}}(\ell ^{-1} \bar S_{\ell ,t}-t < -\delta )$:

$${\mathbb{P}}(\ell^{-1} \bar S_{\ell,t}-t < -\delta) \leqslant e^{\ell\delta/t} \left( 1-\frac\delta{t}\right)^{\ell}. $$

Combining these upper bounds with equation (10), we conclude

$$ \begin{array}{@{}rcl@{}} {\mathbb{P}}(|S_{\ell,t}-t|>\delta) \leqslant e^{\ell\delta/t}\left( 1-\frac{\delta}{t}\right)^{\ell} + e^{-\ell\delta/t}\left( 1+\frac{\delta}{t}\right)^{\ell} =:{\Psi}_{\ell,t}(\delta). \end{array} $$

(11)

We thus find, uniformly in δ ∈ (0,t),

$$ p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) \leqslant p_{ij}(m,m^{\prime};t) + \delta\cdot \sigma+ {\Psi}_{\ell,t}(\delta). $$

Now take δ = ℓ^−α with α > 0. Using elementary Taylor expansions, it can be shown that Ψ_{ℓ, t}(δ) behaves as $\exp (-\ell ^{1-2\alpha }/t^{2})$, which converges to 0 as $\ell \to \infty$ for all α < 1/2. To see this, first note that

$$ e^{\ell\delta/t} \left( 1- \frac\delta{t} \right)^{\ell} = \exp\left( \frac{\ell}{t}\delta + \ell \log\left( 1-\frac{\delta}{t}\right)\right). $$

(12)

Now consider the exponential in the right-hand side of Eq. 12. Plugging in δ = ℓ^−α and using Taylor expansions, one indeed obtains

$$ \frac1{t} \ell^{1-\alpha} + \ell\log \left( 1-\frac1{t}\ell^{-\alpha}\right) = -\frac{1}{t^{2}}\ell^{1-2\alpha} + o(\ell^{1-3\alpha}). $$

A similar analysis can be performed for the other term in the definition of Ψ_{ℓ, t}(δ). We conclude that, for all α < 1/2, Ψ_{ℓ, t}(ℓ^−α) converges to 0 as $\ell \to \infty$. Upon combining the above, and picking $\alpha =\frac {1}{3}$, the desired upper bound follows:

$$ \underset{\ell\to\infty}{\limsup} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) \leqslant \underset{\ell\to\infty}{\limsup}\ p_{ij}(m,m^{\prime};t) + \ell^{-1/3}\cdot \sigma+ {\Psi}_{\ell,t}(\ell^{-1/3}) =p_{ij}(m,m^{\prime};t). $$

We proceed by deriving a lower bound, which is established using elements that resemble those used in the upper bound. It is based on the inequality

$$ \begin{array}{@{}rcl@{}} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) &\geqslant& {\mathbb P}(M_{S_{\ell,t}}= m^{\prime}, X_{S_{\ell,t}} = j | M_{0} = m, X_{0} \\&=&i, |S_{\ell,t}-t|\leqslant\delta)\cdot{\mathbb P}(|S_{\ell,t}-t|\leqslant\delta)\\ &\geqslant& \big(p_{ij}(m,m^{\prime};t)-\delta\cdot \sigma \big)\cdot\big(1- {\mathbb P}(|S_{\ell,t}-t|>\delta)\big) \\&\geqslant& p_{ij}(m,m^{\prime};t) - \delta\cdot \sigma - {\Psi}_{\ell,t}(\delta).\end{array} $$

Pick again δ = ℓ^− 1/3, so as to obtain

$$\liminf_{\ell\to\infty} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) \geqslant p_{ij}(m,m^{\prime};t).$$

The following theorem summarizes the above findings, thus justifying the use of the Erlangization procedure.

Theorem 1

For any $\ell \in {\mathbb N}$, t > 0, and δ ∈ (0,t), with σ defined as in Eq. 2 and Ψ_{ℓ, t}(δ) defined as in Eq. 11,

$$ \left| p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) - p_{ij}(m,m^{\prime};t) \right| \leqslant \delta\cdot \sigma + {\Psi}_{\ell,t}(\delta). $$

(13)

In addition, for any t > 0,

$$\underset{\ell\to\infty}{\lim} p^{(\mathrm{e},\ell)}_{ij}(m,m^{\prime};t) = p_{ij}(m,m^{\prime};t).$$

Note that the advantage of Erlangization is that the number of matrix multiplications is low, in comparison with uniformization. More precisely, picking ℓ a power of two, one just needs to square π_ℓ/t only $\log _{2}\ell$ times. The disadvantage is that the computation of the matrix π_ℓ/t requires the solution of a linear system of dimension D, as argued in Section 3.

In addition, we note that the maximum diagonal element (in absolute terms) σ appears in the error bound of Theorem 1. As a consequence, the upper bound in Eq. 13 tends to be rather generous for some $(m,m^{\prime })$ and (i, j) pairs when the diagonal elements are relatively non-uniform.

5 Performance Analysis of Erlangization

In this section we examine the performance of the Erlangization approximation of P_t, as given by Eq. 9. We compare it with the matrix exponential approach given by Eq. 4 as well as uniformization (5). We study the accuracy (i.e., error) and efficiency (i.e., computational time) of the Erlangization approximation. In the sequel we refer to the Erlangization approach by ‘E’, to the matrix exponential approach by ‘M’, and to the uniformization approach by ‘U’.

In our performance analysis we focus on three qbd processes that are effectively the modulated counterparts of frequently used bd processes. In all three settings the modulating process (also referred to as environmental process) is of dimension 2, irrespectively of the level m ∈{0,1,…,C}. In other words, we have that d_m = d = 2, so that

$$ Q^{(m)} =\left( \begin{array}{cc} -q_{1} & q_{1} \\ q_{2} & -q_{2} \end{array}\right) $$

In addition, we let $\lambda ^{(m)}_{ij} = 0$ for i≠j, which (informally) means that an increase in level cannot occur at the same time as a phase jump. The three settings are parameterized by a function f(m, C), in the sense that

$$ \lambda^{(m)}_{i} = \lambda^{(m)}_{ii} := f(m,C) \lambda_{i}, $$

for a known positive function f(m, C) and parameter $\lambda _{i} \geqslant 0$. Similarly, we let $\mu ^{(m)}_{ij} = 0$ for i≠j, and define

$$ \mu^{(m)}_{i} = \mu^{(m)}_{ii} := g(m,C) \mu_{i}, $$

for a known positive function g(m, C) and parameter $\mu _{i} \geqslant 0$. Hence, there are at most six parameters in these models: q₁, q₂, λ₁, λ₂, μ₁, and μ₂. We proceed by detailing the dynamics underlying the three models.

Experiment 1 (Infinite-server queue)

Here we consider a system, which can also been seen as a population process, in which individuals arrive according to some arrival process and are served in parallel, in the literature also known as an infinite-server queue (Kleinrock 1975; Kulkarni 1995). The special feature is that the Poissonian arrival rate as well as the exponential service rate depend on the state of the modulating process, so that the system at hand is a Markov-modulated infinite-server queue (Anderson et al. 2016; Blom et al. 2016; 2017). This concretely means that f(m, C) = 1 and g(m, C) = m (the latter reflecting that the individuals are served in parallel), so that Λ^(m) = diag{λ₁, λ₂} and ${\mathcal M}^{(m)} = \text {diag}\{m \mu _{1},m \mu _{2}\}$. We impose a truncation at level C.

Experiment 2 (Linear birth-death process)

In this setting we consider the stochastic version of the classical Malthusian growth model, also known as the linear birth-death model (Davison et al. 2020; Karlin and Taylor 1975): the rate upward as well as the rate downward is proportional to the number of individuals present. This concretely means that f(m, C) = m and g(m, C) = m. The rates of moving upward and downward are modulated, which entails that in this case Λ^(m) = diag{mλ₁, mλ₂} and ${\mathcal M}^{(m)} = \text {diag}\{m \mu _{1},m \mu _{2}\}$. We again impose a truncation at C.

Experiment 3 (SIS-type model)

The SIR model is a so-called compartmental model used to describe epidemic growth, that keeps track of the number of susceptible individuals, the number of infectious individuals, and the number of recovered individuals; see e.g. the textbook treatments in (Allen 2003; Andersson and Britton 2000; Daley and Gani 1999). In a related variant, the SIS model, recovered individuals eventually become susceptible again. In this experiment we consider a model of the latter type, which, in the non-modulated context, has the following dynamics. There are C individuals, to be divided into infected and healthy. Let M_t be the number of healthy individuals. When M_t = m, an arbitrary healthy person becomes infected with rate λ(C − m); as a result the rate from m to m + 1 is λm(C − m). Every infected person becomes healthy again independently of the state of all other individuals; as a result, the rate from m to m − 1 is mμ. If we add modulation, then the λ and μ become dependent on the environmental process. We thus get that in this model f(m, C) = m(C − m) and g(m, C) = m, so that the upward rates become Λ^(m) = diag{m(C − m)λ₁, m(C − m)λ₂}, whereas the downward rates are given by ${\mathcal M}^{(m)} = \text {diag}\{m \mu _{1},m \mu _{2}\}$.

We start, in Section 5.1, with an extensive analysis of Experiment 1, the infinite-server queue. In particular we study the impact of the parameters ℓ and C on the accuracy (i.e., error) and efficiency (i.e., computational time) of the Erlangization approximation, and compare these with the other two approaches. In Section 5.2 we consider Experiments 2 and 3.

Importantly, whenever presenting computational times, we report the time it takes to evaluate the entire matrix $P_{t}^{(\mathrm {e},\ell )}$ ($P_{t}^{\text {(m)}}$ and ${P}_{t}^{(\mathrm {u},\ell )}$ likewise), providing us with $p_{ij}^{(\mathrm {e},\ell )}(m,m^{\prime };t)$ for all i, j ∈{1,2} and $m,m^{\prime } = 0,\dots ,C$. Furthermore, we use Matlab’s implementation (⋅) to evaluate the computational times. It is noted that, so as to obtain a reliable estimate, the function (⋅) calls the specified function multiple times, measures the time required each time, and finally outputs the median of all these values.

5.1 Analysis of Experiment 1

We consider Experiment 1 with the parameter values q₁ = 0.015,q₂ = 0.045, λ₁ = 2,λ₂ = 9 and μ₁ = μ₂ = 0.3, and we let C = 60. Observe that in this instance the phase process modulates the arrival rate, but does not affect the service rate. We compute the transition probability $p_{ij}(m,m^{\prime };t)$, as defined in Eq. 3, using the three approaches that we discussed. As a representative illustration, we took i = j = 1, m = 6 and t = 1 for varying $m^{\prime }$, leading to the output that is presented in Table 1. Since the three approaches resulted in almost identical outcomes, Table 1 shows the outcomes for the matrix exponential approach and the absolute differences with the other two approaches. The last row displays the computational time (in seconds) corresponding to the approximation of P_t, which shows that Erlangization performs well compared with the alternative approaches. The values of ℓ for both Erlangization and uniformization are determined by increasing ℓ until the percentage difference between subsequent outcomes of $p_{11}(6,m^{\prime };t)$ was below ε = 10^− 3 for all $m^{\prime } = 0,\dots ,15$. For the Erlangization approach, ℓ was doubled each step, and for the uniformization approach, ℓ was increased by one at a time. This resulted in ℓ = 8192 = 2¹³ and ℓ = 174, respectively. The results in Table 1 indicate that, for these values of ℓ, the accuracy of the three approaches is similar.

Table 1 Infinite-server queue: $p_{ij}(m,m^{\prime };t)$ (and absolute differences) with i = j = 1, m = 6, t = 1 and C = 60

Evidently, computational times increase in C. To compare the computational times of the Erlangization approach and the uniformization approach as fairly as possible, we apply the following procedure to determine the required values of ℓ. We use $P_{t}^{\text {(m)}}$ in Eq. 4 as benchmark, since the sophisticated implementation (⋅) that Matlab is using is claimed to perform highly accurate and has been tested intensively. Then, for both Erlangization and uniformization, we increase ℓ until the percentage difference between the outcome of p₁₁(6,6;t) and the one in $P_{t}^{\text {(m)}}$ is below a chosen tolerance ε > 0. Table 2 shows, for various values of ε, the obtained values of ℓ (which is, by construction, a power of two for Erlangization). Evidently, a smaller error ε can be achieved by increasing ℓ. Importantly, the $\log _{2}\ell$ values for Erlangization are considerably lower than the ℓ values for uniformization, which is indicative of Erlangization being the more efficient approach.

Table 2 Infinite-server queue: The values of ℓ (and, for Erlangization, in addition $\log _{2}\ell$ between brackets) for decreasing values of ε, with C = 60 and using $P_{t}^{\text {(m)}}$ as benchmark

To investigate the impact of C on the computational time, we increase C from 50 to 500 in steps of 50, compute for each C the values of ℓ with ε = 10^− 3 (in the way discussed above, that is), and then use these values of ℓ to evaluate the computational times. Table 3 shows the obtained values of ℓ for the increasing values of C, and Fig. 2 shows the corresponding computational times in seconds.

Table 3 Infinite-server queue: The values of ℓ for the increasing values of C, with ε = 10^− 3 and using $P_{t}^{\text {(m)}}$ as benchmark

Fig. 2

Infinite-server queue: Computational times (in seconds) corresponding to the approximation of P_t with t = 1, for the three different methods. Values of ℓ as displayed in Table 3

From Table 3 we observe that for Erlangization the value of ℓ is not influenced by C, but that for uniformization the value of ℓ increases roughly linearly in C. Furthermore, Fig. 2 reveals that the computational times for the matrix exponential method and Erlangization approach are essentially of the same order. For small values of C, the Erlangization method is (slightly) faster, whereas for higher values of C the matrix exponential method is (slightly) faster. The computational cost of the uniformization method, however, is significantly higher. The latter observation is in line with what we expected: as seen in Table 3, uniformization typically needs a relatively large number of matrix multiplications.

To systematically assess the impact of C on the computational time, which we denote by T, we fit the curve T(C) = αC^β. This we do by applying least squares to T(C) − αC^β, i.e., we determine

$$\min_{\alpha,\beta}\sum\limits_{C\in\{50,\ldots,500\}}(T(C) - \alpha C^{\beta})^{2}.$$

We find that, as a function of C, the cpu time of both the matrix exponential method and Erlangization is superquadratic but subcubic (β = 2.20 and β = 2.57, respectively), whereas the cpu time of uniformization is essentially cubic (β = 3.15). Evidently, these β values serve as an indication only, because they are based on ten observations only.

5.2 Other Experiments

To explore if other settings yield similar results, we investigate the two other experiments as well. We consider Experiment 2 with parameter values q₁ = 0.3,q₂ = 0.9, λ₁ = λ₂ = 0.19, μ₁ = 0.16, μ₂ = 0.08 (i.e., the phase process does not affect the birth rate) and C = 300, and we consider Experiment 3 with parameter values q₁ = 0.1,q₂ = 0.4, λ₁ = 0.0035, λ₂ = 0.01, μ₁ = μ₂ = 0.3 (i.e., the phase process does not affect the recovery rate) and C = 100. We briefly present the results, focusing on the differences with the results of Experiment 1.

First, as in the previous section, we compute the values of ℓ for decreasing values of ε. As the counterparts to the results in Table 2 for Experiment 1, Tables 4 and 5 show the obtained values of ℓ for Experiment 2 and Experiment 3, respectively. We see that the values of ℓ for Erlangization are similar across the three experiments. The $\log _{2}\ell$ values differ at most by one, which corresponds to only one additional matrix multiplication. The results for uniformization, however, are drastically different across the three experiments. This effect could be explained by the fact that the maximum diagonal entry σ, that plays a crucial role in the uniformization approximation (5), depends highly on the functions f(m, C) an g(m, C) chosen.

Table 4 Linear birth-death process: The values of ℓ (and, for Erlangization, in addition $\log _{2}\ell$ between brackets) for decreasing values of ε, with C = 300 and using $P_{t}^{\text {(m)}}$ as benchmark

Table 5 SIS-type model: The values of ℓ (and, for Erlangization, in addition $\log _{2}\ell$ between brackets) for decreasing values of ε, with C = 100 and using $P_{t}^{\text {(m)}}$ as benchmark

Next, we examine again the impact of C on the computational time. As we did in Experiment 1, we increase C from 50 to 500 in steps of 50, compute for each C the values of ℓ with ε = 10^− 3, and use these values of ℓ to evaluate the computational times. Table 6 and 7 show the obtained values of ℓ for the values of C that we considered. Comparing with Experiment 1, we need a slightly higher ℓ in Experiment 2 to obtain the same error ε = 10^− 3. In Experiment 3, however, the ℓ should be increased considerably, but recall that for the Erlangization approach this only requires a few additional matrix multiplications.

Table 6 Linear birth-death process: The values of ℓ for the increasing values of C, with ε = 10^− 3 and using $P_{t}^{\text {(m)}}$ as benchmark

Table 7 SIS-type model: The values of ℓ for the increasing values of C, with ε = 10^− 3 and using $P_{t}^{\text {(m)}}$ as benchmark

Figure 3 shows for each specific approximation the computational times corresponding to the three experiments. The main conclusions from this figure are:

• observing each of the graphs individually, we see that for each of the three computational methods the three experiments roughly take the same amount of computational time (with the SIS-type model taking somewhat longer than the other two models under the uniformization approach, as will be explained in Remark 1 below);

• comparing the three graphs, we see that for uniformization the computational times are substantially higher, while the other two methods require roughly the same computational cost.

Fig. 3

Computational times (in seconds) corresponding to the approximation of P_t with t = 1, for the three experiments and the three different methods; from the top to bottom panel, matrix exponential method, uniformization method and Erlangization method, with values of ℓ as in Tables 3, 6 and 7

When fitting the curve T = αC^β, we observe from Table 8 that the β-values obtained for the linear birth-death process and the SIS-type model align with those found for the infinite-server queue, in the sense that the matrix exponential method and Erlangization yield a β between 2 and 3, whereas uniformization yields a β larger than 3.

Table 8 β values for the different experiments and different approaches

Remark 1

The fact that uniformization is slow for the SIS-type model can be understood as follows. The number of terms needed in Eq. 5, which in turn determines the number of matrix multiplications to be performed, increases in σ, where we recall that σ denotes the (absolute value of) the largest diagonal entry of Q. For the infinite-server model and the linear birth-death model, this largest entry is of the order C. For the SIS-type model, however, recalling that f(m, C) = m(C − m), the largest entry is of the order C². As a consequence, the number of terms in Eq. 5is relatively large, leading to a relatively long computational time.

6 Model Selection

We started our paper with a motivating example: can we statistically distinguish whether data stems from a qbd or from its non-modulated counterpart? We argued that to answer this question, we need machinery to evaluate the likelihood corresponding to a given time series. Now that we have at our disposal techniques to evaluate probabilities of the type (3), we return to our model selection problem of distinguishing between qbd processes and conventional (non-modulated, that is) bd processes. In this section we do so, using both simulated data and real-life data.

We wish to distinguish between the following four scenarios:

• 1. No modulation on neither the birth rate λ nor the death rate μ, i.e., 𝜃 = (λ, μ)

• 2. Modulation on the birth rate λ only (μ₁ = μ₂), i.e., 𝜃 = (q₁, q₂, λ₁, λ₂, μ)

• 3. Modulation on the death rate μ only (λ₁ = λ₂), i.e., 𝜃 = (q₁, q₂, λ, μ₁, μ₂)

• 4. Modulation on both the birth rate λ and the death rate μ, i.e., 𝜃 = (q₁, q₂, λ₁, λ₂, μ₁, μ₂)

We start by considering the setting of Experiment 1 with simulated data, and then use the model of Experiment 2 to analyze the whooping crane data featured in the introduction. We investigate which of these scenarios provides the best fit for the data, using the commonly used Akaike information criterion. This criterion includes a penalty that equals twice the number of estimated parameters (i.e., two times 2, 5, 5, and 6 in the above four scenarios), thus preventing overfitting from happening.

In all experiments below there is a time interval Δ > 0 so that the observations correspond to measurements performed at times $0,{\Delta },2{\Delta },\dots ,n{\Delta }$ for some $n\in \mathbb {N}$. We call these observations m₀,…,m_n. With 𝜃 the vector of parameters, the likelihood is

$$ \mathcal{L}(\theta | m_{0} ,\dots, m_{n}) = {\mathbb{P}}_{\theta}(M_{0} = m_{0} ,\dots, M_{n{\Delta}} = m_{n}). $$

(14)

Regarding scenarios 2, 3, and 4, note that the modulating process is not observed. However, with ${\boldsymbol x}=(x_{0},\ldots ,x_{n})\in \{1,2\}^{n+1},$ we can rewrite Eq. 14 as

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{{\boldsymbol x}\in\{1,2\}^{n+1}}{\mathbb{P}}_{\theta}(M_{0} = m_{0}, X_{0} = x_{0},\dots, M_{n{\Delta} } = m_{n}, X_{n{\Delta}} = x_{n}) \\ & =& \sum\limits_{{\boldsymbol x}\in\{1,2\}^{n+1}} \prod\limits_{i=1}^{n} p_{x_{i-1},x_{i}}(m_{i-1},m_{i};{\Delta}), \end{array} $$

(15)

where it is noted that the probabilities in the last expression are of the type (3), and can be evaluated with the techniques discussed in this paper. Importantly, there is no need to enumerate all paths x ∈{1,2}^n+ 1. Instead we can evaluate Eq. 15 efficiently by, abbreviating $p_{x_{i-1},x_{i}}(m[i])\equiv p_{x_{i-1},x_{i}}(m_{i-1},m_{i};{\Delta })$, evaluating the matrix product

$$ \begin{array}{@{}rcl@{}} {\boldsymbol \alpha}\! \left( \begin{array}{cc} p_{11}(m[1])&p_{12}(m[1])\\ p_{21}(m[1] )&p_{22}(m[1] ) \end{array}\right) \left( \!\begin{array}{cc} p_{11}(m[2])&p_{12}(m[2] )\\ p_{21}(m[2] )&p_{22}(m[2] ) \end{array}\!\right) \cdots\left( \!\begin{array}{cc} p_{11}(m[n])&p_{12}(m[n])\\ p_{21}(m[n])&p_{22}(m[n]) \end{array}\!\right) \!{\boldsymbol 1}, \end{array} $$

(16)

where α = (α₁, α₂) is the distribution of X₀ and 1 is an all-ones vector. Note that the matrices in Eq. 16 appear as blocks in the matrix P_Δ. Maximization of the likelihood gives us the maximum likelihood estimate $\hat \theta$ for 𝜃. As we will discuss below, this likelihood can be used in model selection problems. In the experiments below, all calculations involving probabilities of the type $p_{x_{i-1},x_{i}}(m[i])$ have been performed by the Erlangization approach.

6.1 Simulated Data

We consider the setting of Experiment 1. We simulate data (n = 2000) with parameter values q₁ = 0.015,q₂ = 0.045,λ₁ = 0.2,λ₂ = 0.9,μ = 0.03, Δ = 1 and C = 50. This means that the true model for this data is an infinite-server queue with modulation on λ only. Based on this simulated data, we perform the model selection based on the Akaike information criterion, i.e., using $\textsc {aic} =2 N- 2\log L(\hat \theta )$, with N the dimension of the parameter vector 𝜃.

From Table 9 we observe that the aic value is smallest for scenario 2, which agrees with the ground truth of the simulated data (i.e., it succeeds in finding the scenario with modulation on the parameter λ only). Interestingly, the number of observations has impact on the conclusions drawn. To illustrate this, see Table 10 showing the results using the first 101 data points of the dataset only (i.e., n = 100 instead of n = 2000). The aic value is now minimized by scenario 1, the scenario without modulation, indicating that the dataset is too short to detect the modulation.

Table 9 Experiment 1, simulated data: parameter estimates, loglikelihood value and aic for the four different scenarios (n = 2000), with ℓ = 1024 and C = 50

Table 10 Experiment 1, simulated data: parameter estimates, loglikelihood value and aic for the four different scenarios (n = 100), with ℓ = 1024 and C = 50

6.2 Whooping Crane Population

We proceed by considering the linear birth-death setting of Experiment 2 in relation to the four scenarios mentioned above. We use the whooping crane data (Davison et al. 2020; Stratton 2020), as displayed in Fig. 1, of annual counts of the female population of the whooping crane n = 69. From Fig. 1 we could suspect that a model with modulation could lead to a better fit than a model without modulation. We (conservatively) set C = 200. The outcomes of the model selection procedure are shown in Table 11. As it turns out, the aic value is smallest for scenario 1, i.e., the setting corresponding with no modulation. This is in line with the results that one would obtain using the matrix exponential approach. More specifically, all values of the loglikelihood and aic coincide up to high level of precision. In line with the experiments performed in the previous section, the computational effort of both approaches is roughly similar. One should bear in mind, though, that the number of observations in this dataset is low, making the detection of modulation (involving 5 or 6 parameters) difficult. Additional literature on parameter estimation for linear birth-death models can be found in e.g. Chen and Hyrien (2011), Crawford et al. (2012), Crawford and Suchard (2012), Davison et al. (2020), and Xu et al. (2015).

Table 11 Whooping crane data: parameter estimates using Erlangization, loglikelihood value and aic for the four different scenarios (n = 69), with ℓ = 256 and C = 200

7 Concluding Remarks

We have examined various approaches to compute the time-dependent distribution of qbd processes, with emphasis on the Erlangization approach. This approach has provable asymptotic correctness properties, and is, in terms of computational time, typically relatively fast. The latter property pays off in particular in settings where many time-dependent probabilities have to be evaluated. In this context, one could think of instances in which a function of the time-dependent probabilities is to be optimized over a set of model parameters, e.g. when performing maximum likelihood estimation.

Our study was motivated by model selection problems, in which one wishes to distinguish between models with and without modulation, i.e., between qbd processes and their bd counterparts. Through a series of experiments, with simulated as well as real-life data, we have shown how the techniques for computing time-dependent distributions can play a role in this context.

Our Erlangization approach gives rise to various directions for further research. For the class of qbd processes, the method’s first step (solving the system of linear equations that yield the probabilities at exponential epochs) can exploit the convenient underlying structure, thus allowing an efficient numerical algorithm. We anticipate, however, that Erlangization has the potential to be applied more widely. One could think of multi-type population models, where various types of individuals are considered, which can in turn interact with each other. Another interesting extension concerns the multivariate model in which a population of individuals lives on a network and can move between its nodes. In this respect we refer to our recent paper (de Gunst et al. 2021), approximating time-dependent probabilities in such a network, relying on saddlepoint approximations. The crucial simplification made in de Gunst et al. (2021) is that a discrete-time model is considered, as opposed to the continuous-time model featuring in the present paper. It would therefore be interesting to explore whether an Erlangization-based approach could be developed for the continuous-time setting of such a network population process.