1 Introduction

The significance of water to the natural ecosystem is indisputable. However, the deterioration of water resources has long been a consequence of both natural phenomena and anthropocene activities. In the global panorama, the deterioration of water quality (WQ) represents a primary threat to public health [1]. One of the most widely accepted methods for detecting biological problems associated with aquatic environments is the assessment of WQ. The monitoring of key ecological indicators, which exhibit variations due to seasonal and temporal differences, is a valuable tool for investigating contamination rates [2,3,4]. Many studies conducted to determine the importance of water pollution have reported that water resources play a critical role in protecting the quality of water resources and ensuring human health and the sustainability of ecosystems [5,6,7]. The deterioration of freshwater quality is a consequence of anthropogenic activities that contaminate aquatic habitats. The resulting impact on human health is a problem related to ecosystem degradation, management, and monitoring [8]. Currently, there is no fixed number and type of parameters for assessing WQ. Numerous studies have been conducted to assess WQ, including parameters grouped into indices such as pH, dissolved oxygen, turbidity, and metals. [9, 10]. One of the most efficacious instruments for disclosing information pertaining to WQ is the utilization of the term “water quality index” (WQI), which is a rating component that elucidates the collective impact of disparate WQ parameters. WQI provides a single number that expresses the overall WQ at a given time and place based on various WQ parameters [11].

The fact that artificial neural networks (ANNs) work based on data, adapt to data, and learn by establishing a link between input and output makes them different from many other methods. With these features, ANNs have become a frequently preferred method in the fields of classification, pattern recognition and prediction [12]. WQ modeling has been developed to solve WQ problems with advanced computing using artificial intelligence (AI) techniques. ANNs have helped monitor WQ systems by predicting changes in WQ [13]. Artificial intelligence methods can significantly reduce the costs of water supply and sanitation systems and help ensure compliance with drinking and wastewater treatment quality [14]. ANN models have been used to solve many environmental problems. For example, a number of studies have used ANN models to predict water resource variables such as water quantity and WQ in river systems [15]. Previous studies [16,17,18,19] have applied different machine learning algorithms to analyze ground or surface WQ.

Estimation of WQ plays an important role in environmental monitoring, ecosystem sustainability and aquaculture. Conventional estimation methods cannot predict the linear and non-stationary state of good WQ [20]. Also, traditional methods for calculating WQI are time-consuming and have errors in subdirectory derivatives [21]. The WQI has been adopted as a universal indicator that comprehensively represents the WQ status of the surface water body. Common traditional water quality indices (WQIs) suffer from limitations such as “shadowing” and “uncertainty” [22].

In addition, the accuracy of traditional WQ estimation methods is generally low, and the estimation results have significant autocorrelation [23]. Therefore, the traditional linear forecasting model cannot fully reflect its changing regulation and cannot accurately predict WQ. Reasons for needing mathematical techniques and models that can model and predict WQ efficiently increase in data scale and difficulties in interpreting land use, pollutant loading and disposal, WQ and ecosystem effects [24].

Techniques such as ANNs have gained importance to overcome the problems experienced in traditional WQIs [22]. WQ monitoring plays a vital role in protecting water resources, environmental management and decision-making. Artificial intelligence (AI), based on machine learning techniques, has been widely used in recent years to evaluate and classify WQ [25].

Regarding the simulation and prediction of WQ, adaptive boosting (Adaboost) [26], gradient boosting (GBM) [27], extreme gradient boosting (XGBoost) [28], decision tree (DT) [29, 30], extra trees (ExT) [31], random forest (RF) [26], multilayer perceptron (MLP) [32], radial basis function (RBF) [33], deep feed-forward neural network (DFNN) [34] and convolutional neural network (CNN) [17] have been reported. Among these techniques, the multilayer perceptron (MLP) model has mostly outperformed the others in precision and accuracy [35] and is the most widely used architecture [36]. MLP is a feed-forward ANN model that maps input data sets to appropriate outputs. It uses a supervised learning technique that includes the use of back propagation algorithm [37]. Although there are many ML algorithms, researchers still face problems such as which ML techniques should be applied or which is the most suitable for a particular problem [38]. It is very important to minimize the impact of basin-based variability and complexity and nonlinearity in water quality determination. A robust and flexible model is also needed to improve the accuracy of WQI estimation [21].

As can be seen from the above applied models, many techniques can be applied for WQ estimation. The motivation of our study is the use of single multiplicative neuron model and pi-sigma artificial neural networks, which have not been used before in the modeling of the WQI and allow effective modeling. For this reason, it is necessary to first determine the drinking WQ variables and calculate with a good WQI. Then, it would be more useful and logical to use neural network modeling to map the relationship between them. Due to various problems such as time-consuming and low accuracy of current WQ calculation methods from the studies, it has encouraged to carry out a study with an ANN-based approach. In this research, the WQ of surface water data from southeastern Black Sea Basin was made with the help of artificial neural network (ANN) modeling. The contributions of this study to the literature are as follows.

  • The WQ of surface water bodies was monitoring, and WQIs were calculated.

  • Single multiplicative neuron model and pi-sigma artificial neural networks are firstly used for modeling of WQ.

  • Six different optimal artificial neural networks are proposed for modeling and estimating the surface WQI.

  • Pi-sigma artificial neural network was determined as the best artificial neural network model for modeling the surface WQI.

2 Material and Methods

2.1 Study Area

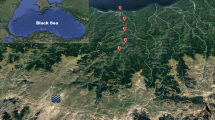
For this study, surface water samples collected from eight different stations for 12 months from the rivers flowing into the southeastern Black Sea were used as raw data to predict WQ using ANN (Fig. 1).

Fig. 1
figure 1

Study location (adapted from Google Earth)

Full size image

2.2 Physicochemical Analysis

In this study, monthly samples were brought to the laboratory and analyzed by applying standard methods. The samples were taken in accordance with the “Water Pollution Control Regulation Sampling and Analysis Methods Communiqué” and were transported to the laboratory environment by keeping them in glass bottles at a temperature of + 4 °C, away from light. After the sample containers were shaken, they were immersed about 15 cm below the water surface and filled. Water temperature (WT), pH, dissolved oxygen (DO), electrical conductivity (EC), and total dissolved solids (TDS) were measured with the YSI 556 MPS. Turbidity (NTU) was measured in the field with the help of WTW brand land-type devices. The other variables for WQ, such as total ammonium nitrogen (TAN), total phosphorus (TP), and biological oxygen demand (BOD) were analyzed on the same day in the laboratory.

2.3 Statistical Analysis

In this paper, statistical analyses were conducted using the SPSS 17.0 for Windows software. The data set utilized in the analyses was collected seasonally and consisted of 96 observations. Descriptive statistics (mean, standard deviation, minimum, and maximum) of the data set were obtained along with statistical calculations.

2.4 Calculation of Water Quality Index (WQI)

WQI is defined as a rating reflecting the combined effect of different WQ parameters. The WQI is an indicator of the quality of any groundwater reservoir in the form of a single number representing a combination of different WQ parameters [39]. The drinking WQI was calculated using the method previously recommended by various research groups [40, 41].

The first WQI calculation method represents the weight attributed to each parameter and is assigned for each parameter from the PCA results based on the eigenvalues for each major component and factor loading and represents the relative importance of each WQ parameter for drinking purposes [42]. Based on these mentioned techniques, WQI was investigated for the water samples. The concentration of each measured parameter is Ci (mg/L) and the standard drinking water values allowed by the surface Si. The whole equation showing drinking WQ is shown below [43, 44].

$${\text{WQI}}_{1} = \sum \left[ {W_{i} x \left( {\frac{{C_{i} }}{{S_{i} }}} \right)} \right] \times 100$$
(1)

In the second WQI calculation method, the following steps were followed. In the first step, each of the eight parameters was assigned a weight (wi) between 1–5 (minimum to highest impact on WQ) based on their impact on health and their importance to the overall quality of drinking water (Table 1). Second, the relative weight (Wi) of the parameters (where n is the number of parameters) is calculated using the following equation [45]:

$$W_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} W_{i} }}$$
(2)
Table 1 Relative weight of the parameters [44]
Full size table

Third, the quality rating scale (qi) was calculated using equality (3). Determined concentration of each used parameter (Ci) and standard safe limit values (Si) is as follows:

$$q_{i} = \frac{{C_{i} }}{{S_{i} }} \times 100$$
(3)

Finally, the WQI2 was calculated using Eq. (4).

$$\mathop \sum \limits_{i = 1}^{n} W_{i} \times q_{i}$$
(4)

WQI2 values calculated at the end of both applications are classified into five categories as follows: WQ is excellent when 0 ≤ WQI < 50; WQ is good when 50 ≤ WQI < 100; when 100 ≤ WQI < 200, the WQ is poor; if 200 ≤ WQI < 300, the WQ is very bad; if WQI ≥ 300, the water is not drinkable [46, 47].

2.5 Artificial Neural Networks (ANN)

ANN, a concept taken from the human mind, is a widely used forecasting method [48]. The neural networks main characteristic is their learning capacity [49]. The concept of an artificial neural network (ANN) is a computational process that attempts to describe and generate a mapping from a multivariate data set as layers of input neurons to one or more hidden layers and an output layer containing one or more output neurons [50]. This makes long calculations and complex conditions easier understandable.

Similarly, assessments of the WQI include complex computations and transformation. In the WQI calculation for each formula, the parameters are formulated with different values or ranges of values for each formula. Therefore, alternatively, an ANN has been used to model the WQI of rivers [32]. Also, WQI determination is also made easier and quicker [51].

The usefulness of ANNs spans many different fields of study, including water resources engineering, hydrogeology, and environmental geology. ANNs are widely used in modeling groundwater and surface water resources [52]. Generally, obtaining optimal ANN models for WQ prediction involves simultaneous training of several networks with a wide variety of neuron counts, input and output activation functions, and training optimization algorithms; finally, the most suitable ANN model is selected for interpretation [53].

Before implementing any data intelligence model, several steps must be implemented to ensure the success of the forecast. One of the most important steps is to determine the best input combination of the model [54]. In this study, single multiplicative neuron model artificial neural network, pi-sigma artificial neural network models and multilayer perceptron were used to predict the result of WQI. In recent years, multilayer perceptron neural networks have been used in many studies for modeling WQ. In this study, we focused on the performance of the multiplicative neuron model artificial neural network and pi-sigma artificial neural network, which can produce more successful prediction results than multilayer perceptron. Multiplicative neuron model artificial neural network and pi-sigma artificial neural network are firstly applied for modeling WQ in the literature.

2.6 Single Multiplicative Neuron Model Artificial Neural Network

The single multiplicative artificial neural network was firstly proposed by [55]. Although the single multiplicative artificial neural network has a simple architectural structure, it is an artificial neural network that can solve complex nonlinear problems. Since it can work with a much less number of neurons and therefore fewer parameters than a multilayer perceptron, its generalization ability is stronger than a multilayer perceptron. The architecture of the single multiplicative artificial neural network is given in Fig. 2.

Fig. 2
figure 2

Architecture of the single multiplicative artificial neural network

Full size image

In the single multiplicative artificial neural network, a nonlinear transformation of the product of the linear transformations of the inputs is calculated as the output. Calculation of the outputs of the single multiplicative artificial neural network with p inputs is carried out with the following formulas:

$$\text{net}={\prod }_{i=1}^{p}\left({w}_{i}\times {\text{input}}_{i}+{b}_{i}\right)$$
(5)
$$\text{output}=\frac{1}{1+\text{exp}(-\text{net})}$$
(6)

The ANN contains a total of 2p weights and biases values. Training this neural network is a problem of estimating 2p parameters. The objective function in the optimization problem can be used as the sum of squares of error. The optimization problem is expressed as follows:

$$\underset{\left\{{w}_{1},\dots ,{w}_{p},{b}_{1},..,{b}_{p}\right\}}{\text{min}}\sum_{j=1}^{n}{\left({\text{output}}_{j}-{\text{target}}_{j}\right)}^{2}$$
(7)

In formula (7), n represents the number of learning examples. The solution to the optimization problem provides the set of parameter values that will enable the network to produce outputs closest to the targets. The optimization problem given by formula (7) can be solved by nonlinear least squares methods as well as by artificial intelligence optimization algorithms such as genetic algorithm and particle swarm optimization. It is well-known that particle swarm optimization can produce very successful results in the training of ANNs. In this study, a particle swarm optimization training algorithm that imitates swarm intelligence developed for numerical optimization problems is preferred. The training algorithm based on PSO is given below in steps.

Algorithm 1.

The training algorithm based on PSO for a single multiplicative artificial neural network [56].

Step 1. The parameters of the training processes are determined.

\(pn:\) The swarm size or particle number

\({c}_{1}\): Social coefficient

\({c}_{2}\): Cognitive coefficient

\(w:\) Inertia weight

\(\varepsilon :\) The error tolerance for relative error difference

\(\text{maxitr}:\) The maximum number of iterations.

The counters are initialized. The restarting strategy counter (rsc) and early stopping counter (esc) are initially taken as zero.

Step 2. The initial positions and velocities are randomly generated as follows:

$${X}_{i,j}^{(0)}\sim \text{Uniform}(\text{0,1})$$
(8)
$${V}_{i,j}^{(0)}\sim \text{Uniform}(-\text{1,1})$$
(9)

\({X}_{i,j}^{(k)}\) is jth position value of ith particle of the population at kth iteration. The positions of an element in a population correspond to the weights and biases values of the neural network, and there are \(2p\).

Step 3. The fitness function values are calculated for each swarm member. The fitness function is selected as the sum of square errors.

$$\text{SSE}={\sum }_{j=1}^{n}{({\text{output}}_{j}-{\text{target}}_{j})}^{2}$$
(10)

Step 4. According to the calculated fitness function values, the best element \(({X}_{\text{best}}^{k})\) in the population is determined as gbest and its fitness value \({(\text{SSE}}_{\text{best}}^{k})\) is saved. Moreover, the Pbest matrix is constituted as a memory for each particle in the swarm.

Step 5. A new swarm is created by replacing the positions of all elements in the swarm with the following equation:

$${V}_{i,j}^{(k+1)}={wV}_{i,j}^{(k+1)}+{c}_{1}{r}_{1}({P\text{best}}_{i,j}^{\left(k\right)}-{X}_{i,j}^{\left(k\right)})+{c}_{2}{r}_{2}({X\text{best}}_{j}^{\left(k\right)}-{X}_{i,j}^{\left(k\right)})$$
(11)
$${X}_{i,j}^{\left(k+1\right)}={X}_{i,j}^{\left(k\right)}+{V}_{i,j}^{\left(k+1\right)}$$
(12)

Step 6. The fitness function values are calculated for each swarm member by using Eq. (11). According to the calculated fitness function values, the best element \(({X}_{\text{best}}^{k})\) in the population and its fitness value \({(\text{SSE}}_{\text{best}}^{k})\) are obtained and compared with \({\text{SSE}}_{\text{best}}^{k-1}\). If \({\text{SSE}}_{\text{best}}^{k}>{\text{SSE}}_{\text{best}}^{k-1}\) , then \({\text{SSE}}_{\text{best}}^{k}={\text{SSE}}_{\text{best}}^{k-1}\).

Step 7. The restarting strategy counter (\(\text{rsc}=\text{rsc}+1\)) is increased, and its value is checked. If the \(\text{rsc}>\text{limit}1\) , then all positions are regenerated by using (8) and (9), and the \(\text{rsc}\) is taken as zero.

Step 8. The early stopping rule is checked. The \(esc\) counter is increased depending on the following condition:

$$\text{esc}=\left\{\begin{array}{c}\text{esc}+1 , \text{if}\, \frac{{\text{SSEbest}}^{\left(k\right)}-{\text{SSEbest}}^{\left(k-1\right)}}{{\text{SSEbest}}^{\left(k\right)}}<\varepsilon \\ 0, \text{otherwise}\end{array}\right.$$
(13)

If \(\text{esc}>\text{limit}2\) is satisfied, the algorithm is stopped otherwise go to Step 5.

2.7 Pi-Sigma Artificial Neural Network

Pi-sigma neural network was firstly proposed by [57]. Pi-sigma artificial neural networks are a high-order type of neural network that is effectively used in time series prediction problems. This model is a sophisticated ANN approach that successfully captures complex structures in time-varying data [58]. Pi-sigma neural network is a high-order neural network proposed as an alternative to multilayer perceptron. Pi-sigma neural network is a type of neural network that uses additive and multiplicative aggregation functions together and performs well in solving prediction problems. Unlike the multilayer perceptron in the pi-sigma artificial neural network, the connection weights between the hidden layer and the input layer are taken as constant and one. Therefore, the number of parameters is less than the multilayer perceptron in the pi-sigma artificial neural network. The architecture of the pi-sigma neural network is given in Fig. 3.

Fig. 3
figure 3

Architecture of the pi-sigma artificial neural network

Full size image

The output of the pi-sigma neural network, which includes p inputs and m hidden layer units, is calculated with the following equations in a few steps.

$${\text{net}}_{j}=\sum_{i=1}^{p}{w}_{i,j}{\text{input}}_{i}+{b}_{j} , j=\text{1,2},\dots ,m$$
(14)
$$\text{output}=f({\prod }_{j=1}^{m}f({\text{net}}_{j}))$$
(15)

Here, \(f\) is the activation function, which is chosen as the logistic function given below in this study.

$$f\left(\text{net}\right)=\frac{1}{1+\text{exp}(-\text{net})}$$
(16)

The ANN contains a total of \(p\times m+m\) weights and biases values. Training this neural network is a problem of estimating (\({w}_{i,j},{b}_{j}) ,i=\text{1,2},\dots ,p , j=\text{1,2}\dots ,m\) parameters. The objective function in the optimization problem can be used as the sum of squares of error. The optimization problem is expressed as follows.

$$\underset{\left\{{w}_{i,j},{b}_{j}/i=\text{1,2},\dots ,p , j=\text{1,2}\dots ,m\right\}}{\text{min}}\sum_{j=1}^{n}{\left({\text{output}}_{j}-{\text{target}}_{j}\right)}^{2}$$
(17)

Pi-sigma neural network can be trained with particle swarm optimization using Algorithm 1. In the algorithm, (17) is used instead of (3) as a fitness function. Also, the number of positions of the particles will be \(p\times m+m\), not \(2\times p\).

2.8 Multilayer Perceptron Artificial Neural Network

The multilayer perceptron is the most commonly used type of neural network. The multilayer perceptron consists of the input layer, hidden layers and output layers. In the literature, the multilayer perceptron containing a single hidden layer has successfully solved many problems (Fig. 4).

Fig. 4
figure 4

Architecture of the multilayer perceptron artificial neural network

Full size image

Calculation of the outputs of a multilayer perceptron with p-input and m hidden layer units is performed with the following formula. Here, \(f\) is the logistic activation function in (16)

$${\text{net}}_{j}=\sum_{i=1}^{p}{w}_{i,j}{\text{input}}_{i}+{b}_{j} , j=\text{1,2},\dots ,m$$
(18)
$${o}_{j}=f({\prod }_{j=1}^{m}f({\text{net}}_{j})) , j=\text{1,2},\dots ,m$$
(19)
$$\text{output}=f(\sum_{j=1}^{n}{v}_{j}{o}_{j}+b)$$
(20)

The ANN contains a total of \(p\times m+2m+1\) weights and biases values. Training this neural network is a problem of estimating (\({w}_{i,j},{v}_{j},{b}_{j},b) ,i=\text{1,2},\dots ,p , j=\text{1,2}\dots ,m\) parameters. The objective function in the optimization problem can be used as the sum of squares of error. The optimization problem is expressed as follows:

$$\underset{\left\{{w}_{i,j},{b}_{j},{v}_{j},b/i=\text{1,2},\dots ,p , j=\text{1,2}\dots ,m\right\}}{\text{min}}\sum_{j=1}^{n}{\left({\text{output}}_{j}-{\text{target}}_{j}\right)}^{2}$$
(21)

Multilayer perceptron artificial neural network can be trained with particle swarm optimization using Algorithm 1. In the algorithm, (21) is used instead of (3) as a fitness function. Also, the number of positions of the particles will be \(p\times m+2m+1.\)

Furthermore, to obtain the best model, the predicted values of the models were compared with each other using the mean square error (RMSE) and mean absolute percentage error (MAPE) criteria. RMSE and MAPE were calculated using the equations given in (22) and (23), respectively. Model training, statistical analysis of parameters, calculation of correlation coefficients, and error analysis mainly implemented on MATLAB 2018b.

RMSE and MAPE values, whose formulas are given below, are given as error criteria.

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum_{t=1}^{n}{\left({\text{output}}_{t}-{\text{target}}_{t}\right)}^{2}}$$
(22)
$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} \left| {\frac{{{\text{output}}_{t} - {\text{target}}_{t} }}{{{\text{target}}_{t} }}} \right|$$
(23)

3 Results

In our study, ANN methods were used to predict the WQI results calculated using WQ parameters. For this purpose, the prediction performance results of single multiplicative neuron model artificial neural network, pi-sigma artificial neural network and multilayer perceptron artificial neural network models, which are statistical tools, were compared using MATLAB to predict the WQI value obtained in the study. Coefficient of determination root-mean-square error (RMSE) and mean absolute percentage error (MAPE) were used to evaluate the quality of the models. By comparing the validation values, it is aimed to select the application with the best prediction performance for WQI.

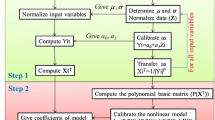
The framework of the proposed methodology consists of four stages: data collection from the study area, analysis of physicochemical parameters, calculation of WQI, application of ANN models and evaluation of model performances, as shown in Fig. 5.

Fig. 5
figure 5

A basic flowchart of the methodology for estimating WQI

Full size image

3.1 Analysis of the Data Set for Traditional Evaluation

The physicochemical variables values obtained from the surface water samples were determined. Average values of physicochemical values are given in Table 2. The mean physicochemical values obtained in our study were determined for WT: 14.05, pH: 7.51, EC: 230.51 μS cm−1, TDS: 0.1694 mg/L, DO: 10.07 mg/L, Turbidity: 27.75 NTU, TP: 0.061 mg/L, TAN: 0.413 mg/L, and BOD: 4.61 mg/L (Fig. 6). Also, Table 2 provides a detailed statistical overview of the data set and factors affecting WQ.

Table 2 Result of physicochemical variables of surface water samples
Full size table
Fig. 6
figure 6

Box plots of physicochemical variables of surface water samples

Full size image

The WQI1 value was between 45 and 199 (minimum and maximum), according to the first calculation method we applied, which was calculated based on the average concentrations for eight different water parameters (Table 3). The average WQI value was 72%, and good WQ was determined. However, unsuitable WQ was also found at different times in the stations.

Table 3 Weights for different variables in surface water samples in this study
Full size table

The WQI2, which we applied as the second method, was evaluated to reveal the drinking WQ of Gelevera Stream. The calculated WQI value was between 55 and 235 (minimum and maximum), and the average value was 86%, and it was determined that it was in the good water category [44]. However, bad water and unsuitable WQ were also encountered at different time intervals on the basis of stations.

Although WQI2 model results require weight assignment for calculation, your results are as accurate as WQI1. It therefore means that the weight assignment made by the authors in this study is correct and justified.

3.2 Proposed Modeling of Water Quality Indices by Using Artificial Neural Networks

For the surface WQ indices calculated with three different methods were modeled with single multiplicative neuron model artificial neural network, pi-sigma artificial neural network models and multilayer perceptron. Single multiplicative neuron model artificial neural network and pi-sigma artificial neural network models are firstly applied for modeling WQ in this paper in the literature. In practice, the inputs of the ANN are the variables used in the calculation of the WQI.

The target value is the previously calculated WQI value. Eight measurements of WQI values for all stations in the last month were used as test data and other data as training data. The data set is randomly divided to two sets as training and test set. The learning algorithm is based on particle swarm optimization. The all ANN applications were conducted in MATLAB by using notebook with Intel(R) Core (TM) i5-4210U CPU 2.40 GHz processor. Optimum neural network architectures and estimations of weights and biases obtained for both WQ indices are given in Figs. 7, 8, 9, 10, 11, 12.

Fig. 7
figure 7

Optimum multilayer perceptron artificial neural network for WQI1

Full size image
Fig. 8
figure 8

Optimum pi-sigma artificial neural network for WQI1

Full size image
Fig. 9
figure 9

Optimum single multiplicative neuron model artificial neural network for WQI1

Full size image
Fig. 10
figure 10

Optimum multilayer perceptron artificial neural network for WQI2

Full size image
Fig. 11
figure 11

Optimum pi-sigma artificial neural network for WQI2

Full size image
Fig. 12
figure 12

Optimum single multiplicative neuron model artificial neural network for WQI2

Full size image

In Table 4, the test set performance of the optimum ANNs used in the modeling of the WQI1 is given.

Table 4 Test performance results for modeling of WQI1
Full size table

When Table 4 is examined, it is seen that the pi-sigma artificial neural network given in Fig. 8 has the lowest RMSE and MAPE values in the modeling of WQI1.

In Table 5, the test set performance of the optimum artificial neural networks used in the modeling of the WQI2 is given.

Table 5 Test performance results for modeling of WQI2
Full size table

When Table 5 is examined, it is seen that the pi-sigma artificial neural network given in Fig. 11 has the lowest RMSE and MAPE values in the modeling of WQI2.

4 Discussion

4.1 Traditional Evaluation

The results of the analyses of the physicochemical parameters of the river water provide us with a comprehensive understanding of the WQ [59]. The effect of temperature on the rate of chemical reaction with respect to water is a very important factor because of its effect on aquatic life and beneficial use of water. In our study, the overall temperature average was determined as 14.05 °C. According to the Surface Water Quality Regulation (2015), the WQ of studied samples is first class. The pH level generally obtained in the study is 7.51, and it is accepted as the first class according to the Surface Water Quality Regulation (2015). The normal pH range of surface waters is between 6.5 and 8.5 [60]. In the statistical analysis of the data, it was determined that the pH changes did not differ between the stations. As a result of the study, we can say that the water is basic. The overall EC level obtained in the study was 230.51 μS cm−1, and it was included in the first class WQ according to the surface (2015). It has been reported that the conductivity in river waters is a maximum of 1000 μS cm−1 according to WHO standards [61].

The average TDS value obtained overall in the study was reported as 0.1694 (ppm). Since TDS values are below 1000 ppm in eight station sources that are the subject of this study, they are in the freshwater class [62].

The average DO level obtained in the study is 10.07 mg/L, and it is first class WQ according to the Surface WQ Regulation (2015). The amount of dissolved oxygen (DO) necessary for the life of aquatic living things should be ≥ 5 mg/L. Dissolved oxygen is one of the most important parameters of water pollution [63]. In the study, the average value of turbidity (NTU) measured from the stations was determined as 8.84.

The average TP level obtained in the study was determined as 0.061 mg/L, and it is included in the second class WQ according to Surface WQ Regulation (2015). Phosphate can enter the aquatic environment naturally, as well as from artificial fertilizers and industrial wastes. As a result of the excessive presence of phosphate in aquatic ecosystems, algae multiply and can cause odor and taste problems in the water [64]. Phosphorus is the most important element of eutrophication in the aquatic environment [65]. In the study, the average level of TAN obtained in general was determined as 0.413 mg/L. The sum of ammonium and ammonia (NH4+  + NH3) is defined as total ammonia (TAN). High ammonia concentrations represent one of the most harmful among the different aquatic environmental problems affecting the fitness of aquatic organism in surface water ecosystems as well as oxygen depletion [66]. The average BOD level obtained in the study was determined as 4.61 mg/L. The BOD is the most important measure of organic pollution. BOD is the amount of oxygen required to stabilize decomposable organic materials by bacteria under aerobic conditions [67]. BOD values in receiving environments close to the discharge point of wastewater are more than 10 mg/L [68]. The main cause of pollution in Gelevera Stream was determined as uncontrolled domestic waste and waste from animal slaughterhouses [69, 70].

The WQI is considered one of the main factors for assessing drinking WQ. This index is the most commonly used evaluation of WQ for drinking purposes [39, 44, 45, 71]. Therefore, in calculating the first method WQI to estimate the suitability of the WQI of Türkiye region in Southeastern Black Sea for drinking purposes, the weights of each parameter (wi) obtained on the basis of the FA/PCA results of eight physicochemical parameters were used for WQIs (Table 3). Krishan et al., 2023 [72] reported that the value of WQI during pre-monsoon (PRM) and post-monsoon (POM) ranged between 72 and 3683 and 51 to 2451 at 50 sampling groundwater stations, respectively. Furthermore, scientists also classified two categories, “Very poor and poor water,” representing 64% of the PRM and 58% of the POM of the collected samples in India. A further drinking WQ assessment study in southwest China used the WQI and reported that the majority of groundwater samples (96%) had EWQI values lower than the WHO drinking standard, which is suitable for drinking purposes [73]. Similarly, through the WQI, Bomadi water was found to be unsuitable for drinking and other domestic purposes and needs to be improved [74]. The present study showed that in WQI1, the average value was 72 and the WQ was found to be “good”, and in WQI2 the average value was 86, and in 82% “good water” 14% “bad water” and 4% “very bad water” for all stations.

4.2 Proposed Methodology for Evaluation

Water pollution is one of the most important environmental problems facing humanity. The main cause of this problem is largely due to the lack of the necessary conditions for forecasting, early warning and solving the problem in emergency situations. Therefore, the provision of an effective monitoring and early warning system to enable smart decision-making and WQ management will be the most important scientific and technological step to be taken [75].

Although the methods tested in this study have never been tried before in WQ assessment, they are original methods. Therefore, the literature is very limited and there is a lack of WQ assessment. The single multiplicative neuron model is a new automatic forecasting method based on a new input significancy test [76]. The results of the single multiplicative neuron (SMN) model, which was applied for the first time in this study for the prediction of WQ, showed performance with RMSE and MAPE values (Table 4; WQI1 for RMSE: 4.731800 and MAPE: 0.051200, Table 5; WQI2 for RMSE: 3.819400 and MAPE: 0.039900, accuracy). Similarly, pi-sigma is another machine learning method that has been found to be underutilized in the assessment of water resources quality prediction. Pi-sigma was able to predict WQI with good performance, showing less error than MLP and SMN model. Based on the statistical parameters, the pi-sigma algorithm showed the highest predictive power for WQI prediction (Table 4; WQI1 for RMSE: 1.976800 and MAPE: 0.023200, Table 5; WQI2 for RMSE: 2.650500 and MAPE: 0.028300, accuracy).

Multilayer perceptron (MLP) model has been applied and validated by most researchers. MLP method was used to estimate the WQI and to find the WQ classification [77, 78, 79]. In the study using machine learning models to predict the WQI in La Buong River, it was found that the RMSE for MLP had a value of 0.132 [38]. It was found that the proposed MLP-ANN model (RMSE = 0.1984) for predicting WQ parameters such as dissolved oxygen using limiting data sets for Ganga River [80]. The results of applied MLP model to estimate the WQI in this study are given in tables above (Table 4; WQI1 for RMSE: 4.349000 and MAPE: 0.051500, Table 5; WQI2 for RMSE: 3.941500 and MAPE: 0.042800, accuracy).

As a result of this study, the comparison of the prediction performance of the model (pi-sigma) that gives the best prediction of WQI with other studies in the literature is given in Table 6.

Table 6 Best prediction of WQI in the literature
Full size table

From Table 6, it is seen that the pi-sigma model with eight input parameters (WT, EC, TDS, DO, Turb., TP, TAN and BOD) outperformed previously developed models such as independent (e.g., GNN and MLP-ANN) and hybrid (SMWOA-LSSVM, FNN and PSO-GA-BPNN). Therefore, pi-sigma has a very different architecture from other ANNs due to its use of both additive and multiplicative structure [81, 89,90,91,92], and more accurate prediction results are compared to other predictive models proposed in the literature.

5 Conclusion

The present study aimed on classifying WQ using machine learning techniques and proposed an intelligent real-time WQ assessment model. Modeling and predicting WQ using AI algorithms is crucial for environmental protection. Artificial intelligence methods can significantly reduce the costs of water supply and sanitation systems and help ensure compliance with drinking and wastewater treatment quality. Therefore, modeling and estimation of WQ to control water pollution are topics that require extensive research.

This article presented surface water sources of the Türkiye region in Southeastern Black Sea data to find out if machine learning could be useful for determining WQ class instead of WQI. The results of the three models were compared, and the pi-sigma model results (RMSE for WQI1: 1.976800 and MAPE: 0.023200, RMSE for WQI2: 2.650500 and MAPE: 0.028300, accuracy) showed a significant superiority over the other two models. In this study, the optimal ANN models are proposed for WQ assessment. This approach aims to avoid the disadvantages of traditional assessment methods such as computational time and complexity. According to the findings of the study, the proposed method provides high prediction accuracy. The findings do not mean that systematic modelling and optimization (SMN), multilayer perceptron (MLP) or particle swarm (PS) models will always outperform other conventional methods. However, in this particular case, the proposed PS-ANN model is suitable and highly efficient for WQ prediction. Moreover, it is presented that the models we have applied in the scope of the study are able to reflect well the nonlinear relationships associated with complex watershed processes. In this context, using machine learning and related technologies to develop innovative solutions to control water pollution, improve WQ and ensure watershed ecosystem security can make significant contributions.

The single multiplicative neuron (SMN) model, multilayer perceptron (MLP) and pi-sigma artificial neural network (PS-ANNs) algorithms, which were specifically selected and compared for water pollution control or WQ improvement, were predicted to provide more effective solutions for these issues. As a result of the comparison, the PS-ANNs algorithm can process more specific types of data or predict certain WQ parameters more accurately. In addition, the difference of the algorithm we have implemented from the others may be that it works faster or more efficiently, which may provide an advantage in the field of application. The aim is to provide information for WQ management, such as the determination of WQ levels, to enable management to respond effectively and quickly in such situations.