Abstract
Information technology applications are crucial to the proper utilization of manufacturing equipment in the new industrial age, i.e., Industry 4.0. There are certain fundamental conditions that users must meet to adapt the manufacturing processes to Industry 4.0. For this, as in the past, there is a major need for modeling and simulation tools in this industrial age. In the creation of industry-driven predictive models for machining processes, substantial progress has recently been made. This paper includes a comprehensive review of predictive performance models for machining (particularly analytical models), as well as a list of existing models' strengths and drawbacks. It contains a review of available modeling tools, as well as their usability and/or limits in the monitoring of industrial machining operations. The goal of process models is to forecast principal variables such as stress, strain, force, and temperature. These factors, however, should be connected to performance outcomes, i.e., product quality and manufacturing efficiency, to be valuable to the industry (dimensional accuracy, surface quality, surface integrity, tool life, energy consumption, etc.). Industry adoption of cutting models depends on a model's ability to make this connection and predict the performance of process outputs. Therefore, this review article organizes and summarizes a variety of critical research themes connected to well-established analytical models for machining processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Today, the capability to combine the flexibility of personalized products with the manufacturing speed and unit cost of mass production is one of the most basic criteria for having a strong economy. A crucial necessity for the mass manufacturing of personalized items is needed for innovative production technologies [1]. Industry 4.0 already relies on advanced intelligent manufacturing for the improvement of extremely flexible parts with low cost and high production rate. The notion is implemented by a fusion of modern engineering technologies in the cyber and physical domains. Industry 4.0 in manufacturing aims to boost productivity, sustainability, agility, and customer attention; it necessitates increases in data sensing, networking, and physical space automation [2]. Subtractive manufacturing plays a leading role in the secondary and tertiary forming requirements of production by proving its excellence in added value, flexibility, and precision. Subtractive manufacturing’s productivity, which is frequently expressed as material removal rate, must be weighed against the form's complexity and precision. By offering the optimal combination of the operation parameters, its sustainability in terms of excellent product quality, energy consumption, environmental effect, and material savings can be further enhanced. Subtractive manufacturing is the general description of forming processes that create the desired geometry of workpieces by cutting material from a solid block and is roughly divided into three subgroups: (i) machining; (ii) abrasive processes; and (iii) non-traditional processes [3, 4].
1.1 Why are Machining Processes Still Important and What are the Limitations and Opportunities in Manufacturing?
Manufacturing processes are thought to be responsible for around 5% of GDP in developed countries [5]. Around the world, investments in subtractive manufacturing infrastructure have constantly been increasing. The global market for machining centers was valued at almost $30 billion and is predicted to increase around $44 billion by 2026, with an annual growth rate of over 5% [2]. Since almost every type of product/part manufactured is directly or indirectly exposed to any machining operation, the most frequent manufacturing method considered is machining [6].
The latest developments in equipment technologies have led to quick and considerable increases in machine tool automation levels, but Industry 4.0 demands the integration of smart technologies and production systems for the digitization of manufacturing activities [7, 8]. Additive manufacturing meets these requirements of Industry 4.0. However, additive manufacturing is known to have some advantages over metal cutting processes, and its initial investment cost, production cost (especially raw material cost), low production speeds, inability to obtain clear shapes, and poor surface quality are still among its major shortcomings. Providing a sustainable hybridization with another manufacturing technology such as machining is an effective short-term remedy to eliminate these deficiencies and effectively complete Industry 4.0 readiness. In this context, hybrid multitasking is a popular arrangement in which pieces near the net form are generated via additive manufacturing; then, subsequently the pure shape is made using superior precision CNC machining processes. It is known that hybrid manufacturing technology has an extensive range of applications during the production of aircraft parts [9]. To summarize, hybridization with additive manufacturing and machining processes can be considered as an alternative application for creating a pure-shaped piece in a single setup as well as in single or multiple workstations. However, the hybridization of these technologies leads to the increased complexity of machining operations that require more extensive sensing abilities and further developments in control technology for the equipment to operate safely and efficiently [2].
1.2 Why is Modeling Necessary in Machining?
According to Industry 4.0, satisfying requirements can be accomplished by integrating information and digital technologies into a manufacturing company's management system during the production stage of a product [10]. This fact is achievable when good integration is created between the machine tool and technical components that are independent of one another, allowing them to monitor each other's state and the process in progress. This necessitates the machine tool and each of its subcomponents to have built-in intelligence along with a series of sensors that allow them to effectively engage in the operational production process [10]. As a result, the efficient utilization of manufacturing equipment is heavily reliant on information technology applications. Also, essential are precise estimations of the outcomes of machining procedures. The usage of such technology needs the evolution of trustworthy models and simulation methodologies for key manufacturing/machining operations. As shown in Fig. 1, modeling can be used to achieve these needs. The reasons behind such modeling are [11]: (i) finding strategies to improve procedures in a timely and practical manner; (ii) enabling accurate process outcomes estimations; (iii) increasing one's understanding of process phases and process design; (iv) using it to gain process monitoring and control capabilities; (v) sustainability; and (vi) adaptation to the new industrial era.
While it is aimed to increase product quality and reduce costs with developments in machine tools and cutting tools along with superior material improvement, their achievement requires predictive models to be used in process planning systems. To achieve this for each workpiece, the following factors must be considered [12]: (i) ideal cutting circumstances; (ii) coolant/lubricant type; (iii) cutting tool type and geometry, and so on. The goal is to use an optimal process plan to satisfy functional design objectives. Process planning must be integrated with the development of predictive performance models. The creation of complex prediction models has recently acquired importance to match the demand. Merchant et al. [13] noted that the database of knowledge regarding processes, tools, materials, and workpiece demands has an important effect on the final state of production. That is, process data and proper models should be used to drive design and production decisions as goals become more complicated. Analytical, computational, experimental, and artificial intelligence (AI)-based hybrid modeling approaches are some of the most common models used for this [14]. Various process models, including process capacity data, combined with advanced simulation tools and AI-based methodologies allow for the management of negative impacts on process performance during the design stage. Moreover, simulation techniques based on mechanical as well as machining process thermal models have proved to be useful in determining cutting process inputs across a wide range of actual parameters in recent years. Simulations can offer a more thorough evaluation of the impacts of several factors on the cutting process than traditional estimates when the empirical and physical components of a thermo-mechanical model are combined [15], as shown in Fig. 2. Aside from the fact that simulation models are critical for ensuring high-quality products and efficient manufacturing, they are also essential for ensuring that basic outputs like tool life and surface quality/integrity are met.
1.3 Motivation, Objectives, and Scope of the Study
For the adaptation of manufacturing processes to Industry 4.0, there are basic requirements that must be met by subtracting and adding manufacturing technologies [16,17,18]. For this, as in the past, there is a great need for modeling and simulation tools in this industrial age. In the creation of industry-driven predictive models for machining processes, substantial progress has recently been made. This article includes a comprehensive review of predictive performance models for machining (particularly analytical models), as well as a list of existing models' strengths and drawbacks. It contains a review of available modeling tools, as well as their usability and/or limits in the monitoring of industrial machining operations. This study includes contributions from practice and the literature, and it is hoped that the paper presents the latest developments as a comprehensive report, and provides readers with an insight into future trends. The goal of process models is to forecast principal variables such as stress, strain, force, and temperature. Therefore, this review article organizes and summarizes a variety of critical research themes connected to well-established analytical models for machining processes. In the end, the new section deals with the models for ductile-to-brittle transition in micro- to macroscale machining has been incorporated to strengthen the idea of the present review article.
2 Analytical Modeling Methods
A mathematical model is an concept of a real system that uses mathematical terminology to describe the system's behavior. To generalize about a subset of reality's parts, structure, and behavior, a model is necessary [19]. Analyzing patterns that can be used to predict future occurrences or outcomes is known as predictive mathematical modeling, which is also known as predictive analytics. An important question to ask in predictive modeling is "What is the most likely event to happen in the future based on known previous behavior?" [20]. To boost efficiency and improve product quality, simulated predictive models can be linked to process planning systems. Predictive performance models can be used to reduce and/or eliminate trial and error procedures in adaptive control for machining operations [12]. Many modeling tools, such as analytical methods, slip-line solutions, empirical procedures, and finite element methods, have been created during the last 50 years by researchers [21]. The manufacturing industry and researchers strive to improve performance indicators of the production process, i.e., surface quality, surface integrity, tool life, chip shape–breakability–evacuation, the accuracy of dimension, burr formation, energy consumption, and others. Optimal conditions for developing the mentioned performance indicators need to employ dynamic forms to track machine tool settings, process, and tool state. The metal cutting processes are principally associated with the following parameters [22, 23]: (i) workpiece material (mechanical properties, physical properties, chemical composition, etc.), (ii) machine tool, (iii) cutting tool (tool material, geometry, coating type, etc.), (iv) cooling type/method, (v) other equipment related to the cutting tool and machine tool, and (vi) others (programming errors, unsuccessful operation, incorrect reactions by operator). In the machining industry, predictive models that can quantitatively anticipate the influence of input factors on output parameters are very significant [24, 25]. Depending on the modeling approach, models could be characterized as semiempirical, physical, or empirical. Analytical, numerical, hybrid, empirical, and AI-based modeling approaches are among the most popular predictive models for cutting operations. Predictive modeling attempts are summarized in Fig. 3 [12].
Modeling approaches in machining processes (adopted and modified from Ref. [12])
As shown in Fig. 3, the quantitative inputs are utilized to estimate the output parameters in two different steps. Cutting force, friction, stresses, strain, and temperature can be predicted with analytical models including slip-line models. In addition, analytical models are proficient at developing tools and give important data for numerical model optimization. However, the complex structure of the machining process still does not make it possible to estimate precisely from all industrial results [26]. Through analytical approaches, the dynamic cutting force has been linked to (i) the instant uncut section of the chip, (ii) the area of the slip plane, and (iii) nonlinear systems. However, supplementary nonlinear factors associated with the cutting process and tool/chip/workpiece interactions prevent most suggested models from effectively predicting the dynamic force [27]. Empirical models are derived from experimental data and can be applied to nearly all machining processes for measurable operation variables. It supplies a simple, quick, and direct prediction of industry-related parameters. However, such models are only valid for the trial range and they require extensive trials, more time, and high cost [28]. Numerical modeling like FEM is another modeling method that is the subject of approximately 18% of the research in this field [11]. FEM has risen to prominence in recent years, particularly for modeling metal cutting operations [29]. Stress, strain, and temperature at primary, secondary, and tertiary shear regions are all calculated using FE models. The hybrid models bring together the powerful features of different methodologies to improve the capability and accuracy of basic models. These are constrained by the capacity of the basic model and need a large amount of data from experiments and/or simulations [28]. Artificial intelligence (AI) has developed a variety of methods to assist in the solution of complicated issues involving human intelligence. The results of various AI tools are far more accurate than previous non-AI-based techniques, and they can accurately anticipate tool wear, surface roughness, and other machining performance characteristics [30,31,32]. Today, huge resources are being invested in the development of AI technology around the world to assist manufacturing industries. However, there are still some difficulties in the practical use of this method [33].
3 Classifications of Analytical Modeling Methods
Several analytical models are developed and used in different machining processes such as turning, milling, drilling, and grinding [34]. Usually, the analytical models are considered in the category of physics-based or mechanistic models. In addition, the finite element model (FEM)-based simulation models are used for the prediction of machining responses. However, the models developed using FEM are not practical to use in the industry due to the need of experimental work and long processing time. Therefore, the analytical models are preferable in that situation. In most of the analytical models, the highest or median temperature at the interface of the cutting tool and workpiece is easily estimated [35, 36]. Similarly, the tool wear [37], cutting forces [38], surface roughness [39], cutting energy [40], chip formation [21] and vibration/chatter [41] are easily calculated/developed with certain analytical models. In another example, it is a well-known fact that the important cost item of machining is the cost of changing the tool that has completed its life and therefore the cost of stopping the process [42]. High temperature during cutting reduces the tool material strength and results in the development of the tool wear. Especially in cutting situations where contact is continuous, such as turning, the temperature caused by friction is high [43, 44]. Therefore, recently analytical and physical mechanics-based modeling methods have been developed. The various models are developed to evaluate the machining performance and the details are given in subsequent sections:
3.1 Cutting Force Models
Cutting forces are the most important parameter that is used to design the structure of machine tools. Several models and algorithms have been developed to detect the high forces and cutting temperatures along with the tool path during the turning process [45, 46]. The cutting tool geometry, material properties, machining parameters, material model concerning the cutting tool–workpiece pair, the mechanical characteristics of the workpiece, and the cutting tool are all inputs of created analytical models [47]. These inputs allow the models to define the quantity of material removed from the specimen at each step regarding the path of the tool, the forces related to cutting in all three directions, and the rise in workpiece temperature as a result of cutting. The cutting parameters in the toolpath can be improved using the results of the model [48]. It is possible to retest the toolpath created with the new parameters, with the developed algorithm, and to optimize the toolpath in terms of cutting forces and workpiece temperature with an iterative method, without ever using the toolpath on the machine. Thanks to these methods, the workpiece and tool costs that need to be used for testing are also reduced, and the desired product is produced faster, more smoothly, and at a lower cost [49].
In turning operation, undesirable tolerance in the workpiece, sudden cutting tool breakage during the operation and excessive wear on the cutting tool are the most common problems [50]. Although there may be different root causes of these problems, they are often caused by excessive cutting forces due to incorrect parameter selection [51]. At this stage, modeling the cutting forces before an operation will ensure that the parameters are selected correctly so that the operation will be carried out smoothly on the first try. Considering all the factors listed above, it is possible to better understand the importance of force modeling along the toolpath for the turning operation [52]. Mechanistic models concerning cutting force production in drilling, turning, and milling were enthusiastically examined. Budak [53] utilized a nonlinear mechanical model suggested by Altintas along with Spence [54] to control the highest cutting force, after they demonstrated that the model-established methodology presented a control routine like adaptive response control. Teramoto et al. [55] suggested an online system concerning a mechanistic procedure model, where the cutting force control is established. Spence along with Altintas [56] utilized a cutting force model-based estimation along with adaptive response control, with prior knowledge of the milling procedure could be utilized to prevent significant overshoot because of response control interval interruption. Likewise, Richards et al. [57] come together with an online adaptive force monitor along with off-line federate optimization established on the mechanistic standard recommended by Fussell et al. [58]. One of the important requirements for the force algorithm to be applied along the toolpath is the development of the intersection algorithm along the toolpath. For instance, the end milling operations were studied by using a model to anticipate cutting force predictions by Vogler et al. [59]. Cutting forces are calculated using a model that incorporates the chip's minimum thickness. For pearlite and ferrite workpieces as well as ductile iron specimens, the authors found that the used model was capable of accurately estimating the magnitude of the cutting forces. Further, to handle machining across diverse cases simultaneously, the end mill is discretized into pivotal pieces. It is listed for each of the flutes that are a part of the workpiece at each time stride. Additionally, this location is compared to the location of the sphere that represents the grain composition in the model centered at \(\left( {x_{Fj} ,y_{Fj} ,z_{Fj} } \right)\) [59]. If:
\({R}_{3i}\) refers to the sphere radius demonstrating the tertiary phase.
The algorithm applied to compute the thickness of the chip consists of the next steps. Primarily, the rotation angle, \({\theta }_{\text{Fi}}\), of flute \({f}_{\text{N}}\left({f}_{\text{N}}\right.\) \(=\text{0,1},\dots \text{N}-1)\) across the tool pass is given as [59]:
where \(\theta =2\pi RPMt/60\), and \(\delta \theta \left({\text{z}}_{\text{Fj}}\right)\) refers to the supplementary angle which should be treated as a cutting-edge spin over the helix angle \(\beta\), as the \(\text{z}\) assortment is varied,
where \(R\) refers to the end mill radius. The center coordinates of the tool, \(\left({\text{x}}_{\text{Ci}},{\text{y}}_{\text{Ci}}\right)\), in the existence of runout could be given as [59]:
\(N\) refers to the flutes number, \({f}_{t}\) represents the feed per flute, \({r}_{0}\) represents the parallel axis offset magnitude, and \(\lambda\) refers to the parallel axis offset locating angle. The cutting-edge coordinates, \(\left({x}_{Fi},{y}_{Fi}\right)\), could then be given as [59]:
In case \(\theta_{{{\text{S}}0}} \le \theta_{{{\text{F}}0}} \le \theta_{{{\text{E}}0}}\), afterward, the present flute is bisecting the surface generated from the chip thickness and the zeroth tool pass for this tool pass is given by [59]:
3.1.1 Orthogonal Cutting
This model is generally called a 2D model, and in this model, the material in the form of chips is removed by the side cutting edge perpendicular to the direction of the tool and workpiece’s relative movement. Therefore, the cutting forces act only in the direction of speed and uncut chip thickness, called the main cutting force (Fc) and the feed force (Ff) [60]. In this model, the rake face, as well as the lowest cutting-edge point, must be taken into account. This is done by taking the thickness of a chip above its minimum point, and after that, the rake angle average is calculated as the angle formed by this line in addition to the normal cutting speed [59].
This assumption is made as a part of the orthogonal cutting approach. Another assumption made in modeling using orthogonal cutting is that the slip area formed during machining on a plane. It is possible to see this assumption in Fig. 4.
Merchant diagram for orthogonal cutting (Copyrights reserved [61])
While modeling with orthogonal cutting, it is possible to construct the Merchant diagram assuming that the cutting is planar and to express the relationship between forces and velocities in a simple trigonometric way by using the angles on the Merchant diagram [62]. One of the important advantages of modeling with the orthogonal cutting method is that this type of modeling can model the effect of different cutting parameters. It is now possible to use orthogonal cutting experiments to predict the consequences of rake angle, cutting velocity, feed value, and depth on the force. The orthogonal cutting test design must incorporate all cutting parameters to represent all cutting variables [63]. Modeling with the orthogonal cutting method has the additional benefit of consistently producing accurate findings for a wide range of experimental parameter values [62]. With the orthogonal cutting technique, the model could be used concerning a variety of cutting operations along with tool geometries devoid of issues. For example, the cutting force can be predicted using a tube cutting orthogonal model obtained by external turning with the tube cutting method. What is critical to remember at this stage is that all simulation parameters must be constrained by higher and lower bounds specified in experimental design specifications, as discussed previously. In a situation where the parameters to be simulated are outside the limits of the parameters included in the experimental design, the orthogonal cutting model gives a result for the force, but since the result obtained at this point will be obtained by extrapolation, it is useful to approach the accuracy of the values cautiously [64].
Although modeling with the orthogonal cutting method gives results reflecting the real situation in most cases, the models obtained by the orthogonal cutting method in very special tool geometries may not yield results at the desired accuracy levels. For example, models obtained by an orthogonal cutting method in special milling tools may give a result, but the results found may not be within the desired error percentages due to the complexity in the geometry of the tool [65]. The specific models obtained by calibration tests using only the tool to be modeled can predict the forces more accurately for that particular tool than the model obtained by the orthogonal cutting method. The specific models obtained by calibration tests using only the tool to be modeled cannot be used to generalize the specific models. Another limitation of modeling with the orthogonal cutting method is that the model obtained cannot model the rake face of the tools [66]. For example, the forces obtained as a result of the cutting tests performed with special chip breaker tools may differ from the forces obtained as a result of cutting with flat tools without a chip breaker [67], but it is not possible to calculate such a situation with a model obtained by the orthogonal cutting method. Another limitation of force modeling with the orthogonal cutting method is that it is specific to the workpiece–tool material pair. In general, the tool materials do not have much influence on the cutting force, but the forces of friction on the tool material surface can affect the cutting force. For this reason, the most accurate approach when modeling with orthogonal cutting is to use the developed model only meant for the tool material–workpiece pair [59]. Chen et al. [68] conducted an analytical model methodology concerning cutting forces in the field of close-orthogonal cutting of Ti6Al4V titanium alloy. An analytical method is utilized to assess chip thicknesses along with forces taking part during the near-orthogonal cutting procedure. The material’s shear flow stress was developed by employing the Johnson–Cook fundamental material principle where the thermal softening behaviors, strain hardening, and strain rate sensitivity are combined. The model forecast is validated through investigational records, where a decent deal in conditions of the typical cutting forces as well as chip thickness is indicated. An assessment of the expected temperatures along with available information achieved by utilizing the finite element process is as well given [68].
It is shown as possessing a radius equal to \({r}_{e}\) on the cutting edge. The angle of clearance concerning the tool is shown by the symbol \({\gamma }_{0}\). In the case of a certain depth penetration p, the interference volume can be calculated as [59]:
The depth penetration quantitatively is similar to the thickness of the chip \({t}_{C}\) for conditions where \({t}_{C}<{t}_{C,\text{min}}\), and is indicated diversely to assert that no chip formation took place during these cases. The computation of the elastic deformation forces could then be [59],
where the continuous force interference and coefficient of friction concerning the elastic deformation force system are denoted by the symbols \({K}_{\text{int}}\) and \({\mu }_{\text{int}}\), respectively.
In the conditions that resulted in chip formation, the orthogonal thrust force, \({F}_{\text{T}}\), is easily transformed into the radial thrust force, \({F}_{\text{rad}}\). The force of cutting is split into two elements, in addition to the longitudinal force, \({F}_{\text{lon}}\), and the tangential force, \({F}_{\text{tan}}\), which are both affected by the inclination angle of the blade. The force of cutting is composed of two elements [59]:
For the situation where no chip formation appeared, the elastic deformation forces are given by [59]:
The longitudinal, differential radial and tangential forces for every slice are further switched into the Cartesian coordinate system as [59]:
The forces are subsequently added to find the total forces [59]:
Yang and Park [69] devised a study to predict the cutting forces that would be used during the ball-end milling operation. The operation of the ball-end milling was thoroughly examined, and a cutting force sample has been created to foresee the immediate force of cutting under certain machining circumstances. The model's conduction was established from an investigation of the ball-end mill cutting geometry in terms of the rake faces plane. The cutting rim of a certain ball-end mill was taken into consideration by way of a sequence of tiny components; also, each cutting-edge component geometry was examined to compute the obligatory parameters concerning the oblique cutting operation under the assumption that every cutting edge was in the same direction as the cutting-edge component. The cutting rim of a specific ball-end mill was taken into consideration through the use of a series of small components, and the geometry of each cutting-edge component was examined. This issue is performed to compute the necessary parameters for the oblique cutting operation under the assumption that every cutting edge was in the same direction as the cutting-edge component.
A diagonal cutting method in the tiny cutting-edge component was investigated by way of a perpendicular cutting operation in the plane consisting of the chip's cutting speed as well as the flow vectors, which was then compared to the original oblique cutting procedure. The authors said that the model could be utilized to value the cutting forces concerning the ball-end milling and that the forces of the anticipated cutting were within the reasonable deal with experiment findings under a range of machining parameters. The coordinate of a cutting-edge point is given by [69]:
where \(R\) refers to the cutter radius, \({\alpha }_{n}\) refers to the plane rake face's normal rake angle, and \(\theta\) refers to the angle concerning the spherical coordinate point. During a dynamical coordinate system, and realizing the infinitesimal length components, \(\Delta x, \Delta y,\) and \(\Delta z\), refers to the angle of inclination, \(i\) has the following connection [69]:
while the effective rake angle, \({\alpha }_{e}\) could be examined using the following equation taking into consideration, Stabler's chip flow standard [69]:
The orthogonal cutting hypothesis is applied for the plane that consists of the chip speed \({V}_{c}\) and the cutting force the cutting velocity \(V\); on the little edge \(\text{OA},\Delta {F}_{\text{r}}\) is analytically stated by [69]:
where \({\tau }_{\text{s}}\) refers to the workpiece shear strength, \(\Delta {A}_{\text{c}}\) represents the undeformed chip cross-sectional area on the tiny edge, \(\phi\) refers to the shear angle, whereas \(\beta\) refers to the rake face friction angle. The undeformed chip cross-sectional area, \(\Delta {A}_{\text{c}},\) is given by [69]:
where \({f}_{\text{e}}\) and \({d}_{\text{e}}\) represent the feed in addition to the cutting depth, respectively, during the \(V-{V}_{\text{c}}\) plane.
If one considers the fact that the comparable cutting depth stands as a practical length concerning the accurate cutting rim, it may be proved by making this connection [69]:
Yet, the infinitesimal length of the cutting edge, \(\Delta a,\) is
while the angle among \(V-a\) plane and \(V-{V}_{c}\) plane \(\gamma\) is [69]:
where \({\eta }_{c}\) refers to the chip flow angle.
By using Stabler's formula, the angle \(\gamma\) has the subsequent link:
In a situation where the cutting speed is enough large when compared to the rate of feed, the cutter can be there supposed static, and its feed average along the \(x\) path, \({f}_{x},\) might be demonstrated through a logical exactness as [69]:
where \({f}_{\text{m}}\) refers to the largest feed average for every cutter and \(\psi\) represents the cutter rotation angle. Since \({f}_{c}\) and \({f}_{\text{c}}\) are explained by [69]:
and
The equivalent cutting depth, \({f}_{\text{e}},\) is eventually specified by:
The infinitesimal cutting force \(\Delta {F}_{\text{r}}\) can be degraded into the subsequent three elements concerning the \(a-b-c\) coordinate:
Converting them into the \(x-y-z\) coordinate gives:
Because the \(x-y-z\) coordinate undergoes rotation in the \(X-Y-Z\) coordinate via the angle \(\psi\), force elements within the latest coordinate exist by:
As previously stated, orthogonal machining information is required to ascertain the infinitesimal force of cutting \(\Delta {F}_{\text{r}}\). End turning experiments concerning the tubes of the thin-walled were employed to generate the information presented here. The obligatory factors in the formula are the angle of shear, \(\phi\), and friction angle, \(\beta\), in addition to shear stress, \({\tau }_{\text{s}}\). Initially, the shear angle could be examined utilizing the subsequent formula from the quantification of the thickness of the quantification.
The friction angle, \(\beta\), could be found via the subsequent equation from the calculation of cutting force elements.
Thereafter, the friction and shear angle is found and shear stress could be evaluated by applying the impractical cutting force formula. Consequently, the experimental outcomes are represented via the following formulas [69]:
3.1.2 Oblique cutting
The method used in mechanistic cutting force modeling is based on the force results collected by performing orthogonal cutting tests [70]. Although most of the cutting work done in practical life is oblique cutting, it is possible to use the model obtained by orthogonal cutting experiments for oblique cutting by performing some transformation operations [69]. It is possible to see the difference between orthogonal and oblique cutting geometries in Fig. 5.
The fundamental difference between these two cutting geometries is that the cutting tool enters the workpiece at an angle equivalent to the cutting-edge inclination angle within the oblique cutting geometries. Orthogonal cutting is characterized by having a tool's blade cut at a 90-degree angle to the workpiece, which eliminates any cutting-edge inclination angle. When using the orthogonal cutting technique for modeling, it is assumed that, as implied by the name, during cutting the edge of the cutter will be orthogonal to the workpiece, resulting in the generation of only two axes of motion: cutting and feeding. It is assumed that the cutting process is modeled as a strain deformation two-dimensional plane with no face spreading when modeling with orthogonal cutting [73].
Fu et al. [74] conducted an analytical model to predict the milling forces of helical end milling established on a machine theory prediction. Milling forces were expected from the key information of specimen material characteristics, cutting conditions, tool geometry, along sorts of milling. The cutting forces of each component of the helical cutter have been estimated analytically by applying the traditional oblique cutting model. The proposed analytical model provided a reasonable settlement for the milling forces when compared with published data derived from the investigative records and the mechanistic model [74]. In Fig. 6, a comparison between the milling forces achieved using the recommended analytical model and the existing data has been illustrated.
Comparison of milling forces achieved through the suggested analytical model as well as the available results (Copyrights reserved) [74]
3.2 Cutting Temperature Models
The generation of heat during machining is a common issue that has a significant impact on the choice of cutting parameters. As with any cutting operation, the heat-affected zones are divided into many phases (Fig. 7). Some of the heat will transfer to the tool depending on the heat transmission coefficient between the tool and the workpiece, leading to diffusion and thermal tensions that will eventually lead to tool wear. Tool life is affected by cutting temperatures, particularly the peak temperature at the chip–tool contact. Determining the temperatures that occur during cutting is crucial for optimizing the process, as tool life is a characteristic that directly influences the efficiency of machining [75].
Heat generation zones in orthogonal cutting process (Copyrights reserved) [75]
There are many analytical and finite element models developed in this regard. The models developed using the finite element method are not practical to use in the industry due to the need for a lot of experimental work and long processing time [76]. In most of the analytical models, the highest or average temperature at the tool–chip interface was calculated. The behavior of the friction occurring in the secondary deformation zone is also taken as sliding friction. There are also models in which the effect of the heat source in the primary deformation zone is neglected [77].
Studies in the literature have generally aimed to improve understanding of the temperature distribution within the chip other than the tool [78]. Moreover, the material behavior in the intended primary region, the effect of heat generation, modeling the heat generated by friction during the secondary region for the two-zone (sticking and sliding) contact state, calculating the temperature distribution by the tool–chip interface, and calculating the thermal properties are the other important focus points in the literature studies [79, 80].
It is the basic model and is typically applied under orthogonal cutting conditions. There has been extensive study into the effects of measuring and analyzing the temperature of the workpiece and the tool tip during machining [81]. Tools' durability and surface quality benefit most from temperature monitoring. By modeling or measuring the heat produced during cutting, tool wear can be predicted, and modeling software can be developed [82]. The generated heat significantly affects the dimensional accuracy, including subsurface damage and residual stress, and the quality of the component. To achieve the desired level of hardness in the workpiece, the process temperature must be precisely regulated [83]. In addition, the process temperature is properly controlled, it can be used to provide the appropriate hardness for the workpiece. In addition, a common method or system that can easily measure temperature in current production processes and is accepted by everyone has not been developed. The temperature has an adverse effect on the performance and efficiency of machining processes. Temperature fluctuations can have a substantial impact on the wear and expansion of tooltips and materials [84]. As cutting speed rises, the temperature of the tool–specimen interface rises exponentially, resulting in an overall increase in wear. Using Weiner's [85] energy dissipation ratio study, Boothroyd [86] and Wright [87] created a similar model. They presumed that the thermal properties of the workpiece were stable regardless of the surrounding temperature. Boothroyd [86] also failed to account for the fact that heat travels along the chip's axis when calculating the contact region's heat dissipation ratio and the consequently constant heat given to the tool. The first cutting temperature models by expert researchers are summarized in Table 1.
Wright [87] on the other hand, accounting for both adhesion and sliding friction, hypothesized that 80% of the heat generated by friction in the contact region is transferred to the chip. To figure out the temperature profile of the rake face, it is first necessary to determine the rise in material temperature within the critical region, \(\Delta Tp\). The product concerning the shear velocity and the shear force is used to determine the rate of work in a parallel-sided, discrete zone, and it may be expressed as [87]:
where \(\rho\) and \(c\) represent the density and specific heat while \(\beta\) refers to the rate of conducted heat backwards into the workpiece. The amount of \(\beta\) might be found by using Boothroyd's standard curve.
Regarding the chip field, the standard heat transfer formula for a movable heat partition applies. The heat conduction in the chip flow direction which is considered negligible can then be given by [87]:
where \({V}_{c}\) refers to the bulk chip velocity and \(K\) represents the thermal diffusivity. This equation’s Laplace transform is given by:
The common solution is:
The constant \(C\) might be found because a further boundary situation is at \(y=0\). At this interface:
where \(k\) refers to the conductivity and \(f(x)\) represents the chip heat flux as examined above. The Laplace transform of this equation is [87]:
and because the derivative of the equation at \(y = 0\) is:
\(C\) may be determined by substitution:
This might be substituted into an equation where \(y=0\)
The inverse transformation of the previous relationship consists of two functions \(F(s)\) and \(1/\sqrt{s}\) might be determined through the convolution theorem so that [87]:
This relationship might currently be estimated for the three sections of the rake face, the zone of sticking friction \(\left({l}_{s}\right)\), and that of sliding friction \(\left({l}_{f}\right)\) in addition to the area further on the contact zone \(\left(>{l}_{s}+{l}_{f}=l\right)\). The function \(f(x-z)\) regarding the heat flux in the chip alters for each of these zones as [87]:
Tool and workpiece are assumed to be semi-infinite environments in an oblique cutting model by Venuvinod and Lau [91]. The slope-moving welding motion was treated with the heat source solution. By expanding on the analyses of Loewen and Shaw [89], the authors were able to create a model that predicts the impact of the slip plane. Without considering the passing of time, Young and Chou [92] measured tool–chip contact temperatures under orthogonal cutting conditions. In their model, heat is considered to be distributed uniformly throughout the cutting plane and the tool–chip contact. In spite of this, they failed to account for heat transfer in the direction of movement. They found that the crack in the chip is where the surface temperature reaches its highest peak in their investigation. Ning and Liang [93] used an analytical system to try and forecast the machining temperature concerning AISI 4340 as well as AISI 1045 steel. According to Johnson–constitutive Cook's model along with orthogonal cutting process mechanics, the model was built. In addition to the stresses determined using the mechanic's system along with the J–C model, the mean temperatures at two shear areas were predicted by lessening the range between the stresses. Cutting force, chip thickness, and Johnson–Cook constants are all examined in their work to foresee temperature throughout the machining of AISI 1045 steel. Numerous sets of chip thicknesses and varying cutting forces as well as offered J–C constants are used to predict temperature. The predicted deviation is greater the larger the insert deviation. It is even possible to estimate the machining temperatures of AISI 4340 steel by utilizing cutting tools of different specifications. Finally, a comparison with other analytical temperature models is used to evaluate the progress and limitations of the temperature model. The authors indicated that this temperature model is capable of being employed for successful and useful machining temperature extrapolation [93]. The organized temperature model was developed according to the mechanics of the cutting procedure and the J–C model [94, 95]. The J–C model is stated as:
in which the five material constants \(A,B,c,n,m\) refer to the yield stress, the strength, the coefficient of the strain rate, the coefficient of strain hardening, and the coefficient of thermal softening, respectively [96, 97]. The shear angle \((\phi )\) is determined as of the chip compression ratio \((\text{r})\) through the supposition of the constant material flow speed at the chip creation area \(\left({t}_{1}V={t}_{2}{V}_{c}\right)\) as:
where \(V,{V}_{c}\) represent the cutting speed and chip speed, respectively; \({t}_{1}\) and \({t}_{2}\) refer to the cutting depth and thickness of the chip, respectively. The shear stream stress at the PSZ could be determined using the cutting mechanics \(\left({k}_{AB}\right)\) along with the J–C model including von Mises yield criterion \(\left( {k_{AB}^{\prime } } \right)\) individually [98, 99] as:
The temperature average at PSZ \(\left({T}_{AB}\right)\) is established by reducing the variation between the shear flow stress \(\left({k}_{AB}\right)\) along with the shear flow stress \(\left( {k_{AB}^{\prime } } \right)\). The stress flow at the SSZ could similarly be determined utilizing the cutting mechanics \(\left({\tau }_{\text{int}}\right)\) plus the J–C model along with von Mises yield criterion \(\left({k}_{\text{int}}\right)\) independently as:
The mean temperature at the SSZ \(\left({T}_{\text{int}}\right)\) is established by way of minimizing the disparity among the shear flow stress \(\left({\tau }_{\text{int}}\right)\) along with the shear flow stress \(\left({k}_{\text{int}}\right).\) Machining process heat modeling and notably the determination concerning the maximum tool–chip interface temperature were investigated for a long period. Analytical [100], semi-analytical [101], and finite element techniques [102, 103] have been utilized to calculate cutting temperatures. Surfaces in contact with air are considered to have boundary conditions that are adiabatic in analytical models because of the complex physics involved. It has been widely assumed that just the sliding friction condition exists by the tool–chip contact; then, it continues to be investigated in this manner.
3.3 Tool Wear and Tool Life Models
When mentioning cutting operations within machining processes, tool wear is an important topic [104]. The relationship of elements during a cutting process leads to several chemical, physical, and thermo-mechanical case that affects the tool wear. It is hard to find one dominant cause of wear in tools since numerous and different combinations of wear mechanisms can be observed such as oxidation or diffusion, adhesion, and abrasion [104]. During the machining process, mainly the tool undergoes wear in the flank, crater, or nose region. A tool is believed to be worn if the price of replacement is lower than the cost when not substituting a tool. The failure of a tool takes place in the case when a tool is no longer able to perform the requested function. The life of a tool can be defined as active life while it is satisfactorily cut, and this life is brought to its end via gradual methods like wear or suddenly mechanisms such as chipping and fracture. As a result of high pressure, sliding speed, temperature, and thermal or mechanical shock in the cutting area of cutting tools, the wear behavior of cutting tools is generally of diverse types such as flank wear and crater wear. Changing cutting situations can affect the type of wear that is now present. The most common wear types are flank and crater wear as shown in Fig. 8.
Flank wear and crater wear (Copyrights reserved) [105]
The tool rake and the interface geometry of the tool and chip are both impacted by crater wear. The tool’s chemical affinity and chip temperature are the two most important parameters that influence crater wear [106]. Flank wear is common because of the tool rubbing with a hard phase in a workpiece causing abrasive or/and adhesive wear [107]. Since the importance of tool management, it is necessary to predict tool life or tool wear using different experimental models. Firstly, it is so important to take into account the reliance on the integration of tool parameters (internal defects, surface integrity, besides material geometry), the workpiece (strength, chemical composition, hardness, etc.) cutting conditions (feed, speed, cutting fluids, cut depth), cutting type (milling, turning, drilling, etc.), and the machine tool (for instance, state of maintenance, stiffness). Several mathematical models are conducted to calculate tool wear [108]. These calculations explain the connection between machining qualities and tool life within a restricted range of cutting settings. Within a narrow assortment of cutting velocities, the Taylor tool life equation describes how cutting velocity affects the tool's life span. The equation can be described as [109]:
where T represents tool life, V is the speed of cutting, and the Taylor constant is represented by C [109]. Taylor equation appears to be useful reasonably when machining low-alloy steels and carbon with various types of materials under semi-roughing environments (depth of cut = 0.050–0.150).
Lorenz concluded that the Taylor equation is suitable for high cutting speeds and short tool life. He incubated a process of shortcut experiments to replace long-run tests of tool life and estimated the results by regression analysis means [110]. Since Taylor's equation only takes into consideration the cutting speed parameter, he derived a new equation to relate other important variables to tool life as the depth of cut, feed, and nose radius. According to Barrow, even typical stress can have an impact on the life span of a tool. According to a new concept, the wear rate of a tool model can be represented as the rate of loss of volume per area, per time on the contact of the tool’s face (flank or rake face). These models necessitate thorough familiarity with the wear systems connected with the materials of the workpiece and the tool, as well as the cutting conditions [111]. Choudhury and Sirinvas [112] studied the expectation of tool wear during turning procedures, and the authors developed a reliable mechanism to find the flank wear, especially upon a turning operation by conducting a mathematical system and then evaluating the model with the test outputs. To conduct the system that was used to estimate the wear of the tool, notable factors such as wear coefficient, tool hardness, diffusion index, and rate of increase in the normal applied load concerning the wear (flank) were taken into consideration. Then, the wear standards of the tool were compared to the flank wear examination values to determine the association coefficient between them. The authors concluded that the correlation coefficient was 0.988 which means the model was valid effectively; also, the results have shown that flank model was dependable and could be used positively in case of tool wear prediction. Some analytical models for tool wear are summarized in Table 2.
Figure 9 shows that the tool gradually wears because of the wear when it undergoes cutting operations.
Gradually wear of the tool (Copyrights reserved) [114]
Machining conditions like cutting depth, turning speed, and geometry of the workpiece and tool all together affect the chip geometry which is generated to calculate the wear of a tool. Pontuale et al. [115] conducted a statistical assessment of the signals concerning tool life monitoring. The authors indicated that signal characteristics of turning operations are important since this model can predict the tool life at certain values by emitting sound signals. Wong and Hamouda used intelligent systems to determine the cutting process parameter of CNC turning. They obtained that the values are beneficial for tool life prediction [116]. Chungchoo and Saini conducted an FNN algorithm for predicting tool wear during cases of CNC turning processes. They indicate that this model predicts the highest depth of crater wear and flank wear typical width accurately [117]. The model consists of the following analytical equations:
where \(T\) refers to the tool life (min) that it needs to acquire a flank wear property of a particular dimension, \(V\) represents the cutting velocity (m min−1), \(N\) is mainly an exponent which relies on cutting terms, and \({C}_{t}\) refers to a constant factor, occasionally known as the Taylor steady, which can correspond to the cutting velocity for \(1\text{ min}\) tool life.
Related trends appear concerning the feed along with DOC; thus, the too life might be stated as [117]:
Like the tool material, the production material has a considerable impression on tool life. The hardness of the work material is considered to be the most straightforward attribute to quantify as well as correlating the tool life. The tool's life span decreases with increasing work material toughness, as one should expect. This equation has been used in several types of research to show that the cutting rate for a long tool life is linked to hardness [117]:
where BHN is the Brinell hardness number, while \(x\) is the BHN exponent.
Mannan et al. [118] developed sound and image analysis methods to monitor the cutting tool's condition. The authors showed that sound and machine analysis mechanisms are suitable for effectively examining the situation of cutting tools (semi-dull, dull, or sharp tool). They included that the CCD camera image evaluation along with microphone sound evaluation successfully distinguished between the types of cutting tools [118]. Albertelli et al. [119] established a tool life model for variables along with constant speed turning. The model was utilized to expect the tool life upon spindle speed variation SSV. The suggested formulation takes into consideration the prime cutting characteristics linked to the SSV. During the study, experimental turning tests were conducted and the collected data was used for the modeling objectives [119]. The authors pointed out that the formulation generated could be applied for predicting the life of tools at adopting SSV and constant spindle machining CSM with an estimated maximum error equal to 6% [119].
3.4 Surface Roughness Models
The surface is principally treated as the major significant feature in the field of engineering surfaces since it has a conclusive impact on the physical and mechanical behavior of machined parts. Such behavior is represented by several properties such as cleanability, fatigue strength, wear resistance, assembly tolerance, coefficient of friction, esthetics, corrosion resistance, and wear rate [120]. The quality concerning a surface is an element of efficiency within the valuation of tool efficiency machining [95, 121]. In addition, surface roughness urges one of the major constraints concerning the assortment of cutting factors and machines in planning the process [122]. Since quality demands by customers are increasing, surface roughness became none of the major important dimensions in the nowadays manufacturing sector. Other significant parameters that affect surface roughness during machining include cut depth, fluids used for cutting, feed, cutting velocity, and tool wear, and relatively small changes in one of these characteristics may lead to an important impact on the surface roughness As a consequence, modeling and quantifying the relation between such parameters and surface roughness is an important topic for researchers [123]. Thus, experimental, analytical, artificial intelligence, and empirical systems have been conducted to foresee the roughness of surfaces. Analytical and experimental models are commonly established on machining theories [123]. Boothroyd and Knight [124], in addition to Groover [125], all together contemplated the influence of nose radius and cutting-edge angles and feed on surface roughness They conducted the subsequent formula to approximate the quixotic roughness value assuming the existence of a nonzero nose radius (r) cutter. The formula is:
where \({S}_{0}\) is the feed (mm/rev or in/rev). r is the cutter nose radius (mm or in), and Ra represents the ideal arithmetic average of surface roughness (mm or in). The previous equation supposes that nose radius along with feed is the major factor that helps in determining the surface geometry [126]. Conversely, if the cutter nose radius r is equal to zero, then the subsequent equation must be used to determine the best surface roughness according to Boothroyd and Knight [124].
where beta and alpha represent the angle of the end cutting edge (ECEA) and the principal cutting-edge angle (MCEA) [124]. Grzesik used a machining-based theory approach to predict surface roughness. The author researched to figure out how tribological associations between the tool and the chip interfaces can monitor the roughness related to a surface generated during turning. Tribological behavior at the chip–tool interface was modeled using Hecky–Ilyuskin plasticity theory and friction molecular–mechanical theory. Because the shift from plowing toward micro-cutting leads to the undeformed least chip thickness, the author concluded that the difference in measured surface roughness and theoretical values was initiated by adhesion by the tool–chip interface. The author calculated the surface roughness theoretically using Branmertz's formula, and he concluded that the proposed model resulted in an efficient evaluation of surface roughness developed by turning [127].
Theoretically, the average roughness \({R}_{at}\) was calculated using the subsequent equation:
where \({r}_{\epsilon }\) symbolizes the corner radius. Otherwise, the theoretical ten-point height \({R}_{zt}\) is generally obtained from the well-known connection, namely:
It must be notable that the above equation is estimated while the accurate equation is:
When it comes to calculating surface roughness in finish turning, Brammertz's formula with the least undeformed chip thickness as a preferred model is eventually taken into account. To put it another way:
Another approach, experimental investigation was carried out by Abouelatta and Madi [128]. The authors inspected the relationship between surface roughness, vibration, and tool life. The authors used an analyzer (FTT) to measure the tool vibrations, whereas S > R was measured via a surtronic 3 + measuring apparatus. The authors pointed out that the results were good enough to predict the surface roughness characteristics as a purpose of both tool vibrations in addition to cutting parameters. The authors used B++, MATLAB, and SPSS to collect and analyze the results. The proportions of the specimen are shown in Fig. 10 [128].
Workpiece dimensions (Copyrights reserved) [128]
In another study, Dhar et al. conducted a comparison study to investigate the impact of dry machining and liquid nitrogen jet condition on the cutting tools. A better surface finish was achieved by using cryogenic cooling, as evidenced by results showing that chipping, abrasion, and built-up edge production were all reduced by cryogenic chilling [129]. Measurement of surface roughness was taken via a Taylor Hobson surtronic apparatus. Two-order models were developed: First-order model covered the cutting velocity at a scale of 110–350 m/min and the second-order model covered the cutting velocity at a scale of 80–495 m/min [130]. Ozel and Karpat researched to predict the tool wear along with surface roughness in dry hard turning procedures by applying neural networks modeling. They used cubic boron nitride (CBN) tools under various cutting conditions, and the test was done by turning AISI H-13 hardened steel. The information collected from the test work regarding measuring tool flank wear and surface roughness was utilized via a neural network model. The authors pointed out that the prediction mechanism was capable of precise tool wear and surface roughness prediction [131]. Liu et al. [39] utilized the UABB procedure to create a mathematical model that predicts surface roughness. When it comes to improving the strength of a material's surface, UABB (ultrasonic-assisted ball burnishing) is a popular choice. The typical burnishing static force is replaced by a sequence of ultrasonic vibrations and traditional burnishing in this mechanism [132]. Although it increases surface hardness, and surface roughness, and introduces higher compressive stress, this approach is effective. A mathematical model, according to the authors, would help examine and anticipate the relationship between test process factors and outcomes, as well as the impact of UABB on surface roughness. To verify that a mathematical model used to determine the surface roughness for a material is accurate, UABB experiments were carried out, which demonstrated that this technique could reduce surface roughness significantly, and the model's calculated values matched the test findings. The authors carried out that the surface roughness dropped and the amplitude increased while the feed rate decreased [39]. The link between height and feed rate in addition to roughness is characterized as follows [39]:
The long semi-axis “a” and the short semi-axis “b” regarding the surface contact could be expressed as follows [39]:
where F indicates the vertical total force; μ1 and μ2 represent the Poisson ratio of both the components added to the ball, respectively. E1 and E2 represent the Young modulus concerning the element and the ball, respectively. E* is the corresponding Young’s modulus. The penetration depth δ could be found using the following equation:
α, β, and λ are the coefficients with values that could be found using the magnitude of θ
where K1 and K′1 are the highest plus the lowest component curvatures, respectively. K2 and K′2 are the highest and lowest curvatures of ball curvatures, respectively. ω refers to the angle between K1 and K2. In this research, the model and the ball are cylindrical and spherical shapes, respectively. Therefore, K1 and K2 were, respectively, calculated as follows [39]:
Therefore,
where \({R}_{1}\) and \({R}_{2}\) are the component and the ball radii [39].
Gadelmawla et al. [133] carried out a study on surface roughness parameters. They illustrated the mathematical definitions for about 59 roughness characteristics. Roughness characteristics could be calculated in either 2D or 3D forms. The authors focused on presenting all roughness characteristics and how to calculate them as shown in Fig. 11 [133].
Definition of the arithmetic average height (Copyrights reserved) [133]
For the turning of AISI 316L stainless steel, an surface roughness model was designed by Galanis et al. [134]. The applied equation shows that the major impact acting on surface roughness was the depth of cut where surface roughness increased as the depth and feed rate increased while surface roughness dropped as cutting velocity increased. The authors concluded that the results obtained experimentally and predicted surface roughness was close to a confidence interval of 95% [134].
3.5 Chip Morphology
Chip morphology is very important in metal cutting operations since slight changes in the formation of a chip process may lead to issues related to surface finish, tool life, and workpiece accuracy, particularly in high-velocity machining conditions. Several factors like machining conditions such as stiffness and cutting tool geometry [135]. Within the framework, the investigation of chip morphology turned into a significant machinability standard. The latter gives information about the material response and stability of the cutting operation [136]. Li et al. [137] presented an investigational report on the behavior of chip morphologies under dry milling at high velocity. Examination of the various parameters concerning the chips was applied including the back surface, free surface in addition to top surface cross section. The shape and structure alterations of both back and free surfaces were resolved via SEM and optical microscope devices. During dry milling of Ti64 alloy, the microstructural analysis specified that chip morphology at a high-velocity range led to a serrated shape. Chip serration degree was more evident as the cutting speed, depth of cut, and feed increased. An important diversity in the chip microstructure including the structure of the serrated tooth and shear bands thickness at various cutting velocities was identified [135]. The authors carried out that the chip formation took place employing catastrophic thermoplastic shear by observing the shear bands via metallurgical analyzing methods. They concluded that X-ray results showed no clue of transformation in phase in the localized shear of the chips [137]. Lizzul et al. [138] also performed the ball-end milling on both additively and traditionally made Ti6Al4V alloy workpieces with an inclination angle of 15, 45, and 75°. Figure 12 shows the experimental setup and the cutter used in milling. Figure 13 shows the SEM pictures of the chips under different cutting conditions, and Fig. 14 shows SEM pictures of the surfaces that have been cut.
Setup of ball-end mills (Copyrights reserved) [138]
Secondary electron SEM images of the chips at varying cutting conditions (Copyrights reserved) [138]
Backscattered electron SEM images of the machined surfaces (Copyrights reserved) [138]
Hernandez et al. [136] developed experimental parametric connections for the geometry of chips of Ti64 alloy under dry machining. Ti64 is considered to be a difficult material when undergoing cutting operations. The authors also studied the chip microstructure and morphology. They used SOM (Stereoscopic optical microscopy) methods to notice the microstructure of the alloy. The test was carried out to assess the power of cutting characteristics on the geometry of the chip Ti64. In this manner, several machining experiments were conducted and different links of cutting characteristics (feed rate, cutting depth, and cutting velocity) were selected during the experiments. Ten specimens for each link of cutting characteristics were machined; therefore, 120 specimens were examined. Du et al. [77] also created a new analytical formula for the tool–chip–workpiece interface friction coefficient, which accounts for the true cutting tool radius rather than the simplified sharp edge. The mean friction coefficient m for high-speed Ti6Al4V machining can be determined using a three-way combination of the innovative analytical formula, FE modeling, and experimental testing. Because of this, the cutting tool has a slightly dull radius and makes only superficial contact with the workpiece during the cutting process (Fig. 15).
Formation of the machined surface. a Cutting edge is assumed sharp; b actual cutting edge with blunt radius (Copyrights reserved) [77]
The shear angle, \(\theta\), could be consequentially determined across its corresponding angle, \(\theta^{{\prime }},\) as shown in Eq. (80).
The shrinkage aspect \((\zeta )\), the segment proportion \(\left({G}_{S}\right)\), and the corresponding chip thickness \(\left({t}_{c}\right)\) could be examined using Eq. (81), respectively, and \(\gamma\) refers to the tool rake angle, taking into consideration the steady volume and the plane strain proposition.
The authors indicated that chip morphology among wide ranges of cutting speed as well as feed remained continuous. Regarding the microstructure of the chip, observation of grain deformation took place [136].
Mhamdi et al. [139] carried out investigational research to explore the chip morphology of AISI D2 hardened steel during turning. It is known that turning operations of steels that have high mechanical characteristics using cutting tools are named as hard turning which is considered a different method within the mechanical sector. During the research, the authors conducted hard turning experiments designed for this steel at various cutting requirements to grasp the chip formation mechanism in a way to gain the best cutting conditions.
The alteration of the process of chip development is correlated with the presence of shear insecurity. This uncertainty derives from a contest among thermal softening \(\partial \overline{\tau }/\partial \gamma\) along with dynamic hardening \(\partial \overline{\tau }/\partial \gamma\) concerning the machined substance. This method could be stated by rules of the substance performance that brings into consideration the feeling toward the strain hardening, the strain amount, plus the thermal lessening. The behavior of the material is thought to be isotropous plus of von Mises sort; it could be stated in the subsequent constitutive structure [139]:
where \(\tau\) refers to the shear stress, \(\gamma\) represents the shear strain, and \(\dot{\gamma }\) refers to the strain rate along with \(\text{T}\) which symbolizes the temperature. The performance is of a thermo-viscoplastic kind. A differential correlation was indicated in the plastic region and it is identified by the index " \(pl\) " [139]:
The explanation from the constitutive rule could be answered by the following equation, wherein the coefficients \({\tau }_{0},k,{\gamma }_{0},a,p\), and \(D\) are determined from certain torsion experiments.
Due to increased demands on materials that are beyond their elastic limitations, workpiece temperatures rise. The temperature rises as the strain rate increases. Consequently, the ensuing equation for energy stability predicts that thermal softening and work hardening lead to an increase in temperature [139]:
where β refers to the coefficient of heat plastic-work, ρ represents the density (kg/m3), and C refers to the particular heat (J/kg °C).
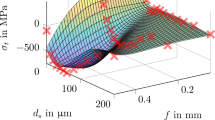
The placement of a mathematical system regarding the divergent cutting force was done via the process of investigational design. A common equivalence of the model is provided by:
wherein the estimates of \({X}_{i}\) are determined by the logarithmic transformation curve of the selected factor's values \(\left({V}_{c},f\right)\) corresponding to the subsequent equation, with \({\text{b}}_{\text{i}}\) coefficients of the formula [139].
with:
Despite all of the necessary computations, a straightforward mathematical sample concerning tangential force \({F}_{t}\) is suggested at this point as a task of the cutting velocity in addition to feed rate.
The authors concluded that increasing cutting velocity decreases the cutting forces in addition to a change in the microstructure of the material [139].
3.6 Vibration Models
Modern technology concerning metalworking of cutting operations is presented by substantial use of high-execution tool materials, indexable cutting appliances, and high velocity of operating elements. The issue of examination of the connection between factors such as tool strength, tool life cycle, surface finish, and precision machining is quiet important. The significance of this issue is growing in nowadays metalworking, identified by the establishment of higher cutting velocities, tools of new material quality requirements, and feed rate. Under any cutting status, metal cutting is accompanied by vibration [140]. The vibrational spectrum character of the system is changed only if the machining conditions were changed, and this system consists of a tool–machine–workpiece [141]. The impact of vibration characteristics on cutting process output parameters is found by a lot of effort [142]. Most researchers think that tools made of materials that do not last very long, like cutting ceramics, cemented carbide, and superhard materials, need a certain amount of vibration when it comes to vibration parameters because above this limit, the tool wear increases dramatically [143]. The increase in frequency decreases the limit amplitude of vibration, and tool life expectancy does not depend just on the vibrational action velocity to cutting velocity ratio [144], but also on the cutting force and friction coefficient [145]. It is known that vibration-supported cutting works well when cutting hard materials [146]. Few authors suggested models for optimizing tool life process characteristics and analyzing the impact of these characteristics on the wear of the tool [147]. Ghorbani et al. [141] developed an analytical and investigational study to consider the connection between vibration and tool life during the cutting process. The authors conducted a mathematical model to show the relation between vibration and tool strength. The relationship between tool parameters, tool life, and elastic vibrations of the system was examined during dynamic and static analysis in addition to cutting operations utilizing cutting tools with various clamping kinds. The authors derived the subsequent findings, depending on the experimental and theoretical investigations. They stated that the vibration effect concerning the wear of the cutting device was industrialized using a specific sample. This model took into consideration the phase shift for various forces and coordinates on the cutting tool rear and rake faces. They also added that the model is effective in predicting relative vibrations among the cutting device and specimen taking into consideration the cutting process and elastic system parameters [141].
An analytical model for the temporary cutting force of elevated velocity supersonic vibration was created by Zhang et al. [148]. When mutually the tool's round cutting edge and its round nose round are brought into concern throughout the cutting process, the micro-machining qualities are examined. For each split cross section of the cutting tool within the typical direction along the cutting side, a transient cutting force is proposed and investigated for each of the four cutting areas (plowing, shearing, tool–chip shearing, and elastic recovery). To the authors' satisfaction, the measured cutting force and model-calculated values matched up nicely. Metal cutting research on chatter vibration is critical because it reduces machining efficiency and compromises the precision of the workpiece. Numerous experiments were conducted to determine the cutting region's final chatter-free width. This property's delicate prediction varies on the cutting active forces, which change according to the cutting circumstances [149]. Analysis of chip thickness increment, cutting velocity, and penetration rate all had a role in the first formulation of the analytical dynamical cutting force expression, which was created by Tobias and Fishwick [150]. The investigational research of active cutting coefficients involves significant endeavor due to their dependency on the circumstances of machining dependence. For cutting dynamic forces during chatter vibration, Kim and Lee [149] devised an analytical model. The concept is centered on the reality that the cutting force that is produced when cutting dynamically changes. The dynamic cutting and statistical cutting coefficients, as well as the static cutting details, both, present these forces. The chatter stability study on a cutting framework with two freedom degrees was performed to confirm the developed model. The equations below were used to derive the dynamic cutting model.
where \({u}_{\text{o}}\) refers to the undeformed chip thickness, \(x\) is the modulation of the cut surface, \({x}_{\text{t}}\) represents the modulation of the work's outer surface, \(\phi\) is the dynamic shear angle, and \({\delta }_{\text{c}}\) is the instantaneous work surface slope developed by the oscillation of the tool being presented by:
where \({v}_{\text{o}}\) refers to the cutting velocity of static cutting and \(\dot{x},\dot{y}\) the vibration speeds in each direction. Supposing that the shear plane is an appropriately thin type, the instantaneous shear length \({l}_{\text{s}}\) is presented by [149]:
The forces acting on the cutting tool upon vibration are shown in Fig. 16.
Forces taking action on the cutting device upon vibration (Copyrights reserved) [149]
In static cutting, the resultant force R is equal to the vectorial amount of the shear force Fs across the shear plane plus the normal force Fn perpendicular to that plane, whereas in dynamic cutting, the resulting force R' is equal to the vectorial totality of the dynamic shear force Fs' plus the normal active force Fn'. The angle between R's route and the immediate cutting direction is \(\beta -\alpha\), since the tool rake and friction angles change during the dynamic cutting procedure. Therefore, the dynamic consequent cutting force \(R^{\prime }\) is exemplified by [149]:
where \({\tau }_{\text{s}}\) refers to the shear stress on the shear plane which is assumed to be regular over this plane, \(\beta\) is the dynamic friction angle amid the tool and chip upon dynamic cutting, \(\alpha\) refers to the dynamic tool rake angle, and \(b\) is the cut width.
The horizontal force component \({F}_{y}\) expressible over the direction of cutting in addition to the vertical force component \({F}_{x}\) normal to that are found, respectively, by the subsequent equations:
To locate the above forces, it is indispensable to predict the three attached variables \({\tau }_{\text{s}},\phi ,\) and \(\beta\) in terms of the distinct cutting parameters (cutting velocity, feed, and tool rake angle). The shear stress \({\tau }_{\text{s}}\) could be specified from the force equilibrium status:
The authors found that the coefficients for this model are easily gained from the static cutting experiments. In addition, a good agreement was seen between experimentally obtained chatter-free cut width and the theoretical prediction of the stable boundary [149]. Tuysuz and Altintas [151] developed an analytical model to measure the damping forces of the machining procedure and low-speed chatter steadiness concerning the process. Sisson et al. [152] examined the impact of cutting side radius, vibration frequency, and clearance angle on the damping procedure experimentally. They demonstrated that as chatter frequencies are increased, the damping effect is shifted to comparatively superior velocities. Wu proposed an orthogonal cutting process dampening model that took the radius of the cutting edge into account. He reasoned that the indentation force became more prominent across the tooltip of the ball-end mill as the cutting velocity decreased [153]. Moufki et al. [154] proposed an analytical sample of cutting chatter vibration. Numerous trials were organized on a CNC lathe, and a unique framework was established to examine vibration in the feed path. As a sample, a tube was employed, and device vibrations were calculated using an eddy current sensor. Chip morphologies, surface roughness, and plus vibration signals were examined for a variety of cutting circumstances to deduce the mechanism's stability limits. The authors then developed a model to monitor the vibration phenomena, combining it with a thermo-mechanical analytical model of cutting to anticipate the cutting dynamic forces and calculate the stability limits. The authors concluded that a comparison of steadiness limits and experimentally determined values yielded a reasonable agreement. The authors' mathematical model is included below. The investigational system and special tool are displayed in Fig. 17, while the typical signals concerning the chip morphology and the surface finish are shown in Fig. 18. Finally, a summary of recent analytical models concerning different parameters related to machining operations is provided in Table 3.
Experimental setup and special tool (Copyrights reserved) [154]
Typical signals concerning the chip morphology and the surface finish (Copyrights reserved) [154]
3.7 The Models for Ductile-to-Brittle Transition in Micro- to Macroscale Machining
Because of their superior qualities, such as high strength, low density, high thermal conductivity, and stable chemical properties, brittle materials are gradually being utilized in high-performance optics, semiconductors, and micro-electromechanical systems, which are undergoing significant advancements. Due to their extreme hardness and poor fracture toughness, brittle materials are classic examples of those that are challenging to cut. As a result, Yoon et al. [177] examine the impact of workpiece surface coatings by considering the ductility or hardness of the material being cut. Similar to the previous study [178], the transition depth of cut, i.e., the uncut chip thickness at which the predominant material response changed from ductile to brittle, was measured quantitatively by observing the machined surface where the crack begins to appear using optical images and cutting force signals (Fig. 19).
Cutting force variations from ductile to brittle region (Copyrights reserved) [177]
Using micro- to macroscale machining simulation, Jiang et al. [179] predicted the cutting behaviors of two-dimensional triaxially braided composites (2DTBC) by focusing on the models for macro-machining and micro-machining (Fig. 20).
Micro- to macroscale machining strategy (Copyrights reserved) [179]
With that in mind, Fig. 20 depicts the investigation of the cutting machine procedure. Micro- and macroscale observations of 2DTBC machining behavior during axial cutting have been the primary focus of research. To investigate the microscopic cutting mechanisms of 2DTBC, first 0°, 30°, 60°, and 90° models are set up. Single-fiber tow's primary material properties may be estimated using the microscale RVE model under six distinct loads [180]. Following this, the mesoscale RVE model is updated with the newly obtained material attributes. The key macroscale characteristics, including axial and transverse Young's modulus, tensile and compressive strengths, and Poisson's ratio, are calculated by performing tensile and compressive responses on 2DTBC using the mesoscale RVE model. Materials parameters are scaled up to the macro-level. Finally, cutting chip formation mechanisms, stress concentrations, damage, etc. are predicted and analyzed using macroscale simulated findings for 2DTBC machining [179]. Some related studies about the models for ductile-to-brittle transition and micro- to macroscale machining are summarized in Table 4.
3.8 Artificial Intelligent Models
Industry 4.0 aims for smart factories to have vertically and horizontally integrated production systems and to ensure that production efficiency, production quality, production time and costs reach the desired values by introducing the Internet of Things (IoT) concept into production. In this process, flexible machines that can interact with each other enable mass production in dark factories. Information is exchanged in production through smart machines and production processes are determined by themselves. During the production, data from smart sensors are collected throughout the process and stored in the cloud center so that necessary decisions can be made. In order for this process to occur, elements such as machines, storage systems and auxiliary equipment/programs must be able to share information with each other and be controlled independently [188].
In smart factories, systems in which physical mechanisms, machines or systems are controlled or monitored by computer-based algorithms are called cyber physical systems (SFS). As a result of R&D activities on SFS within the scope of Industry 4.0, the foundations of smart manufacturing methods were laid [189].
Smart manufacturing applications are given below:
-
Internet of Things (IoT)
-
Artificial intelligence applications
-
Learning robots
-
Cyber physical systems
-
Big data and analysis
-
Cloud technologies
-
Three-dimensional printers
-
Simulation–digital twin
Smart manufacturing applications; reducing resource use, performing lean production, increasing production speed and efficiency, reducing the amount of defective products, shortening the production process, responding quickly to customer demands, shortening inspection and control processes, reducing human–machine interaction, making fast and correct decisions in the production process, It has a usage area in almost every sector with its real-based intervention in the process, early detection and prevention of malfunctions, and most importantly, increasing the competitiveness of the manufacturer [190, 191]. A schematic representation of the production cycle, functional layer, level, and standards used for smart manufacturing applications is given in Fig. 21.
Schematic representation of smart manufacturing applications [192]
In recent years, smart manufacturing applications have found wide use in machining with these positive aspects. Increasing the quality in machining is possible by reducing and controlling the vibrations (chatter) that occur during production. Chatter occurring during machining in turning, milling, grinding and cutting, which are among the most commonly used methods in machining, is of great importance and directly affects the cost and product quality [193, 194].
Predicting what the surface quality will be if the production parameters determined for machining are used and determining the most appropriate machining parameters are undoubtedly among the most important applications used to reduce vibrations that may occur in production. Artificial intelligence-based algorithms are undoubtedly among the most important applications. Artificial intelligence techniques are being used with increasing momentum to reduce tool vibrations and increase quality in machining, with their high accuracy, easy application, and adaptability to every field [195, 196].
In the machining process, artificial intelligence techniques are used for the optimization and prediction of many parameters such as tool material, material and length of the workpiece, rotation speed of the workpiece, depth of cut, feed rate, cutting tool profile, and cutting tool length in order to achieve high quality at optimum cost. The most important artificial intelligence techniques used in the turning process include artificial neural networks (ANN), fuzzy logic meta-heuristic algorithms, wavelet, machine learning, hybrid systems, ANFIS, heuristic-ANN, and heuristic-fuzzy [197, 198]. In addition, in some studies, it is seen that empirical modeling techniques used to determine the relationship between dependent and independent variables are used together with popular artificial intelligence techniques. In addition, Taguchi and ANOVA method are widely used for experimental design and parameter optimization in achieving desired results [199].
4 Challenges and Opportunities
It is illustrated that analytical modeling of machining operations offers quick, precise and fixed results for surface roughness, device life, cutting forces, temperatures, and additional substantial constraints that inhibit the machining of distinct materials. In addition, these models could be directed by employing diverse machining devices and under various environmental circumstances liable for the used material to be machined. Likewise, analytical modeling supports not only the premature prediction of machining progression issues but also in finding good explanations for them before starting the procedure which leads in turn to subordinate material faults and enhancement of certain material possessions such as tool life and surface roughness. Additionally, parameter dependencies are examined briefly. For illustration, new models could be executed to boost the tool life of a material or strengthen its surface thickness of it to evade the ineffective mechanical and tribological performance of the produced material; in that way, the material will gain tougher characteristics and will become further appropriate for vital applications such as those used in the aerospace industry. Likewise, cutting force models could be employed to guesstimate the size of forces that are resourceful for each material, and cutting temperature models aid in finding the finest temperature to be used through cutting approaches for a specific substance in addition to all parameters that might affect this temperature. Tool wear models are also crucial since they assist in expanding the material's tool life by foreseeing suitable conditions of the tool and optimizing tool wear behavior; in addition, surface roughness modeling envisages the appropriate thickness of a material to be used and how to boost this thickness. Although these analytical models are valuable during machining procedures, they have some drawbacks. To begin, some models are limited to particular sorts of issues and materials. They also require utilizing certain difficult modeling theories and calculations which will need a little more duration and complex efforts by employing numerous computational and experimental devices. Besides, the reality frequently varies from the ideal circumstances, and they do not function very well if the data of a particular material is not exactly demonstrated. Similarly, certain data require scaling and certain models may probably not control irrelevant features, and a variety of modeling processes require superior computational costs and devices.
Alongside these analytical modeling procedures, there are future complicated analytical techniques that could contribute to high-level high-performance machining operations. Such models may be used in laser-assisted machining (LAM) which is very important in producing aerospace applications. This will give a better prediction of mechanical and tribological behavior concerning such applications. Also, most materials that used the LAM method require specific parameters and conditions which is an interesting topic to investigate these conditions and parameters using analytical modeling. In addition, machining processes that are coupled with microstructure evolution are considerable since these microstructures have an elevated impact on the machining process such as chip formation and surface integrity. Also conducting analytical models for vibration-assisted machining is important since the latter is used to develop tough and brittle materials. Another future aspect is introducing new modeling methods that give an exact mechanical and tribological performance of different materials. For instance, adding adhesive neural technology sensors to materials will help in collecting parameters influencing various properties of such material; also, it will supply significant data concerning the material's life durability, thickness, temperature impacts, and behavior when subjected to different conditions. These adhesive neural technology sensors could be added to the material before the machining process to predict its behavior and also after production to monitor these characteristics.
5 Conclusions and Future Scope
Due to the complex physics of machining, it is challenging to build a universally accepted model. To increase the efficiency of machining and to determine cutting parameters for the best responses, an analytical model that gives fast and realistic results is needed.
-
There are some basic conditions that users must meet to adapt their manufacturing processes to Industry 4.0. For this reason, as in the past, the importance of modeling and simulation tools is increasing in this industrial age. In this context, recent efforts have been made to develop industry-oriented predictive models such as surface roughness, tool life, cutting force, and temperature for machining processes.
-
Depending on the modeling approach, models can be characterized as quasi-experimental, physical, or empirical. Analytical, numerical, hybrid, empirical, and AI-based modeling approaches are among the most commonly used prediction models for cutting operations. Various machining responses can be predicted effectively with analytical models, including slip-line models. In addition, analytical models are proficient in developing fast and practical tools and provide important data for numerical model optimization. However, the complexity of the machining process still does not make it possible to accurately predict all industrial results.
-
FEM-based simulation models are used for the prediction of processing responses. However, models developed using FEM are not practical for industrial use due to the need for experimental work and long processing time. Therefore, analytical models are preferred. In most analytical models, temperatures at the interface of the cutting zone, tool wear, cutting forces, surface roughness, cutting energy, chip formation, and vibration can be easily calculated with specific analytical models.
-
Although modeling with the orthogonal cutting method gives results reflecting the real situation in most cases, the models obtained by the orthogonal cutting method in very special tool geometries cannot yield results at the desired accuracy levels. Moreover, the model obtained orthogonal cutting method cannot model the rake face of the tools. Another limitation of force modeling with the orthogonal cutting method is that it is specific to the workpiece–tool material pair. For this reason, the most accurate approach when modeling with orthogonal cutting is to use the developed model only meant for the tool material–the workpiece pair.
-
Thermal modeling and determination of the maximum tool–chip interface temperature have been investigated for a long time. Analytical, semi-analytical, and finite element techniques have been extensively used to calculate cutting temperatures. Air-contacting surfaces are assumed to have adiabatic boundary conditions in analytical models due to the complex physics involved. It was widely accepted by the tool–chip contact that only slip friction condition exists, which was further explored as such. Due to some such limitations, a model that predicts cutting temperatures with high accuracy has not yet been effectively presented.
-
Today, machining operations are performed under very different cutting conditions such as dry, conventional cooling, minimum quantity lubrication, cryogenic cooling, and high-pressure cooling. Therefore, there is a great need for models that provide a high precision estimation of temperatures in each environment by including these environments in the models.
-
Because of the importance of tool management, it is essential in manufacturing processes to predict tool life/tool wear using different experimental models. Analytical models have the ability to optimize the process by predicting the tool wear behavior of different materials. The oldest and most popular of these models is Taylor's model. Since this equation only considers the cutting speed parameter, a new equation to relate other important variables such as depth of cut, feed and corner radius to tool life was improved. However, since these are not the only external factors affecting tool wear/life, new high-precision models have been developed that contain many variables related to material and cutting tools.
-
Experimental, analytical, artificial intelligence and empirical systems have been made to help predict the roughness of surfaces. Analytical and experimental models are often built on machining theories. Traditional models have taken into account cutting parameters such as feed, insert radius, cutting speed, and depth of cut to estimate surface roughness. However, for a more precise estimation of surface roughness, factors such as vibration, tool wear, material adhesion, BUE should be also considered.
-
Chatter vibration is critical as it reduces machining efficiency and compromises the precision of the workpiece. Estimates of chatter stability in orthogonal turning, end milling, and 5-axis milling processes are predicted with high precision by new analytical process damping models. Relatively new and more computationally efficient models may be an alternative to currently used empirical models that require significant experimental calibration or computationally finite element modeling approaches.
Data availability
Not applicable.
References
Zawadzki, P.; Żywicki, K.: Smart Product design and production control for effective mass customization in the Industry 4.0 concept. Manag. Prod. Eng. Rev. 3, 105–112 (2016). https://doi.org/10.1515/mper-2016-0030
Iqbal, A.; Zhao, G.; Suhaimi, H.; He, N.; Hussain, G.; Zhao, W.: Readiness of subtractive and additive manufacturing and their sustainable amalgamation from the perspective of Industry 4.0: A comprehensive review. Int. J. Adv. Manuf. Technol. 111, 2475–2498 (2020). https://doi.org/10.1007/s00170-020-06287-6
Knight, W.A.; Boothroyd, G.: Fundamentals of Metal Machining and Machine Tools. CRC Press, Boca Raton (2019)
Shaw, M.C.; Cookson, J.O.: Metal Cutting Principles. Oxford University Press, New York (2005)
Rao, R.V.: Modeling and Optimization of Modern Machining Processes BT—Advanced Modeling and Optimization of Manufacturing Processes: International Research and Development (2011)
Trent, E.M.; Wright, P.K.: Metal Cutting. Butterworth-Heinemann, Oxford (2000)
Cui, Y.; Kara, S.; Chan, K.C.: Manufacturing big data ecosystem: a systematic literature review. Robot. Comput. Integr. Manuf. 62, 101861 (2020). https://doi.org/10.1016/j.rcim.2019.101861
Lu, Y.; Liu, C.; Wang, K.I.-K.; Huang, H.; Xu, X.: Digital Twin-driven smart manufacturing: connotation, reference model, applications and research issues. Robot. Comput. Integr. Manuf. 61, 101837 (2020). https://doi.org/10.1016/j.rcim.2019.101837
Al-Tarifi, M.A.; Filipovic, D.S.: On the design and fabrication of W-band stabilised-pattern dual-polarised horn antennas with DMLS and CNC. IET Microw. Antennas Propag. 11, 1930–1935 (2017)
Zębala, W.; Struzikiewicz, G.; Franczyk, E.: Monitoring of machining in the context of Industry 4.0—case study BT. In: Proceedings of the International Symposium for Production Research 2018 (2019)
Grzesik, W.: Chapter Five—Modelling and Simulation of Machining Processes and Operations (2008)
Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.; Jawahir, I.S.: Recent advances in modelling of metal machining processes. CIRP Ann. 62, 695–718 (2013). https://doi.org/10.1016/j.cirp.2013.05.006
Merchant, M.E.; Dornfeld, D.A.; Wright, P.K.: Manufacturing—its evolution and future. In: Transactions of the North American Manufacturing Research Institute of SME. pp. 211–218 (2005)
van Luttervelt, C.A.; Childs, T.H.C.; Jawahir, I.S.; Klocke, F.; Venuvinod, P.K.; Altintas, Y.; Armarego, E.; Dornfeld, D.; Grabec, I.; Leopold, J.; Lindstrom, B.; Lucca, D.; Obikawa, T.; Shirakashi; Sato, H.: Present situation and future trends in modelling of machining operations progress report of the CIRP Working Group ‘Modelling of Machining Operations.’ CIRP Ann. 47, 587–626 (1998). https://doi.org/10.1016/S0007-8506(07)63244-2
Korkmaz, M.E.; Gupta, M.K.: A state of the art on simulation and modelling methods in machining: future prospects and challenges. Arch. Comput. Methods Eng. (2022). https://doi.org/10.1007/s11831-022-09794-9
Song, Y.-A.; Park, S.: Experimental investigations into rapid prototyping of composites by novel hybrid deposition process. J. Mater. Process. Technol. 171, 35–40 (2006). https://doi.org/10.1016/j.jmatprotec.2005.06.062
Dhakar, K.; Dvivedi, A.: Influence of glycerin-air dielectric medium on near-dry EDM of titanium alloy. Int. J. Addit. Subtractive Mater. Manuf. 1, 328 (2017). https://doi.org/10.1504/ijasmm.2017.10010933
Guo, N.; Leu, M.C.: Additive manufacturing: technology, applications and research needs. Front. Mech. Eng. 8, 215–243 (2013)
Kulakowski, B.T.; Gardner, J.F.; Shearer, J.L.: Dynamic Modeling and Control of Engineering Systems. Cambridge University Press, Cambridge (2007)
Fernández-Martínez, J.L.; Fernández-Muñiz, Z.; Cernea, A.; Kloczkowski, A.: Predictive mathematical models of the short-term and long-term growth of the COVID-19 pandemic. Comput. Math. Methods Med. 2021, 5556433 (2021). https://doi.org/10.1155/2021/5556433
Jawahir, I.S.; Wang, X.: Development of hybrid predictive models and optimization techniques for machining operations. J. Mater. Process. Technol. 185, 46–59 (2007). https://doi.org/10.1016/j.jmatprotec.2006.03.133
Ćwikła, G.: Methods of manufacturing data acquisition for production management—a review. Adv. Mater. Res. 837, 618–623 (2014). https://doi.org/10.4028/www.scientific.net/AMR.837.618
Liang, Q.; Zhang, D.; Wu, W.; Zou, K.: Methods and research for multi-component cutting force sensing devices and approaches in machining. Sensors 16, 1926 (2016). https://doi.org/10.3390/s16111926
Jai Aultrin, K.S.; Dev Anand, M.: Optimization of machining parameters in AWJM process for lead tin alloy using RSM and regression analysis. Int. Rev. Mech. Eng. 9, 136–144 (2015). https://doi.org/10.15866/ireme.v9i2.4791
Gonabadi, H.; Yadav, A.; Bull, S.J.: The effect of processing parameters on the mechanical characteristics of PLA produced by a 3D FFF printer. Int. J. Adv. Manuf. Technol. 111, 695–709 (2020). https://doi.org/10.1007/s00170-020-06138-4
Kozłowski, E.; Mazurkiewicz, D.; Żabiński, T.; Prucnal, S.; Sęp, J.: Machining sensor data management for operation-level predictive model. Expert Syst. Appl. 159, 113600 (2020). https://doi.org/10.1016/j.eswa.2020.113600
Berglind, L.; Ozturk, E.: Modelling of machining processes BT—twin-control: a digital twin approach to improve machine tools lifecycle (2019)
Jawahir, I.S.; Balaji, A.K.; Rouch, K.E.; Baker, J.R.: Towards integration of hybrid models for optimized machining performance in intelligent manufacturing systems. J. Mater. Process. Technol. 139, 488–498 (2003). https://doi.org/10.1016/S0924-0136(03)00525-9
Grzesik, W.; Bartoszuk, M.; Nieslony, P.: Finite difference analysis of the thermal behaviour of coated tools in orthogonal cutting of steels. Int. J. Mach. Tools Manuf 44, 1451–1462 (2004). https://doi.org/10.1016/j.ijmachtools.2004.05.008
Pimenov, D.Y.; Bustillo, A.; Mikolajczyk, T.: Artificial intelligence for automatic prediction of required surface roughness by monitoring wear on face mill teeth. J. Intell. Manuf. 29, 1045–1061 (2018). https://doi.org/10.1007/s10845-017-1381-8
Abellan-Nebot, J.V.; Romero Subirón, F.: A review of machining monitoring systems based on artificial intelligence process models. Int. J. Adv. Manuf. Technol. 47, 237–257 (2010). https://doi.org/10.1007/s00170-009-2191-8
Kim, D.H.; Kim, T.J.Y.; Wang, X.; Kim, M.; Quan, Y.J.; Oh, J.W.; Min, S.H.; Kim, H.; Bhandari, B.; Yang, I.; Ahn, S.H.: Smart machining process using machine learning: a review and perspective on machining industry. Int. J. Precis. Eng. Manuf. Green Technol. 5, 555–568 (2018)
Lee, J.; Davari, H.; Singh, J.; Pandhare, V.: Industrial artificial intelligence for industry 4.0-based manufacturing systems. Manuf. Lett. 18, 20–23 (2018). https://doi.org/10.1016/j.mfglet.2018.09.002
Ghosh, S.; Rao, P.V.: Specific cutting energy modeling for turning nickel-based Nimonic 90 alloy under MQL condition. Int. J. Mech. Sci. 146–147, 25–38 (2018). https://doi.org/10.1016/J.IJMECSCI.2018.07.033
Sugihara, T.; Kobayashi, R.; Enomoto, T.: Direct observations of tribological behavior in cutting with textured cutting tools. Int. J. Mach. Tools Manuf 168, 103726 (2021). https://doi.org/10.1016/j.ijmachtools.2021.103726
Özel, T.: The influence of friction models on finite element simulations of machining. Int. J. Mach. Tools Manuf 46, 518–530 (2006). https://doi.org/10.1016/j.ijmachtools.2005.07.001
Ulutan, D.; Ozel, T.: Machining induced surface integrity in titanium and nickel alloys: a review. Int. J. Mach. Tools Manuf 51, 250–280 (2011). https://doi.org/10.1016/j.ijmachtools.2010.11.003
Khashaba, U.A.; El-Keran, A.A.: Drilling analysis of thin woven glass-fiber reinforced epoxy composites. J. Mater. Process. Technol. 249, 415–425 (2017). https://doi.org/10.1016/j.jmatprotec.2017.06.011
Liu, Z.; Dai, Q.; Deng, J.; Zhang, Y.; Ji, V.: Analytical modeling and experimental verification of surface roughness in the ultrasonic-assisted ball burnishing of shaft targets. Int. J. Adv. Manuf. Technol. 107, 3593–3613 (2020). https://doi.org/10.1007/s00170-020-05261-6
Kumar, R.; Bilga, P.S.; Singh, S.: Multi objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation. J. Clean. Prod. 164, 45–57 (2017). https://doi.org/10.1016/j.jclepro.2017.06.077
Türkeş, E.; Neşeli, S.: A simple approach to analyze process damping in chatter vibration. Int. J. Adv. Manuf. Technol. 70, 775–786 (2014). https://doi.org/10.1007/s00170-013-5307-0
Iqbal, A.; Zhang, H.C.; Kong, L.L.; Hussain, G.: A rule-based system for trade-off among energy consumption, tool life, and productivity in machining process. J. Intell. Manuf. 26, 1217–1232 (2015). https://doi.org/10.1007/s10845-013-0851-x
Yan, P.; Rong, Y.; Wang, G.: The effect of cutting fluids applied in metal cutting process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 230, 19–37 (2015). https://doi.org/10.1177/0954405415590993
Kumar, R.; Sahoo, A.K.; Mishra, P.C.; Das, R.K.: Influence of Al2O3 and TiO2 nanofluid on hard turning performance. Int. J. Adv. Manuf. Technol. 106, 2265–2280 (2020). https://doi.org/10.1007/s00170-019-04754-3
Shrot, A.; Bäker, M.: Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 52, 298–304 (2012). https://doi.org/10.1016/j.commatsci.2011.07.035
Heigel, J.C.; Whitenton, E.; Lane, B.; Donmez, M.A.; Madhavan, V.; Moscoso-Kingsley, W.: Infrared measurement of the temperature at the tool–chip interface while machining Ti–6Al–4V. J. Mater. Process. Technol. 243, 123–130 (2017). https://doi.org/10.1016/j.jmatprotec.2016.11.026
Zhang, X.; Yu, T.; Xu, P.; Zhao, J.: In-process stochastic tool wear identification and its application to the improved cutting force modeling of micro milling. Mech. Syst. Signal Process. 164, 108233 (2022). https://doi.org/10.1016/j.ymssp.2021.108233
Yang, J.; Ai, W.; Liu, Y.; Chen, B.: Kinematics model and trajectory interpolation algorithm for CNC turning of non-circular profiles. Precis. Eng. 54, 212–221 (2018). https://doi.org/10.1016/J.PRECISIONENG.2018.05.014
Williams, J.C.; Boyer, R.R.: Opportunities and issues in the application of titanium alloys for aerospace components. Metals 10, 705 (2020)
Şap, S.: Understanding the machinability and energy consumption of Al-based hybrid composites under sustainable conditions. Lubricants 11, 111 (2023). https://doi.org/10.3390/lubricants11030111
Pecat, O.; Brinksmeier, E.: Tool wear analyses in low frequency vibration assisted drilling of CFRP/Ti6Al4V stack material. Procedia CIRP 14, 142–147 (2014). https://doi.org/10.1016/j.procir.2014.03.050
Li, L.; Deng, X.; Zhao, J.; Zhao, F.; Sutherland, J.W.: Multi-objective optimization of tool path considering efficiency, energy-saving and carbon-emission for free-form surface milling. J. Clean. Prod. 172, 3311–3322 (2018). https://doi.org/10.1016/j.jclepro.2017.07.219
Budak, E.: Improving productivity and part quality in milling of titanium based impellers by chatter suppression and force control. CIRP Ann. Manuf. Technol. 49, 31–36 (2000). https://doi.org/10.1016/S0007-8506(07)62890-X
Altintas, Y.; Spence, A.; Tlusty, J.: End milling force algorithms for CAD systems. CIRP Ann. Manuf. Technol. 40, 31–34 (1991). https://doi.org/10.1016/S0007-8506(07)61927-1
With, T.E.M.; Model, P.: Kouji Teramoto, Kazuaki Iwata and Shinichi Hirai. Department of Computer Controlled Machinery, Faculty of Engineering, Osaka University
Spence, A.; Altintas, Y.: CAD assisted adaptive control for milling. J. Dyn. Syst. Meas. Control. Trans. ASME 113, 444–450 (1991). https://doi.org/10.1115/1.2896430
Richards, N.D.; Fussell, B.K.; Jerard, R.B.: Efficient NC machining using off-line optimized feedrates and on-line adaptive control. In: ASME International Mechanical Engineering Congress and Exposition, pp. 181–191 (2002). https://doi.org/10.1115/IMECE2002-33618
Jerard, R.B.; Fussell, B.K.; Xu, M.; Yalcin, C.: Process simulation and feedrate selection for three-axis sculptured surface machining. Int. J. Manuf. Res. 1, 136–156 (2006). https://doi.org/10.1504/IJMR.2006.011350
Vogler, M.P.; Kapoor, S.G.; DeVor, R.E.: On the modeling and analysis of machining performance in micro-endmilling, part II: cutting force prediction. J. Manuf. Sci. Eng. Trans. ASME 126, 695–705 (2004). https://doi.org/10.1115/1.1813471
Klocke, F.; Raedt, H.-W.; Hoppe, S.: 2D-FEM simulation of the orthogonal high speed cutting process. Mach. Sci. Technol. 5, 323–340 (2001). https://doi.org/10.1081/MST-100108618
Conference, C.D.; Bachrathy, D.; Stepan, G.; Stief, P.; Dantan, J.; Etienne, A.; Siadat, A.: High-speed camera measurements in the mechanical analysis of machining. Procedia CIRP 77, 155–158 (2018). https://doi.org/10.1016/j.procir.2018.08.264
Demir, E.; Mercan, C.: A physics-based single crystal plasticity model for crystal orientation and length scale dependence of machining response. Int. J. Mach. Tools Manuf 134, 25–41 (2018). https://doi.org/10.1016/j.ijmachtools.2018.06.004
Kurniawan, R.; Kiswanto, G.; Ko, T.J.: Micro-dimple pattern process and orthogonal cutting force analysis of elliptical vibration texturing. Int. J. Mach. Tools Manuf 106, 127–140 (2016). https://doi.org/10.1016/j.ijmachtools.2016.03.007
Feldmann, A.; Ganser, P.; Nolte, L.; Zysset, P.: Orthogonal cutting of cortical bone: temperature elevation and fracture toughness. Int. J. Mach. Tools Manuf 118–119, 1–11 (2017). https://doi.org/10.1016/j.ijmachtools.2017.03.009
Abukhshim, N.A.; Mativenga, P.T.; Sheikh, M.A.: Heat generation and temperature prediction in metal cutting: a review and implications for high speed machining. Int. J. Mach. Tools Manuf 46, 782–800 (2006). https://doi.org/10.1016/j.ijmachtools.2005.07.024
Siju, A.S.; Waigaonkar, S.D.: Effects of rake surface texture geometries on the performance of single-point cutting tools in hard turning of titanium alloy. J. Manuf. Process. 69, 235–252 (2021). https://doi.org/10.1016/j.jmapro.2021.07.041
Yılmaz, B.; Karabulut, Ş; Güllü, A.: Performance analysis of new external chip breaker for efficient machining of Inconel 718 and optimization of the cutting parameters. J. Manuf. Process. 32, 553–563 (2018). https://doi.org/10.1016/J.JMAPRO.2018.03.025
Chen, Y.; Li, H.; Wang, J.: Analytical modelling of cutting forces in near-orthogonal cutting of titanium alloy Ti6Al4V. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 229, 1122–1133 (2015). https://doi.org/10.1177/0954406214542967
Yang, M.; Park, H.: The prediction of cutting force in ball-end milling. Int. J. Mach. Tools Manuf 31, 45–54 (1991). https://doi.org/10.1016/0890-6955(91)90050-D
Tahmasebi, E.; Albertelli, P.; Lucchini, T.; Monno, M.; Mussi, V.: CFD and experimental analysis of the coolant flow in cryogenic milling. Int. J. Mach. Tools Manuf 140, 20–33 (2019). https://doi.org/10.1016/j.ijmachtools.2019.02.003
Moufki, A.; Devillez, A.; Dudzinski, D.; Molinari, A.: Thermomechanical modelling of oblique cutting and experimental validation. Int. J. Mach. Tools Manuf 44, 971–989 (2004). https://doi.org/10.1016/j.ijmachtools.2004.01.018
Veiga, F.; Arizmendi, M.; Jiménez, A.; Del, A.G.: Analytical thermal model of orthogonal cutting process for predicting the temperature of the cutting tool with temperature-dependent thermal conductivity. Int. J. Mech. Sci. 204, 106524 (2021). https://doi.org/10.1016/j.ijmecsci.2021.106524
Jomaa, W.; Mechri, O.; Lévesque, J.; Songmene, V.; Bocher, P.; Gakwaya, A.: Finite element simulation and analysis of serrated chip formation during high–speed machining of AA7075–T651 alloy. J. Manuf. Process. 26, 446–458 (2017). https://doi.org/10.1016/J.JMAPRO.2017.02.015
Fu, Z.; Yang, W.; Wang, X.; Leopold, J.: Analytical modelling of milling forces for helical end milling based on a predictive machining theory. Procedia CIRP 31, 258–263 (2015). https://doi.org/10.1016/j.procir.2015.03.013
Barzegar, Z.; Ozlu, E.: Analytical prediction of cutting tool temperature distribution in orthogonal cutting including third deformation zone. J. Manuf. Process. 67, 325–344 (2021). https://doi.org/10.1016/j.jmapro.2021.05.003
Paul, S.: Finite element analysis in fused deposition modeling research: a literature review. Measurement 178, 109320 (2021). https://doi.org/10.1016/j.measurement.2021.109320
Du, M.; Cheng, Z.; Wang, S.: Finite element modeling of friction at the tool-chip-workpiece interface in high speed machining of Ti6Al4V. Int. J. Mech. Sci. 163, 105100 (2019). https://doi.org/10.1016/j.ijmecsci.2019.105100
Carvalho, S.R.; Lima e Silva, S.M.M.; Machado, A.R.; Guimarães, G.: Temperature determination at the chip–tool interface using an inverse thermal model considering the tool and tool holder. J. Mater. Process. Technol. 179, 97–104 (2006). https://doi.org/10.1016/j.jmatprotec.2006.03.086
Fahad, M.; Mativenga, P.T.; Sheikh, M.A.: On the contribution of primary deformation zone-generated chip temperature to heat partition in machining. Int. J. Adv. Manuf. Technol. 68, 99–110 (2013). https://doi.org/10.1007/s00170-012-4711-1
Majumdar, P.; Jayaramachandran, R.; Ganesan, S.: Finite element analysis of temperature rise in metal cutting processes. Appl. Therm. Eng. 25, 2152–2168 (2005). https://doi.org/10.1016/j.applthermaleng.2005.01.006
Parenti, P.; Cazzani, A.; Annoni, M.: Cutting force modelling in green machining of polymer-based metallic feedstock. J. Mater. Process. Technol. 312, 117825 (2023). https://doi.org/10.1016/j.jmatprotec.2022.117825
Baohai, W.; Di, C.; Xiaodong, H.; Dinghua, Z.; Kai, T.: Cutting tool temperature prediction method using analytical model for end milling. Chin. J. Aeronaut. 29, 1788–1794 (2016). https://doi.org/10.1016/j.cja.2016.03.011
Sun, C.; Xiu, S.; Hong, Y.; Kong, X.; Lu, Y.: Prediction on residual stress with mechanical-thermal and transformation coupled in DGH. Int. J. Mech. Sci. 179, 105629 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105629
Ogedengbe, T.S.; Okediji, A.P.; Yussouf, A.A.; Aderoba, O.A.; Abiola, O.A.; Alabi, I.O.; Alonge, O.I.: The effects of heat generation on cutting tool and machined workpiece. In: Journal of Physics: Conference Series, vol. 1378 (2019). https://doi.org/10.1088/1742-6596/1378/2/022012
Wiener, J.H.: Shear-plane temperature distribution in orthogonal cutting. Trans. ASME 77, 1331–1341 (1955)
Boothroyd, G.: Fundamentals of metal machining and machine tools. http://books.google.com/books?id=ttlSAAAAMAAJ (1975)
Wright, P.K.; McCormick, S.P.; Miller, T.R.: Effect of rake face design on cutting tool temperature distributions. J. Eng. Ind. 102, 123–128 (1980). https://doi.org/10.1115/1.3183843
Trigger, K.J.; Chao, B.T.; American Society of Mechanical Engineers: An Analytical Evaluation of Metal-Cutting Temperatures. ASME, New York (1950)
Loewen, E.G.: On the analysis of cutting-tool temperatures. Trans. ASME 76, 217 (1954)
Rapier, A.C.: A theoretical investigation of the temperature distribution in the metal cutting process. Br. J. Appl. Phys. 5, 400–405 (1954). https://doi.org/10.1088/0508-3443/5/11/306
Venuvinod, P.K.; Lau, W.S.: Estimation of rake temperatures in free oblique cutting. Int. J. Mach. Tool Des. Res. 26, 1–14 (1986). https://doi.org/10.1016/0020-7357(86)90191-5
Young, H.T.; Chou, T.L.: Modelling of tool/chip interface temperature distribution in metal cutting. Int. J. Mech. Sci. 36, 931–943 (1994). https://doi.org/10.1016/0020-7403(94)90055-8
Ning, J.; Liang, S.Y.: Evaluation of an analytical model in the prediction of machining temperature of AISI 1045 steel and AISI 4340 steel. J. Manuf. Mater. Process. 2, 74 (2018). https://doi.org/10.3390/jmmp2040074
Akgün, M.; Demir, H.: Optimization and finite element modelling of tool wear in milling of Inconel 625 superalloy. J. Polytech. 24, 391–400 (2021). https://doi.org/10.2339/politeknik.706605
Yaşar, N.: Thrust force modelling and surface roughness optimization in drilling of AA-7075: FEM and GRA. J. Mech. Sci. Technol. 33, 4771–4781 (2019). https://doi.org/10.1007/s12206-019-0918-5
Zhao, W.; Yang, Q.; Mashood, A.; Ning, K.; Anshun, H.: An inverse—identification—based finite element simulation of orthogonal cutting tungsten carbide. J. Braz. Soc. Mech. Sci. Eng. 41, 1–12 (2019). https://doi.org/10.1007/s40430-019-1568-3
Banerjee, B.: The Mechanical Threshold Stress model for various tempers of AISI 4340 steel. Int. J. Solids Struct. 44, 834–859 (2007). https://doi.org/10.1016/j.ijsolstr.2006.05.022
Kargarnovin, M.H.; Faghidian, S.A.; Farjami, Y.; Farrahi, G.H.: Application of homotopy-Padé technique in limit analysis of circular plates under arbitrary rotational symmetric loading using von-Mises yield criterion. Commun. Nonlinear Sci. Numer. Simul. 15, 1080–1091 (2010). https://doi.org/10.1016/j.cnsns.2009.05.030
Zahr Viñuela, J.; Pérez-Castellanos, J.L.: The anisotropic criterion of von Mises (1928) as a yield condition for PMMCs. A calibration procedure based on numerical cell-analysis. Compos. Struct. 134, 613–632 (2015). https://doi.org/10.1016/j.compstruct.2015.08.091
Lalwani, D.I.; Mehta, N.K.; Jain, P.K.: Extension of Oxley’s predictive machining theory for Johnson and Cook flow stress model. J. Mater. Process. Technol. 209, 5305–5312 (2009). https://doi.org/10.1016/J.JMATPROTEC.2009.03.020
Tay, A.A.O.: A review of methods of calculating machining temperature. J. Mater. Process. Technol. 36, 225–257 (1993). https://doi.org/10.1016/0924-0136(93)90033-3
Agmell, M.; Bushlya, V.; M’Saoubi, R.; Gutnichenko, O.; Zaporozhets, O.; Laakso, S.V.A.; Ståhl, J.-E.: Investigation of mechanical and thermal loads in pcBN tooling during machining of Inconel 718. Int. J. Adv. Manuf. Technol. 107, 1451–1462 (2020). https://doi.org/10.1007/s00170-020-05081-8
Li, S.; Sui, J.; Ding, F.; Wu, S.; Chen, W.; Wang, C.: Optimization of milling aluminum Alloy 6061–T6 using modified Johnson-Cook model. Simul. Model. Pract. Theory 111, 102330 (2021). https://doi.org/10.1016/j.simpat.2021.102330
Attanasio, A.; Ceretti, E.; Giardini, C.: Analytical models for tool wear prediction during AISI 1045 turning operations. Procedia CIRP 8, 218–223 (2013). https://doi.org/10.1016/j.procir.2013.06.092
Aslantas, K.; Ucun, İ; Çicek, A.: Tool life and wear mechanism of coated and uncoated Al2O3/TiCN mixed ceramic tools in turning hardened alloy steel. Wear 274–275, 442–451 (2012). https://doi.org/10.1016/j.wear.2011.11.010
Manoj Kumar, B.V.; Kumar, J.R.; Basu, B.: Crater wear mechanisms of TiCN-Ni-WC cermets during dry machining. Int. J. Refract. Met. Hard Mater. 25, 392–399 (2007). https://doi.org/10.1016/j.ijrmhm.2006.12.001
Koren, Y.: Flank wear model of cutting tools using control theory. J. Manuf. Sci. Eng. Trans. ASME 100, 103–109 (1978). https://doi.org/10.1115/1.3439336
Asiltürk, İ; Kuntoğlu, M.; Binali, R.; Akkuş, H.; Salur, E.: A Comprehensive analysis of surface roughness, vibration, and acoustic emissions based on machine learning during hard turning of AISI 4140 steel. Metals 13, 437 (2023). https://doi.org/10.3390/met13020437
Barrow, G.: Tool-life equations and machining economics. In: Proceedings of the Twelfth International Machine Tool Design and Research Conference, pp. 481–493 (1972). https://doi.org/10.1007/978-1-349-01397-5_59
Kiang, T.S.; Barrow, G.: Determination of tool-life equations by step turning test. In: Proceedings of the Twelfth International Machine Tool Design and Research Conference, pp. 379–385 (1972). https://doi.org/10.1007/978-1-349-01397-5_48
Yellowley, I.; Barrow, G.: The stress-temperature method of assessing tool life. In: Proceedings of the Fourteenth International Machine Tool Design and Research Conference, pp. 733–740 (1974). https://doi.org/10.1007/978-1-349-01921-2_94
Choudhury, S.K.; Srinivas, P.: Tool wear prediction in turning. J. Mater. Process. Technol. 153–154, 276–280 (2004). https://doi.org/10.1016/j.jmatprotec.2004.04.296
Luo, Y.: Parametric tool wear estimation solution of HSC appropriate machining. Int. J. Adv. Manuf. Technol. 23, 546–552 (2004). https://doi.org/10.1007/s00170-003-1691-1
Olsson, M.; Bushlya, V.; Lenrick, F.; Ståhl, J.-E.: Evaluation of tool wear mechanisms and tool performance in machining single-phase tungsten. Int. J. Refract. Met. Hard Mater. 94, 105379 (2021). https://doi.org/10.1016/j.ijrmhm.2020.105379
Pontuale, G.; Farrelly, P.A.; Petri, A.; Pitolli, L.: A statistical analysis of acoustic emission signals for tool condition monitoring (TCM). Acoust. Res. Lett. Online 4, 13–18 (2002). https://doi.org/10.1121/1.1532370
Wong, S.V.; Hamouda, A.M.S.: Machinability data representation with artificial neural network. J. Mater. Process. Technol. 138, 538–544 (2003). https://doi.org/10.1016/S0924-0136(03)00143-2
Chungchoo, C.; Saini, D.: On-line tool wear estimation in CNC turning operations using fuzzy neural network model. Int. J. Mach. Tools Manuf 42, 29–40 (2002). https://doi.org/10.1016/S0890-6955(01)00096-7
Mannan, M.A.; Kassim, A.A.; Jing, M.: Application of image and sound analysis techniques to monitor the condition of cutting tools. Pattern Recognit. Lett. 21, 969–979 (2000)
Albertelli, P.; Mussi, V.; Monno, M.: Development of generalized tool life model for constant and variable speed turning. Int. J. Adv. Manuf. Technol. (2021). https://doi.org/10.1007/s00170-021-08017-y
Demirpolat, H.; Binali, R.; Patange, A.D.; Pardeshi, S.S.; Gnanasekaran, S.: Comparison of tool wear, surface roughness, cutting forces, tool tip temperature, and chip shape during sustainable turning of bearing steel. Materials 16, 4408 (2023). https://doi.org/10.3390/ma16124408
Yaşar, N.; Günay, M.: Experimental investigation on novel drilling strategy of CFRP laminates using variable feed rate. J. Brazilian Soc. Mech. Sci. Eng. 41, 150 (2019). https://doi.org/10.1007/s40430-019-1658-2
Yang, K.; Jeang, A.: Statistical surface roughness checking procedure based on a cutting tool wear model. J. Manuf. Syst. 13, 1–8 (1994). https://doi.org/10.1016/0278-6125(94)90012-4
Kant, G.; Sangwan, K.S.: Predictive modelling and optimization of machining parameters to minimize surface roughness using artificial neural network coupled with genetic algorithm. Procedia CIRP 31, 453–458 (2015). https://doi.org/10.1016/j.procir.2015.03.043
Boothroyd, G.: Fundamentals of Metal Machining and Machine Tools. CRC Press, Boca Raton (1988)
Groover, M.P.: Fundamentals of Modern Manufacturing: Materials, Processes, and Systems, 7th edn. Wiley, Hoboken (2019)
Binali, R.; Demirpolat, H.; Kuntoğlu, M.; Salur, E.: Different aspects of machinability in turning of AISI 304 stainless steel: a sustainable approach with MQL technology. Metals 13, 1088 (2023). https://doi.org/10.3390/met13061088
Grzeski, W.: A revised model for predicting surface roughness in turning. Wear 194, 143–148 (1996)
Abouelatta, O.B.; Mádl, J.: Surface roughness prediction based on cutting parameters and tool vibrations in turning operations. J. Mater. Process. Technol. 118, 269–277 (2001). https://doi.org/10.1016/S0924-0136(01)00959-1
Dhar, N.R.; Paul, S.; Chattopadhyay, A.B.: The influence of cryogenic cooling on tool wear, dimensional accuracy and surface finish in turning AISI 1040 and E4340C steels. Wear 249, 932–942 (2001). https://doi.org/10.1016/S0043-1648(01)00825-0
Baradie, M.A.E.: Surface roughness model for turning grey cast iron (154 BHN). Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 207, 43–54 (1993). https://doi.org/10.1243/PIME_PROC_1993_207_060_02
Tuğrul, Ö.; Karpat, Y.: Prediction of surface roughness and tool wear in finish dry hard turning using back propagation neural networks prediction of surface roughness and tool wear in finish dry hard turning using back propagation neural networks. In: 17th International Conference on Production Research, Blacksburg, Virginia, pp. 1–10 (2003)
Teimouri, R.; Amini, S.: Analytical modeling of ultrasonic burnishing process: Evaluation of active forces. Measurement 131, 654–663 (2019). https://doi.org/10.1016/j.measurement.2018.09.023
Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H.: Roughness parameters. J. Mater. Process. Technol. 123, 133–145 (2002). https://doi.org/10.1016/S0924-0136(02)00060-2
Galanis, N.I.; Manolakos, D.E.: Surface roughness prediction in turning of femoral head. Int. J. Adv. Manuf. Technol. 51, 79–86 (2010). https://doi.org/10.1007/s00170-010-2616-4
Li, F.L.; Xia, W.; Zhou, Z.Y.; Zhao, J.; Tang, Z.Q.: Analytical prediction and experimental verification of surface roughness during the burnishing process. Int. J. Mach. Tools Manuf 62, 67–75 (2012). https://doi.org/10.1016/j.ijmachtools.2012.06.001
Hernández, Y.S.; Vilches, F.J.T.; Gamboa, C.B.; Hurtado, L.S.: Experimental parametric relationships for chip geometry in dry machining of the Ti6Al4V alloy. Materials 10, 1260 (2018). https://doi.org/10.3390/ma11071260
Li, A.; Zhao, J.; Zhou, Y.; Chen, X.; Wang, D.: Experimental investigation on chip morphologies in high-speed dry milling of titanium alloy Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 62, 933–942 (2012). https://doi.org/10.1007/s00170-011-3854-9
Lizzul, L.; Sorgato, M.; Bertolini, R.; Ghiotti, A.; Bruschi, S.: Ball end milling machinability of additively and conventionally manufactured Ti6Al4V tilted surfaces. J. Manuf. Process. 72, 350–360 (2021). https://doi.org/10.1016/j.jmapro.2021.10.037
Mhamdi, M.B.; Salem, S.B.; Boujelbene, M.; Bayraktar, E.: Experimental study of the chip morphology in turning hardened AISI D2 steel. J. Mech. Sci. Technol. 27, 3451–3461 (2013). https://doi.org/10.1007/s12206-013-0869-1
Pehlivan, F.: Improvement of machining vibrational stabilization for a CNC lathe in turning of 420 hardened steels by MQL and cryogenic method. J. Mater. Mechatron. A 3, 290 (2022). https://doi.org/10.55546/jmm.1182481
Ghorbani, S.; Kopilov, V.V.; Polushin, N.I.; Rogov, V.A.: Experimental and analytical research on relationship between tool life and vibration in cutting process. Arch. Civ. Mech. Eng. 18, 844–862 (2018). https://doi.org/10.1016/j.acme.2018.01.007
Xiao, X.; Zheng, K.; Liao, W.; Meng, H.: Study on cutting force model in ultrasonic vibration assisted side grinding of zirconia ceramics. Int. J. Mach. Tools Manuf 104, 58–67 (2016). https://doi.org/10.1016/J.IJMACHTOOLS.2016.01.004
Prasad, B.S.; Babu, M.P.: Correlation between vibration amplitude and tool wear in turning: numerical and experimental analysis. Eng. Sci. Technol. an Int. J. 20, 197–211 (2017). https://doi.org/10.1016/J.JESTCH.2016.06.011
Tarng, Y.S.; Young, H.T.; Lee, B.Y.: An analytical model of chatter vibration in metal cutting. Int. J. Mach. Tools Manuf 34, 183–197 (1994). https://doi.org/10.1016/0890-6955(94)90100-7
Kayhan, M.; Budak, E.: An experimental investigation of chatter effects on tool life. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 223, 1455–1463 (2009). https://doi.org/10.1243/09544054JEM1506
Qin, N.; Pei, Z.J.; Treadwell, C.; Guo, D.M.: Physics-based predictive cutting force model in ultrasonic-vibration- assisted grinding for titanium drilling. J. Manuf. Sci. Eng. Trans. ASME. 131, 0410111–0410119 (2009). https://doi.org/10.1115/1.3159050
Thakre, A.A.; Soni, S.: Modeling of burr size in drilling of aluminum silicon carbide composites using response surface methodology. Eng. Sci. Technol. an Int. J. 19, 1199–1205 (2016). https://doi.org/10.1016/J.JESTCH.2016.02.007
Zhang, X.; Sui, H.; Zhang, D.; Jiang, X.: An analytical transient cutting force model of high-speed ultrasonic vibration cutting. Int. J. Adv. Manuf. Technol. 95, 3929–3941 (2018). https://doi.org/10.1007/s00170-017-1499-z
Kim, J.S.; Lee, B.H.: An analytical model of dynamic cutting forces in chatter vibration. Int. J. Mach. Tools Manuf 31, 371–381 (1991). https://doi.org/10.1016/0890-6955(91)90082-E
Tobias, S.A.; Fishwick, W.: The vibrations of radial-drilling machines under test and working conditions. Proc. Inst. Mech. Eng. 170, 232–264 (1956). https://doi.org/10.1243/PIME_PROC_1956_170_028_02
Tuysuz, O.; Altintas, Y.: Analytical modeling of process damping in machining. J. Manuf. Sci. Eng. Trans. ASME. 141, 061006 (2019). https://doi.org/10.1115/1.4043310
Sisson, T.R.; Kegg, R.L.: An explanation of low-speed chatter effects. J. Eng. Ind. 91, 951–958 (1969). https://doi.org/10.1115/1.3591778
Wu, D.W.: Application of a comprehensive dynamic cutting force model to orthogonal wave-generating processes. Int. J. Mech. Sci. 30, 581–600 (1988). https://doi.org/10.1016/0020-7403(88)90101-4
Moufki, A.; Devillez, A.; Segreti, M.; Dudzinski, D.: A semi-analytical model of non-linear vibrations in orthogonal cutting and experimental validation. Int. J. Mach. Tools Manuf 46, 436–449 (2006). https://doi.org/10.1016/j.ijmachtools.2005.04.017
Guo, J.; Li, W.; Wang, S.; Ming, L.: Dynamics analytical model of cutting force in metal cutting processing. Adv. Mater. Res. 308–310, 1211–1214 (2011). https://doi.org/10.4028/www.scientific.net/AMR.308-310.1211
Matsumura, T.; Tamura, S.: Cutting force model in milling with cutter runout. Procedia CIRP 58, 566–571 (2017). https://doi.org/10.1016/j.procir.2017.03.268
Zheng, F.; Han, X.; Hua, L.; Tan, R.; Zhang, W.: A semi-analytical model for cutting force prediction in face-milling of spiral bevel gears. Mech. Mach. Theory 156, 104165 (2021). https://doi.org/10.1016/j.mechmachtheory.2020.104165
Liu, X.; Wang, W.; Jiang, R.; Xiong, Y.; Lin, K.; Li, J.; Shan, C.: Analytical model of cutting force in axial ultrasonic vibration-assisted milling in-situ TiB2/7050Al PRMMCs. Chin. J. Aeronaut. 34, 160–173 (2021). https://doi.org/10.1016/j.cja.2020.08.009
Wang, H.; Qin, X.; Ren, C.; Wang, Q.: Prediction of cutting forces in helical milling process. Int. J. Adv. Manuf. Technol. 58, 849–859 (2012). https://doi.org/10.1007/s00170-011-3435-y
Moufki, A.; Dudzinski, D.; Le Coz, G.: Prediction of cutting forces from an analytical model of oblique cutting, application to peripheral milling of Ti-6Al-4V alloy. Int. J. Adv. Manuf. Technol. 81, 615–626 (2015). https://doi.org/10.1007/s00170-015-7018-1
Shan, C.; Zhang, X.; Shen, B.; Zhang, D.: An improved analytical model of cutting temperature in orthogonal cutting of Ti6Al4V. Chin. J. Aeronaut. 32, 759–769 (2019). https://doi.org/10.1016/j.cja.2018.12.001
Huang, K.; Yang, W.: Analytical model of temperature field in workpiece machined surface layer in orthogonal cutting. J. Mater. Process. Technol. 229, 375–389 (2016). https://doi.org/10.1016/j.jmatprotec.2015.07.008
Zhang, S.; Liu, Z.: An analytical model for transient temperature distributions in coated carbide cutting tools. Int. Commun. Heat Mass Transf. 35, 1311–1315 (2008). https://doi.org/10.1016/j.icheatmasstransfer.2008.08.001
Abouridouane, M.; Klocke, F.; Döbbeler, B.: Analytical temperature prediction for cutting steel. CIRP Ann. Manuf. Technol. 65, 77–80 (2016). https://doi.org/10.1016/j.cirp.2016.04.039
Kara, F.; Aslantaş, K.; Çiçek, A.: Prediction of cutting temperature in orthogonal machining of AISI 316L using artificial neural network. Appl. Soft Comput. 38, 64–74 (2016). https://doi.org/10.1016/j.asoc.2015.09.034
Radulescu, R.; Kapoor, S.G.: An analytical model for prediction of tool temperature fields during continuous and interrupted cutting. J. Manuf. Sci. Eng. Trans. ASME. 116, 135–143 (1994). https://doi.org/10.1115/1.2901923
Usui, E.; Shirakashi, T.; Kitagawa, T.: Analytical prediction of cutting tool wear. Wear 100, 129–151 (1984). https://doi.org/10.1016/0043-1648(84)90010-3
Zhu, D.; Zhang, X.; Ding, H.: Tool wear characteristics in machining of nickel-based superalloys. Int. J. Mach. Tools Manuf 64, 60–77 (2013). https://doi.org/10.1016/J.IJMACHTOOLS.2012.08.001
Van Herreweghe, M.; Verbeke, M.; Meert, W.; Jacobs, T.: A machine learning-based approach for predicting tool wear in industrial milling processes. Commun. Comput. Inf. Sci. 1168, 414–425 (2020). https://doi.org/10.1007/978-3-030-43887-6_34
Sahraoui, Z.; Mehdi, K.; Ben-Jaber, M.: Analytical and experimental stability analysis of AU4G1 thin-walled tubular workpieces in turning process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 234, 1007–1018 (2020). https://doi.org/10.1177/0954405419896115
Altmeppen, J.; Sommerfeld, H.; Koch, C.; Staudacher, S.: An analytical approach to estimate the effect of surface roughness on particle rebound. J. Glob. Power Propuls. Soc. 4, 27–37 (2020). https://doi.org/10.33737/jgpps/118624
Daymi, A.; Boujelbene, M.; Salem; Ben, S.; Hadj Sassi, B.; Torbaty, S.; Sassi, B.H.: Effect of the cutting speed on the chip morphology and the cutting forces. Manuf. Process. Eng. Mater. 781, 77–83 (2009)
Gao, Y.; Sun, R.; Chen, Y.; Leopold, J.: Analysis of chip morphology and surface topography in modulation assisted machining. Int. J. Mech. Sci. 111–112, 88–100 (2016). https://doi.org/10.1016/j.ijmecsci.2016.03.025
Parida, A.K.; Maity, K.: Experimental investigation on tool life and chip morphology in hot machining of Monel-400. Eng. Sci. Technol. Int. J. 21, 371–379 (2018). https://doi.org/10.1016/J.JESTCH.2018.04.003
Salvatore, F.; Mabrouki, T.; Hamdi, H.: Analytical model for chip formation in case of orthogonal machining process. In: AIP Conference Proceedings, vol. 1315, pp. 1621–1626 (2010). https://doi.org/10.1063/1.3552424
Fu, Z.; Zhang, X.; Wang, X.; Yang, W.: Analytical modeling of chatter vibration in orthogonal cutting using a predictive force model. Int. J. Mech. Sci. 88, 145–153 (2014). https://doi.org/10.1016/j.ijmecsci.2014.08.005
Yoon, H.-S.; Kwon, S.B.; Kim, J.-H.; Ahn, S.-H.; Min, S.: Effects of surface coating materials on cutting forces and ductile-to-brittle transition in orthogonal cutting of monocrystalline sapphire. J. Manuf. Process. 84, 375–382 (2022). https://doi.org/10.1016/j.jmapro.2022.09.046
Kwon, S.B.; Nagaraj, A.; Yoon, H.-S.; Min, S.: Study of material removal behavior on R-plane of sapphire during ultra-precision machining based on modified slip-fracture model. Nanotechnol. Precis. Eng. 3, 141–155 (2020). https://doi.org/10.1016/j.npe.2020.07.001
Jiang, H.; Ren, Y.; Liu, Z.: Micro- and macro-scale simulation for axial cutting machining behaviors of 2D tri-axially braided composites. Int. J. Mech. Sci. 156, 1–13 (2019). https://doi.org/10.1016/j.ijmecsci.2019.03.028
Jiang, H.; Ren, Y.; Zhang, S.; Liu, Z.; Nie, L.: Multi-scale finite element analysis for tension and ballistic penetration damage characterizations of 2D triaxially braided composite. J. Mater. Sci. 53, 10071–10094 (2018). https://doi.org/10.1007/s10853-018-2248-x
Wang, H.; Pei, Z.J.; Cong, W.: A mechanistic cutting force model based on ductile and brittle fracture material removal modes for edge surface grinding of CFRP composites using rotary ultrasonic machining. Int. J. Mech. Sci. 176, 105551 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105551
Lai, M.; Zhang, X.; Fang, F.; Bi, M.: Effects of crystallographic orientation and negative rake angle on the brittle-ductile transition and subsurface deformation in machining of monocrystalline germanium. Precis. Eng. 56, 164–171 (2019). https://doi.org/10.1016/j.precisioneng.2018.11.011
Yoon, H.-S.; Lee, S.; Min, S.: Investigation of ductile-brittle transition in machining of yttrium-stabilized zirconia (YSZ). Procedia Manuf. 26, 446–453 (2018). https://doi.org/10.1016/j.promfg.2018.07.052
Huang, W.; Yu, D.; Zhang, X.; Zhang, M.; Chen, D.: Ductile-regime machining model for ultrasonic elliptical vibration cutting of brittle materials. J. Manuf. Process. 36, 68–76 (2018). https://doi.org/10.1016/j.jmapro.2018.09.029
Wang, B.; Liu, Z.; Su, G.; Song, Q.; Ai, X.: Investigations of critical cutting speed and ductile-to-brittle transition mechanism for workpiece material in ultra-high speed machining. Int. J. Mech. Sci. 104, 44–59 (2015). https://doi.org/10.1016/j.ijmecsci.2015.10.004
Arif, M.; Xinquan, Z.; Rahman, M.; Kumar, S.: A predictive model of the critical undeformed chip thickness for ductile–brittle transition in nano-machining of brittle materials. Int. J. Mach. Tools Manuf 64, 114–122 (2013). https://doi.org/10.1016/j.ijmachtools.2012.08.005
Venkatachalam, S.; Li, X.; Liang, S.Y.: Predictive modeling of transition undeformed chip thickness in ductile-regime micro-machining of single crystal brittle materials. J. Mater. Process. Technol. 209, 3306–3319 (2009). https://doi.org/10.1016/j.jmatprotec.2008.07.036
Vogel-Heuser, B.; Hess, D.: Guest editorial Industry 4.0–prerequisites and visions. IEEE Trans. Autom. Sci. Eng. 13, 411–413 (2016). https://doi.org/10.1109/TASE.2016.2523639
Guo, K.; Lu, Y.; Gao, H.; Cao, R.: Artificial intelligence-based semantic internet of things in a user-centric smart city. Sensors 18, 1341 (2018). https://doi.org/10.3390/s18051341
Yang, H.; Kumara, S.; Bukkapatnam, S.T.S.; Tsung, F.: The internet of things for smart manufacturing: a review. IISE Trans. 51, 1190–1216 (2019). https://doi.org/10.1080/24725854.2018.1555383
du Preez, A.; Oosthuizen, G.A.: Machine learning in cutting processes as enabler for smart sustainable manufacturing. Procedia Manuf. 33, 810–817 (2019). https://doi.org/10.1016/j.promfg.2019.04.102
Noor-A-Rahim, M.; John, J.; Firyaguna, F.; Sherazi, H.H.R.; Kushch, S.; Vijayan, A.; O’Connell, E.; Pesch, D.; O’Flynn, B.; O’Brien, W.; Hayes, M.; Armstrong, E.: Wireless communications for smart manufacturing and industrial IoT: existing technologies, 5G and beyond. Sensors 23, 73 (2022). https://doi.org/10.3390/s23010073
Turkes, E.; Orak, S.; Neseli, S.; Yaldiz, S.: A new process damping model for chatter vibration. Measurement 44, 1342–1348 (2011). https://doi.org/10.1016/j.measurement.2011.04.004
Turkes, E.; Orak, S.; Neseli, S.; Yaldiz, S.: Linear analysis of chatter vibration and stability for orthogonal cutting in turning. Int. J. Refract. Met. Hard Mater. 29, 163–169 (2011). https://doi.org/10.1016/j.ijrmhm.2010.10.002
Mirifar, S.; Kadivar, M.; Azarhoushang, B.: First steps through intelligent grinding using machine learning via integrated acoustic emission sensors. J. Manuf. Mater. Process. 4(2), 35 (2020)
Alajmi, M.S.; Almeshal, A.M.: Modeling of cutting force in the turning of AISI 4340 using gaussian process regression algorithm. Appl. Sci. 11(9), 4055 (2021)
Colantonio, L.; Equeter, L.; Dehombreux, P.; Ducobu, F.: A systematic literature review of cutting tool wear monitoring in turning by using artificial intelligence techniques. Machines 9, 351 (2021). https://doi.org/10.3390/machines9120351
Jaisingh Sheoran, A.; Kumar, H.: Fused Deposition modeling process parameters optimization and effect on mechanical properties and part quality: review and reflection on present research. Mater. Today Proc. 21, 1659–1672 (2020). https://doi.org/10.1016/j.matpr.2019.11.296
Korkmaz, M.E.; Günay, M.: Experimental and statistical analysis on machinability of Nimonic80A superalloy with PVD coated carbide. Sigma J. Eng. Nat. Sci. 36, 1141–1152 (2018)
Funding
The authors would like to thank to Karabük University Project Coordinateship Unit with a project number KBÜBAP-22-ABP-010. The research leading to these results has received funding from the Norwegian Financial Mechanism 2014–2021, Project Contract No 2020/37/K/ST8/02795. The authors also acknowledge the “Polısh Natıonal Agency For Academıc Exchange (NAWA) No. PPN/ULM/2020/1/00121” for financial support.
Author information
Authors and Affiliations
Contributions
All authors contribute equally.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Ethical approval and consent to participate
Not applicable.
Consent for publication
The consent to submit this paper has been received explicitly from all co-authors.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Korkmaz, M.E., Gupta, M.K., Sarikaya, M. et al. Analytical Modeling Methods in Machining: A State of the Art on Application, Recent Challenges, and Future Trends. Arab J Sci Eng (2024). https://doi.org/10.1007/s13369-024-09163-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13369-024-09163-7