1 Introduction

Vehicles are indispensable elements of human life. While the first vehicles produced were generally used to carry people and goods, many types produced for different purposes have emerged over time. Considering today's variety of vehicles, it is possible to classify the concept of vehicles as road vehicles used to transport people and goods in daily life and off-road vehicles used for special purposes [1]. One of the most important examples of off-road vehicles is undoubtedly the main battle tanks used in the military field. Main battle tanks are military vehicles with tracks that allow easy movement on the terrain and a weapon system that provides high firepower [2,3,4,5,6,7,8].

There are dynamics that enable the movement of the main battle tank weapon system in the horizontal and vertical axis. The azimuth dynamics provide the movement in the horizontal axis, and the elevation dynamics provide the movement in the vertical axis [6, 7, 9]. In both azimuth and elevation dynamics, the drive is provided by an electric motor and transmitted to the barrel [5, 7, 9]. It is often seen that the barrel usually consists of two or more parts connected [3,4,5,6,7,8]. The aim is to reduce the risk of damage by better distributing the stress and tension occurring in the barrel. If the parts of the barrel do not vibrate uniformly, the barrel is subjected to additional stress and tension, and it becomes difficult to precisely direct the tip of the barrel to the target. For this reason, it is desired to reach a harmony between these two parts, which yields similar vibration characteristics.

A system is defined as a set of components that are brought together to fulfill a specific purpose. System dynamics is the branch of science that involves obtaining mathematical models of these systems in accordance with their nature and generally observing system responses through simulation studies [10]. Although there are systems consisting of only one of the mechanical, electrical, thermal, pneumatic, or hydraulic components, hybrid systems with more than one component are more common today in parallel with technology development [11,12,13,14,15,16,17,18].

Lagrange method, Newton's second law, D’Alembert’s principle, and Hamilton's principle are frequently used to obtain mathematical models of systems [10,11,12, 19]. In addition to these methods, there are also graphical methods for obtaining mathematical models of systems. These methods are the linear graph method and bond graph method [11, 12, 20].

The linear graph method was first introduced by Leonhard Euler in 1736 [21]. The aim of this method is to determine the common points of the components regardless of their type and to obtain the mathematical model of the system by graphical methods. There are many studies in which many systems such as milling machine [22], planar four-bar mechanism and compound pendulum [23], 2-link manipulator, planar slider-crank mechanism, 3 degrees of freedom planar parallel robot [24], flexible plates [25], robotic bevel-gear train [26], flexible multibody systems [27], mass–spring–damper system and two masses with two absorbers [28], the spinning disk [29], which are composed of mechanical components; electrical network [23], composed of electrical components; engine performance [30], double capacity tank level control system [31], which consist of thermal components; four-wheel skid-steer mobile robot [32], a lead-screw-nut mechanism [33], piezoelectric transducers [34], positioning system [35], conveying system [36], condensator speaker [37], industrial paint pumping system [38], auto-leveling system for vehicle-borne platform [39], electrically driven elevator [21], consisting of electrical and mechanical components; electro-hydraulic servo manipulator [40], consisting of electrical and hydraulic components; U-tube system [41], consisting of thermal and hydraulic components; flow-controlled ramp with a mechanical load [42], consisting of hydraulic and mechanical components; electromechanical battery composed of electrical and chemical components [43].

In this study, the elevation dynamics of the weapon system of the main battle tank were modeled, and vibration characteristics of the parts of the barrel were observed. Elevation dynamics consist of many electrical and mechanical components with different functions. In order to benefit from the similarities between these components, the linear graphic method was used as the modeling method. Each step for the linear graph method is shown in Fig. 1. Obtained state equations are solved by simulation studies performed in MATLAB/Simulink environment. The position, velocity, and acceleration graphs of the breech section and muzzle section, as well as the maximum and RMS position velocity and acceleration values, were compared.

Fig. 1
figure 1

The steps of the linear graph method

Full size image

2 Material and Method

This study aims to observe the vibration characteristics of the barrel of the weapon system of the main battle tank in the vertical axis. A physical model representing the physical properties and behavior of the system was first created, and how the system works was explained. Afterward, the mathematical model that would define the mathematical properties and behaviors of the system was obtained by the linear graph method. A simulation process was finally performed to observe the behavior of the system. The material method scheme is presented in Fig. 2.

Fig. 2
figure 2

Material and method scheme

Full size image

2.1 Physical Model

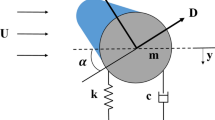
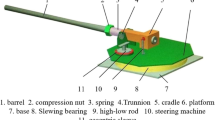
The task of the elevation dynamic, whose schematic diagram is given in Fig. 3a, is to ensure that the weapon system moves on the vertical axis. Figure 3b shows three main parts: the electric motor, the driver, and the barrel (breech section and muzzle section). The propulsion is provided by an electric motor. The resulting torque is transferred to the driver. The driver and pinion are rigidly connected, and their speeds are the same. The movement is transmitted from the driver to the breech section by a pinion rack mechanism. The breech section and muzzle section are hinged to each other [7]. The reaction forces between the components are neglected.

Fig. 3
figure 3

a schematic diagram b components of elevation dynamics [4, 7, 44]

Full size image

2.2 Mathematical Model

Following the steps of the linear graph method in Fig. 1, how the mathematical model of the system is obtained is explained below step by step.

2.2.1 Identification of System Components and Types

In the linear graphics method, the components are classified independently of their type. Based on the classification in Fig. 4, variable definitions for components of the elevation dynamic are made and presented in Table 1.

Fig. 4
figure 4

Classification of components [11]

Full size image
Table 1 Variable definition [11]
Full size table

In the system seen in Fig. 3b, the source element is the motor voltage. This source provides energy to the system. Motor resistance, motor inductance, driver inertia moment, driver viscous friction, breech section inertia moment, muzzle section inertia moment, viscous friction, and spring, which are determined as passive components, behave in the direction of this energy. In addition, there are two-port elements that allow the transition from electrical system to rotational mechanics, from rotational mechanics to translational mechanics, and from translational mechanics to rotational mechanics. These elements are, respectively, the electromechanical conversion element, the pinion rack mechanism and mechanical conversion element (Table 2).

Table 2 Components and types
Full size table

2.2.2 Drawing the Linear Graph, Normal Tree, and Tree Links of the System

Node points were created by determining the places with the across variable. The linear graph is obtained in Fig. 5 by placing the branches of the one-port and two-port elements between the relevant nodes.

Fig. 5
figure 5

Linear graph

Full size image

In order to understand whether there is a contradiction in the system model and to prove that the system is modeled correctly, normal tree and tree links need to be drawn. The main idea is to prevent a closed loop form for drawing the normal tree. Based on this idea, the normal tree (Fig. 6a) is derived by involving active-type A components, a maximum number of passive-type A components, a single branch of two-port components, a maximum number of passive-type D components, and a minimum number of passive-type T components. The branches of the linear graph that do not enter the normal tree form the tree links (Fig. 6b).

Fig. 6
figure 6

a Normal tree b tree links

Full size image

2.2.3 Identification of State, Primary and Secondary Variables

The state variables are the across variables of the passive type A components in the normal tree and the through variables of the passive-type T components in the tree ties. The primary variables are the across variables of the branches in the normal tree, and the through variables of the branches in the tree links, and the secondary variables are the through variables of the branches in the normal tree and the across variables of the branches in the tree links. Table 3 is formed by determining the state variables, primary and secondary variables.

Table 3 State, primary and secondary variables
Full size table

2.2.4 Determination of the Number of Branches, Nodes, and Sources

First, the number of branches, nodes, and sources should be determined. The number of branches is \(B = 16\), the number of nodes is \(N = 9\), and the total number of sources is \(S = 1\) obtained as the number of A-type sources is \(S_{A} = 1\) and the number of T-type sources is \(S_{T} = 0\).

2.2.5 Determination of the Number of Branches, Nodes, and Sources

Obtaining elemental, continuity and compatibility equations: The elemental equation numbered \(B-S\), the continuity equation numbered \(N - 1 - S_{A}\), and the compatibility equations numbered \(B - N + 1 - S_{T}\) should be written for passive components. In this framework, 15 elemental equations, 7 continuity equations, and 8 compatibility equations are presented in Table 4.

Table 4 Elemental, continuity and compatibility equations
Full size table

2.2.6 Obtaining the State Equations in Standard and Matrix form by Making Necessary Arrangements

First of all, secondary variables in the elemental equations are eliminated by making use of continuity equations and compatibility equations. Then, if the variables that are not state variables are destroyed, and necessary adjustments are made, the state equations are obtained as Eqs. (31–36) in standard form and Eq. (37) in matrix form.

$$\frac{{{\text{d}}i_{L} }}{{{\text{d}}t}} = \frac{1}{L}V\left( t \right) - \frac{R}{L}i_{L} - \frac{1}{{LK_{a} }}w_{jd}$$
(31)
$$\frac{{{\text{d}}w_{jd} }}{{{\text{d}}t}} = \frac{1}{{J_{d} K_{a} }}i_{L} - \frac{{c_{d} }}{{J_{d} }}w_{jd} - \frac{{r_{p} }}{{J_{d} }}F_{kd}$$
(32)
$$\frac{{{\text{d}}F_{kd} }}{{{\text{d}}t}} = k_{d} r_{p} w_{jd} + k_{d} x_{tp} w_{j1}$$
(33)
$$\frac{{{\text{d}}T_{kt} }}{{{\text{d}}t}} = k_{t} w_{j1} - k_{t} w_{j2}$$
(34)
$$\frac{{{\text{d}}w_{j1} }}{{{\text{d}}t}} = - \frac{1}{{J_{1} }}T_{kt} - \frac{{c_{t} }}{{J_{1} }}w_{j1} + \frac{{c_{t} }}{{J_{1} }}w_{j2} - \frac{{x_{tp} }}{{J_{1} }}F_{kd}$$
(35)
$$\frac{{{\text{d}}w_{j2} }}{{{\text{d}}t}} = \frac{1}{{J_{2} }}T_{kt} + \frac{{c_{t} }}{{J_{2} }}w_{j1} - \frac{{c_{t} }}{{J_{2} }}w_{j2}$$
(36)
$$\begin{aligned} & \left[\begin{array}{c}\frac{{\text{d}}{i}_{L}}{{\text{d}}t}\\ \frac{{\text{d}}{w}_{jd}}{{\text{d}}t}\\ \frac{{\text{d}}{F}_{kd}}{{\text{d}}t}\\ \frac{{\text{d}}{T}_{kt}}{{\text{d}}t}\\ \frac{{\text{d}}{w}_{j1}}{{\text{d}}t}\\ \frac{{\text{d}}{w}_{j2}}{{\text{d}}t}\end{array}\right]=\left[\begin{array}{cccccc}-\frac{R}{L}& -\frac{1}{L{K}_{a}}& 0& 0& 0& 0\\ \frac{1}{{J}_{d}{K}_{a}}& -\frac{{c}_{d}}{{J}_{d}}& -\frac{{r}_{p}}{{J}_{d}}& 0& 0& 0\\ 0& {k}_{d}{r}_{p}& 0& 0& {k}_{d}{x}_{tp}& 0\\ 0& 0& 0& 0& {k}_{t}& -{k}_{t}\\ 0& 0& -\frac{{x}_{tp}}{{J}_{1}}& -\frac{1}{{J}_{1}}& -\frac{{c}_{t}}{{J}_{1}}& \frac{{c}_{t}}{{J}_{1}}\\ 0& 0& 0& \frac{1}{{J}_{2}}& \frac{{c}_{t}}{{J}_{2}}& -\frac{{c}_{t}}{{J}_{2}}\end{array}\right]\left[\begin{array}{c}{i}_{L}\\ {w}_{jd}\\ {F}_{kd}\\ {T}_{kt}\\ {w}_{j1}\\ {w}_{j2}\end{array}\right]\\&\quad+\left[\begin{array}{c}\frac{1}{L}\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right][V(t)]\end{aligned}$$
(37)

2.3 Simulation Processes

During the simulation process, a Simulink model was created with blocks representing each of the equations of state presented in Eqs. (1–6), and system outputs were obtained versus system input. A schematic diagram of the simulation process is presented in Fig. 7.

Fig. 7
figure 7

Schematic diagram of the simulation process

Full size image

3 Results and Discussion

Simulation studies were carried out in MATLAB/Simulink environment. The relevant parameters are presented in Table 5 [7, 9]. For V(t), which is the system’s input, the sinusoidal input shown in Fig. 8 is preferred.

Table 5 Parameters [7, 9]
Full size table
Fig. 8
figure 8

System input

Full size image

When the input is 20 V, as shown in Fig. 9, the results for the breech and muzzle sections are similar. The angular position, velocity, and acceleration of an angular system are characteristic concepts in terms of system dynamics. The similarity of the angular displacement–time responses of the breech and muzzle sections in the present study is consistent with the studies in the literature. Furthermore, the similarity of the angular velocity and acceleration time responses of the breech and muzzle sections provides a broader scope in terms of reflecting all the characteristics in the system dynamics [3, 5, 7]. As seen in Table 6, the maximum angular displacement, maximum angular velocity, and maximum angular acceleration values are 0.017459 rad, 0.004365 rad/s, 0.004009 rad/s2 for the breech section and 0.017459 rad, 0.004365 rad/s, 0.004182 rad/s2 for the muzzle section, respectively. The RMS angular displacement value for the breech section is 0.010718 rad, the RMS angular velocity value is 0.03094 rad/s, and the RMS acceleration value is 0.001542 rad/s2 while the RMS angular displacement value for the muzzle section is 0.010718 rad, the RMS angular velocity value is 0.003094 rad/s, and the RMS acceleration value is 0.001543 rad/s2. Considering all values, it is seen that the maximum and RMS values are almost identical for the breech and muzzle sections.

Fig. 9
figure 9

a Angular displacement b angular velocity c angular acceleration of breech section and muzzle section

Full size image
Table 6 Maximum and RMS values
Full size table

4 Conclusion

In this study, the elevation dynamics of the weapon system of the main battle tank are modeled by the linear graph method. First of all, system components and types were determined. The system is expressed graphically by obtaining linear graph, normal tree, and tree links of the system. With the help of this graphical expression, the state equations were obtained in standard and matrix form by following the steps of obtaining the state, primary and secondary variables; determining the number of branches, nodes, and sources; and obtaining the elemental, continuity, and compatibility equations. Simulation studies were carried out in MATLAB/Simulink environment. It was observed that the position, velocity, and acceleration time responses of breech and muzzle sections had similar vibration characteristics and that the maximum and RMS position, velocity, and acceleration values were the same or very close. The utilization of the linear graph method in analyzing the elevation dynamics of the weapon system, a critical constituent of the main battle tank, is essential in demonstrating the efficiency of this method in obtaining the mathematical model of systems. In addition, the compatible vibration characteristic of the breech and muzzle sections means that there will be no additional stress and tension and, therefore, no deflection of the barrel from the target. Thus, it has been proven that by realizing the two-piece design, stress and tension can be successfully distributed during the firing. Numerical solution findings obtained through simulation study are a robust tool to evaluate the accuracy of the results. It is expected that the findings of the present study and the results of an experimental study will mainly agree. It should be noted that numerical and mathematical representations ensure us a simplified perspective of the relationships. In other respects, the values which are determined by experimentally can also be impressed by various parameters that may not exist in theoretical models causing some differences between mathematical and experimental findings. That is why it is recommended to perform experimental studies for extensive discussion.