Influence of clearance between cradle and barrel on nonlinear dynamic response of the artillery system

Abstract

The artillery weapon system,characterized as a complex nonlinear mechanical system, is influenced by various factors affecting its muzzle vibration response.In the article, the model of the artillery system with variable cross-section and multistep barrel is established on the basis of the bending deformation equation, and the fundamental frequency equation is obtained, and the auxiliary verification is completed through modal testing and finite element methods. Then, considering the clearance between the barrel and the cradle, the equivalent nonlinear dynamic model of the vertical vibration of the muzzle is established is established. Furthermore, the multi-scale analysis method obtains the amplitude-frequency curve of the equivalent model under sinusoidal excitation, and analyzes the influence of parameters on the response characteristics. Finally, the vibration research system of the model of the artillery system is constructed to study the vibration characteristics of the muzzle. The results show that the equivalent nonlinear dynamic model established in the paper has certain accuracy, which can provide a certain reference for the related research of the artillery system

Article highlights

• 1. An model for predicting the equivalent normal stiffness and fundamental frequency of vertical vibration of the muzzle in variable cross-section and multi-step barrel is established on the basis of quadratic integral method and Rayleigh method

• 2. The impact of clearance and excitation on the response characteristics of the artillery system is examined for providing a reference for the design of the system.

• 3. The accuracy and universality of the equivalent nonlinear dynamic model of the vertical vibration of the muzzle, considering the clearance, were verified by the vibration experiment.

1 Introduction

Relevant research institutions have carried out related research for the purpose of improving the artillery range and shooting accuracy of artillery since the 1870 s. It is roughly divided into three stages. In the first stage, relevant researchers used the theory of structural mechanics to establish a flexible beam model of the artillery weapon system [1]. In the second stage, the multi-rigid body system dynamics was integrated into the research of the artillery weapon system [2, 3]. In the third stage, the research on artillery weapon systems has gradually evolved into a cross-cutting field, involving various theoretical foundations such as modern measurement and control technology, finite element theory, computer theory, ballistics, multi-body dynamics, elastic–plastic mechanics, etc [4]. Kaninskiy, Valeriy et al. [5] consider analytical choice of the digital meter parameters based on DSPS and carried out the simulation model design in order to perform the optimization of its parameters. Rateb Ragaee et al. [6] explores integrating a specialized hydraulic control system with artillery to minimize muzzle disturbances, using flexible modeling, modal analysis for validation and sensitivity analyses on variables affecting firing angles. Y. Budaretskiy et al. [7] analyzed the applied methods of modelling at construction of system of support of decision-making and offerd ways of optimization of system.

The research on artillery weapon systems in China started relatively late. However, due to significant attention at the national level, numerous important research results have been obtained. He Yong et al. [8] derived the equation of motion for the coupled dynamics of rigid and flexible components. They established the finite element model of the artillery barrel, and analyzed the factors affecting the muzzle vibration; Wang De-shi et al. [9] developed a coupled rigid-flexible multibody system model for artillery system dynamics. Tian Jianhui et al. [10]developed a simple “task space” controller for achieving the trade-off between the steady and dynamic tracking and real-time control performance of the pointing system of wheeled self-propelled artillery. Yingfeng Wu et al. [11] examines barrel vibration’s impact on weapon accuracy, using finite element analysis to investigate a multi-barrel system’s vibration characteristics.Dalin Wu et al. [12] built the completely artillery system virtual prototype based on the dynamic theory. Subsequently, the performance variation and failure mechanism of the artillery system were studied by using the method of theoretical analysis, simulation and physical experiment.

The accurate representation of the clearance model for the kinematic pairs in the artillery weapon system is of significant importance for describing its nonlinear dynamic response. Dubowsky and Funnabashi introduced the concept of alternating contact the free states in the motion of mechanical systems and used an equivalent massless spring-damper system to describe collision characteristics [13, 14]. Miedema et al. [15] and Soong et al. [16] extended the two-state model of contact and separation by introducing the multi-state model (contact, separation and collision or transitional), to capture the different phases of relative motion between interacting components within a cycle. Earles introduces a massless-link/spring-damper model to accurately represent the characteristics of motion pairs with clearance [17].

In recent years, many researchers have made new attempts and achieved new research results in the research and model establishment of nonlinear clearance problems in machinery. Z.F. Bai, Y. Zhao et al. [18] proposed a nonlinear hybrid model of revolving joints with backlash. It incorporates elements from the Lankarani-Nikravesh model, utilizes the nonlinear stiffness coefficient and the damping based on an improved elastic foundation model. A.B. Zhu, S.L. He et al. [19] proposed a nonlinear contact pressure distribution model that combines dynamic analysis with wear calculation. This model not only describes the nonlinear relationship between contact pressure and penetration depth, but also avoids the complexity of contact pressure calculation. X.P. Wang et al. [20] proposed a simulation model that considers the influence of different gap sizes, crank speeds and materials on the dynamic response of a multi-body system. While, an experimental platform was built to carry out experimental tests under corresponding working conditions, which further verified the numerical results of the nonlinear impact force model and the dynamic response of the gap joint mechanism.

This study focuses on the vibration analysis of artillery systems. A calculation expression for the fundamental frequency of the vibration of the muzzle is derived using the Rayleigh method and equivalent stiffness.Then, the expression is verified by the modal testing and simulation analysis under constrained boundaries.Furthermore, the amplitude-frequency curve of the equivalent vibration model considering the clearance between barrel and cradle under sinusoidal excitation is obtained using the multi-scale method. Simultaneously, the impact of parameters on the equivalent model is examined. Finally, a research system for vibration characteristics of the artillery system was constructed to investigate the vibration characteristics

2 Dynamics model

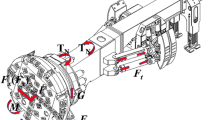
Figure 1 shows the overall scheme of the simplified artillery scale model. The model consists of barrel, compression nut, spring, trunnion, cradle, platform, base, seat ring, level rod, steering machine and eccentric sleeve.

Fig. 1

Simplified artillery scale model

Among them, the barrel and the cradle form a cylindrical pair, and its axial movement is limited by a compression nut and a spring. The cradle and the trunnion form a revolving pair, with the trunnion fixed on the platform rib. The connection between the cradle and the platform is established through a high-low rod assembly.There is a slewing bearing between the platform and the base. The inner ring of the slewing bearing has internal meshing teeth, and the steering wheel has external meshing teeth. The engagement rotation between these teeth is used to adjust the direction of the muzzle. Specifically, rotating the steering mechanism handle enables the barrel to rotate horizontally, while the eccentric sleeve located in the platform hole is utilized to adjust the gear meshing clearance.

2.1 Elastic bending deformation of barrel

2.1.1 Theoretical modeling

Figure 2 shows the schematic diagram of the barrel, and the x-axis of the global coordinate system and the x1-axis, x2-axis, x3-axis of the local coordinate system are established in the barrel.

Fig. 2

Geometric schematic diagram of barrel

The barrel is divided into three sectionsI, II, III.the lengths are$L_1, L_2, L_3$..The inner diameter is d, the largest outer diameter is $D_a$, and the smallest diameter is $D_b$. Since $D_a \ll L_1+L_2+L_3$, it is simplified as a cantilever beam. Among them, Iand II are equal-section beams, and III is a variable-section beam whose section changes continuously. The moment of inertia of any section is $I_x$, and the expression is as follows:

$$\begin{aligned} I\left( x_2\right) =\pi \left( D\left( x_2\right) ^4-d^4\right) / 64 \end{aligned}$$

(1)

Among them, d is the inner diameter of the barrel, $D\left( x_2\right)$ is the outer diameter of the barrel, and its expression is as follows:

$$\begin{aligned} D\left( x_2\right) =\left( D_b-D_a\right) x_2 / L_2+D_a \end{aligned}$$

(2)

Since the deformation of the three-section beam is pure bending deformation, the deflection of each micro-beam section can be obtained by using the quadratic integral method as:

$$\begin{aligned} w(x)=\iint \left( \frac{M(x)}{E I(x)} d x\right) d x+C x+D \end{aligned}$$

(3)

The moment of inertia and bending moment of segment I are $I_1=\pi \left( D_a^4-d^4\right) / 64$ and $M\left( x_1\right) =F\left( L_1+L_2+L_3-x_1\right)$ respectively. The boundary condition are $x_1=0, w_1=0, w_{1, x}=0$.The deflection of the microbeam expression is as follows:

$$\begin{aligned} w_1\left( x_1\right) =\frac{1}{E I_1}\left[ F\left( L_1+L_2+L_3\right) \frac{x_1^2}{2}-F \frac{x_1^3}{6}\right] \end{aligned}$$

(4)

The moment of inertia and bending moment of II are $I_2=\pi \left( D\left( x_2\right) ^4-d^4\right) / 64$ and $M\left( x_2\right) =F\left( L_2+L_3-x_2\right)$respectively.The boundary condition are $x_2=0, w_2=0, w_{2, x}=0$.The deflection of the microbeam expression is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} w_{2, x}\left( x_2\right) =A\left( \psi ^{\prime }\left( x_2\right) +C_2\right) \\ w_2\left( x_2\right) =A\left( \psi \left( x_2\right) +C_2 x_2+D\right) \end{array}\right. \end{aligned}$$

(5)

Here, $A=64 F / \pi D_a^4, C_2=-\psi (0), D=-\psi (0)$. For detailed expressions $\psi (x)$ of $\psi ^{\prime }(x)$ and, see the appendix 1.

The moment of inertia of segment III is $I_3=\pi \left( D_b^4-d^4\right) / 64$, bending moment $M\left( x_3\right) =F\left( L_3-x_3\right)$.The boundary condition are $x_3=0, w_3=0, w_{3, x}=0$.The deflection of the microbeam expression is as follows:

$$\begin{aligned} w_3\left( x_3\right) =\frac{1}{E I_3}\left[ F\left( L_3 \frac{x_3{ }^2}{2}-\frac{x_3{ }^3}{6}\right) \right] \end{aligned}$$

(6)

The beading deformation of the barrel can be solved by the multi reference system method as:

$$\begin{aligned} w(x)=\left\{ \begin{array}{ll} w_1\left( x_1\right) &{} 0<x<L_1 \\ w_{E_1}+\theta _{E_1} x_2+w_2\left( x_2\right) &{} L_1<x<L_1+L_2 \\ w_{E_2}+\theta _{E_2} x_3+w_3\left( x_3\right) &{} L_1+L_2<x<L_1+L_2+L_3 \end{array}\right. \end{aligned}$$

(7)

Here, the relation between local coordinate $x_1, x_2, x_3$ and global coordinate x are $x_1=x, x_2=x-L_1, x_3=x-L_1-L_2$

2.1.2 Finite element simulation

Section 2.1.1 establishes the equation for variable cross-section beams in multiple reference frames using the quadratic integration method. In the following section, using the finite element method will be employed to validate its reliability.

The parameters of the barrel of the scale model are shown in Table 1.

Table 1 Table parameters of the artillery barrel scale model

A finite element model with the same parameters as the barrel is created using the ANSYS software. The solid element type SOLID186 is employed, which features capabilities such as large strain, large deformation, hyperelasticity, plasticity, and stress stiffening, is suitable for simulating various structures with irregular shapes. The finite element model of the barrel is shown in Fig. 3

Fig. 3

Finite element model of barrel

The “Static Structural” module in ANSYS Workbench is selected to perform meshing on the barrel using the sweep method. Since the compression nut and the spring limit the axial movement of the barrel, a fixed constraint is imposed on the end of the barrel to simplify it as a cantilever beam.A concentrated force is applied at the muzzle of the barrel. To obtain an accurate deflection curve of the barrel under the concentrated force, a result path is added from the muzzle to the end of the barrel, and the model is loaded with 2500 substeps.

2.1.3 Theoretical results and FEM analysis

The cloud diagram of the finite element analysis results of the barrel deflection is shown in Fig. 4a, and the comparison between the analytical solution of the deflection curve and the finite element solution is shown in Fig. 4b:

Fig. 4

Finite element analysis results and comparison of barrel

As shown in Fig. 4, it can be observed that under the given variable cross-section beam model and material parameters, the beam is simplified as a cantilever beam by applying typical boundary conditions, and its deflection curve is solved. The finite element analysis results exhibit a high degree of consistency, both in trend and numerical values, with the analytical results. Therefore, the analytical method for solving the deflection curve of the variable cross-section beam demonstrates considerable accuracy and reliability.

2.2 The vertical vibration at the muzzle

2.2.1 Equivalent vertical vibration model

As shown in the following Eq. (7), the deflection $W_{E3}$ of the muzzle can be obtained from Eq. (8):

$$\begin{aligned} w_{E 3}=w_{E 2}+\theta _{E 2} L_3+w_3\left( L_3\right) \end{aligned}$$

(8)

According to Hooke’s law of elastic deformation, the equivalent stiffness of the muzzle is as follows:

$$\begin{aligned} K=F / w_{E 3} \end{aligned}$$

(9)

The bending deformation w(x) of the barrel can be approximated by the following single mode vibration : 

$$\begin{aligned} w(x, t) \approx \phi _i(x) q_i(t) \end{aligned}$$

(10)

Here, $\phi _i(x)$ is normalized special mode function, $\phi _i(x)=w(x) / w_{E 3}, q_i(t)$ is the deflection of the muzzle. The kinetic energy of the barrel is:

$$\begin{aligned} \begin{aligned} T&=\frac{1}{2} M_{e q} q_{i, t}(t)^2=\int _0^{L_1+L_2+L_3} \frac{1}{2} \rho S(x) {\dot{w}}(x, t)^2 d x \\&= \frac{\rho q_{i, t}(t)^2}{2 w_{E 3}{ }^2} \int _0^{L_1+L_2+L_3} S(x) w(x)^2 d x\\&=\frac{\rho q_{i, t}(t)^2}{2 w_{E 3}{ }^2}\left[ \int _ { 0 } ^ { L _ { 1 } } S _ { 1 } \left( x_1 w_1\left( x_1\right) ^2\right. \right. \\&\quad +\int _{L_1}^{L_1+L_2} S_2\left( x_2\right) \left( w_{E_1}+\theta _{E_1} x_2+w_2\left( x_2\right) \right) ^2 d x\\&\quad +\left. \int _{L_1+L_2}^{L_1+L_2+L_3} S_3\left( x_3\right) \left( w_{E_2}+\theta _{E_2} x_3+w_3\left( x_3\right) \right) ^2 d x\right] \end{aligned} \end{aligned}$$

(11)

Here, $S_1\left( x_1\right)$ represents the sectional area of segment I, $S_2\left( x_2\right)$ represents the sectional area of segment II, $S_3\left( x_3\right)$ represents the sectional area of segment III, The specific expressions are as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} S_1\left( x_1\right) =\pi \left( D_a^2-d^2\right) / 4 &{} \quad 0<x_1<L_1 \\ S_2\left( x_2\right) =\pi \left( D\left( x_2\right) ^2-d^2\right) / 4 &{} \quad 0<x_2<L_2 \\ S\left( x_3\right) =\pi \left( D_b^2-d^2\right) / 4 &{} \quad 0<x_3<L_3 \end{array}\right. \end{aligned}$$

(12)

The equivalent mass $M_{eq}$ of the barrel is:

$$\begin{aligned} \begin{aligned} M_{e q}&=\frac{\rho }{w_{E 3}{ }^2}\left[ \int _0^{L_1} S_1\left( x_1\right) w_1\left( x_1\right) ^2\right. \\&\quad +\int _{L_1}^{L_1+L_2} S_2\left( x_2\right) \left( w_{E_1}+\theta _{E_1} x_2\right. \\&\quad +w_2\left( x_2\right) ^2 d x+\int _{L_1+L_2}^{L_1+L_2+L_3} S_3\left( x_3\right) \\&\quad \left. \left( w_{E_2}+\theta _{E_2} x_3+w_3\left( x_3\right) \right) ^2 d x\right] \end{aligned} \end{aligned}$$

(13)

According to the equivalent stiffness and equivalent mass obtained from Eqs. (9) and (13), the natural frequency of the vertical vibration at the muzzle can be calculated as:

$$\begin{aligned} f_1=\frac{1}{2 \pi } \sqrt{\frac{K}{M_e}} \end{aligned}$$

(14)

2.2.2 Verification of equivalent vibration model

Section 2.2.1 predicts the equivalent stiffness of the variable-section barrel and the analytical expressions of the natural frequency of the vertical vibration by using the geometric parameters and material parameters of the variable-section beam.The reliability of the aforementioned approach is further verified through finite element analysis and modal testing.

• (i) Modal testing under constrained boundaries

The hammer impact test, characterized by its simplicity,non-interference with the dynamic characteristics of the tested structure, and broadband excitation provided by the hammer, has been widely applied in the analysis of experimental models.Therefore, in order to avoid the influence of the bending stiffness caused by continuous contact between the exciter’s top rod and the structure, as well as the coupling between the top rod and the structure, the artillery system was mounted on the vibration table for modal testing. The SIMO (Single Input, Multiple Output) method was employed, where the structure was struck with a hammer and triaxial accelerometers were used to measure the response. The modal results in the numerical plane are presented in the following Fig. 5

Fig. 5

The result of modal testing

• (ii) Modal analysis based on simulation software

The finite element model established in Sect. 2.1.2 was imported into the “Pre-Stress Modal” module of WORKBENCH. The same meshing and boundary constraints as described in Sect. 2.1.2 were applied to the barrel. A concentrated force was applied at the muzzle of the barrel. The Lanczos method was employed to extract the modal parameters of the structure [15]. The model was loaded with 2500 substeps, and the first natural frequency obtained is shown in Fig. 6.

Fig. 6

First-order mode shape(28.502Hz)

From the above simulation analysis and modal testing, the analytical solution of the barrel mathematical model, the finite element discrete solution and the experimental solution of the first-order modal natural frequency are obtained, as shown in Table 2 below.

Table 2 The value of the stiffness and natural frequency of the barrel at the muzzle

It can be observed from Table 2 that the natural frequency of the barrel at the muzzle solved by the analytical method is 26.69Hz, which is very close to the experimental value of 26.054Hz, with an error of 2.44%, and is also relatively close to the result of the finite element discrete solution of 28.502Hz. The error is 6.58%. Considering the measurement precision, test methodology and environmental conditions in the experimental modal testing, it can be observed that the analytical solution of the mathematical model of the barrel in this paper exhibits a favorable agreement with the experimental data, substantiating the reliability of the mathematical model proposed in this study

2.3 Nonlinear clearance between cradle and barrel

Contact/collision is common in artillery systems, especially the contact between barrel and cradle. Therefore, it is of great significance to study the effect of the clearance between the barrel and the cradle on the dynamic characteristics of the artillery system for improving the accuracy, stability and reliability of the weapon.

In order to accurately characterize the clearance between the barrel and the support end of the cradle, a piecewise linear contact force model $F_e(y)$ is introduced. the clearance is regarded as a massless rod-spring model, and the contact form between the barrel and the cradle is treated as elastic Collision. The piecewise linear contact force model is shown in the following Eq. (15):

$$\begin{aligned} F_e=\left\{ \begin{array}{ll} k_g y+k_e\left( y+\delta _{\textrm{c}}\right) ,&{} \quad y \le -\delta _{\textrm{c}} \\ k_g y, &{}\quad -\delta _{\textrm{c}}<y<\delta _{\textrm{c}} \\ k_g y+k_e\left( y-\delta _{\textrm{c}}\right) , &{}\quad y \ge \delta _{\textrm{c}} \end{array}\right. \end{aligned}$$

(15)

Here, $\delta _{\textrm{c}}$ represents the clearance between the barrel and the support end of the cradle, $k_g$ and $k_e$ represents equivalent contact stiffness coefficient

The piecewise linear function shown in Eq. (16) is a non-smooth strong nonlinear function. In order to simplify the quantitative calculation and analysis, the cubic nonlinear stiffness is used to regress it. The regression function is as follows:

$$\begin{aligned} F_{e s}=k_1 y+k_2 y^3 \end{aligned}$$

(16)

According to Eqs. (15) and (16), the piecewise linear function and the cubic nonlinear regression function are shown in Fig. 7:

Fig. 7

Piecewise linear function and cubic nonlinear regression function

Assuming the equivalent contact stiffness $k_g=23000 \mathrm {~N} / \textrm{m}, k_e=2000 \mathrm {~N} / \textrm{m}$, we can observe the variations of the first regression coefficient and the third regression coefficient in Eq. (16) as the clearance changes, as shown in Fig. 8.

Fig. 8

The relationship between the regression coefficient of the cubic nonlinear function and the clearance

2.4 Nonlinear dynamics of the muzzle

The vertical vibration of the muzzle will seriously affect the shooting accuracy and stability of the artillery system, so it is of great significance to study it deeply.

The results presented in Table 2 demonstrate a close correspondence between the analytical predictions, finite element solutions, and experimental measurements with respect to the vertical muzzle vibration. The agreement among these values indicates a high level of consistency and concurrence between the analytical method, finite element analysis, and experimental observations. Therefore, when the clearance at support end is considered, the equivalent spring-mass model of the muzzle is shown in Fig. 9:

Fig. 9

The equivalent spring-mass model of the muzzle

The differential equation of motion is shown in Eq. (17):

$$\begin{aligned} M_{e q} \ddot{y}+C {\dot{y}}+K y+F_e(y)=F_0 \sin \omega t \end{aligned}$$

(17)

By considering the motion differential equation represented by Eq. (17) and incorporating the characterization function that captures the nonlinearity of the clearance, namely Eq. (16), The Eq. (18) is derived:

$$\begin{aligned} M_{e q} \ddot{y}+C {\dot{y}}+K y+\left( k_1 y+k_2 y^3\right) =F_0 \sin \omega t \end{aligned}$$

(18)

For convenience of discussion, normalize Eq. (18) dimensionlessly. Assume ${\bar{y}}=\frac{y}{D_a}$, ${\bar{t}}=\frac{t}{T}$, and get Eq. (19):

$$\begin{aligned} \ddot{{\bar{y}}}+\frac{C T}{M_{e q}} \dot{{\bar{y}}}+\frac{\left( K+k_1\right) T^2}{M_{e q}} {\bar{y}}+\frac{k_2 D_a^2 T^2}{M_{e q}} {\bar{y}}^3=\frac{F_0 \sin \omega t T^2}{M_{e q} A} \end{aligned}$$

(19)

Meanwhile, substitute $T=\sqrt{\frac{M_{e q}}{K+k_1}}=\frac{1}{\omega _0}$, and get Eq. (20)

$$\begin{aligned} \ddot{{\bar{y}}}+{\bar{y}}={\bar{F}}_0 \sin \Omega \tau -2 \xi \dot{{\bar{y}}}-\gamma {\bar{y}}^3 \end{aligned}$$

(20)

H ere,${\bar{y}}=y / D_a; \xi =2 C /\left( M_{e q} \omega _0\right) ; \gamma =k_2 D_a^2 /\left( K+k_1\right) ; F_0=F_0 /\left( K+k_1\right) / D_a; \Omega =\omega / \omega _0, \tau =\omega _0 t$.,

3 Resonance response

In practical engineering applications, where $\xi$ and ${\bar{F}}_0$ are considered small quantities, it is convenient to introduce a small parameter ${\mathcal {E}}$ and define the detuning parameter $\sigma$. By doing so, the Eq. (20) can be simplified as:

$$\begin{aligned} \ddot{{\bar{y}}}+{\bar{y}}=\varepsilon \left[ {\bar{f}} \sin (1+\varepsilon \sigma ) \tau -2 \mu \dot{{\bar{y}}}-\lambda {\bar{y}}^3\right] \end{aligned}$$

(21)

In the following, the method of multiple scales is employed to solve the system described by the Eq. (20).The solution of Eq. (21) is provided with the following form:

$$\begin{aligned} {\bar{y}}(T)={\bar{y}}_0\left( T_0, T_1\right) +\varepsilon {\bar{y}}_1\left( T_0, T_1\right) +\ldots \end{aligned}$$

(22)

Here, $T_0$ represents the fast time scale, $T_0=t$ and $T_1$ represents the slow time scale, $T_1=\varepsilon t$ respectively.

Applying Eq. (21) to Eq. (20), the Eq. (22) can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon ^0: D_0^2 {\bar{y}}_0+{\bar{y}}_0=0 \\ \varepsilon ^1: D_0^2 {\bar{y}}_1+{\bar{y}}_1=-2 D_0 D_1 {\bar{y}}_0-2 \mu D_0 {\bar{y}}_0- \\ \lambda {\bar{y}}_0^3+{\bar{f}} \sin \left( T_0+\sigma \textrm{T}_1\right) \end{array}\right. \end{aligned}$$

(23)

The solution of Eq. (22) is expressed as Eq. (23):

$$\begin{aligned} {\bar{y}}\left( T_0, T_1\right) =A\left( T_1\right) e^{i T_0}+{\bar{A}}\left( T_1\right) e^{-i T_0} \end{aligned}$$

(24)

Here, $A\left( T_1\right)$ and ${\bar{A}}\left( T_1\right)$ are complex functions that are conjugate to each other with respect to the time scale.

The Eq. (24) can be obtained by substituting Eq. (23) into Eq. (22) and eliminating its long-term term.

$$\begin{aligned} 2 i({\dot{A}}+\mu A)+3 \lambda A^2 {\bar{A}}-{\bar{f}} e^{i \sigma T_1}=0 \end{aligned}$$

(25)

By substituting into Eq. (24), and separating the real and imaginary components, the Eq. (25) can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{a}}+\mu a-\frac{{\bar{f}}}{2} \sin \varphi =0 \\ a(\sigma -{\dot{\varphi }})-\frac{3}{8} \lambda a^3-\frac{{\bar{f}}}{2} \cos \varphi =0 \end{array}\right. \end{aligned}$$

(26)

Therefore, by rearranging Eq. (25), the amplitude-frequency characteristic equation can be obtained as follows:

$$\begin{aligned} \left( a \sigma -\frac{3 \lambda }{8} a^3\right) ^2+(\mu a)^2=\left( \frac{{\bar{f}}}{2}\right) ^2 \end{aligned}$$

(27)

The following focuses on the amplitude-frequency characteristics of the primary resonance. When the parameters are taken in Table 3, the resonance curve of amplitude-frequency response can be depicted, from which jump phenomenon can be evidently found.

Table 3 Parameter selection of nonlinear dynamic model

Fig. 10

The amplitude jump simulation

The Fig. 10 [20] shows that In the nonlinear system, as the excitation frequency increases, the system’s steady-state vibration reaches point D and then jumps to point B. Conversely, as the excitation frequency decreases, the system’s steady-state vibration reaches point C and then jumps to point E.

3.1 Influence of parameters

By comparing the amplitude-frequency response curves of the system under different parameter settings at the primary resonance, we can observe the influence of each parameter on the vibration state of the system and identify the vibration patterns and trends [21].

3.1.1 Influence of the sinusoidal excitation

The excitation amplitude $F_0$ are selected as 0.1g, 0.2g, 0.3g, 0.4g respectively. The amplitude-frequency response curves corresponding to the excitation are depicted and compared in Fig. 11.

Fig. 11

The primary resonance curves (sinusoidal excitation)

By changing the excitation amplitude, it can be observed that the amplitude-frequency curve slopes toward the direction of frequency decrease with the amplitude $F_0$ increasing. Along with this trend, multiple solutions and amplitude jumps can be observed. The peak frequency also decreases correspondingly, indicating a weakening of the system’s stiffness. Additionally, the peak values of the curve gradually increase, suggesting a progressive amplification of the system response.

3.1.2 Influence of the damping ratio

The damping ratio C are selected as,respectively. The amplitude-frequency response curves corresponding to the damping ratio are depicted and compared in Fig. 12.

Fig. 12

The primary resonance curves (damping ratio)

it can be observed from the figure that variations in damping ratio have a significant impact on the amplitude-frequency curve. Specifically, an increase in damping ratio leads to a reduction in the resonance response amplitude observed in the amplitude-frequency curve, as well as a decrease in the range of frequencies associated with multi-value solutions and discontinuities. These observations indicate an enhanced stability of the system

3.1.3 Influence of the clearance

The clearance values are selected as,respectively.The amplitude-frequency response curves corresponding to the clearance are depicted and compared in Fig. 13.

Fig. 13

The primary resonance curves (clearance)

It can be observed from the figure that variations in the clearance will change the resonance interval of the system. Specifically, an increase in the barrel-cradle clearance causes the amplitude-frequency curve to shift to the left.

4 Experiment on vibration characteristics of the muzzle

In order to accurately investigate the influence of the clearance between the barrel and the cradle on the vibration characteristics of the muzzle, a research system for vibration characteristics of artillery model was constructed. The experiments, which were conducted under the room temperature conditions, studied the effects of the clearance between the barrel and the cradle, as well as the impact of sinusoidal excitation loads on the vibration characteristics of the muzzle.

4.1 Experimental conditions

4.1.1 Construction of the system on vibration characteristics

As shown in Fig. 14,the entire research system is composed of the data acquisition and analysis system, the sensor system, vibration table and control system

Fig. 14

Schematic diagram of the research system for vibration characteristics

The experiment mainly observes the acceleration response and angular velocity response at the muzzle. For this reason, two acceleration sensors (A1 and A2) are arranged at the muzzle, and six acceleration sensors (B1-B6) are arranged at the platform to obtain the acceleration of the platform. The model of the accelerometer is the PCB356A02 triaxial accelerometer with a resonant frequency$\ge$ 25kHz. It has a resolution(1-5kHz) of 0.0005g rms, a measurement range of 500 g, and a sensitivity of 10mV/g. The sampling frequency of the acceleration sensor is 2048Hz

4.1.2 Experimental overview

To capture the pronounced nonlinear system effect resulting from sinusoidal excitation, a sequential arrangement is employed, whereby scale models of the artillery system, exhibiting diverse assembly tolerances, are securely affixed to the extended table. The parameters of the scale model is shown as Table 4 and Fig. 15. Subsequently, a sinusoidal frequency sweep wave is applied to those models, in which the load levels are controlled at 0.1g/0.2g/0.3g/0.4g. The sweep frequency range is 10Hz to 100Hz. The frequency sweep operation advances incrementally and record the response data throughout from A1 acceleration the process.Afterwards, the experimental data is processed, and FFT is used to perform spectral analysis to determine the fundamental frequency of the object (the peak of the amplitude-frequency response).

Table 4 Parameters of the scale model

Fig. 15

Geometric dimensioning and tolerancing of critical components

4.2 Experimental data and result analysis

In order to analyze the amplitude-frequency characteristics in the primary resonance specifically, the amplitude-frequency curves in the frequency range from 15Hz to 45Hz under each condition are intercepted

4.2.1 Comparison between theoretical and experimental results

The comparison of experimental results and theoretical calculations is shown in Figs. 16 and 17. Tables 5 and 6 can be obtained by extracting the fundamental frequency and the corresponding amplitude.

Fig. 16

Comparison of experimental results and theoretical calculations(0.1mm in clearance)

Fig. 17

Comparison of experimental results and theoretical calculations(0.6mm in clearance)

Table 5 Fundamental frequency in 0.1mm clearance

Table 6 Fundamental frequency in 0.6mm clearance

It can be observed from Figs. 16 and  17 that the parameters exhibit similar effects on the nonlinear dynamic characteristics of the artillery system in both sinusoidal sweep vibration experiment and theoretical calculations:

• (1) In the scenario where the clearance value remains constant,the amplitude-frequency curve slopes toward the direction of frequency decrease with the process of increasing the amplitude $F_0$ from 0.1g to 0.4g, indicating a weakening of the system’s stiffness. Additionally, the maximum amplitude of the curve gradually increases.

• (2) In the scenario where the amplitude of excitation remains constant,the amplitude-frequency curve slopes toward the direction of frequency increase with the process of increasing the clearance $\delta _c$, indicating a strengthening of the system’s stiffness. Additionally, the maximum amplitude of the curve in the experiment gradually increases. It is obvious that the enlargement of the clearance value induces a decrement in the damping of the system during the experiment.The clear interpretation can be seen in appendix 2.

It can be observed from Figs. 16 and  17 that the left side of the amplitude-frequency curve of the experiment under each excitation has a jumping phenomenon with a steep increase in the process

It can be observed from Tables 5 and 6 that the theoretical calculations exhibit a high level of consistency with the amplitude-frequency response curves obtained from the experiments, with a maximum error of only 5.9% in 0.1mm clearance and 6.81% in 0.6mm clearance

5 Conclusion

The research shows the following:

• (1) In comparison to the finite element method, The proposed theoretical model of bending deformation and fundamental frequency exhibits a higher level of accuracy and offers computational cost savings. It also overcomes limitations associated with experimental approaches which can’t obtain the stiffness and fundamental frequency instantaneously.

• (2) The maximum amplitude of the amplitude-frequency curve under each excitation also gradually increases and the peak value of the curve shows a decreasing trend, with the increasing of the excitation amplitude, indicating a weakening of the system’s stiffness. What’s more, the left side of the amplitude-frequency curve under each excitation has a jumping phenomenon with a steep increase in the experiment

• (3) The peak value of the amplitude-frequency curve gradually increases with the increasing of the value of the clearance. And the maximum amplitude of the amplitude-frequency curve also gradually increases. Therefore, it is possible to achieve better stability of the muzzle by reducing the clearance between the barrel and the cradle.

• (4) The accuracy and universality of the nonlinear dynamic response were verified by the experiment. Therefore, the calculated characteristics of the system and the results could provide a reference for the design of the subsequent artillery weapon system.

Appendix

(1) The expressions of $\psi (x)$ and $\psi ^{\prime }(x)$ are the followings:

$$\begin{aligned} \begin{aligned} \psi ^{\prime }(x)&=\frac{-1}{81 c^3} 7 L_2\left[ -28 c L_2 \ln \left( c^2+\left( 1-\frac{9 x_2}{28 L_2}\right) ^2\right) \right. \\&\quad +\left( 28 c L_2-9 L_3+19 L_2\right) \ln \left( c-\frac{9 x_2}{28 L_2}+1\right) \\&\quad +\left( 28 c L_2+9 L_3-19 L_2\right) \ln \left( c+\frac{9 x_2}{28 L_2}-1\right) \\&\quad \left. +\left( 38 L_2-18 L_3\right) \tan ^{-1}\left( \frac{1}{c}-\frac{9 x}{28 L_2 c}\right) \right] \\ \psi (x)&=\frac{1}{729 c^3} 7 L_2\left[ \left( 252 c L_2 L_3+532 c L^2\right) \ln \left( 784\left( c^2+1\right) \right. \right. \\&\quad \left. L_2{ }^2-504 L_2 x+81 x^2\right) +2\left( 784 c^2 L_2{ }^2 \right. \\&\quad +\left. 252 L_2 L_3+171 L_2 x-81 L_3 x\right) \tan ^{-1}\left( \frac{1}{c}-\frac{9 x}{28 L_2 c}\right) \\&\quad +\left( 532 L_2{ }^2-1316 c L_2{ }^2-784 c^2 L_2{}^2\right. \\&\quad \left. 52 c L_2 L_3+252 L_2 L_3-81 L_3 x+252 c L_2 x+171 L_2 x\right) \\&\quad \ln \left( c-\frac{9 x_2}{28 L_2}+1\right) +\left( 532 L_2{ }^2+784 c^2 L_2^2\right. \\&\quad 1316 c L_2^2+252 c L_2 L_3-252 L_2 L_3+81 L_3 x\\&\quad \left. +252 c L_2 x-171 L_2 x\right) \ln \left( c+\frac{9 x_2}{28 L_2}-1\right) \\&\quad +1064 L_2^2 \tan ^{-1}\left( \frac{9 x-28 L_2}{28 L_2 c}\right) +\left( 784 c L_2^2+252 c L_2 x\right) \\&\quad \left. \ln \left( c^2+\left( 1-\frac{9 x_2}{28 L_2}\right) ^2\right) \right] \end{aligned} \end{aligned}$$

Here, $c=d / D_a$, d is the inner diameter of the barrel, $D_a$ is the largest outer diameter of the barrel

(2) In section 3.1.1, the variation of resonance peak amplitude and corresponding peak frequency in the range of external excitation force from 0.1g to 0.4g is discussed. It can be seen from Fig 18 that as the excitation force increases, the corresponding resonance peak amplitude increases, and the resonance frequency corresponding to the peak point shifts to the left, that is, the resonance frequency becomes smaller. The experimental part also verified this rule very well.

When the system vibrates, resonance occurs when the frequency of the external excitation is close to or equal to the natural frequency. The natural frequency is a characteristic of the system itself, and its influencing factors are structural stiffness and mass.

Fig. 18

The primary resonance curves (sinusoidal excitation)

For an undamped single-degree-of-freedom system, the formula for calculating the natural frequency is: $f_n=\frac{1}{2 \pi } \sqrt{\frac{k}{m}}$. When there is damping, the formula for calculating its natural frequency is: $f_{\textrm{d}}=f_n \sqrt{1-\xi ^2}$, where is the damping ratio, which has little effect on the natural frequency.

In the model, the mass of the system is a constant, and the reduction of the resonance frequency means the reduction of the natural frequency of the system. From the calculation formula of the natural frequency, the stiffness of the system at this time decreases.