Probabilistic and Fuzzy Nonlinear Discontinuous Aeroelastic Analysis of In-plane FG Panels in Supersonic Flow with Mechanical and Thermal In-plane Loadings

Abstract

This paper is concerned with the uncertain discontinuous nonlinear aeroelastic behavior of in-plane bi-directional functionally graded (FG) metal nanocomposite panels. The panels are subjected to supersonic flow and in-plane mechanical and thermal loadings. This type of FG structures is manufactured using additive manufacturing technologies which might lead to uncertain properties of the manufactured parts due to manufacturing uncertainties, modeling uncertainties in the mathematical and physical formulations used to predict their properties, or uncertainties in the constituent materials properties themselves. These sources of uncertainties might be known with defined probability density functions or defined with uncertain intervals only (fuzzy). Therefore, the mechanical and thermal properties of the nanocomposite material are modeled as uncertain random variables or random fields with known probability distribution function (pdf) or uncertain fuzzy variables or fields with given intervals. The random fields are modeled using the Karhunen–Loève expansion (KLE), and the uncertain output variables are modeled using the Hermite polynomial chaos expansion method (HPCE). The effects of the material properties uncertainties type (fuzzy vs. probabilistic), the cross-correlation between the thermal and mechanical properties, the random fields properties (correlation length, stationary vs. non-stationary, etc.) on the dynamic stability thresholds and the nonlinear limit cycle oscillation are studied.

1 Introduction

The functionally graded structures (FGS) are structures with a continuous spatial variation of one or multiple of their mechanical, thermal, or electrical properties which is done by controlling the spatial variation of the volume fractions of the constituent materials composing the FGS. The concept of a FGS was originated in Japan in the 1980s where scientists and engineers aimed at designing an effective thermal shield of space shuttles that can withstand the intense heat during the reentry, but at the same time match the thermal expansion coefficient of the underlying metallic structure to avoid stress concentrations [1]. Therefore, a functionally graded thermal shield with varying thermal properties across its thickness was invented such that one side is fully metal and the other side is fully ceramic. Since that time, a great progress in the design, the analysis and the manufacturing of FGS is presented by scientists and engineers in many fields ranging from sports equipment, like tennis rackets, to sophisticated medical implants and aerospace parts [2].

Recently, there is a great interest in the design and manufacturing of FGS using multi-materials additive manufacturing (AM) technologies [3,4,5,6,7,8,9]. The advantage of additively manufactured components is the ability to manufacture very intricate shapes with much less material loss compared to the traditional methods (e.g., topology optimized parts), besides that the AM parts can have superior mechanical, thermal, or electrical characteristics due to the multi-materials design strategies. Also, the manufacturing of nanocomposite metal-based components greatly elevated the potentials of AM components as the nano-reinforcement provides much more improvements in the mechanical stiffness and strength properties compared to the micro-reinforcements. A successful production of 3D printed aluminum components were reported in literature with excellent mechanical properties without any defects, such as micro-cracks or agglomeration of the nanoparticles [10,11,12,13]. Also, magnesium-based nanocomposite is gaining more interests because of its light weight which gives it potentials for the aerospace applications [14,15,16].

As for any new technology, there might be uncertainty in the properties of the AM components and these uncertainties must be taken into consideration during the design process. There are two types of uncertainties: aleatoric uncertainty which is an uncertainty that can be quantified and modeled by a probability density function (pdf) through experiments, and epistemic uncertainty which cannot be quantified or modeled by a pdf; like the lack of knowledge of the exact mathematical model of a physical phenomenon, the lack of the measuring equipment to conduct experiments, not enough data to accurately model the uncertainty, etc. [17, 18]. Regarding the uncertain analysis of in-plane FG plates, Hussein and Mulani [19] studied the effect of the material uncertainty on the optimization of in-plane FG carbon nanotube composite plate. The reliability-based optimization was done to satisfy certain maximum displacement criterion under uniform pressure loading. Th uncertain elastic modulus was modeled as a random field and the material distribution was designed using the polynomial expansion of the volume fraction [20, 21]. The same approach is used by Hussein [22] for the uncertain vibration of pre/post-buckled in-plane FG plates. The rest of publications in the literature deal with the uncertainty analysis of through-thickness FG plates; Yang et.al. [23] studied the stochastic static response of FG thick plates under pressure and uniform temperature loadings with material gradation through the plate’s thickness. The mechanical and thermal properties are considered as independent random variables. Chiba and Sugano [24] considered the uncertain static response of a through-thickness FG plate subjected to thermal loadings. The FG plate is assumed to be composed of multi layers of homogenous materials where the thermal conductivity and thermal expansion coefficients of each layer are considered as random variables. An analytical series solution was adopted to estimate the uncertainty in the thermal stresses in the plate. Minh Do et.al [25] investigated the uncertainty quantification of a simply supported through-thickness FG plate under static pressure loading where the elastic modulus is modeled as a random field with imprecise normal probability distribution function such that the mean and the standard deviation of the elastic moduli of the constituent materials are considered as interval uncertain parameters. Talha and Singh [26, 27] analyzed the uncertain thermal buckling and linear vibration of a through-thickness FG thick plate using first-order perturbation stochastic finite element method. The elastic and thermal properties are taken as independent random variables. Shaker et.al. [28] performed a reliability analysis of the free vibration of FG plates using the first-order and the second-order reliability methods where the material properties are taken as independent normal random variables. Karsh et.al. [29] performed a stochastic sensitivity analysis of the free vibration and low-velocity impact response of a through-thickness FG plate. The elastic and mass properties of the materials are considered as random variables. Kitipornchai et.al. [30] studied the random vibration of a laminated FG plate such that the through-thickness FG core is between two homogenous layers. The thermal and elastic properties of the constituent materials are assumed as independent random variables. A parametric study was presented to study the effects of the temperature, the edge support type, the plate’s thickness and aspect ratio on the natural frequencies. Xie and Tian [31] considered the uncertain free vibration of an electric-magneto-elastic FG simply supported plate. The electric, magnetic and elastic properties are assumed to be uncertain interval parameters. Karsh et.al. [32] analyzed the free vibration of a through-thickness FG twisted cantilevered plate with uncertain material properties. Random variable representation of the uncertain parameters is adapted along with neural network finite element framework to quantify the uncertainty level of the natural frequencies. Tomar and Talha [33] investigated the effect of the material uncertainty on the free vibration and the bending response of a skewed sandwich FG plate. The first-order perturbation finite element method is used where the material properties are considered as normal random variables. Macias et.al [34] studied the stochastic free vibration of FG carbon nanotube reinforced plates using a kriging metamodel to quantify the uncertainty in the outputs. The properties of the nanotubes and the matrix materials are taken as random variables. The effect of the through-thickness gradation profile with uncertain parameters is also considered. Trinh and Kim [35] performed an uncertainty analysis of the nonlinear free and forced vibration under uniform harmonic pressure of FG sandwich plates. The plates are considered to have three layers which can be homogenous or FG with random material properties. Jagtap et.al. [36] presented a stochastic nonlinear free vibration of FG plate resting on Winkler nonlinear elastic foundation. The material thermo-elastic parameters and the foundation stiffness coefficients are considered as independent normal random variables. Recently, an isogeometric-based analysis was used for the uncertainty quantification of FG plates. Tran et.al. [37] studied the stochastic vibration of through-thickness FG microplates using higher-order shear deformation theory. The material properties are assumed to be lognormal random variables. Karsh et.al [38]. adopted a radial-basis function based finite element method to investigate the stochastic vibration of cantilevered plates. Kumaraian et.al [39] used a cell-based smoothed finite element method to analyze the effect of the elastic modulus uncertainty on the linear vibration of through-thickness FG plates. Vaishali et.al. utilized a support vector machine learning approach to study stochastic vibration and impact response of FG plates where geometric and material uncertainties are considered. The work in [40,41,42,43,44,45] adopted the spectral isogeometric analysis approach to study the uncertain linear vibration of through-thickness FG plates with where the elastic modulus is modeled as Gaussian random fields.

As can be seen from the literature review, the uncertain nonlinear aeroelastic analysis of in-plane FG plates has not been addressed before. Therefore, this work considers a parametric analysis to study the effect of the material properties uncertainties on the aeroelastic stabilities thresholds of in-plane FG panels and on the limit cycle oscillation in the post-flutter state. The parametric study includes the uncertainty modeling type (fuzzy vs. probabilistic), the cross-correlation effect between the thermal expansion coefficient and the elastic modulus, the mechanical and thermal random fields correlation lengths, and the random fields type (stationary vs. non-stationary). Also the uncertain aeroelastic stability thresholds of in-plane FG plates are compared to the homogenous plates.

2 Mathematical Modeling and Formulations

2.1 Finite Element Formulation

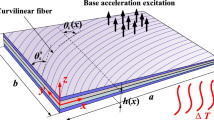
The aeroelastic analysis in this work is done using the finite element method where the panel is discretized into ${N}_{x} \times {N}_{y}$ four-nodded quadrilateral elements. The in-plane axial displacements of the panel’s mid-plane in the x and y directions (${u}_{o} \mathrm{and} {v}_{o}$) are considered to be bilinear functions over each element, while the out-of-plane displacement (${w}_{o}$) is considered to be a third-order function as follows [46]:

$$\begin{aligned} w_{o} \left( {\xi ,\eta } \right) & = a_{o} + a_{1} \xi + a_{2} \eta + a_{3} \xi \eta + a_{4} \xi^{2} + a_{5} \eta^{2} \\ & \quad + a_{6} \xi \eta^{2} + a_{7} \xi^{2} \eta + a_{8} \xi^{3} + a_{9} \eta^{3} + a_{10} \xi \eta^{3} \\ & \quad + a_{11} \eta \xi^{3} \end{aligned}$$

(1.1)

$$u_{o} \left( {\xi ,\eta } \right) = b_{o} + b_{1} \xi + b_{2} \eta + b_{3} \xi \eta$$

(1.2)

$$v_{o} \left( {\xi ,\eta } \right) = c_{o} + c_{1} \xi + c_{2} \eta + c_{3} \xi \eta$$

(1.3)

The non-dimensional coordinates $\xi$ and $\eta$ are the reference element’s local coordinates centered at its center as shown in Fig. 1. Therefore, the mid-plane displacements field can be written in terms of the in-plane nodal degrees of freedom vector $\left\{{q}_{I}\right\}$ and the out-of-plane nodal degrees of freedom vector $\left\{{q}_{o}\right\}$ using shape functions (${\mathcal{N}}_{u} {\mathcal{N}}_{v} \mathrm{and} {\mathcal{N}}_{w}$) as follows:

$$\begin{gathered} w_{o} \left( {\xi ,\eta } \right) = {\mathcal{N}}_{w} \left\{ {q_{o} } \right\} \hfill \\ \left\{ {u_{o} \left( {\xi ,\eta } \right),v_{o} \left( {\xi ,\eta } \right)} \right\} = \left[ {{\mathcal{N}}_{u} {\mathcal{N}}_{v} } \right]^{T} \left\{ {q_{I} } \right\} \hfill \\ \end{gathered}$$

(2)

Fig. 1

a schematic diagram of a panel in a supersonic flow. b reference finite element nomenclature

The formulations of the elemental matrices can be obtained by applying the Hamilton’s principle which can be written in terms of the kinetic energy ($\mathcal{T}$), the strain energy ($\mathcal{U}$) and the external work done (${\mathcal{W}}_{ext}$) as follows:

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta \left( {{\mathcal{T}} - {\mathcal{U}} - {\mathcal{W}}_{ext} } \right)dt = 0$$

(3)

The current analysis deals with thin panels, so the classical plate theory (Kirchhoff–Love plate theory) is adequate to be used which describes the displacement field in terms of the mid-plane displacements as follows [47]:

$$u\left( {x,y,z} \right) = u_{o} \left( {x,y} \right) - z\frac{{\partial w_{o} \left( {x,y} \right)}}{\partial x}$$

(4.1)

$$\,v\left( {x,y,z} \right) = v_{o} \left( {x,y} \right) - z\frac{{\partial w_{o} \left( {x,y} \right)}}{\partial y}$$

(4.2)

$$w\left( {x,y,z} \right) = w_{o} \left( {x,y} \right)$$

(4.3)

Therefore, the nonlinear von Kármán mechanical strains can be written in terms of the mid-plane displacements, The thermal expansion coefficient ($\alpha$) and the temperature change ($\Delta T)$ as follows:

$$\begin{aligned} \vec{\varepsilon } = \left\{ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {2\varepsilon _{{xy}} } \\ \end{array} } \right\} & = \left\{ {\begin{array}{*{20}c} {u_{o} ,_{x} } \\ {v_{o} ,_{y} } \\ {u_{o} ,_{y} + v_{o} ,_{x} } \\ \end{array} } \right\} - z\left\{ {\begin{array}{*{20}c} {w_{o} ,_{{xx}} } \\ {w_{o} ,_{{yy}} } \\ {2w_{o} ,_{{xy}} } \\ \end{array} } \right\} \\ & \quad + \frac{1}{2}\left\{ {\begin{array}{*{20}c} {w_{o} ,_{x}^{2} } \\ {w_{o} ,_{y}^{2} } \\ {2w_{o} ,_{x} w_{o} ,_{y} } \\ \end{array} } \right\} - \alpha \left( {x,y} \right)\Delta T\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ \end{array} } \right\} \\ & = \vec{\varepsilon }_{o} + z\vec{k} + \vec{\varepsilon }_{n} - \vec{\varepsilon }_{T} \\ \end{aligned}$$

(5)

$\mathrm{where} {\overrightarrow{\varepsilon }}_{o}$ is the mid-plane linear strain vector, $\overrightarrow{k}$ is the mid-plane curvature vector, ${\overrightarrow{\varepsilon }}_{n}$ is the mid-plane nonlinear strain vector and ${\overrightarrow{\varepsilon }}_{T}$ is the thermal strain vector. The in-plane stresses ($\overrightarrow{\sigma }={\left\{\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{yy}& {\sigma }_{xy}\end{array}\right\}}^{T}$) can be estimated using the constitutive relation matrix $[C(x,y)]$ which is written in terms of the material elastic modulus $E(x,y)$ and Poisson’s ratio $\upnu (x,y)$ at a point as follows:

$$\vec{\sigma } = \left[ C \right]\vec{\varepsilon } = \frac{{E\left( {x,y} \right)}}{{1 - {\upnu }^{2} \left( {x,y} \right)}}\left[ {\begin{array}{*{20}c} 1 & {{\upnu }\left( {x,y} \right)} & 0 \\ {{\upnu }\left( {x,y} \right)} & 1 & 0 \\ 0 & 0 & {\frac{{1 - {\upnu }\left( {x,y} \right)}}{2}} \\ \end{array} } \right]\vec{\varepsilon }$$

(6)

Hence the variation of the strain energy of an element can be written as follows:

$$\delta {\mathcal{U}} = \iint {\delta \vec{\varepsilon }^{{\text{ T}}} \left[ C \right]\vec{\varepsilon } dV} = \iint {(\delta \vec{\varepsilon }_{o} + z \delta \vec{k} + \delta \vec{\varepsilon }_{n} )\left[ C \right]\left( {\vec{\varepsilon }_{o} + z\vec{k} + \vec{\varepsilon }_{n} - \vec{\varepsilon }_{T} } \right)} J d\xi d\eta dz$$

(7)

where $J$ is the integration Jacobian. The effective elastic and thermal properties of the metal nanocomposite can be computed using the Hashin–Shtrikman upper bound and the Kerner’s model, respectively [48]. The bulk and shear moduli of the nanocomposite ($\mathcal{K},G$) can be written in terms of the metal matrix bulk and shear moduli (${\mathcal{K}}_{m},{G}_{m}$), the nano-reinforcement bulk and shear moduli (${\mathcal{K}}_{p},{G}_{p}$) and the reinforcement volume fraction (${v}_{f}$) as follows:

$${\mathcal{K}} = {\mathcal{K}}_{p} + \left( {1 - v_{f} } \right)\left[ {\frac{1}{{{\mathcal{K}}_{m} - {\mathcal{K}}_{p} }} + \frac{{3v_{f} }}{{3{\mathcal{K}}_{p} + 4G_{p} }}} \right]^{ - 1}$$

(8.1)

$$G = G_{p} + \left( {1 - v_{f} } \right)\left[ {\frac{1}{{G_{m} - G_{p} }} + \frac{{6v_{f} \left( {{\mathcal{K}}_{p} + 2G_{p} } \right)}}{{5G_{p} \left( {3{\mathcal{K}}_{p} + 4G_{p} } \right)}}} \right]^{ - 1}$$

(8.2)

Hence, the Young’s modulus and the Poisson’s ratio of the nanocomposite will be as follows:

$$E = \frac{{9{\mathcal{K}}G}}{{3{\mathcal{K}} + G}} , v = \frac{{3{\mathcal{K}} - 2G}}{{6{\mathcal{K}} + 2G}}$$

(9)

The thermal expansion coefficient of the composite material is written as follows:

$$\begin{aligned} \alpha &= v_{f} \alpha _{p} + \left( {1 - v_{f} } \right)\alpha _{m} {\text{ }} + v_{f} \left( {1 - v_{f} } \right)\left( {\alpha _{p} - \alpha _{m} } \right)\\ & \qquad \times \frac{{{\mathcal{K}}_{p} - {\mathcal{K}}_{m} }}{{v_{f} {\mathcal{K}}_{p} + \left( {1 - v_{f} } \right){\mathcal{K}}_{m} + 3{\mathcal{K}}_{p} {\mathcal{K}}_{m} /4G_{m} }} \end{aligned}$$

(10)

where ${\alpha }_{m}$ is the metal thermal expansion coefficient, while ${\alpha }_{p}$ is the reinforcement thermal expansion coefficient. The variation of the external work done can be computed due to the aerodynamic pressure loading $p(x,y)$ and the applied in-plane loading $\overrightarrow{f}$ as follows:

$$\delta {\mathcal{W}}_{ext} = \iint {\delta w_{o} p\left( {x,y} \right) J d\xi d\eta } + {\oint }\left\{ {\delta u_{o} \delta v_{o} } \right\}^{T} \vec{f} ds$$

(11)

The supersonic aerodynamic pressure loading can be computed using the first-order piston theory which is given in terms of the free stream speed (${V}_{\infty }$), the free stream density (${\rho }_{\infty }$), the non-dimensional aerodynamic pressure$( \lambda )$, the non-dimensional aerodynamic damping coefficient ($g$), a reference elastic modulus ($\overline{E }$), a reference Poisson’s ration ($\overline{\upnu }$), a reference bending stiffness ($\overline{D }=\overline{E}{h }^{3}/12(1-{\overline{v} }^{2})$), a reference material density ($\overline{\rho }$), a reference frequency ( $\overline{\omega }=\sqrt{ \overline{D }/\overline{\rho }h{l}^{4}}$), and the panel’s side length ($l$) and thickness ($h$) as follows [49]:

$$\begin{aligned} & p\left( {x,y} \right) = - \left[ {\frac{{\lambda \bar{D}}}{{l^{3} }}w_{o} ,_{x} + \frac{{g\bar{D}}}{{\bar{\omega }l^{4} }}\dot{w}_{o} } \right] \\ & \lambda = \frac{{\rho _{\infty } V_{\infty }^{2} l^{3} }}{{\bar{D}\sqrt {M_{\infty }^{2} - 1} }},g = \frac{{\rho _{\infty } V_{\infty } \left( {M_{\infty }^{2} - 2} \right)}}{{\bar{\rho }h\bar{\omega }(M_{\infty }^{2} - 1)^{{3/2}} }} \approx \sqrt {\mu \lambda /M_{\infty } } \\ \end{aligned}$$

(12)

The value of the mass ratio $\left(\mu ={\rho }_{\infty }l/ \overline{\rho }h \right)$ over the free stream Mach number (${M}_{\infty }$) is given a value of 0.015. Finally, the variation of the Kinetic energy can be written as follows:

$$\delta {\mathcal{T}} = \iint {\rho h \left( {\delta \dot{w}_{o} \dot{w}_{o} + \delta \dot{u}_{o} \dot{u}_{o} + \delta \dot{v}_{o} \dot{v}_{o} } \right) } J d\xi d\eta$$

(13)

Substituting the expressions of the variational strain energy, the variational external work done and the variational kinetic energy into the Hamilton’s principle along with Eq. 2 yield the aeroelastic system of equations in terms of the nodal degrees of freedom as follows [48, 49]:

$$\begin{aligned} &\left[ {\begin{array}{*{20}c} {M_{o} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } & {M_{I} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{\vec{q}}_{o} } \\ {\ddot{\vec{q}}_{I} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {A_{d} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{\vec{q}}_{o} } \\ {\dot{\vec{q}}_{I} } \\ \end{array} } \right\} \\ & + \left( {\left[ {\begin{array}{*{20}c} {K_{o} - K_{o}^{{\Delta T}} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } & {K_{I} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A_{s} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {N1_{{oo}} } & {N1_{{oI}} } \\ {N1_{{Io}}^{T} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {N2_{{oo}} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} {\vec{q}_{o} } \\ {\vec{q}_{I} } \\ \end{array} } \right\}\\ & = \left\{ {\begin{array}{*{20}c} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{0} } \\ {\vec{F}_{I}^{{\Delta T}} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\vec{F}_{o} } \\ {\vec{F}_{I} } \\ \end{array} } \right\} \end{aligned}$$

(14)

The formulae of these matrices are given in the appendix. For the out-of-plane dynamic analysis, the in-plane inertial forces can be neglected as the in-plane natural frequencies are much higher than the out-of-plane natural frequencies which reduces the system of equation to be written solely in terms of the out-of-plane degrees of freedom as follows:

$$\begin{aligned} &\left[ {M_{o} } \right]\left\{ {\ddot{\vec{q}}_{o} } \right\} + \left[ {A_{{do}} } \right]\left\{ {\dot{\vec{q}}_{o} } \right\} \\ & \qquad + \left( {\left[ {K_{o} - K_{o}^{{\Delta T}} } \right] + \left[ {A_{{so}} } \right] + \left[ {N1_{{oo}} } \right] + \left[ {N2_{{oo}} } \right] + \left[ {\mathbb{N}} \right]} \right)\left\{ {\vec{q}_{o} } \right\} \\ & \quad = \left\{ {\vec{F}_{o} } \right\} + \left\{ {{\vec{\mathfrak{f}}}} \right\} \end{aligned}$$

(15)

The matrix $[{\mathbb{N}}]$ and vector $\{{\mathbb{f}}\}$ can be written as follows:

$$\left[ {\mathbb{N}} \right] = - \left[ {N1_{oI} } \right]\left[ {K_{I} } \right]^{ - 1} \left[ {N1_{Io} } \right]$$

(16)

$$\left\{ {{\vec{\mathfrak{f}}}} \right\} = - \left[ {N1_{oI} } \right]\left[ {K_{I} } \right]^{ - 1} \left( { \vec{F}_{I}^{\Delta T} + \vec{F}_{I} } \right)$$

(17)

2.2 Karhunen–Loève Expansion (KLE) and the Polynomial Chaos Expansion (PCE) for Uncertainty Analysis

The material mechanical and thermal uncertain properties can be either modeled as random variables or random fields. In this study, both approaches are adopted for the parametric analysis. The random field can be numerically represented by the KL expansion method which models the spatial randomness of an uncertain Gaussian property $({\varvec{X}})$ with a mean ${\mu }_{X}(x,y)$ and a standard deviation ${\sigma }_{X}\left(x,y\right)$ in a 2D domain using a finite series with $({n}_{k})$ terms as follows [50]:

$${\varvec{X}}\left( {x,y} \right) = \mu_{X} \left( {x,y} \right) + \sigma_{X} \left( {x,y} \right)\mathop \sum \limits_{i = 1}^{{n_{k} }} {\mathbb{Z}}_{i} \sqrt {\lambda_{i} } \phi_{i} \left( {x,y} \right)$$

(18)

where ${\mathbb{Z}}_{i}$ are independent standard normal variables, while the functions ${\phi }_{i}(x,y)$ and coefficients ${\lambda }_{i}$ are the eigenfunctions and eigenvalues of the auto-correlation function ${\mathbb{C}}(\Delta x,\Delta y),$ respectively, which can be obtained by solving the following integral equation:

$$\iint {{\mathbb{C}}\left( {x - {\mathbb{x}},y - {\mathbb{y}}} \right)\psi \left( {{\mathbb{x}},{\mathbb{y}}} \right){ }d{\mathbb{x}}{ }d{\mathbb{y}} = \lambda \psi \left( {x,y} \right)}$$

(19)

The number of terms in the series expansion depends on the nature of the auto-correlation function which is assumed in this work to be an exponential decaying function with a correlation length (${l}_{c}$) as follows:

$${\mathbb{C}}\left( {x - {\mathbb{x}},y - {\mathbb{y}}} \right) = e^{{ - \frac{{\left| {x - {\mathbb{x}}} \right| + \left| {y - {\mathbb{y}}} \right|}}{{l_{c} }}}}$$

(20)

A single realization of random fields of a standard Gaussian property (${\mu }_{X}\left(x,y\right)=0, {\sigma }_{X}\left(x,y\right)$ =1) with correlation lengths 1, 0.5 and 0.25 for a unit 2D field are shown in Figs.2, 3, 4, respectively. If random variable model is used (${l}_{c}\to \infty$), then the uncertain property can be simply written as follows:

$${\varvec{X}}\left( {x,y} \right) = \mu_{X} \left( {x,y} \right) + \sigma_{X} \left( {x,y} \right){\mathbb{Z}}$$

(21)

Fig. 2

A normalized random field realization $(X-{\mu }_{X})/{\sigma }_{X}$ with ${l}_{c}^{*}=1$

Fig. 3

A normalized random field realization $(X-{\mu }_{X})/{\sigma }_{X}$ with ${l}_{c}^{*}=0.5$

Fig. 4

A normalized random field realization $(X-{\mu }_{X})/{\sigma }_{X}$ with ${l}_{c}^{*}=0.25$

When the mean and the standard deviation of a random field are constants, the field is called a stationary field as in the case of homogenous plates, otherwise the field is considered a non-stationary. In case of correlated uncertain properties ${\varvec{X}}(x,y)$ and ${\varvec{Y}}(x,y)$ with a cross-correlation coefficient (${\rho }_{c}$), the random fields can be simulated using two uncorrelated standard Gaussian random fields $\mathcal{X}\left(x,y\right)$ and $\mathcal{Y}(x,y)$ as follows:

$$\left\{ {\begin{array}{*{20}c} {\user2{X}\left( {x,y} \right)} \\ {\user2{Y}\left( {x,y} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mu _{X} \left( {x,y} \right)} \\ {\mu _{Y} \left( {x,y} \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\sigma _{X} \left( {x,y} \right)} & 0 \\ 0 & {\sigma _{Y} \left( {x,y} \right)} \\ \end{array} } \right]\left[ {\mathcal{A}} \right]\left[ {\sqrt {\mathcal{D}} } \right]\left\{ {\begin{array}{*{20}c} {{\mathcal{X}}\left( {x,y} \right)} \\ {{\mathcal{Y}}\left( {x,y} \right)} \\ \end{array} } \right\}$$

(22)

The matrices $\left[\mathcal{A}\right]$ and $[\mathcal{D}]$ are the eigenvectors matrix and the eigenvalues matrix of the cross-correlation matrix $[\mathcal{C}]$ written as follows:

$$\left[ {\mathcal{C}} \right] = \left[ {\begin{array}{*{20}c} 1 & {\rho_{c} } \\ {\rho_{c} } & 1 \\ \end{array} } \right]$$

(23)

When the probability density function of an uncertain property or variable is not known, the fuzzy uncertainty analysis is used where the uncertain variable is model as an interval with a mid-value ${X}_{m}$, an upper limit ${\overline{X} }^{\beta }$, and a lower limit ${\underline{X}}^{\beta }$ for each $\beta -\mathrm{level}$ cut as shown in Fig. 5 which is known as the possibility function of the uncertain variable. A fuzzy uncertain variable is mathematically represented as follows:

$${\varvec{X}} = X_{m}^{\beta } + \left( {\frac{{{ }\overline{X}^{\beta } - \underline {X}^{\beta } }}{2}} \right){\mathbb{I}},{\mathbb{I}} \in \left[ { - 1,1} \right]$$

(24)

Fig. 5

The possibility curve of a normalized fuzzy uncertain variable

The spatial randomness of a fuzzy uncertain property can be modeled using a modified version of the KLE method to simulate an interval field which treats the fuzzy property as a uniform random field using the cumulative density functions of the standard normal distribution (${\mathcal{F}}_{N}$) and the uniform distribution (${\mathcal{F}}_{U}$) as follows:

$${\varvec{X}}\left( {x,y} \right) = X_{m}^{\beta } \left( {x,y} \right) + \left( {\frac{{{ }\overline{X}^{\beta } - \underline {X}^{\beta } }}{2}} \right) {\mathcal{F}}_{U}^{ - 1} {\mathcal{F}}_{N} \left( {\mathop \sum \limits_{i = 1}^{{n_{k} }} {\mathbb{Z}}_{i} \sqrt {\lambda_{i} } \phi_{i} \left( {x,y} \right)} \right)$$

(25)

For the uncertainty propagation analysis, the uncertain output variables can be quantified either by using a sampling method (e.g., Monte Carlo Sampling, Latin Hyper Cube Sampling LHS, etc.) or by using a metamodel. In this article, the uncertainty of an output variable (${\mathbb{Y}}$) in the probabilistic analysis will be quantified using the polynomial chaos expansion method which represents the uncertain output by a series of orthogonal polynomials with unknown coefficients. The orthogonality is with respect to the pdfs of the input variables. For uncertain normal inputs, Hermite polynomials ${H}_{n}\left({\mathbb{Z}}\right)$ are used as follows [50]:

$${\mathbb{Y}} = \mathop \sum \limits_{j = 0}^{p} c_{n} H_{n} \left( {\mathbb{Z}} \right)$$

(26)

where the Hermite polynomials for a single input are given by the following formula:

$$\begin{aligned} H_{o} \left( {\mathbb{Z}} \right) & = 1, \\ H_{1} \left( {\mathbb{Z}} \right) & = {\mathbb{Z}} \\ H_{n} \left( {\mathbb{Z}} \right) & = {\mathbb{Z}} H_{n - 1} \left( {\mathbb{Z}} \right) - \left( {n - 1} \right)H_{n - 2} \left( {\mathbb{Z}} \right) \\ \end{aligned}$$

(27)

For multiple inputs, the Hermite polynomial in the series expansion will be the tensor product of the polynomials of the input variable. The coefficients of the PCE are estimated using the least square method as follows:

$$\vec{c} = \left( {\left[ {\text{H}} \right]^{T} \left[ {\text{H}} \right]} \right)^{ - 1} \left[ {\text{H}} \right]^{T} {\vec{\mathbb{Y}}}$$

(28)

For Fuzzy uncertainty analysis, only the upper and lower limit of the uncertain output at a certain $\beta -\mathrm{level}$ of the uncertain input variables are required which can be seen as an optimization problem. The KLE transformation given in Eq. 20 for simulating the interval field causes the outputs to be highly nonlinear in the input variables even for a linear physical system which will in turn require high-order PCE with too many coefficients and a large number of code runs that approaches the number of runs of the LHS method. For example, an interval field with 30 inputs and a third-order PCE for an output requires 5456 runs. Therefore, the LHS method is used in this work to estimate the uncertainty limits of the fuzzy outputs.

3 Numerical Results

The nanocomposite panels in this work are made of magnesium as the metal matrix material which has a Young’s modulus of 44 GPa, a Poisson’s ratio of 0.33 and a thermal expansion coefficient of 26 (10^–6) ${{C}^{o}}^{-1}$. The nano-reinforcement is Silicon Carbide particles which have a Young’s modulus of 570 GPa, a Poisson’s ratio of 0.19 and a thermal expansion coefficient of 4 (10^–6) ${{C}^{o}}^{-1}$. Using the upper-bound Hashin–Shtrikman model and the Kerner’s model, the effective mechanical and thermal properties of the nanocomposite can be written as follows [48]:

$$\begin{aligned} \begin{aligned} E & = 44.14 + 289.54v_{f} + 152.67v_{f}^{2} ~~~~\left( {GPa} \right) \\ v & = 0.33 - 0.5160~v_{f} + 1.1816~v_{f}^{2} - 1.248~v_{f}^{3} \\ \rho & = 3200~v_{f} + 1700\left( {1 - v_{f} } \right)~~~\left( {Kg/m^{3} } \right) \\ \alpha & = \left( {26 - 30.69~v_{f} + 10.354~v_{f}^{2} ~} \right)10^{{ - 6}} ~\Delta C^{{o - 1}} \\ \end{aligned}\end{aligned}$$

(29)

The in-plane volume fraction distribution of the nano-reinforcement for clamped and simply supported plates is shown in Figs. 6 and 7, respectively, and can be written using non-dimensional coordinates (${x}^{*}=x/l and {y}^{*}=2y/l$) using the results of a previously done work [48] as follows:

$$\begin{aligned} v_{f}^{cc} \left( {x^{*} } \right) & = 0.2444 + 0.3795x^{*} - 0.3849x^{*2} \\ v_{f}^{cc} \left( {y^{*} } \right) & = 0.0406y^{*} + 0.4142y^{*2} + 0.8470y^{*3} - 0.8426y^{*4} \\ \end{aligned}$$

(30)

$$\begin{aligned} v_{f}^{ss} \left( {x^{*} } \right) & = 0.1621 + 0.6402x^{*} - 0.9457x^{*2} + 1.7592x^{*3} - 1.6116x^{*4} \\ v_{f}^{ss} \left( {y^{*} } \right) & = 1.4892y^{*2} - 0.993y^{*3} \\ \end{aligned}$$

(31)

Fig. 6

The volume fraction distribution of the SiC nano-reinforcement for the FG clamped panel

Fig. 7

The volume fraction distribution of the nano-reinforcement for the FG simply supported panel

This volume fraction distribution is obtained such that the FG panels have a critical flutter dynamic pressure that match that of homogenous panels with a uniform volume fraction of 9% without any in-plane loadings. The overall volume fraction of the FG clamped panel is 6.17%, while for the FG simply supported panel is 7.06%. The considered panels are square with a side length of 0.6 m and a thickness of 3 mm. The panels are discretized into 31 × 31 finite elements for numerical analysis and the material properties random fields and interval fields are simulated for correlation lengths of 0.25, 0.5, 1 and $\infty$. Also, the uncertainty level of the uncertain properties represented by the coefficient of variation (c.o.v. = $\sigma (x,y)/\mu (x,y)$) is modeled either as a uniform field with a value of 5% (Model 1) or as a linear field that depends on the volume fraction of the reinforcement $5 ({v}_{f}/0.2) \%$ (Model 2). The analysis considers two types of in-plane loadings: mechanical bi-axial loading (${f}_{x}={f}_{y}$) where the elastic modulus of the nanocomposite is the only uncertain property, and thermal in-plane loading where the elastic modulus and the thermal expansion coefficient are uncertain properties. The density and the Poisson’s ratio are taken as deterministic properties as their uncertainty levels are very small compared to the other properties [19].

The uncertainty propagation analysis starts with quantifying the uncertainty in the critical flutter non-dimensional dynamic pressure (${\lambda }_{cr}$) and the critical buckling mechanical load (${f}_{cr}$) and the critical buckling temperature change (${\Delta T}_{cr}$). The deterministic value of the critical mechanical buckling load is $({\mathbb{F}}_{cr}=\kappa {\pi }^{2}\overline{D }/{l}^{2})$ where $\kappa$ is 1.867 for the FG simply supported panel and 4.753 for the FG clamped panel, while the deterministic value of the critical buckling temperature change is $({\Delta {\mathbb{T}}}_{cr}=\kappa {\pi }^{2}{h}^{2}/({12(1+\overline{v })\overline{\alpha }l}^{2}))$ where $\kappa$ is 2 for the FG simply supported panel and 5.26 for the FG clamped panel. The reference values with overhead bar sign are taken to of that of the homogenous panels.

3.1 Probabilistic Analysis

The probabilistic analysis of the uncertain stability thresholds is done by using first-order PCEs. The mean and the c.o.v. of the critical non-dimensional dynamic pressure (${\lambda }_{cr}$) without in-plane loading, the critical non-dimensional mechanical buckling load (${f}_{cr}^{*}={f}_{cr}/{\mathbb{F}}_{cr}$) at zero flow speed, and the critical non-dimensional buckling temperature change (${\Delta T}_{cr}^{*}={\Delta T}_{cr}/{\Delta {\mathbb{T}}}_{cr}$) at zero flow speed are given in Tables 1, 2 and 3, respectively. It can be seen that, in general, the model 2 random field yields 50–60% lower uncertainty level in the output random variables compared to the model 1 random field. Both the homogenous and the FG panels show the same uncertainty level for the model 1 random field. For model 2 random field, the FG panels have slightly more uncertainty level compared to the homogenous panels and this difference increases as the correlation length decreases. For example, the FG clamped panel has 5% more uncertainty level for ${l}_{c}^{*}=1$, and 15% more uncertainty level for ${l}_{c}^{*}=0.25$. As the correlation length of the random fields decreases, the outputs uncertainty levels decrease in a quadratic sense for ${l}_{c}\le 1$.

Table 1 The uncertainty analysis results of the critical non-dimensional dynamic pressure (${\lambda }_{cr}$) without in-plane loadings

Table 2 The uncertainty analysis results of the critical non-dimensional mechanical buckling load (${f}_{cr}^{*}$) at zero flow speed

Table 3 The uncertainty analysis results of the critical non-dimensional thermal buckling load ($\Delta {T}_{cr}^{*}$) at zero flow speed

When mechanical in-plane loading is applied to the panels, stability boundaries map can be obtained as shown in Figs. 8 and 9 which show the 6-sigma stability intervals (99.7% confidence interval) for the FG clamped panel and the FG simply supported panel, respectively. The standard deviation in the critical dynamic pressure remains constant as the in-plane mechanical loading increases, while the mean values decrease which yield an approximate linearly increasing function of the flutter uncertainty level in terms of the in-plane loadings. On the other hand, the mechanical buckling uncertainty level decreases as the flow dynamic pressure increases. The case of thermal in-plane loading is more interesting as the cross-correlation between the elastic modulus and the thermal expansion coefficient plays a very important role. Figures 10 and 11 show the 6-sigma stability intervals for the FG clamped panel and the FG simply supported panel, respectively, in the case of model 2 random field with ${l}_{c} \to \infty$. When the elastic modulus and the thermal coefficient are inversely correlated (${\rho }_{c}=-1$), the uncertainty level behavior is similar to the mechanical in-plane loading case, and when they are perfectly correlated (${\rho }_{c}=1$), the uncertainty level in the critical flutter dynamic pressure decreases till it almost vanishes at approximately ${\Delta T}^{*}$=1 for the clamped panel and at ${\Delta T}^{*}=1.65$ for the simply supported panel. To quantify the effect of this cross-correlation, a parametric study is given in Tables 4 and 5 which show a strong nonlinear dependency on the cross-correlation coefficient, especially near ${\rho }_{c}=1$ which in turn depends on the value of the thermal in-plane loading relative to the critical buckling load. Also, it can be concluded that any level of cross-correlation will lead to a decrease in the dynamic pressure uncertainty level as the temperature increases. For the case of uncorrelated material properties, Tables 6 and 7 show a parametric study on the effect of the relative values of the random fields’ correlation lengths on the uncertainty level. The results show that both the elastic modulus and the thermal expansion coefficient have the same weight of effect which is indicated by the nearly symmetric c.o.v. values given in the tables.

Fig. 8

The uncertain stability boundaries of the FG clamped panel with mechanical in-plane loadings (model 1 random field)

Fig. 9

The uncertain stability boundaries the FG simply supported panel with mechanical in-plane loadings (model 1 random field)

Fig. 10

The uncertain stability boundaries of the FG clamped panel with thermal in-plane loadings (model 2 random field ${l}_{c}^{*}=\infty$)

Fig. 11

The uncertain stability boundaries of the FG simply supported panel with thermal in-plane loadings (model 2 random field ${l}_{c}^{*}=\infty$)

Table 4 The effect of the cross-correlation coefficient (${\rho }_{c}$) on the c.o.v. % of the critical dynamic pressure of the clamped panels at ${\Delta T}^{*}$=1. (${\mu }_{\lambda }^{FG}=415.5, {\mu }_{\lambda }^{H}=414$)

Table 5 The effect of the cross-correlation coefficient (${\rho }_{c}$) on the c.o.v. % of the critical dynamic pressure of the simply supported panels at ${\Delta T}^{*}$=1.65. (${\mu }_{\lambda }^{FG}=244, {\mu }_{\lambda }^{H}=242$)

Table 6 The effect of the correlation lengths of the uncorrelated material properties random fields on the c.o.v.% of the critical dynamic pressure of the clamped panels at ${\Delta T}^{*}$=1. (${\mu }_{\lambda }^{FG}=415.5, {\mu }_{\lambda }^{H}=414$)

Table 7 The effect of the correlation lengths of the uncorrelated material properties random fields on the c.o.v. % of the critical dynamic pressure of the simply supported panels at ${\Delta T}^{*}$=1.6. (${\mu }_{\lambda }^{FG}=244, {\mu }_{\lambda }^{H}=242$)

The uncertainty is propagated to the post-flutter response by considering the uncertainty in the limit cycle oscillation (LCO) amplitude at a certain free stream dynamic pressure (${\lambda }_{s}$). Figure 12 shows the 99.7% confidence interval of the non-dimensional LCO amplitude ($W={w}_{max}/h$) for the FG clamped panel at zero in-plane loadings for the model 1 random field with a non-dimensional correlation length of 0.25. The interval boundaries and the back-bone nonlinear response curves are estimated using the fourth-order Runge–Kutta method with a time step of 0.0001 s. The post-flutter uncertainty analysis is performed by using a surrogate model which presents the uncertain critical dynamic pressure in terms of the non-dimensional displacement using a polynomial representation as follows:

$$\lambda_{cr} - \lambda_{s} = a_{1} W + a_{2} W^{2} + a_{3} W^{3}$$

(32)

Fig. 12

The 99.7% confidence interval of the non-dimensional LCO amplitude of the FG clamped panel (model 1 random field with ${l}_{c}^{*}=0.25$)

The coefficients ${a}_{i}{\prime}s$ are determined using the data from curves in Fig. 12 as follows:

$$\begin{aligned} a_{1} & = 2.73019\left( {10} \right)^{ - 3} \lambda_{cr}^{2} - 4.71959 \lambda_{cr} + 2.03624 \left( {10} \right)^{3} \\ a_{2} & = - 9.42266\left( {10} \right)^{ - 3} \lambda_{cr}^{2} + 16.76664 \lambda_{cr} - 7.14187 \left( {10} \right)^{3} \\ a_{3} & = 6.64904\left( {10} \right)^{ - 3} \lambda_{cr}^{2} - 11.57057 \lambda_{cr} + 5.0329 \left( {10} \right)^{3} \\ \end{aligned}$$

(33)

The uncertainty nature of the LCO amplitude depends on the free stream dynamic pressure value which can be seen from Figs. 13, 14, 15 showing the histograms of the LCO amplitude at dynamic pressures of 852, 906, 950, respectively. When the free stream dynamic pressure equals the mean critical dynamic pressure, the LCO amplitude histogram is discontinuous with 50% zero values. For a dynamic pressure at the maximum value of the 6-sigma interval, the histogram is similar to a skewed Rayleigh distribution. For higher dynamic pressure values, the histogram approaches the normal distribution. Table 8 shows the uncertainty parameters of the non-dimensional LCO amplitude for the FG clamped panel in case of the model 2 random field. Analyzing the results in Tables 1 and 8, it can be seen that for a free stream dynamic pressure equals the mean critical dynamic pressure $({\lambda }_{s}=852)$, the mean LCO amplitude varies almost linearly with the critical dynamic pressure c.o.v., while the LCO amplitude c.o.v. remains constant. As the dynamic pressure increases, the distribution of the amplitude approaches the normal distribution with decreasing deviations and skewnesses and the mean seems to be invariant of the random field correlation length. The uncertainty level decreases as the flutter dynamic pressure uncertainty level decreases. On the other hand, as the free stream dynamic pressure decreases below the critical flutter mean value, the mean LCO amplitude decreases to almost zero at the lower end of the confidence interval which lead to an exponential increase in the LCO amplitude c.o.v and the uncertainty level increases as the free stream dynamic pressure decreases. The same uncertain behavior is exhibited by the other panels and in the cases of in-plane loadings, so there is no need to present them.

Fig. 13

The histogram of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=852$ and ${f}^{*}=0$ (model 2 random field $l_c^*\to \infty$)

Fig. 14

The histogram of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=906$ and ${f}^{*}=0$

Fig. 15

The histogram of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=950$ and ${f}^{*}=0$

Table 8 The mean, c.o.v., and skewness of the non-dimensional LCO amplitude of the FG clamped panel at different free stream dynamic pressure values in case of the model 2 random field

3.2 Fuzzy Analysis

Fuzzy uncertainty analysis only estimates the limits of the uncertain outputs at a certain $\beta -\mathrm{level}$ regardless of their probability distribution as stated in Sect. 2.2. In this article, the radius of the fuzzy uncertain inputs at the zero-level is taken as 0.15 of their mid-values which is the fuzzy equivalent of a normal probabilistic input with 5% c.o.v. Fully inverse correlated material properties are considered when simulating the interval fields as it will give the maximum and minimum limits as was concluded from the probabilistic analysis. The uncertainty in the critical dynamic pressure is performed using 4000 LHS which yielded the results in Table 9. Unlike the probabilistic analysis, the correlation length does not have a significant effect on the output limits, so interval input variables analysis is sufficient for this type of uncertainty unless the expected correlation length is very small (e.g., 0.05). Figures 16, 17 and 18 show the possibility curves of the non-dimensional LCO amplitude at free stream non-dimensional dynamic pressures of 415.5, 471.6 and 520, respectively.

Table 9 The fuzzy uncertainty analysis results of the critical non-dimensional dynamic pressure (${\lambda }_{cr}$) for the clamped panels at the $\beta$ zero-level with ${\Delta T}^{*}$=1

Fig. 16

The possibility curve of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=415.5$ and ${\Delta T}^{*}=1$

Fig. 17

The possibility curve of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=471.6$ and ${\Delta T}^{*}=1$

Fig. 18

The possibility curve of the FG clamped panel non-dimensional LCO amplitude at ${\lambda }_{s}=520$ and ${\Delta T}^{*}=1$

4 Conclusions

The work in this paper has dealt with the uncertain aeroelastic analysis of in-plane functionally graded nanocomposite panels using probabilistic and fuzzy approaches. The considered sources of uncertainty are the effective elastic modulus and the effective thermal expansion coefficient of the nanocomposite. The effect of these uncertainties on the stability thresholds (flutter speed) and the limit cycle oscillation (LCO) amplitude have been addressed, and the results can be summarized as follows:

• For the probabilistic approach, the material properties were modeled as random fields with either a uniform coefficient of variation (model 1) or with a reinforcement volume fraction linearly dependent coefficient of variation (model 2). For both models, the uncertainty level in the flutter dynamic pressure decreases in a quadratic sense with decreasing the elastic random field correlation length and it is independent of the boundary condition type.

• Model 2 random field yields approximately 50–60% lower uncertainty levels compared to the model 1 random field.

• For model 1 random field, both the in-plane FG panels and the homogenous panels show the same level of uncertainty in the flutter dynamic pressure, while for model 2 random field, the in-plane FG panels have 5–15% more uncertainty levels for non-dimensional correlation lengths of 1 and 0.25, respectively.

• The application of in-plane mechanical compression loading leads to a linearly increasing uncertainty level in the flutter dynamic pressure. When the in-plane loading equals the critical buckling load at zero free stream speed, the uncertainty level is 70% and 50% higher for the clamped panel and the simply supported panel, respectively, compared to the values at zero in-plane loading.

• For the in-plane thermally loaded panels, the uncertainty level strongly depends on the cross-correlation between the thermal expansion coefficient and the elastic modulus. For a negative perfect cross-correlation, the uncertainty behavior is similar to the mechanically in-plane loading panels. On the other hand, for any other degree of correlation, the uncertainty level decreases as the in-plane loading increases till it vanishes at a certain marginal temperature and then increases again. This marginal temperature depends on the boundary condition type, the cross-correlation coefficient and the random fields model.

• The LCO amplitude uncertainty level and its probability distribution function (pdf) strongly depend on the free stream dynamic pressure (${\lambda }_{s}$) relative to the mean flutter dynamic pressure $({\mu }_{{\lambda }_{f}})$. For ${\lambda }_{s}<$ ${\mu }_{{\lambda }_{f}}$, the amplitude uncertainty level increases as the flutter dynamic pressure uncertainty level decreases and vice versa for the mean amplitude. For ${\lambda }_{s}=$ ${\mu }_{{\lambda }_{f}}$, the uncertainty level seems to be constant as the flutter dynamic pressure uncertainty level, while the mean amplitude decreases. ${\lambda }_{s}>$ ${\mu }_{{\lambda }_{f}}$ the amplitude uncertainty level decreases as the flutter dynamic pressure uncertainty level decreases while the mean amplitude seems unaffected.

• For the fuzzy approach, the possibility curves of the flutter dynamic pressure and the LCO amplitude seems to depend only on the assumed possibility curves of the material properties regardless of the random interval fields correlation lengths.

Finally, the results obtained in this paper are based on assumed probability distribution and parameters, so the future work can be based on estimating the actual uncertainty nature of the material properties produced by an additive manufacturing technology.

Appendix: Expressions of Finite Element Matrices and Vectors

The derivatives of the displacement field can be written in terms of the nodal degrees of freedom as follows [48]:

$$\left\{ {\begin{array}{*{20}c} {w,_{xx} } \\ {w,_{yy} } \\ {2w,_{xy} } \\ \end{array} } \right\} = \left[ {B_{o} } \right]\left\{ {q_{o} } \right\}, \left\{ {\begin{array}{*{20}c} {u,_{x} } \\ {v,_{y} } \\ {u,_{y} + v,_{x} } \\ \end{array} } \right\} = \left[ {B_{I} } \right]\left\{ {q_{I} } \right\}$$

(A.1)

$$\left[ {\Theta } \right] = \left[ {\begin{array}{*{20}c} {w,_{x} } & 0 \\ 0 & {w,_{y} } \\ {w,_{y} } & {w,_{x} } \\ \end{array} } \right], \left\{ {\begin{array}{*{20}c} {w,_{x} } \\ {w,_{y} } \\ \end{array} } \right\} = \left[ {B_{{\Theta }} } \right]\left\{ {q_{o} } \right\}$$

(A.2)

Therefore, the elemental matrices can be written as follows [48]:

$$\left\{\begin{array}{c}{\mathbb{f}}_{x}\\ {\mathbb{f}}_{y}\\ {\mathbb{f}}_{xy}\end{array}\right\}=\left[C\right]\left[{B}_{I}\right]\left\{{q}_{I}\right\}, \left\{\begin{array}{c}{\mathbb{f}}_{x}^{\Delta T}\\ {\mathbb{f}}_{y}^{\Delta T}\\ {\mathbb{f}}_{xy}^{\Delta T}\end{array}\right\}=\alpha \Delta T \left[C\right]\left\{\begin{array}{c}1\\ 1\\ 0\end{array}\right\}$$

(A.3)

$$\left[{\mathbb{F}}\right]=\left[\begin{array}{cc}{\mathbb{f}}_{x}& {\mathbb{f}}_{xy}\\ {\mathbb{f}}_{xy}& {\mathbb{f}}_{y}\end{array}\right], \left[{\mathbb{F}}^{\Delta T}\right]=\left[\begin{array}{cc}{\mathbb{f}}_{x}^{\Delta T}& {\mathbb{f}}_{xy}^{\Delta T}\\ {\mathbb{f}}_{xy}^{\Delta T}& {\mathbb{f}}_{y}^{\Delta T}\end{array}\right]$$

(A.4)

$$\left[{K}^{\Delta T}\right]=h\iint {\left[{B}_{\Theta }\right]}^{T}\left[{\mathbb{F}}^{\Delta T}\right]\left[{B}_{\Theta }\right] J d\xi d\eta$$

(A.5)

$$\left[ {K_{o} } \right] = \frac{{h^{3} }}{12}{\iint }\left[ {B_{o} } \right]^{T} \left[ C \right]\left[ {B_{o} } \right] J d\xi d\eta$$

(A.6)

$$\left[ {K_{I} } \right] = h{\iint }\left[ {B_{I} } \right]^{T} \left[ C \right]\left[ {B_{I} } \right] Jd\xi d\eta$$

(A.7)

$$\left[ {N1_{oI} } \right] = \frac{h}{2}{\iint }\left[ {B_{{\Theta }} } \right]^{{\text{T}}} \left[ {\Theta } \right]^{T} \left[ C \right]\left[ {B_{I} } \right] J d\xi d\eta$$

(A.8)

$$\left[N{1}_{oo}\right]=\frac{h}{2}\iint {\left[{B}_{\Theta }\right]}^{T}\left[{\mathbb{F}}\right] \left[{B}_{\Theta }\right] J d\xi d\eta$$

(A.9)

$$\left[ {N2_{oo} } \right] = \frac{h}{2}{\iint }\left[ {B_{{\Theta }} } \right]^{T} \left[ {\Theta } \right]^{T} \left[ C \right] \left[ {\Theta } \right]\left[ {B_{{\Theta }} } \right] J d\xi d\eta$$

(A.10)

$$\left[ {M_{o} } \right] = \rho h{\iint \mathcal{N}}_{w}^{T} {\mathcal{N}}_{w} J d\xi d\eta$$

(A.11)

$$\left[ {M_{I} } \right] = \rho h{\iint }\left[ {{\mathcal{N}}_{u} {\mathcal{N}}_{v} } \right]^{T} \left[ {{\mathcal{N}}_{u} {\mathcal{N}}_{v} } \right] J d\xi d\eta$$

(A.12)

$$\left[ {A_{S} } \right] = \frac{{\lambda \overline{D}}}{{l^{3} }}{\iint \mathcal{N}}_{w}^{T} {\mathcal{N}}_{w} ,_{x} J d\xi d\eta$$

(A.13)

$$\left[ {A_{d} } \right] = \frac{{g\overline{D}}}{{\overline{\omega } l^{4} }}{\iint \mathcal{N}}_{w}^{T} {\mathcal{N}}_{w} J d\xi d\eta$$

(A.14)

$${\overrightarrow{F}}_{I}^{\Delta T}=\iint {\left[{B}_{I}\right]}^{T}\left\{\begin{array}{c}{\mathbb{f}}_{x}^{\Delta T}\\ {\mathbb{f}}_{y}^{\Delta T}\\ {\mathbb{f}}_{xy}^{\Delta T}\end{array}\right\} J d\xi d\eta$$

(A.15)