1 Introduction

The drilling industry's primary objective of directing a well trajectory toward a distant geological target has necessitated the development of tools and methods for identifying the location and path of the wellbore during drilling. Initially, wells were drilled straight down from the drilling rig to the target spot. However, directional drilling techniques were developed to drill wells with non-vertical trajectories and reach destinations that were not directly beneath the surface. Directional drilling offers an effective approach to accessing challenging targets that cannot be easily reached by vertical drilling. Over time, numerous instruments and methods have been developed for directional drilling, with many companies now providing tools for deflecting and guiding wellbores as well as assessing their inclination and azimuth [1,2,3,4].

The challenging nature of harsh environments presents significant obstacles in the drilling of wells, requiring a high degree of technical expertise and specialized equipment to overcome [5]. One application of directional drilling is extended reach drilling (ERD) [6]. ERD is utilized in developing reservoirs with fewer platforms [7] or smaller sections of a reservoir where an additional platform is not economically feasible. ERD is predicted to become more widespread as the cost of platforms in deeper water and severe environments increases [3, 6]. Previous research suggests that the cost of drilling a horizontal well is approximately 1.4 times that of drilling a vertical well [8]. The advantage of drilling horizontal and directional wells is their ability to access a larger volume of the reservoir and traverse the highest quality zones more effectively than vertical wells, leading to higher production and recovery rates [9]. Efficiently planning the trajectory of directional wells is crucial for minimizing drilling expenses and reducing the potential negative effects of drilling issues. This process presents complex multi-objective optimization challenges [10].

In recent decades, optimization techniques have been widely employed in the oil and gas industry for various purposes such as transport scheduling, process plant optimization, well placement optimization, and different aspects of drilling operations [11,12,13,14,15]. Shokir et al. [11] used the genetic algorithm to design the well path, and Atashnezhad et al. [12] used a single-objective particle swarm optimization algorithm to minimize wellbore length within defined constraints. Yasari et al. [16] applied multi-objective genetic optimization to determine the best and most efficient system of water injection wells, and Guria et al. [13] utilized an elitist non-dominated sorting genetic algorithm to minimize drilling cost, drilling time, and maximize drilling depths with the constraint of fractional drill bit tooth wear. Mansouri et al. [9] proposed another application of multi-objective genetic optimization to optimize a horizontal well trajectory scenario. They provided a detailed description of how their model functioned and analyzed the results for the specific wellbore trajectory chosen. Furthermore, Khosravanian et al. [17] optimized the casing string placement in oil wells in the presence of geological uncertainty. Khosravanian et al. [18] conducted a comparative study to assess multiple metaheuristic algorithms for optimizing complex three-dimensional well-path designs. Mansouri et al. [14] conducted an optimization study aimed at mitigating collision risk in directional drilling by maximizing the separation factor. Their approach sought to optimize the directional well trajectory to ensure minimal overlap with existing wells, thereby reducing the likelihood of collision and the associated risks. Biswas et al. [19] employed objective functions such as true measured depth (TMD), torque, and strain energy to assess the effectiveness of wellbore trajectory design. To address the optimization challenges posed by the 17 tuning variables involved in drilling, they devised a novel approach that combined the cellular automata (CA) technique with the gray wolf optimization (GWO) and particle swarm optimization (PSO) algorithms. This hybridization successfully resolved the optimization objectives associated with drilling and provided a comprehensive solution for achieving optimal results. Huang et al. [20] approached the discrepancy between a planned trajectory and the actual trajectory as a multi-objective optimization problem (MOP) characterized by parameter uncertainties. To address this challenge, they developed a novel methodology called outlier removal (OR-NSGA-II) within the framework of nondominated sorting genetic Algorithm II. This innovative approach effectively resolves the optimization problem by simultaneously optimizing multiple objectives and removing outliers, thereby enhancing the accuracy and reliability of the results. Wendi Huang et al. [21] introduced an innovative optimization method that merges an adaptive penalty function with a multi-objective evolutionary algorithm according to decomposition. This technique effectively tackles the challenges posed by contradictory objectives and nonlinear constraints. Wang et al. [22] introduced a cutting-edge optimization technology for well trajectory and implemented it in 42 wells. The findings of their research demonstrate that this technology is capable of delivering a low-cost and high-efficiency development of horizontal wells in the Cangdong sag. Furthermore, the research outcomes hold significant reference value for the development of analogous regions. Biswas et al. [23] introduced the “Modified Multi-Objective Cellular Spotted Hyena Optimizer” as an innovative solution to address uncertainty in well design. Unlike previous models, this approach excels in identifying isolated minima and exhibits a high convergence rate, making it particularly effective for solving problems with multiple variables. Huang et al. [24] conducted an analysis of the challenges involved in drilling extended-reach wells, using the drilling limit theory as a framework for their investigation. Wood [25] conducted research that highlighted the benefits of utilizing multiple constraints related to different Dogleg severity (DLS) characteristics and the absolute changes in the tool-face angle for optimizing measure depth (MD) of Bezier curves.

Previous studies have primarily concentrated on a single well trajectory, overlooking the provision of a methodology to ascertain the optimal configuration by evaluating various potential drilling trajectories. Furthermore, previous studies have not introduced an automated method, free from the necessity of manual settings and parameters, to choose the finest solution from the set of Pareto optimal solutions. Additionally, the operational aspects, encompassing risk assessment and the requisite drilling tools, have been disregarded in earlier investigations. Therefore, it is of significant importance to present a method capable of simultaneously examining and comparing distinct trajectories, automatically identifying the best solution from the array of optimal choices, and determining the optimal trajectory for diverse trajectories while considering both risk factors and the specialized drilling tools required.

The problem of torque and drag, which results from the friction between the drill string and the borehole wall, is one of the major challenges of extended reach drilling (ERD) [26]. The design of the well has a significant impact on the drilling time, cost, and the torque on the drill string [3, 9]. In the present investigation, a multi-objective genetic algorithm (MOGA) is employed to minimize both well bore length and drill string torque during drilling operations. Moreover, a fuzzy decision-making approach was utilized to select the best solution from Pareto optimal solutions [27, 28]. The TOPSIS method is then utilized to identify the best trajectory based on multiple criteria, such as torque on the drill string, wellbore length, likelihood of keyseat, and number of required tools. The advent of directional drilling technology, particularly the widespread use of diverse down-hole motor tools, measure while drilling tools (MWD), drag reduction oscillators, rotary steerable systems, and agitators, has greatly accelerated the drilling efficiencies of horizontal wells, extended reach wells, multi-branch wells, and other complex-structured wells [29]. However, the implementation of these new tools significantly escalates the cost of drilling operations. Hence, it is advantageous to select a trajectory that necessitates fewer tools.

In this research, the utilization of a genetic algorithm for optimization purposes is discussed. Previous studies have successfully employed the genetic algorithm to optimize the trajectory of a well, confirming its effectiveness in determining the optimal path [9, 11,12,13, 16, 18, 20]. Additionally, the TOPSIS method was employed to select the optimal trajectory, taking into account various criteria such as risk. The flexibility of the TOPSIS method is one of its key advantages, making it a highly suitable option for the well design process. During the well design process, different scenarios may arise. In some cases, a wealth of data is available, with numerous wells having been drilled in the field. In such cases, risk, uncertainty, and other criteria can be accurately assessed and modeled using complex methodologies. Conversely, there are situations where very limited data is accessible, and for example the estimation of risk might rely solely on considering the tension at the Kick-Off Point (KOP), indicating the likelihood of a keyseat occurrence. The TOPSIS method is capable of accommodating both scenarios. It can be seamlessly integrated with sophisticated mathematical risk models to derive an optimal solution, or it can simply employ a straightforward numerical value to assess parameters like risk. This versatility is highly valuable in well design, as specific data may not be obtainable for every well. Therefore, the genetic algorithm and TOPSIS are highly suitable and effective approaches for the well design process. The efficacy of this method for selecting the optimal ERD well path is demonstrated through a case study.

2 Methodology

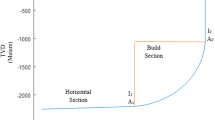
This approach is based on this idea that apart from an optimization technique to identify the optimal path for drilling a well, it is essential to employ a selection method that takes into account all the criteria needed to choose the best path. The design of the well trajectory is a critical factor in the successful operation of ERD wells. The optimal trajectory design aims to achieve long horizontal reaches with the least possible limitations, and there are several approaches available to achieve this goal. As shown in Fig. 1, there are different trajectories that can be used for designing an ERD well [30], each with its own set of advantages and disadvantages. However, it is important to note that the selection of the well path based on a single criterion is not advisable, as this approach does not take into account the multiple factors that can impact the success of the well. Factors such as geological features, drilling technology, and operational limitations and risks can all play a significant role in the selection of the optimal well trajectory. To ensure the success of ERD well operations, it is crucial to conduct a thorough evaluation of all relevant criteria before selecting the well path. This evaluation should take into consideration the geological characteristics of the reservoir, the drilling technology available, and the operational constraints of the project. Only through a comprehensive evaluation of all relevant criteria can the optimal well trajectory be selected, leading to successful ERD well operations.

Fig. 1
figure 1

ERD well trajectory profiles [30]

Full size image

Previous research efforts have employed single-objective and multi-objective optimization techniques to optimize a drilling trajectory of oil and gas wells [9, 11, 12, 18, 19, 21, 31]. However, in some trajectories drilling the trajectory that is optimal may come with some challenges and difficulties, including the need for some tools that inevitably increase drilling costs [32]. For instance, this study demonstrated that drilling an ERD well with a multiple build profile results in the lowest torque. However, this profile also has the highest likelihood of drilling pipe buckling, mainly due to high friction levels in the horizontal section, which necessitates the use of an agitator and rotary steerable system (RSS) [33,34,35]. Furthermore, drilling a completely horizontal layer is a challenging task that requires utmost precision since the drill bit and drill string tend to deviate under their own weight [32, 36, 37]. Additionally, handling drilling cuttings and cleaning the well presents additional problems [30, 38,39,40,41,42]. According to Agbaji [30, 43], in horizontal wells, cuttings tend to accumulate on the lower side of the borehole, creating a continuous and elongated bed of cuttings. The drilling fluid, on the other hand, will flow above the drillpipe. Regardless of the flow rate or viscosity of the mud, mechanical agitation is necessary to displace the cuttings and keep them in motion. Conversely, a well path with higher torque like undersection trajectory presents none of these issues [32]. The findings imply that alongside optimization, a flexible selection approach that comprehensively assesses all the criteria is necessary to select the most suitable drilling path.

The steps of this method are as follows. The first step is to recognize all conceivable trajectories for drilling a well, taking into account the geological features of the formations and the available resources and technologies. Then, a multi-objective genetic algorithm is utilized to find the best well path for each trajectory by minimizing both torque and length. At this step, the optimal parameters for the genetic algorithm to solve the problem should be identified through sensitivity analysis. Then, fuzzy decision-making method was used to choose the best solution. Finally, TOPSIS method was used to choose the best trajectory.

This approach involves identifying all potential drilling trajectories based on geological features, equipment and technologies. The risks associated with each trajectory, such as the likelihood of keyseat formation, which depends on the tension at the build section, are evaluated. Additionally, the required tools for each trajectory, including mud motors, MWDs, agitators, adjustable gauge stabilizers, near-bit subs, and rotary steerable system (RSS), are determined. Then, the optimal trajectory is selected using the TOPSIS method, which considers torque, length, risks, and required tools. A flowchart outlining the method is shown in Fig. 2. Results demonstrate that this approach effectively identifies the optimal well path and assesses the advantages and disadvantages of each trajectory compared to others. The comparison of different trajectories provides useful insights for well design and predicting problems during drilling.

Fig. 2
figure 2

Flowchart of the proposed method

Full size image

This study focuses on the drilling of ERD wells with a vertical depth of 5000 feet and a horizontal deviation of 12,000 feet. These types of wells are commonly used, but drilling them can be very challenging, especially in the 8.5-inch hole, due to the high torque during rotary drilling [24, 44]. Previous surveys conducted by El Sabeh et al. [44] and Huang et al. [24] have shown that ERD wells with a vertical depth of less than 6,500 feet, and even as low as 4,000 feet, are difficult to drill. They showed that 42% of the investigated wells had a vertical depth of less than 6,500 feet, and Huang et al. (2022) studied a well with a vertical depth of 4,000 feet, indicating that ERD wells with true vertical depth (TVD) equal to 4000 feet are common but difficult to drill. Additionally, this study focuses on the Yuri Korchagin field, an offshore oil and gas field in the north sector of the Caspian Sea, located 240 km from Makhachkala and 180 km from Astrakhan. The field was discovered in 2000, developed in 2004, and began production on April 28, 2010, with an expected annual production of 1.2 billion cubic meters of natural gas and 2.5 million tons of crude oil. The productive formations are Volzhski and Neokomian, and the reservoir consists of a 70-m gas cap and a 20-m oil rim [45]. Figure 3 illustrates the Yuri Korchagin field map and the drilled ERD wells in the field.

Fig. 3
figure 3

Yuri Korchagin field map [45]

Full size image

According to Sergey Bogdanov et al. [45, 46], there are 30 development ERD wells that have a step-out of up to 19,000 feet and a vertical depth of 5,118 feet, including production, gas injection, and water injection wells. The Well Construction Team evaluates the drillability of ERD wells using 3D geomechanical models. This study focuses on using ERD wells with the same common dimensions as a case study. The study results reveal the pros and cons of different drilling path types for these wells, compare the various paths in terms of their torque and length, and assess the potential of each path to become the optimal path.

3 Mathematical Modeling

3.1 Wellbore Length

The radius of curvature technique is utilized to determine the well path trajectory, where the curvature and measured depth between two points are computed using specific equations [47]. Additionally, the different angles and elements of the wellbore trajectory are defined using the terms outlined in Fig. 4 [47, 48].

Fig. 4
figure 4

Calculation of the length for a deviated section of the well trajectory [20, 48]

Full size image

To determine the radius of curvature, the MD and the TVD, Eqs. (1)–(3) are used, respectively[19, 23, 47, 48].

$$R=\frac{18000}{\pi . \mathrm{DLS}}$$
(1)
$$\Delta \mathrm{MD}=R\sqrt{{\left({\theta }_{2}-{\theta }_{1}\right)}^{2}({\mathrm{sin}}^{4}\left(\frac{\left({I}_{1}+{I}_{2}\right)}{2}\right)+{\left({I}_{2}-{I}_{1}\right)}^{2})}$$
(2)
$$\Delta \mathrm{TVD}=\frac{180*\Delta \mathrm{MD}(\mathrm{sin}\left({I}_{2}\right)-\mathrm{sin}\left({I}_{1}\right))}{\pi *({I}_{2}-{I}_{1})}$$
(3)

where R is the radius of curvature, DLS is the dogleg severity, \(\theta \) is the azimuth, and I is the inclination angle. The total length of the wellbore is calculated by summing up the measured depths from different segments of the well, as shown in Eq. (4).

$${\mathrm{MD}}_{\mathrm{total}}={\mathrm{MD}}_{\mathrm{KOP}}+{\mathrm{MD}}_{\mathrm{Build} \mathrm{Section}}+{\mathrm{MD}}_{\mathrm{Hold } \mathrm{Section}}$$
(4)

3.2 Torque on the Drill String During Drilling

The soft string model is utilized to determine the torque on a drill string and serves as the basis for the torque objective function. The soft string model operates under the assumption that the drill string resembles a heavy cable resting inside the wellbore, and any stiffness impacts from the drill pipes are disregarded. The calculations only account for the state in which the drill string rotates and not any axial movement up or down. Two general cases are addressed with formulas provided [49].

  1. 1.

    Straight section

  2. 2.

    Curved section

Equations (5) and (6) are used to calculate the torque and tension, respectively, for the straight section of the well.

$${F}_{2}={F}_{1}+Bw\Delta L\mathrm{cos}(I)$$
(5)
$$T=\mu rBw\Delta L\mathrm{sin}(I)$$
(6)

where F is the tension or drag force, T is the torque, B is the buoyancy factor, w is the weight per unit length, \(\Delta L\) is the length of the element, \(\mu \) is the friction coefficient, and r is the pipe radius. The normal force and friction on a drill pipe are not affected by the tension along it in a straight section. Straight sections are mainly dominated by weight, as only the normal weight component creates friction. Figure 5 demonstrates the force balance in a pipe along a straight section. In curved sections, the normal force between the drill string and the borehole is heavily influenced by the axial loading within the pipe. Figure 6 illustrates the force balance for a pipe in a curved section.

Fig. 5
figure 5

Force balance in a pipe along a straight section [20, 49, 50]

Full size image
Fig. 6
figure 6

Force balance for a pipe along a curved section [19, 23, 49]

Full size image

Equations (7) and (8) are utilized to compute the torque and tension for the curved section of the well.

$${F}_{2}={F}_{1}+Bw\Delta \mathrm{L}\left(\frac{\mathrm{sin}\left({\mathrm{I}}_{2}\right)-\mathrm{sin}\left({\mathrm{I}}_{1}\right)}{{\mathrm{I}}_{2}-{\mathrm{I}}_{1}}\right)$$
(7)
$$T=\mu r{F}_{1}\beta $$
(8)
$$\mathrm{cos}\left(\beta \right)=\mathrm{sin}\left({I}_{1}\right)\mathrm{sin}\left({I}_{2}\right)\mathrm{cos}\left({\theta }_{1}-{\theta }_{2}\right)+\mathrm{cos}\left({I}_{1}\right)\mathrm{cos}({I}_{2})$$
(9)

Beta (β) is total directional change [49].

Another objective function in well drilling is the torque on the drill string, denoted by T, which is calculated by summing up the torque in different parts of the wellbore as shown in Eq. (10). The torque calculation begins at the bottom of the drill string, specifically when it reaches the total depth (TD) of the wellbore, and then moves upward in increments toward the wellhead, starting from the horizontal position.

$${T}_{\mathrm{total}}={T}_{\mathrm{KOP}}+{T}_{\mathrm{Build } \mathrm{Section}}+{T}_{\mathrm{Hold } \mathrm{Section}}$$
(10)

3.3 Formulation of the Objective Functions for Optimization

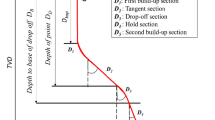
The functions for calculating the length of a wellbore and the torque on a drill string in an extended reach drilling (ERD) well are presented below. The well is divided into various parts such as the Kick-Off Point (KOP), build section, and hold section, as illustrated in Fig. 7.

Fig. 7
figure 7

Different parts of well profile [51]

Full size image

To model the trajectory of a well, it is essential to follow a specific order of equations. The first step is to calculate the measured depth, which is then used to calculate the true vertical depth of the well. The tension force is then determined based on the measured and true vertical depths, and finally, the torque is calculated. The mathematical formulas from Eqs. (11)–(14) provide the calculation for the measured depth in different sections of ERD wells [48, 49, 51].

$${R}_{1}= \frac{18000}{\pi .{\mathrm{DLS}}_{1}}$$
(11)
$${\mathrm{MD}}_{\mathrm{Build} \mathrm{Section}}={R}_{1}\sqrt{{\left({\theta }_{2}-{\theta }_{1}\right)}^{2}({\mathrm{sin}}^{4}\left(\frac{\left({0+I}_{1}\right)}{2}\right)+{\left({I}_{1}-0\right)}^{2})}$$
(12)
$$\begin{aligned}&{\mathrm{MD}}_{\mathrm{Hold} \mathrm{Section}}=({\mathrm{TVD}}_{\mathrm{AG}}-{\mathrm{TVD}}_{\mathrm{AB}}\\ &\quad-({\mathrm{MD}}_{\mathrm{Build Section}}\left(\frac{\mathrm{sin}\left({I}_{1}\right)-\mathrm{sin}(0)}{{I}_{1}-0}\right)))/\mathrm{cos}({I}_{1})\end{aligned}$$
(13)
$${{\mathrm{MD}}_{\mathrm{total}}=\mathrm{TVD}}_{\mathrm{AB}}+{\mathrm{MD}}_{\mathrm{Build } \mathrm{Section}}+{\mathrm{MD}}_{\mathrm{Hold} \mathrm{Section}}$$
(14)

Equations (15)–(18) provide a mathematical model for calculating the true vertical depth of ERD wells.

$${\mathrm{TVD}}_{\mathrm{AB}}=\mathrm{KOP}$$
(15)
$${\Delta \mathrm{TVD}}_{\mathrm{AC}-\mathrm{AB}}=\frac{{\mathrm{MD}}_{\mathrm{Build} \mathrm{Section}}(\mathrm{sin}\left({I}_{1}\right)-\mathrm{sin}\left(0\right))}{({I}_{1}-0)}$$
(16)
$${{\Delta \mathrm{TVD}}_{\mathrm{AG}-\mathrm{AC}}=\mathrm{MD}}_{\mathrm{Hold} \mathrm{Section}}\mathrm{cos}({I}_{1})$$
(17)
$${\mathrm{TVD}}_{\mathrm{total}}={\mathrm{TVD}}_{\mathrm{AB}}+{\Delta \mathrm{TVD}}_{\mathrm{AC}-\mathrm{AB}}+{\Delta \mathrm{TVD}}_{\mathrm{AG}-\mathrm{AC}}$$
(18)

Equations (19)–(22) provide mathematical models for estimating the tension in different parts of ERD wells.

$${F}_{D}=0$$
(19)
$${F}_{C}={F}_{D}+{\mathrm{BwMD}}_{\mathrm{Hold } \mathrm{Section}}\mathrm{Cos}\left({I}_{2}\right)$$
(20)
$${{F}_{B}=F}_{C}+{\mathrm{BwMD}}_{\mathrm{Build} \mathrm{Section}}\left(\frac{\mathrm{sin}\left({I}_{2}\right)-\mathrm{sin}(0)}{{I}_{2}-0}\right)$$
(21)
$${{F}_{A}=F}_{B}+{\mathrm{BwTVD}}_{\mathrm{AB}}\mathrm{Cos}(0)$$
(22)

The torque on the drill string for various segments of ERD wells can be determined using Eqs. (23)–(26).

$${T}_{\mathrm{CD}}=\mu r{\mathrm{BwMD}}_{\mathrm{Hold} \mathrm{Section}}\mathrm{Sin}({I}_{2})$$
(23)
$${T}_{\mathrm{BC}}=\mu r{F}_{C}\beta \& \beta ={I}_{2}$$
(24)
$${T}_{\mathrm{AB}}=0$$
(25)
$${T}_{\mathrm{total}}={T}_{\mathrm{AB}}+{T}_{\mathrm{BC}}+{T}_{\mathrm{CD}}$$
(26)

3.4 Formulation of the Constraints for Optimization

Constraints play a vital role in the field of optimization. During the optimization process, it is crucial to ensure that the variables, which are often referred to as chromosomes, adhere to the specified permissible limits. The evaluation of these variables using objective functions is contingent upon their compliance with the permissible limits as well as satisfying all the imposed restrictions. For example, when the crossover operator is applied to a given dataset, generating new variables, only those parameters that fall within the allowed limits and fulfill all the constraints are accepted. Subsequently, these accepted variables are assessed using the objective functions. The MOGA verifies constraints at three different points: once the initial population is formed, after applying the crossover operation, and after applying the mutation operation.

3.4.1 Maximum Torque and Tension

During the drilling process, it is imperative to maintain the torque and tension levels within permissible limits, while also accounting for the requisite safety margins. In order to accomplish this, it is vital to follow the Eqs. (27)–(28) [47, 52], which present the relevant relationships.

$${T}_{\mathrm{total}} < \frac{\text{Torsional Resistence}}{\text{Safety Factor}}$$
(27)
$${F}_{\mathrm{total}} < \frac{\text{Yield Strength}}{\text{Safety Factor}}$$
(28)

3.4.2 Equivalent Circulation Density (ECD)

Extended reach drilling (ERD) wells, especially those with high inclination angles and long horizontal segments, are susceptible to significant increases in equivalent circulating density (ECD), which can potentially cause formation failure in the heel area. Therefore, it is essential to ensure that the equivalent density remains lower than the fracture pressure of the well. This concern is particularly acute for ERD wells with limited vertical depth. Equation (29) is used to calculate ECD [30, 47].

$${\mathrm{ECD}}_{\mathrm{heel}}=\mathrm{MW}+\frac{\Delta P}{0.052*\mathrm{Length}}$$
(29)

3.4.3 Buckling of Drill Pipes

Buckling is a phenomenon that occurs when a drilling pipe is subjected to an increase in load, causing it to bend or twist. The minimum amount of load required to cause buckling is known as the buckling load, which is dependent on the drilling pipe's weight, properties, and the geometry of the drilling trajectory section. As shown in Fig. 8, there are two types of buckling load: critical buckling load (Fcr) and helical buckling load (Fhel). To determine whether sinusoidal or helical buckling is occurring, the buckling load is compared to other loads such as drag and torque at the point of the drilling trajectory section [53,54,55].

Fig. 8
figure 8

Buckling of pipe, a Sinusoidal buckling, b Helical buckling [53]

Full size image

The types of drilling pipe bending are determined by the degree of deformation. Sinusoidal buckling and helical buckling are two common types of deformation in drilling pipes. Sinusoidal buckling can be seen as a wave-like pattern in the borehole, as shown in Fig. 8a. As the pressure on the drilling pipe increases, it may undergo severe deformation, leading to helical buckling, as illustrated in Fig. 8b. Helical buckling occurs when the pipe spirals into a spiral shape and makes contact with the borehole wall. While sinusoidal buckling has little impact on drilling activities, helical buckling makes it difficult to control the orientation of the drilling pipe and to effectively transfer load to the drilling pipe. When the degree of deflection is significant, the drilling pipe may become immobile or lock-up may occur, resulting in drilling delays and increased costs. Therefore, it is critical to avoid helical buckling in directional drilling, such as horizontal drilling, as it can cause significant damage [53,54,55]. Figure 9 shows a three-dimensional schematic of sinusoidal and helical buckling of drill pipe in wellbore.

Fig. 9
figure 9

Three-dimensional schematic of sinusoidal and helical buckling [37]

Full size image

In this study, the model for buckling load is categorized into two types: critical buckling load and helical buckling load. This classification is determined based on the shape of the drilling trajectory section [33, 36].

Sinusoidal buckling force values of different sections are given in Eqs. (30)–(33) [31, 53].

$${F}_{\mathrm{cr}}(\text{vertical Section})=2.55\sqrt[3]{{\mathrm{EMW}}_{\mathrm{e}}^{2}}$$
(30)
$${F}_{\mathrm{cr}}(\text{build Section})=\frac{4\mathrm{EM}}{\mathrm{Rd}}\left(1+\sqrt{1+\frac{\mathrm{d}{R}^{2}{W}_{e}\mathrm{sin}\left(I\right)}{4\mathrm{EM}}}\right)$$
(31)
$${F}_{\mathrm{cr}}(\text{inclined Section})=2\sqrt{\frac{{\mathrm{EMW}}_{\mathrm{e}}\mathrm{sin}\left(I\right)}{d}}$$
(32)
$${F}_{cr}(\text{horizontal Section})=2\sqrt{\frac{{\mathrm{EMW}}_{\mathrm{e}}}{d}}$$
(33)

Helical buckling force values of different sections are as shown in Eqs. (34)–(37) [31, 53].

$${F}_{\mathrm{hel}}(\text{vertical Section})=5.55\sqrt[3]{{\mathrm{EMW}}_{\mathrm{e}}^{2}}$$
(34)
$${F}_{\mathrm{hel}}(\text{build Section})=\frac{12\mathrm{EM}}{\mathrm{Rd}}\left(1+\sqrt{1+\frac{\mathrm{d}{R}^{2}{\mathrm{W}}_{\mathrm{e}}\mathrm{sin}\left(I\right)}{8\mathrm{EM}}}\right)$$
(35)
$${F}_{\mathrm{hel}}(\text{inclined Section})=2\left(2\sqrt{2}-1\right)\sqrt{\frac{{\mathrm{EMW}}_{\mathrm{e}}\mathrm{sin}\left(I\right)}{d}}$$
(36)
$${F}_{\mathrm{hel}}(\text{horizontal Section})=2\left(2\sqrt{2}-1\right)\sqrt{\frac{{\mathrm{EMW}}_{\mathrm{e}}}{d}}$$
(37)

Equations (30)–(37) provide a comprehensive overview of various parameters and their definitions used in the buckling load model applied in this study. These parameters include the Young's modulus (E), moment of inertia (M), radius of curvature of the drilling trajectory (R), spatial distance between the bore and the wall of the borehole (d), inclination angle (\(I\)), and the effective weight within the drilling trajectory (We). Moment of inertia for drill pipes is calculated using Eq. (38) [31, 47].

$$M=\frac{\pi \left({OD}^{4}-{ID}^{4}\right)}{64}$$
(38)

where OD is outside diameter (in) and ID is inside diameter (in) of pipe.

If the axial load on a structure is less than the critical buckling load, no buckling will occur. When the axial load is between the critical buckling load and the helical buckling load, the structure will buckle sinusoidally. However, if the axial load exceeds the helical buckling load, the structure will buckle in a helical pattern [31].

4 Multi-Objective Genetic Algorithm (MOGA)

John Holland introduced genetic algorithm in the early 1970s [56, 57], and subsequent work by Holland (1975/1992), Goldberg, Rawlins, and Whitley laid the foundations for Gas [58,59,60]. To begin, the GA generates an initial set of random solutions that comply with defined limitations and constraints, known as the population. In each iteration, the GA creates a set of solutions, with the population referring to the set of solutions and each solution being called a chromosome [61]. These chromosomes evolve through generations, with the creation of the next generation, known as offspring, accomplished by either merging two chromosomes from the current generation using a crossover operator or modifying a chromosome using a mutation operator. Chromosomes are evaluated during each generation using measures of fitness, so that fitter chromosomes are more likely to be selected. After several iterations, the algorithm converges to the best solution or chromosome, which represents the optimal or suboptimal solution to the problem. Murata et al. [62, 63] proposed MOGA, which comprises eight steps in each generation. This MOGA utilizes a weighted sum of multi-objective functions to amalgamate them into a scalar fitness function.

4.1 Step 1: Initialization

Generate an initial set of individuals that satisfy the given constraints.

4.2 Step 2: Evaluation

The next step involves computing the objective functions for each chromosome and normalizing them, as different objective functions may have different units. To do so, Eq. (39) is utilized to normalize each objective function.

$${f}_{i}{\prime}=\frac{{f}_{i}-{f}_{i}^{\mathrm{min}}}{{f}_{i}^{\mathrm{max}}-{f}_{i}^{\mathrm{min}}} , i=1, 2, \dots , n$$
(39)

4.3 Step 3: Selection

The fitness value of each chromosome is determined by applying Eq. (40).

$$f(x)={w}_{1}{f}_{1}(x)+{w}_{2}{f}_{2}(x)+...+{w}_{n}{f}_{n}(x)$$
(40)

The combined fitness function f(x) is obtained by multiplying each objective function fi(x) by a constant weight w, summing up the weighted objective functions for a given chromosome x, and then dividing by the number of objective functions n, as shown in Eq. (41).

$${w}_{i}=\frac{{\mathrm{rand}}_{i}}{\sum_{j=1}^{n}{\mathrm{rand}}_{\mathrm{j}}}, i=\mathrm{1,2},...,n$$
(41)

where randi and randj are non-negative random numbers.

Two chromosomes are chosen using selection probability which is illustrated by Eq. (42).

$$P\left(x\right)=\frac{f\left(x\right)-{f}_{\mathrm{min}}\left(\psi \right)}{\sum_{x\in \psi }\left\{f\left(x\right)-{f}_{\mathrm{min}}\left(\psi \right)\right\}}$$
(42)

where \({f}_{\mathrm{min}}\left(\psi \right)\) is as determined using Eq. (43).

$${f}_{\mathrm{min}}\left(\psi \right)=\mathrm{min}\left\{f\left(x\right)|x\in \psi \right\}$$
(43)

4.4 Step 4: Crossover

In this step, the genetic algorithm applies the crossover operation, which is illustrated in Fig. 10.

Fig. 10
figure 10

Crossover mechanism of MOGA [62, 63]

Full size image

4.5 Step 5: Mutation

In this stage, the mutation operation is implemented, as shown in Fig. 11, to introduce genetic diversity into the population.

Fig. 11
figure 11

Mutation mechanism of MOGA [62, 63]

Full size image

4.6 Step 6: Elitist Strategy

The top-performing chromosome is conserved and carried over to the subsequent generation.

4.7 Step 7: Termination Time

Steps 2 to 6 are iterated until the maximum number of iterations is attained.

4.8 Step 8: Final Set of Pareto Optimal Solutions

The MOGA provides a range of Pareto optimal solutions from which the optimal one must be chosen.

Several researchers have employed both single-objective and multi-objective meta-heuristic algorithms for different purposes, such as finding the best neural network training, identifying optimal coefficients for mathematical models, and optimizing various objective functions [64,65,66,67].

5 TOPSIS

TOPSIS, a multi-criteria decision analysis method, was initially introduced by Yoon [68] and further developed by Hwang and Yoon [69]. Subsequent enhancements were made by Yoon [68] and Hwang, Lai, and Liu [70]. This approach is commonly utilized in a variety of fields, including supplier selection, financial performance evaluation, company evaluation, tourism destination evaluation, selecting the most suitable machine, and location selection [71]. TOPSIS is based on the idea that the selected option should have the shortest distance from the positive ideal solution (PIS) and the longest distance from the negative ideal solution (NIS) [72]. To apply TOPSIS, a decision matrix (DM) is first constructed, and the criteria are identified. The DM is then normalized, and the weights for each criterion are determined. Next, a weighted decision matrix is calculated, and the positive and negative ideal solutions are determined. Finally, the distances between each alternative and the ideal alternatives are calculated, and the alternative with the minimum distance to the PIS and the maximum distance to the NIS is selected as the best alternative. In summary, TOPSIS is a robust and widely used decision-making tool that can assist decision-makers in evaluating alternatives in a multi-criterion setting. It provides a systematic and structured approach to decision-making, which can lead to more informed and rational decisions [73, 74]. TOPSIS method involves the following steps:

5.1 Step 1: Decision Matrix

In the TOPSIS method, the initial step involves creating a decision matrix that includes all relevant factors along with their respective quantities, which indicate their level of importance. It is important to note that for some factors, such as the length of a well in well design, a longer length is considered to be unfavorable and therefore a negative parameter. Consequently, a shorter length is considered to be more favorable. Negating the value or calculating the inverse of such parameters can help avoid errors in the decision matrix [74, 75].

5.2 Step 2: Normalized Decision Matrix

The subsequent stage involves creating a normalized decision matrix (NDM), which is accomplished by utilizing Eq. (44).

$$\mathrm{NDM}={R}_{ij}=\frac{{X}_{ij}}{\sqrt{{\sum }_{i=1}^{m}{X}_{ij}^{2}}}$$
(44)

5.3 Step 3: Weighted Decision Matrix

The TOPSIS method assigns varying weights to each selection criterion based on its degree of importance. The weight matrix is multiplied by the normal decision matrix in accordance with Eq. (45) to produce the weighted decision matrix.

$$V={W}_{j}*{\mathrm{NDM}}_{ij}$$
(45)

5.4 Step 4: Positive and Negative Ideal Solution

Positive ideal solution (PIS) and negative ideal solution (NIS) are defined as follows:

PIS = Minimum of V in each column.

NIS = Maximum V in each column.

5.5 Step 5: Separation Distance

The separation distances (S) are calculated using Eqs. (46)–(47).

$${S}_{i}^{+}=\sqrt{{\sum }_{j=1}^{n}({\mathrm{PIS}}_{j}-{V}_{ij}{)}^{2}}$$
(46)
$${S}_{i}^{-}=\sqrt{{\sum }_{j=1}^{n}({\mathrm{NIS}}_{j}-{V}_{ij}{)}^{2}}$$
(47)

5.6 Step 6: Relative Closeness

In accordance with Eq. (48), the determination of the relative closeness (CL) to the ideal solution is executed.

$${\mathrm{CL}}_{i}=\frac{{S}_{i}^{+}}{{S}_{i}^{+}+{S}_{i}^{-}}$$
(48)

6 Case Study

This study involves designing an ERD well with a vertical depth of 5000 ft (1524 m) by considering four trajectories. It is essential to take into account specific limitations while designing each trajectory. The total vertical depth (TVD) is constant in all trajectories. The limitations are based on the design characteristics of each well path, which are detailed in the subsequent tables.

In this study, the following assumptions are considered:

  1. 1.

    The drill string has 0.167 ft radius.

  2. 2.

    The drill string has 0.069 KN/ft weight.

  3. 3.

    The friction factor is 0.2

  4. 4.

    The buoyancy factor is 0.85

  5. 5.

    Drilling fluid density is 9.8 ppg

The drilling equipment utilized in this study was Class N drill pipe, which conforms to the API RP 7G standard, 16th edition, August 1998, with a nominal weight of 15.7 pounds force per foot. This drill pipe has a tensile yield strength of 2593 kilo newtons and a torsional yield strength of 206.5 kN.ft.

The primary objective of this case study is to illustrate the efficacy of the novel method for identifying the optimal well path that minimizes torque on the drill string and wellbore length while taking into account several different criteria, such as risk and the number of tools required. The outcomes obtained via this novel method are heavily influenced by the weights allocated to each criterion. For instance, in one company, the well's length may be less important compared to the torque and the likelihood of a keyseat, while in another company, both factors could be equally significant, leading to varying outcomes. Furthermore, constraints on each trajectory vary depending on the region, and an accurate geological model is required to determine these constraints. In this study, the permissible limits for each trajectory have been considered hypothetically and according to the characteristics of that trajectory.

6.1 Double Build Trajectory Limitations

The profile of the double build trajectory is shown in Fig. 12.

Fig. 12
figure 12

Double build profile [30]

Full size image

The constraints for the double build trajectory used in this study are presented in Table 1, which was taken into consideration during the design of the well trajectory.

Table 1 Limitations of double build trajectory during the design of the well path
Full size table

6.2 Build and Hold Trajectory Limitations

The profile of the build and hold trajectory is shown in Fig. 13.

Fig. 13
figure 13

Build and hold profile [30]

Full size image

The constraints applied to the well trajectory design for the build and hold trajectory are presented in Table 2.

Table 2 Build and hold trajectory constraints
Full size table

6.3 Undersection Trajectory Limitations

As shown in Fig. 14, the undersection trajectory profile is presented below.

Fig. 14
figure 14

Undersection profile [30]

Full size image

This study employed a set of constraints for the undersection trajectory in designing the well path. The specific constraints used are presented in Table 3.

Table 3 Undersection trajectory constraints
Full size table

6.4 Multiple Build Trajectory Limitations

The multiple build trajectory profile is shown in Fig. 15.

Fig. 15
figure 15

Multiple build profile [30]

Full size image

The constraints applied in the well trajectory design of multiple build trajectory are presented in Table 4, as shown in Fig. 15.

Table 4 Multiple build trajectory constraints
Full size table

6.5 Sensitivity Analysis

At the outset, a sensitivity analysis was carried out to identify the optimal parameters of the genetic algorithm that would yield accurate results in a shorter period. The analysis involved evaluating the impact of crossover probability, mutation rate, and population size on the algorithm's performance. The study revealed that increasing these parameters may not necessarily lead to improved algorithm performance.

6.5.1 Crossover Probability

In general, setting a higher value for the crossover probability (Pc) tends to lead to improved algorithm performance and a shorter running time. However, setting it too high may restrict the algorithm from exploring the entire solution space and instead get stuck in a local optimum point. Figure 16 illustrates that increasing the crossover probability enhances the algorithm's performance, but increasing it beyond a certain threshold (0.9) does not result in optimal solutions. Therefore, a value of 0.7 was selected for this study.

Fig. 16
figure 16

Genetic algorithm performance in different crossover probabilities

Full size image

6.5.2 Mutation Rate

In this study, another parameter that was examined through sensitivity analysis is the mutation rate (Mu). Figure 17 demonstrates that an increase in the mutation rate leads to a wider exploration of the solution space. However, this also results in longer processing time. Therefore, the mutation rate was set to 0.2 to balance the search range and processing time.

Fig. 17
figure 17

Genetic algorithm performance in different mutation rates

Full size image

6.5.3 Population Size

The study also looked into the impact of population size on the genetic algorithm's performance. While a larger population can yield better results, it also increases the computational time. Therefore, a population size of 100 was chosen as a reasonable compromise. Figure 18 illustrates the performance of the genetic algorithm across different populations.

Fig. 18
figure 18

Genetic algorithm performance in different populations

Full size image

7 Results and Discussion

As discussed earlier, the optimization of the well path involves two objective functions, minimizing the torque on the drill string and the length of the wellbore, while also taking into account unique constraints associated with each trajectory. To obtain the optimal parameters for this multi-objective optimization problem, a sensitivity analysis was carried out using a genetic algorithm. The analysis allowed for the identification of optimal parameter settings that can deliver accurate results in a shorter time. The obtained optimal parameters for the algorithm are summarized in Table 5.

Table 5 Optimum parameters of the algorithm
Full size table

Furthermore, the MOGA's effectiveness under various parameters was assessed using statistical measures, including spacing metric (SM) and maximum spread (MS). The spacing metric, which is a parameter for measuring distribution based on distance, determines how closely spaced the solutions are. A smaller value of the spacing metric indicates that the solutions are closely positioned, indicating a better distribution of non-dominated solutions. The spacing metric can be computed using Eq. (49) [19].

$$\mathrm{SM}=\sqrt{\frac{1}{\left|P-1\right|}\sum_{i=1}^{\left|P\right|}{\left({d}_{i}-\overline{d }\right)}^{2}}$$
(49)

In this context, \(\overline{d }\) represents the average of all \({d}_{i}\) values, while P denotes the total number of Pareto optimal solutions obtained. The maximum spread (MS) is another metric used to assess the diversity and coverage of the solution space. It represents the greatest distance between the boundary solutions. The calculation for MS is as follows in Eq. (50) [19].

$$\mathrm{MS}=\sqrt{\sum_{i=1}^{P}\mathrm{max}\left(\mathrm{d}\left({a}_{i},{b}_{i}\right)\right)}$$
(50)

In this context, \({a}_{i}\) represents the maximum value, and \({b}_{i}\) represents the minimum value within the \({i}^{\mathrm{th}}\) objective [19].

MOGA was executed multiple times using different parameters, totaling 10 runs. The SM values of the Pareto optimal solutions are presented in Fig. 19 as a box plot, while Fig. 20 displays the box plot of the MS values. Notably, the configuration with a crossover probability of 0.7 and a mutation rate of 0.2 exhibited the lowest average SM. In terms of the MS values, the setup featuring a crossover probability of 0.9 and a mutation rate of 0.2 achieved an MS of 581.5, whereas the configuration with a crossover probability of 0.7 and a mutation rate of 0.2 had an MS of 551.58, both of which surpassed the others. Figure 21 provides an illustrative instance of the optimal solution for MOGA employing different parameters. It is evident that the solution generated by the configuration with a crossover probability of 0.7 and a mutation rate of 0.2 is closer to the minimum values. This correspondence between the parameter values and the minimum values, as shown in Figs. 16 and 17, was also confirmed.

Fig. 19
figure 19

Influence of crossover probability and mutation rate on the spacing metric of the MOGA

Full size image
Fig. 20
figure 20

Impact of crossover probability and mutation rate on the maximum spread metric of the MOGA

Full size image
Fig. 21
figure 21

Impact of varying the crossover probability and mutation rate on the optimal solution produced by the MOGA

Full size image

As shown in Figs. 16, 17, and 18, the algorithm consistently progresses toward finding the minimum value. Through the utilization of crossover and mutation operators, the algorithm is able to explore the entire search space within the permitted limits over a span of 2000 iterations. The outcomes exhibited in Fig. 21 demonstrate that even with varying parameters, the algorithm yields values that exhibit remarkably similar minimum, maximum, and average characteristics, with the fuzzy decision-making method's chosen solution being closely aligned with each other. Subsequently, upon selecting the optimal parameters for the algorithm, the solution with the lowest objective function values, representing the optimal solution, is attained.

Taking into account the objective functions and constraints outlined earlier, the optimization of the well trajectory for four ERD profiles was performed.

The multi-objective function is minimized during the optimization process. The MOGA starts with initialization. A random population of 100 solutions is generated, each of which meets the restrictions. By entering a loop, the objective functions for each solution are calculated, and a fitness score is assigned to each of them depending on the value of these functions. In each generation, the Pareto optimum solutions are allocated to rank one. At least some of the parent solutions are chosen for the following generation. A crossover operator then adjusts the selected parent solutions and generates new solutions. The crossover operator is intended to seek for new solutions that may be more fit than some of the parents. The new enhanced solutions then replace alternatives with low fitness scores that were previously ranked low. Once low-ranking solutions are eliminated, only the most promising options remain. Next, the population undergoes a mutation operator that generates a fresh set of potential solutions for the next generation. The mutation operator is applied to the parents, and the new solutions are accepted or rejected based on their fitness relative to the parent fitness. The mutation step marks the final stage of each iteration. In the analysis conducted for this study, the process sequence or loop was repeated two thousand times. The aim is to minimize both torque and length objective functions concurrently, but it is acknowledged that finding a single solution that meets both objectives is improbable. Therefore, a collection of solutions with equivalent mathematical values is produced. The Pareto set for any two objective functions can be presented graphically as a Pareto frontier which is known as Pareto optimal solutions. Table 6 presents the Pareto frontier for double build trajectory. It is typically observed that Pareto optimum solutions do not repeat across different iterations. However, when the algorithm parameters are optimally chosen, the boundaries representing the maximum, minimum, average values, median, as well as the solution identified through the fuzzy decision-making method, exhibit a remarkable degree of proximity to one another.

Table 6 MOGA Pareto optimum solutions for the double build trajectory
Full size table

Pareto frontier of double build trajectory is shown in Fig. 22. As can be seen, by reducing one of the objective functions, the other function increases, but there is no meaningful relationship between the answers; in other words, for example, the answer that has the shortest length may not have the highest torque.

Fig. 22
figure 22

Pareto optimum solution of double build trajectory. The diamond-shaped point shows the final solution (optimal trade-off) obtained through the use of a fuzzy decision-making system

Full size image

The multi-objective optimization method generates a set of non-dominant Pareto solutions, necessitating a decision-making methodology to determine the optimum Pareto solution. A fuzzy decision-making technique is used in this work to select the best solution (tradeoff) from a set of non-dominant solutions on the Pareto front. Equation (51) is used to compute the fuzzy membership value of the jth objective function [27, 28, 76].

$${\chi }_{j}=\left\{\begin{array}{cc}1& \mathrm{for}\, {\mathrm{OF}}_{j}<{\mathrm{OF}}_{j}^{\mathrm{Min}}\\ \left(\frac{{\mathrm{OF}}_{j}^{\mathrm{Max}}-{\mathrm{OF}}_{j}}{{\mathrm{OF}}_{j}^{\mathrm{Max}}-{\mathrm{OF}}_{j}^{\mathrm{Min}}}\right)& {\mathrm{OF}}_{j}^{\mathrm{Min}}<{\mathrm{OF}}_{j}<{\mathrm{OF}}_{j}^{\mathrm{Max}}\\ 0& \mathrm{for}\, {\mathrm{OF}}_{j}>{\mathrm{OF}}_{j}^{\mathrm{Max}}\end{array}\right.$$
(51)

where \({\mathrm{OF}}_{j}^{\mathrm{Min}}\) and \({\mathrm{OF}}_{j}^{\mathrm{Max}}\) are the objective function's minimum and maximum fitness values, respectively. The function that measures the degree of membership, \({\chi }^{k}\), for each non-dominant solution is mathematically expressed as Eq. (52) [27, 77].

$${\chi }^{k}=\frac{\sum_{i=1}^{{N}_{obj}}{\chi }_{j}^{k}}{\sum_{k=1}^{ND}\sum_{j=1}^{{N}_{obj}}{\chi }_{j}^{k}}$$
(52)

Equation 50 defines the normalized membership function \({\chi }^{k}\) for each non-dominant solution. The symbol ND refers to the number of non-dominated solutions, while Nobj refers to the number of objective functions, which are torque and length in this case. The optimal solution can be determined by selecting the normalized membership function with the highest value of \({\chi }^{k}\) in this process. Table 7 contains the for Pareto optimal solutions of double build trajectory.

Table 7 Normalized membership function for each solution
Full size table

As explained earlier, all these answers have equal mathematical value. The solution in which both functions are at their lowest state on average was chosen. As shown in the table, answer number one has the maximum \({\chi }^{k}\); therefore, this solution was chosen as the optimal state [27, 78]. This process was performed for all trajectories, and the optimal values of each well path were calculated. Results are presented in Table 8. The outcomes of the optimization process are presented in Table 8, along with the optimization trends.

Table 8 Results of optimization for four trajectories
Full size table

The optimization results for the four trajectories studied here were compared based on the minimum length and torque obtained. Multiple build trajectory had the lowest torque and the highest wellbore length, while build and hold trajectory had the highest torque and the lowest wellbore length. These findings are presented in Table 9.

Table 9 Comparative results of optimization on four trajectories
Full size table

Based on the results presented in Fig. 23, it can be concluded that the trajectory with multiple build has the lowest torque, followed by the undersection, double build, and build and hold trajectories, respectively.

Fig. 23
figure 23

Optimum torque of different trajectories

Full size image

As shown in Fig. 24, the trajectory with multiple builds has the highest KOP followed by undersection, double build, and build and hold, respectively. Therefore, increasing KOP leads to a decrease in torque. Accordingly, it can be inferred that it is more advantageous to deviate the well in the lower sections of the wellbore.

Fig. 24
figure 24

Optimum KOP in different trajectories

Full size image

Figure 25 illustrates that the multiple build trajectory has the longest wellbore length compared to the undersection, double build, and build and hold trajectories, which have the second, third, and fourth longest wellbore lengths, respectively.

Fig. 25
figure 25

Optimum length in different trajectories

Full size image

Based on the findings presented in Fig. 26, it can be inferred that as the KOP increases, the torque decreases regardless of the well profile. However, it should be noted that this increase in KOP leads to an increase in MD (measured depth), resulting in longer drilling time and higher costs, which should be taken into account during well design.

Fig. 26
figure 26

Optimum torque, length and KOP in different trajectories compared to each other

Full size image

The build and hold trajectory exhibits the highest level of torque and the lowest MD. Due to the high tension in the build section, there is a high probability of keyseat and fatigue failure. Therefore, the build and hold trajectory is not recommended for drilling an ERD well. The multiple build trajectory, on the other hand, has the minimum torque and maximum MD with a long horizontal section. Due to formation tendency and gravity effect, it is difficult to keep the bit in a horizontal state, and therefore, it is necessary to use RSS, agitator and other special equipment in these wells, which increases the cost. The hold section in the undersection trajectory is not horizontal, which can make drilling easier. In the double build trajectory, the possibility of key seat and fatigue failure decreases compared to the build and hold trajectory because of the low DLS in the first KOP. The results indicate that the ultimate tension in all trajectories is equal, which is demonstrated in Fig. 27. Therefore, drag amount cannot be regarded as a design objective function in this study. However, the tension in different parts of an extended reach drilling (ERD) well is distinct and may impact the well quality and drill pipe design during drilling.

Fig. 27
figure 27

Tension in different parts of four trajectories

Full size image

As previously discussed, it is crucial to note that the level of tension varies across different sections of the trajectories, particularly at the top of the build section in KOP. This is significant as the likelihood of keyseat and fatigue failure is correlated with the tension amount and DLS at KOP. The tension in different parts of the four trajectories is compared in Fig. 27. It can be observed from the figure that the build and hold trajectory has the highest tension in different parts compared to the other trajectories. The double build trajectory, undersection trajectory, and multiple build trajectory have progressively lower tension in different parts.

The crucial factor to consider is the tension level at the KOP. Higher tension at KOP increases the likelihood of keyseat and fatigue failure. Figure 28 demonstrates the tolerance level of each part of different trajectories to tension. The analysis indicates that the build and hold profile has the highest probability of keyseat and fatigue failure, while the multiple build trajectory and undersection have the lowest probability.

Fig. 28
figure 28

Amount of tension tolerated by each part of different trajectories

Full size image

Figure 29 reveals that the build and hold trajectory has the highest tension at KOP compared to the other trajectories, thereby making it the most susceptible to keyseat and fatigue failure. Although the tension at KOP in the double build trajectory is similar to the build and hold trajectory, the double build trajectory has a lower inclination and Dogleg severity, resulting in a lower probability of keyseat and fatigue failure. The multiple build trajectory, on the other hand, has the least amount of tension at KOP.

Fig. 29
figure 29

Amount of torque tolerated by each part of different trajectories

Full size image

The graphical representation in Fig. 29 demonstrates that unlike tension, torque varies in different parts of the ERD wells. Additionally, the graph indicates that the maximum torque in ERD wells is associated with the hold section of the well, highlighting the crucial role of effective hole cleaning in such wells.

7.1 Selection of Best Trajectory Using TOPSIS

As previously stated, each trajectory has its own strengths and weaknesses. Therefore, choosing a well path based on a single criterion is not a recommended practice. The selection of the well path should depend on various criteria, such as the torque on the drill string, the length of the wellbore, and the risk, particularly the probability of keyseat failure, which is determined by the tension at the KOP in each trajectory. The TOPSIS method exhibits a notable attribute of high flexibility. For instance, when formation properties and drilling speed data are accessible, it becomes feasible to accurately calculate the drilling speed for each trajectory by taking into account the well angle, as well as accurately determine the duration and cost of tool usage. However, even in the absence of such detailed information, the TOPSIS method can still be implemented by solely conducting qualitative comparisons among trajectories. In this particular case, the paths were qualitatively assessed based on their requirement for specialized equipment. Deviation drilling, for instance, necessitates drilling equipment as well as survey tools like measurement while drilling (MWD) and well deviation equipment such as whipstock, stabilizer, or motor. Similarly, for multiple build paths, equipment like agitator and RSS are essential, as highlighted by various sources [33,34,35]. In the case of double build path, the complexity of the well path calls for the use of an agitator to enhance drilling operations [79]. Consequently, a rating of 2 was assigned to the double build and undersection trajectories, a rating of 3 for the double build path, and a rating of 4 for the multiple build trajectory to signify the difficulty and challenges associated with each path. Huang et al. (2022) have also presented a method to calculate the difficulty of each ERD well path [24]. If the relevant information is available, this difficulty calculation method can be used with the TOPSIS method to analyze different paths in terms of their difficulty. In this study, the risk associated with each path was proportional to the tension present in the build section of the well, with the values corresponding to the tension in the build section as shown in Fig. 27. The use of decision-making techniques, such as TOPSIS, can aid in the selection of the best trajectory. Figure 30 illustrates the selection criteria utilized in TOPSIS for this study.

Fig. 30
figure 30

Selection criteria of TOPSIS

Full size image

Table 10 presents the proximity of each wellbore trajectory to the ideal state based on the TOPSIS method, which reflects their relative closeness to each other.

Table 10 Relative closeness of each well path
Full size table

Figure 31 illustrates the relative closeness of different ERD well trajectories.

Fig. 31
figure 31

Relative closeness of each well path

Full size image

The results based on the TOPSIS method indicate the relative closeness of ERD well trajectories to the ideal state, as shown in Fig. 28. The undersection trajectory has the highest relative closeness, followed by multiple build, whereas the double build trajectory has the lowest relative closeness. However, it is important to note that practical considerations such as wellbore distortions and deviations must be taken into account during drilling operations. Additionally, drilling several undersection wells from the same platform may not always be feasible due to well collision concerns. Therefore, it is recommended to maintain the well as vertical as possible, similar to the undersection trajectory, until the lower depths, and only then make slight deviations. Alternatively, drilling a single mother well from the platform to the bottom vertical depth and branching off the remaining wells from it could be a better option with the use of new technologies. It can be concluded that choosing a trajectory with characteristics similar to the undersection or multiple build profiles is the best approach for drilling ERD wells.

8 Conclusion

In summary, this study proposes a new approach for optimizing well trajectory design by combining a multi-objective genetic algorithm and TOPSIS method. The results of the study demonstrated that the proposed method can lead to the selection of a better well design by taking into account operational conditions such as risk, cost, and drilling issues, in addition to optimizing torque and length. The undersection trajectory was found to be the best option among different trajectory profiles due to its relatively low torque and tension at KOP, making it less susceptible to keyseat and fatigue failure. On the other hand, the multiple build trajectory had the lowest torque on the drill string, but its inclination was nearly 90 degrees, making it challenging to keep the well in plan, leading to higher costs due to the need for RSS and agitator. The build and hold trajectory had the highest tension at KOP, making it more susceptible to keyseat and fatigue failure. The double build trajectory had tension levels similar to the build and hold trajectory but a lower possibility of keyseat due to its low inclination at KOP. Therefore, the undersection trajectory can be a better option for ERD wells compared to other trajectories. Overall, this study provides valuable insights into the design of ERD wells and highlights the importance of considering multiple operational factors in the optimization process.