Analysis and optimization of control algorithms for RSS^TSP for horizontal well drilling

Abstract

Steering control algorithm plays an important role in a rotary steerable system for horizontal well drilling, including the determination of the well trajectory, vibrations, stability, durability among other variables. This work develops a control algorithm for three static push-the-bit rotary steerable systems (RSS^TSP) (TSP is the abbreviation of “three static push-the-bit”). Based on the structure, mechanism, and working process of the RSS^TSP, mechanical and mathematical models are proposed to determine the required steering force (amplitude and direction) to move the drill bit from a point to another. Additional equations are constructed to overcome the non-uniqueness and then compute the optimal forces for the three pads to achieve the required steering force. Moreover, a new control algorithm of RSS^TSP is developed, considering the steerability, stability, durability, favorable area, unfavorable area, maximum usable magnitude of steering force. The proposed control algorithm is also applied to a new RSS^TSP and tested on a GU-693-P102 well for validation. It is found that each pad force changes smoothly, the drilling tool is stable, and the well trajectory is consistent with the design, demonstrating that our proposed control algorithm is robust and effective for RSS^TSP for horizontal well drilling.

Introduction

With the technological development for unconventional oil and natural gas productions, the numbers of horizontal and three-dimensional multi-target directional wells have increased significantly (Ozkan et al. 2011; Jia et al. 2014; Orem et al. 2014). Drilling equipment not only needs to meet requirements for desired drilling trajectory, but also needs to work reliably in more complex stratum and harsher operating conditions, which presents significant challenges on the drilling technology (John et al. 2000; Kaiser and Yu 2015; Ikonnikova et al. 2015). In recent decades, rotary steerable systems (RSS) have developed very rapidly, in their capability to provide continuous rotation, constant steering, and smoother boreholes (Weijermans et al. 2001; Drummond et al. 2007; Hakam et al. 2014). RSS ensure steering the borehole when drill string is rotating, and are usually used together with a logging while drilling (LWD) system. Geological parameters are analyzed in real time, and then precise control of the directional trajectory is achieved based on geological conditions (Haugen 1998; Tribe et al. 2001; Torsvoll et al. 2010). So far, Schlumberger’s PowerDrive, Baker Hughes’ AutoTrak, and Halliburton’s Geo-Pilot have been the main representative technologies (Stuart et al. 2000; Tribe et al. 2001; Bian et al. 2011; Wang et al. 2014). RSS can be divided into static bias and dynamic bias according to different bias units and can also be divided into push-the-bit and point-the-bit approaches according to different directing principles. PowerDrive and AutoTrak belong to “push-the-bit,” while Geo-Pilot belongs to “point-the-bit” type. PowerDrive is of dynamic bias, while AutoTrak is of static bias (Schaaf 2000; Fontenot et al. 2005; Wang et al. 2014). This article focuses on three static push-the-bit (RSS^TSP) like AutoTrak systems. RSS^TSP have three stretching pads, which press against the well bore thereby causing the bit to press on the opposite side resulting in a direction change (Niu et al. 2013; Wang et al. 2014, Marck and Detournay 2016). Steering control algorithm plays an important role in any RSS^TSP, and a robust control algorithm is the key factor to achieve the desired control effects (Seifabad and Ehteshami 2013; Hakam et al. 2014; Kremers et al. 2015).Because many of these techniques are not available to the public, the research papers for control algorithm for RSS^TSP are very few in the published literature. Zhang and Yu analyzed the configuration and deviation principle of RSS^STP (Zhang 2000). Cheng and Jiang studied control method, using biasing displacement vector (Cheng et al. 2010). Du and Liu studied multi-solution and uncertainty for controlling three pad forces. Models were established with two pads and adapted to adjust and control magnitude and orientation of steering force vector, and another pad extended to wellbore without force (Du et al. 2008). Due to non-unique solutions, Li et al. (2015) proposed to use three pads working at the same time, where one pad force should have a maximum or minimum value determined by relative position of pad and steering forces. The aforementioned papers mainly deal with how to calculate steering force. However, vibrations, stability, and durability were not considered. Therefore, based on the structure and work process of RSS^TSP, this work develops mechanical and mathematical models for the steering force and pad force. A new control algorithm is developed considering factors of steerability, stability, durability, “favorable area,” and “unfavorable area.”

Structure and work process of RSS^TSP

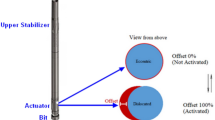
RSS^TSP has three support pads: pad 1, 2, and 3, which are spaced 120° apart from each other, as shown in Fig. 1a, with coordinated movements for rotating spindle, drill string, and bit rotating. The pads are relative static to the rotating outside sleeve. The pads are driven by drilling fluid and stretched out to press against the well bore, thereby causing the bit to press on the opposite side causing a direction change. The support force for each pad is expressed as F₁, F₂, F₃, respectively, as shown in Fig. 1b. The resultant force F of three pad forces forms the total steering force, leading to desired changes in inclination and azimuth, as shown in Fig. 1c.

Fig. 1

Schematic of the structure and pad forces of a typical RSS^TSP

The RSS^TSP works as follows: The value and direction of steering force are first determined based on the current actual point and the expected point on the ground. The steering force is then transmitted downhole. Based on steering force, each pad force is next determined in accordance with predetermined control algorithms downhole. Lastly, the pads are pushed out by applying hydraulic pressure, and the expected steering force and well trajectory are realized. In the whole process, a robust algorithm for steering force and pad force is the key factor for achieving the desired control effects.

Maximum usable steering forces (A _max)

For a given hydraulic pressure applied, the static bias pad has a maximum or minimum support force (F_max or F_min). Because the three pads are 120° apart, the range of the steering force is in a hexagon, as shown in Fig. 2a, b. The hexagon shall have an inner circle and an outer circle, as shown in Fig. 2c.

Fig. 2

Inner circle and outer circle hosting the hexagon of maximum pad force

For a given position of the three pads, if the maximum usable magnitude of steering force (A_max) is within the inner circle and outer circle touching the hexagon, it can only be realized at a point on the hexagon, as shown in Fig. 3. If the steering force is within the inner circle, it can be achieved everywhere. In the actual operation, in order to achieve a steering force in all directions at any time, the steering force must be adjustable in 360°. Therefore, the steering force should be limited in the range within the inner circle. Thus, the maximum usable magnitude of steering force is not F_max, but A_max shown in Fig. 3.

Fig. 3

Vector geometry of the maximum steering force

The maximum usable magnitude of steering force can be expressed as follows:

$$ A_{\hbox{max} } = \frac{\sqrt 3 }{2} \times (F_{\hbox{max} } - F_{\hbox{min} } ), $$

(1)

where F_max is the maximum support force of the pad, F_min is the minimum support force of the pad, and A_max is the maximum usable magnitude of steering force. It is necessary to consider the constraint of A_max in the control algorithm, so as to achieve a desired dogleg, build rate, or walk rate in the actual operations.

Amplitude and direction of the required steering force

Consider a RSS^TSP used in a drilling operation. The amplitude and its direction of the required steering force should be determined based on the current point and orientation of the drill bit and the target point and orientation one would want the drill bit to be.

Amplitude of the required steering force (A _k)

Assume that the current drill bit is at point A (X_A, Y_A, Z_A), and the actual hole inclination angle and azimuth angle are α_A and β_A. The targeted position is at point C (X_C, Y_C, Z_C), and the expected inclination angle and azimuth angle are α_C and β_C. The tangent lines at points A and C intersect at point D, and the normal lines of points A and C intersect at point O, as shown in Fig. 4.

Fig. 4

Current position “A” and targeted position “C”

Let the changes in inclination angle and azimuth angle be Δα_AC and Δβ_AC, and the average inclination angle of points A and C be α₀. The γ of points A and C can be calculated as follows:

$$ \gamma = \frac{{30 \times 360\left| {\sin \frac{{\sqrt {\Delta \alpha_{\text{AC}}^{2} + \Delta \beta_{\text{AC}}^{2} \cdot \sin \alpha_{0}^{2} } }}{2}} \right|^{{}} }}{{\pi \sqrt {(X_{\text{C}} - X_{\text{A}} )^{2} + (Y_{\text{c}} - Y_{\text{A}} )^{2} + (Z_{\text{C}} - Z_{\text{A}} )^{2} } }}, $$

(2)

where $\Delta \alpha_{\text{AC}} = \alpha_{\text{C}} - \alpha_{\text{A}}$, $\Delta \beta_{\text{AC}} = \beta_{\text{C}} - \beta_{\text{A}}$, $\alpha_{0} = \frac{{\alpha_{\text{A}} + \alpha_{\text{C}} }}{2}_{{}}$, γ is the dogleg, α_A is the inclination angle of point “A,” α_c is the inclination angle of point “C,” and α_o is the average inclination angle.

The γ _max of RSS^TSP is usually known and supplied by manufactures under A_max. The work efficiency of RSS^TSP is defined as follows:

$$ A_{k} = \frac{\gamma }{{\gamma_{\hbox{max} } }} \times 100\% , $$

(3)

where γ_max is the dogleg when working under A_max.

If the value of A_k is greater than 100%, it would not be drilled to the target point. In this situation, it is necessary to redesign well trajectory and redetermine target point until the value of A_k is less than 100%.

It can also be expressed using the amplitudes of the steering forces in relation to its maximum usable magnitude, as follows:

$$ A_{k} = \frac{F}{{A_{\hbox{max} } }} \times 100\% , $$

(4)

where F is the steering force.

Therefore, once A_k is obtained, the amplitude of the steering force F can be calculated using Eq. (4).

Direction of steering force (α _k)

The direction angle of steering force (α_k) is defined as clockwise rotation angle from high side to the direction of steering force in the bottomhole plane. The steering force could be broken up into build force and walk force, as shown Fig. 5.

Fig. 5

steering force distribution in bottomhole plane

The “+” indicates increase in “build force” or “walk force,” and the “−” indicates decrease in “build force” or “walk force.” Build rate and walk rate are also determined by steering force and the direction angle of steering force α_k.

With the current point (A) and expected point (C) shown in Fig. 4, the expected build rate (∆α) and the walk rate (∆β) can be obtained using

$$ \Delta \alpha = 30 \times \frac{{\alpha_{\text{c}} - \alpha_{\text{A}} }}{{\Delta D_{m} }}, $$

(5)

$$ \Delta \beta = 30 \times \frac{{\beta_{c} - \beta_{A} }}{{\Delta D_{m} }}, $$

(6)

where Δα is the expected build rate, β_A is the azimuthal angle of point “A,” β_c is the azimuthal angle of point “A,” β_o is the average azimuthal angle, and Δβ is the expected walk rate.

The relations between dogleg γ and α_K, Δα and Δβ (Lapeyrouse et al. 2002) are shown in Fig. 6.

Fig. 6

Diagram for calculating dogleg

Figure 6 shows graphic relationship between α_K Δβ, α₀, and Δα. According to the changes in the inclination and azimuth, α_K can be divided into following nine cases:

$$ _{\text{k}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,\left( {\Delta \alpha > 0\text{,}\Delta \beta = 0} \right), \left( 1 \right)} \\ {\begin{array}{*{20}c} {\arctan \left( {\frac{\Delta \beta \times \sin \alpha 0}{\Delta \alpha }} \right),\left( {\Delta \alpha > 0\text{,}\Delta \beta > 0} \right), \left( 2 \right)} \\ {90, \left( {\Delta \alpha = 0\text{,}\Delta \beta > 0} \right), \left( 3 \right)} \\ {\arctan \left( {\frac{\Delta \beta \times \sin \alpha 0}{\Delta \alpha }} \right) + 180,\left( {\Delta \alpha < 0,\Delta \beta > 0} \right),\left( 4 \right)} \\ \end{array} } \\ {180,\left( {\Delta \alpha < 0\text{,}\Delta \beta = 0} \right),\left( 5 \right)} \\ {\arctan \left( {\frac{\Delta \beta \times \sin \alpha 0}{\Delta \alpha }} \right) + 180,\left( {\Delta \alpha < 0\text{,}\Delta \beta < 0} \right),\left( 6 \right)} \\ \end{array} } \\ {270,\left( {\Delta \alpha = 0\text{,}\Delta \beta < 0} \right), \left( 7 \right)} \\ {\arctan \left( {\frac{\Delta \beta \times \sin \alpha 0}{\Delta \alpha }} \right) + 360,\left( {\Delta \alpha < 0\text{,}\Delta \beta < 0} \right), \left( 8 \right)} \\ {None,\left( 9 \right)} \\ \end{array} } \right) $$

(7)

• 1. Full working to advance the inclination, while the azimuth is not changed.

• 2. Both the inclination angle and azimuth angle are all advanced.

• 3. Full working to increase azimuth, while the inclination is not changed.

• 4. The inclination angle decreased, while the azimuth angle increased.

• 5. Full working to decrease inclination angle, while the azimuth angle is not changed.

• 6. The inclination angle and the azimuth angle all decreased.

• 7. Full working to decrease azimuth, while the inclination is not changed.

• 8. The inclination angle and the azimuth angle all decreased.

• 9. No working. The inclination and the azimuth were controlled by BHA.

A new algorithm for pad forces (F ₁, F ₂, F ₃)

Non-uniqueness for pad forces

When the amplitude A_k and the direction α_k of the required steering force F are determined, a control algorithm is then needed to adjust each pad force to achieve the required steering force. The control variables are these three pad forces. These force vectors constitute a planar concurrent force system in the bottomhole plane, as shown in Fig. 7.

Fig. 7

Three pad forces adjusted to achieve the required steering force F

Figure 7 shows two programs which adjust three pad forces (F₁, F₂, F₃) or (F₁′, F₂′, F₃′) to achieve the same required steering force F. F₁₂ is the resultant force of F₁ and F₂. F₁₂′ is the resultant force of F₁′ and F₂′. The relation between F and F₁, F₂, F₃ can be expressed as follows:

$$ \left\{ \begin{aligned} &F\cos \alpha_{k} = F_{1} \cos \alpha_{1} + F_{2} \cos (\alpha_{1} + 240) + F_{3} \cos (\alpha_{1} + 120) \hfill \\ &F\sin \alpha_{k} = F_{1} \sin \alpha_{1} + F_{2} \sin (\alpha_{1} + 240) + F_{3} \sin (\alpha_{1} + 120) \hfill \\ \end{aligned} \right. $$

(8)

The angle (α₁) between pad 1 and high side is measured by the RSS^TSP system. Once F and α_k are determined, there are three unknown parameters F₁, F₂, and F₃. However, there are only two equations in Eq. (8). The solutions are thus not unique. To determine F₁, F₂, and F₃, an additional equation must be established.

An additional equation for optimal pad force

When a RSS^TSP starts to work, in order to prevent pad damages, forces exerted on each pad should be limited. Initially, the three pads should start simultaneously with the same forces. The initial force can be set as,

$$ F_{\text{ini}} = \frac{{F_{\hbox{max} } + F_{\hbox{min} } }}{2}, $$

(9)

where F_ini is the pad force at the initial working time.

When the RSS^TSP starts to steer the drill bit to a target point, we require a steering force F and direction α_K. One has to decide on whether each of the pad forces is in a “favorable” or “unfavorable” area. Such a decision is made by assessing the direction of each of the pad forces F₁, F₂, and F₃, in relation to the required steering force. If the angle between a pad force and the required steering force is within (− 30°, 30°), the pad force plays a positive role in achieving the required steering force, as shown in the hexagon in Fig. 8. In such cases, the pad force falls in the “favorable” area, and the force of the pad should be:

Fig. 8

Six areas of favorability based on the angle between the directions of each pad force and the required steering force

$$ F_{\text{f}} = \frac{{F_{\hbox{max} } + F_{\hbox{min} } }}{2} + \frac{{F_{\hbox{max} } - F_{\hbox{min} } }}{2}A_{K} , $$

(10a)

where F_f is the pad force on the favorable area and the second term on the right-hand side of Eq. (10a) is the augment of the pad force. On the other hand, if the angle between the pad force and the opposite direction of steering force is within (− 30°, 30°), the pad force plays a negative role in achieving the required steering force. In such cases, the pad force falls in the unfavorable area. The pad force takes big value in favorable area and takes small value in the “unfavorable” area, and the force of the pad should be:

$$ F_{\text{uf}} = \frac{{F_{\hbox{max} } + F_{\hbox{min} } }}{2} - \frac{{F_{\hbox{max} } - F_{\hbox{min} } }}{2}A_{K} , $$

(10b)

where the second term on the right-hand side of Eq. (10b) is the reduction of the pad force. The F_uf is the pad force on the unfavorable area. The bottomhole plane can now be divided into six areas, as shown in Fig. 8. At any point in time, the steering force (determined in “Maximum usable steering forces (A_max)” section) should fall in one of these six areas. The favorable or unfavorable area for one of the pad forces can then be easily determined.

For example, if the required steering force falls in area 1 (in which there is no pad), then area 4 (in which there must be a pad) is an unfavorable area. We thus set the pad force in area 4 with an unfavorable force: F₁ = F _uf, which gives an additional equation to Eq. (8), so that a set of solutions for all the pad forces can be uniquely found. If the steering force falls in area 2 (in which there is a pad), then area 2 is the favorable area. In this case, a favorable force should be assigned to pad 2: F₂ = F _f, which gives an additional equation. If the steering force is in area 3, then area 6 is the unfavorable area and F₃ = F_uf becomes an additional equation. If the steering force is in area 4, then area 4 is the favorable area and F₁ = F_f gives as an additional equation. If the steering force is in area 5, then area 2 is the unfavorable area and F₃ = F_uf becomes an additional equation. If the steering force is in area 6, then area 6 is the favorable area and F₂ = F_f becomes an additional equation.

A new algorithm for pad forces

We are now ready to develop a new algorithm for computing the pad forces. For convenience, we define a $\alpha_{K}^{'} = \alpha_{K} - \alpha_{1}$, which is the relative direction of $\alpha_{K}$ with respect to $\alpha_{1}$, as shown in Fig. 9.

Fig. 9

Relative direction (α ^’ _K ) with respect to direction α₁

As a general convention, α₁ and α_k are all defined as clockwise positive. The relative steering force direction $\alpha_{K}^{'}$ is also defined as clockwise positive with respect to pad 1, and it can be expressed in the following two cases.

$$ \left\{ {\begin{array}{*{20}l} {\alpha_{K}^{'} = \alpha_{K} - \alpha_{1} ;} \hfill & {\alpha_{\text{K}} \ge \alpha_{1} } \hfill \\ {\alpha_{K}^{'} = \alpha_{K} - \alpha_{1} + 360;} \hfill & {\alpha_{K} < \alpha_{1} } \hfill \\ \end{array} } \right. $$

(11)

According to the relative status of the steering force, one of the pads can be determined in either the favorable and unfavorable areas, following the procedure detailed in “Direction of steering force (α_k)” section. Hence, there are six possible situations.

Situation 1:

The steering force is in area 1, as shown in Fig. 10.

Fig. 10

Steering and pad forces when α ^’ _K  > 330 or α ^’ _K  ≤ 30

In Fig. 10, F_1F, F_2F, and F_3F are the force components in the directions of F, respectively, for F₁, F₂, and F₃. F_1f, F_2f, and F_3f are the force components in the normal direction of F, respectively, for F₁, F₂, and F₃. At this situation, $\alpha_{K}^{'} > 330^{^\circ }$ or $\alpha_{K}^{'} \le 30^{^\circ }$, and pad 1 is in a unfavorable area. Then, supplying F₁ = F_uf into Eq. (8), we obtain:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} \cos (\alpha_{K}^{'} - 180) + F_{2} \cos (\alpha_{K}^{'} - 300) + F_{3} \cos (\alpha_{K}^{'} - 60) = A_{\hbox{max} } A_{K} } \hfill \\ {F_{1} \sin (\alpha_{K}^{'} - 180) + F_{2} \sin (\alpha_{K}^{'} - 300) + F_{3} \sin (\alpha_{K}^{'} - 60) = 0} \hfill \\ {F_{1} = F_{\text{uf}} } \hfill \\ \end{array} } \right. $$

(12)

Equation (12) now has unique solutions, and the result is as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{uf}} } \hfill \\ {F_{2} = F_{\text{uf}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} - 60)A_{K} } \hfill \\ {F_{3} = F_{\text{uf}} + \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} + 60)A_{K} } \hfill \\ \end{array} } \right. $$

(13)

Situation 2:

The steering force is in area 2, as shown in Fig. 11.

Fig. 11

Steering and pad forces when 30 < α ^’ _K  ≤ 90

In this situation, pad 3 is in a favorable area, and $30 < \alpha_{K}^{'} \le 90^{^\circ }$, which gives an additional equation of F₃ = F_f. Therefore, a unique solution can be given as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{f}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} + 60)A_{K} } \hfill \\ {F_{2} = F_{\text{f}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} )A_{K} } \hfill \\ {F_{3} = F_{\text{f}} } \hfill \\ \end{array} } \right. $$

(14)

Situation 3:

The steering force is in area 3, as shown in Fig. 12.

Fig. 12

Steering and pad forces when 90 <α ^’ _K  ≤ 150

In this situation, pad 2 is in a unfavorable area, and $90 < \alpha_{\text{K}} '\le 150^{o}$, which gives F₂ = F_uf. The unique solution becomes:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{uf}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (60 - \alpha_{k}^{'} )A_{K} } \hfill \\ {F_{2} = F_{\text{uf}} } \hfill \\ {F_{3} = F_{\text{uf}} + \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} )A_{K} } \hfill \\ \end{array} } \right. $$

(15)

Situation 4:

The steering force is in area 4, as shown in Fig. 13.

Fig. 13

Steering and pad forces when 150 < α ^’ _K  ≤ 210

In this situation, pad 1 is in a favorable area, and $150 < \alpha_{K}^{'} \le 210^{^\circ }$, which supplies F₁ = F_f. Then, the solution is obtained as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{f}} } \hfill \\ {F_{2} = F_{\text{f}} + \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (60 - \alpha_{k}^{'} )A_{K} } \hfill \\ {F_{3} = F_{\text{f}} + \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha \alpha_{k}^{'} + 60)A_{K} } \hfill \\ \end{array} } \right. $$

(16)

Situation 5:

The steering force is in area 5, as shown in Fig. 14.

Fig. 14

Steering and pad forces when 210 <α ^’ _K  ≤ 270

In this situation, pad 3 is in a favorable area, and $210 < \alpha_{K}^{'} \le 270^{^\circ }$, which gives an addition equation of F₃ = F_uf. Then, the result is found as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{uf}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (60 + \alpha_{k}^{'} )A_{K} } \hfill \\ {F_{2} = F_{\text{uf}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} )A_{K} } \hfill \\ {F_{3} = F_{\text{uf}} } \hfill \\ \end{array} } \right. $$

(17)

Situation 6:

The steering force is in area 6, as shown in Fig. 15.

Fig. 15

Steering and pad forces when 270 < α_k′ ≤ 330

In this situation, pad 2 is in a favorable area, and $270 < \alpha_{\text{K}} '\le 330^{o}$, which leads to an addition equation of F₂ = F_f. Then, the result becomes:

$$ \left\{ {\begin{array}{*{20}l} {F_{1} = F_{\text{f}} - \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (60 - \alpha_{k}^{'} )A_{K} } \hfill \\ {F_{2} = F_{\text{f}} } \hfill \\ {F_{3} = F_{\text{f}} + \frac{2\sqrt 3 }{3}A_{\hbox{max} } \sin (\alpha_{k}^{'} )A_{K} } \hfill \\ \end{array} } \right. $$

(18)

Integrating the steer capability, stability, durability, favorable area, unfavorable area, maximum usable magnitude of steering force, a new control algorithm of RSS^TSP can easily be written using Eqs. (12)–(18).

Field tests

The new control algorithm is applied to a RSS^TSP and carried out a field test in a GU-693-P102 well. The RSS^TSP has F_max = 20KN, and F_min = 0.7KN. If α₁ = 30, the pad forces (F₁, F₂, F₃) are changing with the α_k based on the new control algorithm, and the outcome is plotted in Fig. 16.

Fig. 16

Output of the pad forces controlled using the present algorithm for given different α_k

It is shown that each pad force changes smoothly and decreases with decreasing A_k, which reduces drill bit vibration and improves the stability and durability of the RSS^TSP system. The design track and the well trajectory of GU-693-P102 are shown in Fig. 17, where the blue line is the design track and the red line is the well trajectory achieved using the present control algorithm. A is the target spot, and B is the termination spot.

Fig. 17

Well trajectory achieved using the present algorithm against the design track

The results demonstrate the well is consistent with design track as designed. The maximum dogleg rate is 5.92°/30 m, and well trajectory is smooth. It validates that our proposed control algorithm is robust and effective for RSS^TSP systems.

Inclusions

• 1. According to the current and targeted build and walk rates, this work establishes a method to calculate the work efficiency (A_k) and direction of the required steering force (α_K). The calculated results offer key instructions to transmit from ground to downhole for a RSS^TSP drilling process.

• 2. Considering maximum usable magnitude of steering force, steerability, stability, durability, favorable area and unfavorable area, a new algorithm for assigning each pad an optimal force is developed to achieve the required steering force to move the drilling bit from point A to point B.

• 3. The present new control algorithm is applied to a new RSS^TSP, and a field test is carried out in a GU-693-P102 well for validation. It demonstrates that the new control algorithm is robust and effective for RSS^TSP systems.