Entropy Optimization and Slant MHD Mixed Convection Hybrid Nanofluid Flow Within an Oblique Irregular Lid-Driven Enclosure Contains Baffles: Local Thermal Non-equilibrium Model

Abstract

This paper explores the heat transfer by mixed convection within double lid-driven enclosures filled with Cu–Al$_2$O$_3$ hybrid nanofluids. The domain contains T-shaped baffles and is filled with local thermal non-equilibrium (LTNE) porous medium. The wavy boundaries are partially cooled, while the inner baffles have constant heat flux conditions. Mathematical formulations for the system irreversibility in cases of LTNE, constant heat flux conditions and double diffusive are presented and analyzed. The solution methodology is depending on the finite volume scheme in case of non-orthogonal grids. The major results revealed that the alteration of the undulation number $\lambda$ from 1 to 5 gives an augmentation in values of $\theta _\text {f,max}$ up to 4.57%. Also, the increase in the lengths of the baffles causes a reduction in the flow, while $\theta _\text {f,max}$ is rising. Furthermore, the alteration in Ri from 0.5 to 10 gives an augmentation in $\theta _\text {f,max}$ up to 12.97%.

1 Introduction

Recently, a dependable technique to promote the thermal conductivity of conventional liquids such as ethylene glycol, water, and engine oil has been to load nanometer-sized elements of metals, oxides, carbides, nitrides or nanotubes in the regular liquid. Miscellaneous applications of nanoliquid are observed in nanotechnology, particularly in thermal engineering, including the automobile, microfluidics, electronics applications, power stations, microelectronics and processing plants to obtain a highly effective heat transmission performance [1,2,3,4,5,6,7]. Further efforts of scientists and researchers on nanoliquids led to a new sort, namely hybrid nanofluids. This type of fluids have better thermal and heat transmission, rheological, and synergistic features than the traditional mono nanoliquids. Hybrid nanofluids represent an expansion of nanofluids that involve two or more variant sorts of solid nanometer-sized particles merged together in a pure fluid. Now, that hybrid nanoliquid has become the primary desired topic among the scientists to realize the mechanism behind such fluid well. Devi and Devi [8] reported a comparison between hybrid and traditional nanoliquids in terms of the heat transmission attitude. The authors detected that the hybrid nanofluid’s heat transmission rate is greater than the regular nanofluid, even in the existence of a magnetic field. Mahdy et al. [9] simulated numerically free-forced convection flow of a micropolar hybrid nanofluid with an oblique magnetic field in a lid-driven of odd-shaped porous enclosure with radiation impact and discrete heating. A numerical treatment of flow and heat transfer of Ag–MgO–H$_2$O hybrid nanoliquid along a slant permeable stretching shrinking plate was exhibited by Anuar et al. [10]. As observed if the angle of slant and suction factors rise, the gradient of temperature boosts. The hybrid nanoliquid flow in a differentially heated containers loaded by aluminum metal foam or glass spheres as porous media was inspected by Mehryan et al. [11]. The utilizing regular liquid was H$_2$O, and the hybrid nanoelements were Cu–Al$_2$O$_3$. Their outcomes illustrated that the nanoparticles in porous media lessen the rate of heat transfer. MWCNT-Fe$_3$O$_4$-water hybrid nanometer-sized particles have synthesized by Sundar et al. [12], whereas a Ti$_2$O–Cu hybrid nanometer elements have been formed by Madhesh et al. [13]. TiO$_2$–Cu nanosize particles were suspended in water as a base fluid to be a hybrid nanofluid. Radiative attitude of nanoelements with various shapes of nanomaterials inside a permeable domain was simulated using a new technique. To see the characteristics of alumina, water has been developed by Chu et al. [14]. Ramzan et al. [15] introduced an innovative new mathematical pattern to discuss the flow of 3-D tangent hyperbolic nanofluid due to Hall current and Ion slip imposed by a strong magnetic field through a stretching plate. In addition, Chu with other co-authors investigated flow of nanofluid in different cases. [16,17,18,19,20,21].

Fluid flow and heat transmission are irreversible operations, which can be quantified in relationships of entropy optimization. The optimal design of heat transmission operation in variant industries is determined with precision computations of entropy optimization since it illustrates energy losses in a system distinctly. Therefore, entropy optimization is exhibited widely by many authors [22,23,24,25,26,27]. Induced entropy also has been investigated on MHD nanofluid, and Mahmoudi et al. [28] investigated the entropy analysis and improvement of heat transmission in free convection flow using copper CuH$_2$O nanofluid in the existence of a constant magnetic field in a two-dimensional trapezoidal cavity. The outcomes illustrate that at Ra = 10$^4$ and 10$^5$, the strength of the Nusselt number due to nanometer elements boosts with the Hartman number, while at higher values of Rayleigh number, a weakness was noticed. Additionally, it was found that the induced entropy reduces as the nanoparticles are present, but the magnetic field generally rises the magnitude of the induced entropy. Entropy generation has been investigated in different cases by many authors [29,30,31,32].

Besides, as the temperature of the fluid phase $T_\text {f}$ equals that of solid phase $T_\text {s}$ through the flow in porous media, i.e., ($T_\text {f} = T_\text {s}$), hence, the model has one energy equation, this case is known as local thermal equilibrium model LTEM, while the local thermal non-equilibrium model LTNEM is observed if there occurs a contrast among the temperature of the fluid and solid phases, i.e., there is a net heat transfer from one phase to the other, and in this situation, the model has two energy equations. A number of scientists and researchers interested in the case of LTEM [33,34,35,36]. Some of investigations have dealt with LTNEM, Izadi et al. [37] imposed the LTNEM to examine the free convection of CuO–H$_2$O micropolar nanofluids within an enclosure filled by an isotropic porous medium. The authors detected that an increment in the thermal conductivity ratio weakens the thermal resistance of the mixture, and therefore, the rate of heat transfer is boosted. Ahmed and Abd El-Aziz [38] scrutinized the boundary layer nanoliquid flow past a vertical wavy surface immersed in a porous medium utilizing LTNEM. They concluded that as Nield number increases, both of the fluid and porous phases local Nusselt numbers enhance.

Prediction of heat transmission through irregular shapes and baffles in cavities represents a topic of massive significance, and it is noticed in miscellaneous engineering processes. Adis [39] explored the heat transmission within an enclosure with heated base attached to fins to illustrate the impacts of configuration parameters of the fins on the heat transmission of laminar flow. Numerically, Ahmed et al. [40] examined the baffles in exhaust mufflers to improve their transmission loss. The calculations clarify that the temperature of outlet gases reduces by 15% with the change in baffle cut ratio from 75 to 25%. Eva et al. [41] scrutinized combined conduction, convection and radiation heat transmission in a closed horizontal airy enclosure, where its thickness and inner surface emissivity are tested with unchanged heat flux. The authors depicted that the rise in cavity thickness reduces the heat flux. The heat transmission is improved by around 120% utilizing short, thin fins compared with that of cavity with absence of fins. The heating block position within a cavity is filled with nanoliquids. The computations clarify that the solid volume fraction of nanofluid and Rayleigh number boosts the heat transmission that is presented by Sannad et al. [42]. Muthtamilselvan et al. [43] analyzed free-forced convection flow of Cu–H$_2$O nanoliquid in a lid-driven container for variant aspect ratios employing the control volume approach. Finite difference technique for analyzing the natural convection in a partially heated wavy container loaded by nanofluid is introduced by Pop et al. [44]. Abundant published papers depend on simple or irregular enclosures [45,46,47,48].

In the presented contribution, our emphasis is to formulate the mathematical modeling of entropy optimization through double diffusive mixed convection hybrid nanofluid flow and heat transmission attitude in a slant enclosure of wavy walls containing baffles placed in its middle. A slant magnetic field with $\Phi$ of inclination is applied. The LTNEM is imposed between the phases of hybrid nanofluid and porous medium, while the LTEM between the regular fluid (water) and the nanometer particles (alumina and copper) is considered. The impacts of dimensionless factors are interpreted graphically and numerically. The main object of this investigation is to answer the subsequent core questions:

• 1. How fluid thermal and concentrations distributions are affected by the impacts of undulation number, magnetic field factor and variations in the baffles lengths.

• 2. What is the impact of Richardson number on the streamlines, isotherms for both the fluid and solid phases.

• 3. How magnetic field influences the ratio of fluid Bejan number.

• 4. The ratio of the total entropy to the Nusselt number and values of the Nusselt number at the vertical baffle for the variations in porosity, magnetic field and volumetric heat generation/absorption rate.

2 Physical Configuration

Table 1 Thermophysical attributes of water, copper and alumina [9, 48]

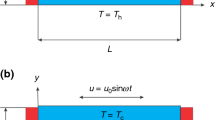
A two-dimensional wavy square enclosure of length H is taken for this investigation with inclination $\alpha$ which filled by an anisotropic porous medium. A steady mixed convection heat transfer of hybrid nanofluid with heat flux is examined with entropy analysis. The bottom wall of the cavity is assumed to be the x-axis with $T_\text {c}$ temperature, while the left vertical wall is considered y-axis. A part of the wavy wall is kept at temperature $T_\text {c}$ and the other parts of the wavy are adiabatic. A heated T-shaped baffles are placed in the middle of the cavity as observed in Fig. 1. The top and bottom walls move with constant velocity $\lambda _\textrm{d} U_0$. MHD is imposed through our contribution to control flow changes in a free-forced convection system. A slant magnetic field of intensity $B_0$ is imposed on left wall of the container with an inclination angle $\Phi$ along the positive horizontal trend, whereas the gravity force direction is downward. Hybrid nanoparticles of copper (Cu) and aluminum dioxide (Al$_2$O$_3$) are immersed in the cavity, and the hybrid nanofluid is simulated as a single-phase homogeneous fluid. The fluid’s Joule heating and viscous dissipation impacts are however ignored. Two energy equations are formulated, namely hybrid nanofluid and porous phase energy equations (LTEM). Table 1 presents the thermophysical properties of the base fluid and the nanoparticles. Under all these mentioned assumptions, the coupled boundary layer continuity, momentum and energy equations, including the boundary conditions, are formulated as [11, 27, 36]:

Fig. 1

Physical model of the problem

Figure 1 to be inserted here

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\rho _\text {hnf}}{\epsilon ^{2}}\left( u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right) =-\frac{\partial \tilde{P}}{\partial x}+\frac{\mu _\text {hnf}}{\epsilon }\left( \frac{\partial ^2 u}{\partial x^2}+\frac{\partial ^2 u}{\partial y^2}\right) \nonumber \\ {}&\quad -\frac{\mu _\text {hnf}}{\tilde{K}}u +g(\rho \beta )_\text {hnf}(T_\text {f}-T_\text {c})\sin \alpha \nonumber \\&\quad +g(\rho \beta ^\star )_\text {hnf}(C-C_\text {c})\sin \alpha \nonumber \\&\quad +\sigma _\text {hnf} B_{0}^{2}(v\sin \Phi \, \cos \Phi -u\sin ^{2}\Phi ) \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\rho _\text {hnf}}{\epsilon ^{2}}\left( u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right) =-\frac{\partial \tilde{P}}{\partial y}+\frac{\mu _\text {hnf}}{\epsilon }\left( \frac{\partial ^2 v}{\partial x^2}+\frac{\partial ^2 v}{\partial y^2}\right) \nonumber \\&\quad -\frac{\mu _\text {hnf}}{\tilde{K}}v +g(\rho \beta )_\text {hnf}(T_\text {f}-T_\text {c})\cos \alpha \nonumber \\&\quad +g(\rho \beta ^\star )_\text {hnf}(C-C_\text {c})\cos \alpha \nonumber \\&\quad +\sigma _\text {hnf} B_{0}^{2}(u\sin \Phi \, \cos \Phi -v\cos ^{2}\Phi ) \end{aligned}$$

(3)

$$\begin{aligned} (\rho c_\text {p})_\text {hnf}\left( u\frac{\partial T_\text {f}}{\partial x}+v\frac{\partial T_\text {f}}{\partial y}\right)&=\epsilon k_\text {hnf} \left( \frac{\partial ^2 T_\text {f}}{\partial x^2}+\frac{\partial ^2 T_\text {f}}{\partial y^2}\right) \nonumber \\&\quad +h_\text {fs}(T_\text {s}-T_\text {f})+{Q_0} \end{aligned}$$

(4)

$$\begin{aligned}&u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y} = D_\text {B}\left( \frac{\partial ^2 C}{\partial x^2}+\frac{\partial ^2 C}{\partial y^2}\right) \end{aligned}$$

(5)

$$\begin{aligned}&(1-{\epsilon })k_\text {s}\left( \frac{\partial ^2 T_\text {s}}{\partial x^2}+\frac{\partial ^2 T_\text {s}}{\partial y^2}\right) +h_\text {fs}(T_\text {f}-T_\text {s})+(1-{\epsilon }){Q_0}=0 \end{aligned}$$

(6)

in where, the proper imposed conditions for the porous wavy enclosure are

On the left side

$$\begin{aligned}{} & {} u=v=0, \,\, T_\text {f}=T_\text {s}=T_\text {c},\quad C=C_\text {c} \nonumber \\{} & {} x=H-AH(1-\cos 2\pi \lambda y/H), \quad 0\le y\le H \end{aligned}$$

On the right side

$$\begin{aligned}{} & {} u=v=0, \,\, T_\text {f}=T_\text {c}=T_\text {s},\quad C=C_\text {c}\nonumber \\{} & {} x=H-AH(1-\cos 2\pi \lambda y/H), \quad 0\le y\le H \end{aligned}$$

On the top side

$$\begin{aligned}{} & {} u=\pm \lambda _\text {d}U_0,\,\,v=0, \partial T_\text {f}/\partial y=\partial T_\text {s}/\partial y=\partial C/\partial y=0, \nonumber \\{} & {} \quad 0\le x\le H, \quad y=H \end{aligned}$$

On the bottom side

$$\begin{aligned}{} & {} u=\pm \lambda _\text {d}U_0,\;\;v=0, \partial T_\text {f}/\partial y=\partial T_\text {s}/\partial y=\partial C/\partial y=0, \nonumber \\{} & {} \quad 0\le x\le H, \quad y=0 \end{aligned}$$

over the inner obestical

$$\begin{aligned}{} & {} \frac{\partial T_\text {f}\left( T_\text {s}\right) }{\partial y}=-\frac{q_\text {w}}{k_\text {hnf}(k_\text {s})},\;\;\frac{\partial C}{\partial y}=\frac{q_\text {m}}{D_\text {B}}, \nonumber \\{} & {} \quad (d-0.5b)H\le x\le (d+0.5b)H,\nonumber \\{} & {} \quad y=(d+0.5b)H\nonumber \\{} & {} \frac{\partial T_\text {f}\left( T_\text {s}\right) }{\partial x}=-\frac{q_\text {w}}{k_\text {hnf}(k_\text {s})},\;\;\frac{\partial C}{\partial x}=\frac{q_\text {m}}{D_\text {B}}, \nonumber \\{} & {} \quad (d-0.5b)H\le y\le (d+0.5b)H,\nonumber \\{} & {} \quad x=0.5H \end{aligned}$$

(7)

where notations appear in governing flow Eqs. (1)–(5) are defined as x and y stand for Cartesian coordinates scaled along the vertical and horizontal walls of the container, respectively, u and v symbolize the hybrid nanofluid velocities along the x- and y- axes, respectively, T denotes the hybrid nanofluid temperature, $\tilde{P}$ indicates the hybrid nanofluid pressure, g indicates the gravity acceleration, K means the permeability and $Q_0$ means the volumetric heat generation/absorption rate.

The dependent factors of the Cu, Al$_2$O$_3$ and water hybrid nanoliquid, i.e., viscosity, density, electrical conductivity, thermal conductivity, heat capacity and effective electrical conductivity are stated as (Mahdy et al. [9, 48]);

$$\begin{aligned} \mu _\text {hnf}= & {} \frac{\mu _\text {nf}}{\left( 1-\varphi _2 \right) ^{2.5}},\quad \mu _\text {nf} =\frac{\mu _\text {bf}}{\left( 1-\varphi _1\right) ^{2.5}} \end{aligned}$$

(8)

$$\begin{aligned} \rho _\text {hnf}= & {} (1-\varphi _2 )\rho _\text {nf}+\varphi _2 \rho _2,\quad \rho _\text {nf} =(1-\varphi _1 )\rho _\text {bf} +\varphi _1 \rho _1\nonumber \\ \end{aligned}$$

(9)

$$\begin{aligned} (\rho c_{p})_\text {hnf}= & {} (1-\varphi _2)(\rho c_{p})_\text {nf}+\varphi _2 (\rho c_{p})_2,\nonumber \\ (\rho c_{p})_\text {nf}= & {} (1-\varphi _1)(\rho c_{p} )_\text {bf}+\varphi _1 (\rho c_{p})_1 \end{aligned}$$

(10)

$$\begin{aligned} (\rho \beta )_\text {hnf}= & {} (1-\varphi _2)(\rho \beta )_\text {nf}+\varphi _2 (\rho \beta )_2,\nonumber \\ (\rho \beta )_\text {nf}= & {} (1-\varphi _1)(\rho \beta )_\text {bf}+\varphi _1 (\rho \beta )_1 \end{aligned}$$

(11)

$$\begin{aligned} \frac{k_\text {hnf}}{k_\text {nf}}= & {} \frac{(k_2 +2k_\text {nf})-2\varphi _2 (k_\text {nf}-k_2)}{(k_2 +2k_\text {nf})+\varphi _2 (k_\text {nf} -k_2)}, \nonumber \\ \frac{k_\text {nf}}{k_\text {bf}}= & {} \frac{(k_1 +2k_\text {bf})-2\varphi _1 (k_\text {bf}-k_1 )}{(k_1 +2k_\text {bf})+\varphi _1 (k_\text {bf} -k_1)} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\sigma _\text {hnf}}{\sigma _\text {nf}}= & {} \frac{(\sigma _2 +2\sigma _\text {nf})-2\varphi _2 (\sigma _\text {nf}-\sigma _2 )}{(\sigma _2 +2\sigma _\text {nf})+\varphi _2 (\sigma _\text {nf} -\sigma _2)}, \nonumber \\ \frac{\sigma _\text {nf}}{\sigma _\text {bf}}= & {} \frac{(\sigma _1 +2\sigma _\text {bf})-2\varphi _1 (\sigma _\text {bf}-\sigma _1 )}{(\sigma _1 +2\sigma _\text {bf})+\varphi _1 (\sigma _\text {bf} -\sigma _2)}, \end{aligned}$$

(13)

where $\varphi _1=\varphi _{\text {Al}_{2}\text {O}_{3}}$ and $\varphi _2 =\varphi _\text {Cu}$. To non-dimensionalize the aforementioned governing Eqs. (1)–(6), the following dimensionless variables are inserted

$$\begin{aligned}&(x,y)=(X,Y)H,\quad (u,v)=(U,V)U_0, \quad P=\frac{\tilde{P}}{\rho _\text {f}U_0^{2}},\nonumber \\&\theta _\text {f} =\frac{\left( T_\text {f}-T_\text {c}\right) k_\text {f}}{q_\text {w}H},\nonumber \\&\theta _\text {s} =\frac{\left( T_\text {s}-T_\text {c}\right) k_\text {s}}{q_\text {w}H},\quad \quad \phi =\frac{\left( C-C_\text {c}\right) D_\text {B}}{q_\text {m}H},\quad D=\frac{d}{H},\nonumber \\&B=\frac{b}{H} \end{aligned}$$

(14)

which mutate the flow governing equations into the non-dimensional subsequent equations in the form

$$\begin{aligned}{} & {} \frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \frac{1}{\epsilon ^{2}}\left( U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}\right) =-\frac{\rho _\text {f}}{\rho _\text {hnf}}\frac{\partial P}{\partial X} +\frac{1}{\hbox {Re} \epsilon } \frac{\nu _\text {hnf}}{\nu _\text {f}}\nonumber \\{} & {} \quad \left( \left( \frac{\partial ^2 U}{\partial X^2}+\frac{\partial ^2 U}{\partial Y^2}\right) -\frac{\epsilon }{\hbox {Da}}U\right) + \hbox {Ra}_\text {c}\phi \sin \alpha +\frac{\beta _\text {hnf}}{\beta _\text {f}} \nonumber \\{} & {} \quad \hbox {Ri} \theta _\text {f}\sin \alpha \!+\!\frac{\rho _\text {f}}{\rho _\text {hnf}}\frac{\sigma _\text {hnf} }{\sigma _\text {f}}\frac{ \hbox {Ha}^{2}}{\hbox {Re}}(V\sin \Phi \,\cos \Phi \!-\!U\sin ^{2}\Phi ) \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \frac{1}{\epsilon ^{2}}\left( U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}\right) =-\frac{\rho _\text {f}}{\rho _\text {hnf}}\frac{\partial P}{\partial Y}\nonumber \\{} & {} \quad +\frac{1}{ \hbox {Re} \epsilon } \frac{\nu _\text {hnf}}{\nu _\text {f}}\left( \left( \frac{\partial ^2 V}{\partial X^2}+\frac{\partial ^2 V}{\partial Y^2}\right) -\frac{\epsilon }{Da}V\right) + \hbox {Ra}_\text {c}\phi \cos \alpha \nonumber \\{} & {} \quad +\frac{\beta _\text {hnf}}{\beta _\text {f}} \hbox {Ri} \theta _\text {f}\cos \alpha \nonumber \\{} & {} \quad +\frac{\rho _\text {f}}{\rho _\text {hnf}}\frac{\sigma _\text {hnf} }{\sigma _\text {f}}\frac{ \hbox {Ha}^{2}}{\hbox {Re}}(U\sin \Phi \,\cos \Phi -V\cos ^{2}\Phi ) \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \hbox {Re} \Pr \frac{(\rho c_\text {p})_\text {hnf}}{(\rho c_\text {p})_\text {f}}\left( U\frac{\partial \theta _\text {f}}{\partial X}+V\frac{\partial \theta _\text {f}}{\partial Y}\right) =\epsilon \frac{k_\text {hnf}}{k_\text {f}} \left( \frac{\partial ^2 \theta _\text {f}}{\partial X^2}+\frac{\partial ^2 \theta _\text {f}}{\partial Y^2}\right) \nonumber \\{} & {} \quad +H^\star (\theta _\text {s}-\theta _\text {f})+Q \end{aligned}$$

(18)

$$\begin{aligned}{} & {} U\frac{\partial \phi }{\partial X}+V\frac{\partial \phi }{\partial Y} =\frac{1}{\hbox {Re} \, \hbox {Sc}}\left( \frac{\partial ^2 \phi }{\partial X^2}+\frac{\partial ^2 \phi }{\partial Y^2}\right) \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \frac{\partial ^2 \theta _\text {s}}{\partial Y^2}+\frac{\partial ^2 \theta _\text {s}}{\partial Y^2} +K_\textrm{d} H^\star (\theta _\text {f}-\theta _\text {s})+K_\text {fs}Q_0=0 \end{aligned}$$

(20)

In the previous non-dimensional equations, the emerging physical factors are expressed mathematically as

$$\begin{aligned}&\Pr =\frac{(\mu c_\textrm{p})_\text {f} }{k_\text {f} },\quad \hbox {Ra}=\frac{g(\rho \beta )_\text {f}(\rho c_\textrm{p})_\text {f} H^{5}\tilde{Q}}{\mu _\text {f} k^2_\text {f}}, \quad \delta =\frac{k_\text {f}\Lambda }{H^2(\rho c_\textrm{p})_\text {f}},\nonumber \\&\hbox {Ha}^2=B_{0}^2 H^2\left( \frac{\sigma _\text {f} }{\mu _\text {f}}\right) , \nonumber \\&\hbox {Da} =\frac{K}{H^{2}},\quad K_\textrm{d}=\frac{k_\text {c}H^{2}}{\nu _\text {f}} \quad R_\textrm{d}=\frac{16\sigma ^\star T_c^3}{3k^\star k_\text {f}} \end{aligned}$$

(21)

In addition, the mutated boundary conditions are

$$\begin{aligned}&\text {On the left side}\nonumber \\&U=V=0, \quad \theta _\text {f}=\theta _\text {s}=\phi =0,\quad X=A(1-\cos 2\pi \lambda Y),\nonumber \\&\quad 0\le Y\le 1 \nonumber \\&\text {On the right side}\nonumber \\&U=V=0, \quad \theta _\text {f}=\theta _\text {s}=\phi =0,\quad X=1-A(1- \cos 2\pi \lambda Y),\nonumber \\&\quad 0\le Y\le 1\nonumber \\&\text {On the top side}\nonumber \\&U=\pm \lambda _\textrm{d},\;\; V=0, \quad \partial \theta _\text {f}/\partial Y=\partial \theta _\text {s}/\partial Y=\partial \phi /\partial Y=0,\nonumber \\&\quad 0\le X\le 1,\quad Y=1 \nonumber \\&\text {On the bottom side}\nonumber \\&U=\pm \lambda _\textrm{d},\;\;V=0, \quad \partial \theta _\text {f}/\partial Y=\partial \theta _\text {s}/\partial Y=\partial \phi /\partial Y=0,\nonumber \\&\quad 0\le X\le 1,\quad Y=0 \nonumber \\&\text {On the inner obestical } \nonumber \\&\partial \theta _\text {f}/\partial X=-k_\text {f}/k_\text {hnf},\;\;\partial \theta _\text {s}/\partial X=\partial \phi /\partial Y=-1,\nonumber \\&\quad X=0.5,\quad D-0.5B\le Y\le D+0.5B\nonumber \\&\partial \theta _\text {f}/\partial Y=-k_\text {f}/k_\text {hnf},\;\;\partial \theta _\text {s}/\partial Y=\partial \phi /\partial Y=-1,\nonumber \\&\quad D-0.5B\le X\le D+0.5B,\quad Y=D+0.5B \end{aligned}$$

(22)

Due to a science and engineering perspective, the physical quantities of curiosity, such as rate of heat transfer in terms of Nusselt number, have plentiful applications. The mathematical expressions for the physical significant amounts of the local Nusselt number of the fluid phase on the vertical and horizontal obesticals are stated as

$$\begin{aligned} \hbox {Nu}_\text {fsv}= & {} \left( \frac{1}{\theta _\text {f}}\right) _{\text {v}}\qquad \hbox {Nu}_\text {fsh} =\left( \frac{1}{\theta _\text {f}}\right) _\text {h} \end{aligned}$$

(23)

$$\begin{aligned} \hbox {Nu}_\text {ssv}= & {} \left( \frac{1}{\theta _\text {s}}\right) _\text {v}\qquad \hbox {Nu}_\text {ssh} =\left( \frac{1}{\theta _\text {s}}\right) _\text {h} \end{aligned}$$

(24)

and the average Nusselt number of the fluid phase is given by

$$\begin{aligned} \hbox {Nu}_\text {mfv}= & {} \frac{1}{B}\int \limits _{D-0.5B}^{D+0.5B} \hbox {Nu}_\text {fsv} \hbox {d}Y,\nonumber \\ \hbox {Nu}_\text {mfh}= & {} \frac{1}{B}\int \limits _{D-0.5B}^{D+0.5B} \hbox {Nu}_\text {fsh} \hbox {d}X \end{aligned}$$

(25)

$$\begin{aligned} \hbox {Nu}_\text {msv}= & {} \frac{1}{B}\int \limits _{D-0.5B}^{D+0.5B} \hbox {Nu}_\text {ssv}\hbox {d}Y,\nonumber \\ \hbox {Nu}_\text {msh}= & {} \frac{1}{B}\int \limits _{D-0.5B}^{D+0.5B} \hbox {Nu}_\text {ssh}\hbox {d}X \end{aligned}$$

(26)

$$\begin{aligned} \hbox {Nu}_\text {mf}= & {} \frac{Nu_\text {mfv}+Nu_\text {mfh}}{2},\nonumber \\ \hbox {Nu}_\text {ms}= & {} \frac{Nu_\text {msv}+Nu_\text {msh}}{2} \end{aligned}$$

(27)

Table 1 to be inserted here

3 Entropy Optimization

Physically, entropy is defined as the measure of irreversibility and signifies a state of unrest in the system and its surroundings. If the heat is not utilized for work completely, the amount of entropy it creates is determined. Entropy optimization of the fluid and solid is formulated as [9, 24]

$$\begin{aligned} S_\text {f}&=\left( \frac{k_\text {eff hnf} }{T_{\text {f}}^{2} }\right) \left\{ \left( \frac{\partial T_\text {f}}{\partial x}\right) ^{2}+\left( \frac{\partial T_\text {f}}{\partial y} \right) ^{2}\right\} \nonumber \\&\quad +\frac{\hbox {RD}}{C}\left\{ \left( \frac{\partial C}{\partial x}\right) ^{2}+\left( \frac{\partial C}{\partial y}\right) ^{2} \right\} \nonumber \\&\quad +\frac{\hbox {RD} }{T_{\text {f}}}\left\{ \frac{\partial T_\text {f}}{\partial x}\frac{\partial C}{\partial x}+\frac{\partial T_\text {f}}{\partial y}\frac{\partial C}{\partial y} \right\} +\left( \frac{\mu _\text {hnf}}{T_{\text {f}}}\right) \nonumber \\&\qquad \left\{ \frac{1}{K}\left( u^{2}+v^{2}\right) +2\left( \left( \frac{\partial u}{\partial x} \right) ^{2}+\left( \frac{\partial v}{\partial y}\right) ^{2}\right) \right. \nonumber \\&\qquad \left. +\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) ^{2} \right\} +\frac{h_\text {fs}}{T_\text {f}T_\text {s}}\left( T_\text {s}-T_\text {f} \right) ^2 \nonumber \\&\qquad +\left( \frac{\sigma _\text {hnf} B_{0}^{2}}{T_{\text {f}}}\right) (u\sin \Phi -v\cos \Phi )^{2} \end{aligned}$$

(28)

$$\begin{aligned} S_\text {s}&=\left( \frac{k_\text {eff s} }{T_{\text {s}}^{2} }\right) \left\{ {\left( {\frac{\partial T_\text {s}}{\partial x}} \right) ^{2}+\left( {\frac{\partial T_\text {s}}{\partial y}} \right) ^{2}} \right\} + \frac{h_\text {fs}}{T_\text {f}T_\text {s}}\left( T_\text {s}-T_\text {f} \right) ^2 \end{aligned}$$

(29)

Due to the dimensionless factors mentioned in Eq. (20), the formulation of the dimensionless entropy optimization may be stated as

$$\begin{aligned} S_\text {f}&=\frac{1}{\left( \theta _{\text {s}}+C_\text {T}\right) ^{2}}\left( \frac{k_\text {hnf} }{k_{\text {f}}^{2} }\right) \left\{ {\left( {\frac{\partial \theta _\text {f}}{\partial X}} \right) ^{2}+\left( {\frac{\partial \theta _\text {f}}{\partial Y}} \right) ^{2}} \right\} \nonumber \\&\quad +\frac{\Omega _2}{\phi +C_\text {c}}\left\{ {\left( \frac{\partial \phi }{\partial X}\right) ^{2}+\left( \frac{\partial \phi }{\partial Y}\right) ^{2}} \right\} \nonumber \\&\quad +\frac{\mu _\text {hnf}\;\;\Omega _1}{\mu _\text {f}\left( \theta _{\text {s}}+C_\text {T}\right) }\nonumber \\&\qquad \left\{ \frac{1}{Da}(U^{2}+V^{2})+2\left( {\left( {\frac{\partial U}{\partial X}} \right) ^{2}+\left( {\frac{\partial V}{\partial Y}} \right) ^{2}} \right) \right. \nonumber \\&\quad \left. +\left( {\frac{\partial U}{\partial yY}+\frac{\partial V}{\partial X}} \right) ^{2} \right\} \nonumber \\&\quad +\frac{\Omega _2 }{\theta _{\text {f}}+C_T}\left\{ {\frac{\partial \theta _\text {f}}{\partial X}\frac{\partial \phi }{\partial X}+\frac{\partial \theta _\text {f}}{\partial Y}\frac{\partial \phi }{\partial Y}} \right\} \nonumber \\&\quad +\frac{H^\star }{(\theta _\text {f}+C_T)(\theta _\text {s}+C_T)}\left( \theta _\text {s}-\theta _\text {f} \right) ^2\nonumber \\&\quad +\left( \frac{\sigma _\text {hnf}}{\sigma _\text {f}}\right) \frac{Ha^2\Omega _1}{\theta _\text {f}+C_T} (U\sin \Phi -V\cos \Phi )^{2} \end{aligned}$$

(30)

$$\begin{aligned} S_\text {s}&=\frac{\Omega _3}{\left( \theta _{\text {s}}+C_\text {T}\right) ^{2} }\left\{ {\left( {\frac{\partial \theta _\text {s}}{\partial X}} \right) ^{2}+\left( {\frac{\partial \theta _\text {s}}{\partial Y}} \right) ^{2}} \right\} \nonumber \\&\quad + \frac{H^\star k_\text {fs}}{(\theta _\text {f}+C_\text {f})(\theta _\text {s}+C_\text {T})}\left( \theta _\text {s}-\theta _\text {f} \right) ^2 \end{aligned}$$

(31)

Fig. 2

Features of $\psi$, $\theta _\text {f}$, $\theta _\text {s}$ and $\phi$ for $\lambda$ = 1, 3, 5 (Top to down)

Fig. 3

Features of $\psi$, $\theta _\text {f}$, $\theta _\text {s}$ and $\phi$for B = 0.1,0.3,0.5 (Top to down)

Herein, the irreversibility rations can be stated by

$$\begin{aligned}{} & {} \Omega _1=\frac{\mu _{\text {f}}}{k_\text {f}(T_\text {f}-T_\text {c})}\left( \frac{\alpha _\text {f}}{H} \right) ^2,\quad \Omega _2= \hbox {RD} \frac{\Delta C}{k_\text {f}},\quad \Omega _3=\frac{k_\text {eff s}}{k_\text {s}},\nonumber \\{} & {} k_=\frac{k_\text {eff s}}{k_\text {s}},\quad k_\text {fs}=\frac{k_\text {f}}{k_\text {s}} \end{aligned}$$

Also, the following Nusselt ration, total entropy generation ration and thermal performance criteria reported by Ilis et al. [26] are defined as

$$\begin{aligned} \hbox {Be}_\text {f} =\frac{S_\text {hf}}{S_\text {f}},\quad \hbox {Be}_\text {s} =\frac{S_\text {hs}}{S_\text {s}} \end{aligned}$$

(32)

In order to provide the impact of nanometer particles, magnetic field and difference of temperature on the average Nusselt number, total induced entropy and Began number, the following Nusselt ration, total induced entropy ration and Began number ration are expressed as

$$\begin{aligned} \hbox {Nu}_\text {mf}^+= & {} \frac{\hbox {Nu}_\text {mf}}{\left( \hbox {Nu}_\text {mf}\right) _{\text {Ha=0}}},\quad S_\text {f}^+ =\frac{S_\text {f}}{\left( S_\text {f}\right) _{\text {Ha=0}}} \end{aligned}$$

(33)

$$\begin{aligned} \hbox {Be}_\text {f}^+= & {} \frac{\hbox {Be}_\text {f}}{\left( \hbox {Be}_\text {f}\right) _{\text {Ha=0}}},\qquad e^+ =\frac{S_\text {f}^+}{\hbox {Nu}_\text {mf}^+} \end{aligned}$$

(34)

4 Results and Discussion

Finite volume procedure in case of non-orthogonal grids has been imposed to get the numerical computations through this paper. A set of illustrations are presented, here, to explore the double-diffusive flow confined a very complex domain filled with hybrid nanofluids. The streamlines $\psi$, suspension temperature $\theta _\text {f}$, solid-phase temperature $\theta _\text {s}$ and mass concentration $\phi$ are examined for higher variations in the undulation number $\lambda =1,3,5$, length of the heat source $B=0.1,0.3,0.5$, nanoparticles (NP) concentration $\varphi =\varphi _1+\varphi _2=0\%,1\%,3\%,5\%$, the Richardson number $\hbox {Ri} =0.5,1$ and 10, the Darcy number $\hbox {Da}=0.1,0.001, 0.00001$, the Hartmann number $\hbox {Ha} =0,25,50,100$, the heat transfer coefficient $H^\star =0.05,5,10,25,100$ and the medium porosity $\epsilon =0.35,0.4,0.45,0.5,0.6.$ Furthermore, the heat transfer coefficients for both the solid and fluids phases are computed against with the aforementioned values of the controlling parameters.

Fig. 2 illustrates the flow features, thermal and concentrations distributions for the alteration of the undulation number $\lambda$. The results disclosed that $\psi$ is represented by two forced eddies near the moving walls with non-active middle area due to the presence of the baffles. The alteration of $\lambda$ causes a weakness of the flow and a reduction in the absolute values of $\psi$. The mixture temperature $\theta _\text {f}$ shows that the convective mode is dominance on their distributions and the growing in $\lambda$ causes an enhancement in its maximum temperature $\theta _\text {f,max}$. However, the solid-phase temperature $\theta _\text {s}$ shows that the conduction mode is dominance and the higher values of $\lambda$ leads to a clear diminishing in values of $\theta _\text {s,max}$. Additionally, the features of the mass concentration revealed that it is concentrated near the top-left and bottom-right corners due to the moving of the upper and lower walls; those pushed the mass in opposite direction of the movements. Here, the growing in $\lambda$ enhances the complexity of the domain, and hence, the suspension flow faces a higher obstruction.

Fig. 3 displays the features of $\psi , \theta _\text {f}, \theta _\text {s}$ and $\phi$ for the variations in the baffles lengths B. It is remarkable that the increase in B enhances the obstruction of the flow, and hence, a clear reduction in values of $\psi$ is given. Also, the upper eddy is shifted toward the outer boundaries as B is increased. However, a clear augmentation in either values of $\theta _\text {f,max}, \theta _\text {s,max}$ or the distributions of $\theta _\text {f}$ and $\theta _\text {s}$ is seen as B is growing. Physically, the inner baffles have the constant heat flux conditions, and hence, the increase in their lengths enhances the heat flux in the flow domain, and as results, the rising in the isotherms is obtained. On the contrary, features of $\phi$ disclosed that the mass concentration is diminishing as B is altered. In the fact, the increase in lengths of the baffles causes a weakness of the buoyancy-induced flow, and hence, the mass concentration is reduced.

Fig. 4

Behaviors of $Nu_\text {mf}$ for various B at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri = 1, Q = 1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 5

Behaviors of $Be_\text {f}$ for various B at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri=1, Q = 1, $\epsilon$ = 0.5, H$^{*}$ = 1

In Figs. 4, 5, behaviors of the fluid heat transfer rate $\hbox {Nu}_\text {mf}$ and fluid Bejan number $\hbox {Be}_\text {f}$ for various values of B and are depicted. The mixed convection mode $(\hbox {Ri}=1)$ is considered, and the value of the heat generation parameter is $Q=1$. It is seen that for all values of B, $\hbox {Nu}_\text {mf}$ is rising as $\varphi$ is altered due to the increase in the mixture thermal conductivity. Also, the heat transfer rate is augmented as the lengths of the baffles are increased due to the increase in the heat flux. On the contrary, a rising in NP concentration causes a reduction in values of $\hbox {Be}_\text {f}$ due to the decrease in the velocity gradients, while the growing in B makes the heat transfer irreversibility more dominance.

Fig. 6

Features of $\psi$, $\theta _\text {f}$, $\theta _\text {s}$ and $\phi$ for Ri = 0.5, 1, 10 (Top to down)

Figs. 6, 7 and 8 illustrate the influences of the Richardson number $(\hbox {Ri}=\hbox {Gr}/\hbox {Re}^2)$ on the features of the streamlines, isotherms for both the fluid and solid phases and iso-concentration together with the Nusselt number for the fluid and solid phases. The flow features show a reduction in values of $\psi _\text {min}$ as Ri grows due to the decrease in the forced flow, while the values of $\theta _\text {f,max}$ are rising. Also, the average heat transfer rate for the fluid phase $\hbox {Nu}_\text {mf}$ is diminishing as either Ri or Ha is altered due to the decrease in the convective flow. Furthermore, the Nusselt number along the vertical baffle is reduced, gradually, as Ri is enhanced due to the decrease in the Reynolds number. In the same context, Figs. 9, 10 display the system entropy for the fluid $S_\text {f}$ and for the solid $S_\text {s}$ for the considered range of Ri and $\varphi$. Two inverse behaviors are noted for $S_\text {s}$ and $S_\text {f}$ when Ri is altered. Here, $S_\text {f}$ is diminishing as Ri is increased due to the invers relation between $S_\text {f}$ and $\theta _\text {f}$, while as Ri increases, $S_\text {s}$ get higher features.

Fig. 7

Behaviors of $Nu_\text {mf}$ for various Ri and Ha at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri =1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 8

Behaviors of $Nu_\text {fsv}$ for various Ri at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri =1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 9

Behaviors of $S_\text {f}$ for various Ri and $\varphi$, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri=1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 10

Behaviors of $S_\text {s}$ for various Ri and $\varphi$, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri =1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 11 illustrates the contours of $\psi , \theta _\text {f}, \theta _\text {s}$ and $\phi$ for the variations in the Darcy number Da. The figure discloses that the flow has a great reduction as Da decreases. In this context, $\psi _\text {min}$ is varied from $-$0.0591891 at $\hbox {Da} =0.1$ to $-$0.0016694 at $\hbox {Da} =0.00001$. This reduction is due to the decrease in the medium’s permeability which makes the flow faces an obstruction due to the medium solid elements. In fact, there is a well-known inverse relation between the fluid speed and $\theta _\text {f,max}$. Therefore, it can be observed that $\theta _\text {f,max}$ is enhanced, clearly, as Da is altered. Further, the iso-concentration lineaments revealed that the alteration of Da enhances the mass concentration within the flow area.

Figs. 12, 13 and 14 depict the ratio of the fluid Bejan number values in the presence/absence of magnetic field $\hbox {Be}_\text {f}^+$, ratio of the total entropy to the Nusselt number $e_\text {f}^+$ and values of the Nusselt number at the vertical baffle $\hbox {Nu}_\text {fsv}$ for the variations in $\epsilon , \hbox {Ha}, H^\star$ and Q. It is noted that $\hbox {Be}_\text {f}^+$ is reduced as the medium porosity $\epsilon$ or the Hartmann number is increased due to the reduction in the convective case. Also, $e_\text {f}^+$ is diminishing as $H^\star$ or Ha is altered due to the Lorentz force. Furthermore, the growing in the heat generation parameter decreases the temperature differences within the flow dominant, and hence, $\hbox {Nu}_\text {fsv}$ gets lower features.

Fig. 11

Features of $\psi$, $\theta _\text {f}$, $\theta _\text {s}$ and $\phi$ for $\hbox {Da}$ = 0.1, 0.001, 0.00001 (Top to down)

5 Conclusions

Conclusion parametric investigations have been carried out for the mixed convection and mass transfer due to the movements of the two-sided edges of two-sided wavy enclosures filled with hybrid nanofluids. Also, T-shaped baffles with constant heat flux conditions were placed in the middle part of the domain. The flow area was filled by LTNE porous elements and an inclined magnetic field together with a heat source/sink has been considered. The finite volume method (FVM) in case of the non-orthogonal grids was applied to solve the mathematical forms, and the irreversibility of the system for the fluid and solid phases was computed. The current analyses led to the following major results:

• 1. The values of $\theta _\text {f,max}$ have an enhancement up to 4.57% when $\lambda$ is altered from 1 to 5.

• 2. The growing in the lengths of the baffles enhances the flow obstruction, and hence, values of $\psi _\text {min}$ are diminishing, while the average heat transfer rate for the suspension is augmented.

• 3. The alteration in Ri from 0.5 to 10 gives an augmentation in $\theta _\text {f,max}$ up to 12.97%

• 4. As Da decreases, the convective transport is reduced while $\theta _\text {f,max}$ is enhanced.

• 5. The increase in the undulation number $\lambda$ from 1 to 5 gives a reduction in the flow up to 5.66%.

• 6. $\hbox {Be}_f^+$ and $e_f^+$ are diminishing, clearly, as Ha is growing.

• 7. The rising in the heat generation parameter causes a reduction in the Nusselt number along the vertical baffles

• 8. The LTNE model gives more realistic results comparing to LTE cases.

• 9. The fluid phase Nusselt number is enhanced as either the nanoparticle volume fraction or the baffles lengths is altered.

Fig. 12

Behaviors of $\hbox {Be}_\text {f}^{+}$ for various $\varepsilon$ and Ha, at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri=1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 13

Behaviors of $e_\text {f}^{+}$ for various $H^{*}$ and Ha, at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri=1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1

Fig. 14

Behaviors of $Nu_\text {fav}$ for various Q at $\varphi$ = 0.05, $\varphi _\text {cu}$ = $\varphi _{\text {Al}_{2}\text {o}_{3}}$ = $\varphi$/2, Ri=1, Q=1, $\epsilon$ = 0.5, H$^{*}$ = 1