1 Introduction

Linear regression is a simple and widely used machine learning algorithm that has received a lot of attention in many fields. In the image recognition area, Naseem et al. [1] proposed a Linear Regression Classification (LRC) algorithm that represents each class's training images independently assuming a linear regression relationship. The algorithm depends on applying the least squares method to find the regression coefficient then decides the class label that gives the smallest reconstruction error. To enhance its performance, Huang and Yang [2] and Zhu et al. [3] proposed to apply principal component analysis (PCA) [4] to extract the vital information from images and reduce the feature vector dimensions. Then, the original data are transformed into a low-dimensional subspace. Finally, LRC is performed on the projected data.

This paper contributes to this literature by proposing a new strategy for classification by performing regression of data in terms of its principal components. A novel formulation of the LRC problem, called Classification by Principal Component Regression (CbPCR), is presented. Moreover, a novel closed-form solution based on this formulation is derived. This classification strategy preserves key data class information and removes redundant and correlated details, yet yielding a more compact solution. Several experiments on public face recognition benchmark databases are reported to provide evidence that the proposed strategy outperforms the original LRC method [1] and its recent variants [2, 3].

The proposed strategy is also extended to color images. PCA techniques [4,5,6] and the existing methods [1,2,3] work in principle on grayscale, single-channel images. They may operate on color images after converting them to grayscale images, thus losing the important color information. Some methods (e.g., [7]) apply LRC to every color channel separately, then select the class having the smallest total prediction error over all color channels. Unlike those methods, inspired by several studies [8,9,10,11,12,13,14], the current paper proposes to use 4D hypercomplex numbers to represent color images. This allows treating the color components of each image pixel as one entity thus considering the correlation between color components. Among the studies [8,9,10,11,12,13,14], two address the LRC problem. Zou et al. [11] proposes a quaternion LRC (QLRC) method that extends the classical LRC algorithm to quaternion space. QLRC converts the quaternion quantities to real ones to circumvent using quaternion derivatives. The recent paper [14] develops closed-form solutions for QLRC from the principles of quaternion calculus. In addition, the current paper proposes novel solutions based on reduced biquaternions (RBs), another hypercomplex space consisting of one real component and 3 imaginary ones. In addition to having commutative algebra—in contrast to quaternions—RBs may be represented using the so-called e1-e2 form [15] that can lead to more time-efficient computation.

The proposed CbPCR formulation is extended to both the quaternion and RB domains to process color images. To that end, the current paper exploits an efficient algorithm derived by the authors in [10] for computing the principal components (eigenvectors) of an RB matrix by casting it as an x + y selection problem [16, 17]. The experimental results on public benchmark databases for color face recognition demonstrate the better performances of the new quaternion and RB-based CbPCR algorithms over competing algorithms [7, 11, 14].

The rest of this paper is organized as follows: Sect. 2 gives a brief history of using 4D hypercomplex domains, namely quaternion and reduced biquaternions, in color image processing, with focus on color face recognition. Section 3 gives some notations and formally defines the problem of our concern here. Section 4 briefly reviews the quaternion and RB domains. Section 5 describes the proposed CbPCR method and its extension to the quaternion and the RB domains. The classification results on two benchmark color face databases are reported in Sect. 6. Section 7 concludes the paper.

2 Related Work

This section briefly reviews the use of 4D hypercomplex domains, namely quaternion, and reduced biquaternions, in representing color image, with focus on their application to color face recognition.

In 1996, Sangwine [18] introduced the idea of using 4D hypercomplex numbers (Quaternion numbers) in color image processing by encoding the pixel’s color components into the three imaginary parts of a quaternion number. Bihan and Sangwine [8] and Pei et al. [19] proposed a Quaternion PCA method, which extracts more informative and robust features from the color image than conventional PCA. In 2011, Sun et al. [20] proposed 2DPCA and bi-dimensional PCA (BDPCA) based on quaternion representation. Also, Javier et al. [21] proposed an independent component analysis algorithm based on quaternions. Years later, Jia et al. [22] presented a 2DPCA based on a quaternion model (2DQPCA) that depends on reducing feature dimension in a row direction. In addition, Liu et al. [23] proposed a quaternion-based maximum margin criterion algorithm. The methods proposed in [20, 22, 23] mainly targeted color face recognition and showed an enhancement in the recognition rate over their grayscale-based counterpart methods.

Using the other 4D domain of reduced biquaternions for the same purpose started rather late. A reduced biquaternion PCA based on reduced biquaternion representation was proposed [10] to represent color images in the typical PCA framework, which takes full advantage of the color characteristics of the image. Recently, a color occlusion face recognition method [24] based on the quaternion non-convex sparse constraint mechanism was proposed.

On the other hand, LRC was originally designed for grayscale images. Zou et al. [11] proposed an LRC model based on quaternion representation to consider the color image information. In [14], an LRC model was developed based on a reduced biquaternion representation. Both works [11, 14] were also applied to the face recognition problem and achieved better performances than the original LRC.

3 Notations and Problem Statement

Let us first give some notations to distinguish between real, quaternion, and reduced biquaternion. Scalars and vectors were denoted using italic and bold lowercase letters, respectively, while matrices are indicated by bold uppercase letters. The number of dots on top of a symbol indicates its intended domain: real (\({\mathbb{R}}\)), complex (\({\mathbb{C}}\)), quaternion (\({\mathbb{Q}}\)), or reduced biquaternion (\({\mathbb{B}}\)). Symbols without any dots on top indicate real or complex quantities, where the intended domain is disambiguated from the context. A quaternion is represented by a symbol with one dot above, while an RB quantity has two dots.

In the context of image classification, the problem of our concern can be defined as follows. Suppose there are L classes in a training set of images, where the l-th class consists of nl images. Each image is of size \(m\times n\). The typical goal of LRC is to find the label of a new probe image \(\mathbf{Y}\) from the given training samples and their labels. Assuming grayscale images, each image \(\mathbf{X}\) \(\in {\mathbb{R}}^{m\times n}\) is represented as a 1D vector \(\mathbf{x}\in {\mathbb{R}}^{mn}\) by stacking the rows, one after another. As such, one can form a matrix \({\mathbf{A}}_{l}=[{\mathbf{x}}_{1}^{l}, {\mathbf{x}}_{2}^{l}, \dots , {\mathbf{x}}_{{n}_{l}}^{l}]\in {\mathbb{R}}^{mn\times {n}_{l}}\) that represents samples from the l-th class. For our work here, a color image is represented as a 1D pure quaternion vector \(\dot{\mathbf{x}}\in {\mathbb{Q}}^{mn}\). Analogously, the color image can be represented as a 1D pure reduced biquaternion vector \(\ddot{\mathbf{x}}\) \(\in {\mathbb{B}}^{mn}\).

4 Hypercomplex Domains

4.1 Quaternions

A quaternion number [25] consists of one real and three imaginary parts: \(\dot{q}={q}_{r}+{q}_{i}i+{q}_{j}j+{q}_{k}k\) (a quaternion number with no real part is called a pure quaternion). The three imaginary parts satisfy:

$$\begin{gathered} i^{2} = j^{2} = k^{2} = - 1,\,{ }ij = - ji = k, \hfill \\ jk = - kj = i,\,{ }ki = - ik = j. \hfill \\ \end{gathered}$$
(1)

The quaternion conjugate is \(\overline{\dot{q} }={q}_{r}-{q}_{i}i-{q}_{j}j-{q}_{k}k,\) and the quaternion norm is \(\left|\dot{q}\right|=\sqrt{\dot{q}\overline{\dot{q}} }\). The Hermitian (conjugate transpose) satisfies \({\left(\dot{\mathbf{P}}\dot{\mathbf{Q}}\right)}^{H}={\dot{\mathbf{Q}}}^{H}{\dot{\mathbf{P}}}^{H}\), see [26] for more details.

Due to the noncommutativity of quaternion multiplication, a quaternion matrix has left and right eigenvalues that may be different [15, 27]. Any quaternion matrix \(\dot{\mathbf{Q}}\in {\mathbb{Q}}^{n\times n}\) can be expressed as: \(\dot{\mathbf{Q}}={\mathbf{Q}}_{1}+{\mathbf{Q}}_{2}j\), where \({\mathbf{Q}}_{1}={\mathbf{Q}}_{r}+i{\mathbf{Q}}_{i}\) and \({\mathbf{Q}}_{2}={\mathbf{Q}}_{j}+i{\mathbf{Q}}_{k}\), with \({\mathbf{Q}}_{r}, {\mathbf{Q}}_{i}, {\mathbf{Q}}_{j,}\mathrm{and }{\mathbf{Q}}_{k}\) being the real and the three imaginary parts of the quaternion matrix \(\dot{\mathbf{Q}}\). The eigenvalues (and eigenvectors) can be calculated from the equivalent complex matrix [27]:

$$\mathcal{H}\left(\dot{\mathbf{Q}}\right):=\left[\begin{array}{cc}{\mathbf{Q}}_{1}& {\mathbf{Q}}_{2}\\ -\overline{{\mathbf{Q} }_{2}}& \overline{{\mathbf{Q} }_{1}}\end{array}\right]\in {\mathbb{C}}^{2n\times 2n},$$
(2)

where the mapping \(\mathcal{H}\left(\boldsymbol{ }.\right)\) transforms a quaternion matrix into an equivalent complex matrix. Thus, there are \(2n\) eigenvalues (eigenvectors) for any \(n\times n\) quaternion matrix.

4.2 Reduced Biquaternions

A reduced biquaternion number also has one real and three imaginary parts: \(\ddot{p}={p}_{r}+{p}_{i}i+{p}_{j}j+{p}_{k}k\), where:

$$\begin{gathered} j^{2} = 1,{ }i^{2} = k^{2} = - 1,\,{ }kj = jk = i, \hfill \\ ji = ij = k,\,{ } ki = ik = - j. \hfill \\ \end{gathered}$$
(3)

In contrast to quaternions, multiplication on the RB domain is commutative. There are two special numbers e1 and e2 [15] such that any RB number can be represented as: \(\ddot{p}={p}_{1}{e}_{1}+{p}_{2}{e}_{2}\), where \({e}_{1}=(1+j)/2, {e}_{2}=(1-j)/2\) and \({p}_{1}=\left({p}_{r}+{p}_{j}\right)+i\left({p}_{i}+{p}_{k}\right), {p}_{2}=\left({p}_{r}-{p}_{j}\right)+i\left({p}_{i}-{p}_{k}\right)\).

Expressing many operations in terms of the e1-e2 forms reduces their complexity. For example, direct RB multiplication requires 16 real multiplications while applying the e1-e2 form requires only 8. The RB norm and Hermitian can be defined in a similar way as quaternion numbers. The RB conjugate [28] is defined as:

$$\overline{\ddot{p} }={p}_{r}-{p}_{i}i+{p}_{j}j-{p}_{k}k.$$
(4)

There are other definitions of conjugate [28,29,30,31] while (4) is the only definition satisfying \(\overline{\ddot{p} }={\overline{p} }_{1}{e}_{1}+{\overline{p} }_{2}{e}_{2}\).

For any \(n\times n\) RB matrix there are \({n}^{2}\) eigenvalues (eigenvectors) (see [10, 15] for proof). The computation of \({n}^{2}\) eigenvalues and their corresponding eigenvectors would increase the computational cost required to find these eigenvalues. The time complexity of finding the t largest eigenvalues will be \(O({n}^{2}t)\). A more efficient algorithm for this purpose was derived in our paper [10] based on the well-known computer science problem x + y selection [16, 17] with time complexity of \(O\left(n t+n {\text{log}}n\right)\).

For an \(m\times n\) RB matrix\(\ddot{\mathbf{P}}\), the Frobenius norm \(\Vert \ddot{\mathbf{P}}\Vert =\frac{1}{\sqrt{2}}\Vert \mathcal{M}\left(\ddot{\mathbf{P}}\right)\Vert\) [14] where \(\mathcal{M}\left(\boldsymbol{ }.\right)\) maps any RB matrix to its complex equivalent matrix:

$$\mathcal{M}\left(\ddot{\mathbf{P}}\right):=\left[\begin{array}{cc}{\mathbf{P}}_{1}& 0\\ 0& {\mathbf{P}}_{2}\end{array}\right]\in {\mathbb{C}}^{2m\times 2n},$$
(5)

where \({\mathbf{P}}_{1}\,\mathrm{ and }\,{\mathbf{P}}_{2}\in {\mathbb{C}}^{m\times n}\) and are defined as \({\mathbf{P}}_{1}=\left({\mathbf{P}}_{r}+{\mathbf{P}}_{j}\right)+i\left({\mathbf{P}}_{i}+{\mathbf{P}}_{k}\right), {\mathbf{P}}_{2}=\left({\mathbf{P}}_{r}-{\mathbf{P}}_{j}\right)+i\left({\mathbf{P}}_{i}-{\mathbf{P}}_{k}\right)\).

5 Proposed Methods

In this section, we review LRC [1], derive the CbPCR for grayscale images and then extend it for color images using the theory of quaternions and RBs.

5.1 Linear Regression Classification (LRC)

The goal of LRC is to infer the correct label of any new probe image \(\mathbf{y}\in {\mathbb{R}}^{mn}\). LRC [1] seeks to represent \(\mathbf{y}\) as a linear combination of the training images of each class by setting up the following real-valued linear regression problem:

$$\underset{{\mathbf{c}}_{l}\in {\mathbb{R}}^{{{\varvec{n}}}_{{\varvec{l}}}}}{\mathrm{min}}{\Vert \mathbf{y}-{\mathbf{A}}_{l}{\mathbf{c}}_{l}\Vert }^{2},l=1, 2, \dots , L,$$
(6)

for which a closed-form solution is found via

$${\widehat{\mathbf{c}}}_{l}={({\mathbf{A}}_{l}^{{\varvec{T}}}{\mathbf{A}}_{l})}^{-1}{\mathbf{A}}_{l}^{{\varvec{T}}}\mathbf{y}.$$
(7)

Then, the predicted vector \({\widehat{\mathbf{y}}}_{l}\) is given by:

$${\widehat{\mathbf{y}}}_{l}={\mathbf{A}}_{l}{\widehat{\mathbf{c}}}_{l}, l=1, 2, \dots , L.$$
(8)

The test sample \(\mathbf{y}\) is eventually assigned to the class with the minimal distance

$$\underset{l}{\mathrm{min}}\Vert \mathbf{y}-{\widehat{\mathbf{y}}}_{l}\Vert , l=1, 2, \dots , L.$$
(9)

5.2 Classification by Principal Component Regression

The idea in our proposed methods is based on the fact that an image (column) in \({\mathbf{A}}_{l}\) can be represented as [4]

$${\widetilde{\mathbf{x}}}_{g}^{l}={{\varvec{\upmu}}}_{l}+\sum_{b=1}^{t}{w}_{g}^{b}{\mathbf{U}}_{l}^{b},$$
(10)

where \({{\varvec{\upmu}}}_{l}\) is the mean vector of the l-th class, and \({\mathbf{U}}_{l}{\in {\mathbb{R}}}^{mn\times t}\) represents the t largest principal components of the class scatter matrix \({{\overline{\mathbf{A}} }_{l}\overline{\mathbf{A}} }_{l}^{T}\) with \({\overline{\mathbf{A}} }_{l}=\left[{(\mathbf{x}}_{1}^{l}-{{\varvec{\upmu}}}_{l}\right), {(\mathbf{x}}_{2}^{l}-{{\varvec{\upmu}}}_{l}), \dots , ({\mathbf{x}}_{{n}_{l}}^{l}-{{\varvec{\upmu}}}_{l})]\in {\mathbb{R}}^{mn\times {n}_{l}}\). That is, an image can be represented as a linear combination of the Eigen-components of the class-specific scatter matrix. The real weights \(\{{w}_{g}^{b}{\}}_{b=1}^{t}\) represent the projections of the g-th image along these components. Huang and Yang [2] and Zhu et al. [3] apply the standard LRC on these weights. Nevertheless, our CbPCR model is defined as:

$$\underset{{\mathbf{c}}_{l}\in {\mathbb{R}}^{t}}{\mathrm{min}}{\Vert \mathbf{y}-{{\varvec{\upmu}}}_{l}-{\mathbf{U}}_{l}{\mathbf{c}}_{l}\Vert }^{2},l=1, 2, \dots , L.$$
(11)

Forcing the gradient of the objective function (11) with respect to \({\mathbf{c}}_{l}\) to vanish, the closed form is found as:

$${\widehat{\mathbf{c}}}_{l}= {({\mathbf{U}}_{l}^{T}{\mathbf{U}}_{l})}^{-1}{\mathbf{U}}_{l}^{T}({\varvec{y}}-{{\varvec{\upmu}}}_{l}).$$
(12)

Since \({\mathbf{U}}_{l}\) is orthonormal,

$${\widehat{\mathbf{c}}}_{l}= {\mathbf{U}}_{l}^{T}(\mathbf{y}-{{\varvec{\upmu}}}_{l}).$$
(13)

The response vector \({\widehat{\mathbf{y}}}_{l}\) is predicted as:

$${\widehat{\mathbf{y}}}_{l}={\mathbf{U}}_{l}{\widehat{\mathbf{c}}}_{l}+{{\varvec{\upmu}}}_{l}, l=1, 2, \dots ,\mathrm{ L}.$$
(14)

The distance between y and the predicted response vector \({\widehat{\mathbf{y}}}_{l}\) is computed as:

$${d}_{l}\left({\varvec{y}}\right)=\Vert \mathbf{y}-{\widehat{\mathbf{y}}}_{l}\Vert , l=1, 2, \dots ,\mathrm{ L},$$
(15)

The test image y is decided to belong to the class minimizing (15).

In order to reduce the computation burden of finding the largest principal components of the class scatter matrix, the common practice [4] was followed by finding first the eigenvectors \({\mathbf{V}}_{l}\in {\mathbb{R}}^{{n}_{l}\times t}\) of the matrix \({\overline{\mathbf{A}} }_{l}^{T}{\overline{\mathbf{A}} }_{l}\), and then the target eigenvectors are computed as:

$${\mathbf{U}}_{l}={\overline{\mathbf{A}} }_{l}{\mathbf{V}}_{l}. l=1, 2, \dots , L.$$
(16)

5.3 Quaternion-based CbPCR

Q-CbPCR is based on the algebra and calculus of quaternion matrices [32] to identify the class to which a new color image belongs. Here a \(m\times n\) training color image is portrayed as a 1D pure quaternion vector \(\dot{\mathbf{x}}\in {\mathbb{Q}}^{mn}\). The columns of matrix \({\dot{\mathbf{A}}}_{l}\in {\mathbb{Q}}^{mn\times {n}_{l}}\) represent samples from the l-th class where each column represents the difference between the training image and the class mean \({\dot{{\varvec{\upmu}}}}_{l}\). A test image \(\dot{\mathbf{y}}\in {\mathbb{Q}}^{mn}\) is represented by setting up the following quaternion regression problem:

$$\underset{{\dot{\mathbf{c}}}_{l}\in {\mathbb{Q}}^{t}}{\mathrm{min}}{\Vert \dot{{\varvec{y}}}-{\dot{{\varvec{\upmu}}}}_{l}-{\dot{\mathbf{U}}}_{l}{\dot{\mathbf{c}}}_{l}\Vert }^{2},l=1, 2, \dots , L,$$
(17)

where \({\dot{\mathbf{U}}}_{l}\) encompasses the key eigenvectors of the quaternion scatter matrix \({\dot{\mathbf{A}}}_{l}{\dot{\mathbf{A}}}_{l}^{H}\) corresponding to the t largest eigenvalues in terms of the quaternion norm as computed by a QPCA technique [8].

Proposition 1:

The closed-form solution of (17) is \({\widehat{\dot{{\varvec{c}}}}}_{l}={\dot{{\varvec{U}}}}_{l}^{H}{(\dot{{\varvec{y}}}}_{l}-{\dot{{\varvec{\upmu}}}}_{l})\).

Proof:

See Appendix 1.

The reconstructed query color image \({\dot{\mathbf{y}}}_{l}\) is computed by:

$${\widehat{\dot{\mathbf{y}}}}_{l}={\dot{\mathbf{U}}}_{l}{\widehat{\dot{{\varvec{c}}}}}_{l}+{\dot{{\varvec{\upmu}}}}_{l}.$$
(18)

Eventually, \(\dot{\mathbf{y}}\) is given the label of the class with the minimal quaternion norm

$$\underset{l}{\mathrm{min}}\Vert \dot{{\varvec{y}}}-{\widehat{\dot{\mathbf{y}}}}_{l}\Vert , l=1, 2, \dots , L.$$
(19)

The proposed quaternion-based representation is depicted in Fig. 1, where a color face image is represented as a linear combination of the mean image and the best t eigenvectors of its class.

Fig. 1
figure 1

Quaternion-based color representation: Column (a) shows original color image. Column (b) gives the closed-form solution of (17) with \(t\)=3. Column (c) depicts the real parts of the principal components in \({\dot{\mathbf{U}}}_{l}\) as grayscale images. Column (d) depicts the imaginary parts of the principal components as color images. First row depicts the real (zero) and imaginary parts of the mean of the training images. Column (e) represents the reconstructed image from (18)

Full size image

5.4 Reduced Biquaternion-based CbPCR

Analogously, RB-CbPCR relies on color image representation using RBs in place of quaternions. Our goal here is to find the correct label of a query color image \(\ddot{\mathbf{y}}\in {\mathbb{B}}^{mn}\) from the given training data matrices \({\ddot{\mathbf{A}}}_{l}\in {\mathbb{B}}^{mn\times {n}_{l}}\) and their true labels. The proposed RB-CbPCR model is set up as:

$$\underset{{\ddot{{\varvec{c}}}}_{l}\in {\mathbb{B}}^{t}}{\mathrm{min}}{\Vert \ddot{{\varvec{y}}}-{\ddot{{\varvec{\upmu}}}}_{l}-{\ddot{\mathbf{U}}}_{l}{\ddot{\mathbf{c}}}_{l}\Vert }^{2},l=1, 2, \dots , L.$$
(20)

where \({\ddot{{\varvec{\upmu}}}}_{l}\) is the mean of the l-th class, and \({\ddot{\mathbf{U}}}_{l}\) represents the eigenvectors of the RB scatter matrix \({\ddot{\mathbf{A}}}_{l}{\ddot{\mathbf{A}}}_{l}^{H}\) corresponding to the t largest eigenvalues in terms of the RB norm as obtained via our efficient RB-based PCA algorithm [10]. By Lemma 2 in [14], it can be proved that (20) is equivalent to:

$$\mathrm{min}{\Vert \mathcal{M}\left(\ddot{\mathbf{y}}\right)-\mathcal{M}\left({\ddot{{\varvec{\upmu}}}}_{l}\right)-\mathcal{M}\left({\ddot{\mathbf{U}}}_{l}\right)\mathcal{M}\left({\ddot{{\varvec{c}}}}_{l}\right)\Vert }^{2},$$
(21)

where a closed-form solution is derived in proposition 2.

Proposition 2:

The closed-form solution of (20) is \({\widehat{\ddot{\mathbf{c}}}}_{l}={\ddot{\mathbf{U}}}_{l}^{H}\left(\ddot{{\varvec{y}}}-{\ddot{{\varvec{\upmu}}}}_{l}\right)\).

Proof: See Appendix 2.

The class-specific reconstructed test image is

$${\widehat{\ddot{\mathbf{y}}}}_{l}={{\ddot{\mathbf{U}}}_{l}\widehat{\ddot{\mathbf{c}}}}_{l}+{\ddot{{\varvec{\upmu}}}}_{l}.$$
(22)

The test image \(\ddot{\mathbf{y}}\) is finally labeled to the class with the minimal RB norm

$$\underset{l}{\mathrm{min}}\Vert \ddot{{\varvec{y}}}-{\widehat{\ddot{\mathbf{y}}}}_{l}\Vert , l=1, 2, \dots , L.$$
(23)

6 Experiments

In this section, the proposed methods are evaluated on two color face recognition benchmark databases: the GATech database [33] and the FERET database [34]. The proposed CbPCR, Q-CbPCR, and RB-CbPCR methods are compared with LRC [1], the quaternion-based QLRC method [11, 14], the RB-based RBLRC method [14], IPCRC [2, 3], and the CLRC method [7]. Note that LRC, IPCRC, and CbPCR work on grayscale images, while the other methods operate on color images.

All experiments are carried out on a pc with an Intel i7 CPU at 2.5 GHz with 8 GB RAM using MATLAB 2015. Quaternion computations are done using the quaternion MATLAB toolbox [35], while RB computations are carried out using our own MATLAB toolbox.

6.1 Experiments on GATech Database

The GATech database [33] consists of 50 (but only 38 are available to us) subjects with 15 images per subject taken in two or three sessions. It experiences several variations in facial expression, pose, illumination, and scale; see Fig. 2a. Following [36], 10 images from each subject were used for training and the remaining 5 for testing.

Fig. 2
figure 2

Sample images from GATech and FERET databases

Full size image

Two factors were studied on the recognition performance: the image size and the number of principal components \(t\). Figure 3 graphs the rank-1 recognition accuracy by all methods versus the image size ranging from 5 to 100% (size 54 × 39 pixels) in steps of 5%. We fix \(t\)=7 per class in our proposed methods and use 266 principal components from the whole training data in the IPCRC method. Expectedly, the performances of the grayscale-based methods are generally worse than those of color-based ones. CbPCR achieves 3% and 4.7% improvement over LRC and IPCRC, respectively. IPCRC is the worst among the three and achieves a peak accuracy of 84.2% compared with respective peak accuracies of 88.9% and 85.8% by CbPCR and LRC.

Fig. 3
figure 3

Rank-1 recognition accuracy on the GATech database by all methods for various image sizes. (Better viewed in color)

Full size image

The color methods offer better performances than the grayscale-based methods except for CLRC which has worse accuracy than CbPCR and a close-performance to LRC with a peak accuracy of 85.8%. The new grayscale-based CbPCR method has a better performance than QLRC and RBLRC till image size 50% then has almost the same performance afterward. The new Q-CbPCR and RB-CbPCR have a close-performance that is better than all other methods. Both have a peak accuracy of 88.95% yielding about 2.28% improvement over QLRC and RBLRC.

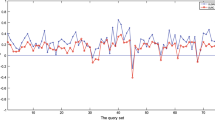
Figure 4 shows the rank-1 recognition accuracy of all methods against \(t=1\) to 9 fixing the image size at 54 × 39 pixels. The number of principal components in IPCRC is taken as the number of classes (38) times \(t\). The accuracies of CLRC, LRC, QLRC, and RBLRC are not dependent on \(t\). IPCRC is the worst overall. As more principal components are used, the proposed CbPCR, Q-CbPCR, and RB-CbPCR offer higher accuracies. For \(t\le 4\), CbPCR and RB-CbPCR have similar performance, while Q-CbPCR tops both methods. Afterward, the performances of Q-CbPCR and RB-CbPCR are better than that of CbPCR. Q-CbPCR tends to offer a slightly better accuracy than RB-CbPCR, where the former has a peak accuracy of 88.95% versus 87.37% for the latter. CbPCR has 86.84% peak accuracy.

Fig. 4
figure 4

Rank-1 recognition accuracy on the GATech database by all methods against number of principal components. (Better viewed in color)

Full size image

An additional experiment is carried out to compare the proposed methods (Q-CbPCR and RB-CbPCR) with existing PCA-based methods: QPCA [8], RBPCA [10], 2DQPCA [22], and 2DRBPCA [10]. Figure 5 graphs the rank-1 recognition accuracies of all these methods versus an image size from 5 to 100% (size 54 × 39 pixels) in steps of 5%. Seven principal components per class are used in the proposed methods, while 266 principal components are employed in QPCA, RBPCA, 2DQPCA, and 2DRBPCA. The performance of 1D PCA methods is the worst. QPCA is worse than RBPCA, with a peak accuracy of 82.63%, while RBPCA has a peak accuracy of 85.78%. Q-CbPCR and RB-CbPCR are the best overall methods, with a peak accuracy of 88.95% compared to 2DQPCA and 2DRBPCA, which achieve peak accuracies of 85.79% and 87.36%, respectively.

Fig. 5
figure 5

Rank-1 recognition accuracy on the GATech database by PCA color methods and the proposed color methods for various image sizes. (Better viewed in color)

Full size image

Finally, the recognition time (in seconds) was studied by taking the average of running each algorithm 10 times on image size \(54\times 39\), with \(t=\) 7 in the proposed methods and 266 principal components in IPCRC, QPCA, RBPCA, 2DQPCA, and 2DRBPCA. As shown in Table 1, QPCA and RBPCA are the slowest while the grayscale-based LRC and IPCRC are the fastest due to their simpler computation. 2DQPCA and 2DRBPCA are faster than Q-CbPCR and RB-CbPCR since the size of the scatter matrix in 2D methods is less than the size of the scatter matrix in the 1D methods. RB-CbPCR is around 1.8 × faster than Q-CbPCR. This is due to the faster computations of RB operations taking advantage of the e1-e2 form and to the faster computation of the RB principal components by our efficient RB-based PCA algorithm [10].

Table 1 Average recognition CPU time (in seconds) over 10 runs of different methods on the GATech database
Full size table

6.2 Experiments on FERET database

The FERET database [34] contains more than 14,000 face images having pose and light variations. In this study, we consider a subset consisting of 115 subjects with 4 images from each subject captured in 3 poses, see Fig. 2b. Two faces are captured at 0° while the other two faces are captured at 15° and − 15°. One frontal image and one with the head rotated 15° were chosen for training, while testing is performed on the other 2 images.

Figure 6 shows the rank-1 recognition accuracy for various image sizes varying from 5 to 100% (48 × 32 pixels) in a step of 5% using \(t=\) 1 in our proposed methods and 115 principal components in IPCRC. Expectedly, the grayscale-based methods have lower accuracy. IPCRC and LRC are close to each other with respective peak accuracies of 79.6% and 80.9%. CbPCR achieves 1.79% and 1.18% improvements over LRC and IPCRC, respectively. QLRC and RBLRC exhibit nearly the same performance with a top accuracy of 81.74%. CLRC performs better than QLRC and RBLRC with a peak of 82.1%. Both Q-CbPCR and RB-CbPCR offer the best overall accuracy of 82.61% at 20% image size. Q-CbPCR shows a slightly better performance than RB-CbPCR for larger image sizes.

Fig. 6
figure 6

Rank-1 recognition accuracy on the FERET database by all methods for various image sizes. (Better viewed in color)

Full size image

Moreover, the average recognition time (in seconds) was assessed by running each algorithm 10 times on image size 48 × 32 using \(\mathrm{t}=\) 1 in the proposed methods and 115 principal components in IPCRC. As shown in Table 2, LRC and IPCRC are the fastest while CLRC is the slowest. Q-CbPCR and RB-CbPCR take less time than QLRC and RBLRC. Moreover, RB-CbPCR is about 1.5 × faster than Q-CbPCR.

Table 2 Average recognition CPU time (in seconds) over 10 runs of different methods on the FERET database
Full size table

7 Conclusions

In this paper, a novel formulation of LRC based on principal component regression has been proposed. This formulation keeps the key information of the data classes while providing more compact closed-form solutions. This formulation is also extended to the quaternion and RB domains to take into account the color information. The specific contributions of this paper are:

  • CbPCR strategy is proposed by performing regression of each data class in terms of its principal components.

  • This CbPCR strategy is extended to the hypercomplex domains of quaternions and RBs to consider color images.

  • The CbPCR closed-form solutions are developed from the principles of real, quaternion and RB domains.

  • Experiments on two color face recognition benchmark databases have showed that the proposed Q-CbPCR and RB-CbPCR have the highest overall accuracy among eight different methods including very recent ones [7, 11, 14]. Moreover, RB-CbPCR is about 1.8 × faster than Q-CbPCR. The grayscale-based CbPCR algorithm has even outperformed some color-based algorithms in the literature in addition to the original grayscale LRC method [1] and its recent variants [2, 3].