1 Introduction

Traveling Salesman Problem (TSP) [1] is one of the most fascinating classes of combinatorial optimization problems. It is difficult to solve by a single mathematical formulation and is often used as an acknowledged criterion to test the performance of algorithms. The TSP problem can be described as a shortest route problem in which a traveler does not repeatedly pass through all the specified cities and finally returns to the initial city. Although for small-scale cities, some mathematical methods can be used to find the route such as cutting planes algorithm [2], branch and cut scheme [3]. However, as the number of cities increases, the amount of computation when using mathematical methods increases exponentially. Especially for large-scale cities, such an approach spent huge amounts of time but did not work well, so the meta-heuristic algorithm was born. Meta-heuristic algorithms, also known as intelligent optimization algorithms, differ from optimization algorithms in that they can construct a feature model based on a specific problem and find a feasible solution under specified constraints. Many scholars have studied meta-heuristic algorithms in order to solve different complex problems, such as genetic algorithm [4], particle swarm optimization [5], grey wolf optimization algorithm [6], whale optimization algorithm [7]. As a typical swarm intelligence algorithm, the ant colony algorithm has excellent ability to find the optimal solution in solving NP-hard problems, which has profound research value and significance.

The ant colony algorithm originated from the doctoral dissertation of M. Dorigo. He simulated the behavior of ants foraging, constructed a route and pheromone update model, and proposed the ant colony optimization algorithm (ACO) [12, 13], which achieved better results in the TSP problem. Later scholars according to their research fields applied ACO to the scheduling problem [8, 9], location routing problem [10, 11], community detection [12, 13], etc., which verify the great performance of ACO.

However, because of the positive feedback of pheromones in the ACO, pheromones will accumulate rapidly on individual routes, resulting in local optima. To alleviate the problem, M. Dorigo further proposed the ant colony system (ACS) [14]. Global and local pheromone update methods were proposed in ACS as well as a local search algorithm was added to improve the performance. Then T. Stutzle proposed the max–min ant system (MMAS) [15], which avoids excessive pheromone accumulation by setting a maximum-minimum threshold of pheromone to control the pheromone concentration within a certain range.

Although these above methods have good performance, they still face problems such as easy to fall into local optimum and slow convergence speed. For these problems, many scholars have proposed their improvement strategies.

The performance improvement of ant colony algorithm is mainly based on the convergence speed and solution accuracy. Zhang, Q. et al. [16] accelerated convergence by reinforcing dynamic pheromone edges. Zhao, D. et al. [17] enhanced convergence speed by cross-searching horizontally and allowing two kinds of ants to exchange information. Li, S. et al. [18] defined a collective action strategy where each ant decides whether to participate in the collective action based on threshold to increase the diversity of the algorithm. Wu, Y. et al. [19] introduced a differential evolution operator to increase the global search capability by modifying the update of the mutation operator.

Besides, some scholars have modified the characteristic model of ACO algorithm. Tam, J.H. et al. [20, 21] optimized the parameters of ACO algorithm by PSO algorithm to improve the solution quality. Abdelbar, A.M. et al. [22, 23] changed the fixed parameters into adjustable parameters to better adapt to different stages of the ant colony algorithm for increasing the accuracy of the solution. Wang, M. et al. [24, 25] added a specified function to the pheromone to improve the solution of the optimal problem. Deng, W. et al. [26] proposed a collaborative strategy based on the crossover variation of genetic algorithm to improve the poor local search ability. Dai, X. et al. [27] combined ACO algorithm with the evaluation function of A* algorithm to enhance the heuristic role of ACO to speed up the convergence. Mohsen, A.M. et al. [28] incorporated the variation factor of the simulated annealing algorithm to increase the diversity of ACO algorithm for more efficient route exploration.

With the increase in city nodes, some scholars found that multiple ant colony [29,30,31,32] have better performance than single colony. Gong, Y. et al. [30] performed a single-objective search with improved pheromone update rules for two colonies and used a heuristic strategy to balance multi-objective optimization to improve algorithm performance. Xu, M. et al. [32] let two populations be, respectively, responsible for solution diversity and convergence speed, and exchange information during exploration to ensure the balance between diversity and convergence speed. Although these improved multiple ant colony algorithms above have good optimization effect, they mostly exchange high-quality information between populations to optimize the algorithms, and the route information of general ants is less studied. But is the route information of a huge number of general ants really worthless? To answer the question, we conducted the present study.

We find that the reason why ants cannot find a better solution in solving TSP is that they fall into local optimum, especially for large-scale cities. When ants explore the solution, the routes taken by elite ants are dominated, making a large accumulation of pheromones and thus failing to find a better solution. To address this situation, we use the routes of general ants as an important reference as well to try to alleviate. We refer to the community detection algorithm [33, 34] to construct the route relationship network and collect the route information of all ants in different populations, finding that the route information of ants in general is extremely diverse, which can improve the situation of getting stuck in stagnation. Meanwhile, the nodes are also divided by the criterion of modularity [35], and the obtained communities balance diversity and stability.

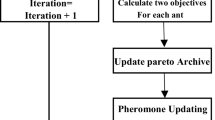
Although some scholars have previously combined community relations with ant colony algorithms, they are used for community detection rather than solving the TSP problem. Noveiri, E. et al. [36] combined pheromones with modularity to find an outer region and then implemented community detection by fuzzy clustering. Romdhane, L. et al. [37] defined an objective function of set purity and density based on the community structure and used the ant colony algorithm to optimize the objective function to classify quality communities that can balance the two metrics. Although they also combined the ant colony algorithm, they did not involve the study of node sparsity and node distance. In this paper, we will improve the ant colony algorithm by incorporating the idea of community detection to balance the relationship between diversity and convergence speed, and propose the multiple ant colony algorithm combining community relationship network to solve the TSP problem. The improved algorithms based on ACO is shown in Fig. 1.

Fig. 1
figure 1

The improved algorithms based on ACO

Full size image

The main contributions and innovations of this study are as follows.

Firstly, we integrate the idea of community detection and sample the route information of all ants. The route relationship network containing node sparsity and distance relationship is constructed by sample processing. Then, we divide the route relationship network into communities with the criterion of modularity, because this approach does not just consider the distance, so the divided communities will increase the diversity of the ant colony algorithm.

Secondly, route exploration is performed with ant colony algorithm in the divided small communities. Benefiting from the structural stability of community detection, routes in small communities have the potential to explore optimal solutions, which can enhance the convergence speed of the algorithm when pheromone guidance is given to multiple swarms. Also, pheromone guidance of non-optimal routes for multiple colonies of ants will increase the diversity and further improve the algorithm performance.

Finally, because of the pheromone guidance of small communities, the exchange of information among multiple colonies during exploration is not limited to distance information, and the sparse relationship of general ants for nodes is also considered. Therefore, the superiority and inferiority mutual aid strategy is used when multiple colonies exchange information to further improve the accuracy of the solution.

The remainder of this study is as follows: Sect. 2 describes ACS, MMAS and community detection algorithms. Section 3 describes in detail the improvement algorithm. Section 4 presents the experimental results of the improved algorithm. Finally, Sect. 5 concludes the work of this study and provides an outlook on future research directions.

2 Related Work

2.1 Ant Colony System

The formula for route construction of ACS is as follows.

$$ S = \left\{ {\begin{array}{*{20}l} {{\text{arg}}\mathop {{\text{max}}}\limits_{{j \in {\text{allowed}}}} \left\{ {\tau _{{ij}} \cdot \eta _{{ij}}^{\beta } } \right\},} & {q \le q_{0} } \\ {s,} & {{\text{else}}} \\ \end{array} } \right. $$
(1)
$$ P_{{ij}} \left( t \right) = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {\frac{{\left[ {\tau _{{ij}} \left( t \right)} \right]^{\alpha } \left[ {\eta _{{ij}} } \right]^{\beta } }}{{\sum\limits_{{s \in {\text{allowed}}}} {\left[ {\tau _{{{\text{is}}}} \left( t \right)} \right]^{\alpha } } \left[ {\eta _{{{\text{is}}}} } \right]^{\beta } }},} & {j \in {\text{allowed}}} \\ {0,} & {\, {\text{else}}} \\ \end{array} } \\ \end{array} } \right. $$
(2)

where \({\tau }_{ij}\left(t\right)\) represents the magnitude of the pheromone between cities i and j at moment t. The starting concentration on each edge is the same, denoted as \({\tau }_{0}.{ \eta }_{ij}\) represents the reciprocal of the distance \({d}_{ij}\) between cities i and j, and \({\eta }_{ij}=1/{d}_{ij}\). \({q}_{0}\) is a constant value in the interval [0,1], q is a random number in the interval [0,1], and \(j\in allowed\) indicates that city j belongs to the set of optional cities outside the taboo table. S denotes the next city that will be selected when \(q\le {q}_{0}\) and s is the selection method of the roulette wheel of Eq. (2).

The update mechanism of ACS is divided into two parts: global pheromone update and local pheromone update.

  • Global pheromone update: After all ants have completed research, the algorithm only updates the pheromones on the current optimal route. Its calculation formula is as follows.

    $${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\rho \Delta {\tau }_{ij}$$
    (3)
    $$ \Delta \tau _{{ij}} = \left\{ {\begin{array}{*{20}l} {1/L_{{{\text{gb}}}} ,{\text{ }}} \hfill & {\, \left( {i,j} \right) \in {\text{Best}}\,{\text{Tour}}} \hfill \\ {0,} \hfill & {\, {\text{else}}} \hfill \\ \end{array} } \right. $$
    (4)

    where \(\rho \) is the global pheromone evaporation rate.\(\Delta {\tau }_{ij}\) is the pheromone increment.\({L}_{\mathrm{gb}}\) is the length of current optimal route.

  • Local pheromone update: Once all ants have completed their iterations, the algorithm performs a local pheromone update for all routes. This shortens the pheromone difference between optimal and non-optimal routes and increases the diversity of the algorithm. The formula is as follows.

    $${\tau }_{ij}\left(t+1\right)=\left(1-\xi \right){\tau }_{ij}\left(t\right)+\xi {\tau }_{0}$$
    (5)

where \({\tau }_{0}\) is the starting concentration on each edge and \(\xi \) is the local pheromone evaporation rate.

2.2 Max–Min Ant System

The main idea of MMAS is to control the pheromone range in a certain interval such that \(\tau \in \left[{\tau }_{\mathrm{min}},{\tau }_{\mathrm{max}}\right]\). When \({\tau }_{ij}\underset{\_}{<}{\tau }_{\mathrm{min}}\), make \({\tau }_{ij}={\tau }_{\mathrm{min}}\); when \({\tau }_{ij}\underset{\_}{>}{\tau }_{\mathrm{max}}\), make \({\tau }_{ij}={\tau }_{\mathrm{max}}\). Where \({\tau }_{\mathrm{min}},{\tau }_{\mathrm{max}}\) are calculated according to Eqs. (6) and (7).

$${\tau }_{\mathrm{max}}=\left(1/\rho \right)\cdot \left(1/{T}^{\mathrm{gb}}\right)$$
(6)
$${\tau }_{\mathrm{min}}={\tau }_{\mathrm{max}}/2n$$
(7)

where \({{\varvec{T}}}^{\mathbf{g}\mathbf{b}}\) is the length of global optimal route and \({\varvec{\rho}}\) is the pheromone evaporation rate.

Based on the limitation of the pheromone range, only the pheromones of the current or global optimal route are updated at the end of each iteration according to Eqs. (8) and (9). This allows the algorithm to explore the routes more efficiently and increases the diversity of the algorithm.

$${{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}}}\left({\varvec{t}}+1\right)=\left(1-{\varvec{\rho}}\right){{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}}}\left({\varvec{t}}\right)+\Delta {{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}}}^{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}$$
(8)
$$\Delta {{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}}}^{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}=1/{\varvec{f}}\left({{\varvec{s}}}^{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}\right)$$
(9)

where \({\varvec{f}}\left({{\varvec{s}}}^{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}\right)\) is the current optimal route or the global optimal route.

2.3 Community Detection

2.3.1 Representation of Complex Networks

Complex networks are generally represented as graphs with nodes and edges, such as \(G=\left(V,E\right)\),where \(V=\left\{1, 2,\dots ,n\right\}\) denotes the set of nodes and \(E\subseteq V\times V\) denotes the set of edges. The nodes and edges are usually represented with the help of the adjacency matrix \({A}_{n\times n}\) when they are processed. Figure 2 shows the community relationship network of 34 members of the karate club community. Equation (10) shows the weights of nodes and edges

Fig. 2
figure 2

Karate club relationship network

Full size image
$${A}_{n\times n}=\left[\begin{array}{ccc}{a}_{11}& \cdots & {a}_{1n}\\ \vdots & \ddots & \vdots \\ {a}_{n1}& \cdots & {a}_{nn}\end{array}\right]$$
(10)

2.3.2 Modularity

The modularity was proposed by Newman to address the notion that the Girvan and Newman algorithm (GN) cannot evaluate the quality of a community. It was widely used to measure the strength of the community structure after network segmentation, as shown in Eq. (11).

$$Q=\sum_{i}^{K}\left({e}_{ii}-{a}_{i}^{2}\right)=\frac{1}{2m}\sum_{v}^{n}\sum_{w}^{n}\left({A}_{vw}-\frac{{\mathrm{d}}_{v}{\mathrm{d}}_{w}}{2m}\right)I\left({c}_{v},{c}_{w}\right)$$
(11)

where K is the number of communities. \({e}_{ii}\) is the proportion of edges inside community i to the total number of edges. \({a}_{i}=\sum_{j=1}^{K}{e}_{ij}\) is the proportion of edges connected to community i to the total number of edges, then \({a}_{i}^{2}\) denotes the proportion of edges in community i to the total number of edges. m is the total number of edges in the network. n is the total number of nodes in the network. \({A}_{vw}\) is the value of the adjacency matrix of node v and w. \({d}_{v}=\sum_{w=1}^{n}{A}_{vw}\) is the degree of node I. \(I\left({c}_{v},{c}_{w}\right)\) is the schematic function, \(I\left({c}_{v},{c}_{w}\right)=1\) when node v and node w belong to the same community, otherwise \(I\left({c}_{v},{c}_{w}\right)=0\).

By dividing the karate club relationship network in Fig. 2 through modularity, we can see that the 34 members are divided into four types of communities, which are closely related within the community and loosely related between the communities in Fig. 3.

Fig. 3
figure 3

Relationship network after community detection

Full size image

3 Proposed Algorithm

3.1 ACO Combined with Community Detection

When the ant colony algorithm uses multiple populations to solve the TSP problem, the communication and collaboration among multiple populations is a great advantage to improve the performance of the algorithm, but most scholars have achieved the improvement of the algorithm performance by exchanging the pheromones and optimal routes among different populations, and there is little research on the social relationship network when all ants of different populations explore the routes. Therefore, this study proposes a community collaboration strategy to study the route structure relationship network among populations with the help of community detection methods from the route relationship network when different populations explore routes, and apply it to solve the TSP problem. In this section, we describe how to construct the route relationship network for the ant colony algorithm.

3.1.1 Route Relationship Network Model

The route network in this study, is a synthetic network that collects the route information provided by all ants of various colonies. As shown in Fig. 4, the route relationship network constructed when ants explore the TSP city set Eil51, each node represents a city and the connection between nodes is an ant route.

Fig. 4
figure 4

Route relation network of TSP city set Eil51

Full size image

3.1.2 Processing of Route Information Samples

As shown in Fig. 4, the route relationship network has a certain complex network structure. With 51 cities as nodes and the exploration routes of all ants as edges, it can be clearly found that some nodes have a certain correlation structure with a significantly dense number of connected edges, while some nodes have few connected edges. In Fig. 4, the city with the number 40 in the lower left corner has more connections with other cities, which proves that this city has very diverse route choices and is a more difficult point to classify in community detection. In contrast, the city with the number 13 has fewer connections to other nodes. Most ants will follow these routes, which are more likely to be high quality routes and easier to classify in community detection, with relatively stable community structure.

Classical datasets such as the Karate dataset only have information about nodes and edges, and connecting edges is not considered for distance, so special treatment is needed to solve the TSP problem. In the ant colony algorithm, ants taking the same route is a sure way to explore better routes. For this problem, this study modifies the adjacency matrix reflecting the route information to be more consistent with the TSP problem by weighting the repeated routes when collecting the route information. When the route sample information is collected and transformed into the adjacency matrix, the adjacency matrix is changed into a weighting matrix by Eq. (12). When node i is not connected to node j, make \({a}_{ij}=0\); when there is a connection, then make \({a}_{ij}\) increment.

$$ a_{{ij}} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}}\, i\, \, \, {\text{and}}\, j\, {\text{are}}\, \, \, \, {\text{not}}\, \, \, \, {\text{connected}}} \hfill \\ {a_{{ij}} + 1,} \hfill & {\, {\text{if}}\, i\, \, \, {\text{and}}\, j\, {\text{are}}\, \, \, {\text{connected}}} \hfill \\ \end{array} } \right. $$
(12)

As shown in Fig. 5, this study used 40 ants for 20 independent sample collections on the city set Eil51, and found that the proportion of connected edges with a weight of 1 was more than 50%, and a total of nearly 70% on the proportion of weights with low weights 1 to 5, which shows that the route network has a more complex relational structure. Also, due to the positive feedback of pheromones, it is not the case that the proportion decreases with higher weights, but starts to increase with higher weights. This reflects that some ants are following the quality ants when exploring.

Fig. 5
figure 5

Graph of the weight share of connected edges

Full size image

In order to avoid affecting the quality of community division by large differences between the upper and lower limits of weights, we use Eqs. (13) and (14) to set an upper weighting limit for the connected edges, which makes the internal differences of the adjacency matrix narrow and increases the diversity of the algorithm.

$$\left(1-v\right)*\mathrm{SUM}\to {A}_{\mathrm{max}}$$
(13)
$$ A_{{ij}} = \left\{ {\begin{array}{*{20}l} {A_{{ij}} ,} & {if\,A_{{ij}} < \,\,[A_{{{\text{max}}}} ]} \\ {[A_{{{\text{max}}}} ],} & {if\,A_{{ij}} \, \ge \,[A_{{{\text{max}}}} ]} \\ \end{array} } \right. $$
(14)

where SUM is the number of connected edges in the adjacency matrix. v is the filtering rate to set the upper limit of the weights. From Fig. 5 we can see that the value of 10% is more appropriate. \({[A}_{\mathrm{max}}]\) meets the number of weights corresponding to the filtering rate, as the upper limit of the weights, and [x] denotes the largest integer no more than x.

3.2 Community Collaboration Strategy

Classical community detection algorithms deal with the relationship between nodes and edges, while the TSP problem is an optimization problem involving distance. This section details how to take advantage of the community structure for better guiding ants to find routes.

Combining Figs. 4 and 5, it can be found that dividing the community is not done just by considering the distance. For city nodes with multiple connected edges, it has a rich diversity of choosing other cities. While for city nodes with fewer connected edges, it indicates that this is the high-quality route that most ants will choose, which can speed up the convergence speed. Therefore, the divided communities satisfy the requirements of the ant colony algorithm for diversity and convergence speed.

As shown in Figs. 6 and 7, firstly, different ant colonies explore the TSP city set according to their own characteristics. When the route information is mature, the route information of each population is collected as samples to construct a route relationship network model. Then the route relationship network is divided into several structurally stable small communities according to the modularity, and in the small communities we use ACS for route exploration to find the shortest closed-loop routes and pheromones.

Fig. 6
figure 6

Schematic diagram of community collaboration strategy

Full size image
Fig. 7
figure 7

Steps of community collaboration strategy

Full size image

Then, we use high-quality pheromones from small communities to guide the inferior populations in multiple populations for improving the search quality of inferior ants. Meanwhile, the superior and inferior populations exchange information to get out of their respective dilemmas when they fall into local optimum.

The three components of collecting route information, community detection, and pheromone guidance are cycled several times to further explore better solutions. In this study, samples were collected once every 500 iterations. In Fig. 6, \({A}_{n\times n}\) is the adjacency matrix of the route relationship network model, and \({P}_{n\times n}\) is the pheromone matrix of each community after merging.

3.2.1 Advantageous Route Guidance

When processing the route samples, an upper weight limit is set for the edges to ensure the quality of community detection. However, the route with the highest weight is the route chosen by most ants and is likely to find the best solution.

Therefore, we enhanced the guidance of high-quality routes when collecting pheromones of optimal routes in small communities to highlight the difference between high-quality routes and common routes. After the sample collection was completed, the weights of the routes were sorted in descending order. In the global pheromone update, the pheromones of the top three edges with the highest weights are guided by Eq. (15) to improve the efficiency of the ants in exploring better solutions.

$${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\rho \left(1/{L}_{\mathrm{gb}}+W/\left(n\cdot {d}_{\mathrm{max}}\right)\right)$$
(15)

where \(\rho \) is the global pheromone evaporation rate. \({L}_{\mathrm{gb}}\) is the length of current optimal route. W is the edge weight. \({d}_{\mathrm{max}}\) is the maximum city distance, and n is the number of cities.

3.2.2 Pheromone Guidance

In dealing with how to solve TSP problems using small divided communities, we use a pheromone guided strategy to complete. We chose to exploit the properties of ACS within small communities to find high-quality solutions faster. Although not all routes explored within each small community are optimal solutions, there exist some routes that are high-quality pieces of optimal solutions.

In summary, this study integrates the pheromones of each small community to integrate a set of high-quality route pheromones, and provides pheromone guidance for multiple groups of ants according to Eqs. (16–18) to guide multiple groups to explore better routes, and also provides samples with better information for the next sample collection of community detection.

$${{\mathrm{Pheromone}}_{i}=\left(1-\sigma \right)\cdot {\mathrm{Pheromone}}_{i}+\upsigma \cdot \mathrm{K}\cdot \mathrm{Pheromone}}$$
(16)
$$ K = \left\{ {\begin{array}{*{20}c} 1 {\it {,\,\,if\,inferior\,population\,is\,ACS\,}} \\ r {\it {,\,\,if\,inferior\,population\,is\,MMAS}} \\ \end{array} } \right. $$
(17)
$$r=\frac{\left({\tau }_{\mathrm{max}}^{\mathrm{MMAS}}-{\tau }_{\mathrm{min}}^{\mathrm{MMAS}}\right)}{\left({\tau }_{\mathrm{max}}^{\mathrm{ACS}}-{\tau }_{\mathrm{min}}^{\mathrm{ACS}}\right)}$$
(18)

where \({\mathrm{Pheromone}}_{i}\) is the pheromone of inferior population.\({\mathrm{Pheromone}}_{c}\) is the combined pheromone collected in the small communities. \(\sigma \) is the guidance weight, for the inferior population, the current optimal route is less effective and should be guided by a slightly larger weight, so \(\sigma =0.6\). K is the conversion coefficient. The transformed pheromone will be more reasonable because the MMAS population has a pheromone range limit, the upper and lower limits of which are different from those of the pheromone of ACS. \({\tau }_{max}^{MMAS}\) and \({\tau }_{min}^{MMAS}\) are the upper and lower limits of the pheromone of MMAS. \({\tau }_{max}^{ACS}\) and \({\tau }_{min}^{ACS}\) are the upper and lower limits of the pheromone of ACS.

3.2.3 Superior and Inferior Mutual Assistance Strategies

When multiple populations consisting of ACS and MMAS exchanged information, the superior population explored the routes with higher precision, but got stuck in stagnation more severely. At this time, although the routes of the inferior population are not very good, their pheromones have better diversity compared with the dominant population. Feeding the pheromones of the inferior population to the superior population, which would increase the possibility of the superior population jumping out of stagnation.

Based on the above principles, we propose superior and inferior mutual assistance strategies, according to Eqs. (19) and (20) to exchange information of multiple populations. The route information of the superior population is transmitted to the inferior population, while the inferior population feeds back the corresponding pheromones to help the superior population explore a better solution.

$$ L_{{{\text{best}}}}^{{{\text{inferior}}}} = \left\{ {\begin{array}{*{20}l} {L_{{{\text{best}}}}^{{{\text{superior}}}} ,} & {\, {\text{if}}\, \, \, {\text{algorithm}}\, \, \, {\text{is}}\, \, \, {\text{stuck}}} \\ {L_{{{\text{best}}}}^{{{\text{inferior}}}} ,} & {{\text{if}}\, \, \, {\text{algorithm}}\, \, \, {\text{is}}\, \, \, {\text{not}}\, \, \, {\text{stuck}}} \\ \end{array} } \right. $$
(19)
$$\tau ^{{{\text{superior}}}} = \left\{ {\begin{array}{*{20}l} {\omega \cdot \tau ^{{{\text{superior}}}} + \left( {1 - \omega } \right)r \cdot \tau ^{{{\text{inferior}}}} } {,\,\,{\text{if}}\,{\text{inferior}}\,{\text{is}}\,{\text{ACS}}} \\ {\omega \cdot \tau ^{{{\text{superior}}}} + \left( {1 - \omega } \right)\frac{1}{r} \cdot \tau ^{{{\text{inferior}}}} } {,{\text{else}}} \\ \end{array} } \right.$$
(20)

where \({L}_{\mathrm{best}}^{\mathrm{inferior}}\) is the shortest route of the inferior population. \({L}_{\mathrm{best}}^{\mathrm{superior}}\) is the shortest route of the superior population. \({\tau }^{\mathrm{superior}}\) is the pheromone of the superior population. \({\tau }^{\mathrm{inferior}}\) is the pheromone of the inferior population. ω is the feedback ratio, and the good route information of the dominant population is also taken into account in the feedback, so \(\omega =0.7\).

3.3 Algorithm Framework

The algorithm framework is shown in Fig. 8, and the orange part is the improvement that differs from the classical algorithm. First, ACS and MMAS jointly explore the optimal routes, and when the sampling frequency is reached, we collect mature route samples to construct a route relationship network with multiple populations. Then we use community detection to delineate small communities with potential quality routes and use ACS for route search.

Fig. 8
figure 8

Algorithm framework

Full size image

Afterward, the pheromones of each small population are integrated and pheromone guidance is applied to multiple populations to form a closed loop of feedback which adjusts the meritocracy of the inferior populations. If the shortest distance is constant over time, the algorithm is judged to be in stagnation, at which point the superior and inferior mutual assistance strategies is used to exchange information and increase the chance of jumping out of stagnation.

figure a

4 Experiment and Simulation

To test the performance of the CACO algorithm, this study uses a simulation environment of Windows 10 system, matlab2016a version, and selects multiple data sets of international standard TSP database for simulation experiments. The number of ants per population is 20, and the maximum number of iterations is 2000 iterations.

4.1 Parameters Setting

4.1.1 ACS and MMAS Parameter Setting

For the ACS algorithm, we conduct the orthogonal experiments with five factors and four levels on the city set Eil51. To ensure the stability of the parameters, data were collected 20 times for each set of parameters and the average solution was taken. Finally, the optimal parameters of the ACS algorithm were determined to be: \(\alpha =1,\beta =4,\rho =0.1,\xi =0.3,q0=0.8\).

Similarly, for the MMAS algorithm, the optimal parameters are: \(\alpha =1,\beta =5,\rho =0.1\).

4.1.2 Parameter Setting for Sample Size

The construction of the route relationship network depends on the collected route information samples, and the number of samples will have a large impact on the modularization performance [38]. In the ant colony algorithm, the number of samples that can be collected in one iteration is a fixed value. For larger cities, it is possible to collect a sparse network of route relationships, making most of the nodes have thin or even no relationships with each other, which results in the inability to form a complete network of relationships. Therefore, we use the minimum route length, the average route length and the average module degree as criteria to determine the parameters by increasing the number of iterations.

The experiments were conducted with 20 ants each from ACS and MMAS, and samples were collected in Pr76 city set for iteration numbers from 1 to 10. To ensure the accuracy of the experiments, 20 independent experiments were conducted. The experimental results are shown in Table 1 and Fig. 7, where \({iter}_{c}\) is the number of sample collection iterations, \({L}_{\mathrm{best}}\) is the minimum route length, \({L}_{ave}\) is the average of the route length, and \({Q}_{\mathrm{ave}}\) is the average of modularity.

Table 1 Pr76 sample collection statistics
Full size table

From Fig. 9, the modularity from one to ten iterations does not vary much and is stable at about 0.71, because the ant routes are different in each iteration instead of repeating only one route, so the structure of the route relationship network is relatively stable even for multiple iterations.

Fig. 9
figure 9

Comparison of Pr76 sample collection

Full size image

Observing the minimum route lengths in Table 1, we can find that the optimal solution for the city set Pr76 is found at iteration numbers 1,3,5,8, when the exploration performance is better. From the average length, the number of iterations is in the local minimum position at 5. Although there is also a tendency to reduce after 10 iterations, it will lead to collecting too many samples and make the route relationship network structure more complicated. The above analysis finally determines the number of sample collection iteration \({iter}_{c}\) is 5.

4.2 Comparison with Traditional Ant Colony Algorithm

To demonstrate the performance of the improved algorithm, we used the TSP, which is recognized to measure the performance of discrete optimization algorithms, as the standard for our experiments. In this section, the performance of the algorithm is analyzed by applying the ACS, MMAS and CACO algorithms to the TSP examples of 28 city sets and comparing the optimal solution \({L}_{\mathrm{best}}\), the average solution \({L}_{\mathrm{ave}}\), the minimum error rate \({E}_{\mathrm{min}}\) and the standard deviation \(STD\) through 20 independent experiments.

The error rate is calculated by Eq. (21) and the average modularity is calculated by Eq. (22). Where \({L}_{\mathrm{opt}}\) is the standard optimal solution of the city set. \({L}_{\mathrm{best}}\) is the optimal solution of the algorithm. \({L}_{i}\) is the final distance of 20 experiments, and \({L}_{ave}\) is the average of the final distance of 20 experiments. These experimental results are shown in Table 2 and Fig. 10.

Table 2 Performance comparison of cities data sets of different sizes
Full size table
Fig. 10
figure 10

Convergence comparison of MMAS, ACS and CACO

Full size image
$${E}_{\mathrm{min}}\left(\%\right)=\left(\frac{{L}_{\mathrm{best}}-{L}_{\mathrm{opt}}}{{L}_{\mathrm{opt}}}\right)\times 100\%$$
(21)
$$\mathrm{STD}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left({L}_{i}-{L}_{\mathrm{ave}}\right)}^{2}}$$
(22)

As shown in Table 2 and Fig. 10, all three algorithms find optimal solutions in the small-scale city sets Eil51, St70, and KroA100. In the medium-scale city sets with the number of cities between 100 and 200, the improved algorithm can find better or optimal solutions for the city set with higher solution accuracy compared with the traditional algorithm, in which the optimal solutions are found for the Ch130 and KroA200 city sets. In the large-scale city sets with more than 200 cities, the improved algorithm can clearly show that the accuracy of the solution is better than the traditional algorithm, and it can keep the minimum error rate within 1%, so it has a better ability of finding the optimal solution.

From (b), (d), (f) and (h) in Fig. 10, we can see the convergence speed and minimum error of CACO. It can find higher precision solutions in a shorter number of iterations and converge quickly in a shorter number of iterations with the pheromone guidance strategy of community detection in the early stage. Later, through the information exchange and mutual assistance of multiple communities, it can realize to jump out of stagnation and further improve the solution accuracy, which better balances the relationship between solution accuracy and convergence speed in the ant colony algorithm.

4.3 Comparison with the Latest Improved Algorithm

To verify the performance of the CACO algorithm, 20 independent experiments were conducted in different size city sets and compared with the latest improved particle swarm optimization algorithm MPSO [39] and wolf swarm optimization algorithm D-GWO [40] so far, and the results are shown in Tables 3 and 4.

Table 3 Comparison of the CACO with MPSO
Full size table
Table 4 Comparison of the CACO with D-GWO
Full size table

As shown in Table 3, both CACO and MPSO can find the optimal solution in the small-scale city sets with the number of cities around 100, but the quality of the optimal solution gradually decreases with the expansion of the city size, starting from KroB150 for MPSO, and the error rate of the optimal solution is greater than 4% starting from the large-scale city set Lin318. In contrast, CACO uses pheromone guidance for multiple populations, which makes the algorithm perform consistently on large-scale city sets and within 1% of the minimum error in the Pr439 city set, indicating that the accuracy of the solution in large-scale city sets is significantly better than MPSO.

The data in Table 4 are more comprehensive, comparing in terms of optimal solution, average solution, minimum error rate, and average error rate. It can be clearly seen that the performance of D-GWO is less stable in the small-scale city sets, and although it can find the approximate optimal solution, it still has some error. While CACO can find the optimal solution in the city sets compared with the number of cities within 150, and the average error rate is within 1%, so the performance is more stable. In larger city sets such as Pr226, although the minimum error rate and average error rate of D-GWO are small with better results, the error rate of the optimal solution of CACO is only 0.004%, which is very close to the optimal solution. In the Pr439 city set, the performance of the D-GWO algorithm decreases significantly, but CACO is able to explore a better optimal route stably due to the guidance of pheromones after community detection, so the global search capability and stability are significantly better than D-GWO.

Overall, CACO has the ability to consistently explore optimal solutions for small sets of cities thanks to the small communities with high quality routes delineated by the route relationship network, allowing the algorithm to quickly find the optimum among high quality routes. At the same time, the pheromones of other routes in the small communities increase the chances that ants will choose other cities when guiding multiple populations, increasing the diversity of the algorithm.

For larger city sets, the exploration accuracy of CACO is high, with the error rate within an acceptable range, and the stability of the solution is strong without much fluctuation, which is mainly due to the great contribution of using community detection and pheromone guidance in the algorithm. The samples of community detection come from the route information of multiple population ants in different periods, so with the increase in iterations, the routes explored by ants are getting closer to the optimal solutions, and the community detection on this basis is beneficial to explore better routes.

4.4 Comparison with Other Improved Algorithms

To further verify the excellent performance of the CACO algorithm, the comparison results of CACO with Hybrid Max–Min ant system (HMMA) [41], Ant colony algorithm based on generalized Jaccard similarity(JCACO) [42], Spider Monkey Optimization(DSMO) [43], parallel cooperative hybrid ant colony optimization(PACO-3Opt) [44] and Heterogenous Adaptive Ant Colony Optimization(HAACO) [45] are added, as shown in Table 5.

Table 5 Comparison of the CACO with other improved algorithms
Full size table

From the number of optimal solutions obtained in different city sets, CACO is significantly better than the other.

algorithms. CACO, JCACO and HAACO can all find optimal solutions in city sets with less than 200 cities with good exploration ability. In the large-scale city set, CACO finds better solutions than other algorithms, and the minimum error rate is less than 1% even in Pr439. Comparing with the average solution, CACO generally has smaller average solutions than other algorithms in large-scale cities, and the stability of the algorithm is better when dealing with more cities.

4.5 Application of the Proposed Algorithm

The above experiments demonstrate the excellent performance of CACO in solving TSP problems, and we will play the advantages of CACO in combination with actual problems in the following. Those red points in Fig. 11 are the general hospitals in Songjiang District, Shanghai, China, located through ArcGIS and Google API.

Fig. 11
figure 11

Hospital location map

Full size image

In the context of COVID-19 affecting the world, assuming that here the medical resources need to be transported to all hospitals at once without interruption, this requirement can be modeled as a TSP problem, and Fig. 12 shows its community detection results and solution routes, with the total route length of 122.653 km and the distance of 40.762 km between A and B.

Fig. 12
figure 12

The optimal results without considering A and B

Full size image

However, the relationship between community nodes in reality changes from time to time. When the situation of hospitals A and B is very urgent, priority should be given to transport resources to hospitals A and B, which cannot be carried out by the ordinary ant colony algorithm. Figure 13 shows the community detection results and solution routes after considering the situation of hospitals A and B. The total route length is 123.873 km, and the distance between A and B is 11.897 km. Although the total length increases by 1%, the distance between A and B is shortened by 71%, which is an obvious improvement.

Fig. 13
figure 13

The optimal results considering A and B

Full size image

5 Conclusion and Future Direction

This study proposes the multiple ant colony algorithm combining community relationship network (CACO), which is different from most scholars who have improved around the route information of better ants. By incorporating the idea of community detection, this study sampled all the route information of different populations of ants to construct a route relationship network model belonging to multiple populations. In this model, community division is performed by modularity, and the small communities are combined with ant colony algorithm for solving the TSP problem. Through the processing of samples and community detection, the divided small communities are structurally stable and have the potential for optimal solutions. At this time, the pheromone of the small community is used to guide the multiple clusters, which speeds up the convergence speed. Also, the pheromones of non-optimal edges increase the diversity of multiple communities, balancing the speed of convergence and diversity.

CACO is compared with the traditional ant colony algorithm and the latest algorithms to date through 28 TSP city sets, and the simulation results show that CACO outperforms other algorithms, as well as better balance between convergence speed and diversity when dealing with large-scale problems.

For future research, we will perform more interdisciplinary combinations. Although ant colony algorithms incorporating community relationship networks can correlate distance with node sparsity, the literature that can be studied is relatively few and limited in thinking. So, there are more optimization studies in theory while relatively simple in application. In the future, more attention will be paid to the combination of complex network structures and intelligent algorithms to solve realistic and more complex problems.