1 Introduction

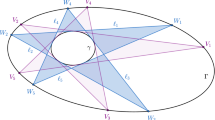
Let C be an oval (by which we mean a simple closed convex plane curve of class \(C^2\) with positive curvature) and \(\alpha \in (0,\pi )\). The set of points at which two support lines of C intersect at angle \(\pi -\alpha \) is called an \(\alpha \)-isoptic \(C_\alpha \) (or simply an isoptic) of C, see Fig. 1. Choosing the coordinate system with origin O inside the curve C, we have the following parametrization of C

$$\begin{aligned} z(t)=p(t)e^{it}+p'(t)ie^{it} \quad \text {for }t\in [0,2\pi ). \end{aligned}$$

Here p is the support function of C (i.e. p(t) is the distance from O to the support line of C perpendicular to \(e^{it}\) at \(z(t)\in C\)).

Fig. 1
figure 1

Construction of an \(\alpha \)-isoptic \(C_{\alpha }\) of a convex curve C for a given \(\alpha \in (0,\pi )\)

Full size image

The \(\alpha \)-isoptics of C for \(\alpha \in (0,\pi )\) can be parametrized (see Cieślak et al. 1991) in terms of the support function

$$\begin{aligned} z_{\alpha }(t) = p(t)e^{it}+\left( -p(t)\cot \alpha +\frac{1}{\sin \alpha }p(t+\alpha )\right) ie^{it} \quad \text {for }t\in [0,2\pi ) \end{aligned}$$

and this parametrization seems to be the main tool in the study of isoptics and their generalizations (Cieślak et al. 1991, 1996; Cieślak and Mozgawa 2022; Dana-Picard et al. 2020; Martini et al. 2011; Michalska 2003; Miernowski and Mozgawa 1997, 2001; Mozgawa 2008, 2009; Rochera 2022; Skrzypiec 2018, 2021; Szałkowski 2005). Isoptics can be considered also in the nonparametric form. However, implicit equations are known only for a small class of curves, see for example (Bakhvalov et al. 1964; Dana-Picard et al. 2020, 2012).

In this paper, we construct parametrizations of orthogonal trajectories to isoptics of ovals, using the solution of a specific Cauchy problem.

The paper is organized as follows. Section 2 provides all necessary definitions and preliminary results, including the formulation of the Cauchy problem used to obtain orthogonal trajectories to isoptics. Next, in Sect. 3, we show how to obtain parametrizations of orthogonal trajectories to isoptics of ovals, which is the main result of the paper. Examples which illustrate orthogonal trajectories to isoptics of some ovals (circles, ellipses, and a curve defined by the support function of class \(C^3\) but not of class \(C^4\)) are presented in Sect. 4. Finally, some open problems involving orthogonal trajectories to isoptics are presented in Sect. 5.

2 Preliminaries and auxiliary lemmas

Let \(p:[0,2\pi ]\rightarrow \mathbb {R}\) be the support function of an oval C and let the radius of curvature

$$\begin{aligned} R(t)=p(t)+p''(t) \end{aligned}$$

of the curve C at the point \(z(t)=p(t)e^{it}+p'(t)ie^{it}\) be positive for all \(t\in [0,2\pi )\). For simplicity, in the following we assume that p and R are defined on \(\mathbb {R}\) and that they are \(2\pi \)-periodic functions. Let \(C_{\alpha }\), \(\alpha \in (0,\pi )\), be the isoptics of C. For \((\alpha ,t)\in [0,\pi )\times \mathbb {R}\) we define

$$\begin{aligned} \lambda (\alpha , t)&= \left\{ \begin{array}{ll} \dfrac{p(t+\alpha )-p(t)\cos \alpha -p'(t)\sin \alpha }{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ 0, &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \\ \mu (\alpha , t)&= \left\{ \begin{array}{ll} -\dfrac{p(t)-p(t+\alpha )\cos \alpha +p'(t+\alpha )\sin \alpha }{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ 0, &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \end{aligned}$$
$$\begin{aligned} \nu (\alpha , t)&= \left\{ \begin{array}{ll} \dfrac{\mu (\alpha , t)}{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ -\frac{1}{2}R(t), &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \\ \rho (\alpha , t)&= \left\{ \begin{array}{ll} \dfrac{p(t)\sin \alpha -p'(t)\cos \alpha +p'(t+\alpha )}{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ R(t), &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \\ \end{aligned}$$

and

$$\begin{aligned} B(\alpha ,t)&= -\mu (\alpha ,t)\sin \alpha =p(t)-p(t+\alpha )\cos \alpha +p'(t+\alpha )\sin \alpha . \end{aligned}$$

It is easy to verify that

$$\begin{aligned}{} & {} \lim _{\alpha \rightarrow 0^+} \lambda (\alpha ,t)=\lim _{\alpha \rightarrow 0^+} \mu (\alpha ,t)=\lim _{\alpha \rightarrow 0^+} B(\alpha ,t)=0, \\{} & {} \lim _{\alpha \rightarrow 0^+} \nu (\alpha ,t)=-\tfrac{1}{2}R(t) \quad \text {and}\quad \lim _{\alpha \rightarrow 0^+} \rho (\alpha ,t)=R(t) \end{aligned}$$

for all \(t\in \mathbb {R}\).

Since \(B(0,t)=0\) and \(\frac{\partial B}{\partial \alpha }(\alpha ,t) = R(t+\alpha )\sin \alpha >0\) for \((\alpha ,t)\in (0,\pi )\times \mathbb {R}\), we have \(B(\alpha ,t)>0\) for \((\alpha ,t)\in (0,\pi )\times \mathbb {R}\). Similarly, we have \(\lambda (0,t)=0\) and \(\frac{\partial \lambda }{\partial \alpha }(\alpha ,t) = \frac{B(t,\alpha )}{\sin ^2\alpha }\), so \(\lambda (\alpha ,t)>0\) and \(\mu (\alpha ,t)= -\frac{B(\alpha ,t)}{\sin \alpha }<0\) for \((\alpha ,t)\in (0,\pi )\times \mathbb {R}\). Moreover, we have

$$\begin{aligned} \lambda ^2(\alpha ,t)+\rho ^2(\alpha ,t) >0 \quad \text {for } (\alpha ,t)\in (0,\pi )\times \mathbb {R}. \end{aligned}$$

For \((\alpha ,t)\in [0,\pi )\times \mathbb {R}\) we define

$$\begin{aligned} H(\alpha , t)= \left\{ \begin{array}{ll} \dfrac{\nu (\alpha ,t)\rho (\alpha ,t)}{\lambda ^2(\alpha ,t)+\rho ^2(\alpha ,t)}, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ -\frac{1}{2},&{} (\alpha ,t)\in \{0\}\times \mathbb {R}. \end{array} \right. \end{aligned}$$

For technical reasons, we define \(H(\alpha ,t)=H(-\alpha ,t)\) for \((\alpha ,t)\in (-\pi ,0)\times \mathbb {R}\).

Fig. 2
figure 2

Geometric interpretation of \(\lambda (\alpha , t)\) and \(\mu (\alpha , t)\) for \(\alpha \in (0,\pi )\) and \(t\in [0,2\pi )\)

Full size image

Lemma 2.1

If p is a \(C^2\) function, then H is continuous in \((-\pi ,\pi )\times \mathbb {R}\).

Proof

Since the functions \(\lambda \), \(\nu \) and \(\rho \) are continuous in \((0,\pi )\times \mathbb {R}\) we only need to prove that H is continuous at (0, t) for all \(t\in \mathbb {R}\), which we obtain by showing that

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \lambda (a,s)=0, \qquad \lim _{(a,s)\rightarrow (0^+,t)} \nu (a,s)=-\frac{1}{2}R(t) \end{aligned}$$

and

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \rho (a,s)=R(t), \end{aligned}$$

where the limits are taken as \((a,s)\rightarrow (0,t)\) with \(a>0\).

For \((a,s)\in [0,\frac{\pi }{2})\times \mathbb {R}\) we define

$$\begin{aligned} f(a,s) = p(s+a)-p(s)\cos a-p'(s)\sin a \quad \text {and}\quad g(a,s) = \sin a, \end{aligned}$$

so that we have

$$\begin{aligned} \lambda (a,s)=\frac{f(a,s)}{g(a,s)},\quad (a,s)\in (0,\tfrac{\pi }{2})\times \mathbb {R}. \end{aligned}$$

Since

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} f(a,s)=\lim _{(a,s)\rightarrow (0^+,t)} g(a,s)=0, \end{aligned}$$

we need some version of l’Hôpital’s rule for multivariable functions. Following the arguments given in the proof of Theorem 2.1 in Lawlor (2012) and the proof of Theorem 4 in Lawlor (2020), let us fix an arbitrary point (0, t), \(t\in \mathbb {R}\), and take any sequence \((a_n,t_n)\rightarrow (0,t)\) such that \(a_n\in (0,\frac{\pi }{2})\) and \(t_n\in \mathbb {R}\). Since the functions \(a\mapsto f(a,t_n)\) and \(a\mapsto g(a,t_n)\) are differentiable in \((0,\frac{\pi }{2})\) and continuous in \([0,\frac{\pi }{2}]\), and \(\frac{\partial g}{\partial a}(a,s)>0\) for \((a,s)\in (0,\tfrac{\pi }{2})\times \mathbb {R}\), we can apply the Cauchy Mean Value Theorem and obtain

$$\begin{aligned} \frac{f(a_n,t_n)}{g(a_n,t_n)} =\frac{f(a_n,t_n)-f(0,t_n)}{g(a_n,t_n)-g(0,t_n)} =\frac{\frac{\partial f}{\partial a}(c_n,t_n)}{\frac{\partial g}{\partial a}(c_n,t_n)}, \end{aligned}$$

where \(c_n\in (0,a_n)\) for all \(n\in \mathbb {N}\). Since \((c_n,t_n)\rightarrow (0^+,t)\), we have

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \frac{f(a,s)}{g(a,s)}&= \lim _{(a,s)\rightarrow (0^+,t)}\frac{\frac{\partial f}{\partial \alpha }(a,s)}{\frac{\partial g}{\partial \alpha }(a,s)} \\&= \lim _{(a,s)\rightarrow (0^+,t)}\frac{p'(s+a)+p(s)\sin a-p'(s)\cos a}{\cos a}=0, \end{aligned}$$

and therefore \(\lim \limits _{(a,s)\rightarrow (0^+,t)} \lambda (a,s)= 0\) for all \( t\in \mathbb {R}\).

The limits of \(\nu (a,s)\) and \(\rho (a,s)\) as \((a,s)\rightarrow (0^+,t)\) can be calculated in the same manner, defining

$$\begin{aligned}&f(a,s) = \mu (a,s)\sin a=-p(t)+p(t+a)\cos a-p'(t+a)\sin a,\\&g(a,s) = \sin ^2 a, \end{aligned}$$

and

$$\begin{aligned}&f(a,s) = p(s)\sin a-p'(s)\cos a+p'(s+a), \\&g(a,s) = \sin a, \end{aligned}$$

respectively. \(\square \)

Lemma 2.2

If p is a \(C^3\) function, then for each \((\alpha _0,t_0)\in (-\pi ,\pi )\times \mathbb {R}\) the Cauchy problem

$$\begin{aligned} \left\{ \begin{array}{l} t'(\alpha )=H(\alpha ,t(\alpha )),\quad \alpha \in (-\pi ,\pi ),\\ t(\alpha _0)=t_0, \end{array} \right. \end{aligned}$$
(1)

has a unique solution.

Proof

Since the continuity of \(\frac{\partial H}{\partial t}\) in \((-\pi ,\pi )\times \mathbb {R}\) implies that in every compact subset of \((-\pi ,\pi )\times \mathbb {R}\) the derivative \(\frac{\partial H}{\partial t}\) is bounded and, consequently, H is locally Lipschitz continuous with respect to t, we only need to prove that \(\frac{\partial H}{\partial t}\) is continuous in \((-\pi ,\pi )\times \mathbb {R}\).

For \((\alpha ,t)\in (0,\pi )\times \mathbb {R}\) we have

$$\begin{aligned} \frac{\partial H}{\partial t} = \frac{\left( \frac{\partial \nu }{\partial t}\rho +\nu \frac{\partial \rho }{\partial t}\right) (\lambda ^2+\rho ^2)-2\nu \rho \left( \lambda \frac{\partial \lambda }{\partial t}+\rho \frac{\partial \rho }{\partial t}\right) }{(\lambda ^2+\rho ^2)^2}. \end{aligned}$$

Moreover, \(\frac{\partial H}{\partial t}(0,t)=0\) for all \(t\in \mathbb {R}\) and \(\frac{\partial H}{\partial t}(-\alpha ,t)=\frac{\partial H}{\partial t}(\alpha ,t)\) for \((\alpha ,t)\in (-\pi ,0)\times \mathbb {R}\). Straightforward calculations yield

$$\begin{aligned} \frac{\partial \nu }{\partial t}(\alpha , t)&=\!\left\{ \!\!\! \begin{array}{ll} -\dfrac{p'(t)-p'(t+\alpha )\cos \alpha +p''(t+\alpha )\sin \alpha }{\sin ^2\alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ -\frac{1}{2}R'(t), &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \\ \frac{\partial \rho }{\partial t}(\alpha , t)&=\!\left\{ \!\!\! \begin{array}{ll} \dfrac{p'(t)\sin \alpha -p''(t)\cos \alpha +p''(t+\alpha )}{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ R'(t), &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \\ \frac{\partial \lambda }{\partial t}(\alpha , t)&=\!\left\{ \!\!\! \begin{array}{ll} \dfrac{p'(t+\alpha )-p'(t)\cos \alpha -p''(t)\sin \alpha }{\sin \alpha }, &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ 0, &{} (\alpha ,t)\in \{0\}\times \mathbb {R}. \end{array} \right. \end{aligned}$$

Continuity of \(\frac{\partial \nu }{\partial t}\), \(\frac{\partial \rho }{\partial t}\) and \(\frac{\partial \lambda }{\partial t}\) in \([0,\pi )\times \mathbb {R}\) can be easily established by using the l’Hôpital’s rule derived in the proof of Lemma 2.1 to calculate the following limits:

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \frac{\partial \nu }{\partial t}(a,s)=-\frac{1}{2}R'(t), \qquad \lim _{(a,s)\rightarrow (0^+,t)} \frac{\partial \rho }{\partial t}(a,s)=R'(t) \end{aligned}$$

and

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \frac{\partial \lambda }{\partial t}(a, s)=0, \quad t\in \mathbb {R}. \end{aligned}$$

Now, we can calculate

$$\begin{aligned} \lim _{(a,s)\rightarrow (0^+,t)} \frac{\partial H}{\partial t}(a,s) =0=\frac{\partial H}{\partial t}(0,t), \end{aligned}$$

and the continuity of \(\frac{\partial H}{\partial t}\) in \((-\pi ,\pi )\times \mathbb {R}\) follows easily. \(\square \)

3 Parametrization of orthogonal trajectories to isoptics of an oval

For \((\alpha ,t)\in [0,\pi )\times \mathbb {R}\) we define

$$\begin{aligned} F(\alpha , t)&= \left\{ \begin{array}{ll} z_{\alpha }(t), &{} (\alpha ,t)\in (0,\pi )\times \mathbb {R},\\ z(t), &{} (\alpha ,t)\in \{0\}\times \mathbb {R}, \end{array} \right. \end{aligned}$$

so that F(0, t) for \(t\in [0,2\pi )\) forms the oval C, while \(F(\alpha ,t)\) for \(t\in [0,2\pi )\) constitutes a single \(\alpha \)-isoptic of C, where \(\alpha \in (0,\pi )\). The function F is continuous in \([0,\pi )\times \mathbb {R}\) and \(C^1\) in \((0,\pi )\times \mathbb {R}\). Moreover, F restricted to \((0,\pi )\times [0,2\pi )\) is injective and the image of \((0,\pi )\times [0,2\pi )\) under F is the exterior of C.

Theorem 3.1

Let C be an oval parametrized in terms of the support function p of class \(C^3\). Orthogonal trajectories to isoptics of C are the curves parameterized by functions \(\gamma _{\tau _0}:[0,\pi )\rightarrow \mathbb {R}^2\) for \(\tau _0\in [0,2\pi )\), defined by

$$\begin{aligned} \gamma _{\tau _0}(\alpha )=F(\alpha ,t(\alpha )), \end{aligned}$$

where \(t:[0,\pi )\rightarrow \mathbb {R}\) is the solution to the Cauchy problem

$$\begin{aligned} \left\{ \begin{array}{l} t'(\alpha )=H(\alpha ,t(\alpha )),\quad \alpha \in (0,\pi ),\\ t(0)=\tau _0. \end{array} \right. \end{aligned}$$
(2)

Proof

Assume that \(t_0\in [0,2\pi )\) and \(\gamma (\alpha )=F(\alpha ,t(\alpha ))\), where \(t:[0,\pi )\rightarrow \mathbb {R}\) is the solution to the Cauchy problem (2) with \(\alpha _0=0\). For each \(\alpha \in (0,\pi )\), the point \(\gamma (\alpha )\) lies on the isoptic \(C_\alpha \). We claim that at the point \(\gamma (\alpha )\) the tangent vector to \(\gamma \) and the tangent vector to the isoptic \(C_\alpha \) are orthogonal for all \(\alpha \in (0,\pi )\).

For \(\alpha \in (0,\pi )\), we have

$$\begin{aligned} \gamma '(\alpha )&=\frac{\partial F}{\partial \alpha } (\alpha ,t(\alpha )) + \frac{\partial F}{\partial t} (\alpha ,t(\alpha ))\cdot t'(\alpha ) \\&=-\nu (\alpha ,t(\alpha ))ie^{it(\alpha )}+\left( -\lambda (\alpha ,t(\alpha ))e^{it(\alpha )}+\rho (\alpha ,t(\alpha ))ie^{it(\alpha )}\right) t'(\alpha ) \\&=-\lambda (\alpha ,t(\alpha ))t'(\alpha )e^{it(\alpha )}+\left( -\nu (\alpha ,t(\alpha ))+\rho (\alpha ,t(\alpha ))t'(\alpha )\right) ie^{it(\alpha )} \end{aligned}$$

and

$$\begin{aligned} z'_{\alpha }(t(\alpha ))&=\frac{\partial F}{\partial t} (\alpha ,t(\alpha )) =-\lambda (\alpha ,t)e^{it(\alpha )}+\rho (\alpha ,t(\alpha ))ie^{it(\alpha )}. \end{aligned}$$

Therefore

$$\begin{aligned}&\hspace{-2em}\left\langle \gamma '(\alpha ), z'_{\alpha }(t(\alpha )) \right\rangle \\&\quad =\lambda ^2(\alpha ,t(\alpha )) t'(\alpha )+(-\nu (\alpha ,t(\alpha ))+\rho (\alpha ,t(\alpha )) t'(\alpha ))\rho (\alpha ,t(\alpha )) \\&\quad =(\lambda ^2(\alpha ,t(\alpha )) + \rho ^2(\alpha ,t(\alpha )) H(\alpha ,t(\alpha )) -\nu (\alpha ,t(\alpha )) \rho (\alpha ,t(\alpha )) \\&\quad =0. \end{aligned}$$

On the other hand, for an arbitrary point P on an isoptic \(C_{\alpha _0}\), where \(\alpha _0\in (0,\pi )\), one can find \(t_0\in [0,2\pi )\) such that \(F(\alpha _0,t_0)=P\) and the solution to the Cauchy problem (1) which goes through \((\alpha _0,t_0)\) reaches some point \((0,T_0)\), where \(T_0\in \mathbb {R}\). Since F and H are \(2\pi \)-periodic in t, there exists \(\tau _0\in [0,2\pi )\) such that the solution to the Cauchy problem (2) goes through P. \(\square \)

Remark 3.2

Orthogonal trajectories to isoptics of an oval C, where C is parametrized in terms of the support function p of class \(C^3\), are regular curves. Indeed, for \(\tau _0\in [0,2\pi )\) and \(\alpha \in (0,\pi )\), we have

$$\begin{aligned} |\gamma '_{\tau _0}(\alpha )|^2=\frac{\lambda ^2(\alpha , t(\alpha ))\nu ^2(\alpha , t(\alpha ))}{\lambda ^2(\alpha , t(\alpha ))+\rho ^2(\alpha , t(\alpha ))}>0. \end{aligned}$$

4 Examples of orthogonal trajectories to isoptics

Example 4.1

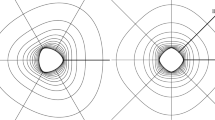
For C being the circle of radius \(r>0\) centered at (0, 0) we have \(p(t)=r\) for \(t\in \mathbb {R}\) and \(H(\alpha ,t)=-\frac{1}{2}\) for \((\alpha ,t)\in [0,\pi )\times \mathbb {R}\). The solution to (2) is

$$\begin{aligned} t(\alpha )=-\frac{1}{2}\alpha +\tau _0,\quad \alpha \in [0,\pi ), \end{aligned}$$

and orthogonal trajectories to the isoptics to the circle C (see Fig. 3) are half-lines

$$\begin{aligned} \gamma (\alpha )=F\left( \alpha ,\tau _0-\frac{1}{2}\alpha \right) =\frac{r}{\cos \frac{\alpha }{2}}e^{i\tau _0},\quad \alpha \in [0,\pi ), \end{aligned}$$

starting from \(z(\tau _0)=re^{i\tau _0}\), where \(\tau _0\in [0, 2\pi )\).

Fig. 3
figure 3

Isoptics of a circle and their orthogonal trajectories

Full size image

Example 4.2

The support function

$$\begin{aligned} p(t)=\sqrt{\cos ^2 t + 4\sin ^2 t}, \quad t\in \mathbb {R}, \end{aligned}$$

defines an ellipse. For \((\alpha ,t)\in (0,\pi )\times \mathbb {R}\) we have

$$\begin{aligned} H(\alpha ,t)=\frac{\mathcal {N}(\alpha ,t)}{\mathcal {D}(\alpha ,t)}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {N}(\alpha ,t)&= -75\sin (2t-\alpha )-295\sin \alpha -45\sin 3\alpha +225\sin (2t+\alpha )\\&\quad \ +34\sin 2\alpha \sqrt{(5-3\cos 2t)(5-3\cos (2t+2\alpha ))}\\&\quad \ -60\sin (2t+2\alpha )\sqrt{(5-3\cos 2t)(5-3\cos (2t+2\alpha ))}\\&\quad \ +18\sin (4t+2\alpha )\sqrt{(5-3\cos 2t)(5-3\cos (2t+2\alpha ))}\\&\quad \ +27\sin (6t+3\alpha )-45\sin (4t+\alpha )+177\sin (2t+3\alpha )\\&\quad \ -135\sin (4t+3\alpha ) \end{aligned}$$

and

$$\begin{aligned} \mathcal {D}(\alpha ,t)&=4\sin \alpha \big (170-126\cos 2t+45\cos 2\alpha -126\cos (2t+2\alpha )\\&\hspace{4.5em} -34\cos \alpha \sqrt{(5-3\cos 2t)(5-3\cos (2t+2\alpha ))}\\&\hspace{4.5em} +30\cos (2t+\alpha )\sqrt{(5-3\cos 2t)(5-3\cos (2t+2\alpha ))}\\&\hspace{4.5em} +45\cos (4t+2\alpha )\big ). \end{aligned}$$

Since we do not have an analytic solution to (2) for \(H(\alpha ,t)=\frac{\mathcal {N}(\alpha ,t)}{\mathcal {D}(\alpha ,t)}\), orthogonal trajectories to the isoptics of the ellipse are obtained numerically, see Fig. 4.

Fig. 4
figure 4

An ellipse, its isoptics, and their orthogonal trajectories

Full size image

Example 4.3

In Fig. 5, also obtained numerically, we present orthogonal trajectories to the isoptics of the curve K defined by the support function

$$\begin{aligned} p(t) = \left\{ \begin{array}{ll} r, &{} t\in [0,\frac{\pi }{2}),\\ r-17a +a\cos 4t +{}\\ \quad {}+4a(5\cos t +5\sin t - 4\sin 2t -\cos 3t +\sin 3t), &{} t\in [\frac{\pi }{2},2\pi ), \end{array} \right. \end{aligned}$$

with \(r=150\) and \(a=1\). The function p is of class \(C^3\) (but not \(C^4\)). The curve K has an axis of symmetry, namely \(y=x\), and coincides with the circle of radius r in the first quadrant.

Fig. 5
figure 5

The isoptics of the curve K (Example 4.3) and their orthogonal trajectories

Full size image

Remark 4.4

Notice that in all the examples presented above, the orthogonal trajectories to the isoptics of the oval, starting at points on any of the axis of symmetry of the oval, are half-lines contained in this axis of symmetry. This observation inspired us to state the following theorem.

Theorem 4.5

If l is an axis of symmetry of an oval C then the orthogonal trajectories to the isoptics of C, starting at points on l, are contained in l.

Proof

The theorem follows easily from the uniqueness of solutions to the problem (1), see Lemma 2.2, and the symmetry of the oval. \(\square \)

5 Open problems

The following questions involving orthogonal trajectories to isoptics are open for future research:

  • Do the sets of points at which the curvature of the isoptics of ovals is extremal form a curve that is orthogonal to the isoptics? We know that the answer is positive for some ovals, e.g., ellipses.

  • Do the sets of points at which the curvature of the isoptics of ovals is equal to zero and the sets of inflection points of orthogonal trajectories to the isoptics coincide? We even do not know if the answer is positive for very simple ovals such as ellipses, but numerical experiments for ellipses suggest so.

  • Are there any other relations between properties of orthogonal trajectories to isoptics and the curvature of the isoptics?