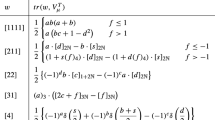On the labelling of characters of Weyl groups of type $F_4$

Abstract

In the literature on finite groups of Lie type, there exist two different conventions about the labelling of the irreducible characters of Weyl groups of type $F_4$. We point out some issues concerning these two conventions and their effect on tables about unipotent characters or the Springer correspondence. Using experiments related to these issues with the computer algebra system CHEVIE, we spotted an error in Spaltenstein’s tables for the generalised Springer correspondence in type $E_7$.

1 Introduction

This note is about certain notational conventions in the representation theory of finite groups of Lie type. General references are the books by Carter (1985), Digne and Michel (2020) and Lusztig (1984a); see also Geck and Malle (2020) for a more recent survey. There are some issues in relation to Weyl groups of type $F_4$. These groups (and related data like generic degrees, Springer representations etc.) occur in a substantial way in a number of situations including:

• The parametrisation of unipotent characters of a Chevalley group $F_4(q)$.

• Degree formulae for unipotent principal series characters of a twisted Chevalley group ${^2\!E}_6(q)$.

• Degrees of unipotent characters of $E_8(q)$ in the Harish-Chandra series above a cuspidal unipotent character of a Levi subgroup of type $D_4$.

• The Springer correspondence for a simple algebraic group of type $F_4$.

• The generalised Springer correspondence for a simple algebraic group of type $E_7$ with respect to a cuspidal datum in a Levi subgroup of type $A_1{\times } A_1{\times } A_1$.

• The generalised Springer correspondence for a simple algebraic group of type $E_8$ with respect to a cuspidal datum in a Levi subgroup of type $D_4$.

In a root system of type $F_4$ there are long roots and short roots, but the picture is highly symmetric and, hence, it often requires some extra care to fix notation and conventions. Unfortunately, this is not always done consistently in the existing literature, which prompted us to write this note. In fact, during the work on Hetz (2023a), there actually occurred some delicate contradictions as a result of a misunderstanding regarding the conventions used in existing tables. (This will be briefly explained in Example 5.2.). Our purpose here is to try to clarify some points in relation to the long/short root issue in type $F_4$. In the course of verifying a number of tables, we actually discovered an error in Spaltenstein’s table for the generalised Springer correspondence in type $E_7$; see Lemma 6.2.

2 Characters of a Coxeter group of type $F_4$

Let W be a Coxeter group of type $F_4$. The basic and widely used reference for the character table of W is Kondo (1965). In that article, W is constructed in a purely group-theoretical way, without reference to an underlying root system. With the notation of Kondo (1965, Prop. 5.1), we have $W=\langle d,a, \tau ,\tau \sigma \rangle$ where $d,a,\tau ,\tau \sigma$ are elements of order 2 that satisfy the following braid relations:

$$\begin{aligned} (d{\cdot } a)^3=(\tau {\cdot }\tau \sigma )^3=(a{\cdot }\tau )^4=1, \quad d{\cdot } \tau =\tau {\cdot } d,\quad d{\cdot }\tau \sigma =\tau \sigma {\cdot } d, \quad a{\cdot } \tau \sigma =\tau \sigma {\cdot } a. \end{aligned}$$

Thus, the corresponding Coxeter diagram is as follows.

The group W has 25 irreducible characters, of degrees 1, 2, 4, 6, 8, 9, 12, 16; we shall denote by $n_j$ the j-th character of degree n in the table in Kondo (1965, p. 152). (This is a standard notation in the existing literature, e.g., Alvis (2005); Carter (1985); Lusztig (1984a); note that Shoji (1980); Spaltenstein (1985) use a slightly different notation for the characters of degree 4.)

Table 1 Irreducible characters for type $F_4$

Table 1 contains some information about the values of the characters on $d,a,\tau ,\tau \sigma$ and $a\tau$. The second column of that table refers to the notation introduced by Carter (1985, p. 413) (where one can also find the complete character table); the third column refers to the a-function, as defined in Lusztig (1984a, 4.1), and printed in Lusztig (1984a, 4.10).

Remark 2.1

There is a group automorphism $\iota :W\rightarrow W$ such that $\iota (d)=\tau \sigma$, $\iota (a)=\tau$, $\iota (\tau ) =a$ and $\iota (\tau \sigma )=d$. This automorphism has order 2 and it induces a permutation of the irreducible characters of W as follows:

$$\begin{aligned} 1_2\leftrightarrow 1_3,\quad 2_1\leftrightarrow 2_3,\quad 2_2\leftrightarrow 2_4,\quad 4_3\leftrightarrow 4_4,\quad 8_1\leftrightarrow 8_3,\quad 8_2\leftrightarrow 8_4,\quad 9_2\leftrightarrow 9_3; \end{aligned}$$

or, with Carter’s notation:

$$\begin{aligned}{} & {} \phi _{1,12}'\leftrightarrow \phi _{1,12}'',\quad \phi _{2,4}'\leftrightarrow \phi _{2,4}'',\quad \phi _{2,16}'\leftrightarrow \phi _{2,16}'',\quad \phi _{4,7}'\leftrightarrow \phi _{4,7}'',\\{} & {} \phi _{8,3}'\leftrightarrow \phi _{8,3}'',\quad \phi _{8,9}'\leftrightarrow \phi _{8,9}'',\quad \phi _{9,6}'\leftrightarrow \phi _{9,6}''. \end{aligned}$$

(All other characters are fixed.)

Remark 2.2

Let $(\phi ',\phi '')$ be a pair of characters that are permuted by the above automorphism $\iota :W \rightarrow W$. By inspection of Table 1 we see that we always have $\phi '(a)= \phi '(d)\le 0$ and $\phi ''(a)=\phi ''(d)\ge 0$. (Hence, this property characterises $\phi '$ and $\phi ''$.)

Remark 2.3

In the following sections, the Coxeter group W will typically arise as the Weyl group of a (crystallographic) root system $\Phi$ of type $F_4$ in some finite-dimensional Euclidean vector space E with scalar product $(\, ,):E\times E\rightarrow \mathbb {R}$. Such a root system contains roots of different lengths, which gives rise to the long/short root issue mentioned in the introduction. Let us fix a set of simple roots $\Pi =\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\subseteq \Phi$, labelled in such a way that $\alpha _1,\alpha _2$ are long and $\alpha _3,\alpha _4$ are short:

Then, denoting by $s_i\in {\text {GL}}(E)$ the reflection with root $\alpha _i$ ($1\leqslant i\leqslant 4$), we have $W\cong \langle s_1,s_2,s_3,s_4\rangle \subseteq {\text {GL}}(E)$. Hence, when referring to the labelling of ${\text {Irr}}(W)$ in Table 1, it is necessary to match the above generators $s_1,s_2, s_3,s_4$ to Kondo’s generators $d,a,\tau ,\tau \sigma$; in other words, one has to specify which of Kondo’s generators should correspond to long roots, and which to short roots. There are precisely two possibilities:

Both (AC) and (L) exist in the literature: Lusztig (1984a, 4.10) explicitly identifies d, a with reflections in long simple coroots and $\tau ,\tau \sigma$ with reflections in short simple coroots. Recall that the coroots are defined by $\alpha ^\vee :=2\alpha /(\alpha ,\alpha )\in E$ for $\alpha \in \Phi$. Then $\Phi ^\vee =\{\alpha ^\vee \mid \alpha \in \Phi \}$ also is a root system of type $F_4$ in E, with simple roots given by $\Pi ^\vee = \{\alpha _1^\vee ,\alpha _2^\vee ,\alpha _3^\vee , \alpha _4^\vee \}$ where now $\alpha _1^\vee , \alpha _2^\vee$ are short, while $\alpha _3^\vee , \alpha _4^\vee$ are long. Hence, Lusztig (1984a, 4.10) chooses (L), while Alvis (2005, p. 6/22), Carter (1985, p. 414) and Geck et al. (1996); Michel (2015) choose (AC).

Working with (AC) or (L) leads to different labels precisely for those irreducible characters that are permuted by the automorphism $\iota :W\rightarrow W$ in Remark 2.1. Concretely, this means for example that the character $2_3$ has value 2 on $s_1,s_2$ with respect to (L), and value 0 on $s_1,s_2$ with respect to (AC).

3 The Iwahori–Hecke algebra of type $F_4$

We shall also need the generic Iwahori–Hecke algebra $\mathscr {H}$ associated with the Coxeter group W of type $F_4$ as defined in Sect. 2. Let $K=\mathbb {Q}(u,v)$ where u, v are commuting indeterminates. Then $\mathscr {H}$ is an associative K-algebra with basis $\{T_w\mid w\in W\}$. As an algebra, $\mathscr {H}$ is generated by the basis elements $T_d,T_a,T_\tau , T_{\tau \sigma }$, subject to the above braid relations and the following quadratic relations:

$$\begin{aligned} T_d^2&=uT_1+(u-1)T_d,\quad T_a^2=uT_1+(u-1)T_a,\\ T_\tau ^2&= vT_1+(v-1)T_\tau ,\quad T_{\tau \sigma }^2=vT_1+(v-1)T_{\tau \sigma }. \end{aligned}$$

It is known that $\mathscr {H}$ is abstractly isomorphic to the group algebra of W over K (an explicit isomorphism is provided by Geck (2011)); furthermore, the specialisation $(u,v)\mapsto (1,1)$ induces a bijection between the irreducible representations of $\mathscr {H}$ and those of W. To give an example (which will also serve as a useful test case later on), we construct representations of $\mathscr {H}$ which specialise to the representations of W with characters $2_1$ and $2_3$.

Example 3.1

By checking that the defining relations for the above generators of $\mathscr {H}$ hold, one obtains two-dimensional matrix representations $\sigma ,\sigma ':\mathscr {H}\rightarrow M_2(K)$ via the following assignments:

$$\begin{aligned} \sigma :&\; T_d\mapsto \left( \begin{array}{rr} u &{} 0\\ 0 &{} u \end{array}\right) , \;T_a\mapsto \left( \begin{array}{rr} u &{} 0 \\ 0 &{} u\end{array}\right) ,\; T_{\tau }\mapsto \left( \begin{array}{rr} -1 &{} 1\\ 0 &{} v\end{array}\right) , \;T_{\tau \sigma }\mapsto \left( \begin{array}{rr} v &{} 0 \\ v &{} -1\end{array}\right) ;\\ \sigma ':&\; T_d\mapsto \left( \begin{array}{rr} u &{} 0\\ u &{} -1 \end{array}\right) ,\;T_a\mapsto \left( \begin{array}{rr} -1 &{} 1 \\ 0 &{} u\end{array}\right) ,\; T_\tau \mapsto \left( \begin{array}{rr} v &{} 0 \\ 0 &{} v\end{array}\right) ,\; T_{\tau \sigma }\mapsto \left( \begin{array}{rr} v &{} 0 \\ 0 &{} v\end{array}\right) . \end{aligned}$$

One easily sees that these are irreducible. We have

$$\begin{aligned} \hbox {trace}(\sigma (T_d))=\hbox {trace}(\sigma (T_a))=2u\quad \hbox {and}\quad \hbox {trace}(\sigma (T_\tau ))=\hbox {trace}(\sigma (T_{\tau \sigma }))=v-1. \end{aligned}$$

Hence, if we specialise $(u,v)\mapsto (1,1)$, then the character of $\sigma$ becomes the character $2_1$ of W. Similarly, $\sigma '$ specialises to the character $2_3$ of W.

Now, we have the one-dimensional representation $\hbox {ind}:\mathscr {H}\rightarrow K$ such that $T_d,T_a\mapsto u$ and $T_\tau ,T_{\tau \sigma } \mapsto v$ (which specialises to the trivial character $1_1$ of W). Then the “generic degree” associated with an irreducible representation $\phi :\mathscr {H}\rightarrow M_d(K)$ is defined by

$$\begin{aligned} D_\phi :=\frac{d\sum _{w\in W} \hbox {ind}(T_w)}{\sum _{w\in W} \hbox {ind} (T_w)^{-1}\hbox {trace}(\phi (T_w))\hbox {trace}(\phi (T_{w^{-1}}))} \in K \quad \hbox {(see Carter (1985, p. 361))} \end{aligned}$$

All of these have been computed previously (see Carter (1985, §13.5) and the references there) but, in the above two cases, we can just perform an explicit computation (using a computer) and obtain:

$$\begin{aligned} D_\sigma =D_{2_1}&=\frac{v^3(v+1)(uv^2+1)(u^2v^2+1)(u^3v^3+1)}{(u^3+1) (u+v)(u^2+v)}, \\ D_{\sigma '}=D_{2_3}&= \hbox { same formula but with the roles of { u},\,{ v} exchanged}. \end{aligned}$$

(See also Carter (1985, p. 450).) Specialising (u, v) to powers of q, where q is a power of a prime, we obtain actual degrees of characters of certain Chevalley groups over $\mathbb {F}_q$; see Carter (1985, Theorem 10.11.5) and Lusztig (1984a, Corollary 8.7).

4 Harish–Chandra series of unipotent characters

Let p be a prime and G be a simple algebraic group over an algebraic closure of $\mathbb {F}_p$. Let q be a power of p and $F:G \rightarrow G$ be a Frobenius map with respect to an $\mathbb {F}_q$-rational structure. Let $B\subseteq G$ be an F-stable Borel subgroup and $T\subseteq G$ be an F-stable maximal torus contained in B. Let $\Phi$ be the root system of G with respect to T and $\Pi \subseteq \Phi$ be the set of simple roots determined by B. Then F induces an action on $\Phi$ which preserves $\Pi$. Let $G^F=G(\mathbb {F}_q)$ and ${\text {Uch}}(G^F)$ be the set of unipotent characters of $G^F$. We have a partition of ${\text {Uch}}(G^F)$ into Harish–Chandra series; furthermore, there is a collection of bijections

$$\begin{aligned} \{\mathscr {S}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {S}})\mid \mathscr {S}\hbox { Harish-Chandra series of } {\text {Uch}}(G^F)\} \end{aligned}$$

where $\mathscr {W}_{\!\mathscr {S}}$ is a certain finite Coxeter group associated to each $\mathscr {S}$. Following Lusztig (1977, 3.25), this is further specified as follows.

• There is a well-defined F-invariant subset $\Pi '\subseteq \Pi$ such that the simple reflections of $\mathscr {W}_{\!\mathscr {S}}$ are indexed by the set ${\overline{\Pi }}$ of F-orbits on $\Pi \setminus \Pi '$; furthermore, there is a certain “parameter function” $\lambda :{\overline{\Pi }} \rightarrow \{ q^n \mid n\in \mathbb {Z}_{\ge 1}\}$.

• The pair $(\mathscr {W}_{\!\mathscr {S}},\lambda )$ determines an Iwahori–Hecke algebra with parameters given by $\{\lambda ({\bar{\alpha }})\mid {\bar{\alpha }} \in {\overline{\Pi }}\}$ (see Lusztig (1977, 3.6)); the degrees of the characters in $\mathscr {S}$ are obtained from the generic degrees of that algebra using the formula in Lusztig (1977, (3.26.1)).

The possibilities for $\Pi '\subseteq \Pi ,{\overline{\Pi }},\lambda$ are explicitly listed in Table II (p. 35) of Lusztig (1977). Let now $\mathscr {S}\subseteq {\text {Uch}}(G^F)$ be a Harish–Chandra series where the associated Coxeter group $\mathscr {W}_{\!\mathscr {S}}$ is of type $F_4$; this situation occurs for $G^F \in \{F_4(q), {^2\!E}_6(q),E_8(q)\}$.

Example 4.1

Let $G^F=F_4(q)$, where we fix the labelling of the simple roots $\Pi \subseteq \Phi$ as in Sect. 2:

Let $\mathscr {S}\subseteq {\text {Uch}}(G^F)$ be the Harish–Chandra series containing the trivial character of $G^F$. Then $\Pi '=\varnothing$, ${\overline{\Pi }}=\Pi$ and $\lambda (\alpha _i)=q$ for $i=1,2,3,4$. Thus, $\mathscr {W}_{\!\mathscr {S}}=W=\langle s_1,s_2,s_3,s_4\rangle$ is the Weyl group of G (where $s_i$ denotes the reflection with root $\alpha _i$); the characters in $\mathscr {S}$ are in bijection with ${\text {Irr}}(W)$. As discussed in Sect. 2, Lusztig (1984a, 4.10) chooses (L), while Carter (1985, p. 414) chooses (AC), so one has to apply the automorphism in Remark 2.1 in order to pass from the notation concerning ${\text {Uch}}(G^F)$ in Lusztig (1984a, p. 371) to Carter’s notation in Table 1.

Remark 4.2

In the setting of Example 4.1, let us write $[\phi ]\in \mathscr {S}$ for the unipotent character corresponding to $\phi \in {\text {Irr}}(W)$. If $(\phi ',\phi '')$ is one of the pairs of characters that are permuted as in Remark 2.1, then $[\phi '], [\phi '']$ have the same degree. Thus, as far as unipotent character degrees are concerned, it is irrelevant whether convention (AC) or convention (L) is chosen. However, a difference occurs when we consider the partition of the unipotent characters into “families” and the parametrisation of the characters inside the various families in terms of finite sets $\mathscr {M}(\mathscr {G})$ (of certain pairs $(x,\sigma )$), as defined in Lusztig (1984a, 4.14) (see also Carter (1985, §13.6)). There are 11 families, two of which contain 4 characters, one of which contains 21 characters, and all the remaining families contain just one character. The 4-element families contain 3 characters of the form $[\phi ]$ for $\phi \in {\text {Irr}}(W)$. For example, one of them is given as follows:

Thus, the two labels $\phi _{2,4}''$ and $\phi _{2,4}'$ in Carter’s table should be exchanged, since Lusztig uses convention (L) and Carter uses convention (AC). The same applies to the other 4-element family, and also to the 21-element family.

Example 4.3

Let $G^F={^2\!E}_6(q)$. Then $\Phi$ is of type $E_6$ and F induces an automorphism of order 2 on $\Phi$. Let again $\mathscr {S}\subseteq {\text {Uch}}(G^F)$ be the Harish-Chandra series containing the trivial character of $G^F$. Then $\Pi '=\varnothing$ and ${\overline{\Pi }}, \lambda$ are given as follows.

Again, $\mathscr {W}_{\!\mathscr {S}}$ is a Coxeter group of type $F_4$. When referring to Kondo’s article for the labelling of ${\text {Irr}}(\mathscr {W}_{\!\mathscr {S}})$, one has to specify whether Kondo’s generators d, a correspond to $\{\alpha _2\}, \{\alpha _4\}$ or to $\{\alpha _3,\alpha _5\},\{\alpha _1,\alpha _6\}$. In other words, one has to specify whether $\lambda$ takes value q on d, a and value $q^2$ on $\tau ,\tau \sigma$, or vice versa. This specification can be reconstructed from the existing tables, as follows.

By Lusztig (1980, Theorem 1.15), there is a bijection between the unipotent characters of the (untwisted) group $E_6(q)$ and those of ${^2\!E}_6(q)$; if $\rho \in {\text {Uch}}(E_6(q))$ corresponds to $\rho '\in {\text {Uch}}({^2\!E}_6(q))$, then the polynomial in q which gives $\rho '(1)$ is obtained from the polynomial which gives $\rho (1)$ by replacing q by $-q$ (and adjusting the sign). The bijection $\rho \leftrightarrow \rho '$ is defined by the tables in Lusztig (1980, 1.10, 1.16). In Lusztig (1980), the characters of $\mathscr {S}$ are denoted $[\phi ]$ for $\phi \in {\text {Irr}}(\mathscr {W}_{\!\mathscr {S}})$. For example, using the information on character degrees in Lusztig (1984a, p. 363), we find that

$$\begin{aligned} \dim [2_1]&=\textstyle {\frac{1}{2}}q^3+ \hbox {higher powers of}~q,\\ \dim [2_3]&=q+ \hbox {higher powers of}~q. \end{aligned}$$

On the other hand, as discussed above, the degrees of these two characters can also be obtained using the generic degrees of the Iwahori–Hecke algebra $\mathscr {H}$ associated with $\mathscr {W}_{\!\mathscr {S}}$ and the parameter function $\lambda$. Using the results of the computations at the end of Sect. 3, and assuming $\lambda (d)=\lambda (a)=q$, $\lambda (\tau )=\lambda (\tau \sigma )=q^2$, we get the same result as above. (If we assume $\lambda (d)=\lambda (a)=q^2$, $\lambda (\tau )=\lambda (\tau \sigma ) =q$, then we get a different result.) Thus, Lusztig must have been using the convention:

and a comparison with the table in Carter (1985, p. 481) shows that the same is also true for Carter. Hence, both Lusztig (1984a) and Carter (1985) use the convention (AC) for the groups $G^F={^2\!E}_6(q)$.

Example 4.4

Let $G^F=E_8(q)$. There is a Harish–Chandra series $\mathscr {S}\subseteq {\text {Uch}}(G^F)$ with corresponding $\Pi '\subseteq \Pi$, ${\overline{\Pi }},\lambda$ as follows (where $\Pi '$ is the subdiagram of type $D_4$ indicated by open circles in the diagram for $E_8$):

Again, $\mathscr {W}_{\!\mathscr {S}}$ is a Coxeter group of type $F_4$. As in the previous example, one has to specify whether $\lambda$ takes value q on Kondo’s generators d, a and value $q^4$ on $\tau ,\tau \sigma$, or vice versa. Actually, this is specified in Lusztig (1984a, p. 361); it is the same convention as in the previous example:

a comparison with the table in Carter (1985, pp. 484–488) shows that the same is also true for Carter. So both Lusztig (1984a) and Carter (1985) use the convention (AC) in the present situation.

One can also do a consistency check, as above. The characters in $\mathscr {S}$ are denoted by $D_4[\phi ]$ for $\phi \in {\text {Irr}}(\mathscr {W}_{\!\mathscr {S}})$. For example, according to the table in Lusztig (1984a, p. 366), the degrees of $D_4[2_1]$ and $D_4[2_3]$ should be

$$\begin{aligned} \dim D_4[2_1]&=\textstyle {\frac{1}{2}}q^{12}+ \hbox {higher powers of }q,\\ \dim D_4[2_3]&=\textstyle {\frac{1}{2}}q^{4}+ \hbox {higher powers of} q, \end{aligned}$$

On the other hand, we can also determine these degrees using the generic degrees of the Iwahori–Hecke algebra associated with $\mathscr {W}_{\!\mathscr {S}}, \lambda$; we get the same result for the degrees precisely when we specify the values of $\lambda$ as above.

Remark 4.5

Let $\mathscr {W}_{\!\mathscr {S}}$ be the finite Coxeter group associated with a Harish–Chandra series $\mathscr {S}\subseteq {\text {Uch}}(G^F)$. Then Lusztig (1976, Theorem 5.9) and Lusztig (1976, (7.7)) do not only show how the type of $\mathscr {W}_{\!\mathscr {S}}$ and the parameter function $\lambda$ are determined from $\Pi '\subseteq \Pi$, but Lusztig (1976, Theorem 5.9) also describes a natural root system ${\overline{\Phi }}$ for $\mathscr {W}_{\!\mathscr {S}}$. One can then check the following:

• (a) In Example 4.3 (where $G^F={^2\!E}_6(q)$), the simple roots in ${\overline{\Phi }}$ corresponding to the F-orbits $\{\alpha _2\}$, $\{\alpha _4\}$ are long, and the other two are short.

• (b) In Example 4.4 (where $G^F=E_8(q)$), the simple roots in ${\overline{\Phi }}$ corresponding to ${\bar{\alpha }}_8$, ${\bar{\alpha }}_7$ are long, and the other two are short.

Thus, as noted before, in both (a) and (b), the choice (AC) is made for matching the simple reflections in $\mathscr {W}_{\!\mathscr {S}}$ (corresponding to the roots in ${\overline{\Pi }}$) with Kondo’s generators $d,a,\tau ,\tau \sigma$.

5 The (generalised) Springer correspondence

Let again p be a prime and G be a simple algebraic group over an algebraic closure of $\mathbb {F}_p$. Let $\mathscr {N}_G$ be the set of all pairs $(C,\mathscr {E})$ where C is a unipotent conjugacy class of G and $\mathscr {E}$ is an irreducible ${\overline{\mathbb {Q}}}_\ell$-local system on C, equivariant for the conjugation action of G. (Here, $\ell$ is a prime $\ne p$.) Let $\mathscr {M}_G$ be the set of all triples $(L,C_0,\mathscr {E}_0)$ (up to G-conjugacy) where L is a Levi subgroup of some parabolic subgroup of G and $(C_0,\mathscr {E}_0)\in \mathscr {N}_L$ is “cuspidal” (see Lusztig (1984b, 2.4, 6.2)). Using intersection cohomology methods, Lusztig (1984b, §6) has defined a natural surjective map $\mathscr {N}_G\rightarrow \mathscr {M}_G$. Following Lusztig (2020), the fibres of that map will be called “unipotent blocks”; they form a partition of $\mathscr {N}_G$. Furthermore, there is a collection of bijections

$$\begin{aligned} \{\mathscr {I}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})\mid \mathscr {I}\hbox { unipotent block of } \mathscr {N}_G\} \end{aligned}$$

where $\mathscr {W}_{\!\mathscr {I}}$ is a certain finite Coxeter group associated to each $\mathscr {I}$; in fact, by Lusztig (1984b, §9), we have $\mathscr {W}_{\!\mathscr {I}}=N_G(L)/L$ where $(L,C_0,\mathscr {E}_0)$ is the triple corresponding to $\mathscr {I}$ under the map $\mathscr {N}_G \rightarrow \mathscr {M}_G$. This is called the generalised Springer correspondence; note that all this does not require an $\mathbb {F}_q$-rational structure on G. If $\mathscr {I}_1$ is the unipotent block containing the pair $(\{1\}, {\overline{\mathbb {Q}}}_\ell )$, then $\mathscr {W}_{\!\mathscr {I}_1}=W$ is the Weyl group of G and the bijection $\mathscr {I}_1 \leftrightarrow {\text {Irr}}(W)$ is the correspondence defined earlier by Springer in the 1970s (up to tensoring by the sign character of W). For example, it is known that $\mathscr {I}_1$ contains all pairs $(C, {\overline{\mathbb {Q}}}_\ell )$ where C is a unipotent conjugacy class of G and ${\overline{\mathbb {Q}}}_\ell$ stands for the trivial local system. We call $\mathscr {I}_1$ the “principal unipotent block” of $\mathscr {N}_G$.

Now assume that G is of exceptional type. The basic reference for the generalised Springer correspondence in this case is Spaltenstein (1985), which completes and extends to small characteristics p earlier work of Springer (for G of type $G_2$), Shoji ($F_4$) and Alvis–Lusztig ($E_6, E_7,E_8$); see the detailed references in Spaltenstein (1985). According to Lusztig (1984b, §15), there are three cases in which there are unipotent blocks $\mathscr {I}\subseteq \mathscr {N}_G$ such that $\mathscr {W}_{\!\mathscr {I}}$ is of type $F_4$; these occur for G of type

$$\begin{aligned} F_4 \;\hbox { (any }p), \quad E_8 \;{ (p=2)}, \quad E_7 \;\hbox { (simply connected and }p\ne 2). \end{aligned}$$

As in the previous section, there are certain issues concerning the conventions used when referring to Kondo’s labelling of ${\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$.

Example 5.1

Let G be of type $F_4$, where we fix the labelling of the simple roots as in the previous section, that is,

As above, let $\mathscr {I}_1\subseteq \mathscr {N}_G$ be the principal unipotent block. Then $\mathscr {W}_{\mathscr {I}_1}=W=\langle s_1,s_2,s_3,s_4 \rangle$ is the Weyl group of G (where $s_i$ is the reflection with root $\alpha _i$). The correspondence $\mathscr {I}_1\leftrightarrow {\text {Irr}}(W)$ was determined by Shoji (1980), with some conditions on the characteristic which were later removed by Spaltenstein (1985). As before, one has to specify which of Kondo’s generators $d,a,\tau ,\tau \sigma$ should correspond to long roots, and which to short roots. Now Shoji explicitly describes the restrictions of the irreducible characters of W to a parabolic subgroup of type $C_3$. So one can deduce from Shoji (1980, 4.3 and Table 4) that Shoji uses the choice (AC) for the labelling of ${\text {Irr}}(W)$. A comparison with the table in Spaltenstein (1985, p. 330) shows that Spaltenstein uses the same choice.

Example 5.2

Let G be of type $E_8$, where $p=2$. By Lusztig (1984b, 15.3), there is a unique unipotent block $\mathscr {I}\subseteq \mathscr {N}_G$ such that $\mathscr {W}_{\!\mathscr {I}}$ is a Coxeter group of type $F_4$. Under the map $\mathscr {N}_G\rightarrow \mathscr {M}_G$, this block corresponds to a triple $(L,C_0,\mathscr {E}_0)$ where L is of type $D_4$ (indicated by open circles in the diagram below). The generators of $\mathscr {W}_{\!\mathscr {I}}$ are indexed by the simple roots indicated by full circles in the diagram below (similarly to Example 4.4):

Again, one has to match ${\bar{\alpha }}_8$, ${\bar{\alpha }}_7$, ${\bar{\alpha }}_6$, ${\bar{\alpha }}_1$ to Kondo’s generators $d,a,\tau ,\tau \sigma$. Now Spaltenstein (1985, p. 327) writes that it makes sense to assign relative root lengths to ${\bar{\alpha }}_8$, ${\bar{\alpha }}_7$, ${\bar{\alpha }}_6$, ${\bar{\alpha }}_1$. In this case, he declares ${\bar{\alpha }}_6$, ${\bar{\alpha }}_1$ to be long, and ${\bar{\alpha }}_8$, ${\bar{\alpha }}_7$ to be short. Since he also refers to Alvis (2005) (with convention (AC)), we are led to the assumption that Spaltenstein uses the following matching with Kondo’s generators:

Note that this is the matching opposite to that in Example 4.4; note also that Spaltenstein’s declaration of relative root lengths for $\mathscr {W}_{\!\mathscr {I}}$ is opposite to that in Remark 4.5(b). (These different declarations actually caused the “delicate contradictions” mentioned in the introduction, and prompted this note.)

That the above assumption is correct has been independently confirmed by the second author in Hetz (2023a, §4.5), via a computation involving characteristic functions of character sheaves and the intersection of Bruhat cells with conjugacy classes. (If the opposite matching is used, then those computations result in a contradiction; see Hetz (2023a, Remark 4.5.33).) The fact that computations of that kind are able to detect properties of the generalised Springer correspondence was subsequently used in order to resolve the last open question concerning the generalised Springer correspondence for G of type $E_8$; see Hetz (2023b).

Example 5.3

Let G be simply connected of type $E_7$, where $p\ne 2$. By Lusztig (1984b, 15.2), there is a unique unipotent block $\mathscr {I}\subseteq \mathscr {N}_G$ such that $\mathscr {W}_{\!\mathscr {I}}$ is a Coxeter group of type $F_4$. Under the map $\mathscr {N}_G\rightarrow \mathscr {M}_G$, this block corresponds to a triple $(L,C_0,\mathscr {E}_0)$ where L is of type $A_1{+}A_1{+}A_1$ (indicated by open circles in the diagram below). The generators of $\mathscr {W}_{\!\mathscr {I}}$ are indexed by the simple roots indicated by full circles in the diagram below:

Similarly to the previous example, Spaltenstein (1985, p. 327) declares ${\bar{\alpha }}_4$, ${\bar{\alpha }}_6$ to be long, and ${\bar{\alpha }}_1$, ${\bar{\alpha }}_3$ to be short. (Note again that this declaration of relative root lengths is opposite to that provided by Lusztig (1976, Theorem 5.9).) Again, we are led to assume that Spaltenstein uses the following matching with Kondo’s generators:

This is confirmed by the computations in the proof of Lemma 6.2 below, in which also one error in Spaltenstein’s table will be corrected. We came across that error via the following remark.

Remark 5.4

Let $\mathscr {I}\subseteq \mathscr {N}_G$ be a unipotent block. Using the bijection $\mathscr {I}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$, we introduce an equivalence relation $\sim$ on ${\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$ as follows. Let $\chi ,\chi '\in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$ and assume that $(C,\mathscr {E})\leftrightarrow \chi$ and $(C',\mathscr {E}')\leftrightarrow \chi '$ under the above bijection; then we write $\chi \sim \chi '$ if $C=C'$. It is shown in Lusztig (2023), that the equivalence classes under $\sim$ for the principal unipotent block $\mathscr {I}_1 \subseteq \mathscr {N}_G$ can be recovered in a purely algebraic way, using operations with characters of Weyl groups. In Lusztig (2020, Conj. 6.11), there is a conjecture in a similar spirit for arbitrary unipotent blocks of $\mathscr {N}_G$. Using CHEVIE, see Michel (2015), we computed the algebraic version of $\sim$ for the unipotent block $\mathscr {I}\subseteq \mathscr {N}_G$ in Example 5.3, where G is of type $E_7$; and we found an inconsistency with the table in Spaltenstein (1985).

6 Computing unipotent blocks

In this section we briefly discuss the explicit computation of unipotent blocks and the generalised Springer correspondence. In particular, this will allow us to resolve the inconsistency in the table in Spaltenstein (1985) mentioned in Remark 5.4.

The main tool is the “multiplicity formula” in Spaltenstein (1985, 1.2(II)) (which is a reformulation of a formula that originally appeared in Lusztig (1984b, §8)). It relates the collection of bijections

$$\begin{aligned} \{\mathscr {I}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})\mid \mathscr {I}\hbox { unipotent block of } \mathscr {N}_G\} \end{aligned}$$

to the analogous collection of bijections

$$\begin{aligned} \{\mathscr {I}'\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'})\mid \mathscr {I}' \hbox { unipotent block of } \mathscr {N}_{M}\} \end{aligned}$$

where M is a Levi subgroup of some parabolic subgroup of G. Recall that we have surjective maps $\mathscr {N}_G\rightarrow \mathscr {M}_G$ and $\mathscr {N}_M \rightarrow \mathscr {M}_M$. Let us fix unipotent blocks $\mathscr {I}\subseteq \mathscr {N}_G$ and $\mathscr {I}'\subseteq \mathscr {N}_M$ which correspond to the same triple in $\mathscr {M}_M$. (Note that $\mathscr {M}_M\subseteq \mathscr {M}_G$.) The latter condition implies that $\mathscr {W}_{\!\mathscr {I}'}$ can be naturally regarded as a parabolic subgroup of $\mathscr {W}_{\!\mathscr {I}}$. To state the multiplicity formula, we need to introduce some further notation.

Let $(C,\mathscr {E}) \in \mathscr {I}$ and $\rho \in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$ correspond to $(C,\mathscr {E})$ under the above bijection. Furthermore, we set $A_G(u):=C_G(u)/ C_G^\circ (u)$ where $u\in C$; then $\mathscr {E}$ corresponds to an irreducible character $\phi \in {\text {Irr}}(A_G(u))$ (see Lusztig (1984b, §0)). Let also $(C',\mathscr {E}')\in \mathscr {I}'$ and $\rho '\in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'})$ correspond to $(C',\mathscr {E}')$ under the above bijection. Furthermore, we set $A_M(u'):= C_M(u')/C_M^\circ (u')$ where $u'\in C'$; then $\mathscr {E}'$ corresponds to an irreducible character $\phi '\in {\text {Irr}}(A_M(u'))$. In this setting, the multiplicity formula states:

$$\begin{aligned}&\hbox {multiplicity of }\rho '\in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'}) \hbox { in the restriction of }\rho \in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})\hbox { to }\mathscr {W}_{\!\mathscr {I}'}\\&\quad =\; \hbox {multiplicity of }\phi \otimes {\overline{\phi }}'\in {\text {Irr}}(A_G(u)\times A_M(u')) \hbox { in }\varepsilon _{u,u'}, \end{aligned}$$

where $\varepsilon _{u,u'}$ is the character of a permutation representation of the direct product $A_G(u)\times A_M(u')$ on a certain finite set $X_{u,u'}$ (defined in Spaltenstein (1985, 1.2)).

Example 6.1

In the above setting, let $\mathscr {I}_1$ be the principal unipotent block of $\mathscr {N}_G$ and $\mathscr {I}_1'$ be the principal unipotent block of $\mathscr {N}_M$. Assume that the bijections $\mathscr {I}_1\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}_1})$ and $\mathscr {I}_1'\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}_1'})$ (that is, the ordinary Springer correspondences) are already known. Now, as remarked earlier, we have $(C,{\overline{\mathbb {Q}}}_\ell ) \in \mathscr {I}_1$ and $(C',{\overline{\mathbb {Q}}}_\ell )\in \mathscr {I}_1'$. The corresponding characters of $A_G(u)$ and $A_M(u')$ are the trivial characters. So, since $\varepsilon _{u,u'}$ is the character of a permutation representation, the right hand side of the multiplicity formula will be a positive integer if $X_{u,u'}\ne \varnothing$, and 0 otherwise. Via the left hand side of the multiplicity formula, this condition can be checked using a computation with the characters of $\mathscr {W}_{\!\mathscr {I}_1}$ and of $\mathscr {W}_{\!\mathscr {I}_1'}$. Assume now that we have a situation where $X_{u,u'}= \varnothing$ and $\mathscr {I}\ne \mathscr {I}_1$, $\mathscr {I}'\ne \mathscr {I}_1'$. Then the right hand side of the multiplicity formula for the pairs $(C,\mathscr {E})\in \mathscr {I}$ and $(C',\mathscr {E}')\in \mathscr {I}'$ will still be 0 (because $X_{u,u'}=\varnothing$) and so the multiplicity of $\rho '\in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'})$ in the restriction of $\rho \in {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$ to $\mathscr {W}_{\!\mathscr {I}'}$ must be 0. If the bijection $\mathscr {I}'\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'})$ is already known, then this rules out many cases on the level of the bijection $\mathscr {I}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$—as pointed out in Spaltenstein (1985, 4.3).

Lemma 6.2

Let G and $\mathscr {I}\subseteq \mathscr {N}_G$ be as in Example 5.3, where G is simply connected of type $E_7$ (with $p\ne 2$) and $\mathscr {W}_{\!\mathscr {I}}$ is of type $F_4$.

• (a) In the table in Spaltenstein (1985, p. 331/332), the characters $\chi _{2,3}$ and $\chi _{8,3}$ of $\mathscr {W}_{\!\mathscr {I}}$ should be interchanged in the column labelled $3A_1'' \;(p\ne 2)$.

• (b) With the adjustment in (a), the statements in Lusztig (2020, Conj. 6.11) are correct for $\mathscr {I}$.

(Here, we use Spaltenstein’s notation for the irreducible characters of $\mathscr {W}_{\!\mathscr {I}}$.)

Proof

(a) We only sketch this. First of all, by Lusztig (1984b, 15.2), $\mathscr {N}_G$ is the union of $\mathscr {I}_1, \mathscr {I}$ and one block consisting of a cuspidal pair when $p\ne 2,3$ (where, as usual, $\mathscr {I}_1$ denotes the principal unipotent block); if $p=3$, then $\mathscr {N}_G$ is the union of $\mathscr {I}_1,\mathscr {I},\mathscr {I}_2$ and three blocks consisting of cuspidal pairs, where $\mathscr {I}_2$ is a block with $\mathscr {W}_{\!\mathscr {I}_2}$ of type $A_1$. We shall assume that $\mathscr {I}_1$ has been determined. By Spaltenstein (1985, 5.5), the block $\mathscr {I}_2$ is also easily determined since $\mathscr {W}_{\!\mathscr {I}_2}$ is of type $A_1$; the cuspidal pairs are listed in the last table of Spaltenstein (1985, p. 337). Thus, we can assume that the subset $\mathscr {I}\subseteq \mathscr {N}_G$ is known.

Now let C be the unipotent class of G denoted by $D_5{+}A_1$, where $\dim \mathfrak {B}_u=6$ and $A_G(u)\cong \mathbb {Z}/2\mathbb {Z}$ for $u\in C$. Consider the pair $(C,\mathscr {E})\in \mathscr {N}_G$, where $\mathscr {E}$ corresponds to the non-trivial character of $A_G(u)$. We have $(C,\mathscr {E})\in \mathscr {I}$. According to Spaltenstein (1982, p. 174), C is obtained by the process of induction (Lusztig and Spaltenstein 1979) from the trivial class of a Levi of type $A_2{+}A_2$. By the transitivity of induction, it will also be induced from a class $C'$ of a Levi M of type $A_5$ containing $A_2{+}A_2$. We choose M such that it contains the Levi L of type $A_1{+}A_1{+}A_1$ (indicated by open circles in Example 5.3). Using weighted Dynkin diagrams and Lusztig and Spaltenstein (1979, Prop. 1.9(b)), we see that $C'$ is the unique unipotent class of M with $\dim \mathfrak {B}_{u'}=6$ und $A_M(u')\cong \mathbb {Z}/2\mathbb {Z}$ ($u'\in C'$).

Consider the pair $(C',\mathscr {E}')\in \mathscr {N}_M$ where $\mathscr {E}'$ corresponds to the non-trivial character of $A_M(u')$. The following information on $(C', \mathscr {E}')$ is obtained via the CHEVIE function UnipotentClasses, see Michel (2015). The pair $(C',\mathscr {E}')$ belongs to the unipotent block $\mathscr {I}'\subseteq \mathscr {N}_{M}$ which corresponds to the same triple in $\mathscr {M}_M\subseteq \mathscr {M}_G$ as $\mathscr {I}$. Furthermore, the parabolic subgroup $\mathscr {W}_{\!\mathscr {I}'}\subseteq \mathscr {W}_{\!\mathscr {I}}$ is of type $A_2$, with simple roots corresponding to ${\bar{\alpha }}_4, {\bar{\alpha }}_6$ (long roots, as in Example 5.3). Under the bijection $\mathscr {I}' \leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}'})$, the corresponding character is the sign character of $\mathscr {W}_{\!\mathscr {I}'}$.

Since C is obtained from $C'$ by induction, we are in the set-up of Spaltenstein (1985, 1.3). This shows that there are subgroups $H\subseteq N \subseteq A_G(u)$ such that H is normal in N with $N/H\cong A_M(u')$; furthermore, the sets $X_{u,u'}$ and $A_G(u)/H$ are isomorphic as sets with $(A_G(u)\times A_M(u'))$-actions. Since $A_G(u)$ and $A_M(u')$ are both isomorphic to $\mathbb {Z}/2\mathbb {Z}$, we must have $H=\{1\}$. Thus, $X_{u,u'}$ and $A_G(u)$ are isomorphic as sets with $(A_G(u) \times A_M(u'))$-actions. Consequently, we find that the right hand side of the multiplicity formula evaluates to 1. Working out the left hand side of that formula (using the CHEVIE function InductionTable), see Michel (2015) we see that only the following characters of $\mathscr {W}_{\!\mathscr {I}}$ can correspond to C: $\chi _{1,3}$, $\chi _{1,4}$, $\chi _{6,1}$, $\chi _{6,2}$, $\chi _{8,3}$, $\chi _{8,4}$. Using also induction of suitable classes from Levi subgroups M of type $A_5{+}A_1$ and $D_6$, one rules out further characters from the above list until the only remaining possibility is $\chi _{8,3}$. Thus, under the bijection $\mathscr {I}\leftrightarrow {\text {Irr}}(\mathscr {W}_{\!\mathscr {I}})$, the pair $(C,\mathscr {E})$ must correspond to the character $\chi _{8,3}$.

For the remaining characters of $\mathscr {W}_{\!\mathscr {I}}$, one proceeds as follows. First one considers all unipotent classes C such that $|A_G(u)|=2$ for $u\in C$. Using similar arguments as above, plus the highly efficient method in Example 6.1, one checks that the entries for these classes in Spaltenstein’s table are correct. It then remains to consider the classes C denoted

$$\begin{aligned} D_6{+}A_1, \quad D_6(a_1){+}A_1, \quad D_6(a_2){+}A_1, \quad D_4(a_1){+}A_1, \end{aligned}$$

where only the following characters of $\mathscr {W}_{\!\mathscr {I}}$ can correspond to any of these classes:

$$\begin{aligned} \chi _{1,2},\quad \chi _{2,3}, \quad \chi _{2,4}, \quad \chi _{4,2},\quad \chi _{6,2}, \quad \chi _{8,1},\quad \chi _{9,4},\quad \chi _{12}. \end{aligned}$$

We now use the method in Example 6.1, with respect to a Levi $M \subseteq G$ of type $D_6$, in order to rule out a number of possibilities. Firstly, we find that only $\chi _{1,2}, \chi _{8,1}$ from the above list can correspond to $D_6{+}A_1$ (in accordance with Spaltenstein’s table); next, one finds that only $\chi _{1,2},\chi _{2,3},\chi _{4,2}$ can correspond to $D_6(a_1){+}A_1$. So the conclusion is that $\chi _{2,3}, \chi _{4,2}$ must correspond to $D_6(a_1){+}A_1$. Similarly, one finds that only $\chi _{2,4},\chi _{9,4}$ can correspond to $D_4(a_1){+}A_1$ and that only $\chi _{2,4},\chi _{6,2},\chi _{12}$ can correspond to $D_6(a_2) {+}A_1$. Hence, again, the conclusion is that $\chi _{6,2},\chi _{12}$ must correspond to $D_6(a_2){+}A_1$. Thus, all entries in Spaltenstein’s table for $E_7$ are found to be correct, with the exception that $\chi _{2,3}$ and $\chi _{8,3}$ need to be exchanged.

(b) This simply follows by inspection of the results of the computation. $\square$