Abstract
It is known that if G is a group such that the centre factor group \(G/\zeta (G)\) is polycyclic, then also the commutator subgroup \(G'\) is polycyclic. The aim of this paper is to describe this situation from a lattice point of view. It is proved that if G is a group admitting a permodularly embedded non-periodic subgroup P such that the interval [G/P] is a polycyclic lattice, then G contains a polycyclic normal subgroup N such that G/N is quasihamiltonian.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A classical theorem of Issai Schur (see Schur (1902)) states that if the centre \(\zeta (G)\) of a group G has finite index, then the commutator subgroup \(G'\) of G is finite. Several results of Schur type were later proved, by replacing the finiteness of the index \(|G:\zeta (G)|\) by a suitable restriction on the factor group \(G/\zeta (G)\). It is known for instance that if G is a group such that \(G/\zeta (G)\) is polycyclic, then also \(G'\) is polycyclic (see for instance Robinson (1972) Part 1, p.115).
A lattice-theoretic approach to Schur’s theorem was adopted in De Falco et al. (2008), by replacing the centre by a normal subgroup with a suitable embedding property. Of course, a subgroup C of a group G lies in the centre \(\zeta (G)\) if and only if \(\langle g,C\rangle \) is abelian for each element g of G, and it was proved in De Falco et al. (2008) that if a group G contains a subgroup M of finite index such that \(\langle g,M\rangle \) has modular subgroup lattice for every \(g\in G\), then there exists a finite normal subgroup N of G such that the subgroup lattice of G/N is modular. A corresponding lattice translation for groups which are Černikov over the centre was given in De Falco et al. (2023), and the aim of this paper is to consider groups which are polycyclic over the centre from a lattice point of view.
Actually, the most striking translation of normality in the subgroup lattice of a group is permodularity and, from the same point of view, the best approximation of abelian groups are groups with a permodular subgroup lattice. The definition of a permodular element of a lattice and also that of a permodular lattice will be explained in details in Sect. 2. We denote by \(\mathcal M\) the class of all groups with a permodular subgroup lattice and say that a subgroup P of a group G is permodularly embedded in G if \(\langle g,P\rangle \) belongs to \(\mathcal M\) for each element g of G.
Let
 be a lattice with least element
be a lattice with least element
 and greatest element I. We say that
and greatest element I. We say that
 is polycyclic if there exists in
is polycyclic if there exists in
 a finite chain of elements
a finite chain of elements

such that
\(a_i\) is a permodular element of
 and the interval
\([a_{i+1}/a_i]\) is distributive and satisfies the maximal condition for each
and the interval
\([a_{i+1}/a_i]\) is distributive and satisfies the maximal condition for each
 , while
, while
 is said to be a supersoluble lattice if each element of the chain (1) can be chosen to be a permodular element of
is said to be a supersoluble lattice if each element of the chain (1) can be chosen to be a permodular element of
 . It is known that a group G is polycyclic (supersoluble respectively) if and only if its subgroup lattice
. It is known that a group G is polycyclic (supersoluble respectively) if and only if its subgroup lattice
 is polycyclic (supersoluble respectively) (see Schmidt 1994, Theorem 6.4.9 and Theorem 6.4.11, respectively).
is polycyclic (supersoluble respectively) (see Schmidt 1994, Theorem 6.4.9 and Theorem 6.4.11, respectively).
Recall that a group G is called quasihamiltonian if \(XY=YX\) for all subgroups X and Y of G. It is known that a group is quasihamiltonian if and only if it is locally nilpotent and has a modular subgroup lattice; in particular, the subgroup lattice of any quasihamiltonian group is permodular. We can now state our main result.
Theorem
Let G be a group containing a permodularly embedded non-periodic subgroup P such that the interval [G/P] is a polycyclic lattice. Then G contains a polycyclic normal subgroup N such that G/N is quasihamiltonian.
As a consequence of the above theorem, a corresponding result can be proved when the interval [G/P] is a supersoluble lattice.
Corollary
Let G be a group containing a permodularly embedded non-periodic subgroup P such that the interval [G/P] is a supersoluble lattice. Then G contains a supersoluble normal subgroup N such that G/N is quasihamiltonian.
We will exhibit an example to show that in our main result the assumption that the subgroup P has elements of infinite order cannot be dropped out. On the other hand, since periodic polycyclic subgroups are finite, it follows from the main result of De Falco et al. (2008) that a statement like our theorem certainly holds in the case of periodic groups. In the final part of the paper, the structure of groups which are not polycylic-by-quasihamiltonian but contain a permodularly embedded subgroup determining a polycyclic interval will be described. Finally, we will also prove that if a group G contains a permodularly embedded arbitrary subgroup P such that [G/P] is a locally polycyclic lattice, then G is locally polycyclic.
Our notation is mostly standard and can be found in Robinson (1996, 1972).
2 Lattice preliminaries
Let
 be a complete lattice with least element
be a complete lattice with least element
 and greatest element I. Recall that an element c of
and greatest element I. Recall that an element c of
 is cyclic if the interval
is cyclic if the interval
 is a distributive lattice satisfying the maximal condition, while an element
is a distributive lattice satisfying the maximal condition, while an element
 is compact if for each subset X of
is compact if for each subset X of
 such that
\(e\le \sup X\) there exist finitely many elements
\(x_1,\ldots ,x_t\) of X such that
\(e\le x_1\vee \cdots \vee x_t\). Moreover, an element x of
such that
\(e\le \sup X\) there exist finitely many elements
\(x_1,\ldots ,x_t\) of X such that
\(e\le x_1\vee \cdots \vee x_t\). Moreover, an element x of
 is covered irreducibly by elements
\(x_1,\ldots ,x_t\) of the interval
is covered irreducibly by elements
\(x_1,\ldots ,x_t\) of the interval
 if, for each cyclic element c of
if, for each cyclic element c of
 , there is
\(i\le t\) such that
\(c\le x_i\) and the set
\(\{ x_1,\ldots ,x_t\}\) is minimal with respect to such property.
, there is
\(i\le t\) such that
\(c\le x_i\) and the set
\(\{ x_1,\ldots ,x_t\}\) is minimal with respect to such property.
An element a of
 is said to be cofinite if there exists in
is said to be cofinite if there exists in
 a finite chain
a finite chain
such that, for every
\(i=0,1,\ldots ,n-1\),
\(a_i\) is a maximal element of the lattice
 and satisfies one of the following conditions:
and satisfies one of the following conditions:
-
\(a_{i+1}\) is covered irreducibly by finitely many elements \(b_1,\ldots b_{n_i}\) of
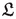 such that
\(b_1\wedge \cdots \wedge b_{n_i}\le a_i\);
such that
\(b_1\wedge \cdots \wedge b_{n_i}\le a_i\); -
for every automorphism \(\varphi \) of the lattice
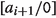 , the element
\(a_i\wedge {a_i}\!\!^\varphi \) is modular in
, the element
\(a_i\wedge {a_i}\!\!^\varphi \) is modular in
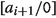 and the lattice
\([a_{i+1}/a_i\wedge {a_i}\!\!^\varphi ]\) is finite.
and the lattice
\([a_{i+1}/a_i\wedge {a_i}\!\!^\varphi ]\) is finite.
A modular element a of
 is called permodular if it satisfies the following con- dition:
is called permodular if it satisfies the following con- dition:
\(\star \) if c is a cyclic element of
 and b is an element of
\([a\vee c/a]\) such that the lattice
\([a\vee c/b]\) is finite, then b is a cofinite element of
\([a\vee c/a]\).
and b is an element of
\([a\vee c/a]\) such that the lattice
\([a\vee c/b]\) is finite, then b is a cofinite element of
\([a\vee c/a]\).
Finally, a modular lattice
 is said to be permodular if every interval of finite length of
is said to be permodular if every interval of finite length of
 is finite; recall here that a partially ordered set
\((S,\le )\) is said to have finite length if there exists a positive integer k such that all chains of S have order at most
\(k+1\). It is easy to show that
is finite; recall here that a partially ordered set
\((S,\le )\) is said to have finite length if there exists a positive integer k such that all chains of S have order at most
\(k+1\). It is easy to show that
 is a permodular lattice if and only if all its elements are permodular.
is a permodular lattice if and only if all its elements are permodular.
In the case of the subgroup lattice
 of a group G, it turns out that the cyclic elements and the compact elements of
of a group G, it turns out that the cyclic elements and the compact elements of
 coincide with the cyclic subgroups and the finitely generated subgroups of G, respectively. Moreover, cofinite elements of
coincide with the cyclic subgroups and the finitely generated subgroups of G, respectively. Moreover, cofinite elements of
 are precisely the subgroups of finite index of G (see Schmidt 1994, Theorem 6.1.10). It is also known that in any soluble group all modular subgroups are permodular.
are precisely the subgroups of finite index of G (see Schmidt 1994, Theorem 6.1.10). It is also known that in any soluble group all modular subgroups are permodular.
The following useful lemma shows in particular that permodular subgroups of finitely generated groups are close to be normal; for a proof of this result we refer to Schmidt (1994), Lemma 6.2.8.
Lemma 2.1
Let G be a group and let P be a permodular subgroup of G. If there exists a finitely generated subgroup E of G such that \(G=\langle P,E\rangle \), then P has finite index in \(P^G\).
Recall that a subgroup X of a group G is said to be permutable in G if \(XY=YX\) for each subgroup Y of G, so that a group is quasihamiltonian if and only if all its subgroups are permutable. Since permutable subgroups are permodular (see for instance Schmidt 1994, Lemma 6.2.2), we have that any quasihamiltonian group has a permodular subgroup lattice. Actually it is known that a subgroup is permutable if and only if it is permodular and serial (see Schmidt 1994, Theorem 6.2.10). Next statement is a direct consequence of Iwasawa’s characterization of non-periodic groups with a modular subgroup lattice (see Schmidt 1994, Theorem 2.4.11).
Lemma 2.2
Let G be a non-periodic group with a modular subgroup lattice. Then G is quasihamiltonian.
We refer to the monograph (Schmidt 1994) for further definitions and results concerning the subgroup lattice of a group.
3 Results and proofs
The first lemma of this section describes the behaviour of permodular subgroups determining a polycyclic interval in the lattice of all subgroups.
Lemma 3.1
Let G be a group and let P be a permodular subgroup of G such that the interval [G/P] is a polycyclic lattice. Then \(P^G/P_G\) is finite and the factor group \(G/P_G\) is polycyclic.
Proof
The factor group \(G/P^G\) has a polycyclic subgroup lattice and so it is polycyclic (see Schmidt 1994, Theorem 6.4.9). Let
be a finite chain in
 such that, for every non-negative integer
\(i<t\), the subgroup
\(P_i\) is permodular in
\(P_{i+1}\) and the interval
\([P_{i+1}/P_i]\) is a distributive lattice satisfying the maximal condition. It follows from Corollary 2.4 of De Falco et al. (2021) that
\(P_{i+1}=\langle P_i,x_i\rangle \) for a suitable element
\(x_i\). Put
\(E=\langle x_0,x_1,\ldots ,x_{t-1}\rangle \), so that
\(G=\langle P,E\rangle \) and hence P has finite index in
\(P^G\) by Lemma 2.1. If the index |G : P| is finite, the group
\(G/P_G\) is finite, and it is soluble (see Schmidt 1994, Theorem 5.2.5).
such that, for every non-negative integer
\(i<t\), the subgroup
\(P_i\) is permodular in
\(P_{i+1}\) and the interval
\([P_{i+1}/P_i]\) is a distributive lattice satisfying the maximal condition. It follows from Corollary 2.4 of De Falco et al. (2021) that
\(P_{i+1}=\langle P_i,x_i\rangle \) for a suitable element
\(x_i\). Put
\(E=\langle x_0,x_1,\ldots ,x_{t-1}\rangle \), so that
\(G=\langle P,E\rangle \) and hence P has finite index in
\(P^G\) by Lemma 2.1. If the index |G : P| is finite, the group
\(G/P_G\) is finite, and it is soluble (see Schmidt 1994, Theorem 5.2.5).
Suppose now that |G : P| is infinite. Then the polycyclic group \(G/P^G\) is infinite and so it contains a torsion-free non-trivial subgroup \(L/P^G\) of finite index (see for instance Robinson (1996), 5.4.15). If a is any element of \(L\setminus P^G\), the subgroup P is normal in \(\langle P,a\rangle \), so that P is normal in L and hence it has only finitely many conjugates in G. Since P has finite index in \(P^G\), it follows that \(P^G/P_G\) is finite. Finally, P is permutable in G (see Schmidt 1994, Theorem 6.2.12) and hence \(P^G/P_G\) is nilpotent (see Schmidt 1994, Theorem 6.2.14). Therefore \(G/P_G\) is polycyclic and the statement is proved. \(\square \)
It is well known that any group with a permodular subgroup lattice is soluble (see Schmidt 1994, Theorem 6.4.3) and so Lemma 3.1 has the following consequence.
Corollary 3.2
Let G be a group containing a permodularly embedded subgroup P such that the interval [G/P] is a polycyclic lattice. Then G is soluble.
Since in any group the centre is contained in all maximal subgroups which are not normal, it is clear that if a group G is polycyclic over the centre, then all maximal subgroups of G have finite index. This fact can be extended to a much more general situation.
Corollary 3.3
Let G be a group containing a permodularly embedded subgroup P such that the interval [G/P] is a polycyclic lattice. Then every maximal subgroup of G has finite index.
Proof
Let M be a maximal subgroup of G. If M is permodular in G, it follows from Lemma 2.1 that the index |G : M| is finite. Suppose now that M is not permodular in G. Application of Lemma 4.9 of De Falco et al. (2021) to the Frattini factor group \(G/\Phi (G)\) yields that P is contained in any maximal subgroup of G which is not permodular. In particular, \(P\le M\) and so M has finite index in G, because \(G/P_G\) is polycyclic by Lemma 3.1. \(\square \)
Proof of the Theorem
By Lemma 3.1 the factor group \(G/P_G\) is polycyclic and \(P_G\) is not periodic. Moreover, \(P_G\) is obviously permodularly embedded in G and so we may suppose without loss of generality that P is a normal subgroup of G and G/P is polycyclic. Since P is not periodic, it follows from Lemma 2.2 that the subgroup \(\langle g,P\rangle \) is quasihamiltonian for each element \(g\in G\). The group G is soluble by Corollary 3.2 and hence, if P has finite index in G, the statement follows from Theorem 3.5 of De Falco et al. (2008).
Suppose now that G/P is infinite, and let E be a finitely generated subgroup of G such that \(G=EP\). Then \(E/(E\cap P)\simeq G/P\) contains a torsion-free non-trivial normal subgroup \(X/(E\cap P)\) such that the index |E : X| is finite. Let x be any element of \(X\setminus P\). Then x has infinite order and \(\langle x\rangle \cap P=\{1\}\). Since P is not periodic and \(\langle x,P\rangle \) is quasihamiltonian, we have by Lemma 2.4.10 of Schmidt (1994) that \(\langle x,P\rangle \) is abelian and hence \([X,P]=\{1\}\). It follows in particular that the subgroup X is normal in G. Since X is finitely generated and \(X/(E\cap P)\) is polycyclic, there exists a finitely generated subgroup Y of X such that \(E\cap P=Y^X\) (see Robinson 1996, 14.1.3). On the other hand, \(E\cap P\) is contained in \(\zeta (X)\), so that \(E\cap P=Y\) is finitely generated and hence X is polycyclic. Since \(\langle gX,PX/X\rangle \) is quasihamiltonian for each \(g\in G\) and the index |G : PX| is finite, it follows again from Theorem 3.5 of De Falco et al. (2008) that the factor group G/X contains a finite normal subgroup N/X such that G/N is quasihamiltonian. Clearly, N is polycyclic and hence the statement is proved. \(\square \)
Proof of the Corollary
By the Theorem there exists a polycyclic normal subgroup N of G such that G/N is quasihamiltonian. Since the normal closure \(P^G\) of P is hypercyclically embedded in G (see De Falco et al. 2021, Corollary 3.2) and the factor group \(G/P^G\) is supersoluble (because it has a supersoluble subgroup lattice), it follows that G is hypercyclic and so also locally supersoluble. Thus N is supersoluble and the statement is proved. \(\square \)
We give now the example showing that the non-periodicity assumption on the subgroup P in the statements of the Theorem and its Corollary cannot be dropped out. First we need the following information.
Lemma 3.4
Let A be a divisible abelian group and let X be a subgroup of Aut(A) containing two elements of infinite order x and y such that
\(\langle x\rangle \cap \langle y\rangle =\{1\}\). If N is a polycyclic normal subgroup of the semidirect product
 , then the lattice
, then the lattice
 is not permodular.
is not permodular.
Proof
Assume for a contradiction that the factor group G/N has a modular subgroup lattice. Since \([ab,g]=[a,g][b,g]\) for all \(a,b\in A\) and \(g\in G\), we have that [A, g] is divisible for each \(g\in G\). If z is any element of \(X\cap N\), the divisible subgroup [A, z] is contained in N, so that \([A,z]=\{1\}\) and hence \(X\cap N=\{1\}\). It follows now from Lemma 2.4.10 of Schmidt (1994) that G/N is abelian. Thus \(G'\le N\) is polycyclic. On the other hand, [A, g] is divisible for each \(g\in G\), whence \([A,g]=\{1\}\) and \(A\le \zeta (G)\), which is of course impossible. \(\square \)
Let p be a prime number and let P be a group of type
\(p^\infty \). It is well known that Aut(P) is isomorphic to the multiplicative group of p-adic integers and so it contains a free abelian subgroup X of rank 2 whose elements fix all elements of P of order p, and of order 4 if
\(p=2\) (see for instance Robinson 1964, p.29). Put
 . Then
\(\langle P,g\rangle \) is quasihamiltonian for each
\(g\in G\) (see Schmidt 1994, Theorem 2.4.11), and so P is a permodularly embedded normal subgroup of G. Moreover, G/P is supersoluble, but it follows from Lemma 3.4 that G is not polycyclic-by-
\(\mathcal M\).
. Then
\(\langle P,g\rangle \) is quasihamiltonian for each
\(g\in G\) (see Schmidt 1994, Theorem 2.4.11), and so P is a permodularly embedded normal subgroup of G. Moreover, G/P is supersoluble, but it follows from Lemma 3.4 that G is not polycyclic-by-
\(\mathcal M\).
If
 is a class of lattices, we say that a lattice
is a class of lattices, we say that a lattice
 is locally
is locally  if the interval
if the interval
 belongs to
belongs to
 for each compact element c of
for each compact element c of
 . Of course, if the class
. Of course, if the class
 is closed with respect to forming sublattices, all lattices in
is closed with respect to forming sublattices, all lattices in
 are also locally
are also locally
 . We will prove that a group G is locally polycyclic if and only it contains a permodularly embedded subgroup P such that [G/P] is a locally polycyclic lattice.
. We will prove that a group G is locally polycyclic if and only it contains a permodularly embedded subgroup P such that [G/P] is a locally polycyclic lattice.
Recall that the FC-centre of a group G is the characteristic subgroup consisting of all elements of G with only finitely many conjugates, or equivalently the set of all \(g\in G\) such that the index \(|G:C_G(g)|\) is finite. It is clear that if a cyclic subgroup \(\langle g\rangle \) is normal in a subgroup of finite index of G, then g belongs to the FC-centre of G.
Lemma 3.5
Let G be a group and let P be a permodularly embedded subgroup of G such that the interval [G/P] is an infinite polycyclic lattice. Then P is contained in the FC-centre of G.
Proof
The group G is soluble by Corollary 3.2 and so it follows from Lemma 3.1 that \(G/P_G\) is an infinite polycyclic group. Then \(G/P_G\) contains a torsion-free non-trivial subgroup \(X/P_G\) such that the index |G : X| is finite. If x is any element of \(X\setminus P_G\), we have that \(\langle x,P\rangle \) is a non-periodic group with modular subgroup lattice and hence it is quasihamiltonian by Lemma 2.2. On the other hand, \(P\cap \langle x\rangle =\{1\}\) and so it follows that all subgroups of P are normal in \(\langle x,P\rangle \) (see Schmidt 1994, Lemma 5.2.7). Therefore every subgroup of P is normal in \(\langle X,P\rangle \) and hence P is contained in the FC-centre of G because the index \(|G:\langle X,P\rangle |\) is finite. \(\square \)
Corollary 3.6
Let G be a finitely generated group containing a permodularly embedded subgroup P such that the interval [G/P] is a polycyclic lattice. Then G is polycyclic.
Proof
Since the factor group \(G/P_G\) is polycyclic by Lemma 3.1, the subgroup \(P_G\) is the normal closure of a finite subset of G and so it follows from Lemma 3.5 that \(P_G\) is finitely generated. It follows that \(P_G\) is supersoluble, because it has a permodular subgroup lattice, and hence G is polycyclic. \(\square \)
Theorem 3.7
Let G be a group containing a permodularly embedded subgroup P such that the interval [G/P] is a locally polycyclic lattice. Then G is locally polycyclic.
Proof
Let E be any finitely generated subgroup of G. Then \(P\cap E\) is a permodularly embedded subgroup of E and the lattice \([E/P\cap E]\simeq \bigl [\langle E,P\rangle /P\bigr ]\) is polycyclic because it is generated by finitely many cyclic elements. Thus E is polycyclic by Corollary 3.6 and so G is locally polycyclic. \(\square \)
In the final part of the paper we describe the structure of groups G which are not polycyclic-by- \(\mathcal M\), although they contain a permodularly embedded subgroup P such that [G/P] is a polycyclic lattice.
Lemma 3.8
Let G be a group with modular subgroup lattice, and let H and K be subgroups of G such that \(H^K=H\) and \(H\cap K=\{1\}\). Then \(X^K=X\) for each subgroup X of H.
Proof
Since the lattice
 is modular and
\(H\cap K=\{1\}\), we have
\(\langle X,K\rangle \cap H=X\) and hence X is normalized by K.
\(\square \)
is modular and
\(H\cap K=\{1\}\), we have
\(\langle X,K\rangle \cap H=X\) and hence X is normalized by K.
\(\square \)
Lemma 3.9
Let G be a non-periodic group and let P be a periodic permodularly embedded subgroup of G. Then P is abelian.
Proof
Let g be an element of infinite order of G. Then \(\langle g,P\rangle \) is a non-periodic group with modular subgroup lattice and so the set of all its elements of finite order is an abelian subgroup (see Schmidt (1994), Theorem 2.4.11). In particular, P is abelian. \(\square \)
Theorem 3.10
Let G be a group containing a permodularly embedded subgroup P such that the interval [G/P] is a polycyclic lattice, and let
\(N=P_G\). If G is not polycyclic-by-
\(\mathcal M\), then N is periodic abelian and there exists a polycyclic normal subgroup L of G such that
 , where E/L is a finitely generated abelian group acting as a faithful group of power automorphisms on NL/L.
, where E/L is a finitely generated abelian group acting as a faithful group of power automorphisms on NL/L.
Proof
The group G is soluble and the factor group G/N is polycyclic by Lemma 3.1. Moreover, G/N is infinite, since otherwise G would contain a finite normal subgroup K such that
 is a modular lattice (see De Falco et al. 2008, Theorem) and hence in particular G would be polycyclic-by-
\(\mathcal M\). Then G is not periodic, while N is periodic by the main theorem, and so also abelian by Lemma 3.9. Let E be a finitely generated subgroup of G such that
\(G=EN\). Since G is locally polycyclic by Theorem 3.7, the subgroup E is polycyclic, and so the normal subgroup
\(V=E\cap N\) of G is finite. Put
\(L/V=C_{E/V}(N/V)\). Then L is a polycyclic normal subgroup of G and
is a modular lattice (see De Falco et al. 2008, Theorem) and hence in particular G would be polycyclic-by-
\(\mathcal M\). Then G is not periodic, while N is periodic by the main theorem, and so also abelian by Lemma 3.9. Let E be a finitely generated subgroup of G such that
\(G=EN\). Since G is locally polycyclic by Theorem 3.7, the subgroup E is polycyclic, and so the normal subgroup
\(V=E\cap N\) of G is finite. Put
\(L/V=C_{E/V}(N/V)\). Then L is a polycyclic normal subgroup of G and

If \(C/L=C_{E/L}(NL/L)\), we have \([N,C]\le L\cap N=V\) and so \(C/L=\{1\}\). Moreover, since NL/L is permodularly embedded in G/L, it follows from Lemma 3.8 applied to all groups of the form \(\langle g\rangle NL/L\), with \(g\in G\), that all subgroups of NL/L are normal in G/L. Therefore E/L acts on NL/L as a faithful group of power automorphisms. In particular E/L is abelian and the proof is complete. \(\square \)
Corollary 3.11
Let G be a group containing a permodularly embedded subgroup P such that the interval [G/P] is a polycyclic lattice. Then G is polycyclic-by- \(\mathcal M\) or abelian-by-polycyclic.
Proof
Suppose that G is not polycyclic-by- \(\mathcal M\), so that \(N=P_G\) is abelian by Theorem 3.10. Moreover, the factor group G/N is polycyclic by Lemma 3.1 and so G is abelian-by-polycyclic. \(\square \)
References
De Falco, M., de Giovanni, F., Musella, C.: The Schur property for subgroup lattices of groups. Arch. Math. (Basel) 91, 97–105 (2008)
De Falco, M., de Giovanni, F., Musella, C.: Modular chains in infinite groups. Arch. Math. (Basel) 117, 601–612 (2021)
De Falco, M., de Giovanni, F., Musella, C.: Groups with a large permutably embedded subgroup. Bull. Aust. Math. Soc. 107, 276–283 (2023)
Robinson, D.J.S.: Groups in which normality is a transitive relation. Proc. Camb. Philos. Soc. 60, 21–38 (1964)
Robinson, D.J.S.: Finiteness Conditions and Generalized Soluble Groups. Springer, Berlin (1972)
Robinson, D.J.S.: A Course in the Theory of Groups, 2nd edn. Springer, New York (1996)
Schmidt, R.: Subgroup Lattices of Groups. de Gruyter, Berlin (1994)
Schur, I.: Neuer Beweis eines Satzes über endliche Gruppen. Proceedings of Symposium Applied Mathematics, pp. 1013–1019. Sitzber. Akad. Wiss., Berlin (1902)
Funding
Open access funding provided by Universitá degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are supported by GNSAGA (INdAM) and are members of AGTA—Advances in Group Theory and Applications (www.advgrouptheory.com).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Falco, M., de Giovanni, F. & Musella, C. A note on groups with a large permodularly embedded subgroup. Beitr Algebra Geom 65, 441–449 (2024). https://doi.org/10.1007/s13366-023-00699-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13366-023-00699-7



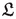 such that
such that
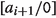 , the element
, the element
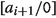 and the lattice
and the lattice