Intersection bodies of polytopes

Abstract

We investigate the intersection body of a convex polytope using tools from combinatorics and real algebraic geometry. In particular, we show that the intersection body of a polytope is always a semialgebraic set and provide an algorithm for its computation. Moreover, we compute the irreducible components of the algebraic boundary and provide an upper bound for the degree of these components.

1 Introduction

This paper studies intersection bodies from the perspective of real algebraic geometry. Originally, intersection bodies were defined by Lutwak (1988) in the context of convex geometry. In view of the notion of $(d-1)$-dimensional cross-section measures and the related concepts of associated bodies (such as intersection bodies, cross-section bodies, and projection bodies), intersection bodies play an essential role in geometric tomography (see Gardner 2006, Chapter 8 and Martini 1994, Section 2.3). In particular, we mention here the Busemann–Petty problem which asks if one can compare the volumes of two convex bodies by comparing the volumes of their sections (Gardner 1994a, b; Gardner et al. 1999; Koldobsky 1998; Zhang 1999b). Moreover, Ludwig showed that the unique non-trivial GL(d)-covariant star-body-valued valuation on convex polytopes corresponds to taking the intersection body of the dual polytope (Ludwig 2006). Due to such results, the knowledge on properties of intersection bodies interestingly contributes also to the (still not systematized) theory of starshaped sets, see Section 17 of the exposition (Hansen et al. 2020).

Recently, there is increased interest in investigating convex geometry from an algebraic point of view (Blekherman et al. 2013; Sinn 2015; Rostalski and Sturmfels 2010; Ranestad and Sturmfels 2011). In this article, we will focus on the intersection bodies of polytopes from this perspective. It is known that in ${\mathbb {R}}^2$, the intersection body of a centrally symmetric polytope centered at the origin is the same polytope rotated by $\pi /2$ and dilated by a factor of 2 (see e.g. Gardner 2006, Theorem 8.1.4). Moreover, if K is a full-dimensional convex body in ${\mathbb {R}}^d$ centered at the origin, then so is its intersection body (Gardner 2006, Chapter 8.1). But what do these objects look like in general? In ${\mathbb {R}}^d$, with $d\ge 3$, they cannot be polytopes (Campi 1999; Zhang 1999a) and they may not even be convex. In fact, for every convex body K, there exists a translate of K such that its intersection body is not convex. This happens because of the important role played by the origin in the construction of the intersection body.

Our main contribution is Theorem 3.2, which states that the intersection body of a polytope is a semialgebraic set, i.e. a subset of ${\mathbb {R}}^d$ defined by a boolean combination of polynomial inequalities. The proof relies on two key facts. First, the volume of a polytope can be computed using determinants. Second, the combinatorial type of the intersection of a polytope with a hyperplane is fixed for each region of a certain central hyperplane arrangement. In Sect. 2, we prove semialgebraicity for the intersection body of polytopes containing the origin, and we generalize the result to arbitrary polytopes in Sect. 3. In Sect. 4, we present an algorithm to compute the radial function of the intersection body of a polytope. An implementation is available at [mat21]. In Sect. 5, we describe the algebraic boundary of the intersection body, which is a hypersurface consisting of several irreducible components, each corresponding to a region of the aforementioned hyperplane arrangement. Theorem 5.6 gives a bound on the degree of the irreducible components. Section 6 focuses on the intersection body of the d-cube centered at the origin (Fig. 4a).

Fig. 1

The intersection body of the icosahedron

2 The intersection body of a polytope is semialgebraic

In convex geometry it is common to use functions in order to describe a convex body, i.e. a non-empty convex compact subset of ${\mathbb {R}}^d$. This can be done e.g. by the radial function. A more detailed introduction can be found in Schneider (2014).

Definition 2.1

Given a convex body $K\subset {\mathbb {R}}^d$, the radial function of K is

$$\begin{aligned} \rho _K : {\mathbb {R}}^d \rightarrow {\mathbb {R}}, \quad x \mapsto \max \left\{ \lambda \in {\mathbb {R}}\mid \lambda x \in K \right\} . \end{aligned}$$

As a convention $\rho _K(0)$ is $\infty$ when $0\in K$ and it is 0 otherwise. An immediate consequence of the definition is that $\rho _K(cx) = \frac{1}{c} \rho _K(x)$ for $c>0$. Therefore, we can equivalently define the radial function on the unit sphere $S^{d-1}$, and then extend to the whole space using the previously mentioned relation. Throughout this paper we will use the following convention: x denotes a vector in ${\mathbb {R}}^d$ whereas u denotes a vector in $S^{d-1}$. With the observation that we can restrict to the sphere, we define the intersection body of K by its radial function, which is given by the volume of the intersections of K with hyperplanes through the origin.

Definition 2.2

Let K be a convex body in ${\mathbb {R}}^d$. Its intersection body is defined to be the set $IK = \{ x\in {\mathbb {R}}^d \mid \rho _{IK}(x) \ge 1 \}$ where the radial function (restricted to the sphere) is

$$\begin{aligned} \rho _{IK}(u) = \text {Vol}_{d-1}(K\cap u^\perp ) \end{aligned}$$

for $u \in S^{d-1}$. We denote by $u^\perp$ the hyperplane through the origin with normal vector u, and by ${{\,\mathrm{Vol}\,}}_i$ the i-dimensional Euclidean volume, for $i \le d$.

We begin our investigation by considering the intersection body of polytopes which contain the origin. For instance, Fig. 1 displays the intersection body of an icosahedron centered at the origin. If the origin belongs to the interior of the polytope P, then $\rho _P$ is continuous and hence $\rho _{IP}$ is also continuous (Gardner 2006). Otherwise we may have some points of discontinuity which correspond to unit vectors u such that $u^\perp$ contains a facet of P; there are finitely many such directions. The intersection body is well defined, but there may arise subtleties when dealing with the boundary. However, we will see later (in Remark 5.2) that for our purposes everything works out. In the following we use notions from polytope theory, such as zonotopes and combinatorial types. For further background on polytopes we refer the reader to Ziegler (1995).

Fig. 2

The two combinatorial types of hyperplane sections of the 3-cube

Example 2.3

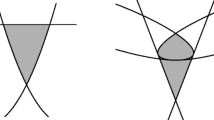
We will use the cube as an ongoing example to illustrate the key concepts used throughout the paper. Let P be the 3-dimensional cube $[-1,1]^3 \subseteq {\mathbb {R}}^3$. If we intersect P with hyperplanes $u^\perp$, for $u\in S^2$, we can observe that there are two possible combinatorial types for $P\cap u^\perp$: it is either a parallelogram (Fig. 2a) or a hexagon (Fig. 2b). There are finitely many regions of the sphere for which the combinatorial type stays the same (see Lemma 2.4). Using this we can parameterize the area of the parallelogram or hexagon with respect to the vector u to construct the radial function of IP. Indeed, as will be shown in the proof of Theorem 2.6, this can be equivalently written to provide a semialgebraic description of the intersection body. In particular, if the intersection is a square, then the radial function in a neighborhood of that point will be a constant term over a coordinate variable, e.g. $\frac{4}{3z}$. On the other hand, when the intersection is a hexagon, the radial function is a degree two polynomial over 3xyz. The intersection body is convex as promised by the theory.

Lemma 2.4

Let P be a full-dimensional polytope in ${\mathbb {R}}^d$. Then there exists a central hyperplane arrangement H in ${\mathbb {R}}^d$ whose maximal open chambers C satisfy the following property. For all $x \in C$, the hyperplane $x^\perp$ intersects a fixed set of edges of P and the polytopes $Q = P \cap x^\perp$ are of the same combinatorial type.

Proof

Let x be a generic vector of ${\mathbb {R}}^d$ and consider $Q = P\cap x^\perp$. The vertices of Q are the points of intersection of $x^\perp$ with the edges of P. Perturbing x continuously, the intersecting edges (and thus the combinatorial type) remain the same, unless the hyperplane $x^\perp$ passes through a vertex v of P. This happens if and only if $\langle x,v \rangle = 0$ and thus the set of normal vectors of such hyperplanes is given by $v^\perp = \{x \in {\mathbb {R}}^d \mid \langle x, v \rangle = 0 \}.$ Taking the union over all vertices yields the central hyperplane arrangement

$$\begin{aligned} H = \{ v^\perp \mid v \text { is a vertex of } P \text { and { v} is not the origin}\}. \end{aligned}$$

Then each open region C of the complement of H contains points x such that $x^\perp$ intersects a fixed set of edges of P. $\square$

The proof of Lemma 2.4 implies that the number of regions we are interested in is the number of chambers of the central hyperplane arrangement H. Let $m = \left( \# \{ v \text { is a vertex of } P\}/\sim \right)$ where $v\sim w$ if $v=\pm w$. Then we have an upper bound for such a number:

$$\begin{aligned} \sum _{j=0}^d \left( {\begin{array}{c}m\\ j\end{array}}\right) \end{aligned}$$

given by the number of chambers of a generic arrangement (Stanley 2007, Prop. 2.4).

Remark 2.5

We note that there are several ways to view the hyperplane arrangement H in Lemma 2.4. For example, since the vertices of P are the normal vectors of the facets of the dual polytope $P^\circ$, we can describe H as the collection of linear hyperplanes which are parallel to facets of $P^\circ$. We also note that H is the normal fan of a zonotope whose edge directions are orthogonal to the hyperplanes of H. The fan $\Sigma$ induced by the hyperplane arrangement H is the normal fan of the zonotope

$$\begin{aligned} Z(P) = \sum _{v \text { is a vertex of } P} [-v, v]. \end{aligned}$$

We will call this zonotope the zonotope associated to P. As will be clarified later in Remark 5.9, the dual body of Z(P) plays an important role in the visualization and the combinatorics of the intersection body IP.

Theorem 2.6

Let $P\subseteq {\mathbb {R}}^d$ be a full-dimensional polytope containing the origin. Then IP, the intersection body of P, is semialgebraic.

Proof

Fix a region $U=C\cap S^{d-1}$ for an open cone C from Lemma 2.4. Then for every $u\in U$ the hyperplane $u^\perp$ intersects P in the same set of edges. Let v be a vertex of $Q=P\cap u^\perp$. Then there is an edge [a, b] of P such that $v = [a,b] \cap u^\perp$. This implies that $v = \lambda a + (1-\lambda ) b$ for some $\lambda \in (0,1)$ and $\langle v,u\rangle =0$. From this we get that

$$\begin{aligned} \lambda = \frac{\langle b, u \rangle }{\langle b-a, u \rangle } \end{aligned}$$

which implies that

$$\begin{aligned} v = \frac{\langle b, u \rangle }{\langle b-a, u \rangle }(a-b)+b = \frac{\langle b, u \rangle a - \langle a, u \rangle b}{\langle b-a, u \rangle }. \end{aligned}$$

In this way we express v as a function of u (for fixed a and b). Let $v_1, \ldots , v_n$ be the vertices of Q and let $[a_i,b_i]$ be the corresponding edges of P.

We now consider the following triangulation of Q: first, triangulate each facet of Q that does not contain the origin, without adding new vertices (this can always be done e.g. by a regular subdivision using a generic lifting function, cf. De Loera et al. 2010, Prop. 2.2.4). For each $(d-2)$-dimensional simplex $\Delta$ in this triangulation, consider the $(d-1)$-dimensional simplex $\text {conv}(\Delta ,0)$ with the origin. This constitutes a triangulation $T = \{\Delta _j : j\in J\}$ of Q, in which the origin is a vertex of every simplex.

Restricting to U, the radial function of the intersection body IP in direction u is the volume of Q, and hence given by

$$\begin{aligned} \rho _{IP}(u) = {{\,\mathrm{Vol}\,}}(Q) = \sum _{j\in J} {{\,\mathrm{Vol}\,}}(\Delta _j). \end{aligned}$$

We can thus compute $\rho _{IP}(u)$ as

$$\begin{aligned} \rho _{IP}(u) = \sum _{j\in J} \frac{1}{d!} \left| \det \left( M_j(u)\right) \right| , \end{aligned}$$

where

$$\begin{aligned} M_j(u) = \begin{bmatrix} v_{i_1}(u) \\ v_{i_2}(u) \\ \vdots \\ v_{i_{d-1}}(u) \\ u \end{bmatrix} = \begin{bmatrix} \frac{\langle b_{i_1}, u \rangle a_{i_1} - \langle a_{i_1}, u \rangle b_{i_1}}{\langle b_{i_1}-a_{i_1}, u \rangle } \\ \vdots \\ \frac{\langle b_{i_{d-1}}, u \rangle a_{i_{d-1}} - \langle a_{i_{d-1}}, u \rangle b_{i_{d-1}}}{\langle b_{i_{d-1}}-a_{i_{d-1}}, u \rangle } \\ u \end{bmatrix} \end{aligned}$$

and the row vectors $\{v_{i_1},v_{i_2}, \ldots , v_{i_{d-1}}\}$ (along with the origin) are vertices of the simplex $\Delta _j$ of the triangulation. Therefore, we obtain an expression $\rho _{IP}(u) = \frac{p(u)}{q(u)}$ for some polynomials $p,q\in {\mathbb {R}}[u_1,\ldots ,u_d]$ without common factors, for $u\in U$. With the same procedure applied to all regions $U_i = C_i \cap S^{d-1}$, for $C_i$ as in Lemma 2.4, we obtain an expression for $\rho \vert _{S^{d-1}}$ that is continuous and piecewise a quotient of two polynomials $p_i,q_i$. It follows from the definition of the radial function that

$$\begin{aligned} IP = \left\{ x \in {\mathbb {R}}^d \mid \rho _{IP}\left( x \right) \ge 1 \right\} = \left\{ x \in {\mathbb {R}}^d \mid \frac{1}{\Vert x\Vert }\rho _{IP}\left( \frac{x}{\Vert x\Vert } \right) \ge 1 \right\} . \end{aligned}$$

Notice that for every $j\in J$ we have the following equality:

$$\begin{aligned} \det \left( M_j\left( \frac{x}{\Vert x\Vert } \right) \right) = \det \begin{bmatrix} v_{i_1}\left( \frac{x}{\Vert x\Vert } \right) \\ \vdots \\ v_{i_{d-1}}\left( \frac{x}{\Vert x\Vert } \right) \\ \frac{x}{\Vert x\Vert } \end{bmatrix} = \det \begin{bmatrix} v_{i_1}\left( x \right) \\ \vdots \\ v_{i_{d-1}}\left( x \right) \\ \frac{x}{\Vert x\Vert } \end{bmatrix} = \frac{1}{\Vert x\Vert } \det \left( M_j\left( x \right) \right) \end{aligned}$$

and therefore, if $\frac{x}{\Vert x\Vert } \in U$,

$$\begin{aligned} \rho _{IP}\left( \frac{x}{\Vert x\Vert } \right) = \sum _{j\in J} \frac{1}{d!} \left| \det \left( M_j\left( \frac{x}{\Vert x\Vert } \right) \right) \right| = \frac{1}{\Vert x\Vert } \sum _{j\in J} \frac{1}{d!} \left| \det \left( M_j\left( x \right) \right) \right| = \frac{p(x)}{\Vert x\Vert q(x)}. \end{aligned}$$

Because the radial function is a semialgebraic map, by quantifier elimination the intersection body is also semialgebraic. More explicitly, let I be the set of indices i such that $\rho _{IP}\big |_{U_i} \ne 0$. Then we can write the intersection body as

$$\begin{aligned} IP&= \bigcup _{i\in I} \left\{ x\in \overline{C}_i \mid \frac{1}{\Vert x\Vert ^2} \cdot \frac{p_i(x)}{q_i(x)} \ge 1 \right\} \\&= \bigcup _{i\in I} \left\{ x\in \overline{C}_i \mid \Vert x \Vert ^2 q_i(x) - p_i(x) \le 0 \right\} . \end{aligned}$$

This expression gives exactly a semialgebraic description of IP. $\square$

Example 2.7

Let P be the regular icosahedron in ${\mathbb {R}}^3$, whose 12 vertices are all the even permutations of $\left( 0, \pm \frac{1}{2}, \pm (\frac{1}{4} \sqrt{5} + \frac{1}{4})\right)$. The associated hyperplane arrangement has $32=12+20$ chambers. The first type of chambers is spanned by five rays and the radial function of IP is given by a quotient of a quartic and a quintic, defined over $\mathbb {Q}(\sqrt{5})$. In the remaining twenty chambers $\rho _{IP}$ is a quintic over a sextic, again with coefficients in $\mathbb {Q}(\sqrt{5})$. This intersection body is the convex set shown in Fig. 1. We will continue the analysis of IP in Example 5.10.

The theory of intersection bodies assures that the intersection body of a centrally symmetric convex body is again a centrally symmetric convex body, as it happens in Example 2.3 and in Example 2.7. On the other hand, given any polytope P (indeed this holds more generally for any convex body) there exists a translation of P such that IP is not convex. This is the content of the next example.

Example 2.8

Let P be the cube $[-1,1]^3 + (1,1,1)$, so that the origin is a vertex of P. The hyperplane arrangement associated to P divides the space in 32 chambers. In two of them the radial function is 0. In six regions the radial function has the following shape (up to permutation of the coordinates and sign):

$$\begin{aligned} \rho (x,y,z) = \frac{2x}{3yz}. \end{aligned}$$

There are then eighteen regions in which the radial function looks like

$$\begin{aligned} \rho (x,y,z) = \frac{2(x+2z)}{3yz}. \end{aligned}$$

In the remaining six regions we have

$$\begin{aligned} \rho (x,y,z) = \frac{2(x^2+2xy+y^2+2xz+z^2)}{3xyz}. \end{aligned}$$

Figure 3 shows two different points of view of IP, which is in particular not convex.

Fig. 3

The intersection body of the cube in Example 2.8 from two different points of view

3 Non-convex intersection bodies

The proof of Theorem 2.6 relies on the fact that the origin is in the polytope. However, if the origin is not contained in P, we can still find a semialgebraic description of IP by adjusting how we compute the volume of $P\cap u^\perp$. The remainder of this section will be dedicated to proving this.

Lemma 3.1

Let $P\subset {\mathbb {R}}^d$ be a full-dimensional polytope, and let $\mathcal {F}$ be the set of its facets. Let p be a point outside of P. For each face $F\in \mathcal {F}$, let $\hat{F}$ denote the set ${\text {conv}}(F\cup \{p\})$. Then the following equality holds:

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(P) = \sum _{F\in \mathcal {F}} {{\,\mathrm{sgn}\,}}(F){{\,\mathrm{Vol}\,}}(\hat{F}) \end{aligned}$$

where ${{\,\mathrm{sgn}\,}}(F)$ is 1 if P and p belong to the same halfspace defined by F, and $-1$ otherwise.

Proof

Let $\hat{P} = {\text {conv}}(P\cup \{p\})$ and denote by $\mathcal {F}^+_p$ the set of facets F of P for which the halfspace defined by F containing P also contains p, possibly on its boundary. Let $\mathcal {F}^-_p = \mathcal {F}\setminus \mathcal {F}^+_p$.

First we will show that $\hat{P} = \bigcup _{F\in \mathcal {F}^+_p} \hat{F}$. The inclusion $\bigcup _{F\in \mathcal {F}^+_p} \hat{F}\subseteq \hat{P}$ follows immediately from convexity. To see the opposite direction, let $q\in \hat{P}$ and consider r to be the ray starting at p and going through q. Either r intersects P only along its boundary, or there are some intersection points also in the interior of P. In the first case $r\cap P \subset F$ and so $q\in \hat{F}$ for some face F, that by convexity must be in $\mathcal {F}^+_p$. On the other hand, if the ray r intersects the interior of the polytope P, denote by a the farthest among the intersection points:

$$\begin{aligned} \Vert a-p\Vert = \max \{\Vert \alpha -p\Vert \mid \alpha \in P\cap r\}. \end{aligned}$$

Let $F_a$ be a facet containing a. Then, q is contained in the convex hull of $F_a \cup \{p\}$, i.e. $\hat{F}_a$. From the definition of a it follows that the halfspace defined by $F_a$ containing p must also contain P, so $F_a\in \mathcal {F}^+_p$ and our statement holds.

Next, we will show that $\bigcup _{F\in \mathcal {F}^-_p} \hat{F} = \overline{\hat{P} \setminus P}$. The pyramid $\hat{F}$ is contained in the closed halfspace defined by F which contains p. By the definition of $\mathcal {F}^-_p$, this halfspace does not contain P thus $\hat{F}\cap P = F$. Also, $\hat{F}~\subseteq ~\hat{P}$ so we have that $\hat{F}\subseteq ~\overline{\hat{P}\setminus P}$ and hence $\bigcup _{F\in \mathcal {F}^-_p} \hat{F}~\subseteq ~\overline{\hat{P} \setminus P}$. Conversely, let $q\in \overline{\hat{P}\setminus P}$. If $q~=~p$ we are done, so assume $q \ne p$. Then, $q = \lambda p + (1-\lambda ) b$ for some $b\in P$, $\lambda \in [0,1)$. Let a be the point at which the segment from p to b first intersects the boundary of P, i.e.

$$\begin{aligned} \Vert a-p\Vert = \min \{\Vert \alpha -p\Vert \mid \alpha \in P, \alpha = tp+(1-t)b \hbox { for } t\in [0,1)\}. \end{aligned}$$

Then by construction there exists a facet $F_a \in \mathcal {F}^-_p$ containing a, such that $q\in \hat{F}_a$. Thus, we have that

$$\begin{aligned} {{\,\mathrm{Vol}\,}}\left( \bigcup _{F\in \mathcal {F}^+_p}\hat{F}\right) = {{\,\mathrm{Vol}\,}}(\hat{P}) = {{\,\mathrm{Vol}\,}}(\hat{P}\setminus P) + {{\,\mathrm{Vol}\,}}(P) = {{\,\mathrm{Vol}\,}}\left( \bigcup _{F\in \mathcal {F}^-_p}\hat{F}\right) + {{\,\mathrm{Vol}\,}}(P). \end{aligned}$$

If $F_1 \ne F_2$ and $F_1, F_2 \in \mathcal {F}^+_p$ or $F_1, F_2 \in \mathcal {F}^-_p$, then the volume of $\hat{F}_1\cap \hat{F}_2$ is zero, therefore

$$\begin{aligned} \sum _{F\in \mathcal {F}^+_p}{{\,\mathrm{Vol}\,}}(\hat{F}) = \sum _{F\in \mathcal {F}^-_p}{{\,\mathrm{Vol}\,}}(\hat{F}) + {{\,\mathrm{Vol}\,}}(P) \end{aligned}$$

and the claim follows. $\square$

Theorem 3.2

Let $P\subset {\mathbb {R}}^d$ be a full-dimensional polytope. Then IP, the intersection body of P, is semialgebraic.

Proof

What remains to be shown is that IP is semialgebraic in the case when the origin is not contained in P, and hence it is not contained in any of its sections $Q = P \cap u^\perp$. From Lemma 3.1, with $p = 0 \in {\mathbb {R}}^d$ we have that

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(Q) = \sum _{F \text { facet of } Q} {{\,\mathrm{sgn}\,}}(F) {{\,\mathrm{Vol}\,}}(\hat{F}) \end{aligned}$$

where $\hat{F}$ is the convex hull of F and the origin. Let $T_F = \{\Delta _j : j\in J_F\}$ be a triangulation of F. We can calculate as in the proof of Theorem 2.6

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(\hat{F)} = \sum _{j\in J_F} \frac{1}{d!} |\det M_j| \end{aligned}$$

where $M_j$ is the matrix whose rows are the vertices of the simplex $\Delta _j \in T_F$ and u. We then follow the remainder of the proof of Theorem 2.6 to see that the intersection body is semialgebraic. $\square$

4 The algorithm

The proofs from Theorems 2.6 and 3.2 lead to an algorithm to compute the radial function of the intersection body of a polytope. In this section, we describe the algorithm. By Remark 2.5, the regions C in which $\rho (x)|_C = \frac{p(x)}{\Vert x \Vert ^2 q(x)}$ for fixed polynomials p(x) and q(x) are defined by the normal fan of the zonotope Z(P). First, we compute the radial function for each of these cones individually, by applying Algorithm 1.

This algorithm has as output the rational function $\rho (x)|_C = \frac{p(x)}{\Vert x \Vert ^2 q(x)}$. Iterating over all regions yields the final Algorithm 2.

An implementation of these algorithms for SageMath 9.2 (The Sage Developers 2021) and Oscar 0.7.1-DEV (The OSCAR Developers 2021) can be found in https://mathrepo.mis.mpg.de/intersection-bodies. We note that in step 2 of Algorithm 1, the implementation uses a regular subdivision of the facets of the polytope Q by lifting the vertices $v_1, \dots , v_m$ along the moment curve $(t^1,\dots ,t^m)$ with $t=3$.

5 Algebraic boundary and degree bound

In order to study intersection bodies from the point of view of real algebraic geometry we need to introduce our main character for this section, the algebraic boundary. For more on the algebraic boundary we refer the reader to Sinn (2015).

Definition 5.1

Let K be any compact subset in ${\mathbb {R}}^d$, then its algebraic boundary $\partial _a K$ is the ${\mathbb {R}}$-Zariski closure of the Euclidean boundary $\partial K$.

Knowing the radial function of a convex body K implies knowing its boundary. In fact, when $0\in {\text {int}} K$ then $x\in \partial K$ if and only if $\rho _K (x) = 1$ (see Remark 5.2 for the other cases). Therefore, using the same notation as in the proof of Theorem 2.6, we can observe that the algebraic boundary of the intersection body of a polytope is contained in the union of the varieties $\mathcal {V}\left( \Vert x \Vert ^2 q_i(x) - p_i(x) \right)$. Indeed, we actually know more: as will be proven in Proposition 5.5, the $p_i$’s are divisible by the polynomial $\Vert x\Vert ^2$, and hence

$$\begin{aligned} \partial _a IP = \bigcup _{i\in I} \mathcal {V}\left( q_i(x) - \frac{p_i(x)}{\Vert x\Vert ^2} \right) \end{aligned}$$

because of the assumption made in the proof of Theorem 2.6 that $p_i,q_i$ do not have common components. That is, these are exactly the irreducible components of the boundary of IP.

Remark 5.2

As anticipated in Sect. 2 there may be difficulties when computing the boundary of IP in the case where the origin is not in the interior of the polytope P. In particular, x is a discontinuity point of the radial function of IP if and only if $x^\perp$ contains a facet of P. Therefore $\rho _{IP}$ has discontinuity points if and only if the origin lies in the union of the affine linear spans of the facets of P. In this case, there are finitely many rays where the radial function is discontinuous and they belong to ${\mathbb {R}}^d \setminus \left( \cup _{i\in I} C_i \right)$, i.e. to the hyperplane arrangement H. If $d=2$, these rays disconnect the space, and this implies that we loose part of the (algebraic) boundary of IP: to the set $\{x\in {\mathbb {R}}^d \mid \rho _{IP}(x) = 1\}$ we need to add segments from the origin to the boundary points in the direction of these rays. However, in higher dimensions the discontinuity rays do not disconnect ${\mathbb {R}}^d$ so $\{x \in {\mathbb {R}}^d \mid \rho _{IP}(x) = 1\}$ approaches the region where the radial function is zero continuously except for these finitely many directions. Therefore there are no extra components of the boundary of IP.

Example 5.3

(Continuation of Example 2.3, cf. Fig. 4a) Starting from the radial function of the intersection body of the 3-cube P, computed using Algorithm 1, we can recover the equations of its algebraic boundary. The Euclidean boundary of this convex body is divided in 14 regions. Among them, 6 arise as the intersection of a convex cone spanned by 4 rays with a hyperplane; they constitute facets, i.e. flat faces of dimension $d-1$, of IP. For example the facet exposed by the vector (1, 0, 0) is the intersection of $3z = 4$ with the convex cone

$$\begin{aligned} \overline{C}_1 = \text {co}\{(1, 0, 1), (-1, 0, 1), (0, 1, 1), (0, -1, 1)\}. \end{aligned}$$

In other words, the variety $\mathcal {V}(3z-4)$ is one of the irreducible components of $\partial _a IP$. The remaining 8 regions are spanned by 3 rays each, and the polynomial that defines the boundary of IP is a cubic, such as

$$\begin{aligned} 6 x y z - 2 x^2 - 4 x y - 2 y^2 - 4 x z + 4 y z - 2 z^2 \end{aligned}$$

in the region

$$\begin{aligned} \overline{C}_2 = \text {co}\{(0, 1, 1), (-1, 1, 0), (-1, 0, 1)\}. \end{aligned}$$

These cubics are in fact, up to a change of coordinates, the algebraic boundary of a famous spectrahedron: the elliptope (Laurent and Poljak 1995). Hence $\partial _a IP$ is the union of 14 irreducible components, six of degree 1 and eight of degree 3.

Remark 5.4

In Plaumann et al. (2021) the authors introduce the notion of patches of a semialgebraic convex body, with the purpose of mimicking the faces of a polytope. In the case of intersection bodies of polytopes, it is tempting to think that each region of Lemma 2.4 corresponds to a patch. Indeed, this happens, for example, for the centered 3-cube in Example 5.3. On the other hand, if $P = [-1,1]^3+(0,0,1)$ then there are 4 regions that define the same patch of the algebraic boundary of IP; therefore there is, unfortunately, no one-to-one correspondence between regions and patches.

Proposition 5.5

Using the notation of Lemma 2.4 and Theorem 3.2, fix a chamber C of H and let $Q = P\cap u^{\perp }$ for some $u\in U = C \cap S^{d-1}$. Then the polynomial $\Vert x\Vert ^2 = x_1^2+\ldots +x_d^2$ divides p(x) and

$$\begin{aligned} \deg \left( q(x) - \frac{p(x)}{\Vert x\Vert ^2} \right) \le f_0(Q). \end{aligned}$$

Proof

For the fixed region C, let T be a triangulation of Q with simplices indexed by J. Then the volume of Q is given by

$$\begin{aligned} \frac{p(x)}{q(x)} = \frac{1}{d!} \sum _{j\in J} \left| \det \left( M_j\left( x \right) \right) \right| \end{aligned}$$

where $M_j$ is the matrix as in the proof of Theorem 2.6. Notice that for each $M = M_j$, we can rewrite the determinant to factor out a denominator (we also write for simplicity $\Delta = \Delta _j$):

$$\begin{aligned} \det (M(x))&= \sum _{\sigma \in S_d} {{\,\mathrm{sgn}\,}}(\sigma ) \prod _{i=1}^d M_{i\sigma (i)} \\&= \sum _{\sigma \in S_d} {{\,\mathrm{sgn}\,}}(\sigma ) x_{\sigma (d)} \prod _{i=1}^{d-1} \frac{\langle b_{i}, u \rangle a_{i\sigma (i)} - \langle a_{i}, u \rangle b_{i\sigma (i)}}{\langle b_{i}-a_{i}, u \rangle } \\&= \prod _{i=1}^{d-1} \frac{1}{\langle b_{i}-a_{i}, u \rangle } \sum _{\sigma \in S_d} {{\,\mathrm{sgn}\,}}(\sigma ) x_{\sigma (d)} \prod _{i=1}^{d-1} \left( \langle b_{i}, u \rangle a_{i\sigma (i)} - \langle a_{i}, u \rangle b_{i\sigma (i)}\right) \\&= \left( \prod _{\begin{array}{c} v_i \in \Delta \\ \text {vertex} \end{array}} \frac{1}{\langle b_{i}-a_{i}, x \rangle } \right) \cdot \det \left( \hat{M}\left( x \right) \right) \end{aligned}$$

where

$$\begin{aligned} \hat{M}(x) = \begin{bmatrix} \vdots \\ \langle b_{i}, x \rangle a_{i} - \langle a_{i}, x \rangle b_{i} \\ \vdots \\ x \end{bmatrix} \end{aligned}$$

and the determinant of $\hat{M}(x)$ is a polynomial of degree d in the $x_i$’s. Note that if we multiply $\hat{M}(x)\cdot x$ we obtain the vector $(0,\ldots ,0,x_1^2+\ldots +x_d^2)$. Hence if $x_1^2+\ldots +x_d^2 = 0$, then $\hat{M}(x)\cdot x = 0$, i.e. the kernel of $\hat{M}(x)$ is non-trivial and thus $\det \hat{M}(x) = 0$. This implies the containment of the complex varieties $\mathcal {V}(\Vert x\Vert ^2) \subseteq \mathcal {V}(\det \hat{M}(x))$ and therefore the polynomial $x_1^2+\ldots +x_d^2$ divides the polynomial $\det \hat{M}(x)$. When we sum over all the simplices in the triangulation T we obtain that

$$\begin{aligned} q(x)&= d! \left( \prod _{\begin{array}{c} v_i \in \Delta \\ \hbox {vertex} \end{array}} \frac{1}{\langle b_{i}-a_{i}, x \rangle } \right) \cdot \left( \prod _{\begin{array}{c} v_i \notin \Delta \\ \hbox {vertex} \end{array}} \frac{1}{\langle b_{i}-a_{i}, x \rangle } \right) \\&= \prod _{\begin{array}{c} v_i \in Q \\ \hbox {vertex} \end{array}} \frac{1}{\langle b_{i}-a_{i}, x \rangle } \end{aligned}$$

and

$$\begin{aligned} p(x) = \sum _{j\in J} \left( \left| \det \left( \hat{M}\left( x \right) \right) \right| \cdot \prod _{\begin{array}{c} v_i \notin \Delta \\ \hbox {vertex} \end{array}} \frac{1}{\langle b_{i}-a_{i}, x \rangle } \right) . \end{aligned}$$

Hence $\deg q \le f_0(Q)$ and $\deg p \le f_0(Q) + 1$, so the claim follows. $\square$

Notice that generically, meaning for the generic choice of the vertices of P, the bound in Proposition 5.5 is attained, because p and q will not have common factors.

Theorem 5.6

Let $P\subset {\mathbb {R}}^d$ be a full-dimensional polytope with $f_1(P)$ edges. Then the degrees of the irreducible components of the algebraic boundary of IP are bounded from above by

$$\begin{aligned} f_1(P) - (d-1). \end{aligned}$$

Proof

We want to prove that $f_0(Q) \le f_1(P) - (d-1)$, for every $Q = P \cap u^\perp$, $u \in S^{d-1} \setminus H$. By definition, every vertex of Q is a point lying on an edge of P, so trivially $f_0(Q) \le f_1(P)$. We want to argue now that it is impossible to intersect more than $f_1(P) - (d-1)$ edges of P with our hyperplane $\mathcal {H}= u^\perp$. If the origin is one of the vertices of P, then all the edges that have the origin as a vertex give rise only to one vertex of Q: the origin itself. There are at least d such edges, because P is full-dimensional, and so $f_0(Q) \le f_1(P) - (d-1)$.

Suppose now that the origin is not a vertex of P, then ${\mathcal {H}}$ does not contain vertices of P. It divides ${\mathbb {R}}^d$ in two half spaces ${\mathcal {H}}_+$ and ${\mathcal {H}}_-$, and so it divides the vertices of P in two families of k vertices in ${\mathcal {H}}_+$ and $\ell$ vertices in ${\mathcal {H}}_-$. Either k or $\ell$ are equal to 1, or they are both greater than one. In the first case let us assume without loss of generality that $k=1$, i.e. there is only one vertex $v_+$ in ${\mathcal {H}}_+$. Then pick one vector $v_-$ in ${\mathcal {H}}_-$: because P is a full-dimensional polytope, there are at least d edges of P with $v_-$ as a vertex. Only one of them may connect $v_-$ to $v_+$ and therefore the other $d-1$ edges must lie in ${\mathcal {H}}_-$. This gives $f_0(Q) \le f_1(P) - (d-1)$.

On the other hand, let us assume that $k,\ell \ge 2$. Then there is at least one edge in ${\mathcal {H}}_+$ and one edge in ${\mathcal {H}}_-$. If $d=3$ these are the $d-1$ edges that do not intersect the hyperplane. For $d>3$ we reason as follows. Suppose that $\mathcal H$ intersects a facet F of P. Then it cannot intersect all the facets of F (i.e. a ridge of P), otherwise we would get $F\subset {\mathcal {H}}$ which contradicts the fact that ${\mathcal {H}}$ does not intersect vertices of P. So there exists a ridge $F'$ of P that does not intersect the hyperplane; it has dimension $d-2\ge 2$ and therefore it has at least $d-1$ edges. Therefore

$$\begin{aligned} f_0(Q) \le f_1(P) - (d-1). \end{aligned}$$

$\square$

Corollary 5.7

In the hypotheses of Theorem 5.6, if P is centrally symmetric and centered at the origin, then we can improve the bound with

$$\begin{aligned} \frac{1}{2} \left( f_1(P) - (d-1) \right) . \end{aligned}$$

Proof

We already know that for each chamber $C_i$ from Lemma 2.4, the degree of the corresponding irreducible component is bounded by the degree of the polynomial $q_i$. This follows from the construction of $p_i$ and $q_i$ in the proof of Theorem 2.6. Specifically, the determinant which gives $p_i/q_i$ comes with the product of $d-1$ rational functions, with linear numerator and denominators, and one linear term. Thus $\deg p_i = \deg q_i + 1$ which implies that $\deg \frac{p_i}{||x||^2} < \deg q_i$. By definition these polynomials are obtained as the least common multiple of objects with shape

$$\begin{aligned} \prod _{\begin{array}{c} v_k \in \Delta _j \\ \hbox {vertex} \end{array}} \frac{1}{\langle b_{k}-a_{k}, x \rangle }. \end{aligned}$$

If P is centrally symmetric, so is Q, and therefore we have the vertex belonging to the edge $[a_k,b_k]$ and also the vertex belonging to the edge $[-a_k,-b_k]$. When computing the least common multiple, these two vertices produce the same factor, up to a sign, and therefore they count as the same linear factor of $q_i$. Hence for every i

$$\begin{aligned} \deg q_i(x) \le \frac{f_0(Q)}{2} \le \frac{1}{2} \left( f_1(P) - (d-1) \right) . \end{aligned}$$

$\square$

Fig. 4

Left: the intersection body of the cube in Example 5.3. Right: the intersection body of the tetrahedron in Example 5.8. Center: the dual body of the zonotope Z(P) associated to both the cube and the tetrahedron. Such a polytope reveals the structure of the boundary divided into regions of these two intersection bodies

Example 5.8

Let P be the tetrahedron in ${\mathbb {R}}^3$ with vertices $(-1, -1, -1), (-1, 1, 1), (1, -1, 1)$, $(1, 1, -1)$. The associated hyperplane arrangement coincides with the one associated to the cube in Example 5.3, so it has 14 chambers that come in two families. The first one consists of cones spanned by four rays, such as $\overline{C}_1$ (see Example 5.3). The polynomial that defines the boundary of IP in this region is a quartic, namely

$$\begin{aligned} q_2(x,y,z) - \frac{p_2(x,y,z)}{\Vert (x,y,z)\Vert ^2} = 6 (x + z) (x - z) (y + z) (y - z) + 4 x^2 z + 4 y^2 z - 4 z^3. \end{aligned}$$

On the other hand the cones of the second family are spanned by three rays: here the section of P is a triangle and the equation of the boundary if IP is a cubic. An example is the cone $\overline{C}_2$ with the polynomial

$$\begin{aligned}&q_1(x,y,z) - \frac{p_1(x,y,z)}{\Vert (x,y,z)\Vert ^2} = 6 (x - y) (x - z) (y + z)\\&- 2 x^2 + 4 x (y + z) - 2 y^2 - 4 y z - 2 z^2. \end{aligned}$$

Note that this region furnishes an example in which the bounds given in Proposition 5.5 and Theorem 5.6 are attained.

Remark 5.9

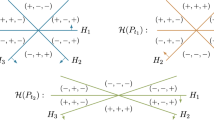
Remark 2.5 together with Proposition 5.5 implies that the structure of the irreducible components of the algebraic boundary of IP is strongly connected with the face lattice of the dual of the zonotope Z(P). More precisely, in the generic case, the lattice of intersection of the irreducible components is isomorphic to the face lattice of the dual polytope $Z(P)^\circ$. Thus, a classification of “combinatorial types” of such intersection bodies is analogous to the classification of zonotopes / hyperplane arrangements / oriented matroids. It is however worth noting, that the same zonotope can be associated to two polytopes $P_1$ and $P_2$ which are not combinatorially equivalent. One example of this instance is a pair of polytopes such that $P_1 = \text {conv}(v_1, \dots , v_n)$ and $P_2 = \text {conv}(\pm v_1, \dots , \pm v_2)$, as can be seen in Fig. 4 for the cube and the tetrahedron. To have a better overview over the structure of the boundary of IP, one strategy is to use the Schlegel diagram of $Z(P)^\circ$. We label each maximal cell by the degree of the polynomial that defines the corresponding irreducible component of $\partial IP$, as can be seen in Figs. 5 and 6.

Example 5.10

(Continuation of Example 2.7, cf. Fig. 1) Let P be the regular icosahedron. In the 12 regions which are spanned by five rays, the polynomial that defines the boundary of IP has degree 5 and it looks like

$$\begin{aligned}&3 ( (\sqrt{5} x + \sqrt{5} y - x + y)^2 - 4z^2) ( (\sqrt{5} x + x + 2 y)^2 - (\sqrt{5} z - z)^2) y \\&\quad + 8 \sqrt{5} x^3 y + 68 \sqrt{5} x^2 y^2 + 72 \sqrt{5} x y^3 + 20 \sqrt{5} y^4\\&\quad - 40 \sqrt{5} x y z^2 - 20 \sqrt{5} y^2 z^2 + 4 \sqrt{5} z^4 \\&\quad + 8 x^3 y + 164 x^2 y^2 + 168 x y^3 + 44 y^4 - 8 x^2 z^2 - 72 x y z^2 - 44 y^2 z^2 + 12 z^4. \end{aligned}$$

In the other 20 regions spanned by three rays, $\partial IP$ is the zero set of a sextic polynomial with the following shape

$$\begin{aligned}&3 ( (\sqrt{5} x + x + 2 y )^2 - ( \sqrt{5} z - z)^2 ) ( (\sqrt{5} y - 2 x - y )^2\\&\quad - ( \sqrt{5} z - z)^2 ) x y + 20 \sqrt{5} x^4 y \\&\quad - 20 \sqrt{5} x^2 y^3 - 4 \sqrt{5} x y^4 + 4 \sqrt{5} y^5 - 4 \sqrt{5} x^3 z^2 - 60 \sqrt{5} x^2 y z^2\\&\quad - 12 \sqrt{5} x y^2 z^2 + 12 \sqrt{5} x z^4 + 44 x^4 y \\&\quad - 8 x^3 y^2 - 44 x^2 y^3 + 12 x y^4 + 12 y^5 - 12 x^3 z^2\\&\quad - 156 x^2 y z^2 - 60 x y^2 z^2 - 8 y^3 z^2 + 28 x z^4. \end{aligned}$$

We visualize the structure of these pieces using the Schlegel diagram in Fig. 5, where the numbers correspond to the degree of the polynomials, as explained in Remark 5.9.

Fig. 5

The Schlegel diagram of $Z(P)^\circ$, in the case where P is the icosahedron from Example 5.10. The labels represent the degrees of the polynomials of $\partial _a IP$

Using this technique we are then able to visualize the boundary of intersection bodies of 4-dimensional polytopes via the Schlegel diagram of $Z(P)^\circ$.

Example 5.11

Let $P = \text {conv}\{(1,1,0,0), (0,1,0,0), (0,-1,0,0), (0,0,-1,0), (0,0,0,-1)\}$. The boundary of its intersection body IP is subdivided in 16 regions. In four of them the equation is given by a polynomial of degree 3, whereas in the remaining twelve regions the polynomial has degree 5. In Fig. 6 we show the Schlegel diagram of

$$\begin{aligned} Z(P)^\circ = \text {conv}\{\pm (1/2, -1/2, 0, 0), \pm (1, 0, 0, 0), \pm (0, 0, 1, 0), \pm (0, 0, 0, 1)\} \end{aligned}$$

with a number associated to each maximal cell which represents the degree of the polynomial in the corresponding region of $\partial IP$.

Fig. 6

The Schlegel diagram of $Z(P)^\circ$ from Example 5.11. There are four cells whose corresponding polynomial in $\partial IP$ has degree 3, including the outer facet; the others correspond to degree 5 polynomials

6 The cube

In this section we investigate the intersection body of the d-dimensional cube $C^{(d)} = [-1,1]^d$, with a special emphasis on the linear components of its algebraic boundary.

Proposition 6.1

The algebraic boundary of the intersection body of the d-dimensional cube $C^{(d)}$ has at least 2d linear components. These components correspond to the 2d open regions from Lemma 2.4 which contain the standard basis vectors and their negatives.

Proof

We show the claim for the first standard basis vector $e_1$. The argument for the other vectors $\pm e_i, i = 1,\ldots , d$ is analogous.

Let C be the region from Lemma 2.4 which contains $e_1$ and consider $U = C\cap S^{d-1}$. For any $u \in U$, the polytope $C^{(d)} \cap u^\perp$ is combinatorially equivalent to $C^{(d-1)}$. Hence we can compute the (signed) volume,

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(C^{(d)} \cap u^\perp ) = \det \begin{bmatrix} v^{(1)} - v^{(0)} \\ \vdots \\ v^{(d-1)} - v^{(0)}\\ u \end{bmatrix} \end{aligned}$$

where $v^{(0)}$ is an arbitrarily chosen vertex of $C^{(d)} \cap u^\perp$ and the remaining $v^{(i)}$ are vertices of $C^{(d)} \cap u^\perp$ adjacent to $v^{(0)}$. Next, we observe that for any vertex v of $C^{(d)} \cap u^\perp$ which lies on the edge [a, b] of $C^{(d)}$, v is the vector

$$\begin{aligned} v = \left( -\frac{1}{u_1}\sum _{j=2}^d a_ju_j,\, a_2,\, \ldots ,\, a_d \right) . \end{aligned}$$

This follows from the formulation of v in the proof of Theorem 2.6 and the fact that $b_1 = -a_1$ and $b_i = a_i$ for $i=2,\ldots ,d$. Combining this with the determinant above gives us the following expression for the radial function restricted to U:

$$\begin{aligned} \rho (u)&= \frac{1}{u_1}\det \begin{bmatrix} -\sum _{j=2}^d (a^{(1)}_j-a^{(0)}_j)u_j &{} a^{(1)}_2-a^{(0)}_2 &{} \cdots &{} a^{(1)}_d-a^{(0)}_d \\ -\sum _{j=2}^d (a^{(2)}_j-a^{(0)}_j)u_j &{} a^{(2)}_2-a^{(0)}_2 &{} \cdots &{} a^{(2)}_d-a^{(0)}_d \\ \vdots &{} \vdots &{} &{} \vdots \\ -\sum _{j=2}^d (a^{(d)}_j-a^{(0)}_j)u_j &{} a^{(d)}_2-a^{(0)}_2 &{} \cdots &{} a^{(d)}_d-a^{(0)}_d \\ u_1^2 &{} u_2 &{} \cdots &{} u_d \end{bmatrix} \end{aligned}$$

where we assume the determinant is nonnegative, else we will multiply by $-1$. Expanding the determinant along the bottom row of the matrix yields

$$\begin{aligned} \rho (u)&= \frac{1}{u_1}\left( u_1^2\det \begin{bmatrix} a^{(1)}_2-a^{(0)}_2 &{} \ldots &{} a^{(1)}_d-a^{(0)}_d \\ a^{(2)}_2-a^{(0)}_2 &{} \ldots &{} a^{(2)}_d-a^{(0)}_d \\ &{} \vdots \\ a^{(d)}_2-a^{(0)}_2 &{} \ldots &{} a^{(d)}_d-a^{(0)}_d \end{bmatrix} + \gamma (u_2,\dots ,u_n)\right) . \end{aligned}$$

where $\gamma (u_2,\dots ,u_d)$ is a polynomial consisting of the quadratic terms in the remaining $u_i$’s. Note that since $\gamma$ does not contain the variable $u_1$ and $\rho$ is divisible by the quadric $u_1^2 + \ldots + u_d^2$ by Proposition 5.5, it follows that

$$\begin{aligned} \rho (u) = \frac{u_1^2 + \ldots + u_d^2}{u_1} \ \det \begin{bmatrix} a^{(1)}_2-a^{(0)}_2 &{} \ldots &{} a^{(1)}_d-a^{(0)}_d \\ a^{(2)}_2-a^{(0)}_2 &{} \ldots &{} a^{(2)}_d-a^{(0)}_d \\ &{} \vdots \\ a^{(d)}_2-a^{(0)}_2 &{} \ldots &{} a^{(d)}_d-a^{(0)}_d \end{bmatrix}. \end{aligned}$$

(1)

Let A be the $(d-1)\times (d-1)$-matrix appearing in this last expression (1). Then finally, by the discussion in Sect. 5, the irreducible component of the algebraic boundary on the corresponding conical region C is described by the linear equation $x_1 = |\det A|$. $\square$

Note that for an arbitrary polytope P of dimension at least 3, the irreducible components of the algebraic boundary $\partial _a IP$ cannot all be linear. This is implied by the fact that the intersection body of a convex body is not a polytope. It is thus worth noting that the intersection body of the cube has remarkably many linear components. We now investigate the non-linear pieces of $\partial _a IC^{(4)}$ of the 4-dimensional cube.

Example 6.2

Let P be the 4-dimensional cube $[-1,1]^4$ and IP be its intersection body. The associated hyperplane arrangement has $8 + 32 + 64 = 104$ chambers. The first 8 are spanned by 6 rays and the boundary here is linear, i.e. it is a 3-dimensional cube. For example, the linear face exposed by (1, 0, 0, 0) is cut out by the hyperplane $w = 2$.

The second family of chambers is made of cones with 5 extreme rays, where the boundary is defined by a cubic equation with shape

$$\begin{aligned} 6 x y z - w^2 - 3 x^2 - 6 x y - 3 y^2 - 6 x z + 6 y z - 3 z^2. \end{aligned}$$

Finally there are 64 cones spanned by 4 rays such that the boundary of the intersection body is a quartic, such as

$$\begin{aligned}&12 w x y z - w^3 - 3 w^2 x - 3 w x^2 - x^3 - 3 w^2 y - 6 w x y - 3 x^2 y - 3 w y^2 - 3 x y^2 \\&\quad - y^3 - 3 w^2 z - 6 w x z - 3 x^2 z + 18 w y z\\&\quad - 6 x y z - 3 y^2 z - 3 w z^2 - 3 x z^2 - 3 y z^2 - z^3. \end{aligned}$$

Proposition 6.1 gives a lower bound on the number of linear components of the algebraic boundary of $IC^{(d)}$. We conjecture that for any $d \in \mathbb {N}$, the algebraic boundary of the intersection body of the d-dimensional cube centered at the origin has exactly 2d linear components. Computational results for $d \le 5$ support this conjecture, as displayed in Table 1. It shows the number of irreducible components of $IC^{(d)}$ sorted by the degree of the component, for $d=2,3,4,5$. The first two columns are the dimension of the polytope, and the number of chambers of the respective hyperplane arrangement H. The third column is the degree bound from Corollary 5.7. The remaining columns show the number of regions whose equation in the algebraic boundary have degree $\deg$, for $\deg =2,\dots , 5$.

Table 1 Number of irreducible components of the algebraic boundary of the intersection body of the d-cube, listed by degree

It is worth noting that the highest degree attained in these examples is equal to the dimension of the respective cube. In particular, the degree bound for centrally symmetric polytopes, as given in Corollary 5.7 is not attained in any of the cases for $d\ge 3$. Finally, note that the number of regions grows exponentially in d, and thus for $d\ge 3$, the number of non-linear components exceeds the number of linear components.